خلاصه

قوس های دایره ای یک عنصر گرافیکی موجود در سیستم های کاداستر بسیاری از کشورها هستند. متأسفانه، این نوع ثبت هندسه مرزهای پاکت، مشکلی است که توسط دستورالعمل های زیرساخت اطلاعات فضایی در اروپا (INSPIRE) مشخصات داده ها در مورد بسته های کاداستر توضیح داده شده است. به دلیل دشواری استفاده از چنین اجسام هندسی، راه حل این مشکل، همانطور که توسط کمیسیون اروپا توصیه شده است، باید نظارت شود. اثر هدف باید یک مدل داده کاداستری باشد که صرفاً بر اساس بخش های خطی باشد. متأسفانه راه حل‌های مبتنی بر رویکرد کلاسیک تبدیل چنین داده‌هایی (مانند قوس‌ها)، همیشه شامل تغییرات یکی از مهمترین ویژگی‌های یک بسته – مساحت آن است. این مقاله پیشنهادی برای حل این مسئله مهم با استفاده از یک الگوریتم ارائه می‌کند، حصول اطمینان از حفظ مساحت بسته ها پس از تبدیل قوس ها به بخش های خطی. علاوه بر این، به جنبه های فنی تغییرات پیشنهادی توجه شد.

کلید واژه ها:

GIS _ قطعات کاداستری ؛ الهام بخش ; قوس دایره ای ؛ تقریب

1. معرفی

در کارهای نقشه کشی و گرافیک، مشکل نمایش یک منحنی معین با استفاده از عناصر تقریبی اغلب پیش می آید. تا به امروز، هیچ محاسبه و الگوریتم هندسی مناسب، ساده و کارآمدی برای انتقال از منحنی ها به زنجیره های چند ضلعی ایجاد نشده است. روش تصحیح شکل توصیف شده توسط Kudas و Wnęk [ 1 ] برای تبدیل چند ضلعی اندازه گیری شده توسط گیرنده های ماهواره ای به یک مستطیل بر اساس مرکز چند ضلعی استفاده می شود. این روش ها ممکن است ارائه صحیح مکان چند ضلعی های اندازه گیری شده موجود در محتوای نقشه های عددی را تسهیل کنند. مشکل زمانی به وجود می آید که لازم باشد عناصر و اشکال موجود در داده های کاداستر جایگزین شوند. اثر ایمای [ 2] مشکل تقریب یک منحنی خطی کسری را توسط منحنی دیگری ارائه می دهد که رئوس آن نشان دهنده درجات متوالی چند جمله ای است. خط منحنی در n نقطه توسط m مستطیل با عرض معین همپوشانی دارد، بنابراین منحنی را به بخش‌هایی تقسیم می‌کند. یک الگوریتم اضافی، کاربرد روش پیشنهادی را با محدود کردن تعداد بخش‌ها ساده می‌کند. روش مشابهی برای تقریب عناصر هندسی، پرز پیشنهاد کرد [ 3]، یک الگوریتم برنامه نویسی پویا برای تقریب خطی منحنی اجرا شده ارائه می دهد. با این حال، الگوریتم برازش منحنی عنصر مؤثری برای جایگزینی منحنی ها نیست. با وجود این، خطاهای موقعیت بین نقاط اصلی و ایجاد شده را به حداقل می رساند (با تعداد عادی نقاط در یک بخش معین).
گریبوف و بادانسکی [ 4 ] امکان استفاده از الگوریتمی را برای تقریب منحنی ها پیشنهاد کردند که تعداد نقاط حاصل از رئوس چندخط را به حداقل می رساند. روش‌های تقریبی خطوط یا بخش‌ها بر اساس افزودن تعداد معینی از نقاط است که به طور قابل توجهی بر کیفیت تبدیل تأثیر نمی‌گذارند. در طول کاهش تعداد رئوس، به اصطلاح فرآیند فیلتراسیون انجام می شود. الگوریتم چند خط را به خوشه هایی با ابعاد معین تقسیم می کند و مسیر آن را با یک خط مستقیم تقریب می زند، بنابراین تعداد راس ها را محدود می کند. چنین روشی کار بر روی اجزای پیچیده را آسان‌تر می‌کند، اما دقت تبدیل و جایگزینی نقاط منحنی را کاهش می‌دهد.
Kolesnikov [ 5 ] ایده جایگزینی قوس های دایره ای با زنجیره های چند ضلعی را ارائه کرد. ایده حل مسئله تقریب منحنی ها با روش های دیجیتال، با حداقل تعداد پاره خط، شامل استفاده از یک الگوریتم سریع و کارآمد برای تقریب خطی، تقریب خطی تکه ای (PWLA) است. اما مشکل ناپیوستگی در گره های تقریب و مشکلات توپولوژیکی در ارائه نتایج نهایی، استفاده از این روش را در بسیاری از زمینه ها غیرممکن می کند. الگوریتم PWLA پیشنهادی را می توان با یک الگوریتم برنامه نویسی پویا جستجو (RSDP) برای به دست آوردن راه حل بهینه در چندین تکرار ترکیب کرد.
روزین [ 6 ] مشکل تداوم خطی منحنی های تقریبی ارائه شده به صورت دیجیتالی با حداقل تعداد قطعات تقسیم کننده خط را در نظر گرفت. چند ضلعی نصب شده در ابتدا با حداکثر خطای تراز کاشته می شود. این الگوریتم را می توان در چندین تکرار در هنگام تبدیل یک منحنی به چند ضلعی استفاده کرد. با این حال، دقت تقریب انجام شده انجام نشده است. عدم کنترل قابلیت اطمینان الگوریتم ممکن است منجر به عدم تشخیص خطاهای ناشی از عناصر خارجی مؤثر بر شکل و مسیر منحنی شود.
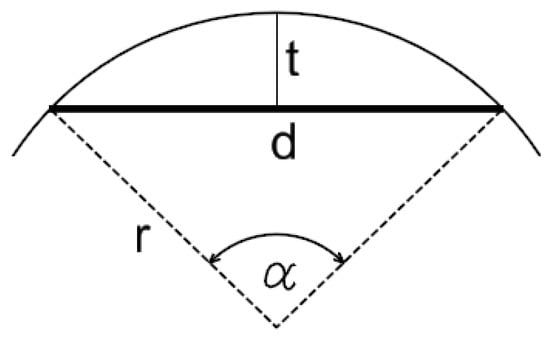
مشکل تبدیل قوس های دایره ای به بخش های خطی مورد بحث در این مقاله شامل تغییر هندسه مرزهای قطعات کاداستری است. روش مورد استفاده تا کنون [ 7 ، 8 ] بر اساس تقسیم یک قوس با استفاده از آکوردها بود ( شکل 1 ). برای پارامتر تعیین کننده درجه تقریب، رایج ترین مورد استفاده، مقدار حدی sagitta t یا حداکثر طول مقطع d بود ( شکل 2 ). متأسفانه این نوع رویکرد، جدای از پیامد اجتناب ناپذیر تغییر روش توصیف محیط بسته، مساحت آن را نیز تغییر می دهد. مساحت بسته یکی از مهمترین پارامترهای توصیف کننده آن است [9 ، 10 ]. سیستم‌های کاداستر که از مساحت به‌دست‌آمده مستقیماً از تعیین تحلیلی آن در هنگام تبدیل داده‌ها استفاده می‌کنند، با مشکل تغییر مساحت مواجه می‌شوند. این می تواند عواقب نامطلوبی داشته باشد. نویسندگان این مقاله با معرفی یک الگوریتم تقریب جدید راه حلی برای این مشکل پیشنهاد کردند که مزیت اصلی آن حفظ مساحت قطعات تقریبی قوس دایره ای است [ 11 ]. علاوه بر این، نویسندگان بر توسعه فناوری تمرکز کردند که تبدیل قوس‌ها به بخش‌ها را بدون نیاز به تغییرات عمده در سیستم‌های کاداستر موجود ممکن می‌سازد.

2. دستورالعمل INSPIRE و شکل مرزهای کاداستر

موضوع کلیدی در زیرساخت داده‌های مکانی مدرن، یافتن نوع مناسب داده برای ادغام با سایر اطلاعات است، نه فقط برای یک کشور یا منطقه، بلکه در سطح بین‌المللی. برای این منظور از اطلاعات دایرکتوری استفاده شد که به صورت نرمال شده راه ارائه اطلاعات به پایگاه را نشان می دهد و امکان استفاده و تبدیل آنها را توسط موجودیت های متوالی نشان می دهد. اصل عملکرد کاداستر بر اساس استاندارد بین المللی ISO 19,152 [ 12 ] بود]، که یکپارچگی داده ها در کاداسترهای ملی و سازگاری داده ها را در سطح بین المللی تضمین می کند. این استاندارد الگوی مدل دامنه مدیریت اراضی (LADM) را تعریف می کند که تمام عناصر مربوط به اداره زمین را پوشش می دهد. این امکان ترکیب اطلاعات مکانی با سایر منابع داده را به شیوه ای منسجم و منسجم فراهم می کند. مدل داده‌های کاداستر نیز در دستورالعمل بین‌المللی زیرساخت اطلاعات فضایی در اروپا (INSPIRE) ارائه شد [ 13 ].
INSPIRE مجموعه‌ای از فعالیت‌های اتحادیه اروپا است که جنبه‌های سازمانی، فنی و قانونی را با خدمات مرتبط مرتبط می‌کند و دسترسی همگانی به پایگاه‌های اطلاعاتی فضایی را ارائه می‌دهد. این سیستم بر اساس زیرساخت داده های مکانی (SDI) کشورهای عضو اتحادیه اروپا است. وظیفه اصلی آن کمک به قانونگذاران در اقدام و اتخاذ تصمیماتی است که ممکن است بر محیط زیست تأثیر بگذارد. تسریع دسترسی به داده ها نیز بسیار مهم است که به نوبه خود بر علاقه مندی به داده های مکانی تأثیر می گذارد. مبنای قانونی SDI دستورالعمل INSPIRE است که توسط پارلمان اروپا صادر شده است. این 34 موضوع در زمینه های ایجاد، ادغام، پردازش، مدیریت و به اشتراک گذاری داده های مکانی را پوشش می دهد. یکی از موضوعات اصلی آن موضوع یک قطعه کاداستری است [ 14 ، 15].
دستورالعمل INSPIRE شامل طرحی است که بوسیله آن بسته های کاداستر باید علامت گذاری و مشخص شوند. از جمله دستورالعمل‌های مربوط به ویژگی‌های اجباری بسته (یعنی مالکیت، مساحت، مراجع ملی، سطح در سلسله مراتب ملی) و ویژگی‌های مربوط به نقاط مرجع و ویژگی‌های فراداده (مخرج مقیاس نقشه یا دقت تخمینی)، هندسه شکل بسته است. نیز معتبر است. مرزهای بسته های کاداستر باید دارای لبه های مطابق با یکدیگر باشند. آنها نباید دارای شکاف توپوگرافی یا همپوشانی توپولوژیکی بین بسته های منفرد باشند. خود مرزها باید به صورت عناصر خطی تعریف، نمایش و نوشته شوند. تمام عناصر فضایی ارائه شده به شکل کاداستر باید با مفروضات “ویژگی ساده” (یک شی هندسی مسطح، با درونیابی خطی بین رئوس مشخص شده تعیین می شود). این تعریف در استاندارد EN ISO 19125-1 مشخص شده است [16 ] – علاوه بر این، با تعیین اینکه تمام درونیابی منحنی ها باید به صورت خطی ارائه شوند، مشخصات مکانی را محدود می کند. علاوه بر این، این استاندارد و همچنین استاندارد ISO 19,107 [ 17 ]، قوانینی را ارائه می دهد که روابط توپولوژیکی و مشخصات هندسی دو شی فضایی مجاور را تعریف می کند. علیرغم توصیه‌های مبنی بر تغییر هندسه قطعات کاداستری و کنار گذاشتن قوس‌های مدور، بسیاری از کشورهای عضو نتوانسته‌اند این تغییرات را دنبال کنند.
به منظور بهبود عملکرد سیستم های کاداستر و بهبود کیفیت و ظرفیت پردازش پایگاه های اطلاعاتی کاداستر، انتقال از قوس های دایره ای به خطوط شکسته توصیه می شود. با این حال، در طول این روش، حفظ ثبات منطقه بسته و دقت موقعیت نقاط مرزی، که باید به طور همزمان وضعیت واقعی و قانونی را نشان دهد، بسیار مهم است.

3. رویکرد قبلی به تقریب کمان های دایره ای

تقریب قوس ها در سیستم های فناوری اطلاعات به تقسیم کمان به قسمت های مساوی محدود شد ( شکل 1 ). نقاط جدید همیشه روی قوس قرار داشتند و پارامتری که درجه تقسیم را تعیین می‌کرد، به اصطلاح ساگیتا t یا طول وتر d ( شکل 2 ) بود [ 7 ، 8 ].

برای محاسبه درجه تقسیم n قوس با زاویه وسط β به دلیل sagitta t از رابطه (1) استفاده می شود:

t = r ∗ ( 1 − cos ( 0.5 ∗ α ) )تی=�∗(1-cos(0.5∗�))

جایی که:

α = 2 ∗ cos قوس ( 1 – t / r )�=2∗قوسcos(1-تی/�)
n = int ( β/ α ) +1�=بین المللی(�/�)+1

برای محاسبه درجه تقسیم n قوس با زاویه β به دلیل طول وتر d از رابطه (4) استفاده می شود:

د= 2 ∗ r ∗ sin ( 0.5 ∗ α )د=2∗�∗گناه(0.5∗�)

جایی که:

α = 2 ∗ قوس گناه (د2 ∗ r)�=2∗قوسگناه(د2∗�)

تعداد کل تقسیمات طبق رابطه (3) محاسبه می شود.

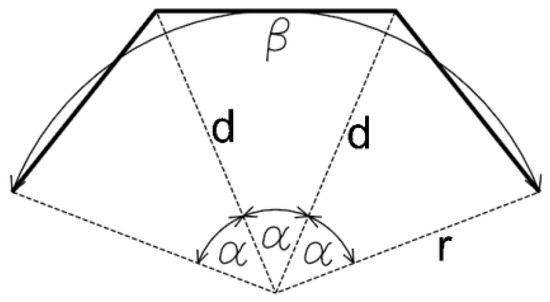
اگر قرار است پارامترها به یکدیگر وابسته باشند، حداکثر ساژیتا و حداکثر طول وتر باید در معیار داده شده قرار گیرند و سپس زاویه α با استفاده از هر دو معادله (2) و (5) محاسبه می‌شود و مقدار زاویه پایین‌تر انتخاب می‌شود. این منجر به تقسیم های زاویه بیشتر β ( n ) می شود. متأسفانه، این رویکرد در حال حاضر منبعی از خطاهای منطقه ای در مفروضات خود است [ 11 ].

4. رویکردی جدید برای تقریب کمان های دایره ای

با توجه به اهمیت ویژگی بسته، که مساحت است، نویسندگان استفاده از فرمول تقریبی را که توسط زیگمونت [ 11 ] توضیح داده شده است، پیشنهاد کردند. برای اهداف عملی ساده شده و در قالب یک معادله برای طول مورد نظر d (6) نوشته شده است ( شکل 3 ).

د=r ∗ (( n – 2 ) ∗ βs i n ( β/ n )+ 1———√− 1 )( n – 2 ); n > 2 د=�∗((�-2)∗�سمن�(�/�)+1-1)(�-2); �>2
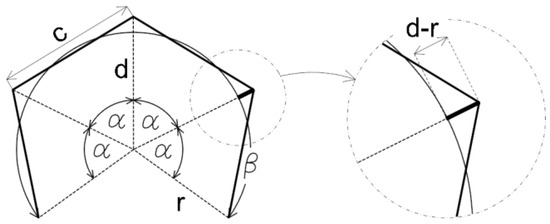
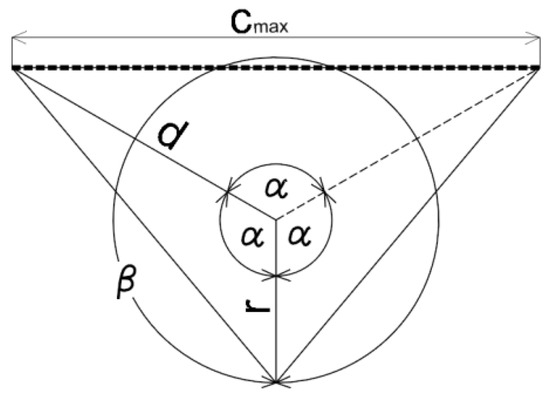
تقریب با تقسیم برای حداقل n = 3 قسمت انجام می شود. به دلایل عملی، تعداد از پیش تعیین شده تقسیمات قوس تقریبی چندان راحت نیست. برای تعیین تعداد n تقسیم با توجه به معیارهای واقعی تر، معادلاتی برای یک قوس واحد (شعاع r = 1) استخراج شد که وابستگی زاویه α را به پارامتر افست نقطه چند ضلعی تقریبی از قوس توصیف می کند ( d – r ) و وابستگی زاویه α به حداکثر طول تقاطع c، یعنی متغیری که چند ضلعی تقریبی را تعریف می کند ( شکل 4 ). این امکان محاسبه سریع درجه مطلوب تقسیم n از زاویه β را فراهم می کند.

5. محاسبه درجه تقسیم زاویه قوس

5.1. محاسبه درجه تقسیم با توجه به حداکثر افست یک نقطه از قوس

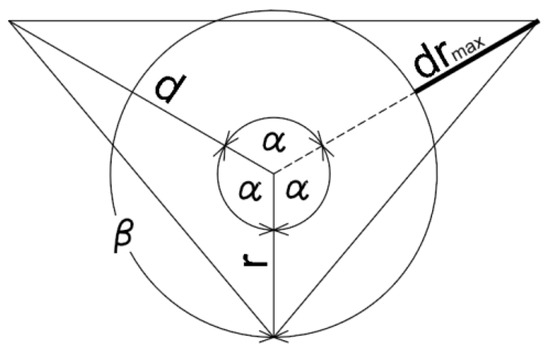
برای تعیین درجه تقسیم n به دلیل بیشینه جابجایی از قوس ( شکل 5 )، معادله رابطه α ( dr ) تقریبی شد. محاسبات برای r = 1 انجام شد ( شکل 6 ). برای حداکثر زاویه α = 120 درجه از رابطه (6)، dr max = 0.873185941935689 به دست آمد. برای r ≠ 1، dr = ( dr o )/ r ، که dr o مقدار آفست واقعی از قوس است.

α ( dr ) =آ1∗ دr2+دr–√∗ (آ2∗ دr +آ3) ؛ 0 < d r ≤ 0.873185941935689�(��)=�1∗��2+��∗(�2∗��+�3); 0<��≤0.873185941935689

که در آن A 1 = 0.433697723021991؛ A 2 = -1.0802363112513. A 3 = 2.83092766791966.

تعداد کل بخش ها محاسبه شد:

n = int (βα) +1،n≥3 �=int(��)+1, �≥3

5.2. محاسبه درجه تقسیم با توجه به حداکثر مقدار سکانت ج

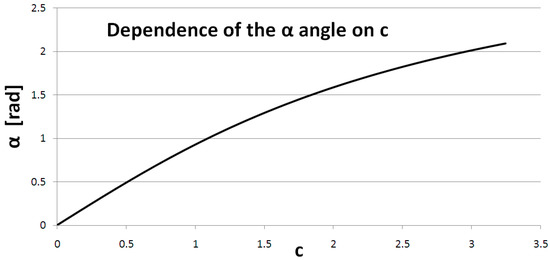
برای تعیین درجه تقسیم n با توجه به حداکثر مقدار سکانت c ( شکل 7 )، معادله رابطه α ( c ) تقریبی شد. محاسبات نیز برای r = 1 انجام شد ( شکل 8 ). برای حداکثر زاویه α = 120 درجه از رابطه (6)، d max = 1.873185941935689 به دست آمد که محاسبه c max = 3.24445322345638 را فعال کرد. برای r ≠ 1، c = c o / r ، که در آن c oمقدار حد واقعی سکنت است.

( ج ) =آ1∗ج6+آ2∗ج5+آ3∗ج4+آ4∗ج3+آ5∗ج2+آ6∗ c +آ7; 0 < c ≤ 3.24445322345638 (�)=�1∗�6+�2∗�5+�3∗�4+�4∗�3+�5∗�2+�6∗�+�7; 0<�≤3.24445322345638

که در آن A 1 = 0.000535037657006; A 2 = −0.008020464613577؛ A 3 = 0.047759867485386; A 4 = −0.128470088893799; A 5 = 0.020621601214003; A 6 = 0.996145055715264; A 7 = 0.000165619038461.

تعداد کل تقسیمات طبق رابطه (8) محاسبه می شود.
با توجه به تقریب های حاصل از روش اعمال شده، مقدار تقسیم بهینه ممکن است کمی متفاوت باشد (1-2 بخش). بنابراین، مرحله نهایی محاسبه باید بررسی شود و احتمالاً درجه تقسیم باید تنظیم شود.

6. تعیین روش تقسیم قوس

الگوریتم تقسیم قوس به تعداد تقسیمات قوس تقریبی نیاز دارد. این مقدار را می توان از معادلات (7) و (9) محاسبه کرد. سوال اساسی مربوط به مقادیر حدی dr و c است. نویسندگان پیشنهاد کردند که مقدار اولویت باید پارامتر dr باشد. مقدار آن در سطح حداکثر خطای موقعیت m P نقطه مرزی نسبت به نقاط شبکه اندازه گیری تعیین می شود. برای انجام تحقیقات تجربی در این کار، حداکثر انحراف خطی نقطه مرزی مطابق با الزامات محلی در سطح m P در نظر گرفته شد.= 0.14 متر اگر لازم است شرایط حاصل از حداکثر طول سکانس برآورده شود، مقدار پایین‌تر برای زاویه محاسبه‌شده α باید همیشه انتخاب شود. مقدار نمونه dr با توجه به مقررات دقت محلی تعیین می شود. چنین رویکردی پذیرش پایداری نقاط مرزی تعیین شده را با توجه به قوس تقریبی امکان پذیر می کند. نقاط جدید حاصل از روش تقریبی توصیف شده “روی قوس قرار دارند” زیرا موقعیت آنها در خطای قابل قبول m P قرار دارد.

7. تست الگوریتم

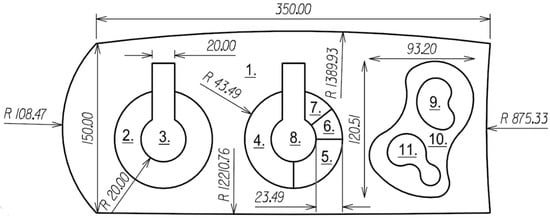
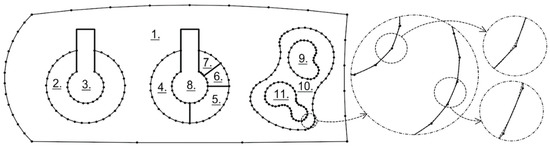
آزمون الگوریتم بر روی یک شی مثال حاوی تنظیمات قوس مختلف انجام شد ( شکل 8 ). به عنوان پارامتر انحراف، dr = 0.14 m در نظر گرفته شد. جدای از مقایسه نتایج با نواحی اصلی و محیط بسته ها، مقایسه ای با روش قبلی تقسیم قوس به وترهای مساوی انجام شد. جدول 1 اطلاعاتی در مورد تقسیم هر یک از قوس ها با استفاده از روش جدید و روش آکوردهای مساوی ارائه می دهد. در مقایسه با روش پیشنهادی و با استفاده از شی آزمایشی حاوی کمان هایی با شعاع های مختلف ( شکل 9 )، شکل 10 و شکل 11 چگالی نقاط قوس تقریبی توسط الگوریتم جدید را نشان می دهد.شکل 10 ) و توسط الگوریتم وتر ( شکل 11 ).
راه حل ارائه شده ( جدول 2 ) بسیار دقیق است. با این حال، توجه داشته باشید که محاسبات از مختصات در قالب “دقت دوگانه” استفاده می کنند. تغییرات مساحت ناشی از گرد شدن مختصات در جدول 3 نشان داده شده است. مختصات جدید X، Y به ترتیب به 1 میلی متر، 1 سانتی متر و 1 dm گرد شدند. نتایج با روش آکوردهای مساوی به دلیل خطاهای ناشی از استفاده از خود روش مقایسه نشد.

دقت ثبت مختصات X، Y نقطه مرزی جدید (تقریبی) مستقیماً به دقت ضبط طول محاسبه شده d (7) بستگی دارد. به عنوان مثال، برای داده های فرضی:

r = 10 متر ; β  =90∘; n = 3�=10 متر; �=90درجه;�=3

مقدار طول زیر (7) در قالب “دقت مضاعف” به دست می آید:

د= 10.35090033 متر د=10.35090033 متر

با قرار دادن این داده (10، 11) در معادله مساحت پاره دایره با قوس تقریبی [ 11 ]:

A = d∗ r ∗ گناه (βn) +n – 22∗د2∗ گناه (βn)آ=د∗�∗گناه(��)+�-22∗د2∗گناه(��)

یک منطقه به دست می آید:

A = 78.5398 متر2آ=78.5398 متر2

برای پاسخ به این سوال که چگونه گرد کردن طول d (11) با دقت μ d (13) بر مساحت تأثیر می گذارد، قانون انتشار خطاها [ 18 ] باید در رابطه (12) اعمال شود:

μآ=∂ A∂ د∗μد= { [ r + ( n − 2 ) ∗ d] ∗ گناه (βn) }∗μد�آ=∂آ∂د∗�د={[�+(�-2)∗د]∗گناه(��)}∗�د

که در آن μ A – خطای ناحیه ناشی از گرد کردن μ d ; ∂ – نماد مشتق جزئی.

به عنوان مثال، برای مقادیر گرد کردن 1 میلی متر، 1 سانتی متر، 1 dm، خطاهای پیش بینی شده μ A منطقه به دست می آید که نتایج آزمون تجربی را تایید می کند ( جدول 3 ):
  • μ d = 0.001 m → μ A = 0.0102 m2 ;
  • μ d = 0.01 m → μ A = 0.1018 m2 ;
  • μ d = 0.1 m → μ A = 1.0175 m2 .
آزمایش های انجام شده نشان می دهد که الگوریتم پیشنهادی راه حل مناسبی برای اهداف کاداستر است. علاوه بر این، تعداد نقاط مرزی در مقایسه با رویکرد قبلی (آکوردهای برابر) کاهش یافت – برای شی مورد آزمایش، این کاهش برابر با 12٪ بود. این یک اثر بسیار مثبت ناشی از استفاده از الگوریتم توصیف شده است. با مقایسه شکل 9 و شکل 10 ، همچنین می توان تناسب بهتری از چند ضلعی تقریبی با کمان های اصلی پیدا کرد. مقررات مربوط به ویژگی های توصیفی قابل قبول نقاط مرزی نیاز به تعدیل دارد. نویسندگان پیشنهاد می کنند برای نشان دادن منبع این نوع نقطه یک ویژگی اضافی اضافه کنید – در این مورد، “نقاط از تقریب قوس”.

8. نتیجه گیری

راه حل پیشنهادی نویسندگان پیشنهادی است که می تواند به حل مشکل قوس ها در سیستم های کاداستر کمک کند. این مسائل نه تنها مربوط به سیستم های کاداستر در اروپا است که الهام بخش این کار بود. در عوض، مشکل گسترده‌تر است و به کشورهای دیگر نیز مربوط می‌شود [ 19 ].
به گفته نویسندگان، راه حل بهینه ذخیره مختصات نقاط محاسبه شده در قالب “دقت دوگانه” است. علاوه بر این، چنین نقاطی باید اطلاعات منبع (وضعیت) را درج می کردند، به عنوان مثال، نقاط محاسبه شده در حدود کمان های دایره ای.
لازم به تاکید است که روش پیشنهادی نویسندگان ممکن است به طور غیرمستقیم به حل مشکلات استفاده از منحنی های دیگر در سیستم های کاداستر کمک کند. بخش بزرگی از تحقیقات علمی در زمینه هندسه شامل تبدیل منحنی های دلخواه به کمان است [ 20 ، 21 ، 22 ، 23 ]. با رویکرد دو مرحله ای به این نوع هندسه، ممکن است اثر نهایی (حفظ مناطق بسته) به روش دقیق اجرا نشود. با این حال، نتایج به‌دست‌آمده ممکن است هنگام توسعه فناوری برای تبدیل هر منحنی به بخش‌های خطی در سیستم‌های کاداستر در نظر گرفته شود.
در سیستم‌های کاداستر موجود در اروپا (و در جهان)، راه‌حل‌هایی غیر از مواردی که در این کار پیشنهاد شده‌اند، قابل استفاده هستند. با توجه به مقررات فنی و قانونی متفاوتی که در کشورهای مختلف در حال اجرا است، نیاز به گسترش دامنه تحقیقات در مورد روش های توصیف قوس های مدور را می بینیم. این مشکل موضوع تحقیقات علمی بعدی نویسندگان خواهد بود.

منابع

  1. کوداس، دی. Wnęk، A. شبیه سازی تعیین مساحت چندضلعی با استفاده از گیرنده های کد تک فرکانس GPS – مطالعه موردی. محاسبه کنید. الکترون. کشاورزی 2019 ، 158 ، 92-101. [ Google Scholar ] [ CrossRef ]
  2. ایمای، اچ. Iri, M. روشهای محاسباتی-هندسی برای تقریب های چند ضلعی یک منحنی. محاسبه کنید. Vis. فرآیند تصویر 1968 ، 36 ، 31-41. [ Google Scholar ] [ CrossRef ]
  3. پرز، جی سی. ویدال، ای. الگوریتمی برای تقریب خطی تکه ای بهینه منحنی های دیجیتالی شده. در مجموعه مقالات یازدهمین کنفرانس بین المللی IAPR در مورد شناسایی الگوها، لاهه، هلند، 30 اوت تا 1 سپتامبر 1992. صص 167-170. [ Google Scholar ]
  4. گریبوف، آ. Bodansky, E. روشی جدید برای تقریب چند خط. در شناخت الگوی ساختاری، نحوی و آماری ؛ LNCS; Springer: برلین/هایدلبرگ، آلمان، 2004; ص 504-511. [ Google Scholar ]
  5. Kolesnikov، A. تقریب خطی تکه ای محدود منحنی های دیجیتال. در مجموعه مقالات نوزدهمین کنفرانس بین المللی 2008 در تشخیص الگو، ICPR’08، تامپا، FL، ایالات متحده آمریکا، 8 تا 11 دسامبر 2008. [ Google Scholar ]
  6. Rosin, P. تکنیک‌هایی برای ارزیابی تقریب‌های چند ضلعی منحنی‌ها. IEEE Trans. الگوی مقعدی ماخ هوشمند 1997 ، 14 ، 659-666. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  7. مرکز راهنمایی ORACLE. راهنمای توسعه دهندگان فضایی. در دسترس به صورت آنلاین: https://docs.oracle.com/cd/B28359_01/appdev.111/b28400/sdo_objgeom.htm#i867636 (در 6 آوریل 2018 قابل دسترسی است).
  8. ESRI. مقاله فنی، پشتیبانی فنی، مشکل: کمان های دایره ای به خطوط متراکم تبدیل می شوند. در دسترس آنلاین: https://support.esri.com/technical-article/000003577 (در 11 مه 2018 قابل دسترسی است).
  9. لای، ال. “خط را کجا بکشیم؟” این یک سوال برنامه ریزی کاربری زمین برای نقشه بردار زمین و شهرساز است. سیاست کاربری زمین 2015 ، 42 ، 619-627. [ Google Scholar ] [ CrossRef ]
  10. والدهئوسل، پ. کونیگ، اچ. Mansberger, R. مرزها و علامت های مرزی میراث فرهنگی اساسی با اهمیت گسترده. ISPRS Ann. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2015 ، II-5/W3 ، 329-334. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  11. Zygmunt، M. تقریب قوس دایره ای با استفاده از چندضلعی. جی. کامپیوتر. Appl. ریاضی. 2017 ، 322 ، 81-85. [ Google Scholar ] [ CrossRef ]
  12. ISO 19152:2012. اطلاعات جغرافیایی – مدل دامنه مدیریت سرزمین (LADM) ; ISO: سازمان بین المللی استانداردسازی: ژنو، سوئیس، 2012. [ Google Scholar ]
  13. اسلادیچ، دی. رادولوویچ، آ. گووداریکا، م. یووانوویچ، دی. Pržulj, D. استفاده از هستی شناسی ها در سیستم های کاداستر. محاسبه کنید. علمی Inf. سیستم 2015 ، 12 ، 1033-1053. [ Google Scholar ] [ CrossRef ]
  14. INSPIRE D2.8.I.6. مشخصات داده ها در مورد بسته های کاداستر – دستورالعمل های فنی. در دسترس آنلاین: https://inspire.ec.europa.eu/id/document/tg/cp (در 20 نوامبر 2019 قابل دسترسی است).
  15. الهام بخشیدن. در دسترس آنلاین: https://inspire.ec.europa.eu (در 24 آوریل 2018 قابل دسترسی است).
  16. PN-EN-ISO 19125-1. اطلاعات جغرافیایی-دسترسی به ویژگی های ساده، قسمت 1: معماری مشترک ; کمیته لهستانی برای استانداردسازی: ورشو، لهستان، 2006.
  17. ISO 19107:2003. اطلاعات جغرافیایی — طرح واره فضایی ; ISO: سازمان بین المللی استاندارد: ژنو، سوئیس، 2003.
  18. گیلانی، محاسبات تنظیم CD : تجزیه و تحلیل داده های مکانی ; جان وایلی و پسران شرکت: Hoboken, NJ, USA, 2010. [ Google Scholar ]
  19. راهنمای تفسیری قوانین نقشه برداری کاداستر . LINZG65700 (6 دسامبر 2011)؛ دولت نیوزلند، دفتر نقشه بردار کل، اطلاعات زمین نیوزلند: ولینگتون، نیوزلند، 2010.
  20. والتون، دی جی؛ Meek، DS تقریب یک مارپیچ مکعبی مسطح Bezier توسط کمان های دایره ای. جی. کامپیوتر. Appl. ریاضی. 1996 ، 75 ، 47-56. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  21. هور، اس. Tae-wan، K. بهترین تقریب G1 مکعبی و G2 کوارتیک Bézier از کمان های دایره ای. جی. کامپیوتر. Appl. ریاضی. 2011 ، 236 ، 1183-1192. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  22. کائوسایها، پ. Dejdumrong، N. مدل سازی منحنی های bézier با استفاده از ترکیبی از تقریب های قوس خطی و دایره ای. در مجموعه مقالات نهمین کنفرانس بین المللی گرافیک کامپیوتری، تصویربرداری و تجسم (CGIV)، هسینچو، تایوان، 25 تا 27 ژوئیه 2012. [ Google Scholar ]
  23. Riškus, A. تقریب یک منحنی مکعبی Bézier توسط کمان های دایره ای و بالعکس. Inf. تکنولوژی کنترل. 2015 ، 35 . [ Google Scholar ] [ CrossRef ]
Ijgi 09 00027 g001 550
شکل 1. رویکرد کلاسیک برای تقریب قوس های دایره ای با استفاده از آکوردها، n = 3.
Ijgi 09 00027 g002 550
شکل 2. روابط بین پارامترهای توصیف کننده قوس.
Ijgi 09 00027 g003 550
شکل 3. تغییر قوس به چند ضلعی، n = 3.
Ijgi 09 00027 g004 550
شکل 4. تغییر قوس به یک چند ضلعی، n = 4.
Ijgi 09 00027 g005 550
شکل 5. حداکثر مقادیر dr برای α = 120 درجه، زمانی که β = 360 درجه، n = 3.
Ijgi 09 00027 g006 550
شکل 6. وابستگی زاویه α به dr ، برای r = 1.
Ijgi 09 00027 g007 550
شکل 7. حداکثر مقادیر c برای α = 120 درجه، زمانی که β = 360 درجه، n = 3.
Ijgi 09 00027 g008 550
شکل 8. وابستگی زاویه α به c ، برای r = 1.
Ijgi 09 00027 g009 550
شکل 9. شی آزمایشی حاوی کمان هایی با شعاع های مختلف (شامل شماره گذاری بسته ها) است، ابعاد برای نشان دادن نسبت های بسته های آزمایشی ساخته شده است.
Ijgi 09 00027 g010 550
شکل 10. آزمایش شیء تقریبی شده توسط الگوریتم جدید.
Ijgi 09 00027 g011 550
شکل 11. شی آزمایشی تقریبی شده توسط الگوریتم وتر.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید