خلاصه
مقادیر بیسابقه دادههای مکانی-زمانی نیاز فوری به کاوش الگوها را در آن برمیانگیزد. تجزیه و تحلیل خوشه بندی در استخراج الگوها از داده های بزرگ با گروه بندی عناصر داده مشابه در خوشه ها مفید است. در مقایسه با روشهای خوشهبندی یک طرفه و همخوشهبندی، روشهای خوشهبندی سهگانه توانایی بیشتری در کاوش الگوهای پیچیده دارند. با این حال، الگوها یا خوشههای کاوششده میتوانند به دلیل وضوحهای زمانی متفاوت دادههای ورودی متفاوت باشند. این مطالعه یک روش مبتنی بر خوشهبندی سهگانه را برای بررسی اثرات تفکیکپذیریهای زمانی مختلف بر روی خوشههای مکانی-زمانی شناساییشده در سریهای زمانی مرجع جغرافیایی (GTS)، یکی از انواع دادههای مکانی-زمانی، ارائه میکند. داده های دمای روزانه هلند در 28 ایستگاه در طول 20 سال برای نشان دادن این مطالعه استفاده شد. داده های دمایی روزانه، ماهانه، و تفکیکپذیریهای سالانه تحت الگوریتم سهگانهسازی میانگین مکعب برگمن با واگرایی I (BCAT_I) قرار گرفتند تا خوشههای مکانی-زمانی را شناسایی کنند، که سپس از نظر الگوهای نمایشدادهشده، ترکیببندیها و عناصر تغییر یافته مقایسه شدند. نتایج تأثیر وضوح زمانی بر خوشههای مکانی-زمانی شناساییشده در دادههای دمای هلند را تأیید میکنند: اکثر ترکیبات خوشهها هنگام تغییر وضوح زمانی دادههای ورودی در GTS متفاوت هستند. با این وجود، تقریباً هیچ تغییری در عناصر در خوشه های خاص (12 ایستگاه در شمال شرق کشور؛ سال 1996، 2010) در تمام قطعنامه های زمانی وجود ندارد، که آنها را به عنوان خوشه های “واقعی” در مجموعه داده مطالعه موردی پیشنهاد می کند. که سپس از نظر الگوهای نمایش داده شده، ترکیب بندی ها و عناصر تغییر یافته با هم مقایسه شدند. نتایج تأثیر وضوح زمانی بر خوشههای مکانی-زمانی شناساییشده در دادههای دمای هلند را تأیید میکنند: اکثر ترکیبات خوشهها هنگام تغییر وضوح زمانی دادههای ورودی در GTS متفاوت هستند. با این وجود، تقریباً هیچ تغییری در عناصر در خوشه های خاص (12 ایستگاه در شمال شرق کشور؛ سال 1996، 2010) در تمام قطعنامه های زمانی وجود ندارد، که آنها را به عنوان خوشه های “واقعی” در مجموعه داده مطالعه موردی پیشنهاد می کند. که سپس از نظر الگوهای نمایش داده شده، ترکیب بندی ها و عناصر تغییر یافته با هم مقایسه شدند. نتایج تأثیر وضوح زمانی بر خوشههای مکانی-زمانی شناساییشده در دادههای دمای هلند را تأیید میکنند: اکثر ترکیبات خوشهها هنگام تغییر وضوح زمانی دادههای ورودی در GTS متفاوت هستند. با این وجود، تقریباً هیچ تغییری در عناصر در خوشه های خاص (12 ایستگاه در شمال شرق کشور؛ سال 1996، 2010) در تمام قطعنامه های زمانی وجود ندارد، که آنها را به عنوان خوشه های “واقعی” در مجموعه داده مطالعه موردی پیشنهاد می کند. اکثر ترکیبات خوشه ها هنگام تغییر وضوح زمانی داده های ورودی در GTS متفاوت هستند. با این وجود، تقریباً هیچ تغییری در عناصر در خوشه های خاص (12 ایستگاه در شمال شرق کشور؛ سال 1996، 2010) در تمام قطعنامه های زمانی وجود ندارد، که آنها را به عنوان خوشه های “واقعی” در مجموعه داده مطالعه موردی پیشنهاد می کند. اکثر ترکیبات خوشه ها هنگام تغییر وضوح زمانی داده های ورودی در GTS متفاوت هستند. با این وجود، تقریباً هیچ تغییری در عناصر در خوشه های خاص (12 ایستگاه در شمال شرق کشور؛ سال 1996، 2010) در تمام قطعنامه های زمانی وجود ندارد، که آنها را به عنوان خوشه های “واقعی” در مجموعه داده مطالعه موردی پیشنهاد می کند.
کلید واژه ها:
خوشه بندی سه گانه ; خوشه های مکانی – زمانی ; سری زمانی ارجاع جغرافیایی ؛ مشکل واحد زمانی قابل تغییر (MTUP) ; دمای هلند
1. معرفی
پیشرفت در تکنیکهای جمعآوری دادهها (مانند سنجش از راه دور، GPS، تلفن همراه و غیره) همراه با خدمات اشتراکگذاری دادهها به طور قابلتوجهی انباشت دادههای مکانی-زمانی را ارتقا داده است [ 1 ، 2 ]. چنین مقادیر بیسابقهای از دادهها در تفکیکپذیریهای مکانی و زمانی چندگانه، نیاز فوری به کاوش الگوها برای به دست آوردن اطلاعات مفید در آن را برمیانگیزد [ 3 ، 4 ]. یکی از انواع رایج دادههای مکانی-زمانی، سریهای زمانی مرجع جغرافیایی (GTS) است، که سریهای زمانی یک یا چند مقدار مشخصهای هستند که در مکانهای ثابت و فواصل زمانی مشاهده میشوند [ 5 ، 6 ]. یک مثال رایج از GTS دمای روزانه ثبت شده در ایستگاه های هواشناسی است.
به عنوان یک کار داده کاوی مهم، خوشه بندی برای کاوش الگوها در GTS با تخصیص عناصر داده مشابه به یک خوشه و عناصر غیر مشابه به عناصر مختلف مفید است [ 7 ، 8 ]. در نتیجه، هم یک نمای کلی از دادهها در سطوح خوشهای و هم بررسی جزئیات روی خوشههای منفرد را ارائه میدهد [ 9 ، 10 ]. با توجه به ابعاد درگیر در تحلیل خوشهبندی، روشهای خوشهبندی برای GTS بهعنوان روشهای خوشهبندی یکطرفه، همخوشهبندی و خوشهبندی سهگانه طبقهبندی میشوند [ 11 ، 12 ].
روشهای خوشهبندی یکطرفه GTS دو بعدی را تجزیه و تحلیل میکنند که معمولاً در یک جدول دادهها با مکانها به عنوان ردیفها و مهرهای زمانی به عنوان ستونها سازماندهی میشوند [ 6 ]. تجزیه و تحلیل را می توان از جنبه مکانی یا زمانی انجام داد. به عنوان مثال، در تجزیه و تحلیل از جنبه فضایی، مکان ها به خوشه های مکان با عناصر داده مشابه در امتداد تمام مهرهای زمانی گروه بندی می شوند ( شکل 1 ب). مطالعات گسترده ای وجود دارد که از روش های خوشه بندی یک طرفه برای تجزیه و تحلیل GTS از جنبه مکانی یا زمانی استفاده می کند [ 13 ، 14 ، 15 ، 16 ]. متفاوت از خوشهبندی یک طرفه، روشهای همخوشهبندی GTS دو بعدی را در جدول دادهها از هر دو جنبه مکانی و زمانی به طور همزمان تجزیه و تحلیل میکنند.6 ، 7 ]. با گروهبندی همزمان مکانها و مُهرهای زمانی به خوشههای مکان و مُهر زمانی، نتایج همخوشهبندی، تقاطعهای آنها، یعنی همخوشهها، با عناصر دادهای مشابه در امتداد مکانها و مُهرهای زمانی هستند ( شکل 1 ج). مطالعات زیادی در مورد تجزیه و تحلیل همخوشهبندی GTS برای اکتشاف الگوهای مکانی-زمانی همزمان انجام شده است [ 17 ، 18 ، 19 ].
روشهای خوشهبندی سهبعدی GTS سهبعدی را تجزیه و تحلیل میکنند که در یک مکعب داده با سه بعد آن به عنوان مکانها، مُهرهای زمانی، و هر سومی، به عنوان مثال، مُهرهای زمانی یا مکانهای دیگر سازماندهی شده است [ 20 ، 21 ]]. برای مثال GTS سه بعدی را با یک بعد مکانی (موقعیت) و دو بعد زمانی تو در تو (مهر زمانی) در نظر بگیرید. با گروهبندی همزمان مکانها و دو مُهر زمانی تو در تو (مثلاً سالها و ماهها) در خوشههای مکان -خوشههای timestamp1 و خوشههای timestamp2- نتایج سهگانهسازی، تقاطعهای آنها، یعنی خوشههای سهگانه، با عناصر داده مشابه در هر سه بعد است. . در مقایسه با روشهای خوشهبندی و همخوشهبندی یکطرفه، روشهای خوشهبندی سهگانه مزایایی در کاوش الگوهای بیشتر در GTS با دادههای دقیقتر و در نتیجه استخراج اطلاعات مفیدتر دارند [ 12 ].
یکی دیگر از مسائل مهم در تجزیه و تحلیل خوشه بندی GTS، وضوح زمانی است. تغییرات تفکیکپذیریهای زمانی در دادههای ورودی میتواند منجر به نتایج خوشهبندی متفاوتی به دلیل اثرات تجمع زمانی شود [ 22 ، 23 ]. در حالی که اثرات تجمع مکانی بر روی الگوهای بررسی شده در داده های مکانی-زمانی به خوبی به عنوان مسئله واحد منطقه قابل اصلاح (MAUP) مورد مطالعه قرار گرفته است، مسائل مربوط به ابعاد زمانی در سال های اخیر توجه را به خود جلب کرده است اما به مطالعات بیشتری نیاز دارد [ 24 ، 25 ، 26 ]. در سال 2011، کلتکین و همکاران. [ 27] ابتدا مسئله واحد زمانی قابل اصلاح (MTUP) را پیشنهاد کرد و آن را در قیاس با MAUP با وضوح زمانی به عنوان یکی از جنبه های ضروری تعریف کرد. پس از آن، چند مطالعه اثرات تفکیکپذیریهای زمانی را بر الگوهای بررسیشده تحلیل کردهاند [ 22 ، 23 ، 28 ، 29 ، 30 ]. در میان آنها، چنگ و آدپژو [ 22 ] اثرات تفکیک زمانی را بر روی خوشه های مکانی-زمانی شناسایی شده در داده های نقطه ای بررسی کردند. با این حال، طبق دانش ما، هیچ مطالعهای برای بررسی اثرات تفکیکهای زمانی بر نتایج خوشهبندی سهگانه در GTS انجام نشده است.
بنابراین، این مطالعه از یک روش مبتنی بر خوشهبندی سهگانه برای بررسی اثرات تفکیکپذیریهای زمانی مختلف بر روی خوشههای مکانی-زمانی شناساییشده در GTS استفاده میکند. دمای روزانه هلند در 28 ایستگاه از سال 1992 تا 2011 به عنوان مجموعه داده مطالعه موردی استفاده می شود. به طور خلاصه، روش خوشهبندی سهگانه برای بررسی مجموعه دادههای دما در رزولوشنهای روزانه، ماهانه و سالانه استفاده میشود و سپس خوشههای مکانی-زمانی شناساییشده در وضوحهای زمانی مختلف برای بررسی تأثیرات آنها مقایسه میشوند. مشارکتهای این مطالعه عبارتند از: (1) این مطالعه آزمایشی را بر اساس یک روش خوشهبندی سهگانه برای استخراج الگوها در GTS طراحی میکند. در مقایسه با سایر روش های خوشه بندی، روش های خوشه بندی سه گانه قابلیت بیشتری در کاوش الگوهای پیچیده و آشکارسازی اطلاعات مفید در داده ها دارند. (2) این مطالعه اثرات تغییر قطعنامه های زمانی را بر روی خوشه های مکانی-زمانی شناسایی شده در GTS بررسی می کند. با مجموعه داده مطالعه موردی، این مطالعه خوشههای شناساییشده را در وضوحهای زمانی مختلف مقایسه میکند و تأثیر تفکیک زمانی را بر نتایج خوشهبندی سهگانه نشان میدهد.
ساختار این مقاله به روش زیر سازماندهی شده است: بخش 2 دادههای دمای روزانه هلند، روش خوشهبندی سهگانه، و آزمایش بر روی تجزیه و تحلیل خوشهبندی سهگانه مجموعه داده در وضوحهای زمانی چندگانه را معرفی میکند. پس از آن، خوشه های مکانی-زمانی شناسایی شده در وضوح های مختلف به طور خلاصه شرح داده شده و سپس در بخش 3 به تفصیل مقایسه می شوند. در نهایت، نتایج در بخش 4 مورد بحث قرار گرفته و نتیجه گیری در بخش 5 ارائه شده است.
2. مواد و روشها
در این بخش ابتدا محدوده مورد مطالعه و مجموعه داده های مطالعه موردی معرفی می شود، سپس روش تجزیه و تحلیل سه خوشه ای توضیح داده می شود و در نهایت گردش کار آزمایش ما شرح داده می شود.
2.1. محدوده مطالعه و مجموعه داده
در این مطالعه، هلند به دلیل قرار گرفتن در اروپا به عنوان منطقه مورد مطالعه انتخاب شده است ( شکل 2 ). در مرز با دریای شمال در شمال و غرب، آب و هوا در این منطقه از هلند بیشتر توسط آب و هوای معتدل دریایی تعیین می شود. در مقابل، آب و هوا در شرق و جنوب هلند بیشتر تحت تأثیر آب و هوای قاره ای کشورهای همسایه آلمان و بلژیک است.
همانطور که در بالا ذکر شد، داده های دمای روزانه هلند جمع آوری شده در 28 ایستگاه طی 20 سال (1992-2011) به عنوان مجموعه داده مطالعه موردی استفاده می شود که از موسسه هواشناسی سلطنتی هلند (KNMI) در دسترس است. برای تولید دادههای ماهانه و سالانه بهعنوان دادههای ورودی با وضوحهای زمانی مختلف برای تجزیه و تحلیل خوشهبندی سهگانه، دادههای روزانه با استفاده از مقدار میانگین جمعآوری شدند که پرکاربردترین روش در کاهش مقیاس دادههای آب و هوا است [ 31 ]. با مختصات ایستگاهها نیز در دسترس KNMI، نقشه چند ضلعی تیسن برای نشان دادن منطقه تحت تأثیر هر ایستگاه تولید شد و برای تجسم نتایج خوشهبندی سهگانه استفاده شد.
2.2. تجزیه و تحلیل سه خوشه ای
از آنجایی که الگوریتم سه خوشهبندی برای اولین بار در سال 2005 ارائه شد، تجزیه و تحلیل خوشهبندی سهگانه برای کاوش الگوها در بسیاری از کاربردها استفاده شده است [ 11 ، 20 ، 21 ، 32 ، 33 ]. به عنوان اولین الگوریتم خوشهبندی سهگانه، TRICLUSTER سه خوشهها را با استفاده از چند گراف از محدودهها و دستههای حداکثر محدود شناسایی میکند. ژائو و زکی [ 20 ] این الگوریتم خوشهبندی سهگانه را برای دادههای بیان ژن برای اکتشاف الگوهای منسجم در طول زمان اعمال کردند. سیم و همکاران [ 32] یک الگوریتم خوشهبندی سهگانه به نام خوشه سهبعدی مرتبط با استخراج (MIC) ایجاد کرد که اطلاعات همبستگی را برای شناسایی خوشههای سهبعدی بسیار همبسته بهینه میکند. آنها از MIC برای تجزیه و تحلیل داده های سهام مالی استفاده کردند. آمار و همکاران [ 33 ] استنتاج ماژول سهطرفه را از طریق نمونهگیری گیبس (TWIGS) پیشنهاد کرد، که از فرض گامای نرمال و نمونهگر گیبس برای استخراج خوشههای سهگانه در مجموعه دادههای بیولوژیکی با ارزش واقعی سه بعدی استفاده میکند. اخیرا، وو و همکاران. [ 21] الگوریتم سه خوشهبندی میانگین مکعب برگمن را با واگرایی I (BCAT_I) توسعه داد. مقادیر اطلاعات مشترک بین سه متغیر را با استفاده از اطلاعات متقابل در زمینه تئوری اطلاعات محاسبه میکند و سپس با بهینهسازی واگرایی اطلاعات متقابل بین مکعب داده اصلی و سه خوشهای، خوشههای سهگانه بهینه را جستجو میکند. آنها BCAT_I را برای تجزیه و تحلیل سری های زمانی داده های دما، که یک مجموعه داده GTS است، اعمال کردند. وو و همکاران [ 12 ] از همین الگوریتم برای شناسایی خوشه های سه گانه در سری های زمانی داده های آلودگی هوا استفاده کرد. همانطور که برای تجزیه و تحلیل GTS ثابت شده است، BCAT_I نیز در این مطالعه استفاده می شود.
برای نشان دادن فرآیند بهینه سازی BCAT_I، داده های دمای ماهانه هلندی به عنوان مثال استفاده می شود. دادههای دما را میتوان در یک مکعب داده سهبعدی سازماندهی کرد که در آن ردیفها ایستگاه، ستونها سال، عمق ۱۲ ماه و عناصر دمای ماهانه هستند. مکعب داده را می توان به عنوان یک ماتریس سه بعدی اتفاقی، O sym ، در بین سه متغیر مشاهده کرد که شامل یک متغیر فضایی در 28 ایستگاه و دو متغیر زمانی تو در تو است که مقادیری را در طول 20 سال و 12 ماه جداگانه می گیرند. ماتریس داده های سه بعدی، تعداد خوشه های ایستگاه، خوشه های سال، و خوشه های ماه پارامترهای ورودی برای BCAT_I هستند در حالی که خروجی سه خوشه بهینه شده است. شبه کد BCAT_I در شکل 3فرآیند بهینه سازی الگوریتم را در سه مرحله خلاصه کرد.
اولین مرحله اولیه سازی تصادفی است که در آن 28 ایستگاه، 20 سال و 12 ماه به ترتیب به طور تصادفی به خوشه های ایستگاه، خوشه های سال و خوشه های ماه نگاشت می شوند. مقدار متوسط هر سه خوشه محاسبه می شود، که برای جایگزینی عناصر در هر سه خوشه و تولید ماتریس سه خوشه استفاده می شود. O^s yمتر�^س�متر. در مرحله بعد، تابع هدف BCAT_I با استفاده از واگرایی اطلاعات بین ماتریس سه بعدی اصلی و سهبعدی ساخته میشود که با نشان داده میشود. Dمن( ⋅ | | ⋅ )�من(⋅||⋅). تابع شباهت بین O sym و را اندازه گیری می کندO^s yمتر�^س�متر. با وجود عناصر مشابه بیشتر در هر سه خوشه و عناصر متفاوت بین سه خوشه، دو ماتریس شبیهتر هستند و تابع هدف مقادیر کمتری دارد. مرحله آخر بهروزرسانی مکرر عضویت خوشه ایستگاه، خوشه سال و ماه برای بهینهسازی تابع هدف است. برای این منظور، همه ایستگاهها در شرایطی که حداقل مقدار تابع هدف به دست میآید به ایستگاهها-خوشههای مربوطه اختصاص داده میشوند (مرحله 3.1). تکالیف یکسان به ترتیب برای تمام سال ها و ماه ها انجام می شود (مرحله 3.2 و 3.3). پس از هر تکرار تخصیص، تابع هدف به طور یکنواخت کاهش می یابد تا زمانی که به همگرایی برسد، یعنی تفاوت بین مقادیر تابع هدف در دو تکرار پیوسته کوچکتر از یک آستانه از پیش تعریف شده است [34 ]. سپس نتایج خوشه بندی سه گانه بهینه به دست می آید.
2.3. آزمایش: سه خوشهبندی دادههای دمای هلند در وضوحهای زمانی چندگانه
برای مقایسه خوشههای مکانی-زمانی شناساییشده در وضوحهای زمانی مختلف، آزمایشی طراحی شد که در آن از الگوریتم BCAT_I در بخش 2.2 برای تجزیه و تحلیل دادههای دمای هلند در وضوحهای روزانه، ماهانه و سالانه استفاده شد. گردش کار آزمایش در شکل 4 نشان داده شده است . ابتدا، برای شناسایی خوشههای مکانی-زمانی در وضوح روزانه، دادههای دمای روزانه هلند در یک مکعب داده سهبعدی با ۲۸ ایستگاه، ۲۰ سال و ۳۶۵ روز (۲۹ فوریه در سالهای کبیسه حذف شد) بهعنوان سه بعد سازماندهی شدند ( شکل ۴).آ). عناصر مکعب داده دمای روزانه هستند. چنین مکعب داده ای را می توان به عنوان یک ماتریس داده سه بعدی با اندازه 28 (ایستگاه) × 20 (سال) × 365 (روز) مشاهده کرد که برای شناسایی ایستگاه ها، خوشه های سال و خوشه های روز تحت BCAT_I قرار گرفت. . دوم، برای شناسایی خوشههای مکانی-زمانی در وضوح ماهانه، دادههای دمای روزانه به طور میانگین برای تولید دادههای دمای ماهانه، که در یک مکعب داده سهبعدی با ایستگاهها، سالها و ماهها بهعنوان سه بعد سازماندهی شدند، میانگینگیری شدند ( شکل 4).ب). عناصر مکعب داده دماهای ماهانه هستند. چنین مکعب داده ای را می توان به عنوان یک ماتریس داده سه بعدی با اندازه 28 (ایستگاه) × 20 (سال) × 12 (ماه) در نظر گرفت، که سپس با استفاده از BCAT_I برای شناسایی ایستگاه-خوشه ها، خوشه های سال و ماه- تجزیه و تحلیل شد. خوشه ها پس از آن، برای شناسایی خوشههای مکانی-زمانی در وضوح سالانه، دادههای دمای سالانه با استفاده از مقدار میانگین در هر سال برای هر ایستگاه از مجموعه داده مطالعه موردی تولید شد. اگرچه در دادههای دمای سالانه فقط دو بعد وجود دارد، یعنی ایستگاهها و سالها، هنوز هم میتوان آن را در یک مکعب داده سهبعدی با ایستگاهها، سالها و 1 به عنوان سه بعدی سازماندهی کرد ( شکل 4).ج) و عناصر مکعب داده دماهای سالانه هستند. BCAT_I برای شناسایی ایستگاهها و خوشههای سال در دادههای دمای سالانه استفاده شد. در نهایت، خوشه های مکانی-زمانی شناسایی شده در وضوح های روزانه، ماهانه و سالانه از نظر الگوهای نمایش داده شده توسط خوشه ها، ترکیبات خوشه ها و عناصر تغییر یافته خوشه ها مقایسه می شوند. از آنجایی که نتایج خوشهبندی سهگانه در این سه وضوح زمانی همگی شامل ایستگاههای خوشهای و خوشههای سال است، برای بررسی تأثیر وضوحهای زمانی مختلف بر نتایج خوشهبندی سهگانه مقایسه شدند.
تجزیه و تحلیل خوشهبندی سهگانه در آزمایش ما به چندین پارامتر از پیش تعریفشده نیاز دارد، به عنوان مثال، تعداد خوشههای ایستگاه، خوشههای سال، خوشههای روز، و خوشههای ماه. با توجه به پارامترها در وضوحهای روزانه، تعداد ایستگاهها، خوشههای سال، و خوشههای روز بهطور تجربی بر اساس مطالعات قبلی روی مجموعه دادههای مشابه، چهار، چهار و هشت تنظیم شدند [ 21 ].]. برای پارامترهای رزولوشن ماهانه، تعداد خوشههای ایستگاه و خوشههای سال هر دو به عنوان چهار برای مقایسه بین وضوحهای زمانی مختلف تعیین شدند. تعداد خوشه های ماه به عنوان چهار با پیش بینی 12 ماه در چهار فصل انتخاب شد. برای پارامترها در تفکیک سالانه، تعداد ایستگاه-خوشه و خوشه-سال چهار برای مقایسه و تعداد خوشه ها در بعد سوم 1 در نظر گرفته شد. علاوه بر این، آستانه از پیش تعریف شده برای رسیدن به همگرایی و تعداد تکرارها تعیین شد. برای تجزیه و تحلیل BCAT_I در تمام وضوحهای زمانی روی 10-6 و 2000 تنظیم شد تا نتایج خوشهبندی سهگانه بهینه را تضمین کند.
3. نتایج
در این بخش، ابتدا خوشه های مکانی-زمانی شناسایی شده توسط BCAT_I در رزولوشن های روزانه، ماهانه و سالانه به طور خلاصه شرح داده می شوند. سپس خوشه ها با وضوح های مختلف از نظر الگوهای نمایش داده شده، ترکیب بندی ها و عناصر تغییر یافته مقایسه می شوند.
3.1. خوشه های فضایی-زمانی در وضوح روزانه
مکعب داده دمای روزانه با اندازه 28 × 20 × 365 در معرض BCAT_I قرار گرفت تا خوشههای مکانی-زمانی را شناسایی کند. پس از تجزیه و تحلیل خوشهبندی سهگانه، 28 ایستگاه، 20 سال و 365 روز به چهار خوشه ایستگاه، چهار خوشه سال و هشت خوشه روز گروهبندی شدند. مضرب های کوچک در شکل 5 الف عناصر درون هر ایستگاه-خوشه و توزیع فضایی آنها در هلند را با رنگ ها نشان می دهند. هر چه رنگ آبی عمیق تر باشد، دمای آن ایستگاه-خوشه کمتر است. جدول زمانی در شکل 5 ب، عناصر درون هر سال-خوشه و توزیع زمانی آنها را از سال 1992 تا 2011، با افزایش دما از سال-خوشه1 به سال-خوشه4 نشان می دهد.
توزیع فضایی ایستگاه-خوشه ها در شکل 5 الف نشان می دهد که چهار منطقه از شمال شرقی به جنوب غربی هلند تقسیم شده اند و الگوهای دمایی افزایشی در این جهت وجود دارد. ایستگاههای خوشهای در شمال شرقی که با آلمان هم مرز هستند، دمای پایینتری دارند در حالی که آنهایی که در جنوب غربی همسایه دریای شمال هستند، دمای بالاتری دارند. چنین نتایجی مؤید این واقعیت است که آب و هوا در شمال شرق کشور بیشتر توسط آب و هوای قاره ای تعیین می شود در حالی که در جنوب غرب بیشتر تحت تأثیر آب و هوای معتدل دریایی است. این نتایج همچنین توسط مطالعات قبلی بر روی داده های دمای هلند [ 21 ، 35 ] پشتیبانی می شود]. توزیع فضایی همچنین نشان می دهد که اکثر عناصر در هر ایستگاه-خوشه از نظر فضایی مجاور هستند. توزیع زمانی خوشههای سال در شکل 5 ب نشان میدهد که از سال 1992 تا 2011، بهویژه در سالهای اخیر پس از 1999، الگوهای دمایی افزایشی کلی وجود دارد. با بالاترین دما در حالی که تنها دو سال (1996 و 2010) متعلق به سال-خوشه 1 با کمترین دما است.
3.2. خوشه های مکانی-زمانی در وضوح ماهانه
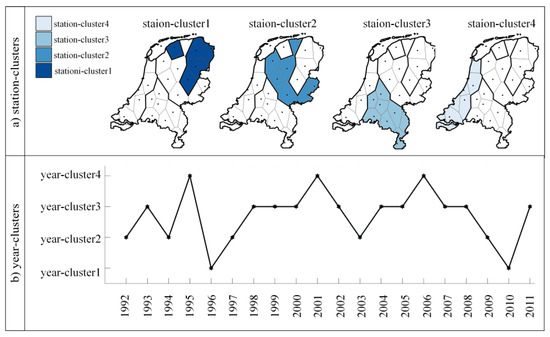
مکعب داده دمای ماهانه با اندازه 28 × 20 × 12 توسط BCAT_I برای شناسایی خوشه های مکانی-زمانی در وضوح ماهانه تجزیه و تحلیل شد. پس از تجزیه و تحلیل، 28 ایستگاه، 20 سال و 12 ماه به چهار ایستگاه – خوشه، چهار سال – خوشه و چهار ماه – خوشه ترسیم شدند. مضرب های کوچک در شکل 6 الف عناصر ایستگاه-خوشه ها و توزیع فضایی آنها در هلند را با رنگ نشان می دهند. رنگ آبی عمیق تر به معنای دمای پایین تر ایستگاه-خوشه است. جدول زمانی خطی در شکل 6 ب، عناصر چهار سال خوشه و توزیع زمانی آنها را از سال 1992 تا 2011 نشان می دهد. دما از سال-خوشه1 به سال-خوشه4 افزایش می یابد.
توزیع فضایی ایستگاه-خوشه ها در شکل 6 الف نیز نشان می دهد که کل کشور به چهار منطقه با افزایش الگوهای دما از شمال شرقی به جنوب غربی تقسیم شده است. با این حال، ایستگاههای خوشهای در جنوب که با شمال بلژیک و دریای شمال هم مرز هستند، دمای بالایی در وضوح ماهانه دارند. شکل 6 a همچنین نشان می دهد که ایستگاه های هر ایستگاه-خوشه از نظر مکانی مجاور هستند. توزیع زمانی خوشه های سال در شکل 6b نشان می دهد که دما از سال 1992 تا 2011 در این وضوح زمانی یک تغییر مداوم را تجربه کرده است. با این وجود، بیش از نیمی از تمام سال ها (13/20) متعلق به خوشه های سال 3 و 4 با دمای بالا است، در حالی که دو سال (1996 و 2010) متعلق به خوشه سال 1 با کمترین دما است.
3.3. خوشه های مکانی-زمانی در وضوح سالانه
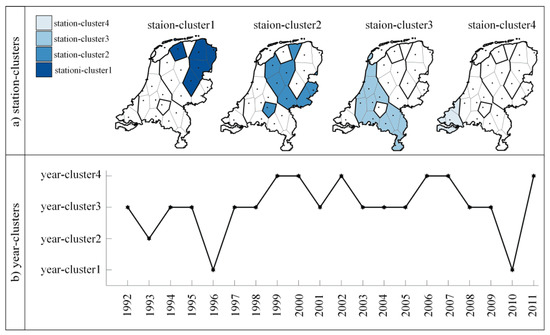
مکعب داده دمای سالانه با اندازه 28 × 20 × 1 در معرض BCAT_I قرار گرفت تا خوشههای مکانی-زمانی در وضوح سالانه شناسایی شود. پس از تجزیه و تحلیل خوشهبندی سهگانه، 28 ایستگاه و 20 سال به چهار ایستگاه-خوشه و چهار خوشه-سال ترسیم شدند. مضرب های کوچک در شکل 7 a توزیع فضایی عناصر را در هر ایستگاه-خوشه در هلند با رنگ ها نشان می دهد: رنگ آبی عمیق تر به معنای دمای پایین تر است. جدول زمانی در شکل 7 ب توزیع زمانی عناصر هر سال-خوشه را از سال 1992 تا 2011 با افزایش دما از سال-خوشه1 به سال-خوشه4 نشان می دهد.
شکل 7 الف نشان می دهد که توزیع فضایی ایستگاه-خوشه ها در تفکیک سالانه همان است که در وضوح روزانه. جدول زمانی خطی در شکل 7 ب، الگوهای دمایی افزایشی کلی دماهای سالانه هلند را از سال 1992 تا 2011 نشان میدهد. بیشتر سالها (17/20) متعلق به خوشههای سال 3 و 4 با دماهای بالا هستند در حالی که سه سال (1993، 1996 و 2010) متعلق به خوشه های سال 1 و 2 با دمای پایین است.
3.4. مقایسه خوشههای مکانی-زمانی در وضوحهای زمانی مختلف
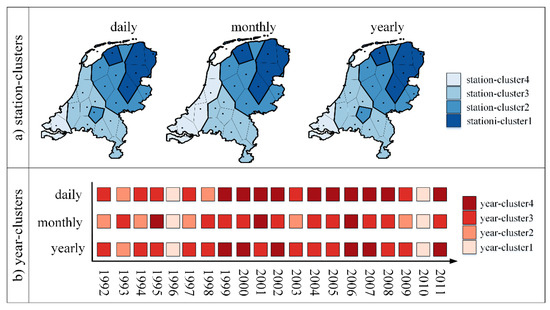
خوشههای ایستگاه و خوشههای سال شناساییشده در دادههای دمای هلند در وضوحهای روزانه، ماهانه و سالانه از نظر الگوهای نشاندادهشده توسط خوشهها، ترکیبها و عناصر تغییر یافته خوشهها مقایسه شدند. برای تسهیل مقایسه، توزیع فضایی ایستگاه-خوشه ها در این سه وضوح زمانی در کنار هم در مضرب های کوچک در شکل 8 الف نشان داده شده است. هر نقشه در مضرب های کوچک، پوشش فضایی ایستگاه-خوشه ها را در یک وضوح زمانی با استفاده از رنگ های آبی عمیق تر برای نشان دادن ایستگاه-خوشه ها با دمای پایین نشان می دهد. نمای مستطیل در شکل 8b برای نمایش توزیع زمانی خوشه های سال در طول 20 سال در این سه وضوح استفاده می شود. این مقایسه ساده خوشههای سال را با وضوحهای مختلف با استفاده از رنگ قرمز تیرهتر برای نشان دادن خوشههای سال با دمای بالاتر فراهم میکند [ 36 ]. علاوه بر این، تعداد عناصری که در هر یک از چهار ایستگاه-خوشه و چهار خوشه سالی از وضوح روزانه به ماهانه، از وضوح روزانه به سالانه و از وضوح ماهانه به سالانه تغییر کرده اند در جدول 1 فهرست شده است. عدد مثبت نشان دهنده افزایش عناصر است، در حالی که عدد منفی به معنای کاهش است.
مضرب های کوچک در شکل 8 a نشان می دهد که حتی اگر ایستگاه-خوشه ها در تمام تفکیک های زمانی الگوهای افزایش دما را از شمال شرقی تا جنوب غربی هلند نشان می دهند، ترکیب ایستگاه-خوشه ها در وضوح ماهانه متفاوت از ترکیب روزانه است. و قطعنامه های سالانه همانطور که در جدول 1 نشان داده شده استچندین ایستگاه در ایستگاه های خوشه 3 و 4 یعنی جنوب غرب کشور تغییر خوشه های ایستگاه را از روزانه به ماهانه و ماهانه به سالانه تجربه کردند. برای مثال station-cluster4 را با بالاترین دما در نظر بگیرید. از رزولوشن روزانه تا ماهانه، چهار ایستگاه دیگر (344 روتردام، 210 والکنبورگ، 240 شیپول، 235 دی کوی) که با دریای شمال هم مرز بودند به این ایستگاه-خوشه تقسیم شدند. از رزولوشن ماهانه تا سالانه، این چهار ایستگاه عضویت خود را در station-cluster4 از دست دادند. چنین تفاوتی به این دلیل است که ایستگاه های جنوب غربی با دمای روزانه و سالانه مشابه، تنوع متفاوتی را در بین دمای ماهانه از خود نشان می دهند. در مقابل، تقریباً هیچ تغییری در عناصر ایستگاه-خوشه 1 و 2 در این سه وضوح زمانی وجود ندارد.
نمای مستطیلی در شکل 8 ب نشان می دهد که اگرچه خوشه های سال در وضوح روزانه و سالانه الگوهای افزایش دما را در طول دوره مورد مطالعه نشان می دهند، ترکیبات خوشه های سال در تمام وضوح های زمانی متفاوت است. همانطور که در جدول 1 نشان داده شده است، خوشه های سال 1 و 2 بیشترین تعداد عناصر تغییر یافته را در وضوح های زمانی مختلف دارند، به ویژه اولی. برای سال-خوشه 1، 10 سال اخیر (1999، 2000، 2001، 2002، 2004، 2005، 2006، 2007، 2008، 2011) با تفکیک روزانه به این خوشه تعلق دارند در حالی که سه سال (19015، 200) شش سال (1999، 2000، 2002، 2006، 2007، 2011) به ترتیب در قطعنامه های ماهانه و سالانه متعلق به آن است. این امکان وجود دارد زیرا خوشه سال در وضوح روزانه فقط شباهت دمای روزانه را برای همه سال ها نشان می دهد و خوشه های سال نیز در وضوح ماهانه و سالانه [ 6 ]. سالهایی با دمای سالانه مشابه ممکن است بین دمای روزانه و ماهانه تفاوتهای متفاوتی داشته باشند.
4. بحث
همانطور که در شکل 8 و جدول 1 نشان داده شده است، حتی اگر عناصر در چندین ایستگاه-خوشه و خوشه سال در وضوح های زمانی مختلف تغییر کرده اند، در ایستگاه های ایستگاه-خوشه 1 و 2 و سال های سال-خوشه 1 در تمام تفکیک های زمانی تغییراتی وجود ندارد یا کم است. این ایستگاه ها شامل پنج ایستگاه در ایستگاه-کلاستر 1 (270 Leeuwarden ، 280 Eelde ، 286 Niewuw Beerta ، 279 Hoogeveen ، 278 Heino) و هفت ایستگاه در ایستگاه-Cluster2 (267 Steverren ، 269 Lelystad ، 273 Markness ، 275 Deelen ، 277 Lauauwwegersoog ، 283 Hupsel, 290 Twenthe) که در شمال شرقی کشور قرار دارند. سالهای سال-خوشه 1 با کمترین دما، سالهای 1996 و 2010 هستند. این خوشههای پایدار نشان میدهند که تفکیکپذیریهای زمانی مختلف دادههای ورودی در تجزیه و تحلیل خوشهبندی سهگانه تأثیری بر آنها ندارند یا تأثیر کمی بر آنها دارند، که میتواند به عنوان خوشههای «واقعی» در مجموعه داده مطالعه موردی [22 ]. برعکس، خوشههای ایستگاه و خوشههای سال با تعداد زیادی از عناصر تغییر یافته در همه وضوحهای زمانی، به عنوان مثال، خوشههای سال 1 و 2، نشان میدهند که اثرات قوی تفکیکپذیریهای زمانی متفاوت بر آنها وجود دارد. این خوشه های ناپایدار نیاز به تجزیه و تحلیل بیشتر در وضوح های زمانی دیگر دارند.
شکل 8 و جدول 1 همچنین نشان می دهد که هیچ تغییری در ترکیبات همه ایستگاه ها از وضوح روزانه به سالانه وجود ندارد، که ممکن است دو وضوح زمانی را به عنوان وضوح زمانی مناسب برای مجموعه داده مطالعه موردی پیشنهاد کند. حتی اگر ایستگاههای همه ایستگاهها در وضوح ماهانه تغییر کردند، اما در وضوحهای روزانه و سالانه ثابت ماندند، که ممکن است به این معنی باشد که این دو وضوح برای تجزیه و تحلیل ایستگاهها-خوشهها در دادههای دمای هلندی مناسب هستند. تحت این شرایط، تجزیه و تحلیل مربوط به ایستگاه-خوشه ها در داده ها می تواند از وضوح درشت، یعنی وضوح سالانه استفاده کند، که به طور قابل توجهی زمان محاسباتی را کاهش می دهد، با توجه به اینکه روش خوشه بندی سه گانه کاملاً زمان بر است [ 12 ].
5. نتیجه گیری ها
این مطالعه یک روش مبتنی بر خوشهبندی سهگانه را برای بررسی تأثیرات تغییر وضوح زمانی دادههای ورودی بر روی خوشههای مکانی-زمانی شناساییشده در GTS ارائه کرد. برای نشان دادن این مطالعه، از دادههای دمای روزانه هلند جمعآوریشده در ۲۸ ایستگاه از سال ۱۹۹۲ تا ۲۰۱۱ استفاده شد. به طور خاص، الگوریتم سه خوشهبندی میانگین مکعب برگمن با واگرایی I (BCAT_I) برای شناسایی خوشههای مکانی-زمانی در دادهها در وضوحهای روزانه، ماهانه و سالانه استفاده شد. سپس، خوشه های مکانی-زمانی شناسایی شده در این سه وضوح از نظر الگوهای نمایش داده شده، ترکیبات، و عناصر تغییر یافته برای بررسی اثرات وضوح زمانی مقایسه شدند.
نتایج نشان میدهد که وضوحهای زمانی در واقع بر خوشههای مکانی-زمانی شناساییشده در یک GTS تأثیر دارند. ترکیب ایستگاهها در رزولوشنهای روزانه و سالانه با وضوح ماهانه متفاوت است و ترکیبات خوشههای سال در همه وضوحها متفاوت است. با این حال، تقریباً هیچ تغییری در ایستگاهها در ایستگاههای خوشههای 1 و 2 (12 ایستگاه در شمال شرق کشور) و در سالهای سال خوشه4 (1996، 2010) در هر سه قطعنامه وجود ندارد که آنها را به عنوان « درست» در مجموعه داده مطالعه موردی. علاوه بر این، ترکیب ایستگاه-خوشه ها در رزولوشن های روزانه و سالانه یکسان است، که ممکن است به عنوان وضوح زمانی مناسب برای تجزیه و تحلیل فضایی مجموعه داده دلالت کند.
به طور خلاصه، روش مبتنی بر خوشهبندی سهگانه پیشنهاد شده در این مطالعه به طور موثر اثرات تفکیک زمانی بر خوشههای مکانی-زمانی شناساییشده در GTS را بررسی میکند. با این حال، یکی از محدودیتهای روش این است که الگوریتم خوشهبندی سهگانه (BCAT_I) مورد استفاده در این مطالعه به دلیل پیچیدگی محاسباتی بالا، به تلاش محاسباتی سنگینی نیاز دارد. بنابراین، کار آینده بر بهینه سازی این الگوریتم خوشه بندی سه گانه برای کاهش زمان اجرای آزمایش متمرکز خواهد بود. علاوه بر این، سایر الگوریتمهای خوشهبندی سهگانه نیز میتوانند در آینده برای صرفهجویی در زمان اجرا مورد استفاده قرار گیرند.
منابع
- لی، ز. یانگ، سی. لیو، ک. هو، اف. جین، بی. مقیاسپذیری خودکار در ابر برای فرآیند کارآمد دادههای بزرگ مکانی. ISPRS Int. J. Geo-Inf. 2016 ، 5 ، 173. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- ساگل، جی. لویدل، ام. Beinat, E. یک رویکرد تجزیه و تحلیل بصری برای استخراج اطلاعات جابجایی شهری مکانی-زمانی از ترافیک شبکه تلفن همراه. ISPRS Int. J. Geo-Inf. 2012 ، 1 ، 256-271. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- شکر، س. جیانگ، ز. علی، RY; افتلی اوغلو، ای. تانگ، ایکس. گونتوری، وی. ژو، ایکس. داده کاوی فضایی و زمانی: یک دیدگاه محاسباتی. ISPRS Int. J. Geo-Inf. 2015 ، 4 ، 2306-2338. [ Google Scholar ] [ CrossRef ]
- میلر، اچ جی; هان، جی. داده کاوی جغرافیایی و کشف دانش: یک مرور کلی. در داده کاوی جغرافیایی و کشف دانش ، ویرایش دوم. Miller, HJ, Han, J., Eds. گروه تیلور و فرانسیس: لندن، انگلستان، 2009; صص 1-26. [ Google Scholar ]
- کیسیلویچ، اس. منزمن، اف. نانی، م. Rinzivillo، S. خوشه بندی فضایی-زمانی. در کتاب داده کاوی و کشف دانش ; Maimon, O., Rokach, L., Eds. Springer: New York, NY, USA, 2010; صص 855-874. [ Google Scholar ]
- وو، XJ; زوریتا میلا، ر. Kraak، MJ سریهای زمانی ارجاعشده جغرافیایی مشترک: کاوش الگوهای مکانی-زمانی در دادههای دمای هلند. بین المللی جی. جئوگر. Inf. علمی 2015 ، 29 ، 624-642. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- هان، جی. کمبر، م. Pei, J. مفاهیم و تکنیک های داده کاوی ; مورگان کافمن MIT Press: برلینگتون، MA، ایالات متحده آمریکا، 2012. [ Google Scholar ]
- مولر، ای. سندووال، ج. مودیگوندا، اس. الیوت، ام. رویکرد مجموعه یادگیری ماشینی مبتنی بر خوشه برای دادههای مکانی: برآورد وضعیت بیمه سلامت در میسوری. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 13. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- آندرینکو، جی. آندرینکو، ن. رینزیویلو، اس. نانی، م. پدرشی، دی. Giannotti، F. خوشهبندی بصری تعاملی مجموعههای بزرگ مسیرها. در مجموعه مقالات سمپوزیوم IEEE در علم و فناوری تجزیه و تحلیل بصری (VAST)، آتلانتیک سیتی، نیوجرسی، ایالات متحده آمریکا، 12 تا 13 اکتبر 2009. [ Google Scholar ]
- وانگ، اچ. دو، ی. سان، ی. لیانگ، اف. یی، جی. وانگ، N. مسیرهای پیچیده خوشهبندی بر اساس شباهت توپولوژیکی و مجاورت فضایی: مطالعه موردی گردابهای اقیانوسی در مقیاس متوسط در دریای چین جنوبی. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 574. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- هنریکس، آر. مادیرا، SC الگوریتم های سه خوشه بندی برای تجزیه و تحلیل داده های سه بعدی: یک بررسی جامع. کامپیوتر ACM. Surv. (CSUR) 2018 , 51 , 95. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- وو، ایکس. چنگ، سی. زوریتا میلا، ر. Song, C. مروری بر روشهای خوشهبندی برای سریهای زمانی جغرافیایی ارجاعشده: از خوشهبندی یکطرفه تا خوشهبندی مشترک و سهگانه. بین المللی جی. جئوگر. Inf. علمی 2020 ، 1–27. [ Google Scholar ] [ CrossRef ]
- میلز، RT; هافمن، اف.ام. کومار، جی. رویکردهای مبتنی بر تحلیل خوشهای هارگرو، WW برای دادهکاوی جغرافیایی-زمانی مجموعههای داده عظیم برای شناسایی تهدیدات جنگل. Proc. محاسبه کنید. علمی 2011 ، 4 ، 1612-1621. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- آندرینکو، جی. آندرینکو، ن. برم، اس. شرک، تی. فون لندزبرگر، تی. باک، پ. کیم، دی. نقشه های خودسازماندهی فضا در زمان و زمان در فضا برای کاوش الگوهای مکانی و زمانی. محاسبه کنید. گر انجمن 2010 ، 29 ، 913-922. [ Google Scholar ] [ CrossRef ]
- هاگناور، جی. Helbich، M. نقشه های خودسازماندهی سلسله مراتبی برای خوشه بندی داده های مکانی و زمانی. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 2026–2042. [ Google Scholar ] [ CrossRef ]
- White, MA; هافمن، اف. هارگرو، دبلیو دبلیو. نمانی، RR یک چارچوب جهانی برای نظارت بر واکنش های فنولوژیکی به تغییرات آب و هوایی. ژئوفیز. Res. Lett. 2005 ، 32 ، L04705. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- وو، ایکس. زوریتا میلا، ر. کراک، ام.-جی. تحلیلی جدید از الگوهای فنولوژیکی بهار در اروپا بر اساس همخوشهبندی جی. ژئوفیز. Res. Biogeosci. 2016 ، 121 ، 1434-1448. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- آندرئو، وی. Izquierdo-Verdiguier، E. زوریتا میلا، ر. رزا، آر. ریزولی، آ. پاپا، الف. شناسایی شرایط فضایی-زمانی مطلوب برای شیوع ویروس نیل غربی با همخوشهبندی سریهای زمانی شاخصهای Modis LST. در مجموعه مقالات IGARSS 2018-2018 IEEE بین المللی زمین شناسی و سمپوزیوم سنجش از دور، والنسیا، اسپانیا، 22 تا 27 ژوئیه 2018. [ Google Scholar ]
- الله، س. داود، ح. داس، SC; خان، HN; خلیل، ع. تشخیص خوشههای بیماری فضا-زمان با اشکال و اندازههای دلخواه با استفاده از رویکرد همخوشهبندی. Geospatial Health 2017 ، 12 ، 567. [ Google Scholar ]
- ژائو، ال. Zaki، MJ Tricluster: الگوریتمی موثر برای استخراج خوشههای منسجم در دادههای ریزآرایه سه بعدی. در مجموعه مقالات کنفرانس بین المللی Acm Sigmod 2005 در مدیریت داده ها، بالتیمور، MD، ایالات متحده آمریکا، 14-16 ژوئن 2005. [ Google Scholar ]
- وو، ایکس. زوریتا میلا، ر. Izquierdo Verdiguier، E. کراک، ام.-جی. سه خوشهبندی سریهای زمانی جغرافیایی مرجع برای تحلیل الگوهای تغییرپذیری درون سالانه دما. ان صبح. دانشیار Geogr. 2018 ، 108 ، 71-87. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- چنگ، تی. Adepeju، M. مسئله واحد زمانی قابل تغییر (MTUP) و تأثیر آن بر تشخیص خوشه فضا-زمان. PLoS ONE 2014 ، 9. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- لیو، ایکس. هوانگ، Q. لی، ز. Wu, M. تأثیر MTUP برای کاوش مسیرهای آنلاین برای مطالعات تحرک انسانی. در مجموعه مقالات اولین کارگاه آموزشی Acm Sigspatial on Prediction of Human Mobility، ردوندو بیچ، کالیفرنیا، ایالات متحده آمریکا، 7 تا 10 نوامبر 2017. [ Google Scholar ]
- Openshaw, S. مسئله واحد قابل تغییر. کتاب های جغرافیایی ; Headley Brothers Ltd. Kent: Norwick, UK, 1983. [ Google Scholar ]
- جیانگ، بی. برانت، SA دیدگاه فراکتالی در مقیاس در جغرافیا. ISPRS Int. J. Geo-Inf. 2016 ، 5 ، 95. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- جوسلین، دی. Louvet, R. تاثیر مقیاس بر چندین معیار مورد استفاده در تجزیه و تحلیل تصویر مبتنی بر شی جغرافیایی: آیا GEOBIA مشکل واحد منطقه ای قابل تغییر (MAUP) را کاهش می دهد؟ ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 156. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- کولتکین، ا. ساباتا، SC; ویلی، دی. ونتوبل، آی. فایستر، اس. کوهن، م. Lacayo، M. مشکل واحد زمانی قابل تغییر. در مجموعه مقالات کارگاه ISPRS/ICA مشکلات پایدار در تجسم جغرافیایی (ICC2011)، پاریس، فرانسه، 2 تا 7 ژوئیه 2011. [ Google Scholar ]
- دی یونگ، آر. de Bruin، S. روندهای خطی در سری های زمانی پوشش گیاهی فصلی و مسئله واحد زمانی قابل تغییر. Biogeosciences 2012 ، 9 ، 71-77. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- وو، ایکس. زوریتا میلا، ر. کراک، ام.-جی. کشف بصری همگام سازی در داده های آب و هوا در وضوح های زمانی متعدد کارتوگر. J. 2013 ، 50 ، 247-256. [ Google Scholar ] [ CrossRef ]
- ژائو، ز. شاو، اس.-ال. یین، ال. نیش، ز. یانگ، ایکس. ژانگ، اف. Wu, S. اثر فواصل نمونهگیری زمانی بر شاخصهای تحرک معمولی انسان بهدستآمده از دادههای مکان تلفن همراه. بین المللی جی. جئوگر. Inf. علمی 2019 ، 33 ، 1471-1495. [ Google Scholar ] [ CrossRef ]
- استرلا، ن. اسپارکس، تی. Menzel، A. روند و پاسخ دما در فنولوژی محصولات در آلمان. گلوب. چانگ. Biol. 2007 ، 13 ، 1737-1747. [ Google Scholar ] [ CrossRef ]
- سیم، ک. آنگ، ز. گوپالکریشنان، وی. کشف خوشه های زیرفضای همبسته در داده های سه بعدی با ارزش پیوسته. در مجموعه مقالات کنفرانس بین المللی IEEE 2010 در مورد داده کاوی، سیدنی، استرالیا، 13 تا 17 دسامبر 2010. [ Google Scholar ]
- عمار، د. یکوتیلی، د. مارون کاتز، آ. هندلر، تی. Shamir, R. یک مدل بیزی سلسله مراتبی برای کشف ماژول انعطاف پذیر در داده های سری زمانی سه طرفه. بیوانفورماتیک 2015 ، 31 ، i17–i26. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- بانرجی، ا. دیلون، آی. گوش، ج. مروگو، اس. Modha، DS یک رویکرد ماکزیمم آنتروپی تعمیم یافته برای همخوشهبندی برگمن و تقریب ماتریس. جی. ماخ. فرا گرفتن. Res. 2007 ، 8 ، 1919-1986. [ Google Scholar ]
- لندرینک، جی. موک، اچ. لی، تی. ون اولدنبورگ، جی. مقیاسپذیری و روند شدید بارشهای ساعتی در دو منطقه آب و هوایی مختلف – هنگ کنگ و هلند. هیدرول. سیستم زمین علمی 2011 ، 15 ، 3033-3041. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- نوکه، تی. شومان، اچ. بوهم، U. روشها برای تجسم دادههای خوشهای اقلیمی. محاسبه کنید. آمار 2004 ، 19 ، 75-94. [ Google Scholar ] [ CrossRef ]
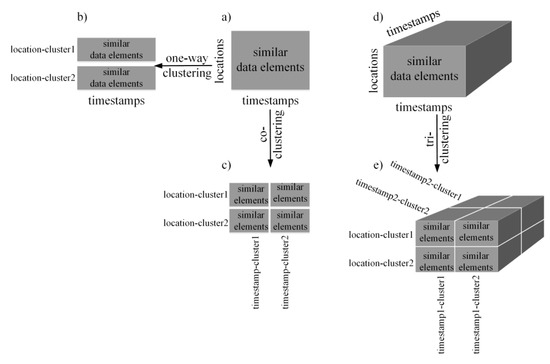
شکل 1. روشهای خوشهبندی یکطرفه ( a ، b )، همخوشهبندی ( a ، c ) و خوشهبندی سهگانه ( d ، e ).
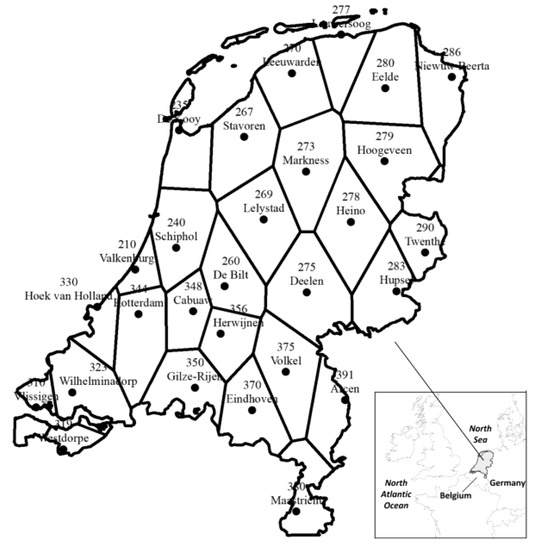
شکل 2. نقشه چند ضلعی های تیسن از ایستگاه های هواشناسی هلند.

شکل 3. فرآیند بهینه سازی BCAT_I با استفاده از داده های دمای ماهانه هلندی مثال زد.
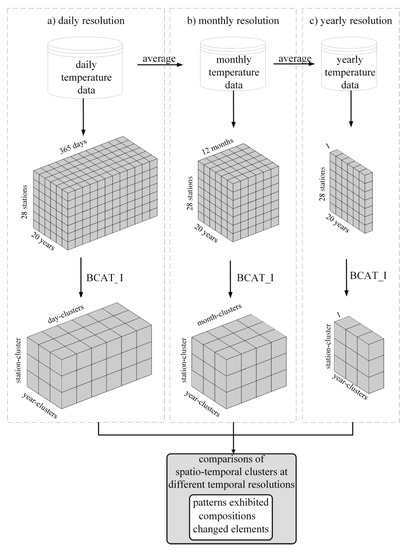
شکل 4. گردش کار تجزیه و تحلیل خوشه بندی سه گانه داده های دمای هلند در قطعنامه های روزانه ( a ) ماهانه ( b ) و سالانه ( c ).
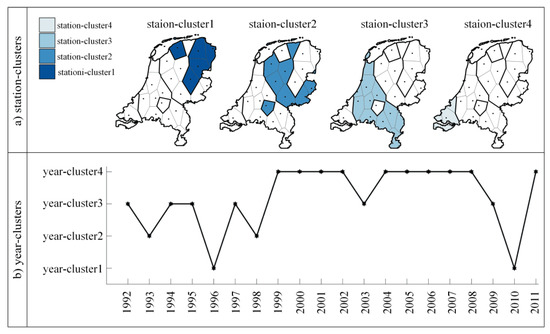
شکل 5. خوشههای فضایی-زمانی (( الف ) خوشههای ایستگاه؛ ( ب ) خوشههای سال) که در دادههای دمای هلند در وضوح روزانه شناسایی شدهاند.
شکل 6. خوشه های مکانی-زمانی (( الف ) خوشه های ایستگاه؛ ( ب ) خوشه های سال)) که در داده های دمای هلند در وضوح ماهانه شناسایی شده اند.
شکل 7. خوشه های مکانی-زمانی (( الف ) ایستگاه-خوشه ها؛ ( ب )- خوشه های سال) شناسایی شده در داده های دمای هلند در تفکیک سالانه.
شکل 8. مقایسه خوشههای ایستگاه ( a ) و خوشههای سال ( b ) در دادههای دمای هلند در وضوحهای روزانه، ماهانه و سالانه.





بدون دیدگاه