یک الگوریتم برنامه ریزی تخلیه مرحله ای کارآمد برای ساختمان های چند خروجی اعمال شده است

خلاصه

هنگامی که تراکم ساکنان ساختمان ها به اندازه کافی زیاد باشد، افراد تخلیه شده مستعد ازدحام در هنگام تخلیه اضطراری هستند، که منجر به طولانی شدن زمان کلی فرار می شود. به خصوص برای ساختمان های چند خروجی، تهیه یک طرح تخلیه موثر یک مشکل چالش برانگیز است. در این مقاله، یک الگوریتم برنامه‌ریزی تخلیه جدید که برای ساختمان‌های چند خروجی اعمال می‌شود، پیشنهاد شده‌است که بر اساس یک مدل شبکه مسیر داخلی است. اولاً، افراد تخلیه شده بر اساس نزدیکی محل خود گروه بندی می شوند، سپس همه گروه ها تقریباً به طور مساوی در چندین منطقه تخلیه طبقه بندی می شوند که هر کدام تنها یک خروجی امن دارند. پس از آن، تمام گروه‌های تخلیه در همان منطقه بر اساس کوتاه‌ترین طول مسیر مرتب‌سازی می‌شوند، سپس پنجره زمانی هر گروه تخلیه که خروجی امن را اشغال می‌کند به نوبه خود محاسبه می‌شود. در صورت ازدحام در خروجی امن، زمان خروج هر گروه تخلیه در دستور ورود خود به تاخیر افتاده است. اهداف الگوریتم پیشنهادی شامل به حداقل رساندن زمان تخلیه کل همه افراد تخلیه شده، زمان سفر هر فرد تخلیه شده، اجتناب از ازدحام ترافیک، متعادل کردن بارهای ترافیکی بین خروجی های مختلف و دستیابی به راندمان محاسباتی بالا است. مطالعات موردی برای بررسی عملکرد الگوریتم ما انجام می شود. تأثیرات تعداد گروه، اندازه گروه، سرعت تخلیه بر روی کل زمان تخلیه در یک شبکه تک خروجی مورد بحث قرار می‌گیرد و روش‌های پارتیشن بندی و تراکم تخلیه بر روی عملکرد و کاربرد در سطوح مختلف تراکم نیز در یک خروجی چندگانه مورد بحث قرار می‌گیرد. شبکه. نتایج نشان می دهد که الگوریتم ما کارایی بالاتری دارد و برای تخلیه با تراکم ساکنین زیاد بهتر عمل می کند.

کلید واژه ها:

تخلیه اضطراری ؛ شبکه مسیر داخلی ; ساختمان های چند خروجی ؛ تخلیه مرحله ای ؛ تراکم، شلوغی

1. معرفی

با توسعه سریع ساخت و ساز شهری و فناوری ساختمان، ساختمان های بزرگ و بیشتری در شهرها ساخته شده اند و ساختارهای داخلی آنها به طور فزاینده ای پیچیده می شود. هنگامی که یک حادثه اضطراری یا فاجعه در داخل ساختمان اتفاق می افتد، ساختار داخلی پیچیده آنها باعث می شود که ساکنان داخل ساختمان به همان سرعتی که یک فاجعه در بیرون رخ می دهد، تخلیه را دشوار کند، که منجر به تراژدی های مکرر می شود. برای امدادگران اضطراری و تخلیه‌کنندگان بسیار مهم است که یک طرح تخلیه اضطراری موثر برنامه‌ریزی کنند [ 1]. دلیل این امر این است که این طرح نه تنها می تواند راه فرار معقولی را برای افراد تخلیه شده در صورت وقوع فاجعه فراهم کند، بلکه زمینه ای را برای امدادگران فراهم می کند تا برنامه نجاتی را تهیه کنند. علاوه بر این، همچنین می‌تواند پیشنهادات معقولی برای چیدمان تأسیسات کنترل آتش و طراحی مسیرهای فرار در داخل ساختمان‌ها ارائه دهد [ 2 ، 3 ].

با توجه به وقوع و گسترش سریع بلایا، لازم است بهترین طرح تخلیه اضطراری در کمترین زمان انجام شود. بنابراین، دو هدف کلیدی یک طرح تخلیه عملی، تضمین کوتاه‌ترین زمان کلی فرار و طراحی طرح در سریع‌ترین زمان ممکن است. تاکنون طرح های تخلیه را می توان تقریباً به عنوان بهینه گرا و شبیه سازی گرا طبقه بندی کرد [ 2]. تحقیق ما به دسته قبلی تعلق دارد و هدف آن توسعه روشی بهینه برای طراحی طرح های تخلیه است. در این مقاله، ما عمیقاً فرآیند تخلیه مرحله‌ای را در محیط‌های شلوغ داخلی تحلیل می‌کنیم و یک الگوریتم ساده و کارآمد برای برنامه‌ریزی مسیر تخلیه مرحله‌ای ارائه می‌کنیم که قادر به مقابله با شبکه‌های چند خروجی است. به طور کلی، تخلیه داخلی یک مشکل تخلیه چند خروجی است. این الگوریتم ابتدا مسئله تخلیه چند خروجی را با متعادل کردن بارهای تخلیه‌کنندگان در همه خروجی‌های اضطراری به یک مسئله تک خروجی تبدیل می‌کند، سپس تخلیه تک خروجی را انجام می‌دهد. مشارکت ما شامل موارد زیر است: 1) برای تخلیه چند خروجی داخلی، یک رویکرد برنامه ریزی تخلیه پارتیشن بندی شده و مرحله ای پیشنهاد شده است که به طور موثر تغییر فوق را تحقق می بخشد و برنامه ریزی تخلیه چند خروجی را ساده می کند. 2) برای تخلیه داخلی تک خروجی، ایده جدیدی برای تعیین توالی فرار تخلیه‌کنندگان با توجه به کوتاه‌ترین طول مسیر پیشنهاد و تأیید شده است که کارایی توسعه طرح تخلیه را بهبود می‌بخشد. علاوه بر این، تخلیه کارآمد تک خروجی به طور موثری کارایی تخلیه چند خروجی را بهبود می بخشد، زیرا تخلیه چند خروجی از تخلیه های چند خروجی یک خروجی در این مقاله تشکیل شده است.

ادامه این مقاله به شرح زیر سازماندهی شده است. بخش 2 کارهای مرتبط را بررسی می کند. بخش 3 مشکل را شرح می دهد. بخش 4 تعاریف و قضایای مرتبط را ارائه می دهد و روش ما را ارائه می دهد. بخش 5 نتایج الگوریتم را نشان می‌دهد، عملکرد و اثربخشی آن را با یک سری آزمایش ارزیابی می‌کند و یک شبیه‌سازی آزمایشی ارائه می‌دهد. بخش 6 مقاله را به پایان می رساند.

2. کارهای مرتبط

از منظر اجرا، لی و همکاران. برنامه های تخلیه را به دو نوع عمده طبقه بندی کنید: طرح های تخلیه خود به خود و طرح های تخلیه سازمان یافته [ 2 ]. اولی با کنترل زیرساخت تخلیه (به عنوان مثال، روشنایی اضطراری آتش سوزی و نشانگر پراکندگی) انجام می شود در حالی که تخلیه کنندگان به طور خود به خود حرکت می کنند اما توسط زیرساخت هدایت می شوند. مورد دوم با کنترل افراد تخلیه شده از جمله زمان حرکت آنها، مسیرهای خروجی امن و غیره محقق می شود. هر نوع طرح تخلیه برای یک سناریوی خاص قابل اجرا است.

با توجه به طرح‌های تخلیه خود به خودی، مدل‌های شبیه‌سازی زیادی برای تحلیل عوامل یا پارامترهای مهمی که بر فرآیند تخلیه تأثیر می‌گذارند یا می‌توانند در ارزیابی عملکرد تخلیه تحت سناریوها و استراتژی‌های مختلف استفاده شوند، ارائه شده‌اند. مدل‌های معمولی موجود شامل مدل‌های مبتنی بر جریان شبکه [ 4 ]، مدل‌های خودکار سلولی (CA) [ 5 ، 6 ]، مدل‌های مبتنی بر عامل [ 7 ، 8 ، 9 ]، مدل‌های نیروی اجتماعی [ 10 ، 11 ]، گاز شبکه LG) مدل‌ها [ 12 ، 13] و غیره. این مدل‌ها با موفقیت برای مطالعه تخلیه جمعیت در موقعیت‌های مختلف به‌دلیل توانایی زیادشان در نمایش برخی از عناصر کلیدی مؤثر بر رفتارهای انسان در طول فرآیند تخلیه، مانند تأثیر تراکم ساکنان اطراف خروجی‌ها [ 14 ، 15 ] و فاصله فضایی بر روی انسان استفاده شده‌اند. رفتار. مدل‌های مبتنی بر جریان به راحتی ساخته می‌شوند در حالی که فاقد تعامل اجتماعی بین تخلیه‌شدگان، رفتار انسان در شرایط اضطراری و نمایش خطرات هستند [ 4 ]]. مدل‌های CA در شبیه‌سازی فرآیند تخلیه در محیط‌های پیچیده بسیار انعطاف‌پذیر و مؤثر هستند، در حالی که در مقایسه با سیستم چند عاملی، دارای عوامل اولیه‌تری هستند که بر روی یک شبکه صلب چیده شده‌اند و با قوانین بسیار ساده با یکدیگر تعامل دارند. مدل‌های ال‌جی مورد خاصی از حالت‌های اتوماتای سلولی را ارائه می‌کنند که از قوانین تصادفی مغرضانه برای شبیه‌سازی جریان متقابل در کانال‌ها یا ارزیابی تأثیر پارامترهای ساختمان بر بازده تخلیه استفاده می‌کنند. مدل‌های مبتنی بر عامل یا مبتنی بر چند عامل می‌توانند انواع مختلفی از عامل‌ها را با ویژگی‌های مختلف نشان دهند و تعاملات آنها پیچیده‌تر است [ 8 ]]، و معایب آنها عموماً از نظر محاسباتی گرانتر از اتوماتای سلولی است. مدل‌های نیروی اجتماعی نوعی مدل پیوسته هستند که از قانون دوم نیوتن برای شبیه‌سازی تخلیه عابر پیاده استفاده می‌کنند و در مدل‌سازی تعاملات بین عابران پیاده خوب هستند، اما کارایی محاسباتی پایینی در شبیه‌سازی تخلیه در ساختمان‌های پیچیده دارند [ 6 ].

این مقاله بر برنامه ریزی تخلیه سازمان یافته متمرکز است که به یک برنامه فرار جامع و موثر برای اهداف تخلیه خاص با توجه به محیط های مختلف فرار نیاز دارد. به طور کلی، این اهداف شامل کاهش درگیری های ترافیکی و به حداقل رساندن کل زمان ترخیص همه افراد تخلیه شده یا زمان تخلیه هر فرد تخلیه شده است. مدل‌های جریان شبکه، مانند مدل‌های جریان حداکثر جریان و مدل‌های جریان کم‌هزینه [ 3 ، 16 ، 17 ، 18 ]، بیشترین استفاده را در بهینه‌سازی جریان تخلیه‌شده دارند، اما آنها کل شبکه را هدف قرار می‌دهند و سعی می‌کنند مبدا را سازماندهی کنند. ، مقصد و مسیرهای تخلیه در سطح مزوسکوپیک جریان دارند. روش برنامه ریزی اعداد صحیح یا برنامه ریزی خطی [ 16 ,19 ]، به عنوان یک الگوریتم دقیق، برای مسائل در مقیاس کوچک قابل استفاده است و معمولاً به پارامترهای اضافی (مثلاً مرزهای پایین یا بالا و غیره) نیاز دارد که معمولاً تخمین از قبل دشوار است. برای تخلیه در مقیاس بزرگ، روش‌های اکتشافی و الگوریتم‌های زمان‌بندی اغلب اتخاذ می‌شوند. اولی، مانند الگوریتم های تکاملی [ 20 ] و بهینه سازی کلنی مورچه ها [ 21 ، 22 ، 23 ]، از نظر کیفیت راه حل ها و زمان محاسبه محدود هستند. دومی به طور کلی روش های دقیقی هستند و برای ادغام اهداف و محدودیت ها در طراحی الگوریتم ها استفاده می شوند [ 2 ، 24 ، 25 ، 26 ].

در فرآیند تخلیه، در صورت وجود ازدحام، ناگزیر منجر به کاهش راندمان فرار و حتی لگدمال شدن حادثه می شود. برای جلوگیری از ازدحام، انتظار ضروری است [ 27 ]. در استراتژی های الگوریتم های زمان بندی دو راه انتظار وجود دارد. یکی در نقطه شروع و دیگری در راه. لی و همکاران یک روش ابتکاری برای ایجاد یک طرح تخلیه مرحله‌ای برای شرایط اضطراری پیشنهاد کرد، اما تنها با یک خروجی ایمن در شبکه اعمال می‌شود و فرض بر این است که سرعت تخلیه‌کنندگان ثابت و برابر است [ 25 ].]. بعداً روش طرح تخلیه مرحله‌ای را از دو جنبه گسترش دادند. یکی این است که آن را برای تخلیه چند خروجی بر اساس مدل شبکه طولانی مدت با متعادل کردن بارهای ترافیک به خروجی های مختلف اعمال کنیم [ 26 ]. مورد دیگر این است که آن را برای تخلیه چند سرعته با یک خروجی مناسب قرار دهید [ 2 ]. اگرچه این الگوریتم‌ها نتایج عالی به دست می‌آورند، محاسبات تکراری شبکه طولانی‌مدت زمان منجر به کارایی پایین آنها می‌شود.

لازم به ذکر است که یکی دیگر از جهت گیری های تحقیقاتی مرتبط با تخلیه اضطراری داخلی، برنامه ریزی پویا یک مسیر تخلیه داخلی بر اساس اطلاعات موقعیت درک شده در زمان واقعی در مورد گسترش یک فاجعه است [ 28 ، 29 ، 30 ، 31 ].]. با این حال، تا کنون، نتایج تحقیقات در این راستا برای شرایط بدون ازدحام داخل ساختمان کاربرد بیشتری دارد. علاوه بر این، فناوری کسب اطلاعات زیست‌محیطی بلایای بلادرنگ در مورد آتش‌سوزی پیشرفت زیادی داشته است، اما همچنان یک کار چالش برانگیز است. به طور دلگرم کننده، ورود شهر هوشمند، دسترسی بلادرنگ به اطلاعات تخلیه داخل ساختمان مانند توزیع افراد تخلیه شده و توسعه یک فاجعه داخلی را ارائه می دهد، که پایگاه داده ای را برای طراحی بلادرنگ طرح تخلیه فراهم می کند. این یکی از دلایلی است که ما به کارایی الگوریتم توجه می کنیم.

3. شرح مشکل

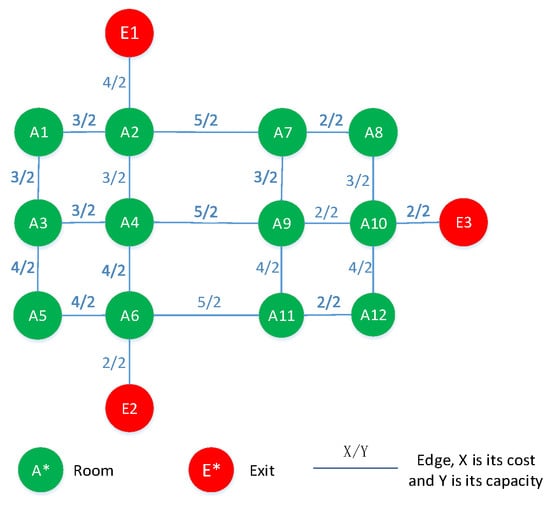
هنگامی که در یک ساختمان با خروجی های متعدد، یک وضعیت اضطراری رخ می دهد، اگر چند نفر ساکن در ساختمان وجود داشته باشد، افراد تخلیه شده نزدیک ترین خروجی را برای فرار انتخاب می کنند. اما اگر تعداد سرنشینان بیشتر باشد، به دلیل محدودیت ظرفیت مسیر فرار، در گوشه ها یا تقاطع های مسیر یا خروجی های ایمنی برای تخلیه شوندگان مستعد ازدحام است که سرعت فرار آنها را کاهش می دهد و زمان کلی تخلیه را طولانی می کند. ، و احتمال خطر را برای آنها افزایش می دهد [ 25 ]. بنابراین، مشکل تخلیه اضطراری داخلی مورد مطالعه در این مقاله این است که چگونه می توان در کوتاه ترین زمان، زمانی که ظرفیت مسیر داخلی محدود است و ممکن است در حین تخلیه ازدحام رخ دهد، همه افراد تخلیه شده از ساختمان های خطرناک با چندین خروجی ایمن فرار کنند. شکل 1نمایش انتزاعی مسئله تخلیه مورد مطالعه را نشان می دهد. سه خروجی ایمنی به نام‌های E1، E2 و E3 در شبکه مسیر داخلی وجود دارد که لبه‌های آن‌ها شامل هزینه و ظرفیت مسیر است. Ai نشان دهنده گره اتاق است. در این مقاله فرض بر این است که ظرفیت های تمامی مکان ها در شبکه مسیر برابر است.

4. روش شناسی

هدف از برنامه ریزی تخلیه اضطراری تخصیص یک زمان حرکت و یک مسیر فرار برای هر فرد تخلیه شده است تا اطمینان حاصل شود که همه سرنشینان داخل خانه می توانند با خیال راحت و منظم به منطقه امن در کمترین زمان فرار کنند. هنگامی که تعداد افراد تخلیه شده زیاد است، معمولاً گروه بندی آنها بر اساس مجاورت مکانی موقعیت هایشان و سپس تخلیه آنها به صورت گروهی مؤثرتر است. یک مسئله کلیدی در طول این روش ازدحام است. برای اجتناب از مشکل، دو استراتژی اغلب در مواقع اضطراری اتخاذ می شود [ 25]. یکی از این راهبردها تخلیه مرحله‌ای است و دیگری تخلیه همزمان. با این حال، در مورد دوم، برای گروه های بعدی سخت است که منتظر بمانند تا زمانی که همه گروه های قبلی به طور کامل از بین بروند. کسی احتمالاً انتظار در شلوغی را رها می‌کند و کورکورانه فرار می‌کند، که درجه ازدحام و کل زمان فرار را افزایش می‌دهد. بنابراین، ما اولی را برای برنامه ریزی فرار اضطراری انتخاب می کنیم.

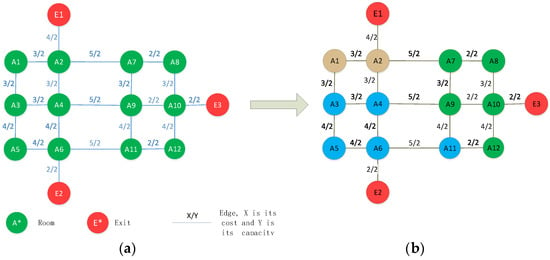
برای یک ساختمان چند خروجی بدون شلوغی، هر خروجی ایمنی منطقه خدماتی مربوط به خود را دارد که در آن تخلیه‌شدگان می‌توانند از کوتاه‌ترین مسیرهای خود به سمت خروجی ایمنی فرار کنند [ 32 ]. هنگامی که یک وضعیت اضطراری رخ می دهد، سرنشینان داخل خانه می توانند از خروجی منطقه تخلیه که در آن قرار دارند فرار کنند. بنابراین، برنامه ریزی تخلیه اضطراری برای یک اضطراری داخلی چند خروجی را می توان به راحتی به برنامه اضطراری یک خروجی داخلی با توجه به مناطق خدماتی خروجی های ساختمان تبدیل کرد ( شکل 2).). با این حال، باید توجه داشت که هدف برنامه‌ریزی تخلیه، تضمین کوتاه‌ترین زمان تخلیه کلی برای همه افراد تخلیه‌شده است، نه کوتاه‌ترین زمان فرار برای یک فرد. زمانی که تراکم سرنشینان داخل خانه بسیار زیاد است یا توزیع آنها غیر یکنواخت است، در منطقه بندی باید این دو عامل را در نظر گرفت. فقط از این طریق می توان تعداد افراد تخلیه شده در هر منطقه تخلیه تقریباً برابر باشد و در نتیجه از تمام خروجی های ایمنی به طور کامل استفاده شود و حداقل زمان تخلیه کل به دست آید.

رویکرد پیشنهادی ما عمدتاً از روش [ 25 ] الهام گرفته شده است که فقط برای مشکل تک خروجی مناسب است. اما رویکرد ما می‌تواند مشکل چند خروجی را به‌خوبی حل کند، به‌ویژه با افراد تخلیه‌شده شلوغ. مسائل کلیدی آن شامل نحوه تبدیل مشکل چند خروجی به مشکل تک خروجی برای حداقل کردن زمان تخلیه کل و چگونگی بهبود رویکرد در [ 25 ] است.] برای به دست آوردن راندمان بالاتر. ابتدا، افراد تخلیه شده بر اساس مجاورت مکانشان گروه بندی می شوند، سپس همه گروه ها تقریباً به طور مساوی در چندین منطقه تخلیه با الگوریتم بهبود یافته Dijkstra با توجه به بار هر خروجی طبقه بندی می شوند. ثانیاً، همه گروه‌های تخلیه در یک منطقه بر اساس کوتاه‌ترین طول مسیر مرتب‌سازی می‌شوند، سپس پنجره زمانی هر گروه تخلیه که خروجی امن را اشغال می‌کند به نوبه خود محاسبه می‌شود. در صورت ازدحام در خروجی امن، زمان خروج هر گروه تخلیه در ترتیب ورود به تاخیر می افتد.

4.1. تخلیه مرحله‌ای برای شبکه تک خروجی

در مورد ازدحام، فرآیند تخلیه شامل عوامل زیادی مانند وزن و ظرفیت شبکه مسیر، تعداد کل و زمان کل تخلیه تخلیه‌شدگان، زمان صدور دستور تخلیه، زمان انتظار، زمان حرکت و فرار است. سرعت هر فرد تخلیه شده و غیره. برای توصیف و تحلیل راحت تخلیه در تئوری، متغیرهای مرتبط در زیر تعریف شده اند.

n : تعداد گروه های تخلیه.

t ₀ : اولین لحظه خروج، یعنی زمانی که دستور تخلیه صادر می شود.

t_{p}^{i}

: زمان مصرف شده توسط گروه فرار i از مبدأ تا خروجی ایمنی E در طول مسیر فرار.

t_{e}^{i}

: زمان صرف شده توسط صف گروه i برای عبور کامل از نقطه ای مانند E در شبکه مسیر.

t_{d}^{i}

: تاخیر زمان خروج گروه فرار i .

t_{l}^{i}

: فاصله زمانی بین گروه i و گروه قبلی آن در طول مسیر.

V : سرعت فرار گروه های فرار.

T : کل زمان تخلیه همه گروه های فرار که زمان از t ₀ تا لحظه ای است که آخرین گروه تخلیه از خروجی اضطراری عبور کرده است.

فرض بر این است که سرعت فرار V هر گروه یکسان است و شبکه تخلیه تنها یک خروجی ایمنی دارد. در عین حال، فرآیند تخلیه مرحله‌ای دارای چهار فرض است:

هر لبه شبکه تخلیه ظرفیت یکسانی دارد و هنگامی که یک گره از شبکه توسط یک گروه اشغال می شود، سایر گروه های فرار نمی توانند از گره عبور کنند.
زمان تاخیر بین دو گروه مجاور برای اطمینان از عدم همپوشانی یا جدا نشدن پنجره های زمانی آنها است.
در طی مراحل فرار مرحله‌ای، هر گروه در کوتاه‌ترین مسیر به سمت خروجی فرار می‌کند.
شبکه تخلیه یک گراف بدون جهت است که در آن هزینه یکسانی برای رفتن یا آمدن به یک لبه خواهد داشت.

در فرآیند تخلیه مرحله‌ای، هر گروه بدون ازدحام در کوتاه‌ترین مسیر خود به خروجی ایمنی می‌رسند. سپس هر گروه به طور متوالی از خروجی عبور می کند تا تخلیه کامل شود [ 25 ]. بر این اساس، کل زمان تخلیه هر گروه را می توان به سه قسمت تقسیم کرد که شامل $t_{e}^{i}$ ، $t_{l}^{i}$ و $t_{p}^{i}$ . کل زمان تخلیه T برابر با زمانی است که خروجی ایمنی در کل فرآیند تخلیه اشغال شده است، بنابراین T را می توان به صورت زیر بیان کرد:

تی = تی 1 پ + \sum 1 n (تی من ل + تی من ه)

(1)

در برنامه ریزی مرحله ای تخلیه، اولین کار کلیدی تعیین ترتیب تخلیه هر گروه است. ما عمیقاً عملیات فرآیند تخلیه مرحله‌ای را تحلیل کردیم و قضیه 1 را به دست آوردیم. این اساس رویکرد پیشنهادی ما است.

قضیه 1.

برای به دست آوردن کوتاه ترین زمان تخلیه کل، همه گروه های فرار باید بر اساس فاصله آنها از خروجی اضطراری به صورت مرحله ای فرار کنند. گروه نزدیک به خروجی اولویت خروج دارد و اگر بین پنجره های زمانی آنها درگیری وجود داشته باشد، گروه دور از خروجی به تعویق خواهد افتاد.

اثبات قضیه 1.

با فرض اینکه گروه Gi و گروه Gi + 1 نیاز به تخلیه دارند و تنها یکی از آنها در فرآیند تخلیه برای محدوده ظرفیت مسیر و گره اجازه عبور دارد. یعنی وقتی یک گروه از خروجی E می گذرد ، گروه های دیگر نمی توانند از آن عبور کنند. سپس در خروجی E (یا تقاطع مسیر) زمانی که دو گروه تخلیه می شوند، چندین موقعیت ممکن است رخ دهد.

وضعیت 1. دو گروه به طور همزمان حرکت می کنند و بدون ازدحام به طور متوالی به خروجی اضطراری می رسند.

همانطور که در شکل 3 نشان داده شده است ، با فرض اینکه Gi قبل از Gi + 1 به خروجی اضطراری E برسد ، شرط عدم ازدحام در خروجی به شرح زیر است:

تی من پ + تی من ه < تی من + 1 پ

(2)

در این زمان، Gi + 1 نیازی به تأخیر در زمان خروج خود ندارد. $t_{d}^{i + 1} = 0$ . کل زمان تخلیه آنها از خروجی E به صورت متوالی می تواند به صورت زیر بیان شود:

تی = تی من پ + تی من ه + تی من + 1 ل + تی من + 1 ه

(3)

وضعیت 2. دو گروه به طور همزمان حرکت می کنند و همزمان به خروجی می رسند و باعث ازدحام می شوند.

گروه Gi و گروه Gi + 1 به طور همزمان به خروجی اضطراری می رسند، یعنی

t_{p}^{i} = t_{p}^{i + 1}

همانطور که در شکل 4 نشان داده شده است. برای جلوگیری از ازدحام Gi و Gi + 1 در خروجی اضطراری، یکی از آنها می تواند بلافاصله شروع به فرار کند در حالی که دیگری باید زمان حرکت خود را به تاخیر بیاندازد و در مبدا منتظر بماند. برای یافتن کوتاه‌ترین زمان تخلیه کلی، زمان تأخیر باید اطمینان حاصل کند که دو گروه به‌طور متوالی از خروجی اضطراری عبور می‌کنند و در عین حال هنگام عبور از خروجی فاصله زمانی وجود ندارد. دو راه حل تخلیه وجود دارد که باید مورد بحث قرار گیرد:

در مواقع اضطراری، Gi بلافاصله حرکت می کند و Gi + 1 زمان حرکت خود را به تاخیر می اندازد. برای $t_{l}^{i + 1} = 0$ ، کل زمان تخلیه آنها به شرح زیر است

$تی = تی من پ + تی من ه + تی من + 1 ه$

(4)
در مواقع اضطراری، Gi + 1 فورا حرکت می کند و Gi زمان حرکت خود را به تاخیر می اندازد. برای $t_{l}^{i} = 0$ ، کل زمان تخلیه آنها به شرح زیر است:

$تی = تی من + 1 پ + تی من + 1 ه + تی من ه$

(5)

زیرا $t_{p}^{i} = t_{p}^{i + 1}$ ، هر یک از آنها را می توان به طور معقولی به تأخیر انداخت تا از ازدحام در هنگام رسیدن همزمان به خروجی جلوگیری شود.

وضعیت 3. دو گروه همزمان حرکت می کنند و به طور متوالی به خروجی می رسند و باعث ازدحام می شوند.

با فرض اینکه Gi قبل از Gi + 1 به E برسد و وقتی Gi + 1 به طور کامل از خروجی عبور نکند، به E برسد، همانطور که در شکل 5 نشان داده شده است ، شرایط برای ازدحام دو گروه است.

t_{p}^{i} < t_{p}^{i + 1}

t_{p}^{i} + t_{e}^{i} > t_{p}^{i + 1}

. برای یافتن کوتاه‌ترین زمان تخلیه کلی، زمان تأخیر باید اطمینان حاصل کند که دو گروه به‌طور متوالی از خروجی اضطراری عبور می‌کنند و در عین حال هنگام عبور از خروجی فاصله زمانی وجود ندارد. دو راه حل تخلیه وجود دارد که باید مورد بحث قرار گیرد:

در مواقع اضطراری، Gi بلافاصله حرکت می کند و Gi + 1 زمان حرکت خود را به تاخیر می اندازد. برای $t_{l}^{i + 1} = 0$ ، کل زمان تخلیه آنها به شرح زیر است

$تی a = تی من پ + تی من ه + تی من + 1 ه$

(6)
در مواقع اضطراری، Gi + 1 فورا حرکت می کند و Gi زمان حرکت خود را به تاخیر می اندازد. برای $t_{l}^{i + 1} = 0$ ، کل زمان تخلیه آنها به شرح زیر است:

$تی b = تی من + 1 پ + تی من + 1 ه + تی من ه$

(7)

زیرا $t_{p}^{i} < t_{p}^{i + 1}$ ، $T a < T b$ . بنابراین، هنگامی که دو گروه تخلیه شلوغ هستند، گروه نزدیک به خروجی اضطراری E ابتدا باید شروع به فرار کنند.

در خاتمه، برای به حداقل رساندن کل زمان تخلیه، یعنی اطمینان از استفاده کامل از خروجی اضطراری، گروه نزدیک به خروجی اضطراری باید اولویت را برای فرار قائل شود. □

در برنامه ریزی مرحله ای تخلیه، دومین کار کلیدی محاسبه زمان خروج تاخیری هر گروه تخلیه است. لی و همکاران از شبکه توسعه یافته زمان برای محاسبه زمان تاخیر هر گروه استفاده کرد [ 25 ]. این روش ابتدا پنجره زمانی هر گره را در مسیر تخلیه اشغال شده توسط هر گروه فرار محاسبه می کند و سپس تأخیر زمان خروج هر گروه را با ترتیب ورود و همپوشانی این پنجره های زمانی محاسبه می کند. فرآیند تکراری منجر به محاسبات اضافی در الگوریتم می شود که منجر به کارایی پایین آن می شود. برای اجتناب از مشکل، ما به طور جامع عملیات فرآیند تخلیه مرحله‌ای را تحلیل کردیم و قضیه 2 را یافتیم که فرآیند محاسبه برنامه‌ریزی تخلیه مرحله‌ای را ساده می‌کند.

قضیه 2.

هنگامی که گروه های تخلیه متراکم هستند، نتیجه محاسبه زمان خروج تاخیری آنها در گره پر ازدحام، مانند خروجی اضطراری است.

اثبات قضیه 2.

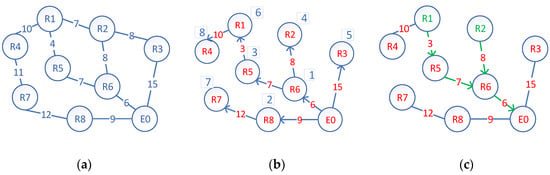
با توجه به مفروضات 3 و 4، در شبکه تخلیه، کوتاه ترین مسیرها از خروجی به سایر گره ها معادل کوتاه ترین مسیرها از سایر گره ها به سمت خروجی است. بنابراین از طریق الگوریتم Dijkstra می توان کوتاه ترین مسیرهای همه گروه ها را به دست آورد تا کوتاه ترین مسیرها از خروجی تا گره هایی که هر گروه در آن قرار دارند محاسبه شود. با توجه به اصل عملکرد الگوریتم Dijkstra، کوتاه‌ترین مسیر از خروجی به هر گره به ترتیب کوتاه‌ترین طول مسیر از کوچک به بزرگ به‌دست می‌آید تا کوتاه‌ترین درخت مسیر را تشکیل دهد. شکل 6 الف یک شبکه تخلیه داخلی است. Ri نشان دهنده یک اتاق و E0 نشان دهنده یک خروجی است. وقتی الگوریتم Dijkstra فراخوانی می شود، به نوبه خود کوتاه ترین مسیرها را پیدا می کند ( P1 (E0-R6 )، P2 ( E0-R8 )، P3 ( E0-R6-R5 )، P4 ( E0-R6-R2 )، P5 ( E0-R3 )، P6 ( E0-R6-R5-R1 )، P7 ( E0-R8-R7 )، P8 ( E0-R6-R5-R1-R4 )) از E0 تا R6 ، R8 ، R5 ، R2 ، R3 ، R1 ، R7 و R4به ترتیب. طول مسیر این مسیرها به نوبه خود افزایش می یابد که عبارتند از 6، 9، 13، 14، 15، 16، 21، 26. این مسیرها کوتاه ترین درخت مسیر را با E0 به عنوان گره ریشه تشکیل می دهند. درخت در شکل 6 ب نشان داده شده است، جایی که عدد مشخص شده روی هر گره نشان دهنده ترتیب به دست آوردن کوتاه ترین مسیر آن هنگام اجرای الگوریتم Dijkstra است. هنگامی که کوتاه ترین مسیر از E0 به هر گره اتاق محاسبه می شود، کوتاه ترین مسیر از هر اتاق تا E0 را می توان با چرخاندن جهت مسیر بدست آورد. شکل 6 ج دو کوتاه ترین مسیر را نشان می دهد. یکی مسیر R1 تا خروجی اضطراری E0 و دیگری مسیر R2 تا E0. آنها در گره R6 یکدیگر را ملاقات می کنند و از R6 تا E0 همپوشانی دارند . □

از روند اجرای الگوریتم Dijkstra می‌توانیم ببینیم که کوتاه‌ترین مسیر هر گره‌ای که کوتاه‌ترین مسیر آن مشخص نشده است، توسط کوتاه‌ترین مسیرهای تعیین‌شده به‌دست می‌آید. بنابراین، هنگامی که مسیرهای تخلیه هر دو گروه تخلیه دارای یک تقاطع باشد، این دو مسیر از تقاطع تا خروجی کاملاً همپوشانی خواهند داشت، همانطور که در شکل 6 ج نشان داده شده است. در فرآیند تخلیه به دلیل اینکه سرعت فرار دو گروه یکسان است، زمان سفر آنها پس از عبور از تقاطع (یعنی از تقاطع تا خروجی اضطراری) نیز برابر است. در نتیجه، محاسبه زمان تاخیر در خروجی یا تقاطع زمانی که دو گروه در تقاطع ازدحام دارند، معادل است. سرعت تخلیه را فرض کنید

V = 1

، G1 نشان دهنده گروه تخلیه است که از R1 شروع می شود .

t_{e}^{1} = 3

; G2 نشان دهنده گروه تخلیه است که از R2 شروع می شود ،

t_{e}^{2} = 5

;

t_{p i}^{1}

زمان تخلیه G1 از R1 به R6 است.

t_{p i}^{2}

زمان تخلیه G2 از R2 به R6 است.

t_{p e}^{1}

زمان تخلیه G1 از R1 به E0 است.

t_{p e}^{2}

زمان تخلیه G2 از R2 به E0 است. سپس زمان تأخیر G1 در تقاطع

t i = t_{p i}^{2} + t_{e}^{2} - t_{p i}^{1}

، و زمان تاخیر G1 در خروجی

t e = t_{p e}^{2} + t_{e}^{2} - t_{p e}^{1}

t_{p e}^{1} - t_{p i}^{1} = t_{p e}^{2} - t_{p i}^{2}

، بنابراین

t i = t e

4.2. الگوریتم پیشنهادی برای شبکه چند خروجی

بر اساس بحث بالا، ما یک الگوریتم برنامه ریزی تخلیه پارتیشن بندی شده و مرحله ای (PSEP) را پیشنهاد می کنیم که برای ساختمان های چند خروجی اعمال می شود. در مورد الگوریتم باید توجه داشت که: الف) برنامه ریزی تخلیه به صورت گروهی پردازش می شود تا پیچیدگی پردازش کاهش یابد. ب) برای همه گروه ها در هر منطقه تخلیه، تخلیه مرحله ای اجرا می شود. ج) به منظور به حداقل رساندن کل زمان تخلیه، هر دو گروه متراکم باید به طور متوالی از خروجی اضطراری عبور کنند و زمان حرکت خود را در هر منطقه به تاخیر انداختند.

4.2.1. توضیحات الگوریتم

کل الگوریتم به دو روش تقسیم می شود. روش اول یک خروجی بهینه را به هر گروه تخلیه اختصاص می‌دهد (همه گروه‌های تخلیه که از یک خروجی عبور می‌کنند متعلق به همان منطقه تخلیه هستند)، و روش دوم زمان خروج هر گروه تخلیه را در همان منطقه محاسبه می‌کند. کد شبه آنها به شرح زیر است.

ورودی: مدل شبکه جاده های داخلی، خروجی ها، سرعت فرار ( V )، اندازه گروه (یکنواخت یا تصادفی) و تعداد گروه ها ( n ).

خروجی: کل زمان تخلیه ( T )، زمان خروج (

t_{d}^{i}

) و مسیر تخلیه برای هر گروه.

نکاتی در مورد رویه 1: خط 5 همه گروه های تخلیه را در شبکه به آرایه N اضافه می کند. خط 6 تمام خروجی های شبکه را به یک آرایه E اضافه می کند. خط 7 تعداد افراد تخلیه شده توسط هر خروجی را به 0 مقداردهی می کند . خطوط 9 تا 14 تعداد تخلیه‌شدگانی را که از هر خروجی عبور می‌کنند مقایسه می‌کنند تا MinE خروجی را با کمترین تخلیه‌کننده پیدا کند. خطوط 15 تا 16 minE را به عنوان نقطه شروع می گیرند، الگوریتم Dijkstra را برای گسترش کوتاه ترین مسیر جدید اجرا کنید. گروهی که در انتهای گره مسیر جدید قرار دارد، minG است. سپس اجازه دهید minGاز طریق MinE تخلیه کنید . در مرحله بعد، تعداد افراد تخلیه شده را که از minE عبور می کنند (خط 19) به روز کنید و minG را از N (خط 20) حذف کنید. بنابراین، یک گروه تخلیه توسط یک حلقه به یک خروجی اختصاص داده می شود. وقتی همه گروه های تخلیه به یک خروجی اختصاص داده می شوند (یعنی تا زمانی که N خالی شود)، حلقه به پایان می رسد.

روش 1 (تخصیص یک خروجی بهینه برای هر گروه تخلیه):

1 عدد صحیح ne // ne تعداد خروجی های شبکه را نشان می دهد.

2 آرایه N[n] // N برای ذخیره همه گروه های تخلیه استفاده می شود.

3 آرایه E[ne] // E برای ذخیره تمام خروجی های ایمنی استفاده می شود.

4 آرایه G[ne] // G برای ذخیره تعداد فعلی تخلیه کنندگان در هر خروجی استفاده می شود.

5 همه گروه های تخلیه را به N اضافه کنید

6 همه خروجی های تخلیه را به E اضافه کنید

7 همه عناصر G را به 0 مقداردهی کنید

8 در حالی که N خالی نیست انجام دهید

9 اجازه دهید minE = 1 // minE متغیری است که برای ثبت شاخص خروجی با حداقل تخلیه کننده ها استفاده می شود.

10 برای e = 2 تا ne //e یک متغیر حلقه محلی است

11 اگر G[e] < G[minE] ، پس

12 اجازه دهید minE = e

13 پایان اگر

14 پایان برای

15 من را به عنوان نقطه شروع در نظر بگیرید

16 الگوریتم Dijkstra را برای گسترش کوتاهترین مسیر جدید اجرا کنید//با مراجعه به شکل 6 a

17 اجازه دهید minG = N[i] // N[i] گروهی است که در انتهای گره مسیر جدید قرار دارد.

18 اجازه دهید minG با عبور از من تخلیه شود

19 تعداد تخلیه‌شدگانی را که از minE عبور می‌کنند به‌روزرسانی کنید

20 minG را از N حذف کنید

21 پایان در حالی که

به طور خلاصه، در طول اجرای رویه 1، یک الگوریتم Dijkstra در هر خروجی وجود دارد، اما فقط الگوریتم Dijkstra در خروجی با کمترین تعداد تخلیه کننده در هر بار اجرا می شود و الگوریتم Dijkstra فقط یک کوتاه ترین مسیر را در هر زمان گسترش می دهد. (یعنی یافتن گروه تخلیه). سپس تعداد تخلیه‌کنندگان تخصیص یافته به هر خروجی تخلیه با یکدیگر مقایسه می‌شود تا مشخص شود که کدام خروجی باید الگوریتم Dijkstra را اجرا کند تا زمانی که همه گروه‌های تخلیه تخصیص داده شوند.

نکاتی در مورد رویه 2: خط 3 تمام گروه های تخلیه در شبکه را به یک آرایه N با طول آرایه n اضافه می کند. خط 4 همه گروه های تخلیه را در N بر اساس کوتاه ترین طول مسیر مرتب می کند. سپس از یک حلقه بیرونی (خط 5) برای پردازش هر ناحیه، یعنی هر خروجی استفاده می شود. دو حلقه داخلی در حلقه بیرونی وجود دارد. اولین حلقه داخلی (خطوط 6 تا 10) برای استخراج همه گروه های تخلیه که از یک خروجی مشابه از N عبور می کنند، استفاده می شود، سپس آنها را به ترتیب به M اضافه می کند . خط 11 باعث می شود گروه 1 در M بلافاصله پس از وقوع یک وضعیت اضطراری حرکت کند و a = 1، جایی که aشماره توالی تخلیه اولین گروه در هر ترکیب تخلیه است که به طور متوالی از خروجی اضطراری عبور می کند. سپس دومین حلقه داخلی (خطوط 12 تا 17) برای محاسبه زمان خروج Gi در M اجرا می شود ، جایی که i از 2 تا m است که تعداد گروه های موجود در همان منطقه است. زمان حرکت Gi به شرح زیر محاسبه می شود:

t_{d}^{i} = t_{p}^{a} + (t_{e}^{a} + \dots + t_{e}^{i - 1}) - t_{p}^{i}

. اگر

t_{d}^{i} > 0

، زمان تأخیر گی است

t_{d}^{i}

. در غیر این صورت، پس از وقوع یک وضعیت اضطراری، Gi فوراً بدون هیچ تأخیری تخلیه می شود و اجازه دهید

a = i

. حلقه داخلی را اجرا کنید تا زمانی که همه گروه‌های تخلیه در M زمان حرکت خود را دریافت کنند، سپس به خط 5 برگردید. وقتی حلقه بیرونی تمام شد و روند به پایان رسید.

روش 2 (محاسبه زمان حرکت هر گروه در هر منطقه):

1 آرایه N[n] // N برای ذخیره همه گروه های تخلیه استفاده می شود

2 آرایه M[n] // M برای ضبط گروه های اختصاص داده شده به همان خروجی استفاده می شود

3 همه گروه های تخلیه را به N اضافه کنید

4 N بر اساس طول مسیر آنها مرتب کنید

5 برای e = 1 به ne // برای پردازش هر منطقه توسط حلقه

6 برای j = 1 تا n // یافتن تمام گروه هایی که از خروجی E[e] توسط حلقه می گذرد

7 اگر N[j] از E[e] عبور کند آنگاه

8 N[j] را به M اضافه کنید

9 پایان اگر

10 پایان برای

11 اجازه دهید

t_{d}^{1} = 0

، a = 1

12 برای i = 2 تا m //برای محاسبه زمان خروج همه گروه هایی که از خروجی E[e] توسط حلقه عبور می کنند

t_{d}^{i} = t_{p}^{a} + (t_{e}^{a} + + t_{e}^{i - 1}) - t_{p}^{i}

14 اگر

t_{d}^{i} < 0

، سپس

t_{d}^{i} = 0

، a = i

16 پایان اگر

17 پایان برای

18 پایان برای

4.2.2. تحلیل پیچیدگی زمانی

در رویه 1، حلقه while n بار و حلقه for ne بار اجرا می شود. علاوه بر این، هنگام اجرای الگوریتم Dijkstra برای گسترش هر گره، طول مسیر همه گره‌ها در شبکه باید n بار مقایسه شود. بنابراین، پیچیدگی زمانی رویه 1 است

O (n (n + n e))

. برای

n e ≪ n

، پیچیدگی زمانی نهایی است

O (n^{2})

در رویه 2، حلقه for خارجی n بار، حلقه داخلی اول برای n بار، حلقه دوم برای m بار اجرا می شود. بنابراین، پیچیدگی زمانی رویه 2 است

O (n e (n + m))

. برای

m \leq n

، پیچیدگی زمانی نهایی است

O (n * n e)

. البته این فرآیند شامل یک فرآیند مرتب سازی با پیچیدگی زمانی نیز می شود

O (n^{2})

یا

O (n \log_{2} n)

هنگامی که الگوریتم PSEP پارتیشن را کامل کرد، هر منطقه معادل یک شبکه تخلیه تک خروجی است. برای یک منطقه، پیچیدگی زمانی محاسبه زمان خروج هر گروه تخلیه است

O (m)

، در حالی که پیچیدگی زمانی تکمیل محاسبه توسط الگوریتم در [ 25 ] است

O (m^{2} \bar{k})

، که در آن m تعداد گروه ها در منطقه است، k تعداد کمان های تمام مسیرهای تخلیه و

\bar{k}

میانگین حسابی k است.

5. مطالعه موردی

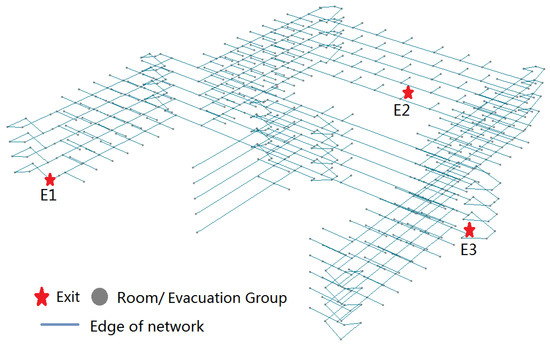
برای تأیید اعتبار و کارایی الگوریتم PSEP، دو آزمون انجام دادیم. یکی برای تأیید صحت و کارایی الگوریتم برای تخلیه تک خروجی استفاده شد. دیگری برای بحث در مورد عقلانیت روش پارتیشن الگوریتم PSEP و مقایسه عملکرد آن با یک الگوریتم موجود. از آنجایی که الگوریتم PSEP بر اساس الگوریتم تخلیه تک خروجی است، هر دو آزمون برای نشان دادن مزایای الگوریتم PSEP ارزشمند هستند. داده های آزمایشی شبکه مسیر سه بعدی ساختمان آموزشی J6 دانشگاه علم و صنعت شاندونگ (SDUST) است، همانطور که در شکل 7 نشان داده شده است.، که در آن هر رأس (یعنی گره) در شبکه یک گروه فرار و هر یال (یعنی قوس) بخشی از مسیر داخلی را نشان می دهد. مدل شبکه از پنج لایه، 818 گره و 853 لبه تشکیل شده است. در طبقه اول، سه خروجی ایمنی وجود دارد: E1 ، E2 و E3 ). در طول آزمایش‌ها، گره‌ها در شبکه مسیر به‌طور تصادفی به‌عنوان گره‌های شروع انتخاب می‌شوند تا محیط تخلیه را در واقعیت شبیه‌سازی کنند.

همه الگوریتم‌های درگیر در سی شارپ توسعه داده شدند و روی نوت‌بوک قابل حمل اجرا می‌شوند که پیکربندی آن به شرح زیر است: CPU i7-6500u، فرکانس اصلی 2.5 گیگاهرتز، حافظه در حال اجرا 12 G و دیسک حالت جامد با ظرفیت 256 G.

5.1. تست های مبتنی بر شبکه تک خروجی

الگوریتم PSEP عمدتاً از الگوریتم [ 25 ] الهام گرفته شده است. ابتدا کارایی و نتایج آنها را با هم مقایسه و بحث می کنیم. علاوه بر این، الگوریتم [ 25 ] فقط برای شبکه تک خروجی مناسب است، بنابراین بخشی از ساختمان آموزشی J6 (یعنی یک منطقه تخلیه با یک خروجی ایمنی) را به عنوان منطقه آزمایشی انتخاب می کنیم تا تأثیر عدد را آزمایش کنیم. از گروه‌های فرار، اندازه گروه‌ها، سرعت فرار و سایر عوامل در کل زمان تخلیه و همچنین کارایی دو الگوریتم. شبکه آزمایشی شامل تنها یک خروجی E1 ، 210 لبه و 210 راس است. هنگامی که الگوریتم PSEP در شبکه تک خروجی اعمال می شود، اولین روش الگوریتم حذف می شود زیرا شبکه تنها یک خروجی دارد.

5.1.1. تأثیر تعداد گروه ها بر کل زمان تخلیه

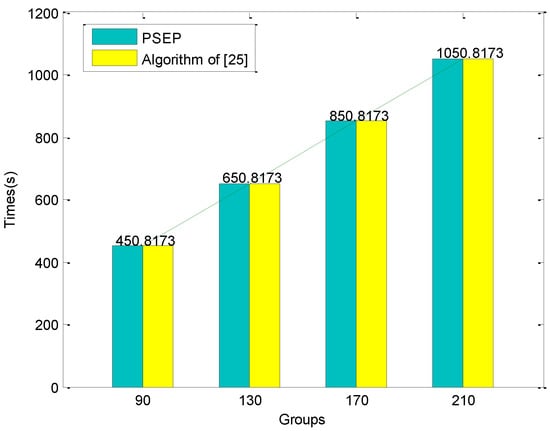
اندازه همه گروه ها 15 متر، سرعت فرار 3 متر بر ثانیه و تعداد گروه های تخلیه به ترتیب 90، 130، 170، 210 تعیین شده است. نتایج آزمون در شکل 8 نشان داده شده است.

شکل 8 نشان می دهد که وقتی اندازه گروه و سرعت فرار هر گروه تخلیه ثابت است، زمان کل تخلیه آنها به صورت خطی با تعداد گروه های تخلیه برای هر دو الگوریتم افزایش می یابد. در عین حال، کل زمان تخلیه دو الگوریتم برابر است.

5.1.2. تأثیر سرعت تخلیه بر کل زمان تخلیه

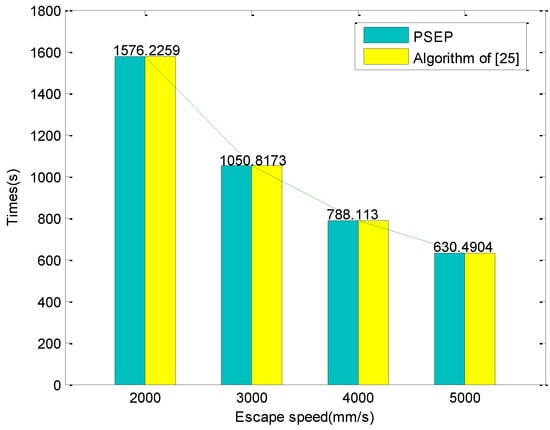
تعداد گروه های تخلیه 210، اندازه گروه 15 متر و سرعت فرار به ترتیب 2، 3، 4 و 5 متر بر ثانیه تعیین شده است. نتایج آزمون در شکل 9 نشان داده شده است.

شکل 9 نشان می‌دهد که وقتی تعداد گروه‌های تخلیه و اندازه گروه ثابت است، کل زمان‌های تخلیه دو الگوریتم با افزایش سرعت فرار کاهش می‌یابد.

5.1.3. تأثیر اندازه گروه بر کل زمان تخلیه

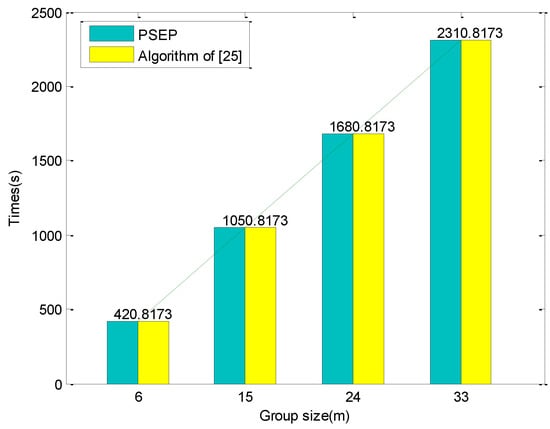
تعداد گروه های تخلیه 210، سرعت فرار 3 متر بر ثانیه و اندازه گروه 6، 15، 24 و 33 متر تعیین شده است. نتایج آزمایش در شکل 10 نشان داده شده است.

شکل 10 نشان می‌دهد که وقتی تعداد گروه‌های تخلیه و سرعت فرار ثابت است، کل زمان‌های تخلیه آنها به صورت خطی با افزایش اندازه گروه برای هر دو الگوریتم افزایش می‌یابد.

5.1.4. مقایسه بازده عملیاتی

اندازه گروه 15 متر، سرعت فرار 3 متر بر ثانیه و تعداد گروه های تخلیه به ترتیب 120، 280، 440، 600، 760، 920 و 1080 تنظیم شده است. آمار آزمون در جدول 1 نشان داده شده است. Td نشان دهنده زمان مصرف شده توسط الگوریتم [ 25 ] و Tp نشان دهنده زمان مصرف شده توسط الگوریتم PSEP است. شکل 11 الف منحنی های زمان مصرف شده توسط دو الگوریتم را نشان می دهد، که از آن می بینیم که مصرف زمان آنها با افزایش تعداد گروه های تخلیه افزایش می یابد، اما زمان مصرف شده توسط الگوریتم PSEP به طور قابل توجهی کمتر از زمان است. الگوریتم [ 25 ]. شکل 11b منحنی نسبت زمان مصرف شده توسط دو الگوریتم را نشان می دهد، که از آن می توان دریافت که هر چه گروه های تخلیه بیشتر باشد، مزیت کارایی الگوریتم PSEP نسبت به الگوریتم [ 25 ] آشکارتر است. وقتی تعداد گروه ها 1080 باشد، Td / Tp به 41465 می رسد.

از سه آزمایش اول می توان دریافت که کل زمان تخلیه دو الگوریتم بدون توجه به شرایط تخلیه یکسان است که درستی الگوریتم پیشنهادی را اثبات می کند. تست 4 نشان می دهد که الگوریتم PSEP بسیار کارآمدتر از الگوریتم [ 25 ] است. دلیل آن این است که محاسبات تکراری زیادی در الگوریتم [ 25 ] وجود دارد]. هر بار که زمان خروج یک گروه تخلیه مشخص می‌شود، لازم است برای هر گروه تخلیه که زمان خروج آن مشخص نشده است، پنجره‌های زمانی خود را در تمام گره‌های مسیر تخلیه خود دوباره محاسبه کند، در حالی که الگوریتم PSEP فقط نیاز به محاسبه پنجره زمانی دارد. از هر گروهی که خروجی را اشغال می کند تا زمان خروج همه گروه های فرار را مشخص کند. علاوه بر این، آزمون های فوق صحت قضایای 1 و 2 را نیز اثبات می کنند.

5.2. تست های مبتنی بر شبکه چند خروجی

بر اساس اصل الگوریتم PSEP، روش پارتیشن و تراکم تخلیه‌کنندگان داخلی دو عامل مهمی هستند که بر زمان کلی تخلیه تأثیر می‌گذارند. بنابراین، ما تأثیر آنها را بر کارایی تخلیه آزمایش کردیم. علاوه بر این، رابطه بین طول مسیر تخلیه و زمان تاخیر هر گروه تخلیه آزمایش می‌شود. عملکرد آن نیز با الگوریتم موجود مقایسه می شود.

5.2.1. تاثیر روش های پارتیشن بندی بر کارایی تخلیه

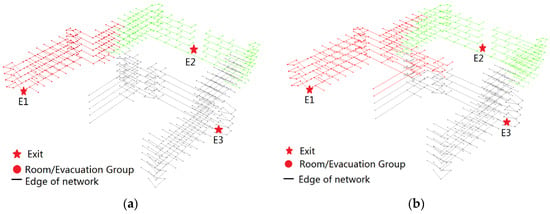
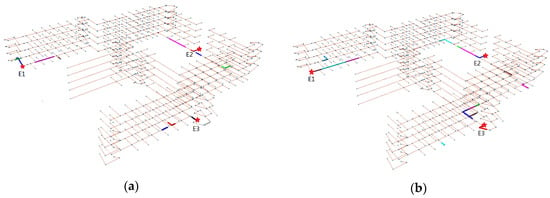
در تئوری، روش پارتیشن مبتنی بر اصل “نزدیکترین تخلیه” زمان تخلیه کلی را زمانی که تراکم تخلیه کنندگان داخلی بیشتر است افزایش می دهد. به منظور تأیید تئوری، ما اصول “نزدیکترین تخلیه” و “تخلیه متعادل” را به ترتیب در الگوریتم PSEP اعمال می کنیم تا تاثیر آنها را بر تخلیه آزمایش کنیم. شکل 12 a شبکه پارتیشن بندی شده داخلی را تنها بر اساس “نزدیکترین تخلیه” نشان می دهد که نزدیکترین خروجی را برای هر گروه پیدا می کند، و شکل 12 ب نشان می دهد که بر اساس “تخلیه متعادل” که باعث می شود هر خروجی تقریباً با در نظر گرفتن تعداد تخلیه شوندگان برابر باشد. هم تعداد افراد تخلیه شده و هم طول مسیر آنها. از شکل 12 قابل مشاهده استکه پارتیشن برخی از گره ها در شبکه مسیر تغییر کرده است. بسیاری از گره‌هایی که در اصل به منطقه E3 تعلق دارند به E1 اختصاص داده می‌شوند، در حالی که ناحیه E1 بخشی از گره‌های ناحیه اصلی E2 را نیز اشغال می‌کند و ناحیه E2 بخشی از گره‌ها را از ناحیه اصلی E3 باز می‌گیرد. علاوه بر این، این گره های تنظیم شده عمدتاً در ناحیه مجاور مناطق اصلی توزیع می شوند.

جدول 2 تعداد گروه های تخلیه، تعداد افراد تخلیه شده از هر منطقه تخلیه و زمان تخلیه کل آنها را در زمانی که الگوریتم PSEP به ترتیب دو روش تقسیم بندی را اتخاذ می کند، نشان می دهد. از جدول می توان دریافت که تعداد گروه های تخلیه هر خروجی هنگام استفاده از اصل “نزدیک ترین تخلیه” متعادل نیست در حالی که هنگام استفاده از اصل “تخلیه متعادل” متعادل هستند. نزدیکترین تخلیه باعث می شود که خروجی های E1 و E2 به طور کامل مورد استفاده قرار نگیرند، که زمان کلی تخلیه را در مقایسه با تخلیه متعادل 265 ثانیه افزایش می دهد. بنابراین، می‌توان نتیجه گرفت که استراتژی پارتیشن مناطق تخلیه تأثیر زیادی بر کارایی تخلیه طرح تخلیه خواهد داشت.

5.2.2. تأثیر تراکم تخلیه بر زمان کل تخلیه

بگذارید چگالی تخلیه ER = EL / NL ، که در آن EL طول کل همه گروه های تخلیه و NL طول کل تمام لبه های شبکه تخلیه است. برای آزمایش تأثیر تراکم تخلیه بر زمان کل تخلیه طرح‌های تخلیه مختلف، نزدیک‌ترین تخلیه و تخلیه متعادل را به ترتیب با تراکم‌های تخلیه مختلف اجرا کردیم. طول کل شبکه مسیر تخلیه 5443.3 متر و تعداد گروه های تخلیه 818 متر است. طول تمام گروه های تخلیه به ترتیب 0.5، 1، 2، 3، 4 و 5 متر تعیین شده است. نتایج آزمون در جدول 3 نشان داده شده است ، جایی که Tnنشان دهنده کل زمان تخلیه نزدیکترین تخلیه و Tb نشان دهنده زمان تخلیه متعادل است. می‌توانیم ببینیم که تخلیه متعادل مزایای آشکاری نسبت به نزدیک‌ترین تخلیه دارد، زمانی که تراکم تخلیه‌کنندگان زیاد است، اما نزدیک‌ترین تخلیه، زمانی که تراکم تخلیه‌کنندگان کوچک است، زمان تخلیه کلی کوتاه‌تری دارد. شکل 13 نشان می دهد که هر چه تراکم افراد تخلیه شده بیشتر باشد، تخلیه متعادل سودمندتر خواهد بود.

5.2.3. شبیه سازی فرآیند تخلیه

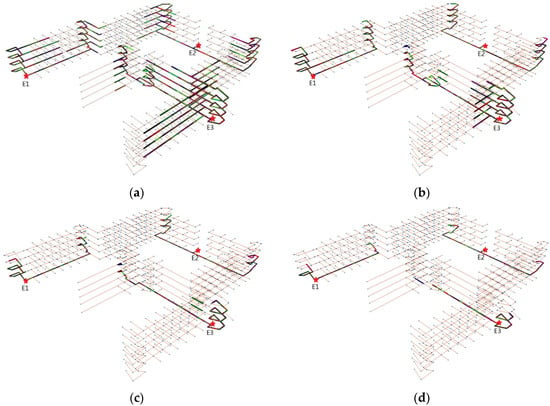
به منظور بررسی بصری اثربخشی الگوریتم خود، کل ساختمان آموزشی J6 SDUST را به عنوان صحنه آزمایش برای شبیه‌سازی فرآیند تخلیه اضطراری با استفاده از نرم‌افزار شبیه‌سازی تخلیه خود در نظر گرفتیم. در صحنه شبیه سازی، رنگ برای شناسایی گروه های مختلف تخلیه استفاده می شود و طول پاره خط نشان دهنده اندازه گروه است. با فرض اینکه زمان شروع تخلیه t0 باشد، سرعت فرار 3 متر بر ثانیه، اندازه گروه تصادفی و مجموع گروه‌های تخلیه 818 باشد. همان زمان در شکل 14 نشان داده شده است ، که در آن (a)-(d) توزیع همه گروه های فرار به ترتیب در t0 + 8 s، t0 + 16، t0 + 24 s و t0 + 32 s است. از شکل 14، می بینیم که بسیاری از بخش های خط رنگارنگ با هم مخلوط شده اند، که نشان می دهد یک منطقه بزرگ ازدحام وجود دارد. بدیهی است که ازدحام جدی سرعت فرار افراد تخلیه شده را کاهش داده و در نهایت منجر به تمدید کل زمان تخلیه می شود.

شکل 15 نتایج شبیه سازی بصری الگوریتم PSEP را نشان می دهد، که در آن (a)-(f) توزیع همه گروه های فرار در t0 + 32 s، t0 + 64 s، t0 + 112 s، t0 + 144 s، t0 + است. به ترتیب 232 ثانیه، t0 + 272 ثانیه. فرآیند شبیه‌سازی نشان می‌دهد که همه گروه‌ها با توجه به زمان حرکت تعیین‌شده بدون ازدحام در مسیر به‌طور منظم فرار می‌کنند و همه گروه‌ها به‌طور متوالی از خروجی اضطراری عبور می‌کنند. همه اینها عملکرد کارآمد کل فرآیند تخلیه را تضمین می کند و زمان کلی تخلیه را کاهش می دهد.

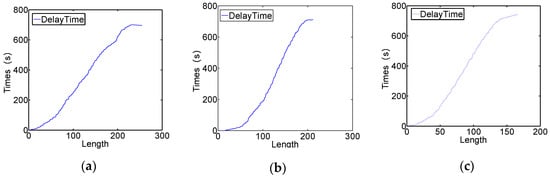
الگوریتم PSEP استراتژی تخلیه پارتیشن بندی شده و مرحله ای را اتخاذ می کند. پس از تکمیل پارتیشن تخلیه، فرآیند تخلیه در هر منطقه مستقل از یکدیگر است. کل زمان تخلیه همه گروه های فرار حداکثر زمان تخلیه هر منطقه است. جدول 4 رابطه بین طول مسیر تخلیه و زمان خروج تاخیری برخی از گروه های تخلیه را در منطقه E1 نشان می دهد و شکل 16 نشان می دهد که همه گروه های تخلیه به ترتیب در مناطق E1، E2 و E3 هستند. می بینیم که زمان خروج تاخیری همه گروه ها در هر منطقه با افزایش طول مسیر تخلیه افزایش می یابد.

5.2.4. رابطه بین طول مسیر تخلیه و زمان تاخیر

جدول 4 رابطه بین طول مسیر تخلیه و زمان تأخیر را در مورد تراکم زیاد افراد تخلیه نشان می دهد. برای به دست آوردن تصویر جامع تری از رابطه آنها، آزمایش دیگری را در مورد تراکم کم افراد تخلیه انجام دادیم. بگذارید همه گروه های تخلیه 2 متر اندازه داشته باشند و سایر شرایط آزمایش ثابت می مانند. جدول 5 طول مسیر تخلیه و زمان خروج با تاخیر گروه های تخلیه جزئی در منطقه E1 را نشان می دهد. شکل 17 رابطه بین طول مسیر تخلیه و زمان خروج تاخیری را برای همه گروه های تخلیه به ترتیب در مناطق E1، E2 و E3 نشان می دهد.

جدول 5 نشان می دهد که زمان تاخیر گروه های تخلیه با افزایش طول مسیر تخلیه آنها به طور کامل افزایش نمی یابد و برخی از آنها استثنایی خواهند بود. این استثنا به دلیل فاصله زمانی بین برخی از گروه های تخلیه مجاور رخ می دهد ( شکل 3) که باعث کاهش زمان خروج با تاخیر گروهی می شود که دیرتر می رسد. برای مثال، اگر پنجره‌های زمانی دو گروه A و B که خروجی یکسانی را اشغال می‌کنند، به ترتیب [23.0، 25.0] و [29.0، 32.0] باشد که همزمان شروع به فرار کنند، با یکدیگر شلوغ نخواهند شد. اما، اگر گروه های جلوتر از A مجبور شوند برای جلوگیری از ازدحام در خروجی، 5 ثانیه به تأخیر بیندازند، پنجره زمانی گروه A که خروجی را اشغال می کند [28.0, 30.0] می شود. برای جلوگیری از ازدحام با گروه A و گروه B باید 1 ثانیه که کمتر از زمان تاخیر گروه A است تاخیر داشته باشد.

5.2.5. مقایسه عملکرد

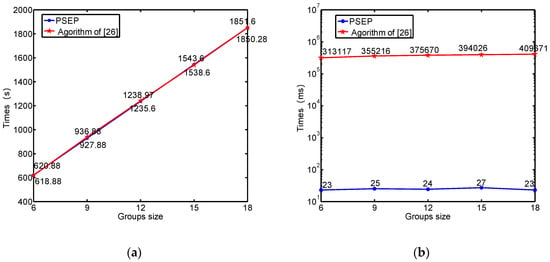
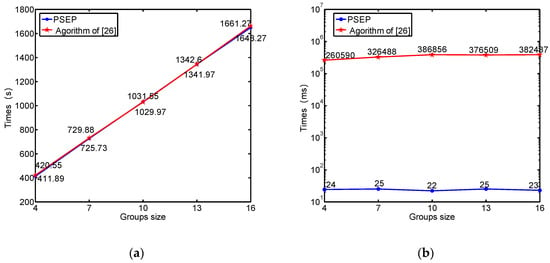
لی و همکاران رویکرد مناسب خود را برای تخلیه تک خروجی به تخلیه چند خروجی در [ 26 ] گسترش دادند. در اینجا، الگوریتم ما با الگوریتم [ 26 ] بر اساس یک مدل شبکه آزمایشی متشکل از 923 گره و 1779 یال مقایسه شده است. سه تا از این گره ها خروجی هستند. هنگامی که اندازه گروه یکنواخت است، نتایج آزمایش در جدول 6 نشان داده شده است ، که در آن Ng و Ne تعداد گروه ها و تعداد افراد تخلیه شده از هر خروجی و Te زمان تخلیه در هر خروجی است. شکل 18 تغییر زمان کل تخلیه و زمان عملیات هر الگوریتم را در زمانی که اندازه گروه به تدریج افزایش می یابد نشان می دهد.

برای واقعی‌تر کردن آزمون، اندازه گروه را به اعداد تصادفی می‌دهیم. هنگامی که اندازه گروه تصادفی است، نتایج آزمون در جدول 7 نشان داده شده است ، که در آن مقدار اندازه گروه یک محدوده است، به این معنی که اندازه گروه می تواند هر مقداری را در این محدوده به طور تصادفی بگیرد. شکل 19 تغییر زمان کل تخلیه و زمان عملیات هر الگوریتم را در زمانی که اندازه گروه به تدریج افزایش می یابد نشان می دهد.

همانطور که در جدول 6 و جدول 7 و شکل 18 و شکل 19 نشان داده شده است، الگوریتم ما و [ 26 ] در زمان تخلیه کلی بسیار نزدیک هستند، اما کارایی برنامه ریزی الگوریتم ما بسیار بیشتر از [ 26 ] است. برای برنامه هایی که نیاز به برنامه ریزی تخلیه سریع یا بلادرنگ دارند، الگوریتم ما مزایای آشکاری دارد.

6. نتیجه گیری

برای تخلیه اضطراری داخلی با تعداد زیادی از تخلیه‌کنندگان، یک الگوریتم برنامه‌ریزی تخلیه پارتیشن بندی شده و مرحله‌ای با در نظر گرفتن ازدحام داخلی پیشنهاد شده است. با توجه به ایده “تخلیه متعادل”، الگوریتم تعداد افراد تخلیه شده را در خروجی های مختلف با الگوریتم بهبود یافته Dijkstra هماهنگ می کند، که کل منطقه تخلیه را تقسیم می کند و تخلیه چند خروجی را به تخلیه تک خروجی تبدیل می کند، بنابراین پیچیدگی را ساده می کند. از پردازش مسئله برای تخلیه تک خروجی، الگوریتم پیشنهادی فقط باید تضاد زمانی بین پنجره‌های زمانی همه گروه‌های تخلیه در خروجی‌ها را در نظر بگیرد، سپس می‌تواند زمان خروج هر گروه را محاسبه کند. در مقایسه با الگوریتم سنتی که تضاد بین پنجره‌های زمانی همه گروه‌های تخلیه را در هر گره از مسیرهای تخلیه برای محاسبه زمان خروج هر گروه در نظر می‌گیرد، محاسبه گره‌های مسیر اضافی را کاهش می‌دهد و کارایی برنامه‌ریزی تخلیه اضطراری را تا حد زیادی بهبود می‌بخشد. . در عمل، الگوریتم PSEP در این مقاله نه تنها بهترین مسیر تخلیه، بلکه زمان خروج بهینه را برای هر گروه ارائه می‌کند تا اطمینان حاصل شود که همه گروه‌ها در حین تخلیه شلوغ نخواهند شد، که عملکرد قوی دارد. شهر هوشمند امکان دسترسی به اطلاعات تخلیه داخلی را در زمان واقعی مانند توزیع افراد تخلیه شده و توسعه یک فاجعه داخلی فراهم می کند که پایگاه داده ای را برای طراحی بلادرنگ یک طرح تخلیه فراهم می کند. طراحی نیاز به کارایی بالای الگوریتم های برنامه ریزی دارد. الگوریتم ما ساده است و دارای مزایای زیادی در بهره وری عملیاتی است که توسعه و تقاضا برای سیستم های تخلیه اضطراری هوشمند و فرماندهی اضطراری را برآورده می کند.

اگرچه الگوریتم PSEP در مورد سرنشینان شلوغ داخلی با تبدیل مسئله تخلیه چند خروجی داخلی به مسئله تخلیه داخل خانه تک خروجی بر اساس اصل “تخلیه متعادل” به نتایج بهتری دست می یابد، اما به دلیل فقدان استدلال و اثبات دقیق ریاضی. در همین حال، استراتژی پارتیشن ممکن است راه حل بهینه جهانی را در زمانی که ساکنان داخل خانه کم هستند به دست نیاورد. بنابراین، ما تأثیر تراکم و توزیع تخلیه‌کنندگان را بر زمان کل تخلیه و اتصال بین همه خروجی‌ها در آینده برای بهینه‌سازی زمان کل تخلیه بیشتر در نظر خواهیم گرفت. علاوه بر این، هنگامی که یک وضعیت اضطراری رخ می دهد، اجازه دهید گروه هایی که ممکن است شلوغ هستند در محل اصلی منتظر بمانند. که برای وقوع بلایای محلی مانند آتش سوزی داخل ساختمان کاربرد ندارد. باید در نظر گرفته شود که یک منطقه خطر بلایای سرپوشیده راه اندازی شود، افراد تخلیه شده در منطقه خطر ابتدا به منطقه ایمنی تخلیه شوند و سپس آنها به خروجی ایمنی تخلیه شوند. ما سعی خواهیم کرد در یک مطالعه بیشتر این موضوع را حل کنیم.

منابع

Kinateder، M. رفتار انسانی در حوادث شدید تونل: اثرات آموزش اطلاعات و رفتار. ترانسپ Res. قسمت F روانشناسی ترافیک. رفتار 2013 ، 17 ، 20-32. [ Google Scholar ] [ CrossRef ]
لی، ایکس. لی، کیو. خو، X. خو، دی. ژانگ، ایکس. یک رویکرد جدید برای توسعه برنامه‌های تخلیه چندسرعته سازمان‌یافته. ترانس. GIS 2018 ، 22 ، 1205-1220. [ Google Scholar ] [ CrossRef ]
شین، ی. کیم، اس. ماه، اول. برنامه ریزی همزمان تخلیه و ورودی در ساختمان مجتمع بر اساس جریان های شبکه پویا. Appl. ریاضی. مدل. 2019 ، 73 ، 545-562. [ Google Scholar ] [ CrossRef ]
Bi, H. Evacuee بهینه‌سازی جریان با استفاده از شبکه G با چندین کلاس از مشتریان مثبت. در مجموعه مقالات بیست و چهارمین سمپوزیوم بین‌المللی IEEE در مورد مدل‌سازی، تحلیل و شبیه‌سازی سیستم‌های کامپیوتری و مخابراتی، لندن، بریتانیا، 19 تا 21 سپتامبر 2016. صص 135-143. [ Google Scholar ] [ CrossRef ]
پلچانو، ن. Malkawi، A. مدل‌های شبیه‌سازی تخلیه: چالش‌ها در مدل‌سازی تخلیه ساختمان‌های مرتفع با رویکردهای اتوماتای سلولی. خودکار ساخت و ساز 2008 ، 17 ، 377-385. [ Google Scholar ] [ CrossRef ]
وانگ، آر. ژو، ال. Liu, J. مطالعه بر روی مدل تخلیه اتوماسیون سلولی بر اساس الگوریتم بهینه‌سازی کلنی مورچه‌ها. چین ساف. علمی J. 2018 ، 28 ، 38-43. [ Google Scholar ] [ CrossRef ]
پان، X. هان، سی. داوبر، ک. قانون، KH یک چارچوب مبتنی بر چند عامل برای شبیه سازی رفتارهای انسانی و اجتماعی در حین تخلیه اضطراری. Ai Soc. 2007 ، 22 ، 113-132. [ Google Scholar ] [ CrossRef ]
رن، سی. یانگ، سی. جین، اس. مدل سازی و شبیه سازی مبتنی بر عامل در تخلیه اضطراری. علوم پیچیده 2009 ، 5 ، 1451-1461. [ Google Scholar ] [ CrossRef ]
چن، ایکس. Zhan، F. مدل سازی و شبیه سازی تخلیه شهری مبتنی بر عامل: اثربخشی نسبی استراتژی های تخلیه همزمان و مرحله ای. جی. اوپر. Res. Soc. 2008 ، 59 ، 25-33. [ Google Scholar ] [ CrossRef ]
پاریسی، DR; Dorso، CO دینامیک میکروسکوپی تخلیه عابر پیاده. فیزیک یک آمار مکانیک. Appl. 2005 ، 354 ، 606-618. [ Google Scholar ] [ CrossRef ]
یانگ، ایکس. دونگ، اچ. وانگ، کیو. چن، ی. هو، ایکس. پویایی جمعیت هدایت شده از طریق مدل نیروی اجتماعی اصلاح شده. فیزیک یک آمار مکانیک. Appl. 2014 ، 411 ، 63-73. [ Google Scholar ] [ CrossRef ]
هلبینگ، دی. ایزوبه، م. ناگاتانی، تی. تاکیموتو، K. شبیه سازی گاز شبکه ای دینامیک تخلیه مورد مطالعه تجربی. فیزیک Rev. E 2003 , 67 , 067101. [ Google Scholar ] [ CrossRef ]
گوا، ایکس. چن، جی. ژنگ، ی. Wei, J. یک مدل گاز شبکه ناهمگن برای شبیه سازی تخلیه عابر پیاده. فیزیک یک آمار مکانیک. Appl. 2012 ، 391 ، 582-592. [ Google Scholar ] [ CrossRef ]
لی، دبلیو. لی، ی. آره.؛ گونگ، جی اچ. شن، اس. هوانگ، ال. لیانگ، JM مدل سازی، شبیه سازی و تجزیه و تحلیل فرآیند تخلیه بر روی پله ها در یک ساختمان کلاس چند طبقه یک مدرسه ابتدایی. فیزیک یک آمار مکانیک. Appl. 2017 ، 469 ، 157-172. [ Google Scholar ] [ CrossRef ]
لیو، اس. یانگ، ال. نیش، تی. لی، جی. تخلیه از یک کلاس درس با توجه به تراکم ساکنان اطراف خروجی. فیزیک یک آمار مکانیک. Appl. 2009 ، 388 ، 1921-1928. [ Google Scholar ] [ CrossRef ]
فلیشر، ال. Skutella، M. حداقل هزینه در طول زمان بدون ذخیره سازی میانی جریان می یابد. در مجموعه مقالات چهاردهمین سمپوزیوم سالانه ACM-SIAM در مورد الگوریتم های گسسته، بالتیمور، MD، ایالات متحده، 12-14 ژانویه 2003. انجمن ریاضیات صنعتی و کاربردی فیلادلفیا: فیلادلفیا، PA، ایالات متحده آمریکا، 2003; جلد 8، ص 66-75. [ Google Scholar ]
ژانگ، ایکس. چانگ، جی. یک مدل تخلیه پویا برای شبکه‌های جریان مختلط عابر پیاده و خودرو. ترانسپ Res. قسمت C Emerg. تکنولوژی 2014 ، 40 ، 75-92. [ Google Scholar ] [ CrossRef ]
ژنگ، ایکس. کای، ال. ژانگ، ام. جینگ، اچ ال. Chen, Y. مدل بهینه‌سازی مسیر تخلیه اضطراری تحت شرایط چند صادراتی. چین ساف. علمی J. 2019 ، 29 ، 180-186. [ Google Scholar ] [ CrossRef ]
استپانوف، آ. اسمیت، JM مسیریابی تخلیه چند هدفه در شبکه های حمل و نقل. یورو جی. اوپر. Res. 2009 ، 198 ، 435-446. [ Google Scholar ] [ CrossRef ]
نیش، ز. لی، کیو. لی، کیو. هان، ال. Shaw, S. یک مدل کارایی فضا-زمان برای بهینه‌سازی حرکات تخلیه خودرو-عابر پیاده درون تقاطع. ترانس. Res. قسمت C Emerg. تکنولوژی 2013 ، 31 ، 112-130. [ Google Scholar ] [ CrossRef ]
نیش، ز. زونگ، ایکس. لی، کیو. لی، کیو. Xiong، S. مسیریابی تخلیه چند هدفه سلسله مراتبی در استادیوم با استفاده از رویکرد بهینه سازی کلونی مورچه ها. J. Trans. Geogr. 2011 ، 19 ، 443-451. [ Google Scholar ] [ CrossRef ]
لی، کیو. نیش، ز. مدل بهینه‌سازی مسیر تخلیه مبتنی بر کلونی مورچه‌ها برای جریان‌های مخلوط عابر پیاده و خودرو. در مجموعه مقالات ششمین کنفرانس بین المللی دینامیک عابر پیاده و تخلیه، ETH، زوریخ، سوئیس، 6-8 ژوئن 2012. Weidmann, U., Kirsch, U., Schreckenberg, M., Eds.; Springer: Cham, Switzerland, 2014; ص 1213-1224. [ Google Scholar ] [ CrossRef ]
وانگ، ال. وانگ، آر. تائو، ک. تحقیق در مورد روش برنامه ریزی مسیر تخلیه با ظرفیت محدود در شبکه های بزرگ مقیاس. علمی Surv. نقشه 2019 ، 35 ، 235-241. [ Google Scholar ] [ CrossRef ]
سبایتی، اچ. محمسنی، HS برنامه ریزی بهینه عملیات تخلیه. ترانس. Res. ضبط 2006 ، 1964 ، 238-246. [ Google Scholar ] [ CrossRef ]
لی، ایکس. هوانگ، بی. لیو، ز. ژانگ، ایکس. Sun, J. یک روش جدید برای برنامه ریزی یک تخلیه مرحله ای. جی. سیست. علمی مجتمع. 2012 ، 25 ، 1093-1107. [ Google Scholar ] [ CrossRef ]
لی، ایکس. لی، کیو. کلارامونت، سی. یک مدل شبکه طولانی مدت برای برنامه ریزی تخلیه مرحله ای. Saf. علمی 2018 ، 108 ، 225-236. [ Google Scholar ] [ CrossRef ]
چاو، WK; Ng، CM زمان انتظار در تخلیه اضطراری پایانه های حمل و نقل عمومی شلوغ. Saf. علمی 2008 ، 46 ، 844-857. [ Google Scholar ] [ CrossRef ]
لیو، اس. Zhu, G. کاربرد فناوری GIS و IOT در تخلیه ساختمان از آتش. Procedia Eng. 2014 ، 71 ، 577-582. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
وانگ، جی. ژائو، اچ. Winter, S. یکپارچه سازی سنجش، مسیریابی و زمان بندی برای تخلیه داخلی. آتش نشانی J. 2015 ، 78 ، 111-121. [ Google Scholar ] [ CrossRef ]
دینگ، ی. او، X. زو، س. لین، اچ. Hu, M. یک روش بهینه سازی پویا در مسیر تخلیه آتش داخلی بر اساس آگاهی از موقعیت واقعی. Acta Geod. کارتوگر. گناه 2016 ، 45 ، 1464-1475. [ Google Scholar ] [ CrossRef ]
ژو، جی. او، پ. لی، دبلیو. کائو، ی. چی، اچ. وانگ، بی. Wang, Y. روش برنامه ریزی پویا مسیر فرار از آتش در فضای داخلی بر اساس شبکه ناوبری. J. جنوب غربی Jiaotong دانشگاه. در مطبوعات. در دسترس آنلاین: https://kns.cnki.net/kcms/detail/51.1277.U.20190320.1146.018.html (دسترسی در 14 ژانویه 2020).
هان، ال. گوا، اچ. ژانگ، اچ. الگوریتمی برای برنامه‌ریزی مسیر که در شرایط اضطراری داخلی چند خروجی استفاده می‌شود. علمی Surv. نقشه 2018 ، 43 ، 105-110. [ Google Scholar ] [ CrossRef ]

شکل 1. شبکه داخلی با خروجی های متعدد.

شکل 2. تبدیل از شبکه مسیر چند خروجی به چندین شبکه مسیر تک خروجی. ( الف ) شبکه مسیر چند خروجی؛ ( ب ) شبکه مسیر چند خروجی پارتیشن بندی شده.

شکل 3. دو گروه به طور متوالی بدون ازدحام به در خروجی می رسند.

شکل 4. دو گروه به طور همزمان به خروجی اضطراری می رسند.

شکل 5. دو گروه به طور متوالی به تقاطع رسیدند و باعث ازدحام شدند.

شکل 6. تصویر تولید کوتاه ترین درخت مسیر و همگرایی دو گروه گریز. ( الف ) شبکه تخلیه داخلی؛ ( ب ) درخت کوتاه ترین مسیر. ( ج ) دو کوتاه ترین مسیر با تقاطع.

شکل 7. مدل شبکه داخلی ساختمان آموزشی J6 SDUST.

شکل 8. مقایسه کل زمان تخلیه آنها با تعداد گروه های تخلیه متفاوت است.

شکل 9. مقایسه کل زمان تخلیه آنها با سرعت فرار متفاوت است.

شکل 10. مقایسه کل زمان فرار آنها با اندازه گروه متفاوت است.

شکل 11. مقایسه کارایی دو الگوریتم. ( الف ) منحنی های زمان مصرف شده توسط دو الگوریتم. ( ب ) نسبت کارایی دو الگوریتم

شکل 12. مقایسه نتایج پارتیشن بندی شده توسط دو روش پارتیشن بندی مختلف. ( الف ) شبکه پارتیشن بندی شده بر اساس نزدیکترین تخلیه. ( ب ) شبکه پارتیشن بندی شده بر اساس تخلیه متعادل

شکل 13. مقایسه کل زمان تخلیه دو استراتژی تحت تراکم تخلیه متفاوت. الف ) تغییر کل زمان تخلیه آنها با افزایش تراکم تخلیه. ( ب ) تغییر کل اختلاف زمان تخلیه با افزایش تراکم تخلیه

شکل 14. شبیه سازی تخلیه همزمان برای شبکه چند خروجی. چهار اسکرین شات در زمان های مختلف به شرح زیر داده می شود: ( a ) t0 + 8 s; ( ب ) t0 + 16 s; ( ج ) t0 + 24 s; ( d ) t0 + 32 s.

شکل 15. شبیه سازی تخلیه پارتیشن بندی شده و مرحله ای برای شبکه چند خروجی. شش اسکرین شات در زمان های مختلف به شرح زیر داده می شود: ( a ) t0 + 32 s; ( ب ) t0 + 64 s; ( ج ) t0 + 112 s; ( d ) t0 + 144 s; ( e ) t0 + 232 s; ( f ) t0 + 272 s.

شکل 16. رابطه طول مسیر تخلیه و زمان خروج تاخیری همه گروه ها در هر منطقه زمانی که تراکم تخلیه زیاد است. ( الف ) منطقه E1؛ ( ب ) منطقه E2. ( ج ) منطقه E3.

شکل 17. رابطه طول مسیر تخلیه و زمان خروج تاخیری همه گروه ها در هر منطقه زمانی که تراکم تخلیه کم است. ( الف ) منطقه E1؛ ( ب ) منطقه E2. ( ج ) منطقه E3.

شکل 18. نتایج مقایسه زمانی که اندازه گروه یکنواخت است. الف ) تغییر کل زمان تخلیه با افزایش تعداد گروهها. ب ) تغییر زمان عملیات با افزایش تعداد گروه ها.

شکل 19. نتایج مقایسه زمانی که اندازه گروه تصادفی است. الف ) تغییر کل زمان تخلیه با افزایش تعداد گروهها. ب ) تغییر زمان عملیات با افزایش تعداد گروه ها.

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

خلاصه

کلید واژه ها:

1. معرفی

2. کارهای مرتبط

3. شرح مشکل

4. روش شناسی

4.1. تخلیه مرحله‌ای برای شبکه تک خروجی

4.2. الگوریتم پیشنهادی برای شبکه چند خروجی

4.2.1. توضیحات الگوریتم

4.2.2. تحلیل پیچیدگی زمانی

5. مطالعه موردی

5.1. تست های مبتنی بر شبکه تک خروجی

5.1.1. تأثیر تعداد گروه ها بر کل زمان تخلیه

5.1.2. تأثیر سرعت تخلیه بر کل زمان تخلیه

5.1.3. تأثیر اندازه گروه بر کل زمان تخلیه

5.1.4. مقایسه بازده عملیاتی

5.2. تست های مبتنی بر شبکه چند خروجی

5.2.1. تاثیر روش های پارتیشن بندی بر کارایی تخلیه

5.2.2. تأثیر تراکم تخلیه بر زمان کل تخلیه

5.2.3. شبیه سازی فرآیند تخلیه

5.2.4. رابطه بین طول مسیر تخلیه و زمان تاخیر

5.2.5. مقایسه عملکرد

6. نتیجه گیری

منابع

قبلیپیش‌بینی‌کننده آبشاری چند مرحله‌ای حرکت عناصر ساختاری در تحلیل تغییر شکل اجسام بزرگ بر اساس عوامل مؤثر بر سری‌های زمانی

بعدیتفاوت در رفتار نگاه عابران پیاده در مسیریابی بین الگوهای جاده های منظم و نامنظم

مطالب مرتبط ...

آموزش مقاله نویسی در رشته ادبیات فارسی

تأثیر همسایگی درونیابی DEM بر عوامل زمین

رگرسیون وزنی جغرافیایی تطبیقی ​​غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

خبرنامه

خبرنامه

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

دسترسی سریع

رگرسیون وزنی جغرافیایی تطبیقی غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب