یک روش ساده سازی حفظ شکل برای مدل های ساختمان شهری

با گسترش مقیاس مدل و بهبود دقت مدل، رندر و نمایش در زمان واقعی مدل های مش سه بعدی غیر ممکن باقی می ماند. برای کاهش چنین فشاری، روش‌های ساده‌سازی مش برای کاهش پیچیدگی ساختاری و در عین حال حفظ ظاهر پیشنهاد شده‌اند. این کار یک روش ساده سازی حفظ شکل را برای مدل های ساختمان شهری معرفی می کند. در مقایسه با روش‌های ساده‌سازی سنتی که فقط حفظ ویژگی‌های هندسی محلی را در نظر می‌گیرند، ما همچنین اشکال کلی مدل‌های ساختمان را برای جلوگیری از فروپاشی با افزایش نرخ ساده‌سازی در نظر می‌گیریم. روش پیشنهادی در چهار مرحله کار می کند. ابتدا، مدل‌های مش را فیلتر می‌کنیم تا ساختارهای مسطح را با حفظ ویژگی‌های واضح ایجاد کنیم. دوم، ما اشکال نواحی مسطح را تشخیص می دهیم. سوم، ما مناطق مسطح و غیر مسطح محدود شده توسط اشکال کلی و ویژگی های هندسی محلی را ساده می کنیم. در نهایت بافت را مجدداً ترسیم می کنیم. آزمایش‌ها اثربخشی این روش را با ارزیابی آن بر روی مدل‌های مختلف ساختمان و مقایسه عملکرد آن با الگوریتم‌های QEM اصلی نشان می‌دهند. علاوه بر این، ما سازگاری فضایی بهتری را در مدل‌های ساختمانی با سطوح مختلف جزئیات (LOD) نسبت به روش‌های سنتی حفظ می‌کنیم.

کلید واژه ها:

مدل سازی شهری ; فیلتر مش ; تشخیص شکل ؛ ساده سازی مش

1. مقدمه

مش های مثلثی بازنمایی محبوب مدل های سه بعدی هستند. یک مدل مش تولید شده از یک خط لوله فتوگرامتری معمولاً شامل صدها میلیون چهره [ 1 ] است که مشکلات زیادی را در ذخیره سازی، انتقال و نمایش به همراه دارد [ 2 ]. با این حال، زمانی که کاربران مدل‌ها را مرور می‌کنند، رندر و نمایش سریع مورد نیاز است. بنابراین، کاهش پیچیدگی ساختاری به طور چشمگیری با حفظ ظاهر ضروری شده است. یعنی هر چه فاصله نزدیکتر باشد، جزئیات مدل های نمایش داده شده بیشتر می شود و بالعکس [ 3 ].

ساده سازی مش یک مشکل طولانی مدت مطالعه شده است، با بسیاری از روش ها توسعه یافته برای کاهش پایدار اندازه مش اصلی بدون تأثیر بر ظاهر آن [ 4 ]. در اینجا، سوال مهم این است که چگونه ساختارهای اصلی و جزئیات کوچک را تعریف کنیم [ 1 ]. روش‌های ساده‌سازی سنتی تنها بر ویژگی‌های هندسی محلی و محدودیت‌های توپولوژیکی تمرکز می‌کنند. تقریب به طور کلی برای مجموعه داده های زمین قابل استفاده است. اما برای ساختمان‌هایی که شکل‌های آنها مسطح است، ویژگی‌های هندسی محلی کافی نیست و اشکال کلی باید شناسایی و حفظ شوند [ 5 ]. در غیر این صورت، مدل مش ممکن است ظاهر اصلی خود را با نرخ ساده سازی بالا از دست بدهد [ 6]. بر اساس تحلیل فوق، روش پیشنهادی ما قرار است ویژگی‌های ساختاری مسطح را حفظ کند. سوال دیگر در مورد نویزهای هندسی و نواقص توپولوژیکی ایجاد شده توسط خط لوله فتوگرامتری است که بیشتر مانع تشخیص ساختارهای مسطح می شود [ 5 ]. برای از بین بردن عیوب و انجام تشخیص شکل، فیلتر مش در مرحله پیش پردازش ضروری است. برای کاهش مقدار داده ها، decimation مش، مانند الگوریتم QEM [ 7 ]، به طور گسترده استفاده می شود، که رئوس را با فروپاشی لبه بر اساس متریک خطای چهارگانه (QEM) [ 1 ] ادغام می کند. الگوریتم های بعدی [ 8 ، 9] انواع معیارهای خطای جدید را برای بهبود کیفیت الگوریتم QEM اصلی پیشنهاد کرد. با این حال، معیارهای خطای فعلی، اشکال کلی را در نظر نمی‌گیرند، که منجر به اعوجاج با افزایش نرخ ساده‌سازی می‌شود.

برای رفع این مشکل، ما یک روش ساده‌سازی حفظ شکل را ارائه می‌کنیم، که مدل‌های مش را فیلتر می‌کند تا ساختارهای مسطح را در عین حفظ ویژگی‌های تیز، تشخیص دهد، اشکال نواحی مسطح را تشخیص می‌دهد، و مناطق مسطح و غیرمسطح محدود شده توسط اشکال کلی و محلی را ساده می‌کند. ویژگی های هندسی در این مقاله، روشی ترکیبی از فیلتر کردن مش و ساده سازی مش اتخاذ شده است. از یک طرف، روش فیلتر شبکه دو طرفه می تواند به تدریج مناطق مسطح را صاف کند و در عین حال ویژگی های تیز را حفظ کند. از سوی دیگر، الگوریتم ساده سازی فروپاشی لبه می تواند تعداد وجوه مثلثی را کاهش دهد. در مقایسه با روش‌های کاهش مشبک سنتی، ما رئوس را به سه نوع طبقه‌بندی می‌کنیم و وزن‌های متفاوتی را با توجه به مناطقی که به آن تعلق دارند، اختصاص می‌دهیم. ترتیب فروپاشی لبه توسط مناطق مسطح شناسایی شده در مرحله قبل برای جلوگیری از فروپاشی با افزایش نرخ ساده سازی محدود می شود. بنابراین، مدل های ساده شده می توانند ساختارهای مسطح و ویژگی های تیز را حفظ کنند.

بقیه مقاله به شرح زیر سازماندهی شده است. ما کارهای مرتبط را در بخش 2 مرور می کنیم . در بخش 3 ، روش ساده سازی پیشنهادی را به تفصیل شرح می دهیم. نتایج تجربی در بخش 4 ارائه و مورد بحث قرار گرفته است. در نهایت، مقاله را در بخش 5 به اختصار خلاصه می کنیم .

2. کارهای مرتبط

الگوریتم‌های ساده‌سازی سنتی به طور مکرر مش ورودی را طبق یک تابع هزینه از بین می‌برند تا ظاهر آن را حفظ کنند تا به نرخ ساده‌سازی مورد نظر برسند [ 4 ]. با توجه به رویه‌های عملیاتی خاص، روش‌های ساده‌سازی فعلی را می‌توان به چهار دسته [ 10 ] تقسیم کرد: کاهش رأس [ 11 ، 12 ]، خوشه‌بندی راس [ 13 ، 14 ]، مش‌های زیربخش [ 15 ، 16 ]، و فروپاشی لبه [ 7 ] ، 17 ]. در میان آنها معمولاً از روش‌های جداسازی مش مبتنی بر فروپاشی لبه استفاده می‌شود. هوپ و همکاران [ 18] اولین کسانی بودند که تابع هزینه را روی لبه ها برای تعیین ترتیب فروپاشی تعریف کردند. به دنبال این ایده، گارلند و همکاران. [ 7 ] یک روش ساده سازی مش را بر اساس متریک خطای چهارگانه (QEM) پیشنهاد کرد. الگوریتم QEM هر راس را با همسایگی خود مرتبط می کند و آن را به عنوان یک ماتریس چهارگانه بیان می کند، که می تواند برای محاسبه هزینه فروپاشی برای هر رأس و یال استفاده شود [ 4 ]. هم کارایی و هم کیفیت ساده سازی را در نظر گرفت و به یک الگوریتم کلاسیک در زمینه ساده سازی مدل های سه بعدی تبدیل شده است. بر اساس الگوریتم اصلی QEM، چندین روش با ترکیب اطلاعات ویژگی، مانند بافت [ 8 ، 9 ]، انحنا [ 19 ، 20 ] توسعه یافته است.]، اطلاعات متقابل [19] توسعه یافته است.21 ] و خواص طیفی [ 22 ]. علاوه بر این، Hoppe و همکاران. [ 23 و 24 ] یک مدل مش پیشرونده و یک الگوریتم مش پیشرونده مبتنی بر دیدگاه را پیشنهاد کردند. لیندستروم و همکاران [ 25 ] یک الگوریتم ساده‌سازی مدل مبتنی بر تصویر را پیشنهاد کرد که متریک خطا را بر روی تصاویر رندر شده از دیدگاه‌های متعدد محاسبه می‌کرد. پردازش موازی [ 26 ، 27 ] برای تسریع فرآیند ساده سازی معرفی شد.

از آنجایی که اشکال ساختمان‌ها به شدت محدود شده‌اند و اطلاعات معنایی نیز پیچیده است، استفاده از روش‌های ساده‌سازی کلی برای مدل‌های ساختمانی سه بعدی به‌طور مستقیم ممکن است منجر به اعوجاج با نرخ ساده‌سازی بالا شود. بنابراین، روش‌های ساده‌سازی هدفمند [ 1 ، 28 ، 29 ، 30 ] برای انطباق با ویژگی‌های ساختمان‌های سه بعدی پیشنهاد شد. لی و همکاران [ 31 ] ویژگی‌های هندسی مدل‌های ساختمانی را به سه دسته طبقه‌بندی کرد و قوانین خاصی برای ساده‌سازی هر نوع ویژگی هندسی پیشنهاد شد. به طور مشابه، وانگ و همکاران. [ 32] رئوس مدل های ساختمان را به راس های مرزی، رئوس سوراخ، و راس های دیگر تقسیم کرد و مدل های محدود شده توسط وابستگی های توپولوژیکی هر نوع راس را ساده کرد.

در این مقاله، مجموعه‌ای از مناطق مسطح را پس از فیلتر کردن مش از پیش تعریف می‌کنیم، رئوس را به سه نوع طبقه‌بندی می‌کنیم و وزن‌های مختلف را با توجه به مناطقی که به آن تعلق دارند، اختصاص می‌دهیم. این روش برای ساختمان هایی با مناطق مسطح بزرگ بسیار مفید است زیرا ظاهر کلی تشخیص داده شده و حفظ شده است تا با افزایش نرخ ساده سازی از فروپاشی جلوگیری شود.

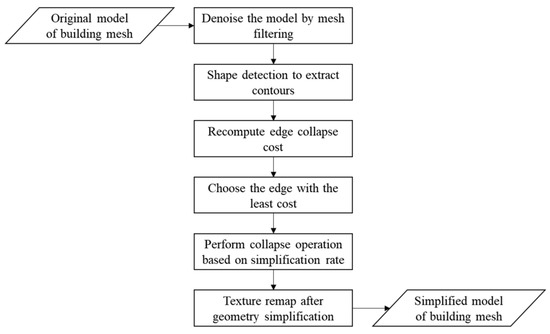
3. روش شناسی

اکثر مدل های سه بعدی فعلی از وجوه مثلثی تشکیل شده اند، بنابراین روش ساده سازی در این مقاله برای مدل های مش مثلثی طراحی شده است. این روش در چهار مرحله کار می کند: (1) مدل اصلی با فیلتر شبکه ای پیش پردازش می شود که مناطق مسطح را صاف می کند و در عین حال ویژگی های واضح را حفظ می کند. (2) مناطق مسطح ناهموار با استفاده از الگوریتم رشد منطقه شناسایی می شوند و مناطق مسطح و مرزهای بین مناطق مجاور با ادغام منطقه و بهینه سازی منطقه به دست می آیند. (3) ما هزینه فروپاشی را برای هر لبه مجدداً محاسبه می کنیم و فروپاشی لبه را با توجه به نتایج تشخیص شکل در مرحله قبل انجام می دهیم. (4) پس از ساده سازی هندسی، بافت را مجدداً ترسیم می کنیم. خط لوله روش پیشنهادی در شکل 1 نشان داده شده است .

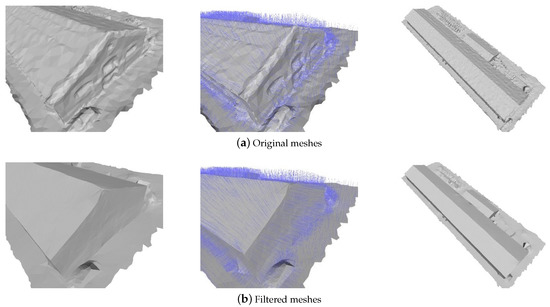
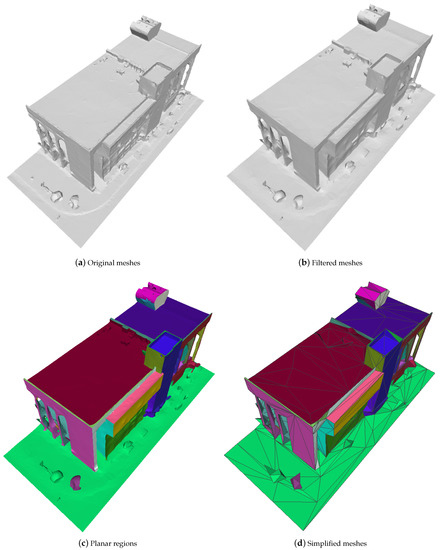
3.1. فیلتر مش

مدل‌های مش مثلثی تولید شده توسط خط لوله فتوگرامتری معمولاً نویزدار هستند، جایی که توزیع نرمال‌های صورت نامنظم است و بیشتر مانع تشخیص ساختارهای مسطح می‌شود. بنابراین، مدل های اصلی نیاز به پیش پردازش دارند. ما از الگوریتم فیلتر شبکه دو طرفه [ 1 ] پیروی می کنیم تا مناطق مسطح به تدریج صاف و در عین حال ویژگی های تیز، مانند لبه ها و گوشه ها را حفظ کنیم [ 33 ].

در این مرحله، نرمال های صورت و رئوس صورت را جدا کرده و آنها را به ترتیب اصلاح می کنیم [ 34 ]. ابتدا نرمال اصلی هر وجه مثلثی محاسبه می شود. سپس، فیلتر دو طرفه را برای هموارسازی این نرمال ها انجام می دهیم و موقعیت های راس مربوطه را به طور مکرر تا زمانی که نیاز برآورده شود، به روز می کنیم. الگوریتم تنها ساختارهای هندسی مدل های مش را اصلاح می کند در حالی که رابطه توپولوژیکی را حفظ می کند. در اینجا، الگوریتم فیلتر معمولی را به تفصیل معرفی می کنیم.

3.1.1. فیلتر معمولی صورت

صورت مثلثی داده شده است $f_{i}$ ، نرمال اولیه به صورت زیر فرموله می شود:

n f من = ( v 2 - v 1 ) \times ( v 3 - v 1 ) ∥ ( v 2 - v 1 ) \times ( v 3 - v 1 ) ∥

(1)

جایی که $v_{1}$ ، $v_{2}$ ، و $v_{3}$ رئوس هستند $f_{i}$ . مخرج نرمال را عادی می کند.

پس از مقداردهی اولیه هر صورت عادی، یک فیلتر دوطرفه اعمال می کنیم تا جهت آن را اصلاح کنیم. مشابه فیلتر تصویر دوطرفه، فیلتر مش دوطرفه شامل دو نوع وزن است: (1) وزن‌های مبتنی بر فاصله فضایی $α_{f_{i} f_{j}}$ ; (2) وزنه های معمولی مبتنی بر مجاورت $β_{f_{i} f_{j}}$ [ 1 ]. دو تابع وزن را می توان مشابه تابع گاوسی تعریف کرد:

α f من f j = انقضا ⎛⎝⎜ - ∥∥ ج f من - ج f j ∥∥ 2 2 σ د من _ 2 ⎞⎠⎟ ، β f من f j = انقضا ⎛⎝⎜ - ∥∥ 1- _ n f من \cdot n f j ∥∥ 2 ( 1 - c o s θ ) 2 ⎞⎠⎟

(2)

جایی که فاصله فضایی بین دو وجه است $f_{i}$ و $f_{j}$ با فاصله اقلیدسی بین مرکز آنها محاسبه می شود $c_{f_{i}}$ و $c_{f_{j}}$ ، $n_{f_{i}}$ و $n_{f_{j}}$ نشان دهنده نرمال دو چهره است، $σ_{d i s}$ واریانس فاصله اقلیدسی است و $θ$ یک آستانه زاویه مشخص شده توسط کاربر است. از نظر تجربی، $θ$ معمولا تنظیم می شود $20 °$ به $30 °$ . تعاریف نشان می دهد که هر دو $α_{f_{i} f_{j}}$ و $β_{f_{i} f_{j}}$ توابع غیر منفی هستند. ارزش $α_{f_{i} f_{j}}$ با افزایش فاصله فضایی بین دو وجه کاهش می یابد. ارزش $β_{f_{i} f_{j}}$ زمانی که جهت دو نرمال به طور قابل توجهی متفاوت باشد، کوچک است. یعنی چهره هایی با وزن کم تأثیر ضعیفی روی یکدیگر دارند.

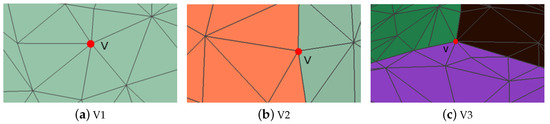
هنگام جست‌وجوی همسایگی یک چهره، باید از چهره‌های ناحیه چین اجتناب کنیم [ 1 ]. در این مقاله، همسایگی را در یک طرح تطبیقی پرس و جو می کنیم. برای یک چهره $f_{i}$ ، همسایگی آن باید دو معیار را برآورده کند: (1) دارای رئوس مشترک با صورت است $f_{i}$ . (2) زاویه بین جهت طبیعی صورت آنها کوچکتر از $θ$ . صورت را اختصاص می دهیم $f_{i}$ یک عادی جدید $\hat{n_{f_{i}}}$ :

n f من^= 1 w من \sum f j \in ن f j آ f من \cdot α f من f j \cdot β f من f j \cdot n f من w من = ∥∥∥∥ \sum f j \in ن f j آ f من \cdot α f من f j \cdot β f من f j \cdot n f من ∥∥∥∥

(3)

جایی که $N_{f_{j}}$ مجموعه همسایگی صورت را نشان می دهد $f_{i}$ ، $A_{f_{i}}$ ناحیه صورت است $f_{i}$ و نرمال جدید $\hat{n_{f_{i}}}$ با یک عامل عادی می شود $w_{i}$ . برای مدل های مش مثلثی که اندازه مش آنها یکسان نیست، همسایگی توپولوژیکی بهتر از همسایگی مبتنی بر فاصله در حین پرس و جو عمل می کند زیرا فقط شامل چهره هایی با جهت گیری های عادی مشابه است [ 1 ]. این مرحله با حفظ ویژگی‌های تیز، نرمی نرمال‌های صورت را درک می‌کند. از طریق چند تکرار فیلتر، نرمال های صورت در همان مناطق مسطح تقریباً همگن خواهند بود.

3.1.2. به روز رسانی موقعیت راس

موقعیت های رأس مدل ها باید با نرمال های چهره جدید به روز شوند. تاوبین و همکاران [ 35 ] موقعیت‌های راس به‌طور مکرر با استفاده از روش نزول گرادیان بر اساس این ویژگی که جهت‌های نرمال‌های صورت متعامد به سه بردار لبه هستند، به‌روزرسانی می‌شوند. با این حال، الگوریتم عملی نیست. سان و همکاران [ 36 ] الگوریتم تکراری دیگری با کارایی بالاتر و اثرات بهتر پیشنهاد کرد. استراتژی تکرار شونده به صورت زیر عمل می کند:

ایکس من “ = ایکس من + 1 | ن v من ( ف ) | \sum f ک \in ن v من (ف) [(ج f ک - v من) \cdot n f ک^] \cdot n f من^

(4)

جایی که $N_{v_{i}} (f)$ مجموعه صورت همسایگی یک حلقه ای رأس است $v_{i}$ ، $c_{f_{k}}$ مرکز صورت است $f_{k}$ ، و $\hat{n_{f_{k}}}$ نرمال فیلتر شده صورت است $f_{k}$ .

به طور مکرر، رئوس به روز شده نرمال های اولیه را در تکرار بعدی تا زمان همگرایی ایجاد می کنند. شکل 2 نتایج فیلتر شبکه ای مدل ساختمان را نشان می دهد.

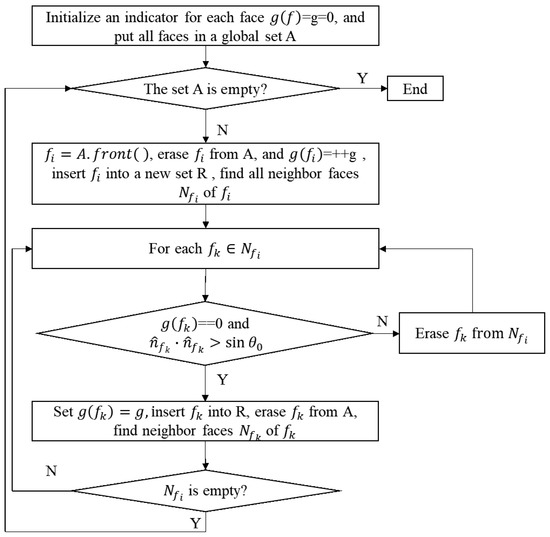
3.2. تشخیص شکل

الگوریتم فیلتر مش تنها ساختارهای هندسی مدل های مش را اصلاح می کند در حالی که رابطه توپولوژیکی را حفظ می کند. مدل های مش اصلاح شده ویژگی های مناطق مسطح و غیر مسطح را بیشتر می کنند. برخلاف مدل‌های سه‌بعدی عمومی، ساختمان‌ها دارای نواحی مسطح‌تر مانند دیوارها، پنجره‌ها و سقف‌ها با ویژگی‌های تیز مانند لبه‌ها و گوشه‌ها هستند. اگر از الگوریتم اصلی QEM برای ساده سازی مش استفاده شود، این مناطق مسطح ممکن است دچار اعوجاج شوند و اشکال کلی ممکن است از بین بروند. بنابراین، نتایج ساده‌سازی را می‌توان با تشخیص اشکال معمولی ساختمان‌ها و انجام ساده‌سازی محدود شده توسط آنها بهبود بخشید.

3.2.1. منطقه در حال رشد

ما نتایج تشخیص هواپیما را با استفاده از الگوریتم رشد منطقه به دست می آوریم. ما یک صورت گروه بندی نشده را انتخاب می کنیم و از چهره های همسایه عبور می کنیم تا جهت گیری های عادی آنها را مقایسه کنیم. اگر جهت‌های دو وجه مشابه باشد، آن‌ها را ادغام می‌کنیم تا زمانی که دیگر چهره‌ای با جهت‌های مشابه وجود نداشته باشد. در نهایت، مجموعه ای از مناطق مسطح درشت را دریافت می کنیم، و هر وجه به یکی از مناطق اختصاص داده شده است [ 37 ]. جزئیات الگوریتم رشد منطقه در شکل 3 نشان داده شده است .

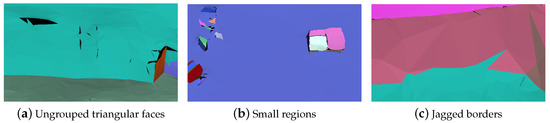
3.2.2. بهینه سازی منطقه

الگوریتم رشد منطقه مجموعه ای از مناطق مسطح درشت را تولید می کند. با این حال، نتایج تشخیص شکل ممکن است به دلیل نویز هندسی و نقص توپولوژیکی ناقص باشد. شکل 4 سه مشکل رایج را نشان می دهد و ما آنها را به صورت زیر خلاصه می کنیم:

(1) صورت های مثلثی گروه بندی نشده. جهت گیری عادی چنین چهره ای با چهره های مجاور آن متفاوت است، بنابراین نمی توان آن را در هیچ منطقه ای گروه بندی کرد.

(2) مناطق کوچک. هدف الگوریتم رشد منطقه تشخیص اشکال کلی مدل‌های ساختمان است. بنابراین، مناطق کوچک باید در مناطق بزرگتر اطراف گروه بندی شوند.

(3) حاشیه های دندانه دار. ممکن است پس از رشد، مرزهای نواحی ناهموار به نظر برسند که بر روند ساده سازی بعدی تأثیر می گذارد.

بنابراین، ما بهینه‌سازی ناحیه را برای اصلاح نتایج تشخیص شکل انجام می‌دهیم. برای هر مشکلی که در بالا ذکر شد، رویکردهای خاصی طراحی شده است. صورت های مثلثی گروه بندی نشده مانند مناطق کوچک حل می شوند. میانگین جهت گیری های نرمال نواحی مجاور آنها را محاسبه کرده و آنها را در ناحیه ای با کوچکترین زاویه گروه بندی می کنیم. اگر منطقه جدید هنوز کوچکتر از آستانه باشد، هر چهره در منطقه باید در یکی از مناطق همسایه خود دوباره گروه بندی شود. ما محدودیتی را تعیین می کنیم که حداقل تعداد وجه ها در یک منطقه نباید کمتر از 10 باشد. برای مرزهای ناهموار، لازم است که چنین مرزهایی هموار شوند. ما چهره های مرزی را فیلتر می کنیم و سپس تعداد چهره ها را در مناطق همسایه می شماریم. هر وجه مرزی در منطقه ای با چهره های بیشتر گروه بندی می شود.

نتایج بهینه شده در شکل 4 در شکل 5 نشان داده شده است. شکل 6 a,b جلوه کامل را نشان می دهد: (1) مناطق مسطح ناهموار با استفاده از الگوریتم رشد ناحیه تشخیص داده می شوند، اما نتایج تشخیص شکل به دلیل نویز ناقص است. (2) مناطق کوچک با توجه به رویکردهای ما به مناطق همسایه گروه بندی شده اند.

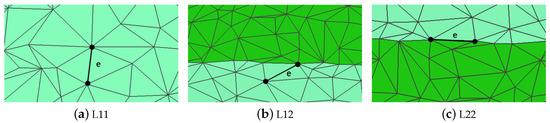
3.3. ساده سازی محدودیت

اصل اساسی الگوریتم edge-collapse ادغام دو راس یک یال در یک راس و حذف لبه و دو وجه مثلثی مجاور آن است. الگوریتم مش ورودی را با توجه به تابع هزینه از بین می‌برد تا زمانی که به نرخ ساده‌سازی مورد نظر برسد. برای تابع هزینه، الگوریتم QEM [ 7 ] یک روش کلاسیک برای محاسبه هزینه فروپاشی است که از مجموع فاصله از یک نقطه تا وجوه مجاور آن به عنوان متریک خطا استفاده می کند. این الگوریتم به دلیل کارایی و کیفیت ساده سازی به طور گسترده مورد استفاده قرار گرفته است. در الگوریتم QEM اصلی، هر رأس با یک ماتریس چهارگانه مرتبط است $Q_{v}$ . چهره داده شده است $p = [a, b, c, d]$ ، مجذور فاصله از یک راس $v = [x, y, z, 1]$ به صورت است:

د (v) 2 = (پ تی v) 2 = v تی (ص پ تی) v = v تی (ک پ) v ک پ = ص پ تی = ⎡⎣⎢⎢⎢⎢ آ 2 a ب یک ج a d a ب ب 2 ب ج ب د یک ج ب ج ج 2 ج د a d ب د ج د د 2 ⎤⎦⎥⎥⎥⎥

(5)

سپس مجموع مجذور فاصله راس v تا تمام وجوه مجاور برابر است با:

Δ v = \sum p \in p l a n e s (v) (پ تی v) 2 = \sum p \in p l a n e s (v) v تی (ص پ تی) v = v تی ⎛⎝ \sum p \in p l a n e s (v) ک پ ⎞⎠ v = v تی س v v

(6)

برای یک لبه $l (v_{i}, v_{j})$ ، ماتریس چهارگانه با جمع ربع های دو رأس آن محاسبه می شود، به عنوان مثال، $Q_{v_{i}} + Q_{v_{j}}$ . در نهایت تابع هزینه لبه را تعریف می کنیم $l (v_{i}, v_{j})$ مانند:

Δ v ¯ = v ¯ تی (س v من + س v j) v ¯

(7)

جایی که $\bar{v}$ یک راس جدید است.

الگوریتم QEM می تواند مدل های سه بعدی کلی را به طور موثر ساده کند. با این حال، ساختمان ها دارای مناطق مسطح بیشتری با ویژگی های تیز هستند. اگر از الگوریتم QEM اصلی برای ساده سازی مش استفاده شود، این مناطق مسطح ممکن است دچار اعوجاج شوند و اشکال کلی ممکن است با افزایش نرخ ساده سازی از بین بروند. بنابراین، ما اشکال معمولی ساختمان‌ها را تشخیص می‌دهیم، ساده‌سازی محدود شده توسط آنها را انجام می‌دهیم و ویژگی‌های تیز مانند لبه‌ها و گوشه‌ها را حفظ می‌کنیم. شایان ذکر است که ما به تعادل بین حفظ ویژگی و کارایی ساده سازی نیاز داریم.

ما در مرحله قبل مجموعه ای از مناطق مسطح را از قبل تعریف کرده ایم و لازم است محدودیت های مربوطه در لبه ها و گوشه ها طراحی شود. همانطور که در شکل 7 و شکل 8 نشان داده شده است، رئوس را به سه نوع طبقه بندی می کنیم و با توجه به مناطقی که به آنها تعلق دارند، وزن های مختلفی را تعیین می کنیم . وزن وجه ها، لبه ها و گوشه ها به ترتیب روی 1، 10 و 100 تنظیم شده است.

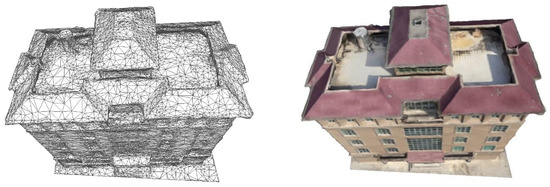
3.4. نقشه برداری مجدد بافت

ما یک روش تولید خودکار را برای مدل‌های رنگی بر اساس تجزیه پچ اتخاذ می‌کنیم. این روش یک مدل بدون بافت را ساده می‌کند، مش را به تکه‌ها تقسیم می‌کند، هر پچ را با وضوح کمتری نسبت به مدل اصلی دوباره مپ می‌کند و در نهایت بافت هر پچ را ادغام می‌کند تا یک مدل بافت ساده‌شده سلسله مراتبی را تشکیل دهد. برای جزئیات بیشتر به ثبت اختراع [ 38 ] مراجعه کنید.

4. نتایج و بحث

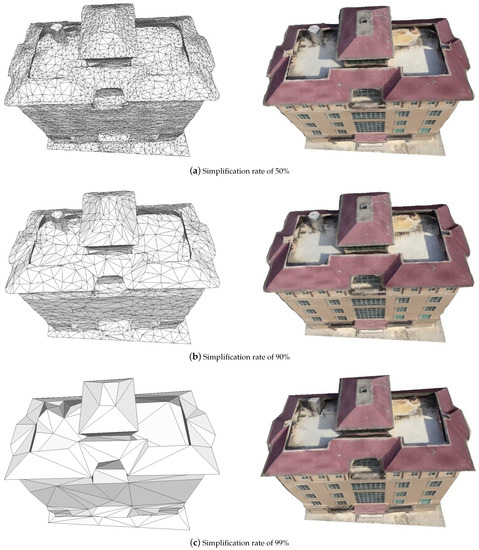
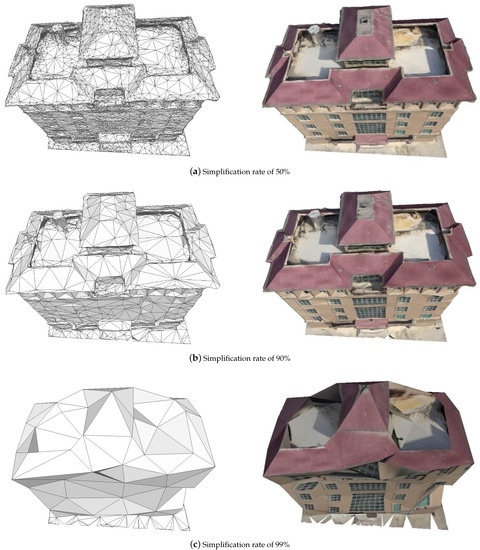
4.1. نتایج ساده سازی

شکل 9 نتایج را در خط لوله روش پیشنهادی نشان می دهد: فیلتر مش، تشخیص شکل و ساده سازی مش. مناطق کوچک در مناطق اطراف بزرگتر برای نتایج ساده سازی سطح بالا گروه بندی می شوند. در مجموع، مدل اصلی دارای 75285 چهره است، در حالی که مدل ساده شده 736 چهره باقی مانده است. نسبت ساده سازی بیش از 99٪ است، اما مدل همچنان ظاهر اصلی را حفظ می کند.

4.2. تحلیل کیفی و کمی

ما نتایج ساده سازی یک مدل ساختمان را با ساختار پیچیده تر مقایسه می کنیم. MeshLab یک نرم افزار پردازش مدل منبع باز با بسیاری از الگوریتم های ساده سازی تعبیه شده است و در اینجا از تابع Quadric Edge Collapse برای مقایسه استفاده می کنیم. شکل 10 مدل اصلی و شکل 11 و شکل 12 را نشان می دهدنتایج ساده‌سازی روش پیشنهادی و الگوریتم QEM را زمانی که نرخ‌های ساده‌سازی به ترتیب 50، 90 و 99 درصد هستند، نمایش می‌دهند. از نتایج می توان دریافت که این دو روش می توانند ساختار کلی مدل اصلی را زمانی که نرخ ساده سازی 50 درصد باشد حفظ کنند. با این حال، روش ما همچنان ظاهر را حفظ می کند در حالی که شکل کلی ساده شده توسط الگوریتم QEM با افزایش نرخ ساده سازی، به ویژه زمانی که به 99٪ می رسد، از بین رفته است. علاوه بر این، بافت را پس از ساده‌سازی هندسی مجدداً ترسیم می‌کنیم و آن را با روش ساده‌سازی بافت در MeshLab مقایسه می‌کنیم.

به جز مقایسه کیفی، نتایج را از نظر کمی نیز مقایسه می کنیم. در اینجا از فاصله هاسدورف به عنوان معیار ارزیابی استفاده می کنیم. از آن قابل مشاهده است جدول 1 قابل مشاهده استکه خطای ساده سازی الگوریتم QEM زمانی که نرخ ساده سازی کم است کمی کمتر از روش ما است. همانطور که نسبت ساده سازی به تدریج افزایش می یابد، مزیت روش ما شروع به نشان دادن می کند. به خصوص زمانی که نرخ ساده سازی به 99 درصد می رسد، خطای ساده سازی روش ما بسیار کمتر از الگوریتم QEM است. منحنی های خطا را بررسی می کنیم و علت تفاوت را پیدا می کنیم. هنگامی که نرخ ساده سازی نسبتاً کم است، مش صفحات مثلثی زیادی را حفظ می کند، بنابراین نتایج ساده سازی دو روش تفاوت چندانی با هم ندارند. با این حال، قبل از ساده سازی، فیلتر مش را انجام می دهیم و ظاهر مدل اصلی را کمی تغییر می دهیم. بنابراین، خطای ساده سازی روش ما یک بستر بالاتر است. با افزایش نرخ ساده سازی، ویژگی های ساختاری مدل کمتر می شود. الگوریتم اصلی QEM فقط ویژگی‌های هندسی محلی را در نظر می‌گیرد و مش را به صورت محلی از بین می‌برد که منجر به اعوجاج شکل کلی می‌شود. روش ما اشکال مناطق مسطح را تشخیص می‌دهد، مش محدود شده توسط نتایج تشخیص را ساده می‌کند و ویژگی‌های تیز مانند لبه‌ها و گوشه‌ها را حفظ می‌کند. از آنجایی که ما وزن‌های بالاتری را به نواحی غیرمسطح اختصاص می‌دهیم، ابتدا نواحی مسطح ساده می‌شوند که تأثیر کمی بر شکل کلی دارد. حتی با نرخ ساده سازی بسیار بالاتر، لبه ها و گوشه های ساختمان آخرین مواردی هستند که باید در نظر گرفته شوند. مش محدود شده توسط نتایج تشخیص را ساده می کند و ویژگی های واضح مانند لبه ها و گوشه ها را حفظ می کند. از آنجایی که ما وزن‌های بالاتری را به نواحی غیرمسطح اختصاص می‌دهیم، ابتدا نواحی مسطح ساده می‌شوند که تأثیر کمی بر شکل کلی دارد. حتی با نرخ ساده سازی بسیار بالاتر، لبه ها و گوشه های ساختمان آخرین مواردی هستند که باید در نظر گرفته شوند. مش محدود شده توسط نتایج تشخیص را ساده می کند و ویژگی های واضح مانند لبه ها و گوشه ها را حفظ می کند. از آنجایی که ما وزن‌های بالاتری را به نواحی غیرمسطح اختصاص می‌دهیم، ابتدا نواحی مسطح ساده می‌شوند که تأثیر کمی بر شکل کلی دارد. حتی با نرخ ساده سازی بسیار بالاتر، لبه ها و گوشه های ساختمان آخرین مواردی هستند که باید در نظر گرفته شوند.

4.3. تحلیل جامع

همانطور که در شکل 13 نشان داده شده است، منطقه ای از ساختمان ها را برای مقایسه ساده انتخاب می کنیم . مدل اصلی دارای 1,841,516 چهره است، در حالی که مدل ساده شده 4280 چهره باقی می ماند که نرخ ساده سازی به 99.8 درصد می رسد. شکل 13 b,c مقایسه بین نتایج ساده شده روش ما و الگوریتم QEM را نشان می دهد. از شکل مشاهده می شود که نتیجه الگوریتم QEM با صورت های مثلثی شکسته و نامنظم فرو ریخته است و بافت مربوطه به دلیل خطای هندسی اشتباه گرفته شده است. با این حال، در مورد نرخ ساده سازی یکسان، اعوجاج شکل کلی مدل ساده شده در این مقاله در محدوده قابل قبولی است، و نقشه مجدد بافت نیز به وضوح قابل تشخیص است.

5. نتیجه گیری ها

این مقاله یک روش ساده را پیشنهاد می‌کند که اشکال کلی ساختمان‌ها را در صحنه‌های شهری حفظ می‌کند. ابتدا، مدل‌های مش را با فیلتر شبکه‌ای پیش پردازش می‌کنیم که جهت طبیعی هر وجه مثلثی را اصلاح می‌کند و موقعیت‌های راس مربوطه را به‌روزرسانی می‌کند. فرآیند فیلتر کردن مناطق مسطح را با حفظ ویژگی های واضح صاف می کند، که عملکرد فرآیند ساده سازی بعدی را بیشتر بهبود می بخشد. سپس، یک الگوریتم در حال رشد ناحیه‌ای را بر روی مدل‌ها اجرا می‌کنیم تا اشکال نواحی مسطح را تشخیص دهیم. پس از فیلتر کردن مش و تشخیص شکل، الگوریتم QEM را برای ساده‌سازی مش بر اساس استراتژی تعریف سلسله مراتبی متریک خطا توسعه می‌دهیم که وزن‌های مختلفی را به مناطق مسطح و غیرمسطح اختصاص می‌دهد. سرانجام، ما یک روش تولید خودکار برای مدل‌های رنگی مبتنی بر تجزیه پچ را برای به دست آوردن مدل‌های بافت ساده سلسله مراتبی اتخاذ می‌کنیم. نتایج تجربی نشان می‌دهد که در مقایسه با الگوریتم QEM اصلی، روش پیشنهادی می‌تواند اشکال کلی مدل‌ها را حفظ کند، به‌ویژه زمانی که نرخ ساده‌سازی بسیار بالا باشد. با این حال، کار این مقاله دارای کاستی هایی است. ابتدا محدوده نواحی و وزن رئوس به صورت دستی تعریف می شوند که روش را در این مقاله محدود می کند. دوم، ما به طور کامل از اطلاعات معنایی مدل های ساختمان استفاده نمی کنیم. چگونگی انجام مدل‌سازی معنایی کامل ساختمان‌ها همچنان نیازمند بررسی است. در آینده، هدف از ساده سازی باید مرتبط ساختن ساختمان ها در سطوح مختلف با توجه به هندسه، توپولوژی،

منابع

لی، ام. Nan, L. ساده سازی مش سه بعدی با حفظ ویژگی برای ساختمان های شهری. ISPRS J. Photogramm. Remote Sens. 2021 , 173 , 135–150. [ Google Scholar ] [ CrossRef ]
بیلجکی، اف. لدوکس، اچ. استوتر، جی. ژائو، جی. رسمی سازی سطح جزئیات در مدل سازی سه بعدی شهر. محاسبه کنید. محیط زیست سیستم شهری 2014 ، 48 ، 1-15. [ Google Scholar ] [ CrossRef ]
مدل‌های هندسی سلسله مراتبی کلارک، JH برای الگوریتم‌های سطح مرئی. اشتراک. ACM 1976 ، 19 ، 547-554. [ Google Scholar ] [ CrossRef ]
پوتامیاس، RA; پلومپیس، اس. Zafeiriou، S. ساده سازی مش عصبی. در مجموعه مقالات کنفرانس IEEE/CVF در مورد دید رایانه و تشخیص الگو، ونکوور، BC، کانادا، 18 تا 24 ژوئن 2022؛ صفحات 18583-18592. [ Google Scholar ]
سالیناس، دی. لافارژ، اف. Alliez، P. از بین بردن شبکه آگاه از ساختار. محاسبه کنید. نمودار. انجمن 2015 ، 34 ، 211-227. [ Google Scholar ] [ CrossRef ]
چانگ، آر. بوتکیویچ، تی. زیمکیویچ، سی. وارتل، ز. پولارد، ن. Ribarsky, W. ساده‌سازی خوانا مدل‌های شهری بافت‌دار. محاسبات IEEE. نمودار. Appl. 2008 ، 28 ، 27-36. [ Google Scholar ] [ CrossRef ]
گارلند، ام. هکبرت، ساده سازی سطح PS با استفاده از معیارهای خطای چهارگانه. در مجموعه مقالات بیست و چهارمین کنفرانس سالانه گرافیک کامپیوتری و تکنیک های تعاملی، لس آنجلس، کالیفرنیا، ایالات متحده آمریکا، 3 تا 8 اوت 1997. ص 209-216. [ Google Scholar ]
گارلند، ام. هکبرت، PS ساده سازی سطوح با رنگ و بافت با استفاده از معیارهای خطای چهارگانه. در Proceedings of the Visualization’98 (Cat. No.98CB36276)، Research Triangle Park, NC, USA, 18-23 اکتبر 1998; صص 263-269. [ Google Scholar ]
Hoppe, H. متریک چهارگانه جدید برای ساده کردن مش ها با ویژگی های ظاهری. در Proceedings of the Visualization’99 (Cat. No. 99CB37067)، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، 24–29 اکتبر 1999; ص 59-510. [ Google Scholar ]
لیو، ایکس. لین، ال. وو، جی. وانگ، دبلیو. یین، بی. Wang, CC تولید مدل‌های قاب سیمی خودنگهدار پراکنده برای چاپ سه بعدی با استفاده از ساده‌سازی مش. نمودار. مدل. 2018 ، 98 ، 14-23. [ Google Scholar ] [ CrossRef ]
شرودر، WJ; زارگه، ج.ا. لورنسن، WE حذف مش های مثلثی. در مجموعه مقالات نوزدهمین کنفرانس سالانه گرافیک کامپیوتری و تکنیک های تعاملی، شیکاگو، IL، ایالات متحده آمریکا، 26-31 ژوئیه 1992; صص 65-70. [ Google Scholar ]
Renze، KJ; Oliver, JH تعمیم یافته بی ساختار. محاسبات IEEE. نمودار. Appl. 1996 ، 16 ، 24-32. [ Google Scholar ] [ CrossRef ]
Rossignac، J.; Borrel, P. تقریب های سه بعدی با وضوح چندگانه برای رندر صحنه های پیچیده. در مدلسازی در گرافیک کامپیوتری ; Springer: برلین/هایدلبرگ، آلمان، 1993; صص 455-465. [ Google Scholar ]
کم، KL; ساده‌سازی مدل Tan، TS با استفاده از خوشه‌بندی راس. در مجموعه مقالات سمپوزیوم 1997 در زمینه گرافیک سه بعدی تعاملی، پراویدنس، RI، ایالات متحده آمریکا، 27-30 آوریل 1997; صص 75-81. [ Google Scholar ]
لونسبری، م. DeRose، TD; وارن، J. تجزیه و تحلیل چند وضوح برای سطوح از نوع توپولوژیکی دلخواه. ACM Trans. نمودار. ToG 1997 ، 16 ، 34-73. [ Google Scholar ] [ CrossRef ]
گوسکوف، آی. ویدیمچه، ک. سولدنز، دبلیو. شرودر، P. مش های معمولی. در مجموعه مقالات بیست و هفتمین کنفرانس سالانه گرافیک کامپیوتری و تکنیک های تعاملی، نیواورلئان، لس آنجلس، ایالات متحده آمریکا، 23 تا 28 ژوئیه 2000; صص 95-102. [ Google Scholar ]
هوپ، اچ. دروز، تی. دوشان، تی. مک دونالد، جی. Stuetzle, W. Mesh بهینه سازی. در مجموعه مقالات بیستمین کنفرانس سالانه گرافیک کامپیوتری و تکنیک‌های تعاملی، آناهیم کالیفرنیا، ایالات متحده آمریکا، 2 تا 6 اوت 1993. صص 19-26. [ Google Scholar ]
هوپ، اچ. دروز، تی. دوشان، تی. مک دونالد، جی. Stuetzle, W. بازسازی سطح از نقاط سازمان نیافته. در مجموعه مقالات نوزدهمین کنفرانس سالانه گرافیک کامپیوتری و تکنیک های تعاملی، شیکاگو، IL، ایالات متحده آمریکا، 26-31 ژوئیه 1992; ص 71-78. [ Google Scholar ]
کیم، اس. جئونگ، دبلیو. تولید کیم، سی. LOD با متریک خطای انحنای گسسته. در مجموعه مقالات کنفرانس دو ملیتی کره اسرائیل، سئول، کره، 10 تا 12 اکتبر 1999; صص 97-104. [ Google Scholar ]
کیم، اس جی. کیم، سی‌چ. لوین، دی. ساده سازی سطح با استفاده از یک هنجار انحنای گسسته. محاسبه کنید. نمودار. 2002 ، 26 ، 657-663. [ Google Scholar ] [ CrossRef ]
کاستلو، پی. اسبرت، ام. چوور، م. Feixas، M. ساده سازی دیدگاه محور با استفاده از اطلاعات متقابل. محاسبه کنید. نمودار. 2008 ، 32 ، 451-463. [ Google Scholar ] [ CrossRef ]
لسکوات، تی. لیو، HTD؛ تیری، جی.ام. جاکوبسون، ا. بوبکور، تی. Ovsjanikov، M. ساده سازی مش طیفی. محاسبه کنید. نمودار. انجمن 2020 ، 39 ، 315–324. [ Google Scholar ] [ CrossRef ]
Hoppe, H. مش های پیشرو. در مجموعه مقالات بیست و سومین کنفرانس سالانه گرافیک کامپیوتری و تکنیک های تعاملی، نیواورلئان، لس آنجلس، ایالات متحده آمریکا، 4 تا 9 اوت 1996. صص 99-108. [ Google Scholar ]
Hoppe, H. پالایش مشهای پیشرونده وابسته به نمایش. در مجموعه مقالات بیست و چهارمین کنفرانس سالانه گرافیک کامپیوتری و تکنیک های تعاملی، لس آنجلس، کالیفرنیا، ایالات متحده آمریکا، 3 تا 8 اوت 1997. ص 189-198. [ Google Scholar ]
لیندستروم، پی. ترک، جی. ساده سازی تصویر محور. ACM Trans. نمودار. (ToG) 2000 ، 19 ، 204-241. [ Google Scholar ] [ CrossRef ]
پاپاژورگیو، ا. Platis, N. ساده سازی مش مثلثی در GPU. Vis. محاسبه کنید. 2015 ، 31 ، 235-244. [ Google Scholar ] [ CrossRef ]
لی، اچ. کیونگ، MH ساده سازی مش موازی با استفاده از فروپاشی درخت تعبیه شده. Vis. محاسبه کنید. 2016 ، 32 ، 967-976. [ Google Scholar ] [ CrossRef ]
نان، ال. Wonka, P. Polyfit: بازسازی سطح چند ضلعی از ابرهای نقطه ای. در مجموعه مقالات کنفرانس بین المللی IEEE در بینایی کامپیوتر، ونیز، ایتالیا، 22 تا 29 اکتبر 2017؛ صص 2353-2361. [ Google Scholar ]
او، جی. گو، ایکس. تان، جی. تانگ، ام. وانگ، سی. روش ساده‌سازی حفظ ظاهر برای مدل‌های ساختمان‌های سه بعدی پیچیده. ترانس. GIS 2019 ، 23 ، 275-293. [ Google Scholar ] [ CrossRef ]
او، جی. چن، بی. تان، جی. ژائو، کیو. Ge, R. روش ساده سازی مدل ساختمانی سه بعدی با در نظر گرفتن مش مدل و ساختار ساختمان. ترانس. GIS 2022 ، 26 ، 1182-1203. [ Google Scholar ] [ CrossRef ]
لی، کیو. سان، ایکس. یانگ، بی. جیانگ، اس. ساده سازی ساختار هندسی مدل های ساختمانی سه بعدی. ISPRS J. Photogramm. Remote Sens. 2013 ، 84 ، 100-113. [ Google Scholar ] [ CrossRef ]
وانگ، بی. وو، جی. ژائو، کیو. لی، ی. گائو، ی. She, J. روش ساده سازی حفظ توپولوژی برای مدل های ساختمان سه بعدی. ISPRS Int. J. Geo-Inf. 2021 ، 10 ، 422. [ Google Scholar ] [ CrossRef ]
بوچ، ام. کوبلت، ال. پالی، ام. آلیز، پی. Lévy، B. پردازش مش چند ضلعی ; CRC Press: Boca Raton، FL، USA، 2010. [ Google Scholar ]
ژنگ، ی. فو، اچ. Au، OKC; Tai, CL فیلتر معمولی دو طرفه برای حذف صدای مش. IEEE Trans. Vis. محاسبه کنید. نمودار. 2010 ، 17 ، 1521-1530. [ Google Scholar ] [ CrossRef ]
Taubin، G. فیلتر شبکه ناهمسانگرد خطی. در گزارش تحقیقاتی IBM ; مرکز تحقیقات IBM TJ Watson: Yorktown Heights, NY, USA, 2001; جلد 1. [ Google Scholar ]
سان، ایکس. Rosin, PL; مارتین، آر. Langbein، F. حذف سریع و مؤثر مش با حفظ ویژگی. IEEE Trans. Vis. محاسبه کنید. نمودار. 2007 ، 13 ، 925-938. [ Google Scholar ] [ CrossRef ]
لافارژ، اف. مالت، سی. ایجاد مدل‌های شهر در مقیاس بزرگ از ابرهای نقطه سه بعدی: رویکردی قوی با نمایش ترکیبی. بین المللی جی. کامپیوتر. Vis. 2012 ، 99 ، 69-85. [ Google Scholar ] [ CrossRef ]
هوانگ، ایکس. ژانگ، اف. Gao, Y. نوعی روش شکل دهی خودکار مدل LOD رنگی که بر اساس بلوک تجزیه می شود. ثبت اختراع چین CN109118588A، 25 سپتامبر 2018. [ Google Scholar ]

شکل 1. خط لوله روش پیشنهادی.

شکل 2. مقایسه مش ها قبل و بعد از فیلتر کردن مش. ( الف ) مش های اصلی. ( ب ) مش های فیلتر شده. (از چپ به راست) مدل های جزئی، معمولی های صورت و مدل های کلی.

شکل 3. خط لوله الگوریتم در حال رشد منطقه.

شکل 4. نمونه هایی از مشکلات رایج در نتایج تشخیص شکل. ( الف ) صورتهای مثلثی گروه بندی نشده. ( ب ) مناطق کوچک. ( ج ) حاشیه های دندانه دار.

شکل 5. نتایج بهینه شده از نمونه های شکل 4 . ( الف ) صورتهای مثلثی گروه بندی نشده. ( ب ) مناطق کوچک. ( ج ) حاشیه های دندانه دار.

شکل 6. مقایسه نتایج تشخیص شکل قبل و بعد از بهینه سازی منطقه. ( الف ) نتایج تشخیص شکل درشت. ( ب ) نتایج تشخیص شکل بهینه شده.

شکل 7. انواع رئوس. ( الف ) رئوس متعلق به یک منطقه است. ( ب ) رئوس متعلق به دو منطقه است. ( ج ) رئوس متعلق به سه منطقه است.

شکل 8. انواع لبه ها. ( الف ) هر دو راس از نوع V1 هستند. ( ب ) یک راس از نوع V1 و دیگری از نوع V2 است. ( ج ) هر دو راس از نوع V2 هستند.

شکل 9. نمونه هایی از نتایج در خط لوله. ( الف ) مش های اصلی (75285 چهره). ( ب ) مش های فیلتر شده. ( ج ) مناطق مسطح. ( د ) مش های ساده شده (736 وجه).

شکل 10. مش های اصلی (36841 وجه).

شکل 11. مش های ساده شده در روش ما. ( الف ) نرخ ساده سازی 50٪ (36841 چهره). ( ب ) نرخ ساده سازی 90% (3682 چهره). ( ج ) نرخ ساده سازی 99% (365 چهره).

شکل 12. مش های ساده شده در الگوریتم QEM. ( الف ) نرخ ساده سازی 50٪ (36841 چهره). ( ب ) نرخ ساده سازی 90% (3682 چهره). ( ج ) نرخ ساده سازی 99% (365 چهره).

شکل 13. مقایسه نتایج ساده سازی در روش ما و الگوریتم QEM. ( الف ) مش های اصلی (1841516 چهره). ( ب ) مش های ساده شده در روش ما با نرخ ساده سازی 99.8٪ (4280 وجه). ( ج ) مش های ساده شده در الگوریتم QEM با نرخ ساده سازی 99.8٪ (4280 چهره).

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

کلید واژه ها:

1. مقدمه

2. کارهای مرتبط