خلاصه

آنتروپی شانون محبوب ترین روش برای کمی سازی اطلاعات در یک سیستم است. با این حال، آنتروپی شانون در اندازه‌گیری داده‌های مکانی، مانند داده‌های شطرنجی، ناتوان در نظر گرفته می‌شود، بنابراین برای چنین مجموعه‌داده‌ای اعمال نشده است. اخیراً، روشی برای محاسبه آنتروپی بولتزمن داده‌های شطرنجی عددی پیشنهاد شده است، اما کارآمد نیست زیرا شامل یک سری فرآیندهای عددی است. هدف ما بهبود کارایی محاسباتی این روش با استفاده از ایده شکستگی سر و دم بود. این مقاله وضعیت شکستگی‌های سر و دم را آرام کرد و داده‌ها را با توزیع دم سنگین طبقه‌بندی کرد. میانگین مقادیر داده در یک کلاس معین به عنوان مقدار نماینده آن در نظر گرفته شد. و این به یک تابع خطی جایگزین شد تا بیان کامل رابطه بین سطح طبقه بندی و آنتروپی بولتزمن به دست آید. این تابع برای تخمین آنتروپی مطلق بولتزمن داده ها استفاده شد. نتایج تجربی ما نشان می‌دهد که روش پیشنهادی هم عملی و هم کارآمد است. زمان محاسبه به حدود 1٪ از روش اصلی در برخورد با هشت کاهش یافت 600×600مدل های ارتفاعی دیجیتال پیکسل

کلید واژه ها:

شکستگی سر/دم ؛ داده های شطرنجی عددی ; آنتروپی مطلق بولتزمن کارایی محاسباتی

1. معرفی

نمایش داده های شطرنجی تعدادی از مزایای مهم را نسبت به گزینه های دیگر ارائه می دهد، از این رو این فناوری در تصاویر ماهواره ای، مدل سازی دیجیتال ارتفاع، نقشه برداری شیب منظره و سایر کاربردها غالب است. مزایای مدل‌سازی داده‌های شطرنجی شامل ساختار داده ساده، سهولت جمع‌آوری داده‌های خاص مکان و مناسب بودن آن برای نمایش سطوح پیوسته است [ 1 ]. کمی سازی اطلاعات مجموعه داده های شطرنجی مدت هاست که یک کار چالش برانگیز بوده و در بسیاری از کاربردها مفید بوده است. به عنوان مثال، اطلاعات نگهداری شده به شکل شطرنجی برای ارزیابی عملکرد ترکیب تصویر استفاده شده است [ 2 ، 3 ، 4]، و به عنوان یک مرجع ضروری برای انتخاب باند در تصویربرداری ابرطیفی [ 5 ، 6 ] در نظر گرفته می شود.
تولید اطلاعات ممکن است از طریق آنتروپی شانون [ 7 ]، که معمولاً در بسیاری از حوزه‌ها، مانند گرافیک کامپیوتری [ 3 ] و بوم‌شناسی منظر [ 8 ، 9 ] استفاده می‌شود، اندازه‌گیری شود. با این حال، کاربرد آنتروپی شانون برای داده‌های فضایی به‌ویژه برای داده‌های شطرنجی مورد تردید قرار گرفته است، زیرا برای کمی کردن اطلاعات مکانی که توزیع فضایی داده‌های شطرنجی را توصیف می‌کند، مناسب نیست [ 10 ].
دو راه حل برای حل این مشکل پیشنهاد شده است: مدل آنتروپی شانون را می توان بهبود بخشید [ 11 ، 12 ، 13 ] یا آنتروپی بولتزمن را می توان به جای آن استفاده کرد [ 14 ، 15 ، 16 ، 17 ، 18 ]. آنتروپی بولتزمن معیار درجه بی نظمی سیستم است و در تئوری، قادر به کمی سازی اطلاعات مکانی داده های شطرنجی است [ 19 ]. اولین روش برای محاسبه آنتروپی بولتزمن داده های شطرنجی عددی اخیرا پیشنهاد شده است [ 18 ]]. این رویکرد یک ماکرو حالت مناسب را تعریف می کند و سپس تعداد ریز حالت ها را تعیین می کند. با استفاده از آنتروپی مطلق بولتزمن، که آنتروپی صفر به عنوان نقطه مرجع خود دارد، روش پیشنهادی قادر به مقایسه داده های شطرنجی مختلف به معنای مطلق است. نتایج تجربی گائو و همکاران. [ 18 ] نشان دادند که روش آنها می تواند اطلاعات مکانی را که در یک ساختار داده شطرنجی نگهداری می شود، ضبط کند. با این حال، این روش کارآمد نیست، زیرا شامل یک سری فرآیندهایی است که از نظر محاسباتی فشرده و زمان بر هستند.
هدف این مطالعه توسعه روشی است که بتواند آنتروپی مطلق بولتزمن داده‌های شطرنجی عددی را به روشی کارآمد برآورد کند. برای انجام این کار، ما یک روش طبقه‌بندی را برای توزیع دم سنگین با الگوی مقیاس‌بندی اتخاذ کردیم، آنتروپی بولتزمن نسبی هر کلاس را تخمین زدیم و آنتروپی بولتزمن مطلق را بر اساس این تخمین‌ها محاسبه کردیم. ما عملکرد این رویکرد را با چندین آزمایش با استفاده از داده‌های شطرنجی عددی آزمایش کردیم.

2. آنتروپی مطلق بولتزمن داده های شطرنجی عددی: محاسبات و مسئله

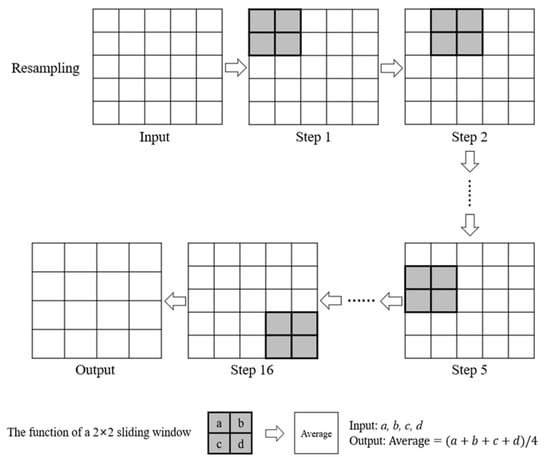
روشی برای محاسبه آنتروپی مطلق بولتزمن یک گرادیان منظره به تفصیل در گائو و همکاران توضیح داده شده است. [ 18 ]. ابتدا باید مجموعه‌ای از ریز حالت‌های مناسب تعریف شود که می‌توان با نمونه‌برداری مجدد از گرادیان منظره اصلی با یک پنجره کشویی انجام داد. 2×2پیکسل، همانطور که در شکل 1 نشان داده شده است. تعداد ریز حالت ها برای هر پنجره کشویی در چشم انداز اصلی به طور منحصر به فرد بر اساس ماکرو حالت مربوطه تعیین شد. آنتروپی نسبی بولتزمن (اسآر)چشم انداز اصلی را می توان با معادله آنتروپی بولتزمن محاسبه کرد

اسآر=کبورود به سیستم(∏من=1متردبلیومن)،

جایی که کبثابت بولتزمن را نشان می دهد (1.38×10-23)، دبلیومنتعداد ریز حالت های ممکن برای است منپنجره کشویی و مترتعداد پنجره های کشویی است. پایه لگاریتم معمولاً روی 2، 10 یا پایه لگاریتم طبیعی تنظیم می شود. ه، بسته به زمینه

یک گرادیان منظره معین را می توان با سلسله مراتبی نشان داد که از جزئی ترین سطح (یعنی منظره اصلی) تا انتزاعی ترین سطح (یعنی یک پیکسل منفرد) را در بر می گیرد، همانطور که در شکل 2 نشان داده شده است. مجموع همه اسآرمقادیر آنتروپی مطلق بولتزمن است ( اسآ) از شیب های چشم انداز، همانطور که در معادله نشان داده شده است

اسآ=∑j=1nاسآر(Lj)

جایی که Ljنشان می دهد jسطح هفتم در سلسله مراتب، اسآر(Lj)آنتروپی نسبی بولتزمن است Lj، و مترتعداد کل سطوح است. پایه لگاریتم معمولاً 2، 10 و یا تنظیم می شود ه.

روش استفاده شده توسط گائو و همکاران. اطلاعات مکانی داده های شطرنجی مانند شیب منظره را کمی می کند. با این حال، فرآیند تکراری برای تعیین تعداد ریز حالت ها برای هر پنجره کشویی آهسته و از نظر محاسباتی سخت است. علاوه بر این، با افزایش ابعاد شیب منظره اصلی، تعداد پنجره های کشویی به طور تصاعدی افزایش می یابد. به عنوان مثال، با افزایش اندازه چشم انداز اصلی از 10×10پیکسل به 100×100پیکسل، تعداد پنجره های کشویی از 81 (9 2 ) به 9801 (99 2 ) افزایش می یابد.
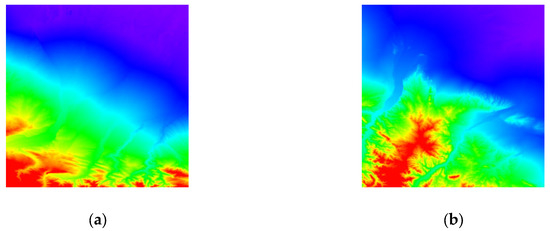
محاسبه آنتروپی مطلق بولتزمن نیز یک فرآیند تکرار است زیرا هر سطح از سطح زیر آن از طریق نمونه‌گیری مجدد به دست می‌آید (به عنوان مثال، L1مشتق شده از L0). هر پیکسل در L1می توان از چهار پیکسل مرتبط تولید کرد L0با این روش به عنوان مثال، میانگین چهار پیکسل در L0مقدار پیکسل مربوطه در است L1. علاوه بر این، مقدار تمام پیکسل ها در L1می توان به دست آورد. با استفاده از ابزار “resample” با گزینه درون یابی دو خطی در نرم افزار ArcGIS، تصویر نشان داده شده در شکل 3 a را از 512×512پیکسل به 256×256پیکسل ها ( شکل 3 ب).
ما یک مقایسه پایه را با محاسبه آنتروپی مطلق بولتزمن برای دو تصویر با اندازه های مختلف ( شکل 3 ) در یک محیط عملیاتی ایجاد کردیم – MATLAB که در ویندوز 10 64 بیتی با CPU Intel Core i7-8750H (2.20 گیگاهرتز، 12.00 گیگابایت رم اجرا می شود. ). ما زمان صرف شده برای محاسبه تعداد ریز حالت ها و همچنین زمان محاسبه کل را ثبت کردیم. نتایج محاسبات پایه در جدول 1 نشان داده شده است. ما دریافتیم که زمان مورد نیاز برای محاسبه تعداد ریز حالت‌ها، بخش بزرگی از کل زمان محاسبه را تشکیل می‌دهد. علاوه بر این، تصویر بزرگتر ( 512×512پیکسل، 1218.5 ثانیه) به زمان محاسباتی حدود هفت برابر بیشتر از تصویر کوچکتر نیاز دارد ( 256×256پیکسل، 173.5 ثانیه)، حتی اگر مساحت آن تنها چهار برابر بزرگتر بود.

3. استراتژی برای برآورد کارآمد آنتروپی بولتزمن مطلق

از آنجایی که مجموع تمام آنتروپی های نسبی بولتزمن، آنتروپی مطلق بولتزمن است، ما رویکرد خود را با این فرض ساده کردیم که آنتروپی نسبی بولتزمن هر سطح را می توان در برابر سطح سلسله مراتب آن ترسیم کرد تا یک منحنی ایجاد کند. مقدار متغیر Lهvهلمخفف سطح در سلسله مراتب شیب منظره است. نمونه ای از این فرآیند در شکل 4 نشان داده شده است . با برون یابی این منحنی، فرآیند پیچیده محاسبه آنتروپی مطلق بولتزمن به فرآیند نسبتاً آسان اضافه کردن مقادیر تمام نقاط روی منحنی تبدیل شد.
دم منحنی همیشه به طور مجانبی به محور x در جهت مثبت نزدیک می شود و بیشتر نقاط دارای مقادیر آنتروپی نسبی بولتزمن کوچکی هستند. این منحنی دارای یک توزیع دم سنگین در نظر گرفته می شود، به این معنی که به طور قابل توجهی به سمت راست منحرف است و می توان آن را دارای یک الگوی “مقیاس بندی” یا “سلسله مراتبی” با “چیزهای بسیار کوچکتر از موارد بزرگتر” توصیف کرد [ 20 ] .
با فرض اینکه شکل منحنی و در نتیجه عملکرد آن را می توان از چندین نقطه تخمین زد، ما توانستیم مقادیر سایر نقاط را پیش بینی کنیم و از آنها برای تخمین آنتروپی مطلق بولتزمن داده های شطرنجی عددی استفاده کنیم. نقاطی که برای تخمین شکل منحنی استفاده کردیم نزدیک به محور y بودند. این نتیجه یک محدودیت اساسی در فرآیند تکراری بود که همیشه با گرادیان اصلی شروع می شود و به ترتیب ادامه می یابد. این نقاط سطح پایین تأثیر زیادی بر مسیر منحنی و مجموع آنتروپی ها دارند که آنها را نسبت به نقاطی با مقادیر کوچکتر بحرانی تر می کند. تخمین شکل منحنی از این نقاط بحرانی منطقی بود. این راه حل برای جلوگیری از محاسبه آنتروپی های نسبی بولتزمن در همه سطوح ایجاد شده است.
با این حال، تخمین عملکرد یک منحنی بر اساس چندین نقطه چالش برانگیز است. همانطور که شکل منحنی پیچیده تر می شود، داده های بیشتری برای نمایش دقیق آن مورد نیاز است [ 21 ]. هنگامی که داده های موجود ناکافی هستند، شکستن منحنی به طبقه بندی های گام به گام بهترین راه برای کاهش پیچیدگی آن است. به عنوان مثال، مک دونالد و همکاران. [ 22] از سه کلاس مختلف برای ساده کردن منحنی استفاده کرد، یک دم پایین، یک فلات و یک دم بالا. ما یک روش طبقه‌بندی مناسب را برای شکستن منحنی، با هدف اضافی استخراج نقاط اساسی با مقادیر آنتروپی نسبی بولتزمن شناسایی کردیم. یک مقدار نماینده برای نشان دادن تمام نقاط در یک کلاس مشخص انتخاب شد، و چندین مقدار معرف به یک تابع برای به دست آوردن بیان کامل آن تابع جایگزین شدند، که سپس برای تخمین آنتروپی های نسبی بولتزمن کلاس های دیگر استفاده شد. در نهایت، آنتروپی مطلق بولتزمن داده های شطرنجی عددی بر اساس این آنتروپی های نسبی بولتزمن تخمین زده شده محاسبه شد.
با پیروی از این خط فکری، این مقاله راهبردی را برای تخمین موثر آنتروپی مطلق بولتزمن به شرح زیر پیشنهاد می‌کند:
  • تجزیه و تحلیل توزیع داده ها و اتخاذ یک روش طبقه بندی مناسب.
  • یک تابع را از طریق یک مقدار نماینده از ضروری ترین کلاس تخمین بزنید و از طریق این تابع، آنتروپی های بولتزمن نسبی تخمین زده شده سایر کلاس ها را بدست آورید.
  • آنتروپی مطلق بولتزمن داده های شطرنجی عددی را بر اساس آنتروپی های نسبی بولتزمن تخمین زده شده محاسبه کنید.

4. محاسبه آنتروپی مطلق بولتزمن بر اساس شکست های سر/دم

در این بخش، رویکرد شکستن سر/دم برای تخمین آنتروپی های نسبی بولتزمن هر کلاس برای یک مجموعه داده شطرنجی عددی داده شده استفاده شده است. کل آنتروپی مطلق بولتزمن را می توان با جمع کردن مقادیر تخمینی آنتروپی نسبی بولتزمن در هر کلاس به دست آورد.

4.1. اتخاذ یک روش طبقه بندی برای توزیع دم سنگین با الگوی مقیاس بندی

نتایج طبقه بندی خوب می تواند الگوهای داده ها را منعکس کند. نتایج طبقه‌بندی کاملاً به روش طبقه‌بندی که برای تقسیم منحنی استفاده می‌شود وابسته خواهد بود، بنابراین اتخاذ یک روش طبقه‌بندی مناسب بسیار مهم است.
اخیراً یک روش طبقه‌بندی برای داده‌ها با توزیع دم سنگین پیشنهاد شده است [ 20 ]. این روش داده ها را بر اساس میانگین حسابی به دو قسمت نامتعادل مرتب می کند – یک سر (بالاتر از میانگین) و یک دم (پایین تر از میانگین). با توجه به اینکه این ساختار نامتعادل ممکن است در سر تکرار شود، این نقاط بیشتر به دو قسمت تقسیم می شوند تا زمانی که نقاط باقی مانده در سر از توزیع دم سنگین پیروی نکنند. تقسیم نهایی نقاط داده بین سر و دم به طور کلی حدود 20% و 80% است [ 23 ]. با این حال، “این شرایط را می توان برای بسیاری از ویژگی های جغرافیایی، مانند 50 درصد یا حتی بیشتر” آرام کرد [ 24 ].
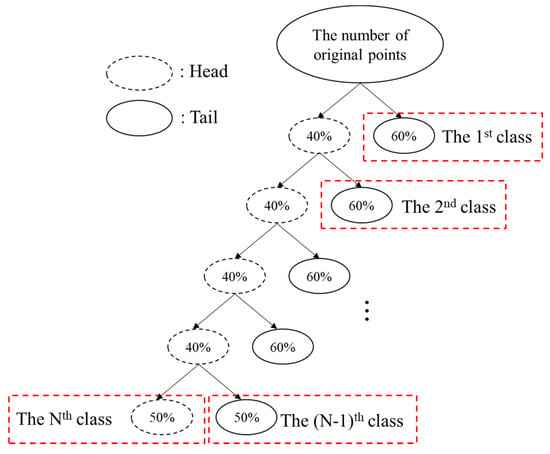
برای تخمین تعداد نقاط موجود در سر و دم هر کلاس، این مقاله از ایده شکستگی سر و دم استفاده کرد و هدف 40٪ از نقاط در سر و 60٪ در دم را تعیین کرد. به عنوان مثال، برای یک شطرنجی عددی که بود 100×80پیکسل، ما 80 سطح را از طریق نمونه گیری مجدد به دست آوردیم، اما 80تیساعتسطح شامل تنها یک واحد بود که شرایط محاسبه تعیین شده توسط گائو و همکاران را برآورده نمی کرد. بنابراین، تعداد نهایی نقاط منحنی 79 بود که 31 نقطه در سر مرتب شد (اعشار به پایین گرد شدند). این تقسیم تا زمانی تکرار شد که تعداد نقاط سر با تعداد نقاط دم برابر شود یا تعداد نقاط سر به 1 برسد. از آنجایی که توزیع دم سنگین در نظر گرفته شده در این مقاله دارای یک الگوی پوسته پوسته شدن بود، حاوی یک تعداد کمی از آنتروپی های نسبی بولتزمن بالا. همانطور که در شکل 5 نشان داده شده است، دم از هر پله یک کلاس در نظر گرفته شد، همانطور که در آخرین مرحله، سر در نظر گرفته شد .
روش طبقه‌بندی مورد استفاده در این مطالعه نه تنها تمام نقاط را در یکی از چندین کلاس طبقه‌بندی می‌کند، بلکه الگوهای داده‌ها را با توزیع دم سنگین منعکس می‌کند. مهم‌تر از آن، مهم‌ترین نقاط را استخراج می‌کند – آن‌هایی که دارای بزرگترین مقادیر آنتروپی نسبی بولتزمن هستند.

4.2. برآورد آنتروپی های نسبی بولتزمن در هر کلاس

از آنجایی که محدوده مقادیر در یک کلاس معین کوچک است، این مقاله استفاده از میانگین نقاط در هر کلاس را به عنوان مقدار آنتروپی نسبی بولتزمن انتخاب کرد.
امتیازهای هر طبقه‌بندی از سر طبقه‌بندی بالا مشتق شده‌اند و نقاط موجود در آخرین طبقه‌بندی باید بالاترین آنتروپی بولتزمن نسبی را داشته باشند. ما آنتروپی‌های نسبی بولتزمن این نقاط را محاسبه کردیم که از طریق استفاده از روشی که از گائو و همکارانش به عاریت گرفته شده بود، تسریع شد. [ 18 ]. میانگین این آنتروپی های نسبی دقیق بولتزمن، آنتروپی نسبی بولتزمن آخرین کلاس است. به همین ترتیب، آنتروپی نسبی دقیق بولتزمن از (ن-1)تیساعتکلاس و (ن-2)تیساعتکلاس را می توان در تئوری محاسبه کرد. با این حال، اگر بخواهیم آنتروپی نسبی بولتزمن دقیق هر کلاس را محاسبه کنیم، مشکل ناکارآمدی را حل نمی‌کنیم.
در عوض، ما از آنتروپی های نسبی بولتزمن دقیق چندین کلاس برای تخمین آنتروپی های نسبی بولتزمن سایر کلاس ها استفاده کردیم. این معتبر است زیرا این آنتروپی های نسبی بولتزمن را می توان تقریباً از طریق یک تابع خطی توصیف کرد. این مقاله تابع خطی را انتخاب کرد y=آ×ایکس. به یاد بیاورید که کلاس اول از طریق (ن-1)تیساعتکلاس همه متعلق به دم است، در حالی که کلاس آخر متعلق به سر است. ما آنتروپی نسبی دقیق بولتزمن را جایگزین کردیم (ن-1)تیساعتکلاس به تابع خطی (یعنی متغیر مستقل است [ن-1]و متغیر وابسته آنتروپی نسبی دقیق بولتزمن است [ن-1]تیساعتکلاس). ما به صورت معکوس پارامتر را حل کردیم αو بیان تابع را بدست آورد. سپس، آنتروپی‌های نسبی بولتزمن را در کلاس‌های باقی‌مانده که متعلق به دم‌ها بودند، محاسبه کردیم.

4.3. محاسبه آنتروپی مطلق بولتزمن بر اساس برآوردها

تا اینجا ما تعداد کلاس ها، تعداد نقاط موجود در هر کلاس و آنتروپی های نسبی بولتزمن هر کلاس را به دست آورده ایم. آنتروپی مطلق بولتزمن مجموعه داده شطرنجی عددی مورد علاقه را می توان به صورت محاسبه کرد

اسآ¯=∑ج=1کاسآر(ج)¯×nج

جایی که اسآ¯بیانگر آنتروپی مطلق بولتزمن تخمینی داده های شطرنجی عددی است، اسآر(ج)¯آنتروپی نسبی کلاس بولتزمن برآورد شده است ج، nجتعداد امتیازات کلاس است  ج، و کتعداد کلاس ها است.

مثلا، اسآر(1)¯و اسآر(2)¯میانگین تمام نقاط در نتیساعتکلاس و (ن-1)تیساعتکلاس به ترتیب آنها را می توان دقیقاً از طریق گائو و همکاران محاسبه کرد. روش [ 18 ].

5. آزمایش تجربی

ما چندین آزمایش از روش پیشنهادی انجام دادیم. همانطور که در شکل 6 نشان داده شده است ، داده های تجربی، به عنوان مثال، چهار جفت مدل رقومی ارتفاع (DEMs)، همان چیزی است که توسط گائو و همکاران استفاده شده است. [ 18 ]. اندازه هر DEM بود 600×600پیکسل، با هر پیکسل نشان دهنده ارتفاع در یک منطقه است. DEM های شکل 6 b2,c2 صاف تر از سایر DEM ها هستند که نشان دهنده درجه نسبتاً کم ناهمگنی است. آنها حاوی ریز حالت های غیرممکن کمتری هستند که آنتروپی بولتزمن مطلق آنها را کاهش می دهد. برای تجزیه و تحلیل بهتر نتایج، نتایج این آزمایش‌ها را با نتایج Gao و همکاران مقایسه کردیم. [ 18 ]، همانطور که در جدول 2 نشان داده شده است.
جدول 2 نشان می دهد که استفاده از روش پیشنهادی ما به طور چشمگیری زمان محاسبه را بین 99.5٪ (از 1482.9 به 7.8 ثانیه) و 99.8٪ (از 2842.2 به 6.9 ثانیه) کاهش داد. با این حال، خطاهای نسبی آنها ناپایدار بود که کوچکترین آنها در 0٪ و بزرگترین آنها به 58.1٪ رسید.

6. بحث

در فرآیند تخمین آنتروپی نسبی بولتزمن هر کلاس، یک تابع خطی را انتخاب کردیم. (y=آ×ایکس)و آنتروپی نسبی دقیق بولتزمن را جایگزین کرد (ن-1)تیساعتبرای حل معکوس پارامتر α (حل معکوس) در تابع خطی قرار می گیرد. این به ما امکان داد که بیان تابع را بدست آوریم. ما مدل‌های تابع دیگری مانند توابع درجه دوم، توابع قانون توان و توابع نمایی را امتحان کردیم، اما توابع خطی نزدیک‌ترین نتایج را به مقادیر واقعی نشان دادند.
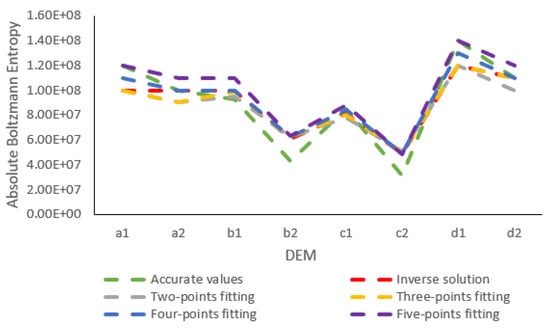
ما از آنتروپی‌های دقیق بولتزمن نسبی چندین کلاس برای تولید یک تابع خطی برازش استفاده کردیم (y=آ×ایکس)، که برای محاسبه آنتروپی های نسبی بولتزمن کلاس های باقی مانده استفاده شده است. برای شناسایی کارآمدترین تعداد نقاط (کلاس‌ها) برای استفاده، آنتروپی‌ها را به ترتیب بر اساس دو، سه، چهار و پنج نقطه مدل‌سازی کردیم. فرض کنید ایکستعداد امتیازات است، کلاس های درگیر از دامنه خواهد بود نتیساعتکلاس به  (ن-(ایکس-1))تیساعتکلاس هنگامی که به DEM تجربی اعمال می شود، نتایج آنتروپی های مطلق بولتزمن به دست آمده توسط مدل هایی با تعداد نقاط مختلف در شکل 7 نشان داده شده است ، با خطاهای نسبی جدول بندی شده در جدول 3 و زمان های محاسبه در شکل 8 و جدول 4 نمایش داده شده است.
ما متوجه شدیم که همه مدل‌ها تخمین‌هایی مشابه مقادیر دقیق دارند، و ما قادر به شناسایی یک رابطه سازگار بین تخمین‌های روش‌های مختلف برای یک DEM معین نبودیم. با استفاده از نقاط بیشتر برای تناسب با تابع خطی، زمان محاسبه افزایش یافت. خطاهای نسبی با استفاده از اتصال با چهار نقطه حداقل و زمان محاسبه قابل قبول بود. از این رو، ما استدلال می کنیم که برازش چهار نقطه مناسب ترین راه حل بود. با بزرگتر شدن اندازه یک شطرنجی عددی، جایگزین کردن تنها یک نقطه در تابع خطی برای به دست آوردن منحنی نهایی ممکن است کافی نباشد. برای هر شطرنجی، تعداد بهینه نقاطی وجود دارد که برای تولید یک تابع خطی مناسب استفاده می‌شود که دقت و همچنین راندمان محاسباتی بالا را به حداکثر می‌رساند.
جدول 3 شکست سیستماتیک مدل ها را در تخمین آنتروپی مطلق بولتزمن DEM b2 و DEM c2 نشان می دهد. به منظور شناسایی دلایل احتمالی این خطای مداوم بالا، ما سطح را در برابر آنتروپی نسبی بولتزمن برای هر هشت DEM ترسیم کردیم، همانطور که در شکل 9 نشان داده شده است.
شیب های منفی DEM b2 و DEM c2 تندتر از شیب های DEM های دیگر است. از شکل 6واضح است که DEM b2 و DEM c2 با توپوگرافی هموارتر نسبت به سایر DEM ها شروع شدند که نشان دهنده ناهمگنی کم است. این ممکن است با فرآیند کاهش وضوح از طریق روش نمونه‌گیری مجدد تشدید شود، که تمایل دارد ناهمگنی را برای تصاویری با ناهمگنی کمتر کاهش دهد. به عبارت دیگر، با کاهش ناهمگونی فضایی، فراوانی ریز حالت‌های غیرممکن کاهش می‌یابد که منجر به کاهش آنتروپی نسبی بولتزمن در هر سطح می‌شود. از آنجایی که ناهمگونی DEM b2 و DEM c2 با اندک شروع شد، آنتروپی نسبی بولتزمن در هر سطح سریعتر از سایر DEM ها کاهش یافت و تعداد نقاط با مقادیر کوچک در دم بیشتر از سایر DEM ها بود. برای DEM b2 و DEM c2، میانگین تمام امتیازات کلاس اول ناچیز بود.
گائو و لی [ 17 ] دریافتند که روش مبتنی بر نمونه‌گیری مجدد آنها هنگام محاسبه آنتروپی مطلق بولتزمن یک گرادیان منظره، که با ترمودینامیک سازگار نیست، توجه بیشتری به مکان‌های مرکزی نسبت به مکان‌های لبه دارد. برای حل این مشکل، آنها یک روش مبتنی بر تجمع را برای محاسبه آنتروپی مطلق بولتزمن پیشنهاد کردند. این روش مشابه روش مبتنی بر نمونه‌برداری مجدد است و می‌توان با تجمیع گرادیان منظره اصلی با یک پنجره کشویی که اندازه آن برابر است، یک حالت کلان مناسب تولید کرد. 2×2پیکسل ها با این حال، این رویکرد همانطور که توسط گائو و لی [ 17 ] به طور کامل توضیح داده شده است، در حین کشویی پنجره، همپوشانی را حذف می کند . این روش تنها زمانی کار می کند که هم طول و هم عرض شیب منظره یکسان باشد 2n، جایی که nیک عدد صحیح مثبت است. دو DEM به دست آمده از ابر داده مکانی ( https://www.gscloud.cn )، با ابعاد 512×512پیکسل ها ( شکل 10 ) برای ارزیابی دقت محاسبه آنتروپی مطلق بولتزمن در جدول 5 تجزیه و تحلیل شدند .
جدول 5 نشان می دهد که خطاهای نسبی ایجاد شده توسط روش مبتنی بر تجمیع کمتر از خطاهای روش مبتنی بر نمونه گیری مجدد است. این امکان وجود دارد که روش مبتنی بر نمونه برداری مجدد برای DEM با ناهمگنی کم مناسب نباشد زیرا با آنالوگ ترمودینامیکی آن مطابقت ندارد.

7. نتیجه گیری و کار آینده

در این مطالعه، ما روشی را برای تخمین کارآمد آنتروپی مطلق بولتزمن داده‌های شطرنجی عددی پیشنهاد و آزمایش کرده‌ایم. روش پیشنهادی ایده شکستگی سر و دم را به عاریت گرفته است تا همه نقاط را در چند کلاس طبقه بندی کند. این طرح طبقه‌بندی نه تنها پیچیدگی منحنی را کاهش می‌دهد، بلکه الگوی مقیاس‌بندی یا سلسله مراتبی یک مجموعه داده را با توزیع دم سنگین منعکس می‌کند. در همین حال، طرح طبقه بندی به طور طبیعی تعداد بهینه کلاس ها و فواصل کلاس ها را تعیین می کند. میانگین مقادیر داده‌ها در یک کلاس معین می‌تواند به عنوان مقدار نماینده آن کلاس عمل کند، زیرا تفاوت‌های بین آنها نسبتاً کم است. این روش پیشنهادی مقدار نماینده را با یک تابع خطی جایگزین می کند. و بیان آن تابع را می توان از طریق حل معکوس به دست آورد. مقادیر معرف باقی مانده را می توان از این تابع تخمین زد. پس از بدست آوردن این تخمین ها، روش آنتروپی مطلق بولتزمن داده های شطرنجی عددی را محاسبه می کند.
نتایج تجربی ما نشان داد که روش پیشنهادی به کارایی محاسباتی بالاتری نسبت به روش قبلی دست می‌یابد که روی داده‌های مشابه گائو و همکاران اعمال شود. [ 18 ]. روش جدید در حدود 99 درصد از زمان محاسبات را هنگامی که روی 8 اعمال می شود، صرفه جویی می کند 600×600DEM های پیکسل با این حال، دو DEM با ناهمگنی کم (DEM b2 و DEM c2) با نرخ خطای بالایی مواجه شدند و خطاهای نسبی شش DEM باقی مانده به اندازه کافی پایدار نبودند. برای حل این مشکل، طیفی از نقاط را برای تناسب با تابع خطی آزمایش کردیم. این نتایج نشان داد که برازش چهار نقطه ای مناسب ترین راه حل است. زمان محاسبات در هنگام برخورد با هشت حدود 98 درصد کاهش یافت 600×600DEM های پیکسل خطاهای نسبی شش DEM ناهمگن نسبتاً پایدار بودند. علاوه بر این، برای بهبود دقت محاسبه، از روش مبتنی بر تجمع [ 17 ] برای جایگزینی روش مبتنی بر نمونه‌گیری مجدد برای بهبود تعداد نقاط درگیر در برازش خطی استفاده کردیم. نتایج نشان داد که این روش توانایی بهبود دقت محاسبه را برای DEM با ناهمگنی کم دارد.
روش پیشنهادی کامل نیست و به تحقیقات گسترده تری نیاز است. این مقاله فرض می‌کند که آنتروپی بولتزمن نسبی همه نقاط در هر مرحله کاهش می‌یابد، و وضعیتی را نادیده می‌گیرد که در آن آنتروپی نسبی بولتزمن یک نقطه منفرد معین بزرگ‌تر از نقطه قبلی است. علاوه بر این، این مقاله درصد کل سر و دم را به ترتیب 40% و 60% تعیین می کند. ممکن است تعداد نقاط سر کمتر از دم بوده باشد اما آنها را گرد کردیم. از این رو، فرآیند طبقه‌بندی تنها زمانی می‌تواند خاتمه یابد که تعداد نقاط سر برابر با 1 باشد. یک شرط پایان جایگزین زمانی است که تعداد نقاط سر بیشتر یا مساوی با نقاط دم باشد [ 20 ]]، که پایان دادن به فرآیند طبقه بندی را زودتر ممکن می سازد.

منابع

  1. Rao، KN Unit-5 مدل های داده GIS و ساختار داده های مکانی. IGNOU . 2017. در دسترس آنلاین: https://egyankosh.ac.in/bitstream/123456789/39613/3/MGY-003E-B2.pdf (در 31 ژانویه 2020 قابل دسترسی است).
  2. بلاش، EP; برایانت، ام. ارزیابی اطلاعات داده های SAR برای ATR. در مجموعه مقالات کنفرانس ملی هوافضا و الکترونیک IEEE 1998، دیتون، OH، ایالات متحده آمریکا، 17 ژوئیه 1998. [ Google Scholar ]
  3. رابرتز، جی دبلیو. Aardt، JAv; احمد، FB ارزیابی روشهای ادغام تصویر با استفاده از آنتروپی، کیفیت تصویر و طبقه بندی چند طیفی. J. Appl. Remote Sens. 2008 , 2 , 1-28. [ Google Scholar ]
  4. رامش، KP; گوپتا، اس. Blasch، آزمایش ادغام تصویر EP برای محتوای اطلاعاتی. در مجموعه مقالات دهمین کنفرانس بین‌المللی 2007 درباره ترکیب اطلاعات، کبک، QC، کانادا، 9 تا 12 ژوئیه 2007. [ Google Scholar ]
  5. باجوا، س. باجسی، پی. گرووز، پ. تیان، ال. داده کاوی تصویر فراطیفی برای انتخاب باند در کاربردهای کشاورزی. ترانس. ASAE 2004 ، 47 ، 895. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  6. سوتوکا، جی.ام. پلا، اف. Klaren، AC انتخاب باند بدون نظارت برای تصاویر چند طیفی با استفاده از نظریه اطلاعات. در مجموعه مقالات هفدهمین کنفرانس بین المللی تشخیص الگو، کمبریج، انگلستان، 26 اوت 2004. [ Google Scholar ]
  7. شانون، سی تئوری ریاضی ارتباطات. بل سیست. فنی J. 1948 , 27 , 379-423. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  8. فن، ی. یو، جی. او، ز. یو، اچ. بای، آر. یانگ، ال. وو، دی. آنتروپی های کاربری/پوشش زمین چین از سال 1990 تا 2010 در سطح شهرستان تغییر می کند. Entropy 2017 , 19 , 51. [ Google Scholar ] [ CrossRef ]
  9. اکستروم، ام. کمی سازی الگوهای فضایی مناظر. آمبیو جی. هوم. محیط زیست 2003 ، 32 ، 573-577. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  10. لی، ز. Huang, P. اقدامات کمی برای اطلاعات مکانی نقشه ها. بین المللی جی. جئوگر. Inf. علمی 2002 ، 16 ، 699-709. [ Google Scholar ] [ CrossRef ]
  11. هارالیک، آر.ام. شانموگام، ک. ویژگی های بافتی Dinstein، IH برای طبقه بندی تصویر. IEEE Trans. سیستم مرد سایبرن. 1973 ، 6 ، 610-621. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  12. برینک، الف. استفاده از اطلاعات مکانی به عنوان کمکی برای حداکثر انتخاب آستانه تصویر آنتروپی. تشخیص الگو Lett. 1996 ، 17 ، 29-36. [ Google Scholar ] [ CrossRef ]
  13. راکشیت، اس. میشا، ع. برآورد محتوای اطلاعاتی ساختاری در تصاویر. در مجموعه مقالات کنفرانس آسیایی در مورد چشم انداز رایانه، برلین/هایدلبرگ، آلمان، 13 تا 16 ژانویه 2006. [ Google Scholar ]
  14. کوشمن، SA ترمودینامیک در بوم شناسی منظر: اهمیت ادغام اندازه گیری و مدل سازی آنتروپی منظر. Landsc. Ecol. 2015 ، 30 ، 7-10. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  15. Cushman، SA محاسبه آنتروپی پیکربندی یک موزاییک منظره. Landsc. Ecol. 2016 ، 31 ، 481-489. [ Google Scholar ] [ CrossRef ]
  16. ورانکن، آی. بودری، جی. اوبینت، ام. ویسر، ام. Bogaert، J. مروری بر استفاده از آنتروپی در بوم‌شناسی منظر: ناهمگونی، غیرقابل پیش‌بینی، وابستگی مقیاس و پیوند آنها با ترمودینامیک. Landsc. Ecol. 2015 ، 30 ، 51-65. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  17. گائو، پی. Li، Z. روش مبتنی بر تجمع برای محاسبه آنتروپی مطلق بولتزمن شیب منظر با سازگاری کامل ترمودینامیکی. Landsc. Ecol. 2019 ، 34 ، 1837–1847. [ Google Scholar ] [ CrossRef ]
  18. گائو، پی. ژانگ، اچ. Li، Z. یک راه حل مبتنی بر سلسله مراتب برای محاسبه آنتروپی پیکربندی شیب های چشم انداز. Landsc. Ecol. 2017 ، 32 ، 1133-1146. [ Google Scholar ] [ CrossRef ]
  19. گائو، پی. ژانگ، اچ. آنتروپی لی، زی بولتزمن برای اطلاعات فضایی داده های شطرنجی. در مجموعه مقالات خلاصه‌های ICA، توکیو، ژاپن، 15 تا 20 ژوئیه 2019. [ Google Scholar ]
  20. Jiang, B. Head/tail breaks: یک طرح طبقه بندی جدید برای داده ها با توزیع دم سنگین. پروفسور Geogr. 2013 ، 65 ، 482-494. [ Google Scholar ] [ CrossRef ]
  21. آندرادیس، جی. لامپریدو، ای. Sherar, P. A Computer Aided Design (CAD) قلم دوزی سیستم دیجیتالی کردن قلم. جی. اتوم. مهندسی کنترل 2015 ، 3 . [ Google Scholar ] [ CrossRef ]
  22. مک دونالد، BD; Rowe، AM تجزیه و تحلیل تجربی و عددی سیستم‌های ذخیره‌سازی هیدروژن هیدرید فلز دینامیک. J. منابع قدرت 2007 ، 174 ، 282-293. [ Google Scholar ] [ CrossRef ]
  23. جیانگ، بی. جیا، قانون T. Zipf برای همه شهرهای طبیعی در ایالات متحده: یک دیدگاه جغرافیایی. بین المللی جی. جئوگر. Inf. علمی 2011 ، 25 ، 1269-1281. [ Google Scholar ] [ CrossRef ]
  24. جیانگ، بی. یین، J. شاخص Ht برای کمی کردن ساختار فراکتال یا مقیاس بندی ویژگی های جغرافیایی. ان دانشیار صبح. Geogr. 2014 ، 104 ، 530-540. [ Google Scholar ] [ CrossRef ]
Ijgi 09 00103 g001 550
شکل 1. نموداری از تکنیک نمونه‌گیری مجدد که برای تولید یک حالت کلان (خروجی) برای یک گرادیان چشم‌انداز استفاده می‌شود (ورودی؛ اصلاح شده از Gao و همکاران [ 18 ]).
Ijgi 09 00103 g002 550
شکل 2. یک نمایش بصری از جمع آنتروپی های نسبی بولتزمن (اسآر)از تمام سطوح برای بدست آوردن آنتروپی مطلق بولتزمن (اسآ) یک گرادیان منظره (اصلاح شده از Gao و همکاران [ 18 ]).
Ijgi 09 00103 g003 550
شکل 3. دو تصویر با وضوح های مختلف: ( الف ) 512×512پیکسل و ( ب ) 256×256پیکسل ها
Ijgi 09 00103 g004 550
شکل 4. تصویری از ( الف ) یک مدل ارتفاعی دیجیتال (DEM) به دست آمده از سایت ابر داده مکانی ( https://www.gscloud.cn ) با اندازه 300×300پیکسل، و ( ب ) منحنی ایجاد شده بین سطح سلسله مراتبی DEM و آنتروپی بولتزمن نسبی آن.
Ijgi 09 00103 g005 550
شکل 5. فرآیند طبقه بندی که از مفهوم شکستگی سر و دم استفاده می کند.
Ijgi 09 00103 g006 550
شکل 6. هشت مدل رقومی ارتفاع، جفت شده با حرف، برگرفته از داده های تجربی گائو و همکاران. [ 18 ].
Ijgi 09 00103 g007 550
شکل 7. مقایسه آنتروپی های مطلق بولتزمن چهار جفت DEM از مقادیر دقیق و تخمین های تولید شده با پنج روش.
Ijgi 09 00103 g008 550
شکل 8. مقایسه زمان محاسباتی مورد نیاز برای چهار جفت DEM از مقادیر دقیق و برآوردهای تولید شده توسط پنج روش.
Ijgi 09 00103 g009 550
شکل 9. نمودارهای سطح در برابر آنتروپی نسبی بولتزمن برای هر یک از هشت DEM. ( a1 – b1 )، ( c1 ) و ( d1 – d2 ) شش نمودار سطح در برابر آنتروپی نسبی بولتزمن برای DEM با ناهمگنی بالا. ( b2 ) و ( c2 ) دو نمودار سطح در برابر آنتروپی نسبی بولتزمن برای DEM با ناهمگنی کم.
Ijgi 09 00103 g010 550
شکل 10. دو DEM به دست آمده از سایت ابر داده های مکانی ( https://www.gscloud.cn ). ( الف ) یک DEM با ناهمگنی کم. ( ب ) DEM دیگر با ناهمگنی کم.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید