خلاصه

با توسعه فناوری یادگیری ماشین، موارد تحقیقاتی برای تخمین فضایی از طریق رویکرد یادگیری ماشین (MLA) علاوه بر تکنیک‌های زمین آماری سنتی در حال افزایش است. MLA این مزیت را دارد که تخمین فضایی بدون فرضیه های ثابت داده ها امکان پذیر است، اما ممکن است نتایج پیش بینی همبستگی فضایی را نادیده بگیرد. در مطالعات اخیر، با استفاده از ماتریس فاصله به جای مختصات خام در نظر گرفته شده است. اگرچه، عملکرد تخمین فضایی را می توان از طریق این رویکرد بهبود بخشید، پیچیدگی محاسباتی MLA به سرعت با افزایش تعداد نقاط نمونه افزایش یافت. در این مطالعه، ما روشی را برای کاهش پیچیدگی محاسباتی MLA با در نظر گرفتن خودهمبستگی فضایی ایجاد کردیم. تحلیل مؤلفه های اصلی برای استخراج ویژگی های فضایی و کاهش ابعاد ورودی ها به آن اعمال می شود. برای تأیید رویکرد پیشنهادی، شاخص کریجینگ به عنوان یک مدل معیار استفاده شد و هر عملکرد MLA هنگام استفاده از مختصات خام، بردار فاصله، و ویژگی‌های فضایی استخراج‌شده از بردار فاصله به عنوان ورودی مقایسه شد. رویکرد پیشنهادی عملکرد را در مقایسه با MLA قبلی بهبود بخشید و عملکرد مشابهی را در مقایسه با کریجینگ نشان داد. ما تأیید کردیم که ویژگی‌های استخراج‌شده دارای ویژگی‌های طبقه‌بندی صلب در برآورد فضایی هستند. بر این اساس، نتیجه می گیریم که این مدل می تواند عملکرد را بهبود بخشد. و هر عملکرد MLA هنگام استفاده از مختصات خام، بردار فاصله و ویژگی‌های فضایی استخراج شده از بردار فاصله به عنوان ورودی مقایسه شد. رویکرد پیشنهادی عملکرد را در مقایسه با MLA قبلی بهبود بخشید و عملکرد مشابهی را در مقایسه با کریجینگ نشان داد. ما تأیید کردیم که ویژگی‌های استخراج‌شده دارای ویژگی‌های طبقه‌بندی صلب در برآورد فضایی هستند. بر این اساس، نتیجه می گیریم که این مدل می تواند عملکرد را بهبود بخشد. و هر عملکرد MLA هنگام استفاده از مختصات خام، بردار فاصله و ویژگی‌های فضایی استخراج شده از بردار فاصله به عنوان ورودی مقایسه شد. رویکرد پیشنهادی عملکرد را در مقایسه با MLA قبلی بهبود بخشید و عملکرد مشابهی را در مقایسه با کریجینگ نشان داد. ما تأیید کردیم که ویژگی‌های استخراج‌شده دارای ویژگی‌های طبقه‌بندی صلب در برآورد فضایی هستند. بر این اساس، نتیجه می گیریم که این مدل می تواند عملکرد را بهبود بخشد.

کلید واژه ها:

یادگیری ماشینی ؛ جنگل تصادفی ; کریجینگ ؛ تخمین فضایی ; ویژگی فضایی ؛ تجزیه و تحلیل اجزای اصلی

1. معرفی

تکنیک کریجینگ [ 1 ] روشی برای تخمین داده های ویژگی برای مکان های ناشناخته با استفاده از داده های شناخته شده است. این به عنوان یک مدل ریاضی توسط بسیاری از دانشمندان ایجاد شده است و به عنوان یک روش معرف برای زمین آمار ظاهر شده است [ 2 ، 3 ، 4 ، 5 ].
اخیراً، روش‌های تخمین فضایی با استفاده از رویکرد یادگیری ماشینی (MLA) به طور فعال پیشنهاد شده‌اند. به طور خاص، الگوریتم جنگل تصادفی [ 6 ]، که کنترل فراپارامترها را نسبتاً ساده می کند و دسترسی به آن از طریق توسعه بسته ها [ 7 ، 8 ] آسان است، به عنوان یک تکنیک نماینده برای تخمین فضایی استفاده شده است [ 9 ، 10 ، 11]. در ابتدا، مختصات فضایی در MLA برای منعکس کردن اطلاعات مکان لازم برای تخمین فضایی استفاده شد. با این حال، زمانی که آنها فقط به صورت مختصات برای یادگیری اطلاعات مکان استفاده می شدند، نتایج الگوی فضایی ظاهر شده در نقطه نمونه را نادیده می گرفتند. به همین دلیل، مقادیر صفت پیش‌بینی‌شده در مدل تمایل به دست‌کم یا بیش‌ازحد برآورد شدن داشتند.
برای غلبه بر این مشکلات با استفاده از فرم مختصات، Hengl و همکاران. [ 12] از فاصله بین تمام نقاط مشاهده به جای فرم مختصات به عنوان ورودی الگوریتم استفاده کرد تا مدل بتواند رابطه فضایی را منعکس کند. وقتی همبستگی فضایی در نظر گرفته شد، عملکرد تخمین فضایی بهبود یافت و تخمین های پایدارتری نسبت به قبل به دست آمد. با این وجود، اگر داده‌های نمونه کوچک باشند، این رویکردها این مضرات را دارند که ممکن است عملکرد کمتر از استفاده از کریجینگ به دلیل کمبود داده‌های آموزشی باشد. برعکس، حتی اگر هزاران مورد یا بیشتر از داده‌های نمونه وجود داشته باشد، متغیر ورودی به‌دست‌آمده با محاسبه فاصله به سرعت افزایش می‌یابد به طوری که هزینه‌های محاسباتی افزایش می‌یابد. این می تواند به نفرین ابعاد منجر شود – یک مشکل رایج در یادگیری ماشین. علاوه بر این،
به طور کلی، مجموعه داده‌های آموزشی و آزمایشی از طریق یک تکنیک تقسیم تصادفی برای تأیید عملکرد آموزش در یادگیری ماشینی تقسیم می‌شوند. با این حال، از آنجایی که داده‌های مکانی عمدتاً دارای یک سوگیری محلی هستند، اگر مجموعه داده‌ها بدون در نظر گرفتن وابستگی مکانی از هم جدا شوند، مدل تخمین ممکن است فقط برای یک منطقه محلی خاص از کل مجموعه داده مناسب باشد یا ممکن است خطای قابل‌توجهی در تأیید عملکرد پیش‌بینی رخ دهد. 13 ، 14 ]. بنابراین، ضروری است که داده های فضایی پارتیشن بندی شده باید به طور مساوی در کل منطقه ترکیب شوند [ 15 ، 16 ].
در این مطالعه، ما یک چارچوب MLA را توسعه دادیم که ویژگی‌های داده‌های مکانی را بر اساس آنچه تاکنون مطالعه شده است، در نظر می‌گیرد. در این چارچوب، برای در نظر گرفتن مسائلی که هنگام آموزش داده های مکانی با استفاده از متغیرهای فاصله رخ می دهد، فرآیند استخراج ویژگی های مکانی از متغیرهای فاصله گنجانده شده است. علاوه بر این، ما الگوریتم جنگل تصادفی را انتخاب کردیم که مطالعات قبلی نشان داده است که عملکرد قوی در تخمین فضایی در میان تکنیک‌های مختلف ML دارد [ 9 ، 10 ، 11 ، 17 ]]، به عنوان یک الگوریتم نماینده برای تمرکز بر بهبود عملکرد از طریق آموزش ویژگی های فضایی استخراج شده از داده های مختصات ورودی. ما انتظار داریم که ویژگی‌های فضایی استخراج‌شده عملکرد MLA را برای تخمین فضایی بهبود بخشد، زیرا آنها دارای ویژگی‌های همبستگی فضایی هستند که با فواصل نشان داده می‌شوند. برای تأیید تأثیر مورد انتظار رویکرد پیشنهادی، از مجموعه داده Meuse که در دسترس عموم است، استفاده شد. یک مجموعه داده گمانه از سئول، کره جنوبی، نیز برای تأیید کاربرد میدانی چارچوب استفاده شد. علاوه بر این، به جای استفاده از سایر متغیرهای کمکی در مدل فضایی، تنها مختصات به عنوان متغیرهای ورودی به منظور تمرکز بر مقایسه اثرات تبدیل آنها بر عملکرد تخمین استفاده شد.

2. نظریه و پیشینه

2.1. اندیکاتور کریجینگ (IK)

در میان تکنیک‌های زمین‌آماری برای تخمین فضایی، شاخص کریجینگ (IK) [ 18 ] یک رویکرد غیر پارامتری است که می‌تواند زمانی که مجموعه داده‌های نمونه کج است یا زمانی که توزیع نرمال ندارد، اعمال می‌شود. علاوه بر این، IK مستقیماً مقدار هدف ناشناخته را پیش‌بینی نمی‌کند، اما مجموعه‌ای از تخمین‌های احتمال K را ارائه می‌دهد [ 18 ، 19 ] که توسط:

i^(x;zk)=FIK(x;zk|n)=Prob{Z(x)≤zk|n}     k=1, …, K�^(�;��)=���(�;��|�)=����{�(�)≤��|�}     �=1, …, �

که در آن n تعداد مشاهدات موجود را برای نمایش درجه ای از همبستگی فضایی در مکان x نشان می دهد ، zk��آستانه k که گسسته کننده دامنه تغییرات مقدار ویژگی z است، و F IK تابع توزیع تجمعی مشروط برای IK است.

برای اعمال IK در تخمین فضایی، مقادیر مشخصه هدف باید با توجه به تعداد معینی از مقادیر آستانه به شاخص تبدیل شوند. اندیکاتورها به صورت توابع باینری کدگذاری می شوند و با توجه به نوع داده به اندیکاتورهای پیوسته یا طبقه ای تبدیل می شوند. معادله (2) تبدیل نشانگر را برای داده های پیوسته نشان می دهد:

i(xa;zk)={1 if  z(xa)≤zk0   otherwise      k=1,…,K�(��;��)={1 ��  �(��)≤��0   ��ℎ������      �=1,…,�

جایی که xa��محل رصد است.

همانند فرآیند کریجینگ معمولی، مدل‌سازی واریوگرام باید با استفاده از شاخص‌های تبدیل‌شده انجام شود. مقادیر شاخص محاسبه شده با استفاده از توزیع احتمال تجمعی مشروط بر اساس هر مقدار آستانه به مقادیر ویژگی مکانی تبدیل می شوند. مقادیر بین مقادیر آستانه عمدتاً با استفاده از درون یابی خطی محاسبه می شوند. زمانی که تفاوت بین مقادیر آستانه زیاد باشد، می توان از روش تقریبی دیگری استفاده کرد [ 4 ، 5 ، 20 ].

2.2. جنگل تصادفی (RF)

جنگل تصادفی (RF) [ 6 ، 21رویکرد ] که یک مشکل را با یادگیری درخت های تصمیم چندگانه حل می کند، یک تکنیک مجموعه ای معرف و روش آماری مبتنی بر داده است. تکنیک درخت تصمیم یک راه حل غیر قابل اعتماد است زیرا عملکرد پیش بینی بسته به داده های آموزشی بسیار متفاوت است. علاوه بر این، همچنین مستعد به تناسب بیش از حد داده های آموزشی خود است. برای غلبه بر این مسائل، روش‌های بسته‌بندی و تقویت، که تکنیک‌های مجموعه‌ای هستند که چندین درخت تصمیم را برای آموزش داده‌ها در نظر می‌گیرند، توسعه و مطالعه شده‌اند. بسته بندی روشی برای جمع آوری درختان اساسی است. برای هر مجموعه داده آموزش داده می شود و از طریق فرآیند بوت استرپ ایجاد می شود تا مجموعه داده ای با همان اندازه ایجاد کند و در عین حال امکان افزونگی در مجموعه داده نمونه را فراهم کند. بنابراین می توان گفت که یک مدل گروه موازی است که هر مدل را به طور مستقل یاد می گیرد. و دارای ویژگی های کاهش واریانس و اجتناب از برازش بیش از حد مدل پیش بینی شده است. RF تقریباً از همان چارچوبی مانند bagging استفاده می کند، اما یک تفاوت این است که به طور تصادفی ویژگی را در شاخه تقسیم گره انتخاب و استفاده می کند [6 ، 21 ، 22 ]. مقادیر پیش‌بینی‌شده از طریق کیسه‌بندی را می‌توان به عنوان مقادیر متوسط ​​مقادیر پیش‌بینی‌شده درختان جداگانه بیان کرد:

θˆB(x)=1B∑b=1Bt∗b(x)�^�(�)=1�∑�=1���*(�)

جایی که b نمونه بوت استرپ منفرد است، B تعداد کل b است، t∗b��*درخت تصمیم فردی برای نمونه b است و:

t∗b(x)=t(x;c∗b1,…,c∗bK)    k=1,…, K��*(�)=�(�;��1*,…,���*)    �=1,…, �

جایی که c∗bk���*K امین نمونه آموزشی با جفت مقادیر برای پاسخ ( y ) و پیش بینی کننده ( x ) است: c∗bk=(xk,yk)���*=(��,��).

از آنجایی که RF می تواند داده ها را بدون تنظیم پیچیده هایپرپارامترها آموزش دهد و می تواند بدون محدودیت برای مسائل کلاس چندگانه اعمال شود، برای مسائل مختلف رگرسیون و طبقه بندی در زمینه های علوم زمین استفاده می شود.

2.3. تجزیه و تحلیل اجزای اصلی (PCA)

PCA [ 23 ، 24 ] یک روش تجزیه و تحلیل چند متغیره است که از روابط بین واریانس و کوواریانس متغیرهای کمی برای یافتن اجزای اصلی (PCs) و به طور تقریبی برای توصیف تغییرات کلی داده های اصلی استفاده می کند. از آنجایی که PCA یک پایه را متعامد با یکدیگر پیدا می کند، در حالی که واریانس را تا حد امکان حفظ می کند، می توان یک فضای با ابعاد بالا را بدون همبستگی خطی به فضایی با ابعاد پایین تبدیل کرد. هر رایانه شخصی برای به حداقل رساندن از دست دادن اطلاعات داده های اصلی محاسبه می شود [ 25 ]. هنگامی که PCA روی داده ها اعمال می شود، یک بردار وزن برای k امین PC به صورت زیر به دست می آید:

wk=argmax ∥w∥ = 1E{(wTXˆk)2}��=argmax ‖�‖ = 1�{(���^�)2}

که w بردار واحد وزن و Xˆk�^�مجموعه داده ای است که k -1th PC را از مجموعه داده اصلی کم می کندX�; Xˆk�^�از رابطه زیر بدست می آید:

Xˆk=X−∑i=1k−1wiwTiX�^�=�−∑�=1�−1������

جایی که Xˆ1�^1همان مجموعه داده اصلی است X�.

از آنجایی که PCA می تواند برای پیش پردازش و تجسم مجموعه داده های با ابعاد بالا استفاده شود، به عنوان یک روش کاهش ابعادی نماینده در زمینه های مختلف تحقیقاتی استفاده می شود. در مسائل رگرسیونی که متغیرهای توضیحی با همبستگی قوی وجود دارد، PCA می تواند تعداد متغیرها را کاهش دهد و عملکرد رگرسیون را بهبود بخشد [ 26 ]. علاوه بر این، برای استخراج متغیرهای جداسازی اصلی در تجزیه و تحلیل خوشه ای [ 27 ، 28 ] یا در پردازش داده ها با نویز بالا [ 29 ، 30 ] استفاده می شود.

3. روش شناسی

به طور کلی، برآوردگرهای مبتنی بر گشتاورهای مرتبه دوم، مانند کریجینگ، به مفروضاتی برای ایستایی مرتبه دوم و ذاتی نیاز دارند که باید در مدل آماری دو نقطه ای از پیش تعریف شوند. در فرآیند مدل‌سازی واریوگرام که این فرضیه‌های ثابت را منعکس می‌کند، دانش تخصصی که می‌تواند ذهنیت متخصصان را درگیر کند برای تنظیم پارامترهای یک واریوگرام ضروری است. در مقابل، MLA به عنوان یک روش پیشنهادی در این مطالعه برای تخمین فضایی، نیازی به فرضیه‌های ثابت داده‌ها و مدل‌سازی واریوگرام ندارد. با این حال، اگر داده‌های مکانی بدون پیش پردازش اضافی و تعصب فضایی در نظر گرفته شوند، ممکن است نتایج پیش‌بینی همبستگی فضایی را نادیده بگیرد. شکل 1فرآیند کریجینگ و روش پیشنهادی برای تخمین فضایی را نشان می دهد. هنگام اعمال کریجینگ برای مسائل فضایی، یافتن نرمال بودن داده های ویژگی هدف ضروری است. اگر توزیع آن توزیع نرمال و اریب نباشد، باید تبدیل شود زیرا برآوردگر کریجینگ به مقادیر داده بزرگ حساس است. دو روش معمولی برای اعمال کریجینگ برای داده های مکانی با چنین چولگی وجود دارد. اولین مورد اعمال کریجینگ معمولی پس از تبدیل داده است. در این مورد، تبدیل Box-Cox شامل تبدیل لگاریتمی معمولاً برای تبدیل داده ها استفاده می شود. با این حال، به طور مشکل ساز، نتایج کریجینگ زمانی که داده ها از طریق اعمال معکوس تبدیل اولیه به تخمین های کریجینگ داده های تبدیل شده، به عقب تبدیل می شوند، سوگیری دارند. مورد دوم استفاده از IK بدون در نظر گرفتن تغییر شکل برگشتی است. با این حال، برای اعمال IK، داده ها باید بر اساس آستانه های خاص به شاخص های جداگانه تبدیل شوند و واریوگرام برای هر شاخص باید به طور جداگانه مدل شود. پس از در نظر گرفتن این نکات، مدل‌سازی واریوگرام با استفاده از داده‌های تبدیل شده انجام شد و با استفاده از مدل واریوگرام نظری در محاسبه کریجینگ، تخمین مکانی انجام شد. در طی این فرآیند، نتایج تبدیل داده‌ها و مدل‌سازی واریوگرام با توجه به دانش متخصص متفاوت است که بر عملکرد تخمین فضایی تأثیر می‌گذارد. متقابلا، مدل‌سازی واریوگرام با استفاده از داده‌های تبدیل شده انجام شد و تخمین فضایی با استفاده از مدل واریوگرام نظری در محاسبه کریجینگ انجام شد. در طی این فرآیند، نتایج تبدیل داده‌ها و مدل‌سازی واریوگرام با توجه به دانش متخصص متفاوت است که بر عملکرد تخمین فضایی تأثیر می‌گذارد. متقابلا، مدل‌سازی واریوگرام با استفاده از داده‌های تبدیل شده انجام شد و تخمین فضایی با استفاده از مدل واریوگرام نظری در محاسبه کریجینگ انجام شد. در طی این فرآیند، نتایج تبدیل داده‌ها و مدل‌سازی واریوگرام با توجه به دانش متخصص متفاوت است که بر عملکرد تخمین فضایی تأثیر می‌گذارد. متقابلا،شکل 1b فرآیند تخمین مکانی را از طریق MLA نشان می دهد که به چهار مرحله اصلی تقسیم می شود: (1) آماده سازی و پردازش داده ها. (II) پارتیشن بندی داده ها. (iii) انتخاب الگوریتم یادگیری ماشینی و بهینه‌سازی فراپارامتر، و (IV) آموزش و تخمین داده‌های مکانی.

3.1. آماده سازی و پردازش داده ها

تخمین فضایی بر اساس MLA نیز یک فرآیند استنتاج داده مبتنی بر مختصات شبیه کریجینگ است. مقدار مشخصه هدف (به عنوان مثال، غلظت آلاینده ها، رسوبات مواد معدنی و ضخامت لایه ها) به عنوان خروجی MLA تنظیم می شود. برای ورودی، اطلاعات مکان (به عنوان مثال، مختصات، ارتفاع) استفاده می شود. اگرچه سایر متغیرهای کمکی موثر بر تخمین مقادیر هدف را می توان گنجاند، ما از مختصات به عنوان ورودی برای مقایسه عملکرد پیش بینی فضایی با توجه به روش های مختلف تحت شرایط داده های یکسان استفاده کردیم. به طور معمول، هنگام استفاده از MLA برای تخمین فضایی، مختصات بدون تغییر شکل استفاده می شود. با این حال، اخیرا، برای تقلید از همبستگی فضایی مورد استفاده در کریجینگ،12 ، 17]. اگرچه انواع مختلفی از الگوریتم محاسبه فاصله وجود دارد، ما از فاصله اقلیدسی برای در نظر گرفتن همبستگی فضایی استفاده کردیم. برعکس، هنگام تبدیل مختصات خام به بردار فاصله، تعداد متغیرهای ورودی با تعداد نقاط نمونه افزایش می‌یابد. به عنوان مثال، اگر 10 نقطه نمونه وجود داشته باشد، یک ماتریس فاصله 10 × 10 محاسبه می شود و هر نقطه نمونه دارای بردار فاصله است که شامل 10 متغیر فاصله است. با این حال، اگر 1000 نقطه نمونه وجود داشته باشد، بردار فاصله ای که به عنوان ورودی استفاده می شود، 1000 متغیر خواهد داشت. در این حالت، پیچیدگی محاسباتی MLA به صورت تصاعدی افزایش می‌یابد که می‌تواند زمان محاسبات را افزایش داده و عملکرد را کاهش دهد. بنابراین، بعد متغیر ورودی با اعمال PCA برای کاهش پیچیدگی محاسباتی MLA کاهش یافت.

3.2. پارتیشن بندی داده ها

برای آموزش و ارزیابی عملکرد MLA، داده‌های نمونه باید به یک مجموعه داده آموزشی و یک مجموعه داده آزمایشی تقسیم شوند. برای پرداختن به مسائل مربوط به حجم زیادی از داده‌های نمونه، تقسیم مجموعه داده‌های آموزشی و آزمایشی بر اساس یک نسبت معین، به اصطلاح روش اعتبار سنجی نگهدارنده، معمول است. با این حال، زمانی که تعداد کمی از نقاط داده نمونه وجود دارد، عملکرد آموزش می تواند به طور قابل توجهی بسته به نسبت جداسازی داده ها کاهش یابد. از این رو، روش اعتبارسنجی k -fold به طور کلی استفاده می شود. همانطور که متد از k پارتیشن داده تشکیل شده و آموزش و اعتبارسنجی k را انجام می دهدچندین بار، این روش این مزیت را دارد که عملکرد پیش‌بینی الگوریتم را برای کل مجموعه داده حتی با مقدار کمی داده ارزیابی می‌کند. هنگام اعمال این روش برای داده‌های مکانی، پارتیشن تاشو منفرد باید به گونه‌ای ترکیب شود که کل منطقه‌ای را که باید تخمین زده شود در نظر بگیرد [ 15 ].

3.3. الگوریتم یادگیری ماشین و بهینه سازی هایپرپارامتر

الگوریتم‌های مختلف یادگیری ماشینی برای حل مشکلات رگرسیون و طبقه‌بندی داده‌های مکانی استفاده شده‌اند. به عنوان مثال، الگوریتم های RF دارای انواع مختلفی هستند که می توانند برای مسائل رگرسیون فضایی استفاده شوند. ما از RF های چندکی استفاده کردیم [ 31] که می تواند واریانس خطای پیش بینی و همچنین مقادیر مشخصه هدف یک منطقه فضایی را محاسبه کند. در MLA، از آنجایی که عملکرد آموزشی الگوریتم بسته به فراپارامترها متفاوت است، بهینه سازی پارامتر ضروری است. در RF، تعداد درختان، اندازه حداقل برگ و تعداد ویژگی‌های گره تقسیم‌بندی، فراپارامترهای معمولی هستند. در مورد تعداد درختان، RF در هنگام افزایش بیش از حد مستحکم تر می شود، اما افزایش عملکرد بیش از یک عدد معین بسیار کم می شود. بنابراین، توصیه می شود آن را روی یک عدد بزرگ در محدوده قابل محاسبه در محیط کامپیوتر محقق قرار دهید [ 32 ].]. در همین حال، بهینه‌سازی فراپارامتر از طریق روش جستجوی شبکه‌ای برای تنظیم اندازه حداقل برگ و تعداد ویژگی‌ها برای گره تقسیم در این مطالعه انجام شد.

3.4. آموزش و برآورد داده های مکانی

هنگامی که پردازش داده های مکانی و تنظیم کلی الگوریتم یادگیری ماشینی تکمیل شد، آموزش و تخمین داده ها با استفاده از MLA مکانی انجام شد. در این مطالعه، روش اعتبارسنجی k -fold بر روی یک مجموعه داده نمونه برای ارزیابی عملکرد پیش‌بینی انجام شد و سپس تخمین فضایی مکان‌های ناشناخته با استفاده از مدل آموزش‌دیده انجام شد.

4. آزمایش کنید

این بخش آزمایش انجام شده برای مقایسه نتایج تخمین فضایی با استفاده از کریجینگ و MLA را توصیف می‌کند. توزیع مقادیر مشخصه هدف در مجموعه داده هایی که باید تخمین زده شوند، که با جزئیات بیشتر در بخش 4.1 توضیح داده شده است ، دارای چولگی مثبت بالایی هستند و حتی دارای مقدار مشخصه صفر هستند. با توجه به ویژگی‌های این داده‌ها، از IK که نیازی به تبدیل برگشتی ندارد، برای تخمین فضایی مرسوم استفاده شد. برای مدل‌سازی واریوگرام نشانگر و اعمال IK، یک بسته نرم‌افزاری auto-IK [ 19] مورد استفاده قرار گرفت. برای MLA، از کتابخانه «TreeBagger» که در جعبه ابزار آمار و یادگیری ماشین MATLAB 2018 گنجانده شده است، استفاده شد. علاوه بر این، آزمایش بر روی پردازنده Intel Core i7-9700K 3.60 گیگاهرتز و مشخصات رم 64 گیگابایتی انجام شد.

4.1. مجموعه داده

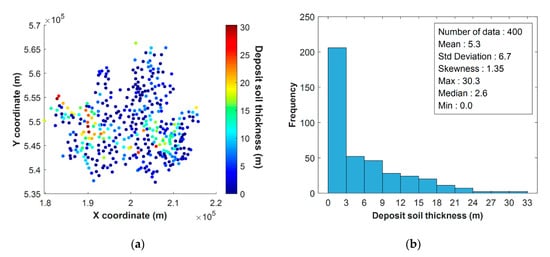
مجموعه داده Meuse [ 33]، که به صورت عمومی در دسترس است، برای ارزیابی عملکرد پیش‌بینی فضایی، و مجموعه داده گمانه سئول برای تأیید کاربرد میدانی روش پیشنهادی استفاده شد. مجموعه داده گمانه حاوی اطلاعات مربوط به ضخامت خاک رسوب‌شده، در سئول، کره جنوبی (37°41’33″–37°71’51″ شمالی، 126°73’41″-127°26’93″ شرقی) است. ، برای توسعه زیرساخت های زیرزمینی بررسی شد. این اطلاعات از اطلاعات بازرسی ژئوتکنیکی ارائه شده توسط سیستم اطلاعات ژئوتکنیکی کره ای DB به دست آمده است. این شامل کد گمانه، اطلاعات مکان (مختصات و ارتفاع)، کد لایه، عمق شروع لایه، عمق انتهای لایه، ضخامت لایه و نام لایه بود. لایه بر اساس طبقه بندی زمینی استاندارد سئول طبقه بندی شد. در این مطالعه،شکل 2 مجموعه داده Meuse را با 155 نقطه نمونه نشان می دهد. شکل 2 a توزیع غلظت روی و شکل 2 b هیستوگرام و آمار پایه غلظت روی را نشان می دهد. شکل 3 a توزیع ضخامت خاک رسوب را نشان می دهد که در 400 داده گمانه گنجانده شده است. شکل 3 ب هیستوگرام و آمار پایه ضخامت ها را نشان می دهد. هنگام تجزیه و تحلیل هیستوگرام ها و آمار، هر دو مجموعه داده مشابه هستند. توزیع مقادیر مشخصه دارای چولگی مثبت بالایی است، به این معنی که توزیع نرمال ندارند. علاوه بر این، بیشتر نقاط نمونه برداری دارای مقادیر مشخصه پایین و تعداد کمی از نقاط دارای مقادیر بسیار بالا هستند.

4.2. راه اندازی آزمایشی

برای مقایسه عملکرد تخمین فضایی، الگوریتم ها و ویژگی های هر روش در جدول 1 ارائه شده است. از آنجایی که مجموعه داده‌های مورد استفاده برای تخمین فضایی به طور معمول توزیع نمی‌شوند، مقادیر ویژگی مکانی باید به یک تبدیل Box-Cox یا شاخص‌هایی برای اعمال کریجینگ تبدیل شوند. در این مطالعه، IK به عنوان یک روش مرجع مقایسه ای با در نظر گرفتن توزیع داده ها و ویژگی ها، از جمله مقدار صفر در مجموعه داده گمانه انتخاب شد. RF برای تخمین فضایی بر اساس MLA استفاده شد. علاوه بر این، MLA بسته به نوع ورودی تبدیل شده و با اعمال PCA به سه روش تقسیم شد.
به طور کلی، هایپرپارامترهایی که به بهینه سازی RF نیاز دارند، اندازه حداقل برگ، تعداد ویژگی های گره تقسیم شده و تعداد درختان هستند. شرح مفصلی از تنظیم دقیق فراپارامترها در کوهن و جانسون [ 34 ] ارائه شده است]. در این مطالعه تعداد درختان 500 عدد تعیین شد تا الگوریتم RF بتواند از طریق آزمون و خطا در برابر برازش بیش از حد مقاوم باشد. در مورد اندازه حداقل برگ و تعداد ویژگی های گره تقسیم، بهینه سازی از طریق روش جستجوی شبکه ای انجام شد. حداقل اندازه برگ به عنوان یک تنظیم پیش فرض کلی برای RF برای رگرسیون روی پنج تنظیم شده است. در این مطالعه، فواصل یک تا پنج به عنوان بازه‌های جستجوی شبکه‌ای متغیر تنظیم شده است. در همین حال، تعداد ویژگی‌های گره تقسیم شده به یک سوم کل تعداد متغیرهای ورودی برای تنظیم پیش‌فرض تنظیم می‌شود. ما از ویژگی های فضایی استخراج شده از بردار فاصله به عنوان متغیر ورودی برای تخمین فضایی MLA استفاده کردیم. بنابراین، در فرآیند کاهش بعد متغیر ورودی با اعمال PCA، تعداد بهینه اجزای استخراج شده بسته به مجموعه داده متفاوت است. با توجه به این، فاصله جستجوی شبکه برای بهینه سازی تعداد ویژگی ها برای گره تقسیم برای هر مورد متفاوت تنظیم شد. به عنوان مثال، در صورتی که تعداد ابعاد کاهش یافته به PCA پانزده در مجموعه داده Meuse باشد، بازه تعداد ویژگی برای گره تقسیم بر روی 1، 3، 6، 9، 12 و 15 تنظیم می شود و بازه حداقل اندازه برگ از یک تا پنج به عنوان فاصله جستجوی شبکه ای تنظیم می شود. بنابراین، فراپارامترهای بهینه با مقایسه نتایج در مجموع 30 مورد تعیین شدند. علاوه بر این، نتایج صد تکرار در هر مورد جستجوی شبکه برای اطمینان از قابلیت اطمینان عملکرد مقایسه شد. بازه جستجوی شبکه برای بهینه سازی تعداد ویژگی ها برای گره تقسیم برای هر مورد متفاوت تنظیم شد. به عنوان مثال، در صورتی که تعداد ابعاد کاهش یافته به PCA پانزده در مجموعه داده Meuse باشد، بازه تعداد ویژگی برای گره تقسیم بر روی 1، 3، 6، 9، 12 و 15 تنظیم می شود و بازه حداقل اندازه برگ از یک تا پنج به عنوان فاصله جستجوی شبکه ای تنظیم می شود. بنابراین، فراپارامترهای بهینه با مقایسه نتایج در مجموع 30 مورد تعیین شدند. علاوه بر این، نتایج صد تکرار در هر مورد جستجوی شبکه برای اطمینان از قابلیت اطمینان عملکرد مقایسه شد. بازه جستجوی شبکه برای بهینه سازی تعداد ویژگی ها برای گره تقسیم برای هر مورد متفاوت تنظیم شد. به عنوان مثال، در صورتی که تعداد ابعاد کاهش یافته به PCA پانزده در مجموعه داده Meuse باشد، بازه تعداد ویژگی برای گره تقسیم بر روی 1، 3، 6، 9، 12 و 15 تنظیم می شود و بازه حداقل اندازه برگ از یک تا پنج به عنوان فاصله جستجوی شبکه ای تنظیم می شود. بنابراین، فراپارامترهای بهینه با مقایسه نتایج در مجموع 30 مورد تعیین شدند. علاوه بر این، نتایج صد تکرار در هر مورد جستجوی شبکه برای اطمینان از قابلیت اطمینان عملکرد مقایسه شد. و فاصله حداقل اندازه برگ از یک تا پنج به عنوان فاصله جستجوی شبکه ای تنظیم می شود. بنابراین، فراپارامترهای بهینه با مقایسه نتایج در مجموع 30 مورد تعیین شدند. علاوه بر این، نتایج صد تکرار در هر مورد جستجوی شبکه برای اطمینان از قابلیت اطمینان عملکرد مقایسه شد. و فاصله حداقل اندازه برگ از یک تا پنج به عنوان فاصله جستجوی شبکه ای تنظیم می شود. بنابراین، فراپارامترهای بهینه با مقایسه نتایج در مجموع 30 مورد تعیین شدند. علاوه بر این، نتایج صد تکرار در هر مورد جستجوی شبکه برای اطمینان از قابلیت اطمینان عملکرد مقایسه شد.

4.3. روش اعتبارسنجی متقابل

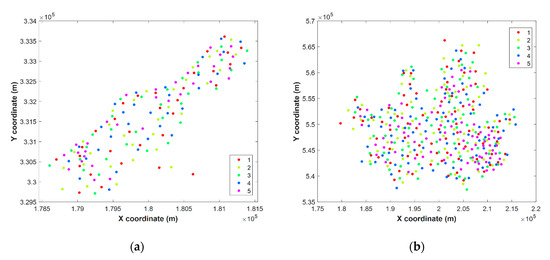
در این مطالعه، از اعتبار سنجی متقابل k-fold استفاده شد، زیرا تعداد داده های نمونه در هر دو مجموعه داده به اندازه کافی برای انجام اعتبار سنجی نگهدارنده بزرگ نبود. مجموعه داده‌ها به پنج تا تقسیم شدند و داده‌های هر بخش در یک منطقه خاص تعصب نداشتند تا از موضوع برون‌یابی در پیش‌بینی فضایی تا حد امکان جلوگیری شود ( شکل 4 ).

4.4. معیارهای عملکرد مدل

برای مقایسه عملکرد IK و MLA، از مربع R (معادله (7)) و ریشه میانگین مربعات خطا (RMSE) (معادله (8)) برای معیارهای عملکرد به همراه آمارهای پایه مانند میانگین، حداقل، و حداکثر مقادیر هر روش از طریق عملکردهای مبتنی بر مقادیر مشخصه پیش‌بینی‌شده از تمام نقاط نمونه تولید شده توسط اعتبارسنجی متقابل پنج برابری مقایسه شد. R-squared توسط:

R2=1−SSresidualsSStotal�2=1−������������������

جایی که SSresiduals�����������مجموع مربعات خطاها در نقاط اعتبارسنجی متقاطع و SStotal�������مجموع مجذورات است (یعنی مجموع مجذور اختلافات بین نقطه نمونه و میانگین آنها).

RMSE= 1n∑an(yˆ(xa)−y(xa))2−−−−−−−−−−−−−−−−−−−−⎷����= 1�∑��(�^(��)−�(��))2

جایی که yˆ(xa)�^(��)مقدار پیش بینی شده است y�در نقطه اعتبارسنجی متقابل xa��و n�تعداد کل نقاط اعتبارسنجی متقابل است.

5. نتایج و بحث

5.1. مدل سازی واریوگرام برای IK

مدل‌سازی واریوگرام برای IK، یک مدل معیار که استانداردی برای مقایسه عملکرد روش‌ها ارائه می‌کند، انجام شد. یک تبدیل شاخص در هر دو مجموعه داده برای انجام مدل‌سازی واریوگرام انجام شد. نه صدک، جدا شده با توجه به نه آستانه، برای تبدیل شاخص اعمال شد. شکل 5 و شکل 6 واریوگرام های تجربی محاسبه شده و واریوگرام نظری مدل سازی شده را به ترتیب برای مجموعه داده های گمانه Meuse و Seoul نشان می دهد. برای محاسبه واریوگرام های نظری از مدل های نمایی، کروی و گاوسی استفاده شد. پارامترهای هر واریوگرام نظری در جدول 2 ارائه شده است. در مورد مدل‌سازی واریوگرام شاخص برای مجموعه داده گمانه سئول، همان واریوگرام از آستانه یک تا آستانه چهار محاسبه می‌شود، همانطور که در شکل 4 نشان داده شده است ، زیرا چهل درصد از مقدار مشخصه هدف صفر است.

5.2. بهینه سازی تعداد رایانه های شخصی

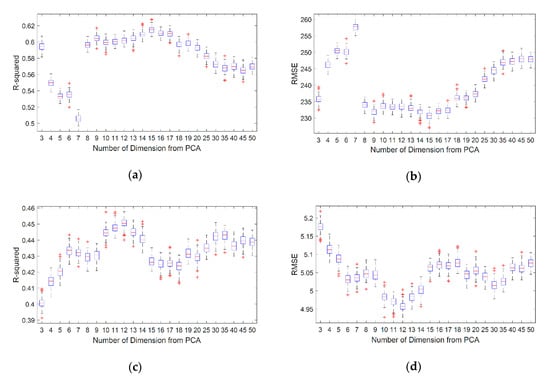
قبل از مقایسه عملکرد هر روش، فرآیند انتخاب تعداد بهینه رایانه‌های شخصی با ارزیابی عملکرد پیش‌بینی با توجه به تعداد رایانه‌های شخصی انجام شد. هر عملکرد از طریق اعتبارسنجی متقابل پنج برابری مورد ارزیابی قرار گرفت. R -squared و RMSE به عنوان معیارهای عملکرد استفاده شد. شکل 7 نتایج ارزیابی R را نشان می دهدمربع و RMSE با توجه به تعداد رایانه های شخصی در مجموعه داده های Meuse و Seoul. از آنجایی که نتایج پیش‌بینی‌شده از هر درخت در RF تصادفی است، پیش‌بینی می‌تواند متفاوت باشد حتی اگر الگوریتم از پانصد درخت تشکیل شده باشد. بنابراین، صد RF با توجه به تعداد رایانه های شخصی انجام شد و هر اجرا در یک باکس پلات نشان داده شد. در نتیجه، بهترین عملکرد زمانی به دست آمد که تعداد رایانه های شخصی پانزده و دوازده برای مجموعه داده های گمانه Meuse و Seoul بود. در نهایت، عملکرد روش پیشنهادی با استفاده از تعداد بهینه رایانه‌های شخصی، با عملکرد روش‌های دیگر مقایسه شد.

5.3. اعتبار سنجی عملکردهای پیش بینی

عملکرد پیش بینی هر روش در جدول 3 مشخص شده است. شکل 8 نمودار جعبه ای را نشان می دهد که R را با هم مقایسه می کند-مقادیر مربع هر روش. برای پیش‌بینی‌های فضایی RF، عملکردها به‌عنوان یک نمودار جعبه نمایش داده می‌شوند زیرا عملکردهای مختلف با توجه به صد تکرار محاسبه شده‌اند. برعکس، برای IK، یک خط در نمودار جعبه نشان داده می شود زیرا بدون توجه به تعداد تکرارها، همان نتیجه به دست می آید. به طور کلی، هنگام مقایسه نتایج پیش‌بینی فضایی هر روش برای هر دو مجموعه داده، محدوده مقادیر هدف (یعنی تفاوت بین مقادیر حداکثر و حداقل) پیش‌بینی‌شده توسط IK از محدوده داده‌های واقعی باریک‌تر بود و انحراف استاندارد کم. دلیل این امر این است که IK کریجینگ معمولی را برای هر شاخص اعمال می کند. بنابراین، مقادیر هدف مناطق در هر شاخص برای تقریبی میانگین آستانه های فردی پیش بینی می شود.
با توجه به این اثر هموارسازی موضعی، دامنه مقادیر پیش بینی شده باریک به نظر می رسد. در مقابل، دامنه مقادیر مشخصه هدف و انحراف استاندارد پیش‌بینی‌شده با اعمال RF نسبتاً بالاتر از IK بود. علاوه بر این، برآوردهای فضایی RF نسبت به IK در پیش‌بینی مقادیر بالای محلی برتری داشتند. دلیل این امر این است که RF می تواند عدم قطعیت تصادفی را با پیش بینی مقادیر هدف متفاوت برای هر درخت منعکس کند. دقت پیش‌بینی فضایی، ارزیابی شده توسط R-squared، نشان داد که IK در مقایسه با RF نسبتاً بالاتر بود. با این حال، RF-PCA دارای دقت یکسان یا بهتر از IK بود. همانطور که در شکل 8 و جدول 3 نشان داده شده استدقت پیش‌بینی فضایی RF-PCA نزدیک به IK، 0.46، برای مجموعه داده سئول بود. علاوه بر این، RF-PCA دقت بالاتری نسبت به IK با دقت پیش‌بینی فضایی 0.62 برای مجموعه داده Meuse داشت. دلیل اینکه دقت پیش‌بینی فضایی RF-PCA بیشتر از سایر روش‌های RF بود این است که عملکرد رگرسیون RF با استفاده از تعداد معینی از رایانه‌های شخصی که دارای ویژگی‌هایی برای توضیح رابطه فضایی بین مشاهدات بودند، بهبود یافت. اثر اعمال PCA در RF به تفصیل در بخش بحث بعدی توضیح داده شده است.

5.4. نتایج نقشه برداری بر روی شبکه های فضایی

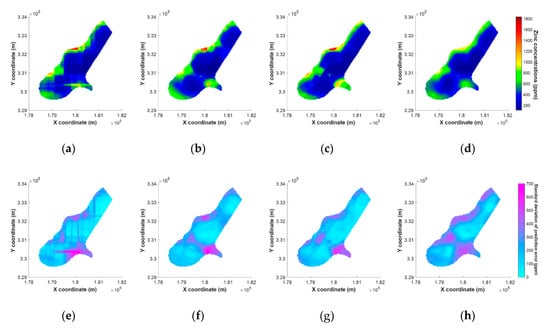
برای مقایسه عملکرد تخمین برای عدم قطعیت فضایی، مقادیر مشخصه پیش‌بینی‌شده به شبکه‌ها، با فاصله معین، برای هر دو مجموعه داده نگاشت شدند. پیش‌بینی فضایی روی 3103 شبکه با فاصله 40 متر برای مجموعه داده Meuse و روی 58074 شبکه با فاصله 100 متر برای مجموعه داده سئول انجام شد. شکل 9 و شکل 10 به ترتیب نتایج پیش بینی فضایی و انحراف استاندارد خطاهای پیش بینی را برای مجموعه داده های Meuse و Seoul نشان می دهد. به طور کلی، همبستگی بین نقشه‌های با استفاده از روش‌های IK و RF بالا بود (هر ضریب همبستگی بالاتر از 0.9 بود).
مقادیر مشخصه روش‌های RF در نزدیکی نقاط پرت محلی بالا پیش‌بینی شد و انحراف استاندارد خطای پیش‌بینی برای هر دو مجموعه داده بسیار بالا بود، همانطور که در شکل 9 و شکل 10 نشان داده شده است.. تأثیر نقاط پرت محلی تا حد زیادی در پیش‌بینی فضایی روش‌های RF منعکس شد. با این حال، در میان روش‌های RF، سخت است که بگوییم RF-Coord یک تکنیک تخمین فضایی مناسب است زیرا نه تنها عملکرد پیش‌بینی نسبتاً پایینی در اعتبارسنجی داشت، بلکه دارای مصنوعات بلوکی نیز بود. در مقابل، RF-Dist الگوهای فضایی را به آرامی، شبیه به IK تخمین زد. این را می توان از نتایج کیسه بندی استنباط کرد، که میانگین نتایج پیش بینی شده درختان منفرد را در نظر می گیرد در حالی که تمام فواصل هر نقطه مشاهده را به عنوان متغیرهای پیش بینی در نظر می گیرد [ 12 ]. RF-PCA در الگوی فضایی اثر هموارسازی ضعیف تری نسبت به RF-Dist دارد، اما روندی جدا از هم محلی است. همانطور که در شکل 9 نشان داده شده استe، روند محلی که در نتیجه RF-PCA ظاهر می‌شود با عبور آرتیفکت مورب از کل نقشه برای مجموعه داده Meuse تأیید می‌شود.

5.5. جلوه ها با استفاده از رایانه های شخصی استخراج شده برای پیش بینی فضایی

RF-PCA عملکرد پیش‌بینی بالاتری را در اعتبارسنجی در مقایسه با روش‌های دیگر نشان داد. با این حال، مشخص شد که مصنوعات ممکن است بسته به روند توزیع مقادیر مشخصه هدف رخ دهند، همانطور که در مجموعه داده Meuse نشان داده شده است ( شکل 9 e). دلیل این مصنوعات این است که هر رایانه شخصی استخراج شده با استفاده از PCA به داده های مکانی دارای یک ویژگی طبقه بندی مکانی صلب است. برای حمایت از این موضوع، تأیید شد که مصنوع جهت مورب زمانی که مقادیر ویژگی فضایی تخمین زده شد، ناپدید شد، به استثنای PC سوم در مجموعه داده Meuse، همانطور که در شکل 11 نشان داده شده است.
شکل 11 a نتیجه RF تنظیم پانزده رایانه شخصی، از جمله رایانه شخصی سوم به عنوان ورودی، و شکل 11 است.b نتیجه RF تنظیم ورودی پس از حذف رایانه سوم در پانزده رایانه است. با نتایج نگاشت، R-squared زمانی که PC سوم گنجانده شد 0.61 بود، اما اگر حذف می شد، عملکرد به 0.54 کاهش می یابد. در نتیجه، PC سوم دارای یک ویژگی طبقه بندی در مورد توزیع غلظت روی است که عملکرد پیش بینی RF را بهبود می بخشد. با این حال، ویژگی طبقه بندی دقیق آن، مصنوعاتی را در نقشه برداری فضایی ایجاد می کند. این همچنین می تواند به عنوان مشکلی دیده شود که می تواند زمانی رخ دهد که متغیرهای یادگیری با تبعیض قوی برای پیش بینی مقادیر در یک رویکرد درختی هستند. بنابراین، لازم است بفهمیم که آیا مصنوعات قابل مشاهده زمانی که یک MLA که مبتنی بر درخت نیست در کارهای آینده اعمال می شود، ایجاد می شود یا خیر.
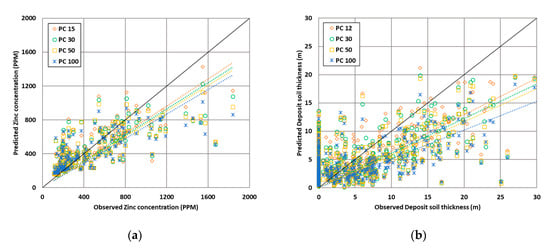
در مقابل، با افزایش بیش از حد تعداد رایانه های شخصی مورد استفاده در RF، دقت پیش بینی فضایی کاهش می یابد و بنابراین مقادیر هدف دست کم گرفته می شوند. شکل 12 نتایج پیش‌بینی را در نمودار پراکندگی پس از اعتبارسنجی متقابل پنج برابری برای هر دو مجموعه داده با توجه به تعداد رایانه‌های شخصی نشان می‌دهد. با افزایش تعداد رایانه های شخصی، شیب خط روند با رهگیری صفر کاهش یافت. از این طریق، فرض بر این بود که RF دست کم گرفته شده است. علاوه بر این، روند پیش‌بینی کمتر برآورد شده با کاهش تدریجی مقادیر میانگین و حداکثر نتایج پیش‌بینی‌شده، همانطور که در جدول 4 توضیح داده شده است، تأیید شد .
فرض بر این است که این اثر به این دلیل اتفاق می‌افتد که رایانه‌های شخصی استخراج‌شده به ترتیب دیرهنگام توانایی توضیح پایینی برای داده‌های اصلی دارند. رایانه‌های شخصی دارای ویژگی‌هایی فقط برای مناطق با مقادیر مشخصه پایین هستند که اکثر داده‌ها را در هر دو مجموعه داده تشکیل می‌دهند. افزودن دقیق مؤلفه‌ها برای تخمین فضایی می‌تواند عملکرد را برای طبقه‌بندی و پیش‌بینی مقادیر هدف مجموعه داده‌ها، مانند جلوه‌های تنظیم دقیق، افزایش دهد. با این حال، اگر رایانه های شخصی بیش از حد اضافه شوند، متغیری که می تواند مقادیر کم ویژگی را در الگوریتم توضیح دهد غالب می شود. این توانایی قابل توضیح را برای نقاط پرت محلی با مقادیر مشخصه بالا در الگوریتم کاهش می دهد و باعث می شود مدل آموزش دیده دست کم گرفته شود.

6. نتیجه گیری

اخیراً موارد تحقیقاتی برای تخمین فضایی از طریق استفاده از MLA علاوه بر تکنیک های زمین آماری سنتی در حال افزایش است. به منظور بهبود عملکرد تخمین فضایی MLA، این مطالعه بر مقایسه تفاوت عملکرد با توجه به نوع تبدیل مختصات متمرکز شده است که می‌تواند به عنوان ورودی‌های اساسی در تخمین فضایی در نظر گرفته شود. ما روشی را پیشنهاد کردیم که از ویژگی های فضایی استخراج شده از بردار فاصله استفاده می کند. در نتیجه، MLA عملکردهای پیش‌بینی و نتایج نقشه‌برداری فضایی شبیه به کریجینگ را نشان داد. شایان ذکر است که عملکرد تخمین مکانی را می توان با حل مشکل افزایش پیچیدگی برای تخمین فضایی MLA به دلیل استفاده از بردار فاصله پیشنهادی در مطالعه قبلی بهبود بخشید.
  • تخمین فضایی از طریق MLA نیازی به فرضیات در مورد ثابت بودن و مدل‌سازی واریوگرام ندارد. علاوه بر این، تبدیل اضافی و تبدیل برگشتی برای متغیرهای هدف مورد نیاز نیست.
  • همبستگی فضایی داده ها را می توان با استفاده از بردار فاصله به عنوان ورودی در MLA در نظر گرفت. با اعمال PCA در بردار فاصله، می توان پیچیدگی متغیر ورودی را کاهش داد. با توجه به این، هزینه محاسباتی MLA کاهش می یابد و عملکرد تخمین مکانی می تواند افزایش یابد.
  • این نتایج تنها با استفاده از مختصات برای تخمین فضایی، بدون افزودن سایر متغیرهای کمکی به دست آمد. بنابراین، روش پیشنهادی می تواند به عنوان روشی برای بهبود عملکرد تخمین در مسائلی که هیچ اطلاعاتی به جز اطلاعات مکان داده های نمونه در هنگام استفاده از MLA وجود ندارد، استفاده شود.
روش پیشنهادی دارای مزایای ذکر شده در بالا است، اما از مسائل مربوط به نقشه برداری فضایی رنج می برد، که باید از طریق تحقیقات اضافی مورد توجه قرار گیرد تا روش را به روشی قوی تر بهبود بخشد. مسائل به شرح زیر است:
  • در نتیجه استفاده از روش پیشنهادی، عملکرد تخمین مکانی بهبود یافته است، اما مصنوعات با توجه به ویژگی‌های الگوریتم مبتنی بر درخت در طول فرآیند نقشه‌برداری رخ داده‌اند که ممکن است بسته به توزیع فضایی داده‌های هدف متفاوت باشد. در کارهای آینده، ما باید نتایج به کارگیری روش پیشنهادی را با تکنیک‌های MLA به غیر از RF مقایسه کنیم یا چگونگی کاهش این اثرات را به روش‌های دیگر مطالعه کنیم.
  • هزینه محاسباتی RF با استفاده از PCA کاهش یافت، اما مقایسه مستقیم هزینه محاسباتی انجام نشد زیرا یک مجموعه داده بزرگ استفاده نشد. در مطالعات آینده، روش پیشنهادی را برای مجموعه داده‌های نقطه‌ای بزرگ اعمال خواهیم کرد و مقرون به صرفه بودن آن را مطالعه خواهیم کرد.
  • مطالعات آینده می تواند شامل کاوش در کاربرد و اثرات تکنیک های مختلف باشد که می تواند به عنوان ابزاری برای استخراج ویژگی های فضایی غیر از PCA مورد استفاده قرار گیرد.

منابع

  1. Krige, DG یک ​​رویکرد آماری به برخی از مشکلات اساسی ارزیابی معدن در Witwatersrand. JS Afr. من هستم. فلز. 1951 ، 52 ، 119-139. [ Google Scholar ] [ CrossRef ]
  2. کرسی، ن. ریشه های کریجینگ. ریاضی. Geosci. 1990 ، 22 ، 239-252. [ Google Scholar ] [ CrossRef ]
  3. ایزاکس، EH; Srivastava, RM مقدمه ای بر زمین آمار کاربردی ; انتشارات دانشگاه آکسفورد: نیویورک، نیویورک، ایالات متحده آمریکا، 1989; شابک 978-0-1950-5013-4. [ Google Scholar ]
  4. Goovaerts, P. Geostatistics for Natural Resources Evaluation ; انتشارات دانشگاه آکسفورد: نیویورک، نیویورک، ایالات متحده آمریکا، 1997; شابک 978-0-1951-1538-3. [ Google Scholar ]
  5. Deutsch، CV; Journel , AG GSLIB: Geostatistical Software Library and User’s Guide , 2nd ed.; انتشارات دانشگاه آکسفورد: نیویورک، نیویورک، ایالات متحده آمریکا، 1998; ISBN 978-0-1951-0015-0. [ Google Scholar ]
  6. بریمن، L. جنگل های تصادفی. ماخ فرا گرفتن. 2001 ، 45 ، 5-32. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  7. لیاو، ا. وینر، ام. طبقه بندی و رگرسیون توسط جنگل تصادفی. R News 2002 , 2 , 18-22. [ Google Scholar ]
  8. رایت، MN; Ziegler, A. Ranger: پیاده‌سازی سریع جنگل‌های تصادفی برای داده‌های با ابعاد بالا در C++ و R. J. Stat. نرم افزار 2017 ، 77. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  9. هنگل، تی. Heuvelink، GBM؛ کمپن، بی. Leenaars، JGB; والش، ام جی؛ شپرد، KD; سیلا، ا. مک میلان، RA; de Jesus, JM; تمنه، ال. و همکاران نقشه برداری از ویژگی های خاک آفریقا با وضوح 250 متر: جنگل های تصادفی به طور قابل توجهی پیش بینی های فعلی را بهبود می بخشد. PLoS ONE 2015 ، 10 ، e0125814. [ Google Scholar ] [ CrossRef ]
  10. نوسبام، م. اسپیس، ک. بالتنسوایلر، ا. گراب، یو. کلر، ا. گرینر، ال. Schaepman، ME; پاپریتز، الف. ارزیابی رویکردهای نقشه برداری دیجیتالی خاک با مجموعه بزرگی از متغیرهای کمکی محیطی. خاک 2018 ، 4 ، 1-22. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  11. جورجانوس، اس. گریپا، تی. Gadiaga، AN; لینارد، سی. لنرت، ام. ونهویسه، اس. امبوگا، ن. ولف، ای. Kalogirou، S. جنگل‌های تصادفی جغرافیایی: گسترش فضایی الگوریتم جنگل تصادفی برای پرداختن به ناهمگونی فضایی در سنجش از دور و مدل‌سازی جمعیت. Geocarto Int. 2019 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  12. هنگل، تی. نوسبام، م. رایت، MN; Heuvelink، GBM؛ Graler, B. جنگل تصادفی به عنوان یک چارچوب عمومی برای مدل سازی پیش بینی متغیرهای مکانی و مکانی- زمانی. PeerJ 2018 , 6 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  13. جوئل، آ. داماد، گیگابایت؛ Svenning، JC; Ejrnaes, R. کاربرد فضایی مدل‌های جنگلی تصادفی برای طبقه‌بندی پوشش گیاهی ساحلی در مقیاس ریز با استفاده از تجزیه و تحلیل شی مبتنی بر عکس‌های هوایی و داده‌های DEM. بین المللی J. Appl. زمین Obs. 2015 ، 42 ، 106-114. [ Google Scholar ] [ CrossRef ]
  14. مایر، اچ. رودنباخ، سی. هنگل، تی. کاتورجی، م. Nauss, T. بهبود عملکرد مدل‌های یادگیری ماشین مکانی-زمانی با استفاده از انتخاب ویژگی رو به جلو و اعتبارسنجی هدف‌گرا. محیط زیست مدل. نرم افزار 2018 ، 101 ، 1-9. [ Google Scholar ] [ CrossRef ]
  15. مایر، اچ. رودنباخ، سی. ولاور، اس. Nauss, T. اهمیت انتخاب متغیر پیش‌بینی‌کننده فضایی در برنامه‌های یادگیری ماشین – حرکت از بازتولید داده به پیش‌بینی فضایی. Ecol. مدل. 2019 ، 411. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  16. والوی، ر. الیت، جی. لاهوز-مونفورت، جی جی. Guillera-Arroita، G. BlockCV: یک بسته r برای ایجاد چین‌های جداشده از نظر فضایی یا محیطی برای اعتبارسنجی متقاطع k-fold مدل‌های توزیع گونه‌ها. روش ها Ecol. تکامل. 2019 ، 10 ، 225-232. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  17. بهرنز، تی. اشمیت، ک. راسل، راو؛ گریس، پی. شولتن، تی. مک میلان، RA مدلسازی فضایی با میدان های فاصله اقلیدسی و یادگیری ماشین. یورو J. Soil Sci. 2018 ، 69 ، 757-770. [ Google Scholar ] [ CrossRef ]
  18. Journel, AG تخمین ناپارامتری توزیع های فضایی. ریاضی. Geosci. 1983 ، 15 ، 445-468. [ Google Scholar ] [ CrossRef ]
  19. Goovaerts، P. AUTO-IK: یک برنامه کریجینگ نشانگر دوبعدی برای مدل‌سازی غیر پارامتری خودکار عدم قطعیت محلی در علوم زمین. محاسبه کنید. Geosci. 2009 ، 35 ، 1255-1270. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  20. رمی، ن. بوچر، ا. Wu, J. زمین آمار کاربردی با SGeMS: راهنمای کاربر . انتشارات دانشگاه کمبریج: نیویورک، نیویورک، ایالات متحده آمریکا، 2009; شابک 978-1-1074-0324-6. [ Google Scholar ]
  21. Ho, TK روش تصادفی زیرفضای برای ساختن جنگل های تصمیم. IEEE TPAMI 1998 ، 20 ، 832-844. [ Google Scholar ]
  22. هستی، تی. طبشیرانی، ر. Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction , 2nd ed.; Springer: نیویورک، نیویورک، ایالات متحده آمریکا، 2013; شابک 978-1-4614-6848-6. [ Google Scholar ]
  23. پیرسون، K. LIII. در خطوط و سطوحی که نزدیکترین تناسب را با سیستم نقاط در فضا دارند. لندن، ادینبورگ دوبلین فیلوس. Mag. J. Sci. 1901 ، 2 ، 559-572. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  24. هتلینگ، H. تجزیه و تحلیل مجموعه ای از متغیرهای آماری به اجزای اصلی. جی. آموزش. روانی 1933 ، 24 ، 417. [ Google Scholar ] [ CrossRef ]
  25. Jolliffe, IT Principal Component Analysis , 2nd ed.; Springer: New York, NY, USA, 2002; شابک 978-0-387-95442-4. [ Google Scholar ]
  26. Wuttichaikitcharoen، P. بابل، M. تجزیه و تحلیل مولفه اصلی و رگرسیون چندگانه برای تخمین بازده رسوب معلق در حوضه های اندازه گیری نشده شمال تایلند. آب 2014 ، 6 ، 2412-2435. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  27. ایواموری، اچ. یوشیدا، ک. ناکامورا، اچ. کواتانی، ت. هامادا، م. هاراگوچی، اس. Ueki، K. طبقه‌بندی داده‌های ژئوشیمیایی بر اساس تجزیه و تحلیل‌های آماری چند متغیره: نقش‌های مکمل تحلیل‌های خوشه‌ای، مؤلفه اصلی و مؤلفه‌های مستقل. ژئوشیمی. ژئوفیز. 2017 ، 18 ، 994-1012. [ Google Scholar ] [ CrossRef ]
  28. کانگ، بی. یونگ، اچ. جونگ، اچ. Choe, J. خصوصیات مخازن کانال سه بعدی با استفاده از فیلتر کالمن مجموعه به کمک تجزیه و تحلیل مؤلفه اصلی. حیوان خانگی علمی 2019 ، 17 ، 182-195. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  29. بیلی، اس. تجزیه و تحلیل مؤلفه اصلی با داده های پر سر و صدا و/یا گمشده. انتشار اختر. Soc. Pac. 2012 ، 124 ، 1015. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  30. مارینوف، تلویزیون؛ میانجی، پ. Arora، R. جریان تجزیه و تحلیل مؤلفه اصلی در محیط پر سر و صدا. در مجموعه مقالات سی و پنجمین کنفرانس بین المللی یادگیری ماشین، PMLR 2018، استکهلم، سوئد، 10 تا 15 ژوئیه 2018؛ جلد 80، ص 3413–3422. [ Google Scholar ]
  31. جنگل‌های رگرسیون چندکی ماین‌هاوزن، N. جی. ماخ. فرا گرفتن. Res. 2006 ، 7 ، 983-999. [ Google Scholar ]
  32. پروبست، پ. Boulesteix، A.-L. تنظیم یا عدم تنظیم تعداد درختان در جنگل تصادفی. جی. ماخ. فرا گرفتن. Res. 2018 ، 18 ، 1-18. [ Google Scholar ]
  33. Rikken، MGJ آلودگی خاک با فلزات سنگین: در تحقیق در مورد تغییرات فضایی، هزینه نقشه برداری و ارزیابی ریسک مس، کادمیوم، سرب و روی در دشت های سیلابی میوس غرب استاین . هلند: گزارش مطالعه میدانی. دانشگاه اوترخت: اوترخت، هلند، 1993. [ Google Scholar ]
  34. کوهن، م. Johnson, K. Applied Predictive Modeling , 1st ed.; Springer: نیویورک، نیویورک، ایالات متحده آمریکا، 2013; شابک 978-1-4614-6848-6. [ Google Scholar ]
Ijgi 09 00587 g001 550
شکل 1. مقایسه رویکردهای برآورد فضایی. تفاوت شماتیک بین ( الف ) کریجینگ و ( ب ) رویکرد یادگیری ماشینی (MLA) برای تخمین فضایی.
Ijgi 09 00587 g002 550
شکل 2. اطلاعات مربوط به مجموعه داده Meuse: ( الف ) توزیع فضایی غلظت روی و ( ب ) یک هیستوگرام با آمار پایه.
Ijgi 09 00587 g003 550
شکل 3. اطلاعات مربوط به مجموعه داده گمانه سئول: ( الف ) توزیع فضایی ضخامت خاک رسوب و ( ب ) یک هیستوگرام با آمار اولیه.
Ijgi 09 00587 g004 550
شکل 4. نتایج تقسیم داده های نمونه به پنج برابر با در نظر گرفتن توزیع فضایی بی طرفانه برای ( الف ) Meuse و ( ب ) مجموعه داده های گمانه سئول.
Ijgi 09 00587 g005 550
شکل 5. واریوگرام های تجربی (نقطه) و نظری (خط) محاسبه شده برای آستانه های ( a ) یک تا ( i ) نه مجموعه داده Meuse.
Ijgi 09 00587 g006 550
شکل 6. واریوگرام های تجربی (نقطه) و نظری (خط) محاسبه شده برای آستانه های ( a ) یک تا ( i ) نه مجموعه داده گمانه سئول.
Ijgi 09 00587 g007 550
شکل 7. نتایج عملکرد تخمین فضایی با توجه به تعداد مؤلفه های اصلی (PC): ( الف ) R -squared و ( b ) RMSE برای مجموعه داده Meuse. ( ج ) R -squared و ( d ) RMSE برای مجموعه داده سئول.
Ijgi 09 00587 g008 550
شکل 8. نتایج عملکرد پیش بینی: ( الف ) مجموعه داده Meuse و ( ب ) مجموعه داده سئول.
Ijgi 09 00587 g009 550
شکل 9. مقایسه پیش‌بینی‌های مبتنی بر هر روش برای مجموعه داده Meuse: غلظت‌های روی پیش‌بینی‌شده (( الف ) جنگل تصادفی با ورودی مختصات (RF-Coord)؛ ( ب ) RF با ورودی فاصله (RF-Dist)؛ ( c ) RF با تجزیه و تحلیل مؤلفه اصلی (RF-PCA)؛ ( d ) کریجینگ نشانگر (IK)) و انحراف استاندارد خطای پیش‌بینی (( e ) RF-Coord؛ ( f ) RF-Dist؛ ( g ) RF-PCA؛ ( h ) IK).
Ijgi 09 00587 g010 550
شکل 10. مقایسه پیش‌بینی‌ها بر اساس هر روش برای مجموعه داده سئول: ضخامت پیش‌بینی‌شده خاک رسوب (( a ) RF-Coord؛ ( b ) RF-Dist؛ ( c ) RF-PCA؛ ( d ) IK) و انحراف استاندارد پیش‌بینی خطا (( e ) RF-Coord؛ ( f ) RF-Dist؛ ( g ) RF-PCA؛ ( h ) IK).
Ijgi 09 00587 g011 550
شکل 11. پیش بینی فضایی از RF-PCA با استفاده از پانزده رایانه شخصی برای مجموعه داده Meuse: ( الف ) شامل رایانه سوم و ( ب ) بدون احتساب رایانه شخصی سوم.
Ijgi 09 00587 g012 550
شکل 12. نتایج اعتبار سنجی متقاطع پنج برابری RF-PCA با توجه به افزایش تعداد رایانه های شخصی برای ( الف ) مجموعه داده Meuse و ( ب ) مجموعه داده سئول.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید