با توسعه شهرنشینی و گسترش جمعیت های شناور، مسکن اجاره ای به یک انتخاب زندگی رایج برای بسیاری از مردم تبدیل شده است و قیمت اجاره مسکن توجه زیادی را از سوی افراد، شرکت ها و دولت به خود جلب کرده است. قیمت‌های اجاره مسکن اساساً بر اساس متغیرهای ساختاری، مکانی و محله‌ای تخمین زده می‌شوند که در میان آنها روابط پیچیده است و به سختی می‌توان آن را به طور کامل با مدل‌های تک بعدی ساده دریافت کرد. علاوه بر این، تأثیر اشیاء جغرافیایی بر قیمت ممکن است با افزایش مقدار آنها متفاوت باشد. با این حال، مدل‌های قیمت‌گذاری موجود معمولاً آن متغیرهای ساختاری، مکانی و همسایگی را به‌عنوان ورودی‌های یک‌بعدی در شبکه‌های عصبی می‌گیرند و اغلب از اثرات انباشته اشیاء جغرافیایی غفلت می‌کنند. که ممکن است منجر به نوسان برآورد قیمت اجاره شود. بنابراین، این مقاله یک مدل قیمت مسکن اجاره را بر اساس شبکه عصبی کانولوشن (CNN) و چگالی فضایی مصنوعی نقاط مورد علاقه (POIs) پیشنهاد می‌کند. CNN می تواند به طور موثر ویژگی های پیچیده را در بین متغیرهای مربوطه مسکن استخراج کند، و متغیرهای دوبعدی مکان و محله، بر اساس تراکم فضایی مصنوعی، به طور موثر اثرات کل تسهیلات شهری را بر قیمت مسکن اجاره ای منعکس می کند و در نتیجه دقت را بهبود می بخشد. از مدل با در نظر گرفتن ووهان، چین، به عنوان منطقه مورد مطالعه، روش پیشنهادی به برآورد قیمت اجاره رضایت‌بخش و دقیق (ضریب تعیین ( این مقاله یک مدل قیمت مسکن اجاره را بر اساس شبکه عصبی کانولوشن (CNN) و تراکم فضایی مصنوعی نقاط مورد علاقه (POIs) پیشنهاد می‌کند. CNN می تواند به طور موثر ویژگی های پیچیده را در بین متغیرهای مربوطه مسکن استخراج کند، و متغیرهای دوبعدی مکان و محله، بر اساس تراکم فضایی مصنوعی، به طور موثر اثرات کل تسهیلات شهری را بر قیمت مسکن اجاره ای منعکس می کند و در نتیجه دقت را بهبود می بخشد. از مدل با در نظر گرفتن ووهان، چین، به عنوان منطقه مورد مطالعه، روش پیشنهادی به برآورد قیمت اجاره رضایت‌بخش و دقیق (ضریب تعیین ( این مقاله یک مدل قیمت مسکن اجاره را بر اساس شبکه عصبی کانولوشن (CNN) و تراکم فضایی مصنوعی نقاط مورد علاقه (POIs) پیشنهاد می‌کند. CNN می تواند به طور موثر ویژگی های پیچیده را در بین متغیرهای مربوطه مسکن استخراج کند، و متغیرهای دوبعدی مکان و محله، بر اساس تراکم فضایی مصنوعی، به طور موثر اثرات کل تسهیلات شهری را بر قیمت مسکن اجاره ای منعکس می کند و در نتیجه دقت را بهبود می بخشد. از مدل با در نظر گرفتن ووهان، چین، به عنوان منطقه مورد مطالعه، روش پیشنهادی به برآورد قیمت اجاره رضایت‌بخش و دقیق (ضریب تعیین ( و متغیرهای مکانی و همسایگی دوبعدی، بر اساس تراکم فضایی مصنوعی، به طور موثر اثرات تجمیع تسهیلات شهری بر قیمت مسکن اجاره‌ای را منعکس می‌کنند و در نتیجه دقت مدل را بهبود می‌بخشند. با در نظر گرفتن ووهان، چین، به عنوان منطقه مورد مطالعه، روش پیشنهادی به برآورد قیمت اجاره رضایت‌بخش و دقیق (ضریب تعیین ( و متغیرهای مکانی و همسایگی دوبعدی، بر اساس تراکم فضایی مصنوعی، به طور موثر اثرات تجمیع تسهیلات شهری بر قیمت مسکن اجاره‌ای را منعکس می‌کنند و در نتیجه دقت مدل را بهبود می‌بخشند. با در نظر گرفتن ووهان، چین، به عنوان منطقه مورد مطالعه، روش پیشنهادی به برآورد قیمت اجاره رضایت‌بخش و دقیق (ضریب تعیین (R2 ) = 0.9097، ریشه میانگین مربعات خطا (RMSE) = 3.5126) در مقایسه با سایر مدل های قیمت گذاری رایج.

کلید واژه ها:

قیمت اجاره مسکن ; POI ; سیستم های اطلاعات جغرافیایی ; یادگیری عمیق

1. مقدمه

اجاره خانه برای بسیاری از مردم در شهرهای مدرن، به ویژه برای افراد جوان و نسبتا کم درآمد، موضوع قابل توجهی است. به دلیل محدودیت‌های مختلف، افراد زیادی مجبورند قبل از داشتن ملک، اجاره مسکن را به عنوان سبک زندگی خود انتخاب کنند [ 1 ، 2 ، 3 ]. با در نظر گرفتن چین به عنوان مثال، در سال های اخیر، اندازه جمعیت های شناور در شهرها به سرعت گسترش یافته است و اکثر جمعیت های شناور مسکن اجاره ای را برای ترتیبات زندگی خود انتخاب می کنند [ 4 ]. در این شرایط، دولت برای تشویق توسعه بازار مسکن اجاره ای، سیاست اجاره و خرید مسکن را با هم ایجاد کرده است .]. با چنین روندی، اجاره مسکن به بخش مهمی از هزینه های روزانه مردم تبدیل می شود و قیمت مسکن به عامل تعیین کننده تری در سرمایه گذاری در املاک تبدیل می شود. قیمت اجاره نیز از سوی دولت در سیاست‌های املاک، برنامه‌ریزی شهرداری و تامین اجتماعی یک موضوع حیاتی در نظر گرفته می‌شود [ 6 ، 7 ]. با این حال، تحقیق در مورد قیمت اجاره مسکن معمولا مکمل قیمت فروش مسکن در بسیاری از مطالعات است و دقت مدل‌های قیمت اجاره کمتر از مدل‌های قیمت فروش است [ 8 ، 9 ]. تخمین های نوسان ممکن است بر چانه زنی افراد و احساسات مرتبط با مسکن اجاره ای تأثیر بگذارد [ 10 ]]، و ممکن است مقررات و سیاست گذاری دولت را در رابطه با برنامه ریزی و مدیریت مسکن عمومی اشتباه کند [ 11 ]. بنابراین، هم دولت و هم افراد ملزومات لازم برای برآورد دقیق‌تر قیمت مسکن اجاره‌ای را بر اساس مدل قیمت‌گذاری قابل اعتمادتر دارند [ 12 ].
از منظر مدل بنیادی قیمت لذت‌گرا (HPM) قیمت مسکن و اجاره مسکن، عوامل مؤثر بر قیمت مسکن را می‌توان به سه نوع زیر تقسیم کرد: متغیرهای ساختاری، متغیرهای مکانی و متغیرهای محله. در میان آنها، متغیرهای مکانی و متغیرهای محله بر اساس محاسبه روابط بین خانه‌ها و تأسیسات شهری مجاور یا نقاط مورد علاقه (POIs)، مانند مناطق تجاری مرکزی (CBDs)، مدارس، بیمارستان‌ها و پارک‌ها هستند. این ویژگی‌های مکانی و محله‌ای متنوع حاوی روابط بسیار پیچیده‌ای هستند و امکانات شهری مربوط به مسکن حاوی مقدار زیادی از ویژگی‌های تراکم فضایی است. اول، روابط پیچیده ای بین متغیرهای ساختاری، مکانی و همسایگی مسکن وجود دارد.13 ، 14 ]. اگر این متغیرها به عنوان یک بردار تک بعدی برای مدل‌سازی در نظر گرفته شوند، مانند حداقل مربعات معمولی (OLS)، رگرسیون وزن‌دار جغرافیایی (GWR)، یا برخی از مدل‌های یادگیری عمیق یک بعدی [ 15 ، 16 ]، دقت پیش‌بینی قیمت محدود خواهد شد. قابل ذکر است، توانایی مدل های یادگیری تک بعدی برای استخراج روابط پیچیده بین متغیرهای عظیم نسبتا محدود است [ 17 ، 18 ، 19 ]]. در مقایسه با ورودی های خطی مدل های یک بعدی، ورودی های شبکه های عصبی دو بعدی شطرنجی و متراکم تر هستند. بنابراین، معماری و ویژگی‌ها در یک مدل دو بعدی بیشتر متمرکز و متمرکز هستند، و توصیف روابط هم افزایی غیرخطی و پیچیده در بین ورودی‌های چندگانه را آسان‌تر می‌کند [ 18 ، 19 ]. بنابراین، یک مدل یادگیری عمیق با بیش از یک بعد برای تحلیل قیمت مسکن ضروری است. در برخی از مدل‌های قیمت مسکن، شبکه‌های عصبی دوبعدی تنها در بخشی از ویژگی‌های تصویر تکمیلی اعمال می‌شوند، اما برای متغیرهای ساختاری، مکانی و همسایگی استفاده نمی‌شوند [ 12 ، 20 ، 21 ، 22 ، 23 .]. با توجه به این محدودیت، این مدل های “نیمه 1 بعدی و نیمه 2 بعدی” نیز جای پیشرفت دارند. از آنجایی که گنجاندن ویژگی‌های تصویری برای تخمین قیمت مسکن ممکن است عملکرد مدل را کاهش دهد [ 24 ]، و از آنجایی که داده‌های چند منبعی معمولاً ممکن است همه نمونه‌ها را پوشش ندهند، استفاده از داده‌های جغرافیایی غیرتصویری برای ساخت یک مدل دقیق قیمت مسکن ممکن و مناسب است. با استخراج بهتر ویژگی های ساختاری، مکانی و همسایگی واحدهای مسکونی.
ثانیاً، پدیده‌های ظاهری تجمع فضایی در تأسیسات شهری و اشیاء جغرافیایی وجود دارد و تأثیر اشیاء جغرافیایی بر قیمت‌گذاری ممکن است با افزایش مقدار آنها به شکلی پیچیده متفاوت باشد. از یک سو، نفوذ بین اشیاء جغرافیایی و مسکن به تدریج با فاصله آنها کاهش می یابد. از سوی دیگر، تأثیر واقعی یک شیء جغرافیایی واحد ممکن است به تدریج با افزایش تعداد اشیاء از همان نوع کاهش یابد، که برخی از مفاهیم و افکار در جغرافیای اقتصادی بر آن دلالت دارند [ 25 ، 26 ].]. با این حال، این اثرات کاهشی ناشی از تجمیع عناصر جغرافیایی به ندرت به طور کامل در مدل‌های قیمت مسکن/اجاره فعلی منعکس می‌شود. اگر متغیرهای مکان و محله از منظر «نزدیک‌ترین فاصله» بیان شوند، مانند فاصله تا نزدیک‌ترین مدرسه، ایستگاه اتوبوس، یا پارک، مانند برخی از مطالعات [ 27 ، 28 ، 29 ].]، تأثیر سایر اشیاء جغرافیایی خوشه‌ای از همان نوع را نمی‌توان در نظر گرفت. با رشد جمعیت، صنعت، بازرگانی و امکانات شهری، این عاملی است که نمی‌توان آن را نادیده گرفت و از دست دادن اطلاعات ناشی از آن ممکن است منجر به کاهش دقت مدل‌های قیمت مسکن یا قیمت اجاره شود. ممکن است ایجاد متغیرهای مکان و همسایگی بر اساس تعداد انواع مختلف POI در محدوده معینی دقیق تر باشد [ 12 , 20 , 30]. با این حال، در این راه، این واقعیت که تأثیر بین اشیاء جغرافیایی با فاصله آنها کاهش می یابد (یعنی قانون اول جغرافیا) مورد توجه قرار نمی گیرد. مدل میدان جغرافیایی (GFM) همچنین می‌تواند برای تولید ویژگی‌های کمی متغیرهای مکان و محله مسکن مورد استفاده قرار گیرد [ 14 ، 31] که قانون اول جغرافیا را در نظر می گیرد. با این حال، GFM این واقعیت را در نظر نمی گیرد که با افزایش تعداد اشیاء از همان نوع، تأثیر واقعی یک شیء جغرافیایی به تدریج کاهش می یابد. به عنوان مثال، در مورد خانه ای که تنها 1 سوپرمارکت در آن نزدیکی است، این سوپرمارکت تأثیر خاصی بر این خانه دارد. وقتی 50 سوپرمارکت در این نزدیکی وجود دارد، هر سوپرمارکت نیز تا حدی بر خانه تأثیر می گذارد، اما تأثیر هر سوپرمارکت ظاهراً کمتر از حالتی است که فقط یک سوپرمارکت در آن حضور دارد. به طور خلاصه، متغیرهای مکان و محله ایجاد شده توسط این روش‌های فعلی ممکن است نادرست باشند، که در نتیجه ممکن است عملکرد مدل قیمت مسکن را کاهش دهد.
از این رو، این مقاله سعی می‌کند مدل قیمت‌گذاری مسکن اجاره‌ای شهری را بررسی کند، و با در نظر گرفتن ووهان، چین، به عنوان مثال، یک مدل قیمت مسکن اجاره‌ای دوبعدی بر اساس یک شبکه عصبی کانولوشن (CNN) و ویژگی‌های چگالی فضایی پیشنهاد می‌کنیم. POI. از یک طرف، CNN می تواند به طور موثر ویژگی های پیچیده را در بین متغیرهای ساختاری، مکانی و همسایگی مسکن استخراج کند. از سوی دیگر، متغیرهای مکان و همسایگی مبتنی بر تراکم فضایی مورد استفاده در این تحقیق می‌توانند ویژگی‌های تراکم فضایی تأسیسات شهری را بر قیمت مسکن اجاره‌ای، از جمله اثر کاهشی ناشی از تجمیع همان نوع عناصر جغرافیایی، بهتر منعکس کنند. در نتیجه دقت مدل را بهبود می بخشد. مسکن اجاره ای و POI های جمع آوری شده از اینترنت مواد قابل توجهی را برای آموزش این روش فراهم می کند. این تحقیق ممکن است اطلاعات تصمیم گیری مناسبی برای افراد و بنگاه ها برای معاملات آنها در بازار مسکن اجاره ای فراهم کند. همچنین ممکن است برای بخش‌های دولتی مرجع تصمیم‌گیری ارزشمندی برای انتخاب مکان‌ها و قیمت‌های مناسب خانه‌های اجاره‌ای عمومی شهری و برای تصمیم‌گیری در مورد سطوح معقول یارانه مسکن در اختیار بخش‌های دولتی قرار دهد.
بقیه مقاله به شرح زیر سازماندهی شده است: بخش 2 کارهای مربوطه را در مورد مدل‌های قیمت فروش و اجاره مسکن، از جمله متغیرهای مکانی و همسایگی در مدل‌های قیمت، مرور می‌کند. بخش 3 مواد و روش های اتخاذ شده در این تحقیق را معرفی می کند. بخش 4 نتایج روش ها و آزمایش های مختلف را مورد بحث و مقایسه قرار می دهد و مدل پیشنهادی را تحلیل می کند. بخش 5 نتیجه گیری و ایده های کاری آینده را ارائه می کند.

2. بررسی ادبیات

2.1. قیمت مسکن و مدل های قیمت اجاره

روش‌های مدل‌سازی قیمت مسکن شامل HPM [ 32 ]، GWR [ 33 ]، روش‌های یادگیری عمیق و انواع آن‌ها است. HPM یک مدل قیمت گذاری اساسی برای قیمت مسکن است که برای اولین بار در حوزه اقتصاد پیشنهاد شد [ 32 ].]. فرض HPM این است که یک فرد نه تنها برای فضای زندگی، بلکه برای سایر عوامل تأثیرگذار، مانند مزایای موقعیت و محیط محله، هزینه مسکن را نیز پرداخت کند. عوامل موجود در مدل HPM را می‌توان به متغیرهای ساختاری (ویژگی‌های ساختمان)، متغیرهای مکانی (ویژگی موقعیت مکانی خانه در شهر، مانند فاصله تا CBD) و متغیرهای محله (ویژگی‌های مربوط به محله، مانند فاصله تا پارک یا بیمارستان نزدیک). شکل کلی HPM رگرسیون خطی چند متغیره (MLR) یا OLS است. HPM به طور گسترده در مطالعات املاک و مستغلات و اجاره مسکن مورد استفاده قرار گرفته است [ 9 ، 27 ، 34]، به دلیل سادگی و توضیح موثر قیمت مسکن. با این حال، HPM کلی بر این فرض استوار است که الگو با مکان‌ها تغییر نمی‌کند، که تفاوت‌های منطقه‌ای و روابط محلی متغیرها را منعکس نمی‌کند و ممکن است منجر به انحراف در دقت مدل‌سازی شود [ 8 ، 33 ، 35 ]. مدل GWR معرفی شده توسط Fotheringham [ 33 ] بر این نگرانی از ناهمگونی فضایی [ 14 ] تمرکز کرده است. در مقایسه با رگرسیون جهانی HPM، GWR به پارامترها اجازه می‌دهد تا با موقعیت‌ها متفاوت باشند و قدرت توضیحی و دقت مناسبی دارد. از این رو، مورد توجه قابل توجهی قرار گرفته و به طور موثر در حوزه اقتصاد و املاک و مستغلات کاربرد دارد [ 14, 35 , 36 ]. با این حال، GWR همچنین فرض کرد که روابط بین متغیرهای مستقل و توضیحی خطی است، که محدودیت آشکاری در مدل‌سازی قیمت مسکن دارد، زیرا الگوهای موجود در قیمت مسکن و اجاره غیرخطی و پیچیده هستند [ 13 ، 37 ]. مطالعات به روز همچنین به معایب GWR در وظایف پیچیده پیش بینی فضایی اشاره کرد [ 8 ، 38 ] و به دلیل قابلیت اطمینان و محدودیت های آن مورد انتقاد قرار گرفت [ 39 ].
در سال‌های اخیر، یادگیری عمیق به یکی از مفیدترین تکنیک‌ها برای مسائل غیرخطی و پیچیده تبدیل شده است و بسیاری از مطالعات در زمینه پیش‌بینی قیمت مسکن، روش یادگیری عمیق را اتخاذ کرده‌اند. در بسیاری از مطالعات، از جمله یادگیری ماشینی و یادگیری عمیق، متغیرهای ساختاری، مکانی و همسایگی معمولاً به عنوان یک بردار تک بعدی برای ورود به مدل ها در نظر گرفته می شوند [ 15 ، 16 ]. در این روش ها، دقت پیش بینی قیمت ممکن است نسبتاً محدود باشد. همانطور که مشخص است، ظرفیت استخراج برای روابط پیچیده بین متغیرهای عظیم در مدل های یادگیری یک بعدی در مقایسه با سایر شبکه های پیچیده نسبتا محدود است [ 17 ، 18 ، 19 ].]. یک شبکه عصبی دو بعدی می تواند متراکم تر باشد و قدرت استخراج و مشخص کردن روابط تعاملی پیچیده بین مقادیر ورودی چندگانه را دارد [ 18 ، 19 ]. بنابراین، شبکه‌های عصبی دو بعدی، مانند شبکه‌های CNN و LSTM، برای بهبود عملکرد مدل‌سازی قیمت مسکن ارزشمند هستند. اگرچه بنسی [ 20] از CNN به عنوان مکمل هنگام استخراج ویژگی‌های تصاویر سنجش از دور در نزدیکی واحدهای مسکونی استفاده کرد، مدل تک بعدی همچنان برای متغیرهای ساختاری، مکانی و همسایگی مورد استفاده قرار گرفت. با توجه به محدود بودن استخراج برای این متغیرها، دقت این روش جای بهبود دارد. به طور مشابه، متن، تصاویر داخل ساختمان یا تصاویر نمای خیابان توسط برخی مطالعات به عنوان ویژگی های اضافی برای مدل سازی قیمت مسکن مورد استفاده قرار گرفت. ژو [ 40 ] از CNN و LSTM هنگام تجزیه و تحلیل متن توضیحات خانه ها استفاده کرد، ژائو [ 23 ] از CNN هنگام استخراج ویژگی های بصری تصاویر داخلی، Fu [ 21 ] و Bin [ 22 ] استفاده کرد.] از CNN برای استخراج ویژگی های تصاویر نمای خیابان در اطراف خانه ها استفاده کرد. در این مطالعات، اگرچه شبکه‌های دوبعدی برای ویژگی‌های اضافی (متن، تصاویر نمای خیابان و غیره) به کار گرفته شد، اما همچنان برای متغیرهای ساختاری، مکانی و محله‌ای که از عوامل حیاتی قیمت مسکن هستند، استفاده نشد. . از این رو، هنوز در این مدل‌های “نیمه یک بعدی و نیمه دو بعدی” جا برای بهبود وجود دارد. یائو [ 17] به طور مستقیم توزیع فضایی انواع مختلفی از اشیاء جغرافیایی، مانند موسسات تجاری یا امکانات آموزشی را در یک شبکه دو بعدی ترسیم کرد و از آن برای یادگیری عمیق قیمت مسکن در مدل CNN همراه با تصاویر سنجش از دور استفاده کرد. از آنجایی که تصویر سنجش از دور و شبکه‌های توزیع انواع مختلف اجسام جغرافیایی ناهمگن هستند، اگر به‌عنوان کانال‌های موازی در CNN وارد شوند، ممکن است ویژگی‌های آنها به طور موثر استخراج نشود. علاوه بر این، ممکن است مدل‌سازی متغیرهای ساختاری و این ویژگی‌ها نیز چالش برانگیز باشد، و چگالی اطلاعات شبکه توزیع هر نوع شیء جغرافیایی زیاد نیست، که ممکن است برای آموزش مدل مفید نباشد. در نتیجه دقت این مدل خیلی بالا نبود. یو [ 30] متغیرهای مکان و محله را دو بعدی کرد و از CNN و LSTM برای پیش بینی قیمت مسکن استفاده کرد. شبکه های دو بعدی در این روش برای متغیرهای مکانی و همسایگی اعمال شد، اما متأسفانه متغیرهای ساختاری تفصیلی را در نظر نگرفتند. اینکه آیا استفاده از لایه های ادغام در CNN برای مشکل رگرسیون قیمت مسکن ضروری است یا خیر، هنوز باید مورد سوال و بررسی قرار گیرد. علاوه بر این، بین [ 24] نشان می دهد که گنجاندن ویژگی های تصویر برای تخمین قیمت مسکن ممکن است عملکرد را کاهش دهد و معمولا داده های چند منبعی ممکن است همه نمونه ها را پوشش ندهند. بنابراین می‌توان با استخراج بهتر ویژگی‌های ساختاری، مکانی و محله‌ای مسکن، از داده‌های جغرافیایی غیرتصویری برای ساخت مدل دقیق قیمت مسکن استفاده کرد.
در بسیاری از مطالعات، بحث قیمت اجاره مسکن معمولا مکمل قیمت فروش مسکن است و دقت مدل‌های قیمت اجاره کمتر از مدل‌های قیمت فروش است. لیبلت [ 9 ] از HPM برای تجزیه و تحلیل قیمت فروش و اجاره مسکن در لایپزیگ، آلمان، به ویژه از نظر فضای سبز استفاده کرد. در تحقیق Won [ 41 ]، یک مدل تاخیر فضایی و مدل خطای فضایی برای بررسی قیمت اجاره در سئول اتخاذ شد. نتایج به دست آمده از مطالعات فوق چندان دقیق نبود. علاوه بر این، Cajias [ 8] به پیچیدگی قیمت مسکن و تقلید از مدل GWR در پیش بینی قیمت مسکن اجاره ای مجتمع اشاره کرد. دقت پایین تخمین ها ممکن است بر چانه زنی و احساسات افراد مرتبط با مسکن اجاره ای تأثیر بگذارد [ 10 ]، و ممکن است مقررات و سیاست گذاری دولت را با توجه به برنامه ریزی و مدیریت مسکن عمومی گمراه کند [ 11 ].]. بنابراین، در حال حاضر، هم دولت و هم افراد ملزومات لازم برای برآورد دقیق‌تر بر اساس مدل قیمت‌گذاری مسکن قابل اعتمادتر را دارند. بر اساس داده‌های POI غیرتصویری، این مقاله سعی می‌کند یک CNN دوبعدی را پیشنهاد کند و یادگیری عمیق را بر روی ویژگی‌های ساختاری، مکانی و محله‌ای مسکن انجام دهد تا مدل قیمت اجاره مسکن دقیق‌تری ایجاد کند، و سعی می‌کند بررسی کند که آیا استفاده از لایه های ادغام در CNN برای مشکل رگرسیون قیمت مسکن ضروری است.

2.2. متغیرهای مکان و همسایگی خانه ها

متغیرهای مکانی و متغیرهای محله مسکن بر اساس محاسبه روابط بین خانه و امکانات شهری مجاور (یا POI) است. در بسیاری از مطالعات مرتبط، این متغیرها از منظر «نزدیک‌ترین فاصله» تولید می‌شوند، مانند «فاصله تا نزدیک‌ترین ایستگاه اتوبوس»، «فاصله تا CBD» و «فاصله تا نزدیک‌ترین بیمارستان» [ 27 ، 28 ].همانطور که در مقدمه توضیح داده شد، اگر مدل‌های قیمت مسکن یا قیمت اجاره تنها بر اساس «نزدیک‌ترین» فواصل تا تسهیلات باشد، اثرات ناشی از جمع‌آوری سایر اشیاء جغرافیایی در نظر گرفته نمی‌شود، که ممکن است منجر به کاهش دقت مدل علاوه بر این، تأثیر اشیاء جغرافیایی بر قیمت مسکن ممکن است با افزایش مقدار آنها به روشی پیچیده متفاوت باشد. بنابراین، ویژگی های کمی یا چگالی اشیاء جغرافیایی باید در هنگام تولید متغیرهای مکان و همسایگی در نظر گرفته شود.
مدل میدان جغرافیایی (GFM) مدلی است که توسط جغرافیدان هاروی پیشنهاد شده است که مفهوم “میدان” را در فیزیک وام گرفته است [ 31 ]. ایده اصلی این است که همه اشیاء جغرافیایی تحت تأثیر یک “میدان جغرافیایی” هستند. میدان جغرافیایی به طور منظم تغییر می کند، و تأثیرات اشیاء جغرافیایی بر چیزهای دیگر، توابع فروپاشی از مکان اصلی خود هستند. جیائو [ 31 ] و لیانگ [ 14 ] از GFM برای ایجاد متغیرهای محل سکونت و محله استفاده کردند، که می تواند به طور منطقی تری درجات تأثیر بین اشیاء جغرافیایی را ارزیابی کند [ 42 ، 43 ]]. با این حال، در دنیای واقعی، با افزایش تعداد اشیاء جغرافیایی، تأثیر واقعی هر شیء منفرد می تواند به تدریج کاهش یابد. به عنوان مثال، تأثیر هر سوپرمارکت زمانی که تنها یک سوپرمارکت در نزدیکی آن وجود دارد، ظاهراً بزرگتر از حالتی است که 50 سوپرمارکت در آن نزدیکی وجود دارد. GFM اثر کاهشی یک عنصر منفرد ناشی از افزایش عناصر از همان نوع را در نظر نمی گیرد. علاوه بر این، بنسی [ 20 ]، یو [ 30 ] و وانگ [ 12] تعداد POI های مختلف را در فاصله معینی از خانه مورد بررسی شمارش کرد و ممکن است در برخی موارد از این فاصله به عنوان فراپارامتر استفاده کند. روش شمارش تعداد POIها قانون اول جغرافیا را در نظر نمی گیرد که تأثیر بین اشیاء جغرافیایی با فاصله کاهش می یابد، بنابراین نتایج آنها ممکن است دارای انحراف نیز باشد. علاوه بر این، تخمین چگالی هسته (KDE) می تواند به طور مستقیم تابع چگالی احتمال را از یک نمونه مشاهده شده بدون تخمین پارامترهای ناشناخته استنتاج کند. بنابراین، ویژگی‌های آماری خوبی را ارائه می‌کند و تخمین‌های چگالی مجانبی را به‌دست می‌آورد. KDE توسط بسیاری از برنامه ها و مطالعات در GIS پذیرفته شده است [ 44 , 45 , 46]، اما کاهش تدریجی تأثیر یک عنصر واحد با افزایش تعداد اشیاء جغرافیایی، مانند GFM را در نظر نمی گیرد.
به طور خلاصه، برخی از مشکلات در تحقیق در مورد مدل های قیمت مسکن اجاره ای شهری وجود دارد. اولاً، روش‌های موجود برای تولید متغیرهای مکان و همسایگی برای ویژگی‌های چگالی اشیاء جغرافیایی به اندازه کافی جامع نیستند، زیرا آنها یا این قانون را در نظر نمی‌گیرند که تأثیر بین اجسام به تدریج با فاصله آنها کاهش می‌یابد، یا این واقعیت را در نظر نمی‌گیرند که واقعی است. تأثیر یک شی واحد به تدریج با افزایش تعداد اشیاء از همان نوع کاهش می یابد، که در نتیجه ممکن است دقت مدل های قیمت گذاری حاصل را کاهش دهد. دوم، روابط پیچیده و غیرخطی بین متغیرهای ساختاری، مکانی و قیمت مسکن محله وجود دارد. مدل های OLS، GWR و یادگیری عمیق موجود معمولاً متغیرها را به شکل بردارهای یک بعدی ترکیب می کنند. بدون ظرفیت استخراج قابل توجهی برای روابط پیچیده بین متغیرها، که ممکن است منجر به عملکرد مدل سازی نسبتاً ناکافی شود. بنابراین، واضح است که برای بهبود دقت مدل قیمت مسکن اجاره ای، روش پیشنهادی باید به طور موثر روابط پیچیده و تراکم فضایی متغیرهای ساختاری، مکانی و همسایگی را مشخص کند. این هدف اصلی این مطالعه است. متغیرهای مکان و محله این هدف اصلی این مطالعه است. متغیرهای مکان و محله این هدف اصلی این مطالعه است.

3. مواد و روش

3.1. چارچوب کلی

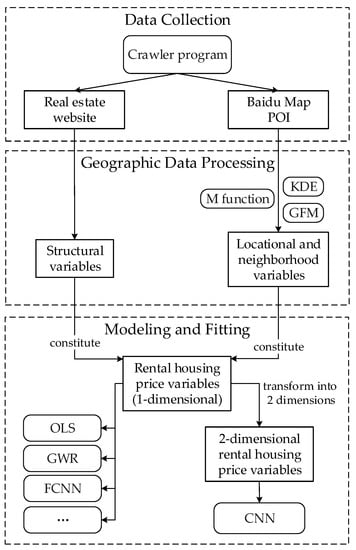
سه مرحله اصلی زیر برای تکمیل کل فرآیند در این مقاله مورد نیاز است ( شکل 1 ): جمع آوری داده ها، پردازش داده های جغرافیایی، و مدل سازی و برازش. ابتدا، ما از یک ابزار خزنده وب برای به دست آوردن داده های مسکن اجاره ای از وب سایت املاک و مستغلات و جمع آوری POI از نقشه بایدو برای منطقه مورد مطالعه (ووهان، چین) استفاده می کنیم. منطقه مورد مطالعه و مواد داده در بخش 3.2 و بخش 3.3 معرفی شده است. دوم، داده‌های به‌دست‌آمده از وب‌سایت املاک معمولاً متغیرهای ساختاری مسکن (شامل در بخش 3.4) را تشکیل می‌دهند.) و POI های Baidu Map نیاز به پردازش داده های جغرافیایی دارند تا به متغیرهای مکانی و همسایگی تبدیل شوند. در این مقاله، ما متغیرهای مکان و همسایگی را بر اساس تراکم فضایی مصنوعی اشیاء جغرافیایی تولید می‌کنیم. برخی از تکنیک‌ها و الگوریتم‌ها، مانند تابع M، KDE، GFM، و دیگران، برای پردازش چگالی فضایی داده‌های POI استفاده می‌شوند که در بخش 3.5 نشان داده شده است . سوم، قیمت‌های اجاره مسکن را می‌توان بر اساس متغیرهای ساختاری، مکانی و محله‌ای به شرح زیر مدل‌سازی کرد: از یک سو، متغیرها را می‌توان به‌عنوان خطوط پایه در مدل‌های قیمت پایه مسکن مانند HPM و GWR (معرفی شده در بخش 3.4) مدل‌سازی کرد.) از سوی دیگر، متغیرهای قیمت مسکن را می توان به دو بعد تبدیل کرد و با مدل پیشنهادی CNN مدلسازی کرد و این رویکرد به تفصیل در بخش 3.6 ارائه و مورد بحث قرار گرفته است .

3.2. منطقه مطالعه

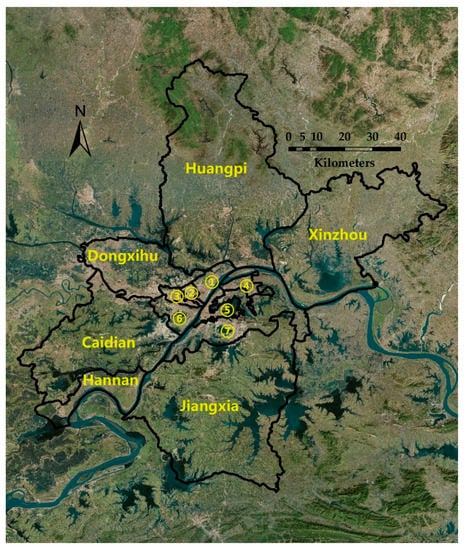
منطقه مورد مطالعه ووهان (29°58′–31°22′ شمالی، 113°41′-115°05′ شرقی)، چین است که مرکز استان هوبی و بزرگترین شهر در مرکز چین است. ووهان مهمترین پایگاه صنعتی و همچنین مرکز علمی و آموزشی در مرکز چین است. همچنین یک مرکز حمل و نقل سراسری در چین است. این شهر دارای 13 ناحیه و مساحت کل 8569.15 کیلومتر مربع است ( شکل 2 ). جمعیت ووهان 12.45 میلیون نفر و تولید ناخالص داخلی 1562 میلیارد یوان در سال 2020 بود [ 47 ]. در میان شهرهای بزرگ چین، ووهان در سال‌های اخیر دارای نسبت بالایی از جمعیت شناور بوده است [ 4 ]]. از آنجایی که اجاره راه اصلی زندگی جمعیت های شناور است، مسکن اجاره ای بازار بسیار بزرگ و فعالی در ووهان دارد.

3.3. جمع آوری داده ها

3.3.1. POI

در مقایسه با داده‌های جغرافیایی سنتی، POI می‌تواند ویژگی‌های مکانی و فعالیت‌های انسانی را با چشم‌اندازی دقیق‌تر و با جزئیات بسیار دقیق‌تر منعکس کند [ 48 ]. در این تحقیق، داده‌های POI جمع‌آوری‌شده از نقشه بایدو برای ایجاد متغیرهای مکانی و همسایگی مسکن اجاره‌ای استفاده شده است. Baidu Map یکی از بزرگترین ارائه دهندگان نقشه الکترونیکی و LBS در چین است. فهرستی از POI ها را می توان در وب سایت Baidu Map با تماس با API های باز یا خدمات اینترنتی آن به دست آورد. ما یک برنامه خزنده ایجاد کردیم و بیش از 550000 نقطه داده POI ووهان را در فوریه 2020 جمع آوری کردیم. POIهای به دست آمده متعلق به 134 نوع ثانویه از 17 نوع اولیه هستند که در جدول 1 فهرست شده است.. تنها POI با نظرات کاربر به عنوان داده های موثر در این تحقیق به کار گرفته شد.
3.3.2. مسکن اجاره ای
داده های مسکن اجاره ای در این مطالعه از Lianjia [ 49 ] که یک وب سایت محبوب برای املاک و مستغلات و مسکن اجاره ای در چین است، گرفته شده است. داده‌های معاملاتی فراوانی از خانه‌های اجاره‌ای در سمت مشتری آن وجود دارد، و داده‌های این وب‌سایت برای تحلیل قیمت مسکن در مطالعات اخیر ثابت شده است [ 50 ، 51 ]]. همه نمونه‌های مسکن اجاره‌ای از برنامه Lianjia به دست آمده و تجزیه می‌شوند. نمونه ها بین مارس و ژوئیه 2020 معامله می شوند و تأثیر زمان را می توان نادیده گرفت (ضریب همبستگی با قیمت اجاره <0.01 است). متغیرهای ساختاری مسکن اجاره ای را می توان به راحتی از این وب سایت دریافت کرد. در میان آنها، کل مسکن اجاره‌ای متعلق به انواع دکوراسیون مدنی و زیبا (که 69 درصد از کل موارد جمع‌آوری شده را تشکیل می‌دهد) را بررسی کردیم و ارزش‌های شدید را حذف کردیم. در نهایت، در مجموع 91906 نمونه اجاره به دست آمد.

3.4. HPM و GWR

HPM یک مدل قیمت اساسی است و برای اولین بار در زمینه اقتصاد پیشنهاد شد [ 32 ]. ماهیت HPM این است که مشتری برای مسکن (یا مسکن اجاره ای) نه تنها برای ساختار یا فضای زندگی، بلکه برای سایر عوامل مرتبط مانند مزایای موقعیت، امکانات شهری و محیط محله نیز هزینه می کند. از منظر اقتصادی، HPM می‌تواند قیمت‌های ضمنی حاشیه‌ای عوامل (متغیرهای) یک خانه را آشکار کند و به طور کلی با استفاده از تحلیل MLR تفسیر می‌شود، که عبارت است از:

که در آن β j نشان دهنده تغییر در قیمت y زمانی است که متغیر j x j تغییر می کند (یعنی قیمت نهایی)، و m تعداد متغیرها است. متغیرهای ساختاری مسکن در جدول 2 نشان داده شده است . متغیرهای مکانی و متغیرهای همسایگی در بخش بعدی مورد بحث قرار می گیرند. HPM یک پایه و چارچوب اساسی برای سایر مدل های قیمت مسکن است. HPM مبتنی بر MLR معمولاً با OLS پیاده سازی می شود و در این مقاله به عنوان مدل “OLS” برچسب گذاری شده است.

مدل کلی OLS همان الگو را در کل منطقه حفظ می‌کند، که ممکن است منجر به انحراف در نتایج زمانی شود که روابط بین متغیرها با مکان‌ها تغییر کند. مدل GWR معرفی شده توسط Fotheringham [ 33 ] بر این نگرانی تمرکز دارد و در واقع یک گسترش جغرافیایی OLS جهانی است. ضرایب ویژگی را می توان به عنوان تغییرات در متغیر وابسته (قیمت) ناشی از متغیرهای مستقل به عنوان توابع نیمه لگاریتمی [ 35 ] تفسیر کرد. GWR یک تکنیک رگرسیون فضایی است که ناهمگونی فضایی را در نظر می گیرد و اجازه می دهد تا پارامترهای محلی با تغییر مختصات تخمین زده شوند. مدل به صورت زیر بیان می شود:

که در آن (u i ، v i ) مختصات مکانی نمونه (مسکن) i ، β k (u i ، v i ) نشان دهنده ضریب رگرسیون k امین متغیر تأثیرگذار نمونه i ، β 0 (u i ، v i ) نشان‌دهنده وقفه فضایی و عبارت خطا را نشان می دهد. β k (u i , v i ) با مختصات (u i , v i ) تغییر می کند و می توان آن را به صورت زیر تخمین زد:

که در آن ماتریس وزن W یک ماتریس n × n است که عناصر خارج از مورب آن همه صفر هستند. برای نمونه i ، عنصر قطری j ام W ij وزن جغرافیایی نمونه i و نمونه j است که نشان دهنده تأثیر جغرافیایی نمونه j بر نمونه i است. متداول ترین تابع برای محاسبه W ij تابع گاوسی است: ، که در آن d ij نشان دهنده فاصله بین نمونه های i و j است، و b نشان دهنده پهنای باند (غیر منفی) است که نشان دهنده درجه اثر فروپاشی مربوط به فاصله است. انتخاب پهنای باند مناسب ( b ) یک کار ضروری برای GWR است و معمولاً بر اساس حداقل معیار اطلاعات Akaike (AICc) است [ 52 ]. در این مطالعه، ما از AICc و تابع گاوسی برای تعیین پهنای باند و وزن های جغرافیایی مدل GWR استفاده می کنیم. از آنجایی که عامل ناهمگونی فضایی در نظر گرفته می‌شود، دقت مدل‌سازی GWR معمولاً بسیار بهتر از OLS جهانی است، زمانی که الگوها و روابط داده‌ها با مکان‌های جغرافیایی متفاوت است.

مدل OLS و GWR مدل های اساسی قیمت مسکن هستند. در این تحقیق از این دو روش به عنوان مبنا برای مقایسه استفاده شده است.

3.5. تراکم فضایی و متغیرهای مکان و همسایگی

3.5.1. مدل سازی چگالی فضایی اجرام جغرافیایی

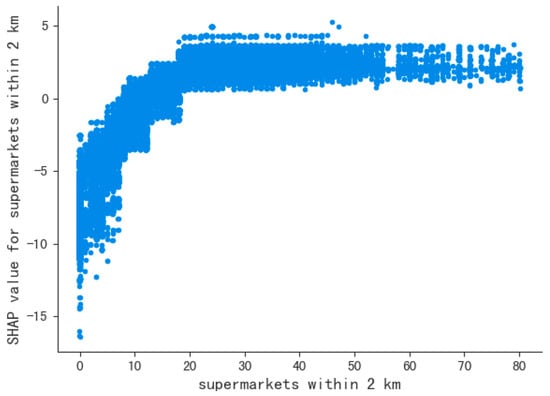
همانطور که در مقدمه ذکر شد، اگر مدل‌های قیمت مسکن یا قیمت اجاره تنها بر اساس «نزدیک‌ترین» فواصل تسهیلات باشد، تأثیرات ناشی از جمع‌آوری سایر عناصر جغرافیایی در نظر گرفته نمی‌شود که ممکن است منجر به کاهش دقت مدل شود. . بنابراین، ویژگی های کمی عناصر جغرافیایی باید در نظر گرفته شود. KDE و GFM معمولاً برای محاسبه اثرات کمی در علم اطلاعات جغرافیایی استفاده می‌شوند و می‌توانند تأثیرات بین عناصر جغرافیایی را به طور منطقی‌تری ارزیابی کنند. با این حال، در دنیای واقعی، با افزایش تعداد اشیاء جغرافیایی، تأثیر واقعی هر شیء منفرد می تواند به تدریج کاهش یابد. مثلا، زمانی که فقط یک سوپرمارکت در آن منطقه قرار دارد، یک سوپرمارکت تنها برای یک فرد مهم تر از زمانی است که پنجاه سوپرمارکت در نزدیکی آن وجود دارد. اثر کاهشی یک شی منفرد با افزایش اشیاء از همان نوع را می توان با تجزیه و تحلیل ارزش Shapley تشخیص داد.53 ]، که یک رویکرد تفسیری برای توضیح مشارکت های محلی متغیرهای مستقل با محاسبه مشارکت های حاشیه ای آنها در تمام ترکیبات متغیر-مقدار ممکن است [ 54 ]. برای متغیر «تعداد سوپرمارکت‌ها در فاصله ۲ کیلومتری واحد مسکونی» (که از این پس «متغیر سوپرمارکت» نامیده می‌شود)، اگر یک توضیح‌دهنده افزودنی Shapley [ 55 ] بر اساس یک رگرسیون XGBoost [ 56 ] برای اجاره مسکن بسازیم. قیمت و متغیر سوپرمارکت را می یابیم (در شکل 3) که با افزایش تعداد سوپرمارکت ها از 0 به تقریبا 20، تأثیر متغیر سوپرمارکت بر قیمت اجاره با تعداد سوپرمارکت ها افزایش می یابد. با این حال، زمانی که تعداد سوپرمارکت‌ها از 20 بیشتر شود، تأثیر متغیر سوپرمارکت‌ها دیگر افزایش نمی‌یابد، و نشان می‌دهد که سهم هر سوپرمارکت در قیمت اجاره مسکن زمانی که تعداد آنها بیشتر از 20 باشد کاهش می‌یابد. KDE و GFM به تدریج آن را در نظر نمی‌گیرند. کاهش تأثیر هر شیء جغرافیایی منفرد با افزایش تعداد اشیاء از نوع مشابه، به این معنی که مدل‌های مکان مبتنی بر این تکنیک‌ها ممکن است کمبودهای خاصی داشته باشند.

تابع M [ 26 ] یک روش اندازه گیری برای تراکم در زمینه های جغرافیای اقتصادی و اقتصاد فضایی است که درجه چگالی را در محدوده شعاع r محاسبه می کند.. تابع M برای اندازه گیری درجه تجمیع یک صنعت خاص نسبت به همه صنایع در یک محدوده معین در نظر گرفته شده است. از طریق تابع M، از آنجایی که فرآیند شامل محاسبه درجه چگالی نسبی یک دسته در مقایسه با همه دسته‌ها، و درجه چگالی نسبی یک منطقه در مقایسه با کل منطقه است، اثر کاهشی یک عنصر واحد با افزایش تعداد اشیاء از همان نوع در واقع صاف می شود. بنابراین، تأثیر چگالی فضایی اشیاء جغرافیایی ممکن است بهتر ارزیابی و کاوش شود. روش‌های مرتبط مبتنی بر تابع M در بسیاری از مطالعات مورد استفاده قرار گرفته‌اند و به نتایج مؤثری دست یافته‌اند [ 57 ، 58 ]. شکل تابع M را می توان به صورت زیر فرموله کرد:

که در آن e iSr نشان دهنده ارزش تولید صنعت S در منطقه با شرکت i م به عنوان مرکز و شعاع r به عنوان محدوده (به استثنای ارزش خود شرکت یکم )، e ir نشان دهنده ارزش تولید همه انواع صنایع موجود در منطقه با مرکزیت شرکت اول و محدوده r (به استثنای ارزش خود شرکت یکم )، N S نشان دهنده تعداد شرکت های متعلق به صنعت S , E S|i است .نشان دهنده ارزش کل تولید صنعت S در کل منطقه تحقیقاتی به استثنای شرکت اول است و E |i نشان دهنده ارزش کل تولید همه انواع صنایع در کل منطقه به استثنای i است.شرکت هفتم تابع M با افزایش تعداد اشیاء از همان نوع، اثر کاهشی عنصر واحد را هموار می کند. از آنجایی که این اصل همولوگ است، اگر از تابع M برای محاسبه داده های عناصر جغرافیایی مانند POI، مسکن، جمعیت استفاده شود، درجات چگالی عناصر جغرافیایی را نیز در محدوده معینی اندازه گیری می کند. بنابراین، از نظر تئوری استفاده از فرم تابع M برای چگالی فضایی POI در این تحقیق امکان پذیر است. با این حال، قابل توجه است که محاسبات در تابع M مبتنی بر انباشت کمی ساده است و این قانون را در نظر نمی گیرد که تأثیر بین اشیاء جغرافیایی به تدریج با فاصله آنها کاهش می یابد، که در KDE و GFM گنجانده شده است. از این رو،

3.5.2. متغیرهای مکانی و همسایگی بر اساس تراکم فضایی مصنوعی
به طور کلی، KDE و GFM این قانون را در نظر می گیرند که تأثیر بین اشیاء جغرافیایی به تدریج با فاصله آنها کاهش می یابد، اما آنها در نظر نمی گیرند که تأثیر واقعی یک شیء جغرافیایی به تدریج با افزایش تعداد اشیاء کاهش می یابد. همان نوع؛ برعکس، تابع M اثر کاهشی یک شی منفرد را با افزایش تعداد همان نوع اشیاء در نظر می‌گیرد، اما از این قانون غفلت می‌کند که تأثیر بین ژئواشیاء با فاصله آنها کاهش می‌یابد. اگر این دو جنبه با هم متحد شوند، بنابراین فرم KDE (الهام گرفته از [ 59 ، 60 ]) یا GFM در تابع M هنگام محاسبه مقادیر ژئواشیاء، هر دو جنبه را می توان در نظر گرفت. شعاعr در تابع M مربوط به پهنای باند مدل KDE یا فاصله نفوذ GFM است.
بنابراین، می‌توانیم از شکلی از تابع M استفاده کنیم که روش KDE یا GFM را برای اندازه‌گیری درجات چگالی فضایی برای تسهیلات (یا POI) در یک منطقه معین در اطراف یک واحد مسکونی در بر می‌گیرد. در مسئله ما، e iSr را می توان با تخمین چگالی هسته (یا امتیاز اثر GFM) POIهای نوع S در ناحیه ای در محدوده r بیان کرد (به استثنای خود POI i )، e ir نشان دهنده چگالی هسته است. تخمین (یا امتیاز اثر GFM) همه انواع POI در محدوده r (به استثنای خود POI i ). N S نشان دهنده تعداد S است-نوع POI. E S|i تخمین چگالی کل هسته (یا نمره کل اثر GFM) POIهای نوع S (به استثنای POI i ) را در کل منطقه نشان می دهد. و E |i تخمین چگالی کل هسته (یا نمره کل اثر GFM) همه انواع POI (به استثنای i) را نشان می دهد.th POI) در کل منطقه. از این منظر، این مدل می تواند هم قانون را در بر گیرد که تأثیر با فاصله اشیاء جغرافیایی کاهش می یابد و هم این واقعیت که تأثیر واقعی یک شیء جغرافیایی واحد به تدریج با افزایش تعداد اشیاء از همان نوع کاهش می یابد. متغیرهای مکان و همسایگی بر اساس این رویکرد ممکن است تعمیم جامع تری از اطلاعات جغرافیایی انباشته را ارائه دهند و ممکن است امکان تجزیه و تحلیل دقیق تری از مسائل مرتبط را فراهم کنند.
در این تحقیق، انواع POI Baidu ( جدول 1) را می توان به متغیرهای مکانی و همسایگی با توجه به قیمت اجاره مسکن در قالب یک تابع M همراه با KDE یا GFM پردازش کرد. این متغیرهای مکانی و همسایگی در این مقاله با عنوان “متغیرهای مکانی و همسایگی مبتنی بر تراکم فضایی مصنوعی” نامگذاری شده‌اند. برای تشخیص اینکه آیا KDE یا GFM ترکیب شده‌اند، می‌توان آنها را به ترتیب به عنوان متغیرهای «مبتنی بر چگالی فضایی مصنوعی (KDE)» یا «مبتنی بر چگالی فضایی مصنوعی (GFM)» تقسیم کرد. برای مقایسه، ما همچنین می‌توانیم متغیرهای مکان و همسایگی را بر اساس «نزدیک‌ترین فاصله» از مسکن تا POI مربوطه تعیین کنیم، و این متغیرها به‌عنوان «متغیرهای مکان و همسایگی مبتنی بر فاصله» برچسب‌گذاری می‌شوند. متغیرهای مکان و همسایگی نیز می‌توانند صرفاً بر اساس محاسبات KDE یا مدل GFM برای POIهای مربوطه تولید شوند و به‌عنوان «متغیرهای مکان و همسایگی مبتنی بر KDE» و «مکانی مبتنی بر GFM و برچسب‌گذاری شوند. متغیرهای همسایگی» به ترتیب. در آزمایش‌های ما، مدل‌های قیمت مسکن اجاره‌ای با متغیرهای مکانی و محله‌ای «مبتنی بر چگالی فضایی مصنوعی»، «مبتنی بر فاصله»، «مبتنی بر KDE» و «مبتنی بر GFM» استفاده شده و برای تعیین اینکه کدام نوع برای بهبود بهتر است، مقایسه می‌شود. مدل. مجموع اعداد POI در اطراف خانه‌های اجاره‌ای در پهنای باند KDE یا در فاصله نفوذ GFM نیز به ترتیب در هر نوع متغیر مکان و محله گنجانده شده‌اند. و آنها به ترتیب به عنوان “متغیرهای مکان و همسایگی مبتنی بر KDE” و “متغیرهای مکان و همسایگی مبتنی بر GFM” ایجاد و برچسب گذاری می شوند. در آزمایش‌های ما، مدل‌های قیمت مسکن اجاره‌ای با متغیرهای مکانی و محله‌ای «مبتنی بر چگالی فضایی مصنوعی»، «مبتنی بر فاصله»، «مبتنی بر KDE» و «مبتنی بر GFM» استفاده شده و برای تعیین اینکه کدام نوع برای بهبود بهتر است، مقایسه می‌شود. مدل. مجموع اعداد POI در اطراف خانه‌های اجاره‌ای در پهنای باند KDE یا در فاصله نفوذ GFM نیز به ترتیب در هر نوع متغیر مکان و محله گنجانده شده‌اند. و آنها به ترتیب به عنوان “متغیرهای مکان و همسایگی مبتنی بر KDE” و “متغیرهای مکان و همسایگی مبتنی بر GFM” ایجاد و برچسب گذاری می شوند. در آزمایش‌های ما، مدل‌های قیمت مسکن اجاره‌ای با متغیرهای مکانی و محله‌ای «مبتنی بر چگالی فضایی مصنوعی»، «مبتنی بر فاصله»، «مبتنی بر KDE» و «مبتنی بر GFM» استفاده شده و برای تعیین اینکه کدام نوع برای بهبود بهتر است، مقایسه می‌شود. مدل. مجموع اعداد POI در اطراف خانه‌های اجاره‌ای در پهنای باند KDE یا در فاصله نفوذ GFM نیز به ترتیب در هر نوع متغیر مکان و محله گنجانده شده‌اند. متغیرهای موقعیتی و همسایگی «مبتنی بر KDE» و «مبتنی بر GFM» برای تعیین اینکه کدام نوع برای بهبود مدل بهترین است، اعمال و مقایسه می‌شوند. مجموع اعداد POI در اطراف خانه‌های اجاره‌ای در پهنای باند KDE یا در فاصله نفوذ GFM نیز به ترتیب در هر نوع متغیر مکان و محله گنجانده شده‌اند. متغیرهای موقعیتی و همسایگی «مبتنی بر KDE» و «مبتنی بر GFM» برای تعیین اینکه کدام نوع برای بهبود مدل بهترین است، اعمال و مقایسه می‌شوند. مجموع اعداد POI در اطراف خانه‌های اجاره‌ای در پهنای باند KDE یا در فاصله نفوذ GFM نیز به ترتیب در هر نوع متغیر مکان و محله گنجانده شده‌اند.
محاسبه مربوط به KDE به صورت زیر اتخاذ می شود: ، جایی که h نمایانگر یک خانه خاص است، j نوع POI است، و p j,k نشان دهنده k امین نقطه در POI های نوع j است. برای POIهای نوع j ، λj ( h ) مقدار تخمینی چگالی آنها در خانه h است، فاصله (h, pj , k ) فاصله بین خانه h و POI pj ,k است و Nj برابر است. تعداد POIهای نوع j . ک(·) تابع هسته KDE است و هسته Epanechnikov به عنوان تابع هسته در این تحقیق پذیرفته شده است. b پهنای باند KDE است، به این معنی که فقط نقاط داخل b برای محاسبه مقدار KDE موثر هستند. پهنای باند هر متغیر با شرطی تعیین می شود که ضریب همبستگی این متغیر تولید شده توسط KDE با قیمت اجاره مسکن به حداکثر برسد.

برای محاسبه مربوط به GFM، برای در نظر گرفتن مقیاس تأثیرات عوامل خارجی، تابع شدت باید با محدود کردن حداکثر فاصله تأثیر محدود شود [ 14 ، 31 ]. تابع شدت خطی با محدودیت دامنه به صورت زیر بیان می شود:

که در آن φ ( x ) شدت میدان (یا امتیاز اثر) در مکان x است و F امتیاز اثر اصلی در فاصله 0 از شی o است که باید با توجه به ویژگی‌های شی محاسبه شود و کیفیت آن را منعکس کند. هدف – شی. d(x) فاصله x تا جسم o ، R حداکثر فاصله تاثیر جسم o ، و r(x) اندازه گیری فاصله نسبی است که با تقسیم d(x) بر R بدست می آید . فاصله نفوذ Rهر متغیر با این شرط تعیین می شود که ضریب همبستگی امتیازات اثر این متغیر با قیمت حداکثر شود، که مشابه فرآیند KDE است. علاوه بر این، برای هر نوع POI، تعداد نظرات هر POI به 5 نوع با الگوریتم K-means [ 61 ] طبقه بندی می شود و GroupID نتیجه به صورت 0 (حداکثر) تا 4 (دقیقه) فهرست می شود. سپس، امتیاز اثر اصلی F هر POI را می توان به صورت F = 1 – GroupID /5.0 تعیین کرد. ظاهراً امتیاز اثر GFM نوع خاصی از POI مربوط به یک خانه، مجموع امتیازات اثر همه POI از این نوع است.

علاوه بر این، در صورتی که ضرایب همبستگی آنها با قیمت اجاره مسکن کمتر از 0.01 باشد (مانند پمپ بنزین، باغ وحش و غیره) متغیرها حذف می شوند.

3.6. متغیرهای دو بعدی قیمت مسکن و مدل CNN

3.6.1. مدل یادگیری عمیق CNN برای قیمت مسکن اجاره ای

قیمت مسکن یک مدل غیرخطی و پیچیده است و با ظهور عصر کلان داده، یادگیری عمیق راه مناسبی برای مقابله با آن فراهم می کند. یادگیری عمیق می تواند به روابط غیرخطی و پیچیده بپردازد [ 17 ، 18 ، 19] در مقادیر ورودی، و چند خطی بودن مشکلی ندارد، که برای مدل‌سازی قیمت مسکن بسیار مهم است. بنابراین، تمام 100 نوع شی جغرافیایی موجود در POI بایدو را می توان به متغیرهای مکانی و همسایگی برای قیمت مسکن اجاره ای پردازش کرد و به همراه متغیرهای ساختاری به مدل یادگیری عمیق وارد کرد. از آنجایی که تعداد متغیرها زیاد است، در این تحقیق این متغیرهای تک بعدی قیمت مسکن را تا کرده و به اشکال دو بعدی تبدیل می کنیم. در یادگیری عمیق، ورودی‌های دو بعدی اطلاعات فشرده‌تری نسبت به فرم تک بعدی دارند و برای استخراج ویژگی‌ها و بهینه‌سازی پارامترها راحت‌تر هستند. مقادیر متغیرهای ساختاری،بخش 3.6.2 . شکل ورودی متغیرهای قیمت مسکن دو بعدی شبیه به تصاویر سنجش از دور است. بنابراین، مدل‌هایی مشابه مدل‌هایی که برای طبقه‌بندی تصویر و استخراج ویژگی‌ها استفاده می‌شوند را می‌توان برای مدل‌سازی متغیرهای قیمت مسکن پس از ایجاد تغییرات تطبیقی ​​اتخاذ کرد.
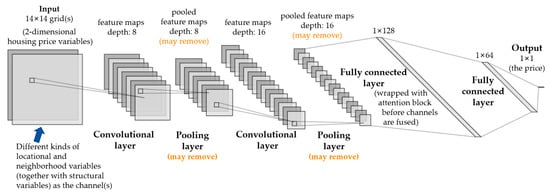
ساختار CNN طراحی شده در مطالعه ما در شکل 4 نشان داده شده است . از آنجایی که مطالعات قبلی نیز اشاره کرده اند که کاهش پیچیدگی CNN برای جلوگیری از تطبیق بیش از حد ضروری است [ 62 ]، و یک مدل پیچیده ممکن است به راحتی پدیده اضافه برازش را برای داده های قیمت مسکن ایجاد کند [ 17 ]]، ساختار CNN همانطور که در شکل نشان داده شده تنظیم شده است. شبکه پیشنهادی شامل یک لایه ورودی، 2 یا 3 لایه کانولوشن، 2 لایه کاملا متصل و یک لایه خروجی است. از آنجایی که لایه‌های ادغام معمولاً برای مسائل طبقه‌بندی به جای مشکلات رگرسیون استفاده می‌شوند، ما آزمایش می‌کنیم که آیا حذف لایه‌های ادغام خوب است یا خیر. برای لایه های کانولوشن، آزمایش می کنیم که اگر 2 یا 3 لایه گنجانده شود، عملکرد بهتری دارد، و همچنین آزمایش می کنیم که اگر اندازه 3 یا 5 برای هسته کانولوشن اعمال شود، کدام بهتر است. اعماق لایه های کانولوشن برای 2 لایه 8، 16 یا برای 3 لایه 8، 16، 32 بر اساس آزمایش های قبلی ما تنظیم شده است. برای دو لایه کاملا متصل، اندازه آنها به ترتیب 128 و 64 است.63 ]. ما همچنین یک عملیات انصراف را در اولین لایه کاملا متصل اعمال می کنیم که به طور تصادفی وزن برخی از نورون ها را غیرفعال می کند و از تطبیق بیش از حد مدل جلوگیری می کند [ 19 ]. از آنجایی که در مطالعات اخیر مکانیسم توجه برای یادگیری عمیق قیمت مسکن موثر نشان داده شده است [ 12 ، 22 ، 24 ، 64 ]، ما الهام گرفته ایم که اولین لایه کاملاً متصل در شبکه خود را با بلوک توجه [ 22 ] بپیچیم.]، که ویژگی های خام را به ویژگی های مورد علاقه تبدیل می کند. ویژگی‌های زیادی وجود دارد که لایه‌های کانولوشن قبل از اینکه وارد لایه‌های کاملاً متصل شوند، استخراج می‌شوند و مکانیسم توجه به شبکه کمک می‌کند تا ویژگی‌های مهمی را که به لایه خروجی (قیمت) کمک می‌کند، که برای نزول گرادیان مناسب هستند، تشخیص دهد. بلوک توجه باید قبل از ادغام کانال ها استفاده شود [ 22 ] و می تواند به صورت زیر فرموله شود: ، . که در آن x بردار ورودی (ویژگی های خام)، y بردار خروجی (ویژگی های مورد توجه)، h بردار نورون ها در لایه کاملاً متصل و w وزن است. بردار Softmax [ 65 ] است که اهمیت ویژگی هایی را که قبلاً با لایه های کانولوشن مشخص شده بودند متمایز می کند. پس از بلوک توجه، انحراف ویژگی ها به طور قابل توجهی تقویت می شود. یعنی y تفاوت قابل ملاحظه‌ای بزرگ‌تری نسبت به x دارد، که به این معنی است که ویژگی‌های اصلی قیمت مسکن اجاره‌ای تحت فشار هستند. لایه ورودی، متغیرهای ساختاری، مکانی و همسایگی 2 بعدی مسکن است که به روش زیر در بخش بعدی نشان داده شده است. (پارامترهای مدل های این مقاله را می توانید در فایل تکمیلی مشاهده کنید .)
3.6.2. تبدیل متغیرهای قیمت مسکن اجاره ای به دو بعدی
قبل از یادگیری عمیق CNN، ما باید متغیرهای قیمت اجاره مسکن (شامل متغیرهای ساختاری، مکانی و همسایگی) را در یک فضای دوبعدی ترسیم کنیم تا داده‌های ورودی شبکه‌های عصبی را در قالب یک تصویر تولید کنیم. علاوه بر این، بهتر است متغیرهای دارای همبستگی بیشتر در موقعیت‌های همسایه در این «تصویر» قرار گیرند، که برای شبکه‌ها برای استخراج ویژگی‌ها از متغیرهای قیمت مسکن اجاره‌ای دوبعدی مؤثر است. همانطور که در شکل 5 نشان داده شده است، برای تبدیل متغیرهای قیمت به دو بعد، 2 مرحله طول می کشد. اولین مرحله کاهش ابعاد است. باید از روشی برای تبدیل هر متغیر قیمت مسکن به یک موقعیت دو بعدی (خام) استفاده شود. مرحله دوم تقسیم و شطرنجی کردن موقعیت ها است. به طور خاص، موقعیت‌های دو بعدی خام به یک شطرنجی درجه دوم تبدیل می‌شوند که می‌تواند سپس به مدل CNN وارد شود.
برای کاهش ابعاد، با فرض اینکه در آزمایش ما N خانه اجاره ای وجود دارد، برای هر متغیر قیمت مسکن اجاره ای N داده وجود دارد، به این معنی که هر متغیر را می توان به عنوان یک بردار N بعدی در نظر گرفت. برای نگاشت این بردارهای N- بعدی به یک فضای دو بعدی، می توان یک روش کاهش ابعاد برای بردارهای با ابعاد بالا اتخاذ کرد. در حال حاضر، روش‌های کاهش ابعاد متداول شامل تجزیه و تحلیل مؤلفه‌های اصلی (PCA) [ 66 ] و تعبیه همسایه تصادفی t-توزیع شده (t-SNE) [ 67 ] است.] و غیره PCA از یک تبدیل خطی برای تبدیل مجموعه ای از متغیرهای با ابعاد بالا به بردارهای مستقل خطی با ابعاد پایین استفاده می کند، با به حداکثر رساندن واریانس داده های پیش بینی شده، و حفظ ویژگی های نقاط داده اصلی تا حد امکان [ 66 ]. روش t-SNE یک الگوریتم کاهش ابعاد غیرخطی است که بر اساس توزیع احتمال پیاده روی های تصادفی بر روی نمودار همسایگی برای یافتن ساختار داخلی داده ها است و می تواند داده های عظیم با ابعاد بالا را به دو یا چند بعد ترسیم کند [ 67 ].]. در مقایسه، PCA نمی تواند رابطه چند جمله ای پیچیده بین ویژگی ها را توضیح دهد، در حالی که داده های کاهش یافته توسط الگوریتم t-SNE می توانند ویژگی های داده های اصلی را بهتر حفظ کنند. یعنی زمانی که نقاط با فواصل مشابه در فضای داده‌های با ابعاد بالا به فضای کم‌بعد نگاشت می‌شوند، فاصله‌ها همچنان مشابه هستند و می‌توانند در موقعیت‌های نسبتاً همسایه بیان شوند [ 68 ، 69 ]. بنابراین، در تحقیق ما از t-SNE برای تبدیل متغیرهای قیمت مسکن اجاره ای به دو بعد.

الگوریتم t-SNE را می توان به طور خلاصه به شرح زیر توصیف کرد: نقاط با ابعاد بالا (متغیرهای قیمت اجاره مسکن) X = x 1 , x 2 , …, x n به منظور ترسیم در فضای کم بعدی Y = y هستند. 1 ، y 2 ، …، y n (دو بعدی در این مطالعه). در ابتدا، t-SNE شباهت مقادیر با ابعاد بالا x i و x j را محاسبه می کند که با p j|i نشان داده می شود. شباهت p j|iاحتمال شرطی این است که x i x j را به عنوان همسایه انتخاب می کند در صورتی که همسایه ها متناسب با چگالی گاوسی در مرکز x i انتخاب شوند :

جایی که σi واریانس تابع گاوسی را نشان می‌دهد که در مرکز مکان با ابعاد بالا x i قرار دارد. شباهت به شکل متقارن تعریف می شود، یعنی p i,j = ( pj |i + p i|j )/2 n که n تعداد نقاط داده است. برای Y هدف کم بعدی ، تعریف بسط داده می شود و شباهت آنها به صورت زیر مدل می شود:

سپس، یک الگوریتم توزیع دم سنگین در فضای کم بعدی برای غلبه بر مشکل ازدحام نقاط داده اعمال می شود [ 67 ]. پس از عملیات بعدی، کاهش ابعاد در t-SNE را می توان تکمیل کرد و داده ها در فضای کم بعدی Y نگاشت می شوند .
فرآیند تقسیم و شطرنجی را می توان به صورت زیر تعمیم داد: اول، فرض کنید داده های هر متغیر قیمت مسکن اجاره ای از طریق t-SNE به 2 بعد کاهش یافته است و “مختصات” دو بعدی آنها ( X ، Y ) به دست می آید. برای این «مختصات»، مختصات میانی آنها ( X me ، Y me) را می توان محاسبه کرد، که می تواند نقطه مرکزی “تصویر” متغیرهای 2 بعدی را نشان دهد. دوم، با توجه به نقطه مرکزی، 4 جهت اطراف آن (بالا چپ، پایین چپ، بالا راست و پایین سمت راست) 4 ربع تشکیل می دهند. برای “مختصات” هر متغیر، آسان است که بدانیم جهت نقطه مرکزی کدام است، تا بدانیم در کدام ربع باید قرار گیرند. سوم، نقاط (متغیرها) در هر ربع را می توان بر اساس “x” آنها مرتب کرد. -مختصات” و به طور مساوی با چندک های “مختصات x” از هم جدا می شوند. سپس، برای هر متغیر می توان چه ردیفی در “تصویر” باشد. در آخر، نقاط (متغیرها) در هر سطر را می توان بر اساس «مختصات y» آنها مرتب کرد و مشخص کرد که در چه ستونی باید باشد.
از مراحل بالا، هر متغیر قیمت مسکن اجاره ای را می توان به یک “پیکسل” از یک شطرنجی ترسیم کرد. مقادیر پیکسل ها را می توان با مقادیر متغیرهای قیمت مسکن پر کرد و پیکسل های بدون پر کردن هیچ متغیری (معمولاً در لبه شطرنجی) را می توان با مقادیر صفر پیش فرض پر کرد. به این ترتیب، در فضای دو بعدی، متغیرهایی با همبستگی بیشتر در موقعیت‌های همسایه قرار می‌گیرند که توانایی شبکه‌ها را برای استخراج ویژگی‌ها از شکل شطرنجی متغیرهای قیمت مسکن اجاره‌ای افزایش می‌دهد.
پنج نوع متغیر مکانی و همسایگی قبلاً برای قیمت خانه ایجاد شده است، به شرح زیر: متغیرهای مبتنی بر فاصله، متغیرهای مبتنی بر KDE، متغیرهای مبتنی بر GFM، متغیرهای مبتنی بر چگالی فضایی مصنوعی (KDE) و مبتنی بر چگالی فضایی مصنوعی (GFM). ) متغیرها آنها به طور جداگانه در شبکه پر می شوند و به مدل 2 بعدی CNN وارد می شوند. علاوه بر این، آنها عملاً می توانند در کنار هم قرار گیرند و شبیه به باندهای مختلف تصاویر، به کانال های موازی در CNN تبدیل شوند. بنابراین، ما به طور جداگانه کانال های دو بعدی متشکل از این نوع متغیرهای قیمت مسکن را ترکیب کرده و آنها را برای آموزش در CNN وارد می کنیم. در طول فرآیند آموزش، اندازه اولیه داده های ورودی 14 × 14 × N است (که Nبستگی به این دارد که آیا ترکیبی از متغیرهای مختلف قیمت مسکن اجاره ای استفاده می شود یا خیر. اگر فقط یک نوع متغیر را وارد کنیم، N = 1; N = 2 یا 3 اگر انواع مختلفی از متغیرها را ترکیب کنیم). در عین حال، مدل ما با مدل های یک بعدی و برخی از مدل های اخیر که در مطالعات دیگر ذکر شده اند مقایسه می شود [ 17 ، 24 ، 30 ].

4. نتایج و بحث

4.1. گروه های آزمایشی و ارزیابی دقت مدل

در این مقاله چهار نوع مدل چارچوب قیمت مسکن اجاره به شرح زیر وجود دارد: OLS، GWR، یک شبکه عصبی کاملا متصل یک بعدی (FCNN) و یک مدل یادگیری عمیق دو بعدی (CNN). همچنین پنج نوع متغیر مکانی و همسایگی به شرح زیر وجود دارد: متغیرهای مبتنی بر فاصله، متغیرهای مبتنی بر KDE، متغیرهای مبتنی بر GFM، متغیرهای مبتنی بر چگالی فضایی مصنوعی (KDE) و متغیرهای مبتنی بر چگالی فضایی مصنوعی (GFM). چهار مدل چارچوب فوق به ترتیب با پنج نوع متغیر تولید و آزمایش شده و نتایج مدل‌سازی مربوطه آن‌ها مورد ارزیابی قرار می‌گیرد. بر اساس نتایج، دقیق‌ترین نوع مدل چارچوب مورد بحث قرار می‌گیرد و اینکه کدام نوع متغیرهای مکانی و همسایگی برای مدل‌سازی قیمت بهتر است، قابل مقایسه است. علاوه بر این، ترکیبات مختلفی از متغیرهای مکانی و همسایگی دو بعدی وارد مدل CNN شده و بهترین مدل برای قیمت اجاره مسکن چیست. برای هر نمونه در مدل های آزمایش شده، مقادیر هر متغیر به 0.0 تا 1.0 نرمال می شود تا از واگرایی مدل جلوگیری شود. کل مجموعه داده به طور تصادفی در هم ریخته شد و به مجموعه آموزشی (70٪) و مجموعه آزمایشی (30٪) برای چهار بار مستقل تقسیم شد و شاخص‌های نهایی میانگین می‌شوند تا نتیجه را نماینده‌تر کند. این مدل‌ها روی رایانه‌ای که با پردازنده Intel i7-9700K و یک پردازنده گرافیکی NVIDIA Titan پیکربندی شده است، آموزش داده می‌شوند. 0 برای جلوگیری از واگرایی مدل. کل مجموعه داده به طور تصادفی در هم ریخته شد و به مجموعه آموزشی (70٪) و مجموعه آزمایشی (30٪) برای چهار بار مستقل تقسیم شد و شاخص‌های نهایی میانگین می‌شوند تا نتیجه را نماینده‌تر کند. این مدل‌ها روی رایانه‌ای که با پردازنده Intel i7-9700K و یک پردازنده گرافیکی NVIDIA Titan پیکربندی شده است، آموزش داده می‌شوند. 0 برای جلوگیری از واگرایی مدل. کل مجموعه داده به طور تصادفی در هم ریخته شد و به مجموعه آموزشی (70٪) و مجموعه آزمایشی (30٪) برای چهار بار مستقل تقسیم شد و شاخص‌های نهایی میانگین می‌شوند تا نتیجه را نماینده‌تر کند. این مدل‌ها روی رایانه‌ای که با پردازنده Intel i7-9700K و یک پردازنده گرافیکی NVIDIA Titan پیکربندی شده است، آموزش داده می‌شوند.

در این تحقیق، ضریب تعیین تعدیل شده (adj R 2 )، ریشه میانگین مربعات خطا (RMSE) و درصد آن (%RMSE) به عنوان شاخص‌های ارزیابی دقت مدل‌ها که از شاخص‌های رایج مورد استفاده در مدل‌های موجود هستند، استفاده می‌شوند. مطالعات [ 20 ، 40 ]:

که در آن y i,o و y i,s مقدار مشاهده شده و پیش بینی شده خانه i است، n تعداد نمونه ها در مجموعه داده، m نشان دهنده تعداد متغیرها است، و نشان دهنده میانگین مقدار مشاهده شده است.

4.2. نتایج مدل های یک بعدی و دو بعدی

برای یافتن یک معماری خوب برای مدل قیمت مسکن اجاره ای، آزمایش ها و مقایسه هایی بر روی انواع مختلف شبکه های عصبی انجام می شود. مدل اول مدل 1 بعدی است که یک FCNN پنج لایه است: لایه ورودی بردار متغیرهای قیمت مسکن اجاره ای یک بعدی است که شامل متغیرهای ساختاری، مکانی و همسایگی می شود. چهار لایه پنهان به ترتیب دارای 200، 120، 100 و 20 نورون هستند. لایه خروجی یک بعد دارد که ارزش قیمت اجاره مسکن است. مدل بعدی CNN دو بعدی است که در بخش 3.6.1 ذکر شده است. اعماق لایه‌های کانولوشن در صورت وجود دو لایه، 8 و 16، یا اگر سه لایه بر اساس آزمایش‌های قبلی ما وجود دارد، 8، 16 و 32 تنظیم می‌شود و اندازه هسته کانولوشن روی سه یا پنج تنظیم می‌شود. . در مجموع 2 × 2 × 2 = 8 مجموعه آزمایش برای مدل CNN انجام شده است. الگوریتم پس انتشار برای آزمایشات در این مطالعه، الگوریتم گرادیان نزول [ 70 ] است. عملکرد کلی از دست دادن مدل های یادگیری عمیق به شرح زیر است: ، جایی که Y نشان دهنده مقدار پیش بینی شده است و Y *نشان دهنده ارزش واقعی است. پارامترهای یادگیری لایه های کاملا متصل به صورت زیر تنظیم می شوند: تنظیم L2 با وزن تنظیم 0.00005 استفاده می شود. اندازه دسته برای هر مرحله آموزش 32 است. نرخ یادگیری اولیه 0.5 است. نرخ فروپاشی نرخ یادگیری 0.99996 است. و میانگین متحرک فروپاشی 0.99996 است. پس از تکمیل فرآیند آموزش، مدل‌ها روی مجموعه آزمایشی اجرا می‌شوند تا دقت برازش و قدرت پیش‌بینی نمونه‌های ناشناخته را تخمین بزنند. متغیرهای مکانی و همسایگی اتخاذ شده در این بخش یکسان نگه داشته می‌شوند، که متغیرهای مکانی و همسایگی مبتنی بر چگالی فضایی مصنوعی (GFM) هستند که با ترکیب تابع M و رویکرد GFM به دست می‌آیند.بخش 4.3 . نتایج انواع دیگر متغیرها نیز در بخش 4.3 مورد بحث قرار گرفته است.
با انجام فرآیند آموزش، همانطور که در شکل 6 نشان داده شده است ، مدل یک بعدی (FCNN) پس از تقریباً 300000 مرحله آموزشی پایدار می شود و مدل دو بعدی (CNN) (برای یک گروه متوسط) پس از تقریباً 150000 مرحله آموزشی به ثبات می رسد. . علاوه بر این، مدل HPM (OLS) و GWR به عنوان گروه های پایه و مدل های یادگیری عمیق اخیر Yao [ 17 ]، Yu [ 30 ] و Bin [ 24 ] نیز برای مقایسه نتایج مدل های پیشنهادی استفاده می شود. (ما بخش تصویر این مدل ها را در نظر نمی گیریم زیرا هیچ داده تصویری در این مطالعه وجود ندارد.) مدل ها به دقت برازش نشان داده شده در جدول 3 در مجموعه های آزمایشی می رسند.
مشاهده می شود که دقت برازش و پیش بینی مدل های دو بعدی ظاهراً بهتر از مدل های یک بعدی است. بنابراین، تبدیل متغیرهای قیمت مسکن اجاره ای به دو بعد می تواند به طور موثر برازش و قابلیت های پیش بینی مدل یادگیری عمیق را بهبود بخشد. از آنجایی که انجمن ها در OLS و GWR به عنوان روابط خطی در نظر گرفته می شوند، دستیابی به دقت افزایش یافته از نظر پیش بینی در مجموعه آزمایش برای آنها دشوار است. ساختار FCNN یک بعدی و نسبتا ساده است که تا حدی در استخراج روابط پیچیده بین متغیرهای عظیم مشکل دارد. شکل 7به طور خلاصه چارچوب اصلی یک مدل FCNN و یک مدل CNN را نشان می دهد. متغیرهای ورودی در یک FCNN بردار و خطی هستند، در حالی که در مدل CNN، متغیرهای ورودی شطرنجی و متراکم هستند. بنابراین، معماری و ویژگی‌های یک مدل CNN متمرکزتر و متمرکزتر است، و دریافت و توصیف روابط پیچیده و تعاملی بین متغیرهای قیمت مسکن اجاره‌ای را برای شبکه آسان‌تر می‌کند. با این حال، در FCNN یک بعدی، ویژگی های متغیرهای ورودی مرتب شده به صورت خطی نسبتا پراکنده هستند و نورون های زیادی برای پیوند دادن آنها مورد نیاز است. هنگامی که متغیرهای ورودی زیادی وجود دارد، FCNN ممکن است پارامترهای اضافی زیادی داشته باشد که می تواند عملکرد را کاهش دهد و مشکلات بیش از حد برازش ممکن است رخ دهد. بدین ترتیب، مدل 1 بعدی ممکن است ظرفیت محدودی برای گرفتن ویژگی های پیچیده متغیرهای عظیم داشته باشد. در نتیجه، CNN دو بعدی می تواند عملکرد مدل سازی قیمت مسکن اجاره ای را بهبود بخشد.
برای مدل‌های دو بعدی CNN، زمانی که اندازه هسته کانولوشن سه است، و دو لایه کانولوشن بدون لایه‌های ادغام وجود دارد (یعنی CNN (3، 2، N))، دقت بهینه است. برای هر پیکربندی از این مدل‌های CNN، وقتی لایه‌های ادغام از چارچوب حذف می‌شوند، همه نتایج بهتر از لایه‌های ادغام خواهند بود. بنابراین، لایه های ادغام CNN برای رگرسیون قیمت مسکن اجاره ای مناسب یا ضروری نیستند. مدل سی‌ان‌ان یو [ 30 ] شامل لایه‌های ادغام می‌شود و روش مفید ترک تحصیل را اعمال نمی‌کند، بنابراین دقت در مقایسه با CNN‌های پیشنهادی در این مقاله کمتر است. روش یائو [ 17] متغیرهای کمتری را در نظر می‌گیرد و ممکن است ویژگی‌های ناهمگونی در شبکه‌های توزیع انواع مختلف ژئواشیاء وجود داشته باشد. بنابراین، اگر ویژگی‌ها به عنوان کانال‌های موازی در یک CNN وارد شوند، ممکن است ویژگی‌ها خیلی موثر استخراج نشوند. همچنین مدل‌سازی متغیرهای ساختاری و ویژگی‌های استخراج‌شده توسط مدل یائو چالش‌برانگیز است، زیرا آنها به طور همزمان آموزش داده نمی‌شوند و در نتیجه، عملکرد آن مدل نسبتاً محدود است. اگرچه درختان رگرسیون تقویت شده توسط Bin [ 24] می تواند به طور موثری عملکرد تخمین قیمت مسکن را بهبود بخشد، از شبکه عصبی یک بعدی برای استخراج ویژگی های متغیرهای ساختاری، مکانی و همسایگی که با ما متفاوت است استفاده می شود، بنابراین دقت در بخشی از داده های غیرتصویری هنوز قابل بهبود است. . هیچ اختلاف زیادی بین مدل های CNN بدون لایه های ادغام در جدول 3 مشاهده نمی شود. بنابراین، تجزیه و تحلیل زیر از مدل های دو بعدی به طور پیش فرض از شبکه CNN (3، 2، N) استفاده می کند.

4.3. نتایج بر اساس انواع مختلف متغیرهای مکان و همسایگی

این بخش اثرات انواع مختلف متغیرهای مکانی و همسایگی را مقایسه می‌کند: متغیرهای مکانی مبتنی بر فاصله، مبتنی بر GFM، مبتنی بر KDE، و مبتنی بر چگالی فضایی مصنوعی (برای GFM و KDE)، در مدل‌های قیمت مسکن اجاره‌ای. این نوع متغیرهای مکانی و همسایگی در مدل‌های چارچوب OLS، GWR، FCNN و CNN (3، 2، N) اعمال می‌شوند و نتایج در جدول 4 نشان داده شده است :
از این جدول مشخص می‌شود که دقت متغیرهای مکانی و همسایگی مبتنی بر چگالی فضایی مصنوعی در همه مدل‌های چارچوب بالاتر از سایرین است. متغیرهای موقعیتی و همسایگی مبتنی بر فاصله فقط شامل ویژگی‌های فاصله اشیاء جغرافیایی مربوط به خانه‌ها، بدون در نظر گرفتن ویژگی‌های کمی می‌شوند. این امر موجب از دست رفتن بسیاری از اطلاعات جغرافیایی می شود و مدل های مبتنی بر این متغیرها نمی توانند به دقت بسیار رضایت بخشی دست یابند. برای متغیرهای مبتنی بر KDE و GFM، اگرچه ویژگی‌های کمی گنجانده شده‌اند، اما این واقعیت را در نظر نمی‌گیرند که تأثیر واقعی یک شیء جغرافیایی به تدریج با افزایش تعداد اشیاء از همان نوع کاهش می‌یابد. با این حال، در متغیرهای مبتنی بر چگالی فضایی مصنوعی (برای GFM و KDE)، شکل تابع M نشان‌دهنده ویژگی‌های تجمع فضایی اشیاء جغرافیایی و امکانات شهری مربوطه است، از جمله اثر کاهشی عنصر واحد با افزایش تعداد اشیاء از همان نوع؛ و روش آماری GFM/KDE تعبیه شده می تواند قانون اول جغرافیا را منعکس کند. بنابراین، در مقایسه با متغیرهای مبتنی بر فاصله، مبتنی بر GFM و مبتنی بر KDE، متغیرهای مکانی و همسایگی مبتنی بر تراکم فضایی مصنوعی، اطلاعات اشیاء جغرافیایی را به‌طور جامع‌تری در نظر می‌گیرند و ویژگی‌های مکانی یک واحد مسکونی را بهتر منعکس می‌کنند. ، که به بهبود دقت برازش مدل قیمت حاصل کمک می کند. شکل تابع M نشان‌دهنده ویژگی‌های تجمع فضایی اشیاء جغرافیایی و امکانات شهری مربوطه، از جمله کاهش اثر یک عنصر واحد با افزایش تعداد اشیاء از همان نوع است. و روش آماری GFM/KDE تعبیه شده می تواند قانون اول جغرافیا را منعکس کند. بنابراین، در مقایسه با متغیرهای مبتنی بر فاصله، مبتنی بر GFM و مبتنی بر KDE، متغیرهای مکانی و همسایگی مبتنی بر تراکم فضایی مصنوعی، اطلاعات اشیاء جغرافیایی را به‌طور جامع‌تری در نظر می‌گیرند و ویژگی‌های مکانی یک واحد مسکونی را بهتر منعکس می‌کنند. ، که به بهبود دقت برازش مدل قیمت حاصل کمک می کند. شکل تابع M نشان‌دهنده ویژگی‌های تجمع فضایی اشیاء جغرافیایی و امکانات شهری مربوطه، از جمله کاهش اثر یک عنصر واحد با افزایش تعداد اشیاء از همان نوع است. و روش آماری GFM/KDE تعبیه شده می تواند قانون اول جغرافیا را منعکس کند. بنابراین، در مقایسه با متغیرهای مبتنی بر فاصله، مبتنی بر GFM و مبتنی بر KDE، متغیرهای مکانی و همسایگی مبتنی بر تراکم فضایی مصنوعی، اطلاعات اشیاء جغرافیایی را به‌طور جامع‌تری در نظر می‌گیرند و ویژگی‌های مکانی یک واحد مسکونی را بهتر منعکس می‌کنند. ، که به بهبود دقت برازش مدل قیمت حاصل کمک می کند. از جمله اثر کاهشی عنصر واحد با افزایش تعداد اشیاء از همان نوع. و روش آماری GFM/KDE تعبیه شده می تواند قانون اول جغرافیا را منعکس کند. بنابراین، در مقایسه با متغیرهای مبتنی بر فاصله، مبتنی بر GFM و مبتنی بر KDE، متغیرهای مکانی و همسایگی مبتنی بر تراکم فضایی مصنوعی، اطلاعات اشیاء جغرافیایی را به‌طور جامع‌تری در نظر می‌گیرند و ویژگی‌های مکانی یک واحد مسکونی را بهتر منعکس می‌کنند. ، که به بهبود دقت برازش مدل قیمت حاصل کمک می کند. از جمله اثر کاهشی عنصر واحد با افزایش تعداد اشیاء از همان نوع. و روش آماری GFM/KDE تعبیه شده می تواند قانون اول جغرافیا را منعکس کند. بنابراین، در مقایسه با متغیرهای مبتنی بر فاصله، مبتنی بر GFM و مبتنی بر KDE، متغیرهای مکانی و همسایگی مبتنی بر تراکم فضایی مصنوعی، اطلاعات اشیاء جغرافیایی را به‌طور جامع‌تری در نظر می‌گیرند و ویژگی‌های مکانی یک واحد مسکونی را بهتر منعکس می‌کنند. ، که به بهبود دقت برازش مدل قیمت حاصل کمک می کند.
علاوه بر این، در تمام آزمایش‌ها، دقت گروه‌های آزمایشی GFM بیشتر از گروه‌های KDE برای همان مدل چارچوب است. از آنجایی که GFM به طور خاص بر مفهوم “نفوذ” تمرکز دارد، که می تواند در ارزیابی تاثیرات بین اشیاء جغرافیایی از KDE جزئیات بیشتری داشته باشد، GFM ممکن است برای تخمین اثرات ژئواشیاء بر مسکن معقول تر باشد، بنابراین منجر به اجاره بالاتر می شود. مدل های قیمت گذاری در عمل، GFM بیشتر تمایل دارد که در مطالعات مربوط به قیمت مسکن استفاده شود [ 14 ، 31 ]، و این تحقیق همچنین از GFM پشتیبانی می کند. در آزمایش‌های زیر، ما نیز تمایل بیشتری به استفاده ترجیحی از روش‌های تعبیه‌شده با GFM داریم.

4.4. نتایج ترکیب های مختلف متغیرهای قیمت مسکن اجاره ای دو بعدی

انواع مختلف متغیرهای قیمت مسکن اجاره ای دو بعدی، از جمله متغیرهای مبتنی بر فاصله، مبتنی بر GFM، مبتنی بر KDE و مبتنی بر چگالی فضایی مصنوعی، عملاً می توانند در کنار هم قرار گیرند و به کانال های موازی در CNN تبدیل شوند، مشابه باندهای مختلف تصاویر بنابراین، ما به طور جداگانه “باندهای تصویر” دو بعدی متشکل از این نوع متغیرهای قیمت مسکن اجاره را ترکیب می کنیم و آنها را برای آموزش در CNN وارد می کنیم. نتایج ترکیبات مختلف متغیرهای دو بعدی در جدول 5 نشان داده شده است. از آنجایی که از نظر تئوری می توان ترکیب های بسیار زیادی را به دست آورد و GFM معمولاً در این تحقیق بهتر از KDE عمل می کند (که در بخش قبل ارائه شد)، برخی از ترکیبات با KDE حذف می شوند.
در میان ترکیب‌های مختلف، «مبتنی بر فاصله + مبتنی بر چگالی فضایی مصنوعی (GFM)» بهترین دقت را هنگامی که به‌عنوان دو کانال برای مدل CNN وارد می‌شود، ارائه می‌کند. با توجه به ویژگی مدل ها و داده های مربوطه، دلایل را می توان به صورت زیر تحلیل کرد:
اولاً، متغیرهای مکان و همسایگی مبتنی بر فاصله، ویژگی‌های فاصله نزدیک‌ترین ژئو شی از نوع خاصی را به مسکن منعکس می‌کنند، در حالی که متغیرهای مبتنی بر تراکم فضایی مبتنی بر GFM و مصنوعی عمدتاً چگالی فضایی ژئواشیاء را در نظر می‌گیرند. بنابراین، اطلاعات موجود در متغیرهای مبتنی بر فاصله به طور قابل توجهی با اطلاعات موجود در دو نوع متغیر دیگر متفاوت است. همانطور که در جدول 6 نشان داده شده استمیانگین ضریب همبستگی بین متغیرهای مبتنی بر چگالی فضایی مصنوعی (GFM) و متغیرهای مبتنی بر GFM نسبتاً بالا است، در حالی که ضرایب همبستگی متوسط ​​(مقادیر مطلق) بین متغیرهای مبتنی بر فاصله و دو نوع دیگر نسبتاً کم است. بنابراین، زمانی که متغیرهای مبتنی بر فاصله و دو نوع متغیر دیگر (یک نوع یا هر دو) در مدل ترکیب شوند، اطلاعات موجود در شبکه غنی می‌شود که به بهبود عملکرد کمک می‌کند. ثانیا، همانطور که از نتایج بخش قبل مشاهده می‌شود، مقادیر دقت با متغیرهای مکانی و همسایگی مبتنی بر چگالی فضایی مصنوعی به وضوح بالاتر از متغیرهای مبتنی بر فاصله و مبتنی بر KDE است. بنابراین در بین گروه های آزمایشی همه ترکیب ها از جمله متغیرهای مبتنی بر چگالی فضایی مصنوعی مزایایی را نشان می دهند. در نهایت، زمانی که هر سه نوع متغیر به عنوان کانال‌های موازی در مدل استفاده می‌شوند، شبکه پیچیدگی بیشتری می‌افزاید اما افزایش قابل توجهی در اطلاعات ایجاد نمی‌کند. از آنجایی که کانال “مبتنی بر GFM” و کانال “بر اساس چگالی فضایی مصنوعی (GFM)” نسبتا مشابه هستند، افزونگی برای مدل مفید نیست و در عوض باعث کاهش دقت می شود.
به طور خلاصه، ترکیب متغیرهای مکانی و همسایگی “مبتنی بر فاصله + مبتنی بر تراکم فضایی مصنوعی (GFM)” به عنوان دو کانال در مدل CNN پیشنهادی برای مدل‌سازی قیمت مسکن اجاره ای در این مقاله بهترین است. این پژوهش بیشتر بر روی داده های جغرافیایی غیرتصویری و متغیرهای ساختاری، مکانی و همسایگی واحدهای مسکونی متمرکز است. شبکه عصبی پیشنهادی برای گسترش داده های تصاویر بسیار سازگار است. ما برای آینده روش پیشنهادی بسیار مشتاق هستیم و قصد داریم آن را با استفاده از تصاویر نمای خیابان یا تصاویر داخلی گسترش دهیم، به محض اینکه داده های مربوطه به اندازه کافی در منطقه مورد مطالعه در دسترس باشد. علاوه بر این،71 ، 72 ]. بررسی اثرات هزینه های ساخت و ساز بر قیمت اجاره مسکن و بهبود مدل قیمت گذاری باید در کارهای آینده مورد توجه قرار گیرد.

5. نتیجه گیری ها

با ووهان به عنوان منطقه مورد مطالعه، این مطالعه از HPM، مدل GWR، یک مدل یک بعدی FCNN و یک مدل دو بعدی CNN برای تخمین قیمت مسکن استفاده می‌کند و دقت این مدل‌ها مقایسه می‌شود. نتایج نشان می‌دهد که CNN دو بعدی با متغیرهای مکانی و همسایگی مبتنی بر چگالی فضایی مصنوعی به بالاترین قیمت مناسب و دقت پیش‌بینی دست می‌یابد. زمانی که اندازه هسته کانولوشن 3 باشد و 2 لایه کانولوشن وجود داشته باشد و لایه های ادغام وجود نداشته باشد، عملکرد CNN پیشنهادی بهینه است. تحقیقات ما نشان می دهد که CNN دو بعدی می تواند به طور موثر قیمت مسکن اجاره ای را با متغیرهای ساختاری، مکانی و همسایگی، که شامل روابط غیرخطی و پیچیده است، مدل کند. و لایه های ادغام برای مشکل رگرسیون قیمت مسکن اجاره ای ضروری نیستند. متغیرهای مکانی و همسایگی مبتنی بر تراکم فضایی مصنوعی مورد استفاده در این تحقیق می‌توانند تأثیر تسهیلات و ژئواشیاء را بر قیمت مسکن اجاره بهتر منعکس کنند و در نتیجه دقت مدل نهایی را بهبود بخشند. ترکیبی از متغیرهای مکانی و همسایگی “مبتنی بر فاصله + مبتنی بر چگالی فضایی مصنوعی (GFM)” به عنوان دو کانال ورودی مدل CNN بهترین دقت را به دست می‌دهد.R 2 = 0.9097، RMSE = 3.5126)، زیرا این ترکیب حاوی اطلاعات نسبتاً گسترده است و افزونگی زیادی ندارد. مدل پیشنهادی ممکن است اطلاعات تصمیم‌گیری مناسبی را در اختیار افراد و شرکت‌ها برای معاملات اجاره مسکن خود قرار دهد. همچنین ممکن است مرجع تصمیم گیری ارزشمندی در مورد مکان ها و قیمت مسکن های اجاره ای عمومی در اختیار دولت قرار دهد.
برخی از بحث های ارائه شده در این مقاله ممکن است به درک مدل های قیمت مسکن اجاره ای کمک کند. اول، در مقایسه با مدل های یادگیری عمیق یک بعدی [ 15 ، 16 ]، معماری و ویژگی های CNN پیشنهادی متراکم تر و متمرکزتر است. بنابراین، CNN بهتر می‌تواند پیچیدگی روابط و تعاملات بین متغیرهای ساختاری، مکانی و همسایگی را مشخص کند و می‌تواند بهتر از FCNN یک بعدی در آزمایش ما عمل کند. دوم، هنگام تولید متغیرهای مکانی و همسایگی، ترکیب تابع M [ 26 ] و GFM [ 14 ، 31 ]] (متغیرهای مبتنی بر چگالی فضایی مصنوعی (GFM)) می‌توانند ویژگی‌های مکانی یک واحد مسکونی را بهتر منعکس کنند. شکل تابع M نشان‌دهنده ویژگی‌های تجمع فضایی اشیاء جغرافیایی و امکانات شهری است و اثر کاهشی یک ژئو شی منفرد را با افزایش تعداد اشیاء از همان نوع در نظر می‌گیرد. علاوه بر این، GFM تعبیه شده این قانون را در نظر می گیرد که تأثیر بین اجسام با فاصله آنها کاهش می یابد. بنابراین، در مقایسه با متغیرهای مبتنی بر فاصله، مبتنی بر GFM و مبتنی بر KDE، متغیرهای مکانی و همسایگی مبتنی بر تراکم فضایی مصنوعی دقت مدل قیمت مسکن اجاره‌ای را افزایش می‌دهند. در نهایت، در مقایسه با سایر مدل‌های منتشر شده، مدل پیشنهادی عموماً بهتر عمل می‌کند. در مدل یائو [ 17]، شبکه های توزیع انواع مختلف اشیاء جغرافیایی (و تصاویر سنجش از دور) ممکن است ناهمگن باشند، و اگر به عنوان کانال های موازی در CNN وارد شوند، ممکن است ویژگی ها به طور موثر استخراج نشوند. علاوه بر این، نحوه ترکیب لایه های کانولوشن با متغیرهای ساختاری در این مدل نیز نیاز به بررسی بیشتر دارد. Yu [ 30 ] لایه های ادغام را از CNN حذف نکرد، که آزمایش شده است که در رگرسیون قیمت مسکن اجاره غیرضروری هستند، بنابراین منجر به عملکرد نسبتا محدود مدل می شود. علاوه بر این، در مدل های نیمه یک بعدی و نیمه دو بعدی (مانند Bin’s [ 24])، شبکه عصبی یک بعدی برای استخراج ویژگی‌های متغیرهای ساختاری، مکانی و همسایگی استفاده می‌شود، بنابراین دقت این مدل‌ها ممکن است هنوز در بخشی از داده‌های غیرتصویری جا برای بهبود داشته باشد. مطمئناً جنبه های پیشرفته این روش ها می تواند راهنمایی برای مطالعات بیشتر در آینده باشد.
در آینده می توان برای این مطالعه بهبودهایی ایجاد کرد. این مطالعه عمدتاً بر روی داده‌های جغرافیایی غیرتصویری و متغیرهای ساختاری، مکانی و همسایگی قیمت مسکن متمرکز است. سایر ویژگی ها مانند ویژگی های توپوگرافی طبیعی، ویژگی های پوشش گیاهی و هزینه های ساخت و ساز، به طور مستقیم در توزیع POI منعکس نمی شوند. تأثیر این عوامل مرتبط بر قیمت مسکن اجاره ای هنوز باید بررسی شود. از آنجایی که مدل ما برای گسترش تصاویر بسیار سازگار است، تصاویر سنجش از راه دور، تصاویر نمای خیابان و تصاویر داخلی را می توان عملاً در روش ما در آینده اعمال کرد. علاوه بر این، شهرهای بیشتر و مکانیسم‌های توجه بیشتری را می‌توان برای شبکه‌های عصبی مدل قیمت اجاره/فروش مسکن آزمایش کرد.

منابع

  1. اندرو، م. هاورین، دی. منصیب، الف. توضیح مسیر تصرف مالک: مقایسه فراآتلانتیک. جی. هاوس. اقتصاد 2006 ، 15 ، 189-216. [ Google Scholar ] [ CrossRef ]
  2. سکو، م. سومیتا، ک. انتخاب تصدی مسکن در ژاپن و پیامدهای رفاه پس از بازنگری قانون حمایت از مستاجر. J. املاک و مستغلات اقتصاد مالی. 2007 ، 35 ، 357-383. [ Google Scholar ] [ CrossRef ]
  3. دونگ، اچ. تأثیر نابرابری درآمد بر مقرون به صرفه بودن اجاره: یک مطالعه تجربی در مناطق بزرگ شهری آمریکا. مطالعه شهری. 2017 ، 55 ، 2106-2122. [ Google Scholar ] [ CrossRef ]
  4. کمیسیون ملی بهداشت، PRC گزارش توسعه جمعیت شناور در چین . چاپ جمعیت چین: پکن، چین، 2018. [ Google Scholar ]
  5. وزارت مسکن و توسعه شهری – روستایی، PRC. اطلاعیه وزارت مسکن و توسعه شهری-روستایی جمهوری خلق چین، شماره 7. 2021. در دسترس آنلاین: https://www.mohurd.gov.cn/gongkai/fdzdgknr/gongkaiwgk/202107/20210708_762874 (دسترسی در 20 اوت 2021).
  6. Saiz, A. مهاجرت و اجاره مسکن در شهرهای آمریکا. J. شهری اقتصاد. 2003 ، 61 ، 345-371. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  7. سو، اس. ژانگ، جی. او هست.؛ ژانگ، اچ. هو، ال. کانگ، ام. کشف تأثیر TOD بر قیمت اجاره مسکن و پیامدهای آن بر برنامه ریزی فضایی: تجزیه و تحلیل مقایسه ای از پنج کلان شهر چین. Habitat Int. 2020 ، 107 ، 102309. [ Google Scholar ] [ CrossRef ]
  8. کاجیاس، م. Ertl، S. اثرات فضایی و غیر خطی در مدل‌سازی لذت‌گرا: آیا مجموعه داده‌های بزرگ مفروضات ما را تغییر خواهند داد؟ سرمایه گذاری J. Prop. مالی 2018 ، 36 ، 32-49. [ Google Scholar ] [ CrossRef ]
  9. لیبلت، وی. بارتکه، اس. شوارتز، N. تجزیه و تحلیل قیمت گذاری لذت بخش از تأثیر فضاهای سبز شهری بر قیمت های مسکونی: مورد لایپزیگ، آلمان. یورو طرح. گل میخ. 2018 ، 26 ، 133-157. [ Google Scholar ] [ CrossRef ]
  10. الله، اف. سپاسگزار، عوامل کلیدی SME موثر بر تصمیمات خرید یا اجاره در سرمایه گذاری هوشمند املاک: یک رویکرد پویایی سیستم با استفاده از داده های موضوع انجمن آنلاین. پایداری 2020 ، 12 ، 4382. [ Google Scholar ] [ CrossRef ]
  11. یو، تی. Song, Y. حل مشکل “آب و هوای سرد” خانه های اجاره ای عمومی – بر اساس تحلیل خرید دولت از خدمات عمومی. اقتصاد چین راهنمای تجارت 2018 ، 32 ، 74-76. [ Google Scholar ]
  12. وانگ، P.-Y. چن، سی.-تی. سو، J.-W. وانگ، T.-Y. هوانگ، اس.-اچ. مدل یادگیری عمیق برای پیش‌بینی قیمت خانه با استفاده از تحلیل داده‌های ناهمگن همراه با مکانیزم خودتوجهی مشترک. دسترسی IEEE 2021 ، 9 ، 55244–55259. [ Google Scholar ] [ CrossRef ]
  13. شیمیزو، سی. کاراتو، ک. نیشیمورا، ک. غیرخطی بودن ساختار قیمت مسکن: ارزیابی سه رویکرد به غیرخطی بودن در بازار مالکیت قبلی توکیو. بین المللی جی. هاوس. علامت. مقعدی 2014 ، 7 ، 459-488. [ Google Scholar ] [ CrossRef ]
  14. لیانگ، ایکس. لیو، ی. کیو، تی. جینگ، ی. فانگ، اف. اثرات عوامل مکانی بر قیمت مسکن جوامع مسکونی: مورد نینگبو، چین. Habitat Int. 2018 ، 81 ، 1-11. [ Google Scholar ] [ CrossRef ]
  15. جیانگ، ز. Shen, G. پیش‌بینی قیمت خانه بر اساس شبکه عصبی پس انتشار در چارچوب یادگیری عمیق Keras. در مجموعه مقالات ششمین کنفرانس بین المللی سیستم ها و انفورماتیک 2019 (ICSAI)، شانگهای، چین، 2 تا 4 نوامبر 2019؛ ص 1408-1412. [ Google Scholar ]
  16. Phan، TD پیش‌بینی قیمت مسکن با استفاده از الگوریتم‌های یادگیری ماشین: مورد شهر ملبورن، استرالیا. در مجموعه مقالات کنفرانس بین المللی 2018 در زمینه یادگیری ماشین و مهندسی داده (iCMLDE)، سیدنی، استرالیا، 3 تا 7 دسامبر 2018؛ صص 35-42. [ Google Scholar ]
  17. یائو، ی. ژانگ، جی. هونگ، ی. لیانگ، اچ. او، جی. نقشه‌برداری قیمت مسکن شهری در مقیاس خوب با ترکیب تصاویر سنجش از راه دور و داده‌های رسانه‌های اجتماعی. ترانس. GIS 2018 ، 22 ، 561-581. [ Google Scholar ] [ CrossRef ]
  18. لکون، ی. بوتو، ال. بنژیو، ی. هافنر، پی. یادگیری مبتنی بر گرادیان برای شناسایی اسناد به کار می رود. Proc. IEEE 1998 ، 86 ، 2278-2324. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  19. هینتون، جنرال الکتریک؛ سریواستاوا، ن. کریژفسکی، آ. سوتسکور، آی. Salakhutdinov، RR بهبود شبکه های عصبی با جلوگیری از سازگاری مشترک آشکارسازهای ویژگی. arXiv 2012 ، arXiv:1207.0580. [ Google Scholar ]
  20. بنی، ای جی؛ رالاپالی، س. گانتی، RK; سریواتسا، م. Manjunath، BS Beyond Spatial Auto-Regressive Models: پیش بینی قیمت مسکن با تصاویر ماهواره ای. در مجموعه مقالات کنفرانس زمستانی IEEE 2017 درباره کاربردهای بینایی کامپیوتری (WACV)، سانتا روزا، کالیفرنیا، ایالات متحده آمریکا، 24 تا 31 مارس 2017؛ صص 320-329. [ Google Scholar ]
  21. فو، ایکس. جیا، تی. ژانگ، ایکس. لی، اس. ژانگ، ی. آیا تصورات صحنه در سطح خیابان بر قیمت مسکن در کلان شهرهای چین تأثیر می‌گذارد؟ تجزیه و تحلیل با استفاده از مجموعه داده های دسترسی باز و یادگیری عمیق. PLoS ONE 2019 , 14 , e0217505. [ Google Scholar ] [ CrossRef ]
  22. بین، جی. گاردینر، بی. لیو، ز. لی، ای. ادغام چند وجهی مبتنی بر توجه برای بهبود ارزیابی املاک: مطالعه موردی در لس آنجلس. اپلیکیشن ابزارهای چندرسانه ای 2019 ، 78 ، 31163–31184. [ Google Scholar ] [ CrossRef ]
  23. ژائو، ی. چتی، جی. Tran, D. یادگیری عمیق با XGBoost برای ارزیابی املاک و مستغلات. در مجموعه مقالات مجموعه سمپوزیوم IEEE 2019 در مورد هوش محاسباتی (SSCI)، Xiamen، چین، 6 تا 9 دسامبر 2019؛ صص 1396–1401. [ Google Scholar ]
  24. بین، جی. گاردینر، بی. دروغ.؛ لیو، زی. تلفیق داده‌های شهری چند منبعی برای ارزیابی ارزش دارایی: مطالعه موردی در فیلادلفیا. محاسبات عصبی 2020 ، 404 ، 70-83. [ Google Scholar ] [ CrossRef ]
  25. Billings, SB; جانسون، EB ضریب مکان به عنوان تخمینگر غلظت صنعتی. Reg. علمی اقتصاد شهری 2012 ، 42 ، 642-647. [ Google Scholar ] [ CrossRef ]
  26. مارکون، ای. Puech, F. اندازه گیری های تمرکز جغرافیایی صنایع: بهبود روش های مبتنی بر فاصله. جی. اکون. Geogr. 2009 ، 10 ، 745-762. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  27. وو، جی. وانگ، ام. لی، دبلیو. پنگ، جی. Huang, L. تاثیر فضای سبز شهری بر قیمت مسکن مسکونی: مطالعه موردی در شنژن. ج. طرح شهری. توسعه دهنده 2015 , 141 , 05014023. [ Google Scholar ] [ CrossRef ]
  28. گنگ، بی. بائو، اچ. لیانگ، ی. مطالعه تأثیر ایستگاه راه آهن پرسرعت بر تغییرات فضایی قیمت مسکن بر اساس مدل لذت‌بخش. Habitat Int. 2015 ، 49 ، 333-339. [ Google Scholar ] [ CrossRef ]
  29. ژانگ، ی. فو، ایکس. Lv، C.; لی، اس. برتری سبزی درک شده عمومی: چارچوبی با استفاده از GWR چند مقیاسی و یادگیری عمیق. بین المللی جی. محیط زیست. Res. بهداشت عمومی 2021 , 18 , 6809. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  30. یو، ال. جیائو، سی. شین، ی. وانگ، ی. وانگ، ک. پیش بینی قیمت مسکن بر اساس یادگیری عمیق. بین المللی جی. کامپیوتر. Inf. مهندس 2018 ، 12 ، 90-99. [ Google Scholar ]
  31. جیائو، ال. لیو، ی. مدل میدان جغرافیایی مبتنی بر ارزیابی لذت جویانه فضاهای باز شهری در ووهان، چین. Landsc. طرح شهری. 2010 ، 98 ، 47-55. [ Google Scholar ] [ CrossRef ]
  32. روزن، اس. قیمت لذت و بازارهای ضمنی: تمایز محصول در رقابت خالص. جی. پولیتی. اقتصاد 1974 ، 82 ، 34-55. [ Google Scholar ] [ CrossRef ]
  33. Fotheringham، AS; ای چارلتون، ام. براندون، سی. رگرسیون وزن‌دار جغرافیایی: تکامل طبیعی روش بسط برای تجزیه و تحلیل داده‌های مکانی. محیط زیست طرح. پاسخ: اقتصادی فضا 1998 ، 30 ، 1905-1927. [ Google Scholar ] [ CrossRef ]
  34. Malpezzi، S. مدل های قیمت گذاری لذت بخش: بررسی انتخابی و کاربردی. خانه اقتصاد سیاست عمومی 2003 ، 67-89. [ Google Scholar ] [ CrossRef ]
  35. وو، سی. بله، X. رن، اف. وان، ی. نینگ، پی. Du، Q. تجزیه و تحلیل داده های رسانه های اجتماعی و فضایی قیمت مسکن در شنژن، چین. PLoS ONE 2016 , 11 , e0164553. [ Google Scholar ] [ CrossRef ]
  36. هوانگ، بی. وو، بی. Barry, M. رگرسیون وزن‌دار جغرافیایی و زمانی برای مدل‌سازی تغییرات مکانی-زمانی قیمت مسکن. بین المللی جی. جئوگر. Inf. علمی 2010 ، 24 ، 383-401. [ Google Scholar ] [ CrossRef ]
  37. Ioannides، YM; روزنتال، اس اس برآورد تقاضاهای مصرف و سرمایه گذاری برای مسکن و تأثیر آنها بر وضعیت تصدی مسکن. کشیش Econ. آمار 1994 ، 76 ، 127-141. [ Google Scholar ] [ CrossRef ]
  38. کامبر، ا. چی، ک. Huy، MQ; نگوین، کیو. لو، بی. Phe، HH; هریس، P. انتخاب متریک فاصله می تواند هم خطی بودن را در رگرسیون دارای وزن جغرافیایی کاهش دهد و هم القا کند. محیط زیست طرح. ب مقعد شهری. علوم شهر 2018 ، 47 ، 489-507. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  39. هاگناور، جی. Helbich، M. یک شبکه عصبی مصنوعی وزن جغرافیایی. بین المللی جی. جئوگر. Inf. علمی 2021 ، 1-21. [ Google Scholar ] [ CrossRef ]
  40. ژو، ایکس. تانگ، دبلیو. لی، دی. مدل سازی اجاره مسکن در منطقه شهری آتلانتا با استفاده از اطلاعات متنی و یادگیری عمیق. ISPRS Int. J. Geo-Information 2019 ، 8 ، 349. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  41. برنده، جی. لی، جی.اس. بررسی چگونگی تعیین اجاره بهای خانه های شهری کوچک: استفاده از مدل سازی لذت جویانه برای مسکن شهری در سئول. پایداری 2017 ، 10 ، 31. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  42. ژو، پی. لیو، ی. چن، ی. زنگ، سی. وانگ، زی. پیش‌بینی توزیع فضایی ساختمان‌های مسکونی بلندمرتبه با استفاده از یک مدل رگرسیون اتولوژیستی مبتنی بر میدان جغرافیایی. جی. هاوس. محیط ساخته شده 2015 ، 30 ، 487-508. [ Google Scholar ] [ CrossRef ]
  43. وو، جی. چن، ایکس. چن، اس. ویژگی های زمانی آب نماها در شهر ووهان و ترجیحات رفتاری مردم بر اساس داده های رسانه های اجتماعی. پایداری 2019 ، 11 ، 6308. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  44. زی، ز. Yan, J. تخمین تراکم هسته تصادفات ترافیکی در فضای شبکه. محاسبه کنید. محیط زیست سیستم شهری 2008 ، 32 ، 396-406. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  45. اندرسون، تخمین چگالی کرنل TK و خوشه‌بندی K-means به نمایه نقاط حادثه خیز جاده‌ای. اسید. مقعدی قبلی 2009 ، 41 ، 359-364. [ Google Scholar ] [ CrossRef ]
  46. انجام دهید، TMT; دوسه، او. میتینن، ام. Gatica-Perez, D. یک روش هسته احتمالی برای پیش بینی تحرک انسان با گوشی های هوشمند. اوباش فراگیر. محاسبه کنید. 2015 ، 20 ، 13-28. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  47. اداره آمار ووهان، جمهوری خلق چین سالنامه آماری ووهان 2021. در دسترس آنلاین: https://tjj.wuhan.gov.cn/tjfw/tjnj/202112/t20211220_1877108.shtml (در 2 نوامبر 2021 قابل دسترسی است).
  48. یو، ی. ژوانگ، ی. بله، AG-O. Xie، J.-Y. ما، سی.-ال. لی، Q.-Q. اندازه گیری استفاده ترکیبی مبتنی بر POI و روابط آنها با سرزندگی محله بین المللی جی. جئوگر. Inf. علمی 2016 ، 31 ، 658-675. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  49. لیانجیا وب سایت پرچمدار لیانجیا. در دسترس آنلاین: https://wh.lianjia.com/ (دسترسی در 2 نوامبر 2021).
  50. لی، اچ. وی، وای. وو، ی. تیان، جی. تجزیه و تحلیل قیمت مسکن در شانگهای با داده های باز: امکانات رفاهی، دسترسی و ساختار شهری. شهرها 2019 ، 91 ، 165–179. [ Google Scholar ] [ CrossRef ]
  51. وو، اچ. جیائو، اچ. یو، ی. لی، ز. پنگ، ز. لیو، ال. Zeng, Z. عوامل تأثیرگذار و مدل رگرسیونی قیمت مسکن شهری بر اساس داده‌های دسترسی باز اینترنت. پایداری 2018 ، 10 ، 1676. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  52. Fotheringham، AS; براندون، سی. چارلتون، ام. رگرسیون وزن‌دار جغرافیایی: تحلیل روابط متغیر فضایی . جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2003. [ Google Scholar ]
  53. Roth, AE The Shapley Value: Essays in Honor of Lloyd S. Shapley ; انتشارات دانشگاه کمبریج: کمبریج، بریتانیا، 1988. [ Google Scholar ]
  54. Rico-Juan، JR; د لاپاز، PT یادگیری ماشینی با قابلیت توضیح یا لذت فضایی؟ تحلیلی از قیمت های درخواستی در بازار مسکن در آلیکانته، اسپانیا. سیستم خبره Appl. 2021 ، 171 ، 114590. [ Google Scholar ] [ CrossRef ]
  55. Lundberg, S. SHAP (توضیحات افزودنی SHapley). در دسترس آنلاین: https://github.com/slundberg/shap (در 2 نوامبر 2021 قابل دسترسی است).
  56. چن، تی. Guestrin, C. Xgboost: A Scalable Tree Boosting System. در مجموعه مقالات بیست و دومین کنفرانس بین المللی ACM SIGKDD در مورد کشف دانش و داده کاوی، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، 13 تا 17 اوت 2016. [ Google Scholar ]
  57. مندز-اورتگا، سی. آرائوزو-کارود، جی.-ام. مکان یابی نرم افزار، بازی های ویدیویی و شرکت های الکترونیک ویرایش: استفاده از داده های میکروجغرافیایی برای مطالعه بارسلونا. J. فناوری شهری. 2019 ، 26 ، 81-109. [ Google Scholar ] [ CrossRef ]
  58. کول مارتینز، ای. مورنو-مونروی، A.-I.; آرائوزو-کارود، جی.-ام. تجمع صنایع خلاق: تجزیه و تحلیل درون شهری برای بارسلونا. پاپ Reg. علمی 2019 ، 98 ، 409-431. [ Google Scholar ] [ CrossRef ]
  59. لانگ، جی. مارکون، ای. Puech، F. اقدامات مبتنی بر فاصله تمرکز فضایی: معرفی یک تابع چگالی نسبی. ان Reg. علمی 2019 ، 64 ، 243-265. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  60. دورانتون، جی. تست Overman، HG برای محلی سازی با استفاده از داده های میکرو جغرافیایی. کشیش Econ. گل میخ. 2005 ، 72 ، 1077-1106. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  61. مک کوئین، جی. برخی روش‌ها برای طبقه‌بندی و تحلیل مشاهدات چند متغیره. در مجموعه مقالات پنجمین سمپوزیوم برکلی در مورد آمار و احتمالات ریاضی، برکلی، کالیفرنیا، ایالات متحده آمریکا، 21 ژوئن تا 18 ژوئیه 1965; جلد 1، ص 281-297. [ Google Scholar ]
  62. ژونگ، ی. فی، اف. Zhang، L. شبکه های عصبی کانولوشنال وصله بزرگ برای طبقه بندی صحنه تصاویر با وضوح فضایی بالا. J. Appl. Remote Sens. 2016 , 10 , 25006. [ Google Scholar ] [ CrossRef ]
  63. نیر، وی. واحدهای خطی Hinton، GE Rectified ماشین‌های بولتزمن محدود را بهبود می‌بخشند. در مجموعه مقالات بیست و هفتمین کنفرانس بین المللی کنفرانس بین المللی در مورد یادگیری ماشین (ICML’10)، حیفا، اسرائیل، 21 تا 24 ژوئن 2010. ص 807-814. [ Google Scholar ]
  64. آشیش، وی. Shazeer, N. پارمار، ن. Uszkoreit، J. جونز، ال. گومز، AN; قیصر، Ł. Polosukhin، I. توجه تمام چیزی است که شما نیاز دارید. در مجموعه مقالات پیشرفت‌ها در سیستم‌های پردازش اطلاعات عصبی، لانگ بیچ، کالیفرنیا، ایالات متحده آمریکا، 4 تا 9 دسامبر 2017. صفحات 5998–6008. [ Google Scholar ]
  65. خو، ک. با، ج. کیروس، آر. چو، ک. کورویل، آ. سالاخودینوف، ر. زمل، آر. Bengio، Y. نمایش، حضور و گفتن: ایجاد شرح تصویر عصبی با توجه بصری. در مجموعه مقالات سی و دومین کنفرانس بین المللی کنفرانس بین المللی در مورد یادگیری ماشین (ICML’15)، لیل، فرانسه، 6 تا 11 ژوئیه 2015. [ Google Scholar ]
  66. وولد، اس. اسبنسن، ک. گلادی، ص. تحلیل مؤلفه های اصلی. شیمی. هوشمند آزمایشگاه. سیستم 1987 ، 2 ، 37-52. [ Google Scholar ] [ CrossRef ]
  67. ون در ماتن، ال. هینتون، جی. تجسم داده ها با استفاده از T-Sne. جی. ماخ. فرا گرفتن. Res. 2008 ، 9 ، 2579-2605. [ Google Scholar ]
  68. لی، دبلیو. سریز، جی. یانگ، ی. هان، اچ. کاربرد t-SNE برای داده های ژنتیکی انسان. J. Bioinform. محاسبه کنید. Biol. 2017 ، 15 ، 1750017. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  69. میائو، آ. ژوانگ، جی. تانگ، ی. سلام.؛ چو، ایکس. لو، S. طبقه بندی واریته مبتنی بر تصویر فراطیفی دانه های ذرت مومی با مدل t-SNE و تجزیه و تحلیل پروکروستس. Sensors 2018 , 18 , 4391. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  70. رودر، اس. مروری بر الگوریتم‌های بهینه‌سازی گرادیان نزول. arXiv 2016 , arXiv:1609.04747. [ Google Scholar ]
  71. ژانگ، اس. میلیاچیو، جی. زندبرگن، PA; Guindani، M. ارزیابی تجربی روش‌های درونیابی سطحی مبتنی بر جغرافیایی برای تنظیم برآورد هزینه ساخت و ساز بر اساس مکان پروژه. J. Constr. مهندس مدیریت 2014 , 140 , 04014015. [ Google Scholar ] [ CrossRef ]
  72. ژانگ، اس. جعلی، SM; لیپیت، سی دی; Migliaccio، GC برآورد عوامل تنظیم مکان برای برآورد هزینه مفهومی بر اساس تصاویر ماهواره ای نور شبانه. J. Constr. مهندس مدیریت 2017 , 143 , 04016087. [ Google Scholar ] [ CrossRef ]
Ijgi 11 00053 g001 550
شکل 1. نمودار جریان کلی تحقیق این مقاله.
Ijgi 11 00053 g002 550
شکل 2. محدوده منطقه مورد مطالعه: ووهان، چین (مناطق شهری عبارتند از: ① جیانگ آن، ② جیانگهان، ③ کیائوکو، ④ کینگشان، ⑤ ووچانگ، ⑥ هانیانگ و ⑦ هونگشان).
Ijgi 11 00053 g003 550
شکل 3. تأثیر محلی “تعداد سوپرمارکت ها در فاصله 2 کیلومتری” بر قیمت مسکن اجاره ای (بر اساس تحلیل ارزش Shapley).
Ijgi 11 00053 g004 550
شکل 4. ساختار مدل CNN برای قیمت مسکن اجاره ای.
Ijgi 11 00053 g005 550
شکل 5. روش تبدیل متغیرهای قیمت اجاره مسکن به دو بعد.
Ijgi 11 00053 g006 550
شکل 6. پارامترهای مشاهده شده در طول فرآیندهای آموزشی: ( الف ) مدل FCNN، و ( ب ) مدل CNN (برای یک گروه متوسط).
Ijgi 11 00053 g007 550
شکل 7. چارچوب اصلی نورون ها در شبکه عصبی ( a ) نمونه ای از مدل FCNN و ( ب ) نمونه ای از مدل CNN.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید