این مقاله کاربرد بالقوه یک نسخه اصلاح شده از الگوریتم ژنتیک مرتب‌سازی غیرمسلط (NSGA)-II را برای برنامه‌ریزی کاربری زمین در جزایر مدیترانه که یک موجودیت جغرافیایی با ویژگی‌های مشابه را تشکیل می‌دهند، بررسی می‌کند. منطقه مورد مطالعه جزیره ناکسوس است که یک جزیره معمولی مدیترانه ای است. به منظور پایش تغییرات کاربری اراضی جزیره برای دوره 1987-2010، طبقه‌بندی مبتنی بر شی از سه تصویر Landsat انجام شده است. طبقه‌بندی کاربری زمین در سال 1987 جمعیت اولیه را برای الگوریتم ژنتیک (GA) تعریف کرد و هدف ارائه سناریوی توسعه بهینه برای جزیره ناکسوس با در نظر گرفتن قوانین، ویژگی‌های زمین‌شناسی و پارامترهای محیطی بود. GA به منظور ایجاد تغییرات کاربری زمین و در عین حال به حداکثر رساندن تناسب تبدیل، فشردگی، استفاده شد. بازده اقتصادی و به حداقل رساندن فرسایش خاک خروجی GA با توسعه واقعی جزیره مقایسه شد. نتایج فرآیند همگرایی الگوریتم پیشنهادی را تایید کرد، در حالی که راه‌حل‌های GA در نهایت یک جبهه پارتو را تشکیل دادند و در تمام اهداف به اندازه کافی عمل کردند. الگوریتم GA کاهش زمین کشاورزی آبی را به میزان 16 درصد، افزایش زمین کشاورزی خشک به میزان 131 درصد و حداکثر مجاز را با محدودیت های تعریف شده افزایش زمین شهری (100 درصد)، بیشتر در قسمت شرقی و مرکزی ناکسوس پیشنهاد کرده است. این تغییرات به طور قابل توجهی با توسعه واقعی جزیره متفاوت است. بازده اقتصادی پس از بهینه سازی 18 درصد افزایش یافت در حالی که فرسایش خاک از 1948 تن در سال به 1843 تن در سال کاهش یافت. نتایج فرآیند همگرایی الگوریتم پیشنهادی را تایید کرد، در حالی که راه‌حل‌های GA در نهایت یک جبهه پارتو را تشکیل دادند و در تمام اهداف به اندازه کافی عمل کردند. الگوریتم GA کاهش زمین کشاورزی آبی را به میزان 16 درصد، افزایش زمین کشاورزی خشک به میزان 131 درصد و حداکثر مجاز را با محدودیت های تعریف شده افزایش زمین شهری (100 درصد)، بیشتر در قسمت شرقی و مرکزی ناکسوس پیشنهاد کرده است. این تغییرات به طور قابل توجهی با توسعه واقعی جزیره متفاوت است. بازده اقتصادی پس از بهینه سازی 18 درصد افزایش یافت در حالی که فرسایش خاک از 1948 تن در سال به 1843 تن در سال کاهش یافت. نتایج فرآیند همگرایی الگوریتم پیشنهادی را تایید کرد، در حالی که راه‌حل‌های GA در نهایت یک جبهه پارتو را تشکیل دادند و در تمام اهداف به اندازه کافی عمل کردند. الگوریتم GA کاهش زمین کشاورزی آبی را به میزان 16 درصد، افزایش زمین کشاورزی خشک به میزان 131 درصد و حداکثر مجاز را با محدودیت های تعریف شده افزایش زمین شهری (100 درصد)، بیشتر در قسمت شرقی و مرکزی ناکسوس پیشنهاد کرده است. این تغییرات به طور قابل توجهی با توسعه واقعی جزیره متفاوت است. بازده اقتصادی پس از بهینه سازی 18 درصد افزایش یافت در حالی که فرسایش خاک از 1948 تن در سال به 1843 تن در سال کاهش یافت. افزایش 131 درصدی زمین های کشاورزی خشک و حداکثر مجاز با محدودیت های تعریف شده افزایش زمین شهری (100 درصد)، بیشتر در قسمت شرقی و مرکزی ناکسوس. این تغییرات به طور قابل توجهی با توسعه واقعی جزیره متفاوت است. بازده اقتصادی پس از بهینه سازی 18 درصد افزایش یافت در حالی که فرسایش خاک از 1948 تن در سال به 1843 تن در سال کاهش یافت. افزایش 131 درصدی زمین های کشاورزی خشک و حداکثر مجاز با محدودیت های تعریف شده افزایش زمین شهری (100 درصد)، بیشتر در قسمت شرقی و مرکزی ناکسوس. این تغییرات به طور قابل توجهی با توسعه واقعی جزیره متفاوت است. بازده اقتصادی پس از بهینه سازی 18 درصد افزایش یافت در حالی که فرسایش خاک از 1948 تن در سال به 1843 تن در سال کاهش یافت.
کلید واژه ها
برنامه ریزی کاربری زمین ، بهینه سازی چند هدفه ، الگوریتم ژنتیک ، NSGA-II ، Landsat ، OBIA
1. مقدمه
منابع نقش برجسته ای در شکل گیری و اجرای سیاست های مرتبط با توسعه پایدار دارند [ 1 ] . با این حال، بررسی راه بهینه ای که منابع باید برای دستیابی به اهداف خاص تخصیص داده شود، یک سرمایه گذاری چالش برانگیز است. نام این مشکلات مشکلات تخصیص منابع (RAPs) [ 2 ] است. زمین یکی از با ارزش ترین منابع است، بنابراین بسیاری از RAP ها مربوط به تخصیص کاربری زمین [ 1 ] است، اصطلاحی که برای توصیف «فرایند تخصیص فعالیت ها یا کاربری های مختلف به واحدهای خاص یک منطقه در یک منطقه» استفاده می شود [ 3 ].] . چنین مسائلی چندهدفه هستند و پیچیدگی محاسباتی قابل توجهی دارند زیرا: 1) پارامترهای چندگانه، گاهی اوقات حتی متناقض باید تحلیل شوند. 2) مجموعه ای از ترکیبات راه حل ممکن باید ارزیابی شود. 3) تعاملات پیچیده بین قطعات زمین اختصاص داده شده باید بررسی شود و 4) آنها به بسیاری از زمینه ها مرتبط هستند [ 3 ] [ 4 ]. به ندرت یک راه حل منحصر به فرد این مسائل پیچیده چند هدفه غیرخطی را به اندازه کافی بهینه می کند. بنابراین این مسائل به عنوان مسائل چند جمله ای غیر قطعی مشخص می شوند و “به روش های اکتشافی برای اجرای فرآیندهای بهینه سازی نیاز دارند” [ 1 ].
جزایر مدیترانه ای واحدهای فضایی متمایز هستند که ویژگی های اقلیمی، زمین شناسی و هیدرولوژیکی و همچنین چشم انداز، تنوع زیستی و فعالیت های اقتصادی مشابهی دارند. ابزارهای مناسب برای تسهیل تخصیص منابع در جزایر مدیترانه مورد نیاز است، موضوعی که اهمیت حیاتی دارد زیرا جزیره‌ای بودن به طور قابل‌توجهی بر منابع موجود و در نتیجه همه سیاست‌های مرتبط تأثیر می‌گذارد.
این مقاله کاربرد بالقوه یک نسخه اصلاح شده از الگوریتم ژنتیک مرتب‌سازی غیرمسلط (NSGA)-II را برای برنامه‌ریزی کاربری زمین در جزایر مدیترانه بررسی می‌کند. با در نظر گرفتن قوانین، ویژگی های زمین شناسی و پارامترهای محیطی، NSGA-II برای ارائه سناریوی توسعه بهینه برای یک جزیره مدیترانه ای استفاده شد. برای این حوزه، الگوریتم ژنتیک (GA) برای معرفی تغییرات کاربری اراضی، در عین به حداکثر رساندن تناسب تبدیل، فشردگی، بازده اقتصادی و به حداقل رساندن فرسایش خاک برنامه‌ریزی شد. NSGA-II یک الگوریتم پرکاربرد و یک استاندارد مقایسه است، بنابراین نویسندگان استفاده از این الگوریتم را به عنوان نقطه شروعی برای تحقیقات خود در مورد تخصیص کاربری زمین در جزایر در نظر می گیرند، در حالی که مطالعات مقایسه ای بیشتری باید توسعه یابد. با توجه به ادبیات [ 5]، NSGA-II GA قبلاً با موفقیت برای حل مسائل تخصیص کاربری زمین که دارای چهار هدف هستند، استفاده شده است، زیرا در مقایسه با سایر الگوریتم های اکتشافی به اندازه کافی عمل می کند. جزیره ناکسوس به عنوان منطقه مورد مطالعه یک جزیره متوسط مدیترانه ای با چشم انداز معمولی مدیترانه ای، سکونتگاه های شهری متوسط، تنوع زیستی و ویژگی های اقلیمی است که فعالیت های اقتصادی آن به طور مساوی بین همه بخش ها توزیع شده و ثروت فرهنگی بی شماری دارد.
علاوه بر اصلاح NSGA-II، این کار تحقیقاتی همچنین به انطباق NSGA-II با جزایر مدیترانه برای بهینه‌سازی کاربری اراضی می‌پردازد، که نیازمند محدودیت‌های بیشتری مانند محدودیت‌های قانونی، الگوهای کاربری/پوشش زمین، فرسایش است. پارامترها و غیره. انتظار می‌رود که نتایج این تحقیق بتواند ابزاری برای حمایت از برنامه‌ریزی کاربری اراضی در جزایر مدیترانه، بر اساس نسخه اصلاح‌شده NSGA-II یا الگوریتم مرتبط دیگری ارائه کند. چنین ابزاری می تواند در بهبود اثربخشی اقتصادی و زیست محیطی اولویت های توسعه پیشنهادی کمک کند. علاوه بر این، ساختار اجتماعی جزایر خاص با تخصیص کاربری‌ها در یک الگوی بهینه در واحدهای فضایی متمایز، که ویژگی‌های کاملاً متفاوتی را برای سرزمین اصلی ارائه می‌دهند، تقویت می‌شود.1 ] .
بخش 2 مروری بر ادبیات روش شناسی های اصلی، مورد استفاده برای مدیریت مسائل چندهدفه، همراه با ویژگی های روش شناسی جبهه پارتو [ 6 ] ارائه می کند. ویژگی ها و عملگرهای اولیه NSGA-II در بخش 3 توضیح داده شده است، در حالی که بخش 4 مواد و روش های مورد استفاده را نشان می دهد. بخش 5 نتایج به دست آمده را خلاصه می کند. در نهایت، مسائل نوظهور برای تحقیقات آینده و همچنین نتیجه گیری این مقاله در بخش 6 خلاصه می شود.
2. بهینه سازی چند هدفه و جبهه پارتو
به منظور حل مشکلات تخصیص کاربری اراضی می توان از دو نوع روش استفاده کرد. نوع اول، روش‌شناسی جمع وزنی است که «مسئله بهینه‌سازی چندهدفه (MOP) را با در نظر گرفتن مجموع وزنی خطی اهداف چندگانه به یک مسئله بهینه‌سازی تک هدفی (SOP) تبدیل می‌کند» [ 3 ]. این روش‌شناسی‌ها می‌توانند «با تنظیم مکرر وزن‌های مرتبط با اهداف مختلف و به‌کارگیری مکرر تکنیک‌های بهینه‌سازی تک‌هدفه، جبهه پارتو را شکل دهند» [ 3 ]] . این روش‌شناسی‌ها ساده هستند و زمانی که برای مقابله با مسائل کاملاً ساختاریافته استفاده می‌شوند، کارایی و اثربخشی بهتری نشان می‌دهند که تعداد محدودی از ترکیب‌های راه‌حل ممکن، تعداد کمی از واحدهای زمین قابل تخصیص و همچنین تعداد کم تکرار برای بهینه‌سازی همه موارد کافی است. اهداف آنها [ 3 ]. با این حال، آنها نیاز به دانش قبلی از مشکل تحت ارزیابی دارند و راه حل های توزیع نابرابر را با نادیده گرفتن جبهه پارتو [ 3 ] [ 7 ] ایجاد می کنند. نوع دوم روش‌شناسی تخصیص کاربری زمین به روشهای اکتشافی [ 8 ] مربوط می‌شود. این روش‌شناسی، تعیین روابط توسعه‌یافته بین اهداف مسئله مورد بررسی را تسهیل می‌کند [ 3] . بسیاری از روشهای محاسباتی اکتشافی با هدف حل مسائل تخصیص منابع گزارش شده‌اند و برجسته‌ترین آنها [ 1 ] عبارتند از: الگوریتم‌های بازپخت شبیه‌سازی شده (SA)، الگوریتم‌های مورچه‌ها و الگوریتم‌های ژنتیک (GA)، که نقش برجسته‌ای در این امر دارند. فرآیند [ 9 ] [ 10 ] . این تکنیک‌های اکتشافی «اگرچه نمی‌توانند ترکیب بهینه کاربری زمین را تضمین کنند، اما می‌توانند یک ترکیب تقریباً بهینه را در یک زمان معقول ایجاد کنند» [ 3 ] با «شبیه‌سازی پدیده‌های فیزیکی، فرآیندهای بیولوژیکی یا رفتار ازدحام» [ 3 ]. در طول دهه‌های گذشته، بسیاری از تلاش‌های تحقیقاتی با هدف اعمال روشهای محاسباتی تکاملی برای حل RAPها در ادبیات گزارش شده است [ 11 ] – [ 17 ]] .
GAها نقش برجسته‌ای در این فرآیند دارند زیرا می‌توانند عملکرد الگوریتم‌های فضایی مورد استفاده برای دستیابی به تخصیص کاربری زمین [ 18 ] را بهبود بخشند، در حالی که تجزیه و تحلیل عوامل مختلف را نیز ممکن می‌سازند (به عنوان مثال فضای راه‌حل بزرگ، مشکلاتی که با عدم قطعیت مشخص می‌شوند). بکارگیری این الگوریتم ها در مسائل برنامه ریزی کاربری اراضی در دو دهه گذشته رونق یافته است. یک الگوریتم ژنتیک چند هدفه با موفقیت توسط متیوز [ 19 ] برای رسیدگی به یک مشکل تخصیص کاربری زمین مورد استفاده قرار گرفت. به منظور به حداقل رساندن فرسایش خاک و به حداکثر رساندن منافع در حوضه آبخیز بریموند در ایران یک الگوریتم خطی چندهدفه توسط نیارکی و کیم [ 20 ] معرفی شد. هوانگ و همکاران [ 3] از سیستم ایمنی مصنوعی برای تخصیص کاربری زمین چند هدفه (AIS-MOLA) GA به منظور یافتن الگوی تخصیص بهینه در مسائل تخصیص در مقیاس بزرگ استفاده کرد. Eldrandaly [ 21 ] یک پلت فرم آنلاین سیستم اطلاعات جغرافیایی (GIS) همراه با برنامه نویسی بیان ژن (GEP) را برای توزیع سه نوع کاربری آزمایشی زمین معرفی کرد. حاجه فروش نیا و همکاران. [ 22 ] مناطق یک پناهگاه حیات وحش را با استفاده از تخصیص زمین چند هدفه (MOLA) GA اختصاص داد. کائو و همکاران [ 23 ] مشکلات تخصیص کاربری زمین را با تعبیه تکنیک های محاسباتی موازی و NSGA-II حل کرد. پورتا و همکاران [ 24 ] یک سیستم ترکیبی ایجاد کرد که الگوریتم های ژنتیک و جاوا را برای ایجاد سناریوهای استفاده از زمین ترکیب می کرد. شایگان و همکاران [ 5] ثابت کرد که NSGA-II در مقایسه با هدف دستیابی-تخصیص زمین چندهدفه (GoA-MOLA) با موفقیت عمل می کند. محققان [ 25 ] یک نسخه اصلاح شده از NSGA-II، به نام NSGA-III، برای رسیدگی به مسائلی ارائه کردند که شامل چهار یا حتی بیشتر هدف می شود، در حالی که نسخه دیگری به نام NSGA-II مبتنی بر نقطه مرجع، مشخص کردن نقاط مرجع را تسهیل می کند. کاربران برای “هدایت جستجو در فضای هدف و تنوع مجموعه پارتو متمرکز را می توان کنترل کرد” [ 26 ].
مشکلات دنیای واقعی به اهداف بسیار و پیچیده مربوط می شود. بنابراین، بررسی اینکه آیا بیش از یک الگوی تخصیص وجود دارد که نتایج نزدیک به بهینه را ایجاد می کند، ضروری است. این فرآیند تخصیص چندهدفه نامیده می‌شود و هدف آن «آشکار کردن راه‌حل‌های ممکن با کارایی نسبی در همه اهداف انتخاب‌شده» [ 3 ] است. اصطلاح بهینه سازی در مسائل چندهدفه برای توصیف فرآیند “ایجاد بهترین سازش ممکن بین اهداف” استفاده می شود [ 27 ].
برجسته‌ترین روش برای آشکار کردن شکل مجموعه‌ای از راه‌حل‌ها به عنوان جایگزین‌های بهینه پارتو [ 6 ] شناخته می‌شود، در حالی که «تصویر آن در فضای عینی، جبهه پارتو نامیده می‌شود» [ 11 ]، که «راه‌حل‌هایی را نشان می‌دهد که عملکرد آنها روی یک هدف است». نمی توان بدون قربانی کردن عملکرد حداقل یکی دیگر را بهبود بخشید» [ 11 ]. این به عنوان بهینه پارتو [ 6 ] شناسایی شده است. معنای مهم در تشکیل جبهه پارتو، مفهوم تسلط پارتو است به این معنی که “یک جایگزین در صورتی که در مقایسه زوجی برای حداقل یک هدف برتری داشته باشد و حداقل عملکرد برابر در بقیه اهداف داشته باشد، بر دیگری غالب می شود” [ 27 ].] . یک راه حل بهینه پارتو زمانی تشکیل می شود که فرآیند تسلط به پایان برسد، بنابراین “مجموعه غیر غالب معمولاً به عنوان تقریبی از جبهه پارتو واقعی استفاده می شود” [ 11 ]. از نظر ریاضی در چنین مسئله ای با k هدف، “یک راه حل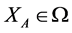 
بر دیگری غالب 
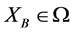می شود اگر” [ 11 ]:
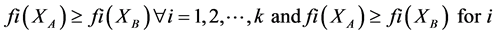(1)
که در آن: fi(x) مقدار تابع هدف هدف i برای حل x است.
X A یک راه حل است.
X B یک راه حل است.
k اهدافی هستند که دنبال می شوند.
3. مدل NSGA-II
در NSGA-II به منظور «مرتب‌سازی جمعیت در جبهه‌های مختلف از روش رتبه‌بندی غیر غالب» استفاده شده است [ 28 ] [ 29 ]. اهداف NSGA-II با توجه به شایگان و همکاران. [ 5 ] عبارتند از: 1) ایجاد جمعیتی از افراد. 2) از سطح غیر سلطه برای رتبه بندی و مرتب سازی هر فرد استفاده کنید. 3) مجموعه های جدیدی از فرزندان ایجاد کنید. 4) قبل از پیشنهاد الگوهای تخصیص جدید، والدین و فرزندان را ترکیب کنید. 5) با تخمین فاصله ازدحام بین هر فرد، یک جبهه پارتو طراحی کنید.
فاصله ازدحام یک پارامتر حیاتی برای NSGA-II است [ 13 ] [ 30 ]. این اصطلاح برای توصیف روشی استفاده می‌شود که “تراکم محلول‌های اطراف یک محلول خاص را تخمین می‌زند” [ 31 ] با ارزیابی “فاصله متوسط بین دو نقطه در دو طرف این نقطه در امتداد محورهای هدف” [ 30 ]. در اکثر مسائل تخصیص، یک حلقه برای تخمین “تمام فواصل ازدحام برای هر راه حل فعال شده” تولید می شود [ 3 ].
یک کروموزوم در NSGA-II طراحی شده است تا راه حل یک مشکل را ترسیم کند، در حالی که ژن های کروموزوم پارامترهای مشکل هستند [ 2 ]. مجموعه ای از کروموزوم ها با استفاده از اولیه سازی، متقاطع و عملگرهای جهش NSGA-II [ 1 ] [ 2 ] تشکیل می شود.
3.1. اپراتور مقداردهی اولیه
انتخاب جمعیت اولیه برای NSGA-II اهمیت حیاتی پیدا می کند [ 1 ] [ 3 ]. مقداردهی اولیه کروموزوم مناسب فرآیند تخصیص را ارزان تر، سریع تر و کارآمدتر می کند، به ویژه در مسائل بزرگ و پیچیده [ 2 ] [ 30 ]. بنابراین، راهنمایی در تولید راه حل های اولیه رضایت بخش ممکن است برای دستیابی به نتایج بهینه اجرا شود.
3.2. اپراتور متقاطع
این عملگر با انجام یک فرآیند تکاملی فعال، الگوهای سلولی مناسبی را طراحی می کند [ 2 ]. یک اپراتور متقاطع “به طور تصادفی ژن ها را بین دو کروموزوم مبادله می کند و به آنها اجازه می دهد تا از این طریق بخش های مفید یک منطقه خاص را پیدا کنند” [ 3 ] [ 31 ]. بسیاری از محققانی که روی مسائل تخصیص کاربری زمین کار می کنند، استفاده از عملگرهای متقاطع دو بعدی را پیشنهاد کرده اند که هنگام کار با داده های مکانی مناسب تر هستند [ 2 ] [ 3 ] [ 5 ] [ 29 ]. با این حال، در این کار از متقاطع باینری استاندارد دو نقطه [ 32 ] استفاده شده است همانطور که بعدا توضیح داده خواهد شد.
3.3. اپراتور جهش
NSGA-II از یک عملگر جهش برای تولید فرزندان یا بهبود فرزندان ایجاد شده توسط اپراتور متقاطع استفاده می کند. “به طور تصادفی یک واحد را انتخاب می کند و کاربری زمین آن را تغییر می دهد تا الگوی بهتری از تخصیص را با توجه به پارامترهای اجرا شده پیدا کند” [ 31 ]. برخی از محققان همچنین عملگرهای جهش خاصی را برای مشکلات تخصیص کاربری زمین پیشنهاد کرده اند [ 2 ]، اما در این کار از یک عملگر جهش عمومی استفاده شده است که مقادیر دو ژن به طور تصادفی انتخاب شده را با هم عوض می کند.
4. مواد و روش ها
در این بخش، ویژگی‌های اصلی منطقه مورد مطالعه، پردازش داده‌ها و فرمول‌بندی مدل تشریح می‌شود.
4.1. منطقه مطالعه
ناکسوس ( شکل 1 ) بزرگترین جزیره جزایر Cyclades یونان است (429 متر مربع). در مرکز دریای اژه (عرض جغرافیایی 37˚6’20” شمالی و طول جغرافیایی 25˚22’35” شرقی) و متعلق به منطقه دریای اژه جنوبی است. زئوس (1004 متر) و فناری (908 متر) بلندترین کوه های جزیره ناکسوس هستند، بنابراین، زمین آن کوهستانی است. زمینه زمین شناسی جزیره ناکسوس از شیست، گنیس و سنگ مرمر در لایه های متناوب با گرانودیوریت و گرانیتوئید تشکیل شده است.
4.2. داده ها
در این مطالعه از GIS و داده های سنجش از دور استفاده شد. داده‌های GIS مورد استفاده لایه‌های GIS مربوط به رودخانه‌ها، دریاچه‌ها، نهرها، جاده‌ها، سایت‌های حفاظت طبیعی ۲۰۰۰، پناهگاه‌های حیات وحش، تالاب‌های جزیره‌ای کوچک بودند که توسط زیرساخت داده‌های فضایی ملی دولت یونان در دسترس بودند [ 33 ]. ساحل اولیه جزیره ناکسوس، که در آن محدودیت های قانونی خاص اعمال می شود، توسط آژانس ملی کاداستر و نقشه برداری یونان ارائه شده است.
برای پایش طول جغرافیایی منطقه مورد مطالعه از سه تصویر Landsat TM برای سال‌های 1987، 2001 و 2010 استفاده شد. این تصاویر با استفاده از نرم افزار Object-Based Image Analysis (OBIA) و به ویژه eCognition Developer نسخه 8.7 طبقه بندی شده اند. تصاویر Landsat TM در همان پروژه درج شدند و
(الف) تصویر Landsat TM از Naxos. ترکیب رنگ 321 (RGB) (ب) طبقه بندی 1987
(ج) طبقه بندی 2001 (د) طبقه بندی 2010
شکل 1 . تصویر Landsat TM از ناکسوس و نتایج طبقه بندی برای سال های 1987، 2001 و 2010.
سه سطح تقسیم بندی ایجاد شده است، یکی برای هر تصویر Landsat TM. تقسیم بندی چند وضوح [ 34پارامترهای ] عبارت بودند از: مقیاس = 3، شکل = 0.3 و فشردگی = 0.5 با در نظر گرفتن همه باندهای حرارتی سه تصویر، برای تولید قطعات یکسان در همه تصاویر. مناطق تمرین و آزمایش بر روی صفحه نمایش با تفسیر عکس با پشتیبانی از حقیقت زمین و داده های جانبی انتخاب شده اند و دو ماسک ایجاد شده است، یکی برای آموزش و دیگری برای آزمایش. مناطق آموزش و آزمایش در مکان‌هایی انتخاب شدند که هیچ تغییر کاربری زمین در طول دوره بیست و سه ساله مورد بررسی اتفاق نیفتاده است، که در همه تصاویر رایج است. هفت طبقه برای طبقه بندی استفاده شده است که عبارتند از: زمین کشاورزی آبی، زمین کشاورزی دیم، علفزار، جنگل، زمین شهری، آب و غیره. مناطق آب با استفاده از قانون تابع عضویت فازی بر اساس NDWI طبقه بندی شدند [ 35] (NDWI > 0، فضای فازی: -0.02 تا 0.02). قوانین استاندارد نزدیکترین همسایه برای بقیه طبقات کاربری زمین استفاده شده است. یک قانون تابع عضویت فازی نیز به رده کاربری اراضی شهری اضافه شده است که اجازه نمی‌دهد بخشی به عنوان زمین شهری در تصویر قدیمی‌تر طبقه‌بندی شود، اگر زمین شهری در تصاویر جدیدتر وجود نداشته باشد. دقت کلی سه طبقه بندی برای سال های 1987، 2001 و 2010 به ترتیب 82، 81 و 84 درصد بود. ضرایب توافق کاپا [ 36 ] 0.79، 0.78 و 0.81 بود. شکل 1 جزیره ناکسوس را به همراه نقشه های کاربری اراضی گردآوری شده نشان می دهد، در حالی که جدول 1 تغییرات دوره ای کاربری ها در منطقه مورد مطالعه را بر اساس آمار این نقشه ها نشان می دهد.
مقایسه بین طبقه‌بندی سال‌های 1987 و 2001 ( جدول 1 ) نشان می‌دهد که طی این سال‌ها در زمین‌های کشاورزی آبی 6 درصد و در زمین‌های کشاورزی دیم 17 درصد افزایش داشته است، در حالی که بیشترین میزان افزایش (60 درصد) مربوط به زمین‌های شهری بوده است. همچنین مقایسه طبقه‌بندی سال 1987 با طبقه‌بندی سال 2010 نشان می‌دهد که اراضی دیم 53 درصد، اراضی کشاورزی آبی 37 درصد و اراضی شهری 112 درصد افزایش یافته است.
4.3. فرمولاسیون مدل و تحقق الگوریتم
این مدل در Ansi C بر اساس برنامه های ارائه شده توسط Deb و همکاران طراحی و ساخته شد. [ 37 ] در وب سایت خود [ 38 ] . برنامه های اصلی به منظور کار با تصاویر طبقه بندی داده های سنجش از راه دور و همچنین سایر لایه های شطرنجی GIS اصلاح شده اند.
مفهوم اساسی برای فرمولاسیون مدل این بود که مجموعه ای از قطعات کاربری زمین را می توان به عنوان یک کروموزوم در نظر گرفت. به دنبال این مفهوم، هر قطعه کاربری زمین همانطور که در بخش 3 توضیح داده شد، به عنوان یک ژن در نظر گرفته می شود. در مورد ما، مجموعه ای از قطعات کاربری زمین از n ردیف (n = 160) و m ستون (m = 122) با فضایی وضوح 216 متر نشان دهنده منطقه مورد مطالعه جزیره ناکسوس است. بنابراین، اگر تمام قطعات کاربری زمین در نظر گرفته شوند، یک کروموزوم با 122 × 160 = 19520 ژن ایجاد می‌شود و هر ژن که به‌عنوان یک متغیر باینری کدگذاری می‌شود، به تعداد کلاس‌های در نظر گرفته شده به تعداد بیت‌های زیر خواهد داشت [ 5 ]:
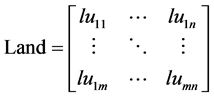(2)
جایی که: زمین کروموزوم است.
lu i, j قطعات کاربری زمین هستند.
هر واحد فضایی (پیکسل) نقشه کاربری زمین به عنوان یک متغیر باینری lu i,j در نظر گرفته می شود و هر کلاس کاربری زمین به عنوان یک متغیر تصمیم گیری فرض می شود، lu [ 5 ]:
(3)
که در آن: 1 = زمین کشاورزی آبی
2 = زمین کشاورزی خشک
3 = علفزار
4 = جنگل ها
5 = شهری
6 = آب
7 = دیگر
در اینجا لازم به ذکر است که در این کار کروموزوم به صورت یک کروموزوم و نه کروموزوم دو بعدی طراحی شده است. اما باید اضافه کرد که جدای از کاربری هایی که به عنوان ژن کدگذاری می شوند
جدول 1 . تغییرات دیاکرونی کاربری اراضی در منطقه مورد مطالعه در هکتار.
کروموزوم، موقعیت مکانی برای هر قطعه کاربری زمین (پیکسل) نیز ذخیره می شود. به این ترتیب، NSGA-II با استفاده از کروموزوم های تک بعدی اعمال می شود و ساده تر و سریع تر است، در حالی که توابع هدف و محدودیت ها در دو بعد اعمال می شوند. با توجه به این طراحی کروموزوم، هیچ عملگر متقاطع دو بعدی نمی تواند اعمال شود و بنابراین عملگر متقاطع باینری دو نقطه ای [ 32 ] به کار گرفته شده است.
در طول تحقق الگوریتم، برخی بهینه‌سازی‌های اساسی و افزودن ویژگی‌ها صورت گرفت. با هدف افزایش سرعت اجرای الگوریتم بهینه‌سازی چند هدفه و کاهش اندازه جمعیت، همه پیکسل‌های طبقه‌بندی در جامعه خوانده نمی‌شوند. کاربر ممکن است کلاس هایی را که باید بدون تغییر باقی بمانند (مانند آب، جنگل ها و غیره) حذف کند. فقط طبقات باقی مانده در جمعیت به حساب می آیند. علاوه بر این، گزینه ای به کاربر داده می شود تا برخی از کلاس ها را قفل کند تا اگر چه این کلاس ها می توانند توسط الگوریتم ژنتیک ایجاد شوند، وصله های فعلی آنها باید بدون تغییر باقی بمانند (یعنی زمین شهری موجود). از آنجایی که مقداردهی اولیه الگوریتم برای همگرایی سریع الگوریتم مهم است، جمعیت اولیه تصادفی نیست. بجای، وضعیت کاربری فعلی/پوشش زمین (از نقشه کاربری زمین شطرنجی یا تصویر طبقه بندی) جمعیت اولیه را مشخص می کند. ویژگی دیگری که به برنامه های اصلی اضافه شده است، توانایی خواندن تعدادی دیگر از لایه های شطرنجی GIS است که می توان از آن استفاده کرد: الف) برای تحقق توابع هدف (یعنی نقشه شیب، نقشه زمین شناسی و غیره). ب) برای اعمال محدودیت ها (به عنوان مثال سایت های حفظ). و ج) به عنوان ماسک برای مناطق خاصی که باید بدون تغییر باقی بمانند و در نتیجه از جمعیت نیز حذف شوند. ب) برای اعمال محدودیت ها (به عنوان مثال سایت های حفظ). و ج) به عنوان ماسک برای مناطق خاصی که باید بدون تغییر باقی بمانند و در نتیجه از جمعیت نیز حذف شوند. ب) برای اعمال محدودیت ها (به عنوان مثال سایت های حفظ). و ج) به عنوان ماسک برای مناطق خاصی که باید بدون تغییر باقی بمانند و در نتیجه از جمعیت نیز حذف شوند.
در جزیره ناکسوس، ایده اصلی این بود که با وضعیت کاربری زمین جزیره در سال 1987 شروع شود، یک سناریوی توسعه بهینه با استفاده از NSGA-II اصلاح شده محاسبه شود و آن‌طور که ارزیابی شده است با توسعه واقعی جزیره مقایسه شود. طبق طبقه بندی 2001 و 2010. بنابراین، ژن‌های جمعیت اولیه تصادفی نبودند، بلکه مستقیماً از تصویر طبقه‌بندی 1987 خوانده شدند. طبقات کاربری زمین آب و جنگل از جمعیت حذف شدند، زیرا این طبقات باید بدون تغییر باقی بمانند. علاوه بر این، یک جزیره کوچک در جنوب شرقی ناکسوس (ایراکلیا) پوشیده شده است. با این استثناها، جمعیت اولیه 70 درصد از 19520 به 6032 ژن کاهش یافت. رده زمین شهری قفل شد، برای اینکه الگوریتم بهینه‌سازی بتواند زمین شهری ایجاد کند اما زمین شهری موجود نباید به هیچ کاربری دیگر تبدیل شود. این لایه‌ها بعداً در بخش‌های مربوطه ارائه می‌شوند که تابع هدف و تعاریف محدودیت را توضیح می‌دهند.
تا آنجایی که به پارامترهای زمان اجرا الگوریتم مربوط می شود، اندازه جمعیت پس از در نظر گرفتن کلاس ها و/یا ماسک های حذف شده مستقیماً از تصویر طبقه بندی خوانده می شود و حداکثر اندازه آن به حافظه فیزیکی رایانه بستگی دارد، زیرا استفاده از حافظه swap بسیار می تواند باشد. افزایش زمان اجرای الگوریتم نرخ احتمال متقاطع و جهش توسط کاربر تعریف می‌شود، اگرچه نرخ احتمال جهش بهینه برابر با 1/(تعداد کل بیت‌ها) است. تکرارهای الگوریتم و همچنین تعداد نسل ها توسط کاربر ارائه می شود. تحقق الگوریتم بر روی یک پردازنده Core Duo E8400 @ 3.0 گیگاهرتز با 8.0 گیگابایت رم و سیستم عامل لینوکس انجام شد. جمعیتی متشکل از 6032 ژن (متغیرهای باینری) با هر کدام 5 بیت (5 کلاس طبقه بندی فعال) تقریباً حداکثر جمعیت قابل استفاده با 8 بود. 0 گیگابایت رم. نرخ بهینه احتمال جهش برای این جمعیت 3.3 × 10 بود-5 ، و نرخ احتمال متقاطع 0.7 استفاده شد.
4.4. توابع و محدودیت های هدف
مشکل توصیف شده در این مطالعه با استفاده از چهار تابع هدف تشکیل شده است که هدف آن به حداکثر رساندن بازده اقتصادی، تناسب تبدیل، فشردگی لکه کاربری زمین و به حداقل رساندن فرسایش خاک است. الگوریتم به گونه ای فرموله شده است که تلاش می کند تمام توابع هدف داده شده را به حداقل برساند، و بنابراین اگر یک تابع باید حداکثر شود (یعنی هدف بازده اقتصادی) از منفی مقدار تابع استفاده می شود.
4.4.1. هدف بازده اقتصادی
الگوهای مختلف کاربری زمین منافع اقتصادی متفاوتی را به همراه دارد. بنابراین، تخصیص کاربری‌ها به گونه‌ای حیاتی است که به حداکثر رساندن سود اقتصادی بدون بدتر شدن اولویت‌های توسعه پایدار باشد. حداکثر بازده اقتصادی (Z 1 ) در سال با استفاده از فرمول (4) محاسبه شد. بر اساس ارزش‌های به‌روز بازار و شواهد تجربی برای جزایر یونان، زمین شهری باید دوازده برابر ارزش زمین‌های علفزار، شش برابر ارزش زمین‌های کشاورزی خشک و سه برابر ارزش زمین‌های کشاورزی آبی ارزیابی شود.
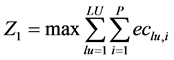(4)
که در آن: Z 1 نشان دهنده هدف بازده اقتصادی است.
ec lu، i بازده اقتصادی ناشی از کاربری زمین lu است که در واحد i اعمال می شود.
lu هر کلاس کاربری زمین است.
LU تعداد کل طبقات کاربری زمین است.
P مخفف کل جمعیت واحدها است.
4.4.2 هدف فشردگی
فشردگی شامل دو مفهوم مجزا است که عبارتند از تداوم و سازگاری. “همسایگی مستلزم این است که تمام سلول‌های دارای کاربری یکسان به هم متصل شوند در حالی که سازگاری سلول‌ها را به خوشه‌ها مرتب می‌کند” [ 1 ]. از تحلیل فوق می توان نتیجه گرفت که سازگاری شامل مجاورت نیز می شود. در این تحقیق از اصطلاح فشردگی برای توصیف این روابط استفاده شده است. فشردگی دسترسی را افزایش می دهد، برابری اجتماعی را ترویج می کند، مصرف انرژی را کاهش می دهد [ 1 ] و به استفاده کارآمد از منابع کمک می کند [ 39 ]. در برنامه ریزی شهری، فشردگی با تراکم بالا و کاربری های مختلط ترکیب می شود. اولویت های پایداری فشردگی را به برابری و عدالت اجتماعی مرتبط می کند [ 40] . اینها اهداف مهمی در مسائل تخصیص کاربری زمین هستند، اما حل آنها دشوار است. مقادیر سازگاری بین کاربری‌ها ( جدول 2 ) پس از تجزیه و تحلیل مرور ادبیات [ 1 ] و شواهد تجربی محاسبه شد.
از فرمول (5) زیر برای محاسبه هدف فشردگی (Z 2 ) استفاده شده است 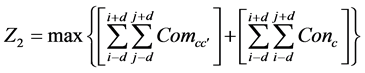[ 5 ]:
(5)
که در آن: Z 2 نشان دهنده هدف فشردگی است.
Com cc سازگاری بین کلاس c و کلاس c است ( جدول 2 ).
Conc تعداد سلول های همسایه سلول (i,j) در همان کلاس را نشان می دهد.
d فاصله جستجو از سلول مرکزی است.
در مدل اصلاح شده NSGA-II، فاصله d می تواند توسط کاربر برای مجاورت و سازگاری به طور مستقل انتخاب شود. در اجرای نهایی مدل توسعه‌یافته d به صورت 1 تعریف شده است که الگوریتم را در اندازه پنجره 3×3 کار می‌کند. این بهترین انتخاب برای هدف سازگاری است زیرا طبقات کاربری زمین واقعاً همسایه را بررسی می کند. مقدار d = 1 برای مجاورت نیز به خوبی کار می کند، در حالی که انتخاب های دیگری مانند d = 2 یا d = 3 منجر به نتایج بدتری برای این مطالعه موردی شد.
4.4.3. هدف مناسب بودن تحول
این تابع هدف تغییر کاربری زمین را از وضعیت فعلی هر قطعه به کاربری جدید بهینه می کند [ 41 ]. در مطالعه موردی ما، از آنجایی که قطعه‌های زمین متعلق به طبقه کاربری «Other» زمین‌های بایر هستند و بنابراین نمی‌توان از آنها برای کشاورزی استفاده کرد، با استفاده از این هدف، این قطعه‌ها ترجیح داده شد تا به زمین شهری تبدیل شوند. علاوه بر این، تبادل نوع کشاورزی مجاز بود، در حالی که علفزارها اجازه داشتند به همه دسته‌های دیگر به غیر از «Other» تبدیل شوند. جدول زیر مقادیر تناسب از به تبدیل استفاده شده برای این هدف را ارائه می دهد ( جدول 3 ).
برای این هدف از فرمول زیر استفاده شده است:
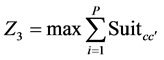(6)
که در آن: Z 3 نشان دهنده هدف مناسب بودن تبدیل است.
کت و شلوار cc ‘ فاکتور تناسب تبدیل برای تبدیل کاربری زمین c به c است.
P کل جمعیت قطعات زمین مورد بررسی است.
جدول 2 . ارزش های سازگاری کاربری زمین
جدول 3 . ارزش های دگرگونی
4.4.4. هدف فرسایش خاک
فرسایش خاک عاملی است که تأثیر جدی بر بهره وری کشاورزی دارد زیرا به شدت بر کیفیت زمین تأثیر می گذارد [ 42 ]. برای محاسبه فرسایش از معادله جهانی تلفات خاک (RUSLE) [ 31 ] [ 43 ] استفاده شد [ 5 ]:
(7)
که در آن: R i ضریب فرسایش بارندگی برای واحد i است.
K i ضریب فرسایش پذیری خاک برای واحد i است.
LS i طول شیب و ضریب شیب واحد i است.
C i ضریب پوشش و مدیریت واحد i است.
P i عامل تمرین پشتیبانی برای واحد i است.
فرمول زیر برای محاسبه فرسایش (Z 4 ) بر حسب تن در سال استفاده شده است [ 5 ]:
(8)
که در آن: Z 4 نشان دهنده هدف فرسایش خاک است.
er lu، i فرسایش کاربری زمین (lu) در واحد i (ton/ha*y) است.
P کل جمعیت قطعات زمین مورد بررسی است.
در یک جزیره کوچک، الگوی و شدت باران را می توان یکنواخت در نظر گرفت و از آنجایی که هیچ داده ای برای منطقه در دسترس نبود، ضریب بارندگی R ثابت در نظر گرفته شده است. هیچ نقشه خاکی برای جزیره در دسترس نبود و بنابراین از نقشه زمین شناسی برای تخمین ک با توجه به خاک موجود در بالا، 5 کلاس برای فاکتور K که در جدول 4 نشان داده شده است، پیشنهاد کرده است .
بنابراین، یک لایه شطرنجی GIS برای ضریب K ایجاد شده و به عنوان ورودی به الگوریتم وارد شده است ( شکل 2 ).
فاکتور LS با SAGA GIS با استفاده از روش پیشنهادی مور و همکاران ایجاد شده است. [ 44 ] و به عنوان یک لایه شطرنجی GIS دیگر در الگوریتم استفاده شد.
تراس های کشت یکی از قدیمی ترین ابزارها برای کاهش تلفات خاک است [ 45 ]. این روش کشت در جزایر به دلیل اثربخشی آنها در توقف یا کاهش از دست دادن خاک بسیار محبوب است. با در نظر گرفتن این موضوع، فاکتورهای C و P با توجه به ادبیات مربوط [ 46 ] [ 47 ] تعریف شده اند ( جدول 5 ).
4.4.6. محدودیت ها
برای به دست آوردن یک الگوی تخصیص کاربری متعادل، شش محدودیت سخت به الگوریتم معرفی شد:
・ سه محدودیت اول مربوط به شیب های مجاز بود. حداکثر شیب قابل قبول برای زمین کشاورزی دیم، زمین کشاورزی آبی و زمین شهری به ترتیب 15، 8 و 25 درصد بود [ 5 ]. برای تحقق این محدودیت، یک نقشه شیب به عنوان لایه شطرنجی GIS ایجاد شده است که به عنوان ورودی الگوریتم استفاده شد ( شکل 3 ). این محدودیت را می توان با فرمول (9) تعریف کرد:
(9)
که در آن: شیب i شیب قطعه کاربری I است.
حداکثر شیب مجاز برای کاربری زمین است.
شکل 2 . لایه شطرنجی فاکتور K GIS.
جدول 4 . برآورد ضریب فرسایش پذیری خاک (K) بر اساس طبقات نقشه زمین شناسی.
جدول 5 . مقادیر فاکتور C و P که استفاده شده است.
محدودیت چهارم در مورد حداکثر زمین قابل تبدیل به زمین شهری اجرا شد. از آنجایی که این مدل برای یک جزیره یونانی اعمال شد، نتایج نسبی سرشماری یونان در 40 سال گذشته در نظر گرفته شد. بر اساس این داده ها یک حد بالای 100٪ افزایش برای قطعات زمین شهری تعیین شد.
(10)
جایی که: Urb i تعداد قطعات کاربری زمین را نشان می دهد که به شهری تبدیل شده اند.
Urb init اولین قطعه کاربری شهری است.
q درصد مطلوب برای حداکثر افزایش شهری است.
P مخفف کل جمعیت واحدها است.
شکل 3 . نقشه شیب جزیره ناکسوس.
همانطور که مدل توسعه یافته مربوط به یک جزیره یونانی است، مفاد مربوطه قانون یونان نیز در نظر گرفته شد. اجازه داده نشد زمین شهری به پناهگاه های حیات وحش، تالاب های جزیره ای کوچک و مناطق شبکه طبیعی 2000 اختصاص یابد. علاوه بر این، محدودیت‌های خاص مربوط به زمین شهری همانطور که در جدول 6 نشان داده شده است، معرفی شده است . تمام این محدودیت‌های جزئی با ایجاد یک لایه شطرنجی ماسک GIS که مناطقی را که در آن دسته طبقه زمین شهری نباید به دلیل مقررات سازمانی معرفی شوند، به عنوان محدودیت پنجم ترکیب شده‌اند ( شکل 4 ).
فرمول زیر (11) محدودیت محدودیت شهری را اعمال می کند:
(11)
جایی که: Urban_mask i مقدار پوشش محدودیت شهری برای قطعه کاربری زمین i است. در مناطق محدود Uran_mask برابر با 0 است.
・ در نهایت، یک محدودیت ششم برای دسته “سایر” اعمال شده است، که اجازه نمی دهد این دسته در مناطقی که قبلا وجود نداشته است تولید شود. برای تحقق این محدودیت، طبقه بندی Landsat TM سال 1987 نیز به عنوان مرجع لایه شطرنجی GIS و در تعریف مسئله الگوریتم استفاده شده است. فرمول زیر (12) این محدودیت را تعریف می کند:
(12)
جایی که: lu i کلاس اختصاص داده شده به واحد کاربری زمین I است.
کلاس i مقدار کلاس رستر مرجع است.
K یک متغیر کمکی است که باید بزرگتر یا مساوی ۰ باشد.
5. نتایج و بحث
الگوریتم پیشنهادی NSGA-II برای 15000 نسل به منظور رسیدگی به اهداف، متغیرها و محدودیت‌های توصیف شده تنظیم شد. اولین راه حل عملی در نسل 166 به دست آمده است و شکل 5 چهار نمودار را نشان می دهد که پیشرفت این فرآیند تکرار را برای ترکیب خاصی از توابع هدف نشان می دهد. در این نمودارها نقاط آبی نشان‌دهنده راه‌حل‌های نسل ۱۷۰، نقاط سریز نشان‌دهنده راه‌حل‌های نسل ۳۵۰، نقاط نارنجی نشان‌دهنده راه‌حل‌های نسل ۲۵۰۰ و نقاط خاکستری نشان‌دهنده راه‌حل‌های نهایی متعلق به آخرین نسل الگوریتم هستند. نمودارهای شکل 5نشان می دهد که راه حل های بهتر به تدریج با توجه به اهداف به دست می آیند در حالی که پراکندگی راه حل ها در بین اهداف دائما محدودتر می شود و در نهایت یک جبهه پارتو را تشکیل می دهد. این نمودار گام به گام به وضوح نشان می دهد
شکل 4 . ماسک محدودیت شهری
(الف) (ب)
(ج) (د)
شکل 5 . فرآیند همگرایی الگوریتم NSGA-II.
جدول 6 . محدودیت های نهادی مربوط به زمین شهری.
فرآیند همگرای الگوریتم پیشنهادی
بررسی اهداف در دو بعد ( شکل 5 (الف)، شکل 5 (ب)) یا سه ( شکل 5 (ج)، شکل 5 (د)) نشان می دهد که الگوریتم به اندازه کافی در تمام اهداف عمل می کند. این روند در شکل 6 نیز نشان داده شده استکه مقدار میانگین هر پیکسل توابع هدف را به نسل های ایجاد شده مرتبط می کند. از آنجایی که مسئله به گونه ای فرموله شده است که همه توابع هدف به حداقل می رسند، مقدار متوسط راه حل های کلی باید با افزایش تعداد تولید کاهش یابد. می توان متوجه شد که کاهش زیادی در نسل 4000 حاصل شده است و الگوریتم می تواند در نسل 5000 خاتمه یابد و راه حل های خوبی ارائه دهد. با این وجود، به نظر می‌رسد که راه‌حل‌های تا حدودی بهتری در حدود نسل 10000 به دست آمده‌اند، در حالی که پس از آن زمان هیچ پیشرفت دیگری حاصل نشد.
تعداد زیادی از راه حل ها (1279 راه حل) در جبهه پارتو قرار دارند و “در صورت در نظر گرفتن نیازهای کیفی کاربران مختلف می توانند برای استخراج راه حل مناسب استفاده شوند” [ 29 ]. سناریوهای مختلفی را می توان ترسیم کرد که کدام راه حل برای یک منطقه خاص بهترین است و اینکه آیا کاربر باید راه حلی با وزن یکسان را ترجیح دهد یا راه حلی که به نفع افراط های تابع هدف خاص باشد. “راه حل ترجیحی با وزن برابر احتمالاً متعادل ترین توزیع کاربری زمین را دارد” [ 29 ] و راه حلی است که ما به عنوان بهترین راه حل در این مطالعه انتخاب کرده ایم.
جدول 7تغییرات کاربری زمین بین طبقه بندی اولیه (1987) و بهترین راه حل NSGA-II را خلاصه می کند. مدل اصلاح شده NSGA-II پیشنهاد کرد که زمین کشاورزی آبی را به میزان 16.2 درصد (کاهش 552 هکتار) به طور عمده با تبدیل آن به زمین کشاورزی خشک و افزایش زمین کشاورزی خشک را به میزان 131.5 درصد (افزایش 2003 هکتار) کاهش دهد. به نظر می رسد کاهش زمین های کشاورزی آبی ناشی از محدودیت های شیب و هدف فرسایش خاک باشد. با این تغییر، الگوریتم بهینه سازی چندهدفه موفق به کاهش فرسایش خاک از 1948 تن در سال به 1843 تن در سال شد. علاوه بر شیب و عوامل فرسایش، از آنجایی که ذخایر آب در جزایر سیکلادس نسبتاً کم است، کاهش اراضی کشاورزی آبی می‌تواند مفید باشد اگرچه بازده اقتصادی را کاهش می‌دهد. یک افزایش چشمگیر توسط الگوریتم در مورد کشاورزی خشک پیشنهاد شده است، و این عمدتاً ناشی از هدف بازده اقتصادی است. مدل NSGA-II همچنین حداکثر مجاز افزایش محدودیت ها را برای زمین شهری (100٪) بیشتر در قسمت شرقی و مرکزی جزیره پیشنهاد می کند. از نظر تئوری، هرچه مناطق شهری بیشتر ساخته شوند، با در نظر گرفتن حد بالایی که بیش از آن تخریب محیط زیست رخ می دهد، بازده اقتصادی بیشتری حاصل می شود. در این چارچوب، همانطور که در بخش محدودیت ها ذکر شد، محدودیت افزایش زمین شهری به 100% نزدیک به واقعیت تنظیم شد. که بالاتر از آن تخریب محیط زیست رخ خواهد داد. در این چارچوب، همانطور که در بخش محدودیت ها ذکر شد، محدودیت افزایش زمین شهری به 100% نزدیک به واقعیت تنظیم شد. که بالاتر از آن تخریب محیط زیست رخ خواهد داد. در این چارچوب، همانطور که در بخش محدودیت ها ذکر شد، محدودیت افزایش زمین شهری به 100% نزدیک به واقعیت تنظیم شد.جدول 1 ). لازم به ذکر است که با اجرای الگوریتم با پارامترهای مختلف (یعنی 5000 نسل) یا تعداد متفاوت دسته بندی قفل شده (یعنی زمین شهری، زمین کشاورزی آبی و زمین کشاورزی دیم) زمین شهری جدید پیشنهادی کم و بیش در همان مناطق قرار داشت. . بازده اقتصادی پس از بهینه سازی 18 درصد افزایش یافت.
در مورد زمین های کشاورزی، الگوریتم NSGA-II، با توجه به اهداف و محدودیت های تعریف شده، پیشنهاد کرد ( شکل 7 ) که برخی از قسمت های جزیره ناکسوس که برای کشاورزی خشک در بخش مرکزی جزیره در طبقه بندی سال 1987 استفاده می شد، باید به علفزار تبدیل شود. به دلیل شیب های ناسازگار با توجه به بهترین راه حل NSGA-II، شیوه های کشاورزی خشک باید عمدتاً به بخش مرکزی و غربی جزیره به دلیل ژئومورفولوژی آن اختصاص داده شود.
علاوه بر این، با توجه به بهترین راه حل NSGA-II، بسیاری از قطعات زمین مورد استفاده برای زمین های کشاورزی آبی در قسمت شرقی جزیره ناکسوس به دلیل شیب های تیز منطقه باید به زمین کشاورزی خشک تبدیل شود. با این حال، کشاورزان، کشاورزی آبی را ترجیح می دهند که با وجود کمبود آب، فرسایش بیشتر خاک و شیب های ناسازگار سودآورتر است.
شکل 6 . میانگین مقدار تابع هدف در هر پیکسل هر نسل.
شکل 7 . طبقه بندی اولیه (1987) و نتیجه بهینه الگوریتم NSGA-II (پس از 15000 نسل).
جزایر Cyclades توریستی هستند و فشار زیادی برای افزایش زمین شهری رخ می دهد که در تعریف مدل NSGA-II به طور جدی مورد توجه قرار نگرفت. این را می توان به وضوح در طبقه بندی سال 2010 مشاهده کرد، زیرا زمین شهری 112٪ در مقایسه با طبقه بندی 1987 افزایش یافته است و بیشتر آن در قسمت جنوب غربی نزدیک به سواحل محبوب جزیره ناکسوس ساخته شده است. بنابراین، برای اینکه الگوریتم بهینه‌سازی چندهدفه نتایج واقعی‌تری ارائه دهد، نیاز به توسعه گردشگری، که درآمد اصلی جمعیت ناکسوس را تشکیل می‌دهد، باید به عنوان تابع هدف دیگری نیز فرموله می‌شد.
این تجزیه و تحلیل نشان می دهد که توسعه بهینه جزیره ناکسوس باید مبتنی بر کشاورزی، به ویژه کشاورزی خشک، همراه با توسعه متوازن و نه یک جانبه شهری/توریستی، به طور یکسان در سراسر جزیره باشد.
جدول 7 . تغییرات کاربری/پوشش زمین بین طبقه بندی اولیه (1987) و بهترین نتیجه NSGA-II تولید شده در طی 15000 نسل.
و نه فقط در اطراف خط ساحلی واقع شده است. با تمرکز بر کلمه “متعادل”، سناریوها و وزن های مختلف برای هر تابع هدف باید در طول انتخاب بهترین راه حل ارزیابی شوند، در حالی که در این مقاله همه اهداف به یک اندازه وزن داده شدند. در مرحله بعد، وزن‌هایی نیز می‌تواند به اهداف فعلی اعمال شود تا مدل پیشنهادی بهبود یابد و نتایج واقعی‌تر تولید شود.
6. نتیجه گیری
مشکلات تخصیص منابع نیازمند پرداختن به اهداف مختلف و معمولاً متضاد است. روش شناسی ابتکاری چند هدفه مبتنی بر پارتو-جلو مکانیزمی را برای حل این چالش فراهم می کند. در تخصیص کاربری اراضی، هدف این روش‌ها تخصیص کاربری‌های خاصی به هر واحد زمین است.
یک الگوریتم اکتشافی با هدف حمایت از مشکلات تخصیص کاربری زمین در جزایر مدیترانه در این مقاله ارائه شده است. الگوریتم پیشنهادی یک نسخه اصلاح‌شده از NSGA-II است که برای تخصیص کاربری‌های زمین در جزایر مدیترانه با در نظر گرفتن قوانین، ویژگی‌های زمین‌شناسی، پارامترهای اقتصادی و زیست‌محیطی تنظیم شده است.
اثربخشی الگوریتم اصلاح‌شده NSGA-II در یک مسئله تخصیص کاربری زمین، که شامل چهار هدف، یعنی رشد بازده اقتصادی، تناسب تبدیل، حداکثر فشرده‌سازی، و کمترین فرسایش خاک ممکن، و همچنین شش محدودیت در رابطه با ژئومورفولوژی، تأیید شد. قوانین و محدودیت های توسعه شهری نتایج نشان داد که الگوریتم به اندازه کافی عمل کرده و احتمالاً می تواند برای پرداختن به اهداف و محدودیت های بیشتر مورد استفاده قرار گیرد.
در مقایسه توسعه پیشنهادی GA با توسعه واقعی جزیره، باید توجه داشت که برای دستیابی به نتایج واقعی‌تر برای برنامه‌ریزی کاربری اراضی در جزایر مدیترانه، الگوریتم بهینه‌سازی چند هدفه باید تعامل توسعه گردشگری را نیز شامل شود. ، زیرساخت های موجود، مالکیت زمین و منابع زیست محیطی. علاوه بر این، با هدف توسعه متوازن‌تر، سناریوها و وزن‌های مختلف برای هر تابع هدف باید در طول انتخاب بهترین راه‌حل مورد ارزیابی قرار گیرد، در حالی که در این مقاله همه اهداف به یک اندازه وزن داده شدند.
NSGA-II یک الگوریتم پرکاربرد و یک استاندارد مقایسه است، بنابراین نویسندگان از این الگوریتم به عنوان نقطه شروعی برای تحقیقات خود در مورد تخصیص کاربری زمین در جزایر مدیترانه استفاده می کنند. این تحقیق به سایر الگوریتم‌های بهینه‌سازی چندهدفه مرتبط برای برنامه‌ریزی کاربری زمین، که برخی از آنها بهتر می‌توانند تعداد بیشتری از اهداف را مدیریت کنند، گسترش خواهد یافت. وزن‌ها، وابستگی‌های متقابل و عدم قطعیت‌ها نیز می‌تواند به توابع و محدودیت‌های هدف به منظور بهبود مدل بهینه‌سازی چند هدفه و تولید نتایج متعادل‌تر تحمیل شود.
بدون دیدگاه