رمزگذاری الگوریتم تبدیل مش مثلثی کواترنر

در فرآیند ساخت اطلاعات جهانی، زمینه های مختلف سیستم های شبکه جهانی گسسته خود را (DGGS) ساخته اند. با توسعه فناوری داده های بزرگ، تبادل داده، یکپارچه سازی و به روز رسانی به تدریج تبدیل به یک روند و همچنین یکپارچه سازی انجمن های مختلف DGGS شده است. با توجه به ناهمگونی DGGS و قوانین رمزگذاری مختلف، نحوه ایجاد قوانین تبدیل کدگذاری و رابطه نگاشت داده بین یک شیء مشابه در DGGS های مختلف، یک فناوری پشتیبانی موثر و کلیدی برای دستیابی به قابلیت همکاری DGGS است. به عنوان نوعی DGGS چند منظوره، مش مثلثی چهارتایی (QTM) به دلیل ساختار ساده اش به یک چارچوب فضایی موثر برای ساخت زمین دیجیتال تبدیل شده است. در حال حاضر، طرح های زیادی برای تحقیقات رمزگذاری QTM وجود دارد، که نقش کلیدی در توسعه QTM ایفا می کند، اما در عین حال منجر به مشکلاتی در ارتباط و ادغام QTM تحت کدگذاری های مختلف می شود. برای حل این مشکل، ویژگی‌های رمزگذاری QTM را بررسی می‌کنیم و سه الگوریتم تبدیل را ارائه می‌کنیم: الگوریتم تبدیل نمونه‌گیری مجدد، الگوریتم تبدیل سلسله مراتبی، و الگوریتم تبدیل ردیف به ستون.

کلید واژه ها:

مش مثلثی چهارتایی ; سیستم های شبکه جهانی گسسته ; رمزگذاری ; تبدیل رمزگذاری ; قابلیت همکاری

1. مقدمه

یک سیستم شبکه جهانی گسسته (DGGS) یک سیستم شبکه ای مناسب برای نمایش زمین است و می تواند به طور نامحدود یک کره را بدون تغییر شکل شبکه آن تقسیم کند. هر سطح زیربخش ساختار منظمی دارد، بنابراین روابط تبدیل دقیقی بین شبکه‌ها در سطوح زیربخش مختلف وجود دارد که یک مدل بیان واحد برای ادغام داده‌های جغرافیایی با توزیع دلخواه و مقیاس‌های مختلف ارائه می‌کند [ 1 ، 2 ، 3 ، 4 ]]. علاوه بر این، یک DGGS با سلسله مراتب گسسته و تداوم جهانی مشخص می شود. با نوع پیش بینی نقشه محدود نمی شود. یک DGGS می‌تواند اساساً مشکلات ذاتی در پیش‌بینی نقشه مسطح، مانند ناپیوستگی داده‌ها، تغییر شکل هندسی، تبدیل‌های مقیاس، و ناسازگاری توپولوژیکی را هنگام مدیریت داده‌های مکانی-زمانی جهانی حل کند [ 5 ، 6 ].

مش مثلثی چهارتایی (QTM) یک DGGS بر اساس یک هشت وجهی منظم محاط شده است [ 7 ]. دارای ویژگی های سازماندهی سلسله مراتبی و مرتب سازی پیوسته [ 8 ] است و همچنین با ویژگی های کروی مطابقت دارد. در سال های اخیر، بسیاری از محققان از ساختار QTM برای کشف استخراج داده های مکانی جهانی و مدیریت چند وضوح [ 9 ]، نمایه سازی سلسله مراتبی داده های مکانی [ 10 ]، ترکیب نقشه و تمایز داده های فازی [ 11 ، 12 ] و ناوبری جهانی استفاده کرده اند. 13]. با این حال، از آنجایی که پیاده‌سازی‌های مختلف QTM از طرح‌های نمایه‌سازی و کدگذاری متفاوتی استفاده می‌کنند، ترجمه داده‌ها از یکی به دیگری می‌تواند مشکل ساز باشد.

مشکل قابلیت همکاری اطلاعات جغرافیایی سابقه طولانی دارد. مانند چارچوب های قبلی GI، قابلیت همکاری DGGS به مانعی برای توسعه بیشتر آن تبدیل شده است [ 14 ]. در سال 2014، کنسرسیوم فضایی باز (OGC) کارگروه استانداردسازی شبکه گسسته جهانی را برای ارتقای پیشرفت قابلیت همکاری DGGS در دامنه ها (یا رشته ها) تأسیس کرد [ 1 ]. به خصوص پس از اینکه OGC استاندارد DGGS را در سال 2017 اعلام کرد، به شدت از این تحقیق حمایت کرد.

به منظور مبادله، یکسان سازی یا استانداردسازی داده های ارائه شده توسط اشکال مختلف DGGS، آریمی ابتدا دسته بندی روش های نمایه سازی مورد استفاده برای DGGS را پیشنهاد کرد و سپس یک فرآیند کلی برای تبدیل آنها تعریف کرد [ 15 ]. لینگیو دو روابط “دوگانگی ضعیف” را بین شبکه شش ضلعی و شبکه مثلثی یا لوزی پیدا کرد و یک رابطه تبدیل یکپارچه بین شبکه‌های ناهمگن و مدل‌های بیان شبکه خط برداری ایجاد کرد [ 16 ]. آریمی به یک الگوریتم تجسم کارآمد پی برد که برای انواع مختلف قابل استفاده بود. شبکه های شش ضلعی [ 17 ] جین بن وجه های مثلثی مجاور یک هشت ضلعی منظم را در یک “ساختار منطقی چهار ضلعی” ترکیب کرد و یک الگوریتم تولید از شبکه های شش ضلعی مختلف را ایجاد کرد.18 ]. Yihang Chen یک رمزگذاری یکنواخت از عناصر ساختاری DGGS را بر اساس ویژگی های توزیع رئوس شبکه پیشنهاد کرد [ 14 ].

به طور خلاصه، تحقیق در مورد QTM و قابلیت همکاری DGGS پیشرفت قابل توجه و نتایج مثمر ثمری داشته است و یکی از مرزهای حوزه علم اطلاعات جغرافیایی است. با این حال، از بحث قبلی می توان دریافت که بسیاری از طرح های رمزگذاری QTM (یعنی نمایه سازی فضایی) وجود دارد و تعیین چگونگی تحقق تبدیل رمزگذاری و اشتراک داده های QTM های مختلف در فرآیند برنامه واقعی به کلید مشکل تبدیل شده است. بنابراین، با توجه به طبقه‌بندی کدگذاری QTM، ما قوانین تبدیل را برای کدگذاری‌های مختلف ایجاد کرده‌ایم و سه الگوریتم را برای ارائه ایده جدیدی برای قابلیت همکاری QTM ارائه کرده‌ایم.

2. رمزگذاری QTM

QTM یک مدل شبکه مثلثی تقریباً منظم است که بر روی یک فضای گسسته کروی محدود 8 × 4 ^نیوتن (N سطح تقسیم فرعی است) ساخته شده است، همانطور که در شکل 1 نشان داده شده است.

رمزگذاری هسته DGGS است، زیرا از نمایه سازی و کاربرد سریع برای محاسبه کارآمد کل تجزیه و تحلیل داده های مکانی پشتیبانی می کند. با توجه به ویژگی‌ها و کاربردهای اصلی شبکه، طرح‌های کدگذاری QTM به شرح زیر است: کدگذاری Goodchild [ 19 ]، رمزگذاری لی و سامت (رم‌گذاری LS) [ 13 ]، کدگذاری چهارتایی [ 20 ]، رمزگذاری داتون [ 7 ]، اصلاح شده رمزگذاری جهت [ 21 ]، رمزگذاری مثلثی چهاردرخت لوزی (رمزگذاری TRQ) [ 22 ]، و رمزگذاری لایه حسابی [ 13 ] و غیره، و ویژگی های ویژگی این رمزگذاری ها در جدول 1 نشان داده شده است.. با توجه به اصل رمزگذاری، آنها را می توان به سه نوع تقسیم کرد: رمزگذاری سلسله مراتبی، رمزگذاری مختصات عدد صحیح و رمزگذاری منحنی پرکننده.

2.1. رمزگذاری

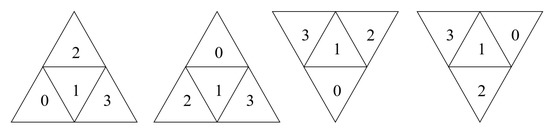
2.1.1. کدگذاری Goodchild

دنباله کدگذاری Goodchild سختگیرانه است. چهار فرزند «مرکز»، «بالا (پایین)»، «چپ» و «راست» به ترتیب با «0»، «1»، «2» و «3» مشخص می شوند، همانطور که در شکل 2 نشان داده شده است. .

2.1.2. رمزگذاری LS

رمزگذاری LS مشابه رمزگذاری Goodchild است که ترتیب رمزگذاری آن نیز جهت ثابتی دارد و تفاوت آن در این است که رمزگذاری فرزند به این صورت است که دو رقم بعد از رمزگذاری والد خود اضافه می کند. قانون آن این است که همانطور که در شکل نشان داده شده است، چهار کودک به ترتیب “بالا (پایین)”، “چپ”، “راست” و “مرکز” با “00”، “01”، “10” و “11” علامت گذاری شوند . 3 .

2.1.3. کدگذاری جهت اصلاح شده

توالی کدگذاری جهت اصلاح شده زمانی که مثلث های رو به بالا و پایین رو به پایین هستند و همگی در خلاف جهت عقربه های ساعت هستند یکسان است. هنگامی که جهت مثلث به سمت بالا است، چهار فرزند «مرکز»، «بالا»، «چپ» و «راست» به ترتیب با «0»، «1»، «2» و «3» مشخص می‌شوند. ، هنگامی که جهت مثلث رو به پایین است، چهار فرزند «مرکز»، «پایین»، «راست» و «چپ» با «0»، «1»، «2» و «3» مشخص می شوند. به ترتیب، همانطور که در شکل 4 نشان داده شده است.

2.1.4. کدگذاری کواترنر

کدگذاری کواترنر نه تنها دارای ویژگی های سلسله مراتبی و تودرتو است، بلکه دارای ویژگی های پیوستگی است که کارایی دسترسی به داده ها را بسیار بهبود می بخشد و به ذخیره رابطه مطلق بین فضاهای مجاور کمک می کند. همانطور که در شکل 5 نشان داده شده است، 4 موقعیت وجود دارد که در آن رمزگذاری های 4 کودک با تقسیم یک شبکه مثلثی شکل می گیرد.

2.1.5. رمزگذاری TRQ

متفاوت از روش های رمزگذاری فوق الذکر که مبتنی بر چهاردرخت هستند، رمزگذاری TRQ بر اساس کدگذاری شبکه لوزی چهاردرخت خطی است. روش آن این است که لوزی را به دو مثلث تقسیم می کنیم، سپس دو مثلث به ترتیب با رمزگذاری شبکه لوزی با پسوندهای “0” و “1”، همانطور که در شکل 6 نشان داده شده است، نشان داده می شوند .

2.1.6. رمزگذاری لایه حسابی

رمزگذاری لایه حسابی را می توان به شماره ردیف و شماره ستون تقسیم کرد، که در آن شماره ردیف مربوط به خط عرض جغرافیایی است، و شماره ستون تعداد شبکه هایی است که در طول همان عرض جغرافیایی از 0 درجه شروع می شود، همانطور که در شکل 7 نشان داده شده است.

2.2. طبقه بندی رمزگذاری

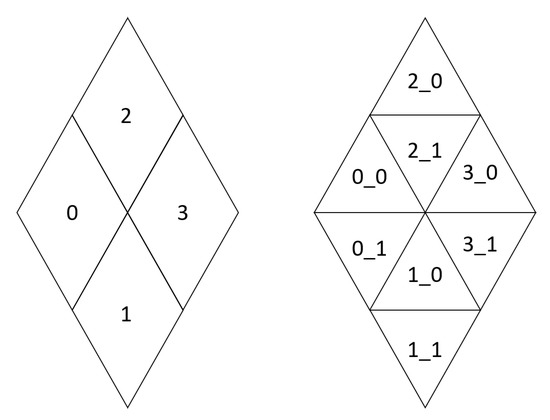
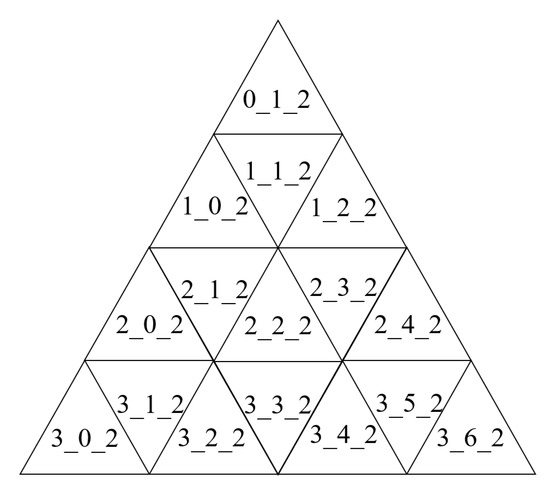
2.2.1. رمزگذاری سلسله مراتبی

مرزهای سلول های والد و فرزند تولید شده توسط تقسیم QTM کاملاً همزمان است. رابطه سلسله مراتبی آنها ساده و واضح است، بنابراین QTM به طور کلی از رمزگذاری سلسله مراتبی برای ایجاد شناسایی شبکه استفاده می کند.

همانطور که در شکل 8 نشان داده شده است ، “الف”، “ب”، “ج” و “د” چهار جهت (مرکز، بالا (پایین)، چپ و راست) کودکان را نشان می دهد که توسط مثلث مرکزی در تقسیم سلسله مراتبی قرار گرفته اند. که برای نمایش مشخصه جهتی رمزگذاری شبکه مثلثی استفاده می شود. با توجه به ترتیب abcd، 1 مورد برای کدگذاری Goodchild و رمزگذاری LS، 2 مورد برای رمزگذاری جهت اصلاح شده و 4 مورد برای کدگذاری چهارتایی وجود دارد، همانطور که در جدول 2 نشان داده شده است.. جهت بودن کدگذاری، فرکانس قضاوت های شمارش را در فرآیند طراحی الگوریتم تعیین می کند. هرچه جهت‌پذیری بالاتر باشد، تبدیل بین کدگذاری QTM مربوطه و مختصات جغرافیایی و الگوریتم همسایه‌یابی پیچیده‌تر می‌شود.

2.2.2. کدگذاری دیگر

روش های رمزگذاری که در بالا توضیح داده شد بر اساس تقسیم بندی چهاردرختی شبکه های مثلثی است. علاوه بر این، روش های رمزگذاری TRQ و رمزگذاری لایه حسابی نیز وجود دارد. رمزگذاری TRQ بر اساس شبکه لوزی چهاردرخت خطی است که برای به اشتراک گذاری داده ها، تبادل و ادغام بین شبکه مثلثی و شبکه لوزی مناسب است. رمزگذاری لایه حسابی متعلق به کدگذاری مختصات عدد صحیح است. مزیت آن اجتناب از محاسبه بازگشتی پیچیده هنگام کدگذاری و تبدیل مختصات مکانی است. محاسبه رابطه مجاور آن ساده است، با این حال، ویژگی های سلسله مراتبی یک شبکه مثلثی را از دست می دهد.

3. روش تبدیل

تبدیل کدهای QTM الگوریتم های اصلی را برای تسهیل ترکیب و اشتراک گذاری داده ها ارائه می دهد و برای اشتراک گذاری داده ها در QTM ها، واردات و صادرات پایگاه های داده QTM و غیره استفاده می شود. بسته به مشکل، کدگذاری سلول شبکه متفاوت است، اما موقعیت آن متفاوت است. و اطلاعات مشخصه موجود در آن ثابت است (تحت طرح یکسان)، همانطور که در شکل 9 نشان داده شده است. محتوای کلیدی تبدیل کدگذاری، ایجاد قوانین نگاشت بین کدهای مختلف است، همانطور که در شکل 10 نشان داده شده است. D(<T>) = { [D(<T>) ] _i |i ∈N} ، که در آن D مجموعه ای از رمزگذاری ها، <T> دسته کدگذاری های QTM و N است.تعداد کل سلول های شبکه در منطقه مورد مطالعه است، مانند D(LS) که به عنوان مجموعه ای از رمزگذاری های LS بیان می شود.

3.1. الگوریتم تبدیل مجدد نمونه گیری

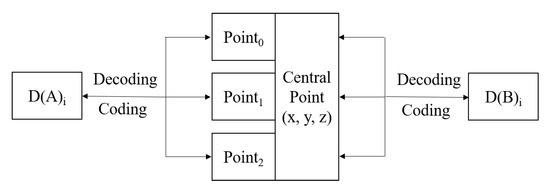
روش تبدیل نمونه‌گیری مجدد، فرآیند محاسبه به‌دست‌آمدن کدکننده D(B) QTM ₂ از مجموعه داده‌های مختصات جغرافیایی نقاط مرکز شبکه مربوط به کدگذاری D(A) QTM ₁ است. فرآیند خاص به شرح زیر است: با توجه به روش تبدیل رمزگذاری و طول و عرض جغرافیایی، D(A) به مجموعه مختصات مکانی تبدیل می شود. ، سپس D(B) را می توان از آن محاسبه کرد همانطور که در شکل 11 نشان داده شده است. در شکل، نقطه ₀ ، نقطه ₁ و نقطه ₂ مختصات 3 رأس شبکه هستند و را می توان با توجه به رابطه (1) به دست آورد.

(1)

3.2. الگوریتم تبدیل سلسله مراتبی

روش تبدیل سلسله مراتبی این است که D(A) _i را از جلو به عقب گام به گام به D(B) _i با توجه به قوانین تخصیص رمزگذاری در فرآیند تقسیم QTM جایگزین کنید.

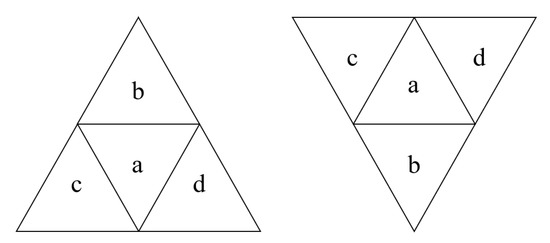
3.2.1. قوانین تبدیل بین Goodchild Encoding و LS Encoding

همانطور که در بالا ذکر شد، کدگذاری Goodchild و رمزگذاری LS ویژگی های یکسانی دارند و تفاوت اصلی این است که شناسه های رمزگذاری برای 4 فرزند متفاوت است. بنابراین، قوانین تبدیل آنها نسبتا ساده است. برای تکمیل تبدیل، فقط باید «0» و «10»، «1» و «00»، «2» و «01» و «3» و «11» را مرحله به مرحله عوض کنیم. با توجه به مطابقت بین دو رمزگذاری، به جز “0” و “1”، بقیه پس از تبدیل پایه برابر هستند. بنابراین، در فرآیند تبدیل کدگذاری، ابتدا می‌توان «0» و «1» در کدگذاری جهت ثابت را جایگزین کرد و سپس رشته کدگذاری چهارتایی به‌دست‌آمده را می‌توان به رشته باینری N-bit که رمزگذاری LS است، تبدیل کرد. در مقایسه با تبدیل مستقیم، این روش تعداد دفعات شمارش در الگوریتم را کاهش می دهد. بنابراین پیچیدگی زمانی الگوریتم تا حد زیادی کاهش می یابد. فرآیند استخراج کدگذاری Goodchild از رمزگذاری LS برعکس است.

3.2.2. قوانین تبدیل بین کدگذاری Goodchild و کدگذاری جهت اصلاح شده

برای کدگذاری جهت اصلاح شده، کدگذاری کودکان چپ و راست مخالف کدگذاری Goodchild در شبکه مثلثی با جهت زیر است. با توجه به سطح تقسیم بندی، جهت مثلث گام به گام از جلو به عقب قضاوت می شود. اگر جهت مثلث رو به پایین باشد، “2” و “3” رد و بدل می شوند. در غیر این صورت هیچ تغییری ایجاد نخواهد شد. جریان الگوریتم در شکل 12 نشان داده شده است ، که در آن GCODE کدگذاری Goodchild است و FCODE رمزگذاری جهت اصلاح شده است.

3.2.3. قوانین تبدیل بین کدگذاری Goodchild و کدگذاری کواترنر

اگرچه روش کدگذاری چهارتایی تداوم شاخص را تضمین می کند و دارای ویژگی منحنی پر کردن فضا یک بعدی است، اما جهت شناسه را قربانی می کند.

Code(Q) رمزگذاری چهارتایی را نشان می دهد و Code(Q)[i] رمزگذاری بیت i-امین کد (Q) است ( i < N ، جایی که N سطح سلسله مراتبی است)، سپس Code[i] بستگی دارد . در کد [i-1] ، و قوانین رمزگذاری آن در جدول 3 با توجه به جهت شبکه مثلثی نشان داده شده است.

«الف»، «ب»، «ج» و «د» در جدول 3 می‌توانند به طور معادل با شناسه‌های «0»، «1»، «2» و «3» از چهار کودک با کدگذاری Goodchild جایگزین شوند. . بنابراین، تبدیل بین کدگذاری چهارتایی و کدگذاری Goodchild را می توان با توجه به قوانین فوق محاسبه کرد.

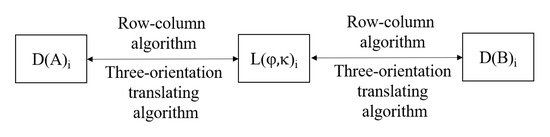
3.3. روش تبدیل ردیف به ستون

کدگذاری Goodchild، رمزگذاری LS، رمزگذاری جهت اصلاح شده و رمزگذاری چهارتایی می توانند تبدیل رمزگذاری را مرحله به مرحله از طریق الگوریتم های بالا تکمیل کنند زیرا به کدگذاری سلسله مراتبی quadtree تعلق دارند. مزیت روش تبدیل سلسله مراتبی این است که از محاسبه اعداد شناور زیادی در روش تبدیل مجدد نمونه گیری اجتناب می کند، اما تنها به رمزگذاری سلسله مراتبی تقسیم چهاردرخت شبکه های مثلثی محدود می شود. با این حال، انواع دیگری از کدگذاری QTM وجود دارد، مانند رمزگذاری مختصات عدد صحیح و رمزگذاری TRQ. به دلیل خاص بودن قوانین رمزگذاری، روش تبدیل سلسله مراتبی برای این نوع رمزگذاری قابل اجرا نیست. در پاسخ به این مشکل، با توجه به ویژگی های توزیع شبکه مثلثی، این فصل یک روش تبدیل ردیف به ستون را پیشنهاد می کند. مجموعه کدگذاری ردیف-ستون مربوط به مجموعه کدگذاری QTM است . اصل اساسی این الگوریتم این است که D(A) _i با توجه به الگوریتم سطر-ستون یا الگوریتم ترجمه سه جهتی به ردیف – ستون شماره L (( φ , κ ) i تبدیل می شود و سپس L( φ, κ ) ) _i از طریق عملیات معکوس به D(B) _i تبدیل می شود، جریان الگوریتم در شکل 13 نشان داده شده است .

3.3.1. الگوریتم تبدیل کدگذاری QTM و شماره ردیف-ستون

شماره سطر-ستون رمزگذاری QTM، رمزگذاری لایه حسابی است که در بخش 2 توضیح داده شده است. همانطور که در شکل 14 نشان داده شده است ، φ شماره ردیف، κ شماره ستون است. برای سهولت درک، شبکه مثلثی را همانطور که در شکل 15 نشان داده شده است به یک شبکه مربع تبدیل می کنیم . در زیر کدگذاری Goodchild را به عنوان مثال در نظر می گیریم، ما به ترتیب از الگوریتم سطر-ستون [ 23 ] و الگوریتم ترجمه سه جهته [ 24 ] برای محاسبه شماره سطر-ستون استفاده می کنیم.

(1) الگوریتم سطر و ستون

محدوده شماره ردیف شبکه های مثلثی در یک ربع φ ∈ [0, 2 ⁿ -1] (از قطب تا استوا) و محدوده شماره ستون κ ∈ [0, 2 φ ] است. فرض کنید کدگذاری شبکه مثلثی کد = C ₀ C ₁ C ₂ C ₃ C ₄ C ₅ … C _n-1 است، که در آن n سطح تقسیم بندی است. عدد سطر-ستون طبق الگوریتم سطر-ستون به شرح زیر محاسبه می شود.

الف. محاسبه شماره ردیف

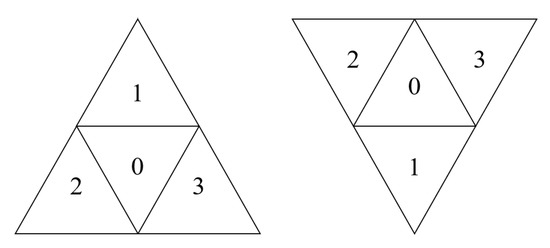
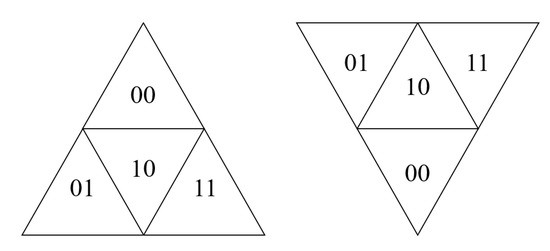
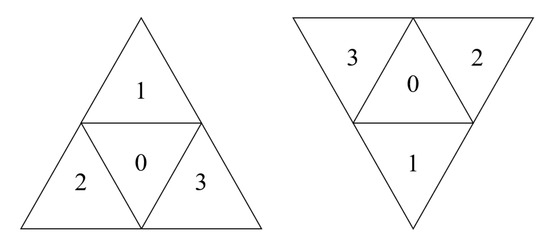
با توجه به جهت شبکه مثلثی والد، یک نشانگر را روی Q قرار دهید . هنگامی که Q = 0، جهت آن به سمت بالا است، و زمانی که Q = 1، جهت آن به سمت پایین است. اگر جهت متفاوت باشد، شماره ردیف مربوط به سلول ها نیز متفاوت است، همانطور که در شکل 14 نشان داده شده است. در شبکه مثلثی هر سطح، 4 خانه را می توان به 2 ردیف تقسیم کرد. اگر جهت سلول به سمت بالا باشد، شناسه شماره ردیف شبکه ای که به عنوان “1” رمزگذاری می شود، “0” و شناسه شماره ردیف شبکه که به صورت “0”، “2” و “3” رمزگذاری می شود، “0” است. 1”. اگر جهت سلول پایین باشد، کاملاً مخالف است. محاسبه شماره ردیف به شرح زیر است: طبق رابطه (2)، یک رشته باینری Str =S ₀S ₁S ₂S ₃ … S _n -1 را می توان محاسبه کرد، در نهایت، شماره ردیف سلول را می توان با تبدیل Str به عدد اعشاری به دست آورد.

(2)

ب. محاسبه شماره ستون

κ را می توان به صورت بازگشتی توسط φ و قوانین رمزگذاری محاسبه کرد. الگوریتم به شرح زیر است. در میان آنها، مقدار اولیه κ و i 0، m = φ _max + 1 = 2 ⁿ است.

①: اگر CODE[i] = 0، پس κ = κ + [2 × ( φ – m /2) + 1]، φ = m – φ – 1، m = m /2.
②: اگر CODE[i] = 1، پس κ = κ , m = m /2;
③: اگر CODE[i] = 2، آنگاه κ = κ , m = m /2, φ = φ − m ;
④: اگر CODE[i] = 3، پس κ = κ + m ، m = m /2، φ = φ − m ;
⑤: محاسبات بالا را تا i = 2 ⁿ -1 تکرار کنید و مقدار κ .

3) رمزگذاری را از شماره ردیف-ستون محاسبه کنید

m = φ _max + 1 = 2 ⁿ ، الگوریتم به شرح زیر است:

①: اگر φ < m /2، پس CODE[i] = 1، m = m /2، φ = φ − m ;
②: اگر φ ≥ m /2، و κ < ( φ +1− m /2)، پس CODE[i] = 2، m = m /2.
③: اگر φ ≥ m /2، و κ ≥ m ∩ κ ≥ ( φ + 1− m / 2)، پس CODE[i] = 3، κ = κ − 2 m ;
④: اگر φ ≥ m /2، و ( φ + 1 – m /2) ≤ κ < m ، آنگاه CODE[i] = 0، κ = κ + m – 2 φ -1، m = m /2، φ = φ − m ;
⑤: محاسبات بالا را تا i = 2 ⁿ -1 تکرار کنید و CODE را خروجی کنید.

(2) الگوریتم ترجمه سه جهتی

الف. محاسبه شماره سطر-ستون

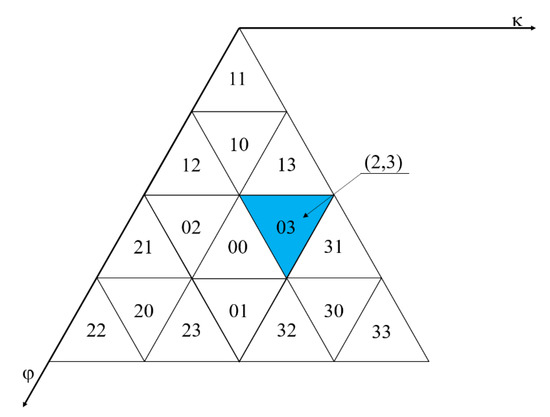
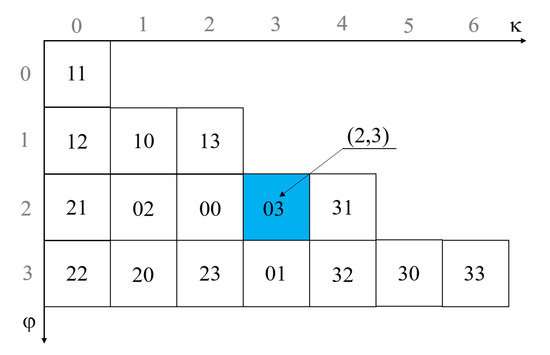
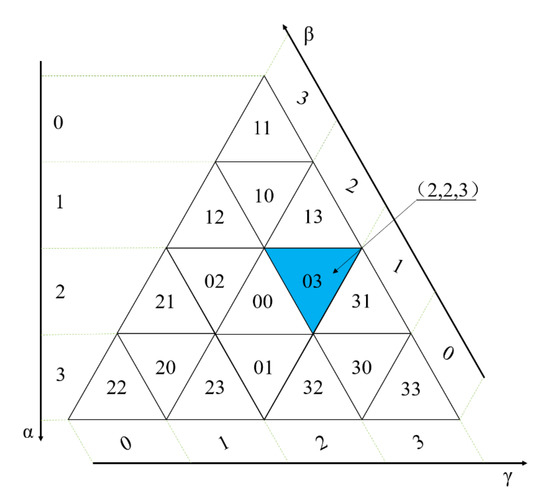
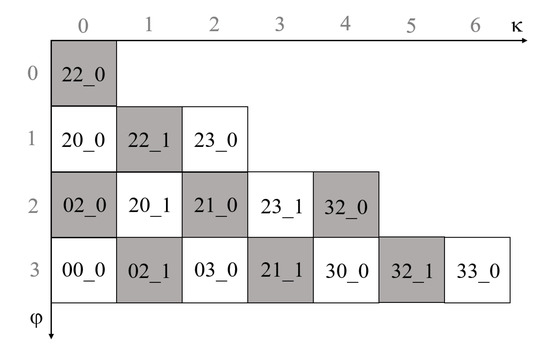
این فصل از سه مختصات جهت گیری برای محاسبه تعداد ردیف-ستون کدگذاری QTM استفاده می کند. سیستم مختصات سه جهتی شبکه های مثلثی در شکل 16 نشان داده شده است ، که α ، β ، γ∈ [0,2 ⁿ -1]. روش محاسبه α از کدگذاری مانند شماره ردیف محاسبه شده در بالا است و محاسبه β و γ مشابه هستند. در نهایت می توان شماره سطر و شماره ستون را طبق رابطه (3) محاسبه کرد.

(3)

ب. رمزگذاری را از شماره ردیف-ستون محاسبه کنید

با توجه به خصوصیات سیستم مختصات سه جهتی، می توان آن را به صورت زیر بدست آورد: اگر جهت شبکه به سمت بالا باشد، α + β + γ = 2 ⁿ ، در غیر این صورت α + β + γ = 2 ⁿ + 1. بنابراین، جهت شبکه مثلثی را می توان با توجه به مجموع α ، β ، و γ تعیین کرد.. در عین حال، به دلیل مختصات ردیف-ستون شبکه مثلثی، وقتی k یک عدد فرد باشد، جهت شبکه رو به پایین است و زمانی که k غیر فرد باشد، جهت شبکه به سمت بالا است. ترکیب این دو ویژگی می تواند منجر به رابطه دیگری بین شماره سطر-ستون و مختصات سه جهتی شود، مانند معادله (4) و معادله (5). ترکیب این دو فرمول می‌تواند مختصات سه جهتی سلول شبکه را از شماره ردیف-ستون محاسبه کند.

(4)

(5)

پس از بدست آوردن مختصات سه جهتی شبکه، جریان الگوریتم محاسبه کدگذاری با توجه به مختصات سه جهتی به شرح زیر است:

①: α , β , γ را به رشته های باینری n بیتی تبدیل کنید Str α _, Str _β , Str _γ , که در آن n سطح زیربخش است.
②: طبق قوانین جدول 4 ، کدگذاری از Strα[i] ، Strβ[i] و Str _γ [i] محاسبه می‌شود و همان مقدار در کدگذاری‌های مربوط به شناسه‌های سه سطح، رمزگذاری مورد نظر است.
③: مراحل بالا را تا پایان محاسبه تکرار کنید.

(3) تحلیل کارایی الگوریتم

ما از تمام شبکه های مثلثی در محدوده هگزاگرام (سطح زیربخش 6-12) به عنوان اشیاء آزمایشی استفاده کردیم و زمان مصرف را به ترتیب با دو الگوریتم بالا محاسبه کردیم و در نهایت نتایج تجربی را مطابق جدول 5 و جدول مقایسه و تجزیه و تحلیل کردیم. 6 . از جمله، محیط سخت افزاری کامپیوتر DELL T3620، پردازنده 8 هسته ای Intel(R) Core (TM) i7-7700 @ 3.60 GHZ، RAM 32.0 Gb و Win10 Professional Edition است.

از طریق تجزیه و تحلیل می توان به نتایج زیر دست یافت:

الف. در الگوریتم تبدیل از رمزگذاری به شماره ردیف-ستون، محاسبه شماره ردیف در الگوریتم سطر-ستون با منطق محاسبه α، β و γ در الگوریتم موقعیت یابی مختصات سه جهتی و اجرای الگوریتم مطابقت دارد. فرآیند ساده است زیرا مصرف زمان آنها عمدتاً در فرآیند محاسبه شناسه باینری از رمزگذاری چهارتایی متمرکز می شود. با این حال، محاسبه شماره ستون در الگوریتم سطر-ستون پیچیده تر است. در فرآیند بازگشتی گام به گام الگوریتم، پارامترهای زیادی وجود دارد که باید محاسبه و تغییر داده شوند. بنابراین، الگوریتم موقعیت یابی مختصات سه جهتی کارآمدتر است. همانطور که در شکل 17 ، شکل 18 ، وجدول 4 ، الگوریتم موقعیت یابی مختصات سه جهتی 1.67 برابر الگوریتم سطر-ستون است.

ب. در الگوریتم تبدیل از شماره ردیف-ستون به کدگذاری، منطق الگوریتم موقعیت یابی مختصات سه جهتی ساده است. با این حال، فرآیند محاسبه رمزگذاری از رشته باینری نسبتاً دشوار است. برعکس، اگرچه منطق الگوریتم سطر-ستون پیچیده است، حجم کار محاسباتی نسبتاً کوچک است. همانطور که در شکل 18 و جدول 5 نشان داده شده است، الگوریتم ردیف-ستون 2.5 برابر الگوریتم موقعیت یابی مختصات سه جهتی است.

به طور خلاصه، ما از الگوریتم موقعیت یابی مختصات سه جهتی و الگوریتم سطر-ستون برای پردازش تبدیل کدگذاری به شماره ردیف-ستون و تبدیل شماره ردیف-ستون به کدگذاری استفاده خواهیم کرد.

3.3.2. الگوریتم تبدیل کدگذاری TRQ و شماره ردیف-ستون

شبکه لوزی مبتنی بر چهاردرخت خطی دارای یک سیستم مختصات رمزگذاری مورتون [ 25 ] است، همانطور که در شکل 19 نشان داده شده است ، جایی که I و J موقعیت شبکه لوزی را نشان می دهند. رمزگذاری مورتون ( _کد M = M ₀M ₁M ₂M ₃ … M _n−1 ) را می توان با Mcode = 2 I + J نشان داد.

(1) محاسبه شماره سطر-ستون

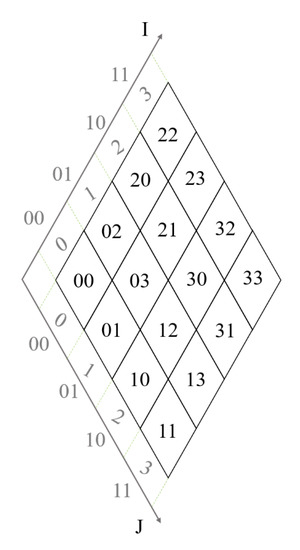
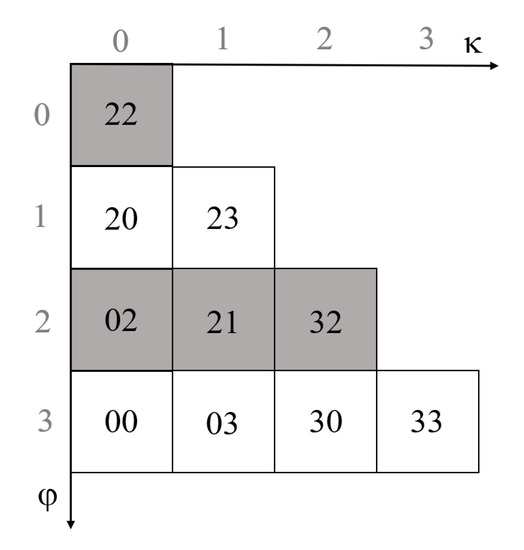
رمزگذاری شبکه‌های مثلثی بر اساس تقسیم‌بندی شبکه‌های لوزی چهاردرخت خطی می‌تواند پسوند «۰» و «۱» در _کد M برای تشخیص مثلث‌های رو به بالا و پایین باشد. با توجه به رابطه (6)، تبدیل بین سیستم مختصات IJ و φκ (همانطور که در شکل 20 نشان داده شده است ) را می توان با استفاده از تبدیل شباهت فضایی تحقق بخشید. در نهایت، با توجه به مطابقت بین شبکه مثلثی و شبکه لوزی (همانطور که در شکل 21 نشان داده شده است ) و جهت گیری شبکه مثلثی، می توان عدد سطر-ستون شبکه مثلثی شکل را با رابطه (7) محاسبه کرد.

(6)

(7)

که در آن ( φT ، _κT₎ و ( _φD_، κD ) به ترتیب اعداد ردیف-ستون شبکه های الماس و مثلث در سیستم مختصات φκ هستند . (I, J) مختصات ردیف-ستون شبکه الماسی در سیستم مختصات IJ است. اگر Q = 0 باشد، جهت مثلث به سمت بالا است و Q = 1 برعکس است. ماتریس چرخش بین سیستم های مختصات مختلف است. و مختصات مبدا سیستم مختصات φκ در سیستم مختصات IJ است.

(2) رمزگذاری را از شماره ردیف-ستون محاسبه کنید.

①: ابتدا مختصات شبکه لوزی شکل φ _D , κ _D ; در سیستم مختصات φκ را می توان با محاسبه معکوس با استفاده از رابطه (8) و شماره ردیف-ستون شبکه مثلثی به دست آورد.
②: سپس از معادله (9) و φ _D , κ _D برای بدست آوردن مختصات شبکه لوزی شکل در سیستم مختصات IJ استفاده می کند و I و J را به کدگذاری شبکه الماس تبدیل می کند.
③: در نهایت، با توجه به جهت مثلث و قوانین رمزگذاری، می توان رمزگذاری TRQ شبکه مثلثی را به دست آورد.

(8)

(9)

4. مقایسه و تحلیل کارایی الگوریتم

ما از داده‌های شبکه بارندگی سالانه 2015 مغولستان داخلی از سطوح 9 تا 13 به عنوان شی آزمایشی استفاده کردیم (داده‌های موسسه علوم جغرافیایی و تحقیقات منابع طبیعی، آکادمی علوم چین https://www.resdc.cn/ ، در 20 دسامبر 2021 مشاهده شد، همانطور که در شکل 22 نشان داده شده است ، و زمان مصرف را به ترتیب با سه الگوریتم بالا محاسبه کرد. در میان آنها، روش ساخت QTM تقسیم قوس بزرگ [ 15 ] است و محیط سخت افزاری همان است که در بالا توضیح داده شد.

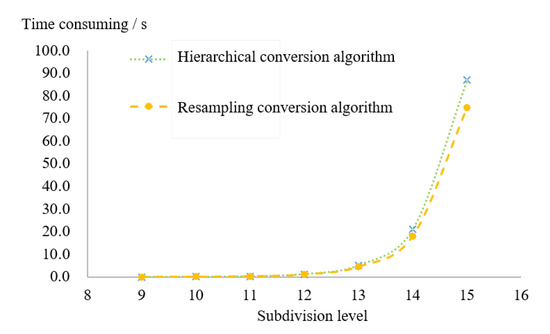
4.1. تحلیل مقایسه ای الگوریتم های تبدیل کدگذاری سلسله مراتبی

(1) تحلیل مقایسه ای الگوریتم نمونه گیری مجدد و الگوریتم تبدیل سلسله مراتبی

هر دوی این الگوریتم ها از روش های بازگشتی استفاده می کنند و پیچیدگی زمانی آنها O(4 ^{n است}). از نظر یک عملیات واحد، الگوریتم تبدیل مجدد نمونه‌برداری عمدتاً مبتنی بر تبدیل بین مختصات رمزگذاری و فضایی است که شامل ضرب عدد ممیز شناور، ریشه مربع و سایر عملیات است و محاسبه پیچیده است. الگوریتم تبدیل سلسله مراتبی تبدیل اعداد صحیح سیستم چهارتایی یا تبدیل بین سیستم چهارتایی و سیستم باینری است و محاسبه نسبتاً ساده است. با این حال، الگوریتم تبدیل مجدد نمونه‌برداری طیف وسیعی از کاربردها را دارد و می‌تواند برای هر تبدیل طرح‌بندی، تقسیم‌بندی و کدگذاری استفاده شود. الگوریتم تبدیل سطح به تبدیل همان طرح ریزی و تقسیم بندی محدود می شود. نتایج تجربی در جدول 7 ، جدول 8 و جدول 9 نشان داده شده استو شکل 23 . تجزیه و تحلیل نشان می دهد که برای تبدیل بین کدگذاری های مختلف، بازده تبدیل الگوریتم تبدیل سلسله مراتبی بهتر از الگوریتم نمونه برداری مجدد است.

(2) تجزیه و تحلیل رابطه بین جهت دهی و بازده تبدیل رمزگذاری

نتایج زیر را می توان با مقایسه رابطه بین بازده تبدیل جهت کدگذاری شده به دست آورد. همانطور که در شکل 24 نشان داده شده است، پیچیدگی قانون نگاشت تبدیل رمزگذاری به پیچیدگی جهت کدگذاری بستگی دارد، و پیچیدگی جهت با بازده تبدیل کدگذاری نسبت معکوس دارد .

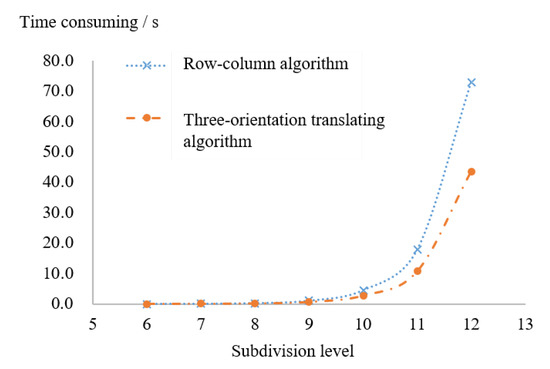
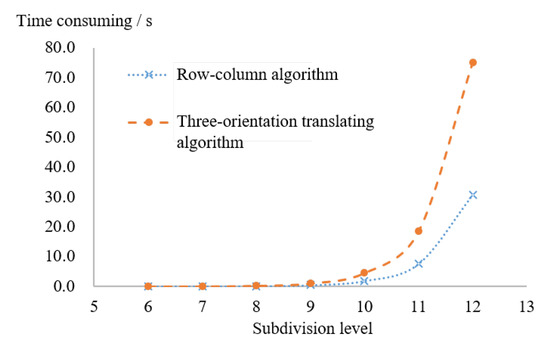
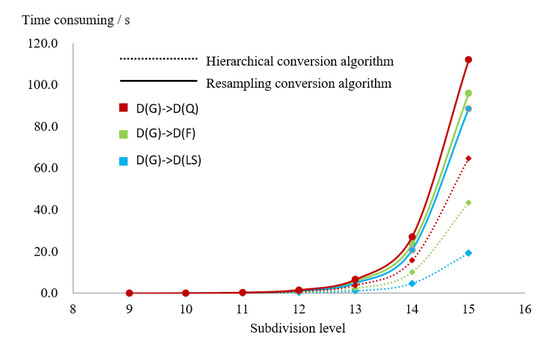
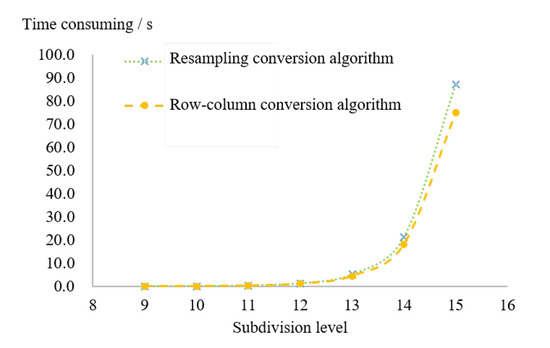
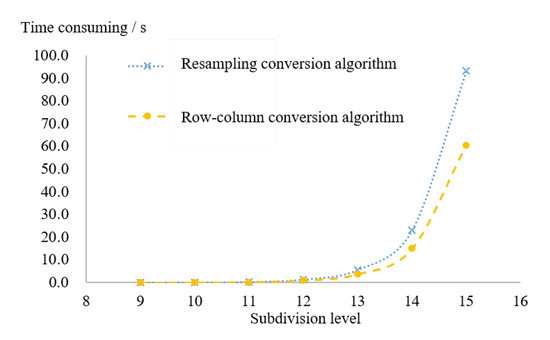
4.2. مقایسه و تحلیل کارایی الگوریتم تبدیل انواع دیگر کدگذاری

برای رمزگذاری TRQ، ویژگی های سلسله مراتبی مثلث ها را ندارد، بنابراین لازم است از «عدد ردیف-ستون» به عنوان واسطه ای برای تبدیل رمزگذاری استفاده شود، بنابراین، الگوریتم تبدیل ردیف به ستون مشابه الگوریتم نمونه گیری مجدد است هر دوی آنها به یک رسانه به عنوان پل برای تبدیل نیاز دارند.اما، مانند الگوریتم تبدیل سلسله مراتبی، الگوریتم تبدیل ردیف به ستون از محاسبه اعداد ممیز شناور اجتناب می کند.تحلیل نتایج تجربی در جدول 10 و جدول 11 و شکل نشان داده شده است. 25 و شکل 26. در مقایسه با الگوریتم تبدیل مجدد نمونه‌برداری، الگوریتم تبدیل ردیف به ستون کارآمدتر است و تفاوت بین راندمان تبدیل کدگذاری Goodchild و رمزگذاری TRQ عمدتاً در پیچیدگی کدگذاری و الگوریتم تبدیل شماره ردیف به ستون منعکس می‌شود.

5. نتیجه گیری ها

این مقاله سه الگوریتم تبدیل را برای رمزگذاری QTM پیشنهاد می‌کند. نتایج اصلی تحقیق به شرح زیر است: اولاً، بر اساس تحقیقات طبقه‌بندی ویژگی‌های رمزگذاری QTM، ما یک ویژگی جهتی برای اندازه‌گیری پیچیدگی تبدیل رمزگذاری ارائه می‌کنیم و بین پیچیدگی جهت و بازده تبدیل رمزگذاری همبستگی منفی وجود دارد. سپس، این مقاله الگوریتم تبدیل مجدد نمونه‌برداری، الگوریتم تبدیل سلسله مراتبی و الگوریتم تبدیل ردیف به ستون کدگذاری QTM را با توجه به رابطه بین کدگذاری و مختصات فضایی، جهت کدگذاری، و رمزگذاری ردیف به ستون شبکه پیشنهاد می‌کند. علاوه بر این، از طریق تأیید تجربی، مشاهده می شود که کارایی الگوریتم تبدیل سلسله مراتبی و الگوریتم تبدیل رتبه بالاتر است. در نهایت، این مقاله یک الگوریتم برای تبادل کدگذاری TRQ و شماره ردیف-ستون پیشنهاد می‌کند و دو روش تبدیل بین کدگذاری QTM و شماره ردیف-ستون را مقایسه می‌کند. نتایج نشان می‌دهد که وقتی تعداد ردیف و ستون توسط QTM محاسبه می‌شوند، الگوریتم موقعیت‌یابی مختصات سه محوره بهتر است، در غیر این صورت الگوریتم سطر-ستون بهتر است. به طور خلاصه، الگوریتم تبدیل کدگذاری ارائه شده در این مقاله، یک مبنای نظری و فنی برای قابلیت همکاری رمزگذاری QTM ارائه می‌کند. در عین حال، الگوریتم تبدیل ردیف به ستون بالا را می توان برای تبدیل بین QTM و شبکه های لوزی نیز اعمال کرد. این مقاله الگوریتمی را برای تبادل کدگذاری TRQ و شماره ردیف-ستون پیشنهاد می‌کند و دو روش تبدیل بین کدگذاری QTM و شماره ردیف-ستون را مقایسه می‌کند. نتایج نشان می‌دهد که وقتی تعداد ردیف و ستون توسط QTM محاسبه می‌شوند، الگوریتم موقعیت‌یابی مختصات سه محوره بهتر است، در غیر این صورت الگوریتم سطر-ستون بهتر است. به طور خلاصه، الگوریتم تبدیل کدگذاری ارائه شده در این مقاله، یک مبنای نظری و فنی برای قابلیت همکاری رمزگذاری QTM ارائه می‌کند. در عین حال، الگوریتم تبدیل ردیف به ستون بالا را می توان برای تبدیل بین QTM و شبکه های لوزی نیز اعمال کرد. این مقاله الگوریتمی را برای تبادل کدگذاری TRQ و شماره ردیف-ستون پیشنهاد می‌کند و دو روش تبدیل بین کدگذاری QTM و شماره ردیف-ستون را مقایسه می‌کند. نتایج نشان می‌دهد که وقتی تعداد ردیف و ستون توسط QTM محاسبه می‌شوند، الگوریتم موقعیت‌یابی مختصات سه محوره بهتر است، در غیر این صورت الگوریتم سطر-ستون بهتر است. به طور خلاصه، الگوریتم تبدیل کدگذاری ارائه شده در این مقاله، یک مبنای نظری و فنی برای قابلیت همکاری رمزگذاری QTM ارائه می‌کند. در عین حال، الگوریتم تبدیل ردیف به ستون بالا را می توان برای تبدیل بین QTM و شبکه های لوزی نیز اعمال کرد. نتایج نشان می‌دهد که وقتی تعداد ردیف و ستون توسط QTM محاسبه می‌شوند، الگوریتم موقعیت‌یابی مختصات سه محوره بهتر است، در غیر این صورت الگوریتم سطر-ستون بهتر است. به طور خلاصه، الگوریتم تبدیل کدگذاری ارائه شده در این مقاله، یک مبنای نظری و فنی برای قابلیت همکاری رمزگذاری QTM ارائه می‌کند. در عین حال، الگوریتم تبدیل ردیف به ستون بالا را می توان برای تبدیل بین QTM و شبکه های لوزی نیز اعمال کرد. نتایج نشان می‌دهد که وقتی تعداد ردیف و ستون توسط QTM محاسبه می‌شوند، الگوریتم موقعیت‌یابی مختصات سه محوره بهتر است، در غیر این صورت الگوریتم سطر-ستون بهتر است. به طور خلاصه، الگوریتم تبدیل کدگذاری ارائه شده در این مقاله، یک مبنای نظری و فنی برای قابلیت همکاری رمزگذاری QTM ارائه می‌کند. در عین حال، الگوریتم تبدیل ردیف به ستون بالا را می توان برای تبدیل بین QTM و شبکه های لوزی نیز اعمال کرد.

منابع

برس، مگابایت؛ پترسون، روابط عمومی؛ استروبل، پ. داو، سی. Sabeur، ZA; گیب، آر جی. Ben, J. Datacubes: دیدگاه سیستم های شبکه جهانی گسسته. کارتوگر. بین المللی جی. جئوگر. Inf. جئوویس. 2019 ، 54 ، 63-71. [ Google Scholar ] [ CrossRef ]
یائو، ایکس. لی، جی. شیا، جی. بن، جی. کائو، کیو. ژائو، ال. ممکن است.؛ ژانگ، ال. Zhu، D. فعال کردن داده های بزرگ مشاهده زمین از طریق محاسبات ابری و DGGS: فرصت ها و چالش ها. Remote Sens. 2019 ، 12 ، 62. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
Kolar, J. نمایش سطح زمین جغرافیایی با استفاده از نمایه سازی جهانی. در مجموعه مقالات دوازدهمین کنفرانس بین المللی ژئوانفورماتیک، Gävle، سوئد، 7-9 ژوئن 2004. صص 321-328. [ Google Scholar ]
ژائو، XS؛ بن، جی. Sun، WB; تانگ، ایکس. مروری بر پیشرفت تحقیقات در شبکه تسلیح زمین. Acta Geod. Et Cartogr. گناه 2016 ، 45 ، 1-14. [ Google Scholar ]
داتون، GH یک سیستم مختصات سلسله مراتبی برای ژئوپردازش و کارتوگرافی . بهار: برلین/هایدلبرگ، آلمان، 1999; پ. 23. [ Google Scholar ]
Goodchild، MF بازاندیشی تاریخچه GIS. ان GIS 2018 ، 24 ، 1-8. [ Google Scholar ] [ CrossRef ]
داتون، جی. مدل‌سازی عدم قطعیت مکان از طریق سلسله مراتبی: دقت پایگاه داده فضایی . تیلور و فرانسیس: لندن، بریتانیا، 1989; صص 125-140. [ Google Scholar ]
هو، ام. زینگ، اچ. ژائو، ایکس. چن، جی. محاسبه رابطه توپولوژیکی پیچیده در شبکه مثلثی چهارگوش سطح کروی. Geomat. Inf. علمی دانشگاه ووهان 2012 ، 37 ، 468-470. [ Google Scholar ]
Fekete، G. ارائه و مدیریت داده های کروی با چهار درخت کروی. در مجموعه مقالات اولین کنفرانس IEEE 1990 در مورد تجسم، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، 23-26 اکتبر 1990. صص 176-186. [ Google Scholar ]
Goodchild، MF; یانگ، اس. ساختار داده های مکانی سلسله مراتبی برای سیستم های اطلاعات جغرافیایی جهانی. نمودار CVGIP. مدل پردازش تصویر 1992 ، 54 ، 31-44. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
داتون، جی. تعمیم نقشه دیجیتال با استفاده از سیستم مختصات سلسله مراتبی. در مجموعه مقالات Auto Carto 13, Bethesda, MD, USA, 7-10 آوریل 1997; ACSM/AS-PRS. صص 367-376. [ Google Scholar ]
داتون، جی. مقیاس، سینوسیته و انتخاب نقطه در تعمیم خطوط دیجیتال. کارتوگر. Geogr. Inf. علمی 1999 ، 26 ، 33-53. [ Google Scholar ] [ CrossRef ]
لی، ام. سامت، ح. پیمایش از طریق مش های مثلثی که به صورت چهاردرخت خطی اجرا می شوند. ACM Trans. نمودار. 2000 ، 19 ، 79-121. [ Google Scholar ] [ CrossRef ]
چن، YH; وانگ، جی ایکس؛ Cao, ZN کدگذاری یکنواخت و روش تولید عناصر ساختاری سیستم‌های شبکه جهانی گسسته. J. Geo-Inf. علمی 2021 ، 23 ، 1382-1390. [ Google Scholar ]
امیری، ع.م. سماواتی، ف. پترسون، P. طبقه بندی و تبدیل برای روش های نمایه سازی سیستم های شبکه جهانی گسسته. بین المللی J. Geo-Inf. 2015 ، 4 ، 320-336. [ Google Scholar ] [ CrossRef ]
Du، LY; بن، جی. Maq, H. الگوریتمی برای ایجاد تبدیل خط گسسته شبکه مثلثی مسطح بر اساس دوگانگی ضعیف. Geomat. Inf. علمی دانشگاه ووهان 2020 ، 45 ، 105-110. [ Google Scholar ]
امیری، ع.م. هریسون، ای. Samavati، F. نقشه های اتصال شش ضلعی برای زمین دیجیتال. بین المللی جی دیجیت. زمین 2015 ، 8 ، 750-769. [ Google Scholar ] [ CrossRef ]
بن، جی. تانگ، ایکس سی; ژو، CH; ژانگ، الگوریتم ساخت و ساز KX سیستم های شبکه شش ضلعی مبتنی بر هشت وجهی. J. Geo-Inf. علمی 2015 ، 17 ، 789-797. [ Google Scholar ]
طلا، سی. مصطفوی، کارشناسی ارشد به سوی GIS جهانی. ISPRS J. Photogramm. Remote Sens. 2000 , 55 , 150-163. [ Google Scholar ] [ CrossRef ]
بارتولدی، جی جی; گلدزمن، پی. نمایه سازی مستمر زیربخش های سلسله مراتبی جهان. بین المللی جی. جئوگر. Inf. علمی 2001 ، 15 ، 489-522. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
وانگ، جی ایکس؛ چن، YH; کائو، ZN; Qin، Z. Shi, Y. الگوریتم همسایه یابی روی شبکه مثلثی چهارتایی با کدگذاری جهت اصلاح شده. علمی Surv. نقشه 2021 ، 46 ، 196-202. [ Google Scholar ]
بای، جی جی. ژائو، XS؛ چن، جی. نمایه سازی شبکه های جهانی گسسته با استفاده از چهاردرخت خطی. Geomat. Inf. علمی دانشگاه ووهان 2005 ، 30 ، 805-808. [ Google Scholar ]
ژائو، XS؛ چن، جی. الگوریتم ترجمه سریع بین کد QTM و هماهنگی طول و عرض جغرافیایی. Acta Geod. کارتوگر. گناه 2003 ، 32 ، 272-277. [ Google Scholar ]
تانگ، ایکس سی; ژانگ، YS؛ Ben, J. الگوریتم ترجمه سه جهت گیری طولانی./lat. هماهنگی و کد QTM همراه با معیار قاضی دقت آن. Geomat. Inf. علمی دانشگاه ووهان 2006 ، 31 ، 27-30. [ Google Scholar ]
وایت، دی. شبکه‌های جهانی از تقسیم‌بندی‌های الماس بازگشتی سطح یک هشت‌وجهی یا ایکو وجهی. محیط زیست نظارت کنید. ارزیابی کنید. 2000 ، 64 ، 93-103. [ Google Scholar ] [ CrossRef ]