روابط کمی بین درجه شباهت توپولوژیکی و تغییر مقیاس نقشه خوشه‌های کانتور چند مقیاسی برای اتوماسیون تعمیم نقشه حیاتی است. با این حال، هیچ روشی برای محاسبه روابط پیشنهاد نشده است. هدف این مقاله پر کردن شکاف با پیشنهاد یک رویکرد جدید است. ابتدا یک درخت کانتور هدایت شده با پیش پردازش خطوط بسته نشده ایجاد کرد و سپس بیان کمی از روابط توپولوژیکی خوشه کانتور را بر اساس درخت کانتور هدایت شده ایجاد کرد. پس از این، از 108 گروه از خوشه‌های کانتور چند مقیاسی با انواع مختلف ژئومورفولوژیکی برای کشف نظم متغیر شاخص‌های توپولوژیکی با مقیاس نقشه استفاده کرد. در نهایت، از 416 نقطه برای محاسبه روابط کمی بین درجه شباهت توپولوژیکی و تغییر مقیاس نقشه با روش برازش منحنی استفاده کرد.

کلید واژه ها:

درجات شباهت توپولوژیکی تعمیم نقشه ; تغییر مقیاس نقشه ; خوشه های کانتور

1. مقدمه

به عنوان یکی از اجزای اساسی روابط فضایی، رابطه تشابه فضایی [ 1 ]، از جمله شباهت گرافیکی [ 2 ، 3 ]، شباهت توپولوژیکی و شباهت معنایی [ 4 ، 5 ] و غیره، به طور گسترده در شناخت فضایی انسان استفاده شده است. 6 ]، تشخیص الگو [ 7 ، 8 ]، و تطبیق داده های مکانی [ 9 ، 10 ، 11 ، 12 ، 13 ]. به خصوص، این یک پایه مهم برای تعمیم خودکار نقشه است [ 14 ، 15] هدایت تعمیم نقشه ها از مقیاس بزرگتر (مثلاً 1:5000) به مقیاس کوچکتر (مثلاً 1:25000) [ 16 ].
کانتور وسیله ای مؤثر برای نمایش توپوگرافی سه بعدی دنیای واقعی بر روی سطوح دو بعدی است [ 17 ]، تعمیم خودکار آن برای کوچک کردن نقشه های توپوگرافی در مقیاس کوچک، تجزیه و تحلیل توپوگرافی بر اساس زمین، و ساخت بردارهای چند مقیاسی ضروری است. پایگاه داده نقشه توپوگرافی در واقع، تعمیم نقشه نوعی تبدیل شباهت فضایی بین نقشه‌های چند مقیاسی است [ 1 ]. نقشه نگاران [ 18 ، 19 ] معتقدند که کلید و هسته تعمیم کانتور، توصیف روابط فضایی و ساختار کانتور است. با این حال، یک رابطه نظم دقیق بین خطوط کانتور وجود دارد، یعنی رابطه فضایی بین خطوط کانتور عمدتاً به رابطه توپولوژیکی اشاره دارد.20 ، 21 ]. بنابراین، بیان کمی روابط توپولوژیکی یک محتوای مهم در مطالعه روابط شباهت فضایی کانتور چند مقیاسی است.
فرآیندهای تعمیم کانتور شامل دو مرحله است: کمیاب سازی و ساده سازی، به عنوان مثال، ادغام تپه های موقعیتی ثانویه. هنگامی که یک نقشه تعمیم داده می شود، اگر فواصل کانتور نقشه اصلی و نقشه حاصل متفاوت باشد، برخی از خطوط باید حذف شوند. این امر به ناچار منجر به تغییر روابط توپولوژیکی بین خطوط می شود. به عنوان مثال، از نظر توپولوژیکی روابطی بین خطوط کانتور L 8 و L 5 یا L 7 وجود دارد، و از نظر توپولوژیکی روابط همسایه بین L 5 و L 7 در نقشه مقیاس بزرگ وجود دارد ( شکل 1 a)، اما این روابط توپولوژیکی دیگر وجود ندارد. L 5 و L 7ادغام می شوند و L 8 در نقشه های مقیاس کوچکتر حذف می شود. تحقیقات موجود نشان داده است که تغییر روابط توپولوژیکی و تغییر مقیاس نقشه یک رابطه کمی در تعمیم نقشه دارد [ 18 ، 19 ]. با این وجود، این موضوع مورد بررسی قرار نگرفته است [ 18 ، 19 ] که مانع از اتوماسیون تعمیم خوشه کانتور می شود.
مطالعات قبلی در مورد روابط توپولوژیکی خطوط [ 22 ، 23 ، 24 ، 25 ] عمدتاً بر روی روابط همسایه تمرکز دارند، اما روابط توپولوژیکی حاوی و روابط توپولوژیک ناپیوسته را در نظر نمی گیرند [ 26 ، 27 ]. از سوی دیگر، روابط توپولوژیکی بین خطوط به طور کلی با استفاده از درختان توصیف می‌شود، اما درخت‌های کانتور در دستاوردهای موجود نمی‌توانند روابط توپولوژیکی را به طور منطقی بیان کنند. به عنوان مثال، در نوعی از درختان کانتور معمولی، خطوط را به عنوان گره و روابط همسایه بین خطوط را به عنوان لبه های اتصال می گیرند [ 26 ]]، روابط بین یک گره والد و گره های فرزند آن، هم روابط همسایه و هم روابط محتوی هستند، و در همان زیردرخت درخت کانتور، به جز روابط همسایه توپولوژیکی بین یک گره و گره والد آن، گره های خواهر و برادر یا گره های فرزند. ، روابط بین این گره و سایر گره ها همگی از نظر توپولوژیکی ناپیوسته هستند. این امر به ناچار منجر به نتایج محاسباتی اشتباه روابط توپولوژیکی بین خطوط می شود [ 1 ، 27 ، 28 ].
به طور خلاصه، هیچ دستاوردی در رابطه کمی بین تغییر مقیاس نقشه و درجه شباهت بین خطوط روی نقشه ها در مقیاس های چندگانه حاصل نشده است. اگرچه توصیف روابط توپولوژیکی بین خطوط کاوش می شود، روابط توپولوژیکی به طور کامل در نظر گرفته نمی شود و به درستی با استفاده از درختان کانتور بدون جهت بیان نمی شود [ 25 ، 26 ]. بنابراین، دستاوردها را نمی توان در تعمیم خوشه های کانتور مانند استخراج کانتور [ 29 ، 30 ] و تعمیم خودکار [ 31 ، 32 ، 33 ، 34 ] استفاده کرد.
ساختار باقی مانده این مقاله به شرح زیر است: بخش 2 مجموعه داده های مورد استفاده در این مطالعه و نحوه پیش پردازش مجموعه داده ها را ارائه می دهد. بخش 3 روش های ساخت درختان کانتور هدایت شده و یک روش بیان کمی برای روابط توپولوژیکی خوشه های کانتور را معرفی می کند. بخش 4 صحت روش های پیشنهادی را با استفاده از آزمایش ها نشان می دهد. بخش 5 روش های پیشنهادی و آزمایش های نشان داده شده در این مطالعه را مورد بحث قرار می دهد. بخش 6 برخی از کلمات پایانی را بیان می کند.

2. مجموعه داده ها و پیش پردازش آنها

2.1. مجموعه داده های تجربی

با توجه به استانداردهای طبقه بندی مختلف [ 35 ، 36 ]، انواع ژئومورفولوژیکی را می توان به زیر کلاس های مختلف ماکرو ژئومورفولوژیکی و زیرگروه های میکرو ژئومورفولوژیکی تقسیم کرد. برای کشف روابط کمی بین تغییر مقیاس نقشه و درجه شباهت توپولوژیکی خوشه‌های کانتور در فضاهای نقشه چند مقیاسی، انواع مختلف مورفولوژیکی بر روی نقشه‌های چند مقیاسی باید بررسی شود. بنابراین، در این مطالعه 108 گروه از خوشه های کانتوری که بیانگر انواع گونه های ژئومورفولوژیکی هستند، انتخاب شدند. هر خوشه کانتور را پوشش می دهد مناطق روی سطح زمین مقیاس نقشه منبع هر خوشه کانتور 1:5000 است و مقیاس هدف خطوط کلی تعمیم یافته متناظر به ترتیب 1:10000، 1:50000، 1:100000 و 1:250000 است.
از بین 108 گروه از خوشه های کانتور، 104 گروه برای بررسی روابط کمی بین تغییر مقیاس نقشه و درجه شباهت توپولوژیکی خوشه های کانتور در فضاهای نقشه چند مقیاسی استفاده می شود، در حالی که چهار گروه دیگر، مقیاس نقشه اصلی و هدف 1 است: 5000، 1:100000، به ترتیب، برای آزمایش یا اعتبار سنجی نتایج روابط کمی استفاده می شود که تغییر فاصله کانتور قبل و بعد از تعمیم بدون تغییر باشد. مجموعه داده ها در مقیاس های چندگانه (1:5000، 1:10000، 1:50،000، 1:100،000، و 1:250،000) روی نقشه ها با فواصل خطوط مختلف ( جدول 1 ) هستند و به صورت دستی توسط نقشه نگاران تعمیم داده می شوند. آنها در قالب های برداری هستند و توسط مرکز ملی ژئوماتیک گانسو (NGCG)، چین ارائه شده اند.
جدول 1 104 گروه از خوشه های کانتور مورد استفاده در این مطالعه را نشان می دهد که سه نوع عمده از انواع ژئومورفولوژیکی کلان (یعنی انواع ژئومورفولوژی لس، انواع کوهستانی و لندفرم های رودخانه ای) و انواع مختلف میکروژئومورفولوژیکی مربوطه را پوشش می دهد.

2.2. پیش پردازش مجموعه داده ها

خطوط در واقعیت پیوسته و بسته هستند. با این حال، یک نقشه تنها یک نمایش جزئی از دنیای واقعی است، و کانتور بر اساس صفحه ذخیره می‌شود، که منجر به کوتاه شدن خطوط کانتور به خطوط کانتور بسته نشده در مرز نقشه می‌شود [ 19 ، 37 ]. ثانیاً، رابطه محتوی نسبت به خطوط کانتور بسته است. علاوه بر این، خطوط کانتور بسته نشده منجر به عدم قطعیت رابطه توپولوژیکی بین خطوط کانتور می شود، که مشکلات غیر ضروری را برای دستیابی خودکار ارتفاع کانتور به همراه خواهد داشت [ 38 ].]. ثالثاً، بسته شدن خطوط کانتور بسته نشده، کارایی ذخیره سازی و بازیابی را بهبود می بخشد و فضای ذخیره سازی را هنگام ساخت ماتریس مجاورت و درخت کانتور بین خطوط کانتور کاهش می دهد. بنابراین، به منظور ساخت درخت های کانتور جهت دار به منظور توصیف روابط توپولوژیکی بین خطوط به طور صحیح و کامل، لازم است خطوط بسته نشده را از قبل پردازش کنیم تا بسته شوند [ 37 ، 38 ، 39 ].
دو شکل ژئومورفولوژیک مخالف وجود دارد: توپوگرافی مثبت و توپوگرافی منفی. فرض کنید خط کانتور در خلاف جهت عقربه های ساعت حرکت می کند، اگر ارتفاعات خط کانتور چپ بیشتر از ارتفاع خط کانتور فعلی باشد، شکل ژئومورفولوژیکی توپوگرافی مثبت است، مانند تپه های فرسوده شده توسط آب جاری معمولی، کوه ها. در غیر این صورت، توپوگرافی منفی است، مانند لندفرم های یخچالی، زمین فانگشان که توسط سنگ های افقی تشکیل شده است [ 28 ]. با در نظر گرفتن توپوگرافی مثبت به عنوان مثال، شکل 2 ایده بسته شدن کانتورهای بسته را نشان می دهد که شامل سه مرحله است: (1) ساخت ماتریس مجاورت بر اساس چند ضلعی های خطوط ورونوی [ 20 ].]؛ (2) تطبیق خطوط بسته نشده با توجه به میدان ارتفاع و ماتریس مجاورت، که شامل تطبیق خطوط تنه و خطوط زیردرخت است. (iii) حل کردن خطوط بسته نشده با توجه به تطبیق فیلد (ID_1) با خطوط بسته، و بازسازی ماتریس مثلثی مجاورت باینری (R (i,j) ) خطوط بسته.

3. روش شناسی

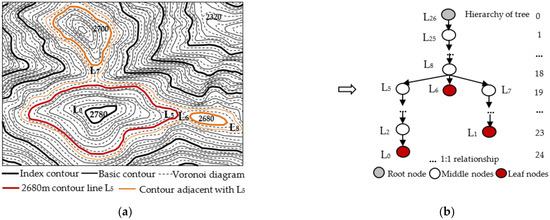
3.1. ساخت درخت کانتور جهت دار

روابط توپولوژیکی بین خطوط به طور کلی با استفاده از درخت توصیف می شود، اما درخت کانتور بدون جهت در دستاوردهای موجود نمی تواند روابط توپولوژیکی را به طور منطقی بیان کند. بنابراین، در اینجا از درختان کانتور جهت دار استفاده می شود که می تواند بر کاستی های درختان کانتور هدایت نشده غلبه کند.
ماهیت ساخت یک درخت کانتور جهت دار تعیین سطح ( k ) گره خطوط واقع در درخت کانتور و قضاوت در مورد حالت اتصال لبه های جهت دار بین گره ها است [ 19 ، 20 ]. برای توپوگرافی مثبت، ارتفاع خطوط با اختلاف مساوی مرتب شده و از گره ریشه مربوط به درونی ترین خطوط قله به گره های برگ کاهش می یابد. بنابراین، با توجه به ارتفاعات و روابط همسایگی خطوط بسته، سطح گره های کانتور واقع در درخت کانتور هدایت شده و نحوه اتصال لبه های جهت دار بین گره ها را می توان تعیین کرد ( شکل 2 ). اینجا، ک= حداکثر{ID_1} + 1 − {ID_1}، در حالی که عکس آن برای توپوگرافی منفی صادق است. گره برچسب گذاری شده گره ریشه است. همان عملیات را برای شاخه فرعی مانند تنه تکرار کرد تا زمانی که تمام گره های برچسب زده شده عبور کنند. اگر گره‌های فرزند گره‌های ریشه برچسب‌گذاری‌شده منحصربه‌فرد نیستند، گره‌های فرزند باید دائماً موقعیت‌های ذخیره‌سازی خود را در فهرست پیوندی پویا تنظیم کنند تا از تلاقی لبه‌های هدایت‌شده اجتناب کنند. درخت کانتور هدایت شده شکل 1 a در شکل 1 b نشان داده شده است.

3.2. روش بیان کمی روابط توپولوژیکی

سه نوع روابط توپولوژیکی بین خطوط وجود دارد: از نظر توپولوژیکی حاوی، از نظر توپولوژیکی همسایه و از نظر توپولوژیکی ناپیوسته. با فرض اینکه M تعداد کل گره ها در یک درخت کانتور جهت دار مربوط به خوشه کانتور با مقیاس نقشه S 1 باشد، i ( i = 1, 2, 3, …, M ) گره جاری است. سطوح درخت کانتور از گره ریشه تا گره های برگ به ترتیب 0، 1، 2، …، k ، …، N است و تعداد کل گره ها در لایه k ( k≤ N ) Pk ( Pk ) است .≤ M ). پاراگراف های زیر محاسبه روابط همسایه توپولوژیکی، محتوی توپولوژیکی و ناپیوسته توپولوژیکی را ارائه می دهند.

3.2.1. رابطه حاوی توپولوژیکی

برای همان زیردرخت یک درخت کانتور هدایت‌شده، روابط بین هر دو گره و گره‌های اجدادش و گره و گره‌های نواده‌اش از نظر توپولوژیکی روابطی هستند. به منظور اجتناب از محاسبه مکرر، فقط موارد اول در نظر گرفته می شود. بنابراین، تعداد کل روابط توپولوژیکی شامل خوشه کانتور در مقیاس را می توان به صورت زیر بیان کرد:

با در نظر گرفتن گره L 6 در شکل 1 b به عنوان مثال، روابط بین گره L 6 و گره های اجداد آن {L 8 , …, L 25 , L 26 } از نظر توپولوژیکی موجود است. بنابراین، عدد کانتور حاوی گره L 6 برابر با سطح k ( k = 19) است که گره L 6 در درخت کانتور هدایت شده قرار دارد. به طور مشابه، تعداد کل خطوط حاوی گره های L 5 و L 7 هر دو 19 است. بنابراین، تعداد کل خطوط حاوی گره های L 5 ، L 6 و L 7در سطح 19 درخت کانتور هدایت شده 57 است. بنابراین، با توجه به تعداد کل گره ها ( ) در هر سطح به جز گره ریشه، تعداد کل روابط حاوی توپولوژیک خوشه کانتور در شکل 1 a 271 است.
3.2.2. رابطه همسایه توپولوژیکی

در یک درخت کانتور جهت دار، روابط همسایه توپولوژیکی بین یک گره والد و گره های فرزند آن یا بین گره های خواهر و برادر وجود دارد، یعنی تعداد کل روابط همسایه از نظر توپولوژیکی. ) گره i به تعداد گره های فرزند و گره های خواهر و برادر آن بستگی دارد، به عنوان مثال، . بنابراین، تعداد کل روابط همسایه توپولوژیکی خوشه کانتور در مقیاس S 1 را می توان به صورت زیر محاسبه کرد:

به منظور اجتناب از محاسبه مکرر، روابط همسایگی توپولوژیکی بین خواهر و برادر فقط باید یک بار محاسبه شود. به عنوان مثال، در شکل 1b، گره های L 5 ، L 6 و L 7 گره های خواهر و برادر یکدیگر هستند، L 5 از نظر توپولوژیکی با L 6 همسایه است ، و L 6 نیز از نظر توپولوژیکی با L 5 همسایه است. در محاسبه فقط اولی در نظر گرفته می شود. بنابراین، تعداد کل روابط همسایه توپولوژیکی مربوط به گره های L 5 ، L 6 و L 7 به ترتیب 2، 1 و 0 است. در شکل 1b، هر گره یک گره فرزند دارد به جز گره L 8 که دارای سه فرزند است و هر یک از گره های دیگر هیچ گره خواهر و برادری ندارند به جز گره های L 5 و L 6 به ترتیب دارای دو و یک هستند. بنابراین، تعداد کل گره های فرزند و خواهر و برادر در شکل 1 ب می باشد و ، به ترتیب. بنابراین، تعداد کل روابط همسایه توپولوژیکی خوشه کانتور در شکل 1 a 35 است.
3.2.3. رابطه گسسته از نظر توپولوژیکی

روابط غیر مجاورت بین خطوط به جز آنهایی که از نظر توپولوژیکی دارای روابط محتوی و همسایه هستند، از نظر توپولوژیکی روابط گسسته نامیده می شوند [ 27 ].]. برای همان زیردرخت یک درخت کانتور جهت دار، به جز روابط همسایه توپولوژیکی بین یک گره و گره والد آن، گره های خواهر و برادر، و گره های فرزند، روابط بین این گره و گره های دیگر همگی از نظر توپولوژیکی ناپیوسته هستند. برای گره‌های متعلق به زیردرخت‌های مختلف، به جز روابط توپولوژیکی ناپیوسته بین یک گره و گره‌های برادر، روابط بین یک گره از این زیردرخت و سایر گره‌های زیردرخت‌های دیگر از نظر توپولوژیکی ناپیوسته هستند، از جمله روابط بین یک گره از این زیردرخت و گره‌های پسرعموی آن یا نوادگان سایر درختان فرعی. علاوه بر این، رابطه همسایه توپولوژیکی و رابطه ناهمگون بین خطوط از نظر کمیت یکدیگر را تکمیل می کنند. از این رو، ، تعداد کل روابط از نظر توپولوژیکی ناپیوسته را می توان به طور غیر مستقیم و کمی با تعداد کل روابط همسایه توپولوژیکی بیان کرد:

با در نظر گرفتن گره L 7 در شکل 1 b به عنوان مثال، روابط بین گره والد L 8 و گره فرزند L 7 از نظر توپولوژیکی موجود است و روابط بین گره L 7 و گره های خواهر و برادر L 5 و L 6 و گره های فرزند آن وجود دارد. از نظر توپولوژیکی همسایه هستند. روابط بین گره L 7 و گره L 2 و گره L 0 از زیردرخت های دیگر از نظر توپولوژیکی ناپیوسته است. در شکل 1 ب، و تعداد کل روابط همسایه توپولوژیکی 35 است. بنابراین، تعداد کل روابط ناهمگون از نظر توپولوژیکی خوشه کانتور در شکل 1 a 430 است.

با توجه به تجزیه و تحلیل فوق، انواع توپولوژیکی مختلف خوشه های کانتور یکدیگر را قطع می کنند و از نظر کمی یکدیگر را تکمیل می کنند. روابط توپولوژیکی بین برخی از گره ها فقط باید یک بار محاسبه شود، به عنوان مثال، روابط همسایه توپولوژیکی بین خواهر و برادر، در حالی که برخی دیگر باید دو بار تکرار شوند، به عنوان مثال، به جز روابط بین گره والدین و گره فرزند، رابطه توپولوژیکی حاوی و از نظر توپولوژیک ناپیوسته رابطه بین گره های اجداد و نوادگان در همان زیردرخت وجود دارد. بنابراین، چگونگی بیان موثر و دقیق روابط توپولوژیکی بین خطوط، کلید و هسته بیان کمی آن است. تعداد کل روابط توپولوژیکی خوشه کانتور در مقیاس را می توان به صورت زیر بیان کرد:

برای خوشه کانتور در شکل 1 a با عمق درخت کانتور هدایت شده 25، تعداد کل روابط توپولوژیکی 736 است.

3.3. فرمولی برای محاسبه شاخص های توپولوژیکی چند مقیاسی

تجزیه و تحلیل در بخش 3.2 نشان می دهد که شاخص های توپولوژیکی مرتبط با بیان کمی توپولوژیکی خوشه کانتور چند مقیاسی شامل نسبت تعداد خطوط بسته چند مقیاسی، نسبت عمق درخت کانتور چند مقیاسی و شباهت توپولوژیکی چند مقیاسی است.

3.3.1. تعریف تغییر فاصله کانتور

فاصله کانتور بازتابی جامع از مقیاس نقشه و زمین است [ 16 ]. تغییر فاصله کانتور را می توان به صورت زیر تعریف کرد: با فرض اینکه دو نقشه کانتور M 1 و M 2 وجود داشته باشد، M 2 یک نقشه تعمیم یافته از M 1 است و فواصل کانتور متناظر آنها به ترتیب d 1 و d 2 است. نسبت تغییر فاصله کانتور (CI) از نامیده می شود به یعنی CI = d 2 /d 1 .
3.3.2. نسبت شاخص توپولوژیکی مقیاس مجاور

نسبت‌های شاخص توپولوژیکی مقیاس مجاور، از جمله نسبت تعداد خطوط بسته مقیاس مجاور، نسبت عمق درختان کانتور مقیاس مجاور، و نسبت تعداد کل توپولوژیکی خوشه‌های کانتور مقیاس مجاور، برای توصیف روند تغییر شاخص‌های توپولوژیکی قبل و بعد استفاده می‌شوند. تعمیم، که برای شناخت فضایی انسان و درک روند تغییر روابط توپولوژیکی چند مقیاسی مهم است. نسبت شاخص توپولوژیکی را می توان به صورت زیر محاسبه کرد:

جایی که، نشان دهنده نسبت شاخص توپولوژیکی قبل و بعد از تعمیم است، مانند نسبت عمق درخت کانتور چند مقیاسی یا نسبت تعداد خطوط بسته، نسبت شاخص توپولوژیکی قبل از تعمیم است و نسبت شاخص توپولوژیکی پس از تعمیم زمانی است که خوشه کانتور از مقیاس تعمیم می یابد مقیاس کردن بودن و . در اینجا، k سطح درخت کانتور هدایت شده است.

3.3.3. شاخص های توپولوژیکی چند مقیاسی

شاخص های توپولوژیکی چند مقیاسی، مانند شباهت توپولوژیکی چند مقیاسی ( S )، نسبت توپولوژیکی حاوی چند مقیاس، و نسبت همسایه توپولوژیکی چند مقیاسی برای توصیف قوانین تغییرات کمی روابط توپولوژیکی چند مقیاسی با تغییر مقیاس نقشه استفاده می شود. که با [ 1 ] قابل اندازه گیری است:

جایی که، نشان دهنده نسبت شاخص های توپولوژیکی چند مقیاسی خوشه کانتور است که با تغییر مقیاس نقشه همبستگی منفی دارد. ; S 1 و S 2 به ترتیب مقیاس نقشه نقشه اصلی و نقشه تعمیم یافته را نشان می دهند. . تعداد کل j امین روابط توپولوژیکی مربوط به مقیاس نقشه را نشان می دهد .

4. آزمایش ها و نتایج

4.1. اعتبارسنجی درختان کانتور هدایت شده

قابلیت اطمینان درخت کانتور ساخته شده صحت بیان کمی روابط توپولوژیکی را تعیین می کند. نتایج تطبیق ارتفاع و کد خطوط بسته نشده در شکل 1 a در جدول 2 ، جدول 3 و جدول 4 نشان داده شده است .
جدول 2 ، جدول 3 و جدول 4 نشان می دهد که 65 کانتور بسته نشده در شکل 1 a مطابقت دارند و 30 کانتور بسته را پس از پیش پردازش تشکیل می دهند، شامل 24 کانتور تنه ( جدول 2 )، پنج کانتور شاخه شاخه فرعی I ( جدول 3 ). ، و یک خط کانتور شاخه شاخه فرعی II ( جدول 4 ). با در نظر گرفتن شکل 1 a به عنوان مثال، شکل 1 b نشان می دهد که درخت کانتور هدایت شده ساخته شده توسط این روش با درخت کانتور بدون جهت ساخته شده توسط سایر روش های موجود سازگار است [ 20 ، 21 ]]، به عنوان مثال، نتیجه ساخت درخت کانتور هدایت شده معقول تر و قابل اعتمادتر است. با در نظر گرفتن شکل 1 b به عنوان مثال، تعداد کل رابطه های توپولوژیکی حاوی محاسبه شده با روش بیان کیفی سنتی بر اساس درخت کانتور بدون جهت [ 1 ] 56 است و تعداد پدران و پسران به ترتیب 27 و 29 است که منجر به تکرار می شود. محاسبات شامل روابط بین پدر و پسر یا پسر و پدر علاوه بر نادیده گرفتن روابط موجود بین اجداد و اعقاب است.

4.2. تحلیل عوامل موثر بر شاخص های توپولوژیکی

عوامل تأثیرگذار شاخص های توپولوژیکی را می توان با تجزیه و تحلیل ویژگی های توزیع شاخص های توپولوژیکی کشف کرد. ) از جمله مقدار متوسط ​​( )، انحراف معیار ( و ضریب تغییرات ( ). انحراف استاندارد نشان دهنده پراکندگی مجموعه ای از آمارها نسبت به میانگین آن است و ضریب تغییرات نشان دهنده نوسان نسبی داده های آماری است [ 40 ]. جدول 5 پراکندگی و نوسانات شاخص های توپولوژیکی انواع مختلف ژئومورفولوژیکی را در مقیاس های مختلف نشان می دهد.
برخی از بینش را می توان از جدول 5 به دست آورد .
(1)
متفاوت از رابطه توپولوژیکی مجزا و همسایه از نظر توپولوژیکی، میانگین تعداد کل رابطه توپولوژیکی حاوی توپوگرافی کوهستانی به طور مداوم بالاتر از شکل زمین رودخانه و ژئومورفی لس است، هر مقیاس نقشه که باشد.
(2)
از انواع مختلف ماکرو ژئومورفولوژیکی در یک دیدگاه مقیاس نقشه، انحراف استاندارد عمق درخت کانتور هدایت‌شده و تعداد کل روابط حاوی توپولوژی مربوط به توپوگرافی کوه‌ها و شکل زمین رودخانه به طور قابل‌توجهی بیشتر از ژئومورفی لس است. با این حال، ضریب تغییرات تعداد کل خطوط بسته کاملاً برعکس است.
(3)
از نظر مقیاس های نقشه های مختلف از انواع ژئومورفولوژیکی یکسان، با کاهش مقیاس نقشه، به جز ضرایب تغییرات تعداد کل خطوط بسته مربوط به توپوگرافی کوه ها و شکل زمین رودخانه بدون تغییر باقی می ماند، انحراف معیار سایر شاخص های توپولوژیکی کاهش می یابد. به تدریج در مقابل، ضریب تغییرات تعداد کل روابط ناپیوسته توپولوژیکی توپوگرافی کوه به تدریج افزایش می یابد.
تجزیه و تحلیل فوق نشان می دهد که هر دو مقیاس نقشه و انواع ژئومورفولوژیکی به طور مشترک بر تفاوت کمی شاخص های توپولوژیکی تأثیر می گذارند، اما مورد اول تمرکز این مطالعه است. بنابراین، به منظور تحقق تعمیم خودکار خوشه های کانتور بر اساس روابط شباهت فضایی چند مقیاسی، مطالب زیر ابتدا روند شاخص های توپولوژیکی چند مقیاسی با تغییر مقیاس نقشه را مورد بحث قرار داده و سپس روابط کمی بین درجه تشابه توپولوژیکی و مقیاس نقشه را مورد بحث قرار داده است. تغییرات با روش برازش منحنی محاسبه شد.

4.3. روندهای کمی شاخص های توپولوژیکی چند مقیاسی

4.3.1. شاخص های توپولوژیکی مقیاس مجاور

شکل 3 روند تغییرات شاخص های توپولوژیکی خوشه های کانتور مقیاس مجاور را از نوع(های) ژئومورفولوژیکی یکسان یا متفاوت نشان می دهد.
دو نتیجه زیر را می توان از شکل 3 گرفت.
(1)
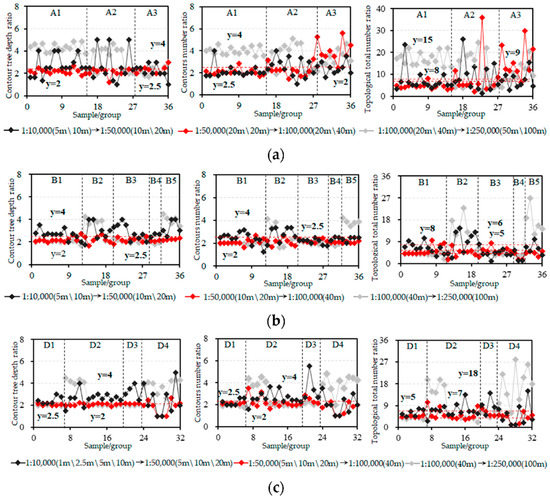
اگرچه نمونه‌های مختلف که به مقیاس نقشه و انواع ریزژئومورفولوژیکی یکسان تعلق دارند، فواصل کانتوری متفاوتی دارند، میانگین نسبت تعداد خطوط یا میانگین نسبت عمق درختان کانتور برابر با نسبت فاصله کانتوری خوشه کانتور مقیاس مجاور است. با این حال، به دلیل تفاوت سطح تسکین، شیب تند و درجه تکه تکه شدن سطح، نسبت عدد خطوط مقیاس مجاور یا نسبت عمق درختان کانتور مقیاس مجاور ثابت نیست اما در اطراف نسبت فاصله کانتور مقیاس مجاور در نوسان است. هنگامی که تغییر مقیاس نقشه 2.5 است، یعنی وقتی خوشه کانتور از 1:100000 به 1:250000 تعمیم داده می شود، شاخص های توپولوژی مقیاس مجاور تمایل بیشتری به فرار دارند.
(2)
متفاوت از اولی، میانگین نسبت عدد کل توپولوژیکی مقیاس مجاور با نسبت فاصله کانتور مربوطه همبستگی مثبت دارد، اما هیچ رابطه تناسبی بین آنها وجود ندارد. به عنوان مثال، زمانی که نسبت فاصله کانتور توپوگرافی کوهستانی {2، 2.5، 4} است، میانگین متناظر نسبت عدد کل توپولوژیکی {5، 6، 8} است. حتی اگر نسبت‌های فاصله کانتور مقیاس مجاور یکسان هستند، تفاوت‌های قابل‌توجهی در نسبت تعداد کل توپولوژیکی برای خوشه‌های کانتور مقیاس مجاور از انواع مختلف کلان ژئومورفولوژیکی وجود دارد، به عنوان مثال، وقتی هر دو اولی 2.5 هستند، دومی 15 و 8 برای ژئومورفی لس و توپوگرافی کوهستانی به ترتیب. بنابراین، بخش‌های زیر روند تشابه توپولوژیکی را بیشتر بررسی می‌کنند (به عنوان مثال،
4.3.2. شاخص های توپولوژیکی چند مقیاسی
درجه تشابه فضایی با افزایش تغییر مقیاس نقشه کاهش می یابد [ 1 ]. با این حال، روابط کمی بین شاخص های توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه هنوز به دست نیامده است. شکل 4 روند درجه تشابه توپولوژیکی چند مقیاسی نوع(های) ژئومورفولوژیکی یکسان یا متفاوت را با تغییر مقیاس نقشه نشان می دهد که می توان با سه نقطه زیر به تفصیل توضیح داد.
(1)
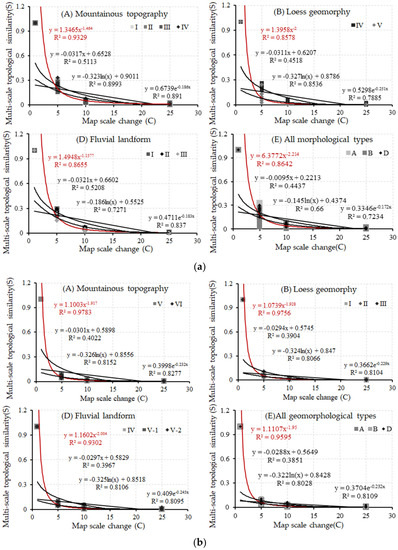
با افزایش تغییر مقیاس نقشه، نسبت شاخص توپولوژیکی چند مقیاسی به تدریج در مقایسه با هر گروه از نمونه ها کاهش می یابد (خط قرمز > سیاه > خاکستری). با این وجود، همه اینها بین گروه های مختلف نمونه درست نیست. به عنوان مثال، در شکل 4 ب، تغییر مقیاس نقشه، تغییر فاصله کانتور و درجه شباهت توپولوژیکی گروه 15 و 30 به ترتیب {10، 4، 0.0772} و {5، 4، 0.0622} است. تغییر فاصله کانتور دو نمونه 4 است و تغییر مقیاس نقشه اولی بیشتر از دومی است، اما درجه شباهت توپولوژیکی اولی نیز بزرگتر از دومی است.
(2)
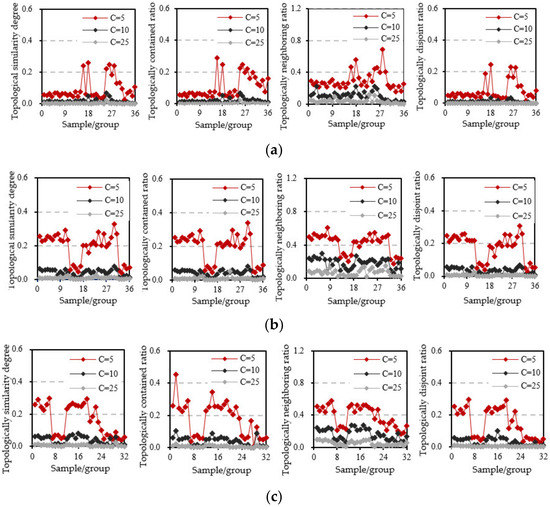
اگرچه تغییر مقیاس نقشه و نوع کلان ژئومورفولوژیکی یکسان است، نسبت های شاخص توپولوژیکی چند مقیاسی انواع مختلف میکروژئومورفولوژیکی به طور قابل ملاحظه ای متفاوت است. به عنوان مثال، همانطور که توسط منحنی قرمز در شکل 4 ب نشان داده شده است، تغییر مقیاس نقشه و نوع کلان ژئومورفولوژیکی گروه های 13-17 و گروه های 1-12 یکسان است، همه متعلق به توپوگرافی کوهستانی هستند، اما نوع میکروژئومورفولوژیکی اولی ارتفاع متوسط ​​و زیاد و کوه‌های برجسته متوسط ​​و دومی ارتفاع متوسط ​​و کوه‌های برجسته متوسط ​​است و درجات شباهت توپولوژیکی چند مقیاسی مربوطه به ترتیب در حدود 06/0 و 24/0 در نوسان است. از جدول 1 می توان آن را شناختکه تغییرات فاصله کانتور گروه 13-17 و گروه 1-12 به ترتیب 4 و 2 است.
(3)
اگر تغییرات فاصله کانتور دو گروه از نمونه ها یکسان باشد، نسبت شاخص های توپولوژیکی متناظر آنها نیز بسیار نزدیک است که همگی حول میانگین آن نوسان می کنند. به عنوان مثال، از شکل 4 ب و جدول 1 می توان فهمید که تغییر فاصله کانتور و نوع کلان ژئومورفولوژیکی گروه های 1-12 و 13-17 یکسان است و نوع میکروژئومورفولوژیکی اولی ارتفاع متوسط ​​است. و کوه‌های برجستگی متوسط، دومی ارتفاع متوسط ​​و بلند و کوه‌های برجسته متوسط، نوع میکروژئومورفولوژیکی متفاوت است، اما درجات شباهت توپولوژیکی چند مقیاسی آنها بسیار نزدیک است که همگی در حدود 0.24 نوسان دارند.
با توجه به تحلیل فوق، نسبت شاخص های توپولوژیکی چند مقیاسی ارتباط نزدیکی با تغییر فاصله کانتور دارد. این نتیجه همچنین نشان داد که “تغییر مقیاس نقشه، نیروی محرکه عینی تعمیم نقشه برداری است [ 10 ]”. بنابراین، این مطالعه بیشتر روابط کمی بین درجه شباهت توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه خوشه کانتور با همان تغییر فاصله کانتور را فرموله کرد.

4.4. روابط کمی بین درجه تشابه توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه

4.4.1. روندهای کمی

جدول 6 درجه شباهت توپولوژیکی چند مقیاسی نوع(های) کلان ژئومورفولوژیکی یکسان یا متفاوت را نشان می دهد.
(1)
با افزایش تغییر مقیاس نقشه، درجه شباهت توپولوژیکی چند مقیاسی و انحراف معیار آن به تدریج کاهش می یابد، اما ضریب تغییرات به تدریج افزایش می یابد. به عنوان مثال، با افزایش تغییر مقیاس نقشه از 5 به 25، انحراف استاندارد متناظر درجه تشابه توپولوژیکی چند مقیاسی توپوگرافی کوهستانی از 0.0849 به 0.0054 کاهش می یابد، اما ضرایب تغییرات از 0.4501 به 0.6993 افزایش می یابد که نشان می دهد با افزایش تغییر مقیاس نقشه، درجه پراکندگی درجه شباهت توپولوژیکی چند مقیاسی به تدریج کاهش می یابد، اما نوسان نسبی بین درجه شباهت توپولوژیکی به تدریج افزایش می یابد. این روند با نتایج در شکل 4 مطابقت دارد.
(2)
اگر فاصله کانتور قبل و بعد از تعمیم بدون تغییر باقی بماند، نسبت شاخص توپولوژیکی چند مقیاسی به 1 تمایل دارد. در آزمایش، چهار گروه از خوشه‌های کانتور چند مقیاسی از انواع مختلف میکروژئومورفولوژیکی انتخاب شدند و از 1:5000 تعمیم داده شدند. به 1:10000، و فاصله کانتور قبل و بعد از تعمیم 5 متر است، و نسبت شماره خط کانتور بسته متناظر، نسبت عمق درخت کانتور و درجه شباهت توپولوژیکی {0.9294، 0.9853، 0.8728}، {1، 1، 1} است، به ترتیب {0.9881، 0.9863، 1} و {1، 1، 0.9669}.

با توجه به تحلیل فوق، توابع مطابق با روند را می توان به صورت زیر فهرست کرد:

شکل 5 نتایج برازش بین درجه شباهت توپولوژیکی و تغییر مقیاس نقشه خوشه های کانتور چند مقیاسی با تغییر فاصله کانتور یکسان را نشان می دهد.

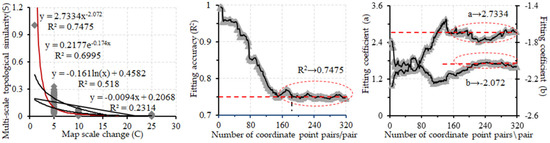
شکل 5 نشان می دهد که تابع توان (فرمول (8)) بهترین تناسب روابط کمی بین درجه شباهت توپولوژیکی و تغییر مقیاس نقشه خوشه کانتور چند مقیاسی با تغییر فاصله کانتور یکسان است، صرف نظر از اینکه یکسان یا متفاوت باشند. نوع(های) ژئومورفولوژیکی، دقت برازش ( R2) تابع قدرت در بین توابع کاندید بالاترین است. دقت فیتینگ کمتر از 0.8578 نیست و حداکثر دقت فیتینگ تا 0.9783 است. هنگامی که تغییر مقیاس نقشه از 1 تا 5 متغیر است، درجه شباهت توپولوژیکی چند مقیاسی به سرعت با افزایش تغییر مقیاس نقشه کاهش می یابد. بنابراین، زمانی که تغییرات فاصله کانتوری خوشه های کانتور یکسان باشد، صرف نظر از اینکه نوع(های) ژئومورفولوژیکی یکسان یا متفاوت باشند، روابط کمی بین درجه تشابه توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه را می توان به صورت کمی با استفاده از توان یکسان بیان کرد. عملکرد:

4.4.2. تأثیر اندازه نمونه بر انواع و دقت عملکرد برازش
هنوز مشخص نیست که آیا انواع تابع برازش بهینه به طور مداوم با افزایش اندازه نمونه تغییر می کند یا خیر. بنابراین، با در نظر گرفتن خوشه کانتور چند مقیاسی با تغییر بازه کانتور یکسان و انواع مختلف ژئومورفولوژیکی کلان به عنوان اشیاء تحقیق، جدول 7 تأثیر حجم نمونه را بر نوع روابط تابع کمی بین شباهت توپولوژیکی چند مقیاسی و مقیاس نقشه نشان می دهد. تغییر دادن.
جدول 7 نشان می دهد که انواع تابع برازش بهینه به طور مداوم با افزایش حجم نمونه تغییر می کند. با این حال، مهم نیست که کدام نوع تغییر بازه کانتور است، تابع توان همیشه بهترین تابع مناسب زمانی است که اندازه نمونه به مقدار مشخصی افزایش یابد. به عنوان مثال، برای خوشه های کانتور چند مقیاسی، که فاصله کانتور آنها {1، 2، 4، 10} است، زمانی که اندازه های نمونه N∈[7، 23]، N∈N+، بهترین تابع برازش یک تابع نمایی است. ، در حالی که N∈[24, 228]، N∈N+، بهترین تابع برازش تابع توان است. بعلاوه، زمانی که فاصله کانتور متعلق به {1، 4، 8، 20} باشد، دقت برازش (R 2) تابع توان همیشه در میان توابع کاندید بالاترین است، یعنی تابع توان همیشه بهترین تابع است. این نتیجه گیری بیشتر تأیید می کند که تابع توان بهترین برای بیان روابط کمی بین درجه شباهت توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه خوشه کانتور با همان تغییر فاصله کانتور است.
از نظر تئوری، یک تناسب کامل R 2 = 1، اما با افزایش حجم نمونه، R 2 کاهش می یابد و در نهایت به مقدار معینی همگرا می شود. بنابراین، با در نظر گرفتن خوشه کانتور با تغییرات بازه کانتور مختلف به عنوان مثال، شکل 6 تأثیر اندازه نمونه را بر دقت و ضرایب برازش نتایج تابع توان نشان می دهد.
همانطور که در شکل 6 نشان داده شده است ، تابع توان ( ) همچنین برای بیان روابط کمی بین درجه تشابه توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه خوشه کانتور با تغییرات فاصله کانتوری متفاوت است. با این حال، دقت برازش تنها 0.7475 است و تجزیه و تحلیل شاخص‌های توپولوژیکی چند مقیاسی در بخش 4.3 نشان می‌دهد که نسبت شاخص‌های توپولوژیکی خوشه کانتور چند مقیاسی ارتباط نزدیکی با تغییر فاصله کانتور دارد. بنابراین، استفاده از تابع توان یکسان برای برازش روابط کمی بین درجه شباهت توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه خوشه کانتور با تغییرات فاصله کانتوری متفاوت، غیرمنطقی است.

5. بحث

برخی از بینش ها را می توان از نتایج تجربی بالا به دست آورد.
روش بیان کمی پیشنهاد شده در این مقاله روابط توپولوژیکی را با استفاده از درخت کانتور جهت دار در نظر گرفته و بیان می کند. در مقایسه با روش بیان کیفی سنتی مبتنی بر درخت کانتور بدون جهت [ 1 ، 21 ]، درخت کانتور جهت دار نه تنها به اندازه کافی همپوشانی و مکمل را بین انواع توپولوژیکی مختلف در نظر می گیرد، بلکه به طور موثر از محاسبات مکرر و حذف روابط توپولوژیکی جلوگیری می کند، بنابراین دقت را بهبود می بخشد. بیان کمی روابط توپولوژیکی همچنین می تواند برای بیان روابط توپولوژیکی اشیاء گروهی دیگر مانند شبکه های خط متقاطع، شبکه های درخت مانند و گروه های چند ضلعی گسسته استفاده شود.
لازم به ذکر است که شاخص های توپولوژیکی چند مقیاسی خوشه های کانتور ارتباط نزدیکی با تغییر فاصله کانتور دارند. این را می توان از دو جنبه زیر تأیید کرد: اولاً، زمانی که فواصل کانتور قبل و بعد از تعمیم بدون تغییر است، میانگین نسبت عددی خطوط مقیاس مجاور یا میانگین نسبت عمق درخت کانتور مقیاس مجاور برابر با نسبت فاصله کانتور مقیاس مجاور است. . در این آزمایش، چهار گروه از خوشه‌های کانتور چند مقیاسی از انواع مختلف میکروژئومورفولوژیکی انتخاب شدند و از 1:5000 به 1:10000 تعمیم داده شدند، فاصله کانتور هر دو 5 متر است و نسبت شماره خط کانتور بسته مربوطه و نسبت عمق درخت کانتور به ترتیب {0.9294، 1، 0.9881،1} و {0.9853، 1، 0.9863،1} است.21 ]، بنابراین این نتیجه گیری با شناخت فضایی انسان سازگار است. ثانیا، زمانی که تغییر مقیاس نقشه و نوع ماکرو ژئومورفولوژیکی یکسان است، نسبت شاخص های توپولوژیکی چند مقیاسی انواع مختلف میکروژئومورفولوژیکی به طور قابل ملاحظه ای متفاوت است. با این حال، زمانی که تغییرات فاصله کانتور یکسان است، نسبت‌های شاخص توپولوژیکی چند مقیاسی بسیار نزدیک هستند که حول میانگین آن در نوسان است.
دلایل روندهای فوق را می توان به صورت زیر توضیح داد: شباهت توپولوژیکی کانتور چند مقیاسی یک قانون تغییر سازگار با تغییر مقیاس نقشه را نشان می دهد. با این حال، نمونه‌های مختلف ویژگی‌های جغرافیایی متفاوتی دارند، مانند درجه تکه تکه شدن زمین، درجه تسکین سطح، و شیب شیب، که منجر به تفاوت قابل‌توجهی در شاخص‌های توپولوژیکی خوشه کانتور با مقیاس نقشه یکسان، مانند شکل زمین بادی و دشت دیلوویا خشک می‌شود. ، توپوگرافی کوهستانی عظیم و توپوگرافی تپه ای شکسته. همین امر برای خوشه های کانتور با مقیاس نقشه و نوع ژئومورفولوژیکی یکسان صادق است. به عنوان مثال، شکل 7خوشه کانتور 1:50000 از همان نوع جغرافیایی را نشان می دهد که تنک بودن و شیب شیب آن تفاوت معنی داری دارد. تعداد خطوط کانتور بسته، عمق درخت کانتور و تعداد کل توپولوژی در شکل 7 ب 1.85، 2.04، و 4.07 برابر شکل 7 a است، اما یک بار چهارم، چهار پنجم و سه پنجم در شکل 7 است.ج به ترتیب فاصله کانتور و درجه شیب شیب، تعداد و تراکم خطوط کانتور، یعنی عمق درخت کانتور را تعیین می کند. درجه تکه تکه شدن زمین، تعداد گره‌ها را در هر سطح از درخت کانتور تعیین می‌کند، این سه عامل با هم منجر به تفاوت‌های قابل‌توجهی در شاخص‌های توپولوژیکی خوشه کانتور در مقیاس مشابه و انواع میکروژئومورفولوژیکی یکسان یا متفاوت می‌شوند.
نتایج تجربی فوق را می توان به طور گسترده در زمینه های شناخت فضایی، استدلال فضایی و طراحی نقشه استفاده کرد. به عنوان مثال، اگر عمق درخت کانتور مقیاس نقشه اصلی و تغییر فاصله کانتور مشخص باشد، عمق درخت کانتور مقیاس هدف را می توان با توجه به نتایج آزمایش بالا استنتاج کرد. رابطه توپولوژیکی بین خطوط را می توان به طور منحصر به فرد با توجه به خوشه کانتور تعیین کرد، و بالعکس، موقعیت همبستگی بین خطوط نیز می تواند بر اساس رابطه توپولوژیکی تعیین شود [ 38 ]]. با توجه به این نتیجه تجربی که میانگین نسبت شماره خطوط کانتور مقیاس مجاور برابر با نسبت فاصله کانتور مقیاس مجاور است، بنابراین، چگالی کانتور باید با توجه به فاصله کانتور قبل و بعد از تعمیم در طراحی نقشه توپولوژیکی مقایسه شود.
علاوه بر این، عملکرد قدرت ( ) برای بیان روابط کمی بین درجه شباهت توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه بهترین است. هنگامی که اعداد نمونه به مقدار معینی افزایش می‌یابد، دقت برازش و ضرایب تابع توان نیز پایدار است. اگرچه روابط کمی بین درجه شباهت توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه را می توان با استفاده از تابع توان یکسان برای خوشه های کانتور چند مقیاسی با تغییرات فاصله کانتوری مختلف بیان کرد، اما دقت برازش تنها 0.7475 است. بنابراین، در مقایسه با خوشه های کانتور چند مقیاسی با تغییرات بازه کانتور متفاوت، منطقی تر است که از تابع توان یکسان برای برازش روابط کمی بین درجه شباهت توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه خوشه کانتور با تغییر فاصله کانتوری یکسان استفاده شود. (ر2 ≥ 0.8578)، صرف نظر از اینکه نوع(های) ژئومورفولوژیکی یکسان یا متفاوت هستند.
نتایج فوق نیز برای تعمیم کانتور اهمیت زیادی دارند. اول، ایجاد رابطه فضایی کانتور و تولید درخت کانتور شرایط و مبنای مناسبی را برای استخراج خطوط ساختاری زمین فراهم می‌کند [ 19 ، 29 ]. به عنوان مثال، با در نظر گرفتن استخراج خط دره، هنگام جستجوی نقاط پایین دره از خطوط کانتور با حداکثر ارتفاع پایین، صحت جستجو و زمان را می توان با کمک درخت کانتور بهبود بخشید. دوم، تعمیم نقشه اساساً یک تبدیل شباهت فضایی بین نقشه‌های چند مقیاسی است که می‌تواند از شباهت فاصله، شباهت توپولوژیکی و شباهت جهت اندازه‌گیری شود [ 1 ، 27 ]]. بنابراین، شباهت توپولوژیکی چند مقیاسی یک محتوای مهم در تحقیق شباهت فضایی کانتور چند مقیاسی [ 19 ] است و برای تحقق تعمیم خودکار کانتور حیاتی است. علاوه بر این، این نتیجه تجربی بیشتر نشان می‌دهد که تحقق تعمیم خودکار خوشه‌های کانتور بر اساس روابط شباهت فضایی چند مقیاسی معقول و امکان‌پذیر است.

6. نتیجه گیری و کارهای آینده

به دست آوردن درجات شباهت توپولوژیکی در میان خوشه های کانتور یکسان در نقشه های چند مقیاسی در تعمیم خودکار نقشه اهمیت دارد. این مقاله یک مدل بیان کمی از روابط توپولوژیکی خوشه کانتور را با ساختن درخت کانتور هدایت شده توسعه داد. بر این اساس، قواعد مختلف کمی شاخص‌های توپولوژیکی، به‌ویژه، درجات شباهت توپولوژیکی خوشه‌های کانتور چند مقیاسی با تغییر مقیاس نقشه بررسی شدند. می توان نتیجه گرفت که شاخص های توپولوژیکی چند مقیاسی خوشه های کانتور ارتباط نزدیکی با تغییر بازه کانتور و تابع توان دارند. )، بهترین تناسب برای بیان روابط کمی بین درجه شباهت توپولوژیکی و تغییر مقیاس نقشه خوشه‌های کانتور چند مقیاسی با تغییر فاصله کانتور یکسان است. این رابطه کمی را می توان با استفاده از تابع توان یکسان بیان کرد، صرف نظر از اینکه آنها از نوع(های) ژئومورفولوژیکی یکسان یا متفاوت باشند. این نتیجه گیری نشان می دهد که تحقق تعمیم خودکار خوشه های کانتور بر اساس روابط شباهت فضایی چند مقیاسی معقول و امکان پذیر است.
در حال حاضر، با توجه به محدود بودن مجموعه داده کانتور در مقیاس بزرگ 1:5000 اعمال شده، تنها از چهار گروه از مجموعه داده ها، که مقیاس نقشه اصلی و هدف مربوطه 1:5000، 1:10000 است، برای اعتبارسنجی نتایج در هنگام نقشه استفاده می شود. تغییر مقیاس بدون تغییر است و پنج نوع مقیاس نقشه در این مطالعه در نظر گرفته شد. با این وجود، آزمایش‌ها نشان می‌دهند که شباهت توپولوژیکی خوشه کانتور چند مقیاسی در تغییر مقیاس کوچک نقشه به شدت تغییر می‌کند (C≤ 5). بنابراین، به منظور ایجاد روابط کمی بین درجه تشابه فضایی و تغییر مقیاس نقشه خوشه‌های کانتور چند مقیاسی، مطالعه آینده ما اندازه‌های نمونه مجموعه داده‌های چند مقیاسی را در مقیاس نقشه بزرگ افزایش می‌دهد که پایه‌ای برای فضایی انسانی فراهم می‌کند.

منابع

  1. Yan، HW; Li, J. روابط شباهت فضایی در فضاهای نقشه چند مقیاسی . Springer International Publishing: Cham, Switzerland, 2014. [ Google Scholar ]
  2. چهرقان، ع. عباسپور، RA ارزیابی درجه تشابه فضایی بین چندخطوط بر روی نقشه های چند مقیاسی و چند منبعی. Geocarto Int. 2017 ، 32 ، 471-487. [ Google Scholar ] [ CrossRef ]
  3. وی، ZW; Guo، QS; چن، ال. لیو، ی. Tong، Y. اندازه‌گیری تشابه شکل بر اساس هم‌ترازی DNA برای ساختمان‌هایی با ویژگی‌های متعامد متعدد. Acta Geod. کارتوگر. گناه 2021 ، 50 ، 1683-1693. [ Google Scholar ]
  4. لی، دبلیو دبلیو; راسکین، آر. گودچیل، اندازه‌گیری شباهت معنایی MF بر اساس دانش کاوی: یک رویکرد شبکه عصبی مصنوعی. بین المللی جی. جئوگر. Inf. علمی 2012 ، 26 ، 1415-1435. [ Google Scholar ] [ CrossRef ]
  5. گائو، XR؛ Yan، HW; اندازه‌گیری شباهت معنایی Lu، XM برای ایجاد تجمع چند ضلعی در فضای نقشه چند مقیاسی. Acta Geod. کارتوگر. گناه 2022 ، 51 ، 95-103. [ Google Scholar ]
  6. لی، بی. Fonseca، F. TDD: یک مدل جامع برای ارزیابی شباهت فضایی کیفی. تف کردن شناخت. محاسبه کنید. 2006 ، 6 ، 31-62. [ Google Scholar ] [ CrossRef ]
  7. ژانگ، ال. Guilbert, E. ارزیابی روشهای تعمیم شبکه رودخانه برای حفظ الگوی زهکشی. بین المللی J. Geo-Inf. 2016 ، 5 ، 230. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  8. Yan، XF; Ai, TH; یانگ، م. یین، اچ. یک شبکه عصبی کانولوشن گراف برای طبقه بندی الگوهای ساختمان با استفاده از داده های برداری فضایی. ISPRS J. Photogramm. Remote Sens. 2019 ، 150 ، 259–273. [ Google Scholar ] [ CrossRef ]
  9. Yan، XF; Ai, TH; یانگ، ام. ساده‌سازی ویژگی‌های مسکونی با روش شناخت شکل و تطبیق الگو. Acta Geod. کارتوگر. گناه 2016 ، 45 ، 874-882. [ Google Scholar ]
  10. فن، HC; Zipf، A.; فو، س. Neis, P. ارزیابی کیفیت برای ایجاد داده های ردپایی در OpenStreetMap. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 700-719. [ Google Scholar ] [ CrossRef ]
  11. ژائو، YP; سان، س. لیو، XG; چنگ، م. یو، تی. روش اندازه‌گیری شباهت معنایی مبتنی بر نهاد جغرافیایی لی، YF و کاربرد آن در تطبیق جاده. Geomat. Inf. علمی دانشگاه ووهان 2020 ، 45 ، 728-735. [ Google Scholar ]
  12. فن، HC; یانگ، BS; Zipf، A.; Rousell, A. یک رویکرد مبتنی بر چند ضلعی برای تطبیق شبکه جاده نقشه خیابان باز با داده های مرجع حمل و نقل منطقه ای. بین المللی جی. جئوگر. Inf. علمی 2016 ، 30 ، 748-764. [ Google Scholar ] [ CrossRef ]
  13. چهرقان، ع. عباسپور، RA یک رویکرد مبتنی بر هندسی برای تطبیق جاده در مجموعه داده‌های چند مقیاسی با استفاده از الگوریتم ژنتیک. کارتوگر. Geogr. Inf. علمی 2018 ، 45 ، 255-269. [ Google Scholar ] [ CrossRef ]
  14. رواس، الف. خودکارسازی تعمیم داده های جغرافیایی. در مجموعه مقالات بیستمین کنفرانس بین المللی کارتوگرافی، پکن، چین، 18 مه 2010; صفحات 1943-1953. [ Google Scholar ]
  15. یانگ، WF; Yan، HW; فرمول Li, J. برای محاسبه درجه شباهت فضایی بین ابرهای نقطه ای روی نقشه های چند مقیاسی که تغییر مقیاس نقشه را به عنوان تنها متغیر مستقل در نظر می گیرند. Geod. ژئودین. 2015 ، 6 ، 113-125. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  16. وانگ، جی. او، ZY; کارتوگرافی Pu، YX ; مطبوعات نقشه برداری و نقشه برداری: پکن، چین، 2016. [ Google Scholar ]
  17. Li، ZL; Sui, HG یک تکنیک یکپارچه برای تعمیم خودکار نقشه های کانتور. کارتوگر. J. 2000 , 37 , 29-37. [ Google Scholar ] [ CrossRef ]
  18. Guo، RZ تجزیه و تحلیل فضایی ; انتشارات آموزش عالی: پکن، چین، 2001. [ Google Scholar ]
  19. Yan، HW; Wang, JY توضیحات رویکردها و خودکارسازی الگوریتم‌های تعمیم برای گروه‌هایی از اشیاء نقشه . انتشارات علمی: پکن، چین، 2009. [ Google Scholar ]
  20. Qiao، CF; ژائو، RL; چن، جی. Chen, YH یک رویکرد مبتنی بر مجاورت داخلی voronoi برای تولید یک درخت کانتور. Geomat. Inf. علمی دانشگاه ووهان 2005 ، 30 ، 801-804. [ Google Scholar ]
  21. ژانگ، ی. فن، اچ. Huang, W. روش تولید درخت کانتور بر اساس مثلث کانتور Delaunay. Acta Geod. کارتوگر. گناه 2012 ، 41 ، 461-474. [ Google Scholar ]
  22. چن، جی. لی، سی ام؛ Li، ZL; طلا، C. مدل 9 تقاطع مبتنی بر ورونوی برای روابط فضایی. ISPRS J. Geogr. Inf. علمی 2001 ، 15 ، 201-220. [ Google Scholar ] [ CrossRef ]
  23. چن، جی. ژائو، RL; روابط همسایه مبتنی بر K-order Li، ZL Voronoi برای تجزیه و تحلیل فضایی. ISPRS J. Photogramm. Remote Sens. 2004 ، 59 ، 60-72. [ Google Scholar ] [ CrossRef ]
  24. Li، ZL; Huang، PZ اقدامات کمی برای اطلاعات فضایی نقشه ها. بین المللی جی. جئوگر. Inf. علمی 2002 ، 16 ، 699-709. [ Google Scholar ] [ CrossRef ]
  25. Qiao، CF; ژائو، RL; چن، جی. Chen, YH روشی برای تولید درخت کانتور بر اساس مجاورت داخلی voronoi. ژئو اسپات. Inf. علمی 2005 ، 8 ، 287-290. [ Google Scholar ]
  26. چن، جی. Qiao، CF; Zhao, RL رویکردی مبتنی بر مجاورت داخلی Voronoi برای ایجاد درخت کانتور. محاسبه کنید. Geosci. 2004 ، 30 ، 355-367. [ Google Scholar ] [ CrossRef ]
  27. Guo، WY; لیو، هی؛ سان، س. یو، AZ; چن، HX A مدل اندازه‌گیری شباهت ترکیبی گروه کانتور برای به‌روزرسانی افزایشی منطقه. J. Geo-Inf. علمی 2019 ، 21 ، 147-156. [ Google Scholar ]
  28. Guo، WY; لیو، هی؛ سان، س. یو، AZ; Ding، ZY یک روش تطبیق خطوط چند منبعی با در نظر گرفتن شباهت ویژگی‌های هندسی. Acta Geod. کارتوگر. گناه 2019 ، 48 ، 643-653. [ Google Scholar ]
  29. Ai, TH استخراج شبکه زهکشی از خطوط کانتور برای تعمیم خط کانتور. ISPRS J. Photogramm. Remote Sens. 2007 ، 62 ، 93-103. [ Google Scholar ] [ CrossRef ]
  30. ژو، ایکس. لی، دبلیو. Arundel، ST یک مدل احتمالی فضایی – زمینه ای برای استخراج ویژگی خطی در زمین تپه ای از داده های DEM با وضوح بالا. بین المللی جی. جئوگر. Inf. علمی 2019 ، 33 ، 666-686. [ Google Scholar ] [ CrossRef ]
  31. Bjorke، JT; Nilsen, S. Wavelets برای ساده‌سازی مدل‌های زمین دیجیتال به کار رفته است. بین المللی جی. جئوگر. Inf. علمی 2003 ، 17 ، 601-621. [ Google Scholar ] [ CrossRef ]
  32. Ai, TH; Li، JZ تعمیم DEM با تشخیص جزئی شاخه دره و پر کردن شبکه. ISPRS J. Photogramm. Remote Sens. 2010 ، 65 ، 198-207. [ Google Scholar ] [ CrossRef ]
  33. ژو، QM; چن، YM تعمیم DEM برای تجزیه و تحلیل زمین با استفاده از روش ترکیبی. ISPRS J. Photogramm. Remote Sens. 2011 ، 66 ، 38-45. [ Google Scholar ] [ CrossRef ]
  34. چن، سی اف. Li، Y. یک روش مبتنی بر حداقل مربع متعامد برای تعمیم DEM. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 154-167. [ Google Scholar ] [ CrossRef ]
  35. وانگ، JY ژئومورفولوژی و تعمیم آن . انتشارات نقشه برداری و نقشه برداری: پکن، چین، 2019. [ Google Scholar ]
  36. چن، WM; ژو، CH; لی، توسط; چای، HX; ژائو، SM استخراج کمی و تجزیه و تحلیل انواع مورفولوژیکی پایه ژئومورفولوژی زمین در چین. جی. جئوگر. علمی 2011 ، 21 ، 771-790. [ Google Scholar ]
  37. Hao, XY نقشه اطلاعات شناسایی و فناوری استخراج ; انتشارات نقشه برداری و نقشه برداری: پکن، چین، 2001. [ Google Scholar ]
  38. Wu، HH GIS و مدل پایه و الگوریتم تعمیم اطلاعات نقشه ; انتشارات دانشگاه ووهان: ووهان، چین، 2012. [ Google Scholar ]
  39. Guo، QS; وو، اچ. Li، PC قوانین رابطه فضایی و ساده سازی گرافیکی پیشرونده خطوط. Geomat. Inf. علمی دانشگاه ووهان 2000 ، 25 ، 31-34. [ Google Scholar ]
  40. Nigel, W. تجزیه و تحلیل داده های جغرافیایی ; Wiley & Sons Ltd.: نیویورک، نیویورک، ایالات متحده آمریکا، 1995. [ Google Scholar ]
Ijgi 11 00268 g001 550
شکل 1. تطبیق کانتور غیر بسته (فاصله کانتور 20 متر است) و مدل درخت کانتور مربوطه آن. ( الف ) نمودار ورونوی و تطبیق خطوط بسته نشده. ( ب ) مدل درخت کانتور جهت دار مربوط به ( a ).
Ijgi 11 00268 g002 550
شکل 2. بسته شدن کانتورهای بسته نشده و ساخت درخت کانتور جهت دار.
Ijgi 11 00268 g003 550
شکل 3. روند تغییرات شاخص های توپولوژیکی خوشه های کانتور مقیاس مجاور. A1-A3، B1-B3، و D1-D4 کدهای نوع انواع مختلف میکروژئومورفولوژیکی را نشان می دهند که در جدول 1 نشان داده شده است. ( الف ) ژئومورفیت لس (36 گروه). ( ب ) توپوگرافی کوهستانی (36 گروه). ج ) شکل زمین رودخانه ای (32 گروه).
Ijgi 11 00268 g004 550
شکل 4. روند درجه تشابه توپولوژیکی چند مقیاسی نوع(های) توپوگرافی یکسان یا متفاوت با تغییر مقیاس نقشه. ( الف ) ژئومورفی لس (36 گروه نمونه). ( ب ) توپوگرافی کوهستانی (36 گروه نمونه). ( ج ) شکل زمین رودخانه ای (32 گروه نمونه).
Ijgi 11 00268 g005 550
شکل 5. برازش نتایج بین درجه شباهت توپولوژیکی چند مقیاسی و تغییر مقیاس نقشه خطوط چند مقیاسی با تغییر فاصله کانتور یکسان. ( الف ) تغییر فاصله کانتور {1، 2، 4، 10} است (57 گروه از مجموعه داده‌های نمونه). ( ب ) تغییر فاصله کانتور {1، 4، 8، 20} است (47 گروه از مجموعه داده‌های نمونه).
Ijgi 11 00268 g006 550
شکل 6. نتیجه برازش خوشه کانتور چند مقیاسی با تغییرات فاصله کانتور متفاوت.
Ijgi 11 00268 g007 550
شکل 7. خطوط 1:50000 با فاصله کانتوری 20 متر و ویژگی های جغرافیایی مختلف توپوگرافی کوه ها. ( الف ) شیب مسطح؛ ( ب ) کمی شیب دار و کمی شکسته. ج ) شیب تند.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید