تعیین چگونگی تخصیص معقول سرپناه در منطقه مرکزی شهر و بهبود کارایی تخلیه از موضوعات مهم در زمینه پیشگیری از بلایای شهری است. این مقاله روش‌شناسی و مدل ریاضی را از حوزه تخلیه اضطراری جمعیت تا بهینه‌سازی مکان پناهگاه معرفی می‌کند. علاوه بر این، یک روش بهینه‌سازی مکان پناهگاه مبتنی بر ترکیب تحلیل شبکه استاتیک و شبیه‌سازی تخلیه پویا پیشنهاد شده‌است. هزینه های ساخت و ساز و زمان تخلیه به عنوان توابع هدف در نظر گرفته می شود. در مرحله اول، بر اساس تحلیل شبکه ایستا، یک قانون تخصیص تخلیه دایره ای بر اساس مدل گرانشی پیشنهاد شده است و سپس الگوریتم ژنتیک برای حل طرح های امکان پذیر با کمترین هزینه ساخت سرپناه طراحی می شود. در مرحله دوم، زمان تخلیه به عنوان هدف بهینه سازی در نظر گرفته می شود. تفاوت سنی پناهندگان، انتخاب مسیرهای تخلیه، و رفتار بزرگسالانی که به کودکان و سالمندان کمک می کنند در یک مدل شبیه سازی تخلیه پویا شبیه سازی شده است. مدل نیروی اجتماعی سنتی برای انجام یک شبیه‌سازی تخلیه منطقه‌ای و تعیین طرح بهینه با کوتاه‌ترین زمان تخلیه بهبود یافته است. در نهایت، منطقه شهری مرکزی شهر Xinyi، استان جیانگ سو، چین، به عنوان یک مورد تجربی در نظر گرفته شده است. مدل نیروی اجتماعی سنتی برای انجام یک شبیه‌سازی تخلیه منطقه‌ای و تعیین طرح بهینه با کوتاه‌ترین زمان تخلیه بهبود یافته است. در نهایت، منطقه شهری مرکزی شهر Xinyi، استان جیانگ سو، چین، به عنوان یک مورد تجربی در نظر گرفته شده است. مدل نیروی اجتماعی سنتی برای انجام یک شبیه‌سازی تخلیه منطقه‌ای و تعیین طرح بهینه با کوتاه‌ترین زمان تخلیه بهبود یافته است. در نهایت، منطقه شهری مرکزی شهر Xinyi، استان جیانگ سو، چین، به عنوان یک مورد تجربی در نظر گرفته شده است.

کلید واژه ها:

پناهگاه ; تجزیه و تحلیل استاتیک/دینامیک ؛ مدل نیروی اجتماعی ; الگوریتم ژنتیک ; بهینه سازی چند هدفه دو مرحله ای

1. مقدمه

پناهگاه ها فضاها و ساختمان های معمولی مجهز به زیرساخت های پشتیبانی اضطراری، امکانات کمکی اضطراری، و تجهیزات و مواد پشتیبانی اضطراری برای امنیت زندگی پناهندگان و نجات متمرکز پس از بلایا هستند [ 1 ]. با توسعه سیستم های طبیعی و اجتماعی که به طور فزاینده ای پیچیده تر می شوند، فراوانی و انواع بلایا در حال افزایش است. ریسک دارای سه جزء اصلی است: وقوع یک رویداد فاجعه بار، آسیب پذیری و قرار گرفتن در معرض. این مطالعه بر اقداماتی برای کاهش مولفه قرار گرفتن در معرض تمرکز دارد. اقدام کلان اصلی برای کاهش قرار گرفتن در معرض، تخلیه است، که شامل کاهش تعداد کاربران و کالاهایی است که می توانند اثرات منفی در هنگام وقوع حوادث اضطراری را تجربه کنند. 2 ].]. بنابراین، تعیین چگونگی تخصیص علمی و بهینه‌سازی مکان پناهگاه‌ها به یک نگرانی فزاینده تبدیل شده است. یک طرح علمی مکان یابی پناهگاه می تواند به طور قابل توجهی تلفات و تلفات اموال را کاهش دهد و می تواند کارایی و ایمنی فرآیند تخلیه پس از بلایا را بهبود بخشد.
محققان مجموعه ای از تحقیقات را در مورد مکان پناهگاه ها انجام داده اند و مدل P-center [ 3 ]، مدل P-median [ 4 ]، مدل پوشش مجموعه [ 5 ]، و مدل حداکثر پوشش [3] را ارائه کرده اند. 6 ]. علاوه بر این، بر اساس مدل کلاسیک، محدودیت‌های فاصله [ 7 ] و محدودیت‌های ظرفیت [ 8 ] اضافه شده‌اند. انواع توابع هدف را می توان به مدل های تک هدفه و چند هدفه تقسیم کرد. برای ساده کردن مسئله، برخی از محققان یک مدل تک هدفه را برای ایجاد مدل مکان در مرحله تحقیقات اولیه اتخاذ کرده اند [ 9 ، 10 ]]، و سپس به حداقل رساندن هزینه ساخت و ساز یا تعداد پناهگاه ها به عنوان هدف بهینه سازی اتخاذ شد. با این حال، به دلیل پیچیدگی بهینه‌سازی مکان پناهگاه‌ها، محققان از ایجاد مدل‌های بهینه‌سازی تک هدفه ناراضی شدند. بنابراین، مدل‌های بهینه‌سازی چند هدفه با ادغام چندین هدف بهینه‌سازی، مانند هزینه ساخت و ساز [ 11 ]، فاصله تخلیه [ 12 ]، زمان [ 13 ]، ایمنی جاده‌های تخلیه [ 14 ] و خطرات بلایا [14] ایجاد شده‌اند. 15 ، 16 ، 17]. متفاوت از مدل‌های مکان تک‌هدفه، راه‌حل مدل‌های مکان چند هدفه، تعادل اهداف چندگانه است و تعداد راه‌حل‌ها معمولاً بیش از یک است. سه روش کلی برای حل مدل بهینه سازی چند هدفه پناهگاه ها وجود دارد: (1) تبدیل مدل بهینه سازی چند هدفه به یک مدل بهینه سازی تک هدفه از طریق وزن دهی [ 18 ]. (2) تبدیل مسئله بهینه سازی پناهگاه چند هدفه به یک مسئله بهینه سازی تک هدفه دو مرحله ای [ 19 ، 20 ]. (3) اتخاذ الگوریتم اکتشافی برای حل جواب بهینه پارتو [ 16 ، 21]. با توجه به سطوح مختلف، ویژگی‌های داخلی، طبقه‌بندی‌ها و عملکردهای مربوط به پناهگاه‌های مختلف، محققان مدل‌های مکان‌یابی پناهگاه چند سطحی را ارائه کرده‌اند [ 21 ، 22 ، 23 ]. به عنوان مثال، بر اساس پناهگاه های موجود در جامعه و تقاضای تخلیه در دوره های مختلف، Ye [ 24 ] یک روش برنامه ریزی تخلیه را بر اساس سناریوهای متعدد در سطح جامعه پیشنهاد کرد. برخی از محققان توزیع مواد امدادی [ 25 ] [ 26 ] و شبیه سازی فرآیند فاجعه را نیز گنجانده اند [ 8 ، 27 ]] به مدل سازی مکان پناهگاه. مدل‌های بهینه‌سازی مکان پناهگاه تغییراتی را از ساده به پیچیده، از یک عامل واحد به انواع عوامل محیطی پیچیده شهری، از سطح کلان به سطح خرد و از سطح منفرد به سطوح چندگانه تجربه کرده‌اند. این پیشرفت‌ها مدل‌های مکان پناهگاه را با جزئیات بیشتری ساخته است، که یک مبنای نظری عملی برای کار عملی فراهم می‌کند.
الگوریتم‌های بهینه‌سازی برای حل مدل‌های بهینه‌سازی مکان پناهگاه‌ها به دو دسته الگوریتم‌های دقیق و تقریبی تقسیم می‌شوند. هنگامی که مدل مکان یابی پناهگاه یک مسئله بهینه سازی تک هدفه بر اساس یک تابع چند جمله ای یا یک مسئله بهینه سازی چند هدفه است که می تواند از طریق روش وزن دهی هدف، روش برنامه ریزی هدف و روش ضریب کارایی به یک تابع تک هدفه تبدیل شود. راه حل های بهینه را می توان با الگوریتم های دقیق، مانند الگوریتم شاخه ای [ 28 ]، روش سیمپلکس و روش آرام سازی لاگرانژ [ 29 ] تعیین کرد.]. فرآیند حل از طریق نرم افزارهای بهینه سازی مانند Lingo و CPLEX پیاده سازی می شود. با این حال، مکان پناهگاه هایی با محدودیت های چند هدفه یک مسئله NP-hard است که حل آن با الگوریتم های دقیق دشوار است. بنابراین، برخی از محققان الگوریتم‌های بهینه‌سازی هوشمند مانند الگوریتم ژنتیک [ 30 ]، الگوریتم بازپخت شبیه‌سازی شده [ 31 ]، الگوریتم ازدحام ذرات [ 12 ، 32 ]، الگوریتم کلونی مورچه [ 33 ] و الگوریتم جستجوی تابو، [ 33 ] و الگوریتم جستجوی تابو را اتخاذ کرده‌اند . برای حل مدل های مکان یابی پناهگاه با محدودیت های چند هدفه. در نهایت، تجسم طرح بهینه بر روی پلت فرم GIS [ 35 ] اجرا می شود.
مطالعاتی که قبلاً توضیح داده شد مبتنی بر روش تحلیل شبکه ایستا هستند و مدل‌های پیشنهادی از نظر محاسبه تقاضای تخلیه و قوانین تخصیص تخلیه با کمبودهای زیر مشخص می‌شوند:
(1) عدم ارضای خواسته های تخلیه در ساعات اوج مصرف. تقاضاهای تخلیه در تحقیقات قبلی بر اساس جمعیت دائمی تعیین شده است [ 27 ، 36 ]. با این حال، به دلیل جدایی محل کار و سکونت در مناطق مرکزی شهری، تفاوت های اساسی در توزیع جمعیت در طول روز و شب وجود دارد [ 37 ، 38 ، 39 ]. تقاضاهای تخلیه تعیین شده توسط یک جمعیت دائمی نمی تواند منعکس کننده توزیع پویای مکانی – زمانی جمعیت باشد و نمی تواند تقاضاهای تخلیه را در طول دوره اوج برآورده کند. و
(2) عدم توجه به روند تخلیه جمعیت و رفتار تخلیه. مدل‌های بهینه‌سازی فعلی معمولاً فرض می‌کنند که عابران پیاده در یک نقطه تقاضا از ترتیبات دولت پیروی می‌کنند و به پناهگاه تعیین‌شده خود می‌روند [ 40 ]، که با فرآیند تخلیه معتبر ناسازگار است. رفتار تخلیه و روانشناسی عابران پیاده، و همچنین تغییرات زمان متغیر ازدحام جاده، قبلا مورد توجه قرار نگرفته است [ 41 ].
از نظر شبیه‌سازی تخلیه اضطراری جمعیت، مدل‌های تخلیه را می‌توان به مدل‌های میکرو، کلان و مزو تقسیم کرد [ 42 ]. از منظر روش تخصیص تخلیه، مدل های تخلیه را می توان به مدل های پویا و استاتیک تقسیم کرد. مدل‌های پویا نشان می‌دهند که عابران پیاده یا وسایل نقلیه جهت حرکت خود را در هر تقاطع انتخاب می‌کنند، در حالی که مدل‌های استاتیک نشان می‌دهند که عابران پیاده یا وسایل نقلیه مسیر از پیش طراحی‌شده را بدون تغییر مسیرهای تخلیه خود در میانه راه دنبال می‌کنند [ 43 ]. مدل‌های کلان [ 44 ] حرکت افراد را به صورت سیال در نظر می‌گیرند و از معادلات دیفرانسیل جزئی در دینامیک سیالات برای توصیف تغییرات متغیر زمان سرعت و چگالی تخلیه استفاده می‌کنند. 45 ].]. این مدل‌ها کارایی محاسباتی بالایی دارند و جزئیات رفتار فردی را در نظر نمی‌گیرند، اما محدودیت‌ها را از شبکه جاده‌ها به جریان شبکه برای بهینه‌سازی تبدیل می‌کنند. با این حال، مدل‌های کلان، متغیرهای حالت را در فواصل زمانی منظم از طریق معادله حالت پویا به‌روزرسانی می‌کنند، که نمی‌تواند تعامل و ناهمگنی بین عابران پیاده را منعکس کند. مدل های مزو بین مدل های خرد و کلان هستند. روش شبیه سازی گسسته برای ردیابی حرکت عابران پیاده در فرآیند تخلیه اتخاذ شده است. مدل های مزو نه تنها با کاهش مقدار محاسبات مشخص می شوند، بلکه بخشی از جزئیات مهم در فرآیند تخلیه را نیز ثبت می کنند. 46 ]]. در نهایت، مدل های خرد افراد را به عنوان ذرات فردی در نظر می گیرند. این مدل‌ها می‌توانند تفاوت‌های بین عابران پیاده را منعکس کنند و توصیف حرکت دقیق‌تر و طبیعی‌تر است. مدل‌های خرد متداول شامل مدل نیروی اجتماعی [ 47 ]، مدل اتوماتای ​​سلولی [ 48 ، 49 ] و مدل چند عاملی [ 50 ، 51 ] و غیره است. شبیه سازی رفتار کاربر در حین تخلیه یک مشکل بسیار پیچیده است، زیرا این رفتار به عوامل مختلفی مانند نوع و ماهیت رویداد خطرناک، ویژگی های اجتماعی-اقتصادی کاربران و وحشت بستگی دارد. 52 ].]. مدل نیروی اجتماعی به دلیل دقت بالا و تداوم قوی به طور گسترده مورد استفاده قرار گرفته است. رفتار تخلیه خاص عابران پیاده، مانند رفتار گله [ 50 ]، رفتار زیر [ 53 ]، اثر سریع یا آهسته و اثر رهبر [ 54 ] را می توان با مدل نیروی اجتماعی شبیه سازی کرد. علاوه بر این، مدل نیروی اجتماعی را می توان با مدل چند عاملی [ 55 ، 56 ] ترکیب کرد تا ناهمگونی دسته های مختلف عابران پیاده را شبیه سازی کند. بنابراین، مدل نیروی اجتماعی در پژوهش حاضر برای انجام شبیه‌سازی تخلیه منطقه‌ای و در نهایت بهینه‌سازی علمی و دقیق مکان پناهگاه‌ها اتخاذ شده است.
در حال حاضر، تحقیق در مورد شبیه‌سازی تخلیه پویا بر روی ساختمان‌های عمومی بزرگ [ 57 ]، ساختمان‌های آموزشی [ 58 ]، متروها [ 59 ] و ساختمان‌های بلند [ 60 ] متمرکز شده است و شبیه‌سازی تخلیه در مقیاس جامعه نادر است. شبیه‌سازی‌های تخلیه منطقه‌ای قبلی، ناهمگونی فضایی سن عابران پیاده [ 61 ] را در نظر نمی‌گرفت، که منجر به انحراف زیادی از نتایج شبیه‌سازی از سناریوهای تخلیه معتبر شده است. مطالعات قبلی نشان داده است که سرعت تخلیه عابران پیاده به طور قابل توجهی با سن همبستگی دارد. 62 ]]. ساختار سنی با انواع کاربری ها و صنایع موجود در فضا بسیار متفاوت است و تفاوت های قابل توجهی در ساختار سنی قطعات مختلف وجود دارد. برای مثال، نسبت افراد مسن در مناطق تجاری کم است، در حالی که در جوامع قدیمی زیاد است. بازده کلی تخلیه قطعات با نسبت بالایی از افراد مسن پایین است، که بر روند کلی تخلیه و پیکربندی فضایی پناهگاه ها تأثیر می گذارد.
بنابراین، این مطالعه روش و مدل شبیه‌سازی تخلیه اضطراری را در بهینه‌سازی مکان پناهگاه‌ها معرفی می‌کند. ابتدا یک مدل تخلیه اضطراری منطقه ای ایجاد می شود که انتخاب مسیرهای تخلیه توسط عابران پیاده را در نظر می گیرد. سه نوع عامل عابر پیاده شامل سالمندان، بزرگسالان و کودکان ایجاد می شود و رفتار بزرگسالانی که به سالمندان و کودکان کمک می کنند در حین تخلیه شبیه سازی می شود. دوم، با ترکیب مزایای مدل سنتی بهینه‌سازی مکان مبتنی بر تحلیل شبکه استاتیک و شبیه‌سازی تخلیه اضطراری پویا، این مطالعه یک روش ترکیبی بهینه‌سازی مکان دو مرحله‌ای استاتیکی/دینامیک را پیشنهاد می‌کند که برای آن تعداد پناهگاه‌ها و کل زمان تخلیه گرفته می‌شود. به عنوان اهداف بهینه سازی تابع هدف بهینه سازی در مرحله اول هزینه ساخت سرپناه است و قوانین تخصیص تخلیه دایره ای بر اساس مدل ثقلی پیشنهاد شده است. سپس الگوریتم ژنتیک برای حل مدل طراحی می شود. بهینه‌سازی در مرحله دوم، مدل تخلیه پویای منطقه‌ای طرح‌های عملی مرحله اول را ایجاد می‌کند. سپس کل زمان تخلیه هر طرح امکان پذیر برای تعیین طرح مکان بهینه با کوتاه ترین زمان تخلیه مقایسه می شود. در نهایت، شهر Xinyi به عنوان یک مورد تجربی برای تأیید امکان‌سنجی و کاربرد روش بهینه‌سازی پیشنهادی بر اساس ترکیب تحلیل استاتیک و شبیه‌سازی دینامیکی در نظر گرفته می‌شود. و قوانین تخصیص تخلیه دایره ای بر اساس مدل گرانشی پیشنهاد شده است. سپس الگوریتم ژنتیک برای حل مدل طراحی می شود. بهینه‌سازی در مرحله دوم، مدل تخلیه پویای منطقه‌ای طرح‌های عملی مرحله اول را ایجاد می‌کند. سپس کل زمان تخلیه هر طرح امکان پذیر برای تعیین طرح مکان بهینه با کوتاه ترین زمان تخلیه مقایسه می شود. در نهایت، شهر Xinyi به عنوان یک مورد تجربی برای تأیید امکان‌سنجی و کاربرد روش بهینه‌سازی پیشنهادی بر اساس ترکیب تحلیل استاتیک و شبیه‌سازی دینامیکی در نظر گرفته می‌شود. و قوانین تخصیص تخلیه دایره ای بر اساس مدل گرانشی پیشنهاد شده است. سپس الگوریتم ژنتیک برای حل مدل طراحی می شود. بهینه‌سازی در مرحله دوم، مدل تخلیه پویای منطقه‌ای طرح‌های عملی مرحله اول را ایجاد می‌کند. سپس کل زمان تخلیه هر طرح امکان پذیر برای تعیین طرح مکان بهینه با کوتاه ترین زمان تخلیه مقایسه می شود. در نهایت، شهر Xinyi به عنوان یک مورد تجربی برای تأیید امکان‌سنجی و کاربرد روش بهینه‌سازی پیشنهادی بر اساس ترکیب تحلیل استاتیک و شبیه‌سازی دینامیکی در نظر گرفته می‌شود. سپس کل زمان تخلیه هر طرح امکان پذیر برای تعیین طرح مکان بهینه با کوتاه ترین زمان تخلیه مقایسه می شود. در نهایت، شهر Xinyi به عنوان یک مورد تجربی برای تأیید امکان‌سنجی و کاربرد روش بهینه‌سازی پیشنهادی بر اساس ترکیب تحلیل استاتیک و شبیه‌سازی دینامیکی در نظر گرفته می‌شود. سپس کل زمان تخلیه هر طرح امکان پذیر برای تعیین طرح مکان بهینه با کوتاه ترین زمان تخلیه مقایسه می شود. در نهایت، شهر Xinyi به عنوان یک مورد تجربی برای تأیید امکان‌سنجی و کاربرد روش بهینه‌سازی پیشنهادی بر اساس ترکیب تحلیل استاتیک و شبیه‌سازی دینامیکی در نظر گرفته می‌شود.
روش پیشنهادی این مطالعه چهار مشارکت دارد: (1) روش شناسی و مدل ریاضی را از زمینه تخلیه اضطراری جمعیت تا بهینه سازی مکان پناهگاه معرفی می کند. کاستی ها در پیکربندی پناهگاه های شهری را می توان به طور شهودی یافت. (2) روش ترکیبی بهینه‌سازی استاتیک/دینامیک نه تنها نمی‌تواند بهینه‌سازی مکان را به طور موثر حل کند، بلکه فرآیند تخلیه جمعیت معتبر را نیز منعکس می‌کند. (3) تقاضاهای تخلیه پویا به دقت تعیین شده است که می تواند تقاضای تخلیه ساکنان را در همه زمان ها برآورده کند. و (4) مدل تخلیه بهبود یافته رفتار کمک بزرگسالان به سالمندان و کودکان، رفتار انتخابی برای مسیرهای تخلیه، و ناهمگونی فضایی ساختار سنی را شبیه‌سازی می‌کند.

2. مواد و روشها

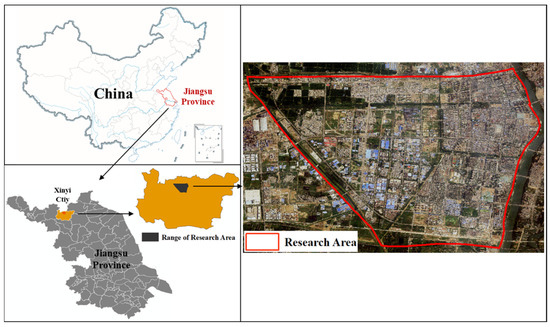
2.1. منطقه مطالعه

منطقه شهری مرکزی شهر Xinyi، استان جیانگ سو، چین، که مساحت کل آن 39.36 کیلومتر مربع است ، به سه دلیل به عنوان منطقه مورد مطالعه انتخاب شد. اولاً، منطقه شهری مرکزی دارای تراکم جمعیت بالا و همچنین شدت ساخت و ساز و توسعه بالایی است. تراکم جمعیت در ساعات اوج بار در گوشه شمال شرقی به 37100 نفر در کیلومتر مربع می رسد. جفت شدن تجمع جمعیت بالا و تراکم فضایی بالا خطر را در طول تخلیه افزایش می دهد. دوم اینکه منطقه مورد مطالعه دارای خطر لرزه ای بالایی است. ناحیه گسلی تانلو از ناحیه شهری مرکزی شهر شینی می گذرد. در 25 ژوئیه 1668، یک زلزله 8.5 ریشتری، که در ناحیه گسل تانلو رخ داد، در نزدیکی شهر تانچنگ، استان شانگدونگ رخ داد. 63 ] رخ داد.] و کانون زمین لرزه تنها 50 کیلومتر با منطقه مورد مطالعه فاصله داشت. ثالثاً، منطقه مورد مطالعه عملکرد ترکیبی بالایی دارد و منعکس کننده مونتاژ چندین صنعت مانند تجارت، مالی، تجارت، سرگرمی و خدمات است و در نتیجه تعداد زیادی از مردم را برای جمع آوری در آنجا جذب می کند. علاوه بر این، توزیع جمعیت بین روز و شب بسیار متفاوت است. شکل 1 موقعیت و محدوده منطقه مورد مطالعه را نشان می دهد.

2.2. جمع آوری و پردازش داده ها

مدل بهینه‌سازی پیشنهادی در این مطالعه مستلزم کسب داده‌های مکانی و جمعیتی در منطقه مورد مطالعه است. داده های به دست آمده شامل موارد زیر است: (1) مکان نقاط تقاضای پناهندگان و تعداد پناهندگان در طول روز و شب. (2) تعداد، مکان و ظرفیت پناهگاه هایی که ساخته شده اند. (3) تعداد، مکان، و ظرفیت پناهگاه های نامزد. (4) کوتاه ترین فاصله شبکه جاده ای از نقاط تقاضای پناهندگان تا پناهگاه ها. و (5) حداکثر فاصله سرویس دهی پناهگاه ها. اهداف تحقیق این مطالعه پناهگاه‌های تجمع اضطراری مقیم مشخص شده در کد چینی مربوطه است، بنابراین حداکثر فاصله خدمات 1500 متر [ 1 ] است.
داده‌های مکانی منطقه مورد مطالعه شامل سطح راه‌های تخلیه و پراکندگی مکانی و مساحت مؤثر پناهگاه‌های فعلی و کاندید است. داده های مکانی از نقشه OpenStreetMap و Gaode مشتق شده اند و از طریق بررسی های میدانی و تصاویر سنجش از دور تکمیل و اصلاح می شوند ( شکل 2 ). منابع اراضی موجود در منطقه مورد مطالعه تفکیک شد و 71 منطقه کاندید قابل استفاده برای سرپناه جدید تعیین شد. همانطور که در جدول 1 گزارش شده است، کوتاه ترین فاصله بین نقاط تقاضا و پناهگاه ها در امتداد شبکه جاده ها توسط الگوریتم Dijkstra [ 64 ] تعیین می شود .

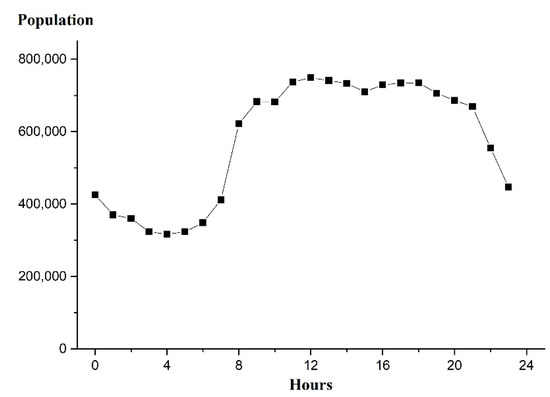
برای به دست آوردن داده های جمعیتی با دقت بالا، جمعیت منطقه مورد مطالعه بیش از 24 ساعت بر اساس داده های سیگنالینگ تلفن همراه چین از 15 دسامبر 2021 تا 28 دسامبر 2021 تعیین شد. شکل 3).). با این حال، این داده های جمعیتی تعداد کل افراد را نشان نمی دهد و نسبت کل جمعیتی که از تجهیزات ارتباطی سیار چینی در منطقه مورد مطالعه استفاده می کنند ناشناخته است. جمعیت شبانه تعیین‌شده توسط داده‌های سیگنالینگ تلفن همراه با اشاره به جمعیت دائمی تصحیح شد، بنابراین نسبت جمعیتی که از تجهیزات ارتباطی سیار چین استفاده می‌کنند که جمعیت دائمی در منطقه مورد مطالعه را تشکیل می‌دهند، آشکار شد. سالنامه آماری Xinyi داده هایی را در مورد جمعیت دائمی ارائه می دهد. منطقه مورد مطالعه شامل محله های Xin’an، Beigou و Mohe است. بر اساس داده های جمعیت ارائه شده توسط سالنامه آماری Xinyi (2020)، تعداد کاربران تلفن همراه چینی در محله های Xin’an، Beigou و Mohe به ترتیب 16.67٪، 15.46٪ و 15 بود. 26 درصد نفوس دایمی سه ولسوالی. داده‌های جمعیت به‌دست‌آمده از داده‌های سیگنال‌دهی تلفن همراه به‌طور متناسب برای تعیین نیازهای تخلیه در هر ساعت از روز تصحیح شد. در نهایت، نسبتی که تعداد پناهندگان برای کل جمعیت در برنامه‌ریزی پناهگاه‌های تجمع اضطراری مقیم به حساب می‌آید، با رابطه (1) تعیین می‌شود.1 ].

که در آن P بی خانمان نشان دهنده تعداد افراد بی خانمان پس از زلزله است. سرانه نشان دهنده سرانه فضای زندگی ساکنان شهری (m2 ) است. A 1 نشان دهنده منطقه آسیب کامل به ساختمان های مسکونی (m2 ) است. A 2 نشان دهنده منطقه آسیب گسترده به ساختمان های مسکونی (m2 ) است. و A 3 نشان دهنده ناحیه آسیب متوسط ​​به ساختمان های مسکونی (m2 ) است. جدول 2 تعداد پناهندگان در هر لحظه و ساختار سنی نقاط تقاضا را نشان می دهد.

WorldPop ( https://www.worldpop.org/ (دسترسی در 8 اکتبر 2020)) داده های شبکه ای را برای تراکم جمعیت در ابعاد 100 متر × 100 متر ارائه می دهد. با توجه به ساختار سنی، WorldPop رده سنی را 5 سال در نظر می گیرد و تعداد افراد از همه گروه های سنی در چین را ارائه می دهد. تعداد و نسبت افراد مسن بالای 65 سال و کودکان زیر 10 سال در هر نقطه تقاضا با تجزیه و تحلیل برهم نهی در ArcGIS تعیین شد ( جدول 2 ).

2.3. ساخت متدولوژی بهینه‌سازی مکان پناهگاه دو مرحله‌ای ترکیبی استاتیک/دینامیک

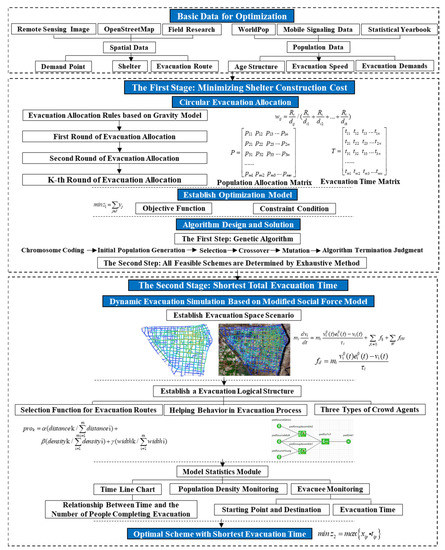
2.3.1. چارچوب کلی تحقیق

بر اساس اصول بهینه سازی انصاف، کارایی و صرفه جویی، تعداد پناهگاه های نوساز و کل زمان تخلیه به عنوان توابع هدف پژوهش حاضر در نظر گرفته شده است. یک روش بهینه سازی پناهگاه دو مرحله ای بر اساس ترکیبی از تجزیه و تحلیل استاتیک و شبیه سازی دینامیکی ایجاد شده است. انصاف نشان می دهد که نتایج بهینه سازی خواسته های تخلیه همه افراد را برآورده می کند. کارایی بیانگر فرآیند تخلیه سریع و به حداقل رساندن زمان تخلیه است. منظور از اقتصاد به حداقل رساندن هزینه ساخت است، یعنی به حداقل رساندن تعداد سرپناه های تازه ساخته شده. در مرحله اول، روش تحلیل شبکه ایستا اتخاذ می شود. و الگوریتم ژنتیک برای تعیین حداقل تعداد پناهگاه هایی طراحی شده است که می تواند نیازهای تخلیه همه افراد را تحت محدودیت ظرفیت پناهگاه و فاصله خدمات برآورده کند. در مرحله دوم، مدل‌های تخلیه دینامیکی طرح‌های امکان‌پذیر شناسایی‌شده در مرحله اول برای تعیین طرح بهینه با کوتاه‌ترین زمان تخلیه کل ایجاد می‌شوند. دلیل ایجاد یک روش ترکیبی بهینه‌سازی دو مرحله‌ای استاتیک/دینامیک به شرح زیر توضیح داده شده است. از یک طرف، در حالی که تحلیل شبکه ایستا سنتی را می توان به سرعت بر اساس الگوریتم هوشمند اکتشافی حل کرد، تفاوت سن پناهندگان، رفتار تخلیه واقعی عابران پیاده و وضعیت شلوغی واقعی جاده تخلیه را در نظر نمی گیرد. . از سوی دیگر،بخش 2.3.3 می‌تواند انتخاب مسیرهای تخلیه، ازدحام بی‌درنگ جاده‌های تخلیه، رفتارهای تخلیه واقعی و تفاوت‌های سنی را منعکس کند. با این حال، اگر بهینه سازی مکان پناهگاه بر اساس شبیه سازی تخلیه پویا تکمیل شود، لازم است هزینه ساخت و زمان تخلیه هر طرح مقایسه شود. تعداد پناهگاه های کاندید m است و i شماره سریال پناهگاه کاندید است، بنابراین تعداد کل طرح های مکان یابی پناهگاه ها به صورت تعیین می شود. . انواع مدل‌های شبیه‌سازی تخلیه باید از طریق روش جامع ایجاد و با یکدیگر مقایسه شوند که منجر به مقدار زیادی محاسبه می‌شود. بنابراین، با ترکیب مزایای دو روش، یک روش بهینه‌سازی مکان پناهگاه دو مرحله‌ای مبتنی بر ترکیب تحلیل استاتیکی و شبیه‌سازی دینامیکی پیشنهاد می‌شود. به طور خاص، این روش شامل موارد زیر است:
(1) جمع آوری داده های پایه. سلسله مراتب جاده، موقعیت مکانی تقاضاهای تخلیه، و پناهگاه ها در منطقه مورد مطالعه از تصاویر سنجش از دور، نقشه های گوگل، نقشه خیابان باز [ 65 ] و تحقیقات میدانی تعیین می شوند. برخی از محققان توزیع مکانی-زمانی جمعیت را بر اساس فناوری‌های کلان داده مانند داده‌های نقطه‌ی علاقه (POI) [ 66 ]، داده‌های سیگنالینگ تلفن همراه [ 67 ]، نقشه‌های حرارتی Baidu [ 68 ] و ورود به سیستم رسانه‌های اجتماعی تعیین کرده‌اند. داده [ 69]. در مطالعه حاضر، منحنی تغییر جمعیت 24 ساعته و تقاضای تخلیه پویا در دوره های مختلف بر اساس داده های سیگنالینگ تلفن همراه تعیین می شود. علاوه بر این، ساختار سنی پناهندگان با داده های WorldPop (https://www.worldpop.org/ (دسترسی در 8 اکتبر 2020)).
(2) هدف بهینه سازی در مرحله اول به حداقل رساندن تعداد پناهگاه ها از طریق تجزیه و تحلیل شبکه ایستا است. ابتدا قانون تخصیص تخلیه دایره ای پیشنهاد شده است. تخصیص تخلیه دایره ای نشان می دهد که پناهندگان در نقطه تقاضا بر اساس مدل جاذبه به پناهگاه های اطراف اختصاص داده می شوند. اگر تعداد پناهندگان پذیرفته شده توسط یک پناهگاه به محدودیت ظرفیت پناهگاه برسد، تخلیه در این زمان متوقف خواهد شد. عابران پیاده که تخلیه نشده اند وارد چرخه بعدی می شوند تا زمانی که همه افراد تخلیه را کامل کنند. دوم، تحت محدودیت های ظرفیت و فاصله خدمات، یک الگوریتم ژنتیک برای حل حداقل تعداد پناهگاه های جدید طراحی شده است. سوم، (B تعداد کل پناهگاه های نامزد است) انواع طرح های کاندیدا.
(3) ایجاد و بهبود مدل تخلیه اضطراری منطقه ای. با توجه به انتخاب مسیرهای تخلیه، این مطالعه مدل نیروی اجتماعی سنتی را بهبود می بخشد و یک تابع انتخاب برای مسیرهای تخلیه ایجاد می کند. علاوه بر این، ناهمگونی فضایی ساختار سنی عابران پیاده و رفتار بزرگسالانی که به کودکان و سالمندان در طول فرآیند تخلیه کمک می کنند، در نظر گرفته می شود. سکوی شبیه‌سازی Anylogic برای شبیه‌سازی فرآیند تخلیه برای تعیین کل زمان تخلیه و شناسایی بخش‌های جاده‌ای متراکم در منطقه مورد مطالعه استفاده می‌شود. و
(4) در مرحله دوم، زمان تخلیه به عنوان تابع هدف برای بهینه‌سازی در نظر گرفته می‌شود و شبیه‌سازی تخلیه اضطراری طرح‌های امکان‌پذیر شناسایی‌شده در مرحله اول تکمیل می‌شود. سپس طرح مکان یابی بهینه پناهگاه با حداقل تعداد پناهگاه و کوتاه ترین زمان تخلیه تعیین می شود.
شکل 4 چارچوب روش شناسی پیشنهادی در این مطالعه را نشان می دهد.
2.3.2. بهینه سازی مرحله اول بر اساس تحلیل شبکه ایستا: در نظر گرفتن هزینه ساخت به عنوان هدف بهینه سازی
  • مفروضات اساسی

مدل بهینه‌سازی چهار فرض را دنبال می‌کند: (1) جاده‌های تخلیه پس از فاجعه، بدون توجه به مسدود شدن جاده‌های تخلیه، ایمن و قابل اعتماد باقی می‌مانند. (2) عرض مؤثر جاده های تخلیه با سلسله مراتب آنها مطابقت دارد. عرض جاده اصلی، جاده فرعی و جاده فرعی به ترتیب 30 متر، 20 متر و 18 متر است [ 70 ]. (3) از نظر مناطق اشغال شده توسط عابران پیاده، کد طراحی مهندسی راه شهری (CJJ 37-2012) [ 71 ] نشان می دهد که عرض گروهی از عابران پیاده 0.75 متر است. علاوه بر این، زمانی که میانگین فاصله 1.22-1.34 متر است، عابران پیاده می توانند آزادانه بدون ازدحام و پایمال شدن حرکت کنند [ 72 ]]. بنابراین، در این مطالعه، فاصله جانبی عابران پیاده 0.75 متر و فاصله طولی 1.34 متر تعیین شده است. و (4) با توجه به تفاوت در ساختار سنی در نقاط مختلف تقاضا، یک روش ساده برای محاسبه میانگین سرعت تخلیه اتخاذ شده است. فرض بر این است که همه افراد در یک نقطه تقاضا با میانگین سرعت تخلیه v ij به پناهگاه ها می روند که با معادله (2) محاسبه می شود.

که در آن p ic ، p ia و p io به ترتیب نشان دهنده نسبت کودکان، بزرگسالان و سالمندان در نقطه تقاضای i هستند و vc، v a و v o به ترتیب نشان دهنده سرعت تخلیه کودکان ، بزرگسالان، و سالمندان در این مطالعه فرض بر این است که یک بزرگسال به یک کودک یا یک شهروند سالمند برای تخلیه کمک می کند و سرعت تخلیه به عنوان مقدار کمتر سرعت تخلیه بین کمک کننده و کمک کننده تعیین می شود. سرعت کودکان، بزرگسالان و افراد مسن به ترتیب 1.05، 1.27 و 1.12 متر بر ثانیه تعیین شد [ 73 ].]. تعداد و نسبت کودکان، بزرگسالان و سالمندان در هر نقطه تقاضا از WordPop تعیین شد.

2.
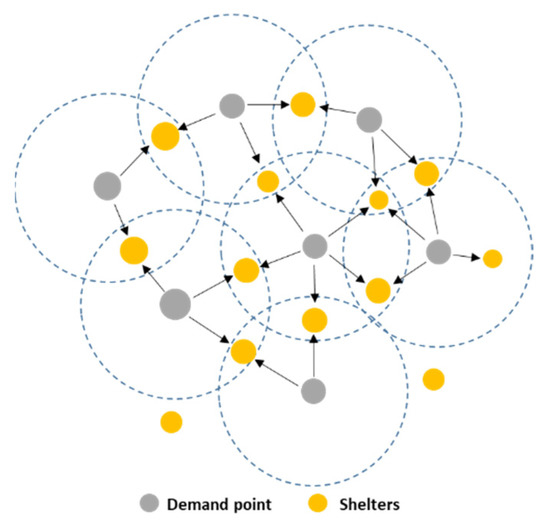
مدل تخصیص تخلیه دایره ای
مسئله بهینه‌سازی مکان پناهگاه شامل دو بخش مکان‌یابی پناهگاه و تدوین طرح تخلیه است. پس از تعیین مکان ها و مناطق ساخت پناهگاه های جدید، لازم است یک طرح توزیع تخلیه برای تخلیه پناهندگان به پناهگاه ها تدوین شود. مدل سنتی فرض می کند که پناهندگان در یک نقطه تقاضا به همان سرپناه اختصاص داده می شوند. در این مطالعه، قوانین تخصیص سنتی بهبود یافته و قوانین تخصیص تخلیه دایره‌ای بر اساس مدل گرانشی پیشنهاد شده‌اند. با توجه به محدودیت فاصله خدمات و ظرفیت سرپناه، افراد در یک نقطه تقاضا می توانند با توجه به فواصل از نقاط تقاضا تا پناهگاه به چندین پناهگاه اختصاص داده شوند. شکل 5).). مدل بهینه‌سازی مکان پناهگاه‌ها که در این مطالعه ایجاد شده است، تغییر پویا تقاضای تخلیه را در نظر می‌گیرد. درخواست های تخلیه در یک روز به 24 دسته تقسیم می شود، یعنی تعداد پناهندگان از ساعت 0:00 تا 24:00. در این بخش، تقاضای تخلیه در ساعت 16:00 به عنوان مثال برای نشان دادن مدل تخصیص دایره ای ارائه شده است.
(الف) تخصیص تخلیه در دور اول

از نظر انتخاب پناهگاه های هدف برای نقاط تقاضا، جمعیت بر اساس مدل ثقلی تخصیص می یابد. جمعیت در هر نقطه تقاضا را می توان به چندین پناهگاه اختصاص داد. قانون مدل جاذبه این است که تعداد پناهندگان در یک نقطه تقاضا بر اساس فواصل از نقطه تقاضا تا پناهگاه ها تخصیص می یابد. پناهگاه های نزدیکتر به نقطه تقاضا پذیرای افراد بیشتری هستند. اگر b پناهگاه در 1500 متر از نقطه تقاضا i وجود داشته باشد ، ضریب وزنی از نقطه تقاضا i تا پناهگاه j با معادلات (3) و (4) تعیین می شود. ضریب وزنی از نقطه تقاضای i تا سرپناه jبا فاصله شبکه جاده از نقطه تقاضا i تا پناهگاه j نسبت مستقیم دارد.

که در آن d ij نشان‌دهنده کوتاه‌ترین فاصله شبکه جاده‌ای از نقطه تقاضای i تا پناهگاه j است. بهترین مسیر تخلیه از هر نقطه تقاضا به پناهگاه های اختصاص داده شده آن با استفاده از الگوریتم Dijkstra [ 64 ] محاسبه می شود. سپس، تعداد پناهندگان از نقطه تقاضا i اختصاص داده شده به پناهگاه j با معادله (5) تعیین می شود:

که در آن w ij وزن تخصیص است، S i کل جمعیت نقطه تقاضا i است ، و p ij تابع ادغام است.

زمانی که تعداد پناهندگان پذیرش شده توسط پناهگاه j در لحظه به حداکثر ظرفیت پناهگاه v j برسد. ، پناهگاه بسته است. در این زمان تعداد افرادی که تخلیه کامل نشده اند وارد چرخه بعدی می شود. لحظه ای است که تعداد افراد دریافت شده توسط پناهگاه j به ظرفیت پناهگاه در سیکل اول می رسد. ماتریس تخصیص جمعیت در ساعت 16:00 در دور اول ( P 1 ( t = 16)) را می توان با رابطه (5) تعیین کرد.

که در آن ستون‌های ماتریس تعداد افرادی است که در دور اول تخلیه را در نقاط تقاضا 1، 2،… m انجام داده‌اند ، و ردیف‌های ماتریس جمعیت دریافت‌شده توسط پناهگاه‌های 1، 2،… n در دور اول هستند. علاوه بر این، نشان دهنده تعداد افرادی است که در اولین دور در پناهگاه j پذیرفته شدند. ارزش به عنوان مجموع ستون j تعیین می شود. نشان دهنده تعداد افرادی است که تخلیه را در دور اول در نقطه تقاضا i انجام دادند. ارزش به عنوان مجموع ردیف i تعیین می شود. تعداد افرادی که در دور اول تخلیه را کامل کرده اند از کل جمعیت اولیه کم می شود تا جمعیت در دور تخصیص بعدی مشخص شود. عرض افقی و فاصله طولی بین عابران پیاده در جاده تخلیه به ترتیب 0.75 متر و 1.34 متر تعیین شده است. با توجه به سلسله مراتب راه در محدوده مورد مطالعه، عرض موثر هر راه تخلیه برابر w متر تعیین می شود. تعداد عابران پیاده که در فضای جانبی در همان زمان جای می گیرند [ w /0.75] است. زمان مورد نیاز برای تخلیه جمعیت از نقطه تقاضا i به پناهگاه j با رابطه (6) تعیین می شود.

سپس، ماتریس زمان تخلیه در دور اول در ساعت 16:00 ( T 1 ( t = 16)) را می توان تعیین کرد.

(ب) تخصیص تخلیه در دور دوم

تعداد افرادی که در دور اول تخلیه را در نقطه تقاضای i انجام دادند ( ) از کل جمعیت تقاضای نقطه i کم می شود تا جمعیت در دور تخصیص دوم مشخص شود ( ). ماتریس توزیع جمعیت و ماتریس زمان تخلیه دور دوم با همان روش محاسباتی مورد استفاده در دور اول تعیین می شود.

اگر تخلیه کامل نشده باشد، دور سوم، چهارم و غیره تا زمانی که همه افراد تخلیه را کامل نکرده باشند، انجام می شود.
(ج) محاسبه کل

بر اساس رابطه (7)، ماتریس های تخصیص جمعیت همه دورها با هم جمع می شوند تا ماتریس تخصیص کل جمعیت در ساعت 16:00 مشخص شود.

که در آن m و n به ترتیب تعداد کل نقاط تقاضا و پناهگاه ها را نشان می دهند.

به همین ترتیب، کل ماتریس زمان تخلیه در ساعت 16:00 توسط رابطه (8) تعیین می شود.

کل زمان تمام افراد برای تکمیل تخلیه را می توان به عنوان حداکثر مقدار عنصر در ماتریس T محاسبه کرد ( t = 16). کل فاصله تخلیه را می توان با رابطه (9) تعیین کرد. جمعیت p ij در هر نقطه تقاضا i و تعداد عابران پیاده دریافت شده توسط هر پناهگاه به ترتیب با معادلات (7) و (8) تعیین می شوند. زمان تخلیه در هر نقطه تقاضا با رابطه (10) محاسبه می شود.

زمان تخلیه ( i ) = حداکثر ( t ij ) i = 1, 2,… m ; j = 1، 2،… n
3.
ایجاد مدل بهینه سازی در مرحله اول

در این تحقیق ارزش، کارایی و به حداقل رساندن هزینه ساخت به عنوان اصول بهینه سازی مکان پناهگاه در نظر گرفته شده است. تعداد پناهگاه های جدید ساخته شده و کل زمان تخلیه به عنوان توابع هدف در مدل بهینه سازی برای ایجاد یک مدل بهینه سازی مکان پناهگاه دو مرحله ای در نظر گرفته شده است. در مرحله اول با محدودیت ظرفیت سرپناه و فاصله سرویس دهی، حداقل تعداد کانکس برای ساخت مشخص می شود. تابع هدف به صورت زیر است:

شرایط محدودیت به شرح زیر است:

در این معادلات، S i ( t ) تعداد پناهندگان در نقطه تقاضا i در لحظه t را نشان می دهد ، v j نشان دهنده ظرفیت پناهگاه j ، J مجموعه پناهگاه ها، j∈ J ، I مجموعه نقاط تقاضا است . i ∈ I و p i,j ( t ) تعداد پناهندگانی را نشان می دهد که از نقطه تقاضا i به پناهگاه j در لحظه t تخلیه می شوند . علاوه بر این، c ijیک ماتریس 0-1 است: اگر فاصله از نقطه تقاضا i تا پناهگاه j کمتر از محدودیت فاصله سرویس دهی شده پناهگاه ها (1500 متر) باشد، مقدار c ij برابر با 1 تعیین می شود. در غیر این صورت، مقدار 0 است. علاوه بر این، x ij و y j متغیرهای تصمیم باینری هستند. اگر پناهگاه j انتخاب شود، مقدار y j برابر 1 تعیین می شود. در غیر این صورت، مقدار 0 است. اگر نقطه تقاضای i توسط پناهگاه j سرویس شود ، مقدار x ij1 تعیین می شود؛ در غیر این صورت، مقدار 0 است. A نشان دهنده تعداد پناهگاه هایی است که ساخته شده اند. شماره سریال پناهگاه های ساخته شده 1، 2، …، A تعیین شده است. B تعداد پناهگاه های نامزد را نشان می دهد. شماره سریال پناهگاه های نامزد به صورت A + 1، A + 2،…، A + B تنظیم شده است.
معادله (11) تابع هدف است که نشان دهنده به حداقل رساندن تعداد سرپناه های تازه ساخته شده است. معادلات (12) – (18) شرایط محدودیت هستند. معادله (12) تضمین می کند که تمام نقاط تقاضا توسط حداقل یک پناهگاه پوشش داده شده است. معادله (13) تضمین می کند که پناهندگان تنها می توانند پناهگاه هایی را در محدوده محدودیت فاصله (1500 متر) انتخاب کنند. معادله (14) تضمین می کند که نقاط تقاضا فقط توسط پناهگاه های انتخاب شده قابل سرویس دهی هستند. معادله (15) تضمین می کند که جمعیت پذیرفته شده توسط پناهگاه در لحظه از ظرفیت آن فراتر نخواهد رفت t بیش از ظرفیت آن نخواهد بود. معادله (16) قیود برای متغیرهای تصمیم باینری را نشان می دهد. معادله (17) تضمین می کند که پناهگاه های ساخته شده انتخاب شده اند (A نشان دهنده تعداد پناهگاه هایی است که ساخته شده اند، در حالی که B نشان دهنده تعداد پناهگاه های نامزد است). در نهایت، معادله (18) تضمین می کند که همه پناهندگان تخلیه را در لحظه t انجام می دهند.
4.
طراحی الگوریتم حل
مدل بهینه‌سازی در مرحله اول از الزامات محدودیت‌های داده شده (محدودیت فاصله، محدودیت ظرفیت و پوشش کامل برای تقاضای پناهگاه) پیروی می‌کند که یک مسئله NP-hard است [ 74 ]. بنابراین، حل مدل از طریق روش جامع و حل‌کننده ریاضی Lingo [ 75 ] مشکل است. بنابراین، در مرحله اول، از الگوریتم ژنتیک [ 76 ] برای حل مدل و تعیین حداقل تعداد پناهگاه k استفاده می شود. فرآیندی که الگوریتم ژنتیک حداقل تعداد پناهگاه ها را تعیین می کند به شرح زیر است.
(الف) کدگذاری کروموزوم
روش کدگذاری کروموزوم در این مطالعه کد باینری است. قاعده نگاشت بین طرح مکان و کد ژنتیکی این است که آیا یک پناهگاه کاندید انتخاب می شود یا نه، در رمزگذاری ژن با 0 و 1 نشان داده می شود. اگر پناهگاه کاندید انتخاب شود، مقدار کدگذاری ژن برابر با 1 تعیین می شود. اگر پناهگاه کاندید انتخاب نشود، مقدار رمزگذاری ژن برابر با 0 تعیین می شود. طول کروموزوم برابر با تعداد پناهگاه های کاندید است. هر نقطه ژن نشان دهنده یک پناهگاه نامزد است و هر کروموزوم نشان دهنده طرح مکان پناهگاه است.
(ب) تولید اولیه جمعیت
در این تحقیق از روش تولید تصادفی برای تولید جمعیت اولیه استفاده شده است. احتمال اینکه هر پناهگاه کاندید انتخاب شود 50% تعیین می‌شود، بنابراین یک سری کروموزوم اولیه تولید می‌شود. اگر اندازه جمعیت اولیه کوچک باشد، الگوریتم مستعد یک نقطه افراطی محلی است. در غیر این صورت، اگر اندازه جمعیت اولیه زیاد باشد، تعداد تکرارها در فرآیند تکامل بسیار افزایش می یابد و در نتیجه کارایی الگوریتم را تحت تاثیر قرار می دهد. برای اجتناب از این دو موقعیت شدید، اندازه جمعیت در این مطالعه 100 تعیین شده است.
(ج) تعیین مقدار تابع تناسب هر طرح مکان
مقدار تابع تناسب استاندارد برای انتخاب کروموزوم ها (یعنی طرح مکان پناهگاه) و قضاوت در مورد شایستگی کروموزوم ها است. در مرحله اول تابع تناسب اندام به عنوان تعداد پناهگاه تعیین می شود. تابع جریمه در محاسبه مقدار تابع تناسب وارد شده است. اگر طرح مکان یابی پناهگاه شرایط محدودیت را برآورده نکند، تعداد پناهگاه های طرح به اضافه 100 مقدار تابع تناسب آن است.
(د) عملیات انتخاب

انتخاب چرخ رولت و استراتژی نخبه گرایی برای تکمیل عملیات انتخاب در این مطالعه اتخاذ شده است. ابتدا مقدار تابع تناسب f k هر کروموزوم در جمعیت محاسبه می شود. احتمال انتخاب هر کروموزوم متناسب با مقدار تابع تناسب آن است. احتمال انتخابی با معادله (19) [ 76 ] تعیین می شود.

علاوه بر این، استراتژی حفظ نخبگان نیز اتخاذ شده است. کروموزوم در جمعیت با بهترین مقدار تابع تناسب به طور مستقیم بدون تطبیق و متقاطع در نسل بعدی کپی می شود، که می تواند اطمینان حاصل کند که ارزش تناسب بهینه نسل کمتر از نسل قبلی نیست.
(ه) عملیات متقاطع
استراتژی متقاطع ترکیبی متقاطع چند نقطه ای و تک نقطه ای در این مطالعه اتخاذ شده است. در مرحله اولیه تکامل، متقاطع چند نقطه ای می تواند تنوع راه حل ها را حفظ کرده و توانایی کاوش الگوریتم را افزایش دهد. در مرحله بعدی، متقاطع تک نقطه ای می تواند همگرایی الگوریتم را تسریع کند و سرعت محاسبات را بهبود بخشد. عملیات متقاطع با احتمال ثابت Pc پذیرفته می شود . ابتدا 10 نقطه متقاطع به طور تصادفی در کروموزوم های والد برای تبادل بلوک های ژنی تنظیم می شود. سپس، متقاطع تک نقطه ای برای تعیین موقعیت متقاطع دو کروموزوم تولید شده توسط متقاطع چند نقطه ای اتخاذ می شود و کروموزوم های نتاج به دست می آیند.
(و) عملیات جهش
در الگوریتم متقاطع، کروموزوم‌های نتاج نه تنها اطلاعات کروموزوم‌های والد را به ارث می‌برند، بلکه با احتمال مشخصی p m جهش می‌یابند . استراتژی جهش اتخاذ شده در این مطالعه این است که یک عدد تصادفی rd∈ ( 0,1) ابتدا برای یک نقطه ژنی تولید می شود. اگر مقدار r d کمتر از p m باشد، مقدار نقطه ژن تغییر می کند. عملیات جهش برای هر نقطه ژن کامل می شود تا زمانی که کروموزوم جدیدی تولید شود.
(ز) قضاوت خاتمه الگوریتم
با در نظر گرفتن زمان و دقت همگرایی، شرایط پایان تکرار شونده به شرح زیر تعیین می شود: (1) راه حل تابع تناسب بهینه در نسل های متوالی بهبود نمی یابد. و (2) جبر تکامل ژنتیکی حداکثر. نقاط ژنی کروموزوم بهینه با طرح بهینه سازی مکان پناهگاه مطابقت دارد. مقدار تابع تناسب کروموزوم بهینه حداقل تعداد پناهگاه ها است.
پس از تعیین حداقل تعداد پناهگاه‌های تازه‌ساخت از طریق الگوریتم ژنتیک، طرح‌هایی که تقاضای تخلیه دینامیکی 24 ساعته را تحت محدودیت‌های ظرفیت پناهگاه و فاصله خدمات برآورده می‌کنند، با روش جامع به‌عنوان طرح‌های مکان‌یابی امکان‌پذیر انتخاب می‌شوند. انواع طرح های نامزد
2.3.3. بهینه سازی مرحله دوم بر اساس شبیه سازی تخلیه پویا: در نظر گرفتن زمان تخلیه به عنوان هدف بهینه سازی
  • شبیه سازی تخلیه منطقه ای بر اساس مدل نیروی اجتماعی

مدل نیروی اجتماعی توسط هلبینگ و همکاران ارائه شده است. [ 77 ] و در الگوریتم اساسی در پلت فرم شبیه سازی Anylogic یکپارچه شده است. مدل نیروی اجتماعی دارای دقت بالا و تداوم قوی است و می تواند رفتار تخلیه خاص عابران پیاده را شبیه سازی کند. علاوه بر این، می توان آن را با مدل چند عاملی [ 55] برای شبیه سازی ناهمگونی انواع مختلف عابران پیاده. مدل نیروی اجتماعی فرض می‌کند که فرآیند تخلیه توسط سه نوع نیروی زیر تعیین می‌شود: (1) نیروی خودران عابران پیاده، که نشان‌دهنده این است که عوامل انسانی فعالانه خود را به سمت تخلیه سوق می‌دهند. (2) نیروی تعامل بین عابران پیاده، که نشان می دهد عوامل انسانی یکدیگر را دفع می کنند تا فاصله معینی را حفظ کنند. و (3) نیروی بین عابران پیاده و محیط، که منعکس کننده اثر دافعه بین عوامل انسانی و محیط است، مانند مرزها و موانع. اصول اولیه مدل نیروی اجتماعی توسط معادلات (20) و (21) [ 75 ] ارائه شده است.

که در آن f d نشان دهنده نیروی خودران عابران پیاده، f ij نشان دهنده تعامل بین عابران پیاده، f iw نشان دهنده تعامل بین عابران پیاده و موانع، mi نشان دهنده وزن عابران پیاده، v i 0 ( t ) نشان دهنده سرعت مورد انتظار است، τ i نشان دهنده زمان شتاب و v i ( t ) نشان دهنده سرعت تخلیه واقعی است.

تحقیقات در مورد رفتار تخلیه جمعیت نشان می دهد که وقتی یک فاجعه رخ می دهد، انتخاب مسیرهای تخلیه تحت تأثیر فواصل از نقاط تقاضا تا پناهگاه ها، تراکم جمعیت و عرض جاده های تخلیه است [ 78 ]. در این مطالعه، از زبان جاوا برای ایجاد یک تابع انتخاب برای مسیرهای تخلیه در پلت فرم Anylogic استفاده شده است. معادله (22) احتمال انتخاب جاده تخلیه k را تعیین می کند و α ، β و γ نشان دهنده ضرایب وزنی هستند. علاوه بر این، فاصله k، چگالی k، و عرض k به ترتیب نشان دهنده فاصله زیر مسیر k هستند، تراکم جمعیت و عرض مسیر تخلیه k .

ضرایب وزن α ، β و γ توسط ویدئویی تعیین می‌شوند که فرآیند تخلیه واقعی را در طول زلزله ضبط کرده است ( https://mvqq.com/z/msite/play-short/index.html?cid=&vid=o08073ef0ll&qqVersion= 0 (دسترسی در 24 اکتبر 2020)). مدل تخلیه اتاق دو خروجی با توجه به فیلم تخلیه معتبر ایجاد شد. این ویدئو روند تخلیه در فاجعه واقعی را ضبط می کند. با استفاده از این ویدیوی معتبر برای تعیین β قابل اعتماد است. آشنایی جمعیت در کلاس با خروجی و مسیر با آشنایی جمعیت با جاده تخلیه و مقصد در مقیاس محله مطابقت دارد. زمانی که ضرایب وزنیα ، β و γ به ترتیب 0.56، 0.24 و 0.2 بودند، نتیجه شبیه سازی به خوبی با سناریوی معتبر مطابقت دارد ( شکل 6 ).
استقرار یک مدل تخلیه منطقه ای بر روی پلت فرم Anylogic شامل چهار مرحله است، یعنی ساخت سناریوی فضای تخلیه، ایجاد ساختار منطقی، تنظیم پارامترهای شبیه سازی و ایجاد ماژول های آماری ( شکل 4 ). ابتدا فضای تخلیه منطقه مورد مطالعه بر اساس داده های جمعیتی و مکانی ایجاد می شود. دوم اینکه با توجه به سرعت های مختلف تخلیه افراد در سنین مختلف، تفاوت ساختارهای سنی در ساختار منطقی در نظر گرفته می شود و سه نوع عامل عابر پیاده یعنی سالمندان، بزرگسالان و کودکان ساخته می شود. سرعت مورد انتظار عابران پیاده در سنین مختلف در جدول 3 گزارش شده است. در فرآیند تخلیه، با افزایش تراکم جمعیت، سرعت تخلیه کاهش می یابد و جهت حرکت همچنان تغییر می کند. سرعت ها و جهت های تخلیه متغیر با زمان توسط مدل نیروی اجتماعی تعبیه شده در پلت فرم Anylogic [ 79 ] تعیین می شود.]. مطابق با فرض مرحله اول، همچنین فرض می شود که یک بزرگسال به یک کودک یا یک فرد مسن کمک می کند تا در مدل شبیه سازی تخلیه تخلیه شود. سرعت تخلیه تجمع به عنوان مقدار کمتر سرعت تخلیه بین کمک کننده و کمک کننده تعیین می شود. سوم، تراکم جمعیت متغیر با زمان در جاده تخلیه، زمان تخلیه، نقطه شروع و مقصد هر عابر پیاده و رابطه بین زمان و تعداد افرادی که تخلیه را تکمیل می‌کنند بر اساس مدل آماری تعیین می‌شود.
2.
فرآیند پیاده سازی برای بهینه سازی در مرحله دوم
در مرحله دوم، مدل نیروی اجتماعی بهبود یافته برای شبیه‌سازی فرآیند تخلیه عابران پیاده ایجاد می‌شود. مدل تخلیه پویا منطقه ای رفتار انتخاب برای مسیرهای تخلیه و تفاوت در ساختار سنی جمعیت را در نظر می گیرد و به طور همزمان محدودیت های ظرفیت و فاصله را تعیین می کند. بر اساس نتایج شبیه سازی تخلیه، کل زمان تخلیه به عنوان تابع هدف در نظر گرفته می شود. طرح مکان یابی پناهگاه با کمترین زمان تخلیه در نهایت انتخاب شد.

در مرحله اول حداقل تعداد کانکس های نوساز k تعیین می شود . در مرحله دوم، از روش جامع برای انتخاب طرح هایی استفاده می شود که نیازهای تخلیه دینامیکی در طول 24 ساعت و محدودیت های ظرفیت پناهگاه و فاصله خدمات را برآورده می کند. انواع طرح ها (B تعداد پناهگاه های نامزد است) به عنوان طرح های امکان پذیر. تابع هدف مرحله دوم در رابطه (23) نشان داده شده است. محدودیت ها با محدودیت های مرحله اول سازگار است. پس از مقایسه زمان کلی تخلیه طرح های قابل اجرا شناسایی شده در مرحله اول، طرح بهینه با حداقل زمان تخلیه کل انتخاب می شود.

که در آن P مجموعه ای از پناهگاه های انتخاب شده در طرح امکان پذیر است، p ∈ P . I مجموعه ای از نقاط تقاضا است، i ∈ I . t ip نشان دهنده زمان تخلیه از نقطه تقاضای i تا پناهگاه انتخابی p است.

3. نتایج و تجزیه و تحلیل

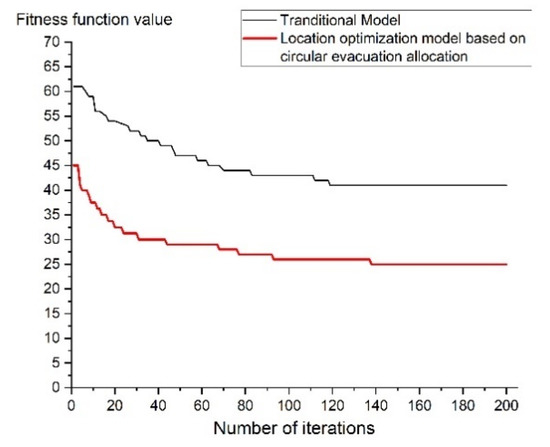
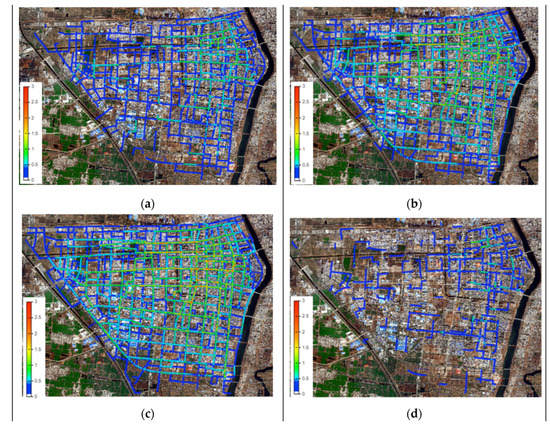
3.1. نتایج بهینه‌سازی مکان پناهگاه بر اساس ترکیب تحلیل استاتیکی و شبیه‌سازی دینامیکی

بر اساس اصول برابری، اقتصادی و کارایی، یک مدل بهینه‌سازی پناهگاه دو مرحله‌ای ایجاد شد. در مرحله اول، با توجه به محدودیت‌های ظرفیت و فاصله خدماتی پناهگاه‌ها، حداقل تعداد کانکس‌های نوساز که بتواند نیاز تخلیه را برآورده کند، تعیین شد. بر اساس الگوریتم ژنتیک طراحی شده، 100 گروه از طرح های مکان یابی به صورت تصادفی به عنوان جمعیت اولیه تعیین شدند. احتمال متقاطع و احتمال جهش در الگوریتم ژنتیک به ترتیب 9/0 و 3/0 تعیین شد. رابطه بین مقدار تابع تناسب و تعداد تکرارها در شکل 7 ارائه شده است. پس از یک محاسبه آزمایشی، زمانی که الگوریتم تا 200 دور تکرار شد، مقدار تابع تناسب به حداقل مقدار رسید و تغییری نکرد. مقدار تابع تناسب اندام به 25 همگرا می شود، که نشان می دهد که لازم است حداقل 25 پناهگاه جدید برای برآورده کردن نیازهای تخلیه پویا در طول 24 ساعت روز ساخته شود. مدل سنتی بهینه‌سازی سرپناه وضعیتی را در نظر نمی‌گیرد که در آن افراد از یک نقطه تقاضا به پناهگاه‌های متعدد دسترسی داشته باشند و فرض بر این است که افراد در یک نقطه تقاضا وارد یک پناهگاه می‌شوند. با مقایسه مدل پیشنهادی بهینه‌سازی مکان مبتنی بر تخصیص تخلیه دایره‌ای با مدل سنتی، تعداد سرپناه‌های نوساز از 42 به 25 کاهش یافت که هزینه ساخت سوله‌ها را تا 40 کاهش می‌دهد.
در مرحله دوم، به شرط تعیین تعداد پناهگاه های نوساز، طرح های مکان یابی امکان پذیر از بین آنها انتخاب شد. طرح ها با روش جامع ( جدول 4 ). طرح‌های قابل اجرا باید محدودیت‌های ظرفیت پناهگاه و فاصله خدمات، و همچنین نیازهای تخلیه پویا در طول 24 ساعت روز را برآورده کنند. بر اساس مدل بهبود یافته نیروی اجتماعی توضیح داده شده در بخش 2 ، مدل های تخلیه منطقه ای از 15 طرح امکان پذیر در جدول 4 ، همانطور که در شکل 8 ارائه شده است، ایجاد شد . شکل 8 روند تخلیه عابران پیاده طرح 14 را از جدول 4 نشان می دهد. الگوی گرافیکی پایین سمت چپ تراکم جمعیت است. تغییر رنگ نشان دهنده تغییر پویا تراکم جمعیت در جاده های تخلیه است. کل زمان تخلیه 15 طرح امکان پذیر درجدول 4 با یکدیگر مقایسه شد و در نهایت طرح مکان یابی بهینه پناهگاه با کمترین زمان تخلیه مشخص شد. جدول 5 زمان تخلیه 15 طرح امکان پذیر را نشان می دهد. توزیع فضایی و مناطق موثر پناهگاه های اضطراری انتخاب شده در شکل 9 نشان داده شده است. چهار پناهگاه با مساحت موثر بین 10000 تا 15000 متر مربع وجود داشت که 16 درصد از کل پناهگاه ها را تشکیل می داد. تعداد پناهگاه هایی با مساحت موثر بین 15000 تا 20000 مترمربع و بین 20000 تا 50000 مترمربع به ترتیب 5 و 11 مورد بود. همچنین 5 پناهگاه با مساحت موثر بیش از 50000 متر مربع وجود داشت .که 20 درصد از کل پناهگاه ها را تشکیل می دهند. بر اساس قوانین تخصیص تخلیه دایره ای فرموله شده در بخش 2.3.2 ، ماتریس تخصیص جمعیت تخلیه و ماتریس زمان تخلیه، و همچنین پناهگاه های هدف برای ساکنان در هر نقطه تقاضا، تعیین شد. شکل 10 جهت تخلیه را در سناریوی تخلیه اضطراری نشان می دهد، که همچنین نشان دهنده ارتباط بین نقاط تقاضا و پناهگاه هایی است که افراد برای ورود به آن انتخاب می کنند. میانگین زمان تخلیه حدود 818 ثانیه و کمترین زمان تخلیه کمتر از 2 دقیقه بود. زمان تخلیه همه افراد کمتر از 30 دقیقه بود. شکل 11توزیع فرکانس زمان تخلیه را نشان می دهد. 57.2 درصد جمعیت در کمتر از 15 دقیقه و 88.5 درصد جمعیت در کمتر از 20 دقیقه تخلیه را کامل کردند. زمان تخلیه پنج نقطه تقاضا بیش از 25 دقیقه بود. در مقایسه با زمان تخلیه قبل از بهینه‌سازی، میانگین زمان تخلیه عابران پیاده از هر نقطه تقاضا از 4822 ثانیه به 818 ثانیه کاهش یافت. راندمان تخلیه 83 درصد افزایش یافت و پراکندگی زمان تخلیه در نقاط مختلف تقاضا به طور قابل توجهی کاهش یافت ( شکل 12 ).

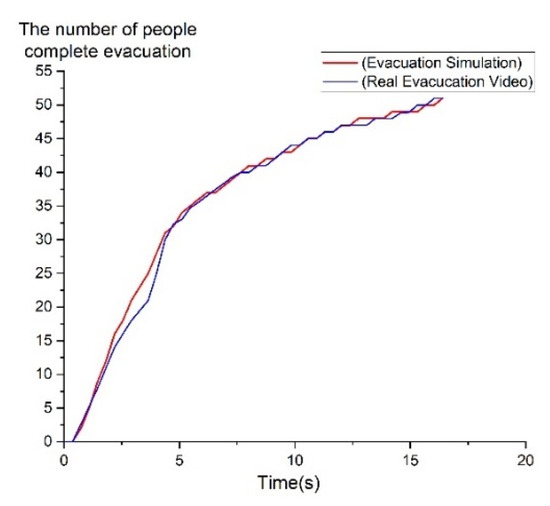
3.2. تایید توسط شبیه سازی تخلیه پویا

بر اساس روش شبیه‌سازی تخلیه منطقه‌ای که در بخش 2.3.3 توضیح داده شد ، مدل‌سازی فضایی و تنظیم پارامتر بر روی پلت فرم Anylgoic تکمیل شد و یک برنامه جاوا برای فرمول‌بندی قوانین انتخاب مسیرهای تخلیه نوشته شد. شبیه سازی تخلیه منطقه مورد مطالعه بر اساس روش ارائه شده در بخش 2 تکمیل شد و تغییرات تعداد افراد تخلیه شده که با گذشت زمان به پناهگاه های اضطراری می رسند به صورت آماری تجزیه و تحلیل شد ( شکل 13).). پس از بهینه سازی، بازده تخلیه منطقه مورد مطالعه به طور قابل توجهی بهبود یافته و زمان تخلیه به طور قابل توجهی کاهش یافت. تنها 1802 ثانیه طول کشید تا همه افراد تخلیه را کامل کنند، که 16.8٪ از کل زمان تخلیه قبل از بهینه سازی است. بنابراین، راندمان تخلیه 83.2٪ بهبود یافته است. زمانی که زمان تخلیه 5 دقیقه بود، 43.1 درصد از عابران پیاده به پناهگاه ها رسیده بودند که 3.2 برابر تعداد افرادی است که قبل از بهینه سازی به پناهگاه ها رسیده بودند. علاوه بر این، 95 درصد از عابران پیاده تخلیه را در 1552 ثانیه کامل کرده بودند که بسیار کوتاهتر از زمان مورد نیاز قبل از بهینه سازی (5513 ثانیه) است ( شکل 13 ).

4. بحث

این مطالعه یک روش سیستماتیک برای بهینه‌سازی مکان پناهگاه‌ها ایجاد کرد. این روش به طور جامع تغییرات متغیر زمان وضعیت ازدحام در جاده‌های تخلیه، رفتار تخلیه جمعیت و روان‌شناسی عابر پیاده را از طریق شبیه‌سازی تخلیه منطقه‌ای در نظر می‌گیرد. مدل شبکه استاتیک سنتی را می توان به سرعت حل کرد و شبیه سازی تخلیه پویا می تواند به طور واقعی فرآیند تخلیه جمعیت را منعکس کند. این مطالعه مزایای تجزیه و تحلیل شبکه استاتیک و شبیه‌سازی تخلیه پویا را برای پیشنهاد یک روش ترکیبی بهینه‌سازی استاتیک/دینامیک ترکیب کرد. در مرحله اول، از دیدگاه مدیران دولتی، هدف بهینه سازی، به حداقل رساندن هزینه ساخت سرپناه تعیین می شود. در مرحله دوم، از دیدگاه پناهندگان، طرح بهینه با کوتاه‌ترین زمان تخلیه کلی از طریق شبیه‌سازی دینامیکی فرآیند تخلیه تعیین می‌شود. این روش بهینه سازی مکان پناهگاه ها را به صورت کارآمد، دقیق و علمی کامل می کند. روش بهینه‌سازی مکان پناهگاه بر اساس ترکیب تحلیل استاتیکی و شبیه‌سازی دینامیکی، این فرض را در روش سنتی، یعنی اینکه عابران پیاده از مسیرهای تعیین‌شده تخلیه می‌کنند، شکسته و فرآیند تخلیه واقعی را به عنوان سیستم مرجع برای شبیه‌سازی دقیق انتخاب در نظر می‌گیرد. مسیرهای تخلیه، تفاوت در سرعت تخلیه ناشی از سنین مختلف و رفتار عابران پیاده که به دیگران کمک می کنند. در مقایسه با روش بهینه‌سازی سنتی، روش پیشنهادی با چهار مزیت زیر مشخص می‌شود: و بهینه سازی مکان یابی پناهگاه ها را به صورت علمی تکمیل می کند. روش بهینه‌سازی مکان پناهگاه بر اساس ترکیب تحلیل استاتیکی و شبیه‌سازی دینامیکی، این فرض را در روش سنتی، یعنی اینکه عابران پیاده از مسیرهای تعیین‌شده تخلیه می‌کنند، شکسته و فرآیند تخلیه واقعی را به عنوان سیستم مرجع برای شبیه‌سازی دقیق انتخاب در نظر می‌گیرد. مسیرهای تخلیه، تفاوت در سرعت تخلیه ناشی از سنین مختلف و رفتار عابران پیاده که به دیگران کمک می کنند. در مقایسه با روش بهینه‌سازی سنتی، روش پیشنهادی با چهار مزیت زیر مشخص می‌شود: و بهینه سازی مکان یابی پناهگاه ها را به صورت علمی تکمیل می کند. روش بهینه‌سازی مکان پناهگاه بر اساس ترکیب تحلیل استاتیکی و شبیه‌سازی دینامیکی، این فرض را در روش سنتی، یعنی اینکه عابران پیاده از مسیرهای تعیین‌شده تخلیه می‌کنند، شکسته و فرآیند تخلیه واقعی را به عنوان سیستم مرجع برای شبیه‌سازی دقیق انتخاب در نظر می‌گیرد. مسیرهای تخلیه، تفاوت در سرعت تخلیه ناشی از سنین مختلف و رفتار عابران پیاده که به دیگران کمک می کنند. در مقایسه با روش بهینه‌سازی سنتی، روش پیشنهادی با چهار مزیت زیر مشخص می‌شود: روش بهینه‌سازی مکان پناهگاه بر اساس ترکیب تحلیل استاتیکی و شبیه‌سازی دینامیکی، این فرض را در روش سنتی، یعنی اینکه عابران پیاده از مسیرهای تعیین‌شده تخلیه می‌کنند، شکسته و فرآیند تخلیه واقعی را به عنوان سیستم مرجع برای شبیه‌سازی دقیق انتخاب در نظر می‌گیرد. مسیرهای تخلیه، تفاوت در سرعت تخلیه ناشی از سنین مختلف و رفتار عابران پیاده که به دیگران کمک می کنند. در مقایسه با روش بهینه‌سازی سنتی، روش پیشنهادی با چهار مزیت زیر مشخص می‌شود: روش بهینه‌سازی مکان پناهگاه بر اساس ترکیب تحلیل استاتیکی و شبیه‌سازی دینامیکی، این فرض را در روش سنتی، یعنی اینکه عابران پیاده از مسیرهای تعیین‌شده تخلیه می‌کنند، شکسته و فرآیند تخلیه واقعی را به عنوان سیستم مرجع برای شبیه‌سازی دقیق انتخاب در نظر می‌گیرد. مسیرهای تخلیه، تفاوت در سرعت تخلیه ناشی از سنین مختلف و رفتار عابران پیاده که به دیگران کمک می کنند. در مقایسه با روش بهینه‌سازی سنتی، روش پیشنهادی با چهار مزیت زیر مشخص می‌شود: تفاوت در سرعت تخلیه ناشی از سنین مختلف و رفتار عابران پیاده که به دیگران کمک می کنند. در مقایسه با روش بهینه‌سازی سنتی، روش پیشنهادی با چهار مزیت زیر مشخص می‌شود: تفاوت در سرعت تخلیه ناشی از سنین مختلف و رفتار عابران پیاده که به دیگران کمک می کنند. در مقایسه با روش بهینه‌سازی سنتی، روش پیشنهادی با چهار مزیت زیر مشخص می‌شود:
(1) نقص در پیکربندی پناهگاه های شهری را می توان به طور مستقیم از طریق شبیه سازی تخلیه اضطراری پیدا کرد. علاوه بر این، زمان کلی تخلیه، تعداد افراد اسکان داده شده در هر پناهگاه، و زمان تخلیه، مسیر تخلیه و پناهگاه هدف نهایی هر عابر پیاده تعیین می‌شود، در نتیجه موقعیت مکانی و پیکربندی ظرفیت پناهگاه‌ها را بهتر هدایت می‌کند.
(2) روش ترکیبی بهینه‌سازی استاتیک/دینامیک پناهگاه‌ها پیشنهاد شده است. مدل شبکه استاتیک سنتی را می توان به سرعت حل کرد و شبیه سازی تخلیه پویا می تواند واقعاً روند تخلیه جمعیت را منعکس کند. بنابراین، روش پیشنهادی مزایای تجزیه و تحلیل شبکه استاتیک و شبیه‌سازی تخلیه دینامیکی را ترکیب می‌کند و تعداد پناهگاه‌ها و زمان کلی تخلیه را به عنوان توابع هدف در نظر می‌گیرد. روش جدید نه تنها بهینه سازی مکان را به طور موثر حل نمی کند، بلکه فرآیند تخلیه جمعیت معتبر را نیز منعکس می کند.
(3) تقاضاهای تخلیه دینامیکی محاسبه می شود. در روش سنتی، تقاضای تخلیه بر اساس جمعیت دائمی محاسبه می‌شود که نمی‌تواند منعکس‌کننده تغییرات مکانی و زمانی جمعیت باشد و نیازهای تخلیه را در دوره اوج برآورده کند. روش پیشنهادی توزیع زمانی و مکانی جمعیت را بر اساس داده های سیگنالینگ تلفن همراه تعیین می کند. بنابراین، تقاضاهای تخلیه پویا به طور دقیق محاسبه می شود تا تقاضای تخلیه ساکنان را در همه زمان ها و در همه مناطق برآورده کند. و
(4) یک مدل تخلیه منطقه ای با توجه به رفتار تخلیه جمعیت و ناهمگونی فضایی ساختار سنی پیشنهاد شد. از طریق توسعه ثانویه برنامه نویسی جاوا بر روی پلت فرم Anylogic، مدل سنتی تخلیه نیروی اجتماعی بهبود یافته است. مدل تخلیه بهبودیافته تابع انتخاب مسیرهای تخلیه را ایجاد می کند و ناهمگونی فضایی سرعت تخلیه ناشی از سنین مختلف عابران پیاده را در نظر می گیرد. علاوه بر این، رفتار کمک بزرگسالان به سالمندان و کودکان در حین تخلیه شبیه سازی شده است.
روش ترکیبی بهینه‌سازی دو مرحله‌ای استاتیک/دینامیک ارائه‌شده در این مطالعه نه تنها می‌تواند در منطقه مرکزی شهری استفاده شود، بلکه می‌تواند در مناطق بزرگ‌تر، به عنوان مثال، کل شهر Xinyi، یا دیگر کلان‌شهرها در چین استفاده شود. مطالعه تجربی در زمینه های بزرگتر در تحقیقات بعدی انجام خواهد شد. در این مطالعه، منطقه مرکزی شهر شینی را به دلیل تراکم جمعیت بالا، خطر لرزه ای بالا و عملکرد ترکیبی بالا انتخاب می کنیم. اما روش پیشنهادی برای سایر حوزه ها مؤثر و معتبر است.
اگرچه این مطالعه چهار مشارکت داشته است، مدل پیشنهادی هنوز دارای کاستی هایی است: (1) ترجیحات افراد برای انواع مختلف پناهگاه ها در مدل تخلیه در نظر گرفته نمی شود. علاوه بر این، هنگامی که یک رویداد خطرناک رخ می دهد، در شرایط تخلیه، مدل های تقاضای مشخص شده و کالیبره شده در شرایط عادی به دلیل تعدد تصمیم گیرندگان نمی توانند مستقیماً اعمال شوند [ 80 ]. ناهمگونی رفتار تخلیه در نظر گرفته نمی شود. و (2) فرض می شود که تمام جاده های تخلیه بدون مانع هستند که با وضعیت واقعی ناسازگار است. پس از وقوع زلزله، برخی از مسیرهای تخلیه توسط آوار ساختمان مسدود می شود.
علاوه بر این، تعیین چگونگی شبیه سازی ترجیحات افراد برای پناهگاه های مختلف و نحوه در نظر گرفتن تأثیر محیط فاجعه بر روند تخلیه، تمرکز تحقیقات آینده خواهد بود. ما می‌توانیم خطر انسداد جاده‌ها و آسیب‌های ساختمانی ناشی از خطرات را با ترکیب فناوری پیشرفته شبیه‌سازی بلایا با شبیه‌سازی تخلیه منطقه‌ای وارد سناریوی تخلیه کنیم تا بتوانیم تقاضاهای تخلیه را با دقت بیشتری تعیین کنیم و فرآیند تخلیه را به‌طور واقعی‌تر منعکس کنیم. علم و دقت فرآیند تخلیه و بهینه سازی مکان پناهگاه بهبود خواهد یافت.

5. نتیجه گیری ها

این مطالعه به معرفی روش‌شناسی و مدل ریاضی در زمینه تخلیه اضطراری جمعیت برای بهینه‌سازی مکان پناهگاه‌ها پرداخته است. از طریق ترکیبی از مزایای تجزیه و تحلیل شبکه استاتیک و شبیه‌سازی تخلیه پویا، یک روش بهینه‌سازی مکان پناهگاه پیشنهاد شد. روش جدید نه تنها می تواند بهینه سازی مکان را به طور موثر حل کند، بلکه فرآیند تخلیه واقعی جمعیت را نیز منعکس می کند. رفتار تخلیه جمعیت و ناهمگونی فضایی ساختار سنی در مدل تخلیه در نظر گرفته شده است. در همین حال، تقاضاهای تخلیه دینامیکی به طور دقیق محاسبه شد تا خواسته‌های تخلیه در همه زمان‌ها برآورده شود. با در نظر گرفتن منطقه شهری مرکزی شهر Xinyi، استان جیانگ سو، چین، به عنوان مثال، امکان سنجی و اثربخشی این روش تایید شد.
(1) مرحله اول با هدف به حداقل رساندن تعداد پناهگاه ها انجام می شود. هنگامی که تعداد تکرارهای الگوریتم ژنتیک به 200 نسل رسید، مقدار تابع تناسب به 25 همگرا شد. بنابراین، برای برآورده کردن نیازهای تخلیه دینامیکی همه ساکنان، 25 پناهگاه جدید مورد نیاز است. در مقایسه با مدل بهینه‌سازی سنتی با فرض اینکه عابران پیاده در نقطه تقاضای یکسان وارد یک پناهگاه می‌شوند، مدل بهینه‌سازی مکان پیشنهادی بر اساس قوانین تخصیص تخلیه دایره‌ای برای کاهش تعداد سرپناه‌های جدید از 42 به 25 و در نتیجه کاهش ساخت پیدا شد. هزینه 40.4٪ و بهبود بهره وری استفاده از منابع فضای پناهگاه. و
(2) در مجموع 25 پناهگاه که خواسته های تخلیه پویا و محدودیت های فاصله و ظرفیت خدمات را برآورده می کردند از 71 پناهگاه کاندید در اولین مرحله بهینه سازی انتخاب شدند و 15 طرح امکان پذیر تعیین شد. در مرحله دوم، کل زمان تخلیه به عنوان هدف بهینه‌سازی در نظر گرفته شد و زمان‌های تخلیه کل 15 طرح امکان‌پذیر برای تعیین طرح مکان بهینه مقایسه شد. پس از بهینه سازی، زمان تخلیه تا 1802 ثانیه کاهش یافت و راندمان تخلیه 83.2٪ افزایش یافت. میانگین زمان تخلیه همه عابران پیاده 818 ثانیه، کوتاه‌ترین زمان تخلیه در 2 دقیقه و طولانی‌ترین زمان تخلیه کمتر از 30 دقیقه بود. زمانی که زمان تخلیه به 5 دقیقه رسید، 43.1 درصد از عابران پیاده به پناهگاه ها رسیده بودند. که 3.2 برابر تعداد عابران پیاده ای است که قبل از بهینه سازی به پناهگاه ها رسیده بودند. علاوه بر این، 95٪ از عابران پیاده تخلیه را در 1552 ثانیه به پایان رسانده اند، که بسیار کوتاه تر از قبل از بهینه سازی (5513 ثانیه) است. در مقایسه با زمان تخلیه قبل از بهینه‌سازی، میانگین زمان تخلیه عابران پیاده از هر نقطه تقاضا از 4822 ثانیه به 818 ثانیه کاهش یافت. علاوه بر این، راندمان تخلیه 83٪ افزایش یافت و پراکندگی زمان تخلیه در نقاط مختلف تقاضا به طور قابل توجهی کاهش یافت. میانگین زمان تخلیه عابران پیاده از هر نقطه تقاضا از 4822 ثانیه به 818 ثانیه کاهش یافته است. علاوه بر این، راندمان تخلیه 83٪ افزایش یافت و پراکندگی زمان تخلیه در نقاط مختلف تقاضا به طور قابل توجهی کاهش یافت. میانگین زمان تخلیه عابران پیاده از هر نقطه تقاضا از 4822 ثانیه به 818 ثانیه کاهش یافته است. علاوه بر این، راندمان تخلیه 83٪ افزایش یافت و پراکندگی زمان تخلیه در نقاط مختلف تقاضا به طور قابل توجهی کاهش یافت.

منابع

  1. GB51143-2015 ; وزارت مسکن و ساخت و ساز شهری – روستایی جمهوری خلق چین. مطبوعات معماری و ساختمان: پکن، چین، 2015. (به زبان چینی)
  2. روسو، اف. Rindon, C. قرار گرفتن در معرض شهری: فعالیت های آموزشی و کاهش خطر. WIT Trans. Ecol. محیط زیست 2014 ، 191 ، 991-1001. [ Google Scholar ]
  3. تسای، CH; Yeh, YL مطالعه ادغام اطلاعات جغرافیایی با تصمیم گیری چندهدفه در مورد تخصیص پناهگاه های مناسب: استفاده از پارک ملی کنگتینگ به عنوان مثال. نات خطرات 2016 ، 82 ، 2133-2147. [ Google Scholar ] [ CrossRef ]
  4. حکیمی، SL مکان های بهینه مراکز سوئیچینگ و مراکز مطلق و میانه های یک نمودار. اپراتور Res. 1964 ، 12 ، 450-459. [ Google Scholar ] [ CrossRef ]
  5. Aly, AA; White, JA فرمول احتمالی مسئله مکان خدمات اضطراری. جی. اوپر. Res. Soc. 1979 ، 29 ، 1167-1179. [ Google Scholar ] [ CrossRef ]
  6. کلیسا، آر. Velle، CR مشکل مکان پوشش حداکثر. پاپ Reg. علمی 1974 ، 32 ، 101-118. [ Google Scholar ] [ CrossRef ]
  7. بایرام، وی. Tansel، BC; یامان، ح. به خطر انداختن سیستم و منافع کاربر در مکان یابی پناهگاه و برنامه ریزی تخلیه. ترانسپ Res. روش قسمت B. 2015 ، 72 ، 146-163. [ Google Scholar ] [ CrossRef ]
  8. گاما، م. سانتوس، BF; Scaparra, MP مدل تخصیص مکان پناهگاه چند دوره ای با دستورات تخلیه برای بلایای سیل. EURO J. Comput. بهینه. 2015 ، 4 ، 299-323. [ Google Scholar ] [ CrossRef ]
  9. کوکاتپه، ا. Ozguven، EE; هورنر، ام. اوزل، اچ. برنامه‌ریزی پناهگاه سازگار با حیوانات خانگی و نیازهای ویژه در فلوریدا جنوبی: یک رویکرد مبتنی بر p-متوسط ​​ظرفیت‌پذیر فضایی. بین المللی J. کاهش خطر بلایا. 2018 ، 31 ، 1207-1222. [ Google Scholar ] [ CrossRef ]
  10. هورنر، مگاوات؛ Ozguven، EE; مارسلین، جی.ام. Kocatepe، A. پناهگاه های طوفان با نیازهای ویژه و جمعیت سالخورده: توسعه یک روش و یک کاربرد مطالعه موردی. بلایا 2018 ، 42 ، 169-186. [ Google Scholar ] [ CrossRef ]
  11. پرانیتفولکرانگ، پ. Huynh، VN; Kanjanawattana، S. یک مدل بهینه‌سازی چند هدفه برای تخصیص مکان پناهگاه در پاسخ به تدارکات امداد بشردوستانه. آسیایی جی شیپ. تدارکات. 2021 ، 37 ، 149-156. [ Google Scholar ] [ CrossRef ]
  12. هو، اف. خو، دبلیو. Li, X. الگوریتم بهینه سازی ازدحام ذرات اصلاح شده برای تخصیص بهینه پناهگاه های اضطراری زلزله. بین المللی جی. جئوگر. Inf. علمی 2012 ، 2 ، 1643-1666. [ Google Scholar ] [ CrossRef ]
  13. شرالی، HD; کارتر، سل؛ Hobeika، AG مدل و الگوریتم مکان تخصیص برای برنامه ریزی تخلیه در شرایط طوفان / سیل. ترانسپ Res. روش قسمت B. 1991 ، 25 ، 439-452. [ Google Scholar ] [ CrossRef ]
  14. ژانگ، ن. هوانگ، اچ. Su، BN تجزیه و تحلیل خطر پویا جاده برای تخلیه عابر پیاده. فیزیک یک آمار مکانیک. برنامه آن است. 2015 ، 430 ، 171-183. [ Google Scholar ] [ CrossRef ]
  15. برزین پور، ف. اسماعیلی، وی. مدل توزیع مکان زنجیره امداد چند هدفه برای مدیریت بلایای شهری. بین المللی J. Adv. Manuf. تکنولوژی 2014 ، 70 ، 1291-1302. [ Google Scholar ] [ CrossRef ]
  16. Doerner، KF; گوجهر، WJ; Nolz، PC برنامه ریزی مکان یابی چند معیاره برای تأسیسات عمومی در مناطق ساحلی مستعد سونامی. OR Spectr. 2009 ، 31 ، 651-678. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  17. لوئیس، AA; لینو، تی. Luís، S. رویکرد چند هدفه برای مکان یابی پناهگاه های اضطراری و شناسایی مسیرهای تخلیه در مناطق شهری. Geogr. مقعدی 2009 ، 41 ، 9-29. [ Google Scholar ]
  18. ژانگ، ایکس. یو، اس. Zhang، X. مدل مکان بهینه شده پناهگاه تجمع اضطراری ساکنان بر اساس محدودیت های چند هدفه. توسعه شهری گل میخ. 2020 ، 27 ، 59-66. [ Google Scholar ]
  19. کونگسومساکساکول، اس. یانگ، سی. چن، الف. مدل تخصیص مکان پناهگاه برای برنامه ریزی تخلیه سیل. جی شرق. انجمن آسیا ترانسپ گل میخ. 2005 ، 6 ، 4237-4252. [ Google Scholar ]
  20. لی، ACY; نوزیک، ال. خو، ن. دیویدسون، آر. مکان یابی پناهگاه و برنامه ریزی حمل و نقل تحت شرایط طوفان. ترانسپ Res. بخش E Logist. ترانسپ Rev. 2012 , 48 , 715-729. [ Google Scholar ] [ CrossRef ]
  21. لی، اچ. ژائو، ال. هوانگ، آر. هو، کیو. برنامه ریزی سلسله مراتبی پناهگاه زلزله در مناطق شهری: موردی برای شانگهای در چین. بین المللی J. کاهش خطر بلایا. 2017 ، 22 ، 431-446. [ Google Scholar ] [ CrossRef ]
  22. چن، ز. چن، ایکس. لی، کیو. چن، جی. سلسله مراتب زمانی پناهگاه ها: یک مدل مکان سلسله مراتبی برای برنامه ریزی پناهگاه زلزله. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 1612-1630. [ Google Scholar ] [ CrossRef ]
  23. ژائو، ایکس. چن، جی. خو، دبلیو. دو، پ. یوان، اچ. یک مدل سلسله مراتبی سه مرحله ای برای مشکل مکان-تخصیص پناهگاه زلزله: مطالعه موردی منطقه چائویانگ، پکن، چین. پایداری 2019 ، 11 ، 4561. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  24. بله، م. وانگ، جی. هوانگ، جی. خو، اس. چن، ز. روش و کاربرد آن برای برنامه ریزی تخلیه در مقیاس جامعه در برابر بلایای زلزله. نات خطرات 2012 ، 61 ، 881-892. [ Google Scholar ] [ CrossRef ]
  25. یی، دبلیو. Ozdamar, L. یک مدل هماهنگی لجستیک پویا برای تخلیه و پشتیبانی در فعالیت های واکنش به بلایا. یورو جی. اوپر. Res. 2007 ، 179 ، 1177-1193. [ Google Scholar ] [ CrossRef ]
  26. ملا، ع.ک. صدوخان، س. داس، پ. Anis، MZ مدل بهینه سازی هزینه و راه حل هایی برای تخصیص پناهگاه و توزیع امداد در سناریوی سیل. بین المللی J. کاهش خطر بلایا. 2018 ، 13 ، 1187-1198. [ Google Scholar ] [ CrossRef ]
  27. فن، سی. ژای، جی. ژو، اس. ژو، اس. ژانگ، اچ. Qiao, P. چارچوب یکپارچه برای برنامه ریزی پناهگاه اضطراری بر اساس ارزیابی ریسک چند خطر و کاربرد آن: مطالعه موردی در چین. نات Hazards Rev. 2017 , 18 , 51-65. [ Google Scholar ] [ CrossRef ]
  28. چن، ز. لی، کیو. چن، جی. مطالعه مکان سلسله مراتبی پناهگاه های اضطراری شهری (Ⅱ): مدل های مکان سه سلسله مراتبی. جی. نات. بلایا 2010 ، 19 ، 13-19. (به چینی) [ Google Scholar ]
  29. لی، ال. جین، م. Zhang, L. برنامه ریزی و مدیریت شبکه پناهگاه با یک مورد در منطقه خلیج فارس. بین المللی J. Prod. اقتصاد 2011 ، 131 ، 431-440. [ Google Scholar ] [ CrossRef ]
  30. هو، اف. یانگ، اس. Xu, W. یک الگوریتم ژنتیک مرتب‌سازی غیرمسلط برای مکان‌یابی و برنامه‌ریزی منطقه‌ای پناهگاه‌های زلزله. بین المللی جی. جئوگر. Inf. علمی 2014 ، 7 ، 1482-1501. [ Google Scholar ] [ CrossRef ]
  31. نگ، دبلیو. پارک، جی. Waller, ST یک مدل دوسطحی ترکیبی برای تخصیص بهینه پناهگاه در تخلیه اضطراری. Comput.-Aided Civ. زیرساخت. مهندس 2010 ، 8 ، 547-556. [ Google Scholar ] [ CrossRef ]
  32. ژائو، ایکس. خو، دبلیو. ممکن است.؛ هو، اف. مدل تخصیص بهینه چند هدفه مبتنی بر سناریو برای پناهگاه‌های اضطراری زلزله با استفاده از الگوریتم بهینه‌سازی ازدحام ذرات اصلاح‌شده: مطالعه موردی در منطقه چائویانگ، پکن، چین. PLoS ONE 2015 ، 12 ، e0144455. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  33. Arnaout، الگوریتم بهینه‌سازی کلنی مورچه JP برای مسئله تخصیص مکان اقلیدسی با تعداد نامعلوم امکانات. جی. اینتل. Manuf. 2011 ، 1 ، 45-54. [ Google Scholar ] [ CrossRef ]
  34. سلمان، اف اس; Yücel، E. مکان تأسیسات اضطراری تحت آسیب تصادفی شبکه: بینش هایی از پرونده استانبول. محاسبه کنید. اپراتور Res. 2015 ، 62 ، 266-281. [ Google Scholar ] [ CrossRef ]
  35. اسکار، RE; Juan, G. طرح آمادگی مبتنی بر سناریو برای سیل. نات خطرات 2014 ، 2 ، 1241-1262. [ Google Scholar ]
  36. یین، ز. لی، اس. یانگ، اس. ژی، ز. روش برآورد خسارت لرزه ای و تلفات لرزه ای. زمین مهندس مهندس Vib. 1990 ، 4 ، 99-108. (به چینی) [ Google Scholar ]
  37. چی، دبلیو. لی، ی. لیو، اس. گائو، ایکس. ژائو، ام. برآورد جمعیت شهری در روز و شب و تجزیه و تحلیل الگوی فضایی آنها: مطالعه موردی منطقه هایدیان، پکن. Acta Geogr. گناه 2013 ، 68 ، 1344-1356. [ Google Scholar ]
  38. آکرمن، الف. الگوی خانوار شهری تغییر جمعیت در طول روز. ان Reg. علمی 1995 ، 29 ، 1-16. [ Google Scholar ] [ CrossRef ]
  39. ژونگ، دبلیو. وانگ، دی. زی، دی. یان، ال. ویژگی های دینامیکی توزیع جمعیت شانگهای با استفاده از داده های سیگنالینگ تلفن همراه. Geogr. Res. 2017 ، 36 ، 972-984. [ Google Scholar ]
  40. ژائو، ایکس. خو، دبلیو. Ma، Y. روابط بین اندازه جمعیت تخلیه، ظرفیت پناهگاه اضطراری زلزله، و زمان تخلیه. بین المللی J. Disaster Risk Sci. 2017 ، 8 ، 457-470. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  41. چانگ، اچ اس. لیائو، CH برنامه ریزی مکان های سرپناه اضطراری بر اساس رفتار تخلیه. نات خطرات 2015 ، 76 ، 1551-1571. [ Google Scholar ] [ CrossRef ]
  42. پید، م. د سیلوا، FN; Eglese، RW یک مدل شبیه سازی برای تخلیه اضطراری. یورو جی. اوپر. Res. 1996 ، 90 ، 413-419. [ Google Scholar ] [ CrossRef ]
  43. کووا، تی جی; جانسون، JP شبیه سازی میکرو تخلیه محله در رابط شهری و سرزمین وحشی. محیط زیست طرح. A 2002 , 34 , 2211-2230. [ Google Scholar ] [ CrossRef ]
  44. Lindell, MK EMBLEM2: یک مدل تخمین زمان تخلیه در مقیاس بزرگ مبتنی بر تجربی. ترانسپ Res. بخش A سیاست سیاست. 2008 ، 42 ، 140-154. [ Google Scholar ] [ CrossRef ]
  45. کلمبو، RM; Rosini, MD جریان های عابر پیاده و شوک های غیر کلاسیک. ریاضی. Methods Appl. علمی 2005 ، 28 ، 1553-1567. [ Google Scholar ] [ CrossRef ]
  46. کیم، اس. جورج، بی. Shekhar, S. برنامه ریزی مسیر تخلیه: اکتشافی مقیاس پذیر. در مجموعه مقالات پانزدهمین سمپوزیوم سالانه بین المللی ACM در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، سیاتل، WA، ایالات متحده آمریکا، 7-9 نوامبر 2007. [ Google Scholar ]
  47. هلبینگ، دی. مولنار، ص. مدل نیروی اجتماعی برای پویایی عابر پیاده. فیزیک Rev. E 1995 , 51 , 4282-4286. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  48. برستد، سی. کلاوک، ک. Schadschneider، A. Zittartz، J. شبیه سازی دینامیک عابر پیاده با استفاده از یک خودکار سلولی دو بعدی. فیزیک A 2001 ، 295 ، 507-525. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  49. او، م. چن، سی. ژنگ، اف. چن، کیو. ژانگ، جی. یان، اچ. Lin, Y. یک بهینه‌سازی مسیر پویا کارآمد برای تخلیه سیل شهری بر اساس اتوماتای ​​سلولی. محاسبه کنید. محیط زیست سیستم شهری 2021 ، 87 ، 101622. [ Google Scholar ] [ CrossRef ]
  50. پان، XS; هان، CS; داوبر، ک. قانون، KH یک چارچوب مبتنی بر چند عامل برای شبیه سازی رفتارهای انسانی و اجتماعی در حین تخلیه اضطراری. AI Soc. 2007 ، 22 ، 113-132. [ Google Scholar ] [ CrossRef ]
  51. کروکس، آ. قلعه، سی. Batty، M. چالش های کلیدی در مدل سازی مبتنی بر عامل برای شبیه سازی جغرافیایی فضایی. محاسبه کنید. محیط زیست سیستم شهری 2008 ، 32 ، 417-430. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  52. روسو، اف. Chilà، G. یک آزمایش نمونه اولیه با استفاده از داده های ترجیحات بیان شده برای مدل سازی تصمیمات تخلیه. WIT Trans. Ecol. محیط زیست 2013 ، 173 ، 743-752. [ Google Scholar ]
  53. یوان، ز. جیا، اچ. لیائو، م. ژانگ، ال. فنگ، ی. تیان، جی. مدل شبیه سازی حرکت خودسازماندهی عابر پیاده با در نظر گرفتن رفتار زیر. جلو. Inf. تکنولوژی الکترون. مهندس 2017 ، 18 ، 1142-1150. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  54. هو، ال. لیو، جی جی. پان، X. وانگ، BH یک مدل تخلیه نیروی اجتماعی با اثر رهبری. فیزیک A 2014 ، 400 ، 93-99. [ Google Scholar ] [ CrossRef ]
  55. Lin, QY; جی، QG; گونگ، SM یک سیستم تخلیه جمعیت در شرایط اضطراری بر اساس مدل دینامیک. در مجموعه مقالات کنفرانس بین‌المللی فناوری‌های تعاملی و سیستم‌های اجتماعی، برلین، آلمان، 23 تا 24 اکتبر 2006. [ Google Scholar ]
  56. هندفورد، دی. راجرز، الف. یک مدل نیروهای اجتماعی مبتنی بر عامل برای رفتارهای تخلیه راننده. Prog. آرتیف. هوشمند 2012 ، 1 ، 173-181. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  57. وی، ز. دینگ، اچ. Tong, W. کاربرد فناوری شبیه سازی گسترش آتش و تخلیه در استادیوم بزرگ. استوک. محیط زیست Res. ارزیابی ریسک 2009 ، 23 ، 433-439. [ Google Scholar ] [ CrossRef ]
  58. Xiao، ML؛ ژانگ، ی. لیو، ب. شبیه سازی تخلیه زلزله کودکان دبستانی در شهر روستایی. نات خطرات 2017 ، 87 ، 1783-1806. [ Google Scholar ] [ CrossRef ]
  59. چن، ی. چن، دبلیو. جفری، BHY; لی، اچ. Zhang, S. شبیه سازی تخلیه اضطراری در شروع اتصال پل بین دریا: مطالعه موردی در ایستگاه مترو خیابان Haicang در خط حمل و نقل ریلی Xiamen. جی. ساخت. مهندس 2020 ، 29 ، 101163. [ Google Scholar ] [ CrossRef ]
  60. زنگ، ی. می، س. لیو، اس. شبیه سازی تخلیه یک ساختمان آموزشی مرتفع با در نظر گرفتن تأثیر موانع. شبیه سازی مدل. تمرین کنید. نظریه 2021 ، 112 ، 102354. [ Google Scholar ] [ CrossRef ]
  61. چنگ، اس. وانگ، ی. Fan, L. A Study on the Optimal Strategies of Optimal Network Road Community در شمال شرق چین بر اساس شبیه سازی تخلیه. آرشیت. J. 2018 ، 2 ، 38-43. (به زبان چینی) [ Google Scholar ]
  62. ورمویتن، اچ. بلین، جی. Boeck، LD; رنیرز، جی. واترز، تی. مروری بر مدل‌های بهینه‌سازی برای مشکلات تخلیه و طراحی عابر پیاده. ساف علمی 2016 ، 87 ، 167-178. [ Google Scholar ] [ CrossRef ]
  63. گو، ق. خو، اچ. یان، ی. ژائو، کیو. لی، ال. منگ، ک. یانگ، اچ. وانگ، جی. جیانگ، ایکس. Ma، D. ساختارهای کم عمق پوسته و تشخیص فعالیت گسل در بخش Xinyi از منطقه گسل تانلو. سیسمول. جئول 2020 ، 42 ، 825-843. [ Google Scholar ]
  64. Dijkstra، EW یادداشتی در مورد دو مشکل در ارتباط با نمودارها. عدد. ریاضی. 1959 ، 1 ، 269-271. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  65. هاکلی، م. Patrick, W. Openstreetmap: نقشه های خیابانی تولید شده توسط کاربر. محاسبات فراگیر IEEE 2008 ، 7 ، 12-18. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  66. ژائو، ی. لی، کیو. ژانگ، ی. Du, X. بهبود دقت نگاشت جمعیت ریز دانه با استفاده از POIهای حساس به جمعیت. Remote Sens. 2019 , 11 , 2502. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  67. وانگ، دی. رن، X. توزیع و ترکیب جمعیت واقعی در فضای شهری از دیدگاه تحرک روزانه انسان. طرح شهری. انجمن 2016 ، 40 ، 33-40. [ Google Scholar ]
  68. وو، زی. Ye, Z. تحقیق در مورد ساختار فضایی شهری بر اساس نقشه حرارتی Baidu: مطالعه موردی در شهر مرکزی شانگهای. طرح شهر. Rev. 2016 , 40 , 33-40. [ Google Scholar ]
  69. چن، اچ. لی، ی. کوین، سی. لیو، جی. Sun، JL مطالعه بر روی توزیع مکانی-زمانی فعالیت های شبانه ساکنان شیان بر اساس میکرو وبلاگ. هوم Geogr. 2015 ، 30 ، 57-63. [ Google Scholar ]
  70. GB/T 51328-2018 ; وزارت مسکن و ساخت و ساز شهری – روستایی جمهوری خلق چین. مطبوعات معماری و ساختمان: پکن، چین، 2018. (به زبان چینی)
  71. CJJ 37-2012 ; وزارت مسکن و ساخت و ساز شهری – روستایی جمهوری خلق چین. مطبوعات معماری و ساختمان: پکن، چین، 2016. (به زبان چینی)
  72. خو، X. Tang, Q. برنامه ریزی راه و ترابری شهری ; چاپ معماری و ساختمان چین: پکن، چین، 2007; ISBN 7112075955. [ Google Scholar ]
  73. گیتس، تی جی; نویس، دی. بیل، AR؛ ون، EN سرعت های پیاده روی توصیه شده برای زمان بندی ترخیص عابر پیاده بر اساس ویژگی های عابر پیاده. در مجموعه مقالات هشتاد و پنجمین نشست سالانه هیئت تحقیقات حمل و نقل، واشنگتن، دی سی، ایالات متحده آمریکا، 22 تا 26 ژانویه 2006. [ Google Scholar ]
  74. جانسون، دی اس ستون کامل بودن NP: راهنمای مداوم. J. Algorithms 1983 , 4 , 87-100. [ Google Scholar ] [ CrossRef ]
  75. وو، جی. Weng, W. سیستم پشتیبانی تصمیم برای مکان های سرپناه شهری. J. Tsinghua Univ. (Sci. Technol.) 2011 ، 5 ، 632-636. [ Google Scholar ]
  76. یانگ، جی. هو، ی. ژانگ، ک. Wu, Y. یک الگوریتم تکامل بهبود یافته با استفاده از الگوریتم ژنتیک رقابت جمعیت و شبکه عصبی BP خود اصلاحی بر اساس چشم انداز تناسب اندام. محاسبات نرم. 2021 ، 25 ، 1751-1776. [ Google Scholar ] [ CrossRef ]
  77. هلبینگ، دی. فرکاس، آی. ویکسک، تی. شبیه سازی ویژگی های دینامیکی وحشت فرار. طبیعت 2000 ، 407 ، 487-490. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  78. یو، جی. ژانگ، سی. ون، جی. لی، دبلیو. لیو، آر. Xu، H. یکپارچه سازی شبیه سازی تخلیه چند عاملی و ارزیابی چند معیاره برای تخصیص فضایی پناهگاه های اضطراری شهری. بین المللی جی. جئوگر. Inf. علمی 2018 ، 32 ، 1884-1910. [ Google Scholar ] [ CrossRef ]
  79. ژو، جی. لی، اس. نی، جی. فن، X. Xia, C. توسعه یک مدل نیروی اجتماعی تجدید نظر شده برای تخلیه اضطراری عابران پیاده در اثر زلزله. Geomat. نات خطر خطرات 2020 ، 11 ، 335-356. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  80. روسو، اف. چیلا، جی. مدل‌های تقاضای سفر یکپارچه برای تخلیه: پلی بین علوم اجتماعی و مهندسی. بین المللی J. Saf. امن مهندس 2014 ، 4 ، 19-37. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Ijgi 11 00262 g001 550
شکل 1. موقعیت و محدوده منطقه مورد مطالعه.
Ijgi 11 00262 g002 550
شکل 2. داده های فضایی ناحیه مرکزی شهری شهر Xinyi.
Ijgi 11 00262 g003 550
شکل 3. تغییرات جمعیت در منطقه مورد مطالعه در طی 24 ساعت.
Ijgi 11 00262 g004 550
شکل 4. چارچوب روش پیشنهادی.
Ijgi 11 00262 g005 550
شکل 5. قوانین تخصیص تخلیه دایره ای از نقاط تقاضا به پناهگاه ها.
Ijgi 11 00262 g006 550
شکل 6. رابطه بین زمان و تعداد افرادی که تخلیه را تکمیل می کنند.
Ijgi 11 00262 g007 550
شکل 7. رابطه بین مقدار تابع تناسب و تعداد تکرارها.
Ijgi 11 00262 g008 550
شکل 8. مدل تخلیه منطقه مورد مطالعه. ( الف ) 5 دقیقه، ( ب ) 10 دقیقه، ( ج ) 15 دقیقه، و ( د ) 25 دقیقه.
Ijgi 11 00262 g009 550
شکل 9. طرح مکان یابی بهینه پناهگاه.
Ijgi 11 00262 g010 550
شکل 10. طرح مکان یابی بهینه پناهگاه.
Ijgi 11 00262 g011 550
شکل 11. طرح مکان یابی بهینه پناهگاه.
Ijgi 11 00262 g012 550
شکل 12. مقایسه توزیع فرکانس زمان تخلیه قبل و بعد از بهینه سازی.
Ijgi 11 00262 g013 550
شکل 13. مقایسه تعداد افرادی که تخلیه را قبل و بعد از بهینه سازی انجام می دهند.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید