کلید واژه ها:
خودهمبستگی فضایی ; تأخیر فضایی ؛ فیلتر بردار ویژه ; یادگیری ماشینی ؛ اعتبار متقابل تو در تو ; پیش بینی جغرافیایی
1. مقدمه
2. کارهای مرتبط
3. روش ها
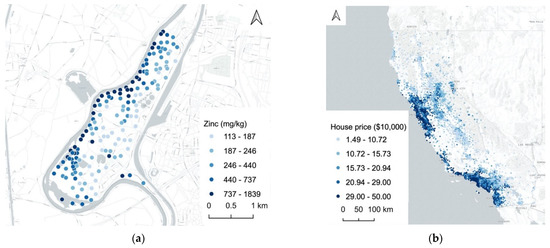
3.1. منابع اطلاعات
3.1.1. مجموعه داده رودخانه میوس
3.1.2. مجموعه داده مسکن کالیفرنیا
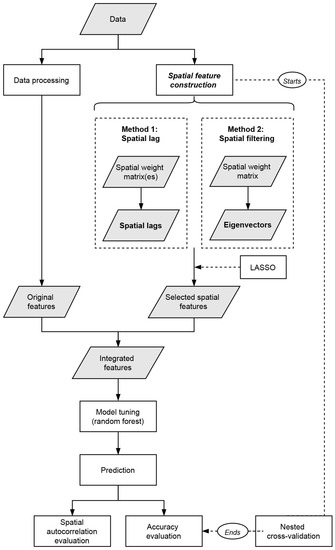
3.2. ساخت و پردازش ویژگی های فضایی
3.2.1. ویژگی های تاخیر فضایی
ویژگیهای تاخیر فضایی، همبستگی مکانی متغیرهای وابسته ( y ) در مناطق اطراف را به تصویر میکشند. تاخیر مکانی مکان i به عنوان مجموع وزنی مقادیر از مکان i تا j محاسبه می شود :
یک ماتریس وزن فضایی ( w ij ) برای ساخت ویژگیهای تاخیر ضروری است. در اصل، ساخت چنین ماتریس وزن فضایی شامل دو رویه است: تعریف همسایگی، و محاسبه وزن های فضایی. همسایگی تعیین می کند که کدام مکان ها به هم مرتبط هستند ( i به j ) و وزن ها قدرت پیوندها را تعیین می کنند. وزن ها را می توان با تنظیمات باینری یا از طریق توابع مبتنی بر فاصله مانند فاصله معکوس و توابع هسته محاسبه کرد. مشخصات مختلف ماتریس نشان دهنده ساختارهای فضایی متفاوت است. با این حال، توافق نظری در مورد انتخاب یک ماتریس وزن فضایی وجود ندارد [ 41]. در این مطالعه، تنظیم باینری یک k-نزدیکترین همسایه استفاده میشود زیرا یک رابط مناسب برای ساخت ماتریس وزن فضایی با تغییر مقدار پارامتر k فراهم میکند. K-نزدیکترین همسایه همچنین یک پیکربندی اتصال تطبیقی را معرفی میکند که در آن تعداد همسایهها ثابت است اما محدوده فاصله بین همسایگان ثابت نیست. ماتریس وزن به صورت ردیفی استاندارد شده است به طوری که ویژگیهای تاخیر نشان دهنده میانگین مقادیر اطراف است. بنابراین، مقادیر وزن عبارتند از:
3.2.2. بردار ویژه فیلتر فضایی
تجزیه ESF بر روی ماتریس انجام می شود
که در آن I یک ماتریس هویت n به n است، 1 یک بردار n در 1 از یک ها است، و W ماتریس وزن فضایی است که توسط Getis و Griffith [ 43 ] تعریف شده است. بردارهای ویژه استخراج شده، الگوهای نقشه پنهان زیرین را ارائه می دهند [ 44 ].
در این مطالعه، ما هسته نمایی مشترک موراکامی و گریفیث [ 20 ] را اتخاذ کردیم زیرا این نویسندگان قابلیت استفاده آن را در مجموعه داده های بزرگ نشان دادند. عناصر ماتریس وزن فضایی به صورت زیر محاسبه می شوند:
که d ij فاصله بین مکان i و j است، و r با حداکثر طول در درخت پوشا حداقلی که همه نمونه ها را به هم متصل می کند، به دست می آید. تا زمانی که هسته نیمه معین است، هسته نمایی را می توان با هر تابع هسته جایگزین کرد تا نیازهای مسائل دیگر را برآورده کند [ 20 ]. با توجه به حجم نمونه و نگرانی محاسباتی تجزیه ویژه، تنها 200 بردار ویژه اول برای داده های مسکن کالیفرنیا تقریبی شده است. برای مجموعه داده Meuse، مقادیر ویژه دقیق بدون تقریب محاسبه می شود.
3.3. مدلهای یادگیری ماشین و محک زدن
3.3.1. جنگل تصادفی
3.3.2. رگرسیون وزنی جغرافیایی
3.4. سنجش عملکرد
- (آ)
-
مجموعه داده را به چین های بیرونی K تقسیم کنید .
- (ب)
-
برای هر تار بیرونی k = 1، 2، …، K : حلقه بیرونی برای ارزیابی مدل:
-
K را به عنوان مجموعه تست بیرونی در نظر بگیرید . چین های باقی مانده را به عنوان مجموعه تمرینی بیرونی، قطار بیرونی بگیرید.
-
قطار بیرونی را به چین های L داخلی تقسیم کنید.
-
برای هر چین داخلی l = 1، 2، …، L : حلقه داخلی برای تنظیم فراپارامتر:
- من.
-
فولد l را به عنوان تست درونی مجموعه تست داخلی و بقیه را به عنوان قطار درونی در نظر بگیرید.
- ii
-
محاسبه ویژگی های فضایی در قطار داخلی .
- III.
-
LASSO تایید شده متقاطع را در قطار داخلی با ویژگیهای فضایی انجام دهید و لامبدا را تعیین کنید با قانون “یک خطای استاندارد”؛ ویژگی های مکانی را با ضرایب غیر صفر انتخاب کنید.
- IV
-
برای هر کاندیدای فراپارامتر، مدلی را در قطار داخلی با مجموعه ویژگی های ترکیبی قرار دهید.
- v
-
ویژگی های فضایی انتخاب شده را در آزمون درونی محاسبه کنید.
- vi.
-
مدل را در آزمون درونی با معیار سنجش ارزیابی کنید.
-
برای هر کاندیدهایپرپارامتر، مقادیر متریک ارزیابی را در تاهای L میانگین کنید و بهترین هایپرپارامتر را انتخاب کنید. در آزمایشهای ما، فراپارامتری که آزمایش شد m try بود.
-
محاسبه ویژگی های فضایی در قطار بیرونی .
-
LASSO تایید شده متقاطع را در قطار بیرونی با ویژگیهای فضایی انجام دهید و لامبدا را تعیین کنید با قانون “یک خطای استاندارد”. ویژگی های مکانی را با ضرایب غیر صفر انتخاب کنید.
-
مدلی را با بهترین هایپرپارامتر در قطار بیرونی آموزش دهید .
-
ویژگی های فضایی انتخاب شده را در آزمون بیرونی محاسبه کنید.
-
مدل را در آزمون بیرونی با معیار سنجش ارزیابی کنید.
-
- (ج)
-
میانگین مقادیر متریک را روی K folds بگیرید و عملکرد تعمیم یافته را گزارش کنید.
3.5. ارزیابی خودهمبستگی فضایی
4. نتایج
4.1. مشخصات مدل ها
4.2. اهمیت متغیرهای توضیحی
4.3. ارزیابی عملکرد – خطای RMSE
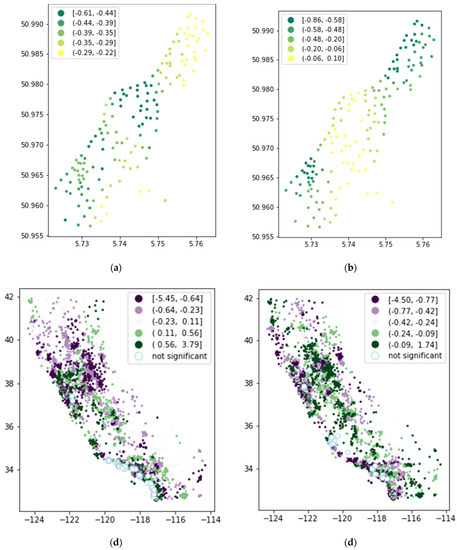
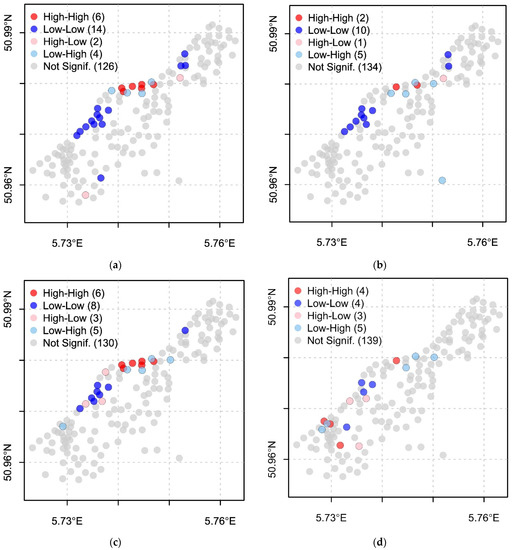
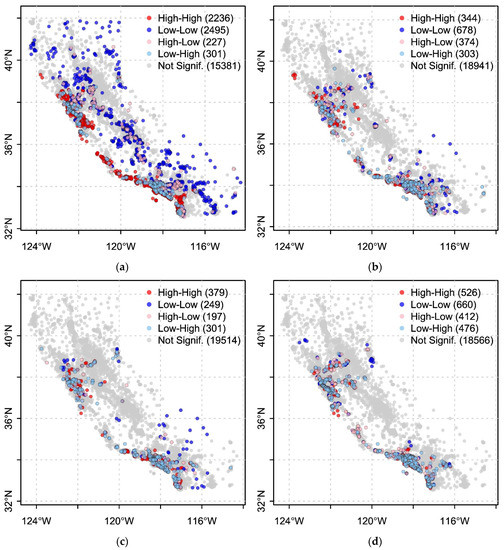
4.4. ارزیابی خودهمبستگی فضایی-محلی و محلی موران
5. بحث
منابع
- Goodchild، MF کیفیت داده های بزرگ (جغرافیایی). دیالوگ هام Geogr. 2013 ، 3 ، 280-284. [ Google Scholar ] [ CrossRef ]
- کیچین، آر. داده های بزرگ و جغرافیای انسانی: فرصت ها، چالش ها و خطرات. دیالوگ هام Geogr. 2013 ، 3 ، 262-267. [ Google Scholar ] [ CrossRef ]
- هافمن، جی. بار سینا، ی. لی، LM; آندریویچ، جی. میشا، س. روبینشتاین، اس ام. رایکرافت، CH یادگیری ماشینی در یک رژیم محدود داده: آزمایشهای تقویت شده با دادههای مصنوعی نظم را در ورقهای مچاله شده آشکار میکند. علمی Adv. 2019 ، 5 ، eaau6792. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
- آگیلار، آر. زوریتا میلا، ر. Izquierdo-Verdiguier، E. De By، RA طبقهبندیکننده گروه چندموقتی مبتنی بر ابر برای نقشهبرداری سیستمهای کشاورزی کوچک. Remote Sens. 2018 , 10 , 729. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Řezník، T. چیتری، جی. Trojanová، K. خط لوله اثبات مفهوم پردازش مبتنی بر یادگیری ماشین برای دانلود تصاویر نیمه خودکار Sentinel-2، فیلتر ابری، طبقه بندی و به روز رسانی مجموعه داده های کاربری زمین/پوشش زمین باز. ISPRS Int. J. Geo-Inf. 2021 ، 10 ، 102. [ Google Scholar ] [ CrossRef ]
- پرادان، AMS؛ کیم، Y.-T. نقشهبرداری حساسیت زمین لغزش کم عمق ناشی از بارندگی در دو حوضه مجاور با استفاده از الگوریتمهای پیشرفته یادگیری ماشین. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 569. [ Google Scholar ] [ CrossRef ]
- زوریتا میلا، ر. گونکالوس، آر. Izquierdo-Verdiguier، E. Ostermann، FO در حال کاوش در شروع بهار در مقیاس قاره ای: نقشه برداری از فنورمنطقه ها و همبستگی دما و فنومتریک مبتنی بر ماهواره. IEEE Trans. کلان داده 2019 ، 6 ، 583–593. [ Google Scholar ] [ CrossRef ]
- رایششتاین، ام. کمپز-والز، جی. استیونز، بی. یونگ، ام. دنزلر، جی. کاروالهایس، ن. پرابهات. یادگیری عمیق و درک فرآیند برای علم سیستم زمین مبتنی بر داده. Nature 2019 ، 566 ، 195-204. [ Google Scholar ] [ CrossRef ]
- کانفسکی، م. پوزدنوخوف، ا. Timonin، V. الگوریتم های یادگیری ماشین برای داده های جغرافیایی. نرم افزارها و ابزارهای نرم افزاری. در مجموعه مقالات چهارمین کنگره بین المللی مدلسازی و نرم افزار محیطی، بارسلون، اسپانیا، 1 ژوئیه 2008; پ. 369. [ Google Scholar ]
- شکر، س. جیانگ، ز. علی، RY; افتلی اوغلو، ای. تانگ، ایکس. گونتوری، VMV؛ ژو، X. داده کاوی فضایی-زمانی: یک دیدگاه محاسباتی. ISPRS Int. J. Geo-Inf. 2015 ، 4 ، 2306-2338. [ Google Scholar ] [ CrossRef ]
- مایکل، FG علم اطلاعات جغرافیایی. بین المللی جی. جئوگر. Inf. سیستم 1992 ، 6 ، 31-45. [ Google Scholar ]
- میلر، HJ نمایش جغرافیایی در تحلیل فضایی. جی. جئوگر. سیستم 2000 ، 2 ، 55-60. [ Google Scholar ] [ CrossRef ]
- Tobler, WR یک فیلم کامپیوتری شبیه سازی رشد شهری در منطقه دیترویت. اقتصاد Geogr. 1970 ، 46 ، 234-240. [ Google Scholar ] [ CrossRef ]
- Anselin, L. اقتصاد سنجی فضایی: روش ها و مدل ها . Springer: Dordrecht, The Netherlands, 1988. [ Google Scholar ] [ CrossRef ][ Green Version ]
- براندون، سی. فاثرینگهام، اس. چارلتون، ام. رگرسیون وزنی جغرافیایی. JR Stat. Soc. سر. D 1996 , 47 , 431-443. [ Google Scholar ] [ CrossRef ]
- لوچل، ام. Axhausen، KW مدل سازی اجاره های مسکونی لذت جویانه برای استفاده از زمین و شبیه سازی حمل و نقل با در نظر گرفتن اثرات فضایی. J. Transp. کاربری زمین 2010 ، 3 ، 39-63. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- ویلر، DC رگرسیون وزنی جغرافیایی. در کتابچه راهنمای علوم منطقه ای ; Springer: برلین/هایدلبرگ، آلمان، 2014; ص 1435-1459. [ Google Scholar ]
- فوئجیو، اف. کلمپ، جی. بررسی عدم قطعیت پیشبینی دادههای مکانی در رویکردهای زمینآماری و یادگیری ماشینی. محیط زیست علوم زمین 2019 ، 78 ، 38. [ Google Scholar ] [ CrossRef ]
- Kleijnen، JPC; ون بیرز، پیشبینی WCM برای دادههای بزرگ از طریق کریجینگ: طرحهای کوچک متوالی و تکشات. صبح. جی. ریاضی. مدیریت علمی 2020 ، 39 ، 199-213. [ Google Scholar ] [ CrossRef ]
- موراکامی، دی. Griffith، DA Eigenvector Spatial Filtering for Large Data Sets: Fixed and Random Effects Approaches. Geogr. مقعدی 2018 ، 51 ، 23-49. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Dormann، CF; مک فرسون، جی.ام. Araújo، MB; بیوند، ر. بولیگر، جی. کارل، جی. دیویس، آر جی. هیرزل، ا. جتز، دبلیو. بوسیدن، WD; و همکاران روشهایی برای محاسبه خودهمبستگی فضایی در تجزیه و تحلیل دادههای توزیع گونهها: مروری. اکوگرافی 2007 ، 30 ، 609-628. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- هنگل، تی. نوسبام، م. رایت، MN; Heuvelink، GBM؛ Gräler، B. جنگل تصادفی به عنوان یک چارچوب عمومی برای مدل سازی پیش بینی متغیرهای مکانی و مکانی-زمانی. PeerJ 2018 , 6 , e5518. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- مایر، اچ. رودنباخ، سی. ولاور، اس. Nauss, T. اهمیت انتخاب متغیر پیشبینیکننده فضایی در برنامههای یادگیری ماشین – حرکت از بازتولید داده به پیشبینی فضایی. Ecol. مدل. 2019 ، 411 ، 108815. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- پوهجانکوکا، ج. Pahikkala، T. نوالاینن، پی. Heikkonen, J. برآورد عملکرد پیشبینی مدلهای فضایی از طریق اعتبارسنجی متقاطع k-fold فضایی. بین المللی جی. جئوگر. Inf. علمی 2017 ، 31 ، 2001–2019. [ Google Scholar ] [ CrossRef ]
- بهرنز، تی. اشمیت، ک. راسل، راو؛ گریس، پی. شولتن، تی. مک میلان، مدل سازی فضایی RA با میدان های فاصله اقلیدسی و یادگیری ماشین. یورو J. Soil Sci. 2018 ، 69 ، 757-770. [ Google Scholar ] [ CrossRef ]
- لی، تی. شن، اچ. یوان، Q. ژانگ، ایکس. ژانگ، ال. تخمین PM2.5 سطح زمین با ترکیب مشاهدات ماهواره و ایستگاه: یک رویکرد یادگیری عمیق ژئو-هوشمند. ژئوفیز. Res. Lett. 2017 ، 44 ، 11985-11993. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- چن، ال. رن، سی. لی، ال. وانگ، ی. ژانگ، بی. وانگ، ز. لی، ال. ارزیابی مقایسه ای رویکردهای زمین آماری، یادگیری ماشینی و ترکیبی برای نقشه برداری محتوای کربن آلی خاک سطحی. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 174. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- فارستی، ال. پوزدنوخوف، ا. تویا، دی. Kanevski، M. مدلسازی بارش شدید با استفاده از الگوریتمهای زمین آمار و یادگیری ماشین. در geoENV VII–Geostatistics for Environmental Applications ; Springer: Dordrecht، هلند، 2010; صص 41-52. [ Google Scholar ]
- هنگل، تی. Heuvelink، GBM؛ کمپن، بی. Leenaars، JGB; والش، ام جی؛ شپرد، KD; سیلا، ا. مک میلان، RA; De Jesus, JM; تمنه، ال. و همکاران نقشه برداری از ویژگی های خاک آفریقا با وضوح 250 متر: جنگل های تصادفی به طور قابل توجهی پیش بینی های فعلی را بهبود می بخشد. PLoS ONE 2015 ، 10 ، e0125814. [ Google Scholar ] [ CrossRef ]
- هنگل، تی. Heuvelink، GBM؛ Rossiter، DG درباره رگرسیون-کریجینگ: از نظریه تا تفسیر نتایج. محاسبه کنید. Geosci. 2007 ، 33 ، 1301-1315. [ Google Scholar ] [ CrossRef ]
- مولر، ای. Sandoval، JSO؛ مودیگوندا، اس. الیوت، ام. رویکرد گروه یادگیری ماشینی مبتنی بر خوشه برای دادههای مکانی: برآورد وضعیت بیمه سلامت در میسوری. ISPRS Int. J. Geo-Inf. 2018 ، 8 ، 13. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- استویانوا، دی. سیسی، م. آپیس، ا. مالربا، دی. Džeroski، S. برخورد با خودهمبستگی فضایی هنگام یادگیری درختان خوشهبندی پیشبینیکننده. Ecol. به اطلاع رساندن. 2013 ، 13 ، 22-39. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- کلمر، ک. کوشیاما، ا. Flennerhag، S. تقویت ساختارهای همبستگی در داده های فضایی با استفاده از مدل های مولد عمیق. در دسترس آنلاین: https://arxiv.org/pdf/1905.09796.pdf (دسترسی در 23 دسامبر 2021).
- کیلی، تی جی; باستیان، ND مدل یادگیری ماشینی هوشیار فضایی. آمار مقعدی حداقل داده ASA Data Sci. J. 2020 ، 13 ، 31-49. [ Google Scholar ] [ CrossRef ]
- زو، ایکس. ژانگ، Q. Xu، C.-Y.; سان، پ. هو، پی. بازسازی دادههای دمای هوای سطحی با وضوح فضایی بالا در سراسر چین: تکنیک یادگیری ماشین مبتنی بر دادههای چندمنبعی جدید ژئوهوشمند. علمی کل محیط. 2019 ، 665 ، 300–313. [ Google Scholar ] [ CrossRef ]
- Pebesma، EJ زمین آمار چند متغیره در S: بسته gstat. محاسبه کنید. Geosci. 2004 ، 30 ، 683-691. [ Google Scholar ] [ CrossRef ]
- بیوند، RS; پبسما، ای. Gómez-Rubio، V. تحلیل داده های مکانی کاربردی با R ، ویرایش دوم. Springer: Berlin/Heidelberg, Germany, 2013. [ Google Scholar ] [ CrossRef ]
- D’Urso، P. Vitale, V. یک خوشه بندی سلسله مراتبی قوی برای داده های جغرافیایی ارجاع داده شده. تف کردن آمار 2020 ، 35 ، 100407. [ Google Scholar ] [ CrossRef ]
- Ejigu، BA; Wencheko، E. معرفی ماتریسهای وزنی وابسته به متغیرهای کمکی در برازش مدلهای خودرگرسیون و اندازهگیری خودهمبستگی فضایی-محیطی. تف کردن آمار 2020 ، 38 ، 100454. [ Google Scholar ] [ CrossRef ]
- سرعت، RK; باری، آر. خودرگرسیون های فضایی پراکنده. آمار احتمالا. Lett. 1997 ، 33 ، 291-297. [ Google Scholar ] [ CrossRef ]
- باومن، دی. دروئت، تی. درای، اس. Vleminckx، J. جداسازی عملکردهای خوب از بد در انتخاب بردارهای ویژه فضایی یا فیلوژنتیکی. اکوگرافی 2018 ، 41 ، 1638-1649. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- دبارسی، ن. LeSage, J. مدلسازی وابستگی انعطافپذیر با استفاده از ترکیبات محدب انواع مختلف ساختارهای اتصال. Reg. علمی اقتصاد شهری 2018 ، 69 ، 48-68. [ Google Scholar ] [ CrossRef ]
- گتیس، ع. گریفیث، DA فیلترینگ فضایی مقایسه ای در تحلیل رگرسیون. Geogr. مقعدی 2002 ، 34 ، 130-140. [ Google Scholar ] [ CrossRef ]
- گریفیث، دی. چون، Y. خودهمبستگی فضایی و فیلتر فضایی. در کتابچه راهنمای علوم منطقه ای ; Springer: برلین/هایدلبرگ، آلمان، 2014; ص 1477-1507. [ Google Scholar ]
- کوپیدو، ک. جوتیچ، پ. Paez, A. الگوهای فضایی مرگ و میر در ایالات متحده: یک رویکرد فیلتر فضایی. بیمه ریاضی. اقتصاد 2020 ، 95 ، 28-38. [ Google Scholar ] [ CrossRef ]
- Paez, A. استفاده از فیلترهای فضایی و تجزیه و تحلیل داده های اکتشافی برای تقویت مدل های رگرسیون داده های مکانی. Geogr. مقعدی 2018 ، 51 ، 314-338. [ Google Scholar ] [ CrossRef ]
- ژانگ، جی. لی، بی. چن، ی. چن، ام. نیش، تی. Liu, Y. مدلسازی رگرسیون فیلتر فضایی بردار ویژه غلظت PM2.5 زمین با استفاده از داده های سنجش از دور. بین المللی جی. محیط زیست. Res. بهداشت عمومی 2018 ، 15 ، 1228. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- دریناس، پ. ماهونی، مگاوات؛ کریستیانینی، ن. در روش نیستروم برای تقریب ماتریس گرم برای بهبود یادگیری مبتنی بر هسته. جی. ماخ. فرا گرفتن. Res. 2005 ، 6 ، 2153-2175. [ Google Scholar ]
- لی، جی. هیپ، AD; پاتر، ا. دانیل، جی جی استفاده از روش های یادگیری ماشین برای درونیابی فضایی متغیرهای محیطی. محیط زیست مدل. نرم افزار 2011 ، 26 ، 1647-1659. [ Google Scholar ] [ CrossRef ]
- تبشیرانی، آر. انقباض و انتخاب رگرسیون از طریق کمند. JR Stat. Soc. سر. روش B. 1996 ، 58 ، 267-288. [ Google Scholar ] [ CrossRef ]
- فریدمن، جی اچ. هستی، تی. Tibshirani, R. مسیرهای منظم سازی برای مدل های خطی تعمیم یافته از طریق نزول مختصات. J. Stat. نرم افزار 2010 ، 33 ، 1-22. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
- کاروانا، آر. کارامپاتزیاکیس، ن. Yessenalina، A. یک ارزیابی تجربی از یادگیری تحت نظارت در ابعاد بالا. در مجموعه مقالات بیست و پنجمین کنفرانس بین المللی یادگیری ماشین، هلسینکی، فنلاند، 5 تا 9 ژوئیه 2008. صص 96-103. [ Google Scholar ]
- بلژیک، م. Drăguţ، L. جنگل تصادفی در سنجش از دور: بررسی برنامهها و جهتهای آینده. ISPRS J. Photogramm. Remote Sens. 2016 ، 114 ، 24–31. [ Google Scholar ] [ CrossRef ]
- Vasan، KK; Surendiran، B. کاهش ابعاد با استفاده از تجزیه و تحلیل مؤلفه اصلی برای تشخیص نفوذ شبکه. چشم انداز علمی 2016 ، 8 ، 510-512. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- عبدالحمد، ر. مسافر، ح. آلسا، ا. فائزی پور، م. Abuzneid، A. ویژگیهای رویکردهای کاهش ابعاد برای تشخیص نفوذ شبکه مبتنی بر یادگیری ماشین. Electronics 2019 ، 8 ، 322. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- بنژیو، ی. دلالو، او. Le Roux, N. نفرین ابعاد برای ماشین های هسته محلی. تکنولوژی Rep. 2005 , 1258 , 12. [ Google Scholar ]
- تنه، GV مشکل ابعاد: یک مثال ساده. IEEE Trans. الگوی مقعدی ماخ هوشمند 1979 ، 1 ، 306-307. [ Google Scholar ] [ CrossRef ]
- ورلیسن، ام. فرانسوا، دی. نفرین ابعاد در داده کاوی و پیش بینی سری های زمانی. در کنفرانس کاری بین المللی شبکه های عصبی مصنوعی ; Springer: برلین/هایدلبرگ، آلمان، 2005; صص 758-770. [ Google Scholar ] [ CrossRef ]
- ما، ال. فو، تی. بلاشکه، تی. لی، ام. تاید، دی. ژو، ز. ما، ایکس. Chen, D. ارزیابی روشهای انتخاب ویژگی برای نقشهبرداری پوشش زمین مبتنی بر شی از تصاویر وسایل نقلیه هوایی بدون سرنشین با استفاده از طبقهبندیکنندههای ماشین بردار تصادفی و جنگلی تصادفی. ISPRS Int. J. Geo-Inf. 2017 ، 6 ، 51. [ Google Scholar ] [ CrossRef ]
- جورجانوس، اس. گریپا، تی. وان هویس، اس. لنرت، ام. شیمونی، م. کالوگیرو، س. Wolff, E. Less is more: بهینهسازی عملکرد طبقهبندی از طریق انتخاب ویژگی در یک برنامه کاربردی شهری مبتنی بر شیء سنجش از دور با وضوح بسیار بالا. GIScience Remote Sens. 2017 ، 55 ، 221-242. [ Google Scholar ] [ CrossRef ]
- سلمر، آر. سیچولسکا، ا. Bełej، M. تحلیل فضایی قیمت مسکن و فعالیت بازار با رگرسیون وزندار جغرافیایی. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 380. [ Google Scholar ] [ CrossRef ]
- چن، D.-R. Truong، K. استفاده از مدلسازی چند سطحی و رگرسیون وزندار جغرافیایی برای شناسایی تغییرات فضایی در رابطه بین معایب سطح مکان و چاقی در تایوان. Appl. Geogr. 2012 ، 32 ، 737-745. [ Google Scholar ] [ CrossRef ]
- سولر، IP; Gemar، G. مدلهای قیمت لذتبخش با رگرسیون وزندار جغرافیایی: کاربرد برای مهماننوازی. جی. مقصد. علامت. مدیریت 2018 ، 9 ، 126-137. [ Google Scholar ] [ CrossRef ]
- ژانگ، ز. چن، RJC; هان، LD; یانگ، ال. عوامل کلیدی مؤثر بر قیمت فهرستهای Airbnb: یک رویکرد وزندار جغرافیایی. پایداری 2017 ، 9 ، 1635. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- علی، ک. کبک، MD; Olfert، MR آیا رگرسیون های وزنی جغرافیایی می توانند تحلیل و سیاست گذاری منطقه ای را بهبود بخشند؟ بین المللی Reg. علمی Rev. 2007 , 30 , 300-329. [ Google Scholar ] [ CrossRef ]
- کیهیل، م. مولیگان، جی. استفاده از رگرسیون وزندار جغرافیایی برای کاوش الگوهای جرم محلی. Soc. علمی محاسبه کنید. Rev. 2007 , 25 , 174-193. [ Google Scholar ] [ CrossRef ]
- چارلتون، ام. Fotheringham، AS رگرسیون وزنی جغرافیایی: آموزش استفاده از GWR در ArcGIS 9.3. 2009. در دسترس آنلاین: https://www.geos.ed.ac.uk/~gisteac/fcl/gwr/gwr_arcgis/GWR_Tutorial.pdf (در 1 ژانویه 2022 قابل دسترسی است).
- اوشان، TM; لی، ز. کانگ، دبلیو. ولف، ال جی. Fotheringham، AS mgwr: پیادهسازی پایتون از رگرسیون جغرافیایی وزندار چند مقیاسی برای بررسی ناهمگونی و مقیاس فضایی فرآیند. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 269. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- شراتز، پی. موئنچو، جی. ایتوریتکسا، ای. ریشتر، جی. برنینگ، الف. تنظیم فراپارامتر و ارزیابی عملکرد الگوریتمهای آماری و یادگیری ماشینی با استفاده از دادههای مکانی. Ecol. مدل. 2019 ، 406 ، 109-120. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- کاولی، جی سی; Talbot، NLC در مورد برازش بیش از حد در انتخاب مدل و سوگیری انتخاب بعدی در ارزیابی عملکرد. جی. ماخ. فرا گرفتن. Res. 2010 ، 11 ، 2079-2107. [ Google Scholar ]
- استون، ام. انتخاب اعتبار متقابل و ارزیابی پیشبینیهای آماری. JR Stat. Soc. سر. روش B. 1974 ، 36 ، 111-133. [ Google Scholar ] [ CrossRef ]
- Anselin، L. نشانگرهای محلی انجمن فضایی-LISA. Geogr. مقعدی 1995 ، 27 ، 93-115. [ Google Scholar ] [ CrossRef ]
- دا سیلوا، آر. Fotheringham، AS مسئله آزمایش چندگانه در رگرسیون وزندار جغرافیایی. Geogr. مقعدی 2016 ، 48 ، 233-247. [ Google Scholar ] [ CrossRef ]
- جورجانوس، اس. گریپا، تی. Gadiaga، AN; لینارد، سی. لنرت، ام. وان هویس، اس. امبوگا، ن. ولف، ای. Kalogirou، S. جنگلهای تصادفی جغرافیایی: گسترش فضایی الگوریتم جنگل تصادفی برای پرداختن به ناهمگونی فضایی در سنجش از دور و مدلسازی جمعیت. Geocarto Int. 2021 ، 36 ، 121-136. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- کالوگیرو، س. جورجانوس، S. SpatialML. بنیاد R برای محاسبات آماری. در دسترس آنلاین: https://cran.r-project.org/web/packages/SpatialML/SpatialML.pdf (در 1 ژانویه 2022 قابل دسترسی است).
- ریستئا، ع. البونی، م. رسچ، بی. گربر، ام اس; لایتنر، ام. توزیع جرم فضایی و پیشبینی رویدادهای ورزشی با استفاده از رسانههای اجتماعی. بین المللی جی. جئوگر. Inf. علمی 2020 ، 34 ، 1708-1739. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- لاماری، ی. فرسکورا، بی. عبدالصمد، ع. آیچبرگ، اس. De Bonviller, S. پیش بینی وقوع جرم فضایی از طریق یک مدل یادگیری گروهی کارآمد. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 645. [ Google Scholar ] [ CrossRef ]
- شائو، کیو. خو، ی. Wu, H. پیشبینی فضایی COVID-19 در چین بر اساس الگوریتمهای یادگیری ماشین و رگرسیون وزندار جغرافیایی. محاسبه کنید. ریاضی. روش ها Med. 2021 ، 2021 ، 7196492. [ Google Scholar ] [ CrossRef ]
- جوان، اس جی. تولیس، جی. Cothren، J. رویکرد اپیدمیولوژی چشم انداز به کمک سنجش از دور و GIS به ویروس نیل غربی. Appl. Geogr. 2013 ، 45 ، 241-249. [ Google Scholar ] [ CrossRef ]
- المالکی، ع. گوکاراجو، بی. مهتا، ن. تکنیکهای رگرسیون یادگیری ماشینی و مکانی مکانی Doss، DA برای تجزیه و تحلیل تأثیر دسترسی به غذا بر مسائل بهداشتی در جوامع پایدار. ISPRS Int. J. Geo-Inf. 2021 ، 10 ، 745. [ Google Scholar ] [ CrossRef ]
- ژو، ایکس. تانگ، دبلیو. لی، دی. مدل سازی اجاره مسکن در منطقه شهری آتلانتا با استفاده از اطلاعات متنی و یادگیری عمیق. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 349. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- چه، م. کلیبردا، م. لیسک، ا. باجات، ب. برآورد عملکرد جنگل تصادفی در مقابل رگرسیون چندگانه برای پیشبینی قیمت آپارتمانها. ISPRS Int. J. Geo-Inf. 2018 ، 7 ، 168. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- آکر، بی. یوان، ام. مدلسازی احتمال وقوع رویداد در فضا و زمان مبتنی بر شبکه: مطالعه موردی تصادفات رانندگی در دالاس، تگزاس، ایالات متحده آمریکا. کارتوگر. Geogr. Inf. علمی 2018 ، 46 ، 21-38. [ Google Scholar ] [ CrossRef ]
- کلر، اس. گابریل، ر. Guth، J. چارچوب یادگیری ماشین برای تخمین سرعت متوسط در شبکه های جاده ای روستایی با داده های نقشه خیابان باز. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 638. [ Google Scholar ] [ CrossRef ]
- دونگ، ال. راتی، سی. ژنگ، اس. پیش بینی ویژگی های اجتماعی-اقتصادی محله ها با استفاده از داده های رستوران. Proc. Natl. آکادمی علمی ایالات متحده آمریکا 2019 ، 116 ، 15447–15452. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- فلدمایر، دی. میش، سی. ساتر، اچ. Birkmann, J. استفاده از داده های OpenStreetMap و یادگیری ماشینی برای تولید شاخص های اجتماعی-اقتصادی. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 498. [ Google Scholar ] [ CrossRef ]
- کرازبی، اچ. دامولاس، تی. جارویس، SA اعتبار متقاطع جاده و زمان سفر برای مدلسازی شهری. بین المللی جی. جئوگر. Inf. علمی 2020 ، 34 ، 98-118. [ Google Scholar ] [ CrossRef ]
- دیگل، پی جی؛ تاون، JA; موید، زمین آمار مبتنی بر مدل RA. JR Stat. Soc. سر. C Appl. آمار 1998 ، 47 ، 299-350. [ Google Scholar ] [ CrossRef ]
- گریفیث، DA توزیع جغرافیایی غلظت سرب خاک: توضیحات و نگرانی ها. URISA J. 2002 ، 14 ، 5-14. [ Google Scholar ]





بدون دیدگاه