کلید واژه ها:
شبکه جاده ای ؛ انتخاب مکان بهینه ؛ داده های ورود ؛ مشخصات کاربر ; درخت جی
1. مقدمه
2. کارهای مرتبط
2.1. شبکه های اجتماعی مبتنی بر مکان (مجموعه داده های LBSN)
2.2. برنامه های کاربردی تجاری
2.3. جستجوهای مکان فروشگاه بهینه
3. بیان مشکل
امتیاز شباهت مشتری CS ( p i , p j ) نشان دهنده رابطه بین مشتریان یک POI p i موجود و دیگری POI p j است . در مرحله بعد، امتیاز تأثیر CI ( Q ، pj ) تأثیر pj را بر مشتریان فروشگاه جدیدی که توسط q افتتاح میشود، نشان میدهد ، که در آن Q = { pP، nP، rP } شرط پرس و جو است که توسط q ارائه میشود . معادله ارزیابی CI( Q , p j ) را می توان به صورت زیر بیان کرد:
کجا | rP | تعداد کل RPOI های تعیین شده توسط q را نشان می دهد . ∑ pi ∈ rP CS ( p i , p j )/| rP | مقدار متوسط روابط بین مشتریان p j و همه RPOI های تعیین شده توسط q است . و α یک متغیر کنترلی است. وقتی p j یک PPOI برای q باشد، آنگاه α = 1 است. وقتی p j یک NPOI برای q باشد، α = -1 است. وقتی p j یک UPOI برای q باشدواضح است که با این فرمول میتوانیم تأثیر احتمالی هر POI بر مشتریان فروشگاه جدید را بر اساس فروشگاههای مرجع، قبل از اینکه q فروشگاه جدید باز کند، تخمین بزنیم. PPOI ها تأثیر مثبتی بر مشتریان فروشگاه جدید دارند، NPOI ها تأثیر منفی بر مشتریان فروشگاه جدید دارند و UPOI ها تأثیری بر مشتریان فروشگاه جدید ندارند. در نهایت، پس از محاسبه تأثیر همه POI ها بر مشتریان فروشگاه جدید، می توانیم امتیاز توصیه هر نقطه (یعنی امتیاز مکان) در شبکه جاده را محاسبه کنیم تا مشخص شود که آیا مکان مناسبی برای فروشگاه جدید است یا خیر. امتیاز مکان به شرح زیر محاسبه می شود:
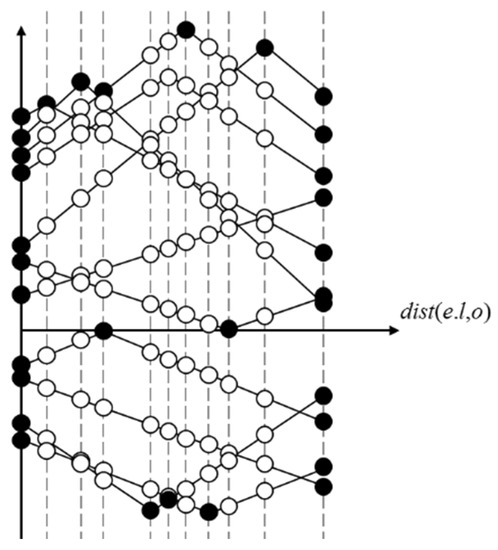
که در آن o هر نقطه داده شده در شبکه جاده را نشان می دهد و dist ( o ، pj ) نشان دهنده کوتاه ترین فاصله جاده بین o و pj در نقشه راه است . توجه داشته باشید که ما از فاصله جاده به جای فاصله اقلیدسی استفاده کردیم زیرا اکثر مردم هنگام سفر در یک شهر، فاصله جاده را در نظر می گیرند. توجه داشته باشید که مقدار کمتر برای LS ( o ، pP ، nP ) مکان بهتری را نشان می دهد. این به این دلیل است که در معادله (2)، CI ( Q ، pj )، تأثیر هر POI pjدر مشتریان فروشگاه جدید در هر پرس و جوی منفرد که توسط q انجام می شود باید یک مقدار ثابت باشد، زیرا CI ( Q , p j ) فقط روابط بین مشتریان p j و RPOI های تنظیم شده توسط q را در نظر می گیرد. در مرحله بعد، اگر p j در معادله (2) یک PPOI باشد، ما می خواهیم o تا حد امکان به p j نزدیک شود زیرا این امر باعث کوچکتر شدن فاصله ( o , pj ) و LS ( o , pP , nP ) می شود.) کوچکتر نیز هست.
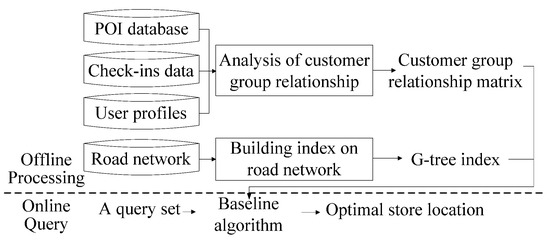
4. الگوریتم پایه
4.1. چارچوب سیستم با استفاده از الگوریتم پایه
4.2. تجزیه و تحلیل شباهت ها بین گروه های مشتری
4.2.1. خوشه بندی مشتریان
4.2.2. شناسایی ویژگی های مشترک
4.2.3. محاسبه امتیاز شباهت مشتری
در این مرحله، CS ( p i ، pj ) ، امتیاز شباهت مشتری بین POIs p i و pj را محاسبه میکنیم . نتیجه در ماتریس M ذخیره می شود . ما CS ( p i , p j ) را به عنوان تعداد مورد انتظار مشتریانی که p i می تواند از p j جذب کند تعریف می کنیم . فرض کنید که گروه مشتریان p i و p j را می توان به ترتیب به صورت { cg i 1 بیان کرد،cg i 2 , …, cg ik } and { cg j 1 , cg j 2 , …, cg jk }. برای هر cg jn از p j ، ابتدا شباهت بین cg jn و همه گروه های مشتریان p i را ارزیابی می کنیم. سپس بالاترین مورد را از بین آنها به عنوان احتمال اینکه اعضای cg jn مشتری p i شوند انتخاب می کنیم. تعداد مشتریان مورد انتظار برابر است با مجموع تعداد مشتریان ضرب در این احتمال. بنابراین، CS( p i , p j ) را می توان به صورت زیر محاسبه کرد:
کجا | cg jn | تعداد مشتریان در cg jn است و cgSIM ( cg jn , cg im ) نشان دهنده درجه شباهت بین گروه های مشتری cg jn و cg im است.
در ادامه ابزارهای محاسبه درجات شباهت بین گروههای مشتری (یعنی cgSIM ( cg jn ، cg im ) در معادله (3)) را معرفی میکنیم. این با استفاده از شکل اصلاح شده شباهت جاکارد به دست می آید. ما از مجموعه مشخصه مشترک برای نشان دادن گروه مشتری استفاده می کنیم و با محاسبه میزان شباهت بین دو مجموعه مشخصه مشترک، درجه شباهت بین دو گروه مشتری را محاسبه می کنیم. شباهت جاکارد J ( A , B ) درجه تشابه بین دو مجموعه A و B را محاسبه می کند [ 26 ]. مقدار J ( A, B ) از 0 تا 1 متغیر است. وقتی A و B یکسان هستند، J ( A , B ) برابر 1 است. وقتی A و B کاملاً متفاوت هستند J ( A , B ) برابر 0 است . J ( A , B ) بنابراین برابر است تقاطع A و B تقسیم بر اتحاد A و B. با این حال، شباهت جاکارد تنها تلاقی و اتحاد دو مجموعه را در نظر می گیرد و توزیع ویژگی های مشترک را در نظر نمی گیرد. بنابراین، ما پیشنهاد میکنیم شباهت جاکارد را با جایگزین کردن تعداد تقاطعهای دو مجموعه مشخصه مشترک با شباهت کل بین توزیعهای مشترک ویژگیهای مشترک اصلاح کنیم. شباهت cgSIM ( cg i , cg j ) بین دو گروه مشتری cg i و cg j را می توان به صورت زیر محاسبه کرد:
که در آن D ( cg , f ) توزیع مشتریان در گروه مشتری cg با توجه به مشخصه مشترک f را نشان می دهد و fSIM (∙,∙) شباهت بین توزیع ویژگی های مشترک است.
ما درجات شباهت بین دو توزیع از ویژگیهای مشترک (یعنی fSIM (∙،∙) در معادله (4)) را با استفاده از شکل اصلاحشده واگرایی جنسن-شانون (JS) محاسبه میکنیم. واگرایی JS [ 27 ] شکل اصلاح شده واگرایی Kullback-Leibler (KL) است. واگرایی KL KLD(Da | Db ) تفاوت بین دو توزیع D a و Db را به صورت زیر اندازه گیری می کند :
با این حال، واگرایی KL تفاوت غیر متقارن را اندازه گیری می کند، به این معنی که KLD ( Da | Db ) برابر با KLD نیست ( Db | D a ) . برای حل این مشکل واگرایی JS (که متقارن است) به صورت زیر محاسبه می شود:
که در آن D m = ( D a + D b )/2. مقدار JSD ( Da | Db ) از 0 تا 1 متغیر است. مقدار JSD ( Da | Db ) متناسب با تفاوت بین توزیعهای D a و Db است . JSD ( D a | D b ) برابر 0 در حداقل اختلاف بین D a و D b استو 1 در حداکثر اختلاف بین D a و D b . از آنجایی که شباهت برعکس تفاوت است، میتوانیم فرمولی برای نمایش شباهت بین دو توزیع از ویژگیهای مشترک به صورت زیر طراحی کنیم:
4.3. ایجاد شاخص نقشه راه
4.4. فرآیند جستجوی آنلاین الگوریتم پایه
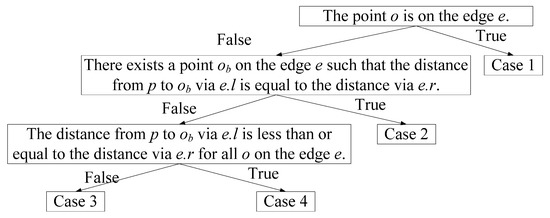
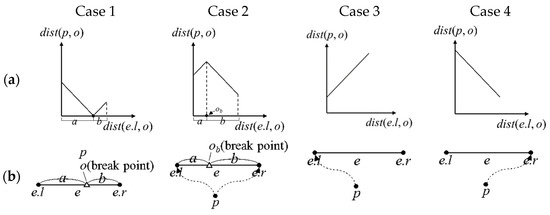
قضیه 1.
اثبات
- مرحله 1.
-
برای هر POI pj ، از معادله (1) و ماتریس امتیاز شباهت مشتری محاسبه شده آفلاین استفاده کنید تا امتیاز تأثیر آن CI ( Q , pj ) را ارزیابی کنید، که در آن Q توسط کاربر پرس و جو داده می شود و برابر با { pP , nP , rP است . }.
- گام 2.
-
نقاط شکست و رئوس تمام یال ها را پیدا کنید.
- مرحله 3.
-
امتیاز مکان تمام نقاط شکست و رئوس تمام لبه ها را محاسبه کنید و راه حل بهینه را انتخاب کنید.
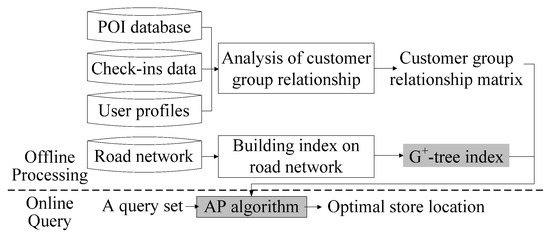
5. الگوریتم هرس مساحت
5.1. کاستی های الگوریتم پایه
5.2. چارچوب سیستم با الگوریتم AP
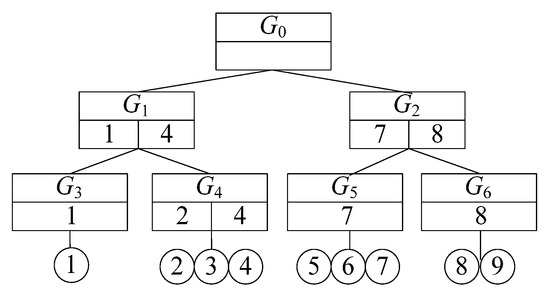
5.3. G + -شاخص درخت
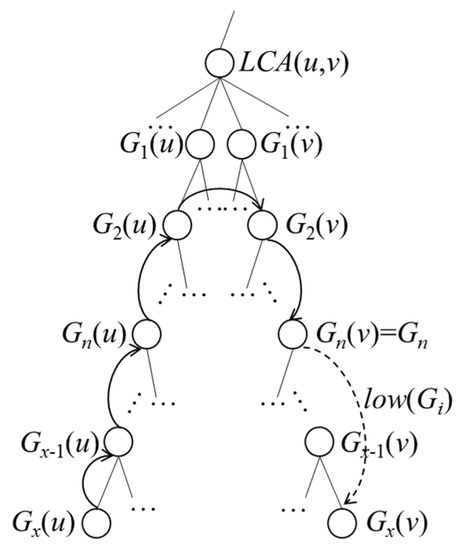
Border low ( G x ): برای دست کم گرفتن فاصله جاده از هر مرز G x تا هر نقطه v در G x استفاده می شود. اگر G x یک گره برگ است، آنگاه کم ( G x ) فاصله جاده از هر مرز کوچکترین G x تا هر نقطه v در G x است. اگر G x یک گره برگ نیست، آنگاه کم ( G x ) فاصله جاده از مرز کوچکترین G است.x تا مرز زیرگره G x +1 به علاوه کم ( G x +1 ). روش محاسبه به شرح زیر است:
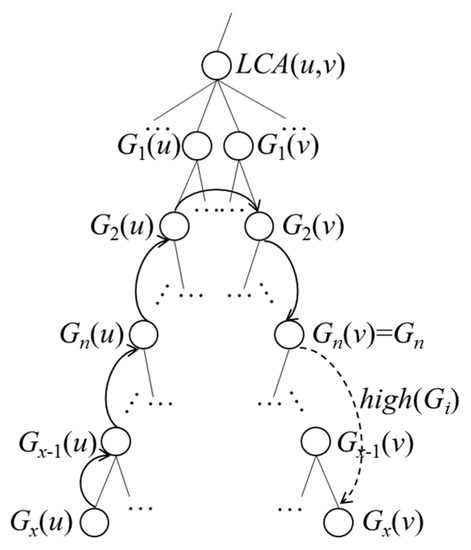
Border high ( G x ): برای تخمین بیش از حد فاصله جاده از هر مرز G x تا هر نقطه v در G x استفاده می شود. اگر G x یک گره برگ است، بالا ( G x ) فاصله جاده از هر مرزی از بزرگترین G x تا هر نقطه v در G x است. اگر G x یک گره برگ نیست، بالا ( G x ) فاصله جاده از مرز بزرگترین G است.x به مرز زیرگره G x +1 به علاوه بالا ( G x +1 ). روش محاسبه به شرح زیر است:
حاشیه maxEdge ( G x ): این طول طولانی ترین یال در G x است. اگر راس سمت چپ e . v l متعلق به G i است، سپس می گوییم که e متعلق به G x است. روش محاسبه به شرح زیر است:
5.4. فرآیند آنلاین الگوریتم AP
o را به عنوان هر نقطه داده شده در هر یال معین در G i در نظر بگیرید. برای POI p ، کران پایینی LB ( Gi ، p ) یک CI ( Q ، p ) × dist ( o ، p ) را تعریف می کنیم. اگر نمره تأثیر p یک عدد مثبت باشد، آنگاه LB ( Gi , p ) برابر است با امتیاز تأثیر ضرب در فاصله کم تخمین زده شده ( o , p ) . اگر نمره نفوذ ازp یک عدد منفی است، سپس LB ( Gi , p ) برابر است با امتیاز تأثیر ضرب در فاصله بیش از حد برآورد شده ( o , p ) . روش محاسبه به شرح زیر است:
در جایی که lowDist ( Gi , p ) یک عدد غیر منفی کوچکتر یا مساوی با فاصله p تا هر راس داده شده در Gi است ، highDist ( Gi , p ) یک عدد غیر منفی بزرگتر یا مساوی با فاصله از p تا هر راس داده شده در G i ، و maxEdge ( G i ) طول طولانی ترین یال در G i است.
قضیه 2.
مجموعه پرس و جو ( pP , nP , rP ) را در نظر بگیرید که در آن p یک POI در pP و nP است. مکان o هر نقطه داده شده در هر یال معین در G i است. بهترین امتیاز مکان در G i باید بزرگتر یا مساوی با مجموع همه LB(G i , p) باشد :
اثبات
قضیه 3.
اثبات
قضیه 4.
اثبات
کد شبه برای الگوریتم AP در الگوریتم 1 نشان داده شده است، جایی که کاربر پرس و جو مجموعه پرس و جو را Q = { pP , nP , rP } وارد می کند.
| الگوریتم 1: الگوریتم هرس مساحت | |
| ورودی: پایگاه داده POI، ماتریس امتیاز شباهت مشتری خروجی: مکان بهینه |
|
| 1 | برای هر p در مجموعه داده POI |
| 2 | ص . w ←set_impact( p ، ماتریس امتیاز شباهت مشتری) |
| 3 | پایان برای |
| 4 | برای هر گره G i در تراورس G + -tree |
| 5 | اگر قضیه 2 برآورده شود |
| 6 | هرس ( G i ) |
| 7 | پایان اگر |
| 8 | if is_leaf_node ( G i ) |
| 9 | نقاط شکست، رئوس←find( G i ) |
| 10 | امتیازات مکان←محاسبه_نمرات (نقاط شکست، رئوس) |
| 11 | راه حل بهینه←به روز رسانی (نمرات مکان) |
| 12 | پایان اگر |
| 13 | پایان برای |
| 14 | بازگشت راه حل بهینه |
- مرحله 1.
-
برای هر POI p ، از معادله (1) و ماتریس امتیاز شباهت مشتری محاسبه شده آفلاین استفاده کنید تا امتیاز تأثیرگذاری آن CI ( Q ، p ) را ارزیابی کنید. (خطوط 1-3)
- گام 2.
-
از G + -tree نقشه راه دیدن کنید و گره درخت بعدی G i را بازیابی کنید . (خط 4)
- مرحله 3.
-
اگر بهترین امتیاز مکان فعلی ≤ ∑ p ∈ pP∪np LB ( G i , p ) باشد، طبق قضیه 2، می توانیم G i را هرس کرده و به مرحله 2 برگردیم. در غیر این صورت، به مرحله 4 بروید (خطوط 5- 7)
- مرحله 4.
-
بررسی کنید که آیا G i یک گره برگ است. اگر یک گره غیر برگ است، به مرحله 2 برگردید. در غیر این صورت، نقاط شکست و رئوس تمام یال ها را در G i پیدا کنید ، امتیازات مکان این نقاط را محاسبه کنید و بهترین راه حل فعلی را به روز کنید. (خطوط 8-12)
- مرحله 5.
-
اگر کل G + -tree بازدید شده است، سپس راه حل بهینه را برگردانید. (خطوط 13-14)
6. الگوریتم هرس مساحت و لبه
6.1. کاستی های الگوریتم AP
6.2. فرآیند آنلاین الگوریتم AEP
قضیه 5.
لبه e و مجموعه پرس و جو ( pP ، nP ، rP ) را در نظر بگیرید. ما به nP ∪ rP به عنوان POI اشاره می کنیم . ما از BP(p,e) برای نشان دادن نقطه شکست POI p در e و از BPs( POIs ,e) برای نمایش مجموعه ای از تمام p در e در POI استفاده می کنیم . بنابرین ما اینها را داریم:
که در آن عبارت قبلی بهترین امتیاز مکان در e است. دومی را می توان به عنوان کران پایین این امتیاز مکان در نظر گرفت.
اثبات
- مرحله 1.
-
برای هر POI p ، از معادله (1) و ماتریس امتیاز شباهت مشتری محاسبه شده آفلاین استفاده کنید تا امتیاز تأثیرگذاری آن CI ( Q ، p ) را ارزیابی کنید.
- گام 2.
-
از G + -tree نقشه راه دیدن کنید و گره درخت بعدی G i را بازیابی کنید .
- مرحله 3.
-
اگر بهترین امتیاز مکان فعلی ≤∑ p ∈ pP∪np LB ( G i , p ) باشد، طبق قضیه 2، می توانیم G i را هرس کرده و به مرحله 2 برگردیم. در غیر این صورت، به مرحله 4 بروید.
- مرحله 4.
-
بررسی کنید که آیا G i یک گره برگ است. اگر یک گره غیر برگ است، به مرحله 2 برگردید. در غیر این صورت، به مرحله 5 بروید.
- مرحله 5.
-
یال بعدی e j را در G i بازیابی کنید .
- مرحله 6.
-
اگر امتیاز بهترین مکان فعلی ≤ ، سپس، طبق قضیه 5، e j را هرس کنید. در غیر این صورت، به مرحله 7 بروید.
- مرحله 7.
-
نقطه شکست یا راس بعدی را در e j پیدا کنید، امتیازات مکان این نقطه را محاسبه کنید و بهترین راه حل فعلی را به روز کنید.
- مرحله 8.
-
اگر تمام نقاط شکست و رئوس در e j در نظر گرفته شده اند، به مرحله 5 برگردید.
- مرحله 9.
-
اگر کل G + -tree بازدید شده است، جواب بهینه را خروجی بگیرید.
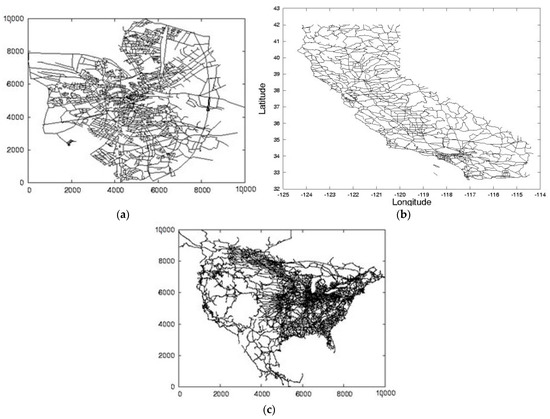
7. آزمایشات
7.1. تنظیمات پارامتر
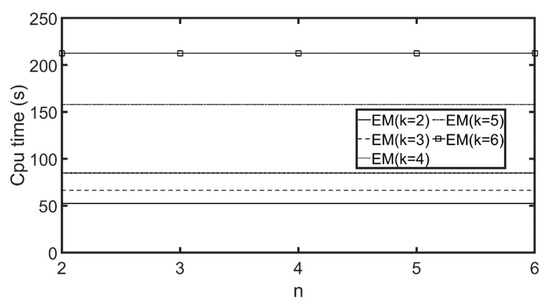
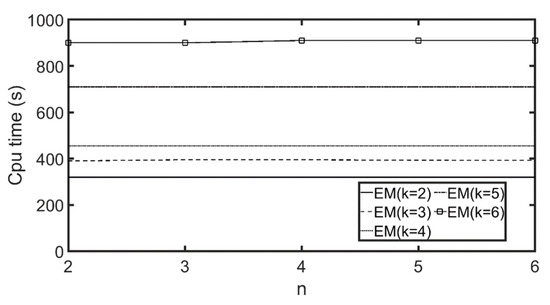
7.2. آزمایشهای مربوط به پردازش آفلاین
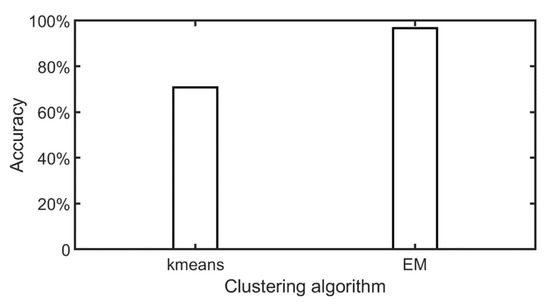
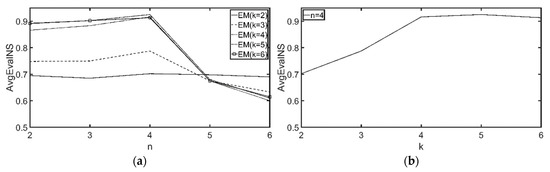
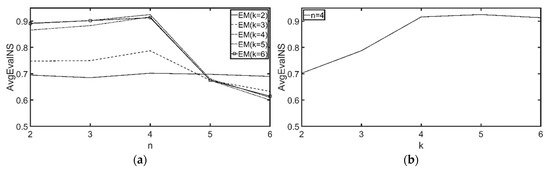
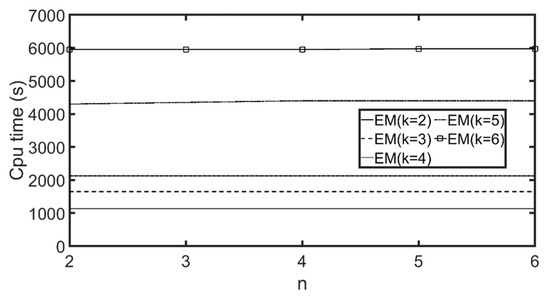
7.2.1. مقایسه دقت روش خوشه بندی
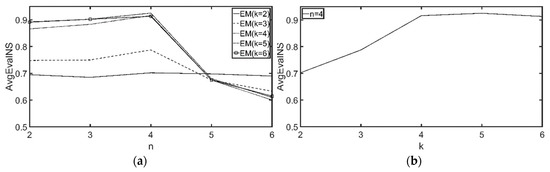
7.2.2. تنظیم تعداد مناسب گروههای مشتری و ویژگیها
7.3. آزمایشهای مربوط به پرس و جو آنلاین
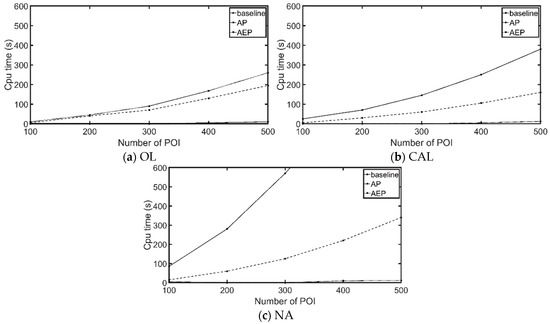
7.3.1. تأثیر تغییرات در poiNum
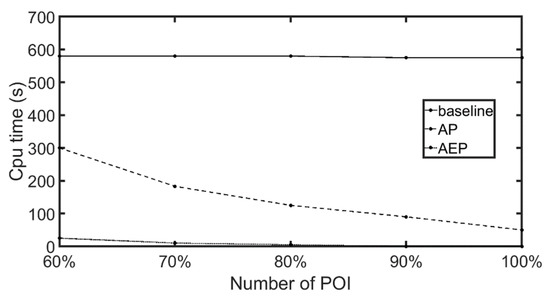
7.3.2. تأثیر تغییرات در نسبت
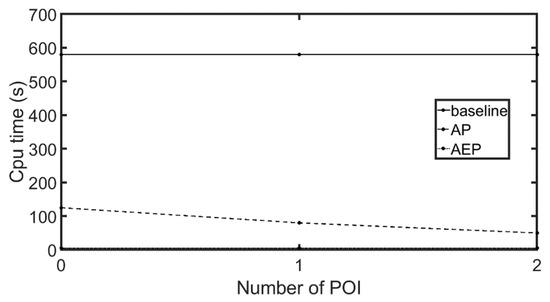
7.3.3. تأثیر تغییرات در poiCent
7.4. مطالعه موردی
8. نتیجه گیری
پیوست A. مثالی از الگوریتم پایه
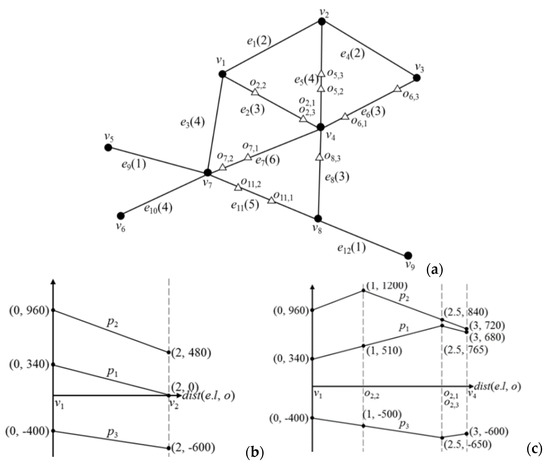
شکل A1 a یک نقشه راه با 9 نقطه و 12 لبه را نشان می دهد. مقادیر داخل پرانتز نشان دهنده طول لبه ها هستند. فرض کنید ماتریس امتیاز شباهت مشتری محاسبه شده توسط سیستم است
و کاربر پرس و جو مجموعه PPOI { p 1 , p 2 }، NPOI set { p 3 } و RPOI set { p 3 } را ارائه می دهد. مکان این POI در جدول A1 نشان داده شده است.
پیوست ب. اثبات قضیه A1
قضیه A1.
مجموعه پرس و جو ( pP , nP , rP ) را در نظر بگیرید که در آن p یک POI در pP و nP است. مکان o هر نقطه داده شده در هر یال معین در G i است. بهترین امتیاز مکان در G i باید بزرگتر یا مساوی با مجموع همه LB (G i , p) باشد:
اثبات



در موارد 3.3-3.4، highDist ( Gi , p ) یک عدد غیر منفی بزرگتر یا مساوی با فاصله p تا هر راس داده شده در G i است و maxEdge ( Gi ) طول طولانی ترین یال در G است . من _ بدین ترتیب،

از طریق موارد 1-4، ما ثابت کرده ایم که dist ( o , p ) × CI ( Q , p ) ≥ LB ( Gi , p ) و از آنجایی که o هر نقطه داده شده در هر یال معین در G i است ، می توانیم استخراج کنیم که
پیوست ج. اثبات قضیه A2
قضیه A2.
اثبات
-
مورد 1. u متعلق به G i است. حداقل فاصله بین هر دو نقطه 0 است زیرا lowDist ( G i , u ) = 0 ≤ 0.
-
مورد 2. u متعلق به G i نیست. همانطور که توسط [ 28 ] نشان داده شده است،
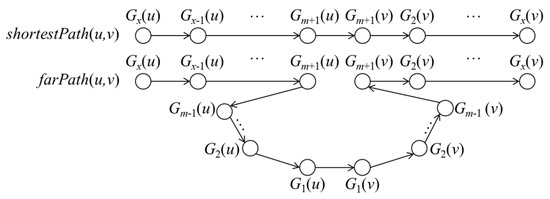
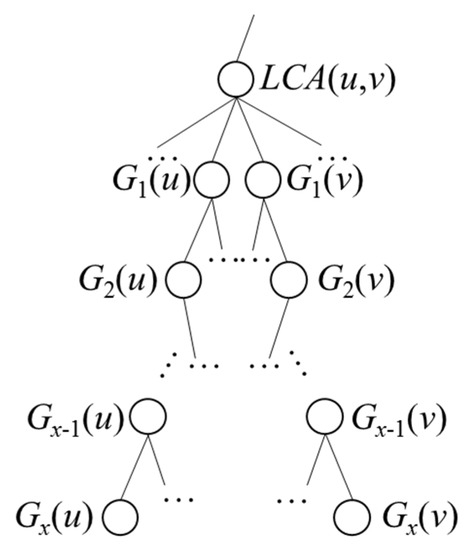
هر مسیری از u به v باید از یک سری گره های درختی G + -G x ( u )، G x -1 ( u )، …، G 1 ( u )، G 1 ( v )، G2 ( v ) عبور کند . ، …، G x ( v ). برای محاسبه فاصله جاده از u تا هر نقطه معین در G i ، از G x ( u )، G عبور می کنیمx −1 ( u )، …، G i . از آنجایی که u به G i تعلق ندارد، G i یکی از گره های بین G x ( u ) و G 1 ( u ) نیست. همانطور که در شکل 7 نشان داده شده است ، اگر G i برابر با G n ( v ) بگذاریم، سپس از همان سری گره های درخت G، G x ( u )، G x -1 ( u )، …، G 1 عبور می کنیم.( u )، …، G n ( v ). بنابراین، حداقل فاصله جاده از u تا هر نقطه معین در G i را می توان به صورت زیر بیان کرد:
که در آن مجموع سه جمله آخر باید بزرگتر یا مساوی باشد
که نشان دهنده کم ( Gn ( v ) ) است. بنابراین، می توانیم معادله (A6) را به صورت زیر بازنویسی کنیم:
سمت راست این معادله برابر با lowDist ( G i , u ) است. بنابراین، ما می توانیم آن را ثابت کنیم
□
پیوست D. اثبات قضیه A3
قضیه A3.
اثبات
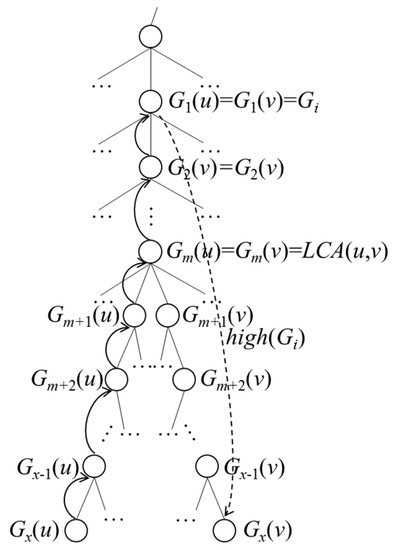
بر اساس شکل 8 ، مانند مورد 2 قضیه A2، اگر G i برابر با G n ( v ) بگذاریم، سپس از همان سری گره های G + -tree عبور می کنیم، G x ( u )، G x -1 ( u )، …، G 1 ( u )، …، G n ( v ). بنابراین، حداکثر فاصله جاده از u تا هر نقطه معین در G i را می توان به صورت زیر بیان کرد:
که در آن جمع چهار جمله آخر کمتر یا مساوی است
حداکثر فاصله جاده از u تا هر نقطه معین در G i را می توان به صورت زیر بیان کرد:
که در آن مجموع شش جمله آخر کمتر یا مساوی است
این کمتر یا مساوی با زیاد است ( G 1 ( v )). بنابراین، می توانیم معادله (A12) را به صورت زیر بازنویسی کنیم:
پیوست E. مثالی از الگوریتم AP




پیوست F. اثبات قضیه A4
قضیه A4.
لبه e و مجموعه پرس و جو ( pP ، nP ، rP ) را در نظر بگیرید. ما به nP ∪ rP به عنوان POI اشاره می کنیم . ما از BP(p,e) برای نشان دادن نقطه شکست POI p در e و از BPs( POIs ,e) برای نمایش مجموعه ای از تمام p در e در POI استفاده می کنیم . بنابرین ما اینها را داریم:
که در آن عبارت قبلی بهترین امتیاز مکان در e است. دومی را می توان به عنوان کران پایین این امتیاز مکان در نظر گرفت.
اثبات
به طور شهودی، میتوانیم موارد زیر را درست ببینیم:
جایی که سمت راست نابرابری نیز برابر است .
در اثبات قضیه 1، نشان دادیم که dist ( o , p )× CI ( Q , p ) یک تابع خطی یا یک تابع خطی تکه ای است و حداقل مقدار آن باید در یک راس { e باشد. ل ، ای _ r } از e یا در BP ( p , e ) از p در e . بنابراین، معادله (A16) را می توان به صورت زیر بازنویسی کرد:
□
پیوست G. مثالی از الگوریتم AEP


منابع
- ژانگ، جی. Ku، W.-S. سان، م. Qin، X. Lu, H. جستجوی مکان بهینه چند معیاره با نمودارهای voronoi همپوشانی. در مجموعه مقالات هفدهمین کنفرانس بین المللی گسترش فناوری پایگاه داده (EDBT)، ادینبورگ، بریتانیا، 29 مارس تا 1 آوریل 2014. صص 391-402. [ Google Scholar ]
- آروانیتیس، ا. دلیگیاناکیس، ا. Vassiliou، Y. پردازش مبتنی بر نفوذ کارآمد پرس و جوهای تحقیقات بازار. در مجموعه مقالات بیست و یکمین کنفرانس بین المللی ACM در مدیریت اطلاعات و دانش، مائوئی، HI، ایالات متحده آمریکا، 29 اکتبر تا 2 نوامبر 2012. صص 1193-1202. [ Google Scholar ]
- شیائو، ایکس. یائو، بی. Li, F. جستجوهای مکان بهینه در پایگاه داده های شبکه جاده ای. در مجموعه مقالات بیست و هفتمین کنفرانس بین المللی مهندسی داده IEEE 2011، واشنگتن، دی سی، ایالات متحده آمریکا، 11 تا 16 آوریل 2011. ص 804-815. [ Google Scholar ]
- لی، سی. یافتن k-مناسب ترین مکان ها با حداقل فاصله متوسط. پایان نامه کارشناسی ارشد، دانشگاه ملی چنگ کونگ، تاینان، تایوان، 2015. [ Google Scholar ]
- لین، ی. وانگ، ای تی. چیانگ، سی. چن، ALP یافتن اهداف با نزدیکترین همسایه مورد علاقه و دورترین همسایه نارضایتی توسط یک جستجوی خط افق. در مجموعه مقالات بیست و نهمین سمپوزیوم سالانه ACM در محاسبات کاربردی، Gyeongju، کره، 24-28 مارس 2014. صص 821-826. [ Google Scholar ]
- ساچاریدیس، دی. Deligiannakis، A. پرسش های انسجام فضایی. در مجموعه مقالات بیست و سومین کنفرانس بین المللی SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، پکن، چین، 2 تا 5 نوامبر 2015. صص 1-10. [ Google Scholar ]
- چی، جی. ژانگ، آر. کولیک، ال. لین، دی. Xue, Y. جستجوی انتخاب مکان کوچک. در مجموعه مقالات بیست و هشتمین کنفرانس بین المللی IEEE در سال 2012 در مهندسی داده، آرلینگتون، VA، ایالات متحده آمریکا، 2 تا 5 آوریل 2012. صص 366-377. [ Google Scholar ]
- سو، آی. هوانگ، ی. چانگ، ی. Shen, I. یافتن مجموع نزدیکترین مثبت و دورترین همسایگان منفی. در مجموعه مقالات کنفرانس بین المللی مهندسی اطلاعات و دانش (IKE)، لاس وگاس، NV، ایالات متحده آمریکا، 16-19 ژوئیه 2012. [ Google Scholar ]
- چهار مربع. در دسترس آنلاین: https://foursquare.com/ (دسترسی در 17 فوریه 2022).
- فیس بوک. در دسترس آنلاین: https://www.facebook.com/ (دسترسی در 17 فوریه 2022).
- چن، YC; هوانگ، اچ. چیو، اس ام. لی، سی. سیستمهای توصیه شریک تبلیغاتی مشترک با استفاده از دادههای شبکههای اجتماعی مبتنی بر مکان. ISPRS Int. J. Geo-Inf. 2021 ، 10 ، 57. [ Google Scholar ] [ CrossRef ]
- یین، دی. میترا، س. ژانگ، اچ. یادداشت پژوهشی – چه زمانی مصرف کنندگان برای نظرات مثبت در مقابل نظرات منفی ارزش قائل می شوند؟ یک بررسی تجربی سوگیری تایید در دهان به دهان آنلاین. Inf. سیستم Res. 2016 ، 27 ، 131-144. [ Google Scholar ] [ CrossRef ]
- کانگ، ال. لیو، اس. گونگ، دی. تانگ، ام. یک سیستم توصیه شخصی نقطهای از علاقه برای تجارت O2O. الکترون. علامت. 2022 ، 31 ، 253-267. [ Google Scholar ] [ CrossRef ]
- چن، ز. لیو، ی. وانگ، RC; شیونگ، جی. مای، جی. طولانی، ج. الگوریتم های کارآمد برای پرس و جوهای مکان بهینه در شبکه های جاده ای. در مجموعه مقالات کنفرانس بین المللی ACM SIGMOD 2014 در مدیریت داده ها، Snowbird، UT، ایالات متحده، 22-27 ژوئن 2014. صص 123-134. [ Google Scholar ]
- خو، ال. مای، جی. چن، ز. لیو، ی. Dai, G. Minsum بر اساس پرس و جو مکان بهینه در شبکه های جاده ای. در مجموعه مقالات کنفرانس بین المللی سیستم های پایگاه داده برای کاربردهای پیشرفته، سوژو، چین، 27 تا 30 مارس 2017. ص 441-457. [ Google Scholar ]
- ژائو، جی. یانگ، اس. هوو، اچ. سان، س. Geng، X. TBTF: یک الگوریتم فاکتورسازی تانسور بایاس متغیر با زمان موثر برای سیستم توصیهگر. Appl. هوشمند 2021 ، 51 ، 4933-4944. [ Google Scholar ] [ CrossRef ]
- کوی، ال. Wang, X. چارچوب آبشاری برای حفظ حریم خصوصی سیستم توصیهکننده نقطهنظر. Electronics 2022 , 11 , 1153. [ Google Scholar ] [ CrossRef ]
- گلال، س. نگی، ن. الشرکاوی، ME CNMF: چارچوب کاهش اخبار جعلی مبتنی بر جامعه. اطلاعات 2021 ، 12 ، 376. [ Google Scholar ] [ CrossRef ]
- لی، اچ. هونگ، آر. زو، اس. Ge, Y. سیستمهای توصیهگر نقطهای از علاقه: دیدگاه فضایی جداگانه. در مجموعه مقالات کنفرانس بین المللی IEEE 2015 در مورد داده کاوی، آتلانتیک سیتی، نیوجرسی، ایالات متحده آمریکا، 14-17 نوامبر 2015. صص 231-240. [ Google Scholar ]
- بائو، جی. ژنگ، ی. Mokbel، MF توصیه مبتنی بر موقعیت و اولویت آگاه با استفاده از داده های شبکه های جغرافیایی-اجتماعی پراکنده. در مجموعه مقالات بیستمین کنفرانس بین المللی پیشرفت در سیستم های اطلاعات جغرافیایی، ردوندو بیچ، کالیفرنیا، ایالات متحده آمریکا، 6-9 نوامبر 2012. ص 199-208. [ Google Scholar ]
- حسیه، ح. لی، سی. Lin, S. Triprec: توصیه مسیرهای سفر از دادههای ثبت ورود در مقیاس بزرگ. در مجموعه مقالات بیست و یکمین کنفرانس بین المللی وب جهانی، لیون، فرانسه، 16-20 آوریل 2012; صص 529-530. [ Google Scholar ]
- لو، ای اچ. چن، سی. Tseng، VS توصیه سفر شخصی با محدودیتهای متعدد با استخراج رفتارهای ورود کاربر. در مجموعه مقالات بیستمین کنفرانس بین المللی پیشرفت در سیستم های اطلاعات جغرافیایی، ردوندو بیچ، کالیفرنیا، ایالات متحده آمریکا، 6-9 نوامبر 2012. ص 209-218. [ Google Scholar ]
- Wen، YT; چو، کی جی. پنگ، WC; یو، جی. Hwang, SW Kstr: توصیه مسیر سفر در افق آگاه از کلمه کلیدی. در مجموعه مقالات کنفرانس بین المللی IEEE 2015 در مورد داده کاوی، آتلانتیک سیتی، نیوجرسی، ایالات متحده آمریکا، 14-17 نوامبر 2015. ص 449-458. [ Google Scholar ]
- وانگ، ایکس. ژانگ، ی. ژانگ، دبلیو. لین، ایکس. به حداکثر رساندن تأثیر آگاه از فاصله در شبکه ژئو اجتماعی. در مجموعه مقالات سی و دومین کنفرانس بین المللی IEEE در مهندسی داده (ICDE)، هلسینکی، فنلاند، 16-20 مه 2016. صص 1-12. [ Google Scholar ]
- جین، ایکس. Han, J. خوشهبندی به حداکثر رساندن انتظار. در دایره المعارف یادگیری ماشین و داده کاوی ; Springer: برلین/هایدلبرگ، آلمان، 2017; صص 480-482. [ Google Scholar ]
- Jaccard, P. Étude comparative de la distribution florale dans une part des alpes et du Jura. گاو نر Soc. وود. علمی نات. 1901 ، 37 ، 547-579. [ Google Scholar ] [ CrossRef ]
- Endres، DM; Schindelin، JE یک معیار جدید برای توزیع احتمال. IEEE Trans. Inf. نظریه 2003 ، 49 ، 1858-1860. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- ژونگ، آر. لی، جی. قهوهای مایل به زرد، KL; ژو، ال. Gong, Z. G-tree: یک شاخص کارآمد و مقیاس پذیر برای جستجوی فضایی در شبکه های جاده ای. IEEE Trans. بدانید. مهندسی داده 2015 ، 27 ، 2175-2189. [ Google Scholar ] [ CrossRef ]
- مجموعه داده های واقعی برای پایگاه های داده فضایی: شبکه های جاده ای و نقاط مورد علاقه. در دسترس آنلاین: https://www.cs.utah.edu/~lifeifei/SpatialDataset.htm (دسترسی در 17 فوریه 2022).
- پروژه OpenStreetMap. در دسترس آنلاین: https://www.openstreetmap.org/ (دسترسی در 14 ژانویه 2019).





بدون دیدگاه