استخراج دقیق اجسام زمینی از تصویر سنجش از دور بر اساس فرآیند نقطه خوشه بندی علامت گذاری

ویژگی های هندسی اجسام زمینی می تواند شکل، کانتور، طول، عرض و توزیع پیکسل اشیاء زمینی را منعکس کند و کاربردهای مهمی در فرآیند تشخیص و تشخیص اشیا داشته باشد. با این حال، ویژگی های هندسی اجسام معمولاً اشکال هندسی نامنظم را نشان می دهند. به منظور برازش دقیق هندسه نامنظم، این مقاله فرآیند نقطه خوشه‌بندی علامت را پیشنهاد می‌کند. در مرحله اول، از نقاط تصادفی در فرآیند والد برای تعیین محل شی زمین استفاده می شود، و نمودار نامنظم ساخته شده توسط نقاط خوشه بندی در فرآیند فرعی به عنوان شناسایی برای تناسب با هندسه شی زمین استفاده می شود. ثانیاً، با فرض اینکه مقادیر اندازه گیری طیفی اجسام زمینی از توزیع گاوسی چند ارزشی مستقل و یکپارچه تبعیت می کنند، مدل اندازه گیری طیفی داده های تصویر سنجش از دور ساخته شده است. سپس مدل استخراج هندسی جسم زمینی تحت چارچوب نظریه بیزی ساخته شده و با الگوریتم مونت کارلو زنجیره مارکوف پرش برگشت پذیر (RJMCMC) برای شبیه سازی توزیع خلفی و تخمین پارامترها ترکیب می شود. در نهایت، مدل استخراج شی بهینه با توجه به معیار احتمال حداکثر پسینی (MAP) حل می‌شود. این مقاله بر روی تصاویر سنجش از دور رنگی آزمایش می کند. نتایج تجربی نشان می‌دهد که روش پیشنهادی نه تنها می‌تواند موقعیت جسم را تعیین کند، بلکه ویژگی‌های هندسی جسم را نیز به طور دقیق برازش می‌دهد. مدل استخراج هندسی جسم زمینی تحت چارچوب نظریه بیزی ساخته شده و با الگوریتم مونت کارلو زنجیره مارکوف پرش برگشت پذیر (RJMCMC) ترکیب شده است تا توزیع خلفی را شبیه سازی کند و پارامترها را تخمین بزند. در نهایت، مدل استخراج شی بهینه با توجه به معیار احتمال حداکثر پسینی (MAP) حل می‌شود. این مقاله بر روی تصاویر سنجش از دور رنگی آزمایش می کند. نتایج تجربی نشان می‌دهد که روش پیشنهادی نه تنها می‌تواند موقعیت جسم را تعیین کند، بلکه ویژگی‌های هندسی جسم را نیز به طور دقیق برازش می‌دهد. مدل استخراج هندسی جسم زمینی تحت چارچوب نظریه بیزی ساخته شده و با الگوریتم مونت کارلو زنجیره مارکوف پرش برگشت پذیر (RJMCMC) ترکیب شده است تا توزیع خلفی را شبیه سازی کند و پارامترها را تخمین بزند. در نهایت، مدل استخراج شی بهینه با توجه به معیار احتمال حداکثر پسینی (MAP) حل می‌شود. این مقاله بر روی تصاویر سنجش از دور رنگی آزمایش می کند. نتایج تجربی نشان می‌دهد که روش پیشنهادی نه تنها می‌تواند موقعیت جسم را تعیین کند، بلکه ویژگی‌های هندسی جسم را نیز به طور دقیق برازش می‌دهد. مدل استخراج شی بهینه با توجه به معیار احتمال حداکثر پسینی (MAP) حل می شود. این مقاله بر روی تصاویر سنجش از دور رنگی آزمایش می کند. نتایج تجربی نشان می‌دهد که روش پیشنهادی نه تنها می‌تواند موقعیت جسم را تعیین کند، بلکه ویژگی‌های هندسی جسم را نیز به طور دقیق برازش می‌دهد. مدل استخراج شی بهینه با توجه به معیار احتمال حداکثر پسینی (MAP) حل می شود. این مقاله بر روی تصاویر سنجش از دور رنگی آزمایش می کند. نتایج تجربی نشان می‌دهد که روش پیشنهادی نه تنها می‌تواند موقعیت جسم را تعیین کند، بلکه ویژگی‌های هندسی جسم را نیز به طور دقیق برازش می‌دهد.

کلید واژه ها:

فرآیند نقطه خوشه بندی علامت ; استخراج شی ; نظریه بیزی ؛ پرش برگشتی زنجیره مارکوف مونت کارلو (RJMCMC)

1. مقدمه

اطلاعات اصلی تصاویر سنجش از دور به طور کلی در چند منطقه کلیدی (مانند جاده ها، رودخانه ها، مخازن، جزایر و غیره) متمرکز است. این مناطقی که مردم به آنها علاقه دارند، در تصاویر سنجش از دور، اشیاء زمینی نامیده می شوند. ویژگی‌های هندسی این اشیاء زمینی نوارها یا چندضلعی‌های ناحیه‌ای هستند که می‌توانند شکل، کانتور، طول و عرض جسم زمین و توزیع پیکسل شی زمین را منعکس کنند [ 1 ]. این ویژگی های هندسی کاربردهای مهمی در فرآیند تشخیص و تشخیص اشیا دارند. بنابراین، چگونگی استخراج دقیق ویژگی‌های هندسی اجسام زمینی در تصاویر سنجش از دور، به یکی از مطالب کلیدی تحقیقاتی محققان تبدیل شده است [ 2 ، 3 ].

روش‌های رایج استخراج ویژگی هندسی اجسام زمینی در تصاویر سنجش از دور شامل روش مبتنی بر تشخیص ویژگی [ 4 ]، روش مبتنی بر یادگیری طبقه‌بندی [ 5 ]، روش مبتنی بر رأی‌گیری Hough [ 6 ، 7 ]، و روش مبتنی بر مدل شیء است. [ 8 ]. با بهبود مستمر وضوح تصویر سنجش از دور در سال های اخیر، روش های استخراج اشیاء تصویر سنجش از دور بر اساس مدل های شی بیشتر مورد استفاده قرار می گیرد. در این میان، روش استخراج شیء مبتنی بر فرآیند نقطه علامت گذاری شده یکی از مؤثرترین روش ها است [ 9 ، 10 ، 11 ].]. در مدل استخراج ویژگی هندسی تصویر سنجش از دور بر اساس فرآیند نقطه علامت‌گذاری شده، موقعیت جسم با فرآیند نقطه تصادفی تعریف شده در حوزه تصویر نشان داده می‌شود و هندسه شی با نشانگر هندسی متصل به تصویر نشان‌دهنده است. نقطه تصادفی [ 12 ]. با این حال، الگوریتم‌های استخراج ویژگی هندسی تصویر سنجش از دور موجود بر اساس فرآیند نقطه مشخص شده، ویژگی‌های عالی و چشم‌انداز توسعه گسترده را نشان می‌دهند. با این حال، علائم با هندسه منظم تعریف می شوند. به عنوان مثال، مستطیل برای استخراج ساختمان ها [ 13 ]، بیضی برای استخراج تاج درختان [ 14 ]، و بخش خط برای استخراج جاده ها [ 15 ] تعریف شده است.]. این نوع روش فقط می تواند اشیاء زمینی منفرد و منظم را استخراج کند که محدودیت های زیادی دارد و کاربرد این نوع روش را محدود می کند. به منظور غلبه بر این نقص، اورتنر و همکاران. (2008) [ 16 ] از دو فرآیند نقطه مشخص شده با هندسه های مختلف (مستطیل و پاره خط) به عنوان علامت استفاده کرد و از الگوریتم زنجیره مارکوف مونت کارلو (MCMC = Markov chain Monte Carlo) برای نمونه گیری مشترک از دو فرآیند نقطه علامت گذاری شده استفاده کرد. با این حال، این روش برای در نظر گرفتن رابطه بین ویژگی‌های هندسی نشان‌داده‌شده توسط این دو گرافیک مختلف دشوار است، که بیان تابع انرژی را برای تحقق تخمین پارامتر بازپخت شبیه‌سازی شده بسیار پیچیده می‌کند. بر اساس کار فوق، لافارژ و همکاران. (2010) [ 17] یک روش استخراج ویژگی هندسی مبتنی بر فرآیند چند نقطه علامت گذاری شده پیشنهاد کرد. این روش با ایجاد یک کتابخانه گرافیکی حاوی انواع گرافیک های هندسی، مدل سازی و استخراج ویژگی های هندسی مختلف را محقق می کند. با این حال، استخراج دقیق ویژگی های هندسی اجسام زمینی با شکل دلخواه هنوز دشوار است. ژائو و همکاران (2018) [ 11 ] یک فرآیند نقطه مشخص شده نامنظم را برای استخراج ویژگی های هندسی لکه های تاریک نشت نفت پیشنهاد کرد. با این حال، این روش فرض می کند که داده های تصویر از توزیع گاما تبعیت می کنند و فقط برای داده های تصویر SAR موثر است.

برای تشخیص اجسام با هندسه نامنظم در تصاویر سنجش از دور رنگی، فرآیند نقطه خوشه‌بندی علامت را پیشنهاد می‌کنیم. ابتدا، توزیع و ویژگی‌های هندسی شی با استفاده از فرآیند نقطه خوشه‌بندی مشخص می‌شود، از نقاط تصادفی در فرآیند والد برای مکان‌یابی شی زمین استفاده می‌شود، و گرافیک نامنظم ساخته شده توسط نقاط خوشه‌بندی در فرآیند فرعی استفاده می‌شود. به عنوان علامت متناسب با شکل هندسی جسم زمین. ثانیاً، با فرض اینکه مقادیر اندازه‌گیری طیفی اجسام زمینی از توزیع گاوسی چند ارزشی مستقل و یکپارچه پیروی می‌کنند، مدل اندازه‌گیری طیفی داده‌های تصویر سنجش از دور رنگی ساخته می‌شود. سپس، مدل استخراج هندسی جسم زمینی تحت چارچوب نظریه بیزی ساخته شده و با الگوریتم مونت کارلو زنجیره مارکوف پرش برگشت پذیر (RJMCMC) ترکیب شده است تا توزیع خلفی را شبیه سازی کند و پارامترها را تخمین بزند. در نهایت، مدل استخراج شی بهینه با توجه به معیار احتمال حداکثر پسینی (MAP) حل می‌شود. ادامه مقاله به شرح زیر تدوین شده است. پس از بررسی اجمالی کار مرتبط، روش تشخیص شی پیشنهادی را معرفی می کنیم. سپس نتایج تجربی و به دنبال آن نتیجه گیری را نمایش می دهیم. ادامه مقاله به شرح زیر تدوین شده است. پس از بررسی اجمالی کار مرتبط، روش تشخیص شی پیشنهادی را معرفی می کنیم. سپس نتایج تجربی و به دنبال آن نتیجه گیری را نمایش می دهیم. ادامه مقاله به شرح زیر تدوین شده است. پس از بررسی اجمالی کار مرتبط، روش تشخیص شی پیشنهادی را معرفی می کنیم. سپس نتایج تجربی و به دنبال آن نتیجه گیری را نمایش می دهیم.

نوآوری های این مقاله عبارتند از:

فرآیند نقطه خوشه بندی علامت برای تناسب با ویژگی های هندسی اشیاء زمینی پیشنهاد شده است.
این مقاله ایجاد مدل داده تصاویر سنجش از دور رنگی را با استفاده از توزیع گاوسی چند ارزشی پیشنهاد می‌کند.
این مقاله شش عملیات متحرک RJMCMC را طراحی می کند که برای تناسب با ویژگی های هندسی اجسام زمینی استفاده می شود.

2. الگوریتم پیشنهادی

داده های سنجش از دور به عنوان مجموعه ای از نقاط گسسته نمونه برداری شده در یک منطقه محدود در صفحه در نظر گرفته می شوند، y = {( x _i , z _i ), i = 1, …, n } که i شاخص پیکسل است. n تعداد کل نقاط داده است. x _i = ( x _1 i , x _2 i ) ∈ S ⊂ R ² مختصات موقعیت شبکه پیکسلی مربوط به نقطه داده i , S است.ناحیه ای است که توسط داده های سنجش از دور (به نام دامنه داده) پوشیده شده است. z _i = ( z _id ، d = 1، …، D ) ^T بردار اندازه گیری طیفی مربوط به پیکسل i است، D بعد داده های نمونه برداری، d شاخص بعد، و T عملیات جابجایی است. .

2.1. مدل هندسی جسم زمینی

با توجه به فرآیند نقطه خوشه‌بندی علامت، مدل هندسی جسم زمین در تصویر سنجش از دور رنگی مدل‌سازی می‌شود. فرآیند نقطه خوشه بندی علامت در حوزه داده S به صورت W = ( U , V ) تعریف می شود و پیکربندی آن w = ( u , v ) فرض می شود. پیکربندی u = { u _j ، j = 1، …، m } فرآیند والد U تعریف شده در S برای توصیف مکان و توزیع فضایی اشیاء زمینی استفاده می‌شود، جایی که jشاخص اجسام زمین است، m تعداد اشیاء است، u _j = ( u _1 j , u _2 j ) ∈ S نشان دهنده موقعیت جسم j است. پیکربندی زیرفرایند خوشه V به صورت v = { v _j , j = 1 , … , m } تعریف می شود که v _j = { v _jg , g = 1, …, k _j } خوشه است مجموعه نقطه مربوط به نقطه تصادفی u _jدر فرآیند والد، v _jg = ( v _1 jg , v _2 jg ) ∈ S مختصات نقطه خوشه g مربوط به نقطه تصادفی u _j است، g شاخص نقطه خوشه، و kj تعداد نقطه خوشه مربوطه است _. به نقطه تصادفی u _j . هر نقطه خوشه در مجموعه نقطه خوشه v _j به ترتیب به هم متصل می شود تا j -امین چند ضلعی v _{j را تشکیل دهد.}، که برای تناسب با هندسه جسم زمین، یعنی علامت مربوط به شی زمین j -ام استفاده می شود.

شکل 1 نمونه ای از مدل سازی هندسه یک شی ویژگی را با استفاده از فرآیند نقطه خوشه بندی علامت نشان می دهد. شکل 1 a فرآیند نقطه خوشه بندی را نشان می دهد. دو فرآیند والد u = { u₁ , u₂ } وجود دارد که با “+” نشان داده می شوند. در نظر گرفتن نقطه تصادفی در فرآیند والد (“+” در شکل) به عنوان مرکز دایره، دو شعاع r ₁ و r ₂توسط توزیع گاوسی تولید می شوند. ناحیه دایره ای مربوطه را ایجاد کنید (در حین ایجاد شعاع، اطمینان حاصل کنید که دو ناحیه دایره ای همدیگر را قطع نمی کنند، برای اطمینان از عدم تلاقی دو جسم زمینی در موقعیت جغرافیایی)، برای ایجاد فرآیند فرعی. هر گره در فرآیند فرعی با “•” نشان داده می شود. همانطور که از شکل مشخص است، v = { v₁ , v₂ }, v₁ = { v₁₁ , v₁₂ , v₁₃ , v₁₄ , v₁₅ , v₁₆ }, v₂ = { v₂₁ ، ج₂₂ ، ج₂₃ ، ج₂₄ ، ج₂₅ }. شکل 1 b فرآیند نقطه خوشه بندی علامت را بر اساس شکل 1 a نشان می دهد . در نظر گرفتن نقاط خوشه در هر فرآیند فرعی در شکل 1 a به عنوان گره و اتصال آنها برای تشکیل یک چندضلعی ساده به عنوان علامت شی مربوطه. مشاهده می شود که در این مثال، فرآیندهای فرعی مربوط به فرآیندهای دو والد به ترتیب دارای شش و پنج نقطه خوشه ای برای تولید شش ضلعی و پنج ضلعی هستند.

2.2. مدل داده تصویر

دامنه داده S به دو دسته تقسیم می شود، S = { S _o , S _b }، که در آن کلاس شی از m چندضلعی تشکیل شده است، یعنی S _o = { S _j ، j = 1، …، m }، S _j ناحیه ای است که توسط پیکسل های موجود در هر چند ضلعی پوشانده شده است.

مقدار اندازه گیری طیفی پیکسل تنظیم شده در ناحیه S _j به صورت z _j = { z _i ( x _i ), x _i ∈ S _j } و مقدار اندازه گیری طیفی پیکسل تنظیم شده در همه مناطق شی به صورت z _o = { بیان می شود. z _j ، j = 1،…، m }. مجموعه اندازه گیری های طیفی پیکسل در ناحیه پس زمینه به صورت _zb = { z i ( x _i ), x _i ∈ بیان می شود _.S _b }. به طور کلی، با فرض اینکه مقادیر اندازه‌گیری طیفی هر پیکسل در تصویر سنجش از دور رنگی از توزیع گاوسی مستقل و چند ارزشی تبعیت می‌کند، مدل داده‌ای تصویر سنجش از دور رنگی z تحت شرط دادن علامت پیکربندی فرآیند نقطه خوشه‌بندی w است.

پzw،θ=∏ایکسمن∈اسبپzمنw،θ×∏j=1متر∏ایکسمن∈اسjپzمنw،θ=∏ایکسمن∈اسب12π3Σبانقضا-12zمن-μبتیΣب-1zمن-μب×∏j=1متر∏ایکسمن∈اسj12π3Σoانقضا-12zمن-μoتیΣo-1zمن-μo

(1)

در میان آنها، θ = ( θb ، θo ) = ( _μb_، Σb _، μo ، _Σo₎_{پارامتر} توزیع گاوسی چند ارزشی است ، μb = ( μbd ، d ₌₁ ، … ، D ) ^T و Σ _b = [ Σ _bdd’ ] _D_×_D بردار متوسط و ماتریس کوواریانس توزیع گاوسی چند ارزشی است که توسط اندازه‌گیری طیفی پیکسل در ناحیه پس‌زمینه رعایت می‌شود.μ _o = ( μ _od , d = 1, …, D )^T و Σ _o = [ Σ _فرد’ ]_D_×_D میانگین بردار و ماتریس کوواریانس توزیع گاوسی چند ارزشی است که با اندازه گیری طیفی پیکسلی شی اطاعت می شود. حوزه.

با فرض اینکه اجزای θ مستقل از یکدیگر هستند، میانگین مقدار μb و _μo از توزیع گاوسی چند ارزشی با میانگین و کوواریانس به صورت ( μ _μ ، Σ μ ₎ ، کوواریانس Σ _b و Σ _o از توزیع گاوسی چند ارزشی با میانگین پیروی می کنند _. و کوواریانس به عنوان ( μ _Σ ، Σ _Σ ). احتمال قبلی θ این است،

پθ=پμپΣ=پμبپμoپΣبپΣo×12π3Σμانقضا-12μب-μμتیΣμ-1μب-μμ×12π3Σμانقضا-12μo-μμتیΣμ-1μo-μμ×12π3ΣΣانقضا-12Σب-μΣتیΣΣ-1Σب-μΣ×12π3ΣΣانقضا-12Σo-μΣتیΣΣ-1Σo-μΣ

(2)

در میان آنها، پارامتر توزیع μ _μ ، Σ _μ ، μ _Σ و Σ _Σ را می توان با توجه به شناخت قبلی θ مشخص کرد.

2.3. مدل استخراج شی زمینی

در این مقاله از قضیه بیزی برای مدلسازی مدل استخراج شی زمینی استفاده شده است. در نظر گرفتن مدل داده های تصویری p ( z | w , θ ) به عنوان مدل احتمال (تابع درستنمایی)، همراه با احتمال قبلی p ( θ ) پارامترهای توزیع و مدل قبلی p ( w ) از پیکربندی هندسی بالا- شی زمینی

قوانین آماری مکان، توزیع و شکل هندسی اجسام زمینی را می توان به عنوان توزیع احتمال پیشینی مشترک پیکربندی ( u ، v ، k ، m ) فرآیند نقطه خوشه بندی علامت توسط گرافیک نامنظم تعریف کرد، یعنی p ( u ، v ، k ، m )، که در آن k = { kj ، _j = 1، …، m } . با فرض اینکه احتمالات قبلی که مکان و هندسه جسم زمین را توصیف می کنند مستقل از یکدیگر هستند، p ( u, v , k , m ) را می توان به صورت زیر نوشت

پw=پتو،v،ک،متر∝پتو|مترپv|متر،کپک|مترپمتر

(3)

علاوه بر این با فرض اینکه هر نقطه تصادفی در فرآیند توصیف اجسام از یکدیگر مستقل است و شکل هندسی اجسام نیز مستقل از یکدیگر است، معادله (3) را می توان به صورت زیر بازنویسی کرد:

پw=پتو،v،ک،متر∝پتو|مترپv|متر،کپک|مترپمتر=پمتر∏j=1مترپتوjپvjپکj

(4)

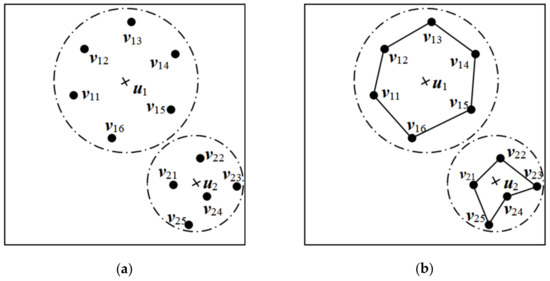
این مقاله از نظریه فرآیند نقطه خوشه‌ای برای مدل‌سازی مکان و شکل هندسی اجسام زمینی استفاده می‌کند. فرآیند نقطه خوشه بندی یک فرآیند نقطه ای است که بر اساس فرآیند نقطه پواسون شکل می گیرد. به طور کلی در نظر گرفته می شود که فرآیند والد آن فرآیند پواسون است. بنابراین دو شرط باید رعایت شود. یکی این است که برای تعداد اشیاء زمینی توزیع شده به طور مساوی در حوزه داده S ، به طور کلی در نظر گرفته می شود که متغیر به طور تصادفی و مستقل با نرخ میانگین ثابت ظاهر می شود و در نظر گرفته می شود که از توزیع پواسون تبعیت می کند. سپس توزیع احتمال p ( m ) تعداد اجسام زمین m را می توان به صورت زیر بیان کرد:

پمتر=پoمنمتر;λمتر=λمترمترمتر!انقضا-λمتر

(5)

که در آن Poi نشان دهنده تابع توزیع پواسون و λ _m پارامتر توزیع پواسون است.

مورد دیگر این است که مکان اشیاء زمین در حوزه داده S به طور کلی مطابق با توزیع یکنواخت در نظر گرفته می شود. یعنی توزیع احتمال p ( u _j ) محل شی زمینی j از توزیع یکنواخت پیروی می کند که می تواند به صورت زیر بیان شود:

پتوj=Unمن اس=اس-1

(6)

که در آن Uni توزیع یکنواخت و | S | نشان دهنده ناحیه دامنه داده S است. در عین حال، با فرض اینکه هر شی مستقل از یکدیگر است، توزیع احتمال p ( u ) مکان همه اشیاء در دامنه داده S به صورت زیر بیان می شود:

پتو=∏j=1مترپتوj=∏j=1مترUnمناس=اس-متر

(7)

از آنجایی که امکان همپوشانی اجسام زمینی از نظر جغرافیایی وجود ندارد، لازم است مکان و توزیع اشیاء زمینی در فرآیند نقطه u محدود شود تا از اشغال اشیاء زمینی مختلف در یک منطقه جلوگیری شود. بنابراین، تابع احتمال تعامل موقعیت جسم زمینی به صورت زیر تعریف می شود:

پتو،تو=∏j=1متر-1∏j”=j+1مترپتوj،توj”

(8)

که در آن p ( u _j , u _j’ ) تابع توزیع احتمال رابطه متقابل بین اشیاء زمینی j و j’ است. برای حذف کامل همپوشانی اشیاء زمینی j و j’ ، p ( u _j , u _j’ ) را می توان به صورت زیر تعریف کرد:

پتوj،توj”=0 اسj∩اسj”≠Φ1 در غیر این صورت

(9)

که در آن S _j و S _j’ مساحت اشغال شده توسط اجسام زمین j و j’ را نشان می دهد و Φ نشان دهنده یک مجموعه خالی است.

پس از مدلسازی مکان و تعداد اجسام زمین (فرایند مادر)، هندسه اجسام زمین (فرایند فرعی) را مدل می کنیم. سپس با فرض اینکه پیکربندی های هندسی اجسام مستقل از یکدیگر هستند، پس

پv=∏j=1مترپvj

(10)

برای نقطه خوشه مجموعه v _j = ( v _jg , g = 1, …, k _j ) برای تناسب با شکل هندسی شی زمین j -ام با فرض اینکه توزیع هر نقطه خوشه مستقل از یکدیگر است استفاده می شود. ، سپس،

پvj=∏g=1کjپvjg

(11)

برای بیان خوشه‌بندی هر نقطه خوشه در فرآیند فرعی خوشه‌بندی به موقعیت هر نقطه تصادفی در فرآیند والد خوشه‌بندی، می‌توان فرض کرد که || u _j – v _jg || ₂ توزیع گاوسی را برآورده می کند،

پvjg=جیتوj-vjg2;μv،σv=12πσvانقضا-توj-vjg2-μv22σv2

(12)

تعداد نقاط خوشه kj مربوط به شی _j توزیع پواسون را با پارامتر λ k _{برآورده} می کند .

پکj=پoمنکj،λک=λککjکj!انقضا-λک

(13)

با فرض اینکه توزیع هندسی هر شی مستقل از یکدیگر است، تعداد فرآیندهای فرعی خوشه بندی هر شی مستقل از یکدیگر است. برای تعداد گره ها در کل تصویر سنجش از دور k = { k _j , j = 1, …, m }، تابع توزیع احتمال باید به صورت

پک=∏j=1مترپکj=∏j=1مترپoمنکj،λک=∏j=1مترλککjکj!انقضا-λک

(14)

سپس مدل نهایی استخراج شی زمینی (یک مدل احتمال پسینی) p ( w , θ | z ) را می توان به صورت زیر بیان کرد:

پw،θ|z∝پz|w،θپθپw=∏ایکسمن∈اس∖اسjپzمنw،θب×∏j=1متر∏ایکسمن∈اسjپzمنw،θj×پθب×∏j=1مترپθj×اس-متر×∏j=1متر∏g=1کj12πσvانقضا-توj-vjg2-μv22σv2×∏j=1مترλککjکj!انقضا-λک×λمترمترمتر!انقضا-λمتر

(15)

2.4. شبیه سازی و بهینه سازی مدل استخراج شی

پس از ایجاد مدل استخراج شی، مدل باید شبیه سازی شود تا راه حل بهینه به دست آید تا استخراج شی بر اساس تصاویر سنجش از دور محقق شود. در این مقاله، الگوریتم RJMCMC برای شبیه‌سازی مدل استخراج شی زمینی (احتمال پسینی) استفاده می‌شود و عملیات متحرک مربوطه به گونه‌ای طراحی شده است که با معیار MAP ترکیب شود تا مکان، کمیت و هندسه اجسام زمین را تعیین کند.

2.4.1. شبیه سازی

با هدف مدل استخراج شی زمینی (احتمال پسینی) بر اساس قضیه بیزی، الگوریتم RJMCMC مربوطه طراحی شده است. علاوه بر پارامترهای موجود در پیکربندی هندسی w شی زمینی، مدل باید پارامترهای توزیع θ مدل توزیع را که توسط داده‌های مشاهده تصویر سنجش از دور رعایت می‌شود، نیز شامل شود. بنابراین، تمام پارامترهای مدل را به عنوان Θ = ( u ، v ، k ، θ ، m ) تنظیم کنید، و مدل احتمال پسینی برای استخراج اشیا را می توان به صورت زیر بازنویسی کرد.

(16)

هنگامی که تعداد اشیاء m و مجموعه گره k تغییر کند، بعد پارامترهای مدل Θ = ( u ، v ، k ، θ ، m ) تغییر خواهد کرد. بنابراین از الگوریتم RJMCMC برای شبیه سازی مدل استخراج شی با ابعاد متغیر استفاده می شود. ایده اصلی این است: برای تنظیم شاخص تکرار نمونه گیری فعلی به عنوان t ، و مجموعه پارامترهای مدل مربوطه Θ⁽^t⁾ است. در تکرار بعدی، نشانگر تکرار t + 1 است و پارامترهای کاندید Θ^*با توجه به پارامترهای مدل Θ⁽^t⁾ ، یعنی Θ^* = Θ^* ( Θ⁽^t⁾ , ζ ) پیشنهاد می شوند. بردار ζ یک بردار تصادفی پیوسته است که برای اطمینان از تعادل ابعادی Θ^* و Θ⁽^t⁾ تعریف شده است که شرایط زیر را برآورده می کند: | Θ^* | = | Θ⁽^t⁾ | ± | ز | ، کجا |⋅| بعد برداری است. به منظور تناسب کامل با شکل هندسی جسم زمینی، عملیات تغییر شکل هندسی جسم زمینی طراحی شده است. این عمدتا شامل: به روز رسانی پارامترهای توزیع θ ، افزودن یا حذف چند ضلعی ها، افزودن یا حذف گره های چند ضلعی، و ادغام چند ضلعی ها است.

اجازه دهید پیکربندی هندسی جسم زمین تحت وضعیت شماره تکرار فعلی t باشد w^( t ) = { w _j^( t ) , j = 1, …, m ^( t ) } = { u^( t ) , v^( t ) } = {( u _j^( t ) , v _j^( t ) ), j = 1, …, m ^( t )}، که در آن vj⁽_t⁾ = { v _jg ، g = 1، …، kj ₍^t⁾^} ، k ⁽^t⁾ = { kj⁽^t⁾^،j = 1، _… ، m ⁽^t⁾ }. بر این اساس، پارامتر توزیع θ⁽^t⁾ = { θ _b⁽^t⁾ , θ _j⁽^t⁾ , j است.= 1، …، m ⁽^t⁾ }.

1.: به روز رسانی پارامترهای توزیع θ

پارامترهای توزیع θ^( t ) = ( μ _b^( t ) , Σ _b^( t ) , μ _o^( t ) , Σ _o^( t ) ) به ترتیب به روز می شوند. با در نظر گرفتن μb ₍^t^) به عنوان مثال، یک پارامتر کاندید جدید μb _* پیشنهاد شده است، و در نظر گرفته می شود که از توزیع گاوسی با میانگین μb ₍^t^{) پیروی می}^کند^.و واریانس ε _b به ترتیب. نرخ پذیرش به روز رسانی پارامتر توزیع μb ₍^t⁾ به صورت زیر تعریف می شود ^:

آ(θ*،θتی)=دقیقه1،پzθ*،wتیپθ*پzθتی،wتیپθتی

(17)

عدد تصادفی γ ~ Uni ([0, 1]) را می گیریم، اگر A ( θ ^* , θ^( t⁾ ) ≥ γ , عملیات به روز رسانی پارامترهای توزیع θ پذیرفته می شود، θ^( t +1) = θ^* . در غیر این صورت، عملیات رد می شود، θ^( t +1) = θ^( t⁾ .

2.: چند ضلعی اضافه کنید

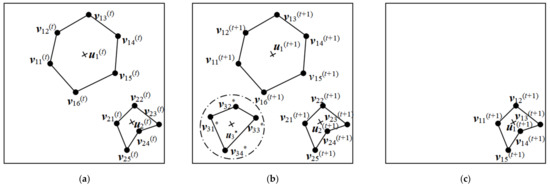
برای افزودن یک عملیات چند ضلعی، اجازه دهید پیکربندی هندسی جسم زمین در حالت تکرار t- امین باشد w^( t ) = { w _j^( t ) , j = 1, …, m ^( t ) } = { u^( t ) , v^( t ) } = {( u _j^( t ) , v _j^( t ) ), j = 1, …, m ^( t )}. در تکرار t +1، یک چند ضلعی اضافه کنید، شاخص چند ضلعی تازه اضافه شده m ^( t⁾ + 1 است و پیکربندی wمترتی+1*=(تومترتی+1*،vمترتی+1*). جایی که، تومترتی+1*~ Uni ( S _b )، vمترتی+1*={vمترتی+1g*،g=1،…،کمترتی+1*}، vمترتی+1g*~Unمن(اسمترتی+1)، کمترتی+1*~پoمنλک. سپس، راضی کنید: برای چند ضلعی دلخواه v _j ، j ∈ {1، …، m ^( t ) }، vمترتی+1g*∩vj=Φ. پس از افزودن عملیات چند ضلعی، پیکربندی نامزد هندسه شی زمین است w*={wتی،wمترتی+1*}. پارامتر توزیع مربوط به چند ضلعی جدید اضافه شده است θمترتی+1*، که از توزیع قبلی از پیش تعریف شده آن استخراج می شود. هنگامی که یک چند ضلعی اضافه می شود، پارامترهای توزیع θ^( t⁾ مدل استخراج شی زمین تغییر نخواهد کرد، بنابراین توزیع احتمال آن تغییر نخواهد کرد. با این حال، پارامترهای ( u^( t⁾ ، v^( t⁾ ، k^( t⁾ ، m ^( t⁾ ) در پیکربندی هندسی w^( t⁾شی زمین با افزایش چند ضلعی ها تغییر می کند، بنابراین توزیع احتمال مربوطه نیز تغییر خواهد کرد. در همان زمان، مدل داده های تصویر سنجش از دور p ( z | θ^( t⁾ , w⁽^t⁾ ) نیز بر این اساس تغییر خواهد کرد. بنابراین، میزان پذیرش عملیات افزودن چند ضلعی به صورت زیر تعریف می شود:

(18)

جایی که، ز=wمترتی+1*،θمترتی+1*بردار حفظ تعادل ابعاد است و p ( ζ ) تابع احتمال بردار پیشنهادی است. zمترتی+1=zمن،ایکسمن∈vمترتی+1*. p _D و p _A به ترتیب احتمال انتخاب عملیات افزودن یا حذف چند ضلعی هستند. اگر یکی از این عملیات در طراحی الگوریتم شبیه‌سازی مدل ترجیح داده نشود، می‌توانیم p _D = p _A را فرض کنیم ، یعنی می‌توانیم چندضلعی‌ها را با احتمال مساوی اضافه یا حذف کنیم.

عدد تصادفی γ ~ Uni ([0, 1]) را می گیریم، اگر A _A ( w^* ) ≥ γ ، عمل جمع چند ضلعی ها پذیرفته می شود، w^( t +1) = w^* . در غیر این صورت، عملیات رد می شود، w^( t +1) = w^( t ) .

3.: حذف چند ضلعی ها

برای حذف یک عملیات چند ضلعی، اجازه دهید پیکربندی هندسی جسم زمین در حالت تکرار t- امین باشد w^( t ) = { w _j^( t ) , j = 1, …, m ^( t ) }. یک چند ضلعی دلخواه v _j^( t ) به طور تصادفی با احتمال مساوی 1/ m ^( t ) از پیکربندی هندسی هدف فعلی w^( t ) انتخاب می شود. پیکربندی هندسی چند ضلعی انتخاب شده w است_j^( t ) = ( u _j^( t ) , v _j^( t ) ) . این چند ضلعی را حذف می کنیم و چند ضلعی های باقی مانده را دوباره ترتیب می دهیم. سپس پیکربندی هندسی جسم به این صورت است w^* = { w _j^* , j = 1, …, m ^( t ) − 1} است. در همان زمان، پارامترهای توزیع مربوط به این چند ضلعی θj⁽_t⁾^{حذف می شوند} . هنگامی که این عملیات انجام می شود، توزیع احتمال پارامترهای توزیع θ^( t⁾ بدون تغییر باقی می ماند. پارامترهای ( u^( t⁾ ، v^( t⁾ ، k^( t⁾ ، m ^( t⁾ ) در پیکربندی هندسی w^( t⁾ شی زمین و مدل داده تصویر سنجش از دور p ( z | θ^( t⁾ ، w⁽^t⁾) تغییر خواهد کرد. در عین حال، این عملیات ابعاد مجموعه پارامتر را نیز تغییر می دهد. برای سادگی، بردار اختیاری برای حفظ تعادل ابعادی ζ = ( _wj⁽^t⁾ ، θj ₍t⁾⁾^است . بنابراین، نرخ پذیرش عملیات چند ضلعی حذف به صورت زیر تعریف می شود:

(19)

جایی که، z _j = { z _i ، x _i ∈ v _j }.

عدد تصادفی γ ~ Uni ([0, 1]) را می گیریم، اگر A _D ( w^* ) ≥ γ , عملیات حذف چند ضلعی ها پذیرفته می شود، w^( t +1) = w^* . در غیر این صورت، عملیات رد می شود، w^( t +1) = w^( t ) .

شکل 2 نمونه هایی از افزودن و حذف چند ضلعی ها است که در شکل 2 a پیکربندی هندسی w^( t⁾ جسم زمین در زمان t را نشان می دهد. علاوه بر این، شکل 2 b,c نمونه هایی از افزودن یا حذف یک چند ضلعی را به ترتیب در زمان t + 1 نشان می دهد.

4.: گره های چند ضلعی را اضافه کنید

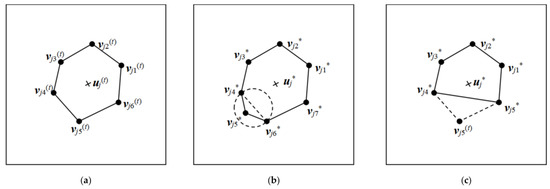
برای هر چند ضلعی معین، گره همسایگی هر گره گرهی است که مستقیماً به گره متصل است و دو گره مستقیماً متصل یک جفت گره همسایگی را تشکیل می دهند. اجازه دهید پیکربندی هندسی جسم زمین در حالت تکرار t ، w^( t ) = { w _j^( t ) , j = 1, …, m ^( t ) } باشد. یک چند ضلعی دلخواه v _j^( t ) به طور تصادفی با احتمال مساوی 1/ m ^( t ) از پیکربندی هندسی هدف فعلی انتخاب می شود.w^( t ). یک جفت گره همسایگی ( v _jg^( t ) , v _jg₊₁^( t ) ) با احتمال مساوی 1/ k _j^( t ) از مجموعه گره v _j^( t ) چند ضلعی انتخاب شده انتخاب کنید. یک نقطه به طور تصادفی به عنوان یک گره نامزد اضافی در ناحیه تقاطع بین دایره با ( _vjg⁽^t⁾ + v _jg₊₁⁽^t⁾ )/2 به عنوان مرکز انتخاب می شود | v_jg^( t )به صورت مجدد مرتب می شوند+ v _jg₊₁^( t ) |/2 به عنوان شعاع و ناحیه قابل مشاهده یال v _jg^( t )v _jg₊₁^( t ) . سپس، گره کاندید بین جفت‌های گره ( vjg⁽^t⁾ , _vjg₊₁⁽_t^{) )}^برای ساخت چند ضلعی کاندید v _j^* وارد می‌شود . در نهایت، گره های چند ضلعی کاندید v _j^*v _j^* = { v _jg^* ، g = 1، …، kj ⁽_t⁾⁺ 1}. بدون از دست دادن عمومیت، گره جدید را به صورت v _jg^* ضبط کنید . هنگامی که این عملیات انجام می شود، توزیع احتمال پارامترهای توزیع θ^( t ) و پارامترهای ( u^( t ) ، m ^( t ) ) در پیکربندی هندسی w^( t )جسم زمینی بدون تغییر باقی می مانند. توزیع احتمال (v^( t ) ، k^( t ) ) و مدل داده‌های تصویر سنجش از دور p ( z | θ^( t ) ، w^( t ) ) تغییر خواهند کرد. در عین حال، این عملیات ابعاد مجموعه پارامتر را نیز تغییر می دهد. برای سادگی، بردار اختیاری برای حفظ تعادل ابعاد ζ = { v _jg^* } است. میزان پذیرش عملیات افزودن گره چند ضلعی به صورت زیر تعریف می شود:

آآVv*،vتی=دقیقه1،پzj*|θjتیپzبj*|θبتیپکjتی+1پv*پدیVپzj*|θبتیپzبj*|θjتیپکjتیپvتیپزپآV

(20)

جایی که z _j^* = S _j^* \ S _j^( t ) ، z _bj^* = S _j^( t ) \ S _j^* ، S _j^* و S _j^( t ) نشان دهنده مساحت های اشغال شده توسط چند ضلعی کاندید v _j^* و چند ضلعی فعلی v _j^( t ) به ترتیب. اگر z _j^*یا z _bj^* یک مجموعه خالی است، تابع چگالی احتمال مشروط مربوطه آن را برابر با 1 قرار می دهیم. p _DV و p _AV به ترتیب احتمال انتخاب عملیات گره چند ضلعی اضافه یا حذف هستند.

عدد تصادفی γ ~ Uni ([0, 1]) را می گیریم، اگر A _AV ( v _j^* , v _j^( t ) ) ≥ γ , عملیات اضافه کردن یک گره چند ضلعی پذیرفته می شود، w^( t +1) = w^* . در غیر این صورت، عملیات رد می شود، w^( t +1) = w^( t ) .

5.: حذف گره های چند ضلعی

اجازه دهید پیکربندی هندسی جسم زمین در حالت تکرار t ، w^( t ) = { w _j^( t ) , j = 1, …, m ^( t ) } باشد. یک چند ضلعی دلخواه v _j^( t ) به طور تصادفی با احتمال مساوی 1 / m ^( t ) از پیکربندی هندسی هدف فعلی w^( t ) انتخاب می شود. سپس، یک گره به طور تصادفی از مجموعه گره های چند ضلعی v _j^(t ) با احتمال مساوی 1 / k _j^( t ) و به صورت v _jg^( t ) ثبت می شود. اگر دو گره همسایگی گره v _jg^( t ) برای یکدیگر قابل مشاهده هستند، گره را حذف کنید و گره های باقیمانده را دوباره ترتیب دهید v _j^* = { v _jg^* , g = 1, …, k _j^( t ) − 1} برای ساخت چند ضلعی کاندید v _j^* .

هنگامی که این عملیات انجام می شود، توزیع احتمال پارامترهای توزیع θ^( t⁾ و پارامترهای ( u^( t⁾ ، m ^( t⁾ ) در پیکربندی هندسی w^( t⁾ جسم زمینی بدون تغییر باقی می مانند. توزیع احتمال پارامترهای ( v^( t⁾ ، k^( t⁾ ) و مدل داده‌های تصویر سنجش از دور p ( z | θ^( t⁾ ،w⁽^t⁾ ) تغییر خواهد کرد. در عین حال، این عملیات ابعاد مجموعه پارامتر را نیز تغییر می دهد. برای سادگی، بردار اختیاری برای حفظ تعادل ابعاد ζ = { v _jg^* } است. نرخ پذیرش عملیات حذف گره چند ضلعی به صورت زیر تعریف می شود:

آدیVv*،vتی=دقیقه1،پzj*|θjتیپzبj*|θبتیپکjتی-1پv*پزپآVپzj*|θبتیپzبj*|θjتیپکjتیپvتیپدیV

(21)

عدد تصادفی γ ~ Uni ([0, 1]) را می گیریم، اگر A _DV ( v _j^* , v _j^( t ) ) ≥ γ , عملیات حذف یک گره چند ضلعی پذیرفته می شود، w^( t +1) = w^* . در غیر این صورت، عملیات رد می شود، w^( t +1) = w^( t ) .

شکل 3 نمونه ای از افزودن و حذف یک گره چند ضلعی است، که در آن شکل 3 a پیکربندی هندسی w^( t⁾ شی زمین در زمان t را نشان می دهد. علاوه بر این، شکل 3 b,c نمونه هایی از افزودن یا حذف یک گره چند ضلعی را به ترتیب در زمان t + 1 نشان می دهد.

6.: ادغام چند ضلعی ها

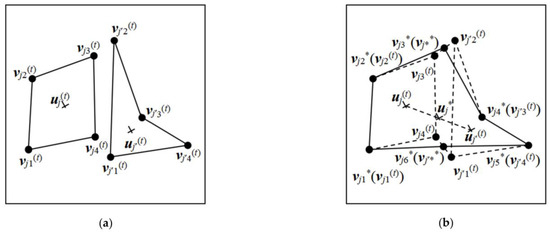
اجازه دهید پیکربندی هندسی جسم زمین در حالت تکرار t ، w^( t ) = { w _j^( t ) , j = 1, …, m ^( t ) } باشد. دو چند ضلعی v _j^( t ) و v _j_‘^( t ) را به طور تصادفی از پیکربندی هندسی شی فعلی w^{( t ) انتخاب کنید.}و سپس فاصله جفت گره آنها را به ترتیب محاسبه کنید. اگر فاصله بین کوتاهترین و فرعی ترین جفت گره کمتر از یک آستانه معین باشد، دو چند ضلعی را با هم ادغام می کنیم. عملیات چند ضلعی ادغام با ادغام جفت گره ها محقق می شود. نقطه وسط کوتاه ترین جفت گره و جفت گره فرعی را به عنوان گره های تازه اضافه شده در نظر بگیرید و آنها را با گره های دیگر ترکیب کنید تا چند ضلعی کاندید v _j^* بسازید . هنگامی که این عملیات انجام می شود، پارامترهای توزیع θ^( t⁾ بدون تغییر باقی می مانند و توزیع احتمال آن بدون تغییر باقی می ماند. پارامترهای ( u^( t⁾ ، v^( t⁾ ،k^( t⁾ , m ^( t⁾ ) در پیکربندی هندسی w^( t⁾ جسم زمین با ادغام چند ضلعی ها تغییر می کند و توزیع احتمال مربوطه آنها نیز تغییر می کند. در همان زمان، مدل داده‌های تصویر سنجش از دور p ( z | θ^( t⁾ , w⁽^t⁾ ) نیز تغییر می‌کند، بنابراین نرخ پذیرش عملیات ادغام چند ضلعی‌ها برابر است با

(22)

جایی که، z _j^* = S _j^* \( S _j^( t ) ∪ S _j’^( t ) ), z _bj^* = ( S _j^( t ) ∪ S _j’^( t ) )\ S _j^* .

عدد تصادفی γ ~ Uni ([0, 1]) را می گیریم، اگر A _M ( w^* ) ≥ γ , عملیات ادغام چند ضلعی ها پذیرفته می شود، w^( t +1) = w^* . در غیر این صورت، عملیات رد می شود، w^( t +1) = w^( t ) .

شکل 4 نمونه ای از چند ضلعی های ادغام شده است، در حالی که شکل 4 a پیکربندی هندسی w^( t⁾ جسم زمین را در زمان t نشان می دهد. علاوه بر این، شکل 4 b مثالی از ادغام چند ضلعی ها در زمان t + 1 را نشان می دهد.

2.4.2. بهینه سازی

معیار MAP ساده ترین طرح بهینه سازی است. هنگامی که احتمال خلفی در مدل استخراج بیزی بزرگترین باشد، راه حل مربوطه نتیجه استخراج شی بهینه است. راه حل بهینه تخمین پارامتر تحت شرایط MAP،

w^،θ^=ارگحداکثرw،θ پw،θ|z

(23)

جایی که Θ^=w^،θ^=تو^،v^،ک^،متر^،θ^حداکثر تخمین احتمال پسینی مجموعه پارامتر است ( w , θ ) = ( u , v , k , m , θ ).

در بین پارامترهای فوق، u = { u _j = ( u _1 j , u _2 j ) ∈ S , j = 1, …, m } که u _j = ( u _1 j , u _2 j ) موقعیت را نشان می دهد. از شی j و m نشان دهنده تعداد اشیاء است. v = { v _j ، j = 1، …، m }، که در آن v _j = { v_jg ، g = 1 ، …،_kj } مجموعه مختصات گره مربوط به شی j است. بنابراین، پیکربندی w = ( u , v ) فرآیند نقطه خوشه‌بندی علامت می‌تواند به طور کامل شی زمین استخراج شده را توصیف کند.

3. نتایج آزمایش

به منظور بررسی صحت الگوریتم پیشنهادی از نظر کمی و کیفی، از تصاویر سنجش از دور رنگی مصنوعی و واقعی برای آزمایش‌ها استفاده می‌شود.

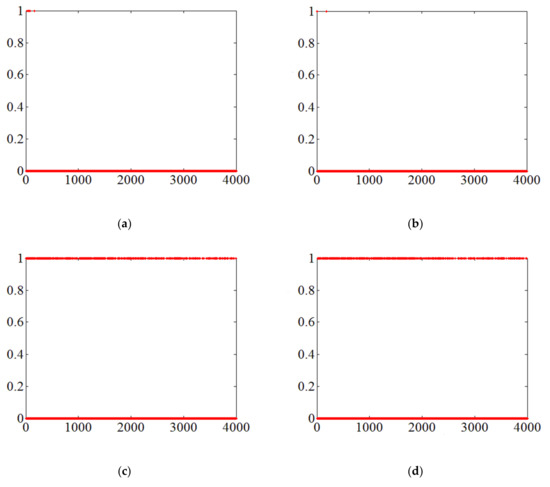
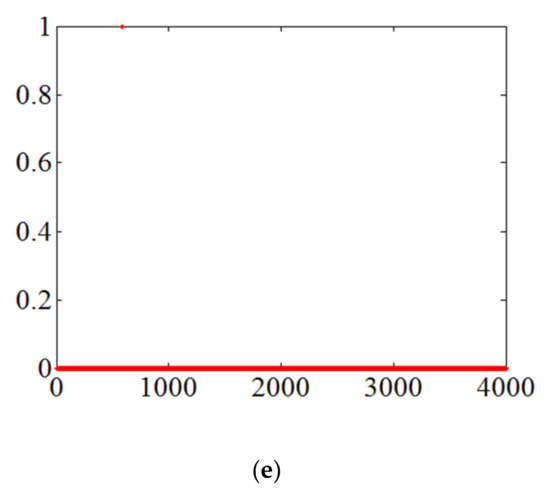
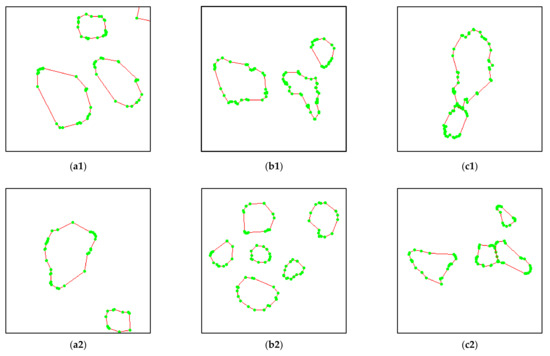
3.1. آزمایش تصویر مصنوعی

با توجه به تصویر الگوی داده شده (همانطور که در شکل 5 الف نشان داده شده است)، دو نوع شی زمینی از زمین های جنگلی و زمین برهنه برای ایجاد یک تصویر 256 × 256 پیکسل (همانطور که در شکل 5 ب نشان داده شده است) به هم متصل می شوند. خط آبی در شکل 5 c طرح کلی شی است.

الگوریتم پیشنهادی برای استخراج اجسام زمین از تصویر مصنوعی در شکل 5 ب استفاده می شود. در طول آزمایش، اگر تعداد تکرارها بیش از حد تنظیم شود، باعث افزونگی زمانی می شود. اگر تعداد تکرارها کم باشد، الگوریتم همگرا نمی شود و برازش ویژگی های هندسی جسم کامل نمی شود. پس از آزمایش‌های زیاد، تعداد تکرارها در این مقاله به 4000 تنظیم شده است. ما آزمایش‌هایی را بر روی پردازنده Intel (R) Core (TM) i7-10510u @ دستگاه 1.80GHz 2.30 GHz انجام دادیم و زمان اجرا حدود 303.403035 ثانیه بود.

در طول آزمایش، هر تکرار شش عملیات طراحی شده را انجام می دهد که پنج عملیات آخر بر هندسه چند ضلعی استفاده شده برای تناسب با اجسام تأثیر می گذارد. جدول 1 تعداد دفعاتی که هر عملیات جابجایی پذیرفته شده است را فهرست می کند. از این میان، عملیات افزودن چند ضلعی ها، حذف چند ضلعی ها و ادغام چند ضلعی ها برای تعیین تعداد اشیا استفاده می شود و دفعات کمتری پذیرفته می شود. عملیات اضافه کردن گره های چند ضلعی و حذف گره های چند ضلعی برای تنظیم شکل چند ضلعی ها استفاده می شود و بارها پذیرفته می شود.

شکل 6 میزان پذیرش پنج عملیات گذشته را نشان می دهد. در میان آنها، عملیات جمع چند ضلعی چهار بار پذیرفته شد که به ترتیب در تکرارهای 26، 49، 62 و 78 اتفاق افتاد، همانطور که در شکل 6 الف نشان داده شده است. عملیات حذف چند ضلعی سه بار پذیرفته شد که به ترتیب در تکرارهای 2، 4 و 185 اتفاق افتاد، همانطور که در شکل 6 ب نشان داده شده است. عملیات ادغام چند ضلعی یک بار پذیرفته می شود، که در تکرار 581 اتفاق می افتد ، همانطور که در شکل 6 e نشان داده شده است. از این سه عملیات برای تعیین تعداد اشیا استفاده می شود. همانطور که در شکل 6 نشان داده شده است، افزودن و حذف گره های چند ضلعی به ترتیب 683 بار و 616 بار بیشتر پذیرفته می شود .c,d برای تنظیم هندسه چند ضلعی.

تعداد کل تکرارهای آزمایش 4000 است و نتایج استخراج شیء هر 20 بار نمایش داده می شود، همانطور که در شکل 7 نشان داده شده است. در میان آنها، شکل 7 a نتیجه اولیه سازی را نشان می دهد. در طول فرآیند اولیه سازی، تعداد فرآیندهای والد داده شده 4 عدد است که با سیم متقاطع سبز رنگ در شکل نشان داده شده است و محدوده خوشه بندی داده شده با دایره آبی رنگ در شکل نشان داده شده است. فرآیندهای فرعی مربوط به فرآیند والد در دایره آبی تولید می شوند. تعداد فرآیندهای فرعی روی 4 تنظیم شده است که در شکل با نقاط قرمز رنگ ثابت نشان داده شده است. فرآیندهای فرعی مربوط به هر فرآیند والد را به ترتیب به هم متصل کنید تا یک چند ضلعی اولیه تشکیل شود، همانطور که در خط قرمز نشان داده شده است، تا یک نتیجه اولیه ایجاد شود.شکل 7 ب نتایج تکرار بیستم را نشان می دهد. در مقایسه با نتایج اولیه سازی ( شکل 7 الف)، مشخص شد که در 20 تکرار اول، عملیات افزودن چند ضلعی پذیرفته نمی شود و عملیات حذف چند ضلعی دو بار پذیرفته می شود که به ترتیب در تکرار دوم و چهارم اتفاق می افتد. شکل 7 ج نتایج تکرار 40 را نشان می دهد. در مقایسه با شکل 7 ب، مشخص شد که در 20 تکرار، یک چند ضلعی اضافه می شود که در تکرار بیست و ششم رخ می دهد و عملیات حذف چند ضلعی دریافت نمی شود. شکل 7 d نتایج تکرار 60 را نشان می دهد. در مقایسه با شکل 7ج، مشخص شد که در 20 تکرار، یک چند ضلعی اضافه می شود که در تکرار 49 رخ می دهد و عملیات حذف چند ضلعی دریافت نمی شود. شکل 7 e نتایج تکرار 80 را نشان می دهد. در مقایسه با شکل 7 d، مشخص شد که در 20 تکرار، عملیات جمع چند ضلعی دو بار پذیرفته شده است که به ترتیب در تکرارهای 62 و 78 اتفاق می افتد و عملیات حذف چند ضلعی پذیرفته نمی شود. شکل 7 f نتایج تکرار 200 را نشان می دهد. در مقایسه با شکل 7 e، مشخص شد که یک عملیات حذف چند ضلعی پذیرفته شده است، که در تکرار 185 رخ می دهد. شکل 7 g نتیجه تکرار 580 را نشان می دهد. در مقایسه با شکل 7f، عملیات افزودن و حذف چند ضلعی ها پذیرفته نمی شود، اما هندسه چند ضلعی ها با افزودن و حذف گره های چند ضلعی تنظیم می شود. شکل 7 h نتایج 600 تکرار را نشان می دهد. در مقایسه با شکل 7 g، مشخص شد که عملیات ادغام چند ضلعی پذیرفته شده است، که در تکرار 581 رخ می دهد. هندسه چند ضلعی با افزودن و حذف پیوسته گره ها تنظیم می شود تا نتیجه نهایی استخراج شی را تشکیل دهد، همانطور که در شکل 7 نشان داده شده است. مشاهده می شود که پس از افزودن، حذف و ادغام چند ضلعی ها، تعداد نهایی چند ضلعی ها با تعداد شیء شکل ها مطابقت دارد.

نتایج آزمایشی نهایی در شکل 8 نشان داده شده است ، که در آن شکل 8 a برای تبدیل نتایج استخراج شی به نتایج تقسیم بندی به منظور ارزیابی کمی نتایج تجربی با استفاده از روش ماتریس سردرگمی است. شکل 8 b نتایج برهم نهی کانتور جسم زمین استخراج شده و تصویر تجربی را برای ارزیابی کیفی نتایج تجربی نشان می دهد. شکل 8c خط کانتور استخراج شده شی زمین را نشان می دهد. نقاط سبز جامد در شکل هر گره را نشان می دهند و خطوط قرمز یکدست برای اتصال هر گره به منظور ایجاد یک چند ضلعی استفاده می شود. طبق نتایج آزمایشی نهایی، اجسام مرکزی، چهار ضلعی، پنج ضلعی و بیضوی به ترتیب با 23، 13، 23 و 21 گره به هم متصل می شوند.

روش پیشنهادی متعلق به روش آماری روشهای سنتی است. روش های آماری معمولاً به واحدهای پردازش پیکسلی و واحدهای پردازش شی گرا تقسیم می شوند. بنابراین، به منظور تأیید اثربخشی آزمایش، مقاله ابتدا از روش آماری استفاده می کند که در آن پیکسل واحد پردازش برای مقایسه است [ 18 ]. ثانیاً، مقایسه با استفاده از روش فرآیند نقطه علامت انجام می شود، که شی را به عنوان واحد پردازش می گیرد اما فقط از مستطیل منظم به عنوان علامت استفاده می کند [ 19 ]. در نهایت، روش مبتنی بر مدل کنتور فعال-فعال، که معمولا در روش‌های سنتی استفاده می‌شود، برای مقایسه استفاده می‌شود [ 20 ]. نتایج تجربی سه الگوریتم مقایسه نشان داده شده استشکل 9 . به منظور ارزیابی کمی نتایج تجربی با استفاده از ماتریس سردرگمی، نتایج تقسیم بندی سه الگوریتم به دست آمده است، همانطور که در شکل 9 a1-c1 نشان داده شده است. به منظور ارزیابی کیفی نتایج تجربی به صورت بصری، نتایج استخراج شیء از سه الگوریتم با تصاویر آزمایشی مطابقت داده شده است، همانطور که در شکل 9 نشان داده شده است.a2–c2. نتایج تجربی نشان می‌دهد که الگوریتم‌های مبتنی بر پیکسل و مدل کانتور فعال اثر بخش‌بندی خوبی بر روی زمین‌های برهنه با اندازه‌گیری طیفی یکنواخت دارند، اما برای مناطق جنگلی با اندازه‌گیری طیفی ناهموار، نویز زیادی در نتایج تجربی ایجاد می‌شود. روش مبتنی بر فرآیند نقطه علامت قانون دارای اثر موقعیت یابی خوبی بر روی اجسام زمین برهنه است اما اثر برازش هندسی ضعیفی دارد.

تصویر الگو ( شکل 5 الف) را به عنوان تصویر استاندارد بگیرید و نتایج تقسیم بندی الگوریتم پیشنهادی و سه الگوریتم مقایسه ( شکل 8 a و شکل 9 a1-c1) را به عنوان تصویر آزمایشی برای ایجاد ماتریس سردرگمی در نظر بگیرید. سپس شاخص دقت را با توجه به ماتریس سردرگمی محاسبه کنید و نتایج در جدول 2 نشان داده شده است.. از جدول می توان دریافت که دقت کاربر در ناحیه پس زمینه و دقت محصول ناحیه شی که بر اساس الگوریتم پیکسل و الگوریتم مدل کانتور فعال هستند از الگوریتم پیشنهادی بالاتر است. این به این دلیل است که توزیع اندازه گیری طیفی ناحیه شی نسبتاً یکنواخت است، بنابراین این دو الگوریتم نتایج تقسیم بندی بهتری برای ناحیه جسم دارند. با این حال، برای منطقه پس‌زمینه با توزیع اندازه‌گیری طیفی پیچیده، دو الگوریتم نویز زیادی تولید می‌کنند که دقت کلی نتایج تجربی را کاهش می‌دهد. اگرچه الگوریتم فرآیند نقطه علامت قانون نویز زیادی تولید نمی کند، اما دقت کلی آن نیز به دلیل اثر برازش ضعیف آن بر روی مرز اجسام زمینی تحت تأثیر قرار می گیرد. به طور کلی،

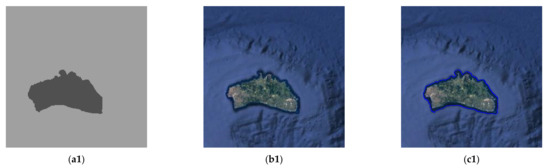
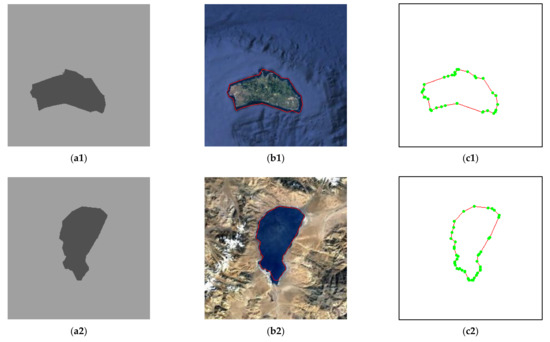
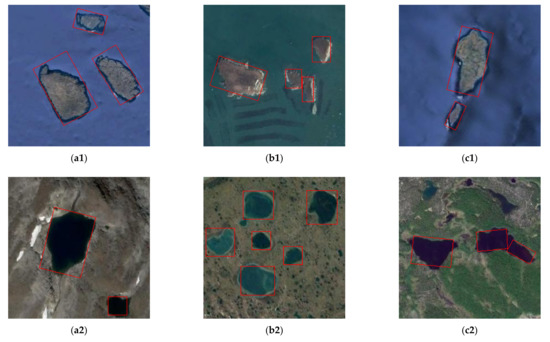
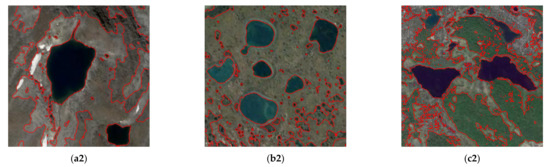
3.2. آزمایش تصویر واقعی

به منظور جلوگیری از ایده‌آل‌سازی بیش از حد تجزیه و تحلیل کمی نتایج تجربی با استفاده از تصاویر مصنوعی، دو تصویر سنجش از دور واقعی [ 21 ] با جزایر و دریاچه‌ها به عنوان اجسام برای آزمایش استخراج شی زمینی انتخاب می‌شوند. خط مرزی با تجزیه و تحلیل بصری از طریق مشاهده انسان تعیین می شود. از آنجایی که برخی از خطاها در خط مرزی جسم تعیین شده توسط دید انسان وجود خواهد داشت، تنها تصویر سنجش از دور با یک شی در آزمایش انتخاب می شود. همانطور که در شکل 10 نشان داده شده است ، شکل 10 b1,b2 به ترتیب تصاویر سنجش از دور جزایر و دریاچه ها هستند. شکل 10 c1,c2 مرزهای جسم تعیین شده به صورت دستی هستند (خط آبی ثابت در شکل). شکل 10a1,a2 الگوهای تصویر استاندارد برای مرزهای شیء تعیین شده مصنوعی برای ارزیابی کمی نتایج تجربی هستند.

الگوریتم پیشنهادی برای آزمایش در شکل 10 b1,b2 استفاده شده است و نتایج تجربی در شکل 11 نشان داده شده است. در میان آنها، شکل 10 c1,c2 نتایج استخراج شی هستند. نقاط سبز جامد در شکل نشان دهنده گره های مورد استفاده برای تشکیل چند ضلعی است و تعداد گره ها به ترتیب 35 و 44 است. هر گروه از گره ها به طور متوالی با خطوط قرمز یکپارچه به هم متصل می شوند تا چند ضلعی را تشکیل دهند که به ترتیب برای جا دادن اجسام جزیره و دریاچه استفاده می شود. چند ضلعی تشکیل شده با تصویر تجربی ( شکل 10 b1,b2) برای ارزیابی بصری قرار می گیرد. نتایج برهم نهی در شکل 11 نشان داده شده استb1، b2. از شکل می توان دریافت که چند ضلعی تشکیل شده توسط نتایج تجربی نه تنها می تواند مکان جزیره و دریاچه را تعیین کند، بلکه به طور دقیق هندسه آنها را نیز مطابقت می دهد. به منظور ارزیابی کمی نتایج تجربی، نتایج شی استخراج شده به نتایج تقسیم بندی تبدیل می شوند، همانطور که در شکل 11 a1,a2 نشان داده شده است.

ما همچنین از سه الگوریتم مقایسه برای آزمایش با شکل 10 b1,b2 استفاده می کنیم و نتایج تجربی در شکل 12 نشان داده شده است. شکل 12 a1-c1 نتایج تقسیم بندی سه الگوریتم مقایسه را در تصویر جزیره و شکل 12 نشان می دهد.a2-c2 نتایج استخراج شی از سه الگوریتم مقایسه را در تصویر جزیره نشان می دهد. در تصویر جزیره، با مقایسه شی جزیره با پس زمینه، می توان دریافت که توزیع اندازه گیری طیفی در ناحیه پس زمینه یکنواخت تر از ناحیه هدف است. بنابراین، در نتایج تجربی بر اساس الگوریتم پیکسل و کانتور فعال، ناحیه شی نویز بیشتری تولید می‌کند، در حالی که در ناحیه پس‌زمینه، نویز فقط در برخی مناطق با توزیع اندازه‌گیری طیفی ناهموار وجود دارد. شکل 12 a3-c3 نتایج تقسیم بندی سه الگوریتم مقایسه را در تصویر دریاچه و شکل 12 نشان می دهد.a4-c4 نتایج استخراج شیء از سه الگوریتم مقایسه را در تصویر دریاچه نشان می دهد. در تصویر دریاچه، توزیع اندازه‌های طیفی پیکسل در ناحیه دریاچه یکنواخت‌تر از ناحیه پس‌زمینه است. بنابراین، در نتایج تجربی بر اساس الگوریتم پیکسل و کانتور فعال، نویز بیشتری در ناحیه پس‌زمینه ایجاد می‌شود. الگوریتم فرآیند نقطه علامت قانون نویز تولید نمی کند، اما اثر برازش مرز ناحیه شی ایده آل نیست، چه برای تصویر جزیره با توزیع شی پیچیده و چه برای تصویر دریاچه با توزیع پس زمینه پیچیده.

ما تصاویر استاندارد تصویر جزیره و تصویر دریاچه (همانطور که در شکل 10 a1,a2 نشان داده شده است) و نتایج تقسیم بندی چهار روش (همانطور که در شکل 11 a1,a2 و شکل 12 a1-c1,a3-c3 نشان داده شده است) مقایسه می کنیم. برای ایجاد ماتریس سردرگمی هر شاخص دقت با توجه به ماتریس سردرگمی محاسبه می شود و نتایج محاسبه در جدول 3 نشان داده شده است.. در نتایج الگوریتم پیکسل و الگوریتم کانتور فعال، تنها دقت کاربر در ناحیه پس‌زمینه و دقت محصول ناحیه شی در تصویر دریاچه بالا است. این به این دلیل است که توزیع اندازه گیری طیفی پیکسل در ناحیه جسم تصویر دریاچه نسبتاً یکنواخت است. در مقایسه با مساحت جسم تصویر دریاچه، توزیع اندازه‌گیری‌های طیفی پیچیده‌تر است، که منجر به دقت نتیجه پایین و کاهش دقت کلی دو الگوریتم می‌شود. دقت الگوریتم فرآیند نقطه علامت قانون بیشتر از این دو الگوریتم است، بنابراین دقت کل نیز بهتر از این دو الگوریتم است. برای الگوریتم پیشنهادی، اگرچه دقت کاربر در ناحیه پس‌زمینه و دقت محصول ناحیه شی در تصویر دریاچه ممکن است کمتر از سه الگوریتم مقایسه باشد. دقت دیگر بالاتر است که دقت کلی الگوریتم را بهبود می بخشد. همچنین از دقت کل، ضریب کاپا و اندازه گیری F1 می توان دریافت که الگوریتم پیشنهادی به طور قابل توجهی بهتر از سه الگوریتم مقایسه است.

شکل 13 شش تصویر انتخاب شده از مجموعه داده های تشخیص اشیاء سنجش از راه دور هوافضا [ 21 ] را نشان می دهد که توسط دانشگاه فناوری نورث وست مشخص شده اند، که همگی 256 × 256 پیکسل هستند. شکل 13 a1-c1 سه تصویر جزیره و شکل 13 را نشان می دهدa2-c2 سه تصویر دریاچه را نشان می دهد. از تصویر می توان دریافت که اندازه های طیفی پیکسل ها در ناحیه پس زمینه تصاویر سه جزیره به طور مساوی توزیع شده اند و اندازه های طیفی پیکسل های شی کاملاً متفاوت است. توزیع اندازه گیری طیفی پیکسل ها در ناحیه پس زمینه سه تصویر دریاچه پیچیده تر است، در حالی که توزیع اندازه گیری طیفی پیکسل های جسم یکنواخت تر است. اشکال هندسی اجسام در این شش تصویر مشخصه های نامنظم را نشان می دهند.

الگوریتم پیشنهادی برای آزمایش تصویر سنجش از دور در شکل 13 استفاده می شود. نتایج تجربی در شکل 14 نشان داده شده است. در شکل، نقاط سبز جامد، گره‌های تشکیل‌دهنده هندسه شی زمین را نشان می‌دهند، و خطوط قرمز ثابت هندسه شی استخراج‌شده را نشان می‌دهند. در میان آنها، شکل 14 a1-c1 نتایج استخراج اجسام جزیره را نشان می دهد و تعداد اشیاء استخراج شده به ترتیب چهار، سه و دو است که با نتایج تفسیر بصری در تصویر آزمایشی یکسان است. شکل 14a2-c2 نتایج دریاچه استخراج شده را نشان می دهد و تعداد اجرام استخراج شده به ترتیب دو، شش و چهار است. نتایج استخراج دو تصویر اول با نتایج تفسیر بصری مطابقت دارد، در حالی که تعداد اجسام سطحی که به صورت بصری در شکل 14 c2 تفسیر شده اند باید 3 باشد. در نتایج تجربی، از دو چند ضلعی برای جا دادن یک شی دریاچه استفاده شده است.

نتایج استخراج شی با تصاویر تجربی برای ارزیابی کیفی، همانطور که در شکل 15 نشان داده شده است، قرار می گیرند . الگوریتم پیشنهادی نه تنها می‌تواند شیء را دقیقاً مکان‌یابی کند، بلکه می‌تواند هندسه آن را هم برای تصاویر جزیره و هم برای تصاویر دریاچه به طور دقیق منطبق کند. هنگامی که یک چند ضلعی نمی تواند برای جا دادن یک شی مورد استفاده قرار گیرد، الگوریتم به طور خودکار چند ضلعی را برای جا دادن یک شی زمین تشخیص می دهد.

در این مقاله، از روش پردازش تصویر مبتنی بر پیکسل برای آزمایش با شش تصویر سنجش از دور در شکل 13 استفاده شده است. نتایج تجربی در شکل 16 نشان داده شده است. در میان آنها، شکل 16 a1-c1 نتایج تجربی سه تصویر جزیره را نشان می دهد. مقادیر اندازه‌گیری طیفی پیکسل در ناحیه شی بسیار متفاوت است، در حالی که مقادیر اندازه‌گیری طیفی پیکسل در ناحیه پس‌زمینه در مقایسه با ناحیه شی نسبتاً کوچک است، که باعث ایجاد نویز بیشتر در ناحیه شی و نویز کمتری در ناحیه پشت می‌شود. شکل 16 c1. شکل 16a2-c2 نتایج تجربی سه تصویر دریاچه را نشان می دهد. مقادیر اندازه‌گیری طیفی پیکسل در ناحیه پس‌زمینه دارای تفاوت زیادی هستند، در حالی که مقادیر اندازه‌گیری طیفی پیکسل در ناحیه هدف تفاوت کمی نسبت به ناحیه پس‌زمینه دارند. بنابراین، در نتایج تجربی، نویز در ناحیه شی نسبتا کمتر و نویز در ناحیه پس‌زمینه نسبتاً بیشتر است.

در این مقاله از الگوریتم فرآیند نقطه علامت گذاری با یک مستطیل به عنوان علامت برای آزمایش بر روی شش تصویر استفاده شده است. نتایج تجربی در شکل 17 نشان داده شده است. شکل 17 a1-c1 نتایج تجربی سه تصویر جزیره را نشان می دهد و تعداد اجسام زمینی استخراج شده به ترتیب سه، چهار و دو است. شکل 17a2-c2 نتایج تجربی سه تصویر دریاچه را نشان می دهد و تعداد اجرام زمینی استخراج شده به ترتیب دو، شش و سه است. شکل هندسی جسم استخراج شده توسط این الگوریتم مستطیل است زیرا علامت از پیش تعریف شده این الگوریتم مستطیل است. یک مستطیل به سختی می‌تواند جسم زمینی را با ویژگی‌های هندسی نامنظم منطبق کند، که دقت کلی نتایج تجربی را کاهش می‌دهد.

در این مقاله از الگوریتم مبتنی بر مدل کانتور فعال برای آزمایش بر روی شش تصویر استفاده شده است. نتایج تجربی در شکل 18 نشان داده شده است. از نتایج تجربی می توان دریافت که نویز بیشتری در نتایج آزمایشی الگوریتم برای تصاویر جزیره ای با تفاوت های زیاد در اندازه گیری های طیفی پیکسل در ناحیه جسم و تصاویر دریاچه با تفاوت های زیاد در اندازه گیری های طیفی پیکسل در ناحیه پس زمینه وجود خواهد داشت. اگرچه نویز کمتری نسبت به الگوریتم مبتنی بر پیکسل وجود دارد، اما موقعیت‌های تصاویر نویز اساساً یکسان است. بنابراین، مشاهده می‌شود که چه الگوریتم مبتنی بر یک پیکسل باشد و چه مدل کانتور فعال، دستیابی به اثر استخراج شیء دقیق‌تر برای مناطق با تفاوت‌های زیاد در اندازه‌های طیفی پیکسل دشوار است.

4. نتیجه گیری

با توجه به نامنظمی بودن شکل هندسی جسم زمینی در تصویر سنجش از دور، بر اساس تئوری فرآیند نقطه هندسی تصادفی، این مقاله یک روش جدید استخراج شی زمینی مبتنی بر فرآیند نقطه خوشه‌بندی علامت پیشنهاد می‌کند و موقعیت، توزیع را بیان می‌کند. و شکل هندسی جسم زمینی. در این مقاله از روش آماری سنتی برای تشخیص استفاده شده است که نیاز به نمونه برداری زیادی دارد، بنابراین سرعت آزمایش کند است. بنابراین، در آزمایش، فقط اشیاء تصویری کوچک با هندسه نامنظم آشکار دارای ویژگی‌های هندسی هستند. در کار آینده، ما می توانیم چگونگی تشخیص سریع شی تصاویر بزرگ یا تصاویر با صحنه های پیچیده تر را در نظر بگیریم.

منابع

Foschini، GJ; Gans, MJ در مورد محدودیت‌های ارتباطات بی‌سیم در محیط محو شدن هنگام استفاده از آنتن‌های متعدد. سیم. پارس اشتراک. 1998 ، 6 ، 311-335. [ Google Scholar ] [ CrossRef ]
ماسودا، ر. Inoue، تشخیص خوشه رویداد نقطه R. از طریق کمند ذوب شده تعمیم یافته بیزی. ISPRS Int. J. Geo-Inf. 2022 ، 11 ، 187. [ Google Scholar ] [ CrossRef ]
هارون، م. شهزاد، م. تشخیص شی چند اندازه فراز، MM با استفاده از تصاویر نوری فضابرد. IEEE J. Sel. بالا. Appl. زمین Obs. Remote Sens. 2020 , 13 , 3032–3046. [ Google Scholar ] [ CrossRef ]
اروس، جی. Loménie, N. چگونه می توان مدل سازی ساختاری را برای وظایف تشخیص اشیاء نقشه برداری در تصاویر ماهواره ای با وضوح بالا در نظر گرفت. تشخیص الگو Lett. 2010 ، 31 ، 1109-1119. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
خو، ی. Xiong، W. Liu, J. الگوریتم جدید تشخیص هدف کشتی بر اساس SVM در تصاویر SAR با وضوح بالا. در مجموعه مقالات کنفرانس بین المللی پیشرفت در پردازش تصویر، بانکوک، تایلند، 25 تا 27 اوت 2017. [ Google Scholar ]
یوکویا، ن. Iwasaki، A. تشخیص شیء بر اساس نمایش پراکنده و رای Hough برای تصاویر سنجش از دور نوری. IEEE J. Sel. بالا. Appl. زمین Obs. Remote Sens. 2015 ، 8 ، 2053–2062. [ Google Scholar ] [ CrossRef ]
چن، اچ. گائو، تی. کیان، جی. چن، دبلیو. Zhang، Y. تبدیل Hough تعمیم یافته تنسور شده برای تشخیص شی در تصاویر سنجش از دور. IEEE J. Sel. بالا. Appl. زمین Obs. Remote Sens. 2020 , 13 , 3503–3520. [ Google Scholar ] [ CrossRef ]
سان، اچ. سان، ایکس. وانگ، اچ. لی، ی. Li، X. تشخیص خودکار هدف در تصاویر سنجش از دور با وضوح بالا با استفاده از مدل کیسه کلمات کدگذاری پراکنده فضایی. IEEE Geosci. سنسور از راه دور Lett. 2011 ، 9 ، 109-113. [ Google Scholar ] [ CrossRef ]
بادلی، ای جی; مدل‌های هندسه تصادفی Lieshout، MNMV در دید سطح بالا. J. Appl. آمار 1993 ، 20 ، 231-256. [ Google Scholar ] [ CrossRef ]
پیواتولو، ا. سبز، تشخیص مرز PJ از طریق چند ضلعی های پویا. JR Stat. Soc.: Ser. B (Stat. Methodol.) 1998 ، 60 ، 609-626. [ Google Scholar ] [ CrossRef ]
ژائو، کیو. ژانگ، اچ. Li، Y. تشخیص نقاط تاریک از تصاویر با شدت SAR توسط یک فرآیند نقطه ای با علائم هندسی نامنظم. بین المللی J. Remote Sens. 2019 , 40 , 774–793. [ Google Scholar ] [ CrossRef ]
دسکامبز، ایکس. Zerubia, J. فرآیند نقطه مشخص شده در تجزیه و تحلیل تصویر. فرآیند سیگنال IEEE Mag. 2002 ، 19 ، 77-84. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
اورتنر، ام. دسکامبز، ایکس. Zerubia, J. استخراج طرح کلی ساختمان از مدل های ارتفاعی دیجیتال با استفاده از فرآیندهای نقطه مشخص شده. بین المللی جی. کامپیوتر. Vis. 2007 ، 72 ، 107-132. [ Google Scholar ] [ CrossRef ]
پرین، جی. دسکامبز، ایکس. Zerubia, J. یک مدل فرآیند نقطه مشخص برای استخراج تاج درخت در مزارع. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد پردازش تصویر، جنوا، ایتالیا، 14 سپتامبر 2005. [ Google Scholar ]
لاکوست، سی. دسکامبز، ایکس. فرآیندهای زروبیا، J. نقطه برای استخراج شبکه خط بدون نظارت در سنجش از دور. IEEE Trans. الگوی مقعدی ماخ هوشمند 2005 ، 27 ، 1568-1579. [ Google Scholar ] [ CrossRef ] [ PubMed ]
اورتنر، ام. دسکامبز، ایکس. Zerubia, J. یک فرآیند نقطه مشخص از مستطیل ها و بخش ها برای تجزیه و تحلیل خودکار مدل های ارتفاعی دیجیتال. IEEE Trans. الگوی مقعدی ماخ هوشمند 2007 ، 30 ، 105-119. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
لافارژ، اف. گیمل فارب، جی. Descombes، X. استخراج ویژگی هندسی توسط یک فرآیند نقطه چند علامت. IEEE Trans. الگوی مقعدی ماخ هوشمند 2009 ، 32 ، 1597-1609. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
شرر، بی. دکتر، م. فوربس، اف. گاربای، سی. عامل تقسیم بندی مبتنی بر مدل مارکوف: کاربرد در اسکن مغز با رزونانس مغناطیسی. آرتیف. هوشمند پزشکی 2009 ، 46 ، 81-95. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
لی، ی. Li, J. تشخیص نشت نفت از تصاویر شدت SAR با استفاده از فرآیند نقطه مشخص شده. سنسور از راه دور محیط. 2010 ، 114 ، 1590-1601. [ Google Scholar ] [ CrossRef ]
دینگ، ک. شیائو، ال. Weng, G. خطوط فعال که توسط انرژی از پیش تنظیم شده محلی برای تقسیم‌بندی سریع تصویر هدایت می‌شوند. تشخیص الگو Lett. 2018 ، 104 ، 29-36. [ Google Scholar ] [ CrossRef ]
چنگ، جی. هان، جی. Lu, X. طبقه بندی صحنه تصویر سنجش از دور: معیار و وضعیت هنر. Proc. IEEE 2017 ، 105 ، 1865-1883. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]

شکل 1. علامت گذاری فرآیند نقطه خوشه بندی برای مدل سازی هندسه شی زمین: ( الف ) فرآیند نقطه خوشه بندی. ( ب ) فرآیند نقطه خوشه بندی علامت.

شکل 2. مثال‌های افزودن و حذف یک چند ضلعی: ( الف ) پیکربندی w^( t ) شی; ( ب ) یک چند ضلعی اضافه کنید. ( ج ) یک چند ضلعی را حذف کنید.

شکل 3. نمونه هایی از افزودن و حذف یک گره چند ضلعی: ( الف ) پیکربندی w^( t ) شی; ( ب ) یک گره چند ضلعی اضافه کنید. ( ج ) یک گره چند ضلعی را حذف کنید.

شکل 4. مثال ادغام چند ضلعی ها: ( الف ) پیکربندی w^( t ) شی. ( ب ) چند ضلعی ها را ادغام کنید.

شکل 5. تصاویر مصنوعی: ( الف ) تصویر الگو. ( ب ) تصویر مصنوعی. ( ج ) کانتور استاندارد.

شکل 6. نرخ پذیرش عملیات های مختلف در طول تکرار: ( الف ) میزان پذیرش چندضلعی های اضافه. ( ب ) میزان پذیرش چند ضلعی های حذف شده. ( ج ) میزان پذیرش گره های چند ضلعی افزودن. ( د ) میزان پذیرش گره های چند ضلعی حذف. ( ه ) میزان پذیرش چند ضلعی های ادغام شده.

شکل 7. فرآیند استخراج شی زمین از تصاویر مصنوعی: ( الف ) مقداردهی اولیه. ( ب ) تکرار بیستم؛ ( ج ) چهلمین تکرار؛ ( د ) تکرار 60; ( ه ) هشتادمین تکرار؛ ( f ) تکرار 200; ( g ) تکرار 580; ( h ) تکرار 600; ( i ) تکرار 4000.

شکل 8. نتایج تجربی تصویر مصنوعی: ( الف ) نتایج تقسیم‌بندی. ( ب ) نتایج استخراج. ( ج ) کانتور را استخراج کنید.

شکل 9. نتایج تجربی الگوریتم مقایسه: ( a1 ) روش مبتنی بر پیکسل. ( ب 1 ) فرآیند نقطه علامت قانون. ( ج 1 ) مدل کانتور فعال; ( a2 ) نتایج تشخیص شیء بر اساس روش پیکسل. ( b2 ) نتایج تشخیص شیء بر اساس فرآیند نقطه علامت قانون. ( c2 ) نتایج تشخیص شیء بر اساس مدل کانتور فعال.

شکل 10. تصاویر تجربی جزیره و دریاچه: ( a1 ) تصویر استاندارد جزیره; ( b1 ) تصویر جزیره; ( ج1 ) کانتور استاندارد جزیره; ( a2 ) تصویر استاندارد دریاچه; ( b2 ) تصویر دریاچه; ( ج2 ) کانتور استاندارد دریاچه.

شکل 11. نتایج استخراج جزیره و دریاچه: ( a1 ) نتایج تقسیم بندی جزیره. ( b1 ) نتایج پوشش کانتور. ( ج1 ) نتایج استخراج جزیره. ( a2 ) نتایج تقسیم بندی دریاچه. ( b2 ) نتایج پوشش کانتور. ( ج2 ) نتایج استخراج دریاچه.

شکل 12. نتایج تجربی الگوریتم مقایسه: ( a1 ) تقسیم بندی جزیره مبتنی بر پیکسل. ( b1 ) تقسیم بندی جزیره علامت قانون. ( c1 ) تقسیم بندی جزیره کانتور فعال. ( a2 ) استخراج جزیره مبتنی بر پیکسل. ( b2 ) استخراج جزیره علامت قانون; ( c2 ) استخراج جزیره کانتور فعال. ( a3 ) تقسیم بندی دریاچه مبتنی بر پیکسل. ( b3 ) تقسیم بندی دریاچه علامت قانون؛ ( ج3 ) تقسیم بندی دریاچه های کانتور فعال. ( a4 ) استخراج دریاچه مبتنی بر پیکسل. ( b4 ) استخراج دریاچه علامت قانون; ( ج4 ) استخراج دریاچه کانتور فعال.

شکل 13. تصاویر سنجش از دور چندطیفی: ( a1 ) تصویر جزیره 1; ( b1 ) تصویر جزیره 2; ( ج 1) تصویر جزیره 3; ( a2 ) دریاچه تصویر 1; ( b2 ) دریاچه تصویر 2; ( ج 2) تصویر دریاچه 3.

شکل 14. نتایج تجربی تصاویر سنجش از دور: ( a1 ) تصویر جزیره 1; ( b1 ) تصویر جزیره 2; ( ج 1) تصویر جزیره 3; ( a2 ) دریاچه تصویر 1; ( b2 ) دریاچه تصویر 2; ( ج 2) تصویر دریاچه 3.

شکل 15. ارزیابی بصری تصاویر سنجش از دور چندطیفی: ( a1 ) تصویر جزیره 1. ( b1 ) تصویر جزیره 2; ( ج 1) تصویر جزیره 3; ( a2 ) دریاچه تصویر 1; ( b2 ) دریاچه تصویر 2; ( ج 2) تصویر دریاچه 3.

شکل 16. نتایج تجربی بر اساس الگوریتم پیکسل: ( a1 ) تصویر جزیره 1; ( b1 ) تصویر جزیره 2; ( ج 1) تصویر جزیره 3; ( a2 ) دریاچه تصویر 1; ( b2 ) دریاچه تصویر 2; ( ج 2) تصویر دریاچه 3.

شکل 17. نتایج تجربی بر اساس الگوریتم فرآیند نقطه علامت گذاری قانون: ( a1 ) تصویر جزیره 1; ( b1 ) تصویر جزیره 2; ( ج 1) تصویر جزیره 3; ( a2 ) دریاچه تصویر 1; ( b2 ) دریاچه تصویر 2; ( ج 2) تصویر دریاچه 3.

شکل 18. نتایج تجربی بر اساس الگوریتم مدل کانتور فعال: ( a1 ) تصویر جزیره 1; ( b1 ) تصویر جزیره 2; ( ج 1) تصویر جزیره 3; ( a2 ) دریاچه تصویر 1; ( b2 ) دریاچه تصویر 2; ( ج 2) تصویر دریاچه 3.

مقالات داخلی و بین المللی

9 نظرات

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

کلید واژه ها:

1. مقدمه