ساده سازی ساختمان یک حوزه تحقیقاتی مهم در تعمیم خودکار نقشه است. تاکنون رویکردهای زیادی توسط محققان ارائه شده است. با این حال، در تغییر مداوم مقیاس ها برای ساختمان ها، حفظ ویژگی های شکل اصلی، مساحت و متعامد بودن ساختمان ها همیشه از نکات کلیدی و دشوار است. بنابراین، این مقاله روشی برای ساده‌سازی پیشرونده برای ساختمان‌ها بر اساس تقسیم‌بندی ساختاری پیشنهاد می‌کند. در این مقاله، ساده‌سازی تکراری اتخاذ شده است که مسئله ساده‌سازی ساختمان را به ساده‌سازی حداقل جزئیات خطوط کلی ساختمان تبدیل می‌کند. اولا، یک ساختار اولویت اصلی ( TPS) تعیین می شود که نشان دهنده کوچکترین جزئیات در طرح کلی ساختمان است. سپس، با توجه به متعامد بودن و ویژگی‌های مقعر- محدب، TPS به‌عنوان 62 زیربخش طبقه‌بندی می‌شوند که ساختار محلی چند ضلعی ساختمان را پوشش می‌دهند. سپس تقسیمات فرعی به چهار نوع ساده سازی تقسیم می شوند. ساختمان برای حذف TPS ساده شده استبه طور مداوم، تا حد امکان ویژگی های زاویه راست و مساحت را حفظ می کند تا زمانی که نتایج محدودیت ها و قوانین ساده سازی را برآورده کند. یک مجموعه داده توپوگرافی (1:1 K) جمع آوری شده از Kadaster برای آزمایش های ما استفاده شد. به منظور ارزیابی الگوریتم، آزمایش‌های زیادی از جمله آزمون‌های ساده‌سازی چند مقیاسی و ساده‌سازی ساختمان‌های معمولی انجام شد که نشان می‌دهد این روش می‌تواند ارائه چند مقیاسی ساختمان‌ها را محقق کند. در مقایسه با روش‌های ساده‌سازی موجود، نتایج مقایسه نشان می‌دهد که روش پیشنهادی می‌تواند ساختمان‌ها را به طور موثر ساده‌سازی کند که دارای مزایای خاصی در حفظ ویژگی‌های شکل، مساحت و مستطیل‌شدن است.

کلید واژه ها:

ساده سازی ساختمان ; ارائه چند مقیاسی ؛ تعمیم کارتوگرافی خودکار

1. مقدمه

ساده سازی ساختمان (گروهی) موضوع مهمی در تعمیم نقشه برداری خودکار نقشه های بزرگ مقیاس است [ 1 ، 2 ، 3 ]. هدف آن این است که ساختمان ها را به طور مختصرتر بسته به مقیاس نقشه یا موضوع، با الزامات خوانایی و نمایش خوب واقعیت نشان دهد [ 4 ]]. ساختمان‌ها به عنوان اشیای مهم دست‌ساخته در نقشه‌های توپوگرافی، دارای ویژگی‌های شکلی منحصربه‌فردی هستند که آن‌ها را از اشیاء طبیعی متمایز می‌کند، مانند مستطیل بودن و متعامد بودن. در نتیجه، بسیاری از الگوریتم‌های ساده‌سازی ساختمان‌ها در سال‌های اخیر برای این هدف پیشنهاد شده‌اند. ساده‌سازی می‌تواند بار شناختی کاربران نقشه را در مقیاس‌های کوچک‌تر کاهش دهد، که به آنها کمک می‌کند روابط ضمنی را به دست آورند. علاوه بر این، ساده‌سازی پیشرونده ساختمان‌ها می‌تواند تجربه بصری «پیوسته» و «زوم بدون پله» را برای کاربران فراهم کند. علاوه بر کاربرد آن در کارتوگرافی سنتی، ساده‌سازی ساختمان‌ها همچنین به ساده‌سازی طرح کلی ساختمان‌های استخراج‌شده از تصاویر سنجش از دور با وضوح بالا کمک می‌کند و شکل ساختمان‌ها را منظم‌تر می‌کند [ 5 ]]. در شناسایی نواحی عملکردی شهری، اشکال ساختمان‌ها در مقیاس‌های مختلف، مبنای مهمی برای استخراج اطلاعات مکانی است [ 6 ، 7 ]. ساده سازی ساختمان معمولاً روی یک ساختمان واحد انجام می شود که عمدتاً مستقل از اطلاعات زمینه ای است. علاوه بر این، گاهی اوقات می توان آن را به طور جداگانه در فرآیند تعمیم نقشه ساخت [ 8 ] انجام داد. این مقاله فقط بر روی ساده سازی طرح های ساختمانی فردی متمرکز است.
ساده سازی ساختمان های منفرد عملیات اساسی در تعمیم نقشه برداری است [ 2 ]. مشکل ساده‌سازی ساختمان، محاسبه ساده‌سازی یک زیربخش معین است، مشروط به محدودیت‌های مختلفی که بر حفظ ویژگی‌های مهم و زیبایی‌شناسی ساختمان‌های ساده‌شده تأثیر می‌گذارد [ 9 ]. برخی از الزامات اساسی در ساده سازی ساختمان وجود دارد. ابتدا ساختمان های ساده شده باید خوانا باشند [ 10]. با کاهش مقیاس، لبه های کوتاهی که طول آنها کوچکتر از آستانه تعیین شده است حذف می شوند. دوم، حفظ یا تقویت ویژگی های اصلی یک ساختمان محدودیت مهم دیگری است، از جمله موقعیت، اندازه، جهت گیری و متعامد بودن. علاوه بر این، ویژگی معمولی شکل باید حفظ شود و شکل قبل و بعد از ساده سازی مشابه حفظ شود. برای مثال، اگر طرح کلی یک ساختمان مانند حرف E به نظر می رسد، ساختمان ساده شده باید از نظر ویژگی های شکل سازگار باشد. به ویژه، ساختمان های ساده شده در تغییر مقیاس پیوسته نقشه ها به صورت تدریجی شکل می گیرند. سوم، روش ساده سازی را می توان برای انواع مختلف ساختمان ها اعمال کرد. برای مثال، برخی روش‌ها ساختمان‌هایی را با ویژگی‌های متعامد فرض می‌کنند [ 11 ،12 ، 13 ]. با این حال، در کلمه واقعی، ساختمان ها نه تنها دارای ویژگی های متعامد هستند، بلکه دارای ویژگی های غیر متعامد نیز هستند [ 14 ]. چندین روش موجود در این زمینه به دلیل طبقه‌بندی و ساده‌سازی نادر انواع سازه‌های ساختمان‌ها با پوشش کامل، از نظر کاربرد محدود هستند.
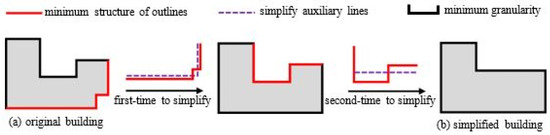
از این رو، در دگرگونی مداوم مقیاس‌ها برای ساختمان‌ها، حفظ ویژگی‌های اصلی، مساحت و متعامد بودن خطوط کلی ساختمان، به‌ویژه برای برخی از ساختمان‌ها با ویژگی‌های غیرمتعامد و اشکال پیچیده، همواره از نکات کلیدی و دشوار است. با توجه به اینکه ماهیت ساده سازی ساختمان حذف، جابجایی و ساخت رئوس بر اساس اصل ساده سازی است [ 15 ]]، ساده سازی ساختمان فرآیند حذف و ادغام حداقل جزئیات به طور مداوم است. ما یک رویکرد ساده سازی ساختمانی پیشرو بر اساس تقسیم بندی ساختاری را پیشنهاد می کنیم. ساده‌سازی تکراری اتخاذ شده است که مشکل ساده‌سازی ساختمان را به ساده‌سازی حداقل جزئیات خطوط کلی ساختمان تبدیل می‌کند. در ابتدا، یک ساختار اولویت اصلی ( TPS ) تعیین می شود که نشان دهنده کوچکترین جزئیات در طرح کلی ساختمان است. سپس با توجه به ویژگی‌های متعامد و مقعر محدب TPS ، نوع ساده‌سازی در چهار نوع ساده‌سازی تعیین می‌شود. ساختمان برای حذف TPS ساده شده استبه طور مداوم، شکل، متعامد بودن و مساحت را تا حد امکان حفظ می کند تا زمانی که ساختمان الزامات ساده سازی را برآورده کند.

2. آثار مرتبط

ساده‌سازی ساختمان‌ها یک مشکل کلاسیک در تعمیم نقشه است، که عنصر اساسی تعمیم زمانی است که اطلاعات “خام” آنقدر پیچیده یا فراوان باشد که به طور کامل در مقیاس نقشه همانطور که وجود دارد بازتولید شود. در آغاز دهه 1940، رایت (1942) [ 16 ] به قابلیت اطمینان علمی نقشه ها اشاره کرد که به طور قطعی به تعمیم بستگی دارد. به گفته وی، ساده سازی و تقویت دو عنصر تعمیم هستند. Raisz (1962) [ 17 ] دیدگاه های مربوط به تعمیم را گسترش داد. به نظر او قواعد خاصی برای تعمیم وجود ندارد که ترکیبی از سه پردازش شده است: تداعی، حذف و ساده سازی. با مراجعه به رابینسون و همکاران. (1978) [ 18]، انتخاب و چهار عنصر تعمیم نقشه‌کشی، ساده‌سازی، طبقه‌بندی، نمادسازی و استقراء در طول تدوین نقشه‌ها اعمال می‌شود. راتاجسکی (1989) [ 19 ] با تمایز دو نوع تعمیم، از موضع رابینسون حمایت کرد: کیفی و کمی. مک مستر و شی (1992) [ 20 ] مدلی را برای تعمیم دیجیتالی ایجاد کردند و سعی کردند به سه سوال پاسخ دهند: چرا، کی و چگونه باید تعمیم داد.
به گفته لی و همکاران. (2005) [ 21 ] و وانگ و همکاران. (2005) [ 22 ]، یک روش مؤثر برای ساده سازی یک ساختمان فردی معمولاً قوانین زیر را در نظر می گیرد:
  • اگر یک ساختمان دارای لبه های کوتاه تر از طول مشخص باشد، باید ساده شود.
  • مشخصات مورفولوژیکی باید تا حد امکان مشابه باشد.
  • مرکز بصری ساختمان بدون تغییر باقی مانده است.
  • شکل متعامد باید حفظ یا تقویت شود.
  • مساحت ساختمان باید تقریباً یکسان باشد.
  • اگر ساختمانی به یک مستطیل یا چهار ضلعی ساده شده باشد، دیگر ساده نمی شود.
بیش از آن، قوانین ساده سازی ساختمان امروزه غنی تر شده است. حفظ مساحت ساختمان ها باید با توجه به هدف نقشه برداری یا موقعیت های خاص تعیین شود. برای ساختمان های کوچک، بزرگ شدن یک روش معمولی است. از سوی دیگر، حفظ منطقه برای اهداف کاداستر مهم است. علاوه بر این، اشکال غیر مستطیلی و حتی شکل های مدور ساختمان ها در بسیاری از شهرها رایج است. بهبود سازگاری الگوریتم های ساده سازی برای ساختمان های مختلف ضروری است.
در حال حاضر، با توجه به نوع داده های مکانی، دو نوع روش ساده سازی ساختمان وجود دارد: روش ساده سازی مبتنی بر شطرنجی و روش ساده سازی مبتنی بر برداری. از آنجایی که این مقاله بر روی روش‌های مبتنی بر برداری تمرکز دارد، روش‌های مبتنی بر شطرنجی به تفصیل معرفی نمی‌شوند. روش های مبتنی بر برداری را می توان به مبتنی بر ساختار محلی، مبتنی بر الگو و مبتنی بر ترکیب طبقه بندی کرد.
در روش های مبتنی بر ساختار محلی، ساختمان ها با حذف جزئیات بی اهمیت یا کوچک ساده می شوند. رویکردی برای ساده‌سازی پلان‌های زمینی ساختمان ارائه شده است که مبتنی بر تکنیک‌های مدل‌سازی نیمه‌فضا و تجزیه سلولی است [ 23 ]. Haunert و Wolff (2008) [ 3 ] یک فرمول برنامه ریزی اکتشافی و یک عدد صحیح را برای ساده سازی ساختمان ها پیشنهاد کردند. بوچین و همکاران (2011) [ 24 ] عملیات edge-move را برای ساده سازی چند ضلعی معرفی کرد. روش حداقل مربعات نیز برای ساده سازی ساختمان استفاده می شود [ 2 ، 12 ، 25 ، 26 ]; Meijers (2016) [ 27] یک الگوریتم ساده مفهومی را برای ساده کردن خطوط کلی ساختمان بر اساس منحنی های افست به دست آمده از اسکلت مستقیم ارائه کرد. با این حال، فرآیند به دست آوردن اسکلت باعث کاهش کارایی می شود. حفظ زوایای قائمه یکی از محدودیت های اصلی درگیر در ساده سازی ساختمان ها است [ 2 ]. یک روش ساده سازی ساخت چند ضلعی با پیچ های قائم الزاویه با در نظر گرفتن حفظ اشکال و نواحی قائم الزاویه مورد بحث قرار گرفته است [ 11 ]. یک رویکرد چند عاملی برای مدل‌سازی اشیاء نقشه‌برداری و درمان در تعمیم، از جمله ساده‌سازی خطوط کلی ساختمان [ 28 ، 29 ] اعمال می‌شود. تکنیک‌های خود بهینه‌سازی قبلاً برای سیستم عاملی که تعمیم‌سازی را انجام می‌دهد مورد مطالعه قرار گرفته است [ 30]. جین و همکاران (2020) [ 31 ] یک روش ساده سازی مرز ساختمانی محدود را بر اساس حداقل مربعات جزئی ارائه کرد، که می تواند جابجایی های هندسی کوچک تری از ساختمان ها را نسبت به روش برازش مبتنی بر حداقل مربعات کلاسیک به دست آورد. یک الگوریتم ساده‌سازی با قضاوت ویژگی‌های ساختار لبه از چهار یا پنج نقطه مجاور [ 15 ، 32 ، 33 ] طراحی می‌شود که به ساده‌سازی انواع مختلف ساختمان‌ها دست می‌یابد. یین و همکاران (2020) [ 34 ] یک روش ساده سازی بازسازی لبه ویژگی برای ساخت چند ضلعی با طرح های فازی پیشنهاد کرد. برخی از انواع نرم افزارهای مورد استفاده برای تعمیم نقشه ها دارای عملکرد بیشتری برای تحقق ساده سازی ساختمان هستند [ 35 , 36، 37 ].
در روش‌های مبتنی بر الگو، ساختمان با جایگزینی با قالب‌های از پیش تعریف‌شده ساده‌سازی می‌شود که شبیه به ساختمان با فرم ساده‌تر است. Rainsford و Mackaness (2002) [ 4 ] یک روش ساده سازی ساختمان را بر اساس تطبیق شکل پیشنهاد کردند که ویژگی های شکل و مساحت را پس از ساده سازی با قابلیت عملی قوی حفظ می کند [ 38 ، 39 ، 40 ، 41 ]. با این حال، به دلیل محدودیت نوع کتابخانه الگو، برای ساده سازی چند ضلعی با ساختارهای پیچیده ایده آل نیست. در روش‌های مبتنی بر ترکیب، الگوریتم‌های مختلف برای دستیابی به کار ساده‌سازی ساختمان ترکیب می‌شوند. یانگ و همکاران با در نظر گرفتن الگوریتم‌های متعدد برای ساده‌سازی ساختمان‌ها. (2021) [ 42] یک رویکرد ترکیبی را ارائه کرد که بهترین نمایش ساده شده یک ساختمان را در میان چهار الگوریتم موجود برای ایجاد کاندیدهای ساده‌سازی با شبکه عصبی پس انتشار شناسایی می‌کند. وی و همکاران (2021) [ 8 ] یک رویکرد ساده سازی ترکیبی ساختمان را بر اساس طبقه بندی ساختار محلی پیشنهاد کرد. سازه های محلی با در نظر گرفتن ویژگی های متعامد و غیر متعامد ساختمان ها طبقه بندی و عملیاتی می شوند. با این حال، ساده سازی ساختمان فردی پایه و اساس رویکردهای ساده سازی ساختمانی ترکیبی است.
اخیراً از روش های سوپرپیکسلی و یادگیری عمیق برای ساده سازی چند ضلعی ها استفاده شده است. شن و همکاران (2018؛ 2019) [ 14 ، 43 ] روش جدیدی برای ساده سازی چند ضلعی ها با استفاده از تقسیم بندی سوپرپیکسلی پیشنهاد کرد. سستر و همکاران (2018) [ 44 ] یک شبکه کانولوشن عمیق را برای وظایف تعمیم کارتوگرافی اعمال کرد. فنگ و همکاران (2019) [ 45 ] شبکه یادگیری عمیق موجود را بهبود بخشید و امکان سنجی روش را اثبات کرد. روش ساده سازی مبتنی بر یادگیری ماشینی بسیار خودکار است، اما به شدت به کیفیت مجموعه آموزشی نمونه بستگی دارد.

3. روش شناسی

مشابه روش ساده سازی تکراری خطوط ارائه شده توسط داگلاس و پوکر (1973) [ 46 ]، ایده اصلی ساده سازی به شرح زیر است: ساده سازی ساختمان فرآیند کاهش جزئیات کوچک خطوط کلی تحت محدودیت های ساده سازی است. یک ساختار حداقلی از خطوط کلی، که حداقل جزئیات را برای ساده سازی ترجیحا ارائه می دهد، می تواند هر بار تعیین شود. ساختمان با تعیین و ساده سازی حداقل سازه به صورت مکرر ساده می شود. همانطور که شکل 1 نشان می دهد، ساختمان اصلی در شکل 1 a به شکل 1 ساده شده است .b پس از دو بار ساده سازی ساختار حداقل. کار اصلی رویکرد ما تعیین و طبقه بندی ساختار حداقل است. سپس به ترتیب الگوریتم ساده سازی ساختار حداقل ارائه می شود.

3.1. مفاهیم اساسی

برای توصیف بهتر، این مقاله پارامترهای زیر را تعریف می کند:
در این مقاله، برای هر چند ضلعی ساختمان فرض کنید بv، که توسط مجموعه ای از رئوس تشکیل شده است v1،v2،⋯،vn. مجموعه زاویه رئوس است θ1،θ2،⋯،θn. زاویه در رأس vمنبه عنوان فرض می شود θمن، به عنوان زاویه لبه نشان داده می شود vمن-1vمندر خلاف جهت عقربه های ساعت حول راس می چرخد vمنبه لبه vمنvمن+1، و θمن∈0درجه،360درجه، به عنوان مثال، θ2زاویه است v2در شکل 2 . طول هر لبه از بvاست v1v2،v2v3،⋯،vn-1vn،vnv1. انواع ساختارهای محلی با توجه به تحدب – تقعر و متعامد رئوس متمایز می شوند. بنابراین، راس با زاویه مسطح، راس متعامد، راس غیر متعامد، راس محدب و راس مقعر به صورت زیر تعریف می شوند. δیک محدوده تحمل در جدول 1 است و δ=10درجهبه طور کلی
راس با زاویه مسطح (FV): زاویه راس را فرض کنید vمنکه در بvمانند θمن، اگر 180درجه-θمن<δ، سپس vمنیک راس با زاویه مسطح است، به عنوان مثال، راس v6در شکل 2 .
راس متعامد (OV): زاویه راس را فرض کنید vمنکه در بvمانند θمن، اگر 90درجه-θمن≤δیا 270درجه-θمن≤δ، سپس vمنیک راس متعامد است، به عنوان مثال، راس v1در شکل 2 .
راس غیر متعامد (NV): زاویه راس را فرض کنید vمنکه در بvمانند θمن، اگر 90درجه-θمن>δو 270درجه-θمن>δ، سپس vمنیک راس غیر متعامد است، به عنوان مثال، راس v5در شکل 2 .

بنابراین، تعریف کنید forتیvمنبرای توصیف متعامد بودن vمن، vمن∈بv:

forتیvمن=OV،90درجه-θمن≤δ ∪ 270درجه-θمن≤δ نV،90درجه-θمن>δ ∩ 270درجه-θمن>δ
راس محدب (CVV): زاویه راس را فرض کنید vمنکه در بvمانند θمن، اگر θمن<180درجه، سپس vمنیک راس محدب است، به عنوان مثال، راس v2در شکل 2 .
راس مقعر (CCV): زاویه راس را فرض کنید vمنکه در بvمانند θمن، اگر θمن>180درجه، سپس vمنیک راس مقعر است، به عنوان مثال، راس v3در شکل 2 .

بنابراین، تعریف کنید fجonvمنبرای توصیف مقعر-محدب از vمن، vمن∈بv:

fجonvمن=سیVV،θمن<180درجه سیسیV،θمن>180درجه

3.2. تعریف راس و ساختار اولویت اول

ساده سازی فرآیند کاهش پیچیدگی یک شکل هندسی با حذف جزئیات است [ 47 ]. در اینجا، اگر یک ساختمان باید ساده شود، ساختار با اولویت بالا ( TPS ) را به عنوان حداقل جزئیاتی که ترجیحاً ساده‌سازی می‌شود، تعریف می‌کنیم. TPS از راس اولویت بالا ( TPV ) و دو راس مجاور آن تشکیل شده است. با توجه به ترتیب رئوس ساختمان ها، دو رأس مجاور به عنوان رأس جلو- مجاور ( FAV ) و پشت-راس مجاور ( RAV ) متمایز می شوند. TPV با استفاده از دو مرحله تعیین می شود:
مرحله 1: یال با کوتاه ترین طول چند ضلعی ساختمان را پیدا کنید که با نشان داده شده است vمنvj، که در آن vمنو vjرئوس مجاور هستند و من<j.
مرحله 2: “مناطق ساختاری” را مقایسه کنید vمنو vj، و راس با مساحت ساختاری کوچکتر را به عنوان TPV انتخاب کنید. اگر «مناطق ساختاری» از vمنو vjمعادل هستند، انتخاب کنید vمنبه عنوان TPV .

ناحیه ساختاری راس را فرض کنید vمنکه در بv به عنوان مشخص می شود استیrآمن، طول دو لبه مجاور است vمن-1vمنو vمنvمن+1به ترتیب، و زاویه در راس vمنبه عنوان مشخص می شود θمن، سپس منطقه سازه ای از vمناست

استیrآمن=vمن-1vمنvمنvمن+1·|گناهθمن|

را بگیرید بv=v1،v2،⋯،v7در شکل 3 ، که باید به عنوان مثال ساده شود. مرحله 1، کوتاه ترین لبه را پیدا کنید v3v4با محاسبه طول لبه های چند ضلعی. مرحله 2، منطقه ساختاری را مقایسه کنید v3و v4همانطور که در شکل 3 نشان داده شده است.

استیrآ3=v2v3v3v4·|گناهθ3|=v2v3v3v4
استیrآ4=v3v4v4v5·|گناهθ4|=v3v4v4v5
در آنجا، θ3و θ4به ترتیب 90 درجه و 270 درجه هستند. v2v3>v4v5، از این رو، استیrآ3>استیrآ4. این v4به عنوان TPV (نشان داده شده با نقطه قرمز)، و ساختار محلی تعیین می شود {v3،v4،v5}TPS است که حداقل جزئیات را در چند ضلعی ساختمان ارائه می دهد. v3FAV است (با نقطه آبی نشان داده شده است) و v5RAV است (با نقطه سبز نشان داده می شود).

3.3. طبقه بندی TPS

از آنجایی که ساختمان ها اشکال مختلفی دارند، طبقه بندی TPS اساس عملیات ساده سازی است. سه راس در TPS وجود دارد که عبارتند از FAV , TPV , RAV . همانطور که جدول 2 نشان می دهد ، TPS را با مقعر-محدب و متعامد بودن سه راس متمایز می کنیم .
طبق جدول 2 ، TPS ها به عنوان 62 زیر کلاس طبقه بندی می شوند که ساختار محلی چند ضلعی ساختمان را پوشش می دهند. به منظور ساده نگه داشتن ویژگی های شکل، 62 زیر کلاس به چهار نوع ساده سازی تقسیم می شوند که شامل 12 حالت ساده سازی است. چهار نوع ساده سازی به شرح زیر است:
  • نوع ساده سازی 1: TPV OV است و OV در دو راس مجاور وجود دارد:
تیپاس∈forتیتیپV=OV، forتیافآV=OV∪forتیآرآV=OV
  • نوع ساده سازی 2: TPV OV است و هیچ OV در دو راس مجاور وجود ندارد:
تیپاس∈forتیتیپV=OV، forتیافآV=نV∩forتیآرآV=نV
  • نوع ساده سازی 3: TPV NV است و متعامد بودن دو راس مجاور متفاوت است:
تیپاس∈forتیتیپV=NV، forتیافآV≠forتیآرآV
  • نوع ساده سازی 4: TPV NV است و متعامد بودن دو راس مجاور یکسان است:
تیپاس∈forتیتیپV=NV، forتیافآV=forتیآرآV

3.4. چارچوب

این مطالعه فقط ساده‌سازی کانتور بیرونی ساختمان‌ها را مورد بحث قرار می‌دهد. با توجه به تقعر- تحدب و متعامد بودن TPV و دو راس مجاور آن، انواع ساده سازی با اتخاذ الگوریتم های ساده سازی مختلف طبقه بندی می شوند. حداقل ساختار یک چند ضلعی ساختمان به طور مکرر ساده می شود تا زمانی که نیاز ساده سازی را برآورده کند. نمودار جریان ساده سازی در شکل 4 نشان داده شده است .
مرحله 1: راس یک چند ضلعی ساختمان را وارد کنید. زوایا، تقعر-تحدب رئوس و طول لبه های چندضلعی را محاسبه کنید.
مرحله 2: رئوس با زاویه مسطح را حذف کنید، یعنی داده های اضافی را حذف کنید.
مرحله 3: تعیین کنید که آیا تعداد رئوس چند ضلعی بیشتر از چهار است یا خیر. اگر بیشتر از چهار است، به مرحله 4 بروید. در غیر این صورت، چند ضلعی ساده نمی شود و رئوس آن خروجی می شود.
مرحله 4: تجزیه و تحلیل کنید که آیا ممنnLهnکمتر است از ε. اگر کمتر از ε، به مرحله 5 بروید؛ در غیر این صورت، چند ضلعی ساده نمی شود و رئوس آن خروجی می شود.
مرحله 5: TPV و TPS چند ضلعی ساختمان را تعیین کنید.
مرحله 6: نوع ساده سازی را با توجه به متعامد بودن و تقعر-تحدب TPV و دو راس مجاور آن تعیین کنید. سپس، ساده سازی را با چهار نوع ساده سازی انجام دهید: انواع ساده سازی 1-4.
مرحله 7: چند ضلعی ساختمان ساده شده را به مرحله 1 منتقل کنید تا ساده سازی تکراری انجام شود تا زمانی که چند ضلعی ساختمان الزامات ساده سازی را برآورده کند.

3.5. روش ساده سازی

یک چند ضلعی ساختمان را می توان با مجموعه ای از رئوس به عنوان نشان داد بv=v1،v2،⋯،vn، و یک لبه به عنوان به={هvک،vمتر|vک،vمتر∈بv}. فرض کنید بvباید ساده شود زیرا ممنnLهnکوچکتر از آستانه است و n>4. این تیپV={vمن|vمن∈بv}، افآV={vمن-1|vمن-1∈بv}، آرآV={vمن+1|vمن+1∈بv}، سپس TPS را می توان با نشان داد{vمن-1،vمن،vمن+1}. چهار نوع روش ساده سازی به شرح زیر است:

3.5.1. نوع ساده سازی 1: TPV OV است و OV در دو راس مجاور وجود دارد

این نوع معمولاً متعلق به چند ضلعی های منظم است که در ساختمان ها رایج است. در فرآیند ساده سازی، مساحت قسمت های پر شده با قسمت های حذف شده برابر است تا مساحت ساختمان حفظ شود. برخی از ساختارهای محلی، به عنوان مثال، مقعر باریک و بلند (محدب)، باید به جای حذف برخی جزئیات، اغراق آمیز باشد. این استیrآاز TPV برای تعیین اغراق استفاده می شود. آستانه اغراق آمیز استیrآاز TPV به عنوان نشان داده شده است γ. چه زمانی استیrآrهآ≥γ، TPS اغراق آمیز خواهد بود. با توجه به تقعر و تحدب سه راس، 8 نوع فرعی وجود دارد که باید ساده شوند:
زیرنوع  1 : تیپاس∈{افآV=سیVV، تیپV=سیVV، آرآV=سیVV، استیrآ<γ}همانطور که شکل 5 a نشان می دهد، یک خط بکشید پ1پ2موازی با لبه هvمن،vمن+1، که در آن پ1روشن است هvمن،vمن-1، و پ2روشن است هvمن+1،vمن+2. توسعه دادن، گسترش پ2پ1و vمن-2vمن-1 برای به دست آوردن یک نقطه متقاطع پ3. مساحت چهارضلعی پ1پ2vمن+1vمنبرابر مثلث است پ1پ3vمن-1. سپس، ساختار محلی {vمن-2،vمن-1،vمن،vمن+1،vمن+2}به عنوان ساده شده است {vمن-2،پ3،پ2،vمن+2}.
زیرگروه  2 : تیپاس∈{افآV=سیسیV، تیپV=سیسیV، آرآV=سیسیV، استیrآ<γ}، اگر |vمنvمن-1≤|vمنvمن+1، از جانب vمن-1یک خط عمودی به لبه بکشید هvمن+1،vمن+2در پ1. سپس، ساختار محلی {vمن-2،vمن-1،vمن،vمن+1،vمن+2}به عنوان ساده شده است {vمن-2،vمن-1،پ1،vمن+2}همانطور که شکل 5 ب نشان می دهد. اگر |vمنvمن-1|>|vمنvمن+1|، از جانب vمن+1یک خط عمودی به لبه بکشید هvمن-1،vمن-2در پ1. سپس، ساختار محلی {vمن-2،vمن-1،vمن،vمن+1،vمن+2}به عنوان ساده شده است {vمن-2،پ1،vمن+1،vمن+2}.
زیرگروه  3 : تیپاس∈{افآV=سیسیV، تیپV=سیسیV، آرآV=سیVV، استیrآ<γ}همانطور که شکل 5 ج نشان می دهد، یک خط بکشید پ1پ3موازی با لبه هvمن-1،vمن، که در آن پ1روشن است هvمن،vمن+1، و پ3روشن است هvمن-2،vمن-1. یک خط بکش پ1پ2موازی با لبه هvمن+1،vمن+2، که در آن پ2در خط است vمن+2vمن+3. مساحت چهارضلعی پ1پ2vمن+2vمن+1برابر با چهار ضلعی است پ1پ3vمن-1vمن. سپس، ساختار محلی {vمن-2،vمن-1،vمن،vمن+1،vمن+2،vمن+3}به عنوان ساده شده است {vمن-2،پ3،پ1،پ2،vمن+3}.
زیرگروه  4 : تیپاس∈{افآV=سیVV، تیپV=سیسیV، آرآV=سیسیV، استیrآ<γ}همانطور که در شکل 5 d نشان داده شده است، یک خط بکشید پ1پ3موازی با لبه هvمن،vمن+1، که در آن پ1روشن است هvمن،vمن-1، و پ3روشن است هvمن+2،vمن+1. یک خط بکش پ1پ2موازی با لبه هvمن-1،vمن-2، که در آن پ2در خط است vمن-2vمن-3. مساحت چهارضلعی پ1پ2vمن-2vمن-1برابر با چهار ضلعی است پ1پ3vمن+1vمن. سپس، ساختار محلی {vمن-3،vمن-2،vمن-1،vمن،vمن+1،vمن+2}به عنوان ساده شده است {vمن-3،پ2،پ1،پ3،vمن+2}. عملیات ساده سازی زیرگروه  3 به دلیل تفاوت در تقعر-تحدب FAV و RAV با زیرگروه 4 مطابقت دارد .
زیرگروه  5 : تیپاس∈{افآV=سیسیV، تیپV=سیVV، آرآV=سیVV، استیrآ<γ}همانطور که در شکل 6 a نشان داده شده است، یک خط بکشید پ1پ3موازی با لبه هvمن+1،vمن+2، که در آن پ1روشن است هvمن،vمن+1، و پ3روشن است هvمن+2،vمن+3. یک خط بکش پ1پ2موازی با لبه هvمن،vمن-1، که در آن پ2در خط است vمن-2vمن-1. مساحت چهارضلعی پ1پ2vمن-1vمنبرابر با چهار ضلعی است پ1پ3vمن+2vمن+1. سپس، ساختار محلی vمن-2،vمن-1،vمن،vمن+1،vمن+2،vمن+3به عنوان ساده شده است {vمن-2،پ2،پ1،پ3،vمن+3}.
زیرگروه  6 : تیپاس∈{افآV=سیVV، تیپV=سیVV، آرآV=سیسیV، استیrآ<γ}همانطور که در شکل 6 ب نشان داده شده است، یک خط بکشید پ1پ3موازی با لبه هvمن،vمن-1، که در آن پ1روشن است هvمن،vمن+1، و پ3روشن است هvمن-1،vمن-2. یک خط بکش پ1پ2موازی با لبه هvمن+1،vمن+2، که در آن پ2در خط است vمن+3vمن+2. مساحت چهارضلعی پ1پ2vمن+2vمن+1برابر با چهار ضلعی است پ1پ3vمن-1vمن. سپس، ساختار محلی vمن-2،vمن-1،vمن،vمن+1،vمن+2،vمن+3به عنوان ساده شده است {vمن-2،پ3،پ1،پ2،vمن+3}. عملیات ساده سازی زیرگروه  5 با زیرگروه 6 مطابقت دارد .
زیرگروه  7 : تیپاس∈{افآV=سیسیV، تیپV=سیVV، آرآV=سیسیV، استیrآ<γ}همانطور که شکل 6 ج نشان می دهد، یک خط بکشید پ4پ5موازی با لبه هvمن-1،vمن-2، که در آن پ4روشن است هvمن،vمن-1، و پ5در خط است vمن-3vمن-2. به طور همزمان یک خط بکشید پ2پ3موازی با لبه هvمن+1،vمن+2، که در آن پ2روشن است هvمن،vمن+1، و پ3در خط است vمن+3vمن+2. خط پ4پ5تقاطع می کند پ2پ3در نقطه پ1. محدودیت این است که نسبت طول از vمنپ4به vمنvمن-1برابر است با نسبت طول vمنپ2به vمنvمن+1. علاوه بر این، مساحت چهار ضلعی پ1پ2vمنپ4برابر است با مجموع مساحت چهارضلعی ها پ4پ5vمن-2vمن-1و پ2پ3vمن+2vمن+1. سپس، ساختار محلی vمن-3،vمن-2،vمن-1،vمن،vمن+1،vمن+2،vمن+3به عنوان ساده شده است {vمن-3،پ5،پ1،پ3،vمن+3}.
زیرگروه  8 : تیپاس∈{افآV=سیVV، تیپV=سیسیV، آرآV=سیVV، استیrآ<γ}همانطور که در شکل 6 d نشان داده شده است، عملیات ساده سازی زیرگروه  8 همانند زیرگروه 7 است که در اینجا تکرار نمی شود.
انواع اغراق : اگر تیپاس∈ استیrآ≥γ، عمل مبالغه انجام می شود. طول کوتاه ترین لبه به εضمن حفظ منطقه پس از اغراق. با توجه به طول لبه هvمن،vمن-1و هvمن،vمن+1. دو نوع وجود دارد: اغراق 1 و اغراق 2.
مبالغه  1 : اگر vمن-1vمن<vمنvمن+1همانطور که شکل 7 a نشان می دهد، اشاره کنید پ1در لبه تعیین می شود هvمن،vمن+1. یک خط بکش پ1پ2موازی با لبه هvمن،vمن-1، که در آن پ2در خط است vمن-1vمن-2. توسعه دادن، گسترش پ2پ1به پ3در حالی که پ2پ3=ε. یک خط بکش پ3پ4موازی با لبه هvمن،vمن+1، که در آن پ4در خط است vمن+1vمن+2. مساحت چهارضلعی پ1پ2vمن-1vمنبرابر با چهار ضلعی است پ1پ3پ4vمن+1. سپس، ساختار محلی vمن-2،vمن-1،vمن،vمن+1،vمن+2به عنوان ساده شده است {vمن-2،پ2،پ3،پ4،vمن+2}.
مبالغه  2 : اگر vمن-1vمن>vمنvمن+1همانطور که شکل 7 ب نشان می دهد، اشاره کنید پ1در لبه تعیین می شود هvمن،vمن-1. یک خط بکش پ1پ2موازی با لبه هvمن،vمن+1، که در آن پ2در خط است vمن+1vمن+2. توسعه دادن، گسترش پ2پ1به پ3در حالی که پ2پ3=ε. یک خط بکش پ3پ4موازی با لبه هvمن،vمن-1، که در آن پ4در خط است vمن-1vمن-2. مساحت چهارضلعی پ1پ2vمن+1vمنبرابر با چهار ضلعی است پ1پ3پ4vمن-1. سپس، ساختار محلی vمن-2،vمن-1،vمن،vمن+1،vمن+2به عنوان ساده شده است {vمن-2،پ4،پ3،پ2،vمن+2}.
3.5.2. نوع ساده سازی 2: TPV OV است و در دو رأس مجاور OV وجود ندارد
زیرگروه  9 : این ساده سازی زیرگروه مستقل از تحدب-تعرفه TPV و رئوس مجاور آن است. همانطور که شکل 8 a نشان می دهد، یک خط بکشید پ1پ2به موازات vمن-1vمن+1، که در آن پ1روشن است هvمن،vمن+1، و پ2روشن است هvمن-1،vمن. طولانی کردن پ1پ2و پ2پ1تقاطع کردن vمن-2vمن-1و vمن+1vمن+2در پ3و پ4، به ترتیب. مساحت مثلث پر شده vمنپ1پ2برابر است با مجموع مساحت مثلث های حذف شده vمن-1پ2پ3و vمن+1پ1پ4. سپس، ساختار محلی vمن-2،vمن-1،vمن،vمن+1،vمن+2به عنوان ساده شده است {vمن-2،پ3،پ4،vمن+2}. در مورد خاص که vمن-2vمن-1و vمن+1vمن+2هم خطی هستند، vمنمستقیم حذف می شود همانطور که شکل 8 ب نشان می دهد، ساختار محلی vمن-2،vمن-1،vمن،vمن+1،vمن+2به عنوان ساده شده است vمن-2،vمن-1،vمن+1،vمن+2.
3.5.3. نوع ساده سازی 3: TPV NV است و متعامد بودن دو راس مجاور متفاوت است
زیرگروه  10 : تیپاس∈افآV=OV، تیپV=نV، آرآV=نV. این ساده‌سازی زیرگروه مستقل از تحدب – تقعر TPV و رئوس مجاور آن است. همانطور که شکل 9 a-c نشان می دهد، یک خط بکشید پ1پ2عمود بر vمن-1vمن، که در آن پ1روشن است هvمن،vمن+1، و پ2روشن است هvمن-1،vمن. فاصله از را نشان دهید vمن+1به هvمن-1،vمنمانند Dمنس. طولانی کردن پ2پ1به پ3در حالی که طول پ2پ3است Dمنس. مساحت مثلث vمنپ1پ2برابر مثلث است vمن+1پ1پ3. سپس، ساختار محلی vمن-2،vمن-1،vمن،vمن+1،vمن+2به عنوان ساده شده است {vمن-2،vمن-1،پ2،پ3،vمن+1،vمن+2}. چه زمانی vمن-1vمنبه موازات است vمن+1vمن+2همانطور که شکل 9 a,b نشان می دهد، پ3، vمن+1، vمن+2پس از ساده سازی هم خط هستند. vمن+1یک راس با زاویه مسطح است که در فرآیند ساده سازی تکراری بعدی حذف خواهد شد، برای جزئیات بیشتر به بخش 3.4 ، مرحله 2 مراجعه کنید.
زیرگروه  11 : تیپاس∈افآV=نV، تیپV=نV، آرآV=OV،عملیات ساده سازی مشابه زیرنوع  10 است که در اینجا به تفصیل ارائه نخواهد شد.
3.5.4. نوع ساده سازی 4: TPV NV است و متعامد بودن دو راس مجاور یکسان است
در این نوع، شکل و ساختار ساختمان ها معمولاً نامنظم است. برای حفظ خصوصیات و مساحت آن تا حد امکان، یک “روش – مقایسه – ساده سازی – منطقه” در اینجا اتخاذ شده است. ایده این است که TPV به موقعیت‌های مختلف جابه‌جا می‌شود و تغییرات مساحت چندضلعی پس از جابجایی را مقایسه می‌کند. سپس موقعیتی با کمترین تغییرات در ناحیه به عنوان موقعیت جدید TPV در نظر گرفته می شود . برای حفظ ویژگی های شکل و زاویه راست ساختمان، موقعیت جابجایی معمولاً با کشیدن خطوط عمود یا متقاطع ساخته می شود.
زیرگروه  12 : تیپاس∈افآV=نV، تیپV=نV، آرآV=نV∪افآV=OV، تیپV=نV، آرآV=OVهمانطور که در شکل 10 نشان داده شده است، رسم کنید vمن-1پ2، vمن+1پ4عمود بر vمنvمن+1و vمنvمن-1، به ترتیب، که در آن پ2در خط است vمنvمن+1، و پ4روشن است vمن-1vمن. سپس، تمدید کنید vمن-2vمن-1و vمن+2vمن+1تقاطع vمن+1vمن، vمن-1vمندر پ1و پ3، به ترتیب. برای vمن، که TPV است، به طور کلی، پنج موقعیت برای جابجایی وجود دارد: پ1، پ2، پ3، پ4، و vمن+1(به این معنا که، vمنحذف می شود). هنگامی که موقعیت جابجایی ساخته شده وجود دارد، منطقه تغییر مربوط به هر موقعیت جابجایی محاسبه می شود. منطقه تغییر مربوط به پ1، که به عنوان نشان داده می شود اسپ1 ، مساحت مثلث است vمن-1vمنپ1. به این معنا که، اسپ1=△vمن-1vمنپ1. به طور مشابه، منطقه تغییر یافته مربوط به پ2، پ3، پ4و vمن+1است اسپ2، اسپ3، اسپ4، و اسvمن+1، به ترتیب، در کجا اسپ2=△vمن-1vمنپ2، اسپ3=△vمنvمن+1پ3، اسپ4=△vمنvمن+1پ4، و اسvمن+1= △vمن-1vمنvمن+1.
اگر اسپ2همانطور که شکل 10 a نشان می دهد، کوچکترین است ،vمنجابجا شده است به پ2. سپس، ساختار محلی vمن-2،vمن-1،vمن،vمن+1،vمن+2به عنوان ساده شده است {vمن-2،vمن-1،پ2،vمن+1،vمن+2}همانطور که در شکل 10 نشان داده شده است. عملیات از اسپ4مثل این هست که اسپ2. اگر اسپ1همانطور که شکل 10 ج نشان می دهد، کوچکترین است ،vمنجابجا شده است به پ1. سپس، vمن-2،vمن-1،vمن،vمن+1،vمن+2به عنوان ساده شده است {vمن-2،پ1،vمن+1،vمن+2}همانطور که در شکل 10 نشان داده شده است. عملیات از اسپ3مثل این هست که اسپ1. اگر اسvمن+1همانطور که شکل 10 e نشان می دهد کوچکترین است ،vمنحذف می شود. سپس، vمن-2،vمن-1،vمن،vمن+1،vمن+2به عنوان ساده شده است {vمن-2،vمن-1،vمن+1،vمن+2}، در شکل 10 نشان داده شده است.

3.6. نمونه ای از فرآیند ساده سازی

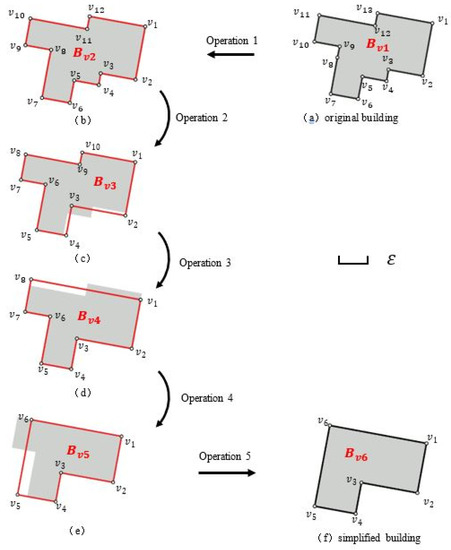
برای نشان دادن فرآیند ساده سازی، ساختمان را در نظر بگیرید بv1=v1،v2،⋯،v13در شکل 11 a به عنوان مثال. فرض کنید که در مقیاس هدف، حداقل دانه بندی است ε. γ=ε2. برای دریافت ساختمان ساده شده بv6=v1،v2،⋯،v6، پنج عملیات وجود دارد:
عملیات 1: گرفتن بv1=v1،v2،⋯،v13به عنوان ورودی زوایا، تقعر-تحدب رئوس و طول لبه های چندضلعی را محاسبه کنید. قبل از هر عملیات ساده سازی، رئوس زاویه مسطح (FV) حذف می شوند. بدین ترتیب، v8که در بv1حذف شده است. ساختمان به صورت ارائه شده است بv2=v1،v2،⋯،v12در شکل 11 ب. تعداد رئوس در بv212 است که بزرگتر از 4 است و ممنnLهnاز بv2کمتر است از ε. از این رو، بv2باید ساده شود.
عملیات 2: بv2ساده شده است به بv3. ابتدا تعیین کنید v4که در بv2به عنوان TPV با پیدا کردن کوتاه ترین لبه هv3،v4و مقایسه مساحت ساختاری v3،v4. سپس، افآV=v3، آرآV=v5، و تیپاس=v3،v4،v5. تیپاس∈forتیتیپV=OV، forتیافآV=OV∪forتیآرآV=OV, که متعلق به Simplification type 1. ناحیه سازه ای از تیپVاست استیrآ4، که کمتر از γ. به عنوان تقعر – تحدب از v3،v4،v5CCV است، CVV، CCV، زیرنوع 7 پذیرفته شده است. ساختمان به صورت ساده شده است بv3=v1،v2،⋯،v10در شکل 11 ج.
عملیات 3: بv3ساده شده است به بv4به صورت مکرر اول، بگیر بv3=v1،v2،⋯،v10به عنوان ورودی برای حذف FV، و هیچ FV در آن وجود ندارد بv3. سپس، به عنوان ممنnLهnاز بv3کمتر است از ε، بv3نیاز به ساده سازی مداوم دارد. که در بv3، v10به عنوان TPV تعیین می شود و تیپاس=v9،v10،v1. تیپاس∈forتیتیپV=OV، forتیافآV=OV∪forتیآرآV=OV، که متعلق به Simplification نوع 1 است v9،v10،v1CCV، CVV، CVV است، زیرگروه 5 پذیرفته شده است. ساختمان به صورت ساده شده است بv4=v1،v2،⋯،v8در شکل 11 د.
عملیات 4: بv4ساده شده است به بv5به صورت مکرر اول، بگیر بv4=v1،v2،⋯،v8به عنوان ورودی برای حذف FV، و هیچ FV در آن وجود ندارد بv4. سپس، به عنوان ممنnLهnاز بv4کمتر است از ε، بv4نیاز به ساده سازی مداوم دارد. که در بv4، v7به عنوان TPV تعیین می شود و تیپاس=v6،v7،v8. تیپاس∈forتیتیپV=OV، forتیافآV=OV∪forتیآرآV=OV، که متعلق به Simplification نوع 1 است v6،v7،v8CCV، CVV، CVV است، زیرگروه 5 پذیرفته شده است. ساختمان به صورت ساده شده است بv5=v1،v2،⋯،v6در شکل 11 e.
عملیات 5: بv5به عنوان خروجی گرفته می شود. اول، بگیر بv5=v1،v2،⋯،v6به عنوان ورودی برای حذف FV، و هیچ FV در آن وجود ندارد بv5. سپس، به عنوان ممنnLهnاز بv5بیشتر است از ε، ساده سازی محدودیت را برآورده می کند. بنابراین، بگیرید بv5=v1،v2،⋯،v6به عنوان نتیجه ساده سازی برای بv1=v1،v2،⋯،v13همانطور که شکل 11 f نشان می دهد.
علاوه بر این، اگر جزئیات کوچکتری از خطوط کلی در انواع ساده سازی ایجاد شود، در فرآیند ساده سازی تکراری حذف خواهد شد.

4. آزمایش و تجزیه و تحلیل

4.1. تعیین شاخص های ارزیابی ساده سازی

برای ارزیابی امکان سنجی و سازگاری روش ما، تغییر در تعداد رئوس ( نتومترسی، تغییر در منطقه ( آrهآسی، تغییر در نسبت رئوس متعامد ( Orتیسی، تغییر موقعیت نقطه مرکزی ( سیتیrپسی، تغییر شکل در جهانی ( اسجیسی، و تغییر شکل در جزئیات ( اسDسی) [ 8 ، 41 ] به عنوان شاخص های ارزیابی انتخاب می شوند که به شرح زیر تعریف می شوند:

فرض کنید یک ساختمان اصلی به عنوان ارائه شده است بorمن=v1،v2،⋯،vnقبل از ساده سازی منطقه از بorمناست آrهآorمن، نقطه مرکزی از بorمناست سیپorمن، و تعداد رئوس متعامد در بorمناست nov. ساختمان ساده شده به صورت ارائه شده است بسمنمتر=v1،،v2،،⋯،vمتر،. منطقه از بسمنمتراست آrهآسمنمتر، نقطه مرکزی از بسمنمتراست سیپسمنمتر، و تعداد رئوس متعامد در بسمنمتراست مترov. ( ایکس0،y0) و ( ایکسس،yس) مختصات هستند سیپorمنو سیپسمنمتر.

نتومترسی=متر-n/n، نتومترسی∈-1،0
آrهآسی=|آrهآسمنمتر-آrهآorمنآrهآorمن|، آrهآسی∈0،∞
Orتیسی=مترovمتر-novn×100%، Orتیسی∈-1،1
سیتیrپسی=ایکس0-ایکسس2+y0-yس2، سیتیrپسی∈0،∞
اسجیسی=آrهآبorمن∩بسمنمتر/آrهآبorمن∪بسمنمتر، اسجیسی∈0،1

جایی که نتومترسینشان می دهد که آیا تعداد رئوس پس از ساده سازی به طور موثر کاهش می یابد یا خیر. آrهآسیشاخصی برای اندازه گیری حفاظت از مساحت است. Orتیسینشان می دهد که آیا ویژگی های متعامد باقی می مانند یا خیر. سیتیrپسیفاصله جابجایی ساختمان را نشان می دهد. اسجیسینشان دهنده تغییر شکل یک ساختمان در سطح جهانی قبل و بعد از ساده سازی است. به همین ترتیب، به منظور مقایسه تغییرات شکل ساختمان ها به طور خاص، اسجیسیبه تصویب رسید.

از آنجایی که خطوط کلی ساختمان دارای رئوس و زوایای قائم کمی هستند، اندازه گیری شباهت شکل ساختمان ها با جزئیات با اتخاذ تابع چرخش مناسب است [ 48 ]. برای یک ساختمان، همانطور که شکل 12 a نشان می دهد، زاویه مماس یک نقطه دلخواه Oدر طرح کلی آن در امتداد یک جهت مرجع (مثلاً محور X ) قرار داردψو تابع چرخش fسبه عنوان رابطه تغییر زاویه مماس تعریف می شود ψدر امتداد طرح کلی آن در جهت خلاف جهت عقربه های ساعت با توجه به طول قوس س(همانطور که شکل 12 ب نشان می دهد). طول کل قوس س1 [ 42 ] است.

این اسDسیبین ساختمان های اصلی و ساده شده به صورت زیر اندازه گیری می شود [ 40 ]:

اسDسی=12πدقیقهϕ∈آر،  تی∈-1،1🔻01forمنس+تی-fسمنمترس+ϕ2دس

جایی که forمنسو fسمنمترسبه ترتیب توابع چرخشی ساختمان های اصلی و ساده شده هستند، t نشان دهنده فاصله ای است که نقطه شروع (نقطه) پدر شکل 12 الف) در امتداد طرح کلی حرکت می کند، و ϕزاویه چرخش را نشان می دهد. دو ساختمان از نظر شکل بیشتر شبیه به هم هستند هر چه ارزش آنها کوچکتر باشد اسDسی[ 15 ].

4.2. آزمایش

روش ما در ArcEngine 10.2 (ESRI، RedLands، CA، USA) با استفاده از C# آزمایش و تأیید شد. داده‌های ساختمان توپوگرافی با 540 ساختمان در هلند، که داده‌های باز در Kadaster است، برای آزمایش‌های ما استفاده شد (در شکل 13 مشاهده می‌شود ). مقیاس داده های ساختمان های اصلی 1:1000 است. در مقیاس 1:25000 ( ε= 7.5 متر)، 540 ساختمان در منطقه خاصی از هلند ساده شد. نتایج ساده سازی در شکل 13 الف نشان داده شده است (سایه خاکستری شکل اصلی ساختمان و خطوط قرمز خطوط ساده شده هستند). پیچیدگی زمانی رویکرد ما T( n ) برای ساده سازی یک ساختمان است، سپس O( n ) ≤ T( n ) ≤ O( n2 )، n تعداد رئوس یک ساختمان است.
با توجه به ساختمان های مختلف با اشکال مختلف در شهرها، روش پیشنهادی از جهانی بودن خوبی برخوردار است. به طور کلی، نتایج ساده‌سازی شکل ساختمانی عادی را بدون ساده‌سازی غیرعادی حفظ می‌کند، که نشان می‌دهد الگوریتم سازگاری خوبی با انواع مختلف ساختمان‌ها دارد. از نمای بزرگ‌شده محلی، همانطور که در شکل 13 b,c نشان داده شده است، ساده‌سازی می‌تواند به طور موثر جزئیات محلی ساختمان‌ها را کاهش دهد و شکل اصلی ساختمان‌ها را که مطابق با عادات ادراک بصری انسان است، حفظ کند. شاخص های ارزیابی نتیجه ساده شده در جدول 3 نشان داده شده است. میانگین آrهآسی0.41٪ است که نشان می دهد روش ما می تواند منطقه را قبل و بعد از ساده سازی حفظ کند. میانگین Orتیسی2.91 درصد افزایش یافت. روش پیشنهادی مرکز بصری ساختمان‌ها را تقریباً بدون تغییر نگه می‌دارد که به طور میانگین ثابت می‌شود سیتیrپسی(0.3878 متر). ارزش اسجیسیمی تواند ساختمان هایی با ناهنجاری های ساده را تشخیص دهد. درصد از اسجیسی≥0.599.81 درصد است که به این معنی است که ساختمان های ساده شکل خود را حفظ می کنند. تنها یک ساختمان با اسجیسیهمانطور که فلش سیاه در شکل 13 a نشان می دهد که به یک مستطیل رضایت بخش ساده شده است، < 0.5 یافت می شود. با این حال، ساده سازی 540 ساختمان 25.53 ثانیه طول می کشد که از نظر بازده زمانی مزیت کمی دارد.

4.3. ساده سازی چند مقیاسی

رویکرد ما برای تغییر مقیاس مداوم ساختمان ها مفید است. برای یک مقیاس هدف معین ( اسجآلهj)، یک ساختمان ( بمن) یک نمایش ساده دارد ( بمنj) مربوط به مقیاس. همانطور که شکل 14 نشان می دهد، 6 ساختمان با شکل پیچیده از بین 540 ساختمان در شکل 13 انتخاب شده اند که به صورت مشخص شده اند. {ب1،ب2،⋯،ب6}. اسجآله=1000، 10000، 12500، 15000، 20000، 22500، 25000. با توجه به مقیاس هدف، هر ساختمان دارای یک نمایش است.
همانطور که در شکل 14 نشان داده شده است ، روش ساده سازی ارائه شده در اینجا به تدریج طرح کلی و جزئیات محلی ساختمان ها را با مقیاس کاهنده ساده می کند، که بیانگر بیان تدریجی و چند مقیاسی ساده سازی است. ما می‌توانیم با تنظیم مقیاس‌ها برای تعیین حداقل دانه‌بندی، فرآیند را درک کنیم. مانند ب11تبدیل به ب17، جزئیات حداقل و غیر مهم ترجیحا حذف می شوند. ساختمان‌های پیچیده به یک ساختمان ساده تبدیل شده‌اند که ویژگی‌های شکل اصلی را نیز حفظ می‌کند، به عنوان مثال، ب17. از آنجایی که ویژگی متعامد ساختمان ها در تبدیل مقیاس پیوسته به خوبی حفظ می شود، نتایج نشان می دهد که روش پیشنهادی ساختمان های مستطیلی را به طور قابل ستایشی ساده می کند، مانند ب21و ب61در شکل 14 . علاوه بر این، روش ما می‌تواند مساحت ساختمان‌ها را قبل و بعد از ساده‌سازی با مقایسه طرح‌های ساده شده و ساختمان‌های اصلی در مقیاس 25000 در شکل 14 ، به جای حذف صرفاً رئوس، حفظ کند. بنابراین، روش پیشنهادی دارای مزایایی در پایدار نگه داشتن نتیجه ساده سازی در تغییر مقیاس پیوسته ساختمان ها است.

4.4. تست ساده سازی ساختمان های معمولی

به منظور ارزیابی رفتار متفاوت روش بر روی اشکال ساختمان‌های معمولی، برخی از ساختمان‌های معمولی (رئوس چند ضلعی ساختمان در جهت عقربه‌های ساعت چیده شده‌اند) را برای آزمایش ساده‌سازی انتخاب کردیم، از جمله ساختمان‌های منظم و ساختمان‌های نامنظم، همانطور که در شکل 15 نشان داده شده است. آ.
① تست وابستگی جهت. ساختمان ها را با زوایای چرخش بچرخانید ω90 درجه در شکل 15 ب. از نتایج ساده‌سازی، نتایج ساده‌سازی ساختمان‌ها در زوایای مختلف همخوانی دارند که تأیید می‌کند روش پیشنهادی به جهت ساختمان‌ها بستگی ندارد. ② تست تغییر دنباله رئوس در خلاف جهت عقربه های ساعت، همانطور که شکل 15 ج نشان می دهد. نتیجه ساده سازی 3 همان نتیجه ساده سازی 1 است، که تأیید می کند که روش ما خروجی یکسانی را برای ساختمان ها ارائه می دهد که در جهت عقربه های ساعت و خلاف جهت عقربه های ساعت کدگذاری شده اند. ③ تست اکستروژن و کشش. در ساده سازی، ساختمان ها ممکن است به درجات مختلف کشیده و اکسترود شوند. ساختمان های شکل 15 d,e با اکسترود کردن و کشش ساختمان ها در شکل 15 به دست می آیند.الف به ترتیب با مقایسه نتایج ساده سازی 1، 4، و 5، نتایج ساده سازی با برخی تفاوت های محلی مشابه است. این نشان می‌دهد که این الگوریتم می‌تواند با توجه به اشکال ساختمان‌های مختلف، ویژگی‌های شکل اصلی ساختمان‌ها را به طور کلی ساده‌سازی کند. ④ تست تنظیم راس شروع. ساختمان های شکل 15 f با تغییر رئوس شروع ساختمان ها در شکل 15 الف به دست می آیند. رئوس شروع به صورت نقاط قرمز رنگ در شکل 15 f نشان داده شده است. نتیجه ساده سازی 6 همان نتیجه ساده سازی 1 است که تأیید می کند که تغییر دنباله رئوس تأثیری بر نتیجه ساده سازی ندارد.

4.5. مقایسه روش

روش پیشنهادی در اینجا با روش ساده‌سازی چهار نقطه‌ای مجاور [ 15 ]، روش ساده‌سازی طبقه‌بندی محلی ساختار [ 8 ]، ابزار ساده‌سازی ساختمان ArcGIS 10.2 (ساختمان ساده)، و روش بازگشتی [ 25 ] با ساده‌سازی 1594 ساختمان در مقایسه شد. مقیاس 1:25000 ( ε= 7.5 متر)، 1:50000 ( ε= 15 متر)، و 1:75000 ( ε= 22.5 متر). مقیاس اصلی آن ساختمان ها 1:1000 است. مشابه روش پیشنهادی، روش ساده‌سازی چهار نقطه‌ای مجاور نیز پردازشی از ساختارهای محلی ارائه می‌دهد. روش ساده سازی طبقه بندی محلی-سازه یک رویکرد ساده سازی ترکیبی ساختمان بر اساس طبقه بندی ساختار محلی و استراتژی عقب نشینی است. ArcGIS یک نرم افزار تجاری کامل است. اصل روش ساده شده مبتنی بر ArcGIS حذف جزئیات غیرضروری، مانند خمیدگی ها و نوسانات خارجی، از یک خط یا مرز منطقه بدون از بین بردن شکل اساسی آن است [ 49 ]. روش بازگشتی یک رویکرد ساده سازی سنتی است که از روش حداقل مربعات استفاده می کند.
به منظور ارائه اثرات ساده سازی هر روش، 85 ساختمان معمولی با اشکال پیچیده و ویژگی های ساختاری متفاوت را از نتایج ساده شده انتخاب کردیم، همانطور که شکل 16 نشان می دهد، از جمله ساختمان های دایره ای شکل. شکل 17 با شمارش شش شاخص ارزیابی ساختمان های ساده شده در آستانه های مختلف ساده سازی به دست آمد.
شکل 16 نشان می‌دهد که تمام روش‌های ساده‌سازی، ویژگی‌های اصلی شکل ساختمان‌ها را حفظ می‌کنند و پیامد مؤثری بر ساختمان‌های معمولی دارند. با این حال، مقایسه اثرات ساده‌سازی نشان می‌دهد که وقتی گستره مقیاس ساده‌سازی بزرگ است، یعنی زمانی که آستانه ساده‌سازی به‌طور قابل‌توجهی بزرگ‌تر از طول لبه‌ها در ساختمان‌ها باشد، روش پیشنهادی برای خطوط اصلی ساختمان‌ها مناسب‌تر است. نتیجه ساده سازی در مقایسه با روش های موجود پایدارتر است. در روش چهار نقطه‌ای مجاور، ویژگی‌های شکل بدیهی است که به دلیل تیز کردن تغییر می‌کنند، همانطور که توسط فلش ​​آبی در شکل 16 نشان داده شده است.ب همانطور که توسط فلش ​​آبی در شکل 16 ج نشان داده شده است، ساختمان های منفرد در روش ساده سازی طبقه بندی محلی-سازه-سازه تغییراتی در شکل دارند . روش ساده سازی ساختمان مبتنی بر ArcGIS نمی تواند مساحت برخی از ساختمان های پیچیده را در طول ساده سازی در نظر بگیرد. علاوه بر این، لبه های کوتاه برخی از ساختمان ها زمانی که حذف نمی شود ε= 22.5 متر، همانطور که توسط فلش ​​آبی در شکل 16 d نشان داده شده است. نتیجه ساده سازی روش بازگشتی به خوبی با شکل ساختمان های اصلی مطابقت ندارد. از آنجا که روش بازگشتی زوایای چرخش را با توجه به حداقل مستطیل مرزی (MBR) ساختمان ها تعیین می کند، این منجر به انحراف جهت برای برخی از ساختمان های پیچیده می شود، همانطور که توسط فلش ​​آبی در شکل 16 نشان داده شده است. ساختمان هایی که با مستطیل های آبی در شکل 16 نشان داده شده اندساختمان های دایره ای شکل هستند. روش پیشنهادی ویژگی های دایره ای شکل را در مقایسه با روش های دیگر حفظ می کند. به طور خاص، روش ساده سازی طبقه بندی محلی-سازه در ساده سازی برخی از ساختمان های دایره ای شکل شکست خورده است. روش مبتنی بر ArcGIS می تواند شکل دایره ای را به عنوان یک کل حفظ کند. با این حال، برخی از ساختارهای کوچک در روش مبتنی بر ArcGIS ساده نشده اند. روش چهار نقطه‌ای مجاور و روش بازگشتی تغییرات نسبتاً زیادی در ویژگی‌های شکل برای ساختمان‌های دایره‌ای شکل دارند.
مقایسه داده های ساده شده ( شکل 17 الف) نشان می دهد که میزان تغییر در تعداد رئوس روش پیشنهادی نزدیک به روش چهار نقطه ای مجاور و روش ساده سازی بازگشتی است. همانطور که در شکل 17 ب نشان داده شده است، از آنجایی که روش پیشنهادی تغییر در مساحت هر نوع ساده سازی را تا حد امکان به حداقل می رساند، روش پیشنهادی نسبت به چهار روش دیگر از نظر حفظ منطقه دارای مزایای خاصی است. با توجه به داده های تجربی، میانگین نرخ تغییر در مساحت روش پیشنهادی 0.0142 درصد است در حالی که برای روش های موجود 10.78 درصد است. در شکل 1ج، الگوریتم پیشنهادی به طور موثر مشخصه راست‌زاویه را با افزایش آستانه ساده‌سازی حفظ می‌کند. به دلیل شکل مستطیلی ساختمان ها، روش بازگشتی می تواند ویژگی های متعامد ساختمان ها را به طور کامل حفظ کند. علاوه بر این، فاصله جابجایی مرکز ساختمان در روش پیشنهادی کمتر از روش‌های دیگر است، همانطور که شکل 17 d نشان می‌دهد. روش پیشنهادی همچنین دارای مزایایی در حفظ مشخصات شکل اصلی است که در شکل 17 e,f قابل اثبات است. با این حال، ساده‌سازی ساختمان‌های جزیره‌ای شکل در الگوریتم پیشنهادی مطالعه نشده است. علاوه بر این، ساده سازی ساختمان بسته به اطلاعات زمینه ای درگیر نیست.

5. نتیجه گیری ها

ساده سازی ساختمان ها یک مشکل کلاسیک در تعمیم نقشه است. ما یک روش ساده‌سازی پیشرونده را برای ساختمان‌ها با در نظر گرفتن حفظ اشکال، متعامد بودن و مساحت ساختمان‌ها به طور همزمان پیشنهاد کردیم. در رویکرد ما، TPS و TPV تعریف شده‌اند که مشکل ساده‌سازی ساختمان را به ساده‌سازی تکراری حداقل ساختار ساختمان‌ها تبدیل می‌کند. با توجه به مقعر- تحدب و متعامد بودن، ساختار محلی TPS به 62 نوع طبقه بندی می شود که می تواند تمام سازه های ساختمان را پوشش دهد. الگوریتم ساده سازی نه تنها الزامات تجسم نقشه را برآورده می کند، بلکه متعامد و مساحت را تا حد امکان حفظ می کند.
برای تأیید روش پیشنهادی، آزمایش‌هایی از جمله آزمایش‌های ساده‌سازی چند مقیاسی و ساختمان‌های معمولی انجام شد. نتایج ساده‌سازی نشان می‌دهد که روش ما برای ساده‌سازی چند مقیاسی ساختمان‌ها که مستقل از جهت و دنباله رئوس ساختمان‌ها است، مناسب است. در مقیاس های چندگانه، ساختمان ها مطابق با قوانین ساده سازی ساده می شوند. در مقایسه با روش ساده‌سازی چهار نقطه‌ای مجاور، روش ساده‌سازی محلی-سازه-طبقه‌بندی، روش ساده‌سازی ساختمان مبتنی بر ArcGIS و روش بازگشتی، روش پیشنهادی، شکل، متعامد بودن و مساحت ساختمان‌ها را با کمترین جابجایی مرکز بهتر حفظ می‌کند. نقطه. با این حال، ما فقط در مورد ساده سازی خطوط کلی ساختمان بحث می کنیم، که فقط یک نوع عملیات در تعمیم نقشه است. روش پیشنهادی باید با سایر عملیات تعمیم ترکیب شود تا به یک نتیجه معقول در آینده دست یابد، به عنوان مثال، تجمیع. علاوه بر این، تحقیقات آتی باید شامل موارد زیر باشد: (1) ساده‌سازی مشترک خطوط داخلی و خارجی ساختمان‌های جزیره‌ای شکل، و ساده‌سازی چند ضلعی سه‌بعدی بر اساس مطالعه خواهد شد.TPS _ و (2) تأثیر ویژگی‌های جغرافیایی منطقه‌ای بر ساده‌سازی ساختمان برای تحقق ساده‌سازی ترکیبی با در نظر گرفتن ویژگی‌های متعدد، نه فقط ساختمان‌های منفرد، در نظر گرفته می‌شود.

اختصارات

مخفف نام و نام خانوادگی
FV راس با زاویه مسطح
OV راس متعامد
NV راس غیر متعامد
CVV راس محدب
CCV راس مقعر
TPV راس اولویت بالا
TPS اولویت-ساختار
FAV جلو – مجاور – رأس
RAV عقب – مجاور – رأس
NumC تغییر در تعداد رئوس
AreaC تغییر در منطقه
OrtC تغییر در نسبت رئوس متعامد
CtrPC تغییر موقعیت نقطه مرکزی
SGC تغییر شکل در جهانی
SDC تغییر شکل در جزئیات

منابع

  1. گوا، آر. Ai, T. ساده سازی و تجمیع چند ضلعی ساختمان در تعمیم خودکار نقشه. جی. ووهان تک. دانشگاه Surv. نقشه 2000 ، 25 ، 25-30. [ Google Scholar ]
  2. Sester, M. تعمیم بر اساس تعدیل حداقل مربعات. بین المللی قوس. فتوگرام Remote Sens. 2000 , 33 , 931-938. [ Google Scholar ]
  3. هاونرت، جی. Wolff, A. ساده سازی بهینه نقشه های زمینی ساختمان. در مجموعه مقالات بیست و یکمین کنگره ISPRS پکن، پکن، چین، 3 تا 11 ژوئیه 2008. صص 372-378. [ Google Scholar ]
  4. رینفورد، دی. Mackaness، W. تطبیق الگو در حمایت از تعمیم ساختمان های روستایی. در مجموعه مقالات دهمین سمپوزیوم بین المللی در مورد مدیریت داده های مکانی، برلین، آلمان، 31 اوت تا 2 سپتامبر 2002. صص 137-151. [ Google Scholar ]
  5. خو، ی. وو، ال. زی، ز. Chen, Z. استخراج ساختمان در تصاویر سنجش از دور با وضوح بسیار بالا با استفاده از یادگیری عمیق و فیلترهای هدایت شده. Remote Sens. 2018 , 10 , 144. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  6. لین، ا. سان، ایکس. وو، اچ. لو، دبلیو. وانگ، دی. ژونگ، دی. وانگ، ز. ژائو، ال. Zhu, J. شناسایی عملکرد ساختمان شهری با ادغام تصاویر سنجش از دور و داده های POI. IEEE J. Sel. بالا. Appl. زمین Obs. Remote Sens. 2021 , 14 , 8864–8875. [ Google Scholar ] [ CrossRef ]
  7. آهنگ، ز. وانگ، اچ. کوین، اس. لی، ایکس. یانگ، ی. وانگ، ی. Meng, P. شناسایی ناحیه عملکردی شهری در سطح ساختمان بر اساس داده‌های انباشته چند ویژگی از تلفن‌های همراه – روشی که مجموعه‌های زمانی چند بعدی را با یک شبکه عصبی SOM ترکیب می‌کند. ISPRS Int. J. Geo-Inf. 2022 ، 11 ، 72. [ Google Scholar ] [ CrossRef ]
  8. وی، ز. لیو، ی. چنگ، ال. دینگ، اس. یک رویکرد ساده سازی ساختمانی مترقی و ترکیبی با طبقه بندی ساختار محلی و استراتژی عقبگرد. ISPRS Int. J. Geo-Inf. 2021 ، 10 ، 302. [ Google Scholar ] [ CrossRef ]
  9. استکوفسکی، آر. میچل، جی. ساده کردن یک بخش فرعی چند ضلعی در عین سادگی. در مجموعه مقالات هفدهمین سمپوزیوم سالانه هندسه محاسباتی، مدفورد، MA، ایالات متحده آمریکا، 3 تا 5 ژوئن 2001. ص 40-49. [ Google Scholar ]
  10. اشتاینیگر، اس. Taillandier، P. Weibel, R. استفاده از تشخیص بافت شهری و یادگیری ماشین برای بهبود تعمیم ساختمان ها. بین المللی جی. جئوگر. Inf. علمی 2010 ، 24 ، 253-282. [ Google Scholar ] [ CrossRef ]
  11. Guo, Q. روش ساده سازی گرافیکی مرز ویژگی منطقه به عنوان زاویه راست. جی. ووهان تک. دانشگاه Surv. نقشه 1999 ، 24 ، 255-258. [ Google Scholar ]
  12. Sester, M. رویکردهای بهینه سازی برای تعمیم و انتزاع داده ها. بین المللی جی. جئوگر. Inf. علمی 2005 ، 19 ، 871-897. [ Google Scholar ] [ CrossRef ]
  13. گائو، ایکس. یان، اچ. لو، ایکس. Wang, Z. شناخت و ساده سازی پیشرونده ساختار لبه کوتاه ساختمان ها با استفاده از مناطق محاسبه. Geomat. Inf. علمی دانشگاه ووهان 2021 ، 46 ، 1782-1790. [ Google Scholar ]
  14. شن، ی. آی، تی. لی، دبلیو. یانگ، م. Feng, Y. روش تجمع چند ضلعی با حفظ ویژگی های جهانی با استفاده از تقسیم بندی سوپرپیکسل. محاسبه کنید. محیط زیست سیستم شهری 2019 ، 75 ، 117-131. [ Google Scholar ] [ CrossRef ]
  15. خو، دبلیو. لانگ، ی. ژو، تی. Chen, L. ساده سازی چند ضلعی ساختمان بر اساس روش چهار نقطه ای مجاور. Acta Geod. کارتوگر. گناه 2013 ، 42 ، 929-936. [ Google Scholar ]
  16. رایت، جی کی نقشه سازان انسان هستند: نظرات در مورد موضوع ذهنی در نقشه ها. Geogr. Rev. 1942 , 32 , 527-544. [ Google Scholar ] [ CrossRef ]
  17. Raisz, E. Principles of Cartography ; Mcgraw-Hill: نیویورک، نیویورک، ایالات متحده آمریکا؛ دانشگاه میشیگان: Ann Arbor, MI, USA, 1962; 315p. [ Google Scholar ]
  18. رابینسون، ا. فروش، ر. موریسون، جی. پادستاوی کارتوگرافی ; PWN: ورشو، لهستان، 1978; 624p. [ Google Scholar ]
  19. Ratajski, L. Metodyka Kartografii Społeczno—Gospodarczej ; Polskie Przedsiębiorstwo Wydawnictw Kartograficznyc: ورشو، لهستان، 1989; 338p. [ Google Scholar ]
  20. مک مستر، آر. شی، تعمیم KS در کارتوگرافی دیجیتال . انجمن جغرافیدانان آمریکایی: واشنگتن، دی سی، ایالات متحده آمریکا، 1992. [ Google Scholar ]
  21. لی، دی. هاردی، پی. خودکارسازی تعمیم ابزارها و مدل ها. در مجموعه مقالات بیست و دومین کنفرانس ICA، A Coruňa، اسپانیا، 9-16 ژوئیه 2005. [ Google Scholar ]
  22. وانگ، اچ. وو، اف. ژانگ، ال. دنگ، اچ. کاربرد مورفولوژی ریاضی و تشخیص الگو برای ساده سازی چند ضلعی ساختمان. Acta Geod. Et Cartogr. گناه 2005 ، 34 ، 269-276. [ Google Scholar ]
  23. کادا، م. Luo, F. تعمیم پلان زمین ساختمان با استفاده از نیم فضا. آرشیو بین المللی فتوگرامتری حسگر از راه دور اسپات. Inf. علمی 2006 ، 36 ، 1-4. [ Google Scholar ]
  24. بوچین، ک. میلمنز، دبلیو. Speckmann, B. روشی جدید برای ساده‌سازی تقسیم‌بندی با کاربردهای تعمیم ناحیه شهری. در مجموعه مقالات نوزدهمین کنفرانس بین المللی ACM Sigspatial در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، شیکاگو، IL، ایالات متحده آمریکا، 1 تا 4 نوامبر 2011. [ Google Scholar ]
  25. Bayer, T. ساده سازی خودکار ساختمان با استفاده از رویکرد بازگشتی. در کارتوگرافی در اروپای مرکزی و شرقی ; Springer: برلین/هایدلبرگ، آلمان، 2009; صص 121-146. [ Google Scholar ]
  26. لخت، من. Touya, G. افزایش ردپای ساختمان با عملیات مربع سازی. جی. اسپات. Inf. علمی 2016 ، 13 ، 33-60. [ Google Scholar ]
  27. Meijers, M. ساده سازی ساختمان با استفاده از منحنی های افست به دست آمده از اسکلت مستقیم. در مجموعه مقالات نوزدهمین کارگاه ICA در مورد تعمیم و بازنمایی چندگانه، هلسینکی، فنلاند، 14 ژوئن 2016. [ Google Scholar ]
  28. بارو، ام. رگنولد، ن. دوچن، سی. هایر، ک. بایج، سی. دمازو، ی. هاردی، پی. Mackaness، W. رواس، ع. Weibel, R. ادغام تکنیک های چند عاملی، شی گرا و الگوریتمی برای بهبود تعمیم خودکار نقشه. در مجموعه مقالات بیستمین کنفرانس بین المللی کارتوگرافی، پکن، چین، 6 تا 10 اوت 2001. صص 2110–2116. [ Google Scholar ]
  29. مارتین، جی. تعمیم خودکار چندضلعی در یک سیستم چند عاملی. Ph.D. پایان نامه، دانشگاه زوریخ، زوریخ، سوئیس، 2003. [ Google Scholar ]
  30. Taillandier، P. دوچن، سی. Drogoul، A. بازنگری خودکار قوانین مورد استفاده برای هدایت فرآیند تعمیم در سیستم ها بر اساس استراتژی آزمون و خطا. بین المللی جی. جئوگر. Inf. علمی 2011 ، 25 ، 1971-1999. [ Google Scholar ] [ CrossRef ]
  31. جین، ی. وی، ال. وانگ، بی. یان، ایکس. لیو، اس. تانگ، X. ساده سازی مرزهای ساختمانی محدود بر اساس روش مجموع حداقل مربعات جزئی. سنسورها Mater. 2020 ، 32 ، 4559. [ Google Scholar ] [ CrossRef ]
  32. لیان، سی. لی، سی. یین، ی. Guo, P. الگوریتم بهبود یافته ساده سازی چند ضلعی بر اساس روش چهار نقطه ای مجاور. علمی Surv. نقشه 2016 ، 41 ، 26-29. [ Google Scholar ]
  33. لی، ال. لی، سی. لو، ایکس. یین، ی. Wu, P. ساده سازی چند ضلعی ساختمان بر اساس روش پنج نقطه ای مجاور. گاو نر Surv. نقشه 2019 ، 3 ، 41-45. [ Google Scholar ]
  34. یین، اس. یان، ایکس. Yan, X. روش ساده سازی چند ضلعی بر اساس بازسازی لبه های ویژگی. Acta Geod. کارتوگر. گناه 2020 ، 49 ، 703-710. [ Google Scholar ]
  35. Bildirici، I. تعمیم ساختمان و جاده با نرم افزار تعمیم تغییر با استفاده از داده های نقشه پایه توپوگرافی ترکیه. کارتوگر. Geogr. Inf. علمی 2004 ، 31 ، 43-54. [ Google Scholar ] [ CrossRef ]
  36. لکودیکس، اف. ترویسان، جی. le Gallic, JM; گوندول، ال. آزمایشات شفافیت برای تعمیم نقشه برداری در تولید. در مجموعه مقالات نهمین کارگاه ICA در مورد تعمیم و بازنمایی چندگانه، پورتلند، OR، ایالات متحده آمریکا، 25 ژوئن 2006. [ Google Scholar ]
  37. استوتر، جی. بائلا، بی. بلوک، سی. بورگاردت، دی. دوچن، سی. پلا، م. رگنولد، ن. Touya, G. آخرین هنر تعمیم خودکار در نرم افزارهای تجاری . EuroSDR: دوبلین، ایرلند، 2010. [ Google Scholar ]
  38. لیو، پی. آی، تی. هو، جی. چنگ، X. ساده سازی ساختمان-چند ضلعی بر اساس تطبیق شکل الگوی نمونه اولیه. Geomat. Inf. علمی دانشگاه ووهان 2010 ، 35 ، 1369-1372. [ Google Scholar ]
  39. آی، تی. چنگ، ایکس. لیو، پی. یانگ، ام. تحلیل شکل و تطبیق الگوی ویژگی‌های ساختمان با روش تبدیل فوریه. محاسبه کنید. محیط زیست سیستم شهری 2013 ، 41 ، 219-233. [ Google Scholar ] [ CrossRef ]
  40. یان، ایکس. آی، تی. یانگ، ام. ساده‌سازی ویژگی‌های مسکونی با روش تطبیق شکل و الگو. Acta Geod. کارتوگر. گناه 2016 ، 45 ، 874-882. [ Google Scholar ]
  41. یان، ایکس. آی، تی. Zhang, X. روش تطبیق و ساده سازی الگو برای ساختن ویژگی ها بر اساس شناخت شکل. ISPRS Int. J. Geo-Inf. 2017 ، 6 ، 250. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  42. یانگ، م. یوان، تی. یان، ایکس. آی، تی. جیانگ، سی. یک رویکرد ترکیبی برای ساده سازی ساختمان با یک ارزیاب از یک شبکه عصبی پس انتشار. بین المللی جی. جئوگر. Inf. علمی 2021 ، 36 ، 280-309. [ Google Scholar ] [ CrossRef ]
  43. شن، ی. آی، تی. وانگ، ال. ژو، جی. رویکردی جدید برای ساده‌سازی ویژگی‌های چندضلعی و خطی با استفاده از تقسیم‌بندی سوپرپیکسلی. بین المللی جی. جئوگر. Inf. علمی 2018 ، 32 ، 2023–2054. [ Google Scholar ] [ CrossRef ]
  44. سستر، ام. فنگ، ی. Thiemann, F. ساخت تعمیم با استفاده از یادگیری عمیق. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2018 ، 42 ، 565-572. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  45. فنگ، ی. تیمن، اف. Sester, M. آموزش تعمیم ساختمان نقشه برداری با شبکه های عصبی کانولوشنال عمیق. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 258. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  46. داگلاس، دی اچ. الگوریتم های Peucker، TK برای کاهش تعداد نقاط مورد نیاز برای نمایش یک خط دیجیتالی یا کاریکاتور آن. Cartographica 1973 , 10 , 112-122. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  47. بوچین، ک. میلمنز، دبلیو. ون رنسن، آ. Speckmann، B. ساده‌سازی و طرح‌واره‌سازی زیربخش‌های چندضلعی حفظ منطقه. ACM Trans. تف کردن سیستم الگوریتم 2016 ، 2 ، 1-36. [ Google Scholar ] [ CrossRef ]
  48. آرکین، ای. جویدن، ال. هاتنلوچر، دی. Kedem، K. Mitchell, JS یک متریک قابل محاسبه کارآمد برای مقایسه اشکال چند ضلعی. Proc. IEEE Trans. الگوی مقعدی ماخ هوشمند 1991 ، 13 ، 209-216. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  49. لی، دی. اتوماسیون تعمیم نقشه: فناوری پیشرفته. در سری کاغذ سفید Esri ; ESRI: دوبلین، ایرلند، 1996. [ Google Scholar ]
Ijgi 11 00393 g001 550
شکل 1. ایده اصلی روش پیشنهادی.
Ijgi 11 00393 g002 550
شکل 2. مثال رئوس.
Ijgi 11 00393 g003 550
شکل 3. تعیین TPV و TPS .
Ijgi 11 00393 g004 550
شکل 4. چارچوب رویکرد ما.
Ijgi 11 00393 g005a 550 Ijgi 11 00393 g005b 550
شکل 5. زیرگروه های ساده سازی 1-4 و عملیات آنها. ( الف ) زیرگروه 1 ، ( ب ) زیرگروه 2 ، ( ج ) زیرگروه 3 ، ( د ) زیرگروه 4 .
Ijgi 11 00393 g006a 550 Ijgi 11 00393 g006b 550
شکل 6. زیرگروه های ساده سازی 5-8 و عملیات آنها. ( الف ) زیرگروه 5 ، ( ب ) زیرگروه 6 ، ( ج ) زیرگروه 7 ، ( د ) زیرگروه 8 .
Ijgi 11 00393 g007 550
شکل 7. انواع اغراق و عملیات آنها: ( الف ) اغراق 1 و ( ب ) اغراق 2 .
Ijgi 11 00393 g008 550
شکل 8. زیرگروه ساده سازی 9 و عملیات آن: ( الف ) زیرگروه 9 و ( ب ) موردی است که vمن-2vمن-1و vمن+1vمن+2هم خطی هستند.
Ijgi 11 00393 g009 550
شکل 9. زیرگروه ساده سازی 10 و عملیات آن: ( a – c ) موارد مختلف زیرنوع 10 هستند.
Ijgi 11 00393 g010 550
شکل 10. زیرگروه ساده سازی 12 و عملیات آن: ( a ، c ، e ) ساختارهای محلی متفاوتی از زیرنوع 12 هستند، و ( b – f ) به ترتیب نتایج ساده شده هستند.
Ijgi 11 00393 g011 550
شکل 11. مثالی از فرآیند ساده سازی: ( الف ) ساختمان اصلی، ( f ) ساختمان ساده شده، و ( ب – ه ) فرآیند ساده سازی هستند.
Ijgi 11 00393 g012 550
شکل 12. تعریف تابع چرخش: ( الف ) زاویه مماس را نشان می دهد ψ، و ( b ) تابع چرخش را نشان می دهد.
Ijgi 11 00393 g013 550
شکل 13. ساده سازی ساختمان ها در مقیاس 1:25000: ( الف ) نتیجه ساده شده در نمای واضح، و ( b ، c ) نماهای بزرگ شده هستند.
Ijgi 11 00393 g014 550
شکل 14. ساده سازی چند مقیاسی ساختمان ها.
Ijgi 11 00393 g015 550
شکل 15. آزمون های ساده سازی ساختمان. ( الف ) ساختمان اصلی و نتیجه ساده شده است. ( ب ) آزمون وابستگی جهت است. ( ج ) آزمون تغییر دنباله رئوس در خلاف جهت عقربه های ساعت است. ( d , e ) آزمون اکستروژن و کشش است. ( f ) تست تنظیم راس شروع است.
Ijgi 11 00393 g016 550
شکل 16. نتایج آزمون مقایسه.
Ijgi 11 00393 g017 550
شکل 17. مقایسه روش های ساده سازی در آستانه های مختلف: ( الف ) NumC ، ( ب ) AreaC ، ( ج ) OrtC ، ( د ) CtrPC ، ( e ) SGC ، ( f ) SDC .

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید