استخراج مناطق فعالیت انسانی از داده های فضایی در مقیاس بزرگ با تراکم های متفاوت

استخراج منطقه فعالیت انسانی، یک موضوع تحقیقاتی محبوب، به استخراج خوشه‌های مکان معنادار از داده‌های فعالیت خام اشاره دارد. با این حال، تراکم های مختلف داده های مکانی در مقیاس بزرگ چالشی را برای روش های استخراج موجود ایجاد می کند. این تحقیق یک چارچوب استخراج منطقه جدید (ELV) را با هدف مقابله با چالش با استفاده از خوشه‌بندی با پارامتر فاصله تطبیقی و یک استراتژی تقسیم‌بندی مجدد با بازیابی نویز پیشنهاد می‌کند. در مرحله اول، یک پارامتر فاصله به طور تطبیقی برای خوشه بندی نقاط با چگالی بالا محاسبه شد، که می تواند عدم قطعیت معرفی شده توسط عوامل ذهنی انسانی را کاهش دهد. ثانیاً، نقاط باقیمانده با توجه به ویژگی‌های فضایی نقاط خوشه‌بندی شده برای قضاوت معقول‌تر نقاط نویز اختصاص داده شدند. سپس، برای مواجهه با مشکل چگالی متفاوت، یک استراتژی تقسیم‌بندی مجدد برای تقسیم‌بندی خوشه‌های مناسب به خوشه‌های کم و چگالی بالا طراحی شد. در نهایت، نقاط نویز تولید شده در مرحله قطعه‌بندی مجدد برای کاهش نویز غیرضروری بازیابی شدند. در مقایسه با سایر الگوریتم‌ها، ELV عملکرد بهتری در مجموعه داده‌های واقعی نشان داد و در شاخص ضریب Silhouette (SC) با بهبود بیش از 16.67 درصد به 0.42 رسید. ELV نتایج خوشه‌بندی قابل اعتمادی را تضمین می‌کند، به‌ویژه زمانی که اختلاف چگالی نقاط فعالیت زیاد است، و می‌تواند در برخی کاربردها، مانند پیش‌بینی مکان و توصیه، ارزشمند باشد. ELV عملکرد بهتری را در مجموعه داده‌های واقعی نشان داد و در شاخص ضریب Silhouette (SC) به 0.42 رسید، با بهبود بیش از 16.67%. ELV نتایج خوشه‌بندی قابل اعتمادی را تضمین می‌کند، به‌ویژه زمانی که اختلاف چگالی نقاط فعالیت زیاد است، و می‌تواند در برخی کاربردها، مانند پیش‌بینی مکان و توصیه، ارزشمند باشد. ELV عملکرد بهتری را در مجموعه داده‌های واقعی نشان داد و در شاخص ضریب Silhouette (SC) به 0.42 رسید، با بهبود بیش از 16.67%. ELV نتایج خوشه‌بندی قابل اعتمادی را تضمین می‌کند، به‌ویژه زمانی که اختلاف چگالی نقاط فعالیت زیاد است، و می‌تواند در برخی کاربردها، مانند پیش‌بینی مکان و توصیه، ارزشمند باشد.

کلید واژه ها:

فعالیت انسانی ؛ استخراج منطقه ; داده های مکانی در مقیاس بزرگ ؛ چگالی متفاوت ؛ الگوریتم خوشه بندی

1. مقدمه

در حال حاضر، حجم عظیمی از داده‌های فعالیت انسانی با اطلاعات برچسب‌گذاری شده جغرافیایی در حال تولید است [ 1 ، 2 ، 3 ]، که فرصتی برای تجزیه و تحلیل عمیق حوزه‌های فعالیت انسانی فراهم می‌کند. حوزه‌های فعالیت عمدتاً به خوشه‌های مکان معنادار استخراج‌شده از داده‌های فعالیت خام اشاره دارند. مسئله چگونگی استخراج اطلاعات ارزشمند از حوزه‌های فعالیت انسانی توجه گسترده‌ای را از زمینه‌های تحقیقاتی مرتبط مختلف، مانند پیش‌بینی تحرک انسان [ 4 ، 5 ]، سیستم‌های توصیه [ 6 ، 7 ، 8 ]، الگوبرداری از مسیر [ 9 ، ] برانگیخته است. 10 ] برانگیخت.] و غیره. با این حال، حوزه‌های فعالیت انسانی را می‌توان به اشکال مختلف استخراج کرد [ 4 ، 11 ، 12 ] که در کاربردهای عملی دشواری‌هایی ایجاد می‌کند. بنابراین لازم است به طور موثر حوزه های فعالیت معناداری استخراج شود که بتواند از نتایج قابل اعتماد پشتیبانی کند و در به کارگیری مطالعات مرتبط مفید باشد.

روش های زیادی برای استخراج مناطق فعالیت پیشنهاد شده است، اما به ناچار از محدودیت های خاصی رنج می برند. یک روش سنتی تخمین چگالی هسته (KDE) [ 13 ، 14 ، 15 ] است که می تواند سطحی با چگالی های مختلف ایجاد کند. با این حال، تعیین مرزهای مناطق و مقدار پهنای باند دشوار است. الگوریتم‌های خوشه‌بندی می‌توانند نقاط را با مرزهای واضح تقسیم کنند و در حال حاضر در استخراج منطقه فعالیت انسانی محبوب هستند [ 16 ، 17 ، 18 ]. K-means [ 19 ، 20] یکی از شناخته شده ترین الگوریتم های خوشه بندی مبتنی بر مرکز است و پیچیدگی زمانی و مکانی کمی دارد، اما از انتخاب تعداد خوشه ها و حساسیت بالای آن به نویز رنج می برد. برخی از مطالعات روش هایی را برای انتخاب یک عدد مناسب به صورت دستی [ 21 ] یا به صورت خودکار [ 22 ] پیشنهاد کردند، اما این برای داده های فضایی در مقیاس بزرگ با چگالی های متفاوت دشوار است. خوشه‌بندی مبتنی بر چگالی، مانند خوشه‌بندی فضایی مبتنی بر چگالی برنامه‌های کاربردی با نویز (DBSCAN) [ 4 ، 23 ، 24 ] و خوشه‌بندی پیک چگالی (DPC) [ 25 ]]، می تواند به طور موثر مشکل نویز را کاهش دهد. استفاده از DBSCAN و DPC با انتخاب پارامترهای مربوط به چگالی محدود شده است که تأثیر زیادی بر نتایج خوشه بندی دارد. اگرچه الگوریتم هایی مانند چند مقیاسی DBSCAN (M-DBSCAN) [ 26 ] و DPC و PSO (PDPC) وجود داشته است. 22 ] وجود داشته است.]، در تلاش برای حل مشکل انتخاب پارامتر، مجموعه داده‌های آزمایشی آن‌ها کوچک بودند و ممکن است برای داده‌های مقیاس بزرگ در این مطالعه مناسب نباشند. علاوه بر این، این دو الگوریتم فقط بر روی مناطق با چگالی بالا تمرکز می کنند و مناطق با تراکم پراکنده را نادیده می گیرند. برای داده‌های فضایی در مقیاس بزرگ (مانند داده‌های مربوط به فعالیت‌های انسانی که چندین شهر را پوشش می‌دهند)، تفاوت در تراکم بسیار زیاد است و بسیاری از مناطق با تراکم نه چندان زیاد ممکن است نادیده گرفته شوند. DBSCAN سلسله مراتبی (HDBSCAN) این مشکل را با معرفی ایده خوشه بندی سلسله مراتبی در DBSCAN کاهش می دهد [ 5 , 27 , 28 , 29]. با این حال، HDBSCAN ممکن است داده های نویز زیادی را در مناطق با تراکم بالا (مانند مراکز شهرها) تولید کند، و برخی از داده های دورتر ممکن است به خوشه هایی در مناطق کم تراکم اختصاص داده شود. بسیاری از مطالعات دیگر الگوریتم‌های خوشه‌بندی جدیدی را در زمینه‌های تحقیقاتی دیگر پیشنهاد کردند [ 30 ، 31 ]، اما به دلیل استفاده از اطلاعات منحصربه‌فرد در زمینه‌های دیگر، جهانی نیستند و کاربرد آن‌ها در استخراج حوزه فعالیت‌های انسانی دشوار است. به طور کلی، کاربرد روش های موجود هنوز به دلیل مشکلات مربوط به انتخاب پارامتر، نویز و تغییرات چگالی محدود است.

در مواجهه با چالش‌های فوق، ما یک چارچوب جدید برای استخراج مناطق فعالیت انسانی از داده‌های فضایی در مقیاس بزرگ با چگالی‌های متفاوت (ELV) پیشنهاد کردیم. در مرحله اول، ما نقاط با چگالی بالا را از داده های خام بر اساس پارامتر فاصله خود انطباق خوشه بندی کردیم. سپس ویژگی‌های فضایی خوشه‌های با چگالی بالا استخراج و برای تخصیص داده‌های کم‌چگالی به خوشه‌های با چگالی بالا استفاده شد. ایده الگوریتم های سلسله مراتبی معرفی شد و همه خوشه ها در نتیجه خوشه اولیه مجدداً تقسیم شدند. این فرآیند چرخه ای است و با توجه به تعداد خوشه ها و داده های نویز تولید شده توسط قطعه بندی مجدد به پایان می رسد. نویز جدید تولید شده در حلقه دوباره با شرایط شل برای بازیابی نویز خوشه بندی شد. در نهایت، چارچوب بر روی سه مجموعه داده واقعی اعمال شد، شامل مجموعه داده های فضایی در مقیاس بزرگ که چندین شهر را پوشش می دهد، و عملکرد بهتری را در مقایسه با سایر روش های پیشرفته نشان داد. روش ما در (1) خوشه‌بندی با پارامتر تطبیقی و ویژگی‌های فضایی استخراج‌شده سودمند است، که می‌تواند تأثیر ذهنی انسان را کاهش دهد و نقاط را بهتر تخصیص دهد. (2) استراتژی بخش‌بندی مجدد با بازیابی نویز، که قابلیت اطمینان مناطق استخراج‌شده از داده‌های مقیاس بزرگ با تراکم‌های متفاوت را تضمین می‌کند. بنابراین، روش ما می تواند بر محدودیت های فوق الذکر روش های موجود غلبه کند. مشارکت های اصلی این کار را می توان به شرح زیر خلاصه کرد: که می تواند تأثیر ذهنی انسان را کاهش دهد و نقاط را بهتر تعیین کند. (2) استراتژی بخش‌بندی مجدد با بازیابی نویز، که قابلیت اطمینان مناطق استخراج‌شده از داده‌های مقیاس بزرگ با تراکم‌های متفاوت را تضمین می‌کند. بنابراین، روش ما می تواند بر محدودیت های فوق الذکر روش های موجود غلبه کند. مشارکت های اصلی این کار را می توان به شرح زیر خلاصه کرد: که می تواند تأثیر ذهنی انسان را کاهش دهد و نقاط را بهتر تعیین کند. (2) استراتژی بخش‌بندی مجدد با بازیابی نویز، که قابلیت اطمینان مناطق استخراج‌شده از داده‌های مقیاس بزرگ با تراکم‌های متفاوت را تضمین می‌کند. بنابراین، روش ما می تواند بر محدودیت های فوق الذکر روش های موجود غلبه کند. مشارکت های اصلی این کار را می توان به شرح زیر خلاصه کرد:

یک مدل خوشه‌بندی جدید برای داده‌های با چگالی بالا با پارامترهای تطبیقی پیشنهاد شده‌است. در مقایسه با روش های موجود، روش ما می تواند عدم قطعیت معرفی شده توسط عوامل ذهنی انسانی را کاهش دهد.
ما روشی را برای تقسیم داده‌های با چگالی کم بر اساس ویژگی‌های فضایی خوشه‌های با چگالی بالا طراحی کردیم، که می‌تواند نویز را منطقی‌تر قضاوت کند.
یک مدل تقسیم‌بندی مجدد ساخته شد که می‌تواند به طور خودکار اثر تقسیم‌بندی مجدد را با توجه به ویژگی‌های خوشه‌بندی قضاوت کند. در مقایسه با روش‌های موجود، بهتر می‌تواند مشکل چگالی متغیر داده‌های فضایی در مقیاس بزرگ را برطرف کند.
یک استراتژی جدید برای بازیابی داده‌های نویز در طول تقسیم‌بندی مجدد ایجاد شد، که می‌تواند از نویز غیرضروری در مقایسه با الگوریتم‌های خوشه‌بندی سلسله مراتبی موجود جلوگیری کند.

ادامه این مقاله به شرح زیر سازماندهی شده است: بخش 2 تحقیقات مرتبط را معرفی می کند. بخش 3 روش شناسی چارچوب ما را شرح می دهد. بخش 4 نتایج آزمایش را مورد بحث قرار می دهد. بخش 5 نتیجه کار را ارائه می دهد.

2. آثار مرتبط

آثار فراوانی در ارتباط با مکان‌های فعالیت انسانی وجود داشته است که پژوهشگران حوزه‌های مختلف را به خود جذب می‌کند. ما ابتدا چندین نوع محبوب از داده‌های فعالیت را معرفی می‌کنیم، سپس الگوریتم‌های اصلی خوشه‌بندی را ارائه می‌کنیم و در آخر کاربردهای احتمالی استخراج مکان فعالیت را نشان می‌دهیم.

انواع مختلفی از داده‌ها که می‌توانند فعالیت انسانی را با اطلاعات برچسب‌گذاری‌شده جغرافیایی توصیف کنند، در کارهای مرتبط مورد استفاده قرار گرفته‌اند، از جمله داده‌های تاکسی [ 18 ، 32 ]، داده‌های تلفن همراه [ 33 ، 34 ]، داده‌های کارت هوشمند [ 35 ]، داده‌های دوچرخه مشترک [ 36 ] ، 37 ]، داده های رسانه های اجتماعی [ 6 ، 8 ] و غیره. داده‌های تاکسی در بسیاری از تحقیقات، مانند تشخیص نقاط مهم [ 38 ]، توصیه سفر [ 39 ] و پیش‌بینی ترافیک استفاده شده است. 40 ]] تحقیقات، با توجه به مقیاس بزرگ داده ها و توصیف تحرک انسان این داده ها ارائه می دهد. اطلاعات مکان داده های تلفن همراه را می توان از شبکه های داده سلولی یا سوابق جزئیات تماس [ 41 ] به دست آورد و برای استخراج الگوی تحرک انسان [ 33 ، 34 ] ارزشمند است . داده های کارت هوشمند عمدتاً رفتار اتوبوس ها و مسافران مترو را ثبت می کنند [ 35 ، 42 ] و در برنامه ریزی شهری مفید هستند. داده های دوچرخه مشترک اخیراً به دلیل حفاظت از محیط زیست و سوابق سفر که در زمینه توریستی مفید هستند بسیار محبوب شده اند [ 43 ]]. اطلاعات تاکسی و کارت هوشمند عمدتاً توسط شرکت های تجاری نگهداری می شود و عمدتاً تنها یک شهر را پوشش می دهد. در حال حاضر به دلیل مسائل مربوط به حریم خصوصی به سختی می توان داده های تلفن همراه و داده های دوچرخه مشترک را به دست آورد. داده های رسانه های اجتماعی توسط افراد به طور فعال ارسال می شود و می توان از رابط های برنامه کاربردی (API) به دست آورد. Foursquare و Gowalla که ورود افراد را ثبت می کنند، منابع داده های رسانه های اجتماعی محبوب هستند [ 6 ، 8 ]، و می توانند رابطه بین افراد و مکان ها را توصیف کنند. مجموعه داده های فلیکر و اینستاگرام، که در تحقیقات زیادی نیز مورد استفاده قرار می گیرند، می توانند عکس های دارای برچسب جغرافیایی [ 44]. علاوه بر این، داده‌های رسانه‌های اجتماعی می‌توانند مقیاس فضایی بسیار بزرگی داشته باشند که برای تحلیل جامع‌تر فعالیت‌های انسانی مفید است. بنابراین، در این تحقیق از مجموعه داده های رسانه های اجتماعی برای تأیید چارچوب پیشنهادی استفاده شد.

الگوریتم‌های خوشه‌بندی مورد استفاده در استخراج ناحیه فعالیت انسانی عمدتاً شامل خوشه‌بندی مبتنی بر مرکز، خوشه‌بندی مبتنی بر چگالی و خوشه‌بندی سلسله مراتبی است. اشبروک و همکاران داده‌های مختصات را با K-means در مکان‌ها خوشه‌بندی کرد و سپس تحرک انسان را پیش‌بینی کرد [ 19 ]. همچنین مطالعات زیادی در رابطه با انتخاب تعداد خوشه‌ها [ 21 ] وجود دارد که یک پارامتر مهم K-means است. برای مثال، سیناگا و همکاران. الگوریتمی را پیشنهاد کرد، K-means بدون نظارت (UK-means)، که می تواند تعداد مناسبی از خوشه ها را بدون تنظیم دستی پیدا کند [ 22 ]. چن و همکاران یک روش خوشه‌بندی جدید بر اساس K-means پیشنهاد کرد که می‌تواند مراکز خوشه‌ای را با توجه به مناطق با تراکم بالا انتخاب کند [ 20 ]]. این روش می تواند با تکرارهای کمتر نتیجه پایدارتری به دست آورد. الگوریتم خوشه‌بندی معروف DBSCAN توسط مارتین و همکاران ارائه شد. برای پایگاه های داده فضایی بزرگ، و نتایج خوشه می تواند اشکال متفاوتی داشته باشد [ 29 ]. DBSCAN در استخراج مناطق فعالیت انسانی محبوب شده است. منطقه منافع (ROI)، استخراج شده توسط DBSCAN، برای توصیف مناطق فعالیت افراد مورد استفاده قرار گرفت و یک مدل پیش بینی بر اساس ROI [ 4 ] ساخته شد. تانگ و همکاران از DBSCAN برای خوشه‌بندی داده‌های تاکسی و تجزیه و تحلیل توزیع مکان‌های حمل و نقل استفاده کرد [ 23 ]. لیو و همکاران M-DBSCAN پیشنهادی برای کاهش عدم قطعیت خوشه بندی از مقیاس های چندگانه [ 26]. این روش مقیاس اندازه های خوشه و تراکم داده های فعالیت افراد را در نظر گرفت. مدل دیگری مبتنی بر چگالی به نام DPC توسط رودریگز بر اساس چگالی مراکز خوشه ای و فواصل بین مراکز پیشنهاد شد [ 25 ]. کای و همکاران PDPC را با ترکیب DPC و بهینه‌سازی ازدحام ذرات (PSO) برای بهبود توانایی جستجوهای جهانی پیشنهاد کرد [ 45 ]]. هم DBSCAN و هم DPC می‌توانند مشکل انتخاب مراکز خوشه‌ای در K-means را بدون اطلاع قبلی برطرف کنند. با این حال، برخی از پارامترهای DBSCAN و DPC مربوط به تعیین چگالی نقاط به سختی انتخاب می شوند و این دو مدل ممکن است برای داده های مقیاس بزرگ با چگالی های متفاوت مناسب نباشند. یک الگوریتم خوشه بندی جدید، HDBSCAN، توسط Campello و همکاران ارائه شد. بر اساس برآورد تراکم سلسله مراتبی [ 27 ]. این روش می تواند عملکرد بهتری را روی داده های چگالی متفاوت در مقایسه با DBSCAN نشان دهد و فقط یک پارامتر دارد. پریت و همکاران از HDBCAN برای خوشه‌بندی عکس‌های دارای برچسب جغرافیایی استفاده کرد و ROI سلسله مراتبی پیدا شد [ 28]. سپس ROI ها برای حاشیه نویسی معنایی مسیرهای استخراج شده از عکس های دارای برچسب جغرافیایی اعمال شدند. میکالیس و همکاران همچنین HDBSCAN را برای استخراج ROI از داده های رسانه های اجتماعی انتخاب کرد و الگوهای سفر گردشگران را تجزیه و تحلیل کرد [ 29 ]. سپس، چندین مورد از محبوب‌ترین مسیرهای سفر که با دنباله‌ای از ROI نشان داده می‌شوند، به‌دست آمدند و نتایج بهتر از روش‌های دیگر بود. با این حال، HDBSCAN ممکن است در نواحی با چگالی زیاد نویز بیش از حد تولید کند و نقاط پرت ممکن است در نواحی با چگالی کم دسته بندی شوند. مطالعات زیادی در رابطه با الگوریتم‌های خوشه‌بندی انجام شده است، اما بسیاری از آنها در زمینه‌های تحقیقاتی دیگر پیشنهاد شده‌اند. برای مثال، سینگ و همکاران. یک الگوریتم خوشه‌بندی جدید برای تجزیه و تحلیل تصاویر پزشکی بیماران مرتبط با COVID-19 پیشنهاد کرد [ 30 ]] و جیانگ و همکاران. الگوریتم دیگری برای تصاویر مغز معرفی کرد [ 31 ]. علاوه بر رشته‌های پزشکی، الگوریتم‌های خوشه‌بندی جدید یا موجود در برخی زمینه‌ها مانند بلایای طبیعی [ 46 ]، تشخیص جامعه [ 47 ]، تقسیم‌بندی تصویر رنگی [ 48 ] و غیره به کار گرفته شده‌اند. همچنین بررسی هایی وجود دارد که انواع مختلفی از الگوریتم های خوشه بندی را نتیجه می دهد [ 49 ، 50 ، 51]. با این حال، این الگوریتم ها معمولا از اطلاعات منحصر به فرد در زمینه های تحقیقاتی دیگر استفاده می کنند و ممکن است برای استخراج منطقه فعالیت از داده های فضایی در مقیاس بزرگ مناسب نباشند. هنوز مطالعه چگونگی بهبود عملکرد استخراج منطقه فعالیت با الگوریتم‌های خوشه‌بندی بیشتر ضروری است. بنابراین، ما ایده سلسله مراتبی را به یک مدل خوشه‌بندی مبتنی بر چگالی جدید برای استخراج مناطق فعالیت معرفی کردیم.

پس از پردازش حوزه های فعالیت، بسیاری از تحلیل ها یا برنامه های کاربردی می تواند ادامه یابد. محمد داده های جنایی را بر اساس DBSCAN برای یافتن نقاط داغ جنایی [ 24 ] دسته بندی کرد. این کار در بالتیمور، مریلند انجام شد و نقاط داغ انواع مختلف حوادث جنایی را به دست آورد. لی و همکاران ابتدا داده های تاکسی را برای استخراج نقاط داغ خوشه بندی کرد و سپس توزیع مکانی-زمانی را تجزیه و تحلیل کرد [ 38 ]. سپس یک شاخص جدید برای ارزیابی جذابیت هات اسپات طراحی شد. یه و همکاران یک رابطه اجتماعی و مکانی قوی بین افراد و مکان‌ها پیدا کرد و یک مدل پیشنهاد مکان بر اساس رابطه [ 6 ]]. این مدل از فیلتر مشارکتی برای امتیاز دادن به مکان ها و به دست آوردن یک نتیجه خوب با مقدار کم محاسبه استفاده می کند. لیان و همکاران یک چارچوب پیشنهاد مکان مقیاس پذیر و انعطاف پذیر برای کاهش مشکل پراکندگی ماتریس های مکان افراد ایجاد کرد [ 8 ]. یک مدل توصیه جدید با معماری دو مرحله ای بر اساس یک ماشین بردار پشتیبان و یک درخت رگرسیون تقویت کننده گرادیان پیشنهاد شد [ 44 ]. این مدل می تواند عملکرد بهتری در شرایط شروع سرد داشته باشد. پیش‌بینی تحرک انسان یکی دیگر از تمرکزهای مهم تحقیقاتی است و هوانگ و همکاران. یک مدل جدید برای پیش بینی مکان های آینده بر اساس AOI های استخراج شده از داده های رسانه های اجتماعی توسط DBSCAN [ 4 ] پیشنهاد کرد.]. چن و همکاران DBSCAN را با HDBSCAN با یک پارامتر تطبیقی برای استخراج AOIها جایگزین کرد [5 ]. سپس، یک مدل بیزی بهبود یافته با ویژگی های وزنی برای پیش بینی مکان های آینده توسعه یافت. طبرج و همکاران دو الگوریتم خوشه‌بندی را با هم ترکیب کرد و آنها را به داده‌های بهداشتی برای تجزیه و تحلیل نقاط داغ شرایط سلامت در هند اعمال کرد [ 52 ]. در مجموع، استخراج حوزه‌های فعالیت معنادار برای اطمینان از تجزیه و تحلیل و کاربردهای قابل اعتماد ارزشمند است.

3. روش شناسی

3.1. توضیحات داده ها

در این تحقیق از سه مجموعه داده واقعی که از یک پلتفرم رسانه اجتماعی (Weibo) به دست آمده بودند استفاده شد. مجموعه داده ها در مناطق مختلف، از جمله منطقه خلیج بزرگ گوانگدونگ-هنگ کنگ-ماکائو (منطقه خلیج بزرگ، GBA)، شانگهای و پکن جمع آوری شدند. مجموعه داده GBA از یک مجموعه داده باز استخراج شده است و می توان آن را در [ 53 ] یافت. شانگهای و پکن از شهرهای مهم و معروف چین به خصوص پکن که پایتخت کشور چین است می باشند. GBA یک تراکم شهری با 11 شهر از جمله هنگ کنگ، ماکائو، شنژن، گوانگژو و غیره است. مطابق جدول 1، مجموعه داده GBA با 12 هفته طولانی ترین بازه زمانی را داشت و دو مجموعه داده دیگر هر دو دارای بازه زمانی یک هفته بودند. از آنجایی که داده‌های GBA 11 شهر را پوشش می‌دهند و دو مجموعه داده دیگر فقط یک شهر را پوشش می‌دهند، فضای مجموعه داده GBA چندین برابر دو مجموعه داده دیگر بود که در کل رکوردها نیز منعکس شد.

مشخصات توزیع فضایی سه مجموعه داده نیز در شکل 1 نشان داده شده است. با توجه به نقشه های حرارتی، توزیع های فضایی بسیار متفاوت بود. مجموعه داده های GBA ( شکل 1 الف) دارای چندین ناحیه هسته بزرگ با تراکم بالا، و برخی مناطق کوچک با تراکم بالا در اطراف نواحی هسته توزیع شده بودند. این مناطق پر تراکم عمدتاً در اطراف مراکز شهر بودند و پراکندگی در هر شهر متفاوت بود. تقریباً همه مناطق در برخی شهرها دارای تراکم بالا بودند، اما فقط مراکز سایر شهرها دارای تراکم بالا بودند. مجموعه داده‌های شانگهای و پکن هر دو دارای مناطق هسته بزرگ با تراکم بسیار بالا بودند و مناطق با تراکم پایین در اطراف مناطق هسته بودند.

علاوه بر این، ما نه تنها از کل مجموعه داده GBA استفاده کردیم، بلکه 7 روز از هفته اول و کل 12 هفته را نیز استخراج کردیم. اطلاعات آماری در شکل 2 نشان داده شده است . تعداد رکوردهای 7 روز تفاوت آشکاری را نشان داد: این تعداد ابتدا افزایش یافت و در 25 دسامبر (روز کریسمس) به اوج خود رسید و سپس تا آخر هفته (28 و 29 دسامبر) شروع به کاهش کرد. مطابق با شکل 2ب، تعداد رکوردها در هفته (از 30-12-2019 تا 05-01-2020) به دلیل روز سال نو بسیار زیاد بود. با این حال در جشنواره بهار کمترین رکورد ثبت شد. دلیل این امر شاید این بوده است که افراد در این 11 شهر در طول جشنواره بهار به خانه بازگشتند و به دلیل COVID-19 نتوانستند به این شهرها برگردند. سپس به دلیل از سرگیری کار، این تعداد به مقادیر زیادی افزایش یافت.

به طور خلاصه، کل مجموعه داده GBA، مجموعه داده شانگهای، مجموعه داده پکن و بخش های مختلف مجموعه داده GBA در آزمایش استفاده شد.

3.2. استخراج مناطق فعالیت انسانی از داده های فضایی در مقیاس بزرگ با تراکم های متفاوت

در این تحقیق از مکان‌های داده‌های فعالیت انسانی برای استخراج منطقه فعالیت استفاده شد. مکان های خام با مختصات ژئودتیکی نشان داده شده و به مختصات صفحه تبدیل شدند. در چارچوب پیشنهادی، ELV، داده های مکان جدید با مراحل زیر پردازش می شوند (نشان داده شده در شکل 3 ):

(1): خوشه بندی تطبیقی نقاط با چگالی بالا. یک روش تطبیقی پارامتر فاصله برای محاسبه چگالی نقاط در داده های مکان پیشنهاد شده است. سپس نقاط با چگالی بالا به عنوان نقاط هسته استخراج می شوند. پارامتر فاصله برای تقسیم نقاط اصلی به خوشه های مختلف استفاده می شود.
(2): تخصیص داده های باقی مانده ویژگی های فضایی خوشه های نقطه هسته استخراج شده است که می تواند تنگی نقاط هسته در هر خوشه را توصیف کند. سپس، ویژگی ها در یک آستانه فاصله ترکیب می شوند. برای یک نقطه باقیمانده، نزدیکترین خوشه نقطه هسته پیدا می شود و فاصله بین آنها با آستانه فاصله برای تخصیص نقطه مقایسه می شود.
(3): تصمیم تقسیم مجدد نتیجه خوشه‌بندی اولیه به‌دست‌آمده از دو مرحله بالا برای تصمیم‌گیری مجدد قطعه‌بندی استفاده می‌شود. به طور خاص، تعداد نقاط در یک خوشه ابتدا برای تصمیم گیری در مورد اینکه آیا این خوشه می تواند دوباره بخش بندی شود استفاده می شود. سپس، نقاط دوباره خوشه بندی می شوند و پارامتر فاصله، تعداد خوشه های جدید و نقاط نویز برای تصمیم گیری در مورد مناسب بودن تقسیم بندی مجدد استفاده می شود.
(4): بازیابی نویز در مرحله تقسیم مجدد، نقاط موجود در خوشه ها ممکن است نویز در نظر گرفته شوند و در نتیجه نقاط نویز زیادی تولید شود. بنابراین، برای هر قطعه‌بندی مجدد، نقاط نویز جدید با توجه به پارامتر فاصله قدیمی که آنها را به یک خوشه اختصاص داده است، مجدداً خوشه‌بندی می‌شوند و پارامتر فاصله جدید از نقاط نویز استخراج می‌شود.

پس از چهار مرحله اصلی می توان به نتیجه نهایی رسید و در ادامه جزئیات چهار مرحله معرفی می شود.

3.2.1. خوشه بندی تطبیقی نقاط با چگالی بالا

در کل چارچوب پیشنهادی، ابتدا نقاط با چگالی بالا استخراج و خوشه‌بندی می‌شوند. بنابراین، تعریف مناسب تراکم بالا برای نقاط موجود در داده های فعالیت انسان ضروری است. به طور معمول، چگالی یک نقطه به عنوان تعداد نقاط در یک محدوده خاص محاسبه می شود. این محدوده معمولاً دایره ای است که نقطه آن مرکز است و شعاع به طور مصنوعی مشخص می شود. سپس مسئله محاسبه چگالی به انتخاب شعاع تبدیل می شود که به آن می گویند. هپسدر روش های دیگر در کاربردهای سنتی، مقادیر متفاوتی از هپستست می شوند و کاربران سعی می کنند با توجه به نتایج بهترین مقدار را پیدا کنند. با این حال، انتخاب یک نتیجه خوب برای داده های در مقیاس بزرگ دشوار است، و هر انتخابی ممکن است از کارایی پایین آنها، به ویژه برای بیش از یک مجموعه داده، رنج ببرد. یک روش پیشنهادی ترسیم نمودار فاصله k است که می تواند روابط فواصل بین نقاط مختلف را توصیف کند. اینجا، کمعمولاً دو برابر ابعاد تنظیم می شود و برای داده های مکانی با دو بعد، ک4 است. در جزئیات، برای یک نقطه، فاصله بین آن و نقاط دیگر محاسبه می شود تا آن را پیدا کنید ک-مین نزدیکترین نقطه، و فاصله ثبت شده است. پس از به دست آوردن فواصل بین تمام نقاط و آنها ک-نزدیکترین نقطه، فواصل به ترتیب از کوچک به بزرگ مرتب می شوند و می توان آنها را به صورت زیر تعریف کرد:

سهqدمنسک(پ)=[دمنسک(پ1)،دمنسک(پ2)،⋯،دمنسک(پمن)،⋯،دمنسک(پn)]

(1)

جایی که پبه مجموعه داده با اشاره دارد nنکته ها؛ پمننقاطی هستند که در پ; دمنسک(پمن)، با 1≤من≤n، تابعی است برای محاسبه فاصله بین پمنو ک-نزدیکترین نقطه؛ سهqدمنسک(پ)دنباله فاصله مرتب شده است. سپس، دنباله را می توان همانطور که در شکل 4 نشان داده شده است ، با فواصل روی محور عمودی Y در برابر نقاط روی محور x افقی ترسیم کرد. از شکل مثال، منحنی حدود 14000 تغییر کرد و ما نقطه نارنجی را به عنوان نقطه آرنج انتخاب کردیم که فاصله آن را می توان به صورت زیر در نظر گرفت. هپس. با این حال، باید توجه داشت که انتخاب ذهنی بود و نقاط موجود در کادر قرمز ممکن است توسط افراد مختلف نقطه آرنج در نظر گرفته شود.

ما یک روش تطبیقی برای استخراج آرنج از شکل برای کاهش عوامل ذهنی پیشنهاد کردیم (نشان داده شده در الگوریتم 1). در واقع، استفاده از فرمول های ریاضی برای نشان دادن منحنی سخت است، اما این مشکل از نقطه نظر هندسی قابل حل است. با مشاهده شکل به راحتی می توان دریافت که انحنای اطراف نقطه آرنج زیاد بوده در حالی که در نقاط دیگر کوچک بوده است. بنابراین می توان سعی کرد انحناها را به صورت ریاضی توصیف کرد و سپس انحنای حداکثر نقطه را استخراج کرد. پس از به دست آوردن مرتب شده است سهqدمنسک(پ)(الگوریتم 1 خط 1-5)، از زوایای هر سه نقطه برای نشان دادن انحناها استفاده می شود و دنباله زوایا را می توان به صورت زیر تعریف کرد (الگوریتم 1 خط 6-9):

الگوریتم 1 : انتخاب پارامتر از هپس

ورودی: تمام نقاط برای خوشه بندی پ

خروجی: هپس

سهqدمنسک(پ)= [ ]
برای پمنکه در پ:
دمنسک(پمن)= فاصله ( پمن، k)//فاصله بین را محاسبه کنید پمنو k -امین نزدیکترین نقطه
سهqدمنسک(پ).append( دمنسک(پمن))
مرتب سازی( سهqدمنسک(پ))
سهqآng(پ)= [ ]
برای دمنسک(پمن)که در سهqدمنسک(پ):
آng(پمن–2،پمن–1،پمن)=آng(پمن–1پمن–2→،پمن–1پمن→)//زاویه سه نقطه پیوسته را محاسبه کنید
سهqآng(پ).append( آng(پمن–2،پمن–1،پمن))
پهلبow= [ ]
برای سمنzهدر محدوده (1, سمنzهمترآایکس):
پهلبow.append( آrgمترمنn(سمترooتیساعتسمنzه(سهqآng(پ))))//نقاط آرنج را استخراج کنید
پهلبow= متوسط( پهلبow)
هپس= دمنسک(پهلبow)
برگشت هپس

سهqآng(پ)=[آng(پ1،پ2،پ3)،آng(پ2،پ3،پ4)،⋯،آng(پمن–2،پمن–1،پمن)،⋯،آng(پn–2،پn–1،پn)]

(2)

جایی که سهqآng(پ)تابعی است برای بدست آوردن دنباله زوایا و آng(پمن–2،پمن–1،پمن)برای محاسبه زاویه سه نقطه پیوسته استفاده می شود. این بر اساس مختصات در کنمودار فاصله، به جای مختصات خام در دنیای واقعی. مختصات یک نقطه پمنهست (من،دمنسک(پمن))و تابع زاویه را می توان به صورت زیر تعریف کرد (الگوریتم 1 خط 8):

آng(پمن–2،پمن–1،پمن)=آng(پمن–1پمن–2→،پمن–1پمن→)

(3)

جایی که پمن–1پمن–2→و پمن–1پمن→بردارهایی هستند که توسط سه نقطه ترکیب شده اند و زاویه به زاویه شامل دو بردار اشاره دارد. نقطه با بیشترین انحنا، نقطه وسط سه نقطه با کوچکترین زاویه است:

پهلبow=آrgمترمنn(سهqآng(پ))

(4)

هنوز این مشکل وجود دارد که ممکن است منحنی به اندازه کافی صاف نباشد و منجر به استخراج اشتباه نقطه آرنج شود. برای افزایش قابلیت اطمینان روش، پنجره های کشویی با اندازه های مختلف از 1 تا سمنzهمترآایکساستفاده می شوند سهqآng(پ)و توالی‌های هموار جدیدی از زاویه‌ها را می‌توان به‌دست آورد، به‌عنوان ثبت سمترooتیساعتسمنzه(سهqآng(پ))جایی که 1≤سمنzه≤سمنzهمترآایکس. مقادیر جدید زاویه ها در دنباله های هموار شده به شرح زیر است:

آngسمنzه(پمن–2،پمن–1،پمن)=آvg(آng(پمن–2–سمنzه/2،پمن–1–سمنzه/2،پمن–سمنzه/2)،⋯،آng(پمن–2،پمن–1،پمن)،⋯،آng(پمن–2+سمنzه/2،پمن–1+سمنzه/2،پمن+سمنzه/2))

(5)

که مقدار متوسط زوایای پنجره کشویی را محاسبه می کند. نقطه آرنج نهایی را می توان به صورت زیر تعریف کرد (الگوریتم 1 خط 10-13):

پهلبow=∑سمنzه=1سمنzهحداکثرآrgمترمنn(سمترooتیساعتسمنzه(سهqآng(پ)))سمنzهحداکثر

(6)

سپس، ارزش سمنzهمترآایکسباید به طور مناسب انتخاب شود، زیرا بیش از حد بزرگ است سمنzهمترآایکسممکن است منجر به اعوجاج در منحنی شود. بنابراین، اجازه دهید سمنzهمترآایکس=n∗تیساعتrسمنzه+1، جایی که تیساعتrسمنzهدرصدی از کل حجم داده است. ارزش تیساعتrسمنzهرا می توان به عنوان یک ثابت بسیار کوچک (1٪) برای حفظ قابلیت اطمینان دنباله هموار تنظیم کرد. سپس، یک مقدار قطع nجتوتیoff=1/تیساعتrسمنzهظاهر می شود. اگر اندازه نقاط کوچکتر از nجتوتیoff، سمنzهمترآایکسهمیشه 1 است و عملکرد صاف کار نمی کند. بنابراین، ما کوچکترین مقدار را تعیین می کنیم سمنzهمترآایکسبه عنوان 2. با این حال، زمانی که اندازه نقاط خیلی بزرگ است ( n≫nجتوتیoff، حلقه محاسبه دنباله هموار شده بزرگ خواهد بود. این از نظر تئوری بر اثربخشی روش تأثیر نمی‌گذارد، اما ممکن است کارایی آن در کاربرد عملی پایین باشد. آستانه دیگری برای محدود کردن تعداد حلقه ها تنظیم شده است. برای مجموعه داده با nجتوتیoffنقاط، اندازه پنجره کشویی باید حداقل کوچکتر از nجتوتیoff/2تا مقدار داده های معتبر بیشتر شود (به عنوان آمتر(vد)) از داده های نامعتبر (به عنوان ثبت شده است آمتر(مند)). برای مجموعه داده با nنکته ها ( n≫nجتوتیoff) آمتر(vد)≫آمتر(مند)اگر اندازه هنوز است nجتوتیoff/2. از این رو، سمنzهمترآایکسرا می توان به صورت زیر تعریف کرد:

سمنzهمترآایکس=حداکثر(2دقیقه(n∗تیساعتrسمنzه+1nجتوتیoff2))

(7)

پس از استخراج خودکار از هپس، نقاط با چگالی بالا را می توان استخراج و خوشه بندی کرد (نشان داده شده در شکل 5 ). در مرحله اول، چگالی نقاط محاسبه می شود، و نقاط با چگالی بالا، با چگالی کمتر از ک، استخراج می شوند (به رنگ نارنجی در شکل وسط شکل 5 ). سپس فرآیند خوشه بندی نقاط با چگالی بالا آغاز می شود. ایده اصلی این است که فاصله بین نقاط در یک خوشه کوچکتر از هپس، و فاصله بین خوشه ها بزرگتر از هپس. بنابراین نقطه اول به صورت تصادفی انتخاب و به عنوان اولین خوشه تنظیم می شود. تمام نقاط با چگالی بالا، با فواصل بین آنها و هر نقطه در خوشه کوچکتر از هپس، متعلق به خوشه است و باید با یک عدد برچسب گذاری شود. سپس، فرآیند روی نقاط باقیمانده چرخه می‌شود تا زمانی که تمام نقاط با چگالی بالا متعلق به برخی خوشه‌ها باشند و برچسب‌گذاری شوند. در قسمت سمت راست شکل 5 ، سه خوشه مختلف با نقاط چگالی بالا استخراج شد. در نهایت مجموعه ای از خوشه ها ( جلتوستیهr1،جلتوستیهr2،⋯،جلتوستیهrj،⋯،جلتوستیهrمتر، 1≤j≤متر) و یک دنباله برچسب خوشه ای از نقاط ( جل(پ)) را می توان بدست آورد:

جل(پ)=[لآبهل1،لآبهل2،⋯،لآبهلمن،⋯،لآبهلn]

(8)

نقاط کم چگالی در فرآیند خوشه‌بندی بالا برچسب‌گذاری نشده‌اند (هنوز در شکل سمت راست شکل 5 با آبی رنگ شده‌اند)، اما برای راحتی همه آنها با -1 برچسب‌گذاری شده‌اند و در قسمت بعدی خوشه‌بندی خواهند شد.

3.2.2. تخصیص داده های باقی مانده

تمام نقاط با چگالی بالا در فرآیند فوق خوشه بندی می شوند و سعی می شود نقاط باقی مانده به خوشه ها اختصاص داده شوند (الگوریتم 2). شکل 6 نمونه ای از تکلیف را نشان می دهد. دو مرحله اصلی برای انتساب وجود دارد، یعنی یافتن خوشه‌های ممکن و قضاوت در مورد مطابقت نقاط با ویژگی‌های خوشه. در مرحله اول، امکان تعلق یک نقطه به یک خوشه با فاصله بین آنها ارزیابی می شود (الگوریتم 2 خط 7-9). در مثال، فاصله بین نقطه انتخاب شده و سه خوشه محاسبه شده است. هر چه فاصله کمتر باشد، امکان بیشتر است. روند یک نقطه ( پمن) به شرح زیر است:

j=آrgمترمنn(دمنستیآnجه(پمن،جلتوستیهrj))1≤j≤متر

(9)

فاصله بین یک نقطه و یک خوشه را می توان در قالب های مختلف تعریف کرد. یک روش استفاده از یک نقطه، مانند مرکز خوشه، برای نشان دادن خوشه است. روش دیگر از مقدار میانگین تمام فواصل بین نقطه هدف و تمام نقاط خوشه استفاده می کند. روش‌ها می‌توانند روی خوشه‌هایی با اشکال محدب به خوبی کار کنند، اما در این تحقیق، اشکال خوشه‌های به‌دست‌آمده بر اساس چگالی می‌تواند نامنظم باشد. بنابراین فقط از مقدار min فواصل بین نقطه هدف و تمام نقاط خوشه استفاده می شود. در ترکیب با معادله (8)، فرآیند یافتن خوشه ممکن را می توان برای یافتن خوشه با نزدیکترین نقطه ساده کرد.

الگوریتم 2 : تخصیص داده های باقی مانده

ورودی: نتیجه خوشه بندی نقاط با چگالی بالا جل(پ)

خروجی: نتیجه خوشه بندی اولیه ثبت شده در به روز شده است جل(پ)

برای jدر محدوده (m):
دآتیآ(جلتوستیهrj)= استخراج شده( جل(پ)، j)//نقاط مرتبط را با توجه به برچسب ها استخراج کنید
دمنس(جلتوستیهrj)= [ ]
برای نقطه در دآتیآ(جلتوستیهrj):
دمنس(جلتوستیهrj).append(mindistance(point))//محاسبه فاصله بین هر نقطه و نزدیکترین نقطه آن در جلتوستیهrj
تیساعتrدمنس(جلتوستیهrj)=مترهآn(دمنس(جلتوستیهrj))+3∗ستید(دمنس(جلتوستیهrj))//محاسبه آستانه فاصله
برای لآبهلمنکه در جل(پ):
اگر لآبهلمن!= −1: ادامه// از نقاط برچسب گذاری شده عبور کنید
j=آrgمترمنn1≤j≤متر(دمنستیآnجه(پمن،جلتوستیهrj))//ممکن ترین خوشه را پیدا کنید
اگر دمنستیآnجه(پمن،جلتوستیهrj)≤تیساعتrدمنس(جلتوستیهrj):
لآبهلمن= j
جل(پ).به روز رسانی( لآبهلمن)
برگشت جل(پ)

در مرحله دوم قضاوت می کنیم که آیا یک نقطه به خوشه ممکن تعلق دارد یا خیر دمنستیآnجه(پمن،جلتوستیهrj)و یک آستانه فاصله ( تیساعتrدمنس) (الگوریتم 2 خط 10-12). در شکل 6 ، ممکن ترین خوشه خوشه 1 است، بنابراین دمنستیآnجه(پمن،جلتوستیهr1)و تیساعتrدمنس(جلتوستیهr1)مقایسه می شوند. ارزش هپساغلب به عنوان آستانه در روش های دیگر استفاده می شود، اما این ویژگی های فضایی مختلف خوشه ها را نادیده می گیرد. به عنوان مثال، دو نقطه و خوشه های ممکن آنها وجود دارد. نقاط یک خوشه بسیار متمرکز هستند و مساحت خوشه (مانند بدنه محدب) بسیار کوچک است. حالت شدید این است که همه نقاط با مختصات یکسانی باشند. برای این مورد، حتی اگر دمنستیآnجه(پمن،جلتوستیهrj)کوچکتر از هپس، نقطه هنوز برای اختصاص دادن به خوشه مناسب نیست. در یک خوشه دیگر، توزیع نقاط پراکنده است و فاصله بین نقاط نزدیک به هپس. بنابراین تخصیص نقطه به این خوشه بسیار مناسب است. بنابراین، آستانه‌های متفاوتی با توجه به توزیع فضایی نقاط در خوشه‌های ممکن تنظیم می‌شوند.

بخشی از فواصل بین نقاط در یک خوشه ممکن برای توصیف توزیع فضایی استفاده می شود (الگوریتم 2 خط 1-6). دلیل استفاده نکردن از تمام فواصل این است که اشکال در این تحقیق نامنظم بوده و ممکن است فاصله بین برخی نقاط بسیار زیاد باشد. برای هر نقطه از خوشه، فاصله بین آن و نزدیکترین نقطه در خوشه محاسبه می شود. سپس یک گروه فاصله از خوشه ( دمنس(جلتوستیهrj)) را می توان برای توصیف توزیع فضایی به دست آورد. حداکثر مقدار در گروه به صورت ثبت می شود مترآایکس(دمنس(جلتوستیهrj))، مقدار میانگین به صورت ثبت می شود مترهآn(دمنس(جلتوستیهrj))، و انحراف معیار به صورت ثبت می شود ستید(دمنس(جلتوستیهrj)). آستانه فاصله یک خوشه ( تیساعتrدمنس(جلتوستیهrj)) به صورت زیر تعریف می شود:

تیساعتrدمنس(جلتوستیهrj)=مترهآn(دمنس(جلتوستیهrj))+3∗ستید(دمنس(جلتوستیهrj))

(10)

در معادله فوق از انحراف استاندارد سه گانه برای حذف آماری نویز استفاده شده است. یک محدوده ارزشی از تیساعتrدمنس(جلتوستیهrj)باید برای افزایش استحکام روش تنظیم شود. نقاط یک خوشه گاهی اوقات ممکن است توزیع ناهمواری داشته باشند و برخی از نقاط نزدیک به هم می توانند منجر به یک توزیع کوچک شوند. تیساعتrدمنس(جلتوستیهrj)، که می تواند صدای زیادی تولید کند. از این رو، مترآایکس(دمنس(جلتوستیهrj))به حد پایین تنظیم شده است، و اگر تیساعتrدمنس(جلتوستیهrj)کوچکتر از مترآایکس(دمنس(جلتوستیهrj))، اجازه دهید تیساعتrدمنس(جلتوستیهrj)=مترآایکس(دمنس(جلتوستیهrj)). حد بالایی تنظیم شده است هپسبرای اطمینان از فیلتر نقاط نویز، و اگر تیساعتrدمنس(جلتوستیهrj)بزرگتر از هپس، اجازه دهید تیساعتrدمنس(جلتوستیهrj)=هپس. این آستانه های خوشه های مختلف را می توان در ابتدا همانطور که در الگوریتم 2 خط 1-6 برای کارایی توضیح داده شده است محاسبه کرد. در نهایت، برچسب یک نقطه باقی مانده ( لآبهلمن) را می توان به صورت زیر تعریف کرد:

لآبهلمن={j منf دمنستیآnجه(پمن،جلتوستیهrj)≤تیساعتrدمنس(جلتوستیهrj)–1 منf دمنستیآnجه(پمن،جلتوستیهrj)>تیساعتrدمنس(جلتوستیهrj)

(11)

پس از به دست آوردن تمام برچسب های نقطه مطابق با معادله (11)، عناصر موجود در معادله (8) سپس به برچسب های مربوطه تبدیل می شوند (الگوریتم 2 خط 10-13) و یک نتیجه خوشه بندی اولیه به دست می آید (قسمت سمت راست شکل 6 ).

3.2.3. تصمیم تقسیم مجدد

نتیجه خوشه بندی اولیه ثبت شده در جل(پ)سپس برای تقسیم بندی مجدد به منظور رسیدگی به مشکل چگالی متغیر داده های فضایی در مقیاس بزرگ استفاده می شود. جریان فرآیند یک تقسیم بندی مجدد در الگوریتم 3 توضیح داده شده است و شکل 7 تقسیم بندی مجدد را در یک خوشه انتخاب شده نشان می دهد. در این مرحله، هر خوشه در جل(پ)با برچسب ها و مختصات آن به عنوان یک مجموعه داده جدید استخراج می شود دآتیآ(جلتوستیهrj)(الگوریتم 3 خط 1-2). سپس، دو مرحله خوشه‌بندی بالا ( بخش 3.2.1 و بخش 3.2.2 ) دوباره روی مجموعه داده جدید پردازش می‌شوند و نتیجه خوشه‌بندی ( جل(دآتیآ(جلتوستیهrj))) برای به روز رسانی عناصر در استفاده می شود جل(پ). پس از پردازش همه خوشه ها، بخش بندی مجدد به صورت دایره ای در به روز شده استفاده می شود. جل(پ). در حلقه، دو مشکل اصلی وجود دارد که باید برطرف شود، یعنی if دآتیآ(جلتوستیهrj)را می توان خوشه بندی کرد (الگوریتم 3 خط 3-9) و اگر جل(دآتیآ(جلتوستیهrj))یک نتیجه خوب برای به روز رسانی است جل(پ)با (الگوریتم 3 خط 10-16).

اولا، دآتیآ(جلتوستیهrj)بررسی می شود تا ببیند آیا می توان آن را خوشه بندی کرد یا خیر، و خوشه 1 در شکل 7 انتخاب شده است. طبق بخش 3.2.1 ، نقاط با چگالی بالا باید استخراج و خوشه بندی شوند. بنابراین، شرط اصلی خوشه این است که حداقل یک نقطه با چگالی بالا وجود داشته باشد، که به معنی تعداد نقاط در دآتیآ(جلتوستیهrj)نباید کوچکتر از k باشد (الگوریتم 3 خط 3-4). اگر عدد شرایط را برآورده کند، روش تطبیقی از هپساستخراج بر روی نقاط برای به دست آوردن یک مقدار جدید استفاده می شود ( هپسj). ارزش هپسjبا مقدار قدیمی مقایسه می شود هپس، که برای تولید استفاده می شد جلتوستیهrj. اگر هپسjکوچکتر از هپس، تقسیم بندی مجدد معنی ندارد (الگوریتم 3 خط 5-7). سپس، دآتیآ(جلتوستیهrj)با روش بخش 3.2.1 و بخش 3.2.2 با استفاده از پارامتر خوشه بندی می شودهپسj.

دوم، نتیجه خوشه بندی جل(دآتیآ(جلتوستیهrj))بررسی می شود تا ببیند آیا به روز رسانی خوب است یا خیر جل(پ)با. تعداد برچسب های مختلف در جل(دآتیآ(جلتوستیهrj))محاسبه می شود و در صورت وجود نویز عدد منهای 1 را بگذارید (الگوریتم 3 خط 10-12). این عدد می‌تواند تعداد مناطق فعالیت معتبر را در این تقسیم‌بندی مجدد توصیف کند و بررسی می‌شود که آیا بزرگ‌تر از 1 است یا خیر. در شکل 7 ، خوشه 1 به سه خوشه جدید تقسیم شده است و نتیجه خوشه‌بندی جدید برای به‌روزرسانی مناسب است. جل(پ). با این حال، زمانی که عدد 1 باشد، بخش‌بندی مجدد نمی‌تواند خوشه‌های جدید استخراج کند و فقط نقاط نویز بیشتری تولید می‌کند. چنین وضعیتی برای استخراج منطقه فعالیت معنی ندارد جل(پ)نباید با آن به روز شود جل(دآتیآ(جلتوستیهrj)). مقادیر مختلف از هپسjاز جانب هپسبه 0 علاوه بر این سعی می شود تا پایداری نتایج روی داده ها را با تعداد بسیار کمی از نقاط افزایش دهند، زمانی که بازگشت الگوریتم 3 -1 است. بررسی نتایج خوشه‌بندی تا زمانی ادامه می‌یابد که تعداد برچسب‌ها از 1 بزرگتر شود، که به این معنی است که پردازش الگوریتم 3 خط 8-16 را با موارد مختلف حلقه کنید. هپسj. اگر هیچ نتیجه ای نتواند شرایط را برآورده کند، جل(پ)در این بخش بندی مجدد به روز نمی شود.

الگوریتم 3 : یکبار تقسیم بندی مجدد

ورودی: نتیجه خوشه بندی اولیه جل(پ)، پارامتر هپس

خروجی: نتیجه تقسیم بندی مجدد در به روز شده ثبت شده است جل(پ)

برای jدر محدوده (m):
دآتیآ(جلتوستیهrj)= استخراج شده( جل(پ)، j)//نقاط مرتبط را با توجه به برچسب ها استخراج کنید
اگر لن( دآتیآ(جلتوستیهrj)) < k:
بازگشت 0//بررسی کنید که آیا تعداد نقاط داده را می توان خوشه بندی کرد
هپسj= الگوریتم 1( دآتیآ(جلتوستیهrj))
اگر هپسj≥ هپس://بررسی کنید که آیا پارامتر می تواند برای خوشه بندی استفاده شود
بازگشت −1
جل(دآتیآ(جلتوستیهrj))= cluster_high_density_points( دآتیآ(جلتوستیهrj)، هپسj)
جل(دآتیآ(جلتوستیهrj))= الگوریتم 2( جل(دآتیآ(جلتوستیهrj)))
num_labels = len( منحصر به فرد جل(دآتیآ(جلتوستیهrj))))//تعداد برچسب های مختلف را محاسبه کنید
اگر -1 اینچ جل(دآتیآ(جلتوستیهrj)):
num_labels = num_labels − 1
اگر num_labels ≤ 1:
بازگشت -1//بررسی کنید که آیا می توان از نتیجه خوشه برای به روز رسانی استفاده کرد
جل(پ).به روز رسانی( جل(دآتیآ(جلتوستیهrj)))
برگشت جل(پ)

با استفاده از دو مرحله بررسی بالا، جدید است جل(پ)می توان به دست آورد، و یک قطعه بندی مجدد به پایان می رسد. دو مرحله (الگوریتم 3) به چرخه جدید ادامه می دهند جل(پ)تا زمانی که نتایج واجد شرایطی وجود نداشته باشد. برای بهبود کارایی حلقه، می‌توان از یک مجموعه برچسب برای ضبط برچسب‌هایی استفاده کرد که نقاط متناظر آن‌ها نیاز به قطعه‌بندی مجدد دارند. اگر نقاط یک خوشه نتوانند دو بررسی فوق را برآورده کنند، برچسب این خوشه از مجموعه برچسب حذف می شود. علاوه بر این، هنگامی که نقاط یک خوشه مجدداً تقسیم می شوند، برچسب قدیمی حذف می شود و برچسب های جدید متفاوت از برچسب های موجود در مجموعه برچسب باید اضافه شوند.

3.2.4. بازیابی نویز

این بخش استراتژی بازیابی نقاط نویز در مرحله تقسیم بندی مجدد را معرفی می کند (الگوریتم 4). بسیاری از روش‌های خروجی نقاط نویز ایجاد نمی‌کنند، اما برای استخراج منطقه فعالیت انسانی به دلیل تصادفی بودن تحرک انسان ضروری است. روش های مبتنی بر چگالی معمولا نقاط را بر اساس چگالی و فاصله بین نقاط به نویز تقسیم می کنند. برای این روش ها نیازی به بازیابی نویز نیست، زیرا فقط یک بار نقاط نویز تولید می کنند. با این حال، حلقه در مرحله تقسیم مجدد به نقاط خوشه ای ادامه می دهد و می تواند نقاط نویز بیشتری نسبت به روش های دیگر ایجاد کند. برخی از برنامه ها فقط بر روی چندین منطقه با چگالی بالا تمرکز می کنند، مانند نقاط مهم، و بسیاری از نقاط بدون تراکم بالا نویز در نظر گرفته می شوند. در چنین شرایطی، بازیابی نویز معنایی ندارد. در این تحقیق، ما سعی کردیم مناطق فعالیت انسانی را با تراکم های مختلف استخراج کنیم. در یک حلقه تقسیم مجدد، نقاطی با چگالی نسبتاً کوچک ممکن است نویز در نظر گرفته شوند، حتی اگر در حلقه قبلی خوشه شده باشند، و چنین نقاطی اهداف بازیابی نویز هستند. که دردر شکل 8 ، نقاط خوشه 3 به دو خوشه تقسیم شده و نقاط زیادی به دلیل اختلاف چگالی نویز در نظر گرفته می شوند. برخی از نقاط نویز را می توان با یک پارامتر بزرگتر بازیابی کرد.

اصل بازیابی نویز شبیه به دو حالتی است که در مورد امکان تقسیم مجدد نقاط قضاوت می کنند. فرآیند بازیابی پس از تقسیم بندی مجدد داده های هر خوشه اضافه می شود ( دآتیآ(جلتوستیهrj)). نقاط نویز از نتیجه خوشه بندی استخراج می شوند ( جل(دآتیآ(جلتوستیهrj))) (الگوریتم 4 خط 1-4). سپس، یک پارامتر فاصله تطبیقی، به عنوان ثبت شد هپسnoمنسهدر صورتی که تعداد نقاط نویز بزرگتر باشد قابل محاسبه است ک(الگوریتم 4 خط 5-7). اکنون سه مقدار مختلف برای پارامتر فاصله وجود دارد، یعنی مقداری که این نقاط را به یک خوشه تقسیم می کند ( هپس، مقداری که نقاط را به عنوان نویز در نظر می گیرد ( هپسj، و مقدار جدیدی که سعی می کند دوباره نقاط را خوشه بندی کند ( هپسnoمنسه). طبق بخش 3.2.3 ، هپسjکوچکتر از هپس، و اگر هپسnoمنسه≤هپسj، این نقاط هنوز سر و صدا هستند، بنابراین حد پایین تر از هپسnoمنسهاست هپسj. چه زمانی هپسnoمنسهبه اندازه کافی بزرگ است، این نقاط، حتی با فواصل بسیار زیاد بین آنها، هنوز هم می توانند خوشه شوند. این برای کاربردهای عملی مناسب نیست، و بنابراین یک حد بالا برای تعیین شده است هپس(الگوریتم 4 خط 8-9).

سپس، نقاط نویز را می توان با استفاده از خوشه بندی کرد هپسnoمنسهبر اساس مراحل معرفی شده در بخش 3.2.1 و بخش 3.2.2 . نتیجه جلnoمنسه(دآتیآ(جلتوستیهrj))برای به روز رسانی عناصر در استفاده می شود جل(پ)، اما برچسب های جدید نقاط نویز نیازی به اضافه شدن به مجموعه برچسب ندارند. دلیل این امر این است که یک حد پایین تر وجود داشته است هپسnoمنسه، به این معنی که خوشه را نمی توان دوباره بخش بندی کرد.

الگوریتم 4 : بازیابی نویز

ورودی: نتیجه خوشه بندی جل(دآتیآ(جلتوستیهrj))، مولفه های هپسو هپسj

خروجی: نتیجه خوشه بندی داده های نویز جلnoمنسه(دآتیآ(جلتوستیهrj))

noise_points = [ ]
برای نقطه در جل(دآتیآ(جلتوستیهrj)):
اگر نقطه نویز باشد:
noise_points.append(point)// استخراج نقاط نویز برای بازیابی از جل(دآتیآ(جلتوستیهrj))
if len(noise_points) < k:
بازگشت 0//بررسی کنید که آیا تعداد نقاط داده‌های نویز را می‌توان خوشه‌بندی کرد
هپسnoمنسه= الگوریتم 1 (نقاط_نویز)
اگر هپسnoمنسه≤ هپسjیا هپسnoمنسه≥ هپس://بررسی کنید که آیا پارامتر می تواند برای خوشه بندی استفاده شود
بازگشت −1
جلnoمنسه(دآتیآ(جلتوستیهrj))= cluster_high_density_points(noise_points, هپسnoمنسه)
جلnoمنسه(دآتیآ(جلتوستیهrj))= الگوریتم 2( جلnoمنسه(دآتیآ(جلتوستیهrj)))
برگشت جلnoمنسه(دآتیآ(جلتوستیهrj))

3.3. الگوریتم های خوشه بندی برای مقایسه

برای تأیید اثربخشی چارچوب پیشنهادی، ELV، سه روش موجود نیز مورد آزمایش قرار گرفت، یعنی خوشه‌بندی پیک چگالی (DPC) [ 25 ]، خوشه‌بندی فضایی مبتنی بر چگالی برنامه‌های کاربردی با نویز (DBSCAN) [ 4 ، 23 ، 24 ]، و DBSCAN سلسله مراتبی (HDBSCAN) [ 5 ، 27 ، 28 ، 29 ]. همانطور که در بخش 1 معرفی شد و بخش 2 معرفی شد، DPC یک الگوریتم خوشه بندی ساده و موثر است که اخیراً ارائه شده است و در بسیاری از زمینه ها استفاده شده است. DBSCAN یک الگوریتم خوشه بندی بسیار معروف و محبوب است و بسیاری از محققین از آن برای استخراج ناحیه فعالیت انسانی استفاده می کنند. HDBSCAN با معرفی ایده خوشه بندی سلسله مراتبی DBSCAN را بهبود می بخشد و در خوشه بندی داده های مکانی موثر است. اصول اولیه و انتخاب پارامترهای سه روش به شرح زیر است:

DPC: این الگوریتم این ایده را معرفی می‌کند که مراکز خوشه‌ای چگالی بالاتری نسبت به نقاط اطراف خود دارند و فواصل بین مراکز زیاد است. بنابراین، الگوریتم داده‌ها را با استخراج نقاط، برآورده کردن ایده، به‌عنوان مراکز خوشه‌ای و سپس تخصیص نقاط دیگر به مراکز، خوشه‌بندی می‌کند. دارای دو پارامتر است که باید به صورت دستی انتخاب شوند، از جمله دمنسو دهn. نقطه ای با چگالی بزرگتر از دهnنقطه با چگالی بالا و نقاط با چگالی بالا با فاصله بین آنها بزرگتر از دمنسمراکز خوشه ای هستند. این الگوریتم همچنین روشی را برای تنظیم پارامترها با توجه به نمودارهای توزیع چگالی و فاصله ارائه می دهد. بنابراین، ما پارامترها را با توجه به روش موجود در مقاله برای هر مجموعه داده و عمدتاً تنظیم می کنیم دمنسو دهnروی 7000 و 50 تنظیم شدند.
DBSCAN: نقاط اصلی در این الگوریتم با توجه به تعداد نقاط موجود در محله ها تعریف می شوند. همانطور که در جدول 2 نشان داده شده است ، یک نقطه اصلی حداقل دارد مترمنnپتیسنقاط با فاصله بین آنها کوچکتر از هپس. برای هر نقطه اصلی، تمام نقاط دیگر را در همسایگی آن پیدا کنید و آنها را به همان خوشه اختصاص دهید. هنگامی که یک خوشه دارای نقاط اصلی جدید است، مرحله قبل را تکرار کنید. پارامتر مترمنnپتیسبر اساس پیشنهاد الگوریتم بر روی دو برابر ابعاد داده تنظیم شده است که در این تحقیق 4 است. پارامتر دیگر، هپس، روی مقادیر مختلف تنظیم شد: 200، 400، 800 و 1600.
HDBSCAN: داده ها ابتدا به یک فرم فاصله جدید بر اساس فاصله هسته برای کاهش تأثیر نویز تبدیل می شوند. یک درخت پوشا حداقل برای توصیف داده ها و تبدیل داده ها به یک سلسله مراتب خوشه ای با ایجاد خوشه هایی برای لبه های درخت پوشا ساخته شده است. خوشه هایی با اندازه های کوچکتر از مترجسنویزها در نظر گرفته می شوند و سپس درخت سلسله مراتب خوشه ای می تواند متراکم شود. در نهایت، خوشه ها را می توان بر اساس شاخصی استخراج کرد که ثبات خوشه ها را اندازه گیری می کند. پارامتر، مترجس، در این تحقیق مقادیر مختلفی از جمله 4، 8، 16 و 32 تعیین شد.

4. نتایج

چارچوب پیشنهادی، ELV، با استفاده از سه مجموعه داده واقعی مورد آزمایش قرار گرفت و با سه روش پیشرفته، از جمله DPC، DBSCAN و HDBSCAN مقایسه شد. در این بخش از داده های روز اول مجموعه داده های GBA به عنوان مثال برای نشان دادن ویژگی های نتایج خوشه بندی الگوریتم های مختلف استفاده شده است. سپس نتایج مقایسه کل مجموعه داده ها بر اساس دو شاخص مورد ارزیابی قرار گرفت و نتایج استخراج چارچوب ما مورد تجزیه و تحلیل قرار گرفت. بر اساس تجزیه و تحلیل بصری و دو اندازه‌گیری، این آزمایش نحوه عملکرد چارچوب پیشنهادی، ELV را در مقایسه با سایر الگوریتم‌های محبوب آزمایش کرد. در نهایت، نتایج آزمایش الگوریتم‌ها را برای تجزیه و تحلیل نقاط قوت و ضعف مورد بحث قرار دادیم.

در این تحقیق، آزمایش‌ها و تحلیل‌ها عمدتاً مبتنی بر پایتون، ArcGIS Pro [ 54 ] و Tableau [ 55 ] بود. ما چارچوب و سایر الگوریتم‌های خود را بر اساس پایتون با کتابخانه‌های مختلفی مانند Pandas [ 56 ]، Numpy [ 57 ]، HDBSCAN [ 58 ]، scikit-learn [ 59 ] و غیره پیاده‌سازی کردیم. نتایج با استفاده از ArcGIS Pro، Tableau و دیگر کتابخانه ها مانند Matplotlib [ 60 ] و Seaborn [ 61 ] تجسم و تجزیه و تحلیل شدند.

4.1. مقایسه عملکرد با استفاده از داده های روز اول مجموعه داده GBA به عنوان مثال

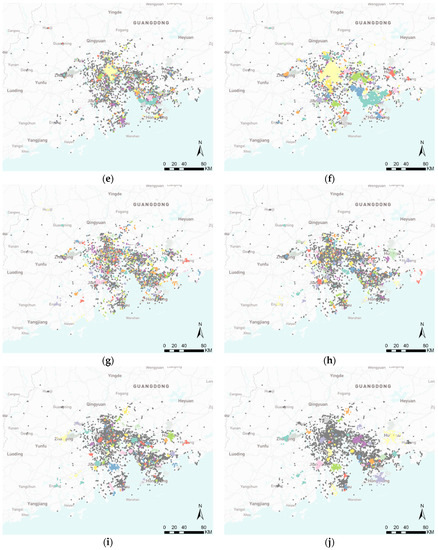
داده های روز اول مجموعه داده GBA با 14248 امتیاز به عنوان نمونه انتخاب شد تا نتایج خوشه ای پایه روش های مختلف را نشان دهد. جدول 3 ویژگی های آماری اصلی نتایج خوشه بندی را شرح می دهد. چارچوب پیشنهادی ما، ELV، بیشترین تعداد خوشه‌ها را به‌دست آورد و به همین ترتیب میانگین تعداد نقاط در هر خوشه کوچک‌ترین بود. HDBCAN 4 دومین خوشه بزرگ را به دست آورد، اما هنوز هم بسیار کوچکتر از ELV بود. کمترین میانگین تعداد امتیازها 6.78 بود که نسبت به تعداد نقاط کامل (14248) بسیار کم و نسبت به سایر روشها نیز کمتر بود. از نقطه نظر فضای جغرافیایی، کل نقاط در مجموع 11 شهر با 56097 کیلومتر مربع توزیع شده است ^.و داده‌ها برای استخراج ناحیه فعالیت انسانی کم بود، بنابراین هر منطقه فعالیت فقط شامل تعداد کمی از نقاط است. بنابراین، اندازه کوچک خوشه ها نسبتا معقول بود. میانگین امتیازهای بدست آمده توسط DBSCAN 200 و HDBSCAN به ترتیب 9.60 و 10.52 بود که نزدیک به ELV بود. تفاوت در مقادیر عمدتاً ناشی از مرحله تقسیم مجدد است که می تواند خوشه های بزرگ را به خوشه های کوچک تقسیم کند. این نشان می دهد که ELV بهتر می تواند مناطق فعالیت ریزدانه را از داده های فضایی در مقیاس بزرگ نسبت به روش های دیگر استخراج کند. علاوه بر این، نسبت نقاط خوشه‌ای HDBSCAN با پارامترهای مختلف همگی کوچکتر از ELV بود. DBSCAN 200 و 400 نقاط نویز زیادی تولید کردند و DBSCAN 800 و 1600 تعداد بسیار کمی از خوشه ها را به دست آوردند. با افزایش پارامتر، میانگین تعداد نقاط در هر خوشه از DBSCAN نیز افزایش یافته است. این نشان دهنده این واقعیت است که DBSCAN نقاط زیادی را در چندین خوشه خوشه بندی می کند و برخی از نقاط نویز به خوشه ها اختصاص داده می شود. در نتیجه، قادر به تشخیص مناطق مختلف فعالیت نبود. به عنوان مثال، نسبت نقاط نویز ایجاد شده توسط DBSCAN 1600 5.92٪ بود، کوچکترین، اما تعداد خوشه ها 211 بود، که به معنای تنها 19.18 خوشه در هر شهر بود. این عدد 19.18 برای مناطق فعالیت انسانی در یک شهر در مقایسه با فعالیت های واقعی انسانی بسیار کم بود. نسبت نقاط نویز تولید شده توسط DBSCAN 1600 5.92% بود، کوچکترین، اما تعداد خوشه ها 211 بود، که به معنای تنها 19.18 خوشه در هر شهر بود. این عدد 19.18 برای مناطق فعالیت انسانی در یک شهر در مقایسه با فعالیت های واقعی انسانی بسیار کم بود. نسبت نقاط نویز تولید شده توسط DBSCAN 1600 5.92% بود، کوچکترین، اما تعداد خوشه ها 211 بود، که به معنای تنها 19.18 خوشه در هر شهر بود. این عدد 19.18 برای مناطق فعالیت انسانی در یک شهر در مقایسه با فعالیت های واقعی انسانی بسیار کم بود.شکل 9 نشان داد که DBSCAN 800 و 1600 نقاط بسیار زیادی را به چندین خوشه تقسیم می کنند که در برخی از مراکز شهر برای استخراج منطقه فعالیت انسانی معنی ندارد. مشکل HDBSCAN این بود که نقاط زیادی به عنوان نویز تخصیص داده شد و برخی از مناطق احتمالی فعالیت قابل شناسایی نبود. عملکرد DPC بدترین بود: تنها 18 خوشه با 45.07 درصد نقاط نویز استخراج کرد. چارچوب پیشنهادی ما نه تنها تعداد زیادی از مناطق فعالیت ریزدانه را استخراج می‌کند، بلکه نویز را نیز در یک نسبت کوچک کنترل می‌کند.

تجسم نتایج نشان داده شده در شکل 9همچنین عملکرد بهتر ELV را در مقایسه با روش های دیگر نشان می دهد. ELV تعداد زیادی خوشه را در مناطق کم و پر چگالی استخراج کرد. به طور خاص، در مناطقی با تراکم بسیار بالا و مقادیر زیادی از نقاط، مانند مراکز شهر، ELV هنوز مناطق مختلف فعالیت را متمایز می کند و خوشه ها را تشکیل می دهد. DPC تنها چندین خوشه با مناطق بزرگ استخراج کرد. DPC فقط بر روی نقاط اصلی با تراکم بسیار بالا متمرکز شده است و برخی از خوشه ها ممکن است به بزرگی یک شهر بوده باشند. علاوه بر این، بسیاری از نقاط فقط با تراکم کمتر نویز در نظر گرفته شدند. DBSCAN 200 نقاط بسیار زیادی تولید کرد و حتی کل منطقه را پوشش داد. DBSCAN 400 قادر به استخراج چندین خوشه فقط در مناطق با تراکم بالا بود و نسبت نقاط نویز بدست آمده همچنان بالا بود. DBSCAN 800 و 1600 نتایج مشابهی با DPC نشان دادند و همین مشکل را داشتند. شکل 9 با جدول 3 مطابقت نداشت . برای مثال، تعداد خوشه‌های به‌دست‌آمده توسط DPC 18 بود، و خوشه‌های به‌دست‌آمده توسط DBSCAN 800 و 1600، 422 و 211 بودند. این معقول است زیرا در شکل 9 ب، فقط چند خوشه بزرگ وجود داشت و خوشه‌های کوچک وجود نداشت ، که به این معنی بود که DPC فقط متمرکز بود. در نقاطی با تراکم بسیار بالا با این حال، در شکل 9 e,f، تعداد زیادی خوشه بسیار کوچک وجود دارد. بنابراین، شباهت‌های بین DBSCAN 800، 1600 و DPC در شکل 9 عمدتاً ناشی از خوشه‌های بزرگ استخراج‌شده مشابه و تفاوت‌های جدول 3 است .به دلیل تعداد زیادی خوشه کوچک ایجاد شده توسط DBSCAN 800 و 1600 بود. نتیجه HDBSCAN 4 بسیار نزدیک به ELV بود، اما همانطور که قبلاً توضیح داده شد، HDBSCAN 4 خوشه های کمتر و نقاط نویز بیشتری به دست آورد. با افزایش پارامتر، HDBSCAN خوشه هایی با تراکم نسبتاً بالاتر استخراج کرد، اما نتیجه HDBSCAN 32 همچنان بهتر از DPC و DBSCAN بود. به طور کلی، ELV برای چنین مجموعه داده ای با مقیاس بزرگ و تراکم های متفاوت مناسب ترین بود.

سپس، ویژگی های خوشه بندی را با توجه به اطلاعات دقیق نشان داده شده در شکل 10 تجزیه و تحلیل کردیم. طبق (الف) چند خوشه حتی بیش از 1000 امتیاز در نتایج DPC و DBSCAN (به جز DBSCAN 200) وجود داشت، اما بیشتر خوشه ها دارای نقاط کوچک بودند. تمرکز بر روی خوشه‌هایی با کمتر از 100 نقطه، (ب) نشان داد که ELV، همه الگوریتم‌های DBSCAN و HDBSCAN 4 توزیع‌های مشابهی داشتند. ترکیب با تجزیه و تحلیل در دو پاراگراف قبلی، DBSCAN ممکن است تنها قادر به استخراج خوشه های مشابه با چگالی کم بوده باشد و در مقایسه با ELV نمی تواند خوشه های موثر را از مناطق با چگالی بالا استخراج کند. با توجه به (ج)، DPC، DBSCAN 1600 و HDBSCAN 32 دارای چند خوشه با مناطق بزرگ بودند. علاوه بر این، مساحت همه خوشه ها در DPC بزرگتر از 5 بود و در (d) نشان داده نشده است. خوشه‌های استخراج‌شده توسط DBSCAN 200 کوچک‌ترین مناطق را داشتند، اما تعداد نقاط در هر خوشه در مقادیر بزرگ‌تر از ELV توزیع شد. مساحت اشغال شده توسط هر نقطه، نسبت مساحت هر خوشه به تعداد نقاط هر خوشه بود. برای تجزیه و تحلیل چگالی خوشه ها محاسبه شد و در (e) و (f) نشان داده شده است. خوشه های استخراج شده توسط DBSCAN همه کوچک بودند زیرا DBSCAN نقاط زیادی را با چگالی بالا به چند خوشه اختصاص داد. یک خوشه در نتیجه HDBSCAN 4 بیشترین مقدار را به دست آورد. دلیل این امر شاید این بوده است که برخی نقاط با تراکم بسیار کم به اشتباه به عنوان خوشه در نظر گرفته شده اند. به جز نتیجه DBSCAN، خوشه ها در نتایج دیگر همگی مقادیر زیادی داشتند. در واقع، بیشتر مقادیر کوچکتر از 1 بودند. نمودار جعبه در (f) نشان داده شده است. مقدار متوسط ELV فقط بزرگتر از مقادیر DBSCAN 200 و 400 بود، اما DBSCAN 200 و 400 نقاط نویز زیادی ایجاد کردند. در نتیجه، ELV خوشه‌هایی را با چگالی بالا و پایین استخراج کرد و مرزهای دسته‌ها را بهتر ارزیابی کرد. در نتیجه عملکرد بهتری با نویز نسبتاً کمتر از خود نشان داد.

با توجه به تجزیه و تحلیل نتایج خوشه‌بندی، ELV و HDBSCAN 4 عملکرد نسبتاً بهتری را نشان دادند، بنابراین ما عملکرد این دو روش را در مناطق با تراکم بالا و کم بیشتر تجزیه و تحلیل کردیم ( شکل 11).). در منطقه با شماره یک، (منطقه 1 به طور خلاصه)، ELV چندین خوشه استخراج کرد، اما HDBSCAN 4 نقاط زیادی را به نویزها اختصاص داد. در منطقه 2، HDBSCAN 4 نویزهای کمی تولید کرد اما نقاط زیادی را به دو خوشه اختصاص داد و خوشه های کمتری را نسبت به ELV استخراج کرد. وضعیت در منطقه 3 بهبود یافته بود، اما HDBSCAN 4 هنوز خوشه های کمتر و نقاط نویز بیشتری داشت. با مشاهده نتیجه خوشه بندی در ناحیه کم چگالی، تعداد نقاط نویز قضاوت شده توسط HDBSCAN 4 کم بود. با این حال، اختصاص دادن نقاط زیادی در مناطق 4 و 5 به تنها دو خوشه نامناسب بود. در واقع، فواصل بین نقاط در مناطق 4 و 5 در فضای جغرافیایی بسیار زیاد بود و نمی‌توانست تنها دو منطقه فعالیت در زندگی واقعی باشد. مناطق تحت پوشش مناطق 4، 5، و 6 همه بزرگ بودند و باید به مناطق کوچک تقسیم می شدند تا مناطق فعالیت را از نظر جغرافیایی نشان دهند. بنابراین، ELV عملکرد بهتری در تجسم نسبت به HDBSCAN 4 نشان داد.

4.2. ارزیابی عملکرد با استفاده از کل مجموعه داده ها بر اساس دو شاخص

در مرحله بعد، ما روش‌ها را روی همه مجموعه‌های داده آزمایش کردیم و دو شاخص محبوب برای ارزیابی عملکرد نتایج استفاده شد، یعنی ضریب شبح (SC) [ 62 ] و شاخص Calinski–Harabasz (CHI) [ 63 ]. این دو شاخص می‌توانند روابط نقاط را در خوشه‌های یکسان و متفاوت توصیف کنند و برای مجموعه‌های داده بدون مقادیر واقعی استفاده می‌شوند. از آنجا که CHI به شدت تحت تأثیر نویز قرار می گیرد، ما محاسبه را به عنوان تغییر دادیم سیاچمن(پ)=سیاچمن(سیپ)rآتیمنo(سیپ)، جایی که سیپبه نقاط خوشه ای بدون نویز اشاره دارد، سیاچمن(سیپ)مقدار CHI نقاط خوشه ای است و rآتیمنo(سیپ)نسبت تعداد است سیپبه تمام نقاط پ. نتایج ارزیابی دقیق روش های مختلف بر اساس SC و CHI در جدول 4 و جدول 5 نشان داده شده است. اشاره شد که هیچ مقدار DPC در مجموعه داده‌های بیش از یک روز وجود ندارد زیرا ما نتوانستیم مجموعه‌های داده را بر اساس DPC خوشه‌بندی کنیم. دلیل این امر این بود که DPC از فواصل بین تمام نقاط استفاده می کند و آنها را ثبت می کند، به این معنی که به فضای ذخیره سازی زیادی نیاز دارد. تعداد رکوردهای داده های یک روز حدود 15000 بود و داده های یک هفته ممکن است حدود هفت برابر این باشد. به همین ترتیب، فاصله بین تمام نقاط به حدود 49 برابر فضای ذخیره سازی داده های یک روز نیاز دارد.

با توجه به دو جدول، چارچوب پیشنهادی ما بهترین عملکرد را نشان داد و حداکثر مقادیر را در تمام مجموعه داده ها و شاخص ها به دست آورد. مقادیر SC ELV در هفت روز حدود 0.30 و در یک هفته حدود 0.40 بود، اما مقدار کل مجموعه داده هنوز 0.42 بدون بهبود قابل توجهی بود. دلیل این امر این بود که داده‌های یک روز کم بود و قادر به ثبت کامل فعالیت‌های انسانی نبودند و داده‌های یک هفته فعالیت‌های انسان را در روزهای کاری و استراحت ثبت می‌کردند. فعالیت های انسانی توصیف شده توسط کل مجموعه داده ممکن است شبیه به یک هفته باشد، بنابراین مقادیر SC نزدیک بودند. مقادیر SC DPC، DBSCAN 800 و 1600 نزدیک و کمی کوچکتر از 0 بودند که با نتایج نشان داده شده در شکل 9 مطابقت داشت.. با این حال، مقادیر CHI DPC، DBSCAN 800، و 1600 بسیار متفاوت بودند. با توجه به جدول 3 و شکل 9 ، تفاوت بین دو شاخص عمدتاً به دلیل نسبت نویز بود. DPC نتایج بصری مشابهی را با DBSCAN 800 و 1600 با چندین خوشه بزرگ مشابه نشان داد، اما DPC خوشه های کوچک را نادیده گرفت و نسبت نویز بزرگتر بود. مقادیر نزدیک نسبت نویز DPC، HDBSCAN 16 و 32 نیز منجر به عملکردهای مشابه در SC و CHI شد. مقادیر SC ELV در مجموعه داده های شانگهای و پکن 0.59 و 0.55 بود که بسیار بزرگتر از مقادیر موجود در مجموعه داده GBA بود زیرا مجموعه داده GBA که 11 شهر را پوشش می دهد بسیار پیچیده تر از مجموعه داده های شانگهای و پکن بود. پیچیدگی را می توان با شکل 1 نیز اثبات کرد، که در آن مجموعه داده GBA مناطق بسیار بزرگتری را پوشش می دهد و تفاوت تراکم از دو مجموعه داده دیگر قابل توجه تر بود. برای همان مجموعه داده، مقادیر CHI ELV به ده ها برابر روش های دیگر رسید. مقدار CHI HDBSCAN 4 بعد از ELV دوم بود، اما شکاف همچنان زیاد بود. علاوه بر این، ELV بزرگترین مقدار CHI را در کل مجموعه داده به دست آورد، اما DBSCAN با پارامترهای مختلف در مقایسه با سایر مجموعه داده‌ها حتی بدتر از کل مجموعه داده را نشان داد. همچنین می توان مشاهده کرد که DBSCAN خوشه های کوچکی را با نقاط نویز زیاد یا فقط چندین خوشه بزرگ در شکل 9 استخراج کرده است. عملکرد در شکل 9 و جدول 4 و جدول 5منعکس کننده ضعف DBSCAN است که نمی تواند با مجموعه داده هایی با تراکم های مختلف سازگار شود. با ترکیب مقادیر SC و CHI، بهبود ELV در مقایسه با روش‌های دیگر در مجموعه داده‌های GBA مهم‌تر از مجموعه داده‌های شانگهای و پکن بود. این نشان دهنده این واقعیت است که ELV برای مجموعه داده های مقیاس بزرگ نسبت به روش های دیگر مناسب تر است.

ما همچنین عملکرد روش های ارزیابی شده در هفته های مختلف را شرح دادیم که در نشان داده شده است شکل 12 نشان داده شده است. مقدار SC ELV در تمام هفته ها بسیار پایدار و بزرگتر از روش های دیگر بود. HDBSCAN با پارامترهای مختلف نیز عملکرد پایداری را نشان داد و مقادیر SC با افزایش پارامتر کاهش یافت. DBSCAN بدترین عملکرد را در تمام هفته ها نشان داد و مقادیر نتوانستند ثابت بمانند. عملکرد DBSCAN آزمایش شده در برخی هفته ها، مانند هفته از 2020-01-20 تا 2020-01-26، بهتر از هفته های دیگر بود. دلیل این امر شاید این بوده است که تعداد رکوردهای هفته های با عملکرد بهتر کم بوده است. عملکرد ارزیابی شده توسط CHI تفاوت هایی را نشان داد، یعنی ELV ابتدا کاهش یافت، به پایین آمد و سپس افزایش یافت. این وضعیت ممکن است ناشی از تعداد رکوردها در یک هفته باشد. مقادیر CHI ممکن است تحت تأثیر حجم داده ها باشد،

سپس تأثیر اختلاف چگالی بر نتایج خوشه‌بندی مورد تجزیه و تحلیل قرار گرفت. برای تعریف اختلاف چگالی، میانگین فاصله نزدیکترین را محاسبه کردیم کامتیاز برای هر امتیاز، متردمنسک(پمن)، به شرح زیر است:

متردمنسک(پمن)=∑ل=1کدمنسل(پمن)ک

(12)

سپس، اختلاف چگالی یک نقطه، دمنff(پمن)، به عنوان مقدار میانگین تفاوت بین میانگین فاصله نقطه و سایر نقاط تعریف شد:

دمنff(پمن)=∑r=1nمتردمنسک(پr)–متردمنسک(پمن)n–1

(13)

در نهایت، تفاوت چگالی کل مجموعه داده ها به عنوان مجموع تفاوت چگالی نقاط تعریف شد. ∑من=1nدمنff(پمن)، که می تواند درجه اختلاف چگالی کلی همه نقاط در مجموعه داده را توصیف کند. این تعریف عمدتاً تعداد نقاط نزدیک به هر نقطه و فواصل بین آنها را در نظر می گیرد. مقدار از هر نقطه منفرد تا کل داده محاسبه شد. بنابراین، می توان از این تعریف برای توصیف اختلاف چگالی استفاده کرد.

شکل 13 تفاوت تراکم تمام هفته ها را نشان می دهد. تفاوت تراکم هفته از 03-02-2020 تا 09-02-2020 کمترین مقدار بود، و هفته های حول و حوش آن زمان جشنواره بهار و جشنواره فانوس را پوشش می داد و همچنین تحت تأثیر شدید COVID-19 قرار گرفت. تفاوت در هفته از 2019-12-30 تا 2020-01-05 به دلیل روز سال نو زیاد بود. این نتایج نشان دهنده این واقعیت است که در طول جشنواره بهار، مردم به شهر خود باز می گردند و در روز سال نو، آنها دوست دارند در شهرهای تحت پوشش مجموعه داده GBA بیرون بروند. چند هفته گذشته نیز اختلافات زیادی داشت، زیرا مردم کار را از سر گرفتند. روابط بین اختلاف چگالی و بهبود ELV در مقایسه با روش‌های دیگر نشان داده شده است شکل 14 نشان داده شده است.. به طور کلی، بهبودها با افزایش اختلاف چگالی افزایش یافته و حتی روابط تقریباً خطی را در برخی از شکل‌ها ارائه کرده‌اند. روابط خطی در شکل 14 e,f که مقایسه با HDBSCAN 4 و 8 را در SC توصیف می کند آشکار نیستند، اما همانطور که در شکل 14 m,n نشان داده شده است در CHI آشکارتر هستند . در نتیجه، ELV عملکرد بهتری را هم در مقادیر بیشتر شاخص‌ها و هم در ثبات بالاتر نشان داد.

4.3. تجزیه و تحلیل نتایج خوشه بندی

در بخش آخر، عملکرد بهتر ELV را نسبت به روش‌های دیگر نشان دادیم و در اینجا ویژگی‌های نتیجه خوشه‌بندی ELV را بیشتر تحلیل می‌کنیم. ویژگی‌های زمانی نتیجه خوشه‌بندی در ساعت مورد بررسی قرار گرفت و سپس سه ویژگی خوشه‌ها مورد بحث قرار گرفت، از جمله اینکه چگونه تعداد نقاط در خوشه‌ها، مساحت خوشه‌ها و تراکم خوشه‌ها در طول هفته‌های مورد مطالعه متفاوت بود.

ویژگی های زمانی نتیجه خوشه بندی در نشان داده شده است شکل 15 نشان داده شده است. تعداد تمام نقاط در ساعت ابتدا از بازه ساعت 0 تا 5 که بیشتر افراد می خوابیدند کاهش یافت، از 6 به 10 افزایش یافت، از 11 به 16 ثابت ماند و در نهایت افزایش یافت. ارزش 2019-12-25 به دلیل روز کریسمس در فواصل ساعتی بیشتر از سایرین بود. مقادیر در آخر هفته (2019-12-28 و 29) نیز بزرگتر از مقادیر در روزهای هفته بود، به جز مقادیر شب و روز کریسمس. به طور عمده، تنوع، روال زندگی افراد مانند خواب، کار و سرگرمی را نشان داد. میانگین تعداد نقاط در هر خوشه می تواند تمرکز مکان فعالیت های انسانی را نشان دهد. مقدار متغیر در (b) حالتی متضاد با (a) نشان داد. هنگامی که بیشتر افراد به رختخواب می روند یا فقط تا دیروقت در خانه می مانند، مقادیر بیشتر از زمان های دیگر بود و نشان داد که مناطق فعالیت متمرکز بودند. با این حال، همچنین تفاوت های زیادی بین (الف) و (ب) وجود داشت که به سادگی برعکس نبودند. موجی در فاصله ساعت 1 ظاهر شد که نشان دهنده این واقعیت بود که ممکن است فعالیت های انسانی در آن زمان تغییر کرده باشد. به عنوان مثال، برخی از افراد ممکن است پس از اضافه کاری یا پس از تفریح و سرگرمی به خانه رفته باشند. همچنین دو پیک محلی در فواصل ساعت 11 و 17 وجود داشت که افراد به کار صبح و بعدازظهر خود پایان می دادند. مقادیر در همان بازه نیز در روزهای مختلف متفاوت بود. بیشترین مقدار در بازه ساعت 5 در 26-12-2019 بود و به همین ترتیب مقدار در همان بازه در 25-12-2019 بسیار کم بود. این نشان داد که افراد پس از روز کریسمس شروع به استراحت خوبی کردند و این پدیده در آخر هفته نیز ظاهر شد. به طور کلی،

تنوع و توزیع هفتگی ویژگی های مختلف در نشان داده شده است شکل 16 نشان داده شده است، که اکنون مورد تجزیه و تحلیل قرار خواهد گرفت. ویژگی k-distance به میانگین فاصله یک نقطه تا نزدیکترین k نقطه آن در یک خوشه اشاره دارد. میانگین تعداد امتیازات در هر خوشه نشان داده شده در (الف) به مقدار حداقل در هفته کاهش یافت (از 10-2-2020 تا 16-02) و سپس افزایش یافت. با ترکیب داده‌های سه هفته نشان‌داده‌شده در (f)، پایین‌ترین نقطه به دلیل حداکثر چگالی در حدود 5 بود. با امتیاز بیش از 7 نسبت به دو هفته دیگر کوچکتر بودند. این بدان معنا بود که افراد دیگر در مکان‌های خاص مانند مراکز تجاری تمرکز نمی‌کردند و همچنین در مکان‌های مختلف مانند رستوران‌های کوچک پراکنده نمی‌شدند. آنها ممکن است به دلیل تأثیر COVID-19 در این هفته خاص در خانه مانده باشند. سپس با تمرکز بر ویژگی مقادیر مساحت، می توان مشاهده کرد که مقادیر حداکثر میانگین مساحت خوشه ها و مساحت اشغال شده توسط هر نقطه هر دو در هفته (از 27-01-2020 تا 02-02) بوده است. دلیل این امر ممکن است این بوده است که افراد در طول جشنواره بهار بیرون می‌رفتند و مکان‌های فعالیت آنها پراکنده می‌شد، که این را می‌توان با فاصله k نشان‌داده‌شده در (e) نیز ثابت کرد. با این حال، مساحت مجموع خوشه ها تغییرات هفتگی متفاوتی را نشان می دهد. قله‌ها و فرورفتگی‌های محلی در (c) مشابه موارد (b) و (d) بودند، اما دامنه نوسانات بسیار متفاوت بود. به عنوان مثال، حداکثر مقدار در هفته (از 2020-02-24 تا 2020-03-01) بود. منطقه مجموع ویژگی ها عمدتاً کل دامنه فعالیت های انسانی را نشان می داد که تحت تأثیر تعداد افراد بود. از این رو، دامنه نوسانات مختلف ممکن است به این دلیل باشد که افراد قبل از جشنواره بهار به خانه رفتند و پس از ضعیف شدن تأثیر COVID-19 به کشور بازگشتند. علاوه بر این، توزیع‌های مساحت و k-فاصله را در هفته‌های خاص، از جمله هفته خاص (27-01-2020 تا 02-02) با حداکثر میانگین مساحت و k-فاصله و هفته‌های اول و آخر تحلیل کردیم. این دو ویژگی عمدتاً در مقادیر کوچک با مساحت 0 تا 0.2 و فاصله k از 0 تا حدود 80 توزیع شده‌اند. هفته خاص تراکم‌های کمتر مقادیر کوچک و تراکم‌های بالاتر از مقادیر بزرگ‌تر در هر دو (g) و (h)، که به معنای پراکنده شدن فعالیت های انسانی بود. هفته اول از نظر مساحت تراکم مقادیر کوچکتر از هفته گذشته و از نظر فاصله k وضعیت معکوس داشت.

در نتیجه، چارچوب پیشنهادی ما، ELV، می‌تواند ویژگی‌های حوزه‌های فعالیت انسانی را با توجه به تجزیه و تحلیل فوق نشان دهد.

4.4. بحث

نقاط قوت و ضعف چهار الگوریتم مقایسه شده در آزمایش فوق در جدول 6 نشان داده شده است که عمدتاً شامل تنظیم پارامتر، کارایی پردازش و عملکرد بر روی داده‌های چگالی متفاوت است. ابتدا روی جنبه تنظیم پارامتر تمرکز می کنیم. الگوریتم پیشنهادی، ELV، به‌ویژه برای داده‌های فضایی در مقیاس بزرگ طراحی شده است و هیچ تنظیم دستی پارامتر ندارد. هزینه عمومیت کم است، به این معنی که ELV ممکن است برای سایر وظایف غیر مرتبط با داده های مکانی مناسب نباشد. سه الگوریتم دیگر همگی کلی هستند و در بسیاری از زمینه های تحقیقاتی قابل استفاده هستند. به خصوص، DBSCAN چنین الگوریتم کلاسیکی است، و هم خودش و هم انواع آن در موقعیت‌های مختلف اعمال شده‌اند [ 4 ، 23 ، 24 ]]. همانطور که دربخش 3.3 ، DPC دارای دو پارامتر است، اما یک روش آسان و مفید برای انتخاب پارامتر ارائه می‌کند، اما همچنان به تنظیم دستی پارامتر برای هر مجموعه داده نیاز دارد. DBSCAN دارای دو پارامتر است و محققان زیادی در مورد نحوه انتخاب پارامترها مطالعه کرده اند، اما تنظیم دستی پارامتر هنوز برای یک کار خاص مهم است. HDBSCAN فقط یک پارامتر دارد و معنی پارامتر واضح است، نقاط min در یک خوشه. در مقایسه با سه الگوریتم دیگر، ELV هیچ تنظیم دستی پارامتر ندارد و می‌تواند به راحتی در کار استخراج منطقه فعالیت انسانی استفاده شود، اما جهانی بودن پایینی دارد و ممکن است در زمینه‌های تحقیقاتی دیگر مفید نباشد.

راندمان پردازش عامل مهم دیگری است که بر کاربرد الگوریتم ها تأثیر می گذارد. در آزمایش، راندمان پردازش از بالا به پایین مرتب شده است DBSCAN، HDBSCAN، ELV، و DPC. زمان دقیق پردازش و استفاده از حافظه در آزمایش ارائه نشد، زیرا کدهای الگوریتم‌ها بر اساس زبان‌های برنامه‌نویسی زیرین مختلف بودند که تأثیر زیادی بر کارایی پردازش داشت. DBSCAN و HDBSCAN از کتابخانه های باز استفاده می کنند [ 58 ، 59]، و راندمان پردازش بسیار بالاتر بود. ما کارایی پردازش را با توجه به اصول اولیه الگوریتم ها تجزیه و تحلیل کردیم. DBSCAN و DPC هر دو دارای جریان های پردازش ساده هستند، اما DBSCAN بالاترین کارایی و DPC کمترین را داشت. عملکرد بد به دلیل ذخیره، خواندن و نوشتن داده های عظیم فاصله بود. برای یک مجموعه داده کوچک، اندازه داده های فاصله کوچک است و DPC می تواند سریع پردازش کند. با این حال، این تحقیق بر روی داده‌های فضایی در مقیاس بزرگ متمرکز شد و DPC کمترین کارایی را نشان داد. در مقایسه با DBSCAN و DPC، جریان های پردازش ELV و HDBSCAN بسیار پیچیده تر هستند زیرا هر دو مفهوم سلسله مراتب را معرفی می کنند. علاوه بر این، ELV ویژگی‌های خوشه‌های منفرد را هنگام اختصاص دادن هیچ نقطه با چگالی بالا در بخش 3.2.2 در نظر می‌گیرد.و مرحله بازیابی نویز را در بخش 3.2.4 اضافه می کند . راندمان ELV می تواند همچنان از DPC زیاد باشد زیرا ELV فقط به بخشی از فواصل بین نقاط نیاز دارد. راندمان پردازش نظری با آن در آزمایش‌ها مطابقت دارد. در واقع، DBSCAN، HDBSCAN و ELV همگی وظیفه استخراج را فقط در چند دقیقه حتی برای داده‌های فضایی بسیار بزرگ (مجموعه داده‌های GBA) تکمیل کردند، اما DPC از مقدار زیادی داده فاصله رنج می‌برد.

سپس بر روی عملکرد نتایج استخراج الگوریتم‌های مختلف تمرکز می‌کنیم. DBSCAN نتایج خوشه بندی بسیار متفاوتی را با پارامترهای مختلف به دست آورد. چه زمانی هپسکوچک بود، DBSCAN مناطق فعالیت ریزدانه را در مناطق با تراکم بالا مانند مراکز شهر استخراج کرد، اما نقاط نویز زیادی ایجاد کرد. برای مناطق کم تراکم مانند حومه شهر، ممکن است خوشه ای وجود نداشته باشد. با بزرگ هپس، DBSCAN به راحتی نقاط با چگالی بالا را با نقاط نویز بسیار کمی استخراج کرد اما نقاط بسیار زیادی را به چندین خوشه تقسیم کرد. به عنوان مثال، یک خوشه ممکن است یک مرکز شهر را پوشش دهد، که برای استخراج منطقه فعالیت معنایی ندارد. عملکرد DPC بسیار شبیه به DBSCAN با استفاده از بزرگ بود هپس. تفاوت بین آنها در این بود که DPC فقط بر روی نقاط با چگالی بالا و DBSCAN تمرکز می کرد، با استفاده از یک بزرگ هپس، هنوز خوشه هایی با نقاط چگالی کم استخراج می شود. HDBSCAN به دلیل مفهوم سلسله مراتب، عملکرد بسیار بهتری نسبت به DBSCAN و DPC نشان داد. با این حال، هنوز نقاط ضعفی داشت که نقاط نویز زیادی را برای تقسیم نقاط با چگالی بالا به خوشه‌های مختلف ایجاد کرد و برخی از نقاط را با فواصل طولانی بین آنها به خوشه‌های مشابه در مناطق کم تراکم اختصاص داد. ELV با در نظر گرفتن ویژگی های خوشه های فردی و بازیابی نقاط نویز عملکرد را بهبود بخشید. در نتیجه، ELV بهترین عملکرد را در داده‌های مکانی با چگالی متفاوت نشان داد.

علاوه بر این، روش‌های ارزیابی نتایج خوشه‌بندی باید مورد بحث قرار گیرد. عمدتاً سه نوع روش برای ارزیابی عملکرد وجود دارد، از جمله تجزیه و تحلیل دستی، ارزیابی نظارت شده، و ارزیابی بدون نظارت [ 21 ، 62 ، 63 ، 64 ، 65 ]. عینی ترین و مؤثرترین نوع ارزیابی تحت نظارت است [ 21 , 64 , 65]. این دقیقاً می تواند توضیح دهد که الگوریتم ها چقدر نقاط را به خوشه های مختلف اختصاص می دهند. با این حال، هیچ ارزش واقعی حوزه های فعالیت انسانی برای استفاده از روش های نظارتی وجود ندارد. بنابراین در این تحقیق از تحلیل دستی و شاخص های ارزیابی بدون نظارت استفاده شد. اطلاعات آماری اصلی نتایج خوشه‌بندی شامل تعداد نقاط در خوشه‌ها، تعداد خوشه‌ها، مساحت خوشه‌ها، نسبت نقاط نویز و غیره استخراج و مقایسه شد. داده های آماری، همراه با تجزیه و تحلیل بصری، به توصیف ویژگی های همه الگوریتم ها کمک کرد، که قبلاً نتیجه گیری شده است. سپس، دو شاخص پرکاربرد، SC و CHI [ 62 ، 63]، برای ارزیابی عملکردها استفاده شد. در واقع، این دو شاخص هر دو بر اساس فواصل داخلی نقاط در خوشه ها و فواصل خارجی بین خوشه ها هستند. اگر اندازه خوشه ها بسیار کوچک باشد، فواصل داخلی نیز کوچک می شود و نشانگرها را بزرگ می کند. با این حال، اندازه کوچک خوشه ها همچنین ممکن است منجر به فاصله های خارجی کوچک بین خوشه ها شود، زیرا خوشه های بیشتر در مناطق محلی می توانند با اندازه های کوچک استخراج شوند. این دو نشانگر با فواصل کوچک خارجی بد می شوند. برای جلوگیری از این امر، برخی نقاط باید به عنوان نقاط نویز در نظر گرفته شوند تا فواصل خارجی بزرگ شوند و نقاط خوشه ای بتوانند شاخص های بالایی را به دست آورند، اما نقاط نویز مقادیر بسیار پایینی دارند که بر شاخص های کل داده ها تأثیر می گذارد. از این رو، الگوریتم ها باید نقاط خوشه ای را با نقاط نویز معاوضه کنند تا شاخص های بالایی به دست آورند. ELV از تقسیم بندی مجدد برای به دست آوردن خوشه های ریز دانه و بازیابی نقاط نویز برای کاهش نسبت نویز استفاده می کند. در نتیجه، عملکرد بهتر با شاخص های بالاتر را می توان با ELV در مقایسه با سایر الگوریتم ها به دست آورد.

در نهایت، الگوریتم پیشنهادی ما، ELV، با سایر تحقیقات مرتبط برای بحث در مورد نوآوری‌ها و مزایای این مطالعه مقایسه می‌شود. بسیاری از مطالعات موجود الگوریتم‌های استخراج را برای نقاط داغ شهری بر اساس انواع مختلف داده‌های فعالیت انسانی پیشنهاد یا استفاده کردند [ 15,18,38 , 66]. مفهوم هات اسپات به مناطقی با تعداد نقاط زیاد اشاره دارد. چنین مناطقی ممکن است جاذبه های توریستی معروف، مراکز تجاری و غیره باشند، اما فقط می توانند بخش کوچکی از فعالیت های انسانی را نشان دهند. بسیاری از مناطق، مانند رستوران ها و سینماها، ممکن است نادیده گرفته شوند. این مطالعه خوشه های ریز دانه را برای نشان دادن مناطق فعالیت انسانی، از جمله مناطق با تراکم بالا و کم، استخراج می کند. بنابراین، توصیف بهتری از فعالیت های انسانی به دست می آید. همچنین مطالعات دیگری وجود دارد که حوزه‌های فعالیت افراد را بر اساس الگوریتم‌های خوشه‌بندی بررسی می‌کند [ 4 ، 5 ، 26 ، 67]. داده‌های مورد استفاده در این مطالعات برای هر پردازش خوشه‌بندی، سوابق فعالیت یک فرد بود. نتایج ویژگی‌های فعالیت‌های افراد را نشان می‌دهد، اما محدود به مشکل پراکندگی داده‌های فضایی یک فرد است. به خصوص برای داده های رسانه های اجتماعی، تنها بخش کوچکی از افراد در این مطالعات انتخاب شدند. علاوه بر این، الگوریتم‌های خوشه‌بندی در مطالعات ممکن است عملکرد بدی را هنگام اعمال آن‌ها در مجموعه داده‌های بسیار پیچیده‌تر از تعداد زیادی از افراد با تراکم‌های متفاوت نشان دهند. این مطالعه ELV را طراحی کرد و عملکرد مجموعه‌های داده با تراکم‌های متفاوت را با پارامتر تطبیقی و استراتژی تقسیم‌بندی مجدد بهبود بخشید. علاوه بر این، این مطالعه بر روی داده‌های فضایی در مقیاس بزرگ متمرکز شد و از مجموعه داده‌های GBA که 11 شهر را پوشش می‌داد استفاده کرد. مطالعات دیگر فقط از مجموعه داده‌هایی استفاده کردند که یک شهر را پوشش می‌داد 4[ 18 ، 26 ] و گستره فضایی بسیار کوچکتر از این مطالعه بود. نتایج خوشه‌بندی استخراج‌شده از مجموعه داده‌های چند شهر با روش ما می‌تواند برای کشف مناطق فعالیت در اتصالات شهرها و تحلیل بهتر روابط بین شهرها مفید باشد. به طور کلی، ELV بهتر می تواند مناطق فعالیت با چگالی متفاوت را از کل مجموعه داده های فضایی در مقیاس بزرگ در مقایسه با مطالعات موجود استخراج کند.

5. نتیجه گیری ها

در این تحقیق، چارچوب جدیدی برای استخراج مناطق فعالیت انسانی از داده‌های فضایی در مقیاس بزرگ با چگالی‌های متفاوت (ELV) پیشنهاد شد. در مرحله اول، یک پارامتر خودکار برای استخراج و خوشه بندی نقاط با چگالی بالا طراحی شد که می تواند عملی بودن را به ویژه در حلقه ها تقویت کند. سپس به نقاط باقیمانده با تراکم کم، برچسب‌های متفاوتی با توجه به ویژگی‌های فضایی خوشه‌های دارای نقاط با چگالی بالا اختصاص داده شد. بر اساس این روش تخصیص، چارچوب قادر به شناسایی بهتر نویزها بود. علاوه بر این، یک استراتژی بخش‌بندی مجدد برای حل چالش نقاط در یک مجموعه داده فضایی در مقیاس بزرگ با تغییرات چگالی بزرگ‌تر توسعه داده شد. در نهایت، نقاط نویز اضافی تولید شده در استراتژی قطعه‌سازی مجدد برای کاهش نویز و دستیابی به استخراج جامع‌تر منطقه بازیابی شدند. این چارچوب بر روی سه مجموعه داده آزمایش شد که یکی از آنها 11 شهر را پوشش می داد و بیش از 1 میلیون نقطه داشت. در مقایسه با روش‌های موجود، از جمله DBSCAN، HDBSCAN و DPC، چارچوب پیشنهادی ما، ELV، بهترین عملکرد را با توجه به شاخص‌ها و تحلیل بصری نشان داد. به طور خاص، زمانی که تفاوت‌های چگالی زیادی وجود داشت، ELV می‌توانست بهتر با شرایط سازگار شود و بهبودهای ELV در مقایسه با سایرین بهتر بود.

در مقایسه با مطالعات موجود، ELV دارای مزایایی در فناوری های نظری و کاربردهای عملی است. هیچ تنظیم دستی پارامتر برای ELV وجود ندارد، که می تواند در زمان تنظیمات پارامتر صرفه جویی کند و عدم قطعیت ایجاد شده توسط عوامل ذهنی انسانی را کاهش دهد. این امر استفاده موثر از ELV را در سناریوهای کاربردی عملی مربوط به استخراج منطقه فضایی فعالیت های انسانی ترویج می کند. روش تخصیص نقاط نویز را با در نظر گرفتن ویژگی های فضایی برای توصیف بهتر شکل مناطق فعالیت متمایز می کند. مدل تقسیم‌بندی مجدد از نظر تئوری باعث می‌شود ELV با چگالی‌های مختلف سازگار شود و نتایج ثابت کرد که ELV خوشه‌های ریز دانه را در مناطق با چگالی بالا و کم استخراج می‌کند. برخی دیگر از الگوریتم‌ها مناطق کم چگالی را نادیده گرفتند و نقاط زیادی را به چندین خوشه تقسیم کردند. این مزیت ELV می تواند به تجزیه و تحلیل جزئیات بیشتر فعالیت های انسانی و مقایسه تفاوت های بین مناطق کم تراکم و بالا کمک کند. بازیابی نویز همچنین مهم است که می تواند نسبت نقاط نویز را که ممکن است شامل مناطق فعالیت احتمالی باشد، کاهش دهد. با ترکیب روش تخصیص و بازیابی نویز، ELV دارای مزایایی در کنترل تأثیر نویز فعالیت‌های تصادفی انسانی با توصیف جامع‌تر از مناطق فعالیت در مقایسه با سایر مطالعات است. این ویژگی ELV در برنامه هایی مانند پیش بینی مکان و توصیه با ارائه مناطق فعالیت دقیق و کامل مفید است. گستره فضایی مناسب برای ELV بسیار بزرگ است و به راحتی می تواند چند شهر را پوشش دهد که نقش مثبتی در تحلیل روابط شهر ایفا می کند. از این رو،

چارچوب پیشنهادی به دلیل استراتژی تقسیم‌بندی مجدد برای مجموعه داده‌های مقیاس بزرگ مناسب است. اولین چالشی که در این مجموعه داده ها با آن مواجه می شود، چگالی های متفاوت آنهاست، به این معنی که بسیاری از الگوریتم های موجود فقط می توانند مناطق با چگالی بالا را استخراج کنند یا نویز بیش از حد تولید کنند. استراتژی تقسیم‌بندی مجدد می‌تواند هم خوشه‌های کم و هم با چگالی بالا را استخراج کند و نویز را می‌توان بازیابی کرد. چالش دیگری که در مجموعه داده های مقیاس بزرگ با آن مواجه می شود، مقدار زیادی محاسبات مورد نیاز است که ممکن است با حجم داده ها به طور تصاعدی رشد کند. بودجه اصلی بر محاسبه فاصله و پرس و جو متمرکز است. برخی از الگوریتم‌ها، مانند DPC، باید داده‌های فاصله زیادی را ثبت کنند و نمی‌توانند روی مجموعه داده‌های مقیاس بزرگ به خوبی کار کنند. ELV می تواند یک کار خوشه بندی کامل را به وظایف فرعی متعدد تقسیم کند، و وظایف فرعی را می توان به دلیل استراتژی تقسیم مجدد تقسیم کرد. بنابراین، چارچوب های محاسباتی توزیع شده را می توان به راحتی در ELV اعمال کرد.

یکی از زمینه هایی که این مطالعه را می توان افزایش داد، با توجه به اندازه گیری فاصله است. این تحقیق فواصل خطی بین نقاط را محاسبه کرد که به طور گسترده در خوشه بندی فضایی استفاده می شود. سایر جنبه های جغرافیایی مانند مسافت طی شده توسط وسایل حمل و نقل مختلف بین نقاط و همچنین زمان سفر را می توان در نظر گرفت. همچنین عناصر جغرافیایی زیادی مانند رودخانه ها و جاده ها وجود دارد که مناطق را به قسمت های مختلف تقسیم می کند. علاوه بر این، شباهت معنایی یکی دیگر از گزینه های خوب برای اندازه گیری فاصله بین نقاط است. در این تحقیق از مجموعه داده های رسانه های اجتماعی استفاده شده است و از داده های متنی می توان برای استخراج اطلاعات معنایی در مورد فعالیت های انسانی استفاده کرد. مضامین فعالیت و وضعیت های احساسی را می توان برای توصیف و تمایز حوزه های فعالیت با معنایی متفاوت استخراج کرد.

منابع

شکر، س. گونتوری، وی. ایوانز، ام آر. یانگ، ک. چالش‌های داده‌های بزرگ فضایی متقاطع تحرک و محاسبات ابری. در مجموعه مقالات یازدهمین کارگاه بین المللی ACM در مورد مهندسی داده برای دسترسی بی سیم و موبایل، اسکاتسدیل، AZ، ایالات متحده آمریکا، 20 مه 2012. صص 1-6. [ Google Scholar ]
لژچینسکی، آ. Crampton, J. مقدمه: داده های بزرگ فضایی و زندگی روزمره. Big Data Soc. 2016 , 3 , 2053951716661366. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
خان، س. Kannapiran, T. فهرست بندی مسائل در مدیریت داده های بزرگ فضایی. در مجموعه مقالات کنفرانس بین المللی پیشرفت در مدیریت علوم مهندسی و فناوری (ICAESMT)-2019، دانشگاه اوتارانچال، دهرادون، هند، 14 مارس 2019. [ Google Scholar ]
Huang، Q. استخراج ردپای آنلاین برای پیش بینی مکان بعدی کاربر. بین المللی جی. جئوگر. Inf. علمی 2017 ، 31 ، 523-541. [ Google Scholar ] [ CrossRef ]
چن، پی. شی، دبلیو. ژو، ایکس. لیو، ز. Fu، X. STLP-GSM: روشی برای پیش‌بینی مکان‌های آینده افراد بر اساس داده‌های رسانه‌های اجتماعی برچسب‌گذاری شده جغرافیایی. بین المللی جی. جئوگر. Inf. علمی 2019 ، 33 ، 2337–2362. [ Google Scholar ] [ CrossRef ]
بله، م. یین، پی. لی، دبلیو.-سی. توصیه مکان برای شبکه های اجتماعی مبتنی بر مکان. در مجموعه مقالات هجدهمین کنفرانس بین المللی SIGSPATIAL در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، سن خوزه، کالیفرنیا، ایالات متحده آمریکا، 2 تا 5 نوامبر 2010. ص 458-461. [ Google Scholar ]
لیم، KH; چان، جی. کاروناسکرا، اس. Leckie, C. توصیه تور و برنامه ریزی سفر با استفاده از رسانه های اجتماعی مبتنی بر مکان: یک نظرسنجی. بدانید. Inf. سیستم 2019 ، 60 ، 1247-1275. [ Google Scholar ] [ CrossRef ]
لیان، دی. ژنگ، ک. Ge، Y. کائو، ال. چن، ای. Xie، X. GeoMF++ توصیه مکان مقیاس‌پذیر از طریق مدل‌سازی جغرافیایی مشترک و فاکتورسازی ماتریس. ACM Trans. Inf. سیستم 2018 ، 36 ، 33. [ Google Scholar ] [ CrossRef ]
جونگ، اچ. Yiu، ML; جنسن، CS; چاو، CC-Y.; موکبل، استخراج الگوی مسیر MMF. در محاسبات با مسیرهای فضایی ; Springer: برلین/هایدلبرگ، آلمان، 2011; صص 143-177. [ Google Scholar ] [ CrossRef ]
سزاریو، ای. کومیتو، سی. تالیا، دی. یک روش اعتبارسنجی جامع برای استخراج الگوی مسیر داده های GPS. در مجموعه مقالات چهاردهمین کنفرانس بین المللی IEEE 2016 در مورد محاسبات قابل اعتماد، خودمختار و ایمن، چهاردهمین کنفرانس بین المللی در مورد هوش فراگیر و محاسبات، دومین کنفرانس بین المللی در مورد هوش و محاسبات بزرگ داده ها و کنگره علوم و فناوری سایبری (DASC/PiComberS) , اوکلند, نیوزلند, 13 اکتبر 2016; صص 819-826. [ Google Scholar ] [ CrossRef ]
یائو، دی. ژانگ، سی. هوانگ، جی. Bi, J. Serm: مدلی تکرارشونده برای پیش‌بینی مکان بعدی در مسیرهای معنایی. در مجموعه مقالات ACM 2017 در کنفرانس مدیریت اطلاعات و دانش، سنگاپور، 6 تا 10 نوامبر 2017؛ ص 2411-2414. [ Google Scholar ]
لیو، کیو. وو، اس. وانگ، ال. Tan, T. پیش‌بینی مکان بعدی: یک مدل تکرارشونده با زمینه‌های مکانی و زمانی. در مجموعه مقالات سی امین کنفرانس AAAI در مورد هوش مصنوعی، فینیکس، AZ، ایالات متحده آمریکا، 12 تا 17 فوریه 2016; جلد 30. [ Google Scholar ]
چینی، اس. تامپسون، ال. Uhlig, S. ابزار نقشه برداری کانون برای پیش بینی الگوهای فضایی جرم. امن J. 2008 , 21 , 4-28. [ Google Scholar ] [ CrossRef ]
Chainey، SP بررسی تأثیر اندازه سلول و اندازه پهنای باند بر روی نقشه‌های کانون جرم تخمین چگالی هسته برای پیش‌بینی الگوهای فضایی جرم. گاو نر Geogr. Soc. لیژ 2013 ، 60 ، 7–19. [ Google Scholar ]
یانگ، ایکس. ژائو، ز. لو، اس. بررسی الگوهای مکانی-زمانی نقاط حساس تحرک انسانی شهری. Sustainability 2016 , 8 , 674. [ Google Scholar ] [ CrossRef ][ Green Version ]
Lawson، AB Hotspot تشخیص و خوشه بندی: راه ها و ابزار. محیط زیست Ecol. آمار 2010 ، 17 ، 231-245. [ Google Scholar ] [ CrossRef ]
شیا، ز. لی، اچ. چن، ی. Liao، W. شناسایی و تعیین حدود مناطق کانونی شهری با استفاده از روش خوشه‌بندی میدان مکانی-زمانی مبتنی بر شبکه. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 344. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
لی، اف. شی، دبلیو. ژانگ، اچ. یک رویکرد خوشه‌بندی دو مرحله‌ای برای تشخیص نقاط کانونی شهری با محدودیت‌های فضایی و زمانی شبکه. IEEE J. Sel. بالا. Appl. زمین Obs. Remote Sens. 2021 , 14 , 3695–3705. [ Google Scholar ] [ CrossRef ]
اشبروک، دی. Starner, T. استفاده از GPS برای یادگیری مکان‌های مهم و پیش‌بینی حرکت بین کاربران متعدد. پارس محاسبات همه جا حاضر. 2003 ، 7 ، 275-286. [ Google Scholar ] [ CrossRef ]
چن، کیو. یی، اچ. هو، ی. خو، X. Li, X. روشی جدید برای انتخاب مراکز خوشه اولیه K-means بر اساس تجزیه و تحلیل Hotspot. در مجموعه مقالات بیست و ششمین کنفرانس بین المللی ژئوانفورماتیک 2018، کونمینگ، چین، 28 تا 30 ژوئن 2018؛ صص 1-6. [ Google Scholar ]
روزنبرگ، ا. Hirschberg, J. V-measure: یک معیار ارزیابی خوشه خارجی مبتنی بر آنتروپی مشروط. در مجموعه مقالات کنفرانس مشترک 2007 در مورد روشهای تجربی در پردازش زبان طبیعی و یادگیری زبان طبیعی محاسباتی (EMNLP-CoNLL)، پراگ، جمهوری چک، 28-30 ژوئن 2007. صص 410-420. [ Google Scholar ]
سیناگا، KP; یانگ، M.-S. الگوریتم خوشه‌بندی K-means بدون نظارت. دسترسی IEEE 2020 ، 8 ، 80716–80727. [ Google Scholar ] [ CrossRef ]
تانگ، جی. لیو، اف. وانگ، ی. وانگ، اچ. کشف تحرک انسان شهری از داده های جی پی اس تاکسی در مقیاس بزرگ. فیزیک آمار مکانیک. Appl. 2015 ، 438 ، 140-153. [ Google Scholar ] [ CrossRef ]
محمد، اف. Baiee, WR تجزیه و تحلیل Hotspot جنایی مبتنی بر GIS با استفاده از تکنیک DBSCAN. در علم و مهندسی مواد، مجموعه مقالات مجموعه کنفرانس IOP، Thi-Qar، عراق، 15-16 ژوئیه 2020 . انتشارات IOP: بریستول، انگلستان، 2020؛ جلد 928، ص. 32081. [ Google Scholar ]
رودریگز، آ. Laio، A. خوشه بندی با جستجوی سریع و یافتن قله های چگالی. Science 2014 ، 344 ، 1492-1496. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
لیو، ایکس. هوانگ، Q. گائو، اس. بررسی عدم قطعیت تشخیص ناحیه فعالیت با استفاده از ردپای دیجیتال با DBSCAN چند مقیاسه. بین المللی جی. جئوگر. Inf. علمی 2019 ، 33 ، 1196-1223. [ Google Scholar ] [ CrossRef ]
Campello، RJGB؛ مولوی، د. Sander, J. خوشه بندی مبتنی بر تراکم بر اساس برآوردهای تراکم سلسله مراتبی. در مجموعه مقالات کنفرانس اقیانوس آرام-آسیا در مورد کشف دانش و داده کاوی، ساحل طلایی، استرالیا، 14-17 آوریل 2013. صص 160-172. [ Google Scholar ]
جارو، پ. تامت، تی. بلند، M. مناطق سلسله مراتبی مورد علاقه. در مجموعه مقالات نوزدهمین کنفرانس بین المللی IEEE در مدیریت داده های تلفن همراه (MDM) 2018، آلبورگ، دانمارک، 25 تا 28 ژوئن 2018؛ صص 86-95. [ Google Scholar ] [ CrossRef ]
کوراکاکیس، م. اسپیرو، ای. میلوناس، پ. Perantonis, SJ بهره برداری از اطلاعات رسانه های اجتماعی به سمت یک سیستم توصیه آگاه از زمینه. Soc. شبکه مقعدی حداقل 2017 ، 7 ، 42. [ Google Scholar ] [ CrossRef ]
سینگ، پی. Bose، SS Ambiguous D-به معنای الگوریتم خوشه‌بندی فیوژن بر اساس نظریه مجموعه‌های مبهم: کاربرد ویژه در خوشه‌بندی تصاویر سی‌تی اسکن COVID-19. سیستم مبتنی بر دانش 2021 ، 231 ، 107432. [ Google Scholar ] [ CrossRef ]
جیانگ، ی. ژائو، ک. شیا، ک. ژو، جی. ژو، ال. دینگ، ی. کیان، پی. الگوریتم خوشه‌بندی فازی چند وظیفه‌ای جدید برای تقسیم‌بندی خودکار تصویر مغز MR. جی. مد. سیستم 2019 ، 43 ، 118. [ Google Scholar ] [ CrossRef ]
لیو، ی. کانگ، سی. گائو، اس. شیائو، ی. Tian, Y. درک الگوهای سفر درون شهری از داده های مسیر تاکسی. جی. جئوگر. سیستم 2012 ، 14 ، 463-483. [ Google Scholar ] [ CrossRef ]
یائو، ز. ژونگ، ی. لیائو، کیو. وو، جی. لیو، اچ. یانگ، اف. درک فعالیت های انسانی و الگوهای تحرک شهری از داده های عظیم تلفن همراه: طراحی پلت فرم و برنامه های کاربردی. IEEE Intell. ترانسپ سیستم Mag. 2020 ، 13 ، 206-219. [ Google Scholar ] [ CrossRef ]
جیانگ، اس. فریرا، جی. گونزالس، MC الگوهای تحرک انسانی مبتنی بر فعالیت استنتاج شده از داده های تلفن همراه: مطالعه موردی سنگاپور. IEEE Trans. کلان داده 2017 ، 3 ، 208-219. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ژونگ، سی. باتی، م. مانلی، ای. وانگ، جی. وانگ، ز. چن، اف. اشمیت، جی. تنوع در نظم: استخراج الگوهای تحرک زمانی در لندن، سنگاپور و پکن با استفاده از داده های کارت هوشمند. PLoS ONE 2016 , 11 , e0149222. [ Google Scholar ]
یانگ، اف. دینگ، اف. Qu، X. Ran, B. برآورد سفرهای شهری با دوچرخه مشترک با داده های شبکه اجتماعی مبتنی بر مکان. پایداری 2019 ، 11 ، 3220. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
کیائو، اس. هان، ن. هوانگ، جی. یو، ک. مائو، آر. شو، اچ. او، س. Wu, X. مدل پیش‌بینی تقاضای دوچرخه مشترک مبتنی بر شبکه عصبی کانولوشنال پویا. ACM Trans. هوشمند سیستم تکنولوژی 2021 ، 12 ، 70. [ Google Scholar ] [ CrossRef ]
کای، ال. جیانگ، اف. ژو، دبلیو. لی، ک. طراحی و کاربرد یک شاخص جذابیت برای نقاط شهری بر اساس داده‌های مسیر GPS. دسترسی IEEE 2018 ، 6 ، 55976–55985. [ Google Scholar ] [ CrossRef ]
کانگ، سی. Qin، K. درک رفتارهای عملیاتی تاکسی ها در شهرها با فاکتورسازی ماتریسی. محاسبه کنید. محیط زیست سیستم شهری 2016 ، 60 ، 79-88. [ Google Scholar ] [ CrossRef ]
ژائو، اس. ژائو، پی. Cui، Y. چارچوب اندازه گیری مرکزیت شبکه برای تجزیه و تحلیل جریان ترافیک شهری: مطالعه موردی ووهان، چین. فیزیک آمار مکانیک. Appl. 2017 ، 478 ، 143-157. [ Google Scholar ] [ CrossRef ]
Lv، Q. کیائو، ی. انصاری، ن. لیو، جی. یانگ، جی. مدل مارکوف پنهان مبتنی بر داده های بزرگ مبتنی بر پیش بینی تحرک فردی در نقاط مورد علاقه. IEEE Trans. وه تکنولوژی 2017 ، 66 ، 5204-5216. [ Google Scholar ] [ CrossRef ]
شن، پی. اویانگ، ال. وانگ، سی. شی، ی. Su، Y. تجزیه و تحلیل خوشه ای و مشخصه ایستگاه های مترو شانگهای بر اساس کارت مترو و داده های کاربری زمین. ژئو اسپات. Inf. علمی 2020 ، 23 ، 352-361. [ Google Scholar ] [ CrossRef ]
چن، سی.-ف. هوانگ، سی.-ای. بررسی اثرات دوچرخه مشترک برای استفاده گردشگری بر تجربه گردشگر و پیامدهای آن. Curr. تور مسائل. 2021 ، 24 ، 134-148. [ Google Scholar ] [ CrossRef ]
سان، ایکس. هوانگ، ز. پنگ، ایکس. چن، ی. لیو، ی. ساخت یک رویکرد توصیه شخصی مبتنی بر مدل برای جاذبه‌های گردشگری از داده‌های رسانه‌های اجتماعی دارای برچسب جغرافیایی. بین المللی جی دیجیت. زمین 2019 ، 12 ، 661–678. [ Google Scholar ] [ CrossRef ]
کای، جی. وی، اچ. یانگ، اچ. ژائو، ایکس. الگوریتم خوشه‌بندی جدید مبتنی بر DPC و PSO. دسترسی IEEE 2020 ، 8 ، 88200–88214. [ Google Scholar ] [ CrossRef ]
ارتباط دادن.؛ چن، اچ. Xu، C.-Y.; یان، پی. لان، تی. لیو، ز. دونگ، سی. ارزیابی خطر سیل ناگهانی بر اساس روش فرآیند تحلیل سلسله مراتبی بهبود یافته و الگوریتم خوشه‌بندی حداکثر احتمال یکپارچه. جی هیدرول. 2020 , 584 , 124696. [ Google Scholar ] [ CrossRef ]
لی، ی. ژو، ی. Shi, J. تشخیص جوامع همپوشانی شبکه اجتماعی بر اساس الگوریتم خوشه‌بندی ترکیبی C-means. حفظ کنید. جامعه شهرها 2019 ، 47 ، 101436. [ Google Scholar ] [ CrossRef ]
اسکویی، AG; هاشم زاده، م. عاشقی، ب. بالافر، MA CGFFCM: کلاستر-وزن و یادگیری گروهی-محلی ویژگی-وزن در الگوریتم خوشه‌بندی فازی C-Means برای تقسیم‌بندی تصویر رنگی. Appl. محاسبات نرم. 2021 ، 113 ، 108005. [ Google Scholar ] [ CrossRef ]
بن عبدالله، AC; بنغابیت، ع. Bouhaddou, I. بررسی الگوریتم های خوشه بندی برای یک زمینه صنعتی. Procedia Comput. علمی 2019 ، 148 ، 291-302. [ Google Scholar ] [ CrossRef ]
احمد، ع. Khan, SS Survey از پیشرفته ترین الگوریتم های خوشه بندی داده های ترکیبی. دسترسی IEEE 2019 ، 7 ، 31883–31902. [ Google Scholar ] [ CrossRef ]
Aggarwal، CC بررسی الگوریتم‌های خوشه‌بندی جریان. در خوشه بندی داده ها ؛ چپمن و هال/CRC: لندن، بریتانیا، 2018؛ صص 231-258. [ Google Scholar ]
طبرج، ام اس; Minz، S. تشخیص نقطه اتصال مبتنی بر مجموعه خشن در داده‌های مکانی. در مجموعه مقالات کنفرانس بین المللی پیشرفت در محاسبات و علوم داده، قاضی آباد، هند، 12 تا 13 آوریل 2019؛ صص 356-368. [ Google Scholar ]
هو، ی. هوانگ، اچ. چن، آ. مائو، X.-L. Weibo-COV: مجموعه داده های رسانه اجتماعی COVID-19 در مقیاس بزرگ از Weibo. در مجموعه مقالات اولین کارگاه آموزشی NLP برای COVID-19 (قسمت 2) در EMNLP 2020، آنلاین، 20 نوامبر 2020؛ انجمن زبانشناسی محاسباتی: کمبریج، MA، ایالات متحده آمریکا، 2020. [ Google Scholar ]
Esri Inc. ArcGIS Pro ; Esri Inc.: Redlands, CA, USA; در دسترس آنلاین: https://www.esri.com/en-us/arcgis/products/arcgis-pro/overview (در 1 ژوئن 2020 قابل دسترسی است).
بات، اس. گرالیس، تی. هارمون، او. Tomolonis, P. Learning Tableau: ابزاری برای تجسم داده ها. جی. اکون. آموزش. 2020 ، 51 ، 317-328. [ Google Scholar ] [ CrossRef ]
McKinney, W. ساختارهای داده برای محاسبات آماری در پایتون. در مجموعه مقالات نهمین کنفرانس علمی پایتون، آستین، TX، ایالات متحده، 28 ژوئن تا 3 ژوئیه 2010. صص 56-61. [ Google Scholar ]
هریس، CR; Millman، KJ; ون در والت، اس جی; گومرز، آر. ویرتانن، پی. کورناپو، دی. ویزر، ای. تیلور، جی. برگ، اس. اسمیت، نیوجرسی؛ و همکاران برنامه نویسی آرایه با NumPy. طبیعت 2020 ، 585 ، 357–362. [ Google Scholar ] [ CrossRef ]
مک اینز، ال. هیلی، جی. Astels, S. hdbscan: خوشه بندی مبتنی بر چگالی سلسله مراتبی. J. نرم افزار منبع باز. 2017 ، 2 ، 205. [ Google Scholar ] [ CrossRef ]
پدرگوسا، اف. واروکو، جی. گرامفورت، آ. میشل، وی. تیریون، بی. گریزل، او. بلوندل، م. پرتنهوفر، پی. ویس، آر. دوبورگ، وی. و همکاران Scikit-Learn: یادگیری ماشینی در پایتون. جی. ماخ. فرا گرفتن. Res. 2011 ، 12 ، 2825-2830. [ Google Scholar ]
Hunter، JD Matplotlib: یک محیط گرافیکی دو بعدی. محاسبه کنید. علمی مهندس 2007 ، 9 ، 90-95. [ Google Scholar ] [ CrossRef ]
Waskom، ML Seaborn: تجسم داده های آماری. J. نرم افزار منبع باز. 2021 ، 6 ، 3021. [ Google Scholar ] [ CrossRef ]
Rousseeuw, PJ Silhouettes: کمکی گرافیکی برای تفسیر و اعتبارسنجی تحلیل خوشه‌ای. جی. کامپیوتر. Appl. ریاضی. 1987 ، 20 ، 53-65. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کالینسکی، تی. Harabasz, J. روش دندریت برای تجزیه و تحلیل خوشه. اشتراک. آمار Methods 1974 ، 3 ، 1-27. [ Google Scholar ] [ CrossRef ]
استرل، آ. Ghosh, J. Cluster ensembles – چارچوبی برای استفاده مجدد از دانش برای ترکیب چند پارتیشن. جی. ماخ. فرا گرفتن. Res. 2002 ، 3 ، 583-617. [ Google Scholar ]
استاینلی، دی. ویژگی‌های شاخص رند تعدیل‌شده هوبرت-زراعی. روانی Methods 2004 , 9 , 386. [ Google Scholar ] [ CrossRef ]
یو، اچ. لیو، پی. چن، جی. وانگ، اچ. تجزیه و تحلیل مقایسه ای روش های تجزیه و تحلیل فضایی برای شناسایی نقاط داغ. اسید. مقعدی قبلی 2014 ، 66 ، 80-88. [ Google Scholar ] [ CrossRef ]
شن، ایکس. شی، دبلیو. چن، پی. لیو، ز. وانگ، ال. مدل جدید برای پیش بینی حرکات افراد در مناطق پویا مورد علاقه. GIScience Remote Sens. 2022 ، 59 ، 250-271. [ Google Scholar ] [ CrossRef ]

شکل 1. نقشه های حرارتی از سه مجموعه داده، یعنی ( الف ) مجموعه داده های GBA، ( ب ) مجموعه داده های شانگهای، و ( ج ) مجموعه داده های پکن. عمق رنگ تراکم را نشان می دهد، با مناطق با رنگ عمیق تراکم بالایی دارند.

شکل 2. نمودار آماری حجم داده ها در تاریخ های مختلف: ( الف ) 7 روز استخراج شده از هفته اول در مجموعه داده GBA. ( ب ) کل 12 هفته در مجموعه داده GBA.

شکل 3. گردش کار ELV با چهار مرحله پردازش اصلی. متوازی الاضلاع داده های خام، داده های پردازش شده و نتایج را نشان می دهند. مستطیل ها به سه مرحله خوشه بندی اشاره دارند و مراحل دیگر مکانیسم های قضاوتی هستند که با الماس نشان داده شده اند.

شکل 4. نمونه ای از نمودار فاصله k که فواصل بین هر نقطه و آن را نشان می دهد. کنزدیکترین همسایگان یک نقطه آرنج به رنگ نارنجی نشان داده شده است و یک کادر قرمز محدوده انتخابی ممکن از نقطه آرنج را توصیف می کند.

شکل 5. جریان پردازش نقاط با چگالی بالا. پارامتر هپستوسط الگوریتم 1 انتخاب می شود و سپس نقاط با چگالی بالا را می توان استخراج و خوشه بندی کرد.

شکل 6. تخصیص داده های باقی مانده. قسمت چپ نمونه هایی از فواصل بین یک نقطه و خوشه ها را نشان می دهد. قسمت سمت راست نتیجه خوشه بندی اولیه را نشان می دهد.

شکل 7. تقسیم بندی مجدد یک خوشه انتخاب شده، شامل بررسی اینکه آیا داده ها را می توان خوشه بندی کرد و آیا باید از نتیجه خوشه بندی برای به روز رسانی نتیجه خوشه بندی استفاده شود.

شکل 8. بازیابی نویز با استفاده از نتیجه تقسیم بندی مجدد خوشه 3. دو خوشه جدید و تعداد زیادی نقاط نویز پس از تقسیم بندی مجدد وجود دارد. سپس، نقاط نویز جدید دوباره خوشه‌بندی می‌شوند و با خوشه‌های 7 و 8 ترکیب می‌شوند تا نتیجه خوشه‌بندی به‌روزرسانی شود.

شکل 9. نتایج خوشه بندی روش های مختلف آزمایش شده بر روی داده های روز اول در مجموعه داده GBA: ( الف ) ELV، ( ب ) DPC، ( ج ) DBSCAN 200، ( د ) DBSCAN 400، ( e ) DBSCAN 800، ( f ) DBSCAN 1600، ( g ) HDBSCAN 4، ( h ) HDBSCAN 8، ( i ) HDBSCAN 16، و ( j ) HDBSCAN 32. نقاط خاکستری رنگ نویز و نقاط با رنگ های دیگر نقاط خوشه ای بودند.

شکل 10. اطلاعات دقیق مربوط به تعداد نقاط و مساحت خوشه ها: ( الف ) نمودار پراکندگی تعداد نقاط در هر خوشه، ( ب ) نمودار جعبه تعداد نقاط در هر خوشه، ( ج ) نمودار پراکندگی از مساحت هر خوشه، ( د ) نمودار مربعی مساحت هر خوشه، ( ه ) نمودار پراکندگی مساحت اشغال شده توسط هر نقطه، و ( f ) نمودار مربعی مساحت اشغال شده توسط هر نقطه.

شکل 11. مقایسه بصری ELV و HDBSCAN در دو ناحیه با تراکم های مختلف بر اساس داده های روز اول مجموعه داده GBA: ( الف ) نتیجه خوشه بندی ELV در یک منطقه با چگالی بالا، ( ب ) نتیجه خوشه بندی HDBSCAN 4 در یک ناحیه با چگالی بالا، ( ج ) نتیجه خوشه‌بندی ELV در ناحیه با چگالی کم، و ( د ) نتیجه خوشه‌بندی HDBSCAN 4 در ناحیه با چگالی کم. علاوه بر این، دایره های جامد نشان دهنده نقاط خوشه ای و مربع های توخالی نقاط نویز هستند.

شکل 12. تغییرات زمانی روش های مختلف ارزیابی شده توسط دو شاخص: ( الف ) SC و ( ب ) CHI.

شکل 13. تفاوت های چگالی مجموعه داده های 12 هفته ای.

شکل 14. تأثیر تفاوت چگالی بر بهبود ELV در مقایسه با روش های دیگر بر روی دو شاخص، یعنی: بهبود SC در مقایسه با ( الف ) DBSCAN 200، ( ب ) DBSCAN 400، ( ج ) DBSCAN 800، ( d ) DBSCAN 1600 . ، ( e ) HDBSCAN 4، ( f ) HDBSCAN 8، ( g ) HDBSCAN 16، و ( h ) HDBSCAN 32. بهبود در CHI در مقایسه با ( i ) DBSCAN 200، ( j ) DBSCAN 400، ( k ) DBSCAN 800، ( l ) DBSCAN 1600، ( m ) HDBSCAN 4، ( n ) HDBSCAN 8، ( o ) HDBSCAN، (16، وص ) HDBSCAN 32.

شکل 15. ویژگی های زمانی مجموعه داده یک هفته و نتیجه خوشه بندی: ( الف ) تعداد تمام نقاط و ( ب ) تعداد میانگین نقاط در هر خوشه.

شکل 16. تغییرات هفتگی ویژگی های مختلف: ( الف ) میانگین تعداد نقاط در هر خوشه، ( ب ) مساحت متوسط خوشه ها، ( ج ) مجموع میانگین مساحت خوشه ها، ( د ) مساحت اشغال شده توسط هر نقطه، و ( ه ) میانگین k-فاصله علاوه بر این، توزیع ( f ) تعداد نقاط، ( g ) مساحت، و ( h ) k-فاصله در هفته‌های خاص نشان داده شد.

مقالات داخلی و بین المللی

9 نظرات

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

کلید واژه ها:

1. مقدمه

2. آثار مرتبط