پیش‌بینی دقیق جریان ترافیک شهری نقشی حیاتی در سیستم حمل‌ونقل هوشمند (ITS) دارد. همبستگی‌های پیچیده بلندمدت و بلندمدت مکانی-زمانی جریان ترافیک چالش مهمی برای کار پیش‌بینی ایجاد می‌کند. اکثر روش‌های تحقیق فعلی تنها بر همبستگی‌های فضایی در مناطق محلی تمرکز می‌کنند و اطلاعات زمینه‌ای جغرافیایی جهانی را نادیده می‌گیرند. گرفتن اطلاعات مکانی از گره‌های دور با استفاده از شبکه‌های عصبی گراف کم عمق (GNN) برای مدل‌سازی همبستگی‌های فضایی دوربرد، چالش برانگیز است. برای رسیدگی به این مشکل، ما یک مدل شبکه کانولوشنی گراف معنایی جهانی مکانی-زمانی جدید (STSGAN) طراحی می‌کنیم که یک شبکه سطح عمیق برای دستیابی به مدل‌سازی همزمان همبستگی‌های مکانی-زمانی است. اولین، ما یک شبکه کانولوشنال توجه گراف (GACN) را برای استخراج اهمیت ویژگی‌های فضایی مختلف و یادگیری همبستگی فضایی مناطق محلی و اطلاعات معنایی فضایی جهانی پیشنهاد می‌کنیم. ساختار پیچیدگی علّی زمانی (TCN) برای گرفتن روابط علی بین زمان‌های بلند-کوتاه مورد استفاده قرار می‌گیرد، بنابراین امکان بررسی یکپارچه همبستگی‌های مکانی و زمانی کلی را فراهم می‌کند. چندین آزمایش بر روی دو مجموعه داده جریان ترافیک در دنیای واقعی انجام شده است، و نتایج نشان می‌دهد که رویکرد ما از چندین خط پایه پیشرفته بهتر عمل می‌کند. بنابراین امکان در نظر گرفتن یکپارچه همبستگی های مکانی و زمانی کلی را فراهم می کند. چندین آزمایش بر روی دو مجموعه داده جریان ترافیک در دنیای واقعی انجام شده است، و نتایج نشان می‌دهد که رویکرد ما از چندین خط پایه پیشرفته بهتر عمل می‌کند. بنابراین امکان در نظر گرفتن یکپارچه همبستگی های مکانی و زمانی کلی را فراهم می کند. چندین آزمایش بر روی دو مجموعه داده جریان ترافیک در دنیای واقعی انجام شده است، و نتایج نشان می‌دهد که رویکرد ما از چندین خط پایه پیشرفته بهتر عمل می‌کند.

کلید واژه ها:

پیش بینی جریان ترافیک ؛ مدل سازی مکانی – زمانی شبکه کانولوشن گراف ; مکانیسم توجه

1. مقدمه

با افزایش شتاب شهرنشینی، افزایش سریع تعداد خودروهای شخصی در شهرها فشار زیادی را بر سیستم ترافیکی موجود وارد کرده است. پیش بینی جریان ترافیک، به عنوان یک جزء ضروری از سیستم های حمل و نقل هوشمند [ 1 ]، به توسعه سیستم های حمل و نقل هوشمند (ITS) در بسیاری از کشورها متعهد شده است، با هدف پیش بینی دقیق شرایط ترافیک در زمان واقعی و ارائه یک مبنای علمی برای بخش حمل و نقل برای بهینه سازی زمان بندی منابع ترافیکی برای کاهش تراکم ترافیک شهری به طور موثر. به دلیل اهمیت پیش‌بینی جریان ترافیک، در سال‌های اخیر توجه بسیاری از محققین را به پیش‌بینی دقیق و بلندمدت ترافیک جلب کرده است.
در شبکه های حمل و نقل شهری وابستگی های مکانی-زمانی پیچیده و بلندمدتی وجود دارد. جریان هر منطقه در شهر تحت تأثیر مناطق مجاور آن و همبستگی معنایی فضایی بین جاده‌های دوردست است. به دلیل حمل و نقل عمومی مانند اتوبوس و تاکسی، وسایل نقلیه دارای تحرک بین منطقه ای هستند. این وضعیت نشان می دهد که با تکامل مشاهدات یک گره، آنها اغلب نه تنها به گره های مجاور آن بلکه به اطلاعات تاریخی گره های دورتر مربوط می شوند [ 2 ]. بنابراین، وجود همزمان وابستگی‌های فضایی بین گره‌های محلی و دور، یعنی وجود همبستگی‌های زوجی معنایی بیشتر بین جاده‌های دورتر، برای پیش‌بینی جریان ترافیک نیز حیاتی است [ 3 ].
دو منطقه در یک شهر با ویژگی های عملکردی جغرافیایی مشابه (مثلاً مناطق خرید یا مسکونی) به شدت به توزیع ترافیک آنها بستگی دارد. با این حال، آنها از نظر فضایی مجاور یا حتی دور از یکدیگر نیستند [ 4 ، 5 ، 6 ]. به عنوان مثال، در شکل 1 ، برای پیش بینی جریان ترافیک نشان داده شده استتی2از اس2، می توان به جریان ترافیک تاریخی اشاره کرد تی1همسایه جغرافیایی خود اس1به دلیل جریان ترافیک منطقه ای. علاوه بر این، جریان ترافیک از اس2در ارتباط است اس5همانطور که در شکل 2 نشان داده شده است، که همچنین یک منطقه مسکونی است ، زیرا عملکردهای منطقه ای و الگوهای زمانی مشابهی دارند. علاوه بر این، جریان ترافیک تاریخی از اس7همچنین باید به دلیل الگوی زمانی بسیار مشابه جریان ترافیک در نظر گرفته شود اس2. الگوهای مشابه جریان ترافیک قبلی را نیز می توان در گره های دور مشاهده کرد که منعکس کننده تعامل بین روابط فضایی چندگانه است. بنابراین، ژانگ و همکاران. [ 7 ] از یک شبکه توجه چند مقیاسی برای یادگیری همبستگی های معنایی فضایی از دیدگاه جهانی برای دستیابی به نتایج پیش بینی دقیق تر استفاده کرد. بنابراین، همبستگی های فضایی دوربرد بین مناطق نقش مهمی را در پیش بینی جریان ترافیک ایفا می کند.
شبکه های عصبی نمودار (GNN) در تحقیقات یادگیری عمیق [ 8 ] استفاده شده است. آنها همچنین به دلیل توانایی قدرتمندشان در گرفتن همبستگی های فضایی از داده های غیر اقلیدسی [ 9 ] به یک رویکرد محبوب برای مشکلات پیش بینی جریان ترافیک تبدیل شده اند. به عنوان مثال، شبکه های کانولوشن گراف مکانی-زمانی (STGCN) [ 10 ]، GraphWaveNet [ 11 ]، شبکه کانولوشن گراف مکانی-زمانی مبتنی بر توجه (ASTGCN) [ 12 ]، و غیره. (GRU)، شبکه‌های حافظه کوتاه‌مدت (LSTM) [ 13 ]، و روش‌های دیگر توانایی بیشتری برای مدل‌سازی وابستگی‌های زمانی یا مکانی دارند، به عنوان مثال، Zhao L و همکاران. [ 14] و دیگران با ترکیب GCN و GRU به نتایج پیش بینی خوبی دست یافته اند.
با این حال، دو مشکل در رویکرد فوق نادیده گرفته شده است: از یک طرف، زمانی که GNN ها اطلاعات توپولوژی فضایی دور را دریافت می کنند، تعداد گره ها در میدان پذیرنده هر گره به طور تصاعدی با افزایش تعداد لایه های شبکه افزایش می یابد. علاوه بر این، خود GNN ها مقیاس پذیری بدتری دارند، و مشکل فشردگی بیش از حد زمانی رخ می دهد که اطلاعات از گره های مختلف با استفاده از GNN های چند لایه جمع آوری می شود [ 15 ، 16 ، 17 ]]، انتشار اطلاعات در بین گره های دور در نمودار را دشوار می کند. ویژگی های تمام گره ها در لایه های عمیق تر به نمایش دقیق همگرا می شوند. این ایرادات عمق شبکه‌های GNN را محدود می‌کند و دستیابی به ویژگی‌های فضایی عمیق‌تر و جامع‌تر را به چالش می‌کشد. از سوی دیگر، مدلسازی تطبیقی ​​همبستگی زمانی بلندمدت برای گرفتن همبستگی فضایی دوربرد حیاتی است. با این حال، زمانی که شبکه‌های عصبی مکرر (RNN)، LSTM و GRU همبستگی طولانی‌مدت را ثبت می‌کنند، به تدریج با افزایش تعداد لایه‌های شبکه، انباشت خطا را معرفی می‌کنند. از انفجار یا ناپدید شدن گرادیان رنج خواهد برد [ 18 ] و به ناچار برخی از اطلاعات ضروری را از دست خواهد داد.
علاوه بر این، تئوری و تحقیقات نشان داده اند که یادگیری ذخیره سری های زمانی بسیار طولانی برای RNN ها دشوار است [ 18 ، 19 ، 20 ]. ASTGCN [ 13 ] و Diffusion Convolutional Recurrent Neural Network (DCRNN) [ 21 ] از یک مکانیسم پیش‌بینی تکراری استفاده می‌کنند که در آن تمام مقادیر پیش‌بینی‌شده برای چندین مرحله زمانی با یک ارزیابی یکنواخت به‌جای تکرارهای مختلف به‌دست می‌آیند. بنابراین، ترکیب وظایف پیش بینی بلند مدت و کوتاه مدت چالش برانگیز است.
برای به دست آوردن وابستگی‌های فضایی محلی و جهانی، ما یک مدل شبکه کانولوشنی توجه گراف جدید را پیشنهاد می‌کنیم تا به طور موثر مشکل فشردن بیش از حد شبکه‌های عصبی گراف چند لایه را حل کرده و به ساخت شبکه‌های عمق دست یابیم. با الهام از الگوریتم دینامیک زمان تاب (DTW) [ 22]، شباهت عملکردی منطقه‌ای توسط ما برای ساخت یک ماتریس مجاورت معنایی استفاده می‌شود تا بتواند همبستگی‌های فضایی دوربرد را ثبت کند. در نهایت، اطلاعات زمینه‌ای مکانی و همبستگی‌های ترافیکی جهانی در مناطق مختلف، نمایش الگوی مکانی-زمانی را افزایش می‌دهند. مشاهدات تاریخی عملی گسترده‌تری برای یادگیری همبستگی‌های طولانی کارآمد غیرخطی و همبستگی‌های زمانی کوتاه‌مدت برای گرفتن همبستگی‌های زمانی جهانی به‌دست می‌آیند. ما یک ساختار شبکه TCN بر اساس مدل‌سازی سری‌های زمانی طراحی کردیم که شامل پیچش اتساع و ماژول‌های باقی‌مانده برای به دست آوردن ویژگی‌های زمانی غیرخطی تاریخی طولانی‌تر است. در نهایت، ماژول TCN با آبشار شبکه توجه گراف ترکیب می‌شود تا همبستگی‌های زمانی طولانی‌تر عمیق‌تر و غنی‌تر به دست آید.
به طور خلاصه، مشارکت های این مقاله به شرح زیر است:
  • ما یک رویکرد مبتنی بر داده را برای ساختن نمودارهای تشابه معنایی طراحی می کنیم، که وابستگی های مکانی و زمانی جهانی پنهان را حفظ می کند. این ماتریس مجاورت مبتنی بر داده می تواند همبستگی های معنایی را استخراج کند که ممکن است در نمودار فضایی وجود نداشته باشد.
  • ما یک مدل STSGAN جدید مبتنی بر شبکه‌های کانولوشنی توجه گراف پیشنهاد می‌کنیم تا به طور موثر مشکل فشردن بیش از حد شبکه عصبی نمودار چند لایه را برطرف کند. ما با موفقیت شبکه‌های عمقی را مدل‌سازی می‌کنیم تا به طور همزمان وابستگی‌های فضایی دوربرد با اهمیت متفاوت را ضبط کنیم. سپس از ماژول پیچیدگی علّی زمانی آبشاری برای تجزیه و تحلیل روابط علی بین زمان بلندمدت و کوتاه‌مدت به‌طور موازی استفاده می‌شود تا به طور همزمان همبستگی‌های زمانی محلی و جهانی داده‌های ترافیک را ضبط کند.
  • آزمایش‌های گسترده‌ای روی دو مجموعه داده ترافیک دنیای واقعی برای ارزیابی منطقی STSGAN در این مقاله انجام شد. در مقایسه با خط پایه پیشرفته، مدل در این مقاله عملکرد پیش‌بینی بهتری در پیش‌بینی 1 ساعته دارد.
ادامه مقاله به شرح زیر تدوین شده است. ما یک نمای کلی از کارهای مربوط به پیش بینی ترافیک در بخش 2 ارائه می دهیم . بخش 3 تعریف مشکل پیش بینی ترافیک را شرح می دهد و اهداف مطالعه را نشان می دهد. چارچوب موجود STSGAN ما و راه حل های مشخصه در بخش 4 به تفصیل آمده است. در بخش 5 ، چندین آزمایش را برای ارزیابی مدل خود طراحی می کنیم. کار ما و جهت کار آینده در بخش 6 خلاصه شده است.

2. کارهای مرتبط

2.1. پیش بینی جریان ترافیک

به عنوان یک مشکل پیش‌بینی مکانی-زمانی معمولی، پیش‌بینی جریان ترافیک در دهه‌های اخیر مورد مطالعه قرار گرفته است. با مطالعات قبل از استفاده از حالت‌های قابل توجهی مانند میانگین متحرک یکپارچه خودکار (ARIMA) [ 22 ]، رگرسیون خودکار برداری (VAR) [ 23 ] و سایر مدل‌های یادگیری ماشین مانند K-نزدیک‌ترین همسایه (KNN) [ 24 ]]. با این حال، این مدل ها فقط همبستگی زمانی را در نظر می گیرند و همبستگی مکانی را نادیده می گیرند. علاوه بر این، روش‌های یادگیری ماشین به شدت بر مهندسی ویژگی‌ها تکیه می‌کنند و باور به همبستگی‌های فضایی با ابعاد بالا را چالش‌برانگیز می‌کند. در سال‌های اخیر، برای توصیف همبستگی فضایی، روش‌های پیش‌بینی مبتنی بر یادگیری عمیق معمولاً کل شهر را به مناطق شبکه‌ای تقسیم می‌کنند و روش‌های مبتنی بر شبکه عصبی کانولوشن (CNN) مانند [ 25 ، 26 ، 27 ] شبکه ترافیک را به عنوان یک تصویر برای استخراج موثر ویژگی های فضایی داده های شبکه. با این حال، این روش‌ها برای داده‌های شبکه طراحی شده‌اند و نمی‌توانند به طور موثر داده‌های حسگر غیراقلیدسی را از توپولوژی جاده‌های دنیای واقعی ضبط کنند [ 28 ، 29 ]]. بنابراین، بیشتر آنها از شبکه های کانولوشن گراف برای گرفتن همبستگی فضایی استفاده می کنند، مانند [ 16 ]. ژائو [ 14 ] از شبکه‌های کانولوشنال نمودار زمانی (T-GCN) برای به دست آوردن توپولوژی شبکه‌های جاده‌ای برای مدل‌سازی همبستگی فضایی استفاده کرد. Guo [ 13 ] یک مدل ASTGCN را پیشنهاد کرد. مکانیسم توجه با پیچیدگی زمانی یکپارچه شده است تا ویژگی‌های مکانی-زمانی پویا داده‌های ترافیک را به تصویر بکشد. بنابراین، اکثر مطالعات کنونی از شبکه‌های کانولوشن گراف برای گرفتن همبستگی‌های فضایی استفاده می‌کنند. برای مثال، STGCN [ 10 ] پیچیدگی نمودار و پیچیدگی زمانی دروازه‌ای را در بلوک‌های پیچیدگی مکانی-زمانی ادغام می‌کند تا همبستگی‌های مکانی-زمانی را بیاموزد. شبکه‌های کانولوشنال گراف سنکرون مکانی-زمانی (STSGCN) [29 ] همبستگی‌های فضایی را با بلوک‌های انحراف زمانی که نمودار و پیچیدگی زمانی دروازه‌ای را برای مدل‌سازی همبستگی‌های مکانی-زمانی یکپارچه می‌کنند، ثبت کرد. با این حال، آن‌ها فقط می‌توانند بین مناطق مجاور یاد بگیرند و نمی‌توانند وابستگی‌های فضایی دوربرد را بگیرند. شبکه نمودار فیوژن تطبیقی ​​مکانی-زمانی (STFAGN) [ 30] لایه‌های کانولوشنال ذوب شده را با ماتریس‌های وابستگی تطبیقی ​​جدید از طریق آموزش سرتاسر ترکیب می‌کند تا وابستگی‌های مکانی-زمانی پنهان به داده‌ها را ضبط کند و وابستگی‌های مکانی-زمانی پنهان را از طریق عملیات همجوشی به‌طور موازی به دست آورد. روش های فوق فرض می کنند که همبستگی فضایی فقط در گره های متناظر یا نزدیک وجود دارد. رویکردهای محلی همبستگی فضایی غیرمحلی بین گره‌ها در شبکه حمل و نقل را در نظر نمی‌گیرند. بیشتر آنها فقط به روابط نزدیکی بین مناطق مختلف فکر می کنند، بنابراین روابط معنایی بین مناطق دیگر را در سطح جهانی نادیده می گیرند.

2.2. شبکه کانولوشن گراف فضایی-زمانی

برونال [ 31 ] در ابتدا شبکه های عصبی گراف را از طریق گسترش طبیعی شبکه های عصبی کانولوشنال (CNN) بر روی داده های گراف ساختاریافته پیشنهاد کرد. در وظایف پیش بینی جریان ترافیک، بسیاری از محققان GCN ها را به گرفتن توپولوژی های فضایی پیچیده اختصاص داده اند [ 6 ، 7 ، 8 ، 9 ، 12 ]. برای مثال، DeepSTN+ [ 7 ] یک مدل کانولوشنی عمیق را برای مدل‌سازی وابستگی‌های فضایی دور بین جریان‌های جمعیت، با استفاده از مکانیسم‌های همجوشی چندگانه برای ثبت روابط پیچیده بین ویژگی‌ها در سطوح مختلف، پیشنهاد کرد. شبکه کانولوشن چند نمودار زمانی (TMGCN) [ 3] شبکه های کانولوشن چند گراف زمانی را برای استخراج مشترک ارتباط معنایی بالقوه و ویژگی های فضایی جهانی پیشنهاد کرد.
استفاده از واحدهای چرخه‌ای RNN و LSTM برای یادگیری همبستگی‌های بلندمدت به تدریج انباشت خطا را معرفی می‌کند و زمان آموزشی اضافی را هزینه می‌کند. محدود به مشکلاتی مانند ناپدید شدن گرادیان و انفجار گرادیان [ 18 ]، که یادگیری ذخیره سازی اطلاعات سری زمانی جامع تر را چالش برانگیز می کند [ 26 ]. بنابراین، برای دستیابی به پیش بینی دقیق تحت شرایط فضایی طولانی مدت و پیچیده. DCRNN [ 21 ] رویکردی برای مدل‌سازی جریان ترافیک به شکل انتشار بر روی نمودارهای جهت‌دار، با استفاده از معماری کد و رمزگشایی و تکنیک‌های نمونه‌برداری برنامه‌ریزی‌شده برای بهبود عملکرد پیش‌بینی بلندمدت، پیشنهاد کرد. شبکه توجه نمودار مکانی-زمانی (STGAT) [ 32] یک مدل معماری دو مسیره مبتنی بر شبکه‌های توجه گراف را برای پردازش سری‌های زمانی طولانی با انباشتن لایه‌های کانولوشن موقتی دردار پیشنهاد کرد. شبکه دینامیکی مکانی-زمانی (STDN) [ 27 ] بیشتر یک تغییر دوره ای مکانیسم توجه را برای یکپارچه سازی اطلاعات منظم بلند مدت پیشنهاد کرد. ژانگ و همکاران [ 33] یک شبکه توجه گراف کانولوشنال مکانی و زمانی عمیق را پیشنهاد می‌کند که از یک شبکه ترانسفورماتور با وضوح چندگانه برای ثبت وابستگی ترافیک بین مناطق مختلف استفاده می‌کند. رویکردهای فوق عمدتاً مبتنی بر همبستگی فضایی محلی هستند و به ندرت ویژگی های جهانی را به تصویر می کشند. در مقابل، مدل STSGAN ما همبستگی مکانی-زمانی را در یک شبکه عصبی کانولوشنال توجه گراف ترکیب می‌کند. ما از ماتریس‌های مجاورت چندگانه استفاده می‌کنیم تا روابط چند تفکیک‌پذیری بین جهانی و محلی را به طور مشترک به تصویر بکشیم، روابط پنهان در سراسر مناطق و بین دوره‌های بلند و کوتاه را بررسی می‌کنیم.

2.3. گراف شبکه توجه

Petar Velickovi [ 34 ] در ابتدا شبکه های توجه گراف (GATs) را پیشنهاد کرد، یک شبکه عصبی کانولوشنال جدید بر اساس داده های شبکه گراف. GATها بر تولید نمایش گره های جدید با تجمیع گره های همسایه و ضرایب توجه تمرکز می کنند تا اهمیت هر گره در نمودار را نسبت به همسایگانش متمایز کنند. تلاش‌های زیادی در پیچیدگی نمودار گنجانده شده است تا مکانیسم‌های توجه را در خود بگنجانند [ 3 ، 27 ، 32 ، 34 ، 35 ]. GAT [ 32 ] در چندین آزمایش معیار برای وظایف مربوط به گراف به نتایج پیشرفته‌ای دست یافته است. مطالعات اخیر [ 36] یک مکانیسم توجه چند بازه ای را برای جمع آوری اطلاعات از مناطق مختلف برای یادگیری خودکار اهمیت فواصل مختلف معرفی کرد. پیش‌بینی ترافیک کوتاه‌مدت با شبکه‌های کانولوشن گراف (LSGCN) [ 37 ] یک شبکه توجه گراف cosAtt را پیشنهاد کرد تا ویژگی‌های فضایی پیچیده را به تصویر بکشد در حالی که وظایف پیش‌بینی بلندمدت و کوتاه‌مدت را برآورده می‌کند. متعاقباً، Graph Multi-Attention Network (GMAN) [ 35 ] یک معماری شبکه رمزگذار-رمزگشا با ماژول های توجه فضایی متعدد برای گرفتن همبستگی های فضایی پیچیده پیشنهاد کرد. به عنوان یک روش مبتنی بر توجه، GMAN به سادگی مجموع امتیازات توجه فضایی همه رئوس را محاسبه می کند. شبکه توجه نمودار مکانی-زمانی تطبیقی ​​(ASTGAT) [ 38] یک شبکه توجه گراف تطبیقی ​​را برای گرفتن وابستگی های فضایی پیشنهاد می کند و یک لایه کانولوشنال گیت-زمان برای مدیریت داده های سری زمانی طولانی طراحی می کند.
روش‌های فوق عملکرد برتر را در پیش‌بینی ترافیک نشان می‌دهند، اما نمی‌توانند همبستگی‌های فضایی جهانی و محلی را در شبکه جاده‌های ترافیکی دریافت کنند. بنابراین، مکانیسم‌های جمع‌آوری توجه توسط ما برای دریافت وابستگی‌های ترافیک محلی و جهانی در سراسر مناطق استفاده می‌شود.

3. مقدمات

در این بخش به تشریح برخی از عناصر ضروری جریان شهری و تعریف مسئله پیش بینی جریان شهری می پردازیم.

تعریف  1.

(گراف شبکه فضایی):
ما جاده را به عنوان یک گراف شبکه نشان می دهیم و از گراف جهت دار استفاده می کنیم جی=(V،E،آ)برای تعریف ساختار توپولوژیکی شبکه راه فضایی. |V|=نمجموعه ای از تمام گره ها (نماینده حسگرها در شبکه جاده ها)، که در آن نتعداد گره ها را در نمودار نشان می دهد. Eمجموعه ای از لبه های متصل بین دو گره را نشان می دهد. آ∈ℝن×ننشان دهنده ماتریس مجاورت است که در آن هر عنصر نمودار جاده فضایی را نشان می دهد جیدرجه اتصال بین گره های مختلف
نمودار فضایی جینشان دهنده همبستگی بین گره های مختلف در بعد فضایی است. روابط شبکه های فضایی با گذشت زمان تغییر نمی کند و ما در کار خود، شبکه فضایی را به صورت یک گراف بدون جهت نشان می دهیم.

تعریف  2.

(جریان ترافیک):
ما تعریف کردیم _ ایکستی،υ∈ℝافبرای نشان دادن تمام بردارهای ویژگی گره υدر زمان تیبا تعداد ویژگی های ورودی اف. ایکسجی(تی)=(ایکستی،1،ایکستی،2،⋯،ایکستی،ن)∈ℝن×اف، تمام مقادیر ویژگی همه گره ها را در زمان مشخص می کند تی، طول مرحله زمانی نشان داده شده با تی، χ=(ایکسجی(1)،ایکسجی(2)⋯،ایکسجی(پ))∈ℝن×اف×پتمام مقادیر ویژه همه گره ها را در برش زمانی تعریف می کند پ. ماتریس سیگنال گراف χوضعیت ترافیک شبکه فضایی را نشان می دهد جیاز نمودار فضایی جیدر برش زمانی پ.

تعریف  3.

(مشکل پیش بینی جریان ترافیک):

هدف پیش‌بینی جریان ترافیک مکانی-زمانی را می‌توان به صورت زیر توصیف کرد: با توجه به کل شبکه ترافیک پبخش های زمانی تاریخی، مشاهدات از نرئوس، به عنوان تعریف شده است χ=(ایکسجی(تی-پ+1)،ایکسجی(تی-پ+2)⋯،ایکسجی(تی))∈ℝن×اف×پ. کارکرد fاز داده های مشاهده ترافیک آموخته می شود پمراحل زمانی تاریخی برای پیش بینی شرایط جریان ترافیک همه رئوس در شبکه جاده ها برای آینده سمراحل زمانی که به صورت مشخص شده است Y=(ایکسجی(تی)،ایکسجی(تی+1)⋯،ایکسجی(تی+س))∈ℝن×اف×س.

(ایکسجی(تی-پ+1)،ایکسجی(تی-پ+2)⋯،ایکسجی(تی))→Y=f(χ ;جی)(Yجی(تی)،Yجی(تی+1)⋯،Yجی(تی+س))،

4. روش شناسی

در یک محیط ترافیکی طبیعی، شرایط ترافیکی در هر منطقه شهر تحت تأثیر مناطق دور و نزدیک است [ 4 ، 5 ، 6 ، 7 ]. بنابراین، ما یک چارچوب شبکه کانولوشنی توجه نمودار معنایی جهانی فضایی-زمانی برای استخراج روابط تکامل مکانی-زمانی جهانی مناطق مختلف پیشنهاد می‌کنیم. STSGAN چارچوب بلوک های متعددی دارد که مدل پیشنهادی در این مقاله در شکل 3 نشان داده شده است .
به طور خاص، ما ویژگی‌های فضایی پنهان را از طریق یک معماری دو مسیره بررسی کردیم، که در آن هر مسیر دارای ساختار یکسانی است تا وابستگی‌های مکانی-زمانی را به تصویر بکشد. یک مسیر از یک ماتریس مجاورت تطبیقی ​​به عنوان ورودی برای مدل‌سازی وابستگی‌های فضایی بین مناطق همسایه در سطح ریزدانه استفاده می‌کند. مسیر دیگر از یک ماتریس مجاورت معنایی جهانی برای مدل‌سازی همبستگی‌های فضایی بین مناطق مختلف از دیدگاه جهانی استفاده می‌کند. دو نوع ماتریس مجاورت به طور همزمان به لایه T-GACN وارد می شوند. فعل و انفعالات بین زمان بلندمدت و کوتاه مدت محلی و جهانی توسط ماژول پیچیدگی علّی زمانی (TCN) ثبت می‌شود: سپس، ورودی به ماژول پیچیدگی توجه گراف داده می‌شود تا به طور همزمان وابستگی‌های فضایی دوربرد را ثبت کند.39 ] و نرمال سازی لایه [ 40 ] در هر ماژول برای تضمین آموزش عمیق و کارآمد مدل. تمام لایه ها در بلوک T-GACN دارای تعداد یکسانی از ابعاد هستند و ویژگی های مکانی-زمانی جامعی را به دست می آورند.

4.1. ساخت نقشه ترافیک

4.1.1. نمودار فضایی مجاورت ترافیک

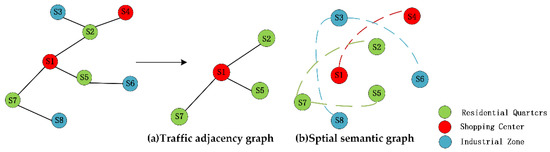
ماتریس مجاورت ترافیک مطابق STGCN ساخته شده است، همانطور که در شکل 4 a نشان داده شده است، تا نزدیکی بین گره ها را با توجه به فاصله هندسی بین گره های مختلف اندازه گیری کند. تابع فاصله مقادیر بین گره های دیگر را تعریف می کند. تابع فاصله به صورت زیر تعریف می شود.

آvمن،vjسپ={هایکسپ(-دvمن،vj2σ2)      ،  منf  هایکسپ(-دvمن،vj2σ2)≥ϵ;0                         ،           oتیساعتهrwمنسه.      ،

فاصله بین گره vمنو گره vjدر رابطه (2) به صورت بیان شده است دvمن،vj: هایپرپارامترها σ2و ϵبرای کنترل پراکندگی ماتریس مجاورت فضایی.
4.1.2. نمودار مکانی معنایی جهانی
همانطور که در شکل 5 نشان داده شده است ، الگوریتم تاب خوردگی زمانی دینامیکی (DTW) [ 22 ، 41 ] می تواند شباهت سری دو زمانی را بهتر از فاصله اقلیدسی منعکس کند. الگوریتم DTW حساسیت عالی به شباهت شکل دارد و نسبت به سایر معیارها برتری دارد [ 39 ]. از آنجا که دو منطقه با ویژگی‌های عملکردی مشابه، الگوهای ترافیک زمانی مشابهی دارند، ما از الگوریتم DTW برای ارزیابی مشابه بودن آنها از نظر عملکرد استفاده کردیم (به عنوان مثال، هر دو متعلق به یک منطقه تجاری هستند). سپس، ما یک نمودار معنایی فضایی جهانی بر اساس شباهت معنایی ساختیم.

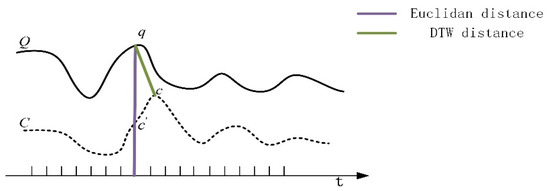
مجموع فاصله اقلیدسی د(qمن،جj)بین مکان های شبکه qمنو جjبه سری های دو زمانه تقسیم می شود. فاصله تجمعی کوچکترین عنصر همسایه که می تواند به نقطه برسد به عنوان فاصله تجمعی نشان داده می شود. γ(من،j). همانطور که در رابطه (3).

γ(من،j)=د(qمن،جj)+مترمنn{γ(من-1،j-1)،γ(من-1،j)،γ(من،j-1)}،

اینجا، γ(من،j)نشان دهنده کوتاه ترین فاصله بین دو گره است س=(q1،q2،⋯،qمن)و سی=(سی1،سی2،⋯،سیj)، بنابراین DTW(س،سی)=  γ(متر،n)به عنوان فاصله نهایی بین گره ها در نظر گرفته می شود سو گره سی، که می تواند شباهت سری دو زمانی را در مقایسه با فاصله اقلیدسی بهتر منعکس کند.

بنابراین، ماتریس مجاورت معنایی را با فاصله DTW به صورت زیر تعریف می کنیم.

آمنjسه={1         ،منf  Dتیدبلیو(سمن،سیj)≤ϵ;0         ،             oتیساعتهrwمنسه.      ،

اینجا، سمنو سیjسری زمانی گره i و گره را نشان می دهدjبه ترتیب، و ϵ را برای کنترل پراکندگی ماتریس مجاورت به 0.6 اختصاص داد.

4.2. شبکه عصبی گراف مبتنی بر توجه

4.2.1. لایه پیچیدگی نمودار فضایی

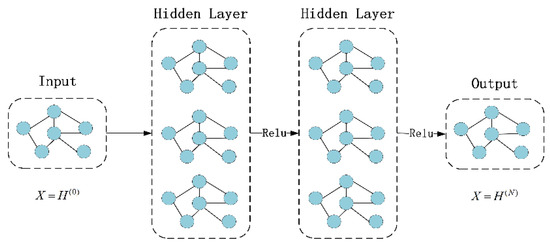
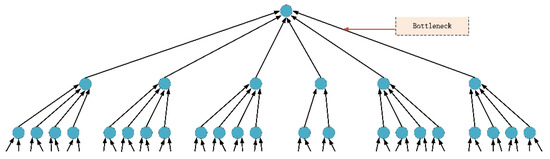
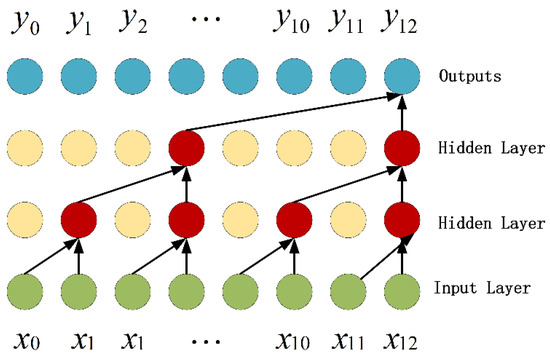
بیشتر کارها از رویکرد GCN برای ثبت همبستگی‌های فضایی در ابعاد منطقه‌ای استفاده می‌کنند، عملیات‌های کانولوشنی سنتی را از داده‌های ساختاریافته به نمودارها گسترش می‌دهند، و آنها را قادر می‌سازد اطلاعات الگوی بدون ساختار پنهان در نمودار را ضبط کنند [ 35 ، 36 ، 37 ]. همانطور که در شکل 6 نشان داده شده است ، ایده GNN این است که اطلاعات مربوط به گره های همسایه را جمع آوری کند تا نمایشی به روز از گره ها تولید کند، و سپس نمایش را با تبدیل طرح ریزی خطی تجمیع کند و در نهایت آن را با غیر خطی فعال کند [ 42 ]. با این حال، چالش‌هایی در مدل‌سازی وابستگی‌های بلندمدت بین داده‌های با ابعاد بالا با استفاده از شبکه‌های کانولوشن گراف وجود دارد. اوری آلون و همکاران [ 17] نشان داد که GNN ها از فشرده سازی بیش از حد در هنگام اتصال سیگنال های راه دور به داده های آموزشی رنج می برند، نمی توانند پیام ها را از گره های مسافت دور هنگام انجام تعاملات از راه دور پخش کنند و در تجمیع ویژگی ها عملکرد ضعیفی دارند.

جیسین(اچ(ل+1))=σ(آ^اچ(ل)دبلیو(ل))،

اچ(ل)نمایش ویژگی ورودی گره است، آ^∈ℝن×نماتریس مجاورت است که نشان دهنده رابطه متقابل بین گره ها و σنشان دهنده تابع فعال سازی غیر خطی است.
برای انتشار تعاملی اطلاعات دوربرد، شبکه عصبی گراف باید تعداد لایه ها را افزایش دهد. با این حال، اثر بدتر است. شکل 7 نشان می دهد که پدیده فشردن بیش از حد رخ می دهد [ 18 ]. بنابراین، ما یک مکانیسم خودتوجهی را در شبکه کانولوشن گراف برای حل مشکل فشردگی بیش از حد شبکه‌های عصبی گراف در گرفتن اطلاعات فضایی دوربرد معرفی می‌کنیم [ 42 ].
4.2.2. لایه توجه نمودار
Velickovic [ 34 ] داده های ساختار گراف را با افزودن یک لایه خودتوجهی به شبکه های عصبی گراف پردازش کرد و نتایج پیشرفته ای را به دست آورد. با الهام از این، ما شبکه عصبی پیچیدگی توجه گراف را با یک لایه توجه به خود اتخاذ کردیم. علاوه بر این، توجه به خود اجازه می دهد تا بازنمایی هر نماد به طور مستقیم با نمایش تمام نمادهای دیگر در دنباله مطلع شود تا توجه به خود بتواند اطلاعات زمینه فضای محلی را به تصویر بکشد. علاوه بر این، مکانیسم توجه به خود به طور موثر وابستگی های جهانی را جذب می کند و می تواند یک دامنه دریافت جهانی عملی ایجاد کند [ 43 ]]. با توجه به اینکه همبستگی فضایی برای گرفتن در فواصل طولانی چالش برانگیز است، بلوک های موازی چند لایه T-GAT برای گرفتن ویژگی های مکانی-زمانی بهتر استفاده می شوند. هر لایه شامل دو بلوک TCN و یک بلوک GACN است. به اشتراک گذاری پارامترهای GAT در بلوک می تواند به کاهش اکستروژن بیش از حد GNN کمک کند تا مدل پیشنهادی ما بتواند یک پیش بینی دوربرد دقیق انجام دهد.
شبکه توجه گراف (GAT) یک لایه خودتوجهی پنهان به GCN اضافه می کند. با پوشاندن لایه توجه به خود، اهمیت متفاوتی به گره‌های مختلف در همسایگی در فرآیند کانولوشن داده می‌شود. با اندازه های مختلف همسایه ها به طور همزمان برخورد می شود. ساختار آن در شکل 7 نشان داده شده است .
در مورد قدرت محاسباتی محدود، مکانیسم توجه، منابع محاسباتی را به گره‌های مهم‌تر اختصاص می‌دهد (به عنوان مثال، ما بر روی گره‌هایی با عملکردهای مشابه در دو منطقه تمرکز می‌کنیم) تا توجه به گره‌های دیگر را کاهش داده و اطلاعاتی را که نمی‌دانیم فیلتر کنیم. اهمیت دادن. این روش می تواند به طور موثری فشار بیش از حد اطلاعات را کاهش دهد و در هنگام برخورد با اطلاعات محلی به اطلاعات عمومی توجه کند.
ورودی شبکه توجه گراف (GAT) مجموعه ای از ویژگی های گره است. ایکس={ایکس1→،ایکس2→،⋯،ایکسن→}∈ℝب×ن×تی×اف، نتعداد گره ها و افتعداد ویژگی های هر گره است. ابتدا آن را جابجا می کنیم و به آن شکل می دهیم ایکستی∈ℝبتی×ن×افو سپس مجموعه جدیدی از ویژگی های گره را تولید کنید ایکس”={ایکس1″→،ایکس2″→،⋯،ایکسن”→}، که خواهد شد ایکسمن”→∈ℝبتی×ن×اف”به عنوان خروجی

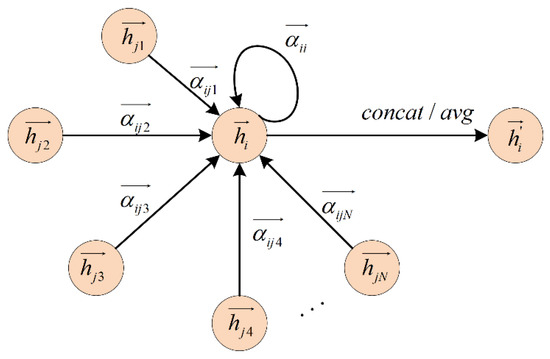
ما یک تابع تبدیل خطی قابل یادگیری را برای تبدیل ویژگی های ورودی به یک نمایش ویژگی سطح بالاتر اتخاذ کردیم. به همین دلیل، تبدیل خطی مشترک دبلیو∈ℝاف×اف”پارامتر با ماتریس وزن به هر گره اعمال می شود. سپس، از مکانیزم توجه مشترک استفاده می کنیم آبرای انجام خود توجهی بر روی هر جفت از ایکسمن→توجه و ایکسj→گره های توجه و امتیازات توجه را به صورت زیر محاسبه کنید:

نمره=آ(ایکسمن→wمن،ایکسj→wj)،  wمن،wj∈اف×اف”،

جایی که wمنو wjاجزای ماتریس وزن هستند و آ(⋯)تابع عملکرد مکانیسم توجه است. به منظور مقایسه و تمایز ضرایب توجه بین گره های مختلف، از تابع softmax برای عادی سازی امتیازات ضریب توجه بین گره های همسایه برای به دست آوردن خروجی زیر استفاده می شود.

آمنj=softmx(نمره)=هایکسپ(نمره)∑ک∈نمنهایکسپ(نمرهمنک)،

ایکسمن”→=σ(∑j∈نمنآمنjایکسj→wj)،

جایی که نمنمجموعه همسایگان گره است مندر نمودار، و σتابع فعال سازی است.

بر اساس شبکه های جاده ای، جاده های مجاور یکدیگر معمولاً شرایط جاده ای مشابهی دارند، همانطور که در شکل 8 نشان داده شده است. ما یک ویژگی توجه گراف جدید برای استخراج موقعیت‌های جاده‌ای مشابه در شبکه‌های ترافیکی طراحی کردیم. در GAT، ما از شبکه توجه گراف جهانی برای یادگیری شباهت هر دو جاده در شبکه ترافیک استفاده کردیم.
ما داده های ترافیک زمانی را با استفاده از TCN موازی می کنیم تا همبستگی های زمانی بلندمدت و کوتاه مدت جهانی را به دست آوریم. به طور خاص، برای ادغام روابط مکانی-زمانی در داده های ترافیک، ما از خروجی مجموعه ویژگی مکانی گره از GAT به عنوان ورودی بلوک TCN بعدی استفاده کردیم. پس از لایه TCN، همبستگی‌های مکانی و زمانی درازمدت شبکه جاده‌ای را به‌دست آوردیم.

4.3. ماژول پیچیدگی علّی زمانی

علاوه بر همبستگی فضایی چند مقیاسی بین گره‌های مختلف که در بالا در نظر گرفتیم، علیت زمانی نیز بین رویدادهای ترافیکی وجود دارد، بنابراین گرفتن وابستگی زمانی طولانی‌مدت گره‌ها نیز بسیار مهم است. مدل های مبتنی بر RNN (به عنوان مثال، LSTM و GRU) به نتایج برجسته ای در تجزیه و تحلیل سری های زمانی دست یافته اند. با این حال، آنها دارای اشکالاتی مانند دشواری مدل در آموزش و تلاش محاسباتی زیاد در استخراج ویژگی های سری طولانی مدت هستند. شبکه های کانولوشنال زمانی توسط Bai S و همکاران مورد ارزیابی قرار گرفتند. [ 44 ] برای اثبات قابلیت ضبط دوربرد کارآمدتر و برتر در مدل‌سازی داده‌های سری زمانی [ 45 ]. بنابراین، معماری TCN نشان داده شده در شکل 9از بسیاری از لایه های کانولوشن علّی با عوامل مقیاس پذیر نمایی تشکیل شده است که دامنه ادراکی را گسترش می دهد. علاوه بر این، پیچش اتساع مقیاس پذیری خوبی دارد و میدان پذیرای بزرگتری را برای گرفتن بهتر وابستگی های فضایی-زمانی دوربرد به دست می آورد.

به طور خلاصه، TCN از یک FCN یک بعدی و یک پیچیدگی علّی [ 43 ، 46 ] تشکیل شده است، و پیچیدگی سببی متسع TCN به صورت زیر فرموله شده است.

yتی=Θ∗تیدایکستی=∑ک=0ک-1wکایکستی-دک،

اینجا، ∗تیدعملگر علّی اتساع با اتساع است دبرای کنترل فاصله پرش، و Θ=[w0،⋯،wک-1]∈ℝکهسته کانولوشن است.

4.3.1. پیچ خوردگی متسع

از آنجایی که فواصل مکانی نقاط مشاهده ما از یکدیگر دور هستند، همبستگی فضایی بین گره ها ممکن است یک ساعت یا حتی بیشتر همبستگی زمانی داشته باشد [ 37 ]. ما یک پیچیدگی TCN 4 لایه را برای استخراج ویژگی های همبستگی زمانی بلندمدت و کوتاه مدت محلی و جهانی قرار می دهیم. ورودی مدل یک سیگنال داده گراف ترافیک سه بعدی با χ∈ℝپ×ن×اف1، و یک پیچیدگی علی گسترده برای تولید استفاده می شود jتیساعتویژگی خروجی گره مندر زمان تیهمانطور که در رابطه (10) نشان داده شده است.

yتی،nمتر=ρ(Θn∗تیدχتیمتر)=ρ(∑من=1افمن∑ک=0ک-1دبلیوn،من،کχتی-دک،منمتر)،

جایی که 1≤n≤افO، yتی،nمتر∈ℝهست nتیساعتویژگی خروجی گره متردر زمان تی، و χتی-دک،nمتر∈ℝهست منتیساعتویژگی ورودی گره متردر زمان تی-دک. هسته Θn∈ℝک×افمنقابل آموزش است افOتعداد ویژگی های خروجی است.

تمام گره‌ها در نمودار شبکه جاده ترافیک با استفاده از همان هسته کانولوشن محاسبه می‌شوند تا ویژگی‌های جدیدی برای هر گره ایجاد کنند. لایه کانولوشن مانند رابطه (11) محاسبه می شود.

y=ρ(Θ∗تیدχ)،

جایی که χ∈ℝپ×ن×افمننشان دهنده مشاهدات تاریخی کل شبکه ترافیک در گذشته است پبرش های زمانی به عنوان ورودی TCN، Θ∈ℝک×افمن×اف0نشان دهنده هسته پیچیدگی علّی و y∈ℝپ×ن×اف0خروجی لایه TCN است.

y(ل+1)=σ(Θل∗تیدy(ل))،

جایی که y(ل)ورودی از است للایه، y(ل+1)خروجی است، y(0)=χ، و د=2(ل)نرخ اتساع است لتیساعتلایه.

4.3.2. اتصال باقیمانده
با الهام از شبکه های باقیمانده [ 39 ]، مشکل هموارسازی بیش از حد را می توان با افزودن اتصالات باقی مانده بین لایه ها کاهش داد. علاوه بر این، ثابت شده است که شبکه‌های باقیمانده یک روش مؤثر برای آموزش شبکه‌های عمیق [ 47 ] هستند که شبکه را قادر می‌سازد اطلاعات را به روشی متقابل انتقال دهد. استفاده از یک شبکه باقیمانده مبتنی بر پیچیدگی برای انجام رابطه فضایی بین دو منطقه در یک شهر از نظر فاصله و مجاورت می‌تواند اطمینان حاصل کند که دقت پیش‌بینی مدل تحت تأثیر ساختار عمیق شبکه عصبی قرار نمی‌گیرد [ 48 ]. در این مقاله، ما یک ماژول باقیمانده همانطور که در شکل 10 نشان داده شده است، می سازیم، که جایگزین یک لایه کانولوشن می شود و به طور موثر مشکل ناپدید شدن گرادیان را برطرف می کند و انتشار ویژگی ها را افزایش می دهد.
برای تضمین پایداری TCN، ما از ماژول های باقیمانده به جای لایه های کانولوشن برای جلوگیری از مشکلاتی مانند ناپدید شدن گرادیان استفاده می کنیم.

4.4. خروجی فیوژن چند ماژول

خروجی‌های اجزای مختلف با هم ترکیب می‌شوند و وزن‌های تأثیر مجاورت و ماتریس معنایی برای هر گره‌ای که از داده‌های تاریخی به دست می‌آید متفاوت است. بنابراین، پس از لایه T-GACN، عملیات ماکزیمم ادغام ابتدا برای تجمیع اطلاعات بر اساس اندازه وزن تأثیر به صورت انتخابی اجرا می‌شود و سپس از طریق لایه max-pooling به نتیجه پیش‌بینی نهایی تبدیل می‌شود. روند محاسبه به شرح زیر است.

Y^=دبلیوآ⊙Y^آ+دبلیوس⊙Y^س،

که در آن ⊙ کثرت هادامارد است و دبلیوآو دبلیوسپارامترهای یادگیری هستند که تأثیر دو ماتریس را بر هدف پیش بینی منعکس می کنند.

از آنجایی که ضرر هوبر نسبت به تلفات خطای مجذور حساسیت کمتری نسبت به نقاط گسسته دارد، ما ضرر هوبر (1992، STSGCN) [ 29 ] را انتخاب می کنیم.

L(Y،Y^)={12(Y-Y^)2              ،|Y-Y^|≤δ;δ|Y-Y^|-12δ2     ،oتیساعتهrwمنسه.  ،

Yو Y^به ترتیب مقدار واقعی و پیش بینی شده مدل هستند و δبه عنوان یک فراپارامتر آستانه برای کنترل دامنه از دست دادن واریانس استفاده می شود.

5. آزمایش کنید

برای ارزیابی عملکرد مدل خود، آزمایش‌های مقایسه‌ای را روی دو مجموعه داده ترافیک بزرگراه در دنیای واقعی انجام دادیم.

5.1. مجموعه داده ها

داده‌های PEMS04 و PEMS08 [ 13 ، 29 ] مورد استفاده در آزمایش‌ها در زمان واقعی هر 30 ثانیه توسط سیستم اندازه‌گیری عملکرد Caltrans (PeMS) جمع‌آوری می‌شوند. این سیستم بیش از 39000 آشکارساز دارد که در آزادراه‌های کلان‌شهرهای کالیفرنیا مستقر شده‌اند. داده‌های خام جریان ترافیک در فواصل زمانی 5 دقیقه جمع‌آوری می‌شوند، به این معنی که 288 مرحله زمانی در جریان ترافیک یک روز وجود دارد. اطلاعات دقیق تر در جدول 1 نشان داده شده است .

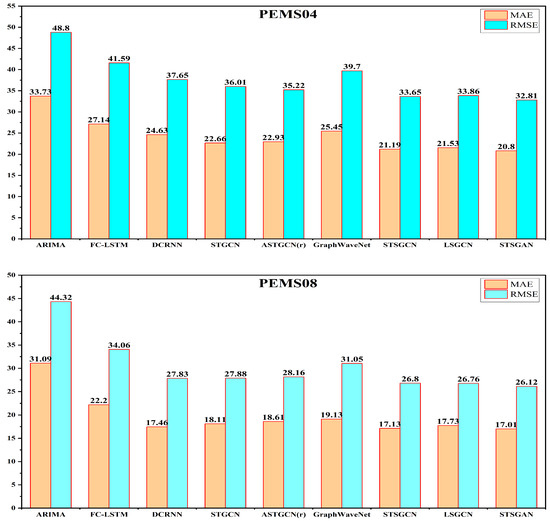
این آزمایش از دو معیار، از جمله MAE (میانگین مطلق خطا) و RMSE (خطای ریشه-میانگین مربع)، برای ارزیابی همه روش ها استفاده می کند، که به طور گسترده برای ارزیابی دقت مشکلات رگرسیون استفاده می شود. برای همه معیارها، هر چه مقدار کمتر باشد، بهتر است. آنها به عنوان تعریف می شوند

MAE(y^من،yمن)=1n∑من=1n|yمن-y^من|،

RMSE(y^من،yمن)=1n∑من=1n(yمن-y^من)2،

5.2. روش های پایه

برای ارزیابی عملکرد مدل خود، آن را با 8 خط پایه مقایسه می کنیم.
  • ARIMA [ 23 ]: مدل میانگین متحرک یکپارچه اتورگرسیو، یک مدل آماری شناخته شده برای تجزیه و تحلیل سری های زمانی، از داده های گذشته برای پیش بینی روندهای آینده استفاده می کند.
  • FC-LSTM [ 49 ]: شبکه‌های حافظه کوتاه‌مدت (LSTM) با واحدهای پنهان کاملاً متصل، یک چارچوب شبکه شناخته شده هستند که در گرفتن وابستگی‌های متوالی قوی هستند.
  • DCRNN [ 21 ] (Li et al., 2017): واحدهای بازگشتی دردار با پیچیدگی نمودار یکپارچه، دینامیک زمانی را با استفاده از سرگردانی تصادفی گراف دو جهته برای شبیه‌سازی وابستگی‌های فضایی ثبت می‌کنند.
  • STGCN [ 10 ]: یک چارچوب یادگیری عمیق برای پیش‌بینی ترافیک از پیچیدگی نمودار و پیچیدگی زمانی دروازه‌دار یک‌بعدی برای گرفتن همبستگی مکانی و همبستگی زمانی استفاده می‌کند.
  • GraphWaveNet (Wu et al., 2019) [ 11 ]: GraphWaveNet کانولوشن گراف تطبیقی ​​را با پیچیدگی گاه به گاه گسترده ترکیب می کند تا به طور خودکار وابستگی های فضایی پنهان را ضبط کند.
  • STSGCN [ 29 ]: مدلی که مستقیماً همبستگی‌های مکانی-زمانی محلی را با استفاده از چندین ماژول زیرگراف محلی و در عین حال ناهمگونی داده‌های مکانی را به طور همزمان ضبط می‌کند.
  • LSGCN [ 37 ]: شبکه کانولوشن گراف کوتاه مدت (LSGCN)، که از بلوک‌های کانولوشنال دردار فضایی با مکانیزم توجه برای ثبت ویژگی‌های مکانی-زمانی استفاده می‌کند.

5.3. تنظیمات پارامتر آزمایشی

ما به ASTGCN [ 13 ] و STSGCN [ 29 ] اشاره می کنیم]، و تمام مجموعه های داده به آموزش، اعتبار سنجی و مجموعه های آزمایشی در نسبت 6:2:2 تجزیه می شوند. به طور خاص، کل مدت زمان مجموعه داده PEMS04 59 روز، با 16992 مرحله زمانی است. بنابراین، 10195 مرحله زمانی اول به عنوان مجموعه آموزشی، 3398 مرحله زمانی به عنوان مجموعه اعتبار سنجی و 3398 گام زمانی به عنوان مجموعه آزمون استفاده می شود. کل مدت زمان مجموعه داده PEMS08 62 روز است که 17856 مرحله زمانی وجود دارد. 10714 مرحله زمانی اول به عنوان مجموعه آموزشی، 3572 مرحله زمانی به عنوان مجموعه اعتبار سنجی و 3572 مرحله زمانی به عنوان مجموعه آزمون استفاده می شود. علاوه بر این، نمونه‌های داده‌های هر بخش جاده را با معادله زیر (17) نرمال می‌کنیم و داده‌های نرمال‌شده را در مدل وارد می‌کنیم، که با تمایز خودکار حالت معکوس و Adam [ 50 ] بهینه شده است.].

ایکس”=ایکس-مترهآn(ایکس)ستید(ایکس)،

ما از یک ساعت داده‌های تاریخی برای پیش‌بینی ساعت بعدی داده‌ها استفاده کردیم و به منظور مقایسه منصفانه، همه نتایج تجربی ما ده بار روی هر مجموعه داده انجام شد.
ما از چارچوب PyTorch برای پیاده‌سازی مدل STSGAN خود استفاده می‌کنیم و همه آزمایش‌ها روی یک سرور لینوکس با محیط آزمایشی (CPU: Intel(R) Core(TM) i7-9900k CPU @ 3.60 GHz، GPU: NVIDIA TITAN RTX 24G کامپایل می‌شوند. ). اندازه پنهان بلوک های TCN به 64، 32 و 64 تنظیم شده است و هر لایه شامل سه بلوک استاندارد است. فراپارامتر نرمال سازی روی 0.8، آستانه های ماتریس مجاورت معنایی و ماتریس مجاورت فضایی به ترتیب روی 0.6 و 0.5 تنظیم شده است و σمقادیر ماتریس‌های مجاورت معنایی و فضایی روی 0.1 و 10 تنظیم شده‌اند. اندازه دسته روی 32، نرخ یادگیری روی 0.001 تنظیم شده است، و مدل با استفاده از بهینه‌ساز Adam با 200 تکرار بهینه شده است.

5.4. نتایج تجربی و تحلیل مقایسه ای

مدل STSGAN ما با خط پایه هشت روش پیشنهادی در دو مجموعه داده دنیای واقعی مقایسه شده است. نتایج آزمایش در جدول 2 نشان داده شده است.
این آزمایش ها برای پاسخ به سؤالات تحقیق زیر خلاصه می شود:
  • RQ1: عملکرد STSGAN برای پیش‌بینی ترافیک کلی در مقایسه با خطوط پایه مختلف چگونه است؟
  • RQ2: چگونه ماژول های فرعی مختلف برای بهبود عملکرد مدل طراحی شده اند؟
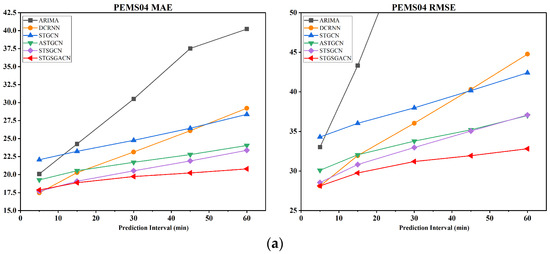
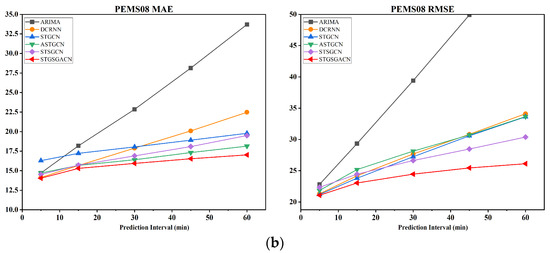
  • RQ3: عملکرد ماژول های طراحی شده در مشکلات پیش بینی بلند مدت چگونه است؟
  • RQ4: تنظیمات پارامتر مدل چگونه بر نتایج تجربی تأثیر می گذارد؟
نتایج در شکل 11 نشان می دهد که STSGAN بالاترین دقت پیش بینی را در مقایسه با سایر خطوط پایه دارد. عمدتاً ARIMA و FC-LSTM فقط همبستگی زمانی را در نظر می گیرند، در حالی که همبستگی مکانی برای عملکرد پیش بینی ضروری است، بنابراین عملکرد پیش بینی آنها بدترین است. DCNN یک روش پیش‌بینی داده‌های مکانی-زمانی مبتنی بر RNN است. با توجه به توانایی برتر برای گرفتن همبستگی زمانی بلندمدت توسط محدودیت‌های گرادیان و مشکلات دیگر از بین می‌رود، دقت پیش‌بینی آن بسیار کمتر از مدل ما است.
اگرچه STGCN، ASTGCN، Graph Wave Net و STSGCN همگی همبستگی زمانی و همبستگی فضایی را در نظر می گیرند، به طور کلی، آنها در مورد مشکل فضایی محلی تحقیق می کنند و رابطه متقابل بین فضایی برد بلند را نادیده می گیرند. روش ما همبستگی فضایی محلی را در نظر می گیرد و تعاملات فضایی دوربرد را برای استخراج ویژگی های جهانی فضا به تصویر می کشد. بنابراین، روش ما عملکرد بهتری نسبت به این روش ها دارد.
شکل 12 اثر افزایش فاصله زمانی پیش بینی را بر عملکرد پیش بینی روش های مختلف نشان می دهد. با افزایش فاصله زمانی پیش‌بینی، دشواری پیش‌بینی نیز افزایش می‌یابد و عملکرد پیش‌بینی مدل کاهش می‌یابد. با این حال، در بیشتر موارد، مدل ما از همه روش‌های پایه برای پیش‌بینی بلندمدت بهتر عمل می‌کند. علاوه بر این، می‌توان از شکل مشاهده کرد که کاهش عملکرد پیش‌بینی مدل ما با افزایش فاصله زمانی نسبتاً کم است و مزیت مدل را برای پیش‌بینی بلندمدت آشکارتر می‌کند.

5.5. آزمایشات فرسایشی

برای ارزیابی بیشتر اثرات اجزای مختلف بر STSGAN، ما چهار ماژول تنوع ساده را بر اساس T-GACN ساختیم. برای بیان آسان، از برخی نمادها برای نشان دادن نام ماژول ها استفاده می شود، از جمله نمودار مجاورت با (L)، گراف معنایی جهانی (S)، لایه توجه گراف (A)، و گراف شبکه عصبی کانولوشنال (G). همه این ماژول ها روی مجموعه داده PEMS04 آزمایش کرده اند و جدول 2 عملکرد پیش بینی T-GACN و انواع مختلف آن را نشان می دهد و نتایج تجربی تجزیه و تحلیل می شوند.
به جز تفاوت‌های فوق، همه سازگاری‌ها تنظیمات پارامتر تجربی مشابهی با T-GACN دارند.
  • T: ماژول پیچیدگی علی زمانی برای پیش‌بینی جریان ترافیک آینده با استفاده از جریان ترافیک تاریخی به عنوان ورودی استفاده شد.
  • T+G: از T به عنوان ماژول پایه استفاده کرد و یک شبکه عصبی کانولوشن گراف (GCN) را برای گرفتن همبستگی های فضایی محلی و جهانی اضافه کرد. این بررسی می کند که آیا زمانی که GCN همبستگی های فضایی دوربرد را ثبت می کند، هموارسازی بیش از حد اتفاق می افتد یا خیر.
  • T+A+G: شبکه عصبی کانولوشنال توجه گراف را برای گرفتن همبستگی های فضایی دوربرد معرفی کنید.
  • T+S+G: به طور مشترک یک ماتریس مجاورت معنایی جهانی برای گرفتن ویژگی‌های فضایی با چشم‌انداز جهانی. در مقایسه با فقدان مکانیسم خود توجه گراف.
به جز تفاوت های فوق، تمام تغییرات تنظیمات مشابه T-GACN هستند.
از جدول 2می‌توان مشاهده کرد که STSGAN MAE و RMSE بهتری نسبت به سایر انواع دارد. تجزیه و تحلیل نتیجه نشان می‌دهد که عملکرد پیش‌بینی مدل زمانی که GCN برای گرفتن ویژگی‌های فضایی یکپارچه می‌شود، افزایش و کاهش نمی‌یابد. پدیده فشرده سازی بیش از حد اطلاعات زمانی رخ می دهد که از GCN برای گرفتن همبستگی فضایی در فواصل طولانی استفاده می شود که منجر به کاهش عملکرد می شود. بنابراین، افزودن ماژول پیچیدگی توجه نمودار می‌تواند به طور موثر پدیده هموارسازی بیش از حد را برای گرفتن ویژگی‌های فضایی دور و بهبود عملکرد مدل کاهش دهد. علاوه بر این، معرفی یک ماتریس مجاورت معنایی برای بهبود عملکرد مدل نشان می‌دهد که می‌تواند ادراک فضایی محلی و جهانی مدل را بهبود بخشد، که به نوبه خود عملکرد پیش‌بینی مدل را بهبود می‌بخشد. از این رو،

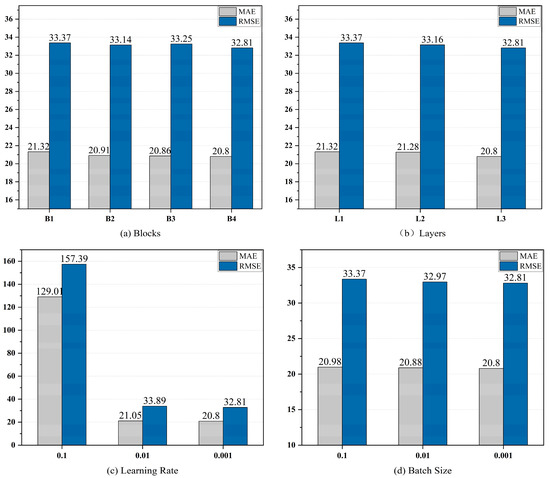
5.6. تأثیر پیکربندی شبکه

برای تحقیق بیشتر که چگونه فراپارامترها و تعداد لایه‌های شبکه بر عملکرد مدل تأثیر می‌گذارند. ما آزمایش هایی را روی پیکربندی های مختلف شبکه انجام دادیم. همه آزمایش‌های زیر از همان تنظیماتی که در بخش 5.3 توضیح داده شده است پیروی می‌کنند، به جز تغییرات در پیکربندی شبکه مورد مطالعه. شکل 13a،b نشان می دهد که B1 نشان می دهد که یک ماژول T-GACN وجود دارد و B4 نشان می دهد که چهار ماژول T-GACN وجود دارد. با افزایش تعداد B (ماژول‌های T-GACN)، می‌توان مشاهده کرد که عملکرد مدل به تدریج در حال بهبود است، که نشان‌دهنده اثربخشی استفاده ما از ماژول‌های پردازش موازی ویژگی‌های مکانی-زمانی است. چهار ماژول T-GACN یک لایه شبکه T-GACN را تشکیل می دهند. L1 نشان دهنده یک شبکه پیکربندی شده با یک لایه از لایه های T-GCAT و L3 نشان دهنده یک شبکه پیکربندی شده با سه لایه از لایه های T-GCAT است. با افزایش عدد L (لایه شبکه T-GACN)، عملکرد پیش‌بینی مدل نیز بهبود می‌یابد. ما متوجه شدیم که با افزایش تعداد لایه‌های شبکه فراتر از دو لایه، عملکرد مدل همچنان بهبود می‌یابد، که نشان می‌دهد استفاده ما از شبکه‌های کانولوشنال توجه می‌تواند به طور موثر مشکل ازدحام بیش از حد GNN را کاهش دهد.
همانطور که از شکل 13 c,d مشاهده می شود، بهترین عملکرد زمانی حاصل می شود که نرخ یادگیری مدل روی 0.001 تنظیم شود. تنظیم اندازه دسته ای مدل، عملکرد شبکه را پایدارتر می کند.

6. نتیجه گیری و کار آینده

در این مقاله، ما STSGAN را پیشنهاد می‌کنیم، یک مدل شبکه عصبی کانولوشنال با توجه به گراف جدید، که با موفقیت بر محدودیت‌های فشار بیش از حد شبکه عصبی گراف غلبه می‌کند و بنابراین همبستگی‌های فضایی و زمانی دوربرد را به تصویر می‌کشد. مدل ما یک ماتریس مجاورت معنایی را معرفی می‌کند و از یک شبکه عصبی کانولوشن گراف با لایه‌های خود توجه برای استخراج ویژگی‌های همبستگی فضایی در سطوح مختلف استفاده می‌کند. یک شبکه کانولوشنال علّی زمانی، وابستگی های زمانی بلندمدت و کوتاه مدت را می آموزد. در نهایت، ماژول فیوژن ویژگی‌های فضایی محلی و جهانی را جمع‌آوری می‌کند تا نمایش الگوی مکانی-زمانی مدل را افزایش دهد. آزمایش های جامع نشان می دهد که روش در این مقاله به طور قابل توجهی بهتر از هشت خط پایه پیشرفته در دو مجموعه داده دنیای واقعی عمل می کند. آزمایش‌های فرسایش اثربخشی GAT پیشنهادی ما را نشان می‌دهد. با این حال، عوامل خارجی مانند آب و هوا و شرایط اضطراری جاده‌ای نیز می‌توانند بر پیش‌بینی جریان ترافیک شهری تأثیر بگذارند. در کار آینده، این اطلاعات خارجی را برای بهبود عملکرد پیش‌بینی مدل در نظر خواهیم گرفت.

منابع

  1. ژانگ، جی. وانگ، FY; وانگ، ک. لین، WH; خو، X. چن، سی. سیستم های حمل و نقل هوشمند مبتنی بر داده: یک نظرسنجی. IEEE Trans. هوشمند ترانسپ سیستم 2011 ، 12 ، 1624-1639. [ Google Scholar ] [ CrossRef ]
  2. ژانگ، ایکس. هوانگ، سی. خو، ی. Xia، L. شبکه‌های توجه نمودار کانولوشنال مکانی-زمانی برای پیش‌بینی جریان ترافیک در سطح شهر. در مجموعه مقالات بیست و نهمین کنفرانس بین المللی ACM در مدیریت اطلاعات و دانش، مجازی، 19 اکتبر 2020؛ صفحات 1853-1862. [ Google Scholar ]
  3. Lv، M. هنگ، ز. چن، ال. زو، تی. جی، اس. شبکه کانولوشن چند گرافی زمانی برای پیش‌بینی جریان ترافیک. IEEE Trans. هوشمند ترانسپ سیستم 2020 ، 22 ، 3337-3348. [ Google Scholar ] [ CrossRef ]
  4. دو، بی. هو، ایکس. سان، ال. لیو، جی. کیائو، ی. Lv، W. پیش‌بینی تقاضای ترافیک بر اساس شبکه عصبی کانولوشنال انتقال پویا. IEEE Trans. هوشمند ترانسپ سیستم 2020 ، 22 ، 1237-1247. [ Google Scholar ] [ CrossRef ]
  5. وانگ، سی. زو، ی. زنگ، تی. لیو، اچ. Yu, J. مدل‌سازی روابط بین ایستگاهی با شبکه کانولوشنال نمودار زمانی برای پیش‌بینی کیفیت هوا. در مجموعه مقالات چهاردهمین کنفرانس بین المللی ACM در جستجوی وب و داده کاوی، مجازی، 8 تا 12 مارس 2021؛ صص 616-634. [ Google Scholar ]
  6. ژانگ، ایکس. هوانگ، سی. خو، ی. شیا، ال. دای، پی. بو، ال. ژنگ، ی. پیش‌بینی جریان ترافیک با شبکه انتشار نمودار مکانی-زمانی. در مجموعه مقالات کنفرانس AAAI در مورد هوش مصنوعی، مجازی، 2 تا 9 فوریه 2021؛ جلد 35، ص 15008–15015. [ Google Scholar ]
  7. لین، ز. فنگ، جی. لو، ز. لی، ی. Jin, D. Deepstn+: شبکه عصبی مکانی-زمانی آگاه از زمینه برای پیش‌بینی جریان جمعیت در کلان شهرها. در مجموعه مقالات کنفرانس AAAI در مورد هوش مصنوعی، هونولولو، HI، ایالات متحده، 27 ژانویه تا 1 فوریه 2019؛ جلد 33، ص 1020–1027. [ Google Scholar ]
  8. وو، زی. پان، اس. چن، اف. لانگ، جی. ژانگ، سی. Philip, SY یک بررسی جامع در مورد شبکه های عصبی گراف. IEEE Trans. شبکه عصبی فرا گرفتن. سیستم 2020 ، 32 ، 4-24. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  9. یان، اس. Xiong، Y. لین، دی. شبکه‌های کانولوشنال نمودار زمانی فضایی برای تشخیص عمل مبتنی بر اسکلت. در مجموعه مقالات سی و دومین کنفرانس AAAI در مورد هوش مصنوعی، نیواورلئان، لس آنجلس، ایالات متحده آمریکا، 2 تا 7 فوریه 2018. [ Google Scholar ]
  10. یو، بی. یین، اچ. Zhu, Z. شبکه‌های کانولوشنال نمودار فضایی-زمانی: یک چارچوب یادگیری عمیق برای پیش‌بینی ترافیک. arXiv 2017 , arXiv:1709.04875. [ Google Scholar ]
  11. وو، زی. پان، اس. لانگ، جی. جیانگ، جی. ژانگ، سی. موج موج گراف برای مدل‌سازی نمودار عمیق مکانی-زمانی. arXiv 2019 ، arXiv:1906.00121. [ Google Scholar ]
  12. گوا، اس. لین، ی. فنگ، ن. آهنگ، سی. وان، اچ. شبکه‌های کانولوشنال نمودار مکانی-زمانی مبتنی بر توجه برای پیش‌بینی جریان ترافیک. در مجموعه مقالات کنفرانس AAAI در مورد هوش مصنوعی، هونولولو، HI، ایالات متحده آمریکا، 27 ژانویه 2019؛ جلد 33، ص 922–929. [ Google Scholar ]
  13. ژائو، ز. چن، دبلیو. وو، ایکس. چن، کامپیوتر; شبکه لیو، جی. LSTM: یک رویکرد یادگیری عمیق برای پیش بینی ترافیک کوتاه مدت. IET Intel. ترانسپ سیستم 2017 ، 11 ، 68-75. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  14. ژائو، ال. آهنگ، ی. ژانگ، سی. لیو، ی. وانگ، پی. لین، تی. Li، H. T-gcn: یک شبکه کانولوشن گراف زمانی برای پیش‌بینی ترافیک. IEEE Trans. هوشمند ترانسپ سیستم 2019 ، 21 ، 3848–3858. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  15. ژو، جی. کوی، جی. هو، اس. ژانگ، ز. یانگ، سی. لیو، ز. Sun، M. گراف شبکه های عصبی: بررسی روش ها و کاربردها. AI Open 2020 ، 1 ، 57–81. [ Google Scholar ] [ CrossRef ]
  16. لی، کیو. هان، ز. بینش Wu، XM Deeper در مورد شبکه های کانولوشن گراف برای یادگیری نیمه نظارت شده. در مجموعه مقالات سی و دومین کنفرانس AAAI در مورد هوش مصنوعی، نیواورلئان، لس آنجلس، ایالات متحده آمریکا، 2 تا 7 فوریه 2018. [ Google Scholar ]
  17. آلون، یو. Yahav, E. در مورد گلوگاه شبکه های عصبی گراف و مفاهیم عملی آن. arXiv 2020 ، arXiv:2006.05205. [ Google Scholar ]
  18. پاسکانو، آر. میکولوف، تی. Bengio، Y. در مورد دشواری آموزش شبکه های عصبی بازگشتی. در مجموعه مقالات کنفرانس بین المللی یادگیری ماشین، PMLR، آتلانتا، GA، ایالات متحده آمریکا، 17-19 ژوئن 2013. ص 1310–1318. [ Google Scholar ]
  19. بنژیو، ی. سیمرد، پ. فراسکونی، پی. یادگیری وابستگی های طولانی مدت با نزول گرادیان دشوار است. IEEE Trans. شبکه عصبی 1994 ، 5 ، 157-166. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  20. روی، ا. روی، KK; احسن علی، ع. امین، م. رحمان، AKM SST-GNN: مدل پیش بینی ترافیک فضایی-زمانی ساده شده با استفاده از شبکه عصبی نمودار. در مجموعه مقالات کنفرانس اقیانوس آرام-آسیا در مورد کشف دانش و داده کاوی، مجازی، 11-14 مه 2021؛ Springer: Cham، سوئیس، 2021; صص 90-102. [ Google Scholar ]
  21. لی، ی. یو، آر. شهابی، ج. لیو، ی. شبکه عصبی تکراری کانولوشنال انتشار: پیش‌بینی ترافیک مبتنی بر داده. arXiv 2017 , arXiv:1707.01926. [ Google Scholar ]
  22. Giorgino, T. محاسبه و تجسم ترازهای تاب خوردگی زمانی پویا در R: بسته dtw. J. Stat. نرم افزار 2009 ، 31 ، 1-24. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  23. ویلیامز، بی.ام. Hoel، LA مدلسازی و پیش بینی جریان ترافیک وسایل نقلیه به عنوان یک فرآیند ARIMA فصلی: مبنای نظری و نتایج تجربی. J. Transp. مهندس 2003 ، 129 ، 664-672. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  24. لو، ز. ژو، سی. وو، جی. جیانگ، اچ. Cui, S. ادغام علیت گرنجر و رگرسیون خودکار برداری برای پیش‌بینی ترافیک شبکه‌های WLAN در مقیاس بزرگ. KSII Trans. اینترنت Inf. سیستم (TIIS) 2016 ، 10 ، 136-151. [ Google Scholar ]
  25. ون لینت، JWC; ون هینسبرگن، سی. مدل‌های پیش‌بینی ترافیک کوتاه‌مدت و زمان سفر. آرتیف. هوشمند Appl. کریت ترانسپ شماره های 2012 ، 22 ، 22-41. [ Google Scholar ]
  26. ما، ایکس. دای، ز. او، ز. ما، جی. وانگ، ی. Wang, Y. یادگیری ترافیک به عنوان تصاویر: یک شبکه عصبی پیچیده عمیق برای پیش بینی سرعت شبکه حمل و نقل در مقیاس بزرگ. Sensors 2017 , 17 , 818. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  27. یائو، اچ. تانگ، ایکس. وی، اچ. ژنگ، جی. لی، زی. بازبینی شباهت مکانی-زمانی: یک چارچوب یادگیری عمیق برای پیش‌بینی ترافیک. در مجموعه مقالات کنفرانس AAAI در مورد هوش مصنوعی، هونولولو، HI، ایالات متحده، 27 ژانویه تا 1 فوریه 2019؛ جلد 33، ص 5668–5675. [ Google Scholar ]
  28. گوا، اس. لین، ی. لی، اس. چن، ز. Wan, H. شبکه‌های عصبی کانولوشنال سه بعدی فضایی-زمانی عمیق برای پیش‌بینی داده‌های ترافیک. IEEE Trans. هوشمند ترانسپ سیستم 2019 ، 20 ، 3913–3926. [ Google Scholar ] [ CrossRef ]
  29. آهنگ، سی. لین، ی. گوا، اس. وان، اچ. شبکه های کانولوشن گراف همزمان مکانی-زمانی: چارچوبی جدید برای پیش بینی داده های شبکه مکانی-زمانی. در مجموعه مقالات کنفرانس AAAI در مورد هوش مصنوعی، نیویورک، نیویورک، ایالات متحده آمریکا، 7 تا 12 فوریه 2020؛ جلد 34، ص 914–921. [ Google Scholar ]
  30. کنگ، ایکس. ژانگ، جی. وی، ایکس. زینگ، دبلیو. Lu, W. شبکه های توجه گراف مکانی-زمانی تطبیقی ​​برای پیش بینی جریان ترافیک. Appl. هوشمند 2022 ، 52 ، 4300-4316. [ Google Scholar ] [ CrossRef ]
  31. برونا، جی. زارمبا، دبلیو. اسلم، آ. LeCun، Y. شبکه های طیفی و شبکه های متصل به صورت محلی روی نمودارها. arXiv 2013 , arXiv:1312.6203. [ Google Scholar ]
  32. هوانگ، ی. بی، اچ. لی، ز. مائو، تی. وانگ، زی استگات: مدل‌سازی تعاملات مکانی-زمانی برای پیش‌بینی مسیر انسان. در مجموعه مقالات کنفرانس بین المللی IEEE/CVF در بینایی کامپیوتر، سئول، کره، 27 اکتبر تا 2 نوامبر 2019؛ ص 6272-6281. [ Google Scholar ]
  33. ژانگ، ایکس. خو، ی. Shao, Y. پیش‌بینی جریان ترافیک با شبکه‌های توجه نمودار کانولوشنال مکانی-زمانی. محاسبات عصبی Appl. 2022 ، 1-23. [ Google Scholar ] [ CrossRef ]
  34. ولیچکوویچ، پ. کوکورول، جی. کازانووا، آ. رومرو، آ. لیو، پی. Bengio، Y. گراف شبکه های توجه. arXiv 2017 , arXiv:1710.10903. [ Google Scholar ]
  35. ژنگ، سی. فن، ایکس. وانگ، سی. Qi، J. Gman: یک گراف شبکه چندتوجهی برای پیش‌بینی ترافیک. در مجموعه مقالات کنفرانس AAAI در مورد هوش مصنوعی، نیویورک، نیویورک، ایالات متحده آمریکا، 7 تا 12 فوریه 2020؛ جلد 34، ص 1234–1241. [ Google Scholar ]
  36. چن، دبلیو. چن، ال. زی، ی. کائو، دبلیو. گائو، ی. Feng, X. شبکه کانولوشن گراف دو جزئی توجه چند بردی برای پیش بینی ترافیک. در مجموعه مقالات کنفرانس AAAI در مورد هوش مصنوعی، نیویورک، نیویورک، ایالات متحده آمریکا، 7 تا 12 فوریه 2020؛ جلد 34، ص 3529–3536. [ Google Scholar ]
  37. هوانگ، آر. هوانگ، سی. لیو، ی. دای، جی. Kong, W. LSGCN: پیش‌بینی کوتاه‌مدت ترافیک با شبکه‌های کانولوشن گراف. در مجموعه مقالات بیست و نهمین کنفرانس مشترک بین المللی هوش مصنوعی، یوکوهاما، ژاپن، 7 تا 15 ژانویه 2020؛ صص 2355–2361. [ Google Scholar ]
  38. یانگ، اس. لی، اچ. لو، ی. لی، جی. آهنگ، ی. Zhou، T. شبکه نمودار همجوشی تطبیقی ​​فضایی و زمانی برای پیش بینی جریان ترافیک کوتاه مدت. ریاضیات 2022 ، 10 ، 1594. [ Google Scholar ] [ CrossRef ]
  39. او، ک. ژانگ، ایکس. رن، اس. Sun, J. یادگیری باقیمانده عمیق برای تشخیص تصویر. در مجموعه مقالات کنفرانس IEEE در مورد دید کامپیوتری و تشخیص الگو، لاس وگاس، NV، ایالات متحده، 27-30 ژوئن 2016. صص 770-778. [ Google Scholar ]
  40. Ba، JL; کیروس، جی آر. نرمال سازی لایه هینتون، جنرال الکتریک. arXiv 2016 , arXiv:1607.06450. [ Google Scholar ]
  41. Berndt، دی جی; کلیفورد، جی. استفاده از تاب خوردگی زمانی پویا برای یافتن الگوها در سری های زمانی. در مجموعه مقالات کارگاه آموزشی KDD، سیاتل، WA، ایالات متحده آمریکا، 30-31 ژوئیه 1994; جلد 10، ص 359–370. [ Google Scholar ]
  42. گیلمر، جی. Schoenholz، SS; رایلی، پی اف. وینیالز، او. ارسال پیام عصبی دال، جنرال الکتریک برای شیمی کوانتومی. در مجموعه مقالات کنفرانس بین المللی یادگیری ماشین، PMLR، سیدنی، استرالیا، 6 تا 11 اوت 2017؛ صص 1263-1272. [ Google Scholar ]
  43. واسوانی، ع. Shazeer, N. پارمار، ن. Uszkoreit، J. جونز، ال. گومز، AN; Polosukhin، I. توجه شما تمام چیزی است که نیاز دارید. Adv. عصبی Inf. روند. سیستم 2017 30 . _ [ Google Scholar ]
  44. بای، اس. Kolter، JZ; کلتون، وی. ارزیابی تجربی شبکه‌های کانولوشنال و تکراری عمومی برای مدل‌سازی توالی. arXiv 2018 , arXiv:1803.01271. [ Google Scholar ]
  45. لیا، سی. ویدال، آر. رایتر، آ. شبکه‌های کانولوشنال موقت Hager، GD: رویکردی یکپارچه برای تقسیم‌بندی اقدام. در مجموعه مقالات کنفرانس اروپایی بینایی کامپیوتر، آمستردام، هلند، 8 تا 16 اکتبر 2016. Springer: Cham, Switzerland, 2016; ص 47-54. [ Google Scholar ]
  46. لانگ، جی. شلهامر، ای. دارل، تی. شبکه های کاملاً پیچیده برای تقسیم بندی معنایی. در مجموعه مقالات کنفرانس IEEE در مورد بینایی کامپیوتری و تشخیص الگو، بوستون، MA، ایالات متحده آمریکا، 7 تا 12 ژوئن 2015. صص 3431–3440. [ Google Scholar ]
  47. گوا، جی. Zhang, T. معماری مکانی-زمانی باقیمانده برای پیش‌بینی تقاضای سفر. ترانسپ Res. قسمت C Emerg. تکنولوژی 2020 , 115 , 102639. [ Google Scholar ] [ CrossRef ]
  48. ژانگ، جی. ژنگ، ی. Qi، D. شبکه‌های باقیمانده مکانی-زمانی عمیق برای پیش‌بینی جریان‌های جمعیتی در سطح شهر. در مجموعه مقالات سی و یکمین کنفرانس AAAI در مورد هوش مصنوعی، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، 4 تا 10 فوریه 2017. [ Google Scholar ]
  49. سوتسکور، آی. وینیالز، او. Le، QV توالی برای یادگیری توالی با شبکه های عصبی. Adv. عصبی Inf. روند. سیستم 2014 ، 27 . [ Google Scholar ]
  50. Kingma، DP; با، جی. آدام: روشی برای بهینه سازی تصادفی. ICLR. 2015. arXiv 2015 , arXiv:1412.6980. [ Google Scholar ]
Ijgi 11 00381 g001 550
شکل 1. تصویری از انواع مختلف همبستگی گره. برای گره اس2، اس1همسایه جغرافیایی آن است در حالی که عملکرد محلی مشابهی دارد اس5.
Ijgi 11 00381 g002 550
شکل 2. مثالی که همبستگی جریان ترافیک را در مناطق عملکردی مشابه نشان می دهد. ترافیک در گره ها جریان دارد اس2و اس5در طول همان دوره
Ijgi 11 00381 g003 550
شکل 3. چارچوب STSGAN. ورودی است χ∈ℝن×اف×پ، جایی که نتعداد گره ها است، پطول گام زمانی است و افویژگی هر گره است. خروجی است Y∈ℝن×س، نمایندگی نسرعت پیش بینی گره در سمراحل زمانی چهار بلوک موازی T-GACN یک لایه T-GACN را در مدل تشکیل می دهند و سه لایه T-GACN برای استخراج ویژگی های با ابعاد بالا به هم متصل شده اند. دو تا از این لایه ها به موازات دو بلوک توجه گراف در هر لایه هستند. شبکه کانولوشنی توجه گراف بین دو پیچیدگی علی زمانی قرار گرفته است.
Ijgi 11 00381 g004 550
شکل 4. ساخت نقشه ترافیک: ( الف ) نمودار مجاورت فضایی ترافیک بر اساس مجاورت ترافیک ساختار یافته است. مناطقی که از لحاظ جغرافیایی به منطقه متصل هستند اس1(مرکز خرید) متصل هستند. ( ب ) نمودارهای مجاورت معنایی جهانی، که در آن مناطق با توابع مشابه دارای الگوهای ترافیکی مشابه هستند، برای اتصال لبه‌ها بین مناطق با عملکردهای مشابه ساخته شده‌اند. به عنوان مثال، مناطق اس2، اس6و اس8محله های مسکونی هستند، بنابراین به هم متصل هستند.
Ijgi 11 00381 g005 550
شکل 5. مثالی از تفاوت بین فاصله اقلیدسی و فاصله DTW.
Ijgi 11 00381 g006 550
شکل 6. شبکه کانولوشن گرافیکی برای استخراج ویژگی های فضایی.
Ijgi 11 00381 g007 550
شکل 7. گلوگاه شبکه های عصبی گراف.
Ijgi 11 00381 g008 550
شکل 8. مثال استفاده از عملیات لایه توجه گراف برای همسایگان اطراف گره 1، که در آن ساعتمن→∈ℝن×افویژگی های گره را نشان می دهد من، نتعداد گره ها و افتعداد امکانات است. ساعتمن”→به روز رسانی ویژگی مخفی است.
Ijgi 11 00381 g009 550
شکل 9. لایه پیچیدگی علّی پسوند چندگانه TCN: ایکس1،ایکس2،⋯،ایکس12دنباله ورودی است و y1،y2،⋯،y12دنباله خروجی است. پذیرفته شده است که طول تاریخچه ورودی شبکه با طول پیش بینی آینده یکسان است.
Ijgi 11 00381 g010 550
شکل 10. یک بلوک باقیمانده شامل دو لایه کانولوشن توسعه یافته و نمودارهای غیر خطی است و WeightNorm و Dropout نیز با هر لایه یکپارچه شده اند تا شبکه را عادی کند.
Ijgi 11 00381 g011 550
شکل 11. زیرشکل های PEMS04 و PEMS08 به ترتیب عملکرد پیش بینی مدل STSGAN ما را روی دو مجموعه داده نشان می دهند. نشان داده شده است که روش ما در مقایسه با هشت مدل پایه دیگر عملکرد بهتری دارد.
Ijgi 11 00381 g012a 550 Ijgi 11 00381 g012b 550
شکل 12. پیش بینی عملکرد روش های مختلف با افزایش فواصل زمانی پیش بینی. ( الف ) نتایج پیش‌بینی روش‌های مختلف بر روی مجموعه داده PEMS04. ( ب ) نتایج پیش‌بینی روش‌های مختلف روی مجموعه داده PEMS08.
Ijgi 11 00381 g013 550
شکل 13. تجزیه و تحلیل پیکربندی شبکه. در ( a )، B1 پیکربندی شبکه را با یک ماژول T-GACN نشان می‌دهد و تعداد ماژول‌های دیگر به‌طور متوالی افزایش می‌یابد. در ( b )، L1 پیکربندی شبکه را با یک لایه T-GACN، و L3 پیکربندی شبکه را با سه لایه T-GACN نشان می دهد. ( c ، d )، به ترتیب، اثرات نرخ یادگیری و اندازه دسته ای را بر روی شبکه تجزیه و تحلیل می کند.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید