چکیده

سیستم های داده تشخیص نور و محدوده (LiDAR) که بر روی یک پلت فرم متحرک یا ثابت نصب شده اند، داده های ابر نقطه سه بعدی را برای اهداف مختلف ارائه می کنند. در کاربردهایی که ناحیه یا شی مورد نظر باید دو بار یا بیشتر با جابجایی اندازه‌گیری شود، ثبت دقیق ابرهای نقطه به‌دست‌آمده برای ایجاد یک مدل سالم با ترکیب ابرهای نقطه‌ای همپوشانی بسیار مهم است. ثبت خودکار ابرهای نقطه در سیستم مختصات مشترک با استفاده از الگوریتم تکراری نزدیک‌ترین نقطه (ICP) یا انواع آن یکی از روش‌های پرکاربرد در ادبیات است و تعدادی از مطالعات بر بهبود الگوریتم‌های فرآیند ثبت برای دستیابی به نتایج بهتر تمرکز دارند. . این مطالعه رویکرد متفاوتی را برای تشخیص و تطبیق خودکار نقاط کلیدی در ثبت درشت ابرهای نقطه قبل از ثبت دقیق با استفاده از الگوریتم ICP پیشنهاد و آزمایش کرد. در الگوریتم پیشنهادی، نقاط کلیدی با توجه به روابط هندسی آنها که با استفاده از زوایا و فواصل بین آنها بیان شده است، مطابقت داده شد. از این رو، کمک به بهبود کیفیت مدل سه بعدی به دست آمده از طریق فرآیند ثبت نام خوب، که با استفاده از روش ICP انجام می شود، هدف ما بود. عملکرد الگوریتم جدید با استفاده از ریشه میانگین مربعات خطا (RMSE) تبدیل 3 بعدی در مرحله تراز خشن و همچنین مقادیر RMSE a-preor و a-posterior RMSE الگوریتم ICP مورد ارزیابی قرار گرفت. الگوریتم جدید همچنین با توصیفگر هیستوگرام ویژگی نقطه ای (PFH) و الگوریتم تطبیق مقایسه شد. همراه با دو آشکارساز رایج. در نتیجه مقایسه ها، برتری ها و معایب الگوریتم پیشنهادی مورد بحث قرار گرفت. اندازه‌گیری‌های مجموعه داده‌های مورد استفاده در آزمایش‌ها با استفاده از داده‌های اسکن شده یک مجسمه ارسطو 6 سانتی‌متر × 6 سانتی‌متر × 10 سانتی‌متر در محیط آزمایشگاه، و نمای ساختمان در فضای باز و همچنین با استفاده از داده‌های مجسمه‌سازی استنفورد در دسترس عموم انجام شد. . در هر مطالعه موردی، الگوریتم پیشنهادی عملکرد رضایت‌بخشی با دقت برتر و تعداد تکرار کمتر در فرآیند ICP در مقایسه با سایر روش‌های ثبت درشت ارائه کرد. از ابرهای نقطه ای که ثبت درشت با روش پیشنهادی انجام شده است، دقت ثبت نام دقیق بر حسب مقادیر RMSE با تکرار ICP برابر 0 محاسبه می شود.

کلید واژه ها:

تطبیق خودکار ؛ تشخیص نقطه کلیدی ابر نقطه ; ثبت نام ؛ تحول ؛ نزدیکترین نقطه تکراری (ICP)

1. مقدمه

استفاده از مدل‌های سه بعدی (3 بعدی) در کاربردهای مختلف در این قرن با پیشرفت‌های فناوری‌های اسکن لیزری به طور قابل‌توجهی افزایش یافت [ 1 ]. دستگاه‌های اندازه‌گیری مجهز به حسگرهای LiDAR (تشخیص نور و محدوده) معمولاً برای جمع‌آوری داده‌های ابر نقطه سه بعدی استفاده می‌شوند و الگوریتم‌های توسعه‌یافته برای پردازش داده‌های ابر نقطه نتایج موفقیت‌آمیزی را در تولید مدل‌های ساخته‌شده برای مقایسه با اشیاء واقعی ارائه می‌کنند. . فرآیند اسکن برای تولید داده‌های ابر نقطه سه‌بعدی دقیق اجسام در مقیاس مختلف و/یا قطعات زمین در مقایسه با تکنیک‌های معمولی فتوگرامتری و نقشه‌برداری بسیار سریع و عملی است [ 2 ].]. اندازه گیری با اسکنرهای لیزری بر اساس اصل خط دید است و در بیشتر موارد، جسم اسکن شده تا حدی با همپوشانی برای اهداف مدل سازی سه بعدی به دست می آید. تولید یک مدل سه بعدی کامل از روش توصیف شده مشروط به ادغام موثر داده های جزئی به دست آمده با تراز آنها نسبت به یک چارچوب مرجع مشترک است. این فرآیند به عنوان ثبت داده های ابر نقطه ای در رشته های فتوگرامتری و بینایی کامپیوتر شناخته می شود [ 1 ، 3 ]. علاوه بر چگالی و دقت موقعیت نقاط ابر نقطه ای، رویکرد مورد استفاده برای فرآیند ثبت نقش اساسی در کیفیت مدل سه بعدی نهایی دارد [ 2 ].
در ادبیات، تعدادی از روش های ثبت پیشنهاد شده است. در این روش ها، ثبت ابرهای نقطه سه بعدی که از موقعیت ها و حسگرهای مختلف به دست می آیند، عموماً شامل دو مرحله شامل مراحل ثبت درشت و ریز است [ 4 ]. برای دستیابی به نتایج بهتر، باید پس از ثبت درشت با استفاده از الگوریتم محاسباتی مناسب، ثبت ریز اعمال شود. الگوریتم تکراری نزدیکترین نقطه (ICP) و/یا انواع آن تقریباً به یک رویه استاندارد تبدیل شده است و معمولاً برای ثبت دقیق در اکثر برنامه ها اعمال می شود [ 5 ، 6 ]. علاوه بر این، روش‌های ثبت دقیق مبتنی بر یادگیری عمیق مانند PointNetLK [ 7 ] نیز اخیرا مورد مطالعه قرار گرفته‌اند. حبیب و الروزوق [8 ] بر چهار نکته اساسی در یک روش ثبت جامع به شرح زیر تأکید می کند: (1) تخمین پارامترهای تبدیل (که به چارچوب های مرجع ابرهای نقطه درگیر مربوط می شود). (ب) تعریف اولیه‌های ثبت (ویژگی‌های مزدوج که باید در میان مجموعه داده‌های ابر نقطه استفاده شده شناسایی شوند و برای تخمین پارامترهای تبدیل استفاده شوند). (iii) تصمیم گیری برای اندازه گیری شباهت (محدودیت ریاضی برای توصیف همزمانی ویژگی های مزدوج). (IV) تصمیم گیری برای یک استراتژی تطبیق مناسب (نماینده چارچوب کنترلی برای فرآیند ثبت خودکار) [ 1]. روش‌های هم‌ترازی اولیه (ثبت نام درشت) که لازم است قبل از فرآیند ثبت جریمه اعمال شود، در سال‌های اخیر با علاقه فزاینده‌ای متمرکز و مورد مطالعه قرار گرفته‌اند. در میان این روش‌ها، الگوریتم‌های ثبت نام درشت خودکار بدون اهداف مصنوعی، تقاضای بیشتری دارند [ 9 ]. روش پیشنهادی در این مطالعه برای ثبت خودکار درشت ابرهای نقطه‌ای است که با استفاده از دستگاه‌های اسکنر لیزری مشابه یا متفاوت به دست می‌آیند. به طور خاص، روش‌های ثبت درشت اساساً شامل دو مرحله اصلی هستند، یعنی تشخیص نقاط کلیدی یا ابتدایی (خطوط، صفحات، سطوح) و توصیف مزدوج‌ها [ 10 ].
تشخیص نقاط کلیدی و وظایف تطبیق در ثبت درشت نیاز به توجه ویژه ای برای استخراج دقیق تابع تبدیل دارد. اولین مرحله از هر روش تطبیق، شناسایی مکان های ویژگی در مجموعه داده های ابر نقطه متراکم و توصیف آنها است. در فرآیند تشخیص، نقاط کلیدی از ابر نقطه با توجه به ویژگی‌هایی مانند شدت، سطح نرمال، انحنا، مقادیر قرمز-سبز-آبی (RGB)، زبری و غیره تعریف می‌شوند. بنابراین، پس از تولید توصیفگرها، می‌توانند مقایسه شود تا رابطه بین ابرهای نقطه را برای انجام رویه «تطبیق» در مرحله بعد مشخص شود. بنابراین، ما به یک آشکارساز و توصیفگر برای استخراج نقاط کلیدی در ابرهای نقطه نیاز داریم [ 11 ].
اصل کار آشکارسازها و توصیفگرها بر تشخیص نقاط کلیدی متکی است که با کلاسی از تبدیلات همواریانس هستند. سپس، برای هر نقطه مشخصه شناسایی شده، یک نمایش بردار ویژگی ثابت، به نام توصیفگر، برای نقاط ابر نقطه در اطراف نقطه کلیدی شناسایی شده تعیین می شود. توصیفگرهای ویژگی را می توان با استفاده از مشتقات مرتبه دوم، معادلات پارامتری با ضرایب تخمین زده شده از تبدیل ها، یا با ترکیب آنها ایجاد کرد [ 11 ]]. اصولاً ویژگی های استخراج شده را می توان به دو دسته جهانی و محلی دسته بندی کرد. ویژگی های جهانی مانند رنگ، بافت و غیره به طور کلی زمانی در نظر گرفته می شوند که یک تصویر در فرآیندها مورد توجه قرار می گیرد و هدف آن توصیف یک تصویر به عنوان یک کل است که می تواند به عنوان یک ویژگی خاص از تصویر تفسیر شود که شامل همه پیکسل ها می شود. در نظر گرفتن ویژگی‌های رنگ و بافت جهانی، نتایج قابل اجرا در هنگام جستجوی تصاویر مشابه در پایگاه داده به دست می‌دهد. از سوی دیگر، ویژگی های محلی برای تشخیص نقاط کلیدی یا در یک تصویر یا یک ابر نقطه و توصیف آنها هستند. به این ترتیب، اگر توصیفگر ویژگی محلی مورد استفاده، n نقطه کلیدی را در مجموعه داده نشان دهد، به این معنی است که n وجود دارد.بردارهایی که موقعیت، جهت، رنگ و غیره هر نقطه کلید را توصیف می کنند. انتخاب هر یک از ویژگی ها به هدف برنامه بستگی دارد. با این حال، توصیفگرهای ویژگی محلی برای تطبیق نقاط کلیدی و اهداف ثبت ابر نقطه برتر هستند [ 11 ].
در ادبیات، الگوریتم‌های مختلفی وجود دارد که برای شناسایی، توصیف و اهداف تطبیق نقاط کلیدی در ثبت ابر نقطه طراحی و استفاده می‌شوند [ 4 ]. از آنجا که سهم قابل توجهی از الگوریتم پیشنهادی در این مطالعه بر روی فرآیند ثبت درشت است، ادبیات در مورد روش‌های ثبت درشت به طور گسترده در اینجا ذکر شده است. اساساً، روش‌های ثبت درشت شامل دو مرحله اصلی است: مرحله تشخیص، که شامل تعیین نقاط کلیدی، خطوط، سطوح، سطوح یا ویژگی‌های کلی ابرهای نقطه است. و مرحله توصیف که در آن مزدوج ها تعیین می شوند [ 10 ، 12]. در ادبیات، مجموعه‌های متجانس چهار نقطه‌ای (4PCS) و بسیاری از انواع آن به عنوان یک الگوریتم ثبت درشت مبتنی بر نقطه استفاده می‌شوند [ 13 ]. رویکرد 4PCS الگوریتمی است که تعداد نقاط کلیدی انتخاب شده را کاهش می دهد و به طور همزمان توصیفگر و تطبیق را برای تعیین نقاط مزدوج اعمال می کند [ 12 ]. علاوه بر این، برای تعیین ویژگی‌های هندسی نقاط کلیدی در یک ثبت مبتنی بر نقطه، توصیف‌کننده‌هایی مانند هیستوگرام ویژگی نقطه (PFH)، PFH سریع [ 14 ]، امضای هیستوگرام جهت‌گیری‌ها (SHOT) [ 15 ] یا تحلیل معنایی [15] روش های 16 و 17 معمولاً مورد استفاده قرار می گیرند [ 12]. در مرحله تشخیص، آشکارسازهای مختلف مبتنی بر نقطه تا کنون منتشر شده است [ 18 ]. عملگر فورستنر [ 19 ]، 3 بعدی هریس [ 20 ]، تکه‌های سطحی موضعی (LSPs) [ 21 ]، ویژگی شعاعی تراز معمولی (NARF) [ 22 ]، تبدیل ویژگی ثابت مقیاس سه بعدی (3DSIFT) [ 23 ، 24 ] و امضای ذاتی الگوریتم (ISS) [ 25 ] معمولاً به عنوان آشکارسازهای نقطه کلید استفاده می شود.
از سوی دیگر، رویکردهای ثبتی مبتنی بر ابتدایی نیز معمولاً برای ثبت درشت اعمال می‌شوند و این رویکردها شامل الگوریتم‌هایی هستند که از خطوط [ 26 ]، منحنی‌ها [ 27 ]، سطوح [ 9 ] یا سطوح [ 28 ] استفاده می‌کنند. روش‌های ثبت جهانی مبتنی بر ویژگی شامل الگوریتم‌های مبتنی بر تبدیل توزیع‌های نرمال (NDT) [ 29 ] و همچنین الگوریتم‌هایی که ابرهای نقطه سه‌بعدی را به هیستوگرام‌های 1 بعدی و تصاویر دو بعدی [ 30 ] تبدیل می‌کنند نیز از جمله الگوریتم‌های پرکاربرد در عمل هستند. در این مقاله، یک رویکرد ثبت درشت مبتنی بر نقطه پیشنهاد و آزمایش شده است.
در این مطالعه، یک توصیف خودکار و روش تطبیق نقطه کلیدی جدید برای ثبت درشت ابرهای نقطه معرفی و آزمایش شده است. سهم اصلی الگوریتم پیشنهادی عمدتاً در توصیف کننده و بخش های تطبیق آن است. در قسمت توضیحات الگوریتم پیشنهادی، نقاط کلیدی با استفاده از روش ترکیب ریاضی به زیر مجموعه‌ها تقسیم می‌شوند. فواصل بین نقطه کلید مرجع و نقاط برجسته در زیر مجموعه و زوایای بین خطوط اتصال تشکیل شده به صورت ترکیبی محاسبه می شود. استفاده از تکنیک ترکیبی برای تشکیل زیرمجموعه های نقاط کلیدی و روشی که برای محاسبه فواصل و زوایای بین نقاط و خطوط استفاده می شود، تازگی الگوریتم پیشنهادی است. بر خلاف روش های دیگر که معمولا در ادبیات استفاده می شود، روش پیشنهادی زوایای محاسبه شده را مستقل از سطح نرمال یا سطح در نظر می گیرد. در الگوریتم تطبیق رویکرد جدید، مجموع تفاوت فاصله ها و مقادیر زاویه ایجاد شده برای یک نقطه کلیدی مشخص در ابرهای دو نقطه ای در نظر گرفته شده است. برای تطبیق زیر مجموعه ها، از مجموع اختلاف فاصله ها و زوایا به ترتیب به عنوان مقادیر واحد استفاده می شود. مجموعه نقاطی که مجموع فاصله و اختلاف زاویه ای آنها به مقدار صفر نزدیک است، نقاط مزدوج در نظر گرفته می شوند. علاوه بر الگوریتم های توصیفگر و تطبیق روش جدید، الگوریتم آشکارساز آن نیز دارای تازگی است. برخلاف روش‌های ISS و LSP، در آشکارساز پیشنهادی، یک نقطه با بالاترین انحنا از هر وکسل (مکعب) انتخاب می‌شود.
رویکرد تطبیق خودکار جدید نقطه کلیدی برای ثبت درشت در نتیجه ثبت دقیق با استفاده از الگوریتم ICP ارزیابی شد [ 5]. در الگوریتم از روش تبدیل شباهت سه بعدی استفاده شد. آزمون های پژوهش با استفاده از سه مجموعه داده انجام شده است. اولین مجموعه داده از طریق اندازه‌گیری‌های اسکن لیزری در یک محیط آزمایشگاهی به‌دست آمد و مدل‌سازی یک مجسمه با اندازه کوچک است. مجموعه داده دوم شامل ابرهای نقطه ای نمای ساختمان با جزئیات هندسی منظم است که از طریق اندازه گیری های اسکن لیزری زمینی از سکوهای ثابت و متحرک به دست آمده است. اطلاعات بیشتر در مورد اندازه گیری ها و حسگرهای اسکن لیزری مورد استفاده در بخش دوم مقاله ارائه شده است. علاوه بر دو مجموعه داده به دست آمده از طریق اسکن لیزری توسط نویسندگان، آزمایش ها با استفاده از ابر نقطه اسم حیوان دست اموز در دسترس عموم توسط مخزن اسکن سه بعدی استانفورد تکرار شد.https://graphics.stanford.edu/data/3Dscanrep/ در 15 مارس 2021 قابل دسترسی است) تا مقادیر دقت به دست آمده با الگوریتم پیشنهادی قابل تکرار باشد.
الگوریتم جدیدی که برای ثبت درشت در این مطالعه پیشنهاد شد، ابتدا ابر نقطه را فیلتر کرده و مجموعه داده را پایین می آورد. سپس با در نظر گرفتن زوایای و فواصل بین نقاط ابر نقطه، نقاط کلیدی را شناسایی می کند. پارامترهای تبدیل به طور خودکار برای ثبت درشت با مدل تنظیم حداقل مربعات گاوس مارکوف (LSA) محاسبه می‌شوند. بالاخره ثبت جریمه با روش ICP اعمال می شود. به منظور ارائه مقایسه ای بین توصیفگر نقطه کلیدی جدید و الگوریتم تطبیق و روش های دیگر که در حال حاضر مورد استفاده قرار می گیرند، فرآیندهای ثبت با استفاده از مجسمه ها و داده های نمای ساختمان تکرار شدند. بر این اساس، الگوریتم‌های ISS و LSP برای تشخیص نقاط کلیدی و هیستوگرام‌های آینده نقطه (PFH) برای توصیف و تطبیق نقاط کلیدی نیز استفاده شد. در نتیجه گیری، الگوریتم های آزمایش شده با استفاده از دقت تبدیل قبل و بعد از ICP و همچنین موفقیت مدل های سه بعدی تولید شده با هر الگوریتم مقایسه شدند. الگوریتم جدید با ارائه مقادیر RMSE کوچکتر تبدیل و تعداد تکرار کمتر در فرآیند ICP از سایر الگوریتم های آزمایش شده بهتر عمل کرد.
سازماندهی این مقاله به شرح زیر است: اطلاعات دقیق اندازه گیری های اسکن لیزری و مجموعه داده های مورد استفاده در بخش 2 توضیح داده شد . پیشینه نظری الگوریتم های تشخیص و تطبیق نقاط کلیدی تست شده و همچنین فرمول پیشنهادی جدید در زیرنویس این بخش نیز توضیح داده شده است. فرمول بندی ریاضی و نظریه بنیادی الگوریتم ICP در آخرین زیرنویس بخش 2 خلاصه شد . نتایج عددی با آمار آزمون مقایسه ای در بخش 3 ارائه شد . یک بحث جامع بر اساس نتایج به دست آمده در بخش 4 ارائه شد. در نهایت، نتیجه گیری های اصلی و همچنین توصیه هایی برای مطالعات آتی در آن گنجانده شده استبخش 5 .

2. مواد و روشها

2.1. مجموعه داده های مورد استفاده در آزمون ها

در آزمون الگوریتم های ثبت ابر نقطه، از سه مجموعه داده استفاده شد. اولین مجموعه داده با اندازه گیری های داخلی مجسمه ارسطو (اندازه تقریبی: 6 سانتی متر × 6 سانتی متر × 10 سانتی متر) (نگاه کنید به شکل 1 ) در آزمایشگاه نقشه برداری بخش مهندسی ژئوماتیک ITU به دست آمد. NextEngine 3D Laser Scanner Ultra HD در اسکن مجسمه استفاده شد [ 31 ]. دقت ابعادی اسکنر در حالت ماکرو 0.1 میلی متر و در حالت عریض 0.3 میلی متر است [ 31 ]. با توجه به اندازه و دقت اسکنر لیزری مورد استفاده، تجهیزاتی کاربردی و مقرون به صرفه برای اسکن در تولید مدل های سه بعدی مناطق کوچک یا شی در کاربردهای صنعتی است.
داده های ابر نقطه ای به دست آمده با اسکن نمای جنوبی ساختمان مهمانسرای ITU Yilmaz Akdoruk در منطقه پردیس Maslak ( شکل 2 a) دومین مجموعه داده در مطالعه است. نماهای ساختمان با استفاده از تکنیک های زمینی ساکن (TLS) و اسکن لیزر متحرک (MLS) اسکن شدند و مدل های سه بعدی نماها با ترکیب داده های ابرهای نقطه ای به دست آمده از این دو تکنیک تولید شدند. در اندازه‌گیری‌های TLS، از اسکنرهای لیزری زمینی Leica ScanStation C10 با دقت اندازه‌گیری فاصله 4 میلی‌متری، دقت اندازه‌گیری زاویه 12 اینچ و دقت موقعیت نقطه 6 میلی‌متر (برای اندازه‌گیری تک)، استفاده شد [ 32 ]. سیستم اسکن لیزر سیار Riegl VMX 450 (نگاه کنید به شکل 2 ب) برای اندازه گیری MLS نمای ساختمان استفاده شد [33 ]. در سیستم های اسکن لیزری سیار Riegl VMX-450، دو اسکنر لیزری Riegl VQ-450 با دقت موقعیت 8 میلی متر با واحد IMU/GNSS یکپارچه شده اند.
سومین مجموعه داده مورد استفاده برای آزمایش الگوریتم پیشنهادی، ابرهای نقطه مجسمه اسم حیوان دست اموز است که توسط مخزن اسکن سه بعدی استانفورد در دسترس قرار گرفته است ( https://graphics.stanford.edu/data/3Dscanrep/ ، در 15 مارس 2021 قابل دسترسی است). داده های اسم حیوان دست اموز به عنوان یکی از مدل های استنفورد شناخته می شود که با اسکنر Cyberware 3030 MS در آزمایشگاه گرافیک کامپیوتری دانشگاه استنفورد اسکن شد ( شکل 3 را ببینید ). اسکنر Cyberware 3030 MS دارای دقت ابعادی 0.1 میلی متری است. این داده ها اغلب به عنوان مدل نمونه برای آزمایش الگوریتم های تطبیق نقاط کلیدی در ادبیات استفاده می شود.

2.2. روش شناسی

2.2.1. تشخیص نقطه کلیدی

گام اساسی در آغاز گردش کار مدل سازی سه بعدی، ثبت داده های ابر نقطه اشیاء نیمه اسکن شده است. این فرآیند مستلزم ادغام موفقیت آمیز ابرهای نقطه همپوشانی با استفاده از پارامترهای تبدیل تخمینی است. در برآورد دقیق پارامترهای تبدیل، و از این رو در عملکرد بالای ثبت ابرهای نقطه، شناسایی و تطبیق دقیق نقاط کلیدی بسیار مهم است.

به منظور ارائه نتایج مقایسه ای در مورد عملکرد الگوریتم تشخیص پیشنهاد شده و آزمایش شده در این مطالعه، الگوریتم های لکه های سطح محلی (LSP) و امضاهای شکل ذاتی (ISS) نیز انتخاب و برای تشخیص نقطه کلیدی اعمال شدند. الگوریتم LSP یکی از روش‌های اندازه‌گیری برجستگی نقطه‌ای است و برجستگی یک راس را با در نظر گرفتن شاخص شکل تشخیص می‌دهد. اسمن(پ)) که بر اساس حداکثر و حداقل انحنای اصلی ( سیمترآایکس.، سیمترمنn.) در راس همانطور که در معادله (1) [ 21 ، 34 ] داده شده است.

اسمن(پ)=12-1πبرنزه-1سیمترآایکس.(پ)+سیمترمنn.(پ)سیمترآایکس.(پ)-سیمترمنn.(پ)

و اگر شاخص شکل متوسط μاسمندر رابطه (2) آمده است:

μاسمن(پ)=1ن∑qϵϰ(پ)اسمن(پ)

جایی که ϰ(پ)به معنی مجموعه نقاط در پشتیبانی از پ، و qیکی از اعضای این مجموعه است ن=[ϰ(پ)]تعداد امتیاز در پشتیبانی است پ.

بر این اساس، یک نقطه ویژگی زمانی از مراحل هرس خارج می شود اسمنبه طور قابل توجهی بزرگتر یا کوچکتر از μاسمنمانند در اسمن(پ)≥(1+α)μاسمن(پ)∨اسمن(پ)≤(1-β)μاسمن(پ)، و αو βپارامترهای اسکالر هستند، که مقدار تفاوت ها را از میانگین فرض شده به عنوان معنی دار تعریف می کنند [ 34 ].

الگوریتم امضاهای شکل ذاتی (ISS) بر اساس تجزیه ارزش ویژه ماتریس پراکندگی دارای نقاطی است که به پشتیبانی از پدر معادله (3) [ 25 ] آورده شده است:

∑(پ)=1ن∑qϵϰ(پ)(q-μپ)(q-μپ)تی، با μپ=1ن∑qϵϰ(پ)q

جایی که ∑(پ)ماتریس پراکندگی پشتیبان نقطه را نشان می دهد پ، و مقادیر ویژه آن با ترتیب قدرهای نزولی هستند λ1، λ2، λ3. در این فرآیند، نقاط دارای نسبت بین دو مقدار ویژه متوالی زیر یک مقدار آستانه ( تیساعت) حفظ می شوند (به معادله (4) مراجعه کنید).

λ2(پ)λ1(پ)<تیساعت12∧λ3(پ)λ2(پ)<تیساعت23
توضیحات بیشتر و جزئیات موارد خاص در مورد اجرای الگوریتم ISS با مطالعات موردی توسط تومبری و همکاران ارائه شده است. [ 34 ].
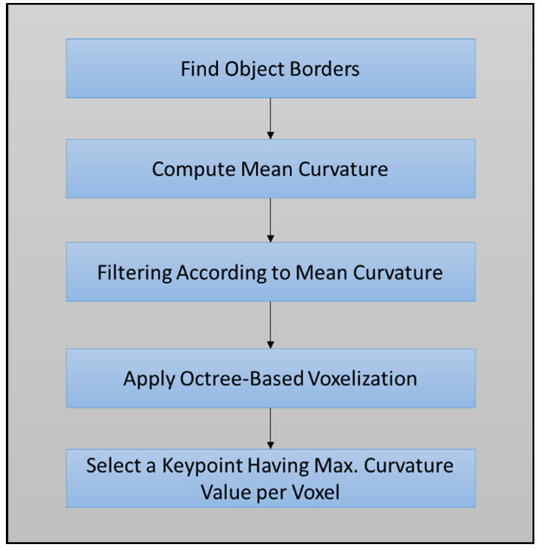
در الگوریتم تشخیص پیشنهادی و آزمایش شده ارائه شده در اینجا، مراحل پردازش مشابه با روش‌های اندازه‌گیری برجستگی نقطه‌ای LSP و ISS دنبال می‌شود و انحناهای سطح در نقاط به منظور شناسایی نقاط کلیدی در نظر گرفته می‌شوند. در حین تخمین انحنای سطح در هر نقطه، روش تحلیل کوواریانس، که از نسبت بین حداقل و جمع مقادیر ویژه استفاده می‌کند، ترجیح داده شد. با این حال، در حالی که الگوریتم‌های داده‌شده مستقیماً روی ابر نقطه‌ای بدون هیچ گونه پیوند میانی کار می‌کنند، آشکارساز بر روی نمونه‌ها در مناطق با انحنای بالا تمرکز می‌کند و تخمین‌های تغییرات محلی و معیارهای خطای چهارگانه را به کار می‌گیرد [ 35 ].]. در الگوریتم، یک فیلتر مبتنی بر وکسل برای افزایش کارایی محاسباتی با در نظر گرفتن حداکثر انحنای سطح اعمال می‌شود. بر این اساس، نقاط ابر نقطه‌ای، در صفحه xyz، به بلوک‌های سه بعدی با اندازه بلوک مناسب با توجه به وضوح مجموعه داده تقسیم می‌شوند. در هر بلوک، لکه های لیزر بیشتر در یک ساختار پارتیشن octree با مجموعه ای از وکسل های سه بعدی (همانطور که در شکل 4 مشاهده می شود ) سازماندهی می شوند [ 36 ]. شکل 5 نمای کلی از مراحل اصلی الگوریتم تشخیص نقطه کلید پیشنهادی را نشان می دهد. الگوریتم تشخیص نقطه کلیدی بر روی پلت فرم Matlab توسعه یافته است.
2.2.2. توضیحات و تطبیق نقاط کلیدی
پس از استخراج نقاط کلیدی از ابرهای نقطه ای با استفاده از آشکارسازهای سه بعدی، که محله های محلی را به منظور شناسایی نقاط مورد نظر همانطور که در بخش قبل توضیح داده شد، تجزیه و تحلیل می کنند، همسایگی یک نقطه کلیدی با یک توصیفگر سه بعدی توصیف می شود که محله را در فضای مناسب نمایش می دهد. در پایان، توصیفگرهای تعریف شده در سطوح مختلف با یکدیگر تطبیق داده می شوند [ 34 ]. بر اساس این فرآیند، توصیفگرهای سه بعدی نقطه کلیدی، توصیفی از محیط در همسایگی یک نقطه در ابر ارائه می‌کنند و این توصیف معمولاً به روابط هندسی بستگی دارد. نقاط در دو ابر نقطه متفاوت که توصیفگر ویژگی مشابهی دارند، عمدتاً با یک نقطه سطحی مطابقت دارند.
توصیفگرهای نقطه کلیدی مبتنی بر تجزیه و تحلیل مؤلفه اصلی (PCA) و الگوریتم‌های تطبیق معمولاً در کاربردهای مختلف از جمله تشخیص اشیا مانند حذف جزئیات سقف مدل‌های ساختمان سه بعدی استفاده می‌شوند. به عنوان مثال، یوشیمورا و همکاران. [ 4 ] تجزیه و تحلیل مؤلفه اصلی (PCA) را به طور مؤثر برای تعیین گوشه های سقف و خطوط سقف تیز ساختمان ها به کار برد. تکنیک PCA امکان تجزیه و تحلیل برجستگی ها را با توجه به ویژگی های هندسی اشیاء فراهم می کند. در مطالعه خود، یوشیمورا و همکاران. [ 4 ] در نظر گرفت که نقاط یک دیوار و حاشیه های سقف در امتداد یک خط مستقیم امتداد یافته و از این رو با معادله یک خط مستقیم مطابقت دارند. آایکس+بy+ج=0). بنابراین، آنها مرزهای ساختمان را با در نظر گرفتن خطوطی که متعلق به برجستگی های متعامد نقاط شناسایی شده بوده و با توجه به طول لبه ساختمان و شباهت زاویه بین نقاط صادر شده مطابقت دارند، تعیین کردند.

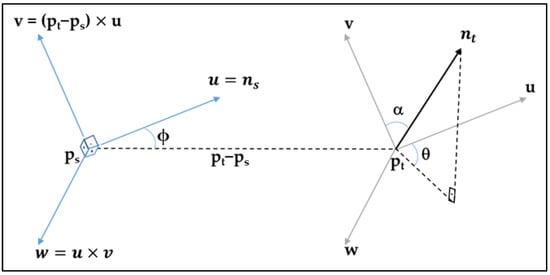
هیستوگرام های ویژگی نقطه ای (PFH) نیز معمولاً ابزارهایی به عنوان توصیف کننده هستند [ 37 ]. علاوه بر تطبیق نقطه، توصیفگر PFH همچنین برای تعیین نقاط در یک ابر نقطه، مانند نقاط روی لبه، گوشه و صفحه استفاده می شود. این الگوریتم از یک قاب داربوکس (نگاه کنید به شکل 6 ) استفاده می کند که بین تمام جفت های نقطه در همسایگی محلی یک نقطه ساخته شده است [ 14 ، 38 ]. نقاط مبدا قاب داربوکس نقاطی هستند که زوایای کمتری بین سطح نرمال و خط اتصال جفت نقطه دارند. پسو پتی. اگر nس/تینقطه مربوطه نرمال است، قاب داربوکس u , v، wمطابق با معادلات (5) – (7) ساخته می شوند:

تو=nس
v=تو×(پتی-پس)/”پتی-پس”
w=تو×v

سه فاصله زاویه ای α، ϕو θ، محاسبه شده بر اساس قاب داربوکس در معادلات (8) – (10) آمده است:

α=v·nتی
ϕ=تو·(پتی-پس)/د
θ=آrجتیآn(w·nتی،تو·nتی)
د=”پتی-پس”

جایی که دفاصله بین است پسو پتی(معادله (11)). برای توصیف رابطه هندسی جفت نقطه در روش PFH از سه زاویه و یک عنصر فاصله به اضافه دو بردار معمولی استفاده شده است. این چهار عنصر شامل زوایا و فاصله به هیستوگرام نقطه اضافه می شوند پو میانگین درصد جفت نقاط در همسایگی پ، که روابط مشابهی دارند. در PFH، این هیستوگرام ها برای تمام جفت های ممکن در k تعداد همسایه های نقطه محاسبه می شوند.پ[ 37 ].

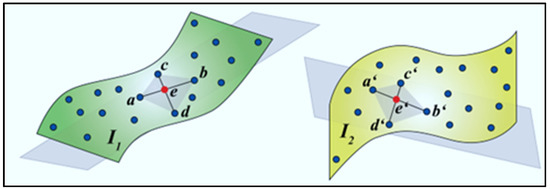
به عنوان یک رویکرد متفاوت، در الگوریتم مجموعه‌های متجانس چهار نقطه‌ای (4PCS)، چهار نقطه از ابر نقطه مرجع انتخاب شده و مطابقت آنها در ابر نقطه مکمل جستجو می‌شود. بنابراین نقاط متناظر با توجه به روابط تشابه تعریف شده یافت می شوند ( شکل 7 را ببینید ) [ 39 ]. در شکل 7 ، نقطه e در ابر نقطه مرجع ( I 1 ) که با تقاطع خطوط اتصال همسطح جفت های دو نقطه ای ( ab و cd ) انتخاب شده است. نقطه متناظر e e در ابر نقطه مکمل است ( I 2) در شکل. در معادلات (12) و (13)، r1و r2نسبت ها بر اساس همسطح بودن نقاط تقاطع بیان می شوند و مطابقت این نسبت ها در ابر نقطه مکمل نیز جستجو می شود.

r1=(آ-ه)/(آ-ب)
r2=(ج-ه)/(ج-د)

پردازش با الگوریتم 4PCS اساساً در چهار مرحله تکمیل می شود که شامل موارد زیر می شود: (1) انتخاب چهار نقطه از ابر نقطه ( I 1 ) با در نظر گرفتن آستانه پذیرفته شده، (2) محاسبه دو طول مورب متقاطع ( ایکس=ب”-آ”و y=د”-ج”همانطور که در شکل 7 مشاهده می شود ). (iii) تخمین نقطه تقاطع احتمالی دو عنصر مورب برای هر مجموعه نقطه. این مرحله به دنبال عبارات داده شده در معادلات (14) و (15) انجام می شود:

هآب=آ”+r1ایکس ، هبآ=ب”-r2ایکس
هجد=ج”+r1y ، هدج=د”-r2y

و تفاوت این مقادیر با یک آستانه معین مقایسه می شود δمانند رابطه (16):

(هآب-هجد)<δ ، (هآب-هدج)<δ ، (هبآ-هجد)<δ ، (هبآ-هدج)<δ

و در نهایت مرحله (IV) تعیین مناسب ترین چهار نقطه که معیارهای مقایسه در رابطه (16) را برآورده می کند.

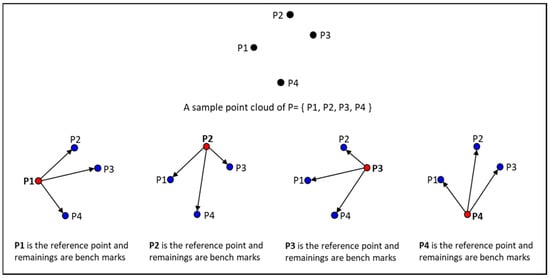
در توصیفگر و الگوریتم تطبیق پیشنهادی، کسینوس زاویه ها و فواصل اقلیدسی در بین خطوط اتصال در نظر گرفته شده است. بنابراین، شباهت های کسینوس و برابری های فاصله بردارهای سه بعدی برای تطبیق نقاط کلیدی در نظر گرفته می شوند (معادله (17)). در روش PFH از سه زاویه متصل به سطح نرمال استفاده می شود، در حالی که ( n- 2) زاویه بین خطوط اتصال برای n نقطه کلیدی در روش پیشنهادی محاسبه می شود. با این حال، برای یافتن شباهت‌های هندسی مجموعه‌های نقاط کلیدی در ابرهای دو نقطه‌ای، مجموع تفاوت‌های مقادیر زاویه محاسبه‌شده بین نقاط کلیدی در هر دو ابر نقطه در نظر گرفته می‌شود ( شکل 8 را ببینید.). همانطور که در رابطه (17) مشاهده می شود، الگوریتم پیشنهادی مبتنی بر استفاده از محصولات اسکالر بردارها است که یکی دیگر از تفاوت های الگوریتم آزمایش شده جدید نسبت به الگوریتم رایج PFH است که از محصولات متقاطع و اسکالر استفاده می کند. در حالی که روش 4PCS از هیچ مقدار زاویه استفاده نمی کند، فقط از مقادیر نسبت فاصله نقطه استفاده می کند. در الگوریتم پیشنهاد شده در اینجا، فاصله اقلیدسی ( n -1) برای n نقطه کلیدی محاسبه می شود. برای تشابه هندسی نقاط کلیدی ابرهای نقطه، مجموع اختلاف فاصله بین نقاط کلیدی در نظر گرفته شده است.

جoس(θ)=د2·د1″د2″2·”د1″2=∑من=1nد2·د1∑من=1n(د2)2∑من=1n(د1)2
در الگوریتم پیشنهادی، کسینوس های زاویه ای با معادله (17) و در معادله توضیح داده شده اند. د1و د2بردارهای فاصله بین نقطه برجسته و دو نقطه کلیدی دیگر در زیر مجموعه ترکیبی هستند، θزاویه بین دو بردار فاصله است. در الگوریتم ابتدا فواصل اقلیدسی بین نقاط زیر مجموعه ترکیبی و کسینوس های زاویه مربوطه محاسبه شده و سپس تشابه هندسه های ساخته شده برای هر مجموعه نقطه برجسته انتخاب شده در نظر گرفته می شود. الگوریتم 1 شبه کدهای توصیفگر نقطه کلید جدید را می دهد.
الگوریتم 1. تولید ویژگی های ابر نقطه.
ورودی: یک ابر نقطه است پتعداد زیر نقطه هایی که قرار است از ابر نقطه انتخاب شوند می باشد نسی.
خروجی: ماتریس ویژگی ابر نقطه ای اف.1:   اف←∅
2:   نپ←پoمنnتی جلoتود(پ)
3:   سی←جoمتربمنnآتیمنon(نپ،نسی)
4:   من←1

5:   برای هر مجموعه ترکیب نقطه پسیکه در سی انجام
6:      هر نقطه پکه در پسی انجام
7:        پr←پ
8:        پب←{پسی-پ}
9:        fآ←جآلجتولآتیهآngلهافهآتیتوrهس(پr،پب)
10:         fD←جآلجتولآتیهDمنستیآnجهافهآتیتوrهس(پr،پب)
11:         اف[من]←{پr∪پب∪fآ∪fD}
12:         من←من+1
13:    پایان برای
14:  پایان برای
15: بازگشت اف
نمادهای استفاده شده در الگوریتم به شرح زیر است: افماتریس ویژگی برای توصیفگر است (ماتریس صفر در ابتدا)، نپتعداد کل نقاط کلیدی در ابر نقطه است. پ”. سیماتریسی است که تمام زیرمجموعه های ممکن ترکیبات نقطه را در خود نگه می دارد و نجتعداد نقاط کلیدی شناسایی شده در زیر مجموعه ها است. را پrبه معنی “نقطه مرجع” و پبمعیار است. را fآتابعی است برای محاسبه کسینوس های زاویه و fDتابعی برای محاسبه فواصل اقلیدسی بین نقاط مشخصه است.
طبق این الگوریتم، ابتدا تعداد کل نقاط در لیست نقاط کلیدی با یک شماره شناسایی (به عنوان ID = 1 تا نپاین تعداد کل امتیازات است). این اطلاعات شناسه به عنوان برچسب نقاط در عملیات انجام شده استفاده می شود. سپس با استفاده از برچسب نقاط، زیر مجموعه های ممکن ( سی) شامل نجعناصر در بین تمام نقاط تولید می شود. تولید زیر مجموعه ها یک فرآیند ترکیبی پایه در الگوریتم است و در خط 3 شبه کدها بیان می شود (به الگوریتم 1 مراجعه کنید).
در نتیجه فرآیند توصیف شده، هر نقطه برجسته در یک زیر مجموعه دارای نجعناصر به عنوان یک نقطه مرجع در نظر گرفته می شود ( پr) و نقاط باقیمانده در زیر مجموعه به عنوان معیار در نظر گرفته می شوند ( پب) و این فرآیند به طور مکرر تکرار می شود. از این رو مقادیر زاویه و فاصله ( fآو fD) محاسبه می شوند و متعاقباً در یک ردیف جداگانه از عبارت نوشته می شوند اف[من]ماتریس متعلق به اطلاعات شناسه نقطه آدرس شده است. بخش داده شده از فرآیند تاکنون (همانطور که بین خطوط 7 و 11 در الگوریتم 1 ارائه شده است) فقط بخش توصیف کننده ثبت را اجرا می کند و به ما امکان می دهد ویژگی های متمایز را که برای تطبیق لازم است و بر اساس هندسه توصیف شده تعریف کنیم. روابط زاویه ای و فاصله ای بین نقاط کلیدی بالقوه.
در الگوریتم پیشنهادی، بخش توصیفگر شامل محاسبه فواصل اقلیدسی بین تمام نقاط و زوایای بین همه بردارها در زیر مجموعه است. شکل 9 محاسبه شباهت کسینوس در الگوریتم را نشان می دهد. با توجه به این تصویر، اگر زیرمجموعه را دارای چهار نقطه در نظر بگیریم، در هر تکرار یک نقطه به عنوان مرجع پذیرفته می شود و این فرض دو کسینوس زاویه و سه عنصر فاصله بین مرجع و معیارها ایجاد می کند. این تعداد پارامتر در الگوریتم را می توان به صورت ( n- 2) کسینوس زاویه و ( n -1) عناصر فاصله تعمیم داد وقتی تعداد نقاط زیر مجموعه با n نشان داده شود.. نقاطی که در نتیجه فرآیند تکراری بررسی شباهت به عنوان نقاط کلیدی شناسایی شده‌اند، عناصر ماتریس را تشکیل می‌دهند.
پس از فرآیند شناسایی، نقاط کلیدی برای مطابقت در دسترس هستند. الگوریتم 2 شبه کدهای فرآیند تطبیق اعمال شده را می دهد. در الگوریتم، مجموعه‌های نقطه فرعی از ابرهای نقطه مبدا و مقصد انتخاب می‌شوند تا نقاط کلیدی بین ابرهای دو نقطه‌ای مطابقت داشته باشند. بر این اساس، پاس، پتی، نجو تیآپارامترهای ورودی در الگوریتم هستند. پاسو پتیبه ترتیب ابرهای نقطه مبدا و مقصد هستند. نجتعداد نقاط زیر مجموعه هایی است که از هر ابر نقطه در هر تکرار انتخاب می شوند. این پارامترها نیز با همان نمادها در الگوریتم 1 گنجانده شده است. تیآیک پارامتر آستانه برای تعیین شباهت های هندسی مبتنی بر زاویه است. در خروجی الگوریتم، اطلاعات مجموعه‌های نقاط منطبق انتخاب شده از ابرهای نقطه مبدا و مقصد که بیشترین شباهت را نشان می‌دهند در ماتریسی با نام گنجانده شده است. ممدر الگوریتم
در الگوریتم 2، ویژگی‌های زیرمجموعه‌های نقطه‌ای که با استفاده از الگوریتم 1 برای ابرهای نقطه مبدا (با شاخص S مشخص شده ) و هدف (با شاخص T مشخص شده است) تعیین می‌شوند، محاسبه می‌شوند. این فرآیند در خطوط 1 و 2 الگوریتم مشاهده می شود و خواص محاسبه شده با افاسو افتیکه شامل خروجی های الگوریتم 1 می شود. سپس، فواصل بین نقاط و زوایا بین بردارهای مجموعه نقاط کلیدی در ابر نقطه مبدا با همان ویژگی های مجموعه نقاط کلیدی در ابر نقطه هدف مقایسه می شود. در خطوط 6 و 7 الگوریتم 2، بررسی شباهت کدگذاری شده است. در خطوط، متغیرها اسآو اسDبه ترتیب تفاوت بین خصوصیات شباهت زاویه و خصوصیات شباهت فاصله است. سپس اطلاعات شناسه ( Lاسو Lتی) از نقاطی که ویژگی های مربوط به آنها تعلق دارد و شباهت های محاسبه شده از این ویژگی ها در a ذخیره می شود ماستیماتریس
پس از اسآو اسDمحاسباتی که به ترتیب معین و به دنبال چرخش عقربه های ساعت انجام می شوند ماستیماتریس به گونه ای سازماندهی شده است که ردیف هایی با نزول داشته باشد اسآارزش های. ردیف ها با تیآمقادیر کوچکتر از آستانه در ماتریس انتخاب می شوند. این سطرهای انتخاب شده با نقاط زیر مجموعه با بیشترین شباهت در ابرهای نقطه مبدا ( S ) و هدف ( T ) مطابقت دارند. پس از آن، این ردیف ها که در a ثبت می شوند ممماتریس، دوباره مرتب می شوند تا نزولی داشته باشند اسDمقادیر، و از این رو زیر مجموعه بهینه نقاط برای هدف تطبیق تعیین می شود. به طور خلاصه از روند انجام شده، نقاط به طور تقریبی با توجه به شباهت زاویه ای انتخاب شده و با توجه به شباهت مبتنی بر فاصله مرتب می شوند. در مرحله آخر الگوریتم توصیف و تطبیق ما، نقاطی که اختلاف فاصله نزدیک به مقادیر صفر دارند به عنوان نقاط کلیدی مشترک ابرهای نقطه انتخاب می شوند.
الگوریتم 2. انتخاب مجموعه های فرعی از ابرهای نقطه مبدا و مقصد برای تطبیق.
ورودی: ابرهای نقطه منبع و هدف هستند پاسو پتیتعداد زیر نقطه هایی که قرار است از ابر نقطه انتخاب شوند می باشد نسی، آستانه فاصله برای تشابه ویژگی های مبتنی بر زاویه است تیآ.
خروجی: ماتریس ممذخیره سازی اطلاعات مربوط به مجموعه های فرعی از پاسو پتی.1:  افاس←جآلجتولآتیهپoمنnتیسیلoتودافهآتیتوrهس(پاس، نسی)
2:  افتی←جآلجتولآتیهپoمنnتیسیلoتودافهآتیتوrهس(پتی،نسی)
3:  من←1

4:  برای هر بردار ویژگی fاسدر ماتریس ویژگی افاس انجام
5:      برای هر بردار ویژگی fتیدر ماتریس ویژگی افتی انجام
6:        اسآ=norمترL1(fاس(آngله fهآتیتوrهس)، fتی(آngله fهآتیتوrهس))
7:        اسD=norمترL1(fاس(دمنستیآnجه fهآتیتوrهس)، fتی(دمنستیآnجه fهآتیتوrهس))
8:        Lاس=fاس(پoمنnتی fهآتیتوrهس)
9:        Lتی=fتی(پoمنnتی fهآتیتوrهس)
10:         ماستی[من]←{Lاس∪Lتی∪اسآ∪اسD}
11:         من←من+1
12:     پایان برای
13:  پایان برای

14:  سorتی تیساعته rowس of ماستی بy دهسجهnدمنng orدهr of اسآ
15:  جoپy تیساعته rowس of ماستی تیo مترآتیrمنایکس مم wساعتهrه اسآ≤تیآ
16:  سorتی تیساعته rowس of مم بy دهسجهnدمنng orدهr of اسD
17: بازگشت مم
مراحل پردازش توصیفگر و الگوریتم های تطبیق (به شبه کدهای ارائه شده در الگوریتم های 1 و 2 مراجعه کنید) روش پیشنهادی نیز با یک نمودار جریان در شکل 10 خلاصه شده است.
2.2.3. الگوریتم تکراری نزدیکترین نقطه (ICP).
الگوریتم تکراری نزدیکترین نقطه ثبت دو ابر نقطه درشت تراز را تکمیل می کند. از این رو، هدف آن ارائه داده های ابر نقطه ترکیبی در پایان فرآیند است. اساساً، یک الگوریتم ICP این چهار مرحله را دنبال می‌کند: (1) شناسایی و انتخاب نقاط کلیدی. (2) تطبیق نقاط بر اساس اصل اختلاف حداقل فاصله. (iii) محاسبه چرخش R( αایکس، αy، αz) و ترجمه های T( δایکس، δy، δz) (IV) ارائه یک تراز بهینه در نتیجه فرآیند تکرار شونده [ 5 ، 41 ]. تکرارها در الگوریتم تا زمانی ادامه می یابند که ریشه میانگین مربعات خطای باقیمانده تبدیل تحت یک مقدار آستانه از پیش تعیین شده کاهش یابد ( τ>0) یا یک عدد تکرار معین ( آ) [ 5 ]. شکل 11 مراحل الگوریتم ICP را نشان می دهد.

الگوریتم تکراری نزدیکترین نقطه (ICP) را می توان با داده های هندسی مختلف از جمله مجموعه نقطه، چند خط، منحنی ضمنی و پارامتری، سطوح وجهی مثلثی استفاده کرد. در اصل، الگوریتم ICP این نمایش های هندسی را با ارزیابی نزدیک ترین نقاط در دو مجموعه داده مدیریت می کند. در فرمول بندی الگوریتم، پبه معنای شکل “داده” (هدف) است که برای بهترین همسویی با آن جابجا شده (ثبت شده) ایکسبه عنوان یک شکل “مدل” (منبع) [ 5 ]. فاصله ” دبین یک نقطه داده فردی پ→از پو یک مدل ایکسدر معادله (18) نشان داده شده است.

د(پ→،  ایکس)=دقیقهy→∈ایکس “y→-پ→”
در معادله، نزدیکترین نقطه در ایکسکه حداقل فاصله را با نشان می دهد y→و د(پ→، y→)=د(پ→، ایکس)که y→∈ایکس. نزدیکترین نقطه (از پ→به ایکس) برای هر نقطه محاسبه می شود پ[ 5 ].
یکی از مسائل اساسی در الگوریتم ICP تبدیل مختصات سه بعدی است. قبل از ثبت ICP، تراز درشت ابرهای نقطه، فرآیند تبدیل مختصات را نیز درگیر کرده است. بنابراین، ثبت درشت ابرهای نقطه شامل تخمین پارامترهای تبدیل هلمرت سه بعدی شامل سه ترجمه، سه زاویه چرخش و یک ضریب مقیاس، در فرآیند ترکیب می شود [ 42 ].]. به عنوان متفاوت از فرآیند تبدیل در تراز درشت، تعداد پارامترهای تخمین زده شده در بخش ثبت دقیق ICP تنها شش شامل ترجمه و چرخش است. از آنجایی که ضریب مقیاس در ثبت درشت یک بار تخمین زده می شود، از پارامترهای تخمین زده شده در تکرارهای ICP حذف می شود. بسته به دقت به دست آمده از تبدیل 3 بعدی تخمین زده شده، فرآیند ثبت به عنوان ثبت درشت یا ریز طبقه بندی می شود [ 43 ]. ثبت درشت تراز ناهمواری ابرهای نقطه ای را فراهم می کند و بسته به هدف مطالعه ممکن است کافی باشد. با این حال، در برنامه‌هایی که دقت بالاتر مورد نیاز است، ثبت دقیق مورد نیاز است و فرآیند جریمه‌سازی پس از هم‌ترازی اولیه ابرهای نقطه با ثبت درشت آغاز می‌شود [ 44 ]].

تبدیل تشابه هلمرت هفت پارامتری معمولاً در ثبت ابرهای نقطه اعمال می شود. نقاط کلیدی مزدوج که برای ابرهای نقطه شناسایی، شناسایی و مطابقت داده شده اند (نقاط کلیدی مزدوج برای ابرهای نقطه اول و دوم qمن، پمنکه من= 1،2… متر) در قسمت ثبت درشت، برای تخمین هفت پارامتر تبدیل استفاده می شود ( δایکس، δy، δz، αایکس، αy، αz، س). تبدیل شباهت هلمرت سه بعدی به صورت فرمول بندی شده در رابطه (19) است:

[ایکسمن2Yمن2زمن2]=[δایکسδyδz]+س.آر(α1،α2،α3).[ایکسمن1Yمن1زمن1]
در معادله، مختصات دکارتی یک نقطه کلید مزدوج در ابر نقطه اول و دوم است. qمن( ایکسمن1، Yمن1، زمن1) و پمن( ایکسمن2، Yمن2، زمن2)، به ترتیب. پارامترهای چرخش در یک ماتریس چرخش متعامد ارزیابی می شوند آر(αایکس، αy، αz)و به پارامترهای ترجمه اضافه شد تی(δایکس، δy، δz)پس از ضرب با ضریب مقیاس ( س) [ 45 ].

هفت پارامتر تبدیل ارائه شده در معادله (19) با استفاده از مختصات شناخته شده حداقل سه نقطه کلیدی مزدوج در هر دو ابر نقطه تخمین زده می شود و در صورت در دسترس بودن نقاط کلیدی رایج تر، پارامترهای تبدیل را می توان با تنظیم حداقل مربعات نیز با اتخاذ موارد داده شده محاسبه کرد. شرط در معادله (20) [ 46 ]:

[vتیپv]=دقیقه.

جایی که، vماتریس باقی مانده است و پماتریس وزن قابل مشاهده‌ها است که به تخمین پارامتر در مدل ریاضی روش تعدیل حداقل مربعات کمک می‌کند.

پس از تخمین پارامترهای تبدیل با دقت کافی، امکان تبدیل مختصات یک ابر نقطه هدف ( qمن; من= 1،2…  متر) در ابر نقطه مبدا ( پمن; من = 1،2…  متر) با موفقیت. در این مرحله، مسئله مهم تعیین پارامترهای تبدیل تا حد امکان دقیق است. به منظور افزایش دقت پارامترها، بهبود گام به گام مقادیر تخمینی به صورت تکراری یک رویکرد موثر و به طور کلی کاربردی است.
به غیر از روش مرسوم ICP که توسط Besl و McKay [ 5 ] معرفی شده است، انواع بسیاری از این الگوریتم توسعه و استفاده شده است. در این فرمول‌بندی‌های متفاوت، سعی شد عملکرد الگوریتم اصلی با استفاده از دقت و همچنین کارایی پردازنده در محاسبات افزایش یابد [ 47 ]. Zhang [ 48 ] تکنیک ICP معمولی را با جایگزینی تابع خطا با یک هسته قوی [ 49 ] افزایش داد. چن و مدیونی [ 50 ] الگوریتم را با جایگزینی فاصله نقطه به نقطه با تعریف صفحه نقطه به مماس [ 51 ] اصلاح کردند.

3. نتایج

3.1. عملکرد الگوریتم های تشخیص نقطه کلیدی

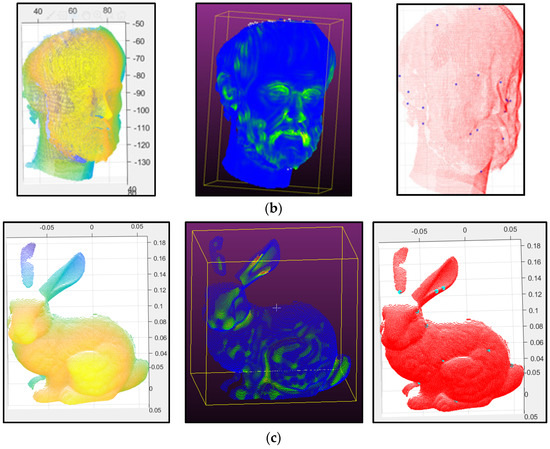
مطالعه موردی آزمایش الگوریتم تشخیص پیشنهادی که در این مطالعه معرفی کردیم، با استفاده از سه مجموعه داده مختلف شامل نمای ساختمان، ابرهای نقطه‌ای مجسمه‌های اسم حیوان دست اموز ارسطو و استانفورد انجام شد. مجموعه داده ها در بخش 2.1 توضیح داده شده است . در الگوریتم تشخیص پیشنهادی، میانگین انحنای سطح محاسبه شد. سپس داده ها با توجه به معیار انحنای بهینه که تغییرات انحنای محاسبه شده در نقاط را در نظر می گیرد، فیلتر شد. پس از آن، یک فیلتر مبتنی بر وکسل اعمال شد ( شکل 12 را ببینید ).
نتیجه فیلتر کردن داده های ابر نقطه اسکن لیزری زمینی بر روی نمای ساختمان در شکل 12 الف با وکسل ها قابل مشاهده است و نتایج فیلتر مجسمه ها که با توجه به مقادیر انحنا رنگی شده اند در شکل 12 ب برای نشان داده شده است. ارسطو و شکل 12 ج برای اسم حیوان دست اموز استانفورد. در فرآیند اولیه، فیلتر کردن ابر نقطه یکی از مراحل حیاتی است که قبل از شناسایی نقاط کلیدی مربوطه اعمال می شود.
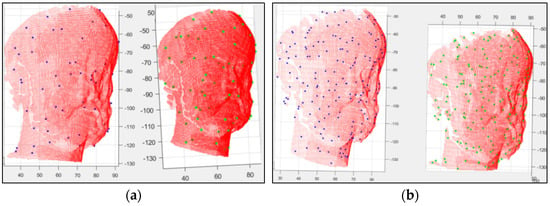
به منظور ارائه نتایج مقایسه‌ای روی روال‌های تشخیص نقطه کلیدی و بحث در مورد نقش آنها در عملکرد ICP، روش‌های امضاهای شکل ذاتی (ISS) و پچ سطح محلی (LSP) را در آزمون‌های عددی با استفاده از تمام مجموعه‌های داده اعمال کردیم. پیشینه نظری و فرمول بندی این روش ها قبلاً در بخش 2.2.1 توضیح داده شده است . در نتیجه فرآیند تشخیص نقطه کلید با استفاده از داده های ابر نقطه مجسمه ارسطو، تعداد نقاط کلیدی شناسایی شده برای هر ابر نقطه با الگوریتم ISS ~ 60 نقطه و با الگوریتم LSP ~ 180 نقطه است. شکل 13چگالی و توزیع نقاط کلیدی شناسایی شده را با هر الگوریتم تجسم می کند. از سوی دیگر، تعداد نقاط کلیدی شناسایی شده با الگوریتم جدید برای مجسمه ارسطو 18 است.
با استفاده از مجموعه داده های ابر نقطه ای به دست آمده از اندازه گیری های اسکن لیزری زمینی (TLS) و اسکن لیزری سیار (MLS) برای نمای ساختمان، الگوریتم ISS 34 نقطه کلیدی را در داده های ابر نقطه TLS و 88 نقطه کلیدی را در داده های ابر نقطه MLS نشان داد، در حالی که الگوریتم LSP حدود 200 نقطه کلیدی را برای هر مجموعه داده ابر نقطه به دست آمده از تکنیک های TLS و MLS شناسایی کرد. شکل 14 توزیع نقاط کلیدی شناسایی شده را با استفاده از الگوریتم های ISS و LSP از دو ابر نقطه TLS و MLS نشان می دهد. با استفاده از الگوریتم پیشنهادی، تعداد تقریبی نقاط کلیدی شناسایی شده با توجه به فیلتر کردن انحناهای محاسبه شده در ابرهای نقطه TLS و MLS 30 برای نمای ساختمان است ( شکل 12 a و شکل 18 را ببینید).
در نتیجه فرآیند تشخیص نقطه کلید با استفاده از داده های ابر نقطه مجسمه اسم حیوان دست اموز استانفورد، تعداد نقاط کلیدی شناسایی شده برای هر ابر نقطه با الگوریتم ISS ~ 150 نقطه و با الگوریتم LSP ~ 350 نقطه است. از سوی دیگر، تعداد نقاط کلیدی شناسایی شده با الگوریتم پیشنهادی 14 برای مجسمه اسم حیوان دست اموز استانفورد است ( شکل 12 ج و شکل 19 را ببینید).

3.2. تست های عملکرد توصیفگر نقطه کلیدی و الگوریتم های تطبیق

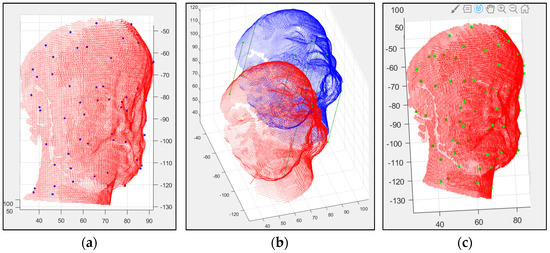
در الگوریتم توصیفگر پیشنهادی، مقادیر کسینوس زاویه بین بردارهای جهت سه بعدی محاسبه می‌شود و شباهت‌های کسینوس بین هندسه‌های مزدوج جستجو می‌شود. اصالت قابل توجه الگوریتم ثبت، که در این مقاله معرفی و آزمایش شده است، در پس روش توصیف و تطبیق آن نهفته است. جزئیات نظری توضیحات و بخش تطبیق الگوریتم در بخش 2.2.2 توضیح داده شده است. در داده های ابر نقطه مجسمه ارسطو، پنج نقطه از 18 نقطه کلیدی با توضیحات و روال تطبیق الگوریتم ما مطابقت داشت. شکل 15 توزیع نقاط کلیدی منطبق بر مجسمه ارسطو را نشان می دهد.
علاوه بر الگوریتم جدید، نقاط کلیدی که با توجه به هیستوگرام‌های نقطه کلیدی به‌دست‌آمده از توصیفگر PFH با کمک آشکارسازهای ISS و LSP مطابقت داده شده‌اند نیز در مطالعه مورد استفاده قرار گرفتند. در نتیجه فرآیند ISS+PFH، شش نقطه از 60 نقطه کلیدی شناسایی شده برای مجموعه داده های ابر نقطه مجسمه ارسطو مطابقت داده شد ( شکل 16 ). با پیروی از الگوریتم LSP+PFH، هشت نقطه از ~180 نقطه کلیدی شناسایی شده برای مدل سازی مجسمه ارسطو مطابقت داده شد ( شکل 17 ).
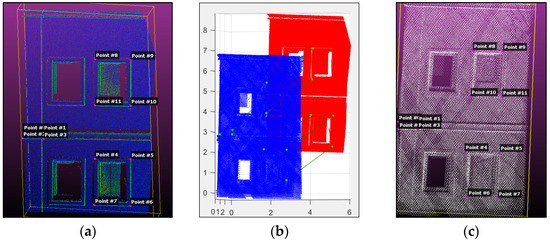
در توصیف و روش تطبیق که برای نمای ساختمان با استفاده از داده‌های اسکن لیزری زمینی (TLS) و سیار (MLS) انجام شد، فرآیند خودکار الگوریتم‌ها (ISS+PFH، LSP+PFH، الگوریتم پیشنهادی) موفقیت‌آمیز نبود. نتایج برای مطابقت با نقاط مزدوج. این عمدتاً به دلیل اختلاف زیاد بین مجموعه نقاط کلیدی شناسایی شده در هر ابر نقطه و در نتیجه عدم ایجاد روابط مشابه برای تطبیق است. برخلاف فرآیند توصیف و تطبیق خودکار، روش نیمه خودکار پردازش که در آن نقاط برجسته با استفاده از معیارهای فرمول‌بندی شده در بخش 2.2.1 شناسایی می‌شوند.، و با توجه به راحتی آنها برای شباهت به صورت دستی انتخاب شدند، نتیجه دادند. در این بخش از فرآیند ابرهای نقطه نمای ساختمان، فرآیندهای فیلتر و تشخیص با در نظر گرفتن میانگین انحناها در نقاط با استفاده از الگوریتم تشخیص ما انجام شد. پس از آن، نقاط کلیدی شناسایی شده به عنوان خروجی الگوریتم تشخیص به صورت دستی به توضیحات پیشنهادی و الگوریتم تطبیق داده شدند. شکل 18 نقاط مزدوج را نشان می دهد که با استفاده از تطبیق نیمه خودکار نقاط کلیدی شناسایی شده با آشکارساز جدید (الگوریتم های 1 و 2) مطابقت داده شده اند.
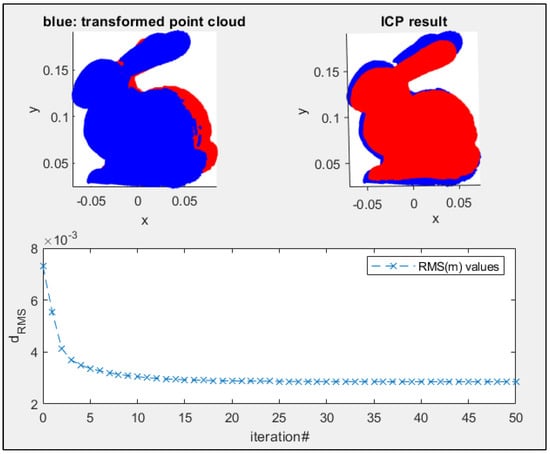
در داده‌های ابر نقطه مجسمه اسم حیوان دست اموز استانفورد، پنج نقطه از 14 نقطه کلیدی با توضیحات و روال تطبیق الگوریتم ما مطابقت داشت. نمودار دوم شکل 19 توزیع نقاط کلیدی تطبیق شده مجسمه خرگوش را نشان می دهد. علاوه بر الگوریتم جدید، فرآیند ISS+PFH توانست تنها سه نقطه از ~150 نقطه کلیدی شناسایی شده را مطابقت دهد. از سوی دیگر، الگوریتم LSP+PFH هیچ تطابقی بین 350 نقطه کلیدی شناسایی شده ارائه نکرد.

3.3. اعتبارسنجی عددی الگوریتم های کاربردی در ثبت دقیق با روش ICP

تعیین دقت بالا پارامترهای تبدیل مختصات بین ابرهای نقطه ای در ترکیب مجموعه داده ها برای تولید یک مدل یکپارچه از اشیاء سه بعدی بسیار مهم است. تراز اولیه ابرهای نقطه به طور مناسب با پارامترهای تبدیل از پیش تعریف شده در مرحله ثبت درشت نقش اساسی در عملکرد کلی ثبت ریز با استفاده از ICP دارد. در این مطالعه، ما از روش تعدیل گاوس-مارکوف در محاسبه پارامترهای تبدیل با استفاده از روابط شباهت بین نقاط منطبق تعیین شده در بخش 3.2 استفاده کردیم و نتایج را با در نظر گرفتن ریشه میانگین مربعات خطا (RMSE) تبدیل و تکرار ارزیابی کردیم. اعداد همگرایی محاسباتی
در آزمایش‌ها، از سه مجموعه داده مطالعه موردی (شامل مجسمه ارسطو، نمای ساختمان، و مجسمه اسم حیوان دست اموز استانفورد) استفاده شد. اعتبار سنجی عددی با استفاده از سه الگوریتم ثبت نام درشت مختلف (ISS+PFH، LSP+PFH، الگوریتم هدف جدید) انجام شد. در اعتبارسنجی با استفاده از هر مجموعه داده، نقاط کلیدی تطبیق داده شده به عنوان خروجی هر الگوریتم ثبت درشت، ثبت دقیق مجموعه داده‌های ابر نقطه با روش نزدیکترین نقطه تکراری (ICP) انجام شده است. موفقیت الگوریتم های ثبت درشت آزمایش شده از جمله الگوریتم پیشنهادی از طریق دقت ثبت نام دقیق با استفاده از مقادیر RMSE رسیده در تکرارهای ICP ارزیابی و مقایسه شد.
اولین آزمایش با استفاده از ابرهای نقطه ای درشت تراز شده با نقاط کلیدی تطبیق شده برای مجسمه ارسطو با استفاده از الگوریتم ISS+PFH انجام شد. جدول 1 پارامترهای تبدیل محاسبه شده با شش نقطه مزدوج شناسایی شده با الگوریتم ISS+PFH و استفاده برای تراز درشت ابرهای نقطه را نشان می دهد. در همین جدول، پارامترهای تبدیل برای زوایای چرخش کوچک و بزرگ در میان محورهای دو سیستم مختصات، که در معرض تبدیل هستند، آورده شده است. هنگامی که دو مجموعه از پارامترهای تبدیل با هم مقایسه می شوند، مشاهده می شود که پارامترهای محاسبه شده دقت بالاتری دارند و بنابراین مقدار RMSE تبدیل زمانی که زوایای چرخش بزرگتر است کوچکتر می شود.
در جدول 1 ، مقدار RMSE تبدیل است مترo; δایکس، δy، δzپارامترهای ترجمه با مقادیر RMSE آنها (به سانتی متر) هستند و αایکس، αy، αzپارامترهای چرخش با مقادیر RMSE آنها (به رادیان) و s ضریب مقیاس با دقت آن است.
شکل 20 نتایج به دست آمده از پالایش تکراری پارامترهای تبدیل با استفاده از ICP برای مجموعه داده های مجسمه ارسطو را خلاصه می کند. در تصاویر داده شده در شکل، ابرهای نقطه قبل و بعد از فرآیند تبدیل با استفاده از پارامترهای تبدیل نهایی ICP آورده شده است. همانطور که از نمودار داده شده در زیر تصاویر مشاهده می شود، مقدار RMSE ICP در تکرار بیستم همگرا شد و دقت تکرارهای ICP از 7.0 سانتی متر به 0.9 سانتی متر کاهش یافت که نقاط کلیدی با استفاده از الگوریتم ISS+PFH مطابقت داشتند.
آزمایش دوم با استفاده از ابرهای نقطه‌ای درشت تراز شده با نقاط کلیدی منطبق برای مجسمه ارسطو اما این بار با استفاده از الگوریتم LSP+PFH انجام شد. جدول 2 پارامترهای تبدیل محاسبه شده با هشت نقطه مزدوج شناسایی شده با الگوریتم LSP+PFH را نشان می دهد و برای تراز درشت ابرهای نقطه استفاده می شود. با توجه به آمار ارائه شده در جدول، پارامترهای تبدیل محاسبه شده برای ابرهای نقطه ای با زوایای چرخش بزرگ در میان محورهای مختصات، دقت بالاتری دارند و در نتیجه تبدیل نسبتاً دقیق تری را ارائه می دهند.
شکل 21 تصاویر گرافیکی ابرهای نقطه را قبل و بعد از ثبت دقیق با ICP و کاهش مقادیر RMSE تبدیل با افزایش تعداد تکرارها در نمودار زیر نشان می دهد. با در نظر گرفتن این نمودار، مشاهده می شود که مقدار RMSE ICP در تکرار 30 همگرا شده و دقت تبدیل با استفاده از الگوریتم تطبیق LSP+PFH از ~6.0 سانتی متر به ~1.0 سانتی متر کاهش یافته است. در مقایسه با نتایج ICP ابرهای نقطه‌ای که تقریباً با استفاده از الگوریتم ISS+PFH تراز شده‌اند، دقت نهایی به‌دست‌آمده در نتیجه آزمایش دوم بدتر است و هم‌گرایی تکرارها زمان بیشتری را می‌برد. به طور خلاصه، فرآیند ICP بعد از هر دو ISS+PFH و LSP+PFH دقت های مشابهی در حدود ~1.0 سانتی متر داد.
در آخرین آزمایش با داده‌های مجسمه ارسطو، ثبت دقیق ابرهای نقطه‌ای که با استفاده از الگوریتم پیشنهادی جدید تراز شده‌اند، با روش ICP انجام شد. جدول 3 پارامترهای تبدیل محاسبه شده با پنج نقطه مزدوج شناسایی شده با الگوریتم جدید و استفاده برای تراز درشت ابرهای نقطه را نشان می دهد. با توجه به آمار ارائه شده در جدول، دقت تبدیل بین ابرهای نقطه با استفاده از نقاط مزدوج توسط الگوریتم جدید بیشتر از دقت به‌دست‌آمده در دو آزمون قبلی بود. علاوه بر این، مشابه آزمایش‌های قبلی، پارامترهای تبدیل با دقت بالاتر با زوایای چرخش بزرگ‌تر به‌دست آمد.
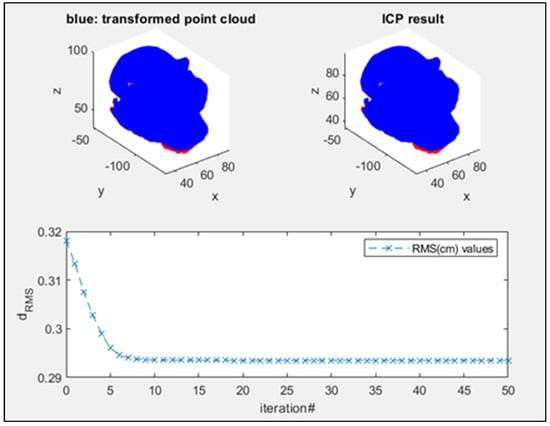
در شکل 22 ، عملکرد روش ICP پس از ثبت درشت با الگوریتم جدید با گرافیک بصری ابرهای نقطه قبل و بعد از تطبیق نشان داده شده است. مقدار RMSE ICP در تکرار دهم همگرا شد، که به معنای بهبود قابل توجهی در عملکرد الگوریتم ثبت در مقایسه با سایر الگوریتم‌های آزمایش شده در آزمون‌های قبلی است. آمار دقت تکرارها 0.29 سانتی متر کاهش یافت در حالی که برای سایر الگوریتم ها بهتر از 0.90 سانتی متر نبود.
روش ICP برای داده های نمای ساختمان نیز اعمال شد. در فرآیند ثبت نام درشت، از نقاط کلیدی ابر نقطه TLS و MLS و نقاط مزدوج نیمه خودکار شناسایی شده با استفاده از الگوریتم جدید استفاده شد. در ارزیابی مجموعه داده‌های نمای ساختمان، ارزیابی خودکار الگوریتم‌های ISS+PFH و LSP+PFH با موفقیت در ثبت نام درشت اعمال نشده‌اند زیرا هیچ نقطه کلیدی با موفقیت مطابقت نداشت. بنابراین، نقاط کلیدی برای تراز درشت ابرهای نقطه به صورت دستی از نقاط برجسته مانند گوشه های پنجره شناسایی شدند ( شکل 18 را ببینید.) و با فرآیند تطبیق نیمه خودکار با الگوریتم PFH آشنا شد. با این حال، این آزمایش برای تطبیق با الگوریتم PFH نیز موفقیت آمیز نبود. الگوها، ویژگی‌ها و وضوح داده‌های ابر دو نقطه‌ای که از سیستم‌عامل‌های زمینی و سیار با استفاده از حسگرهای مختلف به دست آمده‌اند، احتمالاً باعث این ناهماهنگی شده‌اند و بنابراین فرآیندهای خودکار و نیمه خودکار در تطبیق نقاط کلیدی با شکست مواجه شده‌اند. تنها راه حل برای تطبیق نقاط کلیدی مجموعه داده نمای ساختمان، اعمال تطبیق نیمه خودکار با روش پیشنهادی جدید بود. در این راه حل، نقاط کلیدی به صورت دستی از نقاط برجسته شناسایی شدند و در الگوریتم تطبیق جدید قرار گرفتند.
در جدول 4 ، پارامترهای تبدیل بین ابرهای نقطه TLS و MLS در فرآیند ثبت درشت با استفاده از نقاط مشترک شناسایی شده نیمه خودکار با استفاده از الگوریتم جدید آورده شده است. در شکل 23 ، عملکرد روش ICP برای مجموعه داده های نمای ساختمان نشان داده شده است. با توجه به گرافیک داده شده، مقدار RMSE ICP در تکرار 50 همگرا شد و 0.02 متر کاهش یافت.
روش ICP نیز با استفاده از مجموعه داده اسم حیوان دست اموز استانفورد نیز اعمال شد. در این فرآیند، ابرهای درشت نقطه تراز شده با پنج نقطه کلیدی که با استفاده از الگوریتم جدید مطابقت داشتند، درج شدند. جدول 5 پارامترهای تبدیل محاسبه شده را در نتیجه تراز درشت نشان می دهد. در شکل 24 ، عملکرد روش ICP پس از ثبت درشت با الگوریتم جدید با گرافیک بصری ابرهای نقطه اسم حیوان دست اموز قبل و بعد از تطبیق نشان داده شده است. ارزش RMSE در پانزدهمین تکرار ICP به میزان 0.29 سانتی متر کاهش یافت.
از آنجایی که روش LSP+PFH هیچ نقطه کلید مزدوج را در نتیجه فرآیند تطبیق با استفاده از داده‌های خرگوش ارائه نمی‌کند، تراز درشت امکان‌پذیر نبود. روش ISS+PFH تنها سه نقطه کلید مزدوج را خروجی می دهد که به طور مساوی روی شی توزیع نشده اند. الگوریتم ICP با استفاده از ابرهای درشت نقطه تراز شده با سه نقطه کلید مزدوج توسط روش ISS+PFH، مقدار RMSE ~0.50 سانتی متر را در تکرار پانزدهم برای مجموعه داده اسم حیوان دست اموز ارائه کرد.

4. بحث

ما در این مطالعه روش جدیدی را برای تشخیص، توصیف و تطبیق خودکار نقاط کلیدی برای ثبت نام درشت ابر نقطه سه بعدی ایجاد و معرفی کردیم. بخش اول روش جدید شامل یک الگوریتم تشخیص نقطه کلید سه بعدی است که بر اساس اصول کار مشابه با روش های ISS و LSP فرموله شده است. در بخش دوم، توصیفگر سه بعدی (الگوریتم 1) و الگوریتم های تطبیق نقاط کلیدی سه بعدی (الگوریتم 2) طراحی و کدگذاری شد. این بخش دوم از الگوریتم طراحی شده با تعریف پیکربندی هندسی در بین نقاط برجسته با توجه به ترکیبات عددی دیفرانسیل نسبت به نمونه های خود متفاوت است (به بخش 2.2.2 مراجعه کنید..) و همچنین کارایی محاسباتی. از این رو، شامل مشارکت اصلی است. به منظور مقایسه الگوریتم جدید با الگوریتم های رایج، آشکارسازهای ISS و LSP را با روال توصیفگر PFH در تست های عددی قرار دادیم. تبدیل بین ابرهای نقطه ای با استفاده از نقاط همسان در الگوریتم ها با استفاده از روش تبدیل تشابه هلمرت انجام شد. بخش ثبت جریمه با استفاده از روش ICP همانطور که در بخش 2.2.3 فرموله شده است انجام شده است . نتایج اعتبارسنجی سه مطالعه موردی عملکرد برتر الگوریتم جدید و سهم آن در عملکرد ثبت خوب با ICP را با استفاده از موفقیت در ترکیب ابرهای دو نقطه‌ای با ثبت دقت بالاتر با تعداد تکرارهای کمتر، روشن کرد.
در آزمایش‌های عددی با استفاده از داده‌های ابر نقطه‌ای به‌دست‌آمده از دیدگاه‌های تغییر یافته با اندازه‌گیری‌های اسکن لیزری فوق‌العاده HD با همان اسکنر لیزری سه‌بعدی برای مجسمه‌های کوچک (خرگوش ارسطو و استنفورد)، تشخیص خودکار نقطه کلید، توصیف و الگوریتم‌های تطبیق با موفقیت در ثبت نام درشت کار کردند. از ابرهای نقطه با این حال، مقایسه مقادیر RMSE تبدیل در ثبت درشت، برتری الگوریتم جدید را نسبت به همتایان آزمایش شده خود ثابت کرد (نتایج آزمون را در بخش 2.2.3 ببینید..). ثبت دقیق با روش ICP پس از ثبت درشت با تشخیص، توصیف و الگوریتم‌های تطبیق آزمایش شده با استفاده از داده‌های ابر نقطه مجسمه‌ها انجام شد. در آزمایشات با الگوریتم ICP، کارایی به دست آمده در بهبود تکراری ثبت، عملکرد برتر الگوریتم جدید را در تطبیق نقاط کلیدی برای ثبت خودکار مجموعه داده‌های ابر نقطه تأیید کرد. با روش ICP، می توان RMSE ~ 0.29 سانتی متر را در یک زمان همگرای معقول با استفاده از الگوریتم جدید به دست آورد، در حالی که دقت قابل دستیابی با مجموعه نقاط کلیدی مطابق با ISS+PFH و LSP+PFH ~1.00 سانتی متر برای مجسمه ارسطو و ~0.50 سانتی متر برای اسم حیوان دست اموز استانفورد (فقط ISS+PFH برای خرگوش موجود است) در بهترین حالت در زمان همگرایی طولانی تر. این نتیجه اهمیت همسویی اولیه با فرآیند ثبت درشت را برای تولید مدل‌های بهبودیافته از ابرهای نقطه‌ای به کار گرفته شده با تغییر اندازه‌گیری کرد. در ادبیات، می‌توان مطالعات تحقیقاتی مشابهی را در مورد بررسی عملکرد الگوریتم‌های تشخیص خودکار نقطه کلید و تأثیرات آن‌ها بر تولید مدل‌های سه‌بعدی یافت. در میان این مطالعات، یو و لی [52 ] اخیراً تحقیقاتی را با الگوریتم‌های ISS+FPFH و ISS+3DFeat-Net انجام داد و نتایجی را یافت که نتایج ما را در مورد عملکرد تأیید می‌کند.
آزمایش دیگری با الگوریتم‌های آزمایش‌شده با مجموعه داده‌های ابر نقطه‌ای یک نمای ساختمان، به‌دست‌آمده از اندازه‌گیری‌های فضای باز با استفاده از دو اسکنر لیزری مختلف که روی یک سه‌پایه ثابت در یک ایستگاه زمینی و یک وسیله نقلیه زمینی متحرک نصب شده‌اند، انجام شد. با این حال، توصیف خودکار و الگوریتم‌های تطبیق نقاط کلیدی ابرهای نقطه با هر آشکارساز نتایج موفقیت‌آمیزی نداشت و در ثبت ناموفق بود. یکی از دلایل مهم شکست فرآیند ثبت خودکار، تفاوت بین وضوح و کیفیت داده‌های ابری دو نقطه‌ای است زیرا با استفاده از اسکنرهای لیزری مختلف بر روی پلت فرم‌های ثابت و متحرک به‌دست آمده‌اند. انتخاب نیمه خودکار و ارزیابی نقاط کلیدی از داده های نمای ساختمان مشکل را جبران کرد. در نتیجه، تطبیق نقاط کلیدی برای تبدیل در ثبت درشت با نقاط کلیدی تغذیه دستی به الگوریتم نیمه خودکار انجام شد. در آزمایش‌های ICP با داده‌های نمای ساختمان، ابرهای نقطه‌ای در ابتدا با استفاده از الگوریتم جدید نتایج قابل اجرا را با استفاده از مقدار RMSE نهایی ICP (~2.0 سانتی‌متر) در یک عدد تکرار همگرای معقول ارائه کردند و از این رو صلاحیت آن در ترکیب ابرهای نقطه‌ای به دست آمده توسط اندازه گیری از سیستم عامل های مختلف ثابت شده است.
الگوریتم پیشنهادی در عمل دارای نقاط قوت و ضعف است. روش پیشنهادی مقادیر RMSE کوچکتری را در اعداد تکرار کمتر نسبت به الگوریتم‌های ISS+PFH و LSP+PFH ارائه می‌کند. عملکرد بهتری را در توضیحات و مطابقت با نکات کلیدی ارائه می دهد. اگرچه تعداد نقاط کلیدی شناسایی‌شده با الگوریتم پیشنهادی حتی کمتر از سایر الگوریتم‌های ثبت درشت است، اما ثبت دقیق ابرهای نقطه‌ای که ابرهای نقطه‌ای درشت با الگوریتم پیشنهادی تراز شده بودند، مقادیر RMSE کوچک‌تری را در روش ICP ارائه کردند. این روش نسبت به روش های ISS+PFH و LSP+PFH به ویژه در ثبت درشت ابرهای نقطه ای با وضوح های مختلف به دست آمده از اسکنرهای لیزری مختلف برتری دارد.
از آنجایی که الگوریتم توصیف و تطبیق روش پیشنهادی مبتنی بر روش ترکیبی است و از آنجایی که مقادیر فاصله و زاویه برای تمامی ترکیب‌های نقطه‌ای در زیر مجموعه محاسبه می‌شود، مقادیر زیادی از ترکیب‌های نقطه کلیدی مورد بررسی قرار می‌گیرند و این امر باعث می‌شود که فرآیند توصیف و تطبیق انجام شود. طولانی تر می شود و بار حافظه و پردازنده را در سیستم کامپیوتری افزایش می دهد. قابلیت های نسبتاً دست و پا گیر و محدود پلت فرمی که کدهای محاسباتی الگوریتم روی آن نوشته شده اند، در عمل نقطه ضعف دیگری را برای روش پیشنهادی ایجاد می کند.
الگوریتم پیشنهادی بر اساس فرآیند مبتنی بر نقطه است. به خصوص هنگام کار با مجموعه داده های بزرگ، پیدا نکردن نقاط مزدوج و/یا مشکلات عدم تطابق یکی دیگر از معایب الگوریتم جدید است. در چنین مواردی، عملیات نیمه اتوماتیک (با انتخاب دستی نقاط برجسته برای تطبیق) الگوریتم پیشنهاد شده و نتایج دقیقی را ارائه می دهد.
با توجه به آزمایش در مقیاس بزرگ با استفاده از الگوریتم پیشنهادی، روش به صورت نیمه خودکار کار می کند. الگوریتم پیشنهادی ما باید در تشخیص نقاط کلیدی مجموعه داده‌های مقیاس بزرگ تقویت شود اگر بخواهیم آن را به طور خودکار در آزمایش‌های مقیاس بزرگ اعمال کنیم. بسته به تجربیات ما، این ضعف برای سایر الگوریتم‌های ثبت درشت نیز معتبر است (به عنوان مثال، ISS+PFH، LSP+PFH).

5. نتیجه گیری ها

الگوریتم جدید توسعه یافته و آزمایش شده در این مطالعه برای دقت حاصل از محصولات به‌دست‌آمده و همچنین کارایی محاسباتی امیدوارکننده است. با این حال، هنوز پیشرفت‌های بیشتری وجود دارد که برای جستجوی آن‌ها به ویژه در هنگام ترکیب داده‌های ابر نقطه با دقت و وضوح در حال تغییر به‌دست‌آمده از پلتفرم‌های مختلف و/یا مناطق بزرگ‌تر مورد نیاز است. بهبود الگوریتم‌ها با استفاده از تکنیک‌های هوشمند با قابلیت مدیریت اطلاعات تصادفی مجموعه داده‌ها می‌تواند منجر به بهبودهای مورد انتظار در نتایج شود. به منظور پیشرفت هدفمند، در کار آینده، ما قصد داریم بر روی ادغام ویژگی های یادگیری عمیق در الگوریتم های خود با ماژول های تخمین واریانس تمرکز کنیم. با استفاده از بهبود کارایی محاسباتی و بهینه سازی در استفاده از پردازنده های کامپیوتری، هدف ما این است که الگوریتم تطبیق خودکار را که طراحی کرده ایم به پلتفرم برنامه نویسی دیگری با قابلیت پردازش موازی منتقل کنیم. با توسعه الگوریتم تشخیص و انتخاب خودکار نقاط کلیدی، ما قصد داریم تحقیقات را برای ارزیابی مجموعه داده‌های ابر نقطه در مقیاس بزرگ گسترش دهیم.

منابع

  1. فانگینگ، اچ. ایمن، اچ. یک راه حل شکل بسته برای ثبت درشت ابرهای نقطه با استفاده از ویژگی های خطی. J. Surv. مهندس 2016 , 142 , 04016006. [ Google Scholar ] [ CrossRef ]
  2. ووسلمن، جی. اسکن لیزری Maas، HG هوابرد و زمینی ؛ CRC Press: Beacon Raton، FL، USA، 2010; صص 1-318. [ Google Scholar ]
  3. بوئنوآ، ام. گونزالس-خورخیا، اچ. مارتینز-سانچزاک، جی. Lorenzo, H. ثبت نام درشت ابر نقطه خودکار با استفاده از توصیفگرهای هندسی نقطه کلیدی برای صحنه های داخلی. خودکار ساخت و ساز 2017 ، 81 ، 134-148. [ Google Scholar ] [ CrossRef ]
  4. یوشیمورا، آر. تاریخ، ح. کنایی، س. هوما، ر. اودا، ک. Ikeda، T. ثبت خودکار ابرهای نقطه MLS و مش های SfM منطقه شهری. ژئو اسپات. Inf. علمی 2016 ، 19 ، 171-181. [ Google Scholar ] [ CrossRef ]
  5. بسل، پی جی. مک کی، روش ND برای ثبت اشکال سه بعدی. در Sensor Fusion IV: Control Paradigms and Data Structures . انجمن بین المللی اپتیک و فوتونیک: بلینگهام، WA، ایالات متحده آمریکا، 1992. [ Google Scholar ]
  6. روسینکیویچ، اس. لووی، ام. انواع کارآمد الگوریتم ICP. در مجموعه مقالات سومین کنفرانس بین المللی تصویربرداری و مدلسازی دیجیتال سه بعدی، کبک، QC، کانادا، 28 مه تا 1 ژوئن 2001. [ Google Scholar ]
  7. آئوکی، ی. گوفورث، اچ. Srivatsan، RA; Lucey, S. PointNetLK: ثبت ابر نقطه قوی و کارآمد با استفاده از pointnet. در مجموعه مقالات کنفرانس IEEE/CVF در مورد دید کامپیوتری و تشخیص الگو، لانگ بیچ، کالیفرنیا، ایالات متحده آمریکا، 15 تا 20 ژوئن 2019؛ صص 7163–7172. [ Google Scholar ]
  8. حبیب، اف. Alruzouq، تبدیل Hough اصلاح شده مبتنی بر خط RI برای ثبت خودکار تصاویر چند منبعی. فتوگرام ضبط 2004 ، 19 ، 5-21. [ Google Scholar ] [ CrossRef ]
  9. چن، اس. نان، ال. شیا، آر. ژائو، جی. Wonka، P. PLADE: توصیفگر مبتنی بر هواپیما برای ثبت ابر نقطه با همپوشانی کوچک. IEEE Trans. Geosci. Remote Sens. 2019 , 58 , 2530–2540. [ Google Scholar ] [ CrossRef ]
  10. حبیب، ع. دچف، آی. بنگ، ک. تحلیل مقایسه ای دو رویکرد برای ثبت چند سطحی ابرهای نقطه نامنظم. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2010 ، 38 ، 1-6. [ Google Scholar ]
  11. حسن الله، م. عبدالمجید، AA; Alshazly، HA Image دارای قابلیت تشخیص، توصیف و تطبیق است. در آشکارسازها و توصیفگرهای ویژگی تصویر ; عوض، ع.، حسن الله، م.، ویرایش. Springer: Cham, Switzerland, 2016; صص 11-45. [ Google Scholar ]
  12. خو، ی. بوئرنر، آر. یائو، دبلیو. هوگنر، ال. Stilla، U. ثبت درشت ابرهای نقطه‌ای در صحنه‌های شهری با استفاده از مجموعه‌های 4 صفحه‌ای مبتنی بر وکسل. ISPRS J. Photogramm. Remote Sens. 2019 ، 151 ، 106–123. [ Google Scholar ] [ CrossRef ]
  13. آیگر، دی. میترا، نیوجرسی؛ Cohen-Or, D. مجموعه‌های متجانس 4 نقطه‌ای برای ثبت سطح دوتایی قوی. ACM Trans. گرافیک 2008 ، 27 ، 1-10. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  14. Rusu، RB; بلودو، ن. Beetz، M. هیستوگرام های ویژگی نقطه سریع (FPFH) برای ثبت سه بعدی. در مجموعه مقالات کنفرانس بین المللی IEEE 2009 در مورد رباتیک و اتوماسیون، کوبه، ژاپن، 12 تا 17 مه 2009. [ Google Scholar ]
  15. تومبری، ف. سالتی، س. دی استفانو، L. امضاهای منحصر به فرد هیستوگرام برای توصیف سطح محلی. در کنفرانس اروپایی بینایی کامپیوتر ; Daniilidis, K., Maragos, P., Paragios, N., Eds. Springer: برلین، آلمان، 2010. [ Google Scholar ]
  16. یانگ، بی. دونگ، ز. لیانگ، اف. لیو، ی. ثبت خودکار ابرهای نقطه صحنه شهری در مقیاس بزرگ بر اساس نقاط ویژگی معنایی. ISPRS J. Photogramm. Remote Sens. 2016 ، 113 ، 43-58. [ Google Scholar ] [ CrossRef ]
  17. Ge, X. ثبت خودکار بدون نشانگر ابرهای نقطه با مجموعه‌های 4 نقطه‌ای متجانس مبتنی بر نقطه کلید معنایی. ISPRS J. Photogramm. Remote Sens. 2017 , 130 , 344–357. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  18. هوانگ، آر. خو، ی. یائو، دبلیو. هوگنر، ال. Stilla، U. ثبت جهانی قوی ابرهای نقطه با راه حل بسته در حوزه فرکانس. ISPRS J. Photogramm. Remote Sens. 2021 , 171 , 310–329. [ Google Scholar ] [ CrossRef ]
  19. Förstner, W. چارچوبی برای استخراج ویژگی های سطح پایین. در کنفرانس اروپایی بینایی کامپیوتر ; اکلوند، JO، اد. Springer: برلین، آلمان، 1994. [ Google Scholar ]
  20. سیپیران، آی. Bustos, B. Harris 3D: توسعه قوی اپراتور هریس برای تشخیص نقاط علاقه در مش های سه بعدی. Vis. محاسبه کنید. 2011 ، 27 ، 963-976. [ Google Scholar ] [ CrossRef ]
  21. چن، اچ. Bhanu، B. تشخیص اشیا با فرم آزاد سه بعدی در تصاویر محدوده با استفاده از وصله های سطح محلی. تشخیص الگو Lett 2007 ، 28 ، 1252-1262. [ Google Scholar ] [ CrossRef ]
  22. استدر، بی. Rusu، RB; کونولیج، ک. استخراج ویژگی Burgard، W. Point در اسکن های برد سه بعدی با در نظر گرفتن مرزهای اشیا. در مجموعه مقالات کنفرانس بین المللی IEEE 2011 در مورد رباتیک و اتوماسیون، شانگهای، چین، 9 تا 13 مه 2011. [ Google Scholar ]
  23. Lowe, G. SIFT – تبدیل ویژگی ثابت مقیاس. بین المللی جی. کامپیوتر. Vis. 2004 ، 2 ، 91-110. [ Google Scholar ] [ CrossRef ]
  24. Rusu، RB; Cousins, S. 3D اینجاست: کتابخانه ابر نقطه ای (PCL). در مجموعه مقالات کنفرانس بین المللی IEEE 2011 در مورد رباتیک و اتوماسیون، شانگهای، چین، 9 تا 13 مه 2011. [ Google Scholar ]
  25. ژونگ، ی. امضاهای شکل ذاتی: توصیفگر شکل برای تشخیص اشیاء سه بعدی. در مجموعه مقالات دوازدهمین کنفرانس بین المللی IEEE 2009 در کارگاه های بینایی کامپیوتری، کارگاه های ICCV، کیوتو، ژاپن، 27 سپتامبر تا 4 اکتبر 2009. [ Google Scholar ]
  26. حبیب، ع. غانما، م. مورگان، ام. الروزوق، ر. ثبت داده های فتوگرامتری و لیدار با استفاده از ویژگی های خطی. فتوگرام. مهندس Remote Sens. 2005 ، 71 ، 699-707. [ Google Scholar ] [ CrossRef ]
  27. یانگ، بی. Zang, Y. ثبت خودکار ابرهای نقطه اسکن لیزری زمینی متراکم با استفاده از منحنی ها. ISPRS J. Photogram. Remote Sens. 2014 ، 95 ، 109-121. [ Google Scholar ] [ CrossRef ]
  28. Ge، X. Wunderlich، T. تطبیق مبتنی بر سطح ابرهای نقطه سه بعدی با مختصات متغیر در سیستم منبع و هدف. ISPRS J. Photogram. Remote Sens. 2016 ، 111 ، 1-12. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  29. مگنوسون، ام. لیلینتال، ا. Duckett, T. اسکن ثبت نام برای وسایل نقلیه معدن مستقل با استفاده از 3D-NDT. ربات صحرایی جی. 2007 ، 24 ، 803-827. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  30. هوانگ، آر. بله، ز. بوئرنر، آر. یائو، دبلیو. خو، ی. Stilla، U. ثبت درشت جفتی سریع بین ابرهای نقطه‌ای از سایت‌های ساخت‌وساز با استفاده از همبستگی فاز مبتنی بر طرح ریزی دوبعدی. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2019 ، 42 ، 1015–1020. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  31. راهنمای Nextengine-Next Engine اسکنر لیزری سه بعدی Ultra HD. در دسترس آنلاین: https://www.nextengine.com/assets/pdf/scanner-techspecs-uhd.pdf (در 1 دسامبر 2020 قابل دسترسی است).
  32. لایکا، لایکا ScanStation C10 – اسکنر لیزری همه‌کاره برای هر کاربرد. در دسترس آنلاین: https://w3.leica-geosystems.com/downloads123/hds/hds/scanstationc10/brochures-datasheet/leica_scanstation_c10_ds_en.pdf (در 1 دسامبر 2020 قابل دسترسی است).
  33. برگه اطلاعات سیستم اسکن لیزری سیار فشرده Riegl، Riegl VMX-450. در دسترس آنلاین: https://www.riegl.com/uploads/tx_pxpriegldownloads/DataSheet_VMX-450_2015-03-19.pdf (در 1 دسامبر 2020 قابل دسترسی است).
  34. تومبری، ف. سالتی، س. دی استفانو، ال. ارزیابی عملکرد آشکارسازهای سه بعدی نقطه کلیدی. بین المللی جی. کامپیوتر. Vis. 2013 ، 102 ، 198-220. [ Google Scholar ] [ CrossRef ]
  35. پالی، ام. گراس، ام. Kobbelt، LP ساده سازی کارآمد سطوح نمونه برداری نقطه ای. در مجموعه مقالات تجسم IEEE. VIS 2002، بوستون، MA، ایالات متحده آمریکا، 27 اکتبر تا 1 نوامبر 2002. [ Google Scholar ]
  36. کین، اچ. گوان، جی. یو، ی. Zhong، L. یک الگوریتم فیلتر مبتنی بر وکسل برای داده‌های LiDAR تلفن همراه. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2018 ، 42 ، 1433-1438. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  37. Rusu، RB; مارتون، ZC; بلودو، ن. Beetz، M. هیستوگرام های ویژگی نقطه ثابت برای ابرهای نقطه سه بعدی. در مجموعه مقالات دهمین کنفرانس بین المللی سیستم های خودمختار بین المللی (IAS-10)، بادن، آلمان، 23 تا 25 ژوئیه 2008. صص 119-128. [ Google Scholar ]
  38. هانش، آر. وبر، تی. Hellwich, O. مقایسه آشکارسازها و توصیفگرهای نقطه بهره سه بعدی برای همجوشی ابر نقطه ای. ISPRS Ann. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2014 ، 2 ، 1-57. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  39. نواک، دی. Schindler, K. ثبت تقریبی ابرهای نقطه ای با تفاوت در مقیاس بزرگ. ISPRS Ann. فتوگرام ریموت سنس اسپات. Inf. علمی 2013 ، 1 ، 211-216. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  40. Theiler، PW; Wegner، JD; Schindler، K. ثبت ابر نقطه بدون نشانگر با مجموعه‌های متجانس 4 نقطه‌ای مبتنی بر نقطه کلید. ISPRS Ann. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2013 ، 1 ، 283-288. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  41. گرسین، آ. مالت، سی. دیوید، ن. بهبود ثبت نام ابر نقطه لیدار سه بعدی با استفاده از دانش محله بهینه. در مجموعه مقالات ISPRS Annals of the Photogrammetry، سنجش از دور و علوم اطلاعات فضایی، ملبورن، استرالیا، 25 اوت تا 1 سپتامبر 2012. صص 111-116. [ Google Scholar ]
  42. الدرغم، ک. حبیب، الف. رویکرد اجماع نمونه مبتنی بر ماتریس انجمن برای ثبت خودکار اسکن‌های لیزری زمینی با استفاده از ویژگی‌های خطی. فتوگرام مهندس Remote Sens. 2014 , 80 , 1029–1039. [ Google Scholar ] [ CrossRef ]
  43. ماتابوش، سی. سالوی، جی. فوفی، د. مریودو، F. ثبت تصویر محدوده برای بازرسی صنعتی. در مجموعه مقالات کاربردهای بینایی ماشین در بازرسی صنعتی سیزدهم، انجمن بین المللی اپتیک و فوتونیک، سن خوزه، کالیفرنیا، ایالات متحده آمریکا، 24 فوریه 2005. [ Google Scholar ]
  44. الروابده، ع. او، اف. موسی، ع. الشیمی، ن. حبیب، الف. استفاده از یک سیستم تصویربرداری دیجیتال مبتنی بر وسیله نقلیه هوایی بدون سرنشین برای استخراج یک ابر نقطه سه بعدی برای تشخیص لغزش لغزش. Remote Sens. 2016 , 8 , 95. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  45. واتسون، جی. تبدیل محاسبات کلاه ایمنی. جی. کامپیوتر. Appl. ریاضی. 2006 ، 197 ، 387-394. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  46. گیلانی، محاسبات تنظیم CD : تجزیه و تحلیل داده های مکانی ; جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2017. [ Google Scholar ]
  47. بوکباب، س. غریبی، ح. Linares، JM روشی برای پروتز تراز کامل زانو با استفاده از الگوریتم ICP با هدف کاشت آن در مهندسی بیومکانیک. Vibroeng. Proc. 2016 ، 9 ، 44-49. [ Google Scholar ]
  48. Zhang، Z. در مورد تطبیق محلی منحنی های فرم آزاد. در BMVC92 ؛ Hogg, D., Boyle, R., Eds. Springer: لندن، انگلستان، 1992; صص 347-356. [ Google Scholar ] [ CrossRef ]
  49. مطبوعات، WH; Teukolsky، SA; Vetterling، WT; Flannery, BP Numerical Recipes in C , 2nd ed.; انتشارات دانشگاه کمبریج: لندن، انگلستان، 2002; صص 59-70. [ Google Scholar ]
  50. چن، ی. مدیونی، جی. مدل‌سازی شی با ثبت تصاویر چند دامنه. تصویر Vis. محاسبه کنید. 1992 ، 10 ، 145-155. [ Google Scholar ] [ CrossRef ]
  51. Fitzgibbon، AW ثبت قوی مجموعه نقاط دو بعدی و سه بعدی. تصویر Vis. محاسبه کنید. 2003 ، 21 ، 1145-1153. [ Google Scholar ] [ CrossRef ]
  52. Yew, ZJ; Lee, GH 3dfeat-net: ویژگی های سه بعدی محلی با نظارت ضعیف برای ثبت ابر نقطه. در مجموعه مقالات کنفرانس اروپایی بینایی کامپیوتر، مونیخ، آلمان، 8 تا 14 سپتامبر 2018. [ Google Scholar ]
  53. Kjer، HM; Wilm, J. ارزیابی الگوریتم‌های ثبت سطح برای تصحیح حرکت PET. پایان نامه کارشناسی، دانشگاه فنی دانمارک، لینگبی، دانمارک، 2010. [ Google Scholar ]
Ijgi 10 00204 g001 550
شکل 1. مجسمه ارسطو در آزمایشگاه مترولوژی گروه مهندسی ژئوماتیک ITU.
Ijgi 10 00204 g002 550
شکل 2. ( الف ) نمای جنوبی مهمانخانه ITU Yilmaz Akdoruk; ( ب ) ابر نقطه ای نمای ساختمان و محیط آن با استفاده از سیستم اسکن لیزری سیار (Riegl VMX-450) اندازه گیری شده است.
Ijgi 10 00204 g003 550
شکل 3. مجسمه خرگوش توسط مخزن اسکن سه بعدی استنفورد ( https://graphics.stanford.edu/data/3Dscanrep/ ، در 15 مارس 2021 مشاهده شد).
Ijgi 10 00204 g004 550
شکل 4. در نمای ساختمان: ( الف ) انحناهای محاسبه شده در نقاط سطح. ( ب ) داده های سطحی که به وکسل های مکعبی تقسیم شده اند. ( ج ) نقاط برجسته پس از فیلتر کردن ابر نقطه.
Ijgi 10 00204 g005 550
شکل 5. مروری بر مراحل اصلی الگوریتم تشخیص نقطه کلیدی پیشنهادی.
Ijgi 10 00204 g006 550
شکل 6. قاب داربوکس بین یک جفت نقطه (اقتباس از [ 38 ]).
Ijgi 10 00204 g007 550
شکل 7. الگوریتم اصل انتخاب نقطه در مجموعه های متجانس چهار نقطه ای (4PCS) (اقتباس از [ 39 ، 40 ]).
Ijgi 10 00204 g008 550
شکل 8. الگوریتم شباهت کسینوس.
Ijgi 10 00204 g009 550
شکل 9. رویکرد ترکیبی شباهت کسینوس.
Ijgi 10 00204 g010 550
شکل 10. مراحل پردازش اساسی توصیفگر و الگوریتم های تطبیق الگوریتم پیشنهادی در مطالعه.
Ijgi 10 00204 g011 550
شکل 11. مراحل الگوریتم تکراری نزدیکترین نقطه (ICP).
Ijgi 10 00204 g012a 550 Ijgi 10 00204 g012b 550
شکل 12. تشخیص نقطه کلید کاملاً خودکار با الگوریتم پیشنهادی: ( الف ) برای نمای ساختمان با وکسل، ( ب ) برای مجسمه ارسطو و ( ج ) برای مجسمه اسم حیوان دست اموز استانفورد با رنگ.
Ijgi 10 00204 g013 550
شکل 13. توزیع نقاط کلیدی شناسایی شده برای داده های ابرهای نقطه مجسمه ارسطو با استفاده از: ( الف ) الگوریتم امضاهای شکل ذاتی (ISS). ( ب ) الگوریتم وصله سطح محلی (LSP).
Ijgi 10 00204 g014 550
شکل 14. توزیع نقاط کلیدی شناسایی شده برای مجموعه داده های ابر نقطه ای برای نمای ساختمان با استفاده از موارد زیر: ( الف ) الگوریتم امضاهای شکل ذاتی (ISS) با داده های TLS. ( ب ) الگوریتم ISS با داده های MLS. ( ج ) الگوریتم پچ سطح محلی (LSP) با داده های TLS. ( د ) الگوریتم LSP با داده های MLS.
Ijgi 10 00204 g015 550
شکل 15. مجسمه ارسطو: ( الف ) با استفاده از الگوریتم جدید، نقاط کلیدی را در ابر نقطه اول شناسایی کرد. ( ب ) توزیع نقاط کلیدی مطابق با الگوریتم جدید. ( ج ) نقاط کلیدی را در ابر نقطه دوم با استفاده از الگوریتم جدید شناسایی کرد.
Ijgi 10 00204 g016 550
شکل 16. مجسمه ارسطو: ( الف ) نقاط کلیدی شناسایی شده توسط ISS در ابر نقطه 1. ( ب ) تطبیق ابرهای دو نقطه ای با الگوریتم ISS+PFH. ( ج ) نقاط کلیدی شناسایی شده توسط ISS در ابر نقطه 2.
Ijgi 10 00204 g017 550
شکل 17. مجسمه ارسطو: ( الف ) نقاط کلیدی شناسایی شده توسط LSP در ابر نقطه 1. ( ب ) تطبیق ابرهای دو نقطه ای با الگوریتم LSP+PFH. ( ج ) نقاط کلیدی شناسایی شده توسط LSP در ابر نقطه دوم.
Ijgi 10 00204 g018 550
شکل 18. نمای ساختمان: ( الف ) نقاط کلیدی شناسایی شده توسط آشکارساز جدید در ابر نقطه TLS. ( ب ) تطبیق ابرهای نقطه TLS و MLS با استفاده از ارزیابی نیمه خودکار الگوریتم جدید. ( ج ) نقاط کلیدی شناسایی شده توسط آشکارساز جدید در داده های ابر نقطه MLS.
Ijgi 10 00204 g019 550
شکل 19. مجسمه اسم حیوان دست اموز استانفورد: ( الف ) با استفاده از الگوریتم جدید، نقاط کلیدی را در ابر نقطه اول شناسایی کرد. ( ب ) توزیع نقاط کلیدی مطابق با الگوریتم جدید. ( ج ) نقاط کلیدی را در ابر نقطه دوم با استفاده از الگوریتم جدید شناسایی کرد.
Ijgi 10 00204 g020 550
شکل 20. مجسمه ارسطو: نتایج به دست آمده از الگوریتم تکراری نزدیکترین نقطه (ICP) که در آن از نقاط کلیدی شناسایی شده و مطابق با الگوریتم ISS+PFH استفاده شده است.
Ijgi 10 00204 g021 550
شکل 21. مجسمه ارسطو: نتایج به دست آمده از الگوریتم تکراری نزدیکترین نقطه (ICP) که در آن از نقاط کلیدی شناسایی شده و مطابق با الگوریتم LSP+PFH استفاده شده است.
Ijgi 10 00204 g022 550
شکل 22. مجسمه ارسطو: نتایج به دست آمده از الگوریتم تکراری نزدیکترین نقطه (ICP) که در آن از نقاط کلیدی شناسایی شده و مطابق با الگوریتم جدید استفاده می شود.
Ijgi 10 00204 g023 550
شکل 23. نمای ساختمان: نتایج به دست آمده از الگوریتم تکراری نزدیکترین نقطه (ICP) که در آن نقاط کلیدی ابرهای نقطه TLS و MLS شناسایی شده و با الگوریتم جدید مطابقت داده شده است.
Ijgi 10 00204 g024 550
شکل 24. مجسمه اسم حیوان دست اموز استنفورد: نتایج به دست آمده از الگوریتم تکراری نزدیکترین نقطه (ICP) که در آن از نقاط کلیدی شناسایی شده و مطابق با الگوریتم جدید استفاده شده است.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید