یک روش تفکیک فضایی تطبیقی ​​بر اساس مدل ST-ResNet برای پیش‌بینی جرم ملکی ساعتی

چکیده

پلیس پیش‌بینی‌کننده مؤثر می‌تواند گشت‌های پلیس را راهنمایی کند و از جرم و جنایت جلوگیری کند. انتظار می رود پیش بینی جرم ساعتی باعث صرفه جویی در وقت پلیس شود. انتخاب تفکیک مکانی به دلیل ارتباط قوی با دقت پیش‌بینی جرم حائز اهمیت است. در این مقاله، ما یک روش تفکیک فضایی تطبیقی ​​را برای انتخاب بهترین وضوح فضایی برای پیش‌بینی جرم ساعتی پیشنهاد می‌کنیم. مدل ST-ResNet برای پیش‌بینی خطر جرم، با داده‌های جرم تاریخی و داده‌های آب‌وهوا به‌عنوان متغیرهای پیش‌بینی‌کننده استفاده می‌شود.
 برای ارزیابی صحت نتایج از شاخص دقت پیش‌بینی (PAI) استفاده می‌شود. داده های مربوط به جرایم اموال ارتکابی در سوژو، یک شهر بزرگ در چین، به عنوان داده های تحقیق انتخاب شدند. نتایج آزمایش نشان می دهد که وضوح فضایی 2.4 کیلومتر منجر به بهترین عملکرد برای پیش بینی جرم می شود.

کلید واژه ها:

ST-ResNet ; وضوح فضایی ؛ پیش بینی جرم ; جرم مالکیت

1. مقدمه

یکی از اهداف اصلی پیش‌بینی جرم، هدایت کارآمد استقرار پلیس است به گونه‌ای که بتوان با جرایم پیش‌بینی‌شده به طور مؤثر برخورد کرد [ 1 ]. در این زمینه، محققان و پزشکان پلیس در سراسر جهان به طور فزاینده ای به دنبال روش های کارآمد برای پلیس پیش بینی هستند [ 2 ]. بسیاری از انواع داده‌ها برای بهبود کارایی و دقت نتایج پیش‌بینی جرم، از جمله سوابق تاریخی جرم و داده‌های اجتماعی و محیطی استفاده شده‌اند [ 1 ، 3 ، 4 ، 5 ].
مطالعات گذشته نگر با استفاده از سوابق جنایی تاریخی معمولاً با تجزیه و تحلیل نقاط داغ مرتبط هستند. با استفاده از داده های جرایم اخیر، نقاط داغ شناسایی و برای شناسایی جرایم در حال ظهور نقشه برداری می شوند [ 6 ، 7 ]. در این زمینه، کانون های جرم و جنایت در طول زمان پایدار فرض می شوند [ 8 ، 9 ]. این فرض ممکن است برای مناطق با جرم و جنایت درازمدت به دلیل معایب متمرکز به خوبی کار کند [ 10 ]. به منظور بهبود دقت پیش‌بینی‌های کوتاه‌مدت، از جنایات اخیر برای پیش‌بینی مناطق با جرم بالا استفاده می‌شود، به عنوان مثال از طریق مدل‌های فرآیند نقطه‌ای هیجان‌انگیز و رویکردهای تقریباً تکراری [ 11 ، 12 ، 13 ].]. علاوه بر این، نظریه‌های جرم‌شناسی برای تفسیر اینکه چرا جرایم در مکان و زمان خاصی اتفاق می‌افتند پیشنهاد شده‌اند [ 10 ، 14 ، 15 ، 16 ]، و برخی از روش‌ها مانند رگرسیون وزن‌دار جغرافیایی و رگرسیون وزن‌دار جغرافیایی و زمانی برای کشف محیط‌زیست استفاده شده‌اند. عوامل توزیع جرم [ 17 ، 18 ]. با این حال، ماهیت پویای جرم نیازمند روش‌های فعال‌تر است [ 19 ، 20 ].
در عمل، خطر جرم پیش‌بینی‌شده ممکن است برای مدت کوتاهی وجود داشته باشد، اما به دلیل فعالیت‌های غیرمنتظره (مثلاً ناپدید شدن فرصت‌های جرم‌زا) به سرعت از بین می‌رود [ 21 ]. علاوه بر این، یک پنجره زمانی کوچک ممکن است اهمیت داده های تاریخی را کاهش دهد و منجر به نویز بیشتر در پیش بینی جرم شود [ 9 ، 22 ]. این امر پیش‌بینی مؤثر جرایم نوظهور را دشوار می‌کند و موفقیت روش‌های سنتی را برای پیش‌بینی کوتاه‌مدت محدود می‌کند. از این رو، پیش‌بینی کوتاه‌مدت در عمل پلیسی ضروری است.
خوشبختانه، توسعه یادگیری عمیق امکان پیش‌بینی کوتاه‌مدت جنایت را فراهم کرده است که توسط عوامل اجتماعی-اقتصادی و همچنین داده‌های تاریخی جرم تسهیل می‌شود [ 23 ، 24 ، 25 ]. به عنوان مثال، الکساندر و همکاران. از یک مدل شبکه عصبی عمیق برای پیش‌بینی جرم با استفاده از داده‌های جرم تاریخی، داده‌های جمعیتی، سوابق آب‌وهوا و سایت‌های حمل‌ونقل استفاده کرد [ 26 ]. هنگامی که پنجره زمانی کوچک است، مدل شبکه عصبی با انجام محاسبات بیشتر، عملکرد خوبی ندارد. برای رفع این نقص، او و همکاران. یک مدل شبکه باقیمانده عمیق (ResNet) برای بهبود عملکرد مدل در زمانی که پنجره زمانی کوچک است ارائه کرد [ 27 ]]. ژانگ و همکاران این مدل را برای پیش‌بینی جمعیت ساعتی با تطبیق آن با بعد زمان اعمال کرد [ 28 ]. وانگ و همکاران با استفاده از یک مدل ST-ResNet که می‌تواند ساختارهای فضایی را با شبکه‌های عصبی کانولوشن (CNN) ضبط کند و وابستگی‌های زمانی را با شبکه‌های عصبی مکرر (RNNs) یاد بگیرد. یک روش پیش‌بینی جرم ساعتی را بر اساس سوابق آب و هوا و داده‌های جرم تاریخی از لس آنجلس ارائه کرد [ 29 ].
به خوبی شناخته شده است که جرم به طور مساوی در فضا توزیع نشده است [ 30 ، 31 ]. بیشتر جنایات بیشتر در ساعات خاصی از روز انجام می شوند [ 30 ]. ماهیت خوشه‌بندی جرم اغلب با پدیده‌های تکراری و تقریباً تکراری تفسیر می‌شود که برای بسیاری از انواع جرم از جمله سرقت وسایل نقلیه، سرقت‌های خیابانی، سرقت‌های مسکونی و غیره شناسایی شده‌اند [ 32 ، 33 ، 34 ]. پدیده های تکراری و نزدیک به تکرار، رابطه قوی بین مجاورت جنایات در مکان و زمان را تایید می کنند [ 23 ]. روش ناکس اغلب برای تعیین کمیت تأثیر این پدیده استفاده می شود [ 35]. بسیاری از مطالعات ثابت کرده اند که الگوهای تکرار و نزدیک به تکرار در مناطق مختلف متفاوت است. به عنوان مثال، یک الگوی تقریباً تکرار قابل توجه برای 2 ماه در 400 متر در مرسی ساید، انگلستان وجود داشت، اما در نانجینگ، چین، این الگو در 14 روز و 300 متر رخ داد [ 19 ، 36 ]. تجزیه و تحلیل پدیده های تکراری و نزدیک به تکرار برای پیش بینی عملی جرم بسیار مهم است [ 37 ، 38 ].
اندازه سلول شبکه یک پارامتر مهم در پیش‌بینی جرم است و پیش‌بینی‌های جرم نسبت به طرح گسسته‌سازی فضایی مورد استفاده حساس هستند [ 7 ، 31 ، 39 ، 40 ، 41 ]. مشکلات مقیاس مسئله واحد منطقه ای قابل اصلاح می تواند بر نسبت تفاوت مربوط به مناطق اطراف تأثیر بگذارد [ 42 ]. بین انواع جرم و مناطق مورد مطالعه متفاوت است [ 39 ]. برای یافتن یک واحد بهینه برای ترسیم جرم، رویکردهای مختلفی مورد بررسی قرار گرفته است. Oberwittler و Wikström استحکام و یکنواختی درونی را به منظور انتخاب ناحیه بهینه برای رگرسیون تجزیه و تحلیل کردند [ 39]. گرل و همکاران محاسبه همبستگی های درون طبقاتی (ICCs) به عنوان معیاری با مدل سازی خطی سلسله مراتبی برای انتخاب اندازه محیط اطراف بهینه برای درک جغرافیای حوادث آتش سوزی [ 43 ]. مالسون و همکاران شباهت بین الگوهای نقطه فضایی در هر وضوح را برای تعیین یک واحد کافی در هنگام جمع آوری داده های نقطه ای به مناطق برآورد کرد [ 44 ]. راموس و همکاران استحکام متعادل در برابر خطا و یکنواختی داخلی برای تعیین دانه بندی بهینه برای تولید نقشه های جرم قابل اعتمادتر [ 45]. معیارهای واحد بهینه در نقشه برداری جرم بسته به هدف تحلیل جرم متفاوت است. در این مقاله، هنگام انتخاب واحد بهینه، بر دقت پیش‌بینی جرم ساعتی تمرکز می‌کنیم و شاخص دقت پیش‌بینی (PAI) را که می‌تواند سطح دقت نتایج مدل را اندازه‌گیری کند، به عنوان معیاری برای برآورده کردن نیازهای گشت واقعی انتخاب می‌کنیم. [ 6]. مدل یادگیری عمیق ST-ResNet برای استخراج ویژگی یک ماتریس پراکنده از داده های جرم ساعتی ساخته شده است. تأثیر تفکیک‌پذیری‌های فضایی مختلف بر نتایج پیش‌بینی به صورت تکراری تحلیل می‌شود و بالاترین PAI در وضوح بهینه برای مدل محاسبه می‌شود. هزینه زمانی مدل های یادگیری عمیق برای پیش بینی کوتاه مدت بیشتر از مدل های سنتی برای پیش بینی طولانی مدت است. برای کاهش هزینه محاسباتی، ما یک ساختار هرمی سلسله مراتبی را برای ارائه وضوح های مختلف توسط یک فرآیند خودکار اتخاذ می کنیم.
به منظور انتخاب بهترین وضوح فضایی در پیش‌بینی جرم در مقیاس‌های زمانی ساعتی، ما یک روش تفکیک فضایی تطبیقی ​​را پیشنهاد می‌کنیم. یک هرم داده برای به دست آوردن اطلاعات با وضوح های مختلف ساخته شده است. مدل‌های ST-ResNet برای پیش‌بینی جرایم در مقیاس‌های مختلف با تجزیه و تحلیل ناهمگونی جرم و داده‌های آب‌وهوا ساخته شده‌اند. سپس، دقت نتایج پیش‌بینی در هر وضوح بر اساس PAI مقایسه می‌شود. ارزیابی‌های اعتبار و دقت نشان می‌دهد که روش ما می‌تواند به نتایج ایده‌آل پیش‌بینی ساعتی برای برآوردن الزامات خاص پیشگیری و کنترل امنیت عمومی دست یابد.
بقیه این مقاله به شرح زیر سازماندهی شده است. بخش 2 منطقه و داده های مورد مطالعه را تشریح می کند. بخش 3 روش مورد استفاده برای دستیابی به بهترین اثربخشی پیش بینی را تعریف می کند. بخش 4 نتایج پیش بینی را ارائه و مورد بحث قرار می دهد. در نهایت، بخش 5 نتیجه گیری و جهت کار آینده را خلاصه می کند.

2. منطقه مطالعه و داده ها

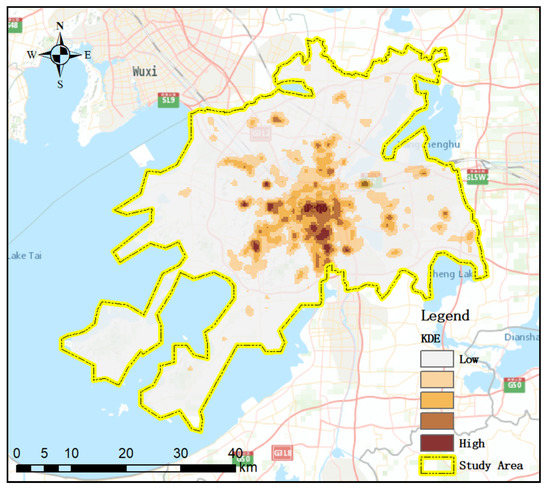
2.1. منطقه مطالعه و داده های جرم ملکی

از نظر آماری، موارد نقض اموال بیش از 70 درصد از جرایم در چین را تشکیل می دهند [ 46 ]. گستره وسیع گشت های مورد نیاز و نیروی پلیس ناکافی منجر به نرخ پایین حل چنین مواردی می شود [ 47 ]. ما می‌توانیم کارایی تخصیص منابع را بهبود بخشیم و مداخلات پیش‌گیرانه مؤثر را با تخصیص صحیح گشت‌ها برنامه‌ریزی کنیم، که می‌توان از طریق پیش‌بینی مؤثر جرم به دست آورد [ 48 ].
شهر سوژو با جمعیتی حدود 10616000 نفر در جنوب شرقی استان جیانگ سو چین واقع شده است. این شهر دارای ششمین تولید ناخالص داخلی در چین است. رودخانه یانگ تسه در شمال سوژو و دریاچه تایهو (سومین دریاچه بزرگ آب شیرین در چین) در غرب سوژو قرار دارد. سوژو یک شهر مهم از مجموعه شهری دلتای رودخانه یانگ تسه در حوضه دریاچه تایهو است که در آن اقتصاد فعال است و حمل و نقل به طور گسترده ای در دسترس است. راه حلی برای پیش‌بینی مؤثر جرم که بتوان در هر منطقه اعمال کرد، برای کمک به پلیس در نظم بخشیدن به نیروی خود و کاهش نرخ جرم ضروری است. از بین پنج منطقه شهرداری سوژو، ما چهار منطقه را انتخاب کردیم که بیش از 80 درصد پرونده های جنایی شهر را از سال 2012 تا 2013 تشکیل می دهند، یعنی منطقه Huqiu، منطقه Gusu، منطقه Wuzhong،
شکل 1 تخمین تراکم هسته تمامی جرایم دارایی (بیش از 130000 مورد) را در منطقه مورد مطالعه از ژانویه 2012 تا اکتبر 2013 نشان می دهد. داده های جرم از اداره پلیس محلی به دست آمده است، و مجموعه داده شامل شماره پرونده، نوع جرم، رخ داده است. زمان، مختصات جغرافیایی و غیره. در این مقاله، انواع جرم هدف ما دزدی، سرقت و سرقت بود که توسط پلیس به عنوان انواع رایج جرایم دارایی در سوژو طبقه بندی می شوند [ 3 ، 49 ، 50 ].

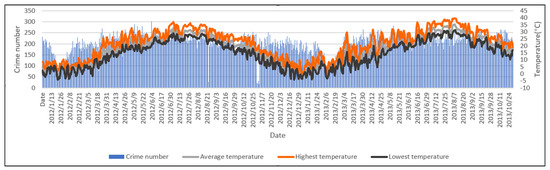
2.2. داده های آب و هوا

آب و هوا می تواند بر نرخ جرم و رفتار مجرمانه تأثیر بگذارد و هر متغیر تأثیر متفاوتی بر انواع مختلف جرم دارد [ 51 ، 52 ، 53 ]. در پیش‌بینی جرایم کوتاه‌مدت، متغیرهای آب‌وهوا پیش‌بینی‌کننده‌های رایج هستند و دما برای پیش‌بینی جرم دارایی مهم است [ 29 ، 54 ]. در این مطالعه، دما را به عنوان تأثیر خارجی مدل انتخاب کردیم. داده‌های میانگین دمای روزانه، بالاترین دما، و داده‌های کمترین دما برای 671 روز از ژانویه 2012 تا اکتبر 2013 از مؤسسه برنامه‌ریزی و طراحی وزارت کشاورزی چین جمع‌آوری شد [ 55 ].

3. روش شناسی

برای بهبود اثربخشی پیش‌بینی جرم ساعتی، ما یک روش تفکیک فضایی تطبیقی ​​را برای انتخاب واحد بهینه برای مدل‌های پیش‌بینی جرم پیشنهاد کردیم. برای پیش بینی خطر جرم از مدل ST-ResNet استفاده شد. PAI برای اندازه گیری دقت نتایج در وضوح های مختلف فضایی استفاده شد [ 29 ]. شکل 2 روند روش را نشان می دهد.
همانطور که در شکل 3 نشان داده شده است، یک هرم داده [ 56 ] برای جمع آوری نقاط به شبکه در مقیاس های چندگانه تولید شد . اکثر خدمات نقشه برداری وب مانند Google Maps و Microsoft Bing Maps از تکنیک هرمی برای ارائه محتوای نقشه بر اساس تقاضا برای کاربران استفاده می کنند [ 57 ، 58 ]. روش گسسته سازی که ما استفاده کردیم مانند این خدمات نقشه برداری وب است. این روش با وضوح درشت شروع می شود و سپس به صورت بازگشتی وضوح های دیگر را تولید می کند. در هر محاسبات مدل ST-ResNet، نقاط به لایه‌ها تجمیع می‌شوند. رزولوشن پایه روی 9.6 کیلومتر تنظیم شده است که مطابق با سطح 12 هرم مطابق با منطقه حداکثر گشت محلی است.
منطقه تحقیقاتی توسط سلول های شبکه ای با وضوح های مختلف پوشیده شده بود. لایه با وضوح بالا دارای شبکه های کوچکی است که یک منطقه کوچک را پوشش می دهد و لایه با وضوح پایین دارای شبکه های بزرگی است که یک منطقه بزرگ را پوشش می دهد. جنایات بر اساس مختصات جغرافیایی و زمان خود در شبکه‌های فضا-زمان تجمیع شدند. تعداد جرایم توسط شبکه شمارش شد و به سلول های مربوطه یک لایه اختصاص داده شد.
برای داده‌های آب‌وهوا، سلول‌های شبکه‌ای یک لایه زمانی مقدار یکسانی دارند، زیرا آب و هوا در منطقه تحقیقاتی همگن است. لایه های ایجاد شده به داده های آموزشی و داده های آزمون تقسیم شدند. از داده های آموزشی برای آموزش مدل ST-ResNet M (همانطور که در بخش 3.1 بحث شد ) و شناسایی پارامترهای بهینه در وضوح فضایی خاص استفاده شد. سپس، خطر جرم با داده های آزمون ارزیابی شده توسط PAI محاسبه شد.
با افزایش سطح لایه d در هرم، وضوح شبکه افزایش می یابد. جنایات دوباره به شبکه های لایه دیگری تجمیع شدند. برای به حداقل رساندن تأثیر تغییرات زمانی جرم، جرایم ارتکابی بیش از 12 ماه به عنوان داده های آموزشی و جرایم انجام شده در ماه بعد برای تأیید صحت مدل انتخاب شدند. این فرآیند به صورت بازگشتی برای زمان‌های معینی انجام شد تا اینکه لایه با بالاترین وضوح به دست آمد. PAI برای ارزیابی دقت محاسبات در مدل گنجانده شد.

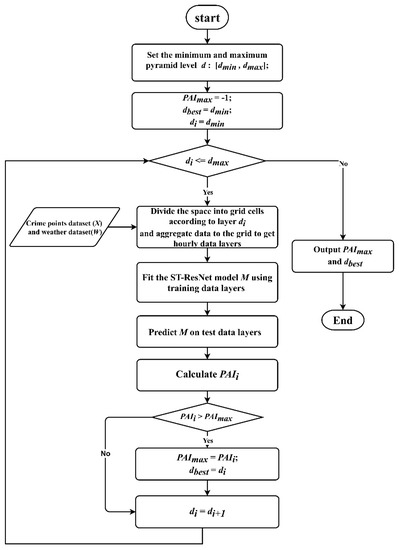
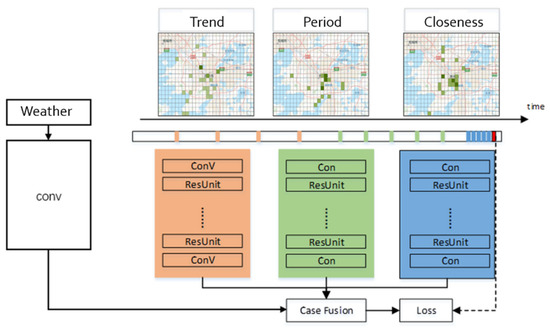
3.1. مدل ST-ResNet

مدل ST-ResNet خطر جرم را بر اساس سوابق آب و هوا و همچنین الگوهای جرم شامل روند، دوره و نزدیکی پیش بینی می کند ( شکل 4 ). روند نشان دهنده تمایل تعداد جرایم به افزایش یا کاهش است. دوره به الگوی دوره ای جرم در مقیاس زمانی معین اشاره دارد. در مقایسه با جنایات دور، جنایاتی که در زمان نزدیکتر به هم انجام می‌شوند، احتمالاً مرتبط هستند. بنابراین، “نزدیک” به فاصله زمانی بین جفت جرم اشاره دارد. به دنبال تحقیقات وانگ (2019)، آزمایش سطوح ساعتی، روزانه و هفتگی را به عنوان فاصله زمانی 3 ویژگی دوره‌ای جرم اتخاذ کرد [ 29 ].
شکل 4 روند مدل ST-ResNet را نشان می دهد. در مرحله کانولوشن، پیچیدگی چند لایه برای اندازه گیری رابطه بین مناطق غیر مجاور انتخاب می شود. 3 مولفه تناوبی و مولفه خارجی (آب و هوا) از طریق یک روش همجوشی مبتنی بر ماتریس پارامتریک ذوب می شوند.
این مدل از توزیع‌های مکانی جرم تاریخی استفاده می‌کند {ایکستی}تی=1nو سوابق آب و هوا {دبلیوتی}تی=1n+1برای پیش بینی توزیع فضایی جرم ایکسn+1در زمان تیn+1، جایی که ایکس1، ایکس2,…, ایکسn+1لایه‌هایی هستند که در مواقعی توزیع‌های فضایی جرم را نشان می‌دهند تی، تی2,…, تیn+1،و دبلیو1، دبلیو2,…, دبلیوn+1لایه های آب و هوا هستند.

برای آموزش مدل، خطای ریشه میانگین مربع (RMSE) بین ماتریس جرم پیش‌بینی‌شده و ماتریس جرم واقعی را به حداقل رساندیم:

آرماسE=1ز∑من(ایکسمن-ایکس^من)2

جایی که ایکسمنارزش واقعی است، ایکس^منمقدار پیش بینی شده است و Z تعداد نقاط داده آموزشی [ 59 ] است.

فرآیند مدل‌سازی به شرح زیر انجام شد: یک مجموعه داده آموزشی (از ژانویه 2012 تا دسامبر 2012) برای آموزش مدل با اعتبارسنجی متقابل (نسبت اعتبار 20٪) و یک مجموعه آزمون (از ژانویه 2013 تا اکتبر 2013) استفاده شد. برای تست مدل نهایی این مدل در چندین تکرار برای انتخاب مدل نهایی، با پارامترهای تنظیم بهینه بر اساس به حداقل رساندن خطای اعتبارسنجی متقابل، آموزش داده شد. سپس با استفاده از مدل نهایی، پیش‌بینی‌هایی درباره مجموعه آزمون انجام دادیم و اثر پیش‌بینی را ارزیابی کردیم. با توجه به این واقعیت که تفاوت‌های فصلی به طور بالقوه بر نتایج تأثیر می‌گذارد، برای هر ماه از مجموعه آزمایشی، ما مکرراً رویدادهای جرم را برای هر تغییر پارامترهای روش‌شناختی پیش‌بینی کردیم. یعنی برای هر تغییر، پیش‌بینی‌هایی با استفاده از یک پنجره چرخان انجام شد (مثلاً هنگام پیش‌بینی ژانویه 2013 با استفاده از 1 سال داده‌های تاریخی، از داده‌های ژانویه 2012 تا دسامبر 2012 برای آموزش استفاده شد. هنگام پیش‌بینی فوریه 2013، از داده‌های فوریه 2012 تا ژانویه 2013 استفاده شد. و غیره): دقت پیش‌بینی برای هر ماه محاسبه شد و سپس برای هر تغییر برای مجموعه آزمون میانگین گرفت.

3.2. ارزیابی دقت

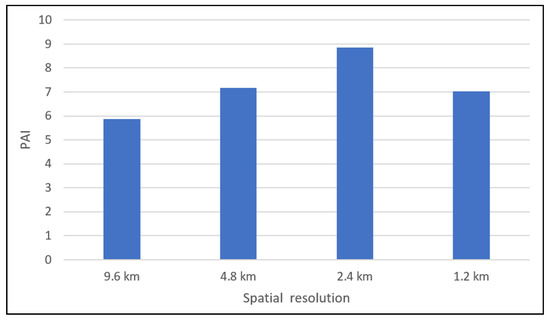
RMSE که تفاوت بین مقادیر پیش‌بینی‌شده و مشاهده‌شده را ارزیابی می‌کند و امتیاز F1 [ 60 ] که دقت و یادآوری را ارزیابی می‌کند، وابسته به مقیاس هستند. یک شاخص ارزیابی پیش‌بینی جرم که معمولاً مورد استفاده قرار می‌گیرد، شاخص دقت پیش‌بینی (PAI) است [ 6 ]. این می تواند برای مقایسه دقت نقاط مهم محاسبه شده با روش های مختلف از طریق محاسبات بسیار ساده استفاده شود و می تواند نتایج پیش بینی را در وضوح ها و بزرگی های مختلف مقایسه کند. شکل کلی این متغیر به صورت زیر است:

پآمن=n/نآ/آ

جایی که nتعداد رویدادهای جرم و جنایت در مناطقی است که وقوع جنایات پیش بینی شده است. نتعداد رویدادهای جرم واقعی در کل منطقه مورد مطالعه است. آمنطقه ای از مناطقی است که وقوع جرم در آن پیش بینی می شود. آمساحت منطقه مورد مطالعه است. PAI را می توان به عنوان نرخ ضربه در مناطقی در نظر گرفت که جرایم با توجه به وسعت منطقه مورد مطالعه پیش بینی می شود. هرچه نرخ ضربه بیشتر و اثر پیش بینی بهتر باشد، PAI بالاتر خواهد بود.

4. نتایج

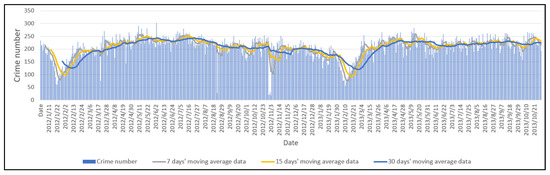
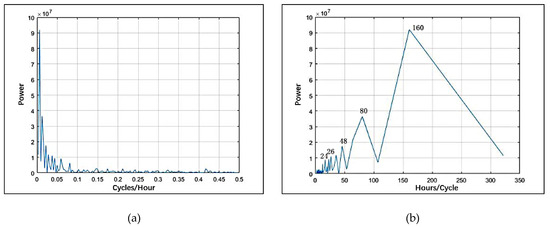
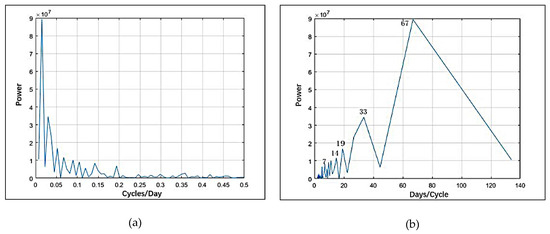
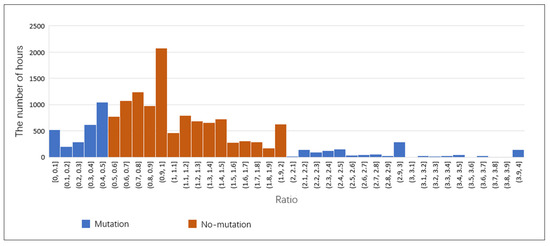
4.1. تحلیل داده ها

خطر جرم که توسط یک ماشین حساب تکراری و تقریباً تکراری اندازه گیری می شود در بین انواع مختلف جرم متفاوت است [ 52 ]. ما مجاورت، تناوب و ناهمگونی جنایات را در مکان و زمان محاسبه کردیم. در نهایت، همبستگی بین تغییرات دما و سطح جرم مورد آزمایش قرار گرفت.
شکل 5 آمار روزانه، داده‌های میانگین متحرک 7 روزه، داده‌های میانگین متحرک 14 روزه و داده‌های میانگین متحرک 30 روزه را برای رویدادهای جرایم دارایی از ژانویه 2012 تا اکتبر 2013 نشان می‌دهد.
ماشین حساب تقریباً تکرار از آزمون ناکس برای تجزیه و تحلیل مختصات در یک بازه زمانی معین توسط شبیه سازی های مونت کارلو برای تشخیص پدیده تکرار نزدیک استفاده می کند [ 61 ]. ما پهنای باند فضایی را 300 متر تعیین کردیم زیرا طول بلوک منطقه مورد مطالعه ما حدود 300 متر است. ما پهنای باند زمانی را 7 روز تنظیم کردیم. فاصله منهتن به این دلیل استفاده شد که نزدیک به یک مسیر واقعی برای محیط های شهری است. جدول 1 سطح خطر جرم را در یک ماتریس تقریباً تکرار نشان می دهد. در مورد منطقه مورد مطالعه ما، یک الگوی تکرار نزدیک برای هفته اول در 300 متر وجود داشت و پدیده تکرار نزدیک با زمان و مسافت ضعیف شد.
برای محاسبه دوره های داده های جرم از روش طیف قدرت [ 62 ] استفاده می شود. قدر مجذور ضرایب فوریه، معیاری از توان است. توان بر روی نیمی از ضرایب محاسبه می شود زیرا نیمی از آنها در بزرگی تکرار می شوند. ما طیف توان را به عنوان تابعی از فرکانس ترسیم کردیم که بر حسب چرخه در ساعت و در روز اندازه‌گیری شد. برای تفسیر آسان‌تر دیدگاه فعالیت چرخه‌ای، ما همچنین توان را به عنوان تابعی از دوره ترسیم کردیم که بر حسب ساعت و روز در هر چرخه اندازه‌گیری می‌شود. شکل 6 طیف توان (الف) و دوره داده های ساعتی (ب) را نشان می دهد. میانگین دوره های گذراندن آزمون معناداری 24 ساعت، 48 ساعت، 80 ساعت و 160 ساعت است. تکرار چرخه کوتاه مدت را می توان در تناوب روزانه مشاهده کرد. شکل 7طیف توان (a) و دوره داده های روزانه (b) را نشان می دهد. میانگین دوره های قبولی در آزمون معناداری 7 روز، 14 روز، 19 روز، 33 روز و 67 روز است. این روند هفتگی داده های جرم را نشان می دهد.
ما نسبت تعداد موارد را در ساعات مجاور محاسبه کردیم، به استثنای برخی از لحظات با موارد غیرعادی بالا یا بدون موارد. سپس، تعداد ساعات مربوط به هر نسبت را از ژانویه 2012 تا اکتبر 2013 محاسبه کردیم. شکل 8 آمار نسبت را نشان می دهد. نود و پنج درصد از ساعت های مجاور دارای نسبت موارد بین 0 تا 4 هستند. با توجه به اینکه تعداد موارد در ساعت کم است، زمان هایی را تعریف کردیم که مقدار نسبت بین 0.5 و 2 بود (یعنی نرخ تغییر دیگر وجود ندارد. بیش از 100٪ به عنوان ساعت بدون جهش و زمان هایی که مقدار نسبت کمتر از 0.5 یا بیشتر از 2 به عنوان ساعت جهش بود. ما همچنین نسبت تعداد موارد را بین دوره های فواصل دو ساعته و فواصل سه ساعته محاسبه کردیم. جدول 2درصد ساعات بدون جهش را در سه موقعیت نشان می دهد. اگرچه درصد ساعات بدون جهش با افزایش فاصله زمانی کاهش یافت، اما همچنان برای هر سه بازه زمانی بالا بود. بنابراین، می توان نتیجه گرفت که بین موارد در لحظات مجاور (1 تا 3 ساعت) تعامل وجود دارد.
شکل 9 تغییرات متغیرهای دمای روزانه و تعداد جرم را نشان می دهد و روند آنها دارای ارتباط خاصی است. با توجه به اینکه منطقه مورد مطالعه جزئی از یک شهر است، تغییرات مکانی قابل توجهی در دما در این منطقه وجود ندارد. بنابراین، ما فقط تأثیر دما را بر داده های جرم در طول زمان تجزیه و تحلیل کردیم. برای بررسی روابط بین متغیرهای دمای روزانه و تعداد جرم از تحلیل همبستگی پیرسون [ 63 ] استفاده شد. جدول 3 نتایج را نشان می دهد. متغیرهای دمای روزانه (دمای متوسط، بالاترین دما و کمترین دما) به طور قابل توجهی همبستگی بالایی دارند. ما بالاترین دمای روزانه را که بیشترین ارتباط را با تعداد جرم دارد، برای استفاده در تحلیل رگرسیون تعداد جرم انتخاب کردیم [ 52]. نتیجه ( 9/30 = R2 ) نشان داد که بالاترین دما می تواند 9/30 درصد از واریانس جرم اموال را توضیح دهد.

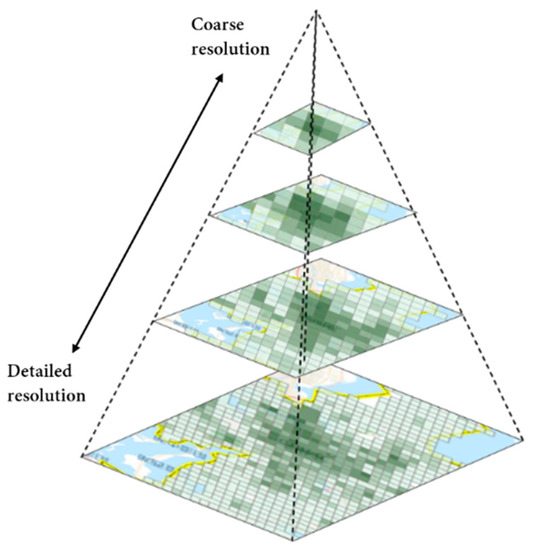
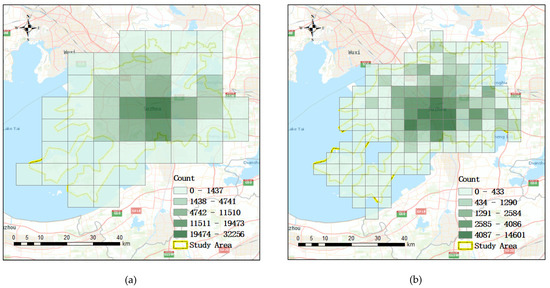
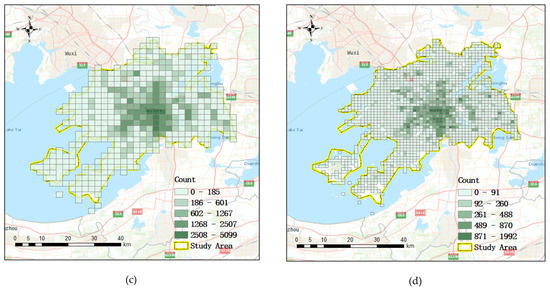
4.2. تجمیع داده ها

شکل 10 توزیع جرم اموال را در تصمیمات مکانی مختلف از ژانویه 2012 تا اکتبر 2013 نشان می دهد. اطلاعات تصمیمات فضایی مختلف منطقه مورد مطالعه در جدول 4 نشان داده شده است . یک ویژگی خوشه‌بندی قوی برای توزیع جرم وجود دارد. موارد عمدتاً در مرکز منطقه مورد مطالعه متمرکز شده اند.

4.3. مدل ST-ResNet برای پیش بینی جرم در سوژو

ما داده های آموزشی از سال 2012 را بین مجموعه آموزشی و مجموعه اعتبار سنجی به نسبت 9:1 تقسیم کردیم. RMSE به عنوان معیار ارزیابی برای تنظیم فراپارامترهای اصلی برای شناسایی پارامترهای بهینه برای مدل‌های ST-ResNet در هر رزولوشن، از جمله اندازه هسته کانولوشن، تعداد هسته‌های پیچشی، عمق شبکه، و طول نزدیکی، دوره و روند استفاده شد. استراتژی توقف اولیه برای جلوگیری از تطبیق بیش از حد [ 64 ، 65 ] اتخاذ شد. روش آموزش زمانی متوقف شد که RMSE مجموعه اعتبارسنجی برای 5 تکرار ضعیف نشد.
ما RMSEها را بین پیش‌بینی‌ها و داده‌های اعتبارسنجی با پارامترهای مختلف در هر وضوح مقایسه کردیم. مدل ST-ResNet بهینه باید با اندازه هسته پیچشی 3×3 ( پیوست A جدول A1 )، 64 هسته پیچشی ( پیوست A جدول A2 )، 8 واحد شبکه باقیمانده ( پیوست A شکل A1 ) و 3 جزء زمانی ساخته شود. (1 ساعت، 1 روز و 1 هفته) ( پیوست A شکل A2 , پیوست A شکل A3 , پیوست A شکل A4، به ترتیب). با توجه به تجزیه و تحلیل قبلی، ثابت شده است که بالاترین دمای روزانه یک عامل خارجی مهم موثر بر جرایم اموال است. در این مدل، بالاترین دمای روزانه را به عنوان جزء خارجی انتخاب کردیم.

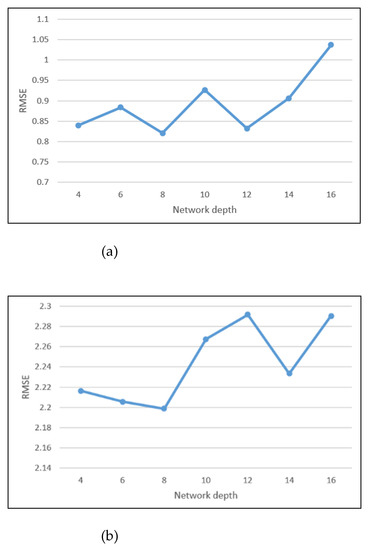
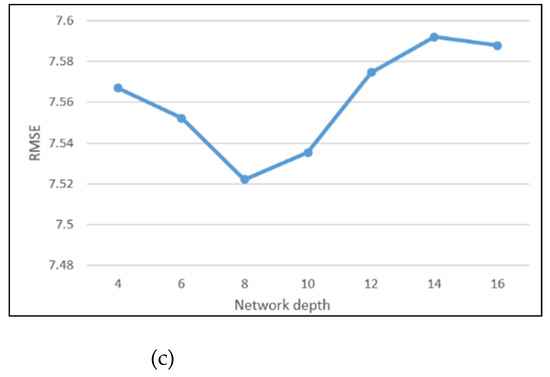
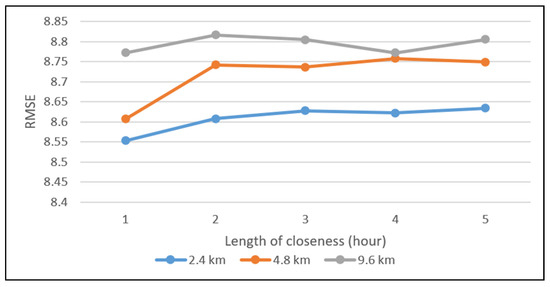
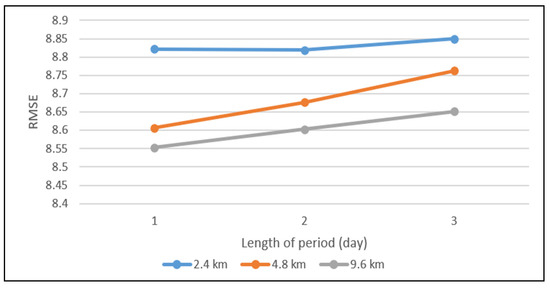
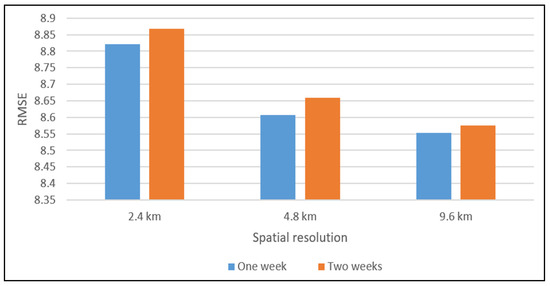
4.4. انتخاب وضوح فضایی بهینه

ما مدل‌هایی را با فراپارامترهای بهینه در وضوح‌های فضایی مختلف (از 1.2 کیلومتر تا 9.6 کیلومتر) اجرا کردیم و PAI نتایج پیش‌بینی را محاسبه کردیم (نشان داده شده در شکل 11 ). بالاترین PAI با وضوح فضایی 2.4 کیلومتر در منطقه مورد مطالعه ما با RMSE = 7.81 به دست آمد.

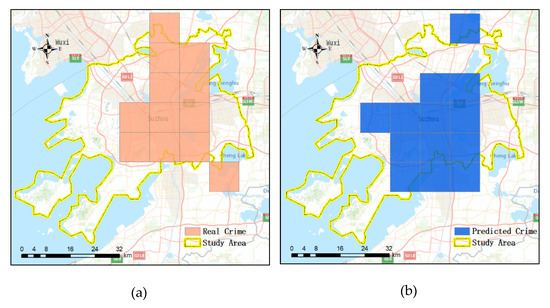
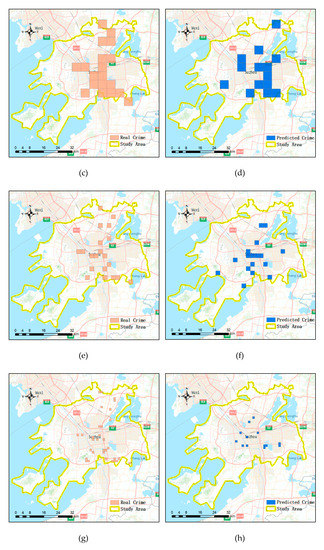
4.5. ارزیابی نتایج پیش بینی

بر اساس نتایج قبلی، مدل ST-ResNet بهینه با وضوح فضایی 2.4 کیلومتر انجام شده است. با مجموعه داده آزمون، ما مقادیر شاخص ارزیابی متوسط ​​آن را برای نتایج پیش‌بینی آن برای PAI = 8.8 محاسبه کردیم.
شکل 12 نتایج پیش‌بینی و توزیع واقعی را در چهار قطعنامه مختلف در ساعت 12 صبح روز 1 ژانویه 2013 نشان می‌دهد. نقشه‌های دودویی اقتباس شده‌اند زیرا شاخص ارزیابی پیش‌بینی جرم PAI به مکانی می‌پردازد که کانون جرم است یا نه (دودویی). شبکه های رنگی نشان دهنده وقوع جنایات است. به طور کلی، نتایج پیش‌بینی واقعی در مراکز شهرها، که مناطقی با تراکم جرم بالا هستند، متمرکز شده‌اند. در مناطق لبه، پیش بینی ها ضعیف هستند. اگر چه شباهت بین نتایج پیش‌بینی و توزیع‌های واقعی با افزایش وضوح کاهش می‌یابد، بین اندازه شبکه و آرایش عملی نیروی پلیس یک مبادله وجود دارد. مقادیر PAI پیش‌بینی با وضوح 1.2 کیلومتر ( شکل 12 ب)، وضوح 2.4 کیلومتر ( شکل 12) به دست می‌آید.d)، وضوح 4.8 کیلومتر ( شکل 12 f)، و وضوح 9.6 کیلومتر ( شکل 12 ساعت) وضوح به ترتیب 2.7، 5.9، 9.8، و 3.3 هستند. سلول‌های شبکه بزرگ‌تر می‌توانند فعالیت‌های مجرمانه بیشتری را ضبط کنند، اما منجر به مشکلاتی برای ترتیبات پلیس می‌شوند. یافتن کانون های جرم و جنایت با اندازه سلول شبکه ای مناسب برای سازماندهی موثر نیروهای پلیس بسیار مهم است.

5. نتیجه گیری و کار آینده

ما یک روش تفکیک فضایی تطبیقی ​​را برای انتخاب بهترین وضوح فضایی برای پیش‌بینی جرم در مقیاس‌های زمانی ساعتی بر اساس مدل ST-ResNet پیشنهاد کردیم. در این مقاله، ویژگی‌های توزیع جرم دارایی و عوامل تأثیر آب و هوای مربوطه را مورد بحث قرار دادیم. روابط تعاملی بین جنایات نزدیک در زمان تایید شد. مشخصه دوره ای جرم در روزها و هفته ها مورد آزمایش قرار گرفت. از نظر فضایی، جرایم اغلب خوشه‌بندی می‌شوند و درجات خوشه‌بندی رویدادهای جرم منطقه‌ای در تفکیک‌های فضایی مختلف متمایز است. یک مدل لایه بندی هرمی برای انجام اطلاعات با وضوح های مختلف ساخته شد. روشی که ما پیشنهاد کردیم می‌تواند دقت مدل پیش‌بینی جرم ساعتی اتخاذ شده در تحقیق وانگ (2019) را با انتخاب وضوح بهینه برای آن بهبود بخشد.29 ]. ما معتقدیم که نتایج فعلی می تواند برای تخصیص کارآمدتر منابع پلیس مورد استفاده قرار گیرد.
در این مطالعه، نتایج نشان داد که واحد تحلیل بهینه نه بهترین و نه وسیع‌ترین واحد در نظر گرفته شده، بلکه یک واحد میانی است. این با تحقیقات راموس و همکارانش مطابقت دارد. (2020) و مالسون و همکاران. (2019) [ 44 ، 45 ]. راموس و همکاران (2020) نقشه های جرم با دانه بندی متوسط ​​را به عنوان قابل اطمینان ترین توصیه می کند، زیرا دانه بندی های درشت ممکن است نقاط جرم و جنایت را بپوشانند و دانه بندی های بسیار ریز ممکن است شمارش جرم را ناپایدار و غیرنماینده کند [ 45 ]]. به طور مشابه، مالسون و همکاران. (2019) نقشه‌های با دانه‌بندی متوسط ​​را برای تجمیع داده‌های نقطه‌ای توصیه می‌کند، زیرا می‌توانند مزایای واحدهای کوچک‌تر را متعادل کنند (ناهمگونی مهمی که احتمالاً در واحدهای بزرگ‌تر پنهان می‌شود در هنگام استفاده از واحدهای کوچک‌تر آشکار است) و اشکالات بزرگ‌تر (از جمله ناپایدار و غیرنماینده) شمارش جرم) [ 44 ].
در مقابل، برخی از محققان به این نتیجه رسیدند که “کوچکتر بهتر است” در انتخاب دانه بندی برای تجزیه و تحلیل جرم [ 39 ، 43 ]. این مطالعات بر تأثیر محیط اجتماعی بر سطح جرم و جنایت از دیدگاه خرد متمرکز است. یک تحلیل ریز نمای ممکن است رابطه بین سطح جرم و عوامل تاثیر آن را در مناطق کوچک ارائه دهد. با این حال، این نتایج را نمی توان برای استقرار پلیس استفاده کرد. روش ما برای یافتن مناسب‌ترین واحد برای بهبود نرخ ضربه نقاط حادثه خیز پیش‌بینی‌شده استفاده می‌شود. انتظار می رود که نتیجه استقرار پلیس محلی را بهبود بخشد و از جرم و جنایت جلوگیری کند.
عوامل زیادی می توانند بر رفتارهای مجرمانه تأثیر بگذارند و تأثیر آنها در موقعیت های مختلف متفاوت است. وقوع جرم معمولاً نتیجه عوامل متعددی است. این مقاله فقط ضریب دما را مورد بحث قرار می دهد و توضیح کمکی کافی نیست. در کارهای آینده عوامل بیشتری در نظر گرفته خواهد شد. تأثیر آنها بر جرم برای بهبود تفسیر جرم برای بهبود دقت پیش‌بینی تجزیه و تحلیل و ترکیب می‌شود.

پیوست اول

جدول A1 RMSEهای بین پیش‌بینی‌ها و داده‌های اعتبارسنجی را در وضوح‌های فضایی مختلف با اندازه‌های هسته پیچشی مختلف فهرست می‌کند. از همان هایپرپارامترها استفاده شد: تعداد هسته کانولوشن = 16، عمق شبکه = 4، طول نزدیکی = 1 ساعت، طول دوره = 1 روز، طول روند = 1 هفته. نتایج نشان داد که 3×3 اندازه هسته کانولوشن بهینه برای مدل است. یک هسته بزرگتر منطقه فضایی بزرگتری را پوشش می دهد، اما برای همان میدان پذیرنده، انباشته شدن هسته های چند لایه کوچک برای تشخیص ویژگی های غیرخطی پیچیده تر از یک هسته بزرگتر تک لایه مفید است [ 66 ].
جدول A2 RMSE های بین پیش بینی ها و داده های اعتبار سنجی را در وضوح های فضایی مختلف با تعداد هسته های کانولوشن متفاوت فهرست می کند. سایر پارامترها ثابت می مانند. تعداد هسته‌های کانولوشن بین 16، 32، 64 و 128 متغیر است. RMSEها در ابتدا با افزایش تعداد هسته‌های کانولوشن کاهش می‌یابند و زمانی که تعداد آن‌ها 64 باشد به حداقل مقادیر خود می‌رسند. اگرچه تعداد زیادی از هسته‌های کانولوشن را می‌توان برای توزیع دقیق ویژگی ها را استخراج کنید، هسته های کانولوشن بیش از حد می تواند منجر به مشکلات بیش از حد برازش شود. تعداد بهینه هسته کانولوشن برای مدل 64 است.
شکل A1 تأثیر عمق شبکه را بر نتایج آموزشی در وضوح های فضایی مختلف نشان می دهد. واحد شبکه باقیمانده عمق شبکه را نشان می دهد. اعماق در مرحله دوم از 4 تا 16 متغیر است. همانطور که شبکه عمیق تر می شود، RMSE ها در ابتدا کاهش می یابند و زمانی که عمق هشت است به حداقل مقادیر خود می رسند. متعاقباً RMSE ها افزایش می یابد. سختی تمرین و نویز در حاشیه شهر با اضافه شدن لایه ها معرفی می شود. بنابراین، عمق شبکه بهینه برای مدل 8 واحد ResNet است.
تأثیر مؤلفه‌های زمانی، از جمله نزدیکی، دوره، و روند در وضوح‌های فضایی مختلف نیز تأیید می‌شود. شکل A2 تغییرات در RMSEها را در وضوح‌های فضایی مختلف با طول‌های نزدیکی متفاوت نشان می‌دهد، که در آن طول دوره را به 1 روز و طول روند را به 1 هفته تعیین می‌کنیم. هنگامی که طول نزدیکی 1 ساعت است، RMSE ها حداقل هستند. در مقایسه با ساعات دور، جرایم بین دو ساعت مجاور بیشتر مرتبط است. شکل A3تغییرات در RMSE ها را در وضوح های فضایی مختلف با طول دوره های مختلف نشان می دهد که در آن طول نزدیکی را به 1 ساعت و طول روند را به 1 هفته ثابت می کنیم. ما می توانیم مشاهده کنیم که RMSE با افزایش طول دوره کاهش می یابد. طول دوره 1 روزه منجر به بهترین RMSE ها می شود، که نشان می دهد دوره های کوتاه مدت سودمند هستند، در حالی که مدل سازی دوره های بلندمدت ممکن است دشوار باشد. شکل A4 تغییرات در RMSEها را در وضوح‌های فضایی مختلف با طول‌های روند متفاوت نشان می‌دهد، که در آن طول نزدیکی را به 1 ساعت و طول دوره را به 1 روز ثابت می‌کنیم. می بینیم که طول روند 1 هفته ای منجر به بهترین عملکرد می شود. مشابه دوره‌ها، گرفتن روندهای بلندمدت ممکن است دشوارتر باشد.
Ijgi 10 00314 g0a1a 550 Ijgi 10 00314 g0a1b 550
شکل A1. RMSE برای وضوح‌های فضایی مختلف و عمق شبکه: ( الف ) RMSE برای عمق‌های مختلف شبکه در وضوح فضایی 9.6 کیلومتر. ( ب ) RMSE برای اعماق شبکه های مختلف با وضوح مکانی 4.8 کیلومتر. ( ج ) RMSE برای اعماق شبکه های مختلف با وضوح فضایی 2.4 کیلومتر.
Ijgi 10 00314 g0a2 550
شکل A2. RMSE در وضوح های فضایی مختلف با طول های مختلف نزدیکی.
Ijgi 10 00314 g0a3 550
شکل A3. RMSE در وضوح های فضایی مختلف با طول زمان های مختلف.
Ijgi 10 00314 g0a4 550
شکل A4. RMSE ها در وضوح های فضایی مختلف با طول های مختلف روند.

منابع

  1. رومنز، آ. هاردینز، دبلیو. اثر تفکیک مکانی-زمانی بر عملکرد مدل پلیسی پیش‌بینی‌کننده. بین المللی J. پیش بینی. 2021 ، 37 ، 125-133. [ Google Scholar ] [ CrossRef ]
  2. هاردینز، دبلیو. رامنز، الف. پلیس پیش بینی به عنوان ابزاری جدید برای اجرای قانون؟ تحولات و چالش های اخیر. یورو جی. جنایت. نتیجه سیاست 2018 ، 24 ، 201-218. [ Google Scholar ] [ CrossRef ]
  3. لیو، ال. جی، جی. آهنگ، جی. آهنگ، جی. لیائو، دبلیو. یو، اچ. Liu, W. Hotspot Prediction of Public Project Crime بر اساس تمایز فضایی جرم و محیط ساخته شده. J. Geo-Inf. علمی 2019 ، 21 ، 1655-1668. [ Google Scholar ] [ CrossRef ]
  4. چن، ایکس. چو، ی. جانگ، SY پیش‌بینی جرم با استفاده از احساسات و آب و هوای توییتر. در مجموعه مقالات سمپوزیوم طراحی مهندسی سیستم و اطلاعات 2015، شارلوتزویل، ویرجینیا، ایالات متحده آمریکا، 24 آوریل 2015. [ Google Scholar ] [ CrossRef ]
  5. آقابابایی، س. مکره چی، م. استخراج محتوای رسانه های اجتماعی برای پیش بینی جرم. در مجموعه مقالات کنفرانس بین المللی IEEE/WIC/ACM 2016 در زمینه هوش وب (WI)، اوماها، NE، ایالات متحده آمریکا، 13 تا 16 اکتبر 2016. [ Google Scholar ] [ CrossRef ]
  6. چینی، اس. تامپسون، ال. Uhlig, S. Utility of Hotspot Mapping برای پیش بینی الگوهای فضایی جرم. امن J. 2008 , 21 , 4-28. [ Google Scholar ] [ CrossRef ]
  7. مولر، جی. پورتر، شبکه چرخشی MD، پیش بینی جرم به حداکثر رساندن PAI. آمار مقعدی حداقل داده 2018 ، 11 ، 227-236. [ Google Scholar ] [ CrossRef ]
  8. جفریس، ای. کاوش چند روشی نقاط داغ جرم و جنایت. در مجموعه مقالات نشست سالانه آکادمی علوم عدالت کیفری، آلبوکرکی، NM، ایالات متحده، 10-14 مارس 1998. صص 10-14. [ Google Scholar ]
  9. آدامز-فولر، تی. نقاط داغ قتل تاریخی: مورد سه شهر. Ph.D. پایان نامه، دانشگاه هاوارد، واشنگتن، دی سی، ایالات متحده آمریکا، 2001. در دسترس آنلاین: https://bit.ly/2Rw7NKc (دسترسی در 5 مه 2021).
  10. سامپسون، RJ; گرووز، ساختار جامعه و جرم و جنایت: آزمایش نظریه بی‌سازمانی اجتماعی. صبح. جی. سوسیول. 1989 ، 94 ، 774-802. در دسترس آنلاین: https://www.journals.uchicago.edu/doi/abs/10.1086/229068 (در 5 مه 2021 قابل دسترسی است). [ CrossRef ][ نسخه سبز ]
  11. مولر، برو؛ کوتاه، مگابایت؛ برانتینگهام، پی جی. شوئنبرگ، FP; تیتا، جنرال الکتریک مدل سازی فرآیند نقطه هیجان انگیز جنایت. مربا. آمار دانشیار 2011 ، 106 ، 100-108. [ Google Scholar ] [ CrossRef ]
  12. Mohler, G. نقشه‌های نقطه‌های مهم فرآیند نقطه‌گذاری شده برای پیش‌بینی جنایت قتل و اسلحه در شیکاگو. بین المللی J. پیش بینی. 2014 ، 30 ، 491-497. [ Google Scholar ] [ CrossRef ]
  13. گور، دبلیو. Olligschlaeger, A. Crime Hot Spot Forecasting: Modeling and Comparative Evaluation خلاصه ; خدمات مرجع عدالت کیفری ملی (NCJRS): Rockville, MD, USA, 2002. در دسترس آنلاین: https://www.ojp.gov/pdffiles1/nij/grants/195168.pdf (در 5 مه 2021 قابل دسترسی است).
  14. کورنیش، دی بی؛ کلارک، RV درک جابجایی جرم: کاربرد نظریه انتخاب عقلانی. جرم شناسی 1987 ، 25 ، 933-948. [ Google Scholar ] [ CrossRef ]
  15. برانتینگهام، پی جی. برانتینگهام، جرم شناسی محیطی PL ; انتشارات سیج: بورلی هیلز، کالیفرنیا، ایالات متحده آمریکا، 1981; در دسترس آنلاین: https://books.google.com/books?id=ITDTAAAAIAAJ (دسترسی در 5 مه 2021).
  16. کوهن، LE; فلسون، ام. تغییرات اجتماعی و روند نرخ جرم و جنایت: رویکرد فعالیت معمول. صبح. اجتماعی Rev. 1979 , 44 , 588-608. [ Google Scholar ] [ CrossRef ]
  17. پوترا، IGB؛ کو، پی اف. Chen, HH تحلیل فضایی اثر آلودگی هوا بر خشونت خانگی و سرقت در نیو ساوت ولز. در مجموعه مقالات چهلمین کنفرانس آسیایی سنجش از دور: پیشرفت فناوری سنجش از دور برای آینده هوشمند، ACRS 2019، Daejeon، کره، 14 تا 18 اکتبر 2019؛ در دسترس آنلاین: https://www.scopus.com/inward/record.url?scp=85085666037&partnerID=8YFLogxK (دسترسی در 5 مه 2021).
  18. ریستئا، ع. کوندی، ا. لایتنر، M. داده های رسانه های جغرافیایی اجتماعی به عنوان پیش بینی کننده ها در یک برنامه GWR برای پیش بینی نقاط داغ جرم (مقاله کوتاه). در مجموعه مقالات دهمین کنفرانس بین المللی علوم اطلاعات جغرافیایی (GIScience 2018)، ملبورن، استرالیا، 28 تا 31 اوت 2018. [ Google Scholar ] [ CrossRef ]
  19. جانسون، SD; Bowers، KJ دزدی به عنوان سرنخی برای آینده: آغاز نقطه داغ آینده نگر. یورو J. Criminol. 2004 ، 1 ، 237-255. [ Google Scholar ] [ CrossRef ]
  20. جانسون، SD; Bowers، KJ پایداری خوشه‌های فضا-زمان سرقت. برادر J. Criminol. 2004 ، 44 ، 55-65. [ Google Scholar ] [ CrossRef ]
  21. هانت، جی.ام. Acton، ST آیا نقاط داغ جنایی حرکت می کنند؟ بررسی اثرات مسئله واحد منطقه ای قابل تغییر و مسئله واحد زمانی قابل تغییر بر پایداری نقطه داغ جرم. Ph.D. پایان نامه، دانشگاه آمریکایی، واشنگتن، دی سی، ایالات متحده آمریکا، 2016. [ Google Scholar ]
  22. پیزا، EL; کارتر، JG پیش بینی آغازگر و رویدادهای تقریباً تکراری در الگوهای جرم و جنایت فضایی-زمانی: تجزیه و تحلیل سرقت مسکونی و سرقت وسایل نقلیه موتوری. عدالت Q. 2018 ، 35 ، 842-870. [ Google Scholar ] [ CrossRef ]
  23. وانگ، بی. ژانگ، دی. ژانگ، دی. برانتینگهام، پی جی. Bertozzi، AL Deep Learning برای پیش‌بینی زمان واقعی جنایت. arXiv 2017 , arXiv:1707.03340. [ Google Scholar ]
  24. کانگ، اچ. کانگ، اچ. پیش‌بینی وقوع جرم از داده‌های چندوجهی با استفاده از یادگیری عمیق. PLoS ONE 2017 , 12 , e176244. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  25. اسکیول، ن. نیکولیس، او. پرالتا، بی. Mateu، J. پیش‌بینی فضایی-زمانی رویدادهای جنایت بالتیمور با استفاده از شبکه‌های عصبی CLSTM. IEEE Access 2020 ، 8 ، 209101–209112. [ Google Scholar ] [ CrossRef ]
  26. Stec، A.; کلابجان، دی. پیش بینی جرم با یادگیری عمیق. arXiv 2018 , arXiv:1806.01486. [ Google Scholar ]
  27. او، ک. ژانگ، ایکس. رن، اس. Sun, J. یادگیری باقیمانده عمیق برای تشخیص تصویر. در مجموعه مقالات کنفرانس IEEE در مورد بینایی رایانه ای و تشخیص الگو (CVPR)، لاس وگاس، NV، ایالات متحده آمریکا، 27 تا 30 ژوئن 2016. [ Google Scholar ] [ CrossRef ][ Green Version ]
  28. ژانگ، جی. ژنگ، ی. Qi، D. شبکه‌های باقیمانده مکانی-زمانی عمیق برای پیش‌بینی جریان‌های جمعیتی در سطح شهر. در مجموعه مقالات کنفرانس AAAI در مورد هوش مصنوعی، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، 4 تا 9 فوریه 2017؛ در دسترس آنلاین: https://ojs.aaai.org/index.php/AAAI/article/view/10735 (دسترسی در 5 مه 2021).
  29. وانگ، بی. یین، پی. برتوزی، آل. برانتینگهام، پی جی. اوشر، اس جی. Xin, J. یادگیری عمیق برای پیش‌بینی جرم در زمان واقعی و سه‌گانه‌سازی آن. چانه. ان ریاضی. سر. B 2019 , 40 , 949–966. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  30. یوتنبوگارد، آ. Ceccato، V. خوشه های فضا-زمان جنایت در استکهلم، سوئد. کشیش Eur. گل میخ. 2012 ، 4. [ Google Scholar ] [ CrossRef ]
  31. برانتینگهام، پی جی. Dyreson، DA; جنایت Brantingham، PL از طریق مخروطی از وضوح دیده می شود. صبح. رفتار علمی 2016 ، 20 ، 261-273. [ Google Scholar ] [ CrossRef ]
  32. هابرمن، CP; راتکلیف، جی اچ چالش‌های پلیسی پیش‌بینی‌کننده سرقت‌های مسلحانه خیابانی تقریباً تکراری. سیاسی J. سیاست سیاست. 2012 ، 6 ، 151-166. [ Google Scholar ] [ CrossRef ]
  33. Bowers، KJ; جانسون، تکرارهای سرقت خانگی SD و خوشه‌های فضا-زمان: ابعاد ریسک. یورو J. Criminol. 2005 ، 2 ، 67-92. [ Google Scholar ] [ CrossRef ]
  34. بلوک، اس. فوجیتا، اس. الگوهای تقریباً تکرار سرقت های موقت و دائم وسایل نقلیه موتوری. جنایت قبلی جامعه ایمن 2013 ، 15 ، 151-167. [ Google Scholar ] [ CrossRef ]
  35. ناکس، EG; بارتلت، ام اس تشخیص تعاملات فضا-زمان. JR Stat. Soc. سر. C (Appl. Stat.) 1964 ، 13 ، 25-30. [ Google Scholar ] [ CrossRef ]
  36. وانگ، ز. لیو، ایکس. تجزیه و تحلیل نقاط داغ سرقت و قربانی شدن تقریباً تکراری در یک شهر بزرگ چین. ISPRS Int. J. Geo-Inf. 2017 ، 6 ، 148. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  37. Bowers، KJ; جانسون، SD; Pease، K. نقطه داغ آینده نگر: آینده نقشه برداری جرم و جنایت؟ برادر J. Criminol. 2004 ، 44 ، 641-658. [ Google Scholar ] [ CrossRef ]
  38. جانسون، SD; Birks، دی جی; مک لافلین، ال. Bowers، KJ; Pease, K. نقشه برداری جنایت آینده نگر در زمینه عملیاتی: گزارش نهایی ; وزارت کشور: لندن، انگلستان، 2007; در دسترس آنلاین: https://bit.ly/3tkAmHV (دسترسی در 5 مه 2021).
  39. اوبرویتلر، دی. Wikström، POH چرا کوچک بهتر است: پیشبرد مطالعه نقش زمینه های رفتاری در علت جرم. در قرار دادن جرم در جای خود: واحدهای تحلیل در جرم شناسی جغرافیایی ; Weisburd, D., Bernasco, W., Bruinsma, G., Eds. Springer: New York, NY, USA, 2009; صص 33-60. [ Google Scholar ] [ CrossRef ]
  40. ویزبرد، دی. گراف، ای آر. یانگ، اس . جرم‌شناسی مکان: بخش‌های خیابان و درک ما از مسئله جرم ؛ انتشارات دانشگاه آکسفورد: آکسفورد، انگلستان، 2012. [ Google Scholar ] [ CrossRef ]
  41. شرمن، LW; گارتین، روابط عمومی؛ بورگر، ME نقاط داغ جنایت غارتگر: فعالیت‌های روتین و جرم‌شناسی مکان. جرم شناسی (بورلی هیلز) 1989 ، 27 ، 27-56. [ Google Scholar ] [ CrossRef ]
  42. اپن شاو، اس. Taylor، PJ یک میلیون یا بیشتر ضرایب همبستگی: سه آزمایش بر روی مسئله واحد سطحی قابل تغییر. در کاربردهای آماری در علوم فضایی ; Wrigley، N.، Ed. پیون: لندن، بریتانیا، 1979; صص 127-144. [ Google Scholar ]
  43. گرل، ام. کوچکترین بهتر است؟ توزیع فضایی آتش سوزی و مسئله واحد منطقه ای قابل تغییر. جی. کوانت. Criminol. 2017 ، 33 ، 293-318. [ Google Scholar ] [ CrossRef ]
  44. مالسون، ن. استین بیک، دبلیو. اندرسن، MA شناسایی وضوح فضایی مناسب برای تحلیل الگوهای جرم و جنایت. PLoS ONE 2019 , 14 , e218324. [ Google Scholar ] [ CrossRef ]
  45. راموس، آر جی. سیلوا، BFA; کلارک، کی سی; Prates، M. خیلی خوب است که خوب باشد؟ مسائل دانه بندی، یکنواختی و خطا در تحلیل جرم فضایی. جی. کوانت. Criminol. 2020 . [ Google Scholar ] [ CrossRef ]
  46. Rui, LI تکامل تاریخی تجاوز به جرم ملکی با موارد مکرر و اقدامات متقابل تحقیق و پیشگیری در 1995-2010. جی. چین. امنیت عمومی مردم دانشگاه (Soc. Sci. Ed.) 2012 ، 28 ، 117-124. [ Google Scholar ]
  47. مایجر، ع. وسلز، ام. پلیس پیش بینی: بررسی مزایا و معایب. بین المللی J. Public Adm. 2019 ، 42 ، 1031–1039. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  48. یانگ، بی. لیو، ال. لان، ام. وانگ، ز. ژو، اچ. Yu, H. یک روش مکانی-زمانی برای پیش‌بینی جرم با استفاده از داده‌های جرم تاریخی و مناطق انتقالی شناسایی‌شده از تصاویر نور شب. بین المللی جی. جئوگر. Inf. علمی IJGIS 2020 ، 34 ، 1740-1764. [ Google Scholar ] [ CrossRef ]
  49. بنسون، BL; کیم، آی. راسموسن، DW; Zhehlke، TW آیا جرم مالکیت ناشی از مصرف مواد مخدر است یا سیاست اجرای مواد مخدر؟ Appl. اقتصاد 1992 ، 24 ، 679-692. [ Google Scholar ] [ CrossRef ]
  50. Sjoquist، DL جرم و جنایت اموال و رفتار اقتصادی: برخی نتایج تجربی. صبح. اقتصاد Rev. 1973 , 63 , 439-446. [ Google Scholar ]
  51. Trujillo, JC; هاولی، پی. تأثیر آب و هوا بر جرم و جنایت در یک منطقه شهری خشن. محیط زیست رفتار 2021 ، 53 ، 69-90. [ Google Scholar ] [ CrossRef ]
  52. پری، جی دی. سیمپسون، من جنایات خشونت آمیز در یک شهر: عوامل تعیین کننده محیطی. محیط زیست رفتار 1987 ، 19 ، 77-90. [ Google Scholar ] [ CrossRef ]
  53. Cohn، EG آب و هوا و جنایات خشونت آمیز. محیط زیست رفتار 2016 ، 22 ، 280-294. [ Google Scholar ] [ CrossRef ]
  54. کوهن، EG; روتون، جی. آب و هوا، روندهای فصلی و جرایم مالکیت در مینیاپولیس، 1987-1988. تجزیه و تحلیل سری زمانی متغیر تعدیل کننده از فعالیت های معمول. جی. محیط زیست. روانی 2000 ، 20 ، 257-272. [ Google Scholar ] [ CrossRef ]
  55. داده های گلخانه ای در دسترس آنلاین: https://data.sheshiyuanyi.com/ (در 8 مارس 2021 قابل دسترسی است).
  56. دی کولا، ال. Montagne، N. سیستم هرمی برای تجزیه و تحلیل شطرنجی چند مقیاسی. محاسبه کنید. Geosci-Uk 1993 ، 19 ، 1393-1404. [ Google Scholar ] [ CrossRef ]
  57. فیل یانگ، سی. وانگ، DW; یانگ، آر. کافاتوس، م. لی، کیو. تکنیک های بهبود عملکرد در GIS مبتنی بر وب. بین المللی جی. جئوگر. Inf. علمی 2005 ، 19 ، 319-342. [ Google Scholar ] [ CrossRef ]
  58. کوین، اس. گاهگان، ام. یک مدل پیش‌بینی برای کاشی‌های متداول در نقشه وب. تی گیس. 2010 ، 14 ، 193-216. [ Google Scholar ] [ CrossRef ]
  59. کورت، جی. Willmott، KM مزایای میانگین خطای مطلق (MAE) نسبت به ریشه میانگین مربعات خطا (RMSE) در ارزیابی میانگین عملکرد مدل. صعود Res. 2005 ، 30 ، 79-82. [ Google Scholar ] [ CrossRef ]
  60. گوت، سی. گاوسیر، ای. یک تفسیر احتمالی از دقت، یادآوری و امتیاز F، با مفهومی برای ارزیابی. در پیشرفت در بازیابی اطلاعات. ECIR. نکات سخنرانی در علوم کامپیوتر ; Losada، DE، Fernández-Luna، JM، Eds. Springer: برلین/هایدلبرگ، آلمان، 2005; جلد 3408. [ Google Scholar ] [ CrossRef ]
  61. راتکلیف، جی اچ. الگوهای Rengert، GF تقریباً تکراری در تیراندازی‌های فیلادلفیا. امن J. 2008 ، 21 ، 58-76. [ Google Scholar ] [ CrossRef ]
  62. تجزیه و تحلیل داده های چرخه ای با FFT. در دسترس آنلاین: https://ww2.mathworks.cn/help/matlab/math/using-fft.html?lang=en (در 8 مارس 2021 قابل دسترسی است).
  63. Spearman, C. نمایش فرمول برای اندازه گیری واقعی همبستگی. صبح. جی روانی. 1907 ، 18 ، 161-169. [ Google Scholar ] [ CrossRef ]
  64. پیوتروسکی، AP; Napiorkowski، JJ مقایسه روش‌هایی برای جلوگیری از برازش بیش از حد در آموزش شبکه‌های عصبی در مورد مدل‌سازی رواناب حوضه. جی هیدرول. 2013 ، 476 ، 97-111. [ Google Scholar ] [ CrossRef ]
  65. لیائو، آر. ون، اچ. وو، جی. آهنگ، اچ. پان، اف. دونگ، ال. پیش‌بینی کانال محو شدن ریلی از طریق یادگیری عمیق. سیم. اشتراک. اوباش محاسبه کنید. 2018 . [ Google Scholar ] [ CrossRef ]
  66. رن، ی. چن، اچ. هان، ی. چنگ، تی. ژانگ، ی. چن، جی. یک مدل یادگیری عمیق ترکیبی یکپارچه برای پیش‌بینی حجم‌های جریان مکانی-زمانی در سطح شهر. بین المللی جی. جئوگر. Inf. علمی 2020 ، 34 ، 802-823. [ Google Scholar ] [ CrossRef ]
Ijgi 10 00314 g001 550
شکل 1. نقشه تراکم هسته برای جرم مالکیت با استفاده از پهنای باند 1 کیلومتر و اندازه شبکه خروجی 300 متر در منطقه مورد مطالعه از ژانویه 2012 تا اکتبر 2013.
Ijgi 10 00314 g002 550
شکل 2. نمودار جریان روش.
Ijgi 10 00314 g003 550
شکل 3. هرمی از شبکه های تجمعی.
Ijgi 10 00314 g004 550
شکل 4. پیش بینی جرم بر اساس مدل ST-ResNet.
Ijgi 10 00314 g005 550
شکل 5. نمودار آمار روزانه و میانگین متحرک رویدادهای جرایم دارایی.
Ijgi 10 00314 g006 550
شکل 6. تحلیل دوره ای داده های جرم ساعتی: ( الف ) نمودار طیف قدرت. ( ب ) نمودار دوره.
Ijgi 10 00314 g007 550
شکل 7. تحلیل دوره ای داده های جرم روزانه: ( الف ) نمودار طیف قدرت. ( ب ) نمودار دوره.
Ijgi 10 00314 g008 550
شکل 8. آمار ساعتی مربوط به نسبت تعداد موارد در فواصل ساعتی مجاور.
Ijgi 10 00314 g009 550
شکل 9. متغیرهای دمای روزانه و توزیع جرم اموال از ژانویه 2012 تا اکتبر 2013.
Ijgi 10 00314 g010a 550 Ijgi 10 00314 g010b 550
شکل 10. توزیع جرم اموال در تصمیمات مکانی مختلف از ژانویه 2012 تا اکتبر 2013: ( الف ) توزیع جرم در تفکیک فضایی 9.6 کیلومتر. ( ب ) توزیع جرم در 4.8 کیلومتر تفکیک فضایی. ( ج ) توزیع جرم در 2.4 کیلومتر تفکیک فضایی. ( د ) توزیع جرم با تفکیک مکانی 1.2 کیلومتر.
Ijgi 10 00314 g011 550
شکل 11. مقادیر PAI پیش‌بینی جرم در تفکیک‌پذیری‌های فضایی مختلف نتایج حاصل می‌شود.
Ijgi 10 00314 g012a 550 Ijgi 10 00314 g012b 550
شکل 12. مقایسه پیش‌بینی‌های مدل و توزیع‌های واقعی: ( الف ) توزیع واقعی رویدادهای جرم مالکیت در وضوح فضایی 9.6 کیلومتر. ( ب ) تجسم نتایج پیش‌بینی در وضوح فضایی 9.6 کیلومتر. ( ج ) توزیع واقعی وقایع جنایت اموال در 4.8 کیلومتر تفکیک فضایی. ( د ) تجسم نتایج پیش‌بینی در وضوح فضایی 4.8 کیلومتر. ( ه ) توزیع واقعی وقایع جنایات دارایی در تفکیک فضایی 2.4 کیلومتر. ( f ) تجسم نتایج پیش‌بینی در وضوح فضایی 2.4 کیلومتر. ( ز ) توزیع واقعی وقایع جنایت اموال در 1.2 کیلومتر تفکیک فضایی. ( h) تجسم نتایج پیش بینی در وضوح فضایی 1.2 کیلومتر.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید