چکیده

:

داده های ابر نقطه ای می توانند به طور دقیق و شهودی رابطه فضایی بین دیوار زغال سنگ و تجهیزات معدنی کاملاً مکانیزه زیرزمینی را منعکس کنند. با این حال، روش غیرمستقیم استخراج ویژگی ابر نقطه ای بر اساس شبکه های عصبی عمیق، بخشی از اطلاعات مکانی ابر نقطه را از دست می دهد، در حالی که روش مستقیم، بخشی از اطلاعات محلی ابر نقطه را از دست می دهد. بنابراین، ما استفاده از شبکه عصبی کانولوشن گراف پویا (DGCNN) را برای استخراج ویژگی‌های هندسی کره در ابر نقطه چهره کاملاً مکانیزه معدن (FMMF) به منظور به دست آوردن موقعیت کره (نشانگر) در ابر نقطه ای FMMF، بنابراین مبنای مستقیمی برای تبدیل بعدی مختصات FMMF به مختصات ژئودزی ملی با کره به عنوان رسانه میانی فراهم می کند. در مرحله اول، ما تولید یک ابر نقطه کره تنوع (مجموعه آموزشی) و یک ابر نقطه FMMF (مجموعه آزمایشی) را تکمیل کردیم. ثانیاً، ما DGCNN را برای افزایش اثر استخراج ویژگی‌های هندسی کره در FMMF بهبود دادیم. در نهایت، ما تأثیر DGCNN بهبود یافته را با PointNet و PointNet++ مقایسه کردیم. نتایج صحت و امکان استفاده از DGCNN برای استخراج ویژگی های هندسی ابرهای نقطه در FMMF را نشان می دهد و روش جدیدی برای استخراج ویژگی ابرهای نقطه در FMMF ارائه می دهد. در عین حال، نتایج تضمین اولیه مستقیمی برای تجزیه و تحلیل داده‌های ابر نقطه FMMF تحت سیستم مختصات ژئودتیک ملی در آینده فراهم می‌کند. این می تواند مبنای موثری برای صاف کردن و تنظیم شیب نوار نقاله های خراش دهنده فراهم کند.

 

1. مقدمه

در حال حاضر، فناوری پردازش داده‌های ابری نقطه‌ای سه‌بعدی بیشتر و بیشتر در زمینه استخراج استفاده می‌شود [ 1 ، 2 ، 3 ]. مرکز ملی مهندسی رباتیک ایالات متحده می تواند با استفاده از داده های ابر نقطه ای به دست آمده توسط اسکنر لیزری سه بعدی، نقشه سه بعدی و با دقت بالا از جاده های زیرزمینی را با موفقیت ترسیم کند و سپس یک حالت استخراج هوشمند بر اساس سه بعدی پیشنهاد دهد. نقشه [ 4 ]. استفاده از داده های ابر نقطه سه بعدی برای توصیف و ترسیم کل FMMF می تواند به طور دقیق و شهودی رابطه موقعیت مکانی بین دیوار زغال سنگ و تجهیزات معدنی کاملاً مکانیزه را منعکس کند [ 5 ، 6 ،7 ، 8]. این می تواند اطلاعات جهت یک نوار نقاله اسکراپر را ارائه دهد تا جابجایی تکیه گاه هیدرولیک را به موقع تنظیم کند. بنابراین، ما نشانگرها را در FMMF مرتب کردیم و سپس نشانگرها را در ابر نقطه ای FMMF یافتیم (در این مطالعه، کره را تحت پشتیبانی هیدرولیک در FMMF قرار دادیم و از کره به عنوان نشانگر استفاده کردیم). در تحقیقات بعدی، ما نشانگر را به عنوان رسانه میانی برای تبدیل داده های ابر نقطه ای FMMF به سیستم مختصات ژئودتیک ملی برای تجزیه و تحلیل در نظر گرفتیم. این نه تنها برای صاف کردن و شیب نوار نقاله اسکراپر و بهبود کارایی معدن و ایمنی معادن زغال سنگ و سایر معادن اهمیت زیادی دارد، بلکه ابزار مهمی برای تحقق استخراج هوشمندانه و بدون سرنشین در زمینه معدن است.
در مقایسه با روش استخراج ویژگی تصویر دو بعدی، روش استخراج ویژگی ابر نقطه سه بعدی یک نوآوری اخیر است. چگونگی تحقق الگوریتم استخراج ویژگی هندسی ابر نقطه ای کارآمد و قوی در این زمینه در سال های اخیر یک مسئله داغ بوده است [ 9 ، 10 ، 11 ، 12 ، 13 ، 14 ]. بسیاری از محققان ویژگی های هندسی ابرهای نقطه ای را با روش های سنتی استخراج کرده اند. به عنوان مثال، سو و همکاران. [ 15 ] یک الگوریتم درج منحنی هیلبرت تطبیقی ​​با زمان شبه خطی برای بهبود کارایی مثلث بندی ابر نقطه ای پیشنهاد کرد. لیو و همکاران [ 16] یک الگوریتم مثلث‌بندی جدید دلونی برای ابرهای نقطه‌ای پیشنهاد کرد که ابر نقطه‌ای را به عناصر مثلثی تقسیم می‌کند و مثلث‌سازی غیرفعال را استخراج می‌کند. ژائو و همکاران [ 17 ] روشی را برای استخراج سریع ویژگی های ابرهای نقطه ای بر اساس شبکه بندی پیشنهاد کرد. این روش ابتدا یک مدل مجازی از ابر نقطه ایجاد می کند، سپس ویژگی های عادی ابر نقطه را افزایش می دهد و از تبدیل فوریه سریع (FFT) برای محاسبه پراش ابرهای نقطه روی شبکه استفاده می کند. این روش از مزایای سرعت بالا و مصرف کم حافظه برخوردار است. دی و همکاران [ 18] معتقد بود که سلول Voronoi ابر نقطه مجاور نقطه منعکس کننده ویژگی های هندسی محلی نقطه مرکزی است و سلول Voronoi در ویژگی مرزی ابر نقطه صفحه ای شکل است. علاوه بر این، سلول Voronoi در تقاطع تکه های سطحی کروی است، و سلول Voronoi در سطح صاف میله ای شکل است، بنابراین ویژگی های ابر نقطه را می توان از شکل هندسی ارائه شده توسط سلول Voronoi استخراج کرد.
با این حال، استخراج ویژگی هندسی ابرهای نقطه‌ای بر اساس مثلث‌بندی فرآیندی زمان‌بر و آسیب‌پذیر در برابر نویز است. مهمتر از همه، وصله مثلثی نمی تواند با توپولوژی سطح واقعی ابرهای نقطه مطابقت داشته باشد [ 19 ، 20 ]. اگرچه روش شبکه بندی ابرهای نقطه ای نیازی به مثلث بندی ندارد، اما روشی ساده و سریع است. با این حال، شبکه به طور کلی حاوی مقدار زیادی از داده های ابر نقطه است، و از آنجایی که شبکه به عنوان واحد اصلی برای استخراج ویژگی های ابر نقطه استفاده می شود، برخی از نقاط ویژگی را می توان حذف کرد [ 21 ، 22 ]]. استخراج ویژگی های ابر نقطه بر اساس روش Voronoi نیاز به تولید یک نمودار Voronoi محلی دارد و انحراف نسبت ارزش ویژه مدل های مختلف ابر نقطه ای زیاد است. بنابراین، تعیین یک مقدار آستانه برای نسبت کلی در نمودارهای ورونوی [ 23 ] دشوار است.
در سال های اخیر، یادگیری عمیق به یک موضوع تحقیقاتی داغ در زمینه بینایی کامپیوتر تبدیل شده است [ 24 ، 25 ، 26 ، 27 ، 28 ]. با توجه به نوع داده شبکه عصبی عمیق (DNN)، روش‌های استخراج ویژگی ابر نقطه‌ای موجود را می‌توان به روش‌های غیرمستقیم و روش‌های مستقیم تقسیم کرد. با استفاده از روش غیر مستقیم، هو و همکاران. [ 29] ویژگی های یک ابر نقطه LiDAR را با استفاده از شبکه عصبی کانولوشن (CNN) استخراج کرد. در ابتدا، همسایگی هر نقطه به چندین مش تقسیم شد تا برآمدگی ابر نقطه سه بعدی بر روی یک صفحه دو بعدی محقق شود. سپس حداکثر، حداقل و میانگین ارتفاعات تمام نقاط در هر شبکه به عنوان مقادیر ویژه سه کانال (قرمز، سبز، آبی) محاسبه شد تا یک نقشه ویژگی برای هر نقطه ایجاد شود و یک CNN با تعداد زیاد آموزش داده شود. مجموعه داده های برچسب گذاری شده ژائو و همکاران [ 30] از روشی استفاده کرد که شامل ایجاد نقشه ویژگی ابر نقطه ای چند مقیاسی و طراحی یک CNN چند مقیاسی برای استخراج ویژگی های ابر نقطه بود. پس از استفاده از CNN چند مقیاسی برای به دست آوردن توزیع احتمال ابر نقطه، از درخت تصمیم برای بهینه سازی نتایج استفاده شد که دقت شبکه را بیشتر بهبود بخشید. پولیتز و همکاران [ 31 ] یک نقشه ارتفاعی با ترکیب یک ابر نقطه هوابرد با یک ابر نقطه تطبیق متراکم ایجاد کرد و سپس مستقیماً از U-Net برای تقسیم‌بندی نقشه ارتفاع تحت تنظیمات پارامترهای مختلف استفاده کرد تا عملکرد استخراج ویژگی U-Net برای این دو مورد بررسی شود. انواع ابر نقطه ای چی و همکاران [ 32] از دانشگاه استنفورد، شبکه عصبی عمیق PointNet را پیشنهاد کرد که مستقیماً یک ابر نقطه سه بعدی را به عنوان ورودی می گیرد. PointNet می‌تواند مستقیماً داده‌های ابر نقطه اصلی را بدون پیش‌پردازش داده‌های ابر نقطه پردازش کند، مانند سایر مدل‌های سنتی شبکه عصبی عمیق (مانند CNN). PointNet می تواند با پردازش هر نقطه به طور مستقل، به تغییر ناپذیری جایگشت دست یابد. از پرسپترون چندلایه (MLP) برای افزایش ابعاد ویژگی هر نقطه استفاده می کند، حداکثر ادغام را به عنوان یک تابع متقارن انجام می دهد تا ویژگی های هر نقطه را ترکیب کند، و در نهایت بردار ویژگی جهانی را برای تکمیل کار تشخیص خروجی می دهد.
با این حال، روش‌های غیرمستقیم استفاده از شبکه‌های عصبی عمیق برای پردازش ابرهای نقطه، همگی باید ابتدا ابر نقطه را تغییر دهند. این تبدیل به ناچار برخی از اطلاعات فضایی ابر نقطه را از دست می دهد، به این معنی که شبکه عصبی عمیق نمی تواند ویژگی های ابر نقطه را به خوبی یاد بگیرد و نمی تواند ابرهای نقطه مختلف را به وضوح تشخیص دهد، که بر طبقه بندی، تقسیم بندی و استخراج ویژگی تاثیر می گذارد. ابرهای نقطه ای در محیط های کاربردی مختلف [ 33]. اگرچه PointNet می‌تواند مستقیماً ویژگی‌های هندسی ابر نقطه را پردازش کند، اما نمی‌تواند اطلاعات محلی را در مدل ابر نقطه جمع‌آوری کند، زیرا فقط ویژگی‌های نقاط مستقل را استخراج می‌کند، که منجر به توانایی ضعیف شبکه برای استخراج ویژگی‌ها از ابر نقطه می‌شود. که بر توانایی تعمیم شبکه نیز تأثیر می گذارد [ 34 ]. DGCNN مبتنی بر شبکه عصبی گراف (GNN) با کمک مفهوم CNN در یادگیری عمیق است. از کانولوشن لبه برای پردازش داده ها در ساختار گراف استفاده می کند و کاربرد گسترده ای در مهندسی زمین شناسی، مهندسی محیط زیست، مهندسی شیمی و غیره داشته است. [ 35 ، 36 ، 37]. DGCNN نیازی به تبدیل داده های ساختار گراف به بردار فضای پیوسته کم بعدی ندارد. بلکه می تواند مستقیماً کل ساختار نمودار را به عنوان ورودی بگیرد (ساختار نمودار در این مطالعه ابر نقطه است). علاوه بر این، عملیات پیچیدگی لبه در DGCNN می‌تواند اطلاعات ویژگی‌های محلی داده‌های ابر نقطه را حفظ کند و از تغییرناپذیری مبادله و تغییر ناپذیری چرخش ساختار آن اطمینان حاصل کند تا اطلاعات ویژگی داده‌های ابر نقطه را به طور مؤثرتری استخراج کند و ویژگی مربوطه را تحقق بخشد. اصطلاح. با توجه به دلایل فوق، ما استفاده از DGCNN را برای استخراج ویژگی‌های هندسی ابرهای نقطه در FMMF پیشنهاد می‌کنیم.
علاوه بر این، با بررسی گزارش‌های موجود در ادبیات، دریافتیم که هیچ مطالعه‌ای در مورد استفاده از DGCNN برای پردازش ابرهای نقطه‌ای FMMF انجام نشده است. علاوه بر این، از ادبیات موجود [ 38 ، 39 ، 40]، می دانیم که DGCNN می تواند به طور موثر ویژگی های ابرهای نقطه ای پل ها و سایت های میراث فرهنگی را یاد بگیرد تا این ابرهای نقطه ای را پردازش کند. با این حال، اینکه آیا DGCNN ساخته شده توسط گروه تحقیقاتی نویسنده می‌تواند در زمینه‌های مهندسی معدن و مهندسی زمین‌شناسی کاربرد داشته باشد و اینکه چقدر در استخراج ویژگی‌های هندسی از ابرهای نقطه‌ای FMMF عمل می‌کند، هنوز نیاز به بررسی و مطالعه دارد. بنابراین، در این تحقیق، کره‌های موجود در ابرهای نقطه‌ای FMMF توسط DGCNN استخراج می‌شوند. این مبنایی را برای تبدیل مختصات بعدی FMMF به مختصات ژئودزیکی با استفاده از کره به عنوان واسطه میانی و سپس برای صاف کردن و تنظیم شیب نوار نقاله اسکراپر فراهم می کند. در عین حال، این برای استخراج هوشمند و بدون سرنشین FMMF مهم است. علاوه بر این،
مشارکت های کار ما را می توان به شرح زیر خلاصه کرد:
(1) به منظور اطمینان از اینکه DGCNN به طور کامل ویژگی های ابر نقطه کروی را یاد می گیرد و استحکام DGCNN را بهبود می بخشد، مقادیر مختلفی نویز را به ابر نقطه کره کامل و کره ناقص اضافه کردیم تا یک مجموعه داده از یک ابر نقطه کره متنوع نتایج ما یک شکاف تحقیقاتی موجود را پر می‌کند که در حال حاضر هیچ مجموعه داده‌ای در مدل شبکه عصبی عمق برای استخراج ویژگی‌های هندسی ابرهای نقطه‌ای وجود ندارد.
(2) با توجه به ویژگی های ابر نقطه، ما روشی را برای استخراج ویژگی های هندسی ابر نقطه بر اساس DGCNN برای به دست آوردن موقعیت کره هدف در FMMF پیشنهاد می کنیم. این مطالعه روش جدیدی را برای استخراج ویژگی ابرهای نقطه‌ای در FMMF ارائه می‌کند و مبنایی را برای تبدیل مختصات بعدی FMMF به مختصات ژئودتیکی با کره به‌عنوان محیط میانی و همچنین پایه‌ای را برای صاف کردن و تنظیم شیب فراهم می‌کند. یک نوار نقاله اسکراپر.
(3) در DGCNN با یک لایه کانولوشن لبه چند لایه، اطلاعات همسایگی استخراج شده توسط پیچیدگی لبه به طور بالقوه می تواند نشان دهنده فاصله بسیار طولانی در فضای اصلی باشد، اما لایه پیچیدگی لبه بیش از حد عمیق باعث برازش بیش از حد می شود که بر استخراج ویژگی تأثیر می گذارد. عملکرد DGCNN ما بهترین تعداد لایه‌های پیچش لبه را برای DGCNN برای پردازش ابر نقطه FMMF تعریف می‌کنیم. علاوه بر این، ما از الگوریتم آدام برای بهبود DGCNN برای حل این مشکل استفاده می‌کنیم که شبکه‌های عصبی احتمالاً از راه‌حل بهینه محلی استفاده می‌کنند. نتایج تحقیق نه تنها خطای موقعیت کره را کاهش می دهد، بلکه سازگاری، توانایی تعمیم و ارزش عملی مدل DGCNN را نیز بهبود می بخشد.
(4) ما تأثیر DGCNN بهبود یافته را با PointNet و PointNet++ در استخراج ویژگی‌های هندسی ابرهای نقطه از FMMF با استفاده از شاخص‌های ارزیابی، مانند خطای موقعیت کره مقایسه کردیم. نتایج نشان می دهد که DGCNN بهبود یافته در همه انواع ارزیابی عملکرد بهتری دارد. این نتایج تضمین اولیه مستقیمی را برای تجزیه و تحلیل پیگیری داده‌های ابر نقطه FMMF تحت سیستم مختصات ژئودزیکی ملی فراهم می‌کند، که می‌تواند مبنای مؤثری برای فرماندهی و کنترل تولید معدن زغال‌سنگ فراهم کند. این برای استخراج شفاف، بدون سرنشین و هوشمند FMMF از اهمیت بالایی برخوردار است.
ساختار باقی مانده مقاله به شرح زیر است. بخش 2 روش های مورد استفاده در کار، از جمله روش تولید یک ابر نقطه کره تنوع، الگوریتم بهینه سازی DGCNN، روش پیچش لبه ابر نقطه، و روش برای یافتن نشانگرها در ابر نقطه FMMF را شرح می دهد. . بخش 3 آزمایش را شرح می دهد، از جمله شرح مجموعه داده ها، جزئیات تجربی، نتایج آزمایشی، و بحث. بخش 4 نتیجه گیری را ارائه می دهد.

2. روش ها

این مطالعه با هدف پر کردن شکاف تحقیقاتی در استخراج ویژگی های هندسی در ابر نقطه ای FMMF در زمینه استخراج هوشمند انجام شده است. علاوه بر این، روش غیرمستقیم استخراج ویژگی ابر نقطه ای مبتنی بر شبکه های عصبی عمیق ابتدا نیازمند تبدیل ابر نقطه است که به ناچار بخشی از اطلاعات فضایی ابر نقطه را از دست خواهد داد. علاوه بر این، روش مستقیم برخی از اطلاعات محلی ابر نقطه را از دست می دهد. در این مقاله، روشی برای استخراج ویژگی هندسی ابرهای نقطه در FMMF بر اساس DGCNN پیشنهاد شده است و ابر نقطه کروی در ابر نقطه FMMF پیدا می‌شود، همانطور که در شکل 1 نشان داده شده است. پیچیدگی لبه (EdgeConv) در بخش 2.3 به تفصیل تجزیه و تحلیل و مطالعه شده است .
نشانگرهای کره ای از مواد لاستیکی ساخته شده اند. نشانگرهای کره اجسام متوسطی هستند که مختصات FMMF را به سیستم مختصات ژئودتیک ملی تبدیل می کنند. این نشانگرهای کره در سر و دم FMMF توزیع شده بودند و سه نشانگر کره در سر و دم وجود داشت. ما فقط نیاز داشتیم که یک نشانگر کره پیدا کنیم. دلیل اینکه ما نشانگرهای کره ای زیادی ترتیب دادیم این بود که به DGCNN اجازه دادیم کره ای را با کمترین خطای موقعیت پیدا کند. ما تمام ابرهای نقطه ای FMMF را با استفاده از LiDAR روی ربات بازرسی جمع آوری کردیم. سپس از DGCNN برای یافتن کره استفاده کردیم، خطای موقعیت هر کره را محاسبه کردیم و در نهایت کره ای را با کمترین خطای موقعیت نمایش دادیم.
همانطور که در شکل 1 نشان داده شده است، ما نویز را به ابر نقطه ای کره و ابر نقطه ای کره ناقص اضافه کردیم تا یک مجموعه آموزشی برای ابر نقطه تشکیل دهیم تا DGCNN به طور کامل ویژگی های ابر نقطه کره را بیاموزد. لایه‌های پیچش لبه در DGCNN به نوبه خود به هم متصل شدند و ویژگی‌های محلی و جهانی ابر نقطه با حداکثر ادغام به دست آمد. در انتهای DGCNN، پرسپترون چند لایه (MLP) برای طبقه بندی ابرهای نقطه ای متصل شد. ما ابر نقطه ای FMMF را به عنوان مجموعه آزمایشی برای DGCNN در نظر گرفتیم. از طریق DGCNN آموزش دیده، ابر نقطه کره را در ابر نقطه FMMF پیدا کردیم. در نهایت ابر نقطه کره را قاب کردیم و خطای موقعیت کره را در کنار آن نمایش دادیم. علاوه بر این،

2.1. روش تولید ابر نقطه کره تنوع

محیط FMMF پیچیده است و ویژگی های ابر نقطه کروی آشکار نیست. به منظور اطمینان از اینکه DGCNN به طور کامل ویژگی های ابر نقطه کروی را یاد گرفته است، در ابر نقطه ای FMMF، DGCNN همچنان می تواند کره را هنگام مواجهه با ابر نقطه کروی کامل و ابر نقطه کروی ناقص تشخیص دهد (بیش از نیمی از کره و کمتر از نیمی از کره). بنابراین، در MATLAB R2019a، موقعیت‌های کره و مکعب به صورت تصادفی تنظیم شد ( شکل 2 ).
همانطور که در شکل 2 نشان داده شده است ، موقعیت های کره و مکعب در فضای مشخص شده تصادفی بوده و مکعب درجات مختلف پوشش کره را تشکیل می دهد. علاوه بر این، به منظور افزایش استحکام DGCNN، همانطور که در شکل 3 و شکل 4 نشان داده شده است، تعداد نقاط مختلف نویز را به ابر نقطه یک کره و ابر نقطه ترکیبی از یک کره و مکعب اضافه کردیم .
همانطور که در شکل 3 و شکل 4 نشان داده شده است، با افزایش تدریجی تعداد نقاط نویز در ابر نقطه کره و ابر نقطه ترکیب تشکیل شده توسط کره و مکعب، موقعیت مکانی نقاط نویز به طور تصادفی تغییر کرد. بنابراین، این نقاط نویز درجات مختلفی از تداخل را در حوزه تشخیص DGCNN ایجاد می کنند.

2.2. الگوریتم بهینه سازی DGCNN

2.2.1. نزول گرادیان تصادفی

به عنوان الگوریتم اصلی الگوریتم بهینه‌سازی شبکه عصبی، ایده اصلی شیب تصادفی (SGD) محاسبه گرادیان در زیر مجموعه‌های تصادفی و دسته‌ای کوچک است. سپس، این به گرادیان واقعی در کل مجموعه داده تقریبی می شود [ 41 ]. همانطور که در معادلات (1) و (2)، SGD به طور مکرر وزن ها را با نمونه های دسته ای کوچک در هر مرحله به روز می کند.

ωتی+1=ωتی+Δωتی،
Δωتی=λ∇wE(ωتی)،

جایی که ωتی+1مقدار وزن در زمان t +1 است. ωتیمقدار وزن در زمان t است. Δωتیعملگر گرادیان در زمان t است، یعنی بخش به روز رسانی وزن هر تکرار. λنرخ یادگیری الگوریتم SGD است، E(ωتی)تابع کاهش وزن است ωتیدر تکرار t و∇wE(ωتی)درجه نردبان وزن است ωدر تابع ضرر در زمان t .

معایب SGD عبارتند از [ 42 ، 43 ]:
(1) برای یک تابع خطای غیر محدب، به راحتی می توان در بهینه محلی قرار گرفت.
(2) انتخاب نرخ یادگیری مناسب برای الگوریتم SGD دشوار است. اگر سرعت یادگیری خیلی کم باشد، سرعت همگرایی ممکن است بسیار کند باشد. اگر نرخ یادگیری خیلی زیاد باشد، همگرایی مانع می شود، که منجر به نوسان وزن نزدیک به راه حل بهینه یا حتی ایجاد واگرایی می شود.
(3) SGD از دسته های تصادفی و کوچکی از داده ها برای محاسبه گرادیان استفاده می کند که مشابه گرادیان واقعی در کل مجموعه داده است، بنابراین چگالی محاسبه را کاهش می دهد و این باعث نویز گرادیان و واریانس می شود.

2.2.2. برآورد لحظه تطبیقی

تخمین گشتاور تطبیقی ​​(آدام) یک الگوریتم بهینه‌سازی است که می‌تواند جایگزین فرآیند نزول گرادیان سنتی شود. این وزن شبکه عصبی را به طور مکرر بر اساس داده های آموزشی به روز می کند [ 44]. الگوریتم آدام با الگوریتم نزولی گرادیان تصادفی سنتی متفاوت است. الگوریتم نزولی گرادیان تصادفی از یک نرخ یادگیری واحد برای به روز رسانی تمام وزن ها استفاده می کند و نرخ یادگیری در طول فرآیند آموزش تغییر نخواهد کرد. آدام نرخ‌های یادگیری مستقل و تطبیقی ​​را برای پارامترهای مختلف با محاسبه تخمین لحظه‌ای مرتبه اول و برآورد لحظه درجه دوم گرادیان طراحی می‌کند. الگوریتم Adam مزایای یک گرادیان تطبیقی ​​(AdaGrad) و ریشه میانگین مربع (RMSProp) را ترکیب می کند. عملکرد عالی در حل مسائل ناپایدار و غیرخطی دارد.
در این مطالعه، ما از الگوریتم Adam برای بهبود DGCNN استفاده کردیم تا این مشکل را حل کنیم که مدل شبکه عصبی به راحتی در راه حل بهینه محلی قرار می گیرد و همچنین مشکلات سرعت همگرایی ضعیف و سرعت یادگیری. فرآیند تکراری استفاده از Adam برای به روز رسانی وزن ها در شکل 5 نشان داده شده است [ 45 ].
در الگوریتم آدم، g گرادیان تابع هدف تصادفی f است. پس از تنظیم پارامترها در مرحله اول، در مرحله t , مقادیر تخمین گشتاور مرتبه اول h t و برآورد گشتاور مرتبه دوم r t با استفاده از معادلات (3) و (4) محاسبه می شود.

ساعتتی=β1ساعتتی–1+(1–β1)gتی،
rتی=β2rتی–1+(1–β2)gتی2،
در معادلات (3) و (4) β1نرخ فروپاشی نمایی تخمین گشتاور مرتبه اول است و β2نرخ فروپاشی نمایی تخمین گشتاور مرتبه دوم است. g1،g2،…gتینشان دهنده گرادیان دنباله گام زمانی است که در آن گرادیان اطاعت می کند gتی~پ(gتی). ما تخمین لحظه مرتبه دوم را مقداردهی اولیه می کنیم r0=0. همانطور که در رابطه (5) نشان داده شده است، با تکرار معادله (4)، می توانیم تابع گرادیان و نرخ واپاشی را در تمام مراحل زمانی بدست آوریم.

rتی=∑من=1تیβ2تی–منgمن2–β2∑من=1تیβ2تی–منgمن2،
برای بدست آوردن معادله (6) هر دو طرف معادله (5) را همزمان به عنوان انتظار در نظر می گیریم:

E[rتی]=E[∑من=1تیβ2تی–منgمن2–β2∑من=1تیβ2تی–منgمن2]=E[gتی2](1–β2)∑من=1تیβ2تی–من+δ=E[gتی2](1–β2تی)+δ،
اگر لحظه مرتبه دوم E[gتی2]پس ایستا است δ=0. در موارد دیگر، δارزش کمی دارد در هر دو مورد فقط (1–β2تی)موارد باقی مانده است بنابراین، زمانی که زمان اولیه یا نرخ پوسیدگی کم است، rتیبه بردار صفر بایاس می شود که باید بردار تقسیم شود (1–β2تی)عبارت برای اصلاح انحراف اولیه. پس از اینکه تخمین گشتاور مرتبه دوم با زمان t اصلاح شد ، معادله (7) به دست می آید.

r^تی=rتی1–β2تی،
پس از اصلاح، به روز رسانی وزن نهایی، همانطور که در رابطه (8) نشان داده شده است، به دست می آید.

ωتی+1=ωتی–ساعت^تیηδ+r^تی،
در معادله (8) ωتی+1وزن در زمان t +1 است، ωتیوزن در زمان t است، ساعت^تینتیجه اصلاح تخمین گشتاور مرتبه اول در زمان t است، r^تینتیجه اصلاح تخمین گشتاور مرتبه دوم در زمان t و ηنرخ یادگیری تعیین شده توسط شبکه است.
طبق تحقیقات موجود [ 46 ]، هنگامی که دو الگوریتم بهینه سازی فوق با یک مدل زین مواجه می شوند، الگوریتم SGD نمی تواند از پایین زین فرار کند (نتیجه الگوریتم SGD حداقل محلی است)، همانطور که در شکل 6 نشان داده شده است.
از نمودار زین در شکل 6 می توان دریافت که نتیجه متناظر الگوریتم SGD در حداقل مقدار محلی مدل زینی گیر کرده است. بنابراین، عملکرد الگوریتم بهینه‌سازی SGD در DGCNN توسط آدام در این مطالعه بهبود یافته است. این مطالعه بر تجزیه و تحلیل اثر DGCNN در استخراج ویژگی‌های هندسی متناظر ابر نقطه در FMMF با استفاده از Adam و SGD به منظور تأیید صحت الگوریتم بهینه‌سازی بهبودیافته تمرکز دارد.

2.3. روش پیچیدگی لبه ابر نقطه ای

پیچیدگی لبه در DGCNN از لبه اتصال بین دو گره به هم پیوسته برای نشان دادن ترکیب اطلاعات ویژگی دو گره به هم پیوسته استفاده می کند، سپس اطلاعات ویژگی چندین گره متصل به گره مرکزی را از طریق یک سری تبدیل غیرخطی جمع می کند تا ویژگی های محلی را بیان کند. گره مرکزی [ 47 ].
در پیچیدگی لبه، k نزدیکترین نقطه برای نقطه مرکزی توسط الگوریتم گراف k-نزدیکترین همسایه (KNN) انتخاب می شود و هر نقطه به نوبه خود به عنوان نقطه مرکزی ساختار نمودار برای محاسبه رابطه لبه، الحاق ویژگی ها و MLP در نظر گرفته می شود. محاسبه هنگامی که کانولوشن لبه لایه به لایه انجام می شود، هر لایه یک ساختار نمودار جدید تولید می کند و یک فضای ویژگی جدید را خروجی می کند. نمودار عملیات پیچیدگی معمولی و پیچیدگی لبه در شکل 7 نشان داده شده است .
همانطور که در شکل 7 نشان داده شده است ، در مقایسه با انحراف سنتی بر روی داده های ساختار یافته اقلیدسی، پیچیدگی لبه از k-نزدیک ترین همسایه ها برای تعریف نزدیک ترین نقطه k به نقطه مرکزی به عنوان ناحیه مجاور نقطه مرکزی استفاده می کند. کانولوشن لبه ابتدا ویژگی های لبه را بین نقطه مرکزی و نقاط مجاور استخراج می کند، سپس ویژگی های لبه را پیچیده می کند. بنابراین، پس از عملیات پیچیدگی لبه، هر گره مرکزی حاوی اطلاعات مشخصه خود و اطلاعات مشخصه گره های k مجاور است. چارچوب پیچیدگی لبه در شکل 8 نشان داده شده است .
همانطور که در شکل 8 نشان داده شده است ، N تعداد کل نقاط در ابر نقطه است، f اطلاعات ابعاد هر نقطه است. (آ1،آ2،…آn)در MLP اطلاعات ابعاد ورودی و اطلاعات ابعاد خروجی هر لایه است و K تعداد گره های مجاور در الگوریتم گراف KNN است.
با نمونه برداری پایین از ابر نقطه هدف، یک ابر نقطه F بعدی با n نقطه به دست آوردیم. ایکس={ایکس1،ایکس2،…،ایکسn}⊆آراف. در این مطالعه، f اطلاعات مختصات هر نقطه مرکزی است (F = 3). در ساختار شبکه عصبی، نورون های هر لایه بر روی خروجی لایه قبلی عمل می کنند، بنابراین از بعد f برای نمایش بعد مشخصه ورودی نورون استفاده می شود. سپس، یک نمودار جهت دار جی=(ν،ε)تنظیم شده است تا ساختار محلی ابر نقطه را با توجه به تعداد نقاط ابر نقطه ای که در آن وجود دارد، نشان دهد v={1،2،…،n}و ε⊆v×vبه ترتیب رئوس و یال های گراف جهت دار را نشان می دهد. در ساختار نمودار، لبه بین نقطه مرکزی و نقطه مجاور را می توان با استفاده از رابطه (9) [ 48 ] بیان کرد:

همنj=ساعتΘ(ایکسمن،ایکسj–ایکسمن)،
در معادله (9) ایکسمننقطه مرکزی است، ایکسjنقطه مجاور نقطه مرکزی است، ساعتΘ: آراف×آراف→آراف“و Θ پارامتر قابل یادگیری است. از این رو، ساعتΘیک تابع فعال سازی غیرخطی است که از پارامتر Θ تشکیل شده است. MLP برای محاسبه ویژگی‌های تمام لبه‌های مرتبط و ویژگی‌های مرکز استفاده می‌شود تا ویژگی‌های ابعاد بالا ساختار نمودار را به‌دست آوریم. خروجی نقطه مرکزی در ساختار نمودار را می توان با استفاده از رابطه (10) بیان کرد:

ایکسمن“=پooلمنngj:(من،j)∈εساعتΘ(ایکسمن،ایکسj–ایکسمن)،
در این مطالعه از DGCNN برای پردازش داده های ابر نقطه ای FMMF استفاده شد. پس از انباشتن تعداد زیادی از لایه‌های شبکه، مدل شبکه عصبی عمیق سنتی به دلیل توانایی نمایش قدرتمند خود به نتایج قابل‌توجهی در بسیاری از مشکلات دست یافت. در لایه پیچیدگی لبه چند لایه DGCNN، اطلاعات همسایگی استخراج‌شده توسط پیچیدگی لبه می‌تواند به طور بالقوه منطقه دوردست را در فضای ابر اصلی نشان دهد. با افزایش تعداد لایه‌های پیچش لبه، میدان پذیرنده بزرگ‌تر و بزرگ‌تر می‌شود و ویژگی‌های گره مرکزی اطلاعات بیشتری از گره‌ها را جمع‌آوری می‌کند. پیچیدگی لبه در DGCNN شامل تجمیع ویژگی‌های گره‌های همسایه است. هنگامی که لایه‌های پیچش لبه در چندین لایه روی هم قرار می‌گیرند، ویژگی‌های بین گره‌ها بسیار صاف و بدون تبعیض هستند. که بر عملکرد شبکه تاثیر می گذارد. بنابراین، این کار تأثیر لایه‌های پیچیدگی لبه‌های مختلف را بر عملکرد DGCNN در آن تحلیل می‌کندبخش 3.1 .

2.4. روش جستجو برای نشانگرها در Point Cloud of FMMF

ابرهای نقطه ای FMMF تجزیه و تحلیل شده در این مطالعه از 43101 سطح معدن زغال سنگ Yujialiang در شمال شرقی شهر Shenmu، استان Shaanxi، چین جمع آوری شد ( شکل 9 ). معدن زغال سنگ Yujialiang یک پایگاه زغال سنگ صادراتی در مقیاس بزرگ گروه انرژی ملی چین است. در عین حال، معدن زغال سنگ Yujialiang یکی از معادن ده میلیون تنی گروه زغال سنگ شندونگ است. معدن زغال سنگ Yujialiang مساحتی معادل 56.33 کیلومتر مربع ، با ذخایر زمین شناسی 504 میلیون تن و ذخایر قابل بازیافت 355 میلیون تن را پوشش می دهد. کیفیت زغال سنگ در میدان معدن عالی است، با ویژگی‌های گوگرد بسیار کم، فسفر بسیار کم، خاکستر بسیار کم و ارزش حرارتی بالا [ 49 ].
طول 43101 صفحه معدن 351.4 متر، طول پیشروی 1809.4 متر، ضخامت درز زغال سنگ 1.0 ~ 1.7 متر، ضخامت متوسط ​​1.5 متر، زاویه شیب 1 ~ 3 درجه، وزن واحد 1.30 است. t/m 3 ، و ارتفاع استخراج 1.4 متر [ 50 ] است. ما یک ربات بازرسی زیرزمینی گران قیمت را در مسیر مخصوص خارج از نوار نقاله اسکراپر در 43101 صفحه ماینینگ نصب کردیم و ابر نقطه کل FMMF توسط تابع LiDAR روی ربات بازرسی به دست آمد ( شکل 10 ).
ما از MATLAB R2019a برای خواندن ابر نقطه ای FMMF جمع آوری شده توسط LiDAR استفاده کردیم. برای مشاهده شهودی، همانطور که در شکل 11 نشان داده شده است، بخشی از ابر نقطه را برای تجسم رهگیری کردیم . خط آبی در ابر نقطه مسیر LiDAR است.
همانطور که در شکل 12 نشان داده شده است، در ابر نقطه ای FMMF، از روش اسکن قاب کشویی برای یافتن ابر نقطه کره استفاده شد .
همانطور که از شکل 12 مشاهده می شود ، قسمت پایین شکل، ابر نقطه ای FMMF است که توسط LiDAR روی ربات بازرسی جمع آوری شده است. در این مطالعه، ما از مدل شبکه عصبی عمق برای عبور و رهگیری ابر نقطه ای FMMF به نوبه خود در مسیر پنجره کشویی استفاده کردیم، سپس قضاوت کردیم که آیا ابر نقطه رهگیری شده دارای ویژگی های یک کره است یا خیر. اگر ویژگی کره در ابر نقطه فعلی وجود داشته باشد، خطای موقعیت بین کره شناسایی شده توسط شبکه عصبی عمق و کره واقعی قابل محاسبه است. در نهایت، کره با کمترین خطای موقعیت را به عنوان نتیجه تشخیص شبکه عصبی عمق در نظر گرفتیم و آن را تجسم کردیم.

3. آزمایش و نتایج

3.1. توضیحات مجموعه داده

ما پس از اضافه کردن سطوح مختلف نویز، ابرهای کره کامل و نقطه کره ناقص را برچسب گذاری کردیم و تولید مجموعه آموزشی ابر نقطه را طبق روشی که در بخش 2.1 توضیح داده شد، تکمیل کردیم . بخشی از مجموعه آموزش ابر نقطه در شکل 13 نشان داده شده است .
در بخش 2.4 ، ابر نقطه FMMF را به دست آوردیم. ما به دنبال یافتن ابر نقطه ای کره در ابر نقطه ای FMMF از طریق DGCNN آموزش دیده بودیم. موقعیت واقعی کره عمدتاً در سر و دم ابر نقطه ای FMMF توزیع شده است. موقعیت ابر نقطه سر و دم در شکل 14 نشان داده شده است .
همانطور که در شکل 14 نشان داده شده است ، بالای شکل نمای اصلی ابر نقطه کل FMMF در جهت Y است. قسمت پایین شکل نمای بالایی ابرهای نقطه سر و دم FMMF در جهت Z است که فضای کوچکتری نسبت به کل FMMF اشغال می کند. هنگامی که قیچی به سر یا دم FMMF می رسد، جهت حرکت را دوباره به من تنظیم می کند.

3.2. جزئیات تجربی

ما یک DGCNN بهبود یافته را برای شناسایی کره در ابر نقطه ای FMMF پیشنهاد می کنیم. این آزمایش بر روی یک ایستگاه کاری با CPU Intel Core-I7 9700 @ 4.70 گیگاهرتز با پردازنده گرافیکی NVIDIA GTX 2080 Super GPU و 16 گیگابایت حافظه ویدیویی انجام شد. پیکربندی نرم افزار شامل PyTorch 1.7.1، Python 3.7.9 و Tensorflow 2.3.0 برای ساخت ساختار DGCNN بود. در الگوریتم گراف KNN، اندازه دسته را 8، دوره ها را 100، مقدار K را 20، و نرخ ترک تحصیل را 0.5 تنظیم کردیم. تابع فعال سازی لایه پیچشی لبه و لایه MLP از ReLU استفاده می کند. تابع از دست دادن تابع از دست دادن آنتروپی متقاطع [ 38 ] بود و بیان ریاضی آن در معادله (11) نشان داده شده است.

لoسس=–1n∑ایکس[yلوگاریتمآ+(1–y)لوگاریتم(1–آ)]،
در معادله (11)، x نمونه، y تگ واقعی، a خروجی پیش بینی شده و n تعداد کل نمونه ها است.
نرخ دقیق (دقت)، نرخ فراخوان (یادآوری)، امتیاز F1 (F1) و خطای موقعیت برای ارزیابی اثر شبکه عصبی استفاده می شود. تعریف ریاضی دقت در رابطه (12) نشان داده شده است.

پrهجمنسمنon=تیپتیپ+افپ،
TP تعداد نمونه هایی است که تگ های واقعی آنها به کلاس مثبت تعلق دارد و مقدار پیش بینی شده آنها نیز کلاس مثبت است و FP تعداد نمونه هایی است که تگ های واقعی آنها متعلق به کلاس منفی است اما مقدار پیش بینی شده آنها کلاس مثبت است. تعریف ریاضی یادآوری در معادله (13) نشان داده شده است.

آرهجآلل=تیپتیپ+افن،
FN تعداد نمونه هایی است که تگ های واقعی آنها به کلاس مثبت تعلق دارد اما مقدار پیش بینی شده آنها کلاس منفی است. تعریف ریاضی F 1 در رابطه (14) نشان داده شده است.

اف1=2×پrهجمنسمنon×آرهجآللپrهجمنسمنon+آرهجآلل،
در ابر نقطه ای FMMF، موقعیت مرکزی واقعی ابر نقطه کروی را می توان با نرم افزار MATLAB R2019a بدست آورد. در این مقاله، خطای موقعیت ابر نقطه کروی در FMMF شناسایی شده توسط DGCNN با مقایسه مقدار شناسایی شده با مقدار واقعی ارزیابی می شود. فرمول محاسبه خطاهای موقعیت کره های مختلف در رابطه (15) نشان داده شده است.

Eمن=(ایکسمن2–ایکسمن1)2+(yمن2–yمن1)2+(zمن2–zمن1)2،
در معادله (15)، i تعداد کره ها است. ایکسمن1،yمن1،zمن1مقدار مختصات مرکز کروی واقعی هستند زمانی که تعداد کره‌های ابر نقطه i است . و ایکسمن2،yمن2،zمن2زمانی که تعداد کره های پردازش شده توسط DGCNN i است، مقدار مختصات مرکز کروی شناسایی شده است . نتیجه حداقل خطای موقعیت کره را به دست آوردیم و نمایش دادیم.
دقت، دقت، فراخوانی و F1 کمیت های بدون بعد هستند. دقت به معنای نسبت نتایج صحیح پیش بینی شده در کل نمونه ها است. دقت به نتایج پیش‌بینی اشاره دارد و نسبت نمونه‌های مثبت واقعی را در نمونه‌های مثبت پیش‌بینی‌شده نشان می‌دهد. یادآوری به نمونه اصلی اشاره دارد و نسبت نمونه های مثبت پیش بینی شده در نمونه های مثبت واقعی را نشان می دهد. F1 میانگین هارمونیک دقت و یادآوری است. بنابراین، هیچ واحدی برای دقت، از دست دادن، دقت، فراخوانی یا F1 وجود ندارد. ضرر برای تخمین درجه ناسازگاری بین مقدار پیش‌بینی‌شده و ارزش واقعی مدل استفاده می‌شود، بنابراین ضرر واحدی ندارد. واحد خطای موقعیت کره m است.

3.3. نتایج تجربی و بحث

3.3.1. مقایسه عملکرد DGCNN با لایه‌های پیچیدگی لبه‌های مختلف

ما تعداد لایه‌های پیچش لبه را در DGCNN تنظیم کردیم. میزان دقت (دقت) و از دست دادن DGCNN در مراحل مختلف هنگام استفاده از تعداد لایه های پیچیدگی لبه های مختلف در شکل 15 و شکل 16 نشان داده شده است.
مشاهده می‌شود که وقتی تعداد لایه‌های پیچش لبه سه باشد، دقت DGCNN بزرگترین و از دست دادن DGCNN کوچکترین است. برای تجزیه و تحلیل و تحقیق شهودی و دقیق، دقت، فراخوانی و امتیاز F1 DGCNN هنگام استفاده از اعداد مختلف لایه پیچشی لبه در شکل 17 نشان داده شده است.
از شکل 17 قابل مشاهده استکه با افزایش تعداد لایه‌های پیچش لبه، دقت، فراخوانی و F1 پدیده اول بالا آمدن و سپس سقوط را نشان می‌دهد. در میان آنها، زمانی که تعداد لایه‌های پیچش لبه سه باشد، دقت، فراخوانی و F1 به ترتیب حداکثر مقادیر خود را 904/0، 937/0 و 920/0 به دست می‌آورند. این به این دلیل است که پیچیدگی لبه در DGCNN شامل عملیات جمع‌آوری گره‌های همسایه است. با افزایش تعداد لایه های پیچش لبه، نقطه مرکزی به طور بالقوه می تواند اطلاعات گره را در فاصله طولانی نشان دهد و سپس به طور کامل و موثر ویژگی های محلی را توصیف کند. با این حال، زمانی که لایه‌های پیچیدگی لبه‌ها بیش از حد وجود داشته باشد، و هر گره حاوی اطلاعات بسیار زیادی از گره‌های دیگر باشد، تبعیض هر گره آشکار نیست و فاقد تبعیض است، و این بر عملکرد شبکه تأثیر می‌گذارد.
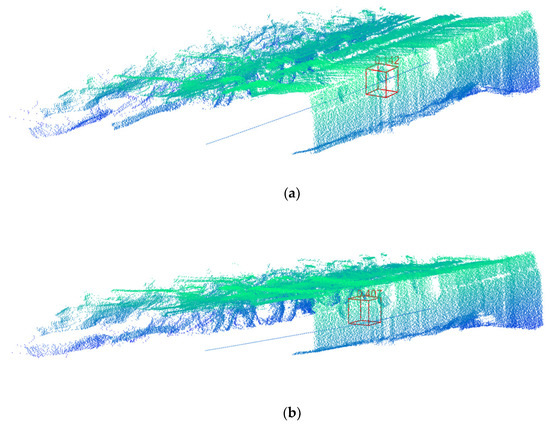
با توجه به مشکل جعبه سیاه شبکه های عصبی عمیق، نمودار خط شکسته موجود، هیستوگرام و سایر اشکال را نمی توان برای ارزیابی واضح DGCNN برای شناسایی اثر ابر نقطه کروی در FMMF بهتر تصویر کرد. ما نتایج ابر نقطه FMMF پردازش شده توسط DGCNN را تجسم کردیم (طول کل FMMF بسیار طولانی است؛ به منظور تسهیل مشاهدات شهودی، ابر نقطه FMMF جزئی را در جایی که کره قرار داشت تجسم کردیم). شکل 18 اثر تشخیص ابر نقطه کره را در زیر تعداد مختلف لایه های پیچشی لبه نشان می دهد.
عدد کنار کادر در شکل 18 نشان دهنده خطای موقعیت بین کره شناسایی شده توسط DGCNN و کره واقعی است. تعداد لایه‌های پیچش لبه DGCNN از یک لایه به هفت لایه افزایش یافت و خطاهای موقعیت به ترتیب 0.343، 0.364، 0.235، 0.142، 0.161، 0.193 و 0.286 متر بود. مشاهده می شود که با افزایش تعداد لایه های پیچشی لبه، خطای موقعیت کره ابتدا کاهش یافته و سپس افزایش می یابد. وقتی تعداد لایه‌های پیچش لبه سه بود، خطای موقعیت کره کوچک‌ترین و عملکرد DGCNN بهترین بود. این یافته‌ها با نتیجه‌گیری بهترین تعداد لایه‌های پیچش لبه DGCNN مطابق با دقت، یادآوری و F1 مطابقت دارند.
در پیچیدگی لبه، ویژگی های لبه K در اطراف نقطه مرکزی برای نشان دادن رابطه بین نقطه مرکزی و نقاط مجاور ساخته شد. مقدار K را در لایه پیچیدگی لبه تنظیم کردیم. دقت، فراخوانی و F1 DGCNN هنگام استفاده از مقادیر مختلف K در شکل 19 نشان داده شده است.
از شکل 19 می توان مشاهده کرد که مقادیر مختلف K بر تأثیر DGCNN تأثیر می گذارد، در حالی که دقت، یادآوری و F1 پدیده ای را نشان می دهد که ابتدا افزایش و سپس سقوط می کند. در میان آنها، زمانی که K 20 بود، دقت، فراخوانی و F1 حداکثر مقدار خود را به دست آوردند. این به این دلیل است که وقتی مقدار K خیلی کوچک بود، نقاط مجاور کمی در اطراف نقطه مرکزی وجود داشت (هر نقطه مجاور و نقطه مرکزی با یک ویژگی لبه نشان داده می شد)، و پیچیدگی لبه در DGCNN نمی توانست ویژگی های محلی را یاد بگیرد. نقطه ابر به خوبی. با این حال، زمانی که مقدار K خیلی بزرگ بود، پیچیدگی لبه ویژگی‌های ابر نقطه را در یک محله بزرگ یاد گرفت، که باعث شد مدل کلی ساده شود و به یادگیری جزئیات محلی ابر نقطه بیفتد.
علاوه بر این، همانطور که در شکل 20 نشان داده شده است، ما اثر تشخیص DGCNN را بر روی ابر نقطه کره در FMMF تحت مقادیر مختلف K بدست آوردیم .
همانطور که از شکل 20 مشاهده می شود ، زمانی که مقدار K 20 بود، خطای موقعیت کره کوچکترین بود، که نشان می دهد زمانی که مقدار K متفاوت است، عملکرد مدل تغییر می کند. بنابراین، این تأثیر بر تأثیر ابر نقطه پردازش DGCNN دارد. علاوه بر این، زمانی که K = 20، اثر DGCNN جستجو برای ابر نقطه کره در FMMF بهترین است.

3.3.2. مقایسه عملکرد DGCNN با الگوریتم‌های بهینه‌سازی مختلف

پس از تعیین تعداد لایه‌های پیچش لبه DGCNN، دقت، فراخوانی و F1 DGCNN تحت الگوریتم‌های بهینه‌سازی مختلف مورد تجزیه و تحلیل قرار گرفت، همانطور که در شکل 21 نشان داده شده است.
همانطور که از شکل 21 مشاهده می شودمقادیر دقت، فراخوان و F1 DGCNN هنگام استفاده از الگوریتم بهینه‌سازی آدام بیشتر از الگوریتم بهینه‌سازی SGD بود و تفاوت‌ها به ترتیب 0.183، 0.161 و 0.173 بود. دلیل این امر این است که نرخ یادگیری همه پارامترها در الگوریتم بهینه سازی SGD یکسان است، که غیر منطقی است زیرا برخی از پارامترها نیازی به تغییر مکرر ندارند، در حالی که برخی از پارامترها نیاز به یادگیری و بهبود مکرر دارند. الگوریتم بهینه‌سازی آدام الگوریتم مومنتوم و الگوریتم RMSProp را ترکیب می‌کند و از تخمین گشتاور مرتبه اول و دوم گرادیان برای تنظیم پویا نرخ یادگیری هر پارامتر استفاده می‌کند.
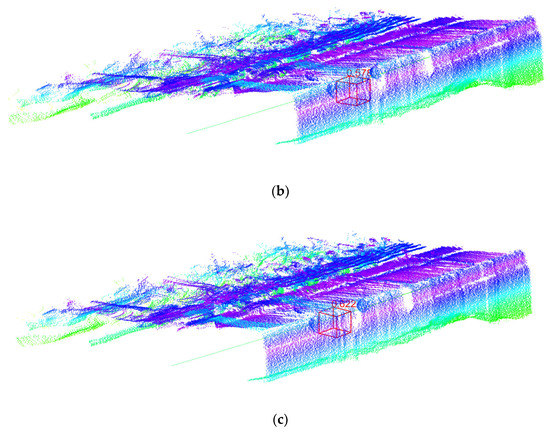
ما DGCNN را با الگوریتم‌های بهینه‌سازی مختلف روی ابر نقطه FMMF اجرا کردیم. به طور مشابه، از آنجا که طول FMMF بسیار زیاد بود، و تعداد ابرهای نقطه به ویژه زیاد بود، به منظور تسهیل مشاهده شهودی، ما مجبور شدیم ابرهای نقطه محلی FMMF واقعی را تجسم کنیم. اثر تشخیص ابر نقطه کروی بر روی ابر نقطه FMMF در شکل 22 نشان داده شده است .
همانطور که از شکل 22 مشاهده می شود ، خطای موقعیت DGCNN با استفاده از الگوریتم بهینه سازی آدام کمتر از الگوریتم بهینه سازی SGD بود و این تفاوت 0.265 متر بود. با توجه به تأثیر تشخیص کره در ابر نقطه ای FMMF، تأثیر الگوریتم بهینه سازی آدم بهتر از الگوریتم بهینه سازی SGD است. بنابراین، ما DGCNN در حال اجرا بر روی ابر نقطه FMMF را به سه لایه از لایه پیچیدگی لبه بهبود دادیم. الگوریتم بهینه سازی مورد استفاده Adam بود.

3.3.3. مقایسه عملکرد شبکه های عصبی مختلف

تفاوت اساسی بین DGCNN و PointNet این است که DGCNN به طور خلاقانه یک ماژول حیاتی به نام پیچش لبه طراحی می کند که DGCNN را قادر می سازد تا ویژگی های محلی ابرهای نقطه را یاد بگیرد. PointNet معادل DGCNN بدون پیچیدگی لبه است [ 47 ]. بنابراین، ما DGCNN بهبود یافته را با PointNet و PointNet+ مقایسه کردیم. این نه تنها نتیجه مقایسه مدل‌های شبکه عصبی عمقی مختلف است، بلکه نتیجه مقایسه با مطالعه فرسایشی DGCNN بدون پیچش لبه است. دقت، نرخ فراخوان و F1 از سه روش در شکل 23 نشان داده شده است.
همانطور که از شکل 23 مشاهده می شوددقت، فراخوانی و F1 به‌دست‌آمده توسط DGCNN بهبودیافته ما بالاتر از موارد به‌دست‌آمده توسط PointNet و PointNet++ است و حداکثر تفاوت‌های دقت، فراخوانی و F1 به ترتیب 0.309، 0.324 و 0.317 بود. دلیل این امر این است که PointNet و PointNet++ هر نقطه داده در ابر نقطه را به عنوان یک موجود جدا شده در نظر می گیرند و هر نقطه در ابر نقطه را به طور مستقل پردازش می کنند و اطلاعات هندسی بین نقاط را نادیده می گیرند، به این معنی که ویژگی های محلی ابر نقطه را از دست می دهند. DGCNN ویژگی‌های همسایگی محلی ابر نقطه را با استفاده از پیچیدگی لبه می‌سازد، که نه تنها ویژگی‌های نقطه فعلی را در نظر می‌گیرد، بلکه ویژگی‌های K نزدیک‌ترین نقطه فعلی را نیز در نظر می‌گیرد. این بدان معنی است که DGCNN می تواند ویژگی های محله محلی را از نمودار محلی متشکل از K نقاط استخراج کند.
به منظور تسهیل مشاهده شهودی، ما ابر نقطه محلی FMMF را تجسم کردیم. اثر تشخیص DGCNN، PointNet، و PointNet++ ما بر روی ابر نقطه کره در FMMF در شکل 24 نشان داده شده است .
همانطور که در شکل 24 نشان داده شده است ، خطای موقعیت به دست آمده توسط DGCNN بهبود یافته ما کمتر از خطای بدست آمده توسط PointNet و PointNet++ است. تفاوت بین DGCNN و PointNet 0.580 متر و تفاوت بین DGCNN و PointNet++ 0.436 متر است. این درستی و امکان سنجی استفاده از DGCNN بهبود یافته برای شناسایی ابر نقطه کروی در ابر نقطه FMMF را نشان می دهد. نتایج تحقیق سازگاری، توانایی تعمیم و ارزش عملی مدل DGCNN را بهبود می‌بخشد و مرجعی برای کاربرد DGCNN در زمینه‌های مرتبط با انرژی و زمین‌شناسی ارائه می‌دهد.
علاوه بر این، سهم پیچیدگی لبه‌های بحرانی در DGCNN به شرح زیر است: اولاً، پیچیدگی لبه‌های بحرانی می‌تواند ویژگی‌های محلی ابر نقطه را استخراج کند، که نقص شبکه عصبی عمق را در این جنبه حل می‌کند. ثانیاً، DGCNN می‌تواند با چیدن لایه‌های پیچیدگی لبه مناسب، یک اثر پردازش ابر نقطه ایده‌آل به دست آورد. علاوه بر این، پیچیدگی لبه نه تنها می تواند ویژگی های محلی ابر نقطه را استخراج کند، بلکه تغییر ناپذیری آرایش ابر نقطه را نیز حفظ می کند. علاوه بر این، به دلیل وجود یک لایه پیچشی لبه، مدل DGCNN می‌تواند اطلاعات ابر نقطه را با به‌روزرسانی پویا ساختار نمودار بین لایه‌ها، بهتر یاد بگیرد.
اگرچه مدل DGCNN بهبود یافته ما در برخورد با ابر نقطه ای FMMF بهتر از PointNet و PointNet++ است، اما خود ابر نقطه دارای ویژگی های پراکندگی و عدم یکنواختی است و FMMF گرد و غبار و کم دید است. در مجموعه آموزشی، هر دو ابر نقطه کره کامل و ابر نقطه کره ناقص به طور مناسب تولید شدند و روش پیشنهادی ما نیز برای مقابله با ابر نقطه FMMF هدف قرار گرفت. بنابراین، روش فعلی دارای این نقص است که نمی تواند وظایف بین دامنه ای را پردازش کند (به عنوان مثال، مراجع [ 51 ، 52 ]). در آینده تحقیقات بیشتری برای بهبود روش فعلی انجام خواهیم داد تا توانایی پردازش وظایف بین دامنه ای را داشته باشد.

4. نتیجه گیری

به منظور به دست آوردن موقعیت کره (نشانگر) در ابر نقطه ای FMMF، این مطالعه مبنایی را برای تبدیل مختصات بعدی FMMF به مختصات ژئودزیکی با استفاده از کره به عنوان رسانه میانی فراهم می کند، سپس مبنایی را برای صاف کردن و تنظیم شیب نوار نقاله اسکراپر. علاوه بر این، برای روش غیرمستقیم استخراج ویژگی ابر نقطه شبکه‌های عصبی عمیق، ابتدا باید ابر نقطه تبدیل شود، که به ناچار بخشی از اطلاعات فضایی ابر نقطه را از دست می‌دهد، در حالی که روش مستقیم قادر به گرفتن آن نیست. اطلاعات محلی ابر نقطه بنابراین، ما روشی را برای استخراج ویژگی‌های هندسی کره در ابر نقطه‌ای FMMF با استفاده از DGCNN پیشنهاد می‌کنیم. اولا، به منظور افزایش استحکام DGCNN، ما سطوح مختلفی از نویز را به ابرهای نقطه کره های کامل و ناقص اضافه کردیم تا تولید مجموعه داده های ابر نقطه ای را تکمیل کنیم. در همان زمان، ما ابر نقطه FMMF جمع آوری شده توسط LiDAR را به عنوان مجموعه آزمایشی در نظر گرفتیم. نتایج شکاف تحقیقاتی مربوط به استفاده از یک مدل شبکه عصبی عمقی را پر می کند که هیچ مجموعه داده ای برای استخراج ویژگی های یک ابر نقطه کروی در ابر نقطه FMMF ندارد. در مرحله دوم، پیچیدگی لبه برای تجمیع اطلاعات ویژگی گره های مجاور به گره مرکزی استفاده می شود. در DGCNN با یک لایه کانولوشن لبه چند لایه، اطلاعات همسایگی استخراج شده توسط کانولوشن لبه به طور بالقوه می تواند نشان دهنده فاصله بسیار طولانی در فضای اصلی باشد، اما لایه پیچیدگی لبه بیش از حد عمیق باعث برازش بیش از حد می شود که بر عملکرد شبکه عصبی تأثیر می گذارد. . از این رو، ما تأثیر DGCNN را در استخراج ویژگی‌های هندسی از ابر نقطه FMMF در هنگام استفاده از تعداد مختلف لایه‌های پیچشی لبه تجزیه و تحلیل کردیم و عملکرد بهینه‌سازی DGCNN را بهبود دادیم. نتایج نشان می‌دهد که با افزایش تعداد لایه‌های پیچش لبه، دقت، فراخوانی و F1 روند اول صعود و سپس نزول را نشان می‌دهند، در حالی که خطای موقعیت روند ابتدا نزول و سپس افزایش را نشان می‌دهد. وقتی تعداد لایه‌های پیچش لبه سه باشد، دقت، فراخوانی و F1 بالاترین و خطای موقعیت کمترین است. اینها به ترتیب 0.9043، 0.9369، 0.9203 و 0.142 هستند. علاوه بر این، تأثیر DGCNN هنگام استفاده از الگوریتم بهینه‌سازی آدام بهتر از الگوریتم بهینه‌سازی SGD است. سرانجام، ما اثر استفاده از DGCNN بهبود یافته را با PointNet و PointNet++ برای شناسایی ابر نقطه یک کره در ابر نقطه FMMF مقایسه کردیم. نتایج نشان می دهد که DGCNN بهبود یافته بهتر از PointNet و PointNet++ است. این امکان سنجی استفاده از DGCNN برای استخراج ویژگی های یک کره در ابر نقطه ای FMMF را نشان می دهد.
بنابراین، این مطالعه روش جدیدی را برای استخراج ویژگی یک کره در ابر نقطه ای FMMF ارائه می دهد و پایه ای را برای تبدیل مختصات بعدی FMMF به مختصات ژئودزی ملی در هنگام استفاده از یک کره به عنوان رسانه میانی فراهم می کند، بنابراین مبنایی را فراهم می کند. برای صاف کردن و تنظیم شیب نوار نقاله اسکراپر. علاوه بر این، این می‌تواند پایه‌ای مؤثر برای فرماندهی و کنترل تولید معدن زغال‌سنگ و مرجعی برای کاربرد DGCNN در زمینه‌های مرتبط با انرژی و زمین‌شناسی فراهم کند. در عین حال، نتایج تضمین اولیه مستقیمی را برای تجزیه و تحلیل داده‌های ابر نقطه‌ای FMMF تحت سیستم مختصات ژئودتیک ملی در آینده فراهم می‌کند، که نه تنها به بهبود کارایی معدن و ایمنی درز زغال‌سنگ کمک می‌کند.

مشارکت های نویسنده

مفهوم سازی، Zhizhong Xing، Shuanfeng Zhao و Wei Guo. روش، Zhizhong زینگ و Shuanfeng ژائو. نرم افزار، Zhizhong Xing، Shuanfeng Zhao و Xiaojun Guo. اعتبار سنجی، Zhizhong Xing، Shuanfeng ژائو و وی گوو. تجزیه و تحلیل رسمی، Zhizhong زینگ، Shuanfeng ژائو و یوان وانگ. تحقیق، Zhizhong زینگ، Shuanfeng ژائو و وی گوو. منابع، Zhizhong Xing، Shuanfeng Zhao و Wei Guo. مدیریت داده، Zhizhong زینگ و Shuanfeng ژائو. نوشتن – آماده سازی پیش نویس اصلی، Zhizhong Xing و Shuanfeng Zhao. نوشتن-بررسی و ویرایش، Zhizhong Xing، Shuanfeng Zhao و Wei Guo. نظارت، Zhizhong زینگ و Shuanfeng ژائو. همه نویسندگان نسخه منتشر شده نسخه خطی را خوانده و با آن موافقت کرده اند.

منابع مالی

این مطالعه توسط برنامه ملی تحقیق و توسعه کلیدی چین (Grant No. 2017YFC0804310) پشتیبانی شد. پروژه های کلیدی تحقیق و توسعه استان شانشی (Grant No. 2020ZDLGY04-05)؛ و پروژه های کلیدی تحقیق و توسعه استان شانشی (Grant No. 2020ZDLGY04-06).

بیانیه هیئت بررسی نهادی

قابل اجرا نیست.

بیانیه رضایت آگاهانه

قابل اجرا نیست.

بیانیه در دسترس بودن داده ها

به اشتراک گذاری داده ها اعمال نمی شود.

قدردانی

نویسندگان از ویراستار برای کمک در ویرایش تشکر می کنند. در آخر، نویسندگان مایلند از نظرات و پیشنهادات ارزشمند داوران در مورد نسخه قبلی نسخه خطی ما تشکر کنند.

تضاد علاقه

نویسندگان اعلام می کنند که هیچ تضاد منافعی ندارند.

منابع

  1. ژنگ، ایکس. او، X. یانگ، ایکس. ما، اچ. یو، ز. رن، جی. لی، جی. ژانگ، اچ. Zhang, J. Terrain Point Cloud Assisted GB-InSAR شیب و روش متمایز کردن روسازی در یک معدن روباز. Sensors 2020 , 20 , 2337. [ Google Scholar ] [ CrossRef ]
  2. ایلیا، آی. لوپاساکیس، سی. Tsangaratos، P. پدیده فرونشست زمین بررسی شده توسط تجزیه و تحلیل فضایی و زمانی منابع آب زیرزمینی، تکنیک های سنجش از دور، و روش جنگل تصادفی: مورد غرب تسالی، یونان. محیط زیست نظارت کنید. ارزیابی کنید. 2018 ، 190 ، 623. [ Google Scholar ] [ CrossRef ]
  3. Tziachris، P. آستونیت، V. Chatzistathis، T. پاپادوپولو، م. Doukas، ID مقایسه مدل‌های یادگیری ماشین و روش‌های زمین آماری ترکیبی با استفاده از متغیرهای محیطی و خاک برای پیش‌بینی pH خاک. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 276. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  4. فکته، اس. دیدریکس، ام. Lato, M. کاربردهای ژئوتکنیکی و عملیاتی برای اسکن لیزری سه بعدی در تونل های مته و انفجار. تون. Undergr. فناوری فضایی 2010 ، 25 ، 614-628. [ Google Scholar ] [ CrossRef ]
  5. یانگ، ایکس. هوانگ، ی. Zhang، Q. استخراج و اندازه گیری خودکار انبارها با استفاده از ابر نقطه سه بعدی و انحنای جهت دار چند مقیاسی. Remote Sens. 2020 , 12 , 960. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  6. ایگناتوویچ استوپار، دی. روزر، جی. Vulić، M. بررسی فتوگرامتری مبتنی بر وسایل نقلیه هوایی بدون سرنشین برای پایش فرونشست معادن بزرگ. Minerals 2020 , 10 , 196. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  7. پال، ا. روزر، جی. Vulić، M. پیش‌بینی فرونشست سطحی در بالای حفاری دیوار بلند زیرزمینی و بر اساس تحلیل ابر نقطه‌ای سه‌بعدی. Minerals 2020 , 10 , 82. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  8. Leśniak، A. Śledź، E. Mirek، K. شناخت دقیق ساختارهای لرزه‌زای فعال شده در حین استخراج زغال‌سنگ زیرزمینی: مطالعه موردی از معدن Bobrek، لهستان. Energies 2020 , 13 , 4622. [ Google Scholar ] [ CrossRef ]
  9. تاچلا، جی. آلتمن، ی. ملادو، ن. مک کارتی، ای. توبین، آر. بولر، جی. تورنرت، جی. مک لافلین، اس. بازسازی سه بعدی بی‌درنگ از داده‌های لیدار تک فوتونی با استفاده از حذف‌کننده‌های ابر نقطه‌ای plug-and-play. نات. اشتراک. 2019 ، 10 ، 1-6. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  10. Alsadik، B. جهت‌گیری زاویه‌ای ایده‌آل لیدارهای چند پرتوی 64 کانالی منتخب برای سیستم‌های نقشه‌برداری سیار. Remote Sens. 2020 , 12 , 510. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  11. کیم، اچ.-اس. سان، سی.-جی. کیم، ام. چو، H.-I.; لی، ام.-جی. ویژگی‌های مکانی بهینه مبتنی بر GIS برای ارزیابی اثر مکان لرزه‌ای در یک منطقه شهری داخلی، کره جنوبی. Appl. علمی 2020 ، 10 ، 7443. [ Google Scholar ] [ CrossRef ]
  12. Cabrera-Barona، P. تأثیر محرومیت چند معیاره شهری و دسترسی فضایی به مراقبت های بهداشتی بر سلامت خود گزارش شده. علوم شهری 2017 ، 1 ، 11. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  13. Zięba-Kulawik، K. اسکوزیلاس، ک. مصطفی، ع. ویزیک، پ. گربر، پی. تلر، جی. عمرانی، H. تغییرات فضایی و زمانی در تراکم ساختمانی سه بعدی با LiDAR و GEOBIA: تحلیل سطح شهر. Remote Sens. 2020 , 12 , 3668. [ Google Scholar ] [ CrossRef ]
  14. پروکوپ، ام. شیخ، س. کیم، K.-S. ثبت ابر نقطه همپوشانی کم با استفاده از تشخیص ویژگی های خط. Remote Sens. 2020 , 12 , 61. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  15. سو، تی. وانگ، دبلیو. Lv، Z. وو، دبلیو. Li, X. FRapid Delaunay مثلث‌سازی برای داده‌های ابر نقطه‌ای توزیع‌شده تصادفی با استفاده از منحنی هیلبرت تطبیقی. محاسبه کنید. نمودار. 2016 ، 54 ، 65-74. [ Google Scholar ] [ CrossRef ]
  16. لیو، ن. لین، بی. Lv، G. زو، ا. ژو، ال. الگوریتم مثلث سازی دلونی بر اساس سازماندهی داده های فضایی دوگانه. PFG-Journal of Photogrammetry. سنسور از راه دور Geoinf. علمی 2019 ، 87 ، 19-31. [ Google Scholar ]
  17. ژائو، ی. شی، سی. کوون، ک. پیائو، ی. پیائو، م. Kim, N. روش محاسبه سریع هولوگرام تولید شده توسط کامپیوتر با استفاده از دوربین عمق با شبکه بندی ابر نقطه ای. انتخاب کنید اشتراک. 2018 ، 411 ، 166-169. [ Google Scholar ] [ CrossRef ]
  18. دی، ت. استخراج منحنی‌های ویژگی مبتنی بر Wang، L. Voronoi برای سطوح منفرد نمونه‌برداری شده. محاسبه کنید. نمودار. 2013 ، 37 ، 659-668. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  19. کشتی.؛ بله، س. Zeng, L. یک استخراج جدید از ساختار داخلی بر اساس ابر نقطه متراکم. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 660. [ Google Scholar ] [ CrossRef ]
  20. تانگ، جی. لی، ی. ژانگ، دبلیو. چن، دی. ژانگ، ز. یانگ، جی. Zhang, J. Point مجموعه چند سطحی جمع آوری ویژگی استخراج بر اساس چند مقیاس حداکثر جمع آوری و LDA برای طبقه بندی ابر نقطه. Remote Sens. 2019 , 11 , 2846. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  21. ژو، تی. پوپسکو، اس. مالامبو، ال. ژائو، ک. Krause، K. از شکل موج های LiDAR تا ابرهای بیش از حد نقطه: یک محصول داده جدید برای مشخص کردن ساختار گیاهی. Remote Sens. 2018 ، 10 ، 1949. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  22. لی، ک. شائو، جی. Guo, D. یک روش پنجره جستجوی چند ویژگی برای تشخیص مرز جاده بر اساس داده های LIDAR. Sensors 2019 , 19 , 1551. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  23. خو، ز. ژانگ، ز. ژونگ، آر. چن، دی. سان، تی. دنگ، ایکس. لی، ز. Qin، C.-Z. ساخت خوشه نقطه ای چندسطحی حساس به محتوا برای طبقه بندی ابر نقطه ای ALS. Remote Sens. 2019 , 11 , 342. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  24. کیان، ز. لیو، ایکس. تائو، اف. ژو، تی. شناسایی مناطق عملکردی شهری با جفت کردن تصاویر ماهواره ای و مسیرهای GPS تاکسی. Remote Sens. 2020 , 12 , 2449. [ Google Scholar ] [ CrossRef ]
  25. هوانگ، تی. ژائو، اس. گنگ، ال. Xu, Q. تخمین عمق تک‌چشمی بدون نظارت بر اساس شبکه عصبی باقیمانده استخراج‌های درشت-تصفیه‌شده برای هواپیماهای بدون سرنشین. Electronics 2019 ، 8 ، 1179. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  26. پتروشانو، دی.-م. کاروتاسو، جی. Căruțașu، NL; Pîrjan, A. مروری بر پیشرفت‌های اخیر در یکپارچه‌سازی مدل‌های یادگیری ماشین با دستگاه‌های حسگر در بخش ساختمان‌های هوشمند با دیدگاهی برای دستیابی به سنجش پیشرفته، بهره‌وری انرژی و مدیریت بهینه ساختمان. Energies 2019 ، 12 ، 4745. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  27. بلو، SA; یو، اس. وانگ، سی. آدم، جی.ام. بررسی لی، جی: یادگیری عمیق در ابرهای نقطه سه بعدی. Remote Sens. 2020 , 12 , 1729. [ Google Scholar ] [ CrossRef ]
  28. پاستوچا، ای. پونیاچ، ای. Ścisłowicz، A.; Ćwiąkała، P. نیویم، دبلیو. Wiącek, P. بازسازی سه بعدی خطوط برق با استفاده از تصاویر پهپاد برای نظارت بر پاکسازی راهرو. Remote Sens. 2020 , 12 , 3698. [ Google Scholar ] [ CrossRef ]
  29. هو، ایکس. یوان، ی. طبقه بندی مبتنی بر یادگیری عمیق برای استخراج DTM از ابر نقطه ای ALS. Remote Sens. 2016 ، 8 ، 730. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  30. ژائو، آر. پانگ، ام. Wang, J. طبقه‌بندی ابرهای نقطه‌ای LiDAR هوابرد از طریق ویژگی‌های عمیقی که توسط یک شبکه عصبی کانولوشنال چند مقیاسی آموخته شده است. بین المللی جی. جئوگر. Inf. علمی 2018 ، 32 ، 960-979. [ Google Scholar ] [ CrossRef ]
  31. پولیتز، اف. Sester, M. بررسی داده های ALS و DIM برای تقسیم بندی معنایی با استفاده از CNN. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی طاق ISPRS. 2018 ، 42 ، 347-354. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  32. Qi، CR; سو، اچ. مو، ک. Guibas، LJ PointNet: یادگیری عمیق در مجموعه های نقطه برای طبقه بندی و تقسیم بندی سه بعدی. در مجموعه مقالات کنفرانس IEEE 2017 در مورد دید رایانه و تشخیص الگو (CVPR)، هونولولو، HI، ایالات متحده آمریکا، 21 تا 26 ژوئیه 2017؛ صص 77-85. [ Google Scholar ]
  33. جوان، م. زیبا، سی. آگوستینیو، اس. گرین، آر. Chen, X. از دست دادن اهمیت و تأثیر آن بر جهت گیری عادی نقطه و ثبت ابر. Remote Sens. 2019 ، 11 ، 1329. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  34. میرسو، ر. سیمیون، جی. Caleanu، CD; Pop-Calimanu، IM یک راه حل مبتنی بر PointNet برای تشخیص حرکت سه بعدی دست. Sensors 2020 , 20 , 3226. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  35. جمال، ع. ویبیسونو، ای. ویکاسونو، اس بی؛ ابیان، MA; حمید، ن. Wisesa، HA; جاتمیکو، دبلیو. Ardhianto، R. تقسیم‌بندی خودکار ساختمان LIDAR بر اساس DGCNN و خوشه‌بندی اقلیدسی. J. Big Data 2020 , 7 , 1-18. [ Google Scholar ] [ CrossRef ]
  36. ژانگ، جی. هو، ایکس. دای، اچ. استخراج Qu، S. DEM از ابرهای نقطه ای ALS در مناطق جنگلی از طریق شبکه پیچیدگی نمودار. Remote Sens. 2020 , 12 , 178. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  37. لی، جی. چانگ، جی. چو، م. تیمیلسینا، اس. سون، ک. کیم، جی. Sohn, K. تکنیک یادگیری عمیق برای تبدیل یک ورق کامپوزیت نانولوله کربن پیزورمقاومتی خام به یک صفحه کلید هوشمند، قابل حمل، یکبار مصرف و بسیار انعطاف پذیر. ACS Appl. ماتر رابط‌ها 2018 ، 10 ، 20862–20868. [ Google Scholar ] [ CrossRef ]
  38. کیم، اچ. کیم، سی. طبقه بندی ابرهای نقطه ای مبتنی بر یادگیری عمیق برای بازرسی پل. Remote Sens. 2020 , 12 , 3757. [ Google Scholar ] [ CrossRef ]
  39. مربیدونی، سی. پیردیکا، آر. پائولانتی، م. کواترینی، آر. Mammoli, R. یادگیری از داده های ابر نقطه مصنوعی برای بخش بندی معنایی ساختمان های تاریخی. ACM J. Comput. فرقه میراث. 2020 ، 13 ، 1-16. [ Google Scholar ] [ CrossRef ]
  40. پیردیکا، آر. پائولانتی، م. ماترون، اف. مارتینی، م. مربیدونی، سی. Malinverni، ES; فروتونی، ای. Lingua، AM Point Cloud Semantic Segmentation با استفاده از چارچوب یادگیری عمیق برای میراث فرهنگی. Remote Sens. 2020 , 12 , 1005. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  41. بلکینا، AC؛ Ciccolella، CO. آنو، آر. هالپرت، آر. اسپیدلن، جی. Snyder-Cappione، JE پارامترهای بهینه شده خودکار برای جاسازی تصادفی همسایه توزیع شده T، تجسم و تجزیه و تحلیل مجموعه داده های بزرگ را بهبود می بخشد. نات. اشتراک. 2019 ، 10 ، 1-12. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  42. ژائو، اس. آویزان شدن.؛ ژائو، کیو. وی، پی. پیش بینی نقاط توجه راننده بر اساس مدل توجه. Appl. علمی 2020 ، 10 ، 1083. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  43. کورتیناس-لورنزو، بی. پرز-گونزالس، اف. آدام و مورچه ها: در مورد تأثیر الگوریتم بهینه سازی بر قابلیت تشخیص واترمارک های DNN. آنتروپی 2020 ، 22 ، 1379. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  44. بالا، کامپیوتر; آیزنرایش، BR; یو، SBM؛ هیدن، توسط; پارک، اچ اس. Zimmermann, J. تخمین خودکار ژست بدون نشانگر در ماکاک‌هایی که آزادانه در حال حرکت هستند با OpenMonkeyStudio. نات. اشتراک. 2020 ، 11 ، 1-12. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  45. Kingma، DP; با، جی. آدام: روشی برای بهینه سازی تصادفی. arXiv 2014 ، arXiv:1412.6980. [ Google Scholar ]
  46. رودر، اس. مروری بر الگوریتم‌های بهینه‌سازی گرادیان نزول. arXiv 2016 , arXiv:1609.04747. [ Google Scholar ]
  47. وانگ، ی. سان، ی. لیو، ز. Sarma, SE; برونشتاین، MM; Solomon، JM Dynamic graph cnn برای یادگیری روی ابرهای نقطه ای. ACM Trans. نمودار. 2019 ، 38 ، 1-12. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  48. او، سی. لی، اس. شیونگ، دی. نیش، پ. Liao، M. بخش بندی معنایی تصویر سنجش از دور بر اساس راهنمای اطلاعات لبه. Remote Sens. 2020 , 12 , 1501. [ Google Scholar ] [ CrossRef ]
  49. گوا، ی. چن، جی. مو، آر. وانگ، ام. بائو، ی. ارزیابی سود اقدامات حفاظت از آب و خاک در شندونگ بر اساس بهینه‌سازی ازدحام ذرات و فرآیند سلسله مراتبی تحلیلی. Water 2020 ، 12 ، 1955. [ Google Scholar ] [ CrossRef ]
  50. جی، ایکس. آهنگ، دی. ژائو، اچ. لی، ی. او، K. تجزیه و تحلیل تجربی ویژگی های منافذ و نفوذپذیری زغال سنگ توسط NMR میدان پایین. Appl. علمی 2018 ، 8 ، 1374. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  51. بنجدیرا، بی. بازی، ی. کوبا، ع. Ouni، K. انطباق دامنه بدون نظارت با استفاده از شبکه های متخاصم مولد برای تقسیم بندی معنایی تصاویر هوایی. Remote Sens. 2019 , 11 , 1369. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  52. لی، ی. شی، تی. ژانگ، ی. چن، دبلیو. وانگ، ز. لی، اچ. یادگیری شبکه تقسیم‌بندی معنایی عمیق تحت محدودیت‌های چندگانه با نظارت ضعیف برای تقسیم‌بندی معنایی تصویر سنجش از دور متقابل. ISPRS J. Photogramm. Remote Sens. 2021 ، 175 ، 20-33. [ Google Scholar ] [ CrossRef ]
Ijgi 10 00482 g001 550
شکل 1. اجرای DGCNN بر روی ابر نقطه FMMF (بالا) و آموزش ابر نقطه هندسی DGCNN (پایین).
Ijgi 10 00482 g002 550
شکل 2. کره ها و ترکیب ها در موقعیت های مختلف فضایی.
Ijgi 10 00482 g003 550
شکل 3. ابر نقطه کره پس از اضافه کردن تعداد مختلف نقاط نویز.
Ijgi 10 00482 g004 550
شکل 4. ابر نقطه ترکیب پس از اضافه کردن تعداد مختلف نقاط نویز.
Ijgi 10 00482 g005 550
شکل 5. جریان اصلی الگوریتم آدم.
Ijgi 10 00482 g006 550
شکل 6. اثرات Adam و SGD بر مدل زین.
Ijgi 10 00482 g007 550
شکل 7. پیچیدگی معمولی و پیچیدگی لبه. ( الف ) نمودار شماتیک یک عملیات کانولوشن معمولی روی داده‌های ساختار یافته اقلیدسی و ( ب ) نمودار شماتیک عملیات پیچش لبه روی داده‌های ابر نقطه‌ای.
Ijgi 10 00482 g008 550
شکل 8. نمودار قاب پیچش لبه.
Ijgi 10 00482 g009 550
شکل 9. موقعیت معدن زغال سنگ Yujialiang.
Ijgi 10 00482 g010 550
شکل 10. ربات بازرسی مورد استفاده در معدن زغال سنگ Yujialiang.
Ijgi 10 00482 g011 550
شکل 11. ابر نقطه ای FMMF.
Ijgi 10 00482 g012 550
شکل 12. جستجوی ابر نقطه کروی روی ابر نقطه FMMF.
Ijgi 10 00482 g013 550
شکل 13. مجموعه داده های ابری چند نقطه ای.
Ijgi 10 00482 g014 550
شکل 14. موقعیت ابر نقطه سر و دم.
Ijgi 10 00482 g015 550
شکل 15. دقت اعداد مختلف لایه های پیچشی لبه.
Ijgi 10 00482 g016 550
شکل 16. از دست دادن تعداد مختلف لایه های پیچش لبه.
Ijgi 10 00482 g017 550
شکل 17. مقدار شاخص ارزیابی هنگام استفاده از اعداد مختلف لایه های پیچشی لبه.
Ijgi 10 00482 g018a 550 Ijgi 10 00482 g018b 550
شکل 18. تأثیر استفاده از تعداد لایه های مختلف پیچشی لبه: ( الف ) 1 لایه، ( ب ) 2 لایه، ( ج ) 3 لایه، ( د ) 4 لایه، ( ه ) 5 لایه، ( f ) 6 لایه، و ( گرم ) 7 لایه.
Ijgi 10 00482 g019 550
شکل 19. مقادیر شاخص ارزیابی هنگام استفاده از مقادیر مختلف K.
Ijgi 10 00482 g020a 550 Ijgi 10 00482 g020b 550
شکل 20. اثر مقادیر مختلف K: ( الف ) K 5 است، ( ب ) K 10 است، ( ج ) K 15 است، ( د ) K 20 است، ( e ) K 25 است، ( f ) K است 30 ، و ( g ) K 35 است.
Ijgi 10 00482 g021 550
شکل 21. مقادیر شاخص ارزیابی DGCNN هنگام استفاده از الگوریتم های بهینه سازی مختلف.
Ijgi 10 00482 g022 550
شکل 22. اثر تشخیص ابر نقطه کره بر اساس الگوریتم های بهینه سازی مختلف: ( الف ) اثر الگوریتم بهینه سازی آدم و ( ب ) اثر الگوریتم بهینه سازی SGD.
Ijgi 10 00482 g023 550
شکل 23. مقایسه اثرات شبکه های عصبی مختلف.
Ijgi 10 00482 g024a 550 Ijgi 10 00482 g024b 550
شکل 24. اثر تشخیص ابر نقطه کره بر اساس شبکه های عصبی مختلف: ( الف ) ما، ( ب ) PointNet، و ( ج ) PointNet++.

دسته‌بندی نشده

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید