بهبود دقت تنظیم نوار لایدار هوابرد با استفاده از داده های ارتفاع و اطلاعات قدرت ویژگی سطح برگرفته از الگوریتم رای گیری تانسور

خلاصه

مختصات فضایی تشخیص نور و محدوده (Lidar)، به ویژه داده های ارتفاع، و داده های شدت ابرهای نقطه ای اغلب برای تنظیم نوار در Lidar در هوا استفاده می شود. با این حال، ناهماهنگی در داده‌های شدت و سپس داده‌های گرادیان شدت به دلیل تغییرات در زوایای فرود و انعکاس در جهت اسکن و تابش نور خورشید در همان مناطق نوارهای مختلف ممکن است باعث ایجاد مشکلاتی در فرآیند تنظیم نوار لیدار شود. به جای شدت لیدار، نوع جدیدی از داده‌ها، به نام داده‌های قدرت ویژگی سطحی که با استفاده از روش رای دهی تانسور به دست می‌آیند، به فرآیند تنظیم نوار با استفاده از روش حداقل مربعات جزئی در این مطالعه معرفی شدند. این داده ها در همان مناطق نوارهای مختلف، به ویژه در سقف ساختمان ها، سازگار هستند.

کلید واژه ها:

لیدار ; تنظیم نوار ؛ الگوریتم رای گیری تانسور ; قدرت ویژگی سطح

1. معرفی

در حال حاضر، سیستم‌های تشخیص نور و محدوده (Lidar) به طور گسترده برای به دست آوردن سریع انواع مختلف داده‌های ابر نقطه‌ای سه‌بعدی (3 بعدی) برای کاهش زمان کار به طور موثر در بسیاری از زمینه‌ها، به ویژه در نقشه‌برداری، مهندسی و ساخت و ساز شهر هوشمند سه بعدی استفاده می‌شوند. مدل‌های زمین دیجیتال از ابرهای نقطه لیدار با استفاده از روش‌های درون‌یابی و فیلتر [ 1 ، 2 ] ساخته شده‌اند. داده های Lidar برای استخراج خطوط کلی ساختمان و متعاقبا بازسازی ساختمان های سه بعدی استفاده شده است [ 3 ، 4 ]. در [ 5]، از یک شبکه عصبی برای طبقه بندی گونه های مختلف گیاهی بر اساس شدت لیدار استفاده شد. علاوه بر این، داده‌های فراطیفی و داده‌های Lidar برای بهبود اطمینان طبقه‌بندی ترکیب شده‌اند [ 6 ، 7 ]. از آنجایی که داده های Lidar را می توان به سرعت به روز کرد، فناوری Lidar برای شناسایی و نظارت بر تغییرات شهری استفاده شده است [ 8 ، 9 ]. علاوه بر این، با استفاده از شکل موج Lidar هوابرد، می توان مناطق شهری و جنگلی را طبقه بندی کرد و جامدات و ساختارهای مات را تجزیه و تحلیل کرد [ 10 ، 11 ، 12 ، 13 ].

به طور کلی، خطاها در داده‌های لیدار را می‌توان به عواملی مانند خطاهای اندازه‌گیری فاصله، خطاهای تعیین جهت واحد اندازه‌گیری اینرسی (IMU)، خطاهای موقعیت‌یابی سیستم ناوبری جهانی ماهواره (GNSS)، خطاهای زمان‌بندی، خطاهای نصب و خطاهای دستگاه نسبت داد. مدل زمینی (در صورت استفاده از سیستم ارتفاعی ارتومتریک) [ 14 ، 15]. دقت موقعیت مکانی با لیدار ممکن است تحت تأثیر این خطاها قرار گیرد. بهبود عملکرد به دست آمده در هنگام استفاده از Lidar، به ویژه بهبود عملکرد هندسی، به کیفیت و دقت مجموعه داده های Lidar بستگی دارد. بنابراین ابتدا داده های لیدار باید کالیبره یا اصلاح شوند. ابزارهای فردی مانند گیرنده های GNSS و IMU و همچنین ادغام آنها با سیستم باید کالیبره شوند. اغلب، یک سیستم Lidar را می توان به طور موثر با استفاده از میدان کالیبراسیون [ 16 ، 17 ، 18 ، 19 ، 20 ] کالیبره کرد. یکی دیگر از روش های کالیبراسیون شامل استفاده از تکه های مسطح مشتق شده از تنظیم بسته فتوگرامتری به عنوان سطوح کنترل به جای یک میدان کالیبره شده است [ 21 ].]. پس از کالیبراسیون، معمولاً می توان به دقت dm مختصات نقطه لیدار دست یافت.

با این حال، ممکن است به دلیل کالیبراسیون ناقص، خطاها همچنان در داده های Lidar وجود داشته باشد. برای کاهش این خطاها، تنظیم نوار اغلب برای اصلاح داده های Lidar اتخاذ می شود. مطالعات معدودی مدل‌های چند جمله‌ای را معرفی کرده‌اند یا سطوح صاف و صاف را در فرآیند تنظیم نوار برای حذف جابجایی‌های اجسام مشابه در نوارهای همپوشانی، به‌ویژه اختلاف ارتفاع، مطابقت داده‌اند [ 22 ، 23 ، 24 ، 25 ].

علاوه بر استفاده از داده‌های ارتفاع در تنظیم نوار لیدار، داده‌های دیگری مانند تصویر هوایی و داده‌های شدت، برای به دست آوردن داده‌های لیدار بسیار دقیق استفاده شده‌اند [ 26 ، 27 ، 28 ]. به عنوان مثال، Burman [ 26 ] و Maas [ 27 ] اختلاف ارتفاع را با استفاده از داده های ارتفاع و شدت نقاط Lidar در تنظیم نوار تصحیح کرده اند. ژانگ و همکاران [ 28 ] از تصاویر مثلثی هوا برای بهبود تنظیم نوار لیدار با تطبیق نقاط مزدوج و ویژگی‌های گوشه ساختمان مزدوج در شدت و تصاویر هوایی استفاده کرد. برای استخراج صحیح و تطبیق ویژگی های سطح، Filin [ 29] یک مدل بازیابی خطا برای سیستم های Lidar ارائه کرد و سطوح اتصال را در نوارهای همپوشانی ایجاد کرد. لی و همکاران [ 30 ] اختلاف ارتفاع بین نوارهای همپوشانی با ویژگی های خطی مزدوج را با استفاده از روش تنظیم تصحیح کرد. به طور خلاصه، کالیبراسیون و تنظیم نوار برای به دست آوردن اطلاعات بسیار دقیق Lidar ضروری است.

اگرچه داده‌های شدت لیدار ممکن است برای متمایز کردن اجسام با توجه به بازتاب‌پذیری مواد مختلف و برای تنظیم نوار استفاده شود، این داده‌ها به راحتی تحت‌تاثیر از دست دادن انتشار لیزر، زوایای تابش نور خورشید و پرتوهای لیزر، زوایای اسکن، تضعیف اتمسفر، زبری سطح، مواد اشیاء و عوامل دیگر بنابراین، داده های شدت معمولاً باید از قبل با پیروی از روش به اصطلاح عادی سازی شدت تصحیح شوند. حتی پس از قرار دادن داده‌های شدت لیدار به روش نرمال‌سازی شدت، تضمین قوام آنها بر روی سطوح یکسان نوارهای مختلف به دلیل عوامل غیرقابل پیش‌بینی مانند قدرت انتشار ناپایدار، واریانس حاشیه‌ای در شرایط جو و مناطق سایه (فقدان بافت) آسان نیست. 31 ،32 ، 33 ]. اگر داده‌های Intensity سازگار باشند، داده‌های مفیدی برای تنظیم نوار Lidar هستند. برخی از محققان با موفقیت چنین داده هایی را برای تنظیم نوار به کار گرفته اند [ 26 ، 27 ، 28 ]. اگر آنها ناسازگار باشند، استفاده از آنها در تنظیم نوار دشوار است.

ثبات در ارتفاع و شدت بین نوارها برای به دست آوردن نتایج تنظیم نوار لیدار با کیفیت بسیار مهم است. مطالعه حاضر بر تنظیم نوار لیدار با استفاده از داده‌های ثابت، یعنی داده‌های ارتفاع و قدرت ویژگی سطح اجسام تمرکز دارد. داده های قدرت ویژگی سطح به دست آمده با استفاده از روش رای گیری تانسور (TVM) اطلاعات هندسی مفیدی را ارائه می دهد [ 3 ، 34 ، 35 ].

در این مطالعه، امکان استفاده از داده‌های ارتفاع با داده‌های قدرت ویژگی سطح برای انجام محاسبات تنظیم نوار لیدار طبق روش پیشنهادی در مطالعات اولیه کار [ 36 ، 37 ] بیشتر مورد بحث و تحلیل قرار می‌گیرد. خواص داده های مقاومت ویژگی سطح در بخش 2 معرفی شده است. با توجه به اینکه تعداد زیادی از پارامترهای سیستم تنظیم نوار لیدار ناشناخته هستند، روش حداقل مربعات جزئی (PLS) معرفی شده در بخش 3 به جای روش حداقل مربعات معمولی (OLS) برای بهبود اثربخشی محاسباتی اتخاذ شده است. آزمایش های انجام شده در این مطالعه در بخش 4 مورد بحث قرار گرفته است. اظهارات پایانی در ارائه شده استبخش 5 .

2. اطلاعات ویژگی های هندسی

قدرت ویژگی سطحی داده‌های لیدار نوعی از داده‌های ویژگی هندسی است که از TVM به دست می‌آید و این داده‌ها می‌توانند برای شناسایی و استخراج ویژگی‌های هندسی ساختمان‌ها استفاده شوند [ 3 ]. شما و لین [ 35 ] از TVM با نقشه های توپوگرافی برای بازسازی ساختمان های سه بعدی از داده های Lidar در هوا استفاده کردند و به نتایج مطلوبی دست یافتند. ما از نتایج استخراج ویژگی هندسی به‌دست‌آمده با TVM، به ویژه داده‌های قدرت ویژگی سطح، برای تنظیم نوار استفاده کردیم.

2.1. قدرت ویژگی هندسی

شما و لین [ 3 ، 35 ] نشان دادید که الگوریتم TVM برای استخراج ویژگی های هندسی از ابرهای نقطه لیدار مناسب است. با استفاده از TVM، ویژگی های هندسی هر نقطه لیدار را می توان با یک تانسور مرتبه دوم به صورت زیر نشان داد [ 34 ]:

تی = (λ 1 - λ 2) v 1 v تی 1 + (λ 2 - λ 3) (v 1 v تی 1 + v 2 v تی 2) + λ 3 (v 1 v تی 1 + v 2 v تی 2 + v 3 v تی 3)

(1)

که در آن λ ₁ , λ ₂ و λ ₃ مقادیر ویژه تانسور T هستند و v₁, v₂, و v₃ بردارهای ویژه متناظر هستند. ویژگی های هندسی یک نقطه لیدار را می توان با توجه به قوانین زیر [ 34 ] دریافت کرد: ویژگی های نقطه ( $λ_{1} \approx λ_{2} \approx λ_{3})$ را می توان بر حسب λ ₃ ، ویژگی های خطی بیان کرد ( $λ_{1} \approx λ_{2} ≫ λ_{3})$ را می توان بر حسب (λ ₂ – λ ₃ ) و ویژگی سطح ( $λ_{1} ≫ λ_{2} \approx λ_{3}$ ) را می توان بر حسب ( λ ₁ – λ ₂ ) بیان کرد. تجزیه دقیق تانسورها و رابطه بین تانسورها و ویژگی های هندسی یک نقطه را می توان با مراجعه به [ 3 ، 34 ] به دست آورد.

رابطه هندسی بین یک نقطه مورد نظر و نقاط مجاور آن در یک منطقه مشخص را می توان از تانسور T در معادله (1) هنگام استفاده از الگوریتم TVM تعیین کرد. پس از پردازش TVM، ویژگی هندسی اصلی یک نقطه را می توان با استفاده از مقادیر ویژه λ ₁ ، λ ₂ و λ ₃ تانسور T با توجه به قوانین ثبت فوق تعیین کرد. نقاط قوت ویژگی هندسی ممکن است تحت تأثیر تعداد نقاط مجاور قرار گیرد. برای غلبه بر این تأثیر، You و Lin [ 3 ] نرمال کردن مقادیر نقاط قوت ویژگی را به شرح زیر پیشنهاد کردند:

قدرت ویژگی سطح: _Cs= ( λ ¹ – λ ₂ )/ λ ₁ ،

قدرت ویژگی خط: _Cl= ( ^λ₂ – λ ₃ )/ λ 1 ،

قدرت ویژگی نقطه: C ^p = λ ₃ / λ ₁ ,

جایی که $0 \leq C^{s}, C^{l}, C^{p} \leq 1$ و $C^{s} + C^{l} + C^{p} = 1 .$ قدرت ویژگی سطح ( $C^{s}$ برای تنظیم نوار در مطالعه ما از داده ها و ارتفاع نقاط لیدار استفاده شد.

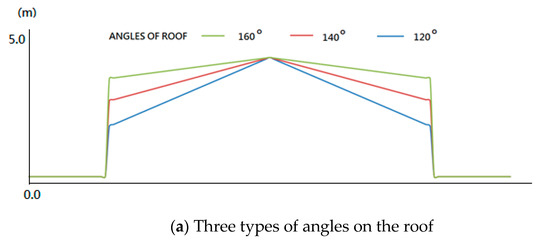
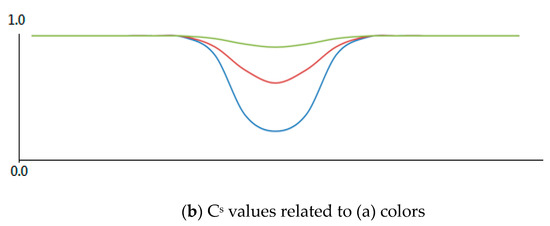
2.2. ویژگی های قدرت ویژگی سطح

در این بخش ابتدا مقاومت ویژگی مهم سطح را بررسی می کنیم

C^{s}

همانطور که در [ 3 ] ذکر شد، ویژگی های نقاط لیدار در یک صفحه . نقاط قوت ویژگی سطح نقاط در صفحات با شیب یکسان تقریباً برابر است و تقریباً به 1 نزدیک می شود. در مقابل، مقاومت ها ممکن است در محل اتصال دو صفحه مجاور با شیب های مختلف، به عنوان مثال، روی سقف ها متفاوت باشد. هر چه اختلاف شیب بین دو صفحه مجاور بیشتر باشد، اهمیت بیشتری دارد

C^{s}

تغییر، همانطور که در شکل 1 نشان داده شده است.

به عنوان مثال، ارتفاع و را نشان می دهیم

C^{s}

تغییر یک ساختمان متشکل از چندین سقف شیروانی با استفاده از داده های واقعی Lidar هوابرد که از قبل با استفاده از روش میدان کالیبراسیون کالیبره شده اند. شکل 2 a-c عکس های هوایی، داده های ارتفاع و

C^{s}

مقادیر سقف های چند شیروانی ساختمان. مقادیر ارتفاع (به عنوان z -data در این مطالعه) خط مقطع

\bar{P Q}

( شکل 2 الف) در شکل 2 ج نشان داده شده است، و

C^{s}

ارزش های

\bar{P Q}

در نوارهای مختلف در شکل 2 f,g نشان داده شده است. اگرچه داده های Lidar از قبل کالیبره شده بودند، همانطور که در شکل 2 e نشان داده شده است، اختلافات ارتفاعی باقی ماندند .

را

C^{s}

مقادیر در صفحات تقریباً یکسان است، به عنوان مثال، صفحات مسطح (به عنوان مثال، زمین) یا سطوح سقف ساختمان ها، صفحات سقف شیبدار یا مسطح، یا سطوح زمین. با این حال

C^{s}

مقادیر خط بخش

\bar{P Q}

در برآمدگی های سقف صفحات سقف مجاور با شیب های دیفرانسیل متفاوت است ( شکل 2 c,d,f). این

C^{s}

مقادیر در همسایگی پشته بام به وضوح با مقادیر دیگر صفحات سقف متفاوت است. با این حال، الگوهای آنها در نوارهای مختلف یک ساختمان بسیار مشابه هستند، همانطور که در شکل 2 f,g نشان داده شده است. مقادیر مقاومت ویژگی سطح اجسام مشابه در نوارهای مختلف سازگار است.

این قوام از

C^{s}

مقادیر را می توان برای تنظیم نوار استفاده کرد. بنابراین، علاوه بر داده های ارتفاع نقاط لیدار،

C^{s}

در این مطالعه از مقادیر نقاط لیدار به عنوان داده های تکمیلی هنگام انجام تنظیم نوار استفاده شد. صفحات سقف مسطح یا صفحات سقف شیبدار و صفحات زمین مسطح که برای آنها

C^{s}

مقادیر اندکی تغییر می کنند، به عنوان مناطقی نامیده می شوند که تابش نور را در آنها نشان می دهند

C^{s}

مقادیر (مناطق SVC) در این مطالعه. این صفحات به رنگ قهوه ای در شکل 2 d نشان داده شده اند. همسایگی پشته های سقف صفحات بام مجاور با شیب های مختلف، نواحی با تغییر ارتفاع در

C^{s}

مقادیر (از این پس، مناطق HVC)، همانطور که با قسمت های آبی در شکل 2 d نشان داده شده است. مناطق سبز در شکل 2 d عبارتند از

C^{s}

تصاویری از درختان یا زیر برس و آنها

C^{s}

مقادیر به طور قابل توجهی متفاوت است. با این حال، چنین ابرهای نقطه توزیع نامرتب برای تنظیم نوار نامناسب هستند و مستثنی هستند. در این مطالعه،

C^{s}

داده های مربوط به مناطق HVC در تنظیم نوار برای مطالعه اثرات داده های مقاومت ویژگی سطح استفاده شد.

3. تنظیم نوار

حتی پس از کالیبره شدن سیستم لیدار ممکن است عدم دقت در داده های لیدار وجود داشته باشد. برای اصلاح چنین عدم دقتی، تنظیم نوار ابزار قدرتمندی است. تنظیم نوار معمولاً شامل استفاده از اختلاف ارتفاع همان شی در مناطق همپوشانی می‌شود و گهگاه شامل استفاده از داده‌های شدت Lidar در صورت وجود داده‌های شدت ثابت است. مدل‌های تبدیل سه، هفت، نه و 12 پارامتری و همچنین مدل‌های چند جمله‌ای، مدل‌های درون‌یابی دوخطی با استفاده از شبکه‌ها، مدل‌های درونیابی خطی با استفاده از شبکه نامنظم مثلثی (TIN)، اصلاحات بر اساس تابع تولید داده‌های لیدار، و روشهای دیگری برای تنظیم نوار لیدار اتخاذ شده است [ 22 ، 23 ، 24 ، 25 ، 26, 27 , 28 ].

از آنجایی که هر روش نرمال شده با شدت با آیتم‌های محدود متفاوتی مرتبط است [ 31 ، 32 ، 33 ]، حفظ شدت ثابت برای یک شیء در نوارهای مختلف حتی پس از عادی‌سازی دشوار است. بنابراین، داده‌های شدت از تنظیم نوار در این مطالعه حذف می‌شوند. به جای داده های شدت، قدرت ویژگی سطح (

C^{s}

) از مقادیر استفاده می شود. z -values (مقادیر ارتفاع) و

C^{s}

مقادیر اشیاء در مناطق همپوشانی نوارهای مختلف به عنوان داده اصلی در طرح تنظیم نوار ما عمل می کنند. علاوه بر این، PLS برای تنظیم نوار به کار گرفته شده است، زیرا مزایایی را از نظر کارایی محاسباتی ارائه می دهد. نقاط مزدوج برای تنظیم، نقاط شبکه ای از مناطق همپوشانی هستند. یک روش درون یابی نیز برای تنظیم مورد نیاز است. جزئیات در مورد شبکه ها و روش درون یابی دوخطی مورد استفاده در این مطالعه را می توان از [ 26 ] به دست آورد.

3.1. مدل های ریاضی و تنظیمات شبکه

هر نوار Lidar به یک مدل تبدیل شباهت هفت پارامتری اختصاص داده می شود و این پارامترها برای جذب خطاهای جابجایی بین نوارهای همپوشانی استفاده می شوند. مدل به صورت زیر بیان می شود:

⎛⎝⎜ ایکس “ y “ z “ ⎞⎠⎟ j من = κ j \cdot R (α j ، β j ، γ j) \cdot ⎛⎝⎜ ایکس y z ⎞⎠⎟ j من + ⎛⎝⎜⎜ تی j ایکس تی j y تی j z ⎞⎠⎟⎟

(2)

که در آن عناصر ماتریس چرخشی $R (α^{j}, β^{j}, γ^{j})$ به شرح زیر است:

R (1 ، 1) = cos β j \cdot cos γ j ، R (1 ، 2) = cos α j \cdot گناه γ j + گناه α j \cdot گناه β j \cdot cos γ j ، R (1 ، 3) = گناه α j \cdot گناه γ j - cos α j \cdot گناه β j \cdot cos γ j ، R (2 ، 1) = - cos β j \cdot گناه γ j ، R (2 ، 2) = cos α j \cdot cos γ j - گناه α j \cdot گناه β j \cdot گناه γ j ، R (2 ، 3) = گناه α j \cdot cos γ j + cos α j \cdot گناه β j \cdot گناه γ j ، R (3 ، 1) = گناه β j ، R (3 ، 2) = - گناه α j \cdot cos β j ، R (3 ، 3) = cos α j \cdot cos β j .

(3)

بالانویس j نشان دهنده شماره نوار است. زیرنویس i نشان دهنده نقطه Lidar i است .

α^{j}, β^{j}, {and γ}^{j}

زوایای چرخشی نوار j را نشان می دهد ،

κ^{j}

عامل مقیاس است،

t_{x}^{j}, t_{y}^{j}, and t_{z}^{j}

پارامترهای تغییر هستند. و (

x_{i}^{j}, y_{i}^{j}, z_{i}^{j}

) و (

{x^{'}}_{i}^{j}, {y^{'}}_{i}^{j}, {z^{'}}_{i}^{j}

) مختصات یک نقطه لیزری قبل و بعد از تبدیل هستند.

یک سری شبکه های مربعی ابتدا در مناطق پروازی برای اتصال نوارهای مختلف تنظیم می شوند. مختصات ( x , y ) هر نقطه شبکه مشخص شده و به صورت زیر محاسبه می شود:

ایکس س = م 0 + G \cdot s ، Y تی = ن 0 + G \cdot t ، s = 0 \dots m ، t = 0 \dots n ،

(4)

جایی که ( $M_{0}, N_{0}$ ) مختصات شناخته شده نقطه اصلی شبکه پیوسته و G طول داده شده یک شبکه مربع است. ارتفاع ( $Z_{s, t})$ و قدرت ویژگی سطح $(C_{s, t})$ از هر نقطه شبکه توابعی از مختصات ( $X_{s}, Y_{t})$ ، به این معنا که، $Z_{s, t}$ = $f_{Z}$ ( $X_{s}, Y_{t})$ و $C_{s, t}$ = $f_{C}$ ( $X_{s}, Y_{t})$ . داده های قدرت ویژگی ارتفاع و سطح هر نقطه لیدار را می توان از نقاط شبکه با استفاده از درون یابی دوخطی [ 26 ] استخراج کرد:

z “ j من = ( ایکس s + 1 ، t + 1 - ایکس “ j من ) ( Y s + 1 ، t + 1 - y “ j من ) جی 2 ز s ، t + ( ایکس “ j من - ایکس s ، t ) ( Y s ، t + 1 - y “ j من ) جی 2 ز s + 1 ، t + ( ایکس s + 1 ، t - ایکس “ j من ) ( y “ j من - Y s ، t ) جی 2 ز s ، t + 1 + ( ایکس “ j من - ایکس s ، t ) ( y “ j من - Y s ، t ) جی 2 ز s + 1 ، t + 1 ،

(5)

سی “ j من = ( ایکس s + 1 ، t + 1 - ایکس “ j من ) ( Y s + 1 ، t + 1 - y “ j من ) جی 2 سی s ، t + ( ایکس “ j من - ایکس s ، t ) ( Y s ، t + 1 - y “ j من ) جی 2 سی s + 1 ، t + ( ایکس s + 1 ، t - ایکس “ j من ) ( y “ j من - Y s ، t ) جی 2 سی s ، t + 1 + ( ایکس “ j من - ایکس s ، t ) ( y “ j من - Y s ، t ) جی 2 سی s + 1 ، t + 1 ،

(6)

با وارد کردن معادله (2) در معادلات (5) و (6) و همچنین “خطاهای کل” v _z و v _C ، معادلات مشاهده پیچیده زیر برای طرح تنظیم نوار ما اتخاذ می‌شوند:

0 + v ز = z j من - z “ j من = اف ز (j ، α j ، β j ، γ j ، تی j ایکس ، تی j y ، تی j z ، ز s ، t ، ز s + 1 ، t ، ز s ، t + 1 ، ز s + 1 ، t + 1 ، ایکس j من ، y j من ، z j من ، ایکس s ، t ، Y s ، t ، ایکس s + 1 ، t ، Y s + 1 ، t ، ایکس s ، t + 1 ، Y s ، t + 1 ، ایکس s + 1 ، t + 1 ، Y s + 1 ، t + 1) ،

(7)

0 + v سی = سی j من - سی “ j من = اف سی (j ، α j ، β j ، γ j ، تی j ایکس ، تی j y ، تی j z ، سی s ، t ، سی s + 1 ، t ، سی s ، t + 1 ، سی s + 1 ، t + 1 ، ایکس j من ، y j من ، ایکس s ، t ، Y s ، t ، ایکس s + 1 ، t ، Y s + 1 ، t ، ایکس s ، t + 1 ، Y s ، t + 1 ، ایکس s + 1 ، t + 1 ، Y s + 1 ، t + 1) ،

(8)

جایی که $x_{i}^{j}, y_{i}^{j}, z_{i}^{j}$ و $C_{i}^{j}$ مقادیر اندازه گیری مختصات و مقدار مقاومت ویژگی سطح را به ترتیب در یک نقطه Lidar نشان می دهد. متغیرهای باقی مانده در توابع F _z و F _C ناشناخته هستند، از جمله پارامترهای تبدیل هر نوار و ارتفاعات و مقادیر مقاومت ویژگی سطح نقاط شبکه.

در مقایسه با نتایج به‌دست‌آمده با استفاده از داده‌های مشاهده ارتفاع به تنهایی، می‌توان انتظار داشت که قابلیت اطمینان نتایج تنظیم نوار هنگام استفاده از داده‌های ارتفاع و قدرت ویژگی سطح بالاتر باشد. قابل توجه، پارامتر

t_{z}^{j}

هنگام استفاده قابل حل نیست

C^{s}

داده های مشاهده به تنهایی، که شبیه به استفاده از داده های شدت در تنظیم است [ 26 ].

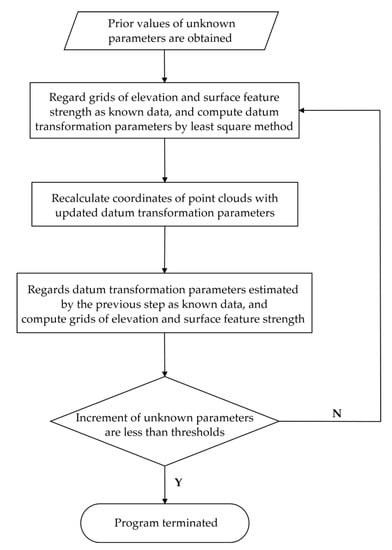
3.2. روش PLS

از آنجایی که تعداد نقاط لیدار و معادلات مشاهداتی مربوطه از نظر تعداد زیاد و معادلات (5) و (6) غیرخطی هستند، یک روش خطی سازی و تکرار برای تنظیم نوار ضروری است. به دلیل تقاضا برای اثربخشی محاسباتی، روش PLS برای تنظیم نوار انتخاب شده است. هلند [ 38 ، 39 ] و یانگ [ 40 ] استفاده از روش PLS را برای کاهش ابعاد پارامترهای ناشناخته برای افزایش کارایی عملیاتی پیشنهاد کرده اند. نتایج تحلیل کدهای منبع برنامه OLS و PLS نشان داد که پیچیدگی زمانی و زمان عملیاتی PLS بیشتر از OLS است. 41 ].]. علاوه بر این، روش PLS ممکن است همبستگی بین پارامترها را کاهش دهد، که ممکن است به یک راه حل قابل اعتمادتر منجر شود [ 42 ].

روش PLS همچنین از اصل حداقل مربعات برای حل مجهولات استفاده می کند. با این حال، تمام پارامترهای ناشناخته را به طور همزمان حل نمی کند. در عوض، پارامترهای ناشناخته را به دو قسمت تقسیم می کند. یک تبدیل متغیر ممکن است برای کاهش همبستگی بین پارامترها استفاده شود [ 42]. اصولاً در ابتدای تنظیم، پارامترهای یکی از قسمت‌ها (که از این به بعد قسمت اول نامیده می‌شود) با تخصیص مقادیر اولیه به آن‌ها به عنوان شناخته شده و پارامترهای قسمت دوم به عنوان مجهولاتی در نظر گرفته می‌شوند که توسط اصل حداقل مربعات هنگامی که پارامترها تخمین زده می شوند، پارامترهای متعلق به قسمت دوم در مرحله تنظیم دوم به عنوان شناخته شده در نظر گرفته می شوند، در حالی که پارامترهای قسمت اول اکنون مجهول در نظر گرفته می شوند. در مرحله تعدیل سوم، پارامترهای قسمت اول برآورد شده در مرحله تعدیل قبلی به عنوان شناخته شده و پارامترهای قسمت دوم اکنون دوباره مجهول در نظر گرفته می شوند. فرآیند تعدیل با چنین تبادل متوالی معلومات و مجهولات ادامه می یابد تا زمانی که تخمین همگرا شود [ 43 ]].

در این تحقیق پارامترهای مجهول به دو بخش ارتفاع و

C^{s}

مقادیر نقاط شبکه پارامترهای قسمت اول و پارامترهای تبدیل مبنا پارامترهای قسمت دوم هستند. نمودار جریانی از روش تنظیم نوار انجام شده در این مطالعه با روش PLS در شکل 3 نشان داده شده است . قبل از تنظیم نوار با استفاده از روش PLS، ارتفاع و استحکام ویژگی سطح شبکه‌ها با توجه به نزدیک‌ترین نقاط مقادیر اولیه تعیین می‌شود. مقدار اولیه پارامتر مقیاس روی 1 و سایر پارامترهای مبنا روی 0 تنظیم شده است. در ابتدای تنظیم نوار، پارامترهای قسمت اول، یعنی ارتفاعات اولیه و

C^{s}

مقادیر نقاط شبکه فوق، اطلاعات شناخته شده در نظر گرفته شده و پارامترهای قسمت دوم، یعنی پارامترهای تبدیل تک تک نوارهای لیدار، با روش OLS برآورد شده است. پس از هر مرحله از تنظیم نوار، مختصات جدید نقاط لیزر با توجه به پارامترهای تبدیل تخمین زده شده جدید به روز می شود. راه حل های نهایی زمانی به دست آمد که روند PLS متوقف شد تا زمانی که تغییرات در پارامترهای ناشناخته (شامل مقادیر شبکه و پارامترهای تبدیل) کمتر از آستانه های مربوطه شود.

اگر داده های Lidar (از جمله z -data و

C^{s}

داده ها) حاوی مقادیر پرت هستند، نتایج تنظیم نوار ممکن است بدتر شود. بنابراین، یک روش تشخیص بیرونی باید در نظر گرفته شود. در این مطالعه، نقاط پرت در داده های لیدار با استفاده از روش قوی [ 44 ] شناسایی شدند. علاوه بر این، داده های مشاهده ای از انواع مختلف، یعنی داده های ارتفاع و

C^{s}

داده ها در این مورد، باید مقادیر صحیح وزن در فرآیند تنظیم اختصاص داده شود. هنگامی که داده‌های مشاهده‌ای فاقد اطلاعات پیشینی صحیح در مورد وزن‌ها هستند، تخمین مؤلفه‌های واریانس باید برای داده‌های مشاهده انواع مختلف انجام شود. ما از تخمین مولفه واریانس هلمرت برای به دست آوردن واریانس های دقیق داده های مشاهده برای دستیابی به تخمین بهینه پارامترهای ناشناخته استفاده کردیم [ 45 ].

4. آزمایش ها و بحث

منطقه مورد مطالعه پوشیده از چهار نوار لیدار در محوطه دانشگاه ملی چنگ کونگ در شهر تاینان، تایوان واقع شده است ( شکل 4 ). مساحت منطقه مورد مطالعه تقریباً 360000 متر مربع ^است . عرض پروازهای A و B تقریباً 350 متر و طول پروازهای A و B 1070 متر بود. عرض پروازهای C و D تقریباً 250 متر و طول پروازهای A و B 570 متر بود. ارتفاع پرواز تقریباً 500 متر از سطح زمین بود. ابرهای نقطه لیدار با استفاده از اسکنر Optech ALTM 30/70 گرفته شدند و چگالی لیدار تقریباً 6 pts/m2 ^بود . اگرچه ابرهای نقطه لیدار در منطقه مورد مطالعه از قبل کالیبره شده بودند، اختلافات به آسانی آشکار بود، همانطور که در تصویر نشان داده شده است. شکل 2 نشان داده شده است، اختلافات به آسانی آشکار بود.ه. بنابراین، روش‌های تنظیم نوار و درون‌یابی شبکه‌ای که در بخش 3 ذکر شده‌اند برای اصلاح چنین تناقضاتی استفاده شد.

ابتدا منطقه مورد مطالعه به صورت شبکه هایی با عرض 1 متر در آزمایش تنظیم شد. مناطق O1، O3، O4، O5 و O7 در شکل 4با دو نوار همپوشانی داشتند و نواحی O2 و O6 توسط سه نوار همپوشانی داشتند. دوم، معادلات مشاهده‌ای (معادلات (7) و (8)) همه نقاط لیدار، به استثنای درختان، زیر برس، زمین و برخی از صفحات چک انتخاب شده در مناطق همپوشانی، با استفاده از روش PLS تنظیم شدند. چند صفحه بام شیبدار یا مسطح و هواپیماهای زمینی به عنوان صفحات چک انتخاب شدند. مشاهدات نقاط لیدار در این هواپیماها در تنظیم استفاده نشد. پس از انجام تنظیم، ارتفاع تنظیم شده و قدرت ویژگی سطح هر نقطه لیدار با استفاده از پارامترهای تبدیل و روش درون یابی بیان شده در معادلات (2)، (5) و (6) محاسبه شد.

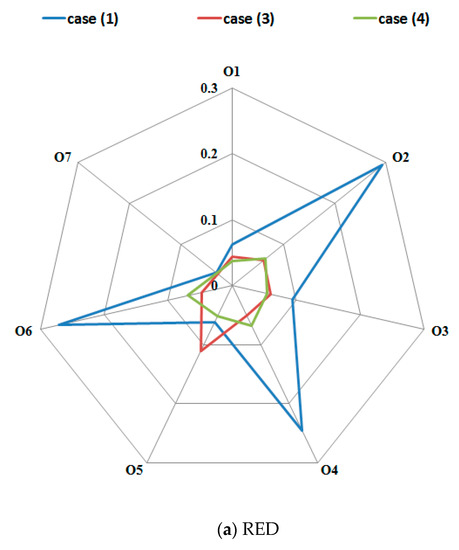
در این مطالعه، دقت نتایج تعدیل با استفاده از دو شاخص کیفیت یعنی انحراف نسبی (RED) و انحراف مطلق (ABD) مورد ارزیابی قرار گرفت. RED با استفاده از تمام باقیمانده‌های مشاهدات در صفحات بررسی به شرح زیر محاسبه شد:

قرمز = \sum ( V ز تی V ز ) n ———-\sqrt ،

(9)

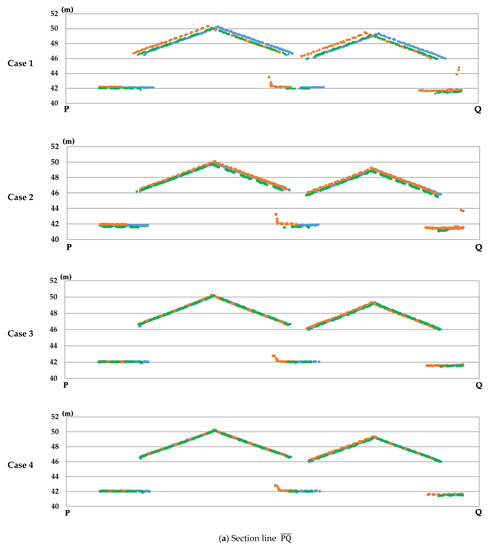
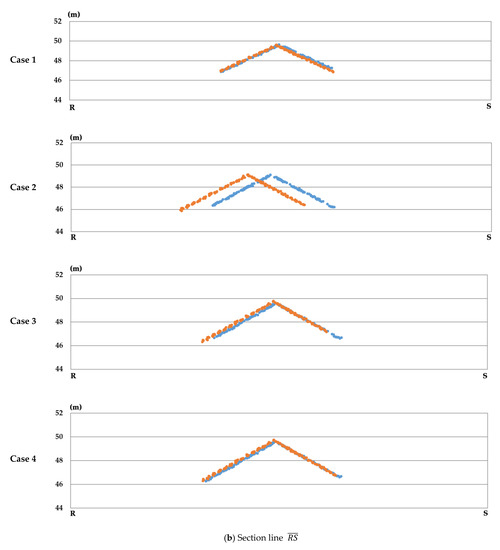
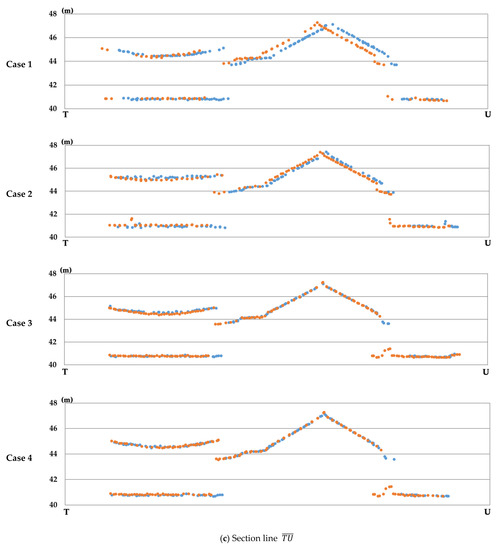
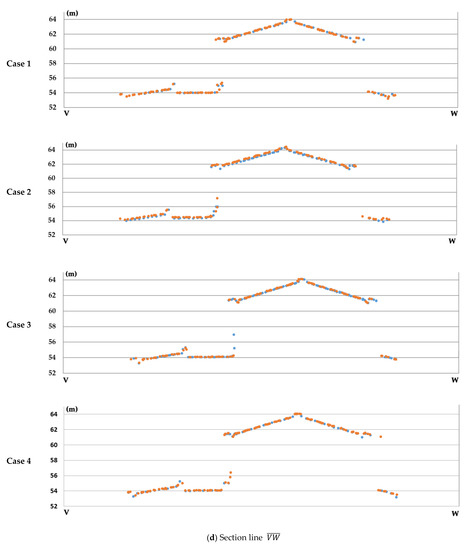
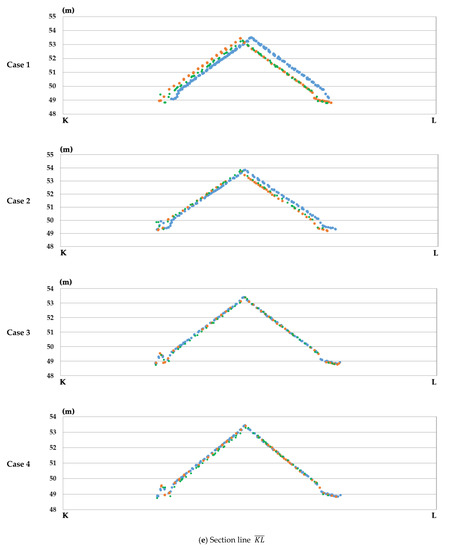
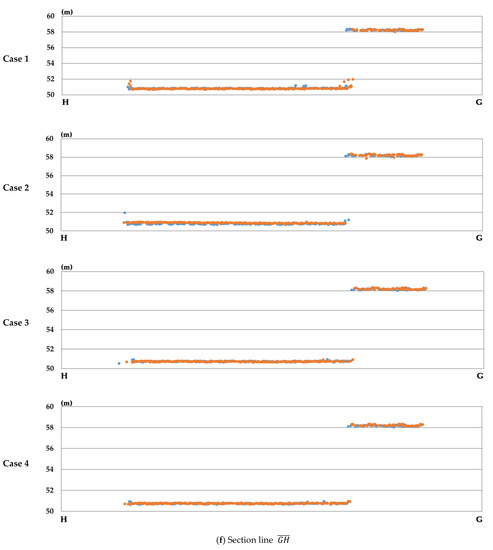
که در آن n تعداد نقاط لیدار است. قرمز را می توان برای آشکار کردن کیفیت تطابق بین نوارها پس از تنظیم استفاده کرد. باقی مانده $v_{z}$ در موارد 2-4 برابر با مقدار z -مشاهده منهای مقدار z تنظیم شده بود، در حالی که در مورد 1، مقدار باقیمانده $v_{z}$ از تفاوت در داده های z کالیبره شده همان شی در نوارهای مجاور محاسبه شد. موارد 1-4 در پاراگراف زیر تعریف شده است.

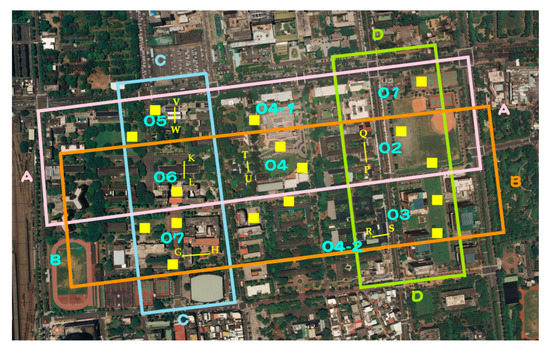
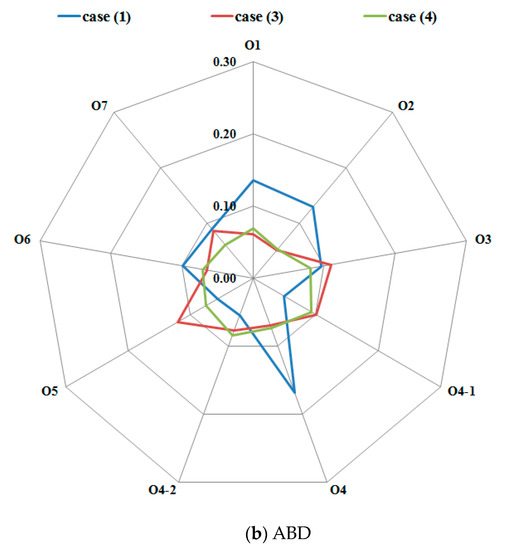
اندازه گیری 20 هواپیمای چک مسطح با استفاده از سه تا پنج نقطه از طریق موقعیت یابی GPS سینماتیک (RTK-GPS) در زمان واقعی با استفاده از گیرنده جی پی اس Leica SR530 انجام شد. چنین صفحات بررسی برای بررسی خارجی نتایج تنظیم استفاده شد ( شکل 4 ). شاخص ABD را می توان به صورت زیر بیان کرد:

ABD = \sum ( ( د w من ) تی \cdot د w من ) n ————-\sqrt ،

(10)

که در آن n مجموع تعداد نقاط بازرسی را در تمام این صفحات بررسی نشان می دهد، $d_{i}^{w} = {z^{'}}_{i}^{w} - \sum_{k = 1}^{m} z_{k, G P S}^{w}$ /m (m = 3~5) نشان دهنده ارتفاع باقی مانده از نقطه لیدار در w امین صفحه تخت است، و $z_{k, G P S}^{w}$ نشان‌دهنده ارتفاع اندازه‌گیری k امین GPS در صفحه مسطح w است. ارتفاعات GPS و ارتفاع نقاط لیدار با مراجعه به سیستم ارتفاعی یکسان در این مطالعه به دست آمد.

برای تجزیه و تحلیل اثرات قدرت ویژگی سطح بر روی طرح تنظیم نوار، ما چهار مورد زیر را برای ارزیابی کیفیت نتایج تنظیم با یا بدون مقادیر مقاومت ویژگی سطح طراحی کردیم. در مورد 1، داده های ارتفاع اولیه ( z -data) پس از کالیبراسیون بدون تنظیم بعدی نوار PLS استفاده شد. در مورد 2، داده های z از نقاط Lidar در مناطق HVC به دست آمده پس از تنظیم نوار استفاده شد. در مورد 3، داده‌های z از نقاط Lidar فقط در نواحی SVC، همانطور که معمولاً در تنظیم Lidar در هوا استفاده می‌شود، استفاده شد. در مورد 4، z -data نقاط Lidar در نواحی SVC و the

C^{s}

داده ها در مناطق HVC استفاده شد. در موارد فوق الذکر،

C^{s}

داده‌ها و z- داده‌های مکان‌های مشابه به طور همزمان در تنظیم استفاده نشدند. z – data استفاده شده در موارد 2-4 مانند موارد استفاده شده در مورد 1 بود.

از آنجا که

C^{s}

داده‌ها در مناطق SVC، مانند سقف‌های صفحه، تقریباً یکسان بودند، برخی از پارامترهای ناشناخته را نمی‌توان در آزمایش‌های ما حل کرد، زمانی که فقط

C^{s}

داده ها در مناطق SVC استفاده شد. در مقابل، z -data معمولاً در نواحی SVC مفید هستند. بنابراین، استفاده از

C^{s}

اطلاعات مربوط به تنظیم نوار در نواحی SVC در این مقاله مورد بحث قرار نگرفته است.

نتایج تعدیل در جدول 1 خلاصه شده است. نتایج تجربی نشان می‌دهد که در مورد 1 که فقط از داده‌های z کالیبره شده و بدون استفاده از تنظیم نوار استفاده شده است، دقت RED 20 سانتی‌متر و دقت ABD 11 سانتی‌متر بوده است. شکل 5 اختلاف بین نوارها را در خطوط مقطع نشان می دهد

\bar{G H}, \bar{K L}, \bar{P Q}

\bar{R S}, \bar{T U}, and \bar{V W}

در موارد 1، 2، 3، و 4. محور آبسیسا جهت را در امتداد خط مقطع و محور عمودی نشان دهنده ارتفاع بر حسب متر است. این اختلافات بر عملکرد برنامه های کاربردی بسیار دقیق با استفاده از داده های Lidar تأثیر منفی می گذارد. نتایج تنظیم مورد 2 بدتر از مورد 1 بود. این نشان می دهد که انجام تنظیم نوار لیدار با استفاده از داده های z در مناطق HVC امکان پذیر نیست. با استفاده از z -data در مناطق SVC (مورد 3)، می توان نتایج بهتری را به دست آورد، همانطور که در جدول 1 خلاصه شده و در شکل 5 نشان داده شده است. همین نتیجه در [ 26 ] به دست آمد.

بر اساس آزمون فرضیه های آماری در سطح معنی داری 95 درصد، نتایج تعدیل به دست آمده در موارد 3 و 4 به طور قابل توجهی برتر از موارد به دست آمده در مورد 1 بود. در مقایسه با مورد 1، نتایج RED و ABD 67 و 21 درصد در مورد 3 بهبود یافتند. به ترتیب و در مورد 4 به ترتیب 72 و 34 درصد. نتایج مورد 4 نسبت به مورد 3 بهتر و دقیق تر بود. در مورد 4، RED و ABD به طور قابل توجهی به ترتیب تقریباً 15 و 17 درصد در مقایسه با مقادیر مربوطه در مورد 3 بهبود یافتند. کیفیت نوار بهبود یافت. نتایج تنظیم با استفاده از داده های z و

C^{s}

داده های به دست آمده با استفاده از z-data به تنهایی برتر بود. به طور کلی، آزمایش ها نشان می دهد که استحکام ویژگی سطح (

C^{s}

) برای بهبود قابل توجه نتایج تنظیم نوار مفید است.

برای تجزیه و تحلیل سطوح بهبود در مناطق مختلف هنگام استفاده

C^{s}

داده ها، نتایج تنظیم به دست آمده در مناطق O1-O7 در متن زیر مورد بحث قرار می گیرند. مقادیر RED و ABD مرتبط در شکل 6 نشان داده شده است. دقت نتایج به دست آمده در مناطق O2، O4 و O6 در مورد 1 بیشتر از نتایج به دست آمده در سایر مناطق بود. خطاها ممکن است ناشی از اختلاف زیاد بین نوارهای A و B باشد، علیرغم این واقعیت که داده های منبع Lidar استفاده شده در این فرآیند از قبل کالیبره شده بودند. پس از تنظیم نوار با استفاده از داده های مورد 3، قرمز همه مناطق به جز O5 به سطح سانتی متر رسید. همانطور که در شکل 4 نشان داده شده است ، این نتیجه به دلیل مناسب بودن کمتر مورد انتظار بود z مناسب مورد انتظار بودنقاط داده از منطقه O5 نسبت به سایر مناطق برای استفاده در تنظیم در دسترس بود. علاوه بر این، داده های موجود از منطقه O5 توزیع ضعیفی داشتند. با این حال، هنگامی که از داده های مورد 4 استفاده شد، دقت بهبود یافت ( شکل 6 ). استفاده از تنظیم نوار برای تصحیح اختلاف بین نوارها، به ویژه اختلاف در ارتفاع، ممکن است همیشه امکان پذیر نباشد، حتی زمانی که داده های z به طور یکنواخت و در یک زمین SVC کافی توزیع شده باشند. اگر z -data به تنهایی استفاده شود، تنظیم نوار ممکن است نتایج ضعیفی به همراه داشته باشد.

با این حال، استفاده از z-data نقاط Lidar در مناطق SVC و

C^{s}

داده های نقاط در مناطق HVC می تواند کیفیت و دقت تنظیم نوار را بهبود بخشد، همانطور که در شکل 5 و شکل 6 نشان داده شده است. قابل توجه، z -data مناطق SVC و

C^{s}

داده های مناطق HVC را می توان به عنوان داده های مکمل برای تنظیم نوار لیدار استفاده کرد.

5. نتیجه گیری ها

در این مطالعه، یک نوع داده جدید Lidar، یعنی قدرت ویژگی سطح مشتق شده از TVM، در تنظیم نوار لیدار معرفی شد. در مقایسه با استفاده از داده های ارتفاع به تنهایی برای تنظیم به روز نوار لیدار هوابرد، استفاده از داده های قدرت ویژگی سطح نقاط Lidar در مناطق HVC به عنوان داده های کمکی می تواند دقت تنظیم نوار را 15 تا 17 درصد بهبود بخشد. نتایج تجربی ما داده های جدید، یعنی قدرت ویژگی سطح، داده های کمکی مفیدی برای تنظیم نوار هستند، به ویژه زمانی که داده های ارتفاعی در مناطق SVC کافی نیستند.

منابع

اوزجان، ق. Ünsalan، C. LiDAR فیلتر کردن داده ها و تولید DTM با استفاده از تجزیه حالت تجربی. IEEE J. Sel. بالا. Appl. زمین Obs. Remote Sens. 2016 , 10 , 360–371. [ Google Scholar ] [ CrossRef ]
رن، ی. چن، ز. چن، جی. هان، ی. وانگ، ی. الگوریتم موازی فرآیند/رشته ترکیبی برای تولید DEM از نقاط LiDAR. ISPRS Int. J. Geo-Inf. 2017 ، 6 ، 300. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
شما، RJ; استخراج ویژگی Lin, BC Building از داده‌های لیدار هوابرد بر اساس الگوریتم رای گیری تانسور. فتوگرام مهندس Remote Sens. 2011 ، 77 ، 1221-1231. [ Google Scholar ] [ CrossRef ]
آلبرز، بی. کادا، م. Wichmann, A. استخراج خودکار و منظم کردن خطوط کلی ساختمان از ابرهای نقطه ای LIDAR در هوا. ISPRS-Int. قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2016 ، 41 ، 555-560. [ Google Scholar ] [ CrossRef ]
ویس، یو. بیبر، پ. لابل، اس. بوهلمان، ک. Zell, A. طبقه بندی گونه های گیاهی با استفاده از حسگر سه بعدی LIDAR و یادگیری ماشینی. در مجموعه مقالات نهمین کنفرانس بین المللی 2010 در مورد یادگیری ماشین و برنامه های کاربردی، واشنگتن، دی سی، ایالات متحده آمریکا، 12-14 دسامبر 2010. صص 339-345. [ Google Scholar ]
فنگ، Q. زو، دی. یانگ، جی. Li، B. ترکیب داده های فراطیفی چند منبعی و LiDAR برای نقشه برداری کاربری زمین شهری بر اساس یک شبکه عصبی پیچیده دو شاخه ای اصلاح شده. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 28. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
پیربهای، ک. موتانگا، او. قرعه کشی، ر. بانگاموابو، وی. اسماعیل، R. تشخیص فراوانی گیاه حشره (Solanum mauritianum) در جنگل کاری مزارع با استفاده از سنجش از دور چند منبعی. ISPRS J. Photogramm. Remote Sens. 2016 , 121 , 167–176. [ Google Scholar ] [ CrossRef ]
عجازی، ع.ک. چچین، پ. Trassoudaine, L. تشخیص و به‌روزرسانی تغییرات در ابرهای نقطه لیدار برای نقشه‌برداری خودکار سه بعدی شهری. ISPRS Ann. فتوگرام سنسور از راه دور Spat Inf. علمی II 2013 ، 2 ، 7-12. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کوین، آر. تیان، جی. Reinartz، P. تشخیص تغییر سه بعدی – رویکردها و برنامه ها. ISPRS J. Photogramm. Remote Sens. 2016 ، 122 ، 41-56. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
مالت، سی. برتار، F. لیدار توپوگرافی شکل موج کامل: پیشرفته ترین. J. Photogramm. Remote Sens. 2009 ، 64 ، 1-16. [ Google Scholar ] [ CrossRef ]
الکساندر، سی. Tansey، K. کادوک، جی. هلند، دی. Tate، NJ Backscatter ضریب به عنوان یک ویژگی برای طبقه‌بندی داده‌های اسکن لیزری هوابرد شکل کامل در مناطق شهری. ISPRS J. Photogramm. Remote Sens. 2010 , 65 , 423-432. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
هاینزل، جی. Koch، B. بررسی پارامترهای LiDAR شکل موج کامل برای طبقه بندی گونه های درختی. بین المللی J. Appl. زمین Obs. Geoinf. 2011 ، 13 ، 152-160. [ Google Scholar ] [ CrossRef ]
هوفل، بی. هالاس، ام. Hagenauer, J. تشخیص پوشش گیاهی شهری با استفاده از داده‌های LiDAR هوابرد با ردپای کوچک با ردپای کوچک کالیبره‌شده. ISPRS J. Photogramm. Remote Sens. 2012 ، 67 ، 134-147. [ Google Scholar ] [ CrossRef ]
Lemmens، MJPM اطلاعات ارتفاع دقیق از ارتفاع سنجی لیزری هوابرد. در مجموعه مقالات سمپوزیوم بین المللی زمین شناسی و سنجش از دور IEEE 1997. سنجش از دور – چشم انداز علمی برای توسعه پایدار، سنگاپور، 3 تا 8 اوت 1997. جلد 1، ص 423-426. [ Google Scholar ]
Schenk, T. مدلسازی و تحلیل خطاهای سیستماتیک در اسکنرهای لیزری هوابرد . گزارش فنی فتوگرامتری شماره 19; گروه مهندسی عمران و محیط زیست و علوم زمین شناسی، دانشگاه ایالتی اوهایو: کلمبوس، OH، ایالات متحده آمریکا، 2001; 40p [ Google Scholar ]
وهر، آ. Lohr، اسکن لیزری هوابرد – مقدمه و نمای کلی. ISPRS J. Photogramm. Remote Sens. 1999 ، 54 ، 68-82. [ Google Scholar ] [ CrossRef ]
سیسانی، ن. Toth, C. بهبود دقت داده های LiDAR با استفاده از اهداف زمینی خاص LiDAR. فتوگرام مهندس Remote Sens. 2007 , 73 , 385-396. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
توث، سی. پاسکا، ای. Brzezinska, D. استفاده از خط کشی های روسازی جاده به عنوان کنترل زمینی برای داده های Lidar. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2008 ، 36 ، 173-178. [ Google Scholar ]
اسکالود، ج. لیچتی، دی. رویکرد دقیق به کالیبراسیون خودکاهشی در اسکن لیزری هوابرد. ISPRS J. Photogramm. Remote Sens. 2006 ، 61 ، 47-59. [ Google Scholar ] [ CrossRef ]
اسکالود، ج. Schaer, P. به سمت خود کالیبراسیون بینایی LiDAR خودکار. در مجموعه مقالات پنجمین سمپوزیوم بین المللی فناوری نقشه برداری موبایل، پادوآ، ایتالیا، 28 تا 31 مه 2007. [ Google Scholar ]
حبیب، اف. Bang، KI; شین، SW; خود کالیبراسیون سیستم Mitishita، E. LiDAR با استفاده از تکه های مسطح از داده های فتوگرامتری. در مجموعه مقالات پنجمین سمپوزیوم بین المللی فناوری نقشه برداری موبایل، پادوآ، ایتالیا، 28 تا 31 مه 2007. [ Google Scholar ]
فریچ، دی. Kilian, J. فیلترینگ و کالیبراسیون اندازه‌گیری‌های اسکنر لیزری. در مجموعه مقالات آرشیو بین المللی فتوگرامتری و سنجش از دور، مونیخ، آلمان، 17 اوت 1994; جلد 2357، ص 227–234. [ Google Scholar ]
کیلیان، ج. هالا، ن. انگلیسی، ام. ضبط و ارزیابی داده های اسکنر لیزری هوابرد. در مجموعه مقالات آرشیو بین المللی فتوگرامتری و سنجش از دور، وین، اتریش، 12 تا 18 ژوئیه 1996; جلد 31، ص 383-388. [ Google Scholar ]
Crombaghs، MJE; دی مین، ای جی; بروگلمن، آر. در مورد تنظیم نوارهای همپوشانی داده های ارتفاع سنج لیزری. بین المللی قوس. فتوگرام Remote Sens. 2000 , 33 , 230-237. [ Google Scholar ]
ووسلمن، جی. Maas، تنظیم HG و فیلتر کردن داده های ارتفاع سنجی لیزری خام. در مجموعه مقالات کارگاه OEEPE در مورد اسکن لیزری هوا و SAR تداخل سنجی برای مدل های ارتفاع دیجیتال دقیق، استکهلم، سوئد، 1-3 مارس 2001. صص 62-73. [ Google Scholar ]
Burman, H. کالیبراسیون و جهت گیری داده های تصویر هوابرد و اسکنر لیزری با استفاده از GPS و INS. Ph.D. پایان نامه، موسسه سلطنتی فناوری، استکهلم، سوئد، 2000. [ Google Scholar ]
Maas, HG Methods for Measuring Height and Planimetry Disconcepances in Airborne Laser Scanner Datas. فتوگرام مهندس Remote Sens. 2002 ، 68 ، 933-940. [ Google Scholar ]
ژانگ، ی. Xiong، X. ژنگ، م. Huang, X. LiDAR Strip Adjustment با استفاده از چند ویژگی منطبق با تصاویر هوایی. IEEE Trans. Geosci. Remote Sens. 2015 ، 53 ، 976-987. [ Google Scholar ] [ CrossRef ]
Filin, S. حذف خطاهای سیستماتیک از داده های اسکن لیزری هوابرد. در مجموعه مقالات کنفرانس IEEE IGARSS 2005، سئول، کره، 25 تا 29 ژوئیه 2005. صص 517-521. [ Google Scholar ]
لی، جی. یو، ک. کیم، ی. Habib، AF تنظیم اختلاف بین نوارهای داده LIDAR با استفاده از ویژگی های خطی. IEEE Geosci. سنسور از راه دور Lett. 2007 ، 4 ، 475-479. [ Google Scholar ] [ CrossRef ]
هوفل، بی. Pfeifer، N. تصحیح داده های شدت اسکن لیزری: داده ها و رویکردهای مدل محور. ISPRS J. Photogramm. Remote Sens. 2007 , 62 , 415-433. [ Google Scholar ] [ CrossRef ]
جوتزی، بی. ناخالص، H. عادی سازی داده های شدت LiDAR بر اساس محدوده و زاویه برخورد سطحی. بین المللی قوس. فتوگرام Remote Sens. 2009 , 38 , 213-218. [ Google Scholar ]
Yan، WY; Shaker, A. تصحیح رادیومتری و عادی سازی داده های شدت LiDAR موجود در هوا برای بهبود طبقه بندی پوشش زمین. IEEE Trans. Geosci. Remote Sens. 2014 , 52 , 7658–7673. [ Google Scholar ]
مدیونی، جی. لی، ام اس; تانگ، CK یک چارچوب محاسباتی برای تقسیم بندی و گروه بندی . Elsevier Science: نیویورک، نیویورک، ایالات متحده آمریکا، 2000; 260p. [ Google Scholar ]
شما، RJ; Lin، BC یک روش پیش‌بینی کیفیت برای بازسازی مدل ساختمان با استفاده از داده‌های لیدار و نقشه توپوگرافی. IEEE Trans. Geosci. Remote Sens. 2011 , 49 , 3471–3480. [ Google Scholar ] [ CrossRef ]
لی، CL; شما، RJ Lidar Strip Adjustment با داده های ارتفاع و قدرت ویژگی. در مجموعه مقالات بیست و نهمین کنفرانس آسیایی سنجش از دور، کلمبو، سریلانکا، 10 تا 14 نوامبر 2008. [ Google Scholar ]
لی، CL; شما، مکانیسم RJ برای تنظیم نوار لیدار با داده های ارتفاع و قدرت ویژگی. در مجموعه مقالات سی امین کنفرانس آسیایی سنجش از دور، پکن، چین، 18 تا 23 اکتبر 2009. [ Google Scholar ]
هلند، IS در ساختار رگرسیون حداقل مربعات جزئی. اشتراک. آمار شبیه سازی محاسبه کنید. 1988 ، 17 ، 581-607. [ Google Scholar ] [ CrossRef ]
هلند، IS جزئی رگرسیون حداقل مربعات و مدل های آماری. Scand. J. Stat. 1990 ، 17 ، 97-114. [ Google Scholar ]
یانگ، PJ فرمول بندی مجدد الگوریتم رگرسیون حداقل مربعات جزئی. SIAM J. Sci. محاسبه کنید. 1994 ، 15 ، 225-230. [ Google Scholar ] [ CrossRef ]
کورمن، تی. استین، سی. ریست، آر. Leiserson, C. Introduction to Algorithms , 3rd ed.; آموزش عالی McGraw-Hill: نیویورک، نیویورک، ایالات متحده آمریکا، 2009. [ Google Scholar ]
رائو، CR; Toutenburg, H. Linear Models: Least Squares and Alternatives , 2nd ed.; Springer: نیویورک، نیویورک، ایالات متحده آمریکا، 1999. [ Google Scholar ]
Grafarend، EW; کروم، اف. اوکه، F. تبدیلات مبدأ ژئودزیکی منحنی. Oceanogr. روشن شد Rev. 1996 , 2 , 135. [ Google Scholar ]
کلاین، اچ. Förstner, W. تحقق تشخیص خودکار خطا در برنامه تنظیم بلوک PAT-M43 با استفاده از برآوردگرهای قوی. بین المللی قوس. فتوگرام Remote Sens. 1984 , 25 , 234-245. [ Google Scholar ]
Helmert، PR Die Ausgleichsrechnung Nach der Methode der Kleinsten Quadrate ; Springer: لایپزیگ، آلمان، 1924. [ Google Scholar ]

شکل 1. مقادیر C برای شیب های مختلف یک سقف شبیه سازی شده و از روش رای گیری تانسور (TVM) مشتق شده است ^.

شکل 2. ( الف ) تصاویر هوایی و خط مقطع

\bar{P Q}

; ( ب ) تصویر ارتفاع؛ ( ج ) ^تصویر C ; ( د ) رنگ سبز: درختان و چمن (HVC)، رنگ آبی: پشته و پله پشت بام (HVC)، و رنگ قهوه ای: صفحات شیبدار، صفحات صفحه، و زمین صفحه (SVC). ( ه ) مقادیر Z (مقادیر ارتفاع) در خط بخش

\bar{P Q}

. رنگ های مختلف نشان دهنده نوارهای مختلف Lidar است. ( f ) و ( g ): مقادیر C ^در خط مقطع

\bar{P Q}

. مقادیر C از TVM مشتق شده است ^.

شکل 3. نمودار جریان تنظیم نوار با استفاده از روش حداقل مربعات جزئی (PLS).

شکل 4. چهار نوار لیدار، یعنی A، B، C و D، و شش خط مقطع، یعنی

\bar{G H}, \bar{K L}, \bar{P Q}

\bar{R S}, \bar{T U}, and \bar{V W}

. مربع های زرد نشان دهنده سطوح بررسی برای محاسبه شاخص انحراف مطلق (ABD) هستند.

شکل 5. بین نوارها در خطوط مقطع

\bar{G H}, \bar{K L}, \bar{P Q}

\bar{R S}, \bar{T U}, and \bar{V W}

در موارد 1، 2، 3، و 4. رنگ های مختلف نشان دهنده نوارهای مختلف است. مقیاس محور آبسیسا 1:280 است.

شکل 6. مقادیر RED و ABD مناطق مختلف در موارد 1، 3، و 4.

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

خلاصه

کلید واژه ها:

1. معرفی

2. اطلاعات ویژگی های هندسی

2.1. قدرت ویژگی هندسی

2.2. ویژگی های قدرت ویژگی سطح

3. تنظیم نوار

3.1. مدل های ریاضی و تنظیمات شبکه

3.2. روش PLS

4. آزمایش ها و بحث

5. نتیجه گیری ها

منابع

قبلیرویکرد تجسم یکپارچه برای ارزیابی زمان واقعی و دینامیکی بلایای طوفان برای دریاهای چین

بعدیتقویت مشارکت با استفاده از سیستم های پشتیبانی برنامه ریزی تعاملی: یک بررسی سیستماتیک

مطالب مرتبط ...

آموزش مقاله نویسی در رشته ادبیات فارسی

تأثیر همسایگی درونیابی DEM بر عوامل زمین

رگرسیون وزنی جغرافیایی تطبیقی غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

خبرنامه

خبرنامه

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

دسترسی سریع

مشاورین هوش پیروزی

بهبود دقت تنظیم نوار لایدار هوابرد با استفاده از داده های ارتفاع و اطلاعات قدرت ویژگی سطح برگرفته از الگوریتم رای گیری تانسور

خلاصه

کلید واژه ها:

1. معرفی

2. اطلاعات ویژگی های هندسی

2.1. قدرت ویژگی هندسی

2.2. ویژگی های قدرت ویژگی سطح

3. تنظیم نوار

3.1. مدل های ریاضی و تنظیمات شبکه

3.2. روش PLS

4. آزمایش ها و بحث

5. نتیجه گیری ها

منابع

قبلیرویکرد تجسم یکپارچه برای ارزیابی زمان واقعی و دینامیکی بلایای طوفان برای دریاهای چین

بعدیتقویت مشارکت با استفاده از سیستم های پشتیبانی برنامه ریزی تعاملی: یک بررسی سیستماتیک

مطالب مرتبط ...

آموزش مقاله نویسی در رشته ادبیات فارسی

تأثیر همسایگی درونیابی DEM بر عوامل زمین

رگرسیون وزنی جغرافیایی تطبیقی ​​غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

خبرنامه

خبرنامه

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

دسترسی سریع

رگرسیون وزنی جغرافیایی تطبیقی غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب