یک روش درون یابی فضایی مبتنی بر شبکه به عنوان ابزاری برای پشتیبانی از تحلیل بازار املاک و مستغلات

خلاصه

توزیع فضایی قیمت‌ها ارتباط تنگاتنگی با بازار املاک و مستغلات شهری دارد. قیمت املاک یکی از شاخص های کلیدی فعالیت اقتصادی است زیرا بر تصمیمات اقتصادی تأثیر می گذارد. تصمیم گیرندگان و مصرف کنندگان اغلب به اطلاعاتی در مورد توزیع مکانی قیمت ها نیاز دارند، اما تحلیل های مکانی-زمانی بازار املاک و مستغلات بر اساس قیمت های نقل شده در مکان های مختلف در طول سال ها (دوران) است. به دلیل این ویژگی خاص، مجموعه داده‌های حاصل پراکنده هستند (در طول سال‌ها متفاوت هستند) و مقایسه آنها دشوار است. به همین دلیل، روش های درون یابی موجود همیشه در تحلیل های بازار املاک موثر نیستند. بنابراین، یک رویکرد متفاوت برای درون یابی قیمت املاک و مستغلات که از تولید سطوح درون یابی پیوسته پشتیبانی می کند و در عین حال مقادیر نقاط اندازه گیری را حفظ می کند، مورد نیاز است. این مقاله روشی را برای جایگزینی داده‌های مکانی پراکنده با یک ساختار GRID منظم پیشنهاد می‌کند. ساختار GRID شی اندازه گیری شده را با یک شبکه منظم از گره ها پوشش می دهد که از درون یابی یکنواخت در هر نقطه از فضای تحلیل شده و مقایسه مدل های درونیابی در دوره های متوالی (سال) پشتیبانی می کند. روش پیشنهادی بر روی یک شی انتخاب شده آزمایش شد. نتایج نشان می‌دهد که ساختار GRID می‌تواند در تحلیل‌های بازارهای املاک و مستغلات بسیار پیچیده که در آن داده‌های ورودی ناقص، نامنظم و پراکنده هستند، استفاده شود. ساختار GRID شی اندازه گیری شده را با یک شبکه منظم از گره ها پوشش می دهد که از درون یابی یکنواخت در هر نقطه از فضای تحلیل شده و مقایسه مدل های درونیابی در دوره های متوالی (سال) پشتیبانی می کند. روش پیشنهادی بر روی یک شی انتخاب شده آزمایش شد. نتایج نشان می‌دهد که ساختار GRID می‌تواند در تحلیل‌های بازارهای املاک و مستغلات بسیار پیچیده که در آن داده‌های ورودی ناقص، نامنظم و پراکنده هستند، استفاده شود. ساختار GRID شی اندازه گیری شده را با یک شبکه منظم از گره ها پوشش می دهد که از درون یابی یکنواخت در هر نقطه از فضای تحلیل شده و مقایسه مدل های درونیابی در دوره های متوالی (سال) پشتیبانی می کند. روش پیشنهادی بر روی یک شی انتخاب شده آزمایش شد. نتایج نشان می‌دهد که ساختار GRID می‌تواند در تحلیل‌های بازارهای املاک و مستغلات بسیار پیچیده که در آن داده‌های ورودی ناقص، نامنظم و پراکنده هستند، استفاده شود.

کلید واژه ها:

توزیع فضایی ; ساختار GRID ; مسکن ; قیمت ملک ؛ بازار املاک و مستغلات

1. معرفی

بازار املاک مسکونی به عنوان “مناطق جغرافیایی که در آن قیمت هر واحد مقدار مسکن (تعریف شده با استفاده از برخی از شاخص های ویژگی های مسکن) ثابت است” [ 1 ] تعریف می شود. توزیع فضایی قیمت ها ارتباط تنگاتنگی با بازار املاک و مستغلات دارد. قیمت املاک یکی از شاخص های کلیدی فعالیت اقتصادی است زیرا بر تصمیمات اقتصادی تأثیر می گذارد و داده های آماری حیاتی را تشکیل می دهد. تصمیم گیرندگان و مصرف کنندگان اغلب به اطلاعاتی در مورد توزیع فضایی قیمت ها نیاز دارند. معاملات املاک را می توان با نقاط (به زبان ساده) نشان داد، و آنها بسیار متمایز هستند، که به طور قابل توجهی تجزیه و تحلیل تغییرات در بازارهای محلی در طول زمان را مختل می کند [ 2 ]]. روش رگرسیون لذت‌گرا و روش فروش تکراری بیشتر در تحلیل‌های بازار املاک و مستغلات استفاده می‌شوند [ 3 ، 4 ، 5 ، 6 ، 7 ، 8 ، 9 ، 10 ، 11 ]. ظهور ابزارهای سیستم اطلاعات جغرافیایی (GIS) به توسعه مدل‌های سطحی با استفاده از روش‌های درون‌یابی فضایی (روش‌های زمین آماری) کمک کرد [ 12 ، 13 ، 14 ، 15 ، 16 ، 17 ]. به گفته چو [ 18]، درون یابی فضایی بر دو فرض اساسی متکی است: سطح متغیر قیمت پیوسته است (بنابراین، مقدار را می توان در هر مکانی تخمین زد)، و متغیر قیمت از نظر مکانی وابسته است (مقدار در یک مکان خاص به مقادیر مربوط می شود. در مکان های اطراف). وجود همبستگی های فضایی بین قیمت های ناشی از اثرات همسایگی توسط بسیاری از نویسندگان مشاهده شده است [ 3 ، 19 ، 20 ، 21 ، 22 ]، و از تحلیل قیمت ها با استفاده از روش های درون یابی مختلف پشتیبانی می کند.

سیستم های اطلاعات مکانی (SIS) برای توصیف، تحلیل، توضیح، تفسیر و پیش بینی پدیده های مختلف در فضای فیزیکی استفاده می شود. روش‌های تجسم داده‌های مکانی نیز از تجزیه و تحلیل مقادیری پشتیبانی می‌کنند که می‌توانند در یک سیستم مرجع مکانی محلی شوند [ 23 ، 24 ]. پایگاه های داده برای به دست آوردن اطلاعات از دوره های مختلف اندازه گیری معرفی می شوند که از تجزیه و تحلیل تغییرات داده ها در طول زمان پشتیبانی می کند. یک سیستم اطلاعات مکانی با در نظر گرفتن بعد زمانی به یک سیستم اطلاعات مکانی پویا (DSIS) تبدیل می شود. DSIS می تواند برای تجزیه و تحلیل داده های فیزیکی یا اقتصادی در یک دوره زمانی معین استفاده شود تا دید جامعی از پدیده های بررسی شده ارائه کند [ 25 , 26]. قابلیت‌های پردازشی سیستم‌های فناوری اطلاعات باید افزایش یابد تا با افزایش مداوم حجم داده‌هایی که در دوره‌های متوالی انباشته می‌شوند، سازگار شود. جستجوی مداوم برای روش‌های جدید تجزیه و تحلیل و تفسیر داده‌ها وجود دارد که می‌توانند در یک سیستم اطلاعات زمین (LIS) یا یک سیستم اطلاعات جغرافیایی (GIS) بومی‌سازی شوند. راه حل های دیجیتال از حوزه های مختلف پردازش داده ها برای توسعه روش های جدید در داده کاوی مکانی (SDM) ترکیب می شوند [ 27 ، 28 ، 29 ].

هدف از این مطالعه ارزیابی کاربرد یک ساختار GRID برای درونیابی سطحی در تحلیل پویایی تغییرات در بازار املاک و مستغلات بود. در این رویکرد، ساختار GRID شبکه منظمی از مربع‌ها را تشکیل می‌دهد که مقادیر آن در گره‌ها (توزیع شده در گوشه‌های مربع‌هایی که اندازه ضلع پایه می‌تواند آزادانه تنظیم شود) توسط الگوریتم‌های درون‌یابی بر اساس نقاط اندازه‌گیری (قیمت مستغلات) تعیین می‌شود. در مجاورت هر گره استفاده از ساختار GRID در تحلیل‌های مکانی-زمانی با ویژگی‌های مشخصه بازار املاک توجیه می‌شود. در ادبیات مرجع، یک تحلیل مکانی-زمانی از بازار املاک و مستغلات بر قیمت‌های به دست آمده در مکان‌های مختلف در سال‌های متوالی (دوران اندازه‌گیری) تکیه دارد. با توجه به این ویژگی خاص، مجموعه داده‌های حاصل پراکنده هستند (در طول سال‌ها متفاوت هستند) و مقایسه آنها دشوار است. موارد فوق به ویژه در مورد درونیابی فواصل طبقاتی و مقایسه آنها در مقیاس مشترک بر اساس یک شبکه نامنظم مثلثی (TIN) که در آن گره های متوالی شبکه مثلثی نشان دهنده قیمت های به دست آمده مستقیماً از بازار املاک و مستغلات است، صدق می کند. استفاده از اندازه‌گیری‌های مستقیم (قیمت‌ها) اغلب مدل‌سازی منطقه مورد تجزیه و تحلیل را با یک شبکه مثلثی یکنواخت غیرممکن می‌کند. مثلث ها دارای ضلع هایی با طول های متفاوت هستند که باعث ایجاد اختلال در درون یابی خطوط ایزوله می شود که فواصل طبقاتی را با دقت یکسان در کل منطقه تشکیل می دهند (شکل 4b,c). در نتیجه، تفاوت‌های بین دوره‌ها را نمی‌توان به‌طور دقیق در مناطقی با چگالی کم داده‌های اندازه‌گیری شده تعیین کرد. از سوی دیگر، تراکم بالای داده، مانع از تجزیه و تحلیل قیمت های شدید می شود. به همین دلیل، TIN همیشه به طور مستقیم برای تحلیل های فضایی توصیه نمی شود. مقایسه مناطقی که داده‌ها در دوره‌های زمانی مختلف (در دوره‌های مختلف) به دست آمده‌اند، به ویژه دشوار است. در نقاط اندازه گیری انتخاب شده، داده ها برای همه دوره ها در دسترس نیستند. بنابراین، مکان های انتخاب شده را نمی توان به طور دقیق مقایسه کرد.

این محدودیت ها نیاز به روش های مختلف درون یابی قیمت را در بازار املاک و مستغلات ایجاد می کند. این مطالعه راه حل های نوآورانه ای را برای تجزیه و تحلیل بازار املاک و مستغلات پیشنهاد می کند و روش های ارائه شده کیفیت تحلیل را بهبود می بخشد. این مقاله روشی را برای جایگزینی داده‌های مکانی پراکنده با یک ساختار GRID معمولی مورد بحث قرار می‌دهد. راه حل های مبتنی بر ساختار GRID پشتیبانی می کنند:

–: کاهش اطلاعات اضافی،
–: کاهش یا حذف اطلاعات اضافی،
–: کاهش حجم مجموعه داده های ذخیره شده در پایگاه های داده،
–: جبران خطاهای اندازه گیری،
–: کاهش تعداد نقاط توصیف کننده یک سطح،
–: تنظیم یکپارچه وضوح شبکه و انطباق وضوح شبکه با مورفولوژی سطح مورد تجزیه و تحلیل،
–: افزایش وضوح گره در سطح مورد بررسی برای دقت بیشتر،
–: انجام تحلیل ها در دوره های اندازه گیری متوالی در مکان های مختلف با تراکم نقاط اندازه گیری متفاوت،
–: عملکرد تحلیل های مقایسه ای در همان نقاط گره که به صورت ریاضی تعیین می شوند،
–: تسریع در مدل سازی و تجسم داده ها،
–: بهینه سازی الگوریتم ها برای پردازش سریعتر داده های دیجیتال،
–: ساده سازی مدل سازی و تحلیل داده های جهت دار (مرتبط با نمایه)،
–: وضوح و شفافیت بیشتر سازمان فضایی داده ها،
–: ترتیب و سازماندهی دقیق ساختار توپولوژیکی داده های ذخیره شده،
–: دسترسی راحت تر به اطلاعات مورد نیاز در فرآیند کاوش داده ها،
–: بایگانی راحت و کارآمد داده ها،
–: بایگانی و مدل سازی داده های چند دوره ای برای یک دوره زمانی خاص،
–: راندمان بالاتر پردازش داده های مکانی در زمان واقعی،
–: کارایی بالاتر سیستم های مدیریت پایگاه داده (DBMS) [ 30 ]،
–: شتاب داده کاوی مکانی (SDM) [ 27 ، 29 ]،
–: تسریع انتقال داده بین سیستم های اطلاعات مکانی (SIS) [ 31 ]،
–: افزایش سرعت دسترسی به داده ها در سرورهای داده مکانی اینترنتی (ISDS) [ 32 ]،
–: ساده سازی ساختار ضبط و خواندن داده ها در مدل های پایگاه داده مکانی (SDB) [ 33 ، 34 ]،
–: تسریع در پردازش درخواست آنلاین فضایی (SOLAP) [ 35 ]،
–: افزایش ظرفیت پردازش داده های پویا SIS (DSIS) [ 26 ].

ویژگی های فوق استفاده جامع از ساختار GRID در مراحل مختلف پردازش داده ها در روش پیشنهادی را توجیه می کند.

موضوع و محدوده فضایی مطالعه و روش تهیه داده های ورودی مورد بحث قرار می گیرد، درون یابی قیمت بر اساس سطوح TIN و GRID مقایسه می شود و شاخص های آماری انتخاب شده در بخش های متوالی مقاله تفسیر می شوند. اصول انتخاب الگوریتم های درون یابی و وضوح ساختار GRID با توجه به موقعیت نقاط اندازه گیری در ناحیه مورد تجزیه و تحلیل در بخش نتایج ارائه شده است. سطوح درون یابی نیز در دوره های اندازه گیری مختلف (سال) مقایسه شدند و مقادیر شاخص های عددی توصیف کننده تغییرات در طول زمان تفسیر شدند.

2. مواد و روشها

2.1. موضوع و محدوده مکانی تحلیل

این مطالعه قیمت آپارتمان های معامله شده در سال های 2005-2014 در شهر اولشتین (لهستان) را در دو شهرک مسکونی مورد تجزیه و تحلیل قرار داد. داده های انباشته شده در 10 دوره اندازه گیری طبقه بندی شدند. میانگین قیمت آپارتمان ها (PLN/m2 ^؛ PLN-Zloty لهستانی) معامله شده در هر دوره داده های ورودی را برای تحلیل های بیشتر تشکیل می دهد. میانگین قیمت به مکان مورد بررسی (ساختمان) در سیستم مرجع اتخاذ شده (WGS 84 Web Mercator) اختصاص داده شد.

مجموعه داده تحلیل شده از نظر عوامل زیر بسیار همگن بود:

–: منابع مسکن مورد بررسی مشابه بودند (فناوری ساخت و ساز یکسان و سال ساخت، راه حل های بازسازی و عایق مشابه، که منجر به سایش فنی و عملکردی مشابهی شد)
–: منابع مورد بررسی توسط همان مدیر مدیریت می شد،
–: املاک تجزیه و تحلیل شده ساختار فشرده ای داشتند،
–: تقاضای بازار ثابت بود،
–: املاک تجزیه و تحلیل شده 16 درصد از منابع مسکن در اولشتین را تشکیل می دهند.
–: تغییرات قیمت آپارتمان در طول زمان مشابه روندهای مشاهده شده در اولشتین و در سراسر لهستان بود.
–: ملک ارزیابی شده به آپارتمان هایی با مساحت متوسط 40 تا 60 متر مربع ^محدود شد.

تجزیه و تحلیل مجموعه داده‌های مربوط به سال‌های 2005 تا 2014 نشان داد که بازار ملک محلی در سال‌های 2005-2007 به طور پویا توسعه یافت و قیمت‌ها به سرعت افزایش یافت و در سال 2007 به اوج خود رسید. رشد بازار در سال‌های متوالی متوقف شد و کاهش مداوم قیمت‌ها در سال 2011 عمیق‌تر شد 2012.

منطقه ارزیابی شده با جزئیات بر اساس سطوح درون یابی تولید شده با استفاده از ساختار GRID تجزیه و تحلیل شد.

2.2. آماده سازی داده های ورودی

برای توسعه یک پایگاه داده تک سطحی، هر رکورد داده در سه فیلد داده نوشته شد. آدرس ساختمان حاوی آپارتمان مورد تجزیه و تحلیل با دو مختصات جغرافیایی نشان داده شد (به عنوان مثال، 53.737152N، 20.489984E). مختصات یک نقطه اندازه گیری در مرکز هندسی ساختمانی که آپارتمان معامله شده در آن قرار داشت تعیین شد. قیمت (P) آپارتمان معامله شده سومین فیلد داده بود. اگر چند آپارتمان در یک ساختمان معامله می شد، از میانگین حسابی قیمت آنها در تحلیل استفاده می شد. مختصات جغرافیایی یک نقطه اندازه گیری (متفاوت در رقم سوم اعشار) به 1,000,000:1 تغییر مقیاس داده شد تا داده های مکانی در یک سیستم همگن تجسم شود. قیمت هر واحد که در قسمت سوم داده وارد شده بود، تغییری نکرده است. داده‌ها برای تجزیه و تحلیل‌های بیشتر به یک پایگاه داده تک سطحی با رکوردهای یکسان شامل فیلدهای N، E و P کاهش یافت. یک مستطیل با مختصات N: 53.735900-53.746248 و E: 20.489660-20.520569 بر روی همه مجموعه‌های داده با اندازه یکسان ترسیم شد تا در تمام مناطق داده با اندازه یکسان تولید شود. دوره ها در مجموعه داده‌های حاصل، تعداد و مکان داده‌ها در سال‌های مورد تجزیه و تحلیل متفاوت بود (سال-تعداد داده‌ها: 2005-80؛ 2006-108؛ 2007-83؛ 2008-115؛ 2009-111؛ 2010-135؛ 2011-127. ؛ 89-2012؛ 96-2013؛ 97-2014). 80–2005; 2006–108; 2007–83; 2008–115; 2009–111; 2010–135; 2011–127; 2012–89; 2013–96; 2014–97). 80–2005; 2006–108; 2007–83; 2008–115; 2009–111; 2010–135; 2011–127; 2012–89; 2013–96; 2014–97).

2.3. مواد و روش ها

2.3.1. درون یابی قیمت در مدل سطح TIN

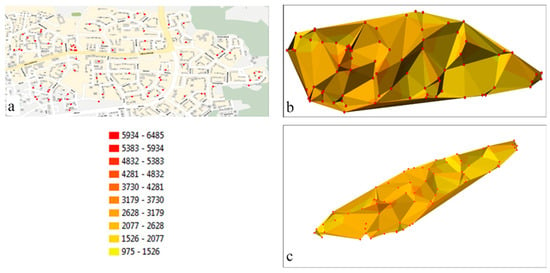
در مثال ارائه شده، داده های قیمت برای سال 2005 مجموعه ای از نقاط پراکنده را ایجاد می کند که با چگالی متفاوت در بخش های مختلف منطقه مورد تجزیه و تحلیل مشخص می شود ( شکل 1 a). الگوی مشابهی در دوره‌های باقی‌مانده مشاهده می‌شود، جایی که مکان‌های نقاط اندازه‌گیری در سال‌های متوالی همپوشانی ندارند.

حداقل و حداکثر مقادیر داده‌ها برای کل دوره تجزیه و تحلیل (2014-2005) در حداقل = 975 PLN / m2 ^و حداکثر = PLN 6485 / m2 تنظیم ^شد تا تمام قیمت‌های ملک را در یک سیستم فضایی همگن نشان دهد. مقادیر به دست آمده سپس به 10 بازه کلاس تقسیم شدند. قیمت‌های ملک درون‌یابی شده با سطح TIN مدل‌سازی شدند که در آن گره‌های متوالی قیمت‌های مستقیم بازار را نشان می‌دادند ( شکل 1)قبل از میلاد مسیح). مقادیر تجزیه و تحلیل شده در سال های متوالی در مکان های مختلف نمونه برداری شدند و مجموعه های پراکنده ای را تشکیل دادند که مقایسه آنها دشوار بود. در نتیجه، تفاوت‌های بین دوره‌ها را نمی‌توان در مناطقی که با چگالی داده‌های کم مشخص می‌شود، به‌دقت تعیین کرد. از سوی دیگر، تراکم بالای داده ها، مانع از تجزیه و تحلیل قیمت های شدید شد. استفاده از اندازه‌گیری‌های مستقیم (قیمت‌ها) اغلب مدل‌سازی منطقه مورد تجزیه و تحلیل را با یک شبکه مثلثی یکنواخت غیرممکن می‌کند. مثلث ها دارای ضلع هایی با طول های مختلف هستند که باعث ایجاد اختلال در درون یابی خطوط ایزوله می شود که فواصل طبقاتی را با دقت یکسان در کل منطقه تشکیل می دهند ( شکل 1).قبل از میلاد مسیح). به همین دلیل، TIN همیشه به طور مستقیم برای تحلیل های فضایی توصیه نمی شود. در برخی از نقاط اندازه گیری، داده ها برای همه دوره ها در دسترس نیستند. بنابراین، مکان های انتخاب شده را نمی توان به طور دقیق مقایسه کرد.

2.3.2. درون یابی قیمت در یک مدل سطح GRID

یک شبکه منظم از گره‌ها که ساختاری از نوع GRID را تشکیل می‌دهند می‌توانند برای تضمین اینکه نقاط با مقادیر انتخاب‌شده به طور یکنواخت در سراسر منطقه مورد تجزیه و تحلیل توزیع شده‌اند استفاده شود [ 36 ، 37 ، 38 ]. شبکه را می توان بر اساس اشکال منظم توسعه داد، اما اغلب از یک شبکه منظم مربع با اضلاع یکسان استفاده می شود. مکان افقی گره های شبکه توسط یک جفت مختصات XY (در این مورد: NE) تعریف می شود که می توانند در یک مکان برای هر دوره نگاشت شوند. مختصات سوم با استفاده از نقاط اندازه گیری (در این مورد: قیمت آپارتمان) واقع در نزدیکی هر گره شبکه مربع تعیین می شود. مقدار در هر گره با درون یابی با یک الگوریتم انتخاب شده تعیین می شود.

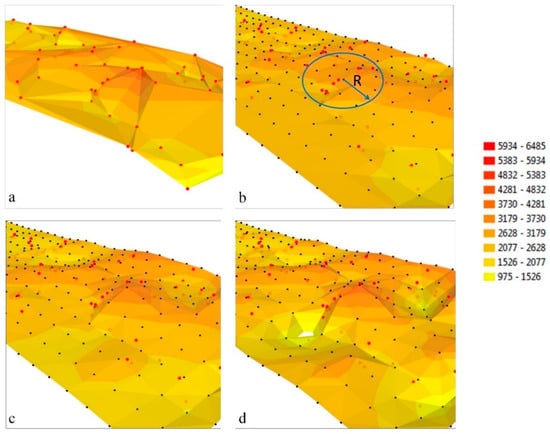
همان قطعه فضا که با سطوح متفاوت تولید شده نشان داده شده است در شکل 2 نشان داده شده است . سطح تولید شده با اندازه گیری های مستقیم یک ساختار TIN است و بر اساس یک شبکه نامنظم مثلثی شکل است ( شکل 2 a). با نقاط اندازه گیری توزیع نامنظم مشخص می شود که مسئول شکل نامنظم سطح تولید شده هستند. در ساختارهای GRID ( شکل 2 b–d)، گره‌هایی که مدل سطح را ایجاد می‌کنند در گوشه‌های مربع‌هایی که به طور منظم توزیع شده‌اند، یافت می‌شوند، و مکان آنها در صفحه XY با یک فاصله فاصله ثابت در هر دو جهت محور کنترل می‌شود. بازه، وضوح یک ساختار GRID را تعیین می کند که می تواند آزادانه تنظیم شود. برخلاف ساختار TIN ( شکل 2a)، یک ساختار GRID ( شکل 2 b-d) شی مورد تجزیه و تحلیل را با یک شبکه گره منظم مدل می کند، که از درون یابی یکنواخت در هر نقطه از سطح تجزیه و تحلیل شده پشتیبانی می کند.

2.3.3. شاخص های آماری

سطوح درون یابی را می توان از تعداد نقاط یکسانی در هر دوره تولید کرد، زمانی که داده های اندازه گیری توزیع نامنظم با یک شبکه منظم از گره ها در یک ساختار GRID جایگزین می شوند. یک مجموعه داده ناهمگن از هر دوره می تواند به یک مجموعه داده همگن (با تعداد مساوی از ویژگی ها) برای تعداد یکسانی از گره ها با وضوح یکسان تبدیل شود. تعداد یکسانی از داده ها در هر سال از مقایسه دوره های متوالی با استفاده از شاخص های آماری پشتیبانی می کند. دوره های انتخاب شده را می توان با مقدار متوسط برای یک دوره معین یا یک مقدار متوسط محاسبه شده برای یک دوره خاص مقایسه کرد. مقادیر تعیین شده در هر گره را می توان در محاسبات آماری استفاده کرد. تجزیه و تحلیل های آماری را می توان با استفاده از شاخص های انتخابی انجام داد [ 39 ،40 ، 41 ]. ویژگی‌های آماری می‌توانند شامل تفاوت در مقادیر تخصیص داده‌شده به هر گره در ساختار GRID (مستقل برای هر دوره) و میانگین حسابی کلی که در آن وزن‌ها به تعداد اندازه‌گیری‌ها در هر دوره تخصیص داده شده است (معادله (1)). این رویکرد می تواند برای مقایسه دقت سطوح درون یابی تولید شده بر اساس گره های GRID با داده های اندازه گیری واقعی استفاده شود.

ایکس ¯ = \sum ک i = 1 ایکس من n من \sum ک i = 1 n من ،

(1)

جایی که:

k – تعداد دوره ها،
xi – میانگین حسابی معمولی مقادیر در یک دوره معین،
ni – تعداد داده ها (تعداد ویژگی ها برابر است با تعداد اندازه گیری ها) در یک دوره معین.

تفاوت میانگین در مقادیر گره های متوالی را می توان به عنوان میانگین معمولی برای هر دوره در نظر گرفت (معادله (2)).

x = \sum n i = 1 ( w من - ایکس ¯ ) n ،

(2)

جایی که:

n – تعداد داده ها (تعداد ویژگی ها برابر است با تعداد گره ها) در یک دوره،
w _i – مقادیر تخصیص یافته به گره ها در یک دوره معین،
$\bar{x}$ – میانگین حسابی داده‌های همه دوره‌ها (معادله (1)).

دوره های متوالی را می توان با استفاده از شاخص هایی مقایسه کرد که سطوح مقایسه شده را بر اساس یک مقدار واحد برای هر دوره توصیف می کند (معادله (3)). در مثال ارائه شده از انحراف استاندارد (معادله (2)) و RMS (معادله (4)) استفاده شده است. انحراف استاندارد در معادله (3) برای ارزیابی تغییرات یک ویژگی در یک مجموعه محاسبه شد. مقدار یک ویژگی در یک مجموعه با مقدار اختصاص داده شده به گره های مختلف در یک دوره معین توصیف شد و تفاوت بین مقادیر گره و مقدار متوسط معمولی برای هر دوره محاسبه شد. این رویکرد از مقایسه تفاوت‌ها در هر دوره (تغییر در هر مجموعه) با دوره‌های دیگر و با میانگین برای یک دوره معین پشتیبانی می‌کند. در مثال های ارائه شده، هر چه انحراف معیار بیشتر باشد، تغییرات در سطوح درون یابی بیشتر است و در نتیجه، تفاوت در قیمت ملک در یک دوره معین بیشتر است. همچنین می توان انحراف معیار را در دوره های متوالی مقایسه کرد تا میزان انحراف یک دوره معین از میانگین دوره مورد بررسی را تعیین کرد.

s = 1 n - 1 \sum n i = 1 (w من - x) 2 ——————\sqrt ،

(3)

جایی که:

n – تعداد داده ها (تعداد ویژگی ها برابر است با تعداد گره ها) در یک دوره معین،
wi – مقادیر اختصاص داده شده به گره ها در یک دوره معین،
x – میانگین معمولی تفاوت در مقادیر گره (معادله (2)).

خوب تناسب بین سطوح درون یابی و سطح مرجع با RMSE مقایسه شده است. در مثال ارائه شده، سطح مرجع شامل سطوح یک صفحه است که توسط مقادیر میانگین کلی ایجاد شده است (معادله (1)). این مقادیر به هر گره مورد استفاده در محاسبات اختصاص داده شد. هرچه RMSE کمتر باشد، تناسب بین سطوح ارزیابی شده بهتر است. در مثال ارائه شده، هرچه RMSE کمتر باشد، قیمت ملک به میانگین دوره مورد تجزیه و تحلیل نزدیکتر است.

R M اس = 1 n \sum n i = 1 (w من - ایکس ¯) 2 —————\sqrt ،

(4)

جایی که:

n – تعداد داده ها (تعداد ویژگی ها برابر است با تعداد گره ها) در یک دوره معین،
w _i – مقادیر تخصیص یافته به گره ها در یک دوره معین،
$\bar{x}$ – میانگین حسابی کلی برای داده های همه دوره ها (معادله ((1)).

3. نتایج

3.1. انتخاب الگوریتم درون یابی

انتخاب یک الگوریتم درون یابی مرحله مهمی در تجزیه و تحلیل استقرار ساختار GRID است. در مثال ارائه شده، سطوح درون یابی برای تحلیل با سه الگوریتم ایجاد شدند: فاصله معکوس تا یک توان، کریجینگ و تابع پایه شعاعی. این رویکرد از مقایسه نتایج درون یابی و انتخاب راه حل بهینه برای تحلیل های بیشتر پشتیبانی می کند.

در طول تولید ساختارهای GRID، مقادیر در گره های درون یابی با استفاده از نقاط اندازه گیری واقع در نزدیکی گره نقشه برداری شده در یک شعاع جستجوی داده شده R محاسبه می شوند ( شکل 2 ب). اندازه شعاع نسبت به وضوح شبکه گره تعیین می شود و یک الگوریتم درون یابی برای کنترل درجه تعمیم سطح توسعه یافته انتخاب می شود [ 42 ، 43 ، 44 ، 45 ، 46 .]. شکل سطح درون یابی تولید شده بر اساس گره های GRID می تواند بسته به الگوریتم اعمال شده و پارامترهای پردازش آن متفاوت باشد. انتخاب الگوریتم درون یابی توسط عوامل زیادی تعیین می شود، به ویژه، توزیع نقاط اندازه گیری، وضوح ساختار تولید شده، تعداد نقاط اندازه گیری جستجو شده در یک شعاع معین، مکان آنها در بخش های اطراف گره و پارامترهای یک الگوریتم درونیابی [ 45 ، 46 ، 47 ، 48 ]. در شکل 2نتایج درون یابی توسط سطوح تولید شده در مدل GRID با فاصله معکوس از الگوریتم های توان (IDP)، کریجینگ (K) و تابع پایه شعاعی (RBF) نشان داده می شود. ریشه میانگین مربعات خطای سطح درون یابی به سطح TIN برای تمام نقاط اندازه گیری (معادله (4)) محاسبه شد تا بهترین الگوریتم درون یابی انتخاب شود. کمترین تناسب رضایت بخش برای سطح تولید شده توسط الگوریتم IDP به دست آمد. مدل‌های سطحی تولید شده با الگوریتم‌های K و RBF تناسب مشابهی را ایجاد کردند و اکسترم‌های محلی در مدل RBF ذکر شدند ( شکل 2 د). دقیق‌ترین مدل‌های GRID توسط الگوریتم K تولید شد و از این الگوریتم برای ایجاد سطوح درون‌یابی در تمام دوره‌ها استفاده شد.

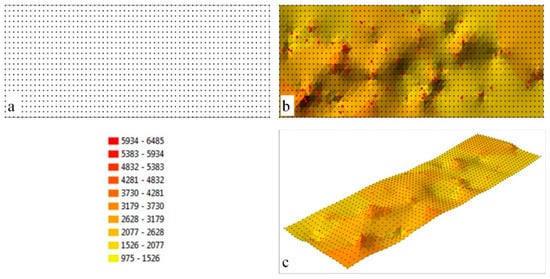
یک مدل سطح تولید شده با ساختار GRID در شکل 3 ارائه شده است . شبکه ای از گره ها با وضوح 0.0005 درجه در منطقه مورد تجزیه و تحلیل در سیستم مختصات اتخاذ شده (WGS 84 Web Mercator) ایجاد شد که از تولید 1386 نقطه مدل پشتیبانی می کند ( شکل 3 a). نقاط اندازه گیری ( شکل 1 الف) برای محاسبه مقدار درونیابی در هر گره با استفاده از الگوریتم K استفاده شد. ساختار GRID حاصل برای تولید سطح درون یابی استفاده شد که در شکل 3 b,c ارائه شده است.

3.2. انتخاب وضوح ساختار GRID

انتخاب پارامترهای ساختاری شبکه مربع ها که مدل تحلیل شده فضای درون یابی را توصیف می کند، مرحله به همان اندازه مهم از تجزیه و تحلیل است. پارامترهای یک ساختار GRID با توجه به وضوح آن انتخاب می شوند که اندازه پایه مربع را در شبکه تعیین می کند و به نوبه خود اندازه میدان پایه را که در آن داده های یک دوره معین را می توان تجزیه و تحلیل کرد، تعیین می کند. مکان گره ها را می توان آزادانه توصیف کرد، که از تنظیم صاف وضوح شبکه با دستورالعمل های دقیق خاص پشتیبانی می کند. دو وضوح از یک ساختار GRID تولید شده بر اساس داده های مشابه ( شکل 1 a) در شکل 4 ارائه شده است.. در حالت اول، ضلع قاعده مربع در 0.0005 درجه تعیین شد که از تولید 1386 گره در شی مورد تجزیه و تحلیل پشتیبانی می کرد. در یک قطعه بزرگ شده از سطح درون یابی، مکان گره های شبکه نسبت به گروه پنج نقطه اندازه گیری استفاده شده در مثال ارائه شده است.

گره های شبکه به دلیل اندازه بزرگ پایه مربع، نقاط اندازه گیری را با هم همپوشانی نمی کنند. مقادیر درون یابی در آن گره ها با مقادیر اندازه گیری شده متفاوت است، که تناسب بدتری بین سطح درون یابی تولید شده و سطح تشکیل شده توسط نقاط اندازه گیری ایجاد می کند. اندازه پایه های مربعی تشکیل دهنده شبکه را می توان با دقت مختصات افقی نقاط اندازه گیری تحلیل شده تعیین کرد. در مثال ارائه شده، خطای تخمین مختصات افقی هر نقطه اندازه‌گیری (مرکز هندسی هر ساختمان) 0.0001 درجه تعیین شد.

افزایش حاصل در وضوح GRID از تولید 32240 گره در شی مورد تجزیه و تحلیل پشتیبانی کرد ( شکل 4 ب). در یک قطعه بزرگ شده از سطح درون یابی، محل گره ها نسبت به همان گروه از پنج نقطه اندازه گیری نشان داده شده است.

وضوح بالاتر از محلی سازی گره ها در نزدیکی نقاط اندازه گیری در حاشیه خطا برای تخمین مختصات افقی هر نقطه اندازه گیری پشتیبانی می کند. وقتی اندازه یک میدان پایه کاهش می‌یابد، داده‌ها را می‌توان با دقت بیشتری تجزیه و تحلیل کرد و تمام خطوطی که فواصل کلاس‌ها را از هم جدا می‌کنند، می‌توانند روان‌تر درون یابی شوند. الگوریتم درونیابی انتخاب شده برای تخصیص مقادیر نزدیک به بازار به گروه‌هایی از گره‌های درون یابی که نزدیک‌ترین نقاط به نقاط اندازه‌گیری هستند، استفاده شد. سطوح ایجاد شده بر اساس گره های شبکه GRID با وضوح 0.0001 درجه می توانند برای تعیین مناطق ارزش دارایی بومی سازی شده در شی مورد تجزیه و تحلیل با دقت داده شده استفاده شوند ( شکل 5).آ). هنگامی که اندازه یک میدان پایه با اندازه اشیاء اندازه‌گیری شده (ساختمان‌ها) تطبیق داده می‌شود، آپارتمان‌های انتخابی می‌توانند در مناطق درون‌یابی ارزش‌های دارایی ( شکل 5 ب) محلی شوند. تأثیر قیمت املاک همسایه بر ارزش شی مورد تجزیه و تحلیل را می توان بررسی کرد.

3.3. تجزیه و تحلیل مدل های عددی

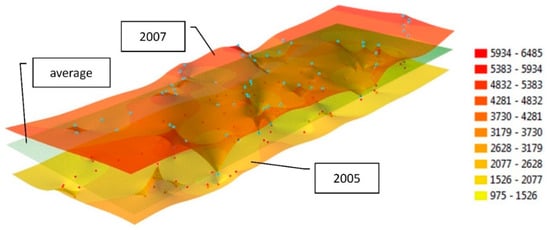
نقاط اندازه گیری با توزیع نامنظم را می توان با یک شبکه گره معمولی جایگزین کرد تا مدل های درون یابی را در طول دوره ها مقایسه کند. سطوح تولید شده را می توان برای مقایسه اندازه گیری های انجام شده در دوره های زمانی مختلف با توزیع و وضوح متفاوت اجسام اندازه گیری شده استفاده کرد. داده های اندازه گیری همچنین می توانند با یک شبکه گره تعریف شده ریاضی جایگزین شوند تا مقادیر تولید شده در دوره های متوالی در هر گره با میانگین قیمت در یک دوره معین، که با یک صفحه افقی نشان داده شده است، مقایسه شود. مکان سه سطح درون یابی (تولید شده بر اساس ساختارهای GRID با وضوح 0.0001 درجه) نسبت به مقدار متوسط برای کل دوره اندازه گیری در شکل 6 ارائه شده است.. میانگین کلی، محاسبه شده با تخصیص وزن به تعداد آپارتمان های معامله شده در سال های متوالی، 3780.80 PLN در متر مربع تعیین ^شد . در مورد اول ( شکل 6 الف)، سطح درون یابی بر اساس داده های سال 2005 ایجاد شد. به استثنای یک مورد، مدل درونیابی در زیر صفحه نشان دهنده میانگین قیمت قرار دارد. دوره ارائه شده (2005) با پایین ترین قیمت املاک و مستغلات مشخص شد.

در مورد دوم ( شکل 6 ب)، یک مدل درون یابی برای مقادیر 2007 ایجاد شد و مختصات افقی گره ها با نمونه اول یکسان بود. در مدل ارائه شده، بیشتر گره های درون یابی بالاتر از میانگین دوره تحلیل شده قرار دارند. این دوره (2007) با بالاترین قیمت املاک و مستغلات مشخص شد. مثال سوم ( شکل 6 ج) یک دوره (2014) را نشان می دهد که در آن قیمت ها به میانگین تقریب می پردازند. در این مورد، مختصات افقی گره ها نیز با موارد ذکر شده در مثال های قبلی یکسان بود.

مدل های سطح تولید شده توسط یک ساختار GRID بر اساس مقادیر شدید از دوره های انتخاب شده می تواند برای تجزیه و تحلیل دامنه نوسانات قیمت ملک در دوره مورد بررسی استفاده شود. در شکل 7 ، مدل های تولید شده برای دوره هایی با مقادیر شدید با یکدیگر و با میانگین دوره مورد تجزیه و تحلیل مقایسه شده اند. با وجود مکان های مختلف نقاط اندازه گیری در هر دوره، می توان آنالیز را در همان گره ها انجام داد ( شکل 7). گره های تولید شده علی رغم تفاوت در چگالی محلی نقاط اندازه گیری به طور یکنواخت توزیع می شوند. افراط محلی، و همچنین مناطقی که با قیمت ملک مشابه مشخص می شوند، می توانند در دوره های مقایسه شده تعیین شوند. گره هایی با مکان های یکسان نیز می توانند برای تعیین تفاوت در مقادیر بین دوره ها و ارائه آنها در یک نمودار دیفرانسیل استفاده شوند. یک نمودار دیفرانسیل تولید شده بر اساس تفاوت قیمت ملک در سال های 2005 و 2007 در شکل 8 ارائه شده است.. نمودار با استفاده از تمام نقاط اندازه گیری در هر دو دوره با شی مورد بررسی تطبیق داده شد. مقادیر محاسبه شده به 10 بازه کلاس مساوی اختصاص داده شد که از شناسایی مناطق قیمتی متفاوت برای مقادیر شدید و متوسط پشتیبانی می کند. تحلیل هایی از این نوع برای تعیین مناطق با بیشترین و کمترین نوسانات قیمت در یک دوره معین و همچنین مناطقی که قیمت ملک در آنها ثابت مانده است انجام می شود.

نمودارهای دیفرانسیل تولید شده برای هر دوره نسبت به میانگین کل دوره تحلیل نیز می‌تواند برای تجسم مناطقی که با قیمت‌های ملک متفاوت مشخص می‌شوند استفاده شود. چنین نمودارهایی زمانی اعمال می شوند که اکستریم های محلی مقادیر شاخص های محاسبه شده را مختل کنند (معادلات (1) – (4)). نمودارها بر اساس تفاوت در مقادیر گره ها و میانگین حسابی قیمت ها برای کل دوره تجزیه و تحلیل تولید می شوند. یک نمودار دیفرانسیل برای سال 2014 در شکل 9 ارائه شده است. فواصل طبقه بندی مقادیر تفاضلی از شناسایی مناطقی پشتیبانی می کند که قیمت ملک در همه دوره ها بالاتر یا کمتر از میانگین است. در مثال ارائه شده، تفاوت ها مثبت (بالاتر از میانگین – با رنگ قرمز مشخص شده) و منفی (زیر میانگین – با سبز مشخص شده) هستند.

3.4. تفسیر شاخص های آماری

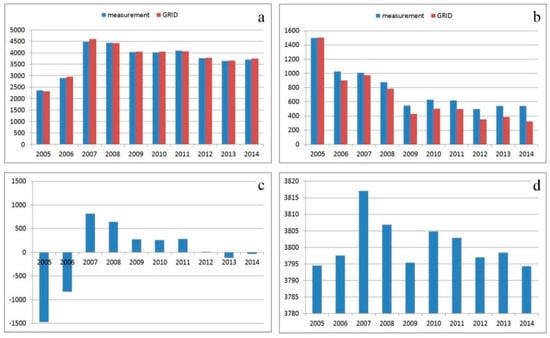
معادلات (1) – (4) برای محاسبه شاخص ها در هر دوره استفاده شد. شاخص های آماری برای دوره های متوالی در شکل 10 ارائه شده است. در شکل 10a،b، شاخص های آماری تعیین شده برای گره های GRID با همان شاخص های محاسبه شده فقط برای نقاط اندازه گیری همراه است. این رویکرد از ارزیابی تناسب بین سطح درون‌یابی GRID و سطح TIN پشتیبانی می‌کند. تغییرات در مقادیر شاخص های محاسبه شده ناشی از تفاوت در تعداد داده ها است. تعداد نقاط اندازه گیری از 80 تا 135 در دوره های مختلف متغیر بود و تعداد گره های درون یابی برای وضوح 0.0001 درجه در 32340 تعیین شد و در طول دوره ها ثابت ماند. درون یابی منجر به تعمیم سطح جزئی می شود. علیرغم تفاوت های جزئی در مقادیر ارائه شده، همبستگی بین دوره های متوالی یکسان است و می توان آنها را با استفاده از ساختار GRID مقایسه کرد.

مقدار متوسط اندازه گیری های محاسبه شده با روش مرسوم و مقدار مطلق میانگین در گره های GRID محاسبه شده با معادله (2) در شکل 10 الف مقایسه شده است. این دو شاخص نشان می‌دهند که میانگین قیمت ملک در سال 2005 کمترین و بالاترین میزان در سال 2007 بوده است. میانگین قیمت در 2009-2011 در 4100 PLN در متر مربع تثبیت شد ^و به سطح پایدار 3700 PLN در متر مربع کاهش ^یافت . 2012–2014.

مقادیر RMSE در معادله (4) محاسبه شده بر اساس داده های اندازه گیری شده و گره های GRID در شکل 10 ب مقایسه شده است. تناسب با مقادیر متوسط سطح تولید شده برای دوره های متوالی در نمودارها ارائه و مقایسه شده است. اندازه‌گیری‌های انجام‌شده در سال 2005 با کمترین تناسب رضایت‌بخش برای صفحه تولید شده بر اساس مقدار متوسط برای دوره مورد بررسی مشخص شد ( شکل 6 a). اکثر مقادیر در سمت صفحه نشان دهنده مقدار متوسط (زیر میانگین) محلی هستند و به استثنای یک مورد، هیچ یک از مقادیر RMSE حاصل را جبران نمی کند. در سال 2007 ( شکل 6ب)، بیشتر مقادیر نیز تنها در یک طرف هواپیما که نشان دهنده میانگین قیمت (بالاتر از میانگین) است، محلی شده بودند، اما در این مورد، همه مقادیر به میانگین نزدیک‌تر بودند. در سال‌های 2009-2014، قیمت‌های ملک مشابه بودند و با روابط مشابه با میانگین قیمت مشخص می‌شدند (تعداد مشابهی از قیمت‌ها بالاتر و پایین‌تر از میانگین آن دوره). بهترین تناسب بین سطح تولید شده توسط میانگین قیمت و سطح درون یابی در سال 2012 و 2014 مشاهده شد ( شکل 6 ج).

تفاوت میانگین در مقادیر اختصاص داده شده به گره های GRID در شکل 10 c ارائه شده است. تفاوت بین ارزش درونیابی شده در یک دوره معین و مقدار تعیین شده توسط میانگین کل دوره محاسبه شد. نمودارها سال هایی را نشان می دهند که در آن اکثر املاک و مستغلات کمتر از میانگین (مقادیر منفی) و بالاتر از میانگین (ارزش مثبت) ارزش گذاری شده اند. قیمت بیشتر اشیا کمتر از میانگین در سال های 2005-2006 و بالاتر از میانگین در سال های 2007-2011 بود. قیمت املاک در سال های 2012 و 2014 نزدیک به میانگین بود که در شکل 10 ب (کمترین RMSE) نشان داده شده است. انحراف استاندارد مقادیر گره در ساختار GRID، محاسبه شده با معادله (3)، در شکل 10 ارائه شده است.د این نمودار حاوی اطلاعاتی در مورد تفاوت در قیمت املاک (تغییرات صفات در یک مجموعه) در هر دوره و همچنین مقادیری است که بیشتر از میانگین متفاوت است. بیشترین تنوع در یک مجموعه داده در سال 2007 ذکر شد ( شکل 6 a). این دوره با مهمترین نوسانات قیمت مشخص شد. داده های شکل 6 a نشان می دهد که این تغییرات به صورت محلی رخ داده اند. کوچکترین نوسانات در قیمت ملک در سالهای 2005، 2009 و 2014 مشاهده شد. سطوح درون یابی ایجاد شده برای آن دوره ها بیشتر شبیه یک صفحه بود ( شکل 6 a,c). بیشترین انحراف از میانگین قیمت در سال 2007 و کمترین انحراف در سال 2014 مشاهده شد ( شکل 10 د).

4. بحث

با توجه به مزایا و پتانسیل قابل توجه یک ساختار GRID، روش تحلیلی ارائه شده جایگزین مناسبی برای روش های درون یابی ارائه می دهد که در حال حاضر در تحلیل های بازار املاک و مستغلات به کار می روند [ 12 ، 13 ، 14 ، 15 ، 16 ، 17 ، 49 .]. انتخاب مناسب ترین الگوریتم درون یابی و وضوح بهینه GRID از تولید سطوح درون یابی پیوسته با حفظ مقادیر نقاط اندازه گیری پشتیبانی می کند. توزیع یکنواخت گره ها در یک ساختار GRID تداوم مدل را حفظ می کند و قطعات گم شده را در سطح مدل شده تکمیل می کند. ساختار نقاط ایجاد یک مدل سطح باید سازماندهی شود تا سرعت تجزیه و تحلیل و بهبود اثربخشی مدل‌سازی و آرشیو داده‌ها را افزایش دهد. هنگامی که یک ساختار GRID استفاده می شود، وضوح گره های شبکه که مدل سطح را تشکیل می دهند نیز می تواند افزایش یابد. هنگامی که تعداد نقاط (گره ها) افزایش می یابد، سطح را می توان با وضوح بیشتری توصیف کرد و تجزیه و تحلیل را می توان در مناطق بدون نقاط اندازه گیری انجام داد.

یک ساختار GRID با وضوح بالاتر از محلی سازی گره ها در نزدیکی نقاط اندازه گیری در حاشیه خطا برای تخمین مختصات افقی هر نقطه اندازه گیری پشتیبانی می کند. وقتی اندازه یک میدان پایه کاهش می‌یابد، داده‌ها را می‌توان با دقت بیشتری تجزیه و تحلیل کرد و تمام خطوطی که فواصل کلاس‌ها را از هم جدا می‌کنند، می‌توانند روان‌تر درون یابی شوند. الگوریتم درون یابی انتخاب شده برای تخصیص مقادیر نزدیک به بازار به گروه هایی از گره های درون یابی واقع در نزدیک ترین نقاط به نقاط اندازه گیری استفاده شد. در یک ساختار TIN با تعداد کمی از نقاط اندازه‌گیری، مدل‌های سطح تولید شده دارای وضوح و کیفیت پایینی هستند [ 50]. موارد فوق همیشه در ساختار GRID که از تولید شبکه‌هایی پشتیبانی می‌کند که در آن وضوح گره‌ها به تنهایی از چگالی نقاط اندازه‌گیری بیشتر است، صادق نیست. وضوح را می توان از طریق استفاده از مربع های پایه با اندازه مورد نیاز و با انجام فرآیند درون یابی بر اساس نقاط اندازه گیری یا گره هایی که قبلاً در یک منطقه خاص ایجاد شده اند، بهبود بخشید. تراکم گره بالاتر از توضیحات دقیق تر مدل در مکان های انتخاب شده و تجزیه و تحلیل دقیق تر در هر نقطه پشتیبانی می کند.

تغییرات در مدل در طول زمان نیز زمانی قابل ارزیابی است که مکان گره های GRID کاملاً ریاضی تعیین شود. هنگامی که از این ساختار استفاده می شود، می توان تحلیل های مقایسه ای را در نقاط مشابه در فضا در دوره های اندازه گیری (سال) مختلف انجام داد. راه حل فوق را می توان برای پیش بینی رفتار فضای مدل سازی شده در طول زمان به کار برد.

روش پیشنهادی همچنین از محلی‌سازی و جبران مادون‌های اندازه‌گیری پشتیبانی می‌کند. در مدل توسعه‌یافته با ساختار GRID، الگوریتم‌های درون‌یابی جبران مقادیر شدید را در سطح معینی از دقت تسهیل می‌کنند. مدل به دست آمده، شکل فضا را به روشی تقریب می زند که تحلیل شکل را تسهیل می کند. موارد فوق بی‌نظمی‌های مدل TIN [ 51 ، 52 ، 53 ، 54 ، 55 ] را جبران می‌کند، در حالی که شکل سطح مورد بررسی را حفظ می‌کند، که تحلیل‌های مربوطه را تسهیل می‌کند. بنابراین یک ساختار GRID می تواند برای تجزیه و تحلیل داده های بسیار پیچیده در بازارهای املاک و مستغلات استفاده شود که با شفافیت کم و در دسترس بودن کم داده های قابل اعتماد مشخص می شود.

مهمتر از همه، توصیف ساختاری دقیق یک مدل سطح به طور قابل توجهی سرعت پردازش و مدل‌سازی داده‌ها را افزایش می‌دهد. موارد فوق تجزیه و تحلیل پایگاه داده و جستجوی اطلاعات مورد نظر را تسریع می بخشد.

رویکرد جهانی برای پردازش ساختارهای GRID در روش پیشنهادی، تجزیه و تحلیل اندازه‌گیری‌های مختلف و فرمول‌بندی مفروضات عملکردی در زمینه‌های مختلف تحقیق را تسهیل می‌کند. مقادیر قابل توجهی از داده ها که ویژگی های اشیاء ارزیابی شده را توصیف می کنند به روشی مشابه (موقعیت شی و ویژگی های شی) ثبت می شوند. بنابراین، روش توسعه یافته را می توان در تجزیه و تحلیل جامع موارد مشابه به کار برد.

عدم وجود داده های مداوم در مورد قیمت املاک و مستغلات در یک مکان معین، مشکل مهمی را در تجزیه و تحلیل بازار املاک و مستغلات ایجاد می کند که نقش کلیدی در عملکرد کل صنعت املاک و مستغلات دارد. راه‌حل پیشنهادی دقت تحلیل‌های فضایی و زمانی چند بعدی بازار املاک و مستغلات را بر اساس داده‌های معاملات پراکنده افزایش می‌دهد. همانطور که در این مطالعه نشان داده شد، مدل‌های GRID از تحلیل‌ها و پیش‌بینی‌های تغییرات در طول زمان، مقایسه‌های پیچیده قیمت‌های املاک در دوره‌های مختلف (سال‌ها) و بایگانی مؤثر منابع هم برای گره‌های GRID منفرد و هم برای کل فضای تحلیل‌شده پشتیبانی می‌کنند. داده‌های مربوط به معاملات بازار همچنین می‌توانند به یک شبکه تعریف شده ریاضی از گره‌ها برای تجزیه و تحلیل و پیش‌بینی مقادیر (قیمت‌ها و ارزش‌های مستغلات) در هر نقطه از زمان با دقت مورد نیاز تبدیل شوند. چنین تحلیل‌هایی را می‌توان در میدان‌های پایه با هر اندازه‌ای با تولید ساختارهای GRID با وضوح آزادانه تنظیم‌شده انجام داد. این رویکرد برای بایگانی و تجزیه و تحلیل داده های بازار املاک و مستغلات از پردازش داده های پویا پشتیبانی می کند. ابزار توصیف شده دقت تحلیل های بازار املاک و مستغلات را افزایش می دهد و از پردازش داده های پویا پشتیبانی می کند و می تواند برای فعالان بازار از جمله خریداران، مستاجران و توسعه دهندگان بسیار مفید باشد. عوامل فوق نقش مهمی را در تجزیه و تحلیل معاملات انجام شده در مقیاس بزرگ ایفا می کنند (شهرها، مناطق یا حتی کشورها) که شامل مجموعه گسترده ای از داده های پراکنده در مورد معاملات، قیمت ها و فواصل زمانی طولانی است. صنعت املاک و مستغلات با پویایی، تغییرپذیری و غیرقابل پیش بینی بالا مشخص می شود و مدل های مبتنی بر ساختارهای GRID می توانند به طور قابل توجهی تجزیه و تحلیل و نظارت املاک را تسهیل کنند.

5. نتیجه گیری ها

روش هایی که بر ساختارهای GRID تکیه دارند، ابزار ارزشمندی برای تحلیل بازار املاک و مستغلات شهری هستند. توزیع فضایی ارزش ها منبع اصلی اطلاعات برای فعالان بازار است. روش‌های درون‌یابی موجود با درجه بالایی از تعمیم و در نتیجه دقت محدود مشخص می‌شوند. این مشکل تا حد زیادی از اثربخشی مدل های تولید شده می کاهد. روش درونیابی پیشنهادی، که بر اساس ساختار GRID توسعه یافته است، با دقت و اثربخشی بسیار بالاتر مشخص می‌شود، که از تحلیل‌های دقیق‌تر و متنوع‌تر قیمت ملک در مکان و زمان پشتیبانی می‌کند. یک سطح درون یابی GRID می تواند برای تجزیه و تحلیل تغییرات در هر نقطه از منطقه مورد بررسی و برای انجام مقایسه با سطوح تولید شده در دوره های دیگر استفاده شود.شکل 3 ج)، تغییرات در مقدار را می توان با دقت بیشتری نسبت به زمانی که یک سطح TIN ( شکل 1 ج) برای همان شی مورد استفاده قرار می گیرد، ارزیابی کرد. در ساختارهای TIN، چگالی، تعداد و مکان نقاط اندازه‌گیری در دوره‌ها متفاوت است و نمی‌توان مستقیماً آنها را با هم مقایسه کرد. در ساختارهای GRID، داده ها را می توان مقایسه کرد زیرا اندازه میدان پایه برای همه دوره ها یکسان است. هر دو قطعه (که توسط گره ها نشان داده می شود) از سطوح درون یابی را می توان با وجود تفاوت در تعداد، مکان و چگالی محلی نقاط اندازه گیری مقایسه کرد. مقایسه را می توان برای هر بازه زمانی انجام داد. مقادیر تخصیص داده شده به گره ها در ناحیه تجزیه و تحلیل شده نیز می تواند در لایه های انتخابی داده در SIS گنجانده شود. این رویکرد از مقایسه با مجموعه داده هایی که در سایر لایه های داده SIS ذخیره شده اند پشتیبانی می کند.

راه حل ارائه شده از تولید هر فضایی که تقریباً فضای واقعی را دارد پشتیبانی می کند و می توان از آن برای کنترل دقت مراحل متوالی رویه و انتخاب توالی های پردازش مناسب در طول کل فرآیند استفاده کرد. استفاده از ساختار GRID در مراحل مختلف پردازش سازماندهی داده ها و بکارگیری مکانیسم های کنترلی مشابه را برای مقایسه دقت مراحل متوالی فرآیند تحلیلی تسهیل می کند. در نتیجه، مراحل پردازش، از جمله تجزیه و تحلیل داده های اندازه گیری شده، تولید یک ساختار GRID و استفاده از آن در کاربردهای مختلف عملی، قابل بهینه سازی است. روش پیشنهادی از پردازش داده های بسیار پویا و اتوماسیون قابل توجه در مراحل متوالی فرآیند پشتیبانی می کند. انسجام مراحل پردازش متوالی تضمین می کند که مجموعه کاملی از داده ها به طور جامع در تجزیه و تحلیل های آماری بررسی می شود. دقت مدل های تولید شده کنترل می شود. بنابراین، مؤثرترین راه‌حل‌ها برای مسائل تحلیل‌شده را می‌توان در هر مرحله از فرآیند تدوین کرد.

منابع

گودمن، ای سی؛ تقسیم بندی بازار مسکن تیبودو، TG. جی. هاوس. اقتصاد 1998 ، 7 ، 121-143. [ Google Scholar ] [ CrossRef ]
جونز، سی. لیشمن، سی. واتکینز، سی. تغییر ساختاری در بازار مسکن شهری محلی. محیط زیست طرح. 2003 ، 35 ، 1315-1326. [ Google Scholar ] [ CrossRef ]
Bourassa, SC; کانتونی، ای. Hoesli، M. وابستگی فضایی، بازارهای فرعی مسکن و پیش‌بینی قیمت مسکن. جی. امور مالی املاک و مستغلات. اقتصاد 2007 ، 35 ، 143-160. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کیس، بی. کلاپ، جی. دوبین، آر. رودریگز، ام. مدلسازی الگوهای قیمتی مکانی و زمانی مسکن: مقایسه چهار مدل. جی. امور مالی املاک و مستغلات. اقتصاد 2004 ، 29 ، 167-191. [ Google Scholar ] [ CrossRef ]
چیانگ، YH; پنگ، TC; چانگ، CO اثر غیرخطی فروشگاه های رفاه بر قیمت املاک مسکونی: مطالعه موردی تایپه، تایوان. Habitat Int. 2015 ، 46 ، 82-90. [ Google Scholar ] [ CrossRef ]
دوبین، آر. پیس، ک. Thibodeau, T. تکنیک‌های خودرگرسیون فضایی برای داده‌های املاک و مستغلات. J. املاک و مستغلات روشن. 1999 ، 7 ، 79-95. [ Google Scholar ] [ CrossRef ]
لیشمن، سی. کاستلو، جی. رولی، اس. واتکینز، سی. عملکرد پیش‌بینی مدل‌های چند سطحی بازارهای فرعی مسکن: تحلیل مقایسه‌ای. مطالعه شهری. 2013 ، 50 ، 1201-1220. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
نایگارد، سی. Meen, G. توزیع قیمت املاک مسکونی لندن و نقش قفل فضایی. مطالعه شهری. 2013 ، 50 ، 2535-2552. [ Google Scholar ] [ CrossRef ]
سرعت، RK; بری، آر. گیلی، OW; سیرمنز، سی اف روشی برای پیش‌بینی مکانی-زمانی با کاربرد قیمت املاک و مستغلات. بین المللی J. پیش بینی. 2000 ، 16 ، 229-246. [ Google Scholar ] [ CrossRef ]
توره، آ. فام، وی اچ. Simon, A. تأثیر پیش از پیش تضاد بر سر تنظیمات زیرساخت بر ارزش املاک مسکونی: مورد مناطق حومه پاریس. مطالعه شهری. 2014 ، 52 ، 2404-2424. [ Google Scholar ] [ CrossRef ]
ژو، پی. لیو، ی. چن، ی. زنگ، سی. وانگ، زی. پیش‌بینی توزیع فضایی ساختمان‌های مسکونی بلندمرتبه با استفاده از یک مدل رگرسیون اتولوژیستی مبتنی بر میدان جغرافیایی. جی. هاوس. محیط ساخته شده 2014 ، 30 ، 487-508. [ Google Scholar ] [ CrossRef ]
کونز، ام. Helbich، M. نقشه برداری زمین آماری قیمت املاک: مقایسه تجربی کریجینگ و کوکریجینگ. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 1904-1921. [ Google Scholar ] [ CrossRef ]
لی، ال. Revesz, P. روش های درون یابی برای داده های جغرافیایی مکانی- زمانی. محاسبه کنید. محیط زیست سیستم شهری 2004 ، 28 ، 201-227. [ Google Scholar ] [ CrossRef ]
مک کلاسکی، WJ; ددیس، WG; لامونت، IG؛ Borst، RA استفاده از ملزهای درونیابی سطحی برای پیش‌بینی ارزش املاک مسکونی. سرمایه گذاری J. Prop. مالی 2000 ، 18 ، 162-176. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
مونترو، جی. لاراز، ب. روش های درونیابی برای داده های جغرافیایی: بازارهای مسکن و تاسیسات تجاری. J. Real Estate Res. 2011 ، 33 ، 233-244. [ Google Scholar ]
پاگورتزی، ای. آسیماکوپولوس، وی. هاتزی کریستوس، تی. فرنچ، ن. ارزیابی املاک و مستغلات: مروری بر روش های ارزش گذاری. سرمایه گذاری J. Prop. مالی 2003 ، 21 ، 383-401. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Szczepańska، A.; سنترا، ا. Wasilewicz-Pszczółkowska، M. اثر سر و صدای ترافیک جاده بر قیمت املاک مسکونی – نمونه ای از یک شهر اروپایی. ترانسپ Res. قسمت D 2015 ، 36 ، 167-177. [ Google Scholar ] [ CrossRef ]
چو، YH کاوش در تحلیل فضایی در سیستم های اطلاعات جغرافیایی . OnWord Press: سانتافه، NM، ایالات متحده آمریکا، 1997. [ Google Scholar ]
باسو، س. Thibodeau، TG تجزیه و تحلیل خودهمبستگی فضایی در قیمت مسکن. جی. امور مالی املاک و مستغلات. اقتصاد 1998 ، 17 ، 61-85. [ Google Scholar ] [ CrossRef ]
Osland, L. یک کاربرد اقتصاد سنجی فضایی در رابطه با مدل سازی قیمت خانه لذت بخش. J. Real Estate Res. 2010 ، 32 ، 289-320. [ Google Scholar ]
تو، ی. سان، اچ. Yu, SM خودهمبستگی های فضایی و تقسیم بندی بازار مسکن شهری. جی. امور مالی املاک و مستغلات. اقتصاد 2007 ، 34 ، 385-406. [ Google Scholar ] [ CrossRef ]
دل جودیس، وی. دی پائولا، پی. توریری، اف. Nijkamp، PJ; Shapira، A. انتخاب های سرمایه گذاری املاک و مستغلات و سیستم های پشتیبانی تصمیم. پایداری 2019 ، 11 ، 3110. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
Goodchild، MF سیستم های اطلاعات جغرافیایی و علم: امروز و فردا. ان GIS 2009 ، 15 ، 3-9. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
لانگلی، پی. Goodchild، MF; مگوایر، دی جی; Rhind، DW سیستم های اطلاعات جغرافیایی و Sience ، ویرایش 3. Wiley: Hoboken، NJ، ایالات متحده، 2011. [ Google Scholar ]
آندرینکو، ن. آندرینکو، جی. تحلیل اکتشافی داده های مکانی و زمانی یک رویکرد سیستماتیک ; Springer: برلین، آلمان، 2006. [ Google Scholar ]
یوهانسون، جی. کرسی، ن. مدل‌های فضایی چند رزولوشن Huang، HC Dynamic. محیط زیست Ecol. آمار 2007 ، 14 ، 5-25. [ Google Scholar ] [ CrossRef ]
هستی، تی. طبشیرانی، ر. فریدمن، جی . عناصر یادگیری آماری. داده کاوی، استنتاج و پیش بینی ؛ Springer Publishing Company: نیویورک، نیویورک، ایالات متحده آمریکا، 2009. [ Google Scholar ]
هوانگ، ی. پی، جی. Xiong، H. الگوهای مکانیابی معدن با رویدادهای نادر از مجموعه داده های مکانی. Geoinformatica 2006 ، 10 ، 239-260. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
میلر، اچ. هان، جی. داده کاوی جغرافیایی و کشف دانش: یک مرور کلی. در داده کاوی جغرافیایی و کشف دانش ; Miller, H., Han, J., Eds. CRC Press: Boca Raton، FL، USA، 2009; صص 1-26. [ Google Scholar ]
Soares, T. پایگاه داده قیاسی. توازی پیاده سازی و کاربردها ; ICLP Springer: برلین/هایدلبرگ، آلمان، 2006. [ Google Scholar ]
هریس، آر. اسلایت، پ. Webber, R. Geodemographies, GIS and Neighborhood Targeting ; Wiley: Chichester، UK، 2005. [ Google Scholar ]
دین، جی. Ghemawat، S. MapReduce: پردازش داده های ساده در خوشه های بزرگ. اشتراک. ACM 2008 ، 51 ، 107-113. [ Google Scholar ] [ CrossRef ]
Masser, L. Spatial Data Lnfrastructure: An Introduction ; ESRI Press: Redlands، CA، USA، 2005. [ Google Scholar ]
Fischer, MM Spatial Analysis and GeoComputation ; Springer: برلین، آلمان، 2006. [ Google Scholar ]
Proulx، MJ; Bédard, Y. مشخصه های اساسی فناوری های OLAP فضایی به عنوان معیارهای انتخاب . اطلاعات مکان: سانتا کلارا، کالیفرنیا، ایالات متحده آمریکا، 2008. [ Google Scholar ]
چن، سی اف. Li، YY; Dai, HL کاربرد پچ Coons برای تولید مدل‌های ارتفاعی دیجیتال مبتنی بر شبکه. بین المللی J. Appl. زمین Obs. Geoinf. 2001 ، 13 ، 830-837. [ Google Scholar ] [ CrossRef ]
Gosciewski، D. Ustalenie wielkości siatki bazowej GRID w zależności od ukształtowania terenu. زسز ناوک. پولیتک. Rzesz. غنچه. Inżynieria Środowiska 2012 ، 59 ، 121-133. [ Google Scholar ]
Raaflaub، LD; کالینز، ام جی اثر خطا در مدل‌های ارتفاعی رقومی شبکه‌ای بر تخمین پارامترهای توپوگرافی. محیط زیست مدل. نرم افزار 2006 ، 21 ، 710-732. [ Google Scholar ] [ CrossRef ]
جوویک، جی. Podgórski، J. Statystyka od Podstaw ; PWE: ورشو، لهستان، 2000. [ Google Scholar ]
Paradysz, J. Statystyka ; Wydawnictwo AE: پوزنان، لهستان، 2005. [ Google Scholar ]
Suchecki , B. Ekonometria Przestrzenna ; Wydawnictwo، CH، اد. بک: ورشو، لهستان، 2010. [ Google Scholar ]
Gosciewski، D. تأثیر توزیع نقاط اندازه گیری در اطراف گره بر دقت درونیابی مدل زمین دیجیتال. جی. جئوگر. سیستم 2013 ، 15 ، 513-535. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Tay، LT; ساگار، BSD; Chuah، HT تجزیه و تحلیل شبکه های ژئوفیزیکی به دست آمده از مدل های ارتفاعی دیجیتال چند مقیاسی: یک رویکرد مورفولوژیکی. IEEE Geosci. سنسور از راه دور Lett. 2005 ، 2 ، 399-403. [ Google Scholar ] [ CrossRef ]
وکسلر، SP ادراک عدم قطعیت مدل ارتفاعی دیجیتال توسط کاربران DEM. URISA J. 2003 ، 15 ، 57-64. [ Google Scholar ]
دنگ، XS; تانگ، ZA درون یابی اسپلاین سطح متحرک بر اساس تابع گرین. ریاضی. Geosci. 2011 ، 43 ، 663-680. [ Google Scholar ] [ CrossRef ]
اردوغان، اس. مقایسه روشهای درونیابی برای تولید مدلهای ارتفاعی دیجیتال در مقیاس میدانی. زمین گشت و گذار. روند. Landf. 2009 ، 34 ، 366-376. [ Google Scholar ] [ CrossRef ]
Gosciewski، D. کاهش تغییر شکل های مدل زمین دیجیتال با ادغام الگوریتم های درون یابی. محاسبه کنید. Geosci. 2014 ، 64 ، 61-71. [ Google Scholar ] [ CrossRef ]
لارسون، ای. فورنبرگ، ب. جنبه های نظری و محاسباتی درونیابی چند متغیره با افزایش توابع پایه تخت. محاسبه کنید. ریاضی. Appl. 2005 ، 49 ، 103-130. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
هو، اس. چنگ، کیو. وانگ، ال. Xie, S. توصیف چندفراکتالی قیمت زمین مسکونی شهری در فضا و زمان. Appl. Geogr. 2012 ، 34 ، 161-170. [ Google Scholar ] [ CrossRef ]
وبستر، آر. Oliver, M. Geostatistics for Environmental Scientists Statistics in Practice ; Wiley: Chichester، UK، 2001. [ Google Scholar ]
Calka، B. برآورد ارزش املاک مسکونی بر اساس خوشه بندی و زمین آمار. Geosciences 2019 ، 9 ، 143. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
Cellmer, R. امکانات و محدودیت های روش های زمین آماری در تحلیل های بازار املاک و مستغلات. مدیریت املاک. ارزش گذاری 2014 ، 22 ، 54-62. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Chica-Olmo, J. پیش‌بینی قیمت مکان مسکن با روش فضایی چند متغیره: کوکریجینگ. J. Real Estate Res. 2007 ، 29 ، 91-114. [ Google Scholar ]
ژانگ، ز. لو، ایکس. ژو، ام. آهنگ، ی. لو، ایکس. کوانگ، ب. مورفولوژی فضایی پیچیده قیمت مسکن شهری بر اساس مدل ارتفاعی دیجیتال: مطالعه موردی شهر ووهان، چین. پایداری 2019 ، 11 ، 348. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
ژانگ، ز. تان، اس. تانگ، W. تحلیل فضایی مبتنی بر GIS از قیمت مسکن و تراکم جاده در مجاورت دریاچه‌های شهری در شهر ووهان، چین. چانه. Geogr. علمی 2015 ، 25 ، 775-790. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]

شکل 1. سطح شبکه نامنظم مثلثی (TIN) که مستقیماً بر اساس نقاط اندازه گیری تولید می شود: ( الف ) توزیع نقاط اندازه گیری. ( ب ) سطح TIN به صورت دو بعدی تجسم شده است. ( ج ) سطح TIN به صورت سه بعدی تجسم شده است. منبع: شرح خود

شکل 2. مقایسه سطوح TIN و GRID تولید شده با الگوریتم های درونیابی مختلف: ( الف ) TIN اصلی. ( ب ) فاصله معکوس تا توان: 2; ( ج ) کریجینگ: خطی. ( د ) تابع پایه شعاعی (RBF): Multilog. منبع: شرح خود

شکل 3. سطح GRID تولید شده بر اساس گره های درون یابی: ( الف ) توزیع گره های درون یابی. ( ب ) سطح درون یابی شده به صورت دو بعدی; ( ج ) سطح درون یابی شده به صورت سه بعدی تجسم شده است. منبع: شرح خود

شکل 4. سطوح درون یابی تولید شده با استفاده از شبکه های GRID با وضوح های مختلف: ( الف ) وضوح 0.0005 درجه. ( ب ) وضوح 0.0001 درجه. منبع: شرح خود

شکل 5. محل مناطق ارزش دارایی در شی مورد تجزیه و تحلیل، ایجاد شده بر اساس ساختار GRID با وضوح 0.0001 درجه (مقیاس مشابه با شکل 7). ( الف ) کل شی (2005)؛ ( ب ) اندازه فیلدهای پایه معادل وضوح GRID است. منبع: شرح خود

شکل 6. محل سطوح درون یابی نسبت به میانگین کلی برای دوره مورد تجزیه و تحلیل. ( الف ، ب ) مقایسه مقادیر شدید در دوره مورد تجزیه و تحلیل (a-2005، b-2007). ( ج ) مکان سطوح (مقادیر) که بهترین تناسب با میانگین دارند (2014). منبع: شرح خود

شکل 7. تجزیه و تحلیل دامنه نوسانات میانگین قیمت ملک بین سالهای 2005 (کمترین مقادیر) و 2007 (بالاترین مقادیر). منبع: شرح خود

شکل 8. مکان مناطق قیمتی تفاضلی بین سال های 2005 و 2007 در منطقه مورد تجزیه و تحلیل، تولید شده برای میدان های پایه در یک ساختار GRID با وضوح 0.0001 درجه. منبع: شرح خود

شکل 9. یک نمودار دیفرانسیل برای میانگین قیمت ها در سال 2014، تولید شده بر اساس ساختار GRID با وضوح 0.0001 درجه. منبع: شرح خود

شکل 10. شاخص های آماری محاسبه شده در سال های متوالی بین ارزش درونیابی شده در یک دوره معین و مقدار تعیین شده توسط میانگین برای کل دوره تحلیل شده. ( الف ) مقایسه قدر مطلق میانگین محاسبه شده از داده های اندازه گیری شده و از گره های GRID. ( ب ) مقایسه RMSE از داده های اندازه گیری شده و از گره های GRID. ( ج ) مقایسه میانگین تفاوت بین گره های GRID. ( د ) مقایسه انحراف استاندارد مقادیر در گره های GRID. منبع: شرح خود

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

خلاصه

کلید واژه ها:

1. معرفی