تجسم عدم قطعیت واریانس حمل و نقل در یک میدان برداری مجموعه ای متغیر با زمان

خلاصه

تجزیه و تحلیل عدم قطعیت یک میدان برداری مجموعه ای متغیر با زمان یک موضوع چالش برانگیز در علم زمین است. به دلیل ساختار پیچیده داده، تعیین کمیت و تجزیه و تحلیل عدم قطعیت یک میدان برداری مجموعه ای با زمان متغیر است. اندازه گیری تفاوت بین مسیرها روشی موثر برای محاسبه عدم قطعیت است. با این حال، معیارهای موجود به اندازه کافی دقیق نیستند یا به موارد پرت حساس هستند. بنابراین، یک ابزار جامع برای تجزیه و تحلیل بیشتر عدم قطعیت الگوهای حمل و نقل مورد نیاز است. در این مقاله، ما یک چارچوب جدید برای کمی‌سازی و تحلیل عدم قطعیت یک میدان برداری مجموعه پیشنهاد می‌کنیم. بر اساس روش فاصله ویرایش کلاسیک بر روی روش توالی واقعی (EDR)، یک متریک قوی و دقیق برای اندازه‌گیری عدم قطعیت خط مسیر پیشنهاد شد. با توجه به تداوم فضایی، ما واریانس حمل و نقل همسایگی یک مکان را محاسبه کردیم و همبستگی عدم قطعیت بین هر مکان و همسایگی آن را با استفاده از Moran’s I محلی ارزیابی کردیم. بر اساس اندازه‌گیری‌های عدم قطعیت پیشنهادی، یک سیستم تجزیه و تحلیل بصری به نام UP-Vis (تجسم مسیر عدم قطعیت) برای بررسی تعاملی عدم قطعیت توسعه داده شد. این یک نمای کلی از عدم قطعیت را ارائه می دهد و از کاوش دقیق الگوهای حمل و نقل در یک مکان انتخاب شده پشتیبانی می کند و امکان مقایسه الگوهای حمل و نقل بین یک مکان و همسایگی آن را فراهم می کند. از طریق خوشه‌بندی مسیر، روندهای اصلی خط مسیر گروه در یک مکان استخراج شد. علاوه بر این، یک علامت برای نمایش مستقیم جهت انتقال و درجه واگرایی هر خوشه طراحی شده است. برای تحلیل عدم قطعیت محله، یک نمای مقایسه ای برای مقایسه الگوهای حمل و نقل بین یک مکان و همسایگی آن با جزئیات طراحی شده است. مجموعه داده های مصنوعی و مجموعه داده های شبیه سازی آب و هوا در آزمایش های ما استفاده شد. ارزیابی و مطالعات موردی نشان داد که چارچوب پیشنهادی می‌تواند عدم قطعیت را به طور موثر اندازه‌گیری کند و به کاربران کمک کند تا الگوهای حمل و نقل عدم قطعیت را به طور جامع کشف کنند.

کلید واژه ها:

تجسم عدم قطعیت ; فیلد برداری مجموعه ; مسیر گروه ; الگوی حمل و نقل ؛ ویرایش فاصله بر اساس دنباله واقعی (EDR)

1. معرفی

عدم قطعیت در حوزه های مختلف مرتبط با علم زمین، مانند هواشناسی و دینامیک سیالات محاسباتی اجتناب ناپذیر است. با بهره‌گیری از قدرت محاسباتی در دسترس، تولید داده‌های مجموعه‌ای که حاوی مجموعه‌ای از خروجی‌های تولید شده از مدل‌های شبیه‌سازی کامپیوتری است، رایج شده است [ 1 ]. این امکان تحلیل شهودی عدم قطعیت در شبیه سازی ها را فراهم می کند.

داده های میدان برداری، مانند جریان باد یا داده های جریان اقیانوسی، معمولاً در فضای جغرافیایی جمع آوری یا شبیه سازی می شوند. تعیین کمیت عدم قطعیت در یک میدان برداری گروهی با تغییر زمان، به دلیل ساختارهای داده پیچیده درگیر دشوار است – معمولاً دارای ابعاد متعدد، مراحل زمانی متعدد و اعضای متعدد مجموعه است. درک عدم قطعیت در یک میدان برداری فضایی برای متخصصان حوزه بسیار مهم است تا بتوانند نتیجه‌گیری قابل اعتماد و تصمیم‌گیری آگاهانه بگیرند. تجسم و تجزیه و تحلیل بصری با تبدیل داده ها و اطلاعات به بازنمایی های بصری تعاملی ، نقش مهمی در توصیف و درک چنین عدم قطعیت ایفا می کند [ 2 ، 3 ]]. با استفاده از تکنیک ها و تعاملات پیوند چند نما، متخصصان حوزه می توانند رفتارهای نامطمئن را تحلیل کرده و الگوهای درونی پدیده های فیزیکی را به طور جامع بررسی کنند [ 5 ، 6 ].

در یک میدان برداری گروهی، یک مسیر گروه مجموعه ای از خطوط مسیر است که از یک مکان مکانی-زمانی در اعضای مختلف گروه ردیابی می شوند. هر یک از این خطوط – یعنی هر یک از اعضای خط مسیر هستند – به معنای یک رفتار حرکتی احتمالی از این مکان است. متخصصان دامنه به مناطقی که اشکال اعضای خط مسیر یا مشابه هستند یا دارای تنوع زیادی هستند، علاقه زیادی دارند، به این معنی که رفتار حرکت به ترتیب قابل پیش بینی یا ناپایدار است. برای مثال، دانشمندان باید عدم قطعیت را هنگام پیش‌بینی روند حمل و نقل یک طوفان درک کنند. کلید آشکارسازی این عدم قطعیت، اندازه‌گیری دقیق شباهت بین مسیرهای گروه است.

اندازه‌گیری‌های شباهت خطوط گروه را می‌توان به دو دسته تقسیم کرد: یکی محاسبه تغییر شکل همسایگی لاگرانژی، با استفاده از روش‌هایی مانند تحلیل مؤلفه اصلی (PCA) [ 7 ] و توان لیاپانوف زمان محدود (FTLE) [7]. 8 ]. واریانس میدان برداری مجموعه با تحلیل واگرایی ذرات همسایگی پس از یک زمان محدود اندازه‌گیری می‌شود. از آنجایی که فقط مکان‌های شروع و پایان اعضای خط مسیر در طول بازه زمانی ثبت می‌شوند، دانشمندان حوزه باید به طور مکرر ذرات را هنگام بررسی واریانس‌ها در مقیاس‌های زمانی مختلف ردیابی کنند.

روش دوم، محاسبه فاصله بین هر جفت از اعضای خط مسیر و میانگین گیری آنها به عنوان مقدار عدم قطعیت نهایی است. دقت این روش ها عمدتاً به انتخاب یا تعریف متریک فاصله بستگی دارد. فاصله اقلیدسی [ 9 ]، تاب خوردگی زمانی پویا (DTW)، و طولانی‌ترین دنباله‌های متداول (LCSS) [ 10 ] برای اندازه‌گیری عدم قطعیت در میدان‌های برداری مجموعه اعمال شده‌اند. فاصله اقلیدسی [ 9 ] ساده و کارآمد است و فاصله نقطه‌ای را به همراه دو عضو مسیر مستقیم محاسبه می‌کند. با این حال، لازم است اعضای خط مسیر دارای طول مساوی باشند، که در یک فیلد برداری این حالت کلی نیست. به عنوان یک روش الاستیک تر، تاب خوردگی زمانی دینامیکی (DTW) [ 11 ، 12] می تواند شکل های مشابه دو مسیر با طول های مختلف را به طور موثر مطابقت دهد. با این حال، فاصله DTW و اقلیدسی هر دو به نقاط دورافتاده که به طور اجتناب ناپذیری در شبیه سازی وجود دارد، به دلیل شکست های گاه به گاه در تولید و جمع آوری داده ها حساس هستند. به منظور رفع این مشکل، طولانی‌ترین زیر دنباله‌های متداول (LCSS) [ 10 ] معرفی شد که روش کنونی پیشرفته است. ایده اصلی آن تعیین کمیت شباهت دو نقطه در اعضای مختلف خط مسیر (با 0 و 1) بر اساس آستانه فاصله است که به دنبال آن می توان طولانی ترین فاصله مشترک بین دو عضو خط مسیر را محاسبه کرد. بنابراین، تأثیرات ناشی از عوامل پرت را می توان تا حد زیادی کاهش داد. با این وجود، LCSS به اندازه کافی دقیق نیست، زیرا تغییرات در تعداد مکان‌های بی‌همتا را نادیده می‌گیرد [ 13 ]] و به تنظیم یک آستانه بستگی دارد.

با توجه به کاستی‌های فوق، یک روش اندازه‌گیری جامع با دقت، مقاوم در برابر نقاط پرت و قابلیت مقایسه خطوط با طول‌های مختلف مورد نیاز است. ویرایش فاصله با پنالتی واقعی (ERP) [ 14 ] و ویرایش فاصله بر روی دنباله واقعی (EDR) [ 13 ]] دو روش اندازه گیری پیشرفته هستند که معمولاً برای مقایسه مسیرهای اجسام متحرک مورد استفاده قرار می گیرند. با این حال، ERP به موارد پرت نیز حساس است. مشابه LCSS، EDR شباهت دو نقطه (با 0 و 1) را بر اساس آستانه فاصله بررسی می کند. بنابراین، نسبت به موارد پرت مقاوم است و می تواند دنباله هایی با طول های مختلف را مدیریت کند. علاوه بر این، می‌تواند نقص دقت LCSS را برطرف کند، زیرا به جای ثبت موقعیت‌های منطبق، فاصله ویرایش را محاسبه می‌کند. بر اساس مزایای EDR، ما یک معیار بهبود یافته به نام AEDR (EDR تطبیقی) را برای اندازه‌گیری شباهت بین اعضای خط مسیر، از طریق محاسبه بیشتر فاصله به صورت تطبیقی در هنگام تطبیق دو نقطه، پیشنهاد می‌کنیم. AEDR نه تنها می‌تواند مشکلات فوق را در روش‌های اندازه‌گیری سنتی حل کند، بلکه باعث بهبود دقت و کاهش وابستگی به آستانه می‌شود. در مقایسه با اندازه‌گیری‌های وابسته به محله، مانند LCSS و EDR کلاسیک. در این مقاله، ما عدم قطعیت محلی (LU) هر شبکه را با استفاده از AEDR تعیین می کنیم. علاوه بر این، ما عدم قطعیت همسایگی فضایی (NU) را نیز محاسبه می کنیم [15 ]، زیرا ساختار همبستگی همسایگی یک ویژگی اساسی میدان برداری است. بر این اساس، همبستگی عدم قطعیت (CU) بین یک مکان و همسایگی آن را می توان با استفاده از Moran’s I محلی [ 16 ] ارزیابی کرد.

علاوه بر این، با استفاده از اندازه‌گیری‌های عدم قطعیت پیشنهادی، ما یک سیستم تجزیه و تحلیل بصری تعاملی به نام UP-Vis (تجسم مسیر عدم قطعیت) را بر اساس اصل طراحی نمای کلی به اضافه جزئیات [ 17 ] توسعه دادیم.]. در سطح جهانی، سیستم ما یک نمای کلی عدم قطعیت ارائه می‌کند، که نتیجه عدم قطعیت خاص همه مکان‌ها و یک نمای طبقه‌بندی را ارائه می‌کند که تحلیل مشترک انواع عدم قطعیت را هدایت می‌کند. هنگامی که کاربران مکان مورد علاقه خود را از نمای کلی انتخاب می کنند، الگوی حمل و نقل دقیق خط مسیر گروه را می توان در نمای خط مسیر و نمای طرح ریزی بررسی کرد. به منظور کاهش بهم ریختگی بصری در تجسم یک مسیر گروه، ما یک علامت (به نام shuttlecock) طراحی کردیم تا روندهای اصلی حمل و نقل و درجات واگرایی مربوطه را به طور مشخص نشان دهد. در مورد تجزیه و تحلیل عدم قطعیت محله، نمای مقایسه تفاوت بین یک مکان و همسایگی آن را نشان می دهد.

به طور کلی، در این مقاله، ما یک چارچوب جامع برای کمی‌سازی و تجزیه و تحلیل عدم قطعیت میدان‌های برداری مجموعه‌ای با زمان متغیر پیشنهاد می‌کنیم. مشارکت های اصلی ما در این کار عبارتند از:

یک روش قوی و موثر برای اندازه گیری عدم قطعیت در یک میدان برداری مجموعه. ما یک روش اندازه‌گیری عدم قطعیت بهبود یافته، AEDR، بر اساس EDR را پیشنهاد می‌کنیم. تأیید شد که نسبت به موارد پرت مقاوم و مؤثرتر از روش‌های اندازه‌گیری سنتی و سایر روش‌های اندازه‌گیری جایگزین، از جمله EDR کلاسیک، LCSS، ERP، DTW، و فاصله اقلیدسی است. بر اساس AEDR، ما عدم قطعیت محلی و عدم قطعیت همسایگی و همبستگی بین آنها را برای برآوردن الزامات تحلیل عدم قطعیت محاسبه کردیم.
یک سیستم تجزیه و تحلیل بصری جامع برای کاوش عدم قطعیت در یک میدان برداری مجموعه ای متغیر با زمان. ما چندین نماهای هماهنگ و یک علامت بصری را بر اساس اصل نمای کلی به اضافه جزئیات طراحی و توسعه دادیم. با استفاده از سیستم تجزیه و تحلیل بصری، کاربران می توانند مکان های مورد علاقه را کشف کنند، الگوهای حمل و نقل را با جزئیات بررسی کنند، و تفاوت بین یک مکان و محله آن را مقایسه کنند.

2. کارهای مرتبط

2.1. تحلیل عدم قطعیت در زمینه برداری

برای تحلیل شبیه‌سازی‌های میدان برداری، دانشمندان بیش از پیش به عدم قطعیت در پدیده‌های علمی توجه کرده‌اند که تأثیر بسیار مهمی بر فرآیندهای تصمیم‌گیری در دنیای واقعی دارد. از آنجایی که یک میدان برداری نامشخص معمولاً متغیر با زمان و چند بعدی است، کمی کردن، تجزیه و تحلیل و تجسم عدم قطعیت بسیار دشوار است. به طور کلی، عدم قطعیت را می توان با یک تابع توزیع احتمال مدل کرد. توزیع گاوسی به دلیل سادگی و کارایی آن معمولاً در کارهای اولیه استفاده می شد. با این حال، از آنجایی که عدم قطعیت در میدان برداری پیچیده معمولاً از توزیع گاوسی پیروی نمی کند، Hazarika و همکاران. [ 3 ] و هالیستر و همکاران. [ 18] بر مشخص کردن عدم قطعیت در زمینه های برداری با دقت بیشتری متمرکز شده است. برای این منظور، روش‌های مبتنی بر PCA برای اندازه‌گیری مؤثر عدم قطعیت یک میدان برداری مجموعه پیشنهاد شده‌اند. این نوع روش تغییر شکل خطی یا تغییر شکل را با اندازه‌گیری ویژگی‌های هندسی یا آماری در یک محله لاگرانژی پس از یک دوره زمانی ارزیابی می‌کند. هومل و همکاران [ 7 ] یک چارچوب مبتنی بر PCA برای مقایسه اعضای گروه مختلف میدان‌های جریان نامشخص ساخت. آنها همچنین با ارزیابی واریانس های حمل و نقل فردی و مشترک، یک فضای طبقه بندی را برای تجسم مجموعه تعریف کردند. FTLE [ 8] روش دیگری است که برای تحلیل ساختار توپولوژیکی میدان های برداری نامشخص ارائه شده است. این نیاز به انجام خطی سازی تغییر شکل دارد. تحلیل واریانس زمان محدود (FTVA) [ 19 ] یک متریک مبتنی بر واریانس و FTLE مانند است که برای تجزیه و تحلیل میدان های جریان ناپایدار پیشنهاد شده است. گوو و همکاران [ 20] سه مفهوم جدید شامل FTLE توزیع ها (FTLE-D)، توزیع FTLE (D-FTLE) و LCS نامشخص (U-LCS) را معرفی کرد که استخراج قطعی FTLE و LCS را برای درک بهتر حمل و نقل گسترش می دهد. رفتارها در فیلدهای بردار مجموعه متغیر با زمان با این حال، FTLE می تواند دقت کمتری را در صورت وجود نقشه برداری غیرخطی قوی داشته باشد. علاوه بر این، این رویکردها بر اساس تغییر شکل همسایگی هستند و نمی توانند عدم قطعیت در زمینه های برداری را به طور کامل توصیف کنند.

2.2. شباهت خط مسیر

به منظور آشکار کردن عدم قطعیت یک میدان برداری گروه، یکی از اساسی ترین رویکردها محاسبه شباهت بین اعضای مختلف گروه است. روش های سنتی مورد استفاده برای اندازه گیری شباهت بین منحنی های سری زمانی شامل فاصله اقلیدسی [ 9 ]، فاصله DTW [ 11 ، 21 ] و رویکردهای مبتنی بر LCSS [ 10 ] است. اخیرا لیو و همکاران. [ 22] LCSS مبتنی بر بلوک را پیشنهاد کرد، که شباهت بین اعضای خط مسیر را از طریق اندازه‌گیری تعداد بلوک‌های مشترکی که از آن عبور می‌کنند محاسبه می‌کند. در مقایسه با فاصله اقلیدسی و DTW، LCSS مبتنی بر بلوک نسبت به موارد پرت مقاوم است، اما اندازه بلوک باید از قبل تعیین شود. استخراج ویژگی های مسیرها و محاسبه تفاوت بین ویژگی های مختلف نیز در مقایسه مسیرهای مختلف موثر بوده است [ 23 ]. بر این اساس مکلولین و همکاران. [ 24 ] با استفاده از مجموعه‌ای از ویژگی‌های مبتنی بر منحنی برای محاسبه امضاهای خط و اندازه‌گیری شباهت بین خطوط جریان، ایده جدیدی را معرفی کرد. آنها از تکنیک تمرکز به اضافه زمینه و یک فیلتر ساده برای تجسم بهتر خطوط جریان استفاده کردند. ویتاکر و همکاران [ 25] جعبه‌های کانتور پیشنهادی، که باکس‌پلات‌هایی را برای تجسم و کاوش مجموعه‌های خطوط تولید می‌کنند. علاوه بر این، آنها یک روش ناپارامتریک جدید [ 26 ] برای تجزیه و تحلیل مجموعه‌های منحنی‌های دو بعدی و سه بعدی ارائه کردند که روش مستقیم‌تری برای تحلیل آماری منحنی‌ها است. علاوه بر این، خوشه بندی برای تشخیص روندهای اصلی و نقاط پرت در رفتارهای مجموعه یا ارائه عدم قطعیت بسیار کارآمد است [ 27 ]. فرستل و همکاران [ 28 ] PCA را برای تبدیل مجموعه‌ای از خطوط جریان به یک فضای اقلیدسی کم‌بعد و خوشه‌بندی آن‌ها در روندهای اصلی در این فضا اتخاذ کرد.

2.3. تجسم میدان برداری

تجسم میدان برداری یکی از چالش برانگیزترین موضوعات در تجسم علمی است. روش‌های فعلی مورد استفاده برای تجسم میدان‌های برداری را می‌توان به طور کلی به سه دسته [ 29 ] طبقه‌بندی کرد: روش‌های تجسم مبتنی بر بافت، مبتنی بر ویژگی و هندسه. بوچن و همکاران [ 30 ] تکنیک های تجسم جریان مبتنی بر بافت را برای تجزیه و تحلیل عدم قطعیت یک میدان برداری دو بعدی با استفاده از مجموعه داده های شبیه سازی سیلندر معرفی کرد. به منظور در نظر گرفتن انسجام ویژگی ها همراه با مهرهای زمانی مختلف، مولدر و همکاران. [ 31 ] یک روش پیش‌بینی-تصحیح پیشنهاد کرد که می‌تواند به دقت مناطق ویژگی را در سری‌های زمانی استنتاج کند. سائر و همکاران [ 32] یک ویژگی را در یک فیلد برداری به عنوان مجموعه وکسلی از داده های حجمی تعریف می کند. بنابراین، مشکل ردیابی ویژگی را می توان با ایجاد تناظر بین داده های ذرات و داده های حجمی به یک مسئله ردیابی ذرات تبدیل کرد. خوشه بندی [ 28 ، 33 ، 34 ] یک روش متداول برای استخراج ویژگی های مکانی یا زمانی میدان های برداری است. فرستل و همکاران [ 28 ] از خوشه بندی سلسله مراتبی برای استخراج روندهای اصلی خطوط جریان گروه استفاده کرد. لی و همکاران [ 35 ] یک روش خوشه‌بندی مسیری را پیشنهاد کرد که خوشه‌بندی را بر روی بخش‌هایی از مسیرها، به جای کل مسیرها انجام می‌داد. گلیف های برداری [ 36] را می توان برای توصیف مستقیم ویژگی های هندسی فیلدهای برداری، به دلیل توانایی آنها در نمایش چندین ویژگی به طور همزمان، گسترش داد. هلاواتچ و همکاران [ 37 ] استعاره رادار را برای نشان دادن جهت‌های جریان به‌وسیله زوایا اتخاذ کرد، جایی که اطلاعات مراحل زمانی با شعاع در مختصات کروی کدگذاری می‌شد. یک علامت تابع توزیع جهت گیری فیبر (ODF) [ 38 ] به عنوان یک بیان دقیق برای عدم قطعیت پیشنهاد شده است. جارما و همکاران [ 39 ] یک علامت لوبولار پیشنهاد کرد، که در آن توابع چگالی احتمال بردار به شکل و جهت لوبولار نگاشت می‌شوند.

3. بررسی اجمالی

چارچوب کلی ما شامل چهار بخش است: تولید داده، اندازه‌گیری شباهت، کمی کردن عدم قطعیت، و تجزیه و تحلیل بصری عدم قطعیت، همانطور که در گردش کار این مقاله نشان داده شده است ( شکل 1).). داده های مورد استفاده در آزمایش ها شامل مجموعه داده های ترکیب شده و مجموعه داده های آب و هوای دنیای واقعی است. برای داده‌های بردار مجموعه اولیه، مسیر مجموعه هر نقطه شبکه با ادغام عددی (روش Runge-Kutta) ردیابی می‌شود. یک متریک بهبود یافته، AEDR، برای اندازه گیری شباهت بین دو عضو خط مسیر پیشنهاد شده است. این روش نسبت به روش‌های معمولی مؤثرتر و قوی‌تر است. با توجه به درجه واگرایی مسیرهای گروه مربوطه، AEDR برای تعیین کمیت عدم قطعیت محلی (LU) و عدم قطعیت همسایگی (NU) هر نقطه شبکه استفاده می‌شود. بر این اساس، همبستگی عدم قطعیت (CU) بین مکان و همسایگی آن محاسبه می‌شود تا نتایج معنادارتری به دست آید.

علاوه بر این، به منظور کمک به درک عدم قطعیت، سیستمی را با استفاده از تکنیک‌های تحلیل بصری توسعه دادیم. نماهای مرتبط چندگانه طراحی و ادغام شدند تا نمای کلی از شرایط عدم قطعیت، الگوهای حمل و نقل مسیرهای گروه و اطلاعات دقیق محله را نشان دهند. بر اساس تجزیه و تحلیل مشترک انواع عدم قطعیت، نمای طبقه بندی یک طبقه بندی برای همه مکان ها ارائه می دهد و ویژگی های مختلف آنها را نشان می دهد. علاوه بر این، برای کمک به درک جزئیات LU در یک مکان انتخاب شده، یک نمای مسیر ارائه می کنیم که هر عضو خط مسیر را نشان می دهد، در حالی که نمای طرح ریزی روابط بین آنها را نشان می دهد. با این حال، خطوط پیچیده ممکن است ناظر را از کشف روندهای حمل و نقل جلوگیری کند. برای حل این مشکل، ما روش خوشه‌بندی DBSCAN بر اساس AEDR را برای اعضای مسیر اعمال می‌کنیم و آنها را به چندین روند مهم اختصاص می‌دهیم. سپس، از طریق طراحی بصری گلیف، روند انتقال و درجه واگرایی هر خوشه می تواند بدون درهم ریختگی وجود داشته باشد. علاوه بر این، بر اساس تکنیک مضرب های کوچک، تفاوت بین یک مکان و همسایگی آن در نمای مقایسه نشان داده می شود، که درک کاربر از NU و CU را تسهیل می کند.

4. محاسبه عدم قطعیت برای میدان برداری مجموعه

در این بخش، متریک بهبود یافته، AEDR را برای محاسبه تفاوت بین مسیرها معرفی و ارزیابی می‌کنیم و محاسبه LU، NU و CU را نشان می‌دهیم.

با توجه به یک میدان برداری متغییر با زمان مجموعه، اجازه دهید P یک مسیر مجموعه ای را نشان دهد که از یک نقطه شبکه q در طول یک دوره زمانی ترسیم شده است. این شامل m اعضای مسیر است و می تواند به صورت نوشته شود

P = P_{1}^{n_{1}}, P_{2}^{n_{2}}, \dots, P_{m}^{n_{m}}

. هر عضو خط راه

P_{i}^{n_{i}} = {(x_{1}^{i}, t_{1}), (x_{2}^{i}, t_{2}), \dots, (x_{n_{i}}^{i}, t_{n_{i}})}

دنباله ای است با

n_{i}

نقاط متوالی اینجا،

n_{i}

تعداد گام های زمانی نمونه در عضو خط مسیر است

P_{i}^{n_{i}}

x_{r}^{i} (1 \leq r \leq n_{i})

یک بردار d بعدی است (که d معمولاً 2 یا 3 است).

4.1. EDR تطبیقی و عدم قطعیت محلی

فاصله ویرایش (ED) [ 40 ]، که به طور گسترده در تشخیص گفتار استفاده شده است، با هدف اندازه گیری شباهت بین دو رشته است. برای دو رشته A و B ،

E D (A, B)

حداقل تعداد عملیات ویرایش مورد نیاز برای تبدیل A به B را نشان می دهد که در آن عملیات ویرایش شامل درج، حذف و جایگزینی است. به طور کلی، هر چه فاصله ویرایش بین دو رشته کمتر باشد، شباهت آنها بیشتر است. برای اعمال این ایده در مقایسه مسیرها، ویرایش فاصله بر روی دنباله واقعی (EDR) [ 13 ] بر اساس ED پیشنهاد شده است که می تواند دنباله هایی از مقادیر واقعی را مدیریت کند. تأیید شده است که در هنگام اندازه گیری شباهت بین مسیرهای حرکت جسم متحرک نسبت به LCSS قوی تر و دقیق تر است. بنابراین، مشخص شد که برای مقایسه خطوط مسیر مناسب است.

برای دو عضو خط راه $P_{i}^{n_{i}}$ و $P_{j}^{n_{j}}$ با $n_{i}$ و $n_{j}$ امتیاز، به ترتیب، یک آستانه فاصله $δ$ باید برای تعیین اینکه آیا دو نقطه در اعضای مختلف خط مسیر می توانند مطابقت داشته باشند تنظیم شود. سپس، طبق تعریف در [ 13 ]، فاصله EDR $E (P_{i}^{n_{i}}, P_{j}^{n_{j}})$ بین $P_{i}^{n_{i}}$ و $P_{j}^{n_{j}}$ را می توان توسط

E(پnمنمن،پnjj) =⎧⎩⎨⎪⎪⎪⎪nمن،nj،m i n ( E(پnمن– 1من،پnj– 1j) + fl ag، ای(پnمن– 1من،پnjj) + 1 ، E(پnمنمن،پnj–1j) + 1 ) ،nj= 0 ،nمن= 0 ،o t h e r w i s e _�(����,����)={��,��=0,��,��=0,���(�(����−1,����−1)+����,�(����−1,����)+1,�(����,����−1)+1),��ℎ������,

(1)

جایی که $P_{i}^{n_{i} - 1}$ و $P_{j}^{n_{j} - 1}$ با حذف آخرین نقطه از $P_{i}^{n_{i}}$ و $P_{j}^{n_{j}}$ به ترتیب و $f l a g$ می تواند 0 یا 1 باشد $| x_{n_{i}}^{i} - x_{n_{j}}^{j} | \leq δ$ ، $f l a g = 0$ ، به این معنی که آخرین نقطه در $P_{i}^{n_{i}}$ با آخرین نقطه در مطابقت دارد $P_{j}^{n_{j}}$ ; در غیر این صورت، $f l a g = 1$ . با این حال، درجه تطابق بین دو نقطه زمانی که با EDR مطابقت داده می‌شوند نادیده گرفته می‌شود که می‌تواند منجر به نتایج نادرست شود. علاوه بر این، مقدار آستانه فاصله $δ$ نتیجه را به شدت تحت تاثیر قرار می دهد و بنابراین تنظیم مناسب دشوار است. برای نشان دادن کاستی‌ها، دو خط سیر تک بعدی را مثال می‌زنیم: $Q = [(1, t_{1}), (2, t_{2}), (3, t_{3}), (4, t_{4})]$ و $R = [(1.9, t_{1}), (1.1, t_{2}), (2.1, t_{3}), (4.9, t_{4})]$ . اگر اجازه دهیم $δ = 1$ ، نتیجه محاسبه شده توسط EDR 0 خواهد بود. با این حال، تفاوت های آشکار بین مسیرها را نباید نادیده گرفت. اگر $δ = 0.8$ ، نتیجه 4 خواهد بود. این به این معنی است که یک تغییر کوچک آستانه ممکن است باعث تغییر زیادی در نتیجه شود. بنابراین، روش سنتی EDR برای اندازه‌گیری تفاوت بین مسیرها به اندازه کافی مؤثر یا دقیق نیست. برای حل این مشکلات، مقدار آن را محاسبه می کنیم $f l a g$ به صورت تطبیقی (همانطور که در زیر نشان داده شده است) زمانی که $| x_{n_{i}}^{i} - x_{n_{j}}^{j} | \leq δ$ ، جایی که اندازه گیری بهبود یافته EDR تطبیقی (AEDR) نامیده می شود.

f l a g = ∣∣ ایکس من n من - ایکس j n j ∣∣ δ .

(2)

از این رو،

f l a g

می تواند یک عدد واقعی در محدوده [0،1] باشد. به این ترتیب، فاصله بین دو نقطه منطبق را می توان به عنوان یک مقدار کوچک (کمتر از 1) و فاصله بین دو نقطه ناهمسان را با 1 اندازه گیری کرد. کاهش.

سپس، شباهت بین دو عضو مسیر $P_{i}^{n_{i}}$ و $P_{j}^{n_{j}}$ را می توان توسط

من هستم (_پ n من من ، پ n j j) = E ( پ n من من ، پ n j j ) m a x ( n من ، n j ) .

(3)

بر اساس شباهت بین هر دو عضو مسیر یک نقطه شبکه q ، عدم قطعیت q را می توان با

L U (ق) = 2 متر ( m - 1 ) (\sum i = 1 m - 1 \sum j = i + 1 متر من هستم (_پ n من من ، پ n j j)) ،

(4)

که در آن m تعداد اعضای مسیر در یک مسیر گروه است.

4.2. ارزیابی

4.2.1. قابلیت آشکارسازی ویژگی ها

از آنجایی که عدم قطعیت در داده های مجموعه فاقد حقیقت پایه است، روش های مختلف اندازه گیری عدم قطعیت را با توجه به ویژگی های خود ارزیابی می کنند. با توجه به وظایف تحلیلی مختلف، دیدگاه‌های زیادی برای ارزیابی دقت اندازه‌گیری عدم قطعیت وجود دارد.

در این مقاله با الهام از کار لیو و همکارانش. [ 22 ]، ما کارایی AEDR را از طریق مقایسه توانایی آن در آشکار کردن ویژگی‌های عدم قطعیت با EDR، DTW، ERP و LCSS کلاسیک ارزیابی می‌کنیم. اگر اندازه‌گیری بتواند ویژگی‌های عدم قطعیت ذاتی را به وضوح نشان دهد، می‌توان آن را مؤثرتر در نظر گرفت. ما از مجموعه داده مصنوعی Double-Gyre (DG) [ 41 ] برای انجام آزمایش‌های ارزیابی استفاده کردیم، که یک مجموعه داده مصنوعی رایج در یک میدان برداری دوبعدی است. روی دامنه تعریف شده است $[0, 2] \times [0, 1]$ ، مانند:

v (x ، y, t) = (- 0.1 π گناه (f (x, t) π) cos (y π) 0.1 π cos (f (x, t) π) گناه (y π) د د ایکس f (x, t))

(5)

f (x, t) = a (t) ایکس 2 + b (t) x

(6)

a (t) = 0.25 sin (t \cdot π / 5)

(7)

b (t) = 1 - 0.5 sin (t \cdot π / 5) ،

(8)

که در آن x و y مختصات موقعیت ها در حوزه، t نشان دهنده مراحل زمانی و بردار v از دو جزء سرعت تشکیل شده است. مجموعه داده های DG مصنوعی یک میدان وابسته به زمان را توصیف می کند، جایی که چرخش ها به طور دوره ای در جهت افقی منبسط و منقبض می شوند. از معادلات (7) و (8)، می توان دریافت که دوره t 10 است. در آزمایش ما، داده های اصلی را روی یک شبکه دکارتی 401 × 201 از $t = 0$ به $t = 30$ . سپس داده های گروهی با 20 عضو با افزودن نویز گاوسی تشکیل شد $(N (0, {0.1}^{2}))$ به داده های مصنوعی اصلی

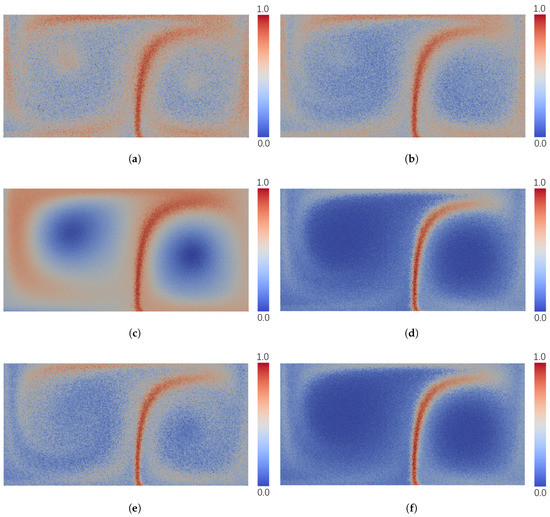
ما عدم قطعیت را برای هر نقطه شبکه داده‌های گروه DG با استفاده از روش‌های اندازه‌گیری بالا محاسبه کردیم.شکل 2نمایش نتایج محاسبه شده را نشان می دهد. برای تسهیل مقایسه، هر نتیجه در محدوده [0،1] نرمال شد. می توان مشاهده کرد که تمام نتایج رندر یک الگوی متمایز با عدم قطعیت بالا را نشان می دهد که می تواند به عنوان جدایی دو چرخ دنده دیده شود. این منطقه از مسیرهای هتروکلینیک تشکیل شده است (شکل 6) که می تواند تحت تأثیر نویز بسیار کمی در جهت معکوس بچرخد. علاوه بر این، سرعت‌های بالایی در مرزهای چرخ‌دنده‌ها وجود دارد که باعث می‌شود ذرات برآمده به سرعت در آنجا واگرا شوند. بنابراین، مرزهای چرخان دارای عدم قطعیت نسبتا بالایی هستند که توسط اکثر اندازه گیری های آزمایشی ارائه شده است. برای نتایج AEDR، EDR کلاسیک، LCSS و فاصله اقلیدسی، این الگو به وضوح قابل تشخیص است، در حالی که الگوی مرزی در نتایج DTW و ERP مشخص نیست.

سرعت کمتر و گردابه بالاتر در مناطق اطراف مراکز چرخ دنده ها در مقایسه با مناطق بیرونی وجود داشت. این بدان معنی است که واریانس مطلق بین اعضای خط مسیری که در اطراف مرکز ردیابی شده اند، در مقایسه با مناطق بیرونی کم است. از سوی دیگر، مسیرهای ترسیم شده از این مناطق در اطراف مراکز چرخش، از منظر محلی، به دلیل گرداب زیاد، بسیار آشفته بود. این نیز باید به عنوان عدم قطعیت بالا در نظر گرفته شود، زیرا واریانس بین اعضای خط مسیر در مقایسه با خودشان به اندازه کافی بالا بود. به طور مشخص، در نتیجه AEDR، مناطق اطراف مراکز چرخش نیز عدم قطعیت نسبتاً بالایی را ارائه کردند. با این حال، سایر روش‌های اندازه‌گیری نتوانستند این ویژگی را دریافت کنند. برای فاصله اقلیدسی، DTW و ERP، این ویژگی نادیده گرفته شد (شکل 2 c,d,f)، زیرا عدم قطعیت محاسبه شده در مرکز چرخش بسیار کم بود و نمی‌توان آن را به‌طور مشخص ارائه کرد. همانطور که برای LCSS و EDR کلاسیک، آنها تفاوت بین نقاط منطبق را در نظر نگرفتند. بنابراین، ویژگی واضح نبود ( شکل 2 b,e). AEDR می تواند این مشکل را حل کند و ویژگی را به وضوح نشان دهد ( شکل 2 a)، زیرا تفاوت بین دو نقطه مطابق را نیز محاسبه می کند.

4.2.2. حساسیت به موارد پرت

مشابه کار لیو و همکاران. [ 22 ]، ما حساسیت به نقاط پرت AEDR و سایر رویکردهای موجود را با انجام دو گروه آزمایش بر روی مجموعه داده های مصنوعی اصلی DG ارزیابی کردیم. ابتدا نویز گاوسی را اضافه کردیم

(N (0, {0.05}^{2}))

به داده های اصلی برای به دست آوردن یک مجموعه داده جدید

{DG}^{'}

(توجه داشته باشید که

{DG}^{'}

داده های مجموعه نیست).

از طریق محاسبه تفاوت بین خطوط مسیر در DG و مسیرهای موجود در ${DG}^{'}$ در همان مکان ها، تفاوت $d^{'}$ برای هر نقطه شبکه می توان به دست آورد. سپس بر اساس ${DG}^{'}$ ، ما 1% از تمام نقاط شبکه را با اضافه کردن نویز بسیار قوی تر یا با تنظیم مولفه سرعت روی 0 ایجاد کردیم. این مجموعه داده را نامیدیم. ${DG}^{″}$ . سپس تفاوت بین مسیرها در DG و ${DG}^{″}$ برای هر نقطه شبکه نیز به عنوان محاسبه شد $d^{″}$ . بنابراین، نرخ تغییر دو مقدار مختلف $d^{'}$ و $d^{″}$ برای هر شبکه از نقطه q برای آشکار کردن تأثیر نقاط پرت استفاده شد که توسط محاسبه شد

د من f f (ق) = | د “ ( ق ) - د “ ( ق ) | د “ ( ق ) .

(9)

ارزش بالاتر از

d i f f (q)

نشان می دهد که نقاط پرت تأثیر بیشتری در نقطه شبکه q داشتند. برای ارائه حساسیت به نقاط پرت در بین تمام نقاط شبکه، تعداد نقاط شبکه را با نرخ تغییر به ترتیب بیش از 1٪، 5٪، 10٪ و 15٪ شمارش کردیم. ما توانایی پنج روش اندازه گیری (DTW، LCSS، ERP، EDR، و AEDR) را برای رسیدگی به موارد پرت مقایسه کردیم و نتایج در جدول 1 نشان داده شده است.. می توان مشاهده کرد که DTW و ERP نسبت به نقاط پرت حساس تر بودند: تحت تأثیر نقاط پرت، بیش از 16٪ از تمام نقاط دارای نرخ تغییر فاصله مسیر بیش از 1٪ و بیش از 2٪ از نقاط دارای نرخ تغییر بیش از 15٪ بودند. نتایج تعجب آور نیستند، زیرا هر دو DTW و ERP بر اساس فاصله اقلیدسی هستند که به نقاط پرت حساس است. در عین حال، تفاوت ناشی از نقاط پرت همراه با فرآیند حمل و نقل انباشته می شود. دیدن اینکه LCSS و EDR کلاسیک نسبت به ERP و DTW بسیار قوی‌تر از ERP و DTW بودند و تعداد نقاط کمتری تغییر می‌کردند. همانطور که در مورد AEDR پیشنهادی، توانایی بسیار بهتری برای رسیدگی به موارد پرت نشان داد. این نتیجه فراتر از انتظار ما بود، زیرا فکر می‌کردیم که محاسبه فاصله نقاط منطبق به طور بالقوه تحت تأثیر نقاط پرت قرار می‌گیرد. با این حال، هنگامی که نقاط پرت باعث می شود دو نقطه ناهمسان به اندازه کافی نزدیک باشند، AEDR به جای نادیده گرفتن مستقیم فاصله، درجه تطابق را اندازه می گیرد، همانطور که در LCSS و EDR کلاسیک وجود دارد. بنابراین، برای این مورد، نتیجه AEDR به شرایط واقعی بدون نقاط پرت نزدیک‌تر بود. این امر می‌تواند حساسیت AEDR را نسبت به LCSS و EDR کلاسیک نسبت به موارد پرت کمتر کند. این مورد یک مورد کلی در آزمایش های ارزیابی ما بود.

4.3. عدم قطعیت و همبستگی همسایگی

ساختار همبستگی همسایگی یک ویژگی اساسی یک میدان برداری است. تجزیه و تحلیل عدم قطعیت یک مکان واحد همراه با همسایگی آن می تواند کاوش ویژگی ها یا ناهنجاری های مهم را تسهیل کند. با توجه به این، ما عدم قطعیت بین اعضای خط مسیر را در همسایگی یک نقطه شبکه محاسبه کردیم و از آن به عنوان یک شاخص مهم برای قضاوت عدم قطعیت استفاده کردیم.

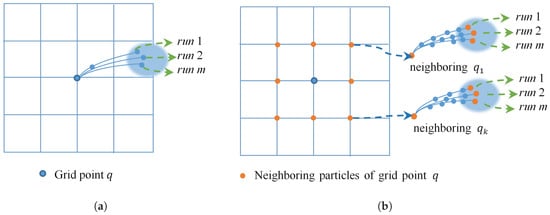
برای نقطه شبکه q ، مجموعه ای از نقاط همسایه را نمونه برداری می کنیم $q_{1}, q_{2}, \dots, q_{h}$ همان طور که در شکل 3 ب نشان داده شده است، در زمان اولیه به طور یکنواخت به q ، و مسیرها را برای همه اعضای گروه در سری زمانی دنبال کنید. برای همسایگی q ، عدم قطعیت را می توان با محاسبه کرد

ن U (ق) = \sum k = 1 ساعت ω ک L U (q ک) ،

(10)

جایی که وزن $ω_{k}$ به صورت زیر محاسبه می شود:

ω ک = 1 د ک \sum ساعت z = 1 1 د z ،

(11)

جایی که $d_{k}$ فاصله بین نقاط شبکه q و $q_{k}$ . این یک نتیجه فازی تر است که وضعیت عمومی عدم قطعیت حمل و نقل را نشان می دهد.

به طور کلی، مقادیر عدم قطعیت نقاط شبکه فضایی مجاور مشابه است. با این حال، معمولاً ناهنجاری هایی وجود دارد که در آن مکان و همسایگی آن متفاوت است. برای تشخیص ناهنجاری‌های بالقوه، موران I محلی [ 16 ] را برای شناسایی خودهمبستگی فضایی محلی معرفی می‌کنیم، به عنوان

سی U (ق) = h ( L U ( ق ) - L U ¯¯¯¯¯ ) \sum ساعت k = 1 ω ک ( L U ( q ک ) - L U ¯¯¯¯¯ ) \sum ساعت k = 1 ( L U ( q ک ) - L U ¯¯¯¯¯ ) 2 ،

(12)

جایی که $\bar{L U}$ میانگین LU در تمام شبکه ها است. سپس، عادی می کنیم $C U (q)$ توسط Z-Score [ 42 ]. بنابراین، مثبت $C U (q)$ همبستگی مکانی مثبت محلی را نشان می دهد، به این معنی که شبکه های مجاور مقادیر عدم قطعیت مشابهی دارند. برعکس منفی $C U (q)$ نشان‌دهنده همبستگی مکانی منفی محلی است، به این معنی که شبکه‌های مجاور مقادیر عدم قطعیت متفاوتی دارند.

4.4. فضای طبقه بندی

به منظور تجزیه و تحلیل جامع واریانس یک نقطه شبکه، یک فضای طبقه بندی می سازیم که در آن محور افقی نشان دهنده مقدار LU و محور عمودی نشان دهنده مقدار NU است. هر نقطه شبکه q را می توان به یک مختصات دو بعدی نگاشت کرد

(L U (q), N U (q))

در این فضا بنابراین، اطلاعات واریانس تمام نقاط شبکه در میدان برداری را می توان در یک نمودار پراکنده مشاهده کرد، که به کاربران کمک می کند تا به وضوح واریانس های کلی میدان برداری نامشخص را شناسایی کنند. همانطور که در شکل 4 الف نشان داده شده است، کل منطقه به چهار قسمت (a-d) به شرح زیر تقسیم می شود:

آ. LU کم و NU کم (منطقه آبی): نقاط شبکه نگاشت شده در این منطقه دارای حمل و نقل پایدار برای اجراهای مختلف گروه هستند و مسیرهای نقاط همسایه آنها بسیار مشابه است. از این منطقه، رفتارهای حمل و نقل قابل پیش بینی در یک میدان برداری نامشخص را می توان یافت.
ب LU کم و NU زیاد (منطقه سبز): رفتارهای انتقال نقاط شبکه نگاشت شده در این منطقه بسیار مشابه است، در حالی که مسیر نقاط همسایه آنها متفاوت است. این ممکن است به این دلیل باشد که میدان سرعت در اطراف این نقاط شبکه ناپایدار است و منجر به تغییر مسیر ذرات همسایه می شود.
ج. LU بالا و NU کم (منطقه نارنجی): نتیجه گیری قابل اعتماد در مورد اینکه آیا رفتارهای حمل و نقل نقاط شبکه نقشه برداری شده در این منطقه پایدار هستند دشوار است. تمام مسیرهای نقاط همسایه آنها بسیار شبیه است، اما واریانس نقاط شبکه متفاوت است. دلیل این پدیده ممکن است این باشد که نقاط شبکه در یک عضو مجموعه خاص پرت هستند یا اینکه میدان سرعت در اطراف نقاط شبکه پایدار است.
د LU بالا و NU زیاد (منطقه قرمز): این ناحیه عدم قطعیت زیادی را نشان می دهد. به این معنی است که واریانس با توجه به تنوع خود یا همسایگانشان آشکار است. بنابراین، می توان نتیجه گرفت که نقاط شبکه نگاشت شده در این منطقه دارای عدم قطعیت زیادی هستند.

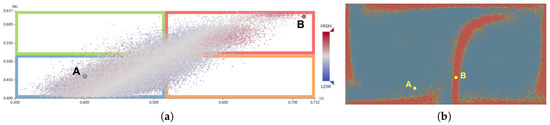
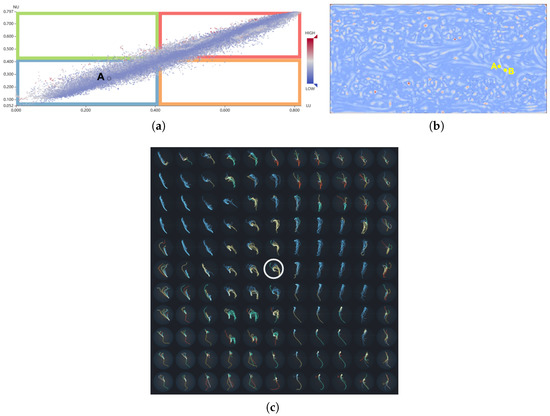
شکل 4 این چهار منطقه را با استفاده از مجموعه داده های DG نشان می دهد (همانطور که در بخش 6.1 توضیح داده شده است). از دیدگاه طبقه بندی ( شکل 4 الف)، واضح است که اکثر نقاط شبکه در ناحیه آبی قرار دارند که مقادیر LU کم و NU پایین را نشان می دهد. به غیر از نقاط موجود در ناحیه آبی، تعداد کمی از نقاط را می توان در مناطق سبز و نارنجی یافت. دلیل این امر را می توان در شکل 4 b مشاهده کرد، جایی که ذرات همسایگی نقاط در مناطق سبز در مناطق آبی و قرمز نمونه برداری شده اند و مقادیر LU این مناطق مخالف هستند. از شکل 4b، می توان مشاهده کرد که نقاط قرمز با نقاط سبز احاطه شده اند، به طوری که نقاط در ناحیه سبز را می توان به عنوان انتقال از حالت ناپایدار به حالت پایدار مشاهده کرد.

برای تجزیه و تحلیل بیشتر زیرفضاهای طبقه بندی شده، رنگ های نقطه ای را با مقادیر CU مربوطه رمزگذاری می کنیم. به طور کلی، زمانی که LU و NU یک نقطه شبکه دارای مقادیر مشابهی هستند، طبیعی است که مقدار CU آن بالا باشد. این بدان معنی است که نقاط ناحیه آبی و قرمز رنگ قرمز تیره تری دارند. برعکس، وقتی LU و NU متفاوت هستند، CU مربوطه کوچک است. این بدان معناست که نقاط مناطق سبز و نارنجی رنگ آبی تیره تری دارند. با این حال، از آنجایی که محله می تواند شرایط پیچیده ای داشته باشد، برخی از نقاط و همسایگی آنها ممکن است همبستگی های غیر آشکار یا حتی همبستگی های منفی را در مناطق آبی و قرمز نشان دهند. به عنوان مثال، همانطور که در شکل 4 a مشخص شده است، نقطه Aدارای LU کم و مقدار NU کم اما مقدار CU پایین. این را می توان با مشاهده اینکه بیشتر نقاط همسایه A دارای مقادیر LU بالایی هستند، اما چندین نقطه همسایه دارای مقادیر LU بسیار پایین هستند. بنابراین، NU و CU نقطه A هر دو مقادیر نسبتا پایینی هستند. به این ترتیب می توان برخی از ناهنجاری های پنهان را بیشتر تشخیص داد.

5. تحلیل بصری عدم قطعیت

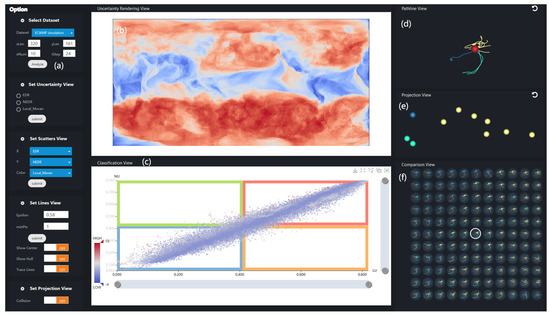
در این بخش، ما بینشی در مورد نحوه انتقال همه اعضای مسیر یک نقطه شبکه در سری زمانی ارائه می دهیم. ما یک سیستم تجزیه و تحلیل بصری تعاملی به نام UP-Vis (تجسم مسیر عدم قطعیت) پیشنهاد می کنیم که رابط های آن در شکل 5 نشان داده شده است. از چهار نما تشکیل شده است: نمای رندر عدم قطعیت، نمای طبقه بندی، نمای مسیر و نمای طرح ریزی. همچنین یک پانل پارامتر وجود دارد که از مدیریت بارگذاری داده، تنظیمات پارامتر و تغییر عنصر تجسم پشتیبانی می کند.

5.1. استخراج الگوی حمل و نقل

خطوط مسیر معمولاً طول‌های متفاوتی دارند، زیرا ممکن است برخی از ذرات در مراحل اولیه از مرز معتبر فرار کنند. برای تجزیه و تحلیل تفاوت آنها در حرکت، Ferstl و همکاران. و جارما و همکاران تمام خطوط مسیر را با تکرار آخرین نقطه خط مسیر در دامنه برای پر کردن موقعیت‌های از دست رفته، طول یکسانی تنظیم کنید [ 28 ، 43 ]. با این حال، این روش ممکن است با توجه به نکات اضافی، خطاها را افزایش دهد. با استفاده از روش ما، شباهت بین هر دو عضو خط مسیر حتی زمانی که طول های متفاوتی داشته باشند را می توان به دست آورد. علاوه بر این، اعضای خط مسیر برای تشخیص مستقیم روندهای حمل و نقل اصلی خوشه‌بندی می‌شوند و در فضای دوبعدی پیش‌بینی می‌شوند تا بینشی در مسیرهای متعلق به همان خوشه ارائه دهند.

ما از الگوریتم tSNE برای تبدیل هر عضو خط مسیر به یک نقطه پراکندگی در فضای دو بعدی استفاده می کنیم. یکی از مزایای tSNE این است که ورودی آن فقط به یک ماتریس فاصله بین اعضا نیاز دارد که می تواند به طور موثر با اندازه گیری AEDR ترکیب شود. از نمای طرح ریزی، رابطه بین خطوط مسیر را می توان با استفاده از فاصله بین نقاط پراکنده بررسی کرد. علاوه بر این، بهم ریختگی بصری یک مسئله رایج در نمودارهای پراکنده است. نقاط همپوشانی می تواند مانع از مشاهده ویژگی های انبوه نشان داده شده در نمای توسط کاربران شود. یک رویکرد رایج اضافه کردن یک کانال بصری جدید است که شفافیت را به هر نقطه پراکنده اضافه می کند. با این حال، برهم نهی شفافیت تعداد نقاط پراکندگی را پنهان می کند. در این صفحه، ما یک استراتژی تشخیص برخورد را معرفی می کنیم که می تواند نقاط همپوشانی را از هم جدا کند و طرح اصلی را تا حد امکان حفظ کند. بنابراین، نمای طرح یک نمایش بصری را امکان پذیر می کند که به طور شهودی روابط بین اعضای مسیر را نشان می دهد.

به منظور استخراج روندهای مختلف یک مسیر گروه، از الگوریتم DBSCAN [ 44 ] برای خوشه بندی اعضای مسیر در هر مسیر گروه استفاده می شود. DBSCAN یک الگوریتم مبتنی بر چگالی است که می‌تواند خوشه‌های شکل دلخواه را بدون تعیین تعداد خوشه‌ها از قبل استخراج کند. علاوه بر این، دارای توانایی قوی در مقاومت در برابر تداخل نویز است و می تواند برای تشخیص مسیرهای دورتر مورد استفاده قرار گیرد. همچنین طبق [ 44 ] به محاسبات کمتری نیاز دارد. DBSCAN به طور گسترده در زمینه تجزیه و تحلیل بصری برای استخراج الگوها و تشخیص ناهنجاری ها، مانند داده های حرکتی [ 45 ] و خطوط جریان [ 46 ] استفاده شده است.

نتایج خوشه بندی را می توان با تنظیم پارامترها تغییر داد

E p s

M i n P t s

. یک بزرگ

E p s

مقدار ممکن است منجر به گروه بندی تمام مسیرها در یک خوشه شود. در ضمن اگر

M i n P t s

خیلی بزرگ است، بسیاری از مسیرها به عنوان نویز تلقی می شوند. با در نظر گرفتن یک مسیر گروه در داده های شبیه سازی آب و هوا (همانطور که در بخش 6.2 توضیح داده شد ) به عنوان مثال، خطوط سبز نشان داده شده در شکل 6 a، اعضای اصلی خط مسیر هستند که خوشه بندی نشده اند. هنگامی که پارامترهای مختلف استفاده می شود، نتایج خوشه بندی مربوطه را می توان به دست آورد. همانطور که در شکل 6 ب نشان داده شده است، اعضای خط مسیر به دو خوشه (رنگ آبی و زرد) دسته بندی شدند.

E p s

0.8 و تنظیم شده است

M i n P t s

بر روی 1 تنظیم شده است. همانطور که در شکل 6 c نشان داده شده است، پس از کاهش

E p s

از 0.8 تا 0.75، اعضای خط مسیر به سه خوشه دسته بندی شدند، جایی که اعضای خط مسیر مشخص شده با رنگ زرد در شکل 6 b بیشتر به دو خوشه تقسیم شدند. علاوه بر این، زمانی که ما افزایش یافته است

M i n P T S

از 1 تا 2، مسیرهای پرت جدا شدند، همانطور که در شکل 6 d نشان داده شده است.

به منظور مقایسه جهانی عدم قطعیت شبکه های مختلف، همان را تنظیم می کنیم

E p s

M i n P T S

برای تمام نقاط شبکه به این ترتیب، درجه واریانس خطوط مسیر را می توان با مشاهده تعداد خوشه هایی که تخصیص داده شد، تشخیص داد. این به این معنی است که هر چه خوشه‌های بیشتری که مسیرها به آنها تقسیم شود، عدم قطعیت شبکه اولیه بیشتر است. در مقایسه با سایر الگوریتم‌های خوشه‌بندی، که نیاز به تعیین تعداد خوشه‌ها دارند، DBSCAN دوستانه‌تر و شهودی‌تر است، زیرا برای کشف عدم قطعیت نیازی به مقایسه واگرایی هر خوشه از شبکه‌های مختلف ندارد. علاوه بر این، الگوریتم‌های خوشه‌بندی و کاهش ابعاد به‌طور یکنواخت در سیستم تجسم ما ادغام می‌شوند، که روابط بین مسیرها را در سطوح جهانی و محلی نشان می‌دهد. علاوه بر این، عملیات برس با استفاده آسان می تواند به کاربران کمک کند تا الگوهای حمل و نقل و جزئیات اعضای مسیر را کشف کنند.

5.2. تجسم شاتل

از نمای خط مسیر که در بخش 5.1 توضیح داده شده است، می‌توانیم ابتدا روند خطوط مسیر را تشخیص دهیم. با این حال، خطوط مسیر در داده‌های دنیای واقعی، با همپوشانی‌ها و تقاطع‌های زیاد، برای تشخیص الگوهای مختلف بسیار پیچیده هستند. برای نمایش جامع و شهودی عدم قطعیت یک نقطه شبکه در یک میدان برداری نامشخص، ما یک گلیف به نام Shuttlecock طراحی کردیم که از یک دایره و چندین “پر” تشکیل شده است. تعداد ویژگی ها برابر است با تعداد خوشه ها. دایره نشان دهنده یک نقطه شبکه در فیلد برداری نامشخص است و رنگ آن مقدار LU را رمزگذاری می کند. نوار رنگ با نمای رندر عدم قطعیت همزمان است. هر چه رنگ قرمز عمیق تر باشد، مقدار LU بالاتر است.

پرها برای نمایش الگوهای اصلی حمل و نقل از یک نقطه شبکه طراحی شده اند. هر پر به عنوان یک کانتور بیرونی رسم می شود که تمام اعضای هر خوشه را به همراه خط مرکزی روند در بر می گیرد. این می تواند به طور شهودی واگرایی هر الگو را توصیف کند. به طور مفصل، برای هر خوشه، نقاط نمونه مساوی را در امتداد هر مسیر انتخاب می کنیم و خطوط چگالی را برای نقاط نمونه داده شده تخمین می زنیم. سپس خط کانتور با کمترین چگالی با رنگی شفاف پر می شود و نمایشی محدب شکل تشکیل می شود. به این ترتیب، برای هر الگوی انتقال، کانتور بیرونی را ترسیم می کنیم. علاوه بر این، خط مسیر با حداقل فاصله AEDR، در مقایسه با سایرین در خوشه، به عنوان مسیر مرکزی انتخاب می‌شود.

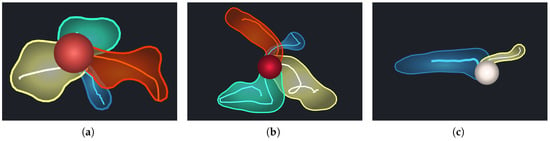
بنابراین، علامت شاتلکاک نه تنها از بهم ریختگی بصری ناشی از ترسیم تمام اعضای خط مسیر جلوگیری می کند، بلکه الگوهای اصلی را به وضوح نشان می دهد، حتی زمانی که تعداد زیادی از اعضای خط مسیر در یک مسیر گروه وجود دارد. از طریق مشاهده اشکال مختلف گلیف برای نقاط مختلف، می‌توانیم به طور موثر عدم قطعیت میدان برداری را در مکان‌های مختلف مقایسه کنیم. شکل 7 نشانه های نتایج خوشه بندی را در شکل 6 b-d نشان می دهد. به عنوان مثال، خطوط مسیر در شکل 6 b به دو خوشه اختصاص داده شده اند، و شکل 7 a طرح کلی و خط مرکزی همه مسیرها را در هر دوی این خوشه ها نشان می دهد. خوشه زرد روند حمل و نقل آشفته تری را نسبت به خوشه آبی نشان می دهد. که دردر شکل 7 b,c، خوشه زرد بیشتر تقسیم شده و مساحت هر خوشه کوچکتر است.

در طول فرآیند طراحی گلیف، چندین جایگزین را نیز در نظر گرفتیم. یکی از گزینه ها نمایش نقاط مسیر تمام مهرهای زمانی در داخل کانتور بود ( شکل 8 a). به این ترتیب، جزئیات واگرایی الگوها را می توان به خوبی حفظ کرد، اما همپوشانی نقاط، شناسایی روندهای اصلی را محدود می کند. همانطور که در شکل 8 ب نشان داده شده است، طرح دیگری برای نمایش نقاط مسیر و مسیرهای مرکزی بود که در زمانی که خوشه های خط مسیر نزدیک بودند، قادر به تشخیص ویژگی ها نبودند. ما همچنین سعی کردیم نقاط مسیر، خطوط مرکزی و خطوط بیرونی را با هم ترکیب کنیم ( شکل 8 ج). با این حال، این طرح به دلیل به هم ریختگی بصری جدی نمی تواند مسیرها و جزئیات مرکزی را به وضوح نشان دهد.

در مقایسه با برخی از طرح‌های متداول تجسم عدم قطعیت، مانند Noodles [ 47 ]، نمودار کانتور [ 25 ]، و غیره، روش ما بر ارائه الگوهای انتقال برای یک مکان واحد با جزئیات تمرکز دارد، به جای ارائه عدم قطعیت کلی کل فیلد داده به طور خاص، Shuttlecock طراحی شده است تا به کاربران کمک کند تا روندهای اصلی را به وضوح درک کنند، نه اینکه مستقیماً مقادیر عدم قطعیت را در علامت رمزگذاری کنند.

5.3. مقایسه با الگوهای همسایگی

همانطور که در بخش 4.3 بحث شد ، ما از NU برای تخمین عدم قطعیت همسایگی یک مکان و محاسبه CU برای نشان دادن همبستگی بین مکان و همسایگی آن استفاده می‌کنیم. الگوهای همبستگی متفاوتی را می توان در نمای طبقه بندی مشاهده کرد ( شکل 4 الف). به طور خاص، برخی از نقاط CU پایین را نشان می دهند، زیرا عدم قطعیت های خود نقطه و نقاط همسایگی آن بسیار متفاوت است. بررسی تفاوت‌های خاص بین خود نقطه شبکه و همسایگی آن مفید است که می‌توان با مقایسه الگوهای حمل و نقل شبکه‌های مختلف در همسایگی آن را حل کرد.

بنابراین، ما یک نمای مقایسه ای طراحی کردیم که شبیه به دوخت کاشی است. خطوط مسیر مکان انتخابی و مکان های همسایه آن را به طور همزمان در کاشی های مجاور ترسیم می کند. شکل 9 موردی از مجموعه داده های آب و هوا را نشان می دهد (همانطور که در بخش 6.2 توضیح داده شده است). هر کاشی دایره ای خاکستری به مکانی چسبانده می شود که تیرگی آن LU مربوطه را کد می کند. محل انتخاب شده را با افزودن یک حاشیه سیاه به کاشی برجسته می کنیم. در داخل هر کاشی، خطوط مسیری که از محل ردیابی می‌شوند، کوچک‌تر شده و بدون محو کردن روند و تنوع ترسیم می‌شوند. برای تقویت کنتراست بین کاشی‌های مختلف، خطوط مسیر را در هر کاشی با همان دسته‌بندی می‌کنیم

E p s

M i n P t s

ارزش های. بنابراین، کاربران می توانند با مشاهده الگوهای استخراج شده با رنگ های مختلف، روند حمل و نقل را در مکان انتخابی و محله آن شناسایی و مقایسه کنند. به عنوان مثال، اعضای خط مسیر که از محل انتخاب شده در شکل 9 ردیابی می شوند، از روندهای مشابهی پیروی می کنند و در یک خوشه طبقه بندی می شوند. به طور مشابه، برخی از کاشی‌ها در قسمت بالا و سمت راست پایین نما، روند اصلی حمل و نقل را به تصویر می‌کشند. با این حال، خطوط مسیر در کاشی های دیگر در جهات مختلف متفاوت است و عدم اطمینان بالایی را نشان می دهد.

6. مطالعه موردی

به منظور نشان دادن اثربخشی روش خود، ما مطالعات موردی را با استفاده از دو مجموعه داده انجام دادیم: مجموعه داده های مصنوعی DG و مجموعه داده های شبیه سازی آب و هوا ECMWF. برای مجموعه داده های DG، ما نتایج بیشتری از الگوهای حمل و نقل عدم قطعیت و همبستگی های همسایگی ارائه می دهیم. برای مجموعه داده های ECMWF، ما روش اندازه گیری پیشنهادی خود را با روش های دیگر مقایسه کردیم و مشاهدات را در تجزیه و تحلیل بصری توصیف کردیم.

6.1. مجموعه داده های مصنوعی دو چرخه

6.1.1. کاوش الگوی حمل و نقل

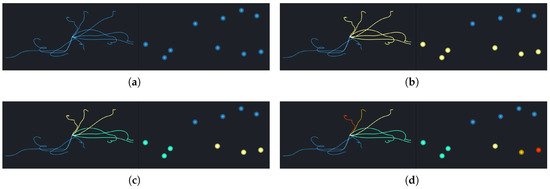
برای اکتشاف بیشتر، ما مکان “A” ( شکل 10 a) را با عدم قطعیت بسیار بالا انتخاب کردیم و الگوی حمل و نقل دقیق را در جداسازی دو چرخان بررسی کردیم. همانطور که در شکل 10 ب نشان داده شده است، دو روند حمل و نقل متضاد را می توان مشاهده کرد که رفتارهای حمل و نقل بسیار ناپایدار را در این منطقه نشان می دهد. هنگامی که نقاط یک خوشه را در نمای طرح ریزی انتخاب می کنیم ( شکل 10 ج)، روند مربوطه برجسته می شود، همانطور که در شکل 10 d نشان داده شده است. این به کارشناسان حوزه کمک می کند تا روندهای حمل و نقل اعضای گروه مربوطه را با پارامترهای ورودی خاص مرتبط کنند.

هنگامی که مکان “B” ( شکل 10 a) را با عدم قطعیت کم انتخاب کردیم، یک روند ثابت ارائه شد، همانطور که در شکل 10 e نشان داده شده است. همانطور که در شکل 10 f نشان داده شده است، همانطور که در شکل 10 نشان داده شده است، خطوط مسیر دارای درهم و برهمی جدی در مرکز چرخش هستند و هیچ ویژگی متمایزی را نمی توان مشاهده کرد. همانطور که در شکل 10 نشان داده شده است، با انجام کاهش ابعاد و خوشه بندی به اعضای خط مسیر بر اساس AEDR، چندین ویژگی پنهان را می توان با برس زدن نقاط خاص بیشتر استخراج کرد.

6.1.2. تحلیل همبستگی همسایگی

برای تجزیه و تحلیل همبستگی همسایگی، رندر NU و CU، نمای طبقه‌بندی و نمای مقایسه برای تسهیل درک کاربر ترکیب می‌شوند. از آنجایی که همه این نماها به هم مرتبط هستند، کاربران می توانند با مشاهده نتیجه NU ( شکل 11 a) یا CU ( شکل 11 ب)، و با پیروی از راهنمای نمای طبقه بندی ( شکل 4 a) و انتخاب یک نقطه مورد علاقه، شروع کنند. نقطه برجسته “B” در نمای طبقه بندی ( شکل 4 الف) نشان دهنده یک همبستگی مثبت بالا بین مکان و همسایگی آن است و با مکان مشخص شده “B” در ارائه CU مطابقت دارد ( شکل 11).ب). این بدان معنی است که منطقه بین دو چرخان دارای CU مثبت است، در حالی که همبستگی در مناطق دیگر آشکار نیست.

علاوه بر این، شکل 11c مقایسه ای از الگوهای حمل و نقل بین مکان مشخص شده “B” در شکل 11 a,b و همسایگی آن را نشان می دهد. مشاهده می شود که الگوهای حمل و نقل محله داخلی به طور کلی با موقعیت مکانی سازگار بود، در حالی که ذرات بیرونی کمی متفاوت بودند. این با استنباط ما مطابقت دارد، زیرا همسایگی داخلی وزن بالاتری نسبت به بیرونی در هنگام محاسبه همبستگی داشت.

6.2. مجموعه داده های شبیه سازی گروه ECMWF

مجموعه داده های شبیه سازی گروه ECMWF از شبیه سازی های هواشناسی در مقیاس بزرگ آب و هوا در مقیاس جهانی تشکیل شده است. داده های سرعت باد در 10 متر بالاتر از سطح دریا در آزمایش ما استفاده شد، جایی که قدرت تفکیک مکانی بود

320 \times 161

. داده‌های خروجی هر سه ساعت یکبار تولید می‌شد و به این ترتیب، هشت مرحله زمانی در روز وجود داشت. ما واریانس های حمل و نقل را در طول سه روز، در مجموع 24 مرحله زمانی تجزیه و تحلیل کردیم. هر تایم گام 10 عضو گروه داشت.

6.2.1. مقایسه و تحلیل الگوی حمل و نقل

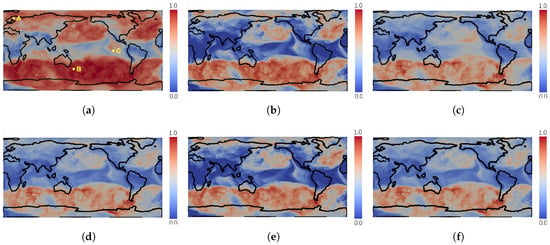
شکل 12 عدم قطعیت محلی میدان سرعت باد را نشان می دهد که توسط AEDR، EDR کلاسیک، فاصله اقلیدسی، DTW، LCSS و ERP محاسبه شده است. به گفته یک متخصص حوزه، پایداری رفتارهای حمل و نقل در میدان باد تا حد زیادی به عوامل جغرافیایی مرتبط است. همانطور که در شکل 12 نشان داده شده استاز دیدگاه جهانی، الگوهای مشابهی در همه نتایج وجود داشت، جایی که مناطق با عدم قطعیت بالا عمدتاً در نیمکره جنوبی قرار داشتند. علاوه بر این، مناطق دریایی به طور کلی دارای عدم قطعیت بالاتری هستند. در مورد قاره ها، آنها معمولاً دارای عدم اطمینان کمتری هستند، در حالی که برخی از مناطق نزدیک دریا نیز درجه کمی از عدم اطمینان را نشان می دهند. این به این دلیل است که شکل گیری و حمل و نقل باد در مناطق دریایی پیچیده تر است و به پارامترهای شبیه سازی آب و هوا حساس تر است. این به طور کلی با انتظارات متخصص دامنه مطابقت داشت. برخی از مناطق با عدم قطعیت نسبتاً بالا در نیمکره شمالی تنها به وضوح توسط AEDR نمایش داده شدند ( شکل 12 a). به عنوان مثال، نقطه “A” در شکل 12a در منطقه ای نزدیک دریا در شمال اروپا واقع شده است که زمین آن کم و هموار است (ارتفاع حدود 135 متر). این مکان تحت تأثیر توده هوای قطبی دریایی و توده هوای قاره است. بنابراین، نقطه “A” دارای عدم قطعیت نسبتا بالایی است ( شکل 12 a)، و الگوی انتقال مربوطه در شکل 13 a نشان داده شده است. باید به عنوان یک الگوی آشفته در مقیاس کوچک در نظر گرفته شود. با این حال، سایر اندازه گیری ها نتوانستند مورد واقعی را آشکار کنند. قدر سرعت کم در مکان “A” منجر به مقادیر کم فاصله اقلیدسی، DTW و ERP شد. در مورد LCSS و EDR کلاسیک، تفاوت تا حد زیادی نادیده گرفته شد، زیرا آنها فاصله بین نقاط مطابق را نادیده گرفتند. در نقطه “B” ( شکل 12الف) واقع در جنوب اقیانوس آرام، سرعت باد معمولاً زیاد است و دائماً در حال تغییر است. برای این مورد، عدم قطعیت بالا ( شکل 12 ) و الگوی حمل و نقل آشفته ( شکل 13 ب) می تواند واقعاً با تمام روش های اندازه گیری ارائه شود. در مورد نقطه C، واقع در اقیانوس آرام در نزدیکی استوا و نزدیک یک قاره، منطقه آن تحت تأثیر بادهای تجاری شمال شرقی و جنوب شرقی قرار گرفت. بنابراین، روند اصلی باد از شرق به غرب بود. با این حال، جریان های نامطلوب کوچک نیز ممکن است در نقطه “C” رخ دهد. همانطور که در شکل 13 نشان داده شده استج، الگوی انتقال نقطه “C” از دو روند متضاد تشکیل شده است. یکی در حال انتقال به دور و دیگری در حال حرکت در نزدیکی مکان است که نشان دهنده وجود رفتارهای نامطمئن است. این مورد مهمی است که متخصصان دامنه می‌خواهند آن را بیابند، زیرا ظاهر گرایش‌های خاص و اعضای گروه مربوطه آنها برای تنظیم پارامترهای مدل شبیه‌سازی مهم هستند. نتایج AEDR می‌تواند این عدم قطعیت را آشکار کند و بهتر با حالت واقعی مطابقت داشته باشد، که به کارشناسان حوزه کمک می‌کند تا چنین الگوهای حمل‌ونقل مهمی را کشف کنند. سایر روش های اندازه گیری نتوانستند عدم قطعیت را به طور دقیق ارائه دهند.

6.2.2. تحلیل همبستگی همسایگی

به منظور تحلیل همبستگی همسایگی، ابتدا بر نمای طبقه بندی تمرکز کردیم ( شکل 14 الف). مشاهده می شود که بیشتر نقاط در نواحی آبی و قرمز ظاهر شده اند. این نشان می دهد که LU و NU آنها به طور کلی سازگار بودند. با این حال، رنگ های نقطه ای نشان می دهد که همبستگی همسایگی در بسیاری از مکان ها منفی بود. برای بررسی این موارد غیرعادی، نقطه A را در شکل 14 a انتخاب کردیم که مقدار CU پایینی داشت. مکان آن در شکل 14 ب مشخص شده است و جزئیات همسایگی آن را می توان در نمای مقایسه بررسی کرد ( شکل 14ج). مشاهده می شود که محله عمدتاً دارای الگوهای حمل و نقل بسیار متفاوت و درجات مختلف عدم قطعیت بوده است. این توضیح می دهد که چرا این مکان با همسایگی خود همبستگی منفی داشته است.

7. بحث

7.1. پیاده سازی و عملکرد

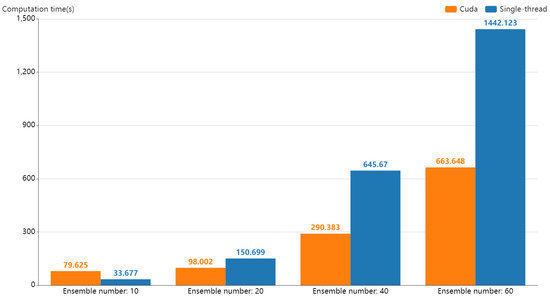
پیاده سازی چارچوب تحلیل بصری ما شامل چندین کار محاسباتی است. محاسبات میدان LU در طبیعت قابل موازی سازی است، زیرا محاسبه برای هر مکان مستقل است. بنابراین، ما آن را به صورت موازی با استفاده از CUDA روی یک پردازنده گرافیکی NVIDIA GT 730 با

(32 \times 32 \times 16 \times 16)

موضوعات. شکل 15زمان محاسبات مجموعه داده های DG را با اعداد مختلف گروه با استفاده از CUDA در مقابل اجرای تک رشته ای نشان می دهد. می توان مشاهده کرد که اجرای CUDA کارایی بالاتری نسبت به اجرای تک رشته ای ارائه می دهد و با افزایش تعداد گروه مزیت بیشتر می شود. با این حال، زمانی که تعداد گروه 10 بود، اجرای تک رشته ای کارآمدتر از اجرای CUDA بود. این به این دلیل بود که پیاده‌سازی CUDA شامل چندین مرحله پیش‌پردازش بود، مانند تقسیم داده‌ها به چند دسته، بارگذاری داده‌ها در GPU و تخصیص رشته‌ها. بنابراین، اگر اندازه داده ها کوچک است، بهتر است از پیاده سازی تک رشته ای استفاده کنید. برای حالت کلی اندازه داده های بزرگ، پیاده سازی CUDA می تواند کارایی محاسبات LU را بهبود بخشد.

علاوه بر این، هنگامی که کاربران سیستم تجزیه و تحلیل بصری را کاوش می کنند، تمام محاسبات و تعاملات در زمان واقعی پاسخ می دهند، از جمله محاسبه آنلاین خوشه بندی و طرح ریزی. با توجه به اینکه DBSCAN و tSNE هر دو نتایج را بر اساس تفاوت بین داده‌ها تولید می‌کنند، برای مسیرهای یک شبکه، نتایج میانی را در پیش پردازش به عنوان ماتریس تفاوت ذخیره می‌کنیم. به این ترتیب، الگوریتم های خوشه بندی و طرح ریزی می توانند هم از ماتریس ها به عنوان ورودی استفاده کنند و هم از تفاوت های محاسباتی مکرر جلوگیری کنند، که سرعت اجرا را بهبود می بخشد. با اجزای غنی در کنترل پنل سیستم ما، تنظیم پارامترهای الگوریتم و بررسی نتایج مربوطه برای کاربران بسیار کارآمد و راحت است.

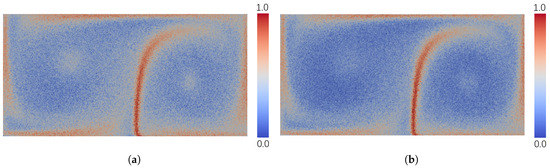
7.2. مولفه های

محاسبه AEDR نسبت به آستانه همسایگی نسبتاً قوی است

δ

. شکل 16 نتایج AEDR را برای مجموعه داده های DG با استفاده از آن نشان می دهد

δ = 20

δ = 30

. ویژگی های کلی ارائه شده در این نتایج سازگار است. استحکام تا آستانه

δ

همچنین با محاسبه فاصله بین نقاط منطبق استفاده شد. اگر تنظیم کنیم

δ

به یک مقدار بسیار کوچک، پایدارترین مکان‌ها پیدا می‌شوند و بیشتر نواحی تغییراتی را در درجات مختلف نشان می‌دهند. به طور مشابه، اگر از مقدار زیادی از استفاده کنیم

δ

برای محاسبه AEDR، منطقه ای با بیشترین عدم قطعیت پیدا می شود. در آزمایش‌هایمان، تنظیم کردیم

δ

به 10-20٪ از طول بعد فضایی کوتاه تر.

در مورد پارامترهای الگوریتم DBSCAN، ما به کاربران اجازه می دهیم آنها را در پانل پارامتر تغییر دهند ( شکل 5 a)، به منظور بررسی نتایج مختلف خوشه بندی و ویژگی های مربوطه.

8. نتیجه گیری و کار آینده

در این مقاله، ما یک روش جدید برای تحلیل عدم قطعیت در یک میدان برداری مجموعه ارائه کرده‌ایم. به منظور اندازه گیری تفاوت بین اعضای خط مسیر به طور موثر، ما یک روش اندازه گیری، AEDR، بر اساس EDR کلاسیک پیشنهاد کردیم. این یک روش اندازه گیری موثرتر است، با استحکام بالا نسبت به نقاط پرت، پشتیبانی از مقایسه بین اعضای خط مسیر با طول های مختلف و دقت بالاتر. بر این اساس، ما عدم قطعیت محله را در نظر گرفتیم و همبستگی بین یک مکان و همسایگی آن را محاسبه کردیم. با استفاده از این اندازه‌گیری‌ها، ما یک سیستم تجزیه و تحلیل بصری، UP-Vis را طراحی و توسعه دادیم تا به کاربران کمک کند تا الگوهای حمل‌ونقل و عدم قطعیت محله را به طور عمیق و جامع تجزیه و تحلیل کنند. ما اعضای مسیر را با استفاده از یک علامت جدید به نام Shuttlecock در روندهای حمل و نقل دسته بندی کردیم. طراحی شده است تا به طور مستقیم روندها و درجات متفاوت آنها را نشان دهد. نمای طبقه بندی و نمای مقایسه می تواند به کاربران کمک کند تا همبستگی همسایگی را عمیق تر درک کنند. نتایج تجربی با استفاده از مجموعه داده های مصنوعی و واقعی، اثربخشی روش ما را نشان داده است.

در آینده، ما قصد داریم داده ها را با وضوح چندگانه و ردیابی ذرات در مقیاس های فضایی مختلف بررسی و تجزیه و تحلیل کنیم. همچنین قصد داریم از خوشه‌بندی گروهی برای به دست آوردن نتایج قوی‌تر برای خوشه‌بندی مسیر استفاده کنیم. علاوه بر این، نماهای بیشتری برای برآوردن نیازهای مختلف و پشتیبانی از تجزیه و تحلیل سه بعدی به سیستم تجزیه و تحلیل بصری اضافه خواهد شد.

منابع

وانگ، جی. هزاریکا، س. لی، سی. شن، تجسم HW و تجزیه و تحلیل بصری داده‌های گروه: نظرسنجی. IEEE Trans. Vis. محاسبه کنید. نمودار. 2018 ، 25 ، 2853-2872. [ Google Scholar ] [ CrossRef ]
ژانگ، اچ. کو، دی. لیو، کیو. شانگ، Q. هو، ی. تجسم عدم قطعیت شن، HW برای تجزیه و تحلیل انجمن های متغیر. Vis. محاسبه کنید. 2018 ، 34 ، 531-549. [ Google Scholar ] [ CrossRef ]
هزاریکا، س. بیسواس، ع. تجسم عدم قطعیت شن، HW با استفاده از تحلیل مبتنی بر کوپول در مدل‌های توزیع مختلط. IEEE Trans. Vis. محاسبه کنید. نمودار. 2018 ، 24 ، 934-943. [ Google Scholar ] [ CrossRef ] [ PubMed ]
لیو، اس. کوی، دبلیو. وو، ی. لیو، ام. نظرسنجی در مورد تجسم اطلاعات: پیشرفت‌ها و چالش‌های اخیر. Vis. محاسبه کنید. 2014 ، 30 ، 1373–1393. [ Google Scholar ] [ CrossRef ]
بیسواس، ع. لین، جی. لیو، ایکس. Shen, HW تجسم مجموعه‌های آب و هوای متغیر با زمان در وضوح‌های چندگانه. IEEE Trans. Vis. محاسبه کنید. نمودار. 2017 ، 23 ، 841-850. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Bonneau، GP; Hege، HC; جانسون، CR; اولیویرا، ام. پاتر، ک. Rheingans، P. شولتز، تی. بررسی اجمالی و آخرین هنر تجسم عدم قطعیت. در تجسم علمی ; Springer: برلین/هایدلبرگ، آلمان، 2014; صص 3-27. [ Google Scholar ]
هومل، ام. اوبرمایر، اچ. گارث، سی. Joy، KI تحلیل بصری مقایسه ای حمل و نقل لاگرانژی در گروه های CFD. IEEE Trans. Vis. محاسبه کنید. نمودار. 2013 ، 19 ، 2743-2752. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
هالر، جی. سطوح مواد متمایز و ساختارهای منسجم در جریان سیال سه بعدی. فیزیک D پدیده غیرخطی. 2001 ، 149 ، 248-277. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
گوا، اچ. یوان، ایکس. هوانگ، جی. Zhu، X. فرارفت و تجزیه و تحلیل خط جریان مجموعه جفت شده. IEEE Trans. Vis. محاسبه کنید. نمودار. 2013 ، 19 ، 2733-2742. [ Google Scholar ]
ولاچوس، م. کولیوس، جی. Gunopulos، D. کشف مسیرهای چند بعدی مشابه. در مجموعه مقالات هجدهمین کنفرانس بین المللی مهندسی داده، سن خوزه، کالیفرنیا، ایالات متحده آمریکا، 26 فوریه تا 1 مارس 2002. صص 673-684. [ Google Scholar ]
کیوگ، ای. راتاناماهاتانا، کالیفرنیا نمایه سازی دقیق تاب خوردگی زمانی پویا. بدانید. Inf. سیستم 2005 ، 7 ، 358-386. [ Google Scholar ] [ CrossRef ]
سالوادور، اس. چان، پی. به سوی تاب برداشتن زمانی دینامیکی دقیق در زمان و مکان خطی. هوشمند داده آنال. 2007 ، 11 ، 561-580. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
چن، ال. اوزسو، MT; Oria، V. جستجوی شباهت قوی و سریع برای مسیر حرکت جسم متحرک. در مجموعه مقالات کنفرانس بین المللی ACM SIGMOD 2005 در مدیریت داده ها، بالتیمور، MD، ایالات متحده آمریکا، 14-16 ژوئن 2005. صص 491-502. [ Google Scholar ]
چن، ال. Ng, R. در مورد ازدواج lp-هنجارها و فاصله ویرایش. در مجموعه مقالات سی امین کنفرانس بین المللی پایگاه های داده بسیار بزرگ – جلد 30، تورنتو، ON، کانادا، 31 اوت تا 3 سپتامبر 2004. صص 792-803. [ Google Scholar ]
پوتکوف، ک. وبر، بی. هژ، HC مکعب های راهپیمایی احتمالی. در انجمن گرافیک کامپیوتری ; کتابخانه آنلاین وایلی: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2011; جلد 30، ص 931–940. [ Google Scholar ]
Anselin، L. شاخص های محلی ارتباط فضایی-LISA. Geogr. مقعدی 1995 ، 27 ، 93-115. [ Google Scholar ] [ CrossRef ]
زو، بی. چن، اچ. تجسم اطلاعات. آنو. Rev. Inf. علمی تکنولوژی 2005 ، 39 ، 139-177. [ Google Scholar ] [ CrossRef ]
Hollister، BE; Pang، A. درونیابی چند متغیری برای تخمین چگالی احتمال مشتق شده از مجموعه. بین المللی J. نامشخص. کمیت 2015 ، 5 . [ Google Scholar ] [ CrossRef ]
اشنایدر، دی. فورمن، جی. رایش، دبلیو. Scheuermann, G. یک روش شبه FTLE مبتنی بر واریانس برای میدان‌های برداری نامشخص ناپایدار. در روش های توپولوژیکی در تجزیه و تحلیل داده ها و تجسم II ; Springer: برلین/هایدلبرگ، آلمان، 2012; صص 255-268. [ Google Scholar ]
گوا، اچ. او، دبلیو. پیترکا، تی. شن، HW; کولیس، اس ام. Helmus، JJ لیاپانوف زمان محدود و ساختارهای منسجم لاگرانژی در جریان‌های ناپایدار نامشخص. IEEE Trans. Vis. محاسبه کنید. نمودار. 2016 ، 22 ، 1672-1682. [ Google Scholar ] [ CrossRef ] [ PubMed ]
یی، BK; جگادیش، ح. فالوتسوس، سی. بازیابی کارآمد توالی های زمانی مشابه تحت تاب برداشتن زمان. در مجموعه مقالات چهاردهمین کنفرانس بین المللی مهندسی داده، اورلاندو، فلوریدا، ایالات متحده آمریکا، 23 تا 27 فوریه 1998. ص 201-208. [ Google Scholar ]
لیو، آر. گوا، اچ. ژانگ، جی. یوان، X. تجسم مقایسه ای مجموعه های میدان برداری بر اساس طولانی ترین دنباله مشترک. در مجموعه مقالات سمپوزیوم IEEE Pacific Visualization 2016 (PacificVis)، تایپه، تایوان، 19 تا 22 آوریل 2016؛ صص 96-103. [ Google Scholar ]
هونگ، اف. بی، سی. گوا، اچ. اونو، ک. یوان، X. چارچوب استفاده مجدد از داده های منحنی انتگرال مبتنی بر فشرده سازی برای تجسم جریان. J. Vis. 2017 ، 20 ، 859-874. [ Google Scholar ] [ CrossRef ]
مک لافلین، تی. جونز، مگاوات؛ لارامی، آر.اس. ملکی، ر. استادان، من. Hansen، CD اقدامات مشابه برای افزایش بذر ساده تعاملی. IEEE Trans. Vis. محاسبه کنید. نمودار. 2013 ، 19 ، 1342-1353. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ویتاکر، RT; میرزرگر، م. کربی، RM کانتور جعبه: روشی برای توصیف عدم قطعیت در مجموعه ویژگی ها از مجموعه های شبیه سازی. IEEE Trans. Vis. محاسبه کنید. نمودار. 2013 ، 19 ، 2713-2722. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
میرزرگر، م. ویتاکر، RT; Kirby, RM Curve boxplot: تعمیم نمودار جعبه برای مجموعه منحنی ها. IEEE Trans. Vis. محاسبه کنید. نمودار. 2014 ، 20 ، 2654-2663. [ Google Scholar ] [ CrossRef ]
دمیر، من. دیک، سی. Westermann, R. نمودارهای چندگانه برای تجسم گروه سه بعدی مقایسه ای. IEEE Trans. Vis. محاسبه کنید. نمودار. 2014 ، 20 ، 2694-2703. [ Google Scholar ] [ CrossRef ]
فرستل، اف. برگر، ک. Westermann, R. نمودارهای تنوع را برای توصیف عدم قطعیت در مجموعه های میدان برداری ساده کنید. IEEE Trans. Vis. محاسبه کنید. نمودار. 2016 ، 22 ، 767-776. [ Google Scholar ] [ CrossRef ]
پست، FH; ورولییک، بی. هاوزر، اچ. لارامی، آر.اس. Doleisch, H. وضعیت هنر در تجسم جریان: استخراج و ردیابی ویژگی. در انجمن گرافیک کامپیوتری ; کتابخانه آنلاین وایلی: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2003; جلد 22، ص 775–792. [ Google Scholar ]
Botchen، RP; ویسکوف، دی. Ertl، T. تجسم تعاملی عدم قطعیت در میدان‌های جریان با استفاده از تکنیک‌های مبتنی بر بافت. در مجموعه مقالات دوازدهمین سمپوزیوم بین المللی در تجسم جریان، گوتینگن، آلمان، 10-14 سپتامبر 2006. صفحات 4051–4056. [ Google Scholar ]
مولدر، سی. استخراج و ردیابی ویژگی Ma، KL Interactive با استفاده از انسجام منطقه. در مجموعه مقالات سمپوزیوم IEEE Pacific Visualization 2009، پکن، چین، 20-23 آوریل 2009. ص 17-24. [ Google Scholar ]
ساور، اف. یو، اچ. Ma، KL ردیابی ویژگی جریان مبتنی بر مسیر در مجموعه داده های ذره/حجم مشترک. IEEE Trans. Vis. محاسبه کنید. نمودار. 2014 ، 20 ، 2565-2574. [ Google Scholar ] [ CrossRef ] [ PubMed ]
هوانگ، دی. لای، جی اچ. Wang، CD Robust گروه بندی با استفاده از مسیرهای احتمال. IEEE Trans. بدانید. مهندسی داده 2015 ، 28 ، 1312-1326. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
هوانگ، دی. وانگ، سی دی; Lai, JH خوشه‌بندی گروهی با وزن محلی. IEEE Trans. سایبرن. 2017 ، 48 ، 1460-1473. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
لی، جی جی; هان، جی. Whang، KY خوشه‌بندی مسیر: یک چارچوب پارتیشن و گروهی. در مجموعه مقالات کنفرانس بین المللی ACM SIGMOD 2007 در مورد مدیریت داده ها، پکن، چین، 11-14 ژوئن 2007. صص 593-604. [ Google Scholar ]
ویتنبرینک، سی ام. Pang، AT; Lodha، SK Glyphs برای تجسم عدم قطعیت در زمینه های برداری. IEEE Trans. Vis. محاسبه کنید. نمودار. 1996 ، 2 ، 266-279. [ Google Scholar ] [ CrossRef ]
هلاواتش، م. لیوب، پی. نواک، دبلیو. Weiskopf، D. گلیف های رادار جریان – تجسم ایستا از جریان ناپایدار با عدم قطعیت. IEEE Trans. Vis. محاسبه کنید. نمودار. 2011 ، 17 ، 1949-1958. [ Google Scholar ] [ CrossRef ]
جیائو، اف. فیلیپس، جی.ام. گور، ی. جانسون، تجسم عدم قطعیت CR در HARDI بر اساس مجموعه‌ای از ODFs. در مجموعه مقالات سمپوزیوم IEEE Pacific Visualization 2012، Songdo، کره، 28 فوریه تا 2 مارس 2012. صص 193-200. [ Google Scholar ]
جارما، م. دمیر، من. کرر، ج. Westermann, R. تحلیل بصری مقایسه ای مجموعه های میدان برداری. در مجموعه مقالات کنفرانس IEEE 2015 در علم و فناوری تجزیه و تحلیل بصری (VAST)، شیکاگو، IL، ایالات متحده آمریکا، 25 تا 30 اکتبر 2015. صص 81-88. [ Google Scholar ]
کدهای باینری Levenshtein، VI که قادر به تصحیح حذف، درج و معکوس هستند. Sov. فیزیک دوکل. 1966 ، 10 ، 707-710. [ Google Scholar ]
Shadden, SC; لکین، اف. Marsden، JE تعریف و خواص ساختارهای همدوس لاگرانژی از شارهای لیاپانوف زمان محدود در جریان های غیر تناوبی دو بعدی. فیزیک D پدیده غیرخطی. 2005 ، 212 ، 271-304. [ Google Scholar ] [ CrossRef ]
کریزیگ، ای. استرود، ک. استفنسون، جی. ریاضیات مهندسی پیشرفته ; جان وایلی پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 1979. [ Google Scholar ]
جارما، م. کرر، ج. Westermann, R. تجزیه و تحلیل بصری مقایسه ای تنوع حمل و نقل در مجموعه های جریان. J. WSCG 2016 ، 24 ، 25-34. [ Google Scholar ]
استر، ام. کریگل، اچ پی؛ ساندر، جی. Xu, X. یک الگوریتم مبتنی بر چگالی برای کشف خوشه ها در پایگاه داده های فضایی بزرگ با نویز. در مجموعه مقالات دومین کنفرانس بین المللی KDD’96 در مورد کشف دانش و داده کاوی، پورتلند، OR، ایالات متحده آمریکا، 2 تا 4 اوت 1996. ص 226-231. [ Google Scholar ]
لندسبرگر، تلویزیون؛ برودکورب، ف. روسکوش، پی. آندرینکو، ن. آندرینکو، جی. Kerren، A. Mobility Graphs: تجزیه و تحلیل بصری دینامیک تحرک انبوه از طریق نمودارهای فضایی-زمانی و خوشه بندی. IEEE Trans. Vis. محاسبه کنید. نمودار. 2015 ، 22 ، 11-20. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
هان، جی. تائو، جی. Wang, C. FlowNet: چارچوب یادگیری عمیق برای خوشه بندی و انتخاب خطوط جریان و سطوح جریان. IEEE Trans. Vis. محاسبه کنید. نمودار. 2018 . [ Google Scholar ] [ CrossRef ]
سانیال، ج. ژانگ، اس. دایر، جی. مرسر، آ. آمبرن، پی. Moorhead، R. Noodles: ابزاری برای تجسم عدم قطعیت مجموعه مدل آب و هوای عددی. IEEE Trans. Vis. محاسبه کنید. نمودار. 2010 ، 16 ، 1421-1430. [ Google Scholar ] [ CrossRef ] [ PubMed ]

شکل 1. گردش کار تجزیه و تحلیل عدم قطعیت در یک میدان برداری مجموعه ای متغیر با زمان.

شکل 2. نتایج معیارهای مختلف: ( الف ) نتیجه AEDR، ( ب ) نتیجه EDR کلاسیک، ( ج ) نتیجه فاصله اقلیدسی، ( د ) نتیجه DTW، ( e ) نتیجه LCSS، و ( f ) نتیجه از ERP

شکل 3. ردیابی مسیر تک مکان و محله: ( الف ) ردیابی مسیر تک مکان و ( ب ) ردیابی مسیر محله.

شکل 4. نمای طبقه‌بندی: ( الف ) چهار ناحیه از فضای طبقه‌بندی و نقاط شبکه نگاشت شده و ( ب ) رندر فیلد برداری اصلی با رنگ‌های استفاده شده در ( a ).

شکل 5. رابط های UP-Vis: ( الف ) پانل پارامتر، ( ب ) نمای رندر عدم قطعیت، ( ج ) نمای طبقه بندی، ( د ) نمای خط مسیر، ( ه ) نمای طرح ریزی، و ( f ) نمای مقایسه.

شکل 6. نتایج خوشه بندی با پارامترهای مختلف: ( الف ) نمای خط مسیر و نمای پیش بینی اعضای خط مسیر قبل از خوشه بندی. ( ب ) نمای خط مسیر و نمای طرح ریزی اعضای خط مسیر خوشه ای با

E p s

= 0.8 و

M i n P t s

= 1; ( ج ) نمای مسیر و نمای طرح ریزی اعضای خط مسیر خوشه ای با

E p s

= 0.75 و

M i n P t s

= 1; و ( د ) نمای مسیر و نمای طرح ریزی اعضای خط مسیر خوشه ای با

E p s

= 0.75 و

M i n P t s

= 2.

شکل 7. Shuttlecock برای خط مسیر گروه: ( الف ) نمایش اعضای خط مسیر خوشه ای با

E p s

= 0.8 و

M i n P t s

= 1; ( ب ) نمایش اعضای خط مسیر خوشه ای با

E p s

= 0.75 و

M i n P t s

= 1; و ( ج ) نمایش اعضای خط مسیر خوشه ای با

E p s

= 0.75 و

M i n P t s

= 2.

شکل 8. طرح های جایگزین: ( الف ) نمایش نقاط مسیر تمام مهرهای زمانی در داخل کانتور. ( ب ) نمایش نقاط مسیر و خطوط مرکزی. و ( ج ) ترکیب نقاط مسیر، خطوط مرکزی، و خطوط بیرونی.

شکل 9. نمای مقایسه ای محل مشخص شده “B” در شکل 14b.

شکل 10. الگوهای انتقال در مجموعه داده های DG: ( الف ) ارائه عدم قطعیت محلی (LU)، ( ب ) الگوی انتقال مکان “A”، ( ج ) نمای پیش بینی مکان “A” با نقاط انتخاب شده، ( d ) روند انتخاب شده، ( ه ) الگوی حمل و نقل مکان “B”، ( f ) الگوی حمل و نقل مکان “C”، و ( ز ) روندهای حمل و نقل پنهان مکان “C” که با مسواک زدن نقاط خاص آشکار می شود.

شکل 11. الگوهای انتقال در مجموعه داده دو چرخه (DG): ( الف ) ارائه عدم قطعیت همسایگی (NU)، ( ب ) ارائه همبستگی عدم قطعیت (CU)، و ( ج ) نمای مقایسه مکان “B” در زیرشکل های ( a , b ).

شکل 12. نتایج LU مجموعه داده ECMWF: ( الف ) نتیجه AEDR، ( ب ) نتیجه EDR کلاسیک، ( ج ) نتیجه فاصله اقلیدسی، ( d ) نتیجه DTW، ( e ) نتیجه LCSS، و ( f ) ) نتیجه ERP.

شکل 13. الگوهای حمل و نقل مکان های مشخص شده در شکل 12 الف: ( الف ) الگوی حمل و نقل در مکان “A”، ( ب ) الگوی حمل و نقل در مکان “B”، و ( ج ) الگوی حمل و نقل مکان “C”.

شکل 14. تجزیه و تحلیل همسایگی داده های ECMWF: ( الف ) نمای طبقه بندی، ( ب ) ارائه CU، و ( ج ) نمای مقایسه مکان “A”.

شکل 15. زمان محاسبه مجموعه داده های مصنوعی DG با اعداد مجموعه مختلف با استفاده از پیاده سازی CUDA و اجرای تک رشته ای.

شکل 16. نتایج AEDR برای مجموعه داده های DG با استفاده از آستانه های مختلف: ( الف ) نتیجه AEDR با

δ = 20

، و ( ب ) نتیجه AEDR با

δ = 30

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

خلاصه

کلید واژه ها:

1. معرفی

2. کارهای مرتبط

2.1. تحلیل عدم قطعیت در زمینه برداری

2.2. شباهت خط مسیر

2.3. تجسم میدان برداری

3. بررسی اجمالی

4. محاسبه عدم قطعیت برای میدان برداری مجموعه

4.1. EDR تطبیقی ​​و عدم قطعیت محلی

4.2. ارزیابی

4.2.1. قابلیت آشکارسازی ویژگی ها

4.2.2. حساسیت به موارد پرت

4.3. عدم قطعیت و همبستگی همسایگی

4.4. فضای طبقه بندی

5. تحلیل بصری عدم قطعیت

5.1. استخراج الگوی حمل و نقل

5.2. تجسم شاتل

5.3. مقایسه با الگوهای همسایگی

6. مطالعه موردی

6.1. مجموعه داده های مصنوعی دو چرخه

6.1.1. کاوش الگوی حمل و نقل

6.1.2. تحلیل همبستگی همسایگی

6.2. مجموعه داده های شبیه سازی گروه ECMWF

6.2.1. مقایسه و تحلیل الگوی حمل و نقل

6.2.2. تحلیل همبستگی همسایگی

7. بحث

7.1. پیاده سازی و عملکرد

7.2. مولفه های

8. نتیجه گیری و کار آینده

منابع

قبلیتغییرات کاربری مکانی – زمانی و پاسخ در الگوی منظر به Hemeroby در یک شهر مبتنی بر منابع

بعدیاستخراج مناطق ساختمانی از فتوگرامتری DSM و DOM با انتخاب خودکار نمونه های آموزشی از داده های DLG تاریخی

مطالب مرتبط ...

آموزش مقاله نویسی در رشته ادبیات فارسی

تأثیر همسایگی درونیابی DEM بر عوامل زمین

رگرسیون وزنی جغرافیایی تطبیقی ​​غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

خبرنامه

خبرنامه

درباره سرزمین فناوری مکانی GISLAND

دسترسی سریع

اطلاعات

دسترسی سریع

4.1. EDR تطبیقی و عدم قطعیت محلی

رگرسیون وزنی جغرافیایی تطبیقی غیر منفی برای تخمین تراکم جمعیت بر اساس نور شب