خلاصه

هنگام کار با داده های منطقه ای از کشورهای مختلف، مسائل مربوط به مقایسه داده ها باید حل شود، از جمله مقایسه منطقه ای. اندازه واحدهای منطقه‌ای متفاوت یک موضوع رایج است که بر نتایج تحلیل‌های اجتماعی-اقتصادی تأثیر می‌گذارد. در این مقاله، ما یک استراتژی برای مقابله با عدم مقایسه منطقه ای داده های اداری در تحقیقات بین المللی معرفی می کنیم. ما یک رویکرد روش‌شناختی مبتنی بر روش درون‌یابی منطقه‌ای پیشنهاد می‌کنیم که استفاده از تحلیل‌های فضایی پیشرفته را تسهیل می‌کند. برای نشان دادن، ما الگوهای فضایی بیکاری را در هفت کشور اروپای مرکزی تحلیل می‌کنیم. ما از یک سطح مکانی (شهری) بسیار دقیق برای آشکار کردن تمایلات محلی استفاده می کنیم. برای داشتن واحدهای قابل مقایسه در کل منطقه، از روش درون یابی منطقه ای استفاده می کنیم. فرآیند پیش‌بینی داده‌ها از واحدهای اداری منبع به ساختار هدف یک شبکه. پس از انتخاب مناسب ترین ساختار شبکه و نمایش داده ها بر روی شبکه، ما یک تجزیه و تحلیل نقطه داغ را برای نشان دادن مزایای ساختار شبکه برای تحلیل های اجتماعی-اقتصادی انجام می دهیم. رویکرد پیشنهادی به دلیل صحت روش‌شناختی و توانایی تفسیر نتایج، پتانسیل زیادی در تحقیقات بین‌المللی دارد.

کلید واژه ها:

درون یابی منطقه ای ; وزن دهی منطقه ساده کریجینگ منطقه ای ; تجزیه و تحلیل نقطه داغ ; قابلیت مقایسه داده ها تحقیقات بین المللی

1. معرفی

ما در عصر داده های باز و کلان زندگی می کنیم. داده های سطح خرد و فردی فضایی برای محققان در سراسر رشته ها در دسترس است. در مورد داده‌های منطقه‌ای آماری، جغرافی‌دانان انسانی و دانشمندان منطقه‌ای معمولاً می‌خواهند با دقیق‌ترین واحدهای موجود، مانند کدهای پستی یا شهرداری‌ها کار کنند. این داده‌ها ما را قادر می‌سازد تا ویژگی‌های محلی را شناسایی کنیم، که ممکن است هنگام کار با واحدهای منطقه‌ای بزرگ‌تر پنهان شوند. با این حال، یافتن تحلیل‌های بین‌المللی خرد منطقه‌ای با استفاده از چنین داده‌های دقیق غیرمعمول است. اگرچه دولت ها پول زیادی را برای هماهنگ سازی داده های خاص کشور سرمایه گذاری می کنند، اما در دسترس بودن داده های قابل مقایسه هنوز مشکل ساز است. می توان آن را در مثالی از تحقیقات تطبیقی ​​بین ملی [ 1 ] یا زیرساخت داده های مکانی [ 2 ] مستند کرد.].
حتی اگر داده‌ها در دسترس باشند، باید هنگام استفاده از داده‌های با جزئیات مکانی مراقب باشید. قبل از انجام تحلیل های آماری و مکانی اغلب به تنظیمات خاصی نیاز است. به طور کلی، زیرساخت‌های داده‌های مکانی منطقه‌ای و محلی سریع‌تر از زیرساخت‌های ملی و جهانی توسعه می‌یابند، زیرا «روش‌های پیچیده‌تر برای هماهنگ‌سازی داده‌ها که از منابع بسیاری با استانداردهای مختلف می‌آیند و شامل تعداد زیادی بازیگر می‌شود» ([ 2 ]، p. 62). بنابراین، جای تعجب نیست که به دلیل در دسترس بودن و مقایسه کم داده ها، تحلیل های بین المللی در سطح خرد منطقه ای وجود نداشته باشد.
هنگام انجام تحلیل های تجربی با استفاده از داده های چندین کشور، چندین موضوع روش شناختی وجود دارد. سه جنبه مقایسه پذیری داده ها بر تحلیل ها تأثیر می گذارد: موضوع (تعاریف، قوانین مختلف، سرشماری در مقابل نمونه ها)، زمان (زمان جمع آوری داده ها، تناوب)، و مکان/منطقه (تحدید فضایی واحدها با اشکال مختلف و اندازه های متوسط). . ساختارهای منطقه ای متفاوت در کشورهای مختلف سومین موضوعی است که می خواهیم به آن بپردازیم. اندازه های مختلف واحد ممکن است مانع از تجزیه و تحلیل و انحراف نتایج شود. در اروپا، اداره آمار EUROSTAT تلاش می کند تا داده های قابل مقایسه از همه کشورهای عضو را از طریق تعیین حدود منطقه ای استاندارد داشته باشد. در حالی که EUROSTAT تا حدی در معرفی واحدهای استاندارد در سطح بالاتر موفق بوده است (NUTS 2)،
هدف اصلی این مقاله معرفی راهبردی در مورد نحوه برخورد با موضوع مقایسه‌پذیری منطقه‌ای است که یکی از بسیاری از موضوعات مرتبط با قابلیت مقایسه داده‌ها است. تفاوت‌های بین سیستم‌های ملی، تحلیل‌ها را مختل می‌کند و بر تفسیر نتایج تأثیر می‌گذارد، که باید زمینه ملی را منعکس کند [ 3 ]. کار با ساختار یکنواخت و منطقه ای به جای سیستم های اداری متفاوت راه حلی برای مسئله مقایسه منطقه ای است. ممکن است استفاده و تفسیر تحلیل‌های فضایی پیشرفته را در تحقیقات بین‌المللی تسهیل کند. بنابراین، تبدیل داده های مکانی منطقه-منطقه باید اعمال شود [ 4]. ما یک رویکرد روش‌شناختی مبتنی بر درون‌یابی منطقه‌ای را به عنوان راحت‌ترین روش برای دستیابی به هدف اصلی پیشنهاد می‌کنیم. ما به طور خاص سؤالات زیر را می پرسیم: مزایای اصلی این رویکرد چیست؟ آیا نقاط قوتش بیشتر از کاستی هایش است؟ سوگیری های احتمالی چیست؟
معمولاً از درون یابی منطقه ای برای محاسبه مجدد از یک ساختار منبع به یک ساختار هدف از پیش تعریف شده استفاده می شود [ 5 ]. ما از این روش به روشی کمی متفاوت استفاده می کنیم تا واحدهای منطقه ای در کشورهای مختلف را به یک ساختار فضایی استاندارد همگن کنیم. این همگن سازی از نظر روش شناختی برای تحلیل های فضایی و آمارهای بعدی بر اساس طرح های وزن دهی فضایی دقیق تر است. علاوه بر این، به ما کمک می کند تا نتایج را با دقت بیشتری تفسیر کنیم. ما این را با مثال خودهمبستگی فضایی (تحلیل نقطه داغ) بیان می کنیم که به آشکار کردن الگوهای فضایی کمک می کند. با این حال، برای مقایسه بهتر داده ها در سیستم های مختلف (مانند کشورها) یا در طول زمان در سطوح مختلف جغرافیایی [ 6]، بهتر است با یک شبکه معمولی کار کنید. برای انجام این کار، ابتدا باید مقادیر را از واحدهای منبع به این شبکه معمولی دوباره محاسبه کنیم. این مقاله دو روش مختلف درون یابی منطقه ای را برای این اهداف در نظر گرفته و آزمایش می کند، (1) وزن دهی منطقه ساده و (2) کریجینگ سطحی.
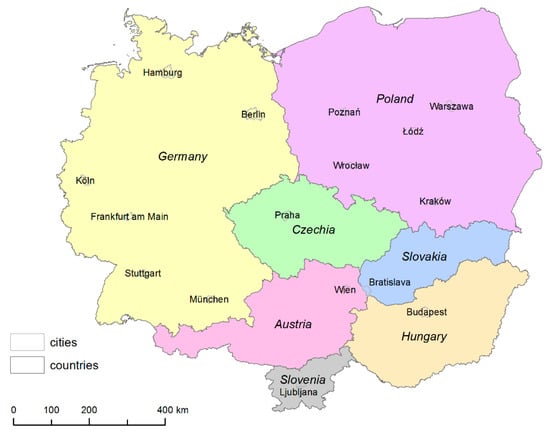
ما این روش را در مورد بیکاری در منطقه ای از اروپای مرکزی متشکل از هفت کشور (اتریش، چک، آلمان، مجارستان، لهستان، اسلواکی و اسلوونی) به نمایش می گذاریم. مسائل مقایسه‌پذیری به‌ویژه در اینجا قابل مشاهده است، به‌ویژه زمانی که ساختار منطقه‌ای بسیار پراکنده در چک (بیش از 6000 شهرداری، به طور متوسط ​​12 کیلومتر مربع) و لهستان (کمتر از 2500 شهرداری با میانگین بیش از 120 کیلومتر مربع) را مقایسه کنید. علاوه بر تفاوت اندازه ساختار منطقه ای در کشورهای مربوطه، تفاوت بین اندازه شهرداری در این کشورها بسیار زیاد است. به عنوان مثال، پراگ دارای مساحت 496 کیلومتر مربع است که بیش از 30 برابر بزرگتر از میانگین شهرداری چک است. به عنوان یک مجموعه داده آزمایشی، از داده های بیکاری در سال 2010 استفاده کردیم.

2. تبدیل داده های مکانی از طریق درونیابی منطقه ای

موضوع تبدیل داده های مکانی بین دو سیستم مختلف از واحدهای فضایی به طور سنتی یک موضوع چالش برانگیز در ادبیات مکانی است [ 4 ، 7 ، 8 ]. در زمین آمار، تبدیل داده های مکانی اغلب به عنوان مشکل تغییر پشتیبانی (COSP) نامیده می شود [ 5 ، 7 ]. بسته به نوع منبع و داده های فضایی هدف (نقطه، خط، مساحت، سطح)، ما می توانیم بین بسیاری از COSP ها با استفاده از تکنیک های درون یابی فضایی مختلف تمایز قائل شویم. برای اهداف خود، ما از روش درون یابی منطقه ای و COSP منطقه-مساحت استفاده می کنیم. برای شرح و بررسی دقیق COSP و تکنیک های درون یابی فضایی، [ 4 ، 7 ] را ببینید.
درون یابی مساحتی (یا تخمین سطح متقابل) ما را قادر می سازد تا مقادیر را از یک تحدید چند ضلعی به دیگری محاسبه کنیم. این به عنوان “مجموعه ای از روش هاست که می تواند یک ویژگی کلی از یک سیستم واحد منطقه ای را بر اساس سیستم دیگری که از نظر مکانی ناسازگار است، تخمین بزند که داده های ویژگی در آن جمع آوری شده است” ([ 9 ]) درک می شود.]، پ. 645). به طور کلی، درون یابی منطقه ای تبدیل داده ها از یک مجموعه چند ضلعی به مجموعه دیگر است، یعنی از ساختار منطقه ای مبدا به ساختار منطقه ای هدف. این به ما اجازه می دهد تا مقیاس را تغییر دهیم، به عنوان مثال، سطح منطقه ای داده های مورد مطالعه را کاهش دهیم یا ارتقا دهیم. بنابراین می‌توان پدیده‌ها را در تراکت‌های سرشماری از داده‌های شهرداری پیش‌بینی کرد و بالعکس. بسیاری از روش‌ها و تکنیک‌های درونیابی با داده‌ها و الزامات فرضی متفاوت توسعه داده شده‌اند [ 10 ]. دو رویکرد اساسی، روش های نقشه برداری و زمین آماری (سطح محور) [ 5 ] است.
رویکردهای کارتوگرافی درون یابی منطقه ای بر اساس وزن دهی به وسیله ناحیه همپوشانی بین واحدهای منبع (شهرداری) و هدف (سلول های شبکه) [ 5 ] است. ما از ساده ترین شکل، روش وزن دهی منطقه ای ساده استفاده می کنیم. در این روش از اندازه ناحیه منبع و هدف برای وزن دادن به مقادیر ناحیه منبع استفاده می شود که حجم جمعیت اصلی را حفظ می کند. یکی از محدودیت های این روش ساده این است که توزیع یکنواخت جمعیت در هر منطقه منبع (شهرداری) فرض می شود [ 9 ، 11 ]] که به ندرت در واقعیت جغرافیایی صادق است. با این حال، این موضوع در مورد ما مطرح نیست، زیرا هدف ما تشخیص الگوهای فضایی کلی است، نه برآورد دقیق مقیاس خرد. سایر تکنیک‌های پیشرفته‌تر با این انتظار واقع‌بینانه‌تر سروکار دارند که مناطق منبع ناهمگن هستند اما ساختاری ناشناخته دارند [ 12 ].
روش های زمین آماری سطح تولید می کنند و اغلب به عنوان سطح گرا [ 5 ] نامیده می شوند. ما از یک تکنیک درونیابی زمین آماری استفاده می کنیم که نظریه کریجینگ را به داده های جمع آوری شده روی چند ضلعی ها مانند شمارش گسسته گسترش می دهد. این تکنیک با روش های درونیابی زمین آماری استاندارد که اندازه های چند ضلعی را در نظر نمی گیرند و با داده های نقطه ای یا مرکز به عنوان نماینده داده های چند ضلعی کار می کنند متفاوت است. در درونیابی منطقه ای بر اساس تکنیک جداسازی کریجینگ [ 13]، جمع آوری مجدد داده های چند ضلعی از شهرداری ها به یک شبکه منظم یک فرآیند دو مرحله ای است. اول، یک سطح پیش‌بینی صاف از داده‌های یک ساختار منطقه‌ای منبع، شهرداری‌ها در مورد ما ایجاد می‌شود. به دلیل ماهیت داده‌های ما، که در شهرداری‌ها در یک دوره خاص اندازه‌گیری می‌شوند، ما از درون‌یابی منطقه‌ای برای شمارش رویدادها استفاده می‌کنیم. این تکنیک سطحی را ایجاد می‌کند که شانس اصلی شناسایی یک فرد (15 تا 64 ساله، در مورد ما بیکار) را در یک مکان خاص پیش‌بینی می‌کند. سطح پیش بینی شده را می توان به عنوان یک نقشه چگالی تفسیر کرد. برای ساخت یک مدل معتبر و یافتن سطح با کمترین خطای استاندارد، از واریوگرافی تعاملی استفاده کردیم. دوم، سطح پیش‌بینی به مجموعه جدید چندضلعی‌ها تجمیع می‌شود.
برای اهداف ما، ما دو روش درون یابی منطقه ای، وزن دهی منطقه ساده و کریجینگ منطقه ای را اعمال و مقایسه می کنیم. قبل از اینکه بتوانیم از هر دو روش استفاده کنیم، لازم است یک ساختار منطقه ای هدف را انتخاب کنیم. ما تصمیم گرفتیم یک ساختار شبکه ای منظم ایجاد کنیم که در بسیاری از مطالعات جمعیت یافت می شود [ 14 ، 15 ]. ما این کار را در کل منطقه مورد مطالعه انجام دادیم تا تفاوت‌های اندازه شهرداری را در کشورهای مربوطه هماهنگ کنیم. ما از بهترین گرید بر اساس آمار برازش استفاده می کنیم. مهم است که تأکید شود که این افزایش یا کاهش مقیاس نیست، بلکه همگن سازی است. در نتیجه، ما همچنان می‌توانیم با جزئیات فضایی کافی کار کنیم. درون یابی بیش از حد پراکنده پواسون به ما امکان می دهد تعداد شمارش ها را برای هر مربع مشخص شده در یک شبکه منظم پیش بینی کنیم.

هر COSP، از جمله درون یابی منطقه ای، خطای تبدیل ایجاد می کند. خطای احتمالی درون یابی منطقه ای را می توان با دو معیار تعریف شده توسط سیمپسون [ 16 ] تخمین زد: درجه سلسله مراتب و درجه تناسب. این معیارها میزان برآورد درگیر در فرآیند تبدیل داده از یک سیستم فضایی به سیستم دیگر را بیان می کند. درجه سلسله مراتب برای کل منطقه مورد مطالعه برابر است با نسبت تمام مناطق منبع (شهرداری) که به طور کامل در هر یک از مناطق هدف (شبکه ها) قرار می گیرند [ 8 ، 16 ]. شواهدی از لانه سازی می دهد. درجه سلسله مراتب [ 16 ] به صورت زیر محاسبه می شود:

∑منj(wمنj،منf (wمنj=1))n*100

جایی که i = یک واحد فضایی منبع (شهرداری)، j = یک واحد فضایی هدف (سلول شبکه)، w ij = نسبت شهرداری که با سلول شبکه همپوشانی دارد، و n = تعداد واحدهای منبع (شهرداری). درجه تناسب برای کل منطقه مورد مطالعه، نسبت مجموع حداکثر وزن هر واحد منبع (شهرداری) و تعداد همه واحدهای منبع (شهرداری) است [ 8 ، 16 ]. میزان همپوشانی بین دو سیستم فضایی را اندازه گیری می کند. این اندازه گیری دقیق تر است زیرا تشخیص می دهد که مرزهای شهرداری ممکن است نزدیک به مرزهای سلول شبکه باشد حتی زمانی که دقیقاً با آنها مطابقت ندارند. درجه تناسب [ 16] به صورت زیر محاسبه می شود:

∑من(حداکثرwمنj)n*100

که در آن max w ij حداکثر نسبت همپوشانی شهرداری i به شبکه j است. همانند سایر محققانی که با درون یابی منطقه ای سروکار دارند [ 8 ، 17 ]، ما نیز از این دو معیار سیمپسون برای تخمین «خوبی تناسب» بین ساختار منطقه ای واقعی و ساختارهای منظم با اندازه های شبکه متفاوت استفاده می کنیم.

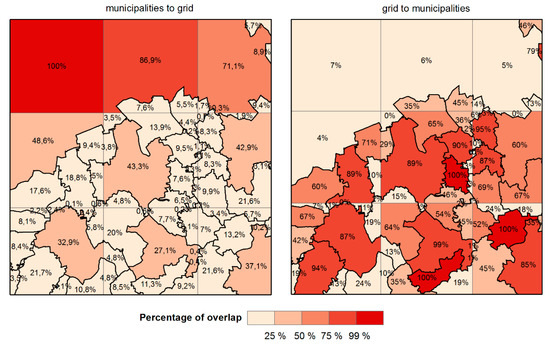
این آمار برازش برای انتخاب بهترین ساختار شبکه هدف مناسب استفاده شد. ابتدا، همپوشانی بین شهرداری‌ها و ساختار شبکه را برای اندازه‌های مختلف سلول‌های شبکه ارزیابی کردیم. ما هر دو جهت این درجات را در نظر می گیریم: شهرداری ها به شبکه (چگونه شهرداری ها در شبکه قرار می گیرند) و شبکه به شهرداری ها (نحوه تناسب شبکه با ساختار شهرداری). تفاوت بین محاسبات درصد همپوشانی برای درجه تناسب با تجسم در شکل 1 به بهترین شکل مستند شده است.. معمولاً فقط از یک جهت استفاده می شود. در مورد استفاده ما، داشتن حداکثر تعادل ممکن بین این دو جهت مهم است. از آنجایی که ما به دنبال بهترین راه حل مناسب هستیم و ساختار هدف مشخصی نداریم، از درجه تناسب به عنوان “تناسب دو طرفه” استفاده می کنیم.

3. منطقه اروپای مرکزی به عنوان یک مطالعه موردی

منطقه اروپای مرکزی (CER) به عنوان یک منطقه مطالعه موردی برای آزمایش استراتژی ما برای مقابله با داده های تجربی عمل می کند. ما داده‌های بیکاری قابل مقایسه را در سطح مکانی (شهرداری) بسیار دقیق در یک منطقه جغرافیایی بین‌المللی نسبتاً بزرگ جمع‌آوری کردیم. منطقه مورد مطالعه شامل هفت کشور اروپای مرکزی است: اتریش، چک، آلمان، مجارستان، لهستان، اسلواکی و اسلوونی. این هفت کشور الزامات ما را برآورده کردند و یک منطقه مطالعاتی بزرگ مناسب برای اهداف روش شناختی ما ایجاد کردند – این یک منطقه فشرده با ساختارهای منطقه ای مختلف (اندازه های شهرداری) است. همچنین به دلیل الگوهای فضایی قابل توجه بیکاری، پتانسیل تجزیه و تحلیل های تجربی بعدی را دارد. ما از ادراک مشکل ساز و تحدید حدود اروپای مرکزی آگاه هستیم [ 18]، اما ما از عبارت منطقه اروپای مرکزی (CER) در سراسر مقاله استفاده می کنیم. CER در شکل 2 نشان داده شده است .
هنگام تجزیه و تحلیل داده های منطقه ای، باید با مشکل واحد منطقه قابل تغییر (MAUP) مواجه شد. MAUP هر زمان که ما با داده های انبوه مکانی کار می کنیم، صرف نظر از رشته علمی، ایجاد می شود. این مشکل شناخته شده حساسیت نتایج را به انتخاب دلخواه واحدهای تجمع فضایی نشان می دهد که در آن تجزیه و تحلیل انجام می شود [ 19 ، 20 ]. زمانی که از ساختار منطقه ای کمتر تکه تکه (در نتیجه انباشته تر) استفاده می شود، نتایج احتمالاً مغرضانه هستند [ 21 ، 22 ].
با انتخاب حدود یا منطقه بندی مختلف، می توان به نتایج بسیار متفاوت یا حتی متناقضی دست یافت. بنابراین تفسیر نتایج تحت تأثیر ساختار منطقه ای انتخاب شده مورد استفاده قرار می گیرد. برای کاهش مشکل MAUP، می توان از دقیق ترین داده های موجود استفاده کرد، همانطور که در اینجا انجام دادیم. در این مورد، شهرداری ها (LAU2—واحدهای اداری محلی در اتحادیه اروپا) هستند. با این حال، تفاوت های زیادی در ساختارهای منطقه ای در کشورهای مربوطه وجود دارد، جدول 1 را ببینید .
مشکل دیگر داده است. اولاً، بسیاری از ویژگی های اجتماعی-اقتصادی در چنین سطح دقیقی در دسترس نیستند. دوم، تعریف یک مشخصه اغلب در کشورهای مربوطه متفاوت است و این مسئله مقایسه پذیری داده ها باید حل شود. نرخ بیکاری به عنوان یکی از معدود ویژگی های اقتصادی موجود در سطح مکانی دقیق و ضروری انتخاب شد. از آنجایی که نرخ بیکاری در هر کشور کمی متفاوت تعریف می شود، ما به یک تعریف مشترک بسنده کرده ایم. نرخ بیکاری همانطور که در این مقاله تعریف می کنیم، سهم افراد بیکار (جویندگان کار) در بین جمعیت 15 تا 64 ساله است. ما از داده های سال 2010 (بیکاران در اکتبر 2010 و جمعیت در 31 دسامبر 2010) استفاده می کنیم که از منابع رسمی آماری در کشورهای مورد مطالعه به دست آمده است. لازم به ذکر است که با توجه به تعریف متفاوتی که در این مقاله از بیکاری استفاده شده است، نتایج با آمار رسمی منتشر شده قابل مقایسه نبوده و کمتر از نرخ های موجود در جاهای دیگر است. برای آمار توصیفی بیکاری در کشورهای مورد مطالعه ر.کجدول 2 .
حتی زمانی که مناسب‌ترین داده‌ها انتخاب شده‌اند، موضوع ساختارهای منطقه‌ای نسبتاً غیرقابل مقایسه حل‌نشده باقی می‌ماند. بنابراین، ما روش درون یابی منطقه ای را اعمال می کنیم. این ساختارهای منطقه ای متفاوت در کشورهای مورد مطالعه را به یک ساختار شبکه ای منظم برای کل منطقه مورد مطالعه تبدیل می کند. با این حال، ما هنوز باید بهترین اندازه شبکه خاص را انتخاب کنیم. ما این کار را با استفاده از آمار برازش انجام می دهیم. ابتدا، همپوشانی بین شهرداری‌ها و ساختار شبکه را برای اندازه‌های مختلف سلول‌های شبکه ارزیابی کردیم. ما هر دو جهت این درجات را در نظر می گیریم: شهرداری ها به شبکه (چگونه شهرداری ها در شبکه قرار می گیرند) و شبکه به شهرداری ها (نحوه تناسب شبکه با ساختار شهرداری).
ما از دو معیار سیمپسون برای تخمین «خوبی تناسب» بین ساختار منطقه‌ای واقعی شهرداری‌ها و سازه‌های منظم با اندازه‌های شبکه متفاوت در حال تغییر از 1 تا 10 کیلومتر با تاخیر 1 کیلومتری استفاده می‌کنیم. مقادیر حاصل از درجه سلسله مراتب و درجه تناسب برای 10 ساختار شبکه مختلف در شکل 3 نشان داده شده است.. بر اساس تعداد سلول ها (نزدیک به تعداد شهرداری ها، 28937) و بالاترین تعادل بین درجه تناسب برای مسیرهای شبکه به شهرداری و شهرداری به شبکه، توصیه می کنیم از شبکه با سلول های 6 × 6 استفاده کنید. کیلومتر برای این منطقه خاص. انتخاب شبکه 6 کیلومتری با تقاطع نمودارهای شهرداری به شبکه و شبکه به شهرداری هر دو درجه تناسب و درجه سلسله مراتب قابل مشاهده است. هنگام افزایش یا کاهش اندازه سلول ها، درجه در یک جهت افزایش می یابد اما در جهت دیگر به طور قابل توجهی کاهش می یابد. هدف این است که هر دو جهت درجه را به حداکثر برسانیم.
در جدول 3 ، خوب بودن آمار برازش برای ساختار شهرداری و شبکه 6 کیلومتری در تمامی کشورهای مورد مطالعه مشاهده می شود. از این ارقام، تفاوت‌ها در ساختار منطقه‌ای مشخص است، لهستان و چک بزرگترین نقاط پرت هستند. در چک، ساختار منطقه‌ای بسیار پراکنده با درجه نسبتاً کم تناسب در جهت شبکه به شهرداری ثبت شده است (شهرداری‌ها کوچکتر از شبکه هستند). در لهستان، کمترین ساختار تکه تکه شده از کشورهای مورد مطالعه با درجه نسبتاً پایین تناسب در جهت شهرداری ها به شبکه مستند شده است (شهرداری ها بزرگتر از شبکه هستند). با این حال، اندازه شبکه انتخابی 6 کیلومتری بهترین درجه تناسب متوسط ​​را برای هر دو جهت و همه کشورهای مورد مطالعه دارد.
با این حال، ممکن است مشکلی با قرارگیری دقیق شبکه معمولی وجود داشته باشد. بنابراین، ما مکان های مختلف شبکه را با توجه به درجه تناسب آزمایش کرده ایم. ما شبکه 6 کیلومتری را در هر جهت 1 کیلومتر تغییر دادیم (هر دو محور x و y) و 36 محل قرارگیری شبکه ممکن را آزمایش کردیم. برای هر 6 کیلومتر قرار دادن شبکه، درجه تناسب را برای هر دو جهت (شهرداری به شبکه و شبکه به شهرداری) اندازه‌گیری کردیم. مقادیر حاصل از درجه برازش اندازه گیری شده تفاوت معنی داری ندارند (با حداکثر درجه برازش 62.44، حداقل 62.18 و میانگین 62.31). بنابراین، ممکن است نتیجه بگیریم که قرارگیری شبکه برای نتایج ما مهم نیست.
هنگامی که داده ها در یک شبکه منظم هستند، می توانیم داده ها را با استفاده از روش های مکانی استاندارد مانند همبستگی مکانی محلی تجزیه و تحلیل کنیم. خودهمبستگی فضایی به شناسایی الگوی فضایی بیکاری، خوشه های فضایی احتمالی یا محورهای توسعه کمک می کند. در این مقاله، ما از تحلیل نقطه داغ، به‌ویژه آمار فضایی Getis–Ord (Gi*) استفاده می‌کنیم [ 23 ، 24]. این نوع خوشه‌های زیاد و کم پایین (در سطوح معنی‌داری مختلف) را تجسم می‌کند و نقاط داغ و نقاط سرد از نظر آماری معنی‌دار را شناسایی می‌کند. برای ایجاد یک نقطه داغ از نظر آماری معنی دار، یک پدیده با ارزش بالا باید توسط پدیده های دیگر با ارزش های بالا نیز احاطه شود. هنگام استفاده از تجزیه و تحلیل نقطه داغ، مفهوم مجاورت مهم است. مجاورت با استفاده از وزنه های فضایی تعیین می شود. طرح وزن دهی فضایی تعریف می کند که کدام واحدها (شهرداری ها، در مورد ما) برای محاسبه تجزیه و تحلیل نقطه داغ نزدیک در نظر گرفته می شوند. انتخاب وزن فضایی متفاوت ممکن است بر نتایج نهایی تأثیر بگذارد. برای بحث در مورد اهمیت وزن های فضایی، [ 25 ] را ببینید]. اگرچه انتخاب یک طرح وزن دهی فضایی خاص دلخواه است و بر نتایج نهایی تأثیر می گذارد، بر اساس شواهد از ادبیات [ 25 ]، ما این موضوع را مهم نمی دانیم. اهمیت وزن فضایی نیز با درون یابی منطقه ای که داده ها را قبل از انجام تجزیه و تحلیل نقطه داغ تنظیم می کرد، کاهش می یابد. در این مقاله از مجاورت ملکه ( مرتبه 1) در تجزیه و تحلیل نقطه داغ استفاده می کنیم.

4. نتایج تجربی

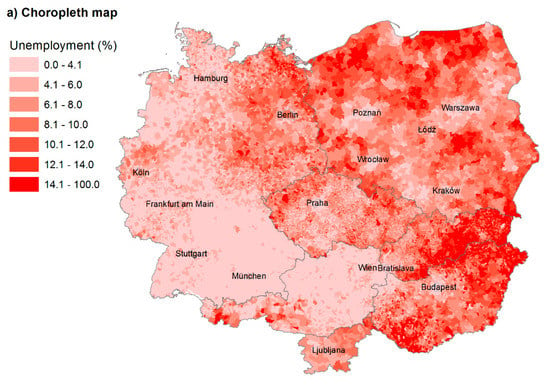
ابتدا، الگوهای فضایی بیکاری در منطقه CER توسط یک نقشه choropleth تجسم شده است ( شکل 4 a را ببینید). 28937 شهرداری وجود دارد. حتی از این تجسم ساده، تفاوت شدید بین بیکاری در غرب و شرق و همچنین سطوح بیکاری مطلوب تر در تجمعات بزرگتر قابل مشاهده است. با این حال، نقشه نسبتاً پراکنده است و جدای از نتایج ذکر شده، تفسیر آن دشوار است. واحدهای بزرگتر تسلط دارند و توجه ما را به خود جلب می کنند (مانند شهرداری های لهستان یا شهرهای بزرگتر). علاوه بر این، اندازه‌های مختلف شهرداری‌ها در کشورهای مورد مطالعه اجازه تفسیر خوشه‌های فرامرزی را نمی‌دهند.
پس از داشتن سطح بیکاری، می‌توانیم به تحلیل نقطه داغ، یعنی آمار فضایی Getis–Ord (Gi*) ادامه دهیم [ 23 ، 24 ]. تجزیه و تحلیل نقطه داغ در قالب یک نقشه خوشه ای ارائه شده است ( شکل 4 ب). برای مثال، اگر داده‌های بیکاری را داشته باشیم، می‌توانیم بررسی کنیم که آیا مقادیر بیکاری در شهرداری‌های نزدیک به هم شبیه‌تر است یا خیر. اگر آنها وجود داشته باشند، خودهمبستگی فضایی مثبت وجود دارد و یک خوشه (انواع زیاد- زیاد یا کم-پایین) تشکیل می شود. اگر مقادیر به طور تصادفی در فضا توزیع شوند، هیچ همبستگی مکانی وجود ندارد. ما کل CER را به عنوان یک سیستم، بنابراین با یک میانگین در نظر می گیریم.
نقاط سرد (آبی) سطح پایین بیکاری را نشان می دهد، در حالی که نقاط داغ (قرمز) سطوح بالای بیکاری را نشان می دهد. شکاف غرب به شرق هنوز قابل مشاهده است. با این حال، در حالی که مرز بین آلمان غربی سابق و آلمان شرقی مبهم است، مرز آلمان – چک از سمت باواریا و مرز اتریش – چک بسیار تیز هستند، یک استثناء محور کم ارتفاع است که از پراگ کشیده شده است. به نظر می رسد این مرز تاریخی از اینرسی بالایی برخوردار است. علاوه بر این، از آنجایی که بیکاری با بازار کار مرتبط است، مرز در مورد مرزهای ملی با مانع زبانی (آلمان – چک و اتریش – چک) به طور قابل توجهی تیزتر است.
بلوک غرب یک خوشه بزرگ کم-پایین را تشکیل می دهد با یک استثنا، منطقه روهر، که دارای یک خوشه بالا با نرخ بیکاری بالاتر است. در بقیه منطقه، خوشه‌های بزرگ با ارتفاعات کم و کم در اطراف مراکز جمعیتی وجود دارد. در همه کشورهای شرق این شکاف (برلین، پراگ، پوزنان، ورشو، وروتسواف، کراکوف، براتیسلاوا، بوداپست، لیوبلیانا) نقاط سردی از بیکاری کم در تراکم‌های بزرگتر و نقاط داغ بیکاری بالا در مناطق مشکل‌ساز مانند شرق اسلواکی وجود دارد. شرق و جنوب غربی مجارستان یا شمال غربی و شمال شرقی لهستان. حتی ممکن است محورهای توسعه بین بزرگترین تجمعات شکل بگیرد. یک محور از پراگ به آلمان و اتریش در جنوب و وروتسواو و پوزنان در شمال امتداد دارد. در داخل لهستان، محورهای اولیه بین ورشو وجود دارد، کراکوف، وروتسواف و پوزنان. از پوزنان، می تواند بیشتر به سمت برلین کشیده شود و لهستان را به موز آبی پیوند دهد.26 ]. با این حال، برای بررسی این اثرات، نتایج باید در یک بازه زمانی طولانی‌تر مورد مطالعه قرار گیرند.
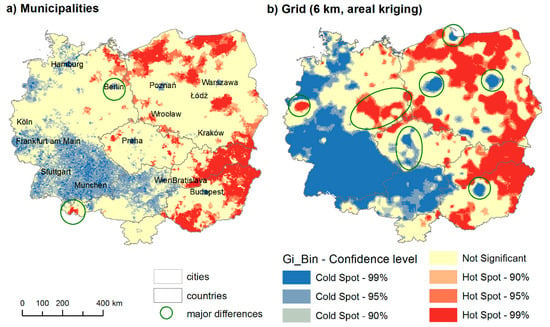
شکل 5نتایج تجزیه و تحلیل نقطه داغ بیکاری محاسبه شده در شبکه منظم 6 کیلومتری با 28.395 مربع با استفاده از درون یابی منطقه ای را نشان می دهد. هنگام استفاده از درون یابی منطقه ای، سطح حاصل صاف تر است. شهرداری های کوچک با ارزش های افراطی را منحل می کند، مانند شهرداری با نرخ بیکاری 100 درصد در حالی که یک ساکن بیکار دارد. بنابراین، تصویر کلی واضح تر است. مقایسه بین نقشه های خوشه ای بر اساس وزن دهی ساده منطقه و کریجینگ مساحتی تفاوت بین محاسبه این دو روش را نشان می دهد. در وزن دهی ساده منطقه، مردم (جمعیت 15 تا 64 و بیکار) به سادگی دوباره توزیع می شدند. در کریجینگ منطقه ای، روش جستجو برای مدلی است که نتایج را هموار کند. به اندازه روش وزن دهی ساده افراط را نشان نمی دهد. بدین ترتیب، نقشه به دست آمده با روش کریجینگ منطقه ای فشرده تر (با خوشه های جدا شده کمتر) و تفسیر آسان تر است. تقسیم غرب به شرق و نقاط سرد در توده های بزرگتر در مقایسه با نتایج به دست آمده با روش وزن دهی ساده، حتی بیشتر قابل مشاهده است.
تفاوت بین تجزیه و تحلیل نقطه داغ بیکاری در شهرداری‌ها و شبکه (6 کیلومتر، کریجینگ منطقه) به خوبی نشان می‌دهد که این روش‌شناسی ارزش زیادی اضافه نمی‌کند و به‌طور قابل‌توجهی تفسیر نهایی را بهبود می‌بخشد ( شکل 6 را ببینید).). هنگامی که تفاوت ها نسبتاً بزرگ هستند (مانند در مورد تفاوت غرب-شرق در بیکاری)، تجزیه و تحلیل نقطه داغ یا حتی یک نقشه choropleth ساده معمولاً کافی است. با این حال، اگر تفاوت ها آنقدر بزرگ نباشند (مانند بیکاری در چک، اسلواکی و لهستان)، درون یابی منطقه ای (کریجینگ منطقه ای در این مورد) توصیف دقیق تری از واقعیت را به ما ارائه می دهد. نتایج آنچنان تحت تأثیر مقادیر پرت نیستند، چه مقادیر شدید در برخی شهرداری‌ها، چه در شهرداری‌های بسیار کوچک یا بزرگ. تفاوت های اصلی در شکل 6 مشخص شده است. تحلیل ها پتانسیل تجربی عظیم روش درونیابی منطقه ای را در تحقیقات بین المللی نشان می دهد. به طور خاص، به نظر می رسد این روش برای مطالعه محورهای توسعه بالقوه مناسب باشد.
از دیدگاه تجربی، تحلیل‌های انجام‌شده نور جدیدی را بر تحقیقات تجربی بین‌المللی در مورد مسائل مرزی می‌تاباند. همانطور که پتراکوس و توپالوگلو [ 27 ] بیان کردند، مشخص نیست که آیا مناطق مرزی ذاتاً از همکاری های فرامرزی سود می برند یا اینکه مناطق حاشیه ای باقی می مانند که با وجود موقعیت جغرافیایی نزدیک خود، عمیقاً تحت تأثیر یکپارچگی اقتصادی و سیاسی قرار نگرفته اند. هنگام استفاده از نرخ بیکاری به عنوان نماینده ای برای توسعه اقتصادی [ 28 ]، مرزهای ملی همچنان بیشتر به عنوان یک مانع به نظر می رسد تا یک پل. این احتمالاً با وابستگی بیکاری به بازار کار مرتبط است، که شکل گیری آن در سراسر مرزهای ملی دشوار است، به ویژه هنگامی که یک مانع زبانی وجود دارد [ 29 ]]. ممکن است این فرضیه وجود داشته باشد که ویژگی‌های اقتصادی مختلف (مانند تولید ناخالص داخلی) کمتر تحت تأثیر مرز ملی است. از سوی دیگر، سطح درآمد احتمالاً مانند بیکاری به بازار کار مرتبط است. بنابراین، مرزهای ملی می تواند تأثیر قوی داشته باشد.

5. نتیجه گیری ها

هدف اصلی مقاله معرفی یک استراتژی در مورد نحوه برخورد با موضوع مقایسه منطقه ای است که یکی از بسیاری از موضوعات کلی مرتبط با قابلیت مقایسه است [ 3 ]. پرداختن به این موضوع به ویژه در تحقیقات بین المللی اهمیت دارد. با دو موقعیت مرتبط است: (1) ساختارهای منطقه ای متفاوت دو یا چند سیستم مختلف (مانند کشورها)، و (2) تغییر ساختارهای منطقه ای در زمان (تغییر در حدود منطقه ای). ما یک استراتژی با استفاده از درون یابی منطقه ای برای همگن سازی بهتر ساختارهای منطقه ای مختلف به یک ساختار شبکه ای معرفی کرده ایم. این رویکرد ما را قادر می سازد تا تجزیه و تحلیل داده های مکانی را مؤثر کنیم.
هر تبدیل داده، خطای ایجاد می کند که تحت تأثیر تفاوت بین واحدهای منبع و واحدهای هدف قرار دارد. ابتدا، انتخاب مناسب ترین ساختار هدف (مانند یک شبکه معمولی)، اندازه واحدها و موقعیت آن مهم است. برای انجام این کار، ما استفاده از دو معیار را پیشنهاد می کنیم. درجه سلسله مراتب (تودرتو) و درجه تناسب (همپوشانی) [ 16]. این دو معیار خطای مربوط به تبدیل از منبع به واحد هدف را بیان می کنند. معمولاً از این معیارها برای تعیین کمیت تناسب بین ساختار منبع و هدف استفاده می شود. با این حال، اگر نیاز به انتخاب مناسب ترین ساختار هدف دارید، پیشنهاد می کنیم از تناسب دو طرفه (منبع به هدف و هدف به منبع) و انتخاب ساختار هدف با حداکثر تناسب متوسط ​​استفاده کنید. در مثال منطقه اروپای مرکزی و شهرداری‌ها به‌عنوان ساختار منبع، ما یک شبکه 6 کیلومتری را در یک موقعیت خاص بر اساس این رویکرد انتخاب کردیم. برای یک منطقه مختلف یا واحدهای منبع مختلف، می توان بهترین اندازه و موقعیت شبکه را با استفاده از همان رویکرد پیدا کرد.
دوم، ما دو روش درون یابی منطقه ای را به کار بردیم که مناسب ترین روش برای تحقیق ما است، (i) وزن دهی منطقه ساده و (ب) کریجینگ منطقه ای. ما نحوه اجرای صحیح این روش ها را نشان داده ایم و مهم ترین موضوعات مرتبط با آنها را مورد بحث قرار داده ایم. روش‌های استاندارد تجزیه و تحلیل فضایی، مانند تجزیه و تحلیل نقطه داغ، برای تحلیل پدیده‌های فضایی مناسب‌تر از روش‌های غیرمکانی هستند (به تفاوت نقشه choropleth مراجعه کنید). روش های درون یابی منطقه ای حتی در تحقیقات منطقه ای بین المللی مناسب تر هستند. در مقایسه با روش‌های دیگر (مانند نقشه کروپلث و تحلیل نقطه داغ بر اساس داده‌های شهری)، چندین مزیت مهم شناسایی شد. اول از همه، درون یابی منطقه ای در مواردی که تفاوت های دو یا چند سیستم (کشور) زیاد است، بینش های جدیدی به ارمغان نمی آورد. مانند تفاوت کلی غرب و شرق. با این حال، در مواردی که تفاوت ها چندان قابل مشاهده نیستند، درون یابی منطقه ای می تواند تفسیر نهایی را به طور قابل توجهی تغییر دهد. این زمانی قابل مشاهده است که نقشه های ایجاد شده توسط تجزیه و تحلیل نقاط داغ شهرداری و کریجینگ منطقه ای مقایسه شوند. این به طور خاص در مناطقی با مراکز منطقه ای مهم (مانند شهرهای بزرگ در لهستان) که اندازه های قابل توجهی متفاوتی دارند، مهم است. به طور کلی، روش‌های درون‌یابی منطقه‌ای تحت‌تاثیر نقاط پرت نیستند (هم از نظر مقادیر شدید و هم از نظر اندازه‌های فضایی بسیار متفاوت). برای اهداف و اهداف ما، کریجینگ منطقه ای بهترین گزینه بود. با این حال، اگر اهداف تحقیق متفاوت باشد، لازم نیست این یکسان باشد. در مواردی که تفاوت ها چندان قابل مشاهده نیستند، درون یابی منطقه ای می تواند تفسیر نهایی را به طور قابل توجهی تغییر دهد. این زمانی قابل مشاهده است که نقشه های ایجاد شده توسط تجزیه و تحلیل نقاط داغ شهرداری و کریجینگ منطقه ای مقایسه شوند. این به طور خاص در مناطقی با مراکز منطقه ای مهم (مانند شهرهای بزرگ در لهستان) که اندازه های قابل توجهی متفاوتی دارند، مهم است. به طور کلی، روش‌های درون‌یابی منطقه‌ای تحت‌تاثیر نقاط پرت نیستند (هم از نظر مقادیر شدید و هم از نظر اندازه‌های فضایی بسیار متفاوت). برای اهداف و اهداف ما، کریجینگ منطقه ای بهترین گزینه بود. با این حال، اگر اهداف تحقیق متفاوت باشد، لازم نیست این یکسان باشد. در مواردی که تفاوت ها چندان قابل مشاهده نیستند، درون یابی منطقه ای می تواند تفسیر نهایی را به طور قابل توجهی تغییر دهد. این زمانی قابل مشاهده است که نقشه های ایجاد شده توسط تجزیه و تحلیل نقاط داغ شهرداری و کریجینگ منطقه ای مقایسه شوند. این به طور خاص در مناطقی با مراکز منطقه ای مهم (مانند شهرهای بزرگ در لهستان) که اندازه های قابل توجهی متفاوتی دارند، مهم است. به طور کلی، روش‌های درون‌یابی منطقه‌ای تحت‌تاثیر نقاط پرت نیستند (هم از نظر مقادیر شدید و هم از نظر اندازه‌های فضایی بسیار متفاوت). برای اهداف و اهداف ما، کریجینگ منطقه ای بهترین گزینه بود. با این حال، اگر اهداف تحقیق متفاوت باشد، لازم نیست این یکسان باشد. این زمانی قابل مشاهده است که نقشه های ایجاد شده توسط تجزیه و تحلیل نقاط داغ شهرداری و کریجینگ منطقه ای مقایسه شوند. این به طور خاص در مناطقی با مراکز منطقه ای مهم (مانند شهرهای بزرگ در لهستان) که اندازه های قابل توجهی متفاوتی دارند، مهم است. به طور کلی، روش‌های درون‌یابی منطقه‌ای تحت‌تاثیر نقاط پرت نیستند (هم از نظر مقادیر شدید و هم از نظر اندازه‌های فضایی بسیار متفاوت). برای اهداف و اهداف ما، کریجینگ منطقه ای بهترین گزینه بود. با این حال، اگر اهداف تحقیق متفاوت باشد، لازم نیست این یکسان باشد. این زمانی قابل مشاهده است که نقشه های ایجاد شده توسط تجزیه و تحلیل نقاط داغ شهرداری و کریجینگ منطقه ای مقایسه شوند. این به طور خاص در مناطقی با مراکز منطقه ای مهم (مانند شهرهای بزرگ در لهستان) که اندازه های قابل توجهی متفاوتی دارند، مهم است. به طور کلی، روش‌های درون‌یابی منطقه‌ای تحت‌تاثیر نقاط پرت نیستند (هم از نظر مقادیر شدید و هم از نظر اندازه‌های فضایی بسیار متفاوت). برای اهداف و اهداف ما، کریجینگ منطقه ای بهترین گزینه بود. با این حال، اگر اهداف تحقیق متفاوت باشد، لازم نیست این یکسان باشد. روش‌های درون‌یابی منطقه‌ای تحت‌تاثیر نقاط پرت نیستند (هم از نظر مقادیر شدید و هم از نظر اندازه‌های فضایی بسیار متفاوت). برای اهداف و اهداف ما، کریجینگ منطقه ای بهترین گزینه بود. با این حال، اگر اهداف تحقیق متفاوت باشد، لازم نیست این یکسان باشد. روش‌های درون‌یابی منطقه‌ای تحت‌تاثیر نقاط پرت نیستند (هم از نظر مقادیر شدید و هم از نظر اندازه‌های فضایی بسیار متفاوت). برای اهداف و اهداف ما، کریجینگ منطقه ای بهترین گزینه بود. با این حال، اگر اهداف تحقیق متفاوت باشد، لازم نیست این یکسان باشد.
علاوه بر این، موارد بالقوه زیادی برای استفاده از این روش در تحقیقات تجربی گرا وجود دارد. مهم است که به یاد داشته باشید که تجزیه و تحلیل، همانطور که در این مقاله ارائه شده است، باید در یک سری زمانی برای ارزیابی تکامل الگوهای فضایی انجام شود. هماهنگ سازی مناطق جغرافیایی برای یک سری زمانی تخمین ها ضروری است زیرا مرزها در طول زمان تغییر می کنند. ناهماهنگی های زمانی در مرزهای منطقه ای یک مسئله عملی بزرگ در تحلیل های تکاملی جغرافیایی است. به طور خاص، در اروپا، تعداد و مرزهای شهرداری ها همچنان در طول زمان تغییر می کند. درون یابی منطقه ای امکان تبدیل ساختار منطقه ای به عقب و جلو در زمان را فراهم می کند و بنابراین یک سیستم منطقه ای سازگار را تشکیل می دهد [ 17 ]]. روش پیشنهادی می تواند به طور موثر برای تفسیر دینامیک تکاملی مورد استفاده قرار گیرد.
از نقطه نظر تجربی، منطقه اروپای مرکزی به دلیل تغییر نقش مرزهای مورد مطالعه بسیار جالب است. ممکن است توجه ویژه ای به ظهور محورهای توسعه در سراسر منطقه اروپای مرکزی شود. علاوه بر این، باید از ویژگی‌های متفاوتی استفاده کرد، به‌ویژه آنهایی که کمتر تحت تأثیر مؤسسات با اینرسی بالاتر، مانند بازار کار قرار می‌گیرند. چالش این است که داده‌های با جزئیات فضایی کافی برای این نوع تحلیل پیدا کنیم. تمرکز دقیق‌تری را می‌توان به مرزهای ملی در داخل بلوک شرق یا جاهای دیگر که میراث تاریخی به اندازه پرده آهنین قوی نیست، معطوف کرد. علاوه بر مرزهای ملی، انواع دیگری از مرزها نیز قابل بررسی است. به عنوان مثال مرزهای تاریخی زیادی در داخل منطقه مورد مطالعه وجود دارد.

منابع

  1. Burkhauser، RV; لیلارد، DR سهم و پتانسیل هماهنگ سازی داده ها برای تحقیقات تطبیقی ​​بین ملی. J. Comp. پالیسی آنال. Res. تمرین کنید. 2005 ، 7 ، 313-330. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  2. ادرزی، ب. شرایط عمومی زیرساخت داده های مکانی. بین المللی جی. نات. مهندس علمی 2018 ، 12 ، 57–62. [ Google Scholar ]
  3. بوناکورسی، آ. دارائو، سی. لپوری، بی. Slipersaeter، S. شاخص‌های موسسات آموزش عالی فردی: پرداختن به مشکلات داده‌ها و مسائل مقایسه‌پذیری. Res. Eval 2007 ، 16 ، 66-78. [ Google Scholar ] [ CrossRef ]
  4. Arbia, G. اثر آماری تبدیل داده ها: یک چارچوب کلی پیشنهادی. در صحت پایگاه داده های مکانی ; Goodchild، MF، Gopal، S.، Eds. تیلور و فرانسیس: لندن، بریتانیا، 1989; صص 249-259. شابک 978-0850668476. [ Google Scholar ]
  5. آرنتز، م. Wilke, R. کاربرد درونیابی منطقه نقشه برداری به داده های اداری آلمان. Asta-Adv. آمار مقعدی 2007 ، 91 ، 159-180. [ Google Scholar ] [ CrossRef ]
  6. لو، اس. گوان، ایکس. یو، دی. دنگ، ی. Zhou، L. تجزیه و تحلیل چند مقیاسی نابرابری منطقه ای بر اساس مدل میدان فضایی: مطالعه موردی چین از سال 2000 تا 2012. Isprs Int. J. Geo-Inf. 2015 ، 4 ، 1982-2003. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  7. گوتوی، کالیفرنیا؛ جوان، LJ ترکیب داده های فضایی ناسازگار. مربا. آمار Assoc 2002 , 97 , 632-648. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  8. هالیسی، ای. تای، ای. برنز، آ. ویلت، جی. پیپینز، ال. لوئیس، بی. گراهام، اس. فلانگان، بی. Buchanan Lunsford، N. تغییر مقیاس جغرافیایی: مقایسه ترکیب جمعیت و وزن منطقه با سایر روش های درونیابی. Int J. Health Geogr. 2017 ، 16 ، 29. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  9. کیو، اف. ژانگ، سی. ژو، ی. توسعه یک پسوند ArcGIS درونیابی منطقه ای و یک مطالعه تطبیقی. گیسی. Remote Sens. 2012 ، 49 ، 644-663. [ Google Scholar ] [ CrossRef ]
  10. جگا، IM; کامبر، ای جی. Tate, NJ مقایسه روش‌های درون‌یابی فضایی در مقیاس‌های مختلف فضایی. Ssrg Int. J. Geoinf. جئول علمی 2017 ، 4 ، 12-22. [ Google Scholar ]
  11. Goodchild، MF; لام، NS-N. درون یابی منطقه ای: گونه ای از مسئله سنتی فضایی. ژئو فرآیند. 1980 ، 1 ، 297-312. [ Google Scholar ]
  12. لی، تی. پولار، دی. کورکوران، جی. استیمسون، R. مقایسه تکنیک‌های تفکیک فضایی که برای تخمین جمعیت برای جنوب شرق کوئینزلند (SEQ)، استرالیا اعمال می‌شود. Appl. Gis 2007 ، 3 ، 1-16. [ Google Scholar ]
  13. کریوروچکو، ک. گریبوف، آ. Krause، E. درونیابی منطقه ای چند متغیره برای داده های پیوسته و شمارش. Procedia Environ. علمی 2011 ، 3 ، 14-19. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  14. دایچمن، یو. بالک، دی. یتمن، جی. تغییر داده های جمعیت برای کاربردهای بین رشته ای: از سرشماری تا شبکه . مرکز داده ها و برنامه های اجتماعی و اقتصادی (CIESIN، کلمبیا): نیویورک، نیویورک، ایالات متحده آمریکا، 2001; در دسترس آنلاین: https://sedac.ciesin.columbia.edu/gpw-v2/GPWdocumentation.pdf (در 3 مارس 2019 قابل دسترسی است).
  15. داوسون، تی. Sandoval، JSO؛ ساگان، وی. کرافورد، تی. تحلیل فضایی رابطه بین پوشش گیاهی و فقر. Isprs Int. J. Geo-Inf. 2018 ، 7 ، 83. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  16. Simpson, L. جداول تبدیل جغرافیا: چارچوبی برای تبدیل داده ها بین واحدهای جغرافیایی. Int J. Popul Geogr. 2002 ، 8 ، 69-82. [ Google Scholar ] [ CrossRef ]
  17. نورمن، پی. ریس، پی. بویل، پی. دستیابی به سازگاری داده ها در مکان و زمان: ایجاد مناطق جغرافیایی سازگار. بین المللی جی پوپول. Geogr. 2003 ، 9 ، 365-386. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  18. بلاها، JD; نواچک، الف. چگونه اروپای مرکزی درک و تحدید می شود. میت اوسترر. Geogr. Ges. 2016 ، 158 ، 193-214. [ Google Scholar ] [ CrossRef ]
  19. Openshaw, S. مسئله واحد منطقه ای قابل تغییر (CATMOG 37) ; Geo Books: Norwich, UK, 1984; پ. 41. [ Google Scholar ]
  20. Wong، DWS مسئله واحد منطقه ای قابل تغییر (MAUP). در SAGE Handbook of Spatial Analysis ; Fotheringham, AS, Rogerson, PA, Eds. SAGE: لندن، انگلستان، 2009; صص 105-123. [ Google Scholar ]
  21. نلسون، جی کی. بروور، کالیفرنیا ارزیابی پایداری داده ها در ساختارهای تجمع در مقیاس های فضایی: بازبینی مشکل واحد منطقه ای قابل تغییر. کارتوگر. Geogr. Inf. علمی 2017 ، 44 ، 35-50. [ Google Scholar ] [ CrossRef ]
  22. نتردووا، پ. نوسک، وی. بررسی تنوع و الگوهای جغرافیایی ویژگی های جمعیت: دیدگاه های منطقه ای و فضایی. موراو. Geogr. 2017 ، 25 ، 85-94 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  23. گتیس، ع. Ord, JK تجزیه و تحلیل ارتباط فضایی با استفاده از آمار فاصله. Geogr. مقعدی 1992 ، 24 ، 189-206. [ Google Scholar ] [ CrossRef ]
  24. Ord، JK; Getis، A. آمار خودهمبستگی فضایی محلی: مسائل توزیعی و یک کاربرد. Geogr. مقعدی 1995 ، 27 ، 286-306. [ Google Scholar ] [ CrossRef ]
  25. نوسک، وی. Netrdová، P. اندازه گیری جنبه های فضایی متغیر. مقایسه خودهمبستگی فضایی با تجزیه منطقه ای در تحقیقات بین المللی بیکاری. تاریخچه Soc. Res. 2014 ، 39 ، 292-314. [ Google Scholar ] [ CrossRef ]
  26. نتردووا، پ. نوسک، V. الگوهای فضایی بیکاری در اروپای مرکزی: محورهای توسعه در حال ظهور فراتر از موز آبی. J. Maps 2016 ، 12 ، 701–706. [ Google Scholar ] [ CrossRef ]
  27. پتراکوس، جی. توپالوگلو، ل. جغرافیای اقتصادی و ادغام اروپا: اثرات بر مناطق مرزی خارجی اتحادیه اروپا. Int J. Public Pol. 2008 ، 3 ، 146-162. [ Google Scholar ] [ CrossRef ]
  28. Lewandowska-Gwarda، K. رگرسیون وزنی جغرافیایی در تحلیل بیکاری در لهستان. Isprs Int. J. Geo-Inf. 2018 ، 7 ، 17. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  29. بوساو، ک. ون میترن، م. سانسن، جی. مایجرز، ای. استورم، تی. لوو، ای. درودر، بی. Witlox، F. برنامه ریزی برای اقتصادهای تراکم در یک منطقه چند مرکزی: پیش بینی یک منطقه اصلی کلان شهری کارآمد در فلاندر. یورو جی. اسپات. توسعه دهنده 2018 ، 69 ، 1-26. [ Google Scholar ] [ CrossRef ]
Ijgi 09 00126 g001 550
شکل 1. محاسبات درصد همپوشانی درجه تناسب، جهت شهرداری به شبکه و شبکه به شهرداری. منبع: © EuroGeographics برای مرزهای اداری، کمیسیون اروپا، Eurostat/GISCO.
Ijgi 09 00126 g002 550
شکل 2. منطقه اروپای مرکزی مورد مطالعه. منبع: © EuroGeographics برای مرزهای اداری، کمیسیون اروپا، Eurostat/GISCO.
Ijgi 09 00126 g003 550
شکل 3. درجه تناسب و درجه سلسله مراتب بین ساختار منطقه ای شهرداری ها و ساختارهای شبکه با اندازه سلول های شبکه متفاوت.
Ijgi 09 00126 g004a 550 Ijgi 09 00126 g004b 550
شکل 4. نقشه Choropleth ( a ) و تجزیه و تحلیل نقطه داغ ( b ) از بیکاری در سال 2010 در شهرداری در CER. منبع: © EuroGeographics برای مرزهای اداری، کمیسیون اروپا، Eurostat/GISCO.
Ijgi 09 00126 g005 550
شکل 5. تجزیه و تحلیل نقطه داغ بیکاری در یک شبکه 6 کیلومتری، وزن منطقه ساده ( a ) و کریجینگ منطقه ( b ). منبع: © EuroGeographics برای مرزهای اداری، کمیسیون اروپا، Eurostat/GISCO.
Ijgi 09 00126 g006 550
شکل 6. مقایسه تحلیل نقطه داغ بیکاری در شهرداری ها ( a ) و شبکه ( b -6 کیلومتر، کریجینگ منطقه). منبع: © EuroGeographics برای مرزهای اداری، کمیسیون اروپا، Eurostat/GISCO.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید