خلاصه
کلید واژه ها:
جبر نمودار ; RDF فضایی و زمانی مشخصات نحوی
1. معرفی
2. کارهای مرتبط
2.1. جبر برای داده های مکانی و زمانی
2.2. جبر نمودارهای RDF
3. معناشناسی RDF مکانی و زمانی و جبر نمودار
3.1. معناشناسی فضای زمانی RDF
تعریف 1.
- ●
-
s نام منبع و s ∈ R ∪ B است.
- ●
-
p یک نام خصوصیت و p∈ R است.
- ●
-
o یک مقدار است و o ∈ R ∪ B ∪ K ∪ I ∪ S.
- ●
-
t ∈ I داده های زمانی است.
- ●
-
l ∈ S داده های مکانی است.
تعریف 2.
- ●
-
V = s ∪ محدوده (U) مجموعه ای از رئوس است.
- ●
-
E = {(r, r’)} مجموعه ای از یال ها از r تا r’ است که در آن ∀r، r’ ∈ V است.
- ●
-
F (r، r’) = {f | (r, f: <t, l>, r’) ∈ G} مجموعه ای از نگاشت E است که در آن ∀r، r’ ∈ V* است.
- ●
-
λ مجموعه ای از برچسب ها است که توسط رئوس یا لبه ها ارائه می شود.
- ●
-
T ∈ محدوده (f s-t ∪ f p-t ).
- ●
-
L ∈ محدوده (f s-l ∪ f p-l ).
تعریف 3.
- ●
-
وقتی G 1 ، G 2 نمودارهای پایه stRDFS هستند، G 1 |= G 2 فقط در صورتی که G 1 (Ti) |= G 2 (Ti) و G 1 (Si) |= G 2 (Si).
- ●
-
وقتی G 1 , G 2 گراف های stRDFS هستند، G 1 |= G 2 فقط اگر μ 1 (G 1 ) برای هر نمونه گراف پایه G 1 ، یک نمونه گراف پایه μ 2 (G 2 ) از G 2 و μ وجود داشته باشد. 1 (G 1 ) |= μ 2 (G 2 ).
تعریف 4.
- ●
-
G’ بزرگترین مجموعه در جهان (G) است که همه واژگان RDF را اضافه می کند، که می تواند به صورت tcl (G) بیان شود، جایی که G ⊆ G’ یا G |= G’.
- ●
-
بسته شدن بلوک G به صورت scl (G) بیان می شود. این یک گراف RDF مکانی-زمانی است که با ∪ Si, Ti (cl(G (Si ∪ Ti)) Si, Ti تعریف شده است که در آن cl(G (Si ∪ Ti) بسته شدن دلخواه گراف RDF G (Si ∪ Ti) است.
قضیه 1.
اثبات قضیه 1.
قضیه 2.
اثبات قضیه 2.
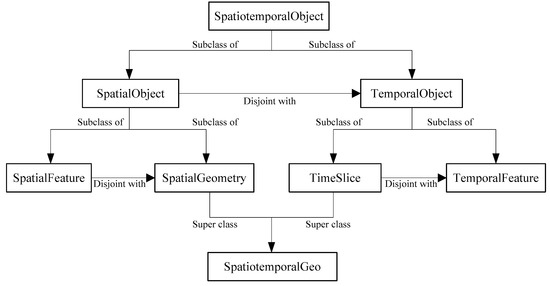
3.2. کلاسها و توضیحات فضایی-زمانی در دامنه مکانی-زمانی
به عنوان مثال، یک گیرنده صوتی بزرگ وجود دارد که پس از دریافت، برنامه های مربوطه را برای تجزیه و تحلیل امواج صوتی فراخوانی می کند. کلاس نرم افزار دارای نمونه های Program1 و Program2 است که انواع آنها به ترتیب JavaProgram و PythonProgram هستند. کلاس گیرنده دارای نمونه های Receiver1 و Receiver2 است و نوع Receiver2 SoundWaveReceiver است. ما مدل stRDF و مدل stRDFS را با توصیف اطلاعات مکانی-زمانی مقایسه میکنیم. مدل stRDF به شرح زیر است:
| مثال: برنامه 1 | rdf: نوع | مثال: JavaProgram |
| مثال: program2 | rdf: نوع | مثال: PythonProgram |
| مثال: برنامه 1 | om: رویه | مثال: برنامه شمارش |
| مثال: program2 | om: رویه | مثال: برنامه خروجی |
| مثال: برنامه 1 | om: hasPro1Call | مثال: گیرنده 2 |
| مثال: program2 | om: hasPro2Call | مثال: گیرنده 2 |
| مثال: گیرنده 2 | rdf: نوع | مثال: SoundWaveReceiver |
| مثال: گیرنده 2 | ssn: اندازه گیری می کند | مثال: صدا |
| مثال: گیرنده 2 | ssn: hasLocation | مثال: مکان 1 |
| مثال: مکان 1 | strdf: دارای مسیر | “( t = 8t و t = 18t یا 9t ≤ t ≤ 14t) و k = 0t و ((20.9°N < L <21°N و 45.8°E < D <= 46°E) یا ( L = 21° N و D = 46°E))” ^^ strdf: SemiLinearPointSet. |
در مدل stRDF، strdf: hasTrajectory داده های مکانی-زمانی را توصیف می کند که به عنوان مقدار ویژگی strdf در نظر گرفته می شود: hasTrajectory برای Location1. در مدل stRDF، فقط دادههای مکانی-زمانی در کل موجودیتها را میتوان در بعد مکانی-زمانی ثبت کرد، در حالی که دادههای مکانی-زمانی در قسمت خاصی از شیء نمیتوانند. به عنوان مثال، مدل stRDF نمی تواند داده های مکانی را در t = 8t نشان دهد و داده های زمانی را هنگامی که جسم در موقعیت قرار دارد (L = 21°N و D = 46°E) ثبت کند. در همان زمان، اگر یک مقدار مشخصه در یک زمان خاص یا در یک موقعیت مکانی خاص تغییر کند، stRDF داده های نادرست را ثبت می کند. مدل stRDFS این مشکل را به صورت زیر حل می کند:
| مثال: برنامه 1 | rdf: نوع | مثال: JavaProgram |
| مثال: program2 | rdf: نوع | مثال: PythonProgram |
| مثال: برنامه 1 | om: رویه | مثال: برنامه تجزیه و تحلیل |
| مثال: program2 | om: رویه | مثال: برنامه تجزیه و تحلیل |
| مثال: برنامه 1 | om:hasPro1Call | مثال: گیرنده 2 |
| مثال: program2 | om: hasPro2Call | مثال: گیرنده 2 |
| مثال: گیرنده 2 | rdf: نوع | مثال: SoundWaveReceiver |
| مثال: گیرنده 2 | ssn: اندازه گیری می کند | مثال: صدا |
| مثال: گیرنده 2 | ssn: hasLocation1 | مثال: مکان 1 |
| مثال: گیرنده 2 | ssn: hasLocation2 | مثال: مکان 2 |
| om: hasPro1Call | strdfs: SpatiotemporalGeo | t = 8 t و t = 18t و k = 0t و (20.9°N < L <21°N و 45.8°E < D <= 46°E)” ^^ strdfs: SemiLinearPointSet |
| om: hasPro2Call | strdfs: SpatiotemporalGeo | “9t ≤ t ≤ 14t و L = 21°N و D = 46°E و k = 0t” ^^ strdfs: SemiLinearPointSet |
| ssn: hasLocation1 | strdfs: SpatialGeometry | “(20.9° شمالی < L < 21° شمالی و 45.8° شرقی < D <= 46° شرقی)” ^^ strdfs: SemiLinearPointSet |
| ssn: hasLocation2 | strdfs: SpatialGeometry | “( L = 21 درجه شمالی و D = 46 درجه شرقی)” ^^ strdfs: SemiLinearPointSet |
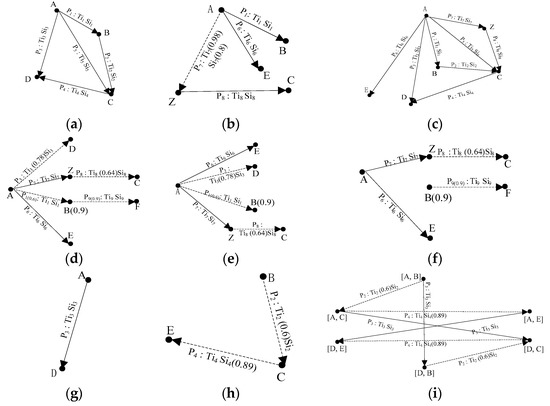
3.3. جبر نمودار RDF فضایی و زمانی
تعریف 5.
- ●
-
V = V A ∪ V B
- ●
-
E = E A ∪ E B
- ●
-
F = F A ∪ F B
- ●
-
Π N T = Π N T A ∪ Π N T B
- ●
-
Π k T = min (Π N T A , Π N T B )
- ●
-
L = L A ∪ L B .
تعریف 6.
- ●
-
V = V A ∩ V B
- ●
-
E = E A ∩ E B
- ●
-
F = F A ∩ F B
- ●
-
Π N T = Π N T A ∩ Π N T B
- ●
-
Π k T = دقیقه (Π N T A , Π N T B )
- ●
-
L = L A ∩ L B .
تعریف 7.
- ●
-
E = E A – E B
- ●
-
V مجموعه رئوس E است.
- ●
-
F مجموعه ای از نگاشت E است.
- ●
-
T مجموعه داده زمانی F است.
- ●
-
L مجموعه داده فضایی F است.
تعریف 8.
- ●
-
V = V A × V B
- ●
-
E = {(u, u 2 )(u, v 2 )| u ∈ V A , u 2 v 2 ∈ E B } ∪ {(u 1 , ω)(v 1 , ω)| ω ∈ V B , u 1 v 1 ∈ E A }
- ●
-
F مجموعه ای از نگاشت E است.
- ●
-
T مجموعه داده زمانی F است.
- ●
-
L مجموعه داده فضایی F است.
قضیه 3.
- ●
-
A ∪ B یک گراف stRDFS است.
- ●
-
A ∩ B یک گراف stRDFS است.
- ●
-
A – B یک گراف stRDFS است.
- ●
-
A × B یک گراف stRDFS است.
تعریف 9.
- ●
-
V P مجموعه محدودی از رئوس است.
- ●
-
E P مجموعه ای محدود از لبه های جهت دار است.
- ●
-
F p مجموعه ای از نگاشت های E p است.
- ●
-
T P یک مجموعه داده زمانی است.
- ●
-
L P یک مجموعه داده فضایی است.
- ●
-
R e = {R 1 R 2 , R 1 |R 2 , R+, ε} مجموعه ای از قوانین فیلتر است که E p را توصیف می کند که در آن R یک قانون فیلتر را نشان می دهد.
4. مشخصات نحو RDF فضایی و زمانی
- ●
-
کلمه کلیدی SELECT مشخصات نتیجه پرس و جو را تعیین می کند. به دنبال آن بقیه پرس و جو قرار می گیرد: لیست شناسه های نتیجه پرس و جو.
- ●
-
کلمه کلیدی FROM محدوده پرس و جو را مشخص می کند که معمولاً یک مجموعه داده مکانی-زمانی یا چندین نمودار stRDFS است.
- ●
-
کلمه کلیدی WHERE نشان دهنده پرس و جو واقعی است و به دنبال آن معیارهای پرس و جو که با الگویی مطابق با برخی از نمودارهای stRDFS که با متغیرها جایگزین شده اند ارائه می شود. الگوهای پیچیده تر نیز مجاز به شکل گیری با برخی عملگرهای جبری هستند. این حالت را می توان نه تنها برای پرس و جو از یک مجموعه داده مکانی-زمانی، بلکه برای چندین مجموعه داده مکانی-زمانی نیز استفاده کرد.
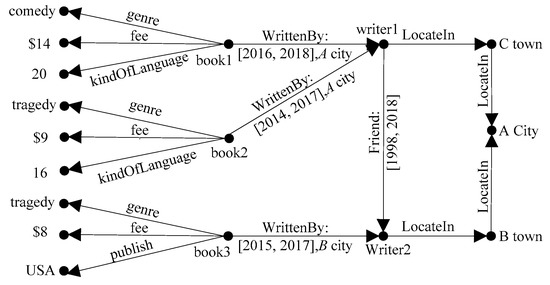
مثال 1.
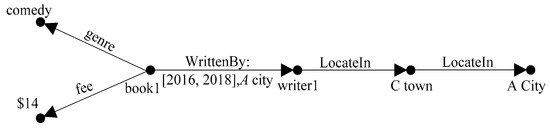
مثال 2.
مثال 3.
5. نتیجه گیری و کار آینده
منابع
- Lassila، O. چارچوب توصیف منابع (RDF) مدل و مشخصات نحو، توصیه W3C. در دسترس آنلاین: https://www.w3.org/TR/PR-rdf-syntax (در 22 فوریه 1999 قابل دسترسی است).
- باتساکیس، اس. پتراکیس، EGM نشان دهنده دانش زمانی در وب معنایی: رویکرد 4 بعدی فلوئنت توسعه یافته. در ترکیبی از روش ها و کاربردهای هوشمند ; Springer: برلین/هایدلبرگ، آلمان، 2011; صص 55-69. [ Google Scholar ]
- لوتز، سی. ولتر، اف. Zakharyaschev, M. منطق های توصیف زمانی: یک بررسی. در مجموعه مقالات پانزدهمین سمپوزیوم بین المللی در نمایندگی و استدلال زمانی، مونترال، QC، کانادا، 16-18 ژوئن 2008. صص 3-14. [ Google Scholar ]
- رید، TW; مک میکین، دی. Reitsma، F. نمایش روابط فضایی در شهرهای هوشمند با استفاده از هستی شناسی ها. در فناوری نوآوری اطلاعات در شهرهای هوشمند ; Springer: برلین، آلمان، 2018; صص 33-45. [ Google Scholar ]
- کیم، جی جی؛ شین، IS; لی، YS; ماه، J.-Y. سیستم های مدیریت هستی شناسی مکانی-زمانی برای معنایی. وب اطلاعات 2016 ، 19 ، 4237-4254. [ Google Scholar ]
- تاپولت، جی. Bernstein، A. RDF زمانی کاربردی: پرس و جوی زمانی کارآمد از داده های RDF با SPARQL. در مجموعه مقالات کنفرانس وب معنایی اروپا، کرت، یونان، 31 مه تا 4 ژوئن 2009. اسپرینگر: برلین/هایدلبرگ، آلمان؛ صص 308-322. [ Google Scholar ]
- هرناندز، دی. هوگان، ا. Krötzsch، M. Reifying RDF: چه چیزی با Wikidata خوب کار می کند؟ در مجموعه مقالات یازدهمین کارگاه بین المللی در مورد سیستم های پایگاه دانش وب معنایی مقیاس پذیر، بیت لحم، PA، ایالات متحده آمریکا، 11 اکتبر 2015. [ Google Scholar ]
- گوتیرز، سی. هورتادو، سی. Vaisman, A. Temporal rdf. در مجموعه مقالات کنفرانس وب معنایی اروپا، کرت، یونان، 2005، 29 مه تا 1 ژوئن. اسپرینگر: برلین/هایدلبرگ، آلمان؛ صص 93-107.
- Pugliese، A.; اودریا، او. زیربرهمانیان، در مقابل مقیاس RDF با زمان. در مجموعه مقالات هفدهمین کنفرانس بین المللی وب جهانی، پکن، چین، 21-25 آوریل 2008; ص 605-614. [ Google Scholar ]
- کنسولی، اس. مونگیوویچ، ام. Nuzzolese، AG; پرونی، س. پرسوتی، وی. Recupero، DR; Spampinato، D. یک مدل داده شهر هوشمند بر اساس بهترین روش و اصول معناشناسی. در مجموعه مقالات بیست و چهارمین کنفرانس بین المللی وب جهانی، فلورانس، ایتالیا، 18 تا 22 مه 2015; صص 1395–1400. [ Google Scholar ]
- کوباراکیس، م. Kyzirakos، K. مدلسازی و جستجوی فراداده در وب حسگر معنایی: مدل stRDF و زبان پرس و جو stSPARQL. در مجموعه مقالات کنفرانس وب معنایی گسترده، کرت، یونان، 30 مه تا 3 ژوئن 2010. اسپرینگر: برلین/هایدلبرگ، آلمان؛ صص 425-439. [ Google Scholar ]
- شنگ، جی ال. سو، ی.ال. Wang, WD یک رویکرد فراکتالی جدید برای توصیف تخلخل/نفوذپذیری/تراکم پذیری شکست القایی در مخازن غیر متعارف تحریک شده. J. Petroleum Sci. مهندس 2019 ، 179 ، 855–866. [ Google Scholar ] [ CrossRef ]
- ژائو، اچ. خو، ال. گوا، ز. لیو، دبلیو. ژانگ، Q. نینگ، ایکس. لی، جی. Shi, L. یک گردش کار جدید و سریع بهینه سازی سیلاب بر اساس راندمان تزریق مشتق شده از INSIM با یک کاربرد میدانی. J. Petroleum Sci. مهندس 2019 ، 179 ، 1186-1200. [ Google Scholar ] [ CrossRef ]
- هوانگ، ال. هو، ی. لی، ی. کیشور کومار، PK؛ کولی، دی. Dey, A. مطالعه نمودارهای نوتروسوفیک منظم و نامنظم با کاربردهای واقعی. ریاضیات 2019 ، 7 ، 551. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- نیکیتوپولوس، پی. ولاچو، ع. دولکریدیس، سی. Vouros، GA پردازش موازی و مقیاس پذیر پرس و جوهای RDF مکانی-زمانی با استفاده از Spark. GeoInformatica 2019 . [ Google Scholar ] [ CrossRef ]
- فراسینکار، اف. هوبن، GJ; ودووجاک، ر. بارنا، P. RAL: جبری برای پرس و جو RDF. وب جهانی 2004 ، 7 ، 83-109. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- رابرتسون، روابط سه گانه EL: جبری برای وب معنایی. در مجموعه مقالات کارگاه بین المللی وب معنایی و پایگاه های داده، تورنتو، کانادا، 29 تا 30 اوت 2004. [ Google Scholar ]
- چن، ال. گوپتا، ا. Kurul، ME جبر پرس و جوی RDF با آگاهی معنایی. در مجموعه مقالات کنفرانس بین المللی مدیریت داده ها (COMAD)، حیدرآباد، هند، 20-22 دسامبر 2005. [ Google Scholar ]
- جامور، اف. عبدالعزیز، ط. Kalnisk، P. نمایشی از magiq: رویکرد جبر ماتریسی برای حل پرس و جوهای گراف rdf. در مجموعه مقالات بنیاد VLDB، ریودوژانیرو، برزیل، 27 تا 31 اوت 2008. صفحات 1978-1981. [ Google Scholar ] [ CrossRef ]
- تاکار، اچ. پانجانی، دی. اوئر، اس. ویدال، ام.-ای. به سمت جبر نمودار یکپارچه برای تطبیق الگوی نمودار با گرملین. مجموعه مقالات کنفرانس بین المللی پایگاه داده و برنامه های کاربردی سیستم های خبره، لیون، فرانسه، 28 تا 31 اوت 2017. اسپرینگر: چم، آلمان؛ صص 81-91. [ Google Scholar ]
- کورکولز، جی. González، P. مشخصات یک زبان پرس و جو فضایی بر روی GML. در مجموعه مقالات نهمین سمپوزیوم بین المللی ACM در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، آتلانتا، GA، ایالات متحده آمریکا، 9 تا 10 نوامبر 2001. [ Google Scholar ]
- پان، اف. Hobbs, JR Temporal Aggregates در OWL-Time. در مجموعه مقالات کنفرانس FLIRS، Clearwater Beach، FL، ایالات متحده آمریکا، 15-17 مه 2005. صص 560-565. [ Google Scholar ]
- براتیس، ای. پتراکیس، EGM; باتساکیس، اس. ماریس، ن. پاپاداکیس، N. TOQL: زبان جستجوی هستی شناسی زمانی. در مجموعه مقالات سمپوزیوم بین المللی پایگاه های داده مکانی و زمانی، آلبورگ، دانمارک، 8 تا 10 ژوئیه 2009. Springer: برلین/هایدلبرگ، آلمان، 2009; صص 338-354. [ Google Scholar ]
- Moffitt، VZ; استویانوویچ، جی. جبر نمودار زمانی. در مجموعه مقالات شانزدهمین سمپوزیوم بین المللی زبان های برنامه نویسی پایگاه داده، مونیخ، آلمان، 1 سپتامبر 2017; پ. 10. [ Google Scholar ]
- پری، م. شث، ا. آرپینار، آی بی; حکیم پور، ف. تحلیل معنایی مکانی و زمانی. در کتابچه راهنمای تحقیقات ژئوانفورماتیک ; IGI Global: Hershey، PA، USA، 2009; صص 161-170. [ Google Scholar ]
- حکیم پور، ف. عالم-مزا، بی. پری، م. Sheth، A. پردازش داده های فضایی-مضمونی برای وب معنایی. در وب جغرافیایی ؛ Springer: لندن، انگلستان، 2009; صص 79-89. [ Google Scholar ]
- پری، م. جین، پی. Sheth، AP SPARQL-ST: گسترش SPARQL برای پشتیبانی از پرس و جوهای فضایی و زمانی. Geos. سمنت. سمنت. وب 2011 ، 12 ، 61-86. [ Google Scholar ]
- بای، ال. Xu, C. جبر پرس و جوی فضایی-زمانی مبتنی بر XML بومی. در کتابچه راهنمای تحقیق در مورد تکنیک های نوآورانه پردازش پرس و جو پایگاه داده ; IGI Global: Hershey, PA, USA, 2015; صص 275-293. [ Google Scholar ]
- بای، ال. Zhu، L. یک جبر برای داده های فضایی و زمانی فازی در XML. دسترسی IEEE 2019 ، 7 ، 22914–22926. [ Google Scholar ] [ CrossRef ]
- Cyganiak، R. جبر رابطهای برای SPARQL . آزمایشگاه سیستم های رسانه های دیجیتال HP Laboratories Bristol. HPL-2005-170: بریستول، انگلستان، 2005; جلد 35، ص. 9. [ Google Scholar ]
- پری، م. Herring, J. OGC GeoSPARQL-یک زبان پرس و جو جغرافیایی برای داده های RDF. پیاده سازی OGC. استاندارد 2012 ، 40. [ Google Scholar ]
- نبرد، آر. Kolas, D. Geosparql: فعال کردن یک وب معنایی جغرافیایی. وب معنایی J. 2011 ، 3 ، 355-370. [ Google Scholar ] [ CrossRef ]
- نبرد، آر. کولاس، دی. فعال کردن وب معنایی جغرافیایی با پارلمان و geosparql. وب معنایی 2012 ، 3 ، 355-370. [ Google Scholar ] [ CrossRef ]
- زو، سی. پال، ا. Dey, A. مفاهیم جدید نمودارهای فازی تصویری با کاربرد. ریاضیات 2019 ، 7 ، 470. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- ما، ز. لی، جی. Yan, L. مدل سازی داده های فازی و عملیات جبری در RDF. سیستم مجموعه های فازی 2018 ، 351 ، 41-63. [ Google Scholar ] [ CrossRef ]
- دی، ع. پال، ا. بلند، HV فازی حداقل پوشا درخت با فاصله نوع 2 طول قوس فازی: فرمول و یک الگوریتم ژنتیک جدید. محاسبات نرم. 2019 ، 1-12. [ Google Scholar ] [ CrossRef ]
- نیتا، ک. Savnik، I. یک روش اجرای پرس و جو توزیع شده برای مدیران ذخیره سازی RDF. در مجموعه مقالات دهمین کارگاه بین المللی در مورد سیستم های پایگاه دانش وب معنایی مقیاس پذیر که با سیزدهمین کنفرانس بین المللی وب معنایی، ریوا دل گاردا، ترنتینو، ایتالیا، 19 تا 23 اکتبر 2014 برگزار شد. [ Google Scholar ]
- راویندرا، پی. کیم، اچ اس. Anyanwu، K. جبر میانی برای بهینه سازی تطبیق الگوی نمودار RDF در MapReduce. در مجموعه مقالات کنفرانس وب معنایی گسترده، برلین، آلمان، 2011; اسپرینگر: برلین/هایدلبرگ، آلمان؛ صص 46-61. [ Google Scholar ]
- وانگ، دی. زو، ال. ژائو، D. g st -Store: موتوری برای نمودار RDF بزرگ که اطلاعات مکانی و زمانی را یکپارچه می کند. در مجموعه مقالات هفدهم EDBT/ICDT، آتن، یونان، 24 تا 28 مارس 2014. صص 652-655. [ Google Scholar ]
- تره فرنگی؛ لی، کی. کیم، YH; چوی، جی جی. جانگ، هستی شناسی مکانی-زمانی GS برای وب معنایی. موسسه بین المللی اطلاعات (توکیو). اطلاعات 2015 ، 18 ، 329-334. [ Google Scholar ]
- پری، م. Sheth، AP; حکیم پور، ف. جین، پی. پشتیبانی از پرس و جوهای پیچیده موضوعی، مکانی و زمانی بر روی داده های وب معنایی. در مجموعه مقالات دومین کنفرانس بین المللی معناشناسی جغرافیایی، مکزیکو سیتی، مکزیک، 29 تا 30 نوامبر 2007. ص 228-246. [ Google Scholar ]
- پرز، جی. آرناس، م. گوتیرز، سی. معناشناسی و پیچیدگی SPARQL. در مجموعه مقالات پنجمین کنفرانس بین المللی وب معنایی، آتن، GA، ایالات متحده آمریکا، 5-9 نوامبر 2006. صص 30-43. [ Google Scholar ]
- پری، م. استرادا، ا. داس، اس. Banerjee, J. توسعه برنامه های GeoSPARQL با Oracle Spatial و Graph. در مجموعه مقالات ISWC، بیت لحم، PA، ایالات متحده آمریکا، 11-15 اکتبر 2015. صص 57-61. [ Google Scholar ]
- وانگ، دی. زو، ال. Zhao, D. gst-store: Querying Large Spatio-Temporal RDF Graphs. اطلاعات اطلاعات مدیریت 2017 ، 1 ، 84-103. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]







بدون دیدگاه