خلاصه

نمونه‌برداری مکانی پیچیده جغرافیایی معمولاً با مسائل مختلف بهینه‌سازی چند هدفه مواجه می‌شود، که برای آن‌ها الگوریتم‌های بهینه‌سازی چندهدفه مؤثر برای کمک به پیشرفت این زمینه بسیار مورد نیاز است. برای بهبود کارایی محاسباتی فرآیند بهینه‌سازی چند هدفه، روش بازپخت شبیه‌سازی شده چند هدفه آرشیو شده (AMOSA) -II به عنوان یک روش بهینه‌سازی چند هدفه موازی بهبود یافته برای نمونه‌برداری فضایی جغرافیایی پیچیده پیشنهاد شده‌است. بر اساس روش AMOSA، چندین زنجیره مارکوف برای گسترش زنجیره سنتی تک مارکوف استفاده می شود. فناوری موازی سازی چند هسته ای بر اساس زنجیره های چند مارکوف به کار گرفته شده است. محدودیت tabu-archive برای جلوگیری از جستجوهای مکرر برای راه حل های بهینه طراحی شده است. دو مورد مورد بررسی قرار گرفت: یکی با شش مشکل تست سنتی معمولی، و دیگری برای کاربردهای بهینه سازی نمونه برداری فضایی خاک. شش شاخص عملکرد از دو مورد مورد تجزیه و تحلیل قرار گرفت – زمان محاسباتی، همگرایی، خلوص، فاصله، فاصله دقیقه و جابجایی. نتایج نشان داد که AMOSA-II در مقایسه با AMOSA و NSGA-II عملکرد بهتری داشت که در به دست آوردن راه‌حل‌های بهینه ترجیحی مؤثرتر بود. AMOSA-II را می توان به عنوان وسیله ای عملی برای اعمال در سایر بهینه سازی های پیچیده مکانی جغرافیایی در نظر گرفت.

کلید واژه ها:

بهینه سازی چند هدفه ؛ AMOSA-II ; چندین زنجیره مارکوف ؛ موازی سازی

1. معرفی

در فضاهای پیچیده جغرافیایی، سناریوهای نمونه‌برداری مکانی معمولاً در اهداف نمونه‌گیری مختلف و عوامل نظارتی مختلف دخالت دارند که منجر به تنوع و پیچیدگی اهداف نمونه‌گیری می‌شود. اهداف اصلی نمونه‌برداری فضایی عمدتاً شامل برآورد، درونیابی، بازرسی، طبقه‌بندی و تشخیص است [ 1 ]. این اهداف نمونه‌برداری همیشه بر اساس موقعیت‌های مختلف ترکیب می‌شوند – مانند تخمین پارامترهای واریوگرام و دقت نقشه‌برداری، یا برای برآورد میانگین جمعیت و درونیابی. مسائل نمونه‌گیری فضایی چندهدفه از چنین اهداف نمونه‌گیری چندگانه ناشی می‌شوند [ 2 ، 3]. علاوه بر این، عوامل متعددی برای هر نمونه در یک نظرسنجی مورد نیاز است. به عنوان مثال، بررسی خاک مستلزم جمع آوری عوامل فلزات سنگین و عوامل غذایی در یک نمونه است یا پایش هواشناسی مستلزم مشاهده عواملی مانند دما، رطوبت و فشار هوا است. نمونه برداری برای شاخص های نظارتی چندگانه یک مسئله نمونه برداری فضایی چند هدفه با فضاهای ویژگی چندگانه را تشکیل می دهد [ 4 ، 5 ]. علاوه بر این، هنگامی که اهداف نمونه‌گیری چندگانه با عوامل نمونه‌گیری متعدد ترکیب می‌شوند، چنین مسائل نمونه‌گیری فضایی چندهدفه بسیار پیچیده‌تر می‌شوند.
مسائل بهینه سازی چندهدفه گسترده نمونه برداری فضایی را می توان به دو روش بهینه سازی مستقیم و غیرمستقیم مورد بررسی قرار داد. در بهینه سازی غیرمستقیم، چندین هدف با وزن دهی به یک تابع هدف تبدیل می شوند و با روش بهینه سازی تک هدف بهینه می شوند [ 6 ، 7 ، 8 ]. به عنوان مثال، بروس خطای تخمین روند و خطای درون یابی فضایی را با وزن دهی در واریانس کریجینگ جهانی میانگین فضایی گنجانید [ 8 ]]. برای به دست آوردن الگوی بهینه در گسترش فضاهای جغرافیایی و ویژگی استفاده شد. با این حال، در اکثر شرایط، اهداف چندگانه را نمی توان با وزن دهی خودسرانه به یک هدف واحد تبدیل کرد، زیرا مفهوم نماینده آنها اساساً متفاوت است – به عنوان مثال، هزینه نظارت و کیفیت نمونه ها. ادغام چندین هدف با واحدهای اندازه گیری مختلف به دلیل وزن دهی غیرعلمی است. علاوه بر این، تعیین وزن برای تأثیر قصد ذهنی بحث‌برانگیز است و بهینه‌سازی برای هر یک از اهداف چندگانه نمی‌تواند تضمین شود. بنابراین، استفاده از روشی که بتواند به طور مستقیم چندین هدف را برای نمونه‌برداری مکانی پیچیده جغرافیایی بهینه کند، ضروری است.
روش‌های بهینه‌سازی چندهدفه مستقیم مسائل را به‌منظور دستیابی به راه‌حل‌های بهینه پارتو با ایجاد معاوضه بین اهداف متعدد حل می‌کنند [ 9 ، 10 ، 11 ، 12 ، 13 ، 14 ، 15 ]. مقادیر متناظر توابع چند هدفه راه‌حل‌های بهینه پارتو بهینه پارتو است که بدون بدتر شدن اهداف دیگر نمی‌توان آن را بیشتر بهبود بخشید. الگوریتم بازپخت شبیه سازی شده چند هدفه آرشیو شده (AMOSA) یک روش بهینه سازی مستقیم چند هدفه ساده و پرکاربرد است [ 16 ]. توسط Lark به نمونه‌گیری فضایی برای بهینه‌سازی طراحی نمونه‌گیری چندهدفه معرفی شد [17 ]. با استفاده از این الگوریتم، دو هدف برای نمونه‌برداری از خاک به‌طور مستقیم بهینه‌سازی شد و مجموعه‌ای از راه‌حل‌های نمونه‌برداری بهینه ارائه شد که در نتیجه شایستگی الهام‌بخش این الگوریتم در نمونه‌برداری مکانی جغرافیایی آشکار شد. با این وجود، کارایی روش AMOSA عملکرد بهینه‌سازی نمونه‌برداری آن را محدود می‌کند. تکمیل بهینه‌سازی در مورد کاربردی Lark یک فرآیند زمان‌بر بود. در عمل، فضای نمونه برداری جغرافیایی به طور کلی بسیار پیچیده تر است [ 18 ، 19 ، 20 ]]، و زمان صرف شده توسط فرآیند بهینه سازی به طور قابل توجهی طولانی تر است. با این حال، ارائه طرح‌های نمونه‌گیری بهینه در زمان با بهینه‌سازی کارآمد، مهم است. بنابراین، به منظور دستیابی به کاربرد فشرده برای سناریوهای مختلف بهینه‌سازی نمونه‌برداری چندهدفه، کارایی AMOSA نیازمند بهبود بیشتر است.
در این مقاله، یک روش بهینه‌سازی چندهدفه موازی بهبود یافته از AMOSA، که AMOSA-II نامیده می‌شود، برای بهبود کارایی فرآیند بهینه‌سازی نمونه‌برداری مکانی در فضای پیچیده جغرافیایی پیشنهاد شده‌است. بهبودهای AMOSA عمدتاً به سه جنبه مربوط می شود. (1) طراحی چندین زنجیره مارکوف برای تقویت شدت درجه جستجو برای تسریع روند همگرایی ساخته شده است. (2) فناوری موازی سازی بر اساس زنجیره های چند مارکوف برای افزایش بیشتر بازده تکرار بدون همگرایی زودرس ایجاد شده است. (3) محدودیت tabu-archive برای جلوگیری از بازسازی راه حل هایی که قبلا جستجو شده اند برای صرفه جویی در زمان محاسباتی اضافی اضافه شده است.
بقیه این مقاله به روش زیر سازماندهی شده است: ادبیات موجود در مورد بهینه سازی چندهدفه نمونه برداری مکانی جغرافیایی در بخش 2 بررسی می شود . روش AMOSA-II در بخش 3 توضیح داده شده است . مورد با شش مشکل آزمایش سنتی و مورد استفاده شده برای نمونه برداری خاک در مطالعات قبلی برای تجزیه و تحلیل عملکرد AMOSA-II در بخش 4 و بخش 5 مورد مطالعه قرار گرفته است. تنظیم پارامترهای مرتبط برای AMOSA-II بیشتر در بخش 6 مورد بحث قرار گرفته است. نتیجه گیری در بخش 7 ارائه شده است.

2. بررسی ادبیات

برای نمونه گیری مکانی پیچیده جغرافیایی، به دلیل محدودیت منابع، زمان و فناوری، همیشه مطلوب است که یک بررسی نمونه برای اهداف چندگانه انجام شود. مسائل نمونه‌گیری مکانی جغرافیایی برای اهداف بهینه‌سازی چندگانه متفاوت است. هنگام برخورد با نمونه گیری شبکه، لازم است تعادلی بین فاصله شبکه و دقت نقشه برداری بر اساس بودجه موجود بدست آید [ 21 ، 22 ]. هنگامی که هیچ دانش قبلی از یک منطقه خاص از نظر ویژگی های تغییرات وجود ندارد، برآورد پارامتر واریوگرام و درونیابی اهداف نمونه گیری هستند که باید بهینه شوند [ 2 ، 8 ]]. گاهی اوقات، مدیریت تفاضلی باید بر اساس درجه هدف بررسی انجام شود، و انتظار می‌رود که نمونه‌برداری برای اهداف طبقه‌بندی و تشخیص، منعکس‌کننده توزیع درجه باشد [ 23 ، 24 ]. هنگامی که داده‌های متغیرهای کمکی مناطق خاص فراوان است، با اهداف تخمین روند جمعیت و درونیابی، انتظار می‌رود نقاط نمونه برای توزیع یکنواخت در هر دو فضای جغرافیایی و ویژگی بهینه شوند [ 25 ]. علاوه بر این، زمانی که دانش قبلی در مورد پارامترهای واریوگرام وجود نداشته باشد و اطلاعات مربوط به متغیرهای کمکی در دسترس باشد، سناریوی نمونه‌گیری پیچیده می‌شود و باید در فضای جغرافیایی، فضای ویژگی و توزیع جفت نقطه برای دستیابی به تخمین جمعیت، تخمین واریوگرام و درون یابی بهینه‌سازی شود.26 ]. مورد حتی پیچیده تر این است که برای درونیابی دقیق و تخمین جمعیت باید از چند متغیره نمونه برداری شود [ 27 ، 28 ].
در حوزه نمونه‌گیری مکانی، ابزار رایج برای مسائل بهینه‌سازی نمونه‌گیری چندهدفه، انتقال چندین هدف به یک هدف واحد با وزن‌دهی است. اولین بار توسط ون گرونیگن برای بهینه سازی هدف ترکیبی با معیارهای مرتبط برای نمونه برداری محیطی فضایی [ 29 ، 30 ، 31 ]، الگوریتم بازپخت شبیه سازی شده فضایی (SSA) به عنوان یکی از پرکاربردترین رویکردها در فرآیند بهینه سازی نمونه گیری غیرمستقیم به کار گرفته شد. بروس از الگوریتم SSA برای بهینه سازی واریانس کریجینگ جهانی میانگین مکانی استفاده کرد که شامل خطای تخمین روند و خطای درونیابی فضایی است [ 8 ].]. وبستر شرحی از فرآیند بهینه سازی دقیق با این الگوریتم ارائه کرد، با هدف اطمینان از تناسب طراحی نمونه هم برای تخمین واریوگرام و هم برای درونیابی کریجینگ [ 32 ]. گائو با استفاده از SSA برای بهینه‌سازی نقاط نمونه که به طور مساوی در فضاهای مشخصه و جغرافیایی پخش می‌شوند، یک روش نمونه‌گیری ابرمکعب لاتین شرطی فضایی پیشنهاد کرد [ 26 ]. علاوه بر این، گاربور الگوریتم SSA را در نمونه‌برداری فاز دوم برای بهینه‌سازی اهداف نقشه‌برداری چند متغیره خاک اعمال کرد [ 4 ]]. در این تحقیقات، وزن برای ترکیب اهداف چندگانه مستلزم در نظر گرفتن دانش تخصصی یا برآورد مدل است. با این وجود، به طور کلی چالش برانگیز است که رابطه بین اهداف چندگانه با وزن های تعیین شده منعکس شود، که نسبتاً دلخواه است. حتی نتیجه تخمین مدل با عدم قطعیت وجود دارد، بدون ذکر موقعیت هایی که به دلیل آن اهداف چندگانه درگیر اساساً متفاوت هستند. علاوه بر این، نتیجه بهینه‌سازی – که می‌تواند صرفاً جواب نمونه بهینه را برای هدف ترکیبی منعکس کند – نمی‌تواند بهینه‌سازی را برای هر یک از اهداف چندگانه تضمین کند. علاوه بر این، اثر بهینه‌سازی هر هدف ناشناخته است که توسط وزن ترکیب می‌شود.
توسعه علم و فناوری کامپیوتر شاهد ظهور رویکردهای بهینه سازی مستقیم چندهدفه مستقیم در زمینه های دیگر بوده است. این واقعیت کمک می کند تا فرصتی برای کاربرد این رویکردها در نمونه برداری های پیچیده جغرافیایی فراهم شود. این رویکردهای بهینه سازی مستقیم عمدتاً به سه نوع اصلی تعلق دارند: سری الگوریتم ژن (مانند MOGA [ 9 ]، NSGA [ 10 ] و NSGA-II [ 11 ])، سری الگوریتم تکامل (مانند PAES [ 12 ] و PESA-). II [ 13 ]) و سری بازپخت شبیه سازی شده (مانند SMOSA [ 14 ]، PSA [ 15 ] و AMOSA [ 16 ]]). این روش‌ها، که می‌توانند به بیش از یک راه‌حل بهینه به شیوه‌ای هوشمندانه و بدون در نظر گرفتن وزن یا محدودیت کمک کنند، به طور گسترده در زمینه‌های متعددی مانند طراحی شبکه حسگر بی‌سیم [ 33 ، 34 ]، طرح معمول [ 35 ، 36 ] استفاده می‌شوند. اعزام کار [ 37 ، 38 ، 39 ، 40 ]، پیکربندی سیستم مهندسی [ 41 ، 42 ، 43 ] و غیره. AMOSA، که به عنوان یکی از الگوریتم‌های نماینده عمل می‌کند، با دو جنبه منحصر به فرد مشخص می‌شود: میزان تسلط موجود بین راه‌حل‌ها و آرشیو برای ذخیره راه‌حل‌های بهینه [ 16 ]]. میزان تسلط باعث می‌شود به تدریج به سمت منطقه‌ای که راه‌حل‌های بهینه جهانی وجود دارد، جست‌وجو کنید، در نتیجه احتمال خروج از جستجوی محلی بر اساس معیار متروپلیس را تضمین می‌کند. آرشیو با اندازه محدود برای ذخیره راه حل های بهینه طراحی شده است که بر یکدیگر تسلط ندارند. اهداف چندگانه در فرآیند بهینه‌سازی با یکدیگر مواجه می‌شوند، که باعث می‌شود راه‌حل‌های بهینه پارتو در نهایت بایگانی شوند. در مقایسه با سایر روش‌های بهینه‌سازی چندهدفه، به‌ویژه NSGA-II که به طور قابل توجهی مورد استفاده قرار می‌گیرد، AMOSA قادر به دستیابی به مجموعه راه‌حل پارتو بهتر با کارایی بالاتر است [ 16 ، 44 ]. این ثابت می کند که در بهینه سازی مسائل با تعداد زیادی از اهداف، شایستگی بیشتری دارد.
AMOSA برای اولین بار توسط Lark در سال 2016 در زمینه نمونه برداری فضایی معرفی شد [ 17 ]. یک مورد فرضی برای به تصویر کشیدن روشی که در آن روش AMOSA در بهینه‌سازی نمونه‌گیری چندهدفه استفاده می‌شود، طراحی شد. بر اساس بهینه‌سازی مستقیم و همزمان روی اهداف چندگانه، نیازی به در نظر گرفتن تخصیص غیرقابل تحمل وزن‌ها نبود و بیش از یک طرح نمونه‌برداری بهینه ارائه کرد. لارک این ایده را داشت که می‌توان AMOSA را در دیگر سناریوهای نمونه‌گیری مکانی پیچیده جغرافیایی، مانند نمونه‌گیری برای درونیابی، نمونه‌برداری اضافی یا نمونه‌برداری فضایی غیر ثابت، به کار برد.
با این حال، کارایی AMOSA در واقع به عنوان یک گلوگاه عمل می کند که عملکرد آن را برای کاربرد گسترده در بهینه سازی چند هدفه نمونه برداری فضایی پیچیده محدود می کند. با در نظر گرفتن کیس آزمایشی Lark به عنوان مرجع، برای هر بار اجرا روی یک پردازنده 3.4 گیگاهرتزی با 8 گیگابایت رم تقریباً 10 ساعت طول می کشید. AMOSA به یک زنجیره مارکوف مجهز است که منجر به تکرار ذاتی متوالی می شود، فرآیند تکرار نمی تواند موازی شود و نسبتاً وقت گیر است. همانطور که در بالا نشان داده شد، برای مسائل نمونه‌برداری بهینه‌سازی چندهدفه مشترک و پیچیده است که در اهداف نمونه‌گیری چندگانه و شاخص‌های نظارتی متعدد درگیر شوند. این بدان معناست که فرآیند بهینه‌سازی زمان‌برتر خواهد بود. علاوه بر این، در مواجهه با فضای نمونه برداری با پوشش جغرافیایی زیاد و ناهمگونی بالا [18 ]، کمیت محاسباتی فوق‌العاده بزرگ است. از این رو، بهبود کارایی AMOSA برای سناریوهای بهینه‌سازی نمونه‌برداری چند هدفه از فضای پیچیده جغرافیایی ضروری است.

3. روش شناسی

3.1. چارچوب AMOSA-II

روش AMOSA-II برای نمونه برداری فضایی بر اساس AMOSA توسعه یافته است. عمدتاً کارایی بهینه سازی را از نظر سه جنبه بهبود می بخشد. اول، چندین زنجیره مارکوف برای گسترش زنجیره اصلی و منفرد مارکوف طراحی شده است. هر یک از این زنجیره ها به طور مستقل تکرار می شوند و سپس اطلاعات را پس از تکرارهای خاص به اشتراک می گذارند. زنجیره های بیشتر باعث تقویت درجه جستجو و تسریع روند همگرایی می شود. فناوری موازی سازی چند هسته ای بر اساس چندین زنجیره مارکوف معرفی شده است. یک زنجیره مارکوف یک فرآیند سریال سازی است که موازی کردن آن دشوار است و بنابراین باعث بازده تکرار محدود می شود. با این حال، موازی سازی برای چندین زنجیره امکان پذیر می شود و به بهبود بیشتر بازده تکرار کمک می کند. علاوه بر این، یک تابو آرشیوبرای ذخیره راه حل های جستجو شده طراحی شده است. نیازی نیست راه حل جدیدی که در آرشیو تابو وجود دارد دوباره با راه حل های بهینه مقایسه شود و سپس با اجتناب از چنین فرآیند مقایسه ای تکراری و نامعتبر در زمان محاسباتی صرفه جویی می شود.
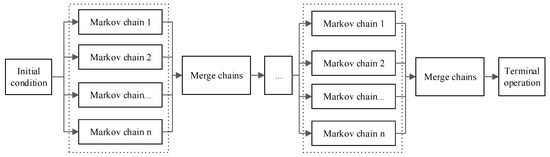
طرح گردش کار الگوریتم AMOSA-II در شکل 1 ارائه شده است . مراحل اساسی الگوریتم AMOSA-II در زیر توضیح داده شده است.
مرحله 1: پارامترهای فهرست شده را تنظیم کنید: دمای اولیه، Tmax ; نسبت بازپخت، آلفا ؛ حداکثر تعداد راه حل های موجود در بایگانی زنده که در نهایت بازگردانده می شوند، HL ; بیشترین تعداد راه حل در آرشیو زنده که عملیات خوشه بندی را راه اندازی می کند، SL ; تعداد دفعات بازپخت، eiter ; عدد تکرار در دمای فعلی، iiter .
مرحله 2: دو بایگانی را راه‌اندازی کنید – یکی برای ذخیره راه‌حل‌های بهینه، بایگانی زنده ، و دیگری برای ذخیره راه‌حل‌های جستجو شده، تابو-آرشیو . چند راه حل اولیه با استفاده از یک تکنیک ساده تپه نوردی یافت می شود. اینها بدون تسلط بر یکدیگر باقی می مانند و سپس به دو بایگانی اضافه می شوند.
مرحله 3: چندین زنجیره مارکوف ایجاد کنید. چندین زنجیره مارکوف با پشتیبانی از فناوری موازی سازی چند هسته ای به صورت موازی بر اساس رشته های متعدد اجرا می شوند.
مرحله 4: در هر زنجیره، بایگانی تابو به عنوان آرشیو فرعی، بایگانی زنده به عنوان آرشیو فرعی در نظر گرفته می شود ، و یک راه حل به طور تصادفی از آرشیو فرعی به عنوان راه حل فعلی زنجیره انتخاب می شود. ، جریان-sln .
مرحله 5: در هر زنجیره، یک راه حل جدید با اغتشاش تصادفی جریان-sln تولید می شود و وجود آن در آرشیو فرعی مورد قضاوت قرار می گیرد. اگر در بایگانی فرعی نیست، به عنوان راه‌حل جدید، new-sln در نظر گرفته می‌شود ، و بایگانی فرعی با بایگانی new-sln به‌روزرسانی می‌شود و اگر اندازه آن از SL بیشتر باشد، به اندازه HL خوشه‌بندی می‌شود . در غیر این صورت باید راه حل جدیدی ایجاد شود.
مرحله 6: در هر زنجیره، رابطه تسلط بین جریان-sln و new-sln را با قانون قضاوت بر اساس AMOSA مقایسه کنید.
مرحله 7: در هر زنجیره، آرشیو فعلی-sln ، زیر زنده را بر اساس خروجی مقایسه به روز کنید.
مرحله 8: فرآیند بالا، از مراحل 4 تا 7، با تکرارهای تکراری تکرار می شود.
مرحله 9: پس از تکرار دوم، دمای فعلی tau توسط tau=tau * alpha آنیل می شود .
مرحله 10: مراحل 3 تا 9 را تکرار کنید، پس از زمان‌های بازپخت مشخص، آرشیوهای زیر زنده و زیر تابو آرشیو را در تمام زنجیره‌های مارکوف ادغام کنید. آرشیو ترکیبی از آرشیوهای زیر زنده باید به گونه‌ای مدیریت شود که متشکل از راه‌حل‌هایی باشد که بر یکدیگر تسلط ندارند و اگر اندازه آن از SL بیشتر باشد به اندازه HL خوشه‌بندی می‌شوند . در نهایت، آرشیو زنده با آرشیو ترکیبی پردازش شده به روز می شود.
مرحله 11: مراحل 3 تا 10 را با تکرار تکرار کنید تا زمانی که شرط پایانی برآورده شود.

3.2. چند زنجیره مارکوف

چندین زنجیره مارکوف از یک زنجیره بازپخت شبیه‌سازی شده جدا می‌شوند و نمی‌توانند به طور مستقل رشد کنند – یعنی به طور همزمان یا ناهمزمان – بلکه اطلاعات را در لحظات خاصی به اشتراک می‌گذارند [ 45 ]]. موازی سازی با فناوری چند هسته ای در فرآیند بهینه سازی برای آنها امکان پذیر می شود. چندین زنجیره مارکوف راه‌حل‌های بهینه را از طریق تکرارهای خود به دست می‌آورند که مقیاس جستجو را در مقایسه با یک زنجیره مارکوف به میزان زیادی گسترش می‌دهد. هنگامی که شرط ترکیب برآورده شد، راه حل های بهینه از همه زنجیره ها مقایسه می شوند و بهینه ترین راه حل ها به دست می آیند و به عنوان ورودی مرحله تکرار بعدی برای همه زنجیره ها در نظر می گیرند. همگرایی با تعامل اطلاعاتی تسریع می شود. بنابراین، کارایی بهینه‌سازی در نتیجه زنجیره‌های مارکوف متعدد بهبود می‌یابد.
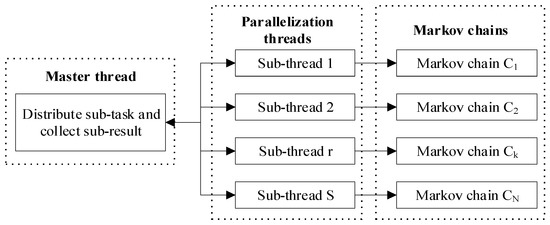
در روش AMOSA-II، چندین زنجیره مارکوف برای تکرار همزمان طراحی شده‌اند. حالت عملیات خاص در شکل 2 ارائه شده است . بر اساس شرایط اولیه یکسان، هر زنجیره مارکوف به طور مستقل با فرکانس یکسان رشد می کند و راه حل های غیر غالب خود را می گیرد. پس از آن، تمام زنجیره‌ها برای استخراج راه‌حل‌های بهینه ترکیب می‌شوند که به عنوان ورودی‌های مرحله تکرار بعدی برای هر زنجیره در نظر گرفته می‌شوند. تکرار مرحله ای و ترکیب تا زمانی که شرایط خاتمه برآورده شود ادامه می یابد.
در طول رشد مستقل، برای هر زنجیره مارکوف، آرشیو زنده و بایگانی تابو به ترتیب به عنوان آرشیو زیر زنده و زیر تابو آرشیو در نظر گرفته می‌شوند . یک راه حل به طور تصادفی به عنوان راه حل فعلی فعلی-sln از آرشیو زیر زنده مربوطه انتخاب می شود و سپس جریان-sln به طور تصادفی مختل می شود تا یک راه حل جدید تشکیل شود که اگر در زیر مجموعه مربوطه نباشد به عنوان new-sln در نظر گرفته می شود. tabu-archive . هر راه حل تازه تشکیل شده باید به آرشیو فرعی مربوطه اضافه شود . رابطه سلطه بین new-slnو جریان-sln با قاعده قضاوت مورد قضاوت قرار می گیرد و سپس آرشیو زیر زنده مربوطه و جریان-sln به صورت مشروط به روز می شود. هر زنجیره باید همان فرکانس را تکرار کند.
در مرحله ترکیب، هر زنجیره دارای آرشیو زیر زنده و زیر تابو آرشیو به روز شده خود است . همه آرشیوهای فرعی بایگانی ترکیب می شوند و همه راه حل ها برای به روز رسانی آرشیو tabu استخراج می شوند . راه‌حل‌های همه آرشیوهای زیر زنده جمع‌آوری شده و با یکدیگر مقایسه می‌شوند تا رابطه سلطه را قضاوت کنند. پس از آن، راه حل های بهینه بدون تسلط در نهایت در آرشیو زنده ذخیره می شوند . از طریق ترکیب همه زنجیره‌ها، بایگانی زنده و بایگانی تابو به‌روزرسانی می‌شوند و به عنوان ورودی زیر آرشیو زنده و زیر تابو آرشیو در نظر گرفته می‌شوند.هر زنجیره در مرحله تکرار بعدی.

3.3. موازی سازی بر اساس چند زنجیره مارکوف

بر اساس چندین زنجیره مارکوف، فناوری موازی سازی چند هسته ای در AMOSA-II برای بهبود کارایی بهینه سازی به کار گرفته شده است. با توسعه سریع علوم کامپیوتر، فناوری موازی سازی چند هسته ای عملکرد محاسباتی بسیار خوبی را نشان داده است [ 46 ، 47 ]]. با استفاده از این فناوری، وظیفه اصلی به چند کار فرعی تقسیم می شود که به عنوان الگوهای خاصی به چندین پردازنده اختصاص داده می شود. این پردازنده ها می توانند هسته های کامپیوترهای مشابه یا متفاوت باشند. سپس، این وظایف فرعی به صورت مستقل و همزمان اجرا می شوند، روند اجرای هر زیرکار به وظایف دیگر بستگی ندارد. هنگامی که تمام وظایف فرعی تکمیل می شود، نتایج همه وظایف فرعی بر اساس مکانیسم های خاص و خروجی به عنوان نتیجه یکپارچه کار اصلی جمع آوری می شود. یک زنجیره مارکوف یک فرآیند سریال‌سازی است که نمی‌توان آن را به وظایف فرعی موازی تجزیه کرد. برای چندین زنجیره مارکوف، هر یک به طور مستقل تکرار می شود، و نتایج تکراری باید پس از تکرارهای خاص ترکیب شوند. بنابراین، فناوری موازی سازی چند هسته ای را می توان برای چندین زنجیره مارکوف اعمال کرد.
طرح موازی سازی بر اساس چندین زنجیره مارکوف در شکل 3 ارائه شده است . بر اساس یک کامپیوتر با کارایی بالا که با چندین هسته پیکربندی شده است، رشته اصلی ابتدا باید برای رشته های فرعی S اعمال شود و سپس کل کار تکراری مبتنی بر زنجیره های مارکوف متعدد را به وظایف فرعی متعدد تجزیه کند. این وظایف فرعی به صورت پویا بین رشته‌های فرعی توزیع می‌شوند و از داشتن یک زیرمجموعه اطمینان حاصل می‌شود. هنگامی که یک کار فرعی از یک رشته فرعی تکمیل شد و سپس یک کار فرعی دیگر فراخوانی می شود. همانطور که همه موضوعات فرعی تمام زیر کارها را تکمیل می کنند، نتایج همه کارهای فرعی توسط رشته اصلی جمع آوری می شود و به عنوان خروجی کل کار تکراری
به منظور دستیابی به موازی سازی بر اساس زنجیره های چند مارکوف، تابع sfClusterApplyLB یکپارچه در بارش برف بسته (ارائه شده در پلت فرم R) استفاده می شود [ 48 ]. این فقط به چند پارامتر نیاز دارد – مانند اندازه هسته‌ها برای موازی‌سازی و توابع یا آرگومان‌هایی که باید فراخوانی شوند – و به عملیات موازی‌سازی خاص، مانند تجزیه وظیفه یا تخصیص نخ مربوط نمی‌شود. علاوه بر این، یادگیری و استفاده از آن برای توسعه دهندگان بسیار راحت است. علاوه بر این، تابع sfClusterApplyLBمی‌تواند در مقایسه با سایر توابع موازی‌سازی به تعادل بار دست یابد، که به این معنی است که وقتی یک رشته وظیفه فرعی خود را کامل می‌کند، بلافاصله زیرکار بعدی را فراخوانی می‌کند بدون اینکه منتظر بماند تا همه رشته‌های دیگر وظایف فرعی خود را تکمیل کنند. بنابراین، حالت متعادل کننده بار می تواند با استفاده کامل از نخ ها و کاهش زمان بیکاری، کارایی محاسباتی را بهبود بخشد.

3.4. محدودیت Tabu-Archive

محدودیت tabu-archive بر اساس عملیات جستجوی tabu طراحی شده است تا از راه حل های جستجوی مکرر جلوگیری شود. از آنجایی که امکان چندین بار جستجوی یک راه حل وجود دارد، عملیات جستجوی تابو یک روش سنتی برای جلوگیری از جستجوی مکرر در بهینه سازی است [ 49 ]. در AMOSA-II، یک تابو آرشیو بدون محدودیت اندازه برای ذخیره راه‌حل‌هایی طراحی شده است که قبلاً توسط تمام زنجیره‌های مارکوف جستجو شده‌اند، و توسط تمام زنجیره‌های مارکوف به‌عنوان زیر آرشیو تابوی خودشان به اشتراک گذاشته می‌شود . علاوه بر این، هر یک از آرشیوهای فرعی در هنگام تشکیل یک راه حل جدید در طی فرآیند تکرار خود به روز می شوند، و سپس تمام آرشیوهای فرعی در مرحله ترکیب برای به روز رسانی ترکیب می شوند.tabu-archive . در طول فرآیند تکرار مستقل، هنگامی که یک راه حل جدید توسط اغتشاش تصادفی تشکیل شد، لازم است قضاوت کنیم که آیا راه حل در آرشیو فرعی زنجیره مربوطه وجود دارد یا خیر. اگر بایگانی شود، راه حل تازه تشکیل شده باید نادیده گرفته شود و برای به دست آوردن راه حل جدید دیگری، آشفتگی دیگری انجام شود. تمام راه حل های تازه تشکیل شده هر زنجیره مارکوف به آرشیو فرعی مربوطه اضافه می.
با توجه به این واقعیت که جستجوی مکرر یک راه حل منجر به زمان محاسباتی اضافی بدون بهینه سازی می شود، محدودیت tabu-archive برای کمک به صرفه جویی در زمان بهینه سازی طراحی شده است. در غیاب محدودیت tabu-archive، راه‌حل‌هایی که در روش‌های قبلی پیدا شده‌اند ممکن است با اغتشاش جستجو شوند. سپس، روابط سلطه آن با راه حل های دیگر در آرشیو زندهمکررا مورد قضاوت قرار خواهد گرفت با این حال، فرآیند قضاوت پیچیده و زمان بر است. علاوه بر این، بدون هیچ گونه بهبودی در همگرایی راه‌حل‌های بهینه، نامعتبر است و در نهایت، این امر باعث افزایش زمان محاسباتی می‌شود. در مقابل، با محدودیت tabu-archive، راه حل تکراری را می توان حذف کرد، و از فرآیند داوری نامعتبر اضافی اجتناب کرد. در نتیجه، در زمان محاسباتی اضافی صرفه جویی می شود و راندمان بهینه سازی کلی بهبود می یابد.

3.5. تحلیل پیچیدگی

پیچیدگی AMOSA-II بر اساس روش AMOSA تجزیه و تحلیل شد. همانطور که در بالا نشان داده شد، روش AMOSA-II دارد n( n>1) زنجیر مارکوف و آموزا تنها یکی دارند که تفاوت اصلی بین آنهاست. فن آوری موازی سازی چند هسته ای با مترنخ ها بر اساس چندین زنجیره مارکوف اعمال می شود. سپس، زمان محاسباتی برای چندین زنجیره مارکوف برای یک زنجیره مارکوف در تکرارهای مساوی در دمای فعلی یکسان است. با این حال، برای توزیع پایدار محلول‌ها، تعداد تکرارها در دمای فعلی برای AMOSA-II کمتر از AMOSA با مزیت زنجیره‌های متعدد است. بنابراین، تعداد کل تکرارها برای AMOSA-II کمتر از AMOSA است. بخش‌های دیگر روش پیشنهادی AMOSA-II تقریباً مشابه روش AMOSA است. همانطور که توسط Bandyopadhyay [ 16 ] نشان داده شده است، پیچیدگی AMOSA به روش زیر بیان می شود.

سیoمترپلهایکسمنتیy=O(تیoتیآلمنتیهr×ن×(م+ورود به سیستم(ن)))

جایی که تیoتیآلمنتیهrمخفف تعداد کل تکرارها است، ناندازه آرشیو HL و متعداد اهداف است.

بر اساس تجزیه و تحلیل فوق، پیچیدگی AMOSA-II به صورت زیر بیان می شود.

سیoمترپلهایکسمنتیy=O(تیoتیآلمنتیهrn×ن×(م+ورود به سیستم(ن))

3.6. شاخص های عملکرد

انتظار می‌رود که یک روش بهینه‌سازی چندهدفه خوب، راه‌حل‌های بهینه رضایت‌بخش را به طور کارآمد ارائه دهد. زمان محاسباتی یک شاخص عملکرد برای منعکس کننده کارایی همگرایی به مجموعه راه حل بهینه پارتو است. علاوه بر این، مجموعه ای برجسته از راه حل های بهینه به دست آمده با روش بهینه سازی چند هدفه باید دو شرط را برآورده کند [ 50 ]]. یکی این است که جبهه پارتو، متشکل از راه حل های بهینه، باید تا حد امکان به جبهه پارتو واقعی همگرا باشد. مورد دیگر این است که راه حل های بهینه باید تا حد امکان متنوع باشند. به منظور ارزیابی عملکرد راه‌حل‌های بهینه به‌دست‌آمده از روش بهینه‌سازی چند هدفه با توجه به این دو شرط، پنج شاخص عملکرد پیشنهاد شده‌اند که در زمینه بهینه‌سازی چندهدفه به طور گسترده پذیرفته شده‌اند. اینها عبارتند از: همگرایی [ 11 ]، خلوص، فاصله، فاصله حداقل [ 51 ] و جابجایی [ 52 ]. فرمول ها و توضیحات پارامترهای این شش شاخص در جدول 1 فهرست شده است.
همگرایی کمی کردن درجه همگرای مجموعه راه حل بهینه پارتو به مجموعه بهینه پارتو شناخته شده است. هر چه مقدار کمتر باشد، مجموعه به دست آمده به مجموعه شناخته شده تقریبی بیشتری دارد. خلوص عبارت است از ارزیابی میزان مشارکت مجموعه های راه حل های مختلف. این مجموعه راه‌حل‌ها ابتدا جمع‌آوری می‌شوند تا مجموعه راه‌حل بهینه نهایی و سپس نسبت راه‌حل‌های بهینه از یک مجموعه راه‌حل خاص، که بخشی از مجموعه راه‌حل بهینه نهایی نیز هستند را تشکیل دهند. این مقدار برای منعکس کردن درجه مشارکت آن، بین 0 و 1 محاسبه می‌شود. شاخص فاصله می تواند یکنواختی راه حل های بهینه را نشان دهد، و شاخص فاصله حداقل برای جبران نقصی که شاخص فاصله ممکن است نتایج اشتباهی را برای موارد شدید به همراه داشته باشد، ایجاد شده است، حتی اگر گاهی اوقات ممکن است عملکرد ضعیفی داشته باشد. هر چه مقادیر این شاخص ها کمتر باشد، جواب ها یکنواخت تر می شوند. شاخص جابجایی برای تخمین اختلاف بین مجموعه راه حل به دست آمده و جبهه شناخته شده پارتو استفاده می شود. هر چه مقدار کمتر باشد، همگرایی و تنوع راه حل های بهینه به دست آمده بهتر است.

4. تست عملکرد در مسائل آزمون سنتی

4.1. مورد آزمایش

به منظور تجزیه و تحلیل عملکرد بهینه‌سازی AMOSA-II برای مسائل بهینه‌سازی چند هدفه، مورد آزمایش بر اساس مسائل آزمایشی سنتی به‌عنوان روشی که به طور گسترده توسط سایر مطالعات استفاده می‌شود، طراحی شده است [ 11 ، 13 ، 16 ]. انواع مختلف جلو پارتو برای مسائل مختلف بهینه سازی چند هدفه وجود دارد. شکل ممکن است محدب یا غیر محدب باشد و توزیع ممکن است پیوسته یا ناپیوسته، یکنواخت یا غیر یکنواخت باشد. از طرف انواع مختلف جبهه پارتو، شش مسئله تست سنتی برای آزمایش عملکرد روش AMOSA-II انتخاب شده است. اینها عبارتند از: ZDT1، ZDT2، ZDT3، ZDT4، ZDT6 [ 50 ]، و DTLZ2 [ 53]. اطلاعات دقیق در مورد عملکردها و ویژگی های شکل جبهه های پارتو در جدول 2 فهرست شده است.

4.2. طراحی آزمایش

بر اساس شش مسئله تست سنتی، عملکرد AMOSA-II با نسخه بهبود نیافته آن AMOSA و NSGA-II که یک روش بهینه‌سازی چند هدفه پرکاربرد در زمینه‌های دیگر با راندمان محاسباتی بالا است مقایسه می‌شود [ 54 ، 55 ، 56 ] . برای همه الگوریتم‌ها، مسائل آزمون به ترتیب با مجموعه‌های یکسانی از راه‌حل‌ها مقداردهی اولیه شدند. برای دو الگوریتم قبلی، اغتشاش تصادفی برای ایجاد یک راه حل جدید استفاده شد – HL 100 و SL بود.برای هر مشکل 110 بود. در همین حال، روش سنتی انتخاب، متقاطع و جهش برای به دست آوردن محلول های فرزندان برای NSGA-II استفاده می شود و اندازه مجموعه راه حل آن برای هر مشکل 100 بود. برای AMOSA-II و AMOSA، دمای اولیه و نسبت بازپخت به عنوان آزمایش مقایسه الگوریتم AMOSA مورد استفاده توسط Bandyopadhyay [ 16 ] قرار گرفت که 200 و 0.8 بود. برای NSGA-II، احتمال متقاطع 0.9 و احتمال جهش 1/ l بود ( l طول رشته است)، که هر دو توسط گلدبرگ [ 57 ] توصیه شده است. برای AMOSA-II، سه زنجیره مارکوف، سه رشته موازی وجود داشت. تکرار مربوطه برای هر شش مشکل 50، 50، 50، 20، 20 و 50 بود و به ترتیبتکرار 15، 15، 15، 10، 10 و 7 بود، فرکانس ترکیبی مربوطه 7، 7، 7، 2، 2 و 5 بود. برای AMOSA، تعداد تکرار برای هر شش مسئله 500 بود. برای NSGA-II ، اعداد نسل 240، 240، 240، 110، 110 و 300 بودند. جبهه پارتو واقعی با 200 راه حل برای هر مسئله آزمایشی بر اساس تعریف ارائه شده توسط Deb [ 50 ] به دست آمد. این سه الگوریتم، توابع چند هدفه مرتبط، و استخراج راه‌حل‌ها در جبهه پارتو واقعی برای شش مسئله آزمایشی بر اساس زبان R کدگذاری شدند. مشکلات سنتی روی رایانه شخصی با رم 128 گیگابایتی و چهار پردازنده (CPU Inter R Xeon R e7-4850، 2.20 گیگاهرتز، 14 هسته) آزمایش شدند.

4.3. نتایج

بر اساس طرحی که در بخش 4.2 نشان داده شده است ، آزمایش‌های AMOSA-II، AMOSA و NSGA-II ده بار برای هر مسئله آزمایشی انجام شد. شاخص های عملکرد هر مسئله با شمارش میانگین مقدار و انحراف معیار (SD) ده دور به دست آمد.
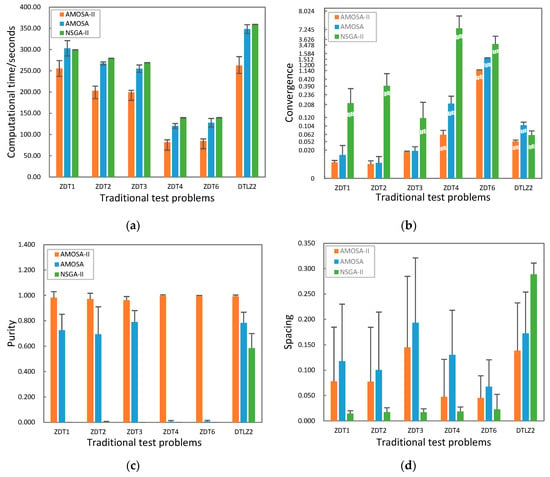
نتایج شاخص های عملکرد در شکل 4 آمده است. برای هر شش مشکل تست، زمان محاسباتی برای AMOSA-II به طور مشخص کمتر از زمان AMOSA و NSGA-II است. همگرایی AMOSA-II کمی بیشتر از AMOSA و NSGA-II است و خلوص AMOSA-II به طور قابل توجهی بیشتر از دو الگوریتم دیگر است. دو شاخص نشان می دهد که AMOSA-II عملکرد همگرایی بهتری نسبت به AMOSA و NSGA-II دارد. شاخص های فاصله و فاصله دقیقه AMOSA-II کمتر از AMOSA است، که نشان می دهد AMOSA-II پوشش یکنواخت تری از جبهه پارتو را در مقایسه با AMOSA به دست می آورد. شاخص های فاصله و فاصله دقیقه AMOSA-II و NASG-II تمایل به نوسان دارند، که نشان می دهد که یکنواختی پوشش راه حل های بهینه با دو الگوریتم بستگی به مورد دارد. جابجایی AMOSA-II کمتر از AMOSA و NSGA-II است.
علاوه بر این، شاخص های SD مربوطه برای هر الگوریتم، که با خط خطای نمودار میله ای در شکل 4 نشان داده شده است.، تحلیل می شود. SD زمان محاسباتی برای AMOSA-II قابل مقایسه با AMOSA است، اما بالاتر از NSGA-II است، که به این معنی است که زمان محاسباتی برای AMOSA-II به اندازه NSGA-II پایدار نیست. این تا حدی به این دلیل است که تعداد راه حل های بهینه جستجو شده در هر تکرار برای AMOSA-II و AMOSA تغییر می کند. بر اساس تعداد متفاوت راه‌حل‌ها، میزان عملیات داوری متغیر است و زمان عملیات خوشه‌بندی نیز تضمین نمی‌شود که پایدار باشد. با این حال، برای NSGA-II، تعداد راه‌حل‌ها در هر نسل ثابت است که آن را از نظر زمان محاسباتی بسیار پایدارتر می‌کند. شاخص‌های SD همگرایی، خلوص و جابجایی برای AMOSA-II کمتر از شاخص‌های AMOSA و NSGA-II است، که نشان می‌دهد کیفیت راه‌حل‌های بهینه پایدارتر است.
بر اساس نتایج این شش شاخص، در مقایسه با AMOSA و NSGA-II، AMOSA-II جواب های بهینه را با همگرایی بهتر در زمان کمتر به دست آورد، یکنواختی AMOSA-II بهتر از AMOSA است اما نه NSGA-II که بستگی به مورد دارد پایداری زمان اجرای آن با AMOSA قابل مقایسه است اما به خوبی NSGA-II نیست و کیفیت راه حل های بهینه آن پایدارتر از دو راه حل دیگر است.

5. تحلیل عملکرد در نمونه گیری فضایی

5.1. مورد آزمایش

به منظور آزمایش عملکرد کاربرد AMOSA-II برای بهینه‌سازی نمونه‌گیری مکانی پیچیده جغرافیایی، مورد مطالعه توسط Lark [ 17 ] استفاده شد.] برای نمونه برداری خاک از اینجا وارد می شود. در این مورد، میدانی که باید نمونه برداری شود مربع است و هر ضلع آن 100 متر است. اما قسمتی که در مرکز گوشه سمت راست و با شعاع 40 متر قرار دارد، وجود ندارد. همانطور که لارک توضیح داد، کیفیت آماری فضایی و کارایی نمونه‌برداری دو نکته کلیدی هستند که باید در طراحی نمونه‌گیری در نظر گرفته شوند. کیفیت آماری مکانی را می توان با خطای استاندارد نمونه تخمین زد که انتظار می رود برای پوشش فضایی بهتر نقاط نمونه کمتر باشد. علاوه بر این، راندمان نمونه برداری را می توان با فاصله کل تا تمام نقاط نمونه منعکس کرد که انتظار می رود به حداقل برسد. بین پوشش مکانی و کارایی نمونه‌برداری معاوضه‌هایی وجود دارد. به طور کلی، راندمان نمونه برداری بهتر ممکن است منجر به پوشش فضایی ضعیف شود. و پوشش فضایی خوب می تواند منجر به راندمان نمونه برداری ضعیف شود. بنابراین، روش بهینه‌سازی چند هدفه را می‌توان برای به دست آوردن طرح‌های نمونه‌گیری بهینه که این دو جنبه را برآورده می‌کند، به کار برد.

در این حالت اولین تابع هدف، واریانس میانگین نمونه است. برای دستیابی به پوشش فضایی خوب بهینه شده است. همبستگی مکانی متغیر خاک در این منطقه به صورت واریوگرام کروی که دامنه آن 100 متر، واریانس ناگت 500 و واریانس همبسته 4500 در نظر گرفته شده است، سپس واریانس میانگین نمونه بر اساس فرمول های زیر با داده های داده شده برآورد می شود. پارامترهای واریوگرام [ 58 ]:

σمتر2=2n∑من=1nγ¯(ایکسمن،ب)-1n2∑من=1n∑j=1nγ(ایکسمن-ایکسj)-γ¯(ب،ب)
γ¯(ایکسمن،ب)=🔻ایکسک∈بoγ(ایکسمن-ایکسک)دایکسک
γ¯(ب،ب)=🔻ایکسک∈ب0🔻ایکسل∈بoγ(ایکسک-ایکسل)دایکسلدایکسک

جایی که ایکسمننشان دهنده مختصات منسایت نمونه و γواریوگرام دو سایت در دامنه است ب.

یکی دیگر فاصله کل تا تمام نقاط نمونه است. بهینه سازی حداقل فاصله کل را به دست می آورد. مکان‌های شروع و خروج در پایین سمت چپ دامنه با مختصات (0، 0) قرار دارند و کوتاه‌ترین مسیر برای بازدید از مجموعه‌ای از نقاط نمونه کاندید بر اساس روش Sol_TSP تخمین زده می‌شود که یک دو لبه است. روش بهبود تبادل در بسته TSP توسط پلتفرم R [ 59 ] یکپارچه شده است.

5.2. طراحی آزمایش

بر اساس مورد نمونه‌گیری فضایی بهینه‌سازی چند هدفه، عملکرد کاربردی AMOSA-II با AMOSA و NSGA-II مقایسه می‌شود. پنج گروه آزمایشی با حجم نمونه (HL) 20، 40، 60، 80 و 100 به صورت زیر طراحی شده اند. برای همه آزمایش‌ها با دو الگوریتم قبلی، تنظیمات پارامتر مربوطه در مورد لارک به اشتراک گذاشته شد. حجم نمونه 20، دمای اولیه 1 و نسبت بازپخت 0.99 بود. SL به ترتیب 30، 50، 70، 90 و 110 تنظیم شد. برای AMOSA-II، 20 زنجیره مارکوف و 20 رشته موازی سازی وجود داشت. فرکانس ترکیب 8 و تعداد تکرار کل به ترتیب 3200 در پنج آزمایش بود. برای AMOSA، تعداد کل تکرار 2000 بود. برای NSGA-II، احتمال متقاطع 0.9، احتمال جهش 0.1 بود.جدول 3 . کد این توابع چند هدفه ارائه شده در کار لارک در این مقاله استفاده شده است. این مورد آزمایشی روی رایانه شخصی با 128 گیگابایت رم و چهار پردازنده (CPU Inter R Xeon R e7-4850، 2.20 گیگاهرتز، 14 هسته) انجام شد.
علاوه بر این، آزمایش‌های مرتبط برای تجزیه و تحلیل بیشتر کارایی AMOSA-II از سه جنبه انجام شد. آزمایش A برای تجزیه و تحلیل اثر تعداد زنجیره های مارکوف بر بازده عملیاتی، آزمایش B برای تجزیه و تحلیل اثر تعداد رشته های موازی سازی بر بازده عملیاتی و آزمایش C برای تجزیه و تحلیل اثر فرکانس ترکیبی بر بازده عملیاتی طراحی شده است. . برای هر مورد پنج گروه آزمایشی فرعی با حجم نمونه (HL) 20، 40، 60، 80 و 100 به روش زیر طراحی شده است. برای همه گروه ها، دمای اولیه 1، نسبت بازپخت 0.99 بود، و SL به ترتیب 30، 50، 70، 90 و 110 تنظیم شد. تنظیمات پارامترها برای آزمایش های A، B، و C در جدول 4 آمده است. .

5.3. نتایج

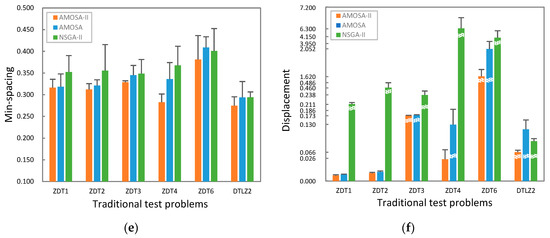
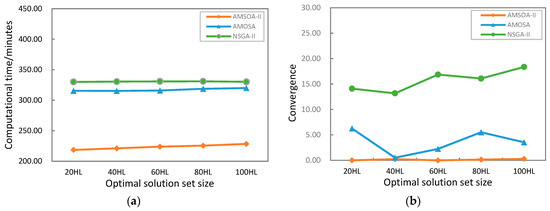
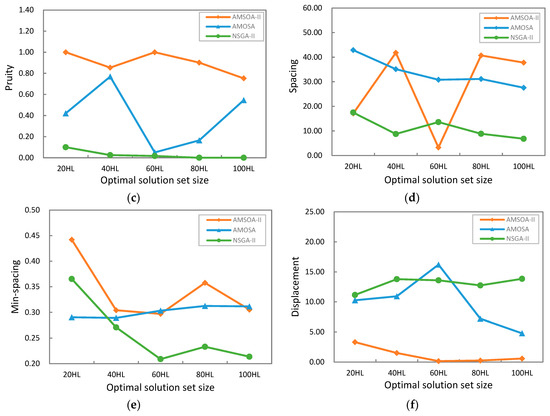
بر اساس طرحی که در بخش 5.2 نشان داده شده است ، AMOSA-II، AMOSA و NSGA-II برای بهینه‌سازی نمونه‌برداری از خاک استفاده می‌شوند. نتایج شاخص های عملکرد در شکل 5 فهرست شده است . برای همه اندازه‌های مجموعه راه‌حل بهینه (20HL، 40HL، 60HL، 80HL، و 100HL)، همانطور که در شکل 5 الف نشان داده شده است، زمان محاسباتی AMOSA-II تقریباً 223 دقیقه است، و زمان محاسباتی AMOSA تقریباً 316 دقیقه و NSGA است. -II حدود 330 دقیقه است. زمان همگرایی AMOSA-II تقریباً 40٪ کمتر از AMOSA و 47٪ کمتر از NSGA-II است. شکل 5 ب نشان می دهد که همه شاخص های همگرایی AMOSA-II کمتر از شاخص های AMOSA و بسیار پایین تر از شاخص های NSGA-II هستند. شکل 5c نشان می دهد که تمام شاخص های خلوص AMOSA-II نزدیک به 1 هستند و شاخص های خلوص AMOSA برای اندازه مجموعه محلول بهینه با 20HL، 40HL و 100HL کمتر از 0.8 و برای 60HL، 80HL نزدیک به 0 هستند. علاوه بر این، شاخص‌های خلوص NSGA-II برای همه اندازه‌های مجموعه تقریباً 0 است. شاخص‌های همگرایی پایین‌تر و شاخص‌های خلوص بالاتر برای تمام اندازه‌های مجموعه راه‌حل بهینه نشان می‌دهد که راه‌حل‌های بهینه به‌دست‌آمده توسط AMOSA-II بسیار همگراتر از راه‌حل‌های به‌دست‌آمده توسط AMOSA هستند. و NSGA-II. همانطور که در شکل 5 نشان داده شده استd،e، شاخص های فاصله AMOSA-II با اندازه های مجموعه محلول 40HL، 80HL، و 100HL بالاتر از شاخص های AMOSA و NSGA-II است، در حالی که شاخص های فاصله کوتاه AMOSA-II با اندازه های 20HL، 40HL و اندازه مجموعه محلول 80HL بالاتر از AMOSA و NSGA-II است. این نشان می دهد که تنوع یا یکنواختی مجموعه های محلول به دست آمده توسط AMOSA-II نسبت به AMOSA یا NSGA-II برتر یا حتی بدتر نیست. همانطور که در شکل 5 نشان داده شده استf، شاخص‌های جابجایی همه اندازه‌های مجموعه راه‌حل بهینه بر اساس AMOSA-II بسیار بالاتر از شاخص‌های AMOSA و NSGA-II هستند. این نشان می دهد که راه حل های بهینه تولید شده توسط AMOSA-II بسیار همگراتر و متنوع تر از راه حل های تولید شده توسط AMOSA و NSGA-II هستند. نتایج شاخص‌های جابه‌جایی با نتایج شاخص‌های فاصله و فاصله حداقل یکسان نیست، و این از این ایده حمایت می‌کند که شاخص‌های فاصله و فاصله به اندازه کافی برای نشان دادن درجه یکنواختی راه‌حل‌ها در موارد خاص کافی نیستند. که توسط Bandyopadhyay [ 16]. بر اساس چهار شاخص زمان محاسباتی، همگرایی، خلوص و جابجایی، برای مورد کاربرد بهینه‌سازی نمونه‌برداری خاک، می‌توان استنباط کرد که AMOSA-II کارایی بهینه‌سازی را با راه‌حل‌های بهینه‌تری نسبت به راه‌حل‌های ارائه‌شده توسط AMOSA و NSGA-II بهبود بخشید.
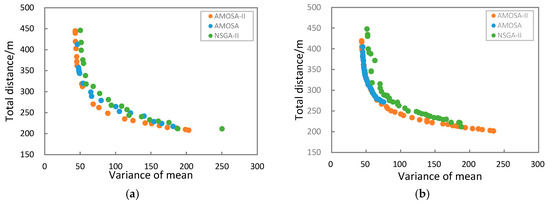
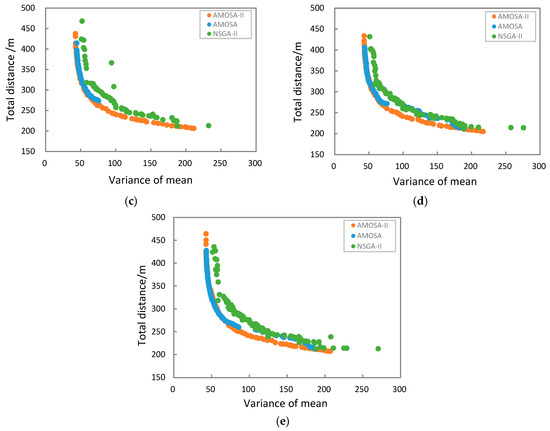
بر اساس نتیجه بهینه سازی به دست آمده با AMOSA-II، AMOSA و NSGA-II، گسترش راه حل های بهینه آنها در شکل 6 ارائه شده است . نتایج نشان می‌دهد که راه‌حل‌های بهینه از AMOSA-II نسبت به AMOSA و NSGA-II، راه‌حل‌های بیشتری را نشان می‌دهند، که نشان می‌دهد که راه‌حل‌های بهینه AMOSA-II همگراتر هستند. گسترش مجموعه راه حل بهینه به دست آمده با AMOSA-II نسبتاً یکنواخت تر است، در حالی که راه حل های بهینه به دست آمده با الگوریتم های AMOSA و NSGA-II نسبتاً نابرابرتر پخش می شوند. این با نتایج فوق در مورد شاخص‌های فاصله و فاصله دقیقه ناسازگار است و این استدلال را که دو شاخص به طور دقیق یکنواختی توزیع مجموعه راه‌حل را توصیف نمی‌کنند، که توسط Bandyopadhyay اعلام شده است، پشتیبانی می‌کند.16 ]. در نتیجه، بهینه‌سازی نمونه‌برداری چند هدفه خاک با AMOSA-II نه تنها برای کارایی محاسباتی، بلکه برای هم‌گرایی و یکنواختی مجموعه راه‌حل بهینه بهبود می‌یابد.

6. بحث

روش AMOSA-II بر اساس الگوریتم بازپخت شبیه سازی شده توسعه یافته است: تنظیم پارامترهای اولیه عملکرد اجرای برنامه بازپخت شبیه سازی شده را تعیین می کند. همانطور که در بخش 3.1 نشان داده شد ، پارامترهای اولیه کلیدی مربوطه عبارتند از: دمای حداکثر ( Tmax )، نسبت بازپخت ( آلفا )، تعداد تکرارها ( iiter ) و شرایط پایانی. حداکثر دما به عنوان دمای اولیه برای بدست آوردن کل فضای محلول در نظر گرفته می شود و روش های مختلفی برای انتخاب آن توسط Suman و Kumar [ 60 ] توصیه شده است.]. نسبت پذیرش یک شاخص کلیدی است که باید در نظر گرفته شود. در AMOSA-II، دمای اولیه به همان شیوه ای تنظیم می شود که در AMOSA برای به دست آوردن نرخ پذیرش اولیه تقریباً 50٪ [ 16 ]. برنامه بازپخت سرعت تغییر دما را تعیین می کند. برنامه بازپخت متناسب در روش پیشنهادی استفاده می شود و مقدار آلفا را می توان بر اساس نیاز بین 0.5 و 0.99 تنظیم کرد [ 60 ]. پارامتر iiter تعداد تکرارها را در هر دما نشان می دهد. تعیین مقدار تکرار باید وضعیت واقعی را در نظر بگیرد [ 60]، اما معیار اصلی اطمینان از جستجوی کارآمد برای توزیع پایدار محلول ها در هر دما است. شرط پایانی را می توان به روش های مختلفی مانند دمای حداقل، تعداد تکرارهای کل یا محدودیت های مقدار اهداف چندگانه تنظیم کرد [ 60 ]. در AMOSA-II، تعداد کل تکرارها به عنوان حاصل ضرب تعداد تکرارها در هر دما ( iiter ) و تعداد دفعات بازپخت ( eiter ) توصیه می شود . علاوه بر این، اندازه محدودیت سخت و نرم HL و SL بایگانی زنده را می توان بسته به نیاز کاربر تنظیم کرد — هیچ معیار مشخصی برای این کار وجود ندارد.
تأثیر بر کارایی AMOSA-II از نظر سه جنبه – تعداد زنجیره‌ها، تعداد رشته‌های موازی‌سازی و فرکانس ترکیب، در ادامه بیشتر مورد بحث قرار می‌گیرد.
ابتدا، تأثیر تعداد زنجیره‌های مارکوف بر بازده الگوریتم بر اساس آزمایش A تحلیل می‌شود. همانطور که در شکل 7 نشان داده شده است.زمان اجرا به تدریج از 150 دقیقه به تقریباً 220 دقیقه با افزایش تعداد زنجیره‌های مارکوف افزایش یافت، که به این معنی است که زنجیره‌های بیشتر زمان اجرا را افزایش می‌دهند. علاوه بر این، زنجیره‌های بیشتر به معنای جستجوی فشرده‌تر برای راه‌حل‌های بهینه است و زنجیره‌های کمتر به معنای جستجوی ناکافی احتمالی است که ممکن است بر عملکرد راه‌حل‌های بهینه تأثیر بگذارد. با این حال، تعداد بیش از حد زنجیره‌ها می‌تواند منجر به زمان اجرای فوق‌العاده شود که برای ارائه راه‌حل‌های بهینه در زمان مورد نیاز غیرقابل قبول است. بنابراین تعداد زنجیره های مارکوف باید از نظر زمان عملیات قابل قبول و کیفیت راه حل های بهینه مناسب باشد.
سپس، تأثیر هسته‌های موازی‌سازی مختلف بر بازده الگوریتم بر اساس آزمایش B تحلیل می‌شود. همانطور که در شکل 8 نشان داده شده است.با افزایش تعداد هسته ها، زمان اجرا از 900 دقیقه اولیه (5 هسته) به 280 دقیقه (20 هسته) کاهش یافت و سپس ثابت ماند. در این حالت فقط 20 هسته برای موازی سازی می تواند از کامپیوتر با 56 هسته نهایت استفاده را ببرد و نیازی به موازی سازی تمام هسته های کامپیوتر نیست. برعکس، گرفتن هسته‌های غیرضروری بیشتر به معنای هسته‌های کمتر برای کارهای دیگر، هدر رفتن منابع محاسباتی و قربانی کردن کارایی سایر وظایف است. بنابراین، تعداد هسته های موازی سازی باید بیش از نیمی از پیکربندی رایانه باشد، که نه تنها کارایی در حال اجرا را تضمین می کند، بلکه فضای محاسباتی را نیز ذخیره می کند.
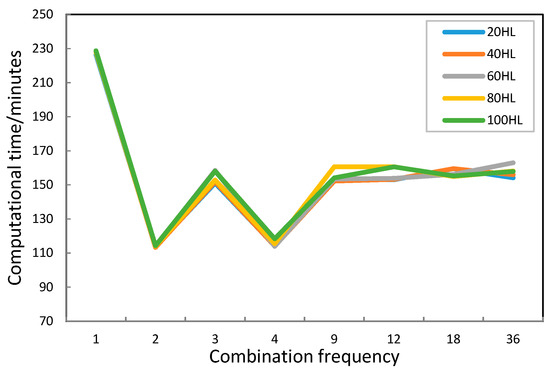
علاوه بر این، تأثیر فرکانس‌های ترکیبی مختلف بر کارایی الگوریتم بر اساس آزمایش C مورد بحث قرار گرفته است. همانطور که در شکل 9 نشان داده شده است.زمان اجرا از 230 دقیقه در ابتدا به تقریبا 160 دقیقه پس از نوسان کاهش یافت و سپس ثابت ماند در حالی که فرکانس ترکیب افزایش یافت. نتیجه نشان می دهد که فرکانس ترکیبی بالاتر منجر به کارایی بیشتر می شود. با این حال، فرکانس ترکیبی بیش از حد بالا ممکن است منجر به عملکرد همگرایی بد راه‌حل‌های بهینه شود، زیرا هر زنجیره قبل از ترکیب به اندازه کافی تکرار نمی‌شود و سپس همگرایی راه‌حل‌های بهینه به‌دست‌آمده ناکافی می‌شود. به این ترتیب، تقاضا برای عملکرد راه حل های بهینه و زمان اجرا قابل قبول باید با هم در نظر گرفته شوند تا فرکانس ترکیب را تنظیم کنیم.
بر اساس بحث فوق، در کاربرد عملی نمونه برداری فضایی AMOSA-II، زمان اجرای قابل قبول، شدت جستجو و پیکربندی رایانه باید به طور جامع در هنگام تنظیم تعداد زنجیره های مارکوف، تعداد هسته های موازی سازی و فرکانس ترکیب در نظر گرفته شود. در صورت وجود، یک کامپیوتر یا دسته ای از رایانه ها با عملکرد محاسباتی فوق العاده بالا توصیه می شود. هنگام اجرای AMOSA-II با یک رایانه خاص، اگر نیاز به تأکید بر صرفه جویی در زمان اجرا و در عین حال اطمینان از درجه خاصی از شدت جستجو باشد، زنجیره های مارکوف کمتر ممکن است بهتر باشد. هسته های موازی سازی را می توان تقریباً در دو تا سه چهارم کل تنظیم کرد و فرکانس ترکیبی می تواند بیشتر باشد. اگر نیاز به تاکید بر شدت جستجو و حصول اطمینان از مقدار قابل قبولی از زمان اجرا است، سپس زنجیره های مارکوف بیشتری را می توان تنظیم کرد. پیشنهاد می شود که فرکانس ترکیبی نباید بیش از حد باشد. هسته های موازی سازی با همین توصیه ارائه می شوند.
اگرچه راندمان بهینه‌سازی بهبود یافته است، اما محدودیت‌هایی برای AMOSA-II وجود دارد. راه اغتشاش تصادفی به اندازه کافی برای ایجاد راه حل های بهینه جدید موثر نیست، زیرا ممکن است راه حل های نامعتبری را دریافت کند که بسیار پایین تر از راه حل های بایگانی شده هستند. علاوه بر این، نقاط دور از راه‌حل‌های بهینه می‌تواند منجر به جستجوی بهینه محلی شود که در نتیجه بر جستجوی بهینه جهانی تأثیر می‌گذارد. با این حال، اقدامات خاصی برای روش پیشنهادی برای مقابله با چنین موارد پرت وجود ندارد. این محدودیت‌ها بینش‌هایی را برای تحقیقات آینده فراهم می‌کنند، مکانیسم اغتشاش خاصی را می‌توان برای شکل‌دهی راه‌حل‌های جدید نامعتبر و جستجوی راه‌حل‌های بهینه به طور کارآمد توسعه داد. علاوه بر این، برخی از استراتژی ها را می توان برای دستیابی به راه حل های بهینه با توزیع متنوع تر و یکنواخت طراحی کرد. در تحقیقات آتی بهینه سازی نمونه برداری فضایی،

7. نتیجه گیری

با هدف بهبود کارایی محاسباتی فرآیند بهینه‌سازی برای نمونه‌برداری فضایی که معمولاً با میدان‌های نمونه‌برداری بزرگ و اهداف چندگانه پیچیده سروکار دارد، یک روش بهینه‌سازی چندهدفه موازی بهبود یافته برای نمونه‌برداری فضایی، AMOSA-II، در این مقاله پیشنهاد شده‌است. چندین زنجیره مارکوف در AMOSA-II برای جستجوی فشرده راه‌حل‌های بهینه برای جایگزینی زنجیره تکی که در AMOSA استفاده می‌شود، طراحی شده‌اند و اطلاعات بهینه‌سازی این زنجیره‌ها پس از تعداد معینی از تکرار برای ارتقای همگرایی بین آنها به اشتراک گذاشته می‌شود. مکانیسم موازی سازی برای تسریع بیشتر فرآیند تکرار استفاده می شود. محدودیت tabu-archive برای جلوگیری از جستجوی مکرر برای صرفه جویی در زمان محاسباتی نامعتبر طراحی شده است. دو مورد تجربی برای تجزیه و تحلیل عملکرد بهینه‌سازی AMOSA-II با مقایسه با AMOSA و NSGA-II انجام شد. مورد شش مسئله آزمایش سنتی معمولی راه‌حل‌های بهینه بهتری را در مدت زمان کمتری با استفاده از AMOSA-II نسبت به مواردی که از دو روش دیگر استفاده می‌کنند دریافت کرد، که کارایی بهینه‌سازی بهبود یافته روش پیشنهادی را ثابت می‌کند. در حالت دیگر، نتایج بهینه‌سازی نمونه‌برداری فضایی خاک نشان می‌دهد که AMOSA-II عملکرد بهتری دارد که در به دست آوردن طرح‌های نمونه‌برداری مطلوب در مقایسه با AMOSA و NSGA-II مؤثرتر است. در نهایت، پیشنهاد می‌شود که زمان اجرای قابل قبول، شدت جستجو و پیکربندی رایانه باید به طور جامع در نظر گرفته شود تا تعداد زنجیره‌های مارکوف تعیین شود. رشته های موازی سازی و فرکانس ترکیبی هنگام استفاده از AMOSA-II برای بهینه سازی نمونه برداری فضایی چند هدفه. با محدودیت‌های روش پیشنهادی، انتظار می‌رود پژوهش‌های آینده مکانیسم‌های اغتشاش را برای شکل‌دهی راه‌حل‌های معتبرتر و ایجاد استراتژی برای به دست آوردن توزیع متنوع‌تر راه‌حل‌های بهینه ایجاد کنند. در نتیجه، AMOSA-II را می توان به عنوان یک روش عملی برای استفاده در سایر مسائل پیچیده بهینه سازی نمونه برداری مکانی جغرافیایی با اهداف چندگانه در نظر گرفت.

منابع

  1. De Gruijter، JJ; بروس، دی جی; Bierkens، MFP; Knotters، M. نمونه برداری برای نظارت بر منابع طبیعی ; Springer: برلین، آلمان، 2006. [ Google Scholar ]
  2. زیمرمن، طراحی شبکه بهینه DL برای پیش‌بینی فضایی، تخمین پارامتر کوواریانس و پیش‌بینی تجربی. Environmetics 2006 ، 17 ، 635-652. [ Google Scholar ] [ CrossRef ]
  3. Heuvelink، GBM؛ بروس، دی جی; de Gruijter، JJ بهینه سازی پیکربندی نمونه برای نقشه برداری دیجیتالی خواص خاک با کریجینگ جهانی. در نقشه برداری خاک دیجیتال. دیدگاه مقدماتی ; Lagacherie, P., Mcbratney, AB, Voltz, M., Eds. Elisevier: آکسفورد، انگلستان، 2007; صص 137-154. [ Google Scholar ]
  4. Szatmári، G. لازلو، پی. تاکاچ، ک. سابو، جی. باکاچی، ز. کوس، اس. Pásztor, L. بهینه سازی نمونه برداری فاز دوم برای اهداف نقشه برداری خاک چند متغیره: مطالعه موردی از یک منطقه شراب، مجارستان. Geoderma 2018 ، 352 ، 373-384. [ Google Scholar ] [ CrossRef ]
  5. واشات، ر. Heuvelink، GBM؛ Borůvka, L. بهینه سازی طراحی نمونه برداری برای نقشه برداری چند متغیره خاک. ژئودرما 2010 ، 155 ، 147-153. [ Google Scholar ] [ CrossRef ]
  6. بالاری، د. دی بروین، اس. برگت، AK ارزش اطلاعات و محدودیت‌های تحرک برای نمونه‌برداری با حسگرهای موبایل. محاسبه کنید. Geosci. 2012 ، 49 ، 102-111. [ Google Scholar ]
  7. زو، ز. Stein، ML طراحی نمونه‌گیری فضایی برای پیش‌بینی با پارامترهای تخمین زده شده. جی. آگریک. Biol. محیط زیست آمار 2006 ، 11 ، 24-44. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  8. بروس، دی جی; Heuvelink، GBM بهینه سازی الگوهای نمونه برای کریجینگ جهانی متغیرهای محیطی. ژئودرما 2007 ، 138 ، 86-95. [ Google Scholar ] [ CrossRef ]
  9. کارلوس، MF; پیتر، جی اف مروری بر الگوریتم های تکاملی در بهینه سازی چند هدفه. تکامل. محاسبه کنید. 1995 ، 3 ، 1-16. [ Google Scholar ]
  10. سرینیواس، ن. Deb، K. بهینه سازی چند هدفه با استفاده از مرتب سازی غیر غالب در الگوریتم های ژنتیک. تکامل. محاسبه کنید. 1995 ، 2 ، 221-248. [ Google Scholar ] [ CrossRef ]
  11. دب، ک. پراتاپ، ا. آگاروال، اس. میاریوان، تی. الگوریتم ژنتیک چندهدفه سریع و نخبه: NSGA-II. IEEE Trans. تکامل. محاسبه کنید. 2002 ، 6 ، 182-197. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  12. جاشوا، DK; دیوید، WC تقریب جبهه بدون تسلط با استفاده از استراتژی تکامل آرشیو شده پارتو. تکامل. محاسبه کنید. 2000 ، 8 ، 149-172. [ Google Scholar ]
  13. دیوید، سی. نیک، RJ; جاشوا، DK; مارتین، JO PESA-II: انتخاب مبتنی بر منطقه در چند هدف تکاملی. در مجموعه مقالات کنفرانس محاسبات ژنتیکی و تکاملی (GECCO-2001)، سانفرانسیسکو، کالیفرنیا، ایالات متحده آمریکا، 7 تا 11 ژوئیه 2001. ص 283-290. [ Google Scholar ]
  14. سومان، ب. بازپخت شبیه سازی شده چند هدفه – یک تکنیک فراابتکاری برای بهینه سازی چند هدفه یک مسئله محدود. پیدا شد. محاسبه کنید. تصمیم می گیرد. علمی 2002 ، 27 ، 171-191. [ Google Scholar ]
  15. Suman, B. مطالعه الگوریتم های مبتنی بر بازپخت شبیه سازی شده برای بهینه سازی چند هدفه یک مسئله محدود. محاسبه کنید. شیمی. مهندس 2004 ، 28 ، 1849-1871. [ Google Scholar ]
  16. Bandyopadhyay، S.; سها، س. Maulik، U. Deb، K. الگوریتم بهینه سازی چندهدفه مبتنی بر بازپخت شبیه سازی شده: AMOSA. IEEE Trans. تکامل. محاسبه کنید. 2008 ، 12 ، 269-283. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  17. Lark، RM بهینه سازی چند هدفه نمونه برداری فضایی. تف کردن آمار 2016 ، 18 ، 412-430. [ Google Scholar ] [ CrossRef ]
  18. چنگ، سی ایکس; شی، پی جی. آهنگ، CQ; گائو، JB داده های بزرگ جغرافیایی: فرصتی جدید برای مطالعه پیچیدگی جغرافیا. Acta Geogr. گناه 2018 ، 73 ، 1397–1406. [ Google Scholar ]
  19. شن، اس. بله، SJ; چنگ، سی ایکس; آهنگ، CQ; گائو، جی بی؛ یانگ، جی. نینگ، LX؛ سو، ک. ژانگ، T. پایداری و مقیاس‌های زمانی متناظر دینامیک رطوبت خاک در طول تابستان در حوضه رودخانه بابائو، شمال غربی چین. جی. ژئوفیس. Res. اتمس. 2018 ، 123 ، 8936-8948. [ Google Scholar ] [ CrossRef ]
  20. ژانگ، تی. شن، اس. چنگ، سی ایکس; آهنگ، CQ; Ye, SJ تجزیه و تحلیل همبستگی طولانی مدت دما و رطوبت خاک در دامنه های A’rou، حوضه رودخانه بابائو. Atmospheres 2018 , 123 , 12606–12620. [ Google Scholar ] [ CrossRef ]
  21. Burgess, TM; وبستر، آر. مکبراتنی، AB درونیابی بهینه و نقشه برداری همسانی خواص خاک: IV. استراتژی نمونه یورو J. Soil Sci. 1981 ، 32 ، 643-659. [ Google Scholar ] [ CrossRef ]
  22. مک براتنی، AB; وبستر، آر. Burgess, TM طراحی طرح‌های نمونه‌گیری بهینه برای تخمین محلی و نگاشت متغیرهای منطقه‌ای شده. نظریه و روش. محاسبه کنید. Geosci. 1981 ، 7 ، 331-334. [ Google Scholar ]
  23. جوانگ، ک. لیائو، دبلیو. لیو، تی. تسوئی، ال. لی، دی. نمونه برداری اضافی بر اساس آستانه تنظیم و واریانس کریجینگ برای کاهش احتمال ترسیم کاذب در یک سایت آلوده. علمی کل محیط. 2008 ، 389 ، 20-28. [ Google Scholar ] [ CrossRef ]
  24. Meirvenne، MV; Goovaerts، P. ارزیابی احتمال تجاوز از آستانه آلودگی کادمیوم خاک مخصوص سایت. Geoderma 2001 ، 102 ، 75-100. [ Google Scholar ] [ CrossRef ]
  25. هنگل، تی. دیوید، GR; Stein، A. استراتژی های نمونه برداری خاک برای پیش بینی فضایی با همبستگی با کمکی. اوست J. Soil Res. 2003 ، 41 ، 1403-1422. [ Google Scholar ] [ CrossRef ]
  26. گائو، بی بی. پان، YC; چن، زی. وو، اف. رن، XH; Hu، MG یک روش نمونه‌برداری از لاتین هایپرمکعب شرطی فضایی برای نقشه‌برداری با استفاده از داده‌های جانبی. ترانس. GIS 2016 ، 20 ، 735-754. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  27. لین، YP; چو، اچ جی; هوانگ، یل. تانگ، CH; روحانی، س. پایش و شناسایی تغییرات منظر مکانی-زمانی در تصاویر سنجش از دور چندگانه با استفاده از روش نمونه‌برداری لایه‌های مشروط لاتین هایپرمکعب و شبیه‌سازی زمین آماری. محیط زیست نظارت کنید. ارزیابی کنید. 2011 ، 177 ، 353-373. [ Google Scholar ] [ CrossRef ]
  28. Ge، Y. وانگ، جی اچ. Heuvelink، GBM؛ جین، آر. لی، ایکس. وانگ، JF نمونه‌برداری بهینه‌سازی طراحی یک شبکه حسگر بی‌سیم برای نظارت بر فرآیندهای اکوهیدرولوژیکی در حوضه رودخانه بابائو، چین. بین المللی جی. جئوگر. Inf. علمی 2014 ، 29 ، 92-110. [ Google Scholar ] [ CrossRef ]
  29. Van Groenigen، JW; Stein، A. بهینه سازی محدود نمونه برداری فضایی با استفاده از بازپخت شبیه سازی شده پیوسته. جی. محیط زیست. کیفیت 1998 ، 27 ، 1078-1086. [ Google Scholar ] [ CrossRef ]
  30. Van Groenigen، JW; سیدریوس، دبلیو. Stein، A. بهینه سازی محدود نمونه برداری از خاک برای به حداقل رساندن واریانس کریجینگ. ژئودرما 1999 ، 87 ، 239-259. [ Google Scholar ] [ CrossRef ]
  31. Van Groenigen، JW تأثیر پارامترهای واریوگرام بر طرح‌های نمونه‌برداری بهینه برای نقشه‌برداری با کریجینگ. ژئودرما 2000 ، 97 ، 223-236. [ Google Scholar ] [ CrossRef ]
  32. ریچارد، دبلیو. موری، ال. نمونه برداری بایگانی برای علوم و مدیریت زیست محیطی ; Routledge: Oxon، UK، 2013. [ Google Scholar ]
  33. وادوکس، ا. بروس، دی جی; Heuvelink، GBM بهینه سازی طراحی نمونه برای نقشه برداری خاک با جنگل تصادفی. Geoderma 2019 , 355 , 11. [ Google Scholar ] [ CrossRef ]
  34. توکلی صومعه، س. رضوانی، MH چند هدفه قرار دادن تابع شبکه مجازی با استفاده از رویکرد فراابتکاری NSGA-II. جی. ابرکامپیوتر. 2019 ، 75 ، 6451-6487. [ Google Scholar ] [ CrossRef ]
  35. Xue, Y. برنامه‌ریزی مسیر ربات متحرک با الگوریتم ژنتیک مرتب‌سازی غیرمسلط. Appl. علمی بازل 2018 ، 8 ، 2253. [ Google Scholar ] [ CrossRef ][ Green Version ]
  36. رایات، ف. موسوی، م. بزرگی امیری، الف. مشکل مسیریابی مکان-موجودی-موجودی قابل اعتماد دوهدفه با سفارش مجدد جزئی تحت خطرات اختلال: رویکرد AMOSA اصلاح شده. Appl. محاسبات نرم. 2017 ، 59 ، 622-643. [ Google Scholar ] [ CrossRef ]
  37. معماری، ع. رحیم، آرا; حسن، ع. Ahmad, R. تنظیم شده NSGA-II برای بهینه سازی کل هزینه و سطح خدمات برای یک شبکه توزیع به موقع. محاسبات عصبی Appl. 2017 ، 28 ، 3413-3427. [ Google Scholar ]
  38. ربیعی، م. زندیه، م. رمضانی، ص. مشکل زمانبندی کارگاه انعطاف پذیر جزئی دوهدفه: رویکردهای NSGA-II، NRGA، MOGA و PAES. بین المللی J. Prod. Res. 2012 ، 50 ، 7327-7342. [ Google Scholar ] [ CrossRef ]
  39. کاوه، ع. مغانی، RM; جوادی، SM انتخاب رکورد حرکت زمین با استفاده از الگوریتم های بهینه سازی چند هدفه: یک مطالعه تطبیقی. دوره زمانی. پلی تک. مدنی مهندس 2019 ، 63 ، 812-822. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  40. سعادت پور، م. افشار، ع. خوشکام، ح. مدل تخصیص بار زباله چند هدفه چند آلاینده برای رودخانه ها با استفاده از الگوریتم بازپخت شبیه سازی شده بایگانی شده همراه با QUAL2Kw. J. Hydroinform. 2019 ، 21 ، 397–410. [ Google Scholar ] [ CrossRef ]
  41. آن، اچ. گرین، دی. Johrendt، J. اسمیت، ال. بهینه سازی چند هدفه طراحی مسیر بارگذاری در شکل دهی لوله چند مرحله ای با استفاده از MOGA. بین المللی جی. ماتر. فرم. 2013 ، 6 ، 125-135. [ Google Scholar ] [ CrossRef ]
  42. آرورا، آر. کاوشیک، SC; Arora، R. بهینه‌سازی چند هدفه و چند پارامتری ژنراتور ترموالکتریک دو مرحله‌ای در پیکربندی‌های سری الکتریکی و موازی از طریق NSGA-II. انرژی 2015 ، 91 ، 242-254. [ Google Scholar ] [ CrossRef ]
  43. پانگ، جی. ژو، اچ. Tsai، Y.-C. چو، اف.-دی. یک الگوریتم بازپخت شبیه‌سازی شده پراکنده برای مسئله زمان‌بندی دوهدفه برای ایستگاه مرطوب تولید نیمه‌رسانا. محاسبه کنید. مهندسی صنعتی 2018 ، 123 ، 54-66. [ Google Scholar ]
  44. 44. دانیال، ص. کریستوف، بی. مارتین، ک. مارتا، جی. منندز، م. Sainz-Palmero، GI; برتراند، سی ام. کلاون، اف. بنیتز، JM بهینه سازی چند هدفه برای برنامه های تعمیر و نگهداری راه آهن. جی. کامپیوتر. مدنی مهندس 2018 ، 32 ، 1-11. [ Google Scholar ]
  45. چندی، جی. سونگو، ک. رامکومار، بی. پارکز، اس. Banerjee, P. ارزیابی استراتژی های آنیل شبیه سازی شده موازی با کاربرد در قرار دادن سلول استاندارد. IEEE Trans. محاسبه کنید. به دس کمک کرد. یکپارچه سازی سیستم مدار. 1997 ، 16 ، 398-410. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  46. بورین، ای. Devloo, PRB; ویرا، جی اس. Shauer, N. نرم افزار مهندسی شتاب دهنده بر روی پردازنده های چند هسته ای مدرن. Adv. مهندس نرم افزار 2015 ، 84 ، 77-84. [ Google Scholar ] [ CrossRef ]
  47. ری، آر. گورونگ، آ. داس، بی. بارتوچی، ای. بوگومولوف، اس. Grosu, R. XSpeed: تجزیه و تحلیل دسترسی سریع در پردازنده های چند هسته ای. در سخت افزار و نرم افزار: تأیید و آزمایش. HVC 2015. نکات سخنرانی در علوم کامپیوتر ; Springer: Cham, Switzerland, 2015. [ Google Scholar ]
  48. مانوئل، JAE; یوخن، ک. کریستین، پی. مارکوس، اس. Esmeralda, V. آموزش عملی برای محاسبات موازی با R. Comput. آمار 2011 ، 26 ، 219-239. [ Google Scholar ]
  49. گلاور، اف. Taillard، E. راهنمای کاربران برای جستجوی تابو. ان اپراتور Res. 1993 ، 41 ، 1-28. [ Google Scholar ] [ CrossRef ]
  50. Deb، K. بهینه سازی_چند هدفی با استفاده از الگوریتم های تکاملی . Wiley: Wiltshire، UK، 2001. [ Google Scholar ]
  51. سانگامیترا، بی. پال، SK; Aruna، B. GAs چندهدفه، شاخص های کمی، و طبقه بندی الگو. IEEE Trans. سیستم مرد سایبرن. قسمت B Cybern. 2004 ، 34 ، 2088-2099. [ Google Scholar ]
  52. سانگامیترا، بی. سریپارنا، اس. طبقه بندی بدون نظارت: اقدامات مشابه، رویکردهای کلاسیک و فراابتکاری، و کاربردها . Springer: برلین، آلمان، 2013. [ Google Scholar ]
  53. دب، ک. تیله، ال. لومانز، ام. Zitzler, E. مسائل آزمون بهینه سازی چندهدفه مقیاس پذیر. در مجموعه مقالات کنگره 2002 محاسبات تکاملی. CEC’02 (Cat. No.02TH8600)، هونولولو، HI، ایالات متحده آمریکا، 12–17 مه 2002; صص 825-830. [ Google Scholar ]
  54. ترکسون، RF؛ یان، اف. علی، MKA; لیو، بی. Hu, J. مدل‌سازی و بهینه‌سازی چند هدفه عملکرد موتور و انتشار هیدروکربن از طریق استفاده از کد مهندسی به کمک رایانه و الگوریتم ژنتیک NSGA-II. پایداری 2016 ، 8 ، 72. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  55. ارشد، محمدرضا; ابیدو، MA; سالم، ا. Elsayed, AH بهینه سازی عوامل وزنی مدل کنترل گشتاور پیش بینی کننده موتور القایی با استفاده از NSGA-II با تصمیم گیری TOPSIS. دسترسی IEEE 2019 ، 7 ، 177595–177606. [ Google Scholar ] [ CrossRef ]
  56. Bandyopadhyay، S.; پال، SK طبقه بندی و یادگیری با استفاده از الگوریتم های ژنتیک کاربرد در بیوانفورماتیک و هوش وب . Springer: Heidelberg/Berlin، آلمان، 2007. [ Google Scholar ]
  57. گلدبرگ، الگوریتم های ژنتیک DE در جستجو، بهینه سازی و یادگیری ماشینی ؛ ادیسون-وسلی: نیویورک، نیویورک، ایالات متحده آمریکا، 1989. [ Google Scholar ]
  58. وبستر، آر. الیور، کارشناسی ارشد روش های آماری در بررسی منابع خاک و زمین ; دانشگاه آکسفورد: آکسفورد، انگلستان، 1991; جلد 86، ص 1149–1150. [ Google Scholar ]
  59. مایکل، اچ. Kurt, H. TSP-Infrastructure برای مشکل فروشنده دوره گرد. J. Stat. نرم افزار 2007 ، 23 . [ Google Scholar ]
  60. سومان، بی. کومار، پی. بررسی بازپخت شبیه سازی شده به عنوان ابزاری برای بهینه سازی تک و چند هدفه. جی. اوپر. Res. Soc. 2006 ، 57 ، 1143-1160. [ Google Scholar ] [ CrossRef ]
Ijgi 09 00236 g001 550
شکل 1. طرح گردش کار الگوریتم بازپخت شبیه سازی شده چند هدفه آرشیو شده (AMOSA)-II.
Ijgi 09 00236 g002 550
شکل 2. طرح چندین زنجیره مارکوف.
Ijgi 09 00236 g003 550
شکل 3. موازی سازی بر اساس چندین زنجیره مارکوف.
Ijgi 09 00236 g004a 550 Ijgi 09 00236 g004b 550
شکل 4. شاخص های عملکرد AMOSA-II، AMOSA، و NSGA-II با مسائل تست سنتی (ZDT1، ZDT2، ZDT3، ZDT4، ZDT6، و DTLZ2): ( الف ) زمان محاسباتی. ( ب ) همگرایی؛ ج ) خلوص؛ ( د ) فاصله؛ ( ه ) فاصله ی دقیقه؛ ( و) جابجایی .
Ijgi 09 00236 g005a 550 Ijgi 09 00236 g005b 550
شکل 5. شاخص های عملکرد AMOSA-II، AMOSA، و NSGA-II با اندازه مجموعه راه حل بهینه (20HL، 40HL، 60HL، 80HL، و 100HL): ( الف ) زمان محاسباتی. ( ب ) همگرایی؛ ج ) خلوص؛ ( د ) فاصله؛ ( ه ) فاصله ی دقیقه؛ ( و) جابجایی .
Ijgi 09 00236 g006a 550 Ijgi 09 00236 g006b 550
شکل 6. توزیع راه حل های بهینه بر اساس AMOSA-II، AMOSA، و NSGA-II با اندازه های مختلف محلول بهینه: ( a ) 20HL; ( ب ) 40HL; ( ج ) 60HL; ( د ) 80HL; ( ه ) 100HL.
Ijgi 09 00236 g007 550
شکل 7. زمان محاسباتی بر اساس اعداد مختلف زنجیره مارکوف.
Ijgi 09 00236 g008 550
شکل 8. زمان محاسباتی بر اساس تعداد مختلف هسته های موازی سازی.
Ijgi 09 00236 g009 550
شکل 9. زمان محاسباتی بر اساس فرکانس های ترکیبی مختلف.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید