درک فرم شهری چینی: الگوی فراکتال جهانی شبکه های خیابانی در 298 شهر

خلاصه

فرم شهری را می توان با بسیاری از عناصر شهر، مانند خیابان ها، منعکس کرد. یک شبکه خیابانی به عنوان ستون فقرات یک شهر عمل می کند و ساختار فیزیکی شهر را منعکس می کند. اقدامات توپولوژیکی شبکه خیابانی و توزیع‌های آماری به طور گسترده در سال‌های اخیر مورد بررسی قرار گرفته‌اند، اما مطالعات قبلی به ندرت توزیع سنگین اتصالات خیابانی را از منظر فراکتال مشخص کرده‌اند. توزیع دم بلند اتصالات خیابانی می‌تواند بر اساس تعریف جدید و سوم فراکتال باشد: یک مجموعه یا الگوی فراکتال است اگر مقیاس چیزهای کوچک بسیار بیشتر از چیزهای بزرگ حداقل دو بار تکرار شود. تعداد الگوهای مقیاس‌گذاری تکراری خیابان‌های کم‌تر نسبت به خیابان‌هایی که به خوبی متصل هستند، به اندازه‌گیری سلسله‌مراتب مقیاس‌بندی یک شبکه خیابانی کمک زیادی می‌کند. علاوه بر این، این ما را قادر می سازد تا کسری بالقوه شبکه های خیابانی شهری را در مقیاس ملی بررسی کنیم. در این رابطه، مطالعه حاضر با هدف کمک به مورفولوژی شهری در چین از طریق بررسی همه‌جای شهرهای فراکتال از لنز شبکه‌های خیابانی است. برای انجام این کار، ما صدها هزار خیابان طبیعی را از حدود 4.5 میلیون بخش خیابان در 298 شهر چین تولید کردیم و تشخیص قانون قدرت و همچنین سه معیار فراکتال را که از تعریف سوم فراکتال پدید آمدند، اتخاذ کردیم. نتایج نشان می دهد که تقریباً همه شهرها از نظر اتصالات خیابانی دارای ساختار فراکتالی هستند. علاوه بر این، تجزیه و تحلیل رگرسیون چندگانه ما نشان می‌دهد که کسر بودن شبکه‌های خیابانی با وضعیت اجتماعی-اقتصادی شهری و با مصرف انرژی همبستگی منفی دارد. از این رو،

کلید واژه ها:

فرم شهری ؛ خیابان های طبیعی ؛ تعریف سوم فراکتال ; مقیاس بندی سلسله مراتب ; قانون قدرت

1. معرفی

به طور گسترده ای شناخته شده است که ویژگی های جغرافیایی مانند کوه ها و رودخانه ها نه صاف و نه منظم هستند، بنابراین نمی توان آنها را به طور دقیق بر اساس هندسه اقلیدسی توصیف کرد. در عوض، هندسه فراکتال ظرفیت پر کردن این شکاف را دارد. خود کلمه “فرکتال” از لاتین سرچشمه گرفته و به معنای واقعی کلمه “شکسته” یا “نامنظم” است. توسعه هندسه فراکتال از طریق سه تعریف انجام شد، که همه آنها بر اصطلاح “شباهت خود” متمرکز هستند: بخشی از یک شی یا الگو شبیه به کل است [ 1 ، 2 ، 3 ]. برای تعریف اول و دوم، فراکتال ها به اشکالی اطلاق می شود که به طور دقیق یا از نظر آماری مشابه خود هستند. یک مثال کلاسیک از اشکال کاملاً مشابه منحنی کوخ [ 4] که قطعات آن دقیقاً کپی های کوچک شده منحنی اصلی است. Mandelbrot [ 5 ] با افزودن مقداری تصادفی به آن «نسخه‌های مقیاس‌شده» سخت‌گیری را کاهش داد تا منحنی ساخته‌شده قادر به توصیف ویژگی‌های دنیای واقعی، مانند خط ساحلی باشد. خود شباهت های دقیق و آماری، هر دو یک توان قانون توان یا بعد فراکتال را از رابطه قانون توان بین تعداد کپی ها در فراکتال و مقیاسی که در آن اندازه گیری می شود حفظ می کنند. از آنجایی که رابطه قانون قدرت برای دیدن فراکتال های دنیای واقعی بسیار سخت است، جیانگ و یین [ 6 ]] این نیاز آماری را با بررسی اینکه آیا الگوی مقیاس بندی (مقیاس های بسیار کوچکتر از مقیاس های بزرگ) یک فراکتال حداقل دو بار تکرار می شود، این نیاز آماری را بیشتر کاهش داد. در تعریف سوم، تمرکز خود شباهت دیگر بر شکل هندسی نیست، بلکه بیشتر بر الگوی تکرارشونده مقیاس‌بندی آمار در میان کل‌های فرعی داده‌های مشتق‌شده تکراری است.

فضای شهری الگوهای فراکتال را از دو منظر اصلی به نمایش می گذارد. از نظر ریخت شناسی، حجم وسیعی از ادبیات شواهد فراکتالی را از بسیاری از عناصر شهری ارائه می دهد – به عنوان مثال، مناطق ساخته شده، کاربری های زمین، خیابان ها، و اشکال مرزی [ 7 ، 8 ، 9 ، 10 ، 11 ، 12 ]، و تکامل آنها یا رشد (به عنوان مثال، [ 13 ، 14 ، 15]). از نظر عملکردی، فعالیت‌های انسانی در داخل یک فضای شهری، به‌ویژه آن‌هایی که با داده‌های رسانه‌های اجتماعی مبتنی بر مکان آشکار می‌شوند، در ساختاری فراکتال‌مانند که شامل اقلیتی از مکان‌های با تراکم بالا و اکثریت مکان‌های کم تراکم است، تجمع می‌یابند که به صورت مکانی از مرکز شهر به سمت حاشیه [ 16 ، 17 ]. همچنین ادعا می‌شود که چنین پیکربندی فضایی فعالیت‌های انسانی شبیه ساختار فراکتالی سیستم‌های مکان مرکزی است [ 18 ]]. در میان عناصر شهری فوق الذکر، خیابان های شهری بیشتر برای درک شکل و عملکرد شهر مورد استفاده قرار می گیرند. از یک سو، خیابان ها محیط فیزیکی یک شهر را نشان می دهند و انسجام سازمان فضایی آن را به نمایش می گذارند. از سوی دیگر، فعالیت‌ها یا حرکات شهری انسان تا حد زیادی در شبکه خیابان‌ها محدود می‌شوند. بنابراین، بررسی شهرهای فراکتال از منظر شبکه های خیابانی به منظور دستیابی به بینش های جدید در مورد محیط فضایی زیربنایی یک شهر، پیکربندی آن و فعالیت های انسانی در آن مهم است.

شبکه‌های خیابانی به‌عنوان یک نوع خاص از شبکه‌های پیچیده که گره‌ها و پیوندها در فضای جغرافیایی قرار دارند، به‌طور طبیعی به‌عنوان نمایش گراف مدل‌سازی می‌شوند، که در آن نمودار دوگانه (گره‌ها به عنوان خیابان، پیوندها به عنوان تقاطع، [ 19 ]) ما را قادر می‌سازد خیابان را تجزیه و تحلیل کنیم. پیکربندی ساختاری از طریق مجموعه ای از اقدامات توپولوژیکی بر اساس نظریه گراف [ 20 ، 21 ] و رویکردهای نحوی فضا [ 22 ]. مشابه بسیاری دیگر از شبکه‌های پیچیده دنیای واقعی، مانند شبکه‌های اجتماعی و تعاملات پروتئینی، نمودار دوگانه شبکه‌های خیابانی با توجه به توزیع قانون توان درجات گره، تمایل به داشتن یک ویژگی فراکتال یا مقیاس‌بندی دارند [ 20 ، 23 ].]، یا رابطه قانون توان بین تعداد محفظه های غیر همپوشانی که کل شبکه را پوشش می دهند و اندازه آنها [ 24 ، 25 ، 26 ]. با این حال، از آنجایی که مدل قانون قدرت برای اندازه‌گیری فراکتالی که توزیع آماری آن از قانون غیر قدرتی پیروی می‌کند، بسیار سخت است، اما به نظر می‌رسد که دارای ویژگی‌های دم چربی است (مثلا، log-normal)، ارزیابی اینکه آیا شبکه‌های خیابانی فراکتالی هستند یا خیر. تنوع زیادی از شهرها چالش برانگیز است. سپس، این مقاله با انگیزه استفاده از تعریف سوم فراکتال، که محدودیت قانون توان را با در نظر گرفتن انواع دیگر توزیع دم سنگین به عنوان پشتیبان فرکتالیته، برای شناسایی الگوی فراکتالی جهانی شبکه‌های خیابانی در گستره فضایی وسیع باز می‌کند.

یکی دیگر از عوامل محرک این تحقیق، داده های بزرگ جغرافیایی است. در دسترس بودن محدود داده ها و منابع محاسباتی در گذشته منجر به ایجاد دامنه فضایی نسبتاً باریکی از آثار متعلق به شبکه های خیابانی شهری شده است. یعنی سطح محله یا شهر [ 27 ]. داده‌های بزرگ فرصت‌های بی‌سابقه‌ای را برای محققین فراهم می‌کند تا به مجموعه‌های داده‌های مکانی در مقیاس عظیم دست یابند. به عنوان مثال، از طریق OpenStreetMap (OSM)، یک پلت فرم اطلاعات مکانی داوطلبانه، ما قادر به دستیابی و پردازش شبکه خیابانی در سراسر کشور یا حتی در سراسر جهان هستیم که فرصت‌های جدیدی را برای بررسی شکستگی‌های خیابانی در سطوح بین شهری در یک کشور یا در سراسر کشورها ایجاد می‌کند. 28]. نه تنها می توان به شبکه راه های ملی دسترسی داشت، بلکه به سایر مقادیر شهری ملی نیز می توان به راحتی دسترسی داشت، مانند تولید ناخالص داخلی (GDP) و انتشار CO ₂ . این امکان را برای ما باز می کند تا رابطه بین پیکربندی شبکه خیابانی و شاخص های انرژی، زیست محیطی و اقتصادی شهری را باز کنیم. مطالعات قبلی در مقیاس شهری گزارش کرده‌اند که خیابان‌هایی با ویژگی‌های فراکتال می‌توانند به افزایش سرمایه اجتماعی و کاهش انتشار گازهای گلخانه‌ای به دلیل کارایی بزرگ‌تر شبکه‌های خیابانی کمک کنند (به عنوان مثال، [ 26 ، 29 ]). این مطالعه چنین تحلیل اکتشافی را در مقیاس کشور انجام می دهد.

سهم این مطالعه سه برابر است. اولاً، ما از نمایش خیابانی طبیعی (یک خیابان پیوسته به جای بخش‌ها یا رئوس بی‌معنی آن؛ به جزئیات در بخش 2.2 مراجعه کنید ) برای شناسایی ساختار فراکتال یا مقیاس‌بندی استفاده کردیم. ما خیابان‌های طبیعی را برای تقریباً تمام شهرهای استانی در چین با موفقیت پردازش و استخراج کرده‌ایم، که می‌تواند منبع داده‌ای ارزشمند برای جامعه تحقیقاتی باشد. دوم، ما یک روش ابتکاری در ترکیب معیارهای فراکتال مختلف تحت چارچوب نظری تعریف سوم طراحی کردیم. شروع از ht-index ناشی از شکستگی سر/دم [ 6]، می‌توانیم فرکتالیته شبکه خیابانی را برای هر شهر جداگانه و پیچیدگی کلی همه شبکه‌های خیابانی را در مقیاس کشور ارزیابی کنیم. در مرحله بعد، به دلیل عدم حساسیت شاخص ht، ما از دو گزینه استفاده کردیم: نرخ تجمعی رشد (CRG, [ 30 ]) و نسبت مناطق در یک نمودار با اندازه رتبه (RA, [ 31 ]). جزئیات بیشتر را در بخش 2.3 ببینید). ما دریافتیم که استفاده از آنها به طور جمعی می تواند شهرها را در یک سلسله مراتب مقیاس بندی متمایز کند، و این امکان را فراهم می کند تا درک جامع تر و منظم تر از اشکال شهری چینی را فرموله کنیم. در نهایت، ما به دنبال روابط بین فرکتالیته شبکه‌های خیابانی و انواع مختلف معیارهای شهری بودیم و قدرت توضیحی فراکتال‌های شهری را بر وضعیت اجتماعی-اقتصادی شهری و مصرف انرژی در مقیاس ملی ارزیابی کردیم.

ادامه این مقاله به شرح زیر است. بخش 2 مجموعه داده ها و چارچوب روش شناختی پیشنهادی را معرفی می کند. بخش 3 تجسم و نتایج آماری را در مورد الگوی فراکتال جهانی در بیش از 300 شهر در چین و همچنین همبستگی بین هر متریک فراکتال و کمیت شهری ارائه می‌کند. بخش 4 بیشتر ساختار فراکتالی شبکه های خیابانی را مورد بحث قرار می دهد، قبل از اینکه بخش 5 نتیجه گیری کند و به مسیرهای تحقیقاتی آینده اشاره کند.

2. داده ها و روش ها

2.1. داده ها و پردازش داده ها

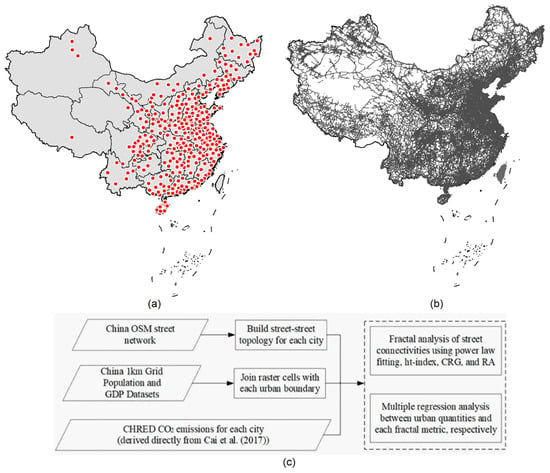
_{در این مطالعه از سه مجموعه داده استفاده شد: (1) مرزهای 298 شهر، ( 2} ) شبکه خیابان های ملی، و (3) مجموعه داده های شبکه چین از تولید ناخالص داخلی، جمعیت و انتشار CO2. همانطور که در شکل 1 نشان داده شده است ، ما 298 شهر در سطح استانی را انتخاب کردیم که در سراسر چین به عنوان مناطق مورد مطالعه پراکنده شده بودند. هر مرز شهر بیشتر به عنوان واحد پردازش داده پذیرفته می شود. شبکه ملی خیابان از پلتفرم Geodata رایگان GEOFABRIK در آلمان دانلود شد [ 32 ]. ما از جعبه ابزار ArcGIS Interoperability Toolbox استفاده کردیمبرای پردازش مجموعه بزرگ چند خط با انواع جاده ها به 4,419,603 بخش برای اطمینان از اینکه راس انتهایی هر بخش محل اتصال خیابان است که در آن حداقل سه چند خط قطع می شوند و سپس کل مجموعه قطعات را با استفاده از هر مرز شهری برش دادیم تا شهر را به دست آوریم. خیابان های همسطح داده های شبکه ملی تولید ناخالص داخلی و جمعیت از پایگاه داده های منابع ملی و محیط زیست آکادمی علوم چین [ 33 ] تهیه شده است. داده‌ها در سال 2015 جمع‌آوری شدند و با فناوری سنجش از دور با وضوح زمین 1 کیلومتر فضایی شدند (برای جزئیات بیشتر این رویکرد، [ 34 ] را ببینید). آمار تولید ناخالص داخلی و جمعیت در سطح شهر با تجمیع مقادیر سلول در هر مرز شهر با موفقیت محاسبه شد. _{CO 2} در سطح شهرانتشار مستقیماً از کار قبلی [ 35 ] مشتق شد که آمارهای مرتبط بر اساس CHRED (پایگاه داده انتشار با وضوح بالا چین؛ جزئیات بیشتر را در [ 36 ] ببینید) ارائه می‌کند. _{توجه داشته باشید که انتشار CO 2} در مقیاس شهری در کار Cai و همکاران [ 35 ] فقط برای 283 شهر در دسترس است.

2.2. تبدیل از توپولوژی قطعه-بخش به توپولوژی خیابان-خیابان

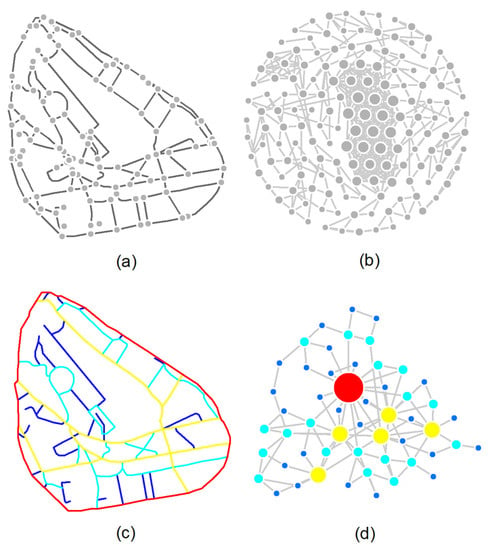
توپولوژی بخش-بخش به طور گسترده ای در سیستم های GIS فعلی پذیرفته شده است. به عنوان مثال، پسوند ArcGIS Network Analyst ، تجزیه و تحلیل شبکه را بر اساس رابطه بین بخش هایی که در یک گره تقاطع خیابان از هم جدا شده اند، ایجاد می کند. توپولوژی بخش-بخش یا به طور کلی تجزیه و تحلیل مبتنی بر بخش، قابل توجه است زیرا بسیاری از کاربردهای شهری مانند ناوبری را ارائه می دهد. با این حال، توپولوژی بخش-بخش اساساً یک چشم انداز هندسی است زیرا واحد مدل سازی شبکه خیابانی بر اساس اولیه های هندسی، مانند نقاط، چند خط و چند ضلعی ها است. اولیه های هندسی فضا را به صورت مکانیکی نشان می دهند، زیرا طول ها یا اتصالات آنها تمایل به پیروی از توزیع نرمال دارند ( شکل 2 a,b).

برای مشاهده ارگانیک‌تر فضا، می‌توان توپولوژی بخش-بخش را به توپولوژی خیابان-خیابان تبدیل کرد. خیابان به مفهوم «خیابان طبیعی» یا «خیابان نام‌گذاری شده» اشاره دارد که از مجموعه‌ای از بخش‌های مجاور با تداوم خوب یا نام‌های مشترک تشکیل شده است [ 37 ]. تداوم خوب را می توان به عنوان زوایای انحراف کوچک (یعنی آنهایی که کوچکتر از 45 درجه است) در سراسر جفت قطعه مجاور درک کرد. در مقایسه با بخش‌ها، خیابان‌هایی مانند واحد مدل‌سازی در ادراک ما منسجم و معنادار هستند [ 22 ]. علاوه بر این، توپولوژی خیابان-خیابان به ما اجازه می دهد تا شبکه خیابان را از دیدگاه شبکه پیچیده بررسی کنیم [ 38]، از آنجایی که طول خیابان ها و اتصالات تحت چنین تنظیماتی تمایل دارند بدون مقیاس یا ناهمگن باشند، که نشان دهنده خیابان های کوتاه تر/کمتر نسبت به خیابان های طولانی/با اتصال خوب است ( تصویر 2 ). اگرچه ممکن است طول خیابان با اتصال خیابان همبستگی داشته باشد، ما فقط از اتصال خیابان برای آزمایش‌های زیر استفاده کرده‌ایم زیرا طول خیابان فردی عامل اصلی برای درک فضای شهری نیست. این را می توان به راحتی با این واقعیت درک کرد که معمولاً یک خیابان با اتصال خوب در یک شهر یافت می شود، در حالی که یک خیابان طولانی اغلب خیابانی با اتصال خوب نیست و معمولاً در حومه شهر یافت می شود.

2.3. تجزیه و تحلیل فراکتالی اتصالات خیابانی

ساختار فراکتالی شبکه‌های خیابانی شهری را می‌توان با قانون قدرت یا سایر مدل‌های توزیع سنگین در رابطه با اتصالات خیابان مشخص کرد. از آنجایی که ممکن است مدل قانون قدرت برای شناسایی یک فراکتال بسیار سخت‌گیرانه باشد، ما سلسله‌مراتب مقیاس‌بندی خیابان‌ها را با استفاده از شکاف‌های سر/دم [ 39 ] استخراج می‌کنیم و سه معیار – ht-index، CRG و RA را برای اندازه‌گیری فرکتالیته بالقوه محاسبه می‌کنیم. شبکه خیابانی

2.3.1. تشخیص قانون قدرت

یک مدل قانون توان را می توان با رابطه (1) بیان کرد:

y = ایکس - α .

(1)

ساده‌ترین راه برای شناسایی توزیع قانون توان، رتبه‌بندی مقادیر داده‌ها از بزرگ‌ترین به کوچک‌ترین و سپس ایجاد نمودار log-log از داده‌های مرتب‌شده است. اگر داده ها دقیقاً از توزیع قانون قدرت پیروی کنند، توزیع یک خط مستقیم خواهد بود. با این حال، برای این روش مقابله با بالا و پایین های آشفته در دم برای بسیاری از مجموعه داده های دنیای واقعی بسیار دشوار است [ 40 ]. برای رسیدگی به این مشکل، یک روش قوی با استفاده از تخمین حداکثر احتمال، پیشنهاد شده توسط Clauset و همکاران. [ 41 ]، می تواند به تشخیص دقیق اینکه آیا داده ها قانون قدرت هستند یا نه کمک کند. این روش ابتدا توان قانون توان را بررسی می کند $α$ که با معادله (2) نشان داده می شود:

α = 1 + n ⎡⎣ \sum i = 1 n لوگاریتم ایکس من ایکس m i n ⎤⎦ - 1

(2)

جایی که $x_{m i n}$ کوچکترین مقداری است که داده ها از آنجا توزیع شده اند. محدوده قابل قبول برای توان $α$ از 1 تا 3 است. برای آزمایش اینکه چقدر داده ها می توانند با قانون قدرت مطابقت داشته باشند، Clauset et al. [ 41 ] انجام تست کولموگروف-اسمیرنوف را پیشنهاد می کند. این آزمون داده ها را با نمونه ها بر اساس توزیع قانون توان ایده آل با استفاده از مقادیر x-min و آلفای مشتق شده مقایسه می کند. سپس مقدار p -value شاخص خوبی از برازش ، که از 0 تا 1 متغیر است، تولید و برای تعیین میزان تناسب داده‌ها با یک مدل قانون توان استفاده می‌شود. اگر p -value $\geq$ 0.01، ما مجموعه ای از داده ها را می پذیریم که با قانون قدرت توزیع شوند.

2.3.2. ادغام Ht-Index، CRG، و RA برای اندازه گیری فراکتال

جیانگ و یین [ 6 ] سومین تعریف فراکتال را به عنوان «عود ریزهای بسیار بیشتر از بزرگ‌ها» ارائه کردند و شاخص ht متریک جدیدی را القا کردند که از طرح طبقه‌بندی جدید شکستگی‌های سر/دم [ 39 ] می‌آید. برای توضیح بیشتر، با توجه به داده‌هایی با توزیع دم سنگین، همیشه می‌توانیم داده‌ها را به مقادیر بسیار کوچک (یعنی دم) و چند مقدار بزرگ (سر) تقسیم کنیم. توجه داشته باشید که عدم تعادل بین درصد سر و درصد دم وجود دارد (مثلاً 60/40). عملیات شکاف را تقسیم سر/دم می گویند. ما می‌توانیم این تقسیم‌بندی را به‌طور مکرر در قسمت سر داده اعمال کنیم تا زمانی که درصد سر و دم به‌روز شده به تعادلی مانند 50/50 برسد. کل فرآیند نشان می دهد که چگونه روش سر/دم شکسته می شود [ 39] آثار. از آنجایی که فرآیند بازگشتی است، معمولاً به یک سری مقادیر میانگین دست پیدا می کنیم. تعداد مقادیر میانگین به دست آمده $i$ به علاوه یک به اصطلاح ht-index است که در رابطه (3) بیان شده است:

ht = i + 1

(3)

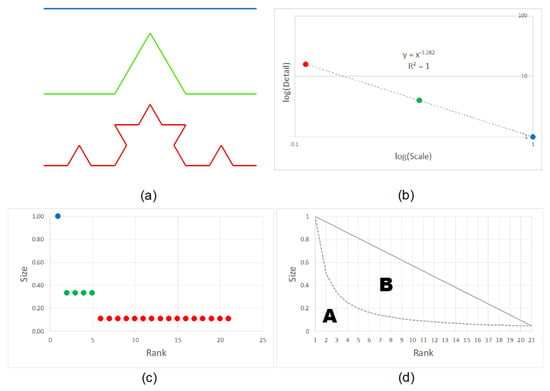
شکل 3 a سه تکرار اول منحنی کخ [ 4 ] را نشان می دهد. اولین تکرار شامل یک بخش با مقیاس 1 است. بخش دوم شامل چهار بخش با مقیاس 1/3 است. سوم شامل 16 بخش با مقیاس 1/9 است. بعد فراکتال، یعنی توان قانون توان بین جزئیات و مقیاس‌های آن، برابر است با شیب نمودار log-log همانطور که در شکل 3 ب نشان داده شده است. برای اعمال روش شکستن سر/دم، همه مقیاس‌های منحنی کوخ را از بزرگ‌ترین تا کوچک‌ترین رتبه‌بندی می‌کنیم (نمودار اندازه رتبه، شکل 3 ج). مقدار ht-index القایی منحنی کخ 3 است، به این معنی که الگوی مقیاس بندی بخش های کوتاه بسیار بیشتر از قطعات طولانی دو بار ظاهر می شود. دو مقدار میانگین محاسبه شد: m ₁

= \frac{16 * \frac{1}{9} + 4 * \frac{1}{3} + 1 * 1}{21} \approx

0.195 و متر _مربع

= \frac{4 * \frac{1}{3} + 1 * 1}{5}

\approx

0.46. به این ترتیب، می‌توانیم سه سطح سلسله مراتبی مقیاس‌پذیری منحنی را استخراج کنیم: 16 بخش که مقیاس آن زیر m2 است، چهار بخش که مقیاس آن بین m ₁ و m2 است و _یک بخش که مقیاس آن بالاتر از m ₁_است.پیشنهاد ht-index در بسیاری از جنبه های محاسبه کسر بودن یک ویژگی جغرافیایی مهم است. ht-index استفاده از سایر مدل‌های ریاضی توزیع دم سنگین را برای تعیین کمیت یک فراکتال گسترش می‌دهد. علاوه بر این، از آنجایی که بعد فراکتال بر تغییر مقیاس ها در بین مراحل مختلف تکرار تمرکز نمی کند، شاخص ht مکمل بعد فراکتال از نظر اندازه گیری رشد یک فراکتال در حین انجام تکرار است. با این حال، ht-index از تمایز دو فراکتال با الگوهای کمی متفاوت اما مقدار ht-index یکسان رنج می برد، زیرا مقدار ht-index به صورت یک عدد صحیح قالب بندی شده است. برای حل عدم حساسیت شاخص ht، چندین متریک فراکتال مانند CRG و RA توسعه داده شده است [ 30 ، 31 ].

CRG با جمع کردن نسبت های بین مقادیر میانگین متوالی محاسبه می شود که با رابطه (4) بیان می شود:

CRG = ⎧⎩⎨⎪⎪⎪⎪⎪⎪ 0, متر 1 ، \sum متر من + 1 متر من ، i = 0 i = 1 من > 1

(4)

جایی که $i$ نشان دهنده i _امین مقادیر در طول فرآیند شکستن سر/دم است. با در نظر گرفتن منحنی Koch در شکل 3 a دوباره به عنوان مثال کار، CRG آن برابر m ₂ / m ₁ = 0.46/0.2 = 2.38 است که از مقادیر اعشاری پشتیبانی می کند، به طوری که CRG می تواند رشد یک فراکتال را با حساسیت بیشتری ثبت کند.

RA شاخصی است که میزان توزیع مقادیر عددی دم بلند را بررسی می کند. برای محاسبه RA، می‌توانیم نسبت بین مساحت دو چند ضلعی A و B را بر اساس توزیع رتبه‌ای به دست آوریم ( شکل 3d)، همانطور که با رابطه (5) نشان داده شده است.

RA = اس آ اس آ + اس ب

(5)

جایی که $S$ مساحت یک چندضلعی است که توسط خط توزیع تشکیل شده است.

در مجموع، می توان گفت که شاخص ht متریک اولیه ای است که مسئول توصیف فراکتال است. شاخص‌های CRG و RA تا حد زیادی جایگزین‌های شاخص ht بودند و مزیت اصلی آن‌ها گرفتن حساسیتی است که ht-index نمی‌تواند. به طور خاص، CRG تفاوت‌های بین هر دو سطح سلسله مراتبی متوالی را جمع‌بندی می‌کند، در حالی که RA فاصله کلی کل جمعیت را از یک توزیع دم سنگین تا یک توزیع نرمال خلاصه می‌کند. در اینجا، ما دو تکرار دیگر از یک منحنی کوخ را برای تصویر واضح‌تر اضافه می‌کنیم. مانند جدول 1 و شکل 4نشان می دهد، CRG و RA به طور غیرخطی با تکرار تغییر می کنند، در حالی که مقادیر ht-index خطی به نظر می رسد. همچنین جالب است بدانید که CRG و RA مکمل یکدیگر هستند. از آنجایی که CRG یک روند صعودی است که محدوده آن [0 است،

\infty)

(هرچه CRG بالاتر باشد، داده ها سطوح سلسله مراتبی مقیاس بندی بیشتری دارند)، در حالی که RA از 1 به 0 رو به پایین است (هرچه RA کمتر باشد، داده ها با دم سنگین تر توزیع می شوند). همراه با CRG و RA، می‌توانیم فراکتال‌ها را با سلسله‌مراتب مقیاس‌بندی یکسان یا همان مقدار شاخص ht متمایز کنیم. با این حال، در حال حاضر، این سه معیار به ندرت برای درک جامع تر از یک فراکتال ترکیب می شوند. در این مطالعه، ما ht-index، CRG و RA را برای پیاده‌سازی تحلیل فراکتالی اتصالات خیابان برای هر شبکه خیابان شهری ادغام می‌کنیم.

2.4. تجزیه و تحلیل رگرسیون

مطالعات قبلی رشد سیستم شهری در سطح استان چین را با استفاده از مقادیر شهری ارزیابی کرده‌اند. برای مثال، تولید ناخالص داخلی و جمعیت [ 42 ]. این مطالعه ارتباط بین مقادیر شهری چین و ساختار خیابان را با الگوی فراکتال شناسایی شده بررسی می‌کند. برای انجام این کار، ما یک تحلیل رگرسیون چندگانه انجام می دهیم تا روابط بین معیارهای فراکتال و شاخص های شهری جمع آوری شده از جمله عوامل اجتماعی-اقتصادی (GDP و جمعیت) و انتشار کربن را باز کنیم. جدای از سه معیار فراکتال، مطالعه قبلی [ 43 ] را با معرفی مساحت شهر، تعداد خیابان‌ها (#خیابان‌ها) و طول کل خیابان‌ها دنبال می‌کنیم. $l_{\forall S t r e e t s}$ ) به عنوان متغیرهای مدل رگرسیون برای تخمین جامع قدرت توضیحی اقدامات پیکربندی شبکه خیابانی بر وضعیت اجتماعی و اقتصادی شهرها. ما از لگاریتم برخی از معیارها استفاده می کنیم تا همه متغیرها را در یک مقدار مشابه مقیاس کنیم. بنابراین، مدل رگرسیون چندگانه به شکل زیر است که معادله (6) نشان می دهد:

ورود به سیستم (G D P) = β 0 + β 1 * log (A r e a) + β 2 * ورود به سیستم (# S t r e e t s) + β 3 * ثبت نام (ل \forall اس t r e e t s) + β 4 * h t + β 5 * سی R G + β 6 * R A._

(6)

ما همچنین دو مدل رگرسیون چندگانه را به ترتیب با log (جمعیت) و log (انتشار CO ₂ ) به عنوان متغیر وابسته اجرا می کنیم. تحلیل همبستگی بر اساس ابزار رگرسیون در نرم افزار مایکروسافت اکسل انجام شد.

3. نتایج و بحث

3.1. الگوی فراکتال جهانی 298 شبکه خیابان شهری

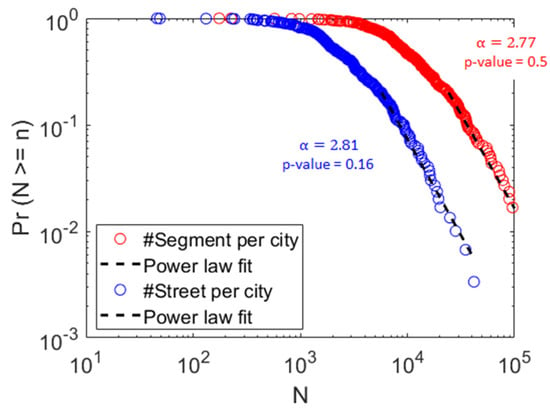
خیابان های طبیعی برای تمام شبکه های خیابانی شهری ایجاد شدند. تعداد بخش ها و تعداد خیابان ها از 173360 و 34924 (شانگهای) تا 175 و 49 (Wuzhishan) متغیر بود. تعداد بخش‌ها و تعداد خیابان‌ها برای هر شهر، هر دو از توزیع قانون قدرت تبعیت می‌کنند ( شکل 5 ). تعداد خیابان های حاصل برای هر شهر به طور متوسط 4.4 برابر کمتر از تعداد بخش ها است. ما روش شکستن سر/دم را بر روی تعداد خیابان‌ها برای همه شهرها اعمال کردیم و شاخص ht برابر با 4 را تولید کردیم. از جدول 2 ، اشاره کردیم که هر درصد سر بسیار پایین بود (حدود 30٪). این نشان می دهد که با توجه به مجموعه داده های ارائه شده توسط OSM، تنها تعداد کمی از شهرها بیش از 10000 خیابان دارند و اکثر شهرها دارای 4000 خیابان یا کمتر هستند.

در مرحله بعد، شاخص های ht را بر حسب اتصالات خیابانی برای هر شهر محاسبه کردیم. تقریباً همه شهرها دارای مقدار شاخص ht بزرگتر یا مساوی 3 بودند، به جز یک شهر (وژیشان) که مقدار شاخص ht آن تنها 1 بود. چهار شهر برتر از نظر شاخص ht عبارتند از شانگهای، دونگوان، هانگژو و جین‌هوا که همگی در مناطق بسیار توسعه‌یافته چین واقع شده‌اند (مثلاً در اطراف دلتای رودخانه یانگ تسه). اکثر شهرهای مهم، مانند شهرداری‌های مستقیماً زیر نظر دولت مرکزی و شهرهای مرکز استان، دارای شاخص‌های ht بالای 5 هستند .بیش از 80 درصد شهرها دارای شاخص های ht بالاتر از 4 هستند، که نشان می دهد در هر یک از این شهرها، الگوی مقیاس بندی خیابان های با اتصال بسیار کمتر نسبت به خیابان های با اتصال خوب، حداقل چهار بار تکرار می شود. این سطوح سلسله مراتبی مقیاس‌بندی زیربنایی در مقیاس شهر به ما کمک می‌کند تا همه‌جای الگوهای فراکتالی شبکه‌های خیابانی شهری چین را شناسایی کنیم. ما همچنین تشخیص قدرت-قانون را برای درجه اتصال هر شبکه خیابان شهری انجام دادیم. در مجموع، 199 شهر وجود دارد که اتصالات خیابانی آنها از آزمون قانون قدرت عبور می کند. ما نگاهی دقیق‌تر به شهرهایی با سطح سلسله مراتبی خیابانی یکسان (یعنی همان مقدار شاخص ht) انداختیم و روند آشکاری را یافتیم که شبکه‌های خیابانی با مقدار شاخص ht بالاتر تمایل به قبولی در آزمون سخت‌گیرانه قانون قدرت دارند.جدول 3 ).

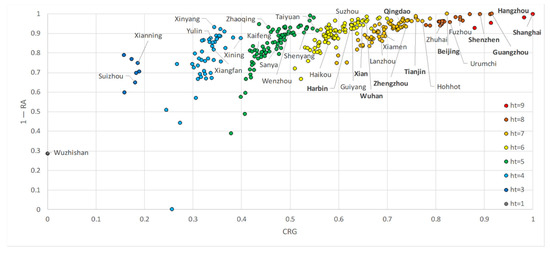
برای بررسی دقیق‌تر شبکه‌های خیابانی شهری، شاخص‌های CRG و RA را برای هر شهر محاسبه کردیم. برای اهداف تجسم، ما هر دو CRG و RA را در محدوده [0، 1] نرمال کردیم و از 1 – RA برای نشان دادن نتایج به منظور حفظ مقادیر CRG و RA در یک جهت استفاده کردیم. یعنی هرچه سمت راست بالا بیشتر باشد، شهر فراکتال بیشتری دارد ( شکل 5 ). به طور خاص، می توان گفت که محور x نشان دهنده افزایش اختلاف مجموع هر دو سطح سلسله مراتبی متوالی است، در حالی که محور y نزدیکی توزیع قانون قدرت را نشان می دهد.

طرح را می توان از هر دو دیدگاه جهانی و محلی توضیح داد ( شکل 6 و شکل 7 ، به ترتیب). در سطح جهانی، توزیع شهرهای با استفاده از CRG و RA تا حد زیادی از توزیع با استفاده از شاخص ht پیروی می کند. با این حال، به دلیل افزایش زیاد حساسیت، تفاوت‌های بین شهرها در همان یا در بین شاخص‌های ht مختلف را می‌توان به طور موثر تشخیص داد. به عنوان مثال، شانگهای، که هم بزرگترین CRG و هم 1 – RA را دارد، با شاخص ht 9، فراکتال ترین شهر در میان چهار شهر برتر بود. پکن، با شاخص ht 7 اما یک قانون قدرت کامل (آلفا = 0.58، p -value = 0.26، و 1 – RA = 1)، در بالاترین سطح و جالب‌تر از آن، در وسط شهرهایی قرار داشت که شاخص‌های ht داشتند. 8 بودند.

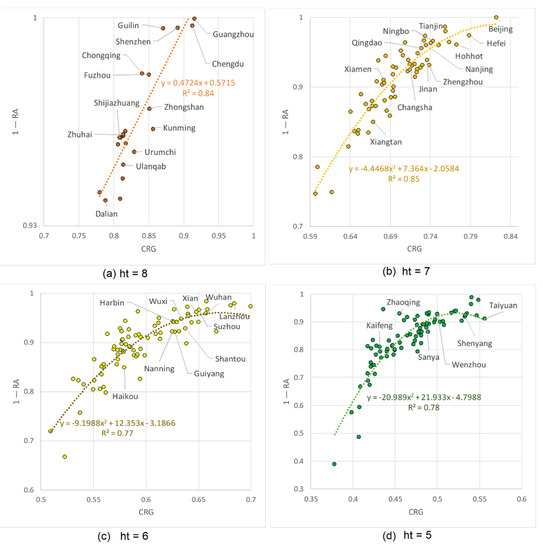
به صورت محلی، می‌توانیم تشخیص دهیم که CRG و RA در هر شاخص ht همبستگی بسیار خوبی دارند، زیرا شهرهایی با مقدار شاخص ht یکسان در اطراف خط روند خوشه‌بندی و توزیع شده‌اند ( شکل 6 ). به عنوان مثال، همبستگی بین CRG و RA را می توان با استفاده از یک تابع چند جمله ای مرتبه دوم به بهترین نحو نشان داد که ht-index = 5، 6، و 7 ( شکل 7 b-d)، در حالی که CRG به طور خطی با RA زمانی که ht همبستگی دارد. -index = 8 ( شکل 7آ). همبستگی خوب حاکی از رابطه مثبت بین مجموع اختلافات بین سطوح سلسله مراتبی و نزدیک بودن به قانون قدرت بودن است. از آنجایی که CRG و RA 100٪ همبستگی ندارند، خط روند، در این رابطه، به عنوان یک “حکم‌کش” عمل می‌کند تا آنچه را که در یک الگوی فراکتال مهم‌تر است متمایز کند: قانون توان بیشتر (بالاتر از خط روند) یا رشد بیشتر بین سطوح سلسله مراتبی آن (زیر خط روند). از شکل 7، ما برای هر نمودار همبستگی یک چیز مشترک پیدا کردیم: در بیشتر موارد، شهرهایی با وضعیت اقتصادی بالاتر (براساس تولید ناخالص داخلی شهری مشتق شده) یا وضعیت سیاسی (اگر مرکز استان یا شهر تحت حکومت مرکزی باشند) در سمت راست بالا قرار دارند. بخشی از ناحیه شکل یا بالای خط روند. این نشان می دهد که درجه اتصال در شبکه های خیابانی در شهرهای توسعه یافته به سمت توزیع قانون قدرت حرکت می کند، اما در شهرهای کمتر توسعه یافته کمتر.

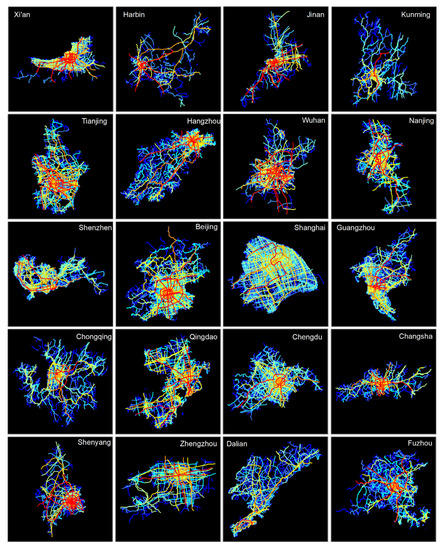
اجازه دهید در 20 شهر برتر چین (رتبه‌بندی شده بر اساس تولید ناخالص داخلی) بزرگنمایی کنیم تا ظاهر الگوهای فراکتال را در شهرهای معرف مشاهده کنیم. همانطور که جدول 4 نشان می دهد، الگوی فراکتال برای هر یک از این شهرهای توسعه یافته قابل توجه بود که با شاخص ht بزرگ و آمار قانون توان نشان داده شد. توجه داشته باشید که فقط اتصالات خیابانی نانجینگ غیرقانونی توزیع شده بود و به همین دلیل است که نانجینگ در زیر خط روند قرار داشت ( شکل 6 ج). سلسله مراتب زیربنایی شبکه های خیابانی شهری از نظر اتصالات خیابانی را می توان به طور موثر با طیفی از رنگ ها از آبی تا قرمز در شکل 8 تجسم کرد.. علیرغم اشکال مختلف مرزهای مختلف شهرها، الگوی فراکتالی فراگیر خیابان‌های بسیار کم‌تر نسبت به خیابان‌های با اتصال خوب بین این شهرها قابل توجه بود. کمبود خطوط قرمز (مرتبط ترین خیابان ها) در مقابل تعداد زیادی خطوط آبی (فقیرترین خیابان های متصل)، به علاوه خیابان های دیگر در میان، ساختار شهری را به شکل فراکتال شکل داده است.

3.2. همبستگی بین متریک های فراکتال و کمیت های شهری

بررسی چگونگی ارتباط الگوی فراکتال زیربنایی با مقادیر شهری بر اساس تحلیل رگرسیون چندگانه انجام شد که نتایج در جدول 5 نشان داده شده است. مقادیر تنظیم R ² مناسب بودن مدل ها هستند. همراه با معیارهای سنتی خیابان، مقادیر R2 ^برای تولید ناخالص داخلی شهری (0.57) بزرگترین بود و به ترتیب جمعیت (0.459) و CO _{2 به دنبال آن بودند.}انتشار (0.285). ما همچنین مقادیر معناداری را با استفاده از آزمون t محاسبه کردیم و اطمینان حاصل کردیم که روابط بین متغیرهای مستقل و متغیر وابسته در سطح معنی‌داری 1% معنی‌دار است. به طور کلی، می توان مشاهده کرد که شاخص ht نسبت به سطح معنی داری کمتر از CRG یا RA عمل می کند. ما پیشنهاد می کنیم که CRG یا RA قابل توجه تر از ht-index احتمالاً به دلیل افزایش حساسیت آن است.

جدول 5 اثرات انواع مختلف اقدامات پیکربندی خیابان را بر وضعیت اجتماعی-اقتصادی شهری (log (GDP) و log (جمعیت)) و مصرف انرژی (log (CO ₂ )) خلاصه می کند. کسری شبکه های خیابانی به طور مثبت با تولید ناخالص داخلی و جمعیت مرتبط است، در حالی که همبستگی منفی جزئی با انتشار CO2 _دارد . جالب است بدانید که معیارهای فراکتال خیابانی تأثیر ضعیف تری نسبت به معیارهای سنتی خیابانی دارند، مانند

l_{\forall S t r e e t s}

و #خیابان ها در حالی که تاثیر قوی تری نسبت به وسعت شهر دارند. به طور خاص، افزایش یک واحدی در

l_{\forall S t r e e t s}

با افزایش 1.66 واحدی تولید ناخالص داخلی شهری همراه است که حدود 4 برابر بیشتر از افزایش یک واحدی در CRG است. به همین ترتیب، افزایش جمعیت با افزایش یک واحدی در

l_{\forall S t r e e t s}

پنج برابر با کاهش یک واحدی در RA، ceteris paribus است. توجه داشته باشید که کاهش RA با افزایش شاخص ht و CRG مطابقت دارد، زیرا مقادیر RA کوچکتر به معنای فراکتال های قابل توجه تر است. برای انتشار CO ₂ ، افزایش یک واحدی در طول کل خیابان و تعداد خیابان ها به ترتیب با 1.02 واحد و 1.57 واحد افزایش در ارتباط است، در حالی که افزایش یک واحدی در RA (فرکتال کمتر) با 0.035- مرتبط است. افزایش واحد

4. بحث بیشتر در مورد این مطالعه

باز بودن و دستیابی به داده های بزرگ جغرافیایی به ما کمک می کند تا اشکال شهری را در هر دو سطح درون شهری و بین شهری تجزیه و تحلیل و درک کنیم. شبکه های خیابانی تا حد زیادی تصویری کلی از یک محیط فیزیکی شهری را منعکس می کنند. بر اساس خیابان‌های طبیعی مشتق‌شده از ۲۹۸ شهر، می‌توانیم ساختار فراکتالی و آمار مقیاس‌بندی شبکه‌های خیابانی شهری چین را شناسایی کرده و الگوی فراکتال جهانی را در میان طیف وسیعی از فضاهای شهری پیدا کنیم. در این بخش، روش‌شناسی توسعه‌یافته و نتایج به‌دست‌آمده و چگونگی کمک آنها به دانش ما در مطالعات شهری فعلی چین را بیشتر مورد بحث قرار می‌دهیم.

ویژگی های جغرافیایی در اصل فراکتال هستند، همانطور که فضای شهری که مجموعه بزرگی از ویژگی های جغرافیایی را در بر می گیرد. اختراع سومین تعریف فراکتال [ 6 ] ما را قادر می سازد تا الگوی فراکتال جهانی را در مقیاس های مختلف فضای جغرافیایی درک کنیم. باید تاکید کرد که با توجه به دیدگاه درست، تقریباً تمام ویژگی های جغرافیایی را می توان به صورت فراکتال دید. به عنوان مثال، کار قبلی شکستگی اساسی را از یک منحنی صاف فردی بررسی می کند [ 1] از منظر خمش های بازگشتی به جای رئوس یا بخش های موجود در آن. به طور مشابه، برای مجموعه‌ای از ویژگی‌های خطی – یعنی شبکه خیابانی – باید به جای توپولوژی بخش – بخش یا اتصال – اتصال برای دیدن فراکتال، دیدگاه توپولوژی خیابان-خیابان را در نظر گرفت. در این مطالعه، ما از چنین دیدگاهی استفاده کردیم و الگوی فراکتالی جهانی شبکه‌های خیابانی را در بین بیش از 298 شهر با موفقیت نشان دادیم.

الگوی فراکتال جهانی شناسایی‌شده شبکه‌های خیابانی شهری را می‌توان به صورت کمی با توزیع قانون قدرت اتصالات خیابان و سلسله‌مراتب مقیاس‌بندی زیربنایی دریافت کرد. توزیع قانون قدرت به طور گسترده در پدیده های طبیعی و اجتماعی مشاهده می شود و معمولاً به عنوان شاخصی برای پایداری در نظر گرفته می شود [ 29 ]]. تشخیص قانون قدرت برای هر شهر با استفاده از روش برآورد حداکثر احتمال قوی انجام شد و به ما کمک می‌کند تشخیص دهیم که حدود 67 درصد از شبکه‌های خیابانی شهری چین ماهیت قانون قدرت دارند. برای 33 درصد باقی‌مانده شهرها، سطوح سلسله مراتبی مقیاس‌بندی که از شکستگی‌های سر/دم به دست می‌آیند، الگوهای فراکتالی خیره‌کننده خیابان‌های بسیار کم‌تر نسبت به خیابان‌های با اتصال خوب را نشان می‌دهد. بنابراین، شاخص ht نسبت به معیارهای قانون قدرت با توجه به شناسایی الگوی فراکتال جهانی شبکه‌های خیابانی چینی برتر است. علاوه بر این، ht-index برای تمایز شبکه های خیابانی شهری در سلسله مراتب مختلف مقیاس بندی خوب است. دو جایگزین آن، CRG و RA، به ما کمک می کنند تا شهرهایی را که در یک سلسله مراتب مقیاس بندی یکسان هستند، به دلیل افزایش حساسیت متمایز کنیم. در این رابطه،

این مطالعه همچنین تلاش کرد تا قدرت توضیحی فرکتالیته شبکه‌های خیابانی بر وضعیت اجتماعی-اقتصادی شهری و مصرف سوخت را تخمین بزند. از آنجایی که شاخص‌های شهری مانند تولید ناخالص داخلی معمولاً با عوامل متعدد یک شبکه خیابانی مرتبط هستند، این مطالعه رویکرد رگرسیون چندگانه را با درگیر کردن سایر معیارهای هندسی شبکه خیابانی سنتی به منظور نزدیک‌تر کردن مدل به واقعیت و کاهش احتمال مخدوش شدن اتخاذ کرد. اثرات در نتیجه، مقدار ضریب همبستگی R2 مدل رگرسیون چندگانه، مانند مورد GDP (R ²⁼ 0.57)، بالاتر از یک مدل رگرسیون منفرد بر اساس یک ویژگی هندسی خیابانی یا متریک فراکتال است (به عنوان مثال ، R ² = 0.41 با

l_{\forall S t r e e t s}

فقط یا R2 ⁼ 0.23 فقط با CRG). بنابراین، می‌توان گفت که چندین معیار شبکه خیابانی برای تحلیل اکتشافی هر کمیت شهری مناسب هستند تا اندازه‌گیری واحد.

تجزیه و تحلیل رگرسیون چندگانه ما بیشتر نشان می‌دهد که شهرهایی با الگوهای خیابانی فراکتال برجسته‌تر (یعنی سطوح سلسله مراتبی مقیاس‌پذیر شبکه‌های خیابانی آنها) تمایل به وضعیت اقتصادی بهتری دارند. نتایج تجزیه و تحلیل فراکتالی در جدول 4 همچنین تأیید می کند که اکثر شهرهای فراکتال، کلانشهرهای سطح بالا در چین مانند پکن و شانگهای هستند. اگر نگاه دقیق تری به ضریب بیندازیم

β

، لازم به ذکر است که اثر مثبت از

l_{\forall S t r e e t s}

وضعیت اجتماعی-اقتصادی شهری قوی تر از هر یک از سه معیار فراکتال است. این نشان می‌دهد که توسعه اقتصادی یک شهر مستقیم‌تر با جزئیات هندسی شبکه خیابان‌های آن نشان داده می‌شود تا الگوی فراکتالی زیربنایی. با این حال، این بدان معنا نیست که معیارهای فراکتال معنادار کمتری دارند. همانطور که توسط نتایج تجزیه و تحلیل رگرسیون با انتشار CO2 نشان داده _شده است ، ساختار فراکتالی یک شبکه خیابانی می تواند به بهره وری انرژی یک شهر کمک کند. نشانه های مخالف از

β

بین متریک های فراکتال و

l_{\forall S t r e e t s}

نشان می دهد که شکستگی های خیابانی می توانند متفاوت از ویژگی های هندسی خیابان عمل کنند. در این راستا، fractality شبکه های خیابانی می تواند مکمل مفیدی برای اقدامات سنتی پیکربندی شبکه خیابانی باشد.

5. نتیجه گیری ها

یک شهر نه تنها از مناطق یا ساختمان‌های ترافیکی تشکیل شده است، بلکه مجموعه‌ای از خیابان‌های منسجم است. این مقاله الگوی فراکتال جهانی 298 شهر در چین را از منظر شبکه های خیابانی بررسی می کند. این مقاله از ادغام سه معیار فراکتال – ht-index، CRG و RA – برای تجزیه و تحلیل فراکتال یا مقیاس‌بندی اتصالات خیابانی استفاده می‌کند. نتایج نشان می‌دهد که تقریباً همه شهرها دارای ساختار فراکتالی هستند، زیرا تعداد سطوح سلسله مراتبی مقیاس‌بندی شبکه خیابانی برای هر شهر بالاتر یا مساوی 3 است. ما ثابت کرده‌ایم که CRG و RA می‌توانند تا حد زیادی عدم حساسیت ht- را جبران کنند. فهرست مطالب. بعلاوه، نتایج تحلیل رگرسیون چندگانه نشان می‌دهد که ساختار فراکتالی شبکه خیابان‌های شهری به طور مثبت با وضعیت اجتماعی-اقتصادی شهری و با مصرف انرژی شهری همبستگی منفی دارد. تحقیقات بیشتر بر روی کاربرد جهانی بودن الگوی فراکتال در چارچوب تعریف سوم برای برنامه ریزی شهری یا تصمیم گیری شهری با درگیر کردن سایر ویژگی های هندسی (مانند آزیموت) و ساختاری (مانند بین بین) شبکه های خیابانی و شاخص های شهری دقیق تر

منابع

ما، دی. جیانگ، ب. منحنی صاف به عنوان یک فراکتال در تعریف سوم. Cartographica 2018 ، 53 ، 203-210. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
بوئینگ، جی. اندازه گیری پیچیدگی فرم و طراحی شهری. شهری دس. بین المللی 2018 ، 23 ، 281-292. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
گائو، پی. کوشمن، SA; لیو، جی. آره.؛ شن، اس. Chang, C. Fracl: ابزاری برای توصیف fractality شیب منظره از دیدگاهی جدید. ISPRS Int. J. Geo-Inf. 2019 ، 8 ، 466. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
Koch، H. Sur une courbe ادامه بدون مماس، obtenue par une ساخت و ساز géométrique élémentaire روی یک منحنی پیوسته بدون مماس قابل ساخت از هندسه ابتدایی. Arkiv Matematik 1904 ، 1 ، 681–704. [ Google Scholar ]
ماندلبروت، بی. طول ساحل بریتانیا چقدر است؟ خود شباهت آماری و بعد کسری. Science 1967 , 156 , 636-638. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
جیانگ، بی. یین، J. Ht-شاخص برای تعیین کمیت ساختار فراکتال یا مقیاس بندی ویژگی های جغرافیایی. ان دانشیار صبح. Geogr. 2014 ، 104 ، 530-541. [ Google Scholar ] [ CrossRef ]
باتی، م. Longley، P. شهرهای فراکتال: هندسه شکل و عملکرد . انتشارات آکادمیک: لندن، بریتانیا، 1994. [ Google Scholar ]
باتی، م. کاروالیو، آر. هادسون اسمیت، ا. میلتون، آر. اسمیت، دی. Steadman, P. مقیاس‌بندی و آلومتری در هندسه‌های ساختمانی لندن بزرگ. یورو فیزیک J. B 2008 , 63 , 303-314. [ Google Scholar ] [ CrossRef ]
تانیر، سی. توماس، آی. وویدل، جی. فرانکهاوزر، پی. رویکرد فراکتالی برای شناسایی مرزهای شهری. Geogr. مقعدی 2011 ، 43 ، 211-227. [ Google Scholar ] [ CrossRef ]
تانیر، سی. توماس، I. تعریف و مشخص کردن مرزهای شهری: تحلیل فراکتالی شهرهای نظری و شهرهای بلژیکی. محاسبه کنید. محیط زیست سیستم شهری 2013 ، 41 ، 234-248. [ Google Scholar ] [ CrossRef ]
توماس، آی. فرانکهاوزر، پی. ابعاد فراکتال ردپای ساخته شده: ساختمان ها در مقابل جاده ها. شواهد فراکتالی از آنتورپ (بلژیک). محیط زیست طرح. ب مقعد شهری. علوم شهر 2013 ، 40 ، 310-329. [ Google Scholar ] [ CrossRef ]
شریواستاوا، ا. رائو، PSC; McGrath، GS خود شباهت و ویژگی های مقیاس بندی فراکتال جزایر حرارتی درون شهری برای شهرهای مختلف جهانی. فیزیک Rev. E 2019 , 100 , 032142. [ Google Scholar ] [ CrossRef ] [ PubMed ][ Green Version ]
شن، جی. بعد فراکتالی و رشد فراکتالی مناطق شهری. بین المللی جی. جئوگر. Inf. علمی 2002 ، 16 ، 419-437. [ Google Scholar ] [ CrossRef ]
مهاجری، ن. Gudmundsson، A. تکامل و پیچیدگی شبکه های خیابانی شهری. Geogr. مقعدی 2014 ، 46 ، 345-367. [ Google Scholar ] [ CrossRef ]
نیلسون، ال. گیل، جی. امضای رشد شهری ارگانیک. در ریاضیات مورفولوژی شهری ; D’Acci، L.، Ed. Birkhäuser: بازل، سوئیس، 2019؛ صص 93-121. [ Google Scholar ]
وو، ال. ژی، ی. سویی، ز. لیو، ی. تحرک انسانی درون شهری و انتقال فعالیت: شواهدی از داده های ورود به شبکه های اجتماعی. PLoS ONE 2014 ، 9 ، e97010. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ما، دی. توشیهیرو، او. اوکی، تی. جیانگ، بی. بررسی ناهمگونی حرکت‌های شهری انسانی با استفاده از توییت‌های دارای برچسب جغرافیایی. بین المللی جی. جئوگر. Inf. علمی 2020 . [ Google Scholar ] [ CrossRef ]
جیانگ، بی. Ren, Z. فضای جغرافیایی به عنوان یک ساختار زنده برای پیش بینی فعالیت های انسانی با استفاده از داده های بزرگ. بین المللی جی. جئوگر. Inf. علمی 2019 ، 33 ، 764-779. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
پورتا، اس. کروسیتی، پی. Latora، V. تحلیل شبکه ای خیابان های شهری: رویکرد دوگانه. Physica A 2006 , 369 , 853-866. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کروسیتی، پی. لاتورا، وی. پورتا، س. اقدامات مرکزیت در شبکه های فضایی خیابان های شهری. فیزیک Rev. E 2006 , 73 , 036125. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
کرکلی، ا. باربوسا، اچ. بارتلمی، ام. Ghoshal, G. از مرکزیت میانی در شبکه های خیابانی تا متغیرهای ساختاری در نمودارهای مسطح تصادفی. نات. اشتراک. 2018 ، 9 ، 2501. [ Google Scholar ] [ CrossRef ]
جیانگ، بی. کلارامونت، سی. تحلیل توپولوژیکی شبکه های خیابانی شهری. محیط زیست طرح. B طرح. دس 2004 ، 31 ، 151-162. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
ما، دی. عمر، آی. سندبرگ، ام. جیانگ، بی. چرا توپولوژی در پیش‌بینی فعالیت‌های انسانی اهمیت دارد؟ محیط زیست طرح. ب مقعد شهری. علوم شهر 2019 ، 46 ، 1298-1313. [ Google Scholar ] [ CrossRef ]
ژانگ، اچ. Li، Z. فراکتالیته و خود شباهت در ساختار شبکه های جاده ای. ان دانشیار صبح. Geogr. 2012 ، 102 ، 350-365. [ Google Scholar ] [ CrossRef ]
لو، ز. ژانگ، اچ. ساوتورث، اف. Crittenden، J. ابعاد فراکتال شبکه های جاده ای منطقه شهری و اثرات آن بر محیط ساخته شده شهری. Ecol. اندیک. 2016 ، 70 ، 285-296. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
لان، تی. لی، ز. ژانگ، اچ. مقیاس‌بندی آلومتریک شهری در زیر شکست ساختاری شبکه‌های جاده‌ای. ان دانشیار صبح. Geogr. 2019 ، 109 ، 943-957. [ Google Scholar ] [ CrossRef ]
کروکس، AT; کرویتورو، آ. جنکینز، ا. مهابیر، ر. آگوریس، پ. Stefanidis، A. داده های بزرگ تولید شده توسط کاربر و مورفولوژی شهری. محیط ساخته شده 2016 ، 42 ، 396-414. [ Google Scholar ] [ CrossRef ]
بوئینگ، جی. اطلاعات فضایی و خوانایی فرم شهری: داده های بزرگ در ریخت شناسی شهری. بین المللی J. Inf. مدیریت 2019 ، 102013. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
صلات، س. بوردیک، L. پیچیدگی شهری. سلسله مراتب مقیاس، بهره وری انرژی و ایجاد ارزش اقتصادی. در شهر پایدار VII: بازآفرینی شهری و پایداری . Pacetti, M., Passerini, G., Brebbia, CA, Latini, G., Eds. WIT Press: بوستون، MA، ایالات متحده آمریکا، 2012; جلد 155، صص 97–107. [ Google Scholar ]
گائو، رایانه شخصی؛ لیو، ز. Xie، MH; تیان، ک. شاخص لیو، جی. CRG: شاخص ht حساس تر برای فعال کردن نماهای پویا از ویژگی های جغرافیایی. پروفسور Geogr. 2016 ، 68 ، 533-545. [ Google Scholar ] [ CrossRef ]
گائو، رایانه شخصی؛ لیو، ز. تیان، ک. لیو، جی. مشخص کردن شرایط ترافیکی از منظر ناهمگونی مکانی-زمانی. ISPRS Int. J. Geo-Inf. 2016 ، 5 ، 34. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
ژئوفابریک. در دسترس آنلاین: https://download.geofabrik.de/ (دسترسی در 10 نوامبر 2019).
پایگاه داده منابع ملی و محیط زیست آکادمی علوم چین. در دسترس آنلاین: https://www.resdc.cn/ (در 15 نوامبر 2019 قابل دسترسی است).
لیو، اچ. جیانگ، دی. یانگ، ایکس. لو، سی. رویکرد فضایی سازی به تولید ناخالص داخلی شبکه 1 کیلومتری با پشتیبانی سنجش از دور. Geo-Inf. علمی 2005 ، 7 ، 120-123. [ Google Scholar ]
کای، بی. وانگ، جی. یانگ، اس. مائو، ایکس. مجموعه داده های انتشار CO ₂ شهر کائو، L. چین : بر اساس داده های شبکه بندی شده انتشار با وضوح بالا در چین. مردم چین منبع. محیط زیست 2017 ، 27 ، 7085–7093. (به زبان چینی) [ Google Scholar ]
کای، بی. لیانگ، اس. ژو، جی. وانگ، جی. کائو، ال. کو، س. خو، ام. یانگ، زی. پایگاه داده انتشار با وضوح بالا (CHRED) با منابع انتشار نقطه‌ای، داده‌های انتشار شبکه‌بندی شده، و داده‌های اجتماعی-اقتصادی تکمیلی. منبع. حفظ کنید. بازیافت. 2018 ، 129 ، 232-239. [ Google Scholar ] [ CrossRef ]
جیانگ، بی. ژائو، اس. یین، جی. جاده های طبیعی خود سازماندهی شده برای پیش بینی جریان ترافیک: مطالعه حساسیت. J. Stat. مکانیک. تئوری Exp. 2008 ، 2008 ، 07008. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
نیومن، MEJ ساختار و عملکرد شبکه های پیچیده. SIAM Rev. 2003 , 45 , 167-256. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Jiang, B. Head/tail breaks: یک طرح طبقه بندی جدید برای داده ها با توزیع دم سنگین. پروفسور Geogr. 2013 ، 65 ، 482-494. [ Google Scholar ] [ CrossRef ]
نیومن، قوانین قدرت MEJ، توزیع پارتو و قانون Zipf. تحقیر کردن فیزیک 2005 ، 46 ، 323-351. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
کلاوزت، ا. شالیزی، CR; نیومن، توزیع‌های قانون قدرت MEJ در داده‌های تجربی. SIAM Rev. 2009 , 51 , 661-703. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
زوند، دی. Bettencourt، LMA رشد و توسعه در شهرهای سطح استان در چین. PLoS ONE 2019 , 14 , e0221017. [ Google Scholar ] [ CrossRef ]
مهاجری، ن. گودموندسون، آ. انتشارات فرانسوی، JR CO ₂ در رابطه با پیکربندی شبکه خیابانی و اندازه شهر. ترانسپ Res. قسمت D Transp. محیط زیست 2015 ، 35 ، 116-129. [ Google Scholar ] [ CrossRef ]

شکل 1. (رنگ آنلاین) توزیع فضایی ( الف ) 298 شهر انتخاب شده، ( ب ) شبکه خیابانی ملی، و ( ج ) چارچوب روش شناختی در این مطالعه.

شکل 2. (رنگ آنلاین) تبدیل از توپولوژی بخش-بخش به توپولوژی خیابان-خیابان. (توجه: از منظر شبکه ای از بخش های خیابان و خیابان ها، توپولوژی قطعه-بخش (پانل های a و b ) یک ساختار مکانیکی است که فاقد الگوی مقیاس بندی کوچکتر از بزرگ است، در حالی که توپولوژی خیابان-خیابان (پانل های c و d) ) ارگانیک است، زیرا چنین الگویی را به وضوح دارد).

شکل 3. (رنگ آنلاین) اشکال هندسی سه تکرار اول منحنی کخ ( a ) و آمار مقیاس بندی زیربنایی آنها برای نشان دادن سه معیار فراکتال. توجه: ( ب ) رابطه قانون توان بین تعداد بخشها و مقیاسها است. ( ج ) همه مقیاس‌ها را از بزرگ‌ترین تا کوچک‌ترین برای محاسبات ht-index و CRG رتبه‌بندی می‌کند. ( د ) دو نوع ناحیه در نمودار اندازه رتبه برای محاسبه RA

شکل 4. (رنگ آنلاین) با استفاده از پنج تکرار اول منحنی کخ برای نشان دادن CRG و RA مکمل ht-index از نظر حساسیت گرفتن.

شکل 5. توزیع قانون قدرت #بخش ها و #خیابان ها در هر شهر (توجه: # = شماره).

شکل 6. (رنگی آنلاین) نمای یکپارچه CRG و RA از اتصالات خیابانی برای 298 شهر. (توجه: نام شهرهای برتر بر اساس تولید ناخالص داخلی به صورت پررنگ است).

شکل 7. (رنگ آنلاین) همبستگی بین CRG و RA برای شهرهایی با شاخص ht یکسان. توجه: پانل های ( a )، ( b )، ( c )، و ( d ) به ترتیب همبستگی با شاخص ht 8، 7، 6 و 5 هستند.

شکل 8. (رنگ آنلاین) الگوی فراکتال خیابان‌های کم‌تر نسبت به خیابان‌های با اتصال خوب در 20 شهر برتر بر اساس تولید ناخالص داخلی در چین. (توجه: طیف رنگی برای تجسم ساختار خیابان شهر اتخاذ شده است، قرمز و آبی به ترتیب نشان دهنده بهترین خیابان های متصل و فقیرترین خیابان ها هستند؛ رنگ های دیگر (در فیروزه ای، زرد و نارنجی) نشان دهنده خیابان های بین این دو هستند. ).

مقالات داخلی و بین المللی

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ

برای نوشتن دیدگاه باید وارد بشوید.

مشاورین هوش پیروزی

خلاصه

کلید واژه ها:

1. معرفی