خلاصه

در برنامه‌ریزی شهری و مدیریت حمل‌ونقل، ویژگی‌های محوری خیابان‌های شهری از اقدامات حیاتی است که باید در نظر گرفته شود. مرکزیت می‌تواند به درک ویژگی‌های ساختاری شبکه‌های ترافیکی متراکم که بر زندگی و فعالیت انسان در شهرها تأثیر می‌گذارد کمک کند. بسیاری از شهرها خیابان‌های شهری را طبقه‌بندی می‌کنند تا به ذینفعان گروهی از دستورالعمل‌های خیابانی را برای بازسازی احتمالی جدید مانند پیاده‌روها، حاشیه‌ها و عقب‌نشینی‌ها ارائه دهند. تحقیقات حمل و نقل همواره شبکه های خیابانی را به عنوان ارتباط بین مناطق مختلف شهری در نظر می گیرد. طبقه بندی عملکرد خیابان نقش هر عنصر از شبکه خیابان شهری (USN) را تعریف می کند. برخی از عوامل بالقوه مانند ترکیب کاربری زمین، خدمات در دسترس، هدف طراحی و سیاست‌های مدیران می‌توانند بر الگوی حرکت مسافران شهری تأثیر بگذارند. در این مطالعه، نه معیار مرکزیت برای طبقه بندی جاده های شهری در چهار شهر برای ارزیابی اهمیت ساختاری بخش های خیابان استفاده می شود. در کار ما، رمزگذار خودکار حذف نویز پشته‌ای (SDAE) عملکرد یک خیابان را پیش‌بینی می‌کند، سپس از رگرسیون لجستیک به عنوان یک طبقه‌بندی کننده استفاده می‌شود. طبقه‌بندی‌کننده پیشنهادی ما می‌تواند بین چهار کلاس مختلف که از وزارت حمل‌ونقل ایالات متحده (USDT) پذیرفته شده‌اند تمایز قائل شود: جاده شریانی اصلی، جاده شریانی کوچک، جاده جمع‌آوری و جاده محلی. مدل مبتنی بر SDAE نشان داد که پیکربندی‌های شبکه منظم با الگوهای تکراری در شکل‌گیری عملکرد شبکه‌های جاده‌ای در مقایسه با آن‌هایی که نظم کمتری در ساختار فضایی خود دارند، تأثیر بیشتری دارند. رمزگذار خودکار حذف نویز پشته‌ای (SDAE) عملکرد یک خیابان را پیش‌بینی می‌کند، سپس از رگرسیون لجستیک به عنوان یک طبقه‌بندی استفاده می‌شود. طبقه‌بندی‌کننده پیشنهادی ما می‌تواند بین چهار کلاس مختلف که از وزارت حمل‌ونقل ایالات متحده (USDT) پذیرفته شده‌اند تمایز قائل شود: جاده شریانی اصلی، جاده شریانی کوچک، جاده جمع‌آوری و جاده محلی. مدل مبتنی بر SDAE نشان داد که پیکربندی‌های شبکه منظم با الگوهای تکراری در شکل‌گیری عملکرد شبکه‌های جاده‌ای در مقایسه با آن‌هایی که نظم کمتری در ساختار فضایی خود دارند، تأثیر بیشتری دارند. رمزگذار خودکار حذف نویز پشته‌ای (SDAE) عملکرد یک خیابان را پیش‌بینی می‌کند، سپس از رگرسیون لجستیک به عنوان یک طبقه‌بندی استفاده می‌شود. طبقه‌بندی‌کننده پیشنهادی ما می‌تواند بین چهار کلاس مختلف که از وزارت حمل‌ونقل ایالات متحده (USDT) پذیرفته شده‌اند تمایز قائل شود: جاده شریانی اصلی، جاده شریانی کوچک، جاده جمع‌آوری و جاده محلی. مدل مبتنی بر SDAE نشان داد که پیکربندی‌های شبکه منظم با الگوهای تکراری در شکل‌گیری عملکرد شبکه‌های جاده‌ای در مقایسه با آن‌هایی که نظم کمتری در ساختار فضایی خود دارند، تأثیر بیشتری دارند. جاده جمع کننده و جاده محلی. مدل مبتنی بر SDAE نشان داد که پیکربندی‌های شبکه منظم با الگوهای تکراری در شکل‌گیری عملکرد شبکه‌های جاده‌ای در مقایسه با آن‌هایی که نظم کمتری در ساختار فضایی خود دارند، تأثیر بیشتری دارند. جاده جمع کننده و جاده محلی. مدل مبتنی بر SDAE نشان داد که پیکربندی‌های شبکه منظم با الگوهای تکراری در شکل‌گیری عملکرد شبکه‌های جاده‌ای در مقایسه با آن‌هایی که نظم کمتری در ساختار فضایی خود دارند، تأثیر بیشتری دارند.

کلید واژه ها:

شبکه حمل و نقل شهری ; طبقه بندی عملکرد خیابان ; رمزگذاری خودکار حذف نویز انباشته ; یادگیری عمیق ؛ اقدامات مرکزیت ; فراگیری ماشین

1. معرفی

رفت و آمدهای شهری با استفاده از اتومبیل، وظایف روزانه مهمی برای اکثر ساکنان شهر است. سیستم خیابان های شهری یک شبکه حیاتی است که مکان ها و افراد را در داخل و در سراسر مناطق شهری به هم متصل می کند. سیستم خیابان شهری را می توان به طور موثر به عنوان یک شبکه با استفاده از نظریه گراف مدل کرد و رفت و آمدها به حرکات محدود شبکه تبدیل می شوند [ 1 ]] هر بخش از شبکه مسئول انتقال ترافیک به سمت مقصد است. داشتن اطلاعات در مورد عناصر شبکه با اهداف خاص برای برنامه ریزان و مهندسان بسیار مهم است. این اهداف از سفرهای طولانی مدت تا خدمات رسانی به سفرهای محله ای به مراکز خرید مجاور را شامل می شود. طبقه‌بندی عملکردی راه‌ها نقشی را که هر عنصر از شبکه راه‌ها برای برآوردن نیازهای کاربر ایفا می‌کند، مشخص می‌کند. پیکربندی فضایی شبکه خیابانی محدودیت هایی را در الگوهای حرکتی از طریق شبکه ایجاد می کند. تأثیر پیکربندی فضایی شبکه خیابان بر جریان ترافیک توسط چندین محقق مورد مطالعه قرار گرفته است [ 2 , 3 , 4 , 5 , 6 , 7]. با این حال، در کار ما، از پیکربندی فضایی شبکه برای طبقه‌بندی عملکرد خیابان‌های جداگانه استفاده می‌شود.
طبقه بندی عملکردی خیابان ها نقشی را که هر عنصر از شبکه خیابان شهری (USN) در شبکه حمل و نقل شهری ایفا می کند، تعریف می کند. خیابان‌ها معمولاً با توجه به ویژگی‌ها و نوع خدمات به یک طبقه کاربردی اختصاص می‌یابند. 8] ارائه می کنند. خیابان ها به کاربر کمک می کند تا به مکان فعلی خود دسترسی داشته باشد و از آن به سمت مقصد خارج شود. بر اساس مفاهیم عملکرد خیابانی ارائه شده توسط وزارت حمل و نقل ایالات متحده (USDoT)، خیابان هایی که سطح بالایی از تحرک را ارائه می دهند “شریانی”، خیابان هایی که سطح بالایی از دسترسی را فراهم می کنند “محلی” نامیده می شوند متوازن از نظر تحرک و دسترسی به آنها “گردآورنده” گفته می شود. بر اساس مفاهیم ذکر شده مربوط به طبقه بندی عملکردی خیابان ها، USN ها به دو گروه اصلی شریانی و غیر شریانی با کلاس های اصلی و کوچک به عنوان زیر کلاس های گروه شریانی و خیابان جمع کننده و محلی به عنوان زیر کلاس غیر شریانی طبقه بندی می شوند. گروه شریانی. شکل 1نمونه هایی از چندین شبکه خیابانی را نشان می دهد که بر اساس عملکرد طبقه بندی شده اند.
طبقه بندی عملکردی خیابان (SFC) اهمیت بیشتری فراتر از هدف خود به عنوان ابزاری برای شناسایی نقش خاص خیابان ها در حرکت وسایل نقلیه از طریق USN دریافت کرده است. SFC برای توصیف عملکرد سیستم راهداری، معیارها و اهداف توسط چندین آژانس حمل و نقل استفاده شده است. با هدف داشتن رویکرد مبتنی بر عملکرد بیشتر برای آژانس‌های حمل‌ونقل، SFC در اندازه‌گیری نتایج به‌طور عمده برای حفظ، تحرک و ایمنی مورد توجه قرار خواهد گرفت. تا کنون، SFC بر اساس قوانین خیابانی به دست آمده است و بر اساس ویژگی هایی مانند تحرک، دسترسی، طول سفر، محدودیت سرعت، حجم، میانگین ترافیک روزانه سالانه (AADT)، مایل سفر با وسیله نقلیه (VMT) و غیره طبقه بندی شده است. شواهد نشان می دهد که طبقه بندی تنها بر اساس عناصر مورد بحث کافی نیست، و خیابان ها را نمی توان به درستی طبقه بندی کرد. در بسیاری از موارد، اختصاص یک کلاس کاربردی به یک خیابان ساده است. با این حال، تصمیم گیری بین طبقه بندی مجاور بسیار چالش برانگیز است. به عنوان مثال، تصمیم گیری در مورد اینکه آیا یک خیابان معین به عنوان شریان کوچک یا جمع کننده عمل می کند می تواند مورد بحث قرار گیرد، زیرا یک خیابان می تواند یک شریان کوچک بر اساس AADT و یک کلکتور بر اساس VMT باشد. تصمیم گیری بین تخصیص شریانی اصلی و شریانی جزئی می تواند چالش برانگیزتر باشد. زیرا یک خیابان طبق AADT می تواند یک شریان کوچک و یک کلکتور بر اساس VMT باشد. تصمیم گیری بین تخصیص شریانی اصلی و شریانی جزئی می تواند چالش برانگیزتر باشد. زیرا یک خیابان طبق AADT می تواند یک شریان کوچک و یک کلکتور بر اساس VMT باشد. تصمیم گیری بین تخصیص شریانی اصلی و شریانی جزئی می تواند چالش برانگیزتر باشد.
ما یک استراتژی جدید برای تخصیص SFC بر اساس ساختار فضایی خیابان ها و نقش آنها در شبکه پیشنهاد می کنیم. تحقیقات ما نشان می دهد که نقش خیابان ها بیش از جابجایی ترافیک است. خیابان ها اسکلت اساسی شبکه حمل و نقل هستند، بنابراین توصیف نقش هر خیابان در شبکه مفهومی قابل توجه است. ساختار فضایی خیابان ها در شبکه یکی از ویژگی های اساسی شبکه است، اما به آن توجه کافی نشده است. پیکربندی USN با استفاده از ویژگی های معنایی تجزیه و تحلیل شده است [ 3 ، 4 ، 5 ]، با کار اخیر تجزیه و تحلیل USN با استفاده از توپولوژیک [ 2 ] ] و هندسی [ 9 ]]. سیستم طبقه بندی عملکردی (FCS) در دهه 1970 به عنوان پایه ای برای ارتباط بین طراحان و برنامه ریزان توسعه یافت [ 10 ، 11 ]. این یک چارچوب رایج برای طبقه بندی جاده ها بر اساس تحرک و دسترسی است [ 12 ، 13 ، 14 ، 15 ]. کاربرد FCS گسترش یافته است و اکنون در کل فرآیند توسعه پروژه مورد استفاده قرار می گیرد و بر تمام مراحل توسعه پروژه حمل و نقل، از برنامه ریزی و برنامه ریزی تا طراحی تا تصمیمات نگهداری و بهره برداری تأثیر می گذارد [ 16 ، 17 ، 18 ، 19 ].
مرکزیت [ 2 ] یکی از مهمترین مفاهیم در تحلیل شبکه های اجتماعی است. ویژگی‌های ساختاری فضایی گره‌ها (خیابان‌ها) در یک شبکه را توصیف می‌کند. معیارهای متعددی مانند بین بودن، نزدیکی، مرکزیت درجه، مرکزیت بردار ویژه، مرکزیت اطلاعات، بین جریان و شاخص راش [ 2 ] ایجاد شده است. اقدامات مرکزیت به صورت جداگانه در نظر گرفته شده است [ 7 ، 20 ] در نظر گرفته شده است، در درجه اول در مورد اینکه چگونه بر جریان ترافیک تاثیر می گذارد. رگرسیون آماری ساده و مدل‌های یادگیری ماشین سنتی برای SFC استفاده شده‌اند، اما تنها بر اساس یک یا دو معیار مرکزیت [ 7 ]]. با توجه به پیچیدگی ساختار فضایی USN پارامترها و اندازه گیری های بیشتری برای مدل سازی مناسب SFC مورد نیاز است. برای در نظر گرفتن معیارهای مرکزیت در شبکه‌های شهری، الگوهای خیابان‌ها و جاده‌ها بر اساس نظریه گراف در نظر گرفته می‌شوند که به استخراج ویژگی‌های توپولوژی فضایی خیابان‌ها کمک می‌کند. هدف از اندازه گیری مرکزیت یافتن مهم ترین مکان های مرکزی در شبکه و ویژگی های آنهاست که نقش محوری در نظارت بر کارایی و دسترسی شبکه های حمل و نقل ایفا می کنند [ 21 , 22 , 23 , 24]. مرکزیت ها می توانند به تحلیلگران کمک کنند تا شبکه های پیچیده را به طور موثرتری درک کنند. از نظر فنی، اندازه‌گیری‌های مرکزیت الهام‌بخش کار ما شدند، جایی که برای کمک به کاربران دامنه در کشف داده‌های حمل‌ونقل شهری و ارائه ویژگی‌های مهم اولیه از شبکه‌های جاده‌ای برای انجام تحلیل سطح بالاتر در شبکه حمل‌ونقل شهری استفاده می‌شوند [ 25 ، 26 ].
برخی از مطالعات تجربی رابطه بین پیکربندی فضایی ساختار شهر و ترافیک در خیابان های شهر را نشان می دهند [ 6 ، 9 ، 23 ، 27 ، 28 ، 29]. در کنار سایر مطالعات، تحقیقات زیادی سعی شده است با بررسی ویژگی‌های ساختاری شبکه‌های خیابانی، الگوهای حرکتی افراد را آشکار کند. پارامترهای زیادی از جمله ویژگی‌های هندسی شبکه، رفتار حرکت راننده و توزیع فضایی کاربری‌های شهری در توزیع ترافیک تأثیرگذار هستند. علاوه بر این، تحقیقات نشان داده است که این پارامترها تحت تأثیر ساختار فضایی شبکه قرار دارند. به عنوان مثال، ساختار فضایی شبکه شهری تأثیر زیادی بر رفتار انسان و تقاضا برای انجام سفرهای درون شهری دارد [ 6 ، 30 ، 31 ]. اولین باری که یک شبکه عصبی خود سازماندهی نقشه (SOM) در تعمیم شبکه شهری توسط کوهونن [ 32 ] استفاده شد.]. کوهونن در شبکه خود ویژگی های توپولوژیکی، هندسی و معنایی خیابان ها را در نظر گرفته است. جیانگ و هری [ 1 33 ] از SOM و شبکه عصبی پس انتشار (BPNN) برای تعمیم شبکه شهری بر اساس طرح شهر قبل از طراحی شهر استفاده کرد. نتایج آنها در مقایسه با نتایج به دست آمده با SOM به تنهایی بهبود را نشان داد. ] از شبکه عصبی SOM برای خوشه بندی خیابان ها بر اساس ویژگی های آنها استفاده کرد. در سال 2012، ژو [
شبکه‌های عصبی چندلایه عمیق سطوح یادگیری غیرخطی زیادی دارند که به آنها اجازه می‌دهد تا توابع بسیار غیرخطی و بسیار متغیر را به طور فشرده یاد بگیرند، و جذابیت زیادی در زمینه‌های مختلف تحقیقات علوم زمین پیدا کرده‌اند [ 34 ، 35 ، 36 ، 37 ، 38 ]، به ویژه در تحلیل مسئله برنامه ریزی شهری [ 17 ، 39 ، 40 ]. Lv و همکاران [ 40] شروع به استفاده از شبکه‌های عصبی عمیق معروف به رمزگذار خودکار پشته‌ای (SAE) برای پیش‌بینی جریان ترافیک روی یک مجموعه داده بزرگ کرد. در اجرای خود، آنها بیش از 93 درصد را برای پیش بینی جریان ترافیک به دست آوردند. آنها مدل خود را با برخی تکنیک های سنتی مانند ماشین بردار پشتیبان (SVM)، جنگل تصادفی (RF) و شبکه عصبی پس انتشار (BPNN) مقایسه کردند و SAE [ 41 ] به نتایج بهتری دست یافت. در تحقیقی دیگر، اطلاعات شرایط آب و هوایی نامناسب در ارتباط با خودروها به ویژگی های ورودی برای مدل یادگیری عمیق برای پیش بینی جریان ترافیک [ 42 ] اضافه می شود. آنها به دنبال ارتباط بین شرایط آب و هوایی و پیش بینی جریان ترافیک بودند. توانایی یادگیری عمیق برای پردازش داده های بزرگ [ 34 ، 43 ، 44]، با در نظر گرفتن همبستگی بیشتر بین مجموعه‌های داده و حل پیچیدگی و غیرخطی بودن مجموعه‌های داده، ما را بر آن داشت تا در تحلیل عملکرد خیابان‌ها تجدید نظر کنیم. در کار ما، به دلیل داشتن ساختار جدولی در داده‌های ورودی، یک مدل یادگیری عمیق لایه‌ای حریصانه برای یادگیری ویژگی بدون نظارت برای درک غیرخطی بودن داده‌های ورودی اعمال می‌شود و سپس از رگرسیون لجستیک به عنوان طبقه‌بندی‌کننده استفاده می‌شود. مدل SDAE، به عنوان یکی از بهترین مدل‌های بدون نظارت از نظر لایه‌های حریص، برای حل مشکل آموزش شبکه‌های عمیق استفاده شد [ 45 ]. برای ارزیابی عملکرد مدل، چندین مدل یادگیری ماشین مانند رگرسیون لجستیک، پرسپترون چند لایه (MLP) [ 46 ]، SVM [ 47 ] و RF [ 48 ] را مقایسه می‌کنیم.]، با SDAE در چهار شهر با ساختارهای فضایی متفاوت. چهار شهر مورد استفاده تهران، ایران هستند. اصفهان، ایران؛ Enschede، هلند؛ و پاریس، فرانسه و شکل 1 ساختار فضایی آنها را نشان می دهد.
مطالعه ما روشی را پیشنهاد می‌کند که می‌تواند مفهوم اساسی شیوه یک شبکه، یعنی ساختار فضایی یک شبکه خیابانی را بررسی کند. ابتدا ثابت می‌کنیم که می‌توانیم عملکرد یک خیابان را با اندازه‌گیری فضایی در درصد قابل قبولی استخراج کنیم و سپس روش طبقه‌بندی پیشنهادی را برای طبقه‌بندی خیابان‌هایی که به یک کلاس کاربردی خاص تعلق ندارند، پیشنهاد می‌کنیم. در این کار، ابتدا USN به عنوان یک شبکه با استفاده از نظریه گراف [ 1]، سپس ساختار فضایی USN با استفاده از 9 اندازه گیری مرکزی برای درک بهتر پیچیدگی شبکه به SFC توصیف می شود. برای استفاده از SFC، از مدل یادگیری غیرخطی قدرتمندی به نام یادگیری عمیق استفاده شده است تا از توانایی آن در درک پیچیدگی USN و عملکرد خیابان استفاده شود. مطالعه ما ویژگی‌های ساختاری هر کلاس عملکردی را در دنیای واقعی بررسی می‌کند. سهم عمده این مقاله به شرح زیر خلاصه می شود.
  • با توجه به چالش طبقه‌بندی عملکردی خیابان‌ها بر اساس ساختار فضایی خیابان‌ها، عمدتاً معیارهای مرکزیت.
  • توسعه یک مدل یادگیری عمیق بدون نظارت برای بهبود دقت طبقه‌بندی عملکردی خیابان در مقایسه با تکنیک‌های سنتی.
  • تحلیل اهمیت هر معیار مرکزیت در طبقه بندی عملکردی خیابان با استفاده از تکنیک جنگل تصادفی.
  • بررسی تأثیر نظم شبکه خیابانی بر طبقه‌بندی عملکردی خیابان.
در این مطالعه، ما یک رمزگذار خودکار حذف نویز پشته‌ای (SDAE) [ 41 ] را انتخاب می‌کنیم، زیرا یکی از بهترین مدل‌های یادگیری بدون نظارت از نظر لایه‌ای حریصانه است [ 45 ، 49 ] ]. اگرچه داده‌های ورودی ما برچسب‌گذاری شده‌اند، ما از SDAE برای یادگیری ویژگی‌ها و وزن‌ها به شیوه‌ای بدون نظارت، حریصانه و لایه‌ای استفاده می‌کنیم، در حالی که تنظیم دقیق نظارت شده برای تنظیم بیشتر وزن‌های شبکه برای طبقه‌بندی با استفاده از داده‌های برچسب‌گذاری شده استفاده می‌شود. برای طبقه بندی تنظیم دقیق، ما رگرسیون لجستیک را اعمال کردیم، اما تکنیک های دیگر کار می کنند. ما مدل یادگیری عمیق خود را با چهار مدل یادگیری ماشین سنتی مقایسه می کنیم.
بقیه مقاله کار ما را به تفصیل شرح می دهد، با بخش 2 توضیح SDAE و تشریح معیارهای مرکزی که ما استفاده کردیم. بخش 3 روش ارزیابی ما از پیاده سازی ما را با استفاده از چهار مجموعه داده مختلف ارائه می دهد. نتایج عددی حاصل از آزمایش‌های ما در بخش 4 مورد بحث قرار می‌گیرد و بخش 5 نتیجه‌گیری‌های ما را ارائه می‌کند.

2. مواد و روشها

در این بخش مدل‌سازی شبکه خیابانی بر اساس تئوری گراف و استخراج معیارهای مرکزیت مورد استفاده در این تحقیق برای آموزش مدل توضیح داده می‌شود. علاوه بر این، مدل یادگیری عمیق SDAE ما مورد بحث قرار گرفته است. شکل 2یک شماتیک از کل فرآیند SFC بر اساس معیارهای مرکزیت با استفاده از یک مدل یادگیری عمیق است. در مرحله اول، USN برای 4 شهر مختلف مورد مطالعه در این کار با استفاده از نظریه گراف مدل‌سازی شده است. سپس 9 معیار مرکزیت برای همه شهرها محاسبه شده و طبقات عملکردی آنها از پایگاه داده استخراج می شود. سپس مدل یادگیری عمیق SDAE برای SFC اعمال می شود. علاوه بر این، نتایج با مدل‌های یادگیری ماشین سنتی مقایسه می‌شوند. در نهایت، اهمیت هر معیار مرکزیت بر اساس تکنیک جنگل تصادفی در نظر گرفته می‌شود، همچنین تأثیرات نظم شبکه خیابانی بر SFC بر اساس نسبت اختلاط مورد بحث قرار می‌گیرد.

2.1. مدل سازی USN با استفاده از نظریه گراف

برای مدل سازی شبکه خیابان های شهری ابتدا باید مفهوم دقیق هر نوع خیابان تعریف شود و دوم مدل ریاضی برای نمایش شبکه در نظر گرفته شود. سه روش برای تعریف عنصر اصلی در یک شبکه خیابانی وجود دارد: خط محوری [ 50 ]، خیابان‌های قطعه‌ای، و ضربه [ 51 ]. خطوط محوری در نظریه نحو فضا برای مدل‌سازی خیابان‌ها استفاده شد. یک خط محوری نشان دهنده طولانی ترین کانال هایی است که مردم در یک شهر از آن عبور می کنند. مفهوم دیگری که برای تعریف یک خیابان استفاده می شود، خیابان های قطعه ای است، که اتصال بین دو تقاطع در شبکه خیابان است. سکته مغزی راه دیگری برای تعریف مفهوم خیابان است. ایده اصلی ساخت یک قطعه جاده به صورت سکته مغزی توسط تامسون و ریچاردسون [ 51 ] ارائه شد]. اصل اساسی بسیار ساده بود: “عناصری که به نظر می رسد در یک جهت دنبال می شوند، تمایل به گروه بندی دارند” که از مضمون “اصل تداوم خوب” در یک چشم انداز بصری پیروی می کند [ 33 ]. در این فرآیند، یک معیار هندسی ساده، زاویه انحراف که انحراف از 180 درجه زاویه بین دو بخش جاده است، به عنوان معیاری برای قضاوت در مورد اینکه کدام دو بخش جاده باید به هم متصل شوند، استفاده شد. پیشنهاد شد از زاویه انحراف کوچک بین 40 تا 60 درجه استفاده شود [ 52] به عنوان آستانه ای برای اطمینان از اینکه تمام ضربه ها از اصل تداوم خوب پیروی می کنند. علاوه بر این، در مقایسه با سایر روش‌های موجود برای مدل‌سازی موجودیت خیابان، سکته مغزی معمولاً نتایج بهتری در پیش‌بینی الگوهای حرکتی افراد در شبکه‌های شهری ارائه می‌کند [33 ] و برای مدیریت ترافیک و زمان بندی در شبکه های شهری مناسب است [ 1 ].
روند ساخت سکته مغزی از یک بخش جاده دلخواه شروع می شود. هنگام رسیدن به یک تقاطع با حداقل دو بخش جاده دیگر، لازم است تصمیم بگیرید که با سه استراتژی بالقوه به کدام یک متصل شوید: خود تناسب، بهترین تناسب، و هر بهترین مناسب [ 1 ]. استراتژی بهترین تناسب، هر جفت بخش جاده را برای مقایسه در نظر می گیرد و جفتی را با کمترین زاویه انحراف برای الحاق انتخاب می کند. نتایج بهینه با استفاده از بهترین تناسب به دست خواهد آمد، زیرا این استراتژی تمام الحاقات ممکن را در هر تقاطع در نظر می گیرد (برای اطلاعات بیشتر به کار در [ 33 مراجعه کنید]). شبکه خیابان را می توان با یک نمودار اتصال، متشکل از رئوس و یال ها نشان داد. نمایشی از شبکه خیابانی وجود دارد که ابتدا بر اساس یک نمودار اولیه است، که در آن تقاطع ها به گره ها و خیابان ها به لبه ها تبدیل می شوند. در مرحله دوم، از یک نمودار دوگانه استفاده می شود که در آن خیابان ها گره و تقاطع ها لبه هستند. در مطالعه ما، ما از بهترین روش برای ساخت سکته‌ها و همچنین نمودارهای دوگانه برای ارائه موجودیت‌های خیابان با در نظر گرفتن جهت خیابان‌ها استفاده می‌کنیم. علاوه بر این، به خیابان ها وزن هایی داده می شود که متناسب با طول آنها در دنیای واقعی تعیین می شود. نتایج استفاده از این روش در شکل 1 نشان داده شده است.

2.2. اقدامات مرکزیت

به منظور تجزیه و تحلیل ساختار فضایی یک شبکه، نیاز به اقداماتی برای تعیین کمیت ویژگی‌های ساختاری هر خیابان در آن شبکه‌ها وجود دارد. معیارهای کمی که برای ارزیابی ویژگی‌های ساختاری شبکه‌ها استفاده می‌شوند، به عنوان «معیارهای مرکزی» شناخته می‌شوند. در این تحقیق، در مجموع از 9 معیار برای ارزیابی اهمیت ساختاری هر خیابان استفاده شده است. برای ارزیابی اهمیت ساختاری یک خیابان، استفاده از بیش از یک معیار ضروری است. از آنجایی که یک معیار واحد اهمیت خیابان را از یک منظر مورد توجه قرار می دهد، استفاده از انواع معیارهای ارزیابی می تواند به ما کمک کند تا از جنبه های مختلف به فضای مشکل نگاه کنیم. اقدامات مورد استفاده در این مطالعه در زیر مورد بحث قرار گرفته است.

2.2.1. بین مرکزیت

مرکزیت بین ( CB��) تعداد دفعاتی که یک گره توسط کوتاه ترین مسیری که همه جفت گره ها را در شبکه به هم وصل می کند پیموده می شود. CB��، برای گره i ، با معادله ( 1 ) تعریف می شود:

CBi=1(N−1)(N−2)∑j=1;k=1;j≠knjk(i)njk���=1(�−1)(�−2)∑�=1;�=1;�≠����(�)���

جایی که njk���تعداد کوتاه ترین مسیر بین گره های j و k است، N تعداد کل گره ها و njk(i)���(�)تعداد کوتاهترین مسیرهایی است که شامل گره i است. به طور کلی، گره هایی با بینایی بالاتر بیشتر در هدایت و انتقال جریان در شبکه نقش دارند، بنابراین نقش مهمی در ارتباطات گره ایفا می کنند [ 53 ]. در این مطالعه از مرکزیت بین‌بینی برای شناسایی خیابان‌هایی که نقش پل ارتباطی بین کوتاه‌ترین مسیرهای توپولوژیکی مختلف دارند، استفاده می‌شود. با توجه به تعریف، به نظر می رسد این اقدام برای تشخیص خیابان های پرتردد یا شریانی مناسب باشد. شکل 3 تمام معیارهای مرکزیت را نشان می دهد که شامل مرکزیت بین ( شکل 3 الف) برای تهران، ایران USN است.

2.2.2. ورودی/خارجی و وزنی درون/خارج مدرک

بر اساس تعریف فریمن [ 54 ]، درجه یک گره کانونی i(degi)�(����)مجاورت در شبکه است که به معنی تعداد گره های متصل مستقیم به گره کانونی i است :

degini=∑j=1Naمن ج������=∑�=1����
degouti=∑j=1Naمن ج�������=∑�=1����

جایی که i گره کانونی، j همه گره های دیگر، N تعداد کل گره ها و a ماتریس مجاورت است. برای استفاده از این معیار در یک شبکه هدایت شده و وزن دار، باید جهت و وزن اتصال را در نظر گرفت. از نظر جهت اتصال، این اندازه به دو معیار تقسیم می شود: درجه، degini������و درجه بالاتر، degouti�������. Indegree تعداد اتصالات منتهی به یک گره معین است و outdegree تعداد اتصالاتی است که از آن گره قابل دسترسی است. درجه به طور کلی به مجموع وزن ها در هنگام تجزیه و تحلیل شبکه های وزن داده شده است [ 55 ]. با توجه به وزن شبکه، این معیار به دو معیار تقسیم می شود: درجه وزنی، wdegini�������و درجه بالاتر وزنی، wdegouti��������(یعنی مجموع وزن اتصال منتهی به یک گره معین یا قابل دسترسی از آن گره)،

wdegini=∑j=1Nwij�������=∑�=1����
wdegouti=∑j=1Nwij��������=∑�=1����

اگر گره i به گره j متصل باشد، w ماتریس مجاورت وزنی است ، و چه زمانی wij���بزرگتر از 0 است، بین گره های i و j ارتباط وجود دارد . در شبکه خیابان های شهری، درجه هر خیابان نشان دهنده تعداد خیابان هایی است که مستقیماً به آن خیابان دسترسی دارند که می تواند میزان دسترسی خیابان ها را در شبکه شهری اندازه گیری کند. برای استفاده از این معیار در شبکه خیابانی دارای وزن و جهت، جهت و وزن خیابان ها (طول) نیز باید در نظر گرفته شود. شکل 3 b-e معیارهای درجه، درجه، درجه برتر وزنی و مرکزیت وزنی در درجه را برای تهران نشان می دهد.

2.2.3. ضریب خوشه بندی

ضریب خوشه بندی محلی CLcc����به احتمال وجود دو گره مجاور که متصل هستند اشاره دارد. این به عنوان تعداد اتصالات موجود بر تعداد اتصالات ممکن بین همسایگان گره محاسبه می شود. بنابراین، نتیجه بین 0 و 1: 0 در صورت عدم وجود ارتباط بین همسایگان و 1 در صورت وجود همه اتصالات ممکن است [ 6 ]،

CLcci=NaijNpij�����=��������

جایی که Naij����تعداد اتصالات واقعی و Npij����تعداد اتصالات ممکن بین گره های i و j است. وجود ارتباط بین گره های مجاور به این معنی است که آنها می توانند جریان شبکه را مستقیماً بدون نیاز به واسطه ارسال و دریافت کنند. خیابانی با ضریب خوشه‌بندی بالا به این معنی است که خیابان‌های مجاور آن به یکدیگر دسترسی مستقیم دارند. در نتیجه برای رسیدن به دیگران نیازی به عبور از آن خیابان نیست، بنابراین ترافیک کاهش می یابد. برعکس، اگر ارتباط مستقیمی بین همسایگان یک خیابان وجود نداشته باشد، آن خیابان نقش اساسی تری در عبور افراد به مقصد دارد. شکل 3 f معیارهای مرکزیت ضریب خوشه بندی را برای تهران نشان می دهد.

2.2.4. میانگین وزنی رتبه مرکزیت (WACR)

این اندازه گیری برای ارزیابی میزان کنترل هر گره بر روی جریان شبکه ایجاد شده است. مقدار بالاتر این اندازه گیری وضعیت مهم تری از انتقال جریان ورودی گره در کل شبکه را نشان می دهد [ 20 ].

WACRi=ki∑ms=1(wis+∑wiqwqs)2(s∈Ni,q∈Niandq≠s)�����=��∑�=1�(���+∑������)2(�∈��,�∈��and�≠�)

جایی که wمن _���نسبت درجه در گره s به مجموع درجه در همه گره های مجاور i است و m اندازه مجموعه است. Ni��. شکل 3 i معیارهای مرکزیت WACR را برای تهران نشان می دهد.

2.2.5. مرکزیت رتبه صفحه

PageRank یک فناوری کلیدی در پشت موتور جستجوی گوگل است که ارتباط و اهمیت هر یک از صفحات وب را تعیین می کند. محاسبه آن از طریق یک نمودار وب انجام می شود که در آن گره ها و پیوندها صفحات وب و لینک های داغ را نشان می دهند [ 56 ]. گراف وب یک گراف جهت‌دار است، به‌عنوان مثال، یک پیوند از صفحه A به B به معنای اتصال مستقیم دیگری از B به A نیست. ایده اصلی رتبه صفحه این است که یک گره با رتبه بالا، گره‌ای است که گره‌های با رتبه بالا به آن اشاره می‌کنند [ 56 ]. یک تعریف بازگشتی PageRank برای رتبه بندی صفحات وب منفرد در پایگاه داده هایپرپیوندی استفاده می شود. به طور رسمی به شرح زیر تعریف می شود [ 6 ]،

PRLcci=1−dn+d∑j∈ON(i)PR(j)nj������=1−��+�∑�∈��(�)��(�)��

که در آن n تعداد کل گره ها است. ON(i)��(�)همسایگان طرح کلی است (یعنی گره هایی که به گره i اشاره می کنند ). PR(i)��(�)و PR(j)��(�)به ترتیب امتیازات رتبه گره های i و j هستند. nj��تعداد گره های طرح گره j را نشان می دهد . و d یک عامل میرایی است که معمولاً روی آن تنظیم می شود 0.850.85برای رتبه بندی صفحات وب در شبکه خیابان‌های شهری، این معیار به این معناست که اگر فردی مسیرهای شبکه شهری را به‌طور تصادفی انتخاب کند، خیابان‌هایی که دارای رتبه صفحه بالا هستند، به احتمال زیاد همان مسیرهای عبوری هستند. شکل 3 h معیارهای مرکزیت رتبه صفحه را برای تهران نشان می دهد.

2.2.6. مرکزیت نزدیکی

نزدیکی به عنوان معکوس انصاف تعریف می شود، که به نوبه خود مجموع فواصل تا همه گره های دیگر است [ 54 ]. هدف پشت این اقدام شناسایی گره هایی بود که می توانستند به سرعت به دیگران دسترسی پیدا کنند. این اندازه گیری می کند که تا چه اندازه گره i به تمام گره های دیگر در امتداد کوتاه ترین مسیرها نزدیک است و با معادله ( 9 ) تعریف می شود:

CCi=N−1∑j∈G;j≠idij���=�−1∑�∈�;�≠����

جایی که dij���کوتاه ترین طول مسیر بین است i و j است که در یک نمودار با ارزش تعریف شده است، به عنوان کوچکترین مجموع طول یال در تمام مسیرهای ممکن در نمودار بین i و j . شکل 3 g معیارهای مرکزیت نزدیکی را برای تهران نشان می دهد.

2.3. اندازه‌گیری نظم: پیکربندی فضایی یک شبکه خیابان شهری

پیکربندی فضایی یک شبکه شهری در شهرهای مختلف کاملاً متفاوت است زیرا در زمان‌های مختلف و در بافت‌های مختلف ساخته می‌شوند. عوامل اجتماعی، فرهنگی و سیاسی بر پیکربندی و چیدمان خیابان ها در شهرهای مختلف تأثیر می گذارد. در برخی شهرها پیکربندی جاده ها به خوبی منضبط و از یک الگوی یکنواخت پیروی می کند، در حالی که در برخی دیگر آشفته است و الگوی خاصی در آنها نمی توان یافت. برای ارزیابی پیکربندی‌های مختلف، به یک اندازه‌گیری کمی نیاز داریم، زیرا دو پیکربندی بصری متفاوت ممکن است از نظر نظم ساختاری مشابه باشند. نرخ اختلاط الگوریتمی برای تعیین سطح نظم ساختاری در یک شبکه است.

برای توضیح میزان اختلاط، فردی را در نظر بگیرید که به طور تصادفی در یک شبکه راه می‌رود، در طول این پیاده‌روی تصادفی، ممکن است از برخی گره‌های جدید بازدید کند یا از گره‌هایی عبور کند که قبلا دیده شده‌اند. پس از انجام چندین مرحله، فرکانس عبور از یک گره کاهش می یابد تا زمانی که به یک مقدار ثابت همگرا شود. فرکانس عبور از یک گره بر اساس تعداد دفعاتی که واکر از یک گره عبور می کند تقسیم بر تعداد کل حرکت ها محاسبه می شود. ثابت شده است که این فرکانس متناسب با درجه گره است و به صورت معادله ( 10 ) [ 57 ] محاسبه می شود:

πi=deg(i)E�من=ده�(من)�

جایی که deg(i)���(�)درجه گره و E تعداد کل پیوندها است. نرخ کاهشی که در فرکانس تقاطع برای گره های شبکه رخ می دهد، معیاری است که برای ارزیابی سطح نظم ساختاری یک شبکه استفاده می شود [ 58 ]. این اندازه گیری به عنوان معادله ( 11 ) تعریف می شود:

η=limt→∞supmaxi,j∣∣p(t)−πiij∣∣1t�=لیمتی→∞شامحداکثرمن،�|پمن�(تی)-�من|1تی

جایی که η�حداقل مرزهای بالایی یا supremum است. طبق تعریف، مازاد مجموعه S که زیرمجموعه A است، در صورت وجود، کوچکترین کمیتی است که بزرگتر یا مساوی هر یک از اعضای مجموعه S است. نرخ اختلاط معیاری بین 0 تا 1 است که بر اساس سطح نظم در ساختارهای فضایی تعیین می شود.

2.4.رمزگذار خودکار حذف نویز انباشته

رمزگذارهای خودکار نوع خاصی از شبکه عصبی پیشخور با ساختار متقارن هستند که از یک لایه ورودی، یک لایه پنهان و یک لایه خروجی تشکیل شده است [ 59 ، 60 ]. لایه میانی که گلوگاه نامیده می شود، برای بازسازی ورودی ها تا حد امکان آموزش داده شده است. قانون تنگنا این است که داده های ورودی را به یک کد با ابعاد پایین تر فشرده می کند تا رمزگذار خودکار را مجبور کند تا آموزنده ترین ویژگی ها (ویژگی های پنهان) را بیاموزد. رمزگذار خودکار دارای سه بخش کاربردی است: رمزگذاری برای رمزگذاری پیش بینی کننده های ورودی و یادگیری ویژگی های پنهان، رمزگشایی برای بازسازی نمایش با استفاده از آخرین ویژگی ها، و یک تابع ضرر برای محاسبه خطاهای بازسازی [ 59 ، 60 ]. ]. شکل 4تصویری از رمزگذار خودکار ارائه می دهد.

در رمزگذار خودکار، هم رمزگذار و هم رمزگشا شبکه‌های عصبی پیش‌خور کاملاً متصل هستند و اندازه ویژگی‌های ورودی و ویژگی‌های بازسازی‌شده باید یکسان باشد. با این حال، لایه گلوگاه قلب یک رمزگذار خودکار است و تغییر آن به فرد اجازه می‌دهد تا معماری را دستکاری کرده و عملکرد را افزایش دهد [ 59 ، 61 ]. به طور کلی، تعداد گره ها در هر لایه، مهمترین هایپرپارامتر برای رمزگذارهای خودکار، بیشتر برای لایه گلوگاه است. هرچه اندازه کوچکتر با تعداد پیش‌بینی‌کننده‌های ورودی مقایسه شود، نمایش معنادارتری را به همراه خواهد داشت. پس انتشار تکنیکی است که اغلب برای آموزش رمزگذارهای خودکار استفاده می شود. در ادامه فرمول های ( 12 ) و ( 13 ).) در مورد ساختار اساسی یک رمزگذار خودکار بحث کنید. رمزگذار خودکار ساده از یک رمزگذار و رمزگشا تشکیل شده است که توسط دو ماتریس وزن و دو بردار بایاس تعریف شده است:

y=f(x)=s1(w1(x)+b1)�=�(�)=�1(�1(�)+�1)
r=g(x)=s2(w2(x)+b2)�=�(�)=�2(�2(�)+�2)

که در آن f و g به ترتیب توابع رمزگذاری و رمزگشایی هستند که با وزن‌های w و بایاس‌های b تعیین می‌شوند و s1س1و s2س2توابع فعال سازی را که معمولا غیرخطی هستند نشان می دهد. تابع فعال سازی چندین ورودی از لایه های قبلی دریافت می کند، مجموع وزنی این ورودی ها را محاسبه می کند و خروجی ها را بر اساس تابع خود تولید می کند. تابع Sigmoid رایج ترین تابع فعال سازی برای رمزگذارهای خودکار است [ 59 ]. هدف یک رمزگذار خودکار بهینه سازی w و b به منظور به حداقل رساندن خطای مدل سازی است. دو روش رایج بهینه سازی مورد استفاده برای رمزگذارهای خودکار، آنتروپی متقابل [ 49 ] و حداقل میانگین مربعات خطا [ 62 ] است. ] است. پس انتشار برای به روز رسانی وزن ها و بایاس ها برای به حداقل رساندن خطای بازسازی استفاده می شود.

همانطور که قبلاً بحث شد، یکی از راه‌های افزایش عملکرد رمزگذار خودکار، افزودن لایه‌های بیشتر، ایجاد رمزگذارهای خودکار پشته‌ای (SAE) است. SAE یک مدل یادگیری عمیق بدون نظارت است که دارای چندین لایه برای مدل سازی بهتر پیچیدگی داده های ورودی است. روشی برای وادار کردن SAE به یادگیری ویژگی‌های مفید، اضافه کردن نویز تصادفی به ورودی‌های آن و بازیابی داده‌های اصلی بدون نویز است. به این ترتیب، رمزگذار خودکار نمی تواند به سادگی ورودی را در خروجی خود کپی کند، زیرا ورودی نیز حاوی نویز تصادفی است. این رمزگذار خودکار حذف نویز پشته‌ای (SDAE) نامیده می‌شود [ 40 ، 59 ].
یک SDAE از تمام مزایای هر شبکه عمیق مانند قدرت بیان بیشتر برخوردار است. این تکنیک یک مدل آموزش لایه های حریصانه است و اولین بار توسط هینتون [ 45 ] ارائه شد. الگوریتم رایجی که برای بهینه‌سازی وزن‌ها و بایاس‌ها در رمزگذارهای خودکار استفاده می‌شود، شیب نزولی تصادفی (SGD) است. در هر مرحله، گرادیان تابع هدف مربوط به پارامترها، جهت تندترین شیب را نشان می‌دهد و به الگوریتم اجازه می‌دهد تا پارامترها را برای جستجوی حداقل تابع تغییر دهد. علاوه بر این، برای محاسبه گرادیان های لازم، پس انتشار اعمال می شود [ 40 ، 59]. برای استفاده از شبکه SDAE برای طبقه بندی عملکرد خیابان، باید یک طبقه بندی استاندارد به عنوان لایه بالایی اضافه کنیم. در این مقاله، یک لایه رگرسیون لجستیک در بالای شبکه برای طبقه‌بندی عملکرد خیابان نظارت شده قرار می‌دهیم. SDAE به علاوه طبقه بندی کننده کل مدل معماری عمیق نشان داده شده در شکل 4 را شامل می شود.

3. نتایج

این بخش نحوه مقایسه نتایج مدل پیشنهادی خود را با چهار مدل یادگیری ماشین دیگر توضیح می‌دهد. مجموعه داده‌هایی را که استفاده کردیم، معیارهای به کار گرفته شده، مدل‌هایی که با آن‌ها مقایسه کردیم، نحوه تنظیم آن مدل‌ها و در نهایت نتایج طبقه‌بندی عملکرد خیابان را توصیف می‌کنیم.

3.1. توضیحات داده ها

برای استخراج معیارهای مرکزیت، محورهای اصلی تمامی جاده ها با استفاده از روش قطعه خیابان مدلسازی شده است. این بدان معنی است که جاده بین دو اتصال متوالی به عنوان یک بخش مجزا در شبکه در نظر گرفته می شود. بخش های خیابان مدل شده برای ساخت سکته مغزی استفاده شد. این ضربه‌ها با استفاده از بهترین روش‌ها ساخته شده‌اند. جهت های خیابان نیز در طراحی سکته ها در نظر گرفته شد. در این تحقیق از مجموعه داده های چهار شهر مختلف استفاده شده است. خیابان‌های هر شهر بر اساس قابلیت‌های جاده شریانی اصلی (PAr)، جاده شریانی کوچک (MAr)، جاده جمع‌آوری (Cr) و جاده محلی (Lr) به چهار کلاس گروه‌بندی می‌شوند. برای هر خیابان، 9 ویژگی مرکزی متفاوت تعیین شده است و اطلاعات آماری هر 9 معیار مرکزیت در این موارد خلاصه شده است.جدول 1 . پس از پیش پردازش داده ها، بردار ویژگی ساختاری برای هر ضربه محاسبه می شود، سپس بردارها در محدوده [-1،1] نرمال می شوند. از آنجایی که یک سکته مغزی متشکل از چندین بخش خیابان با عملکردهای مختلف در دنیای واقعی است، معیارهای ساختاری هر ضربه به تمام بخش‌های تشکیل‌دهنده خیابان اختصاص داده می‌شود. از طریق تمام پیاده سازی های مختلف مدل یادگیری ماشین، 75%75%از اقدامات برای آموزش استفاده می شود و 25%25%برای آزمایش.

3.2. تنظیم الگوریتم

ما چهار مدل رایج یادگیری ماشین، یعنی رگرسیون لجستیک (LR)، پرسپترون چند لایه (MLP)، ماشین‌های بردار پشتیبانی (SVM) و جنگل تصادفی (RF) را برای مقایسه با مدل پیشنهادی SDAE برای استفاده در SFC انتخاب کردیم. طبقه‌بندی‌کننده‌های یادگیری ماشین و یادگیری عمیق معمولاً دارای پارامترهایی هستند که باید توسط کاربر تنظیم شوند که به عنوان hyperparameters شناخته می‌شوند. تنظیم فراپارامتر شامل انتخاب مقادیری برای این فراپارامترها است که منجر به عملکرد بهینه یک مدل می شود. فراپارامترهای مورد استفاده برای هر یک از مدل های یادگیری ماشین سنتی و مدل SDAE ما در جدول 2 آورده شده است. مقادیر فراپارامتر بر اساس تکنیک جستجوی شبکه ای [ 63 ] انتخاب می شوند ] با اعتبارسنجی متقابل [63] انتخاب می شوند. 64 ] انتخاب می شوند.]. به هر هایپرپارامتر فهرستی از مقادیر گسسته داده می شود و برای هر ترکیبی از فراپارامترهای مختلف، یک آموزش اعتبارسنجی متقابل 5 برابری استفاده می شود. داده ها به پنج قسمت مساوی تقسیم می شوند و هر بخش به عنوان داده های آزمایشی استفاده می شود، در حالی که بقیه داده ها (چهار قسمت دیگر) برای آموزش استفاده می شود و اعتبار متقاطع 5 برابری می دهد. مجموعه ای از فراپارامترهایی که بالاترین دقت طبقه بندی را به دست می آورند به عنوان هایپرپارامترهای مورد استفاده انتخاب می شوند.
برازش بیش از حد یک مشکل رایج در همه مدل‌های یادگیری ماشینی و یادگیری عمیق است. تطبیق بیش از حد به این معنی است که مدل در داده های آموزشی بسیار خوب عمل می کند اما در داده های آزمایشی (داده های دیده نشده) عملکرد خوبی ندارد. منظم سازی تکنیکی برای تعمیم یک مدل است و به نوبه خود، عملکرد مدل را روی داده های آزمایشی دیده نشده بهبود می بخشد تا مشکل اضافه برازش را بهبود بخشد. منظم‌سازی تأثیر یکسانی بر یادگیری ماشینی و یادگیری عمیق دارد اما به روش‌های متفاوت. در یادگیری ماشین، منظم‌سازی ضرایب را جریمه می‌کند، اما در یادگیری عمیق، ماتریس‌های وزن گره‌ها را جریمه می‌کند [ 45 ]. ].
برای طراحی معماری مدل SDAE که استفاده کردیم، تعداد متفاوتی از لایه‌های پنهان و تعداد نورون‌ها برای هر لایه مورد آزمایش قرار گرفت. SDAE بر اساس نزول گرادیان تصادفی آموزش داده شده است 75%75%از یک مجموعه داده، و آزمایش 20 بار تکرار می شود تا تغییرپذیری فرآیند ارزیابی شود. مدل آموزش‌دیده در نهایت بر روی داده‌های آزمایشی، باقی‌مانده‌های دیده نشده، ارزیابی می‌شود 25%25%از یک مجموعه داده در این آزمایش، تعداد نورون‌های لایه پنهان را از 1 تا 20 تغییر می‌دهیم تا تعداد بهینه را تعیین کنیم و همچنین تعداد لایه‌های پنهان را از دو به سه تغییر می‌دهیم. بر اساس 95%95%فاصله اطمینان و تخمین خطای استاندارد برای 20 تکرار، در نهایت به 10 نورون بهینه برای لایه اول و پنج نورون برای لایه دوم یا گلوگاه می رسیم. به طور کلی، برای یک مدل SAE سه راه برای کنترل بیش از حد برازش وجود دارد: اضافه کردن یک عبارت جریمه در تابع ضرر (اصطلاح تنظیم) برای کنترل وزن‌ها، اضافه کردن نویز به داده‌های ورودی برای وادار کردن مدل SAE به یادگیری ویژگی‌های اطلاعاتی بیشتر، و پراکندگی رمزگشایی با غیرفعال کردن برخی از گره ها در هر لایه به طور تصادفی. برای جلوگیری از برازش بیش از حد، 0- 30%30%نویز به داده های ورودی (فقط لایه اول) اضافه می شود تا مدل رمزگذار خودکار حذف نویز انباشته شده را برآورده کند و بر اساس نتایج، 10%10%مقدار بهینه بود. علاوه بر این، برای مدت تنظیم، 0.0010.001بر اساس تکنیک جستجوی شبکه ای بین مقادیر در محدوده 0 تا انتخاب می شود 0.00010.0001برای جلوگیری از رشد وزن ها در مدل یادگیری عمیق و بیش از حد برازش.
LR یک مدل یادگیری ماشینی معیار رایج است و ساده ترین مدلی است که در این کار استفاده می شود. عبارت منظم‌سازی مورد استفاده در مدل LR بر اساس یک استراتژی جستجوی شبکه‌ای برای یافتن مقدار بهینه، با انتخاب 1، در محدوده (0.1-10) آزمایش شد. علاوه بر این، برای بهینه سازی مدل LR دو تکنیک مختلف آزمایش شده است: SGD و حافظه محدود برویدن-فلچر-گلدفارب-شانو (LBFGS) [ 65]؛ LBFGS بهترین تکنیک بهینه سازی برای استفاده در این کار بود. برای پیکربندی مدل MLP، تعداد لایه‌های پنهان، تعداد نورون‌ها در هر لایه، نوع تابع فعال‌سازی، تکنیک بهینه‌سازی و نرخ یادگیری در ترکیب‌های مختلف آزمایش می‌شوند تا بهترین پیکربندی برای مدل MLP پیدا شود. برای تکنیک بهینه‌سازی LBFGS، سه لایه پنهان و 100 نورون برای هر یک از آنها که توسط تابع فعال‌سازی ReLU فعال می‌شوند، بهترین هایپرپارامترها برای مدل MLP بودند. برای SVM، یک هسته RBF به عنوان یکی از بهترین روش‌های هسته در مدل‌های یادگیری ماشین مبتنی بر هسته آزمایش می‌شود. مقادیر C، یک عبارت منظم‌سازی، و گاما به‌عنوان فراپارامتر برای هسته RBF بر اساس استراتژی جستجوی شبکه‌ای یافت شد: به ترتیب 1 و 10 برای C و گاما. در این کار از RF به عنوان یکی از بهترین مدل های مجموعه استفاده شده است. در فرآیند آموزش RF، دو روش برای کنترل بیش از حد برازش وجود دارد: محدود کردن تعداد گره ها در هر برگ یا محدود کردن عمق درختان. بر اساس یک جستجوی شبکه ای، مقادیر بهینه برای هر دو این دو ابرپارامتر برای RF 5 برای حداکثر عمق و 4 برای حداقل تعداد گره در هر برگ بود.

3.3. نتایج تجربی

مدل SDAE پیشنهادی ما به همراه چهار مدل یادگیری ماشین برای طبقه‌بندی عملکرد خیابان‌های شبکه در چهار شهر مختلف استفاده شد. در این بخش، نتایج برای همه مدل ها نشان داده شده و مورد بحث قرار می گیرد. برای در نظر گرفتن تأثیر مقدار داده های ورودی برای الگوریتم های مختلف یادگیری ماشین و همگرایی فرآیند آموزش، منحنی های یادگیری برای مدل های مختلف ارائه شده است. هر یک از پیش‌بینی‌کننده‌های ورودی، یا ویژگی‌های ورودی، نقش متفاوتی را ایفا می‌کنند و سطح اهمیت متفاوتی در عملکرد نهایی یک مدل دارند. در این بخش اهمیت هر یک از پیش بینی کننده های ورودی مورد توجه و بحث قرار گرفته است. علاوه بر این، تأثیر منظم بودن خیابان شبکه و رابطه بین منظم بودن هر شهر بر نتایج طبقه‌بندی مورد بحث قرار می‌گیرد.

ارزیابی دقت یک گام اساسی در ارزیابی عملکرد و کارایی طبقه‌بندی‌کننده‌های مختلف است. در این بخش، نتایج مدل های مختلف پیاده سازی شده بر روی داده های واقعی محاسبه می شود. برای ارزیابی عملکرد طبقه‌بندی‌کننده‌های مختلف، به ماتریس سردرگمی نگاه می‌کنیم. R2�2، و ریشه میانگین مربعات خطا (RMSE). ماتریس سردرگمی جدولی است که اغلب برای توصیف عملکرد تکنیک های طبقه بندی استفاده می شود (برای اطلاعات بیشتر در مورد ماتریس سردرگمی به کار در [ 66 ] مراجعه کنید). دقت کلی (OA) بر اساس این مدل، نسبت تعداد کل پیش‌بینی‌های صحیح است. متریک اندازه گیری F بر اساس دقت (P) و یادآوری (R) است (P نسبت موارد مثبت پیش بینی شده است که درست بوده و R همان مثبت واقعی است) و به صورت محاسبه می شود.

F1=2PRP+R�1=2���+�
RMSE [ 67 ] به طور منظم در مطالعات ارزیابی مدل استفاده می شود. RMSE تفسیر کاملی از توزیع خطا در محدوده ارائه می دهد [0,1][0,1]، جایی که مقادیر نزدیک به صفر بهتر است. علاوه بر این، برای ارزیابی بهترین پیش بینی R2�2استفاده شده است [ 68 ]، محدوده این متریک بین [0,1][0,1]، جایی که مقادیر نزدیک به 1 بهتر است. برای بقیه مقاله، OA برای داده های آموزشی به عنوان “OA-Tr” و OA برای مجموعه داده های آزمایشی به عنوان “OA-Te” مشخص می شود. علاوه بر این، امتیاز F1 برای کلاس‌های PAR، MAr، Cr و Lr به ترتیب به‌عنوان «F1-PAR»، «F1-MAR»، «F1-Cr» و «F1-Lr» مشخص می‌شود.
نتایج طبقه‌بندی مدل‌های یادگیری ماشین و یادگیری عمیق پیاده‌سازی ما در جدول 3 ، جدول 4 ، جدول 5 و جدول 6 برای چهار شهر ارائه شده است. نتایج برای همه مجموعه‌های داده نشان می‌دهد که یادگیری ماشین و یادگیری عمیق می‌توانند عملکرد خیابان را تنها بر اساس ویژگی‌های ساختاری خیابان‌ها پیش‌بینی و طبقه‌بندی کنند. همانطور که نتایج در جدول 3 ، جدول 4 ، جدول 5 و جدول 6 نشان داده شده است، SDAE توانسته است بیش از 90 درصد دقت پیش بینی را برای خیابان های نمونه آموزشی و آزمایشی شهرها ایجاد کند که بالاتر از همه مدل های پیشنهادی در این آزمایش
دقت کلی برای مجموعه داده های آزمایشی (OA-Te) است 92%92%، 89%89%، 92%92%، و 92%92%به ترتیب برای اصفهان، انشده، تهران و پاریس. نتایج به این نتیجه می‌رسد که ساختار فضایی خیابان‌ها نقش مهمی در شکل‌گیری عملکرد جاده‌های شهری دارد، زیرا عملکرد خیابان‌ها تنها با استفاده از ویژگی‌های ساختاری و فضایی قابل تشخیص است.
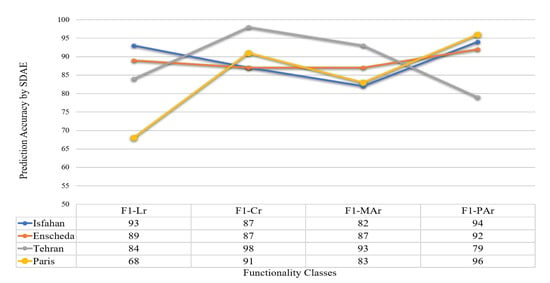
بر اساس نتایج امتیاز F1 پیشنهادی برای هر طبقه از عملکرد خیابانی، می توان بیان کرد که هر کلاس عملکرد دارای یک الگوی ساختاری خاص است که قابل تشخیص است. نمودار نشان داده شده در شکل 5 نتایج پیش‌بینی مدل SDAE را برای آزمایش مجموعه داده‌های نمونه هر کلاس از عملکرد خیابان نشان می‌دهد. همانطور که در نمودار نشان داده شده است، اکثر خطاها در کلاس های عملکرد در مشابه ترین کلاس ها رخ داده است. بنابراین، طبقه‌بندی اشتباه بیشتر بین کلاس‌هایی اتفاق می‌افتد که مشابه هستند، نه بین کلاس‌هایی که از نظر ساختاری کاملاً متفاوت هستند. به عنوان مثال، طبقه بندی اشتباه برای Cr اتفاق می افتد زیرا کلاس های Lr از نظر ساختاری و مکانی مشابه هستند و برای دو کلاس جاده های اولیه یکسان هستند. شکل 5نشان می‌دهد که دقت تشخیص کلاس PAR بالاتر از MAr و قابل تشخیص‌تر است زیرا ویژگی‌های فضایی MAr بسیار نزدیک به PAR است و همین تحلیل برای کروم که دقت کمتری نسبت به Lr دریافت کرده است.

4. بحث

علاوه بر SFC، تأثیر منظم بودن شهرها بر طبقه بندی، اهمیت هر معیار مرکزیت و نقش یادگیری عمیق برای چنین پردازش داده های بزرگ در این بخش مورد بحث قرار گرفته است.

4.1. منظم بودن شهرها و تأثیر آن بر نتایج طبقه بندی

ارزیابی تأثیر الگوهای ساختاری بر شکل‌دهی عملکرد جاده‌ها در دنیای واقعی بسیار مهم است. به نظر می رسد که پیکربندی و ساختار فضایی به طور قابل توجهی بر نحوه توزیع این الگوها تأثیر می گذارد. سطوح مختلف نظم در ساختارهای شبکه تأثیرات متفاوتی بر شکل‌دهی عملکرد جاده‌های شهری در دنیای واقعی دارد. برای بررسی این ایده، سطح نظم ساختاری برای همه شهرها با استفاده از نسبت اختلاط معادلات (10) و (11) محاسبه شده است. علاوه بر این، نتایج طبقه‌بندی با سطح نظم در هر شبکه مقایسه می‌شود. شکل 6 سطح نظم ساختاری (نرخ اختلاط) شهرها در محور X و دقت طبقه بندی کل آنها را در محور Y نشان می دهد.
بر اساس نتایج ارائه شده در شکل 6برای نرخ اختلاط طبقه بندی کلی برای همه شهرهای مختلف، می توان نتیجه گرفت که ماهیت سلسله مراتبی جاده ها در مناطق شهری نیز بر اساس ویژگی های ساختاری آنها آشکار می شود. با توجه به نتایج، می توان استنباط کرد که در شبکه های با پیکربندی منظم (که در آن الگوی مشابه در شبکه تکرار می شود)، بین عملکرد یک جاده و ویژگی های ساختاری آن رابطه قوی وجود دارد. به عبارت دیگر، در شبکه‌های معمولی مانند تهران و اصفهان که نرخ اختلاط و دقت کلی بالاتری را پیشنهاد می‌کردند، ساختار فضایی تأثیر زیادی در شکل‌گیری کلاس عملکرد در خیابان‌های دنیای واقعی نشان داد. از سوی دیگر، برای شهرهایی که در این مطالعه ترتیب خیابان‌ها در آنها کمتر منظم است، مانند پاریس یا انشده با کمتر از 72%72%نرخ اختلاط و کمتر از دقت کلی کمتر، ساختار فضایی موجود تأثیر کمتری بر شکل‌دهی عملکردهای خیابان دارد که منجر به الگوهای ساختاری ضعیف در هر کلاس عملکردی می‌شود. در پایان، برای مطالعه موردی در پژوهش حاضر، سطح نظم ساختاری در پیکربندی فضایی شبکه‌های شهری عامل مؤثری در شکل‌گیری کارکرد راه‌های شهری است، هرچند در سایر شهرها نیاز به بررسی بیشتر است.

4.2. اهمیت هر ویژگی مرکزی

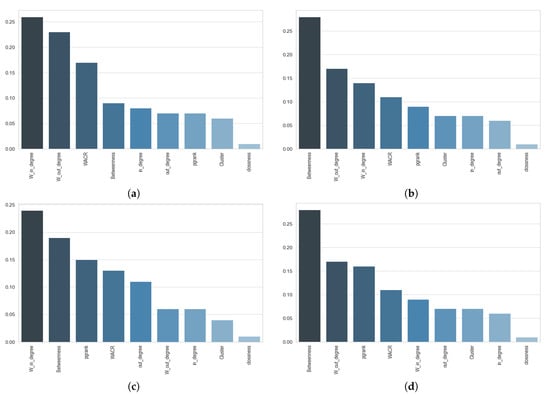
شکل 7 اهمیت سهم هر ویژگی را در طبقه بندی برای هر چهار مجموعه داده آزمایشی نشان می دهد. محور افقی نشان دهنده ویژگی و محور عمودی درصد اهمیت است. مهمترین ویژگی برای هر شهر بالاترین ستون در نمودار است. اهمیت هر ویژگی بر اساس مفاهیم جنگل تصادفی محاسبه می شود، زیرا وزن ناخالصی گره با احتمال رسیدن به آن گره کاهش می یابد. احتمال گره با تعداد نمونه هایی که به گره می رسند، تقسیم بر تعداد کل نمونه ها محاسبه می شود. هر چه مقدار بالاتر باشد، ویژگی مهمتر است [ 69 ].
با توجه به نتایج در شکل 7، برای پاریس و انشده، بین بودن مهم ترین ویژگی و برای تهران و اصفهان یکی از مهم ترین ویژگی ها است. به طور کلی، این به معنی بین بودن مهمترین ویژگی در پیش بینی عملکرد خیابان و حتی الگوهای حرکتی است. این نتیجه نشان می‌دهد که کوتاه‌ترین مسیر، نقشی محوری در یافتن مقصد برای افراد دارد. خیابان‌های شلوغ بیشتر به کوتاه‌ترین مسیر در شبکه کمک می‌کنند، که دلیل آن این است که همه شهرها از بین بودن یکی از مهمترین ویژگی‌ها هستند. با توجه به این واقعیت، محاسبه بین خیابان ها منجر به پیش بینی بهتر میزان ترافیک می شود. محاسبه بین بین بودن در شبکه می تواند به طراحی بهتر برای خیابان سازی جدید کمک کند.
بعد از بین بودن، وزن دهی در داخل و خارج از مهمترین ویژگی ها بیشتر برای اصفهان و تهران است. مدرک خیابانی (دانشگاهی و تحصیلی) به داشتن ارتباطات بیشتر و کاربرد بیشتر در استفاده افراد برای رسیدن به مقصد کمک می کند. برای اصفهان و تهران با سطح منظمی بالاتر، به دلیل سازماندهی و نظم بالای شبکه خیابانی، اهمیت بین‌المللی در بالاترین حد نیست و همه خیابان‌ها سهم نزدیکی در حمل ترافیک دارند. در درجات وزنی، خیابان‌های با وزن بالاتر ارتباط بیشتری با جاده‌های شریانی اولیه دارند که در شهرهای عادی مانند اصفهان و تهران سهم بیشتری در پیش‌بینی ترافیک دارند. نزدیکی برای همه شهرهای مورد مطالعه ما کمترین اهمیت را دارد زیرا مردم اکثراً در کوتاه ترین مسیر به مقصد خود رانندگی می کنند.

4.3. یادگیری عمیق برای پردازش داده های بزرگ

در این دنیای علمی که به سرعت در حال رشد است و امکان جمع آوری کلان داده ها، یادگیری عمیق نقش مهمی در راه حل های کلان داده ایفا می کند. به جز داشتن حجم زیاد، تنوع زیاد و ویژگی پیچیدگی داده های بزرگ یک چالش بزرگ برای شبکه های عصبی کم عمق و یادگیری ماشین سنتی است. در این کار، ما یک مجموعه داده بزرگ برای چهار شهر با پیچیدگی و غیرخطی بالا اعمال کردیم. متریک RMSE بر اساس رگرسیون خطی برای همه مجموعه داده ها می باشد 0.690.69، 0.720.72، 0.650.65، و 0.720.72به ترتیب برای اصفهان، انشده، تهران و پاریس. این نتایج برای رگرسیون خطی RMSE به غیرخطی بودن بالای مجموعه داده‌های ما اشاره می‌کند.
برخلاف یادگیری ماشین سنتی و شبکه‌های عصبی کم عمق، مدل‌های یادگیری عمیق از توابع غیرخطی عظیمی بهره می‌برند که می‌توانند نمایش و پیچیدگی ویژگی‌ها را بیاموزند. مهم‌تر از همه، مدل‌های یادگیری بدون نظارت در لایه‌های حریص مانند SDAE می‌توانند ویژگی‌های پنهان (مهم‌ترین ویژگی‌های پیش‌بینی‌کننده‌های ورودی برای تغذیه به طبقه‌بندی‌کننده) را در سطح ارائه بالاتر بیاموزند. جدول 3 ، جدول 4 ، جدول 5 و جدول 6عملکرد SDAE را بهتر از LR و شبکه های عصبی کم عمق نشان می دهد: SVM و جنگل تصادفی. علاوه بر این، LR به‌عنوان طبقه‌بندی‌کننده به‌طور جداگانه استفاده می‌شود تا نشان دهد ویژگی‌های تولید شده توسط SDAE در سطح بالاتری از نمایش، قابل تفکیک‌تر از داده‌های ورودی خام هستند و بر اساس نتایج ارائه‌شده در جدول 3 ، جدول 4 ، جدول 5 و جدول 6 ، SDAE+LR بهتر از LR به عنوان یک طبقه بندی کننده یادگیری نظارت شده کار می کرد. این به این دلیل است که SDAE ویژگی‌ها را به روشی غیرخطی بر اساس تکنیک لایه‌ای حریصانه یاد می‌گیرد و ویژگی‌های جدیدی را که ترکیبی از ویژگی‌های موجود هستند تولید می‌کند، سپس LR با استفاده از این ویژگی‌های جدید بر اساس داده‌های برچسب‌گذاری شده مربوطه طبقه‌بندی می‌کند.
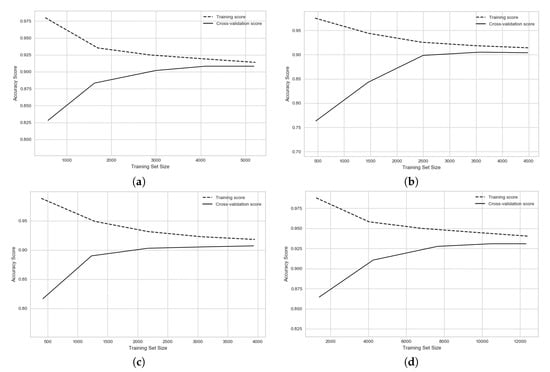
وقتی از مدل‌های یادگیری ماشینی و یادگیری عمیق استفاده می‌کنیم، می‌خواهیم خطاها را تا حد امکان پایین نگه داریم. دو منبع اصلی خطا برای مدل های یادگیری ماشین وجود دارد: سوگیری و واریانس. مقداری که تخمین با تغییر مجموعه داده آموزشی تغییر می کند واریانس نامیده می شود و بایاس تعداد خطاهای ناشی از فرض خطی بودن مجموعه داده است. برای در نظر گرفتن واریانس و سوگیری پیش بینی توسط مدل های مختلف، مجموعه داده ها به مجموعه های آموزشی و اعتبار سنجی جداگانه تقسیم می شوند. در این تحقیق از تکنیک اعتبارسنجی متقابل 5 برابری استفاده شده است. منحنی یادگیری بهترین تکنیک برای بررسی این دو منبع خطا است که برای مدل‌های یادگیری عمیق در شکل 8 و تمامی مدل‌های یادگیری ماشین برای اصفهان در شکل 9 نشان داده شده است.. محور افقی اندازه مجموعه آموزشی و محور عمودی دقت است (به جای آن می تواند خطا باشد). منحنی های یادگیری نشان داده شده در شکل 8 برای مدل SDAE نشان می دهد که این مدل بهترین نتایج را برای تمام شهرهای آزمایش شده با بهترین همگرایی ارائه کرده است. یک همگرایی خوب به این معنی است که الگوریتم می تواند غیرخطی بودن و پیچیدگی ویژگی های ورودی را مدل کند و الگوریتم برای درک رفتار ویژگی های ورودی برای مدل سازی به نمونه های آموزشی بیشتری نیاز ندارد.
در شکل 9منحنی یادگیری برای تمامی مدل های یادگیری ماشین برای اصفهان به تصویر کشیده شده است. مدل MLP-3-100-RELU-LBFGS قادر به پیش‌بینی بوده است، اما همچنان با ارائه دقت پایین، مشکل بایاس کم وجود دارد. SVM یک شرایط همگرایی خوب و واریانس خوب اما بایاس و ضعف کم برای پیش‌بینی پیچیدگی و غیرخطی بودن ویژگی‌ها ارائه کرد. مدل‌های RF دقت بالاتری را با بایاس بالا و واریانس کم ارائه می‌دهند، اما همچنان مشکلی وجود دارد که در وسط و حتی انتهای دو خط سبز و قرمز یک شکاف بزرگ وجود دارد، به این معنی که این مدل هنوز به داده‌های بیشتری برای آموزش مدل نیاز دارد. به یک نرخ خطای خوب همگرا شود. بر اساس منحنی یادگیری برای مدل رگرسیون لجستیک، واضح است که این مدل نتوانسته است پیچیدگی و غیرخطی بودن تمامی ویژگی های آموزشی را به خوبی پیش بینی کند. زیرا اول از همه، دقت پیش‌بینی خوب نیست، بنابراین میزان خطای تمرین بالاست (مشکل کم تعصب). علاوه بر این، به نظر می‌رسد که این مقدار داده برای این مدل‌ها زیاد است، زیرا در ابتدا بین دو خط یادگیری فاصله وجود ندارد (مشکل واریانس بالا، ناحیه وسیع اطراف خط)، بنابراین این مدل‌ها نمی‌توانند پیچیدگی را پیش‌بینی کنند. ویژگی های ورودی، و، همانطور که می بینیم، نتایج نیز خوب نیستند.

5. نتیجه گیری ها

مطالعات زیادی در مورد درک نقش ساختارهای فضایی در الگوی حرکت فردی انجام شده است. مطالعه حاضر دو دیدگاه جدید در مورد مطالعه ساختاری فضایی در شبکه‌های شهری ارائه می‌کند. در این پژوهش از 9 معیار مختلف سازه ای برای بررسی تأثیر ساختاری فضایی بر شکل‌دهی عملکرد راه‌های شهری استفاده شد. تکنیک‌های مختلف یادگیری ماشین، مانند رگرسیون لجستیک، MLP، SVM، و جنگل تصادفی، در کنار یک مدل یادگیری عمیق به نام رمزگذاری خودکار حذف نویز پشته‌ای، برای آشکار کردن الگوهای موجود در هر کلاس عملکردی از جاده‌های شهری استفاده می‌شوند. برای دستیابی به این هدف، مجموعه‌ای آموزشی از بخش‌های خیابان، که با بردار ویژگی و کلاس عملکرد آنها تعریف شده‌اند، به مدل‌های مختلف داده شد.
نتایج نشان می دهد که با دقت قابل قبول ارائه شده توسط SDAE، می توان عملکرد خیابان ها را تنها بر اساس ویژگی های ساختاری فضایی آن ها پیش بینی کرد. این بدان معناست که برای هر کلاس عملکردی در دنیای واقعی، یک الگوی ساختاری فضایی خاص وجود دارد، و ویژگی‌های ساختاری خیابان‌ها در یک کلاس عملکرد کاملاً مشابه به نظر می‌رسد. می توان نتیجه گرفت که ساختار فضایی شبکه های شهری عامل موثری در شکل گیری نقش و اهمیت هر خیابان در دنیای واقعی است. به عبارت دیگر، اهمیت ساختاری برخی از راه‌های شهری باعث شده است که از آن‌ها بیشتر از سایر راه‌ها استفاده شود که به نوبه خود منجر به تغییرات فیزیکی در ویژگی‌های جاده برای انطباق با نیازهای ترافیکی بالا می‌شود. در نتیجه بیشتر این جاده ها به جاده های معروف با ظرفیت بالا تبدیل می شود. بیشتر به عنوان جاده های شریانی شناخته می شود. از سوی دیگر، برخی دیگر از جاده ها به دلیل موقعیت مکانی خود در شبکه های شهری، معمولاً توسط مسافران کمتری مورد استفاده قرار می گیرند. این وضعیت منجر به تبدیل این جاده ها به جاده های دسترسی می شود که به جاده های فرعی معروف هستند.
نتایج طبقه‌بندی همچنین سلسله مراتبی را ارائه کرد که به طرز جالبی شبیه سلسله مراتب مفهومی جاده در دنیای واقعی بود. به عبارت دیگر، اگرچه این طبقه‌بندی صرفاً با اعمال ویژگی‌های سازه‌ای انجام شد، اما نتایج آن دقیقاً به همان روشی که جاده‌های شهری انجام می‌دادند ترتیب داده شد. این بدان معناست که در تمام کلاس‌های عملکردی که توسط مدل‌های یادگیری ماشین و یادگیری عمیق پیش‌بینی شده‌اند، اکثر خطاها در مشابه‌ترین کلاس‌ها رخ داده است. وقتی متوجه می‌شویم که مجموعه داده آموزشی هیچ اطلاعاتی در مورد ترتیب کلاس‌های عملکردی ندارد و سلسله‌مراتب حاصل در طبقه‌بندی فقط بر اساس ویژگی‌های ساختاری رخ داده است، قابل توجه خواهد بود. همچنین نتایج نشان داد که در شبکه های منظم که در آن یک الگوی فضایی در نقاط مختلف شهر تکرار می شود، مدل یادگیری عمیق توانست کلاس عملکرد دنیای واقعی را با دقت بیشتری پیش بینی کند. این نشان می دهد که در شبکه های منظم، یک الگوی ساختار فضایی برجسته در هر کلاس عملکردی در مقایسه با شبکه های کمتر منظم وجود دارد. به این معنی که در شبکه‌های منظم، ساختارها و پیکربندی‌های فضایی تأثیر بیشتری در شکل‌گیری نقش‌های خیابانی در دنیای واقعی دارند. از سوی دیگر، در شبکه‌های کمتر منظم، اهمیت ساختار فضایی در شکل‌گیری عملکرد خیابان کاهش می‌یابد که به نوبه خود الگوهای ساختاری ضعیفی را در هر کلاس عملکردی در دنیای واقعی ایجاد می‌کند. در نتیجه، سطح نظم ساختاری در شبکه‌های شهری عامل کلیدی در شکل‌گیری عملکرد و اهمیت خیابان‌ها در دنیای واقعی است.

منابع

  1. جیانگ، بی. هری، ال. انتخاب خیابان ها از یک شبکه با استفاده از نقشه های خودسازماندهی. ترانس. GIS 2004 ، 8 ، 335-350. [ Google Scholar ] [ CrossRef ]
  2. Borgatti، SP Centrality و جریان شبکه. Soc. شبکه 2005 ، 27 ، 55-71. [ Google Scholar ] [ CrossRef ]
  3. پورتا، اس. کروسیتی، پی. Latora، V. تحلیل شبکه ای خیابان های شهری: رویکرد دوگانه. فیزیک یک آمار مکانیک. برنامه آن است. 2006 ، 369 ، 853-866. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  4. بلانچارد، پی. ولچنکوف، دی. تحلیل ریاضی شبکه‌های فضایی شهری . Springer Science & Business Media: برلین/هایدلبرگ، آلمان، 2008. [ Google Scholar ]
  5. کازرانی، ع. زمستان، S. مرکزیت میانی می تواند جریان ترافیک را توضیح دهد. در مجموعه مقالات دوازدهمین کنفرانس بین المللی AGILE در علم اطلاعات جغرافیایی، هانوفر، آلمان، 2 تا 5 ژوئن 2009. صفحات 1-9. [ Google Scholar ]
  6. جیانگ، بی. لیو، سی. نمایش های توپولوژیکی مبتنی بر خیابان و تجزیه و تحلیل برای پیش بینی جریان ترافیک در GIS. بین المللی جی. جئوگر. Inf. علمی 2009 ، 23 ، 1119-1137. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  7. گائو، اس. وانگ، ی. گائو، ی. لیو، ی. درک ویژگی‌های جریان ترافیک شهری: بازنگری در مرکزیت بین‌المللی. محیط زیست طرح. B طرح. دس 2013 ، 40 ، 135-153. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  8. وزارت حمل و نقل آمریکا طبقه بندی عملکردی بزرگراه: مفاهیم، ​​معیارها و رویه ها . USDoT: واشنگتن، دی سی، ایالات متحده آمریکا، 2013.
  9. پن، ا. هیلیر، بی. بنیستر، دی. Xu, J. مدل سازی پیکربندی شبکه های حرکت شهری. محیط زیست طرح. B طرح. دس 1998 ، 25 ، 59-84. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  10. ترنر، اف سی بزرگراه کمک های فدرال سال 1970 و سایر لوایح مرتبط برای تحویل به کمیته فرعی جاده های کمیته امور عمومی سنا آماده شد. در دسترس آنلاین: https://rosap.ntl.bts.gov/view/dot/43207 (در 2 ژوئن 2020 قابل دسترسی است).
  11. استاماتیادیس، ن. کرک، ای. کینگ، ام. چلمن، آر. توسعه یک سیستم طبقه بندی عملکردی چندوجهی حساس به زمینه. Adv. ترانسپ گل میخ. 2019 ، 47 ، 5-20. [ Google Scholar ]
  12. حسن، یو. وایت، ا. Al Jassmi, H. مروری بر تحول سیستم های حمل و نقل جاده ای: آیا ما برای گام بعدی در حمل و نقل پایدار با هوشمندی مصنوعی آماده هستیم؟ Appl. سیستم نوآوری. 2020 ، 3 ، 1. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  13. هان، بی. سان، دی. یو، ایکس. آهنگ، دبلیو. Ding, L. طبقه بندی شبکه های خیابانی شهری بر اساس ویژگی های شبکه درخت مانند. پایداری 2020 ، 12 ، 628. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  14. زینگ، اچ. Meng, Y. اندازه‌گیری مناظر شهری برای طبقه‌بندی عملکرد شهری با استفاده از معیارهای فضایی. Ecol. اندیک. 2020 , 108 , 105722. [ Google Scholar ] [ CrossRef ]
  15. کاسترو، جی تی. Vistan، EFL یک سیستم اطلاعات جغرافیایی برای دسترسی روستایی: توسعه پایگاه داده و کاربرد ارزیابی چند معیاره برای برنامه ریزی شبکه راه در مناطق روستایی. در برنامه ریزی شهری و ترانزیت ; Springer: برلین، آلمان، 2020؛ صص 277-288. [ Google Scholar ]
  16. سامیت، SH; Akhter, S. C-به معنی خوشه بندی و طبقه بندی عمیق عصبی-فازی برای اندازه گیری وزن جاده در سیستم مدیریت ترافیک. محاسبات نرم. 2019 ، 23 ، 4329–4340. [ Google Scholar ] [ CrossRef ]
  17. مائده، ک. تاکاهاشی، س. اوگاوا، تی. Haseyama، M. شبکه پیوند عملکردی تصادفی بردار عمیق مبتنی بر کدگذاری پراکنده برای طبقه‌بندی پریشانی سازه‌های جاده‌ای. Comput.-Aided Civ. زیرساخت. مهندس 2019 ، 34 ، 654-676. [ Google Scholar ] [ CrossRef ]
  18. احمدزی، ف. رائو، KL; الفت، س. ارزیابی و مدل سازی شبکه های راه های شهری با استفاده از نمودار یکپارچه شبکه راه های طبیعی (رویکردی مبتنی بر GIS). J. Urban Manag. 2019 ، 8 ، 109–125. [ Google Scholar ] [ CrossRef ]
  19. Van HIEP، D.; SODIKOV، J. نقش طبقه بندی عملکردی بزرگراه ها در مدیریت دارایی جاده. جی شرق. انجمن آسیا ترانسپ گل میخ. 2017 ، 12 ، 1477-1488. [ Google Scholar ]
  20. ژانگ، اچ. Li, Z. شبکه من وزنی برای تشکیل ساختار سلسله مراتبی شبکه های جاده ای. بین المللی جی. جئوگر. Inf. علمی 2011 ، 25 ، 255-272. [ Google Scholar ] [ CrossRef ]
  21. کروسیتی، پی. لاتورا، وی. پورتا، س. مرکزیت در شبکه های خیابان های شهری. آشوب میان رشته ای. J. Nonlinear Sci. 2006 ، 16 ، 015113. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  22. جاستن، آ. مارتینز، اف جی. Cortés، CE استفاده از محدودیت‌های فضا-زمان برای انتخاب مکان‌های فعالیت اختیاری. J. Transp. Geogr. 2013 ، 33 ، 146-152. [ Google Scholar ] [ CrossRef ]
  23. ژونگ، سی. آریسونا، اس ام. هوانگ، ایکس. باتی، م. اشمیت، جی. تشخیص پویایی ساختار شهری از طریق تحلیل شبکه فضایی. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 2178-2199. [ Google Scholar ] [ CrossRef ]
  24. برلی، جی. دوکروت، سی. مارتین، آر. ستن، اس. تأثیر متقابل در حال تغییر بین شهرهای اروپایی و شبکه های حمل و نقل بین وجهی (دهه 1970-2010). در شهرهای بندری اروپا در حال گذار ; Springer: برلین، آلمان، 2020؛ ص 241-263. [ Google Scholar ]
  25. او هست.؛ یو، اس. وی، پی. فانگ، سی. تحلیل شبکه طراحی فضایی شبکه‌های خیابانی و مکان‌های فعالیت‌های سرگرمی اوقات فراغت: مطالعه موردی ووهان، چین. حفظ کنید. جامعه شهرها 2019 ، 44 ، 880-887. [ Google Scholar ] [ CrossRef ]
  26. Ližbetin, J. روش شناسی برای تعیین مکان پایانه های حمل و نقل بین وجهی برای توسعه سیستم های حمل و نقل پایدار: مطالعه موردی از اسلواکی. پایداری 2019 ، 11 ، 1230. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  27. هیلیر، بی. پن، ا. هانسون، جی. گراجوسکی، تی. Xu, J. حرکت طبیعی: یا پیکربندی و جاذبه در حرکت عابر پیاده شهری. محیط زیست طرح. B طرح. دس 1993 ، 20 ، 29-66. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  28. هیلیر، بی. آیدا، اس. شبکه و اثرات روانی در حرکت شهری. در مجموعه مقالات کنفرانس بین المللی نظریه اطلاعات فضایی، الیکوت ویل، نیویورک، ایالات متحده آمریکا، 14 تا 18 سپتامبر 2005. Springer: برلین، هایدلبرگ، 2005; صص 475-490. [ Google Scholar ]
  29. تسیوتاس، دی. Polyzos، S. معرفی یک معیار مرکزیت جدید از تحلیل شبکه حمل و نقل در یونان.ان اپراتور Res. 2015 ، 227 ، 93-117. [ Google Scholar ] [ CrossRef ]
  30. راتی، سی. فرانسوی، دی. پولسلی، آر.ام. ویلیامز، اس. مناظر موبایل: استفاده از داده های مکان از تلفن های همراه برای تجزیه و تحلیل شهری.محیط زیست طرح. B طرح. دس 2006 ، 33 ، 727-748. [ Google Scholar ] [ CrossRef ]
  31. چن، سی. چن، جی. باری، جی. الگوی روزانه سواری حمل و نقل: مطالعه موردی سیستم متروی شهر نیویورک.J. Transp. Geogr. 2009 ، 17 ، 176-186. [ Google Scholar ] [ CrossRef ]
  32. Kohonen, T. Self-Organizing Maps ; سری Springer در علوم اطلاعات; Springer: برلین، آلمان، 2001; جلد 30. [ Google Scholar ]
  33. ژو، Q. حذف انتخابی شبکه های جاده ای در نمایش چند مقیاسی. دکتری پایان نامه، دانشگاه پلی تکنیک هنگ کنگ، هنگ کنگ، چین، 2012. [ Google Scholar ]
  34. وانگ، پی. خو، دبلیو. جین، ی. وانگ، جی. لی، ال. لو، کیو. وانگ، جی. پیش‌بینی حجم ترافیک در محل مقطع تعیین‌شده در آزادراه از داده‌های جمع‌آوری عوارض منطقه‌ای بزرگ. دسترسی IEEE 2019 ، 7 ، 9057–9070. [ Google Scholar ] [ CrossRef ]
  35. لنجانی، ع. دایک، اس جی. بیلیونیس، آی. Yeum، CM; کامیا، ک. چوی، جی. لیو، ایکس. Chowdhury، AG به سوی جمع‌آوری و تجزیه و تحلیل داده‌های پس از رویداد کاملاً خودکار: ادغام اطلاعات قبل از رویداد و پس از رویداد. مهندس ساختار. 2020 ، 208 ، 109884. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  36. کمانگیر، ح. رهنمون فر، م. دابز، دی. پادن، جی. فاکس، جی. شبکه موجک هیبریدی عمیق برای تشخیص مرز یخ در تصاویر رادرا. در مجموعه مقالات IGARSS 2018-2018 IEEE بین المللی زمین شناسی و سمپوزیوم سنجش از دور، والنسیا، اسپانیا؛ 2018; صص 3449–3452. [ Google Scholar ]
  37. پاشایی، م. کمانگیر، ح. استارک، ام جی. Tissot، P. بررسی و ارزیابی معماری‌های یادگیری عمیق برای نقشه‌برداری کارآمد پوشش زمین با تصاویر فرافضایی UAS: مطالعه موردی بر روی یک تالاب. Remote Sens. 2020 , 12 , 959. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  38. پاشایی، م. استارک، ام جی. کمانگیر، ح. بری هیل، جی. وضوح تصویر تکی مبتنی بر یادگیری عمیق: تحقیقی برای بازسازی صحنه متراکم با فتوگرامتری UAS. Remote Sens. 2020 ، 12 ، 1757. [ Google Scholar ] [ CrossRef ]
  39. گلوروت، ایکس. بوردس، آ. Bengio، Y. شبکه های عصبی یکسو کننده پراکنده عمیق. در مجموعه مقالات چهاردهمین کنفرانس بین المللی هوش مصنوعی و آمار، فورت لادردیل، فلوریدا، ایالات متحده آمریکا، 11 تا 13 آوریل 2011; جلد 15 JMLR. صص 315-323. [ Google Scholar ]
  40. Lv، Y.; دوان، ی. کانگ، دبلیو. لی، ز. Wang، FY پیش‌بینی جریان ترافیک با داده‌های بزرگ: رویکرد یادگیری عمیق IEEE Trans. هوشمند ترانسپ سیستم 2015 ، 16 ، 865-873. [ Google Scholar ] [ CrossRef ]
  41. وینسنت، پی. لاروچل، اچ. لاجوئی، آی. بنژیو، ی. Manzagol، PA رمزگذاری خودکار حذف نویز انباشته: یادگیری نمایش های مفید در یک شبکه عمیق با معیار حذف نویز محلی. جی. ماخ. فرا گرفتن. Res. 2010 ، 11 ، 3371-3408. [ Google Scholar ]
  42. کوسدویدی، ا. سوآ، ر. Karray، F. بهبود پیش بینی جریان ترافیک با اطلاعات آب و هوا در اتومبیل های متصل: یک رویکرد یادگیری عمیق. IEEE Trans. وه تکنولوژی 2016 ، 65 ، 9508-9517. [ Google Scholar ] [ CrossRef ]
  43. لطف اللهی، م. سیاوشانی، م.ج. زاده، RSH; صابریان، ام. بسته عمیق: یک رویکرد جدید برای طبقه بندی ترافیک رمزگذاری شده با استفاده از یادگیری عمیق. محاسبات نرم. 2017 ، 24 ، 1999–2012. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  44. لنجانی، ع. دایک، اس. بیلیونیس، آی. Yeum، CM; چوی، جی. لوند، آ. مقاره، الف. ترکیب اطلاعات شبکه های عصبی کانولوشنال سلسله مراتبی برای تشخیص منبع فعالیت در ساختمان های هوشمند. ساختار. مانیتور سلامت. 2019 . [ Google Scholar ] [ CrossRef ]
  45. هینتون، جنرال الکتریک؛ اوسیندرو، اس. Teh, YW یک الگوریتم یادگیری سریع برای شبکه های باور عمیق. محاسبات عصبی 2006 ، 18 ، 1527-1554. [ Google Scholar ] [ CrossRef ]
  46. هایکین، اس. شبکه های عصبی: یک بنیاد جامع . Prentice Hall PTR: Upper Saddle River, NJ, USA, 1994; شابک 978-0-13-147139-9. [ Google Scholar ]
  47. اسمولا، ای جی; Schölkopf, B. A Tutorial on Support Vector Regression. آمار محاسبه کنید. 2004 ، 14 ، 199-222. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  48. سوتنیک، وی. لیاو، ا. تانگ، سی. کولبرسون، جی سی. شریدان، آر.پی. جنگل تصادفی Feuston، BP: یک ابزار طبقه‌بندی و رگرسیون برای طبقه‌بندی ترکیبات و مدل‌سازی QSAR. جی. شیمی. Inf. محاسبه کنید. علمی 2003 ، 43 ، 1947-1958. [ Google Scholar ] [ CrossRef ]
  49. بنژیو، ی. لامبلین، پی. پوپوویچی، دی. Larochelle, H. Greedy لایه عاقلانه آموزش شبکه های عمیق. در پیشرفت در سیستم های پردازش اطلاعات عصبی ; انتشارات MIT: کمبریج، MA، ایالات متحده آمریکا، 2007; صص 153-160. [ Google Scholar ]
  50. هیلیر، بی. هانسون، جی . منطق اجتماعی فضا . انتشارات دانشگاه کمبریج: کمبریج، انگلستان، 1989. [ Google Scholar ]
  51. تامسون، آرسی Richardson, DE یک رویکرد نظریه گراف برای تعمیم شبکه جاده ای. در مجموعه مقالات هفدهمین کنفرانس بین المللی کارتوگرافی – دهمین مجمع عمومی ICA، بارسلون، ES، اسپانیا، 3 تا 9 سپتامبر 1995. صفحات 1871-1880. [ Google Scholar ]
  52. چودری، او. Mackaness، W. تعمیم شبکه جاده های روستایی و شهری: استخراج 1: 250000 از OS MasterMap . موسسه جغرافیا، دانشکده علوم زمین، دانشگاه ادینبورگ: ادینبورگ، انگلستان، 2006. [ Google Scholar ]
  53. برندز، U. الگوریتم سریع‌تر برای مرکزیت میانی. جی. ریاضی. اجتماعی 2001 ، 25 ، 163-177. [ Google Scholar ] [ CrossRef ]
  54. شفاف سازی مفهومی فریمن، LC مرکزیت در شبکه های اجتماعی.Soc. شبکه 1978 ، 1 ، 215-239. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  55. اپسهل، تی. Panzarasa, P. خوشه بندی در شبکه های وزنی Soc. Networks 2009 ، 31 ، 155-163. [ Google Scholar ] [ CrossRef ]
  56. برین، اس. Page, L. آناتومی یک موتور جستجوی وب فرامتنی در مقیاس بزرگ.محاسبه کنید. شبکه سیستم ISDN 1998 ، 30 ، 107-117. [ Google Scholar ] [ CrossRef ]
  57. Lovász, L. Random walks on graphs: a Survey. شانه. Paul Erdos Is Eighty 1993 , 2 , 1-46. [ Google Scholar ]
  58. لوواس، ال. وینکلر، پی. اختلاط پیاده‌روی‌های تصادفی و سایر انتشارات روی یک نمودار . مجموعه یادداشت های سخنرانی انجمن ریاضی لندن; انتشارات دانشگاه کمبریج: کمبریج، انگلستان، 1995; صص 119-154. [ Google Scholar ]
  59. چارت، دی. چارت، اف. گارسیا، اس. دل عیسی، ام جی; هررا، اف. آموزش عملی در رمزگذارهای خودکار برای ترکیب ویژگی های غیرخطی: طبقه بندی، مدل ها، نرم افزار و دستورالعمل ها. Inf. فیوژن 2018 ، 44 ، 78-96. [ Google Scholar ] [ CrossRef ]
  60. لی، دبلیو. فو، اچ. یو، ال. گونگ، پی. فنگ، دی. لی، سی. کلینتون، N. یادگیری عمیق مبتنی بر رمزگذار خودکار پشته‌ای برای طبقه‌بندی تصاویر سنجش از راه دور: مطالعه موردی نقشه‌برداری پوشش زمین آفریقا. بین المللی J. Remote Sens. 2016 , 37 , 5632–5646. [ Google Scholar ] [ CrossRef ]
  61. کمانگیر، ح. کالینز، دبلیو. تیسوت، پی. کینگ، SA مدل یادگیری عمیق برای پیش بینی طوفان های تندری در 400 کیلومتر مربع از حوزه های جنوب تگزاس استفاده می شود. هواشناسی Appl. 2020 ، 27 ، e1905. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  62. وانگ، ز. Bovik، AC میانگین مربعات خطا: آن را دوست دارم یا ترک می کنم؟ نگاهی جدید به معیارهای وفاداری سیگنال فرآیند سیگنال IEEE Mag. 2009 ، 26 ، 98-117. [ Google Scholar ] [ CrossRef ]
  63. برگسترا، جی. Bengio، Y. جستجوی تصادفی برای بهینه سازی هایپرپارامتر. جی. ماخ. فرا گرفتن. Res. 2012 ، 13 ، 281-305. [ Google Scholar ]
  64. فوشیکی، تی. برآورد خطای پیش‌بینی با استفاده از اعتبارسنجی متقاطع K-fold. آمار محاسبه کنید. 2011 ، 21 ، 137-146. [ Google Scholar ] [ CrossRef ]
  65. زو، سی. برد، RH; لو، پی. Nocedal، J. الگوریتم 778: L-BFGS-B: زیربرنامه های فرترن برای بهینه سازی محدود محدود در مقیاس بزرگ. ACM Trans. ریاضی. نرم افزار (TOMS) 1997 ، 23 ، 550-560. [ Google Scholar ] [ CrossRef ]
  66. Story، M. و Congalton، RG ارزیابی دقت: دیدگاه کاربر. فتوگرام مهندس از راه دور. Sens. 1986 , 52 , 397-399. [ Google Scholar ]
  67. چای، تی. Draxler، RR ریشه میانگین مربعات خطا (RMSE) یا میانگین خطای مطلق (MAE)؟ – استدلال هایی علیه اجتناب از RMSE در ادبیات. Geosci. مدل Dev. 2014 ، 7 ، 1247-1250. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  68. کامرون، AC; Windmeijer، FA یک اندازه گیری مربع R از خوبی برازش برای برخی از مدل های رگرسیون غیرخطی رایج. جی. اکونوم. 1997 ، 77 ، 329-342. [ Google Scholar ] [ CrossRef ]
  69. لوپ، جی. وهنکل، ال. سوترا، ا. Geurts، P. درک اهمیت متغیر در جنگل های درختان تصادفی. در پیشرفت‌ها در سیستم‌های پردازش اطلاعات عصبی 26، مجموعه مقالات سیستم‌های پردازش اطلاعات عصبی (NIPS)، دریاچه تاهو، نوادا، 5-8 دسامبر 2013 . Neural Information Processing Systems Foundation, Inc.: San Diego, CA, USA; صص 431-439.
Ijgi 09 00456 g001 550
شکل 1. طبقات عملکردی شبکه خیابان های شهری در چهار شهر مختلف.
Ijgi 09 00456 g002 550
شکل 2. شماتیک یا سیستم ما که طبقه بندی عملکرد خیابان را بر اساس معیارهای مرکزیت با استفاده از یک مدل یادگیری عمیق انجام می دهد.
Ijgi 09 00456 g003 550
شکل 3. همه 9 معیار مرکزیت تولید شده برای تهران، ایران.
Ijgi 09 00456 g004 550
شکل 4. ( الف ) ساختار اساسی یک رمزگذار خودکار شامل یک ورودی x است که از طریق یک رمزگذار (عملکرد f) روی رمزگذاری y نگاشت می شود. این رمزگذاری به نوبه خود با استفاده از رمزگشا (عملکرد g) به بازسازی r نگاشت می شود. ( ب ) ساختار رمزگذار خودکار Denoising Stacked (SDAE) که در این کار استفاده شده است.
Ijgi 09 00456 g005 550
شکل 5. امتیاز SDAE F1 عملکرد هر کلاس.
Ijgi 09 00456 g006 550
شکل 6. نرخ اختلاط منظم بودن شهرها در مقابل دقت کلی SDAE.
Ijgi 09 00456 g007 550
شکل 7. اهمیت ویژگی ها برای ( الف ) اصفهان، ( ب ) انشده، ( ج ) تهران، و ( د ) پاریس.
Ijgi 09 00456 g008 550
شکل 8. منحنی های یادگیری برای مدل SDAE: ( الف ) اصفهان، ( ب ) انشید، ( ج ) تهران، و ( د ) پاریس.
Ijgi 09 00456 g009 550
شکل 9. منحنی یادگیری مدل های یادگیری ماشین برای اصفهان.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید