خلاصه

Industry 4.0 شامل طیف گسترده ای از فرآیندهای توسعه در مدیریت تولید و تولید زنجیره ای است. در حال حاضر، تلاش زیادی برای اتوماسیون ساخت و کنترل خودکار تولید وجود دارد. این قصد منجر به افزایش نیاز به روش‌های با کیفیت بالا برای دیجیتالی کردن و بازسازی اشیا، به ویژه در زمینه مهندسی معکوس می‌شود. نرم افزار اسکن متداول بر اساس الگوریتم های شناخته شده می تواند اشیاء صاف را به درستی پردازش کند. با این وجود، آنها معمولاً برای مدل های پیچیده شکل با ویژگی های تیز قابل استفاده نیستند. تعداد نقاط روی لبه ها به دلیل اصل اسکن لیزری و گاهی اوقات وضوح اسکن پایین بسیار محدود است. بنابراین، یک مشکل بازسازی لبه درست رخ می دهد. همین مشکل در بسیاری از کاربردهای اسکن لیزری دیگر ظاهر می‌شود، به عنوان مثال، در نمایش ساختمان‌ها از اسکن‌های لیزری هوا برای مدل‌های سه بعدی شهر. ما روی روشی برای حفظ و بازسازی ویژگی های تیز تمرکز می کنیم. ما شرح مفصلی از هر سه مرحله کلیدی ارائه می‌دهیم: تقسیم‌بندی ابر نقطه، تشخیص لبه، و نمایش صحیح لبه B-spline. الگوریتم تشخیص ویژگی مبتنی بر روش رشد منطقه مرسوم است و ما مقدار ورودی بهینه آستانه انحنا را با استفاده از رگرسیون حداقل مربعات لگاریتمی استخراج می‌کنیم. نمایش لبه بعدی بر روی الگوریتم تکراری تقریب B-spline است که در آن ما خطای نامتقارن وزنی را با استفاده از نسبت طلایی محاسبه می‌کنیم. مجموعه مثال ها نشان می دهد که روش ما نتایج بهتر یا قابل مقایسه با روش های دیگر می دهد. به عنوان مثال، در نمایش ساختمان ها از اسکن لیزری هوا برای مدل های سه بعدی شهر. ما روی روشی برای حفظ و بازسازی ویژگی های تیز تمرکز می کنیم. ما شرح مفصلی از هر سه مرحله کلیدی ارائه می‌دهیم: تقسیم‌بندی ابر نقطه، تشخیص لبه، و نمایش صحیح لبه B-spline. الگوریتم تشخیص ویژگی مبتنی بر روش رشد منطقه مرسوم است و ما مقدار ورودی بهینه آستانه انحنا را با استفاده از رگرسیون حداقل مربعات لگاریتمی استخراج می‌کنیم. نمایش لبه بعدی بر روی الگوریتم تکراری تقریب B-spline است که در آن ما خطای نامتقارن وزنی را با استفاده از نسبت طلایی محاسبه می‌کنیم. مجموعه مثال ها نشان می دهد که روش ما نتایج بهتر یا قابل مقایسه با روش های دیگر می دهد. به عنوان مثال، در نمایش ساختمان ها از اسکن لیزری هوا برای مدل های سه بعدی شهر. ما روی روشی برای حفظ و بازسازی ویژگی های تیز تمرکز می کنیم. ما شرح مفصلی از هر سه مرحله کلیدی ارائه می‌دهیم: تقسیم‌بندی ابر نقطه، تشخیص لبه، و نمایش صحیح لبه B-spline. الگوریتم تشخیص ویژگی مبتنی بر روش رشد منطقه مرسوم است و ما مقدار ورودی بهینه آستانه انحنا را با استفاده از رگرسیون حداقل مربعات لگاریتمی استخراج می‌کنیم. نمایش لبه بعدی بر روی الگوریتم تکراری تقریب B-spline است که در آن ما خطای نامتقارن وزنی را با استفاده از نسبت طلایی محاسبه می‌کنیم. مجموعه مثال ها نشان می دهد که روش ما نتایج بهتر یا قابل مقایسه با روش های دیگر می دهد. در نمایش ساختمان ها از اسکن لیزری هوا برای مدل های سه بعدی شهر. ما روی روشی برای حفظ و بازسازی ویژگی های تیز تمرکز می کنیم. ما شرح مفصلی از هر سه مرحله کلیدی ارائه می‌دهیم: تقسیم‌بندی ابر نقطه، تشخیص لبه، و نمایش صحیح لبه B-spline. الگوریتم تشخیص ویژگی مبتنی بر روش رشد منطقه مرسوم است و ما مقدار ورودی بهینه آستانه انحنا را با استفاده از رگرسیون حداقل مربعات لگاریتمی استخراج می‌کنیم. نمایش لبه بعدی بر روی الگوریتم تکراری تقریب B-spline است که در آن ما خطای نامتقارن وزنی را با استفاده از نسبت طلایی محاسبه می‌کنیم. مجموعه مثال ها نشان می دهد که روش ما نتایج بهتر یا قابل مقایسه با روش های دیگر می دهد. در نمایش ساختمان ها از اسکن لیزری هوا برای مدل های سه بعدی شهر. ما روی روشی برای حفظ و بازسازی ویژگی های تیز تمرکز می کنیم. ما شرح مفصلی از هر سه مرحله کلیدی ارائه می‌دهیم: تقسیم‌بندی ابر نقطه، تشخیص لبه، و نمایش صحیح لبه B-spline. الگوریتم تشخیص ویژگی مبتنی بر روش رشد منطقه مرسوم است و ما مقدار ورودی بهینه آستانه انحنا را با استفاده از رگرسیون حداقل مربعات لگاریتمی استخراج می‌کنیم. نمایش لبه بعدی بر روی الگوریتم تکراری تقریب B-spline است که در آن ما خطای نامتقارن وزنی را با استفاده از نسبت طلایی محاسبه می‌کنیم. مجموعه مثال ها نشان می دهد که روش ما نتایج بهتر یا قابل مقایسه با روش های دیگر می دهد. ما شرح مفصلی از هر سه مرحله کلیدی ارائه می‌دهیم: تقسیم‌بندی ابر نقطه، تشخیص لبه، و نمایش صحیح لبه B-spline. الگوریتم تشخیص ویژگی مبتنی بر روش رشد منطقه مرسوم است و ما مقدار ورودی بهینه آستانه انحنا را با استفاده از رگرسیون حداقل مربعات لگاریتمی استخراج می‌کنیم. نمایش لبه بعدی بر روی الگوریتم تکراری تقریب B-spline است که در آن ما خطای نامتقارن وزنی را با استفاده از نسبت طلایی محاسبه می‌کنیم. مجموعه مثال ها نشان می دهد که روش ما نتایج بهتر یا قابل مقایسه با روش های دیگر می دهد. ما شرح مفصلی از هر سه مرحله کلیدی ارائه می‌دهیم: تقسیم‌بندی ابر نقطه، تشخیص لبه، و نمایش صحیح لبه B-spline. الگوریتم تشخیص ویژگی مبتنی بر روش رشد منطقه مرسوم است و ما مقدار ورودی بهینه آستانه انحنا را با استفاده از رگرسیون حداقل مربعات لگاریتمی استخراج می‌کنیم. نمایش لبه بعدی بر روی الگوریتم تکراری تقریب B-spline است که در آن ما خطای نامتقارن وزنی را با استفاده از نسبت طلایی محاسبه می‌کنیم. مجموعه مثال ها نشان می دهد که روش ما نتایج بهتر یا قابل مقایسه با روش های دیگر می دهد. الگوریتم تشخیص ویژگی مبتنی بر روش رشد منطقه مرسوم است و ما مقدار ورودی بهینه آستانه انحنا را با استفاده از رگرسیون حداقل مربعات لگاریتمی استخراج می‌کنیم. نمایش لبه بعدی بر روی الگوریتم تکراری تقریب B-spline است که در آن ما خطای نامتقارن وزنی را با استفاده از نسبت طلایی محاسبه می‌کنیم. مجموعه مثال ها نشان می دهد که روش ما نتایج بهتر یا قابل مقایسه با روش های دیگر می دهد. الگوریتم تشخیص ویژگی مبتنی بر روش رشد منطقه مرسوم است و ما مقدار ورودی بهینه آستانه انحنا را با استفاده از رگرسیون حداقل مربعات لگاریتمی استخراج می‌کنیم. نمایش لبه بعدی بر روی الگوریتم تکراری تقریب B-spline است که در آن ما خطای نامتقارن وزنی را با استفاده از نسبت طلایی محاسبه می‌کنیم. مجموعه مثال ها نشان می دهد که روش ما نتایج بهتر یا قابل مقایسه با روش های دیگر می دهد.

کلید واژه ها:

تشخیص لبه ؛ ابر نقطه ; مهندسی معکوس ; اسپلاین ; صنعت 4.0 ; اسکن سه بعدی ؛ مدل سه بعدی

 

 

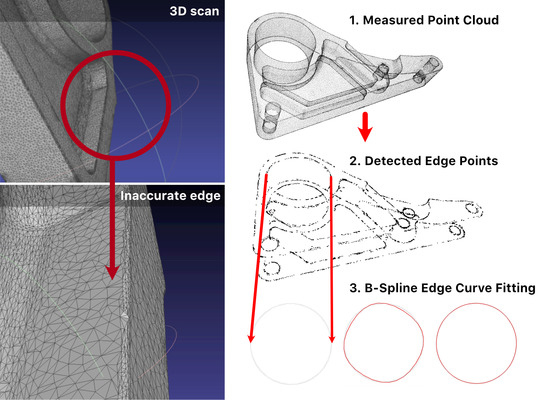
چکیده گرافیکی

1. معرفی

Industry 4.0 گرایش به سمت اتوماسیون و تبادل داده در فناوری ها و فرآیندهای تولید است. کارخانه‌های Industry 4.0 دارای ماشین‌هایی هستند که با اتصال بی‌سیم و حسگرها، به سیستمی متصل شده‌اند که می‌تواند کل خط تولید را تجسم کند و به تنهایی تصمیم‌گیری کند. تولید هوشمند دسته وسیعی از تولید است که از تولید یکپارچه کامپیوتری، سطوح بالای سازگاری و تغییرات سریع طراحی، فناوری اطلاعات دیجیتال و آموزش نیروی کار فنی انعطاف‌پذیرتر استفاده می‌کند [ 1 ، 2 ].
کار ما بخشی از اتوماسیون در ساخت و مهندسی معکوس را برای تغییرات طراحی پوشش می دهد. در دسترس بودن گسترده سنسورهای عمق تجاری ارزان یا تنظیمات چند دوربینی منجر به استفاده متداول از آنها در مهندسی ساخت، به ویژه در توسعه سریع محصول می شود [ 3 ]. بنابراین، ابر نقطه تبدیل به نوع معمولی نمایش مورد استفاده به عنوان مثال، در مهندسی معکوس (RE) و نمونه سازی سریع (RP) شده است. دقت، سرعت اسکن و تنوع الگوریتم های پردازش، شرایط مناسبی را برای استفاده رایج از آن ایجاد می کند.
یک مشکل کلیدی در ادغام RE/RP، همانطور که در [ 4 ] ذکر شد، تبدیل مجموعه ای از نقاط متراکم به دست آمده در فرآیند RE به یک مدل برازش است که می تواند مورد استفاده قرار گیرد. در شکل 1 ، فرآیند مهندسی معکوس توضیح داده شده است.
معمولاً اسکنرهای سه بعدی با نرم‌افزاری ارائه می‌شوند که یک شی فیزیکی را در راه‌اندازی دو فازی ایجاد می‌کنند: بازسازی مدل CAD از داده‌های نقطه اسکن شده و سپس خروجی مدل STL. با این حال، روش های اجرا شده معمولاً فقط برای اشیاء ساده و صاف کافی است. اشیاء پیچیده‌تر با سوراخ‌ها، لبه‌های تیز یا گوشه‌ها اغلب به دانش قبلی در مورد نحوه ویرایش داده‌های اسکن شده نیاز دارند. پس از پردازش داده ها زمان بر است و به طور بالقوه می تواند منجر به خطا شود. ما الگوریتمی را ارائه می کنیم که به طور خودکار ویژگی های واضح را در داده های ابر نقطه دلخواه تشخیص می دهد. الگوریتم ما بر اساس یک روش رشد منطقه اصلاح شده است. مقدار ورودی به الگوریتم تنها یک پارامتر است – آستانه برداری عادی θن(مقدار شروع بهینه و توضیحات در بخش 2.1 ارائه شده است ). الگوریتم رشد منطقه نقاط مسطح را حذف می کند و نقاط باقی مانده احتمالاً نقاط لبه هستند.
قبل از فرآیند ساخت نهایی یا پرینت سه بعدی، یک مدل صحیح برای تولید STL [ 5 ] و برش های بعدی ضروری است [ 4 ، 6 ]. شکل 2 بخش مشکل ساز رایج (حاشیه های ناهموار و نادرست) را نشان می دهد که اغلب رخ می دهد. برای حل این مشکل، در بخش 3.2 ما نمایش لبه جدید را بر اساس تقریب B-spline پیشنهاد می کنیم. ارزیابی خطای نامتقارن بر اساس تابع زنگ با وزن دهی با استفاده از نسبت طلایی [ 7 ] برای بهبود نمایش لبه مدل ها است.
علاوه بر این، تقریب B-spline ما نیز برای برش مستقیم STL از ابرهای نقطه‌ای که خطوط مقطع (منحنی‌ها) را مستقیماً بدون بازسازی مدل استخراج می‌کند، کافی است. نمای کلی این روش ها به عنوان مثال در [ 8 ] است. تقریب B-spline ارائه شده را می توان بدون محدودیت در این روش برش استفاده کرد زیرا بدیهی است که به طور تکراری خطای شکل منحنی لایه را به حداقل می رساند.

کار قبلی

تقسیم بندی و طبقه بندی ابر نقطه ای نقش کلیدی در پردازش ابر نقطه ای در استفاده از RE/RP ایفا می کند. تقسیم بندی فرآیند گروه بندی ابرهای نقطه ای به چندین ناحیه همگن با ویژگی های مشابه است در حالی که طبقه بندی مرحله ای است که این مناطق را برچسب گذاری می کند. روش‌های تقسیم‌بندی به دسته‌های زیادی تقسیم می‌شوند و انتخاب روش‌ها به منطقه مورد نظر، تراکم نمونه‌برداری، کیفیت داده‌ها و ساختار صریح ابر نقطه بستگی دارد. می‌توانیم از طبقه‌بندی شرح داده شده در [ 9 ، 10 ] استفاده کنیم: روش‌های رشد منطقه، روش‌های مبتنی بر لبه، برازش مدل و روش‌های ترکیبی.
بیشتر روش‌ها با رشد منطقه‌ای شروع می‌شوند که Besl [ 11 ] برای تقسیم‌بندی تصاویر در نظر گرفته بود. الگوریتم رشد منطقه بعداً در دو نسخه مختلف به سه بعدی گسترش یافت: unseeded [ 12 ] و seeded [ 13 ]. رشد منطقه در بسیاری از کاربردهای مختلف استفاده می شود، به عنوان مثال، استخراج ویژگی ها و سطوح مسطح از ابرهای نقطه رخنمون سه بعدی [ 14 ]، تقسیم بندی سطح، و استخراج خطوط ویژگی لبه از قطعات شکسته شده آثار [ 15 ] یا مدل سازی محیط شهری [ 16 ] و همچنین مدلسازی سه بعدی شهر (بررسی ادبیات به عنوان مثال، در [ 17 ]).
رشد منطقه اغلب بهبود می یابد. به عنوان مثال، Demaris و همکاران. [ 18 ] لبه‌های تیز بسته را با استفاده از ناحیه در حال رشد با نرمال‌هایی که با ساختن یک شبکه محلی و صفحات حداقل مربعات از طریق نزدیک‌ترین نقاط همسایگی ارائه می‌شوند، تشخیص دهند. تشخیص صحیح لبه توسط نظریه گراف (درخت پوشا حداقل) ارائه شده است. در [ 16 ]، مرحله رشد منطقه بر روی یک نمایش ابر نقطه ورودی وکسل شده مبتنی بر octree برای استخراج بخش‌های اصلی انجام می‌شود.
روش‌های مبتنی بر لبه معمولاً با ابرهای نقطه‌ای که به تصاویر محدوده تبدیل می‌شوند استفاده می‌شوند [ 19 ]. استفاده از ویژگی‌های سطح بالا (تکنیک گروه‌بندی خط اسکن) به‌عنوان بخش‌بندی اولیه به جای پیکسل‌های منفرد، سرعت محاسباتی بالا را تضمین می‌کند. با این حال، این تشخیص لبه برای داده های پر سر و صدا قابل استفاده نیست.
روش های برازش مدل فرض می کند که یک سطح را می توان به عنوان ترکیبی از اشکال هندسی ساده و متعارف توصیف کرد (بازسازی ضد آب). روش‌های ابتدایی از RANSAC برای یافتن قوی صفحات، کره‌ها، استوانه‌ها، مخروط‌ها و torii استفاده می‌کنند [ 20 ]. با این حال، مشکلی در نویز وجود دارد، هر گونه جزئیات ریزدانه احتمالاً به عنوان نویز با پیشین اولیه در نظر گرفته می شود، اگر نتوان آنها را به عنوان اتحادیه ای از موارد اولیه کوچکتر نشان داد (یک بررسی در [ 21 ] توضیح داده شده است). راه‌حل جزئی، روش‌های ترکیبی است که از روش‌های اولیه با دیگر قبلی استفاده می‌کند [ 22 ].
روش های رشد منطقه ای، لبه محور و برازش مدل نیازی به پیش پردازش ندارند، اما روش های تقسیم بندی دیگری بر اساس پیش پردازش وجود دارد. این الگوریتم‌ها می‌توانند ناقص بودن داده‌ها را بازسازی کنند [ 23 ، 24 ] یا یک شبکه مثلثی از ابر نقطه داده شده بسازند [ 25 ، 26 ، 27 ]. پس از آن، مش تشکیل شده را می توان با استفاده از هندسه دیفرانسیل گسسته پردازش کرد که در آن حد محلی سطح خطوط لبه را تشخیص می دهد [ 25 ] یا روش های جبری مبتنی بر چند جمله ای های دو متغیره [ 27 ]. باید توجه داشته باشیم که برخی از این روش ها با روش های یادگیری ماشین کار می کنند [ 28 ].
پس از تقسیم‌بندی و طبقه‌بندی ابر نقطه‌ای، ما به یک نمایش صحیح مدل و جداسازی (معمولا STL) با برش‌های بعدی برای استخراج تولید افزودنی مبتنی بر لایه نیاز داریم [ 29 ]. رویکردهای مختلفی وجود دارد که فناوری های مختلف را ترکیب می کند. روش سنتی STL به عنوان مثال در [ 30 ] توضیح داده شده است. سطوح B-spline یا NURBS اغلب استفاده می شوند، به عنوان مثال، نویسندگان در [ 31 ، 32 ] برش مستقیم از NURBS را بدون STL ارائه می دهند. همچنین مدل B-Rep متشکل از صفحات، کره ها، استوانه ها و مخروط ها از یک شبکه سه بعدی برای برش مناسب است [ 33 ، 34]. برخی از نویسندگان بازسازی مدل را حذف کرده و تولید مستقیم کانتور مقطعی را انجام می دهند. برای مثال، نویسندگان در [ 35 ] از اسکلت منحنی مدل برای برش دادن لبه های مش سطح استفاده می کنند. برازش منحنی B-Spline لایه‌هایی که در آن انحنای منحنی با روش برازش دایره تعیین می‌شود در [ 8 ] ارائه شده است.
توسعه شبکه های عصبی و یادگیری عمیق نیز تحقیقات در تجزیه و تحلیل ابر نقطه را لمس می کند. برخی از روش‌ها امیدوارکننده هستند، اما هنوز هیچ رویکردی برای همه وجود ندارد. مرور روش ها به عنوان مثال در [ 36 ، 37 ، 38 ] پوشش داده شده است.
ادبیات حاضر شامل بیشتر اصول شناخته شده اخیر است. سهم اصلی علمی در بهبودها و کاربردهای آنهاست. برای مثال، کار [ 39 ] (منتشر شده در سال 2020) از نمایش B-spline و محاسبات عادی با استفاده از انحنای نرمال که مستقیماً توسط مشتقات جزئی سطح محاسبه می‌شود، استفاده می‌کند. حذف مقدار آستانه از پیش تعریف شده ایده اصلی در [ 40 ] (منتشر شده در سال 2019) است. نویسندگان ترکیب فیلتر فضایی مبتنی بر FFT و تشخیص مرز را پیشنهاد می‌کنند، که با هم اجازه می‌دهند تا سطوحی با نویز کم را از داده‌های ابر نقطه تولید کنند. Ref [ 41 ] ساده سازی ابر نقطه حساس به ویژگی را ارائه می دهد که بر اساس رگرسیون بردار پشتیبانی غیر حساس است.
مزایای روش های شناخته شده (رشد منطقه ای یا PCA) آشکار است – استحکام، سهولت محاسبه، الگوریتم های پایدار. به همین دلیل، ما این روش‌های کلاسیک را انتخاب کردیم و ایده اصلی ما (1) ساده‌سازی و تنظیم خودکار مقادیر ورودی (شرح شده در بخش 2.1 ) بود (2) یافتن ارزیابی خطای بهینه در نمایش B-spline که برای اشیاء مهندسی مناسب است. مشکل محاسبه خطا در بخش 2.2 توضیح داده شده است و ما وزن دهی نامتقارن را بر اساس جیره طلایی پیشنهاد کردیم.

2. روش ها و مواد

اجزای متداول مهندسی صنایع از سطوح مسطح، صاف یا منحنی تشکیل شده است. تفاوت قابل اندازه گیری در نرمال یا انحنای سطح در اکثر سطوح مدل نسبتاً کم است. بر خلاف آن، در همسایگی یک ویژگی تیز، مانند لبه یا گوشه تیز، تغییر قابل توجهی در نرمال و انحنای سطح وجود دارد. بنابراین، اگر تمام نقاط سطوح مسطح، صاف یا منحنی را حذف کنیم، نقاط باقیمانده نقاطی هستند که روی ویژگی های تیز هستند. با در نظر گرفتن این ایده، روش خود را، مشابه [ 42 ]، بر روی تجزیه و تحلیل مقادیر ویژه ماتریس کوواریانس برای نزدیکترین همسایه k هر نقطه ایجاد می کنیم. ما از رشد منطقه برای یافتن سطوح مسطح یا مدل‌های منظم استفاده می‌کنیم [ 43] اما برای حذف نقاط با انحنای کم ( بخش 2.1 ).
مقادیر ورودی مهم منطقه در حال رشد، آستانه نرمال و انحنا هستند. تنظیم آنها به طور قابل ملاحظه ای نتایج تقسیم بندی را تغییر می دهد، اما انتخاب آنها غیرمعمول و به خصوص برای مبتدیان دشوار است. ما همبستگی هندسی بین این دو مقدار را پیدا می کنیم و مقدار اولیه بهینه را که در مورد اشیاء مهندسی منظم قابل استفاده است محاسبه می کنیم. این در زیر بخش های زیر توضیح داده شده است. این رویکرد در برابر نویز قوی است و برای تقریب بعدی B-spline مناسب است.
تقریب B-spline به دلیل خواص خوب و محاسبات شناخته شده آن انتخاب شد. فرآیند تکراری کیفیت کافی را تضمین می کند. محاسبه خطا بر اساس فاصله وزنی نامتقارن است (فاصله نامتقارن در [ 44 ] ارائه شده است) اما در مورد ما، وزن با نسبت طلایی توصیف شده است. اندازه گیری نامتقارن جایگزین نقاط پرت شده و منحنی را از اثر زیگزاگ محافظت می کند. این رویکرد در بخش 2.2 توضیح داده شده است . منحنی B-Spline محاسبه شده می تواند لبه ها را در ابرهای نقطه ای نشان دهد. علاوه بر این، تقریب B-Spline توصیف شده نیز می‌تواند در روش‌های برش مستقیم استفاده شود.

2.1. تشخیص نقاط لبه

پردازش یک ابر نقطه مشخص با تقسیم بندی در حال رشد منطقه شروع می شود. محاسبات نرمال سطحی بر اساس تجزیه و تحلیل مؤلفه اصلی (PCA) [ 45 ] است که از یک تبدیل متعامد برای تبدیل مجموعه ای از مشاهدات متغیرهای احتمالاً همبسته به مجموعه ای از مقادیر متغیرهای خطی غیر همبسته استفاده می کند. توضیحات در بخش 2.1.1 است.
یال ها را می توان با نگاشت گاوس نیز طبقه بندی کرد [ 42 ، 46 ، 47 ]. بردارهای نرمال نقطه ای بر روی کره گاوس پیش بینی می شوند و خوشه بندی بعدی نوع نقطه (گوشه، لبه، مسطح) را متمایز می کند. این روش زمان بر است به طوری که ما از منطقه در حال رشد استفاده می کنیم.

2.1.1. PCA – تخمین عادی

اولین مرحله در الگوریتم PCA، محاسبه ماتریس کوواریانس C برای هر نقطه P در ابر نقطه است.

سی=1ک∑من=1ک(پمن-پ¯)·(پمن-پ¯)تی،

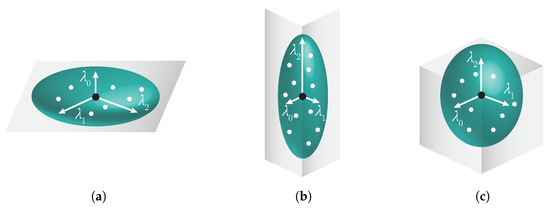
جایی که پ¯مرکز k -نزدیکترین نقاط همسایگی است پمن،من=1،2،⋯کاز یک نقطه P مقادیر ویژه ( λ0،λ1،λ2) و بردارهای ویژه ( v1→،v→2،v→3) از این ماتریس بیضی کوواریانس را تعریف می کند . ما بین این سه مورد تمایز قائل می شویم:

  • (λ0≤λ1≤λ2)∧(λ1≈λ2)
  • (λ0≤λ1≤λ2)∧(λ0≈λ1)
  • (λ0≤λ1≤λ2)∧(λ0≈λ1≈λ2).
این نوع بیضی های کوواریانس همسایگی نقطه داده شده را تعریف می کنند ( شکل 3 a-c). در مورد یک بیضی شکل ( (λ0≤λ1≤λ2)∧(λ1≈λ2)، نقطه به وضوح در یک منطقه تقریبا مسطح است و بردار ویژه مربوط به کوچکترین مقدار ویژه نقطه نرمال است.
2.1.2. منطقه در حال رشد – مقدار آستانه نرمال اولیه تیساعتrθن
الگوریتم تقسیم بندی در حال رشد منطقه معمولاً به پارامترهای ورودی نیاز دارد: حداقل و حداکثر اندازه خوشه، k -نزدیکترین نقطه همسایه، آستانه نرمال تیساعتrθنو آستانه انحنا تیساعتrθسی. ارزش θنزاویه بین نرمال های دو نقطه ای و θسیانحنا است. آنها به شدت بر نتایج تقسیم بندی تأثیر می گذارند و از نظر هندسی به شدت به هم متصل هستند. تنظیم مقادیر اولیه غیر شهودی و کاربر پسند نیست، به طوری که ما بر برآورد خودکار بهینه تمرکز می کنیم. θن.

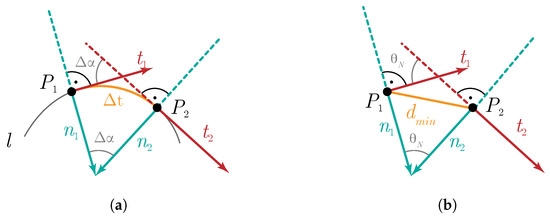
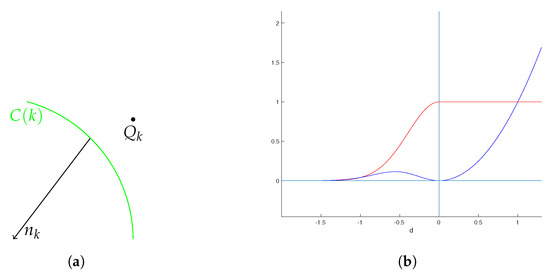
شکل 4 a تعریف انحنا را نشان می دهد θاز منحنی l در نقطه پ1. در حد به عنوان Δتی→0، ما بدست می آوریم:

θ=لیمΔتی→0ΔαΔتی

در مورد ابر نقطه، پارامتر را در نظر می گیریم Δتیبه عنوان حداقل فاصله دمترمنnخط بین دو نقطه مجاور ( شکل 4 ب). انحنا θسیمحاسبه می شود

θسی=θندمترمنn.
بنابراین، تقسیم بندی در حال رشد منطقه را می توان تنها با یک پارامتر کنترل کرد – آستانه برداری عادی تیساعتrθن. بخش زیر فرآیند مقدار اولیه ایده آل را شرح می دهد تیساعتrθن.
مجموعه ای از ابرهای نقطه آزمایش را آماده کردیم ممن،من=1،2،…،6برای پوشش طیف اشکال مختلف از ساده تا پیچیده ( شکل 5 ). این داده‌های ابر نقطه‌ای توسط ATOS Compact Scan 2M بدست آمدند. ما محدوده آزمایشی از حداکثر مقادیر آستانه برداری عادی را تنظیم کردیم. تیساعتrθن=1،…،15. به این معنی که تقسیم بندی تمام نقاط خوشه هایی را که آستانه بردار نرمال کمتر از آن است حذف می کند تیساعتrθن. اجازه دهید noتوتیتعدادی از نقاط حذف شده باشد و nمنnچندین نقطه در یک ابر نقطه باشد.

ما الگوریتم رشد منطقه را روی مجموعه داده های خود با پارامترها اعمال کردیم تیساعتrθنو تعداد نقاط حذف شده را محاسبه کردیم noتوتی. درصد امتیاز باقیمانده به صورت زیر تعریف می شود:

پهrجن=noتوتیnمنn·100.

متوجه می شویم که وابستگی بین تیساعتrθنو پهrجندارای پیشرفت لگاریتمی است، رگرسیون لگاریتمی بهترین انتخاب برای محاسبه وابستگی است:

تیساعتrθن=ب1لوگاریتم(پهrجن)+ب0،ب0،ب1∈آر.

نمودارها و نتایج نهایی در بخش 3.1 آمده است.

2.2. B-Spline Edge Representation

اتصالات B-spline متعلق به ابزارهای مورد علاقه برای پردازش مجموعه ای از نقاط داده سازماندهی نشده و احتمالاً پر سر و صدا در گرافیک کامپیوتری، بینایی کامپیوتر و CAD/CAM است. مزیت اصلی تقریب B-spline بر اساس فرمول شناخته شده B-spline است [ 48 ]:

سی(تو)=∑من=0nبمن،پ(تو)پمن،

جایی که بمن،پ(تو)تابع پایه B-spline درجه p با نقاط کنترل است پمن. پارامتر u از بازه گره غیر تناوبی و غیر یکنواخت است تو=<تو0،تو1،…،توn+پ+1>. تنظیم کردیم تو0=0و توn+پ+1=1.

اجازه دهید {سک}ک=0مترمجموعه نقاط ورودی باشد. الگوریتم برازش نقاط کنترل را جستجو می کند پمن، وکتور گره تومنحنی spline تعریف شده در رابطه ( 6 ) و همچنین پارامترها تو^={تو^ک}ک=0مترکه معادله را برآورده کرد:

سک=∑من=0nبمن،پ(تو^ک)پمن

و سی(تو0)=سی(0)=س0، سی(توn+پ+1)=سی(1)=سمتر.

ابتدا شکل منحنی اولیه را محاسبه می کنیم. نویسندگان در [ 44 ] با دایره اولیه (مرکز دایره در میانگین ابر نقطه، شعاع حداکثر فاصله یک نقطه تا مرکز است) یا یک بیضی کار می کنند که محورهای اصلی توسط PCA محاسبه می شوند. ما با روش پرکاربرد وتر و مرکزگرا شروع می کنیم. روش آکوردال پارامترها را به صورت زیر محاسبه می کند:

تو^0=0;تو^متر=1;تو^ک=تو^ک-1+|سک-سک-1|د

جایی که د=∑ک=1متر|سک-سک-1|. روش گریز از مرکز مشابه است، ما فقط جذر طول خط را اضافه می کنیم. روش گریز از مرکز در مواردی که داده ها چرخش های تند داشته باشند، مرتبط تر است.

در مرحله دوم، بردار گره را تنظیم می کنیم توبا این شرط که هر دهانه گره حداقل دارای یک گره باشد تو^ک.دهانه های گره داخلی با [ 49 ] تعریف می شوند:

من=fلoor(jد)،α=jد-من،توپ+j=(1-α)تو^من-1+αتو^من،j=1،…،n-پ

و عملکرد fلoorبزرگترین عدد صحیح است من≤jد.

پس از آن، مختصات نقاط کنترل پمنبا تکنیک استاندارد برازش حداقل مربعات خطی [ 48 ] تقریب می‌شوند. ما تابع را کوچک می کنیم:

f=|∑ک=1متر-1سک-سی(تو^ک)|2

ما می توانیم راه حل را به صورت ماتریسی (سیستم از n-1×n-1معادلات) به صورت:

(بتیب)پ=آر

که در آن ماتریس B B نشان دهنده تابع B-spline درجه p است که برای همه ارزیابی شده است تو^ک، ک=1،…،n-1. ماتریس پنقاط کنترل و بردار مورد نظر هستند آربردار است n-1نکته ها:

آر=∑ک=1متر-1ب1،پ(تو^ک)آرک⋮∑ک=1متر-1بn-1،پ(تو^ک)آرک

و

آرک=سک-ب0،پ(تو^ک)س0-بn،پ(تو^ک)سمتر،ک=1،…،متر-1.

معادله ( 11 ) را می توان با حذف گاوسی حل کرد زیرا ماتریس بتیبمثبت قطعی و به خوبی شرطی شده است.

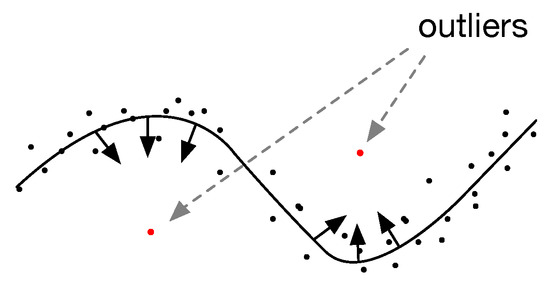
ما باید در طول فرآیند تکرار با مشکل اصلی برخورد کنیم: انتخاب اندازه گیری فاصله تا تعیین خطا. فرمول‌بندی مسئله ساده است، ما نقاط داده سازمان‌یافته (در مورد ما نقاط لبه احتمالی) با توزیع غیریکنواخت با نویز قابل‌توجه داریم. این مسئله را می توان به عنوان یک مسئله بهینه سازی غیرخطی فرموله کرد. با توجه به نقاط ورودی {سک}ک=0متر، می خواهیم نقاط کنترل را محاسبه کنیم پمنکه یک تابع هدف کلی را به حداقل می رساند [ 44 ]:

f=12∑ک=1nد2(پ(تو)،سک)+λfس

د2(پ(تو)،سک)فاصله نقطه است سکبه منحنی پ(تی)، fساصطلاح منظم سازی برای اطمینان از منحنی صاف است، λوزن است fس.در الگوریتم ما با اندازه گیری فاصله نقطه وزنی نامتقارن کار می کنیم. ما یک اصطلاح خطای جدید را در معادله ( 15 ) معرفی می کنیم که بر اساس جیره طلایی است. این تضمین می کند که نقاط داخلی (در همان سمت یک بردار معمولی) تأثیر کمتری نسبت به بیرونی دارند. این مزیت نقاط پرت مشکل ساز را حذف می کند و شکل منحنی را بهبود می بخشد ( شکل 6 ).

فاصله دکفاصله علامت گذاری شده نقطه است سکو نزدیکترین نقطه در منحنی B-spline محاسبه شده. دکاگر نکته مثبت باشد سکدر همان سمت معمولی است nک– شکل 7 الف را ببینید. این اصطلاح خطا عبارت است از:

wφ(دک)=1φ+φ-دک2σ2برایدک<01برایدک≥0

ک=0،1،2⋯،متر، جایی که σعرض انتقال تابع وزن را با توجه به فاصله علامت گذاری شده تعریف می کند. ارزش φنسبت طلایی است 1.61803398875.تابع هدف یک شکل دارد:

fφ=∑ک=0مترwφ(دک)دک2،

تابع وزن دهی wφ(دک)و تابع هدف fφدر شکل 7 ب مدل شده اند.

خطای نامتقارن قسمت هایی را که دقت منحنی در آنها کافی نیست تشخیص می دهد. بهبود با درج گره موضعی انجام می شود. ما پارامتر را می دانیم تو¯کاز نزدیکترین نقطه منحنی سی(توک¯)برای هر سک.بنابراین، ما همه گره ها را وارد می کنیم توک¯در قسمت های ناکافی و با استفاده از طرح درج گره، منحنی را دوباره محاسبه کنید. اگر توک¯∈<توک،توک+1)، سپس نقاط کنترل جدید پ¯منهستند:

پ¯من=βمنپمن+(1-βمن)پمن-1

جایی که

βمن=تو¯ک-تومنتومن+پ-تومنبرایک-پ+1≤من≤ک1برایمن≤ک-پ0برایمن≥ک+1

در قسمت هایی که خطا زیاد است، گره جدید را به مقدار نزدیکترین نقطه منحنی اضافه می کنیم. ما بهبود پیشنهادی را روی مجموعه ابرهای نقطه آزمایش کردیم سی1،سی2،سی3،سی4و سی5. نتایج آزمون و مقایسه کامل در بخش 3 آمده است.

3. نتایج و بحث

این بخش شامل دو بخش اصلی است: برآورد پارامتر آستانه نرمال و برازش B-spline با یک خطای نامتقارن جدید. در بخش اول، ما یک سری از اشیاء آزمایشی را ساختیم – از موارد تقریباً مسطح گرفته تا موارد پیچیده با سوراخ. ما این مدل ها را با الگوریتم رشد منطقه ای پیش بردیم و با استفاده از روش پیشنهادی خود ( بخش 2.1.2 ) مقدار بهینه آستانه نرمال را تخمین زدیم. این مقدار را می توان به عنوان یک مقدار آستانه ورودی جهانی تنظیم کرد. کاربران نهایی بی تجربه الگوریتم تشخیص لبه به هیچ کتابچه راهنمای پیچیده ای در مورد نحوه کنترل نتایج نیاز ندارند.
مرحله دوم شامل یک الگوریتم برازش B-spline برای نمایش لبه است. ورودی این قسمت نقاطی هستند که در مرحله اول شناسایی می شوند. خطای نامتقارن با نسبت طلایی (معادله ( 15 )) در فرآیند تکرار همانطور که در بخش قبل توضیح داده شد استفاده می شود. روی مجموعه منحنی های مختلف (صاف، پیچیده) نتایج را نشان می دهیم و با روش [ 44 ] مقایسه می کنیم.
الگوریتم تشخیص ویژگی در Microsoft Visual Studio C++ با Point Cloud Library 1.8.0 پیاده سازی شد. تقریب B-spline در MATLAB R2018a برنامه ریزی شد. مجموعه داده های ابر نقطه ای توسط ATOS Compact Scan 2M به دست آمد. تست بر روی MacBook Pro، 2.6 گیگاهرتز Intel Core i7، 16 گیگابایت 1600 MHz DDR3، NVIDIA GeForce GT 750M 2048 MB، SSD ارائه شده است.

3.1. تخمین آستانه نرمال تیساعتrθن

اولین تجزیه و تحلیل تاثیر پارامتر را بررسی می کند تیساعتrθن. مجموعه ابرهای نقطه آزمایش ممن،من∈〈1،6〉در شکل 5 آمده است. اجازه دهید سمنnچندین نقطه در ابر نقطه داده شده باشد ( جدول 1 ).

ما الگوریتم رشد منطقه را روی مجموعه داده های خود با پارامترهای اولیه اعمال کردیم تیساعتrθن∈ن، تیساعتrθن=1،…،15و تعداد نقاط حذف شده را پیدا می کنیم noتوتی. درصد امتیازات باقیمانده به صورت زیر محاسبه می شود:

پهrجن=noتوتیnمنn·100.

جدول A1 نتایج به دست آمده از تجزیه و تحلیل مقادیر مختلف را ارائه می دهد تیساعتrθن. ما می توانیم ببینیم که ارزش پهrجنبه شدت با پیچیدگی مدل مرتبط است.
جدول A2 (ستون میانی) نمودارهای نقطه ای مقادیر را نشان می دهد تیساعتrθنو پهrجن. ما می توانیم ببینیم که به طور مستقل بر روی پیچیدگی مدل، پیشرفت لگاریتمی دارد. بنابراین، وابستگی بین تیساعتrθنو پهrجنمی توان به طور کلی با رگرسیون لگاریتمی با استفاده از رابطه ( 5 ) توصیف کرد. معادلات و نمودارهای نهایی در جدول A2 (ستون آخر) آمده است.

ما می خواهیم بهترین مقدار ورودی ممکن را تعیین کنیم تیساعتrθنکه برای ابرهای نقطه مشترک مدل های مهندسی قابل استفاده است. ما با معادله رگرسیون متوسط ​​(میانگین معادلات جدول A2 ) شروع می کنیم:

θاستی≈آر(ایکس)=-2.45·لوگاریتم(ایکس)+6.06.

مقدار بهینه از پهrجبه طور تجربی 1-6٪ تنظیم شده است. بنابراین، ارزش های تیساعتrθندر فاصله هستند 〈آر(1)،آر(6)〉. بدیهی است که دریافت می کنیم:

آر(1)=-2.45·لوگاریتم(1)+6.06≤θاستی≤-2.45·لوگاریتم(6)+6.06=آر(6)6.06≤θاستی≤1.67.

میانگین حسابی آر(1)و آر(6)است θoپتی=3.86به عنوان یک مقدار اولیه پیش فرض در الگوریتم تشخیص ویژگی پیشنهادی تنظیم شده است. در مورد نتایج ناکافی، این مقدار را می توان به صورت تدریجی تغییر داد. جدول 2 نتایج تقسیم بندی مدل ها را نشان می دهد ممن،من=1،2،…،6با استفاده از مقدار اولیه پیش فرض θoپتی=3.86. بدیهی است که نتایج کافی است و این مقدار به کاربران بی تجربه کمک می کند تا بدون هیچ گونه آگاهی قبلی از انحنا یا آستانه معمولی، تقسیم بندی را شروع کنند. با اعمال تغییر تدریجی این مقدار، نتایج برای به دست آوردن کیفیت کافی برای استفاده واقعی بهبود می یابد.
ما روش خود را با رویکردهای مشابه ارائه شده در [ 18 ، 47 ] مقایسه کردیم. ما مجموعه ای مشابه از مدل ها را برای ارزیابی ساختیم ( شکل 8 را ببینید ). مقدار اولیه آستانه انحنا روی مقدار اولیه از پیش تعریف شده تنظیم شد θنو این مقدار به صورت تدریجی تغییر کرد تا بهترین نتایج حاصل شود.
در جدول 3 ، مدل در ستون (الف)، تفاوت قابل توجهی بین نتایج وجود دارد – قطعات سیلندر نادرست تشخیص داده شده در نتایج [ 18 ]. روش ما با تیساعتrθن=4نتایج قابل مشاهده بهتری ارائه می دهد.
مدل‌های (b)، (c) و (d) مشابه مدل‌های [ 47 ] هستند. می بینیم که روش ما نتایج قابل مقایسه ای ارائه می دهد. در مورد این مدل‌ها، باید ارزش آن را کاهش می‌دادیم θنزیرا این مدل ها دارای سطوح مسطح زیادی هستند.

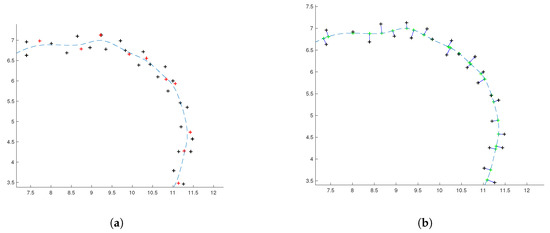
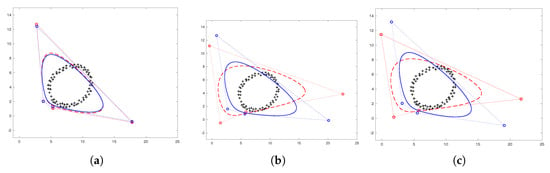
3.2. فیتینگ منحنی B-Spline

این بخش نتایج تقریب B-spline پیشنهادی شرح داده شده در بخش 2.2 را ارائه می دهد. ما محاسبات را روی مجموعه منحنی ها آزمایش کردیم سیمن، من=1،…،5( شکل 9 ). منحنی ها از ابرهای نقطه ای استخراج شدند – منحنی مربع (200 × 200 میلی متر) از مدل مکعبی، دایره (شعاع 200 میلی متر) از مدل استوانه ای. مدل‌های باقی‌مانده در استودیو Blender برای اثبات تطبیق‌پذیری الگوریتم تولید شدند. جدول 4 تعداد نقاط این منحنی ها را نشان می دهد.

مجموعه نقاط منحنی با استفاده از اتصالات منحنی B-spline ارائه شده با درج گره تطبیقی ​​آزمایش شد. دشوارترین بخش تنظیم بهینه محاسبه خطا بود – چگونه می توان کیفیت تقریب را در صورتی که شکل صحیح را ندانیم اندازه گیری کرد. روش رایج محاسبه خطا با فاصله نقطه ای کار می کند که استحکام را ارائه می دهد. فاصله مماس [ 50 ] همگرایی بسیار سریعتری را فراهم می کند. فاصله مجذور با وزن دهی نامتقارن [ 44 ، 51 ] از هر دو سود می برد و یک روش پایدار را انجام می دهد. ما از وزن دهی نامتقارن استفاده کردیم، اما یک ارزیابی جدید از خطای نامتقارن پیشنهاد کردیم:

fφ،ک2=wφ،ک(دک)دک2،جایی کهwφ(دک):=1φ+φ-دک2σ2برایدک<01برایدک≥0

ک=0،1،2⋯،متر،

آستانه خطا را روی 1 میلی متر قرار می دهیم. در شکل 10 a، منحنی B-spline اولیه (خط آبی چین) را می بینیم که با روش وتر و روش حداقل مربع شرح داده شده در بخش 2.2 محاسبه شده است. نقاط قرمز نقاط کنترل B-spline جدید و صلیب های سیاه نقاط در ابر نقطه هستند. شکل 10 ب فاصله نقاط ابر نقطه تا منحنی برازش (قطعات خط آبی) را نشان می دهد.
مقدار خطای نامتقارن تعیین می کند که آیا ما وارد کردن گره را ادامه دهیم و نقاط کنترل جدیدی را در موقعیت های نادرست وارد کنیم. شکل 11 نتیجه تکرار دوم اتصالات B-spline را نشان می دهد. ما روش [ 44 ] را پیاده سازی کردیم و محاسبات ارائه شده توسط معادله ( 22 ) را پیشنهاد کردیم. میانگین خطای تقریب را محاسبه کردیم Eمترو Egoلددر جدول 5 (ما تنظیم کردیم σ=0.02،0.09،0.1). ما می توانیم آن را در مورد σ=0.09و σ=0.1خطا کمتر است و شکل منحنی به وضوح بهتر است ( شکل 11 را ببینید ).
جدول A3 نتایج متفاوتی را با تعداد نقاط کنترل و خطای نامتقارن مربوطه نشان می دهد. بدیهی است که الگوریتم در مورد سازه های مختلف قابل اجرا است و با نقاط گوشه به خوبی کار می کند.

4. نتیجه گیری

سهم اصلی این مقاله روشی است که تشخیص و نمایش لبه‌های قطعات مهندسی اسکن شده را بهبود می‌بخشد. این ناحیه چالش برانگیز است زیرا دستگاه اسکن (معمولاً یک اسکنر سه بعدی) اغلب نمی تواند لبه های تیز را با مقدار کافی از نقاط اندازه گیری شده بپوشاند. بنابراین، تکنیک های مورد استفاده در نمایش صحیح شکل شی مشکل دارند. برای تنظیم دقیق اشیاء اسکن شده به یک کار وقت گیر دستی در برخی از برنامه های تجاری نیاز است. مقاله ما گردش کار کلی تشخیص خودکار لبه در ابر نقطه دلخواه و پس از آن نمایش صحیح لبه با استفاده از خطوط را شرح می دهد. ما یک راه حل کاربرپسند مبتنی بر یک پارامتر کنترلی ارائه می دهیم که می تواند با اشکال مختلف قطعات مهندسی و همچنین سایر اسکن های سه بعدی به طور کلی کار کند. این روش به عنوان مثال برای بازسازی لبه های تیز ساختمان ها بر اساس اسکن لیزری هوا نیز مناسب است. چگالی نقاط اندازه گیری شده نیز توانایی الگوریتم ها را برای بازسازی شکل دقیق دیوارها محدود می کند. تنظیم ساده یک پارامتر کنترلی برای نوع خاصی از شیء اسکن شده می تواند نتایج را به طور قابل ملاحظه ای بهبود بخشد.
به عنوان اولین مرحله از الگوریتم خود، از تقسیم بندی استاندارد در حال رشد منطقه استفاده کردیم. ما بخشی از الگوریتم تجزیه و تحلیل مؤلفه اصلی (PCA) را که برای محاسبات عادی ضروری است، بهبود دادیم. ما یک سری آزمایش با اشکال متغیر (از تقریباً مسطح تا پیچیده) انجام دادیم و با استفاده از حساب هندسی و روش‌های عددی، متغیر جدید – آستانه برداری عادی را پیاده‌سازی کردیم. تیساعتrθن. پس از آن، این مقدار بهینه محاسبه شده را به عنوان مقدار شروع تنظیم می کنیم. کاربران می توانند به صورت تدریجی این آستانه را با توجه به شکل شیء تغییر دهند. استفاده از یک مقدار به هم پیوسته برای کنترل نتیجه برای کاربران نهایی که قادر به درک همه پارامترهای الگوریتم نیستند مناسب تر و بسیار راحت تر است. روش رشد منطقه ای نقاط مسطح را حذف می کند و نقاط باقیمانده نقاط لبه احتمالی هستند.
مرحله بعدی چالش برانگیز بود. نحوه محاسبه خطای نمایش لبه زمانی که نقاط لبه صحیح از دست رفته است. ما انتخاب کردیم که با روش تکرار شونده B-spline با استفاده از فاصله نقطه وزن نامتقارن کار کنیم. دلایل در بخش 3 مورد بحث قرار گرفته است. ما تصمیم گرفتیم از نسبت طلایی به عنوان یک پارامتر استفاده کنیم ( بخش 2.2 ). این تضمین می کند که نقاط داخلی (در همان سمت یک بردار معمولی) تأثیر کمتری نسبت به بیرونی دارند و نتیجه از نظر نوری “کامل” است. این مزیت نقاط پرت مشکل ساز را از بین می برد و شکل منحنی را بهبود می بخشد. ما الگوریتم را در برابر نویز مقاوم کردیم و از اثر زیگزاگ جلوگیری کردیم.
کار ما پسوندهای احتمالی زیادی دارد. مهندسی معکوس به شدت با فناوری چاپ سه بعدی مرتبط است. صحت اشیاء چاپ شده به برش های مناسب (G-code) بستگی دارد. اولین پیگیری می تواند تنظیم روش برش B-spline باشد. علاوه بر این، تجسم اشیاء اسکن شده را می توان بهبود بخشید. تقریب نقاط منحنی را می توان به شبکه مثلثی اضافه کرد. پیشرفت قابل توجهی می تواند ادغام T-splines باشد. T-spline شبکه نامنظم را فعال می کند و ما می توانیم لبه های تیز را با استفاده از بردارهای مختلف گره محلی نشان دهیم. مطمئناً بسیاری از حوزه های علمی از پیشرفت های عظیم در شبکه های عصبی و یادگیری عمیق بهره می برند. تحلیل ابر نقطه ای نیز از این قاعده مستثنی نیست.38 ].

اختصارات

در این نسخه از اختصارات زیر استفاده شده است:

RP نمونه سازی سریع
RE مهندسی معکوس
CAD طراحی به کمک رایانه
PCA تجزیه و تحلیل مؤلفه های اصلی
STL زبان استاندارد Tessellation
NURBS غیر یکنواخت منطقی B-spline

پیوست اول

جدول
جدول A1. جدول از تیساعتrθنو پهrجنبرای همه ابرهای نقطه آزمایش
جدول
جدول A2. جدول داده ها و رگرسیون لگاریتمی برای همه ابرهای نقطه آزمایش.
جدول
جدول A3. مقایسه تقریب منحنی B-spline ابرهای آزمایشی، CP تعداد نقاط کنترل است، wφمیانگین خطای وزنی است.

منابع

  1. دیویس، جی. ادگار، تی. پورتر، جی. برنادن، جی. سارلی، م. ساخت هوشمند، هوشمندی ساخت و عملکرد پویای تقاضا. محاسبه کنید. شیمی. مهندس 2012 ، 47 ، 145-156. [ Google Scholar ] [ CrossRef ]
  2. وایدیا، س. امباد، پ. Bhosle, S. Industry 4.0—A Glimpse. Procedia Manuf. 2018 ، 20 ، 233-238. [ Google Scholar ] [ CrossRef ]
  3. چوآ، CK; لئونگ، KF; Lim, CS Rapid Prototyping: Principles and Applications. در نمونه سازی سریع: اصول و کاربرد . انتشارات علمی جهانی: سنگاپور، 2010. [ Google Scholar ]
  4. کیو، ی. ژو، ایکس. Qian, X. برش مستقیم داده های ابری با توپولوژی تضمین شده برای نمونه سازی سریع. بین المللی J. Adv. Manuf. تکنولوژی 2011 ، 53 ، 255-265. [ Google Scholar ] [ CrossRef ]
  5. لیوسو، ام. الرو، اس. مارتینز، جی. لوفور، اس. Attene, M. از مدل های سه بعدی تا چاپ های سه بعدی: مروری بر خط لوله پردازش. محاسبه کنید. نمودار. انجمن 2017 ، 36 ، 1-24. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  6. چوی، S.-H. Samavedam, S. مدل سازی و بهینه سازی نمونه سازی سریع. محاسبه کنید. Ind. 2002 , 47 , 39-53. [ Google Scholar ] [ CrossRef ]
  7. سن، SK; آگاروال، RP نسبت طلایی در علم، به عنوان منبع توالی تصادفی، محاسبه آن و فراتر از آن. جی. کامپیوتر. ریاضی. Appl. 2008 ، 56 ، 469-498. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  8. جاویدراد، ر. Pourmoayed، بازسازی منحنی Contour AR از داده های ابری برای نمونه سازی سریع. ربات. محاسبه کنید. یکپارچه سازی Manuf. 2011 ، 27 ، 397-404. [ Google Scholar ] [ CrossRef ]
  9. گریلی، ای. منا، اف. Remondino، F. مروری بر الگوریتم های تقسیم بندی و طبقه بندی ابرهای نقطه ای. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2017 ، XLII-2/W3 ، 339–344. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  10. نگوین، ا. Le, B. تقسیم بندی ابر نقطه سه بعدی: یک بررسی. در مجموعه مقالات ششمین کنفرانس IEEE در مورد رباتیک، اتوماسیون و مکاترونیک (RAM)، مانیل، فیلیپین، 12-15 نوامبر 2013. ص 225-230. [ Google Scholar ]
  11. بسل، پی جی؛ جین، تقسیم بندی RC از طریق برازش سطحی با مرتبه متغیر. IEEE Trans. الگوی مقعدی ماخ هوشمند قوس. 1988 ، 10 ، 167-192. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  12. نهار، م. علی سوجان رحمان، م. بهبود الگوریتم رشد منطقه تک دانه در تقسیم بندی تصویر. گلوب. جی. کامپیوتر. علمی تکنولوژی 2018 ، 18 ، 15-22. [ Google Scholar ]
  13. آدامز، آر. Bischof، L. منطقه بذر در حال رشد. IEEE Trans. الگوی مقعدی ماخ هوشمند قوس. 1994 ، 6 ، 641-647. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  14. وانگ، ایکس. زوآ، ال. شینا، ایکس. رنا، ی. Qina، Y. یک رویکرد در حال رشد منطقه برای استخراج خودکار شکستگی رخنمون از یک ابر نقطه سه بعدی. محاسبه کنید. Geosci. 2017 ، 99 ، 100-106. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  15. خو، جی. ژو، ام. وو، زی. شوی، دبلیو. Ali, S. جداسازی سطحی قوی و استخراج خطوط لبه از قطعات شکسته شده آثار. جی. کامپیوتر. دس مهندس 2015 ، 2 ، 79-87. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  16. Vo، AV; تروونگ-هنگ، ال. Laefer، DF; منطقه برتولتو، M. Octree در حال رشد برای تقسیم‌بندی ابر نقطه‌ای. ISPRS J. Photogramm. Remote Sens. 2015 ، 104 ، 88-100. [ Google Scholar ] [ CrossRef ]
  17. نی، اچ. لین، ایکس. نینگ، ایکس. Zhang، J. تشخیص لبه و ردیابی خط ویژگی در ابرهای نقطه سه بعدی با تجزیه و تحلیل ویژگی های هندسی. Remote Sens. 2016 , 8 , 710. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  18. دماریس، ک. واندرستریتن، دی. ولودین، تی. Roose, D. تشخیص لبه های تیز بسته در ابرهای نقطه ای با استفاده از تخمین عادی و نظریه گراف. محاسبه کنید. به دس کمک کرد. 2007 ، 39 ، 267-283. [ Google Scholar ]
  19. جیانگ، XY; بونک، اچ. Meier، U. بخش بندی تصویر با برد سریع با استفاده از تقسیم بندی های ابتدایی سطح بالا. در مجموعه مقالات سومین کارگاه آموزشی IEEE در مورد کاربردهای بینایی کامپیوتری، ساراسوتا، FL، ایالات متحده آمریکا، 2 تا 4 دسامبر 1996. صص 83-88. [ Google Scholar ]
  20. اشنابل، آر. وال، آر. Klein, R. Efficent Ransac برای تشخیص شکل ابر نقطه ای. محاسبه کنید. نمودار. انجمن 2007 ، 26 ، 214-226. [ Google Scholar ] [ CrossRef ]
  21. برگر، ام. تالیاساکی، آ. Seversky، LM; آلیز، پی. Guennebaud، G. لوین، جی. سیلوا، سی تی بررسی بازسازی سطح از ابرهای نقطه ای. محاسبه کنید. انجمن نمودار 2016 ، 36 ، 301-329. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  22. لافارژ، اف. Alliez, P. بازسازی سطح از طریق ساختار مجموعه نقطه. در انجمن گرافیک کامپیوتری ; Benes, B., Chen, M., Eds. وایلی: نیویورک، نیویورک، ایالات متحده آمریکا، 2013; ص 225-234. [ Google Scholar ]
  23. وانگ، ام. جو، م. فن، ی. گوا، اس. لیائو، م. یانگ، اچ. Komura, T. بازسازی 3 بعدی سطوح ابر نقطه ای ناقص با تقسیم بندی و بهبود ویژگی ها. دسترسی IEEE 2019 ، 7 ، 15272–15281. [ Google Scholar ] [ CrossRef ]
  24. یین، ک. هوانگ، اچ. ژانگ، اچ. گونگ، ام. کوهن-اور، دی. Chen, B. Morfit: بازسازی سطح تعاملی از ابرهای نقطه ناقص با توپولوژی منحنی محور و کنترل هندسه. ACM Trans. نمودار. 2014 ، 33 ، 202. [ Google Scholar ] [ CrossRef ]
  25. هیلدبرانت، ک. پولثیر، ک. Wardetzky، M. Smooth دارای خطوط روی مش های سطحی است. در سمپوزیوم Eurographics در مورد پردازش هندسه ; Desbrun, M., Pottmann, H., Eds. انجمن Eurographics: Aire-la-Ville، سوئیس، 2005; صص 85-90. [ Google Scholar ]
  26. اوتاکه، ی. Belyaev, A. تشخیص خودکار برآمدگی ها و دره های ژئودزیکی در سطح چند ضلعی. جی سه بعدی. تصاویر 2001 ، 15 ، 127-132. [ Google Scholar ]
  27. استیلیانو، جی. استخراج خطوط Farin، G. Crest از مش های سه بعدی. در روش های سلسله مراتبی و هندسی در تجسم علمی ; Farin, G., Hamann, B., Hagen, H., Eds. Springer: برلین، آلمان، 2003; صص 69-81. [ Google Scholar ]
  28. توتونی، س. دسوزا، ا. دونوان، آر. رائو، پی کی; کنگ، ز. Borgesen, P. طبقه‌بندی تغییرات ابعادی در قطعات ساخته شده افزودنی از داده‌های ابر نقطه‌ای سه بعدی اسکن شده با لیزر با استفاده از رویکردهای یادگیری ماشین. J. Manuf. علمی مهندس 2017 ، 139 ، 142-149. [ Google Scholar ]
  29. بنیر، آر. ساب سول، جی. گسکایر، جی. لو برتون، اف. Puech, W. فرآیند جامع مهندسی معکوس از مش های سه بعدی تا مدل های CAD. محاسبه کنید. به دس کمک کرد. 2013 ، 45 ، 1382–1393. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  30. ژانگ، ز. Sanjay, J. یک الگوریتم برش بهبود یافته با ساخت کانتور کارآمد با استفاده از فایل های STL. بین المللی J. Adv. Manuf. تکنولوژی 2015 ، 80 ، 1347–1362. [ Google Scholar ] [ CrossRef ]
  31. ما، دبلیو. اما، WC; او، برش تطبیقی ​​مبتنی بر P. NURBS برای نمونه سازی سریع کارآمد. محاسبه کنید. به دس کمک کرد. 2004 ، 36 ، 1309-1325. [ Google Scholar ] [ CrossRef ]
  32. اوروپالو، دبلیو. پیگل لس، ا. روزن، پی. Rajab, K. ایجاد ابرهای نقطه ای برای برش اشیاء آزاد برای چاپ سه بعدی. محاسبه کنید. به دس کمک کرد. Appl. 2017 ، 14 ، 242-249. [ Google Scholar ] [ CrossRef ]
  33. شی، ک. کای، سی. وو، زی. Yong, J. تولید ساختار برش و پشتیبانی برای چاپ سه بعدی به طور مستقیم بر روی مدل های B-rep. Vis. محاسبه کنید. Ind. Biomed. هنر 2019 ، 2 ، 3. [ Google Scholar ] [ CrossRef ]
  34. ژائو، جی. ما، جی. فنگ، جی. Xiao، W. روش‌های تولید مسیر و برش غیرمسطح برای ساخت افزودنی‌های روباتیک. بین المللی J. Adv. Manuf. تکنولوژی 2018 ، 96 ، 3149. [ Google Scholar ] [ CrossRef ]
  35. کرسلین، جی. حقیقی، پ. جاجونگ، پی. رامنات، اس. سوترادار، ا. شاه، جی جی بازیابی شکل مقطعی خودکار ساختارهای انشعاب سه بعدی از ابر نقطه. جی. کامپیوتر. دس مهندس 2018 ، 5 ، 368-378. [ Google Scholar ] [ CrossRef ]
  36. لیو، دبلیو. سان، ج. لی، دبلیو. هو، تی. وانگ، پی. یادگیری عمیق در مورد ابرهای نقطه و کاربرد آن: یک بررسی. Sensors 2019 , 19 , 4188. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  37. گریفیث، دی. Boehm, J. A Review on Deep Learning Techniques for 3D Sensed Data Classification. Remote Sens. 2019 , 11 , 1499. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  38. گوا، ی. وانگ، اچ. هو، کیو. لیو، اچ. لیو، ال. بننامون، ام. یادگیری عمیق برای ابرهای نقطه سه بعدی: یک بررسی. arXiv 2019 ، arXiv:abs/1912.12033. [ Google Scholar ] [ CrossRef ]
  39. لی، دی. کوان، آی. وو، سی. وو، جی. تامیر، د. Rishe، N. بهینه سازی بازسازی سطح B-Spline برای حفظ ویژگی شارپ. در مجموعه مقالات دهمین کارگاه و کنفرانس سالانه محاسبات و ارتباطات (CCWC)، لاس وگاس، NV، ایالات متحده، 6 تا 8 ژانویه 2020؛ صص 359-364. [ Google Scholar ]
  40. مینیو، سی. پیرس، اس جی; Summan, R. الگوریتم های جدید برای تشخیص مرز ابر نقطه سطحی سه بعدی و بازسازی لبه. جی. کامپیوتر. دس مهندس 2019 ، 6 ، 81–91. [ Google Scholar ] [ CrossRef ]
  41. مارکوویچ، وی. یاکوویویچ، ز. Miljkovic، Z. ویژگی ساده سازی ابر نقطه سه بعدی حساس با استفاده از رگرسیون بردار پشتیبان. فنی گز. 2019 ، 27 ، 985–994. [ Google Scholar ]
  42. بازازیان، د. Casas, JR; روئیز-هیدالگو، جی. استخراج لبه سریع و قوی در ابرهای نقطه سازمان نیافته. در مجموعه مقالات کنفرانس بین المللی محاسبات تصویر دیجیتال: تکنیک ها و کاربردها (DICTA)، آدلاید، استرالیا، 23 تا 25 نوامبر 2015. صص 1-8. [ Google Scholar ]
  43. وانگ، YX; وانگ، جی. چن، ایکس. چو، تی. لیو، ام. Yang, T. ویژگی استخراج و بازسازی سطح از اجزای صنعتی با استفاده از تقسیم بندی چند مرحله ای و بهینه سازی. Remote Sens. 2018 , 10 , 1073. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  44. موروالد، تی. بالزر، جی. Vincze, V. مدلسازی مناطق متصل در ابرهای نقطه مسطح دلخواه با تقریب B-spline قوی. ربات. Auton. سیستم 2008 ، 76 ، 141-151. [ Google Scholar ] [ CrossRef ]
  45. Jolliffe، تجزیه و تحلیل مؤلفه اصلی فناوری اطلاعات ؛ Springer: نیویورک، نیویورک، ایالات متحده آمریکا، 1986; پ. 487. [ Google Scholar ]
  46. بانچوف، تی. گافنی، تی. مک کروری، سی. جام های نقشه گاوس. در یادداشت های تحقیق در ریاضیات ; پیتمن: لندن، بریتانیا، 1982. [ Google Scholar ]
  47. وبر، سی. هامن، اس. Hagen, H. روش‌های تشخیص ویژگی در ابر نقطه. در تجسم مجموعه داده های بزرگ و بدون ساختار – کارگاه IRTG ; Middel, A., Scheler, I., Hagen, H., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Bodega Bay, CA, USA, 2010; ص 90-99. [ Google Scholar ]
  48. پیگل، ال. Tiller, W. The NURBS Book ; Springer: نیویورک، نیویورک، ایالات متحده آمریکا، 1997. [ Google Scholar ]
  49. de Boor, C. A Practical Guide to Splines ; Springer: نیویورک، نیویورک، ایالات متحده آمریکا، 2001. [ Google Scholar ]
  50. بلیک، ا. Isard, M. The Active Contours ; Springer: نیویورک، نیویورک، ایالات متحده آمریکا، 1998. [ Google Scholar ]
  51. وانگ، دبلیو. پوتمن، اچ. لیو، ی. برازش منحنی‌های B-spline برای اشاره به ابرها با به حداقل رساندن فاصله مربعی مبتنی بر انحنا. ACM Trans. نمودار. 2006 ، 25 ، 214-238. [ Google Scholar ] [ CrossRef ]
Ijgi 09 00422 g001 550
شکل 1. فرآیند مهندسی معکوس.
Ijgi 09 00422 g002 550
شکل 2. قسمت های مشکل دار در لبه ها.
Ijgi 09 00422 g003 550
شکل 3. انواع بیضی کوواریانس ( a ) مایل ( b ) پرولات ( c ) شبیه به یک کره.
Ijgi 09 00422 g004 550
شکل 4. ( الف ) انحنای منحنی، ( ب ) تخمین انحنا در یک ابر نقطه ای.
Ijgi 09 00422 g005 550
شکل 5. ابرهای نقطه آزمایش: ( الف ) مffl، ( ب ) م2، ( ج ) م3، ( د ) م4، ( ه ) م5، ( f ) م6.
Ijgi 09 00422 g006 550
شکل 6. مثالی از نقاط پرت.
Ijgi 09 00422 g007 550
شکل 7. ( الف ) بردار عادی در طرف مقابل نقطه است سک، فاصله دکمنفی است، ( ب ) نمودارهای توابع wφ(خط قرمز) و fφ(خط آبی).
Ijgi 09 00422 g008 550
شکل 8. مجموعه ای از مدل های آزمایش برای مقایسه ( a ) مشابه مدل در [ 18 ]، ( b – d ) مشابه مدل های [ 47 ].
Ijgi 09 00422 g009 550
شکل 9. مجموعه ابرهای نقطه آزمایش: ( الف ) سی1، ( ب ) سی2، ( ج ) سی3، ( د ) سی4، ( ه ) سی5.
Ijgi 09 00422 g010 550
شکل 10. ( الف ) منحنی اولیه B-spline نقاط ابری (صلیب های سیاه) و نقاط کنترل جدید (صلیب های قرمز)، ( ب ) فاصله نقاط ابر نقطه و خط منحنی محاسبه شده.
Ijgi 09 00422 g011 550
شکل 11. مقایسه تکرار دوم با استفاده از روش [ 44 ] (خط قرمز) و روش پیشنهادی با معادله ( 22 ) (خط آبی). مقادیر مختلف از σ: ( الف ) σ=0.02، ( ب ) σ=0.09، ( ج ) σ=0.1.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید