الگوریتم تقسیم نقطه پایه برای ایجاد خطوط اسکلت چندضلعی در نمونه دریاچه ها
خلاصه
این مقاله الگوریتم Base Point Split (BPSplit) را برای ایجاد یک اسکلت چندضلعی پیچیده بر اساس مجموعهای از دادههای برداری توصیفکننده دریاچهها و رودخانهها ارائه میکند. یکی از ویژگی های کلیدی الگوریتم BPSplit این است که به نقاط پایه که منبع یا دهانه یک رودخانه یا یک جریان را نشان می دهند وابسته است. مقادیر ورودی نقاط پایه، شکل اسکلت حاصل از چند ضلعی های پیچیده را تعیین می کند. اسکلت های مختلفی را می توان با استفاده از نقاط پایه مختلف تولید کرد. نقاط پایه برای تقسیم مرزهای چند ضلعی پیچیده به بخش ها اعمال می شوند.
تقسیم بندی از انتخاب لبه های شبکه نامنظم مثلثی (TIN) در داخل چند ضلعی های پیچیده پشتیبانی می کند. نقاط میانی لبه های TIN انتخاب شده مبنایی برای تولید یک اسکلت است. این الگوریتم چند ضلعی های پیچیده با حفره های متعدد را مدیریت می کند و همه حفره ها را به حساب می آورد. این مقاله روشی را برای اصلاح یک اسکلت پیچیده با سوراخ های متعدد پیشنهاد می کند. در رویکرد مورد بحث، لبه های اسکلت که معیارهای از پیش تعیین شده را برآورده نمی کنند (به عنوان مثال، قرار گرفتن اسکلت بین سوراخ های مرکز چند ضلعی) به طور خودکار حذف می شوند. الگوریتمی برای صاف کردن خطوط زیگزاگ پیشنهاد شد.
کلید واژه ها:
اسکلت مستقیم ؛ شبکه هیدروگرافی ; مدل سازی شبکه
1. معرفی
راهحلهای خودکار برای پردازش دادههای برداری مربوط به آبهای سطحی و رودخانهها کاربردهای عملی زیادی دارند و میتوان از آنها برای تولید اسکلت یک شبکه هیدروگرافی استفاده کرد. این امر با استفاده از الگوریتم های تولید انجام می شود. روش های تولید مختلفی در ادبیات شرح داده شده است، از جمله موارد زیر:
-
تبدیل محور میانی [ 1 ، 2 ، 3 ];
-
تبدیل محور وتر [ 4 ];
-
اسکلت مستقیم [ 5 ، 6 ];
-
مثلث سازی دلونی [ 6 , 7 , 8 , 9 ];
-
الگوریتم Splitarea [ 10 ، 11 ];
-
دیگر [ 12 ، 13 ، 14 ].
در روش های توصیف شده، فرآیند رسم خطوط اسکلت با تولید اسکلت پایه آغاز می شود. در مراحل متوالی، لبههای اسکلت انتخاب شده اصلاح و حذف میشوند تا کاربرد نتایج بهبود یابد. اسکلت ها با استفاده از روش های مختلف اصلاح می شوند، از جمله تصحیح [ 7 ، 15 ]، استخراج [ 8 ]، استخراج ویژگی سلسله مراتبی [ 16 ]، فیلتراسیون [ 17 ، 18 ] و تعمیم [ 19 ]. انواع مختلفی از مثلث ها در چند ضلعی ها شناسایی می شوند که با استفاده از روش های مبتنی بر شبکه های نامنظم مثلثی (TIN) تولید می شوند [ 7 ، 10 ، 20] .]. رویکردهای مختلف برای تولید لبه های اسکلت برای انواع مثلث های مختلف در ادبیات [ 7 ، 10 ، 20 ] ارائه شده است ( شکل 1 ). در مثلث نوع 1، یک ضلع بخشی از خط مرزی چند ضلعی است و دو ضلع باقیمانده چند ضلعی را قطع می کنند. در مثلث نوع 2، دو ضلع قطعاتی از خط مرزی چندضلعی هستند. رئوس یک مثلث نوع 3 روی خط مرزی چند ضلعی قرار دارند و هیچ یک از اضلاع مثلث با مرز چند ضلعی همپوشانی ندارند. موارد فوق در مورد مثلث نوع 4 نیز صدق می کند.
در ادبیات [ 8 ، 10 ، 14 ]، اسکلت ها بر اساس تجزیه و تحلیل محیط اطراف چند ضلعی تولید شدند و همسایگان در سمت راست و چپ مرزهای چند ضلعی شناسایی شدند. شناسایی همسایگان همیشه آسان نیست، و در برخی موارد، منطقه مورد تجزیه و تحلیل باید گسترش یابد [ 10 ]. این فرآیند به ویژه زمانی دشوار است که چند ضلعی های پیچیده حاوی حفره هایی (جزایر روی بدنه های آبی) باشند.
در مطالعه قبلی [ 14 ]، نویسندگان یک روش ساده شده را برای ایجاد خط مرکزی یک چندضلعی دراز در مثال جزیره رودخانه به کار بردند. دادههای توپولوژیکی که همسایگی چند ضلعی را که یک کانال رودخانه را نشان میدهد توصیف میکند برای انتخاب لبههای TIN که کانال رودخانه را در جهت عمود بر جریان رودخانه قطع میکنند، استفاده شد. وجود یک جزیره بر روی رودخانه این روند را پیچیده می کرد زیرا روابط همسایگی بین مرز جزیره و مرز چپ و راست کانال رودخانه باید در نظر گرفته می شد. نویسندگان به این نتیجه رسیدند که الگوریتم پیشنهادی باید در تجزیه و تحلیل سایر اشیاء با اشکال مختلف، به ویژه در شبکههای متشکل از تعداد زیادی آب متصل [ ] آزمایش و اصلاح شود (ص. 17) ..
چنین تلاشهایی در مطالعه فعلی برای حذف کاستیهای الگوریتم توصیفشده قبلی، که در آن روابط همسایگی بین مرزهای چند ضلعی و چند ضلعیهای همسایه باید در نظر گرفته میشد، انجام شده است. این کار به ویژه در چند ضلعی های حاوی سوراخ های متعدد چالش برانگیز بود.
هدف از این مطالعه توسعه الگوریتمی برای تولید اسکلتهای چندضلعی پیچیده بود که عناصر یک شبکه هیدروگرافی پیچیده را نشان میدهد، مانند سیستم دریاچههایی که توسط رودخانهها یا دریاچههایی با جزایر متعدد به هم متصل شدهاند. سایر خطوط جریان مانند رودخانه هایی که از دریاچه ها می گذرند نیز در شبکه هیدروگرافی شناسایی شده اند. برای اینکه چنین خطوطی در اسکلت چند ضلعی نمایش داده شوند، نقاطی در مرز دریاچه که ورودی و خروجی رودخانه را مشخص میکنند باید در الگوریتم در نظر گرفته شوند. در راه حل پیشنهادی، این نقاط به عنوان نقاط پایه (BP) نامیده شدند. نقاط پایه به طور قابل توجهی بر شکل اسکلت چند ضلعی تأثیر می گذارد. در راه حل مورد بحث، تعداد نامحدودی از نقاط پایه را می توان در مرز یک چندضلعی پیچیده که نشان دهنده یک دریاچه است، شناسایی کرد. تنها شرط این است که نقاط پایه روی خط مرزی چند ضلعی قرار گیرند زیرا شکل اسکلت تولید شده را تعیین می کنند. اهمیت نقاط پایه در الگوریتم در عنوان این مقاله منعکس شده است.
الگوریتم توسعه یافته در چندین کار تحقیقاتی به کار گرفته شد. اولین کار این بود که بررسی کنیم که آیا الگوریتم طراحی شده می تواند یک اسکلت با شکل مناسب در ابتدای فرآیند ایجاد کند و آیا می توان آن را در موارد مختلف اعمال کرد. شکل اسکلت حاصل با محل نقاط پایه در مرز یک چندضلعی پیچیده (مرز یک جسم آبی) تعیین شد. این نکات برای کاربرد عملی اسکلت تولید شده مهم هستند. نقاط شناسایی شده گره های آویزان در اسکلت های چندضلعی های پیچیده خواهند بود. این اسکلت برای ایجاد یک مدل هندسی از یک شبکه هیدروگرافی به منظور مدل سازی یا ناوبری هیدروگرافی استفاده خواهد شد. دومین وظیفه تحقیقاتی بررسی توانایی الگوریتم پیشنهادی برای تولید اسکلت برای چند ضلعیهایی با حفرههای متعدد (جزایر روی بدنههای آبی) بود، که در آن مکان اسکلت بین جزایر به طور خودکار بر اساس معیارهای از پیش تعیین شده اصلاح شد. سومین کار شامل جستجوی راه حلی بود که در آن اسکلت را بتوان با حذف اثرات زیگزاگ تعمیم داد. از رویکرد میانگین متحرک اصلاح شده استفاده شد.
مطالعه حاضر با استفاده از ابزارهای برنامه نویسی در نرم افزار ArcGIS (ESRI) [ 21 و 22 ] و الگوریتم های توسعه یافته توسط نویسندگان در پایتون انجام شد.
2. روش ها و مواد
2.1. اولین کار تحقیقاتی – مشخص کردن الگوریتم Bpsplit
اولین کار تحقیقاتی بر این فرض تکیه داشت که شکل مورد انتظار یک اسکلت را می توان در مرحله آماده سازی داده ها تعریف کرد. چند ضلعی تجزیه و تحلیل شده نشان دهنده یک بدنه آبی است و یکی از عناصر یک شبکه هیدروگرافی متشکل از دریاچه هایی است که توسط یک رودخانه به هم متصل شده اند. شبکه هیدروگرافی بر اساس داده های برداری توسعه یافته است. الگوریتم Base Point Split (BPSplit) ایجاد شد. نقاط پایه که به طور قابل توجهی بر اسکلت تولید شده تأثیر می گذارد در مرحله اول تعریف شد. لبه های مدل مثلث سازی دلونی (شبکه نامنظم مثلثی، TIN) در داخل چند ضلعی عناصر کلیدی الگوریتم بودند. در راه حل های کلاسیک شامل مدل های TIN، اسکلت بر اساس تمام لبه های TIN در داخل چند ضلعی با استفاده از راه حل هایی که برای انواع مثلث های TIN اعمال می شود، تولید می شود.شکل 1 ). سپس اسکلت اصلاح می شود [ 10 ].
در مطالعه قبلی نویسندگان [ 14 ] و در مطالعه فعلی، لبه های TIN انتخاب شده برای تولید یک اسکلت استفاده شد. در مطالعه قبلی، لبه های TIN بر اساس روابط توپولوژیکی بین مرزهای چند ضلعی و چند ضلعی های همسایه انتخاب شدند. در این مطالعه، لبه های TIN بر اساس مجموعه ای از نقاط پایه اتخاذ شده انتخاب شدند. نقاط پایه بر روی مرز یک چند ضلعی، به عنوان مثال، در سرچشمه یا دهانه رودخانه ای که یک دریاچه را قطع می کند، قرار گرفتند. نقاط پایه گره های آویزان در اسکلت حاصل را تشکیل می دهند.
در الگوریتم توسعهیافته، نقاط پایه خط مرزی چند ضلعی را به بخشهایی تقسیم میکنند. هر بخش مرزی در یک نقطه پایه شروع و به پایان می رسد. تکنیک تقسیم بندی برای انتخاب لبه های TIN استفاده می شود. لبه های TIN که بخش های مختلف خط مرزی را لمس می کنند از مجموعه لبه های TIN واقع در داخل چند ضلعی انتخاب می شوند. لبه های TIN که نقاط پایه را لمس می کنند از این زیر مجموعه حذف می شوند. نقاط میانی لبه های TIN انتخاب شده و نقاط پایه مبنایی برای تولید اسکلت یک شبکه هیدروگرافی است. برای ترکیب این نقاط در یک اسکلت به داده های بیشتری نیاز است. در روشهای کلاسیک TIN، یک اسکلت با استفاده از ساختارهای تعریفشده برای انواع مثلثها ایجاد میشود ( شکل 1).). مثلث ها در راه حل پیشنهادی تحلیل نمی شوند. لبه های TIN انتخاب شده برای تقسیم چند ضلعی (به عنوان مثال، یک چند ضلعی نشان دهنده یک دریاچه) به مجموعه ای از چند ضلعی های کوچکتر استفاده می شود. لبه های اسکلت بر اساس نقاط میانی لبه های TIN انتخاب شده و نقاط پایه ایجاد می شوند. لبه ها بین نقاط واقع در مرز یک قطعه چند ضلعی منفرد ایجاد می شوند.
الگوریتم پیشنهادی یک نسخه بهبود یافته از راه حل پیشنهادی قبلی است [ 14 ]. الگوریتم توسعه یافته به صورت گرافیکی در شکل 2 در زیر ارائه شده است . داده های ورودی چند ضلعی پیچیده و مجموعه ای از نقاط پایه بودند. مجموعه نقاط پایه توسط کاربر تهیه می شود.
روش انتخاب لبه های TIN (7) که دو بخش مختلف از مرز را لمس می کنند، یک ملاحظات مهم در الگوریتم BPSplit است. راه حل ساده ای برای تحقق این نیاز پیشنهاد شد. در راه حل قبلی [ 14 ]، لبه های TIN با شناسایی روابط توپولوژیکی بین خطوط مرزی و مناطق مجاور انتخاب شدند. این راه حل در دریاچه هایی با تعداد زیادی جزیره بسیار پر زحمت است. در الگوریتم پیشنهادی، لبه های TIN بر اساس روابط توپولوژیکی ساده انتخاب می شوند. روابط بین خطوط مرزی یک چند ضلعی پیچیده و نواحی مجاور نیازی به تعیین نیست.
دو ابزار پیشنهادی که در الگوریتم به کار رفته اند در زیر توضیح داده شده اند.
2.1.1. روش انتخاب لبههای TIN که دو بخش مرزی متفاوت را در الگوریتم BPSplit لمس میکنند.
فرآیند انتخاب لبه های TIN نقش مهمی در الگوریتم BPSplit ایفا می کند. لبه های TIN بر اساس بخش هایی از مرزهای چند ضلعی انتخاب می شوند. لبه های TIN که بخش های مرزی مختلف را لمس می کنند انتخاب می شوند. روابط بین لبه های TIN و بخش های مرزی چند ضلعی باید برای این منظور تعیین شود. این با تجزیه و تحلیل روابط توپولوژیکی در طول پردازش داده ها انجام می شود. مجموعه ای از نقاط که رئوس لبه های TIN را تشکیل می دهند تولید می شود. به این نقاط شناسه لبه های TIN (TIN_ID) در جداول مشخصه اختصاص داده شده است ( شکل 3 ب).
مجموعه داده به دست آمده دو برابر بیشتر از لبه های TIN راس دارد. در نتیجه، جدول ویژگی شامل دو نقطه با TIN_ID یکسان است ( شکل 3 ب). در مرحله بعد، الگوریتم بخش های مرزی را با رئوس TIN که آنها را لمس می کند، به هم متصل می کند. شناسه بخش مرزی (BoundarySegment_ID) که رئوس TIN را لمس می کند در جدول ویژگی گنجانده شده است ( شکل 3 ج). این دادهها برای انتخاب شناسه لبههای TIN در تماس با بخشهای مرزی مختلف استفاده میشوند. الگوریتم مقادیر TIN_ID و BoundarySegment_ID ( شکل 4 ) را با هم مقایسه می کند و مقادیر BoundarySegment_ID را انتخاب می کند که برای مقادیر مشابه TIN_ID متفاوت است. در مثال مورد بحث (در بخش 3.1.1) 1029 لبه TIN از مجموعه کلی 3374 لبه TIN انتخاب شد. در مرحله بعد، لبه های TIN که نقاط پایه را لمس می کنند از مجموعه لبه های TIN انتخاب شده حذف شدند.
2.1.2. تولید یک اسکلت بر اساس بخش های یک چند ضلعی پیچیده، نقاط پایه و نقاط میانی لبه های TIN انتخاب شده
این اسکلت با الگوریتمهای اختصاصی که توسط نویسندگان در پایتون بر اساس کتابخانه GDAL و تغییرات خود پیادهسازی شدهاند، تولید شد. الگوریتم پیشنهادی یک راهحل ساده ارائه میکند: اسکلت یک چند ضلعی پس از حذف لبههای TIN بیاهمیت و یالهایی که نقاط پایه را لمس میکنند، تولید میشود. داده های ورودی بخش های یک چند ضلعی پیچیده و مجموعه ای از نقاط (نقاط پایه و نقاط میانی لبه های TIN انتخاب شده) بودند. ابزار توسعه یافته برای تولید و صاف کردن اسکلت در مخزن داده ها و نرم افزار ارائه شده است.
2.1.3. مقایسه الگوریتم های BPSplit و Splitarea
در سال 2016، Meijers و همکاران. [ 10 ] الگوریتم Splitarea را برای تولید اسکلت های چندضلعی که نشان دهنده آب هستند، پیشنهاد کرد. در این مطالعه، الگوریتم Splitarea به عنوان یک روش کلاسیک مورد استفاده قرار گرفت. مطالعه مورد استناد نویسندگان را برای انجام تحقیق حاضر ترغیب کرد. الگوریتم Base Point Split (BPSplit) با مقایسه آن با الگوریتم Splitarea [ 10 ] توصیف شد. مراحل متوالی فرآیند تولید اسکلت شامل الگوریتم های مقایسه شده در جدول 1 و شکل 5 ارائه شده است . این ارائه به چند ضلعی های توسعه یافته توسط Meijets و همکاران متکی است. [ 10 ]. مراحل متوالی فرآیند تولید اسکلت شامل الگوریتم های مقایسه شده در ارائه شده استجدول 1 و شکل 5 .
مراحل پردازش داده های پی در پی در شکل 5 ارائه شده است . در راه حل ارائه شده توسط Meijets و همکاران. [ 10 ]، یک اسکلت بر اساس تمام لبه های TIN تولید می شود و در مراحل متوالی برای ارائه عملکرد مورد نیاز اصلاح می شود. در رویکردی که شامل الگوریتم BPSplit است، مجموعه ای از نقاط پایه تولید می شود. در مثال ارائه شده، نقاط پایه با سه نقطه روی خط مرزی چند ضلعی نشان داده می شوند. از نقاط پایه برای تقسیم مرز چند ضلعی به قطعات استفاده شد و از قطعات برای انتخاب لبههای TIN استفاده شد که بخشهای مختلف خطوط مرزی را لمس میکنند، اما نقاط پایه را لمس نمیکنند. یک اسکلت بر اساس نقاط میانی لبه های TIN انتخاب شده و نقاط پایه ایجاد شد.
2.1.4. تنظیم اسکلت با الگوریتم BPSplit
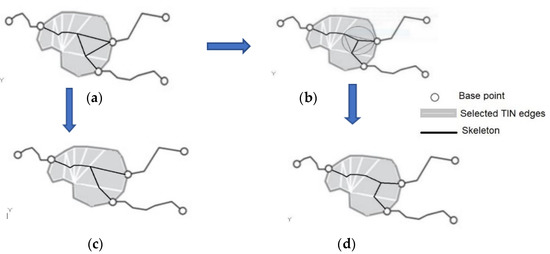
اسکلت تولید شده با الگوریتم BPSplit می تواند حاوی حلقه ها باشد ( شکل 6 و شکل 7 ). از اسکلت به دست آمده می توان برای مدل سازی شبکه های ناوبری استفاده کرد. شبکه هیدروگرافی مدل شده نباید دارای حلقه باشد. دو روش برای حذف حلقه ها وجود دارد. در روش اول، یک حلقه با یک مرکز حلقه جایگزین می شود ( شکل 6 b,d). این راه حل در ادبیات برای مثلث های نوع 3 استفاده شده است ( شکل 1 ). روش دوم شامل ابزاری برای ایجاد کوتاه ترین مسیر بین منبع و دهانه رودخانه است (ابزار درخت پوشا نیز می تواند مورد استفاده قرار گیرد). نتایج تولید شده توسط ابزار کوتاه ترین مسیر برای ایجاد یک اسکلت بدون حلقه ترکیب می شوند ( شکل 6ج).
اسکلت های تولید شده با استفاده از چهار روش مختلف در شکل 7 ارائه شده است . اسکلت های تولید شده با استفاده از راه حل های پیشنهاد شده توسط [ 10 ] در شکل 7 a,b ارائه شده است. اسکلت های تولید شده با استفاده از راه حل های پیشنهادی در این مطالعه در شکل 7 c,d ارائه شده است.
نتایج ارائه شده در شکل 7 متفاوت است. راه حل پیشنهادی در شکل 7 c دارای کمترین تعداد لبه است. هیچ راه حل خوب و بدی وجود ندارد زیرا هر راه حلی درست است. با این حال، تعدد الگوریتم های موجود نشان می دهد که هیچ راه حل ایده آل واحدی وجود ندارد. کاربرد راه حل پیشنهادی باید توسط کاربران ارزیابی شود. طول کل لبه های اسکلت را می توان مقایسه کرد. تناسب اسکلت با خطوط رودخانه را می توان ارزیابی کرد، اما این رویکرد نیاز به تجزیه و تحلیل هیدروگرافی اضافی دارد. پیچیدگی های الگوریتم نشان داده شده در جدول 1 و شکل 5 را می توان با هم مقایسه کرد. الگوریتم BPSplit ساده تر از الگوریتم Splitarea است.
2.1.5. خلاصه ای از الگوریتم BPSplit
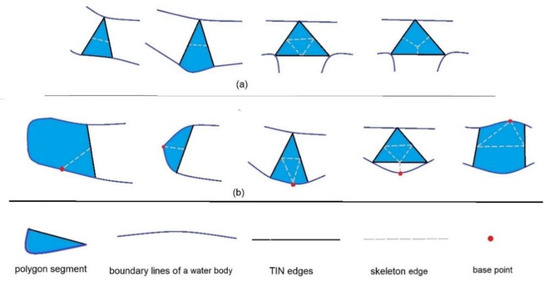
الگوریتم BPSplit یک اسکلت چند ضلعی را با استفاده از نقاط پایه و نقاط میانی لبه های TIN انتخاب شده ایجاد می کند. الگوریتم بر انواع مختلف قطعات چندضلعی ( شکل 8 الف) و اتصالات مختلف با نقاط پایه ( شکل 8 ب) در فرآیند تولید یک اسکلت متکی است.
الگوریتم BPSplit پیشنهادی بر روشهای تولید اسکلت کلاسیک مبتنی بر لبههای TIN است. روابط بین مرزهای چند ضلعی و چند ضلعی های همسایه در سمت راست و چپ در نظر گرفته نمی شود. یک اسکلت بر اساس قوانین قابل اعمال برای انواع مشخص شده قطعات چند ضلعی، و همچنین قوانین اضافی، با مکان های مختلف نقاط پایه تولید می شود ( شکل 8 ).
2.2. روش شناسی مرتبط با وظیفه تحقیق دوم – چند ضلعی با سوراخ
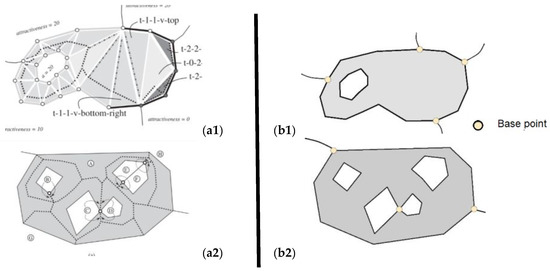
کار تحقیق دوم بر این فرض تکیه داشت که مکان یک اسکلت نشان دهنده یک چندضلعی با سوراخ های متعدد (جزایر روی بدنه های آبی) می تواند به طور خودکار بین جزایر مطابق با معیارهای از پیش تعیین شده تغییر یابد. در راه حل های نرم افزاری انتخاب شده، از جمله ESRI، حفره ها در طول تولید اسکلت حذف می شوند. این ساده ترین راه حل است. در رویکرد توصیف شده توسط Meijers و همکاران. [ 10 ]، حفره ها در نظر گرفته شدند و مکان خاص آنها در داخل چند ضلعی در نظر گرفته شد ( شکل 9 (a1,a2)). مورد خاصی که سوراخ های داخل یک چند ضلعی با هم تماس پیدا می کنند در شکل 9 (a2) ارائه شده است. این راه حل نیز از کار Meijers و همکاران الهام گرفته شده است. [ 10]. داده های الگوریتم BPSplit ( شکل 9 (b1,b2)) بر اساس چند ضلعی های پیچیده ارائه شده در [ 10 ] تهیه شد ( شکل 9 (a1,a2)).
اسکلت ها با استفاده از الگوریتم BPSplit بر اساس چند ضلعی های پیچیده ارائه شده توسط [ 10 ] تولید شدند. در مرحله اول، نقاط پایه به عنوان نقاط مشترک واقع در مرز چند ضلعی و خطوطی که خطوط چند ضلعی را لمس می کنند، شناسایی شدند. چهار نقطه پایه برای چندضلعی پیچیده در شکل 8 ب مشخص شد. سه نقطه پایه برای چند ضلعی در شکل 9 (b2) شناسایی شد، اما دو نقطه در مرز خارجی چند ضلعی قرار داشت، در حالی که نقطه سوم در مرز دو سوراخ در تماس قرار داشت (نقطه سوم برای ایجاد لبههای اسکلت بین جزایر).
مجموعه نقاط پایه برای تقسیم بندی مرزهای یک چندضلعی پیچیده استفاده شد. بخش های مرزهای چند ضلعی با رنگ های مختلف در شکل 10 مشخص شده اند . مرزهای سوراخ های داخل چند ضلعی بخش های جداگانه ای را تشکیل می دهند. اسکلت های چند ضلعی با الگوریتم BPSplit تولید شدند. لبه های TIN بر اساس رئوس یک چند ضلعی پیچیده و همچنین نقاط میانی لبه های چند ضلعی تولید شدند. این نقاط باید به خطوط مرزی اضافه میشدند، زیرا در آزمایشهای اولیه که نقاط اضافه نمیشدند، لبههای منفرد اسکلتهای تولید شده با روش BPSplit جزیرهها را قطع میکردند. این نتیجه به تعداد ناکافی نقاط در مرز چند ضلعی برای تولید لبه های TIN با الگوریتم BPSplit اشاره می کند. در نرم افزار ESRI [ 21]، هنگامی که خط مرکزی یک چند ضلعی با استفاده از ابزار Polygon to Centerline ایجاد می شود، نقاط به طور پیش فرض خوشه بندی می شوند.
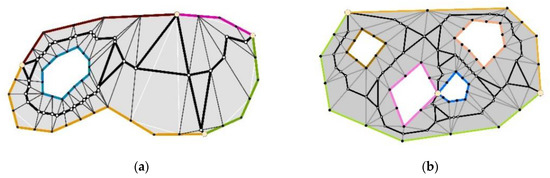
اسکلت های تولید شده توسط الگوریتم BPSplit در شکل 10 a,b ارائه شده است. اسکلت ها سوراخ های داخل چند ضلعی را احاطه کرده اند و دارای حلقه هایی هستند. حلقهها را میتوان با مرکزهای حلقه بر اساس قانون قابل اعمال برای مثلثهای نوع 3 جایگزین کرد ( شکل 1 ، شکل 3 d و شکل 6 a).
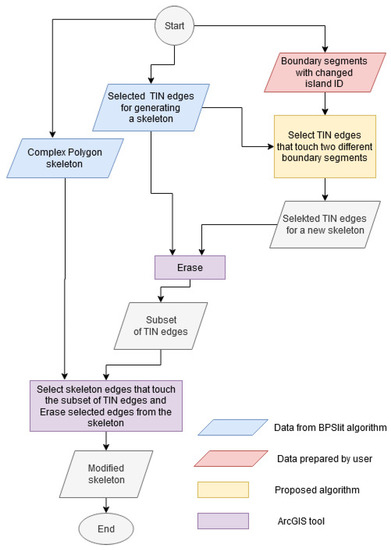
در کار تحقیق دوم، نویسندگان فرض کردند که اسکلت هایی که همه سوراخ های داخل چند ضلعی ها را تشکیل می دهند، می توانند بر اساس نیاز اصلاح شوند. نمودار یک الگوریتم برای اصلاح یک اسکلت در شکل 11 ارائه شده است .
فرآیند اصلاح یک اسکلت در مثالی از اسکلت های نشان داده شده در شکل 12 ارائه خواهد شد .
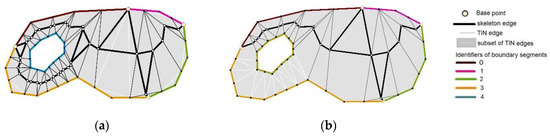
الگوریتم BPSplit یک اسکلت بر اساس نقاط میانی لبه های TIN انتخاب شده ایجاد می کند. لبه های TIN انتخاب شده باید دو بخش مرزی چند ضلعی متفاوت را لمس کنند. یک چند ضلعی با یک سوراخ منفرد دارای بخش هایی از خط مرزی خارجی و خط مرزی سوراخ است که به عنوان قطعه متوالی در نظر گرفته می شود. اگر شناسه مرز سوراخ با شناسه یک بخش منفرد از مرز خارجی جایگزین شود، اسکلتی بین سوراخ و آن بخش از مرز خارجی ایجاد نخواهد شد. این محلول روی یک چند ضلعی با یک سوراخ اعمال شد ( شکل 10آ). فرض بر این بود که یک اسکلت نباید در جنوب سوراخ قرار گیرد. بنابراین، شناسه سوراخ با شناسه بخش مرز خارجی واقع در جنوب سوراخ جایگزین شد. در نتیجه، به سوراخ و بخش مرز خارجی شناسههای یکسانی اختصاص داده شد. لبه های TIN که سوراخ و بخش تجزیه و تحلیل شده مرز خارجی را لمس می کنند در فرآیند انتخاب لبه های TIN در نظر گرفته نشده اند. زیر مجموعه ای از لبه های TIN را می توان با مقایسه انتخاب لبه های TIN با الگوریتم BPSplit بر اساس داده های منبع ( شکل 12 الف) و انتخاب لبه های TIN بر اساس شناسه اصلاح شده خط مرزی سوراخ ایجاد کرد ( شکل 12) .ب). زیر مجموعه لبه های TIN تفاوت بین مجموعه های TIN است. برای اصلاح اسکلت، لبههای اسکلت که لبههای TIN را از زیر مجموعه لبههای TIN بالا لمس میکنند، حذف شدند. اسکلت تولید شده بر اساس داده های منبع در شکل 12 الف و اسکلت اصلاح شده در شکل 12 ب نشان داده شده است. تغییرات در رنگ مرز سوراخ و زیر مجموعه لبه های TIN برای اصلاح اسکلت در شکل 12 ب ارائه شده است.
راه حل های دیگر را می توان برای چند ضلعی های پیچیده حاوی تعداد زیادی سوراخ اعمال کرد ( شکل 10 ب):
-
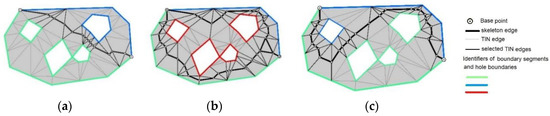
برای خودکارسازی فرآیند، به هر مرز حفره (مرز جزیره) میتوان یک شناسه مربوط به نزدیکترین بخش از مرز چند ضلعی خارجی (بر اساس مرکز سوراخ) اختصاص داد. لبه های TIN بین سوراخ ها و خطوط مرزی خارجی در فرآیند انتخاب لبه های TIN نادیده گرفته می شوند. لبه های چند ضلعی اصلاح شده بین سوراخ ها، روی خط مرکزی چند ضلعی قرار خواهند گرفت ( شکل 13 a).
-
اگر یک شناسه واحد به همه سوراخ ها اختصاص داده شود، لبه های TIN بین سوراخ ها در هنگام انتخاب خودکار لبه های TIN در نظر گرفته نمی شوند ( شکل 13 ب). لبه های اسکلت نزدیک دو مرز چند ضلعی خارجی قرار خواهند گرفت ( شکل 13 ب).
-
شناسه یک بخش انتخاب شده از مرز چند ضلعی خارجی را می توان به خطوط مرزی سوراخ ها (جزایر) انتخاب شده اختصاص داد. لبه های TIN بین سوراخ های انتخاب شده در نظر گرفته نمی شوند. لبه های TIN بین سوراخ های انتخاب شده و بخش های انتخاب شده از مرز خارجی نیز در نظر گرفته نمی شوند ( شکل 13 ج).
سومین وظیفه تحقیق در بخش 3.3.3 بر اساس مثال مورد بحث ارائه شده است. نمودار جریانی از الگوریتم برای تعمیم اسکلت در شکل 14 ارائه شده است .
3. اعتبارسنجی الگوریتم در مجموعه داده های بزرگ
الگوریتم BPSplit برای تولید اسکلت یک شبکه هیدروگرافی بر اساس داده های برداری از پایگاه داده اشیاء توپوگرافی در مقیاس 1:10000 (BDOT_10) استفاده شد. پایگاه داده توسط خدمات مدیریت دولتی بر اساس تصاویر هوایی ایجاد شده است. دادههای مربوط به دریاچهها و رودخانهها از پایگاه داده انتخاب شدند و از آنها برای ارائه عملکرد الگوریتم BPSplit استفاده شد.
3.1. استفاده از الگوریتم BPSplit برای مجموعه های مختلف از نقاط پایه در یک شی انتخاب شده
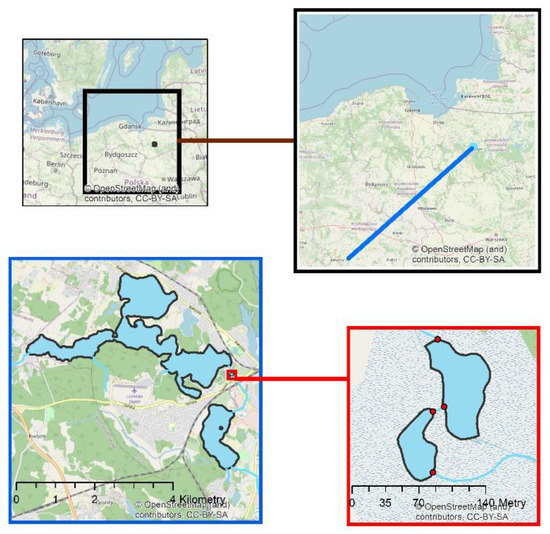
در مثال اول، الگوریتم برای تولید اسکلت یک شبکه هیدروگرافی متشکل از دو دریاچه بزرگ و دو دریاچه کوچک که توسط یک رودخانه به هم متصل شدهاند، و همچنین جریانهای فصلی به بزرگترین دریاچهها اعمال شد (شکل 15 ) . همه دریاچه ها با چند ضلعی های پیچیده نشان داده می شوند. رودخانه از میان هر چهار دریاچه می گذرد. رودخانه و نهرهای فصلی با خطوط نشان داده شده اند.
اسکلت شبکه هیدروگرافی بر اساس داده های منبع در مراحل زیر تولید شد:
-
مجموعه ای از نقاط پایه نشان دهنده ورودی و خروجی رودخانه در دریاچه ها ایجاد شد.
-
مجموعه نقاط پایه برای تقسیم مرزهای چند ضلعی های پیچیده استفاده شد.
-
لبه های TIN در داخل چند ضلعی های پیچیده بر اساس رئوس چند ضلعی و نقاط پایه تولید شدند.
-
لبههای TIN که بخشهای مختلف مرزهای چندضلعی پیچیده را لمس میکنند، اما نقاط پایه را لمس نمیکنند، انتخاب شدند.
-
نقاط میانی لبه های TIN انتخاب شده تولید شد.
-
چند ضلعی های پیچیده به بخش هایی تقسیم شدند.
-
لبه های اسکلت بین نقاط میانی لبه های TIN انتخاب شده و بین نقاط میانی لبه های TIN و نقاط پایه ایجاد شد.
شبکه هیدروگرافی مدل شده از اسکلت های چندضلعی پیچیده و خطوط رودخانه تشکیل شده است.
دو راه حل برای تولید اسکلت شبکه هیدروگرافی استفاده شد. در راه حل اول، اسکلت بر اساس دریاچه های بررسی شده و رودخانه ای که از میان دریاچه ها می گذرد ایجاد شد. هشت نقطه پایه برای نشان دادن مکان هایی که رودخانه در داخل و خارج از دریاچه های مورد تجزیه و تحلیل جریان دارد، ایجاد شد. جریان های فصلی ورودی به دریاچه های مورد بررسی در راه حل دوم در نظر گرفته شد و یازده نقطه پایه ایجاد شد.
در راه حل سوم، اسکلت بزرگترین دریاچه به منظور جهت یابی مدل سازی شد. نقاط جذاب در ساحل دریاچه به عنوان نقاط پایه انتخاب شدند. راه حل ها در بخش های بعدی ارائه شد
3.1.1. تولید اسکلت شبکه هیدروگرافیک بر پایه دریاچه ها و یک رودخانه
در راه حل اول، رودخانه Kortówka که از میان چهار دریاچه تجزیه و تحلیل شده می گذرد با یک خط نشان داده شد. هشت نقطه مبنا که مکانهای جریان رودخانههای ورودی و خروجی دریاچههای مورد مطالعه را مشخص میکردند، انتخاب شدند. نقاط پایه برای تقسیم مرزهای دریاچه به 9 بخش، از جمله یک بخش نشان دهنده مرز جزیره استفاده شد ( شکل 16 ).
بخش های مرزی برای انتخاب لبه های TIN که نقش مهمی در روند توسعه اسکلت بازی می کنند استفاده شد. اسکلت های چند ضلعی دریاچه بر اساس نقاط میانی لبه های TIN انتخاب شده و مجموعه نقاط پایه تولید شدند ( شکل 17 ).
شبکه بر اساس بخش های چند ضلعی که با تقسیم چند ضلعی ها با لبه های TIN انتخاب شده به دست آمد، تولید شد ( شکل 18 ). فقط چند بخش شکل مثلث نوع 1 داشتند. مثلث های نوع 1 در توده های آبی باریک با خط ساحلی یکنواخت مواجه می شوند، در حالی که مثلث های نوع 3 در مجاورت جزایر یافت می شوند. خطوط اسکلت در این بخش ها (مثلث ها) طبق قانون ارائه شده در شکل 8 رسم شد .
3.1.2. تولید اسکلت شبکه هیدروگرافیک بر اساس دریاچه ها، یک رودخانه و سه نهر
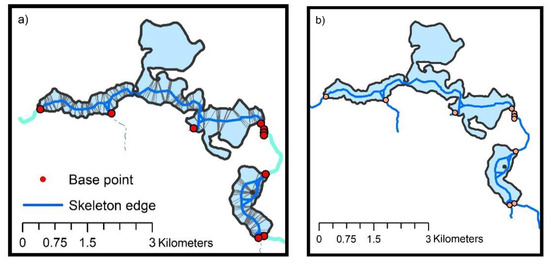
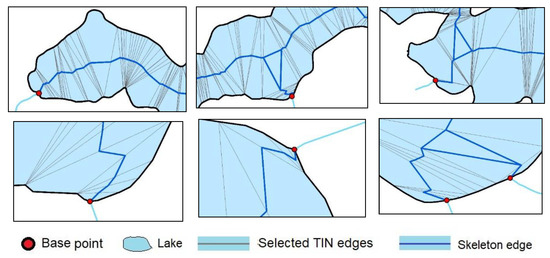
در راه حل دوم، رودخانه اصلی که تمام دریاچه های مورد تجزیه و تحلیل را قطع می کند و سه جریان فصلی که به این دریاچه ها می ریزد در فرآیند تولید اسکلت در نظر گرفته شد. تعداد نقاط پایه نسبت به راه حل قبلی سه افزایش یافت. این نقاط به مرزهای چند ضلعی اضافه شد که نشان دهنده دو دریاچه بزرگ است. مکان نقاط پایه، لبه های TIN انتخاب شده، اسکلت های تولید شده در دریاچه ها و جریان های فصلی در شکل 19 ارائه شده است . اشکال هندسی در بخش های مرزی که نقاط پایه را لمس می کنند در شکل 20 نشان داده شده است .
3.1.3. تولید اسکلت برای ناوبری در بزرگترین دریاچه با خط ساحلی متنوع
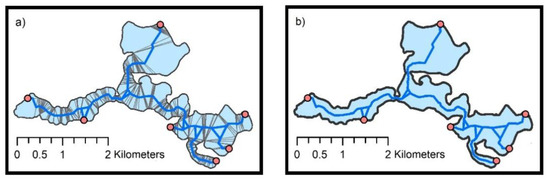
راه حل سوم فقط شامل بزرگترین دریاچه و همچنین نقاط پایه است که جذاب ترین مکان ها را در ساحل دریاچه نشان می دهد. اسکلت تولید شده را می توان برای ناوبری استفاده کرد ( شکل 21 ).
3.2. نتایج ایجاد شده توسط الگوریتم BPSplit در دریاچه ای با جزایر متعدد
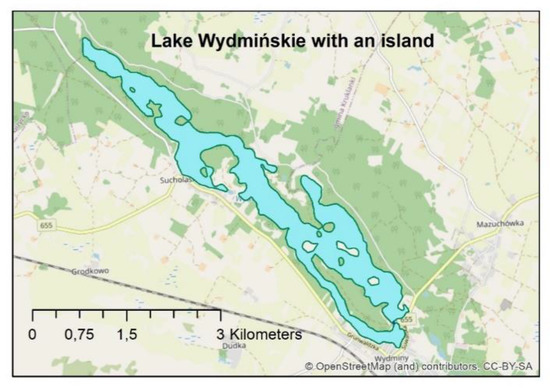
در راه حل بعدی، الگوریتم BPSplit بر روی یک چند ضلعی پیچیده که دارای حفره های زیادی بود، آزمایش شد. شی مورد مطالعه دریاچه Wydmińskie بود که با خط ساحلی متنوع و جزایر متعدد مشخص می شود ( شکل 22 ). یک اسکلت به منظور ناوبری تولید شد. نقاط پایه نشان دهنده نقطه پرتاب و نقاط پهلوگیری در ساحل دریاچه انتخاب شدند.
داده ها با الگوریتم BPSplit پردازش شدند. نتایج تبدیل های متوالی در شکل 23 ارائه شده است . اسکلت تولید شده در شکل 24 نشان داده شده است .
اسکلت ارائه شده بر اساس موقعیت نقاط پایه ایجاد شده است و کل دریاچه (چند ضلعی) را پوشش نمی دهد. اسکلت مناطق قابل توجهی در اطراف نقاط پایه انتخاب شده را به خود اختصاص می دهد. اسکلت تمام جزایر را می پوشاند. لبه های اسکلت در دو طرف جزایر ایجاد شد.
3.3. اصلاح یک اسکلت معرف چند ضلعی با حفره های زیاد – اعتبار سنجی راه حل ارائه شده در کار تحقیقی دوم
این فرض که یک اسکلت بین جزایر را می توان به طور خودکار تغییر داد در مثال دریاچه Wydmińskie ( شکل 24 ) به عنوان اسکلت پایه تأیید شد. لبه های TIN انتخاب شده برای ساخت اسکلت پایه و TIN انتخاب شده پس از اصلاح شناسه جزیره در فرآیند اصلاح استفاده شد. باید به تفاوت بین این مجموعه ها، یعنی زیر مجموعه ای از لبه های TIN توجه شود. اسکلت پایه با حذف لبه های اسکلت که لبه های زیر مجموعه ای از TIN را لمس می کنند، اصلاح شد.
دو تغییر شامل تغییرات خودکار در شناسه مرزهای جزیره در زیر ارائه شده است. نموداری از الگوریتم اصلاح اسکلت با تغییر شناسه مرزهای سوراخ در شکل 11 ارائه شده است .
3.3.1. اصلاح اسکلت پایه برای ایجاد اسکلت بین جزایر در مرکز دریاچه با اختصاص شناسه نزدیکترین بخش از مرز چند ضلعی به مرزهای جزیره
اسکلت پایه با جایگزینی شناسه مرزهای جزیره با شناسه نزدیکترین بخش مرز خارجی دریاچه اصلاح شد. هنگامی که شناسه مرزهای جزیره اصلاح شد، مجموعه جدیدی از لبههای TIN که بخشهای مختلف مرز چند ضلعی را لمس میکردند انتخاب شد. مجموعه پایه لبه های TIN با مجموعه جدید لبه های TIN مقایسه شد و زیر مجموعه ای از لبه های TIN بر اساس تفاوت بین مجموعه های مقایسه شده ایجاد شد. اسکلت پایه با حذف لبه های لمس زیر مجموعه لبه های TIN اصلاح شد. فرآیند اصلاح در شکل 25 ارائه شده است . شناسه های جدید مرزهای جزیره به صورت رنگی در شکل 25 الف مشخص شده اند. زیر مجموعه لبه های TIN برای اصلاح اسکلت در شکل 25 ارائه شده استب فرآیند حذف لبه های اسکلت که زیر مجموعه لبه های TIN را لمس می کنند در شکل 25 ج نشان داده شده است. اسکلت حاصل در شکل 25 d ارائه شده است.
3.3.2. اصلاح اسکلت دریاچه برای به دست آوردن اسکلتی که بین جزایر قرار ندارد وقتی که مرزهای جزیره یک شناسه یکسان اختصاص داده شود
اگر به تمام مرزهای جزیره یک شناسه اختصاص داده شود، اسکلت دریاچه تغییر یافته در امتداد مرزهای خارجی دریاچه قرار خواهد گرفت و بین جزایر قرار نخواهد گرفت. مراحل متوالی روش اصلاح اسکلت، که طی آن لبههای اسکلت پایه که زیر مجموعه لبههای TIN را لمس میکنند، حذف شدند، در شکل 26 ارائه شدهاند .
یک اسکلت پایه با سوراخ نیز می تواند با تغییر شناسه مرزهای جزیره بر اساس ویژگی های جزیره اصلاح شود. رویه های توصیف شده را می توان برای پیش بینی نتیجه چنین تغییراتی به کار برد.
3.3.3. تعمیم اسکلت (هموارسازی) – اعتبار سنجی سومین وظیفه تحقیقاتی
در اکثر راه حل هایی که اسکلت ها بر اساس لبه های TIN تولید می شوند، چند ضلعی های مقعر و چند ضلعی های دارای سوراخ (جزایر) با حضور حلقه ها و جلوه های زیگزاگ مشخص می شوند. سومین کار تحقیقاتی با صاف کردن اسکلت دریاچه Wydmińskie تأیید شد ( شکل 24 ). الگوریتم در نمودار در شکل 14 ارائه شده است . با استفاده از یک الگوریتم توسعه یافته توسط نویسندگان در پایتون، حلقه با مرکزهای حلقه جایگزین شد ( شکل 27 ). یک روش مشابه در محلول برای مثلث های نوع 3 اعمال شد. حذف حلقه تعداد گره ها را در اسکلت کاهش می دهد.
اکثر چند ضلعی های تولید شده بر اساس لبه های TIN دارای اثرات زیگزاگی هستند. هنگامی که چند ضلعی دارای عرض یکنواخت باشد، اثرات زیگزاگ حداقل است، و در چند ضلعی های با عرض متفاوت گسترده تر است ( شکل 27 c و شکل 28 a). روش های مختلف ساده سازی خط در ادبیات [ 23 ، 24 ، 25 ، 26 ، 27 ] توضیح داده شده است. یک روش هموارسازی جایگزین، که نوعی از رویکرد میانگین متحرک است، در این مطالعه پیشنهاد شد. در این رویکرد، بخش های اسکلت با بخش های جدید بر اساس نقاط میانی قطعات اسکلت متوالی جایگزین می شوند ( شکل 28) .ب). برای جلوگیری از تشکیل حلقههای جدید در حین هموارسازی، نقاط نشاندهنده گرههای شبکه به عنوان نقاط ثابت در نظر گرفته شدند. مجموعه نقاط پایه با مجموعه نقاط ثابت ترکیب شد. فرض بر این بود که مکان نقاط ثابت در حین هموارسازی تغییر نمی کند. مراحل (تکرار) متوالی روش هموارسازی در شکل 28 c,d ارائه شده است و نتیجه در شکل 29 نشان داده شده است .
در تکرارهای متوالی فرآیند هموارسازی، مکان جسم حاصل باید در داخل چند ضلعی کنترل شود.
4. نتیجه گیری
این مقاله یک نسخه بهبود یافته از الگوریتم توسعه یافته قبلی را برای تولید اسکلت های چندضلعی های پیچیده پیشنهاد می کند [ 14 ]. راه حل ارائه شده از کار Meijers و همکاران الهام گرفته شده است. [ 10 ].
نام الگوریتم BPSplit نشان می دهد که نقاط پایه نقش مهمی در فرآیند تولید اسکلت دارند. نقاط پایه انتخاب شده در خط مرزی چند ضلعی تضمین می کند که اسکلت مرز چند ضلعی را لمس می کند. این نقاط پایه، گره های انتهایی لبه های آویزان اسکلت خواهند بود.
در الگوریتم توسعهیافته، راهحلهای پیشنهادی برای شناسایی نقاط پایه، انتخاب لبههای TIN مهم برای تولید یک اسکلت، و اصلاح لبههای اسکلت بین جزایر به دلیل سادگی قابل توجه به نظر میرسند. این راه حل ها عناصر جدید در نسخه بهبود یافته الگوریتم ارائه شده قبلی [ 14 ] را تشکیل می دهند.
بنابراین، الگوریتم BPSplit پیشنهادی یک روش جایگزین برای تولید اسکلتهای چندضلعی است. این الگوریتم را می توان برای مجموعه های مختلف داده های برداری مکانی و موارد خاص اعمال کرد. الگوریتم BPSplit برای تولید اسکلت چند ضلعی به مجموعه ای از نقاط پایه در خط مرزی چندضلعی نیاز دارد. نقاط پایه شکل اسکلت تولید شده را تعیین می کنند و در انتخاب لبه های TIN نقش مهمی دارند. لبه های TIN برای تولید اسکلت بر اساس روابط توپولوژیکی ساده که در طول پردازش داده های ساده شناسایی می شوند، انتخاب می شوند. مجموعه نقاط پایه از تعیین شرایط اولیه در فرآیند تولید اسکلت پشتیبانی می کند.
الگوریتم پیشنهادی بر روی مجموعه دادههایی با هندسه متنوع، بر اساس مجموعههای مختلف نقاط پایه، اعتبارسنجی شد. این الگوریتم اولین کار تحقیقاتی را تایید کرد و فرض کرد که شکل پیشبینی شده اسکلت تولید شده را میتوان تعریف کرد.
در دریاچههایی با جزایر متعدد (چند ضلعیهایی با سوراخهای متعدد)، الگوریتم BPSplit لبههای اسکلتی بین جزایر و بین جزایر و مرزهای خارجی دریاچه ایجاد میکند. مکان اسکلت بین جزایر توسط کاربر قابل تغییر است. مثال های ارائه شده، کار تحقیق دوم را تایید می کند.
سومین کار تحقیقاتی نیز با حذف حلقه ها و صاف کردن اسکلت بر اساس گره های تعریف شده و نقاط پایه به عنوان نقاط ثابت با موفقیت تأیید شد.
چندین آزمایش با استفاده از انواع مختلف اشکال چند ضلعی ارائه شد. نتایج الگوریتم BPSplit با راه حل های دیگر قابل مقایسه است. سادگی راه حل، تحقیقات بیشتر در این زمینه را تشویق می کند.
منابع
- لی، DT تبدیل محور میانی یک شکل مسطح. IEEE Trans. الگوی مقعدی ماخ هوشمند 1982 ، 4 ، 363-369. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- چین، اف. اسنوئینک، جی. وانگ، کالیفرنیا در حال یافتن محور میانی یک چندضلعی ساده در زمان خطی. در سمپوزیوم بین المللی الگوریتم ها و محاسبات ; Springer: برلین/هایدلبرگ، آلمان، 1995. [ Google Scholar ]
- کریمی پور، ف. قندهاری، م. LeDoux، H. ترسیم حوضه از محور داخلی شبکه های رودخانه. محاسبه کنید. Geosci. 2013 ، 59 ، 132-147. [ Google Scholar ] [ CrossRef ]
- پراساد، ال. تجزیه و تحلیل مورفولوژیکی اشکال. CNLS Newsl. 1997 ، 139 ، 1-18. در دسترس آنلاین: https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.57.3204 (در 12 نوامبر 2020 قابل دسترسی است).
- اپشتاین، دی. Erickson, J. Raising Roofs, Crashing Cycles, and Playing Pool: کاربردهای یک ساختار داده برای یافتن تعاملات زوجی. گسسته. محاسبه کنید. Geom. 1999 ، 22 ، 569-592. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- طلا، C. مدلسازی فضایی: نمودارهای ورونوی. در دایره المعارف بین المللی جغرافیا: مردم، زمین، محیط زیست و فناوری ؛ Richardson, D., Castree, N., Goodchild, MF, Kobayashi, A., Liu, W., Marston, RA, Eds. Wiley: Hoboken، NJ، ایالات متحده، 2017. [ Google Scholar ]
- لی، سی. یین، ی. وو، پی. Wu, W. روش تشخیص و تصحیح الگو برای خطوط اسکلت در مرزهای پچ کوچک. ترانس. GIS 2020 . [ Google Scholar ] [ CrossRef ]
- لی، سی. دای، ز. یین، ی. Wu, P. روشی برای استخراج خطوط پارتیشن از تکههای بلند و باریک که ویژگیهای ساختاری را در بر میگیرد. ترانس. GIS 2019 ، 23 ، 349–364. [ Google Scholar ] [ CrossRef ]
- آی، تی. که، اس. یانگ، م. Li, J. تولید پاکت و سادهسازی چند خطوط با استفاده از مثلثسازی Delaunay. بین المللی جی. جئوگر. Inf. علمی 2016 ، 31 ، 297-319. [ Google Scholar ] [ CrossRef ]
- مایجرز، ام. ساوینو، اس. Van Oosterom, P. SPLITAREA: الگوریتمی برای تقسیم وزنی چهره ها در زمینه یک پارتیشن مسطح. بین المللی جی. جئوگر. Inf. علمی 2016 ، 30 ، 1522-1551. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Meijers, M. اطلاعات جغرافیایی مقیاس متغیر ; Nederlandse Commissie voor Geodesie، کمیسیون ژئودتیک هلند: دلفت، هلند، 2011; پ. 236. [ Google Scholar ]
- آگنر، دبلیو. Aurenhammer، F. Jüttler, B. در مورد محورهای مثلثی چندضلعی ها. Inf. روند. Lett. 2015 ، 115 ، 45-51. [ Google Scholar ] [ CrossRef ]
- وانگ، ز. Yan, H. الگوریتمی برای استخراج خطوط اسکلت اصلی چند ضلعی ها بر اساس جهت های گسترش اصلی. در مجموعه مقالات کنفرانس بین المللی 2011 در الکترونیک، ارتباطات و کنترل (ICECC)، نینگبو، چین، 9 تا 11 سپتامبر 2011. صص 125-127. [ Google Scholar ] [ CrossRef ]
- لواندویچ، ای. Flisek، P. روشی برای ایجاد خط مرکزی یک چند ضلعی دراز در مثالی از یک جریان آب. ISPRS Int. J. Geo-Inf. 2020 ، 9 ، 304. [ Google Scholar ] [ CrossRef ]
- لی، سی. یین، ی. وو، پی. لیو، ایکس. Guo, P. بهبود روش حذف لرزش و تصحیح توپولوژی برای خط تقسیم تکه های باریک و طولانی. ISPRS Int. J. Geo-Inf. 2018 ، 7 ، 402. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- وانگ، تی. استخراج اسکلت بهینه چندضلعی بر اساس تحلیل سلسله مراتبی. بین المللی قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2009 ، 28 ، 272-276. [ Google Scholar ]
- گیسن، جی. میکلوس، بی. پالی، ام. تقریب محور میانی اشکال مسطح از اتحاد توپ ها: یک الگوریتم ساده تر و قوی تر. در مجموعه مقالات کنفرانس هندسه محاسباتی کانادا، اتاوا، ON، انتاریو، 20-22 اوت 2007. صص 105-108. [ Google Scholar ]
- گیسن، جی. میکلوس، بی. پالی، ام. Wormser, C. تبدیل محور مقیاس. در مجموعه مقالات بیست و پنجمین سمپوزیوم سالانه هندسه محاسباتی، آرهوس، دانمارک، 8 تا 10 ژوئن 2009. صص 106-115. [ Google Scholar ] [ CrossRef ]
- Haunert، JH; Sester, M. استفاده از اسکلت مستقیم برای تعمیم در یک محیط نمایش چندگانه. در مجموعه مقالات کارگاه ICA در مورد تعمیم و بازنمایی چندگانه، لستر، بریتانیا، 20 تا 21 اوت 2004. [ Google Scholar ]
- Szombara, S. مقایسه روش های مورد استفاده در کارتوگرافی برای اسکلت سازی اشیاء منطقه. Geoinf. پول 2015 ، 14 ، 85-94. [ Google Scholar ]
- ESRI 2020، ArcGIS. در دسترس آنلاین: https://www.esri.pl/ (در 12 نوامبر 2020 قابل دسترسی است).
- ESRI. ابزار: خطوط مرکزی را از ویژگی های Polygon ایجاد می کند. 2020. در دسترس آنلاین: https://pro.arcgis.com/en/pro-app/tool-reference/topographic-production/polygon-to-centerline.htm (در 12 نوامبر 2020 قابل دسترسی است).
- داگلاس، دی اچ. الگوریتم های Peucker، TK برای کاهش تعداد نقاط مورد نیاز برای نمایش یک خط دیجیتالی یا کاریکاتور آن. کارتوگر. بین المللی جی. جئوگر. Inf. جئوویس. 1973 ، 10 ، 112-122. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Li، ZL; Openshaw, S. الگوریتمهای تعمیم خودکار خط بر اساس یک اصل طبیعی تعمیم عینی. بین المللی جی. جئوگر. Inf. سیستم 1992 ، 6 ، 373-389. [ Google Scholar ] [ CrossRef ]
- کیان، اچ. ژانگ، ام. Wu, F. یک رویکرد سادهسازی جدید بر اساس روش منحنی تقسیم اریب برای خطوط کانتور. ISPRS Int. J. Geo-Inf. 2016 ، 5 ، 153. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- شی، دبلیو. Cheung, C. ارزیابی عملکرد الگوریتم های ساده سازی خط برای تعمیم برداری. کارتوگر. J. 2006 ، 43 ، 27-44. [ Google Scholar ] [ CrossRef ]
- Kozioł, K. Znaczenie punktów stałych obiektu w processie upraszczania (اهمیت نقاط ثابت در فرآیند ساده سازی). Archiwum Fotogrametrii، Kartografii i Teledetekcji 2012 ، 23 ، 169-177. [ Google Scholar ]
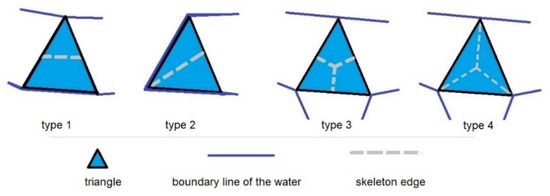
شکل 1. انواع مثلث: نوع 1 – مثلث پیوندی، نوع 2 – مثلث گوش، انواع 3 و 4 – مثلث های شاخه ای.
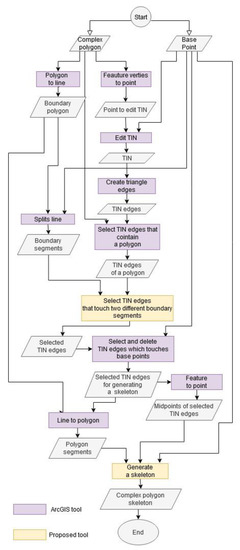
شکل 2. نمودار جریان الگوریتم تقسیم نقطه پایه (BPSplit).

شکل 3. روابط توپولوژیکی در طول پردازش داده ها: ( الف ) جدول ویژگی لبه های شبکه نامنظم مثلثی (TIN). ( ب ) جدول ویژگی رئوس لبه TIN با شناسه راس (Point_ID) و مقادیر TIN_ID. ( ج ) جدول ویژگی رئوس لبه TIN که بخش های مرزی را لمس می کند (شامل مقادیر BoundarySegment_ID).
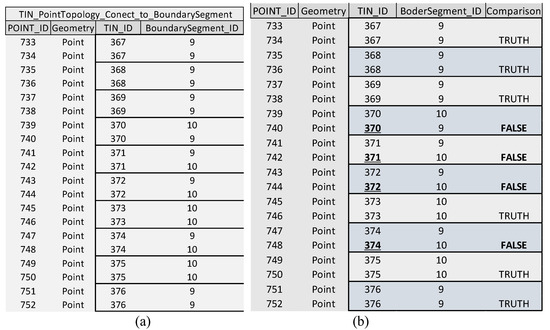
شکل 4. انتخاب لبه های TIN (TIN_ID) بر اساس o: ( الف ) ویژگی های رئوس TIN بر اساس روابط توپولوژیکی در طول پردازش داده ها. ( ب ) شناسه لبههای TIN انتخاب شده بر اساس مقادیر FALSE (370، 371، 372، 374، و غیره).
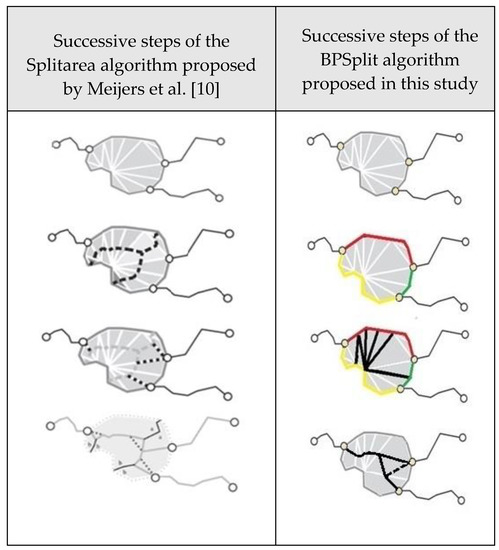
شکل 5. مراحل متوالی فرآیند تولید الگوریتم با استفاده از الگوریتم های Splitarea [ 10 ] و BPSplit. عملیات شامل داده های جدول 1 مشاهده شد.
شکل 6. حذف حلقه ها از یک اسکلت: ( الف ) اسکلت با یک حلقه; ( ب ) حلقه با مرکز حلقه جایگزین شده است (مثلث نوع 3). ( ج ) اسکلت با استفاده از ابزارهای تحلیل شبکه اصلاح شده است. ( د ) اسکلت حاصل که در آن حلقه با مرکز حلقه جایگزین شد.

شکل 7. اسکلت های همان چند ضلعی که با روش اسکلت مستقیم ( a ) تولید شده اند [ 6 ]. ( ب ) الگوریتم Splitarea [ 10 ]; ( ج ، د ) الگوریتم BPSplit و تنظیم اسکلت.
شکل 8. ویرایش لبه های اسکلت بر اساس انواع مختلف قطعات چند ضلعی: ( الف ) انواع مختلف قطعات چند ضلعی با لبه های اسکلت. ( ب ) مکان های مختلف نقاط پایه در بخش ها با تجسم لبه های اسکلت.
شکل 9. چند ضلعی های پیچیده با سوراخ: ( a1 ، a2 ) بر اساس کار Meijers و همکاران است. [ 10 ]؛ ( b1 , b2 ) چند ضلعی های پیچیده با یک سوراخ و سوراخ های متعدد را برای آزمایش نشان می دهد.
شکل 10. اسکلت های تولید شده توسط الگوریتم BPSplit بر اساس داده های فضایی ارائه شده در شکل 9 : ( الف ) اسکلت یک چند ضلعی با یک سوراخ. ( ب ) اسکلت یک چند ضلعی با چهار سوراخ.
شکل 11. فلوچارت الگوریتمی که اسکلت چند ضلعی را با تغییر شناسه های جزیره اصلاح می کند.
شکل 12. اسکلت های تولید شده برای چند ضلعی با سوراخ: ( الف ) اسکلت تولید شده بر اساس داده های منبع. ( ب ) اسکلت اصلاح شده با این فرض که اسکلت نباید در جنوب سوراخ قرار گیرد (شناسه جزیره با تغییر رنگ مرز جزیره اصلاح شد).
شکل 13. اصلاح اسکلت بر اساس سه معیار: ( الف ) اسکلت باید در مرکز چند ضلعی پیچیده بین سوراخ ها (جزایر) قرار گیرد. ( ب ) اسکلت باید سوراخ ها (جزایر) را حذف کند و باید در امتداد مرز خارجی چند ضلعی پیچیده قرار گیرد. ( ج ) اسکلت را نیز می توان با تغییر شناسه مرزهای سوراخ تغییر داد.
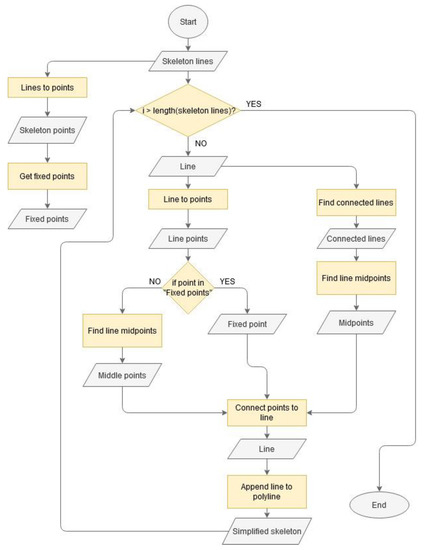
شکل 14. نمودار جریانی از الگوریتم برای تعمیم اسکلت.
شکل 15. شی مورد تجزیه و تحلیل – چهار دریاچه که توسط یک رودخانه با جریان های فصلی که به دریاچه ها می ریزند به هم متصل شده اند.
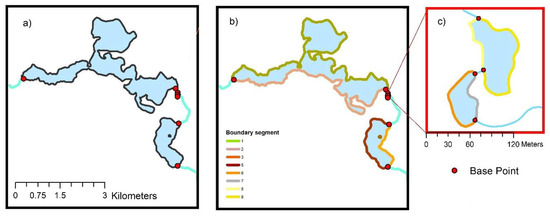
شکل 16. داده های منبع برای تولید اولین اسکلت بر اساس 8 نقطه پایه و 9 بخش از مرزهای چندضلعی (دریاچه): ( الف ) دریاچه ها با مکان نقاط پایه. ( ب ) تقسیم بندی خطوط مرزی دریاچه ها. ج ) دو دریاچه کوچک با بخشهایی از خطوط مرزی آنها .
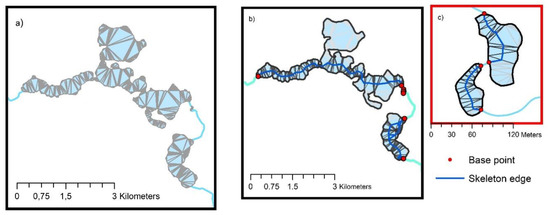
شکل 17. اسکلت یک شبکه هیدروگرافی تولید شده با الگوریتم BPSplit بر اساس نقاط پایه انتخاب شده: ( الف ) لبه های TIN در چند ضلعی ها (دریاچه ها). ( ب ) لبه های TIN انتخاب شده؛ ( ج ) دو دریاچه کوچک با لبه های TIN انتخاب شده.
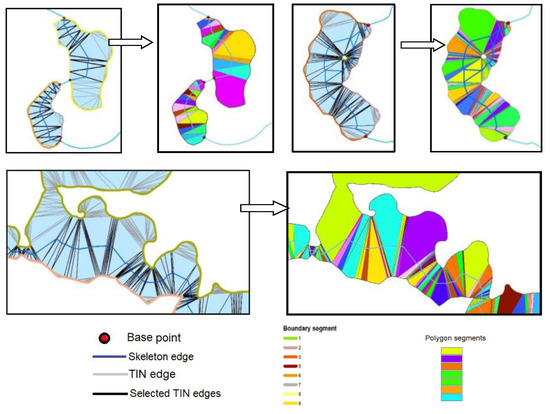
شکل 18. نمونه هایی از بخش های چند ضلعی مختلف برای تولید یک اسکلت بر اساس نقاط میانی لبه های TIN انتخاب شده. چند قطعه دارای شکل مثلث های نوع 1 و 3 از شکل 8 هستند .
شکل 19. اسکلت شبکه هیدروگرافی تولید شده بر اساس 11 نقطه پایه در چهار دریاچه، یک رودخانه که همه دریاچه ها را قطع می کند، و سه جریان فصلی که به دریاچه های مورد تجزیه و تحلیل می ریزد: ( الف ) فرآیند تولید. ( ب ) نتایج.
شکل 20. اشکال هندسی مختلف در بخش های مرزی نزدیک به نقاط پایه.
شکل 21. اسکلت یک چند ضلعی که بر اساس 7 نقطه پایه ایجاد شده است که مکان های جذابی را در ساحل دریاچه نشان می دهد. اسکلت را می توان برای ناوبری استفاده کرد. ( الف ) فرآیند تولید؛ ( ب ) نتایج.
شکل 22. دریاچه Wydmińskie با جزایر متعدد.
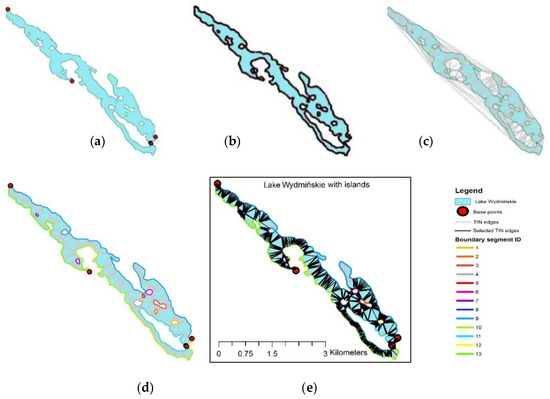
شکل 23. تبدیل داده ها در فرآیند تولید اسکلت: ( الف ) مکان نقاط پایه، ( ب ) رئوس یک چندضلعی پیچیده که دریاچه تحلیل شده را نشان می دهد. ( ج ) لبه های TIN تولید شده. ( د ) لبه های TIN در داخل چندضلعی پیچیده که دریاچه تجزیه و تحلیل شده را نشان می دهد، با تجسم بخش های مرزی. ( ه ) تجسم فرآیند، با نشان دادن لبه های TIN انتخاب شده برای تولید اسکلت.
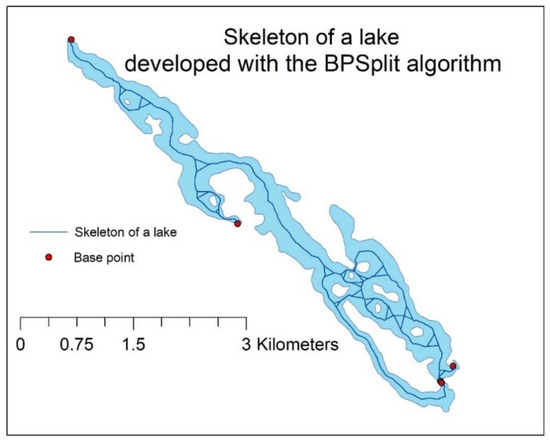
شکل 24. اسکلت یک دریاچه با جزایر متعدد که با الگوریتم BPSplit بر اساس مجموعه پذیرفته شده از نقاط پایه توسعه یافته است.
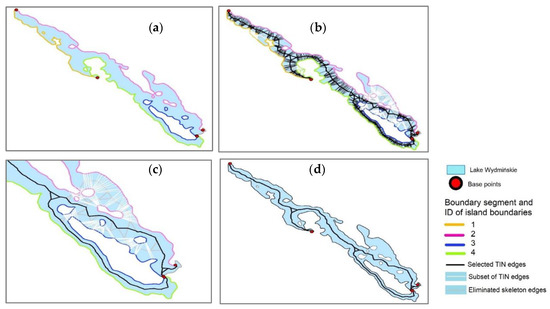
شکل 25. اصلاح اسکلت پایه برای به دست آوردن یک اسکلت در مرکز چند ضلعی بین جزایر: ( الف ) به مرزهای جزیره شناسه های جدیدی اختصاص داده می شود و تغییرات حاصل با رنگ مشخص می شوند. ( ب ) زیر مجموعه ای از لبه های TIN برای اصلاح اسکلت با رنگ سفید مشخص شده است. ( ج ) حذف لبه های اسکلت که لبه های TIN را لمس می کنند. ( د ) اسکلت حاصل.
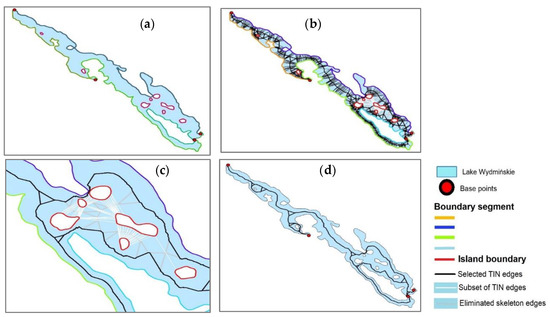
شکل 26. اصلاح اسکلت پایه برای به دست آوردن یک اسکلت واقع در امتداد مرزهای خارجی دریاچه زمانی که مرزهای همه جزایر یک شناسه یکسان اختصاص داده می شود: (الف) به بخش های مرزهای جزیره شناسه های جدید اختصاص داده می شود و خطوط مرزی جزیره مشخص می شوند. با همان رنگ؛ ( ب ) زیر مجموعه لبه های TIN برای اصلاح اسکلت با رنگ سفید مشخص شده است. ( ج ) حذف لبه های اسکلت که زیر مجموعه لبه های TIN را لمس می کنند. ( د ) اسکلت حاصل.
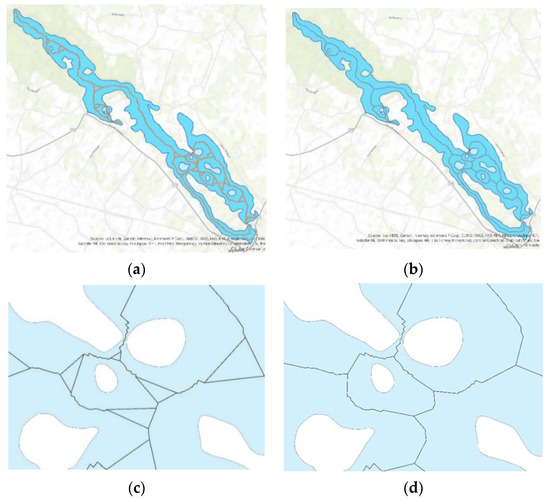
شکل 27. مدل اسکلت: ( الف ) مدل با حلقه ها. ( ب ) مدلی که در آن حلقه ها با مرکزهای حلقه جایگزین شدند. ( ج ، د ) قطعات اسکلت قبل و بعد از برداشتن حلقه.
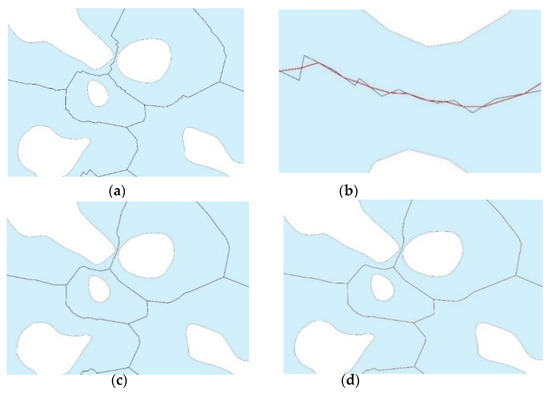
شکل 28. حذف اثرات زیگزاگ در اسکلت شبکه با ایجاد نقاط ثابت در گره های شبکه: ( الف ) اثرات زیگزاگ در شبکه. ( ب ) تجسم روش هموارسازی. ( ج ) نتایج هموارسازی پس از اولین تکرار. ( د ) نتایج هموارسازی پس از تکرار دوم.
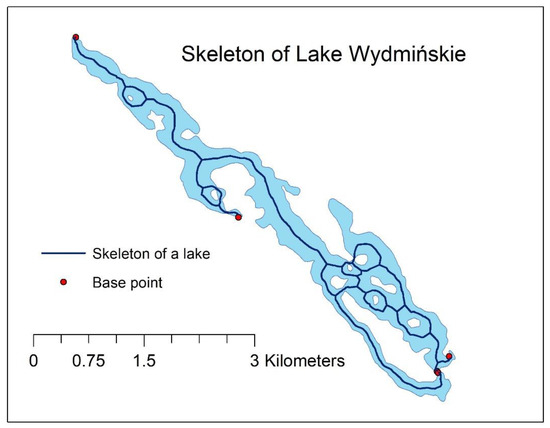
شکل 29. مدلی از اسکلت شبکه تولید شده در یک چند ضلعی هندسی پیچیده که دریاچه ویدمینسکی را بر اساس مجموعه نقاط پایه اتخاذ شده پس از حذف حلقه و دو تکرار از روش هموارسازی برای حذف اثرات زیگزاگی نشان می دهد.






بدون دیدگاه