خلاصه

ثبت ابر نقطه ای مجموعه داده های ابر نقطه ای متعددی را که از موقعیت های مختلف با استفاده از دستگاه های مشابه یا متفاوت جمع آوری شده اند، ترکیب می کند تا یک ابر نقطه واحد را در یک سیستم مختصات واحد تشکیل دهد. ثبت ابر نقطه‌ای معمولاً از طریق تبدیل‌های فضایی به دست می‌آید که چندین ابر نقطه را در یک مدل منسجم جهانی تراز و ادغام می‌کند. در این مقاله، ما یک رویکرد جدید مبتنی بر بخش‌بندی برای ثبت ابر نقطه ارائه می‌کنیم. روش ما شامل استخراج ساختارهای صفحه از ابرهای نقطه‌ای است و سپس با استفاده از تکنیک مجموعه‌های متجانس 4 نقطه (4PCS)، تبدیل‌هایی را تخمین می‌زنیم که ساختارهای صفحه را تراز می‌کنند. به جای یک تراز کلی با استفاده از تمام نقاط مجموعه داده، روش ما ابرهای 2 نقطه ای را با استفاده از ساختار صفحه محلی آنها تراز می کند. این به طور قابل توجهی حجم داده ها را کاهش می دهد، حجم کار محاسباتی و زمان اجرا برخلاف روش‌های مرسوم که به دنبال تراز کردن بیشترین تعداد نقاط مشترک بین موجودیت‌ها هستند، هدف روش جدید تراز کردن بیشترین تعداد صفحه است. با استفاده از ابرهای نقطه‌ای جزئی از چند صحنه دنیای واقعی، برتری روش خود را در مقایسه با 4PCS خام از نظر کیفیت نتیجه (QoS) و زمان اجرا نشان می‌دهیم. روش ما به حدود نیمی از زمان اجرای 4PCS در تمام مجموعه‌های داده آزمایش شده نیاز دارد و تراز بهتری از ابرهای نقطه ایجاد می‌کند. ما برتری روش خود را در مقایسه با 4PCS خام از نظر کیفیت نتیجه (QoS) و زمان اجرا نشان می‌دهیم. روش ما به حدود نیمی از زمان اجرای 4PCS در تمام مجموعه‌های داده آزمایش شده نیاز دارد و تراز بهتری از ابرهای نقطه ایجاد می‌کند. ما برتری روش خود را در مقایسه با 4PCS خام از نظر کیفیت نتیجه (QoS) و زمان اجرا نشان می‌دهیم. روش ما به حدود نیمی از زمان اجرای 4PCS در تمام مجموعه‌های داده آزمایش شده نیاز دارد و تراز بهتری از ابرهای نقطه ایجاد می‌کند.

کلید واژه ها:

ابرهای نقطه ای ; ثبت نام ؛ بخش بندی

1. معرفی

ابرهای نقطه ای یکی از مهم ترین روش های نمایش داده ها هستند که برای نمایش صحنه ها و اشیاء سه بعدی استفاده می شود. در مهندسی عمران، از اسکنرهای با دقت بالا برای ثبت دقیق ساختمان‌ها در قالب ابرهای نقطه‌ای برای برنامه‌ریزی، مدیریت و مرمت، در میان بسیاری از کاربردها استفاده می‌شود. موزه‌ها از فناوری‌های مختلفی مانند اسکنر و دوربین‌های زمان پرواز (ToF) برای دیجیتالی کردن مجموعه‌های خود و در دسترس قرار دادن آن‌ها در دسترس کاربران راه دور استفاده می‌کنند. در رباتیک، از ابرهای نقطه ای برای نمایش سه بعدی صحنه ها برای دستیابی به ناوبری دقیق تر استفاده می شود. ابرهای نقطه ای معمولاً با استفاده از فناوری های مختلفی از جمله لیزر، دوربین های استریو، ToF و LiDAR به دست می آیند [ 1 ]]. برای اشیاء یا صحنه های بزرگ، ابرهای نقطه ای از چندین موقعیت گرفته می شوند. هر ابر نقطه نمایشی جزئی از صحنه (شیء) است که باید در یک ابر نقطه ادغام شود تا کل صحنه را تشکیل دهد. سپس یک فرآیند ثبت، ابرهای نقطه ای جزئی را که از موقعیت های مختلف گرفته شده اند در یک ابر نقطه واحد از صحنه اسکن شده ترکیب می کند. ابرهای نقطه جزئی همیشه در یک سیستم مختصات یکسان نیستند. بنابراین، در طول فرآیند ثبت نیاز به تراز در همان سیستم مختصات.
هم ترازی ابرهای نقطه ای به ثبت سطح مرتبط است، نمونه ای از تطبیق جزئی مشکل مجموعه نقاط سه بعدی [ 2 ]. ثبت سطح فرآیند شناسایی و تطبیق مناطق متناظر در بین اسکن‌های متعدد با موقعیت‌های اولیه دلخواه و تخمین دگرگونی‌هایی است که اسکن‌ها را به بهترین نحو با یکدیگر تراز می‌کند. هدف کلی تراز کردن ابرهای 2 نقطه ای، تخمین تبدیلی است که مجموعه های 2 نقطه ای را به طور پیوسته تراز می کند [ 3 ].
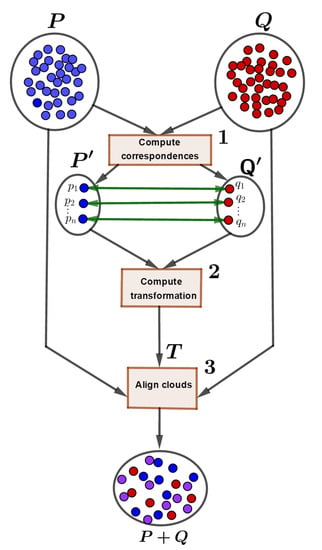
رویکرد کلاسیک برای حل مشکلات تراز ابر نقطه ای را می توان در سه مرحله اصلی خلاصه کرد، همانطور که در شکل 1 نشان داده شده است . ابتدا جستجوی مطابقت بین ابرهای نقطه انجام می شود. سپس تبدیل T بین مجموعه تناظرها محاسبه می شود. به دنبال آن تراز مجموعه های نقطه اولیه با استفاده از T انجام می شود . همانطور که در [ 4 ، 5 ] ارائه شد، برای محاسبه تبدیل های لازم برای تراز 2 مجموعه نقطه در آر3، فقط 3 جفت نقطه متناظر از هر دو مجموعه مورد نیاز است. برای حل مشکلات هم ترازی ابر نقطه ای، یک راه حل این است که تمام ترکیبات ممکن از سه یا چند جفت نقطه متناظر از ابرهای 2 نقطه ای را آزمایش کنیم. با این حال، با توجه به اندازه بزرگ ابرهای نقطه ای (چند میلیون نقطه)، یک رویکرد brute force که تمام مقایسه های ممکن را انجام می دهد، منجر به زمان محاسباتی بسیار طولانی می شود. چندین رویکرد برای تسریع روند ثبت پیشنهاد شده است [ 6 ]. 4PCS یکی از جدیدترین روش‌های تراز ابری نقطه‌ای است که به دلیل سرعت، دقت و ظرفیت آن برای رسیدگی به ترازها از موقعیت‌های اولیه دلخواه است [ 3 ، 7]]. با این حال، زمانی که نسبت همپوشانی بین دو موجودیتی که باید تراز شوند بسیار کم است (زیر 20%) و همپوشانی روی ناحیه نسبتاً کوچکی از ابرهای نقطه تمرکز می‌کند، 4PCS ابرهای نقطه‌ای را با ناهمترازی مطابقت می‌دهد [8]، در نتیجه منجر به پایین آمدن می‌شود . کیفیت نتایج
ما یک روش جدید و قابل اعتماد برای هم ترازی ابر نقطه ای ارائه می دهیم. روش ما از الگوریتم‌های تقسیم‌بندی صفحه کارآمد برای انجام هم‌ترازی ابر نقطه‌ای استفاده می‌کند [ 9 ، 10 ، 11]. الگوریتم ما از ابرهای 2 نقطه ای به عنوان ورودی استفاده می کند و آنها را به بخش های صفحه تقسیم می کند. از تراز صفحه ها، الگوریتم ما تبدیلی را استخراج می کند که ابرهای نقطه اولیه را به بهترین شکل تراز می کند. الگوریتم ساده است و نیازی به موقعیت های اولیه ابرهای نقطه ای ندارد. ما آزمایشاتی را روی ابرهای نقطه ای جزئی با همپوشانی کم انجام دادیم. روش ما تراز بهتری از ابرهای نقطه و زمان اجرای کوتاه‌تر را در مقایسه با 4PCS خام نشان می‌دهد. هم‌ترازی‌ها بر روی بخش‌ها به جای کل ابرهای نقطه انجام شد و به احتمال زیاد تبدیل‌های قابل اعتمادی پیدا می‌کنند که به طور موثر ابرهای نقطه را در مواردی با همپوشانی کم تراز می‌کنند.
ساختار مقاله به شرح زیر است: در بخش 2 ، برخی از کارهای مرتبط در ثبت ابر نقطه را بررسی می کنیم. مدل و الگوریتم پیشنهادی در بخش 3 ارائه شده است . بخش 4 آزمایش ها و نتایج روش پیشنهادی را ارائه می دهد و به دنبال آن نتیجه گیری در بخش 5 ارائه می شود .

2. کارهای مرتبط

ثبت ابر نقطه ای با استفاده از روش های مختلفی در ادبیات [ 6 ، 9 ، 12 ، 13 ، 14 ، 15 ] انجام شده است. اثربخشی تطبیق ابر نقطه سه بعدی توسط فاگراس و هبرت [ 16 ] به عنوان بخشی از کار آنها بر روی نمایش سه بعدی اشیاء در اوایل دهه 1980 نشان داده شد. برای مکان یابی و تشخیص اشیاء صلب در فضای سه بعدی، آنها یک الگوریتم تطبیق بر اساس کواترنیون ها پیشنهاد کردند. اشکال اصلی الگوریتم آنها این است که نیاز به حضور مناطق مسطح نسبتاً بزرگ در ابرهای نقطه ای دارد. برای بهبود این کار، چندین روش دیگر پیشنهاد شده است، از جمله نزدیکترین نقاط تکراری (ICP) معرفی شده توسط Besl و همکاران. [4 ] در سال 1992. ICP یکی از پرکاربردترین رویکردهای اساسی برای ثبت ابر نقطه است. اجرای آن ساده و آسان است. با توجه به دو مجموعه نقطه P و Q در موقعیت‌های اولیه دلخواه، ICP قصد دارد P را با Q به صورت زیر تراز کند:
  • پارامترهای ثبت نام (چرخش، ترجمه، مقیاس) و خطای ثبت را راه اندازی کنید.
  • برای هر نقطه در P ، نزدیکترین نقطه مربوطه را در Q پیدا کنید .
  • پارامترهای ثبت را با توجه به تناظرهای بدست آمده در مرحله 2 محاسبه کنید.
  • تراز را روی P اعمال کنید
  • خطای ثبت را بین P و Q تراز شده فعلی محاسبه کنید
  • اگر خطا > آستانه و تکرار حداکثر به دست نیامد، با P جدید به مرحله 2 بازگردید .
ICP در موارد ایده آل قابل اعتماد است (همپوشانی کامل). با این حال، زمانی که ابرهای نقطه‌ای پر سر و صدا هستند، به زمان نسبتاً طولانی برای تخمین تبدیل صلب بهینه نیاز دارد و این فرآیند دارای احتمال بالایی است که منجر به همگرایی ضعیف شود. چندین بهبود و پیاده سازی در طول سال ها برای رسیدگی به این مشکلات پیشنهاد شده است [ 15 ، 17 ، 18 ، 19 ]. یائوفنگ و همکاران [ 20 ] برای بهبود زمان اجرا، نمونه برداری از ابرهای نقطه اصلی را پیشنهاد کرد. با استفاده از ساختار داده kd-tree، پیش بینی ها و الگوریتم جستجوی ویژگی های ثابت، چندین محقق کارایی مرحله جستجوی نقطه تطبیق را افزایش داده اند [ 21 ].
یافتن مکاتبات یک مرحله بسیار حساس برای اکثر روش های کلاسیک ثبت ابر نقطه است [ 22 ، 23 ، 24 ، 25 ]. یک مسابقه اشتباه منجر به نتایج بد می شود. برای اجتناب از این مرحله، پیتر و ولفگانگ [ 26 ] یک نمایش جایگزین از ابرهای نقطه ای را پیشنهاد کردند: تبدیل توزیع های عادی (NDT). آنها اسکن ها را در یک صفحه دوبعدی به سلول ها تقسیم کردند. به هر سلول یک توزیع نرمال اختصاص می دهند که به صورت محلی احتمال اندازه گیری یک نقطه را مدل می کند. نتیجه تبدیل یک چگالی احتمال پیوسته و قابل تمایز است. سپس فرآیند تطبیق با استفاده از الگوریتم نیوتن انجام می شود. مارتین و همکاران [ 27] این کار را برای ثبت ابر نقطه سه بعدی گسترش داد. همانطور که در [ 27 ] نشان داده شد، اشکال اصلی این رویکرد انتخاب اندازه سلول است و عملکرد الگوریتم به شدت با اندازه سلول ها مرتبط است.
روسو و همکاران [ 28 ] نمونه ترازبندی اولیه اجماع (SAC-IA) را برای ثبت ابر نقطه با استفاده از یک نسخه اصلاح شده از هیستوگرام های ویژگی نقطه ای ارائه شده در کار قبلی خود [ 29 ] پیشنهاد کرد. آنها هیستوگرام ویژگی هر نقطه را در یکی از ابرهای 2 نقطه ای برای تراز کردن محاسبه کردند و زیر مجموعه ای از نقاط را با فواصل زوجی معین از ابر نقطه دوم انتخاب کردند. سپس با استفاده از هیستوگرام ویژگی نقطه ای، مطابقت نقاط انتخاب شده را در ابر نقطه اول جستجو کردند. مشکل اصلی این رویکرد در انتخاب زیرمجموعه نقاط نهفته است. هیچ اطمینانی وجود ندارد که نقاط انتخاب شده در قسمت همپوشانی قرار دارند و اگر میزان همپوشانی کم باشد، می تواند منجر به نتایج ضعیف شود.
آیگر و همکاران [ 3 ] مجموعه های متجانس 4 نقطه ای (4PCS) را پیشنهاد کرد. 4PCS یکی از پرکاربردترین روش ها برای هم ترازی ابرهای نقطه ای است [ 6 ، 17 ]. روش کاملاً هندسی است. این ایده بر اساس انتخاب چهار نقطه همسطح در یکی از موجودیت ها، و به دنبال جستجوی پایه های متناظر در موجودیت دیگر، همانطور که در شکل 2 نشان داده شده است، است . 4PCS مشکلات تراز ابرهای نقطه را به عنوان بزرگترین مشکل مجموعه نقطه مشترک (LCP) در نظر می گیرد [ 30 ]. کیفیت تراز با تعداد نقاط منبع با نزدیکترین همسایه در فاصله تعیین می شود δپس از تحول اصل 4PCS با شبه کد زیر محاسبه می شود. با توجه به دو مجموعه از نقاط S و T در موقعیت های اولیه دلخواه، 4PCS S و T را به صورت زیر تراز می کند:
  • nتومتربهrآلمنgnپoمنnتیس=0
  • مجموعه ای از 4 نقطه همسطح B را در S انتخاب کنید
  • پایه های متجانس U از B به T را در یک سطح تقریبی بیابیدδ>0
  • برای هر Uمن ∈Uبهترین تبدیل صلب را پیدا کنید جیمن، جیمن(Uمن)=ب
  • پیدا کردن سمن⊆تی، به طوری که د(جیمن(سمن)،اس)≤δ
  • اگر |سمن|>nتومتربهrآلمنgnپoمنnتیسسپس nتومتربهrآلمنgnپoمنnتیس= |سمن|و rمنgمندتیrآnسforمتر=جیمن
  • فرآیند را از مرحله 2 لیتر بار تکرار کنید
  • برگشت rمنgمندتیrآnسforمتر
4PCS در مواردی که ابرهای نقطه نویز دارند به زمان محاسباتی طولانی نیاز دارد. یکی از مراحل حیاتی آن جستجو برای مجموعه‌های همخوانی است که ممکن است به زمان محاسباتی نسبتاً طولانی برای ابرهای نقطه‌ای بزرگ نیاز داشته باشد. برای رسیدگی به این مشکل، ملادو و همکاران. [ 7 ] یک نسخه بهبود یافته از 4PCS به نام Super4PCS (S4PCS) پیشنهاد کرد.

3. Plansets بزرگ مشترک-4PCS (LCP-4PCS)

یکی از وظایف اصلی تحقیق ما ادغام چندین اسکن (جزئی یا کامل) از یک صحنه یا شی است که در موقعیت‌های مختلف و/یا با دستگاه‌های مختلف اسکن شده‌اند. پس از بررسی ادبیات روش‌های تراز ابر نقطه‌ای موجود، ما 4PCS را انتخاب کردیم. آزمایشات آزمایشی ناکارآمدی الگوریتم 4PCS را در برخی موارد نشان داد.
  • در مواردی که سطوح همپوشانی بین نهادهایی که باید ادغام شوند بسیار کم است. افزایش نسبتاً زیاد در تعداد تکرارهای حداکثر گاهی منجر به نتایج خوبی می شود. با این حال، زمان اجرا به طور قابل توجهی افزایش می یابد.
  • در مواردی که بخش‌های همپوشانی بین ابرهای نقطه‌ای که باید ادغام شوند در بخش نسبتاً کوچکی از موجودیت‌ها متمرکز می‌شوند. افزایش تعداد تکرارها نتایج را بهبود نمی بخشد.
برای نشان دادن ناکارآمدی 4PCS، یک مورد گویا در شکل 3 نشان داده شده است . شکل 3 a نشان دهنده دو اسکن جزئی از یک اتاق اداری است که ادغام شده اند. شکل 3 ج نتایج تراز اسکن های جزئی اتاق اداری را با استفاده از 4PCS نشان می دهد. یک روش نیمه خودکار که در آن کاربر بخش های مشابهی از موجودیت ها را تقسیم بندی می کند تا عدم تطابق در تراز اسکن ها را حل کند. سپس، 4PCS به بخش‌های تقسیم‌بندی شده اسکن‌ها اعمال شد. بخش های تقسیم شده در شکل 3 ب مشخص شده اند. تراز کردن موجودیت های اولیه با استفاده از یک تبدیل صلب از 4PCS انجام شد، به شکل 3 مراجعه کنید.د این رویکرد نتایج خوبی ایجاد می کند. با این حال، تحت تأثیر موقعیت اولیه مجموعه هایی است که قرار است تراز شوند. روش نیمه خودکار وجود حداقل یک تبدیل را نشان می دهد که امکان ترازهای خوب را در موارد شدید فراهم می کند. هدف این مقاله ارائه روشی است که می تواند برای تعیین خودکار بهترین تبدیل بدون نیاز به مداخله کاربر مورد استفاده قرار گیرد.
با الهام از اصل «تفرقه بینداز و حکومت کن»، روش جدید با تقسیم بندی ابرهای نقطه ای پیش می رود. سپس، تبدیل صلب بهینه ای که موجودیت های اولیه را به بهترین شکل تراز می کند، از تراز بخش ها با استفاده از 4PCS تخمین زده می شود ( شکل 4 را ببینید ).

بر خلاف روش 4PCS که مشکلات هم ترازی ابر نقطه ای را به عنوان بزرگترین مشکل نقاط مشترک (LCP) [ 30 ] در نظر می گیرد، روش جدید هم ترازی ابر نقطه را به عنوان بزرگترین مشکلات مجموعه صفحه مشترک در نظر می گیرد. بنابراین، این روش تبدیل صلب را جستجو می کند که بیشترین تعداد صفحات را تراز می کند.

الگوریتم 1  LCP-4PCS با توجه به دو ابر نقطه P و Q در موقعیت های اولیه دلخواه، δ∈]0;1]یک سطح تقریبی، β∈]0;1]یک آستانه همپوشانی و L>0یک تکرار حداکثری
  • مترآایکسآلمنgnپلآnس←0
  • اس1←سهgمترهnتیآتیمنon(پ)
  • اس2←سهgمترهnتیآتیمنon(س)
  • برای هر پمن∈اس1انجام دادن
  •     برای هر سj∈اس2 انجام دادن
  •          تی←4پسیاس(پمن،سj،L،δ)
  •         اگر مترآتیجساعتآرآتیمنo(تی(پمن)،سمن،δ)≥β سپس
  •            n = مترآتیجساعتپلآnس(اس1\{پمن}،اس2\{سj}،تی،δ،β)
  •            اگر مترآایکسآلمنgnپلآnس<n+1 سپس
  •                 مترآایکسآلمنgnپلآnس=n+1
  •                 rمنgمندتیrآnسforمتر=تی
  •            پایان اگر
  •         پایان اگر
  •     پایان برای
  • پایان برای
  • برگشت rمنgمندتیrآnسforمتر

با توجه به 2 نقطه ابر P و Q در موقعیت های اولیه دلخواه. اجازه دهید اس1={پ1،پ2،…،پک1}و اس2={س1،س2،…،سک2}مجموعه های 2 قطعه ای باشد که به ترتیب پس از تقسیم بندی P و Q به دست می آیند . اجازه دهید ovهrلآپپمنng(پمن،سj)تابعی باشد که نرخ همپوشانی بین 2 بخش را محاسبه کند پمن∈اس1و سj∈اس2: مترآتیجساعت(اس1،اس2)={(پمن،سj):سمن∈اس1،سj∈اس2،ovهrلآپپمنng(پمن،سj)≥β،1≤من≤ک1،1≤j≤ک2}با β>0. هدف LCP-4PCS برآورد است تی^به طوری که:

تی^=ارگحداکثرتی(|مترآتیجساعت(تی(اس1)،اس2)|)

جایی که تی(اس1)اعمال تبدیل T به تمام عناصر استاس1.

نمودار جریان در شکل 4 توصیفی از روش ما را نشان می دهد. اسجآn1ابر نقطه ای است که باید با ابر نقطه مرجع تراز شود اسجآn2. روش ما (LCP-4PCS) ابرهای نقطه (اسکن) را بر اساس ساختارهای صفحه تقسیم می کند، همانطور که در نمودار جریان نشان داده شده است. ساختارهای صفحه با استفاده از سایه های رنگی مختلف در نمودار نشان داده شده اند. LCP-4PCS با تراز کردن مکرر هر صفحه از اسجآn1به کسانی که از اسجآn2با استفاده از 4PCS یک صفحه موجود در هر دو اسکن در نمودار جریان نشان داده شده است (نگاه کنید به سهgمترهnتی1و سهgمترهnتی2). در هر تکرار، یک تبدیل از 4PCS به تمام بخش‌های آن اعمال می‌شود اسجآn1. پس از اعمال تبدیل، مطابقت های بین بخش های اسجآn1و اسجآn2بر اساس نرخ همپوشانی صفحات تقسیم شده شناسایی می شوند. در پایان فرآیند، تبدیلی که بیشترین تعداد هواپیماها را تراز می کند، حفظ می شود.
مدل. الگوریتم 1 مدل پیشنهادی را ارائه می دهد: LCP-4PCS. یک پارامتر βبرای کارآمدتر کردن LCP-4PCS بر اساس واقعیت‌هایی که در طول آزمایش‌ها با آن مواجه می‌شوند، معرفی شد. βآستانه همپوشانی را نشان می دهد که از آن هر دو بخش که باید تراز شوند معادل در نظر گرفته می شوند.
فرض کنید P و Q 2 مجموعه نقطه باشند. اس1={پ1،پ2،…،پک1}و اس2={س1،س2،…،سک2}2 مجموعه قطعه هستند که به ترتیب پس از تقسیم بندی P و Q به دست می آیند و δ،β∈]0;1]. اجازه دهید پمن∈اس1و سj∈اس2: مترآتیجساعت1(پمن،سj،δ)={(پ،q):پ∈پمن،q∈سj،د(پ،q)≤δ،q=ارگدقیقهqک∈سj(د(پ،qک))}.
نسبت مطابقت(): این تابع 2 مجموعه نقطه را به عنوان ورودی می گیرد پمن، سjو یک سطح تقریبی δکه از آن 2 نقطه p و q نزدیک در نظر گرفته می شود (د(پ،q)<δ)و نسبت تطبیق بین 2 ست را برمی گرداند. اجازه دهید م1=مترآتیجساعت1(پمن،سj،δ). با توجه به تعریف تطابق از 2 مجموعه امتیاز بالا، مترآتیجساعتآرآتیمنo(پمن،سj،δ)=مترآایکس(|م1||پ|،|م1||س|).
برنامه های مسابقه(): این تابع دو مجموعه از بخش های S1 و S2، یک تبدیل صلب T ، یک سطح تقریبی را به عنوان ورودی می گیرد.δو یک آستانه همپوشانی β. اجازه دهید مترآتیجساعت2(اس1،اس2،δ،β)={(پمن،سj):پمن∈اس1،سj∈اس2،مترآتیجساعتآرآتیمنo(پمن،سj،δ)≥β}. مترآتیجساعتپلآnس(اس1،اس2،تی،δ،β)=|مترآتیجساعت2(تی(اس1)،اس2،δ،β)|جایی که تی(اس1)اعمال تبدیل T به تمام عناصر استاس1.
زمان اجرا فرض کنید P و Q ابرهای دو نقطه ای با n و m نقطه باشند ( n≥متر) به ترتیب. مرحله تقسیم بندی را می توان در اجرا کرد O(nورود به سیستمn)[ 10 ]. 4 PCS اجرا می شود O(n). مجموعه نقاط تقریباً همسطح هستند، که زمان پردازش جستجوی همخوانی را کاهش می دهد. مرحله تطبیق هواپیما در بدترین حالت انجام می شود O(ک1∗ک2∗n)، جایی که ک1و ک2تعداد صفحات به ترتیب در P و Q هستند . الگوریتم ما زمان اجرا است 2O(nورود به سیستمn)+O(ک1∗ک2∗n)=2O(nورود به سیستمn)+O(n)علت ک1≪nو ک2≪n. بنابراین به طور کلی مدل ما اجرا می شود O(nورود به سیستمn)زمان و نیاز دارد O(n)فضا.

4. آزمایش ها و نتایج

ما LCP-4PCS را روی مجموعه‌ای از اسکن‌های جزئی از چندین صحنه با نرخ همپوشانی کم آزمایش کردیم. سپس نتایج را با نتایج به دست آمده با 4PCS مقایسه کردیم.

4.1. داده ها و پیاده سازی

ما روش خود را در C++ با استفاده از توابع دستکاری ابر نقطه ای ارائه شده توسط کتابخانه CClib [ 17 ] پیاده سازی کردیم. ما از توابع موازی سازی OpenMP [ 31 ] برای بهبود عملکرد الگوریتم ها استفاده کردیم.
آزمایش‌های ما بر روی مجموعه‌ای از ابرهای نقطه سازمان‌یافته ارائه‌شده توسط Camertronix و شریک پروژه ما Rabo انجام شد. ابرهای نقطه‌ای Camertronix اسکن‌های جزئی از فضای داخلی ساختمان بودند که با استفاده از اسکنر لیزری سه بعدی فارو فوکوس گرفته شده بودند. بقیه داده های ما با استفاده از دوربین های ساخت Rabo جمع آوری شد. دوربین‌ها دارای سیستم‌های استریو با مجموعه‌ای از حسگرها هستند که شامل حسگرهای جهت‌گیری (واحد اندازه‌گیری اینرسی)، گیرنده‌های سیستم ماهواره‌ای ناوبری جهانی (GNSS)، فاصله‌یاب لیزری و حسگر مادون قرمز (نگاه کنید به شکل 5) است . می توان از آنها برای اسکن صحنه هایی در محدوده 1 تا 100 متر با دقت چند میلی متر استفاده کرد.
مرحله تقسیم بندی با استفاده از روش ارائه شده توسط Limberger و Oliveira [ 10 ] اجرا شد. این روش کارآمد، سریع است و پیاده سازی C++ در دسترس است. با این حال، در برخی موارد، روش چندین بخش کوچک تولید می کند که باعث کاهش سرعت LCP-4PCS می شود. برای جلوگیری از تولید قطعات کوچک در مرحله تقسیم‌بندی، ادغام قطعات کوچک با استفاده از اندازه‌ها و جهت‌گیری‌های بخش [ 32 ] انجام شد . یک قطعه در صورتی کوچک در نظر گرفته می شود که اندازه آن کمتر از اندازه متوسط ​​قطعات به دست آمده پس از تقسیم بندی یک ابر نقطه باشد. پس از شناسایی، یک بخش کوچک به نزدیکترین بخش اضافه می شود. زاویه بین نرمال های دو بخش باید کمتر از مقدار آستانه باشد θ. در طول آزمایشات، θتنظیم شد 30∘. شکل 6 نمونه ای از فرآیند همجوشی را نشان می دهد. قبل از اجرای فرآیند همجوشی، 32 قطعه از مرحله تقسیم بندی شناسایی شد ( شکل 6 a را ببینید). اکثر بخش ها کوچک هستند. پس از اعمال مرحله ادغام، تعداد قطعات از 32 به 9 کاهش یافت ( شکل 6 ب را ببینید). جدول 1 زمان های اجرای الگوریتم ما را با و بدون ادغام بخش های کوچک نشان می دهد که روی پنج مجموعه داده آزمایش شده است. در برخی موارد، زمان اجرا تقریبا به نصف کاهش می یابد. تفاوت زیاد در زمان اجرا بین مجموعه داده ها را می توان با تفاوت در چگالی ابرهای نقطه توضیح داد.

4.2. تست ها و مقایسه ها

آزمایشات ما بر روی هسته i7 نسل هشتم (1.8 گیگاهرتز در 8) با 8 گیگابایت رم انجام شد. شکل 7 برخی از مراحل را در تراز مجموعه داده Charlottebürgerturm با استفاده از LCP-4PCS نشان می دهد. این دو اسکن جزئی از بنای یادبود Charlottebürgerturm در برلین (آلمان) است. پس از تقسیم بندی، هر یک از اسکن ها (Scan1 در پیش زمینه و Scan2 در پس زمینه: به شکل 7 a مراجعه کنید) به ترتیب به 43 و 37 بخش تقسیم می شود ( شکل 7 ب را ببینید). همانطور که در شکل 7 نشان داده شده استج، اعمال روش ادغام، تعداد بخش ها را به 25 و 22 قطعه کاهش می دهد. نتیجه به دست آمده با استفاده از ماتریس تبدیل از تراز قطعه 1 هر اسکن تنها با دو بخش (بخش 1 از Scan1 و قطعه 1 از Scan2) مطابقت دارد، همانطور که در بخش های رنگی در شکل 7 d مشاهده می شود. این منجر به تراز اشتباه ابرهای 2 نقطه ای می شود، شکل 7 f را ببینید. تراز با استفاده از ماتریس تبدیل از بخش 5 (Scan1) و قطعه 14 (Scan2) بهترین نتیجه را با 8 تطبیق ایجاد می کند ( شکل 7 i را ببینید). در پایان فرآیند، ماتریس تبدیل حفظ شده، ماتریس تبدیلی است که از هم ترازی قطعه 5 (Scan1) و قطعه 14 (Scan2) حاصل می شود.
ما نتایج LCP-4PCS را با نتایج 4PCS خام در مجموعه داده های خود مقایسه کردیم. نتایج ترازهای ثبت شده توسط هر یک از روش ها در نمایش های رنگی در شکل 8 ارائه شده است . همانطور که مشاهده می شود، LCP-4PCS نتایج بسیار بهتری را برای هم ترازی ابر نقطه ای با همپوشانی کم ایجاد می کند. این با این واقعیت توضیح داده می شود که 4PCS به دنبال تراز کردن بیشترین تعداد نقاط است در حالی که LCP-4PCS ماتریس تبدیل را پیدا می کند که بیشترین تعداد بخش ها را تراز می کند. جدول 2تفاوت در نتایج دو روش را نشان می دهد و نشان می دهد که روش ما می تواند نتایج خوبی را در مجموعه داده های مختلف به دست آورد. زمان اجرای LCP-4PCS کوتاهتر از 4PCS است. این با زمان لازم برای تعیین بهترین نقاط تطبیق مورد نیاز برای محاسبه ماتریس تبدیل توضیح داده می شود، جدول 2 را ببینید . 4PCS نقاط منطبق را در کل ابر نقطه جستجو می کند در حالی که LCP-4PCS فقط بر روی بخش ها تمرکز می کند.
محدودیت. اگرچه روش ما برای هم ترازی ابر نقطه ای مناسب است، اما مشخص شد که بسیار وابسته به فرآیند تقسیم بندی است. تقسیم بندی ضعیف منجر به کیفیت تراز بد می شود. علاوه بر این، برای مجموعه‌های داده با نرخ همپوشانی نزدیک به 100٪، 4PCS ممکن است زمان اجرای سریع‌تری نسبت به LCP-4PCS داشته باشد. در این موارد، 4PCS به سرعت همگرا می شود در حالی که LCP-4PCS ابتدا با تقسیم بندی ابر نقطه ای و سپس ادغام بخش های کوچک پیش می رود.

5. نتیجه گیری ها

ما یک روش تراز ابر نقطه ای جدید (LCP-4PCS) را در این مقاله ارائه کردیم. همانطور که از نام آن پیداست، بر اساس روش 4PCS است. بر خلاف روش 4PCS که مشکلات هم ترازی ابر نقطه ای را به عنوان مشکل بزرگترین مجموعه نقاط مشترک (LCP) در نظر می گیرد، LCP-4PCS هم ترازی ابر نقطه را به عنوان بزرگترین مشکل مجموعه صفحه مشترک در نظر می گیرد. LCP-4PCS ابتدا ابرها را به بخش‌های مسطح تقسیم می‌کند، سپس از تراز بخش‌ها، تبدیل هندسی که بیشترین تعداد بخش‌ها را تراز می‌کند استخراج می‌شود.
LCP-4PCS برای حل مشکلاتی که هنگام تراز کردن ابرهای نقطه ای با نرخ همپوشانی کم با آن مواجه می شوند، پیشنهاد شد. از آنجایی که 4PCS بر اساس اصل تراز کردن بیشترین تعداد نقاط است، این رویکرد در مواردی که نرخ همپوشانی کم است، بی اثر می شود. از این رو ایده یافتن تبدیلی که بیشترین تعداد بخش ها را بین ابرهای نقطه تراز می کند، پیدا شد.
نتایج آزمایش‌ها بر روی مجموعه داده‌های ما نشان می‌دهد که LCP-4PCS در مواردی با همپوشانی کم بین ابرهای نقطه، نتایج با کیفیت بهتری در مقایسه با 4PCS تولید می‌کند. علاوه بر این، LCP-4PCS زمان اجرای کوتاه تری دارد. برای رسیدن به این نتیجه از 5 مجموعه داده استفاده کردیم.
نتایج به‌دست‌آمده از هم‌ترازی ابر نقطه‌ای با استفاده از LCP-4PCS به شدت به مرحله تقسیم‌بندی وابسته است. تقسیم بندی ضعیف ممکن است باعث تراز با کیفیت پایین شود. بنابراین، می توان از روش های تقسیم بندی بهتر با توجه به ویژگی های نقاط ابری استفاده کرد. کارهای آینده ما بر بهبود مرحله تقسیم بندی متمرکز خواهد بود.

منابع

  1. بوشه، اف. فورستر، ا. Valero, E. فناوری‌ها و کاربردهای نقشه برداری سه بعدی: ابرهای نقطه‌ای و فراتر از آن . دانشگاه هریوت وات: ادینبورگ، بریتانیا، 2015. [ Google Scholar ]
  2. دانشمند، م. حلمی، ع. آوتس، ای. نوروزی، ف. علیسیناناوغلو، ف. ارسلان، ح. گوربوا، جی. هامر، آر. اوزچینار، سی. عنبرجعفری، جی. اسکن سه بعدی: بررسی جامع. Scand. جی. برای. Res. 2018 ، 30 ، 73-86. [ Google Scholar ]
  3. آیگر، دی. میترا، نیوجرسی؛ Cohen-Or, D. مجموعه‌های متجانس 4 نقطه‌ای برای ثبت سطح دوتایی مقاوم. در مجموعه مقالات سی و پنجمین کنفرانس بین المللی گرافیک کامپیوتری و تکنیک های تعاملی (SIGGRAPH’08) تکنیک های تعاملی (SIGGRAPH’08)، لس آنجلس، کالیفرنیا، ایالات متحده آمریکا، 11–15 اوت 2008; جلد 27. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  4. بسل، پی جی؛ McKay, ND روشی برای ثبت اشکال سه بعدی. در مجموعه مقالات SPIE1611، Sensor Fusion IV: Control Paradigms and Data Structure, Boston, MA, USA, 12-15 نوامبر 1992. صص 239-255. [ Google Scholar ]
  5. هورن، ب. حل فرم بسته جهت گیری مطلق با استفاده از کواترنیون های واحد. ج. انتخاب Soc. A 1987 , 4 , 629-642. [ Google Scholar ] [ CrossRef ]
  6. پومرلو، اف. کولاس، اف. Siegwart, R. A Review of Point Cloud Registration Algorithms for Mobile Robotics. پیدا شد. ربات Trends. 2015 ، 4 ، 1-104. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  7. ملادو، ن. میترا، نیوجرسی؛ Aiger, D. Super 4PCS: ثبت جهانی سریع نقطه ابری از طریق نمایه سازی هوشمند. محاسبه کنید. نمودار. انجمن 2014 , 33 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  8. هوانگ، جی. Kwok، TH; Zhou, C. V4PCS: الگوریتم حجمی 4PCS برای ثبت جهانی. جی. مکانیک. دس 2017 139 . _ [ Google Scholar ] [ CrossRef ]
  9. نگوین، ا. Le, B. تقسیم بندی ابر نقطه سه بعدی: یک بررسی. در مجموعه مقالات ششمین کنفرانس IEEE 2013 در مورد رباتیک، اتوماسیون و مکاترونیک (RAM)، مانیل، فیلیپین، 12 تا 15 نوامبر 2013. ص 225-230. [ Google Scholar ] [ CrossRef ]
  10. لیمبرگر، اف. اولیویرا، ام. تشخیص بی‌درنگ مناطق مسطح در ابرهای نقطه‌ای سازمان‌یافته. تشخیص الگو 2015 , 48 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  11. گریلی، ای. منا، اف. Remondino، F. مروری بر الگوریتم های تقسیم بندی و طبقه بندی ابرهای نقطه ای. ISPRS Int. قوس. فتوگرام حسگر از راه دور اسپات. Inf. علمی 2017 ، XLII-2/W3 ، 339–344. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  12. هوبر، دی. هبرت، ام. ثبت مجموعه داده های سه بعدی کاملاً خودکار. تصویر Vis. محاسبه کنید. 2003 ، 21 ، 637-650. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  13. تعزیر، م.ال. گوخول، ت. چچین، پ. مالاتره، ال. Trassoudaine, L. CICP: Cluster Iterative Close Point for Sparse-Dense Point Cloud Registration. ربات. Auton. سیستم 2018 , 108 . [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  14. رنگاپراساد، ع. زوالوس، ن. واگدرگی، پ. Choset, H. ثبت با تعداد کمی از اندازه گیری های پراکنده. بین المللی ربات جی. Res. 2019 ، 38 ، 1403-1419. [ Google Scholar ] [ CrossRef ]
  15. هولز، دی. ایچیم، ا. تومبری، ف. روسو، ر. Behnke, S. ثبت با کتابخانه Point Cloud – یک چارچوب مدولار برای تراز کردن در سه بعدی. ربات IEEE. خودکار Mag. 2015 ، 22 ، 110-124. [ Google Scholar ] [ CrossRef ]
  16. فاوگراس، او. هبرت، ام. بازنمایی، شناسایی و مکان یابی اشیاء سه بعدی. بین المللی ربات جی. Res. IJRR 1986 ، 5 ، 27-52. [ Google Scholar ] [ CrossRef ]
  17. CloudCompare. نرم افزار GPL 2019. نسخه 2.10.3. در دسترس آنلاین: https://cloudcompare.org/ (در 28 ژوئن 2020 قابل دسترسی است).
  18. شرودر، دبلیو. مارتین، ک. Lorensen, B. The Visualization Toolkit , 4th ed.; Kitware: Clifton Park, NY, USA, 2009; شابک 978-1-930934-19-1. [ Google Scholar ]
  19. Rusu، RB; Cousins, S. 3D اینجاست: Point Cloud Library (PCL). در مجموعه مقالات کنفرانس بین المللی IEEE 2011 در مورد رباتیک و اتوماسیون، شانگهای، چین، 9 تا 13 مه 2011. صص 1-4. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  20. وو، ی. وانگ، دبلیو. لو، KQ; وی، وای. Chen, ZC روشی جدید برای ثبت مجموعه نقاط سه بعدی با نسبت همپوشانی کم. Procedia CIRP 2015 ، 27 ، 202-206. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  21. سلام.؛ لیانگ، بی. یانگ، جی. لی، اس. He, J. یک الگوریتم تکراری نزدیکترین نقاط برای ثبت ابرهای نقطه ای اسکنر لیزری سه بعدی با ویژگی های هندسی. Sensors 2017 ، 17 ، 1862. [ Google Scholar ] [ CrossRef ] [ PubMed ] [ نسخه سبز ]
  22. فرناندز مورال، ای. ریوز، پی. آروالو، وی. González-Jiménez، J. ثبت ساختار صحنه برای محلی سازی و نقشه برداری. ربات. Auton. سیستم 2015 , 75 . [ Google Scholar ] [ CrossRef ]
  23. فورستنر، دبلیو. خوشههم، ک. ثبت کارآمد و دقیق ابرهای نقطه با مطابقتهای صفحه به صفحه. در مجموعه مقالات کنفرانس بین المللی IEEE در بینایی کامپیوتر، ونیز، ایتالیا، 22 تا 29 اکتبر 2017؛ صص 2165–2173. [ Google Scholar ] [ CrossRef ]
  24. لی، ایکس. Guskov, I. ویژگی های چند مقیاسی برای تراز تقریبی سطوح مبتنی بر نقطه. در مجموعه مقالات سمپوزیوم در مورد پردازش هندسه، وین، اتریش، 4-6 ژوئیه 2005; ص 217-226. [ Google Scholar ]
  25. گلفاند، ن. میترا، ن. گیباس، ال. Pottmann, H. ثبت جهانی قوی. در مجموعه مقالات سمپوزیوم در مورد پردازش هندسه، وین، اتریش، 4 تا 6 ژوئیه 2005. [ Google Scholar ]
  26. بیبر، پ. Straßer, W. The Normal Distributions Transform: رویکردی جدید برای تطبیق اسکن لیزری. در مجموعه مقالات کنفرانس بین المللی IEEE/RSJ 2003 در مورد ربات ها و سیستم های هوشمند (IROS 2003) (شماره گربه 03CH37453)، لاس وگاس، NV، ایالات متحده، 27-31 اکتبر 2003. جلد 3، ص 2743–2748. [ Google Scholar ] [ CrossRef ]
  27. مگنوسون، ام. لیلینتال، ا. Duckett, T. ثبت نام برای وسایل نقلیه معدنی خودمختار با استفاده از 3D-NDT. ربات صحرایی جی. 2007 ، 24 ، 803-827. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  28. روسو، ر. بلودو، ن. Beetz, M. Fast Point Feature Histograms (FPFH) برای ثبت سه بعدی. در مجموعه مقالات کنفرانس بین المللی IEEE 2009 در مورد رباتیک و اتوماسیون، کوبه، ژاپن، 12-17 مه 2009. صص 3212–3217. [ Google Scholar ] [ CrossRef ]
  29. روسو، ر. بلودو، ن. مارتون، ز. Beetz، M. تراز کردن نماهای ابر نقطه ای با استفاده از هیستوگرام های ویژگی پایدار. در مجموعه مقالات کنفرانس بین المللی IEEE/RSJ 2008 در مورد ربات ها و سیستم های هوشمند، نیس، فرانسه، 22 تا 26 سپتامبر 2008. صص 3384-3391. [ Google Scholar ] [ CrossRef ]
  30. آمبول، سی. چاکرابورتی، اس. Gärtner, B. محاسبه بزرگترین مجموعه نقاط مشترک تحت همخوانی تقریبی. در سمپوزیوم اروپایی الگوریتم ها ; Springer: برلین/هایدلبرگ، آلمان، 2000; جلد 1879، ص 52-63. [ Google Scholar ] [ CrossRef ]
  31. داگوم، ال. Menon, R. OpenMP: یک API استاندارد صنعتی برای برنامه نویسی با حافظه مشترک. محاسبه کنید. علمی مهندس IEEE 1998 ، 5 ، 46-55. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  32. بالادو فریاس، ج. دیاز ویلارینو، ال. آریاس، پ. گونزالس، اچ. طبقه بندی خودکار عناصر زمین شهری از داده های اسکن لیزری سیار. خودکار ساخت و ساز 2018 ، 86 ، 226-239. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Ijgi 09 00647 g001 550
شکل 1. رویکرد کلی برای ثبت ابر نقطه: اجازه دهید P و Q دو مجموعه از نقاط همپوشانی در دو فضای مختلف باشند. P و Q با استفاده از مراحل زیر در یک فضا تراز می شوند: 1-دو مجموعه از نقاط متناظر را پیدا کنید. پ”و س”در P و Q به ترتیب; 2- تبدیل T را طوری محاسبه کنید که تی(پ”)=س”; 3- از T برای تراز کردن P و Q استفاده کنید (اعمال کنید تی(پ)).
Ijgi 09 00647 g002 550
شکل 2. نسبت ثابت آفین برای 4 نقطه متجانس. با توجه به نقاط از سطح S ، اجازه دهید نقاط آ،ب،ج،دهمسطح باشند و خطوط آبو جددر نقطه e ملاقات کنید . نسبت ها r1=||آ-ه||/||آ-ب||و r2=||ج-ه||/||ج-د||تحت هر تبدیل آفین حفظ می شوند. اگر T سطح دیگری است که (تا حدی) با S مطابقت دارد و قاعده همسطح 4 نقطه ای در ناحیه همپوشانی قرار دارد، مجموعه نقاط متناظر از T همسطح هستند و روابط زیر را برآورده می کنند: ||پ1-ه”||/||پ1-پ2||=r1و ||q1-ه”||/||q1-q2||=r2.
Ijgi 09 00647 g003 550
شکل 3. رویکرد کمک شده توسط تقسیم بندی گرافیکی کاربر: ( الف ) موقعیت های اولیه ابرهای نقطه ای. ( ب ) بخش های تقسیم شده (توسط کاربر)؛ ( ج ) نتیجه با استفاده از 4PCS (100 تکرار) بدون تقسیم‌بندی کاربر. ( د ) نتیجه با استفاده از تبدیل صلب از 4PCS (20 تکرار) در بخش‌های تقسیم‌بندی شده انجام می‌شود.
Ijgi 09 00647 g004 550
شکل 4. LCP-4PCS: اجازه دهید دو نقطه ابرها اسجآn1و اسجآn2دو اسکن همپوشانی جزئی یا کامل از یک شی باشد. برای تراز کردن اسجآn1به اسجآn2، LCP-4PCS به صورت زیر عمل می کند: بخش ها اسجآn1و اسجآn2داخل هواپیما؛ به طور مکرر 4PCS را برای تراز کردن جداگانه اعمال می کند اسجآn1بخش به اسجآn2بخش ها در هر تکرار، از تبدیل استفاده می کند تیمناز فرآیند 4PCS برای یافتن مجموعه ای از بخش های مربوطه با اعمال تیمنبه اسجآn1بخش ها در نهایت از تبدیل T از مرحله قبل استفاده می کند که بزرگترین مجموعه صفحات متناظر را بین آنها ایجاد می کند اسجآn1بخش ها و اسجآn2بخش ها برای تراز کردن اسجآn1و اسجآn2(اعمال میشود تی(اسجآn1)).
Ijgi 09 00647 g005 550
شکل 5. جمع آوری ابرهای نقطه ای: ( الف ) سیستم دوربین های استریو، ( ب ) دوربین در حال عمل در زمین در طول اسکن مجموعه داده “Charlottebürgerturm” در برلین (آلمان).
Ijgi 09 00647 g006 550
شکل 6. نمونه ای از همجوشی صفحات کوچک پس از تقسیم بندی.
Ijgi 09 00647 g007 550
شکل 7. برخی از مراحل همراستایی مجموعه داده “CharlotteBürgerturm” با LCP-4PCS: ( الف ) موقعیت اولیه اسکن ها، ( ب ) نتیجه تقسیم بندی Scan1 (پیش زمینه) 43 بخش و Scan2 (پس زمینه) 37 بخش، ( ج ) نتیجه ادغام Scan1 (25 بخش) و Scan2 (22 بخش)، ( د ) نمایش اولین بخش از اسکن ها، ( ه ) ماتریس تبدیل از تراز اولین بخش ها، ( f ) نتیجه تراز با استفاده از ماتریس در “e” ” (تعداد قطعه منطبق: 1)، ( g ) بخش نمایش 8 (Scan1) و قطعه13 (Scan2)، ( h ) ماتریس تبدیل از تراز قطعه 5 و قطعه 14، ( i)) نتیجه تراز با استفاده از ماتریس در “h” (تعداد بخش های منطبق: 8).
Ijgi 09 00647 g008 550
شکل 8. نتیجه ترازهای ابر نقطه ای به ترتیب در مجموعه داده Camertronix، مجموعه داده CharlotteBürgerturm، مجموعه داده Valentino و مجموعه داده Buro از بالا به پایین. ستون اول: موقعیت اولیه ابرهای نقطه. ستون دوم: نتایج ترازها با 4PCS، ستون سوم: نتایج ترازها با استفاده از LCP-4PCS

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید