یک رگرسیون موازی وزندار جغرافیایی مبتنی بر CUDA برای دادههای جغرافیایی در مقیاس بزرگ
خلاصه
CUDA ; GWR ; محاسبات موازی ; داده های جغرافیایی در مقیاس بزرگ
1. معرفی
2. مدل GWR و الگوریتم اتمیزاسیون
2.1. بررسی GWR
2.1.1. مدل GWR
مدل GWR OLR را گسترش میدهد و فاکتور مکان را برای بیان تغییرات فضایی ضرایب معرفی میکند. به عبارت دیگر موارد زیر را داریم:
جایی که yمن��متغیر رگرسیون (متغیر وابسته) در مکان i است ، (تومن،vمن)(��,��)مختصات (معمولاً طول و عرض جغرافیایی) اولین نقطه نمونه در منطقه مورد مطالعه را نشان می دهد. βمتر(تومن،vمن)��(��,��)نشان دهنده ضریب k امین نقطه نمونه بر اساس تابعی با متغیرهای مستقل است تومن��و vمن��، ایکسمن _���m امین متغیر پیش بینی کننده (متغیر مستقل) را بیان می کند و εمن��عبارت خطا را نشان می دهد و n حجم نمونه است. شرایط لازم برای رابطه (2) را می توان به صورت زیر بیان کرد:
برای سادگی، معادله (1) به صورت خلاصه شده است
متغیرهای مربوط به GWR را می توان در قالب ماتریس تعریف کرد. ماتریس متغیر مستقل X�با فرم زیر قابل محاسبه است:
2.1.2. تابع هسته وزن فضایی
وجود دارد n�شرایط وزن فضایی wij���بین دو نقطه نمونه ( i=j�=�مجاز است) در منطقه مورد مطالعه. در مدل GWR معمولاً نشان دادن ماتریس وزن است Wi��به عنوان یک ماتریس مربع مورب:
در حال حاضر، اشکال مختلفی از تابع هسته وزن وجود دارد wij���، و بیشترین استفاده را Bi-Square و Gaussian می کنند. دو تابع را می توان به صورت معادلات (6) و (7) بیان کرد:
جایی که dij���نشان دهنده فاصله بین دو نقطه نمونه ( i�و jj) و bw��پارامتر پهنای باند را نشان می دهد که می تواند نه تنها به عنوان آستانه همسایگان بلکه به عنوان ضریب تضعیف فاصله در تابع هسته وزن تفسیر شود.
2.1.3. رگرسیون مدل
برآورد ضریب رگرسیون β^i�^�در موقعیت i�تعریف شده است
مقدار رگرسیون Y^من�^�از نقطه رگرسیون من�بر اساس β^من�^�می توان از آن تخمین زد
جایی که ایکسمن��نشان دهنده بردار ردیف i در ماتریس استایکس�. ماتریس کلاه نقش بسیار مهمی در تحلیل باقیمانده مدل رگرسیون خطی دارد. این مطالعه به معرفی ماتریس کلاه می پردازد اس�به GWR. ماتریکس اس�را می توان به صورت زیر بیان کرد:
2.1.4. معیارهای انتخاب پهنای باند بهینه
کلید کشف پهنای باند بهینه b w��در حال به حداقل رساندن است یک Iسیج����نمره. روش های انتخاب حلقه و انتخاب طلایی برای به دست آوردن کمترین در دسترس هستند یک Iسیج����ارزش. جستجوی پهنای باند بهینه b w��از معیار تخمین پارامتر جدایی ناپذیر است. معیار یک Iسیج����[ 29 ] توسط Brunsdon و همکاران معرفی شده است. (2002) [ 30 ] برای انتخاب پهنای باند بهینه تابع وزن. فرمول خاص را می توان به صورت بیان کرد
باقی مانده ε�را می توان با داده های نمونه محاسبه کرد Y�و نتیجه رگرسیون Y^�^:
برآورد بی طرفانه واریانس خطای تصادفی به صورت بیان شده است σ^2�^2:
جایی که RSS مجموع مجذور باقیمانده ها را نشان می دهد، t r ( S)��(�)ردی از ماتریس کلاه است اس�، و n – 2 t r ( S) + t r (استیاس)�−2��(�)+��(���)درجه آزادی موثر GWR را نشان می دهد. در بیشتر موارد، t r (استیاس)��(���)تقریبا برابر است t r ( S)��(�)( t r (استیاس) ≈tr ( S)��(���)≈��(�)، و بدین ترتیب، معادله (14) فوق را می توان به صورت ساده سازی کرد
2.2. اتمیزه کردن مدل GWR
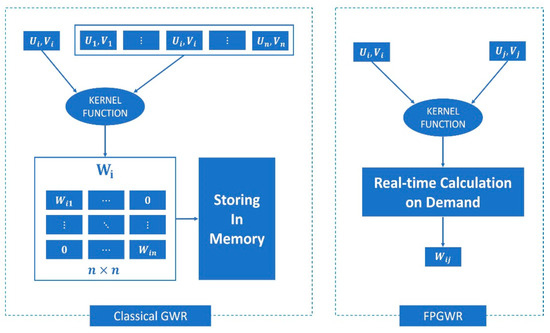
همانطور که در بالا ذکر شد، فرآیند رگرسیون مدل GWR شامل دو مرحله ثابت است: انتخاب پهنای باند بهینه و تشخیص مدل. اکثر بسته های موجود که الگوریتم GWR را پیاده سازی کرده اند توسط حالت سریال پشتیبانی می شوند. در مقایسه با حالت موازی، حالت سریال پیامدهای نامطلوبی برای محاسبه رگرسیون دارد. ظروف محاسباتی با توان محاسباتی نامتناهی با نمونه های بسیار بزرگ بارگذاری می شوند. زمان اجرا همراه با رشد اندازه نمونه، به دنبال یک توان یا حتی یک رابطه نمایی [ 31 ] بوجود می آید. در این مقاله، این یک راه حل عملی برای طراحی الگوریتم 1 (اتمیزه کردن) در کاهش پیچیدگی محاسبه رگرسیون GWR است.
| الگوریتم 1 فرآیند اتمی – حداقل واحد الگوریتم ها. |
فرآیند اتمی: بهینه سازی جستجوی پهنای باند با به حداقل رساندن امتیاز AIC
|
2.2.1. ماتریس متوسط
OLR را می توان با فرم ماتریس زیر محاسبه کرد:
بر اساس OLS، ضریب رگرسیون β^�^برآورد می شود از
بعد، نتیجه رگرسیون Y^�^OLR را می توان به صورت زیر بیان کرد:
با تجزیه و تحلیل جامع معادلات (8)، (9)، (17)، و (18)، میتوان ماتریس میانی را پیدا کرد. M�که در تمام مدل های رگرسیون تخمین بی طرفانه از طریق OLS وجود دارد. با موارد زیر قابل محاسبه است:
ماتریس XT��را می توان با تعریف کرد
که در آن p تعداد متغیرهای مستقل است. ضرب ماتریس XT��و ماتریس مربع مورب Wi��خاص است ماتریس حاصل A�را می توان به صورت زیر بیان کرد:
به طور مشابه، ماتریس B�را می توان به صورت نوشتاری
جایی که ماتریس B�یک ماتریس مربع با p+1�+1ابعاد در کاربردهای عملی، p+1�+1معمولا کمتر از 10 است ، به این معنی که نادیده گرفتن زمان صرف شده توسط عملیات معکوس برای ماتریس قانونی است. B�.
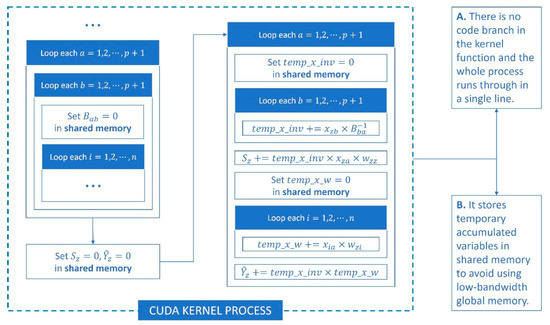
2.2.2. پیاده سازی الگوریتم اتمیزاسیون
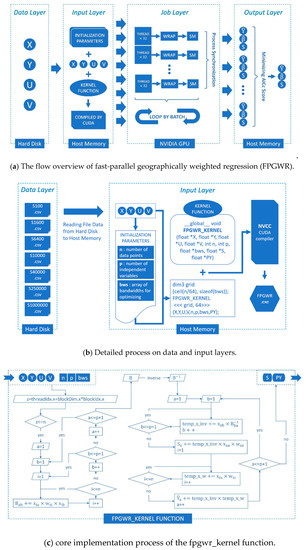
3. CUDA Enabled FPGWR
3.1. بهینه سازی عملکرد هسته CUDA
3.2. پیاده سازی FPGWR بر اساس CUDA
4. نتایج و بحث
4.1. منبع اطلاعات
4.1.1. مجموعه داده های شبیه سازی
منطقه آزمایش به صورت یک مساحت مربع [ 34 ] با نمایش داده می شودl�طول اضلاع، که در آن نقاط نمونه به طور مساوی توزیع می شوند. پس از تنظیم اندازه نمونه هر ردیف به c�، تعداد کل نمونه ها را می توان به صورت بیان کرد n=c×c�=�×�. فاصله بین دو نمونه مجاور با محاسبه می شود Δl=l/(c−1)Δ�=�/(�−1). گوشه پایین سمت چپ به عنوان مبدا سیستم مختصات تعریف می شود. بیان برای محاسبه موقعیت نمونه ها توسط
که در آن mod مخفف تابع باقی مانده است و کف نشان دهنده تابع گرد کردن است.
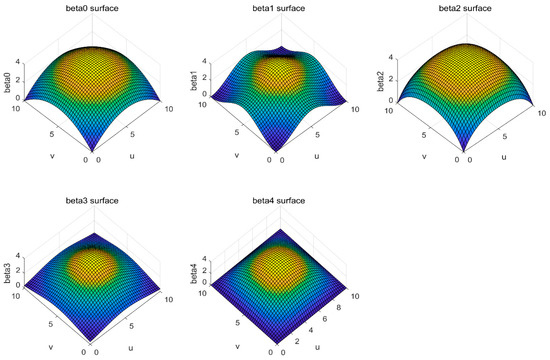
داده های نمونه توسط مدل GWR زیر تولید می شود. در رابطه (24) به صورت زیر از پیش تعریف شده است:
برای یکسان سازی ابعاد ضرایب رگرسیون β�، همه مقادیر به بازه محدود می شوند (0,βmax)(0,����)( βmax����ثابت ثابت است). ضرایب β�5 عملکرد را به شرح زیر دنبال کنید :
4.1.2. مجموعه داده تست Zillow
مجموعه داده تست Zillow [ 26 ] زیرمجموعه ای از مجموعه داده های دارایی Zillow است که از اطلاعات مسکن یک خانواده در منطقه شهری لس آنجلس تشکیل شده است. بیان ریاضی مجموعه داده به صورت معادله (30) بیان می شود. مجموعه داده به همراه الگوریتم FastGWR در GitHub منبع باز است ( https://github.com/Ziqi-Li/FastGWR ). این مقاله هشت مجموعه داده (1 k، 2 k، 5 k، 10 k، 15 k، 20 k، 50 k و 100 k) را برای آزمایش مقایسه ای از مخزن GitHub دانلود کرده است.
4.1.3. مجموعه داده گرجستان
مجموعه داده جورجیا [ 33 ] شامل زیرمجموعه ای (ویژگی های جمعیتی-اجتماعی) از سرشماری 1990 ایالات متحده در ایالت جورجیا است. مختصات نقاط داده در مرکز شهرستان ها تنظیم می شود، بنابراین 159 رکورد حاوی ویژگی های جمعیت شهرستان در مجموعه داده وجود دارد. مدل را می توان به صورت معادله (31) تعریف کرد:
4.2. تست مشخصات و محیط
4.3. نتایج
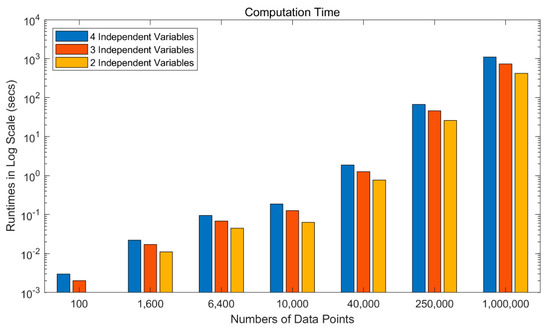
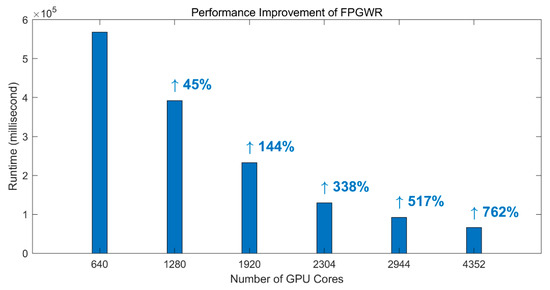
4.3.1. عملکرد FPGWR
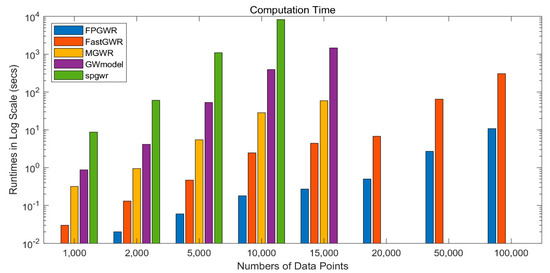
4.3.2. مقایسه FPGWR و سایر GWR
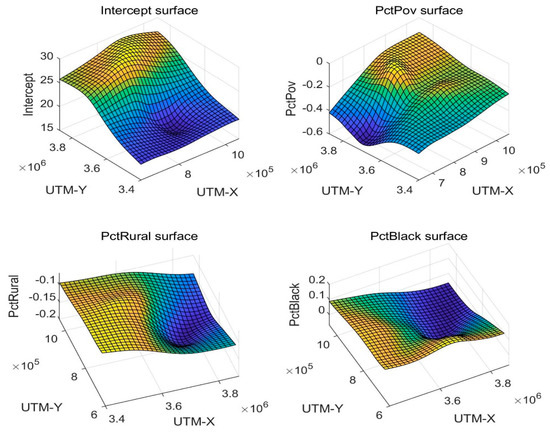
4.3.3. اعتبارسنجی دقت نتیجه
4.4. بحث
4.4.1. حافظه
4.4.2. زمان
5. نتیجه گیری ها
منابع
- توچ، ای. لرنر، بی. بن زیون، ای. بن گال، I. تجزیه و تحلیل داده های تحرک انسان در مقیاس بزرگ: بررسی روش ها و کاربردهای یادگیری ماشین. بدانید. Inf. سیستم 2019 ، 58 ، 501-523. [ Google Scholar ] [ CrossRef ]
- وکستروم، سی. کوجالا، آر. ملادنوویچ، MN; ساراماکی، جی. ارزیابی انتقال در مقیاس بزرگ در شبکه های حمل و نقل عمومی با استفاده از داده های جدول زمانی باز: مورد گسترش مترو هلسینکی. J. Transp. Geogr. 2019 ، 79 ، 102470. [ Google Scholar ] [ CrossRef ]
- هیکس، جی ال. آلتوف، تی. سوسیچ، ر. کوهار، پ. بوستیانچیچ، بی. کینگ، AC; Leskovec، J. Delp، SL بهترین روشها برای تجزیه و تحلیل دادههای بهداشتی در مقیاس بزرگ از ابزارهای پوشیدنی و برنامههای گوشیهای هوشمند. رقم NPJ. پزشکی 2019 ، 2 ، 1-12. [ Google Scholar ] [ CrossRef ]
- تاسار، اُ. تارابالکا، ی. Alliez, P. یادگیری افزایشی برای تقسیم معنایی داده های سنجش از دور در مقیاس بزرگ. IEEE J. Sel. بالا. Appl. زمین Obs. Remote Sens. 2019 , 12 , 3524–3537. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- لی، ز. هوانگ، Q. جیانگ، ی. Hu, F. SOVAS: یک سیستم تحلیلی بصری آنلاین مقیاس پذیر برای تجزیه و تحلیل داده های آب و هوایی بزرگ. بین المللی جی. جئوگر. Inf. علمی 2020 ، 34 ، 1188-1209. [ Google Scholar ] [ CrossRef ]
- میلر، اچ جی; Goodchild، جغرافیای داده محور MF. GeoJournal 2015 ، 80 ، 449-461. [ Google Scholar ] [ CrossRef ]
- شیا، جی. هوانگ، اس. ژانگ، اس. لی، ایکس. لیو، جی. شیو، دبلیو. Tu, W. DAPR-tree: یک طرح نمایه سازی داده های مکانی توزیع شده با الگوهای دسترسی به داده ها برای حمایت از طرح های Digital Earth. بین المللی جی دیجیت. زمین 2020 ، 1-16. [ Google Scholar ] [ CrossRef ]
- آجی، ع. وانگ، اف. وو، اچ. لی، آر. لیو، کیو. ژانگ، ایکس. Saltz, J. Hadoop-GIS: یک سیستم ذخیره سازی داده های مکانی با کارایی بالا بر روی MapReduce. در مجموعه مقالات کنفرانس بین المللی VLDB Endowment در مورد پایگاه های داده بسیار بزرگ، ترنتو، ایتالیا، 26 تا 30 اوت 2013. جلد 6. [ Google Scholar ]
- وو، QY; سو، KY؛ Zou، ZJ یک روش مبتنی بر کاهش نقشه برای محاسبه موازی مبدا و مقصد مسافران اتوبوس از دادههای حمل و نقل عظیم. J. Geo Inf. علمی 2018 ، 20 ، 647-655. [ Google Scholar ]
- ویلکینسون، بی. Allen, M. برنامه نویسی موازی ; Prentice Hall: Upper Saddle River، نیوجرسی، ایالات متحده آمریکا، 1999. [ Google Scholar ]
- گونگ، ز. تانگ، دبلیو. بنت، دی. Thill، J.-CF شبیهسازی مبتنی بر عامل موازی از تعاملات فضایی در سطح فردی در یک محیط محاسباتی چند هستهای. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 1152-1170. [ Google Scholar ] [ CrossRef ]
- تانگ، دبلیو. فنگ، دبلیو. جیا، ام. تجزیه و تحلیل الگوی نقطه فضایی بسیار موازی: تابع K ریپلی با استفاده از واحدهای پردازش گرافیکی شتاب گرفت. بین المللی جی. جئوگر. Inf. علمی 2015 ، 29 ، 412-439. [ Google Scholar ] [ CrossRef ]
- ژانگ، جی. زو، تبر; Huang، Q. یک رویکرد برآورد چگالی هسته تطبیقی با شتاب GPU برای تجزیه و تحلیل الگوی نقطه ای کارآمد در داده های بزرگ فضایی. بین المللی جی. جئوگر. Inf. علمی 2017 ، 31 ، 2068–2097. [ Google Scholar ] [ CrossRef ]
- ساندریک، آی. ایونیتا، سی. چیتو، ز. داردالا، م. ایریمیا، ر. Furtuna، FT استفاده از CUDA برای تسریع مدلسازی انتشار عدم قطعیت برای ارزیابی حساسیت زمین لغزش. محیط زیست مدل. نرم افزار 2019 ، 115 ، 176-186. [ Google Scholar ] [ CrossRef ]
- استویانوویچ، ن. Stojanovic، D. موازی سازی الگوریتم انباشت جریان چندگانه با استفاده از cuda و openacc. ISPRS Int. J. Geo Inf. 2019 ، 8 ، 386. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- پی، تی. آهنگ، سی. گوا، اس. شو، اچ. لیو، ی. دو، ی. ما، تی. ژو، سی. استخراج داده های جغرافیایی بزرگ: هدف، مفاهیم و مسائل تحقیقاتی. جی. جئوگر. علمی 2020 ، 30 ، 251-266. [ Google Scholar ] [ CrossRef ]
- براندون، سی. Fotheringham، AS; چارلتون، ME رگرسیون وزندار جغرافیایی: روشی برای کاوش غیرایستایی فضایی. Geogr. مقعدی 1996 ، 28 ، 281-298. [ Google Scholar ] [ CrossRef ]
- ژانگ، پی. یانگ، دی. ژانگ، ی. لی، ی. لیو، ی. سن، ی. ژانگ، دبلیو. گنگ، دبلیو. رانگ، تی. لیو، ی. و همکاران بررسی مجدد نیروهای محرک آلودگی فاضلاب صنعتی چین بر اساس مدل GWR در سطح استان. جی. پاک. تولید 2020 , 262 , 121309. [ Google Scholar ] [ CrossRef ]
- وو، دی. روابط متفاوت مکانی و زمانی بین ردپای اکولوژیکی و عوامل مؤثر در استانهای چین با استفاده از رگرسیون وزندار جغرافیایی (GWR). جی. پاک. تولید 2020 ، 261 ، 121089. [ Google Scholar ] [ CrossRef ]
- یوان، ی. غار، م. خو، اچ. ژانگ، سی. کاوش روابط فضایی متغیر بین سرب و آل در خاک های شهری لندن در مقیاس منطقه ای با استفاده از رگرسیون وزنی جغرافیایی (GWR). جی. هازارد. ماتر 2020 , 393 , 122377. [ Google Scholar ] [ CrossRef ]
- هونگ، آی. Yoo, C. تجزیه و تحلیل واریانس فضایی عوامل تعیین کننده قیمت Airbnb با استفاده از رویکرد چند مقیاسی GWR. Sustainability 2020 , 12 , 4710. [ Google Scholar ] [ CrossRef ]
- وو، اس. وانگ، ز. دو، ز. هوانگ، بی. ژانگ، اف. لیو، آر. رگرسیون وزنی شبکه عصبی از نظر جغرافیایی و زمانی برای مدلسازی روابط غیر ثابت فضایی و زمانی. بین المللی جی. جئوگر. Inf. علمی 2020 ، 1–27. [ Google Scholar ] [ CrossRef ]
- بیوند، ر. یو، دی. ناکایا، تی. گارسیا لوپز، MA Package SPGWR ; بسته نرم افزاری R; بنیاد R برای محاسبات آماری: وین، استرالیا، 2020. [ Google Scholar ]
- گولینی، آی. لو، بی. چارلتون، M. GWmodel: یک بسته R برای کاوش ناهمگونی فضایی با استفاده از مدلهای وزندار جغرافیایی. J. Stat. نرم افزار 2015 ، 63 ، 1-50. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- اوشان، TM; لی، ز. کانگ، دبلیو. ولف، ال جی. Fotheringham، AS mgwr: پیادهسازی پایتون از رگرسیون وزندار جغرافیایی چند مقیاسی برای بررسی ناهمگونی و مقیاس فضایی فرآیند. ISPRS Int. J. Geo Inf. 2019 ، 8 ، 269. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- لی، ز. Fotheringham، AS; لی، دبلیو. Oshan, T. Fast Geographically Weighted Regression (FastGWR): یک الگوریتم مقیاس پذیر برای بررسی ناهمگونی فرآیند فضایی در میلیون ها مشاهده. بین المللی جی. جئوگر. Inf. علمی 2019 ، 33 ، 155-175. [ Google Scholar ] [ CrossRef ]
- Tran، HT; نگوین، اچ تی. Tran، VT رگرسیون وزندار جغرافیایی در مقیاس بزرگ در Spark. در مجموعه مقالات هشتمین کنفرانس بین المللی دانش و مهندسی سیستم ها (KSE) 2016، هانوی، ویتنام، 6 تا 8 اکتبر 2016؛ صص 127-132. [ Google Scholar ]
- فاستر، SA; Gorr، WL یک فیلتر تطبیقی برای تخمین پارامترهای متغیر مکانی: کاربرد برای مدلسازی ساعات پلیس صرف شده در پاسخ به تماسهای خدمات. مدیریت علمی 1986 ، 32 ، 878-889. [ Google Scholar ]
- Akaike, H. نگاهی جدید به شناسایی مدل آماری. IEEE Trans. خودکار کنترل 1974 ، 19 ، 716-723. [ Google Scholar ]
- براندون، سی. Fotheringham، AS; چارلتون، ام. آمار خلاصه وزنی جغرافیایی – چارچوبی برای تجزیه و تحلیل داده های اکتشافی محلی. محاسبه کنید. محیط زیست سیستم شهری 2002 ، 26 ، 501-524. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- هریس، آر. سینگلتون، ا. گروس، دی. براندسون، سی. Longley، P. رگرسیون وزنی جغرافیایی توانمند گرید: مطالعه موردی مشارکت در آموزش عالی در انگلستان. ترانس. GIS 2010 ، 14 ، 43-61. [ Google Scholar ]
- شرکت انویدیا محاسبه معماری دستگاه یکپارچه (CUDA). در دسترس آنلاین: https://developer.nvidia.com/cuda-toolkit (در 6 اکتبر 2020 قابل دسترسی است).
- Fotheringham، AS; براندون، سی. چارلتون، ام. رگرسیون وزندار جغرافیایی: تحلیل روابط متغیر فضایی . جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2002. [ Google Scholar ]
- ژانگ، اچ. Mei, C. برآورد حداقل انحراف مطلق محلی مدلهای ضریب متغیر مکانی: رویکردهای رگرسیون وزندار جغرافیایی قوی. بین المللی جی. جئوگر. Inf. علمی 2011 ، 25 ، 1467-1489. [ Google Scholar ]
- مشتاق، DL; زهورجان، ج. Lazowska، ED Speedup در مقابل بهره وری در سیستم های موازی. IEEE Trans. محاسبه کنید. 1989 ، 38 ، 408-423. [ Google Scholar ]
- یانگ، ال. سان، ایکس. Li, Z. چارچوبی کارآمد برای پردازش موازی سنجش از دور: ادغام الگوریتم کلونی زنبورهای مصنوعی و فناوری چند عاملی. Remote Sens. 2019 , 11 , 152. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]






بدون دیدگاه