یک روش سریع جدید برای محاسبات Viewshed در DEM از طریق حداکثر ادغام و حداقل ارتفاع مورد انتظار

خلاصه

محاسبات نمای یک مدل رقومی ارتفاع (DEM) نقش مهمی در یک سیستم اطلاعات جغرافیایی ایفا می کند، اما زمان محاسباتی بالای مورد نیاز یک مشکل جدی برای کاربرد عملی است. تاکنون، روش‌های اصلی محاسبات viewshed شامل روش خط دید، روش صفحات مرجع، و غیره است. بر اساس این الگوریتم‌های کلاسیک، یک الگوریتم جدید برای محاسبات viewshed در این مقاله پیشنهاد شده است: الگوریتم عروسک ماتریوشکا.
دوره-آموزش-حرفه-ای-gis
از طریق یک عملیات ادغام، حداقل ارتفاع مورد انتظار DEM به عنوان حداکثر ادغام با حداقل ارتفاع مورد انتظار در بهینه سازی محاسبات دیدگاه معرفی می شود. این برای افزایش کارایی و سازگاری محاسبه محدوده دید است. نتایج تجربی نشان می دهد که الگوریتم مزایای آشکاری در سرعت محاسبات دارد.

کلید واژه ها:

محاسبات viewshed ; DEM ; حداکثر جمع آوری ; حداقل ارتفاع مورد انتظار

چکیده گرافیکی

1. معرفی

محاسبات Viewshed رابطه بصری بین نقاط روی یک نقطه مشاهده جغرافیایی خاص را تعیین می کند [ 1 ]. به طور گسترده ای در زمینه های مختلفی مانند سیستم اطلاعات جغرافیایی (GIS) [ 1 ]، مدیریت منظر [ 2 ]، ارزیابی چشم انداز [ 3 ] و ناوبری [ 4 ] و سایر موارد [ 5 ] استفاده شده است. به عنوان مثال، با استفاده از تجزیه و تحلیل دیدگاه، می توان مناطق مرئی و نامرئی را از مدل های رقومی ارتفاع (DEMs) در مناطق کوهستانی تشخیص داد و مقیاس منطقه را برای اقدامات جنگلی برای بهبود اثر مناظر کوهستانی تعیین کرد [6] .]. در سال های اخیر با تحقیق و توسعه بیشتر در تئوری و کاربردهای مرتبط، روش های موجود به نتایج خوبی دست یافته اند. با این حال، کاستی های بسیار کمی نیز وجود دارد. الگوریتم‌های تحلیل دیدگاه کنونی به‌ویژه با داده‌های زمین فضایی در مقیاس بزرگ بسیار زمان‌بر هستند [ 7 ]. اشکال دیگر این است که این الگوریتم‌ها از ویژگی‌های زمین برای ساده‌سازی محاسبات مربوطه استفاده کامل نمی‌کنند.
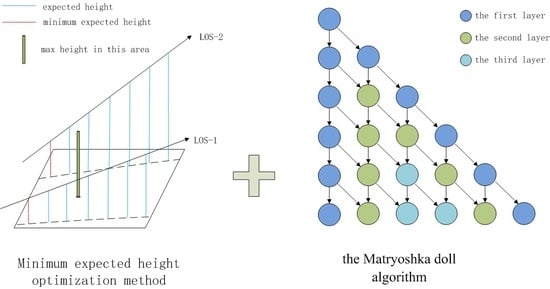
در این مقاله، یک روش محاسباتی جدید پیشنهاد شده است که تأثیر زمین بر روی دید را در نظر می‌گیرد و مفهوم حداکثر عملیات جمع‌آوری و حداقل ارتفاع مورد انتظار را برای بهبود کارایی محاسبه دامنه بصری معرفی می‌کند. مشارکت های این مقاله به شرح زیر است. ابتدا، مشابه یادگیری عمیق، حداکثر ادغام DEM معرفی می شود و همراه با حداقل ارتفاع مورد انتظار، کارایی محاسباتی viewshed بهبود می یابد. تا آنجا که می دانیم، ما اولین کسی هستیم که حداکثر جمع آوری را در محاسبات viewshed معرفی می کنیم. دوم، یک الگوریتم viewshed ساده شده به نام عروسک Matryoshka توسعه داده شد.
بقیه این مقاله به شرح زیر سازماندهی شده است. در بخش 2 ، ما ساختار داده را برای نمایش یک سطح ارائه می کنیم و برخی از الگوریتم های مهم را برای محاسبات viewshed مرور می کنیم. در بخش 3 ، الگوریتم پیشنهادی و مراحل اجرای آن را شرح می‌دهیم. بخش 4 به طور تجربی عملکرد بین الگوریتم پیشنهادی و الگوریتم‌های موجود را مقایسه می‌کند. در نهایت، نتیجه‌گیری و راه‌های تحقیقات آتی در بخش 5 ارائه شده است .

2. کارهای مرتبط

2.1. نمایندگی زمین

در یک سیستم GIS، نمایش‌های مختلفی از یک سطح وجود دارد، اما شبکه‌های مستطیلی و شبکه‌های نامنظم مثلثی (TIN)، همانطور که در شکل 1 [ 8 ] نشان داده شده است، بیشترین استفاده را دارند.
DEM یک شبیه‌سازی دیجیتالی از زمین با استفاده از داده‌های ارتفاعی محدود (یعنی بیان دیجیتالی مورفولوژی سطح زمین) است، همانطور که در شکل 2 نشان داده شده است . از مجموعه ای از آرایه های عددی مرتب شده برای نشان دادن ارتفاع زمین استفاده می کند که به طور گسترده در سراسر ژئومورفولوژی استفاده می شود [ 9 ]. این شاخه ای از مدل های دیجیتال زمین است. تمام مقادیر دیگر ویژگی زمین را می توان از DEM مشتق کرد.
شبکه مستطیلی منظم مجموعه داده مقادیر ارتفاع در موقعیت مختصات صفحه است [ 10 ]. مزیت شبکه مستطیلی DEM این است که ظرفیت ذخیره سازی آن به راحتی فشرده و ذخیره می شود که استفاده و مدیریت آن را آسان می کند [ 11]]. از سوی دیگر، از آنجایی که هر نقطه ای که TIN را تشکیل می دهد، داده اصلی است، TIN از از دست دادن دقت درون یابی جلوگیری می کند. بنابراین، می توان از آن برای تخمین نقاط ویژگی و خطوط ژئومورفولوژی استفاده کرد، که زمین پیچیده را با دقت بیشتری نسبت به شبکه مستطیلی نشان می دهد. با این حال، TIN برای برخی از کاربردها مانند تجزیه و تحلیل شیب و جنبه سطح در GIS کمتر از DEM مناسب است. علاوه بر ذخیره مختصات سه بعدی آن، توپولوژی شبکه نیز تنظیم شده است. در نتیجه، به طور کلی برای طیف وسیعی از عکاسی هوایی برای به دست آوردن مقادیر عددی استفاده می شود.
دوره-آموزش-حرفه-ای-gis

2.2. روش برای محاسبه دید

دو روش اصلی برای محاسبات viewshed وجود دارد: روش محاسبه دیدگاه مبتنی بر خط دید (LOS) و روش صفحات مرجع. در حال حاضر، استفاده از الگوریتم LOS برای محاسبه دید یک زمین رایج است. الگوریتم LOS فقط از رابطه هندسی ساده بین نقاط برای قضاوت در مورد دید زمین استفاده می کند. پین [ 12 ] تجزیه و تحلیل دید بر اساس خط دید را به سه تجزیه و تحلیل دید تقسیم کرد: همبستگی نقطه، همبستگی مسیر، و همبستگی منطقه ای. فلوریانی و همکاران [ 13 ] روش شیب کلیدی را پیشنهاد کرد که به موجب آن با محاسبه شیب بین نقطه دید و نقطه هدف، حداکثر شیب و به روز رسانی پویا محاسبه می شود، همانطور که در شکل 3 نشان داده شده است.. این روش شیب هر نقطه را نیز محاسبه می کند تا بازدهی الگوریتم کم باشد. فرانکلین و همکاران [ 14 ] الگوریتم دایره متحدالمرکز را بر اساس LOS پیشنهاد کرد که با معرفی فاصله ثابت از نقطه دید، محاسبات را بهبود می بخشد. روش R3 [ 15 ] یک الگوریتم دیدگاه دقیق‌تر است، که یک LOS جداگانه از نقطه ناظر به هر نقطه اجرا می‌کند و تعیین می‌کند که آیا هر ارتفاعی در LOS مانع آن می‌شود یا خیر. پیچیدگی آن O(n 3 ) است. R2 [ 16 ] یک نسخه ساده شده از R3 است که دقت را کاهش می دهد اما کارایی الگوریتم را بهبود می بخشد. پیچیدگی R2 O(n2 ) است.
الگوریتم صفحات مرجع [ 17 ] یک صفحه مرجع ایجاد می کند که یک نقطه هدف، دو نقطه کمکی و نقطه دید (همانطور که در شکل 4 نشان داده شده است ) را برای تعیین دید هر هدف در بر می گیرد. بنابراین، بازده محاسباتی بالاتر از الگوریتم LOS است. الگوریتم سریال پیشنهاد شده توسط وو و همکاران. [ 18 ] داده‌های DEM با وضوح بالا را بخش‌بندی می‌کند، و از الگوریتم سطوح مرجع برای تعیین دید نقاط هدف استفاده می‌کند.

2.3. روش‌هایی برای بهینه‌سازی الگوریتم‌های دامنه بصری

در سال های اخیر، کاربردهای محاسبات موازی در محاسبات viewshed ظاهر شده است. اینها عمدتاً از تقارن داده های DEM و تکنیک های موازی سازی برای تسریع در تعیین میدان دید استفاده می کنند. فریرا و همکاران [ 19 ] محاسبات موازی بر روی زمین‌های شبکه برای پیاده‌سازی الگوریتم Van طراحی کرد. با استفاده از مدل حافظه مشترک، الگوریتم موازی اثرات شتاب متفاوتی را با توجه به تعداد رشته ها ایجاد می کند. به عنوان مثال، هنگامی که از 16 رشته همزمان استفاده می شود، الگوریتم می تواند تا 12 برابر سرعت داشته باشد. Osterman [ 20 ] موازی سازی الگوریتم r.los را توسعه داد. الگوریتم موازی برای سیستم‌های GIS امیدوارکننده است زیرا زمان‌های اجرا را در کارت‌های گرافیک NVIDIA افزایش می‌دهد.
اجرای الگوریتم LOS در [ 21 ] شامل محاسبه اندازه گام متغیر است، که در آن هر چه یک نقطه DEM از نقطه مشاهده دورتر باشد، فاصله گام برای انتخاب نقاط DEM بزرگتر است. اگرچه این امر محاسبات را کاهش می دهد، استراتژی فاصله گام با در نظر نگرفتن عوامل زمین نسبتاً ساده است و در نتیجه جزئیات را در مناطق پیچیده زمین مانند مناطق تپه ای از دست می دهد.

3. روش پیشنهادی

این مقاله بر اساس الگوریتم‌های نمای کلاسیک، یک روش محاسباتی جدید را پیشنهاد می‌کند که کارایی محاسباتی آن را به شرح زیر بهبود می‌بخشد. ابتدا بر اساس الگوریتم LOS و الگوریتم صفحات مرجع، الگوریتم عروسک ماتریوشکا پیشنهاد شد که محاسبات را ساده می کند. دوم، حداکثر ادغام معرفی شده است، و مفهوم حداقل ارتفاع مورد انتظار پیشنهاد شده است، که کارایی الگوریتم پیشنهادی را با توجه به اطلاعات زمین بهبود بخشید.
نمودار جریان الگوریتم پیشنهادی در شکل 5 نشان داده شده است . اول از همه، max-pooling برای یافتن حداکثر مقدار هر بلوک داده اعمال شد (شرح شده در بخش 3.1 ). پس از انتخاب نقاط مشاهده، ارتفاع سایر داده های DEM با توجه به انحنای زمین (شرح شده در بخش 3.2 ) کالیبره شد. سپس از الگوریتم عروسک ماتریوشکا برای محاسبه نمای مربوط به نقاط مشاهده استفاده شد (شرح شده در بخش 3.3 ). محاسبه با استفاده از نتایج عملیات حداکثر ادغام قبلی و حداقل ارتفاع مورد انتظار هر منطقه (شرح شده در بخش 3.4 ) ساده شد.

3.1. ادغام داده های ارتفاعی

ادغام یک روش رایج کاهش ابعاد در یادگیری عمیق است. روش های رایج ادغام، ادغام عمومی و ادغام همپوشانی [ 22 ] است. با محاسبه حداکثر یا میانگین داده ها در یک پنجره کشویی، تمام داده های ویژگی در یک پنجره کشویی با یک مقدار نشان داده می شوند و در نتیجه بعد ویژگی کاهش می یابد.
بر اساس ادغام در یادگیری عمیق، این مقاله یک روش بهبود یافته را با افزودن یک عملیات حداکثر ادغام پیشنهاد کرد. در داده های DEM، با استفاده از یک پنجره کشویی با مساحت ثابت (1 کیلومتر × 1 کیلومتر)، از روش جمع آوری حداکثر، همانطور که در شکل 6 نشان داده شده است ، برای محاسبه حداکثر ارتفاع یک منطقه استفاده می شود.

3.2. تصحیح داده مدل رقومی ارتفاع (DEM).

از آنجایی که زمین را می توان به عنوان یک کره عظیم در نظر گرفت، زمانی که هدف از نقطه مشاهده دور باشد، ارتفاع رصد هدف کمتر از ارتفاع واقعی آن در سطح زمین خواهد بود. این اثر در شکل 7 نشان داده شده است .
در بسیاری از الگوریتم‌های محاسباتی [ 23 ، 24 ]، از آنجایی که دامنه تشخیص کوچک است، مدل محاسباتی یک زمین منحنی را به یک صفحه ساده می‌کند. این مدل نسبتاً ساده است و دامنه تشخیص میدان دید در صورت کوچک بودن نمی تواند به شدت تحت تأثیر قرار گیرد. اگر دامنه بزرگ باشد (مانند قله کوه)، ارتفاع نسبی هدف دور کمتر از ارتفاع مطلق آن خواهد بود. برخی از نقاط هدف قابل مشاهده در مدل صفحه به دلیل اثرات انحنا در مدل کروی قابل مشاهده نیستند، بنابراین خطا تأثیر زیادی بر نتایج محاسبه دامنه بصری دارد. در این مقاله روشی برای اصلاح ارتفاع برای اهداف دور معرفی شد.
شعاع استوایی زمین 1/6378 کیلومتر و شعاع قطبی 8/6356 کیلومتر [ 25 ] است که تفاوت این دو شعاع تنها 3/0 درصد است. در کاربردهای کلی، زمین را می توان به یک کره کامل با شعاع 6371 کیلومتر ساده کرد.

هنگامی که فاصله از نقطه مشاهده تا نقطه هدف D باشد ، ارتفاع واقعی نقطه هدف باید کاهش یابد. Δساعتبرای محاسبه تأثیر انحنای زمین بر ارتفاع نقطه هدف، جایی که Δساعتبه شرح زیر تعیین می شود:

D2+آر2=(آر+Δساعت)2⇒D2=2آر⋅Δساعت+Δساعت2⇒Δساعت=D22آر+Δساعت⇒Δساعت≈D22آر

که در آن R شعاع زمین است. جدول 1 اثر فاصله و انحنای زمین را بر تخمین ارتفاع با استفاده از رابطه (1) نشان می دهد.

با توجه به ویژگی های داده های DEM، می توان آن را به هشت زیر منطقه با تقارن کامل در هشت جهت تقسیم کرد: شرق (E)، جنوب (S)، غرب (W)، شمال (N)، شمال شرق (NE)، جنوب شرق. (SE)، جنوب غربی (SW) و شمال غربی (NW) [ 23 ] همانطور که در شکل 8 نشان داده شده است . بنابراین، با توجه به این ویژگی هندسی، داده های یک منطقه را می توان پردازش کرد و داده های کالیبراسیون را می توان با رابطه فاصله متناظر بین نقاط داده در مناطق دیگر کپی کرد.

3.3. حداقل ارتفاع مورد انتظار

بسیاری از روش‌های محاسبه viewshed [ 7 ، 8 ] انحنای نیمرخ بین تمام نقاط DEM و نقاط مشاهده را محاسبه می‌کنند. این از نظر محاسباتی ناکارآمد است زیرا بسیاری از محاسبات غیر ضروری هستند. به عنوان مثال، اگر دشتی پشت یک کوه بزرگ واقع شده باشد، نمی توان تمام نقاط دشت را مشاهده کرد و بنابراین نیازی به محاسبه نیست. همچنین در مناطق کوهستانی یا دشتی، هر چه نقاط داده ارتفاعی دورتر باشند، احتمال مشاهده آنها کمتر است. بنابراین، برخی از الگوریتم‌ها متغیر فاصله گام را ارائه می‌کنند [ 21] در محاسبه LOS، در حالی که فاصله بین نقاط ارتفاع بیشتر می شود، بنابراین پارامتر اندازه گام نقطه ارتفاع نیز به تدریج افزایش می یابد و در نتیجه محاسبه کاهش می یابد. با این حال، این روش زمین را در نظر نمی گیرد، که فقط کارایی خاصی را در مناطق دشت بهبود می بخشد. بنابراین، در مناطقی مانند تپه‌ها که تغییرات ارتفاع شدیدتری دارند، خطای مشخصی بین مرز مرئی و مرز واقعی محاسبه‌شده با عملیات ساده شده وجود خواهد داشت و در نتیجه دقت کاهش می‌یابد.
به دلیل انسداد توسط موانع، زمانی که الگوریتم LOS منطقه خاصی را تشخیص می دهد، یک زاویه گام وجود دارد. از آنجایی که LOS از یک سری نقاط DEM در منطقه عبور می کند، ارتفاع مورد نیاز نقاط در LOS در ناحیه منطقه محاسبه می شود که مطابق با حداقل ارتفاع نقاط قابل مشاهده در منطقه همانطور که در شکل 9 نشان داده شده است . . حداقل ارتفاع مورد انتظار اولین نقطه در منطقه را حداقل ارتفاع مورد انتظار می نامند.
هنگامی که حداکثر ارتفاع منطقه کمتر از حداقل ارتفاع مورد انتظار باشد، نمی توان همه نقاط منطقه را مشاهده کرد. این بدان معنی است که نقاط موجود در منطقه را می توان نادیده گرفت و نقاط واحد بعدی را می توان مستقیماً همانطور که در شکل 10 نشان داده شده است بررسی کرد . از آنجایی که هر منطقه از بیش از یک LOS عبور می کند، این روش می تواند محاسبه ناحیه دید را تا حد زیادی تسریع کند.
از آنجایی که بالاترین ارتفاع روی زمین 8848 متری کوه قومولانگما است که معمولاً به عنوان کوه اورست شناخته می شود، زمانی که حداقل ارتفاع مورد انتظار یک منطقه بیشتر از 8848 متر باشد، پس در محیط زمین، منطقه پیگیری به طور کامل در نظر گرفته می شود. در تئوری نامرئی است و تشخیص زیر متوقف می شود.

3.4. الگوریتم عروسک ماتریوشکا

نقطه LOS نزدیک نقطه مشاهده چندین بار محاسبه می شود، بنابراین بازده الگوریتم بسیار کمتر از الگوریتم صفحات مرجع است. در این مقاله، یک الگوریتم LOS بهبود یافته پیشنهاد شده است که از درس‌هایی از سطوح مرجع استفاده می‌کند، که می‌تواند تعداد مقایسه‌های مکرر را تا حد زیادی کاهش دهد، در نتیجه کارایی الگوریتم را بهبود بخشد.
به دلیل خاص بودن داده های DEM، می توان آن را به هشت بخش متقارن ساختاری تقسیم کرد که هر کدام شبیه مثلث پاسکال است. هر لایه از مثلث یک نقطه بیشتر از لایه قبلی دارد و یک نقطه در لایه بالایی بر روی قابل مشاهده بودن دو نقطه مجاور در لایه بعدی تأثیر می گذارد. طبق الگوریتم صفحات مرجع، هر نقطه شی هدف نسبت به دو نقطه کمکی بین جسم و ناظر قابل مشاهده است، همانطور که در نشان داده شده است. شکل 11 نشان داده شده است، قابل مشاهده است.. الگوریتم صفحات مرجع از دو نقطه کمکی (یعنی دایره های سبز و سفید) همراه با نقطه ناظر برای تشکیل صفحه ای استفاده می کند تا مشخص کند آیا نقطه شی هدف قابل مشاهده است یا خیر. با این حال، در فرآیند محاسبه الگوریتم، دو نقطه کمکی نقش های متفاوتی را برای زوایای مختلف مشاهده ایفا می کنند.
بر اساس الگوریتم LOS و الگوریتم صفحات مرجع، الگوریتم جدیدی به نام الگوریتم عروسک ماتریوشکا، همانطور که در شکل 12 نشان داده شده است، پیشنهاد شد که می تواند به سرعت دید یک بخش خاص از یک منطقه را محاسبه کند.
الگوریتم در یک زیر منطقه نشان داده شده است و مراحل آن به شرح زیر است:
مرحله 1. گره ریشه به عنوان نقطه قضاوت فعلی برای تعیین دید نقطه هدف انتخاب می شود.
مرحله 2. از الگوریتم LOS برای محاسبه دید نقاط در سطح پایین تر و در جهت 45 درجه استفاده کنید.
مرحله 3. از نقطه قضاوت و دو نقطه همسایگی برای تشکیل صفحه مرجع استفاده کنید و میزان دید نقطه میانی دو لایه بعدی را در زیر نقطه قضاوت محاسبه کنید.
مرحله 4. نقطه میانی دو لایه زیر نقطه قضاوت فعلی را به عنوان نقطه قضاوت جدید در نظر بگیرید و مرحله 2 را تکرار کنید تا آخرین لایه داده پردازش شود.
از آنجایی که الگوریتم عروسک ماتریوشکا میزان دید نقاط را از لایه بیرونی به درونی همانطور که در شکل 13 نشان داده شده است محاسبه می کند و مشابه ساختار عروسک ماتریوشکا است، همانطور که در شکل 14 نشان داده شده است ، الگوریتم عروسک ماتریوشکا نامیده شد.

3.5. تعیین محدوده میدان های دیداری با ضرب چنگال

محاسبات مرسوم نمای LOS، ارتفاع بین نقاط روی LOS و نقطه مشاهده را به منظور تعیین دید آنها، مشابه مقایسه شیب و مقایسه زاویه اوج، مقایسه می‌کند. کوهن [ 26 ] روش ضرب را پیشنهاد کرد و سپس روش افزایشی را مطرح کرد. ایده خاص تعیین رابطه انسداد بین نقاط LOS با نتیجه حاصلضرب متقاطع بردار است. در این مقاله روش کوهن [ 26] برای ترکیب موثر حاصل ضرب بردار و روش افزایشی استفاده شد. افزایش حاصلضرب متقاطع برداری برای تعیین نقطه مرئی و افزایش ارتفاع برای پرداختن به نقطه غیر قابل مشاهده استفاده می شود. عملیات ترکیبی به طور قابل توجهی زمان عملیات مورد نیاز را کاهش می دهد.

اجازه دهید Vهyهیک نقطه مشاهده را نشان می دهد، در حالی که پ1و پ2نقاط توپوگرافی در یک زمین هستند. همانطور که در شکل 15 نشان داده شده است ، دو بردار، Vهyهپ1→و Vهyهپ2→، می تواند برای تعیین اینکه آیا جهت بردار استفاده می شود پ1پ2→چپ یا راست نسبت به Vهyهپ1→توسط محصول متقاطع برداری. پ2را می توان نسبت به Vهyه، اگر و فقط اگر جهت از پ1پ2→به سمت چپ نسبت به است Vهyهپ1→، در غیر این صورت با استفاده از آن قابل مشاهده نخواهد بود

(پ1-Vهyه)×(پ2-Vهyه)=(U1-Uهyه)⋅(اچ2-اچهyه)-(U2-Uهyه)⋅(اچ1-اچهyه)=U1⋅(اچ2-اچهyه)-U2⋅(اچ1-اچهyه)
اجازه دهید U*نشان دهنده فاصله یک نقطه * تا نقطه مشاهده، و اچ*ارتفاع نقطه * است. برای آزمایش هر نقطه با استفاده از رابطه (2) فقط به دو ضرب و سه تفریق نیاز است. روش حاصلضرب متقاطع برداری برای تعیین دید استفاده می شود و پیچیدگی آن O(n) است.

از آنجایی که نقاط نامرئی واقع در زیر LOS دارای پیوستگی محلی هندسی هستند، نقاط نامرئی با محاسبه افزایشی در جهت عمودی برای جستجوی ناحیه مقعر مبهم پردازش می‌شوند. هنگامی که حاصل ضرب بردار با یک نقطه غیر قابل مشاهده روبرو می شود، برای تعیین ارتفاع نقاط بعدی به یک الگوی ناحیه مبهم در یک دره تبدیل می شود. هر نقطه توپوگرافی بعدی تا زمانی که ارتفاع با نقطه LOS مطابقت نداشته باشد قابل مشاهده نیست تا زمانی که یک نقطه قابل مشاهده دوباره ظاهر شود. فرض کنید پمنقابل مشاهده است و نکته بعدی پمن+1نیست، الگوریتم تعیین می کند که پمن+1نقطه قابل مشاهده نیست معیار تصمیم گیری از Vهyهبه پمنبه عبارت دیگر، شیب LOS است،

م=اچ1-اچهyهU1-Uهyه=اچ1-اچهyهU1
از آنجایی که طول گام در جهت H 1 است، ارتفاع LOS مربوطه در بالای آن است پمن+1است ساعت=ساعتمن+متر. بنابراین، ما فقط باید شیب را در ارتفاع نقطه فعلی برای آزمایش دید اضافه کنیم و سپس با مقایسه ارتفاع، دید را تایید کنیم. بنابراین، محاسبه پیمایش در ناحیه مبهم تنها یک اضافه است. پیچیدگی محاسبات viewshed با بررسی بیشتر ناحیه مبهم در دره زمین کاهش می یابد.
دوره-آموزش-حرفه-ای-gis

4. آزمایش و تجزیه و تحلیل

سه آزمایش برای تجزیه و تحلیل زمان محاسباتی مورد نیاز و دقت الگوریتم پیشنهادی با استفاده از دو مجموعه داده با وضوح‌های فضایی مختلف طراحی شد. برای وضوح 10 متر از DLR (DLR مخفف Deutsches Zentrum für Luft- und Raumfahrt است و STRM X-SAR DEM ایجاد شده توسط مرکز هوافضای آلمان DLR) و برای وضوح 30 متر از ASTER– استفاده کردیم. GDEM (Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Model) V2. آزمایش‌ها در دو منطقه (هر منطقه حدود 40 کیلومتر مربع ، همانطور که در شکل 16 نشان داده شده است ) در حومه شهر چانگشا، چین انجام شد .
ابتدا از الگوریتم عروسک ماتریوشکا و الگوریتم R3 برای محاسبه ناحیه دید در همان نقطه مشاهده داده های مشابه استفاده کردیم و قابلیت اطمینان الگوریتم را تأیید کردیم. دوم، ما از الگوریتم عروسک ماتریوشکا و یک الگوریتم موجود برای آزمایش دو ناحیه مختلف استفاده کردیم و زمان محاسباتی مورد نیاز هر الگوریتم را مقایسه کردیم. علاوه بر این، اثر بهینه سازی حداکثر و حداقل ارتفاع مورد انتظار به ترتیب بر روی زمین های کوهستانی و دشت آزمایش شد. سوم، تفاوت در دقت بین الگوریتم پیشنهادی و روش سنتی بر روی مجموعه داده‌های DEM با وضوح‌های مختلف و زمین‌های مختلف تعیین شد.
الگوریتم R3، یک روش دقیق اما زمان‌بر [ 14 ]، برای محاسبه دیدگاه مورد استفاده قرار گرفت تا امکان مقایسه دقت نتایج محاسباتی الگوریتم عروسک ماتریوشکا را فراهم کند. شکل 17 اثر الگوریتم را نشان می دهد. اگرچه برخی جزئیات تا حدی در نتایج الگوریتم پیشنهادی وجود ندارد، اما این دو نتیجه مشابه بودند.

4.1. تجزیه و تحلیل زمان محاسباتی

چندین الگوریتم بر روی مجموعه داده DEM با رزولوشن 10 متر با محدوده های مختلف آزمایش شدند و زمان محاسباتی مورد نیاز الگوریتم های مختلف در شکل 18 نشان داده شده است . ابتدا مشاهده می شود که به دلیل تعداد کم درونیابی، الگوریتم پیشنهادی و الگوریتم صفحات مرجع به زمان کمتری نیاز دارند. از سوی دیگر، با توجه به الگوریتم درون یابی، روش تقریبی R2 [ 14 ] به زمان بسیار بیشتری با داده های با وضوح بالا نیاز داشت.
عملکرد الگوریتم بهینه سازی به ترتیب در مناطق کوهستانی و دشتی مورد آزمایش قرار گرفت. نتایج در شکل 19 نشان داده شده است . از آنجایی که زمین کوهستانی پیچیده است و بسیاری از مناطق فرعی نیاز به تضاد دارند، عملکرد الگوریتم مشخص نبود. از سوی دیگر، به دلیل تک زمین، بسیاری از مناطق فرعی در صفحه با شرایط بهینه‌سازی مطابقت دارند و اثر بهینه‌سازی کلی قابل توجه بود.
مشاهده می شود که الگوریتم عروسک ماتریوشکا از نظر زمان محاسباتی مورد نیاز بهتر از روش محاسباتی viewshed موجود بوده است. علاوه بر این، روش بهینه‌سازی جدید می‌تواند محاسبات را در زمین‌های مختلف، به‌ویژه در زمین‌های دشت، ساده‌سازی کند.

4.2. تجزیه و تحلیل دقت

طبق [ 14 ]، R3 یک روش دقیق است و R2 بهترین عملکرد را با توجه به دقت روش های تقریب دارد. بنابراین، با مراجعه به [ 27 ]، از نتیجه R3 به عنوان حقیقت زمین برای تعیین دقت الگوریتم پیشنهادی با مقایسه تفاوت با R2 و صفحه مرجع استفاده شد.
آزمایش به دو گروه تقسیم شد. گروه اول بر روی داده های DEM با وضوح های مختلف و گروه دوم بر روی زمین های مختلف از همان DEM انجام شد. به منظور قابل مقایسه کردن نتایج، مجموعه های تفاضل و تقاطع، همانطور که در شکل 20 نشان داده شده است ، در ارزیابی نتایج معرفی شدند.

دقت الگوریتم پیشنهادی با مقایسه تعداد نقاط قابل مشاهده تعیین شده توسط دو الگوریتم در یک نقطه مشاهده مورد تجزیه و تحلیل قرار گرفت. عدم تشابه شکل بین آنها با استفاده از محاسبه شد

Dمنffهrهnتی آرآتیه=نvمنسمنبله*-نvمنسمنبلهآر3نvمنسمنبلهآر3

و شباهت بین آنها با استفاده از

اسمنمترمنلآr آرآتیه=نvمنسمنبله*∩نvمنسمنبلهآر3نvمنسمنبلهآر3

جایی که نvمنسمنبله*نشان دهنده مجموع نقاط داده ای است که توسط الگوریتم در نقطه خاصی از مجموعه داده قابل مشاهده است. مقدار کوچک نرخ مختلف به معنای دقت بالا است. نرخ مشابه، نسبت نقاط قابل رویت صحیح نسبت به نقاط دید حقیقت است، جایی که مقدار بزرگ به معنای دقت بالا است. مشاهده می شود که مجموع نرخ مشابه و نرخ متفاوت لزوما برابر با 1 نیست. این به این دلیل است که در نقطه بازرسی، تعداد نقاط قابل مشاهده توسط R3 با سایر الگوریتم ها برابر نیست. شکل 21 و شکل 22 نتایج مقایسه را نشان می دهد. برای شکل 21 ، شش نقطه زمین اول استفاده شده، داده های DEM با وضوح 10 متر، و شش نقطه دوم زمین، داده های DEM با وضوح 30 متر بودند.شکل 21همچنین نشان می دهد که روش پیشنهادی عملکرد خوبی در هر دو مجموعه داده وضوح دارد.

برای شکل 22 ، شش نقطه زمین اول در دشت و شش نقطه زمین دوم در منطقه کوهستانی بودند. شکل 22 نیز نشان می دهد که روش پیشنهادی عملکرد خوبی در زمین های مختلف دارد.
هر دو شکل 21 و 22 نشان می دهند که دقت الگوریتم پیشنهادی به وضوح داده های DEM و زمین درگیر مرتبط است. شکل 23 نشان می دهد که چگونه الگوریتم پیشنهادی از نقاط داده DEM موجود برای تقریب نقاط داده در LOS استفاده می کند. دقت الگوریتم با وضوح DEM همبستگی مثبت دارد و با سطح تغییر زمین نسبت معکوس دارد.
دوره-آموزش-حرفه-ای-gis

5. نتیجه گیری ها

این مقاله بر اساس الگوریتم معمول مورد استفاده محاسبات viewshed، الگوریتم عروسک ماتریوشکا را پیشنهاد کرد. این الگوریتم با افزودن max-pooling و معرفی حداقل ارتفاع مورد انتظار، کارایی محاسباتی را با توجه به زمین بهبود می‌بخشد. علاوه بر این، دقت الگوریتم پیشنهادی به وضوح DEM و زمین مرتبط است.
مزیت اصلی روش پیشنهادی ما این است که الگوریتم عروسک ماتریوشکا با حداکثر ادغام و حداقل ارتفاع مورد انتظار راندمان محاسبات دید را به طور قابل توجهی افزایش می دهد، به خصوص در زمین صفحه زیرا ارتفاع مورد انتظار به تدریج افزایش می یابد، اما حداکثر ارتفاع هر فرعی افزایش می یابد. منطقه نسبتا کوچک است. علاوه بر این، از آنجایی که الگوریتم پیشنهادی به طور خودکار محدوده بصری را با توجه به ویژگی‌های سطح زمین از جمله شعاع و بالاترین ارتفاع تعیین می‌کند، می‌توان از آن در سایر اجرام آسمانی مانند ماه و مریخ استفاده کرد. با این حال، شعاع ماه و مریخ کوچکتر از زمین است، بنابراین تأثیر انحنای روی ارتفاع باید دوباره محاسبه شود و تأثیر در این مکان ها، به ویژه برای ماه، باید آشکارتر باشد. روش پیشنهادی محدودیت هایی دارد. روش پیشنهادی نمی تواند با مجموعه داده DEM با وضوح چندگانه مانند مجموعه داده NED (مجموعه داده های ارتفاعی ملی) تطبیق یابد [28 ] با رزولوشن 10 متر و زیر مجموعه وضوح 30 متر، زیرا فقط برای داده های تک وضوح معتبر است.
بهبود کارایی الگوریتم با محاسبات موازی مبتنی بر GPU کار تحقیقاتی آینده ما است. علاوه بر این، الگوریتم می تواند از حداکثر مقدار جهانی (بالاترین ارتفاع زمین) به عنوان پارامتر برای خاتمه محاسبات استفاده کند و سپس حداکثر مقدار منطقه را به عنوان پارامتر خاتمه با توجه به مکان و سایر پارامترها انتخاب کند، بنابراین بیشتر بهبود کارایی الگوریتم

منابع

  1. فلوریانی، ل. Magillo، P. الگوریتم‌های محاسبه دید در زمین‌ها: یک بررسی. محیط زیست طرح. B طرح. دس 2003 ، 30 ، 709-728. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  2. سیلیس، جی. Statuto، D.; Picuno، P. ساختمان‌های مزرعه بومی و منظر روستایی: یک رویکرد جغرافیایی برای مدیریت یکپارچه آنها. پایداری 2020 ، 12 ، 4. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  3. Palmer, JF سهم یک مدل ارزیابی منظر مبتنی بر GIS در یک رویکرد علمی دقیق برای ارزیابی تأثیر بصری. Landsc. طرح شهری. 2019 ، 189 ، 80-90. [ Google Scholar ] [ CrossRef ]
  4. لوپز-سانچز، ن. گومز-گونزالس، JI زیارتگاه های گدیر (کادیز، اسپانیا) به عنوان مراجع برای ناوبری. تجزیه و تحلیل دید GIS. Archaeol را باز کنید. 2019 ، 5 ، 284-308. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  5. سرویلا، آر. تبیک، س. ویاس، جی. مریدا، م. Romero، LF Total 3D-viewshed map: Quantifying the Visible Volume in Digital Elevation Models. ترانس. GIS 2017 ، 21 ، 591-607. [ Google Scholar ] [ CrossRef ]
  6. لی، کی. Seo, JI; کیم، KN; لی، ی. کوئون، اچ. کیم، جی. کاربرد تحلیل‌های زیبایی‌شناختی دید و فضایی در شیوه‌های جنگل برای بهبود مناظر کوهستانی در جمهوری کره. پایداری 2019 ، 11 ، 2687. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  7. تبیک، س. زاپاتا، EL; Romero، LF محاسبه همزمان کل نماها روی شبکه های بزرگ با وضوح بالا. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 804-814. [ Google Scholar ] [ CrossRef ]
  8. هائو-نگوین، تی. Duy، TN; Tra-Duong، A. یک الگوریتم جدید برای محاسبات viewshed در زمین شطرنجی. در مجموعه مقالات دومین کنفرانس بین المللی 2018 در مورد پیشرفت های اخیر در پردازش سیگنال، ارتباطات و محاسبات (SigTelCom 2018)، هوشی مین، ویتنام، 29 تا 31 ژانویه 2018؛ صص 56-60. [ Google Scholar ]
  9. Heritage, GL; میلان، دی جی; بزرگ، ARG؛ تأثیر فولر، IC استراتژی نظرسنجی و مدل درونیابی بر کیفیت DEM. ژئومورفولوژی 2009 ، 112 ، 334-344. [ Google Scholar ] [ CrossRef ]
  10. ژائو، ی. پادمنابان، ع. وانگ، اس. یک رویکرد محاسباتی موازی برای تجزیه و تحلیل دیدگاه داده‌های زمین بزرگ با استفاده از واحدهای پردازش گرافیکی. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 363-384. [ Google Scholar ] [ CrossRef ]
  11. ژو، Q. چن، ی. تعمیم DEM برای تجزیه و تحلیل زمین با استفاده از روش ترکیبی. ISPRS J. Photogramm. Remote Sens. 2011 ، 66 ، 38-45. [ Google Scholar ] [ CrossRef ]
  12. Lv، P. ژانگ، جی. لو، ام. Li, L. تجزیه و تحلیل دید زمین بر اساس خط دید. محاسبه کنید. مهندس Appl. 2006 ، 8 . [ Google Scholar ]
  13. فلوریانی، LD; مارزانو، پ. Puppo، E. ارتباط خط دید در مدل های زمین. بین المللی جی. جئوگر. Inf. سیستم 1994 ، 8 ، 329-342. [ Google Scholar ] [ CrossRef ]
  14. فرانکلین، WR; ری، CK; مهتا، اس. الگوریتم های هندسی برای مکان یابی باتری های موشکی پدافند هوایی. Res. پروژه نبرد 1994 , 2756 . [ Google Scholar ]
  15. کائوچیچ، بی. Zalik, B. مقایسه الگوریتم های viewshed در نقاط با فاصله منظم. در مجموعه مقالات هجدهمین کنفرانس بهار در زمینه گرافیک کامپیوتری، Budmerice، اسلواکی، 24-27 آوریل 2002; صص 177-183. [ Google Scholar ]
  16. فرانکلین، WR; Ray, C. بالاتر لزوماً بهتر نیست: الگوریتم‌های دید و آزمایش‌ها. در پیشرفت در تحقیقات GIS، مجموعه مقالات ششمین سمپوزیوم بین المللی در مورد مدیریت داده های فضایی، ادینبورگ، اسکاتلند، 5-9 سپتامبر 1994 . تیلور و فرانسیس: ابینگدون، بریتانیا، 1994; جلد 2، ص 751–770. [ Google Scholar ]
  17. وانگ، جی. رابینسون، جی جی; White, K. ایجاد دیدگاه‌ها بدون استفاده از خطوط دید. فتوگرام مهندس Remote Sens. 2000 , 66 , 87-90. [ Google Scholar ]
  18. وو، اچ. پان، م. یائو، ال. Luo, B. یک الگوریتم سریال مبتنی بر پارتیشن برای تولید viewshed در DEM های عظیم. بین المللی جی. جئوگر. Inf. علمی 2007 ، 21 ، 955-964. [ Google Scholar ] [ CrossRef ]
  19. فریرا، CR; آندراد، MVA؛ Magalhães، SVG; فرانکلین، WR; Pena، GC یک الگوریتم موازی برای محاسبات دید در زمین های شبکه. J. Inf. مدیریت داده ها 2014 ، 5 ، 171. [ Google Scholar ]
  20. Osterman، A. پیاده‌سازی ماژول r.cuda.los در GIS منبع باز GRASS با استفاده از محاسبات موازی روی کارت‌های گرافیک NVIDIA CUDA. Elektrotehniski Vestn. 2012 ، 79 ، 19-24. [ Google Scholar ]
  21. هینز، AM; Van Vuuren، JH Terrain وابسته به موقعیت مکانی تاسیسات از طریق تخمین سریع پویا و پویا viewshed فاصله در یک محیط شطرنجی. در مجموعه مقالات کنفرانس سالانه 2013 انجمن تحقیقات عملیات آفریقای جنوبی، Stellenbosch، آفریقای جنوبی، 15-18 سپتامبر 2013. صص 112-121. در دسترس آنلاین: https://connection.ebscohost.com/c/proceedings/96160513/42nd-orssa-annual-conference (در 5 اکتبر 2020 قابل دسترسی است).
  22. کریژفسکی، آ. سوتسکور، آی. هینتون، GE Imagenet طبقه بندی با شبکه های عصبی کانولوشن عمیق. در مجموعه مقالات بیست و ششمین کنفرانس سالانه کنفرانس سیستم های پردازش اطلاعات عصبی، دریاچه تاهو، NV، ایالات متحده، 3-6 دسامبر 2012. ص 1097-1105. در دسترس آنلاین: https://conference.researchbib.com/view/event/10123 (در 5 اکتبر 2020 قابل دسترسی است).
  23. دوو، دبلیو. لی، ی. Wang, Y. یک الگوریتم زمانبندی با دانه بندی ریز برای تحلیل موازی XDraw viewshed. علوم زمین آگاه کردن. 2018 ، 11 ، 433-447. [ Google Scholar ] [ CrossRef ]
  24. فیشر، الگوریتم PF و عدم قطعیت اجرا در تحلیل دیدگاه. بین المللی جی. جئوگر. Inf. سیستم 1993 ، 7 ، 331-347. [ Google Scholar ] [ CrossRef ]
  25. چمبات، اف. Valette، B. میانگین شعاع، جرم و اینرسی برای مدل‌های زمین مرجع. فیزیک سیاره زمین. اینتر 2001 ، 124 ، 237-253. [ Google Scholar ] [ CrossRef ]
  26. یا، DC؛ لرزش، الف. دید و مناطق مرده در نقشه‌های زمین دیجیتال. محاسبه کنید. نمودار. انجمن 1995 ، 14 ، 171-180. [ Google Scholar ] [ CrossRef ]
  27. یو، جی. وو، ال. هو، کیو. یان، ز. ژانگ، اس. یک الگوریتم سطح بصری مصنوعی برای محاسبه دید با در نظر گرفتن دقت و کارایی. محاسبه کنید. Geosci. 2017 ، 109 ، 315-322. [ Google Scholar ] [ CrossRef ]
  28. گش، دی. اویموئن، م. گرینلی، اس. مجموعه داده های ارتفاعی ملی. فتوگرام مهندس Remote Sens. 2002 ، 68 ، 5-32. [ Google Scholar ]
Ijgi 09 00633 g001 550
شکل 1. نمایش داده های مختلف بین مدل رقومی ارتفاع (DEM) ( a ) و نامنظم مثلثی (TIN) ( b ). DEM داده شطرنجی است، در حالی که TIN داده های مثلثی نامنظم است.
Ijgi 09 00633 g002 550
شکل 2. نمونه ای از داده های DEM. داده های DEM هر منطقه را می توان به عنوان یک نمودار نشان داد. هر نقطه در نمودار مربوط به یک نقطه نمونه برداری در منطقه است. سطح خاکستری یک نقطه نشان دهنده مقدار ارتفاع آن است، جایی که هر چه سطح خاکستری بزرگتر باشد (یعنی روشن تر)، ارتفاع بالاتر است.
Ijgi 09 00633 g003 550
شکل 3. محاسبات Viewshed در الگوریتم خط دید (LOS). الگوریتم یک پرتو را از نقطه دید (یعنی نقطه مرکزی شبکه) به نقطه هدف (یعنی بیرونی ترین نقطه ای که با پرتو قطع می شود) ترسیم می کند و ارتفاع نقطه مرجع در LOS با درون یابی به دست می آید.
Ijgi 09 00633 g004 550
شکل 4. محاسبات Viewshed در الگوریتم صفحات مرجع. دو نقطه مجاور بین نقطه دید (یعنی نقطه مرکزی شبکه) و نقطه هدف (یعنی دورترین نقطه سبز از نقطه دید) به عنوان نقاط کمکی انتخاب شدند. خطوط نقطه چین سه نوع نقطه را برای تشکیل یک صفحه مرجع در بر می گیرد. رابطه بین هدف و هواپیما تعیین می کند که آیا نقطه هدف قابل مشاهده است یا خیر.
Ijgi 09 00633 g005 550
شکل 5. نمودار جریان الگوریتم پیشنهادی.
Ijgi 09 00633 g006 550
شکل 6. عملیات ادغام حداکثر مقدار را در هر ناحیه مشخص شده استخراج می کند. اندازه پنجره کشویی عملیات ادغام برابر با اندازه گام است، بنابراین دامنه هر نتیجه ادغام با هم قطع نمی شود.
Ijgi 09 00633 g007 550
شکل 7. تأثیر انحنای زمین بر ارتفاع یک جسم دور. هر چه فاصله (D) یک جسم از یک نقطه مشاهده بیشتر باشد، اختلاف ارتفاع h بیشتر است و بنابراین ارتفاع مشاهده شده در سطح زمین کمتر می شود.
Ijgi 09 00633 g008 550
شکل 8. داده های DEM به هشت زیر منطقه تقسیم شدند. هر منطقه فرعی به صورت چرخشی متقارن (یا متقارن آینه ای) با یک منطقه فرعی دیگر با رابطه فاصله متناظر بین نقاط داده است.
Ijgi 09 00633 g009 550
شکل 9. ارتفاع مورد انتظار و حداقل ارتفاع مورد انتظار در ناحیه ای که با متوازی الاضلاع محدود شده است.
Ijgi 09 00633 g010 550
شکل 10. حداکثر ارتفاع منطقه ای و حداقل ارتفاع مورد انتظار. LOS-1 و LOS-2 نشان دهنده LOS نقاط مشاهده مختلف هستند و حداقل ارتفاعات مورد انتظار متفاوتی در یک منطقه دارند. هنگامی که LOS یک ناحیه محدود شده توسط متوازی الاضلاع را تشخیص می دهد، ابتدا حداقل ارتفاع مورد انتظار را محاسبه می کند و سپس آن را با حداکثر مقدار در منطقه مقایسه می کند. اگر حداقل ارتفاع مورد انتظار کوچکتر از حداکثر منطقه باشد، می تواند مستقیماً به منطقه بعدی برود.
Ijgi 09 00633 g011 550
شکل 11. قضاوت دید: میزان دید بین نقطه مشاهده و نقطه هدف به ارتفاع دو نقطه کمکی بین آنها مربوط می شود. هنگامی که زاویه مشاهده (که با فلش نقطه‌دار مشخص می‌شود) متفاوت است، وزن‌های دید دو نقطه مرجع متفاوت است.
Ijgi 09 00633 g012 550
شکل 12. مراحل در الگوریتم پیشنهادی عروسک ماتریوشکا. فقط یک چرخه محاسبه برای هر بخش از داده ها نشان داده می شود و مرحله 1 نقطه قضاوت فعلی را انتخاب می کند (الگوریتم را ببینید). ( a ) یک نمودار شماتیک مرحله 1 الگوریتم است و فقط بیرونی ترین گره های آبی تیره در محاسبه این مرحله نقش دارند. ( ب ) نمودار شماتیک مرحله دوم است و گره های سبز رنگ در لایه دوم در محاسبه این مرحله شرکت می کنند. ( ج ) مشابه دو مرحله قبل است، فقط گره های آبی روشن در محاسبه شرکت می کنند.
Ijgi 09 00633 g013 550
شکل 13. یک نمودار شماتیک از الگوریتم عروسک ماتریوشکا. برای هر چرخه، داده‌های درگیر در عملیات از لایه‌های بیرونی به لایه‌های داخلی حرکت می‌کنند که شبیه شکل تودرتو عروسک ماتریوشکا است.
Ijgi 09 00633 g014 550
شکل 14. عروسک ماتریوشکا: این عروسک از چند عروسک چوبی توخالی تشکیل شده است. از آنجایی که ترتیب محاسبه مشابه ساختار اسباب بازی است، الگوریتم پیشنهادی الگوریتم عروسک ماتریوشکا نام گرفت.
Ijgi 09 00633 g015 550
شکل 15. تعیین دید با استفاده از روش محصول متقاطع برداری. فقط تعیین جهت چرخش لازم است پ1پ2→نسبت به Vهyهپ1→برای تعیین اینکه آیا پ2قابل مشاهده است، کجا Vهyهنقطه مشاهده است و پ1و پ2نقاط توپوگرافی روی زمین هستند.
Ijgi 09 00633 g016 550
شکل 16. تصاویر زمین مناطق آزمایشی را نشان می دهند. ( الف ) منطقه نسبتاً مسطح با برخی تپه‌های کم ارتفاع. و ( ب ) یک منطقه کوهستانی.
Ijgi 09 00633 g017 550
شکل 17. مقایسه نتایج با داده های DEM (رزولوشن 30 متر): ( الف ) محدوده میدان بینایی محاسبه شده با استفاده از الگوریتم عروسک ماتریوشکا. و ( ب ) viewshed با استفاده از الگوریتم عروسک R3 محاسبه شده است. تفاوت در نتایج در دایره های قرمز در ( a ) محصور شده است.
Ijgi 09 00633 g018 550
شکل 18. مقایسه زمان محاسباتی مورد نیاز الگوریتم های مختلف.
Ijgi 09 00633 g019 550
شکل 19. تأثیر روش حداکثر تجمع- حداقل ارتفاع مورد انتظار. اثر شتاب سطح صفحه آشکارتر بود.
Ijgi 09 00633 g020 550
شکل 20. نمودار شماتیک مجموعه های تقاطع و تفاضل. ( الف ) مجموعه تفاوت (BA)؛ و ( ب ) مجموعه تقاطع (A∩B).
Ijgi 09 00633 g021 550
شکل 21. تأثیر وضوح DEM بر الگوریتم ها: ( الف ) تأثیر وضوح DEM بر نرخ متفاوت هر الگوریتم. و ( ب ) تأثیر وضوح DEM بر نرخ متفاوت هر الگوریتم.
Ijgi 09 00633 g022 550
شکل 22. تأثیر زمین بر الگوریتم ها: ( الف ) تأثیر زمین بر نرخ مشابه هر الگوریتم. و ( ب ) تأثیر زمین بر نرخ متفاوت هر الگوریتم.
Ijgi 09 00633 g023 550
شکل 23. نشان دادن تفاوت بین الگوریتم پیشنهادی و روش سنتی. الگوریتم پیشنهادی از داده‌های DEM (که با نقاط آبی مشخص می‌شوند) برای تقریب داده‌های درون‌یابی (که با نقاط قرمز مشخص می‌شوند) در LOS استفاده می‌کند. تقریب با زمین های مختلف و وضوح DEM متفاوت است.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید