چکیده

:

پیش‌بینی دقیق ترافیک در زمان واقعی، یک مشکل فنی اصلی در برابر پیاده‌سازی سیستم حمل‌ونقل هوشمند است. با این حال، با توجه به وابستگی‌های مکانی و زمانی پیچیده در میان جریان‌های ترافیک، همچنان چالش برانگیز است. در بعد فضایی، به دلیل اتصال شبکه جاده ای، جریان ترافیک بین جاده های متصل ارتباط تنگاتنگی دارد. در بعد زمانی، اگرچه گرایشی بین نقاط زمانی مجاور وجود دارد، اما اهمیت نقاط زمانی دور لزوما کمتر از زمان های اخیر نیست، زیرا جریان های ترافیکی نیز تحت تأثیر عوامل خارجی قرار می گیرند. در این مطالعه، یک شبکه کانولوشن گراف زمانی توجه (A3T-GCN) پیشنهاد شد تا به طور همزمان دینامیک زمانی جهانی و همبستگی های فضایی در جریان ترافیک را به تصویر بکشد. مدل A3T-GCN روند کوتاه مدت را با استفاده از واحدهای بازگشتی دروازه ای می آموزد و وابستگی مکانی را بر اساس توپولوژی شبکه جاده از طریق شبکه کانولوشن گراف می آموزد. علاوه بر این، مکانیسم توجه برای تنظیم اهمیت نقاط زمانی مختلف و جمع‌آوری اطلاعات زمانی جهانی برای بهبود دقت پیش‌بینی معرفی شد. نتایج تجربی در مجموعه داده‌های دنیای واقعی، اثربخشی و استحکام A3T-GCN پیشنهادی را نشان می‌دهد. ما بهبودهایی را در RMSE 2.51-46.15٪ و 2.45-49.32٪ نسبت به خطوط پایه برای SZ-taxi و Los-loop مشاهده می کنیم. در همین حال، دقت ها به ترتیب 0.95-89.91٪ و 0.26-10.37٪ بیشتر از خطوط پایه برای SZ-taxi و Los-loop هستند. مکانیسم توجه برای تنظیم اهمیت نقاط زمانی مختلف و جمع‌آوری اطلاعات زمانی جهانی برای بهبود دقت پیش‌بینی معرفی شد. نتایج تجربی در مجموعه داده‌های دنیای واقعی، اثربخشی و استحکام A3T-GCN پیشنهادی را نشان می‌دهد. ما بهبودهایی را در RMSE 2.51-46.15٪ و 2.45-49.32٪ نسبت به خطوط پایه برای SZ-taxi و Los-loop مشاهده می کنیم. در همین حال، دقت ها به ترتیب 0.95-89.91٪ و 0.26-10.37٪ بیشتر از خطوط پایه برای SZ-taxi و Los-loop هستند. مکانیسم توجه برای تنظیم اهمیت نقاط زمانی مختلف و جمع‌آوری اطلاعات زمانی جهانی برای بهبود دقت پیش‌بینی معرفی شد. نتایج تجربی در مجموعه داده‌های دنیای واقعی، اثربخشی و استحکام A3T-GCN پیشنهادی را نشان می‌دهد. ما بهبودهایی را در RMSE 2.51-46.15٪ و 2.45-49.32٪ نسبت به خطوط پایه برای SZ-taxi و Los-loop مشاهده می کنیم. در همین حال، دقت ها به ترتیب 0.95-89.91٪ و 0.26-10.37٪ بیشتر از خطوط پایه برای SZ-taxi و Los-loop هستند. 32 درصد بیش از خطوط پایه برای SZ-taxi و Los-loop، به ترتیب. در همین حال، دقت ها به ترتیب 0.95-89.91٪ و 0.26-10.37٪ بیشتر از خطوط پایه برای SZ-taxi و Los-loop هستند. 32 درصد بیش از خطوط پایه برای SZ-taxi و Los-loop، به ترتیب. در همین حال، دقت ها به ترتیب 0.95-89.91٪ و 0.26-10.37٪ بیشتر از خطوط پایه برای SZ-taxi و Los-loop هستند.

 

1. مقدمه

پیش بینی ترافیک جزء مهمی از سیستم های حمل و نقل هوشمند و بخش مهمی از برنامه ریزی و مدیریت حمل و نقل و کنترل ترافیک است [ 1 ، 2 ، 3 ، 4 ]. پیش‌بینی دقیق ترافیک در زمان واقعی به دلیل وابستگی‌های مکانی-زمانی پیچیده یک چالش بزرگ بوده است. وابستگی زمانی به این معنی است که وضعیت ترافیک با زمان تغییر می کند که با تناوب و گرایش آشکار می شود. وابستگی فضایی به این معنی است که تغییرات در وضعیت ترافیک تابع توپولوژی ساختاری شبکه‌های جاده‌ای است که با انتقال وضعیت ترافیک بالادست به بخش‌های پایین دست و اثرات گذشته‌نگر وضعیت ترافیک پایین‌دست در بخش بالادست آشکار می‌شود [ 5 ].]. از این رو، در نظر گرفتن ویژگی های زمانی پیچیده و ویژگی های توپولوژیکی شبکه راه ها برای تحقق وظیفه پیش بینی ترافیک ضروری است.
مدل های پیش بینی ترافیک موجود را می توان به مدل های پارامتریک و مدل های ناپارامتریک تقسیم کرد. مدل های پارامتری رایج عبارتند از میانگین تاریخی، سری های زمانی [ 6 ، 7 ]، رگرسیون خطی [ 8 ] و مدل های فیلتر کالمن [ 9 ]. اگرچه مدل‌های پارامتریک سنتی از الگوریتم‌های ساده استفاده می‌کنند، اما به فرضیه‌های ثابت بستگی دارند. این مدل‌ها نه می‌توانند غیرخطی بودن و عدم قطعیت وضعیت‌های ترافیکی را منعکس کنند و نه بر تداخل رویدادهای تصادفی مانند تصادفات رانندگی غلبه کنند. مدل های ناپارامتریک می توانند این مسائل را به خوبی حل کنند زیرا می توانند قوانین آماری داده ها را به طور خودکار با داده های تاریخی کافی یاد بگیرند. مدل‌های ناپارامتریک رایج عبارتند از k-nearest [ 10]، رگرسیون برداری پشتیبانی (SVR) [ 11 ، 12 ]، منطق فازی [ 13 ]، شبکه بیزی [ 14 ] و مدل های شبکه عصبی [ 15 ].
اخیراً، مدل‌های شبکه عصبی عمیق به دلیل توسعه سریع یادگیری عمیق، توجه گسترده‌ای را از سوی محققان به خود جلب کرده است [ 16 ، 17 ، 18 ]. شبکه‌های عصبی بازگشتی (RNN)، حافظه کوتاه‌مدت (LSTM) [ 19 ]، و واحدهای بازگشتی دروازه‌ای (GRUs) [ 20 ] با موفقیت در پیش‌بینی ترافیک استفاده شده‌اند، زیرا می‌توانند از مکانیسم‌های گردش خود استفاده کنند و وابستگی زمانی را مدل کنند [ 21 ]. ، 22 ، 23]. با این حال، این مدل‌ها فقط تغییرات زمانی وضعیت ترافیک را در نظر می‌گیرند و از وابستگی مکانی غفلت می‌کنند. بسیاری از محققان شبکه های عصبی کانولوشنال (CNN) را در مدل های خود برای توصیف وابستگی فضایی معرفی کرده اند. وو و همکاران [ 24 ] یک چارچوب ترکیبی ویژگی برای پیش‌بینی کوتاه‌مدت جریان ترافیک با ترکیب CNN با LSTM طراحی کرد. این چارچوب ویژگی‌های فضایی جریان ترافیک را از طریق یک CNN تک بعدی ثبت کرد و تغییرات کوتاه‌مدت و تناوب جریان ترافیک را با دو LSTM بررسی کرد. کائو و همکاران [ 25] یک مدل پایان به انتها به نام شبکه کانولوشن مکرر زمانی تعاملی (ITRCN) پیشنهاد کرد که جریان شبکه تعاملی را به تصاویر تبدیل کرد و جریان های شبکه را با استفاده از CNN ضبط کرد. ITRCN همچنین ویژگی های زمانی را با استفاده از GRU استخراج کرد. یک آزمایش ثابت کرد که خطای پیش‌بینی این روش به ترتیب 14.3 و 13.0 درصد بیشتر از GRU و CNN بود. یو و همکاران [ 26 ] همبستگی فضایی و دینامیک زمانی را توسط شبکه‌های کانولوشنی مکرر مکانی-زمانی (SRCN) بر اساس شبکه عصبی پیچیده عمیق (DCNN) و LSTM به دست آورد. آنها همچنین برتری SRCN را بر اساس بررسی داده های شبکه ترافیک در پکن ثابت کردند. سان و همکاران [ 27] یک مدل چند شاخه ای مبتنی بر یادگیری عمیق به نام شبکه پیش بینی جریان ترافیک (TFFNet) برای پیش بینی جریان ترافیک کوتاه مدت پیشنهاد کرد. TFFNet از یک چارچوب کاملاً پیچیده چند لایه برای استخراج وابستگی های فضایی سلسله مراتبی از مقیاس های محلی به جهانی استفاده می کند.
اگرچه CNN برای داده‌های اقلیدسی [ 28 ]، مانند تصویر و شبکه‌ها قابل استفاده است، اما همچنان در شبکه‌های ترافیکی که دارای ساختارهای غیراقلیدسی هستند، محدودیت‌هایی دارد. در سال های اخیر، شبکه کانولوشن گراف (GCN) [ 29 ]، که می تواند بر محدودیت های ذکر شده غلبه کند و ویژگی های ساختاری شبکه ها را به تصویر بکشد، به سرعت توسعه یافته است [ 30 ، 31 ، 32 ]]. علاوه بر این، RNN ها و انواع آن ها از پردازش متوالی در طول زمان استفاده می کنند و برای به خاطر سپردن آخرین اطلاعات مناسب تر هستند، بنابراین برای گرفتن گرایش های کوتاه مدت در حال تکامل مناسب هستند. با این حال، یکی از مشکلات این مدل ها این است که عملکرد آنها با افزایش افق پیش بینی کاهش می یابد. علاوه بر این، اهمیت نقاط زمانی مختلف را نمی توان تنها با نزدیکی زمان تشخیص داد. همانطور که Pavlyuk در [ 33 ] پیشنهاد کرد، تعریف ساختار مکانی – زمانی جریان ترافیک نیز باید شامل روابطی باشد که از نظر زمانی دور هستند. وابستگی های طولانی مدت (مثلاً وابستگی های دوره ای) که در بازه های زمانی بزرگ پنهان شده اند باید در نظر گرفته شوند. بنابراین، مکانیسم هایی که قادر به یادگیری همبستگی های جهانی در توالی های زمانی ورودی طولانی هستند مورد نیاز است.
به همین دلیل، یک GCN زمانی توجه (A3T-GCN) برای کار پیش‌بینی ترافیک پیشنهاد شد. A3T-GCN GCN ها و GRU ها را ترکیب می کند و مکانیزم توجه را معرفی می کند [ 34 ، 35 ]. نه تنها می‌تواند وابستگی‌های مکانی-زمانی را بگیرد، بلکه می‌تواند اطلاعات تغییرات کلی را تنظیم و جمع‌آوری کند. A3T-GCN برای پیش بینی ترافیک بر اساس شبکه های جاده ای شهری استفاده می شود.
بقیه مقاله به شرح زیر سازماندهی شده است. بخش 2 مدل پیشنهادی را معرفی می کند. در بخش 3 ، عملکرد A3T-GCN را با مجموعه داده های ترافیک دنیای واقعی، از جمله تجزیه و تحلیل نتایج پیش بینی، تجزیه و تحلیل اغتشاش، و تفسیر تجسم ارزیابی می کنیم. ما مقاله را در بخش 4 به پایان می رسانیم .

2. روش ها

2.1. تعریف مشکلات

در این مطالعه، پیش‌بینی ترافیک برای پیش‌بینی وضعیت‌های ترافیکی آینده با توجه به وضعیت‌های ترافیکی تاریخی در جاده‌های شهری انجام می‌شود. به طور کلی، وضعیت ترافیک می تواند به جریان ترافیک، سرعت و تراکم اشاره کند. در این مطالعه وضعیت ترافیک تنها به سرعت ترافیک اشاره دارد.
تعریف  1.

شبکه راه G: ساختار توپولوژیکی شبکه راه شهری به شرح زیر است جی=(V،E)، جایی که V={v1،v2،⋯،vن}مجموعه ای از بخش های جاده و N تعداد بخش های جاده است. E مجموعه ای از لبه ها است که ارتباط بین بخش های جاده را منعکس می کند. تمام اطلاعات اتصال در ماتریس مجاور ذخیره می شود آ∈آرن×ن، که در آن سطرها و ستون ها توسط بخش های جاده نمایه می شوند و مقدار هر ورودی نشان دهنده اتصال بین بخش های جاده مربوطه است. مقدار ورودی صفر است اگر ارتباطی بین جاده ها و یک وجود نداشته باشد (گراف وزنی نشده) یا غیر منفی (گراف وزنی) در غیر این صورت.
تعریف  2.

ماتریس ویژگی ایکسن×پ: سرعت ترافیک در یک بخش جاده به عنوان ویژگی گره های شبکه مشاهده می شود و با ماتریس ویژگی بیان می شود. ایکس∈آرن×پ، که در آن P تعداد ویژگی های ویژگی گره است، یعنی طول سری زمانی تاریخی. ایکسمننشان دهنده سرعت ترافیک در تمام بخش ها در زمان i است.
بنابراین، پیش‌بینی ترافیک، مدل‌سازی وابستگی‌های زمانی و مکانی را می‌توان به عنوان یادگیری یک تابع نگاشت f بر اساس شبکه جاده‌ای G و ماتریس ویژگی X شبکه جاده مشاهده کرد. سرعت ترافیک لحظه های T آینده به صورت زیر محاسبه می شود:

ایکستی+1،⋯،ایکستی+تی=fجی;ایکستی–n،⋯،ایکستی–1،ایکستی،

که در آن n طول یک سری زمانی مشخص و T طول سری زمانی است که باید پیش بینی شود.

2.2. مدل GCN

GCN ها مدل های نیمه نظارتی هستند که می توانند ساختارهای گراف را پردازش کنند. آنها پیشرفتی از CNN در زمینه های نموداری هستند. GCN ها در بسیاری از کاربردها، مانند طبقه بندی تصویر [ 36 ]، طبقه بندی اسناد [ 28 ] و یادگیری بدون نظارت [ 29 ] به پیشرفت های زیادی دست یافته اند . حالت کانولوشن در GCN ها شامل پیچش های طیف و دامنه فضایی [ 36 ] است. اولی در این مطالعه به کار گرفته شد. پیچیدگی طیف را می توان به عنوان حاصل ضرب سیگنال x در نمودار و فیلتر شکل تعریف کرد gθ(L)، که در دامنه فوریه ساخته شده است: gθ(L)∗ایکس=Ugθ(Uتیایکس)، جایی که θیک پارامتر مدل است، L ماتریس لاپلاسی گراف است، U بردار ویژه ماتریس لاپلاسی نرمال شده است. L=منن–D–12آD–12=UλUتی، و Uتیایکسنمودار تبدیل فوریه x است. x را نیز می توان ارتقا داد ایکس∈آرن×سی، جایی که C به تعداد ویژگی ها اشاره دارد.
با توجه به ماتریس مشخصه X و ماتریس A مجاور ، GCN ها می توانند با انجام عملیات کانولوشنال طیف با در نظر گرفتن گره گراف و حوزه های مجاور مرتبه اول گره ها، عمل کانولوشنی را در CNN های قدامی جایگزین کنند. علاوه بر این، یک قانون انتشار سلسله مراتبی برای روی هم قرار دادن چندین شبکه اعمال می شود. یک مدل GCN چند لایه در [ 29 ] به صورت زیر بیان می شود:

اچل+1=σD˜–12 آ^ D˜–12 اچل θل،

جایی که آ˜=آ+مننیک ماتریس مجاور با ساختارهای خود اتصال است، مننیک ماتریس هویت است، D˜یک ماتریس درجه است، D˜منمن=∑jآ˜منj، اچل∈آرن×لخروجی لایه l است، θلپارامتر لایه l و است σ(·)یک تابع فعال سازی است که برای مدل سازی غیرخطی استفاده می شود.

به طور کلی، یک مدل GCN دو لایه [ 29 ] را می توان به صورت زیر بیان کرد:

fایکس،آ=σآ^ آرهLUآ^ ایکس دبلیو0دبلیو1،

که در آن X یک ماتریس ویژگی است. A ماتریس مجاور است. و آ^=D˜–12 آ˜ D˜–12یک مرحله پیش پردازش است که در آن آ˜=آ+مننماتریس مجاور گراف G با ساختار خود اتصال است. دبلیو0∈آرپ×اچماتریس وزن از لایه ورودی به لایه واحد پنهان است که در آن P طول زمان و H تعداد واحدهای پنهان است. دبلیو1∈آراچ×تیماتریس وزن از لایه پنهان به لایه خروجی است. fایکس،آ∈آرن×تینشان دهنده خروجی با طول پیش بینی T و آرهLU()یک تابع فعال سازی غیرخطی رایج است.

GCNها می‌توانند ساختارهای توپولوژیکی شبکه‌های جاده‌ای و ویژگی‌های بخش‌های جاده‌ای را با تعیین رابطه توپولوژیکی بین بخش جاده مرکزی و بخش‌های جاده اطراف رمزگذاری کنند. بر این اساس می توان وابستگی فضایی را گرفت. در یک کلام، این مطالعه وابستگی فضایی را از طریق مدل GCN آموخت [ 29 ].

2.3. مدل GRU

وابستگی زمانی وضعیت ترافیک یکی دیگر از مشکلات کلیدی است که مانع پیش‌بینی ترافیک می‌شود. RNN ها مدل های شبکه عصبی هستند که داده های متوالی را پردازش می کنند. با این حال، محدودیت‌هایی در پیش‌بینی بلندمدت در RNN‌های سنتی به دلیل معایب از نظر ناپدید شدن گرادیان و انفجار مشاهده می‌شود [ 37 ]. LSTM [ 19 ] و GRUs [ 20 ] انواعی از RNN ها هستند که به طور موثر مشکلات را میانجیگری می کنند. LSTM و GRU اساساً اصول اساسی یکسانی دارند. هر دو مدل از مکانیسم های دروازه ای برای حفظ اطلاعات بلند مدت استفاده می کنند و به طور مشابه در وظایف مختلف انجام می دهند [ 38]. در مقایسه با GRUها، LSTM دارای یک سلول حافظه اضافی است و واحدهای ورودی بیشتری را برای کنترل جریان اطلاعات تطبیق می دهد. بنابراین، GRU ساختار نسبتاً ساده‌تری دارد، پارامترهای کمتری دارد و محاسبه و پیاده‌سازی آسان‌تر است [ 39 ].
در مدل حاضر، وابستگی زمانی توسط یک مدل GRU گرفته شد. فرآیند محاسبه به شرح زیر معرفی می شود، جایی که ساعتتی–1حالت پنهان در t − 1 است، ایکستیسرعت ترافیک در لحظه فعلی است و rتیدروازه تنظیم مجدد برای کنترل درجه نادیده گرفتن اطلاعات وضعیت در لحظه قبل است. اطلاعات بی ربط به پیش بینی را می توان رها کرد. اگر دروازه تنظیم مجدد 0 را خروجی دهد، اطلاعات ترافیک در لحظه قبل نادیده گرفته می شود. اگر گیت تنظیم مجدد عدد 1 را به دست آورد، اطلاعات ترافیک لحظه قبل به طور کامل به لحظه بعدی وارد می شود. توتیدروازه به روز رسانی است و برای کنترل کمیت اطلاعات وضعیت در لحظه قبلی که به حالت فعلی آورده می شود استفاده می شود. در همین حال، جتیمحتوای حافظه ذخیره شده در لحظه جاری است و ساعتتیوضعیت خروجی در لحظه فعلی است.

توتی=σ(دبلیوتو∗ایکستی،ساعتتی–1+بتو)
rتی=σ(دبلیوr∗ایکستی،ساعتتی–1+بr)
جتی=tanh(دبلیوجایکستی،(rتی∗ساعتتی–1)+بج)
ساعتتی=توتی∗ساعتتی–1+(1–توتی)∗جتی.
GRU ها وضعیت ترافیک را در لحظه فعلی با استفاده از حالت پنهان در لحظه قبلی و اطلاعات ترافیک در لحظه فعلی به عنوان ورودی تعیین می کنند. GRUها روند تغییرات اطلاعات ترافیک تاریخی را هنگام ثبت اطلاعات ترافیک در لحظه فعلی به دلیل مکانیزم دروازه ای حفظ می کنند. از این رو، این مدل می‌تواند ویژگی‌های تغییرات زمانی پویا را از داده‌های ترافیک دریافت کند، یعنی این مطالعه از یک مدل GRU برای یادگیری روند تغییرات زمانی وضعیت ترافیک استفاده کرده است.

2.4. مدل توجه

مدل توجه بر اساس مدل رمزگذار – رمزگشا تحقق می یابد. این مدل در ابتدا در کارهای ترجمه ماشین عصبی [ 40 ] استفاده شد. امروزه، مدل‌های توجه به طور گسترده برای تولید شرح تصویر [ 34 ]، سیستم‌های توصیه [ 41 ] و طبقه‌بندی اسناد [ 42 ] اعمال می‌شوند. با توسعه سریع چنین مدل هایی، مدل های توجه موجود را می توان به انواع مختلفی تقسیم کرد، مانند توجه نرم و سخت [ 40 ]، توجه جهانی و محلی [ 43 ] و توجه به خود [40]. 35 ].]. در مطالعه حاضر، از یک مدل توجه نرم برای یادگیری اهمیت اطلاعات ترافیک در هر لحظه استفاده شد و سپس بردار زمینه ای که می تواند روند تغییرات کلی وضعیت ترافیک را بیان کند برای وظایف پیش بینی ترافیک آینده محاسبه شد.
فرض کنید که یک سری زمانی ایکسمن(من=1،2،⋯،n)، که در آن n طول سری زمانی است، معرفی شده است. فرآیند طراحی مدل های توجه نرم به شرح زیر معرفی می شود. اول، حالات پنهان ساعتمن(من=1،2،⋯،n)در لحظات مختلف با استفاده از CNN (و انواع آنها) یا RNN (و نوع آنها) محاسبه می شوند و به صورت بیان می شوند. اچ={ساعت1،ساعت2،⋯،ساعتn}. دوم، یک تابع امتیازدهی برای محاسبه امتیاز/وزن هر حالت پنهان طراحی شده است. سوم، یک تابع توجه برای محاسبه بردار زمینه طراحی شده است سیتیکه می تواند اطلاعات تنوع ترافیک جهانی را توصیف کند. در نهایت نتایج خروجی نهایی با استفاده از بردار زمینه به دست می آید. در مطالعه حاضر، این مراحل در فرآیند طراحی دنبال شد، اما به جای آن یک ادراک چند لایه به عنوان تابع امتیازدهی اعمال شد.
به ویژه، ویژگی ها ساعتمندر هر لحظه به عنوان ورودی هنگام محاسبه وزن هر حالت پنهان بر اساس مکانیسم توجه استفاده شد. خروجی های مربوطه را می توان از طریق دو لایه پنهان به دست آورد. وزن هر مشخصه αمنتوسط یک تابع شاخص نرمال شده Softmax (معادله ( 8 ))، که در آن w(1)و ب(1)وزن و انحراف لایه اول هستند و w(2)و ب(2)به ترتیب وزن و انحراف لایه دوم هستند.

همن=w(2)(w(1)اچ+ب(1))+ب(2)
αمن=انقضا(همن)∑ک=1nانقضا(هک).
در نهایت تابع توجه طراحی شد. فرآیند محاسبه بردار زمینه سیتیکه اطلاعات تغییرات ترافیک جهانی را پوشش می دهد در معادله ( 10 ) نشان داده شده است.

سیتی=∑من=1nαمن∗ساعتمن.

2.5. مدل A3T-GCN

A3t-GCN بهبود کار قبلی ما به نام شبکه Convolutional Graph (T-GCN) [ 31 ] است. مکانیسم توجه برای وزن‌دهی مجدد به تأثیر وضعیت‌های ترافیکی تاریخی و در نتیجه گرفتن روند تغییرات جهانی وضعیت ترافیک معرفی شد. ساختار مدل در شکل 1 نشان داده شده است .
مدل T-GCN با ترکیب GCN و GRU ساخته شد. ابتدا، n مرحله زمانی داده های ترافیکی تاریخی در مدل T-GCN برای به دست آوردن n حالت پنهان ( h ) وارد شد که ویژگی های مکانی-زمانی را پوشش می داد: {ساعتتی–n،⋯،ساعتتی–1،ساعتتی}. محاسبه T-GCN در معادلات (11)-(14) [ 31 ] نشان داده شده است، جایی که ساعتتی–1خروجی در t – 1 است. GC فرآیند کانولوشنی گراف است. توتیو rتیگیت های به روز رسانی و تنظیم مجدد به ترتیب در t هستند. جتیمحتوای ذخیره شده در لحظه فعلی است. ساعتتیحالت خروجی در لحظه t است و W و b به ترتیب وزن و انحراف در فرآیند تمرین هستند.

توتی=σ(دبلیوتو∗[جیسی(آ،ایکستی)،ساعتتی–1]+بتو)
rتی=σ(دبلیوr∗[جیسی(آ،ایکستی)،ساعتتی–1]+بr)
جتی=tanh(دبلیوج∗[جیسی(آ،ایکستی)،(rتی∗ساعتتی–1)]+بج)
ساعتتی=توتی∗ساعتتی–1+(1–توتی)∗جتی).
سپس، حالت‌های پنهان به مدل توجه داده شد تا بردار زمینه‌ای که اطلاعات تغییرات ترافیک جهانی را پوشش می‌دهد، تعیین کند. به ویژه، وزن هر ساعت توسط Softmax با استفاده از ادراک چند لایه محاسبه شد: {آتی–n،⋯،آتی–1،آتی}. بردار زمینه که اطلاعات تغییرات ترافیک جهانی را پوشش می دهد با مجموع وزنی محاسبه شد. در نهایت، نتایج پیش‌بینی با استفاده از لایه کاملاً متصل خروجی شد.
در مجموع، ما A3T-GCN را برای تحقق پیش بینی ترافیک پیشنهاد کردیم. شبکه راه های شهری به صورت یک شبکه نموداری ساخته شد و وضعیت ترافیک در بخش های مختلف به عنوان ویژگی های گره توصیف شد. ویژگی‌های توپولوژیکی شبکه جاده‌ای توسط یک GCN برای به دست آوردن وابستگی فضایی گرفته شد. تنوع دینامیکی ویژگی‌های گره توسط یک GRU برای به دست آوردن تمایل زمانی محلی وضعیت ترافیک گرفته شد. سپس روند تغییرات جهانی وضعیت ترافیک توسط مدل توجه، که منجر به تحقق پیش‌بینی دقیق ترافیک می‌شد، ثبت شد.

2.6. عملکرد از دست دادن

هدف آموزش به حداقل رساندن خطاهای بین سرعت واقعی و پیش بینی شده در شبکه راه است. سرعت واقعی و پیش بینی شده در مقاطع مختلف در t با Y و بیان می شودY^، به ترتیب. بنابراین، تابع هدف A3T-GCN به صورت زیر نشان داده شده است. اولین عبارت با هدف به حداقل رساندن خطا بین سرعت واقعی و پیش بینی شده است. ترم دوم Lrهgیک اصطلاح عادی سازی است که برای جلوگیری از برازش بیش از حد مساعد است. λیک هایپر پارامتر است.

لoسس=“Yتی–Yتی^“+λLrهg.

3. آزمایشات

3.1. توضیحات داده ها

دو مجموعه داده ترافیک دنیای واقعی، یعنی مجموعه داده مسیر تاکسی (SZ-taxi) در شهر شنژن و مجموعه داده آشکارساز حلقه (Los-loop) در لس آنجلس، استفاده شد. هر دو مجموعه داده به سرعت ترافیک مرتبط هستند. از این رو، سرعت ترافیک به عنوان اطلاعات ترافیکی در آزمایش‌ها در نظر گرفته می‌شود. مجموعه داده تاکسی SZ مسیر تاکسی شنژن از 1 ژانویه تا 31 ژانویه 2015 است. در مطالعه حاضر، 156 جاده اصلی منطقه لوهو به عنوان منطقه مورد مطالعه انتخاب شدند، بنابراین اندازه ماتریس مجاورت تاکسی SZ برابر است با 156×156. مجموعه داده Los-loop در بزرگراه شهرستان لس آنجلس در زمان واقعی توسط آشکارسازهای حلقه جمع آوری شد. در مجموع 207 حسگر به همراه سرعت ترافیک آنها از 1 مارس تا 7 مارس 2012 انتخاب شدند. اندازه ماتریس مجاورت حلقه Los بنابراین است 207×207.

3.2. معیارهای ارزیابی

برای ارزیابی عملکرد پیش‌بینی مدل، خطای بین سرعت واقعی ترافیک و نتایج پیش‌بینی‌شده بر اساس معیارهای زیر ارزیابی می‌شود [ 31 ]:
(1) ریشه میانگین مربعات خطا (RMSE):

آرماسE=1من∑j=1م∑من=1ن(yمنj–yمنj^)2.
(2) میانگین خطای مطلق (MAE):

مآE=1من∑j=1م∑من=1نyمنj–yمنj^.
(3) دقت:

آججتوrآجy=1–“Y–Y^“اف“Y“اف،

که در آن F هنجار فروبنیوس است که جذر مجموع مجذور مطلق عناصر در ماتریس را محاسبه می کند.

(4) ضریب تعیین ( آر2):

آر2=1–∑j=1م∑من=1ن(yمنj–yمنj^)2∑j=1م∑من=1ن(yمنj–Y¯)2.
(5) امتیاز واریانس توضیح داده شده ( vآr):

vآr=1–VآrY–Y^VآrY،

جایی که yمنjو yمنj^به ترتیب اطلاعات ترافیک واقعی و پیش بینی شده نمونه زمانی j در جاده i هستند. N تعداد گره های موجود در جاده است. M تعداد نمونه های زمانی است. Y و Y^مجموعه ای از yمنjو yمنj^به ترتیب و Y¯میانگین Y است.

به ویژه از RMSE و MAE برای اندازه گیری خطای پیش بینی استفاده شد. مقادیر کوچک RMSE و MASE منعکس کننده دقت پیش بینی بالا هستند. دقت برای اندازه گیری دقت پیش بینی استفاده می شود و مقدار دقت بالا ترجیح داده می شود. آر2و vآrضریب همبستگی را محاسبه کنید، که توانایی نتیجه پیش‌بینی را برای نمایش داده‌های واقعی اندازه‌گیری می‌کند: هر چه مقدار بزرگ‌تر باشد، اثر پیش‌بینی بهتر است.

3.3. تجزیه و تحلیل نتایج تجربی

فراپارامترهای A3T-GCN شامل نرخ یادگیری، دوره و تعداد واحدهای پنهان است. در آزمایش، نرخ یادگیری و دوره به صورت دستی، بر اساس تجربیات، برای هر دو مجموعه داده 0.001 و 5000 تنظیم شد و پارامترها به طور تصادفی از یک توزیع نرمال مقداردهی اولیه شدند. ما مدل را روی تعداد واحدهای مخفی مختلف (8، 16، 32، 64، 100، 128) آزمایش کردیم و اعدادی را انتخاب کردیم که بهترین عملکرد را گزارش کردند، یعنی 64 برای مجموعه داده SZ-taxi و 100 برای Los-loop. مجموعه داده
در مطالعه حاضر 80 درصد داده های ترافیکی به عنوان مجموعه آموزشی و 20 درصد مابقی داده ها به عنوان مجموعه آزمون استفاده شد. اطلاعات ترافیکی در 15، 30، 45 و 60 دقیقه آینده پیش بینی شده بود. نتایج پیش‌بینی‌شده با نتایج مدل میانگین تاریخی (HA)، مدل میانگین متحرک یکپارچه رگرسیون خودکار (ARIMA)، SVR، مدل GCN و مدل GRU مقایسه شد. A3T-GCN از دیدگاه‌های دقت، قابلیت‌های پیش‌بینی مکانی-زمانی، قابلیت پیش‌بینی بلندمدت و قابلیت ثبت ویژگی جهانی مورد تجزیه و تحلیل قرار گرفت.

3.3.1. دقت پیش بینی بالا

جدول 1 و جدول 2مقایسه مدل‌های مختلف و دو مجموعه داده واقعی را از نظر دقت پیش‌بینی طول‌های مختلف سرعت ترافیک نشان می‌دهد. نتایج بهینه را در جداول پررنگ می کنیم، و * به این معنی است که مقادیر به اندازه ای کوچک هستند که قابل چشم پوشی هستند، که نشان می دهد اثر پیش بینی مدل ضعیف است. دقت پیش‌بینی مدل‌های شبکه عصبی (مانند A3T-GCN و GRU) بالاتر از مدل‌های دیگر (مانند HA، ARIMA، و SVR) است. با توجه به سری زمانی 15 دقیقه، RMSE و دقت HA به ترتیب تقریباً 9.22٪ بیشتر و 4.24٪ کمتر از A3T-GCN هستند. RMSE و دقت ARIMA به ترتیب تقریباً 46.15% بیشتر و 39.01% کمتر از A3T-GCN هستند. RMSE و دقت SVR به ترتیب تقریباً 5.95٪ بیشتر و 2.81٪ کمتر از A3T-GCN هستند. در مقایسه با GRU، RMSE و دقت HA به ترتیب تقریباً 6.88٪ بیشتر و 3.32٪ کمتر هستند. RMSE و دقت ARIMA به ترتیب تقریباً 44.76% و 38.07% هستند. RMSE و دقت SVAR به ترتیب تقریباً 3.52٪ و 1.87٪ هستند. این نتایج عمدتاً ناشی از توانایی‌های برازش غیرخطی ضعیف HA، ARIMA، و SVAR با توجه به داده‌های ترافیکی پیچیده و متغیر است. وقتی از ARIMA استفاده می شود، پردازش داده های طولانی مدت غیر ثابت دشوار است. علاوه بر این، ARIMA با میانگین گیری خطاهای بخش های مختلف سود می برد. داده های برخی از بخش ها ممکن است برای افزایش خطای نهایی نوسان زیادی داشته باشند. از این رو، ARIMA کمترین دقت پیش بینی را نشان می دهد. RMSE و دقت SVAR به ترتیب تقریباً 3.52٪ و 1.87٪ هستند. این نتایج عمدتاً ناشی از توانایی‌های برازش غیرخطی ضعیف HA، ARIMA، و SVAR با توجه به داده‌های ترافیکی پیچیده و متغیر است. وقتی از ARIMA استفاده می شود، پردازش داده های طولانی مدت غیر ثابت دشوار است. علاوه بر این، ARIMA با میانگین گیری خطاهای بخش های مختلف سود می برد. داده های برخی از بخش ها ممکن است برای افزایش خطای نهایی نوسان زیادی داشته باشند. از این رو، ARIMA کمترین دقت پیش بینی را نشان می دهد. RMSE و دقت SVAR به ترتیب تقریباً 3.52٪ و 1.87٪ هستند. این نتایج عمدتاً ناشی از توانایی‌های برازش غیرخطی ضعیف HA، ARIMA، و SVAR با توجه به داده‌های ترافیکی پیچیده و متغیر است. وقتی از ARIMA استفاده می شود، پردازش داده های طولانی مدت غیر ثابت دشوار است. علاوه بر این، ARIMA با میانگین گیری خطاهای بخش های مختلف سود می برد. داده های برخی از بخش ها ممکن است برای افزایش خطای نهایی نوسان زیادی داشته باشند. از این رو، ARIMA کمترین دقت پیش بینی را نشان می دهد. داده های برخی از بخش ها ممکن است برای افزایش خطای نهایی نوسان زیادی داشته باشند. از این رو، ARIMA کمترین دقت پیش بینی را نشان می دهد. داده های برخی از بخش ها ممکن است برای افزایش خطای نهایی نوسان زیادی داشته باشند. از این رو، ARIMA کمترین دقت پیش بینی را نشان می دهد.
نتایج مشابهی را می توان برای Los-loop گرفت. مدل A3T-GCN می تواند عملکرد پیش بینی بهینه تمام معیارها را در دو مجموعه داده واقعی به دست آورد، بنابراین اعتبار و برتری مدل A3T-GCN در وظایف پیش بینی ترافیک مکانی-زمانی را اثبات می کند.

3.3.2. اثربخشی مدل‌سازی وابستگی‌های مکانی و زمانی

برای آزمایش مزایای نمایش ویژگی‌های مکانی و زمانی داده‌های ترافیکی به طور همزمان در A3T-GCN، مدل A3T-GCN با GCN و GRU مقایسه می‌شود.
شکل 2 نتایج را بر اساس SZ-taxi نشان می دهد. خطای پیش‌بینی A3T-GCN کمتر از GCN (فقط با در نظر گرفتن ویژگی‌های مکانی) در 15، 30، 45 و 60 دقیقه پیش‌بینی ترافیک کمتر نگه داشته می‌شود، همانطور که در نشان داده شده است.همانطور که در شکل 2آ. در مقایسه با GCN، A3T-GCN به ترتیب در 15، 30، 45 و 60 دقیقه سری زمانی پیش‌بینی ترافیک، تقریباً 31.11، 31.08، 30.94 درصد و 30.78 درصد RMSE کمتری به دست می‌آورد. در مقایسه با GRU (فقط با در نظر گرفتن ویژگی های زمانی)، A3T-GCN تقریباً 2.51٪ RMSE کمتر در پیش بینی ترافیک 15 دقیقه، تقریباً 4.19٪ RMSE کمتر در پیش بینی ترافیک 30 دقیقه، تقریبا 4.99٪ RMSE کمتر در سری زمانی 45 دقیقه و تقریباً به دست می آورد. 2.55٪ RMSE کمتر در سری زمانی 60 دقیقه. در مجموع، همانطور که در شکل 2 ب نشان داده شده است، خطای پیش‌بینی A3T-GCN کمتر از GRU در پیش‌بینی ترافیک 15، 30، 45 و 60 دقیقه نگه داشته می‌شود .
نتایج مبتنی بر Los-loop مشابه نتایج مبتنی بر SZ-taxi است. همانطور که در شکل 3 الف نشان داده شده است، خطای پیش‌بینی A3T-GCN در 15، 30، 45 و 60 دقیقه پیش‌بینی ترافیک کمتر از GCN نگه داشته می‌شود . A3T-GCN تقریباً 34.67٪، 28.05٪، 24.08٪ و 23.38٪ RMSE های کمتری را در 15، 30، 45 و 60 دقیقه سری زمانی پیش بینی ترافیک به دست می آورد. همانطور که برای مقایسه با GRU نشان داده شده در شکل 3 ب، A3T-GCN تقریباً 2.45٪ RMSE کمتر در پیش بینی ترافیک 15 دقیقه، تقریبا 4.50٪ RMSE کمتر در پیش بینی ترافیک 30 دقیقه، تقریبا 4.98٪ RMSE کمتر در سری زمانی 45 دقیقه به دست می آورد. و تقریباً 7.35٪ RMSE کمتر در سری زمانی 60 دقیقه.
شکل 2 و شکل 3 نشان می دهد که A3T-GCN به ترتیب قابلیت پیش بینی بهتری نسبت به GCN و GRU دارد. به عبارت دیگر، مدل A3T-GCN می‌تواند ویژگی‌های توپولوژیکی فضایی شبکه‌های جاده‌ای شهری و ویژگی‌های تغییرات زمانی وضعیت ترافیک را به طور همزمان ثبت کند، به این معنی که در مقایسه با GRU و GCN برتری را در افق‌های پیش‌بینی مختلف حفظ می‌کند.

3.3.3. قابلیت پیش بینی بلند مدت

قابلیت پیش‌بینی بلندمدت A3T-GCN برای پیش‌بینی سرعت ترافیک در افق‌های پیش‌بینی 15، 30، 45 و 60 دقیقه آزمایش شد. مقایسه RMSE مدل های مختلف تحت افق های پیش بینی مختلف در شکل 4 الف نشان داده شده است. RMSE A3T-GCN کمترین مقدار در تمام طول سری های زمانی است. روند تغییرات RMSE و دقت، که به ترتیب خطای پیش‌بینی و دقت A3T-GCN را در افق‌های پیش‌بینی مختلف منعکس می‌کند، در شکل 4 نشان داده شده است.ب ما می توانیم مشاهده کنیم که RMSE با افزایش طول سری زمانی افزایش می یابد، در حالی که دقت کاهش می یابد. هر دو کمی تغییر می کنند و ثبات خاصی را نشان می دهند. در مقایسه با GRU (که از سایر خطوط پایه بهتر است)، A3T-GCN دارای انحراف استاندارد تقریباً 0.03 در RMSE است، در حالی که انحراف GRU تقریباً 0.06 است.
نتایج پیش بینی بر اساس Los-loop در شکل 5 نشان داده شده است و قوانین منسجم یافت می شوند. در مجموع، A3T-GCN قابلیت پیش‌بینی بلندمدت خوبی دارد. همانطور که در شکل 5 الف نشان داده شده است، می تواند بهترین عملکرد را در افق های پیش بینی 15، 30، 45 و 60 دقیقه حفظ کند . شکل 5 ب نشان می دهد که نتایج پیش بینی A3T-GCN با تغییرات در افق های پیش بینی اندکی تغییر می کند و در نتیجه ثبات خاصی را نشان می دهد. در مقایسه با GRU (که عملکرد بهتری از سایر خطوط پایه دارد)، A3T-GCN دارای انحراف استاندارد تقریباً 0.76 در RMSE است، در حالی که انحراف استاندارد GRU تقریباً 0.91 است. بنابراین، A3T-GCN برای کارهای پیش بینی ترافیک کوتاه مدت و بلند مدت قابل استفاده است.

3.3.4. اثربخشی معرفی توجه به جذب تنوع جهانی

A3T-GCN و T-GCN برای آزمایش برتری گرفتن تنوع جهانی مقایسه شدند. نتایج در جدول 3 نشان داده شده است. مدل A3T-GCN تقریباً 0.86٪ RMSE کمتر و تقریباً 0.32٪ دقت بالاتری نسبت به مدل T-GCN در سری زمانی 15 دقیقه نشان می دهد. تقریباً 1.31٪ RMSE کمتر و تقریباً 0.48٪ دقت بالاتر در سری زمانی 30 دقیقه. تقریباً 1.14٪ RMSE کمتر و تقریباً 0.43٪ دقت بالاتر تحت پیش بینی ترافیک 45 دقیقه. و تقریباً 0.99٪ RMSE کمتر و تقریباً 0.37٪ دقت بالاتر در سری زمانی 60 دقیقه.
از این رو، خطای پیش‌بینی A3T-GCN کمتر از T-GCN است، اما دقت اولی در افق‌های مختلف پیش‌بینی ترافیک بالاتر است، در نتیجه قابلیت ثبت ویژگی‌های جهانی مدل A3T-GCN را اثبات می‌کند.

3.4. تجزیه و تحلیل اغتشاش

نویز در مجموعه داده های دنیای واقعی اجتناب ناپذیر است. بنابراین، تجزیه و تحلیل اغتشاش برای آزمایش استحکام A3T-GCN انجام شد. در این آزمایش دو نوع نویز تصادفی به داده های ترافیک اضافه شد. نویز تصادفی از توزیع گاوسی تبعیت می کند ن∈(0،σ2)، جایی که σ∈(0.2،0.4،0.8،1،2)و توزیع پواسون پ(λ)، جایی که λ∈(1،2،4،8،16). مقادیر ماتریس نویز به [0، 1] نرمال شد.
نتایج تجربی بر اساس SZ-taxi در شکل 6 نشان داده شده است. نتایج اضافه کردن نویز گاوسی در شکل 6 الف نشان داده شده است، که در آن محورهای x و y تغییرات در σو به ترتیب در معیارهای ارزیابی مختلف. رنگ های مختلف معیارهای مختلفی را نشان می دهند. به طور مشابه، نتایج اضافه کردن نویز پواسون در شکل 6 ب نشان داده شده است. مقادیر معیارهای ارزیابی مختلف بدون توجه به تغییرات در اساساً یکسان باقی می مانند σ/λ. از این رو، مدل پیشنهادی به طور قابل توجهی می تواند در برابر نویز مقاومت کند.
شکل 7 a,b نشان می دهد که نتایج تجربی بر اساس Los-loop با نتایج تجربی بر اساس SZ-taxi مطابقت دارد. بنابراین، مدل A3T-GCN می تواند به طور قابل توجهی در برابر نویز مقاومت کند و همچنان نتایج پیش بینی پایداری را تحت اختلالات گاوسین و پواسون به دست آورد.

3.5. تجزیه و تحلیل تصویری

نتایج پیش‌بینی مدل A3T-GCN بر اساس دو مجموعه داده واقعی برای توضیح خوب مدل تجسم شده‌اند.
(1) SZ-taxi: ما نتیجه یک جاده را در 27 ژانویه 2015 تجسم می کنیم. نتایج تجسم برای سری های زمانی 15، 30، 45 و 60 دقیقه در شکل 8 نشان داده شده است.
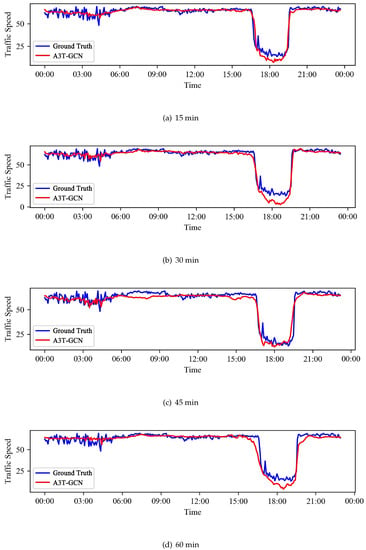
(2) Los-loop: به طور مشابه، یک داده آشکارساز حلقه را در مجموعه داده Los-loop تجسم می کنیم. نتایج تجسم برای 15، 30، 45 و 60 دقیقه در شکل 9 نشان داده شده است.
در مجموع، سرعت ترافیک پیش‌بینی‌شده روند تغییرات مشابهی را با سرعت واقعی ترافیک در طول‌های سری زمانی مختلف نشان می‌دهد، که نشان می‌دهد مدل A3T-GCN در کار پیش‌بینی ترافیک صلاحیت دارد. این مدل همچنین می تواند روند تغییرات سرعت ترافیک را ثبت کند و نقاط شروع و پایان ساعات شلوغی را تشخیص دهد. همانطور که توسط تناسب A3T-GCN با افت ناگهانی در ساعات شلوغی در شکل 9 پیشنهاد شده است، مدل A3T-GCN ترافیک ترافیک را به طور دقیق پیش‌بینی می‌کند، در نتیجه اعتبار آن را در پیش‌بینی ترافیک بلادرنگ اثبات می‌کند.

4. نتیجه گیری

یک روش پیش‌بینی ترافیک به نام A3T-GCN برای ثبت پویایی‌های زمانی جهانی و همبستگی‌های مکانی به طور همزمان و تسهیل پیش‌بینی ترافیک پیشنهاد شده است. شبکه راه های شهری به صورت یک نمودار ساخته می شود و سرعت ترافیک در جاده ها به عنوان ویژگی های گره های روی نمودار توصیف می شود. در روش پیشنهادی، وابستگی‌های فضایی توسط GCN بر اساس ویژگی‌های توپولوژیکی شبکه راه‌ها گرفته می‌شوند. در همین حال، تغییرات دینامیکی سرعت‌های ترافیک تاریخی متوالی توسط GRU ثبت می‌شود. علاوه بر این، روند تغییرات زمانی جهانی توسط مکانیسم توجه ضبط و جمع‌آوری می‌شود. در نهایت، مدل پیشنهادی A3T-GCN بر روی کار پیش‌بینی ترافیک مبتنی بر شبکه جاده شهری با استفاده از دو مجموعه داده واقعی، یعنی SZ-taxi و Los-loop آزمایش می‌شود. ما بهبودهای RMSE 2.51-46 را مشاهده می کنیم. 15٪ و 2.45-49.32٪ بیش از خطوط پایه برای SZ-taxi و Los-loop، به ترتیب. در همین حال، دقت ها به ترتیب 0.95-89.91٪ و 0.26-10.37٪ بیشتر از خطوط پایه برای SZ-taxi و Los-loop هستند. نتایج نشان می‌دهد که مدل A3T-GCN از نظر دقت پیش‌بینی در طول‌های مختلف افق پیش‌بینی نسبت به HA، ARIMA، SVR، GCN، GRU، و T-GCN برتر است و در نتیجه اعتبار آن را برای پیش‌بینی ترافیک بلادرنگ اثبات می‌کند.

مشارکت های نویسنده

مفهوم سازی، جیاندونگ بای و جیاوئی زو. روش، آهنگ یوجیائو. نرم افزار Jiandong Bai و Yujiao Song. گزینش داده ها، لینگ ژائو، ژیشیانگ هو و رونگهوا دو. نوشتن – آماده سازی پیش نویس اصلی، جیاندونگ بای و جیاوئی ژو. تجسم، آهنگ یوجیائو. نظارت، جیاوئی زو و هایفنگ لی. همه نویسندگان نسخه منتشر شده نسخه خطی را خوانده و با آن موافقت کرده اند.

منابع مالی

این تحقیق توسط بنیاد ملی علوم طبیعی چین تأمین مالی شد (شماره های کمک مالی 41571397، 41871364). و صندوق های تحقیقات بنیادی (شماره 2019zzts881) برای دانشگاه های مرکزی دانشگاه مرکزی جنوب.

تضاد علاقه

نویسندگان هیچ تضاد منافع را اعلام نمی کنند.

منابع

  1. Huang، HJ مدلسازی پویا شبکه های حمل و نقل شهری و تحلیل رفتارهای سفر آن. چانه. جی. مناگ. 2005 ، 2 ، 18-22. [ Google Scholar ]
  2. جیان، ی. فن، ب. سنتز پیشرفت تحقیق پیش بینی جریان ترافیک کوتاه مدت. ترانسپ شهری چین 2012 ، 10 ، 73-79. [ Google Scholar ]
  3. جینگ، ال. Wei, G. خلاصه ای از روش های پیش بینی جریان ترافیک. جی. هایو. ترانسپ Res. توسعه دهنده 2004 ، 3 ، 82-85. [ Google Scholar ]
  4. گائو، ال. لیو، ایکس. لیو، ی. وانگ، پی. دنگ، م. زو، س. لی، اچ. اندازه‌گیری آسیب‌پذیری توپولوژی شبکه جاده‌ای با انحنای ریسی. فیزیک یک آمار مکانیک. برنامه آن است. 2019 ، 527 ، 121071. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  5. دونگ، سی جی. شائو، CF; Zhuge، CX; Meng, M. ویژگی‌های مکانی و زمانی برای ترافیک شلوغ در بزرگراه شهری. J. دانشگاه پکن. تکنولوژی 2012 ، 38 ، 1242-1246، 1268. [ Google Scholar ]
  6. احمد، ام اس; کوک، تحلیل واقعیت افزوده داده‌های سری زمانی ترافیک آزادراه با استفاده از تکنیک‌های Box-Jenkins . سابقه تحقیقات حمل و نقل: واشنگتن، دی سی، ایالات متحده آمریکا، 1979. [ Google Scholar ]
  7. هاج، وی جی. کریشنان، آر. آستین، جی. پولاک، جی. جکسون، تی. پیش بینی کوتاه مدت جریان ترافیک با استفاده از یک شبکه عصبی باینری. محاسبات عصبی Appl. 2014 ، 25 ، 1639-1655. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  8. سان، اچ. ژانگ، سی. Ran، B. پیش بینی بازه برای سری های زمانی ترافیک با استفاده از پیش بینی خطی محلی. در مجموعه مقالات کنفرانس بین المللی IEEE در مورد سیستم های حمل و نقل هوشمند، واشنگتن، WA، ایالات متحده آمریکا، 3 تا 6 اکتبر 2004. [ Google Scholar ]
  9. اوکوتانی، آی. استفاندس، YJ پیش‌بینی دینامیکی حجم ترافیک از طریق نظریه فیلتر کالمن. ترانسپ Res. روش قسمت B. 1984 ، 18 ، 1-11. [ Google Scholar ] [ CrossRef ]
  10. آلتمن، NS مقدمه ای بر رگرسیون ناپارامتریک هسته و نزدیکترین همسایه. صبح. آمار 1992 ، 46 ، 175-185. [ Google Scholar ]
  11. وو، CH; هو، جی.ام. لی، دی. پیش‌بینی زمان سفر با رگرسیون بردار پشتیبان. IEEE Trans. هوشمند ترانسپ سیستم 2005 ، 5 ، 276-281. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  12. فو، جی. آویزان شدن.؛ لو، اف. Xu, Z. مدل پیش‌بینی جریان ترافیک کوتاه‌مدت بر اساس رگرسیون ماشین بردار پشتیبان. J. دانشگاه جنوب چین تکنولوژی 2013 ، 41 ، 71-76. [ Google Scholar ]
  13. یین، اچ. وانگ، SC; خو، جی. Wong، CK پیش‌بینی جریان ترافیک شهری با استفاده از رویکرد عصبی فازی. ترانسپ Res. قسمت C 2002 ، 10 ، 85-98. [ Google Scholar ] [ CrossRef ]
  14. سان، اس. ژانگ، سی. یو، جی. رویکرد شبکه بیزی برای پیش بینی جریان ترافیک. IEEE Trans. هوشمند ترانسپ سیستم 2006 ، 7 ، 124-132. [ Google Scholar ] [ CrossRef ]
  15. چتینر، BG; ساری، م. بورات، او. مدل پیش‌بینی جریان ترافیک مبتنی بر شبکه عصبی. ریاضی. محاسبه کنید. Appl. 2010 ، 15 ، 269-278. [ Google Scholar ]
  16. نقره، دی. شریتویزر، جی. سیمونیان، ک. آنتونوگلو، آی. هوانگ، آ. گئز، آ. هوبرت، تی. بیکر، ال. لای، م. بولتون، ای. تسلط بر بازی Go بدون دانش بشر. طبیعت 2017 ، 550 ، 354–359. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  17. موراویک، م. اشمید، ام. برچ، ن. لیسی، وی. موریل، دی. بارد، ن. دیویس، تی. واو، ک. جوهانسون، ام. Bowling، M. DeepStack: هوش مصنوعی در سطح متخصص در پوکر بدون محدودیت heads-up. Science 2017 , 356 , eaam6960. [ Google Scholar ]
  18. یوان، اچ. لی، جی. بررسی پیش بینی ترافیک: از داده های مکانی- زمانی تا حمل و نقل هوشمند. اطلاعات علمی مهندس 2021 ، 6 ، 63-85. [ Google Scholar ] [ CrossRef ]
  19. گریوز، الف. حافظه کوتاه مدت. محاسبات عصبی 1997 ، 9 ، 1735-1780. [ Google Scholar ]
  20. چو، ک. Merrienboer، BV; بهداناو، د. Bengio, Y. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches. arXiv 2014 ، arXiv:1409.1259. [ Google Scholar ]
  21. روی، اف. زو، ز. Li, L. استفاده از روش های شبکه عصبی LSTM و GRU برای پیش بینی جریان ترافیک. در مجموعه مقالات کنفرانس آکادمیک جوانان انجمن اتوماسیون چینی، ووهان، چین، 11 تا 13 نوامبر 2016. [ Google Scholar ]
  22. لینت، JWCV؛ Hooqendoorn, SP; Zuvlen، پیش‌بینی زمان سفر آزادراه HJV با شبکه‌های عصبی حالت-فضا: مدل‌سازی پویایی حالت-فضا با شبکه‌های عصبی مکرر. ترانسپ Res. ضبط J. Transp. Res. هیئت 2002 ، 1811 ، 347-369. [ Google Scholar ]
  23. ژائو، اف. Zeng، GQ; Lu، KD EnLSTM-WPEO: پیش‌بینی کوتاه‌مدت جریان ترافیک توسط گروه LSTM، یکپارچه‌سازی وزن NNCT، و بهینه‌سازی شدید جمعیت. IEEE Trans. وه تکنولوژی 2019 ، 69 ، 101-113. [ Google Scholar ] [ CrossRef ]
  24. وو، ی. Tan، H. پیش‌بینی کوتاه‌مدت جریان ترافیک با همبستگی مکانی-زمانی در یک چارچوب یادگیری عمیق ترکیبی. arXiv 2016 , arXiv:1612.01022. [ Google Scholar ]
  25. کائو، ایکس. ژونگ، ی. یون، ز. جیانگ، دبلیو. Zhang، W. شبکه کانولوشن مکرر زمانی تعاملی برای پیش بینی ترافیک در مراکز داده. دسترسی IEEE 2017 ، 6 ، 5276–5289. [ Google Scholar ] [ CrossRef ]
  26. یو، اچ. وو، زی. وانگ، اس. وانگ، ی. Ma، X. شبکه‌های کانولوشنال مکرر فضایی و زمانی برای پیش‌بینی ترافیک در شبکه‌های حمل‌ونقل. Sensors 2017 , 17 , 1501. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  27. سان، اس. وو، اچ. Xiang، L. پیش بینی جریان ترافیک در سطح شهر با استفاده از یک شبکه عصبی پیچیده عمیق. Sensors 2020 , 20 , 421. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  28. دیفرارد، ام. برسون، ایکس. Vandergheynst، P. شبکه‌های عصبی کانولوشن روی نمودارها با فیلتر کردن طیفی سریع محلی. Adv. عصبی Inf. روند. سیستم 2016 ، 29 ، 3844-3852. [ Google Scholar ]
  29. Kipf، TN; ولینگ، ام. طبقه بندی نیمه نظارت شده با شبکه های کانولوشن گراف. arXiv 2016 , arXiv:1609.02907. [ Google Scholar ]
  30. لی، ی. یو، آر. شهابی، ج. Liu, Y. Graph Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. arXiv 2017 , arXiv:1707.01926. [ Google Scholar ]
  31. ژائو، ال. آهنگ، ی. ژانگ، سی. لیو، ی. وانگ، پی. لین، تی. دنگ، م. Li، H. T-gcn: یک شبکه کانولوشن گراف زمانی برای پیش‌بینی ترافیک. IEEE Trans. هوشمند ترانسپ سیستم 2019 ، 21 ، 3848–3858. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  32. یو، بی. لی، ی. Sohn، K. پیش‌بینی سرعت ترافیک جاده‌ای با در نظر گرفتن وابستگی‌های مکانی-زمانی در سطح منطقه بر اساس یک شبکه عصبی کانولوشنال گراف (GCN). ترانسپ Res. قسمت C Emerg. تکنولوژی 2020 ، 114 ، 189-204. [ Google Scholar ] [ CrossRef ]
  33. Pavlyuk، D. انتخاب و استخراج ویژگی در پیش‌بینی ترافیک مکانی-زمانی: مروری بر ادبیات سیستماتیک. یورو ترانسپ Res. Rev. 2019 , 11 , 1-19. [ Google Scholar ] [ CrossRef ]
  34. خو، ک. با، ج. کیروس، آر. چو، ک. کورویل، آ. سالاخوتدینوف، ر. زمل، آر. Bengio، Y. نمایش، حضور و گفتن: ایجاد شرح تصویر عصبی با توجه بصری. arXiv 2015 ، arXiv:cs.LG/1502.03044. [ Google Scholar ]
  35. واسوانی، ع. Shazeer, N. پارمار، ن. Uszkoreit، J. جونز، ال. گومز، AN; قیصر، Ł. Polosukhin، I. توجه شما تمام چیزی است که نیاز دارید. در پیشرفت در سیستم های پردازش اطلاعات عصبی ; Curran Associates, Inc.: Long Beach, CA, USA, 2017; صفحات 5998–6008. [ Google Scholar ]
  36. برونا، جی. زارمبا، دبلیو. اسلم، آ. Lecun، Y. شبکه های طیفی و شبکه های محلی متصل روی نمودارها. arXiv 2013 , arXiv:1312.6203. [ Google Scholar ]
  37. بنژیو، ی. سیمرد، پ. فراسکونی، پی. یادگیری وابستگی های طولانی مدت با نزول گرادیان دشوار است. IEEE Trans. شبکه عصبی 2002 ، 5 ، 157-166. [ Google Scholar ] [ CrossRef ]
  38. چانگ، جی. گلچهره، سی. چو، ک. Bengio، Y. ارزیابی تجربی شبکه‌های عصبی بازگشتی دروازه‌ای در مدل‌سازی توالی. arXiv 2014 ، arXiv:cs.NE/1412.3555. [ Google Scholar ]
  39. چو، ک. Merrienboer، BV; گلچهره، سی. باهداناو، دی. بوگارس، اف. شونک، اچ. Bengio، Y. بازنمایی عبارت یادگیری با استفاده از رمزگذار-رمزگشا RNN برای ترجمه ماشینی آماری. arXiv 2014 ، arXiv:1406.1078. [ Google Scholar ]
  40. بهداناو، د. چو، ک. Bengio، Y. ترجمه ماشین عصبی با یادگیری مشترک تراز و ترجمه. arXiv 2014 ، arXiv:cs.CL/1409.0473. [ Google Scholar ]
  41. شیائو، جی. بله، اچ. او، X. ژانگ، اچ. وو، اف. ماشین‌های عامل‌سازی توجه Chua، TS: یادگیری وزن تعاملات ویژگی‌ها از طریق شبکه‌های توجه. arXiv 2017 ، arXiv:cs.LG/1708.04617. [ Google Scholar ]
  42. پاپاس، ن. Popescu-Belis، A. شبکه های توجه سلسله مراتبی چند زبانه برای طبقه بندی اسناد. arXiv 2017 , arXiv:1707.00896. [ Google Scholar ]
  43. Luong، MT; فام، اچ. منینگ، رویکردهای موثر CD برای ترجمه ماشین عصبی مبتنی بر توجه. arXiv 2015 ، arXiv:1508.04025. [ Google Scholar ]
Ijgi 10 00485 g001 550
شکل 1. چارچوب A3T-GCN.
Ijgi 10 00485 g002 550
شکل 2. SZ-taxi: اثربخشی مدل‌سازی وابستگی‌های مکانی و زمانی. ( الف ) مقایسه RMSE بین A3T-GCN و GCN (فقط ویژگی های فضایی را ثبت می کند). عملکرد بهتر A3T-GCN تحت افق های پیش بینی مختلف، اثربخشی A3T-GCN را در گرفتن ویژگی های زمانی اضافی در مقایسه با GCN تأیید می کند. ( ب ) مقایسه RMSE بین A3T-GCN و GRU (فقط ویژگی های زمانی را ثبت می کند). عملکرد بهتر A3T-GCN تحت افق های پیش بینی مختلف، اثربخشی A3T-GCN را در گرفتن ویژگی های فضایی اضافی در مقایسه با GRU تأیید می کند.
Ijgi 10 00485 g003 550
شکل 3. Los-loop: اثربخشی مدل‌سازی وابستگی‌های مکانی و زمانی. ( الف ) مقایسه RMSE بین A3T-GCN و GCN (فقط ویژگی های فضایی را ثبت می کند). عملکرد بهتر A3T-GCN تحت افق های پیش بینی مختلف، اثربخشی A3T-GCN را در گرفتن ویژگی های زمانی اضافی در مقایسه با GCN تأیید می کند. ( ب ) مقایسه RMSE بین A3T-GCN و GRU (فقط ویژگی های زمانی را ثبت می کند). عملکرد بهتر A3T-GCN تحت افق های پیش بینی مختلف، اثربخشی A3T-GCN را در گرفتن ویژگی های فضایی اضافی در مقایسه با GRU تأیید می کند.
Ijgi 10 00485 g004 550
شکل 4. SZ-taxi: توانایی پیش بینی بلند مدت. ( الف ) RMSE A3T-GCN و خطوط پایه تحت افق های پیش بینی مختلف. ( ب ) تغییرات در RMSE و دقت A3T-GCN تحت افق های پیش بینی مختلف.
Ijgi 10 00485 g005 550
شکل 5. Los-loop: توانایی پیش بینی بلند مدت. ( الف ) RMSE A3T-GCN و خطوط پایه تحت افق های پیش بینی مختلف. ( ب ) تغییرات در RMSE و دقت A3T-GCN تحت افق های پیش بینی مختلف.
Ijgi 10 00485 g006 550
شکل 6. SZ-taxi: تجزیه و تحلیل اغتشاش. ( الف ) عملکرد A3T-GCN پس از افزودن اغتشاش گاوسی به مجموعه داده تاکسی SZ. ( ب ) عملکرد A3T-GCN پس از افزودن اختلال پواسون به مجموعه داده تاکسی SZ.
Ijgi 10 00485 g007 550
شکل 7. Los-loop: تجزیه و تحلیل اغتشاش. ( الف ) عملکرد A3T-GCN پس از افزودن اغتشاش گاوسی به مجموعه داده Los-loop. ( ب ) عملکرد A3T-GCN پس از افزودن اغتشاش پواسون به مجموعه داده Los-loop.
Ijgi 10 00485 g008 550
شکل 8. نتایج تجسم برای افق پیش بینی 15، 30، 45، 60 دقیقه (SZ-taxi).
Ijgi 10 00485 g009 550
شکل 9. نتایج تجسم برای افق پیش بینی 15، 30، 45، 60 دقیقه (Los-Loop).

دسته‌بندی نشده

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید