خلاصه

حجم اطلاعات جمع آوری شده در مورد زمین بسیار زیاد شده است. با این اطلاعات، تقاضا برای یکپارچه سازی، پردازش، تجسم و توزیع این داده ها به وجود می آید تا بتوان از آن برای حل مشکلات دنیای واقعی استفاده کرد. برای پرداختن به این موضوع، به یک ساختار اطلاعاتی با دقت طراحی شده نیاز است که تمام اطلاعات مربوط به زمین را در قالبی مناسب ذخیره کند، به طوری که بتوان به راحتی از آن برای حل طیف گسترده ای از مشکلات استفاده کرد. ایده ای که ما بررسی می کنیم این است که یک سیستم شبکه جهانی گسسته (DGGS) با استفاده از سه وجهی Disdyakis (DT) به عنوان چند وجهی اولیه ایجاد کنیم. ما برای کاهش اعوجاج و سرعت بخشیدن به پرس و جوها، یک طرح ساده، بسته، با مساحت مساوی را تطبیق داده ایم. ما یک معکوس شکل بسته کارآمد برای این طرح ریزی استخراج کرده ایم که می تواند در جستارهای مهم DGGS استفاده شود. ساختار حاصل با استفاده از اطلسی از نقشه های اتصال نمایه می شود. با استفاده از محاسبات ساده مدولار، می‌توانیم پرس‌و‌جوهای نقطه به سلول، همسایگی و سلسله مراتبی را در شبکه آدرس دهی کنیم، که اجازه می‌دهد این پرس‌وجوها در زمان ثابت انجام شوند. ما اعوجاج زاویه ای ایجاد شده توسط DGGS خود را با مقایسه آن با DGGS ایکوساهدرون سنتی با استفاده از یک طرح ریزی مشابه ارزیابی کرده ایم. ما نشان می‌دهیم که شبکه ما اعوجاج زاویه‌ای را کاهش می‌دهد در حالی که امکان رندر زمان واقعی داده‌ها را در سراسر جهان فراهم می‌کند. ما اعوجاج زاویه ای ایجاد شده توسط DGGS خود را با مقایسه آن با DGGS ایکوساهدرون سنتی با استفاده از یک طرح ریزی مشابه ارزیابی کرده ایم. ما نشان می‌دهیم که شبکه ما اعوجاج زاویه‌ای را کاهش می‌دهد در حالی که امکان رندر زمان واقعی داده‌ها را در سراسر جهان فراهم می‌کند. ما اعوجاج زاویه ای ایجاد شده توسط DGGS خود را با مقایسه آن با DGGS ایکوساهدرون سنتی با استفاده از یک طرح ریزی مشابه ارزیابی کرده ایم. ما نشان می‌دهیم که شبکه ما اعوجاج زاویه‌ای را کاهش می‌دهد در حالی که امکان رندر زمان واقعی داده‌ها را در سراسر جهان فراهم می‌کند.

کلید واژه ها:

سیستم های شبکه جهانی گسسته ; زمین دیجیتال ؛ طرح ریزی مساحت مساوی ; مدل سازی هندسی

1. معرفی

در عصر مدرن، ما به طور فزاینده ای در حال جمع آوری مقادیر زیادی از اطلاعات در مورد زمین هستیم. زتابایت‌های زیادی از داده‌ها در حال حاضر در دسترس هستند و روزانه بیشتر جمع‌آوری می‌شوند [ 1 ، 2 ]. استفاده از این داده‌ها از آزمایش‌ها و تحلیل‌های پیچیده گرفته تا استفاده روزانه توسط عموم مردم برای اطمینان از آگاهی کامل از تصمیماتشان، متغیر است. برای انجام این وظایف، داده ها معمولاً باید در صفات و مقیاس های مختلف ترکیب شوند. به عنوان مثال، ترکیب الگوهای آب و هوای جهانی با وضوح بالا، موقعیت و هندسه دارایی های تجاری و احتمال بی ثباتی سیاسی برای ارزیابی ریسک بیمه. بنابراین، ما به ابزاری برای یکپارچه‌سازی، تحلیل، شبیه‌سازی، توزیع و تجسم این داده‌ها نیاز داریم تا بتوان از آن برای حل مشکلات دنیای واقعی استفاده کرد.2 ].
در نتیجه، ایده زمین دیجیتال (DE) دنبال شد. در مراحل اولیه DE، بسیاری از ایده ها از نقشه کشی سنتی به یک محیط دیجیتال گسترش یافت و نمایش مجازی نقشه های مسطح سنتی استاندارد شد [ 3 ]. در یک DE مبتنی بر نقشه، داده‌های زمین با استفاده از هر یک از گونه‌های چندگانه پیش‌بینی نقشه، که بسیاری از آن‌ها امروزه هنوز در حال استفاده هستند، به یک نقشه مسطح پیش‌بینی می‌شوند [ 4 ]. سپس با استفاده از روش‌های اقلیدسی مرسوم می‌توان تحلیل را در محیط مسطح انجام داد. با این حال، طرح زمین بر روی یک نقشه مسطح باعث ایجاد اعوجاج قابل توجه و اجتناب ناپذیر می شود که خطاهایی را در تجزیه و تحلیل ایجاد می کند [ 5 ].
گلوب ها جایگزینی برای نقشه های مسطح هستند که اعوجاج بسیار کمتری ایجاد می کنند [ 3 ]. در حالی که کره های فیزیکی به راحتی مقیاس بندی نمی شوند و تولید آنها دشوار است، یک DE فرصتی برای رفع برخی از کاستی های کره های فیزیکی [ 3 ] فراهم می کند. با یک کره، تجزیه و تحلیل را می توان به طور مستقیم در فضای کروی انجام داد و نتایج دقیق را تولید کرد. با این حال، این تحلیل‌ها ممکن است از نظر محاسباتی گران قیمت باشند. در برخی موارد، حتی ممکن است تکنیک‌هایی برای انجام تحلیل مستقیم در فضای کروی وجود نداشته باشد. به همین دلیل، بسیاری از سیستم‌های DE هنوز از نقشه‌های مسطح منفرد به عنوان بازنمایی زیربنایی خود استفاده می‌کنند [ 3 ].
با انگیزه تمایل به کاهش اعوجاج و مواجهه با چالش محاسبات کارآمد، تقریب های چند وجهی زمین مورد بررسی قرار گرفته اند. تقریب سطح زمین با یک چندوجهی محدب، اعوجاج را به طور کامل حذف نمی کند، اما به طور قابل توجهی آن را کاهش می دهد در حالی که اجازه می دهد هر وجهی از چند وجهی به عنوان یک نقشه مسطح در نظر گرفته شود [ 6 ]. چهره های بیشتر در چند وجهی امکان تقریب نزدیکتر از زمین و کاهش بیشتر اعوجاج را فراهم می کند [ 6 ].
یک سیستم شبکه جهانی گسسته (DGGS) یک DE مبتنی بر چند وجهی است که در آن سطح زمین به سلول‌های اغلب منظم و با وضوح چندگانه گسسته می‌شود. این سلول‌ها به‌طور منحصربه‌فردی فهرست‌بندی می‌شوند و به‌عنوان مکان‌گیر برای داده‌های مکانی مرتبط با مکان مربوطه روی زمین استفاده می‌شوند. DGGS به طور کلی از چهار بخش تشکیل شده است:
  • چند وجهی اولیه: درشت ترین گسسته سازی زمین به سلول
  • طرح ریزی: نقشه برداری بین هر نقطه روی زمین و نقطه متناظر در چند وجهی ( شکل 1 را ببینید ) .
  • نمایه سازی: اختصاص یک شناسه منحصر به فرد به هر سلول
  • پالایش: راهی برای تقسیم سلسله مراتبی سلول‌های درشت به سلول‌های ظریف‌تر و ایجاد سلول‌هایی با وضوح چندگانه
علیرغم حجم قابل توجهی از تحقیقات در مورد چگونگی بهترین انتخاب این اجزا، هر DGGS با ویژگی‌های خاصی در ذهن و با معاوضه‌های انجام شده برای دستیابی به اهداف خاص توسعه داده می‌شود. یکی از این ویژگی ها این است که سلول های DGGS باید در تمام وضوح های پشتیبانی شده دارای مساحت مساوی باشند. علاوه بر این، سلول ها باید تا حد امکان فشرده باشند (تقریباً باید منطقه بزرگی از دایره مرزی خود را اشغال کنند). در ترکیب، این دو ویژگی به سلول ها اجازه می دهد تا داده های مکانی را با دقت بیشتری نشان دهند. DGGS همچنین باید امکان عملیات کارآمد، از جمله پرس و جوهای نقطه ای، پرس و جوهای همسایگی و پیمایش سلسله مراتب را فراهم کند. در ارتباط با انتخاب چندوجهی اولیه، یک برآمدگی (و معکوس آن) از کره به این چندوجهی مورد نیاز است. طرح انتخابی باید ویژگی های فوق را برای سلول های چند وجهی و همتایان کروی آنها در تمام وضوح حفظ کند. همچنین باید اعوجاج ایجاد شده در سلول های مسطح حاصل را تا حد امکان کاهش دهد.
انتخاب اینکه از کدام چند وجهی اولیه استفاده شود، انگیزه بسیاری از عوامل مختلف است و منجر به فهرست‌های متعددی از ویژگی‌های ایده‌آل برای برآورده شدن آنها شده است [ 7 ، 8 ]. جامدات افلاطونی و برخی از جامدات باستانی، مانند ایکوسادرون کوتاه، در حال حاضر به عنوان چند وجهی اولیه برای ساختن DGGS استفاده می شوند [ 2 ]]. جامدات افلاطونی گزینه‌های خوبی هستند زیرا سطح‌ها مساحت و فشرده هستند. علاوه بر این، تقارن و منظم بودن این چند وجهی امکان پرس و جوهای کارآمد را فراهم می کند. برای بسیاری از جامدات افلاطونی، چندین طرح ریزی ایجاد شده است که معیار مساحت مساحت را حفظ می کند. این پیش‌بینی‌ها معمولاً با یک نقشه‌برداری تکه‌ای که با دقت بر روی هر وجه از چندوجهی اولیه تعریف شده است، ساخته می‌شوند. در حالی که می توان منطقه را حفظ کرد، حذف همزمان اعوجاج زاویه ای و شکل غیرممکن است ( شکل 2 را ببینید ). میزان اعوجاج تولید شده نه تنها به نوع نقشه برداری تکه ای بستگی دارد، بلکه به نزدیکی چهره های چند وجهی به سطح زمین نیز بستگی دارد. بنابراین، انتخاب یک چند وجهی با وجه های بیشتر مفید است که اعوجاج را کاهش می دهد [6 ]. یکی دیگر از ویژگی های مهم پیش بینی های DGGS هزینه محاسباتی آنها است، زیرا بسیاری از عملیات مهم DGGS از پروجکشن استفاده می کنند. به عنوان مثال، به منظور ارائه داده ها در سراسر سطح زمین، داده ها باید از ساختار داده چند وجهی که در آن ذخیره می شوند به موقعیت خود در کره زمین برعکس پیش بینی شوند. تمام نقاط هندسه ای که برای رندر کردن کره استفاده می شود، نیاز به انجام این عملیات برای ایجاد یک رندر دقیق دارند، که ایجاب می کند این عملیات کارآمد باشد. این پیش بینی ها می توانند یک گلوگاه قابل توجه در یک DGGS باشند و کار برای افزایش سرعت آنها انجام شده است [ 9 ، 10 ]]. یک چالش مهم برای تحقیقات DGGS، یافتن چند وجهی اولیه جدید و پیش‌بینی‌های حفظ منطقه مرتبط است که باعث کاهش بیشتر زاویه و اعوجاج شکل و در عین حال حفظ عملیات سریع و کارآمد DGGS می‌شود.
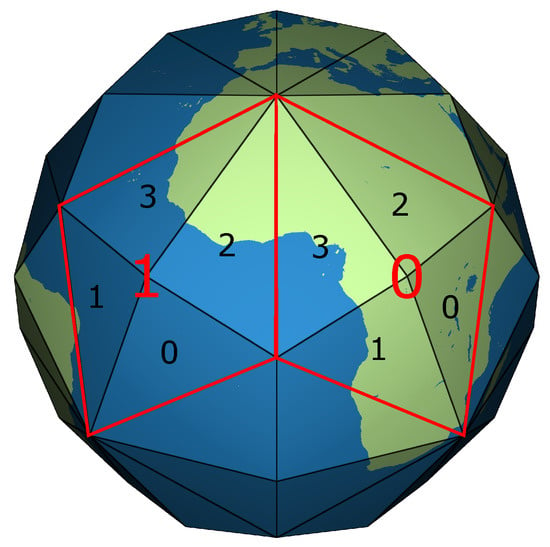
برای پرداختن به این چالش، ما یک DGGS جدید را معرفی می کنیم که از سه ضلعی Disdyakis (DT) به عنوان چند وجهی اولیه استفاده می کند ( شکل 1 را ببینید).). DT یک جامد کاتالانی با 120 وجه مثلثی یکسان است که در آن همه رئوس روی یک کره قرار دارند. این چند وجهی به این دلیل انتخاب شد که بیشترین چهره را در بین سایر جامدات کاتالونیایی دارد. در این چند وجهی کروی و محدب، تمام وجوه مجاور، تصاویر آینه ای یکسانی از یکدیگر در امتداد لبه مجاور خود هستند و وجه ها فشرده هستند. هنگامی که چند وجهی اولیه به یک DT تغییر می کند، سایر اجزای DGGS باید مجدداً بازبینی و به طور بالقوه اصلاح شوند. اشکال صورت DT با اشکال در جامدات افلاطونی متفاوت است و برجستگی های موجود یا کار نمی کنند یا باید برای سازگاری با این تغییر اصلاح شوند. به عنوان مثال، طرح ریزی با مساحت مساوی اسنایدر را می توان برای ایکوساهدر کوتاه استفاده کرد، اما انتظار دارد وجه های پنج ضلعی و شش ضلعی منظم که در DT وجود ندارند [ 13 ]]. برای ایجاد یک طرح ریزی با مساحت مساوی برای DT، ما طرح دایره بزرگ مبتنی بر راس مساحت را که توسط van Leeuwen و Strebe [ 14 ] پیشنهاد شده بود، اصلاح می کنیم. برای حفظ فشردگی مثلث ها در طول پالایش، از پالایش مثلث 1:4 طولانی ترین یال استفاده می کنیم [ 15 ]. برای پشتیبانی از عملیات کارآمد، ما یک طرح نمایه سازی با الهام از اطلس نقشه های اتصال (ACM) [ 16 ] توسعه می دهیم. با استفاده از برخی محاسبات ساده مدولار، ما به پرس و جوهای مکانی روی شبکه با الگوریتم های زمان ثابت پرداخته و عملیات مهمی مانند پرس و جوهای همسایگی، روابط والد/فرزند و پرس و جوهای نقطه ای را اجرا می کنیم.
به منظور ارزیابی DGGS خود، ما اعوجاج زاویه‌ای را در سطوح بین یک DGGS با استفاده از یک ایکوساهدر به عنوان چند وجهی اولیه و DGGS جدید مقایسه می‌کنیم. ما نشان می‌دهیم که DGGS ما میانگین اعوجاج زاویه‌ای را تقریباً یک ضریب چهار کاهش می‌دهد در حالی که پرس‌وجوهای دقیق و کارآمد را حفظ می‌کند و به طور قابل‌توجهی ویژگی‌های DGGS مطلوب را قربانی نمی‌کند. به طور خلاصه، کمک های اصلی این کار ایجاد یک سیستم جدید DGGS است که ناحیه را حفظ می کند و پرس و جوهای سریع را حفظ می کند و در عین حال اعوجاج زاویه ای را نیز کاهش می دهد.

2. کارهای مرتبط

یک همکاری جهانی از مشاغل، سازمان‌های دولتی، سازمان‌های تحقیقاتی و دانشگاه‌ها به نام کنسرسیوم فضایی باز (OGC) برای تسهیل استفاده و کاربرد داده‌های مکانی ایجاد شد [ 8 ]. OGC استانداردی برای ساخت DGGS ایجاد کرده است و ویژگی های مطلوب DGGS را تعریف می کند. مجموعه قابل توجهی از کارهای تحقیقاتی برای دسته بندی، مقایسه و ارزیابی DGGS [ 2 ، 7 ، 17 ، 18 وجود دارد.]. DGGS با انتخاب چهار جزء دسته بندی می شوند: چند وجهی اولیه، طرح ریزی، نمایه سازی و پالایش. ارزیابی DGGS عموماً به شکل اندازه‌گیری اعوجاج نقشه‌های ایجاد شده، اندازه‌گیری مساحت و فشردگی سلول‌های ایجاد شده، اندازه‌گیری ویژگی‌های نمونه‌گیری شبکه برای اطمینان از دقت و کارایی محاسبات آماری، و اندازه‌گیری عملکرد و کارایی پرسش‌های DGGS حاصل می‌شود. . در زیر، تحقیقات انجام شده در مورد هر یک از این مؤلفه ها را بررسی می کنیم و همچنین به برخی از DGGS های اخیر نگاه می کنیم.

2.1. چند وجهی اولیه

به عنوان روشی برای ذخیره سازی و بازیابی داده ها، ایده هایی از ساختارهای داده پارتیشن بندی فضایی موجود (به عنوان مثال، Quadtree، Octree، R-tree، kd tree و BSP) اغلب مورد استفاده قرار می گیرند، اما به طور خاص برای فضای کروی برای مدیریت داده ها در سطح طراحی شده اند. زمین [ 17 ]. همه این ساختارها به منظور تسریع عملیات بازیابی به تقسیم بندی سلسله مراتبی فضا متکی هستند. این سوال را مطرح می کند که چگونه می توان زمین را برای بازیابی کارآمد داده ها تقسیم بندی کرد. یک DGGS بر روی ایده های این ساختارهای پارتیشن بندی فضایی گسترش می یابد که در آن سلسله مراتب سلول های حاصل برای نمایش داده ها با وضوح چندگانه استفاده می شود. تلاش های اولیه برای ساخت DGGS از خطوط طول و عرض جغرافیایی استفاده می کرد [ 19]. سلول‌ها با برداشتن گام‌های گسسته در طول و عرض جغرافیایی ساخته شدند و وضوح چندگانه را می‌توان به راحتی با پالایش نقطه میانی ساده در هر بعد به دست آورد. مزایای این شبکه ها سادگی آنها با همسایه مستقیم و پیمایش سلسله مراتبی و همچنین رمزگذاری کارآمد مختصات طول و عرض جغرافیایی به سلول های مربوطه است. با این حال، این شبکه‌ها مشکل‌ساز هستند، زیرا سلول‌ها نه سطح مساوی و نه معیارهای فشردگی را برآورده نمی‌کنند [ 7 ]. علاوه بر این، نواحی قطبی شبکه با رئوس ظرفیت بالا منحط شده‌اند که فشردگی را در این مناطق کاهش می‌دهد و باعث ایجاد مشکلاتی در تجزیه و تحلیل داده‌ها می‌شود.
به منظور رسیدگی به محدودیت‌های مساحت و فشردگی، شبکه‌های منحط (اغلب به نام ایگلو) پیشنهاد شده‌اند که هنوز گام‌های مجزا در طول و عرض جغرافیایی برمی‌دارند، اما گاهی اوقات اندازه پله‌های خود را در سراسر شبکه تغییر می‌دهند تا سلول‌هایی با مساحت برابر تولید کنند [ 20 ، 21 ] . این باعث ایجاد نواحی منحط شبکه در انتقال بین اندازه های پله می شود که می تواند پیمایش همسایه و سلسله مراتب را پیچیده کند و همچنین باعث ایجاد چالش هایی مشابه با شبکه های عرض-طول جغرافیایی سنتی شود.
روش دیگری برای تقسیم زمین از کمان‌های دایره‌ای کوچک برای ساخت سلول‌هایی با مساحت مساوی مستقیماً روی کره استفاده می‌کند [ 22 ]. این روش از انحطاط شبکه های ایگلو جلوگیری می کند. با این حال، پیچیدگی محاسباتی بازیابی و تجزیه و تحلیل برای این نوع شبکه به طور قابل توجهی افزایش یافته است. به عنوان مثال، آزمایش مهار یک نقطه در داخل یک سلول نیاز به یک پیمایش سلسله مراتبی از شبکه دارد که در هر سطح، محدودیت در سلول های فرزند باید آزمایش شود.
بسیاری از تکنیک‌های اخیر از یک چندوجهی استفاده می‌کنند که رئوس آن روی یک کره قرار دارد تا زمین را تقسیم کند. کمان‌های دایره‌ای بزرگ، رئوس را به هم متصل می‌کنند که پارتیشن کروی شکل را ایجاد می‌کنند [ 23 ، 24 ]. اکثر این تکنیک ها از جامدات افلاطونی استفاده می کنند زیرا معیارهای مساحت و فشردگی را برآورده می کنند. اجازه دادن به چند وجهی با وجه به طور قابل توجهی بیشتر از جامدات افلاطونی یک چالش است، زیرا برخی از خواص مطلوب جامدات افلاطونی باید قربانی شوند تا امکان وجود وجه های بیشتر فراهم شود. کار برای ساخت شبکه‌هایی با استفاده از چند وجهی ژئودزیکی با وجوه مثلثی زیاد انجام شده است، اما حفظ مساحت و فشردگی برابر دشوار است [ 25 ]]. چگونگی توزیع بهترین رئوس در سراسر کره و تعریف اتصال آنها به منظور برآورده کردن این محدودیت ها، حوزه ای از تحقیقات در حال انجام است. کار اخیر ماسی از بهینه‌سازی یک پارتیشن‌بندی ورودی معین استفاده می‌کند و رئوس را روی کره حرکت می‌دهد تا سلول‌های فشرده و مساحتی ایجاد کند [ 25 ]. به طور کلی، این روش‌ها فقط می‌توانند به مساحت مساوی نزدیک شوند و سلول‌هایی با اشکال و اندازه‌های مختلف تولید کنند که بازیابی و تجزیه و تحلیل داده‌ها را به‌طور قابل توجهی پیچیده می‌کند. روش دیگری توسط لی و مورتاری از تقسیم بندی کروی استفاده می کند که با یک ایکوساهدر شروع می شود تا سلول های فشرده با مساحت مساوی را بسازد [ 15 ]. با این حال، در سطوح بالاتر تقسیم بندی، این شبکه انحطاط هایی مشابه شبکه های ایگلو ایجاد می کند.

2.2. فرافکنی

برای به دست آوردن مزایای تجزیه و تحلیل سریع داده ها، ما نیاز به یک نقشه برداری بین شبکه کروی و فضای مسطح مربوطه داریم تا امکان تحلیل ساده تر با استفاده از روش های اقلیدسی را فراهم کنیم. به طور سنتی، این با استفاده از طرح ریزی نقشه انجام می شود. پیش بینی های اولیه برای نگاشت کره به یک صفحه پیوسته ایجاد شد که اعوجاج اجتناب ناپذیری ایجاد می کند [ 5 ]. بسیاری از شبکه‌های فعلی یک پیش‌بینی ساده را انتخاب می‌کنند که منطقه را حفظ نمی‌کند، اما امکان بازیابی سریع‌تر داده‌ها را در سراسر زمین فراهم می‌کند [ 23 ، 24 ، 25 ]. در حالت ایده آل، این پیش بینی ها بایدحفظ مساحت برابر و خواص فشردگی پارتیشن بندی فضایی اصلی ما. در روش اخیر گورسکی و همکاران، سلول‌های حاصل مساحت مساوی دارند و برآمدگی مورد استفاده ترکیبی از برجستگی مساحت مساوی استوانه‌ای لامبرت و برآمدگی کلینیون منقطع [ 26 ] است. این دو پیش بینی در حالی که منطقه را حفظ می کنند و امکان وضوح چندگانه را در سراسر شبکه فراهم می کنند، اعوجاج زاویه ای قابل توجهی را در نقشه های مسطح ایجاد می کنند.
در اوایل سال 1525، پیشنهاد شد که زمین باید به صورت تکه تکه بر روی بسیاری از سطوح مسطح مربوط به وجوه چند وجهی پرتاب شود، که امکان اعوجاج بسیار کمتری را فراهم می کند [ 27 ]. فیشر در اثری منتشر نشده که در سال 1946 به آن ارجاع داده شد، طرحی با مساحت مساوی به چهره یک ایکوسادرون ارائه کرد [ 28 ]. با حفظ منطقه، این طرح ناپیوستگی در نقشه و اعوجاج زاویه ای قابل توجهی ایجاد کرد. در سال 1992، اسنایدر کار فیشر را با حذف ناپیوستگی ها و کاهش اعوجاج زاویه ای بهبود بخشید [ 13 ].]. برجستگی اسنایدر همچنین اجازه می دهد تا بر روی صورت های یک ایکوساهدر کوتاه (یک جامد باستانی) که دارای وجه های بیشتری از هر جامد افلاطونی است و امکان اعوجاج زاویه ای کمتری را نیز دارد. این طرح در برخی از DGGS های فعلی به دلیل خواص نمونه گیری مطلوب سلول ها و خواص اعوجاج نسبتاً خوب در مقایسه با جایگزین ها استفاده می شود [ 11 ، 29 ]. با این حال، این پیش بینی از نظر محاسباتی گران است و یک گلوگاه قابل توجه برای تجزیه و تحلیل کارآمد داده ها [ 9 ، 10 ] است. علاوه بر این، همانطور که در شکل 2 مشاهده می شود، همچنان اعوجاج زاویه ای قابل توجهی وجود دارد .
برای مقابله با این چالش ها، مقدار قابل توجهی کار برای توسعه پیش بینی های ساده و حفظ سطح برای جامدات افلاطونی انجام شده است. Rosca و Plonka به ترتیب برای مکعب و هشت ضلعی یک شکل بسته و برجستگی حفظ منطقه ایجاد کرده اند [ 30 ، 31 ]. در این برجستگی‌ها، بخش‌هایی از نواحی کلاهک‌های کروی و مثلث‌های مسطح برای برآمدگی برابر می‌شوند. به دلیل سادگی و ویژگی مساحت آن، برای ساخت یک DGGS کامل استفاده شده است [ 32 ].
در کار van Leeuwen و Strebe، دو پیش بینی مساحت مساوی به شکل بسته پیشنهاد شده است که برای هر چند وجهی با وجوه مثلثی کار می کند [ 14 ]. در این برجستگی ها، با تقسیم یک مثلث کروی با استفاده از کمان های دایره ای بزرگ و کوچک، یک عنصر مساحت بینهایت کوچک ایجاد می شود. سپس این عنصر مساحت بینهایت کوچک با استفاده از خواص مثلثهای مشابه به یک عنصر مسطح بینهایت کوچک نگاشت می شود. آنها این طرح را برای تمام جامدات افلاطونی اعمال می کنند و پیشنهاد می کنند که می توان از چند وجهی دیگر استفاده کرد.

2.3. پالایش و انواع سلول

پالایش به طور کلی بستگی زیادی به انتخاب چند وجهی اولیه دارد زیرا فقط اصلاحات خاصی برای اشکال سلول اولیه خاصی کار می کنند. اشکال سلولی به طور کلی شامل مثلث، چهار ضلعی و شش ضلعی است (بعضی از شبکه ها از سلول هایی با شکل نامنظم استفاده می کنند که در اینجا در نظر گرفته نشده است). مهدوی امیری، آلدرسون و سماواتی بررسی خوبی در مورد پالایش ها و انواع سلول ارائه می دهند [ 2 ]. مثلث ها به دلیل ساده بودن برای ارائه سودمند هستند. چهارضلعی ها برای داشتن نمایه سازی مبتنی بر آرایه ساده خوب هستند و شش ضلعی ها فشردگی و خواص نمونه گیری خوبی دارند [ 33]. طرح های پالایش تمایل دارند تا حد امکان سلول های فرزند را برای هر سلول والد بخواهند تا از داده ها در مقیاس های مختلف پشتیبانی کنند. برای سلول های مثلثی و چهار ضلعی، اصلاحات 1:4 و 1:9 وجود دارد که سلول های مسطح مساحتی را تولید می کنند و خواص نسبتا خوبی برای نمونه برداری دارند [ 24 ، 34 ، 35 ]. سلول های شش ضلعی معمولاً از اصلاح 1:3 استفاده می کنند اما از این که کودکان بخشی از والدین خود نیستند رنج می برند [ 16 ].

2.4. نمایه سازی

نمایه سازی برای کارایی عملیات روی DGGS [ 36 ] انتخاب می شود. این شامل کارایی پرس و جوهایی مانند پیمایش نقطه، همسایه و سلسله مراتب است. باید یک رابطه ساده بین مکان در طول و عرض جغرافیایی یک نقطه و شاخص داده شده به سلول مربوطه وجود داشته باشد. این مهم است زیرا بیشتر داده ها به شکل طول و عرض جغرافیایی می آیند، بنابراین داشتن این رابطه ساده به معنای ذخیره سازی و بازیابی کارآمد داده ها است [ 37 ]. برای پرس‌و‌جوهای همسایگی، این سودمند است که شاخص‌های سلول‌های همسایه تا حد امکان شبیه به انجام پرس‌وجوهای محدوده کارآمد باشند [ 38 ]]. بازیابی بلوک های پیوسته حافظه از یک پایگاه داده کارآمد است و هنگام بازیابی داده ها برای سلول های همسایه از گم شدن حافظه پنهان جلوگیری می کند. برای پیمایش سلسله مراتبی، همچنین باید یک رابطه ساده بین شاخص یک سلول و والدین و فرزندان آن وجود داشته باشد.
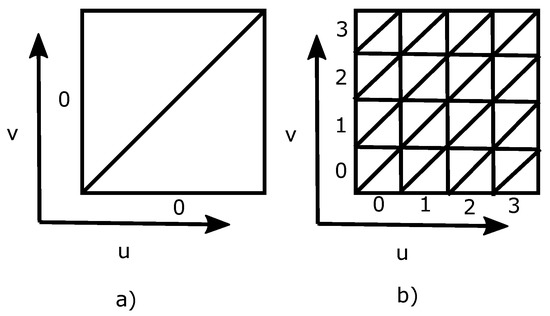
روش های نمایه سازی به طور کلی به سه دسته تقسیم می شوند: سلسله مراتبی، منحنی پرکننده فضا و مبتنی بر مختصات [ 2 ]. در نمایه سازی سلسله مراتبی، فرزندان یک سلول یک پیشوند یا یک پسوند را از نمایه والدین خود به ارث می برند. دو مزیت این روش پیمایش سلسله مراتبی و تعیین ساده وضوح یک سلول معین است. برای منحنی‌های پرکننده فضا، یک منحنی از دامنه سلول‌ها عبور می‌کند و سلول‌ها به ترتیبی که منحنی آنها را قطع می‌کند ایندکس می‌شوند ( شکل 3 را ببینید).). اغلب، منحنی را می‌توان برای شاخص‌سازی وضوح‌های دقیق‌تر شبکه اصلاح کرد. مزیت این روش این است که منحنی را می توان برای دادن شاخص های مشابه به سلول های همسایه تعریف کرد که امکان پرس و جوهای محدوده کارآمد را فراهم می کند. در نمایه سازی مبتنی بر مختصات، یک سیستم مختصات بر روی دامنه سلول ها تعریف می شود و سلول ها بر اساس برداشتن گام های گسسته در امتداد جهت مختصات ایندکس می شوند. مزیت در اینجا این است که بسیاری از عملیات کارآمد و ساده هستند، اما این روش برای شبکه‌های معمولی که در آن سلول‌ها همه اندازه و شکل هستند، بهترین کار را دارد.
روش های ترکیبی نیز توسعه یافته اند که از ترکیبی از این رویکردها استفاده می کنند. یک مثال نقشه های Atlas of Connectivity است که می تواند برای مش های نیمه منظم استفاده شود [ 16 ]. در این تکنیک، منحنی فضا، پر کردن را می توان برای چند وجهی اولیه استفاده کرد در حالی که نمایه سازی مبتنی بر مختصات می تواند برای بخش های منظم شبکه استفاده شود. انواع مختلفی از این روش های نمایه سازی وجود دارد. برای درمان کامل، به مرجع [ 36 ] مراجعه کنید.

2.5. DGGS

برای ساخت DGGS، یک چند وجهی اولیه، طرح ریزی، پالایش و نمایه سازی به طور کلی بسته به ویژگی های مورد نظر سیستم حاصل انتخاب می شود. چندین اثر انتخاب های مختلف و ویژگی های آنها را بررسی و بحث می کنند [ 2 ، 8 ، 18 ].
DGGS از جامدات افلاطونی به عنوان چند وجهی اولیه از اوایل سال 1968 ایجاد شده است [ 39 ]. انتخاب های رایج مکعب، هشت وجهی و ایکو وجهی هستند. این مکعب از نظر تاریخی انتخاب شده است زیرا چهار وجهی آن می تواند برای گسترش طبیعی ساختار داده چهاردرخت به سطح زمین استفاده شود [ 32 ، 40 ، 41 ]. این امکان ذخیره سازی و بازیابی کارآمد داده ها را فراهم می کند. هم‌سویی محورهای وجه‌های مکعب همچنین به پرس‌وجوهای نقطه‌ای ساده اجازه می‌دهد تا تعیین کنند که یک نقطه در کدام وجه قرار دارد . 42]. با این حال، این دو جامد افلاطونی تقریب ضعیفی از کره هستند و برآمدگی های تعریف شده روی آنها تمایل به ایجاد اعوجاج قابل توجهی دارند [ 43 ]. DGGS های اخیر تمایل دارند از ایکوساهدر به عنوان چند وجهی اولیه برای خواص اعوجاج بهتر آن استفاده کنند [ 43 ، 44 ، 45 ، 46 ]. بسیاری از DGGS های اخیر نیز از پیش بینی های مساحت مساوی از وجه های چند وجهی استفاده می کنند که لزوماً اعوجاج زاویه ای ایجاد می کند. هدف اصلی برای DGGS تعریف پیش بینی هایی بوده است که این اعوجاج را کاهش می دهد [ 43 ]. برخی از DGGS نیز از ایکوساهدر کوتاه شده به عنوان چند وجهی اولیه خود استفاده می کنند [ 11]. دو مزیت اصلی عبارتند از پتانسیل اعوجاج کمتر ناشی از افزایش تعداد وجه ها و خواص نمونه برداری خوب شبکه های شش ضلعی. با این حال، شبکه‌های شش ضلعی برای اصلاح و نمایه‌سازی ایده‌آل نیستند، زیرا کودکان نمی‌توانند پارتیشنی از والدین خود باشند، و ارائه آنها به سادگی مثلث نیست.
روند در کارهای اخیر افزایش تعداد چهره‌ها در چند وجهی برای کاهش اعوجاج و در عین حال استخراج طرح‌ریزی با مساحت مساوی برای تکمیل DGGS بوده است. ما این روند را با انتخاب DT به عنوان چند وجهی اولیه خود ادامه می دهیم، که دارای مثلث ترین وجه ها در بین هر شکل کروی محدب با ویژگی تصویر آینه ای و مثلث های فشرده است. سپس طرح دوم را از van Leeuwen و Strebe تغییر می دهیم تا با چند وجهی اولیه ما کار کند. ما این کار را با ارائه سریع و کارآمد همسایه و پیمایش سلسله مراتبی تکمیل می کنیم. DGGS ما در مقایسه با DGGS با استفاده از جامدات افلاطونی و ایکوز وجهی کوتاه، مساحت و خواص فشردگی برابر را حفظ می‌کند و در عین حال اعوجاج زاویه‌ای را به طور قابل توجهی کاهش می‌دهد.

3. ایجاد DT DGGS

برای کاهش اعوجاج ایجاد شده از طرح ریزی، DT را به عنوان چند وجهی اولیه برای DGGS خود معرفی می کنیم. با این حال، این تغییر ما را ملزم می کند که سایر اجزای DGGS را در محل اقامت اصلاح کنیم. ما این اجزا را در زیر ارائه می دهیم.

3.1. چند وجهی اولیه

به منظور کاهش اعوجاج زاویه‌ای، باید از یک چند وجهی کروی اولیه مناسب – با تعداد وجه‌های بیشتر از گزینه‌های فعلی – و یک پیش‌نمایش حفظ منطقه مربوطه استفاده کنیم. پروجکشن توسعه یافته توسط van Leeuwen و Strebe انتخاب خوبی است زیرا کارآمد است و دارای اعوجاج زاویه ای کم است. با این حال، این طرح مستلزم آن است که چهره های چند وجهی اولیه تصاویر آینه ای از یکدیگر در امتداد لبه مجاور خود باشند. فقط چند وجهی کروی خاصی می تواند این معیار را برآورده کند. اینها شامل جامدات افلاطونی، برخی از جامدات کاتالان و دو هرم هستند. دو هرم‌ها این مزیت را دارند که تعداد چهره‌ها را مجاز می‌کنند، اما خاصیت فشرده‌سازی ضعیفی برای تعداد زیادی از وجه‌ها دارند ( شکل 4 را ببینید.). جامدادی کاتالان اجازه می دهد تا چهره های بیشتری نسبت به جامدات افلاطونی ایجاد شود، بنابراین آنها انتخاب ارجح هستند.
از جامدات کاتالونیایی، یکی با بیشترین وجهی که به بهترین شکل به یک کره تقریب می‌کند، DT است – دارای 120 وجه مثلث مقیاسی یکسان – که آن را به بهترین انتخاب برای برآورده کردن اهداف ما تبدیل می‌کند ( شکل 1 را ببینید ). از آنجایی که چهره ها یکسان هستند، هر طرحی که به صورت جداگانه روی هر یک از وجه ها اعمال شود تضمین می شود که در امتداد لبه های چهره ها پیوسته باشد زیرا مناطق را به طور یکسان بر روی وجه هایی با شکل یکسان ترسیم می کند. علاوه بر این، وجوه دارای مناطق کروی مساوی هستند که وقتی با یک برآمدگی مساوی ترکیب می شوند، معیار مساحت مساحت را برآورده می کنند. هنگامی که از یک DT به عنوان چند وجهی اولیه استفاده می کنیم، مقداری فشردگی سلول ها را از دست می دهیم. یکی از معیارهای فشردگی یک ناحیه کروی، فشردگی استاندارد منطقه است [ 7] که به مساحت کروی و محیط منطقه و همچنین شعاع کره نیاز دارد. حداکثر فشرده مثلث متساوی الاضلاع است. فشردگی یک مثلث DT حدود 88 درصد از یک مثلث متساوی الاضلاع در یک ایکو وجهی (0.727246:0.824773) برای کره ای به شعاع 1 است.

3.2. طرح ریزی منطقه مساوی

ویژگی‌های DT آن را به کاندیدای ایده‌آل برای انطباق با طرح Slice and Dice ارائه شده توسط van Leeuwen و Strebe تبدیل می‌کند، زیرا دارای اعوجاج زاویه‌ای کم است اما به خاصیت تقارن آینه‌ای که DT دارد نیاز دارد [ 14 ]. تقارن و منظم بودن مش تضمین می کند که می توانیم پرس و جوهای کارآمد داشته باشیم و بنابراین سرعت و سادگی عملیات DGGS سنتی را از دست نمی دهیم.

3.3. طرح حفظ منطقه برش و تاس

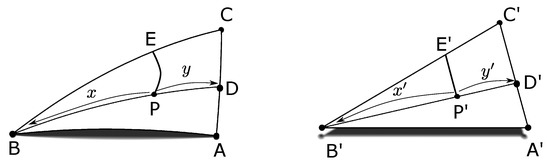
برای نمایش نقاط روی زمین به و از نقاط روی DT، طرح Slice and Dice ارائه شده توسط van Leeuwen و Strebe نیاز به تغییرات جزئی دارد [ 14 ]. همانطور که در مرجع [ 14 ] توضیح داده شد، به منظور ترسیم یک مثلث کروی آبسیبه یک مثلث مسطح آ”ب”سی”( شکل 5 را ببینید ) با مقیاس مساحت ثابت، دو مثلث به سلول های بینهایت کوچک تقسیم می شوند. تا زمانی که سلول ها با یک مقیاس مساحت ثابت در همه جای مثلث به یکدیگر نگاشت می شوند، نگاشت مساحتی برابر است. در مرحله اول طرح ریزی (نگاه کنید به شکل 5 )، یک نقطه P در مثلث کروی آبسیقرار است بر روی یک نقطه ناشناخته پیش بینی شود پ”درون مثلث مسطح آ”ب”سی”. برای اینکه سطح برآمدگی مساوی باشد، مثلث کروی از طریق نقطه P و یک تقسیم بندی مربوطه از طریق نقطه پیش بینی شده تقسیم می شود. پ”به گونه ای ایجاد می شود که مقیاس منطقه ای برای قطعاتی که قرار است پیش بینی می شوند حفظ شود. برای انجام این کار، مرکز طرح ریزی به عنوان راس B در مثلث کروی انتخاب می شود. کمان های دایره ای بزرگ که از راس B سرچشمه می گیرند و از قوس دایره ای بزرگ عبور می کنند آسیدر نقطه D در مثلث کروی به خطوط مستقیمی که از راس سرچشمه می‌گیرند، پیش بینی می‌شود ب”و لبه عبور آ”سی”در نقطه D”در مثلث مسطح قوس دایره ای بزرگی که از B تا نقطه P سرچشمه می گیرد، مثلث کروی را به دو قسمت با مساحت تقسیم می کند تیبالاو تیپایین. همانطور که در مرجع [ 14 ] نشان داده شده است، تقسیمات کروی و مسطح با پارامترسازی خطی تناسب دارند. آ”سی”جایی که تو”و v”در شکل 5 نشان داده شده است :

تیپایینتیبالا+تیپایین=تیپایین”تیبالا”+تیپایین”=تو”تو”+v”.

در مرحله دوم طرح ریزی مساحت مساوی ( شکل 6 را ببینید )، فواصل زاویه ای x و y که با نقطه P تعریف شده اند از قوس دایره ای بزرگ که از راس B نشات می گیرد حل می شوند . فاصله ها ایکس”و y”در امتداد خط قبلی ما ساخته شده است ب”D”به گونه ای تعیین می شوند که برای تمام نقاط پیش بینی شده مقیاس مساحت ثابتی وجود داشته باشد:

ایکس”2(ایکس”+y”)2=1-cos(ایکس)1-cos(ایکس+y).
از آنجایی که این برای تمام نقاط ممکن P در مثلث کروی صادق است، این بدان معناست که مناطق بینهایت کوچک محدود به آن نقاط نیز مساحت یکسانی خواهند داشت.
برای مثلث ها در DT، روش ما دو تغییر جزئی در روش ارائه شده توسط van Leeuwen و Strebe دارد. ابتدا، روش آنها مثلث های متساوی الاضلاع را در جامدات افلاطونی به شش قطعه برش می دهد تا به طور جداگانه نمایش داده شوند، اما این مرحله برای DT غیر ضروری است. از آنجا که چهار وجه DT با یک وجه از مثلث ضلعی لوزی (RT) مطابقت دارد، می‌توانیم از راس در مرکز هر لوزی به عنوان مرکز طرح برای هر وجه استفاده کنیم. ثانیاً، آنها در داخل مثلث‌های خود یک زاویه قائم فرض می‌کنند، که امکان ساده‌سازی در محاسبه مساحت‌های کروی و زوایای کروی را فراهم می‌کند. با این حال، مثلث ها در DT این زاویه راست را ندارند.

3.4. پروجکشن معکوس برای DT

به منظور انجام تمام عملیات DGGS، طرح ریزی باید شامل یک نقشه برداری معکوس از نقاط روی چند وجهی به نقطه مربوطه در کره باشد. در حالت ایده‌آل، این نگاشت معکوس باید کارآمد و دقیق باشد تا عملیاتی را که در آن نقاط بسیاری نیاز به انجام آن دارند، امکان پذیر کند. رندر کردن یکی از این عملیات است که در آن هندسه مسطح سلول ها باید معکوس شود تا داده ها از حوزه چند وجهی به مکان های مربوطه روی زمین منتقل شود. در وضوح بالا، این عملیات می تواند در صدها هزار نقطه مورد نیاز باشد. در نشریه ون لیوون و استربه، آنها معکوس فرافکنی خود را ارائه نمی دهند و معلوم می شود که بی اهمیت است. ما یک معکوس شکل بسته برای طرح Slice و Dice پیدا کرده‌ایم که در زیر ارائه می‌کنیم. برای ساده کردن نمادگذاری، ایکسY^برای فاصله زاویه ای بین X و Y ، دو راس روی یک مثلث کروی.
برای طرح معکوس، یک نقطه داده شده پ”در مثلث مسطح به نقطه مربوطه P در مثلث کروی نگاشت شده است ( شکل 5 را ببینید ). ساخت ما برای نگاشت معکوس بر اساس مراحل معکوس از طرح ریزی رو به جلو است. ما این کار را با حل D به گونه ای انجام می دهیم که نسبت موجود در رابطه ( 1 ) برقرار باشد و سپس P را به گونه ای حل می کنیم که نسبت موجود در رابطه ( 2 ) برقرار باشد. روش ما برای یافتن D و سپس P بر اساس رویکرد لی و مورتاری [ 15 ] است، جایی که ما به دنبال فاصله زاویه ای هستیم. آD^و x به گونه ای که بتوانیم دو درون یابی خطی کروی (SLERP) انجام دهیم [ 47 ]. ابتدا یک SLERP از نقطه A به نقطه C با فاصله زاویه ای آD^و سپس از نقطه B به سمت نقطه D با فاصله زاویه ای x ، پس از آن نقطه P را دقیقاً پیدا کرده ایم. برای انجام این کار، فقط باید فواصل زاویه ای را محاسبه کنیم آD^و x _

برای شروع، خط ناشی از آن را حل می کنیم ب”از طریق پ”ملاقات با مثلث مسطح در نقطه D”. حل نقطه D”به سادگی تقاطع دو خط همسطح است. حالا نسبت مساحت مثلث ها را تعریف کنید ب”آ”D”به آ”ب”سی”مانند

متر=حوزه(ب”آ”D”)حوزه(آ”ب”سی”).

از اینجا، قوس دایره ای بزرگ را حل می کنیم که مثلث کروی را به مناطق متناسب مربوطه برش می دهد. راه حل یک مشکل مشابه توسط لی و مورتاری [ 15 ] ارائه شده است. با این حال، راه حل آنها محدود به موردی است که در آن متر=1/2. در اینجا رویکرد آنها را برای حل نقطه D داده شده گسترش می دهیم0<متر<1. از آنجایی که D با A و C همسطح است، می توان آن را با استفاده از SLERP با فاصله زاویه ای ناشناخته بیان کرد آD^به شرح زیر است:

D=1گناه(آسی^)(سیگناه(آD^)+آگناه(آسی^-آD^)).

به منظور پیدا کردن آD^، باید زوایای r و d را از شکل 5 پیدا کنیم. ابتدا توجه کنید که با استفاده از فرمول اضافی کروی ژیرار و نسبت مساحت مثلث m مان، می توانیم مجموع زوایای r و d را به صورت زیر حل کنیم.

حوزه(آبسی)=آ+ب+ج-π.
حوزه(آبD)=آ+r+د-π=متر(حوزه(آبسی)).

تنظیم مجدد می گیریم

Y=r+د=متر(آ+ب+ج-π)-آ+π.

می توانیم بیان کنیم آD^با استفاده از قانون کروی سینوس ها بر حسب Y و r به صورت زیر:

گناه(آD^)=گناه(r)گناه(آب^)گناه(Y-r).

برای یافتن r ، از همان رویه لی و مورتاری در مرجع [ 15 ] استفاده می کنیم. اشتقاق آنها در زیر با نماد ما تکرار می شود. استفاده از قانون کسینوس های کروی روی مثلث آبDما گرفتیم

cos(Y-r)=گناه(r)گناه(آ)cos(آب^)-cos(r)cos(آ).

با گسترش سمت چپ با استفاده از هویت اختلاف زاویه برای کسینوس و حل برای r به دست می‌آییم

برنزه(r)=cos(Y)+cos(آ)گناه(آ)cos(آب^)-گناه(Y).

اکنون می توانیم Y و r را جایگزین کنیم تا فاصله زاویه ای را پیدا کنیم آD^با استفاده از رابطه ( 8 ) و با استفاده از معادله ( 4 ) نقطه D را بیابید .

هنگامی که نقطه D را با استفاده از معادله ( 4 ) بدست آوریم، اکنون باید فاصله زاویه ای x را برای تکمیل معکوس پیدا کنیم. برای انجام این کار، ما می توانیم برای cos(ایکس+y)با

cos(ایکس+y)=ب·D.

سپس می توانیم از طول های شناخته شده استفاده کنیم ایکس”و y”همچنین cos(ایکس+y)برای حل x با تنظیم مجدد معادله ( 2 ) برای بدست آوردن

ایکس=آرکوس(1-(1-cos(ایکس+y)ایکس”2(ایکس”+y”)2)).

موقعیت نقطه P در امتداد دایره بزرگ بDمی توان با استفاده مجدد از رابطه ( 4 ) به صورت زیر محاسبه کرد:

پ=1گناه(بD^)(سیگناه(ایکس)+آگناه(بD^-ایکس)).
در نتیجه، ما یک طرح معکوس شکل بسته برای طرح ریزی مساحت مساوی ارائه شده توسط van Leeuwen و Strebe [ 14 ] استخراج کرده ایم. راه حل ما بر توابع مثلثاتی ساده بدون نیاز به حل معادلات غیرخطی تکراری تکیه دارد، همانطور که در مورد طرح منطقه مساوی اسنایدر [ 13 ] وجود دارد. این امکان نمایش کارآمد از زمین را فراهم می کند.

3.5. پالایش و نمایه سازی

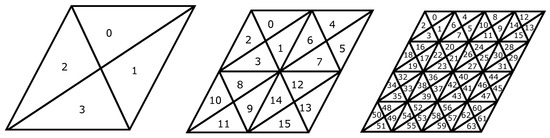
برای تعریف یک سیستم شبکه با وضوح چندگانه با استفاده از DT، به یک روش پالایش نیاز داریم. بسیاری از گزینه های اصلاحی برای DGGS وجود دارد که در مرجع [ 2 ] به تفصیل آمده است. شکل 7 برخی از انتخاب های رایج برای پالایش مثلث ها را نشان می دهد. از آنجایی که مثلث های اولیه یک DT متساوی الاضلاع نیستند و ما می خواهیم مساحت و فشردگی را حفظ کنیم، لازم است از اصلاحاتی مانند (a)، (c) یا (d) در شکل 7 استفاده کنیم. اصلاح 1:3 نشان داده شده در (ب) نامطلوب است زیرا برنامه های کاربردی بازگشتی باعث کاهش نامحدود در فشردگی با افزایش سطح تقسیم بندی می شوند. شکل 7(ج) و (د) این مشکل را ندارند و آنها را برای پالایش DGGS رایج تر می کند. برای هر دو اصلاح (c) و (d)، لازم است که نقطه میانی لبه‌ها با M ، N و P مشخص شود. توجه کنید که یال با نشان داده شده است پندر پالایش (ج) با مVدر اصلاح (d)، که در آن M نقطه وسط طولانی ترین لبه مثلث اصلی است.
به منظور نمایه سازی سیستم شبکه خود برای پرس و جوهای کارآمد، از نقشه های اطلس ارتباط (ACM) [ 16 ] استفاده می کنیم. ACM روشی است که برای مش های نیمه منظم حاصل از اصلاحات تکراری (مثلاً سطوح تقسیم بندی) توسعه یافته است. در این روش، نامنظمی مش پایه متفاوت از ساختار منظم ناشی از پالایش تکراری مدیریت می شود. به عنوان مثال، یک ساختار داده نیمه لبه [ 48 ] را می توان برای اتصال نامنظم مش پایه استفاده کرد در حالی که اتصال منظم ناشی از اصلاح را می توان با استفاده از روابط جبری ساده که در مرجع [ 16 ] شرح داده شده است، مدیریت کرد.
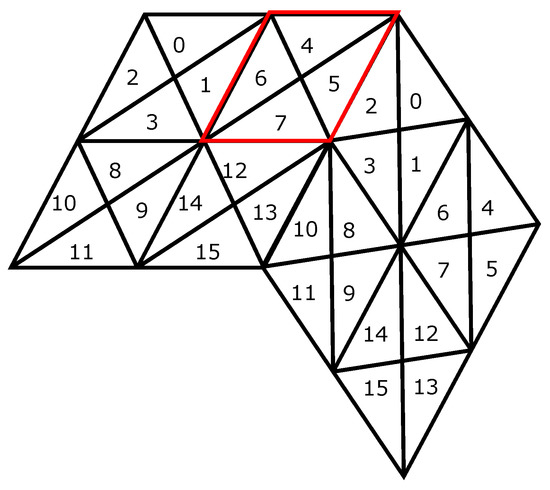
برای سیستم شبکه DT، ما از یک طرح خاص برای 30 وجه مربوط به وجه های RT استفاده می کنیم ( شکل 8 را ببینید ). این 30 چهره به صورت مارپیچی نمایه شده اند. اتصال بین این چهره ها در یک آرایه 30 × 30 که در آن هر ورودی ذخیره می شود (من،j)تبدیل بین صورت i و صورت j را در صورت مجاورت ذخیره می کند. برای نمایه سازی سلول های داخل هر وجه لوزی، از الگوی منظم ایجاد شده توسط پالایش بهره می بریم. به عنوان مثال، اعمال پالایش سنتی 1:4 به DT اجازه می دهد تا نقشه اتصال در مرجع [ 16 ] برای نمایه سازی موثر سلول های حاصل استفاده شود ( شکل 9 را ببینید ). برای اصلاح ترکیبی 1:4، ما یک اصلاح در ترتیب ردیف اصلی را پیشنهاد می کنیم. در این روش، مثلث های درون لوزی ها با استفاده از بلوک های شکل Z، همانطور که در شکل 10 نشان داده شده است، نمایه سازی می شوند.. برای تمایز بین سطوح زیربخش مختلف، سطح تفکیک آن سلول به شاخص سلول الحاق می شود. این طرح به دلیل سادگی و کارایی پرس و جوهای به دست آمده انتخاب شده است.

4. اتصال و مکان

از آنجایی که چند وجهی اولیه DGGS ما تغییر کرده است، باید به جستارهای مهمی مانند نقطه به سلول، دسترسی همسایگی و پیمایش سلسله مراتب بپردازیم. ما نشان می‌دهیم که همه این پرس‌وجوها با استفاده از محاسبات ساده در زمان ثابت انجام می‌شوند و بدون در نظر گرفتن وضوح شبکه، آنها را کارآمد می‌کنند.

4.1. پرس و جوهای همسایگی

برای یافتن همسایگان یک سلول معین در شبکه خود، از ساختار داده ACM ارائه شده در بخش قبل استفاده می کنیم. از آنجایی که چند وجهی اولیه ما منحط نیست، همه مثلث ها دقیقاً سه همسایه یال دارند و به دلیل انتخاب طرح نمایه سازی ما، یافتن دو همسایه بی اهمیت است. این دو همسایه باید در لوزی کوچکی که سلول اصلی در آن قرار دارد ساکن شوند ( شکل 11 را ببینید.). برای یافتن همسایه سوم، وضعیت پیچیده تر است. ابتدا باید تصمیم بگیریم که سلول مورد نظر در مرز اطلس است که بسته به اینکه سلول مورد نظر در مرز بالا، پایین، چپ یا راست باشد چهار حالت دارد. اگر سلول پرس و جو روی مرز باشد، سپس با بررسی ساختار داده ACM که جهت همسایگان هر سلول پایه را ذخیره می کند، در مورد جهت گیری نسبی سلول همسایه تصمیم می گیریم ( شکل 8 را ببینید).). بسته به جهت سلول های همسایه نسبت به یکدیگر، دو حالت وجود دارد (توجه داشته باشید که برای یک مش کلی، می تواند 9 مورد باشد، اما با ساخت، ما اجبار کرده ایم که مش ما فقط دو مورد داشته باشد). یک تبدیل خطی به ما امکان می دهد از سیستم مختصات سلول فعلی به سیستم همسایه تغییر کنیم. سطر و ستون تبدیل شده به ما یک ردیف و شماره ستون در سلول پایه همسایه می دهد و این شاخص همسایه را به ما می دهد. اگر سلول مورد نظر در مرز اطلس نباشد، وضعیت بسیار ساده تر است و دارای چهار حالت مربوط به مثلث های بالا، پایین، چپ و راست است ( شکل 11 را ببینید ). به عنوان مثال، در شکل 11، شاخص پنج در لوزی قرمز کوچک دارای همسایه دو در لوزی قاعده مجاور است. این همسایگان به جهت گیری نسبی دو لوزی پایه بستگی دارد که در ساختار داده ACM ذخیره می شود.

4.2. پرس و جوهای سلسله مراتبی

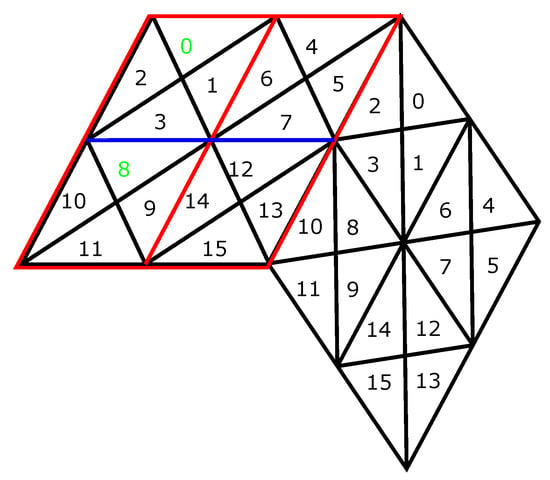
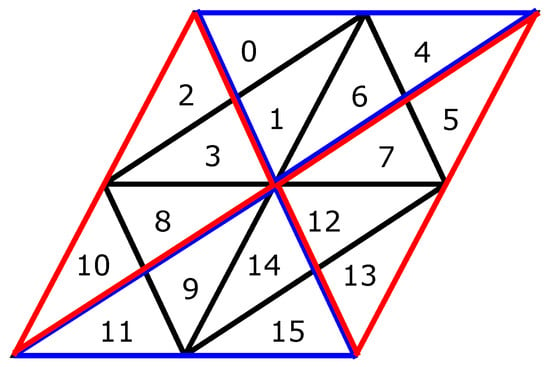
برای پیدا کردن والد یک سلول معین در شبکه، ابتدا شماره سطر و ستون سلول را در لوزی پایه پیدا می کنیم. برای مثالی از سطرها و ستون ها، شکل 12 را ببینید . در مرحله بعد، شاخص شروع بالا و پایین لوزی کوچک را در یک سطح وضوح درشت تر از سطح فعلی می یابیم (به برچسب های سبز در شکل 12 مراجعه کنید). پس از آن، با توجه به سطر و ستونی که قبلاً حل شده بود، شاخص والد را حل می کنیم (توجه داشته باشید که والدین نصف تعداد سطرها و ستون ها را دارند). بر اساس شاخص داخل لوزی کوچک در یک سطح وضوح درشت تر از سطح فعلی، می توانیم با استفاده از 16 مورد نشان داده شده در شکل 13 ، سلول والد را حل کنیم . فرزندان یک سلول با استفاده از معکوس این فرآیند محاسبه می شوند.

4.3. پرس و جو نقطه به سلول

برای یافتن شاخص سلولی که نقطه ای در مختصات طول و عرض جغرافیایی داده شده است، ابتدا مثلثی را در DT می یابیم که حاوی نقطه است. برای سرعت بخشیدن به این بخش از پرس و جو، ما DT را با محور طول جغرافیایی به گونه ای تراز کرده ایم که یک راس ظرفیت ده در هر دو قطب شمال و جنوب قرار دارد ( شکل 14 را ببینید ). یال‌هایی را که از این دو راس سرچشمه می‌گیرند، تراز می‌کنیم تا با مضرب‌های هم‌تراز شوند 2π/10رادیان طول جغرافیایی
برای یافتن سلول حاوی نقطه داده شده P ، ابتدا تعیین می کنیم که کدام وجه F از DT حاوی P است ( شکل 14 را ببینید ). سپس، فرزند F را در وضوح خاصی می یابیم که حاوی P است. برای یافتن F ، صرفاً بررسی طول جغرافیایی نقطه به ما امکان می دهد جستجوی خود را به 12 مثلث ممکن محدود کنیم. برای تمایز بین 12 باقیمانده، بررسی می کنیم که آیا نقطه در بالا یا پایین لبه های این مثلث ها قرار دارد. این کار با استفاده از جستجوی دودویی انجام می شود که در آن حداکثر باید 5 یال آزمایش شود تا مثلث به طور منحصر به فرد تعیین شود.

در مرحله بعد، برای یافتن فرزندان F در وضوح s حاوی P ، نقطه خود را از کره به F با استفاده از طرح طرح ریزی منطقه مساوی که در بخش 3.2 توضیح داده شده است، نشان می دهیم . پس از آن، نقطه پیش بینی شده خود را بیان می کنیم پ”به عنوان مختصات باریسنتریک ( u و v ) مثلث مسطح F ، که شماره سطر و ستون نمایه سلولی را که حاوی نقطه است به ما می دهد. هنگامی که سطر و ستون را در اختیار داریم، بررسی نهایی را انجام می دهیم تا مشخص کنیم کدام یک از چهار مثلث در آن سطر و ستون حاوی نقطه P است. برای این کار ابتدا تعداد سطرها و ستون های n را از وضوح s با پیدا می کنیم

n=2س-1.

سپس ردیف r و ستون c نقطه را پیدا می کنیم:

r=⌊v∗n⌋،و
ج=⌊تو∗n⌋.

از آنجایی که مثلث مسطح به طور مساوی به ردیف ها و ستون ها تقسیم می شود، لوزی کوچک حاوی نقطه را به ما می دهد. برای اینکه بفهمیم کدام مثلث حاوی نقطه است، یک ردیف و ستون افست پیدا می کنیم که جزء کسری کوتاه شده از عملیات کف بالا است. این به ما یک افست در لوزی کوچک می دهد. سپس این افست را در برابر توابع آزمایش می کنیم y=ایکسو y=1-ایکسبرای تعیین مثلث ما o را به عنوان عدد مثلث محاسبه شده از چهار در داخل لوزی کوچک تعریف می کنیم. شاخص مثلث نهایی ما i پس از آن است

من=2س+1∗r+(4∗ج)+o.

5. نتایج

برای ارزیابی DGGS جدید، ما اعوجاج زاویه‌ای Slice و Dice را بر روی وجه‌های یک DT به Slice و Dice بر روی وجه‌های یک DGGS ایکوس وجهی مقایسه می‌کنیم. برای اندازه‌گیری اعوجاج زاویه‌ای، از این واقعیت استفاده می‌کنیم که یک دایره بینهایت کوچک روی زمین به یک بیضی بینهایت کوچک در سلول مسطح ما کشیده می‌شود. محور اصلی و فرعی ( a و b ) بیضی پیش بینی شده مقدار اعوجاج زاویه ای d ایجاد شده توسط برآمدگی را طبق فرمول زیر [ 14 ] کمیت می کند.

د=2∗آرکسینآ-بآ+ب
از نظر هندسی، کمیت d حداکثر اختلاف زاویه (از -πبه π) بین یک نقطه روی یک دایره و نقطه متناظر روی بیضی با محور اصلی a و محور کوچک b . تطابق بین دایره و بیضی توسط تبدیل مقیاس‌پذیری ایجاد می‌شود که دایره را روی بیضی ترسیم می‌کند. این تغییر در زاویه، تغییر موضعی در بلبرینگ لازم برای حرکت بین نقاط روی نقشه مسطح است.
برای تخمین اعوجاج ایجاد شده توسط برش و تاس، دایره های ریز زیادی را در سراسر مثلث کروی خود توزیع می کنیم ( شکل 15 را ببینید ). ما این دایره ها را روی مثلث مسطح قرار می دهیم و محورهای اصلی و فرعی خود را پیدا می کنیم. استفاده از d در معادله 18 تخمینی از اعوجاج را در تمام مراکز دایره نمونه‌برداری شده ارائه می‌کند. میانگین و انحراف معیار اعوجاج زاویه ای برای هر دو DT و ایکوسادرون را می توان در جدول 1 یافت .
برای تجسم توزیع اعوجاج، مقادیر مطلق d را به مقادیر مقیاس خاکستری نشان داده شده در شکل 16 نگاشت کرده ایم . در این شکل، حداکثر مقدار مطلق d موجود در ایکو وجهی را به رنگ سفید و حداقل قدر مطلق d موجود در ایکوسا وجهی را به رنگ سیاه ترسیم کرده ایم. ما از همان محدوده مقادیر اعوجاج برای نگاشت مقیاس خاکستری برای هر دو ایکوساهدر و DT استفاده کرده ایم. ما در شکل 16 می بینیم که تمام صورت DT سیاه است که نشان دهنده یک پیشرفت قابل توجه است.
شکل 17 خروجی سیستم ما را نشان می دهد و تاثیر اعوجاج زاویه ای کم را بر هندسه شبکه حاصل نشان می دهد. وضوح این شبکه پنج است و زمین را به 30720 مثلث تقسیم می کند.
علاوه بر این، ما یک DGGS کاملاً کاربردی را با استفاده از روش‌های پیشنهادی پیاده‌سازی کرده‌ایم. شکل 18 تجسم دما را در سراسر زمین با استفاده از داده های ماهانه دو ساله نشان می دهد که به صورت خطی بین ماه ها و به صورت دوخطی بر روی رئوس DT درون یابی شده است. ما می‌توانیم این داده‌ها را در سراسر زمین در زمان واقعی جستجو و تجسم کنیم.

6. نتیجه گیری

در این مقاله، یک DGGS مساوی جدید با استفاده از DT معرفی کرده‌ایم. برای پشتیبانی از این چند وجهی اولیه جدید، ما طرح Slice و Dice را برای داشتن یک شکل بسته معکوس و روش‌های اصلاح و نمایه‌سازی برای این سیستم شبکه‌ای گسترش داده‌ایم. DGGS جدید ما اعوجاج زاویه ای را در مقایسه با سایر DGGS کاهش می دهد و در عین حال حفظ منطقه را در تمام سطوح وضوح حفظ می کند. ما نشان داده ایم که DGGS جدید ما می تواند برای پشتیبانی از پرس و جوهای سریع و کارآمد در سراسر سطح زمین پیاده سازی شود.

کار آینده

تعدادی مسیر برای کاوش در آینده وجود دارد. اول، تحقیقات بیشتر در مورد دیگر چند وجهی ممکن است جایگزین‌های مناسبی را در اینجا فراهم کند. اجازه دادن به کاربر برای تعیین معاوضه بین ویژگی های مختلف برای یک مشکل یا برنامه خاص، بهترین چند وجهی ممکن را برای هر مورد استفاده می دهد. ما همچنین می‌خواهیم طرح‌های نمایه‌سازی مختلف را برای کمک به محل حافظه برای سلول‌های همسایه بررسی کنیم. طرح نمایه سازی ما کارایی پرس و جوهای همسایگی را با محل حافظه معامله کرد. به خصوص با بالا رفتن وضوح، از دست دادن حافظه پنهان در طول پرس و جوها می تواند به گلوگاه قابل توجهی برای عملکرد سیستم تبدیل شود، و انتخاب های مختلف برای طرح نمایه سازی ممکن است روشی را که ویژگی های ذخیره سازی بهتری دارد، امکان پذیر کند. سوال باقیمانده دیگر این است که آیا می‌توانیم شبکه‌هایی با سلول‌های مساحت مساوی پیدا کنیم که برای کاهش بیشتر اعوجاج، چهره‌های بیشتری نسبت به DT دارند یا خیر. این یک سوال تحقیقاتی باز است که چگونه می توان شبکه هایی با مساحت مساوی بر روی کره بدون تولید مناطق منحط ساخت.

اختصارات

در این نسخه از اختصارات زیر استفاده شده است:

DE زمین دیجیتال
DGGS سیستم شبکه جهانی گسسته
DT سه ضلعی دیسدیاکیس
RT سه ضلعی لوزی

منابع

  1. یائو، ایکس. لی، جی. شیا، جی. بن، جی. کائو، کیو. ژائو، ال. یو، م. ژانگ، ال. زو، دی. فعال کردن داده‌های رصد بزرگ زمین از طریق محاسبات ابری و DGGS: فرصت‌ها و چالش‌ها. Remote Sens. 2019 ، 12 ، 62. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  2. مهدوی امیری، ع. آلدرسون، تی. سماواتی، اف. بررسی زمین دیجیتال. محاسبه کنید. نمودار. 2015 ، 53 ، 95-117. [ Google Scholar ] [ CrossRef ]
  3. Goodchild، MF بازاندیشی تاریخچه GIS. ان Gis 2018 , 24 , 1-8. [ Google Scholar ] [ CrossRef ]
  4. Tomlinson, R. Environmental Information Systems. در مجموعه مقالات اولین سمپوزیوم یونسکو/IGU در سیستم های اطلاعات جغرافیایی، اتاوا، ON، کانادا، 28 سپتامبر تا 2 اکتبر 1970. [ Google Scholar ]
  5. گاوس، KF تحقیقات عمومی سطوح منحنی 1827 و 1825. طبیعت 2012 ، 66 ، 316-317. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  6. سلیمان، ی. اسلپچف، دی. جرثقیل، K. تکینگی های مخروطی بهینه برای صاف کردن منسجم. ACM Trans. نمودار. 2018 ، 37 ، 4. [ Google Scholar ] [ CrossRef ]
  7. کیمرلینگ، جی. سحر، ک. سفید، دی. Song, L. مقایسه ویژگی‌های هندسی شبکه‌های جهانی. کارتوگر. Geogr. Inf. علمی 2013 ، 26 ، 271-288. [ Google Scholar ] [ CrossRef ]
  8. پرس، م. گیب، آر. سماواتی، ف. پترسون، پی. اندرو راجرز، جی. بن، جی. Dow, C. OGC سیستم شبکه جهانی گسسته (DGGS) Core Standard ; کنسرسیوم فضایی باز: Wayland، MA، ایالات متحده آمریکا، 2017. [ Google Scholar ]
  9. هریسون، ای. مهدوی امیری، ع. سماواتی، اف. تحلیل بهینه سازی های معکوس اسنایدر. در معاملات در علوم محاسباتی شانزدهم ; Gavrilova, M., Tan, C., Eds. یادداشت های سخنرانی در علوم کامپیوتر; Springer: برلین/هایدلبرگ، آلمان، 2012; جلد 7380، صص 134–148. [ Google Scholar ]
  10. هریسون، ای. مهدوی امیری، ع. سماواتی، اف. بهینه سازی طرح چند وجهی معکوس اسنایدر. در مجموعه مقالات کنفرانس بین المللی 2011 در دنیای سایبر (CW)، کلگری، AB، کانادا، 4 تا 6 اکتبر 2011. صص 136-143. [ Google Scholar ]
  11. نوآوری PYXIS. PYXIS چگونه کار می کند. در دسترس آنلاین: https://www.pyxisinnovation.com/pyxwiki/index.php?title=How_PYXIS_Works (در 1 آوریل 2020 قابل دسترسی است).
  12. پترسون، شبکه ژئودزیکی روابط عمومی ISEA3H مصور. در دسترس آنلاین: https://en.wikipedia.org/wiki/File:Geodesic_Grid_(ISEA3H)_illustrated.png (در 7 مه 2020 قابل دسترسی است).
  13. اسنایدر، جی. پیش‌بینی نقشه مساحتی برای گلوب‌های چندوجهی. Cartographica 1992 ، 29 ، 10-21. [ Google Scholar ] [ CrossRef ]
  14. لیوون، دی. Strebe، D. رویکرد “برش و تاس” به معادل سازی منطقه در پیش بینی های نقشه چند وجهی. کارتوگر. Geogr. Inf. علمی 2006 ، 33 ، 269-286. [ Google Scholar ] [ CrossRef ]
  15. لی، اس. Mortari, D. الگوریتم تقسیم مساحت شبه برابر برای نقاط یکنواخت روی یک کره با کاربرد برای هر توزیع داده های جغرافیایی. محاسبه کنید. Geosci. 2017 ، 103 ، 142-151. [ Google Scholar ] [ CrossRef ]
  16. مهدوی امیری، ع. هریسون، ای. Samavati، F. نقشه های اتصال شش ضلعی برای زمین دیجیتال. بین المللی جی دیجیت. زمین 2014 ، 8 ، 750-769. [ Google Scholar ] [ CrossRef ]
  17. هوانگ، اس. شیباساکی، آر. کاسویا، م. Takagi, M. مطالعه تطبیقی ​​بر روی طرح‌های تسلیت کروی برای GIS جهانی. Geocarto Int. 1998 ، 13 ، 3-14. [ Google Scholar ] [ CrossRef ]
  18. آلدرسون، تی. پرس، م. شیائوپینگ، دی. مهدوی امیریاند، ع. سماواتی، اف. بسترهای دیجیتال زمین. در کتابچه راهنمای زمین دیجیتال ; Springer: سنگاپور، 2019؛ صص 25-54. [ Google Scholar ]
  19. Brooks, D. Grid Systems for Earth Radiation Budget Experiment Applications ; یادداشت فنی ناسا: همپتون، ویرجینیا، ایالات متحده آمریکا، 1981.
  20. کریتندن، آر. Turok, N. دقیقاً پیکسل‌سازی‌های آزیموتالی آسمان. arXiv 1998 ، arXiv:0712.0157. [ Google Scholar ]
  21. Leopardi، P. تقسیم کره واحد به مناطقی با مساحت مساوی و قطر کوچک. الکترون ETNA ترانس. عدد. مقعدی 2006 ، 25 ، 309-327. [ Google Scholar ]
  22. آهنگ، ال. کیمرلینگ، آ. سحر، ک. توسعه شبکه جهانی مساحت مساوی توسط زیربخش دایره کوچک . مرکز ملی اطلاعات و تحلیل جغرافیایی: سانتا باربارا، کالیفرنیا، ایالات متحده آمریکا، 2002. [ Google Scholar ]
  23. داتون، جی. رمزگذاری و مدیریت داده های مکانی با مش های مثلثی سلسله مراتبی. در مجموعه مقالات هفتمین سمپوزیوم در مورد مدیریت داده های فضایی، دلفت، هلند، 12 تا 16 اوت 1996. ص 505-518. [ Google Scholar ]
  24. Szalay، ع. گری، جی. فکته، جی. Kunszt، PZ; Kukol، PZ; تاکار، الف. نمایه سازی کره با مش مثلثی سلسله مراتبی . تحقیقات مایکروسافت: ردموند، WA، ایالات متحده آمریکا، 2005. [ Google Scholar ]
  25. Massey, N. ردیابی ویژگی در شبکه مثلثی مساحت سلسله مراتبی. محاسبه کنید. Geosci. 2012 ، 44 ، 42-51. [ Google Scholar ] [ CrossRef ]
  26. گورسکی، ک. هیوون، ای. باندی، ا. واندلت، بی. هانسن، اف. راینکه، ام. Bartelman، M. HEALPix: چارچوبی برای گسسته سازی با وضوح بالا و تجزیه و تحلیل سریع داده های توزیع شده در کره. اخترفیزیک. J. 2005 ، 622 ، 759-771. [ Google Scholar ] [ CrossRef ]
  27. Dürer, A. Unterweisung der Messung mit dem Zirkel und Richtscheit: Faksimiledruck nach der Urausgabe vom Jahre 1525 ; Stocker-Schmid، دانشگاه میشیگان: دیترویت، MI، ایالات متحده آمریکا، 1966. [ Google Scholar ]
  28. برادلی، پیش‌بینی مساحت مساوی پس از میلاد بر روی ایکوساهدر. Geogr. Rev. 1946 , 36 , 101-104. [ Google Scholar ] [ CrossRef ]
  29. بن، جی. تانگ، ایکس. ژو، سی. Zhang، K. الگوریتم ساخت سیستم های شبکه شش ضلعی مبتنی بر هشت وجهی. J. Geo-Inf. علمی 2015 ، 17 ، 789-797. [ Google Scholar ]
  30. روشکا، دی. پلونکا، جی. شبکه های کروی یکنواخت از طریق طرح ریزی مساحت مساوی از مکعب به کره. جی. کامپیوتر. Appl. ریاضی. 2011 ، 236 ، 1033-1041. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  31. روشکا، دی. پلونکا، جی. پیش بینی حفظ منطقه از هشت وجهی منظم به کره. نتایج ریاضی 2012 ، 62 ، 429-444. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  32. امیری، ع.م. بوجانی، ف. سماواتی، اف. زمین دیجیتال یک به دو. در پیشرفت در محاسبات بصری ; ببیس، جی، بویل، آر، پروین، بی، کوراسین، دی، لی، بی، پوریکلی، اف.، زوردان، وی، کلوسوفسکی، جی.، کوکیلارت، اس.، لو، ایکس، و همکاران، ویرایش. Springer: برلین/هایدلبرگ، آلمان، 2013; صص 681-692. [ Google Scholar ]
  33. اسنایدر، جی. میچل، دی. نقشه برداری کارآمد نمونه برداری از تصاویر کروی . تحقیقات مایکروسافت: ردموند، WA، ایالات متحده آمریکا، 2001. [ Google Scholar ]
  34. داتون، جی. یک سیستم مختصات سلسله مراتبی برای ژئوپردازش و کارتوگرافی . نکات سخنرانی در علوم زمین; Springer: برلین/هایدلبرگ، آلمان، 1999; جلد 79. [ Google Scholar ]
  35. Goodchild، MF; Shiren, Y. ساختار داده های مکانی سلسله مراتبی برای سیستم های اطلاعات جغرافیایی جهانی. نمودار Cvgip. مدل. فرآیند تصویر 1992 ، 54 ، 31-44. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  36. مهدوی امیری، ع. سماواتی، ف. پترسون، P. طبقه بندی و تبدیل برای روش های نمایه سازی سیستم های شبکه جهانی گسسته. Isprs Int. J. Geo-Inf. 2015 ، 4 ، 320-336. [ Google Scholar ] [ CrossRef ]
  37. ژو، ال. لیان، دبلیو. Lv، G. زو، تبر; Lin, B. الگوریتم رمزگذاری و رمزگشایی کارآمد برای شبکه جهانی گسسته مثلثی بر اساس استراتژی تبدیل ترکیبی. محاسبه کنید. محیط زیست سیستم شهری 2018 ، 68 ، 110-120. [ Google Scholar ] [ CrossRef ]
  38. بوهم، سی. پرداچر، م. Plant، C. یک منحنی جدید هیلبرت برای حلقه‌های حفظ مکان حافظه پنهان. IEEE Trans. Big Data 2018 ، PP ، 1. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  39. سحر، ک. سفید، دی. کیمرلینگ، A. سیستم شبکه جهانی گسسته. کارتوگر. Geogr. Inf. علمی 2003 ، 30 ، 121-134. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  40. البرزی، ح. Samet، H. افزایش SAND با مدل داده کروی. در مجموعه مقالات کنفرانس بین المللی شبکه های جهانی گسسته، سانتا باربارا، کالیفرنیا، ایالات متحده آمریکا، 26 تا 28 مارس 2000. [ Google Scholar ]
  41. سفید، RA; Stemwedel، SW مکعب کروی چهار ضلعی و چهار درخت برای همه داده های آسمان. اختر. داده آنال. نرم افزار سیستم 1992 ، 25 ، 379. [ Google Scholar ]
  42. وایت، دی. شبکه‌های جهانی از زیربخش‌های الماس بازگشتی سطح یک هشت‌وجهی یا ایکو وجهی. محیط زیست نظارت کنید. ارزیابی کنید. 2000 ، 64 ، 93-103. [ Google Scholar ] [ CrossRef ]
  43. سفید، دی. کیمرلینگ، آ. سحر، ک. Song, L. مقایسه اعوجاج مساحت و شکل در پارتیشن‌های بازگشتی بر اساس چند وجهی کره. بین المللی جی. جئوگر. Inf. علمی 1998 ، 12 ، 805-827. [ Google Scholar ] [ CrossRef ]
  44. صدورنی، ر. آراکاوا، ا. مینتز، ی. ادغام معادله گردابی باروتروپیک غیر واگرا با یک شبکه شش‌ضلعی-ایکو وجهی برای کره. صبح. هواشناسی Soc. 1968 . [ Google Scholar ] [ CrossRef ]
  45. باومگاردنر، جی آر. فردریکسون، PO گسسته سازی ایکو وجهی دو کره. سیام جی. نومر. مقعدی 1985 ، 22 ، 1107-1115. [ Google Scholar ] [ CrossRef ]
  46. فکته، جی. Treinish، L. Sphere quadtrees: یک ساختار داده جدید برای پشتیبانی از تجسم داده های کروی توزیع شده. In Proceedings of the Electronic Imaging: Advanced Devices and Systems, Santa Clara, CA, USA, 11–16 فوریه 1990. [ Google Scholar ]
  47. Shoemake، K. متحرک کردن چرخش با منحنی های کواترنیون. محاسبات SIGGRAPH. نمودار. 1985 ، 19 ، 245-254. [ Google Scholar ] [ CrossRef ]
  48. Kettner, L. CGAL User and Reference Manual 5.0.2. در دسترس آنلاین: https://doc.cgal.org/latest/Manual/index.html (در 7 مه 2020 قابل دسترسی است).
Ijgi 09 00315 g001 550
شکل 1. طرح ریزی بین چند وجهی و زمین. تقارن آینه ای در امتداد لبه های تمام مثلث های مجاور در سه ضلعی Disdyakis (DT) وجود دارد.
Ijgi 09 00315 g002 550
شکل 2. طرح ریزی منطقه مساوی اسنایدر بر روی یک شبکه شش ضلعی منظم انجام شده است [ 11 ]. در حالی که نواحی شش ضلعی های پیش بینی شده حفظ می شوند، اشکال و زوایای آن حفظ نمی شود. تصویر اصلاح شده از [ 12 ]، دارای مجوز Creative Commons BY-SA 3.0.
Ijgi 09 00315 g003 550
شکل 3. از چپ به راست، منحنی های پرکننده فضاهای هیلبرت، پیانو، سیرپینسکی و مورتون. ترتیب بازدید منحنی از سلول ها، نمایه سازی را تعیین می کند. تصاویر گرفته شده از [ 36 ]، دارای مجوز Creative Commons BY 4.0.
Ijgi 09 00315 g004 550
شکل 4. دو هرم با 64 وجه. همه چهره ها یکسان هستند و تصاویر آینه ای از یکدیگر در امتداد لبه مجاور هستند، اما با افزایش تعداد چهره ها، فشردگی مثلث ها ایجاد مثلث های بلندتر و باریک تر را کاهش می دهد.
Ijgi 09 00315 g005 550
شکل 5. نقطه P مثلث کروی را قطع می کند آبسیبه دو قسمت با یک قوس دایره ای بزرگ که از راس B سرچشمه می گیرد. نقطه پ”در یک مثلث مسطح معین آ”ب”سی”به گونه ای حل می شود که رابطه در معادله 1 برقرار است.
Ijgi 09 00315 g006 550
شکل 6. توجه کنید که مناطق بDسیو بپEهر دو بخش از یک کلاهک کروی هستند. مساحت یک کلاهک کروی متناسب با زاویه ای است که در برابر مساحت آن قرار می گیرد بDسیمتناسب است 1-cos(ایکس+y)و مساحت بپEمتناسب است 1-cos(ایکس). همچنین توجه کنید که مناطق ب”D”سی”و ب”پ”E”مثلث های مشابه هستند مساحت مثلث های مسطح مشابه با مجذور طول ضلع آنها و مساحت مثلث متناسب است ب”D”سی”متناسب است (ایکس”+y”)2و مساحت ب”پ”E”متناسب است ایکس”2.
Ijgi 09 00315 g007 550
شکل 7. پالایش رایج مثلث ها شامل ( a ) 1:2 ( b ) 1:3 و ( c ) 1:4 است. در ( d ) نشان داده شده است، یک طرح پالایش ترکیبی 1:4 نیز می‌تواند توسط دو برنامه پالایش 1:2 در ( a ) ایجاد شود.
Ijgi 09 00315 g008 550
شکل 8. سه ضلعی لوزی (RT) زیر مجموعه ای از رئوس و لبه های DT است. دو صورت لوزی و نمایه سازی لوزی به رنگ قرمز نشان داده شده اند. نمایه سازی سیاه با لوزی های شکل 10 مطابقت دارد .
Ijgi 09 00315 g009 550
شکل 9. ( الف ) نقشه‌های اتصال را می‌توان به دو مثلث مجاور نسبت داد تا یک دامنه چهار ضلعی با پارامتر u و v از 0 تا 1 تشکیل دهند. در نقشه اتصال که می تواند با پارامترهای u و v نمایه شود .
Ijgi 09 00315 g010 550
شکل 10. نمونه ای از طرح نمایه سازی در قطعنامه های 1، 2 و 3 از چپ به راست. توجه داشته باشید که این برای هر لوزی در RT تکرار می شود. این الگوهای Z شکل در لوزی‌های کوچک در امتداد ردیف‌ها و ستون‌های لوزی‌های کوچک به ترتیب اصلی تکرار می‌شوند. ما لوزی های کوچک را ردیف به ردیف فهرست می کنیم، که بیشتر در سطح وضوح 3 در سمت راست مشهود است.
Ijgi 09 00315 g011 550
شکل 11. شاخص های سلولی دو لوزی پایه مجاور. توجه داشته باشید که برای هر سلول c در لوزی کوچکی که با قرمز نشان داده شده است، دو همسایه در شاخص قرار دارند. ج⊕1و ج⊕2. این در مورد هر شاخصی در هر لوزی کوچک صادق است. همسایه نهایی بستگی به این دارد که آیا در مرز بین لوزی ها قرار داریم یا نه.
Ijgi 09 00315 g012 550
شکل 12. لوزی که با رنگ قرمز مشخص شده است، وقتی سطوح زیربخش را کاهش دهیم، به لوزی والد تبدیل می شود. سطرها با یک خط آبی – ستون ها با یک خط قرمز تقسیم می شوند. شاخص های سبز شروع دو بلوک متوالی از شاخص ها در لوزی قرمز هستند. همانطور که در شکل 13 مشاهده می شود، شاخص های خاص بخشی از والدین خاص می شوند .
Ijgi 09 00315 g013 550
شکل 13. سلول های والد با رنگ های آبی و قرمز مشخص شده اند. توجه داشته باشید که 16 سلول کودک چهار والد را در لوزی تشکیل می دهند.
Ijgi 09 00315 g014 550
شکل 14. یک DT با کمان دایره ای بزرگ (طول جغرافیایی) بین قطب شمال و جنوب که با رنگ قرمز مشخص شده است. ناحیه بین این کمان ها شامل 12 مثلث پایه است. یک نقطه P روی زمین را می‌توان به سرعت بررسی کرد تا ببینیم آیا در پارتیشن ایجاد شده توسط کمان‌های قرمز به سادگی با بررسی طول آن قرار دارد یا خیر. خطوط چین نشان دهنده سطح زیربخش بعدی است. مختصات باریسنتریک نقطه درون مثلث پایه تعیین می کند که سلول فرزند P در کدام سلول قرار دارد.
Ijgi 09 00315 g015 550
شکل 15. دایره های روی وجه کروی یک DT که با رنگ آبی نشان داده شده اند به صورت بیضی روی وجه مسطح یک DT که با رنگ سبز نشان داده شده است، پیش بینی می شود. می بینیم که اعوجاج زاویه ای جزئی است زیرا محور اصلی و فرعی بیضی ها به هم نزدیک هستند.
Ijgi 09 00315 g016 550
شکل 16. ( الف ) اعوجاج زاویه ای که به یک مقدار مقیاس خاکستری در سراسر یک وجه ایکوساهدر نگاشت شده است. ( ب ) اعوجاج زاویه ای نگاشت شده به یک مقدار خاکستری در سطح یک DT. سیاه اعوجاج کم و سفید اعوجاج زیاد است. ما برای مقایسه مستقیم از یک نقشه برداری در مقیاس خاکستری برای هر دو استفاده کرده ایم.
Ijgi 09 00315 g017 550
شکل 17. DT به وضوح 5 تقسیم شده است. اعوجاج زاویه ای در امتداد لبه ها قابل مشاهده نیست.
Ijgi 09 00315 g018 550
شکل 18. داده های دما درون یابی شده در سراسر سیستم شبکه جهانی گسسته DT (DGGS). مناطق سرد آبی و مناطق قرمز گرم هستند. این داده ها را می توان در زمان واقعی در سراسر زمین جستجو و تجسم کرد.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید