PolySimp: ابزاری برای ساده سازی چند ضلعی بر اساس سلسله مراتب مقیاس بندی زیربنایی

خلاصه

تعمیم نقشه فرآیندی است برای کاهش محتویات یک نقشه یا داده ها برای نشان دادن درست یک ویژگی(های) جغرافیایی در مقیاس کوچکتر. در طی چند سال گذشته، روش تفکر فراکتالی به عنوان پارادایم جدیدی برای تعمیم نقشه پدیدار شده است. یک ویژگی جغرافیایی را می توان با توجه به دیدگاه مقیاس بندی، به عنوان یک فراکتال در نظر گرفت، زیرا شکل خشن، نامنظم و غیرصاف آن ذاتاً سلسله مراتب مقیاس پذیری قابل توجهی از عناصر بسیار کوچکتر از عناصر بزرگ را در خود دارد. الگوی چیزهای کوچک به مراتب بیشتر از چیزهای بزرگ توزیع دم سنگین است. در این مقاله، ما سلسله مراتب مقیاس بندی را برای تعمیم نقشه به ویژگی های چند ضلعی اعمال می کنیم. برای انجام این کار، ابتدا سلسله مراتب مقیاس بندی یک فراکتال کلاسیک را بررسی می کنیم: دانه برف کوخ. سپس کارهای قبلی را که از الگوریتم داگلاس-پیکر استفاده می‌کردند، مرور می‌کنیم.
دوره-آموزش-حرفه-ای-gis
که نقاط مشخصه را در یک خط مشخص می کند تا سه نوع معیار توزیع شده در دم بلند را به دست آورد: طول خط پایه (d)، فاصله عمود بر خط مبنا (x)، و مساحت تشکیل شده توسط x و d (مساحت). مهمتر از آن، ما استفاده از سه معیار را به سایر روش‌های رایج تعمیم نقشه‌کشی گسترش می‌دهیم. به عنوان مثال، روش ساده سازی خم، روش Visvalingam-Whyatt، و روش تجزیه سلسله مراتبی، که هر یک از آنها هر چند ضلعی را به مجموعه ای از خم ها، مثلث ها یا بدنه های محدب به عنوان واحدهای هندسی اساسی برای ساده سازی تجزیه می کنند. سپس سطوح مختلف جزئیات چند ضلعی را می توان با انتخاب بازگشتی قسمت سر واحدهای هندسی و حذف قسمت دم با استفاده از شکستگی سر/دم، که یک طرح طبقه بندی جدید برای داده ها با توزیع دم سنگین است، به دست آورد. از آنجایی که در حال حاضر ابزارهای کمی وجود دارد که بتوان به آسانی ساده سازی چند ضلعی را از چنین منظر فراکتالی انجام داد، ما PolySimp را توسعه داده ایم، ابزاری که چهار الگوریتم ذکر شده را برای ساده سازی چند ضلعی بر اساس سلسله مراتب مقیاس بندی زیربنایی آن یکپارچه می کند. خط ساحلی بریتانیا برای نشان دادن سودمندی این ابزار انتخاب شد. می توان انتظار داشت که ابزار توسعه یافته کاربرد روش تفکر فراکتال را به نمایش بگذارد و به توسعه تعمیم نقشه کمک کند.

کلید واژه ها:

تعمیم نقشه کشی ; مقیاس بندی ویژگی های چند ضلعی ; تجزیه و تحلیل فراکتال ؛ سر/دم می شکند

1. معرفی

پرداختن به مسائل جهانی مانند محیط زیست، آب و هوا و اپیدمیولوژی برای سیاست‌گذاری یا تصمیم‌گیری مربوط به برنامه‌ریزی فضایی و توسعه پایدار نیازمند اطلاعات مکانی است که شامل انواع ویژگی‌های جغرافیایی در هر سطح از جزئیات است. در علم اطلاعات جغرافیایی، اصطلاح تعمیم نقشه برای رفع این نیاز ابداع شده است [ 1 ، 2 ، 3 ، 4 ]. به زبان ساده، تعمیم نقشه، بخش‌های اساسی اصلی داده‌های منبع یا نقشه را در سطوح مختلف جزئیات نگه می‌دارد، بنابراین عناصر با ویژگی‌های حیاتی کمتر را حذف می‌کند [ 5 ، 6 ]]. به عبارت دیگر، هدف از تعمیم کاهش محتویات یا پیچیدگی یک نقشه یا داده ها برای نشان دادن درست ویژگی(های) جغرافیایی به میزان کمتری است. تعمیم ارتباط نزدیکی با مقیاس نقشه دارد که به نسبت بین اندازه گیری روی نقشه و اندازه گیری در واقعیت اشاره دارد [ 7 ]. با کاهش مقیاس، ساده کردن و/یا حذف برخی از اشیاء جغرافیایی برای قابل تشخیص کردن ویژگی های نقشه اجتناب ناپذیر است.
تعمیم یک شی جغرافیایی را می توان به عنوان کاهش عناصر هندسی آن (به عنوان مثال، نقاط، خطوط، و چندضلعی) درک کرد. ساده‌ترین راه برای انجام ساده‌سازی، حذف نقاط در یک بازه زمانی مشخص است (یعنی هر n نقطه ، [ 8 ]). با این حال، ممکن است اغلب در حفظ شکل اصلی شکست بخورد زیرا از شکل جهانی شی و روابط همسایه بین عناصر هندسی حاوی آن غفلت می کند. به منظور حفظ شکل اولیه در سطوح درشت‌تر، مطالعات مرتبط در چندین دهه گذشته از دیدگاه‌های مختلف، از جمله کوچک‌ترین اجسام مرئی [ 9 ]، ناحیه مؤثر [ 10 ]، سازگاری توپولوژیکی [ 11 ] کمک بزرگی کردند.]، زوایای انحراف و باندهای خطا [ 12 ]، انحنای شکل [ 13 ]، سیستم‌های چند عاملی (پروژه AGENT؛ [ 14 ، 15 ])، و راه‌حل‌های ریاضی مانند روش گرادیان مزدوج [ 16 ]، مبتنی بر فوریه تقریب [ 17 ]، و غیره. مخزن انباشته روش‌ها و الگوریتم‌های ساده‌سازی راه‌حل‌های مفیدی را برای حفظ شکل هسته بر اساس معیارهای مختلف ارائه می‌دهند، اما آنها به ندرت نتایج ساده‌سازی شده مؤثر را با مقیاس‌های نقشه مرتبط می‌کنند.
در سال های اخیر، هندسه فراکتال [ 18 ] به عنوان پارادایم جدید برای تعمیم نقشه پیشنهاد شده است. نورمانت و تریکو [ 19 ] یک الگوریتم مبتنی بر بدنه محدب برای ساده سازی خط طراحی کردند در حالی که ابعاد فراکتال را برای مقیاس های مختلف حفظ کردند. لام [ 20 ] اشاره کرد که فراکتال ها می توانند الگوهای فضایی را مشخص کنند و به طور موثر روابط بین ویژگی های جغرافیایی و مقیاس ها را نشان دهند. جیانگ و همکاران [ 5] یک قانون جهانی برای تعمیم نقشه ایجاد کرد که کاملاً در چارچوب تفکر فراکتال-هندسی است. این قانون جهانی است زیرا چیزهای کوچک بسیار بیشتری نسبت به چیزهای بزرگ در سطح جهان در فضای جغرافیایی و در مقیاس های مختلف وجود دارد. این واقعیت نسبت نامتعادل بین چیزهای بزرگ و کوچک – همچنین به عنوان ماهیت فراکتال ویژگی های جغرافیایی شناخته می شود – به عنوان قانون مقیاس بندی فرموله شده است [ 21 ، 22 ، 23 ]. جیانگ با الهام از ساختار فراکتالی ذاتی و آمار مقیاس بندی ویژگی های جغرافیایی [ 24 ]] پیشنهاد کرد که یک نقشه در مقیاس بزرگ و نقشه مقیاس کوچک آن یک رابطه بازگشتی یا تودرتو دارند و نسبت بین مقیاس های بزرگ و کوچک نقشه باید با نسبت مقیاس بندی تعیین شود. در این رابطه، ماهیت فراکتال یا قانون مقیاس‌بندی می‌تواند تا حدی به راهنمایی بهتری از تعمیم نقشه نسبت به قانون رادیکال تاپفر [ 25 ]، با توجه به آنچه که باید تعمیم داده شود و میزانی که می‌توان آن را تعمیم داد، بیان کرد. تعمیم یافته است.
برای مشخص کردن ماهیت فراکتالی ویژگی‌های جغرافیایی، یک طرح طبقه‌بندی جدید به نام شکستگی‌های سر/دم [ 26 ] و متریک القایی آن، شاخص ht [ 27 ] می‌تواند به طور موثر برای به دست آوردن سلسله‌مقیاس‌بندی تعداد زیادی از کوچک‌ترین، تعداد بسیار کمی از بزرگترین، استفاده شود. و برخی در بین کوچکترین و بزرگترین (جزئیات بیشتر را در بخش 2.2 و ضمیمه A ببینید). سلسله‌مراتب مقیاس‌بندی ناشی از شکستگی‌های سر/دم می‌تواند منجر به تعمیم خودکار نقشه از یک ویژگی نقشه ریز دانه به مجموعه‌ای از نقشه‌های درشت‌تر شود. بر اساس یک سری از مطالعات قبلی، شیوه‌های نقشه‌برداری یا به طور خاص تعمیم نقشه، می‌تواند به عنوان فرآیندهای سر و دم به کار رفته برای ویژگی‌ها یا داده‌های جغرافیایی در نظر گرفته شود. این نوع تفکر در ادبیات مورد توجه فزاینده ای قرار گرفته است (به عنوان مثال، [ 28 , 29 , 30 , 31 , 32]). با این حال، با توجه به اینکه تفکر هندسی فراکتال، به ویژه پیوند دادن با سلسله مراتب مقیاس خود ویژگی نقشه، هنوز برای تعمیم نقشه نسبتاً جدید است، مشکل عملی فقدان ابزاری برای تسهیل محاسبه معیارهای فراکتالی مرتبط است که بتواند فرآیند تعمیم نقشه را هدایت کند. .
هدف کار حاضر توسعه چنین ابزاری برای پیشبرد کاربرد تفکر فراکتال-هندسی در شیوه‌های تعمیم نقشه است. مشارکت‌های این مقاله را می‌توان برحسب سه جنبه اصلی آن توصیف کرد: (1) معیارهای هندسی مورد استفاده در مطالعه قبلی [ 5 ] را به سه الگوریتم ساده‌سازی چندضلعی دیگر معرفی کردیم. (2) ما متوجه شدیم که الگوی فراکتالی یک ویژگی چند ضلعی در همه جا در الگوریتم‌های انتخاب شده وجود دارد که توسط آمار مقیاس‌بندی معیارهای هندسی از همه انواع نشان داده می‌شود. و (3) ابزار توسعه‌یافته (PolySimp) می‌تواند استخراج خودکار یک نمایش چند‌مقیاسی از یک ویژگی چند ضلعی را بر اساس شکستگی‌های سر/دم و ht-index القا شده آن امکان‌پذیر کند.
بقیه این مقاله به شرح زیر سازماندهی شده است. بخش 2 روش‌های ساده‌سازی چند ضلعی مرتبط را مرور می‌کند و کاربرد سلسله‌مراتب مقیاس‌بندی را در آن نشان می‌دهد. بخش 3 ابزار PolySimp را در رابطه با رابط کاربری، عملکرد و ملاحظات الگوریتمی آن معرفی می کند. در بخش 4 ، ساده‌سازی خط ساحلی بریتانیا با استفاده از الگوریتم‌های معرفی‌شده انجام شده و مقایسه‌هایی بین الگوریتم‌های مختلف و معیارهای هندسی انجام شده است. بحث در بخش 5 و در ادامه با نتیجه گیری در بخش 6 ارائه شده است.

2. روش ها

2.1. الگوریتم های مرتبط برای ساده سازی چند ضلعی

این ابزار بر روی ساده سازی چند ضلعی تمرکز دارد که یکی از شاخه های اصلی در زمینه تعمیم نقشه است. همانطور که در ادبیات GIS [ 33 ] تعریف شده است، ساده سازی چند ضلعی با نمادشناسی گرافیکی سر و کار دارد، که منجر به فرآیند ساده سازی یک ویژگی چند ضلعی می شود که منجر به نمایش فضایی چند مقیاسی می شود [ 34 ]. با توجه به مستندات نرم افزار ArcGIS [ 35 ] (ESRI 2020) و پلتفرم های منبع باز مانند CartAGEn [ 36 ، 37 ]، واحد هندسی یک ویژگی چند ضلعی که باید ساده شود بر اساس نقاط، خم ها و سایر واحدهای سطحی آن دسته بندی می شود. به ترتیب مثلث و بدنه محدب.
رایج ترین الگوریتم حذف نقطه احتمالاً الگوریتم داگلاس-پیکر (DP) است [ 38]، که می تواند به طور موثر شکل اساسی یک چند خط را با یافتن و حفظ نقاط مشخصه و در عین حال حذف سایر موارد بی اهمیت حفظ کند. این الگوریتم به صورت بازگشتی اجرا می شود. با شروع با یک قطعه با پیوند دو انتهای یک چندخط، نقطه ای را با حداکثر فاصله از آن پاره خط تشخیص می دهد. اگر فاصله کمتر از یک آستانه معین باشد، نقاط بین انتهای قطعه حذف خواهند شد. در غیر این صورت، دورترین نقطه را نگه می دارد و آن را با انتهای هر بخش وصل می کند و مراحل قبلی را در قسمت های جدید ایجاد شده تکرار می کند. این الگوریتم زمانی متوقف می‌شود که تمام فاصله‌های حداکثر شناسایی‌شده کمتر از آستانه داده‌شده باشد. الگوریتم DP را می توان با تقسیم یک چند ضلعی به دو قسمت (چپ و راست یا بالا و پایین) اعمال کرد. یکی از راه‌های تقسیم عینی یک چند ضلعی، استفاده از قطعه‌ای است که دورترین جفت نقطه را به هم مرتبط می‌کند، مانند خط مورب یک مستطیل. به این ترتیب، هر قسمت از یک چند ضلعی را می توان به عنوان یک چند خط پردازش کرد که الگوریتم DP می تواند روی آن اعمال شود.
Visvalingam و Whyatt [ 10 ] که از رویکرد حذف نقطه تکامل یافته اند، یک روش مبتنی بر مثلث (VW) را برای انجام ساده سازی ارائه کردند. هر مثلث مربوط به یک راس و دو همسایه مستقیم آن است، به طوری که اهمیت یک راس را می توان با اندازه مثلث مربوط به آن اندازه گیری کرد. بنابراین، فرآیند ساده سازی چند ضلعی به طور مکرر آن راس های بی اهمیت (مثلث های کوچک) را حذف می کند. این روش با استفاده از صافی، چولگی و تحدب مثلث بیشتر بهبود یافت [ 39 ]. بعدها، وانگ و مولر [ 40] الگوریتم ساده سازی خم (BS) را پیشنهاد کرد که خم ها را به عنوان واحدهای اساسی برای ساده سازی چند خط/چند ضلعی برای حفظ بهتر شکل نقشه برداری چند خط/چند ضلعی تعریف می کند. به بیان ساده، یک خط/چند ضلعی از خم های متعددی ساخته شده است که هر کدام از مجموعه ای از نقاط متوالی با علامت زوایای خمشی یکسان تشکیل شده است. سپس فرآیند ساده سازی زیر تبدیل به حذف بازگشتی خم هایی می شود که ویژگی های هندسی آنها اهمیت کمی دارد.

یکی دیگر از الگوریتم های مبتنی بر واحد منطقه ای، تجزیه سلسله مراتبی یک چندضلعی است (HD; [ 41 ]). این یک شی چند ضلعی را به مجموعه ای از مستطیل های حداقل محدود یا بدنه های محدب تجزیه می کند. این الگوریتم همچنین به صورت بازگشتی کار می کند. در هر تکرار، یک بدنه محدب برای هر جزء چند ضلعی می سازد، سپس تفریق/تفاوت بین مؤلفه چند ضلعی و همتای محدب آن را استخراج می کند و از آن در تکرار بعدی استفاده می کند تا زمانی که جزء چند ضلعی به اندازه کافی کوچک شود یا درجه محدب آن بزرگتر از یک باشد. آستانه از پیش تعیین شده در نهایت، تمام بدنه های محدب مشتق شده در یک ساختار درختی ذخیره می شوند و با یک عدد تکرار مربوطه مشخص می شوند. بر اساس هندسه های پایه ساخت یافته، می توانیم چند ضلعی اصلی را با استفاده از معادله زیر استخراج کنیم:

پoلygon=∑ک=0n(-1)ک آک

که در آن k عدد تکرار و  آکبدنه محدب است که در تکرار k تنظیم شده است.

الگوریتم تجزیه سلسله مراتبی انتقال تدریجی یک شی چند ضلعی را فراهم می کند. با توجه به این معادله، می‌تواند یک شی چند ضلعی را در سطوح مختلف جزئیات با افزودن یا تفریق یک مجموعه بدنه محدب در تکرار مرتبط به دست آورد. توجه داشته باشید که مطالعه حاضر فقط یک بدنه محدب را برای توضیح بیشتر در نظر گرفته است.
دوره-آموزش-حرفه-ای-gis

2.2. ساده سازی چند ضلعی با استفاده از سلسله مراتب مقیاس ذاتی آن

این مطالعه برای انجام تعمیم بر اساس سلسله مراتب مقیاس بندی یک ویژگی چندضلعی بر روش شکستگی سر/دم تکیه داشت. شکستن سر/دم در ابتدا به عنوان یک روش طبقه بندی برای داده ها با توزیع دم سنگین [ 26 ] توسعه یافت. با توجه به داده‌هایی با توزیع دم سنگین، میانگین حسابی داده‌ها را به سر (درصد کوچک با مقادیر بالاتر از میانگین، به عنوان مثال، <40 درصد) و دم (درصد بزرگ با مقادیر کمتر از میانگین) تقسیم می‌کند. به این ترتیب، به طور بازگشتی قسمت سر را به یک سر و دم جدید جدا کرد تا اینکه مفهوم مقادیر بسیار کوچکتر از مقادیر بزرگ نقض شد. تعداد دفعاتی که می توان تقسیم سر/دم را به اضافه 1 اعمال کرد، شاخص ht است [ 27 ]]. به عبارت دیگر، ht-index تعداد دفعاتی را نشان می‌دهد که الگوی مقیاس‌بندی عناصر بسیار کوچک‌تر از عناصر بزرگ تکرار می‌شود، بنابراین سلسله‌مراتب مقیاس‌بندی داده‌ها را به تصویر می‌کشد. در مجموع، داده‌هایی با توزیع دنباله‌دار به طور ذاتی دارای یک سلسله مراتب مقیاس‌بندی هستند که برابر با مقدار شاخص ht است: تعداد الگوهای تکرارشونده چیزهای کوچک‌تر از موارد بزرگ در داده‌ها.
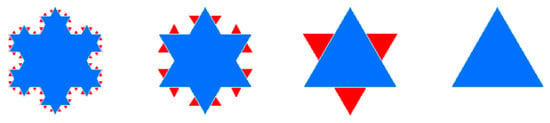
با سلسله مراتب مقیاس بندی، تعمیم نقشه را می توان با استفاده از شکست های سر/دم با انتخاب بازگشتی قسمت سر به عنوان نتیجه تعمیم یافته در سطح بعدی انجام داد تا زمانی که قسمت سر دیگر دم سنگین نباشد [ 5 ]. صرفاً به این دلیل است که هد شبیه به کل مجموعه داده است که دارای یک سلسله‌مراتب مقیاس‌پذیر است. اجازه دهید از دانه‌ی برف Koch برای نشان دادن نحوه عملکرد شکستن سر/دم برای ساده‌سازی چند ضلعی استفاده کنیم. شکل 1دانه برف اصلی را نشان می دهد که شامل 64 مثلث متساوی الاضلاع با اندازه های مختلف است. به طور دقیق تر، 48، 12، 3، و 1 مثلث با طول لبه های 1/27، 1/9، 1/3 و 1 وجود داشت. طول لبه هر مثلث بدیهی است که از توزیع دم سنگین پیروی می کند. بنابراین، می‌توانیم ساده‌سازی چند ضلعی را با استفاده از شکاف‌های سر/دم بر اساس طول لبه انجام دهیم. میانگین اول این است متر1=1×1+3×13+12×19+48×12764= 0.08، که مثلث ها را به 16 مثلث بالا تقسیم می کند متر1و 48 مثلث زیر متر1. بنابراین، آن 16 مثلث نمایانگر قسمت سر هستند (16/64 = 0.25، <40%) و به عنوان اولین نتیجه تعمیم یافته انتخاب شدند ( شکل 1 ). بقیه را می توان به همین ترتیب انجام داد. میانگین دوم متر2=1×1+3×13+12×19160.21 = به به دست آوردن یک نتیجه ساده تر شامل سر جدید با چهار مثلث کمک کرد ( شکل 1 ). در نهایت، تنها یک مثلث بالاتر از میانگین سوم وجود داشت متر3=1×1+3×134= 0.5، که آخرین نتیجه ساده شده بود ( شکل 1 ). می توان مشاهده کرد که سه سطح تعمیم در طول فرآیند شکستن سر/دم به دست آمد که با سلسله مراتب مقیاس بندی همه مثلث ها سازگار بود.
همانطور که مثال بالا نشان می دهد، شکستن سر/دم راهی موثر و ساده برای ساده کردن یک شی چند ضلعی است که سلسله مراتب مقیاس بندی را دارد. با این حال، دانه‌ی برف کوخ فقط یک مدل ریاضی تحت تفکر فراکتالی است تا یک چندضلعی واقعی. سپس این سوال مطرح می‌شود که چگونه می‌توانیم چنین الگوی مقیاس‌بندی یک چندضلعی معمولی را که درک سلسله‌مراتب مقیاس‌بندی آن بسیار دشوارتر از دانه‌ی برف کوخ است، تشخیص دهیم. در اینجا ما سه معیار هندسی را معرفی کردیم: x، d، و مساحت هر جسم چندضلعی که بر دو الگوریتم فوق الذکر تکیه دارد.
مطالعات قبلی (به عنوان مثال، [ 5 ، 42 ]) سه معیار ذکر شده را بر اساس الگوریتم DP پیشنهاد کرده اند. همانطور که شکل 2 a نشان می دهد، x فاصله دورترین نقطه C از قطعه ای است که دو انتهای یک چند خط (AF) را به هم متصل می کند. d طول بخش AF است. و مساحت برابر است با مساحت مثلث ACF (x*d/2). در این مطالعه، ما این سه معیار را برای روش‌های VW، BS و HD نیز با توجه به نوع واحدهای ساده‌سازی منطقه‌ای خود محاسبه کردیم. با در نظر گرفتن روش HD به عنوان مثال، همانطور که می دانیم چند ضلعی به مجموعه ای از بدنه های محدب تجزیه می شود، این سه معیار را می توان به صورت شکل 2 تعریف کرد.b نشان می دهد: x دورترین نقطه C از طولانی ترین لبه بدنه محدب (AE) است. d طول بلندترین لبه AE است. و مساحت بدنه محدب ABCDE است.
هر سه معیار چهار الگوریتم به صورت بازگشتی مشتق شده اند. جیانگ و همکاران [ 5 ] نشان داد که معیارهای x و x/d بر اساس روش DP، توزیع دم سنگینی را نشان می‌دهند. بنابراین، هر سه معیار روش DP که روی ویژگی چند ضلعی اعمال می‌شوند، با یک سلسله مراتب مقیاس‌بندی واضح هستند. برای سه الگوریتم دیگر، اندازه واحد ساده‌سازی منطقه‌ای مشتق‌شده نیز تمایل به توزیع دم بلند دارد ( شکل A1 را در پیوست A ببینید.). در اینجا دوباره از روش HD برای مثال استفاده کردیم: با توجه به اینکه چند ضلعی اصلی به اندازه کافی پیچیده بود، نواحی تمام بدنه‌های محدب به‌دست‌آمده به‌طور اجتناب‌ناپذیری دارای سلسله‌مراتب مقیاس‌بندی هستند، همانطور که دو معیار دیگر از آنجایی که همبستگی زیادی با مساحت داشتند. برای توصیف شهودی تر، دانه برف Koch دوباره به عنوان یک نمونه کار استفاده شد.
شکل 3 تجزیه دانه های برف کوچ را مطابق با رابطه (1) نشان می دهد. این فرآیند در تکرار 2 متوقف می شود زیرا تمام اجزای چند ضلعی به شکل مثلث هستند که درجه محدب آن 1 است. در مجموع 67 بدنه محدب وجود داشت. به وضوح می توان مشاهده کرد که بدنه های محدب کوچک بیشتر از بدنه های بزرگ هستند. اگر بر روی ناحیه این بدنه های محدب شکاف های سر/دم اعمال کنیم، می توان دریافت که الگوی پوسته پوسته شدن دو بار تکرار می شود. توجه داشته باشید که دانه‌های برف کخ بسیار پیچیده‌تر از چند ضلعی نقشه‌کشی بود که معمولاً بیش از 10 تکرار داشت. در این راستا، ما می‌توانیم الگوی پوسته پوسته‌های محدب تجزیه شده یک جسم چندضلعی را از طریق x، d و ناحیه بر اساس الگوریتم HD تشخیص دهیم. این اصل برای روش های VW و BS نیز کار می کند.

3. توسعه یک ابزار نرم افزاری: PolySimp

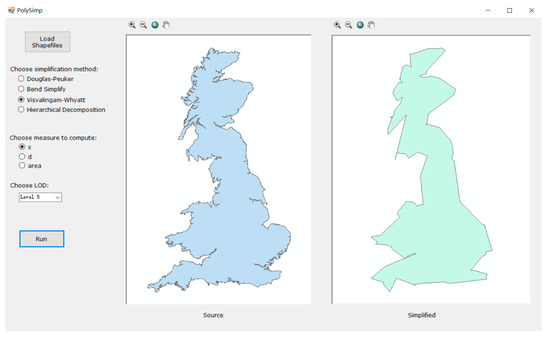
در حال حاضر ابزارهای کمی وجود دارد که با استفاده از چهار الگوریتم از منظر فراکتال ساده سازی چند ضلعی را به راحتی انجام دهیم. برای پرداختن به این موضوع، ما یک ابزار نرم افزاری (به نام PolySimp) در این مطالعه برای تسهیل محاسبه سه معیار معرفی شده و اجرای تعمیم ایجاد کردیم ( شکل 4).). این ابزار نرم افزاری با Microsoft Visual Studio 2010 با Tools for Universal Windows Apps پیاده سازی شد. تابع تعمیم توسط انواع داده ArcEngine و رابط های NET Framework 4.0 انجام شد. ابزار نرم افزار برای انجام عملکردهای زیر طراحی شده است. اولین تابع یک تابع ورودی است. ابزار باید قادر باشد (الف) یک داده چند ضلعی را بارگذاری کند و (ب) نتایج را به نمایشگر نقشه داخلی ارائه دهد. فایل های داده را می توان در قالب Shapefile تهیه کرد که بیشترین استفاده را در محیط GIS فعلی دارد. تابع دوم تابع خروجی است که بر اساس معیارهای انتخاب شده، نتیجه ساده سازی چند ضلعی را تولید می کند. یعنی الگوریتم، نوع اندازه گیری و سطح جزئیاتی که باید تعمیم داده شود. وقتی تعمیم کامل شد، نتیجه در پانل دوم در سمت راست نشان داده شده است. این ابزار نرم افزاری را می توان درمواد تکمیلی .
همانطور که برای ملاحظات الگوریتمی، ابزار نرم افزار ساده سازی چند ضلعی را با اعمال روش شکستن سر/دم برای هر یک از سه معیار به ترتیب انجام می دهد. نمودارهای جریان در شکل 5کل روش نحوه اجرای توابع توسط ابزار را ارائه دهید. با توجه به یک سری مقادیر برای هر یک از سه معیار (x، d، و مساحت) از طریق چهار الگوریتم، ابتدا آن واحدهای ساده‌کننده را تولید کردیم. به عنوان مثال، نقاط، خم ها، مثلث ها، یا بدنه محدب. برای واحدهای منطقه، ما مطمئن شدیم که واحدهای ساده‌سازی مشتق‌شده در بهترین سطح به خاطر مقیاس‌بندی محاسبات سلسله مراتبی هستند. از آنجایی که فولکس‌واگن می‌تواند هر مثلث را با هر نقطه مرتبط کند، ما فقط قوانین الگوریتم‌های BS و HD را تعیین می‌کنیم: برای BS، تا زمانی که علامت زاویه عطف تغییر می‌کند، خم را تشخیص می‌دهیم، به طوری که کوچک‌ترین خم می‌تواند یک مثلث باشد. برای HD، شرط توقف را در تجزیه یک چند ضلعی تنظیم می کنیم که به موجب آن هر جزء چند ضلعی تجزیه شده باید دقیقاً محدب باشد، صرف نظر از اینکه چقدر کوچک است. سپس، ما آن واحدهای ساده‌سازی را که مقادیر آن‌ها بزرگ‌تر از میانگین (در قسمت سر) بودند، حفظ کردیم، واحدهایی را که مقادیر کوچک‌تر از میانگین داشتند (در دم) حذف کردیم. ما معتقد بودیم که آنها بخش مهمی از یک چند ضلعی هستند و نگهداری بازگشتی آنها می تواند به حفظ شکل هسته در سطوح مختلف کمک کند. این روند ادامه داشت تا زمانی که قسمت سر دیگر اقلیت نبود (> 40٪). هر بار که یک چند ضلعی ساده شده تولید می شد، قسمت سر دوباره محاسبه می شد. توجه داشته باشید که هنگام ادغام بدنه های محدب در قسمت سر با استفاده از روش HD، اضافه یا تفریق بدنه محدب به تعداد تکرار آن بستگی دارد (به معادله (1) مراجعه کنید). ما معتقد بودیم که آنها بخش مهمی از یک چند ضلعی هستند و نگهداری بازگشتی آنها می تواند به حفظ شکل هسته در سطوح مختلف کمک کند. این روند ادامه داشت تا زمانی که قسمت سر دیگر اقلیت نبود (> 40٪). هر بار که یک چند ضلعی ساده شده تولید می شد، قسمت سر دوباره محاسبه می شد. توجه داشته باشید که هنگام ادغام بدنه های محدب در قسمت سر با استفاده از روش HD، اضافه یا تفریق بدنه محدب به تعداد تکرار آن بستگی دارد (به معادله (1) مراجعه کنید). ما معتقد بودیم که آنها بخش مهمی از یک چند ضلعی هستند و نگهداری بازگشتی آنها می تواند به حفظ شکل هسته در سطوح مختلف کمک کند. این روند ادامه داشت تا زمانی که قسمت سر دیگر اقلیت نبود (> 40٪). هر بار که یک چند ضلعی ساده شده تولید می شد، قسمت سر دوباره محاسبه می شد. توجه داشته باشید که هنگام ادغام بدنه های محدب در قسمت سر با استفاده از روش HD، اضافه یا تفریق یک بدنه محدب به تعداد تکرار آن بستگی دارد (به معادله (1) مراجعه کنید).

4. مطالعه موردی و تجزیه و تحلیل

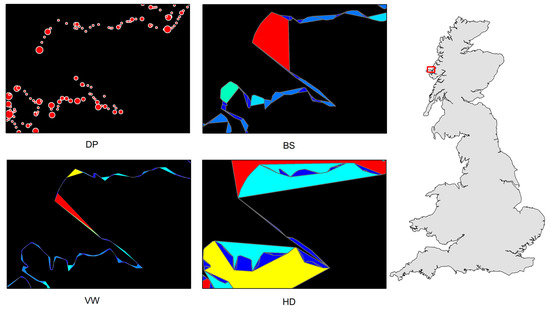
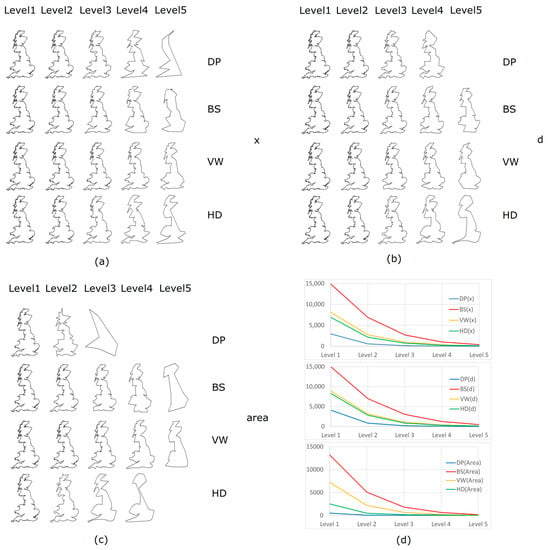
خط ساحلی بریتانیا به عنوان مطالعه موردی برای نشان دادن نحوه عملکرد PolySimp انتخاب شد. از آنجایی که شکل خط ساحلی بریتانیا (قطعاً یا به طور کامل) به طور گسترده به عنوان مطالعات موردی برای DP، BS و VW مورد استفاده قرار گرفته است، ما از آن برای نشان دادن اینکه چگونه سلسله‌مراتب مقیاس‌بندی می‌تواند برای ساده‌سازی چند ضلعی اعمال شود و بر این اساس مقایسه کنیم، استفاده کردیم. ما سلسله مراتب مقیاس را از DP، BS، VW، و HD با داده های منبع بهتر که حاوی 23601 راس (تقریبا 10 برابر بیشتر از مورد استفاده شده توسط [ 5 ]) با استفاده از PolySimp بود استخراج کردیم. هر دو تعداد واحدهای ساده کننده برای DP و VW 23601 بود که با تعداد رئوس مطابقت داشت. برای BS و HD، به ترتیب 10883 خم و 10639 بدنه محدب وجود داشت ( شکل 6 ). میز 1میانگین زمان اجرای هر سطح از جزئیات را بین روش های مختلف ساده سازی نشان می دهد. شایان ذکر است که استخراج بدنه محدب و بازسازی چند ضلعی ساده شده برای الگوریتم HD هزینه بیشتری نسبت به سه الگوریتم دیگر داشت، زیرا به بسیاری از عملیات اتحاد/تفاوت چند ضلعی نیاز دارد. پس از آزمایش با داده های منبع با محاسبه سه پارامتر آن واحدهای ساده کننده برای هر الگوریتم، تجزیه و تحلیل مقیاس را انجام دادیم و متوجه شدیم که همه آنها حداقل چهار سطح سلسله مراتبی مقیاس بندی دارند، به این معنی که الگوی اندازه های کوچک بسیار بیشتر از اندازه های بزرگ است. کمتر از سه بار عود کرد ( جدول 2 ). به عبارت دیگر، ما یک الگوی فراکتال یا مقیاس جهانی از ویژگی چند ضلعی را در چهار الگوریتم ساده‌کننده مشاهده کردیم.
سطوح سلسله مراتبی مقیاس با سطوح جزئیات خط ساحلی مطابقت دارد. پنج سطح بالای چند ضلعی های ساده شده از چهار الگوریتم در شکل 7 ارائه شده است. با توجه به انواع مختلف واحدهای هندسی، تعداد رئوس منبع حفظ شده در هر سطح به طور چشمگیری از الگوریتمی به الگوریتم دیگر متفاوت است ( جدول 3)). به طور خاص، روش BS بیشترین امتیاز را حفظ می کند (به طور متوسط ​​تقریباً 45٪ از امتیازات در هر سطح حفظ می شود) و به دنبال آن VW (36٪)، HD (35٪) و DP (23٪) قرار دارند. برای هر الگوریتم، باید تاکید کرد که اگر از ناحیه برای کنترل تعمیم استفاده کنیم، تعداد نقاط به شدت کاهش می‌یابد که منجر به کمترین سطوح جزئیات می‌شود. در مقابل، استفاده از پارامتر x می تواند بیشتر سطوح را ایجاد کند. نه تنها تعداد نقاط، بلکه اشکال تعمیم یافته نیز با یکدیگر متفاوت هستند. با وجود نتایج ساده شده در سطح پنجم، روش‌های مبتنی بر واحد چند ضلعی (به ویژه VW و HD) می‌توانند به حفظ شکل صاف‌تر و طبیعی‌تر از الگوریتم مبتنی بر واحد نقطه (DP) کمک کنند.
دوره-آموزش-حرفه-ای-gis

5. بحث

برای نشان دادن ابزار ساده سازی چند ضلعی بر اساس سلسله مراتب مقیاس بندی اساسی، ما این ابزار را در خط ساحلی بریتانیا اعمال کردیم. این مطالعه سه معیار هندسی از پیش تعریف شده – x، d و مساحت – را از روش DP به سه روش دیگر آورد. یعنی به ترتیب روش های VW، BS و HD. هر یک از سه معیار در چهار الگوریتم توزیع شده با دم سنگین است. چنین الگوی مقیاس‌بندی نشان می‌دهد که ماهیت فراکتال فقط در مدل‌های ریاضی (مانند دانه‌های برف کوخ) وجود ندارد، بلکه در یک ویژگی جغرافیایی نیز وجود دارد. با آمار دم چربی، شکستن سر/دم می تواند به عنوان یک ابزار قدرتمند برای استخراج سلسله مراتب مقیاس ذاتی و کمک به تقسیم خم ها، مثلث ها و بدنه های محدب به سر و دم به صورت بازگشتی استفاده شود. آن عناصر منطقه ای در سر، اجزای حیاتی چند ضلعی در نظر گرفته می شوند و سپس برای عملیات بعدی انتخاب می شوند. در نتیجه، ما دریافتیم که اکثر اشکال ساده شده در چندین سطح قابل قبول هستند، که از سودمندی تفکر فراکتال-هندسی در تعمیم نقشه‌کشی پشتیبانی می‌کند. بر اساس یافته‌ها، نتایج و بینش‌هایی را که از این مطالعه به دست آوردیم، بیشتر مورد بحث قرار دادیم.
برای بررسی عمیق تر، مساحت (S)، محیط (P) و ضریب شکل (P/S) را برای هر نتیجه ساده شده محاسبه کردیم. شکل 8 نشان می دهد که چگونه آنها به ترتیب در مورد هر الگوریتم با پارامترهای مختلف تغییر می کنند. با سه نوع معیار محاسبه شده (S، P، و P/S)، می‌توانیم عملکرد روش‌های ساده‌سازی مختلف را که توسط سلسله مراتب مقیاس‌بندی اساسی هدایت می‌شوند اندازه‌گیری و مقایسه کنیم. در حالت ایده‌آل، منحنی هر متریک در هر سطح از جزئیات مسطح خواهد بود، به این معنی که اشکال چند ضلعی ساده‌شده تا حداکثر میزان اولیه حفظ می‌شوند. به عبارت دیگر، یک منحنی تند می تواند یک اعوجاج ناخوشایند را نشان دهد (به عنوان مثال، سطح 3 روش DP در شکل 7 ج و شکل 8 ج). به طور کلی، ما می توانستیم ازشکل 8 که روش های VW و HD می توانند شکل اساسی تری را در سطوح مختلف نسبت به DP و BS، صرف نظر از نوع متریک، به دست آورند. باید توجه داشت که منحنی متریک BS در برخی موارد صاف تر از منحنی VW یا HD به نظر می رسد (به عنوان مثال، شکل 8 i). با این حال، نتیجه ساده شده در هر سطح با استفاده از روش BS امتیازهای بسیار بیشتری (حدود 50٪) نسبت به استفاده از VW یا HD ( جدول 3) حفظ کرد.). در این رابطه، BS کارایی کمتری داشت. در مقابل، شیب‌های بزرگ منحنی‌های متریک DP اغلب ممکن است ناشی از افت شدید نقاط باشد. بنابراین، ما حدس زدیم که نتایج الگوریتم‌های VW و HD تعادل خوبی بین تعداد نقاط مشخصه و شکل هسته چند ضلعی به دست آورد که منجر به عملکرد بهتر در این مطالعه شد.
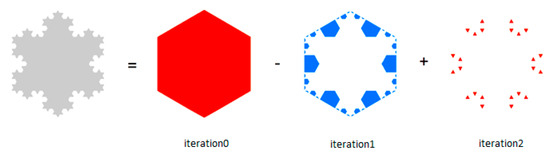
بر اساس مقایسه نتایج، شکل‌های چنین مرز پیچیده‌ای با استفاده از روش‌های VW و HD با x، حتی در آخرین سطح، به بهترین وجه حفظ می‌شوند. منطقه بدترین پارامتر در این زمینه است زیرا منجر به سطوح کمتر جزئیات و اشکال نامناسب می شود ( شکل 7 و شکل 8 ). احتمالاً مساحت به صورت x ضربدر d عمل می کند، بنابراین اثر هر اندازه گیری منفرد را ضعیف می کند. برای توضیح دلیل، ما دوباره از دانه برف Koch استفاده کردیم. شکل 1 نشان می دهد که فرآیند تعمیم توسط d هدایت می شود و در صورت استفاده از x نتیجه یکسانی خواهد بود. با این حال، استفاده از ناحیه منجر به یک سری متفاوت از تعمیم می شود زیرا مثلث های بیشتری در بازگشت اول حذف خواهند شد ( شکل 9).) این توضیح می دهد که چرا تعداد رئوس به طور قابل توجهی نسبت به دو معیار دیگر کاهش یافته است. از آنجایی که x پارامتر بهتری از d است، ما حدس زدیم که ارتفاع ویژگی های بیشتری از یک هندسه نامنظم را نسبت به طولانی ترین لبه آن ثبت می کند. این امر مستلزم مطالعه بیشتر است.
شایان ذکر است که همه الگوریتم ها به صورت بازگشتی کار می کنند. فرآیند هر الگوریتم را می توان به عنوان یک ساختار درختی نشان داد، که یک گره نشان دهنده یک نقطه بحرانی یا یک عنصر منطقه ای از یک ویژگی چند ضلعی است. با وجود تفاوت گره، ساختار درختی بین دو الگوریتم نیز اساساً متفاوت است. درخت از الگوریتم DP یک درخت باینری است [ 43]، از آنجایی که یک ویژگی خط به طور مکرر توسط دورترین نقطه و دو انتهای قطعه پایه به دو قسمت تقسیم می شود. بنابراین، هر گره می تواند حداکثر دو فرزند داشته باشد. با این حال، الگوریتم‌های دیگر، یک درخت N-ary را بدون چنین محدودیتی تولید می‌کنند، زیرا تعداد فرزندان هر گره والد به تعداد خم، مثلث یا قسمت‌های مقعر متعلق به گره بستگی دارد. از این نظر، الگوریتم‌های ساده‌سازی مبتنی بر واحد سطحی درختی کمتر صلب و ارگانیک‌تر از درخت مبتنی بر نقطه ایجاد می‌کنند که با ساختار پیچیده یک شی جغرافیایی که به طور طبیعی فرمول‌بندی می‌شود، همخوانی بیشتری دارد. بنابراین، نتایج ساده سازی VW و HD طبیعی تر و روان تر از DP هستند.
با استفاده از روش پیشنهادی، نتایج ساده شده به طور خودکار می توانند به عنوان یک نمایش چند مقیاسی عمل کنند، زیرا هر سطح از جزئیات را می توان در یک نقشه مقیاس کوچکتر به صورت بازگشتی حفظ کرد. مثالی از خط ساحلی بریتانیا را در نظر بگیرید که با استفاده از روش HD با x تعمیم داده شده است. ما نسبت مقیاس بندی این مثال را با استفاده از توان x تمام بدنه های محدب داده های چند ضلعی اصلی محاسبه کردیم. مقدار توان 1.91 بود بنابراین نسبت مقیاس بندی را می توان تقریباً 1/2 تنظیم کرد. لازم به ذکر است که این ایده از MapGen [ 44 ] سرچشمه گرفته است. شکل 10سری نقشه به دست آمده را نشان می دهد که از آن می توانیم ببینیم که نتیجه ساده شده در هر سطح به خوبی با کاهش مقیاس مطابقت دارد. در این رابطه، ما بیشتر تأیید می‌کنیم که تفکر فراکتال-هندسی ما را به یک نقشه‌برداری یا تعمیم نقشه هدف می‌برد [ 24 ]]، که در آن هیچ مقدار یا آستانه ای از پیش تعیین شده برای کنترل فرآیند تعمیم داده نمی شود. به عبارت دیگر، تعمیم یک ویژگی چند ضلعی را می توان از طریق سلسله مراتب مقیاس ذاتی آن انجام داد، و نسبت مقیاس بندی سری نقشه، که به طور عینی از توزیع دنباله بلند معیارهای هندسی به دست می آید (به عنوان مثال، توان قانون توان)، می تواند مورد استفاده قرار گیرد. نتایج ساده شده را به درستی ترسیم کنید. بنابراین، ما بر این باوریم که ماهیت فراکتال یک ویژگی جغرافیایی خود یک مرجع مؤثر و مهمتر از آن، یک روش جدید برای تفکر و انجام تعمیم نقشه فراهم می کند.

6. نتیجه گیری

ویژگی های جغرافیایی ذاتاً فراکتال هستند. سلسله مراتب مقیاس بندی که به طور درونزا توسط یک فراکتال وجود دارد، می تواند به طور طبیعی سطوح مختلف جزئیات یک شکل را توصیف کند و در نتیجه می تواند به طور موثر تعمیم نقشه برداری را هدایت کند. در این مقاله، PolySimp را برای استخراج سلسله‌مراتب مقیاس‌بندی بر اساس چهار الگوریتم معروف: DP، BS، VW و HD پیاده‌سازی کردیم و بر این اساس ساده‌سازی چند ضلعی را انجام دادیم. ما مطالعه قبلی را با معرفی سه معیار هندسی از پیش تعریف شده DP به سه الگوریتم دیگر گسترش دادیم. در نتیجه، ابزار نرم‌افزاری می‌تواند محاسبات آن معیارها را تسهیل کند و از آنها برای به‌دست آوردن نمایش چندمقیاسی از یک ویژگی چند ضلعی استفاده کند. جدای از تعمیم، ما دریافتیم که معیارهای محاسبه شده همچنین می توانند برای توصیف یک ویژگی چند ضلعی به عنوان یک فراکتال از طریق سلسله مراتب مقیاس بندی زیرین آن استفاده شوند. امیدواریم این ابزار نرم افزاری کاربرد روش تفکر فراکتال را به نمایش بگذارد و به توسعه تعمیم نقشه کمک کند.
برخی از مسائل نیاز به تحقیقات بیشتری دارد. در این کار، اگرچه PolySimp می تواند یک چند ضلعی منفرد را به یک سری از جزئیات سطح پایین تر تعمیم دهد، اما کاربرد ابزار برای ساده سازی چند ضلعی، به ویژه برای آن دسته از چند ضلعی ها با مرز مشترک، هنوز در نظر گرفته نشده است. این به منظور حفظ نه تنها شکل هسته یک چند ضلعی، بلکه برای حفظ ثبات توپولوژی آن بیشتر بهبود خواهد یافت. علاوه بر این، ما فقط نمایش چند ضلعی دو بعدی را در نظر گرفتیم. در آینده استفاده از PolySimp برای محاسبه سلسله مراتب مقیاس بندی یک چند ضلعی سه بعدی و انجام تعمیم نقشه برداری بر این اساس با اعمال شکست های سر/دم بسیار امیدوارکننده خواهد بود.

پیوست الف. سلسله مراتب مقیاس بندی واحدهای هندسی برگرفته از الگوریتم های DP، BS، و VW

این ضمیمه بخش 2.2 را با نشان دادن الگوی مقیاس بندی واحدهای هندسی یک فراکتال کلاسیک – دانه برف کخ تکمیل می کند. سه نوع عنصر هندسی (یعنی نقاط مشخصه، خم ها و مثلث ها) به ترتیب از روش های DP، BS و VW مشتق شده اند. شکل A1 سطوح سلسله مراتبی مقیاس بندی را برای هر نوع عنصر هندسی با توجه به پارامتر x نشان می دهد، که در آن تعداد سطوح برای DP سه، برای BS دو و برای VW سه است. از این رو، می‌توانیم الگوهای مقیاس‌بندی مشابهی را در ابعاد کوچک‌تر از بزرگ‌ها در سه روش تشخیص دهیم. آن «بزرگ ها» – عناصر هندسی به رنگ قرمز یا سبز – ضروری ترین بخش را نشان می دهند و بنابراین می توانند شکل دانه های برف را در سطحی درشت تر تشکیل دهند.
Ijgi 09 00594 g0a1 550
شکل A1. (رنگ آنلاین) تصویر ساده سازی واحدهای هندسی در بین الگوریتم های DP، BS، و VW با استفاده از دانه برف Koch و نتیجه تعمیم در سطح اول. (توجه: اندازه هر نوع واحد ساده‌سازی، مانند نقاط، مثلث‌ها و خم‌ها، سلسله‌مراتب مقیاس‌بندی زیرین را شامل می‌شود که شامل تعداد زیادی کوچک (به رنگ آبی)، چند عدد بزرگ (قرمز) و برخی در بین ( به رنگ سبز)، که همه آنها می توانند برای راهنمایی تعمیم نقشه برداری استفاده شوند).

منابع

  1. باتنفیلد، BP; مک مستر، RB تعمیم نقشه: ایجاد قوانین برای بازنمایی دانش . گروه لانگمن: لندن، بریتانیا، 1991. [ Google Scholar ]
  2. Mackaness، WA; رواس، ع. Sarjakoski، LT تعمیم اطلاعات جغرافیایی: مدل سازی نقشه برداری و کاربردها ; الزویر: آمستردام، هلند، 2007. [ Google Scholar ]
  3. استوتر، جی. پست، م. ون آلتنا، وی. نیجهویس، آر. Bruns, B. تعمیم کاملاً خودکار نقشه 1:50k از داده 1:10k. کارتوگر. Geogr. Inf. علمی 2014 ، 41 ، 1-13. [ Google Scholar ] [ CrossRef ]
  4. بورگاردت، دی. دوچن، سی. Mackaness، W. چکیده اطلاعات جغرافیایی در یک جهان غنی از داده ها: روش ها و کاربردهای تعمیم نقشه . Springer: برلین، آلمان، 2014. [ Google Scholar ]
  5. جیانگ، بی. لیو، ایکس. جیا، تی. مقیاس بندی فضای جغرافیایی به عنوان یک قانون جهانی برای تعمیم نقشه. ان دانشیار صبح. Geogr. 2013 ، 103 ، 844-855. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  6. ویبل، آر. جونز، CB Computational Perspectives on Map Generalization. GeoInformatica 1998 ، 2 ، 307-315. [ Google Scholar ] [ CrossRef ]
  7. مک مستر، آر.بی. Usery، EL یک دستور کار تحقیقاتی برای علم اطلاعات جغرافیایی ; CRC Press: لندن، انگلستان، 2005. [ Google Scholar ]
  8. تعمیم نقشه عددی Tobler، WR ; گروه جغرافیا، دانشگاه میشیگان: Ann Arbour، MI، ایالات متحده آمریکا، 1966. [ Google Scholar ]
  9. لی، ز. Openshaw, S. الگوریتم‌هایی برای تعمیم خودکار خطوط بر اساس یک اصل طبیعی تعمیم عینی. بین المللی جی. جئوگر. Inf. سیستم 1992 ، 6 ، 373-389. [ Google Scholar ] [ CrossRef ]
  10. Visvalingam، M. وایات، تعمیم خط JD با حذف مکرر نقاط. کارتوگر. J. 1992 ، 30 ، 46-51. [ Google Scholar ] [ CrossRef ]
  11. Saalfeld، A. ساده سازی خط سازگار از نظر توپولوژیکی با الگوریتم داگلاس-پوکر. کارتوگر. Geogr. Inf. علمی 1999 ، 26 ، 7-18. [ Google Scholar ] [ CrossRef ]
  12. گوکگوز، تی. سن، ا. ممدو اوغلو، ا. Hacar, M. یک الگوریتم جدید برای ساده‌سازی نقشه‌برداری رودخانه‌ها و دریاچه‌ها با استفاده از زوایای انحراف و باندهای خطا. ISPRS Int. J. Geo-Inf. 2015 ، 4 ، 2185-2204. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  13. کولانوفسکی، بی. آگوستینیاک، جی. Latos, D. تعمیم خطوط نقشه برداری بر اساس تجزیه و تحلیل شعاع انحنا. ISPRS Int. J. Geo-Inf. 2018 ، 7 ، 477. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  14. Ruas, A. Modèle de Généralisation de Données Géographiques à Base de Contraintes et D’autonomie. دکتری Thesis, Université Marne La Vallée, Marne La Vallée, France, 1999. [ Google Scholar ]
  15. تویا، جی. دوچنه، سی. Taillandier، P. گفوری، ج. رواس، ع. Renard، J. سیستم های چند عاملی برای تعمیم نقشه برداری: بازخورد از تحقیقات گذشته و در حال انجام. گزارش فنی ؛ LaSTIG، équipe COGIT. hal-01682131; IGN (Institut National de l’Information Géographique et Forestière): Saint-Mandé، فرانسه، 2018؛ در دسترس آنلاین: https://hal.archives-ouvertes.fr/hal-01682131/document (در 6 اکتبر 2020 قابل دسترسی است).
  16. هری، ال. سارجاکوسکی، تی. تعمیم گرافیکی همزمان مجموعه داده های برداری. GeoInformatica 2002 ، 6 ، 233-261. [ Google Scholar ] [ CrossRef ]
  17. Zahn، CT; توصیفگرهای Roskies، RZ فوریه برای منحنی های بسته صفحه. IEEE Trans. محاسبه کنید. 1972 ، C-21 ، 269-281. [ Google Scholar ] [ CrossRef ]
  18. مندلبروت، بی . هندسه فراکتالی طبیعت . WH Freeman and Co.: New York, NY, USA, 1982. [ Google Scholar ]
  19. نورمانت، اف. Tricot, C. ساده سازی فراکتال خطوط با استفاده از بدنه محدب. Geogr. مقعدی 1993 ، 25 ، 118-129. [ Google Scholar ] [ CrossRef ]
  20. لام، فراکتال های NSN و مقیاس در ارزیابی و نظارت محیطی. در مقیاس و جغرافی . Sheppard, E., McMaster, RB, Eds. Blackwell Publishing: Oxford, UK, 2004; ص 23-40. [ Google Scholar ]
  21. باتی، م. لانگلی، پی. Fotheringham، S. رشد شهری و شکل: مقیاس بندی، هندسه فراکتال، و تجمع محدود انتشار. محیط زیست طرح. یک اقتصاد. فضا 1989 ، 21 ، 1447-1472. [ Google Scholar ] [ CrossRef ]
  22. باتی، م. Longley، P. شهرهای فراکتال: هندسه شکل و عملکرد . انتشارات آکادمیک: لندن، بریتانیا، 1994. [ Google Scholar ]
  23. بتنکورت، LMA؛ لوبو، جی. هلبینگ، دی. کونرت، سی. غرب، رشد GB، نوآوری، مقیاس‌پذیری و سرعت زندگی در شهرها. Proc. Natl. آکادمی علمی ایالات متحده آمریکا 2007 ، 104 ، 7301-7306. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  24. جیانگ، ب. ماهیت فراکتال نقشه ها و نقشه برداری. بین المللی جی. جئوگر. Inf. علمی 2015 ، 29 ، 159-174. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  25. تاپفر، اف. Pillewizer, W. اصول انتخاب. کارتوگر. J. 1966 ، 3 ، 10-16. [ Google Scholar ] [ CrossRef ]
  26. Jiang, B. Head/tail breaks: یک طرح طبقه بندی جدید برای داده ها با توزیع دم سنگین. پروفسور Geogr. 2013 ، 65 ، 482-494. [ Google Scholar ] [ CrossRef ]
  27. جیانگ، بی. یین، J. شاخص Ht برای کمی کردن ساختار فراکتال یا مقیاس بندی ویژگی های جغرافیایی. ان دانشیار صبح. Geogr. 2014 ، 104 ، 530-541. [ Google Scholar ] [ CrossRef ]
  28. لانگ، ی. شن، ی. جین، XB نقشه برداری مناطق شهری در سطح بلوک برای همه شهرهای چین. ان صبح. دانشیار Geogr. 2016 ، 106 ، 96-113. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  29. طولانی، Y. بازتعریف سیستم شهری چین با داده های جدید در حال ظهور. Appl. Geogr. 2016 ، 75 ، 36-48. [ Google Scholar ] [ CrossRef ]
  30. گائو، رایانه شخصی؛ لیو، ز. Xie، MH; تیان، ک. شاخص لیو، جی. CRG: شاخص ht حساس تر برای فعال کردن نماهای پویا از ویژگی های جغرافیایی. پروفسور Geogr. 2016 ، 68 ، 533-545. [ Google Scholar ] [ CrossRef ]
  31. گائو، رایانه شخصی؛ لیو، ز. تیان، ک. لیو، جی. مشخص کردن شرایط ترافیکی از منظر ناهمگونی مکانی-زمانی. ISPRS Int. J. Geo-Inf. 2016 ، 5 ، 34. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  32. لیو، پی. شیائو، تی. شیائو، جی. Ai، T. مدل نمایش چند مقیاسی چند خط بر اساس شکستگی سر/دم. بین المللی جی. جئوگر. Inf. علمی 2020 . [ Google Scholar ] [ CrossRef ]
  33. مولر، جی سی. لاگرانژ، جی پی. Weibel, R. GIS and Generalization: Methodology and Practice ; تیلور و فرانسیس: لندن، بریتانیا، 1995. [ Google Scholar ]
  34. لی، زی. بنیاد الگوریتمی بازنمایی فضایی چند مقیاسی . CRC Press: لندن، انگلستان، 2007. [ Google Scholar ]
  35. ESRI. نحوه کار Simplify Line و Simplify Polygon در دسترس آنلاین: https://desktop.arcgis.com/en/arcmap/latest/tools/cartography-toolbox/simplify-polygon.htm (در 15 ژوئیه 2020 قابل دسترسی است).
  36. تویا، جی. لخت، من. Duchêne, C. CartAGEn: یک بستر تحقیقاتی منبع باز برای تعمیم نقشه. در مجموعه مقالات کنفرانس بین المللی کارتوگرافی 2019، توکیو، ژاپن، 15 تا 20 ژوئیه 2019؛ صفحات 1-9. [ Google Scholar ]
  37. CartAGEn. الگوریتم های ساده سازی خط 2020. در دسترس آنلاین: https://ignf.github.io/CartAGEen/docs/algorithms.html (در 6 اکتبر 2020 قابل دسترسی است).
  38. داگلاس، دی. Peucker, T. الگوریتم‌هایی برای کاهش تعداد نقاط مورد نیاز برای نمایش یک خط دیجیتالی یا کاریکاتور آن. می توان. کارتوگر. 1973 ، 10 ، 112-122. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  39. ژو، اس. کریستوفر، تعمیم خط آگاه از شکل BJ با ناحیه موثر وزنی. در تحولات در مدیریت داده‌های فضایی، مجموعه مقالات یازدهمین سمپوزیوم بین‌المللی مدیریت فضایی، زوریخ، سوئیس . فیشر، پی اف، اد. Springer-Verlag: برلین/هایدلبرگ، آلمان، 2005; صص 369-380. [ Google Scholar ]
  40. وانگ، ز. مولر، JC تعمیم خط بر اساس تجزیه و تحلیل ویژگی های شکل. کارتوگ. Geogr. Inf. سیستم 1998 ، 25 ، 3-15. [ Google Scholar ] [ CrossRef ]
  41. آی، تی. لی، ز. Liu, Y. انتقال پیشرونده داده های برداری بر اساس مدل انباشت تغییرات. در تحولات در مدیریت داده های مکانی ; Springer-Verlag: هایدلبرگ، آلمان، 2005; صص 85-96. [ Google Scholar ]
  42. ما، دی. جیانگ، ب. منحنی صاف به عنوان یک فراکتال در تعریف سوم. Cartographica 2018 ، 53 ، 203-210. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  43. سستر، ام. برنر، سی. واژگانی برای توصیف فرآیند چند مقیاسی برای انتقال سریع و تجسم مداوم داده‌های مکانی. محاسبه کنید. Geosci. 2009 ، 35 ، 2177-2184. [ Google Scholar ] [ CrossRef ]
  44. جیانگ، بی. روش‌ها، دستگاه و برنامه رایانه‌ای برای استخراج خودکار نقشه‌های مقیاس کوچک. ثبت اختراع ایالات متحده WO 2018/116134، PCT/IB2017/058073، 28 ژوئن 2018. [ Google Scholar ]
Ijgi 09 00594 g001 550
شکل 1. (رنگ آنلاین) فرآیند ساده‌سازی دانه‌های برف کوخ که توسط شکستگی‌های سر/دم هدایت می‌شود. (توجه: چند ضلعی های آبی در هر پانل قسمت های سر را نشان می دهند، در حالی که مثلث های قرمز قسمت دم را نشان می دهند که برای هدف تعمیم باید به تدریج حذف شود).
Ijgi 09 00594 g002 550
شکل 2. (رنگ آنلاین) تصویر معیارهای هندسی برای ( الف ) واحد ساده سازی مبتنی بر نقطه (به عنوان مثال، الگوریتم داگلاس-پوکر (DP)) و ( ب ) واحد مبتنی بر منطقه (به عنوان مثال، ساده سازی خمشی (BS) و سلسله مراتبی تجزیه الگوریتم چند ضلعی (HD).
Ijgi 09 00594 g003 550
شکل 3. (رنگ آنلاین) تصویر الگوریتم HD با استفاده از دانه برف Koch به عنوان مثال کار. توجه داشته باشید که اندازه بدنه‌های محدب مشتق‌شده دارای یک سلسله‌مراتب مقیاس‌بندی قابل‌توجه است که به مراتب بیشتر از بدنه‌های بزرگ است.
Ijgi 09 00594 g004 550
شکل 4. ابزار ساده سازی نقشه برداری ویژگی های چند ضلعی بر اساس سلسله مراتب مقیاس ذاتی آن.
Ijgi 09 00594 g005 550
شکل 5. نمودار جریان برای انجام ساده سازی چند ضلعی بر اساس شکست های سر/دم برای هر الگوریتم.
Ijgi 09 00594 g006 550
شکل 6. (رنگ آنلاین) واحدهای هندسی اساسی بخشی از خط ساحلی بریتانیا (اشاره به کادر قرمز در پانل سمت راست) برای هر الگوریتم ساده سازی چند ضلعی که توسط PolySimp مشتق شده است. (توجه: پانل‌های سمت چپ یک سلسله‌مراتب مقیاس‌بندی واضح از پانل‌های کوچک‌تر از پانل‌های بزرگ را نشان می‌دهند که با اندازه نقطه یا رنگ وصله نمایش داده می‌شوند).
Ijgi 09 00594 g007 550
شکل 7. (رنگ آنلاین) نتایج ساده شده خط ساحلی بریتانیا در سطوح مختلف جزئیات از طریق چهار الگوریتم از نظر شکل چند ضلعی بر اساس x ( a )، d ( b ) و مساحت ( c ). و تعداد نقاط مربوطه ( d ) به ترتیب.
Ijgi 09 00594 g008 550
شکل 8. (رنگ آنلاین) تغییر شکل نتایج ساده شده خط ساحلی بریتانیا در پنج سطح جزئیات، که با مساحت چند ضلعی (پانل‌های a – c )، محیط (پانل‌های e – g )، و ضریب شکل (پانل‌های h –) نشان داده شده است. j ).
Ijgi 09 00594 g009 550
شکل 9. (رنگ آنلاین) اولین تکرار فرآیند ساده‌سازی دانه‌های برف کوخ بر اساس ناحیه هدایت می‌شود (توجه داشته باشید: مثلث‌های قرمز قسمت دمی هستند که باید در سطح اول حذف شوند).
Ijgi 09 00594 g010 550
شکل 10. (رنگ آنلاین) یک نمایش چند مقیاسی با نسبت مقیاس 1/2 از نتیجه ساده شده از سطح 1 تا 5 (پانل های a – e ) خط ساحلی بریتانیا با استفاده از الگوریتم HD.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید