خلاصه

اندازه‌گیری شباهت بین یک جفت مسیر اساس بسیاری از روش‌های خوشه‌بندی فضایی-زمانی است و کاربردهای گسترده‌ای در کاوی الگوی مسیر دارد. با این حال، اکثر معیارهای شباهت مسیر در ادبیات مبتنی بر مدل‌های دقیقی هستند که عدم قطعیت ذاتی در داده‌های مسیر ثبت شده توسط حسگرها را نادیده می‌گیرند. روش‌های محاسباتی یا استخراج سنتی که دقت و دقت مسیرها را فرض می‌کنند، در نتیجه خطر عملکرد ناکافی یا بازگشت نتایج نادرست را دارند. برای پرداختن به این مشکل، یک مدل بیضی اصلاح‌شده را پیشنهاد می‌کنیم که هم خطای درون‌یابی و هم خطای موقعیت‌یابی را با استفاده از ویژگی‌های حرکت مسیر برای محاسبه پارامترهای شکل بیضی در نظر می‌گیرد. یک روش سنجش تشابه تخصصی با در نظر گرفتن عدم قطعیت به نام اندازه گیری شباهت مسیر نامشخص (UTSM) بر اساس مدل نیز پیشنهاد شده است. ما این رویکرد را به صورت تجربی بر روی داده‌های مصنوعی و دنیای واقعی تأیید می‌کنیم و نشان می‌دهیم که UTSM نه تنها در برابر نویز و نقاط پرت قوی‌تر است، بلکه در برابر فرکانس‌های نمونه مختلف و نمونه‌برداری ناهمزمان از مسیرها نیز تحمل بیشتری دارد.

کلید واژه ها:

مدل بیضی ; سنجش تشابه ; عدم قطعیت ؛ ویژگی های حرکتی

1. معرفی

همراه با زیرساخت‌های جدید عظیمی که برای ارتباطات نسل بعدی ساخته می‌شود، حسگرهای GPS سالانه میلیون‌ها نفر در خودروها، تلفن‌های همراه، ربات‌ها و بسیاری از اجسام متحرک دیگر نصب می‌شوند. این حسگرها به طور مداوم مکان های حامل را ضبط می کنند و تعداد زیادی مسیر از انواع مختلف اشیاء را ایجاد می کنند. نحوه استخراج اطلاعات جالب پنهان در داده های مسیر محور تحقیقات بسیاری است. پیشرفت‌های زیادی در مدل‌سازی مسیر و الگوکاوی حاصل شده است، از جمله کار بر روی اندازه‌گیری شباهت مسیر.
اندازه‌گیری‌های شباهت مسیر برای خوشه‌بندی یا طبقه‌بندی حرکت فضایی اساسی هستند [ 1 ، 2 ]، و پرس و جوهای شباهت را می‌توان به طور گسترده در بسیاری از کاربردهای داده کاوی فضایی، مانند یافتن الگوی گروه/گله اجسام متحرک، تشخیص نقاط پرت مکانی-زمانی، و پیش‌بینی آب و هوا به کار برد. یا آب و هوا مانند مسیر طوفان. اطلاعات در مورد شباهت در الگوهای حرکتی می تواند مدیران ترافیک را قادر سازد تا رفتار مشکوک را پیدا کنند و ایمنی و امنیت را افزایش دهند [ 1 ].
با این حال، داده‌های مسیر زندگی واقعی برای بسیاری از برنامه‌ها به اندازه کافی قابل اعتماد نیستند، زیرا مجموعه داده‌های جمع‌آوری‌شده از حسگرهای موبایل اغلب به دلیل نویز و رکوردهای ناپیوسته نادرست و نادرست هستند [ 3 ]]. در دنیای واقعی، دینامیک اجسام متحرک در چارچوب مرجع مکانی-زمانی آنها از نظر ماکروسکوپی پیوسته و دقیق است. با این حال، در طول فرآیند ثبت، انتشار و محاسبه، این پویایی ها به صورت نقاط نمونه برداری مکانی-زمانی گسسته یا چند خطوط پیوسته درون یابی بیان می شوند، که به ناچار برخی عدم قطعیت را به همراه دارد. در بیشتر موارد، نیازهای تحلیل و کاربرد را می توان با وجود برخی عدم قطعیت در داده ها برآورده کرد. با این حال، در برخی سناریوها، به دلیل عواملی مانند خرابی سنسور یا تأثیر محیط، فرکانس نمونه‌برداری الزامات قانون نمونه‌گیری نایکویست را برآورده نمی‌کند، که ممکن است باعث ایجاد خطاهای بزرگ در بازسازی مسیر شود و منجر به نتایج محاسباتی اشتباه شود. حتی اگر بتوانیم داده های مسیر دقیق را جمع آوری کنیم، ما نمی توانیم فرض کنیم که به دلیل افزایش تقاضای حفاظت از حریم خصوصی مصرف کنندگان، آنها در دسترس باقی می مانند. بنابراین، نیاز به مدل‌ها و الگوریتم‌های جدیدی نیز وجود دارد که با داده‌های تار کار می‌کنند.
یکی دیگر از نگرانی‌های اصلی در اندازه‌گیری شباهت بین مسیرها این است که فرکانس‌های نمونه‌گیری مختلف و یک استراتژی نمونه‌گیری ناهمزمان باعث قضاوت‌های نادرست می‌شوند. مقایسه شباهت نشان داده شده در شکل 1 را در نظر بگیرید : مسیرهای واقعی P و Q در شکل 1 a نزدیکتر از P و R هستند. با این حال، به دلیل فرکانس نمونه برداری کم و توزیع ناهمگون نقاط نمونه، مسیرهای بازسازی شده در شکل 1 b به دست آمده با درون یابی خطی نتیجه معکوس را نشان می دهد: R بیشتر شبیه P است تا Q.
برای کاهش این نوع قضاوت نادرست تحت شرایط فعلی کیفیت داده، باید عدم اطمینان را در نظر بگیریم. در این کار، مشارکت های اصلی ما به شرح زیر است:
  • ما یک مدل بیضی اصلاح‌شده برگرفته از [ 4 ] را پیشنهاد می‌کنیم که می‌تواند عدم قطعیت در یک مسیر را با محاسبه دینامیکی پارامترهای شکل مدل بر اساس ویژگی‌های حرکت هر بخش از مسیر، توصیف کند.
  • ما یک معیار تشابه جدید بر اساس مدل ارائه می‌کنیم که اندازه‌گیری شباهت مسیر نامشخص (UTSM) نامیده می‌شود. تایید شده توسط آزمایش‌ها بر روی داده‌های مصنوعی و داده‌های دنیای واقعی، UTSM توانایی بهتری برای مقایسه شباهت بین مسیرها نشان می‌دهد و همچنین در برابر نویز و نقاط پرت قوی‌تر است و فرکانس‌های نمونه مختلف و نمونه‌برداری ناهمزمان را تحمل‌تر می‌کند.
بقیه مقاله به شرح زیر سازماندهی شده است: بخش 2 مفاهیم اساسی مربوط به معیارهای تشابه مسیر را معرفی می کند، بیانیه رسمی مسئله را ارائه می دهد و جدولی از قراردادهای نمادهای مورد استفاده در مقاله ارائه می دهد. بخش 3 کارهای مرتبط و فناوری فعلی را بررسی می کند. مدل بیضی بازطراحی شده ما و روش اندازه گیری شباهت در بخش 4 پیشنهاد شده است . بخش 5 آزمایش ها و نتایج اعتبار سنجی را ارائه می دهد، در حالی که بخش 6 مقاله را به پایان می رساند و به کارهای آینده نگاه می کند.

2. مقدمات و تعریف مسئله

2.1. مفاهیم اساسی

  • مسیر فضایی و زمانی

    خط سیر فضا-زمان یک منحنی پیوسته است که از حرکت یک جسم متحرک در فضای اقلیدسی در یک دوره معین تشکیل می شود. مورفولوژی مسیر را می توان با یک تابع پیوسته به دقت توصیف کرد. با این حال، در واقعیت، موقعیت مکانی جسم متحرک عموماً توسط یک سنسور در فرکانس ثابت یا تصادفی ثبت می‌شود. مسیر حرکت جسم معمولاً با دنباله ای از موقعیت های حاوی اطلاعات مکانی و زمانی نشان داده می شود، مانند:

    پس0،تی0،س1،تی1،…،سn-1،تیn-1

    که در آن تعداد نقاط نمونه برداری از کل مسیر و سمنموقعیت جسم متحرک در نقطه زمانی است تیمن. در کاربردهای عملی، سمنبه طور کلی یک مختصات دو بعدی یا سه بعدی است. این مقاله عمدتاً بر روی مسیرها در فضای دو بعدی تمرکز دارد، بنابراین با ترکیب اطلاعات زمانی، نقطه نمونه‌برداری را می‌توان به صورت ( ایکسمن،yمن،تیمن).

  • خطای درون یابی
    از آنجایی که داده‌های ثبت‌شده حسگر، دنباله‌ای از نقاط نمونه‌برداری هستند که در زمان و مکان پیوسته نیستند، نقاط نمونه‌گیری عموماً به ترتیب زمانی به هم متصل می‌شوند تا مورفولوژی کلی مسیر را توصیف کنند. شکاف داده بین نقاط نمونه گیری مجاور معمولاً با درون یابی خطی پر می شود و مسیر به یک خط چند ضلعی تبدیل می شود. درون یابی اساساً یک تخمین و تقریب داده های از دست رفته است و به ناچار عدم قطعیت را در شکاف بین نقاط نمونه گیری مجاور ایجاد می کند. خطای معرفی شده توسط این روش در این مقاله خطای درون یابی (InE) نامیده می شود.
  • خطای موقعیت یابی
    به دلیل محدودیت دقت سنسورهای موقعیت یابی یا شدت سیگنال های مختلف مناطق مختلف، داده های موقعیت یابی نقاط نمونه گیری در یک مسیر معمولاً دارای مقدار مشخصی خطا هستند. به این خطای اندازه گیری نیز می گویند. میانگین دقت مکانی یک گیرنده GPS استاندارد نزدیک به دو متر به صورت افقی در فاصله اطمینان 95% [ 5 ] و در مناطق مسدود به دلیل سیگنال ضعیف بدتر است. در این مقاله، این نوع خطا به عنوان خطای موقعیت یابی (PoE) تعریف شده است.
  • شباهت مسیر
    معیار تشابه یا تابع شباهت عموماً یک تابع با ارزش واقعی است که شباهت بین دو شی را کمی می کند. تشابه مسیر به درجه شباهت بین یک جفت مسیر از جمله موقعیت مکانی، روند شکل، ویژگی های حرکت و غیره اشاره دارد که با هم می توانند شباهت کلی حرکت آنها را اندازه گیری کنند. فاصله یک معیار تشابه معمولی است، مانند فاصله اقلیدسی، فاصله هاسدورف، فاصله فریشت و غیره. با این حال، فاصله با شباهت نسبت معکوس دارد. هرچه فاصله بین دو مسیر کمتر باشد، شباهت آنها بیشتر است. همچنین می توان از یک مدل شباهت تعریف شده مصنوعی برای بیان شباهت بین مسیرها استفاده کرد. در کاربردهای عملی، 0،1برای مقایسه ناهمگن
    عملکرد معیارهای مختلف شباهت مسیر در بخش 3 بیشتر مورد بحث قرار خواهد گرفت .

2.2. بیان مسأله

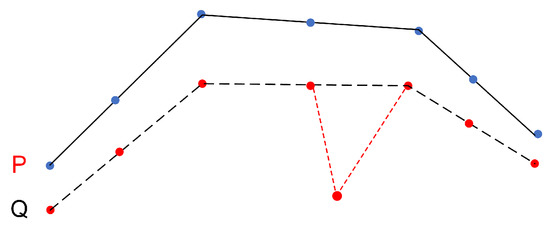
مشکل ما به طور رسمی به صورت زیر تعریف می شود: با توجه به دو مسیر P و Q، یک معیار شباهت نرمال شده با S(P, Q) برای دو مسیر پیدا کنید که شرایط زیر را برآورده می کند:

0<اسپ،س≤1اسپ،س=اسس،پاسپ،پ=1

به عبارت دیگر، متریک غیر منفی، متقارن و بازتابی است. علاوه بر محدودیت‌های معمول، هنگام طراحی مدل اندازه‌گیری، باید دو نوع عدم قطعیت، یعنی خطای درون‌یابی و خطای موقعیت‌یابی را نیز در نظر بگیریم. برای سادگی، فرض می کنیم که فواصل زمانی بین جفت های متوالی نقاط لنگر برابر است.
نمادهایی که ما استفاده می کنیم در جدول 1 فهرست شده اند

3. کارهای مرتبط

3.1. مدل های داده مسیر مکانی-زمانی

می‌توان گفت که قدمت مدل‌های مسیر به دهه 1970 بازمی‌گردد، زمانی که محققان در تلاش بودند راه جامع‌تر و مؤثرتری برای توصیف داده‌های آب و هوا و پیش‌بینی تغییرات آب و هوا و آب و هوا بیابند. در سال 1972، یک مدل مسیر سه بعدی عددی برای داده های باد در [ 6 ] پیشنهاد شد که برای پیش بینی دما و نقطه شبنم عملیاتی بود. از آن زمان به بعد، مدل‌های داده مسیر متعددی پیشنهاد شده‌اند، مانند برخی از مدل‌های مشتق‌شده از مدل‌های کلاسیک داده‌های مکانی-زمانی عمومی مانند STER [ 7 ]، MADS [ 8 ]، و دیگر مدل‌های برجسته طراحی‌شده تحت پس‌زمینه‌های کاربردی خاص مانند مدل محدودیت [ 9 ] مدل توقف حرکت [ 10 ]، و مدل مبتنی بر رویداد [ 11]. در بیشتر موارد، فقط اطلاعات مکان در مُهرهای زمانی استفاده می‌شود و فرض می‌شود که دقیق هستند. برخی تحقیقات بر روی اطلاعات معنایی اجسام متحرک تمرکز کرده اند [ 12 ، 13 ، 14 ]. در میان آنها، یک مدل خاص وجود دارد که سزاوار توجه ویژه است به نام مدل چند دانه بندی [ 15 ]. از یک شکل مهره مانند برای توصیف منطقه مسیر احتمالی که یک جسم متحرک ممکن است بین دو نقطه لنگر طی کند استفاده می کند. دو مفهوم کلیدی پشت این مدل عبارتند از: مهره نجات و گردنبند. مدل مهره خط حیات از چارچوب جغرافیای زمانی [ 16 ] مشتق شده است. اساس ریاضی آن در [ 17 , 18 , 19 ] بیشتر توضیح داده شد ., 20 , 21 , 22 ] شامل مسیر فضا-زمان و منشور فضا-زمان، دو عنصر اساسی جغرافیای زمانی. مدل مهره مکانی-زمانی با موفقیت برای عدم قطعیت معرفی شده توسط نمونه برداری و نمایش درونیابی داده های مسیر حساب می کند. مدل عدم قطعیت پیشنهادی ما از لحاظ نظری بر اساس مدل مهره است.

3.2. عدم قطعیت در مسیرهای مکانی-زمانی

اکثر تحقیقات قبلی که به عدم قطعیت در مسیرها پرداخته بودند، بر خطای درون یابی تمرکز داشتند [ 23 ، 24 ]. مدل‌ها و روش‌های موجود که عدم قطعیت فضایی را در نظر می‌گیرند شامل مدل محدوده دایره‌ای [ 25 ]، مدل سیلندر [ 26 ]، مدل شبکه [ 27 ]، مدل مهره [ 15 ] (همچنین مدل چند دانه‌ریزی نیز نامیده می‌شود) یا منشور ST. مدل [ 17 ، 19] و غیره که عمدتاً موقعیت های ممکن اجسام متحرک بین نقاط نمونه گیری مجاور و احتمال توزیع آنها را در اشکال هندسی مختلف توصیف می کنند. دست زدن به مهره ها به دلیل بدنه سه بعدی آنها که معیارهای مکانی و زمانی را با هم ترکیب می کند، آسان نیست. یک روش کلاسیک کاربردی این است که یک مهره را بر روی یک صفحه دوبعدی به صورت بیضی، همانطور که در شکل 2 نشان داده شده است، نشان دهیم . تحقیقات زیادی بر اساس بیضی پیش بینی شده انجام شده است، مانند محاسبات دسترسی و پیش بینی امکان توزیع مکان [ 28 ، 29 ، 30 ].
روش معمول برای رسیدگی به عدم قطعیت در مسیرها این است که فرض کنیم موقعیت اشیاء متحرک در فواصل زمانی بین نقاط نمونه برداری با توزیع خاصی مطابقت دارد. به عنوان مثال، یک رویکرد [ 31 ] ابتدا فضا-زمان بین نقاط نمونه برداری را گسسته می کند و سپس یک روش راه رفتن تصادفی را برای شبیه سازی موقعیت جسم متحرک بین دو نقطه نمونه گیری ثابت اتخاذ می کند، به طوری که یک توزیع احتمال دسترسی تقریبی بر روی گسسته است. شبکه مکانی-زمانی را می توان به دست آورد. اثری دیگر [ 28] استفاده از روش راه رفتن تصادفی و مدل حرکت براونی را بهبود بخشید و توزیع احتمال اجسام متحرک را در یک منطقه مسیر بالقوه (PPA) در یک حوزه مکانی – زمانی پیوسته توصیف کرد. با این حال، هر دوی آنها خطای موقعیت یابی نقاط لنگر [ 4 ] را نادیده می گیرند.

3.3. اقدامات تشابه مسیر

3.3.1. متریک فاصله هندسی

فاصله یک معیار رایج برای تشابه شی است. معمولاً فرض بر این است که فاصله با شباهت نسبت معکوس دارد. اندازه‌های فاصله مینکوفسکی مانند فاصله اقلیدسی، فاصله منهتن، فاصله چبیشف و انواع آنها معیارهای شهودی شباهت مسیر هستند. همچنین برخی دیگر از روش‌های اندازه‌گیری به‌طور خاص طراحی شده‌اند مانند فاصله کسینوس و فاصله هاسدورف، که بر ویژگی‌های هندسی تمرکز می‌کنند، یا فاصله همینگ، فاصله جاکارد، و فاصله همبستگی، که بر روی ویژگی‌های آماری تمرکز می‌کنند. مساحت بین یک جفت مسیر نیز می تواند به عنوان اندازه گیری فاصله استفاده شود [ 32 ]. با این حال، اکثر این روش ها ویژگی زمانی مسیرها را نادیده می گیرند.
3.3.2. متریک فاصله بر اساس زمان
برای غلبه بر کمبود معیارهای هندسی مبتنی بر هندسی و در نظر گرفتن نظم زمانی یا زمانی، اقدامات فاصله یا شباهت مبتنی بر زمان متعددی پیشنهاد شده است، مانند فاصله Frechet، DTW [ 33 ]، LCSS [ 34 ]، ERP [ 35 ]، EDR [ 35]. 36 ، Swale [ 37 ]، STLIP [ 38 ] و NWED [ 39 ]. تحقیقات زیادی برای بهبود کارایی محاسباتی این روش‌های کلاسیک یا انطباق مدل‌های اندازه‌گیری آنها برای کاربرد عملی انجام شده است. با این حال، بیشتر راه‌حل‌ها فرض می‌کنند که یک مسیر در ویژگی مکانش دقیق است.

3.3.3. تشابه معیارهایی که عدم قطعیت را در نظر می گیرند

کار اخیر [ 4 ] مدل اصلی مسیر بیضوی [ 23 ] را برای توصیف محدوده قابل دسترسی یک مسیر مسیر بهبود بخشید. این فرض حداکثر سرعت را در مدل اصلی حذف کرد و آن را با فاصله حد بالایی تقریبی جایگزین کرد. سپس معیارهای تشابه، اشتراک و تداوم را تعریف و محاسبه کرد. در نهایت، یک بیان شباهت جامع به دست آمد. با این حال، آنها به سادگی فاصله اقلیدسی نقاط لنگر مجاور را با یک ضریب ثابت گسترش دادند تا پارامترهای بیضی را تعیین کنند. به عبارت دیگر، همه بیضی ها دارای یک خروج از مرکز بودند، که نمی تواند وضعیت واقعی عدم قطعیت را در طول مسیر توصیف کند. کار [ 40] روشی برای تعیین کمیت شباهت مسیر به عنوان یک بازه، به جای یک مقدار واحد، به نام تخمین فاصله فاصله مسیر، پیشنهاد کرد تا عدم قطعیت ناشی از نرخ‌های نمونه‌گیری مختلف و نمونه‌گیری ناهمزمان را به دست آورد. مدل تخمین بر اساس یک ناحیه مرزی دایره ای با شعاع متناسب با حداکثر سرعت تخمین زده شده بود. در حالی که این ناحیه مرزی دایره ای می تواند مشکل نمونه برداری ناهمزمان را تا حد معینی حل کند، حداکثر سرعت به طور دلخواه به عنوان حداکثر مقدار میانگین سرعت هر جفت نقطه لنگر متوالی تعیین شد. همچنین برخی از معیارهای شباهت مجموعه فازی بر اساس تئوری فازی وجود دارد که در طبقه بندی شکل استفاده شده است [ 41 ].
به طور خلاصه، کار مرتبط در مورد اندازه گیری شباهت به صورت شکل 3 نشان داده شده است .
برای غلبه بر این محدودیت کار قبلی، ما یک مدل بیضی اصلاح‌شده جدید پیشنهاد می‌کنیم که یک مسیر را به‌عنوان زنجیره‌ای از بیضی‌های به هم پیوسته نشان می‌دهد، که پارامترهای شکل آن به‌طور دینامیکی توسط ویژگی‌های حرکت بخش‌های مجاور محاسبه می‌شوند. سپس از مدل جدید برای طراحی یک معیار تشابه استفاده می کنیم که برای خطای درون یابی و خطای موقعیت قوی تر است.

4. رویکرد پیشنهادی

4.1. مدل بیضی اصلاح شده

مدل مهره سنتی مسیر ممکنی را که یک جسم متحرک می تواند بین دو نقطه لنگر متوالی (که نقاط نمونه نیز نامیده می شود) طی کند، در نظر می گیرد [ 15 ]. شیب مهره با حداکثر سرعت جسم متحرک تعیین می شود. با این حال، در موارد واقعی، اجسام متحرک احتمالاً با حداکثر سرعت به حرکت خود ادامه نمی دهند. بنابراین، در یک صفحه نمایش دوبعدی، شکل بیضی پیش بینی شده نباید همیشه با حداکثر سرعت تعیین شود، که اغلب به طور دلخواه تعیین می شود. در کار ما، برای بهبود منطقی بودن توصیف موقعیت ممکن بین نقاط لنگر، هنگام تعیین پارامترهای شکل یک بیضی نامشخص، ویژگی‌های حرکت را در نظر می‌گیریم.

4.1.1. مدل اولیه بدون خطای موقعیت یابی

همانطور که نمودار شکل 4 نشان می دهد، ما دو نقطه لنگر مجاور را به عنوان نقاط کانونی E( پمن،پمن+1). آنچه از بیضی ناشناخته باقی می ماند طول محور نیمه فرعی است، یعنی. ب . به طور شهودی، b عدم قطعیت دامنه عمودی جسم متحرک به دلیل خطای درون یابی را نشان می دهد. هسته روش ما تخمین این محدوده با استفاده از ویژگی های حرکتی است که بخش های مجاور را منعکس می کند.
خطای درون یابی از درون یابی خطی، متداول ترین روش درون یابی، که منجر به شکست در انعکاس تغییر حالت های حرکت می شود، نشات می گیرد. هرگونه تغییر جهت بین دو نقطه لنگر متوالی از قلم افتاده و به سادگی با یک خط مستقیم جایگزین می شود. محدوده یک منطقه مسیر ممکن با سرعت و تغییر جهت حرکت مرتبط است. می‌توانیم از ویژگی‌های حرکتی مربوط به بخش‌های محله برای تقریب وضعیت واقعی استفاده کنیم. علاوه بر سرعت و شتاب، ویژگی‌های مهم دیگری مانند سینوسی و زاویه چرخش وجود دارد که می‌تواند ویژگی‌های حرکت، به‌ویژه جهت حرکت و تغییر آن را منعکس کند. از آنجایی که مدل بیضی بر پایه بخش ها است تا نقاط منفرد،ب .

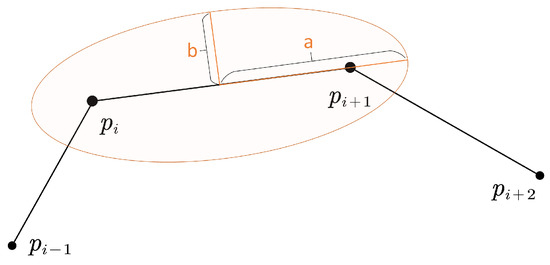
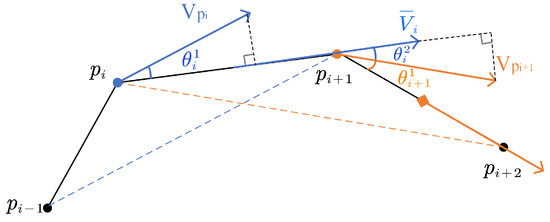
بگیر سهgمترهnتی(پمن،پمن+1)در شکل 5 به عنوان مثال، زاویه چرخش از اختلاف جهت بین سرعت متوسط ​​(بر حسب بردار) به دست می آید. سهgمترهnتی(پمن-1،پمن+1)، سهgمترهnتی(پمن،پمن+1)، و سهgمترهnتی(پمن،پمن+2)، یعنی:

θمن1=∠پمن-1،پمن+1-∠پمن،پمن+1θمن2=∠پمن،پمن+2-∠پمن،پمن+1

که در آن ∠ به معنای زاویه بین بردار و خط افقی است.

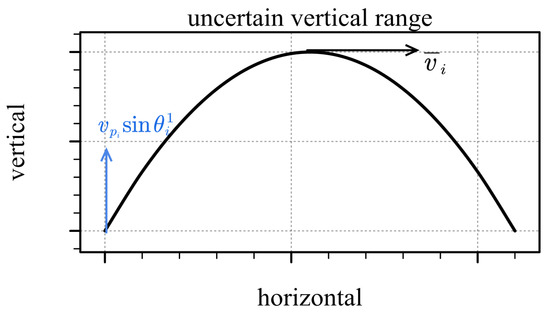
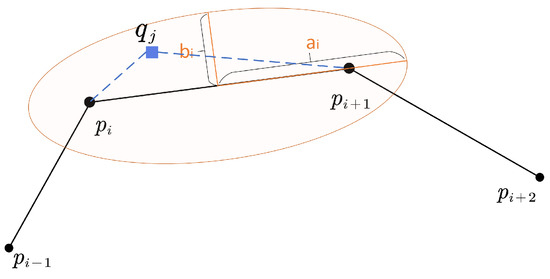
یک فرضیه شهودی این است که محدوده عدم قطعیت عمودی با مولفه سرعت در جهت عمودی متناسب است. همانطور که شکل 6 نشان می دهد، مولفه عمودی سرعت vپمنگناهθمنکمی تواند منجر به فاصله عمودی از 12vپمنگناهθمنک·Δتی2تا زمانی که مولفه به صفر برسد. زمان کاهش سرعت تنظیم شده است Δتی2زیرا جسم متحرک باید به نقطه لنگر برگردد پمن+1. ما می توانیم دو فاصله عمودی نامشخص حاصل از سرعت شروع و سرعت پایان قطعه را بدست آوریم. بنابراین، می‌توانیم مقدار محور نیمه فرعی b را با محاسبه میانگین دو فاصله عمودی نامشخص تخمین بزنیم:

ب=12vپمنگناهθمن12·Δتی2+vپمن+1گناهθمن22·Δتی2=18Δتیvپمنگناهθمن1+vپمن+1گناهθمن2

پارامترهای بیضی اصلاح شده بدین ترتیب هستند:

ج=12دهتوجپمن،پمن+1ب=18Δتیvپمن|گناهθمن1|+vپمن+1|گناهθمن2|آ=ب2+ج2

مثال ها:
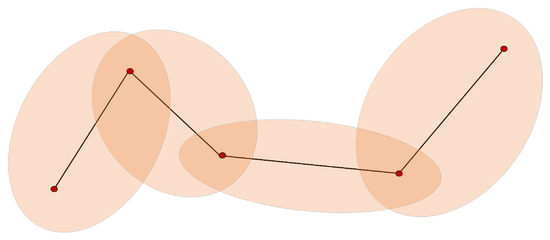
  • اگر یک قطعه تقریباً با هر دو همسایه‌اش جهت یکسانی داشته باشد، b آن بسیار کوچک خواهد بود، و گریز از مرکز نسبتاً بزرگ است، به عنوان مثال، ناحیه عدم قطعیت قطعه یک بیضی باریک است ( شکل 7 )، که با معمول ما سازگار است. تصور اینکه جسمی که در یک خط مستقیم حرکت می کند، تمایل به عدم قطعیت مکان کمتری دارد. برای معیار تشابه ارائه شده در بخش زیر، این نوع منحنی‌های «مستقیم» به دلیل ناحیه کوچکتر عدم قطعیت، شباهت کمتری با یکدیگر دارند.
  • قطعه ای با زوایای چرخشی بزرگ نسبت به همسایگانش b بزرگتر خواهد داشت که به خروج از مرکز کوچکتر و بیضی گسترده تر کمک می کند ( شکل 8 ). این پدیده همچنین با این درک شهودی مطابقت دارد که جسمی که در زوایای تند حرکت می کند، تمایل به عدم قطعیت مکان بیشتری دارد. برای اندازه‌گیری شباهت پیشنهادی، این نوع منحنی‌های «پیچ‌پیچ» تمایل بیشتری به داشتن شباهت بیشتر با یکدیگر در نتیجه ناحیه همپوشانی بزرگ‌تر از گستره‌های عدم قطعیت مجاور دارند.
4.1.2. مدل در نظر گرفتن خطای موقعیت یابی
همانطور که در شکل 9 نشان داده شده است، معرفی خطای موقعیت یابی، یک زاویه افست اضافی به زاویه چرخش اصلی قطعه اضافه می کند.

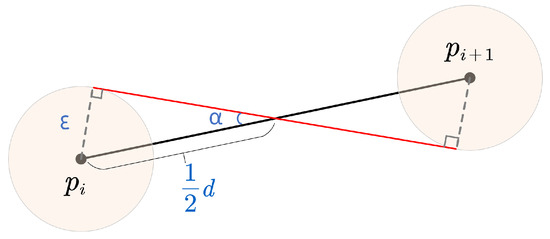
زاویه افست ناشی از خطای موقعیت یابی را می توان با موارد زیر بدست آورد:

گناهα=ε12د=2εد

ما از میانگین دقت مکانی یک گیرنده استاندارد GPS به عنوان خطای اندازه گیری موقعیت استفاده می کنیم، به عنوان مثال، ε=2متر[ 5 ]. در بیشتر موارد، خطا به مراتب کمتر از فاصله بین دو نقطه لنگر متوالی است. 2εدمقدار بسیار کمی است و همینطور است α. با توجه به گسترش سری تیلور:

گناهα=∑ک=0∞-1ک2ک+1!α2ک+1=α-α33!+α55!-…≈α→0α

بنابراین، در شرایط یک خطای اندازه گیری موقعیت منظم، تقریباً می توانیم به دست آوریم: α≈گناهα=2εد، و زاویه چرخش اصلاح شده قطعه است θمنک+2εد،ک=1،2.

بنابراین، پارامترهای بیضی اصلاح شده نهایی که هر دو InE و PoE را در نظر می گیرند عبارتند از:

ج=12دهتوجپمن،پمن+1=12دب=18Δتیvپمنگناهθمن1+2εد+vپمن+1گناهθمن2+2εدآ=ب2+ج2

اگر نقاط لنگر بسیار نزدیک به یکدیگر باشند، می توانیم از فرمول اصلی زاویه افست استفاده کنیم α=آرکسین2εد. بنابراین، محور نیمه اصلی b خواهد بود:

ب=18Δتیvپمنگناهθمن1+آرکسین2εد+vپمن+1گناهθمن2+آرکسین2εد

4.2. اندازه گیری تشابه مسیر نامشخص

با توجه به مدل بیضی اصلاح شده ما، یک مسیر را می توان با زنجیره ای از بیضی ها با پارامترهای شکل مختلف نشان داد. یک مدل شباهت بر اساس توصیف عدم قطعیت طراحی شده است. ابتدا باید یک مفهوم کلیدی به نام تطبیق تعریف کنیم. اگر نقطه لنگر پمندر P در داخل بیضی قطعه قرار دارد qj،qj+1سپس در Q پمنمطابقت دارد qj،qj+1یا پمنمطابق شکل 10 با E(Q) مطابقت دارد . در غیر این صورت، پمنبا Q مطابقت ندارد.
در روش ما، هر نقطه لنگر در یک مسیر باید بر شباهت کلی تأثیر بگذارد. اصول طراحی مدل شباهت عبارتند از:
  • هر مسابقه بین P و Q تأثیر مثبتی بر روی خواهد داشت اس(پ،س).
  • یک تطابق مداوم افزایش بیشتری را به همراه خواهد داشت اس(پ،س).
  • عدم تطابق اثر غیر مثبتی بر اس(پ،س)یعنی بدون اثر یا اثر منفی.

معیار تشابه پیشنهادی ما بر اساس مدل بیضی اصلاح شده به شرح زیر است:

سqj=انقضا-دقیقهf∈پمن،پمن+1دqj،fآمن·کqjکqj=جاریطولازادامه مسابقهqمناستتطبیق0qمناستناهماهنگ

برای هر نقطه لنگر در هر دو مسیر، سهم آن را در شباهت نهایی بر اساس موقعیت و بیضی تطبیق آن محاسبه می کنیم، مانند شکل 10 . سهم نقطه qjبا نشان داده می شود سqj. توجه داشته باشید که سqjحاوی یک ضریب ضرب است که با نشان داده شده است ک(qj)، و به آن ضریب پیوستگی می گویند که از اصل دوم گرفته شده است. ک(qj)برای هر نقطه لنگر به روز می شود تا طول فعلی تطابق ادامه یابد. مقدار اولیه آن صفر است و اگر نقطه فعلی با یک بیضی از مسیر دیگر مطابقت داده شود، یک افزایش می یابد. زمانی که نقطه فعلی با هیچ بیضی مطابقت نداشته باشد به صفر بازنشانی می شود. پس از آن، می‌توانیم شباهت غیر عادی را با جمع‌بندی سهم هر نقطه لنگر به دست آوریم:

اسپ،س=12∑من=0n-1سqمن+∑j=0متر-1سپj

از آنجایی که معیار تشابه منفرد را در یک ضریب پیوستگی ضرب می‌کنیم، می‌توانیم معیار شباهت کلی را با تقسیم حداکثر تداوم عادی کنیم:

ناسپ،س=12∑من=0n-1سqمن/∑من=1n-1من+∑j=0متر-1سپj/∑j=1متر-1j

ناسپ،سبنابراین UTSM نهایی ما می شود. از تعریف فرمول به راحتی می توان ثابت کرد که UTSM الزامات غیر منفی، متقارن و بازتابی بودن را برآورده می کند.

4.3. الگوریتم ها

ما از دو الگوریتم برای محاسبه شباهت پیشنهادی مسیرهای نامشخص بر اساس مدل بیضی اصلاح شده خود استفاده کردیم. یکی shape_estimator در الگوریتم 1 است که پارامترهای شکل بیضی را با توجه به ویژگی های متحرک محاسبه شده توسط موقعیت هر نقطه لنگر گام به گام تخمین می زند. دیگری UTSM_calculator Algorithm 2 است که مقدار UTSM یک جفت مسیر را با پیمایش مسیر با استفاده از دو حلقه مختلف محاسبه می‌کند. پیچیدگی محاسباتی کلی بود O(پq)، که در آن p و q نشان دهنده طول (یعنی تعداد نقاط لنگر) دو مسیر هستند.
الگوریتم 1: shape_estimator.
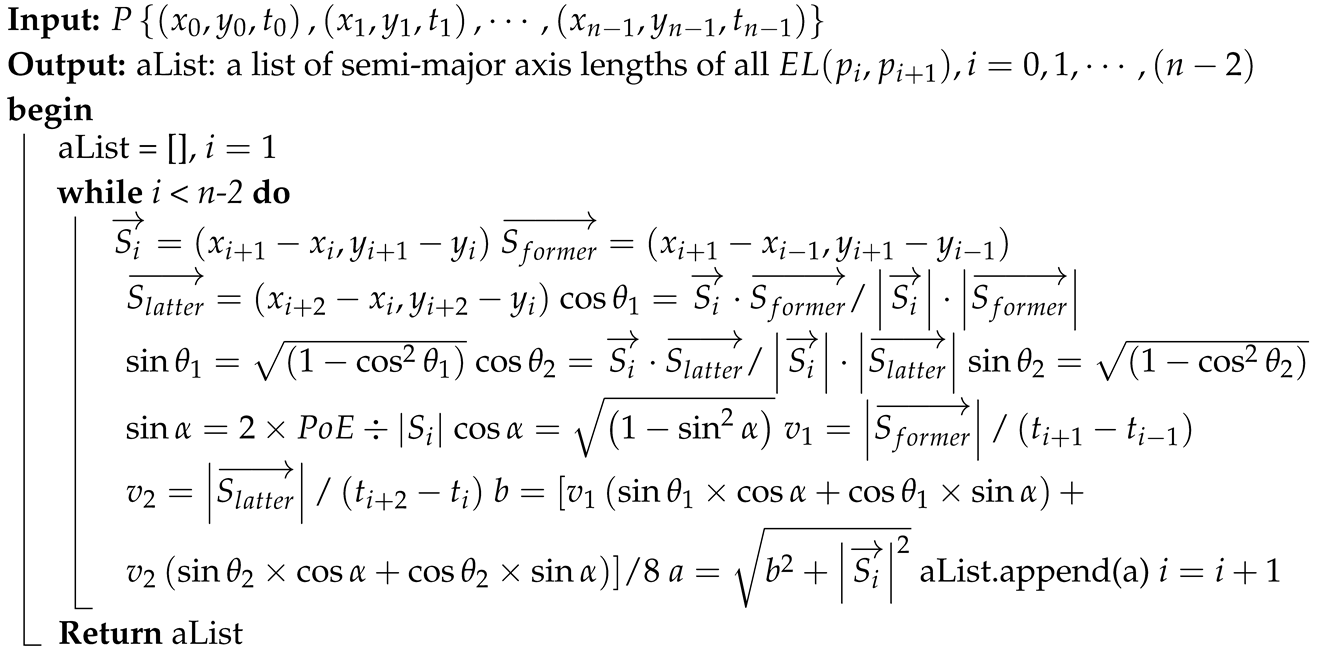Ijgi 08 00518 i001
الگوریتم 2: UTSM_calculator.
Ijgi 08 00518 i002

5. ارزیابی تجربی

اهداف آزمایش های زیر عبارتند از:
  • ارزیابی اثربخشی UTSM در اندازه گیری شباهت بین مسیرها.
  • استحکام UTSM نسبت به نقاط پرت، نرخ‌های نمونه‌گیری مختلف و نمونه‌گیری ناهمزمان را تأیید کنید.
ما از داده های دنیای واقعی و داده های مصنوعی برای آزمایش ویژگی های خاص استفاده کردیم.

5.1. تنظیم آزمایش

داده های دنیای واقعی:
  • کاداستر دریایی: این مجموعه داده AIS دریایی تقریباً 30 ویژگی را برای 150000 کشتی در سراسر قلمرو ایالات متحده با فرکانس یک خواندن GPS در دو تا 10 ثانیه ثبت می کند. هر مسیر شامل تعداد مختلفی از نقاط لنگر از 10 تا 3000 بود.
  • مجموعه داده T-Drive: این شامل مسیرهای بدون استخوان است که از داده های مسیر واقعی سفرهای تاکسی نیویورک استخراج شده است. داده های نمونه ای که ما استفاده کردیم حاوی بیش از 20000 مسیر بود. هر مسیر شامل 100 تا 500 نقطه لنگر بود.
این دو مجموعه داده را می توان با لینک های موجود در مواد تکمیلی در انتهای مقاله دانلود کرد.
داده های مصنوعی:
  • مسیرهای شبیه سازی شده با نقاط پرت: ما برخی از نقاط پرت را به مسیرهای اصلی دنیای واقعی اضافه کردیم.
  • مسیرهای شبیه‌سازی شده با نرخ‌های نمونه‌گیری متفاوت: ما عملیات نمونه‌گیری مجدد را با فواصل مختلف بر اساس مسیرهای واقعی انتخاب شده انجام دادیم.
  • مسیرهای ناهمزمان مصنوعی: ما به صورت دستی نقاط را به صورت ناهمزمان از منحنی سینوسی در فرکانس های تقلیل ناپذیر نمونه برداری کردیم.
محیط:
آزمایش ها با استفاده از برنامه Python 3.6 بر روی یک پردازنده Intel® Core™ i7-4710MQ @ 2.50 گیگاهرتز با 16 گیگابایت رم و سیستم عامل Ubuntu 18.04 LTS انجام شد.
روش های پایه:
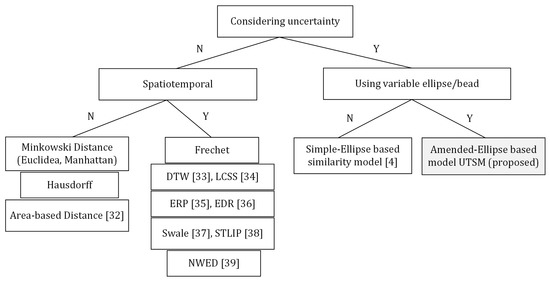
  • اندازه گیری مبتنی بر فاصله: فاصله Hausdorff، فاصله Frechet، DTW [ 33 ]، LCSS [ 34 ]، ERP [ 35 ]، EDR [ 36 ] و فاصله مبتنی بر ناحیه [ 32 ].
  • اندازه گیری تشابه با در نظر گرفتن عدم قطعیت: شباهت مبتنی بر بیضی ساده [ 4 ].

5.2. ارزیابی و بحث

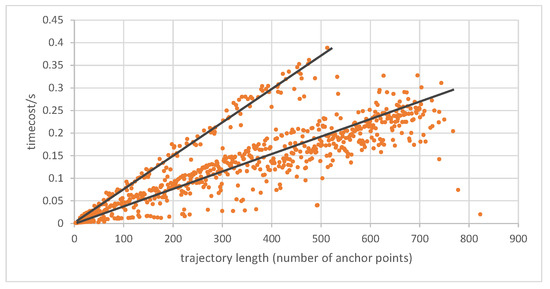
5.2.1. کارایی محاسباتی

برای ارزیابی کارایی مدل UTSM، هر دو کاداستر دریایی و مجموعه داده T-Drive به عنوان ورودی برای الگوریتم‌های ما استفاده شدند. شباهت UTSM بین یک مسیر به طور تصادفی انتخاب شده با بقیه در همان محیط محاسبه شد. همانطور که طول مسیرها (یعنی تعداد نقاط لنگر در مسیرها) متفاوت بود، زمان مصرف محاسبات UTSM بین مقیاس میلی ثانیه و ثانیه پخش شد. نتیجه کلی در شکل 11 نشان داده شده است .
بدیهی است که زمان-هزینه رابطه خطی مثبتی با طول مسیرها دارد. برای دقیق تر، دو خط روند خطی متمایز از نقاط پراکندگی وجود دارد. خط روند با شیب کمتر با مجموعه داده کاداستر دریایی مطابقت دارد که شامل هندسه نسبتاً صافی از مسیرهای کشتی است. خط روند دیگر با شیب بیشتر با مجموعه داده T-Drive مطابقت دارد که شامل مسیرهای خودروها با پیچ های بیشتر است. همچنین نشان داد که زمان و هزینه محاسبه UTSM با مورفولوژی هندسی ناشی از ویژگی‌های متحرک مسیرها مرتبط است.
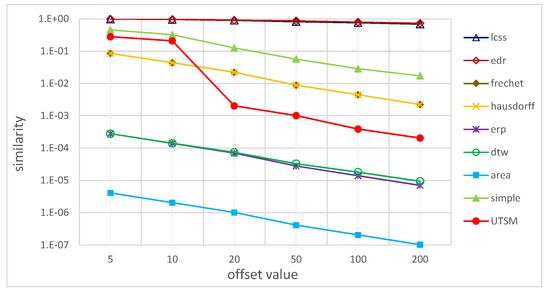
5.2.2. اثربخشی
ما افست های مختلفی را به هر نقطه لنگر یک مسیر دنیای واقعی از مجموعه AISdatastre Marine Cadastre اضافه کردیم و سپس شباهت بین اصلی و آفست را با استفاده از معیارهای شباهت مختلف محاسبه کردیم. نتایج در جدول 2 و شکل 12 نشان داده شده است. توجه داشته باشید که برای شبیه سازی مقدار شباهت یکنواخت، ما یک تبدیل مقدار مبتنی بر فاصله را انجام دادیم تا آن را به شباهت تبدیل کنیم. فرمول تبدیل است اس=1-ه-1D، که در آن S نشان دهنده شباهت و D نشان دهنده مقدار فاصله است. این به این دلیل بود که شباهت مبتنی بر فاصله می تواند به بازه [0، 1] تبدیل شود، مهم نیست مقدار فاصله چقدر بزرگ باشد.
از نتیجه، می بینیم که با افزایش افست اضافه شده به صورت دستی، تمام معیارهای شباهت کاهش یافت. با این حال، اقدامات مختلف شروع شد و در سطوح مختلف کاهش یافت. هنگامی که افست نسبتاً کوچک بود (یعنی پنج یا 10)، در مقایسه با میانگین فاصله بین نقاط لنگر، برخی از معیارهای مبتنی بر فاصله مانند مساحت، ERP، DTW، Hausdorff و Frechet نسبتاً بزرگ بودند، به طوری که شباهت مربوطه بسیار کوچک برای منعکس کردن شباهت واقعی مسیرهای نمونه. هنگامی که مقدار افست بزرگتر تنظیم شد (یعنی 200)، برخی از معیارها مانند LCSS و EDR، بزرگ باقی ماندند (> 0.6)، که نشان داد آنها معیارهای شباهت خوبی نیستند. علاوه بر این، معیارهای مبتنی بر LCSS و EDR به یک مقدار آستانه معقول در الگوریتم‌های خود نیاز داشتند تا یک مقدار معنی‌دار به دست آورند. که کاربرد آنها را در بسیاری از سناریوها محدود می کند. در مقابل، UTSM و مدل بیضی ساده با یک مقدار مناسب شروع شدند (یعنی 0.2 تا 0.5) و روند کاهشی معقولی را نشان دادند که می‌تواند با موفقیت شباهت واقعی را منعکس کند. این پدیده همچنین اثربخشی در نظر گرفتن عدم قطعیت هنگام اندازه‌گیری شباهت مسیر را نشان داد. با این حال، UTSM پیشنهادی ما نسبت به مدل ساده بیضی حساس‌تر بود، زمانی که افست به فاصله مسیرهای نقاط لنگر نزدیک شد. مجموعه داده کاداستر دریایی AIS موقعیت گسسته سفرهای کشتی را در فرکانس دو تا ۱۰ ثانیه زمانی که کشتی در حال حرکت بود، ثبت کرد، که به این معنی است که فاصله بین هر جفت نقطه همسایه در مسیر یک کشتی حدود ۵ تا ۳۰ متر است (با توجه به سرعت متوسط ​​ماهیگیری معمولی یا کشتی های باری). در این حساب، وقتی یک افست فراتر از آن فاصله اضافه می کنیم، مقدار شباهت باید به سطح پایینی کاهش یابد تا مشخصه واقعی مسیرها را منعکس کند. این یک شواهد قوی است که مدل UTSM ما می تواند با موفقیت فاصله نامشخص مسیرها را ثبت کند.
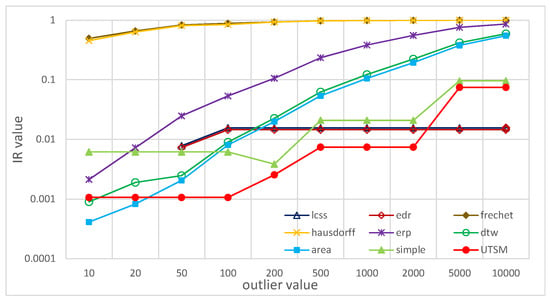
5.2.3. استحکام نسبت به موارد پرت
در این آزمایش، ما مسیرهای نسبتاً طولانی را از مجموعه داده T-Drive انتخاب کردیم و مانند شکل 13 ، نویزهایی با اندازه های مختلف به چندین نقطه لنگر در مسیر اضافه کردیم . نقاط نویز به طور تصادفی از مسیر انتخاب شدند و این نشان دهنده یک درصد از تمام نقاط لنگر بود.
برای انعکاس تأثیر نقطه پرت اضافه شده، ما یک تغییر کوچک برای مسیر اصلی و نویز انجام دادیم و شباهت آنها را به ترتیب با اصلی محاسبه کردیم. دو شباهت به عنوان نشان داده شده است سمنمترorمنgمنnو سمنمترnoمنسهد. ما همچنین یک نسبت نفوذ (IR) را به عنوان تعریف کردیم منآر=سمنمترnoمنسهد-سمنمترorمنgمنn/سمنمترorمنgمنnبرای نشان دادن درجه تأثیر برجستگی اضافه شده. شکل 14 نشان می دهد منآرنتیجه اقدامات شباهت های مختلف
از نتیجه، می‌توانیم ببینیم که تحت اندازه‌های پرت مختلف، مدل‌های اندازه‌گیری که عدم قطعیت را در نظر می‌گیرند، به عنوان مثال، مدل ساده بیضی و UTSM پیشنهادی ما، مقادیر IR کوچک‌تری نسبت به روش‌های دیگر داشتند، به‌خصوص زمانی که نویز اضافه‌شده بزرگ شد. UTSM حتی بهتر از مدل بیضی ساده عمل کرد، که نشان داد UTSM استحکام بهتری نسبت به نقاط پرت در مسیر دارد.
اشاره کرد که LCSS و EDR همچنین دارای مقدار IR کوچکی در اندازه های مختلف نویز هستند. این به این دلیل بود که مقدار آستانه ورودی آنها با توجه به نویز اضافه شده به صورت دستی تنظیم شده بود.
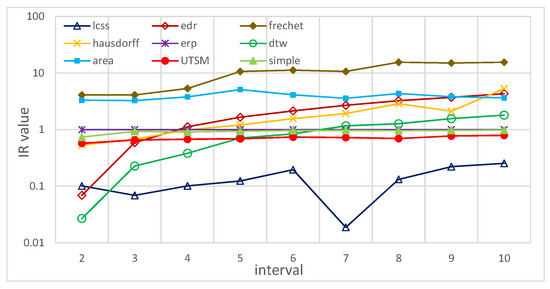
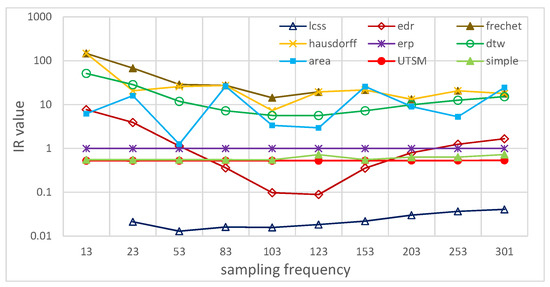
5.2.4. تحمل به نرخ های مختلف نمونه برداری
در این آزمایش، ما دوباره یک مسیر نسبتا طولانی را از مجموعه داده T-Drive انتخاب کردیم و یک عملیات نمونه‌گیری مجدد روی آن با فواصل زمانی مختلف برای شبیه‌سازی نرخ‌های نمونه‌گیری مختلف از داده‌های مسیر انجام دادیم. شکل 15 نمونه ای از عملیات نمونه گیری مجدد است.
همانند آزمایش در V.ب.3، ما همچنین یک افست کوچک به مسیرهای اصلی و نمونه برداری مجدد انجام دادیم و سپس شباهت را با مسیر اصلی محاسبه کردیم. IR نیز برای نشان دادن تأثیر فرکانس‌های نمونه بر روی مدل‌های شباهت محاسبه شد. نتیجه در شکل 16 نشان داده شده است .
از نتیجه، می‌توانیم ببینیم که مدل UTSM پیشنهادی ما نیز استحکام خوبی برای نرخ نمونه‌گیری نشان داد. بیضی نامشخص مورد استفاده در شباهت محاسباتی می تواند تا حدی بر اثر منفی داده های از دست رفته غلبه کند. UTSM مقدار IR نسبتاً کوچکتری نسبت به مدل بیضی ساده داشت زیرا UTSM ویژگی های حرکت را در نظر می گرفت. پارامترهای شکل محاسبه شده به صورت دینامیکی آن می تواند بهتر از بیضی ساده در هنگام برخورد با نقاط لنگر از دست رفته کار کند.
اشاره شد که LCSS در اکثر موارد کمترین مقدار IR را داشت. این به این دلیل بود که مدل LCSS می‌توانست هنگام محاسبه شباهت، نقاط گمشده یا عدم تطابق ذاتی را نادیده بگیرد.
5.2.5. تحمل به نمونه گیری ناهمزمان
جدای از نرخ نمونه برداری، نمونه گیری ناهمزمان نیز بخش مهمی از ناهمگونی مسیر است. در این آزمایش، با نمونه‌برداری از منحنی سینوسی پیوسته در فرکانس‌های مختلف که بر یکدیگر قابل تقسیم نبودند، مسیرهای ناهمزمان ایجاد کردیم. شکل 17 نمونه ای از دو مسیر نمونه برداری ناهمزمان را نشان می دهد.
برای ارزیابی تأثیر نمونه‌گیری ناهمزمان، یک فرکانس ثابت (یعنی 100) را به عنوان معیار در نظر گرفتیم و شباهت را با مسیرهای نمونه‌برداری شده در فرکانس‌های دیگر محاسبه کردیم (یعنی 13، 23، 53، 83، 103، 123، 153، 203، 253 و 301)، که بر اساس معیار قابل تقسیم نبودند. مقادیر IR مدل های مختلف اندازه گیری در شکل 18 نشان داده شده است.
از نتیجه، می توان مشاهده کرد که LCSS کمترین مقدار IR را داشت. این نیز به این دلیل بود که الگوریتم LCSS ذاتاً می تواند هنگام محاسبه شباهت از نقاط گمشده یا بی همتا چشم پوشی کند. این ویژگی به تحمل بهتر استراتژی‌های نمونه‌گیری مختلف کمک کرد، اما تأثیر منفی بر انعکاس شباهت واقعی مسیرها، به عنوان آزمایش داشت. V.ب.2نشان داده شده.
EDR زمانی که فرکانس نمونه‌برداری نزدیک به فرکانس معیار بود، مقدار IR پایینی داشت، اما اگر فرکانس دورتر می‌رفت، عملکرد بدتری داشت. بنابراین، اساسا، جدای از LCSS، در مقایسه با مدل‌های دیگر، UTSM پیشنهادی ما بر اساس بیضی اصلاح‌شده دارای مقدار IR پایین‌تری در بیشتر موارد بود، که به این معنی است که تحمل بهتری نسبت به نمونه‌گیری ناهمزمان نشان می‌دهد.
5.2.6. خلاصه
برای ارائه واضح تر عملکرد معیارهای شباهت مختلف در سناریوهای مختلف، تمام نتایج آزمایش را در جدول 3 خلاصه می کنیم . اگر یک مدل اندازه گیری در سناریوی خاص در سه رتبه برتر قرار گیرد، علامت چک داده می شود.
جدول 3 نشان می دهد که UTSM پیشنهادی ما تنها معیاری بود که در هر چهار شاخص ارزیابی در سه رتبه برتر قرار گرفت، که نشان می دهد UTSM می تواند به عنوان یک معیار شباهت موثر و پایدار در مجموعه داده های مسیر چند منبع یا ناهمگن استفاده شود.

6. نتیجه گیری و کار آینده

مدل بیضی اصلاح شده پیشنهادی ما با موفقیت به عدم قطعیت موجود در مسیرها پرداخت. هم خطای درون یابی و هم خطای موقعیت یابی را در نظر گرفت. با محاسبه پارامترهای شکل بیضی به صورت دینامیکی بر اساس ویژگی‌های حرکت، هر بخش در یک مسیر با یک بیضی با برون‌مرکزی متفاوت مطابقت دارد که ناحیه عدم قطعیت بخش را به‌طور تطبیقی ​​توصیف می‌کند. اندازه گیری شباهت پیشنهادی UTSM بر اساس مدل می تواند شباهت را در یک مقدار نرمال شده به تصویر بکشد، که می تواند تأثیر عدم قطعیت را به طور موثر منعکس کند. در مقایسه با کار [ 4]، مدل اصلاح شده ما به جای استفاده از حداکثر سرعت، ویژگی های حرکت را هنگام تعیین پارامترهای شکل بیضی مربوطه در نظر گرفت. علاوه بر این، تأثیر خطای موقعیت در مدل ما در نظر گرفته شد. هنگام طراحی مدل شباهت UTSM، ما بر تطابق پیوسته در سهم اضافی مقدار شباهت نهایی تأکید کردیم که این نیز یک پیشرفت قابل توجه بود. تایید شده توسط آزمایش‌ها بر روی داده‌های مصنوعی و دنیای واقعی، UTSM نسبت به سایر معیارهای کلاسیک استحکام بهتری نسبت به نویز و نقاط پرت نشان داد. همچنین نسبت به نرخ‌های نمونه‌گیری مختلف و نمونه‌گیری ناهمزمان در مسیرها تحمل بیشتری داشت. با این حال، روش پیشنهادی ما به دلیل گام اضافی در هنگام محاسبه پارامترهای بیضی عدم قطعیت، پیچیدگی محاسباتی نسبتاً بالاتری داشت.
برای کارهای آینده، مدل بیضی اصلاح‌شده را می‌توان برای انطباق با خطای موقعیت شرطی یا متغیر زمان اصلاح کرد، و تحقیقات بیشتری برای گسترش مدل عدم قطعیت به مسیرهای محدود شبکه مورد نیاز است. برای اندازه‌گیری شباهت بر اساس مدل نامشخص، ما همچنین قصد داریم UTSM را بهبود بخشیم تا با داده‌های مسیر نمونه‌برداری فواصل مساوی سازگار شود و اندازه‌گیری را برای برنامه‌های خوشه‌بندی مسیر اتخاذ کنیم. علاوه بر این، الگوریتم های موازی باید برای بهبود کارایی پرس و جوهای شباهت در مجموعه داده های مقیاس بزرگ طراحی شوند. از منظر کاربرد عملی، ما قصد داریم مدل پیشنهادی خود را در کارهای مرتبط با مسیر مختلف، مانند جستجوی شباهت مسیر، به عنوان مثال، یافتن دسته‌های خاصی از پرندگان که مسیر مهاجرت مشابهی دارند، یا تطبیق نقشه، به کار ببریم،

منابع

  1. توهی، ک. داکهام، ام. اقدامات شباهت مسیر. Sigspatial Spec. 2015 ، 7 ، 43-50. [ Google Scholar ] [ CrossRef ]
  2. راناچر، پ. Tzavella، K. چگونه حرکت را مقایسه کنیم؟ مروری بر اقدامات شباهت حرکتی فیزیکی در علم اطلاعات جغرافیایی و فراتر از آن کارتوگر. Geogr. Inf. علمی 2014 ، 41 ، 286-307. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  3. یان، ز. پدر و مادر، سی. اسپاکاپیترا، اس. چاکرابورتی، دی. یک مدل ترکیبی و بستر محاسباتی برای مسیرهای فضایی- معنایی. در وب معنایی: تحقیقات و کاربردها ; Springer: برلین/هایدلبرگ، آلمان، 2010; صص 60-75. [ Google Scholar ]
  4. فورتادو، ع. آلوارس، LOC؛ پلکیس، ن. تئودوریدیس، ی. بوگورنی، وی. آشکارسازی عدم قطعیت حرکت برای تحلیل شباهت مسیر قوی. بین المللی جی. جئوگر. Inf. علمی 2018 ، 32 ، 140-168. [ Google Scholar ] [ CrossRef ]
  5. تیم محصولات جی پی اس. گزارش تجزیه و تحلیل عملکرد سیستم موقعیت یابی جهانی (GPS) سرویس موقعیت یابی استاندارد (SPS) ; تیم محصول GPS: واشنگتن، دی سی، ایالات متحده آمریکا، 2014. [ Google Scholar ]
  6. Reap, RM یک مدل مسیر سه بعدی عملیاتی. J. Appl. هواشناسی 1972 ، 11 ، 1193-1202. [ Google Scholar ] [ CrossRef ]
  7. تریفونا، ن. جنسن، مدل‌سازی داده‌های مفهومی CS برای کاربردهای فضایی و زمانی. Geoinformatica 1999 ، 3 ، 245-268. [ Google Scholar ] [ CrossRef ]
  8. پدر و مادر، سی. اسپاکاپیترا، اس. Zimányi، E. مدل های مفهومی فضایی-زمانی: ساختارهای داده + فضا + زمان. در مجموعه مقالات سمپوزیوم بین المللی ACM در مورد پیشرفت در سیستم های اطلاعات جغرافیایی، کانزاس سیتی، MO، ایالات متحده آمریکا، 2-6 نوامبر 1999. صص 26-33. [ Google Scholar ]
  9. کوپر، جی. لیبکین، ال. Paredaens, J. Database Constraint ; Springer Science and Business Media: برلین، آلمان، 2013. [ Google Scholar ]
  10. اسپاکاپیترا، اس. پدر و مادر، سی. دامیانی، ام.ال. Macedo، JAD; پورتو، اف. وانگنوت، سی. دیدگاه مفهومی در مسیرها. دانستن داده ها مهندس 2008 ، 65 ، 126-146. [ Google Scholar ] [ CrossRef ]
  11. Hornsby، KS; کول، اس. مدل سازی اجسام مکانی متحرک از دیدگاه مبتنی بر رویداد. ترانس. GIS 2007 ، 11 ، 555-573. [ Google Scholar ] [ CrossRef ]
  12. لیو، اچ. اشنایدر، ام. اندازه گیری تشابه مسیرهای جسم متحرک. در مجموعه مقالات کارگاه بین المللی Acm Sigspatial درباره ژئواستریمینگ، ردوندو بیچ، کالیفرنیا، ایالات متحده آمریکا، 6 نوامبر 2012. [ Google Scholar ]
  13. وانگ، اچ. هان، اس. کای، ز. صادق، س. ژو، ایکس. مطالعه اثربخشی بر روی معیارهای شباهت مسیر. در مجموعه مقالات بیست و چهارمین کنفرانس پایگاه داده استرالیا، آدلاید، استرالیا، 29 ژانویه تا 1 فوریه 2013. [ Google Scholar ]
  14. یینگ، جی جی. لو، ای اچ. لی، دبلیو. ونگ، تی. شباهت کاربر Tseng، VS Mining از مسیرهای معنایی. در مجموعه مقالات دومین کارگاه بین المللی ACM SIGSPATIAL در مورد شبکه های اجتماعی مبتنی بر مکان، سن خوزه، کالیفرنیا، ایالات متحده آمریکا، 2 نوامبر 2010. صص 19-26. [ Google Scholar ]
  15. هورنسبی، ک. Egenhofer، MJ مدل سازی اجسام متحرک بر روی دانه بندی های متعدد. ان ریاضی. آرتیف. هوشمند 2002 ، 36 ، 177-194. [ Google Scholar ] [ CrossRef ]
  16. Hägerstraand, T. در مورد افراد در علم منطقه چطور؟ پاپ Reg. علمی 1970 ، 24 ، 7-24. [ Google Scholar ] [ CrossRef ]
  17. میلر، HJ مدل‌سازی دسترسی با استفاده از مفاهیم منشور فضا-زمان در سیستم‌های اطلاعات جغرافیایی. بین المللی جی. جئوگر. Inf. سیستم 1991 ، 5 ، 287-301. [ Google Scholar ] [ CrossRef ]
  18. نویتنز، تی. ون دی وگه، ن. ویتلوکس، اف. De Maeyer, P. منشور فضا-زمان مبتنی بر شبکه سه بعدی. جی. جئوگر. سیستم 2008 ، 10 ، 89-107. [ Google Scholar ] [ CrossRef ]
  19. میلر، HJ نظریه اندازه گیری برای جغرافیای زمانی. Geogr. مقعدی 2005 ، 37 ، 17-45. [ Google Scholar ] [ CrossRef ]
  20. داونز، جی. بره، دی. هایزر، جی. لورام، آر. اسمیت، ZJ; O’Neal، BM کمی کردن تعاملات مکانی-زمانی حیوانات با استفاده از منشورهای احتمالی فضا-زمان. Appl. Geogr. 2014 ، 55 ، 1-8. [ Google Scholar ] [ CrossRef ]
  21. آهنگ، ی. میلر، اچ جی; ژو، ایکس. Proffitt, D. مدلسازی احتمالات بازدید در منشورهای زمان شبکه با استفاده از تکنیک های مارکوف. Geogr. مقعدی 2016 ، 48 ، 18-42. [ Google Scholar ] [ CrossRef ]
  22. کویجپرز، بی. میلر، اچ جی; عثمان، دبلیو. منشورهای جنبشی: گنجاندن محدودیت های شتاب در منشورهای فضا-زمان. بین المللی جی. جئوگر. Inf. علمی 2017 ، 31 ، 2164-2194. [ Google Scholar ] [ CrossRef ]
  23. Pfoser، D.; جنسن، CS ثبت عدم قطعیت بازنمایی‌های شی متحرک. در سمپوزیوم بین المللی پایگاه های داده فضایی ; Springer: برلین، آلمان، 1999; صص 111-131. [ Google Scholar ]
  24. جونگ، اچ. لو، اچ. ساثه، س. Yiu, ML مدیریت عدم قطعیت در حال تحول در پایگاه داده های مسیر. IEEE Trans. دانستن مهندسی داده 2013 ، 26 ، 1692-1705. [ Google Scholar ] [ CrossRef ]
  25. فرنتزوس، ای. گراتسیاس، ک. تئودوریدیس، ی. در مورد تأثیر عدم قطعیت مکان در پرس و جو فضایی. IEEE Trans. دانستن مهندسی داده 2008 ، 21 ، 366-383. [ Google Scholar ] [ CrossRef ]
  26. ترایچفسکی، جی. ولفسون، او. Hinrichs، K. چمبرلین، اس. مدیریت عدم قطعیت در پایگاه داده های اشیاء متحرک. ACM Trans. سیستم پایگاه داده (TODS) 2004 ، 29 ، 463-507. [ Google Scholar ] [ CrossRef ]
  27. ژانگ، ام. چن، اس. جنسن، CS; Ooi، BC; Zhang, Z. نمایه سازی موثر اجسام متحرک نامشخص برای پرس و جوهای پیش بینی. Proc. VLDB Enddow. 2009 ، 2 ، 1198-1209. [ Google Scholar ] [ CrossRef ]
  28. آهنگ، ی. Miller, HJ شبیه سازی توزیع احتمال بازدید در منشورهای فضا-زمان مسطح. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 104-125. [ Google Scholar ] [ CrossRef ]
  29. میلر، HJ Time Geography و Space-Time Prism. در دایره المعارف بین المللی جغرافیا: مردم، زمین، محیط زیست و فناوری ها . وایلی: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2016؛ صص 1-19. [ Google Scholar ]
  30. لی، جی. میلر، اچ جی در حال تجزیه و تحلیل دسترسی جمعی با استفاده از منشورهای فضا-زمان متوسط. ترانسپ Res. قسمت D: Transp. محیط زیست 2019 ، 69 ، 250–264. [ Google Scholar ] [ CrossRef ]
  31. زمستان، اس. یین، ZC عناصر جغرافیای زمانی احتمالی. GeoInformatica 2011 ، 15 ، 417-434. [ Google Scholar ] [ CrossRef ]
  32. جکل، CF; ونتر، جی. ونتر، نماینده مجلس؛ استاندر، ن. هفتکا، RT اندازه‌گیری تشابه برای شناسایی پارامترهای مواد از حلقه‌های پسماند با استفاده از تحلیل معکوس. بین المللی جی. ماتر. فرم. 2019 ، 12 ، 355-378. [ Google Scholar ] [ CrossRef ]
  33. کیوگ، ای. راتاناماهاتانا، کالیفرنیا نمایه سازی دقیق تاب خوردگی زمانی پویا. دانستن Inf. سیستم 2005 ، 7 ، 358-386. [ Google Scholar ] [ CrossRef ]
  34. ولاچوس، م. کولیوس، جی. Gunopulos، D. کشف مسیرهای چند بعدی مشابه. در مجموعه مقالات هجدهمین کنفرانس بین المللی مهندسی داده، سن خوزه، کالیفرنیا، ایالات متحده آمریکا، 26 فوریه تا 1 مارس 2002. [ Google Scholar ]
  35. چن، ال. Ng, R. در مورد ازدواج lp-هنجارها و فاصله ویرایش. در مجموعه مقالات سی امین کنفرانس بین المللی پایگاه های داده بسیار بزرگ – جلد 30، تورنتو، ON، کانادا، 31 اوت تا 3 سپتامبر 2004. صص 792-803. [ Google Scholar ]
  36. لی، سی. اوزسو، MT; Oria، V. جستجوی شباهت قوی و سریع برای مسیر حرکت جسم متحرک. در مجموعه مقالات کنفرانس بین المللی Acm Sigmod در مدیریت داده ها، بالتیمور، MD، ایالات متحده آمریکا، 14-16 ژوئن 2005. [ Google Scholar ]
  37. مورس، MD؛ Patel, JM روشی کارآمد و دقیق برای ارزیابی شباهت سری های زمانی. در مجموعه مقالات کنفرانس بین المللی ACM SIGMOD 2007 در مدیریت داده ها، پکن، چین، 12 تا 14 ژوئن 2007. صص 569-580. [ Google Scholar ]
  38. پلکیس، ن. کوپاناکیس، آی. مارکتوس، جی. نتوتسی، آی. آندرینکو، جی. تئودوریدیس، ی. جستجوی تشابه در پایگاه های داده مسیر. در مجموعه مقالات سمپوزیوم بین المللی در بازنمایی و استدلال زمانی، آلیکانته، اسپانیا، 28 تا 30 ژوئن 2007. [ Google Scholar ]
  39. دوج، اس. لاوب، پی. ارزیابی تشابه حرکت با استفاده از نمایش نمادین مسیرها. بین المللی جی. جئوگر. Inf. علمی 2012 ، 26 ، 1563-1588. [ Google Scholar ] [ CrossRef ]
  40. نادریسال، س. کولیک، ال. بیلی، جی. اندازه گیری فاصله موثر و همه کاره برای مسیرهای مکانی و زمانی. حداقل داده دانستن کشف کنید. 2019 ، 33 ، 577-606. [ Google Scholar ] [ CrossRef ]
  41. باکور، ال. علیمی، ع.م. جان، RI چند یادداشت در مورد معیارهای شباهت فازی و کاربرد در طبقه بندی اشکال تشخیص جملات عربی و موزاییک. بین المللی IAENG جی. کامپیوتر. علمی 2014 ، 41 ، 81-90. [ Google Scholar ]
Ijgi 08 00518 g001 550
شکل 1. مثال اعوجاج شباهت مسیر.
Ijgi 08 00518 g002 550
شکل 2. مهره ST و بیضی مسطح.
Ijgi 08 00518 g003 550
شکل 3. روش های اندازه گیری شباهت مسیر.
Ijgi 08 00518 g004 550
شکل 4. بیضی نامشخص یک قطعه درونیابی.
Ijgi 08 00518 g005 550
شکل 5. ویژگی های حرکتی یک قطعه.
Ijgi 08 00518 g006 550
شکل 6. تخمین محدوده عمودی نامشخص بر اساس زاویه چرخش.
Ijgi 08 00518 g007 550
شکل 7. یک خط “مستقیم” با بیضی های باریک.
Ijgi 08 00518 g008 550
شکل 8. یک خط “سیم پیچ” با بیضی های گسترده.
Ijgi 08 00518 g009 550
شکل 9. زاویه افست ناشی از خطای موقعیت.
Ijgi 08 00518 g010 550
شکل 10. نقطه لنگر و بیضی تطبیق آن.
Ijgi 08 00518 g011 550
شکل 11. اندازه گیری شباهت مسیر نامشخص (UTSM) محاسبه زمان-هزینه مسیرهای با طول های مختلف.
Ijgi 08 00518 g012 550
شکل 12. شباهت های بین مسیرهای با افست های مختلف.
Ijgi 08 00518 g013 550
شکل 13. یک مسیر با نقطه بیرونی.
Ijgi 08 00518 g014 550
شکل 14. نسبت نفوذ (IR) در فواصل دورافتاده مختلف.
Ijgi 08 00518 g015 550
شکل 15. نمونه برداری مجدد با فواصل دو و سه.
Ijgi 08 00518 g016 550
شکل 16. IR در فواصل مختلف نمونه گیری مجدد.
Ijgi 08 00518 g017 550
شکل 17. یک جفت مسیر نمونه برداری ناهمزمان.
Ijgi 08 00518 g018 550
شکل 18. IR مسیرهای نمونه برداری ناهمزمان.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید