آموزش GIS : فاصله و اهمیت آن در سیستم اطلاعات جغرافیایی

سیستم اطلاعات جغرافیایی (GIS)و پایش مخاطرات زیست‌محیطی تحت تغییرات آب و هوا: بررسی گسترده

آموزش GIS : فاصله و اهمیت آن در سیستم اطلاعات جغرافیایی

آموزش GIS : فاصله و اهمیت آن در سیستم اطلاعات جغرافیایی:فاصله یک مفهوم مرکزی در جغرافیا است و در نتیجه انواع مختلفی از عملیات وجود دارد که از مفهوم فاصله استفاده می کنند. این مقاله کوتاه به معرفی معیارهای متداول فاصله، هدف عملیات فاصله‌ای، انواع مختلف عملیات و ملاحظات و همچنین کاربردهای نمونه در حوزه فیزیکی و اجتماعی می‌پردازد. عملیات فاصله می تواند بر روی داده های برداری یا شطرنجی انجام شود، اما عملیات و نتایج ممکن است متفاوت باشد. هنگام انجام عملیات فاصله، مهم است که به یاد داشته باشید که چگونه فاصله در حین انجام عملیات مفهوم سازی می شود.

فاصله به عنوان یکی از مفاهیم مهم در GIS، به معنای فاصله فیزیکی بین دو نقطه یا شیء است. در سیستم اطلاعات جغرافیایی، فاصله می‌تواند به عنوان یکی از متغیرهای مهم در تحلیل داده‌های مکانی مورد استفاده قرار گیرد.

اهمیت فاصله در GIS به دلیل این است که این مفهوم می‌تواند به عنوان یکی از شاخص‌های مهم در تحلیل داده‌های مکانی مورد استفاده قرار گیرد. به عنوان مثال، در تحلیل داده‌های مکانی برای شناسایی الگوهای جغرافیایی، فاصله می‌تواند به عنوان یکی از شاخص‌های مهم مورد استفاده قرار گیرد. همچنین، در تحلیل داده‌های مکانی برای مدل‌سازی توزیع جمعیت، فاصله می‌تواند به عنوان یکی از شاخص‌های مهم مورد استفاده قرار گیرد.

در GIS، فاصله می‌تواند به صورت دو بعدی و سه بعدی محاسبه شود. در فاصله دو بعدی، فاصله بین دو نقطه در صفحه نقشه محاسبه می‌شود، در حالی که در فاصله سه بعدی، فاصله بین دو نقطه در فضا محاسبه می‌شود. همچنین، در GIS می‌توان از مفهوم فاصله منطقی نیز استفاده کرد که به معنای فاصله بین دو نقطه بر اساس موانع موجود در مسیر می‌باشد.

در نتیجه، فاصله به عنوان یکی از مفاهیم مهم در GIS، می‌تواند به عنوان یکی از شاخص‌های مهم در تحلیل داده‌های مکانی مورد استفاده قرار گیرد. همچنین، محاسبه فاصله در دو بعد و سه بعد و همچنین استفاده از مفهوم فاصله منطقی، می‌تواند در تحلیل داده‌های مکانی مورد استفاده قرار گیرد.

توضیحات موضوع:

تعاریف
اندازه گیری های مشترک فاصله در GIS
عملیات از راه دور

1. تعاریف

فضا : فضا در این زمینه به طور کلی به عنوان گستره سه بعدی بی حد و مرزی است که در آن اشیا و رویدادها موقعیت و جهت نسبی دارند .

فضای اقلیدسی : فضای اقلیدسی یک فضای متریک است، یعنی فضایی که در آن مفهوم فاصله بین دو نقطه و ویژگی های آن به طور بدیهی تعریف شده و قابل اندازه گیری است. در فضای اقلیدسی می توان مکان (x,y) یک شی را دانست و همچنین می توان فاصله و جهت بین آنها را کمی کرد.

نقطه : یک نقطه در فضا با استفاده از مختصات (x,y) مکان را نشان می دهد.

ویژگی : یک ویژگی یک شی یا رویداد واقع در فضا است. شی ممکن است یک مکان واحد باشد (مانند یک چاه)، که می تواند با استفاده از یک نقطه نشان داده شود، ممکن است یک موجودیت گسترده تر مانند یک رشته کوه را نشان دهد، یا ممکن است نشان دهنده پدیده پیچیده تری باشد، مانند محل درختان بیمار در یک جنگل کاج. .

2. اندازه گیری های مشترک فاصله در GIS

قانون اول جغرافیا بیان می کند که “همه چیز به هر چیز دیگری مربوط است، اما چیزهای نزدیک بیشتر از چیزهای دور مرتبط هستند” (توبلر، 1970). فاصله تجسم کمی مفهوم نزدیک و دور است. در نتیجه، “فاصله” یک مفهوم مرکزی در جغرافیا است که بسیاری از مفاهیم بیشتر بر اساس آن ساخته شده اند. به بیان ساده، فاصله معیاری است که به شما امکان می دهد فضای قابل پیمایش بین دو ویژگی را اندازه گیری کنید. شکل 1 چهار راه مختلف برای پیمایش بین دو نقطه را نشان می دهد. از شکل مشخص است که با توجه به دو نقطه در فضا، راه های مختلفی وجود دارد که می توان از یکی به دیگری رسید. راه های مختلف که در آن فضا طی می شود، روش های مختلفی برای محاسبه فاصله ایجاد می کند. در این مبحث ابتدا روش های رایج محاسبه فاصله در GISc را قبل از معرفی عملیات متداول فاصله معرفی می کنیم. توجه داشته باشید که برای انجام اکثر عملیات فاصله ممکن است از چندین روش اندازه گیری فاصله استفاده شود. انتخاب اندازه گیری فاصله مورد استفاده ممکن است به طور قابل توجهی نتایج عملیات را تغییر دهد.

2.1 فاصله اقلیدسی

فاصله اقلیدسی متداول ترین اندازه گیری فاصله است. با توجه به دو نقطه، $\dpi{100} \small P_{1}(x_{1}، y_{1})، P_{2}(x_{2}، y_{2})$ در فضای دوبعدی اقلیدسی، فاصله اقلیدسی کمترین فاصله بین آنها را «همانطور که کلاغ پرواز می کند» است. از نظر ریاضی، فاصله اقلیدسی (E) به صورت زیر تعریف می شود:

$E(P_{1}، P_{2}) = \sqrt{(x_{1}-x_{2})^{2}+ (y_{1}-y_{2})^{2}}$

علاوه بر اطلاعات موقعیت مکانی دو بعدی، اگر ارتفاع نیز وجود داشته باشد، دو نقطه با 3 مختصات (x، y، z) تعریف می شوند و فرمول فاصله اقلیدسی بین آنها به شرح زیر است:

$\small E(P_{1},P_{2})=\sqrt{(x_{1}-x_{2})^{2} + (y_{1}-y_{2})^{2} + (z_{1}-z_{2})^{2}}$

2.2 فاصله منهتن

فضای بین دو نقطه P1 و P2 به ندرت خالی است. با توجه به قرارگیری ویژگی‌ها بین دو نقطه، ممکن است نتوان مسیر مستقیم «همانطور که کلاغ پرواز می‌کند» را طی کرد. در مورد شهرهای برنامه ریزی شده، جاده ها اغلب در زوایای قائم با یکدیگر برخورد می کنند و شهر را به مجموعه ای از بلوک ها تقسیم می کنند و مسافر را مجبور می کند که فقط در جهت های شرقی-غربی یا شمال-جنوب سفر کند (شکل 1). در چنین حالتی، کوتاه ترین فاصله بین دو نقطه با استفاده از رنگ قرمز در شکل 1 نشان داده شده است. این فاصله، فاصله منهتن (M) یا فاصله تاکسی نامیده می شود و به صورت زیر اندازه گیری می شود:

$\small M(P_{1},P_{2}) = \چپ | x_{1}-x_{2} \right | + \ چپ | y_{1}-y_{2} \right |$

جالب اینجاست که بر خلاف فاصله اقلیدسی که فقط یک کوتاه ترین مسیر بین دو نقطه P1 و P2 دارد، هنگام استفاده از فاصله منهتن، می توان چندین مسیر کوتاه بین این دو نقطه وجود داشت. در شکل 1، خطوط مسیرهای قرمز، زرد و آبی همگی دارای کوتاه ترین طول مسیر 12 هستند، در حالی که فاصله کوتاه ترین مسیر اقلیدسی نشان داده شده با رنگ سبز دارای طول 8.5 است.

به بیان دقیق، فاصله منهتن یک متریک دو بعدی است که در هندسه متفاوتی نسبت به فضای اقلیدسی تعریف شده است، که در آن حرکت فقط به جهت شمال-جنوب، شرق-غرب محدود می شود.

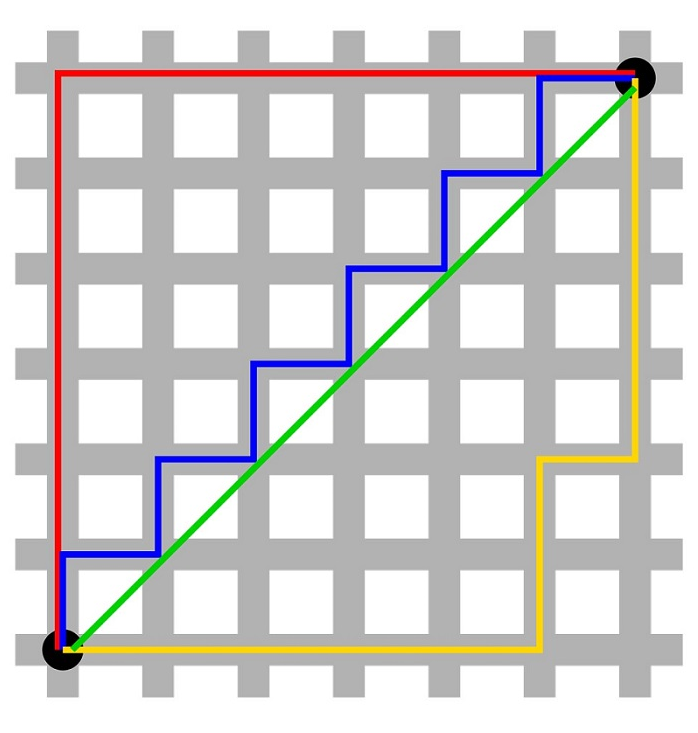
شکل 1. فاصله اقلیدسی و فاصله منهتن. خط سبز مسیر اقلیدسی را بین دو نقطه نشان می دهد در حالی که خطوط قرمز، آبی و زرد مسیرهای منهتن را بین دو نقطه نشان می دهد. هر سه مسیر منهتن فاصله منهتن یکسانی دارند. (تصویر از Wikimedia Commons )

2.3 فاصله هزینه

در یک منظره، سهولت عبور از هر قسمت از منظره ممکن است یکنواخت نباشد. به عنوان مثال، توپوگرافی منظره ممکن است عبور از قسمت های خاصی را سخت تر از سایر قسمت ها کند (لی، لارسون و رکس، 2005). علاوه بر این، ممکن است موانعی (به عنوان مثال کوه ها، حصارها) وجود داشته باشد که ممکن است قسمت های خاصی از چشم انداز را از دسترس دیگران خارج کند. بنابراین، برای چنین مواردی، فاصله بین ویژگی‌ها را می‌توان با «هزینه» پیمایش اندازه‌گیری کرد (داگلاس، 1994؛ تاملین، 2010). فاصله هزینه اغلب به شکل رستر در دسترس است که به آن سطح هزینه می گویند، جایی که ارزش هر پیکسل نشان دهنده هزینه عبور از آن پیکسل است. نمونه ای از چنین شطرنجی، شطرنجی شیب محاسبه شده از یک مدل ارتفاعی دیجیتال (DEM) است. مقدار این سطح هزینه نشان دهنده شیب است، که میزان سختی سفر در مسیرهای خاص را نشان می دهد. برای یافتن هزینه پیمایش بین دو نقطه روی این سطح، باید تمام مقادیر پیکسل‌هایی را که مسیر از آن‌ها عبور می‌کند، اضافه کرد. مقدار هزینه نهایی باید با مسافت واقعی طی شده بین دو نقطه ضرب شود تا فاصله هزینه بدست آید.

2.4 فاصله ژئودزیکی

در حالی که فاصله‌های اقلیدسی و منهتن برای اندازه‌گیری فاصله بر روی داده‌های پیش‌بینی‌شده مناسب هستند، برای سطوح غیراقلیدسی مانند یک کره، که اغلب برای نمایش زمین استفاده می‌شود، مناسب نیستند. کوتاه‌ترین فاصله بین دو نقطه P1 و P2 روی سطح یک کره، با طول و عرض جغرافیایی ( $\small \Phi _{1}،\lambda _{1}$ ) و ( $\small \Phi _{2}،\lambda _{2}$ ) که بر حسب رادیان اندازه‌گیری می‌شود، یعنی فاصله ژئودزیکی (G)، توسط قانون کروی کسینوس‌ها به صورت زیر به دست می‌آید:

$\small G=r\Delta \sigma$

$\small where، \Delta \sigma = \left \{ sin(sin(\varphi _{1})) \cdot sin(sin(\varphi _{2})) + cos(cos(\varphi _{1} )) \cdot cos(cos(\varphi _{2})) \cdot cos(cos(\Delta \lambda)) \راست \}$

$\small and, \Delta \lambda = \left | \lambda _{1} - \lambda _{2} \right |$

بگذارید $x_{2}، y_{2}$ با مختصات ( $x_{2}، y_{2}$ ) و ( $x_{2}، y_{2}$ ) برآمدگی نقاط P1 و P2 روی یک سطح صاف باشد. اجازه دهید eفاصله بین نقاط p1 و p2 در صفحه باشد. بین اندازه گیری فاصله G و e تفاوت وجود دارد. این انحراف زمانی بیشتر می شود که این دو مکان در سطح کره از هم دورتر باشند (شکل 2). بنابراین، هنگام استفاده از اندازه‌گیری‌های فاصله، در نظر گرفتن مکان نقاط روی سطح زمین و پیش‌بینی استفاده‌شده روی داده‌ها مهم است. اگر مکان ها در عرض های جغرافیایی بالاتر قرار داشته باشند، پیش بینی های نامناسب ممکن است هنگام استفاده از عملیات فاصله باعث خطاهای تجزیه و تحلیل شود. اصطلاح فاصله دایره بزرگ گاهی اوقات برای اشاره به فاصله ژئودزیکی زمانی که زمین به عنوان یک کره مدل می شود استفاده می شود. اصطلاح فاصله ژئودتیکی کلی‌تر است زیرا نشان‌دهنده کوتاه‌ترین مسیر روی یک سطح منحنی (مثلاً کره یا بیضی) است که به عنوان فاصله دایره بزرگ کوتاه‌ترین مسیر روی یک کره است، اما نه در همه بیضی‌ها. از آنجایی که فاصله دایره بزرگ فاصله بین دو نقطه روی سطح کره را اندازه می گیرد، نشان دهنده کوتاه ترین مسیر بین دو مکان روی زمین است (کارنی، 2013). بنابراین، هنگام نگاه کردن به یک نقشه مسطح، ممکن است به نظر برسد که یک هواپیما مسیر طولانی‌تری را طی می‌کند، اما در واقع مسیر ژئودزیکی را دنبال می‌کند که هنگام نمایش بر روی نقشه دچار اعوجاج می‌شود.

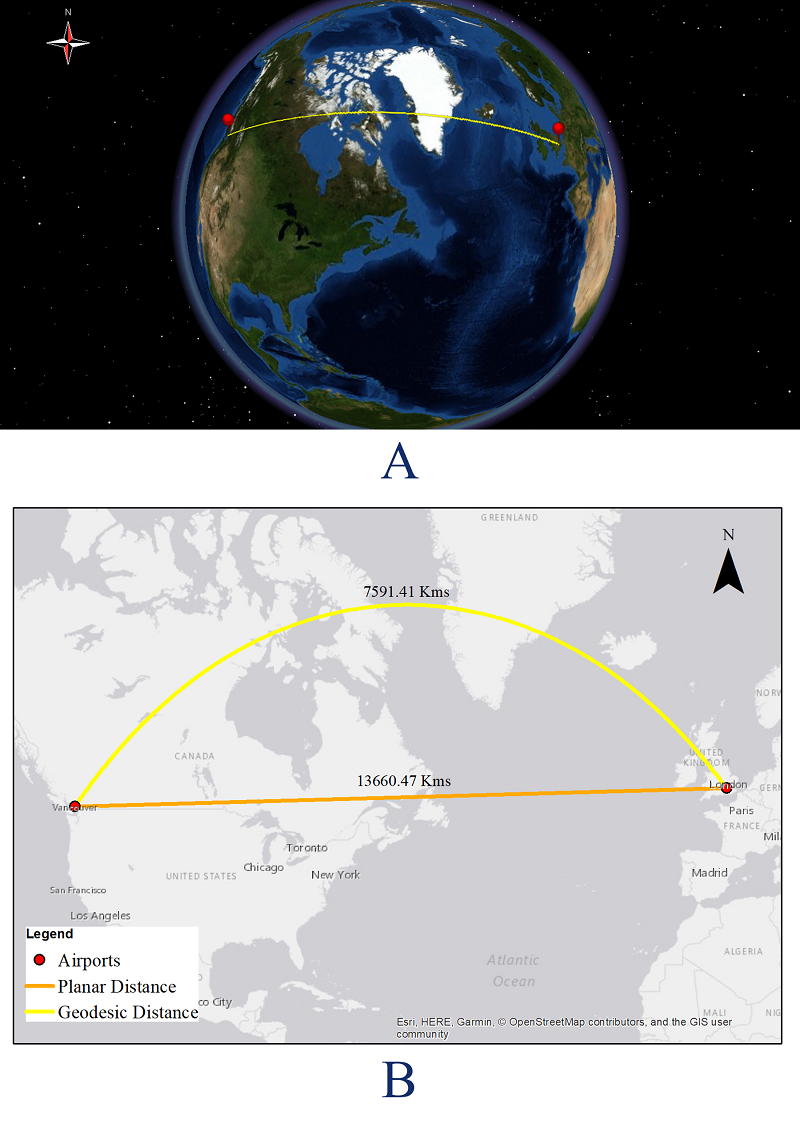
شکل 2. شکل بالا (A) فاصله ژئودزیکی بین فرودگاه هیترو، لندن و فرودگاه بین المللی ونکوور، کانادا را نشان می دهد. تصویر زیر (B) طرح فاصله ژئودزیکی را بر روی نقشه به همراه فاصله مسطح بین دو مکان نشان می دهد.

2.5 فاصله شبکه

همه فضاها را نمی توان به صورت پیوسته بین دو نقطه طی کرد. به عنوان مثال، در یک شبکه جاده ای، حرکت از نقطه ای به نقطه دیگر در امتداد جاده ها است. چنین ساختاری با استفاده از شبکه ای متشکل از گره ها (تقاطع ها) که توسط لبه ها (جاده ها) به هم متصل شده اند نشان داده می شود. شبکه های اجتماعی همچنین از ساختار گره و لبه برای به تصویر کشیدن روابط (به عنوان یال) بین موجودیت ها (که با گره ها مشخص می شوند) استفاده می کنند. فاصله با شمارش تعداد گره های میانی که در نتیجه امید از گره به گره در امتداد لبه ها پیموده شده اند اندازه گیری می شود. با این حال، برای محاسبه کوتاه ترین فاصله بین دو گره در یک شبکه، یک فرمول ساده کافی نیست. الگوریتم هایی مانند الگوریتم Dijkstra برای محاسبه کوتاه ترین مسیر در شبکه مورد نیاز است.

توجه داشته باشید که در مورد شبکه‌های جاده‌ای، حرکت لزوماً از گره به گره (نشان دهنده تقاطع‌ها) نیست، بلکه ممکن است در امتداد لبه‌های معرف جاده‌ها پیوسته باشد. در چنین حالتی، فاصله بین دو نقطه در شبکه راه را می توان با جمع کردن فاصله، بخش به بخش محاسبه کرد. این اندازه گیری اغلب فاصله شبکه جاده یا به اختصار فاصله شبکه نامیده می شود.

3. عملیات از راه دور

این بخش انواع مختلف عملیات فاصله ای را که معمولاً در GIS استفاده می شود، شرح می دهد. بسیاری از موضوعات به تفصیل در فصل های دیگر فهرست شده در بخش «موضوعات مرتبط» پوشش داده شده است. خوانندگان تشویق می شوند برای درمان جامع تر به این فصل ها نگاه کنند.

3.1 بافرها

بافرها با ایجاد مرزی از یک فاصله معین در اطراف یک ویژگی، نواحی پروگزیمال را مشخص می کنند. یکی از متداول ترین وظایف در GIS این است که بفهمیم چه چیزی در نزدیکی یا همسایگی یک مکان قرار دارد. به عنوان مثال، یک دانشمند حفاظت می خواهد مناطق حایل ساحلی ایجاد کند تا از نهرها در برابر تأثیر کاربری های زمین های مجاور محافظت کند (Xiang، 1993). این سوال را می توان با ایجاد بافرهایی در فاصله مورد نیاز در اطراف نهرها برای ترسیم مناطق حفاظت شده حل کرد. بافر یک ویژگی جغرافیایی ناحیه‌ای است که در آن کوتاه‌ترین فاصله از هر مکان در منطقه تا ویژگی کمتر یا مساوی یک فاصله آستانه است.

3.2 ایزوکرون

فاصله را می توان بر حسب زمان نیز تعریف کرد. با توجه به یک بازه زمانی ثابت، می‌توان حلقه‌های بافر مانندی را در اطراف یک ویژگی ترسیم کرد که نشان‌دهنده حداکثر مسافتی است که یک جسم ممکن است در آن فاصله طی کرده باشد، اگر جهت حرکت مشخص نباشد یا مهم نباشد (شکل 3). این حلقه‌های فاصله‌ای مبتنی بر زمان به نام ایزوکرون شناخته می‌شوند (میلر و بریدول، 2009؛ اوسالیوان، موریسون، و شیرر، 2000). ایزوکرون های نشان داده شده در شکل 3 شبکه راه های زیرین را به حساب می آورند. بنابراین، فاصله به عنوان فاصله شبکه محاسبه می شود و هر چند ضلعی نشان دهنده فاصله بالقوه ای است که می توانست از مرکز در هر فاصله زمانی 5 دقیقه طی شود، اگر سرعت وسیله نقلیه حداکثر 100 کیلومتر در ساعت بود. ایزوکرون ها در سناریوهایی مانند دستگیری سارق مفید هستند. پس از گزارش یک جنایت، پلیس ممکن است تصور کلی از سرعت حرکت یک ماشین در منطقه داشته باشد. با آگاهی از سرعت و محل وقوع جرم، پلیس ممکن است برای تعیین محل نصب موانع، ایزوکرون ها را محاسبه کند. توجه داشته باشید که ایزوکرون ها ممکن است دایره های کاملی نباشند. از آنجایی که حرکت خودرو به شبکه جاده محدود می شود، فاصله ممکن است در امتداد جاده ها محاسبه شود (فاصله شبکه جاده) و نه “همانطور که کلاغ پرواز می کند” همانطور که با فاصله اقلیدسی اندازه گیری می شود (شکل 3).

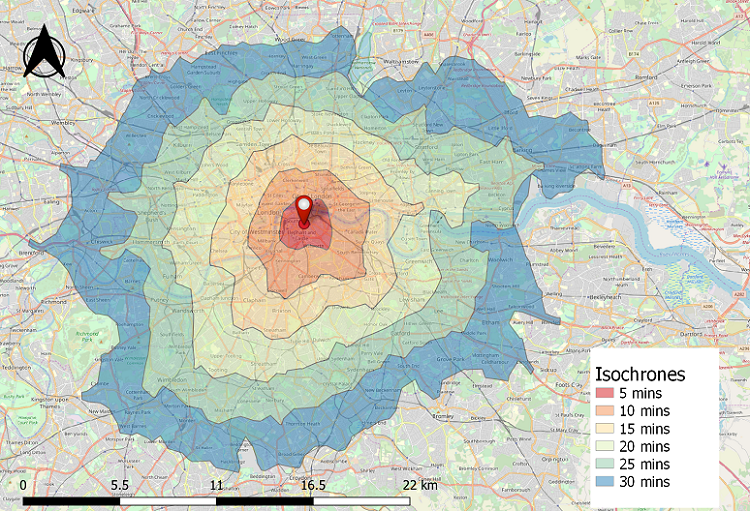
شکل 3. ایزوکرون ها حداکثر فاصله سفر ممکن را از نقطه قرمز مرکزی در هر فاصله 5 دقیقه ای با حداکثر سرعت سفر محدود به 100 کیلومتر در ساعت نشان می دهند.

3.3 ماتریس فاصله

با توجه به مجموعه ای از ویژگی ها، فاصله بین هر جفت ویژگی را می توان در ماتریسی به نام ماتریس فاصله ذخیره کرد (شکل 4). ماتریس فاصله ممکن است یک بار محاسبه شود و هر زمان که فاصله بین ویژگی ها مورد نیاز است به عنوان جدول جستجو استفاده شود. ماتریس فاصله معکوس اصلاحی از ماتریس فاصله است و معکوس فاصله بین ویژگی ها را به جای فواصل واقعی ذخیره می کند (Anselin, 1992). این برای صرفه جویی در زمان محاسباتی در مراحل بعدی تجزیه و تحلیل فضایی است که ممکن است نیاز به همبستگی خودکار یا خوشه‌بندی بین مشاهدات داشته باشد. بنابراین، هنگامی که فاصله به عنوان جایگزینی برای اندازه گیری شباهت استفاده می شود، ویژگی های نزدیکتر باید وزن بیشتری داشته باشند. چندین آمار فضایی، مانند Moran’s I و Getis Ord G*، می توانند به ماتریس فاصله به عنوان ورودی نیاز داشته باشند.

ویژگی های توپوگرافی روی چشم انداز، عبور از یک منظره را سخت تر می کند. با توجه به توزیع ویژگی‌ها، سهولت سفر بین نقاط P1 و P2 ممکن است از P2 تا P3 متفاوت باشد (حتی P2 و P1، زمانی که اختلاف ارتفاع وجود دارد) حتی اگر فاصله اقلیدسی یکسانی داشته باشند. ماتریس هزینه مانند ماتریس فاصله به نظر می رسد اما میزان سختی رسیدن از یک مکان به مکان دیگر را ذخیره می کند. بنابراین، هنگام استفاده از آمارهایی که از ماتریس فاصله استفاده می کنند، بسته به سناریوی کاربردی، ممکن است مهم باشد که ماتریس هزینه را با ماتریس فاصله ضرب کنیم و ماتریس فاصله هزینه را برای ارائه به عنوان ورودی تولید کنیم. بسته به سناریوی برنامه، این تضمین می‌کند که واقعیت‌های روی زمین عبور از چشم‌انداز در نظر گرفته می‌شوند. همچنین، بسته به سناریوی برنامه و در دسترس بودن داده‌ها، روش های مختلفی برای ایجاد ماتریس فاصله هزینه یا سطح وجود خواهد داشت. همانطور که قبلا ذکر شد، هزینه ممکن است به صورت تصویر شطرنجی نیز ارائه شود.

در مورد مجموعه داده های شبکه مانند جاده ها، یک ماتریس فاصله به نام ماتریس مبدا-مقصد (OD) اغلب ایجاد می شود که کوتاه ترین فاصله را بین مجموعه ای از مکان ها ذخیره می کند.

در مورد همه انواع ماتریس هایی که در بالا بحث شد، بسته به اینکه فاصله/هزینه رسیدن از نقطه P1 به نقطه P2 برابر با رفتن از P2 به P1 باشد، ماتریس ممکن است متقارن یا نامتقارن باشد. یک سناریوی مثال زمانی که ممکن است ماتریس های نامتقارن مورد نیاز باشد، زمانی است که محدودیت های شبکه های جاده ای مانع از طی کردن مسیر مشابه با سفر جلو در سفر برگشت می شود. بنابراین، ماتریس های فاصله امکان رمزگذاری فواصل ناهمسان سنجی بین نقاط را فراهم می کنند.

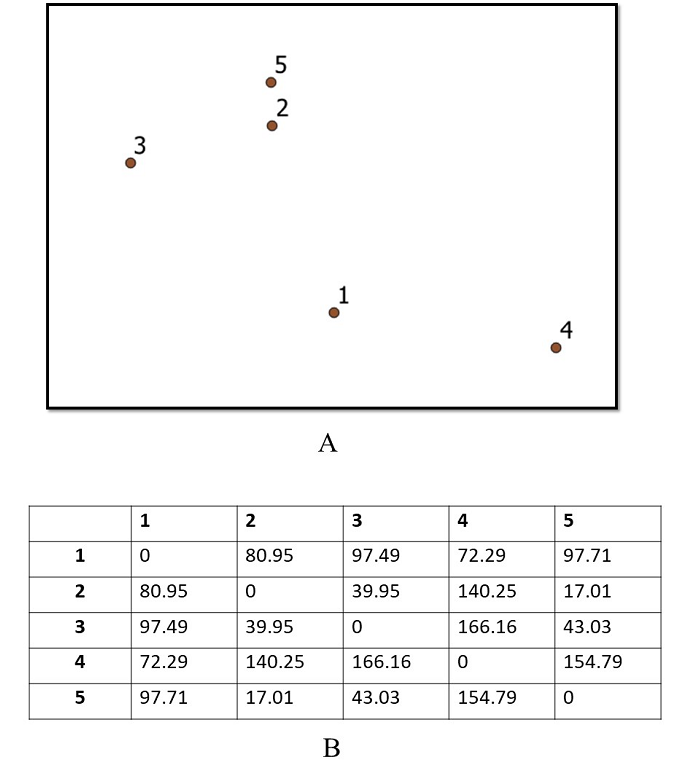
شکل 4. نقاط تصادفی در فضای اقلیدسی (A) و ماتریس فاصله متناظر آن (B). سطر اول و ستون اول ماتریس نشان دهنده شناسه نقطه است، هر ورودی در ماتریس نشان دهنده فاصله بین دو نقطه بر حسب متر است.

3.4 K-نزدیکترین همسایه ها

مجاورت، همانطور که با نزدیکی ویژگی ها بیان می شود، نیز در بسیاری از برنامه ها مورد توجه قرار می گیرد. نزدیکترین همسایگان یک ویژگی گاهی اوقات تأثیر قابل توجهی بر ویژگی مورد علاقه دارند. به عنوان مثال، هنگام راه‌اندازی یک مکان خرده‌فروشی جدید، یک تحلیلگر ممکن است علاقه‌مند باشد تا نزدیک‌ترین رقبای خود را در کجا قرار دهد. چنین عملیاتی به عنوان k-نزدیکترین همسایه (به اختصار k-NN) شناخته می شود که k نشان دهنده تعداد همسایگان مورد علاقه است. k-NN ها را می توان از ماتریس فاصله در صورتی که از قبل محاسبه شده باشد، یا با افزایش تدریجی شعاع جستجو در صورت عدم وجود ماتریس فاصله، پیدا کرد. توجه داشته باشید که در حالی که هر دو بافر و k-NN برای یافتن ویژگی های پروگزیمال استفاده می شوند، برخلاف بافرها، الگوریتم k-NN نیازی به دانش قبلی از شعاع جستجو ندارد. بنابراین، هنگامی که ویژگی ها در فضا پراکنده می شوند،

3.5 فروپاشی فاصله

ویژگی‌های نزدیک به هم شبیه هستند، اما با افزایش فاصله، شباهت بین ویژگی‌ها کاهش می‌یابد. فرآیندهای جغرافیایی زیربنایی که این الگوی فضایی را ایجاد می کنند، با افزایش فاصله از منبع، قدرت خود را از دست می دهند. بنابراین، فروپاشی فاصله روشی برای مدل‌سازی تأثیر فرآیندهای جغرافیایی به عنوان تابعی از فاصله است تا مشخص شود که ویژگی‌های مختلف چقدر با یکدیگر تعامل خواهند داشت. برهمکنش فضایی بین ویژگی ها به طور کلی فرض می شود که عملکرد فروپاشی صاف با توجه به فاصله دارد (آنسلین، 1998). بسته به سناریوی کاربردی، نرخ فروپاشی به صورت یک تابع خطی، درجه دوم یا نمایی مدل‌سازی می‌شود (Krivoruchko، 2011، ص 302). مدل‌سازی فروپاشی فاصله گام مهمی برای تکنیک‌های زمین‌آماری مانند کریجینگ است. یک مثال ساده از کاهش فاصله این است، هنگام تلاش برای مدل‌سازی فراوانی پوشش گیاهی که به فاصله تا منابع آب بستگی دارد. مدل‌سازی چگونگی تغییر فراوانی با فاصله از منبع آب مهم است. استفاده از مدل درجه دوم فروپاشی فاصله در این مورد منجر به کاهش بسیار شدید فراوانی با فاصله نسبت به استفاده از مدل خطی می شود.

فروپاشی فاصله همچنین می تواند برای یافتن ناحیه نفوذ و تعیین ویژگی های متقابل استفاده شود. به عنوان مثال، مدل‌های گرانش معمولاً برای مدل‌سازی مهاجرت افراد بین شهرها استفاده می‌شوند (Foot & Milne, 1984; Karemera, Oguledo, & Davis, 2000; Plane, 1984). در چنین مدلی، جریان مردم به توده (مثلاً جمعیت، فرصت اقتصادی) شهر و فاصله بین شهرها بستگی دارد. کاهش فاصله ممکن است به عنوان معکوس مجذور فاصله مدل شود تا این واقعیت را توضیح دهد که هر چه شهرها دورتر باشند، احتمال حرکت افراد کمتر می شود. بنابراین، احتمال تعامل دو شهر با افزایش فاصله کاهش می یابد.

3. 6 خود همبستگی

ممکن است ویژگی ها به طور یکنواخت در فضا توزیع نشوند. در واقع، با توجه به قانون اول جغرافیا، ویژگی های مشابه تمایل دارند نزدیک به یکدیگر قرار گیرند. همبستگی خودکار معیاری از شباهت ویژگی های مجاور را ارائه می دهد. به منظور اندازه گیری خودهمبستگی با استفاده از آماری مانند Global Moran’s I، باید میانگین فاصله بین ویژگی ها در فرآیند مشاهده شده را با فاصله متناظر در صورتی که ویژگی ها توسط یک فرآیند تصادفی تولید شده اند مقایسه کرد (لی، کالدر، و کرسی، 2007). . بنابراین، دانستن فاصله بین ویژگی‌ها یک شاخص کلیدی برای این است که آیا مشاهدات تولید شده توسط فرآیند زیربنایی در فضا خوشه‌بندی شده‌اند یا خیر.

3.7 خوشه بندی

خوشه‌ها توسط گروهی از ویژگی‌ها تعریف می‌شوند که نزدیک‌تر از یک فرآیند تصادفی به یکدیگر قرار دارند. در حالی که معیارهای خودهمبستگی جهانی تمایل ویژگی‌های یک مجموعه داده را به خوشه‌بندی کمی می‌کند، مکان خوشه‌ها را مشخص نمی‌کند. برای یافتن مکان خوشه‌های منفرد، به جای بررسی یکباره کل مجموعه داده، باید زیرمجموعه‌های ویژگی‌های به‌هم پیوسته فضایی ارزیابی شوند. ساده‌ترین راه برای پیدا کردن خوشه‌ها با نگاه کردن به گروهی از ویژگی‌ها برای تعیین اینکه آیا میانگین فاصله بین ویژگی‌ها (تراکم) بیشتر از همسایگی آن است یا خیر. این ایده توسط متریک Local Moran’s I گرفته شده است.

3.8 فروشنده دوره گرد

مسئله فروشنده مسافر بر اساس تحلیل کوتاه‌ترین مسیر در مجموعه داده‌های شبکه است تا کارآمدترین مسیر را برای بازدید از یک سری مکان‌ها و بازگشت به مبدا پیدا کند. راندمان در اینجا را می توان بر حسب مسافت طی شده، زمان یا هر روش مناسب دیگری اندازه گیری کرد. دستیابی به راه حل دقیق برای این مشکل از نظر محاسباتی دشوار است، به خصوص زمانی که تعداد شهرها زیاد باشد. اما، الگوریتم‌های اکتشافی می‌توانند برای یافتن راه‌حل‌های دقیق منطقی برای مشکل فروشنده دوره گرد مورد استفاده قرار گیرند (اورپونن، 1990؛ شارما، میوک، و دارماراج، 2005). یک تغییر رایج از مشکل فروشنده دوره گرد در GIS به عنوان مشکل مسیریابی وسیله نقلیه نامیده می شود. یک مثال کاربردی از مشکل فروشنده دوره گرد، فروشنده ای است که سعی می کند به بهترین نحو در مجموعه ای از مکان های برنامه ریزی شده برای فروش محصولات خود سفر کند. بدین ترتیب،

3.9 نزدیکترین تسهیلات

با توجه به یک شبکه جاده و اطلاعات در مورد تأسیسات واقع در طول شبکه، تجزیه و تحلیل نزدیکترین تسهیلات، نزدیکترین تسهیلات را به هر مکان مورد علاقه تعیین می کند. این تحلیل از الگوریتم های کوتاه ترین مسیر استفاده می کند و برای شرایط اضطراری مفید است. به عنوان مثال، در صورت اورژانس پزشکی، کاربر ممکن است نیاز داشته باشد که بداند نزدیکترین مرکز بیمارستان در کجا واقع شده است.

3.10 منطقه خدمات

Service Area یکی دیگر از عملیات های مبتنی بر شبکه است و مشابه isochrones است. در این حالت، با توجه به موقعیت مکانی (معمولاً به عنوان تسهیلات، مانند ایستگاه آتش نشانی، ایستگاه پلیس) در یک شبکه جاده ای، منطقه خدمات منطقه جغرافیایی را پیدا می کند که می توان از تأسیسات در یک دوره زمانی معین به آن دسترسی داشت. و بالعکس. بنابراین در این عملیات زمان سفر تعیین کننده مسافت است. تجزیه و تحلیل منطقه خدمات می تواند به اطمینان حاصل شود که محله های مختلف به اندازه کافی از امکانات شهری برخوردار هستند کمک می کند.

منابع:

Anselin, L. (1992). تجزیه و تحلیل داده های مکانی با GIS: مقدمه ای بر کاربرد در علوم اجتماعی. تحقیقات سیستمی، 1-54.

Anselin, L. (1998). زیرساخت های تحقیقاتی GIS برای تحلیل فضایی بازارهای املاک و مستغلات. مجله تحقیقات مسکن، 9 (1)، 113-133. DOI: 10.5555/jhor.9.1.e523670p713076p1

داگلاس، دی اچ (1994). مسیر کم هزینه در GIS با استفاده از سطح هزینه انباشته و خطوط شیبدار. Cartographica: The International Journal for Geographic Information and Geovisualization، 31 (3)، 37-51. DOI: 10.3138/D327-0323-2JUT-016M

Foot, DK, & Milne, WJ (1984). برآورد مهاجرت خالص در یک مدل گرانش چند منطقه ای توسعه یافته مجله علوم منطقه ای، 24 (1)، 119-133. DOI: 10.1111/j.1467-9787.1984.tb01023.x

گتیس، ا. (2009). ماتریس وزن های فضایی تحلیل جغرافیایی، 41 (4)، 404-410.

Karemera, D., Oguledo, VI, & Davis, B. (2000). تحلیل مدل جاذبه مهاجرت بین المللی به آمریکای شمالی اقتصاد کاربردی، 32 (13)، 1745-1755. DOI: 10.1080/000368400421093

کارنی، CFF (2013). الگوریتم های ژئودزیک مجله ژئودزی، 87 (1)، 43-55. DOI: 10.1007/s00190-012-0578-z

کریوروچکو، ک. (2011). تجزیه و تحلیل داده های آماری مکانی برای کاربران GIS . Redlands: Esri Press.

لی، اچ، کالدر، کالیفرنیا، و کرسی، ن. (2007). فراتر از موران I: آزمون وابستگی فضایی بر اساس مدل خودرگرسیون فضایی. تحلیل جغرافیایی، 39 (4)، 357-375. DOI: 10.1111/j.1538-4632.2007.00708.x

لی، ایکس، لارسون، سی ام، و رکس، AB (2005). ایجاد بافر روی سطوح نقشه کشی و علم اطلاعات جغرافیایی، 32 (3)، 195-212. DOI: 10.1559/1523040054738945

Miller, HJ, & Bridwell, SA (2009). یک نظریه میدانی برای جغرافیای زمانی. سالنامه انجمن جغرافیدانان آمریکایی، 99 (1)، 49-75. DOI: 10.1080/00045600802471049

O’Sullivan, D., Morrison, A., & Shearer, J. (2000). استفاده از GIS دسکتاپ برای بررسی دسترسی به وسیله حمل و نقل عمومی: یک رویکرد هم زمان مجله بین المللی علوم اطلاعات جغرافیایی، 14 (1)، 85-104. DOI: 10.1080/136588100240976

Orponen, P. (1990). در مورد کاهش تقریبی حفظ: مشکلات کامل و اقدامات قوی (نسخه تجدید نظر شده).

Plane, DA (1984). فضای مهاجرت: نقشه برداری مدل گرانشی دوگانه از جدایی نسبی بین ایالتی. سالنامه انجمن جغرافیدانان آمریکایی، 74 (2)، 244-256. DOI: 10.1111/j.1467-8306.1984.tb01451.x

سرکار، دی.، سیبر، آر.، و سنگوپتا، آر. (2016). ملاحظات علم GIS در شبکه های اجتماعی فضایی. در JA Miller, DO Sullivan, & N. Wiegand (Eds.), Lecture Notes in Computer Science (جلد 1، صفحات 85-98) . انتشارات بین المللی Springer. DOI: 10.1007/978-3-319-45738-3_6

Sharma, O., Mioc, D., Anton, F., & Dharmaraj, G. (2006). الگوریتم تقریب فروشنده دوره گرد برای شبکه های جاده ای واقعی. در ISPRS WG II/1،2،7، VII/6 سمپوزیوم بین‌المللی مدل‌سازی فضایی-زمانی، استدلال فضایی، تحلیل فضایی، داده‌کاوی و ترکیب داده (STM 2005)، پکن، چین تیلور و فرانسیس. مجموعه کتاب های ISPRS پیشرفت در تحلیل مکانی-زمانی

Tobler، WR (1970). یک فیلم کامپیوتری شبیه سازی رشد شهری در منطقه دیترویت. جغرافیای اقتصادی، 46 ، 234. DOI: 10.2307/143141

تاملین، دی (2010). انتشار امواج شعاعی هزینه سفر در یک شبکه مجله بین المللی علم اطلاعات جغرافیایی، 24 (9)، 1391–1413. DOI: 10.1080/13658811003779152

اهداف یادگیری:

انواع فاصله (اقلیدسی، منهتن، شبکه، فاصله دایره بزرگ) را متمایز کنید و توصیف کنید که باید برای اندازه گیری نقطه به نقطه در مطالعات موردی مختلف شامل سفر، حرکت حیوانات، کاربردهای شهری و انتشار منطقه ای استفاده شود.
توضیح دهید که چگونه یک عملیات فاصله می تواند یک متغیر باینری، یک متغیر ترتیبی یا یک متغیر پیوسته تولید کند.
سناریوهایی را توصیف کنید که عملیات فاصله برای تجزیه و تحلیل جغرافیایی مورد نیاز است (ایجاد خط مشی، اندازه گیری کاهش فاصله، تعیین مناطق خدماتی، و تعیین احتمالات تعامل).
مواردی را توصیف کنید که خروجی یک عملیات فاصله یک چند ضلعی، خط، سطح شطرنجی یا ماتریس عددی باشد.

سوالات ارزشیابی آموزشی:

توضیح دهید که چرا روش های مختلف سفر باعث ایجاد فواصل متفاوت می شود.
هزینه ها و مزایای یک بافر چند حلقه در سطح فاصله اقلیدسی را توضیح دهید.
نحوه اعمال عملیات فاصله را برای مجموعه ای از نقاط، خطوط یا چند ضلعی ها توضیح دهید.
دقت بین بافرهای بردار و شطرنجی و نقش اندازه سلول در تولید بافرهای شطرنجی را مقایسه کنید.
چه نوع قوانین دنیای واقعی وجود دارد که از طریق استفاده از عملیات فاصله GIS برای مدلسازی محیط ساخته شده اجرا می شود؟
چند مفهوم عمده در جغرافیا که نیاز به عملیات از راه دور دارند را نام ببرید.
نمونه هایی از بافرهای تولید شده بر اساس محاسبه هزینه جابجایی را شرح دهید.

سیستم اطلاعات جغرافیایی

آموزش GIS : فاصله و اهمیت آن در سیستم اطلاعات جغرافیایی

آموزش GIS : فاصله و اهمیت آن در سیستم اطلاعات جغرافیایی

قبلیاهمیت فاصله و جهت در GIS

بعدی شکل زمین، سطح دریا و ژئوئید

مطالب مرتبط ...

آموزش مقاله نویسی با هوش مصنوعی:تجربه ای متفاوت

همه چیز درباره تحلیل فضایی

تکنیک های تحلیل فضایی و استفاده از آنها در تجارت

بدون دیدگاه

دیدگاهتان را بنویسید لغو پاسخ