اهمیت فاصله و جهت در GIS

سیستم اطلاعات جغرافیایی (GIS)و پایش مخاطرات زیست‌محیطی تحت تغییرات آب و هوا: بررسی گسترده

اهمیت فاصله و جهت در GIS :همانطور که فاصله، جهت نیز نقش مهمی در GIS ایفا می کند. این مقاله ابتدا روش های مختلف اندازه گیری جهت را به صورت کمی یا کیفی خلاصه می کند. فرمول ها و مثال ها ارائه شده است. در ادامه، تفاوت های اساسی فاصله و جهت در توصیف روابط فضایی بررسی می شود. ویژگی‌های زاویه‌ها در زمینه GIS تأکید می‌شود. و طبقه بندی هر دو جهت اصلی و تصویری نشان داده شده است. با تمرکز بر عملیات کمی، عملیات جهت‌گیری مختلف بر اساس عواملی مانند مدل داده‌های زیربنایی (بردار یا شطرنجی) و اینکه آیا اثر جهت به طور صریح یا ضمنی در داده‌ها تعبیه شده است، طبقه‌بندی و توضیح داده می‌شوند.

توضیحات موضوع:

تعاریف
جهت اندازه گیری در GIS
عملیات جهت دار در GIS
فاصله در مقابل جهت

1. تعاریف

جهت : جهت در GIS عموماً به معنای موقعیتی است که یک ویژگی جغرافیایی به سمت آن حرکت می کند یا رو به رو می شود. معمولاً به صورت یک بردار در فضای اقلیدسی نشان داده می شود.

زاویه : اندازه گیری کمی جهت است.

اثر جهت : مشابه اثر فاصله، اثر جهت تاثیر جهت را در فرآیند جغرافیایی و الگوی تولید شده آن به تصویر می‌کشد.

همسانگردی : همسانگردی به معنای یکنواختی در همه جهات است در حالی که ناهمسانگردی نشان دهنده وجود تنوع در جهات مختلف است.

2. اندازه گیری جهت در GIS

مانند فاصله، جهت به عنوان راهی برای توصیف روابط بین ویژگی های جغرافیایی استفاده می شود. به طور خاص، اغلب برای نشان دادن مکان و حرکت ویژگی های جغرافیایی استفاده می شود. قبل از اینکه ما فناوری هایی مانند جی پی اس داشته باشیم، اجداد ما با بررسی رابطه بین جهت حرکت یک قایق و جهت گیری آن به سمت قطبی، مسیریابی در دریا را آموخته بودند. توسعه هندسه درک ما از جهت را بیشتر کرد و مهمتر از همه، راهی برای اندازه گیری کمی و در نتیجه مقایسه جهت ها در اختیار ما قرار داد. این مقاله اندازه گیری جهت را از منظر کمی و کیفی مورد بحث قرار می دهد.

2.1 جهت کمی

مفهوم زاویه برای اندازه گیری کمی جهت استفاده می شود. برای انجام این کار، ابتدا باید یک جهت اولیه و یک جهت تعریف کرد که در شکل 1 نشان داده شده است.

در GIS، جهت عمدتاً در یک صفحه (یا فضای اقلیدسی) مورد مطالعه قرار می گیرد، در حالی که جهت معمولاً به عنوان یک بردار با استفاده از مختصات دو نقطه (به عنوان مثال، مبدا و مقصد) نشان داده می شود. به عنوان مثال، در سیستم مختصات دکارتی دو نقطه P ₁ وجود دارد : ( x ₁ , y ₁ ) و P ₂ : (x ₂ , y ₂ ) و جهت آنها به صورت بردار تعریف می شود $\underset{P_1P_2}{\rightarrow}$ : (Δ x , Δ y ) ، که در آن Δ x = x ₂ – x ₁ و Δ y = y ₂ – y₁ . اگر یکی از محورهای متعامد جهت اولیه در نظر گرفته شود (مثلاً محور x ) و جهت گیری به سمت محور دیگر (مثلاً محور y ) به عنوان جهت تعریف شود، آنگاه زاویه بردار را می توان به صورت زیر محاسبه کرد $\textup{\, tan}\: \theta = \frac{\Delta _y}{\Delta _x} \: \textup{or}\: \: \theta = tan ^{-1} \frac{\Delta _y }{\Delta _x}$ : این به صورت هندسی در شکل 1.B نشان داده شده است.

برخلاف سیستم مختصات دکارتی، سیستم مختصات قطبی روش ساده‌تری برای اندازه‌گیری زاویه جهت در صفحه اقلیدسی است. در واقع از زاویه به صراحت برای تشکیل مختصات دو بعدی استفاده می شود. همانطور که شکل 1.C نشان می دهد، در سیستم مختصات قطبی که در آن L محور قطبی و O قطب است، مکان یک نقطه به صورت ( θ, r ) نشان داده می شود که θ زاویه جهت و r فاصله از آن است. قطب به نقطه هدف

مختصات را می توان بین سیستم مختصات دکارتی و سیستم مختصات قطبی تبدیل کرد. فرمول های خاصی را می توان تقریباً در هر کتاب درسی هندسه یافت. سیستم مختصات دکارتی به طور گسترده در GIS استفاده می شود، بنابراین بحث های زیر از آن به عنوان سیستم مختصات پیش فرض برای بحث در مورد ویژگی ها و عملیات جهت ها استفاده می کنند. همچنین شایان ذکر است که این سیستم های مختصات را می توان از یک صفحه به یک کره نیز گسترش داد. در یک کره، دو زاویه، به عنوان مثال، طول و عرض جغرافیایی، اغلب برای مکان یابی یک نقطه استفاده می شود.

در سیستم مختصات دکارتی، حتی اگر جهت اولیه با محور هم تراز نباشد، امکان اندازه گیری زاویه نیز وجود دارد. به طور خاص می توان از زاویه برای اندازه گیری رابطه بین دو جهت دلخواه استفاده کرد که در این سیستم به صورت دو بردار نمایش داده می شوند. برای مثال، در شکل 1.D دو بردار وجود دارد $\underset{u}{\rightarrow}$ : (Δ x ₁₂ , Δ y ₁₂ ) و $\underset{v}{\rightarrow}$ : (Δ x ₃₄ , Δ y ₃₄ ) ; زاویه θ بین این دو جهت به صورت cos θ = محاسبه می شود $\frac{\vec{u}\cdot\vec{v}}{|\vec{u}|\cdot|\vec{v}|}$ . تفاوت بین زاویه‌های شکل‌های 1.B و 1.D ناشی از مفاهیم همسانگردی ثابت و شعاعی است (Zhu et al., 2019).

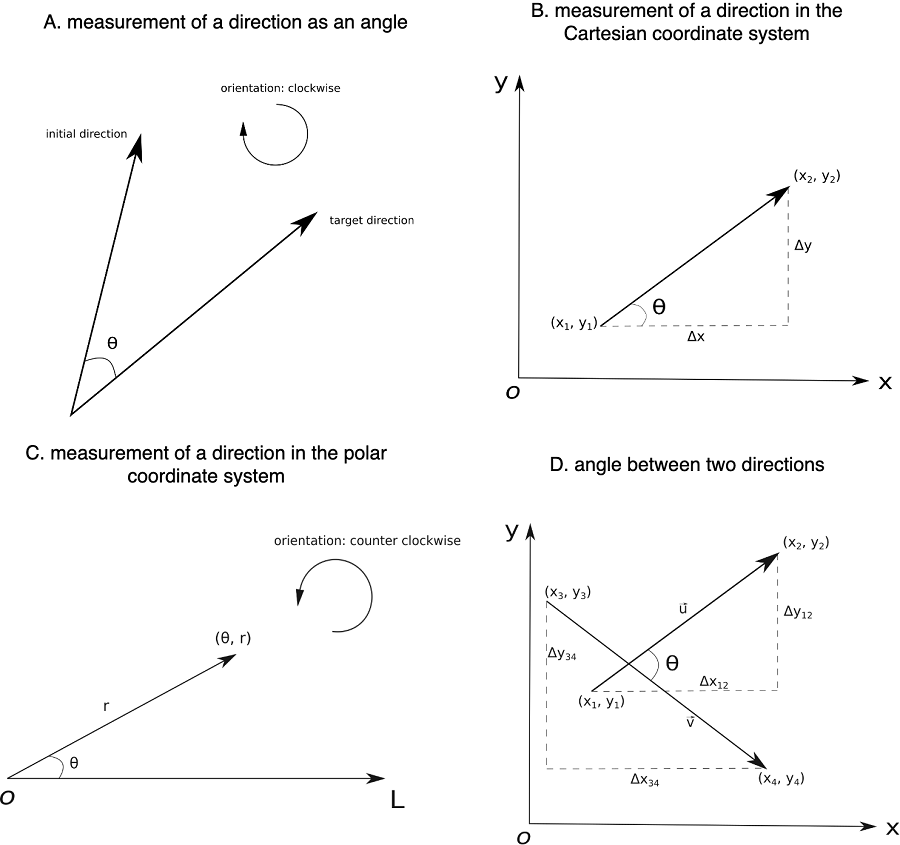
شکل 1. اندازه گیری جهت. منبع: نویسندگان

زاویه ها معمولاً با استفاده از واحد درجه (º) یا رادیان (راد) تعیین می شوند. محدوده درجه از 0 درجه تا 360 درجه است و می تواند اعشاری یا در قالب “درجه-دقیقه-ثانیه” (1º = 60′ = 360″) باشد. محدوده رادیان از 0 تا 2π است. بین درجه و رادیان برابر است با 1º = $\frac{\pi}{180}راد$ . هیچ محدودیتی در مورد استفاده از واحد در GIS وجود ندارد، اما در عمل، اگر از زاویه در محاسبات ریاضی استفاده شود، معمولاً از واحد رادیان استفاده می شود، در حالی که اگر هدف، ناوبری باشد. یا برای تجسم زوایا روی نقشه ها، واحد درجه اغلب به کار می رود. بعلاوه، اگرچه تعریف زاویه از مقادیر منفی پشتیبانی نمی کند، معمولاً از علامت منفی برای نشان دادن اینکه جهت در جهت مخالف است استفاده می شود. به عنوان مثال، اگر جهت با – θ اندازه گیری می شوددر سیستم مرجع شکل 1.A، به این معنی است که جهت θ از جهت اولیه در جهت خلاف جهت عقربه های ساعت فاصله دارد. از طرف دیگر، همان زاویه را می توان به صورت 360 – θ (بر حسب درجه) یا 2π – θ (بر حسب رادیان) اندازه گیری کرد.

2.2 جهت گیری کیفی

برخلاف رابطه کمی که بر محاسبات هندسی متکی است، جهت کیفی مبتنی بر مقایسه بدون استفاده از مقادیر عددی است. این بخش دو نوع جهت کیفی کلاسیک را توضیح می دهد: کاردینال و تصویری و همچنین مبهم بودن آنها در زبان طبیعی.

2.2.1 دستورالعمل های اصلی

جهت‌های اصلی به شمال، جنوب، شرق و غرب دسته‌بندی می‌شوند (و در یک دانه‌بندی دقیق‌تر، چهار جهت دیگر را می‌توان اضافه کرد: شمال شرقی، شمال غربی، جنوب شرقی و جنوب غربی). اینها اغلب در ناوبری و نجوم استفاده می شوند. با استفاده از جهت های اصلی، جهت اولیه به عنوان خط شمال به جنوب تعریف می شود که مرجع “شمال” را تعیین می کند. چندین مرجع پرکاربرد “شمال” وجود دارد. شمال واقعی (یا شمال جغرافیایی) از قطب شمال به عنوان مرجع استفاده می کند و در امتداد جهت خطوط طول جغرافیایی قرار دارد. برای تعیین محل قطب شمال، مردم در زمان های قدیم از ستاره هایی مانند قطبی استفاده می کردند، در حالی که اخیراً قطب نما ژیروسکوپی طراحی شده بود که تحت تأثیر زمان روز یا شرایط آب و هوایی قرار نمی گرفت. دومین مورد رایج “شمال” توسط یک قطب نما مغناطیسی اندازه گیری می شود. و به طور مناسب شمال مغناطیسی نامیده می شود. در این مرجع، “شمال” به جای محور چرخش زمین، با خطوط نیروی مغناطیسی زمین همسو می شود. در نهایت، برای نقشه های پیش بینی شده (به عنوان مثال، مرکاتور عرضی جهانی)، “شمال” گاهی اوقات به عنوان شبکه شمالی شناخته می شود که به صورت محلی برای مناطق یا شبکه ها تعریف می شود و با نصف النهار مرکزی هم تراز است. شایان ذکر است که جهت خطوط شمال به جنوب در این سیستم های مرجع مختلف در اکثر موارد با یکدیگر همسو نیستند. برای تجسم جهت اصلی، اغلب از قطب نما رز استفاده می شود. که به صورت محلی برای زون ها یا شبکه ها تعریف می شود و با نصف النهار مرکزی همسو می شود. شایان ذکر است که جهت خطوط شمال به جنوب در این سیستم های مرجع مختلف در اکثر موارد با یکدیگر همسو نیستند. برای تجسم جهت اصلی، اغلب از قطب نما رز استفاده می شود. که به صورت محلی برای زون ها یا شبکه ها تعریف می شود و با نصف النهار مرکزی همسو می شود. شایان ذکر است که جهت خطوط شمال به جنوب در این سیستم های مرجع مختلف در اکثر موارد با یکدیگر همسو نیستند. برای تجسم جهت اصلی، اغلب از قطب نما رز استفاده می شود.

جهت اصلی را می توان با استفاده از مفهوم آزیموت و یاتاقان تعیین کرد. از نظر آزیموت، جهت اولیه می تواند هر یک از “شمال” فوق الذکر باشد و جهت آن در جهت عقربه های ساعت است. زاویه آزیموت از 0 درجه (شمال)، تا 90 درجه (شرق)، 180 درجه (جنوب) و 270 درجه (غرب)، تا 360 درجه (دوباره شمال و منطبق با 0 درجه) متغیر است. یاتاقان همچنین از یکی از خطوط شمالی-جنوبی فوق الذکر به عنوان مرجع استفاده می کند، اما جهت گیری می تواند در جهت عقربه های ساعت یا خلاف جهت عقربه های ساعت باشد که از “شمال” یا “جنوب” شروع می شود. بنابراین، زاویه برای یاتاقان از 0º تا 90º متغیر است. یک فرمت معمولی یاتاقان مانند: شمال 25 درجه غربی است، به این معنی که جهت هدف 25 درجه از جهت اصلی “شمال” فاصله دارد، و جهت آن به سمت غرب است، یعنی خلاف جهت عقربه های ساعت (شکل 2).

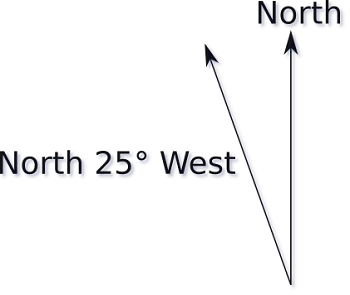
شکل 2. نمونه ای از بلبرینگ. منبع: نویسندگان

تاکنون، جهت ها همه در فضای اقلیدسی مورد بحث قرار گرفته اند. با این حال، زمانی که فضا منحنی است (فضای غیر اقلیدسی)، جهت در فواصل طولانی باید متفاوت عمل کند. به عنوان مثال، جهت یک دایره بزرگ در سطح زمین، آزیموت واقعی نامیده می شود که زاویه آن دائماً در طول نصف النهارهای متوالی تغییر می کند. اما در مواردی که دایره بزرگ با استوا یا هر نصف النهار منطبق باشد، آن را آزیموت ثابت می نامند (کمپبل، 1993).

2.2.2 جهت های فرافکنی

برخلاف جهت‌های اصلی، که از یک سیستم مرجع جهانی استفاده می‌کنند، جهت‌های تصویری یک دیدگاه محلی را اتخاذ می‌کنند. نمونه هایی از جهت های تصویری (سه تایی) عبارتند از: بین، قبل، چپ، و غیره. اینها اغلب در زندگی روزمره ما استفاده می شوند و از یک چارچوب مرجع ذاتی یا دیکتیک استفاده می کنند (جهت های اصلی از یک چارچوب مرجع بیرونی استفاده می کنند). کلمنتینی (2013) یک مدل 5 تقاطع را برای طبقه بندی جهت های پرتابی سه تایی در بین سه ویژگی جغرافیایی بدون اشاره به هیچ چارچوب مرجع تعریف کرد (شکل 3 را ببینید). برای استنباط روابط تصویری سه تایی بر اساس موارد مشاهده شده، کلمنتینی و همکاران. (2019) سیستم استدلالی را پیشنهاد کرد که هم قوانین جایگشت و هم ترکیب را اعمال می کرد.

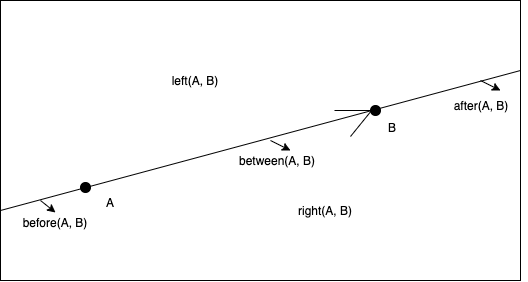
شکل 3. مدل پنج تقاطع برای روابط تصویری سه تایی بین نقاط. منبع: نویسندگان

2.2.3 ابهام در جهت گیری های کیفی

بسیاری از این جهات کیفی ذکر شده با برخی حروف اضافه انگلیسی مطابقت دارند که اغلب در راهیابی روزانه، روباتیک و پاسخگویی به سؤالات جغرافیایی استفاده می شود (رتز-اشمیت، 1988). به عنوان مثال، ما از جهت کلامی مسیر استفاده می کنیم، مانند چرخش کمی به چپ در گذرگاه بعدی، برای کمک به ناوبری. با این حال، استفاده از چنین جهت های کیفی در زبان طبیعی می تواند مبهم باشد. به عنوان مثال، هنگام استفاده از جهت های تصویری، چارچوب مرجع اغلب مبهم است، بنابراین یک عامل شناختی باید برای تفسیر آنها به زمینه ها تکیه کند (بیتمن، 2010). برای مثال، ریچر و کلیپل (2007) با تمرکز بر جهت مسیر، یک رویکرد محاسباتی را برای ابهام‌زدایی از روابط جهتی کمی بین نقطه تصمیم و نقطه عطف ایجاد کردند. این نوع چارچوب محاسباتی ابهام‌زدایی را بیشتر تسهیل می‌کند،

3. عملیات جهت دار در GIS

جهت در انواع مطالعات و کاربردهای فضایی اعمال شده است. معمولی ترین آنها استفاده از جهت، به ویژه جهت کیفی، برای استدلال فضایی است (فرکسا، 1991، فرانک، 1996، کلمنتینی، 2009). از آنجایی که استدلال فضایی کیفی می تواند به خودی خود یک موضوع واحد باشد و اغلب به عنوان یک نوع عملیات GIS اجرا نمی شود، این مقاله به تفصیل در مورد آن بحث نمی کند. در عوض، عملیات کمی که جهت را برای درک الگوهای فضایی اعمال می‌کنند، مورد بحث قرار خواهند گرفت.

3.1 جهت در تعاملات فضایی

تعامل فضایی معمولاً به عنوان جریان‌های بین موجودیت‌های جغرافیایی تعریف می‌شود، که در آن جریان اغلب به‌عنوان یک بردار نشان داده می‌شود که هم اطلاعات فاصله و هم جهت را در خود جای داده است (هاینز و فاثرینگهام، 1984). از آنجایی که جهت به صراحت در تعریف جریان ها گنجانده شده است، بسیاری از عملیات از این گروه جهت را در نظر گرفته اند. در زیر چند نمونه آورده شده است.

3.1.1 عملیات شطرنجی پایه

برای محاسبه جهت هر سلول در یک شطرنجی، معمولاً از عملیات جهت جریان در GIS استفاده می شود. این عملیات جهت سلول ها را به عنوان شیب دارترین نزول ویژگی هدف در همسایگی محاسبه می کند. یک مثال، محاسبه جنبه در مدل رقومی ارتفاع (DEM) است. به طور مشابه، انباشت جریان، انباشت (وزن دار) جریان ها را به سلول هدف پایین شیب محاسبه می کند. این عملیات مبتنی بر جریان به شدت در کاربردهای هیدرولوژیکی (مثلاً برای تعیین جریان جریان) استفاده می شود. عملیات اساسی دیگر جهت اقلیدسی است که جهت هر سلول را به نزدیکترین منبع مشخص می کند. همچنین عملیات آماری اساسی برای توصیف الگوی جهت ها وجود دارد. مثلا، میانگین جهت دار از نظر آماری نشان دهنده روند جهتی کلی جریان ها و واریانس زاویه ای نشان دهنده انحراف آماری جریان ها از میانگین جهت است. آمارهای پیشرفته تر در مورد جهت های جریان را می توان در Mardia و Jupp (2009) یافت.

3.1.2 فیلدهای برداری (یا فیلدهای جریان)

میدان برداری داده های شطرنجی را با استفاده از نمادهای برداری تجسم می کند، که هم مقدار و هم جهت جریان را نشان می دهد. یک مثال میدان جریان باد است که در شکل 4 نشان داده شده است. همانطور که مشاهده می شود، هر سلول شطرنجی به عنوان نمادی با طول نشان دهنده بزرگی باد و فلش نشان دهنده جهت آن نشان داده شده است. به لطف ماهیت پیوستگی میدان برداری، تکنیک هایی برای درونیابی میدان برداری توسعه داده شده است، که مشابه درونیابی بر روی میدان های عمومی است، اما جهت نیز در آن گنجانده شده است. خوانندگان تشویق می شوند برای جزئیات بیشتر به کار توبلر (1975) مراجعه کنند.

شکل 4. نمونه ای از یک فیلد برداری. منبع: اسری.

3.1.3 Moran’s I مبتنی بر برداری

برای اندازه‌گیری کمی همبستگی فضایی بردارها (جریان‌ها)، Moran’s I مبتنی بر برداری طراحی شده است، که یک تعمیم از Moran’s I سنتی با جهت اضافه شده در فرمول است. به طور خاص، این عملیات مشاهده اسکالر اصلی در موران I را با بردار جایگزین می کند که به صورت زیر فرموله می شود:

$\frac{n}{\sum_i\sum_j w_{ij}} \frac{\sum_i\sum_jw_{ij}(\vec{m_i}-\overline{\vec{m}}) \cdot (\vec{m_j} -\overline{\vec{m}})}{\sum_i(\vec{m_i}-\vec{m}) \cdot (\vec{m_i}-\vec{m})}$ ،

جایی که $\underset{m_i}{\rightarrow} \: = (x_{i}^{D} - x_{i}^{O}, y_{i}^{D}-y _{i}^{O} )$ و $\overline{\vec{m_i}} = (\overline{x_i}^D - \overline{x_i}^O , \overline{y_i}^D - \overline{y_i}^O)$ ، و بردار با مبدا ( $x_{i}^{O}، y_{i}^{O}$ ) و مقصد ( $x_{i}^{D}، y_{i}^{D}$ ) تعریف می شود.

ماتریس وزن فضایی w با در نظر گرفتن محله مبدا یا محله مقصد یا حتی هر دو تعیین می شود. بحث های مفصل را می توان در لیو و همکاران (2015) یافت. علاوه بر I موران، سایر معیارهای خودهمبستگی فضایی (یعنی C Geary) نیز می توانند با درج جهت به نسخه برداری تعمیم داده شوند.

3.1.4 خوشه بندی جریان ها

مانند خوشه‌بندی نقطه‌ای فضایی، تشخیص خوشه‌ای جریان‌های فضایی به عنوان یک تکنیک ضروری برای درک الگوی جریان‌ها در نظر گرفته می‌شود. بر خلاف خوشه‌بندی نقطه‌ای مکانی (که در آن فقط فاصله برای مدل‌سازی مجاورت فضایی استفاده می‌شود)، خوشه‌بندی جریان فضایی جهت جریان‌ها را در نظر می‌گیرد. رویکردهای متعددی برای جریان‌های خوشه‌ای وجود دارد که جهت یا به طور صریح (ژو و همکاران، 2019، یائو و همکاران، 2018) یا به طور ضمنی گنجانده شده است (تائو و تیل، 2016). تا زمانی که مجاورت فضایی با گنجاندن جهت اندازه گیری شود، یک روش خوشه بندی سنتی (مانند تحلیل K ریپلی و نقطه داغ) می تواند اتخاذ شود.

3.2 جهت در ساختارهای فضایی

علاوه بر جریان های فضایی، اطلاعات جهت نیز می تواند برای کمک به درک ساختار فضایی الگوهای نقطه ای و داده های زمین آماری مورد استفاده قرار گیرد. در این موارد، اطلاعات جهت‌دهی به‌صراحت در نمایش ویژگی‌های جغرافیایی (مثلاً نقطه یا سلول) مانند جریان مبتنی بر بردار گنجانده نمی‌شود، اما برای تحلیل روابط بین ویژگی‌های جغرافیایی در جریان محاسبه می‌شود. همانطور که در مورد اثر فاصله، این نوع اطلاعات به نام اثر جهت نامیده می شود.

3.2.1 اثر جهت در الگوهای نقطه فضایی

برای تعیین کمیت الگوی جهت نقاط فضایی، ابتدا می توان یک بیضی انحراف استاندارد اعمال کرد که در آن جهت محور اصلی با روند جهتی الگوی نقطه همسو می شود (شکل 5 را ببینید). در مرحله بعد، یک تابع K وابسته به زاویه (Ohser and Stoyan، 1981) می تواند برای تشخیص وجود خوشه نقطه ای وابسته به جهت استفاده شود. در نهایت، الگوریتم خوشه‌بندی مبتنی بر چگالی ناهمسانگرد (Mai et al., 2018) برای خوشه‌بندی این نقاط به گروه‌هایی با جهت چگالی نقطه‌ای در نظر گرفته شده، اختیاری است. عملیات جهت‌گیری پیشرفته‌تر برای مطالعه ناهمسانگردی الگوهای نقطه‌ای مکانی را می‌توان در راجالا و همکاران (2018) یافت.

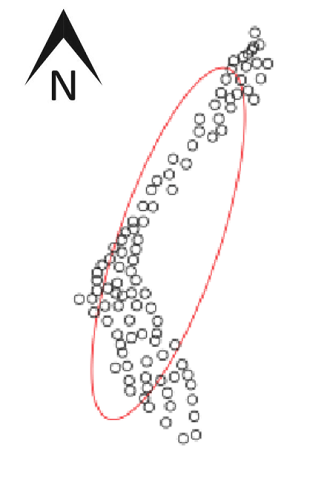
شکل 5. مثالی از بیضی انحراف استاندارد برای یک الگوی نقطه فضایی. منبع: نویسندگان

3.2.2 اثر جهت در داده های زمین آماری

مدل‌های زمین آماری پرکاربرد، مانند کریجینگ، نسخه‌های ناهمسانگرد خود را نیز دارند، که در آن وابستگی فضایی و همسانگردی به طور مشترک از طریق یک نیم متغیره جهت‌دار مدل‌سازی می‌شوند. این یک تعمیم از روش semivariogram سنتی است اما در امتداد جهات مختلف (به عنوان مثال، شمال-جنوب، غرب-شرق، و غیره) ایجاد شده است. شکل 6 نمونه ای از استفاده از نیم متغیره جهت دار را برای بررسی الگوی فضایی غلظت روی در یک منطقه نشان می دهد. مشاهده می‌شود که در جهات مختلف، نیم‌واریوگرام‌های تجربی متفاوت هستند، که این واقعیت را آشکار می‌کند که این الگوی فضایی ناهمسانگرد است.

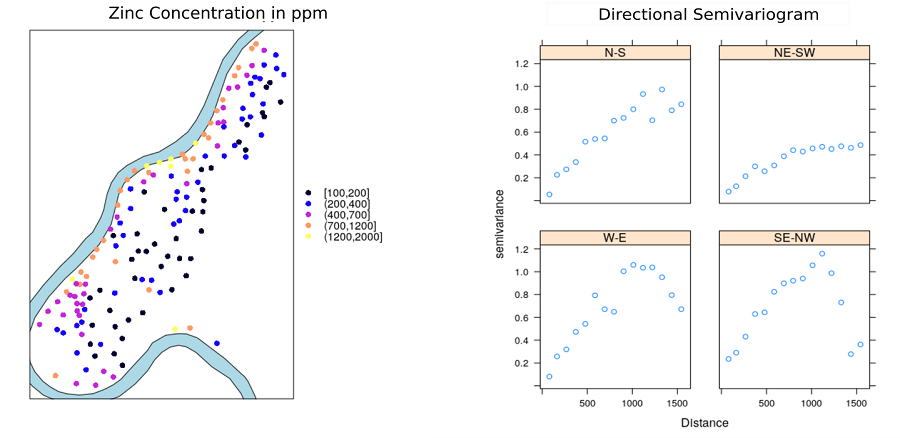
شکل 6. نمونه ای از نیم متغیره جهت دار. منبع: ژو و همکاران 2019.

گام بعدی در کریجینگ، برازش این نیمه متغیرهای جهت‌نمای تجربی به عنوان یک تابع کوواریانس پیوسته است. بسته به این که آیا ناهمسانگردی هندسی (که در آن محدوده های نیمه متغیر جهتی متفاوت است) یا ناهمسانگردی ناحیه ای (که در آن هر دو محدوده و آستانه برای جهات مختلف متفاوت هستند)، می توان مدل های ناهمسانگرد متعددی را اعمال کرد. ایده کلیدی زیربنای این عملیات، تبدیل میدان جغرافیایی ناهمسانگرد اولیه به میدان همسانگرد از طریق یک سری تبدیل، مانند چرخش و ترجمه است. به این ترتیب، مدل‌های نیمه‌واریوگرام ایزوتروپیک سنتی می‌توانند برای برازش داده‌های ناهمسانگرد استفاده شوند. برای جزئیات بیشتر، خوانندگان تشویق می شوند که فصل 4 Goovaerts (1997) را مرور کنند.

3.3 سایر عملیات جهت دار

علاوه بر عملیات جهتی فوق الذکر، بسیاری از عملیات معمولی GIS نسخه جهت دار خود را نیز دارند. به عنوان مثال، عملیات بافر محبوب یک نسخه ناهمسانگرد دارد که بافر مبتنی بر شکل نامیده می شود (Mu، 2008)، که در آن سرعت فرآیند بافر در جهات مختلف بسته به شکل چند ضلعی های Voronoi ساخته شده از یک مجموعه هندسی متفاوت است. مثال دیگر ماتریس وزن شبکه است که برای تحلیل شبکه فضایی توسعه یافته است (ارماگون و لوینسون، 2018). متفاوت از ماتریس وزن فضایی، یک ماتریس وزن شبکه اطلاعات توپولوژیکی مانند جهت لبه را در تحلیل شبکه فضایی رمزگذاری می کند. علاوه بر این، برای بررسی اثر جهت، ژو و همکاران. (2019) یک واریوگرام زاویه‌ای را به عنوان قیاس با نیم‌واریوگرام مبتنی بر فاصله پیشنهاد کرد. که در آن روابط بین ویژگی‌های جغرافیایی صرفاً بر اساس زاویه‌ها و نه فاصله‌ها مدل‌سازی می‌شوند. با این حال، شایان ذکر است که با وجود موفقیت این روش ها در دانشگاه، در حال حاضر به ندرت در میان فروشندگان GIS یافت می شوند.

4. فاصله در مقابل جهت

هر دو به عنوان اساسی ترین مفهوم در GIS، فاصله و جهت ارتباط نزدیکی دارند. فاصله یک کمیت اسکالر است که فاصله دو مکان را اندازه می گیرد در حالی که زاویه ها جهت بین دو مکان را اندازه می گیرند. توصیف رابطه فضایی بین دو جسم در فضای اقلیدسی یا کروی (مثلاً تعیین مکان یک شی با اشاره به مبدا) به فاصله و جهت نیاز دارد که منجر به کمیت برداری می شود. به عنوان مثال، اگر مختصات نقطه A را بدانیم و نقطه B دیگری در فاصله 500 متری از آن وجود داشته باشد، مکان نقطه B مشخص نیست. فقط زمانی که جهت بین نقطه A و B نیز ارائه شود (مثلاً B در شمال A باشد)، می‌توانیم مکان B را با اشاره به A تعیین کنیم. به همین ترتیب، اگر فقط بدانیم که B در شمال A است، مکان آن نمی‌تواند یا ثابت شود

علیرغم ارتباط نزدیک، فاصله و جهت در GIS نقش متفاوتی دارند. به عنوان مثال، فاصله اغلب برای توصیف روابط ایستا بین دو جسم استفاده می شود در حالی که جهت نشان دهنده روند پویا است. دو سناریوی متضاد می توانند آن را توضیح دهند: دو جسم می توانند از نظر فاصله نزدیک باشند اما بر اساس جهت از یکدیگر دور می شوند. دو جسم که از یکدیگر دور هستند ممکن است به سمت یکدیگر حرکت کنند. اساساً، فاصله رابطه فضایی بین دو نقطه را اندازه گیری می کند در حالی که جهت رابطه بین دو بردار را نشان می دهد که هر کدام از حداقل دو نقطه تشکیل شده است. این به وضوح با تعریف فوق الذکر از زاویه، که رابطه بین جهت هدف و یک جهت اولیه است (این دو جهت به عنوان بردار در فضای اقلیدسی نشان داده می شود) مثال زده می شود. از این رو،

منابع:

آکسوی، اس.، و سینبیس، آر جی (2009). تصویر کاوی با استفاده از محدودیت های فضایی جهت دار IEEE Geoscience and Remote Sensing Letters، 7(1)، 33-37. DOI: 10.1109/LGRS.2009.2014083

بیتمن، جی (2010). زبان و فضا: رویکرد معنایی دو سطحی مبتنی بر اصول مهندسی هستی‌شناسی مجله بین المللی فناوری گفتار، 13(1)، 29-48. DOI: 10.1007/s10772-010-9069-x

Bateman, JA, Hois, J., Ross, R., & Tenbrink, T. (2010). هستی شناسی زبانی فضا برای پردازش زبان طبیعی هوش مصنوعی، 174(14)، 1027-1071. DOI: 10.1016/j.artint.2010.05.008

کمپبل، جی (1993). استفاده و تحلیل نقشه دوبوک: Wm. سی. براون.

کلمنتینی، ای. (2013). روابط جهتی و چارچوب های مرجع. GeoInformatica، 17 (2)، 235-255. DOI: 10.1007/s10707-011-0147-2

کلمنتینی، ای.، اسکیادوپولوس، اس.، بیلن، آر.، و تارکینی، اف. (2009). سیستم استدلالی از روابط تصویری سه تایی. IEEE Transactions on Knowledge and Data Engineering، 22(2)، 161-178. DOI: 10.1109/TKDE.2009.79

ارماگون، ا.، و لوینسون، دی (2018). مقدمه ای بر ماتریس وزن شبکه تحلیل جغرافیایی، 50(1)، 76-96. DOI: 10.1111/gean.12134

فرانک، AU (1996). استدلال فضایی کیفی: جهت های اصلی به عنوان مثال. مجله بین المللی علم اطلاعات جغرافیایی، 10(3)، 269-290. DOI: 10.1080/02693799608902079

فرکسا، سی (1991). استدلال فضایی کیفی. در جنبه های شناختی و زبانی فضای جغرافیایی (ص 361-372). اسپرینگر، دوردرخت DOI: 10.1007/978-94-011-2606-9_20

Goovaerts، P. (1997). زمین آمار برای ارزیابی منابع طبیعی انتشارات دانشگاه آکسفورد بر حسب تقاضا.

Haynes، KE، & Fotheringham، AS (1984). مدل‌های برهمکنش گرانشی و فضایی (جلد 2). بورلی هیلز، کالیفرنیا: سیج.

Liu, Y., Tong, D., & Liu, X. (2015). اندازه گیری خودهمبستگی فضایی بردارها. تحلیل جغرافیایی، 47(3)، 300-319. DOI: 0.1111/gean.12069

مای، جی.، یانوویچ، ک.، هو، ی.، و گائو، اس. (2018). ADCN: یک الگوریتم خوشه‌بندی مبتنی بر چگالی ناهمسانگرد برای کشف الگوهای نقطه فضایی با نویز. معاملات در GIS، 22(1)، 348-369. DOI: 10.1111/tgis.12313

Mardia، KV، و Jupp، PE (2009). آمار جهت (جلد 494). جان وایلی و پسران

مو، ال (2008). یک روش بافر مبتنی بر شکل. محیط و برنامه ریزی ب: برنامه ریزی و طراحی، 35(3)، 399-412. DOI: doi.org/10.1068/b33046

Ohser, J., & Stoyan, D. (1981). در مورد تجزیه و تحلیل مرتبه دوم و جهت گیری فرآیندهای نقطه ثابت مسطح. مجله بیومتریک، 23 (6)، 523-533. DOI: 10.1002/bimj.4710230602

Rajala، T.، Redenbach، C.، Särkkä، A.، & Sormani، M. (2018). مروری بر تحلیل ناهمسانگردی الگوهای نقطه فضایی آمار فضایی، 28، 141-168. DOI: 10.1016/j.spasta.2018.04.005

رتز اشمیت، جی (1988). دیدگاه های مختلف در مورد حروف اضافه فضایی. مجله هوش مصنوعی، 9(2)، 95-95. DOI: doi.org/10.1609/aimag.v9i2.678

Richter, KF, & Klippel, A. (2006, سپتامبر). قبل یا بعد: حروف اضافه در سیستم های فضایی محدود. در کنفرانس بین المللی شناخت فضایی (ص 453-469). اسپرینگر، برلین، هایدلبرگ. DOI: 10.1007/978-3-540-75666-8_26

تائو، آر، و تیل، جی سی (2016). تشخیص خوشه فضایی در داده های جریان مکانی تحلیل جغرافیایی، 48(4)، 355-372. DOI: 10.1111/gean.12100

Tobler، WR (1970). یک فیلم کامپیوتری شبیه سازی رشد شهری در منطقه دیترویت. جغرافیای اقتصادی، 46(sup1)، 234-240.

Tobler, W. (1975). الگوهای تعامل فضایی مجله سیستم های محیطی 6، 271-301.

Worboys، MF، & Duckham، M. (2004). GIS: دیدگاه محاسباتی پرس CRC.

Yao, X., Zhu, D., Gao, Y., Wu, L., Zhang, P., & Liu, Y. (2018). یک روش خوشه‌بندی جریان مکانی-زمانی گام به گام برای کشف روندهای تحرک دسترسی IEEE، 6، 44666-44675. DOI: 0.1109/ACCESS.2018.2864662

ژو، آر.، کیریاکیدیس، پی سی، و یانوویچ، ک. (2017، مه). فراتر از جفت: تعمیم دوقطبی جغرافیایی برای کمی سازی الگوهای فضایی در زمینه های جغرافیایی. در کنفرانس بین المللی سالانه علوم اطلاعات جغرافیایی (صص 331-348). اسپرینگر، چم. DOI: 10.1007/978-3-319-56759-4_19

ژو، آر.، یانوویچ، ک.، و مای، جی. (2019). ساختن جهت شهروند درجه یک از قانون اول جغرافیای توبلر. معاملات در GIS، 23(3)، 398-416. DOI: 10.1111/tgis.12550

اهداف یادگیری:

روش های مختلف اندازه گیری جهت را به صورت کمی شرح دهید.
خصوصیات ذاتی زاویه ها را شناسایی کنید و نحوه اتصال آنها را با عملیات جهتی نشان دهید.
پنج نوع جهت کیفی را نام ببرید و چارچوب های مرجع را برای هر کدام مشخص کنید.
ارزیابی کنید که آیا عملیات جهت دهی مورد نیاز است و در چه نوع هایی.

سوالات ارزشیابی آموزشی:

دو جزء لازم برای اندازه گیری جهت را فهرست کنید و اهمیت آنها را از نظر عملیات جهتی توضیح دهید.
اثر جهت را توضیح دهید و مثال بزنید.
از نظر توصیف روابط فضایی، بین فاصله و جهت تمایز قائل شوید.
سناریوهایی را که در آنها عملیات جهت دار مورد نیاز است را شرح دهید.

سیستم اطلاعات جغرافیایی

قبلیچرخه حیات توسعه سیستم (SDLC) : طراحی، توسعه، آزمایش و استقرار برنامه های کاربردی GIS

بعدیآموزش GIS : فاصله و اهمیت آن در سیستم اطلاعات جغرافیایی

مطالب مرتبط ...

اهمیت GIS در برنامه ریزی و مدیریت منابع آب

سیستم اطلاعات جغرافیایی:100 تعریف در یک صفحه

تعریف برنامه استراتژیک GIS وجهت آن

2 نظرات

دیدگاهتان را بنویسید لغو پاسخ