تأثیر همسایگی درونیابی DEM بر عوامل زمین

خلاصه

عوامل توپوگرافی مانند شیب و جهت پارامترهای اساسی در به تصویر کشیدن ساختار و مورفولوژی سطح زمین هستند. ما تأثیر تعداد نقاط در همسایگی یک روش درون یابی مدل رقومی ارتفاع (DEM) را بر شیب میانگین، جنبه میانگین و RMSE شیب و جنبه از DEM درونیابی شده مطالعه می‌کنیم. از آنجایی که روش حداقل مربعات متحرک (MLS) می تواند خواص ذاتی و سایر ویژگی های یک سطح را حفظ کند، این روش برای درونیابی DEM انتخاب می شود. سه منطقه حاوی انواع مختلف ویژگی های توپوگرافی برای مطالعه انتخاب شده است. داده های شبیه سازی شده از سطح گاوس نیز برای مقایسه استفاده می شود. ابتدا، تأثیر تعداد نقاط بر روی ریشه میانگین مربعات خطای DEM (RMSE) تحلیل می‌شود. DEM RMSE در سه منطقه مورد مطالعه به تدریج با تعداد نقاط در همسایگی کاهش می یابد. علاوه بر این، تأثیر تعداد نقاط در همسایگی بر شیب میانگین و جنبه میانگین در سراسر توپوگرافی‌های مختلف از طریق تحلیل رگرسیون مورد مطالعه قرار گرفت.
دوره آموزش حرفه ای gis
 این دو متغیر به طور متفاوتی به تغییرات زمین پاسخ می دهند. با این حال، RMSE های شیب و جنبه در تمام مناطق مورد مطالعه از نظر لگاریتمی با تعداد نقاط همسایگی مرتبط است و با افزایش تعداد نقاط همسایگی، مقادیر به طور یکنواخت کاهش می‌یابند. با نقاط بیشتر در همسایگی، RMSE های شیب و جنبه به تفاوت های توپوگرافی حساس نیستند و روندهای یکسانی برای سه کمیت مورد مطالعه مشاهده می شود. نتایج برای سطح گاوس مشابه است. سرانجام، این مطالعه توزیع فضایی خطاهای شیب و جنبه را تحلیل می‌کند. خطای شیب در پشته ها، دره ها، مناطق شیب دار و لبه های خندق متمرکز است در حالی که خطای جنبه در پشته ها، دره ها و مناطق مسطح متمرکز است. با نقاط بیشتر در همسایگی، تعداد سلول های شبکه ای که در آنها خطای شیب بیشتر از 15 درجه است به تدریج کاهش می یابد. با انواع زمین و منابع داده مشابه، اگر کارایی محاسبه نگران کننده نباشد، نقاط کافی در محدوده خودهمبستگی فضایی باید در همسایگی تجزیه و تحلیل شود تا دقت شیب و جنبه به حداکثر برسد. با این حال، انتخاب بین 10 تا 12 نقطه در محله مقرون به صرفه است. و مناطق مسطح با نقاط بیشتر در همسایگی، تعداد سلول های شبکه ای که در آنها خطای شیب بیشتر از 15 درجه است به تدریج کاهش می یابد. با انواع زمین و منابع داده مشابه، اگر کارایی محاسبه نگران کننده نباشد، نقاط کافی در محدوده خودهمبستگی فضایی باید در همسایگی تجزیه و تحلیل شود تا دقت شیب و جنبه به حداکثر برسد. با این حال، انتخاب بین 10 تا 12 نقطه در محله مقرون به صرفه است. و مناطق مسطح با نقاط بیشتر در همسایگی، تعداد سلول های شبکه ای که در آنها خطای شیب بیشتر از 15 درجه است به تدریج کاهش می یابد. با انواع زمین و منابع داده مشابه، اگر کارایی محاسبه نگران کننده نباشد، نقاط کافی در محدوده خودهمبستگی فضایی باید در همسایگی تجزیه و تحلیل شود تا دقت شیب و جنبه به حداکثر برسد. با این حال، انتخاب بین 10 تا 12 نقطه در محله مقرون به صرفه است. نقاط کافی در محدوده خودهمبستگی فضایی باید در همسایگی تجزیه و تحلیل شود تا دقت شیب و جنبه به حداکثر برسد. با این حال، انتخاب بین 10 تا 12 نقطه در محله مقرون به صرفه است. نقاط کافی در محدوده خودهمبستگی فضایی باید در همسایگی تجزیه و تحلیل شود تا دقت شیب و جنبه به حداکثر برسد. با این حال، انتخاب بین 10 تا 12 نقطه در محله مقرون به صرفه است.

کلید واژه ها:

مدل رقومی ارتفاع (DEM) ; نقاط همسایه ; شیب ; جنبه

1. معرفی

یک مدل رقومی ارتفاع (DEM) داده‌های اساسی را برای تجزیه و تحلیل فضایی سیستم‌های اطلاعات جغرافیایی نشان می‌دهد که به طور گسترده در زمینه‌های هیدرولوژی [ 1 ]، خاک [ 2 ]، شکل زمین [ 3 ، 4 ]، زمین‌شناسی [ 5 ]، کشاورزی [5] کاربرد دارد. 6 ، و کاربردهای نظامی [ 7 ، 8 ]. عوامل توپوگرافی مانند شیب و جهت استخراج شده بر اساس DEM نه تنها پارامترهای مهم برای توصیف ساختار و مورفولوژی سطوح توپوگرافی هستند، بلکه متغیرهای اساسی مدل‌های ژئوآنالیز، مانند شبیه‌سازی فرآیند سطح، هیدرولوژیکی، فرسایش خاک و طبقه‌بندی کاربری اراضی هستند. مدل‌ها [ 9 ، 10, 11 , 12 , 13 ]. شیب در برآورد پاسخ هیدرولوژیکی اساسی است. مقدار شیب بر زمان رسیدن یک هیدروگراف به اوج خود تأثیر می گذارد [ 14 ]. جنبه در استخراج متغیرهای هیدرولوژیکی مانند تجمع جریان، جهت جریان، مرزهای حوضه آبریز و شبکه های جریان یا متغیرهای محیطی مانند شاخص رطوبت و تابش خورشیدی بسیار مهم است [15 ] . دقت شیب و جنبه در تحلیل دیجیتال زمین مهم است.
یک DEM برای تحقق شبیه‌سازی دیجیتالی سطح زمین با داده‌های ارتفاعی زمین محدود است [ 16 ]. روش ساخت آن شامل ساخت مستقیم و ساخت غیر مستقیم است [ 17]: یعنی درونیابی از طریق نقاط نمونه برای تولید DEM یا ساختن یک شبکه نامنظم مثلثی (TIN) از طریق نقاط و سپس درونیابی آن برای تولید DEM. روش ساخت و ساز مستقیم ارتفاع نقاط درون یابی را با وزن دهی خطی نقاط نمونه برداری در همسایگی تخمین می زند. روش ساخت غیر مستقیم شامل داده های TIN در مراحل میانی و نتایج میانی است. از آنجایی که داده‌های ویژگی توپوگرافی را می‌توان به یک TIN اضافه کرد، دقت DEM به‌دست‌آمده در نتیجه تا حدی بهبود می‌یابد. در همین حال، با توجه به این واقعیت که ساختار داده TIN پیچیده است، الگوریتم تجزیه و تحلیل بر اساس TIN بسیار پیچیده است. از این رو، نتایج میانی داده‌های TIN عمدتاً کنار گذاشته می‌شوند. در نتیجه این روش بازدهی پایینی دارد. منابع داده مورد استفاده برای DEM ها روندی از تنوع را نشان می دهد،18 ]. در این میان، داده‌های ابر نقطه‌ای تشخیص نور و محدوده (LIDAR) می‌توانند DEM با دقت بالا تولید کنند. این به تدریج تبدیل به راه اصلی برای به دست آوردن DEM های با دقت بالا می شود [ 12 ]. از طریق طبقه بندی داده های ابر نقطه، نقاط ارتفاعی زمین به دست می آید. سپس یک DEM با دقت بالا با روش درون یابی مستقیم یا روش ساخت غیر مستقیم ساخته می شود. با رواج داده‌های ابر نقطه‌ای و داده‌های فتوگرامتری، روش درونیابی مستقیم مزایای بیشتری نسبت به روش ساخت غیرمستقیم ارائه می‌دهد که در آن هیچ مرحله میانی مورد نیاز نیست. علاوه بر این، یک DEM با دقت بالا را می توان در ترکیب با نقاط ویژگی توپوگرافی به دست آورد.
در میان کاربردهای مختلف DEM، مشکلات مورد توجه عبارتند از دقت DEM، عامل زمین استخراج شده، و تأثیر تفکیک DEM بر نتیجه و غیره [7 ، 11 ، 12 ، 13 ، 14 ، 15 ، 19 . , 20 , 21 , 22 , 23 , 24]. گائو (1997) دقت DEM را با وضوح های مختلف برای نمایش های زمین مورد مطالعه قرار داد و رابطه بین چگالی کانتور، وضوح DEM و خطای میانگین مربعات ریشه DEM (RMSE) را ایجاد کرد: وقتی وضوح DEM کاهش می یابد، دقت شبیه سازی سطح ابتدا به آرامی کاهش می یابد، سپس به شدت کاهش می یابد. علاوه بر این، تأثیر زیادی از وضوح بر روی شیب استخراج شده از DEM وجود دارد. با این حال، میانگین شیب به طور قابل توجهی تحت تاثیر قرار نمی گیرد در حالی که انحراف معیار شیب به شدت تحت تاثیر قرار می گیرد. گائو (1998) بیشتر تأثیر فاصله نمونه برداری بر روی شیب و مقادیر جنبه استخراج شده از DEM را مطالعه کرد و دریافت که این جنبه به فاصله نمونه برداری حساس نیست در حالی که شیب به آن بسیار حساس است، حتی در مناطق مسطح. حدود 90 درصد از واریانس در شیب و جنبه به دلیل خطای DEM است. فلورینسکی (2000) تأثیر توپوگرافی را بر توزیع فضایی رطوبت خاک تجزیه و تحلیل کرد. ابتدا، رابطه بین وضوح DEM و متغیرهای توپوگرافی ایجاد شد. سپس DEM با وضوح مناسب به منظور استخراج شیب، انحنای صفحه، انحنای مقطع و انحنای متوسط ​​انتخاب شد و وابستگی رطوبت خاک به متغیرهای توپوگرافی فوق مورد بررسی قرار گرفت. با این روش می توان یک DEM با وضوح مناسب انتخاب کرد تا متغیر توپوگرافی استخراج شده نزدیک ترین مقدار ویژگی توپوگرافی واقعی را داشته باشد. Kienzle (2004) اثر تفکیک DEM را بر عوامل توپوگرافی مرتبه اول شیب و جهت، عوامل زمین مرتبه دوم انحنای پروفیل و انحنای صفحه، و عامل توپوگرافی یکپارچه شاخص رطوبت مطالعه کرد. وضوح DEM بهینه برای استخراج عوامل توپوگرافی مختلف از طریق بازرسی KS مورد تجزیه و تحلیل قرار گرفت. در ترکیب با نتایج تحلیل خطای شیب، مشخص شد که شیب استخراج‌شده بالاترین دقت را برای وضوح DEM 7.5 متر در زمین پیچیده و 20 متر در زمین صاف دارد، در حالی که سایر عوامل زمین وضوح بهینه قابل‌توجهی ندارند. وقتی وضوح DEM کاهش می یابد، RMSE DEM به صورت خطی افزایش می یابد و RMSE انحنای پروفیل، انحنای صفحه و شاخص رطوبت توپوگرافی به صورت لگاریتمی افزایش می یابد. در حالی که سایر عوامل زمین تفکیک بهینه قابل توجهی ندارند. وقتی وضوح DEM کاهش می یابد، RMSE DEM به صورت خطی افزایش می یابد و RMSE انحنای پروفیل، انحنای صفحه و شاخص رطوبت توپوگرافی به صورت لگاریتمی افزایش می یابد. در حالی که سایر عوامل زمین تفکیک بهینه قابل توجهی ندارند. وقتی وضوح DEM کاهش می یابد، RMSE DEM به صورت خطی افزایش می یابد و RMSE انحنای پروفیل، انحنای صفحه و شاخص رطوبت توپوگرافی به صورت لگاریتمی افزایش می یابد.
مک مستر (2002) تأثیر تفکیک DEM بر شبکه های حوضه استخراج شده را مورد مطالعه قرار داد. دقت شبکه های حوضه استخراج شده از DEM با وضوح های مختلف با دو روش کمی مورد تجزیه و تحلیل قرار گرفت: یک روش محاسبه فاصله بین شبکه حوضه استخراج شده و خطوط شبکه حوضه اندازه گیری شده و روش دیگر محاسبه طول حوضه اندازه گیری شده بود. شبکه در محدوده بافر شبکه حوضه استخراج شده. نتایج نشان داد که شبکه حوضه استخراج شده از نظر دقت موقعیت از شبکه حوضه اندازه گیری شده پایین تر است. با این حال، شاخه های حوضه مرتبه اول و دوم استخراج شدند. موگلن (2001) تأثیر تفکیک DEM بر شیب و جنبه و همچنین تأثیر بیشتر آن بر مدل‌های هیدرولوژیکی را مورد مطالعه قرار داد. با کاهش وضوح، مقدار شیب نیز کاهش می یابد اما زمان رسیدن جریان ها به مقادیر اوج خود افزایش می یابد. رابر (2007) اثر فاصله گذاری اسمی LIDAR بر نتایج شبیه سازی یک مدل هیدرولیک را تجزیه و تحلیل کرد. نتایج تأیید کرد که مرزهای منطقه سیلاب نسبت به فاصله پست حساس هستند. وایز (2007) تأثیر روش‌های مختلف ساخت DEM را بر مدل‌های هیدرولوژیکی مطالعه کرد. آگیلار (2005) و همکاران. تاثیر انواع مختلف ژئومورفیک، چگالی نمونه‌برداری و روش‌های درون‌یابی بر دقت DEM را مطالعه کرد. وازه (2010) و همکاران. تأثیر دقت و وضوح DEM بر شاخص توپوگرافی را مورد مطالعه قرار داد. چاو (2009) و همکاران. تأثیر تراکم نمونه‌برداری مکانی و وضوح DEM بر میانگین شیب را بررسی کرد. DEM با رزولوشن های مختلف اثرات مختلفی بر روی شبیه سازی سطح، شیب و جنبه استخراج شده و نتایج شبیه سازی مدل دارند. هرچه رزولوشن کمتر باشد، اثر صاف کنندگی روی سطح آشکارتر است. نقاط نمونه برداری برای تخمین ارتفاع نقاط درونیابی شده در طول ساخت DEM استفاده می شود. بسیاری از محققان تأثیر چگالی نمونه‌برداری و روش‌های درون‌یابی را بر دقت DEM، تأثیر تفکیک DEM بر شیب و جنبه، و تأثیر فاصله نمونه‌گیری و فاصله پست LIDAR بر شیب و جنبه مورد مطالعه قرار داده‌اند. با این حال، تأثیر تعداد نقاط نمونه برداری در همسایگی درون یابی بر دقت DEM و عوامل زمین استخراج شده به ندرت در نظر گرفته شده است. بسیاری از محققان تأثیر چگالی نمونه‌برداری و روش‌های درون‌یابی را بر دقت DEM، تأثیر تفکیک DEM بر شیب و جنبه، و تأثیر فاصله نمونه‌گیری و فاصله پست LIDAR بر شیب و جنبه مورد مطالعه قرار داده‌اند. با این حال، تأثیر تعداد نقاط نمونه برداری در همسایگی درون یابی بر دقت DEM و عوامل زمین استخراج شده به ندرت در نظر گرفته شده است. بسیاری از محققان تأثیر چگالی نمونه‌برداری و روش‌های درون‌یابی را بر دقت DEM، تأثیر تفکیک DEM بر شیب و جنبه، و تأثیر فاصله نمونه‌گیری و فاصله پست LIDAR بر شیب و جنبه مورد مطالعه قرار داده‌اند. با این حال، تأثیر تعداد نقاط نمونه برداری در همسایگی درون یابی بر دقت DEM و عوامل زمین استخراج شده به ندرت در نظر گرفته شده است.
دقت شیب و جنبه استخراج شده توسط DEM به خطای DEM، وضوح DEM، الگوریتم تعیین شیب و جنبه و پیچیدگی زمین بستگی دارد [ 11 ، 25 ]. منبع داده، نوع ژئومورفیک، روش ساخت و تفکیک DEM ممکن است بر دقت یک DEM تأثیر بگذارد [ 15 ، 18 ]. در میان منابع مختلف داده DEM، داده‌های فتوگرامتری و داده‌های LIDAR دقت بالاتری دارند. با این حال، داده های بررسی توپوگرافی و داده های کانتور منابع داده ضروری هستند. تقریباً همه کشورها دارای داده های کانتور در مقیاس های مختلف هستند که هزینه اکتساب پایینی دارد. در همین حال، داده های LIDAR شامل سایبان های گیاهی و نقاط زمین است، بنابراین داده های کانتوری که فقط شامل ارتفاع زمین هستند غیر قابل تعویض باقی می مانند [13 ]. اگرچه DEM ها ممکن است بر اساس یک منبع داده ساخته شوند، دقت DEM زمانی که از روش های درونیابی متنوع استفاده می شود، می تواند متفاوت باشد. با توجه به Kienzle (2004)، روش وزن دهی معکوس فاصله (IDW) برای نمونه برداری از نقاط توزیع نامنظم مناسب نیست، زیرا به احتمال زیاد باعث ایجاد اثر چشم گاو نر می شود، در حالی که DEM های ساخته شده توسط اسپلاین های منظم با روش کشش و ANUDEM دارای دقت های بالاتر با این حال، طبق گفته آگیلار (2005)، در میان تمام روش های درون یابی سنتی، مانند همسایه طبیعی (NN)، ANUDEM، کریجینگ معمولی (OK) و روش چند چهارگانه (MQ)، MQ زمانی بهترین است که برای داده های سنجش از دور استفاده شود. مانند LIDAR. چن (2016) یک روش MQ-M را ارائه کرد که بر اساس روش MQ با موارد دورافتاده در داده های سنجش از دور سازگارتر است [ 26]]. DEM های مختلف با روش های درون یابی متنوع و با پارامترهای مختلف یا تعداد متفاوت نقاط نمونه محلی برای تخمین ارتفاع نقاطی که قرار است درونیابی شوند ساخته می شوند. سپس متغیرهای توپوگرافی استخراج شده نیز متفاوت هستند [ 27 ]. به عنوان مثال، توان تابع وزن IDW به طور کلی 2 در نظر گرفته می شود، اما ممکن است 1 یا 3 نیز باشد. برخی از مطالعات نشان داده اند که نتایج زمانی بهتر است که به عنوان 2 در نظر گرفته شود، در حالی که نتیجه درون یابی حساسیت زیادی به آن ندارد. توان [ 7 ]. هنوز مشخص نیست که آیا پارامترهای سایر روش های درون یابی تأثیر قابل توجهی بر DEM و متغیرهای توپوگرافی دارند یا خیر.
در میان روش های محاسبه شیب و جنبه، روش های ارائه شده توسط هورن (1981) و زونبرگن و تورن (1987) به طور گسترده ای استفاده شده است [ 28 ، 29 ]. الگوریتم هورن برای دستور SLOPE ArcInfo و الگوریتم ارائه شده توسط Zevenbergen و Thorne برای دستور CURVATURE در ArcInfo استفاده می شود. به گفته جونز (1998)، الگوریتم ارائه شده توسط Zevenbergen و Thorne بهترین است و پس از آن الگوریتم ارائه شده توسط Horn [ 30]]. الگوریتم شیب و جنبه یک شبکه DEM کاملاً بالغ است. نگرانی در این مطالعه نیست. این مقاله بر تاثیر روی یک DEM و همچنین بر دقت شیب و جنبه زمانی که منبع داده برای ساخت DEM، وضوح DEM ساخته شده، الگوریتم‌های شیب و جنبه، و روش درون یابی برای ساخت DEM یکسان هستند، تمرکز می‌کند. تعداد نقاط نمونه برداری محلی انتخاب شده برای برآورد ارتفاع نقاط افزایش می یابد.
در این مقاله، نقاط نمونه برداری و داده های خط کانتور از سه ناحیه از انواع مختلف ژئومورفیک شامل منطقه خندق لس، منطقه تپه ای لس و منطقه کوهستانی مرتفع اتخاذ شده و از روش حداقل مربعات متحرک (MLS) برای ساخت استفاده شده است. DEM ها به منظور مطالعه تفاوت در DEM های ساخته شده و شیب و جنبه استخراج شده برای تعداد مختلف نقاط جستجو در همسایگی.

2. مواد و روشها

2.1. منطقه مطالعه

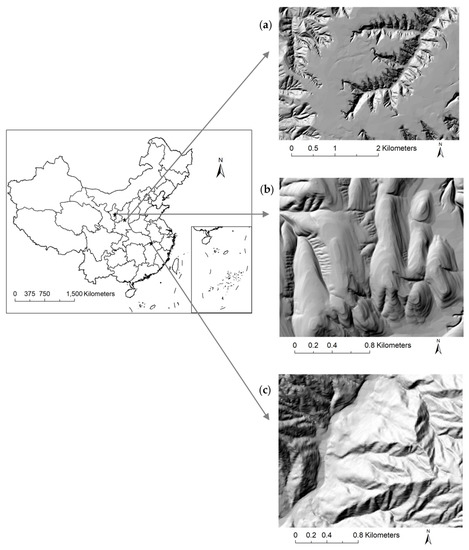
این مطالعه شامل سه سایت مطالعاتی با انواع مختلف زمین است ( شکل 1). منطقه مطالعه 1 و منطقه مطالعه 2 شامل یک تپه لس واقع در فلات لس در شمال مرکزی چین است. در این منطقه فلات لس، انواع ژئومورفیک عمدتاً شامل دشت ها، حوضه ها، نواحی تپه ای، تپه های لس، خندق های فلات و دشت های آبرفتی و ویژگی های ژئومورفیک عمدتاً شامل دشت ها، پشته ها و تپه های لس است. مشخصه این منطقه خندق‌های فراوان، شکل‌های زمین پاره پاره، و نقش برجسته‌های توپوگرافی بزرگ است. دامنه ارتفاعی 200-3000 متر است و فرسایش خاک و از دست دادن آب و خاک شدید است. علاوه بر این، منطقه مورد مطالعه 1 از نظر شکل زمین یک خندق لس است. عمدتاً مسطح با بخش کوچکی از آبکندهای عمیق است و فرسایش سطحی نسبتاً سبک است. منطقه مورد مطالعه 2 از نظر شکل زمین یک تپه / خط الراس لس است. تپه های لس نسبتاً مسطح و کوچک هستند، یک قوس آشکار وجود دارد، طول شیب کوچکتر است. و شیب به وضوح تغییر می کند. منطقه مطالعه 3 در جنوب شرقی منطقه لوشان چین واقع شده است. کوه لوشان کوهی مرتفع است که در اثر بالا آمدن زمین ساختی به وجود آمده است که ارتفاع قله‌های آن بیشتر در حدود 1300 متر، بلندترین قله تا 1473 متر ارتفاع دارد و در دو طرف آن صخره‌های شیب‌دار به صورت نردبانی با تغییرات زیاد در ارتفاع و شیب وجود دارد. .
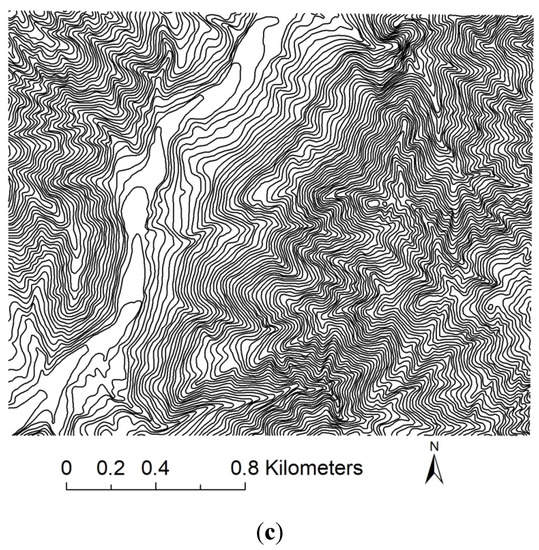
خطوط کانتور از داده های دیجیتالی نقشه های توپوگرافی به دست می آیند ( شکل 2) فاصله کانتور 10 متر است و نقاط نمونه برداری ارتفاعی از نقشه های توپوگرافی جمع آوری شده است. از آنجایی که نقاط نمونه برداری از ارتفاع بسیار پراکنده هستند، خطای DEM به دست آمده از طریق درونیابی نسبتاً بزرگ است. بنابراین، ما خطوط کانتور را به نقاطی پراکنده کردیم تا با نقاط نمونه برداری ارتفاعی مورد استفاده برای ساخت و ساز DEM ترکیب شوند. رزولوشن DEM 5 متری تولید شده توسط اداره دولتی نقشه برداری و نقشه برداری به عنوان مرجع در نظر گرفته شده است. DEM ساخته شده با درونیابی نقطه نمونه برداری نیز دارای وضوح 5 متر است. DEM تولید شده توسط اداره دولتی نقشه برداری و نقشه برداری توسط یک TIN ساخته شده با خطوط کانتور با فواصل کانتور 5 متر درونیابی می شود. با توجه به محدودیت‌های اندازه‌گیری، همیشه درجاتی از خطا در داده‌های مکانی وجود دارد [ 31]]. هیچ به اصطلاح “ارزش واقعی” در داده ها در علوم زمین وجود ندارد و تنها داده های با دقت بالا می توانند به عنوان داده های مرجع قابل قبول و معقول در نظر گرفته شوند [ 32 ].
نقاط نمونه برداری در هر منطقه مورد مطالعه برای حذف نقاطی با مقادیر مختصات افقی و مختصات عمودی یکسان از قبل پردازش شدند. پس از پیش پردازش به ترتیب 85071، 29988 و 47989 نقطه نمونه برداری در مناطق مطالعه 1-3 باقی مانده است.

2.2. داده های شبیه سازی شده

از آنجایی که مقادیر شیب و جنبه واقعی سطح زمین واقعی را نمی توان بدست آورد، از یک آزمایش عددی استفاده می شود. ما از داده های شبیه سازی شده برای مقایسه نتایج حاصل از مناطق مورد مطالعه استفاده کردیم. داده های شبیه سازی شده شامل نقاط نمونه برداری و یک DEM مرجع استخراج شده از سطح گاوس است. فرمول به شرح زیر است:

z = A [ 1- _(ایکسمتر)2]ه–(ایکسمتر)2–(yn+ 1 )2– B [ 0.2 (ایکسمتر) –(ایکسمتر)3–(yn)5]ه–(ایکسمتر)2–(yn)2–Ce–( (ایکسمتر) +1)2–(yn)2� =آ[1-(ایکسمتر)2]ه-(ایکسمتر)2-(�n+1)2-ب[0.2(ایکسمتر)-(ایکسمتر)3-(�n)5]ه-(ایکسمتر)2-(�n)2-Ce-((ایکسمتر)+1)2-(�n)2
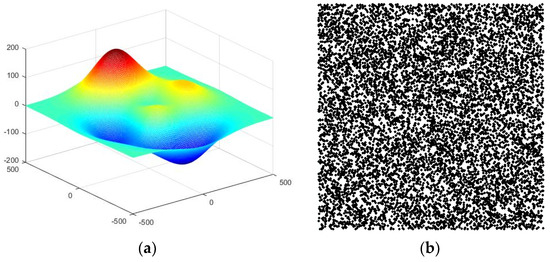
A، B، C، m و n پارامترهایی هستند که می توانند شکل یک سطح را تغییر دهند: A = 60، B = 200، C = 6، m = 200، و n = 200. محدوده x و y است [ -500، 500]. سطوح همانطور که در شکل 3 نشان داده شده است . اندازه سلول شبکه 5 است. نقاط نمونه برداری به طور تصادفی از سطوح گاوس پراکنده می شوند ( شکل 3 ب). تعداد نقاط پراکنده 10000 است.

2.3. مواد و روش ها

تأثیر نقاط همسایگی بر شیب و جنبه استخراج شده از DEM تمرکز ما است، از جمله تأثیر بر DEM RMSE، شیب میانگین، جنبه متوسط ​​و RMSE شیب و جنبه. همبستگی بین نقاط در همسایگی و RMSEهای شیب و جنبه برقرار است. پردازش داده ها شامل موارد زیر است: (1) مجموعه نقاط نمونه برداری. (2) ساخت یک DEM با وضوح 5 متر. (3) استخراج شیب و جنبه بر اساس ArcGIS [ 28 ]. (3) محاسبه شیب متوسط ​​و جنبه میانگین. (4) محاسبه RMSEهای شیب و جنبه. و (5) محاسبه خطای مطلق و خطای نسبی شیب و همچنین خطای جنبه.
از طریق چهار آزمایش، حساسیت خطاهای شیب و جنبه به نقاط در همسایگی تجزیه و تحلیل می‌شود:
  • آزمایش 1: رابطه بین تعداد نقاط در همسایگی و DEM RMSE
  • آزمایش 2: رابطه بین تعداد نقاط همسایگی و شیب میانگین و جنبه میانگین
  • آزمایش 3: رابطه بین تعداد نقاط در همسایگی و RMSEهای شیب و جنبه
  • آزمایش 4: توزیع فضایی خطاهای شیب و جنبه

روش MLS یک روش محلی برازش سطح و یک رویکرد آماری است که برای بازسازی سطح استفاده می شود. می تواند ماهیت ذاتی یک سطح را حفظ کند، مقدار تقریبی یک سطح را به دقت محاسبه کند، و به نقاط پرت با نقاط گسسته حساس نیست [ 33 ]. MLS با توابع پایه خطی و توابع گاوسی به عنوان توابع وزن بر اساس MATLAB تحقق می یابد. فرمول تابع وزن به صورت زیر است:

w ( r ) =⎧⎩⎨ه–r2β2–ه–β21- _ه–β2 r ≤ 10 r > 1   ،�(�)={ه-�2�2-ه-�21-ه-�2 �≤10   �>1،
r =( x- _ایکسمن)2+( y–yمن)2—————-√/دmI،�=(ایکس-ایکسمن)2+(�-yمن)2/دmI،

d mI شعاع دامنه پشتیبانی گره x I است . β یک ثابت است و مقدار آن 3.0 است. مقادیر پارامتر در رویکرد MLS ثابت نگه داشته می‌شوند و تأثیر تفاوت‌ها در توابع پایه و پارامترها بر روی DEM خارج از محدوده این مطالعه است. وضوح DEM ساخته شده در طول آزمایش یکنواخت است. اگرچه، در مورد داده های LIDAR، مقادیر پارامترهای روش درون یابی و تعداد نقاط در همسایگی مورد توجه نیستند [ 34]]، تأثیر آنها بر داده های دیجیتالی نقشه های توپوگرافی را نمی توان نادیده گرفت. داده های دیجیتالی برای نقشه های توپوگرافی از داده های LIDAR از نظر دقت و تراکم نمونه پایین تر هستند. بنابراین، پیشنهاد می شود به دنبال روشی برای بهبود دقت در ساخت DEM باشید.

از آنجایی که توابع پایه خطی در روش MLS اتخاذ می‌شوند، تعداد نقاط همسایه باید بیشتر یا مساوی سه باشد. به منظور بهبود دقت درونیابی، به طور کلی نقاط نمونه برداری بیشتری برای تخمین انتخاب می شوند، بنابراین تعداد نقاط جستجو از پنج نقطه شروع می شود. وقتی شعاع همسایگی بزرگتر از فاصله خودهمبستگی فضایی باشد، خطای DEM افزایش می یابد. بنابراین، محدوده تعداد نقاط در همسایگی 5-20 است.

2.3.1. آزمایش 1: رابطه بین تعداد نقاط در همسایگی و DEM RMSE

با توجه به تعداد نقاط همسایگی، ما DEM i با وضوح 5 متر می سازیم (i = 5، 6، 7، 8، …، 20)، داده های مرجع DEM 0 را به عنوان مقادیر واقعی در نظر می گیریم، RMSE های DEM مربوطه را به صورت محاسبه می کنیم. EDEM i (i = 5، 6، 7، 8، …، 20)، و رابطه بین تعداد نقاط در همسایگی و DEM RMSE را بررسی کنید. فرمول DEM RMSE [ 20 , 35 ] به صورت زیر نشان داده شده است:

RMSE =1n∑nk = 1(زک–zک)2—————√،RMSE=1n∑ک=1n(زک-zک)2،

n مقدار مقادیر مشاهده شده، Z k مقدار واقعی نقطه مشاهده شده و z k مقدار مشاهده شده است. در این مقاله، n حاصلضرب تعداد ردیف DEM و شماره ستون، Z k ارتفاع یک سلول شبکه در DEM 0 و z k ارتفاع سلول مربوطه در DEM i است .

2.3.2. آزمایش 2: رابطه بین تعداد نقاط در همسایگی و شیب متوسط ​​و جنبه میانگین
با استفاده از روش Hone’s ArcGIS [ 28 ]، 14 شبکه شیب و جنبه به ترتیب به عنوان شیب i و جنبه i بر اساس DEM i استخراج می شوند (i = 5, 6, 7, 8, …, 20). شیب میانگین و جهت میانگین به ترتیب به صورت MeanSlope i و MeanAspect i استخراج می‌شوند و رابطه بین تعداد نقاط همسایگی و شیب متوسط ​​و جنبه میانگین ایجاد می‌شود. شیب میانگین، مقدار متوسط ​​شیب تمام سلول های شبکه در شیب i است . جنبه میانگین، مقدار میانگین جنبه تمام سلول های شبکه در Aspect i است .
2.3.3. آزمایش 3: رابطه بین تعداد نقاط در همسایگی و RMSEهای شیب و جنبه

شبکه های شیب و جنبه استخراج شده از DEM 0 به ترتیب شیب 0 و جنبه 0 به عنوان مرجع هستند، RMSE های شیب و جنبه به عنوان ESlope i و EAspect i بیشتر محاسبه می شوند، و رابطه بین RMSE های شیب و جنبه و تعداد. از نقاط محله ایجاد شده است. خطای جنبه برای هر سلول شبکه طبق فرمول زیر محاسبه می شود:

EAمن ، ( ر ، ج )= {( 360 −∣∣جنبهمن ، ( ر ، ج )–جنبه0 , ( r , c )∣∣) %180، ∣∣جنبهمن ، ( ر ، ج )–جنبه0 , ( r , c )∣∣> 180∣∣جنبهمن ، ( ر ، ج )–جنبه0 , ( r , c )∣∣، ∣∣جنبهمن ، ( ر ، ج )–جنبه0 , ( r , c )∣∣≤ 180،EAمن،(r،ج)={(360-|جنبهمن،(r،ج)-جنبه0،(r،ج)|)%180، |جنبهمن،(r،ج)-جنبه0،(r،ج)|>180|جنبهمن،(r،ج)-جنبه0،(r،ج)|، |جنبهمن،(r،ج)-جنبه0،(r،ج)|≤180،
EA خطای جنبه، r شماره ردیف شبکه و c شماره ستون شبکه است. از آنجایی که جنبه یک مقدار چرخه است، اگر مقدار واقعی 1 درجه و مقدار محاسبه شده 359 درجه باشد، خطای جنبه باید 2 درجه باشد نه 358 درجه. بنابراین، خطای جنبه را نمی توان با تفریق مستقیم به دست آورد. با محدوده 180 درجه، خطای جنبه محاسبه شده طبق فرمول (5) می تواند از مشکل بالا جلوگیری کند.
2.3.4. آزمایش 4: توزیع فضایی خطاهای شیب و جنبه
با توجه به شیب i و جنبه i (i = 5، 6، 7، …، 20) برای هر منطقه مورد مطالعه و شیب 0 و جنبه 0 ، شبکه های خطای مطلق و خطای نسبی شیب محاسبه شده توسط ArcGIS به ترتیب AESlope i و RESlope هستند. i و شبکه خطای جنبه EA i است . نقشه های توزیع خطا برای شیب از طریق آمار روی تمام سلول های شبکه بزرگتر از 15 در AESlope i و بیشتر از 100٪ در RESlope i ساخته شده است .

2.4. فرضیه ها

انتظار می رود تغییر وضوح DEM منجر به تغییرات در عوامل زمین مانند شیب و جنبه شود [ 10 ، 12 ، 24 ]. دنگ (2007) معتقد بود که با کاهش وضوح DEM، مقدار متوسط ​​شیب به ترتیب کاهش می یابد [ 36 ]. چاو (2009) کشف کرد که وضوح DEM و شیب میانگین یک رابطه لگاریتمی دارند و با کاهش وضوح، شیب میانگین کاهش می یابد [ 12 ]. زیادت (2007) دریافت که با افزایش اندازه شبکه DEM، RMSE شیب به تدریج کاهش می یابد [ 10]]. بنابراین می توان به طور منطقی فرض کرد که نقاط بیشتر در همسایگی درون یابی باعث تغییر در عوامل زمین مانند شیب و جهت می شود. نقاط بیشتر در همسایگی ممکن است باعث افزایش شعاع محله شود. بنابراین، نقاط نمونه برداری بیشتری در برآورد ارتفاع سلول شبکه DEM شرکت می کنند. با این حال، مشخص نیست که آیا و چگونه نقاط بیشتری در همسایگی بر شیب و مقادیر جنبه استخراج شده از DEM تأثیر می گذارد یا خیر. بنابراین، یک فرضیه صفر ممکن است تنظیم شود:
(1)
با نقاط بیشتر در همسایگی، میانگین شیب و مقادیر ابعاد میانگین تغییر نمی کند، به عنوان مثال:
MeanSlope 5 = MeanSlope 6 = … = MeanSlope 20
MeanSlope 5 = MeanAspect 6 = … = MeanAspect 20
(2)
با نقاط بیشتر در همسایگی، RMSE شیب و جنبه تغییر نمی کند، به عنوان مثال:
ESlope 5 = ESlope 6 = … = ESlope 20
ESlope 5 = EAspect 6 = … = EAspect 20

3. نتایج

3.1. مورفولوژی زمین مناطق مورد مطالعه

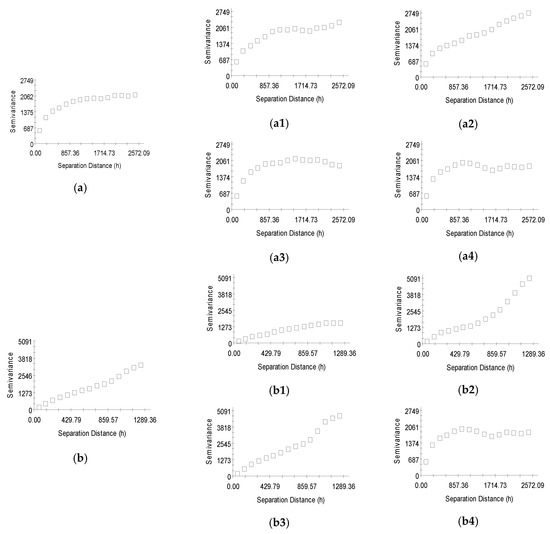
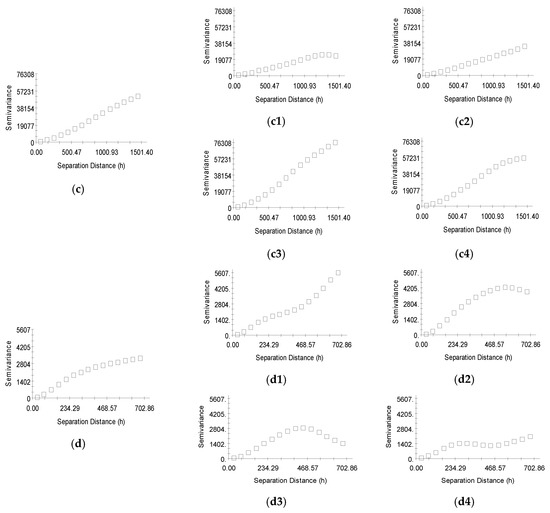
برای هر منطقه مورد مطالعه و داده های شبیه سازی شده، حداقل، حداکثر، میانگین، میانه، انحراف معیار و ضریب تغییرات (CV) ارتفاعات از نقاط نمونه گیری محاسبه می شود ( جدول 1 ). ساختار فضایی ارتفاعات با استفاده از نیم متغیره ها برای جهات 0 درجه، 45 درجه، 90 درجه و 135 درجه تعیین شده توسط GS+ ارزیابی می شود ( شکل 4 ). نسبت آستانه قطعه (N/S) برای تعیین کمیت استحکام ساختار فضایی ارتفاعات استفاده می شود. نقاط قوت از ضعیف (N/S > 0.6)، متوسط ​​(0.3 <N/S <0.6) تا قوی (N/S <0.3) [37 ] متفاوت است. مقادیر N/S سه ناحیه مورد مطالعه و داده های شبیه سازی شده همگی کمتر از 0.3 هستند. همبستگی فضایی مناطق مورد مطالعه و داده های شبیه سازی شده قوی است.
قطعه نشان می دهد که تنوع ارتفاع شامل تغییرات غیرقابل توضیح یا تصادفی است. به جز عامل خطاهای داده، قطعات پیچیدگی زمین سه منطقه مورد مطالعه و داده های شبیه سازی شده را در مقیاس های دقیق تر نشان می دهند. مقادیر قطعه از کوچک به بزرگ به ترتیب با داده های شبیه سازی شده، منطقه مطالعه 2، منطقه مطالعه 1 و منطقه مطالعه 3 مطابقت دارد. سطح داده های شبیه سازی شده صاف ترین، و سطح زمین منطقه مطالعه 3 پیچیده ترین است.
بر اساس نیمه متغیرهای جهت، تغییرات و دامنه در جهت شمال (0 درجه) و جهت شمال شرق (45 درجه) بزرگتر از سایر جهات در منطقه مطالعه 1 است. جهت گیری خندق ها در منطقه مطالعه 1 عبارتند از مطابق با دو جهت (0 درجه، 45 درجه). در منطقه مورد مطالعه 2، تغییرات و دامنه در جهت شمال شرقی (45 درجه) و جهت شرقی-غربی (90 درجه) بیشتر است. در منطقه مورد مطالعه 3، تغییرات و دامنه در جهت شرقی-غربی (90 درجه) بیشتر است. تغییرات و دامنه در جهت شمال (0 درجه) بزرگتر از جهات دیگر داده های شبیه سازی شده است. علاوه بر این، تغییر در جهت شمال غربی (135 درجه) نشان دهنده برخی از دوره های تناوب است. جهت حداکثر و حداقل خود همبستگی با جهت گیری ویژگی های زمین تعیین می شود.38 ].
محدوده نیم متغیره های مناطق مورد مطالعه 1-3 و داده های شبیه سازی شده به ترتیب 448 متر، 2347 متر، 985 متر و 676 متر است ( جدول 2 ). حداکثر شعاع محلات با 20 نقطه از مناطق مطالعه 1-3 و داده های شبیه سازی شده به ترتیب 258 متر، 150 متر، 114 متر و 58.32 متر است. بنابراین، حداکثر شعاع محله با 20 نقطه از هر منطقه مورد مطالعه و داده های شبیه سازی شده از محدوده نیم متغیره های مربوطه فراتر نمی رود.

3.2. رابطه بین تعداد نقاط همسایگی و DEM RMSE

شیوه نمونه گیری از نقاط در این تحقیق، نمونه گیری نامنظم است. بررسی الگوی توزیع مکانی نقاط نمونه برداری ضروری است. ابزار میانگین نزدیکترین همسایه تحت ابزارهای آمار فضایی ArcGIS برای محاسبه شاخص نزدیکترین همسایه (NNI) و میانگین مقدار فاصله نزدیکترین همسایه هر منطقه مورد مطالعه و داده های شبیه سازی شده استفاده می شود (جدول 3 ) . هنگامی که مقدار NNI کوچکتر از 1 باشد، نشان دهنده توزیع تجمعی، زمانی که مقدار NNI برابر با 1 باشد، نشان دهنده توزیع تصادفی و زمانی که NNI بزرگتر از 1 باشد، نشان دهنده توزیع پراکنده است.
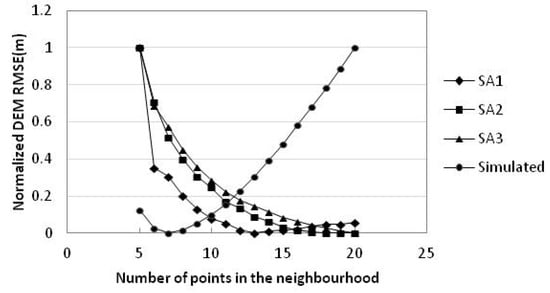
DEM RMSE هر منطقه مورد مطالعه و داده های شبیه سازی شده در جدول 4 نشان داده شده است. DEM RMSE منطقه مورد مطالعه 1 از 3.14 متر به 2.72 متر کاهش یافت و سپس به تدریج به 2.75 متر افزایش یافت. DEM RMSE منطقه مورد مطالعه 2 از 1.64 متر به 1.44 متر کاهش یافت و تمایل به حفظ ثبات داشت. DEM RMSE منطقه مورد مطالعه 3 از 11.72 متر به 4.9 متر کاهش یافت که بیشترین دامنه را داشت. با افزایش نقاط در همسایگی، DEM RMSE های سه منطقه مورد مطالعه همه تمایل به کاهش دارند، و زمانی که تعداد نقاط همسایگی 5 تا 10 باشد، RMSE های DEM به طور چشمگیری کاهش می یابد. منطقه مطالعه 2 دارای کمترین مقدار میانگین فاصله نزدیکترین همسایه است و سطح در سه ناحیه مطالعه صاف است که DEM RMSE آن کوچکترین است. مقدار نقطه درونیابی برای انتخاب نقاط نمونه برداری نزدیک از نقاط نمونه برداری دور دقیق تر است. میانگین فاصله نزدیکترین همسایه منطقه مطالعه 3 کوچکتر از منطقه مطالعه 1 است، اما CV آن بزرگتر از منطقه مطالعه 1 است،
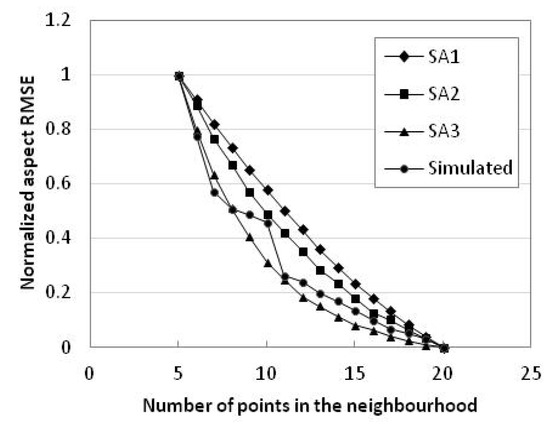
تفاوت های زیادی در محدوده DEM RMSE در سه منطقه مورد مطالعه وجود دارد. برای مقایسه تغییرات DEM RMSE در انواع مختلف زمین به وضوح، همه مقادیر RMSE نرمال شده اند ( شکل 5 ). هنگامی که نقاط محله افزایش می یابد، منطقه مطالعه 2 و منطقه مطالعه 3 در قانون تغییر DEM RMSE نسبتا مشابه هستند، در حالی که منطقه مطالعه 1 با دو منطقه مورد مطالعه دیگر متفاوت است. علاوه بر این، هنگامی که نقاط همسایه از 5 به 11 افزایش می یابد، RMSE های DEM به سرعت کاهش می یابد. هنگامی که نقاط همسایگی بزرگتر از 11 باشد، RMSEهای DEM تمایل دارند به تدریج پایدار باشند. وقتی نقاط همسایه 11 تا 13 باشد، یک نقطه عطف نرخ تغییر DEM RMSE وجود دارد و محدوده شامل مقدار مشترک شماره نقطه در همسایگی به صورت 12 است [12] .]. مجدداً مقدار پیش‌فرض عدد نقطه در روش‌های درون‌یابی ArcGIS مانند IDW، کریجینگ و اسپلاین نیز 12 است. تعداد همسایه‌های 12 که به‌عنوان یک مقدار تجربی در نظر گرفته می‌شوند، عقلانیت خاصی دارد و برای سه حوزه مورد مطالعه اینجا قابل استفاده است.
DEM RMSE داده های شبیه سازی شده کاملاً متفاوت از مناطق مورد مطالعه است ( شکل 5 ). DEM RMSE ابتدا کاهش می یابد و سپس افزایش می یابد. نقطه عطف 7 نقطه در محله است.

3.3. رابطه بین تعداد نقاط همسایگی و شیب متوسط ​​و جنبه میانگین

دقت DEM بر کیفیت عوامل زمین استخراج‌شده تأثیر می‌گذارد و بیشتر بر کیفیت نتایج تجزیه و تحلیل زمین که بر این عوامل زمین مربوط می‌شود تأثیر می‌گذارد [ 39 ، 40 ، 41 ، 42 ]. برای تعداد متفاوتی از نقاط در همسایگی، دقت متفاوتی از DEM i (i = 5، 6، 7، …، 20) از طریق درون یابی به دست می آید، و مقادیر میانگین شیب و ابعاد میانگین استخراج شده نیز متفاوت است ( جدول 5 و جدول 6 ، شکل 6 و شکل 7). دامنه تغییرات سه ناحیه مورد مطالعه و داده های شبیه سازی شده همگی کوچکتر از 1 هستند. میانگین شیب داده های شبیه سازی شده به صورت خطی با افزایش تعداد نقاط در همسایگی کاهش می یابد. بر اساس انحراف معیار شیب میانگین، مقدار شیب متوسط ​​با افزایش تعداد نقاط در همسایگی تغییرات بسیار کمی دارد. به طور خاص، انحراف معیار منطقه مطالعه 1 بزرگتر از منطقه مطالعه 2 یا منطقه مطالعه 3 است. این نشان می دهد که میانگین مقدار شیب منطقه مورد مطالعه 1 نسبت به تغییر همسایگی حساس است. ضرایب معادله رگرسیون ( جدول 7) برای منطقه مطالعه 1 و منطقه مورد مطالعه 2 به ترتیب 0.0538- و 0.0079- است، که همچنین نشان می دهد که منطقه مطالعه 1 تغییر بیشتری در مقدار میانگین شیب دارد. مقادیر میانگین شیب منطقه مورد مطالعه 1 و منطقه مطالعه 2 با افزایش تعداد نقاط همسایگی کاهش می یابد در حالی که مقدار شیب متوسط ​​منطقه مطالعه 3 افزایش می یابد.
با توجه به شیب i (i = 5، 6، 7، …، 20) برای هر منطقه مورد مطالعه ( شکل 8 )با افزایش تعداد نقاط در همسایگی، حداکثر مقدار شبکه شیب در سه منطقه مورد مطالعه کاهش می یابد. حداقل مقادیر شیب بین 0 تا 5 درجه برای منطقه مطالعه 2 و منطقه مطالعه 3 نسبت آنها کاهش می یابد. نسبت مقادیر شیب بیش از 40 درجه در سه منطقه مورد مطالعه کاهش می یابد. نسبت مقادیر شیب بین 5 تا 10 درجه در منطقه مطالعه 1 افزایش یافته است. نسبت مقادیر شیب بین 5 تا 20 درجه در منطقه مطالعه 2 افزایش یافته است. و نسبت مقادیر شیب بین 15 و 40 درجه در منطقه مورد مطالعه 3 افزایش یافته است. این نتایج مشابه یافته های تحقیق در مورد تأثیر فواصل نمونه برداری بر روی شیب ها است که توسط گائو (1998) انجام شده است. به گفته گائو، با افزایش فاصله نمونه برداری، شیب میانه افزایش می یابد در حالی که مقادیر حداکثر و حداقل شیب و دامنه مقادیر شیب کاهش می یابد. هنگامی که مقدار فاصله نمونه برداری بسیار زیاد است، مقادیر شیب کوچکتر دره ها در شیوع افزایش می یابد در حالی که مقادیر شیب بزرگتر پشته ها بیشتر می شود. فواصل نمونه برداری بزرگتر نقش تعمیم قوی تری بر روی لندفرم ها دارند: بسیاری از ویژگی های توپوگرافی جزئی ناپدید می شوند و ویژگی های اصلی حفظ می شوند.11 ].
منطقه مطالعه 1 در بیشتر قسمت ها مسطح است اما شامل چند خندق عمیق است. ترکیب این دو نوع توپوگرافی مختلف باعث می شود که مقدار شیب متوسط ​​در منطقه مورد مطالعه 1 به شدت تغییر کند. منطقه مطالعه 2 و منطقه مطالعه 3 از نظر توپوگرافی نسبتاً همگن هستند، با تغییر کمی در مقدار میانگین شیب.
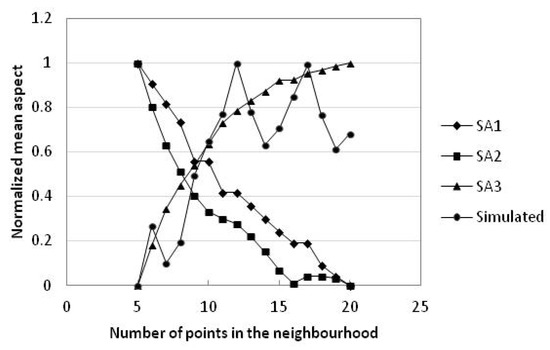
داده های شبیه سازی شده کمترین تغییر را در بعد میانگین دارند و پس از آن منطقه مورد مطالعه 2 و منطقه مطالعه 3 قرار دارند و منطقه مطالعه 1 دارای بیشترین تغییر در بعد میانگین است. انحراف معیار جنبه میانگین نیز از همین ترتیب پیروی می کند. با توجه به معادله رگرسیون ( جدول 8 )، بعد میانگین و نقاط همسایه دارای یک رابطه چند جمله ای درجه دوم هستند. میانگین جنبه های منطقه مطالعه 1 و منطقه مطالعه 2 با افزایش تعداد نقاط در همسایگی کاهش می یابد، اما جنبه میانگین منطقه مطالعه 3 به تدریج افزایش می یابد و جنبه میانگین داده های شبیه سازی شده در کل افزایش می یابد. افزایش جهت نشان می دهد که جهت رو به رو در جهت عقربه های ساعت جابجا می شود، در حالی که کاهش جهت نشان می دهد که جهت روبرو در خلاف جهت عقربه های ساعت تغییر می کند.

3.4. رابطه بین تعداد نقاط در همسایگی و RMSEهای شیب و جنبه

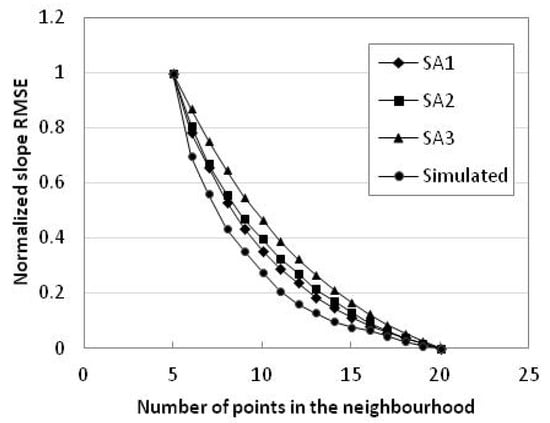
با نقاط بیشتر در همسایگی، RMSEهای شیب و جنبه سه ناحیه مورد مطالعه و داده های شبیه سازی شده همگی کاهش می یابند و رابطه آنها با تعداد نقاط همسایه لگاریتمی است ( جدول 9 و جدول 10 ، شکل 9 و شکل 10 ). . بنابراین فرض صفر رد می شود. با توجه به مقدار ESlope i (i = 5, 6, 7, …, 20) ( جدول 11)، داده های شبیه سازی شده دارای کمترین RMSE شیب هستند و پس از آن منطقه مورد مطالعه 2 و سپس منطقه مطالعه 1 قرار دارد و منطقه مطالعه 3 دارای بیشترین RMSE شیب است. داده های شبیه سازی شده فقط دارای خطاهای گرد کردن و خطاهای گسسته سازی هستند. از این رو، شیب RMSE و جنبه RMSE بسیار کوچک هستند. اگرچه منطقه مطالعه 1 عمدتاً مسطح است، شیب های تند در داخل خندق ها گنجانده شده است و زمین پاره پاره شده است که باعث ایجاد RMSE بزرگتر در شیب می شود. اگرچه منطقه مورد مطالعه 2 نیز شامل تپه‌ها می‌شود، اما در سطح نسبتاً صاف با ویژگی‌های جزئی کمتر است و این نیز یکی از دلایل RMSE کوچک‌تر شیب آن است. منطقه مطالعه 3 شیب دار با ویژگی های زمین دقیق تر است. RMSE شیب آن بزرگترین است. وقتی تعداد نقاط همسایه کوچکتر (بزرگتر) از 12 باشد، سه ناحیه مورد مطالعه دارای شیب بزرگتر (کوچکتر) شیب RMSE هستند. با این حال، RMSE شیب همچنان کاهش می یابد. این روند مشابه تغییر DEM RMSE است که وقتی تعداد نقاط همسایه کوچکتر از 12 باشد سریعتر کاهش می یابد و زمانی که بیشتر از 12 است تقریباً پایدار می شود. بنابراین، در این مورد، 12 می تواند با توجه به کارایی و دقت به عنوان تعداد نقاط همسایه در نظر گرفته شود.
مطالعات موجود بیشتر بر روی تأثیر وضوح DEM بر دقت شیب و جنبه تمرکز دارند. به عنوان مثال، چانگ و تسای (1991) و هاجسون (1998) معتقد بودند که وقتی اندازه سلول شبکه افزایش می یابد، خطاهای شیب و جنبه افزایش می یابد [ 25 ، 43 ]. وارن (2004) کشف کرد که شیب های استخراج شده از یک DEM با وضوح 1 متر کمی بهتر از شیب های DEM با وضوح 2-5 متر است و به طور قابل توجهی نسبت به DEM با وضوح 12.5 متر برتری دارد [44] .]. تأثیر عدد نقطه در همسایگی بر دقت شیب و جنبه از گرایش مخالف پیروی می کند. این همیشه درست نیست که هر چه محله کوچکتر باشد، نتیجه بهتر است. زیادت (2007) کشف کرد که در مورد داده های کانتور، زمانی که شیب با استفاده از یک پنجره 5×5 از طریق یک DEM با سلول های شبکه بزرگتر استخراج شد، شیب استخراج شده دقت بالاتری داشت. دقت شیب افزایش یافت اما دقت DEM با افزایش اندازه سلول شبکه کاهش یافت [ 10]. دیدگاه در مطالعه او این بود که، هرچه سلول های شبکه بزرگتر باشد، دقت شیب بالاتر است، مشابه نتیجه گیری در اینجا با استفاده از خطوط نوع داده مشابه. با این حال، تأثیر تفکیک پذیری بر دقت DEM برخلاف همسایگی در اینجا است. تأثیر تفکیک پذیری بر روی زمین به مراتب بیشتر از تأثیر شماره نقطه در همسایگی بر روی زمین است. هموارسازی زمین و تعمیم ناشی از تغییر وضوح بسیار آشکار است. بر اساس فرمول تابع وزن گاوسی، زمانی که نقطه نمونه برداری در همسایگی به نقطه ای که قرار است درون یابی می شود نزدیکتر باشد، مقدار وزن آن بزرگتر و سهم آن در نتیجه نهایی بیشتر است. اگرچه تعداد نقاط همسایگی افزایش می‌یابد، اما تأثیر آن توسط تابع وزن محدود می‌شود. از این رو،
با توجه به EAspect i (i = 5, 6, 7, …, 20) ( جدول 12 )، از نظر RMSE جنبه برای مناطق مورد مطالعه و داده های شبیه سازی شده، از کوچکترین به بزرگترین داده های شبیه سازی شده، منطقه مطالعه 3 ترتیب داده شده است. منطقه مطالعه 2، و منطقه مطالعه 1. این کاملا با رتبه بندی آنها از نظر خطای شیب متفاوت است. منطقه مورد مطالعه 3 یک منطقه کوهستانی مرتفع با شیب های تندتر و خطای جنبه آن کوچکترین است. منطقه مورد مطالعه 1 بیشتر از زمین مسطح تشکیل شده است و خطای جنبه آن بزرگترین است. با توجه به معادله رگرسیون ( جدول 9 و جدول 10).) خطاها در شیب و جنبه برای زمین های مشابه و منابع داده را می توان به منظور تعیین تعداد مناسب نقاط در همسایگی تخمین زد.

3.5. توزیع فضایی خطاهای شیب و جنبه

در بخش قبل، تجزیه و تحلیل آماری RMSEهای شیب و جنبه در هر منطقه مورد مطالعه در حالی که تعداد نقاط محله افزایش یافته بود، انجام شد، اما این تنها به آمار عددی محدود شد. در این بخش، توزیع فضایی خطاهای شیب و جنبه ترسیم شده است ( شکل 11 و شکل 12 ). چانگ و تسای (1991) کشف کردند که خطای شیب عمدتاً در مناطق شیب تند متمرکز است، در حالی که خطای جنبه عمدتاً در مناطق مسطح متمرکز است [ 25 ]. نتیجه تحقیق در اینجا تقریباً با این نتیجه گیری مطابقت دارد. به دلیل فضای محدود، تنها نقشه های خطا که تعداد نقاط همسایه ده نقطه است در اینجا فهرست شده است ( شکل 11 ).
ناحیه مسطح و کف دره منطقه مورد مطالعه 1 دارای خطای شیب نسبی بزرگتری هستند اما مقدار شیب اصلی منطقه مسطح بسیار کوچک است. بنابراین خطای مطلق بسیار ناچیز باقی می ماند و می توان تاثیر این قسمت را کاملا نادیده گرفت. لبه و داخل خندق در منطقه مورد مطالعه 1 با تغییرات توپوگرافی فوق العاده هر دو دارای خطاهای شیب مطلق بزرگتری هستند. در منطقه مورد مطالعه 2، قله کوه دشت/ خط الراس شکل و منطقه مسطح دارای خطای شیب نسبی بزرگتر و قله و دره دارای خطای شیب مطلق بزرگتر هستند. در منطقه مورد مطالعه 3 خطای شیب نسبی در قسمت مسطح و خطای مطلق در پشته ها، دره ها و کناره های شیب های تند متمرکز است. به طور خلاصه، خطای شیب در پشته ها، دره ها، شیب های تند و نواحی لبه خندق متمرکز است.
خطای جنبه منطقه مورد مطالعه 1 در منطقه مسطح متمرکز است. به غیر از مناطق مسطح، خطای جنبه در منطقه مورد مطالعه 2 نیز در پشته ها و دره ها متمرکز است. خطای جنبه در منطقه مورد مطالعه 3 در نزدیکی حوضه و خط حوضه، یعنی پشته ها و دره ها و همچنین طبقات ملایم دره ها متمرکز است. به طور خلاصه، خطای جنبه در پشته ها، دره ها و مناطق مسطح متمرکز است. مقادیر جنبه به علائم مثبت و منفی مقادیر مشتق در جهت x یا y یک نقطه روی سطح حساس هستند.
با نقاط بیشتر در همسایگی، مناطق با خطای شیب بزرگتر به تدریج کاهش می یابد. هنگامی که تعداد نقاط جستجو در محله از 5 به 20 افزایش می یابد، نسبت سلول های شبکه با خطای شیب مطلق بالای 15 درجه در منطقه مطالعه 1 از 8.53 درصد به 4.73 درصد کاهش می یابد، نسبت سلول های شبکه با خطاهای شیب مطلق بالای 15 درصد کاهش می یابد. درجه در منطقه مورد مطالعه 2 از 4.48 درصد به 1.58 درصد کاهش می یابد و نسبت سلول های شبکه با خطای شیب مطلق بالای 15 درجه در منطقه مطالعه 3 از 21.91 درصد به 6.24 درصد کاهش می یابد. به طور کلی، با نقاط بیشتر در همسایگی، خطاهای شیب و جنبه به تدریج کاهش می یابد.
با توجه به نقشه های سایه تپه DEM i (i = 5، 6، …، 20) ( شکل 13 )، DEM های ساخته شده توسط داده های کانتور درجات مختلفی از اشکال پلکان را نشان می دهند. مناطق مسطح بین دو خط کانتور مجاور در پشته ها وجود دارد. با افزایش تعداد نقاط در همسایگی، پله های سطح زمین به تدریج کاهش می یابد. پله ها دلیل اصلی تمرکز خطاهای شیب و جنبه در پشته ها، دره ها و نواحی لبه گودال ها هستند. علاوه بر این، منجر به دست کم گرفتن پیک و بیش از حد ارزیابی می شود.

4. بحث و نتیجه گیری

این مطالعه تأثیر تعداد نقاط همسایگی را به عنوان پارامتر روش درونیابی، بر شیب میانگین، میانگین وجه و RMSE شیب و جهت مورد بررسی قرار داد. MLS به عنوان یک روش برازش سطح موضعی، دارای خواص مهمی است، مانند حفظ خواص ذاتی سطح، شبیه سازی دقیق سطح، و غیر حساس بودن به نقاط پرت با نقاط گسسته. این مطالعه از روش MLS برای ساخت DEM برای سه منطقه مطالعاتی انتخاب شده از انواع مختلف زمین استفاده کرد. داده های شبیه سازی شده از سطوح گاوس با نتایج حاصل از مناطق مورد مطالعه مقایسه شد. منابع داده های سه منطقه مورد مطالعه، کانتور هستند. این تفسیر یافته ها را به منابع داده مشابه، مقیاس های فضایی و مدل های محاسباتی محدود می کند.
از نتایج همه آزمایش‌ها، تأثیر تعداد نقاط همسایگی بر شیب و جنبه مشهود بود. با امتیازهای بیشتر در محله،
(1)
RMSEهای DEM سه منطقه مورد مطالعه به تدریج کاهش یافت، اما DEM RMSE داده های شبیه سازی شده ابتدا کاهش یافت و سپس افزایش یافت.
(2)
ميانگين شيب و ميانگين ابعاد منطقه مورد مطالعه 1 و منطقه مطالعه 2 به تدريج کاهش يافت. میانگین شیب و بعد میانگین منطقه مطالعه 3 افزایش یافت. میانگین شیب داده های شبیه سازی شده به صورت خطی کاهش یافت. و جنبه میانگین داده های شبیه سازی شده به صورت موجی افزایش یافت.
(3)
شیب RMSEs و جنبه RMSE سه منطقه مورد مطالعه و داده های شبیه سازی شده به صورت لگاریتمی کاهش یافت.
(4)
سلول های شبکه با خطای شیب مطلق بیشتر از 15 درجه کاهش یافته است.
صرف نظر از نوع زمین، روند شیب و جهت تغییر RMSE با تغییر در تعداد نقاط محله تقریباً یکسان است. هر چه نقاط همسایگی در تخمین ارتفاع سلول شبکه DEM درگیرتر باشد، شیب و جنبه استخراج شده دقیق تر است. بنابراین، برای منابع داده‌های مشابه، مقیاس‌ها و تراکم‌های نقاط نمونه‌برداری، وجود نقاط همسایگی کافی برای درون‌یابی DEM‌ها می‌تواند منجر به دستیابی به شیب‌ها و جنبه‌های دقیق‌تر شود. با این حال، نقاط همسایگی بیشتر برای درون یابی DEM ها منجر به کاهش بازده محاسباتی می شود. زمانی که تعداد نقاط همسایه کمتر از 10 بود، RMSEهای شیب و جنبه به سرعت کاهش یافت، در حالی که وقتی تعداد نقاط همسایه از 12 بیشتر بود، RMSEها به آرامی کاهش یافتند. هم در نتایج حاصل از سه حوزه مطالعه و هم در داده های شبیه سازی شده. از این رو، حفظ بین 10 تا 12 نقطه در محله یک انتخاب اقتصادی است.
روش درون یابی زمانی باید در نظر گرفته شود که چگالی نمونه برداری کم باشد. هنگامی که تراکم نمونه‌برداری بالا باشد، تفاوت‌های کمی بین روش‌های درون‌یابی مختلف وجود دارد، صرف‌نظر از مورفولوژی شکل زمین [ 37 ]. تراکم نمونه برداری برای مناطق مورد مطالعه و برای داده های شبیه سازی شده همگی کم است. نتایج ممکن است با استفاده از روش های مختلف درونیابی متفاوت باشد.
کسب دانش در مورد شکل زمین قبل از درون یابی بسیار مهم است. برای توصیف و مدل‌سازی ساختارهای فضایی سه ناحیه مورد مطالعه و داده‌های شبیه‌سازی شده از نیم‌واریوگرام‌ها استفاده شد. استحکام ساختارهای فضایی ارتفاعات می تواند بر دقت DEM های درونیابی شده تأثیر بگذارد. کراوچنکو معتقد بود که اگر ساختار فضایی ضعیف باشد، نتایج درونیابی دقیق را می توان تنها از طریق نمونه گیری بسیار فشرده به دست آورد [ 45]]. در این مطالعه، تراکم نمونه‌گیری برای مناطق مورد مطالعه و داده‌های شبیه‌سازی شده کم بود و ساختارهای فضایی همگی قوی بودند. شیب ها و جنبه های استخراج شده از DEM های مناطق مورد مطالعه و داده های شبیه سازی شده قابل مقایسه هستند. علاوه بر این، همسایگان درگیر در تخمین ارتفاع نقاط درونیابی باید در محدوده خود همبستگی فضایی باشند تا تخمین دقیقی به دست آید. حداکثر جهت های خودهمبستگی فضایی جهت گیری ویژگی های زمین را توصیف می کند.
نقاط گسسته از کانتورها می توانند DEM هایی با شکل پلکانی در درون یابی ایجاد کنند. با افزایش نقاط همسایگی، پله ها به تدریج کاهش می یابد. این دلیل اصلی بزرگتر بودن RMSEهای شیب های استخراج شده از DEM های درونیابی شده در زمانی است که تعداد نقاط همسایگی در روش درونیابی کمتر بود. مناطق مسطح بین دو خط کانتور مجاور در مناطق شیب ملایم DEM های درون یابی زمانی که تعداد نقاط همسایگی کمتر بود مشاهده شد. این امر باعث تخمین نادرست جهت جریان آب در آنالیزهای هیدرولوژیکی شد. بنابراین، استفاده از DEM های درونیابی شده از منابع داده کانتور در شبیه سازی جریان آب را توصیه نمی کنیم. در مقیاس‌هایی مانند مقیاس‌های موجود در این مطالعه، اگر داده‌های کانتور تنها منبع داده موجود باشد، برای مثال تعداد کافی نقاط همسایگی، 20 یا بیشتر، باید در درونیابی DEM ها برای کاهش خطاهای شیب های استخراج شده و مناطق مسطح از DEM ها دخالت داشته باشند. سپس، DEM های درونیابی شده توسط تعداد بیشتری از نقاط همسایگی از داده های کانتور ممکن است عملاً در تحلیل های هیدرولوژیکی استفاده شوند. بدیهی است که داده های کانتور منبع داده ایده آلی برای ساخت DEM ها نیستند.
توزیع فضایی خطاهای شیب و جنبه مورد تجزیه و تحلیل قرار گرفت. خطای شیب در پشته‌ها، دره‌ها، شیب‌های تند و نواحی لبه خندق و خطای جنبه در پشته‌ها، دره‌ها و مناطق مسطح متمرکز بود. این مشکل را می توان با افزودن داده های ویژگی مانند خطوط خط الراس، خطوط دره و خطوط شانه دره ها و انتخاب نقاط کافی در همسایگی در درونیابی ساخت و ساز DEM حل کرد.
این مقاله مرجعی برای انتخاب نقاط در همسایگی با استفاده از روش درونیابی، در ساخت DEM ارائه می دهد. اگر شکل زمین و منبع داده مشابه مناطق مورد مطالعه در اینجا باشد، می توان شیب و خطاهای جنبه را با توجه به معادلات رگرسیون تخمین زد تا تعداد بهینه نقاط در همسایگی انتخاب شود. تمام پارامترها در روش درونیابی، به جز تعداد نقاط همسایگی، ثابت هستند. در یک DEM، منابع داده های زیادی، روش های مختلف ساخت و ساز و شکل های مختلف زمین وجود دارد و تأثیر پارامترهای متعدد روش درونیابی بر روی DEM و دقت شیب و جنبه بسیار پیچیده است. این مطالعه مقدماتی است. تنها سه منطقه مورد مطالعه از انواع مختلف زمین انتخاب شدند. تغییر در شیب و خطاهای جنبه با افزایش نقاط در همسایگی درون یابی در سایر مناطق نوع زمین نیاز به تحقیق بیشتر دارد. یکی دیگر از تمرکزهای تحقیقاتی آینده، تأثیر تعداد نقاط محله بر شیب و جنبه زمانی است که از نقاط نمونه برداری با توزیع ها، تراکم ها و مقیاس های مختلف استفاده می شود و وضوح های مختلف DEM ساخته می شود.

منابع

  1. روئدا، ا. Noguera, JM; مارتینز-کروز، سی. یک الگوریتم سیلاب برای استخراج شبکه های زهکشی از مدل های ارتفاعی دیجیتال پردازش نشده. محاسبه کنید. Geosci. 2013 ، 59 ، 116-123. [ Google Scholar ] [ CrossRef ]
  2. بهرنز، تی. زو، تبر; اشمیت، ک. Scholten، T. تجزیه و تحلیل زمین دیجیتال چند مقیاسی و انتخاب ویژگی برای نقشه برداری دیجیتالی خاک. ژئودرما 2010 ، 155 ، 175-185. [ Google Scholar ] [ CrossRef ]
  3. فلورس-پریتو، ای. Quénéhervé، G. باکوفر، اف. شهزاد، ف. Maerker، M. تفسیر مورفوتکتونیکی حوضه ماکویونی در شمال تانزانیا با استفاده از داده‌های DEM و SAR. ژئومورفولوژی 2015 ، 248 ، 427-439. [ Google Scholar ] [ CrossRef ]
  4. کوکوولاس، IK; زیگوری، وی. نیکولاکوپولوس، ک. Verroios، S. رساله در مورد ژئومورفولوژی تکتونیکی گسل های فعال: اهمیت استفاده از یک مدل ارتفاع دیجیتال جهانی. جی. ساختار. جئول 2018 . پذیرفته شده. [ Google Scholar ] [ CrossRef ]
  5. میکسنر، جی. گریمر، جی سی. بکر، ا. شیل، ای. Kohl, T. مقایسه مدل‌های مختلف ارتفاعی دیجیتال و تصاویر ماهواره‌ای برای تحلیل خطی: مفاهیمی برای شناسایی و آرایش فضایی مناطق گسلی در سنگ‌های زیرزمینی کریستالی جنگل سیاه جنوبی (آلمان). جی. ساختار. جئول 2017 ، 108 ، 256-268. [ Google Scholar ] [ CrossRef ]
  6. مکرم، م. حجتی، م. تحلیل مورفومتریک نهر به عنوان یکی از منابع آبیاری اراضی کشاورزی با استفاده از قدرت تفکیک مکانی بالا مدل رقومی ارتفاعی (DEM). محاسبه کنید. الکترون. کشاورزی 2017 ، 142 ، 190-200. [ Google Scholar ] [ CrossRef ]
  7. Aguilar، JF; آگوئرا، اف. Aguilar، AM; کارواخال، F. اثرات مورفولوژی زمین، تراکم نمونه برداری، و روش های درونیابی بر دقت DEM شبکه. فتوگرام مهندس Remote Sens. 2005 ، 71 ، 805-816. [ Google Scholar ] [ CrossRef ]
  8. چن، سی. لی، ی. Dai, H. کاربرد پچ Coons برای تولید مدل‌های ارتفاع دیجیتال مبتنی بر شبکه. بین المللی J. Appl. رصد زمین. Geoinf. 2011 ، 13 ، 830-837. [ Google Scholar ] [ CrossRef ]
  9. فلورینسکی، VI دقت متغیرهای توپوگرافی محلی به دست آمده از مدل های رقومی ارتفاع. بین المللی جی. جئوگر. Inf. علمی 1998 ، 12 ، 47-61. [ Google Scholar ] [ CrossRef ]
  10. زیاد، اثر MF فواصل کانتور و اندازه سلول شبکه بر دقت DEMs و مشتقات شیب. ترانس. GIS 2007 ، 11 ، 67-81. [ Google Scholar ] [ CrossRef ]
  11. Gao, J. تاثیر فواصل نمونه برداری بر قابلیت اطمینان متغیرهای توپوگرافی نقشه برداری شده از DEM های شبکه در مقیاس میکرو. بین المللی جی. جئوگر. Inf. علمی 1998 ، 12 ، 875-890. [ Google Scholar ] [ CrossRef ]
  12. چاو، TE; هاجسون، EM اثرات پس‌فاصله لیدار و تفکیک DEM به میانگین برآورد شیب. بین المللی جی. جئوگر. Inf. علمی 2009 ، 23 ، 1277-1295. [ Google Scholar ] [ CrossRef ]
  13. عاقلانه، اثر MS روش‌های مختلف ایجاد DEM بر نتایج یک مدل هیدرولوژیکی. محاسبه کنید. Geosci. 2007 ، 33 ، 1351-1365. [ Google Scholar ] [ CrossRef ]
  14. موگلن، جنرال الکتریک؛ اثرات هارتمن، GL Resolution بر پارامترهای مدل‌سازی هیدرولوژیکی و دبی اوج جی هیدرول. مهندس 2001 ، 6 ، 490-497. [ Google Scholar ] [ CrossRef ]
  15. Kienzle، S. اثر وضوح شطرنجی DEM بر مشتقات مرتبه اول، مرتبه دوم و زمین مرکب. ترانس. GIS 2004 ، 8 ، 83-111. [ Google Scholar ] [ CrossRef ]
  16. تانگ، جی. پیشرفت DEM و تجزیه و تحلیل زمین دیجیتال در چین. Acta Geogr. گناه 2014 ، 69 ، 1305-1325. [ Google Scholar ]
  17. Li، ZL; Zhu, Q. مدل ارتفاعی دیجیتال ; انتشارات دانشگاه ووهان: ووهان، چین، 2003. [ Google Scholar ]
  18. موکرجی، اس. جوشی، KP; موکرجی، اس. قوش، ع. Garg، DR; Mukhopadhyay, A. ارزیابی دقت عمودی مدل منبع باز دیجیتال ارتفاعی (DEM). بین المللی J. Appl. رصد زمین. Geoinf. 2013 ، 21 ، 205-217. [ Google Scholar ] [ CrossRef ]
  19. فلورینسکی، VI; Kuryakova، GA تعیین اندازه شبکه برای مدل‌سازی زمین دیجیتال در بررسی‌های منظر – با توزیع رطوبت خاک در مقیاس میکرو. بین المللی جی. جئوگر. Inf. علمی 2000 ، 12 ، 47-61. [ Google Scholar ] [ CrossRef ]
  20. Gao, J. وضوح و دقت نمایش زمین توسط DEM های شبکه در مقیاس میکرو. بین المللی جی. جئوگر. Inf. علمی 1997 ، 11 ، 199-212. [ Google Scholar ] [ CrossRef ]
  21. قیاسی عقیعی، ی. Willgoose, GR; De Troch، FD اثرات تفکیک عمودی و مقیاس نقشه مدل رقومی ارتفاع بر پارامترهای ژئومورفولوژیکی مورد استفاده در هیدرولوژی. هیدرول. روند. 1995 ، 9 ، 363-382. [ Google Scholar ] [ CrossRef ]
  22. Mcmaster، JK اثرات وضوح مدل رقومی ارتفاع بر موقعیت شبکه جریان مشتق شده. منبع آب Res. 2002 ، 38 ، 1042. [ Google Scholar ] [ CrossRef ]
  23. رابر، جی. جنسن، جی آر. هاجسون، من؛ تولیس، جی. دیویس، کارشناسی; Berglund، J. تاثیر فاصله گذاری اسمی LIDAR بر دقت DEM و تعیین منطقه سیل. فتوگرام مهندس Remote Sens. 2007 ، 73 ، 793-804. [ Google Scholar ] [ CrossRef ]
  24. وازه، ج. تنگ، جی. Spencer, G. تأثیر دقت و وضوح DEM بر شاخص های توپوگرافی. محیط زیست مدل. نرم افزار 2010 ، 25 ، 1086-1098. [ Google Scholar ] [ CrossRef ]
  25. چانگ، KT; Tsai، BW اثر وضوح DEM بر روی شیب و نقشه برداری. کارتوگر. Geogr. Inf. سیستم 1991 ، 18 ، 69-77. [ Google Scholar ] [ CrossRef ]
  26. چن، سی. لیو، اف. لی، ی. یان، سی. لیو، جی. یک روش درون یابی قوی برای ساخت مدل های ارتفاعی دیجیتال از داده های سنجش از دور. ژئومورفولوژی 2016 ، 268 ، 275-287. [ Google Scholar ] [ CrossRef ]
  27. فرانک، آر. درون یابی داده های پراکنده: آزمون های برخی از روش ها. ریاضی. محاسبه کنید. 1982 ، 38 ، 181-200. [ Google Scholar ]
  28. شاخ، سایه‌اندازی تپه BKP و نقشه بازتاب. Proc. IEEE 1981 ، 69 ، 14-47. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  29. Zevenbergen، LW; تورن، CR تجزیه و تحلیل کمی توپوگرافی سطح زمین. فرآیند سطح زمین Landf. 1987 ، 12 ، 47-56. [ Google Scholar ] [ CrossRef ]
  30. Jones, KH مقایسه الگوریتم های مورد استفاده برای محاسبه شیب تپه به عنوان ویژگی DEM. محاسبه کنید. Geosci. 1998 ، 24 ، 315-323. [ Google Scholar ] [ CrossRef ]
  31. Goodchild، MF سخنرانی اصلی: سمپوزیوم در مورد دقت پایگاه داده فضایی. در مجموعه مقالات سمپوزیوم در مورد دقت پایگاه داده فضایی، ملبورن، استرالیا، 19-20 ژوئن 1991. صص 1-16. [ Google Scholar ]
  32. فانک، سی. کرتین، ک. گودچایلد، م. مونتلو، دی. Noronha, V. فرمول‌بندی و آزمایش مدلی از میدان‌های اعوجاج موقعیتی. در ارزیابی دقت مکانی: عدم قطعیت اطلاعات زمین در منابع طبیعی ; Lowell, K., Jaton, A., Eds. ان آربر پرس: چلسی، MA، ایالات متحده آمریکا، 1998; صص 131-137. [ Google Scholar ]
  33. فلیشمن، اس. کوهن-اور، دی. Silva، CT دارای حداقل مربعات متحرک مستحکم با ویژگی های تیز. ACM Trans. گر (TOG) 2005 ، 24 ، 544-552. [ Google Scholar ] [ CrossRef ]
  34. لوید، سی دی; اتکینسون، PM استخراج DEMS از داده های LIDAR با کریجینگ. بین المللی J. Remote Sens. 2002 ، 23 ، 2519-2524. [ Google Scholar ] [ CrossRef ]
  35. گونگ، جی. لی، ز. زو، س. سویی، اچ. ژو، ی. اثرات عوامل مختلف بر دقت DEMs: یک بررسی تجربی فشرده. فتوگرام مهندس Remote Sens. 2000 , 66 , 1113-1117. [ Google Scholar ]
  36. دنگ، ی. ویلسون، جی پی؛ وابستگی های تفکیک بائر، BO DEM ویژگی های زمین در سراسر یک چشم انداز. بین المللی جی. جئوگر. Inf. علمی 2007 ، 21 ، 187-213. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  37. چاپلوت، وی. داربوکس، اف. بورنان، اچ. لگوئدویس، اس. سیلورا، ن. Phachomphon، K. دقت تکنیک های درونیابی برای استخراج مدل های ارتفاعی دیجیتال در رابطه با انواع شکل زمین و چگالی داده ها. ژئومورفولوژی 2006 ، 77 ، 126-141. [ Google Scholar ] [ CrossRef ]
  38. لیو، اچ. Jezek، CK بررسی الگوهای خطای DEM با واریوگرام های جهت دار و تحلیل فوریه. Geogr. مقعدی 1999 ، 31 ، 249-266. [ Google Scholar ] [ CrossRef ]
  39. Bolstad، PV; استو، تی. ارزیابی دقت DEM: ارتفاع، شیب و جنبه. فتوگرام مهندس Remote Sens. 1994 , 60 , 1327-1332. [ Google Scholar ]
  40. لوپز، سی. آزمایشی بر روی بهبود دقت ارتفاعی DEM های مشتق شده از نظر فتوگرامتری. بین المللی جی. جئوگر. Inf. علمی 2002 ، 16 ، 361-375. [ Google Scholar ] [ CrossRef ]
  41. لی، جی. اسنایدر، پی کی; فیشر، PF مدل‌سازی اثر خطاهای داده بر استخراج ویژگی از مدل‌های ارتفاعی دیجیتال. فتوگرام مهندس Remote Sens. 1992 ، 58 ، 1461-1467. [ Google Scholar ]
  42. واکر، جی پی؛ Willgoose، GR در مورد تأثیر دقت مدل ارتفاعی دیجیتال بر هیدرولوژی و ژئومورفولوژی. منبع آب Res. 1999 ، 35 ، 2259-2268. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  43. هاجسون، EM مقایسه زوایا از الگوریتم‌های شیب/جهت سطح. کارتوگر. Geogr. Inf. سیستم 1998 ، 25 ، 173-185. [ Google Scholar ] [ CrossRef ]
  44. وارن، اس دی؛ هومن، ام جی; اورسوالد، ک. میتاسووا، H. ارزیابی روش‌های تعیین شیب با استفاده از داده‌های رقومی ارتفاع. کاتنا 2004 ، 58 ، 215-233. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  45. کراوچنکو، AN تأثیر ساختار فضایی بر دقت روشهای درونیابی. علم خاک Soc. صبح. J. 2003 , 67 , 1564-1571. [ Google Scholar ] [ CrossRef ]
Ijgi 08 00030 g001 550
شکل 1. موقعیت و توپوگرافی سه منطقه مورد مطالعه: نقشه های سایه تپه ایجاد شده از DEM های مرجع 5 متری برای ( الف ) منطقه مطالعه 1، ( ب ) منطقه مطالعه 2، ( ج ) و منطقه مطالعه 3.
Ijgi 08 00030 g002a 550 Ijgi 08 00030 g002b 550
شکل 2. نقشه های کانتور: ( الف ) منطقه مطالعه 1، ( ب ) منطقه مطالعه 2، و ( ج ) منطقه مطالعه 3. فاصله کانتور 10 متر است.
Ijgi 08 00030 g003 550
شکل 3. سطح و نقاط پراکنده داده های شبیه سازی شده. ( الف ) سطح ایجاد شده توسط فرمول (1) و ( ب ) نقاط به طور تصادفی از سطح پراکنده شده است.
Ijgi 08 00030 g004a 550 Ijgi 08 00030 g004b 550
شکل 4. نیمه متغیرهای جهت ارتفاعات. نیم متغیره های همسانگرد ( الف ) منطقه مطالعه 1، ( ب ) منطقه مطالعه 2، ( ج ) منطقه مطالعه 3، و ( د ) داده های شبیه سازی شده. نیم متغیره ناهمسانگرد (0°) از (a1) منطقه مطالعه 1، ( b1 ) منطقه مطالعه 2، ( c1 ) منطقه مطالعه 3، و ( d1 ) داده های شبیه سازی شده. نیمه متغیریگرام ناهمسانگرد (45 درجه) از ( a2 ) منطقه مطالعه 1، ( b2 ) منطقه مطالعه 2، ( c2 ) منطقه مطالعه 3، و ( d2 ) داده های شبیه سازی شده. نیم متغیره ناهمسانگرد (90 درجه) از ( a3 ) ​​منطقه مطالعه 1، ( b3 ) منطقه مطالعه 2، ( c3 )) منطقه مطالعه 3، و ( d3 ) داده های شبیه سازی شده. نیمه متغیریگرام ناهمسانگرد (135 درجه) از ( a4 ) منطقه مطالعه 1، ( b4 ) منطقه مطالعه 2، ( c4 ) منطقه مطالعه 3، و ( d4 ) داده های شبیه سازی شده.
Ijgi 08 00030 g005 550
شکل 5. نمودار DEM RMSE سه منطقه مطالعه و داده های شبیه سازی شده بر اساس تعداد نقاط در همسایگی.
Ijgi 08 00030 g006 550
شکل 6. نمودار شیب متوسط ​​با تعداد نقاط در همسایگی در مناطق مطالعه 1-3 و داده های شبیه سازی شده.
Ijgi 08 00030 g007 550
شکل 7. نمودار ابعاد میانگین با تعداد نقاط در همسایگی در مناطق مطالعه 1-3 و داده های شبیه سازی شده.
Ijgi 08 00030 g008a 550 Ijgi 08 00030 g008b 550
شکل 8. هیستوگرام درجه شیب با تعداد سلول های شبکه در مناطق مورد مطالعه 1-3. 5 درجه در هر درجه وجود دارد. ستون‌های چپ به راست در هر گروه به ترتیب با تعداد سلول‌های شبکه هر درجه شیب در شیب i (i = 5، 6، 7، …، 20) مطابقت دارند. هیستوگرام ( الف ) منطقه مطالعه 1، ( ب ) منطقه مطالعه 2، و ( ج ) منطقه مطالعه 3.
Ijgi 08 00030 g009 550
شکل 9. نمودار شیب RMSE با تعداد نقاط در همسایگی در مناطق مطالعه 1-3 و داده های شبیه سازی شده.
Ijgi 08 00030 g010 550
شکل 10. نمودار جنبه RMSE با تعداد نقاط در همسایگی در مناطق مطالعه 1-3 و داده های شبیه سازی شده.
Ijgi 08 00030 g011 550
شکل 11. توزیع فضایی خطای شیب (قسمت های آبی در ( a – c ) به ترتیب نشان دهنده تمام سلول های شبکه ای منطقه مطالعه 1، منطقه مطالعه 2، و منطقه مطالعه 3 با خطاهای نسبی بیشتر از 100٪ است؛ قسمت های آبی در ( d – f ) به ترتیب تمام سلول های شبکه منطقه مورد مطالعه 1، منطقه مطالعه 2 و منطقه مطالعه 3 را با خطاهای شیب مطلق بیشتر از 15 درجه نشان می دهد.
Ijgi 08 00030 g012 550
شکل 12. توزیع فضایی خطاهای جنبه (( a – c ) به ترتیب نشان دهنده توزیع فضایی خطاهای جنبه منطقه مطالعه 1، منطقه مطالعه 2، و منطقه مطالعه 3 است.
Ijgi 08 00030 g013 550
شکل 13. نقشه های سایه انداز تپه تولید شده از DEM برای ( الف ) DEM 5 منطقه مطالعه 1، ( ب ) DEM 5 منطقه مطالعه 2، ( ج ) DEM 5 منطقه مطالعه 3، ( د ) DEM 20 منطقه مطالعه 1 ، ( ه ) DEM 20 منطقه مطالعه 2 و ( f ) DEM 20 منطقه مطالعه 3.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید