جستجو ...

تطبیق خودکار داده‌های ساختمان چندمقیاس بر اساس برچسب‌گذاری آرامش و ترکیب الگوها

مقالات داخلی و بین المللی تطبیق خودکار داده‌های ساختمان چندمقیاس بر اساس برچسب‌گذاری آرامش و ترکیب الگوها

خلاصه

با تقاضای فزاینده فوری برای ترکیب نقشه و به‌روزرسانی به موقع داده‌ها، تطبیق داده‌ها به یک مسئله حیاتی در کلان داده و جامعه GIS تبدیل شده است. با این حال، انحراف غیر صلب، همگن سازی شکل، و تفاوت‌های مقیاس نامشخص در داده‌های ساختمانی جمع‌سپاری و رسمی رخ می‌دهد، که باعث ایجاد چالش‌هایی در ترکیب مجموعه داده‌های ساختمانی ناهمگن از منابع و مقیاس‌های مختلف می‌شود. بنابراین، این مقاله یک روش تطبیق داده‌های ساختمان خودکار را بر اساس برچسب‌گذاری آرامش و ترکیب‌های الگو پیشنهاد می‌کند. روش پیشنهادی ابتدا تمام اشیاء تطبیق احتمالی و ترکیب‌های الگو را برای ایجاد یک جدول تطبیق تشخیص می‌دهد و چهار شباهت جغرافیایی را برای هر جفت نامزد تطبیق محاسبه می‌کند تا یک ماتریس تطبیق احتمالی را مقداردهی کند. بعد از آن، اطلاعات زمینه‌ای جفت‌های تطبیق نامزد همسایه برای اصلاح اکتشافی ماتریس تطبیق مبتنی بر شباهت جغرافیایی برای دستیابی به سازگاری تطبیق متنی بررسی می‌شود. سه مطالعه موردی برای نشان دادن اینکه روش پیشنهادی دقت تطبیق بالایی را به دست می‌آورد و تطابق‌های مختلف 1:1، 1:M و M:N را به درستی شناسایی می‌کند، انجام شده است. این نشان می‌دهد که روش تطبیق برچسب‌گذاری آرامش در سطح الگو می‌تواند به طور موثر بر مشکلات همگنی شکل و انحراف غیر صلب غلبه کند، و در عین حال حساسیت ضعیفی به تفاوت‌های مقیاس نامشخص دارد، و یک راه‌حل کاربردی برای ترکیب داده‌های جمع‌سپاری و ساختمان رسمی ارائه می‌دهد. سه مطالعه موردی برای نشان دادن اینکه روش پیشنهادی دقت تطبیق بالایی را به دست می‌آورد و تطابق‌های مختلف 1:1، 1:M و M:N را به درستی شناسایی می‌کند، انجام شده است. این نشان می‌دهد که روش تطبیق برچسب‌گذاری آرامش در سطح الگو می‌تواند به طور موثر بر مشکلات همگنی شکل و انحراف غیر صلب غلبه کند، و در عین حال حساسیت ضعیفی به تفاوت‌های مقیاس نامشخص دارد، و یک راه‌حل کاربردی برای ترکیب داده‌های جمع‌سپاری و ساختمان رسمی ارائه می‌دهد. سه مطالعه موردی برای نشان دادن اینکه روش پیشنهادی دقت تطبیق بالایی را به دست می‌آورد و تطابق‌های مختلف 1:1، 1:M و M:N را به درستی شناسایی می‌کند، انجام شده است. این نشان می‌دهد که روش تطبیق برچسب‌گذاری آرامش در سطح الگو می‌تواند به طور موثر بر مشکلات همگنی شکل و انحراف غیر صلب غلبه کند، و در عین حال حساسیت ضعیفی به تفاوت‌های مقیاس نامشخص دارد، و یک راه‌حل کاربردی برای ترکیب داده‌های جمع‌سپاری و ساختمان رسمی ارائه می‌دهد.

کلید واژه ها:

تطبیق ساختمان ; برچسب زدن آرامش ; ترکیبات الگوی ؛ مقیاس های چندگانه ؛ ترکیب نقشه

1. معرفی

در زمینه شهرنشینی و کلان داده، توسعه سریع اکتساب داده های مکانی باعث رشد انفجاری مجموعه داده های مکانی شده است. به طور خاص، با محبوبیت اطلاعات جغرافیایی داوطلبانه (VGI)، به روز رسانی داده های مکانی در حال تغییر قابل توجهی از به روز رسانی فعال از بالا به پایین به به روز رسانی جمعی از پایین به بالا است [1 ] . از یک سو، داده‌های جغرافیایی جمع‌سپاری شده نقش مهمی در تولید مدل‌های سه بعدی شهر یا نقشه‌های راه بسیار دقیق دارند [ 2 ، 3 ، 4 ]. از سوی دیگر، استفاده از داده‌های مکانی موجود برای غنی‌سازی اطلاعات ساختمان تولید شده توسط کاربر ضروری است. 5]]. در کاربردهای عملی، بخش‌ها یا داوطلبان مختلف مجموعه‌های داده‌های جغرافیایی مختلف را با دقت‌های مختلف، مقیاس‌های مختلف یا تمرکز موضوعی متفاوت جمع‌آوری می‌کنند. این مجموعه داده‌های جغرافیایی ناهمگن نمی‌توانند به طور موثر با یکدیگر تعامل داشته باشند، که منجر به مشکلات جداسازی اطلاعات می‌شود. این یک مسئله حیاتی در جامعه GIS است که مجموعه داده‌های جغرافیایی چندمنبعی و ناهمگن را در یک محصول داده غنی شده یا به موقع با دقت هندسی بالاتر و اطلاعات ویژگی‌های دقیق ادغام کنند [ 6 ، 7]]. هدف تطبیق داده ها شناسایی اشیاء نقطه، خطی یا ناحیه مرتبط بین دو یا چند مجموعه داده جغرافیایی در یک منطقه یا همپوشانی است که به طور گسترده به عنوان مرحله اساسی ترکیب داده ها و به روز رسانی نقشه در نظر گرفته می شود. موضوع مقاله ساخت تطبیق چند ضلعی است.
به دلیل مشارکت آماتور و بازرسی کیفیت محدود، تناقضات داده ها (مانند تفاوت های مقیاس ناهموار، اختلافات هندسی بزرگ و توصیف های معنایی متنوع) احتمالاً بین داده های مکانی جمعی و معتبر [8] رخ می دهد . محققان دریافته‌اند که مجموعه داده‌های جمع‌سپاری با سطوح ناهماهنگ جزئیات (LOD) و مقیاس‌های نامشخص مشخص می‌شوند [ 9 ]. این ناهماهنگی در LODها ممکن است منجر به شیوع 1:M و M:N مطابقت بین مجموعه داده‌های مختلف شود. علاوه بر این، محتوای تولید شده توسط کاربر ممکن است از نظر هندسی دقیق و ساختار معنایی کمتری داشته باشد، به ویژه در مناطق روستایی یا توسعه نیافته [ 10]]. این چالش‌های بزرگی را برای تطبیق مجموعه داده‌های جمع‌سپاری و معتبر ایجاد می‌کند. به طور خاص، تطبیق چند ضلعی های ساختمانی چند مقیاسی با برخی از مشکلات پیچیده همراه است. اولاً، همگن سازی شکل و جهت اشیاء ساختمانی و انحرافات غیر صلب بین مجموعه داده های مختلف، تشخیص اشیاء تطبیق 1:1 با شکل ها و چیدمان های مشابه را دشوار می کند [11 ] . همانطور که در شکل 1 نشان داده شده است، اکثر اشیاء چند ضلعی ساختمان به صورت مستطیل های منظم با انحرافات غیر صلب نشان داده می شوند که به سختی می توان آنها را بر اساس مقایسه شباهت شکل مطابقت داد. ثانیا، LODهای ناسازگار منجر به شباهت کم اشیاء تطبیق 1:M و M:N می شود. همانطور که در نشان داده شده است شکل 1 نشان داده شده استب، تناظرهای 1:0، 1:M، N:1 و M:N زیادی با شباهت کم وجود دارد. از این رو، این مقاله بر روی موضوع خاص تطبیق چند ضلعی های ساختمانی چند مقیاسی با رویکرد برچسب زدن آرامش بهبود یافته تمرکز می کند.
ادامه مقاله به شرح زیر تدوین شده است. در بخش 2 ، اطلاعات مربوط به تطبیق داده ها بررسی می شود. بخش 3 یک روش تطبیق ساختمان بهبود یافته را بر اساس برچسب زدن آرامش و ترکیب الگو ارائه می دهد. بخش 4 نتایج تجربی را تشریح می کند و برخی تحلیل های ارزیابی را برای نشان دادن کارایی و استحکام روش پیشنهادی انجام می دهد. در نهایت، نتیجه گیری و کارهای آتی در پایان مقاله بیان شده است.

2. بررسی ادبیات

تطبیق داده‌ها برای یافتن اشیاء یا موقعیت‌های یکسان بین مجموعه داده‌های جغرافیایی چندگانه که موجودیت دنیای واقعی یکسان را منعکس می‌کنند توسعه داده شد [ 12 ، 13 ، 14 ]. یافتن تناقضات بین تصاویر به‌روز و مجموعه داده‌های مکانی موجود، ابزار مهمی برای دستیابی به تشخیص تغییر و به‌روزرسانی داده‌ها بود [ 15 ، 16 ]. این مقاله به تطبیق اشیاء ساختمان بردار می پردازد و بنابراین بررسی مختصری در تطبیق داده های برداری انجام می دهد.
با توجه به انواع شی، تطبیق داده های برداری را می توان به تطابق شی نقطه، خطی و ناحیه طبقه بندی کرد. برای تطبیق نقاط، روش‌های تصمیم‌گیری چند معیاره برای مطابقت با POI (نقاط مورد علاقه) از پلت‌فرم‌های شبکه‌های اجتماعی مختلف توسعه یافته‌اند [ 17 ، 18 ]. برای تطبیق خطی، اکثر مطالعات شباهت های متعدد (مانند هندسه، معنایی، توپولوژی) و استراتژی های تطبیق مبتنی بر گره، مبتنی بر قوس، چند ضلعی یا ترکیبی را مقایسه کرده اند [19 ، 20 ، 21 ، 22 ، 23 ] . پیشرفت‌های اخیر برچسب‌گذاری آرامش، رگرسیون لجستیک و الگوریتم‌های ژنتیک را برای بهبود عملکرد تطبیق شبکه جاده‌ها معرفی کرده‌اند [ 24] .25 ، 26 ]. دو و همکاران [ 27 ] توصیفات هستی شناسی و اپراتورهای همجوشی را برای ادغام داده های جاده معتبر و جمع سپاری طراحی کرد. لیو و همکاران [ 28 ] یک روش بافر پیشرونده برای به روز رسانی نقشه های راه با داده های OSM (OpenStreetMap) پیشنهاد کرد. یانگ و همکاران [ 29 و 30 ] از خوشه بندی فضایی و برازش شکل برای استخراج مطابقت های مرتبط با الگوی بین POI های ناهمگن و شبکه جاده ها استفاده کرد. آی و همکاران [ 31 ] درختان سلسله مراتبی خمشی را برای تطبیق داده های کانتور و شبکه های رودخانه برای تشخیص ناسازگاری هندسی ساخت.
اگرچه مطالعات متعددی به تطبیق مجموعه‌های داده‌های جاده‌ای مختلف یا معتبر اختصاص داده شده است، توجه کمی به تطبیق شی منطقه (به عنوان مثال، ساخت چند ضلعی) [ 32 ] شده است . تطبیق چند ضلعی ساختمان عمدتاً بر شناسایی مطابقت‌های سطح شی [ 33 ] و جفت‌های نقطه مزدوج بین اشیاء همسان [ 34 ] متمرکز است. آی و همکاران [ 35 ] و فن و همکاران. [ 32 ] توصیفگرهای فوریه و توابع چرخشی را برای اندازه گیری شباهت شکل اجسام چندضلعی ساختمان محاسبه کرد. وانگ و همکاران [ 36 ] یک رویکرد شبکه عصبی پس انتشار برای تعیین انطباقی وزن شباهت های چندگانه پیشنهاد کرد. دو و همکاران [ 37] مکان و اطلاعات واژگانی را برای تعیین ساختمان های منطبق با نامزد در نظر گرفت و سپس از استدلال فضایی برای اصلاح آنها استفاده کرد. سمال و همکاران [ 38 ] و کیم و همکاران. [ 39 ] زمینه جغرافیایی را برای اصلاح همگن سازی شکل و انحرافات غیر صلب ترکیب کرد. ژانگ و همکاران [ 40 ] شباهت‌های شکل و اطلاعات زمینه‌ای را برای یافتن جفت‌های منطبق با همسایه‌ها ترکیب کرد. مطالعات فوق فقط اطمینان تطبیق اشیاء تطبیق 1:1 را محاسبه کردند و احتمال تطابق کلی 1:M، N:1 و M:N اشیاء تطبیق را نادیده گرفتند. هوه و همکاران [ 41] تکنیک تعبیه گراف و خوشه‌بندی سلسله مراتبی تجمعی را برای کشف اشیاء ساختمانی متناظر چند مقیاسی به کار برد. با این حال، به دلیل همگن سازی شکل، انحرافات غیر صلب، و مطابقت های پیچیده چند مقیاسی، تطبیق داده های چند ضلعی ساختمانی در مقیاس چندگانه هنوز یک کار چالش برانگیز است. بنابراین، این مقاله یک رویکرد جدید برای تطبیق چند ضلعی‌های ساختمانی چند مقیاسی بر اساس برچسب‌گذاری آرامش و ترکیب‌های الگو پیشنهاد می‌کند. روش پیشنهادی عمدتاً مدل تطبیق برچسب‌گذاری آرامش [ 40 ، 42 ] را با در نظر گرفتن تطابق همزمان با اشیاء متعدد (یعنی ترکیب‌های الگو) گسترش می‌دهد.

3. روش شناسی

روش‌های سنتی برچسب‌گذاری آرامش [ 24 ، 40 ] کل اطمینان تطابق متناظرهای 1:M و M:N را نادیده می‌گیرند و ممکن است میانگین احتمال تطابق چندین شیء به طور همزمان با یک شیء مشابه را کاهش دهند. از این رو، این مقاله ترکیب‌های الگوی بالقوه را برای مدل‌سازی روابط تطبیق 1:M و M:N بررسی می‌کند. به طور کلی، رویکرد پیشنهادی شامل دو مرحله اصلی است که به شرح زیر است:
●
اشیاء ساختمانی مطابق با نامزد را بر اساس تجزیه و تحلیل بافر شناسایی کنید، اشیاء همسایه را در ترکیبات الگو جمع آوری کنید، و شباهت های جغرافیایی بین اشیاء منطبق با نامزد و ترکیبات الگو را برای مقداردهی اولیه ماتریس تطبیق محاسبه کنید.
●
سازگاری های متنی بین جفت های تطبیق همسایه را محاسبه کنید تا به طور مکرر ماتریس تطبیق اولیه را به روز کنید، جفت های تطبیق را بر اساس ماتریس تطبیق همگرا انتخاب کنید و آنها را از طریق تشخیص تضاد منطبق اصلاح کنید.
بگذارید دو مجموعه داده ساختمانی R = { r i | باشند i = 1، …، m } و T = { t j | j = 1، …، n }. ما فرض می کنیم که R مجموعه داده مرجع و T یک مورد هدف است. از یک طرف، به دلیل LOD های ناسازگار بین مجموعه داده های ساختمانی دارای انبوه و معتبر، اثبات اینکه آیا T دارای LOD بالاتری نسبت به S است مشکل است ، که منجر به مشکل تطبیق جهت می شود [ 24]]. از سوی دیگر، از آنجایی که روش‌های سنتی برچسب‌گذاری آرامش، اطمینان‌های تطبیق کلی را برای کاردینالیته‌های چندگانه نادیده می‌گیرند، این مقاله اشیاء تطبیق کاندید را در ترکیب‌های الگو جمع‌آوری می‌کند تا تطابق همزمان با اشیاء متعدد را نشان دهد. همانطور که در شکل 2 نشان داده شده است , rp 1 … rp m ‘ و tp 1 … tp m ‘ ترکیبات الگوی جمع شده در R و T هستند . این مقاله نه تنها احتمال تطبیق اشیاء مجزا را محاسبه می‌کند ( r i , t j ترکیب‌های الگو را نیز محاسبه می‌کند. r i , tpj ) یا ( rp i , tj ) برای تشکیل یک ماتریس تطبیق . پس از آن، تأثیرات سازگار اشیاء همسایه و ترکیب‌های الگو در نظر گرفته می‌شوند تا به‌طور اکتشافی ماتریس تطبیق اولیه برای یک سازگاری تطبیق جهانی به‌روزرسانی شود.

3.1. مقدمه‌سازی احتمال تطبیق در در نظر گرفتن ترکیب‌های الگوی چند مقیاسی

با توجه به چارچوب تطبیق برچسب‌گذاری آرامش، ماتریس تطبیق ابتدا بر اساس شباهت‌های جغرافیایی محلی (به عنوان مثال، موقعیت، جهت، ناحیه و شکل) شکل گرفت. یکی از مشارکت‌های این مقاله این است که ما اشیاء تطبیق نامزد همسایه را در ترکیب‌های الگوی جمع‌آوری کردیم و احتمالات اشیاء و ترکیب‌های الگوی جداگانه را برای مدل‌سازی مطابقت‌های 1:1، 1:M و M:N محاسبه کردیم. برای کاهش پیچیدگی محاسباتی، یک تحلیل بافر برای فیلتر کردن ویژگی‌های تطبیق غیرممکن اجرا شد.

3.1.1. تشخیص اشیاء تطبیق نامزد و ترکیب الگوها

یک عملیات بافر می تواند به طور عملی تمام اشیاء تطبیق ممکن بین دو مجموعه داده جغرافیایی را در یک مرجع فضایی یکسان تشخیص دهد [ 28 ]. مطالعات قبلی از یک آستانه بافر تجربی برای تشخیص تطبیق نامزد استفاده کرده اند [ 21 ، 24 ]. ما شبکه مثلث Delaunay ( DT R ) را برای مرکز ساختمان در R ساختیم . آستانه بافر ε به عنوان میانگین طول لبه DT R پس از حذف تمام لبه های بلند سراسری و محلی طبق روش دنگ و همکاران تنظیم شد. [ 43 ]. مجموعه تطبیق نامزد هر شی r iبه عنوان آن اشیایی در T تعیین شد که در ناحیه بافر ε r i قرار می گیرند ، یعنی CR i = { t j | t j ∈ T و t j در بافر ( r i , ε )}. به طور مشابه، مجموعه تطبیق نامزد اشیاء tj در مجموعه داده T را می توان به صورت CT j = { r i | r i ∈ R و r i در بافر (t j ، ε )}.
به دلیل LOD های ناسازگار، یک شی ساختمان ممکن است با چندین شی در مجموعه داده های جغرافیایی-فضایی دیگر مطابقت داشته باشد. همانطور که در شکل 3 الف نشان داده شده است، شی r i دارای چهار شیء تطبیق کاندید است. یعنی CR 1 = { t 1 , …, t 4 }. از نظر تئوری، شرایط تطبیق C 4 0 + C 4 1 + C 4 2 + C 4 3 + C 4 4 = 2 4 وجود دارد ، همانطور که در شکل 3 نشان داده شده است.b–f. با این حال، استراتژی تطبیق احتمالی سطح شی ممکن است یک جفت منطبق 1:1 را شناسایی کند، اما سایر اشیاء منطبق با احتمالات کمی کمتر را نادیده بگیرد. از این رو، لازم است اشیاء تطبیق نامزد همسایه را به عنوان یک ترکیب الگوی کامل برای مدل‌سازی مکاتبات برچسب‌گذاری آرامش چند مقیاسی جمع آوری کنیم.
برای اندازه‌گیری شباهت کلی با بیش از یک شیء منطبق با نامزد، باید آنها را در یک چندضلعی کامل، به نام ترکیب الگو، جمع کنیم. به طور مفصل، برای یک مجموعه تطبیق کاندید، ما به طور مکرر دو شیء ساختمانی نزدیک را جمع آوری کردیم و در نهایت یک شی چند ضلعی به دست آوردیم تا ترکیب الگوی آن مجموعه تطبیق کاندید را نشان دهد. به عنوان مثال، همانطور که در شکل 4 الف نشان داده شده است، ابتدا t 1 و t 2 را به عنوان M( t 1 , t 2 ) به هم نزدیکتر کردیم و سپس M( t 1 ، t 2 ) و t 3 را به عنوان M( t) نزدیکتر کردیم.1 ، t 2 ، t 3 ). برای تجمیع دو شیء ساختمانی مجزا، یک الگوریتم تقریب بدنه محدب ایجاد شد که شامل سه مرحله زیر است:
●
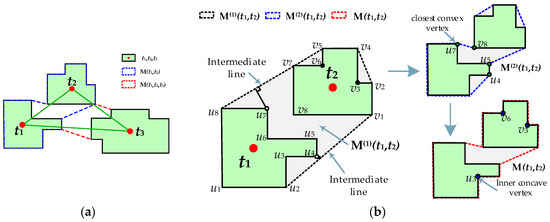
مرحله 1: بدنه محدب دو شیء ساختمانی را به عنوان چند ضلعی ادغام شده اولیه کنید.
●
مرحله 2: به طور مکرر نقاط محدب نزدیک به خطوط میانی را اضافه کنید تا چند ضلعی ادغام شده را اصلاح کنید.
●
مرحله 3: برای اصلاح بیشتر چند ضلعی ادغام شده، نقاط مقعر داخلی را در اشیاء t 1 و t 2 وارد کنید.
همانطور که در شکل 4 ب نشان داده شده است، برای دو شی t 1 = < u 1 , …, u 8 > و t 2 = < v 1 , …, v 8 >، بدنه محدب ابتدا به عنوان ترکیب الگوی M (1) مقداردهی اولیه شد. ( t 1 , t 2 ) = < u 1 , u 2 , v 1 , v 2 , v 4 , v 5 , v 7 ,u 8 > که دو بخش s 1 = < u 2 , v 1 > و s 2 = < v 7 , u 8 > به عنوان خطوط میانی یافت شد که رئوس t 1 و t 2 را به هم متصل می کند . ثانیاً، نقاط محدب نزدیک به خطوط میانی (به عنوان مثال، u 7 ، u 4 ، v 8 و u 5 ) به طور مکرر اضافه شدند تا ترکیب الگو به صورت M (2) اصلاح شود ( t 1، t 2 ). در نهایت، نقاط مقعر داخلی در اشیاء t 1 و t 2 (به عنوان مثال، u 3 ، v 3 و v 6 ) برای اصلاح ترکیب الگو به عنوان M( t1 ، t2 ) درج شدند .
فرض کنید یک شی r i دارای P اشیاء منطبق با نامزد است (| CR i | = P )، مجموعه ترکیبی الگوی تطبیق نامزد از r i به صورت CRP i = { CRP i 2 … CRP i p … CRP i P } تعریف می شود. ، که در آن CRP i p به معنای زیر مجموعه ترکیب الگو است که شامل اشیاء چند ضلعی p است. به طور مشابه، فرض کنید یک شی t j دارای Q باشداشیاء تطبیق نامزد (| CT j | = Q )، مجموعه ترکیبی الگوی تطبیق نامزد t j به صورت CTP j = { CTP j 2 , …, CTP j q … CTP j Q } تعریف می شود که در آن CTP j q به معنی زیر مجموعه ترکیب الگو که حاوی اشیاء چند ضلعی q است. از این رو، بر اساس تشخیص تطبیق نامزد و ترکیب الگوهای همسایه، جدول تطبیق نامزد به صورت c_Table = {( r i , t j ایجاد شد.)| r i ∈ R , t j ∈ CR i ∪ CRP i یا r i ∈ CT j ∪ CTP j , t j ∈ T } که به طور ساده به عنوان یک جدول تطبیق نامزد توصیف می شود c_Table = ( r i , t j ), i = 1…( m + m ‘)، j = 1…( n + n ‘).
3.1.2. محاسبه شباهت های جغرافیایی و احتمالات تطبیق اولیه

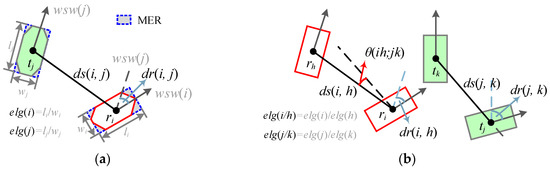
برای هر جفت تطبیق نامزد ( ri , tj ) در جدول تطبیق نامزد c_Table ، چهار شباهت هندسی، یعنی شباهت موقعیت sim p ، شباهت جهت sim o ، شباهت ناحیه sim a ، و شباهت شکل sim محاسبه شد. ماتریس تطبیق نامزد را مقداردهی اولیه کنید. فرمول ها به شرح زیر فهرست شده اند.

سمنمترپ(من،j)=1-دس(من،j)ε، سمنمترآ=دقیقه{آrهآ(من)،آrهآ(j)}حداکثر{آrهآ(من)،آrهآ(j)}سمنمترo(من،j)=1-دr(من،j)π/2، سمنمترس=دقیقه{هلg(من)،هلg(j)}حداکثر{هلg(من)،هلg(j)}

همانطور که در شکل 5 نشان داده شده است، ds ( i ، j ) به معنای فاصله مرکز بین دو جسم r i و t j است ، dr ( i ، j ) جهت گیری وزنی آماری دیوار آنها را نشان می دهد [ 44 ] تفاوت، elg (*) نسبت محور اصلی به فرعی حداقل مستطیل محصور (MER) را نشان می دهد و مساحت (*) مساحت چند ضلعی را اندازه می گیرد. پس از آن، احتمال تطابق اولیه به صورت زیر محاسبه می شود:

پمنj=سمنمتر(من،j)∑تیک∈سیآرمن∪سیآرپمنسمنمتر(من،ک)سمنمتر(من،j)=سمنمترپ(من،j)∗سمنمترo(من،j)∗سمنمترآ(من،j)∗سمنمترس(من،j)

که در آن t k ∈ CR i ∪ CRP i , sim ( i , j ) مجموع شباهت جغرافیایی ( r i , t j ) است و sim ( i , k ) نیز همینطور است. sim p ، sim o ، sim a و sim s شباهت های موقعیت، جهت، مساحت و شکل هستند که با فرمول (1) محاسبه می شوند.

در نظر گرفتن همه ترکیب‌های الگوی تطبیق کاندیدای ممکن زمان‌بر است. بنابراین، جفت‌های تطبیق نامزد با sim p < T pos ، sim o < T dir ، sim a < T ناحیه ، و sim s < T shp از جدول c حذف شدند و ماتریس تطبیق نامزد اولیه به صورت m_Matrix = ( p ij ) M × N ، M ≤ m +m ‘، N ≤ n + n ‘.

3.2. تطابق احتمال آرامش بر اساس اطلاعات متنی چند مقیاسی

احتمال تطابق اولیه فقط شباهت های هندسی محلی را در نظر می گیرد و تأثیرات روابط تطبیق همسایه را نادیده می گیرد. الگوریتم برچسب‌گذاری آرامش، اطلاعات متنی جفت‌های تطبیق نامزد همسایه را به عنوان یک ضریب سازگاری برای به‌روزرسانی اکتشافی احتمال تطابق مبتنی بر شباهت محلی مدل‌سازی می‌کند.

3.2.1. تعریف رابطه همسایگی و ضریب سازگاری

از آنجایی که هیچ رابطه همسایگی صریحی در مجموعه داده های ساختمان ذخیره نمی شود، برخی از محققان از شعاع ثابت، شبکه مثلثی و نمودار مجاورت برای جستجوی اشیاء همسایه محلی استفاده کرده اند [ 38 ، 40 ]. برای شی ساختمان مرجع r i در R ، مثلث Delaunay را ساختیم و اشیاء متصل مرتبه اول و ترکیبات الگو را به عنوان مجموعه همسایه آن Ɲ ( r i ) تعریف کردیم. برای شی ساختمان هدف t j در T ، اشیاء و ترکیبات الگو در بافر ( tj , ε) به عنوان مجموعه همسایه Ɲ ( tj ) تعیین شدند . به طور خاص، برای یک ترکیب الگو r u ‘ = { r a , …, r b }، Ɲ ( r u ‘) به عنوان یک مجموعه تفریق تعریف شد، Ɲ ( r a )∪…∪ Ɲ ( r b )-{ r a … r b }.

بر اساس تعریف روابط همسایه، اطلاعات زمینه‌ای جفت‌های همسایه کاندید-تطبیق به عنوان یک ضریب سازگاری با توجه به فرمول (3) [40] که هر دو موقعیت نسبی و مطلق، جهت‌گیری، شکل و روابط منطقه را ترکیب می‌کند، کمیت‌سازی شد.

سی(منj;ساعتک)=سمنمتر(من،j)·∏تو=14rهلتو(منj;ساعتک)

در جایی که C ( ij ; hk ) نشان دهنده ضریب سازگاری بین دو جفت همجوار ( ri , tj ) و ( rh , tk ) است، sim ( i , j ) شباهت جغرافیایی مطلق محاسبه شده توسط فرمول ( 2)، و rel u ( ij ؛ hk ) ( u = 1…4) چهار رابطه هندسی نسبی بین آنها را نشان می دهد که به ترتیب به عنوان فرمول (4) – (7) محاسبه می شوند.

rهل1(منj;ساعتک)=rدمنس∗rدمنr∗rrآتیمنo{rدمنس=1-|دس(من،ساعت)-دس(j،ک)|حداکثرrمتر∈ن(rمن)،تیn∈ن(تیj){دس(من،متر)،دس(j،متر)}rدمنr=1-θ(منساعت،jک)π/2rrآتیمنo=1-دس(من،ساعت)حداکثرrمتر∈ن(rمن){دس(من،متر)}
rهل2(منj;ساعتک)=1-|دr(من،ساعت)-دr(j،ک)|π/2
rهل3(منj;ساعتک)=11+(هلg(من/ساعت)-هلg(j/ک))2
rهل4(منj;ساعتک)=11+(آrهآ(من/ساعت)-آrهآ(j/ک))2
rel 1 ( ij ; hk )، rel 2 ( ij ; hk )، rel 3 ( ij ; hk ) و rel 4 ( ij ; hk ) نشان دهنده موقعیت نسبی، جهت گیری، شکل و روابط مساحت بین دو نامزد همسایه است. به ترتیب جفت ( r i , tj ) و ( r h , t k ) . همانطور که در شکل 5 ب نشان داده شده است، ds ( i ،h ) و dr ( i , h ) به معنای فاصله مرکز و تفاوت جهت بین دو شیء ساختمانی همسایه r i و r h است ، Ɲ ( r i ) مجموعه همسایه شی r i را نشان می دهد و θ ( ih ؛ jk ) برابر است. زاویه بین دو بردار مرکز rمنrساعت→و تیjتیک→. elg ( i / h ) و مساحت ( i / h ) نسبت شاخص کشیدگی و نسبت مساحت بین دو شیء ساختمانی همسایه r i و r h هستند ، همچنین elg ( j / k ) و مساحت ( j / k ) نیز انجام می‌شود.
3.2.2. آرامش ماتریس تطبیق و انتخاب جفت های تطبیق نهایی
ضریب سازگاری محاسبه‌شده در بالا، سازگاری هندسی نسبی بین دو جفت همسایه نامزد تطبیق را اندازه‌گیری می‌کند. با این حال، احتمالاً بیش از یک جفت همسایه کاندیدا وجود دارد. فرآیند برچسب‌گذاری آرامش، تأثیرات همه جفت‌های تطبیق نامزد همسایه (که شاخص‌های پشتیبانی فرعی نیز نامیده می‌شوند) را در یک شاخص حمایت کل ترکیب می‌کند و ماتریس تطبیق مبتنی بر هندسی را به‌روزرسانی می‌کند. در پرتو تناظرهای چند مقیاسی 1:M و M:N، تأثیرات ترکیب الگوهای همسایه نیز باید در شاخص کل حمایت ادغام شود. به طور مفصل ، شاخص کل حمایت از یک جفت تطبیق نامزد ( ri , tj ) به صورت زیر محاسبه شد :
●

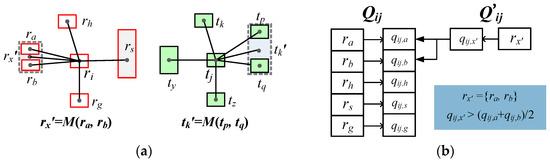
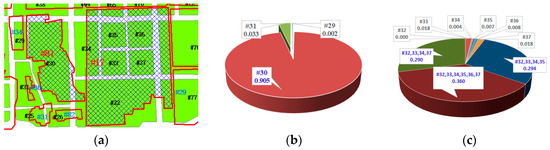
شاخص‌های پشتیبانی فرعی همه اشیاء مجزا و ترکیب‌های الگوی مجاور را طبق فرمول (8) محاسبه کنید، که به دو صف جداگانه Q ij و Q ‘ ij تقسیم می‌شوند . Q ij اندیس های پشتیبانی فرعی اشیاء مجاور همسایه و Q ‘ ij شاخص های پشتیبانی فرعی ترکیب های الگوی همسایه را ذخیره می کند. برای جفت منطبق با نامزد ( ri , tj ) در شکل 6 a ، دو صف شاخص پشتیبانی فرعی Q ij و Q ij ‘ در فهرست شده اند .شکل 6 ب.

qمنj،ساعت=حداکثرسک∈سیآرساعت∪سیآرپساعت{سی(منj;ساعتک)پ(ساعت،ک)}،rساعت∈نمن یا نپمن
●
Q ij ‘ را به ترتیب صعودی از تعداد شیء موجود در ترکیب الگوی همسایه عبور دهید و قضاوت کنید که آیا شاخص پشتیبانی فرعی آن بزرگتر از میانگین شاخص پشتیبانی اشیاء شامل آن است یا خیر . اگر بله، شاخص پشتیبانی فرعی آن ترکیب الگو جایگزین شاخص‌های پشتیبانی فرعی مربوط به اشیاء موجود در Q ij می‌شود . همانطور که در شکل 6 ب توضیح داده شده است، شاخص پشتیبانی فرعی q ij , x ‘ از r x ‘ = { r a , r b } بزرگتر از میانگین q ij , a استو q ij , b , بنابراین q ij , x ‘ جایگزین مقادیر q ij , a و q ij , b در Q ij می شود .
●
هنگامی که تمام عناصر Q ij ‘ پیموده می شوند و با مراحل بالا قضاوت می شوند، میانگین شاخص های پشتیبانی فرعی در Q ij به عنوان شاخص کل پشتیبانی q ij از ( r i , t j ) محاسبه می شود.

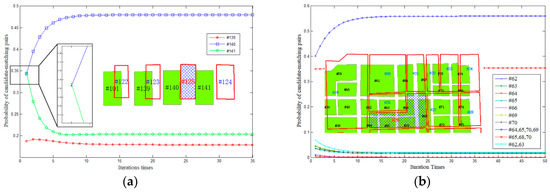
هنگامی که کل شاخص‌های پشتیبانی همه جفت‌های تطبیق نامزد مشخص شد، تکرار ماتریس تطبیق جغرافیایی مشابه طبق فرمول (9) [ 24 ] اجرا شد. فرآیند برچسب‌گذاری آرامش تا زمانی ادامه می‌یابد که اختلاف احتمال بین دو تکرار کمتر از آستانه از پیش تعریف‌شده δ باشد .

پمنjr+1=پمنjr+qمنjr1+∑ساعت∈سیاسمنqمنساعتr
بر اساس ماتریس تطبیق همگرا، جفت‌های تطبیق با حداکثر احتمال تطابق در هر ردیف ابتدا انتخاب و در یک صف MQueue وارد شدند . سپس، هر جفت منطبق A را در MQueue بررسی کنید . هنگامی که یک جفت تطبیق B دیگری در MQueue وجود دارد که شامل یک یا چند شیء ساختمانی رایج است، ممکن است دو جفت تطبیق تطابق یا یک جفت تطبیق M:N تقسیم بر چندین جفت تطبیق 1:M یا M:1 باشد. برای تمایز شرایط فوق، شباهت هندسی کلی Sim ( A ∪ B ) ادغام A و B را محاسبه کردیم . اگر سیم (A ∪ B ) بزرگتر از Sim ( A ) و Sim ( B ) است، A و B در یک جفت منطبق M:N A ∪ B ادغام می شوند . در غیر این صورت، یکی با احتمال تطابق بالاتر رزرو می شود و دیگری با احتمال کمتر با جفت با احتمال بالاتر بعدی جایگزین می شود. پس از آن، MQueue به عنوان جفت تطبیق نهایی بین دو مجموعه داده ساختمان R و T تعیین شد .

4. آزمایش و تجزیه و تحلیل

یک مجموعه داده ساختمان ساختگی و دو مجموعه داده واقعی ساختمان در شهر شیان، چین و دالاس در ایالات متحده آمریکا برای تأیید کارایی و قابلیت اطمینان روش پیشنهادی استفاده شد. همانطور که در جدول 1 فهرست شده است، مقیاس های فضایی دو مجموعه داده ساختمان شیان به عنوان 1:250000 و 1:200000 شناخته می شوند، اما تفاوت های مقیاس نامشخصی در مجموعه داده های شبیه سازی شده و مجموعه داده دالاس از منابع وب یافت شد. در جدول 1 ، T pos ، T dir ، T ناحیه ، T shp چهار آستانه تشابه برای جفت های منطبق با نامزد فیلتر شده از بخش 3.1.2 و δ هستند.آستانه همگرا برای فرآیند برچسب زدن آرامش است که در بخش 3.2.2 بیان شده است .
شکل 7 نتیجه تطبیق اولیه داده‌های ساختمان ساختگی را بر اساس شباهت هندسی محلی و نتایج تطبیق تولید شده توسط روش برچسب‌گذاری آرامش در سطح شی و روش سطح الگوی پیشنهادی را نشان می‌دهد. از شکل 7 الف می توان دریافت که چندین خطای آشکار در نتایج تطبیق مبتنی بر شباهت به دلیل انحرافات غیر صلب و همگن شدن شکل رخ می دهد. اگرچه روش برچسب‌گذاری آرامش در سطح شیء پیشرفت بزرگی از نظر یافتن یک سازگاری مطابق متنی است، همانطور که در شکل 7 ب نشان داده شده است، هنوز برخی از جفت‌های تطبیق 1:M و M:N وجود دارد که توسط استراتژی تطبیق سطح شی نادیده گرفته می‌شوند. شکل 7c نشان می دهد که جفت های مختلف تطبیق 1:M و M:N به درستی با روش پیشنهادی بر اساس برچسب زدن آرامش و ترکیبات الگو شناسایی می شوند. نتایج تطبیق داده‌های شیان و داده‌های دالاس در شکل 8 نشان داده شده است ، که نشان می‌دهد روش پیشنهادی می‌تواند به طور قوی تناظر پیچیده اشیاء ساختمانی را با تفاوت‌های مقیاس بزرگ و نامشخص شناسایی کند.

با مقایسه نتایج تطبیق با تطبیق دستی، سه شاخص دقت – دقت P ، Recall R و مقدار F – طبق فرمول (10) محاسبه شد. tp نشان‌دهنده جفت‌های تطبیق واقعی است که توسط روش ما شناسایی شده‌اند، fp نشان‌دهنده جفت‌های تطبیق نادرست است که توسط روش ما شناسایی شده‌اند، و fn به معنای جفت‌های تطبیق واقعی است که توسط روش ما حذف شده‌اند. از جدول 2 می توان دریافت که هم میزان دقت و هم نرخ فراخوان بالاتر از 90٪ است و دقت های آشکار بالاتری با روش ما نسبت به روش برچسب زدن آرامش در سطح شی به دست آمده است.

پ=تیپتیپ+fپ،آر=تیپتیپ+fn،اف=2×پ×آرپ+آر
شکل 9 احتمال تغییر جفت های تطبیق نامزد از اشیاء #125 و #26 را در طول فرآیند برچسب گذاری آرامش نشان می دهد. همانطور که در شکل 9 نشان داده شده است، فرآیند برچسب‌گذاری آرامش، جفت‌های تطبیق تقلبی (#125 → #141) و جفت‌های تطبیق واقعی (#125 → #140) را با ادغام اطلاعات زمینه‌ای جفت‌های تطبیق همسایه برای اصلاح اکتشافی شباهت محلی به درستی متمایز می‌کند. ماتریس تطبیق مبتنی بر این نشان می دهد که روش پیشنهادی می تواند به طور موثر بر تطابق نادرست ناشی از همگن سازی شکل و انحراف غیر صلب غلبه کند. در همین حال، همانطور که در شکل 9 نشان داده شده استب، روش تطبیق سطح الگو به درستی یک جفت تطبیق پیچیده 1:M از (#26 → #64، 65، 70، 69) را با در نظر گرفتن ترکیب‌های الگو در مدل برچسب‌گذاری آرامش، شناسایی می‌کند. این نشان می‌دهد که روش ما می‌تواند به‌طور مؤثری مطابقت‌های مختلف 1:M و M:N را که احتمالاً توسط روش تطبیق سطح شی از دست رفته‌اند، بیابد.
توزیع احتمال تطبیق شی #81 و #17 در شکل 10 a به ترتیب در شکل 10 b,c توضیح داده شده است. مشاهده می شود که هم مطابقت شی 1:1 (#81 → #30) و هم تطابق ترکیبی الگوی 1:M (#17 → #32، 33، 34، 35، 36، 37) به طور قابل اعتمادی از نظر یک بزرگ شناسایی می شوند. شکاف احتمال این نشان می‌دهد که روش ما نسبت به روش برچسب‌گذاری آرامش در سطح شی، نسبت به تفاوت‌های مقیاس فضایی حساس‌تر است.
جدول 3 دو نمونه منطبق از ترکیب الگوها را نشان می دهد. برای شی r A ، جدول 3 چهار تناظر نامزد برتر را فهرست می کند. می توان مشاهده کرد که احتمال تطبیق ( rA → {t a, tb, tc, td } ) به صورت 0.218 محاسبه شده است که ظاهراً بیشتر از سایر اشیاء تطبیق با نامزد یا ترکیبات الگو است . برای شی r B و r C ، بهترین جفت تطبیق با بیشترین احتمال تطبیق به صورت M 1 = ( r B محاسبه شد.به ترتیب → { t e , t f }) و M 2 = ( r C → { t e , t g }). از آنجایی که M 1 و M 2 حاوی یک شی مشترک t e هستند ، این دو جفت تطبیق در نهایت در یک جفت تطبیق M:N ادغام شدند M = ({ r A , r B } → { t e , t f , t g}) با مقایسه شباهت های جغرافیایی آنها. این بیشتر نشان‌دهنده عملکرد خوب روش ما در شناسایی روابط تطبیق پیچیده 1: M و M: N بین داده‌های ساختمان چند مقیاسی ناهمگن است.

5. نتیجه گیری ها

تطبیق اشیاء یک مرحله ضروری از ترکیب نقشه و به روز رسانی داده ها است. تطبیق داده های ساختمان در مقیاس چندگانه با مشکلاتی مانند همگن سازی شکل، انحرافات غیر صلب و تفاوت های مقیاس نامشخص مواجه است. این مقاله یک روش تطبیق خودکار ساختمان را بر اساس برچسب‌گذاری آرامش و ترکیبات الگو پیشنهاد می‌کند. روش پیشنهادی روش تطبیق برچسب‌گذاری آرامش در سطح شی را گسترش داد و یک مدل تطبیق احتمالی با در نظر گرفتن تطبیق شی 1:1 و تطبیق ترکیب الگوی 1:M ساخت. نتایج تجربی نشان می‌دهد که فرآیند برچسب‌گذاری آرامش، اطلاعات متنی را در نظر می‌گیرد، و به طور قابل اعتمادی دقت تطبیق و عدم حساسیت به انحرافات غیر صلب و همگن‌سازی شکل را افزایش می‌دهد. علاوه بر این، ترکیب‌های الگو به‌طور جدیدی در مدل تطبیق احتمالی ادغام می‌شوند و به طور موثر عملکرد را برای مطابقت با مجموعه داده‌های ساختمان جمع‌سپاری با تفاوت‌های مقیاس فضایی بزرگ و نامشخص بهبود می‌بخشند. کار آینده بر مدل‌سازی تطبیق پوچ و انتخاب بهینه جفت‌های تطبیق نامزد برای بهبود استحکام روش ما تمرکز خواهد کرد.

منابع

  1. جیانگ، بی. اطلاعات جغرافیایی داوطلبانه و جغرافیای محاسباتی: دیدگاه های جدید. در جمع سپاری دانش جغرافیایی ; Sui, D., Elwood, S., Goodchild, M., Eds. Springer: Dordrecht، هلند، 2013; صص 125-138. [ Google Scholar ]
  2. Goetz, M. به سمت تولید مدل‌های بسیار دقیق 3D CityGML از OpenStreetMap. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 845-865. [ Google Scholar ] [ CrossRef ]
  3. برگمن، سی. Oksanen, J. Conflation of OpenStreetMap و داده های ردیابی ورزشی موبایل برای مسیریابی خودکار دوچرخه. ترانس. GIS 2016 ، 20 ، 848-868. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  4. یانگ، دبلیو. آی، تی. Lu, W. روشی برای استخراج اطلاعات مرزهای جاده از مسیرهای GPS وسایل نقلیه جمع سپاری. Sensors 2018 , 18 , 1261. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  5. هچت، ر. کونز، سی. Hahmann, S. اندازه گیری کامل بودن ردپای ساختمان در OpenStreetMap در مکان و زمان. ISPRS Int. J. Geo-Inf. 2013 ، 2 ، 1066-1091. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  6. رویز، جی جی؛ آریزا، FJ; Ureña، MA; Blázquez، EB تلفیق نقشه دیجیتال: بررسی فرآیند و پیشنهادی برای طبقه بندی. بین المللی جی. جئوگر. Inf. علمی 2011 ، 25 ، 1439-1466. [ Google Scholar ] [ CrossRef ]
  7. دالیوت، اس. داهیندن، تی. شولز، ام جی; بولجن، ج. سستر، ام. یکپارچه سازی ساختارهای شبکه نمایش های مختلف هندسی. EMP Surv. Rev. 2013 , 45 , 428-440. [ Google Scholar ] [ CrossRef ]
  8. سستر، ام. ارسنجانی، ج. کلامر، آر. بورگاردت، دی. Haunert، JH یکپارچه سازی و تعمیم اطلاعات جغرافیایی داوطلبانه. در چکیده اطلاعات جغرافیایی در جهان غنی از داده ; Burghardt, D., Duchêne, C., Mackaness, W., Eds.; انتشارات بین المللی Springer: چم، سوئیس، 2014; صص 119-155. [ Google Scholar ]
  9. تویا، جی. براندو اسکوبار، سی. تشخیص تناقضات سطح جزئیات در مجموعه داده‌های اطلاعات جغرافیایی داوطلبانه. کارتوگر. بین المللی جی. جئوگر. Inf. جئوویس. 2013 ، 48 ، 134-143. [ Google Scholar ] [ CrossRef ]
  10. بارون، سی. نیس، پ. Zipf، A. چارچوبی جامع برای تحلیل کیفی نقشه خیابان باز ذاتی. ترانس. GIS 2014 ، 18 ، 877-895. [ Google Scholar ] [ CrossRef ]
  11. خو، جی. وو، اف. کیان، اچ. Ma, F. الگوریتم تطبیق حل و فصل با استفاده از روابط شباهت فضایی به عنوان محدودیت. Geomat. Inf. علمی دانشگاه ووهان 2013 ، 38 ، 484-488. [ Google Scholar ]
  12. Saalfeld, A. Conflation: Automated map Compilation. بین المللی جی. جئوگر. Inf. علمی 1988 ، 2 ، 217-228. [ Google Scholar ] [ CrossRef ]
  13. کیلر، بی. هوانگ، دبلیو. هاونرت، جی. جیانگ، جی. تطبیق مجموعه داده‌های رودخانه در مقیاس‌های مختلف. در یادداشت های سخنرانی در اطلاعات جغرافیایی و نقشه برداری ; Sester, M., Bernard, L., Paelke, V., Eds. Springer: برلین/هایدلبرگ، آلمان، 2009; صص 135-154. [ Google Scholar ]
  14. پورعبدالله، ع. مورلی، جی. فلدمن، اس. جکسون، ام. به سوی نقشه خیابان باز معتبر: تلفیق شبکه جاده ای نقشه های ملی OSM و سیستم عامل OpenData. ISPRS Int. J. Geo-Inf. 2013 ، 2 ، 704-728. [ Google Scholar ] [ CrossRef ]
  15. چن، سی.-سی. Knoblock، C. شهابی، سی. تلفیق خودکار داده‌های بردار جاده با تصوير قاعده. GeoInformatica 2006 ، 10 ، 495-530. [ Google Scholar ] [ CrossRef ]
  16. ژانگ، جی. یک مدل ترکیبی متجانس برای ترکیب تصاویر ماهواره ای و پایگاه داده جاده. Ph.D. پایان نامه، دانشگاه فنی مونیخ، مونیخ، آلمان، 2013. [ Google Scholar ]
  17. مک کنزی، جی. یانوویچ، ک. Adams, B. یک روش وزنی چند ویژگی برای تطبیق نقاط مورد علاقه ایجاد شده توسط کاربر. کارتوگر. Geogr. Inf. علمی 2014 ، 41 ، 125-137. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  18. شفلر، تی. شیرو، آر. Lehmann, P. تطبیق نقاط مورد علاقه از سایت های مختلف شبکه های اجتماعی. در KI 2012: Advances in Artificial Intelligence ; Goebel, R., Tanaka, Y., Wahlster, W., Siekmann, J., Eds. Springer: برلین/هایدلبرگ، آلمان، 2012; ص 45-248. [ Google Scholar ]
  19. شیونگ، دی. Sperling، J. تطبیق نیمه خودکار برای یکپارچه سازی پایگاه داده شبکه. ISPRS J. Photogramm. Remote Sens. 2004 ، 59 ، 35-46. [ Google Scholar ] [ CrossRef ]
  20. ژانگ، ام. منگ، ال. یک رویکرد تطبیق جاده ای تکراری برای ادغام داده های پستی. محاسبه کنید. محیط زیست سیستم شهری 2007 ، 31 ، 598-616. [ Google Scholar ] [ CrossRef ]
  21. موستیر، اس. Devogele, T. تطبیق شبکه ها با سطوح مختلف جزئیات. GeoInformatica 2008 ، 12 ، 435-453. [ Google Scholar ] [ CrossRef ]
  22. فن، اچ. یانگ، بی. Zipf، A.; Rousell, A. رویکردی مبتنی بر چند ضلعی برای تطبیق شبکه‌های جاده‌ای OpenStreetMap با داده‌های معتبر. بین المللی جی. جئوگر. Inf. علمی 2016 ، 30 ، 748-764. [ Google Scholar ] [ CrossRef ]
  23. صفرا، ای. کانزا، ی. ساگیو، ی. Doytsher, Y. تطبیق موقت شبکه های جاده ای بردار. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 114-153. [ Google Scholar ] [ CrossRef ]
  24. یانگ، بی. ژانگ، ی. Luan، X. یک رویکرد آرامش احتمالی برای تطبیق شبکه های جاده ای. بین المللی جی. جئوگر. Inf. علمی 2013 ، 27 ، 319-338. [ Google Scholar ] [ CrossRef ]
  25. تانگ، ایکس. لیانگ، دی. Jin, Y. روش تطبیق شی جاده خطی برای ادغام بر اساس بهینه سازی و رگرسیون لجستیک. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 824-846. [ Google Scholar ] [ CrossRef ]
  26. چهرقان، ع. عباسپور، RA یک رویکرد مبتنی بر هندسی برای تطبیق جاده در مجموعه داده‌های چند مقیاسی با استفاده از الگوریتم ژنتیک. کارتوگر. Geogr. Inf. علمی 2018 ، 45 ، 255-269. [ Google Scholar ] [ CrossRef ]
  27. دو، اچ. آناند، اس. آلچینا، ن. مورلی، جی. هارت، جی. لیبوویچی، دی. جکسون، ام. Ware, M. ادغام اطلاعات مکانی برای داده های برداری جاده معتبر و منبع جمعیت. ترانس. GIS 2012 ، 16 ، 455-476. [ Google Scholar ] [ CrossRef ]
  28. لیو، سی. شیونگ، ال. هو، ایکس. Shan, J. یک روش بافر پیشرونده برای به روز رسانی نقشه راه با استفاده از داده های نقشه خیابان باز. ISPRS Int. J. Geo-Inf. 2015 ، 4 ، 1246-1264. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  29. یانگ، بی. ژانگ، ی. Lu, F. رویکرد مبتنی بر هندسی برای ادغام POI های VGI و شبکه های جاده ای. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 126-147. [ Google Scholar ] [ CrossRef ]
  30. یانگ، بی. Zhang، Y. روش استخراج الگو برای ترکیب شبکه‌های جاده‌ای جمع‌سپاری با POI. بین المللی جی. جئوگر. Inf. علمی 2015 ، 29 ، 786-805. [ Google Scholar ] [ CrossRef ]
  31. آی، تی. یانگ، م. ژانگ، ایکس. Tian, ​​J. تشخیص و تصحیح ناسازگاری بین شبکه های رودخانه و داده های کانتور توسط دانش محدودیت فضایی. کارتوگر. بین المللی جی. جئوگر. Inf. Geov. 2015 ، 42 ، 79-93. [ Google Scholar ] [ CrossRef ]
  32. فن، اچ. Zipf، A.; فو، س. Neis, P. ارزیابی کیفیت برای ایجاد داده های ردپایی در OpenStreetMap. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 700-719. [ Google Scholar ] [ CrossRef ]
  33. گوسلن، جی. سستر، ام. ادغام مجموعه داده های علم زمین و نقشه دیجیتال آلمانی با استفاده از رویکرد تطبیق. در مجموعه مقالات بیستمین انجمن بین المللی فتوگرامتری و کنگره سنجش از دور، استانبول، ترکیه، 12 تا 23 ژوئیه 2004. صص 1249-1254. [ Google Scholar ]
  34. ها، ی. یو، ک. Heo, J. تشخیص جفت نقطه مزدوج برای تراز نقشه بین دو مجموعه داده چند ضلعی. محاسبه کنید. محیط زیست سیستم شهری 2011 ، 35 ، 250-262. [ Google Scholar ] [ CrossRef ]
  35. آی، تی. چنگ، ایکس. لیو، پی. یانگ، ام. تحلیل شکل و تطبیق الگوی ویژگی‌های ساختمان با روش تبدیل فوریه. محاسبه کنید. محیط زیست سیستم شهری 2013 ، 41 ، 219-233. [ Google Scholar ] [ CrossRef ]
  36. وانگ، ی. چن، دی. ژائو، ز. رن، اف. Du, Q. یک رویکرد مبتنی بر شبکه عصبی پس انتشار برای تطبیق ویژگی های چندگانه در انتشار به روز رسانی. ترانس. GIS 2015 ، 19 ، 964-993. [ Google Scholar ] [ CrossRef ]
  37. دو، اچ. آلچینا، ن. جکسون، ام. هارت، جی. روشی برای تطبیق داده های جغرافیایی معتبر و منبع جمعیت. ترانس. GIS 2016 . [ Google Scholar ] [ CrossRef ]
  38. سمال، ع. ست، اس. Cueto، K. یک رویکرد مبتنی بر ویژگی برای ترکیب منابع جغرافیایی. بین المللی جی. جئوگر. Inf. علمی 2004 ، 18 ، 459-489. [ Google Scholar ] [ CrossRef ]
  39. کیم، جو. یو، ک. هیو، جی. Lee, WH یک روش جدید برای تطبیق اشیاء در دو مجموعه داده جغرافیایی مختلف بر اساس زمینه جغرافیایی. محاسبه کنید. Geosci. 2010 ، 36 ، 1115-1122. [ Google Scholar ] [ CrossRef ]
  40. ژانگ، ایکس. آی، تی. استوتر، جی. ژائو، ایکس. تطبیق داده‌های چند ضلعی‌های ساختمانی در مقیاس‌های چندگانه نقشه با اطلاعات متنی و آرامش بهبود یافته است. ISPRS J. Photogramm. Remote Sens. 2014 ، 92 ، 147-163. [ Google Scholar ] [ CrossRef ]
  41. ها، ی. کیم، جی. لی، جی. یو، ک. Shi, W. شناسایی جفت‌های مجموعه شی متناظر چند مقیاسی بین دو مجموعه داده چندضلعی با هم‌خوشه‌بندی سلسله مراتبی. ISPRS J. Photogramm. Remote Sens. 2014 ، 88 ، 60-68. [ Google Scholar ] [ CrossRef ]
  42. ژانگ، ی. هوانگ، جی. دنگ، م. نیش، ایکس. Hu, J. تطبیق برچسب‌گذاری آرامش برای مجموعه داده‌های مسکونی چند مقیاسی بر اساس الگوهای همسایه. Geomat. Inf. علمی دانشگاه ووهان 2018 ، 43 ، 1098-1105. [ Google Scholar ]
  43. دنگ، م. لیو، کیو. چنگ، تی. Shi, Y. یک الگوریتم خوشه‌بندی فضایی تطبیقی ​​مبتنی بر مثلث‌سازی دلونی. محاسبه کنید. محیط زیست سیستم شهری 2011 ، 35 ، 320-332. [ Google Scholar ] [ CrossRef ]
  44. دوچن، سی. بارد، اس. باریلو، ایکس. رواس، ع. ترویسان، جی. Holzapfel, F. توصیف کمی و کیفی جهت گیری ساختمان. در مجموعه مقالات پنجمین کارگاه آموزشی در مورد پیشرفت در تعمیم خودکار نقشه، پاریس، فرانسه، 28-30 آوریل 2003. ICA، کمیسیون تعمیم نقشه: بارسلون، اسپانیا، 2003. [ Google Scholar ]
Ijgi 08 00038 g001 550
شکل 1. مشکلات پیچیده در تطبیق چند ضلعی های ساختمانی در مقیاس: ( الف ) همگن سازی شکل و انحرافات غیر صلب بین ویژگی های ساختمان. ( ب ) تطابق 1:M و M:N ناشی از سطوح ناسازگار جزئیات (LOD).
Ijgi 08 00038 g002 550
شکل 2. مدل تطبیق برچسب‌گذاری آرامش با در نظر گرفتن اشیاء مجزا و ترکیب‌های الگو: ( الف ) نمایش گرافیکی. ( ب ) نمایش ماتریسی.
Ijgi 08 00038 g003 550
شکل 3. ترکیبات تطبیق احتمالی یک شیء ساختمانی r i : ( الف ) یک شیء ساختمانی r i و اشیاء منطبق با نامزد آن t 1 … t 4 . ( ب ) r i مطابقت با هیچ; ( ج ) r i مطابقت با یک شی. ( د ) r i مطابقت با دو شی; ( e ) r i مطابقت با سه شی. ( f ) r i مطابقت با چهار شی.
Ijgi 08 00038 g004 550
شکل 4. تجمیع اشیاء منطبق با نامزد همسایه در ترکیبات الگو: ( الف ) تجمیع دو یا چند شیء بر اساس فواصل مرکز. ( ب ) تجمیع دو جسم بر اساس تقریب بدنه محدب.
Ijgi 08 00038 g005 550
شکل 5. محاسبه شباهت هندسی مطلق و ضریب سازگاری نسبی: ( الف ) شباهت هندسی مطلق بین جفت های تطبیق نامزد. ( ب ) ضریب سازگاری نسبی بین جفت‌های تطبیق نامزد همسایه. MER: حداقل مستطیل محصور.
Ijgi 08 00038 g006 550
شکل 6. ادغام شاخص‌های پشتیبانی فرعی اشیاء مجزا و ترکیب‌های الگوی مجاور در یک شاخص پشتیبانی کل: ( الف ) اشیاء مجزای مجاور و ترکیب‌های الگوی ( ri , tj ) . ( ب ) ادغام همه شاخص‌های پشتیبانی فرعی در یک شاخص کل پشتیبانی.
Ijgi 08 00038 g007 550
شکل 7. مقایسه نتایج تطبیق داده‌های ساختمان ساختگی: ( الف ) جفت‌های تطبیق اولیه بر اساس شباهت هندسی محلی. ( ب ) جفت‌های تطبیق شناسایی شده توسط روش برچسب‌گذاری آرامش در سطح شی. ( ج ) جفت‌های تطبیق شناسایی شده با روش برچسب‌گذاری آرامش در سطح الگو.
Ijgi 08 00038 g008 550
شکل 8. نتایج تطبیق داده‌های شیان و دالاس: ( الف ) نتایج تطبیق داده‌های شیان با تفاوت‌های مقیاس آشکار. ( ب ) نتایج تطبیق داده‌های دالاس با تفاوت‌های مقیاس نامشخص.
Ijgi 08 00038 g009 550
شکل 9. تغییر احتمال تطبیق در طول فرآیند برچسب‌گذاری آرامش: ( الف ) تغییر احتمال جفت‌های منطبق با نامزد شی #125. ( ب ) تغییر احتمال جفت‌های تطبیق نامزد شی 26.
Ijgi 08 00038 g010 550
شکل 10. مقایسه احتمال تطبیق با یک شی منفرد و تطبیق همزمان با چندین شی: ( الف ) شی #81 و #17 در R و اشیاء تطبیق نامزد آنها در T. ( ب ) مقایسه احتمال تطبیق همه جفت‌های تطبیق نامزد شماره 81. ( ج ) مقایسه احتمال تطبیق همه جفت‌های تطبیق نامزد شماره 17.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید