داده و ماهیت آن :آنچه که باید درباره داده ها بدانید

داده و ماهیت آن :آنچه که باید درباره داده ها بدانید عنوان پستی است که من قصد دارم درباره آن صحبت کنم .امیدوارم این پست که از فصل دوم کتاب جغرافیای محاسباتی من انتخاب شده است لذت ببرید .ممنون میشم که نظرات خودتان را در این باره با من به اشتراک بگذارید.

نویسنده:

دکتر سعید جوی زاده

2-1 مقدمه

به طور کلی داده، نمودی از وقایع، معلومات، رخدادها، پدیده­ ها و مفاهیم می­ باشد. در علم جغرافیا با دو دیدگاه به داده نگاه می­ شود.

الف)دیدگاه غیر مکانی (توصیفی)؛

ب) دیدگاه مکانی.

در آمار کلاسیک از داده­ های غیر مکانی (توصیفی) و در آمار فضایی از داده­ های مکانی استفاده می­ شود. داده ­های غیر مکانی، شامل اطلاعات ثبت شده برای توصیف پدیده ­هاست و داده ­های مکانی به داده­ هایی اطلاق می­ شود که مختصات زمینی عوارض و موقعیت مکانی پدیده ­ها را نشان می­ دهد. این ویژگی­ ها در بخش ­های این فصل توضیح داده می­ شود.

-2 تفاوت داده و اطلاعات

داده شامل مواد خام آماری است که از واقعیت­ها و ارقامی تشکیل می­شود و تشریح کمی-کیفی مشخصه­های پدیده و یا واحدهای مورد نظر را بر عهده دارد. داده­ها شامل اعداد، گزارش­ها، نقشه­ها، جداول و نمودارهایی است که از منابع مختلف جمع­آوری و بدون هیچ گونه پردازشی به صورت خام ارائه می­شود.

داده و ماهیت آن :آنچه که باید درباره داده ها بدانید

اطلاعات، داده­هایی است که پس از پردازش برای دستیابی به مقاصد مختلف مورد توجه قرار می­گیرند. در واقع اطلاعات عبارت است از نتایج فرآیندهای انجام شده بر روی داده­ها برای دستیابی به واقعیت­ها، روابط و نمایش ساختارهای پیچیده.

به طور کلی داده­های جغرافیایی را می­توان به دو دستۀ داده­های مکانی و غیر مکانی (توصیفی) تقسیم کرد. داده­های مکانی به داده­هایی اطلاق می­شود که مختصات زمینی عوارض و موقعیت مکانی پدیده­ها را نشان می­دهد. این داده­ها در دو شکل رستری و برداری قابل نمایش و استفاده است. داده­های غیر مکانی (توصیفی) شامل اطلاعات ثبت شده برای توصیف پدیده­هاست.

داده­های جغرافیایی به دو شکل پیوسته و ناپیوسته هستند. داده­های پیوسته داده­هایی هستند که در همه جای سطح زمین وجود دارند مانند ارتفاع از سطح دریا، دما، و باران. داده­های ناپیوسته در همه جا یافت نمی­شوند. مانند معدن آهن، جنگل، رودخانه، روستا، خانه، دریاچه، چاه آب و غیره. داده­های ناپیوسته در حقیقت عارضه­های جغرافیایی را تشکیل می­دهند. عارضه­های جغرافیایی می­توانند به صورت نقطه، خط و سطح دیده شوند. در بخش بعدی راجع به این نوع عارضه­ها بحث می­شود. معمولاً داده­های ناپیوسته شمارش می­شوند. فراوانی عارضه­ها یا در داخل واحد­های طبیعی یا مصنوعی شمرده می­شوند.

داده­های پیوسته در نقاط معینی از سطح زمین اندازه گیری می­شوند. اندازه دما یا نم نسبی در ایستگاه­های هواشناسی تعیین می­شود. برای استفاده از این داده­ها در نقاط فاقد داده از فرآیند درون­یابی استفاده می­شود. برای درونیابی داده­های پیوسته سطح زمین به واحد­های کوچکی بنام پیکسل تقسیم می­شود. در فصل­های بعدی راجع به درونیابی بحث می­شود.

داده­های جغرافیایی در مقیاس­های اسمی، رتبه­ای، فاصله­ای و یا نسبتی تعریف می­شوند.

مقياس اسمي: در اين مقياس داده­ها شكل گروه يا طبقه به خود مي­گيرند. طبقۀ مونث در قبال مذكر، حاضر يا غايب، موفق يا ناموفق، زير ميانگين يا بالاي ميانگين، انگليسي يا آمريكايي، آلماني، ايراني، فرانسوي. انواع پوشش­ها و کاربری­های زمین. انواع ناحیه­های جغرافیایی. به عبارت كلي­تر در اين نوع مقياس فقط تعلق يا عضويت يك داده به يك گروه يا طبقه مشخص مي­شود. بر روی زمین معمولاً طبقات اسمی مانند گروه­های مختلف پوشش زمین و یا ناحیه­های مختلف حرارتی ایران در کنار هم قرار دارند و با همدیگر همسایه هستند. از این جهت به این طبقات داده­ها، واحد­های همجوار هم گویند. در هر طبقه کاربری زمین، نوع استفاده از زمین در همه جای آن یکسان است. در یک منطقه جنگلی همه جا جنگل است. اما در ناحیه­های حرارتی همه جا دما یکسان نیست بلکه متوسط دما در آن ناحیه با متوسط دمای ناحیه مجاور فرق دارد. به عبارت دیگر در ناحیه­های جغرافیایی معمولاً ارزش نقاط مختلف داخل ناحیه معدل­گیری و ساده شده است.

مقياس ترتيبي: عارضه­ها و سطح زمین از نظر داشتن یک ارزش و صفت ویژه درجه­بندي مي­شوند. مثلاً شهرها به شهرهاي پرجمعيت، متوسط، كم جمعيت. هتل­ها به چهار ستاره، سه ستاره، دو ستاره، تك ستاره، وضع سطح بهداشت يك شهر به عالي، بسيار خوب، خوب، متوسط، ضعيف، بسيار ضعيف، بد درجه­بندی می­شوند. در اين نوع مقياس­بندي، فاصله بين درجه يا رتبه­ها معلوم نيست و يا اينكه دقيق نيست. در هر موردي مي­تواند يك معيار خاصي را به خود بگيرد. مثلاً شهر درجه 1 شهري باشد كه بهترين هتل و دبيرستان و دانشگاه دارد، شهر درجه دو شهري كه مثلاً دانشگاه ندارد. باد درجه 1 يا غالب با باد درجه 2 از نظر دفعات وزش فرق دارد ولي چقدر معلوم نيست. فقط كمتر از آن باشد كافي است. البته مقياس درجه­اي يا ترتيبي يك نوع طبقه­بندي است كه محقق با توجه به معلومات كلي خود انجام مي­دهد.

مقياس فاصله­اي: در اين حالت نيز همانند مقياس­هاي قبلي عضوها براساس ارزشي از همديگر فاصله دارند ولي اندازه فاصله مشخص است. مثلاً تهران در مقياس دما از يزد 4 درجه فاصله دارد. فاصله بين دو عضو متوالي مي­تواند به صورت عدد صحيح يا اعشاري باشد. در اين درجه­بندي، داده­ها صفر مبنايي ندارند. مثلاً نمي توان گفت كه يك شهر دما ندارد. مثلاً دماي صفر درجه مبنا نيست و اندازه­ها مي­توانند تا بينهايت ادامه يابند. اگرچه فاصله بين اعضاي متوالي مشخص است ولي اندازه فاصله­ها نمي­توانند نسبتي از همديگر باشند. براي مثال نمي توان گفت كه دماي 20 درجه دو برابر دماي 10 درجه ارزش دارد.

مقياس نسبتي: اين مقياس همانند مقياس فاصله­اي است با دو تفاوت. اولاً مبناي صفر مطلق دارد يعني ممكن است ارزش يك متغيير در عضوي هيچ باشد. یعنی اینکه ارزش متغيير اندازه­هاي منفي نمي­پذيرد. مثلاً بارش در مقابل دما. بارش مقياس نسبتي دارد ولي دما مقياس فاصله­اي. ثانياً ارزش­هاي اعضا قابل تقسيم به همديگر هستند. يعني مي­توان گفت 200 ميليمتر بارش دو برابر 100 ميليمتر بارش ارزش دارد.

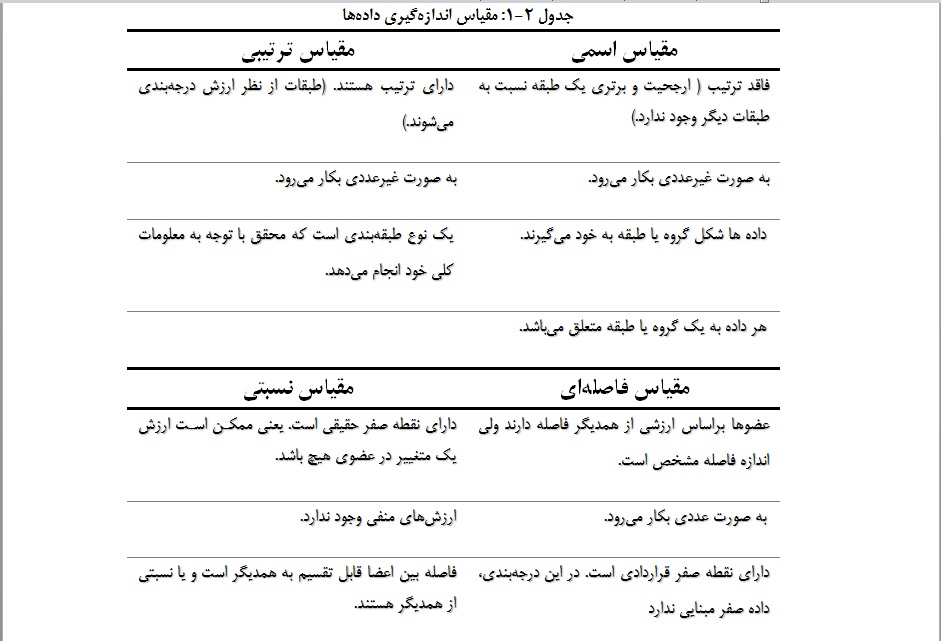
به سخن كوتاه، در مقياس اسمي عضو به يك طبقه یا ناحیه تعلق پيدا مي­كند و تفاوت طبقات از همديگر براساس يك مقياس يا درجه مشخص نيست، بلكه كيفي است. اما در مقياس ترتيبي تفاوت بين طبقات بر اساس درجه­بندي يك ارزش معيني انجام شده است ولي فاصله بين طبقات مساوي نيست و قابل اندازه­گيري هم نيست.  فقط مي­دانيم كه طبقه يا رده اول بهتر از رده دوم است. ولي نمي­دانيم چند برابر بزرگ است. در مقياس فاصله­اي، فاصله بين اعضا قابل اندازه­گيري ولي قابل تقسيم به همديگر نيست. در مقياس نسبتي فاصله بين اعضا قابل تقسيم به همديگر است و يا نسبتي از همديگر هستند.در مقياس نسبتي ارزش­هاي منفي وجود ندارد. مقياس­هاي اسمي و ترتيبي قابل پردازش با روش­هاي آماري متداول نيستند و به تعبير ديگر مي­توان آن­ها را اطلاعات كيفي نامگذاري كرد. اما مقياس­هاي فاصله­اي و نسبتي قابل پردازش هستند و به آن­ها داده­هاي پارامتري يا كمّي گويند. مقياس­هاي اسمي و ترتيبي داده­هاي ناپارامتري یا کیفی ناميده مي­شوند. جدول 2-1 خلاصه­ای از مقیاس اندازه­گیری داده­ها را نشان می­دهد.

-3 الف) فرم داده­های غیر مکانی (توصیفی)

داده­هاي توصيفي كه تشريحي و موضوعي نيز ناميده مي­شوند، ارائه دهندۀ تمامي اجزاي غير مکانی نظير: نام (مالك، شهر) شماره (پارسل، خانه) اندازه­هاي كمي و كيفي (شوري خاك، حجم، تعداد و كيفيت درختان جنگل) نوع (سنگ مادر و خاك) و خلاصه هر نوع مشخصه مرتبط با فرم مکانی مي­باشد.

2-3-1 جداول توصیفی

جداول توصیفی، نمودارها و برخی از شاخص­های آماری از جمله روش­هایی هستند که برای توصیف داده­ها به کار می­روند. داده­های توصیفی معمولاً به صورت جداول توصیفی نشان داده می­شوند. ساختار جداول توصیفی مشتمل بر سطر­ها و ستون­هایی است. سطرها با عنوان رکورد و ستون­های جدول توصیفی، با عنوان فیلد معرفی می­شوند. نمونه­ای از جداول توصیفی در جدول 2-2 و 2-3 نشان داده شده است. برخي از آماردانان معتقدند كه نمايش تصويري به درک ساختار دروني داده­ها كمك مؤثرتري می­کند. راجع به نمودارهای کاربردی در جغرافیا و شاخص­های توصیفی در فصل­های بعدی توضیح داده می­شود.

هر چند در آمار کلاسیک ممکن است جدول توصیفی مربوطه دارای مختصات طول و عرض جغرافیایی باشد ولی تا زمانی که نقشه به کار گرفته نشود و مختصات جغرافیایی به طور کاربردی در پژوهش در نظر گرفته نشود کاری جز آمار کلاسیک انجام نشده است.
2-4 ساختارهای داده­های غیر مکانی (توصیفی)
تنوع زيادي در ساختار داده­هاي توصيفي وجود دارد كه عمدتاً از تكامل يكديگر حاصل شـده انـد مهمترين این ساختارها عبارتست از:
الف) ساختار داده تخت
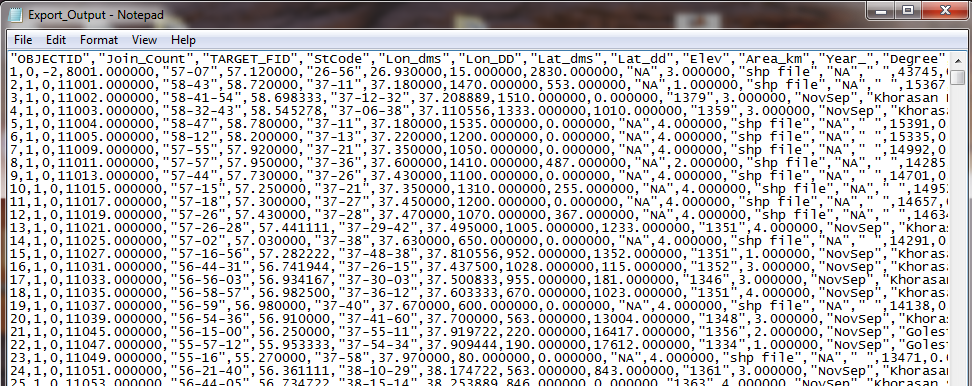
در ساده­ترين حالت، ساختار داده­هاي تخت را مي­توان در يک فايل متني ارائه کرد. در اين حالت معمولاً عنوان هر توصيف در يک ” ” قرار گرفته و مقادير هر توصيف با جداکننده­ها (معمولاً کاما) از يکديگر متمايز مي­شوند (يوجي، 2012). براي نمونه ساختار داده­هاي تخت مربوط به ويژگي­هاي برخي از ايستگاه­هاي هیدرومتري ايران در شکل 2-1 نشان داده شده است.

شکل 2-1: ساختار داده تخت مربوط به برخي از ايستگاه­هاي هيدرومتري ايران (منبع: نگارندگان)

ب) ساختار سلسله مراتبي

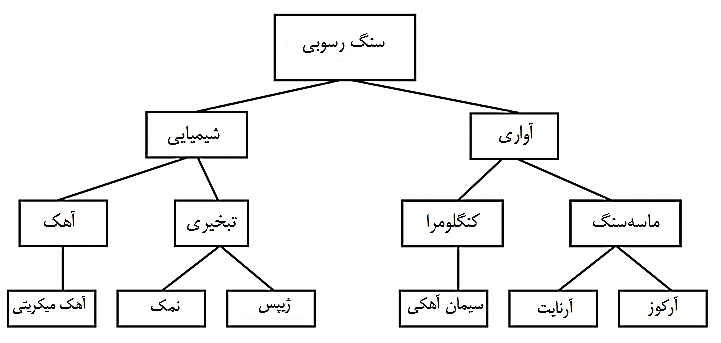
در این نوع از بانک­های اطلاعاتی، اطلاعات به صورت درختی در اختیار کاربران قرار می­گیرد. داده­ها در بخش­هایی به نام قطعه ذخیره می­شوند. قطعه بالای هرم ریشه نامیده می­شود. ریشه به صورت رابطه پدر – فرزندی به قطعات زیرین وصل می­شود. قطعه پدر می­تواند چندین فرزند داشته باشد، ولی هر فرزند فقط یک پدر دارد.این نوع پایگاه داده دو اشکال عمده داشت. اول اینکه به دلیل نوع ساختار خود از جامعیت خوبی برخوردار نبود چون به دلیل افزونگی داده باعث ناسازگاری در بانک اطلاعاتی می­شد و دوم اینکه اشکال ساختاری داشت یعنی با حذف و اضافه کردن رکوردها کل ساختار پایگاه داده باید تغییر می­کرد (توني و فلورنس 2016). براي نمونه در شکل 2-2 ساختار سلسله مراتبي در بانک اطلاعاتي مربوط به سنگ­هاي رسوبي نشان داده شده است.

شکل 2-2: ساختار سلسله مراتبي ذخيره داده¬هاي مربوط به سنگ¬هاي رسوبي (منبع: نگارندگان)

ج) ساختار شبکه­ اي

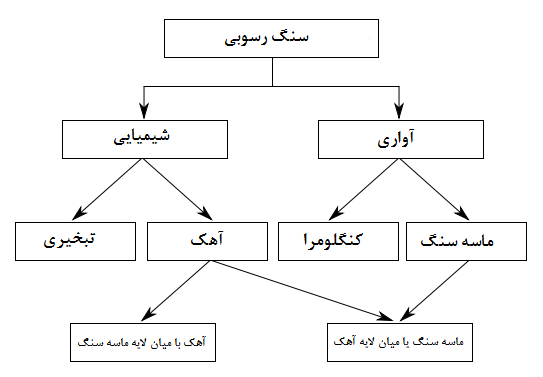
در واقع حالت تغییر یافته مدل بانک اطلاعاتی سلسله مراتبي است. این دو مدل به سادگی قابل تبدیل به یکدیگر هستند. در مدل سلسله مراتبي می­توان یک عامل را به چندین عامل پیوند داد ولی در مدل شبکه­ای می­توان چندین عامل را به چندین عامل پیوند داد. اگر چه با اجازه دادن ایجاد سیکل اشکال اول مدل سلسله مراتبي (عدم جامعیت) برطرف می­شود اما مشکل ساختاری همچنان پابرجا بود (تورستن و مولوني 2014). در شکل 2-3 ساختار شبکه­ای داده­هاي مربوط به سنگ­هاي رسوبي نشان داده شده است.

شکل 2-3: ساختار شبکه¬اي ذخيره داده¬هاي مربوط به سنگ¬هاي رسوبي

د) ساختار رابطه ­ای

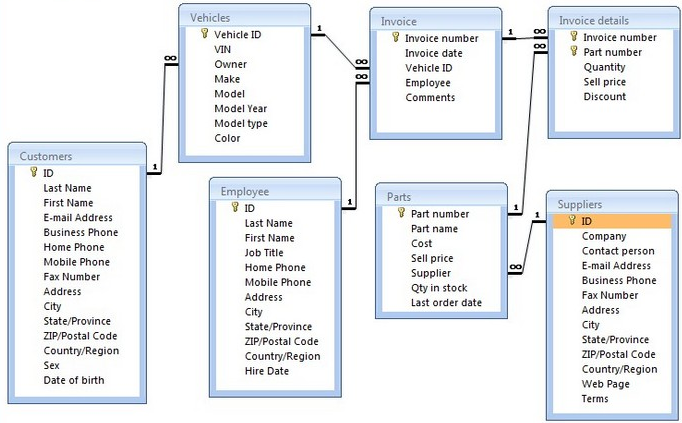
در این مدل، داده‌ها به صورت مجموعه­ای از جداول دو بعدی ذخیره می­شوند که توسط فیلدهای کلیدی (فیلدهای مشترک) به هم وصلمی­شوند. در واقع یک کلاس عارضه توسط یک جدول با فیلدهای مشترک ارائه می‌شود. جدول به نامهای رابطه یا چندتایی نیز نامیده می­شود. مزایاي اين ساختار عبارتند از: 1) انعطاف پذیری بالا و عدم محدودیت در پرسش­دهی یا به عبارت دیگر امکان انجام جستجو در هر جدول و بر اساس هر فیلد توصیفی؛ 2) عدم نیاز به ذخیره­سازی جدول الحاقیو جلوگیری از تولید افزونگی؛ 3) نرمال بودن جداول که باعث ایجاد انسجام و حداقل افزونگی می­شود؛ 4) افزونگی کمتر نسبت به مدل­های سلسله مراتبی و شبکه­ای؛ 5) دارای پایه تئوری دقیق و ریاضی؛ 6) سادگی ساختار؛ 7) سادگی ایجاد تغییرات و 8) رایج­ترین مدل در نرم‌افزارهای تجاری  و کاربردهای  به علت انعطاف پذیری بالا. همچنين از معايب اين ساختار مي­توان به مواردي چون: 1) سخت بودن پیاده سازی و اجرا؛ 2) کارآیی کمتر و کند بودن سیستم به دليل عدم وجود اتصالات فیزیکی یا اشاره­گرها 3) مناسب نبودن برای کار با اشیاء پیچیده و 4) میزان بالای بروز اشتباهات منطقی به علت انعطاف پذیری بالای مدل (نوئل، 1991). در شکل 2-4 نمونه­اي از ساختار رابطه­اي نشان داده شده است.

شکل 2-4: ساختار رابطه¬اي ذخيره داده¬هاي مربوط به مشتريان، کارمندان، وسايل نقليه و اجناس يک فروشگاه (منبع http://www.hpkclasses.ir)

-5 ب) فرم داده­های مکانی

مدل­های فرم مکانی ساختار و توزیع عوارض را در مکان جغرافیایی ارائه می­کند. مدل فرم مکانی پاسخ­گوی دو سوال است: 1) چه چیز؟ و 2) کجاست؟ در مدل فرم مکانی، جهان واقعی (کره زمین) به صورت یک مدل شبیه­سازی (نقطه، خط و سطح) تبدیل می­شود. برای نمونه تعدادی چندضلعی که بر روی یک صفحه یا نقشه مختصات­دار ترسیم شده است. نشاندهنده فرم داده­های مکانی است چرا که بیانگر شکل پدیده (در این جا چندضلعی) و همچنین محل قرارگیری آن می­باشند (توبلر 1989). مدل فرم مکانی به دو دسته مدل برداریو رستری تقسیم می­شود:

2-5-1 مدل­های برداری

در مدل ­برداري اشيا يا پدیده­ها در جهان واقعي به وسيله عناصر هندسـي نمـايش داده مي­شوند. بدين معنا كه موقعيت هر شي به وسيله مختصات آن و توسط نقاط، خطـوط و سطوح مشخص
مي­شود. در اين مدل موقعيت هر نقطه به­طور دقيق بـا يـك جفـت مختصات  در يك سيستم مختصات معين ارائه مي­گردد كه روابـط همـسايگي را نيز مي­توان به آن افزود، بدين معنا كه نقاط آغاز و پايان يك خـط و همچنـين سـطوح مجاور آن­ها را تعيين نمود . اين ساختار در ارائه موقعيت پديده­هـا دقـت بـالايي دارد و بنابراين براي تشريح موقعيت مکاني پدیده­هاي نقطه­اي، خطي و سطحي بسيار مناسب مي­باشد.

الف) نقاط

هر نقطه نشاندهنده یک موقعیت منحصر به فرد در فضا می­باشد، برای نمونه یک مسجد و یا مدرسه، که با استفاده از علائم کارتوگرافی در نقشه­های شهری قابل نمایش هستند. معمولاً از نقاط برای نمایش عوارضی استفاده می­شود که نتوان آن­ها را با خطوط و سطوح نمایش داد (مانند چاه­ها و دکل­های برق. از نقاط برای نمایش عوارضی می­توان استفاده کرد که دارای امتداد و مساحت نیستند). در شکل تعدادی پدیده نقطه­ای نشان داده شده است.

شکل 2-5: پديده¬هاي واقعي که معمولاً به صورت نقطه¬اي ذخيره مي¬شوند.

ب) خطوط

خطوط نشاندهنده نقاط با ویژگی­های یکسان هستند. برای نمونه، جاده­ها و یا مسیرهای لوله­گذاری، نمایش دهنده عوارض خیلی باریک و بسیار کم عرضی هستند که دارای طول می­باشد اما فاقد سطح هستند. منحنی میزان در روی نقشه توپوگرافی نیز پدیده­هایی خطی محسوب می­شوند. در روی نقشه توپوگرافی هر منحنی میزان نو8434.وئوظک92232عی خط هم ارزش است که ارزش عددی آن در تمام نقاط یکسان می­باشد. از خطوط هم ارزش می­توان برای نمایش پدیده­های مختلف مانند میزان بارندگی، تراکم آلودگی آلاینده­های هوا در محیط­های شهری و یا سطح ایستابی سفره­های آب زیرزمینی استفاده کرد. در شکل تعدادی پدیده نقطه­ای نشان داده شده است.

ج) سطوح

نشاندهنده یک محدوده فضایی همگونی در داخل یک چندضلعی می­باشند. برای نمونه محدوده جنگلی و یا تمامیت یک کشور به خصوص در محدوده­های سیاسی خود که توسط چندضلعی­های بسته نشان داده شده است. در شکل تعدادی پدیده از نوع محدوده­ای نشان داده شده است.

2-5-2 ساختار مدل رستری

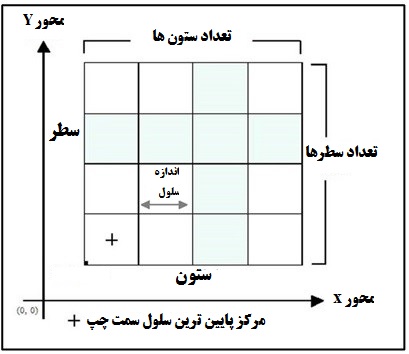
رستر شامل مجموعه اي از نقاط يا سلول­هايي است كه عوارض زمين را در يـك شـبكه منظم مي­پوشاند و به كمك شماره­هاي رديف و ستون آن­هـا، آدرس­دهـي مـي­شـود. كوچكترين عنصر تشكيل دهنده رستر، پیکسل يا سلول ناميده مـي­شـود كه ارزش هـر يك از آن­ها، نمايانگر اطلاعات طیفی یا توصيفي عارضه زميني است. بين سـلول­هـاي يك داده رستري هيچ رابطه منطقي وجود ندارد و هر سلول تنها داراي يك ارزش است كه نمايانگر يك ويژگي مانند جمعيت، كاربري، نوع خاك و . . . خواهد بود. تصاویر ماهواره­ای، عکس­های هوایی، نقشه­های کاغذی اسکن شده، مدل­های رقومی ارتفاعی دارای ساختار رستری می­باشند (جوی­زاده و همکاران، 1396). در شکل اجزای یک لایه رستری نشان داده شده است.

شکل 2-8: اجزای لایه¬های رستری

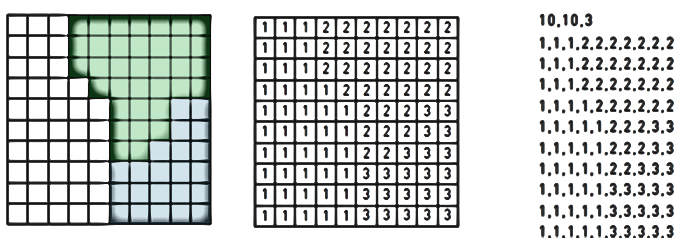
در مدل رستري به هر سلول يك كد يا مقدار ارزش اختصاص داده مي­شود كه در واقع معرف نوع عارضه است. همچنین هر سلول نمايشگر مساحتي از سطح زمين است كه اين مقدار مساحت به ضريب تفكيك پـذيري مـدل بـستگي دارد. در شکل 2-9 چگونگی کد­گذاری به سلول­ها در لایه­های رستری نشان داده شده است.

شکل 2-9: کدگذاري سلول¬ها در داده¬هاي رستري

در مدل رستری عوارض نقطه­ای با یک سلول منفرد، عوارض خطی با رشته­ای از پیکسل­های ممتد و سطوح با پهنه یا مجموعه­ای از پیکسل­های متصل به هم نمایش داده می­شود. به واسطه همین نوع نمایش، عوارض این مدل نسبت به مدل برداری دارای قابلیت تحلیلی بسیار بالاتری است. داده­های رستری به نسبت داده­های برداری از تنوع بیشتری برخوردار هستند (جوی­زاده و همکاران، 1396). در شکل 2-10 چگونگی نشان دادن پدیده­های سطح زمین با مدل­های برداری و رستری نشان داده شده است.

شکل 2-10: داده¬های رستری و برداری

داده­ها را با روش­های متعددی می­توان وارد مدل رستری نمود. برای نمونه با اسکن کردن و تبدیل داده­ها به تصویر، تبدیل داده­های برداری به داده­های رستری با انواع نرم افزار­ها و یا دریافت داده­ها به صورت رقومی از دیگر ورودی­ها مانند تصاویر ماهواره­ای می­توان به داده­های رستری دست یافت.

لایه­های رستری را به دو صورت اعداد صحیح و اعشاری می­توان ارزش­گذاری کرد. ارزش گذاری با اعداد صحیح در رابطه با داده­هایی است که دارای رتبه­بندی یا طبقه­بندی هستند، برای نمونه داده­های مربوط به نقشه تراکم پوشش گیاهی یک منطقه که تراکم زیاد را با عدد 1، تراکم متوسط با عدد 2، و تراکم کم با عدد 3 ارزش گذاری شده­اند. از مزایای این روش ارزش­گذاری استفاده از آنها در جدول اطلاعاتی لایه رستری است.

ارزش گذاری با اعداد اعشاری در رابطه با عوارضی به کار می­رود که دارای داده­های پیوسته هستند، برای نمونه مقدار ارتفاع، مقدار بارندگی یا درجه حرارت و… یک لایه رستری اعشاری، می­تواند شامل اعدادی مانند 26/ 1002 ، 90/ 1500 و …. باشد. فرمت اعشاری حجم بیشتری را نسبت به فرمت اعداد صحیح به خود اختصاص می­دهد.

ابعاد و اندازه پیکسل­ها در مدل رستری نشان دهنده درجه وضوح و قدرت تفکیک آن می­باشد هر چه ابعاد لایه رستری کوچکتر باشد، لایه رستری از وضوح بیشتری برخوردار است و برای نمایش دقیق­تر عوارض مناسب­تر می­باشد. البته به همان میزان که ابعاد پیکسل­ها کوچکتر
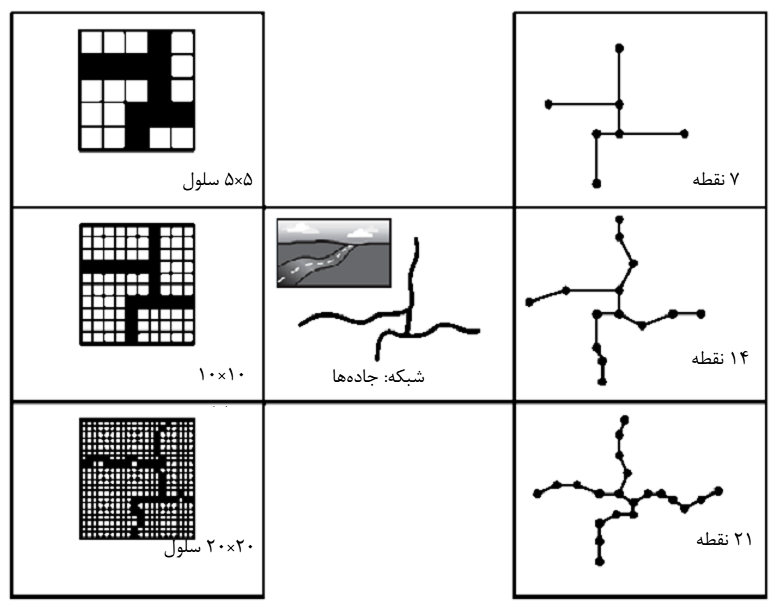
می­شود حجم ذخیره­سازی آن نیز بیشتر می­شود. هر دو مدل برداری و رستری قابلیت تبدیل به یکدیگر را دارند ولی در هر رفت و برگشت تعدادی از ارزش داده­ها دچار تغییراتی می­شوند، اعمال دقت بیشتر و استفاده از روش­های مناسب­تر می­تواند از بروز این مشکل جلوگیری کند و یا آن را به حداقل برساند .در شکل 2-11 تأثیر قدرت تفکیک بر وضوح داده­های رستری و برداری نشان داده شده است.

شکل 2-11: تأثير تغيير قدرت تفکيک بر وضوح داده¬هاي رستري و برداري

2-5-3 پیچیدگی­های جهان واقعی و مدلسازی

مشکلات متعددی در رابطه با ساده­سازی پیچیدگی­های جهان واقعی با مدل­های برداری و رستری وجود دارد. که از میان آن­ها می­توان به ماهیت پویایی جهان واقعی، تعیین عوارض گسسته و پیوسته و مقیاس کار اشاره کرد. جهان واقعی ساکن نیست برای نمونه در یک ناحیه جنگلی درختان روییده و قطع می­شوند، رود­ها طغیان می­کنند و شهر­ها گسترش می­یابند. ماهیت پویایی جهان باعث دشوار شدن تعریف عارضه در پروژه­های مرتبط با سیستم اطلاعات جغرافیایی می­شود (لاورینی، 2000). این دشواری­ها را می­توان مشتمل بر موارد زیر دانست:

الف) نماد سازی عوارض

معمولاً انتخاب نوع و نماد عارضه در مدل سازی دشوار می­باشد. برای نمونه تصمیم­گیری در مورد این که بهترین شیوه برای نشان دادن جنگل استفاده از مجموعه­ای از نقاط است (نشان دادن موقعیت درختان به صورت جدا از هم) یا استفاده از یک ناحیه (چندضلعی) دشوار است.

ب) نمایش تغییرات

چگونگی ارائه تغییرات زمانی پدیده­ها نیز دشوار است. برای نمونه ممکن است جنگلی که با یک ناحیه نشان داده شده است با گذشت زمان آنچنان فرسوده شود که گروه پراکنده­ای از درختان را شامل شده و در آن صورت با استفاده از نقاط بهتر بتوان آن را نشان داد.

ج) نگرش متفاوت

گر چه ممکن است ماهیت فیزیکی عوارض ثابت باشد اما درک ما از ساختار جغرافیایی آن­ها می­تواند با توجه به هدف کار متفاوت باشد. بازدید کننده از یک درّه جنگلی ممکن است به نقشه شبکه راه­های منطقه به عنوان عوارض خطی بنگرد در حالی که برای مهندسین راه­سازی که باید سطح جاده را بعد از فصل زمستان تعمیر کنند، جاده­ها نوعی عوارض سطحی محسوب می­شوند.

گاهی اوقات تعیین مرز عوارض دشوار می­باشد. برای نمونه در یک ناحیه جنگلی مرز مشخصی بین واحدهای مختلف گونه­های گیاهی وجود ندارد زیرا معمولاً در یک منطقه گذر، درختان با گیاهان ناحیه مجاور در هم می­آمیزند. در این مورد، چنانچه بخواهیم جنگل را به وسیله یک چندضلعی نشان دهیم، نمی­توان مرز دقیقی را تعیین نمود به نظر یک بوم­شناس، پوشش گیاهی می­تواند عارضه­ای پیوسته باشد که با یک عارضه نشان داده می­شود در حالی که برای یک جنگلبان بهتر است گیاهان به صورت مجموعه­ای از عوارض ناحیه­ی منفصل نشان داده شوند. بنابراین تعیین نوع عارضه­ای که در مدل­سازی جهان واقعی به کار می­رود در برخی موارد کار ساده­ای نیست.

خلاصه :

– فرم داده­های مکانی به مکان پدیده مرتبط می­شود. فرم توصیفی داده­ها در مورد چیستی فرم مکانی داده­ها بحث می­کند.

– مدل فرم مکانی به دو دسته مدل برداری و رستری تقسیم می­شود.

– در مدل­برداري اشيا يا پدیده­ها در جهان واقعي به وسيله عناصر هندسـي نمـايش داده مي­شوند. بدين معنا كه موقعيت هر شي به وسيله مختصات آن و توسط نقاط، خطـوط و سطوح مشخص مي­شود.

– نقطه در مدل برداری نشاندهنده یک موقعیت منحصر به فرد در فضا می­باشد، برای نمونه یک مسجد و یا مدرسه

– خطوط در مدل برداری نشاندهنده نقاط با ویژگی­های یکسان هستند. برای نمونه، جاده­ها و یا مسیرهای لوله­گذاری، نمایش دهنده عوارض خیلی باریک و بسیار کم عرضی هستند که دارای طول می­باشد اما فاقد سطح هستند.

– سطوح در مدل برداری نشاندهنده یک محدوده فضایی همگونی در داخل یک چندضلعی
می­باشند. برای نمونه محدوده جنگلی

– رستر شامل مجموعه اي از نقاط يا سلول­هايي است كه عوارض زمين را در يـك شـبكه منظم مي­پوشاند و به كمك شماره­هاي رديف و ستون آن­هـا، آدرس­دهـي مـي­شـود.

– كوچكترين عنصر تشكيل دهنده رستر، پیکسل يا سلول ناميده مـي­شـود.

– ابعاد و اندازه پیکسل­ها در مدل رستری نشان دهنده درجه وضوح و قدرت تفکیک آن می­باشد هر چه ابعاد لایه رستری کوچکتر باشد، لایه رستری از وضوح بیشتری برخوردار است و برای نمایش دقیق­تر عوارض مناسب­تر می­باشد.

– هر دو مدل برداری و رستری قابلیت تبدیل به یکدیگر را دارند ولی در هر رفت و برگشت تعدادی از ارزش داده­ها دچار تغیراتی می­شوند، اعمال دقت بیشتر و استفاده از روش­های مناسب­تر می­تواند از بروز این مشکل جلوگیری کند و یا آن را به حداقل برساند .

– تنوع زيادي در ساختار داده­هاي توصيفي وجود دارد كه عمدتاً از تكامل يكديگر حاصل شـده انـد. ساختار داده تخت، ساختار سلسله مراتبی، ساختار شبکه­ای و مدل رابطه­ای از مهمترين ساختارها هستند.

– در ساده­ترين حالت، ساختار داده­هاي تخت را مي­توان در يک فايل متني ارائه کرد. در اين حالت معمولاً عنوان هر توصيف در يک ” ” قرار گرفته و مقادير هر توصيف با جداکننده­ها (معمولاً کاما) از يکديگر متمايز مي­شوند.

– در ساختار سلسله مراتبی، اطلاعات به صورت درختی در اختیار کاربران قرار می­گیرد. داده­ها در بخش­هایی به نام قطعه ذخیره می­شوند.

– قطعه بالای هرم در ساختار سلسله مراتبی ریشه نامیده می­شود.

– ساختار شبکه­ای در واقع حالت تغییر یافته مدل بانک اطلاعاتی سلسله مراتبي است. در مدل سلسله مراتبي می­توان یک عامل را به چندین عامل پیوند داد ولی در مدل شبکه­ای می­توان چندین عامل را به چندین عامل پیوند داد.

– در مدل رابطه­ای، در واقع یک کلاس عارضه توسط یک جدول با فیلدهای مشترک ارائه می‌شود.

منابع مطالعاتی بیشتر

[1].Anselin, L., Syabri, I. and Kho, Y., (2006), GeoDa: An Introduction to Spatial Data Analysis. Geographical Analysis 38, 5–22.

[2].Bivand, R. S., Pebesma, E. J. and Gomez-Rubio, V., (2008). Applied Spatial Data Analysis with R . Springer. 378p.Chambers, J.M., (2009). Software for Data Analysis: Programming with R .Springer. 498p.

[3].Couclelis, H., (1992), People manipulate objects (but cultivate fields): Beyond the rastervector debate in gis. in frank, a., u., campari, i. and formentini, u. (eds.). Theories and Methods of Spatio-Temporal Reasoning in Geographic Space, 639:65–77.

[4].Grandchamp, E. (2010), Raster-vector cooperation algorithm for GIS GeoProcessing.

[5].Heywood, I., Cornelius, S. and Carver, S., (2006), Introduction to Geographical Information Systems. Pearson Prentice Hall, New York. Lo, C. P. and A. K. W. Yeung. (2007). Concepts and Techniques of Geographic Information Systems. Pearson Education Inc. 532 pp.

[6].Schneider, M. (1999), Uncertainty management for spatial data in databases: fuzzy spatial data types, in: Advances in Spatial Databases, Lecture Notes in Computer Science, vol. 1651, Springer, Berlin, pp. 330–351.

[7].Wiegand, N., et al., (2007), “A Task-Based Ontology Approach to Automate Geospatial Data Retrieval”, In Transactions in GIS, vol. 11, issue 3, pp. 355–376.

[8].Zandbergen, P.A. (2008), Positional Accuracy of Spatial Data: Non-Normal Distributions and a Critique of the National standard for Spatial Data Accuracy, In Transactions in GIS, vol. 12, issue 1, pp. 103–130.