راهکارهای جستجو در تخمین گرهای زمین آماری

راهکارهای جستجو در تخمین گرهای زمین آماری-موسسه چشم انداز-آموزش کاربردی GIS و RS

مقدمه

به طور کلی، انتخاب رویکرد ها و راهکار های مناسب جستجو، کنترل کنندۀ تعداد مشاهدات مورد استفاده در فرآیند تخمین است، و یکی از مهم ترین موضوعات در به کارگیری تخمین­ گرهای زمین آماری محسوب می ­گردد. بهینه­ سازی رویکردهای جستجو، در برگیرندۀ پاسخگویی به پرسش زیر است:

آیا به تعداد کافی، نمونه در مجاورت محل تخمین وجود دارد؟

آیا تعداد زیادی نمونه در همسایگی محل تخمین وجود ندارد؟

آیا نمونه­ های واقع در همسایگی محل تخمین، زاید و اضافی هستند؟

آیا نمونه­ های واقع در مجاورت محل تخمین، مرتبط با موضوع تخمین هستند؟

پرسش­ های اول تا سوم، از نقطه ­نظر تخمین گرهایی که قادرند با بیش از یک (و حتی سه نمونه) نمونه در تخمین سر و کار داشته باشند (مانند کریجینگ و یا تخمین گرهای معکوس فاصله)، حائز اهمیت هستند. در تخمین گرهای هندسی (مانند روش چندضلعی تیسن)، الگوی توزیع مکانی نمونه ­ها تعیین کنندۀ نمونه­ های مورد استفاده در فرآیند تخمین است. از سوی دیگر، در به کارگیری تخمین­ گرهایی که قادر به کاربرد تعداد نامحدودی نمونه در تخمین هستند، معمول ترین راهکار جستجو، عبارت از استفاده از نمونه ­هایی است که در فضای (یا پنجره) جستجوی معین و مشخصی قرار می­ گیرند.

پرسش چهارم از هر دو نقطه نظر کاربردی و نظری، حائز اهمیت است. زیرا، پاسخ به این پرسش، تعیین کنندۀ این واقعیت است که آیا نمونه­ های واقع در همسایگی محل تخمین، متعلق به گروه و جمعیت نقطۀ مورد تخمین می ­باشند یا خیر؟ بدیهی است که این پرسش، برای تمامی تخمین گرها مهم است.

تعریف و تعیین فضای جستجو

همان گونه که در مقدمه اشاره شد، برای روش­ های تخمینی که فاقد محدودیت در به کارگیری مشاهدات مجاور در تخمین هستند، روش معمول، عبارت از انتخاب نمونه­ ها از طریق تعیین محدودۀ جستجو است. تعریف فضای جستجو از طریق محدودۀ همسایگی با مرکزیت منطبق بر محل تخمین صورت می گیرد. سمت­ گیری و امتدادهای جغرافیایی فضای جستجو، وابسته به الگوی ناهمسان گردی موجود در ساختار پیوستگی مکانی متغیر مطالعه است. چنانچه مقادیر عددی نمونه ­ها در جهت مشخص جغرافیایی، پیوستگی بیشتری از خود نشان دهند، آن گاه سمت ­گیری محدودۀ جستجو، به گونه ­ای خواهد بود که محور اصلی آن به موازات جهت حداکثر پیوستگی قرار می ­گیرد. بدیهی است که دسترسی به مستندات کافی به منظور تبین و مدلسازی ناهمسان گردی ضروری است. در صورت فقدان ناهمسان گردی، یعنی همسان گرد بودن الگوی پیوستگی مکانی داده ­ها، محدودۀ جستجو به شکل فضای دایره مانند تعریف می ­گردد.

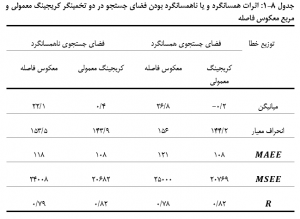
اثرات همسانگرد و یا ناهمسانگرد بودن محدودۀ جستجو بر تخمین، با استفاده از داده­ های متغیر V و تخمین­ گرهای کریجینگ معمولی و مربع معکوس فاصله، مورد مطالعه قرار گرفتند و نتایج حاصل در جدول زیر نشان داده شده است.

همان گونه که ملاحظه می­ شود، به کارگیری فضای جستجو ناهمسان گرد در مقایسه با فضای جستجوی همسان گرد، باعث ارتقا و بهبود تخمین ( هر چند اندک) شده است. شاید یکی از دلایل بهبود اندک تخمین­ ها، ناشی از این واقعیت باشد که محورهای ناهمسان گردی انتخاب شده برای الگوی پیوستگی مکانی داده ­ها، از جامعیت خوبی در کل منطقۀ مطالعاتی برخوردار نمی­ باشند و تنها انعکاسی از الگوی پراکنش مکانی داده ­ها در بخش یا بخش­ هایی از منطقه مطالعاتی هستند.

کفایت تعداد نمونه­ های واقع در همسایگی محل تخمین

پس از تعیین فضای جستجو، جهت و نسبت ناهمسان گردی آن، بایستی در مورد تعداد نمونه ­هایی که در این فضا قرار می ­گیرند تصمیم ­گیری نمود. محدودۀ جستجو باید به قدر کافی بزرگ باشد، تا در برگیرندۀ تعداد کافی نمونه به منظور حصول به تخمین ­های مناسب باشد. بدیهی است که بزرگی محدودۀ جستجو توسط الگوی هندسی نمونه ­ها تعیین می ­گردد. چنانچه نمونه ­ها بر روی شبکه ­ای منظم ( یا شبه منظم) واقع شده باشند؛ آن گاه محدودۀ جستجو را می­ توان به گونه ­ای تعریف نمود که حداقل، در برگیرندۀ 4 نمونۀ نزدیک به محل تخمین باشد. در عمل، محدودۀ جستجو بایستی به قدر کافی وسیع باشد تا حداقل، 12 نمونه را در گیرد.

در شرایطی که نمونه ­ها به طور نامنظم در فضای نمونه ­برداری پراکنده شده ­اند، محدودۀ جستجو بایستی اندکی بزرگتر از متوسط فاصلۀ بین نمونه ­ها (D ̅) انتخاب گردد:

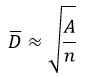
که  A: کل ناحیه تحت پوشش به وسیله نمونه ­ها؛ n تعداد نمونه­ ها می باشد.

ازدیاد نمونه ­های واقع در همسایگی محل تخمین

در بخش قبلی، به قسمتی از پرسش مربوط به بزرگی محدودۀ جستجو پاسخ داده شد. پاسخ مزبور، تنها در برگیرندۀ حداقل اندازۀ ممکن برای محدودۀ جستجو است، که توسط الگوی نمونه ­برداری و ژئومتری داده ­ها تعیین می­ گردد. حال، پرسش اصلی در برگیرندۀ این موضوع است که محدودۀ جستجو تا چه اندازه می­ تواند وسیع و بزرگ باشد. قبل از پاسخ به این پرسش، بایستی به دو اصل حاکم بر تخمین گرهای زمین آماری اشاره کرد:

– به کارگیری تعداد بیشتری از نمونه­ های واقع در فضای جستجو، منجر به افزایش حجم و زمان محاسبات می­ گردد.

– برقراری فرضیات ایستایی، با به کارگیری نمونه­ های بسیار دور از محل تخمین، بیش از پیش، مورد شک و تردید قرار می ­گیرند.

در به کارگیری تخمینگر کریجینگ معمولی، توجه به دو نکتۀ بالا ضروری است. حجم و تعداد محاسبات مورد نیاز جهت دستیابی به اوزان کریجینگ، با توان سوم تعداد نمونه­ های مورد استفاده جهت هر تخمین متناسب است. اگر تعداد نمونه ­های واقع در فضای جستجو، دو برابر گردند؛ حجم محاسبات، هشت برابر افزایش پیدا می­ کنند.

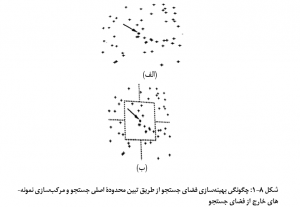
مشکل مربوط به حجم محاسبات را می­ توان از طریق ترکیب چند نمونه که در فواصل دورتر از محل تخمین قرار گرفته­ اند، و ایجاد نمونه ­های مرکب مرتفع کرد. همان گونه که در شکل زیر نشان داده شده است، به جای در نظر گرفتن 50 نمونۀ واقع در فضای همسایگی محل تخمین، با  مرکب سازی نمونه ­ها، تنها از 16 نمونه جهت تخمین می­ توان استفاده کرد. آن­ها مشتمل بر 12 نمونه به عنوان نزدیک ترین نمونه­ های منفرد به محل تخمین و 4 نمونۀ مرکب، که حاصل از ترکیب 38 نمونل منفرد هستند، می­ باشند. در عمل، سیستم محاسباتی کریجینگ را می ­توان برای شرایط وجود نمونه­ های مرکب، سازگار و تعدیل نمود؛ به گونه ­ای که وزن تخصیصی به یک نمونۀ مرکب، به طور مساوی بین نمونه ­های منفرد تشکیل دهندۀ آن توزیع گردد.

در رابطه با اصل دوم، بایستی خاطر نشان ساخت که استفاده از مدل ایستایی، به کارگیری فضاهای جستجوی بسیار وسیع و بزرگ را توصیه نمی­ کند. اگرچه از منظر مدل مورد استفاده توسط تخمین گر، نمونه ­های بیشتر (صرف­نظر از فاصلۀ آن­ها تا محل تخمین) همیشه باعث بهبود تخمین می­ شوند؛ لیکن صادق بودن آن در شرایط واقعی، همیشه مورد شک و تردید است. به دیگر سخن، با وسیع ­تر نمودن پنجرۀ جستجو، مدل سازی نمونه­ های دورافتاده (هر چند درون فضای جستجو) به عنوان پیشامد و نتیجۀ ممکن تابع تصادفی ایستا، بسیار دشوار است. بدین ترتیب، بین واقعیت پدیده و مدل نظری مورد استفاده جهت توصیف آن پدیده، بیش از پیش، دوگانگی و افتراق مفهومی ایجاد می­ گردد. بنابراین، با محدود کردن و بهینه ­سازی فضا و پنجرۀ جستجو، امکان بیشتری جهت مفهوم­ سازی مدل تابع تصادفی ایستا و انطباق آن با واقعیت ذاتی پدیدۀ مورد مطالعه فراهم می­ آید. در نتیجه، اختلاف بین خصوصیات آماری پدیده (پارامترها) و آن­ هایی که متعلق به مدل هستند (آماره ­ها)، به حداقل رسانده می ­شود.

نکتۀ مهم دیگر که ذکر آن ضروری استف مربوط به تصور نادرستی است که از فضای جستجو و ارتباط آن با دامنۀ واریوگرام وجود دارد. معمولاً تصور می­ گردد که محدوده و شعاع جستجو، نبایستی ماورای مقدار عددی دامنۀ واریوگرام قرار گیرد. تجارب نشان داده ­اند که چنان­چه تعداد معدودی نمونه در محدودۀ دامنۀ واریوگرام واقع گردند و سپس، اقدام به افزودن نمونه ­های دیگر ( که فاصله ­شان با محل تخمین، ماورای مقدار عددی دامنۀ واریوگرام است)، شود؛ آن گاه غالباً بهبود و ارتقای تخمین­ های زمین آماری را به دنبال خواهند داشت.