خلاصه
کلید واژه ها:
خوشه بندی محدود ; قیمت مسکن ؛ سرریز درون شهری ; اثر موج دار ; زنجیره مارکوف فضایی
1. معرفی
-
مداخلات دولت محلی بر روی حباب بازار مسکن تنها تأثیری حاشیه ای بر سرریز بازار مسکن ایجاد می کند. آنها در دراز مدت انتقال سرریز را تغییر نمی دهند.
-
نیروهای محرک سرریز بازار مسکن به دو بازار فرعی واقع در اطراف تونگژو هدایت می شوند، شهری جدید که برنامه ریزی شده است تا شهر اقماری بزرگ پکن باشد و به بسیاری از منابع ارزشمند پزشکی، آموزشی و اداری مجهز شود. بنابراین، جهت انتقال سرریز در پکن بسیار با اولویت سیاست سازگار است.
-
نیروهای محرک و مکانیسم پشت سرریزهای درون شهری در پکن به طور قابل توجهی متمایز از عواملی است که در پشت سرریزهای بین شهری به طور گسترده مستند شده اند. شکل موج دار سرریز دیگر غالب نیست. در مقابل، اثر مهاجرت ناشی از شکاف قیمت و الگوی فضایی دو نیروی اصلی هستند که باعث سرریز درون شهری در پکن میشوند، اگرچه آنها کماهمیتترین نیروها در مطالعات سرریز بین شهری در نظر گرفته میشوند.
-
این مقاله یک روش فضا-زمان جدید را برای مطالعه سرریز قیمت مسکن با ادغام مدل زنجیره مارکوف و خوشهبندی محدود پیشنهاد میکند.
-
تفاوتهایی که در اینجا بین سرریزهای بازار مسکن درون شهری و بین شهری آشکار میکنیم، میتواند تحقیقات آتی را، هم نظری و هم تجربی، ترویج کند.
-
انواع مختلف شوکهای سیاستی میتوانند از نظر تأثیر بر مکانیسم سرریز بلندمدت، که بینشی را برای حوزه تنظیم بازار مسکن فراهم میکند، بهطور قابلتوجهی متفاوت باشند.
2. داده ها و روش ها
2.1. توضیحات داده ها
2.2. مدل زنجیره مارکوف
در هر زمان ثابت t و t + 1�+1، سرریز بین مکان ها متر0،متر1∈ م�0,�1∈�را می توان به طور طبیعی به عنوان وقوع رویدادی که قیمت در آن تغییر می کند شناسایی کرد متر1�1در حین t + 1�+1به همان روشی که در متر0�0در طول تی . به عبارت دیگر اگر r را a نشان دهیم{ – 1 ، 1 }{−1,1}تابع ارزش به گونه ای است که r ( t , m )�(�,�)ارزش می گیرد – 1−1، اگر در مکان m و زمان t ، قیمت مسکن کاهش یابد، و اگر قیمت جهش کند، 1، آنگاه سرریز از متر0�0به متر1�1در زمان t و t + 1�+1به صورت زیر شناسایی می شود:
فرآیند سرریز به معنای زیر ماکارویی است: برای هر بار t ، سرریز بین هر دو مکان به طور تصادفی اتفاق میافتد، با احتمال وقوع صرفاً به بازار فرعی که مکان از محل به آن تعلق دارد و بازار فرعی که مکان به آن متعلق است، بستگی دارد. . به طور رسمی، احتمال وقوع را می توان در سطح زیر بازار تعریف کرد و به صورت a بیان کرد | پ| × | پ||�|×|�|ماتریس انتقال ثابت ماکاروف، با نشان داده شده است تی�( | . ||.|تعداد عناصر یک مجموعه است)، به طوری که برای هر پمن��و پj��با متر0∈پمن،متر1∈پj�0∈��,�1∈��
با توجه به ماتریس انتقال ثابت مارکوف تی�و پانلی از داده های قیمت
در جایی که T تعداد زمان مشاهده است، میتوانیم رویه مورد بحث در مرجع [ 54 ] را برای تخمین ورودیها اتخاذ کنیم.تی�; به طور رسمی، دو تخمینگر وجود دارد که میتوان آنها را استخراج کرد، که هر دو برای تعداد مکانهای مشاهدهشده بسیار سازگار هستند:
از آنجایی که هر دو برآوردگر ( 4 ) و ( 5 ) با تیمن ، ج��,�، باید مجانبی با یکدیگر برابر باشند. علاوه بر این، با پیروی از ادبیات [ 54 ]، میتوان نتیجه گرفت که آمار زیر که از دو تخمینگر به دست آمده است به طور مجانبی از یک χ2�2توزیع با درجات آزادی | پ| ⋅ ( تی− 2 )|�|·(�−2):
2.3. خوشه بندی K-Means محدود
تعداد کل زیرمنطقه ها | پ||�|و محدوده جغرافیایی آنها در مدل زنجیره مارکوف فضایی هنوز ناشناخته است. برای تکمیل تنظیم مدل، یک گزینه این است که مناطق اداری و/یا کد پستی را به عنوان مجموعه پارتیشن در نظر بگیرید. پ�. با این حال، فشرده سازی مناطق اداری/کد پستی به نقاط در یک محیط درون شهری مناسب نیست، زیرا ممکن است اطلاعات مهم ارتباطات اقتصادی بین مکان های مختلف را از دست بدهد. در این بخش یک روش مبتنی بر داده برای شناسایی مجموعه پارتیشن ارائه می کنیم پ�. روش جدید روش استنتاج استاندارد ماتریس انتقال را ترکیب می کند تی�با خوشه بندی k-means از طریق افزودن مجموعه ای از شرایط محدودیت به مسئله بهینه سازی مرتبط با خوشه بندی k-means. این روش جدید اساساً نوعی خوشه بندی محدود است که در ادبیات مطالعه شده است [ 49 ، 50 ، 51 ، 52 ]، در حالی که در محیط ما، محدودیت از مدل زنجیره مارکوف فضایی به روش مشتری مشتق شده است. به طور رسمی، خوشه بندی محدود را می توان به عنوان یک مسئله بهینه سازی محدود به صورت زیر بیان کرد:
جایی که اسک��یک پارتیشن K- fold از کل نمونه است. x بردار ویژگی است که نشان دهنده ارزش تمام ویژگی های مرتبط با یک واحد مسکونی در نمونه است. ویژگی ها باید شامل مختصات جغرافیایی دوبعدی هر شبکه و سایر ویژگی های متصل به آن شبکه و مهم برای تجزیه و تحلیل، مانند نرخ رشد قیمت محلی باشد. ابعاد مرتبط با مختصات به صورت c نشان داده می شود . ایکسج��نمایانگر بردار x بر روی ابعاد c است. تحت این نماد، ( 7 ) دقیقاً تابع هدف برای خوشه بندی k-means استاندارد با تابع شباهت به عنوان فاصله اقلیدسی روی نقشه است که به طور گسترده در ادبیات مورد بحث قرار گرفته است [ 55 ].
در شرایط فعلی، شکل خاص محدودیت ها ( 8 ) و معنای اقتصادی آنها از انتقال زنجیره مارکوف فضایی سرریزها در میان بازارهای فرعی مسکن به عنوان ضربه مشتق شده است:
جایی که χ2پ، ⋅��,·2و χ2⋅ ،پ“�·,�′2هستند χ2�2آمار به دست آمده در ( 6 ). τ| پ| ⋅ ( تی− 2 ) ، α�|�|·(�−2),�هست 1 – α1−�سطح چندکی a χ2�2توزیع با درجه آزادی بودن | پ| ⋅ ( تی− 2 )|�|·(�−2).
محدودیت ( 9 ) از ویژگی ثابت مدل زنجیره ماکاروف ( 2 ) ناشی می شود. در واقع، زمانی که مدل زنجیره مارکوف واقعی که دادههای سرریز قیمت مشاهدهشده را تولید میکند، ثابت باشد، تحت بازیابی صحیح بازارهای فرعی پنهان، فرضیه صفر زیر باید برقرار باشد:
2.4. تخمین چگالی کرنل و تجزیه و تحلیل هات اسپات
در داده های اولیه، قیمت مسکن به هر واحد مسکونی پیوست شده است. چنین قیمت هایی به طور مستقیم در طول زمان قابل مقایسه نیستند. برای تسهیل تجزیه و تحلیل، ما از روش تخمین چگالی هسته استفاده کردیم و دادههای قیمت را در سطح واحد مسکونی به قیمت در سطح مکان جمع کردیم. در جزئیات، ما منطقه مورد مطالعه را به مجموعه ای از 1000متر × 1000متر1000m×1000mزیرمنطقه ها را مربع و مراکز آنها را به عنوان مجموعه شبکه ها انتخاب کردند (تحلیل اولیه نشان می دهد که 1000متر1000mانتخاب بهینه است زیرا اندازه شبکه بزرگتر از 1000متر1000mتمایل به پنهان کردن تفاوت های محلی دارد و به دلیل اینکه اندازه شبکه کوچکتر از 1000متر1000mمی تواند ویژگی های محلی را اغراق کند). سپس از روش چگالی هسته گاوسی برای تخمین قیمت تجربی در هر شبکه استفاده شد. به طور رسمی، ما دریافتیم:
جایی که جپمن���مختصات جغرافیایی (طول و عرض جغرافیایی) است که با رکورد تراکنش یکم مرتبط است. جj��مختصات جغرافیایی مرتبط با شبکه j است. مترتی��تعداد کل کل معاملات جمع آوری شده بر حسب سه ماهه t است. K تابع چگالی گاوسی دو بعدی استاندارد با میانگین صفر است. بتی��عرض هسته است که انتخاب شده است σ⋅متر–13تی�·��−13، جایی که σ�میانگین انحراف استاندارد طول و عرض جغرافیایی تمام واحدهای مسکونی نمونه است. چنین انتخابی از عرض هسته تضمین می کند که به عنوان مترتی→ ∞��→∞، قیمت تجربی در احتمال به ارزش صدق آن همگرا می شود. برای زمان ثابت t ، پt ، i��,�و پ^t ، j�^�,�به ترتیب قیمت مسکن در اولین رکورد معامله و قیمت تخمینی مسکن در شبکه j می باشد.
به طور رسمی، Getis-Ord را محاسبه کردیم جیمن∗��*آماری برای چگالی توزیع رکوردهای تراکنش در نزدیکی هر شبکه از طریق فرمول زیر:
جایی که ایکس¯�¯( wمن¯¯¯¯��¯) میانگین تجربی بردار است {ایکس1, … ,ایکسn}{�1,…,��}( {wمن 1, … ,wمن n}{��1,…,���}). x ( : = {ایکس1, … ,ایکسn}:={�1,…,��}) بردار است که یک ویژگی مرتبط با هر شبکه را نشان می دهد j ∈ { 1 , … , n }�∈{1,…,�}; wمن��( : = {wمن 1, … ,wمن n}:={��1,…,���}) بردار وزن مربوط به یک شبکه i با هر است wمن ج���وزنی است که شبکه i به شبکه j اختصاص می دهد. n تعداد تمام شبکه هاست. اسایکس��و اسwمن���انحرافات استاندارد تجربی مرتبط با بردار x و هستندwمن��به ترتیب. ⟨ . ، . ⟩.,.حاصل ضرب داخلی دو بردار در فضای اقلیدسی n بعدی را نشان می دهد.
در تنظیمات فعلی، ویژگی x به عنوان چگالی توزیع تجربی همه تراکنشهای نمونه انتخاب شده است. ساختار چگالی فضایی یک شبکه به شرح زیر است:
جایی که همه جپمن���، جj��، و K به همان معنی در ( 11 ) است. m تعداد کل سوابق معاملات در تمام سه ماهه است. و b به همان روشی که در ( 11 ) انتخاب شده است.
وزن wمن ج���همچنین از طریق تابع هسته گاوسی به صورت زیر انتخاب می شود:
با همان انتخاب عرض هسته برای چگالی تجربی ( 13 ).
2.5. فاصله هاسدورف
فاصله هاسدورف یک متریک محبوب است که فاصله بین دو مجموعه را اندازه گیری می کند. به طور گسترده در بسیاری از زمینه ها، مانند تطبیق تصویر و ارزیابی کارایی خوشه بندی [ 58 ، 59 ] استفاده شده است. با توجه به تعریف ساده آن از طریق یک عملیات حداقل، می توان آن را به یک آزمون فرضی با یک فرم بسیار ساده از توزیع فرضیه صفر توسعه داد. آزمایش حاصل می تواند بررسی کند که آیا مناطق تحت پوشش دو مجموعه از نقاط نمونه روی نقشه یکسان هستند یا خیر. به طور رسمی، فاصله Hausdorff به صورت زیر تعریف می شود:
جایی که اس1�1و اس2�2دو منطقه فرعی باز در منطقه X روی نقشه هستند. d یک متریک پیش فرض X است و در تنظیمات ما می تواند به عنوان متریک اقلیدسی در تعریف شود آر2�2. فاصله هاسدورف داچ��یک متریک کاملاً تعریف شده از مجموعه همه زیرمجموعه های X با فضای داخلی باز است [ 59 ]، به این معنی که دارای ویژگی است داچ(اس1،اس2) = 0��(�1,�2)=0اگر و تنها اگر اس1=اس2�1=�2دارایی های. نسخه تجربی داچ��را می توان از طریق نمونه های تصادفی از اس1�1و اس2�2مانند زیر:
جایی که ایکسمن��اولین نمونه توزیع شده مستقل ( iid ) است که به طور یکنواخت از منطقه کشیده شده است اس1�1; yمن��آنالوگ است ایکسمن��برای منطقه اس2�2.
توجه داشته باشید که ( 16 ) را می توان حتی بدون دانستن محدوده دقیق تعریف کرد اس1�1و اس2�2; حداقل دانش تعریف شده ( 16 ) فقط این است که x و y دو مجموعه از نمونه iid از دو منطقه هستند. بنابراین، ( 16 ) را می توان به عنوان آزمون فرضی برای بررسی فرضیه صفر که مناطق اس1�1و اس2�2پشت دو نمونه ایکسمن��شن yمن��s یکسان هستند. به طور رسمی:
2.6. تکامل شدت سرریز
در این بخش، روشی را برای کمی سازی دینامیک چند دوره ای انتقال سرریز معرفی می کنیم. همانطور که مشخص است، توان n ام ماتریس گذار مارکوین احتمال انتقال دوره n را می دهد. یعنی
جایی که تیnمن ، ج��,��هست من ج��ورود هفتم از تیn��، n ام توان از تی�.
فرض کنید نیروی تصادفی که بازار فرعی مسکن را بالا و پایین می کند به طور مساوی بین همه خرده بازارها توزیع شده است (توزیع اولیه غیر اطلاعاتی). فرمول زیر شدت ترانزیت خالص تجمعی را نشان می دهد ( C ICI) نیروی تصادفی در بین بازارهای فرعی تا زمان t :
جایی که 11نشان دهنده یک بردار ردیف K بعدی است که تمام ورودی ها ثابت 1 هستند. K تعداد زیر بازارهایی است که برابر با کاردینالیته است | پ||�|و می توان با خوشه بندی محدود تعیین کرد. برای هر بار tC IتیCI�یک بردار K بعدی است. برای هر l ∈ { 1 , … , K}�∈{1,…,�}، مقدار در بعد l از C IتیCI�نشاندهنده احتمال/شدت تجمعی است که نیروهای تصادفی در تمام دورههای زمانی، حداکثر تا زمان t ، به زیر بازار اول سرریز میشوند .
3. نتایج
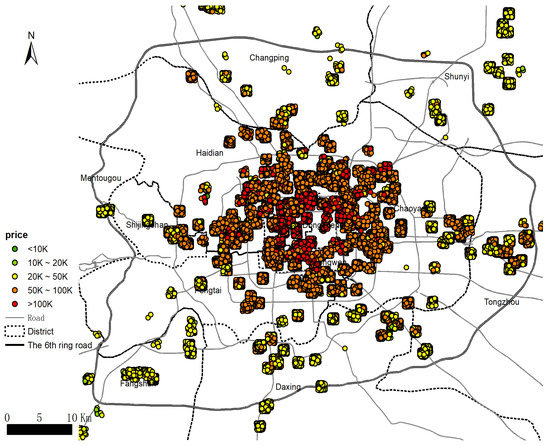
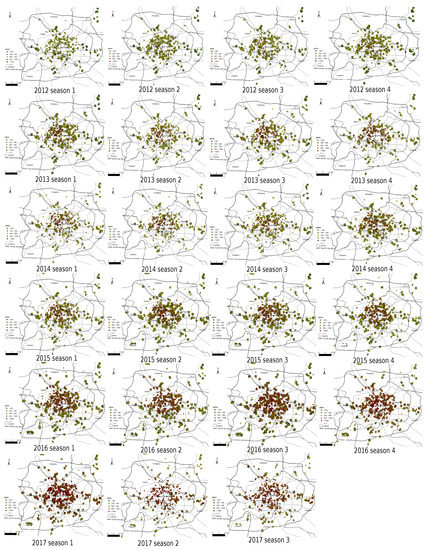
3.1. منطقه مطالعه
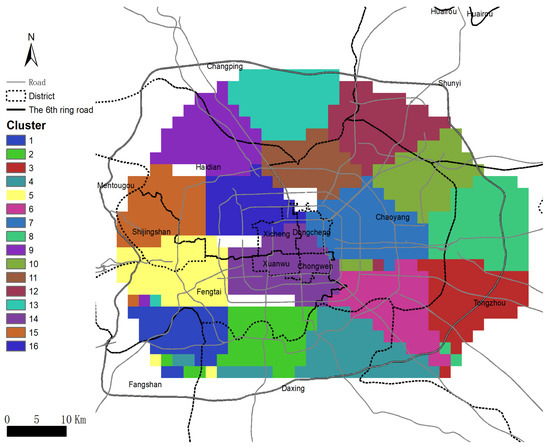
3.2. مرزهای بازار مسکن و بازارهای فرعی در پکن
3.3. تجزیه و تحلیل استحکام توسط شوک سیاست
برای تشخیص شوکهای یکباره و دائمی، ما دوباره خوشهبندی محدود را در دو بازه زمانی مجزا اجرا کردیم که (1) قبل از Q3 2013 و (2) بعد از Q3 2013 بود. آزمون تغییر ساختاری در مورد محدوده و مکان هر خرده بازار و احتمالات انتقال بین بازارهای فرعی انجام شد. فرضیه صفر همیشه این بود که در طول دو دوره، هیچ تغییر ساختاری وجود نخواهد داشت، که برای آن دو مجموعه آزمون فرضیه را در نظر گرفتیم:
اچ10�01بر اساس فاصله تجربی هاسدورف ( 16 ) (به بخش روش مراجعه کنید) بین یک بازار فرعی آزمایش شده است.اسمن��از این فرض که هیچ تغییر ساختاری در کل دوره جمعآوری دادهها و بازار فرعی ایجاد نشده است اسلمن∗��*�نزدیکترین به اسمن��تولید شده قبل از ( l = 1�=1) و بعد از ( l = 2�=2) زمان، سه ماهه سوم 2013، زمانی که سیاست مداخله آغاز شد. بنابراین، تست از اچ10�01بررسی می کند که آیا تغییرات مبتنی بر مکان و/یا محدوده برای بازارهای فرعی وجود دارد یا خیر.
3.4. عوامل موثر بر سرریز
در این بخش، تحلیل رگرسیون انجام شده برای شناسایی عواملی که قویترین ارتباط را با شدت انتقال سرریز دارند، توصیف میکنیم. در میان همه عوامل، ما عمدتاً نگران تأثیرات فاصله، تفاوت قیمت، تفاوت مساحت و مکان بین بازارهای فرعی بر احتمالات انتقال بودیم، زیرا تجزیه و تحلیل اولیه نشان داد که در بین همه متغیرهای کمکی جایگزین، این پنج کلاس متغیر برای محاسبه کافی هستند. در بالا 90 درصد90%از کل تغییرات احتمالات انتقال. به طور رسمی، معادله رگرسیون را به شکل زیر برآورد می کنیم:
و برای بررسی استحکام، معادله رگرسیون جایگزین را نیز در نظر گرفتیم:
جایی که پمن ، ج��,�احتمالات انتقال بین i و j هستند. دمن s t a n cهمن ، ج���������,�فاصله مرکزی بین دو بازار فرعی است (یعنی فاصله اقلیدسی بین مراکز دو بازار فرعی). و p r i c e _ دمنfمن ج�����_�����میانگین تفاوت قیمت است (یعنی تفاوت بین میانگین های درون خوشه ای دو بازار فرعی). εمن ، ج��,�باقی مانده است. ( 20 ) با ( 21 ) تفاوت دارد به این معنا که آیا مکان نسبی بین بازارهای فرعی ترانزیت ورودی و خروجی یا مکان دقیق آنها دخیل است. در ( 20 )، مکان دقیق از طریق طول و عرض جغرافیایی مراکز زیر بازارهای ترانزیت خروجی و ترانزیت ورودی گنجانده شده است که اطلاعات بیشتری را ارائه می دهد.
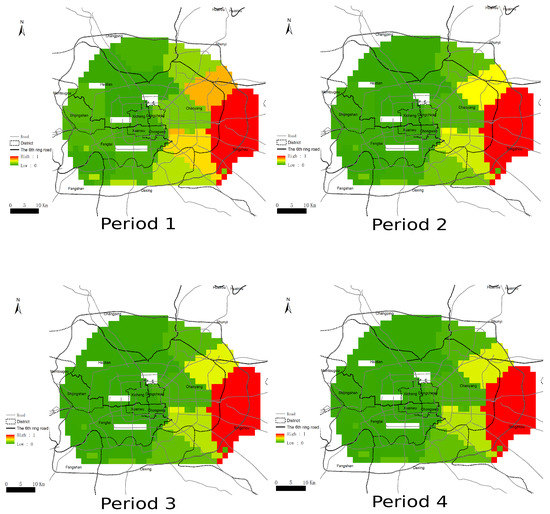
3.5. شدت انتقال سرریزهای چند دوره ای
4. بحث
5. نتیجه گیری ها
منابع
- اشورث، جی. Parker, SC مدل سازی قیمت مسکن منطقه ای در بریتانیا. اسکات ج. اقتصاد سیاسی. 1997 ، 44 ، 225-246. [ Google Scholar ] [ CrossRef ]
- پترسون، دبلیو. هالی، اس. گادوین، پی. بریتانیا، جی. کار بیشتر بر روی مدل اقتصادی تقاضا و نیاز برای مسکن اجتماعی . دفتر لوازم التحریر: لندن، انگلستان، 2002. [ Google Scholar ]
- Cook, S. همگرایی قیمت های منطقه ای مسکن در بریتانیا. مطالعه شهری. 2003 ، 40 ، 2285-2294. [ Google Scholar ] [ CrossRef ]
- دو، س. وو، سی. بله، X. رن، اف. Lin, Y. ارزیابی اثرات منظر بر قیمت مسکن در چین شهری. Tijdschriftvoor Economische En Sociale Geografie 2018 ، 109 ، 525–541. [ Google Scholar ] [ CrossRef ]
- هلمز، ام جی; گریمز، الف. آیا همگرایی بلندمدت بین قیمتهای مسکن منطقهای در بریتانیا وجود دارد؟ مطالعه شهری. 2008 ، 45 ، 1531-1544. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- باروس، سی. گیل آلانا، ال. پین، جی. آزمون های همگرایی و رفتار حافظه طولانی در قیمت مسکن ما بر اساس ایالت. جی. هاوس. Res. 2013 ، 23 ، 73-87. [ Google Scholar ]
- چاو، WW; Fung، MK; چنگ، الف. همگرایی و سرریز قیمت مسکن در شهرهای چین. Appl. اقتصاد 2016 ، 48 ، 4922-4941. [ Google Scholar ] [ CrossRef ]
- دیفوسکو، ا. دینگ، دبلیو. فریرا، اف. Gyourko, J. نقش سرریز قیمت در رونق مسکن آمریکا. J. شهری اقتصاد. 2018 ، 108 ، 72-84. [ Google Scholar ] [ CrossRef ]
- کوهن، جی پی. Zabel, J. انتشار قیمت مسکن محلی. اقتصاد املاک و مستغلات. 2018 . نمای اولیه [ Google Scholar ] [ CrossRef ]
- آلپر، او. ارطغرل، ح. Coskun، Y. مدلی پویا برای سرریز قیمت مسکن با شواهدی از بازارهای ایالات متحده و بریتانیا. J. Cap. علامت گذاری. گل میخ. 2018 ، 2 ، 70-81. [ Google Scholar ]
- پیجنبرگ، ک. بعد فضایی قیمت مسکن در ایالات متحده. مطالعه شهری. 2017 ، 54 ، 466-481. [ Google Scholar ] [ CrossRef ]
- برنده، جی. لی، جی اس در حال بررسی چگونگی تعیین اجاره خانههای شهری کوچک: استفاده از مدلسازی لذتبخش فضایی برای مسکن شهری در سئول. پایداری 2018 ، 10 ، 31. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- رنگان، جی. Sun، X. سرریزهای بازار مسکن در آفریقای جنوبی: شواهدی از یک مدل تخمینی اقتصاد باز کوچک DSGE. امپراتور اقتصاد 2018 ، 58 ، 1-24. [ Google Scholar ]
- کاکان، ای. دمیرر، آر. گوپتا، آر. Uwilingiye, J. عدم قطعیت سیاست اقتصادی و رفتار گله داری: شواهدی از بازار مسکن آفریقای جنوبی. Adv. تصمیم می گیرد. علمی 2019 ، 23 ، 1-25. [ Google Scholar ]
- لی، اس. بله، X. لی، جی. گونگ، جی. Qin, C. تحلیل فضایی و زمانی قیمت مسکن در چین: چشم انداز کلان داده. Appl. تف کردن مقعدی سیاست 2017 ، 10 ، 421-433. [ Google Scholar ] [ CrossRef ]
- Meen, G. قیمتهای منطقهای خانه و اثر امواج: تفسیری جدید. خانه گل میخ. 1999 ، 14 ، 733-753. [ Google Scholar ] [ CrossRef ]
- مورفی، ا. Muellbauer, J. توضیح قیمت خانه های منطقه ای در بریتانیا . گروه اقتصاد، کالج دانشگاهی دوبلین: دوبلین، ایرلند، 1994. [ Google Scholar ]
- تاجانی، ف. مورانو، پی. سائز پرز، نماینده مجلس؛ دی لیدو، اف. Locurcio، M. تحلیل پویا چند متغیره و مدلهای پیشبینی حبابهای دارایی آینده: کاربردهای تجربی در بازارهای مسکن کلانشهرهای اسپانیا. پایداری 2019 ، 11 ، 3575. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- Stein, JC قیمت ها و حجم معاملات در بازار مسکن: مدلی با اثرات پیش پرداخت. QJ Econ. 1995 ، 110 ، 379-406. [ Google Scholar ] [ CrossRef ]
- گوردون، I. محدودیت های مسکن و بازار کار در مهاجرت در سراسر تقسیم شمال-جنوب. خانه Natl. اقتصاد 1990 ، 75-89. [ Google Scholar ]
- قیمت خانه هولمنز، AE : تغییرات در طول زمان در سطح ملی و فرعی ؛ وزارت محیط زیست لندن: لندن، بریتانیا، 1990. [ Google Scholar ]
- وو، سی. بله، X. رن، اف. وان، ی. نینگ، پی. Du، Q. تجزیه و تحلیل داده های رسانه های اجتماعی و فضایی قیمت مسکن در شنژن، چین. PLoS ONE 2016 , 11 , e0164553. [ Google Scholar ] [ CrossRef ]
- هولمنز، ا. چه بر سر شکاف شمال-جنوب در قیمت مسکن و بازار مسکن آمده است. خانه مالی Rev. 1995 , 96 , 25-31. [ Google Scholar ]
- وو، سی. بله، X. دو، س. Luo, P. اثرات فضایی دسترسی به پارک ها بر قیمت مسکن در شنژن، چین. Habitat Int. 2017 ، 63 ، 45-54. [ Google Scholar ] [ CrossRef ]
- هوی، ای. وانگ، Z. احساسات بازار در بازار مسکن خصوصی. Habitat Int. 2014 ، 44 ، 375-385. [ Google Scholar ] [ CrossRef ]
- مونرو، ام. Maclennan، D. تغییرات درون شهری در قیمت مسکن: گلاسکو 1972-1983. خانه گل میخ. 1987 ، 2 ، 65-81. [ Google Scholar ] [ CrossRef ]
- فادیگا، ام ال. وانگ، ی. تحلیل مؤلفه های مشاهده نشده چند متغیره از بازار مسکن ما. جی. اکون. مالی 2009 ، 33 ، 13-26. [ Google Scholar ] [ CrossRef ]
- ژانگ، ام. منگ، ایکس. وانگ، ال. Xu, T. توسعه ترانزیت شکل دهنده شهرنشینی: شواهدی از بازار مسکن در پکن. Habitat Int. 2014 ، 44 ، 545-554. [ Google Scholar ] [ CrossRef ]
- ژانگ، اس. Guldmann، JM دسترسی، تنوع، کیفیت محیطی و پویایی جمعیت درون شهری و محل اشتغال. رشد چانگ. 2010 ، 41 ، 85-114. [ Google Scholar ] [ CrossRef ]
- کربی، DK; LeSage, JP تغییرات در زمان رفت و آمد به محل کار طی دوره 1990 تا 2000. Reg. علمی اقتصاد شهری 2009 ، 39 ، 460-471. [ Google Scholar ] [ CrossRef ]
- جونز، سی. لیشمن، سی. واتکینز، سی. مهاجرت درون شهری و بازارهای فرعی مسکن: نظریه و شواهد. خانه گل میخ. 2004 ، 19 ، 269-283. [ Google Scholar ] [ CrossRef ]
- شلینگ، مدل های دینامیک TC تفکیک. جی. ریاضی. اجتماعی 1971 ، 1 ، 143-186. [ Google Scholar ] [ CrossRef ]
- کوی، سی. گیرتمن، اس. Hooimeijer، P. توزیع درون شهری مهاجران ماهر: مطالعات موردی شانگهای و نانجینگ. Habitat Int. 2014 ، 44 ، 1-10. [ Google Scholar ] [ CrossRef ]
- ژنگ، اس. Peiser، RB; ژانگ، دبلیو. ظهور اقتصادهای خارجی در پکن: شواهدی از تغییرات دستمزد درون شهری. Reg. علمی اقتصاد شهری 2009 ، 39 ، 449-459. [ Google Scholar ] [ CrossRef ]
- کبک، MD; ریکمن، دی اس؛ علی، ک. Olfert، MR Agglomeration سرریز و شیب دستمزد و هزینه مسکن در سراسر سلسله مراتب شهری. J. Int. اقتصاد 2009 ، 78 ، 126-140. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- Njoh، AJ روابط بین سازمانی و اثربخشی در زمینه سیاست مسکن در حال توسعه. Habitat Int. 1996 ، 20 ، 253-264. [ Google Scholar ] [ CrossRef ]
- لی، ز. لی، ایکس. وانگ، ال. شهرسازی گمانه زنی و ساخت شهرهای دانشگاهی در چین: موردی از شهر دانشگاهی گوانگژو. Habitat Int. 2014 ، 44 ، 422-431. [ Google Scholar ] [ CrossRef ]
- کروپکا، دی جی؛ نونان، مناطق توانمندسازی DS، تغییر محله و مسکن تحت اشغال. Reg. علمی اقتصاد شهری 2009 ، 39 ، 386-396. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- کلیتون، جی. لینگ، دی. Naranjo، A. ارزش گذاری املاک تجاری: اصول در مقابل احساسات سرمایه گذار. جی. امور مالی املاک و مستغلات. اقتصاد 2009 ، 38 ، 5-37. [ Google Scholar ] [ CrossRef ]
- ژو، جی. اندرسون، RI بررسی تجربی رفتار گله داری در بازار reit ایالات متحده. جی. امور مالی املاک و مستغلات. اقتصاد 2013 ، 47 ، 83-108. [ Google Scholar ] [ CrossRef ]
- والنتینی، پ. ایپولیتی، ال. Fontanella، L. مدل سازی قیمت مسکن ما توسط مدل های معادلات ساختاری پویا فضایی. ان Appl. آمار 2013 ، 7 ، 763-798. [ Google Scholar ] [ CrossRef ]
- Tsai، اثر سرریز IC بین بازارهای مسکن منطقه ای و ملی در بریتانیا. Reg. گل میخ. 2015 ، 49 ، 1957-1976. [ Google Scholar ] [ CrossRef ]
- هاردینگ، جی پی؛ روزنبلات، ای. یائو، وی. اثر مسری خواص سلب شده. J. شهری اقتصاد. 2009 ، 66 ، 164-178. [ Google Scholar ] [ CrossRef ]
- دانشوری، ن. کلورتی، تی. Kader، A. اثرات کوتاه مدت خود قیمت و سرریز املاک مسکونی پریشان: مورد سقوط مسکن. J. Real Estate Res. 2011 ، 33 ، 179-207. [ Google Scholar ]
- لئونارد، تی. مورداک، جی. اثرات همسایگی سلب مالکیت. جی. جئوگر. سیستم 2009 ، 11 ، 317. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- Rogers, W. کاهش اثرات محله سلب مالکیت در طول زمان. خانه بحث سیاست 2010 ، 20 ، 687-706. [ Google Scholar ] [ CrossRef ]
- ایهلانفلد، ک. Mayock، T. تاثیر فروش REO بر محله ها و ساکنان آنها. جی. امور مالی املاک و مستغلات. اقتصاد 2016 ، 53 ، 282-324. [ Google Scholar ] [ CrossRef ]
- دل جودیس، وی. دی پائولا، پی. فورته، اف. Manganelli، B. ارزیابی املاک و مستغلات با رویکرد بیزی و روش مونت کارلو ترکیبی زنجیره مارکوف: یک کاربرد در یک منطقه شهری مرکزی ناپل. Sustainability 2017 , 9 , 2138. [ Google Scholar ] [ CrossRef ][ Green Version ]
- وو، سی. Sharma, R. طبقه بندی بازار فرعی مسکن: نقش مجاورت فضایی. Appl. Geogr. 2012 ، 32 ، 746-756. [ Google Scholar ] [ CrossRef ]
- واگستاف، ک. کاردی، سی. راجرز، اس. شرودل، اس. K-محدود به معنی خوشه بندی با دانش پیش زمینه است. Icml 2001 ، 1 ، 577-584. [ Google Scholar ]
- باسو، س. بانرجی، ا. Mooney، RJ Active نیمه نظارت برای خوشهبندی محدود زوجی. در مجموعه مقالات کنفرانس بین المللی SIAM در سال 2004 در مورد داده کاوی، دریاچه بوئنا ویستا، FL، ایالات متحده آمریکا، 22-24 آوریل 2004. صص 333-344. [ Google Scholar ]
- دیاز-والنزوئلا، آی. لویا، وی. مارتین-باتیستا، ام جی; سناتور، اس. Vila, MA تولید محدودیت های خودکار برای خوشه بندی نیمه نظارت شده: تجربیات با طبقه بندی اسناد. محاسبات نرم. 2016 ، 20 ، 2329-2339. [ Google Scholar ] [ CrossRef ]
- بونهوم، اس. Manresa، E. الگوهای گروهبندی ناهمگونی در دادههای تابلویی. Econometrica 2015 ، 83 ، 1147-1184. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- کانگ، دبلیو. آزمونهای مشروط و مشترک ری، SJ برای اثرات فضایی در مدلهای زنجیره مارکوف گسسته پویایی توزیع درآمد منطقهای. ان Reg. علمی 2018 ، 61 ، 73-93. [ Google Scholar ] [ CrossRef ]
- وو، سی. بله، X. رن، اف. Du, Q. چارچوب داده محور اصلاح شده برای تقسیم بندی بازار مسکن. ج. طرح شهری. توسعه دهنده 2018 , 144 , 04018036. [ Google Scholar ] [ CrossRef ]
- گتیس، ع. Ord, JK تجزیه و تحلیل ارتباط فضایی با استفاده از آمار فاصله. Geogr. مقعدی 1992 ، 24 ، 189-206. [ Google Scholar ] [ CrossRef ]
- Ord، JK; Getis، A. آمار خودهمبستگی فضایی محلی: مسائل توزیع و یک برنامه کاربردی. Geogr. مقعدی 1995 ، 27 ، 286-306. [ Google Scholar ] [ CrossRef ]
- گیرس، جی اف. Touya, G. ارزیابی کیفیت مجموعه داده openstreetmap فرانسوی. ترانس. GIS 2010 ، 14 ، 435-459. [ Google Scholar ] [ CrossRef ]
- دنگ، م. لی، ز. Chen, X. فاصله Hausdorff طولانی برای اشیاء فضایی در gis. بین المللی جی. جئوگر. Inf. علمی 2007 ، 21 ، 459-475. [ Google Scholar ]
- اداره ملی آمار. سالنامه آماری شهر چین ; انتشارات آمار: پکن، چین، 2016.
- زو، آر. Wu, X. خطرات و پتانسیل ها در بازار املاک پکن. بیومد. J. Sci. فنی Res. 2018 ، 9 ، 7406–7413. [ Google Scholar ]
- وانگ، اف. گائو، X. الگوی فضایی انتقالی قیمت مسکن در پکن: عوامل و مفاهیم. بین المللی کشیش اسپات. طرح. حفظ کنید. توسعه دهنده 2014 ، 2 ، 46-62. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
- لین، جی. ژانگ، الف. کلان شهرهای چین در تحول: سیاست نولیبرالیزه کردن، کالاسازی زمین و توسعه ناهموار در پکن. جئوگر شهری. 2017 ، 38 ، 643-665. [ Google Scholar ] [ CrossRef ]
- تاجانی، ف. مورانو، پی. توره، سی. دی لیدو، اف. تحلیلی از تأثیر مالیات بر دارایی بر قیمت مسکن در منطقه آپولیا (ایتالیا). ساختمانها 2017 ، 7 ، 67. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
- Meen، G. تجمع فضایی، وابستگی فضایی و قابلیت پیش بینی در بازار مسکن انگلستان. خانه گل میخ. 1996 ، 11 ، 345-372. [ Google Scholar ] [ CrossRef ]
|
در دسترس بودن نمونه : نمونه هایی از این تحقیق از نویسندگان در دسترس است.
|





بدون دیدگاه