خلاصه

بسیاری از سیستم های فضایی دنیای واقعی را می توان به عنوان شبکه مفهوم سازی کرد. در این مفهوم سازی ها، گره ها و پیوندها به ترتیب اجزای سیستم و تعاملات آنها را نشان می دهند. تحلیل شبکه سنتی از معیارهای تئوری گراف برای مجموعه داده های شبکه ایستا استفاده می کند. با این حال، علاقه اخیر در بازنمایی و تحلیل شبکه های در حال تکامل نهفته است. رویکردهای اتوماتای ​​شبکه موجود ساختارهای شبکه در حال تکامل را شبیه‌سازی می‌کنند، اما نمایش شبکه‌های در حال تکامل تعبیه‌شده در فضای جغرافیایی یا ادغام داده‌های مکانی واقعی را در نظر نمی‌گیرند. بنابراین، هدف این مطالعه ادغام اتوماتای ​​شبکه با سیستم‌های اطلاعات جغرافیایی (GIS) برای توسعه یک چارچوب مدل‌سازی جدید، اتومات شبکه جغرافیایی (GNA)، برای نمایش و تحلیل سیستم‌های فضایی پویا پیچیده به عنوان شبکه‌های مکانی در حال تکامل است. چارچوب GNA برای دو مطالعه موردی شامل نمایش شبکه فضایی (1) مدل بازی زندگی کانوی و (2) مدل تفکیک شلینگ اجرا و ارائه شده است. ساختارهای شبکه فضایی در حال تکامل شبیه‌سازی شده با استفاده از نظریه گراف اندازه‌گیری می‌شوند. نتایج به‌دست‌آمده نشان می‌دهد که ادغام مفاهیم علوم اطلاعات جغرافیایی، سیستم‌های پیچیده و نظریه شبکه ابزار جدیدی برای نمایش و تحلیل سیستم‌های فضایی پیچیده ارائه می‌دهد. چارچوب مدل‌سازی GNA ارائه‌شده هم کلی و هم انعطاف‌پذیر است و برای مدل‌سازی انواع پدیده‌های مکانی واقعی و توصیف و کاوش ساختار شبکه، دینامیک و تکامل سیستم‌های فضایی واقعی مفید است.

کلید واژه ها:

اتوماتای ​​شبکه جغرافیایی ; سیستم های اتومات جغرافیایی ; شبکه های پیچیده ؛ علم شبکه ; سیستم های اطلاعات جغرافیایی و علم ; سیستم های پیچیده

1. معرفی

همانطور که داده‌های مکانی به طور فزاینده‌ای در دسترس می‌شوند، شبکه‌ها به عنوان یک چارچوب مفهومی قدرتمند برای نمایش و تحلیل مجموعه‌ای از سیستم‌های فضایی پیچیده در زمینه‌های اجتماعی، شهری و زیست‌محیطی استفاده می‌شوند [ 1 ، 2 ، 3 ]. مفهوم‌سازی سیستم‌های فضایی پیچیده به‌عنوان شبکه‌ها از پایین به بالا آغاز می‌شود، جایی که اجزای سیستم به‌عنوان گره‌های جغرافیایی مرجع و تعاملات بین اجزا به‌عنوان پیوند نشان داده می‌شوند. مجموعه ای از تعاملات محلی بین گره ها ساختار شبکه جهانی را تشکیل می دهند. نمایش سیستم‌های فضایی پیچیده به‌عنوان شبکه، یک جعبه ابزار توسعه‌یافته برای تحلیل ارائه می‌دهد [ 4 ، 5 ]]. به طور خاص، نظریه گراف را می توان برای توصیف ساختارهای فضایی پدیده های واقعی و کشف رابطه محکم بین ساختار فضایی و دینامیک فضایی به کار برد.
پویایی شبکه را می توان بین پویایی در یک شبکه یا پویایی شبکه ها [ 6 ] تشخیص داد. در حالت اول، اطلاعات یا مواد به صورت پویا از طریق مجموعه ای از گره ها و پیوندهای مرتب شده فضایی منتشر می شوند. به عنوان مثال، در اکولوژی، پویایی مکانی-زمانی پراکندگی گونه ها به شدت به ساختار فضایی ویژگی های زیستگاه در سراسر چشم انداز وابسته است [ 3 ]. به همین ترتیب، در اپیدمیولوژی، پویایی مکانی-زمانی گسترش بیماری با استفاده از ساختار فضایی شبکه های تماس انسانی [ 7 ] پیش بینی می شود. در یک بافت شهری، انواع شبکه های حمل و نقل، پویایی تحرک انسان را تعیین می کنند [ 8 ]. دومی، پویایی ازشبکه به تغییرات پویا در ساختار شبکه اشاره دارد که به عنوان تکامل شبکه نیز شناخته می شود. در این فرآیند، گره‌ها و پیوندها اضافه می‌شوند، حذف می‌شوند، مجدداً سیم‌کشی می‌شوند یا ویژگی‌ها در مکان و زمان تغییر می‌کنند [ 9 ]. تکامل شبکه به عنوان تابعی از پویایی خود شبکه، تعاملات بین شبکه و ماتریس اطراف، و پویایی که به طور محکم با ساختار شبکه مرتبط است، رخ می دهد [ 10 ]. به عنوان مثال، پویایی پراکندگی گونه ها ممکن است به نوبه خود بر اتصال چشم انداز تأثیر بگذارد، پویایی گسترش بیماری ممکن است شبکه تماس انسانی را تغییر دهد و ترافیک ممکن است به خیابان ها آسیب برساند و مجبور به بسته شدن آنها شود یا نیاز به ساخت خیابان های جدید برای کاهش ازدحام داشته باشد. بنابراین تکامل شبکه های حمل و نقل را وادار می کند.
تکامل شبکه به خوبی درک نشده است زیرا مجموعه داده های دقیق که پدیده های واقعی را به عنوان شبکه ها در مکان و زمان جغرافیایی نشان می دهند به دلیل فقدان مجموعه داده های مناسب محدود شده اند. تجزیه و تحلیل شبکه فضایی متعارف تمایل دارد بر توصیف و فهرست نویسی ساختارهای شبکه فضایی استاتیک یا بررسی تأثیر ساختارهای شبکه فضایی ساکن بر پویایی فضایی تمرکز کند. برخی از نمونه‌های آن عبارتند از کاوش فرآیندهای اصیل سازی در شبکه ایستا از املاک مسکونی [ 11 ]، پویایی پراکندگی اکولوژیکی بر روی شبکه‌های اتصال چشم‌انداز ساکن [ 3 ، 12 ]، پویایی تحرک در شبکه‌های جاده ایستا [ 13 ، 14 ]]، و اپیدمی در شبکه های تماس ساکن [ 7 ، 15 ] و در شبکه های خطوط هوایی [ 16 ].
مدل‌هایی که پدیده‌هایی مانند دینامیک شکارچی-شکار [ 17 ]، رشد قارچ [ 9 ] و اپیدمی‌های انسانی [ 18 ] را به‌عنوان شبکه‌های غیرفضایی در حال تکامل نشان می‌دهند، با اعمال قوانین فرعی نشان‌دهنده پویایی شبکه برای ساختارهای شبکه که ساختار شبکه را تغییر می‌دهند، توسعه یافته‌اند. خودش در طول زمان این روش به عنوان خودکار شبکه (NA) رسمیت یافت [ 9 ، 19] که در آن توپولوژی شبکه در طول زمان تغییر می کند. با این حال، این چارچوب‌های NA پیشنهادی با سیستم‌های اطلاعات جغرافیایی (GIS) ادغام نشده‌اند و از داده‌های مکانی واقعی استفاده نمی‌کنند. علیرغم تقاضا برای تغییر از معیارهای توصیفی ساختارهای شبکه فضایی به مطالعه شبکه های فضایی پیچیده در حال تکامل که علاقه دیرینه به بررسی ارتباط بین ساختار شبکه فضایی و دینامیک فضا-زمان را تسهیل می کند، NA هنوز انجام نشده است. در کاربرد پدیده‌های دینامیکی زمین‌فضایی مورد بررسی قرار گرفت.
بنابراین، اهداف این مطالعه ادغام مفاهیم علم اطلاعات جغرافیایی (GIScience) و سیستم‌ها (GIS)، سیستم‌های پیچیده و نظریه شبکه برای (1) پیشنهاد یک چارچوب نظری برای یک رویکرد مدل‌سازی جدید به نام اتوماتای ​​شبکه جغرافیایی (GNA) است. که برای نمایش و تحلیل سیستم های فضایی پیچیده به عنوان شبکه های در حال تکامل استفاده می شود، (2) چارچوب نظری پیشنهادی را با توسعه و اجرای دو مدل GNA بر اساس بازی زندگی کانوی [ 20 ] و مدل تفکیک فضایی شلینگ [ 21 ، 22 ] نشان می دهد.]، و (3) تئوری گراف را برای تجزیه و تحلیل چندین شبکه فضایی در حال تکامل مختلف و رفتار آنها به کار می‌برند. مدل‌های GNA پیشنهادی ابزاری را برای توضیح واضح چارچوب GNA فراهم می‌کنند تا بتوان آن را به راحتی در یک پدیده جغرافیایی دنیای واقعی اعمال کرد. در ابتدا، زمینه نظری برای هر دو رویکرد مدل‌سازی GNA و همچنین نظریه گراف مورد استفاده برای تجزیه و تحلیل خروجی‌های GNA ارائه شده است. در مرحله بعد، چارچوب مدل‌سازی GNA در کاربرد نسخه شبکه صریح فضایی بازی زندگی کانوی [ 20 ] و مدل تفکیک شلینگ [ 21 ، 22 ] ارائه می‌شود.] برای نشان دادن چارچوب GNA و بررسی تغییرات در ساختار و پویایی شبکه همانطور که در مکان و زمان تکامل می‌یابند. در نهایت، استفاده از چارچوب GNA در کاربرد برای طیف وسیعی از پدیده‌های مکانی مورد بحث قرار می‌گیرد.

2. خودکار شبکه جغرافیایی (GNA)

این بخش ابتدا چارچوب کلی مدل‌سازی GNA را برای نمایش شبکه پدیده‌های فضایی دنیای واقعی ارائه می‌کند و در مرحله دوم پیش‌زمینه نظری را برای کاربرد نظریه گراف برای تحلیل خروجی‌های SN شبکه فضایی GNA معرفی می‌کند.

2.1. چارچوب مدل سازی GNA

خودکار شبکه جغرافیایی (GNA) یک نمایش ریاضی از یک سیستم پیچیده یا بخش هایی از یک سیستم به عنوان یک شبکه فضایی در حال تکامل است و می تواند به صورت زیر بیان شود:

جینآ=[Uن،اسن، جی، آر، سی، Δتی]

که در آن اجزای یک GNA عبارتند از (1) یک شبکه فضایی SN متشکل از مجموعه ای از گره های N و مجموعه ای از پیوندهای L که نشان دهنده یک سیستم یا بخشی از یک سیستم مورد علاقه است که در طول زمان تکامل می یابد. (2) یک ساختار زیربنایی شبکه سازمان ملل که بر شبکه فضایی SN مورد نظر تأثیر می گذارد و به طور بالقوه تحت تأثیر قرار می گیرد . (3) همسایگی(های) J که گره های همسایه را تعریف می کند. (4) قوانین انتقال R که دینامیک سیستم بین گره های همسایه را شبیه سازی می کند. (5) هزینه اتصال C که مقاومت ماتریس بین گره های همسایه یا فرآیند تکامل شبکه را اندازه گیری می کند. و (6) زمان، جایی که توپولوژی شبکه فضاییSN در زمان t + 1 تابعی از شبکه فضایی SN ، شبکه زیربنایی UN ، همسایگی J و قوانین انتقال اعمال شده R و هزینه های اتصال C در زمان t است.

رویکرد GNA می‌تواند برای مدل‌سازی انواع پدیده‌ها با اجرای هر مرحله به تفصیل در جدول 1 عملیاتی شود .
چارچوب GNA به داده‌های به‌دست‌آمده از منابع مختلف از جمله داده‌های مکانی مصنوعی، داده‌های مکانی واقعی، و داده‌هایی از ادبیات به عنوان ورودی برای مقداردهی اولیه مکان گره، پارامترسازی گره‌ها و اجرای ماتریس شبکه و هرگونه موانع جغرافیایی بالقوه نیاز دارد. این نوع داده ها همچنین برای پارامترسازی قوانین انتقال و هزینه اتصال مورد نیاز هستند. مجموعه های داده مستقل از توسعه مدل برای آزمایش مدل مورد نیاز است.
در مرحله 1، یک سیستم یا بخشی از یک سیستم مورد علاقه به عنوان یک شبکه فضایی در حال تکامل SN مفهوم سازی می شود . به عنوان مثال، در نمایش شبکه و تجزیه و تحلیل الگوهای مکانی-زمانی هجوم حشرات جنگلی [ 23 ]، می توان شبکه ای از گره ها را به نمایندگی از توده های جنگلی تصور کرد که برخی از آنها با گونه های حشره مهاجم آلوده شده اند. اگر فاصله بین یک گره توده جنگلی آلوده vمنو یک گره توده جنگلی بدون آلودگی vjکمتر از حداکثر فاصله پراکندگی گونه حشره مهاجم، گره است vjآلوده خواهد شد با گذشت زمان، با تشدید آلودگی حشرات جنگلی، تعداد گره هایی که آلوده می شوند افزایش می یابد. بنابراین مجموعه گره‌هایی که آلوده می‌شوند گره‌هایی هستند که مورد توجه اولیه مدل‌ساز هستند، زیرا تکامل آنها را می‌توان با استفاده از نظریه گراف اندازه‌گیری و تحلیل کرد. بنابراین، شبکه فضایی SN نشان دهنده یک شبکه هجوم است، که در آن گره ها نشان دهنده توده های جنگلی آلوده و پیوندها نشان دهنده حرکت دسته ای از حشرات مهاجم بین گره ها هستند. البته، ساختار شبکه سازمان ملل متحد نیز وجود دارد که ثابت است. این شبکه از تمام گره های توده جنگلی تشکیل شده است و از آن به عنوان شبکه اتصال چشم انداز یاد می شود. شبکه زیربنایی UN نقش عمده ای در رفتار SN ایفا می کندو در بسیاری از موارد، SN می تواند سازمان ملل را تحت تأثیر قرار دهد زیرا جنگل ها در پاسخ به هجوم حشرات از بین می روند و از شبکه حذف می شوند.
همانطور که در مثال بالا نشان داده شد، اغلب اتفاق می افتد که یک شبکه فضایی مورد علاقه اولیه SN بر اساس یک شبکه زیربنایی UN شکل می گیرد ( شکل 1 a) که در آن UN شبکه زیربنایی است، SN شبکه فضایی است، J شبکه تعریف شده است. همسایگی، R قوانین انتقال، C هزینه اتصال، و Δt افزایش زمان مدل GNA است. این نوع GNA را می توان با عبارت (1) تعریف کرد.

در موردی که کمتر رایج است، جایی که هیچ شبکه زیربنایی سازمان ملل وجود ندارد و شبکه به عنوان تابعی از ساختار خود تکامل می‌یابد ( شکل 1 ب)، یک شبکه فضایی مورد علاقه SN مستقل از یک شبکه زیربنایی تشکیل می‌شود. بنابراین، عبارت GNA (1) اصلاح شده و به صورت زیر ارائه می شود:

جینآ=[اسن، جی، آر، سی، Δتی]

هر دو شبکه فضایی در حال تکامل SN تولید شده توسط GNA و شبکه زیربنایی UN از مجموعه ای از گره های N تشکیل شده است که اجزای یک سیستم را نشان می دهد. جفت گره ها توسط پیوندهای L به هم متصل می شوند که نشان دهنده تعاملات یا روابط بین اجزای سیستم است. شبکه فضایی SN را می توان به صورت زیر بیان کرد:

اسن=[نس،Lس]

یک شبکه زیربنایی سازمان ملل نیز می تواند به صورت زیر بیان شود:

Uن=[نتو،Lتو]

مجموعه گره های N و پیوندهای L در شبکه فضایی SN یا شبکه زیربنایی UN بیشتر به صورت زیر بیان می شوند:

ن=[v1، v2، …، vn] جایی که v است آ گره که در را تنظیم از گره ها ن; n است را عدد از گره ها که در ن.
L=[ه1، ه2، …، همتر] جایی که ه است آ ارتباط دادن که در را تنظیم از پیوندها L; متر است را عدد از پیوندها که در L.
هر گره v و پیوند e در مجموعه گره‌های N و پیوندهای L توسط چندین ویژگی فضایی، غیرمکانی و شبکه تعریف می‌شوند ( جدول 2 ). گره‌های N با ویژگی‌های فضایی‌شان، مهم‌تر از همه موقعیت جغرافیایی تعریف می‌شوند که به نوبه خود اندازه‌گیری فاصله جغرافیایی d بین هر دو گره را تسهیل می‌کند. بسته به نوع پدیده ای که مجموعه گره ها نشان می دهند، ویژگی های هندسی دیگری مانند مساحت و محیط ممکن است مورد توجه قرار گیرند. گره های N نیز با ویژگی های شبکه مانند تعداد و لیست اتصالات یک گره v تعریف می شونددارای گره های دیگر در شبکه یا وزن گره است. وزن مقداری است که به یک گره اختصاص داده می شود و می تواند برای تعیین کمیت مقدار جریان، اهمیت، تناسب یا اولویت در مجموعه ای از گره های N استفاده شود.
پیوندهای L نیز با ویژگی‌های فضایی آن‌ها تعریف می‌شوند که کمی با ویژگی‌های فضایی گره‌ها متفاوت است. در حالی که گره های N همیشه در فضای جغرافیایی تعبیه شده اند، در بیشتر موارد، پیوندهای L اینگونه نیستند. استثنا یک شبکه مسطح مانند شبکه راه است که در این صورت طول پیوند مورد توجه است. پیوندها همچنین حاوی ویژگی شبکه مهم وزن پیوند هستند که می‌تواند برای تعیین کمیت جریان افراد، مواد یا اطلاعات بین گره‌ها استفاده شود. پیوندها یا یک طرفه یا دو طرفه هستند، به این معنی که جریان به ترتیب در یک یا هر دو جهت رخ می دهد. هر دو گره N و پیوند Lدارای ویژگی‌های غیر مکانی هستند که ویژگی‌های کمی یا کیفی هستند که برای توصیف گره یا پیوند شبکه استفاده می‌شوند.
قوانین انتقال R برای نمایش دینامیک دنیای واقعی بین عناصر سیستم و تعیین تکامل شبکه فضایی SN طراحی شده‌اند . قوانین انتقال در بیشتر موارد برای گره اعمال می شود vمنهمسایگی J ، به عنوان مجموعه ای از گره ها تعریف می شود vjمتصل به گره vمنبه نوعی توسعه قوانین انتقال R به این بستگی دارد که آیا دینامیک فضایی در یک شبکه نمایش داده می شود یا یک شبکه. در مورد نمایش دینامیک در یک شبکه، قوانین انتقال R ممکن است در جایی که شبکه فضایی SN با شبکه زیربنایی UN در تعامل است تعریف شود . به عنوان مثال، در مرحله زمانی t ، گره vمندر SN پیوندی به گره تشکیل می دهد vjدر گره UN ifvjمقداری وزن دارد گره ها vjکه دارای این شرایط هستند گره را تشکیل می دهند vمنمحله جی . در مورد نمایش دینامیک یک شبکه، توسعه قوانین انتقال R به تعامل بین گره‌ها در SN بستگی دارد . برای مثال، در مرحله زمانی t ، اگر کمتر از سه گره در نزدیکی مشخصی به گره وجود داشته باشد vمن، یک گره جدید vjدر این مجاورت ایجاد می شود و پیوندی بین گره تشکیل می شود vمنو گره vj. گره ها vjگره هایی که این شرایط مبتنی بر فاصله را برآورده می کنند vمنمحله جی . هزینه اتصال C مقاومت فضای جغرافیایی بین گره ها را برای ایجاد پیوند بین گره ها یا تولید گره های جدید ارزیابی می کند. این فضای بین گره ها به عنوان ماتریس هزینه نامیده می شود. مقاومت در این زمینه ممکن است تابعی از فاصله بین گره ها یا مناسب بودن کم ماتریس برای اتصال گره ها یا تخم ریزی گره های جدید باشد.
سازماندهی فضایی و توپولوژیکی شبکه فضایی SN و در برخی موارد UN ، به ویژه اینکه چه گره هایی با چه پیوندهایی به چه گره هایی متصل می شوند، به ترتیب در ماتریس های مجاورت NxN A SN و A UN ثبت می شوند. در این جداول، وجود پیوند بین دو گره در یک شبکه با استفاده از مقدار 1 و جایگزین با استفاده از مقدار 0 ثبت شده است.
در مورد شبیه سازی دینامیک در یک شبکه، قوانین انتقال اعمال شده R و هزینه های اتصال C بر UN زیربنایی شبکه تأثیر می گذارد ، که به نوبه خود بر SN شبکه فضایی تأثیر می گذارد و بنابراین اطلاعات ثبت شده در ماتریس های مجاورت را در هر مرحله زمانی تغییر می دهد. بنابراین، تکامل شبکه فضایی SN با هر مرحله زمانی تعریف می‌شود که در آن ماتریس مجاورت در مرحله زمانی بعدی t + 1 تابعی از شبکه زیربنایی UN ، همسایگی J ، قوانین تولیدی R ، هزینه اتصال C است.و ماتریس مجاورت در زمان قبلی t . در مورد شبیه سازی دینامیک یک شبکه، قوانین انتقال اعمال شده R و هزینه های اتصال C ، SN فضایی شبکه را تغییر می دهد و بنابراین اطلاعات ثبت شده در ماتریس مجاورت را در هر مرحله زمانی تغییر می دهد. بنابراین، تکامل شبکه فضایی SN در جایی تعریف می‌شود که ماتریس مجاورت در مرحله زمانی بعدی t + 1 تابعی از همسایگی J ، قوانین تولیدی R ، هزینه اتصال C و ماتریس مجاورت در زمان قبلی t است.

2.2. تجزیه و تحلیل شبکه فضایی GNA با استفاده از نظریه گراف

خروجی یک GNA دنباله ای از شبکه های فضایی در حال تکامل SN است که یک پدیده دنیای واقعی را در مکان و زمان نشان می دهد. این نمایش مفید است زیرا ساختار شبکه های فضایی را می توان با استفاده از معیارهای تئوری گراف مشخص کرد [ 24 ، 25 ، 26 ، 27 ]. ویژگی‌های ساختاری و دینامیکی شبکه‌های دنیای واقعی اغلب برخی یا بسیاری از ویژگی‌های مشابه چهار نوع گراف نظری کاملاً تعریف شده را نشان می‌دهند: منظم، تصادفی، دنیای کوچک و بدون مقیاس. این نوع نمودارها را می توان با استفاده از چند معیار ساده تئوری نمودار جهانی از جمله میانگین درجه <k> ، توزیع درجه P(k) از یکدیگر متمایز کرد.، میانگین ضریب خوشه بندی < C> و طول مسیر متوسط ​​<l> ( جدول 3 ). هر نوع نمودار را می توان در یک زمینه غیر فضایی یا فضایی در نظر گرفت. در یک زمینه غیر فضایی، مکان گره ها هیچ نگرانی ندارد، اما در عوض، نحوه اتصال گره ها به گره های دیگر است. در یک بافت فضایی، گره ها دارای موقعیت مکانی در فضای جغرافیایی هستند.
شبکه‌هایی که ویژگی‌های نمودارهای معمولی را نشان می‌دهند از مجموعه‌ای از گره‌ها و پیوندها تشکیل شده‌اند که هر گره دقیقاً همان تعداد پیوندهای درجه k را دارد [ 28 ]. یک نمودار منظم که غیر فضایی است به گونه ای ارائه می شود که مکان مکانی گره ها را در نظر نمی گیرد، بلکه به نحوه اتصال گره ها مربوط می شود. به عنوان مثال، گره ها ممکن است در یک دایره مرتب شوند که در آن هر گره به گره های همسایه خود متصل است. آرایش دایره ای از نظر مکانی بی معنی است، اما برای درک بهتر توپولوژی گراف انتخاب شده است. یک نمودار منظم فضایی ممکن است به گونه‌ای مرتب شود که گره‌های جغرافیایی مرجع آن به گونه‌ای سازماندهی شوند که تمام پیوندها با طول یکسان d باشند.و همه گره ها دارای درجه یکسانی k هستند. در هر صورت، از آنجایی که همه گره‌ها به نزدیک‌ترین همسایگان خود متصل هستند، نمودارهای منظم غیرمکانی و فضایی دارای ضریب خوشه‌بندی بالایی هستند < C> . اتصالات محلی منجر به متوسط ​​طولانی‌ترین طول مسیر <l> بین جفت گره‌ها در شبکه می‌شود.
برخلاف نمودارهای معمولی، ویژگی‌های نمودارهای تصادفی غیرمکانی به طور قابل توجهی با نمودارهای فضایی تصادفی متفاوت است. شبکه هایی که ویژگی های نمودارهای تصادفی غیرمکانی را نشان می دهند از گره هایی تشکیل شده اند که به طور تصادفی به گره های دیگر متصل می شوند [ 29 ]. از آنجایی که نمودار غیرمکانی است، ارتباط بین گره ها تحت تأثیر فاصله بین آنها قرار نمی گیرد. نمودارهای تصادفی که غیرمکانی هستند با توزیع درجه P(k) تعریف می شوند که در آن همه گره ها دارای درجه k مشابه هستند. این درجه متوسط ​​کاملاً تعریف شده توزیع درجه پواسون P(k) را تولید می کند . از آنجایی که هر دو گره به صورت تصادفی به هم متصل می شوند، میانگین ضریب خوشه بندی < C> و میانگین طول مسیر<l> بسیار کوچک هستند. یک گراف تصادفی غیر فضایی نیز به عنوان گراف Erdos–Renyi (ER) به نام دو ریاضیدانی که برای اولین بار مفهوم نمودارهای تصادفی را معرفی کردند، شناخته می‌شود.
دو نوع اصلی از نمودارهای فضایی تصادفی وجود دارد. نوع اول به عنوان یک نمودار هندسی تصادفی (RGG) نامیده می شود که از گره هایی تشکیل شده است که به طور تصادفی در فضای جغرافیایی قرار دارند. برخلاف یک نمودار تصادفی غیرمکانی، گره‌ها در یک RGG به طور تصادفی به هم متصل نمی‌شوند، بلکه اگر فاصله بین دو گره در آستانه فاصله انتخاب شده d [ 30 ] باشد، به گره‌های دیگر متصل می‌شوند. آستانه فاصله d را می توان با استفاده از فاصله اقلیدسی، منهتن یا ژئودزیکی تعریف کرد [ 31]. ویژگی‌های RGGها با نمودارهای تصادفی غیرمکانی سنتی متفاوت است زیرا آستانه فاصله باعث ایجاد خوشه‌بندی موضعی بین گره‌های مجاور و فقدان اتصالات دوردست می‌شود که مشخصه بسیاری از شبکه‌های واقعی جاسازی شده فضایی است [ 25 ]. گنجاندن فضای جغرافیایی به عنوان یک محدودیت در ساختار شبکه، بازنمایی واقعی تری از پدیده های واقعی را نسبت به شبکه های غیر فضایی ارائه می دهد. بنابراین، RGGها به عنوان مدلی برای درک بهتر بسیاری از پدیده‌های واقعی از شبکه‌های مخابراتی گرفته تا شبکه‌های اجتماعی استفاده شده‌اند. نوع دوم گراف فضایی تصادفی به عنوان نمودار ER فضایی نامیده می شود. در این نمایش گره ها به صورت تصادفی در فضای جغرافیایی توزیع می شوند و بر اساس احتمال p به صورت تصادفی به هم متصل می شوند .
نمودارهای دنیای کوچک، هم همتایان غیرمکانی و هم مشابه فضایی آنها، با ساختاری مشخص می شوند که بین نمودارهای معمولی که اصلاً تصادفی نیستند و نمودارهای تصادفی که کاملاً تصادفی هستند قرار می گیرد [ 32 ]. مانند یک گراف معمولی، اکثر گره‌ها در گراف‌های دنیای کوچک به نزدیک‌ترین همسایگان خود متصل هستند، اما تعداد کمی از گره‌ها به گره‌های دور متصل هستند. این نوع گراف همچنین هنگام ترسیم نمودار توزیع درجه به صورت هیستوگرام، توزیع درجه پواسون P(k) تولید می کند. با این حال، نمودارهای دنیای کوچک با نمودارهای معمولی یا تصادفی متفاوت هستند، زیرا چند اتصال دور بین گره‌ها ضریب خوشه‌بندی متوسط ​​بالایی را تولید می‌کنند ، اما به طور چشمگیری طول متوسط ​​مسیر را کاهش می‌دهند.<l> . شبکه‌های اجتماعی معمولاً ویژگی‌های نمودارهای دنیای کوچک را نشان می‌دهند، جایی که تنها چند آشنای متوسط ​​بین هر دو نفر در جهان وجود دارد. پویایی در یک شبکه دنیای کوچک مانند انتقال اطلاعات یا ویروس بسیار کارآمد است. به طور خاص، به دلیل این طول متوسط ​​کوتاه <l> ، انتقال اطلاعات یا انتشار یک ویروس از گره i به گره j می تواند تنها با چند واسطه رخ دهد.
شبکه‌ها، اعم از غیر مکانی یا فضایی، با ویژگی‌های مشخصه گراف‌های بدون مقیاس معمولاً دارای توزیع درجه P(k) هستند که در آن تعداد کمی از گره‌ها دارای درجه نامتناسب بزرگ و اکثر گره‌ها دارای درجه بسیار کمی هستند [ 33 ]. این یک توزیع درجه بدون مقیاس با میانگین ضریب خوشه‌بندی پایین < C> و طول مسیر متوسط ​​کوچک <l> ایجاد می‌کند.. براباسی و آلبرت (1999) شبکه‌های دارای توزیع قانون قدرت را به عنوان شبکه‌های «بدون مقیاس» معرفی می‌کنند، زیرا همان توزیع قانون قدرت در تمام مقیاس‌های شبکه باقی می‌ماند. این ساختار شبکه با رشد و پیوست ترجیحی توضیح داده می شود، به این معنی که با شکل گیری شبکه، احتمال اضافه شدن یک پیوند جدید به گره وجود دارد. vمنمتناسب با درجه k آن گره است و می تواند منجر به تشکیل هاب هایی با تعداد غیرعادی زیاد لینک شود. این نوع شبکه ها در برابر حملات تصادفی قوی هستند، با این حال، از دست دادن یک هاب در یک حمله هدفمند باعث شکست سیستم می شود [ 34 ]. درجه گره تنها عاملی نیست که به پیوست ترجیحی کمک می کند [ 35 ] و تغییرات متعددی پیشنهاد شده است که احتمال اضافه شدن پیوند جدیدی به گره وجود دارد. vمنمتناسب با سن گره است [ 36 ، 37 ].
معیارهای تئوری گراف جهانی را می توان برای توصیف ساختارهای شبکه کلی، برای ارائه بینشی به دینامیک فضایی که در آن ساختارها رخ می دهد، برای مقایسه بین سیستم های مختلف، و برای مقایسه بین همان سیستمی که در طول زمان تکامل می یابد، استفاده کرد. برخی از معیارهای مهم تئوری گراف جهانی در جدول 3 ارائه شده است که یک تصویر فوری کامل از ساختار شبکه ارائه می دهد که شامل تعداد گره n ، تعداد پیوندهای m ، میانگین درجه <k> ، توزیع درجه P(k) ، میانگین است. ضریب خوشه بندی <C> و میانگین کوتاه ترین طول مسیر <l>. این معیارهای خاص برای توصیف ساختارهای شبکه تولید شده توسط مدل‌های GNA که در بخش‌های زیر ارائه شده‌اند، استفاده می‌شوند.

3. مطالعات موردی خودکار شبکه جغرافیایی

در بخش‌های بعدی، کاربرد چارچوب GNA پیشنهادی برای نسخه شبکه صریح فضایی بازی زندگی GNA GOL و تفکیک GNA SEG شلینگ ارائه شده است. هر دو مدل با استفاده از زبان برنامه نویسی جاوا در محیط توسعه یکپارچه Eclipse با استفاده از جعبه ابزار شبیه سازی عامل متخلخل بازگشتی (Repast) [ 38 ] توسعه یافته اند.

3.1. GNA Game of Life GNA GOL

بازی زندگی به عنوان اولین مطالعه موردی برای ارائه چارچوب GNA انتخاب شده است زیرا یک مدل شناخته شده از یک سیستم نظری است که ذاتاً ساده است و در مکان و زمان عمل می کند. بازی اصلی زندگی یک خودکار سلولی است که توسط جان کانوی در سال 1970 ساخته شد و برای شبیه‌سازی دینامیک تولید مثل، مرگ و بقای سلول‌ها در یک شبکه طراحی شد. اعمال این پویایی ها برای گره ها در یک شبکه امکان کاوش در تکامل شبکه فضایی، به ویژه رشد و انقباض شبکه فضایی را فراهم می کند زیرا گره ها در طول زمان اضافه و حذف می شوند. بنابراین، این مطالعه موردی یادگیری گسترده تر در مورد پویایی و تکامل شبکه های فضایی را تسهیل می کند.

3.1.1. چارچوب مدل سازی GNA GOL

مدل GNA GOL یک شبکه فضایی در حال تکامل SN را شبیه‌سازی می‌کند که به یک گراف هندسی تصادفی زیربنایی (RGG) شبکه UN محدود شده است. بر اساس عبارت (1)، GNA GOL را می توان به صورت زیر ارائه کرد:

جینآجیOL=[UنجیOL،اسنجیOL، جی، آر، سی، Δتی]

که در آن GNA GOL تابعی از شبکه زیربنایی است UنجیOL، شبکه فضایی مورد علاقه اسنجیOL، محله J ، قوانین انتقال آر، هزینه اتصال سی، و زمان Δتی.

RGG UN GOL اساسی است که در آن مجموعه ای از گره های N به طور تصادفی در فضای جغرافیایی و تعداد کل گره ها n = 2000 قرار گرفته اند. تعداد گره های n برای نشان دادن روش GNA انتخاب شد. گره vمنو گره vjدر مجموعه گره ها ، N توسط یک پیوند به هم متصل می شوند و بنابراین اگر فاصله اقلیدسی d ij بین آنها کمتر از 1 کیلومتر باشد، گره های همسایه در نظر گرفته می شوند. محدوده داده شده برای d همسایگی J را برای هر گره تعریف می کند. از آنجایی که توزیع فضایی همه گره‌ها تصادفی است و نه یک مجموعه منظم، گره‌ها در UN GOL تعداد گره‌های همسایه یکسانی ندارند. این با فرمولیسم سنتی نسخه CA از بازی زندگی متفاوت است که بر روی یک مجموعه فضایی منظم عمل می کند که در آن همه سلول ها دقیقاً به همان تعداد همسایه دارند. هر گره در مجموعه گره‌های N را می‌توان با مکان آن تعریف کرد ( x, yمختصات)، فواصل d بین گره های همسایه و حالت “زنده” یا “مرده” آن. در نهایت هر گره با ویژگی های شبکه محلی خود از جمله درجه k ، ضریب خوشه بندی C و کوتاه ترین طول مسیر l تعریف می شود.
شبکه فضایی SN GOL از گره هایی با ویژگی های فضایی و شبکه یکسان تشکیل شده است، با این حال، گره ها در این شبکه فقط می توانند در حالت “زنده” باشند. قوانین انتقال نشان دهنده پویایی تولید مثل، مرگ و بقا در شبکه UN GOL که در آن گره ها اضافه می شوند، حذف می شوند و به مرور زمان سیم کشی می شوند، اعمال می شوند، بنابراین یک شبکه فضایی در حال تکامل از گره های “زنده” SN GOL تولید می شود که می تواند تجزیه و تحلیل شود. چهار قانون گذار R بر اساس بازی زندگی [ 20 ] وجود دارد که در زمان t به GOL سازمان ملل اعمال می شود و GOL و UN GOL را تعیین می کند .SN GOL در زمان t + 1، به شرح زیر است:
R1 – برای شبیه سازی پویایی کم جمعیت، هر گره زنده vمنبا تعدادی یا کمتر از همسایگان زنده j می میرد و از شبکه فضایی SN GOL حذف می شود .
R2 – برای شبیه سازی پویایی بقای بهترین، هر گره زنده vمندقیقاً با تعدادی همسایه زنده وضعیت زنده خود و در نتیجه جایگاه خود را در شبکه فضایی SN GOL حفظ می کند .
R3 – برای شبیه سازی پویایی جمعیت بیش از حد، هر گره زنده vمنبا تعدادی یا بیشتر از همسایگان زنده j می میرد و از فضایی SN GOL حذف می شود .
R4 – برای شبیه سازی پویایی تولید مثل، هر گره مرده vمندقیقاً با تعدادی همسایه زنده، j تبدیل به یک گره زنده می شود و به شبکه فضایی SN GOL اضافه می شود.
اگرچه تأثیر ماتریس هزینه بر پویایی سیستم به طور رسمی در بازی سنتی زندگی بررسی نشده است، یک مانع در GNA GOL برای نشان دادن استفاده از هزینه اتصال C در چارچوب GNA معرفی شده است. هزینه اتصال C به شرح زیر است:
C1 – یک پیوند نمی تواند بین گره تشکیل شود vمنو گره vjاگر مانع را قطع کند
برای هر مدلی که اجرا می شود، ساختار شبکه زیربنایی UN GOL همیشه یکسان است، اگرچه حالت گره ها تغییر می کند. UN GOL و متعاقباً SN GOL در زمان t 0 مقداردهی اولیه می شود که در آن 50٪ از 2000 گره به طور تصادفی به عنوان “زنده” انتخاب می شوند. شبکه زیربنایی UN GOL در GNA GOL یک فرآیند به روز رسانی گره هماهنگ را پیاده سازی می کند. ابتدا تعداد گره های همسایه زنده برای هر گره در شبکه زیربنایی UN GOL محاسبه می شود . دوم، قوانین انتقال Rاعمال می شوند و وضعیت هر گره بر اساس تعداد همسایگان زنده آن تغییر می کند. در نهایت تعداد جدید گره های زنده محاسبه می شود. اگر گره زنده باشد، گره باقی می ماند یا بخشی از شبکه فضایی مورد علاقه SN GOL می شود و به همسایگان زنده خود متصل می شود. GNA GOL برای 20 مرحله زمانی اجرا می شود که پس از آن شبکه فضایی در حال تکامل SN GOL به تعادل می رسد و اکثر گره ها راضی می شوند.
3.1.2. سناریوهای GNA GOL
دو سناریو با تنظیم قوانین انتقال R1-R4 مدل GNA GOL برای نشان دادن رفتارهای فضایی مختلف شبیه‌سازی‌شده با استفاده از شبکه‌های فضایی در حال تکامل SN GOL ایجاد شد. سناریوی 1 از قوانین انتقال R ارائه شده در جدول 4 برای ایجاد یک شبکه فضایی استفاده می کند که در طول زمان رشد و گسترش می یابد. برای تقویت یک شبکه در حال رشد، قوانین به گونه‌ای کالیبره می‌شوند که داشتن همسایه‌های بیشتر مطلوب باشد، به‌عنوان مثال، پارامتر x به‌گونه‌ای انتخاب می‌شود که تولیدمثل و افزایش جمعیت تشویق شود در حالی که از کمبود جمعیت جلوگیری می‌شود. سناریوی 2 از قوانین انتقال R ارائه شده در جدول 4 استفاده می کندبرای ایجاد یک شبکه فضایی که در طول زمان و مکان کوچک و کاهش می یابد. برای تقویت یک شبکه در حال کوچک شدن، قوانین طوری کالیبره می‌شوند که داشتن همسایه‌های کمتر مطلوب است، یعنی پارامتر x انتخاب می‌شود تا از تولیدمثل و افزایش جمعیت جلوگیری شود و جمعیت کم تشویق شود. در هر دو سناریو، هزینه اتصال C1 یکسان باقی می ماند، جایی که یک پیوند نمی تواند بین گره ایجاد شود vمنو گره vjاگر مانع را قطع کند. چندین نمونه واقعی از سیستم ها به عنوان شبکه وجود دارد که ممکن است این نوع رفتارهای مکانی-زمانی را نشان دهند. یک شبکه در حال رشد، که در آن تعداد گره‌ها و پیوندها به طور مداوم در طول زمان افزایش می‌یابد، می‌تواند نماینده هر نوع پدیده مبتنی بر انتشار مانند گسترش گونه‌های مهاجم، انتقال بیماری، انتشار ویروس‌های رایانه‌ای، گسترش شهری، سیل و شبکه‌های ارتباطی باشد. یک شبکه در حال کوچک شدن، که در آن گره‌ها به طور مداوم از شبکه حذف می‌شوند، ممکن است نماینده فرآیندهایی مانند جنگل‌زدایی، از دست دادن زیستگاه به دلیل گونه‌های مهاجم، از دست دادن زمین‌های کشاورزی و خشکسالی باشد. GNA به شبیه‌سازی این دو نوع تکامل شبکه محدود نمی‌شود، زیرا تکامل شبکه از قوانین انتقال پیاده‌سازی شده برای نشان دادن پویایی مکان بین گره‌ها پدید می‌آید.
3.1.3. نتایج GNA GOL
خروجی GNA GOL مجموعه‌ای از شبکه‌های فضایی SN GOL است که به عنوان تابعی از قوانین انتقال R که در شبکه زیربنایی UN GOL اعمال می‌شوند، تکامل می‌یابند . به طور خاص، ساختار شبکه در حال تکامل SN GOL اندازه‌گیری شده توسط ساختار گراف هندسی تصادفی زیربنایی (RGG) UN GOL محدود می‌شود و بنابراین GNA GOL در هر دو سناریو یک شبکه فضایی در حال تکامل SN GOL ایجاد می‌کند که RGG نیز هست. ساختار شبکه زیربنایی UN GOL اجازه ظهور یک شبکه فضایی مورد علاقه را نمی دهد.SN GOL که دارای خواص انواع گراف های دیگر مانند بدون مقیاس یا کوچک است. بر اساس ساختار شبکه فضایی در حال تکامل تصادفی SN GOL تولید شده توسط GNA GOL ، ساختارهای شبکه مشاهده و اندازه‌گیری شده در اینجا RGGها را مشخص می‌کنند زیرا به پویایی‌هایی که باعث رشد و کاهش پاسخ‌ها می‌شوند پاسخ می‌دهند. از آنجایی که بسیاری از انواع پدیده های واقعی توسط RGG ها نشان داده و مدل می شوند، مهم است که درک کنیم که چگونه فرآیندهایی که بر روی ساختار RGG عمل می کنند ممکن است تحت تاثیر تغییرات در ساختار آنها قرار گیرند. در بخش زیر، نتایج شبیه‌سازی GNA GOL به‌دست‌آمده ارائه شده و شبکه فضایی در حال تکامل SN GOL با استفاده از معیارهای تئوری گراف مورد تجزیه و تحلیل قرار می‌گیرد.

نتایج شبیه سازی GNA GOL

نتایج شبیه سازی به دست آمده از هر دو سناریو در شکل 2 ارائه شده است. در هر دو سناریو، پس از مقداردهی اولیه، 50% از گره ها به طور تصادفی به عنوان “زنده” انتخاب می شوند ( شکل 2 a).
سناریوی 1 – استفاده از قوانین انتقال R توسعه یافته برای شبیه سازی رشد شبکه فضایی در ابتدا پیکربندی را تشکیل می دهد که از خوشه های ضخیم گره ها تشکیل شده است ( شکل 2 ب). از آنجایی که قوانین انتقال R یک عدم تعادل به نفع بازتولید گره (R4) و بقا (R2) ایجاد می کند، خوشه ها در طول زمان گسترش می یابند زیرا گره های “مرده” نزدیک به لبه خوشه ها در نهایت همسایه های “زنده” کافی دارند که برای آنها لازم است. برای تکثیر و پیوستن به شبکه فضایی SN GOL ( شکل 2ج-ه). به این ترتیب، شبکه به عنوان یک کل در طول زمان رشد می کند که گویی در حال گسترش است. ساختارهای زنجیره‌ای و حلقه‌مانند زمانی تشکیل می‌شوند که فضای داخلی هر خوشه به دلیل جمعیت زیاد می‌میرد و قسمت‌های بیرونی هر خوشه به دلیل کمبود جمعیت می‌میرند و بقیه گره‌های خوشه با تعداد پیوندهای صحیح تا مرحله زمانی بعدی زنده می‌مانند. پیکربندی های حلقه مانند و الگوهای تکرار شونده مانند الگوهایی هستند که در نسخه اصلی بازی زندگی تولید شده اند.
سناریوی 2 – استفاده از قوانین انتقال R توسعه یافته برای شبیه سازی انقباض شبکه فضایی در ابتدا مجموعه ای پراکنده از خوشه ها را تشکیل می دهد، جایی که برخی از خوشه ها به شبکه فضایی بزرگتر متصل هستند و برخی دیگر متصل نیستند ( شکل 2 f). این نتیجه قوانین انتقال R است که برای کاهش بازتولید گره و حذف بقای گره طراحی شده است. در نتیجه، شبکه به سرعت منقبض می شود تا زمانی که شبکه به دنباله ای تکرار شونده از پیکربندی های حلقه مانند نسبتا پایدار کاهش می یابد ( شکل 2 g–i). به محض اینکه پیکربندی ناپایدار تولید می‌شود که منجر به از دست دادن یا افزایش گره‌ها می‌شود، شبکه فرو می‌پاشد و همه گره‌ها به دلیل کمبود جمعیت می‌میرند.

نتایج تجزیه و تحلیل شبکه فضایی GNA GOL

روندهای عمومی – شبکه فضایی در حال تکامل SN GOL با تعداد گره‌ها n ، تعداد پیوندهای m ، میانگین ضریب خوشه‌بندی <C> ، میانگین درجه گره‌های زنده <k> ، و میانگین طول مسیر <l> مشخص می‌شود. هر تکرار برای سناریو 1 ( شکل 3 الف) و سناریو 2 ( شکل 3)ب). به طور کلی، در سناریوی 1، اندازه شبکه در طول زمان به طور پیوسته افزایش می یابد. سرعت رشد در مراحل اولیه سریعتر است و در مراحل بعدی کندتر می شود زیرا شبکه پیکربندی پایداری پیدا می کند و گره های مرده کمتری برای تولید مثل و پیوستن به شبکه به عنوان گره های زنده در دسترس هستند. در سناریوی 2، اندازه شبکه در طول زمان تنها با چند مرحله زمانی کاهش می‌یابد که در آن تعداد گره‌ها قبل از کاهش کمی افزایش می‌یابد. نتایج نشان می دهد که اقدامات شبکه جمع آوری شده برای شبکه کوچک شونده ( شکل 3 ب) نویزتر از اقدامات شبکه جمع آوری شده برای شبکه در حال رشد است ( شکل 3)آ). در شبکه در حال رشد، در تمام مراحل زمانی، تعداد گره ها و لینک ها بیشتر از مرحله زمانی قبلی است. در سناریوی کوچک شدن شبکه، در برخی مراحل زمانی، تعداد گره ها و لینک ها قبل از کاهش شدید افزایش می یابد. این نویز تابعی از اعمال قوانین برای ازدیاد جمعیت است. گره ها زنده می مانند، تکثیر می شوند و به گره های دیگر سیم کشی می شوند. همانطور که درجه آنها در طول زمان افزایش می یابد، از آستانه ساختار تعیین شده توسط R3 فراتر می رود و سپس در تکرار بعدی می میرد.
همبستگی بین معیارهای تئوری گراف – جدول 5 همبستگی بین معیارهای نظریه گراف به دست آمده از شبکه های فضایی تولید شده در سناریوی 1 ( جدول 5 الف) و سناریو 2 ( جدول 5 ب) را نشان می دهد.
سناریوی 1: بر اساس نتایج ارائه شده در جدول 5 الف، ساختار شبکه فضایی رو به رشد SNGOL یک همبستگی مثبت قوی بین تعداد گره ها و تعداد پیوندها، میانگین طول مسیر و درجه متوسط ​​را نشان می دهد. برعکس، یک همبستگی منفی قوی بین میانگین ضریب خوشه‌بندی و تعداد گره‌ها، تعداد پیوندها، میانگین طول مسیر و میانگین درجه وجود دارد.
سناریوی 2: ساختار شبکه در حال انقباض SN GOL همبستگی مثبت قوی تا متوسطی را بین تعداد گره ها و تعداد پیوندها، میانگین، طول مسیر و درجه متوسط ​​نشان می دهد ( جدول 5 ب). یک همبستگی منفی متوسط ​​تا ضعیف بین میانگین ضریب خوشه‌بندی و تعداد گره‌ها ، تعداد پیوندها، میانگین طول مسیر و میانگین درجه وجود دارد.
به طور کلی، برای شبکه های فضایی در حال تکامل SN GOL شبیه سازی شده در همه سناریوها، با افزایش اندازه RGGها، تعداد پیوندها، میانگین طول مسیر و درجه متوسط ​​افزایش می یابد در حالی که ضریب خوشه بندی کاهش می یابد. برعکس، با کوچک شدن RGGها، تعداد پیوندها، طول مسیر متوسط ​​و درجه متوسط ​​نیز کاهش می‌یابد، در حالی که ضریب خوشه‌بندی افزایش می‌یابد. این یافته‌ها از این نتیجه‌گیری حمایت می‌کنند که اندازه‌گیری‌های نظریه گراف به اندازه شبکه وابسته هستند [ 39 ]. این همبستگی ها به ویژه جالب هستند زیرا رابطه بین اندازه شبکه و سایر معیارهای تئوری گراف به خوبی درک نشده است و به ندرت در ادبیات به ویژه در مورد شبکه های صریح فضایی مورد بررسی قرار گرفته است.
توزیع مدرک . هنگامی که یک شبکه در حال تکامل تحت رشد قرار می‌گیرد (سناریوی 1) و اندازه شبکه افزایش می‌یابد، درجه گره افزایش می‌یابد که یک توزیع درجه با چوله منفی سمت چپ ایجاد می‌کند ( شکل 4 a). هنگامی که یک شبکه در حال تکامل تحت انقباض قرار می گیرد (سناریوی 2)، گره ها حذف می شوند، گره های باقی مانده با درجه کوچکتر باقی می مانند، و توزیع درجه با یک انحراف مثبت سمت راست ایجاد می شود ( شکل 4 ب).
بازی زندگی یک مدل شناخته شده از یک سیستم فضایی نظری است که به عنوان مطالعه موردی برای نشان دادن چارچوب مدل سازی GNA به وضوح انتخاب شده است، با این حال GNA GOL ارائه شده است.مجموعه داده های جغرافیایی واقعی را در بر نمی گیرد. در مورد کاربرد جغرافیایی چارچوب مدل‌سازی GNA برای پدیده‌های دنیای واقعی، عناصر GNA شامل وضعیت شبکه اولیه، شبکه زیربنایی، قوانین انتقال، هزینه اتصال و وضوح مکانی و زمانی باید طراحی شود تا به درستی منعکس کننده یک سیستم دنیای واقعی خاص باشد و شامل داده های مکانی باشد تا امکان توسعه GNA، کالیبراسیون، تجزیه و تحلیل حساسیت به شرایط و پارامترهای اولیه و اعتبارسنجی را فراهم کند. این فرآیند برای طراحی هر دستگاه خودکار سلولی یا برای یک مدل مبتنی بر عامل یکسان خواهد بود. در بخش بعدی، مدل دومی که داده‌های مکانی واقعی را در چارچوب مدل‌سازی GNA ادغام می‌کند، ارائه می‌شود.

3.2. تفکیک GNA شلینگ GNA SEG

شلینگ [ 21 ، 22] مدلی را ارائه کرده است که با استفاده از یک قانون توانست الگوهای فضایی تفکیک انسانی، خودسازماندهی افراد ناهمگن را در خوشه‌هایی از افراد «یکسان» به تصویر بکشد. این قانون به این صورت است: اگر فردی از ترکیب دیگرانی که در همسایگی خود زندگی می کنند ناراضی باشد، فرد تا زمانی که راضی شود به جای دیگری نقل مکان می کند. این قانون راهی برای مدل‌سازی فرآیندهای اجتماعی بسیار پیچیده فراهم می‌کند که افراد را بر اساس شباهت‌های زبان، علایق، جنسیت، قومیت، شغل، دیدگاه‌های سیاسی، تحصیلات، زبان و غیره به هم نزدیک می‌کند. کار شلینگ برای بررسی اثرات تنظیمات پارامتر از جمله تحمل فردی، اندازه محله، ساختارهای جمعیتی، و توابع ابزاری که منجر به تفکیک می شود، گسترش یافته است [ 40 ، 41 ]]. در سایر مطالعات تحقیقاتی، مدل ها بر اساس داده های واقعی [ 42 ، 43 ، 44 ] پارامتر بندی می شوند. در بسیاری از موارد، جداسازی به عنوان شبکه مدل‌سازی می‌شود [ 45 ، 46 ، 47 ، 48 ]، با این حال، نمایش شبکه و تجزیه و تحلیل فرآیندهای فضایی جداسازی با استفاده از داده‌های مکانی واقعی مورد بررسی قرار نگرفته است.
در این بخش، GNA دوم توسعه یافته است. مدل GNA SEG یک نمونه اولیه برای نمایش الگوهای تفکیک در یک محیط شهری است. مدل ارائه شده پیشرفته‌تر از مدل GNA GOL است زیرا داده‌های مکانی واقعی را تشکیل می‌دهد که یک شبکه زیربنایی را تشکیل می‌دهد، به چندین نوع همسایگی گره که قوانین انتقال برای آن‌ها پیاده‌سازی می‌شوند، دسترسی پیدا می‌کند، و پویایی بین چندین نوع گره مختلف را بررسی می‌کند. در این شبکه، برخلاف GOL، تکامل شبکه با اضافه کردن یا حذف گره ها مشخص نمی شود، بلکه سیم کشی مجدد تعداد مشابهی از گره ها در طول زمان تغییر مکان می دهد.

3.2.1. چارچوب مدل سازی GNA SEG

مدل GNA SEG یک شبکه فضایی در حال تکامل SN را شبیه‌سازی می‌کند که به یک شبکه فضایی زیربنایی سازمان ملل از املاک مسکونی شهری محدود می‌شود. بنابراین، بر اساس عبارت (1)، GNA SEG را می توان به صورت زیر ارائه کرد:

جینآاسEجی=[UناسEجی،اسناسEجی، جی، آر، سی، Δتی]

که در آن GNA SEG تابعی از شبکه زیربنایی است UناسEجی، شبکه فضایی مورد علاقه به هم پیوسته محکم اسناسEجی، محله J ، قوانین انتقال آر، هزینه اتصال سی، و افزایش زمان Δتی.

شبکه فضایی زیربنایی UN SEG ساخته شده است که تعداد کل گره ها n = 20213 باشد. هر گره vمندر مجموعه گره‌های N نشان‌دهنده مکان واقعی املاک مسکونی خالی از سکنه واقع در چندین محله در شهر ونکوور، کانادا از جمله West End، Downtown Vancouver، Hastings Sunrise، Strathcona و Grandview Woodland است. مکان خواص از داده‌های مکانی واقعی تولید شده توسط شهر ونکوور به‌دست می‌آید و می‌تواند به عنوان داشتن یک الگوی فضایی خوشه‌ای مشخص شود. املاک مسکونی تنها در چند محله ونکوور در این مطالعه گنجانده شده‌اند و بنابراین تعداد گره‌ها را به منظور حفظ کارایی محاسباتی محدود می‌کنند. در شبکه فضایی زیربنایی UN SEG ، گره vمنو گره vjدر مجموعه گره ها ، N توسط یک پیوند به هم متصل می شوند و بنابراین اگر فاصله اقلیدسی d ij کوچکتر از محدوده J همسایگی معین باشد ، در این مورد d ij <= 50 متر باشد، خصوصیات همسایه در نظر گرفته می شوند. مقدار همسایگی با محاسبه میانگین فاصله نزدیکترین همسایه بر حسب متر انتخاب شد. از آنجایی که همسایگی با مجاورت تعریف می شود، نمودار یک نمودار هندسی در نظر گرفته می شود. با این حال، چون گره ها به طور تصادفی در فضای جغرافیایی توزیع نمی شوند، شبکه زیربنایی RGG در نظر گرفته نمی شود.
برای هر مدل اجرا شده، ساختار شبکه زیربنایی UN SEG همیشه یکسان است. هر گره و پیوند در مجموعه گره های N و پیوندهای L برای شبکه فضایی زیربنایی UN SEG را می توان با ویژگی های فضایی آن از جمله مکان ( مختصات x، y ) و فواصل d بین گره های دیگر تعریف کرد. هر گره همچنین می تواند با حالت “اشغال” یا “غیر اشغال” مشخص شود. در نهایت هر گره با ویژگی های شبکه محلی خود تعریف می شود، جایی که هر گره مجزا دارای یک درجه k ، یک ضریب خوشه بندی C و یک طول مسیر کوتاه l است.
شبکه فضایی SN SEG از گره هایی تشکیل شده است که نشان دهنده مکان خانواده هایی است که دارایی های مرکز شهر ونکوور را اشغال می کنند. فرض بر این است که هر ملک فقط یک خانواده را اشغال می کند. گره‌ها در شبکه فضایی SN SEG دارای ویژگی‌های فضایی و شبکه‌ای مشابه شبکه زیربنایی UN SEG هستند، با این حال، گره‌ها دارای دو حالت «کلاس A » یا «کلاس B » هستند. گره vمنو گره vjاگر d ij <= 50 m باشد ، در شبکه فضایی توسط یک پیوند به هم متصل می شوند . SN SEG در زمان t 0 مقداردهی می شود که در آن از 20213 گره نشان دهنده املاک مسکونی، 33% خالی، 33% توسط کلاس A و 33% توسط کلاس B اشغال شده است. تخصیص اولیه خانواده ها به املاکی که از کلاس A یا کلاس B هستند به همان اندازه محتمل است.
شبکه فضایی SN SEG از پویایی تفکیک بین گره های خانواده همسایه در شبکه فضایی SN SEG و گره های دارایی اشغال نشده در شبکه زیربنایی UN SEG پدید می آید . علاوه بر این، شبکه فضایی SN SEG با در دسترس بودن خواص در شبکه زیربنایی UN SEG محدود شده است. دو قانون انتقال R وجود دارد که در زمان t اعمال می شود و SN SEG را در زمان t + 1 تعیین می کند. برای اجرای آنها دو نوع همسایگی J در نظر گرفته شده است. محلهJ A فقط گره های خانواده همسایه را در نظر می گیرد vjاز گره خانواده vمنموجود در شبکه فضایی SN . محله J B فقط گره های ملکی اشغال شده و غیر اشغال شده همسایه را در نظر می گیرد vjاز گره خانواده vمندر شبکه زیربنایی UN SEG . قوانین انتقال R به شرح زیر است:
R1 – بر اساس تعریف محله J A ، اگر گره vمنهمسایگی از نسبت بالاتری از همسایگان کلاس مخالف تشکیل شده است، گره ناراضی است و به مکان خالی جدید منتقل می شود.
R2 – بر اساس تعریف محله J B ، اگر گره vمنهمسایگی از نسبت بالاتری از دارایی های غیر اشغالی نسبت به املاک اشغال شده تشکیل شده است، گره ناراضی است و به مکان خالی جدید منتقل می شود.
هر گره دارایی در شبکه زیربنایی UN SEG گره‌های دارایی مجاور خود را ردیابی می‌کند، خواه اشغال نشده باشند، اشغال شده توسط کلاس A ، یا اشغال شده توسط کلاس B. این اطلاعات توسط گره خانواده استفاده می شود vمنبرای درک ترکیب محله و تعیین اینکه آیا از موقعیت آن راضی است یا خیر. GNA SEG برای 20 مرحله زمانی اجرا می شود، پس از آن مدل به تعادل می رسد و اکثر عوامل راضی هستند به این معنی که حرکت کمی فراتر از 20 مرحله زمانی وجود دارد.
3.2.2. نتایج GNA SEG
خروجی های GNA SEG شامل یک سری شبکه های فضایی SN SEG است که به عنوان تابعی از قوانین انتقال R که به شبکه فضایی SN SEG و همچنین تعاملات بین SN SEG و UN SEG اعمال می شود، تکامل می یابند . در بخش زیر، نتایج شبیه‌سازی برای GNA SEG به‌دست‌آمده ارائه می‌شود و شبکه فضایی در حال تکامل SN SEG با استفاده از معیارهای تئوری گراف تحلیل می‌شود.

نتایج شبیه سازی GNA SEG

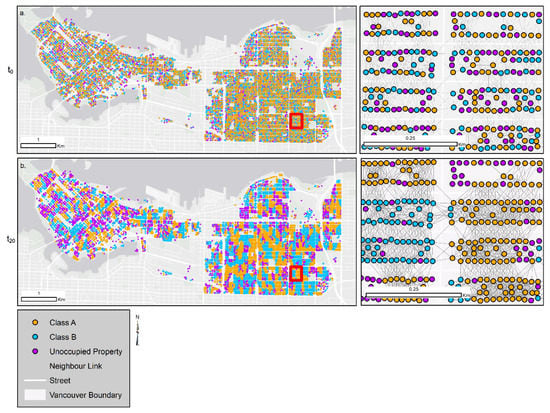
نتایج شبیه سازی به دست آمده از GNA SEG در شکل 5 ارائه شده است. این مدل در زمان t 0 مقداردهی اولیه می شود که در آن یک سوم از املاک مسکونی در محله های انتخابی ونکوور به طور تصادفی به عنوان اشغال شده توسط کلاس A اختصاص داده می شود ، یک سوم از املاک مسکونی به طور تصادفی به عنوان اشغال شده توسط کلاس B اختصاص داده می شود ، و یکی یک سوم از املاک مسکونی خالی مانده است ( شکل 5 الف). نقشه داخلی شکل 5 a ترکیب تصادفی طبقات چند بلوک شهر و نحوه اتصال آنها را با جزئیات نشان می دهد. در زمان t 20، تقریباً همه گره ها از مکان خود راضی هستند ( شکل 5 ب). نقشه داخلی برای شکل 5 ب توزیع جغرافیایی تصادفی دیگر گره ها را نشان می دهد، اما در عوض، ویژگی هایی که در مجاورت قرار دارند توسط گره هایی از همان کلاس اشغال می شوند.

نتایج تجزیه و تحلیل شبکه فضایی GNA SEG

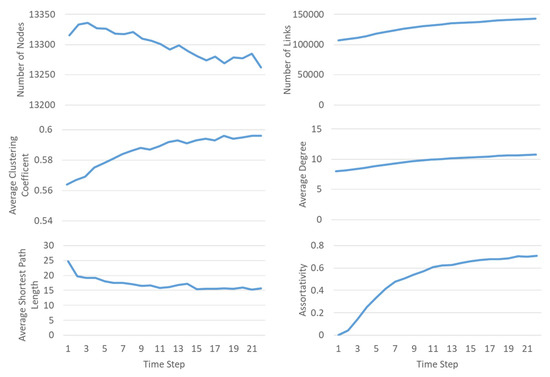
روندهای عمومی – شبکه فضایی در حال تکامل SN SEG را می توان به صورت کوچک یا در حال رشد توصیف نکرد، بلکه سیم کشی مجدد را انجام داد، به این معنی که اتصالات بین گره ها در طول زمان با تغییر مکان گره ها تغییر می کند. شبکه فضایی SN SEG با معیارهای تئوری گراف زیر مشخص می‌شود: تعداد گره‌ها n ، تعداد پیوندهای m ، میانگین ضریب خوشه‌بندی <C> ، میانگین درجه گره‌ها <k> ، میانگین طول مسیر <l> ، و طبقه‌بندی، محاسبه شده برای هر مرحله زمانی ( شکل 6 ). Assortativity درجه یکسان بودن گره های متصل را اندازه گیری می کند، در این مورد، درجه ای که گره های متعلق به کلاس هستند.A به کلاس A و بالعکس متصل می شوند. اگر مجموعه ای برای شبکه 1 باشد، گره ها فقط به گره های هم کلاس متصل می شوند. بنابراین، مجموعه‌بندی اندازه‌گیری نظریه گراف قادر است درجه تفکیک در شبکه فضایی را کمی کند و مفید است زیرا تمام تعاملات فضایی را در کل منطقه مورد مطالعه خلاصه می‌کند.
به طور کلی، تعداد گره‌های متصل به شبکه فضایی SN SEG با گذشت زمان کمی کاهش می‌یابد زیرا برخی از گره‌ها به مکان‌هایی بدون همسایه می‌روند و راضی می‌شوند. برعکس، تعداد لینک ها در طول زمان افزایش می یابد. این را می توان به این طریق توضیح داد که در ابتدا، بلوک های شهری متشکل از بسیاری از ویژگی ها حاوی چندین ویژگی خالی از سکنه هستند ( شکل 5 یک ورودی). املاک اشغال نشده به شبکه فضایی SN SEG متصل نیستند ، در عوض شبکه زیربنایی UN SEG را تشکیل می دهند.. این امر هم میانگین درجه و هم ضریب خوشه بندی املاک اشغال شده را کاهش می دهد زیرا بسیاری از املاک مسکونی مجاور در مجاورت یک گره خالی از سکنه هستند. بر اساس قانون گذار R2 ، گره‌های خانواده در شبکه فضایی SN SEG در صورتی که دارایی‌های اشغال نشده بیشتر از خواص اشغال‌شده در همسایگی آنها وجود داشته باشد، ناراضی هستند. بنابراین، با گذشت زمان، خوشه‌های املاک مسکونی شهری اشغال شده همگن و خوشه‌هایی از املاک غیرمسکونی تشکیل می‌شوند ( شکل 5 b inset). از آنجایی که برخی از بلوک‌های شهری دیگر دارای خاصیت خالی از سکنه نیستند، درجه و ضریب خوشه‌بندی این گره‌ها افزایش می‌یابد. در نتیجه این رفتار، میانگین ضریب خوشه بندی و میانگین درجه شبکه فضاییSN SEG با گذشت زمان افزایش می یابد و طول مسیر متوسط ​​را کاهش می دهد. در نهایت، دسته بندی به طور قابل توجهی در طول زمان از 0.0 به 0.7 افزایش می یابد، زیرا شبکه به طور فزاینده ای جدا می شود.
همبستگی بین معیارهای تئوری گراف – جدول 6 همبستگی بین معیارهای نظریه گراف به دست آمده از شبکه های فضایی تولید شده SN SEG را نشان می دهد. توجه به این نکته مهم است که برخی از همبستگی‌های بین معیارهای نظریه گراف تابعی از پویایی فضایی است که در شبکه رخ می‌دهد. به عنوان مثال، فرآیندهای تفکیک، طبقه‌بندی را افزایش می‌دهند و به طور همزمان میانگین ضریب خوشه‌بندی را افزایش می‌دهند که به نوبه خود یک همبستگی مثبت قوی بین این دو معیار ایجاد می‌کند.
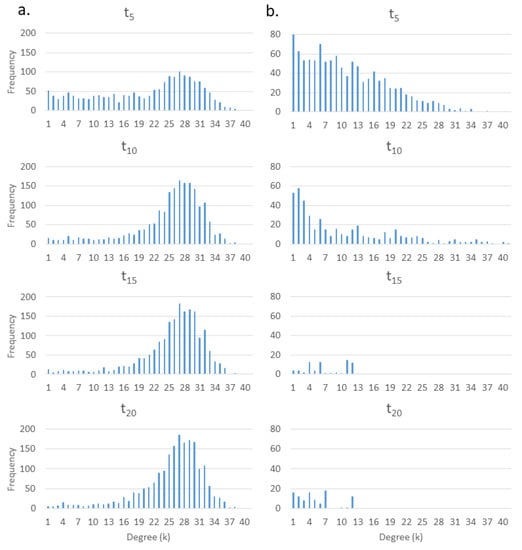
توزیع درجه – توزیع درجه یک توزیع پواسون است و با تغییر شبکه فضایی SN SEG در طول زمان نسبتاً پایدار می ماند. به طور خاص، توزیع درجه برای t 5 ، t 10 ، و t 15 با شاخص پراکندگی 0.98 مشخص می شود. توزیع درجه ابتدا کمی به سمت راست منحرف می‌شود، قبل از اینکه نرمال‌تر شود با شاخص پراکندگی 0.99، زیرا میانگین درجه کمی همانطور که در شکل 7 نشان داده شده است افزایش می‌یابد .
هنگام مقایسه نتایج به‌دست‌آمده برای دو مطالعه موردی، تعداد گره‌ها و تعداد پیوندها در شبکه فضایی SN SEG به شدت همبستگی منفی دارند و در شبکه فضایی SN GOL همبستگی قوی مثبت دارند . این تابعی از قوانین انتقال در شبکه فضایی SN SEG است که سیم‌کشی مجدد شبکه را به پیکربندی با پیوندهای بیشتر مجبور می‌کند که تعداد کمتری از گره‌های خانواده را بهتر برآورده کند. علاوه بر این، SN SEGیک RGG نیست زیرا گره ها به طور تصادفی سازماندهی نشده اند، بلکه در عوض خوشه بندی می شوند. با وجود این تفاوت‌ها بین انواع شبکه، چهار همبستگی وجود دارد که در هر دو خروجی مدل مطالعه موردی GNA صادق است. در تمام شبکه‌های تولید شده توسط هر دو مدل، (1) تعداد گره‌ها و میانگین ضریب خوشه‌بندی همبستگی قوی منفی دارد، (2) تعداد گره‌ها و میانگین طول مسیر همبستگی مثبت دارد، (3) تعداد پیوندها و درجه متوسط همبستگی قوی مثبت، و (4) میانگین طول مسیر و میانگین ضریب خوشه بندی قویاً همبستگی منفی دارد. GNA توسعه یافتهSEG مدلی است که با هدف ارائه چارچوب مدل سازی GNA طراحی شده است که یک مجموعه داده مکانی واقعی را پیاده سازی می کند. نمونه اولیه GNA SEG توسعه‌یافته بسیار مقیاس‌پذیر است و بنابراین نقطه شروعی را فراهم می‌کند که پارامترسازی آسان را با استفاده از داده‌های واقعی اضافی در آینده تسهیل می‌کند.

4. بحث و نتیجه گیری

این مطالعه چارچوب مدل‌سازی جدید اتوماتای ​​شبکه جغرافیایی (GNA) را معرفی می‌کند که می‌تواند برای نمایش و تحلیل سیستم‌های مکانی-زمانی پیچیده به عنوان شبکه‌های در حال تکامل و پویا استفاده شود. رویکرد مدل‌سازی GNA پیشنهادی ارائه‌شده در این مطالعه در چارچوب مدل‌سازی بزرگ‌تر سیستم‌های خودکار جغرافیایی (GAS) [ 49 ، 50 ]، مجموعه‌ای از رویکردهای مدل‌سازی جغرافیایی که شامل اتوماتای ​​سلولی (CA) و مدل‌سازی مبتنی بر عامل (ABM) است، تناسب دارد. چارچوب‌های مدل‌سازی GAS با شبیه‌سازی فعل و انفعالات سطح محلی که رفتار در سطح سیستم از آن پدیدار می‌شود، به دنبال کشف پیچیدگی‌های ذاتی پدیده‌های جغرافیایی واقعی هستند. در حالی که GNA به طور مجزا تعاملات بین گره ها را با استفاده از پیوندها نشان می دهد، CA نشان دهنده پویایی محلی بین سلول ها است.51 ] و ABM ها تعاملات بین افراد یا “عامل ها” را نشان می دهند [ 52 ، 53 ]. مانند رویکرد مدل‌سازی GNA پیشنهادی، CA و ABM تحت چارچوب نظری GAS با سیستم‌های اطلاعات جغرافیایی (GIS) و مجموعه‌های داده‌های مکانی همراه شده‌اند و برای مدل‌سازی انواع پدیده‌های جغرافیایی واقعی با مطالعات اولیه در شهری استفاده شده‌اند [ 54 ، 55 ] ، اجتماعی [ 56 ] و سیستم های زیست محیطی [ 57 ]. افزودن رویکرد مدل‌سازی GNA پیشنهادی به موقعیت نظری بهتر سایر روش‌های مدل‌سازی که به نوعی ترکیبی هستند، کمک می‌کند، از جمله برای مثال اتومات‌های سلولی نمودار [ 58 ] و ABM‌های مبتنی بر شبکه [ 59 ،60 ، 61 ].
در حالی که رویکرد مدل‌سازی GNA پیشنهادی به خوبی در چارچوب GAS قرار می‌گیرد، اما فاصله زیادی با CA مبتنی بر سلول کلاسیک و ABM مبتنی بر بردار حفظ می‌کند. رویکرد توسعه‌یافته GNA برای استفاده صریح از نمایش‌های شبکه، همسایگی‌های مبتنی بر شبکه، قوانین انتقال مبتنی بر شبکه، و تحلیل شبکه با استفاده از نظریه گراف برای شبیه‌سازی پدیده‌های پیچیده مکانی-زمانی طراحی شده است. چارچوب مدل‌سازی GNA با GAS سنتی شامل CA و ABM متفاوت است، زیرا به‌دلیل دیدگاه صریح منحصربفرد آن از روابط مبتنی بر شبکه و تعاملات بین ویژگی‌های فضایی که با پیوندها و ماتریس مجاورت NxN A نشان داده می‌شود، متفاوت است.. چارچوب مدل‌سازی GNA بر نمایش، تحلیل و تجسم داده‌های رابطه‌ای، تعاملات و جریان‌ها تأکید دارد.
در CA و ABM، قوانین انتقال برای شبیه‌سازی روابط، تعاملات و جریان‌ها پیاده‌سازی می‌شوند، اما آنها اغلب به طور صریح نمایش داده نمی‌شوند و یا به‌طور مجزا اندازه‌گیری نمی‌شوند. در عوض، نحوه پاسخگویی سیستم به این تعاملات اندازه گیری می شود. GNA چارچوب مدل‌سازی انعطاف‌پذیرتری نسبت به CA سنتی ارائه می‌کند که در آن گره‌ها ممکن است متحرک باشند، ممکن است چندین نوع همسایگی تعریف‌شده داشته باشند که قوانین انتقال برای آن‌ها پیاده‌سازی شده‌اند، و رفتار غیر قطعی در سطح سیستم. علاوه بر این، GNA نمایش صریح برهمکنش‌ها را به‌عنوان پیوند ارائه می‌دهد و بنابراین دید «اشعه ایکس» از مدل را ارائه می‌کند که می‌تواند برای اندازه‌گیری و تجسم مجموعه‌های بزرگی از تعاملات بین اجزای یک سیستم به‌گونه‌ای که ABM‌ها به طور سنتی انجام نمی‌دهند، استفاده شود.
«شبکه‌ها همه جا هستند» عبارتی است که در بسیاری از مطالعات که تحقیقات شبکه را مرور می‌کنند یافت می‌شود که در نهایت به ماهیت میان رشته‌ای و سودمندی انتزاع سیستم‌های واقعی در شبکه‌های پویا فضایی پیچیده می‌پردازد. این نشان دهنده پتانسیل GNA برای پیاده سازی در بسیاری از کاربردهای دیگر مکانی برای نمایش، توصیف و تحلیل انواع سیستم های پیچیده است. شبکه‌های فضایی پیچیده یک تناسب طبیعی برای نمایش و تحلیل روابط و تعاملات هستند و به این ترتیب، چارچوب مدل‌سازی GNA یک رویکرد ایده‌آل برای کاربردهایی است که تعامل، روابط، پویایی و جریان‌های بین مجموعه‌ای از مؤلفه‌ها مورد توجه هستند. پتانسیل کاربرد گسترده است و شامل حرکت و جریان اطلاعات، مردم، منابع، پول، گونه های زیست محیطی، انرژی، بیماری، و وسایل حمل و نقل در طول زمان و در سراسر نقاط در فضای جغرافیایی. طبیعتاً مطالعه روابط فضایی و غیرمکانی بین افراد نیز کاربرد ایده آلی برای این رویکردهای مدل سازی است. علاوه بر این، رویکرد مدل‌سازی GNA پیشنهادی برای درک بهتر تعاملات بین دو یا چند سیستم محکم مرتبط در مکان و زمان مانند تعاملات بین سیستم‌های سیاست، اجتماعی و محیطی ایده‌آل خواهد بود. چارچوب مدل‌سازی GNA پیشنهادی با هدف جایگزینی سایر گازهای گازی توسعه‌یافته و همچنین ادعا نمی‌کند که بهتر از آن است، اما در عوض، ابزار جدیدی برای نمایش و عدسی جدیدی برای تجزیه و تحلیل پدیده‌های پیچیده مکانی-زمانی ارائه می‌دهد. مطالعه روابط فضایی و غیر فضایی بین افراد نیز یک کاربرد ایده آل برای این رویکردهای مدل سازی است. علاوه بر این، رویکرد مدل‌سازی GNA پیشنهادی برای درک بهتر تعاملات بین دو یا چند سیستم محکم مرتبط در مکان و زمان مانند تعاملات بین سیستم‌های سیاست، اجتماعی و محیطی ایده‌آل خواهد بود. چارچوب مدل‌سازی GNA پیشنهادی با هدف جایگزینی سایر گازهای گازی توسعه‌یافته و همچنین ادعا نمی‌کند که بهتر از آن است، اما در عوض، ابزار جدیدی برای نمایش و عدسی جدیدی برای تجزیه و تحلیل پدیده‌های پیچیده مکانی-زمانی ارائه می‌دهد. مطالعه روابط فضایی و غیر فضایی بین افراد نیز یک کاربرد ایده آل برای این رویکردهای مدل سازی است. علاوه بر این، رویکرد مدل‌سازی GNA پیشنهادی برای درک بهتر تعاملات بین دو یا چند سیستم محکم مرتبط در مکان و زمان مانند تعاملات بین سیستم‌های سیاست، اجتماعی و محیطی ایده‌آل خواهد بود. چارچوب مدل‌سازی GNA پیشنهادی با هدف جایگزینی سایر گازهای گازی توسعه‌یافته و همچنین ادعا نمی‌کند که بهتر از آن است، اما در عوض، ابزار جدیدی برای نمایش و عدسی جدیدی برای تجزیه و تحلیل پدیده‌های پیچیده مکانی-زمانی ارائه می‌دهد. رویکرد مدل‌سازی GNA پیشنهادی برای درک بهتر تعاملات بین دو یا چند سیستم محکم مرتبط در مکان و زمان مانند تعاملات بین سیستم‌های سیاست، اجتماعی و محیطی ایده‌آل خواهد بود. چارچوب مدل‌سازی GNA پیشنهادی با هدف جایگزینی سایر گازهای گازی توسعه‌یافته و همچنین ادعا نمی‌کند که بهتر از آن است، اما در عوض، ابزار جدیدی برای نمایش و عدسی جدیدی برای تجزیه و تحلیل پدیده‌های پیچیده مکانی-زمانی ارائه می‌دهد. رویکرد مدل‌سازی GNA پیشنهادی برای درک بهتر تعاملات بین دو یا چند سیستم محکم مرتبط در مکان و زمان مانند تعاملات بین سیستم‌های سیاست، اجتماعی و محیطی ایده‌آل خواهد بود. چارچوب مدل‌سازی GNA پیشنهادی با هدف جایگزینی سایر گازهای گازی توسعه‌یافته و همچنین ادعا نمی‌کند که بهتر از آن است، اما در عوض، ابزار جدیدی برای نمایش و عدسی جدیدی برای تجزیه و تحلیل پدیده‌های پیچیده مکانی-زمانی ارائه می‌دهد.
مدل‌های GNA ارائه‌شده با موفقیت پدیده‌های فضایی پویا را به عنوان شبکه‌ها نشان می‌دهند که با استفاده از دو مطالعه موردی نشان داده شده‌اند. کمی سازی ساختارهای شبکه شبیه سازی شده با استفاده از معیارهای شبکه می تواند درک جدیدی از پدیده ها را آشکار کند. در مثال بازی زندگی، معیارهای شبکه راهی برای تعیین کمیت رفتارهای رایج پدیده‌های مکانی-زمانی مانند رشد و انقباض ارائه می‌دهند. در مثال تفکیک، مشخص می‌شود که طبقه‌بندی اندازه‌گیری شبکه می‌تواند برای کمی کردن تفکیک در سطح فردی و به طور کلی بسیار مفید باشد. این یک چالش با شاخص‌های تفکیک سنتی بوده است که تمایل دارند تفکیک را در واحدهای اندازه‌گیری مختلف خلاصه کنند، یعنی مرزهای سرشماری و به این ترتیب مشمول مشکل واحد منطقه‌ای قابل تغییر هستند.
مثال بازی زندگی GNA GOL ارائه شده در این مطالعه تحقیقاتی، تکامل ساختارهای شبکه متشکل از گره‌هایی را شبیه‌سازی می‌کند که از نظر جغرافیایی ارجاع داده شده‌اند. نمونه تفکیک GNA SEG از داده‌های GIS واقعی برای منطقه مورد مطالعه در شهر ونکوور استفاده می‌کند تا مکان واقعی گره‌ها را نشان دهد که در آن هر گره نشان‌دهنده یک ملک مسکونی در شهر است. یک تفاوت کیفی بین دو مطالعه موردی وجود دارد که در آن سطح ادغام GIS از GNA GOL به GNA SEG افزایش یافته است.ادغام GIS و اتوماتای ​​شبکه و در نتیجه ارائه چارچوب اتوماتای ​​شبکه جغرافیایی از سه طریق سودمند است: (1) ساختار و دینامیک شبکه را می توان به داده های جغرافیایی مرجع که پدیده های دنیای واقعی را نشان می دهد پیوند داد، (2) تصویرسازی جغرافیایی شبکه های فضایی در حال تکامل شبیه سازی شده ارجاع جغرافیایی به یک منطقه مورد مطالعه، و (3) هر دو تجزیه و تحلیل فضایی با استفاده از GIS و تجزیه و تحلیل شبکه ساختارهای شبکه فضایی تولید شده را می توان به کار گرفت.
حتی اگر GNA SEG داده‌های مکانی واقعی را برای تشکیل شبکه زیربنایی UN SEG ترکیب می‌کند، کار آینده ممکن است بر پارامترهای اضافی و آزمایش و اعتبارسنجی مدل کامل تمرکز کند. اعتبار سنجی مدل به عنوان میزان توافق بین ساختارهای شبکه فضایی شبیه سازی شده و الگوهای فضایی دنیای واقعی مشاهده شده در نظر گرفته می شود، که باید با استفاده از مجموعه داده هایی که مستقل از توسعه و کالیبراسیون مدل هستند ارزیابی شوند. کار آینده مستلزم کاوش رویکردهای اعتبارسنجی مدل مناسب برای مقایسه شبکه های در حال تکامل با مجموعه داده های واقعی است، حتی در مواجهه با کمبود داده مانند رویکرد اعتبار سنجی NEAT [ 62 ].
در نتیجه، این مطالعه اتوماتای ​​شبکه جغرافیایی (GNA)، یک رویکرد مدل‌سازی توسعه‌یافته برای شبیه‌سازی سیستم‌های فضایی به عنوان شبکه‌های فضایی پیچیده در حال تکامل را ارائه می‌کند. تازگی رویکرد GNA در توانایی آن برای نشان دادن اتصال محکم بین ساختار شبکه فضایی و پویایی شبکه است که منجر به تکامل فضا-زمان شبکه می شود. رویکرد GNA اذعان می‌کند که برای بسیاری از پدیده‌ها، تکامل شبکه در فضای جغرافیایی رخ می‌دهد، و بنابراین داده‌های مکانی و سیستم‌های اطلاعات جغرافیایی می‌توانند برای نمایش و تحلیل سیستم‌های واقعی مورد استفاده قرار گیرند. چارچوب مدل‌سازی GNA یک رویکرد سیستمی پیچیده را با شبیه‌سازی تعاملات فضایی محلی بین گره‌های جغرافیایی مرجع که توسط پیوندهایی که از آن یک شبکه پیچیده پدید می‌آید، اتخاذ می‌کند. در نهایت، این رویکرد یک کلاس جدید از GAS در کنار مدل‌های ABM و CA است. این چارچوب با استفاده از نمایش شبکه فضایی دو مدل GNA از جمله بازی زندگی کانوی و مدل تفکیک شلنگ اجرا می‌شود که در آن قوانین انتقال پیاده‌سازی شده پویایی بین گره‌ها را در سطح محلی شبیه‌سازی می‌کنند و ساختار شبکه فضایی را تغییر می‌دهند، که به نوبه خود بر پویایی بین گره ها سپس از نظریه گراف برای توصیف و اندازه گیری ساختار و رفتار شبکه های شبیه سازی شده استفاده می شود. رویکرد توسعه‌یافته GNA هم کلی و هم انعطاف‌پذیر است به طوری که می‌توان آن را برای نمایش و تحلیل بسیاری از سیستم‌های جغرافیایی واقعی از جمله شهری، اجتماعی و زیست‌محیطی به کار برد و پتانسیل استفاده در فرآیندهای کشف دانش و تصمیم‌گیری را دارد. این چارچوب با استفاده از نمایش شبکه فضایی دو مدل GNA از جمله بازی زندگی کانوی و مدل تفکیک شلنگ اجرا می‌شود که در آن قوانین انتقال پیاده‌سازی شده پویایی بین گره‌ها را در سطح محلی شبیه‌سازی می‌کنند و ساختار شبکه فضایی را تغییر می‌دهند، که به نوبه خود بر پویایی بین گره ها سپس از نظریه گراف برای توصیف و اندازه گیری ساختار و رفتار شبکه های شبیه سازی شده استفاده می شود. رویکرد توسعه‌یافته GNA هم کلی و هم انعطاف‌پذیر است به طوری که می‌توان آن را برای نمایش و تحلیل بسیاری از سیستم‌های جغرافیایی واقعی از جمله شهری، اجتماعی و زیست‌محیطی به کار برد و پتانسیل استفاده در فرآیندهای کشف دانش و تصمیم‌گیری را دارد. این چارچوب با استفاده از نمایش شبکه فضایی دو مدل GNA از جمله بازی زندگی کانوی و مدل تفکیک شلنگ اجرا می‌شود که در آن قوانین انتقال پیاده‌سازی شده پویایی بین گره‌ها را در سطح محلی شبیه‌سازی می‌کنند و ساختار شبکه فضایی را تغییر می‌دهند، که به نوبه خود بر پویایی بین گره ها سپس از نظریه گراف برای توصیف و اندازه گیری ساختار و رفتار شبکه های شبیه سازی شده استفاده می شود. رویکرد توسعه‌یافته GNA هم کلی و هم انعطاف‌پذیر است به طوری که می‌توان آن را برای نمایش و تحلیل بسیاری از سیستم‌های جغرافیایی واقعی از جمله شهری، اجتماعی و زیست‌محیطی به کار برد و پتانسیل استفاده در فرآیندهای کشف دانش و تصمیم‌گیری را دارد. سپس از نظریه گراف برای توصیف و اندازه گیری ساختار و رفتار شبکه های شبیه سازی شده استفاده می شود. رویکرد توسعه‌یافته GNA هم کلی و هم انعطاف‌پذیر است به طوری که می‌توان آن را برای نمایش و تحلیل بسیاری از سیستم‌های جغرافیایی واقعی از جمله شهری، اجتماعی و زیست‌محیطی به کار برد و پتانسیل استفاده در فرآیندهای کشف دانش و تصمیم‌گیری را دارد. سپس از نظریه گراف برای توصیف و اندازه گیری ساختار و رفتار شبکه های شبیه سازی شده استفاده می شود. رویکرد توسعه‌یافته GNA هم کلی و هم انعطاف‌پذیر است به طوری که می‌توان آن را برای نمایش و تحلیل بسیاری از سیستم‌های جغرافیایی واقعی از جمله شهری، اجتماعی و زیست‌محیطی به کار برد و پتانسیل استفاده در فرآیندهای کشف دانش و تصمیم‌گیری را دارد.

منابع

  1. اسکلاتو، اس. نولاس، ا. لامبیوت، آر. Mascolo، C. ویژگی های اجتماعی- فضایی شبکه های اجتماعی مبتنی بر مکان آنلاین. مجموعه مقالات پنجمین کنفرانس بین المللی AAAI در وبلاگ ها و رسانه های اجتماعی، بارسلون، اسپانیا، 17-21 ژوئیه 2011; صص 329-336. [ Google Scholar ]
  2. ژونگ، سی. آریسونا، اس ام. هوانگ، ایکس. باتی، م. اشمیت، جی. تشخیص پویایی ساختار شهری از طریق تحلیل شبکه فضایی. بین المللی جی. جئوگر. Inf. علمی 2014 ، 28 ، 2178-2199. [ Google Scholar ] [ CrossRef ]
  3. Fortuna، MA; گومز-رودریگز، سی. Bascompte، J. ساختار شبکه فضایی و تداوم دوزیستان در محیط های تصادفی. Proc. R. Soc. B Biol. علمی 2006 ، 273 ، 1429-1434. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  4. کویلو، سی. Guo, D. هموارسازی اقدامات مکانی در شبکه های تعامل فضایی. محاسبه کنید. محیط زیست سیستم شهری 2013 ، 41 ، 12-25. [ Google Scholar ] [ CrossRef ]
  5. سرکار، دی. آندریس، سی. چپمن، کالیفرنیا؛ سنگوپتا، R. متریک برای توصیف ساختار شبکه و اهمیت گره در شبکه های اجتماعی فضایی. بین المللی جی. جئوگر. Inf. علمی 2019 ، 33 ، 1017–1039. [ Google Scholar ] [ CrossRef ]
  6. گراس، تی. سایاما، اچ. شبکه های تطبیقی. در شبکه های تطبیقی: نظریه، مدل ها و کاربردها . Gross, T., Sayama, H., Eds. Springer: هایدلبرگ، آلمان، 2009; صص 1-8. [ Google Scholar ]
  7. بانسال، اس. بخوانید، جی. پوربهلول، بی. مایرز، لس آنجلس ماهیت پویا شبکه های تماس در اپیدمیولوژی بیماری های عفونی. جی بیول. دین 2010 ، 4 ، 478-489. [ Google Scholar ] [ CrossRef ]
  8. بالکان، دی. کولیزا، وی. گونسالوز، بی. متعجب.؛ راماسکو، جی جی. Vespignani، A. شبکه های تحرک چند مقیاسی و گسترش فضایی بیماری های عفونی. Proc. Natl. آکادمی علمی ایالات متحده آمریکا 2009 ، 106 ، 21484–21489. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  9. اسمیت، دی.م. اونلا، جی.-پی. لی، سی اف; Fricker، MD; جانسون، اتوماتای ​​شبکه NF: ساختار و عملکرد جفت در شبکه های پویا. Adv. سیستم پیچیده 2011 ، 14 ، 317-339. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  10. Barthelemy، M. مورفوژنز شبکه های فضایی . Springer International Publishing: Cham, Switzerland, 2018. [ Google Scholar ]
  11. O’Sullivan، D. به سمت مدل سازی فضایی در مقیاس خرد از gentrification. جی. جئوگر. سیستم 2002 ، 4 ، 251-274. [ Google Scholar ] [ CrossRef ]
  12. شهری، دی. کیت، تی. اتصال چشم انداز: دیدگاه نظری گراف. اکولوژی 2001 ، 82 ، 1205-1218. [ Google Scholar ]
  13. دوکروت، سی. Notteboom، T. شبکه جهانی کشتیرانی دریایی: ساختار فضایی و پویایی منطقه ای. گلوب. شبکه 2012 ، 12 ، 395-423. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  14. جیانگ، بی. سلسله مراتب خیابان: اقلیتی از خیابان ها اکثریت جریان ترافیک را تشکیل می دهند. بین المللی جی. جئوگر. Inf. علمی 2009 ، 23 ، 1033-1048. [ Google Scholar ] [ CrossRef ]
  15. بیان، ال. Liebner, D. مدل شبکه ای برای پراکندگی بیماری های واگیر. ترانس. GIS 2007 ، 11 ، 155-173. [ Google Scholar ] [ CrossRef ]
  16. کولیزا، وی. بارات، ا. بارتلمی، ام. Vespignani، A. نقش شبکه حمل و نقل هوایی در پیش بینی و قابل پیش بینی اپیدمی های جهانی. Proc. Natl. آکادمی علمی ایالات متحده آمریکا 2006 ، 103 ، 2015-2020. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  17. بوکارا، ن. Cheong، K. رفتار بحرانی یک مدل SIS شبکه خودکار احتمالی برای گسترش یک بیماری عفونی در جمعیتی از افراد در حال حرکت. J. Phys. یک ریاضی Gen. 1993 , 26 , 3707. [ Google Scholar ] [ CrossRef ]
  18. بوکارا، ن. رابلین، او. Roger, M. Automata شبکه شکارچی-شکار مدل با تعقیب و گریز. فیزیک Rev. E 1994 , 50 , 4531. [ Google Scholar ] [ CrossRef ]
  19. سایاما، اچ. Laramee, C. Generative network automata: چارچوبی تعمیم یافته برای مدلسازی پویایی شبکه تطبیقی ​​با استفاده از بازنویسی نمودار. در شبکه های تطبیقی: نظریه، مدل ها و کاربردها . Gross, T., Sayama, H., Eds. Springer: هایدلبرگ، آلمان، 2009; صص 311-332. [ Google Scholar ]
  20. کانوی، جی. بازی زندگی. علمی صبح. 1970 ، 223 ، 4. [ Google Scholar ]
  21. شلینگ، مدل های TC از تفکیک. صبح. اقتصاد Rev. 1969 , 59 , 488-493. [ Google Scholar ]
  22. شلینگ، مدل های دینامیک TC تفکیک. جی. ریاضی. اجتماعی 1971 ، 1 ، 143-186. [ Google Scholar ] [ CrossRef ]
  23. اندرسون، تی. Dragicevic، S. رویکرد خودکار شبکه جغرافیایی برای مدل‌سازی سیستم‌های اکولوژیکی پویا. Geogr. مقعدی 2020 ، 52 ، 3-27. [ Google Scholar ] [ CrossRef ]
  24. نیومن، ME ساختار و عملکرد شبکه های پیچیده. SIAM Rev. 2003 , 45 , 167-256. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  25. Barthélemy، M. شبکه های فضایی. فیزیک Rep. 2011 , 499 , 1-101. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  26. لوئیس، علم شبکه TG: نظریه و عمل . جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2011. [ Google Scholar ]
  27. باراباسی، ع.-ال. علوم شبکه ; انتشارات دانشگاه کمبریج: کمبریج، بریتانیا، 2016. [ Google Scholar ]
  28. بوکالتی، اس. لاتورا، وی. مورنو، ی. چاوز، م. هوانگ، دی.-یو. شبکه های پیچیده: ساختار و پویایی فیزیک Rep. 2006 , 424 , 175-308. [ Google Scholar ] [ CrossRef ]
  29. Erdős، P. Rényi, A. در مورد تکامل نمودارهای تصادفی. انتشار ریاضی. Inst. آویزان شد. آکادمی علمی 1960 ، 5 ، 17-60. [ Google Scholar ]
  30. دال، جی. کریستنسن، ام. نمودارهای هندسی تصادفی. فیزیک Rev. E 2002 , 66 , 016121. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  31. آنتونیونی، آ. Tomassini، M. همبستگی های درجه در نمودارهای هندسی تصادفی. فیزیک Rev. E 2012 , 86 , 037101. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  32. واتس، دی جی؛ استروگاتز، SH دینامیک جمعی شبکه‌های «جهان کوچک». Nature 1998 , 393 , 440. [ Google Scholar ] [ CrossRef ]
  33. آلبرت، آر. جونگ، اچ. باراباسی، ع.-ال. قطر وب جهانی طبیعت 1999 ، 401 ، 130-131. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  34. کوهن، آر. ارز، ک. بن-آوراهام، دی. هاولین، اس. انعطاف پذیری اینترنت در برابر خرابی های تصادفی. فیزیک کشیش لِت 2000 ، 85 ، 4626. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  35. Udny Yule، G. یک نظریه ریاضی تکامل، بر اساس نتایج دکتر JC Willis، FRS. فیلوس ترانس. R. Soc. لندن. سر. B 1925 , 213 , 21-87. [ Google Scholar ]
  36. جونگ، اچ. ندا، ز. باراباسی، ع.-ال. اندازه گیری دلبستگی ترجیحی در شبکه های در حال تکامل EPL (Europhys. Lett.) 2003 ، 61 ، 567. [ Google Scholar ] [ CrossRef ] [ نسخه سبز ]
  37. دسوزا، آر.ام. بورگس، سی. Chayes، JT; برگر، ن. Kleinberg، RD ظهور دلبستگی ترجیحی تعدیل شده از بهینه سازی. Proc. Natl. آکادمی علمی ایالات متحده آمریکا 2007 ، 104 ، 6112-6117. [ Google Scholar ] [ CrossRef ] [ PubMed ][ نسخه سبز ]
  38. Simphony, R. Repast Simphony نسخه 2.4 ; دانشگاه شیکاگو: شیکاگو، IL، ایالات متحده آمریکا، 2016. [ Google Scholar ]
  39. Van Wijk، BC; استام، سی جی; Daffertshofer، A. مقایسه شبکه‌های مغزی با اندازه‌های مختلف و چگالی اتصال با استفاده از نظریه گراف. PLoS ONE 2010 ، 5 ، e13701. [ Google Scholar ] [ CrossRef ] [ PubMed ]
  40. آریباس-بل، دی. Nijkamp، P. پوت، جی. معیارهای جداسازی چقدر می تواند متنوع باشد؟ نتایج شبیه‌سازی مونت کارلو یک مدل مبتنی بر عامل. محیط زیست طرح. یک اقتصاد. فضا 2016 ، 48 ، 2046–2066. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  41. سینگ، آ. وینشتاین، دی. ویس، مدل تفکیک H. شلینگ: پارامترها، مقیاس‌بندی و تجمع. Demogr. Res. 2009 ، 21 ، 341-366. [ Google Scholar ] [ CrossRef ]
  42. بننسون، آی. عمر، آی. هاتنا، E. مدل‌سازی پویایی مسکونی شهری مبتنی بر نهاد: مورد یافو، تل آویو. محیط زیست طرح. B طرح. دس 2002 ، 29 ، 491-512. [ Google Scholar ] [ CrossRef ]
  43. فلینت اشری، اس. تفکیک خرد از نوع شلینگ در یک منطقه حصیدی در استمفورد-هیل. خانه گل میخ. 2018 ، 33 ، 1038-1059. [ Google Scholar ] [ CrossRef ]
  44. پرز، ال. دراگیسویچ، اس. Gaudreau، J. یک مدل مبتنی بر عامل جغرافیایی از پویایی شهری فضایی جمعیت مهاجر: مطالعه جزیره مونترال، کانادا. PLoS ONE 2019 , 14 , e0219188. [ Google Scholar ] [ CrossRef ]
  45. فاگیولو، جی. والنته، ام. Vriend، NJ جداسازی در شبکه ها. جی. اکون. رفتار عضو. 2007 ، 64 ، 316-336. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  46. Banos، A. اثرات شبکه در مدل تفکیک شلینگ: شواهد جدید از شبیه‌سازی مبتنی بر عامل. محیط زیست طرح. B طرح. دس 2012 ، 39 ، 393-405. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  47. Netto، VM; سوآرس، نماینده مجلس؛ Paschoalino, R. شبکه های جدا شده در شهر. بین المللی J. Urban Reg. Res. 2015 ، 39 ، 1084-1102. [ Google Scholar ] [ CrossRef ]
  48. کوی، ز. هوانگ، Y.-A. تبادل خانه و تفکیک مسکونی در شبکه ها. بین المللی J. Game Theory 2017 ، 46 ، 125–147. [ Google Scholar ] [ CrossRef ]
  49. بننسون، آی. Torrens, P. Geosimulation: Automata-based Modeling of Urban Phenomen ; جان وایلی و پسران: وست ساسکس، بریتانیا، 2004. [ Google Scholar ]
  50. تورنس، PM؛ Benenson، I. سیستم های خودکار جغرافیایی. بین المللی جی. جئوگر. Inf. علمی 2005 ، 19 ، 385-412. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  51. وایت، آر. Engelen، G. مدل سازی یکپارچه با وضوح بالا از پویایی فضایی سیستم های شهری و منطقه ای. محاسبه کنید. محیط زیست سیستم شهری 2000 ، 24 ، 383-400. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  52. کروکس، آ. قلعه، سی. Batty، M. چالش های کلیدی در مدل سازی مبتنی بر عامل برای شبیه سازی جغرافیایی فضایی. محاسبه کنید. محیط زیست سیستم شهری 2008 ، 32 ، 417-430. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  53. تورنس، مدل‌های مبتنی بر عامل PM و علوم فضایی. Geogr. Compass 2010 , 4 , 428-448. [ Google Scholar ] [ CrossRef ]
  54. وایت، آر. Engelen، G. اتوماتای ​​سلولی به عنوان اساس مدل سازی منطقه ای پویا یکپارچه. محیط زیست طرح. B طرح. دس 1997 ، 24 ، 235-246. [ Google Scholar ] [ CrossRef ]
  55. باتی، م. زی، ی. Sun، Z. مدلسازی دینامیک شهری از طریق اتوماتای ​​سلولی مبتنی بر GIS. محاسبه کنید. محیط زیست سیستم شهری 1999 ، 23 ، 205-233. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  56. Gimblett، HR یکپارچه‌سازی سیستم‌های اطلاعات جغرافیایی و تکنیک‌های مدل‌سازی مبتنی بر عامل برای شبیه‌سازی فرآیندهای اجتماعی و اکولوژیکی ؛ انتشارات دانشگاه آکسفورد: نیویورک، نیویورک، ایالات متحده آمریکا، 2002. [ Google Scholar ]
  57. DeAngelis، DL; Mooij، WM مدل‌سازی فردی فرآیندهای اکولوژیکی و تکاملی. آنو. کشیش اکول. تکامل. سیستم 2005 ، 36 ، 147-168. [ Google Scholar ] [ CrossRef ]
  58. O’Sullivan، D. Graph-cellular automata: یک مدل شهری و منطقه ای گسسته تعمیم یافته. محیط زیست طرح. B طرح. دس 2001 ، 28 ، 687-705. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
  59. بلومنفلد-لیبرتال، ای. پرتغالی، J. شهرهای شبکه: رویکرد شبکه پیچیدگی به پویایی و توسعه شهری. در تحلیل جغرافیایی و مدلسازی ساختار و دینامیک شهری ; جیانگ، بی.، یائو، ایکس.، ویرایش. Springer: New York, NY, USA, 2010; صص 77-90. [ Google Scholar ]
  60. پیرس، بی. کروکس، AT مدل‌سازی ظهور شورش‌ها: یک رویکرد شبیه‌سازی زمین. محاسبه کنید. محیط زیست سیستم شهری 2017 ، 61 ، 66-80. [ Google Scholar ] [ CrossRef ]
  61. اندرسون، TM; Dragićević، S. مدل مبتنی بر عامل شبکه برای شبیه‌سازی ساختار شبکه فضایی پویا سیستم‌های اکولوژیکی پیچیده. Ecol. مدل. 2018 ، 389 ، 19-32. [ Google Scholar ] [ CrossRef ]
  62. اندرسون، تی. رویکرد Dragicevic، S. NEAT برای آزمایش و اعتبارسنجی مدل‌های مبتنی بر عامل شبکه جغرافیایی. بین المللی جی. جئوگر. Inf. علمی 2020 ، در دست چاپ. [ Google Scholar ] [ CrossRef ][ نسخه سبز ]
Ijgi 09 00270 g001 550
شکل 1. پویایی شبکه های فضایی پیچیده SN ( a ) یک شبکه اولیه مورد علاقه SN که در طول زمان تکامل می یابد و ( b ) در یک شبکه SN که در آن شبکه مورد علاقه در طول زمان به عنوان تابعی از یک شبکه زیربنایی UN تکامل می یابد .
Ijgi 09 00270 g002 550
شکل 2. بر اساس ( a ) حالت اولیه، شبکه های فضایی در حال تکامل SN GOL تولید شده از GNA GOL برای سناریوی 1 در مراحل زمانی ( b ) t 5 ، ( c ) t 10 ، ( d ) t 15 ، (د) ارائه شده است. e ) t 20 و سناریو 2 در مراحل زمانی ( f ) t 5 ، ( g ) t 10 ، ( h ) t 15 ، ( i ) t 20.
Ijgi 09 00270 g003 550
شکل 3. تعداد محاسبه‌شده گره‌ها، تعداد پیوندها، میانگین ضریب خوشه‌بندی، میانگین درجه و طول مسیر برای شبکه فضایی به‌دست‌آمده SN GOL همانطور که در فضا و زمان ایجاد شده از ( الف ) سناریوی 1: رشد شبکه و ( ب ) سناریوی 2: انقباض شبکه.
Ijgi 09 00270 g004 550
شکل 4. توزیع درجه محاسبه شده برای هر شبکه فضایی در حال تکامل SN GOL همانطور که در طول زمان ایجاد می شود از ( الف ) سناریوی 1: رشد شبکه و ( ب ) سناریو 2: انقباض شبکه.
Ijgi 09 00270 g005 550
شکل 5. بر اساس ( a ) حالت اولیه، شبکه فضایی در حال تکامل SN SEG تولید شده از GNA SEG ارائه شده است که به طور فزاینده ای در ( b ) t 20 جدا می شود . نقشه های درونی برای هر مرحله زمانی برای هر یک ارائه شده است که ترکیب محله ها را به ترتیب در t 0 و t 20 نشان می دهد.
Ijgi 09 00270 g006 550
شکل 6. مقادیر به‌دست‌آمده برای تعداد گره‌ها، تعداد پیوندها، میانگین ضریب خوشه‌بندی، میانگین درجه، میانگین طول مسیر، و طبقه‌بندی برای شبکه فضایی SN SEG همانطور که در مکان و زمان تکامل می‌یابد.
Ijgi 09 00270 g007 550
شکل 7. توزیع درجه به دست آمده برای هر شبکه فضایی در حال تکامل SN SEG همانطور که در طول زمان تکامل می یابد.

مقالات داخلی و بین المللی

مطالب مرتبط ...

بدون دیدگاه

دیدگاهتان را بنویسید