1. معرفی
رویدادهای فعالیت های انسانی عمدتاً با مکان های قابل تعریف و مهرهای زمانی وقوع مرتبط هستند. اطلاعات مکانی و زمانی جمع آوری شده از این رویدادها ممکن است نه تنها الگوهای فضایی فعالیت ها در دوره های مختلف، بلکه تکامل فرآیندهای مکانی در طول زمان را نیز تشکیل دهد [ 1 ]. رویدادهای فعالیت انسانی را می توان به عنوان داده های نقطه ای با اطلاعات مکانی و زمانی ثبت کرد، که به دلیل سنسورهای مقرون به صرفه، اینترنت به طور گسترده در دسترس و فناوری مکانی در حال پیشرفت دائماً در دسترس هستند. داده های مربوط به رویدادهای فعالیت انسانی از منابع متعددی به دست می آید که در دسترس هستند و منتظر راه های جدیدی برای تجزیه و تحلیل و تفسیر هستند [ 2 ].
آمار مکانی و مکانی-زمانی، خانوادهای از شاخصهای غیر گرافیکی، معمولاً برای توصیف خودهمبستگی مکانی/مکانی با اندازهگیری درجاتی که اجسام در فضا و در طول زمان همبستگی یا خوشهبندی دارند، استفاده میشود. خود همبستگی مکانی و زمانی رویدادهای فعالیت انسانی می تواند به عنوان یک مرجع اساسی برای نظارت بر تکامل رویدادها برای تسهیل ارزیابی اثرات زیست محیطی استفاده شود. رویدادهای فعالیت انسانی، که به دلیل سطوح خود همبستگی مکانی و زمانی مورد مطالعه قرار گرفتهاند، شامل مشاهده زیستگاههای حیوانات یا جوامع گیاهی در معرض خطر/در معرض خطر، جنایات، تجارت بینمنطقهای یا بینالمللی، یا حتی پدیدههای اخیر مانند پستهای رسانههای اجتماعی و بسیاری از اشکال دیگر پویایی رفتاری انسان [ 3 ، 4 ،5 ، 6 ، 7 ].
در اکثر مطالعات موجود، این روشها بیشتر بر ارزیابی همبستگی مکانی-زمانی یک نوع واحد از رویدادهای فعالیت انسانی تمرکز دارند. با این حال، کار با رویدادهایی با بیش از یک نوع، دو چالش اصلی دارد. اولاً، از آنجایی که اغلب تصور میشود رویدادها ارتباط نزدیکی با محیطهای جغرافیایی خود دارند، همه دستهبندی رویدادها اغلب دارای سطوح مشابهی از خوشهبندی مکانی-زمانی در نظر گرفته میشوند. با این حال، در برخی موارد، با توجه به یکسان بودن همه رویدادها، ارتباط و تأثیرات تعاملی بین دستههای مختلف رویدادهای فعالیت نادیده گرفته میشود. بنابراین، عوامل کلیدی مؤثر بر خودهمبستگی مکانی – زمانی یک نوع خاص از رویداد ممکن است شناسایی نشوند. دومین، جنبه های مکانی و زمانی را باید از منظر فیزیکی متفاوت در نظر گرفت زیرا مکان و زمان اغلب در واحدهای مختلف اندازه گیری می شوند. این دو بعد نباید در یک معادله به طور مستقیم مشابه بسیاری از روش های موجود ترکیب شوند. این مسائل توسعه و استفاده از معیارهای خودهمبستگی مکانی-زمانی رویدادهای فعالیت انسانی را به شدت محدود کرده است.
برای پر کردن این شکاف روششناختی، روشی برای اندازهگیری سطح خوشهبندی مکانی-زمانی یا خودهمبستگی مکانی-زمانی در توزیع مجموعهای از رویدادهای فعالیت انسانی با دستههای دوتایی یا چندگانه پیشنهاد شده است. ما رابطه مکانی-زمانی بین رویدادها را با استفاده از مدل Voronoi (برای بعد مکانی) و یک مدل پنجره کشویی (برای بعد زمانی) مدلسازی کردیم. این شاخص توسعهیافته، همبستگی توزیع مکانی-زمانی رویدادهای باینری یا چند طبقهای را مشخص میکند. روش پیشنهادی برای نشان دادن امکانسنجی و کاربرد آن بر روی دادههای شبیهسازی شده و دنیای واقعی اعمال شد.
سهم این مقاله دوگانه است. اول، یک مدل پنجره کشویی مبتنی بر Voronoi برای پشتیبانی از تحلیل مکانی و زمانی رویدادهای جغرافیایی با اطلاعات ویژگیهای دستهبندی متعدد پیشنهاد شدهاست. این مدل همبستگی مکانی-زمانی را در بین رویدادهای فعالیت انسانی که به عنوان نقاط گسسته نشان داده شده اند، ارزیابی می کند. می توان از آن برای اندازه گیری سطوح خوشه بندی مکانی-زمانی برای پشتیبانی از تجزیه و تحلیل بعدی استفاده کرد. دوم، اهمیت روابط بین دستههایی از رویدادها در مجموعه داده برجسته میشود. با بهترین دانش ما، این اولین شاخصی است که همبستگی توزیع مکانی-زمانی را برای داده های نقطه ای دسته های مختلف مشخص می کند.
2. بررسی ادبیات
نشان داده شده است که بسیاری از رویدادها دارای همبستگی مکانی/فضایی زمانی هستند که ممکن است تحت تأثیر عوامل اجتماعی-اقتصادی و/یا محیط فیزیکی در این مکان ها قرار گیرد [ 8 ، 9 ، 10 ]]. ما در مورد کارهای قبلی در مورد خودهمبستگی مکانی و خودهمبستگی مکانی-زمانی بحث می کنیم. به عنوان یک روش کلی، تجزیه و تحلیل رویدادهای جغرافیایی اغلب از ارزیابی اینکه آیا سطح مشخصی از خوشهبندی مکانی/مکانی در میان آنها وجود دارد، شروع میشود. اگر چنین خوشهبندی یافت شود، آنگاه فرض کردیم که عوامل خاصی در این مکانها یا در نزدیکی آنها ممکن است بر توزیع رویدادها برای به دست آوردن چنین الگوهای خوشهبندی تأثیر گذاشته باشند. اگر خوشه بندی مطلوب باشد، گام منطقی بعدی شناسایی عوامل تأثیرگذار برای ترویج خوشه بندی خواهد بود. از طرف دیگر، اگر چنین خوشهبندی نامطلوب باشد، شناسایی عوامل تأثیرگذار مستلزم سیاستگذاری یا اقدامات مناسب برای کاهش سطح خوشهبندی است.
2.1. الگوی فضایی رویدادها
روشهایی برای اندازهگیری سطوح خودهمبستگی فضایی در میان رویدادهای جغرافیایی با اطلاعات ویژگیهای مقیاس فاصله و نسبت موجود است. مطالعات بسیاری با استفاده از چنین روش هایی برای یافتن نقاط داغ/نقاط سرد پدیده های جغرافیایی انجام شده است [ 11 ، 12 ، 13 ، 14 ، 15 ، 16 ، 17 ، 18 ]. بنابراین می توان اقدامات مناسبی را در این مکان ها انجام داد. این روش ها بر اساس آمار فضایی مانند موران I، نسبت نزدیکترین همسایه (NNR) [ 19 ] است.] و آمار G. در سالهای اخیر، روشهای جدیدی برای مقابله با دادههای بزرگ مانند برآورد همبستگی خودکار فضایی با دادههای شبکه بزرگ توسعه یافته است [ 20 ].
این روشها برای کار با مجموعههای داده طراحی شدهاند، که در آن همه دادهها دارای یک دسته هستند یا همه رویدادها یکسان در نظر گرفته میشوند. در حالی که قادر به اندازهگیری سطح خوشهبندی فضایی در مجموعهای از دادههای نقطهای هستند که از همان دسته/نوع هستند، این روشها هنگام کار با دادههای نقطهای دستههای باینری یا چندگانه مفید نیستند [ 21 ].
2.2. الگوی فضایی و زمانی رویدادها
خودهمبستگی مکانی-زمانی به همبستگی رویدادها در درون خود بر فضا و در طول زمان اشاره دارد. این نشان دهنده میزان خوشه یا پراکندگی رویدادهای ویژگی های مشابه است. برخی از مطالعات اخیراً منتشر شده، شروع به گسترش آمار فضایی به آمار مکانی – زمانی کردهاند. این مطالعات شامل تحقیقاتی است که خودهمبستگی مکانی-زمانی را با توسعه آمار فضا-زمان خاص، استفاده از مکعب های فضا-زمان یا استفاده از اسکن های فضا-زمان اندازه گیری می کند [ 8 ، 9 ، 10 ،]. این آثار توانایی ما را از ارزیابی میزان خوشهبندی رویدادها در فضا تا اندازهگیری نحوه خوشهبندی رویدادها در فضا و در طول زمان گسترش دادهاند. این پیشرفت مهم است زیرا راهی برای تجزیه و تحلیل فرآیندهای پویا ارائه می دهد که رویدادهای فعالیت انسانی ممکن است در فضا و در طول زمان تکامل یافته باشند.
برای اندازهگیری سطح خودهمبستگی مکانی-زمانی در مجموعهای از رویدادهای جغرافیایی، برخی از مطالعات رویدادها را در یک بازه زمانی گروهبندی کردهاند تا همبستگی مکانی را برای هر دوره زمانی محاسبه کنند. سپس نتایج با تجزیه و تحلیل سری های زمانی [ 22 ، 23 ، 24 ، 25 ] تجزیه و تحلیل می شوند. مطالعات دیگر نقاط را در مناطق جمع کرده و از چند ضلعی ها به عنوان واحدهای تحلیلی فضایی برای ساختن ساختار مجاورت فضایی چند ضلعی های مرتبط با فرکانس نقاط در چند ضلعی ها استفاده کرده اند. به عنوان مثال، [ 26] از این رویکرد برای طراحی یک مدل خودرگرسیون فضایی برای مطالعات اکولوژیکی استفاده کرد. نمونه های دیگر از قیمت مسکن به عنوان یک ویژگی مکانی-زمانی مرتبط با مجموعه ای از مکان های خانه برای بررسی تغییرات مکانی-زمانی قیمت مسکن استفاده کردند [ 3 ، 27 ، 28 ]. در این موارد و بسیاری موارد دیگر، رویدادها از نظر مکانی-زمانی خوشه بندی شدند، زیرا ویژگی های آنها تحت تأثیر شرایط محلی محیط آنها فرض می شد. بدیهی است که تأثیرات زمانی عوامل تأثیرگذار در هنگام استفاده از روشهای اندازهگیری خودهمبستگی فضایی نامشخص است. نتایج تحلیلی احتمالاً تنها به عنوان رویدادهای فضایی در نظر گرفته شده و معتبر هستند [ 29 ].
برخی از کارها تلاش کرده اند تا خودهمبستگی مکانی-زمانی رویدادهای فعالیت انسانی را بر اساس روش های تحلیل چند متغیره مانند توسعه و کاربرد موران I فضایی-زمانی جهانی با استفاده از وزن های مکانی و وزن های زمانی ساختار یافته جداگانه شناسایی کنند [ 30 ، 31 ، 32 ، 33 ، 34 ، 35 ، 36 ، 37 ] یا تقویم فضا-زمان [ 38 ]. این شاخص ها برای اندازه گیری سطح خودهمبستگی مکانی-زمانی در برخی از پدیده های جغرافیایی استفاده شده است [ 32 , 39 , 40 , 41]. با این حال، ادغام مکان و زمان باید با دقت بیشتری در نظر گرفته شود.
از منظر فیزیکی، منطقی نیست که ویژگیهای مکانی و زمانی رویدادها را به یک شکل در نظر بگیریم. این به این دلیل است که تفاوت های قابل توجهی بین چگونگی ارتباط رویدادها با یکدیگر در مکان و زمان وجود دارد [ 42 ]. به عنوان مثال، دو رویداد ممکن است ارتباط متقابلی در فضا داشته باشند که در مدلهای تعامل فضایی توضیح داده شده است. با این حال، رویدادهای قبلی ممکن است روی رویدادهای جاری تأثیر بگذارند، اما برعکس نه. بنابراین، ادغام مستقیم ابعاد مکانی و زمانی داده های جغرافیایی باید به دقت مورد بازنگری قرار گیرد. به عنوان مثال، سطح خوشه بندی مکانی-زمانی در مجموعه ای از رویدادها ممکن است به عنوان ایجاد شده توسط فرآیندهای تصادفی در نظر گرفته شود [ 28 ، 43 ]]، اگر فرض شود که رخدادها دارای سطوح خاصی از تصادفی هستند. R-tree برای تعریف نقاط همسایه مکانی-زمانی و ارزیابی شاخص K ریپلی مکانی-زمانی [ 44 ] استفاده می شود. در مطالعه دیگری در مورد روندهای مکانی و زمانی رویدادها، مدل های خودرگرسیون مکانی برای داده هایی با ویژگی های مکانی و زمانی استفاده شد [ 26 ].
این مطالعات سطوح خودهمبستگی مکانی-زمانی یک دسته از رویدادها را ارزیابی کردند. مطالعه ما با هدف بررسی و اندازهگیری سطوح خودهمبستگی توزیع مکانی-زمانی یک دسته از رویدادها در صورت همزیستی با رویدادهای دستههای دیگر انجام شد.
3. روش
برای درک بهتر و اندازه گیری سطح همبستگی توزیع مکانی-زمانی رویدادهای فعالیت انسانی، یک روش جدید، خود همبستگی توزیع رویدادهای فعالیت انسانی (DAE) پیشنهاد شده است. این روش به ویژه زمانی مفید است که، برای مثال، رویدادهای مورد مطالعه دارای انواع یا دسته بندی های متعدد باشند. به عنوان مثال، رویدادهای جنایی در یک منطقه در یک دوره زمانی خاص متفاوت است، به عنوان مثال، آنها می توانند سرقت های تجاری یا مسکونی، قتل، یا سرقت باشند. DAE پروندههای سرقت، شاخصی است که سطح خودهمبستگی توزیع پروندههای سرقت را با در نظر گرفتن سایر انواع پروندههای جرم به عنوان دیگر انواع رویدادهای جرم اندازهگیری میکند.
در بیشتر آمارهای فضایی، اندازهگیری خودهمبستگی مکانی-زمانی بین مجموعهای از رویدادها را میتوان در برابر یک فرضیه صفر که فرض میکند رویدادها خوشهبندی نشدهاند، آزمایش کرد. اگر شاخصی که سطح خودهمبستگی مکانی-زمانی را اندازه گیری می کند از نظر آماری به طور معنی داری با سطحی که توزیع تصادفی مکانی-زمانی را نشان می دهد متفاوت باشد، گفته می شود که سطح اندازه گیری شده خود همبستگی مکانی-زمانی از نظر آماری برای حمایت از رد این فرضیه صفر معنادار است.
3.1. مدل پنجره کشویی مبتنی بر Voronoi
یکی از راه های تقسیم بندی فضای اشغال شده توسط مجموعه ای از نقاط (رویدادها) ساختن چند ضلعی های تیسن است [ 45 , 46 , 47 , 48] (همچنین به عنوان چند ضلعی Voronoi شناخته می شود) با استفاده از نقاط به عنوان مرکز چند ضلعی. هر چند ضلعی یک نقطه دارد که به عنوان مرکز چندضلعی عمل می کند. هر مکانی در یک چند ضلعی تیسن به مرکز چندضلعی نزدیکتر از هر چندضلعی دیگر است. از نظر فضایی، همسایگان تیسن را میتوان با ساختن مثلث دلونی که تمام نقاط را به شبکهای از مثلثهایی که زوایای داخلی آنها حداکثر شده است، تعیین کرد. اگر دو نقطه (مرکز) توسط یک یال مثلث دلونی به هم متصل شوند، این دو نقطه همسایه تیسن در نظر گرفته میشوند که نشان میدهد آنها مرکز دو چند ضلعی تیسن مجاور هستند (آنها حداقل بخشی از مرزهای چند ضلعی را به اشتراک میگذارند). لبه های چند ضلعی های تیسن را می توان با نیمسازهای عمود بر لبه های مثلث دلون ترسیم کرد. سپس چنین نیمسازهایی دوباره جمع می شوند تا چندضلعی های تیسن را تشکیل دهند. نمودار چند ضلعی های تیسن به عنوان نمودار ورونوی شناخته می شود و روشی که یک فضا به چند ضلعی های تیسن تقسیم می شود به عنوان تسلاسیون تیسن شناخته می شود. در بیشتر آمارهای فضایی که نقاط را تجزیه و تحلیل میکنند، تسلیت تیسن برای ساختن ساختار همسایگی فضایی در میان رویدادهایی که بهعنوان نقاط نمایش داده میشوند، استفاده میشود.
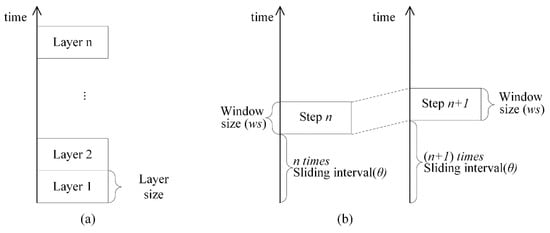
با توجه به ویژگیها و واحدهای تحلیلی، که در آن روابط مکانی و زمانی بین نقاط رویداد متفاوت است، ادغام مستقیم وزنهای مکانی و زمانی با ضرب ماتریس وزنهای مکانی و ماتریس وزنهای زمانی فضای زیادی برای بحث باقی میگذارد [ 42 ]. بنابراین، ما نمیتوانیم با گسترش مستقیم نمودار ورونوی برای همه رویدادها از دوبعدی به سه بعدی، تعیین کنیم که آیا هر یک از جفت رویدادها همسایههای مکانی-زمانی هستند یا خیر (مثلاً، روابط همسایگی زمانی متقابلاً درست نیستند در حالی که روابط همسایگی مکانی ممکن است درست باشد). یکی از راهحلهای ممکن برای مسئله مطالعات موجود، تقسیم رویدادها به یک سری از بازههای زمانی مداوم است که به آن مدل لایهای گفته میشود ( شکل 1).الف)، با هر بازه زمانی یک لایه زمانی در نظر گرفته شود.
مدل لایهای یک مشکل بالقوه را تجربه میکند، به شرح زیر: اگر گروهبندی رویدادها بر اساس ماه و دو رویداد دقیقاً در پایان یک ماه اتفاق میافتد (مثلاً در 31 ژانویه 2019 و 1 فوریه 2019)، در این صورت آنها در لایههای مختلف خواهند بود. بدیهی است که این دو رویداد باید از نظر زمانی مجاور باشند، اما مدل لایهای آنها را به دو لایه متفاوت جدا میکند. برای جلوگیری از این مشکل، ما یک مدل پنجره کشویی را، همانطور که در شکل 1 b نشان داده شده است، با تعیین پویا رویداد در یک لایه تعریف کردیم. با توجه به یک بازه زمانی مانند یک هفته به عنوان اندازه پنجره کشویی ws ، و ساختار لایه همانطور که در شکل 1 ب توضیح داده شده است، لغزش پنجره زمانی، با فاصله کشویی θ، از پایین شروع می شود و به سمت بالا ادامه می یابد.
ما یک مدل جدید ایجاد کردیم، یعنی مدل پنجره کشویی مبتنی بر Voronoi با ترکیب مدل پنجره کشویی و مدل Voronoi. برای ساختن یک ساختار همسایگی مکانی-زمانی استفاده می شود. در این مدل، کشویی پنجره در تمام مدت زمان تکرار میشود تا رویدادهای مجاور مکانی-زمانی را بر اساس ساختار Voronoi فضایی پیدا کند. الگوریتم کامل در الگوریتم 1 نشان داده شده است:
| الگوریتم 1. ساخت ماتریس وزن مکانی-زمانی با الگوریتم پنجره کشویی. |
ورودی :
-
n = تعداد رویدادها،
-
هماهنگ = مکان رویدادها،
-
ts = زمان وقوع رویدادها،
-
ws = اندازه پنجره،
-
θ = اندازه گام کشویی
خروجی : ماتریس وزن فضایی و زمانی
-
1: ماتریس وزن مکانی-زمانی با اندازه n * n ایجاد کنید و همه عناصر را روی 0 تنظیم کنید.
-
2: در حالی که زمان آخرین رویدادها>= لبه به روز رسانی ویندوز فعلی
-
3: xs = [ ]، ys = [ ]
-
4: برای هر رویداد واقع در ویندوز فعلی
-
5: مختصات x و y رویداد را به xs و ys اضافه کنید
-
6: پایان برای
-
7: tri = Delaunay ( xs , ys )
-
8: برای ساده سازی در سه:
-
9: برای هر دو رأس در ساده
-
10: برای مجاورت دو راس در ماتریس فضایی-زمانی روی 1 تنظیم کنید
-
11: پایان برای
-
12: پایان برای
-
13: پنجره اسلاید با اندازه گام θ
-
14: پایان در حالی که
-
15: ماتریس بازگشت
|
3.2. ارزیابی خودهمبستگی توزیع رویدادهای فعالیت انسانی (DAE) رویدادها
پس از ساختن ساختار ارتباط مکانی-زمانی در میان رویدادهای فعالیت انسانی، DAE را با گسترش آمار شمارش مشترک [ 49 ]، یک آمار فضایی قابل استفاده برای دادههای چند ضلعی با ویژگیهای باینری یا چند طبقهای محاسبه کردیم.
بگذارید دسته هدف رویدادها “سیاه” و دسته دیگر رویدادها “قرمز” باشد. با چنین علامت گذاری می توانیم مستقیماً DAE آنها را بر اساس آمار Joint Count ارزیابی کنیم. آمار شمارش مشترک شاید سادهترین معیار آماری همبستگی خودکار فضایی مجموعهای از چند ضلعیهای دوتایی یا چند طبقهای باشد، بهویژه زمانی که فقط مقولهای باشد. اطلاعات ویژگی برای توصیف ویژگی های رویدادها و زمانی که تعداد چند ضلعی ها در هر دسته بسیار متفاوت است، در دسترس است. آمار شمارش مشترک می تواند ابزار بسیار خوبی برای حل مشکل اندازه گیری همبستگی خودکار بین دو دسته رویداد باشد. در نظر گرفتن رویدادهای مکانی-زمانی با یک ویژگی طبقه بندی شده (مانند علامت گذاری به عنوان سیاه و قرمز)، یک آمار تعداد مشترک گسترده را می توان با استفاده از تعداد اتصالات بین رویدادهای همسایه فضایی و زمانی محاسبه کرد. لطفاً توجه داشته باشید که چند ضلعیها در آمار شمارش مشترک فضایی به حجمهای فضا-زمان در آمار شمارش مشترک مکانی-زمانی گسترش مییابند. به طور خاص، بخش مرزی بین دو چند ضلعی مجاور فضایی، اتصال نامیده می شود. یک اتصال می تواند مرز بین دو چند ضلعی سیاه، بین دو چند ضلعی قرمز، یا بین یک چند ضلعی سیاه و یک چند ضلعی قرمز باشد. برای ساده نگه داشتن مسائل، ما همچنان به وجه مرزی بین دو حجم مجاور از لحاظ مکانی-زمانی به عنوان یک پیوست اشاره می کنیم. قطعه مرزی بین دو چند ضلعی مجاور فضایی را اتصال می گویند. یک اتصال می تواند مرز بین دو چند ضلعی سیاه، بین دو چند ضلعی قرمز، یا بین یک چند ضلعی سیاه و یک چند ضلعی قرمز باشد. برای ساده نگه داشتن مسائل، ما همچنان به وجه مرزی بین دو حجم مجاور از لحاظ مکانی-زمانی به عنوان یک پیوست اشاره می کنیم. قطعه مرزی بین دو چند ضلعی مجاور فضایی را اتصال می گویند. یک اتصال می تواند مرز بین دو چند ضلعی سیاه، بین دو چند ضلعی قرمز، یا بین یک چند ضلعی سیاه و یک چند ضلعی قرمز باشد. برای ساده نگه داشتن مسائل، ما همچنان به وجه مرزی بین دو حجم مجاور از لحاظ مکانی-زمانی به عنوان یک پیوست اشاره می کنیم.
دسته بندی های ممکن پیوندها، در مورد دسته های باینری سیاه و قرمز، سیاه-سیاه، سیاه-قرمز یا قرمز-سیاه و قرمز-قرمز هستند (که در آن سیاه یا قرمز به حجم خاصیت سیاه یا حجمی از ویژگی های سیاه اشاره دارد. خاصیت قرمز).
فرض کنید J تعداد اتصالات Black–Black باشد. یک شاخص R برای شناسایی DAE برای رویدادهای “سیاه”، مانند رابطه (1) تعریف شده است:
که در آن k تعداد همه رویدادها (یعنی جلدها) است. p نسبت J به k است. و S خطاهای استاندارد چنین اعداد مورد انتظار پیوندهای سیاه-سیاه است. اگر از فرض نرمال بودن پیروی کنیم، که فرض میکند احتمال قرمز یا سیاه بودن هر حجم معینی از یک فرآیند تصادفی پیروی میکند، میتوان مقدار خطاهای استاندارد را از تابع چگالی احتمال با ویژگیهای توزیع نرمال به صورت زیر محاسبه کرد:
m نشان دهنده موارد زیر است:
خودهمبستگی توزیع و اهمیت آماری آن از توزیع یک دسته از رویدادها با مقدار R تعیین میشود. اگر R مثبت باشد، دستهبندی فعالیت ارزیابیشده از نظر مکانی-زمانی بیشتر از رویدادهای دستههای دیگر خوشهبندی میشود. مشابه بیشتر آمارهای مکانی، مقدار شاخص R به تنهایی مفید نیست. سطحی از اهمیت آماری باید این مقدار شاخص را همراهی کند. در این مورد، اهمیت آماری R با استفاده از فرمول امتیاز Z محاسبه میشود و تابع چگالی احتمال مرتبط از توزیع نرمال پیروی میکند. به عنوان مثال، زمانی که مقدار R بزرگتر از 1.96 است، خودهمبستگی توزیع به طور قابل توجهی در سطح 0.05 خوشه بندی می شود، و زمانی که مقدار R کمتر از 1.96- باشد، خودهمبستگی توزیع در سطح 0.05 پراکنده می شود.
در نهایت، آزمون سطح معناداری یک آزمون دو دنباله از فرضیه صفر است (بدون همبستگی مکانی-زمانی) با توجه به اینکه R می تواند مثبت یا منفی باشد.
4. آزمایش ها و نتایج
4.1. داده ها
برای ارزیابی کامل روش پیشنهادی (DAE)، سه گروه از داده های شبیه سازی شده را طراحی کردیم. هر گروه داده 1500 رویداد داشت. موقعیتهای هر رویداد با مختصات x ، y ، و t آنها، جایی که ( x ، y ) یک مکان مکانی را تعریف میکند، و t یک مهر زمانی را تعریف میکند.
در گروه 1، رویدادها بر اساس فرض تصادفی سازی ایجاد شدند که x ، y ، و tمختصات به طور تصادفی بین 0 و 1 توزیع شد. رویدادهای فعالیت با یک فرآیند تصادفی به “سیاه” یا “قرمز” اختصاص داده شدند. در گروه 2، رویدادها بر اساس فرض عادی سازی با محوریت (0.5، 0.5، 0.5) با انحراف استاندارد مختصات روی 0.2 ایجاد شدند. رویدادها با یک فرآیند تصادفی به “سیاه” یا “قرمز” اختصاص داده شدند. در گروه 3 رویدادها شامل سه دسته بودند که بر اساس فرض توزیع دوجمله ای ایجاد شدند. دسته اول رویدادهایی که با “سیاه” مشخص شده اند در اطراف (0.7، 0.7، 0.7) با انحراف استاندارد 0.05 توزیع شده اند. دسته دوم رویدادهایی که با “آبی” مشخص شده اند در اطراف (0.3، 0.3، 0.3) با انحراف معیار 0.1 توزیع شده اند، و رویدادهای دسته سوم، که x ، y ، و t هستند.به طور تصادفی بین 0 و 1 توزیع شدند، “قرمز” مشخص شدند. برای فعال کردن آزمون های مقایسه ای، تعداد رویدادهای هر دسته در هر گروه یکسان نگه داشته شد. مجموعه ای از مثال ها برای توزیع مکانی و زمانی رویدادها در هر گروه در شکل 2 a-c نشان داده شده است.
4.2. تنظیم آزمایش
آزمایشها از موران I [ 11 ، 41 ] و نسبت نزدیکترین همسایه (NNR) [ 50 ] استفاده کردند.] به عنوان روش های پایه برای مقایسه با DAE. Moran’s I یک ضریب پرکاربرد است که همبستگی فضایی کلی یک مجموعه داده را اندازه گیری می کند. مقدار بالاتر ضریب به معنای همبستگی فضایی بالاتر بین رویدادهای منطقه است. NNR به عنوان نسبت میانگین فاصله مشاهده شده بین نزدیکترین رویدادهای همسایه به میانگین فاصله مورد انتظار بر اساس یک توزیع تصادفی فرضی با تعداد یکسانی از ویژگیها که همان مساحت کل را پوشش میدهند، محاسبه میشود. این یک ابزار اساسی برای بررسی خوشه بندی مجموعه ای از نقاط گسسته است. مقدار NNR از 0 (کاملاً خوشهای) تا 1 (تصادفی) تا 2.149 (کاملاً پراکنده) متغیر است. در این مقاله، دو مدل و روش پیشنهادی (DAE) شش شاخص برای بررسی اثربخشی روش پیشنهادی تشکیل دادند.
برای موران کلاسیک I که سطح خودهمبستگی فضایی را در بین نقاط داده اندازهگیری میکرد، این آزمایش در ابتدا انتساب زمانی رویدادهای فعالیت را حذف کرد. در ابتدا فضا را به شبکه ای 10 در 10 از 100 سلول هم اندازه (0.1 × 0.1) تقسیم کرد. تعداد رویدادهای داخل هر سلول شبکه به عنوان ویژگی سلول شبکه در نظر گرفته شد. پس از آن، ما هر سلول شبکه را به عنوان یک منطقه در نظر گرفتیم و مقدار I موران شبکه را محاسبه کردیم.
برای موران I [ 41 ] فضایی-زمانی که خود همبستگی مکانی-زمانی مکعب زمان-فضا را اندازهگیری کرد، آزمایش فضای فعالیت را به یک حجم مکعبی 10 در 10 در 10 با اندازه 1000 (0.1 × 0.1 × 0.1) تقسیم کرد. به طور مشابه، تعداد رویدادهایی که در هر مکعب می افتد به عنوان ویژگی آن استفاده می شود. در نهایت هر مکعب را یک حجم در نظر گرفتیم و Moran’s I هر مکعب را بررسی کردیم.
برای NNR کلاسیک، آزمایش پارامتر “منطقه” مطالعه را 1 تنظیم کرد و سپس نسبت مطابق با مختصات x و y آن رویدادها محاسبه شد.
برای NNR فضایی-زمانی، این از NNR کلاسیک با گسترش فاصله فضایی در مدل به فاصله فضا-زمان مشتق شد. فاصله بین رویداد a (x1, y1, t1) و رویداد b (x2, y2, t2) با استفاده از فاصله اقلیدسی محاسبه شد (یعنی فاصله(a,b) = sqrt((x2 – x1) 2 + (y2 – y1) 2 + (t2 – t1) 2 ) متعاقباً با تنظیم اندازه منطقه مورد مطالعه بر روی 1 نسبت محاسبه شد.
برای روش DAE پیشنهادی، آزمایشها را پس از تنظیم پارامتر ws (اندازه ویندوز) در هر یک از دو آزمایش به 1 و 0.2 انجام دادیم. هنگامی که ws روی 1 تنظیم شد، همه رویدادها در یک پنجره زمانی قرار گرفتند و شاخص تمایل داشت که همبستگی توزیع مکانی رویدادها را نسبت به خودهمبستگی توزیع مکانی-زمانی ارزیابی کند.
ما یک آزمون 100 جایگشتی برای ارزیابی مقادیر دقت شش شاخص انجام دادیم و مقدار میانه R و p-value در هر گروه به عنوان نتیجه گروه ثبت شد.
4.3. نتایج
همانطور که در بخش 4.1 ذکر شدرویدادهای “سیاه” در گروه 2 و گروه 3 و رویدادهای “آبی” در گروه 3 سه مورد بودند که توزیع آنها با فرض عادی سازی شبیه سازی شد. نتیجه موران I و ST موران I از سه مورد نشان داد که آن رویدادها در سطح معناداری 001/0 همبستگی خودکار داشتند. تمام مقادیر NNR و ST NNR در سه مورد بیشتر از 0 بود و از نظر آماری در سطح 0.05 معنیدار بود. به عبارت دیگر، چهار شاخص با موفقیت همبستگی عادی سازی را شناسایی کرده بودند، در حالی که رویداد «سیاه» در گروه 1 و رویداد «قرمز» در گروه 3 دو موردی بودند که با فرض تصادفی سازی شبیه سازی شدند. چهار شاخص Moran’s I، ST Moran’s، NNR و ST NNR بسیار نزدیک به 0 بودند، که نشان می دهد آنها سطوح خودهمبستگی بین رویدادها را به طور موثر اندازه گیری می کنند. به طور خلاصه، چهار شاخص هنگام اندازهگیری سطوح خودهمبستگی مکانی/مکانی، مقادیر معقولی را به دست آورده بودند. با این حال، نقص آنها این بود که نمیتوانستند تفاوت خودهمبستگی توزیع بین دو رویداد دستهای را که خودهمبستگی جزئی نامیده میشود، شناسایی کنند. مفهوم خودهمبستگی جزئی شبیه به ضریب رگرسیون جزئی در مدل رگرسیون چند متغیره است. خود همبستگی رویدادهای یک دسته خاص را اندازه گیری می کند در حالی که همه رویدادهای دسته های دیگر را به عنوان نوع دوم در نظر می گیرد. فقدان ابزار برای محاسبه خودهمبستگی جزئی می تواند محدودیت روش های کلاسیک باشد. بنابراین ما انگیزه انجام این مطالعه را داشتیم. نقص آنها این بود که نتوانستند تفاوت خودهمبستگی توزیع را بین دو رویداد طبقه بندی کنند که خود همبستگی جزئی نامیده می شود. مفهوم خودهمبستگی جزئی شبیه به ضریب رگرسیون جزئی در مدل رگرسیون چند متغیره است. خود همبستگی رویدادهای یک دسته خاص را اندازه گیری می کند در حالی که همه رویدادهای دسته های دیگر را به عنوان نوع دوم در نظر می گیرد. فقدان ابزار برای محاسبه خودهمبستگی جزئی می تواند محدودیت روش های کلاسیک باشد. بنابراین ما انگیزه انجام این مطالعه را داشتیم. نقص آنها این بود که نتوانستند تفاوت خودهمبستگی توزیع را بین دو رویداد طبقه بندی کنند که خود همبستگی جزئی نامیده می شود. مفهوم خودهمبستگی جزئی شبیه به ضریب رگرسیون جزئی در مدل رگرسیون چند متغیره است. خود همبستگی رویدادهای یک دسته خاص را اندازه گیری می کند در حالی که همه رویدادهای دسته های دیگر را به عنوان نوع دوم در نظر می گیرد. فقدان ابزار برای محاسبه خودهمبستگی جزئی می تواند محدودیت روش های کلاسیک باشد. بنابراین ما انگیزه انجام این مطالعه را داشتیم. خود همبستگی رویدادهای یک دسته خاص را اندازه گیری می کند در حالی که همه رویدادهای دسته های دیگر را به عنوان نوع دوم در نظر می گیرد. فقدان ابزار برای محاسبه خودهمبستگی جزئی می تواند محدودیت روش های کلاسیک باشد. بنابراین ما انگیزه انجام این مطالعه را داشتیم. خود همبستگی رویدادهای یک دسته خاص را اندازه گیری می کند در حالی که همه رویدادهای دسته های دیگر را به عنوان نوع دوم در نظر می گیرد. فقدان ابزار برای محاسبه خودهمبستگی جزئی می تواند محدودیت روش های کلاسیک باشد. بنابراین ما انگیزه انجام این مطالعه را داشتیم.
لازم به ذکر است که حتی در ارزیابی خودهمبستگی مکانی-زمانی مطلق (در مقابل جزئی)، NNR مکانی-زمانی دارای محدودیت هایی است. مقادیر R آن باید تقریباً 1 برای زیرگروه رویدادهای “سیاه” در گروه 1 و برای زیر گروه رویدادهای “قرمز” در گروه 3 باشد زیرا رویدادهای “سیاه” برای توزیع تصادفی شبیه سازی شده اند. R باید برای رویدادهای زیر گروه “سیاه” در گروه 2 کمتر از 1 باشد زیرا توزیع داده ها با فرض عادی سازی شبیه سازی شده است. علاوه بر این، آنها باید مقدار p حداقل 0.05 در سه زیر گروه داشته باشند، زیرا همبستگی توزیع رویدادها در سه زیر گروه از نظر آماری معنی دار نبود.
با توجه به جدول 1 ، روش DAE پیشنهادی با موفقیت توزیع دسته هدف رویدادها را در برابر سایر دستهبندی رویدادها ارزیابی کرد. هنگامی که رویدادهای هدف در گروههای مختلف توزیعهای مشابه داشتند، R فضایی-زمانی بسیار کم بود، با تقریباً 0.5 p-value در زیرگروههای رویداد «سیاه» در گروه 1 و گروه 2. رویدادهای سه زیر گروه در گروه 3 دارای سطوح مختلف بودند. همبستگی توزیع: یک مقدار R بالا نشان می دهد که دسته هدف متفاوت از دسته های دیگر توزیع شده است. علاوه بر این، سه R به تدریج همراه با کاهش درجات تجمع سه دسته از رویدادها کاهش یافت.
5. بحث
5.1. تأثیر نسبت فعالیت هدف
برای بررسی اینکه آیا نسبت رویدادهای هدف در برابر سایرین بر مقادیر شاخص محاسبهشده تأثیر میگذارد، فرض کردیم که دادهها تحت سه توزیع مختلف هستند: تصادفی، توزیع نرمال استاندارد و توزیع دوطبیعی، و آزمایشها را با نسبتهای «سیاه» تکرار کردیم. از 0.1 تا 0.9 (یعنی 10٪ و 90٪ از تمام نقاط رویداد در یک مجموعه داده شبیه سازی شده). برای هر آزمایش، اندازه پنجره کشویی ( ws ) روی 0.1، فاصله لغزشی θ روی 0.01، و تعداد جایگشت ها روی 100 تنظیم شد. میانه مقادیر شاخص به دست آمده و مقادیر p مربوط به آنها در جدول 2 فهرست شده اند .
جدول 2 نشان می دهد که تمام مقادیر R بسیار نزدیک به 0 بودند، اما هیچ کدام در نسبت رویدادهای “سیاه” در داده ها تحت فرض تصادفی سازی یا عادی سازی تفاوت معنی داری نداشتند. در گروه 3، توزیع دو جمله ای، مقادیر R از 15.664 به 4.037 کاهش یافت، در حالی که نسبت رویدادهای “سیاه” از 0.1 (10٪) به 0.9 (90٪) در مجموعه داده های شبیه سازی شده افزایش یافت. این یافته به این دلیل است که تعداد رویدادهایی که با علامت “سیاه” مشخص شده اند، بیشتر از نیمی از تعداد کل همه رویدادها است. اما زمانی که تعداد یک دسته کمتر از تعداد کل دسته های دیگر فعالیت ها بود، اینطور نبود.
5.2. تاثیر اندازه پنجره کشویی اندازه و اندازه مرحله
با استفاده از مدل DAE، اندازه پنجرههای کشویی ( ws ) و اندازه گام ( θ ) باید روی مقادیر R تأثیر بگذارد. با توجه به اینکه توزیع دادههای “سیاه” در گروه 3 با هر شش شاخص معنیدار بود، ما از همان دادههای شبیهسازی شده گروه 3 در بخش 4 برای انجام آزمایشهای بیشتر برای تأیید تأثیر اندازه پنجره و اندازه گام استفاده کردیم. مقادیر ws مورد استفاده در آزمایشها از 0.05 تا 0.5 با افزایش θ از 0.005 تا 0.05 شروع شد. مقادیر R میانه هر 100 جایگشت در جدول 3 a فهرست شده است.
جدول 3 الف نشان می دهد که اندازه پنجره به طور معنی داری با نتایج همبستگی دارد. باید توجه داشت که بایاس می تواند وجود داشته باشد زیرا توزیع فضایی x ، y و توزیع زمانی t به طور بسیار مشابهی با فرض و پارامترهای یکسان کنترل شده و تولید می شود.
با این حال، شواهد روشنی وجود نداشت که نشان دهد نتایج به اندازه گام مرتبط هستند. در حالت ایدهآل، θ باید تا حد امکان کوچک باشد تا پنجره به آرامی حرکت کند و بنابراین روابط زمانی و مکانی بین رویدادها را بهتر نشان دهد. برای بررسی بهتر تاثیر اندازه گام، یک θ بسیار کوچک ، 0.001، را به عنوان پایه θ در نظر گرفتیم . سپس، D x را برای ارائه انحراف بین مقادیر R در خط مبنا و Rx در نظر گرفتیم ، که وقتی θ روی x تنظیم شد به دست آمد . D x توسط | محاسبه شد R 0.001 – Rx |، همانطور که در جدول 3 فهرست شده است.
همانطور که در جدول 3 نشان داده شده است ، با افزایش θ ، میانگین D θ نیز افزایش یافت . D θ کوچکتر به این معنی است که مقادیر R انحراف کمتری با نتایج نظری داشتند و بهتر تصور میشد. این نشان می دهد که شاخص پیشنهادی ترجیح می دهد که θ باید تا حد امکان کوچک باشد. با این حال، یک θ کوچکتر مستلزم تکرار بیشتر فرآیند Delaunay است که زمانبر است.
ما معتقدیم که ws یک MTUP (مشکل واحد زمانی قابل تغییر) ایجاد می کند. برای رویدادهای دنیای واقعی، واحدهای طبیعی زمان مانند سال، ماه، هفته، روز، انتخاب های خوبی برای ws خواهند بود. علاوه بر این، بازه زمانی همه رویدادها برای ثبت دقیق تاثیر زمانی باید از ده ها ws عبور کند. برای θ ، هرچه کوچکتر باشد بهتر است.
5.3. تجزیه و تحلیل عملکرد
از آنجایی که داده های رویداد به طور فزاینده ای تولید و در دسترس قرار می گیرند، مدل ها و روش های جدیدی برای رسیدگی به حجم زیادی از داده های رویداد مورد نیاز است. برای بررسی رابطه بین هزینه زمان محاسبه و حجم دادههای رویداد، آزمایشهایی را با استفاده از چهار مجموعه داده نمونه با اندازههای مختلف انجام دادیم که به ترتیب شامل 1000 رویداد، 10000 رویداد، 100000 رویداد و 1000000 رویداد بودند. زمان های استفاده شده در محاسبه سه شاخص ST Moran’s I، ST NNR و شاخص پیشنهادی (R) ثبت و در جدول 4 ارائه شده است.
همانطور که در جدول 4 نشان داده شده است ، زمان های محاسبه برای شاخص ST Moran’s I و ST NNR با افزایش حجم نمونه به سرعت افزایش یافت. در مقابل، روش ما در مدیریت مقدار زیادی داده کارآمدتر بود. زمان مورد نیاز شاخص پیشنهادی با افزایش حجم نمونه افزایش یافت که نشان دهنده رابطه خطی با حجم نمونه بود. علاوه بر این، سربار زمانی به دو پارامتر ws و θ مرتبط بود :
- (1)
-
هنگامی که ws بزرگتر بود، رویدادهای بیشتری در هر پنجره زمانی افتاد و در هر مدل دلونی درگیر شد، بنابراین نیاز به زمان محاسبه بیشتری داشت.
- (2)
-
هنگامی که مقدار θ کوچکتر بود، زمان بیشتری برای ساخت مثلث دلونی مورد نیاز بود و در نتیجه زمان محاسبات کلی بیشتری داشت.
5.4. برنامه دنیای واقعی – موردی از سوابق تماس برای خدمات
در این مطالعه موردی از مجموعه داده تماس برای خدمت در پورتلند، اورگان، با مختصات جغرافیایی و مهرهای زمانی استفاده شد. دادهها از وبسایت رسمی چالش پیشبینی جنایت در زمان واقعی ( https://nij.gov/funding/Pages/fy16-crime-forecasting-challenge.aspx ، در تاریخ 19 مه 2017) دانلود شده است. در مجموع 95 دسته از رویدادها در داده های تماس برای سرویس دانلود شده ثبت شد که نشان دهنده 208083 مورد رویداد واقع در پورتلند در طول آن زمان بود.
با توجه به اینکه جمعیت ممکن است ارتباط نزدیکی با تعداد تماس ها [ 51 ] داشته باشد، تراکم جمعیت و تماس در هر کیلومتر مربع توسط مناطق سرشماری نقشه برداری می شود، همانطور که در شکل 3 a,b نشان داده شده است. از این ارقام، سطوحی از خوشه بندی فضایی در توزیع جمعیت و تماس ها را می توان به صورت بصری مشاهده کرد.
ما روی 10 تراکت برتر تمرکز کردیم که شماره تماس آنها در بین تراکت ها بالاترین بود. همانطور که در جدول 5 نشان داده شده است ، تعداد انباشته تماس های 10 دسته برتر تماس برای خدمات، بیش از 50 درصد از تعداد کل تماس ها از همه دسته ها بود.
برای بررسی الگوهای فضایی بر اساس دستههای فراخوانی، آنها را با استفاده از Moran’s I با دو واحد فضایی، یعنی تراکتها و گروههای بلوک سرشماری ارزیابی کردیم. علاوه بر این، مقادیر نسبت نزدیکترین همسایه (NNR) با استفاده از پارامترهای پیشفرض برای هر یک از 10 دسته تماس برتر محاسبه شد. نتایج در جدول 6 a,b نشان داده شده است.
جدول 6 a,b سطوح مطمئناً معنی دار آماری خوشه بندی فضایی را با توجه به همه دسته های فراخوانی نشان می دهد. با این حال، تشخیص اینکه کدام دسته فراخوانی، الگوی فضایی را نشان میدهد که به طور قابلتوجهی متفاوت از همه دستههای فراخوانی است، زیرا همه الگوهای فضایی از نظر آماری به طور قابلتوجهی برای این مجموعه دادهها خوشهبندی شدهاند. بنابراین، تجزیه و تحلیل این رویدادها برای شناسایی الگوی توزیع خودهمبستگی بر روی دستههای تماس مختلف ضروری است. ما خودهمبستگی مکانی و زمانی جزئی را برای هر دسته از رویدادها با استفاده از روش پیشنهادی ارزیابی کردیم و نتایج در جدول 7 نشان داده شده است.
جدول 7تفاوت قابل توجه بین دسته های تماس مختلف را نشان می دهد. R در دسته های UNWNT، WELCKP و WELCK کمتر از 1.96 بود. اگرچه آنها به طور قابل توجهی از نظر مکان و زمان خوشه بندی شده بودند، به نظر می رسد در مقایسه با دسته های تماس دیگر به طور قابل توجهی پراکنده هستند. چنین نتیجه ای نشان می دهد که دسته های فراخوانی با مقادیر R مطلق کوچک ممکن است عوامل فضایی خاصی نداشته باشند که می تواند منبع این فراخوان ها را تحت تأثیر قرار دهد. از طرف دیگر، دستههای DISTP، SUSP، THEFT، AREACK و HAZARD ویژگیهای تجمع نسبی مکانی-زمانی آشکاری دارند، همانطور که با اقدامات همبستگی جزئی آنها نشان داده شده است. این یافته نشان می دهد که آنها می توانند ارتباط نزدیکی با محیط های فضایی خاص و عوامل دیگر داشته باشند. این شرایط تنها زمانی امکان پذیر است که سطوح خودهمبستگی جزئی محاسبه شود.
جدول 6 همچنین نشان میدهد که سطوح DAE (زمانی که ws روی هفت روز تنظیم شده بود) همه دستههای تماس از نظر آماری معنیدارتر از الگوی فضایی (زمانی که ws روی 365 روز تنظیم شده بود) هر دسته تماس معینی بود. این یافته نشان می دهد که الگوهای زمانی در این رویدادهای فراخوانی نباید نادیده گرفته شوند.
6. نکات پایانی
برای تشخیص بهتر خودهمبستگی توزیع رویدادهای فعالیت انسانی، روش جدیدی برای اندازهگیری سطوح خودهمبستگی در مجموعهای از رویدادها پیشنهاد شد. با این روش، ما یک مدل پنجره کشویی مبتنی بر Voronoi ساختیم تا مشکل یافتن همسایگان مکانی-زمانی در میان رویدادهای فعالیت انسانی را حل کنیم. این مدل بر اساس یکپارچهسازی ابعاد فضا و زمان در حالی که ناهمگونی مکانی-زمانی را در بین رویدادهای مکانی-زمانی حفظ میکند، است. ما همچنین خواص و کاربرد این روش را با استفاده از آن در داده های شبیه سازی شده و مطالعه موردی داده های دنیای واقعی تجزیه و تحلیل و نشان دادیم. نتایج تجربی نشان داد که روش پیشنهادی میتواند سطح خودهمبستگی مکانی-زمانی را در مجموعهای از رویدادها بررسی و اندازهگیری کند.
با این حال، این مطالعه هنوز دارای محدودیت هایی است که ممکن است نیاز به تحقیقات بیشتری داشته باشد. اولاً، استفاده از تنها یک مطالعه موردی ممکن است مغرضانه باشد زیرا زمانی که روش پیشنهادی در مطالعات موردی مختلف استفاده میشود، نتایج متفاوتی به دست میآید. سوابق فراخوان خدمت مورد استفاده در اینجا فقط به منظور نشان دادن رویه های روش شناختی و بررسی اثربخشی روش ها است. ممکن است با استفاده از روش پیشنهادی برای مجموعه دادههای بیشتر با ویژگیهای مختلف، کارهای بیشتری در زمینه طبقهبندی سوابق فراخوان برای سرویس به دستههای مختلف مورد نیاز باشد. علاوه بر این، مدل پنجره کشویی فاقد ابزاری برای تعریف اندازه بهینه پنجره جهانی است. در کاربردهای عملی، چنین اندازههای پنجره ممکن است به نحوه توزیع دسته خاصی از رویدادها بستگی داشته باشد.
در امتداد بعد زمانی، رویدادهای جغرافیایی می توانند رویدادهای دیگر را به روشی متفاوت از ابعاد مکانی تحت تأثیر قرار دهند. به عنوان مثال، رویدادهای گذشته ممکن است بر چگونگی تحول رویدادهای جاری تأثیر بگذارد، اما برعکس تأثیر نمی گذارد. به طور مشابه، اثراتی که برخی رویدادها ممکن است بر روی دیگران بگذارند، ممکن است تأثیرات تأخیر زمانی داشته باشند. قالب فعلی روش مورد بحث در مقاله این اثرات را در نظر نمی گیرد. علاوه بر این، فرکانس رویدادها باید ارزیابی شود تا ببینیم آیا آنها دارای هر چرخه زمانی هستند، که در هنگام تعیین اندازه پنجره زمانی مناسب در تجزیه و تحلیل مهم است.
در نهایت، مانند تقریباً در تمام آمارهای مکانی، مسئله مرز نیز باید در اینجا شناسایی شود. به طور معمول، یک منطقه حائل را می توان برای گنجاندن رویدادهای جغرافیایی از مناطق همسایه در مجموعه داده برای تجزیه و تحلیل ساخت. البته این تنها زمانی امکان پذیر است که چنین داده هایی در دسترس باشند.







بدون دیدگاه