1. معرفی
تشخیص تغییر ساختمان از
داده های سنجش از دور یک فناوری مهم در
تغییر پوشش زمین،
ارزیابی بلایا و
نظارت بر شهر است [ 1 ، 2 ، 3 ]. ساختمان ها جزء اصلی یک شهر را تشکیل می دهند و استخراج ساختمان و تشخیص تغییر ساختمان به دلیل پیچیدگی صحنه های شهری همچنان وظایف چالش برانگیزی هستند [ 4 ]. از آنجایی که روشهای سنتی تفسیر بصری دستی و برداری زمانبر و پرهزینه هستند، روشهای تشخیص تغییر ساختمان خودکار و قوی به کانون تحقیقاتی در زمینه فتوگرامتری و سنجش از دور تبدیل شدهاند [5 ] .
در چند سال گذشته، یک سری روشهای تشخیص خودکار تغییر ساختمان از دادههای سنجش از دور توسعه یافتهاند. متداولترین منابع دادهای که برای تشخیص تغییرات ساختمان استفاده میشوند،
تصاویر و دادههای LiDAR هستند. در روش مبتنی بر تصویر، از ویژگی های طیفی، زمینه ای، هندسی تصاویر و
شاخص مورفولوژیکی ساختمان (MBI) برای استخراج ساختمان ها استفاده می شود [ 4] .]. با این حال، روش های پیشرفته مبتنی بر تصاویر هنوز با چالش های عمده زیر روبرو هستند: (1) انسداد و سایه بین ساختمان ها. (2) به راحتی تحت تأثیر عواملی مانند فصول و دقت ثبت نام. (3) دشواری در تشخیص ساختمان ها از سایر سازه های ساخته شده توسط انسان، مانند جاده ها. (4) فقدان اطلاعات ارتفاع، که توسعه تشخیص تغییر ساختمان سه بعدی را محدود می کند [6 ].
با افزایش اکتساب داده های LiDAR، بسیاری از مطالعات تشخیص تغییر ساختمان بر اساس ابر نقطه LiDAR [ 7 ] انجام شده است. روشهای مبتنی بر LiDAR شامل روشهای مبتنی بر DSM، مبتنی بر ابر نقطهای و مبتنی بر ترکیب دادهها میشوند. 8]]. هر روشی مزایا و معایب خود را دارد. روش مبتنی بر DSM می تواند به طور موثر از اطلاعات ارتفاع تولید شده از داده های LiDAR بدون تأثیر سایه ها و تغییرات فصل استفاده کند. با این حال، ممکن است از خطاهای درون یابی و از دست دادن اطلاعات رنج ببرد. روش مبتنی بر ابر نقطه ای مستقیماً از ویژگی های هندسی داده های اصلی استفاده می کند. ابر نقطه به طور کلی باید به وکسل، سوپروکسل یا اشیاء قطعهبندی شده تقسیم شود. تقسیم بندی و طبقه بندی ابر نقطه ای هنوز یک کار چالش برانگیز است. روش همجوشی داده ها از اطلاعات هندسی ابر نقطه و اطلاعات طیفی تصویر استفاده کامل می کند که می تواند ساختمان ها را از پوشش گیاهی به طور موثر متمایز کند. با این وجود، عدم قطعیت در ثبت داده های چند منبع وجود دارد،
با محدودیت منابع داده، این مقاله بر روی تشخیص تغییر ساختمان بر اساس DSM تمرکز دارد. DSM های تولید شده توسط داده های LiDAR در زمان های مختلف می توانند اطلاعات ارتفاع ارزشمندی را برای تشخیص تغییرات ساختمان ارائه دهند. علاوه بر این، تغییرات ساختمان را می توان با استفاده از مجموعه ای از تکنیک های پردازش تصویر شناسایی کرد. روش های تشخیص تغییر ساختمان مبتنی بر DSM را می توان به سه دسته دسته بندی کرد. دسته اول روش تفاضل DSM است که مناطق تغییر یافته ساختمان را با تفریق ساده بین DSMها شناسایی می کند [ 9 ، 10 ، 11 ، 12]. دقت تشخیص تغییر نهایی ممکن است تحت تأثیر کیفیت DSM ها و ثبت اشتباه باشد. مراحل پس از پردازش همیشه برای اصلاح نقشه تشخیص تغییر ساختمان پیشنهاد می شود. دسته دوم روش ترکیب اطلاعات [ 13 ، 14 ، 15 ، 16 ، 17 ] است. این اطلاعات ارتفاع از DSM ها را با اطلاعات دیگر مانند اطلاعات طیفی یا بافتی از تصاویر سنجش از راه دور ادغام می کند. این رویکرد می تواند به نتایج خوبی دست یابد، اما اطلاعات دیگر همیشه در بسیاری از موارد در دسترس نیست. دسته سوم روش پس از طبقه بندی است [ 18 ، 19 ، 20] که به دقت استخراج ساختمان بستگی دارد. ابتدا، تقسیمبندی و طبقهبندی برای استخراج ساختمانها اعمال میشود و سپس ناحیه تغییر و نوع تغییر ساختمانها با بررسی سازگاری ساختمانها در دو مقطع زمانی تعیین میشود. این روش می تواند به دقت بالایی برسد، اما با دقت استخراج ساختمان مشخص می شود و برای تشخیص ساختمان های کوچک چندان موثر نیست.
تجزیه و تحلیل تصویر مبتنی بر شی از شی تقسیم بندی به عنوان واحد اصلی تجزیه و تحلیل استفاده می کند که می تواند دقت نتایج تشخیص تغییر ساختمان را بر اساس DSM ها بهبود بخشد. الگوریتمهای تقسیمبندی تصویر متعددی برای کارهای مختلف پردازش تصویر پیشنهاد شدهاند، از جمله (1) روش آستانهگذاری [ 21 ]، (2) روش رشد منطقه [ 22 ]، (3) روش مبتنی بر لبه [ 23 ] و (4) ) روش های مبتنی بر نظریه های دیگر [ 24 ]. روش های تقسیم بندی مختلف برای اهداف مختلف مناسب هستند. با توجه به اینکه ادغام ناحیه آماری (SRM) می تواند با فساد نویز قابل توجه مقابله کند، انسدادها را کنترل کند و بخش بندی های حساس به مقیاس را انجام دهد [ 25 ]، در این مقاله استفاده شده است.
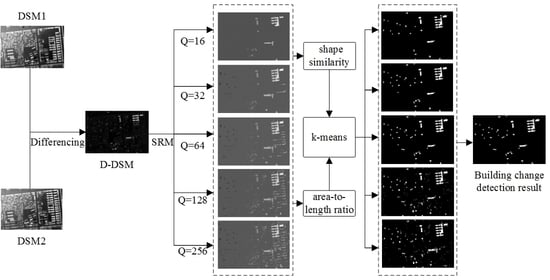
در این مقاله، یک رویکرد جدید تشخیص تغییر ساختمان شی گرا پیشنهاد شده است که از ادغام منطقه آماری (SRM) و یک مدل شباهت زمینه شکل استفاده می کند. اول، پردازش تفاوت بر روی داده های DSM در دو نمونه زمانی انجام می شود تا داده های تفاوت D-DSM تولید شود. سپس داده های تفاوت D-DSM با استفاده از الگوریتم SRM با مقیاس های مختلف تقسیم می شود س=2n (n=1،2،⋯،8). سوم، مقادیر متوسط اشیاء تقسیمبندی شده محاسبه میشود و آستانهای برای تشخیص تغییرات اولیه تعیین میشود. با فرض اینکه تغییرات ساختمان معمولاً مستطیلی هستند، از مدل شباهت زمینه شکل برای محاسبه شباهت شکل بین اشیاء نتیجه تشخیص تغییر اولیه و ساختمانها و به دست آوردن شاخص شباهت و هزینه تطبیق استفاده میشود. در نهایت، روش خوشهبندی
k-means بر اساس شاخص شباهت و نسبت مساحت به طول برای خوشهبندی اشیاء تغییر یافته در ساختمانهای تغییر یافته و سایر ساختمانها اجرا میشود. تقسیم بندی
SRM می تواند نویز “نمک و فلفل” ناشی از روش مبتنی بر پیکسل را کاهش دهد. بافت شکل می تواند تغییرات ساختمان را از سایر انواع تغییرات متمایز کند، و نسبت مساحت به طول می تواند تغییرات تشخیص نادرست ناشی از خطاهای ثبت ساختمان های بلند را حذف کند. بنابراین، روش پیشنهادی می تواند به طور موثری دقت نتایج تشخیص تغییر ساختمان را بهبود بخشد.
2. مواد و روشها
2.1. داده ها
محل مطالعه در شهر Lianyungang، استان جیانگ سو، چین واقع شده است. مرکز منطقه مورد مطالعه در نزدیکی 118°56’20” شرقی و 34°43’08” شمالی قرار داشت. مجموعه دادههای آزمایشی دو DSM بود که از دادههای LiDAR در سالهای 2017 و 2018 بهترتیب با 1،122،573 و 1،062،337 امتیاز تهیه شد. داده های نقطه LiDAR در فرمت LAS 1.2 ذخیره شدند و چگالی نقطه LiDAR بین 2-3 نقطه بر متر مربع (ppm) بود. داده های LiDAR با استفاده از Terrascan TM در DSM با وضوح 0.5 متر درونیابی شدند . DSMها (2126 × 1426) در شکل 1 a,b نشان داده شده اند و داده های تفاوت D-DSM تولید شده توسط پردازش تفاوت در شکل 1 c نشان داده شده است. حقیقت اصلی ایجاد شده از طریق تجزیه و تحلیل بصری نشان داده شده است شکل 1 نشان داده شده استد پوشش اراضی این منطقه مورد مطالعه شامل ساختمان ها (بیشتر مستطیل شکل)، جاده ها، خاک برهنه و پوشش گیاهی (علف و درخت) است.

2.2. روش شناسی
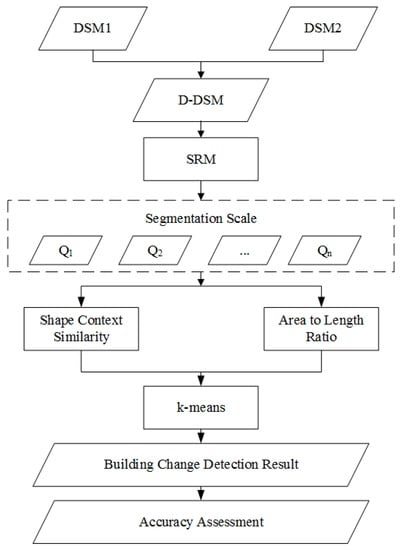
جدول زمانبندی روش پیشنهادی تشخیص تغییر ساختمان در شکل 2 خلاصه شده است . این رویکرد شامل سه مرحله اصلی است: تقسیم بندی SRM، محاسبه شباهت شکل، و تشخیص تغییر ساختمان. جزئیات هر مرحله در بخش های بعدی توضیح داده شده است.
2.2.1. بخش بندی D-DSM با استفاده از SRM
پردازش تفاوت بر روی دادههای DSM در دو نمونه زمانی انجام میشود تا دادههای تفاوت D-DSM تولید شود. سپس تقسیم بندی تصویر اجرا می شود [ 25 ]. ابتدا، SRM بر روی D-DSM ها برای تولید اشیا انجام می شود و سپس تشخیص تغییر ساختمان شی گرا انجام می شود. در SRM، تصویر مشاهده شده X شامل متر×nپیکسل ها با باند L ، و هر مقدار پیکسل به مجموعه تعلق دارد {0،1،2،⋯،g}(در عمل خواهیم داشت g=255). با فرض اینکه X* نتیجه تقسیم بندی بهینه است، هر مقدار باند پیکسل در تصویر مشاهده شده X با نمونه برداری مجدد در سطح Q از هر پیکسل در X به دست می آید. مقدار پیکسل X* از 0 تا g / Q متغیر است . Q یک متغیر تصادفی مستقل است که مقیاس تقسیم بندی را تنظیم می کند. با افزایش مقدار Q ، اشیاء بیشتری تقسیم بندی می شوند .
SRM عمدتاً با تکرار بین گزاره ادغام و ترتیب ادغام به تقسیم بندی تصویر دست می یابد. محمول ادغامی پ(آر،آر”)را می توان به صورت زیر تعریف کرد:
جایی که آرو آر”مناطق در تصویر X را نشان می دهد، آر¯آو آر¯آ”میانگین مقادیر باند را نشان می دهد آکه در آرو آر”، به ترتیب. ب(آر،آر”)به صورت فرموله شده است:
جایی که δثابت است، |آر|و |آر”|اعداد پیکسل را نشان دهید |آر|و |آر”|، به ترتیب. تنظیم کردیم δ=1/(6|من|2)، و |من|عدد پیکسل تصویر X را نشان می دهد.
اگر پ(آر،آر”)=درست است، واقعی، آرو آر”ادغام می شوند. برای ترتیب ادغام، تابع fمی توان برای مرتب سازی پیکسل ها در X استفاده کرد:
جایی که پو پ”پیکسل ها در X هستند، پآو پآ”مقادیر خاکستری پیکسل ها هستند پو پ”در باند آبه ترتیب. تقسیم بندی تصویر را می توان با تکرار ساده به دست آورد. مقادیر متوسط اشیاء تقسیمبندی شده بر اساس D-DSM محاسبه میشود و یک آستانه برای تشخیص تغییرات اولیه تعیین میشود. در این آزمایش مقدار آستانه 41 (میانگین به اضافه انحراف معیار) تعیین شد.
2.2.2. محاسبه تشابه شکل با استفاده از مدل زمینه شکل
اشکال ساختمان معمولاً منظم و بیشتر مستطیل هستند. بنابراین، زمینه شکل پیشنهادی توسط لینگ و جاکوبز [ 26 ] برای محاسبه شباهت شکل بین اشیاء و ساختمانهای تغییر یافته معرفی میشود. شایان ذکر است که برای محاسبه شباهت اجسام تغییر یافته در این سایت آزمایشی فقط از ساختمان هایی با اشکال مستطیلی استفاده می شود. اگر ساختمان های تغییر یافته دارای اشکال دیگری هستند، باید از اشکال ساختمان های قبلی بیشتر برای ایجاد نتایج تشخیص دقیق تر استفاده شود. مراحل خاص تشابه زمینه شکل به شرح زیر است:
(1) نقاط جدا شده در اشیاء تغییر یافته تولید شده توسط بخش بندی SRM را حذف کرده و تولید کنید nنقاط نمونه در مرز اشیاء برای نشان دادن شکل اجسام تغییر یافته.
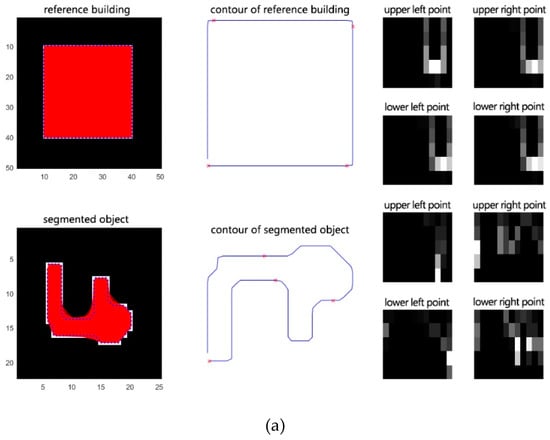
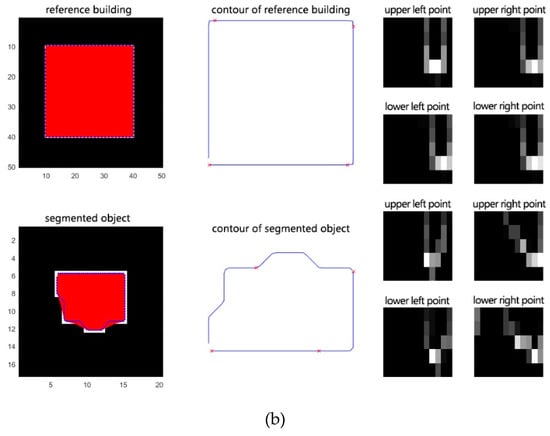
(2) زمینه شکل را برای تمام نقاط نمونه ایجاد کنید. همانطور که در شکل 3 الف نشان داده شده است، کوتاه ترین مسیر بین نقطه لبه است پو یک نقطه لبه دیگر qبه عنوان فاصله داخلی تعریف می شود که با نشان داده می شود د(پ،q); زاویه کوچکتر بین مماس در پو فاصله درونی د(پ،q)به عنوان زاویه داخلی تعریف می شود که با نشان داده می شود θ(پ،q). در نظر گرفتن د(پ،q)و θ(پ،q)به عنوان یک بردار، و نقطه پمی تواند تولید کند n-1بردارها برای بقیه n-1نکته ها. با توجه به حداکثر فاصله و زاویه بردار در نقطه پ، فاصله داخلی و زاویه داخلی را می توان به دو دسته تقسیم کرد nدو nθفواصل، به ترتیب. برای نقطه شکل پ، هیستوگرام ساعتتولید شده توسط آن n-1بردارها را می توان به صورت زیر محاسبه کرد:
جایی که ک∈{1،2،⋯،ک}،ک=nدnθ، و صندوقچه(ک)نشان دهنده تعداد بردارهایی است که در این بازه قرار می گیرند. شکل 3 ب شکل یک ساختمان استخراج شده را نشان می دهد و شکل 3 c,d هیستوگرام بافت شکل نقطه نمونه را نشان می دهد. ز1و نقطه نمونه ز2، به ترتیب. سرانجام، nهیستوگرام های تولید شده توسط nبرای محاسبه شباهت دو شکل از نقاط استفاده می شود.
(3) شباهت دو نقطه را می توان با محاسبه حداقل هزینه تطبیق نقطه نمونه بدست آورد. پمنو نقطه نمونه qj. توزیع بافت شکل نقاط نمونه در شکل 3 c,d نشان داده شده است. اجازه دهید سیمنjهزینه تطبیق این دو نقطه را نشان می دهد. این χ2از آمار آزمون می توان برای محاسبه هزینه مسابقه استفاده کرد [ 27 ]:
جایی که ساعتمن(ک)و ساعتj(ک)هیستوگرام ها را در نشان دهید پمنو qjبه ترتیب و کتعداد سطل های هیستوگرام است. جایگشت πباید هزینه کل مسابقه را به حداقل برساند اچ(π)بر اساس nنکات نمونه:
الگوریتم برنامه نویسی پویا برای حل مسئله تطبیق و هزینه تطبیق استفاده می شود اچ(π)برای توصیف شباهت شکل بین اشکال اشیاء تغییر یافته و اشکال ساختمان ها استفاده می شود. برای جزئیات، لطفاً به لینگ و جاکوبز [ 26 ] مراجعه کنید. به طور کلی، هر چه تعداد نقاط نمونه شکل بیشتر باشد، دقت نتایج تطبیق بیشتر است. در این مقاله، ما تنظیم کردیم n=50،nد=5،nθ=12.
2.2.3. تشخیص تغییر ساختمان با استفاده از الگوریتم K-Means
هنگام انجام تشخیص تغییر ساختمان بر اساس نتایج شباهت شکل، شکل تشخیص نادرست ناشی از ثبت اشتباه ساختمانهای بلند بسیار شبیه به ساختمانهای تغییر یافته است. معمولاً در اطراف لبه ساختمان ها پخش می شود که با مساحت کوچک و شکل باریک مشخص می شود، در حالی که ساختمان های تغییر یافته معمولاً دارای مناطق بزرگ هستند. بنابراین، نسبت مساحت به طول محاسبه می شود. نسبت مساحت به طول برای خطاهای ثبت نسبتاً کوچک است، در حالی که نسبت مساحت به طول ساختمانهای تغییر یافته نسبتاً بزرگ است.
الگوریتم k-means برای خوشه بندی شباهت شکل و نسبت مساحت به طول اشیاء تغییر یافته در نتایج تشخیص تغییر اولیه استفاده می شود. ساختمانهای تغییریافته شباهت شکلی بالایی با شکل ساختمان و مقادیر نسبتاً زیادی نسبت مساحت به طول دارند و سایر ویژگیهای تغییر یافته شباهت شکل کمی با شکل ساختمان و مقادیر نسبتاً کوچک نسبت مساحت به طول دارند. اشیاء تقسیم شده به دو نوع خوشه بندی می شوند: ساختمان های تغییر یافته و تغییرات دیگر.
برای ارزیابی کمی عملکرد رویکرد پیشنهادی برای تشخیص تغییر ساختمان، از سه شاخص برای ارزیابی نتایج استفاده شد:
- (1)
-
تشخیص های از دست رفته ( MD ): تعداد پیکسل های بدون تغییر در نقشه تشخیص تغییر که در مقایسه با نقشه مرجع زمینی به اشتباه طبقه بندی شده اند. نرخ تشخیص از دست رفته پمتربا نسبت محاسبه می شود پمتر=مD/ن0×100%، جایی که ن0تعداد کل پیکسل های تغییر یافته شمارش شده در نقشه مرجع زمینی است.
- (2)
-
آلارم های کاذب ( FA ): تعداد پیکسل های تغییر یافته در نقشه تشخیص تغییر که در مقایسه با مرجع زمینی به اشتباه طبقه بندی شده اند. میزان تشخیص نادرست پfبا نسبت محاسبه می شود پf=افآ/ن1×100%، جایی که ن1تعداد کل پیکسل های بدون تغییر شمارش شده در نقشه مرجع زمینی است.
- (3)
-
مجموع خطاها ( TE ): تعداد کل خطاهای تشخیص شامل تشخیص اشتباه و اشتباه است که مجموع FA و MD است . میزان خطای کل پتیبا نسبت توصیف می شود پتی=(افآ+مD)/(ن0+ن1)×100%.
3. نتایج و بحث
آزمایش ها بر روی رایانه شخصی با سرعت کلاک 3.6 گیگاهرتز و 16.00 گیگابایت رم انجام شد. برای برنامه ریزی روش پیشنهادی از MATLAB 2019 استفاده شد.
در الگوریتم SRM، پارامتر Q مقیاس تقسیم بندی تصویر را کنترل می کند. وقتی مقدار Q بزرگتر باشد، وصله های دقیق تری در نتایج تقسیم بندی وجود خواهد داشت. وقتی مقدار Q کوچکتر باشد، فقط اشیاء با مساحت بزرگ می توانند قطعه بندی شوند. تنظیم کردیم س∈{16،32،64،128،256}برای تجزیه و تحلیل اثر مقیاس تقسیم بندی بر دقت نتیجه تشخیص تغییر. شکل 4 نتایج تقسیم بندی تولید شده توسط مقادیر مختلف Q را نشان می دهد . همانطور که در شکل 4 الف نشان داده شده است، زمانی که Q = 16، اشیاء با مساحت بزرگ و مقدار تغییر بزرگ به اشیاء مستقل تقسیم شدند. با افزایش Q ، مانند Q = 256، اشیاء با جزئیات بیشتر به اشیاء مستقل تقسیم شدند. زمانی که Qخیلی کوچک بود، فقط اشیاء اصلی در دادههای DSM تفاوت را میتوان به بخشهای کامل تقسیم کرد، و نتیجه تقسیمبندی تولید شده خیلی درشت بود، که منجر به خطاهای تشخیص از دست رفته بیشتر شد. با این حال، شایان ذکر است که اشیاء کامل، اصلی و اساسی تغییر یافته هنوز می توانند به اشیاء مستقل تقسیم شوند. وقتی Q خیلی بزرگ باشد، وصله های دقیق تری در نتیجه تقسیم بندی و خطاهای تشخیص نادرست بیشتری وجود خواهد داشت. به عنوان مثال، برای ساختمان های بلند، تغییرات ناشی از خطاهای ثبت را می توان تشخیص داد که دقت نتایج تشخیص تغییر ساختمان را کاهش می دهد. بنابراین، تعیین مقدار مناسب پارامتر تقسیم بندی Q برای تولید نتایج تشخیص تغییرات با دقت بالا ضروری است.
بر این اساس، زمینه شکل برای محاسبه شباهت بین شکل ساختمان و شی قطعه بندی شده استفاده شد. همانطور که در شکل 5 الف نشان داده شده است، زمانی که تفاوت شکل بین شی قطعه بندی شده و ساختمان زیاد بود، هیستوگرام زمینه شکل محاسبه شده نقاط مشخصه مربوطه بسیار متفاوت بود. هنگامی که شکل شی قطعه بندی شده بسیار شبیه به ساختمان بود، هیستوگرام زمینه شکل نقاط مشخصه مربوطه پس از محاسبه نسبتا مشابه بود، همانطور که در شکل 5 ب نشان داده شده است. بنابراین، هر چه شی قطعه قطعه شده بیشتر به شکل ساختمان شباهت داشته باشد، شباهت محاسبه شده بیشتر و تطبیق نهایی کمتر خواهد بود.
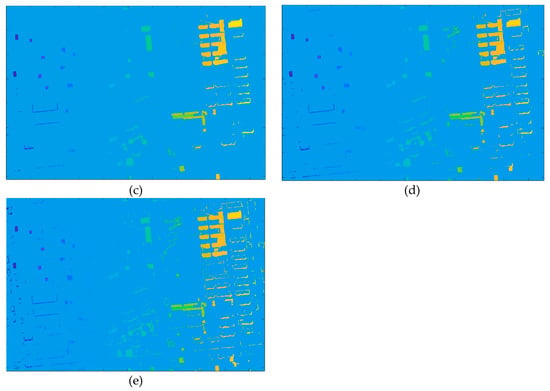
شباهت شکل بین شی قطعه بندی شده و ساختمان محاسبه شده توسط زمینه شکل در شکل 6 نشان داده شده است . هنگامی که شباهت شکل بین جسم تقسیم شده و ساختمان بیشتر باشد، در تصویر روشن تر به نظر می رسد و بالعکس. از شکل 6 می توان دریافت که برای اشیاء قطعه بندی شده در تمام مقیاس ها، شباهت شکل بین ساختمان های اصلی تغییر یافته و ساختمان مرجع زیاد بود و شباهت محاسبه شده سایر طبقات تغییر یافته کم بود. بنابراین، زمانی که مقیاس تقسیمبندی Q = 32، نتایج شباهت شکل میتواند تغییرات ساختمان را به خوبی توصیف کند. همانطور که در شکل 6 نشان داده شده است، همانطور که مقیاس تقسیم بندی افزایش یافت، تغییرات جزئی تر به اشیاء مستقل تقسیم شدندبودن. به خصوص برای ساختمان های بلند، تغییرات ناشی از خطاهای ثبت به اشیاء مستقل تقسیم شد و شکل آنها مشابه شکل ساختمان بود، همانطور که در شکل 6 d و e نشان داده شده است. بنابراین، استخراج خودکار ساختمان های تغییر یافته به طور مستقیم بر اساس شباهت شکل، به ویژه برای منطقه با تغییرات ساختمان های بلند دشوار است.
سپس نسبت سطح به طول محاسبه شد. نسبت مساحت به طول خطاهای ثبت معمولاً کمتر از 3 و نسبت مساحت به طول ساختمانهای کوچک معمولاً بیشتر از 6 بود. بنابراین از تشابه شکل و نسبت مساحت به طول به طور مشترک برای تشخیص ساختمان استفاده شد. تغییر می کند.
الگوریتم k -means برای خوشهبندی شباهت شکل و نسبت مساحت به طول اشیاء تقسیمبندی شده استفاده شد و اشیاء تقسیمبندی شده به دو نوع ساختمانهای تغییر یافته و تغییرات دیگر خوشهبندی شدند. نتایج تشخیص تغییر ساختمان در شکل 7 نشان داده شده است . از شکل می توان دریافت که وقتی Q = 16، تنها ساختمان هایی با مساحت زیاد یا تغییرات زیاد قابل تشخیص هستند. دلیل اصلی این است که مقدار Q بسیار کوچک بود و نقشه تقسیمبندی ایجاد شده ناهموار بود و در نتیجه ساختمانهای کوچک شناسایی نشدند. با افزایش مقدار Q ، ساختمانهای تغییر یافته بیشتری با مساحتهای کوچکتر را میتوان تشخیص داد زیرا Q بزرگتر بودارزش یک نقشه تقسیم بندی دقیق تری ایجاد کرد. هنگامی که Q = 32 و 64، نتیجه تشخیص تغییر ساختمان به دست آمده بسیار شبیه به داده های مرجع زمینی بود و می توانست به طور موثر ساختمان های شناسایی نادرست ناشی از ثبت را حذف کند. هنگامی که Q = 256، به دلیل نتایج تقسیمبندی بسیار خوب، تغییرات نادرست بسیاری در نتایج تشخیص وجود داشت.
جدول 1 دقت نتایج تشخیص تغییر ساختمان را تحت مقادیر مختلف Q نشان می دهد . از جدول می توان دریافت که دقت نتایج تشخیص تغییر با افزایش مقدار Q در ابتدا افزایش می یابد. هنگامی که Q = 32 و 64، نتایج تشخیص تغییر ساختمان ایجاد شده دارای نرخ خطای کل مشابهی بود. پس از آن، با افزایش مقدار Q ، میزان خطای کل نیز افزایش یافت. هنگامی که Q = 64، ضریب کاپا بالاترین بود. به طور کلی، دقت نتایج تشخیص تغییر ساختمان تولید شده در Q = 32 و 64 به طور کلی سازگار و شبیه به داده های مرجع زمینی بود.
برای اثبات اثربخشی روش پیشنهادی، آن را با برخی از روشهای تشخیص تغییر موجود (CD) مانند مدل کانتور فعال (CV) [28]، مجموعه سطح چند مقیاسی ( MLS ) [ 29 ]، MLS+MRF (29) مقایسه شد. Markov Random Filed)، و c-means اطلاعات محلی فازی (FLICM) [ 30 ]، و یک روش تشخیص تغییر ساختمان بر اساس طبقه بندی CNN (شبکه های عصبی کانولوشنال). نتایج در شکل 8 نشان داده شده است . تمام مقادیر پارامتر μ که طول کانتور فعال را تنظیم می کند، در CV، MLS و MLS+MRF روی 0.1 و مقدار پارامتر تنظیم شد. αدر MRF که تعادل بین طیف و اطلاعات فضایی را تنظیم میکند روی 0.5 تنظیم شد. شکل 8 a-d نقشه های تغییر ایجاد شده توسط CV، MLS، MLS+MRF و FLICM را به ترتیب نشان می دهد. همه این نقشه ها مقدار زیادی نویز “نمک و فلفل” دارند. شکل 8 e نقشه تغییر ساختمان تولید شده توسط روش طبقه بندی CNN را نشان می دهد که می تواند به طور موثر سر و صدا را سرکوب کند اما دارای برخی آلارم های کاذب ناشی از خطاهای ثبت ساختمان های بلند است. شکل 8 f نقشه تغییر ساختمان تولید شده با روش پیشنهادی را نشان می دهد که نزدیک ترین به نقشه مرجع زمین است. دلیل آن این است که از اشیاء تقسیمبندی شده به جای پیکسلهای منفرد استفاده میشود و شباهت شکل و نسبت مساحت به طول میتواند به طور موثر تشخیص نادرست را حذف کند.
پنج شاخص شامل تشخیص از دست رفته، آلارم های کاذب، کل خطاها، ضریب کاپا و زمان محاسبه برای ارزیابی کمی اثربخشی روش پیشنهادی استفاده شد. نتایج تجربی کمی در جدول 2 نشان داده شده است . نرخ تشخیص از دست رفته Pm ، نرخ تشخیص نادرست Pf ، نرخ خطای کل P tضریب کاپا و زمان محاسبه روش پیشنهادی به ترتیب 05/16، 71/0، 14/1، 8/0 و 29 ثانیه بود. برخلاف روشهای دیگر مورد استفاده در این مطالعه، روش پیشنهادی کمترین آلارمهای کاذب را ایجاد کرد و کل خطاها و سطوح تشخیص از دست رفته و زمان محاسبه در مقایسه با روشهای دیگر رضایتبخش بود. علاوه بر این، روش پیشنهادی بالاترین ضریب کاپا را در مقایسه با روشهای دیگر تولید کرد که نشان میدهد نقشه تغییر ساختمان سازگاری بهتری با نقشه مرجع زمینی دارد. روش طبقهبندی CNN میتواند به دقت تشخیص رضایتبخشی دست یابد، اما آموزش مدل CNN زمان زیادی میبرد.

4. نتیجه گیری
روشی برای تشخیص تغییر ساختمان بر اساس مدل شباهت زمینه شکل در این مقاله ارائه شده است. اول، تفاوت دادههای D-DSM با پردازش تفاوت از دادههای DSM در دو نمونه زمانی تولید شد. سپس دادههای تفاوت D-DSM با استفاده از الگوریتم SRM با مقیاسهای مختلف تقسیمبندی میشود و یک آستانه تجربی برای ایجاد تشخیص تغییر اولیه تنظیم شد. شباهت شکل بین اشیاء تغییر یافته نتیجه تشخیص تغییر اولیه و ساختمانها با استفاده از یک مدل شباهت زمینه شکل محاسبه شد و نسبت مساحت به طول برای اشیاء تغییر یافته نیز برای حذف هشدارهای کاذب ناشی از ثبت اشتباه ایجاد شد. در نهایت، روش خوشهبندی k-means بر اساس شاخص شباهت و نسبت مساحت به طول برای تهیه نقشه تغییر ساختمان اجرا شد.Q در یک محدوده مشخص. هنگامی که مقدار Q 32 یا 64 بود، دقت تشخیص تغییر ساختمان ایجاد شده تقریباً یکسان بود. تقسیم بندی SRM می تواند نویز “نمک و فلفل” ناشی از روش مبتنی بر پیکسل را کاهش دهد.
نتایج تجربی نشان داد که روش پیشنهادی میتواند به طور موثر تغییرات ساختمان را بر اساس دادههای DSM در مقایسه با سایر روشهای رایج CD تشخیص دهد. شباهت بین اشیاء تقسیمبندی شده و ساختمان محاسبهشده توسط بافت شکل میتواند به طور موثر تغییرات ساختمان را استخراج کند و نسبت مساحت به طول میتواند تغییرات تشخیص نادرست ناشی از خطاهای ثبت ساختمانهای بلند را حذف کند و دقت را بهبود بخشد. تشخیص تغییر ساختمان
با این حال، فقط ساختمانهای مستطیلی برای محاسبه شباهت برای اشیاء تغییر یافته استفاده شد، که ممکن است منجر به تشخیص نادرست برای ساختمانهای تغییر یافته با اشکال دیگر شود. از اشکال ساختمان های قبلی بیشتر در کارهای آینده برای ایجاد نتایج تشخیص دقیق تر استفاده خواهد شد.















بدون دیدگاه