توصیف نموداری داده های جغرافیایی

توصیف نموداری داده های جغرافیایی-موسسه چشم انداز-آموزش کاربردی GIS و RS

مقدمه

اگرچه توصيف هاي مقداري بسياري از ويژگي­ هاي نهان سري­ هاي آماري را بيان مي­ كنند ولي مشاهده عيني اين ويژگي­ ها اثر پايدارتري در مغز انسان ايجاد مي­ كند. بدين جهت برخي از آمار دانان (توكي، 1977) معتقدند كه نمايش تصويري ساختار دروني داده­ ها كمك مؤثرتري دارد. در توصيف­ هاي نموداري اطلاعات بيشتري از ساختار دروني داده ها آشكار مي شود. بدين جهت به اين روش­ هاي توصيفي تحليل اكتشافي داده ­ها نيز مي­ گويند. در اين فصل به معرفی نمودارهای مختلف و کاربردی در جغرافیا پرداخته می­ شود. برخی از این نمودارها که معرفی می­ شوند تنها در مکان کاربرد دارند.

الف) مهم ترین نمودارهای کاربردی

کلیۀ نمودار هایی که در این بخش معرفی می­ شوند هم در توصیف داده های غیر مکانی و مکانی کاربرد دارند. البته در توصیف مکانی، نمودار مربوطه به نقشه ­ای از مکان متصل می­ شود. که این امر باعث می­ شود توصیفات بر روی مکان بهتر مشاهده شود. بخش (ب) نمودارهای مکانی و پیاده ­سازی نمودار با نقشه را نشان می­ دهد.

نمودار جعبه­ ای

اين نمودار برای توصیف تغییرات داده و در نتیجه نرمال بودن آن­ها به کار می­ رود. در این نمودار از یک جعبه برای نمایش فاصله بین چارک اول و سوم استفاده می­ شود و یک خط در داخل جعبه، میانه (چارک دوم) را مشخص می ­کند. مقادیر حداقل و حداکثر داده­ ها و بنابراین داده­ های دورافتاده خارج از جعبه واقع می­ شوند و به راحتی می­ توان آن­ها را شناسایی کرد.

همان طور که در شکل 6-1 مشاهده می­ شود تراز آب زیر زمینی در آبخوان بوشکان بین 500 تا 540 متر بالاتر از سطح دريا قرار دارد. از آن­ جا که فاصله چارک اول تا میانه نسبت به فاصله چارک سوم تا میانه کمتر به نظر می­ رسد می­ توان مطرح نمود که در آبخوان بوشکان بیشتر مناطق دارای تراز آب مشابه با مقدار میانه هستند. همچنين یک داده دور افتاده نيز در میانه این دشت وجود دارد که از نظر هيدروژئولوژي بايستي تفسير شود.

لازم به ذکر است که هر چه طول جعبه کوتاه تر باشد درجه تراکم یا یکسانی داده ­ها بیشتر است و همچنین در صورت متقارن بودن داده ­ها طول چارک اول و چارک سوم نیز مساوی خواهد بود. در اين نمودار محل ميانه و چارك ­ها تحت تأثير اعضاي داراي ارزش ­هاي بسيار بالا يا پائين قرار نمي­ گيرند و از اين نظر مقاوم ناميده مي­ شوند.

نحوۀ به دست آوردن کمترین و بیشترین مشاهده در نمودار جعبه­ ای به ترتیب در معادلۀ (6-1) و (6-2) نشان داده شده است.

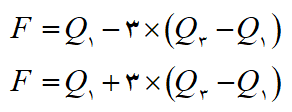
نمودار پراکنش

در طبیعت حوادث متعددی اتفاق می­ افتد که بین آن­ها همبستگی وجود دارد. چنانچه افزایش در یک متغیر، منجر به افزایش یا کاهش یک متغیر دیگر شود، گفته می­ شود که بین این دو متغیر، همبستگی وجود دارد. با توجه به خاصیت همبستگی که بین بازه

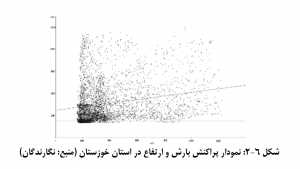
می ­باشد. هر اندازه |ρ| به یک نزدیک تر باشد این همبستگی قوی­ تر می­ باشد، به عبارت دیگر یافته­ های  گرایش زیاد دارند که اطراف یک خط راست باشند. برای نمونه، نمودار پراکنش بارش و ارتفاع در استان خوزستان در شکل 6-2 حاکی از عدم ارتباط قوی بین دو متغیر است.

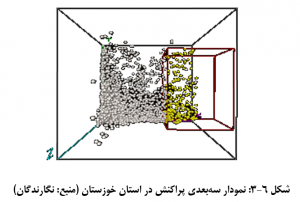
در صورتی که لازم باشد ارتباط بین سه متغیر به طور همزمان مورد ارزیابی قرار گیرد نمودار سه بعدی پراکنش، نمودار مناسبی است (رابینسون، 1956). این نمودار شامل سه محور z، y، x است، که بر روی هر محور یک متغیر بررسی می­ شود. البته ترسيم اين نمودار اولاً مشكل است و ثانياً تفسير و تعبير آن­ها آسان نيست. در نتيجه چندان متداول نيستند. برای نمونه، در استان خوزستان سه متغیر بارش، ارتفاع و شیب از طریق نمودار سه­ بعدی پراکنش که در شکل 6-3 نشان داده شده مورد بررسی قرار داده، بارش بر روی محور x، ارتفاع بر روی محور y و شیب بر روی محور z قرار دارد. این نمودار می ­تواند به شناسایی مکان­ هایی بپردازد که مورد توجه پژوهشگر است. برای نمونه اگر هدف پیدا کردن مکان یا مکان­ هایی است که دارای بارش زیاد، شیب کم و ارتفاع آن مناطق دارای نوسان باشد، از طریق کادر مستطیلی به راحتی می­ توان مکان­ هایی که این ویژگی را دارند شناسایی کرد و حتی می ­توان این مناطق را بر روی نقشه نشان داد.

البته روي محورها مي ­توان جايگاه شاخص­ هايي چون پایین ترین، چارك اول، ميانه، ميانگين، چارك سوم، و بالاترين را مشخص كرد. نمودار پراكنش علاوه بر آشكارسازي تمام ويژگي­ هاي مشخص شده در نمودار هاي جعبه ­اي يا شاخه و برگ، امكان مقايسه بين دو متغيير و همانگي تغييرات مشاهدات در دو متغيير را هم نشان مي ­دهد. از روي اين نمودار مي ­توان فهميد كدام متغيير پراكنده­ تر و كدام متمركز تر يا يكنواخت­ تر است. شدت تغييرات كدام بيشتر است. تغييرات متغييرها همسو است يا مخالف هم، هماهنگي تغييرات خطي است يا غيرخطي.

در صورتی که تعداد متغیرها زیاد باشد، ماتریس پراکنش نگار تهیه می­ شود. شکل زیر چهار نمودار پراکنش نگار دما و متغیرهای مکانی (طول، عرض و ارتفاع) را برای ایستگاه­ های استان کرمان نشان می­ دهد. در ردیف اول رابطۀ دما (محور yها) با ارتفاع (ردیف اول، ستون دوم)، عرض جغرافیایی (ردیف اول، ستون سوم) و طول جغرافیایی (ردیف اول، ستون چهارم) نشان داده می­ شود. در ریف دوم شکل زیر، دما در محور x قرار می ­گیرد. محور yها شامل ارتفاع است. در این بخش از شکل، رابطه دما-ارتفاع در ردیف دوم- ستون اول، ارتفاع-طول جغرافیایی در ردیف دوم، ستون سوم و رابطه ارتفاع- عرض جغرافیایی در ردیف دوم ستون چهارم جای گرفته است. بقیه ردیف ­ها و ستون­ ها، به شکل مشابه قابل تعبیر است. در قطر تصویر نیز محل قرارگیری رابطه هر متغیر با خودش است که با نام آن متغیر جایگزین شده است. قابل ذکر است که هر یک از این نمودارها به شکل منفرد و مستقل قابل ترسیم است. این تلفیق برای بیان این واقعیت است که گاهی رابطۀ چندین متغیر توأم را می ­توان نیز ترسیم کرد (عساکره، 1390).

نمودار هیستوگرام

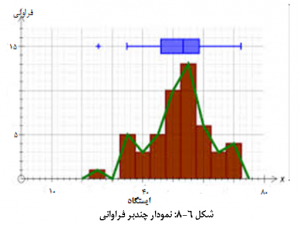
یکی از روش­ های سودمند سازمان ­دهی داده ­ها، تشکیل جدول فراوانی و نمایش گرافیکی آن در قالب هیستوگرام است. همان طور که در فصل های قبل نیز اشاره شد، جدول فراوانی، در واقع، تعداد دفعاتی که مقادیر مشاهده شده در دامنه­ های عددی مشخص (کلاس­ های عددی) قرار می­ گیرند را ثبت می ­کند. جدول فراوانی 100 دادۀ مربوط به متغیر V در جدول 6-1 ارائه شده است. اطلاعات موجود در جدول مذکور را می­ توان به صورت گرافیکی و به شکل نمودار هیستوگرام نشان داد. معمولاً جهت ترسیم هیستوگرام، از کلاس­های عددی با دامنۀ ثابت استفاده می­ شود. در این صورتف ارتفاع هیستوگرام، متناسب با تعداد مشاهداتی است که در هر کلاس قرار گرفته ­اند. هیستوگرام داده­ های متغیر V در شکل 6-5 نشان داده شده است.

نمودار فراوانی تجمعی

گاهی اوقات، بهتر است که داده ­ها را به صورت صعودی (یا نزولی) مرتب نمود و سپس، اقدام به تهیۀ جدول فراوانی (تجمعی) و توصیف گرافیکی توزیع فراوانی (تجمعی) کرد. برای نمونه، در مطالعات الودگی خاک به عناصر سنگین و یا توزیع عناصر و املاح در خاک­ های مبتلا به نمک، اطلاع از فراوانی تجمعی یا تعداد مشاهداتی که دارای مقادیر عددی بیشتر (یا کمتر) از یک حد بحرانی (معین و تعریف شده) هستند، بسیار مهم می باشند.

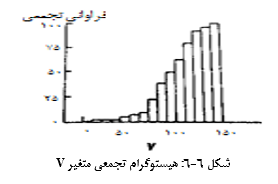
جدول فراوانی تجمعی متغیر V (با در نظر گرفتن عرض کلاس 10 پی­پی­ام) به همراه هیستوگرام تجمعی آن در جدول 6-2 و شکل 6-6 نشان داده شده­اند. همان گونه که ملاحظه می ­شود، هیستوگرام تجمعی، در حکم یک تابع غیر نزولی می­ باشد که بین 0 تا 100 درصد در تغییر می­ باشد. بدیهی است که با دانستن یکی از درصد فراوانی و یا درصد فراوانی تجمعی می ­توان دیگری را محاسبه نمود (محمدی، 1385).

نمودار میله­ ای

نمودار میله ­ای وسیلۀ دیگر برای نمایش نموداری داده ­های کمی گسسته و کیفی است. این نوع نمودار با شکلی شبیه میله نمایش داده می شود. پهنای ستون در همه طبقات به یک اندازه است. ستون ها نباید به هم بچسبند ولی اندازه فاصله از همديگر مي ­تواند متغير باشد. در شکل زیر متوسط وضعیت انواع خشکسالی (با شاخص SPI) مناطق غرب کشور با نمودار میله­ ای نشان داده شده است.

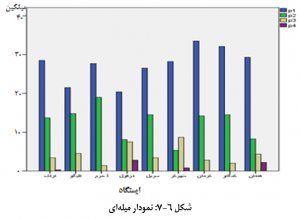
نمودار چندبر فراوانی

این نمودار مشابه نمودار مستطیلی است اما با این تفاوت که از نقطه میانی کران طبقات برای محور افقی استفاده می کند و ستون­ ها را نیز به وسیله نقاط جایگزین می­ کند و سپس از اتصال این نقاط نمودار رسم می­ شود.

نمودارهای احتمال نرمال (Q-Q) و لوگ نرمال

چنان چه توزیع داده ­ها، نرمال و یا نزدیک به نرمال باشند؛ نتایج حاصل از تخمین آماری از دقت بالاتری برخوردار خواهند بود.

نمودار احتمال نرمال، یک نمودار فراوانی تجمعی است که به تحلیل ­گر کمک می­ کند تا میزان شباهت و نزدیکی توزیع داده ­ها به توزیع نرمال را بررسی کند. محور عمودی این نمودار به گونه­ ای مقیاس ­بندی شده است تا در صورت نرمال بودن توزیع داده ­ها، فراوانی تجمعی، به صورت خطی مستقیم بر روی نمودار پدیدار گردند. نمودار احتمال متغیر V (برای 100 مشاهده) در شکل 6-9 نشان داده شده است. همان گونه که مشاهده می ­گردد، علی رغم این که بخش اعظم داده­ ها، به ویژه بدنۀ میانی داده­ ها، بر روی خط مستقیم واقع شده است؛ لیک (مقادیر بسیار کوچک و بسیار بزرگ) از خط مستقیم، انحراف نشان می ­دهند.

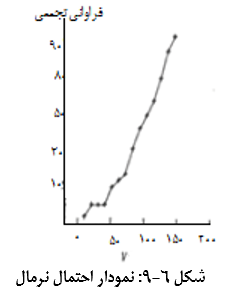
انحراف از توزیع نرمال، عموماً به دلیل وجود مقادیر کرانه ­ای است. گاهی اوقات، مقادیر کرانه ­ای به عنوان داده ­های پرت و یا ناشی از خطاهای مختلف محسوب می ­شوند و بایستی مورد بررسی و بازبینی دقیق قرار گیرند.

در صورت انحراف داده ­ها از توزیع نرمال، از مدل توزیع لوگ نرمال جهت توصیف داده­ ها استفاده می­ شود. یک متغیر، هنگامی دارای توزیع لوگ نرمال است که پراکنش لگاریتم مقادیر عددی آن به صورت نرمال توزیع یافته باشد.

به منظور بررسی توزیع لوگ نرمال، از مقیاس لگاریتمی محور افقی نمودار احتمال نرمال استفاده می ­گردد. هرگاه فراوانی تجمعی به شکل خط راست باشد، می­ توان نتیجه گرفت که توزیع داده­ ها لوگ نرمال است. نمودار احتمال لوگ نرمال متغیر V در شکل 6-10 نشان داده شده است. با توجه به شکل تقعر مانند نمودار مزبور، داده ­های مورد نظر از توزیع لوگ نرمال پیروی نمی­ کنند.

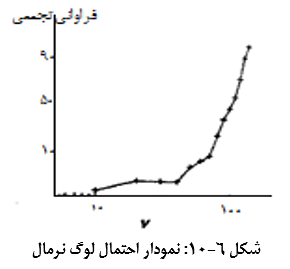
از نمودارهای احتمال می ­توان به عنوان ابزار مناسبی جهت بررسی وجود یا عدم وجود جمعیت­ های چندگانۀ اماری در مجموعۀ داده ­ها استفاده کرد. اگر چه وجود هر گونه پیچ و تاب در نمودار ، نبایستی بلافاصله به حضور چندین جمعیت تعبیر گردد؛ لیکن، چنین رفتاری می ­تواند حاکی از تغییرات خصوصیات و مشخصه­ های آماری داده­ ها در دامنه ­های عددی مختلف باشد. لذا بررسی و کشف دلایل مربوط، ضروری است (محمدی، 1385).

نمودار دایره ­ای

در اين نمودار فراواني طبقات به جاي نمايش با يك نمودار توسط قطاع ­هاي يك دايره نشان داده مي ­شود. در اين دايره مساحت دايره حجم كل داده ­ها را تشكيل مي ­دهد و هر طبقه به نسبت فراواني خودش درصدي از مساحت آن را به خود اختصاص مي­ دهد. تقسيم مساحت دايره به نسبت فراواني ­هاي طبقات از روي محيط آن انجام مي­ شود. كل داده ها 360 درجه منظور مي ­شود و آن را به نسبت فراواني ­ها بين طبقات تقسيم مي كنند. نقاط مرزي بين طبقات بوسيله خطي به مركز دايره وصل مي­ شود.

فراوانی نسبی عامل*360 = درجه هر طبقه

جدول زیر توزیع فراوانی بارش سالانه ایستگاه آبادان را نشان می ­دهد. نمودار دایره­ای در شکل 6-11 نشان داده شده است.

نمودار ساقه و برگ

برای رسم نمودار ساقه و برگ به این شکل عمل می­ شود. رقمی را که تغییرات کمی دارد به عنوان ساقه و رقمی را که تغییرات آن زیادتر هست به عنوان برگ لحاظ می­ شود. از روي اين نمودار بسياري از ويژگي هايي نهفته سري آشکار مي شود. گروه داراي بيشترين فراواني اعضا، بالاترين و پائين ترين عضو، درجه تراكم يا پراکندگی اعضا و جايگاه اين پراکندگی يا تراكم مشاهده مي شود. نمودار ساقه و برگ نموداری مناسب برای تشخیص دادن نرمال بودن داده می­ باشد. شکل 6-12 نمونه-ای از نمودار ساقه و برگ را نشان می­ دهد.

ب) نمودار های کاربردی در مکان

ویژگی مهم در نمودارهای مکانی، توجه عمده به مکان جغرافیایی محل نمونه ­ها است. وضعیت مورد مطالعه در داده ­های مکانی را با کمک نرم افزارهایی مانند GIS می ­توان بر روی مکان در قالب نقشه نشان داد.

نمودار H- پراکنش

نمودار H- پراکنش، نموداری است که جفت مقادیر عددی یک متغیر که با فاصلۀ معین و در جهت جغرافیایی مشخص از یکدیگر واقع شده ­اند، را نشان می­ دهد. در نمودارهای H- پراکنش، نمایه­ های X و y، بیانگر مختصات جغرافیایی محل نمونه ­ها هستند. موقعیت هر نمونه را می ­توان توسط یک آرایه بیان کرد. فاصلۀ بین دو نمونه را نیز می ­توان به همین ترتیب توصیف کرد.

شکل 6-13، نحوۀ تعیین و نشان دادن جفت داده ­ها و محاسبۀ فاصلۀ بین آن­ها را نشان می­ دهد. حروف x و y، نشانگر مختصات جغرافیایی و مکانی داده­ ها هستند. برای نمونه، داده ­های مربوط به متغیرهای U و V، بر روی یک شبکۀ 10 در 10 متر مربعی قرار گرفته ­اند. موقعیت جغرافیایی آن­ها از X =11 تا X =20 شرقی و از y =241 تا y =250 شمالی امتداد دارد. بدیهی است که x و y را می­ توان در واحد مسافتی ( مانند متر-کیلومتر) و یا به صورت طول و عرض جغرافیایی (درجه، دقیقه و ثانیه) بیان کرد.

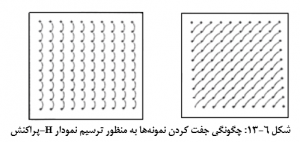
بدین ترتیب موقعیت هر نمونه (نقطه) را بر اساس x و y مشخص و معینی می ­توان بیان داشت. در شکل 6-14، موقعیت یک نمونه در(xi,yi) را می­ توان به صورت ti نوشت. ti، در واقع آرایه ­ای از موقعیت نقاط می ­باشد. به همین ترتیب، نقطۀ واقع در (xj,yj) را می­ توان به صورت tj بیان کرد. فاصلۀ جدا کنندۀ دو نقطۀ i و j، عبارت از tj-ti است که می­ توان به صورت جفت مختصات (xj-xi,yj-yi) آن را نشان داد. در پردازش آماری آرایه ­های فاصله­ ای، در نظر گرفتن جهت (برای نمونه، از نقطۀ i به j و یا بالعکس) حائز اهمیت است. بنابراین، hij، نشان دهندۀ آرایۀ فاصله ­ای بین نقطۀ i به سمت نقطۀ j است. در مقابل، hij، بیانگر جهت آرایۀ فاصله ­ای از j به i می ­باشد.

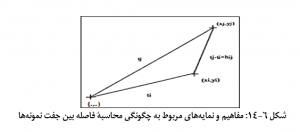
چنانچه نمودار H- پراکنش برای یک متغیر مانند V ترسیم گردد؛ آن گاه نمودار H- پراکنش V-V، در برگیرندۀ اطلاعات مربوط به مقادیر عددی یک متغیر است. در این نمودار، محور افقی را با (V(t و محور عمودی را با (V(t+h می توان نشان داد. بدین ترتیب، مختصات x یک نقطه، مطابق با مقدار متغیر V در یک موقعیت معین می باشد و مختصات y، عبارت از مقدار متغیر در نقطه ای با فاصله و جهت h (که از نقطۀ قبلی قرار گرفته است) می باشد. برای نمونه، (h =0,1) به این معنی است که جفت کردن موقعیت داده ها به گونه ای صورت گرفته است که مختصات شرقی آن ها یکسان می باشد؛ لیکن، در جهت مختصات شمالی دارای فاصلۀ دقیقاً 1 متری از یکدیگر هستند. بدیهی است که مجموعه ای از نمودار پراکنش با فاصله های مختلف h را می توان ترسیم کرد.
همانگونه که در شکل 6-15 ملاحظه می گردد، چگونگی جفت کردن داده ها که با فاصلۀ دقیقاً 1 متری و در جهت شمالی-جنوبی و همچنین، جهت شمال شرقی به جنوب غربی، از هم واقع شده اند، به خوبی نشان داده شده است. جفت کردن نمونه ها را می توان برای شرایط (h =0,2) و در همان جهت قبلی انجام داد. جهت ترسیم نمودار پراکنش ، موقعیت نمونه ها بایستی به گونه ای با یکدیگر جفت گردند که در هر دو جهت شمالی و شرقی به اندازۀ 1 متر از یکدیگر فاصله داشته باشند.
شکل و الگوی ابر نقاط بر روی نمودار H- پراکنش، بیانگر درجۀ پیوستگی مکانی داده ها در فواصل و جهات مورد نظر است. چنان چه مقادیر داده ها (که در فاصلۀ معینی یکدیگر واقع شده اند) شبیه به هم باشند؛ آن گاه ابر جفت نقاط در اطراف خط 45 درجه ( که مبدأ مختصات می گذرد قرار می گیرد. هر قدر، درجۀ شباهت و یکسانی مقادیر داده ها کاهش یابد؛ میزان پراکندگی و انتشار جفت داده ها حول خط 45 درجه نیز افزایش می یابد.
نمودار H- پراکنش متغیر V با در نظر گرفتن 4 فاصلۀ جدا کنندۀ (h =0,4)، (h =0,3)، (h =0,2)،(h =0,1) و در جهت مشخص شمالی –جنوبی در شکل 6-16 نشان داده شده است. نکتۀ جالب توجه در این مجموعه نمودارها آن است که با افزایش فاصله، از به ، پراکندگی جفت نقاط حول خط 45 درجه بیشتر می گردد. علاوه بر آن، وجود برخی جفت داده ها که به گونه ای مشکوک، دور از خط 45 درجه و جدا از بقیۀ جفت داده ها واقع شده اند، کاملاً بر روی نمودارها مشخص می باشند. بدین ترتیب، با استفاده از نمودار H- پراکنش می توان نحوۀ پراکندگی مکانی داده ها را به صورت تصویری مورد بررسی قرار داد.

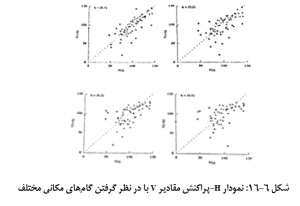
مطالعۀ الگوی مکانی پراکنش داده­ ها توسط نمودار H- پراکنش، مستلزم تهیۀ مجموعۀ بسیار زیادی از این نمودارها در فواصل و جهات مختلف است. زیرا تغییرات مکانی، نه تنها وابسته به فاصلۀ بین نمونه ­ها هستند؛ بلکه در جهات مختلف جغرافیایی نیز می­ تواند رفتاری متفاوت از خود نشان دهند.

برای نمونه، در یک فرآیند الودگی نقطه­ ای، تغییرات غلظت آلاینده، نه تنها وابسته به فاصلۀ محل نمونه­ برداری تا منبع انتشار آلودگی (مانند دودکش یک کارخانه) است؛ بلکه متأثر از وزش بادهای غالب در منطقۀ مطالعاتی نیز می ­باشد. عامل اخیر می­ تواند آلاینده را به صورت ترجیحی و در جهات جغرافیایی مشخص پراکنده سازد (محمدی، 1385).

نمودار هماهنگی خطوط موازی

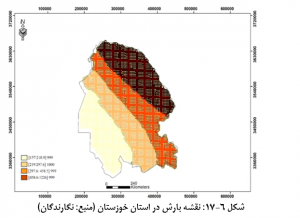
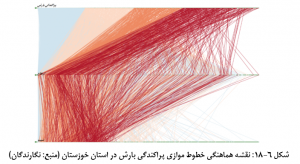
به ازای هر یک از متغیرها یک خط مستقیم در زیر هم رسم می­ شود. مقادیر مربوط به هر متغیر بر روی خط مربوطه در نظر گرفته می ­شود. در این نمودار متغیر مورد مطالعه اصلی از جنبه ­های مختلفی چون انحراف معیار، چارک، و … می­ تواند طبقه بندی شود. سپس متغیر طبقه بندی شده با دیگر متغیرها ارزیابی می­ شود. برای نمونه بارش در استان خوزستان را بر اساس پراکندگی (انحراف معیار) طبقه بندی کرده و آن را با دو متغیر ارتفاع و شیب مورد ارزیابی قرار داده پراکندگی بارش در قسمت شمال و شمال شرقی و شرق خوزستان به مراتب زیاد است و این ناحیه، مناطقی هستند که بیشترین بارش در سطح استان خوزستان را دارند (شکل 6-17 را ببینید). با استفاده از نمودار هماهنگی خطوط موازی در شکل 6-18 این نتیجه به دست آمده که این مناطق از نظر ارتفاعی متفاوت هستند اما شیب کمی را نسبت به سایر مناطق به خود اختصاص می ­دهند (جوی زاده و همکاران، 1396).