28 اصول GIS
28.1 بررسی اجمالی
جنبههای فضایی دادههای شما میتواند بینشهای زیادی در مورد وضعیت شیوع بیماری و پاسخ به سؤالاتی از قبیل:
- کانون های فعلی بیماری کجا هستند؟
- نقاط مهم در طول زمان چگونه تغییر کرده اند؟
- دسترسی به امکانات بهداشتی چگونه است؟ آیا به بهبودی نیاز است؟
تمرکز فعلی این صفحه GIS برای رسیدگی به نیازهای اپیدمیولوژیست های کاربردی در واکنش به شیوع بیماری است. ما روش های اصلی تجسم داده های مکانی را با استفاده از بسته های tmap و ggplot2 بررسی خواهیم کرد . همچنین برخی از روشهای اساسی مدیریت دادههای مکانی و روشهای پرس و جو را با بسته sf بررسی خواهیم کرد . در نهایت، به طور خلاصه به مفاهیم آمار فضایی مانند روابط مکانی، خودهمبستگی مکانی و رگرسیون فضایی با استفاده از بسته spdep خواهیم پرداخت .
28.2 اصطلاحات کلیدی
در زیر برخی از اصطلاحات کلیدی را معرفی می کنیم. برای آشنایی کامل با GIS و تجزیه و تحلیل فضایی، پیشنهاد می کنیم یکی از دوره های آموزشی یا دوره های طولانی تر فهرست شده در قسمت مراجع را مرور کنید.
سیستم اطلاعات جغرافیایی (GIS) – GIS چارچوب یا محیطی برای جمع آوری، مدیریت، تجزیه و تحلیل و تجسم داده های مکانی است.
نرم افزار GIS
برخی از نرم افزارهای محبوب GIS امکان تعامل نقطه و کلیک را برای توسعه نقشه و تجزیه و تحلیل فضایی فراهم می کنند. این ابزارها دارای مزایایی مانند عدم نیاز به یادگیری کد و سهولت انتخاب دستی و قرار دادن آیکون ها و ویژگی ها بر روی نقشه هستند. در اینجا دو مورد محبوب وجود دارد:
ArcGIS – یک نرم افزار تجاری GIS که توسط شرکت ESRI توسعه یافته است، که بسیار محبوب اما بسیار گران است
QGIS – یک نرم افزار رایگان منبع باز GIS که تقریباً هر کاری را که ArcGIS می تواند انجام دهد، انجام می دهد. می توانید QGIS را از اینجا دانلود کنید
استفاده از R بهعنوان یک GIS در ابتدا میتواند ترسناکتر به نظر برسد، زیرا به جای «نقطه و کلیک»، یک «واسط خط فرمان» دارد (شما باید برای به دست آوردن نتیجه دلخواه کدنویسی کنید). با این حال، اگر نیاز به تولید مکرر نقشه ها یا ایجاد تجزیه و تحلیل قابل تکرار داشته باشید، این یک مزیت بزرگ است.
داده های فضایی
دو شکل اولیه داده های مکانی مورد استفاده در GIS داده های برداری و شطرنجی هستند:
داده های برداری – رایج ترین فرمت داده های مکانی مورد استفاده در GIS، داده های برداری از ویژگی های هندسی رئوس و مسیرها تشکیل شده است. داده های مکانی برداری را می توان به سه نوع پرکاربرد تقسیم کرد:
- نقاط – یک نقطه از یک جفت مختصات (x,y) تشکیل شده است که نشان دهنده یک مکان خاص در یک سیستم مختصات است. نقاط ابتدایی ترین شکل داده های مکانی هستند و ممکن است برای نشان دادن یک مورد (به عنوان مثال خانه بیمار) یا یک مکان (به عنوان مثال بیمارستان) روی نقشه استفاده شوند.
- خطوط – یک خط از دو نقطه متصل تشکیل شده است. خطوط دارای طول هستند و ممکن است برای نشان دادن چیزهایی مانند جاده ها یا رودخانه ها استفاده شوند.
- چند ضلعی – یک چند ضلعی از حداقل سه پاره خط تشکیل شده است که توسط نقاطی به هم متصل شده اند. ویژگی های چند ضلعی دارای طول (یعنی محیط منطقه) و همچنین اندازه گیری مساحت هستند. چند ضلعی ممکن است برای یادداشت یک منطقه (به عنوان مثال یک روستا) یا یک ساختار (یعنی منطقه واقعی یک بیمارستان) استفاده شود.
داده های شطرنجی – یک قالب جایگزین برای داده های مکانی، داده های شطرنجی ماتریسی از سلول ها (به عنوان مثال پیکسل) است که هر سلول حاوی اطلاعاتی مانند ارتفاع، دما، شیب، پوشش جنگل و غیره است. اینها اغلب عکس های هوایی، تصاویر ماهواره ای و غیره هستند. رسترها همچنین می توانند به عنوان “نقشه های پایه” در زیر داده های برداری استفاده شوند.
تجسم داده های مکانی
برای نمایش بصری دادههای مکانی روی نقشه، نرمافزار GIS از شما میخواهد که اطلاعات کافی در مورد مکانهایی که ویژگیهای مختلف باید در ارتباط با یکدیگر باشند، ارائه دهید. اگر از داده های برداری استفاده می کنید، که برای اکثر موارد استفاده درست است، این اطلاعات معمولاً در یک فایل شیپ ذخیره می شود:
Shapefiles – یک shapefile یک قالب داده رایج برای ذخیره داده های فضایی “بردار” متشکل از خطوط، نقاط یا چند ضلعی است. یک shapefile منفرد در واقع مجموعه ای از حداقل سه فایل است – .shp، .shx و dbf. همه این فایل های فرعی باید در یک پوشه (پوشه) مشخص وجود داشته باشند تا شکل فایل قابل خواندن باشد. این فایل های مرتبط را می توان در یک پوشه ZIP فشرده کرد تا از طریق ایمیل ارسال شود یا از یک وب سایت دانلود شود.
شکل فایل حاوی اطلاعاتی در مورد خود ویژگی ها و همچنین محل قرارگیری آنها در سطح زمین خواهد بود. این مهم است زیرا در حالی که زمین یک کره است، نقشه ها معمولاً دو بعدی هستند. انتخابهای مربوط به نحوه «مسطحسازی» دادههای مکانی میتواند تأثیر زیادی بر ظاهر و تفسیر نقشه حاصل داشته باشد.
سیستم های مرجع مختصات (CRS) – CRS یک سیستم مبتنی بر مختصات است که برای مکان یابی ویژگی های جغرافیایی در سطح زمین استفاده می شود. دارای چند جزء کلیدی است:
- سیستم مختصات – سیستم های مختصات بسیار زیادی وجود دارد، بنابراین مطمئن شوید که مختصات شما از کدام سیستم است. درجات طول و عرض جغرافیایی رایج است، اما می توانید مختصات UTM را نیز ببینید .
- واحدها – بدانید که چه واحدهایی برای سیستم مختصات شما هستند (مثلاً درجات اعشاری، متر)
- Datum – یک نسخه مدل شده خاص از زمین. اینها در طول سالها بازنگری شدهاند، بنابراین مطمئن شوید که لایههای نقشه شما از دادههای یکسانی استفاده میکنند.
- فرافکنی – اشاره ای به معادله ریاضی که برای نمایش زمین واقعاً گرد بر روی یک سطح صاف (نقشه) استفاده شد.
به یاد داشته باشید که می توانید داده های مکانی را بدون استفاده از ابزارهای نقشه برداری که در زیر نشان داده شده است، خلاصه کنید. گاهی اوقات یک جدول ساده بر اساس جغرافیا (مثلا منطقه، کشور و غیره) تنها چیزی است که لازم است!
28.3 شروع به کار با GIS
چند مورد کلیدی وجود دارد که باید داشته باشید و برای تهیه نقشه در مورد آنها فکر کنید. این شامل:
- یک مجموعه داده – این می تواند در قالب داده های مکانی باشد (مانند فایل های شکل، همانطور که در بالا ذکر شد) یا ممکن است در قالب فضایی نباشد (به عنوان مثال فقط به عنوان یک csv).
- اگر مجموعه داده شما در قالب فضایی نیست، به یک مجموعه داده مرجع نیز نیاز خواهید داشت . دادههای مرجع شامل نمایش مکانی دادهها و ویژگیهای مرتبط حاوی مطالب، مکان و اطلاعات آدرس ویژگیهای خاص است.
- اگر با مرزهای جغرافیایی از پیش تعریف شده کار می کنید (به عنوان مثال، مناطق اداری)، فایل های شکل مرجع اغلب به صورت رایگان برای دانلود از یک سازمان دولتی یا سازمان به اشتراک گذاری داده در دسترس هستند. وقتی شک دارید، یک مکان خوب برای شروع این است که «[regions] shapefile» را در گوگل جستجو کنید.
- اگر اطلاعات آدرس دارید، اما طول و عرض جغرافیایی ندارید، ممکن است لازم باشد از یک موتور کدگذاری جغرافیایی برای دریافت داده های مرجع مکانی برای سوابق خود استفاده کنید.
- ایده ای در مورد اینکه چگونه می خواهید اطلاعات موجود در مجموعه داده های خود را به مخاطبان هدف خود ارائه دهید. انواع مختلفی از نقشه ها وجود دارد، و مهم است که در مورد اینکه کدام نوع نقشه با نیازهای شما مطابقت دارد، فکر کنید.
انواع نقشه برای تجسم داده های شما
نقشه Choropleth – نوعی نقشه موضوعی که در آن از رنگ ها، سایه ها یا الگوها برای نشان دادن مناطق جغرافیایی در رابطه با ارزش یک ویژگی استفاده می شود. برای مثال مقدار بزرگتر را می توان با رنگ تیره تر نسبت به مقدار کوچکتر نشان داد. این نوع نقشه به ویژه هنگام تجسم یک متغیر و نحوه تغییر آن در مناطق تعریف شده یا مناطق ژئوپلیتیکی مفید است.
نقشه حرارتی چگالی موردی – نوعی نقشه موضوعی که در آن از رنگ ها برای نشان دادن شدت یک مقدار استفاده می شود، اما از مناطق یا مرزهای ژئوپلیتیکی تعریف شده برای گروه بندی داده ها استفاده نمی کند. این نوع نقشه معمولاً برای نشان دادن “نقاط داغ” یا مناطقی با تراکم یا تمرکز نقاط بالا استفاده می شود.
نقشه چگالی نقطه – یک نوع نقشه موضوعی است که از نقاط برای نشان دادن مقادیر ویژگی در داده های شما استفاده می کند. این نوع نقشه بهتر است برای تجسم پراکندگی داده های شما و اسکن بصری برای خوشه ها استفاده شود.
نقشه نمادهای متناسب (نقشه نمادهای درجه بندی شده) – یک نقشه موضوعی شبیه به نقشه choropleth، اما به جای استفاده از رنگ برای نشان دادن مقدار یک ویژگی، از نماد (معمولا یک دایره) در رابطه با مقدار استفاده می کند. به عنوان مثال یک مقدار بزرگتر را می توان با یک نماد بزرگتر از یک مقدار کوچکتر نشان داد. بهترین استفاده از این نوع نقشه زمانی است که می خواهید اندازه یا کمیت داده های خود را در مناطق جغرافیایی تجسم کنید.
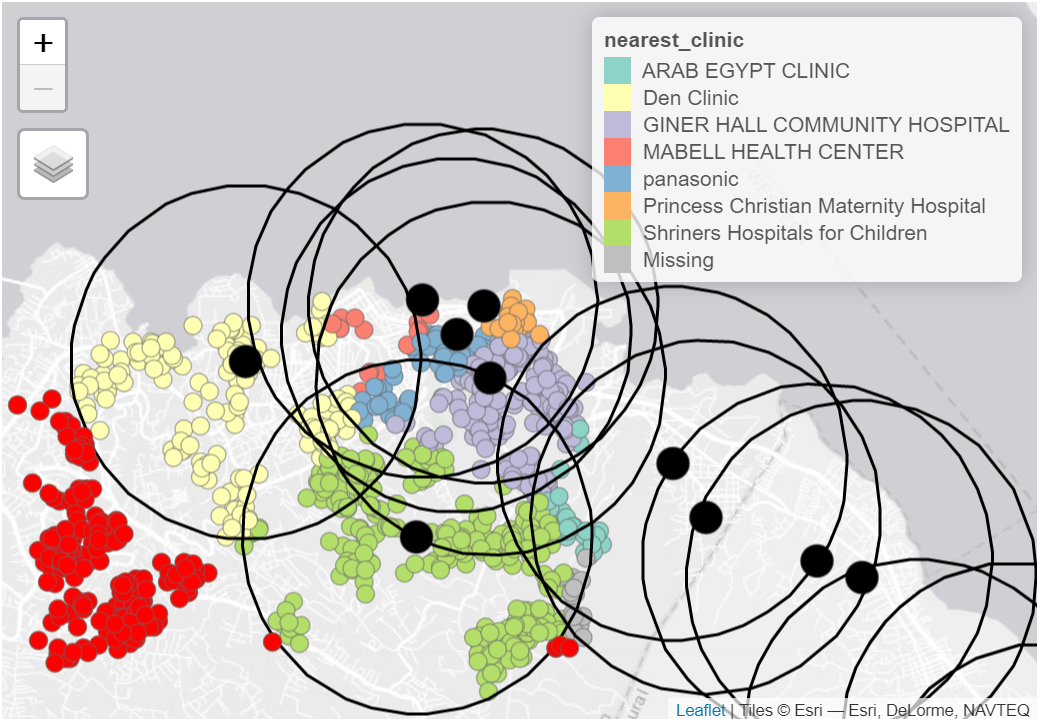
همچنین می توانید چندین نوع تجسم مختلف را برای نشان دادن الگوهای جغرافیایی پیچیده ترکیب کنید. به عنوان مثال، موارد (نقطه) در نقشه زیر با توجه به نزدیکترین مرکز بهداشتی خود رنگ می شوند (به افسانه مراجعه کنید). دایرههای قرمز بزرگ، حوضههای آبریز تأسیسات بهداشتی را با شعاع معین نشان میدهند، و نقاط قرمز روشن آنهایی را که خارج از هر محدوده حوضهای قرار دارند، نشان میدهند:
توجه: تمرکز اصلی این صفحه GIS بر زمینه پاسخ به شیوع شیوع میدانی است. بنابراین محتویات صفحه دستکاری ها، تجسم ها و تحلیل های داده های مکانی پایه را پوشش می دهد.
28.4 آماده سازی
بسته ها را بارگیری کنید
این قطعه کد بارگیری بسته های مورد نیاز برای تجزیه و تحلیل را نشان می دهد. p_load()در این کتاب راهنما از Pacman تاکید می کنیم که در صورت لزوم بسته را نصب کرده و برای استفاده بارگذاری می کند. همچنین میتوانید بستههای نصبشده را با library()از پایه R بارگیری کنید . برای اطلاعات بیشتر در مورد بستههای R به صفحه مبانی R مراجعه کنید.
pacman::p_load(
rio, # to import data
here, # to locate files
tidyverse, # to clean, handle, and plot the data (includes ggplot2 package)
sf, # to manage spatial data using a Simple Feature format
tmap, # to produce simple maps, works for both interactive and static maps
janitor, # to clean column names
OpenStreetMap, # to add OSM basemap in ggplot map
spdep # spatial statistics
)
میتوانید یک نمای کلی از تمام بستههای R که با دادههای مکانی سروکار دارند را در CRAN “Spatial Task View” مشاهده کنید .
نمونه داده های موردی
برای اهداف نمایشی، ما با یک نمونه تصادفی از 1000 مورد از linelistچارچوب داده اپیدمی شبیهسازی شده ابولا کار خواهیم کرد (از لحاظ محاسباتی، کار با موارد کمتر در این کتاب راهنمای نمایش آسانتر است). اگر میخواهید دنبال کنید، برای دانلود فهرست خط «پاک» (به عنوان فایل rds) کلیک کنید.
از آنجایی که ما نمونهای تصادفی از موارد میگیریم، نتایج شما ممکن است کمی متفاوت از آنچه در اینجا نشان داده شده است، زمانی که کدها را به تنهایی اجرا میکنید، به نظر برسد.
دادهها را با import()تابع از بسته rio وارد کنید (این نوع فایلها مانند xlsx.، .csv.، .rds را مدیریت میکند – برای جزئیات به صفحه واردات و صادرات مراجعه کنید ).
# import clean case linelist
linelist <- import("linelist_cleaned.rds")
سپس یک نمونه تصادفی از 1000 ردیف را با استفاده sample()از پایه R انتخاب می کنیم.
# generate 1000 random row numbers, from the number of rows in linelist
sample_rows <- sample(nrow(linelist), 1000)
# subset linelist to keep only the sample rows, and all columns
linelist <- linelist[sample_rows,]
اکنون میخواهیم این را linelistکه دیتافریم کلاس است، به یک شی از کلاس «sf» (ویژگیهای فضایی) تبدیل کنیم. با توجه به اینکه لیست خط دارای دو ستون “lon” و “lat” است که نشان دهنده طول و عرض جغرافیایی محل سکونت هر مورد است، این کار آسان خواهد بود.
ما از بسته sf (ویژگی های فضایی) و عملکرد آن st_as_sf()برای ایجاد شی جدیدی که فراخوانی می کنیم استفاده می کنیم linelist_sf. این شی جدید اساساً شبیه لیست خط است، اما ستونها lonبه latعنوان ستون مختصات تعیین شدهاند، و یک سیستم مرجع مختصات (CRS) برای زمانی که نقاط نمایش داده میشوند، اختصاص داده شده است. 4326 مختصات ما را بر اساس سیستم جهانی ژئودتیک 1984 (WGS84) مشخص می کند – که برای مختصات GPS استاندارد است.
# Create sf object
linelist_sf <- linelist %>%
sf::st_as_sf(coords = c("lon", "lat"), crs = 4326)
دیتافریم اصلی اینگونه linelistبه نظر می رسد. در این نمایش، ما فقط از ستون date_onsetو geometry(که از فیلدهای طول و عرض جغرافیایی بالا ساخته شده و آخرین ستون در قاب داده است) استفاده خواهیم کرد.
DT::datatable(head(linelist_sf, 10), rownames = FALSE, options = list(pageLength = 5, scrollX=T), class = 'white-space: nowrap' )
شکل فایلهای مرز مدیریت
سیرالئون: شکل فایلهای مرزی مدیریت
از قبل، ما تمام مرزهای اداری سیرالئون را از وبسایت تبادل دادههای بشردوستانه (HDX) در اینجا دانلود کردهایم . همچنین، میتوانید این و همه دادههای نمونه دیگر را برای این کتابچه راهنما از طریق بسته R ما دانلود کنید، همانطور که در صفحه راهنمای دانلود و دادهها توضیح داده شده است .
حال برای ذخیره شیپ فایل سطح 3 مدیریت در R می خواهیم کارهای زیر را انجام دهیم:
- شکل فایل را وارد کنید
- نام ستون ها را پاک کنید
- ردیفها را فیلتر کنید تا فقط مناطق مورد علاقه حفظ شود
read_sf()برای وارد کردن یک شکل فایل از تابع sf استفاده می کنیم . مسیر فایل از طریق ارائه می شود here(). – در مورد ما فایل در پروژه R ما در زیرپوشههای “data”، “gis” و “shp” با نام فایل “sle_adm3.shp” قرار دارد (برای اطلاعات بیشتر به صفحات Import and export و R projects مراجعه کنید ) . شما باید مسیر فایل خود را ارائه دهید.
clean_names()سپس از بسته سرایدار برای استاندارد کردن نام ستون های shapefile استفاده می کنیم . ما همچنین filter()فقط از ردیفهایی با نام admin2 «Western Area Urban» یا «Western Area Rural» استفاده میکنیم.
# ADM3 level clean
sle_adm3 <- sle_adm3_raw %>%
janitor::clean_names() %>% # standardize column names
filter(admin2name %in% c("Western Area Urban", "Western Area Rural")) # filter to keep certain areas
در زیر می توانید نحوه ظاهر شکل فایل پس از وارد کردن و تمیز کردن را مشاهده کنید. به سمت راست بروید تا ببینید که چگونه ستونهایی با سطح مدیریت 0 (کشور)، سطح سرپرست 1، سطح سرپرست 2 و در نهایت سطح مدیریت 3 وجود دارد. هر سطح دارای یک نام کاراکتر و یک شناسه منحصر به فرد “pcode” است. pcode با هر افزایش سطح مدیریت گسترش می یابد، به عنوان مثال SL (سیرا لئون) -> SL04 (غربی) -> SL0410 (منطقه غربی روستایی) -> SL040101 (کویا روستایی).
داده های جمعیت
سیرالئون: جمعیت بر اساس ADM3
این داده ها را می توان دوباره از HDX (لینک اینجا ) یا از طریق بسته R epirhandbook ما که در این صفحه توضیح داده شده است ، بارگیری کرد . ما import()برای بارگذاری فایل csv. استفاده می کنیم. ما همچنین فایل وارد شده را clean_names()برای استاندارد کردن نحو نام ستون ارسال می کنیم.
# Population by ADM3
sle_adm3_pop <- import(here("data", "gis", "population", "sle_admpop_adm3_2020.csv")) %>%
janitor::clean_names()
در اینجا فایل جمعیت شبیه به آن است. به سمت راست بروید تا ببینید که چگونه هر حوزه قضایی دارای ستون هایی با maleجمعیت، femaleجمعیت، totalجمعیت و تفکیک جمعیت در ستون ها بر اساس گروه سنی است.
خدمات درمانی
سیرالئون: امکانات داده سلامت از OpenStreetMap
مجدداً مکانهای مراکز درمانی را از HDX از اینجا یا از طریق دستورالعملهای موجود در صفحه راهنمای دانلود و داده دانلود کردهایم .
شکل فایل نقاط تسهیلات را با وارد میکنیم read_sf()، دوباره نام ستونها را تمیز میکنیم و سپس فیلتر میکنیم تا فقط نقاطی را با عنوان «بیمارستان»، «درمانگاه» یا «پزشکان» برچسبگذاری کنیم.
# OSM health facility shapefile
sle_hf <- sf::read_sf(here("data", "gis", "shp", "sle_hf.shp")) %>%
janitor::clean_names() %>%
filter(amenity %in% c("hospital", "clinic", "doctors"))
در اینجا چارچوب داده به دست آمده است – برای دیدن نام و مختصات تأسیسات به سمت راست بروید .geometry
28.5 مختصات رسم
ساده ترین راه برای رسم مختصات XY (طول/طول جغرافیایی، نقاط)، در این مورد، ترسیم آنها به عنوان نقاط مستقیماً از شی ای است linelist_sfکه در قسمت آماده سازی ایجاد کردیم.
بسته tmap قابلیت های نقشه برداری ساده را برای هر دو حالت استاتیک (حالت “نقاط”) و تعاملی (حالت “نمایش”) تنها با چند خط کد ارائه می دهد. نحو tmap شبیه به ggplot2 است، به طوری که دستورات به یکدیگر اضافه می شوند . جزئیات بیشتر را در این خط مشروب بخوانید .+
- حالت tmap را تنظیم کنید . در این مورد ما از حالت “Plot” استفاده خواهیم کرد که خروجی های ثابت تولید می کند.
tmap_mode("plot") # choose either "view" or "plot"در زیر، نقاط به تنهایی ترسیم شده اند. tm_shape()با linelist_sfاشیاء ارائه می شود. سپس نقاط را از طریق اضافه می کنیم tm_dots()و اندازه و رنگ را مشخص می کنیم. از آنجا که linelist_sfیک شی sf است، ما قبلاً دو ستون را که حاوی مختصات lat/long و سیستم مرجع مختصات (CRS) هستند تعیین کرده ایم:
# Just the cases (points)
tm_shape(linelist_sf) + tm_dots(size=0.08, col='blue')
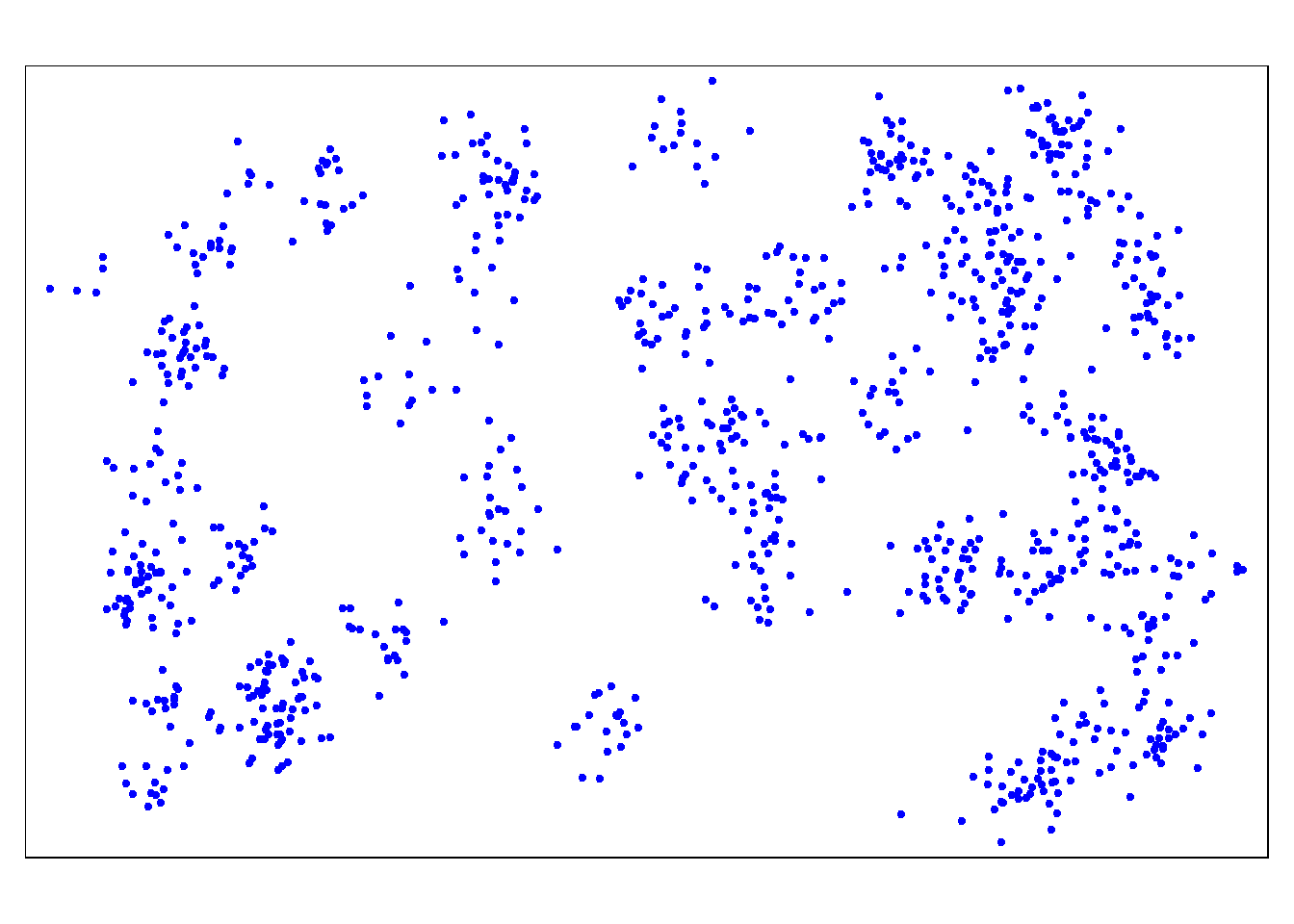
به تنهایی، نکات چیز زیادی به ما نمی گوید. بنابراین ما باید مرزهای اداری را نیز ترسیم کنیم:
tm_shape()دوباره از (به مستندات مراجعه کنید) استفاده می کنیم ، اما به جای ارائه شکل فایل نقاط مورد، شکل فایل مرز اداری (چند ضلعی ها) را ارائه می دهیم.
با bbox =آرگومان (bbox مخفف “Bounding Box”) می توانیم مرزهای مختصات را مشخص کنیم. ابتدا نمایش نقشه را بدون bboxو سپس با آن نشان می دهیم.
# Just the administrative boundaries (polygons)
tm_shape(sle_adm3) + # admin boundaries shapefile
tm_polygons(col = "#F7F7F7")+ # show polygons in light grey
tm_borders(col = "#000000", # show borders with color and line weight
lwd = 2) +
tm_text("admin3name") # column text to display for each polygon
# Same as above, but with zoom from bounding box
tm_shape(sle_adm3,
bbox = c(-13.3, 8.43, # corner
-13.2, 8.5)) + # corner
tm_polygons(col = "#F7F7F7") +
tm_borders(col = "#000000", lwd = 2) +
tm_text("admin3name")
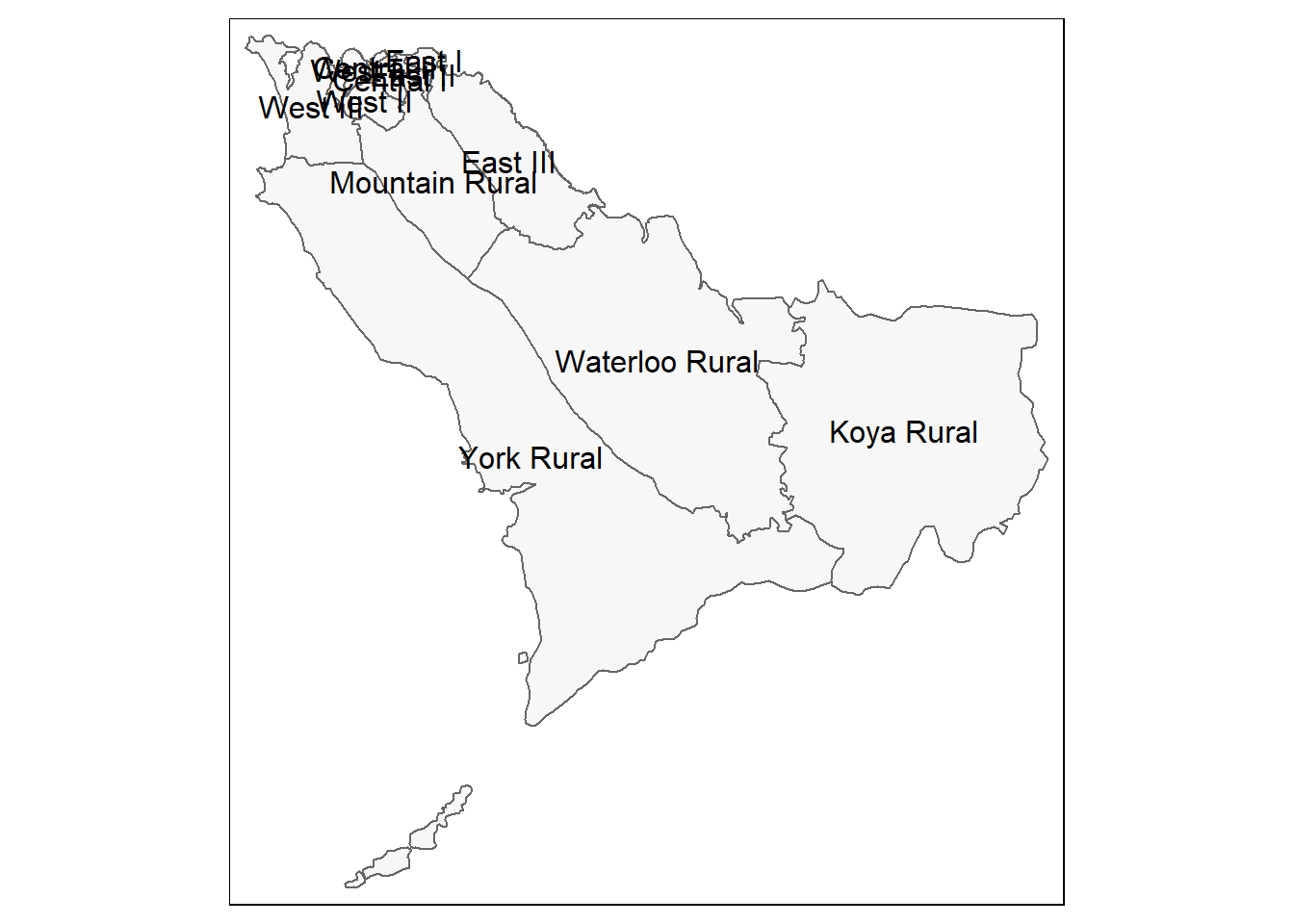
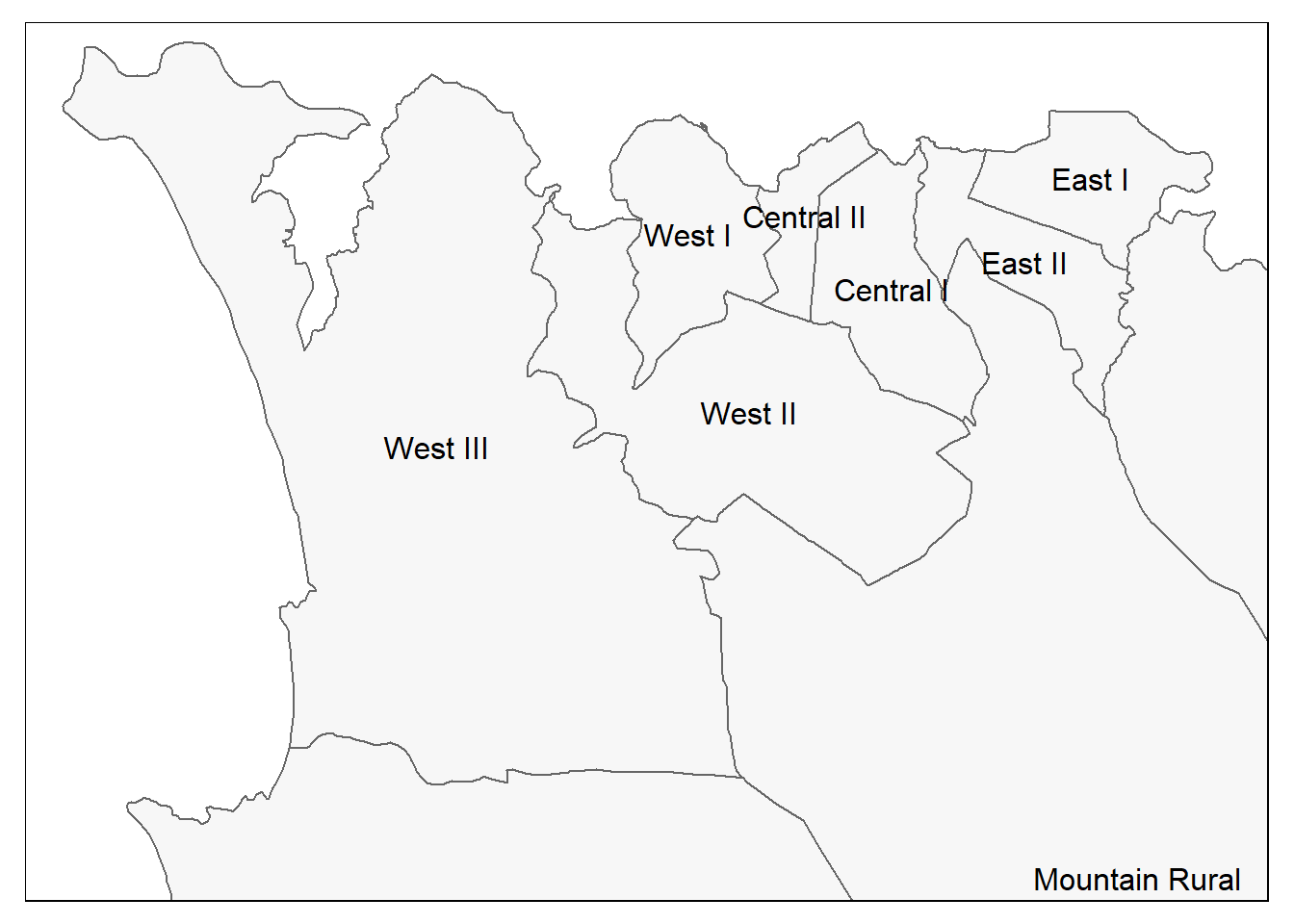
و حالا هر دو نقطه و چند ضلعی با هم:
# All together
tm_shape(sle_adm3, bbox = c(-13.3, 8.43, -13.2, 8.5)) + #
tm_polygons(col = "#F7F7F7") +
tm_borders(col = "#000000", lwd = 2) +
tm_text("admin3name")+
tm_shape(linelist_sf) +
tm_dots(size=0.08, col='blue', alpha = 0.5) +
tm_layout(title = "Distribution of Ebola cases") # give title to map
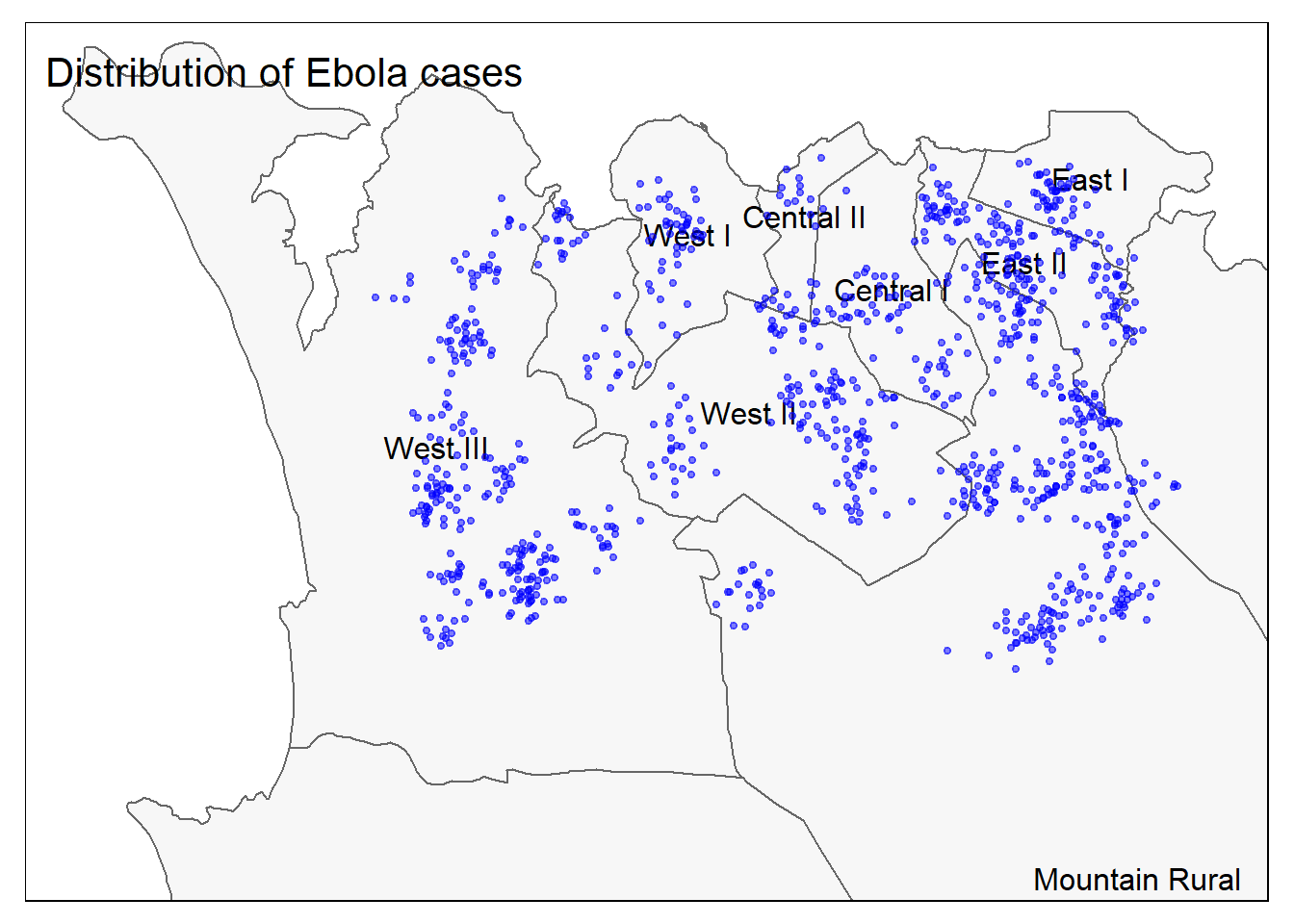
برای خواندن یک مقایسه خوب از گزینه های نقشه برداری در R، این پست وبلاگ را ببینید .
28.6 اتصالات فضایی
ممکن است با اتصال داده ها از یک مجموعه داده به مجموعه دیگر آشنا باشید . چندین روش در صفحه داده های پیوستن این کتابچه مورد بحث قرار گرفته است. اتصال فضایی هدفی مشابه دارد اما روابط فضایی را تحت تأثیر قرار می دهد. به جای تکیه بر مقادیر مشترک در ستونها برای تطبیق صحیح مشاهدات، میتوانید از روابط فضایی آنها استفاده کنید، مانند قرار گرفتن یک ویژگی در دیگری، یا نزدیکترین همسایه به دیگری، یا در یک بافر با شعاع معین از دیگری و غیره.
بسته sf روش های مختلفی را برای اتصالات فضایی ارائه می دهد. مستندات بیشتر در مورد روش st_join و انواع اتصالات فضایی را در این مرجع مشاهده کنید .
نقاط در چند ضلعی
واگذاری فضایی واحدهای اداری به پرونده ها
در اینجا یک معمای جالب وجود دارد: لیست موارد حاوی هیچ اطلاعاتی در مورد واحدهای اداری پرونده ها نیست. اگرچه جمعآوری چنین اطلاعاتی در مرحله جمعآوری دادههای اولیه ایدهآل است، اما میتوانیم واحدهای اداری را بر اساس روابط فضایی آنها به موارد جداگانه اختصاص دهیم (یعنی نقطه با یک چندضلعی قطع میشود).
در زیر، مکانهای موردی (نقاط) خود را با مرزهای ADM3 (چند ضلعیها) قطع میکنیم:
- با لیست خط (امتیاز) شروع کنید
- پیوستن فضایی به مرزها، تنظیم نوع اتصال در “st_intersects”
select()فقط برای نگه داشتن برخی از ستون های مرز اداری جدید استفاده کنید
linelist_adm <- linelist_sf %>%
# join the administrative boundary file to the linelist, based on spatial intersection
sf::st_join(sle_adm3, join = st_intersects)تمام ستون های از sle_admsبه لیست خط اضافه شده اند! اکنون هر پرونده دارای ستون هایی است که سطوح اداری را که در آن قرار می گیرد، نشان می دهد. در این مثال، ما فقط میخواهیم دو تا از ستونهای جدید (سطح مدیریت 3) را نگه داریم، بنابراین select()نام ستونهای قدیمی و فقط دو ستون مورد علاقه را داریم:
linelist_adm <- linelist_sf %>%
# join the administrative boundary file to the linelist, based on spatial intersection
sf::st_join(sle_adm3, join = st_intersects) %>%
# Keep the old column names and two new admin ones of interest
select(names(linelist_sf), admin3name, admin3pcod)در زیر، صرفاً برای نمایش، میتوانید ده مورد اول را ببینید و اینکه حوزههای قضایی سطح سرپرست 3 (ADM3) آنها بر اساس محل تلاقی فضایی نقطه با اشکال چندضلعی، پیوست شدهاند.
# Now you will see the ADM3 names attached to each case
linelist_adm %>% select(case_id, admin3name, admin3pcod)## Simple feature collection with 1000 features and 3 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -13.27276 ymin: 8.447753 xmax: -13.20545 ymax: 8.490227
## Geodetic CRS: WGS 84
## First 10 features:
## case_id admin3name admin3pcod geometry
## 1804 fc6146 West III SL040208 POINT (-13.26622 8.467828)
## 3370 7b7e0c East II SL040204 POINT (-13.21043 8.476803)
## 675 6254ff Mountain Rural SL040102 POINT (-13.20937 8.462601)
## 1035 64ad98 Mountain Rural SL040102 POINT (-13.21327 8.468354)
## 4213 fd4705 West III SL040208 POINT (-13.26002 8.455182)
## 279 04ebc8 Central I SL040201 POINT (-13.23286 8.47862)
## 2855 c70ead Mountain Rural SL040102 POINT (-13.22476 8.479803)
## 4939 198a37 West II SL040207 POINT (-13.23424 8.466239)
## 1380 d6f195 East II SL040204 POINT (-13.21833 8.479677)
## 1912 097ab6 Mountain Rural SL040102 POINT (-13.24052 8.453057)اکنون می توانیم موارد خود را بر اساس واحد اداری توصیف کنیم – کاری که قبل از پیوستن فضایی قادر به انجام آن نبودیم!
# Make new dataframe containing counts of cases by administrative unit
case_adm3 <- linelist_adm %>% # begin with linelist with new admin cols
as_tibble() %>% # convert to tibble for better display
group_by(admin3pcod, admin3name) %>% # group by admin unit, both by name and pcode
summarise(cases = n()) %>% # summarize and count rows
arrange(desc(cases)) # arrange in descending order
case_adm3## # A tibble: 10 × 3
## # Groups: admin3pcod [10]
## admin3pcod admin3name cases
## <chr> <chr> <int>
## 1 SL040102 Mountain Rural 279
## 2 SL040208 West III 243
## 3 SL040207 West II 157
## 4 SL040204 East II 128
## 5 SL040201 Central I 57
## 6 SL040206 West I 48
## 7 SL040203 East I 45
## 8 SL040202 Central II 20
## 9 SL040205 East III 19
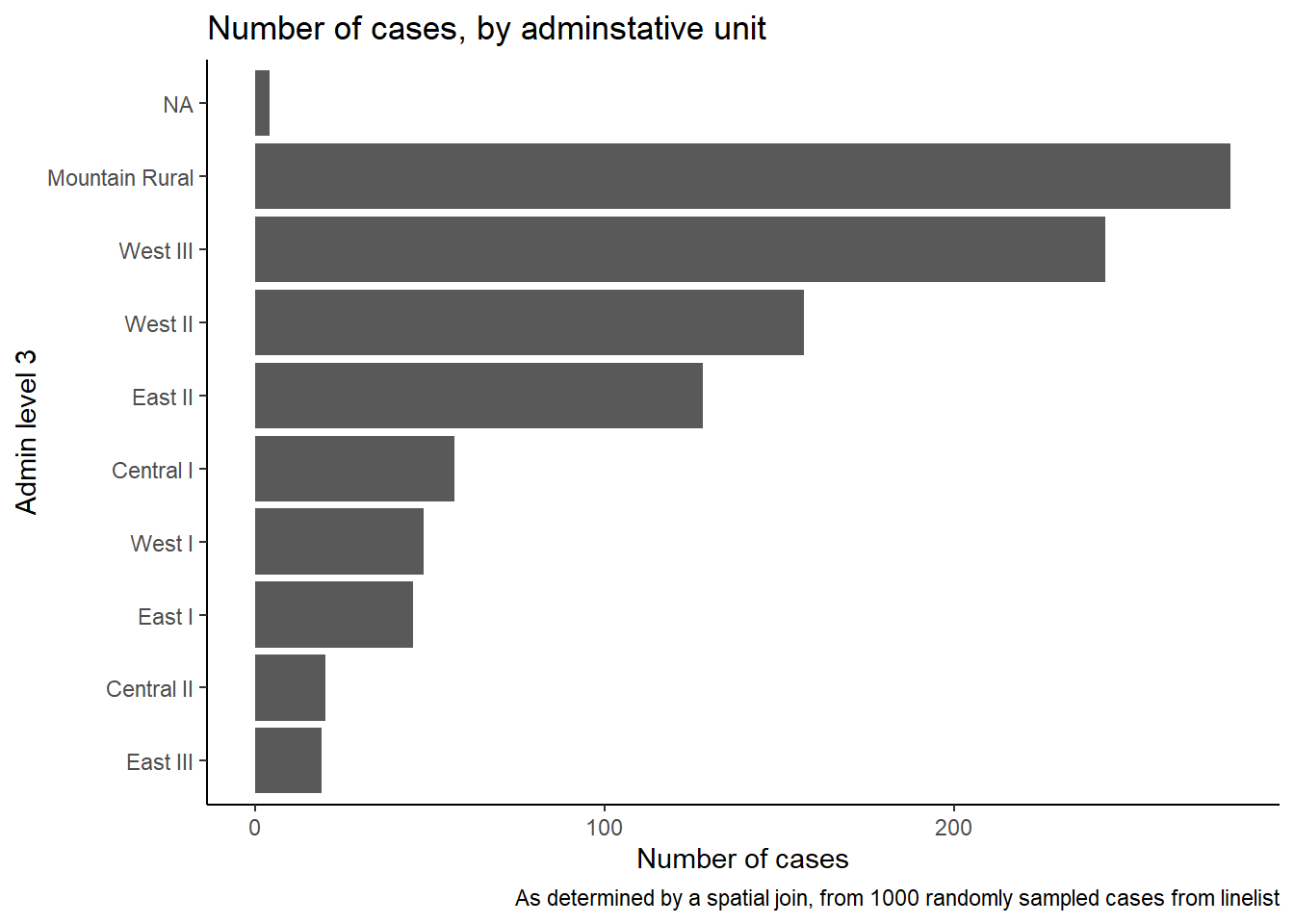
## 10 <NA> <NA> 4ما همچنین می توانیم یک طرح نواری از شمارش موارد توسط واحد اداری ایجاد کنیم.
در این مثال، ما ggplot()با علامت شروع میکنیم linelist_adm، به طوری که میتوانیم توابع فاکتور را اعمال کنیم، مانند fct_infreq()اینکه میلهها را بر اساس فرکانس مرتب میکند (برای نکات به صفحه Factors مراجعه کنید ).
ggplot(
data = linelist_adm, # begin with linelist containing admin unit info
mapping = aes(
x = fct_rev(fct_infreq(admin3name))))+ # x-axis is admin units, ordered by frequency (reversed)
geom_bar()+ # create bars, height is number of rows
coord_flip()+ # flip X and Y axes for easier reading of adm units
theme_classic()+ # simplify background
labs( # titles and labels
x = "Admin level 3",
y = "Number of cases",
title = "Number of cases, by adminstative unit",
caption = "As determined by a spatial join, from 1000 randomly sampled cases from linelist"
)
نزدیکترین همسایه
نزدیکترین مرکز بهداشتی / حوضه آبریز را پیدا کنید
ممکن است دانستن اینکه مراکز درمانی در رابطه با نقاط داغ بیماری در کجا قرار دارند مفید باشد.
میتوانیم از روش اتصال st_nearest_feature از st_join()تابع ( بسته sf ) برای تجسم نزدیکترین مرکز بهداشتی به موارد فردی استفاده کنیم.
- ما با لیست خط شکل فایل شروع می کنیم
linelist_sf - ما به صورت فضایی به آن ملحق می شویم
sle_hfکه مکان های مراکز درمانی و کلینیک ها (نقاط) است.
# Closest health facility to each case
linelist_sf_hf <- linelist_sf %>% # begin with linelist shapefile
st_join(sle_hf, join = st_nearest_feature) %>% # data from nearest clinic joined to case data
select(case_id, osm_id, name, amenity) %>% # keep columns of interest, including id, name, type, and geometry of healthcare facility
rename("nearest_clinic" = "name") # re-name for clarity
میتوانیم در زیر (۵۰ ردیف اول) ببینیم که هر مورد اکنون دادههایی در مورد نزدیکترین کلینیک/بیمارستان دارد.
می بینیم که “دن کلینیک” نزدیک ترین مرکز درمانی برای حدود 30% موارد است.
# Count cases by health facility
hf_catchment <- linelist_sf_hf %>% # begin with linelist including nearest clinic data
as.data.frame() %>% # convert from shapefile to dataframe
count(nearest_clinic, # count rows by "name" (of clinic)
name = "case_n") %>% # assign new counts column as "case_n"
arrange(desc(case_n)) # arrange in descending order
hf_catchment # print to console
## nearest_clinic case_n
## 1 Den Clinic 376
## 2 Shriners Hospitals for Children 305
## 3 GINER HALL COMMUNITY HOSPITAL 179
## 4 panasonic 61
## 5 Princess Christian Maternity Hospital 33
## 6 ARAB EGYPT CLINIC 21
## 7 <NA> 16
## 8 MABELL HEALTH CENTER 9برای تجسم نتایج، می توانیم از tmap استفاده کنیم – این بار حالت تعاملی برای مشاهده آسان تر
tmap_mode("view") # set tmap mode to interactive
# plot the cases and clinic points
tm_shape(linelist_sf_hf) + # plot cases
tm_dots(size=0.08, # cases colored by nearest clinic
col='nearest_clinic') +
tm_shape(sle_hf) + # plot clinic facilities in large black dots
tm_dots(size=0.3, col='black', alpha = 0.4) +
tm_text("name") + # overlay with name of facility
tm_view(set.view = c(-13.2284, 8.4699, 13), # adjust zoom (center coords, zoom)
set.zoom.limits = c(13,14))+
tm_layout(title = "Cases, colored by nearest clinic")
بافرها
همچنین میتوانیم بررسی کنیم که چند مورد در فاصله 2.5 کیلومتری (30 دقیقه) پیادهروی از نزدیکترین مرکز بهداشتی قرار دارند.
توجه: برای محاسبات دقیقتر فاصله، بهتر است شی sf خود را مجدداً به سیستم پیشبینی نقشه محلی مربوطه مانند UTM (زمین بر روی یک سطح مسطح) پرتاب کنید. در این مثال، برای سادگی، ما به سیستم مختصات جغرافیایی سیستم ژئودتیک جهانی (WGS84) (زمین در یک سطح کروی / گرد نشان داده شده است، بنابراین واحدها بر حسب درجه اعشار هستند) پایبند خواهیم بود. ما از تبدیل کلی استفاده خواهیم کرد: 1 درجه اعشاری = ~ 111 کیلومتر.
اطلاعات بیشتر در مورد پیش بینی نقشه ها و سیستم های مختصات را در این مقاله esri مشاهده کنید . این وبلاگ در مورد انواع مختلف طرح ریزی نقشه و نحوه انتخاب یک طرح مناسب بسته به منطقه مورد علاقه و زمینه نقشه/تحلیل شما صحبت می کند.
ابتدا یک بافر دایره ای با شعاع 2.5 کیلومتر در اطراف هر مرکز بهداشتی ایجاد کنید. st_buffer()این کار با تابع tmap انجام می شود . از آنجایی که واحد نقشه در درجات اعشاری لات/بلند است، “0.02” به این ترتیب تفسیر می شود. اگر سیستم مختصات نقشه شما بر حسب متر است، عدد باید بر حسب متر ارائه شود.
sle_hf_2k <- sle_hf %>%
st_buffer(dist=0.02) # decimal degrees translating to approximately 2.5km
در زیر ما خود مناطق حائل را رسم می کنیم که عبارتند از:
tmap_mode("plot")
# Create circular buffers
tm_shape(sle_hf_2k) +
tm_borders(col = "black", lwd = 2)+
tm_shape(sle_hf) + # plot clinic facilities in large red dots
tm_dots(size=0.3, col='black')
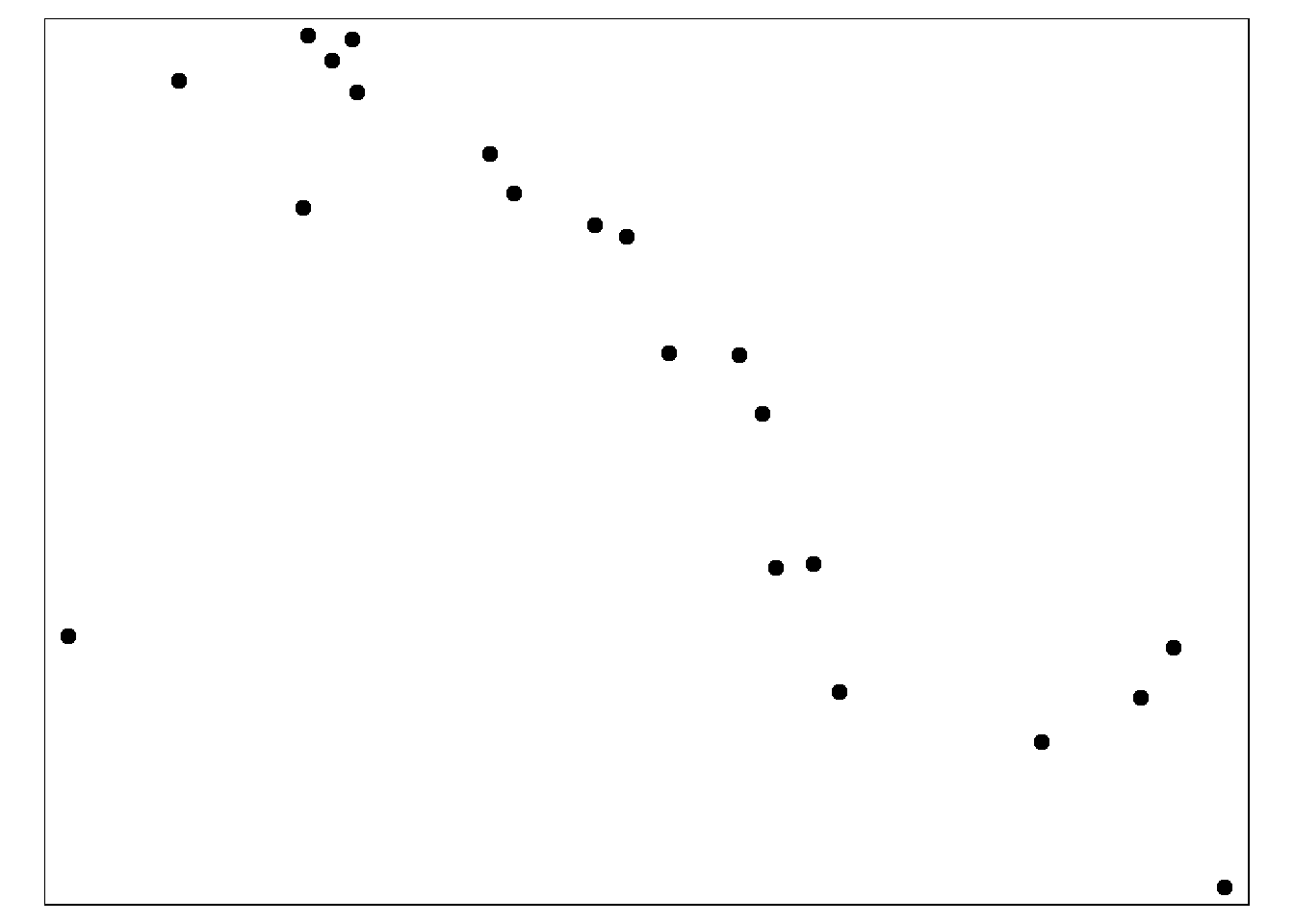
**دوم ، این بافرها را با موارد (نقاط) با استفاده از st_join()و نوع join st_intersects* قطع می کنیم. یعنی داده های بافرها به نقاطی که با آنها تقاطع دارند وصل می شوند.
# Intersect the cases with the buffers
linelist_sf_hf_2k <- linelist_sf_hf %>%
st_join(sle_hf_2k, join = st_intersects, left = TRUE) %>%
filter(osm_id.x==osm_id.y | is.na(osm_id.y)) %>%
select(case_id, osm_id.x, nearest_clinic, amenity.x, osm_id.y)اکنون میتوانیم نتایج را بشماریم: nrow(linelist_sf_hf_2k[is.na(linelist_sf_hf_2k$osm_id.y),])از 1000 مورد با هیچ بافری قطع نمیشود (این مقدار وجود ندارد)، و بنابراین بیش از 30 دقیقه پیادهروی از نزدیکترین مرکز بهداشتی زندگی کنید.
# Cases which did not get intersected with any of the health facility buffers
linelist_sf_hf_2k %>%
filter(is.na(osm_id.y)) %>%
nrow()## [1] 1000ما می توانیم نتایج را به گونه ای تجسم کنیم که مواردی که با هیچ بافری تلاقی نداشته اند به رنگ قرمز ظاهر شوند.
tmap_mode("view")
# First display the cases in points
tm_shape(linelist_sf_hf) +
tm_dots(size=0.08, col='nearest_clinic') +
# plot clinic facilities in large black dots
tm_shape(sle_hf) +
tm_dots(size=0.3, col='black')+
# Then overlay the health facility buffers in polylines
tm_shape(sle_hf_2k) +
tm_borders(col = "black", lwd = 2) +
# Highlight cases that are not part of any health facility buffers
# in red dots
tm_shape(linelist_sf_hf_2k %>% filter(is.na(osm_id.y))) +
tm_dots(size=0.1, col='red') +
tm_view(set.view = c(-13.2284,8.4699, 13), set.zoom.limits = c(13,14))+
# add title
tm_layout(title = "Cases by clinic catchment area")
سایر اتصالات فضایی
مقادیر جایگزین برای آرگومان joinشامل (از مستندات )
- st_contains_properly
- st_contains
- st_covered_by
- st_covers
- st_crosses
- st_disjoint
- st_equals_exact
- st_equals
- st_is_in_distance
- st_nearest_feature
- st_overlaps
- st_touches
- st_within
28.7 نقشه های Choropleth
نقشه های Choropleth می توانند برای تجسم داده های شما بر اساس منطقه از پیش تعریف شده، معمولاً واحد اداری یا منطقه بهداشتی مفید باشند. به عنوان مثال، در واکنش به شیوع این امر می تواند به هدف گذاری تخصیص منابع برای مناطق خاص با نرخ بروز بالا کمک کند.
اکنون که نام واحدهای اداری به همه موارد اختصاص داده شده است (به بخش پیوندهای فضایی، در بالا مراجعه کنید)، میتوانیم نقشهبرداری تعداد موارد را بر اساس منطقه (نقشههای choropleth) شروع کنیم.
از آنجایی که ما همچنین داده های جمعیتی را توسط ADM3 داریم، می توانیم این اطلاعات را به جدول case_adm3 ایجاد شده قبلی اضافه کنیم.
ما با دیتافریم ایجاد شده در مرحله قبل شروع می کنیم case_adm3که جدول خلاصه ای از هر واحد اداری و تعداد موارد آن است.
- داده های جمعیت
sle_adm3_popبا استفاده از aleft_join()from dplyr بر اساس مقادیر مشترک در سراسر ستونadmin3pcodدرcase_adm3چارچوب داده و ستونadm_pcodeدرsle_adm3_popقاب داده به هم متصل می شوند. به صفحه مربوط به پیوستن به داده ها مراجعه کنید ). select()برای حفظ ستون های مفید –totalکل جمعیت است- موارد در هر 10000 نفر به عنوان یک ستون جدید با محاسبه می شود
mutate()
# Add population data and calculate cases per 10K population
case_adm3 <- case_adm3 %>%
left_join(sle_adm3_pop, # add columns from pop dataset
by = c("admin3pcod" = "adm3_pcode")) %>% # join based on common values across these two columns
select(names(case_adm3), total) %>% # keep only important columns, including total population
mutate(case_10kpop = round(cases/total * 10000, 3)) # make new column with case rate per 10000, rounded to 3 decimals
case_adm3 # print to console for viewing
## # A tibble: 10 × 5
## # Groups: admin3pcod [10]
## admin3pcod admin3name cases total case_10kpop
## <chr> <chr> <int> <int> <dbl>
## 1 SL040102 Mountain Rural 279 33993 82.1
## 2 SL040208 West III 243 210252 11.6
## 3 SL040207 West II 157 145109 10.8
## 4 SL040204 East II 128 99821 12.8
## 5 SL040201 Central I 57 69683 8.18
## 6 SL040206 West I 48 60186 7.98
## 7 SL040203 East I 45 68284 6.59
## 8 SL040202 Central II 20 23874 8.38
## 9 SL040205 East III 19 500134 0.38
## 10 <NA> <NA> 4 NA NAبرای نگاشت به این جدول با شکل فایل چند ضلعی ADM3 بپیوندید
case_adm3_sf <- case_adm3 %>% # begin with cases & rate by admin unit
left_join(sle_adm3, by="admin3pcod") %>% # join to shapefile data by common column
select(objectid, admin3pcod, # keep only certain columns of interest
admin3name = admin3name.x, # clean name of one column
admin2name, admin1name,
cases, total, case_10kpop,
geometry) %>% # keep geometry so polygons can be plotted
drop_na(objectid) %>% # drop any empty rows
st_as_sf() # convert to shapefile
نقشه برداری از نتایج
# tmap mode
tmap_mode("plot") # view static map
# plot polygons
tm_shape(case_adm3_sf) +
tm_polygons("cases") + # color by number of cases column
tm_text("admin3name") # name display
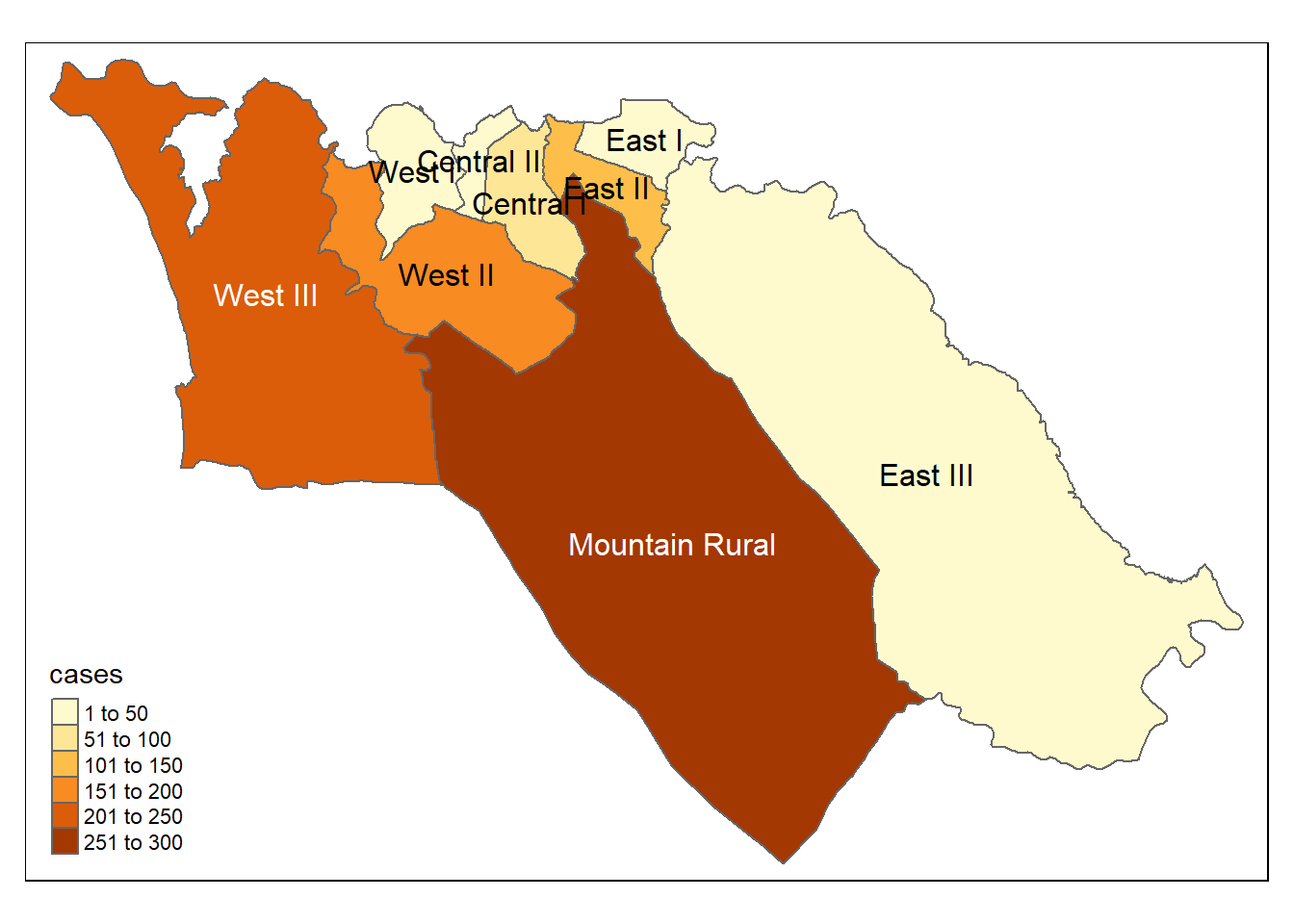
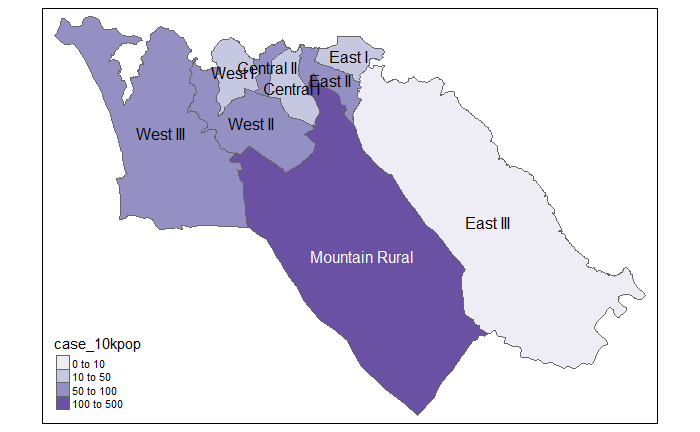
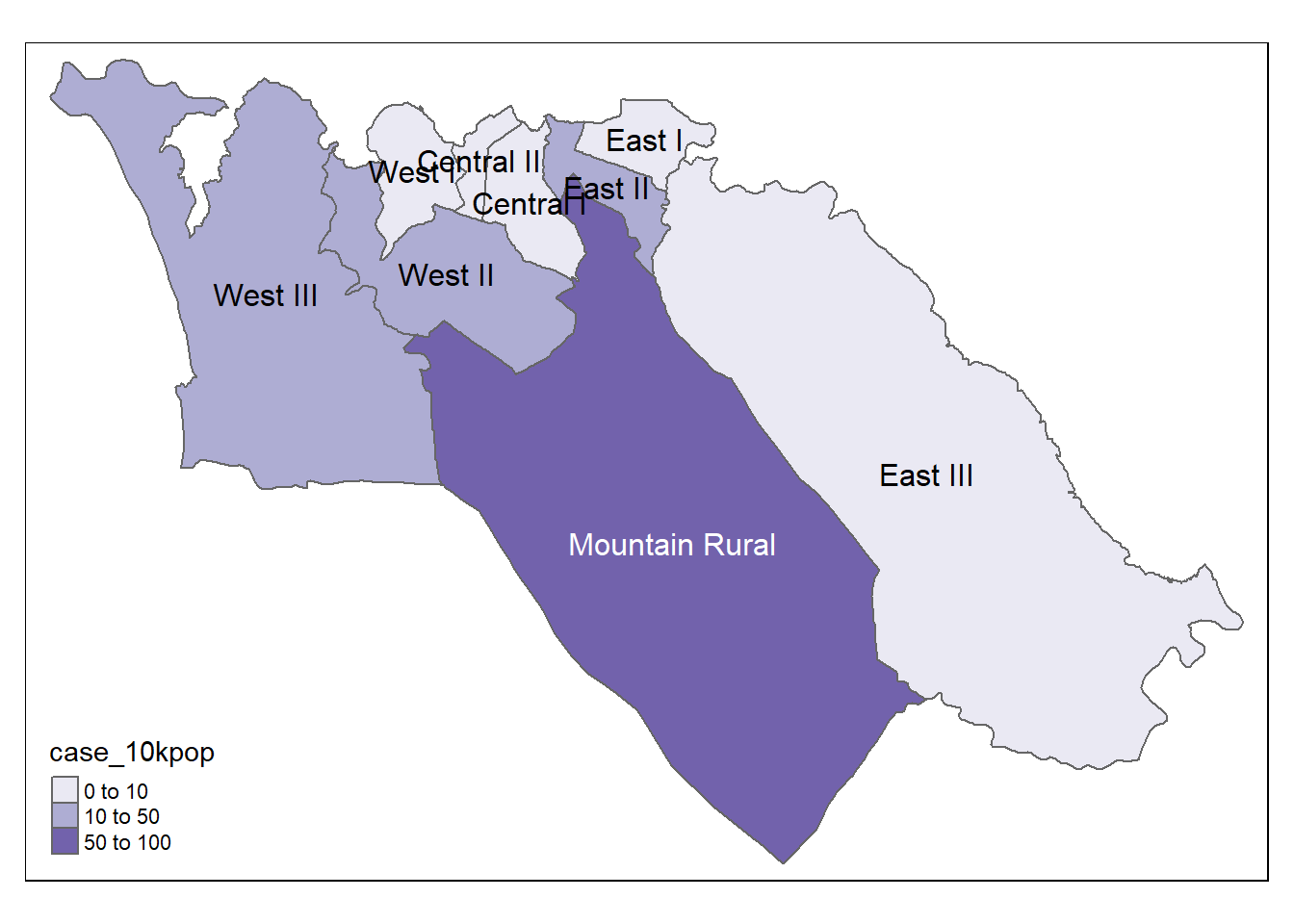
ما همچنین می توانیم نرخ بروز را ترسیم کنیم
# Cases per 10K population
tmap_mode("plot") # static viewing mode
# plot
tm_shape(case_adm3_sf) + # plot polygons
tm_polygons("case_10kpop", # color by column containing case rate
breaks=c(0, 10, 50, 100), # define break points for colors
palette = "Purples" # use a purple color palette
) +
tm_text("admin3name") # display text
28.8 نقشه برداری با ggplot2
اگر قبلاً با استفاده از ggplot2 آشنا هستید ، می توانید به جای آن از آن بسته برای ایجاد نقشه های ایستا از داده های خود استفاده کنید. این geom_sf()تابع بر اساس ویژگی هایی (نقاط، خطوط یا چند ضلعی) در داده های شما، اشیاء مختلفی را ترسیم می کند. به عنوان مثال، شما می توانید geom_sf()در یک داده با هندسه چند ضلعی برای ایجاد یک نقشه choropleth ggplot()استفاده کنید.sf
برای نشان دادن نحوه کار، میتوانیم با شکل فایل چند ضلعی ADM3 که قبلاً استفاده کردیم شروع کنیم. به یاد داشته باشید که اینها مناطق مدیریت سطح 3 در سیرالئون هستند:
sle_adm3## Simple feature collection with 12 features and 19 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -13.29894 ymin: 8.094272 xmax: -12.91333 ymax: 8.499809
## Geodetic CRS: WGS 84
## # A tibble: 12 × 20
## objectid admin3name admin3pcod admin3ref_n admin2name admin2pcod admin1name admin1pcod admin0name admin0pcod date
## * <dbl> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <chr> <date>
## 1 155 Koya Rural SL040101 Koya Rural Western A… SL0401 Western SL04 Sierra Le… SL 2016-08-01
## 2 156 Mountain Rural SL040102 Mountain Ru… Western A… SL0401 Western SL04 Sierra Le… SL 2016-08-01
## 3 157 Waterloo Rural SL040103 Waterloo Ru… Western A… SL0401 Western SL04 Sierra Le… SL 2016-08-01
## 4 158 York Rural SL040104 York Rural Western A… SL0401 Western SL04 Sierra Le… SL 2016-08-01
## 5 159 Central I SL040201 Central I Western A… SL0402 Western SL04 Sierra Le… SL 2016-08-01
## 6 160 East I SL040203 East I Western A… SL0402 Western SL04 Sierra Le… SL 2016-08-01
## 7 161 East II SL040204 East II Western A… SL0402 Western SL04 Sierra Le… SL 2016-08-01
## 8 162 Central II SL040202 Central II Western A… SL0402 Western SL04 Sierra Le… SL 2016-08-01
## 9 163 West III SL040208 West III Western A… SL0402 Western SL04 Sierra Le… SL 2016-08-01
## 10 164 West I SL040206 West I Western A… SL0402 Western SL04 Sierra Le… SL 2016-08-01
## 11 165 West II SL040207 West II Western A… SL0402 Western SL04 Sierra Le… SL 2016-08-01
## 12 167 East III SL040205 East III Western A… SL0402 Western SL04 Sierra Le… SL 2016-08-01
## # ℹ 9 more variables: valid_on <date>, valid_to <date>, shape_leng <dbl>, shape_area <dbl>, rowcacode0 <chr>,
## # rowcacode1 <chr>, rowcacode2 <chr>, rowcacode3 <chr>, geometry <MULTIPOLYGON [°]>ما می توانیم left_join()از تابع dplyr برای اضافه کردن داده هایی که می خواهیم به شی shapefile نگاشت استفاده کنیم. case_adm3در این مورد، ما از چارچوب داده ای که قبلا ایجاد کردیم برای خلاصه کردن تعداد پرونده ها بر اساس منطقه اداری استفاده می کنیم . با این حال، میتوانیم از همین رویکرد برای ترسیم هر داده ذخیرهشده در یک قاب داده استفاده کنیم.
sle_adm3_dat <- sle_adm3 %>%
inner_join(case_adm3, by = "admin3pcod") # inner join = retain only if in both data objects
select(sle_adm3_dat, admin3name.x, cases) # print selected variables to console## Simple feature collection with 9 features and 2 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -13.29894 ymin: 8.384533 xmax: -13.12612 ymax: 8.499809
## Geodetic CRS: WGS 84
## # A tibble: 9 × 3
## admin3name.x cases geometry
## <chr> <int> <MULTIPOLYGON [°]>
## 1 Mountain Rural 279 (((-13.21496 8.474341, -13.21479 8.474289, -13.21465 8.474296, -13.21455 8.474298, -...
## 2 Central I 57 (((-13.22646 8.489716, -13.22648 8.48955, -13.22644 8.489513, -13.22663 8.489229, -1...
## 3 East I 45 (((-13.2129 8.494033, -13.21076 8.494026, -13.21013 8.494041, -13.2096 8.494025, -13...
## 4 East II 128 (((-13.22653 8.491883, -13.22647 8.491853, -13.22642 8.49186, -13.22633 8.491814, -1...
## 5 Central II 20 (((-13.23154 8.491768, -13.23141 8.491566, -13.23144 8.49146, -13.23131 8.491294, -1...
## 6 West III 243 (((-13.28529 8.497354, -13.28456 8.496497, -13.28403 8.49621, -13.28338 8.496086, -1...
## 7 West I 48 (((-13.24677 8.493453, -13.24669 8.493285, -13.2464 8.493132, -13.24627 8.493131, -1...
## 8 West II 157 (((-13.25698 8.485518, -13.25685 8.485501, -13.25668 8.485505, -13.25657 8.485504, -...
## 9 East III 19 (((-13.20465 8.485758, -13.20461 8.485698, -13.20449 8.485757, -13.20431 8.485577, -...برای ایجاد نمودار ستونی از تعداد موارد بر اساس منطقه، با استفاده از ggplot2 ، میتوانیم geom_col()به صورت زیر فراخوانی کنیم:
ggplot(data=sle_adm3_dat) +
geom_col(aes(x=fct_reorder(admin3name.x, cases, .desc=T), # reorder x axis by descending 'cases'
y=cases)) + # y axis is number of cases by region
theme_bw() +
labs( # set figure text
title="Number of cases, by administrative unit",
x="Admin level 3",
y="Number of cases"
) +
guides(x=guide_axis(angle=45)) # angle x-axis labels 45 degrees to fit better
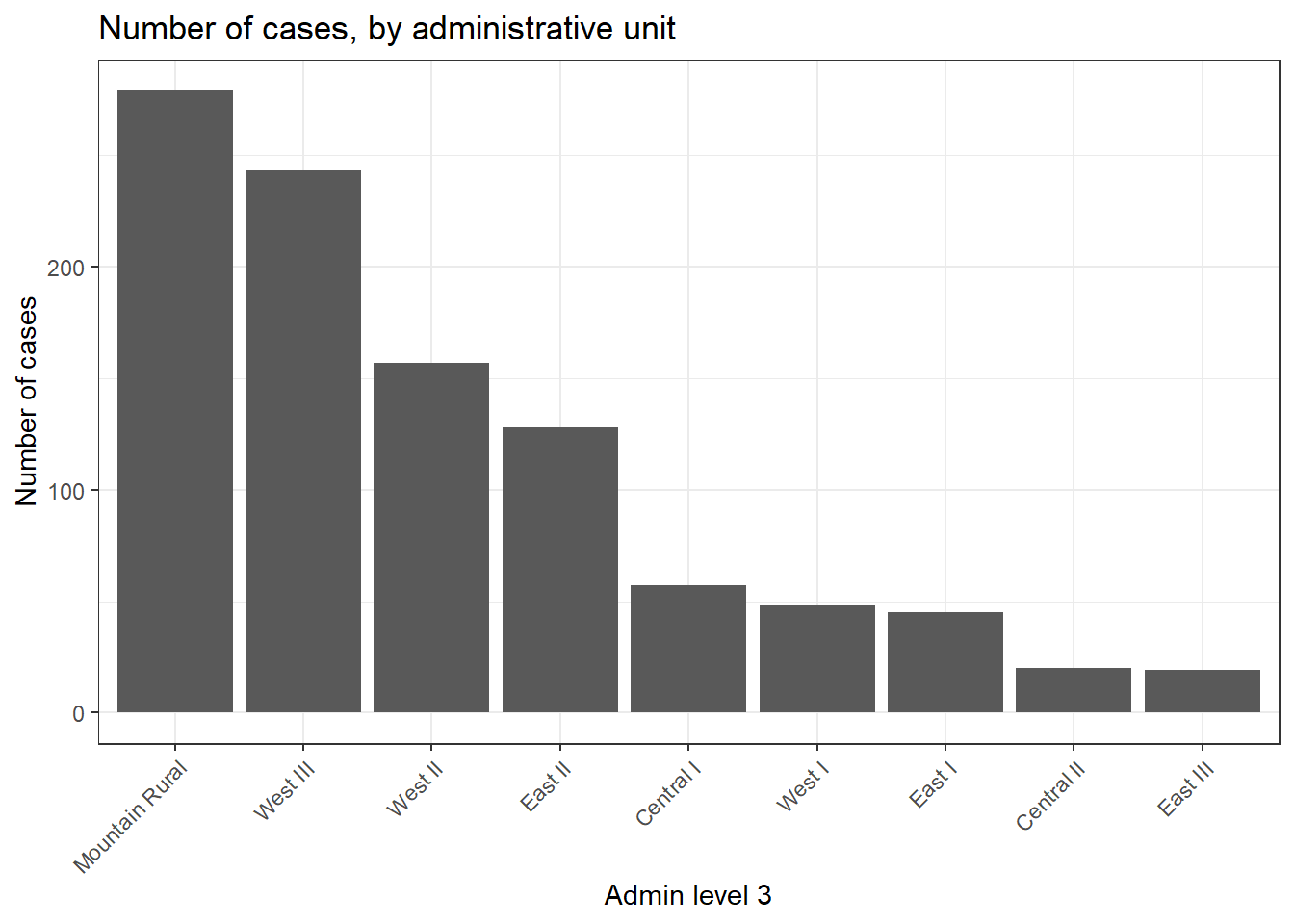
اگر بخواهیم از ggplot2 برای ایجاد یک نقشه choropleth از تعداد موارد استفاده کنیم، میتوانیم از نحو مشابه برای فراخوانی تابع استفاده کنیم geom_sf():
ggplot(data=sle_adm3_dat) +
geom_sf(aes(fill=cases)) # set fill to vary by case count variable
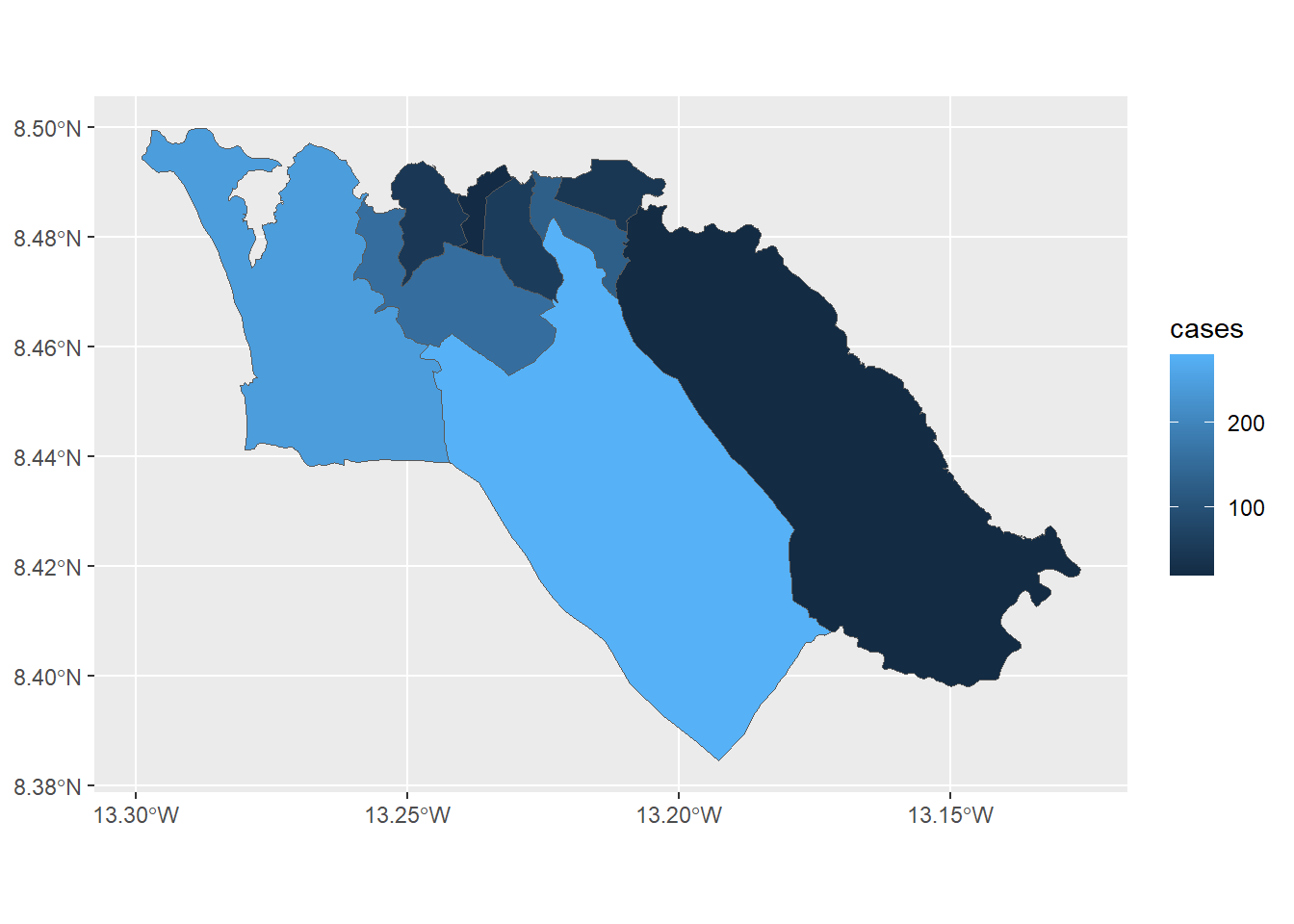
سپس میتوانیم ظاهر نقشه خود را با استفاده از دستور زبانی که در سراسر ggplot2 سازگار است، سفارشی کنیم ، برای مثال:
ggplot(data=sle_adm3_dat) +
geom_sf(aes(fill=cases)) +
scale_fill_continuous(high="#54278f", low="#f2f0f7") + # change color gradient
theme_bw() +
labs(title = "Number of cases, by administrative unit", # set figure text
subtitle = "Admin level 3"
)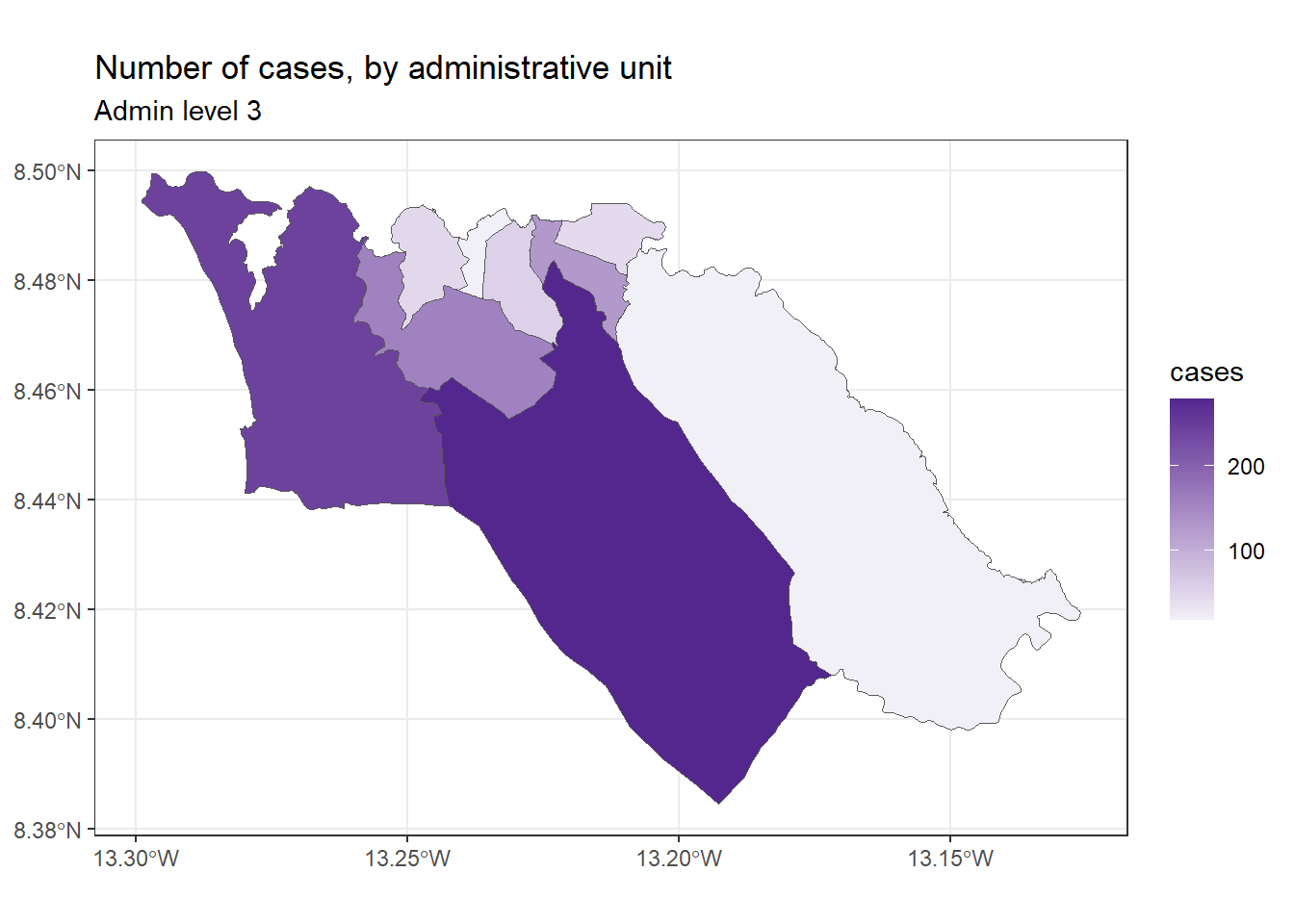
برای کاربران R که راحت با ggplot2 کار می کنند ، geom_sf()پیاده سازی ساده و مستقیمی را ارائه می دهد که برای تجسم های اولیه نقشه مناسب است. برای کسب اطلاعات بیشتر، geom_sf() vignette یا کتاب ggplot2 را بخوانید .
28.9 بیس مپ
نقشه خیابان باز
در زیر نحوه دستیابی به نقشه پایه برای نقشه ggplot2 با استفاده از ویژگی های OpenStreetMap را شرح می دهیم. روش های جایگزین شامل استفاده از ggmap است که نیاز به ثبت نام رایگان در Google دارد ( جزئیات ).
OpenStreetMap یک پروژه مشترک برای ایجاد یک نقشه قابل ویرایش رایگان از جهان است. داده های موقعیت جغرافیایی زیربنایی (مانند مکان شهرها، جاده ها، ویژگی های طبیعی، فرودگاه ها، مدارس، بیمارستان ها، جاده ها و غیره) خروجی اولیه پروژه در نظر گرفته می شود.
ابتدا بسته OpenStreetMap را بارگذاری می کنیم ، که از آن نقشه پایه خود را دریافت می کنیم.
سپس، شی را ایجاد می کنیم که با استفاده از mapتابع بسته OpenStreetMap ( مستندات ) تعریف می کنیم. ما موارد زیر را ارائه می دهیم:openmap()
upperLeftوlowerRightدو جفت مختصات که حدود کاشی نقشه پایه را مشخص می کنند- در این مورد ما حداکثر و حداقل را از ردیف های لیست خطی قرار داده ایم، بنابراین نقشه به صورت پویا به داده ها پاسخ می دهد.
zoom =(در صورت تهی بودن به طور خودکار تعیین می شود)type =کدام نوع از نقشه پایه – ما چندین احتمال را در اینجا فهرست کرده ایم و کد در حال حاضر از اولین ([1]) “osm” استفاده می کند.mergeTiles =ما TRUE را انتخاب کردیم تا پایهها همه در یک ادغام شوند
# load package
pacman::p_load(OpenStreetMap)
# Fit basemap by range of lat/long coordinates. Choose tile type
map <- OpenStreetMap::openmap(
upperLeft = c(max(linelist$lat, na.rm=T), max(linelist$lon, na.rm=T)), # limits of basemap tile
lowerRight = c(min(linelist$lat, na.rm=T), min(linelist$lon, na.rm=T)),
zoom = NULL,
type = c("osm", "stamen-toner", "stamen-terrain", "stamen-watercolor", "esri","esri-topo")[1])
اگر همین الان این نقشه پایه را با استفاده autoplot.OpenStreetMap()از بسته OpenStreetMap رسم کنیم ، می بینید که واحدهای روی محورها مختصات طول و عرض جغرافیایی نیستند. از یک سیستم مختصات متفاوت استفاده می کند. برای نمایش صحیح خانه های کیس (که در lat/long ذخیره می شوند)، این باید تغییر کند.
autoplot.OpenStreetMap(map)
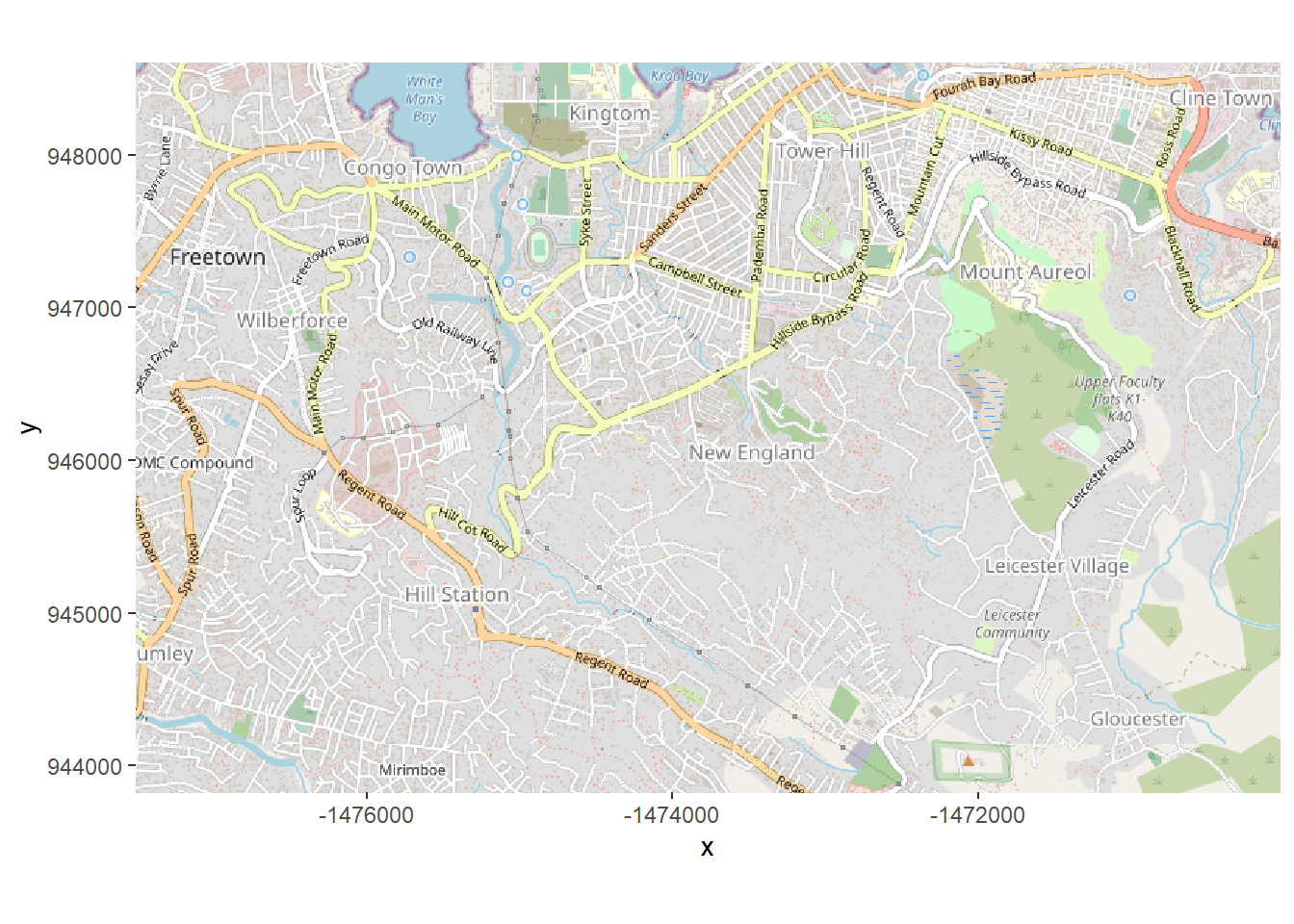
openproj()بنابراین، ما می خواهیم نقشه را با تابع بسته OpenStreetMap به طول و عرض جغرافیایی تبدیل کنیم . ما نقشه پایه mapو همچنین سیستم مرجع مختصات (CRS) مورد نظر خود را ارائه می دهیم. ما این کار را با ارائه رشته کاراکتر “proj.4” برای طرح ریزی WGS 1984 انجام می دهیم، اما شما می توانید CRS را به روش های دیگری نیز ارائه دهید. ( برای درک بهتر رشته proj.4 به این صفحه مراجعه کنید)
# Projection WGS84
map_latlon <- openproj(map, projection = "+proj=longlat +ellps=WGS84 +datum=WGS84 +no_defs")
حالا وقتی طرح را ایجاد می کنیم می بینیم که در امتداد محورها مختصات طول و عرض جغرافیایی هستند. سیستم مختصات تبدیل شده است. اکنون موارد ما در صورت همپوشانی به درستی رسم می شوند!
# Plot map. Must use "autoplot" in order to work with ggplot
autoplot.OpenStreetMap(map_latlon)
برای اطلاعات بیشتر آموزش ها را اینجا و اینجا ببینید.
28.10 نقشه های حرارتی چگالی منحنی
در زیر نحوه دستیابی به یک نقشه حرارتی چگالی منحنی از موارد، بر روی نقشه پایه، با یک لیست خط (یک ردیف در هر مورد) را شرح می دهیم.
- همانطور که در بالا توضیح داده شد، کاشی نقشه پایه را از OpenStreetMap ایجاد کنید
- موارد
linelistاستفاده از ستون های طول و عرض جغرافیایی را ترسیم کنید - نقاط را با استفاده
stat_density_2d()از ggplot2 به یک نقشه حرارتی چگالی تبدیل کنید ،
هنگامی که ما یک نقشه پایه با مختصات lat/long داریم، می توانیم موارد خود را با استفاده از مختصات lat/long محل اقامت آنها در بالا رسم کنیم.
با ساختن تابع autoplot.OpenStreetMap()برای ایجاد نقشه پایه، توابع ggplot2 به راحتی در بالا اضافه می شوند، همانطور که در geom_point()زیر نشان داده شده است:
# Plot map. Must be autoplotted to work with ggplot
autoplot.OpenStreetMap(map_latlon)+ # begin with the basemap
geom_point( # add xy points from linelist lon and lat columns
data = linelist,
aes(x = lon, y = lat),
size = 1,
alpha = 0.5,
show.legend = FALSE) + # drop legend entirely
labs(x = "Longitude", # titles & labels
y = "Latitude",
title = "Cumulative cases")
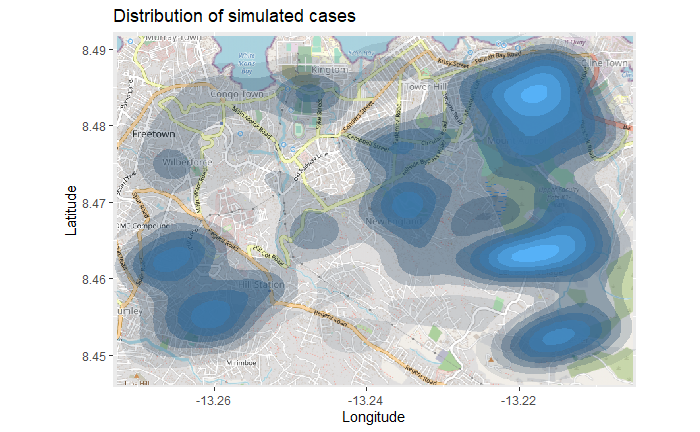
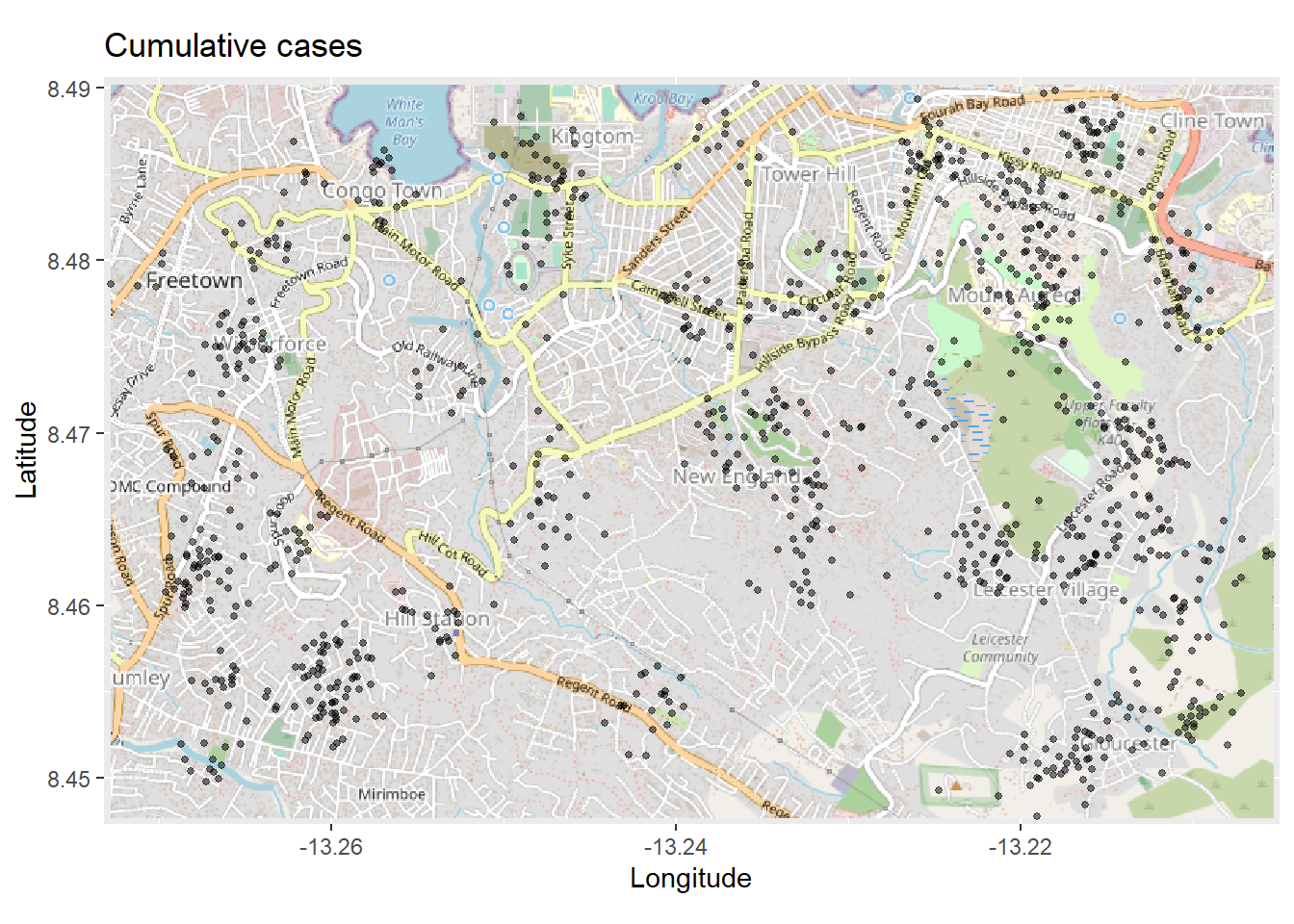 تفسیر نقشه بالا ممکن است دشوار باشد، به خصوص با همپوشانی نقاط. بنابراین می توانید با استفاده از تابع ggplot2
تفسیر نقشه بالا ممکن است دشوار باشد، به خصوص با همپوشانی نقاط. بنابراین می توانید با استفاده از تابع ggplot2stat_density_2d() یک نقشه چگالی دوبعدی ترسیم کنید . شما هنوز از مختصات lat/lon لیست خطی استفاده می کنید، اما یک تخمین چگالی هسته دو بعدی انجام می شود و نتایج با خطوط کانتور نمایش داده می شوند – مانند یک نقشه توپوگرافی. مستندات کامل را اینجا بخوانید .
# begin with the basemap
autoplot.OpenStreetMap(map_latlon)+
# add the density plot
ggplot2::stat_density_2d(
data = linelist,
aes(
x = lon,
y = lat,
fill = ..level..,
alpha = ..level..),
bins = 10,
geom = "polygon",
contour_var = "count",
show.legend = F) +
# specify color scale
scale_fill_gradient(low = "black", high = "red")+
# labels
labs(x = "Longitude",
y = "Latitude",
title = "Distribution of cumulative cases")
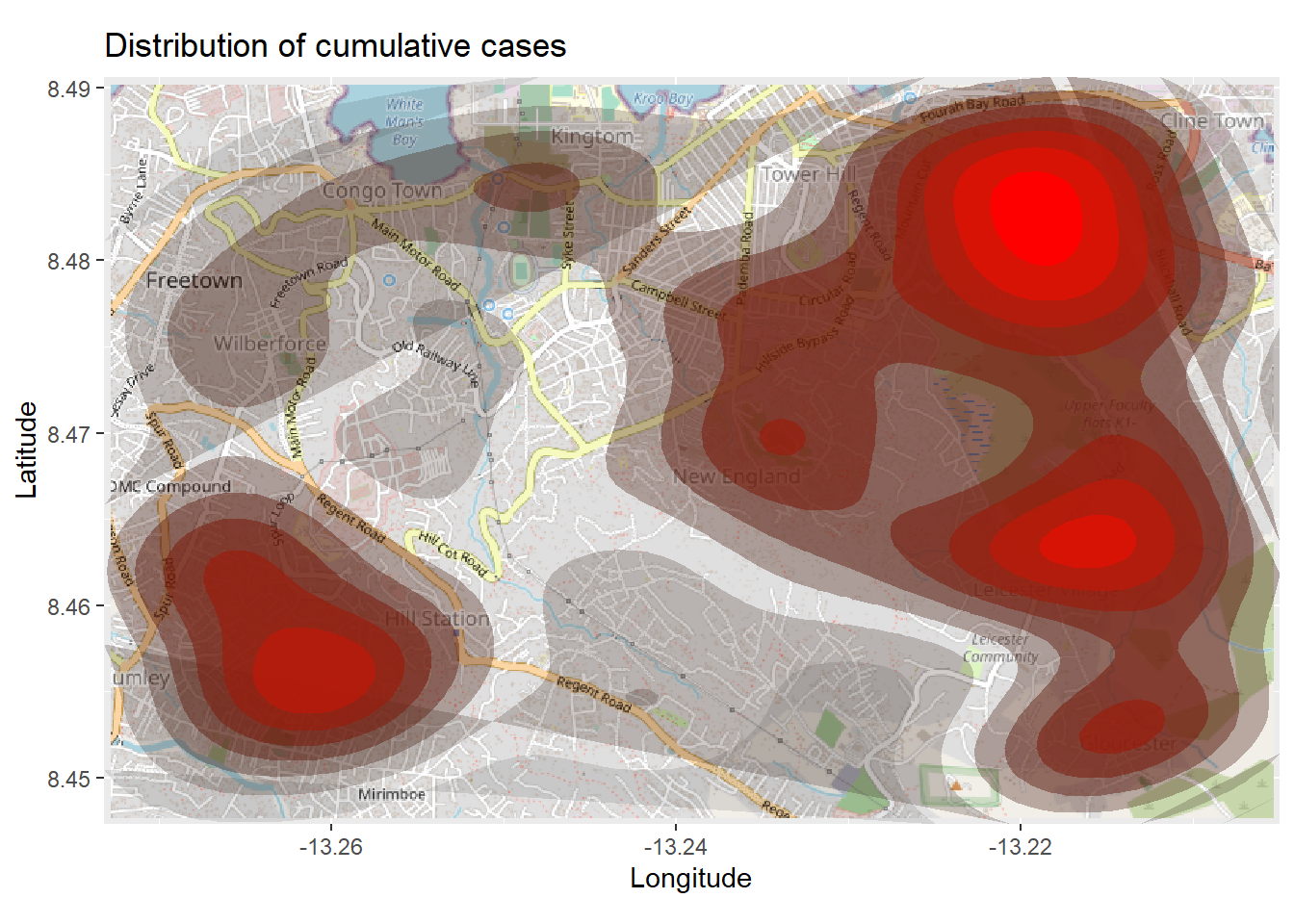
نقشه حرارتی سری زمانی
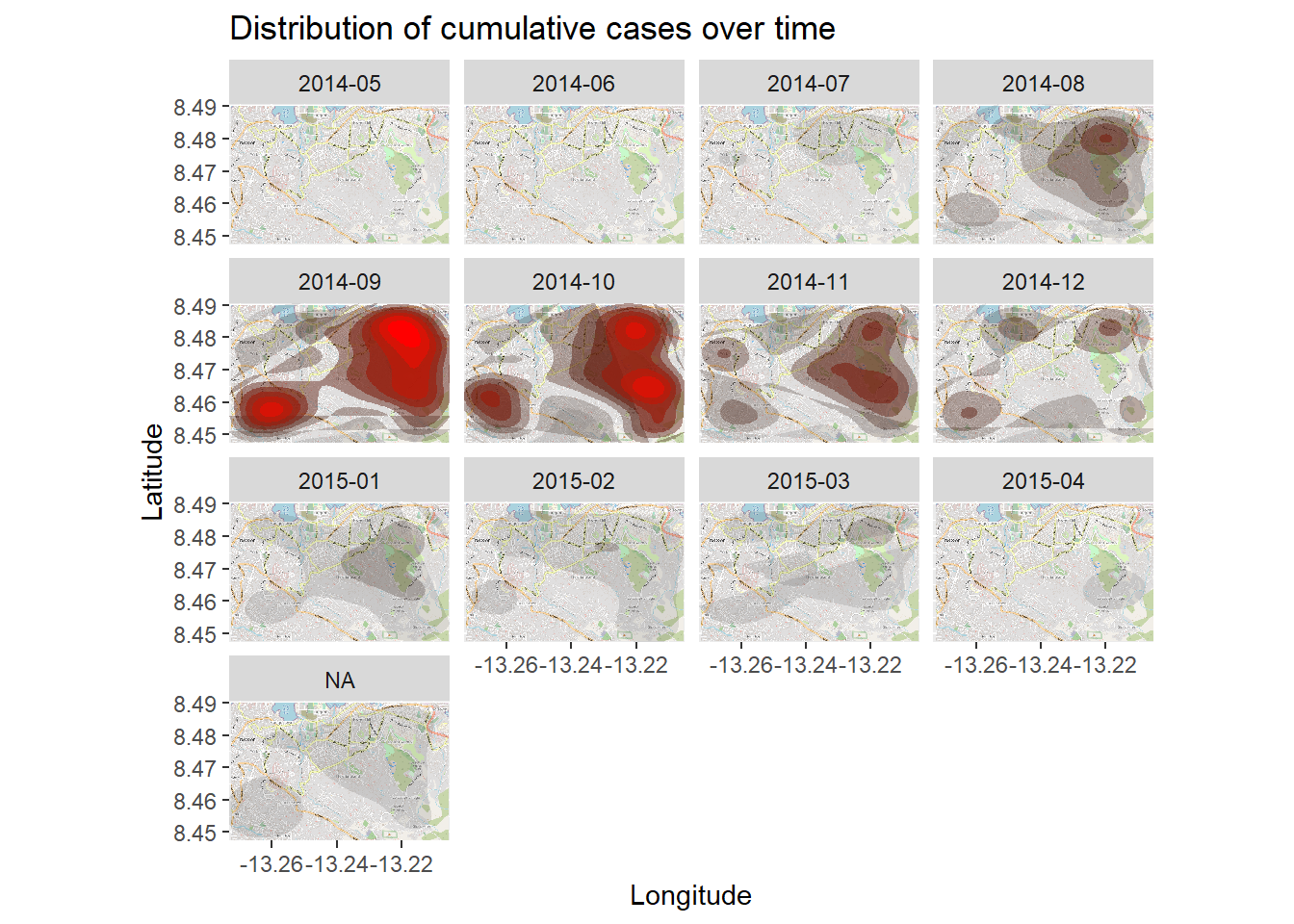
نقشه حرارتی چگالی بالا موارد تجمعی را نشان می دهد . ما میتوانیم شیوع بیماری را در طول زمان و مکان با رویارویی با نقشه حرارتی بر اساس ماه شروع علائم بررسی کنیم ، همانطور که از لیست خط مشتق شده است.
ما با linelistایجاد یک ستون جدید با سال و ماه شروع شروع می کنیم. تابع format()پایه R نحوه نمایش تاریخ را تغییر می دهد . در این مورد ما “YYYY-MM” را می خواهیم.
# Extract month of onset
linelist <- linelist %>%
mutate(date_onset_ym = format(date_onset, "%Y-%m"))
# Examine the values
table(linelist$date_onset_ym, useNA = "always")
##
## 2014-05 2014-06 2014-07 2014-08 2014-09 2014-10 2014-11 2014-12 2015-01 2015-02 2015-03 2015-04 <NA>
## 7 9 31 90 199 179 128 112 60 52 53 29 51اکنون، ما به سادگی فیتینگ را از طریق ggplot2 به نقشه حرارتی چگالی معرفی می کنیم. facet_wrap()با استفاده از ستون جدید به عنوان ردیف اعمال می شود. برای وضوح، تعداد ستونهای فاکتور را روی 3 قرار میدهیم.
# packages
pacman::p_load(OpenStreetMap, tidyverse)
# begin with the basemap
autoplot.OpenStreetMap(map_latlon)+
# add the density plot
ggplot2::stat_density_2d(
data = linelist,
aes(
x = lon,
y = lat,
fill = ..level..,
alpha = ..level..),
bins = 10,
geom = "polygon",
contour_var = "count",
show.legend = F) +
# specify color scale
scale_fill_gradient(low = "black", high = "red")+
# labels
labs(x = "Longitude",
y = "Latitude",
title = "Distribution of cumulative cases over time")+
# facet the plot by month-year of onset
facet_wrap(~ date_onset_ym, ncol = 4)
28.11 آمار فضایی
بیشتر بحث ما تا کنون بر روی تجسم داده های مکانی متمرکز بوده است. در برخی موارد، ممکن است علاقه مند به استفاده از آمار فضایی برای تعیین کمیت روابط مکانی ویژگی ها در داده های خود باشید. این بخش مروری بسیار کوتاه از برخی مفاهیم کلیدی در آمار فضایی ارائه میکند و منابعی را پیشنهاد میکند که در صورت تمایل به انجام تحلیلهای فضایی جامعتر برای کشف آنها مفید خواهد بود.
روابط فضایی
قبل از اینکه بتوانیم هر گونه آمار مکانی را محاسبه کنیم، باید روابط بین ویژگی ها را در داده های خود مشخص کنیم. راههای زیادی برای مفهومسازی روابط فضایی وجود دارد، اما یک مدل ساده و رایج برای استفاده، مدل مجاورت است – بهویژه، که ما انتظار داریم یک رابطه جغرافیایی بین مناطقی که دارای مرز مشترک یا “همسایه” هستند، وجود داشته باشد.
ما میتوانیم روابط مجاورت بین چند ضلعیهای مناطق اداری را در دادههایی که با بسته spdepsle_adm3 استفاده کردهایم کمیت کنیم . ما مجاورت ملکه را مشخص می کنیم ، به این معنی که اگر مناطقی در امتداد مرزهای خود حداقل یک نقطه مشترک داشته باشند، همسایه خواهند بود. جایگزین، مجاورت روک است، که مستلزم آن است که مناطق دارای یک لبه باشند – در مورد ما، با چند ضلعی های نامنظم، تمایز بی اهمیت است، اما در برخی موارد انتخاب بین ملکه و روک می تواند تأثیرگذار باشد.
sle_nb <- spdep::poly2nb(sle_adm3_dat, queen=T) # create neighbors
sle_adjmat <- spdep::nb2mat(sle_nb) # create matrix summarizing neighbor relationships
sle_listw <- spdep::nb2listw(sle_nb) # create listw (list of weights) object -- we will need this later
sle_nb## Neighbour list object:
## Number of regions: 9
## Number of nonzero links: 30
## Percentage nonzero weights: 37.03704
## Average number of links: 3.333333round(sle_adjmat, digits = 2)## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## 1 0.00 0.20 0.00 0.20 0.00 0.2 0.00 0.20 0.20
## 2 0.25 0.00 0.00 0.25 0.25 0.0 0.00 0.25 0.00
## 3 0.00 0.00 0.00 0.50 0.00 0.0 0.00 0.00 0.50
## 4 0.25 0.25 0.25 0.00 0.00 0.0 0.00 0.00 0.25
## 5 0.00 0.33 0.00 0.00 0.00 0.0 0.33 0.33 0.00
## 6 0.50 0.00 0.00 0.00 0.00 0.0 0.00 0.50 0.00
## 7 0.00 0.00 0.00 0.00 0.50 0.0 0.00 0.50 0.00
## 8 0.20 0.20 0.00 0.00 0.20 0.2 0.20 0.00 0.00
## 9 0.33 0.00 0.33 0.33 0.00 0.0 0.00 0.00 0.00
## attr(,"call")
## spdep::nb2mat(neighbours = sle_nb)ماتریس چاپ شده در بالا روابط بین 9 منطقه در sle_adm3داده های ما را نشان می دهد. نمره 0 نشان می دهد که دو منطقه همسایه نیستند، در حالی که هر مقداری غیر از 0 نشان دهنده یک رابطه همسایه است. مقادیر در ماتریس به گونه ای مقیاس بندی می شوند که هر ناحیه دارای وزن کل ردیف 1 باشد.
یک راه بهتر برای تجسم این روابط همسایه، ترسیم آنها است:
plot(sle_adm3_dat$geometry) + # plot region boundaries
spdep::plot.nb(sle_nb,as(sle_adm3_dat, 'Spatial'), col='grey', add=T) # add neighbor relationships
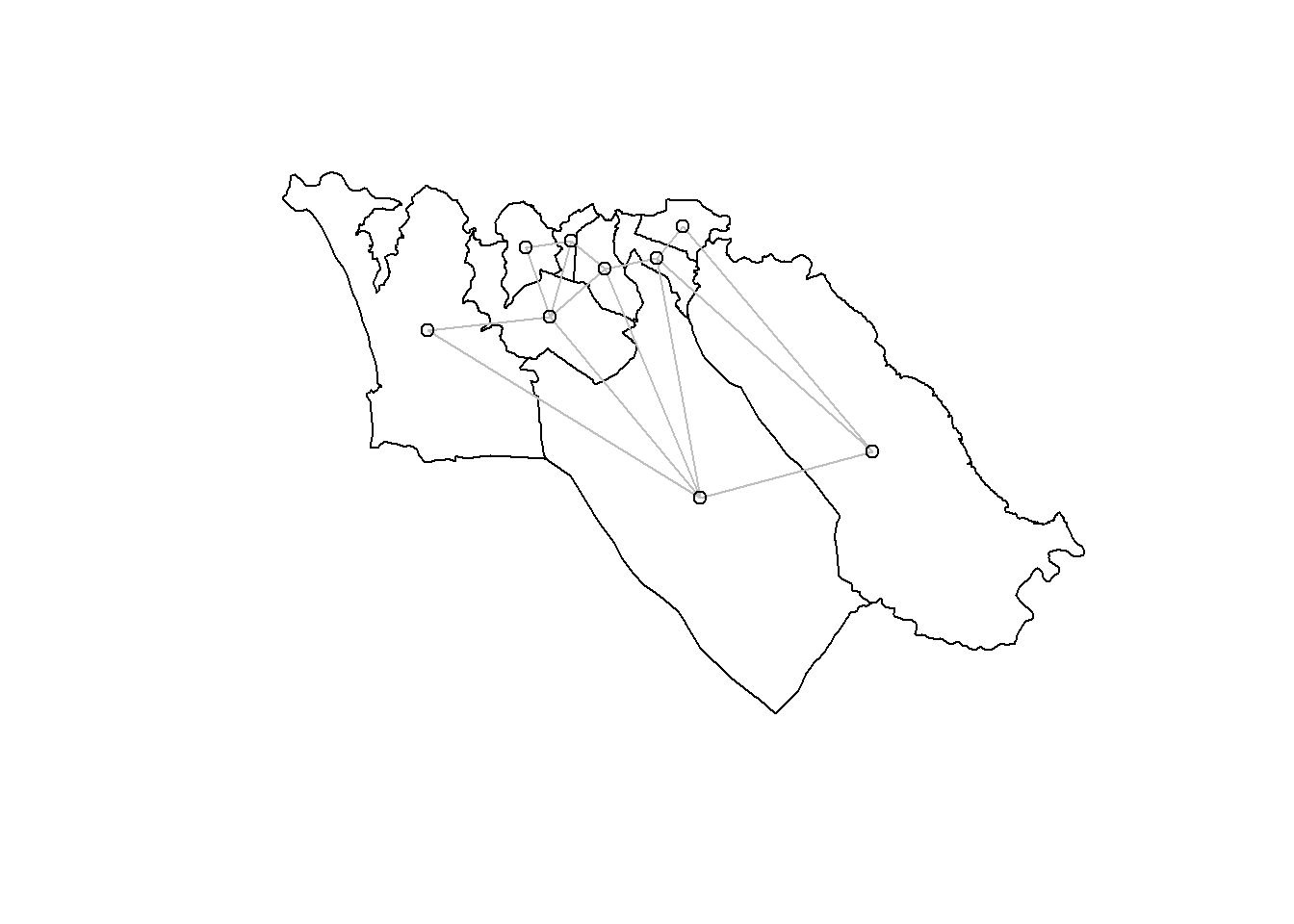
ما از یک رویکرد مجاورت برای شناسایی چند ضلعی های همسایه استفاده کرده ایم. همسایه هایی که ما شناسایی کردیم گاهی اوقات همسایه های مبتنی بر مجاورت نامیده می شوند . اما این تنها یک راه برای انتخاب مناطقی است که انتظار می رود رابطه جغرافیایی داشته باشند. رایجترین رویکردهای جایگزین برای شناسایی روابط جغرافیایی، همسایگان مبتنی بر فاصله ایجاد میکنند . به طور خلاصه این موارد عبارتند از:
- K-نزدیکترین همسایه – بر اساس فاصله بین مرکزها (مرکز دارای وزن جغرافیایی هر ناحیه چند ضلعی)، n نزدیکترین ناحیه را به عنوان همسایه انتخاب کنید. همچنین ممکن است یک آستانه نزدیکی حداکثر فاصله مشخص شود. در spdep ، می توانید استفاده کنید
knearneigh()(به مستندات مراجعه کنید ). - همسایگان آستانه فاصله – همه همسایگان را در آستانه فاصله انتخاب کنید. در spdep ، این روابط همسایه را می توان با استفاده از
dnearneigh()(به مستندات مراجعه کنید ) شناسایی کرد.
خودهمبستگی فضایی
قانون اول جغرافیایی که اغلب به آن اشاره می شود، بیان می کند که “همه چیز به هر چیز دیگری مربوط است، اما چیزهای نزدیک بیشتر از چیزهای دور مرتبط هستند.” در اپیدمیولوژی، این اغلب به این معنی است که خطر یک پیامد سلامتی خاص در یک منطقه خاص بیشتر شبیه به مناطق همسایه آن است تا مناطق دور. این مفهوم به عنوان خودهمبستگی فضایی رسمیت یافته است – ویژگی آماری که ویژگی های جغرافیایی با مقادیر مشابه در کنار هم در فضا جمع می شوند. معیارهای آماری خودهمبستگی فضایی را می توان برای تعیین کمیت میزان خوشه بندی فضایی در داده های شما، مکان یابی محل وقوع خوشه بندی و شناسایی الگوهای مشترک خود همبستگی فضایی استفاده کرد.بین متغیرهای متمایز در داده های شما این بخش مروری بر برخی از معیارهای متداول خودهمبستگی فضایی و نحوه محاسبه آنها در R می دهد.
Moran’s I – این یک آمار خلاصه جهانی از همبستگی بین مقدار یک متغیر در یک منطقه و مقادیر همان متغیر در مناطق همسایه است. آمار Moran’s I معمولاً از 1- تا 1 متغیر است. مقدار 0 نشان دهنده عدم وجود الگوی همبستگی فضایی است، در حالی که مقادیر نزدیک به 1 یا -1 نشان دهنده خودهمبستگی مکانی قوی تر (مقادیر مشابه نزدیک به هم) یا پراکندگی فضایی (غیر مشابه). مقادیر نزدیک به هم) به ترتیب.
به عنوان مثال، ما یک آمار موران I را برای تعیین کمیت همبستگی مکانی در موارد ابولا که قبلاً ترسیم کردیم محاسبه خواهیم کرد (به یاد داشته باشید که این زیرمجموعه ای از موارد از چارچوب داده اپیدمی شبیه سازی شده است linelist). بسته spdep تابعی دارد moran.testکه می تواند این محاسبه را برای ما انجام دهد:
moran_i <-spdep::moran.test(sle_adm3_dat$cases, # numeric vector with variable of interest
listw=sle_listw) # listw object summarizing neighbor relationships
moran_i # print results of Moran's I test##
## Moran I test under randomisation
##
## data: sle_adm3_dat$cases
## weights: sle_listw
##
## Moran I statistic standard deviate = 1.6673, p-value = 0.04773
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic Expectation Variance
## 0.22324408 -0.12500000 0.04362563خروجی تابع moran.test()یک آمار Moran I را به ما نشان می دهد round(moran_i$estimate[1],2). این نشاندهنده وجود همبستگی مکانی در دادههای ما است – بهویژه، اینکه مناطقی با تعداد مشابه موارد ابولا احتمالاً نزدیک به هم هستند. مقدار p ارائه شده توسط moran.test()در مقایسه با انتظارات تحت فرضیه صفر عدم همبستگی فضایی ایجاد میشود و در صورت نیاز به گزارش نتایج یک آزمون فرضیه رسمی میتوان از آن استفاده کرد.
Local Moran’s I – ما می توانیم آمار موران I (جهانی) محاسبه شده در بالا را برای شناسایی خودهمبستگی فضایی محلی تجزیه کنیم. یعنی برای شناسایی خوشه های خاص در داده هایمان. این آمار، که گاهی به آن آمار نشانگر محلی انجمن فضایی (LISA) نیز گفته می شود ، میزان خودهمبستگی فضایی را در اطراف هر منطقه به طور خلاصه نشان می دهد. می تواند برای یافتن نقاط “گرم” و “سرد” روی نقشه مفید باشد.
برای نشان دادن یک مثال، میتوانیم Local Moran’s I را برای تعداد موارد ابولا استفاده شده در بالا با تابع local_moran()spdep محاسبه و ترسیم کنیم :
# calculate local Moran's I
local_moran <- spdep::localmoran(
sle_adm3_dat$cases, # variable of interest
listw=sle_listw # listw object with neighbor weights
)
# join results to sf data
sle_adm3_dat<- cbind(sle_adm3_dat, local_moran)
# plot map
ggplot(data=sle_adm3_dat) +
geom_sf(aes(fill=Ii)) +
theme_bw() +
scale_fill_gradient2(low="#2c7bb6", mid="#ffffbf", high="#d7191c",
name="Local Moran's I") +
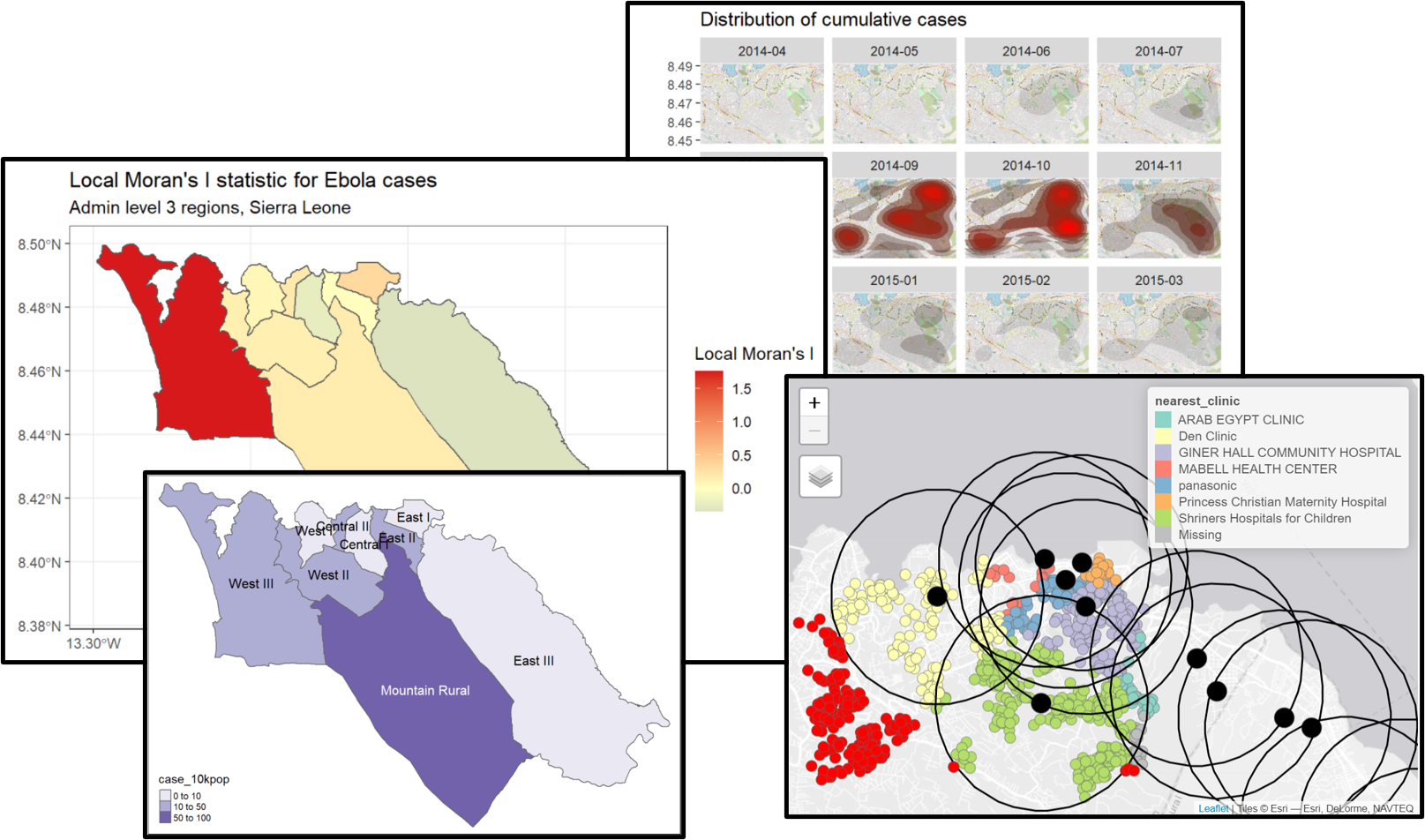
labs(title="Local Moran's I statistic for Ebola cases",
subtitle="Admin level 3 regions, Sierra Leone")
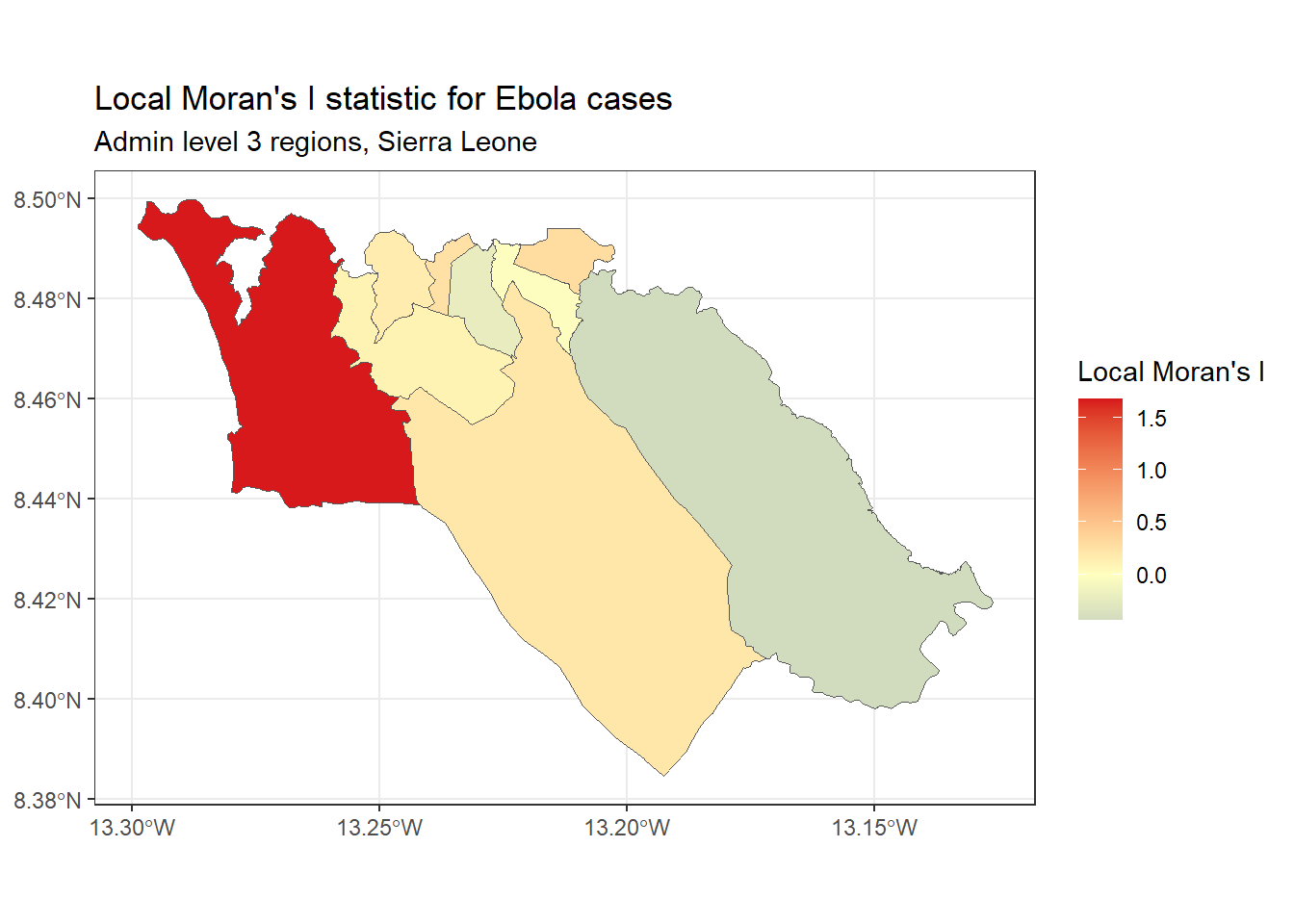
Getis-Ord Gi* – این آمار دیگری است که معمولاً برای تجزیه و تحلیل هات اسپات استفاده می شود. تا حد زیادی، محبوبیت این آمار به استفاده از آن در ابزار تجزیه و تحلیل نقطه داغ در ArcGIS مربوط می شود. بر این فرض استوار است که معمولاً تفاوت در مقدار متغیر بین مناطق همسایه باید از توزیع نرمال پیروی کند. از یک رویکرد z-score برای شناسایی مناطقی استفاده می کند که مقادیر قابل توجهی بالاتر (نقطه داغ) یا به طور قابل توجهی کمتر (نقطه سرد) یک متغیر مشخص در مقایسه با همسایگان خود دارند.
میتوانیم آمار Gi* را با استفاده localG()از تابع spdep محاسبه و ترسیم کنیم :
# Perform local G analysis
getis_ord <- spdep::localG(
sle_adm3_dat$cases,
sle_listw
)
# join results to sf data
sle_adm3_dat$getis_ord <- as.numeric(getis_ord)
# plot map
ggplot(data=sle_adm3_dat) +
geom_sf(aes(fill=getis_ord)) +
theme_bw() +
scale_fill_gradient2(low="#2c7bb6", mid="#ffffbf", high="#d7191c",
name="Gi*") +
labs(title="Getis-Ord Gi* statistic for Ebola cases",
subtitle="Admin level 3 regions, Sierra Leone")
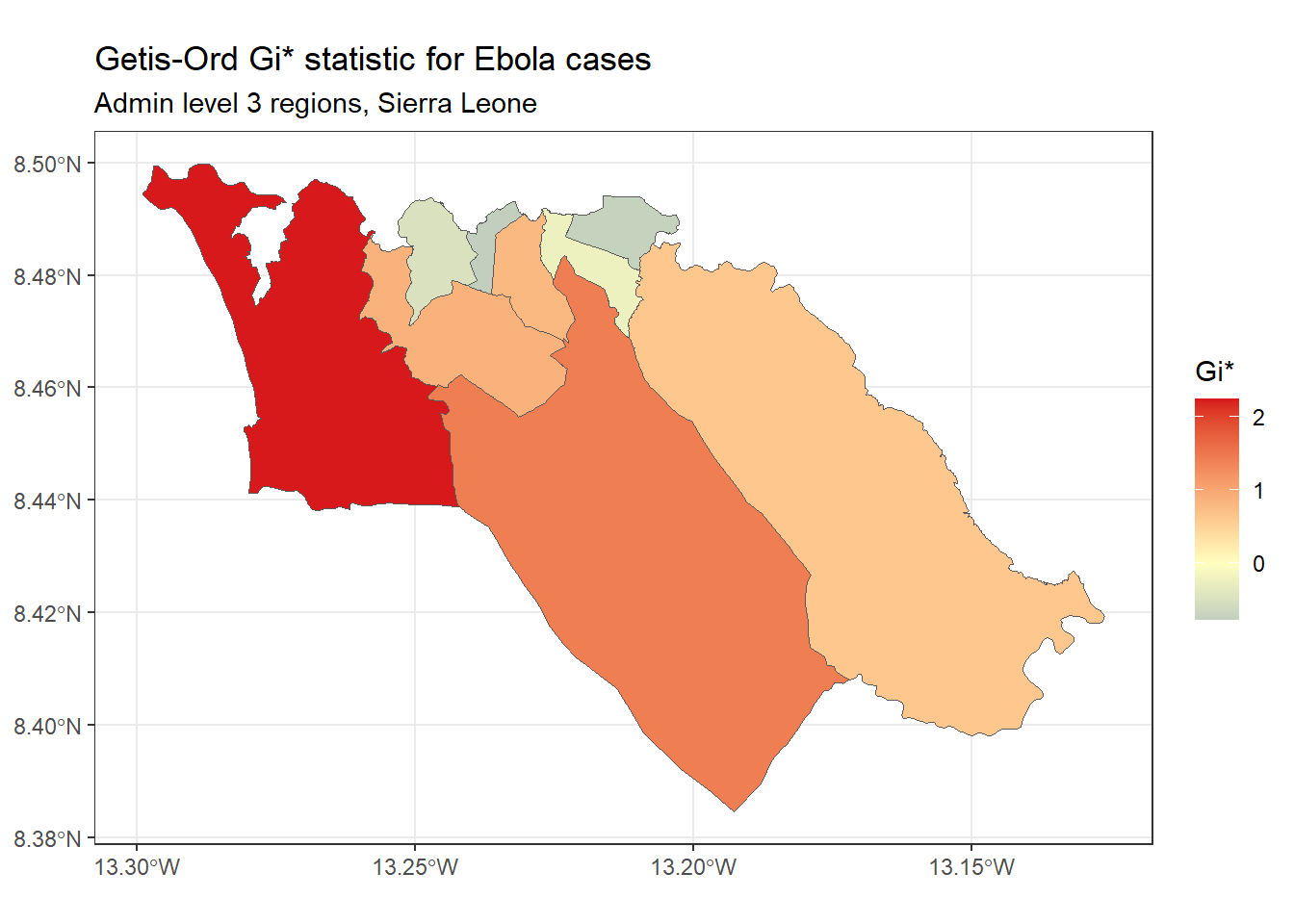
همانطور که می بینید، نقشه Getis-Ord Gi* کمی متفاوت از نقشه Local Moran’s I است که قبلا تهیه کردم. این نشان می دهد که روش مورد استفاده برای محاسبه این دو آمار کمی متفاوت است. اینکه کدام یک را باید استفاده کنید بستگی به مورد استفاده خاص شما و سوال تحقیق مورد علاقه شما دارد.
آزمون L لی – این یک آزمون آماری برای همبستگی فضایی دو متغیره است. این به شما امکان میدهد آزمایش کنید که آیا الگوی فضایی یک متغیر x شبیه الگوی فضایی متغیر دیگری، y است که فرض میشود از نظر فضایی با x مرتبط است یا خیر .
برای مثال، بیایید آزمایش کنیم که آیا الگوی فضایی موارد ابولا از اپیدمی شبیهسازی شده با الگوی فضایی جمعیت همبستگی دارد یا خیر. برای شروع، باید یک populationمتغیر در sle_adm3داده های خود داشته باشیم. میتوانیم totalاز متغیری sle_adm3_popکه قبلاً بارگذاری کردیم، استفاده کنیم.
sle_adm3_dat <- sle_adm3_dat %>%
rename(population = total) # rename 'total' to 'population'
ما میتوانیم به سرعت الگوهای فضایی دو متغیر را در کنار هم مجسم کنیم تا ببینیم آیا شبیه به هم هستند یا خیر:
tmap_mode("plot")
cases_map <- tm_shape(sle_adm3_dat) + tm_polygons("cases") + tm_layout(main.title="Cases")
pop_map <- tm_shape(sle_adm3_dat) + tm_polygons("population") + tm_layout(main.title="Population")
tmap_arrange(cases_map, pop_map, ncol=2) # arrange into 2x1 facets
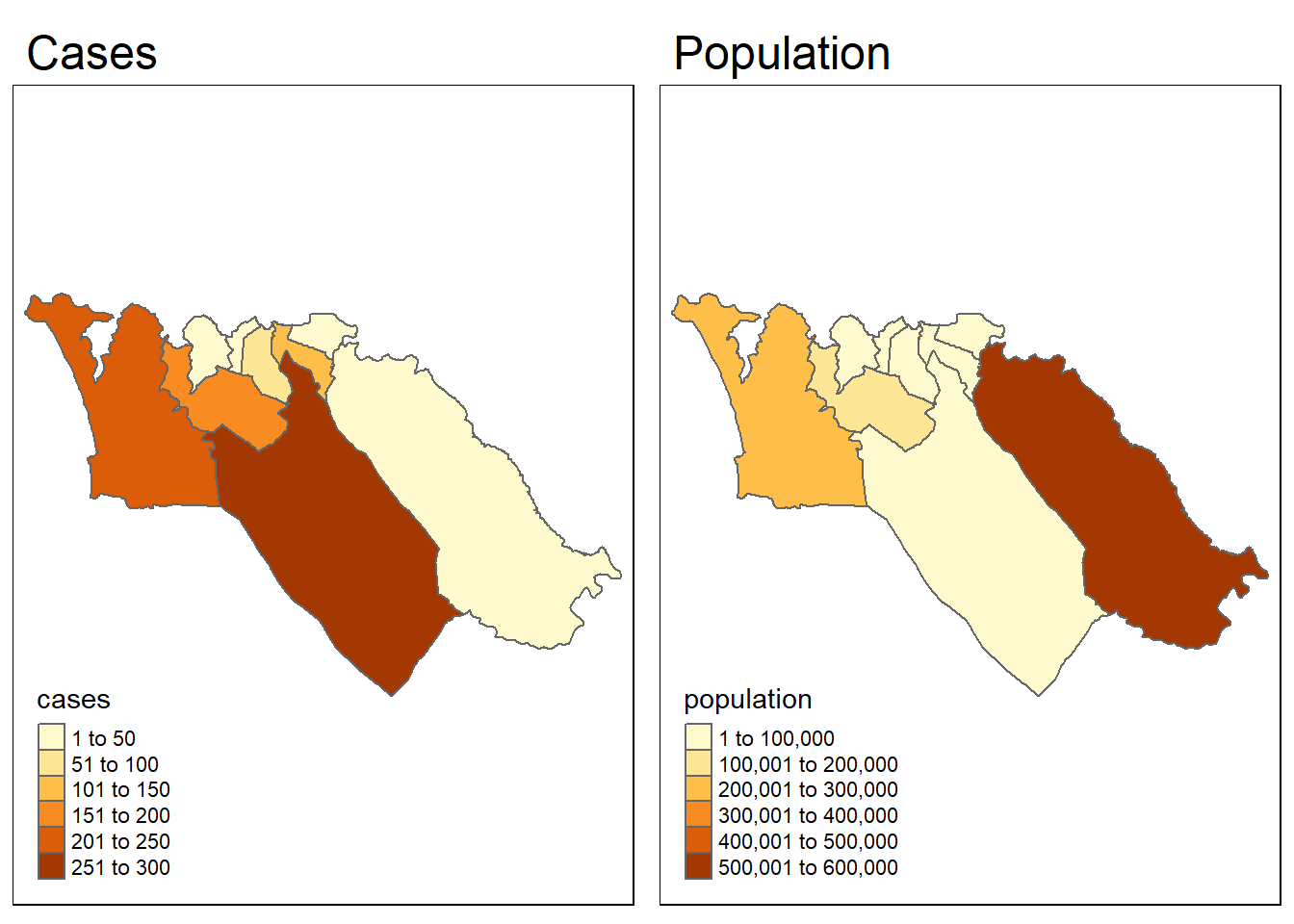
از نظر بصری، الگوها متفاوت به نظر می رسند. میتوانیم از lee.test()تابع در spdep برای آزمایش آماری استفاده کنیم که آیا الگوی خودهمبستگی مکانی در دو متغیر مرتبط است یا خیر. اگر همبستگی بین الگوها وجود نداشته باشد، آمار L نزدیک به 0، اگر همبستگی مثبت قوی وجود داشته باشد (یعنی الگوها مشابه هستند) نزدیک به 1 خواهد بود و اگر همبستگی منفی قوی وجود داشته باشد، نزدیک به 1- خواهد بود. الگوها معکوس هستند).
lee_test <- spdep::lee.test(
x=sle_adm3_dat$cases, # variable 1 to compare
y=sle_adm3_dat$population, # variable 2 to compare
listw=sle_listw # listw object with neighbor weights
)
lee_test##
## Lee's L statistic randomisation
##
## data: sle_adm3_dat$cases , sle_adm3_dat$population
## weights: sle_listw
##
## Lee's L statistic standard deviate = -0.74905, p-value = 0.7731
## alternative hypothesis: greater
## sample estimates:
## Lee's L statistic Expectation Variance
## -0.12330323 -0.04007484 0.01234575خروجی بالا نشان می دهد که آماره L لی برای دو متغیر ما برابر است round(lee_test$estimate[1],2)که نشان دهنده همبستگی منفی ضعیف است. این امر ارزیابی بصری ما را تأیید می کند که الگوی موارد و جمعیت به یکدیگر مرتبط نیستند، و شواهدی را ارائه می دهد که الگوی فضایی موارد کاملاً نتیجه تراکم جمعیت در مناطق پرخطر نیست.
آماره Lee L می تواند برای ایجاد این نوع استنباط در مورد رابطه بین متغیرهای توزیع شده مکانی مفید باشد. با این حال، برای توصیف ماهیت رابطه بین دو متغیر با جزئیات بیشتر، یا تنظیم برای گیج کننده، تکنیک های رگرسیون فضایی مورد نیاز است. این موارد به طور خلاصه در بخش زیر توضیح داده شده است.
رگرسیون فضایی
ممکن است بخواهید استنتاج های آماری در مورد روابط بین متغیرها در داده های مکانی خود داشته باشید. در این موارد، در نظر گرفتن تکنیک های رگرسیون فضایی مفید است – یعنی رویکردهایی به رگرسیون که به صراحت سازماندهی فضایی واحدها را در داده های شما در نظر می گیرند. برخی از دلایلی که ممکن است لازم باشد مدلهای رگرسیون فضایی را به جای مدلهای رگرسیون استاندارد مانند GLM در نظر بگیرید، عبارتند از:
- مدل های رگرسیون استاندارد فرض می کنند که باقیمانده ها از یکدیگر مستقل هستند. در حضور خود همبستگی فضایی قوی ، باقیماندههای یک مدل رگرسیون استاندارد احتمالاً از نظر مکانی همبستگی خودکار دارند، بنابراین این فرض را نقض میکند. این می تواند منجر به مشکلاتی در تفسیر نتایج مدل شود که در این صورت یک مدل فضایی ترجیح داده می شود.
- مدلهای رگرسیون نیز معمولاً فرض میکنند که تأثیر متغیر x روی همه مشاهدات ثابت است. در مورد ناهمگونی فضایی ، اثراتی که میخواهیم تخمین بزنیم ممکن است در فضا متفاوت باشد، و ممکن است ما علاقهمند باشیم که این تفاوتها را کمی کنیم. در این مورد، مدلهای رگرسیون فضایی انعطافپذیری بیشتری برای تخمین و تفسیر اثرات ارائه میدهند.
جزئیات رویکردهای رگرسیون فضایی خارج از محدوده این کتاب راهنما است. این بخش به جای آن یک نمای کلی از رایج ترین مدل های رگرسیون فضایی و استفاده از آنها ارائه می دهد و شما را به منابعی ارجاع می دهد که در صورت تمایل به کاوش بیشتر در این زمینه ممکن است مفید باشند.
مدلهای خطای مکانی – این مدلها فرض میکنند که عبارات خطا در واحدهای فضایی همبستگی دارند، در این صورت دادهها مفروضات یک مدل استاندارد OLS را نقض میکنند. مدلهای خطای فضایی گاهی اوقات به عنوان مدلهای خودرگرسیون همزمان (SAR) نیز شناخته میشوند . آنها می توانند با استفاده از errorsarlm()تابع موجود در بسته spatialreg (توابع رگرسیون فضایی که قبلاً بخشی از spdep بودند ) مناسب شوند.
مدلهای تاخیر فضایی – این مدلها فرض میکنند که متغیر وابسته برای یک منطقه i نه تنها تحت تأثیر مقدار متغیرهای مستقل در i ، بلکه تحت تأثیر مقادیر آن متغیرها در مناطق همسایه i نیز قرار میگیرد . مانند مدلهای خطای فضایی، مدلهای تاخیر مکانی نیز گاهی اوقات به عنوان مدلهای خودبازگشت همزمان (SAR) توصیف میشوند . lagsarlm()آنها می توانند با استفاده از تابع موجود در بسته spatialreg مناسب شوند .
بسته spdep شامل چندین تست تشخیصی مفید برای تصمیم گیری بین مدل های استاندارد OLS، تاخیر فضایی و خطای مکانی است . این تستها که تشخیص ضریب لاگرانژ نامیده میشوند، میتوانند برای شناسایی نوع وابستگی فضایی در دادههای شما و انتخاب مدل مناسبتر استفاده شوند. از این تابع lm.LMtests()می توان برای محاسبه تمام تست های ضریب لاگرانژ استفاده کرد. Anselin (1988) همچنین یک ابزار نمودار جریان مفید برای تصمیم گیری از کدام مدل رگرسیون فضایی بر اساس نتایج آزمونهای ضریب لاگرانژ ارائه میکند:
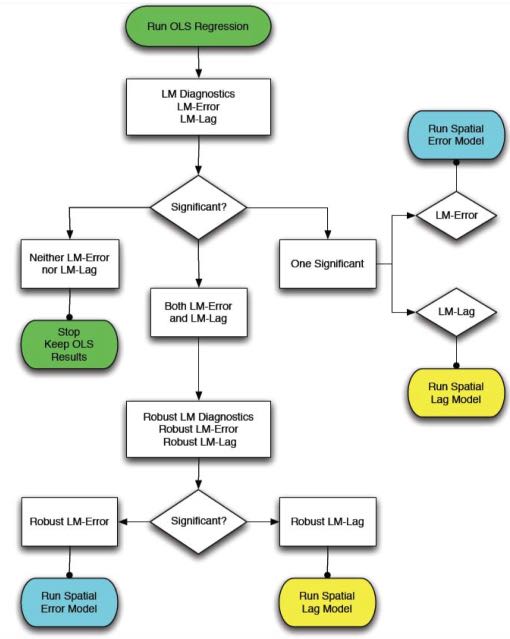
مدلهای سلسله مراتبی بیزی – رویکردهای بیزی معمولاً برای برخی از کاربردها در تحلیل فضایی، معمولاً برای نقشهبرداری بیماری استفاده میشوند . آنها در مواردی که داده های موردی به طور پراکنده توزیع می شوند (به عنوان مثال، در مورد یک پیامد نادر) یا از نظر آماری “پر سر و صدا” ترجیح داده می شوند، زیرا می توان از آنها برای ایجاد تخمین های “هموار” خطر بیماری با در نظر گرفتن فضای پنهان زمینه ای استفاده کرد. روند. این ممکن است کیفیت برآوردها را بهبود بخشد. آنها همچنین به محقق اجازه میدهند تا الگوهای همبستگی فضایی پیچیدهای را که ممکن است در دادهها وجود داشته باشد، از پیش تعیین کند (از طریق انتخاب قبلی)، که میتواند تغییرات وابسته به فضایی و مستقل را در متغیرهای مستقل و وابسته به حساب آورد. در R، مدل های سلسله مراتبی بیزی را می توان با استفاده از CARbayes مناسب کردبسته (رجوع کنید به تصویر ) یا R-INLA (به وب سایت و کتاب درسی مراجعه کنید ). R همچنین می تواند برای فراخوانی نرم افزارهای خارجی که تخمین بیزی انجام می دهند، مانند JAGS یا WinBUGS استفاده شود.


بدون دیدگاه