هدف یادگیری
- هدف از این بخش آشنایی با مفاهیم و اصطلاحات مربوط به سطوح GIS، نحوه ایجاد آنها و نحوه استفاده از آنها برای پاسخ به سؤالات فضایی خاص است.
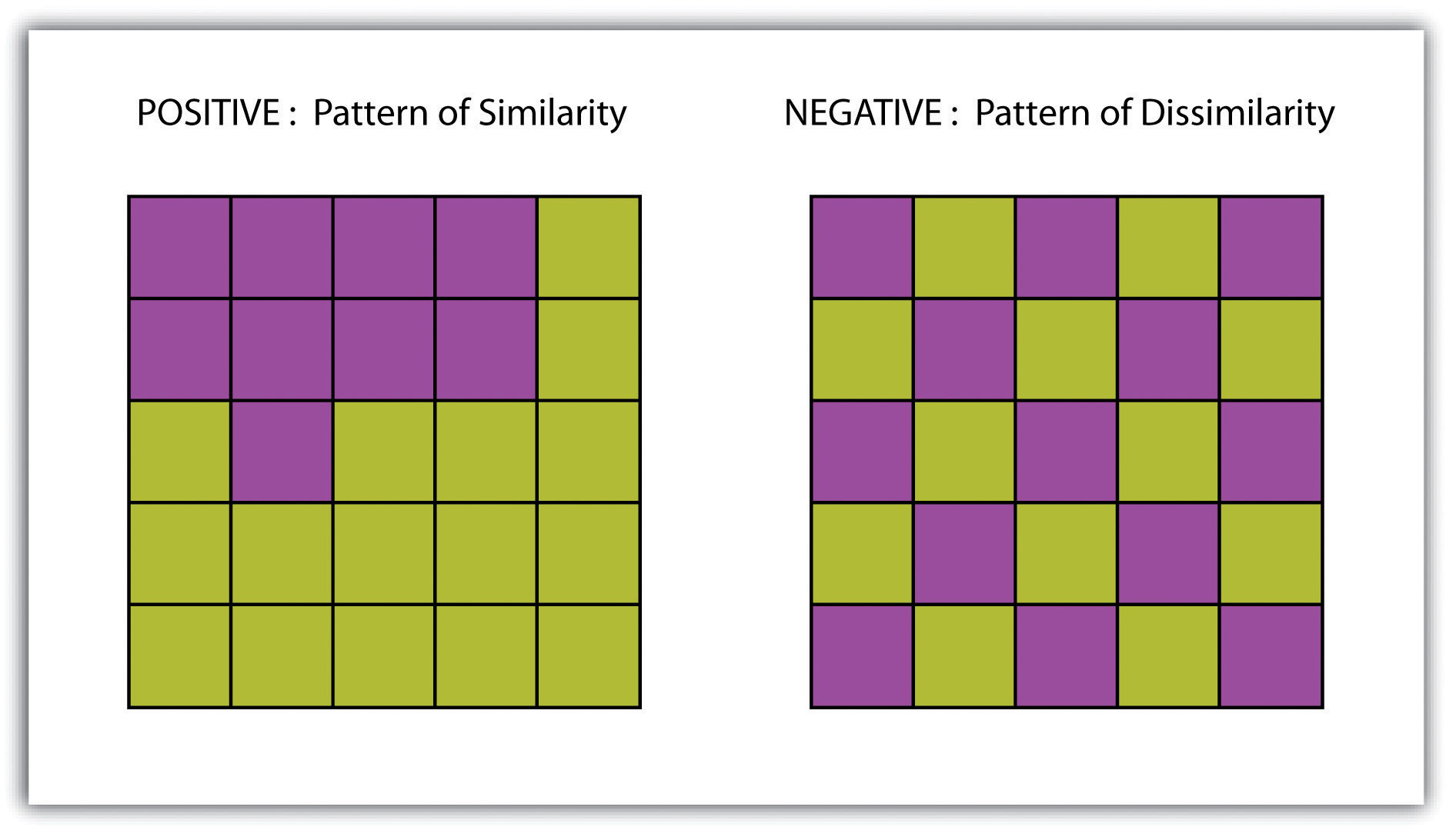
سطح یک مجموعه داده برداری یا شطرنجی است که حاوی یک مقدار مشخصه برای هر محلی در سراسر گستره آن است. به یک معنا، همه مجموعه داده های شطرنجی سطح هستند، اما همه مجموعه داده های برداری سطح نیستند. سطوح معمولاً در یک سیستم اطلاعات جغرافیایی (GIS) برای تجسم پدیدههایی مانند ارتفاع، دما، شیب، جنبه، بارندگی و غیره استفاده میشوند. در یک GIS، تجزیه و تحلیل سطح معمولاً بر روی مجموعه داده های شطرنجی یا TIN ها انجام می شود (شبکه نامنظم مثلثی؛ فصل 5 “مدیریت داده های جغرافیایی” ، بخش 5.3.1 “فرمت های فایل برداری”، اما می توان از خطوط ایزوله یا آرایه نقطه ای نیز استفاده کرد. درون یابی برای تخمین مقدار یک متغیر در یک مکان نمونه برداری نشده از اندازه گیری های انجام شده در مناطق نزدیک یا مجاور استفاده می شود. روشهای درونیابی فضایی از مرام نظری قانون اول جغرافیای توبلر استفاده میکنند، که میگوید «همه چیز به هر چیز دیگری مرتبط است، اما چیزهای نزدیک بیشتر به هم مرتبط هستند تا چیزهای دور». در واقع، این اصل اساسی خودهمبستگی فضایی مثبت ، ستون فقرات بسیاری از تحلیل های فضایی را تشکیل می دهد ( شکل 8.9 “خودهمبستگی فضایی مثبت و منفی” ).
شکل 8.9 خود همبستگی فضایی مثبت و منفی
ایجاد سطوح
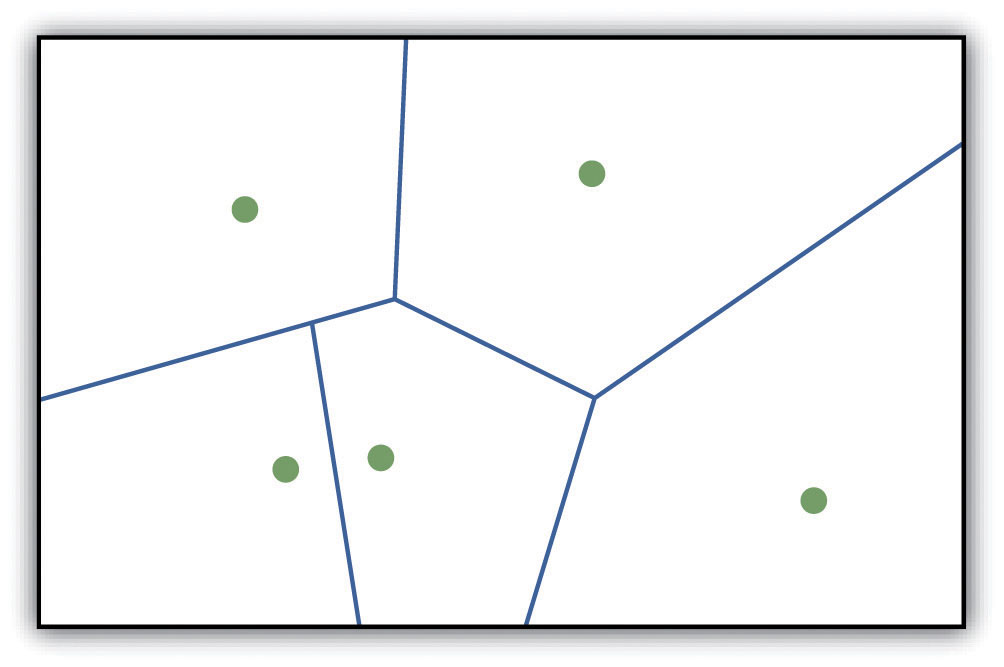
توانایی ایجاد سطح یک ابزار ارزشمند در GIS است. با این حال، ایجاد سطوح شطرنجی اغلب با ایجاد یک سطح برداری شروع می شود. یکی از روش های رایج برای ایجاد چنین سطح برداری از داده های نقطه ای، از طریق تولید چندضلعی های تیسن (یا ورونوی) است. چند ضلعی های Thiessen مناطقی هستند که به صورت ریاضی ایجاد می شوند که حوزه نفوذ را در اطراف هر نقطه از مجموعه داده نسبت به سایر نقاط تعریف می کنند ( شکل 8.10 “یک سطح برداری ایجاد شده با استفاده از چند ضلعی های Thiessen”). به طور خاص، مرزهای چند ضلعی به عنوان نیمسازهای عمود بر خطوط بین هر جفت از نقاط همسایه محاسبه می شوند. سپس چند ضلعی های تیسن مشتق شده را می توان به عنوان سطوح بردار خام استفاده کرد که اطلاعات ویژگی را در کل ناحیه مورد نظر ارائه می دهد. یک مثال رایج از چند ضلعی های تیسن ایجاد یک سطح بارندگی از مجموعه ای از مکان های نقطه باران سنج است. با استفاده از برخی تکنیکهای طبقهبندی مجدد، این چند ضلعیهای تیسن را میتوان به راحتی به نمایشهای شطرنجی معادل تبدیل کرد.
شکل 8.10 یک سطح برداری ایجاد شده با استفاده از چند ضلعی های Thiessen
در حالی که ایجاد چند ضلعی های تیسن منجر به یک لایه چند ضلعی می شود که به موجب آن هر چند ضلعی یا ناحیه شطرنجی یک مقدار واحد را حفظ می کند، درون یابییک تکنیک آماری بالقوه پیچیده است که ارزش تمام نقاط مجهول بین نقاط شناخته شده را تخمین می زند. سه روش اساسی مورد استفاده برای ایجاد سطوح درون یابی عبارتند از: spline، وزن معکوس فاصله (IDW) و سطح روند. روش درون یابی اسپلاین یک منحنی هموار را از طریق مجموعه نقاط ورودی شناخته شده برای تخمین مقادیر ناشناخته و مداخله ای مجبور می کند. درون یابی IDW مقادیر مکان های ناشناخته را با استفاده از فاصله تا مقادیر نزدیک و شناخته شده تخمین می زند. وزنی که روی مقدار هر مقدار نزدیکی قرار میگیرد، نسبت معکوس با فاصله مکانی آن از محل هدف است. بنابراین، هر چه نقطه پروگزیمال دورتر باشد، وزن کمتری در تعیین مقدار نقطه هدف دارد. سرانجام،
روش های درونیابی بسیار پیچیده دیگری مانند کریجینگ وجود دارد. کریجینگ یک تکنیک پیچیده زمین آماری است، شبیه به IDW، که از نیمه متغیرها برای درونیابی مقادیر یک لایه نقطه ورودی استفاده می کند و بیشتر شبیه به تحلیل رگرسیون است (Krige 1951). Krige, D. 1951. یک رویکرد آماری به برخی از ارزش گذاری های معدن و مشکلات وابسته در Witwatersrand . پایاننامهی کارشناسی ارشد. دانشگاه ویت واترسرند جزئیات روش کریجینگ در اینجا پوشش داده نخواهد شد، زیرا این خارج از محدوده این متن است. برای اطلاعات بیشتر در مورد کریجینگ، به متون مروری مانند Stein (1999) مراجعه کنید. Stein, M. 1999. درون یابی آماری داده های فضایی: برخی نظریه ها برای کریجینگ . نیویورک: اسپرینگر.
برعکس، داده های شطرنجی نیز می توانند برای ایجاد سطوح برداری استفاده شوند. به عنوان مثال، نقشه های ایزولاین از خطوط پیوسته و غیر همپوشانی تشکیل شده اند که نقاط با ارزش برابر را به هم متصل می کنند. ایزولاین ها بسته به نوع اطلاعاتی که مدل می کنند، نام های مشخصی دارند (به عنوان مثال، ارتفاع = خطوط کانتور، دما = ایزوترم، فشار بارومتریک = ایزوبارها، سرعت باد = ایزوتاچ ها) شکل 8.11 “خطوط کانتور مشتق شده از DEM”یک نقشه ارتفاعی ایزولاین را نشان می دهد. از آنجایی که مقادیر ارتفاع این مدل رقومی ارتفاع (DEM) از 450 تا 950 فوت متغیر است، خطوط کانتور در ارتفاعات 500، 600، 700، 800 و 900 فوت در سراسر وسعت تصویر قرار می گیرند. در این مثال، فاصله کانتور، که به عنوان فاصله عمودی بین هر خط کانتور تعریف شده است، 100 فوت است. فاصله کانتور توسط کاربر در هنگام ایجاد سطح تعیین می شود.
شکل 8.11 خطوط کانتور مشتق شده از DEM

خوراکی های کلیدی
- درون یابی فضایی برای تخمین مقادیر ناشناخته یافت شده بین نقاط داده شناخته شده استفاده می شود.
- خودهمبستگی مکانی زمانی مثبت است که ویژگیهای نقشهبرداری شده خوشهبندی شوند و زمانی منفی است که ویژگیهای نقشهبرداری شده به طور یکنواخت توزیع شوند.
- چند ضلعی های تیسن ابزار ارزشمندی برای تبدیل آرایه های نقطه ای به سطوح چند ضلعی هستند.
تمرینات
- یک مثال از پنج پدیده در دنیای واقعی که خود همبستگی فضایی مثبت را نشان می دهند، بیاورید.
- یک مثال از پنج پدیده در دنیای واقعی که همبستگی فضایی منفی را نشان می دهند، بیاورید.


بدون دیدگاه